16. Аппроксимация производных конечными разностями

Апроксимация производных конечными разностями

• diff(X) — возвращает конечные разности смежных элементов массива X. Если X — вектор, то diff(X) возвращает вектор разностей соседних элементов [Х(2)-Х(1) Х(3)-Х(2) ... X(n)-X(n-D], у которого количество элементов на единицу меньше, чем у исходного вектора X. Если X — матрица, то diff(X) возвращает матрицу разностей столбцов: [X(2:m, :)-X(l:m-l. :)];

• Y = diff(X.n.dim) — возвращает конечные разности для матрицы X по строкам или по столбцам в зависимости от значения параметра dim. Если порядок п равен величине dim или превышает ее, то diff возвращает пустой массив.

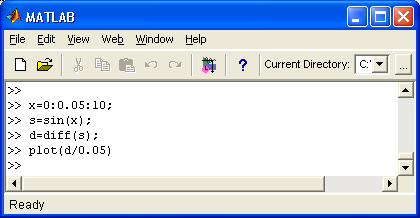
Используя функцию diff, можно строить графики производных заданной функции. Пример этого показан ниже:

» Х=0:0.05:10; 

» S=sin(X); 

» D=diff(S): 

» plot(D/0.05)

Для получения приближенных численных значений производной от функции sin(.r) вектор конечно-разностных значений D поделен на шаг точек по х. Как и следовало ожидать, полученный график очень близок к графику функции косинуса (рис. 16.2). Обратите внимание, что по оси х отложены номера элемента* вектора X, а не истинные значения х.

Пакет расширения Symbolic Math Toolbox позволяет выполнять дифференциро вание функций в аналитическом виде, т. е. точно. Это, однако, не всегда нужно

Рис. 16.2. Приближенный график производной от функции sin(x)