Главное меню
Вы здесь
16.4 Бинарная логистическая регрессия
16.4 Бинарная логистическая регрессия
С помощью метода бинарной логистической регрессии можно исследовать зависимость дихотомических переменных от независимых переменных, имеющих любой вид шкалы.
Как правило, в случае с дихотомическими переменными речь идёт о некотором событии, которое может произойти или не произойти; бинарная логистическая регрессия в таком случае рассчитывает вероятность наступления события в зависимости от значений независимых переменных.
Вероятность наступления события для некоторого случая рассчитывается по формуле
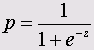
где z= b1*X1 + b2хХ2+ ...+ bnxXn+ a ,
X1 — значения независимых переменных, b1 — коэффициенты, расчёт которых является задачей бинарной логистической регрессии, а — некоторая константа.
Если для р получится значение меньшее 0,5, то можно предположить, что событие не наступит; в противном случае предполагается наступление события.
В качестве примера рассмотрим два диагностических теста из области медицины на предмет обнаружения карциномы (злокачественной опухоли) мочевого пузыря: подсчет количества (типизация) Т-клеток и тест LAI. Результатами первого теста являются значения, принадлежащие к интервальной шкале, а тест LAI дает дихотомический результат: "положительно" или "отрицательно".
Оба теста были проведены со здоровыми людьми и заведомо больными пациентами. Результаты представлены в следующей таблице:
Коллектив | Типизация t-клеток | LAI | Коллектив | Типизация t-клеток | LAI |
болен | 48.5 | положи-тельно | болен | 73.5 | положи-тельно |
болен | 55.5 | положи-тельно | здоров | 61.1 | положи-тельно |
болен | 57.5 | положи-тельно | здоров | 62.5 | отрица-тельно |
болен | 58.5 | положи-тельно | здоров | 63.5 | отрица-тельно |
болен | 61.0 | положи-тельно | здоров | 64.5 | положи-тельно |
болен | 61.5 | положи-тельно | здоров | 69.5 | положи-тельно |
болен | 61.5 | положи-тельно | здоров | 70.0 | отрица-тельно |
болен | 6,2.0 | положи-тельно | здоров | 70.0 | отрица-тельно |
болен | 62.0 | положи-тельно | здоров | 71.0 | положи-тельно |
болен | 62,0 | положи-тельно | здоров | 71,5 | положи-тельно |
болен | 62.5 | положи-тельно | здоров | 71.5 | отрица-тельно |
болен | 63.0 | положи-тельно | здоров | 72.0 | отрица-тельно |
болен | 63.5 | положи-тельно | здоров | 73.0 | отрица-тельно |
болен | 65.0 | положи-тельно | здоров | 76.0 | отрица-тельно |
болен | 65.0 | отрица-тельно | здоров | 72.5 | отрица-тельно |
болен | 66.5 | отрица-тельно | здоров | 73.0 | отрица-тельно |
болен | 66.5 | отрица-тельно | здоров | 73.5 | отрица-тельно |
болен | 66.5 | положи-тельно | здоров | 74.0 | отрица-тельно |
болен | 68.5 | положи-тельно | здоров | 75.0 | отрица-тельно |
болен | 69.0 | отрица-тельно | здоров | 77.0 | отрица-тельно |
болен | 71.0 | положи-тельно | здоров | 77.0 | отрица-тельно |
болен | 71.0 | положи-тельно | здоров | 78.5 | отрица-тельно |
болен | 71.0 | положи-тельно |
|
|
|
Если сначала посмотреть на результаты типизации Т-клеток, то можно заметить, что здесь для здоровых людей значения в среднем выше, чем для больных. Следовательно, исходя из значений, получившихся при типизации Т-клеток, можно попытаться, вывести вероятность наличия карциномы мочевого пузыря.
Приведенные в таблице данные находятся в файле hkarz.sav. Больным присвоена кодировка 1, а здоровым 2; для теста LA1 кодировка 0 соответствует положительному результату, а 1 отрицательному.
-
Откройте файл hkarz.sav.
-
Выберите в меню Analyze... (Анализ) Regression... (Регрессия) Binary logistic... (Бинарная логистическая)
Открывается диалоговое окно Logistic Regression (Логистическая регрессия).
-
Поместите переменную gruppe (группа), содержащую информацию о принадлежности к одному или второму коллективу (больным или здоровым), в поле для зависимых переменных, а переменную tzell — в поле ковариат. Результаты теста LAI сначала мы не будем использовать в расчёте.
Рис. 16.16: Диалоговое окно -Ogistic Regression (Логистическая регрессия).
В качестве метода использования переменных в вычислениях предварительно установлен метод Enter (Вложение), при котором в расчёт одновременно вовлекаются :-:е переменные объявленные ковариатами. Альтернативой здесь являются прогрессивная и обратная селекции. В случае наличия лишь одной ковариаты, как в указаном примере, для расчёта подходит только предварительно установленный метод.
Кнопка Select» (Выбрать) предоставляет возможность отбора определённых случаев для дальнейшего анализа.
Используя кнопку Categorical... (Категориальные) Вы можете подготовить для расчета категориальные переменные (то есть переменные, принадлежащие к номинальной шкале). На этом мы остановимся более подробно, рассматривая второй пример.
При помощи кнопки Save... (Сохранить) Вы можете добавить в файл дополнительные переменные; активируйте к примеру в разделе Predicted Values (Спрогнозированные значения) предварительные установки Probabilities (Вероятности) и Принадлежность к группе.
Нажав на кнопку Options... (Опции), Вы сможете организовать вывод дополнительных статистических характеристик, различных диаграмм и произвести некоторые дополнительные установки. В данном расчёте мы этого делать не будем.
-
Начните расчёт нажатием ОК.
Наиболее важные результаты приведены в нижеследующей таблице, причём в 10 версии SPSS они уже выводятся в новой табличной форме.
Omnibus Tests of Model Coefficients (Универсальный критерий коэффициентов модели)
Chi-square (Хи-квадрат) | Df | Sig. (Значимость) | ||
Step 1 (ШаМ) 1 | Step (Шаг) | 18,789 | 1 | ,000 |
Block (Блок) | 18,789 | 1 | ,000 | |
Model (Модель) | 18,789 | 1 | ,000 |
Model Summary (Сводная таблица модели)
Step (Шаг) | -2 Log likelihood (-2 логарифмическое правдоподобие) | Сох & Snell R Square (R-квадрат Кокса и Шнела) | R Square Nadelkerkes (R-квадрат Наделькеркеса) |
1 | 43,394 | ,341 | ,456 |
Качество приближения регрессионной модели оценивается при помощи функции подобия. Мерой правдоподобия служит отрицательное удвоенное значение логарифма этой функции (-2LL). В качестве начального значения для -2LL применяется значение, которое получается для регрессионной модели, содержащей только константы. После добавления переменной влияния tzell значение -2LL равно 43,394; это значение на 18,789 меньше, чем начальное. Подобное снижение величины означает улучшение; разность обозначается как величина хи-квадрат и является очень значимой.
Это означает, что начальная модель после добавления переменной tzell претерпела значительное улучшение. Если при наличии некоторого количества независимых переменных анализ производится не при помощи метода вложения, а пошаговым образом, то получающиеся изменения отображаются в разделах "Блок" и "Шаг". При этом, если Вы производили ввод переменных в блочной форме, то показатель в разделе "Блок" приобретает особое значение.
Два других выведенных показателя, названные именами Кокса & Шела и Наделькеркеса, являются мерами определённости. Они также как и при линейной регрессии указывают на ту часть дисперсии, которую можно объяснить с помощью логистической регрессии. Мера определённости по Коксу и Шелу имеет тот недостаток, что значение равное 1 является теоретически не достижимым; этот недостаток устранен благодаря модификации данной меры по методу Наделькеркеса. Часть дисперсии, объяснимой с помощью логистической регрессии, в данном примере составляет 45,6 %.
Далее приводится классификационная таблица, в которой наблюдаемые показатели принадлежности к группе (1 = болен, 2 = здоров) противопоставляются предсказанным на основе рассчитанной модели.
Classification Table (Классификационная таблица) а
Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
GRUPPE (Группа) | Percentage Correct (Процентный показатель верных показателей) | ||||
Krank (болен) | Gesund (здоров) | ||||
Шаг 1 | GRUPPE (Группа) | Krank (болен) | 18 | 6 | 75,0 |
| Gesund (здоров) | 4 | 17 | 81,0 | ||
| Overall Percentage (Суммарный процентный показатель) |
| 77,8 | |||
a. The cut value is ,500 (Разделительное значение равно ,500)
Из таблицы можно сделать вывод о том, что из общего числа больных, равного 24, тестом были признаны таковыми только 18 (в медицинской диагностике в таких случаях говорят о "строго положительных" результатах). Остальных 6 называют "ложно отрицательными"; они были признаны тестом здоровыми, хотя и являются больными. Из общего числа здоровых, равного 21, тестом были признаны таковыми только 17 ("строго отрицательные"), 4 признаны больными, хотя они и являются здоровыми ("ложно положительные"). В общем, правильно были распознаны 35 случаев из 45, это составляет 77,8 %.
В заключении выводятся результаты о рассчитанных коэффициентах и проверке их значимости:
Variables in the Equation (Переменные в уравнении)
|
| В (Коэф-фициент регрессии В) | S.E. (Стандарт- ная ошибка) | Wald (Вальд) | df | Sig. (Значи-мость) | Ехр (В) |
Step 1 (Шаг 1)а | TZELL | ,278 | ,082 | 11,599 | 1 | ,001 | 1,321 |
| Constant (Константа) | -19,005 | 5,587 | 11,571 | 1 | ,001 | ,000 |
a. Variable(s) entered on step 1: TZELL (Переменные, введенные на шаге 1: TZELL)
Проверка значимости отличия коэффициентов от нуля, проводится при помощи статистики Вальда, использующей распределение хи-квадрат, которая представляет собой квадрат отношения соответствующего коэффициента к его стандартной ошибке.
В приведенном примере получились сверх значимые коэффициенты а = -19,005 bt = 0,278. При помощи этих двух значений коэффициентов мы можем для каждого значения Т-типизации рассчитать вероятность р. К примеру, для некоего обследуемого со значением Т-типизации 72 получим
z= - 19,005+ 0,278x72= 1,018
и таким образом
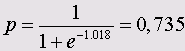
Рассчитанная вероятность р всегда указывает на исполнение предсказании, которое соответствует большей из двух кодировок зависимых переменных, в данном случае — на исполнение предсказания "здоров". Следовательно, рассматриваемый человек является здоровым с вероятностью 0,735.
Рассчитанная вероятность для всех случаев и связанная с ней принадлежность к группе кодировка 1 для болен и 2 для здоров) добавлены к файлу под именами рге_1 и pgr_l.
Теперь подключим к нашему анализу тест LAI. Дополнительно к переменной tzell теперь в поле ковариат поместите и переменную lai.
Расчёт выдаст сначала заметно снизившееся значение -2LL (хи-квадрат = 25,668) и следующую классификационную таблицу. Доля правильно спрогнозированных диагнозов незначительно выросла (с 77,8 % до 80,0 %).
Classification Table (Классификационная таблица)а
|
Observed (Наблюдаемый показатель) |
Predicted (Спрогнозировано) |
||||
|
Группа |
Percentage Correct (Процентный показатель верных показателей) |
||||
| Krank (болен) | Gesund (здоров) | ||||
|
Шаг 1 |
GRUPPE (Группа) | Krank (болен) |
20 |
4 |
83,3 |
| Gesund (здоров) |
5 |
16 |
76,2 |
||
| Overall Percentage (Суммарный процентный показатель) |
80,0 |
||||
а. The cut value is ,500 (Разделительное значение равно ,500)
Количество ложно отрицательных диагнозов снизилось на 2, а количество ложно положительных повысилось на 1. Для коэффициентов получим:
Variables in the Equation (Переменные в уравнении)
|
| В (Коэф0 фициент регрессии В) | S.E. Стандартная ошибка) | Wald (Вальд) | df | Sig. (Значи0 мость) | Ехр (В) |
Stepl (UJarlf | TZELL | ,201 | ,094 | 4,574 | 1 | 0,32 | 1,222 |
LAI | 2,205 | ,877 | 6,324 | 1 | ,012 | 9,074 | |
Constant (Константа) | -14,645 | 6,328 | 5,356 | 1 | ,021 | ,000 |
a. Variable(s) entered on step 1: TZELL, LAI. (Переменные, вводимые на шаге 1: TZELL, LAI)
Для обследуемого с типизированным числом Т-клеток равным 72 получилась вероятность оказаться здоровым р = 0,735. Если в дополнении к этому и тест LAI отрицателен (кодировка 1), то эта же вероятность рассчитывается следующим образом:

Вероятность, оказаться здоровым, при наличии данных уже двух диагностических методов значительно возросла.
Ещё один пример из области медицины, теперь уже с большим количеством независимых переменных, должен помочь нам разобраться в пошаговом методе анализа. Кроме того, в состав независимых переменных будет включена категориальная переменная.
Для данного примера в некоторой клинике со специальными автоматизированными методиками лечения были накоплены данные о пациентах с тяжёлыми (или даже смертельными) повреждениями лёгких. Из большого количества переменных были выбраны следующие:
Имя переменной | Расшифровка |
out | Исход (0 = скончался, 1 = выздоровел) |
alter (возраст) | Возраст |
bzeit | Время проведения искусственного дыхания в часах |
kob | Концентрация кислорода в воздушной массе для искусственного |
дыхания | |
адд | Интенсивность искусственного дыхания |
gesch (пол) | Пол (1 = мужской, 2 = женский) |
gr | Рост |
ursache (причина) | Причина повреждения лёгких (1 = несчастный случай, 2 = воспаление лёгких, 3 = прочее) |
Наряду с переменной out (исход), имеются переменные, при первом же взгляде на которые можно понять, что они с ней связаны. Причина повреждения лёгких является категориальной переменной, которая перед проведением анализа должна быть преобразована в несколько дихотомических переменных (к примеру, несчастный случай: да — нет).
Вопрос, на который нам предстоит найти ответ, звучит так: какое влияние на вероятность выздоровления оказывают отобранные переменные.
-
Откройте файл lunge.sav.
-
После выбора соответствующего меню в диалоговом окне Logistic Regression (Логистическая регрессия) переменной out присвойте статус независимой переменной, а всем остальным (кроме пг) присвойте статус ковариат. Здесь, как и при множественной линейной регрессии, ввод ковариат Вы можете производить по блокам.
Из-за вовлечения в анализ большого количества переменных компьютер должен решить, какие из них в конечном случае будут отобраны для использовании в уравнении вероятности. Поэтому здесь должен быть выбран не метод вложения, который включает в расчёт все переменные, а один из пошаговых методов.
Метод прямой селекции начинается с использования одних лишь констант на стартовом этапе , а затем последовательно подключаются переменные, которые демонстрируют сильную корреляцию с зависимыми переменными. Далее опять следует проверка того, какие переменные должны быть исключены, причём в качестве критерия проверки выбирается либо статистика Вальдовского (Wald), либо функция правдоподобия, либо один из вариантов, называемых "условной статистикой" (которые, однако, не рекомендуются). Метод обратной селекции сначала берёт в расчёт все переменные, а затем в обратном порядке происходит исключение малозначимых переменных.
-
Выберите в качестве метода Forward: LR (Прямой:LR) и щёлкните на кнопке Categorical... (Категориальные), чтобы поместить переменную ursache в поле, предусмотренное для категориальных ковариат.
Количество образовываемых "фиктивных" дихотомических переменных должно быть всегда на 1 меньше, чем число количество заданных категорий. Категория, оказавшаяся лишней, называется эталонной категорией и, в соответствии с предварительными установками, является последней категорией. При помощи поля контрастов Contrast) Вы можете управлять особенностями вовлечения в анализ образованных Фиктивных переменных; при контрасте равном Deviation (Отклонение) все категории кроме эталонной будут проверяются относительно суммарного эффекта.
-
Установите контраст Deviation (Отклонение) и при помощи щелчка на Continue (Далее) вернитесь в исходное диалоговое окно.
-
Начните расчёт нажатием ОК.
Вы можете проследить, какие переменные вовлекаются в анализ и как улучшается вероятность прогноза после вовлечения каждой новой переменной. На завершающей стати анализа присутствуют четыре переменные, а именно: возраст, время проведения искусственного дыхания, рост и концентрация кислорода в воздушной массе для искусственного дыхания.
Точность исполнения прогноза, которая достигается при использовании этих четыpex переменных, составляет 71,0 %; её можно увидеть в нижеследующей классификанионной таблице на стр 25.
Classification Table (Классификационная таблица)а
| Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
| Outcome (Исход) | Percentage Correct (Процентный показатель верных прогнозов) | ||||
| gestorben (скончался) | ueberlebt (выздоровел) | ||||
|
Step 1 (Шаг)
|
Outcome (Исход) | gestorben (сконча-лся) | 29 | 34 | 46,0 |
| ueberlebt (выздоро- вел) | 14 | 54 | 79,4 | ||
| 63,4 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
|
Step 2 Шаг 2)
|
Outcome (Исход) | gestorben (сконча- лся) | 32 | 31 | 50,8 |
| ueberlebt (выздоро- вел) | 16 | 52 | 76,5 | ||
| 64,1 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
| StepS (Шаг 3) | Outcome (Исход) | gestorben (сконча- лся) | 33 | 30 | 52,4 |
| ueberlebt (выздоро- вел) | 19 | 49 | 72,1 | ||
| Overall Percentage (Суммарный процентный показатель) | 62,6 | ||||
| Step 4 (Шаг 4) | Outcome (Исход) | gestorben (сконча-лся) | 37 | 26 | 58,7 |
| ueberlebt (выздоро- вел) | 12 | 56 | 82,4 | ||
| 71,0 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
a. The cut value is ,500 (Разделительное значение равно ,500)
Прогноз оправдался для 58,7 % умерших пациентов и для 82,4 % выздоровевших. Значения коэффициента Ь. и константы а для расчёта вероятности (выздоровления) находятся в следующей таблице:
Variables in the Equation (Переменные в уравнении)
В Коэф-фициент регрессии В) | S.E. (Стандар-тная ошибка) | Wald (Валь-довский) | df | Sig. (Значи- мость) | Ехр (В) | ||
Шаг 1а | BZEIT | -,081 | ,028 | 8,482 | 1 | ' ,004 | ,922 |
Конста- нта | 1,104 | ,385 | 8,205 | 1 | ,004 | 3,017 | |
Шаг 2b | GR | ,038 | ,017 | 5,109 | 1 | ,024 | 1,039 |
BZEIT | -,073 | ,028 | L 6,688 | 1 | ,010 | ,930 | |
Конста- нта | -5,460 | 2,924 | L 3,487 | 1 | ,062 | ,004 | |
Шаг 3c | КОВ | -2,678 | 1,264 | 4,489 | 1 | ,034 | ,069 |
GR | ,037 | ,017 | 4,622 | 1 | ,032 | 1,038 | |
BZEIT | -,077 | ,029 | 6,866 | 1 | ,009 | ,926 | |
Конста- нта | -2,995 | 3,192 | ,880 | 1 | ,348 | ,050 | |
Шаг 4d | ALTER (возраст) | -.037 | ,017 | 4,653 | 1 | ,031 | ,963 |
КОВ | -3,028 | 1,302 | 5,410 | 1 | ,020 | ,048 | |
GR | ,044 | ,017 | 6,650 | 1 | ,010 | 1,045 | |
BZEIT | -,062 | ,029 | 4,639 | 1 | ,031 | ,940 | |
Конста- нта | -2,884 | 3,079 | ,877 | 1 | ,349 | ,056 |
a. Variable(s) entered on step 1: BZEIT. (Переменные, вводимые на шаге 1: BZEIT.)
b. Variable(s) entered on step 2: GR. (Переменные, вводимые на шаге 2: GR.)
с. Variable(s) entered on step 3: КОВ. (Переменные, вводимые на шаге 3: КОВ.)
d. Variable(s) entered on step 4: ALTER. (Переменные, вводимые на шаге 4: ALTER.)
Если мы рассмотрим случай с 30-тилешим пациентом, с ростом 180 см, которому делали искусственное дыхание в течении 10 часов при концентрации кислорода в смеси равной 0,7, то исходя из соотношения
z= - 2,884- 0,037x30- 0,062x10+ 0,044x180- 3,028x0,7= 1,12В получим вероятность выздоровления
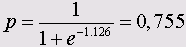
следовательно, вероятность выздоровления пациента равна 0,755