Главное меню
Вы здесь
16.2 Множественная линейная регрессия
16.2 Множественная линейная регрессия
В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи в конце концов становится невозможно представить графически.
В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения
у = b1-х1+b2-х2+... + bn-хn+а,
где n — количество независимых переменных, обозначенных как х1 и хn, а — некоторая константа.
Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.
В качестве примера рассмотрим стоматологическое обследование 1130 человек, в котором исследуется вопрос необходимости лечения зубного ряда, измеряемой при помощи так называемого показателя CPITN, в зависимости от набора различных переменных.
При этом зубной ряд был разделён на секстанты, для которых и происходило определение показателя CPITN. Этот показатель может принимать значения от 0 до 4, где 0 соответствует здоровому состоянию, а 4 наибольшей степени развития заболевания. Затем значения показателя CPITN для всех секстант были усреднены.
Файл zahn.sav содержит следующие переменные:
Имя переменной | Расшифровка |
cpitn | Усредненное значение CPITN |
alter | Возраст |
g | Пол (1 = мужской, 2 = женский) |
s | Образование (1 = специальное школьное, 2 = неполное школьное, 3 = среднее, 4 = аттестат зрелости, 5 = высшее образование) |
pu | Периодичность чистки зубов (1 = меньше одного раза в день, 2 = один раз в день, 3 = два раза в день, 4 = долее двух раз в день) |
zb | Смена зубной щётки (1 = каждый месяц, 2 = каждые три месяца, 3 = раз в полгода, 4 = ещё реже) |
beruf (профессия) | Профессия (1 = государственный служащий/служащий, 2 = рабочий/профессиональный рабочий, 3 = занятость в области медицины, 4 = военный) |
Переменные cpitn и alter принадлежат к интервальной шкале, а переменные s, pu и zb при более подробном рассмотрении можно отнести к порядковой шкале, так что они могут быть подвергнуты регрессионному анализу. Переменная g относится к номинальной шкале, но в то же время является дихотомической. Поэтому если при оценке результатов обратить внимание на полярность, то и эта переменная так же может быть вовлечена в регрессионный анализ. Однако, переменная beruf относится к номинальной шкале и имеет более двух (а именно четыре) категории. Поэтому, без дополнительной обработки ее нельзя применять в дальнейших расчётах.
В данном случае можно прибегнуть к специальному трюку: разложить переменную beruf на четыре, так называемых, фиктивных переменных, с кодировками отвечающими О (действительно) и 1 (ложно). В файл добавляются четыре новые переменные: berufl-beruf4, которые поочередно соответствуют четырём различным кодировкам переменной beruf. Так, к примеру, переменная berafl указывает на то, является ли данный респондент государственным служащим/работником (кодировка 1) или нет (кодировка 0).
-
Откройте файл zahn.sav.
-
Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная)
-
Поместите переменную cpitn в поле для зависимых переменных, объявите переменные: alter, berafl, bеrа0, beru0, beruf4, g, pu, S.H zb независимыми.
Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных, установленный по умолчанию. Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной. Для множественного анализа следует выбрать один из пошаговых методов. При прямом методе независимые переменные, которые имеют наибольшие коэффициенты частичной корреляции с зависимой переменной пошагово увязываются в регрессионное уравнение. При обратном методе начинают с результата, содержащего все независимые переменные и затем исключают независимые переменные с наименьшими частичными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент не оказывается незначимым (в данном случае уровень значимости равен 0,1).
Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу. При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно.
-
Выберите пошаговый метод, но воздержитесь от блочной формы ввода данных, не задавайте больше ни каких дополнительных расчётов и начните вычисление нажатием ОК.
Model Summary (Сводная таблица модели)
Model (Модель) | R | R Square (Коэф- фициент детерми- нации) | Adjusted R Square (Скорректи- рованный R-квадрат) | Std. Error of the Estimate (Станда- ртная ошибка оценки) |
1 2 3 4 5 | ,452а ,564b ,599с ,609d ,613е | ,204 ,318 ,359 ,371 ,375 | ,203 ,317 ,358 ,369 ,373 | ,8316 ,7698 ,7467 ,7402 ,7380 |
a. Predictors: (Constant), Alter (Влияющие переменные: (константа), возраст)
b. Predictors: (Constant), Alter, Putzhaeufigkeit (Влияющие переменные: (константа), возраст, периодичность чистки)
c Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки)
d Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование)
е. Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung, Arbeiter/Facharbeiter (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник) .
Из первой таблице следует, что вовлечение переменных в расчет производилось за пять шагов, то есть переменные возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник поочерёдно внедрялись в уравнение регрессии. Для каждого шага происходит вывод коэффициентов множественной регрессии, меры определённости, смещенной меры определённости и стандартной ошибки.
К указанным результатам пошагово присоединяются результаты расчёта дисперсии (см. гл. 16.1.1), которые здесь не приводятся. Также, пошаговым образом, производится вывод соответствующих коэффициентов регрессии и значимость их отличия от нуля.
Coefficients (Коэффициенты) a
| Model (Модель) | UnStan- dardized Coefficients (He стандарти-зированные коэф- фициенты) | Standa- rdized Coefficients (Стандарти-зированные коэф-фициенты) | Т | Sig. (Значи мость) | ||
| В | Std. Error (Станда- ртная ошибка) | ß (Beta) | ||||
| (Constant) (Константа) Alter (Возраст) | 1,295 3,31 Е-02 | ,071
,002 |
,452 | 18,220 17,006 | ,000 ,000 | |
| 2 | (Константа) Возраст Перио- дичность чистки | 3,024 3.20Е-02 -,604 | ,142
,002 ,044 |
,437
-,339 |
21,317 17,765 -13,756 | ,000 ,000 ,000 |
| 3 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки | 1,903 3.25Е-02 -,439 ,253 | ,191
,002 ,047 ,030 |
,443
-,246 ,222 |
9,976 18,555 -9,376 8,473 | ,000 ,000,
,000 ,000 |
| 4 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки Образование | 2,188 3,31 Е-02 -,391 ,226 -,115 | ,199
,002 ,048 ,030 ,025 |
,451
-,220 ,199 -,116 |
10,992 19,011 -8,235 7,498 -4,580 | ,000 ,000
,000 ,000 ,000 |
| 5 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки Образование Рабочий/ Профес- сиональный работник |
2,022 3.20Е-02 -,379 ,229 -8.3Е-02 ,143
|
,208 ,002 ,048 ,030 ,028 ,052
|
,437 -,213 ,201 -,084 ,075
|
9,743 18,041 -7,964 7,613 -2,983
2,757 |
,000 ,000 ,000 ,000 ,003
,006 |
а. Dереnаdеnt variable: Mittlerer CPITN-Wert (Зависимая переменная: усреднённое значение CPITN)
Вдобавок ко всему для каждого шага анализируются исключённые переменные. В вышеприведенной таблице в объяснениях нуждаются лишь коэффициенты ß. Это — регрессионные коэффициенты, стандартизованные соответствующей области значений, они указывают на важность независимых переменных, вовлечённых в регрессионное уравнение.
Уравнение регрессии для прогнозирования значения CPITN выглядит следующим образом:
cpitn = 0,032•alter - 0.379•рu + 0,229•zb - 0,083•s + 0,143- benif 2 + 2,022
Для 40-летнего рабочего с неполным школьным образованием, который ежедневно чистит зубы один раз в день и меняет щётку раз в полгода, с учётом соответствующих кодировок, получается следующее уравнение:
cpitn = 0,032•40-0,379•2 + 0,229•3- 0,083•2 + 0,143•1 + 2,022 = 3,208
При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков, на которых мы здесь останавливаться не будем. Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
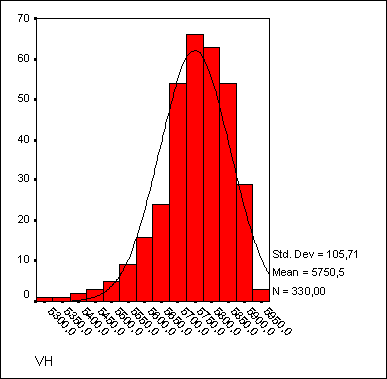
Важным моментом является анализ остатков, то есть отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (то есть не систематически) и подчиняться нормальному распределению. Это можно проверить, если с помощью кнопки Charts... (Диаграммы) построить гистограмму остатков. В приведенном примере наблюдается довольно хорошее согласование гистограммы остатков с нормальным распределением.
Проверка на наличие систематических связей между остатками соседних случаев (что, однако, является уместным только при наличии так называемых данных с продольным сечением), может быть произведена при помощи теста Дарбина-Ватсона (Durbin-Watson) на автокорреляцию. Этот тест вычисляет коэффициент, лежащий в диапазоне от 0 до 4. Если значение этого коэффициента находится вблизи 2, то это означает, что автокорреляция отсутствует. Тест Дарбина-Ватсона можно активировать через кнопку Statistics (Статистические характеристики). В данном примере тест дает удовлетворительное значение коэффициента, равное 1,776.
Ещё одной дополнительной возможностью является задание переменной отбора в диалоговом окне Linear Regression (Линейная регрессия). Здесь, с помощью кнопки Rule... (Правило) в диалоговом окне Linear Regression: Define Selection Rule (Линейная регрессия: ввод условия отбора), Вы получаете возможность при помощи избирательного признака сформулировать условие, которое будет ограничивать количество случаев, вовлеченных в анализ.
Рис. 16.14: Гистограмма остатков