8. Численные расчеты — пакет NumericalMath

Численные расчеты — пакет NumericalMath

Пакет расширения NumericalMath содержит множество полезных функций для тех, кто имеет дело с численными расчетами. В их числе функции для выполнения высокоточных аппроксимаций рациональными функциями, численного интегрирования и дифференцирования, вычисления пределов функций, решения уравнений, разложения в ряд и т. д. Ниже описано подавляющее большинство функций этого расширения. Исключены лишь отдельные функции, представляющие ограниченный интерес и несложные для самостоятельного изучения (в подпаке-mах Butcher, Microscope и ComputerArithmetic).

Аппроксимация аналитических функций — Approximations

Подпакет Approximations содержит ряд функций для улучшенной рациональной аппроксимации аналитических функций. Для рациональной интерполяции и аппроксимации функций по заданным значениям абсцисс служит следующая функция:

• Rationallnterpolation [f, {x,m, k}, {x ₁ , x ₂ , ...,.x _m+k+1 } ] — возвращает аппроксимирующее функцию f выражение в виде отношения полиномов а степенью полинома числителя m и знаменателя k в абсциссах, заданных списком {x _l ,x ₂ ,...,x _m+jt+1 }.

Пример применения этой функции:

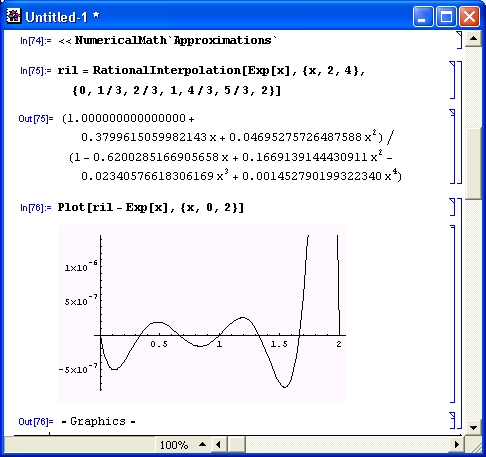
<<NumericalMath `Approximations`

ril = Rationallnterpolation[ Exp[x], {х, 2, 4}, {0, 1/3, 2/3, 1, 4/3, 5/3, 2}]

Построим график погрешности аппроксимации, то есть график разности функ ии ril и Ехр [х] — он представлен на рис. 11.22.

Нетрудно заметить, что если в центральной части области аппроксимации погрешность мала (менее 5-10- ⁷ ), то у правого края она резко возрастает.

Представленная функция может использоваться и в иной форме:

Rationallnterpolation[f,{х, m, k},{x, xmin, xmax}]

Рис. 11.22. График погрешности рациональной аппроксимации экспоненциальной функции

В данном случае выбор абсцисс осуществляется автоматически в интервале от xmin до mах. В отличие от первого случая, когда абсциссы могли быть расположены неравномерно, в данном случае расположение их будет равномерным. Приведем пример аппроксимации функции синуса в интервале от n до n:

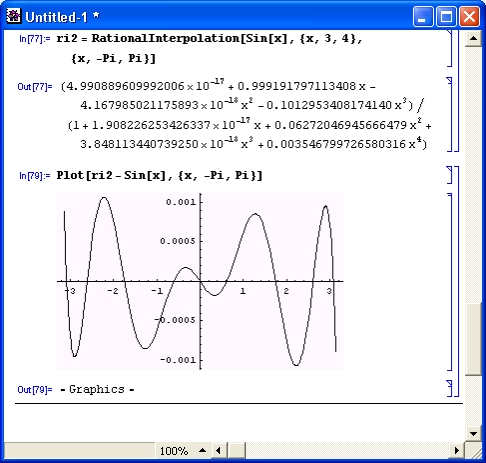
ri2 = RationalInterpolation[Sin[x],{x,3,4},{x,-Pi,Pi}]

Интересно оценить погрешность аппроксимации. Для этого достаточно построить график разности аппроксимирующей и аппроксимируемой функций. Это построение представлено на рис. 11.23. Любопытно, что хотя максимальная погрешность и значительна, резких выбросов погрешности в данном случае нет.

Рис. 11.23. График погрешности аппроксимации синусоидальной функции

При рациональной аппроксимации можно задать опции WorkingPrecision и Bias со значениями по умолчанию $MachinePrecision и 0 соответственно. Опция Bias обеспечивает автоматическую расстановку узлов интерполяции. При Bias->0 обеспечивается симметрирование выбросов погрешности, дающее наименьшее ее значение в пиках. Ниже приведен пример интерполяции (аппроксимации) экспоненциальной функции в интервале изменения х от 0 до 2:

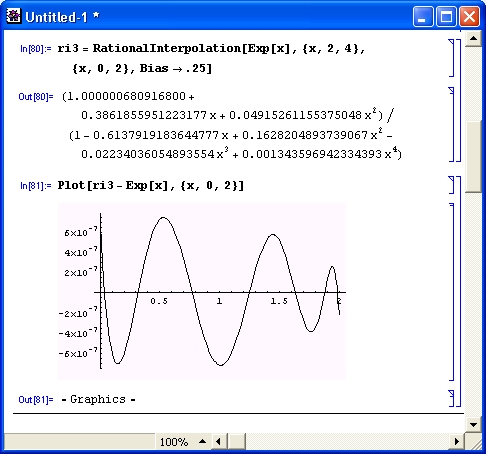
ri3 = RationalInterpolation[Exp[x],{x,2,4},{x,0,2},Bias->.25]

Построение графика погрешности (рис. 11.24) показывает, что правильным выбором центра интерполяции можно существенно уменьшить ее погрешность. Теперь большая погрешность наблюдается в левой части графика. Однако резкого выброса погрешности в данном случае нет.

Рис. 11.24. Погрешность аппроксимации экспоненты при выборе опции Bias->.25

Из приведенных примеров ясно, что рациональная аппроксимация способна дать существенное уменьшение погрешности при некотором оптимальном расположении узлов аппроксимации и выравнивании погрешностей по абсолютной величине в точках минимумов и максимумов кривой погрешности. Это лежит в основе так называемой минимаксной аппроксимации. Она реализуется следующей функцией:

• MiniMaxApproximation[f,{x,{xmin,xmax},m,k}] — возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax:
• MiniMaxApproximation [f, approx, {x, {xmin, xmax} ,m, k} ] —возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax с возможностью выбора метода аппроксимации approx.

Эта аппроксимация использует итерационный алгоритм вычислений. Они начинаются с первого шага, на котором используется функция Rational Interpolation. Затем аппроксимация последовательно улучшается применением алгоритма Ремеза, лежащего в основе этого вида аппроксимации.

Функция MiniMaxApproximation возвращает два списка — первый с координатами абсцисс, при которых наблюдается максимальная погрешность, второй содержит рациональную функцию аппроксимации. Ниже представлен пример аппроксимации экспоненциальной функции:

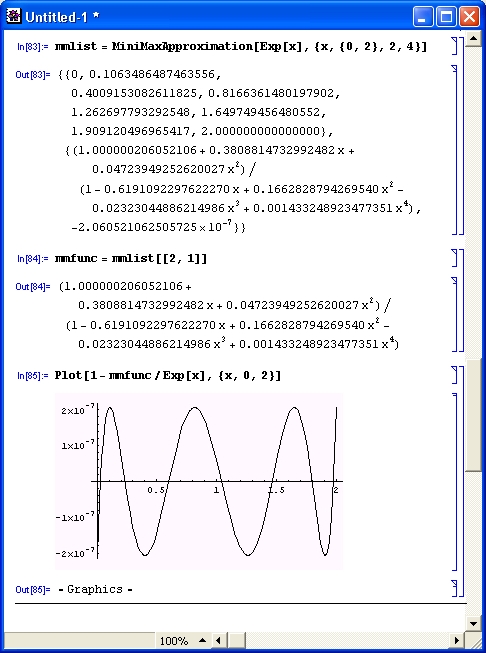
mmlist = MiniMaxApproximation[Ехр[х], {х, {0, 2}, 2, 4}]

Выделим формулу аппроксимации:

mmfunc = mmlist[[2, 1]]

Теперь можно построить график погрешности аппроксимации (рис. 11.25).

Рис. 11.25. График погрешности при минимаксной аппроксимации экспоненциальной функции

Следует отметить, что малость абсолютной ошибки для ряда функций (например, тригонометрических) может приводить к большим относительным погрешностям в точках, где функции имеют нулевые значения. Это может привести к отказу от выполнения аппроксимации вследствие исчерпания числа итераций (опция Maxlterations по умолчанию имеет значение 20). Такой случай наблюдается, например, при исполнении следующей команды:

MiniMaxApproximation[Cos[x], {х, {1, 2}, 2, 4}]

Делением функции на (x-Pi/2) можно исключить эту ситуацию:

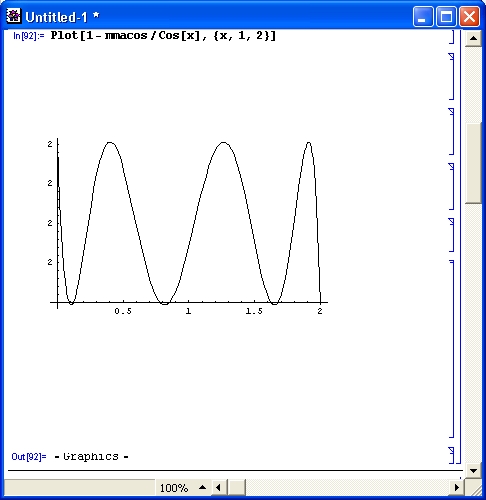
MiniMaxApproximation[Cos[x]/(x-Pi/2),{*,{1!,2},2,4}] [[2,1]]

График погрешности для этого примера представлен на рис. 11.26. Обратите внимание на то, что в этом примере погрешность аппроксимации не превышает (б...7)-10- ¹⁰ .

В приложении дан список функций общей рациональной интерполяции (аппроксимации) для аналитических зависимостей, заданных параметрически. Примеры применения этого довольно редкого вида аппроксимации можно найти в справочной базе данных системы Mathematica. Там же можно найти дополнительные соображения по уменьшению погрешности аппроксимации.

Рис. 11.26. График погрешности при минимаксной аппроксимации функции косинуса

Нули функций Бесселя — BesselZeros

В подпакете BesselZeros определены функции, дающие список аргументов функций Бесселя в их первых п нулевых точках: BesselJZeros [mu, n], Bessel-YZeros[mu,n], BesselJPrimeZeros[mu,n], BesselYPrimeZeros[mu,n] и др. Ввиду редкого использования функций этого класса ограничимся парой примеров их применения:

<<NumericalMath`BesselZeros`

BesselJZeros[0, 5]

{2.40483, 5.52008, 8.65373, 11.7915, 14.9309}

BesselJYJYZeros[2, 6/5, 3, WorkingPrecision -> 20]

{15.806622444176579073, 31.46556009153683, 47.1570167108650315}

Поиск корней уравнений с интерполяцией — InterpolateRoot

Подпакет InterpolateRoot дает средства для ускоренного и более точного поиска корней уравнений по сравнению с соответствующими функциями ядра. Достигается это за счет применения интерполяции функции, корни которой ищутся. Под-пакет задает функцию InterpolateRoot [f, {х, a, b} ], которая находит корень функции f в интервале х от а до b. Вместо функции f можно задавать уравнение eqn. Возможны опции AccuracyGoal->Automatic, Maxlterations->15, WorkingPrecision->$MachinePrecision и ShowProgress->False (указаны принятые по умолчанию значения).

Примеры применения данной функции (n — число итераций):

<<NumericalMath` InterpolateRoot`

n = 0; FindRoot[n++; Exp[x] == 2, {x, 0, 1},

WorkingPrecision -> 100, AccuracyGoal -> 95]

{x->

0.693147180559945309417232121458176568075500134360255 2541206800094933936219696947156058633269964186876}

n

17

n = 0; f[x_] := (n++; Exp[x]-2) /; NumberQ[x]

InterpolateRoot[f[x], {x, 0, 1), WorkingPrecision -> 100,

AccuracyGoal -> 95]; n 10

InterpolateRoot[Exp[x] ==2, {x, 0, 1},ShowProgress -> True,

WorkingPrecision -> 40]

{0, 0.58197670686932642439}

{21, 0, -0.12246396352039524100}

{1, 0.7019353037882764014443370764853594873432}

{21, 20, 0.0130121629575404389120930392554}

{3,0.6932065772065263165289985793736618546663}

{21, 20, 0.000062480788747713548804773113708}

{6, 0.6931471932603933841618726058237307884661}

{21, 20, 1.26443483693584888038460396742xHT8}

{12, 0.693147180559945119457822446

95590259222308309027205042483074}

{40, 20, -1.89953767048152086910014102216x 10-16}

{24, 0.6931471805599453094172321214

5786257157118117337249076750141}

Реализация интервальных методов —IntervalRoots

Иногда важно не найти приближенное значение корня, а уточнить интервал, в котором он находится. В подпакете IntervalRoots для этого используется ряд известных методов, реализованных следующими функциями:

• IntervalBisection [f ,x, int, eps] — находит корень функции f(x) путем уточнения исходного интервала int с заданной погрешностью eps методом половинного деления;
• IntervalSecant [f ,x, int, eps] — находит корень функции f(x) путем уточнения исходного интервала int с заданной погрешностью eps методом секущей;
• IntervalNewton [ f, x, int, eps ] — находит корень функции/(x) путем уточнения исходного интервала int с заданной погрешностью eps методом Ньютона (касательной).

Во всех функциях можно опциями задать максимальное число рекурсий (Max-Recursion) и погрешность (WorkingPrecision). Примеры применения этих функций даны ниже:

<<NumericalMath`IntervalRoots`

IntervalBisection[Sin[x], x, Interval[{2., 8.}], .1]

Interval[{3.125, 3.218750000000001}, {6.218750000000003, 6.312500000000006}]

IntervalBisection[Sin[x], x, Interval[{2., 8.}], .01]

Interval[{3.125, 3.17188}, {6.26563, 6.3125}]

IntervalBisection[Sin[x], x, Interval[{2., 8.}], .01, MaxRecursion -> 10]

Interval[{3.13672, 3.14258}, {6.27734, 6.2832}]

IntervalSecant[Sin[x], x, Interval[{2., 8.}], .01]

Interval[{3.14159, 3.1416}, {6.28316, 6.28321}]

IntervalSecant[Sin[x], x, Interval[{2., 8.}], .01]

Interval[{3.14159, 3.1416}, {6.28316, 6.28321}]

IntervalBisection[Sin[x], x,

Interval[{2, 8}], .1, WorkingPrecision -> Infinity]

Табличное численное интегрирование — Listlntegrate

Встроенная в ядро функция NIntegrate вычисляет определенные интегралы при известной подынтегральной функции. Однако нередко, например при экспериментах, такая функция задается таблицей или списком значений. В подпакете List-Integrate имеются функции для решения этой задачи — табличного интегрирования:

• Listlntegrate [ {yl, y2,..., yn} ,h] — возвращает численное значение интеграла для функции, заданной списком ординат yi при заданном шаге h по х;
• Listlntegrate [ {yl, y2,..., yn}, h, k] — возвращает численное значение интеграла для функции, заданной списком ординат yi при заданном шаге h по х, используя k точек каждого подинтервала;
• Listlntegrate [ {{xl, yl}, {х2, у2 },..., {хп, уп}}, k] — возвращает численное значение интеграла для функции, заданной списком координат {х.., у.}. используя k точек для каждого подынтервала.

Примеры применения данной функции:

<<NumericalMath`Listlntegrate`

data = Tablet n^2, {n, 0, 7}]

{0, 1, 4, 9, 16, 25, 36, 49}

ListIntegrate[data, 1]

343/3

Listlntegrate[{{0,0},{1,1},{2,4},{5,25},{7,49}},2] 241/2

При проведении интегрирования для данных, заданных таблично, можно использовать интерполяцию:

арр = Listlnterpolation[data,{{0,7}}] Integrate[app[x],{x,0,7}]

343/3

Integrate[Interpolation[{{0,0},{1,1},{2,4}, {5,25}, {7,49}},

InterpolationOrder->l][x],{x,0,7}]

241/2

 

Численное вычисление пределов — NLimit

В подпакете N limit определена функция

Nlimit[expr,х->х0]

для численного вычисления пределов выражений ехрг (см. примеры ниже):

<<NumericalMath` NLimit`

NLimit[Zeta[s] - l/(s-l), s->l]

0.577216

N[EulerGamma]

0.577216

С помощью команды Options [NLimit] можно просмотреть опции, которые используются функцией NLimit по умолчанию. В этом подпакете задано также вычисление бесконечных сумм Эйлера EulerSum[f, { i, imin, Infinity} ]. Например:

EulerSum[(-l)^k/(2k + 1) , {k, 0, Infinity}]

0.785398

EulerSumt(-1)^k/(2k +1), {k, 0, Infinity},

WorkingPrecision->40, Terms->30, ExtraTerms->30]

0.78539816339744830961566084579130322540

%- N[Pi/4, 40]

-2.857249565x 10-29

Имеется также функция вычисления производной в численном виде:

• ND [ f, х, хО] — вычисляет первую производную f(x) в точке х0;
• ND[f, {x,n} ,х0] — вычисляет п-ю производную f(X) в точке х0. Пример вычисления производной:

ND[Exp[Sin[x]], х, 2]

-1.03312

Options[ND]

{WorkingPrecision-> 16, Scale-> 1, Terms-> 7, Method-> EulerSum]

В некоторых случаях вычисления могут быть ошибочными. Тогда следует использовать опции — особенно опцию выбора метода Method. Помимо метода по умолчанию (EulerSum) можно использовать NIntegrate (метод интегрирования по формуле Коши).

Численное вычисление остатка — N Residue

В подпакете NResidue имеется функция вычисления остатка NResidue [expr, {x, x0} ] в точке х=х0:

<<NumericalMath` NResidue`

NResidue[1/z, {z, 0}]

1. + 6.35614x 10-18 I

Residue[f, {z, 1.7}]

0

NResidue[f, {z, 1.7}]

0.259067 - 1.9353xl0-17I

l/((z+.2+.5 I)(z+.2-.5 I)) /. z -> 1.7

0.259067 + 0. I

Options[NResidue]

Обратите внимание на возможные опции для этой функции в последнем примере.

Численное разложение в ряд — NSeries

Подпакет NSeries вводит функцию NSeries [f, {x,xO,n}], которая дает численный ряд, аппроксимирующий функцию f(x) в окрестности точки х = х ₀ , включая термы от (х -х ₀ ) ^-n до (х - х ₀ ) ^п .

Примеры применения данной функции:

<<NumericalMath`NSeries`

NSeries[Sin[х], {х, -2, 2}]

Rationalize[Chop[%]]

Rationalize[Chop[NSeries[Log[x], {x, 1, 5}, Radius -> 1/8]]]

Rationalize[Chop[NSeries[Exp[x], {x, 0, 5},

WorkingPrecision -> 40, Radius -> 1/8]]]

Rationalize[Chop[NSeries[Exp[x], {x, 0, 5}, Radius -> 4]]]

Chop[NSeries[Zeta[s], {s, 1, 3}]]

Вычисление коэффициентов формулы интегрирования Ньютона—Котесса — NewtonCotes

Функция NIntegrate, имеющаяся в ядре системы Mathematica, реализует метод интегрирования Гаусса—Кронрода. Еще одним известным методом интегрирования является метод Ньютона—Котесса, сводящий интегрирование к вычислению взвешенных ординат функции в равномерно расположенных точках оси абсцисс. Для реализации метода используются следующие функции:

• NewtonCotesWeights [n, a, b] — возвращает список весовых коэффициентов и абсцисс узловых точек {wi, xi} для квадратуры Ньютона—Котесса на интервале от а до b;
• NewtonCotesError [n, f, a, b] — возвращает погрешность формулы Ньютона—Котесса для заданной функции f.

Примеры применения этих функций представлены ниже:

<<NumericalMath` NewtonCotes`

NewtonCotesWeights[5, 0, 10]

NewtonCotesError[5, f, 0, 10]

NewtonCotesError[5, f, a, a+h]

NewtonCotesWeights[5, -0, 10, QuadratureType -> Open]

NewtonCotesError[5, f, 0, 10, QuadratureType -> Open]

Обратите внимание на то, что приведенные формулы готовят данные для численного интегрирования методом Ньютона—Котесса, но не выполняют самого интегрирования.

Что нового мы узнали?

В этом уроке мы научились:

• Пользоваться алгебраическими функциями пакета Algebra.
• Применять вычислительные функции пакета Calculus.
• Работать с функциями дискретной математики из пакета DiscreteMath.
• Производить геометрические расчеты с помощью пакета Geometry.
• Выполнять алгебраические вычисления с помощью пакета LinearAlgebra.
• Пользоваться расширенными функциями теории чисел из пакета NumberTheory.
• Осуществлять численные расчеты с помощью пакета NumericalMath.