Главное меню
Вы здесь
4. Пакет дискретной математики DiscreteMath
Пакет дискретной математики DiscreteMath
Пакет DiscreteMath задает набор функций дискретной математики. Это прежде всего функции комбинаторики и работы с графами (более 230 функций). Мы вынуждены рассмотреть их только выборочно.
Комбинаторика и ее функции — Combinatorica и CombinatorialFunctions
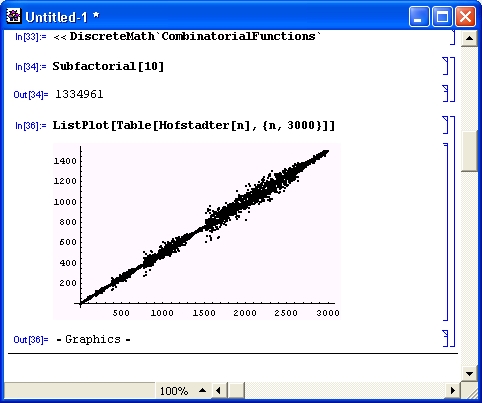
Несколько функций комбинаторики (Factorial, Factorial2, Binomial, Multinomial, Pochhammer и Fibonacci) могут использоваться без загрузки пакетов расширения. Рисунок 11.5 демонстрирует работу подпакета Combinatorial-Functions (функции комбинаторики). Определения функций этого пакета есть в справочной базе данных.
Рис. 11.5. Примеры работы с подпакетом функций комбинаторики
Подпакет Combinatorica задает определение ряда функций комбинаторики и теории графов. Ниже представлены имена функций комбинаторики.
| Функции перестановок и сочетаний | |
| Backtrack | BinarySearch |
| Binary Subsets | DerangementQ |
| Derangements | Distinct Permutations |
| EquivalenceClasses | EquivalenceRelationQ |
| Equivalences | Eulerian |
| FromCycles | FromlnversionVector |
| GrayCode | HeapSort |
| Heapify | HideCycles |
| Index | InversePermutation |
| Inversions | InvolutionQ |
| Josephus | Ksubsets |
| Lexicographic Permutations | LexicographicSubsets |
| MinimumChangePermutations | MultiplicationTable |
| NextKSubset | Next Permutation |
| NextSubset | NthPermutation |
| NthSubset | NumberOf Derangements |
| NumberOf Involutions | NumberOf Permu tat ion sByCycles |
| PermutationGroupQ | PermutationQ |
| Permute | Polya |
| RandomHeap | RandomKSubset |
| RandomPermutation | RandomPermutationl |
| RandomPermutation2 | RandomSubset |
| RankPermutation | RankSubset |
| RevealCycles | Runs |
| SamenessRelation | SelectionSort |
| SignaturePermutation | StirlingFirst |
| StirlingSecond | Strings |
| Subsets | ToCycles |
| ToInversionVector | TransitiveQ |
Следует отметить, что ввиду обилия функций даже в справочной системе даны примеры лишь для избранных функций. Для ознакомления с назначением конкретной функции достаточно исполнить команду ?Имя_функции, например:
<<DiscreteMath`Combinatorica`
?Permute
Permute[l, p] permutes list 1 according to permutation p.
?KSubsets
KSubsets[l, k] gives all subsets of set 1 containing exactly k
elements, ordered lexicographically.
KSubsets[{l, 2, 3, 4, 5}, 2]
{{1, 2}, {1, 3), {1, 4}, {1, 5}, {2, 3), {2, 4}, {2, 5}, {3, 4}, {3, 5}, (4, 5}}
<< DiscreteMath`Combinatorica`
MinimumChangePermutations[{1,2,3}]
{{1, 2, 3}, {2, 1, 3}, {3, 1, 2}, {1, 3, 2}, {2, 3, 1}, {3, 2, 1}}
Map[RankPermutation, Permutations[{1,2,3,4}]]
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23}
InversePermutation[{4,8,5,2,1,3,7,6}]
(5, 4, 6, 1, 3, 8, 7, 2}
Polya[Table[ RotateRight[Range[8],i], {i,8}], m]
1/8 (4m+2m2 +m4 +m8)
Table[NthSubset[n,a,b,c,d], {n,0,15}]
{{}, {a}, {b}, {a, b}, {c}, {a, c}, {b, c}, {a, b, c}, {d}, (a, d}, {b, d}, {a, b, d}, {c, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}
Вторая группа функций комбинаторики представлена следующими функциями.
| Функции разделения, композиции и картин Янга | |
| CatalanNumber | Compositions |
| ConstructTableau | DeleteFromTableau |
| DurfeeSquare | EncroachingListSet |
| FerrersDiagram | FirstLexicographicTableau |
| . Insert IntoTableau | LastLexicographicTableau |
| Longest IncreasingSubsequence | NextComposition |
| Next Part it ion | NextTableau |
| NumberOf Compos it ions | NumberOf Partitions |
| NumberOf Tableaux | PartitionQ |
| Partitions | RandomComposition |
| RandomPartition | RandomTableau |
| TableauClasses | TableauQ |
| TableauxToPermutation | Tableaux |
| TransposePartition | TransposeTableau |
Ha рис. 11.6 показано несколько примеров работы с некоторыми из этих функций.
Рис. 11.6. Примеры работы с функциями разделения, композиции и картин Янга
Этих примеров достаточно, чтобы заинтересованный читатель по их образцу и подобию изучил свойства и возможности нужных ему функций комбинаторики.
Mathematica имеет самые обширные возможности решения задач, связанных с графами. Задание графов и манипуляции с ними также включены в пакет комбинаторики. Они представлены четырьмя группами функций.
| Представление графов | ||
| AddEdge | AddVertex | Breadth'FirstTraversal |
| ChangeEdges | ChangeVertices | CircularVertices |
| CompleteQ | Contract | DeleteEdge |
| DeieteVertex | DepthFirstTr aversal | Diameter |
| DilateVertices | Distribution | Eccentricity |
| Edges | EmptyQ | FromAd j acencyLists |
| FromOrderedPairs | FromUnorderedPairs | GraphCenter |
| GraphComplement | InduceSubgraph | M |
| MakeSimple | MakeUndirected | Normal! zeVerticesPointsAndLines |
| Pseudograph | RadialEmbedding | Radius |
| RankGraph | RankedEmbedding | ReadGraph |
| RemoveSelf Loops | RootedEmbedding | RotateVertices |
| ShakeGraph | ShowGraph | ShowLabe 1 edGr aph |
| SimpleQ | Spectrum | SpringErrbedding |
| ToAdjacencyLists | ToOrderedPairs | ToUnorderedPairs |
| TranslateVertices | UndirectedQ | UnweightedQ |
| Vertices | WriteGraph | |
Одной из самых важных функций этой группы является функция ShowGraph (показать граф). Она обеспечивает визуальное представление графа, заданного аргументом функции. Покажем работу избранных функций этой группы на нескольких примерах.
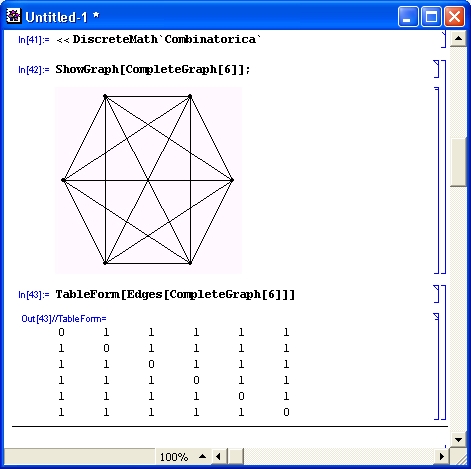
На рис. 11.7 показано построение полного графа и его таблицы. Параметром графа является число 6, характеризующее число узловых точек графа, соединенных друг с другом.
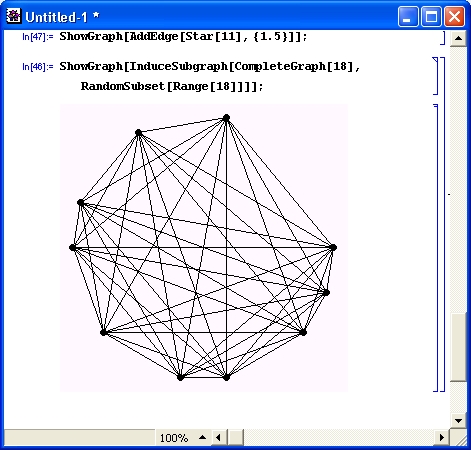
Изменяя значение параметра графа, можно получить множество других графов. На рис. 11.8 показан вид двух разных графов. Верхний граф — многолучевая звезда с добавленным отрезком, полученная с помощью функции AddEdge. Первый аргумент задает исходный граф (в нашем случае — звезду с 11 узлами), а второй — соединяемые отрезком прямой точки. Нижний рисунок иллюстрирует построение подграфа.
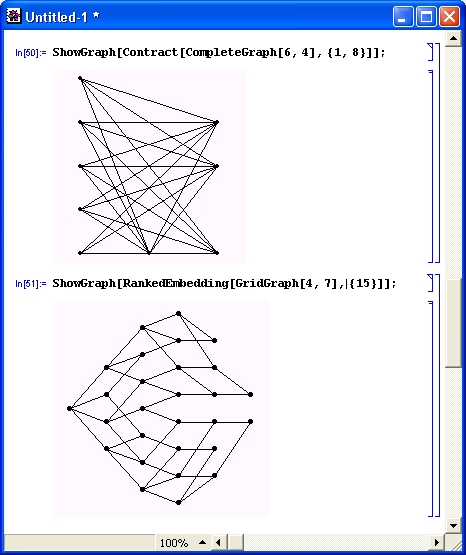
Еще пара графов представлена на рис. 11.9. Этот рисунок иллюстрирует применение функций Contract и GridGraph. Последняя из них строит сеточный граф.
Рис. 11.7. Пример построения полного графа и его таблицы
Рис. 11.8. Построение графа звезды и подграфа
Рис. 11.9. Примеры построения графов с помощью функций Contractn GridGraph
Приведенный выше набор функций позволяет строить практически любые виды графов и обеспечивает высокую степень их визуализации.
| Создание графов | ||
| CartesianProduct | CirculantGraph | CodeToLabeledTree |
| CompleteGraph | Cycle | DegreeSequence |
| EmptyGraph | ExactRandomGraph | ExpandGraph |
| Functional-Graph | GraphDif ference | Graphlnter section |
| GraphJoin | GraphPower | GraphProduct |
| GraphSum | GraphUnion | GraphicQ |
| GridGraph | Hypercube | IncidenceMatrix |
| IntervalGraph | LabeledTreeToCode | LineGraph |
| MakeGraph | NthPair | Path |
| RandomGraph | RandomTree | RandomVertices |
| RealizeDegreeSequence | RegularGraph | RegularQ |
| Turan | Wheel | - |
Рисунок 11.10 показывает применение функций GraphUnion (верхний график) и GraphProduct (нижний график).
Рис. 11.10. Создание графов с помощью функций GraphUnion и GraphProduct С действием других функций нетрудно ознакомиться самостоятельно.
| Свойства графов | ||
| ArticulationVertices | Automorphisms | Bi Connected Components |
| BiconnectedQ | BipartiteQ | Bridges |
| ChromaticNumber | Chromatic Polynomial | CliqueQ |
| Connected Components | ConnectedQ | DeBruijnSequence |
| DeleteCycle | EdgeChromatic Number | EdgeColoring |
| EdgeConnectivity | Element | EulerianCycle |
| EulerianQ | ExtractCycles | FindCycle |
| Girth | GraphPower | HamiltonianCycle |
| HamiltonianQ | Harary | HasseDiagram |
| IdenticalQ | Independent SetQ | IsomorphicQ |
| Isomorphism | IsomorphismQ | MaximumClique |
| Maximum lndependentSet | Minimum VertexCover | OrientGraph |
| PartialOrderQ | PerfectQ | SelfComplementaryQ |
| StronglyConnected Components | TopologicalSort | TransitiveClosure |
| TransitiveReduction | TravelingSalesman | TravelingSalesman Bounds |
| TreeQ | Trianglelnequality | TwoColoring |
| VertexColoring | VertexConnectivity | VertexCoverQ |
| WeaklyConnected Components | ||
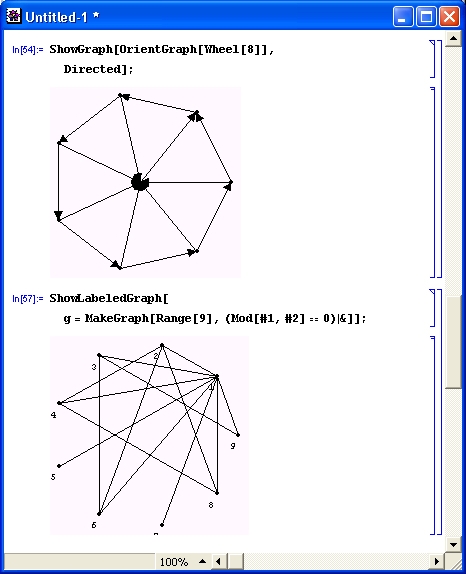
Рисунок 11.11 (сверху) показывает применение функции OrientGraph для построения ориентированного графа, который представляется стрелками. Там же (снизу) показано применение функции ShowLabeledGraph для построения графа с маркированными числами вершинами. Напомним, что функция ShowGraph позволяет наблюдать графы без маркировки вершин.
Рис. 11.11. Построение графов — ориентированного (сверху) и с маркированными вершинами (снизу)
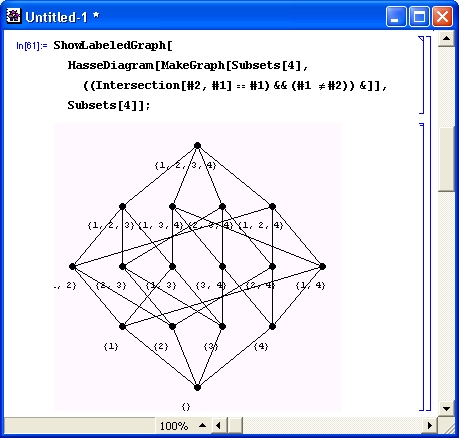
Построение широко используемой в теории графов диаграммы Хассе (Hasse) иллюстрирует рис. 11.12.
| Алгоритмическая теория графов | ||
| AllPairsShor test Path | BipartiteMatchin | Cofactor |
| Dijkstra | FindSet | GraphPower |
| InitializeUnionFind | Maxima IMatching | MaximumAntichain |
| MaximumSpanningTree | MinimumChainPartition | MinimumSpanningTree |
| NetworkFlowEdges | Networks' low | NumberOfSpanningTrees |
| PathConditionGraph | PlanarQ | Shortest PathSpanningTree |
| ShortestPath | StableMarriage | UnionSet |
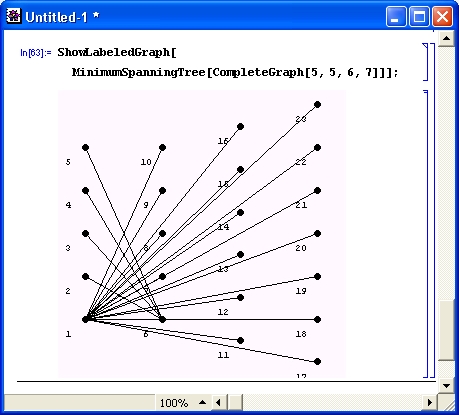
Рисунок 11.13 показывает действие функции MinimumSpanningTree с выводом графа с метками узловых точек.
Риc. 11.12. Построение диаграммы Хассе
Риc. 11.13. Пример применения функции MinimumSpanningTree
В целом следует отметить, что набор функций в области создания, визуализации и теории графов весьма представителен, так что специалисты в области графов могут найти в этом наборе как типовые, так и уникальные средства.
Функции вычислительной геометрии — ComputationalGeometry
В подпакете ComputationalGeometry заданы следующие функции, относящиеся к геометрическим поверхностям:
- ConvexHull [ { {xl, yl...}, {х2, у2,...},...] — вычисляет выпуклость оболочки в точках плоскости;
- DelaunayTriangulation[ {{xl,yl...}, {х2, у2,...},...] — вычисляет триангуляцию Делоне (разбивку на выпуклые треугольники) в точках плоскости;
- DelaunayTriangulationQ [ {{xl, yl...}, {х2, у2,...},...}, trival] — тестирует триангуляцию Делоне в точках плоскости; ,
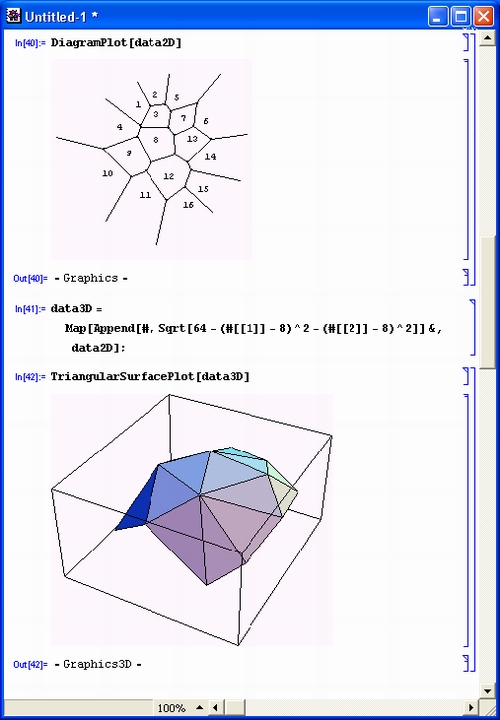
- DiagramPlot [ {{xl, yl...}, {х2, у2,...},...] — построение диаграммы по заданным точкам (после списка параметров возможны спецификации в виде списков diagvert, diagval);
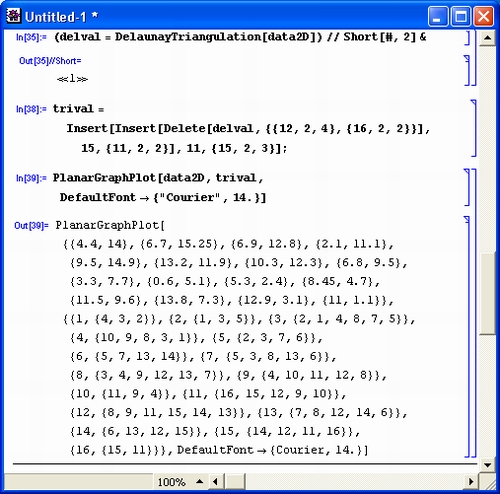
- PlanarGraphPlot [{ {xl, yl...}, {x2, y2,...},...] — построение планарного графа по заданным точкам (после списка параметров возможна спецификация в виде списка indexlist или vals);
- TriangularSurfacePlot [ {{xl,yl, zl}, {x2,y2, z2 },...] — строит поверхность из треугольников по заданным точкам;
- VoronoiDiagramm[ {{xl, yl...}, {х2, у2,...},...] — вычисляет данные для построения диаграммы Вороного.
Примеры применения этих функций приведены ниже:
<<DiscreteMath`ComputationalGeometry`
ConvexHull[{{0,2}, {1,1}, {0,0}, {2,0}, {1,2}}]
{4, 5, 1, 3}
delval = (DelaunayTriangulation[{{l,2J, {0,3}, {1,1}}]) // Short[#,2]&
{{1, {2, 3}}, {2, {3, 1}}, {3, {1, 2}}}
VoronoiDiagram[{{l,2}, {0,3}, {1,1}}]
{{{-0.50000000000000, 1.5000000000000},
Ray [{- 0.50000000000000, 1.5000000000000},
{1.5000000000000, 3.5000000000000}],
Ray [ {- 0.50000000000000, 1.5000000000000},
{2.0000000000000,1.50000000000000}],
Ray[ {- 0.50000000000000, 1.5000000000000},
{-2.5000000000000, 0.50000000000000} ]},
{{1, {1, 3, 2}}, {2, {1, 2, 4}}, {3, {1, 4, 3}}}}
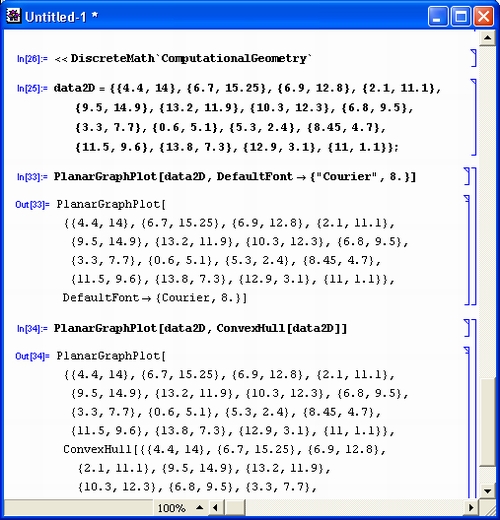
Рисунок 11.14 показывает задание на плоскости массива точек data2D, построение планарного графа и его выпуклой огибающей с помощью функции Convex-Hull.
Рис. 11.14. Пример построения планарного графа и его выпуклой огибающей Выполнение триангуляции Делоне иллюстрирует рис. 11.15.
Рис. 11.15. Выполнение триангуляции Делоне
Наконец, на рис. 11.16 показаны результаты действия еще двух функций — построение диаграммы и триангуляция в пространстве.
Рис. 11.16. Построение диаграммы (сверху) и триангуляция в пространстве (снизу)
Дискретные функции единичного скачка и импульса — KroneckerDelta
В подпакете KroneckerDelta системы Mathematica 3 заданы дискретные функции единичного скачка и единичного импульса:
- DiscreteStep [n] — возвращает единичный скачок при целом n=0;
- DiscreteStep [n1, n2,...] — функция многомерного единичного скачка;
- KroneckerDelta [n] — возвращает 1 при целом n=0 и 0 во всех других случаях;
- KroneckerDelta [n1, n2,...] — многомерная функция Кронекера.
Примеры использования этих функций в одномерном варианте представлены ниже:
<<DiscreteMath` KroneckerDelta`
Table[DiscreteStep[n], {n, -3, 3}]
{0, 0, 0, 1, 1, 1, 1}
Table[DiscreteStep[n], {n, -3, 3, 1/2}]
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1}
Table[KroneckerDelta[n], {n, -2, 2, 1/2}]
{0, 0, 0, 0, 1, 0, 0, 0, 0}
Sum[KroneckerDelta[n— a]f[n], {n, -Infinity, Infinity}]
f[a]
Sum[( (KroneckerDelta[n]— KroneckerDelta[n-1]) -
(KroneckerDelta[n-1]— KroneckerDelta[n-2]) ) f[n], {n, -Infinity, Infinity}]
f[0]-2f[l] +f[2]
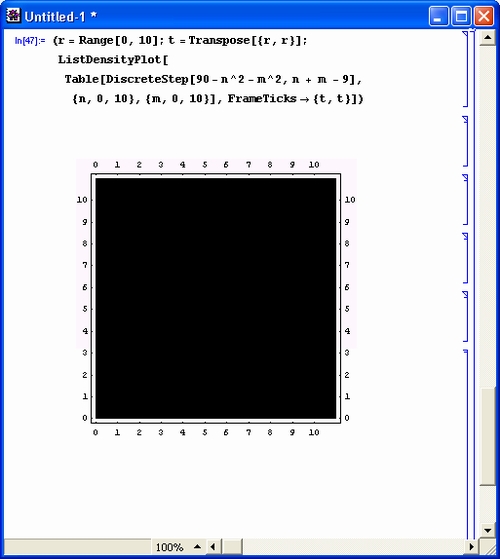
Рисунок 11.17 иллюстрирует применение функции единичного скачка в двумерном случае.
Рис. 11.17. Пример применения функции скачка в двумерном случае
В системе Mathematica 4 функция KroneckerDelta стала встроенной. В данный подпакет входят еще две функции:
- SimplifyDiscreteStep [ехрr] — упрощение выражения ехрг с функциями дискретного скачка;
- SimplifyKroneckerDelta [ехрг] — упрощение выражения ехрг с дельта-функцией Кронекера.
Действие этих функций демонстрируют следующие примеры:
DiscreteStep[n - 1] (KroneckerDelta[n - 2] + DiscreteStep[n, m] DiscreteStep[m - 1]) // SimplifyDiscreteStep
DiscreteStep[-1+m]
DiscreteStep[-l+m] + KroneckerDelta[-2+n]
(f[n] + KroneckerDelta[n]) DiscreteStep[n-l] // SimplifyKroneckerDelta
DiscreteStep [ -1 + n] f [ n]
Дискретные перестановки — Permutations
В подпакете Permutations определен ряд функций дискретных перестановок:
- RandomPermutation [n] — случайные перестановки из n элементов;
- Ordering [list] — дает перестановки в установленном списком list порядке;
- ToCycles [perm] — дает циклическую декомпозицию для списка list;
- FromCycles [ {cicl, cic2,...}] — возвращает перестановки из циклических декомпозиций cic1, cic2, ...;
- PermutationQ [list] — возвращает True, если список list представляет перестановки, и False в ином случае.
Работа функций поясняется следующими примерами:
<<DiscreteMath`Permutations`
RandomPermutation[16]
{16, 12, 11, 5, 3, 4, 9, 14, 2, 8, 15, I, 13, 7, 10, 6}
ToCycles[%]
{{16, 6, 4, 5, 3, 11, 15, 10, 8, 14, 7, 9, 2, 12, 1}, {13}}
FromCycles[%]
{16, 12, 11, 5, 3, 4, 9, 14, 2, 8, 15, 1, 13, 7, 10, 6}
Ordering[%]
{12, 9, 5, 6, 4, 16, 14, 10, 7, 15, 3, 2, 13, 8, 11, 1}
Решение рекуррентных разностных уравнений — RSolve
Для решения рекуррентных разностных уравнений в подпакет RSolve введены следующие функции:
- RSolve [eqn, a [n] , n] — решает рекуррентное уравнение для а [n];
- RSolve [eqn, a, n] — решает рекуррентное уравнение для функции а;
- RSolvet {eqnl, eqn2,...}, {al, a2,...},n] — решает систему рекуррентных уравнений, представленных списками.
Ниже представлены примеры применения данных функций:
<<DiscreteMath` RSolve`
RSolve[a[n+l] == 2 a[n], a[n], n]
{{a[n] -> 2nC[l]}}
RSolve[a[n] == a[n-l] + a[n-2], a[0] == a[l] == 1, a[n], n]
RSolve[ a[0] == a[l] == 2,
(n+1) (n+2) a[n+2]- 2 (n+1) a[n+l]- 3 a[n] == 0, a[n], n]
Подпакет Tree содержит функции создания и применения древовидных структур, именуемых деревьями. Вот эти функции:
- MakeTree [list] — создает дерево по информации, представленной в списке list;
- TreeFind [tree, x] — возвращает позицию наименьшего элемента, превосходящего х в списке list, представляющем дерево.
Действие этих функций поясняют следующие примеры:
<<DiscreteMath` Tree`
MakeTree[{el, e2, е3, е4}]
{{e2, 2), {{el, 1}, {}, {}}, {{e3, 3}, {}, {{e4, 4}, {}, {}}}}
tree = MakeTree[{8.5, 1.2, 9.1, 3.4, 5., 7.6 ,6.4}]
{{6.4, 4}, {{3.4, 2}, {{1.2, 1}, {}, {}}, {{5., 3}, {}, {}}},
{{8.5, 6}, {{7.6, 5}, {}, {}}, {{9.1, 7}, {},{}}}}
TreeFind[tree, 1.2]
1 . .
TreeFind[tree, 1]
0
Для визуализации деревьев служат следующие функции:
- TreePlot [tree] — строит график дерева tree;
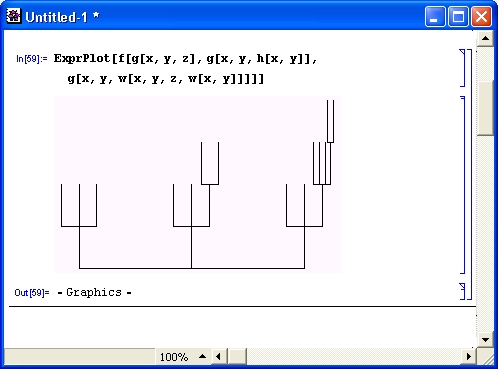
- ExprPlot [expr] — строит график, представляющий ехрг в виде дерева.
Примеры построения графиков деревьев представлены на рис. 11.18. Верхнп; график построен по данным дерева tree, определенного в приведенных выи: примерах, а нижний — по данным случайного дерева.
Построение графиков деревьев по выражению ехрг с помощью функции ExprPlot демонстрирует рис. 11.19.
Рис. 11.18. Примеры визуализации деревьев
Рис. 11.19 . Построение графиков деревьев с помощью функции ExprPlot