Главное меню
Вы здесь
3. Пакет вычислительных функций Calculus
Пакет вычислительных функций Calculus
Пакет расширения Calculus содержит представительный набор функций для решения дифференциальных уравнений, задания функций единичного скачка и импульса, выполнения операций с векторами, преобразований Фурье и Лапласа, выполнения спектрального анализа и синтеза, расширенного вычисления пределов и проведения аппроксимаций аналитических функций. Для открытия пакета используется команда Calculus`
Решение дифференциальных уравнений — DSolvelntegrals
Многие нелинейные дифференциальные уравнения не имеют общего решения. В под-пакете DSolvelntegrals определены функции, позволяющие найти решения в форме полного интеграла:
- Completelntegral [eqn, u [х, у,...], {х, у...} ] — создает полный интеграл для дифференциального уравнения, касательного к и [х, у,...];
- Differential Invariants [ {eqnsl, eqns2,...}, {u [х] , v [х] ,...}, х} — возвращает список дифференциальных инвариантов для простых переменных {u[x] ,v[x] ,...} и х;
- Differential Invariants [ {eqnsl, eqns2,...}, {u, v,...}, х} — возвращает список дифференциальных инвариантов для простых переменных {u, v,...} и х;
Применение этих функций поясняют следующие примеры:
<<Calculus`DSolvelntegrals`
Completelntegral[
Derivative[0, 1][u][х, у] == (u[x, у] +
x^2*Derivative[l, 0][u][x, y]^2)/y, u[x,y], {х,у}]
Completelntegral[-u[x, у] +
(2 + y)*Derivative[0, 1][u] [x, y] +
x*Derivative[l, 0][u][x, y] + 3*Derivative[l, 0][u][x, y]^2 == 0,
u[x,y], {x,y}, IntegralConstants->F]
Differentiallnvariants[
{U`[X] == -(U[X] (U[X] +V[X])),
V`-[x] == V[x] (u[x] +V[x])},{u, v}, x]
Дельта-функция Дирака — DiracDelta
В подпакете DiracDelta системы Mathematica 3 задано определение двух полезных функций Дирака:
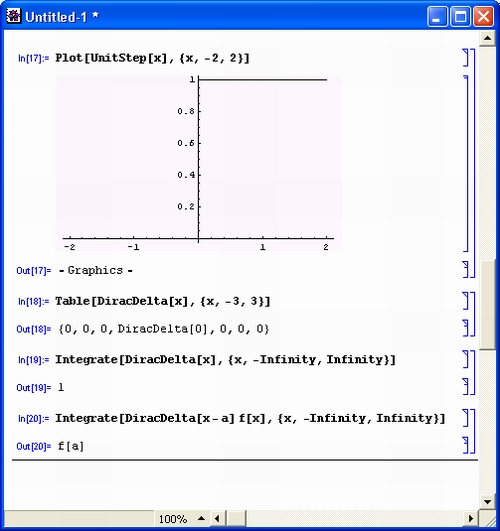
- UnitStep [х] — возвращает функцию с единичным скачком при х = 0 (дает значение 0 при х < 0 и 1 при х > 1);
- DiracDelta [x] — возвращает дельта-функцию Дирака, которая является импульсом с единичной площадью, бесконечно малой шириной в точке х = 0 и бесконечно большой амплитудой.
Рисунок 11.1 поясняет применение этих функций. Функция UnitStep имеет простую графическую иллюстрацию, тогда как построение графика функции DiracDelta в принципе невозможно — эта функция представляет собой линию бесконечно большой высоты в точке х - 0. Обратите внимание на то, что интеграл от функции Дирака при интегрировании от -°° до +°° равен 1.
Рис. 11.1. Робота с функцией единичного скачка и дельта-функцией Дирака
Обе описанные функции широко применяются при решении задач автоматического регулирования и при математическом моделировании систем и устройств. Поэтому в системе Mathematica 4 они перешли в разряд встроенных функций.
Улучшенное вычисление пределов — Limit
Подпакет Limit не создает новых функций. Он просто переопределяет встроенную функцию Limit, так что ограничимся примерами его применения:
<<Calculus` Limit`
Limit[Е^х^х/ Е^х^(2 х), x->Infinity]
0
Limit [Е^х^х— Е^х^ (2 х) , x->Infinity]
-бесконечность
Limit[E:x ExpIntegralE[2, ArcTan[E^x]- Pi/2] -E^x- x, x->Infinity]
1 - EulerGamma - I л
Limit[Zeta[l+x, v] - 1/x, x->0]
-PolyGamma[0, v] ,
Limit[x^0 PolyGamma[2,x], x->Infinity] .
0
Limit[x^2 PolyGamma[2,x], x->Infinity]
-1
Limit[x^3 PolyGamma[2,x], x->Infinity]
-бесконечность
Работа скорректированной функции наиболее эффективна при вычислении пределов от выражений, содержащих специальные математические функции, и пределов при х, стремящемся к бесконечности.
Рациональная аппроксимация аналитических функций — Fade
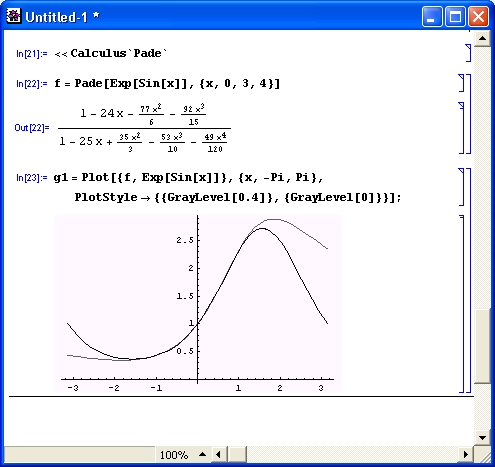
Полиномиальная аппроксимация и обычное разложение функций в ряд Тейлора нередко дают слишком большую погрешность. Уменьшение ее возможно при представлении аппроксимирующей функции в виде отношения двух полиномов разной степени. В подпакете Fade определены две функции для рациональной аппроксимации Паде:
- Pade[f, {x,x0,m,k}] — возвращает выражение для аппроксимации Паде функции f(x) в окрестностях точки х0 в виде отношения двух полиномов степеней m и k;
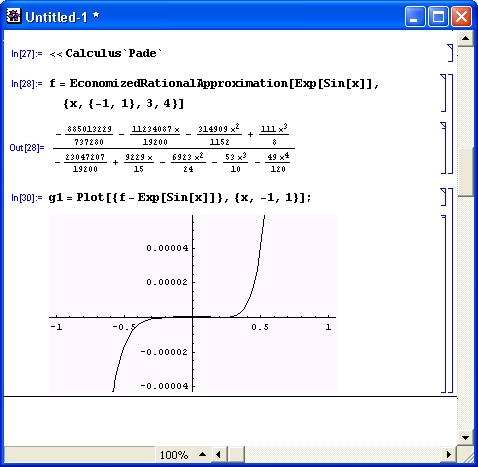
- EconomizedRationalApproximation [f, {х, {xmin, xmax}, m, k} ] —возвращает выражение для осуществления экономичной рациональной аппроксимации функции f(x) в интервале {xmin, xmax} в виде отношения двух полиномов степеней m и k.
Аппроксимация Паде является расширением полиномиальной аппроксимации, обеспечивающим повышенную точность представления функции. На рис. 11.2 представлен пример выполнения аппроксимации Паде с построением графика исходной функции (темная линия) и аппроксимирующей функции (более светлая линия).
Рис. 11.2. Пример, осуществления аппроксимации Паде
Пример осуществления экономичной рациональной аппроксимации показан на рис. 11.3. Здесь также дана визуализация аппроксимации в виде наложенных друг на друга графиков исходной и аппроксимирующей функций.
Рис. 11.3. Пример осуществления экономичной рациональной аппроксимации
Экономичная рациональная аппроксимация обычно позволяет получить приемлемую погрешность при меньшей степени полиномов числителя и знаменателя аппроксимирующей функции. В ограниченной области {xmin, xmax} эта аппроксимация нередко позволяет получить погрешность менее сотых долей процента (рис. 11.4). На этом рисунке показан график погрешности в виде разности между значениями аппроксимирующей и аппроксимируемой функций.
Рис. 11.4. Пример осуществления экономичной рациональной аппроксимации с построением графика погрешности
Несмотря на обширные возможности выбора средств аппроксимации, все же надо отметить, что они уступают таковым у конкурента системы Mathematica — Maple V R4/R5, где функций для осуществления аппроксимации больше.
Векторный анализ —VectorAnalysis
Подпакет VectorAnalysis содержит множество функций, используемых при выполнении векторного анализа. Здесь надо иметь в виду, что речь идет не о векторах как представителях одномерных массивов, которые рассматривались ранее. В данном случае вектор — это направленный отрезок прямой в пространстве, заданном той или иной системой координат.
Системы координат и их преобразования
Заметная часть функций подпакета VectorAnalysis относится к заданию и преобразованию координат:
- Coordinates [ ] — возвращает имена переменных текущей системы координат;
- Coordinates [coordsys] — возвращает имена переменных системы координат coordsys;
- SetCoordinates [coordsys] — устанавливает систему координат coordsys с текущими переменными;
- Coordinates [coordsys, {vars}] — устанавливает систему координат coordsys с переменными, заданными списком {vars }.
Ниже даны названия систем координат и соответствующие им представления.
| Наименование | Представление |
| Прямоугольные | Cartesian [х, у, z] |
| Цилиндрические | Cylindrical [r, theta, z] |
| Сферические | Spherical [r, theta, phi] |
| Параболические цилиндрические | ParabolicCylindrical [u, v, z] |
| Параболические | Paraboloidal [u, v, phi] |
| Эллиптические цилиндрические | EllipticCylindrical [u, v, z, a] |
| Вытянутые сфероидальные | ProlateSpheroidal [xi, eta, phi, a] |
| Сплющенные сфероидальные | OblateSpheroidal [xi, eta, phi, a] |
| Биполярные | Bipolar[u, v, z, a] |
| Бисферические | Bispherical [u, v, phi, a] |
| Тороидальные | Toroidal [u, v, phi, a] |
| Конические | Conical [lambda, mu, nu, a, b] |
| Конфокальные эллипсоидальные | ConfocalEllipsoidal [lambda, rnu, nu, a, b, c] |
| Конфокальные параболические | ConfocalParaboloidal [lambda, mu, nu, a, bj |
Например, параболическую систему координат можно задать следующим образом:
SetCoordinates[Paraboloidal[x, у, z] ]
Paraboloidal [x, у, z]
{CoordinateSystem, Coordinates[]}
{Paraboloidal, {x, y, z}}
Ряд функций служит для контроля и установки параметров систем координат:
- CoordinateRanges [ ] — возвращает пределы изменения переменных текущей координатной системы;
- Parameters [ ] — возвращает параметры текущей координатной системы;
- ParametersRanges [ ] — возвращает пределы изменения параметров текущей координатной системы;
- CoordinateRanges [coordsys] — возвращает пределы изменения переменных координатной системы coordsys;
- Parameters [coordsys] — возвращает параметры координатной системы coordsys;
- ParametersRanges [coordsys] — возвращает пределы изменения параметров координатной системы coordsys;
- SetCoordinates [coordsys, {vars,param} ] — устанавливает параметры текущей координатной системы как параметры coordsys с переменными vars и параметрами param.
Ниже представлены примеры применения этих функций:
CoordinateRanges[]
{0<Х<бесконечности,0<Y<бесконечность,-л<Z<=л}
Parameters[]
{}
ParameterRanges[ ]
Coordinates[Conical], CoordinateRanges[Conical]
{{Llanibda, Мmu, Nnu}, {-бесконечность< Llambda< бесконечность, l< Mmu2 < 4, Nnu2< 1}}
Parameters[Bipolar],ParameterRanges[Bipolar]
{{1}, 0< #1<бесконечность}
Для преобразования координат служат следующие функции:
- CoordinatesToCartesian [pt] — преобразование текущих координат в декартовы;
- CoordinatesToCartesian [pt, coordsys] — преобразование координат coordsys в декартовы;
- CoordinatesFromCartesian [pt] — преобразование из декартовых координат в текущие;
- CoordinatesFromCartesian [pt, coordsys] — преобразование из декартовых координат в координаты coordsys.
Эти примеры демонстрируют преобразования координат:
CoordinatesToCartesian[{I, Pi/3, Pi/3}, Spherical]
CoordinatesToCartesian [u, v, phi}, Bipolar]
CoordinatesFromCartesian [ {x, y, z} , Bipolar]
{-2Im[ArcCoth[x+ Iy]] , 2Re[ArcCoth[x+ Iy] ] , z}
Функции векторного анализа
Помимо функций для задания и преобразования систем координат подпакет Vector An a lysis содержит ряд функций собственно векторного анализа:
- DotProduct [vl, v2] — возвращает скалярное произведение векторов vl и v2, заданных в текущей системе координат;
- CrossProduct [vl,v2] — возвращает векторное произведение векторов vl и v2, заданных в текущей системе координат;
- ScalarTripleProduct [vl, v2, v3 ] — возвращает тройное скалярное произведение для векторов vl, v2 и v3, заданных в текущей системе координат;
- DotProduct [vl, vl, coordsys ] — возвращает скалярное произведение векторов vl и v2, заданных в системе координат coordsys;
- CrossProduct [vl, v2, coordsys] — возвращает векторное произведение векторов vl и v2, заданных в системе координат coordsys.
Примеры выполнения этих операций представлены ниже:
SetCoordinates[ParabolicCylindrical[ ]]
ParabolicCylindrical[Uu, W, Zz]
DotProduct[{1.2, 1.1, 0}, {5.4, -2, 1.2}]
-12.8093
CrossProduct[{1.2, 1.1, 0}, {5.4, -2, 1.2}]
{-1.78157, 0.0774597, -17.8476}
ScalarTripleProduct[{1, 0, 1}, {1, 1, 0}, {0, 1, 1}, Cartesian]
2
Для вычисления производной дуги служат функции:
- ArcLengthFactor [ { fx, f у, f z}, t] — дает дифференциал длины дуги, заданной параметрически с параметром t в текущей системе координат;
- ArcLengthFactor [ {fx, f у, fz}, t, coordsys] — дает дифференциал длины дуги, заданной параметрически с параметром t в системе координат coordsys
Примеры вычисления дифференциалов и длин дуг с помощью этих функций:
param = {Cos[t], Sin[t], t}
{Cos[t], Sin[t], t}
ArcLengthFactor[ param, t, Cartesian] //Simplify
корень из 2
f[x_, y_, z_] := x^2 y^2 z
Integrate[ f[param] ArcLengthFactor[
param, t, Cartesian], {t, 0, 2 Pi}] // Simplify
Ряд функций служит для создания матрицы Якоби (матрицы частных производных) и вычисления относящихся к ней понятий:
- JacobianMatrix [ ] — возвращает матрицу Якоби, определенную в текущих координатах;
- JacobianMatrix [pt] — возвращает матрицу Якоби в точке pt и в текущих координатах;
- JacobianMatrix [coordsys] — возвращает матрицу Якоби, определеннук в системе координат coordsys;
- JacobianMatrix [pt, coordsys] — возвращает матрицу Якоби в точке pt, определенную в системе координат coordsys;
- JacobianDeterminant [], JacobianDeterminant [pt] и т. д. — вычисление детерминанта матрицы Якоби при указанных выше определениях;
- ScaleFactor [ ], ScaleFactor [pt] и т. д. — вычисление масштабного фактора при указанных выше определениях.
Применение этих функций поясняют следующие примеры:
JacobianMatrix[Cartesian[x, у, z]]
{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}
JacobianMatrix[Spherical[r, t, p] ]
{{Cos[p] Sin[t] , rCos[p] Cos[t] ,-rSin[p] Sin[t]},
{Sin[p] Sin[t] , rCos[t] Sin[p] , rCos[p] Sin[t]},
{Cos[t] , -rSin[t], 0}}
JacobianDeterminant[Spherical[r, t, p] ]
r^2Sin[t]
Integrate[r^2 JacobianDeterminant[ Spherical[r, theta, phi]],
{r, 0, 2}, {theta, 0, Pi}, {phi, -Pi, Pi}]
128n/5
Следующие функции определяют ряд характеристик векторного поля:
- Div[f] — возвращает дивергенцию векторного поля f в текущей системе координат;
- Curl [f ] — возвращает вихрь (ротор) векторного поля f в текущей системе координат;
- Grad[f ] — возвращает градиент векторного поля f в текущей системе координат;
- Laplasian [f] — возвращает лапласиан векторного поля f в текущей системе координат;
- Вiharmonic [f] — возвращает лапласиан лапласиана векторного поля f в текущей системе координат;
- Div [f, coordsys], Curl [f, coordsys] и т. д. — указанные выше функции в системе координат coordsys.
Приведем примеры использования этих функций:
Laplacian[x*y^2*z^3,ProlateSpheroidal[х, у, z]]
(Csc[y] Csch[x] (y2z3Cosh[x] Sin [у] +
2xyz3Cos[y] Sirih[x] +2xz3Sin[y] Sinh[x] +
6xy2zCsc[y] Csch[x] (Sin[y]2+ Sinh[x]2))) /
(Sin[y]2+Sinh[x]2)
Grad[x^2 y^3 z^4,ProlateSpheroidal[x, у, z]]
Вариационные методы —VariationalMethods
Подпакет VariationaLMethods содержит функции для реализации вариационных методов. Напомним, что вариационные методы заменяют минимизацию функционала, заданного на некотором бесконечномерном линейном пространстве, задачами его минимизации на последовательности конечномерных подпространств. Функционал в системе Mathematica задается следующим образом:
F=
f[u[x], u'(x),x]dx
В данный подпакет включены следующие функции:
- VariationalD [f, u [х] , х] — дает первую вариационную производную для функционала f одной переменной х;
- VariationalD [f, u [х, у,...] , {х, у,...} ] — дает первую вариационную производную для функционала ряда переменных;
- VariationalD [f, {u [х, у,...], v [х, у],...}, {х, у,...} ] — дает список первых вариационных производных для функционала ряда переменных;
- EulerEquations [f, u [х] , х] — дает равенство Эйлера при f с одной переменной;
- EulerEquations [f, u [х, у,...], {х, у,...} ] — дает равенство Эйлера при f с рядом переменных;
- EulerEquations [f, {u [х, у,...] , v [х, у,...],...}, {х, у,...} ] — дает список с равенствами Эйлера при f с рядом переменных;
- Firstlntegral [ f, u [х] , х] — дает первый интеграл с f, определенной для одной переменной х;
- Firstlntegral [f, {u [х, у,...] ,v [х, у,...],...}, {х, у,...} ] — дает первый интеграл при f с рядом переменных;
- Firstlntegral[u] — дает первый интеграл, ассоциированный с переменной и.
Применение данных функций поясняют следующие примеры:
<<Calculus `VariationalMethods`
VariationalD[y[x] Sin[l+y'[x]], y[x], x]
-Cost 1 +У [x]] y'[x] + Sin[l + y'[x]] d+y[x] y'[x])
EulerEquations[ m1^2 theta1[t]^2/2+m g 1 Cos[theta[t]], theta[t], t]
-Im(gSin[theta[t]] + 1 theta''[ t]) == 0
Firstlntegrals[m(r'[t]^2+r[t]^2 phi'[t]^2)/ 2-U[r], r[t],phi[t], t]
{Firstlntegral[phi] ->-mr[ t]2 phi' [ t] , Firstlntegral[t] -> 1/2 (2U[r] + m (r[t]2phi'[t]2 + r^t]2)) }
Помимо указанных функций подпакет содержит функцию VariationalBound для представления границ и значений функционала. Ввиду громоздкости записи параметров этой функции ограничимся примерами ее применения:
VariationalBound[(-u[r] D[r^2 u'[r],r]/r^2-2u[r]^2/r)r^2,
u[r]^2 r^2,u[r], r,0,Infinity,(a-r)E^(-b r),a,b]
{-0.25, (a-> 2., b-> 0.5}}
VariationalBound[-u[x,у](D[u[x,y],x,2]+
D[u[x,y],y,2]) -2u[x,y],u[x,y],x,-a,a,y,-a,a,
(x^2-a^2)(y^2-a^2)(al+a2(x^2+y^2)),al,a2]
С полными возможностями этой функции можно ознакомиться по справочной базе данных (раздел Add-ons).