Глава 5 Работа со вставками

Глава 5 Работа со вставками

5.1. Подменю позиции Insert (Вставка) главного меню

Установка любого объекта в окно редактирования называется вставкой MathCAD реализует различные механизмы вставки — от просто вывода шаблона объекта до вставки объекта, созданного в другом приложении, через буфер обмена. В версии MathCAD 7 0 все виды вставок включены в новую позицию главного меню Insert (Вставка).

При активизации этой позиции появляется подменю со следующими операциями:

Graph (Графика) — вставка шаблонов графики, Matrix... [Ctrl+M] (Матрица) — вставка шаблонов матриц и векторов, Function... [Ctrl+F] (Функция) — вставка шаблонов встроенных функций, Unit... [Ctrl+U] (Единицы) — вставка единиц измерений размерных величин;

Picture [Ctrl+T] (Рисунок) — вставка шаблона импортируемого рисунка;

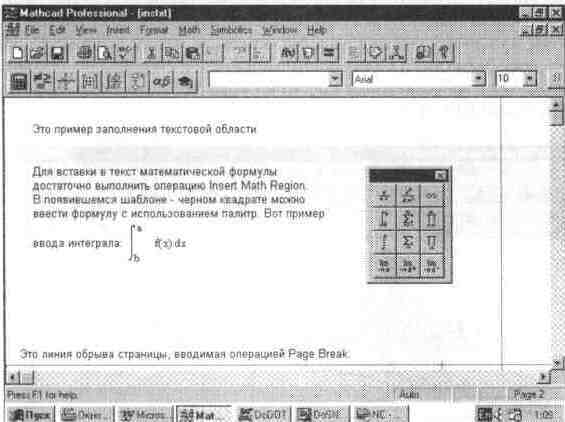
Math Region — вставка в текстовую область (Математическая область) шаблона математической области;

Text Region (Текстовая область) — вставка текстовой области;

Page Break (Разрыв страницы) — вставка линии разрыва страницы;

Hyperlink (Гиперссылка) — вставка гиперссылки;

Reference... (Ссылка) — вставка обращения к заданному файлу активизацией кнопки,

Component... (Компонент) — вставка других компонентов системы, Object... (Объект) — вставка объекта с установлением динамической связи с порождающим его приложением.

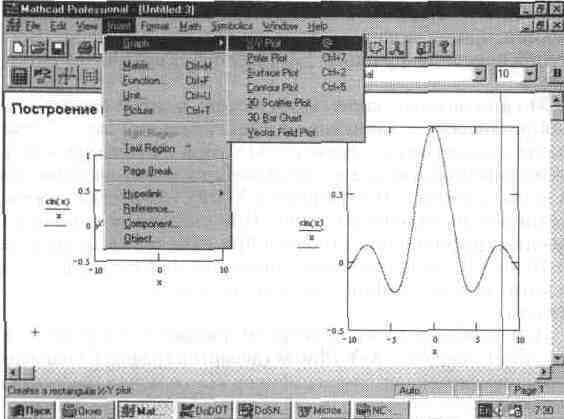
Вид подменю позиции Insert главного меню показан на рис. 5.1. Для создания графиков в системе MathCAD имеется программный графический процессор. Основное внимание при его разработке было уделено обеспечению простоты задания графиков и их модификации с помощью соответствующих опций. Процессор позволяет строить самые разные графики, например в декартовой и полярной системах координат, трехмерные поверхности, графики уровней и т д

Для построения графиков используются шаблоны Их перечень содержит подменю Graph (Графика) в позиции Insert (Включение) главного меню Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически Поэтому для начального построения графика того или иного вида достаточно задать тип графика В подменю Graph содержится список из семи основных типов графиков. Они позволяют выполнить следующие действия X-Y Plot® (Декартов — создать шаблон двумерного графика график) в декартовой системе координат,

Рис. 5.1 Экран системы с открытым подменю Insert

Polar Plot [Ctrl+7] — создать шаблон графика в полярной системе (Полярный график) координат, Surface Plot [Ctrl+2] — создать шаблон для построения трехмерного (График поверхности) графика, Contour Plot [Ctrl+5] — создать шаблон для контурного графика (Карта линий уровня) трехмерной поверхности, 3D Scatter Plot создать шаблон для графика в виде точек (Точечный график) (фигур) в трехмерном пространстве, 3D Bar Chart (Трехмерная создать шаблон для изображения в виде гистограмма) совокупности столбиков в трехмерном про странстве, Vector Field Plot — создать шаблон для графика векторного (Векторное поле) поля на плоскости

Вид окна системы с подменю Insert Graph показан на рис 5.1. В этом подменю видны команды создания шаблонов указанных выше типов графиков В окне редактирования показаны также два одинаковых графика, но в разных местах и разного размера

5.2. Установка шаблона двумерных графиков (X-Y Plot @)

Графики в системе MathCAD могут иметь различные размеры и перемещаться в окне редактирования документа. Для наиболее распространенных графиков в декартовой и в полярной системах координат в MathCAD предусмотрен упрощенный и очень удобный способ построения графиков без предварительного задания функции и ранжирования независимой переменной.

Именно так построены графики на рис 5 1 Для упрощенного построения двумерных графиков некоторой функции f(x) надо вывести их шаблон, по вертикали указать эту функцию, а по горизонтали — независимую переменную х. Таким образом можно строить на одном рисунке и графики многих функций, просто опишите их у вертикальной оси, используя запятые для разделения описаний функций. Графики будут построены линиями разного типа и цвета.

Можно вначале записать функцию, а затем вывести шаблон графика;

функция окажется записанной у вертикальной оси, и останется только указать независимую переменную у горизонтальной оси. Такой простой способ наверняка порадует начинающих пользователей, плохо сознающих (на первых порах), что графики в MathCAD всегда строятся по векторам и матрицам их отдельных точек. При указанном упрощенном способе построения графиков они строятся при изменении независимой переменной от -10 до+10. В дальнейшем операцией форматирования этот диапазон и все иные данные графиков можно изменить (это называют изменением формата).

Для вывода шаблона двумерной графики в декартовой системе координат служит операция X-Y Plot® (декартов график). Она выводит в текущее положение курсора шаблон графиков 2D-rana или графиков в декартовых координатах. Напоминаем, что это обычный график на плоскости с воображаемыми (или действительно нарисованными) осями Х (горизонтальная) и Y (вертикальная), расположенными под прямым углом друг к другу.

Каждая точка декартова графика характеризуется своими координатами х и у=f(х), где х — абсцисса точки, а у — ее ордината. Точки соединяются друг с другом разнообразными линиями (сплошной, пунктирной и т. д.). Могут быть показаны и исходные (узловые) точки графика в виде жирных точек, квадратиков, кружков и т. д.; возможно и построение на одном рисунке графиков нескольких функций.

Перед применением этой команды необходимо определить функции, графики которых должны строиться, и изменение их аргумента (например, х) в заданном интервале. Впрочем, простые функции, если они в дальнейшем не используются, можно указать в шаблоне самого графика. Далее надо приблизительно наметить место левого верхнего угла графика и установить на него графический курсор. Затем следует ввести команду (используя соответствующую позицию меню или нажав клавиши, задающие символ @).

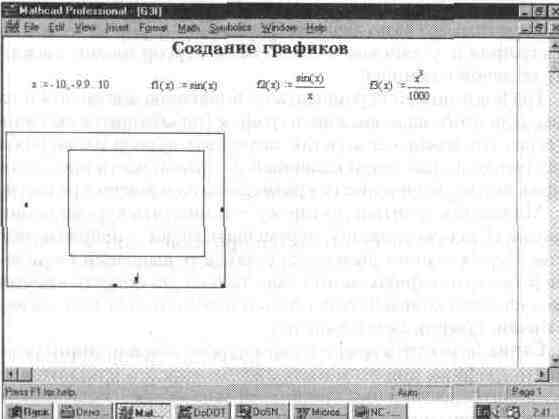
Рис. 5.2 показывает задание трех функций и вывод шаблона графика (внизу).

Незаполненный шаблон графика представляет собою большой пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат будущего графика. В средние шаблоны данных надо поместить имя переменной (х у оси абсцисс) и задать формулы для функций (у у оси ординат). Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Чтобы перемещать по шаблонам метку их выбора и выделения, следует использовать клавиши перемещения курсора. Можно выбрать шаблон данных и прямо с помощью мыши, указав нужный шаблон ее курсором и нажав левую клавишу мыши.

Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически. Недостаток тут в том, что масштабы, скорее всего, окажутся

Рис. 5.2 Задание трех функций и вывод незаполненного шаблона графика

не вполне удобными (например, будут представлены неокругленными десятичными цифрами), для представления целиком всего графика в максимальном размере. Рекомендуется всегда вначале использовать автоматическое масштабирование и лишь затем изменять масштабы на более подходящие.

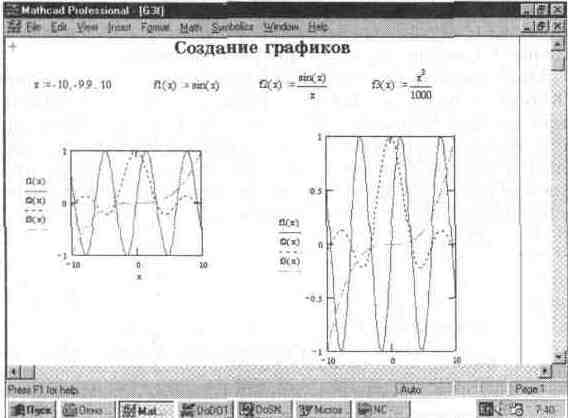
Чтобы произошло построение графика в автоматическом режиме вычислений, достаточно вывести курсор за пределы графического объекта. В ручном режиме вычислений для этого нужно еще нажать клавишу F9. При построении область графика во время вычислений ординат функций покрывается зеленой штриховкой, затем графики функций появляются в шаблоне (см. рис. 5.3).

Если что-либо в построенном графике не вполне удовлетворяет пользователя, можно применить описанные ниже операции изменения его формата.

Рис. 5.3 Пример построения двух графиков трех функций

Эти операции позволяют изменять заданные по умолчанию параметры графиков. Заметим, что окно задания форматов графиков появляется, если выделить график и, установив в его области курсор мыши, дважды быстро щелкнуть ее левой клавишей.

Графики можно перемещать по полю окна документа и изменять их размеры Для этого надо выделить график (он обводится сплошной линией) Проще всего это можно сделать так. поместить курсор мыши в область графика и щелкнуть один раз левой клавишей В правой части рис 5 3 показан тот же график после увеличения его размеров и завершения редактирования формата

Можно поступить и по-иному — поместить курсор мыши вблизи графика и, нажав ее левую клавишу, перемещать мышь в направлении графика наискосок Курсор начнет вычерчивать область выделения в виде прямоугольника из черных пунктирных линий Как только эта область захватит график и он тоже окажется обведен пунктирным прямоугольником, надо отпустить клавишу мыши График будет выделен

Стоит поместить графический курсор вблизи линий рамки, выделяющей область графика, при этом изображение курсора изменится: вмесго маленького красного крестика оно приобретет вид ладони. Если теперь нажать левую клавишу мыши и начать ее перемещать, то весь шаблон графика будет перемещаться по окну Установите его в нужное место и отпустите левую клавишу мыши. Рисунок окажется на новом месте.

Для изменения размеров рисунка нужно точно подвести графический курсор к специальным шаблонам на рамке, выделяющей рисунок Эти шаблоны имеют вид маленьких черных прямоугольников. Изображение курсора при этом заменяется на двустороннюю стрелку, указывающую, в каких направлениях можно растягивать рисунок. Нажав левую клавишу мыши, можно захватить соответствующую сторону или угол шаблона рисунка и, не отпуская клавишу, начать растягивать или сжимать шаблон. После того как клавиша будет отпущена, рисунок перестроится в новых размерах. Сжимать и растягивать графики можно в вертикальном, горизонтальном и диагональном направлениях

При любом виде выделения рисунка нажатие клавиши F3 стирает рисунок в окне и переносит его в буфер обмена. Переместив курсор, установленный на месте левого верхнего окна бывшего графика, в новое место и нажав клавишу F4, можно перенести рисунок на это место

Особо следует отметить возможность помещения текстовых комментариев в область графиков. Для этого вначале надо подготовить их в стороне от графика и выделить пунктирной линией Затем поместив курсор мыши в область текста, надо нажать ее левую клавишу и перенести текстовый блок в область рисунка. Установив текст в нужном месте, отпустите клавишу мыши Если при этих операциях или снятии выделений нанесенные на рисунок надписи исчезают, воспользуйтесь командой восстановления изображения на экране — Ctrl+R

Этим методом не стоит злоупотреблять, так как надписи сверху, снизу и сбоку графиков (в пределах области их определения) можно создавать с по мощью соответствующих средств задания формата графиков Они будут описаны несколько позже Такие надписи никогда не исчезают Чтобы надписи были на русском языке, следует использовать соответствующие наборы шрифтов. Поскольку шрифт в процессе ввода текста менять нельзя, есть определенные трудности с созданием таких надписей на русском языке

5.3. Установка шаблона графиков в полярной системе координат (Polar Plot)

В полярной системе координат каждая точка задается углом W, радиусом и длиной радиус-вектора R(W). График функции обычно строится при изменении угла W в определенных пределах, чаще всего от 0 до 2р. Опция Polar Plot (Полярный график) выводит шаблон таких графиков, показанный на рис. 5.4. Этот шаблон имеет форму окружности и содержит шаблоны данных.

Рис. 5.4 Шаблон графиков типа Polar Plot

Перед построением таких графиков надо задать изменение ранжированной переменной W(или с другим именем) в заданных пределах. После вывода шаблона следует ввести W в шаблон снизу и функцию R(W) в шаблон справа, а также указать нижний предел изменения длины радиус-вектора R(W) — Rmin и шаблоне справа внизу и верхний предел — Rmax в шаблоне справа и сверху.

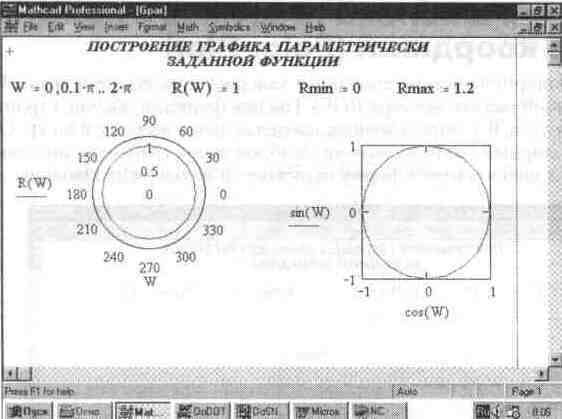
На рис. 5.5 показано построение графиков в полярной системе координат:

слева — по описанному шаблону, справа — с помощью шаблона обычной двумерной графики X-Y Plot. Сейчас R(W)=i, так что в обоих случаях строится окружность (если дисплей имеет различные масштабы по вертикали и горизонтали, окружность превратится в эллипс).

При построении графика в полярной системе координат с использованием шаблона обычного 1рафика в прямоугольной системе координат надо по оси Х установить R(W)-cos(W), а по оси Y — R(W)-sin(W). Построение графиков в полярной системе координат с помощью шаблона обычной графики X-Y Plot в ряде случаев даже более предпочтительно, поскольку в математической литературе графики параметрически заданных функций чаще всего строятся именно таким образом. При задании даже простых функций R(W) графики в полярной системе координат могут иметь весьма причудливый вид.

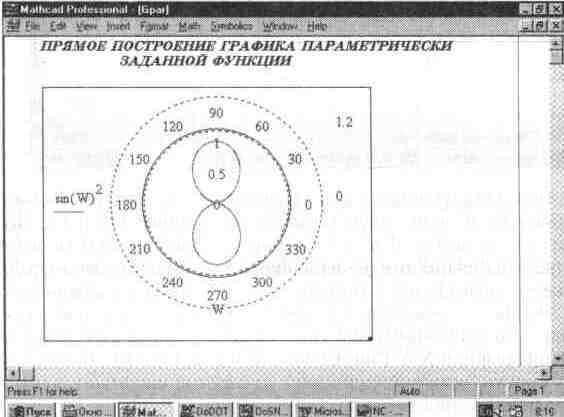
Надо также отметить новую возможность прямого построения графиков функций в полярной системе координат, без определения диапазона изменения независимой переменной W. Пример такого построения дан на рис. 5.6.

Рис. 5.5 Графики функций в полярной системе координат

Рис. 5.6 Пример прямого построения графика параметрически заданной функции

При прямом построении графика достаточно просто заполнить ее шаблон. Саму функцию надо описать ее уравнениями, которые вписываются на места шаблонов по осям Х и Y. Стоит вывести графический курсор мыши из области графика, как последний будет построен.

5.4. Установка шаблона трехмерных графиков (Surface Plot)

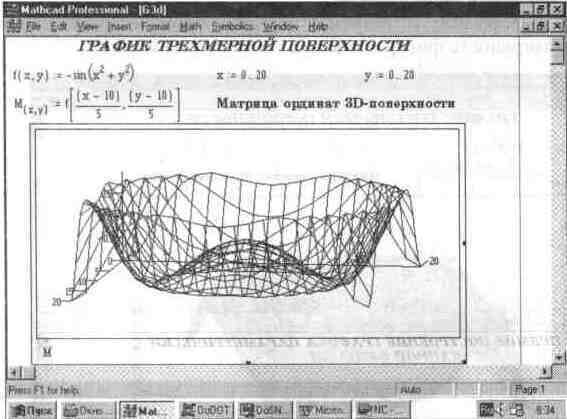
Эта операция служит для построения трехмерной поверхности Z(X, Y), предварительно представленной матрицей М ординат Z. При этом выводится шаблон графика, левый верхний угол которого помещается в место расположения курсора. Шаблон, в свою очередь, содержит единственный шаблон данных — темный прямоугольник у левого нижнего угла основного шаблона. В него надо занести имя матрицы со значениями ординат ЗD-поверхности. Разумеется, прежде чем строить график ЗD-поверхности, нужно ее определить математически. На рис. 5.7 показан пример такого определения.

Рис. 5.7 Задание и построение трехмерной поверхности без удаления невидимых линий

Наглядность представления трехмерных поверхностей зависит от множества факторов: масштаба построений, углов поворота фигуры относительно осей, применения алгоритма удаления невидимых линий или отказа от него, использования функциональной закраски и т. д. Для изменения этих параметров следует использовать операцию установки формата графика (см. далее). На рис. 5.8 показано то же построение, что и описанное выше, но с применением алгоритма удаления невидимых линий.

Рис. 5.8 Задание и построение трехмерной поверхности с удалением невидимых линий

Нетрудно заметить, что применение алгоритма удаления невидимых линий делает рисунок трехмерной поверхности намного более наглядным. Дальнейшее повышение наглядности восприятия 3D-поверхностей обеспечивается применением функциональной закраски. По существу, она дает дополнительную информацию о третьем измерении; в нашем случае, чем ниже расположена поверхность фигуры, тем она темнее (см. рис. 5.9).

Рис. 5.9 Задание и построение трехмерной поверхности с функциональной закраской

С помощью описываемых ниже команд изменения формата можно получить множество разновидностей 3D-графики. В частности, возможен вывод координатных осей. "параллелепипеда", обрамляющего фигуру, и иных деталей подобных графиков, например титульных надписей.

Поскольку график строится на основе матрицы, содержащей только координаты высот фигуры, то истинные масштабы по осям Х и Y не известны и на рисунках не проставляются. Могут, впрочем, выводиться просто порядковые номера элементов матриц в заданном направлении (по Х и по Y). Надо также следить за тем, как сформировать векторы Х и Y, с тем чтобы фигура выглядела естественно и занимала нужное место в пространстве. Все это несколько затрудняет быстрое создание графиков трехмерных поверхностей нужного вида.

Большие возможности дает несколько иной способ задания трехмерных поверхностей — в параметрическом виде. При этом приходится формировать три матрицы — X, Y и Z — и указывать их в шаблоне в виде X, Y, Z. В Главе 14 (в разделе 14.1) дан ряд примеров такого задания трехмерных поверхностей.

5.5. Установка шаблона контурных ЗD-графиков (Contour Plot)

Еще один широко распространенный тип графиков для представления трехмерных поверхностей — график из линий равного уровня. Такие графики широко применяются, например, в картографии. Операция Contour Plot (Карта линий уровня) служит для построения шаблона таких графиков. Он подобен шаблону, описанному в предыдущем разделе (кстати, как и предшествующие выводу шаблона действия по созданию матрицы М).

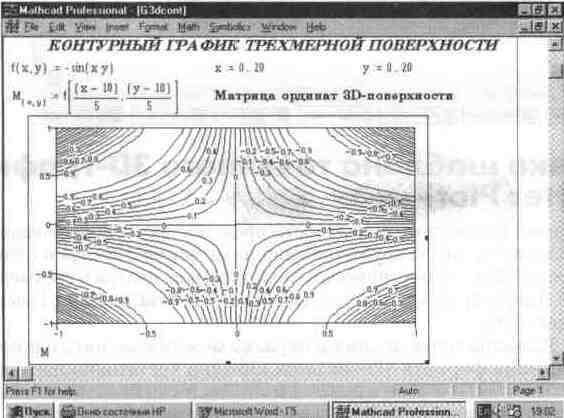
На рис. 5.10 показано построение контурного графика в виде линий равного уровня. Численные значения уровней для разных кривых графика представлены рядом цифр.

Рис. 5.10 Контурный график 3D-поверхности

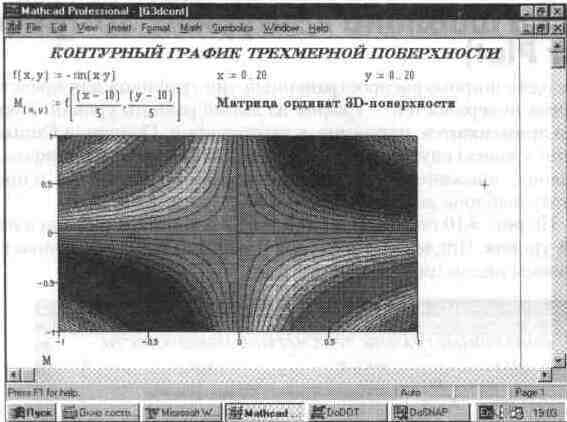
Такое представление графика удобно для количественных оценок. Однако в большинстве случаев указание количественных значений уровней загромождает график. Возможно задание высот 3D-поверхности с помощью функциональной окраски. Тогда можно выполнить построение этой поверхности в виде распределения плотности окраски (см. рис. 5.11).

При использовании цветной функциональной окраски описанные выше типы графиков выглядят весьма впечатляюще. Но неплохие результаты получаются и при задании монохромных графиков. В этом случае гамма цветов заменяется просто разной плотностью серого цвета, от ярко-белого до черного.

Иногда контурные графики получаются даже более информативными, чем просто трехмерные поверхности. У последних нередко одни части поверхности закрывают другие. Например, пик на переднем плане может закрыть меньшие пики или впадины на заднем плане. У контурных графиков такого эффекта нет, и на них легко обнаруживаются все пики и впадины, правда, при достаточно большом числе линий равного уровня и малом расстоянии между ними.

Рис. 5.11 График распределения плотности ЗD-поверхности

5.6. Установка шаблона точечного ЗD-графика (3D Scatter Plot)

Нередко трехмерные поверхности представляют в виде находящихся в этом пространстве точек, кружочков или иных фигур. Каждая из этих фигур несет информацию о геометрическом положении ее центра в трехмерном пространстве. Такой график создается операцией 3D Scatter Plot (Точечный график) — см. рис. 5.12.

Размеры точек, их вид и окраску можно изменять с помощью команды изменения формата ЗD-графика. Обычно достаточно наглядными являются графики с малыми фигурами, расположенными внутри параллелепипеда Однако в целом наглядность таких графиков не очень высока. Их стоит использовать не для показа трехмерных поверхностей, а лишь для демонстрации расположения на них небольшого числа объектов. Объекты могут быть не только в виде точек, но и иных фигур, крестиков, окружностей, квадратов и др

Рис.5.12 График ЗD-поверхности в виде разбросанных в пространстве точек

5.7. Установка шаблона SD-графиков в виде гистограммы (3D Bar Chart)

Весьма pacпpocтраненной формой представления ЗD-поверхностей является также представление ее рядом трехмерных столбиков, высота которых определяется значением координаты z(x, у) Для этого используется операция 3D Bar Chart (Трехмерная гистограмма) — см рис 513

Рис.5.13 Представление ЗD-поверхности трехмерными столбиками

Подобные графики широко применяются при анализе сложных статистических данных, например представленных тремя независимыми переменными Обычно их построение считается высшим пилотажем, но MathCAD превращает этот процесс в обыденную операцию При этом, как видно из рис. 513, достаточно наглядным является представление столбиками и сложных трехмерных поверхностей

5.8. Установка шаблона ЗD-графиков с векторным представлением (Vector Field Plot)

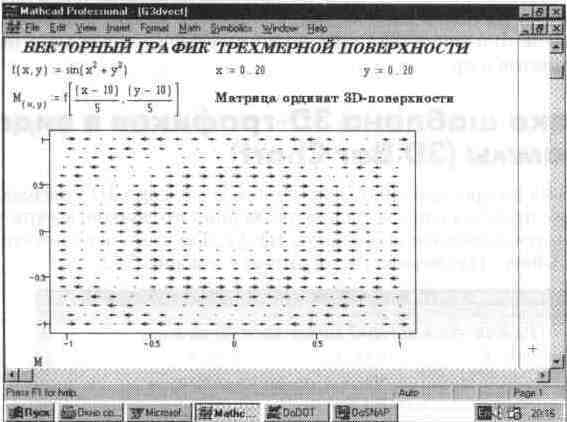
Еще один вид представления ЗD-поверхности векторное представление Оно задается построением коротких стрелочек векторов Стрелка обращена острием в сторону нарастания высоты поверхности, а плотность расположения стрелок зависит от скорости этого нарастания На рис 514 показан пример подобного графика Для его построения используется команда Field Plot (Векторное поле)

Рис. 5.14 Представление 3D-поверхности векторами

Эти графики применяются редко из-за трудностей построения множества стрелок, для каждой из которых надо рассчитывать градиент поля Но MathCAD дает удобную возможность широкого применения этого вида графиков Он особенно подходит для представления электромагнитных, тепловых, гравитационных и иных полей

5.9. Установка шаблона матриц и векторов (Matrix...)

Операция Matrix... (Матрицы) обеспечивает задание векторов или матриц Как известно, матрица является заданным своим именем объектом в виде массива данных MathCAD использует одномерные массивы — векторы и двумерные — собственно матрицы

Матрица характеризуется числом строк (Rows) и числом столбцов (Columns). Таким образом, число элементов матрицы или ее размерность равны Rows x Columns Элементами матриц могут быть числа, константы, пере менные и даже математические выражения Соответственно матрицы могут быть численными и символьными

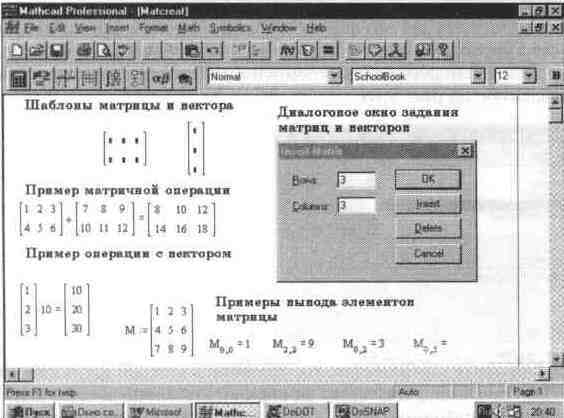
Если использовать операцию Matrix..., то в текущем окне появится не большое окошко, позволяющее задать размерность вектора или матрицы (см рис 515 справа) Для этого нужно указать число строк Rows и число сголбцов Columns Нажав клавишу Enter или указав курсором мыши на изображение клавиши Insert (Вставить) в окошке, можно вывести шаблон матрицы или вектора (вектор имеет один из параметров размерности, равный 1)

Шаблон содержит обрамляющие скобки и темные маленькие прямоугольники, обозначающие места ввода значений (числовых или символьных) для элементов вектора или матрицы. Один из прямоугольников можно сделать активным (отметив его курсором мыши). При этом он заключается в уголок. Это указывает на то, что в него будут вводиться значения соответствующего элемента. С помощью клавиш перемещения курсора можно по горизонтали пробежаться по всем прямоугольникам и ввести все элементы вектора или матрицы.

Рис. 5.15 Вывод шаблонов вектора и матрицы и их заполнение

Пока идет ввод элементов векторов или матриц, пустые шаблоны отображаются без каких-либо комментариев. Однако, если закончить ввод до полного заполнения шаблонов, система выведет сообщение об ошибке — незаполненный шаблон приобретет красный цвет. Вывод несуществующей матрицы или ошибочное указание ее индексов также отображается красным цветом.

Если использовать операцию Insert (Включение) при уже выведенном шаблоне матрицы, то матрица расширяется и ее размер увеличивается. Кнопка Delete (Стирание) позволяет убрать расширение матрицы, вычеркнув из нее строку или столбец.

Каждый элемент матрицы характеризуется индексированной переменной, и его положение в матрице обозначается двумя индексами: один указывает номер строки, другой — номер столбца. Для набора индексированной переменной прежде надо ввести имя переменной, а затем перейти к набору индексов нажатием клавиши, вводящей символ]. Прежде указывается индекс строки, а затем через запятую индекс столбца. Примеры вывода индексированных переменных (элементов матрицы М) также даны на рис. 5.14.

Вырожденная в одну строку или в один столбец матрица является вектором. Его элементы — индексированные переменные с одним индексом. Нижняя граница индексов задается значением системной переменной ORIGIN. Обычно ее значение задают равным 0 или 1.

5.10. Вывод функций (Choose function...)

Как правило, при подготовке документов имена функций пользователь вводи г самостоятельно. Поскольку функций, встроенных в систему, очень много (около 250), запомнить их все довольно сложно. Это и не нужно, ведь в MathCAD есть средство для ввода имен функций из их общего списка (каталога).

Операция Choose function... (Вставить функцию) выполняет следующие действия:

• выводит полный перечень встроенных в ядро системы функций;

• кратко поясняет назначение каждой функции;

• позволяет корректно ввести шаблон с именем функции в место расположения курсора, установленного в математическом выражении.

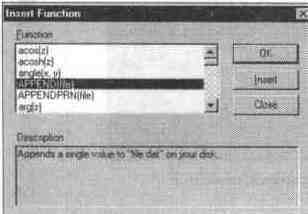
Для реализации этих возможностей команда выводит диалоговое окно, показанное на рис. 5.16.

Рис. 5.16 Диалоговое окно встроенных функций

Обратите внимание на то, что запись каждой функции дается в полной синтаксической форме. Это исключает довольно частые ошибки в формулах, вызванные неточностями записи функций. На месте параметров в выведенной функции имеются шаблоны данных для их ввода. Приведенное окно дает полный список встроенных в систему MathCAD функций и является хорошим средством для ознакомления с ними.

5.11. Установка единиц измерения размерных величин (Units...)

Операция Units... (Единицы) служит для установки единиц измерения размерных величин в заданной системе. Размерные величины широко используются в физических и в научно-технических расчетах.

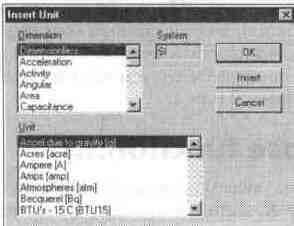
При использовании операции Units... появляется окно, имеющее список размерных величин Dimension и относящихся к ним единиц измерения Unit. В окне есть также указание на то, какая система единиц System используется. Вид окна показан на рис. 5.17. По умолчанию используется система единиц SI.

Рис. 5.17 Диалоговое окно вставки единиц измерения размерных величин

Операция Options... в подменю Math главного меню служит для смены используемой системы единиц

Окно вставки единиц измерения размерных величин имеет три кнопки Insert — вставляет выбранную единицу измерения с сохранением окна, OK — вставляет выбранную единицу измерения и закрывает окно, Cancel — отменяет операцию вставки размерных величин

При работе с размерными величинами MathCAD производит необходимые преобразования и выводит числовые значения величин вместе с единицами их измерения

5.12. Установка шаблона импортируемого рисунка (Picture)

Ценной возможностью систем MathCAD является импорт графических файлов, создаваемых другими графическими системами, например графическими редакторами класса PaintBrush, системами AutoCAD, PCAD и др Это позво ляет включать в документы MathCAD высококачественные графические иллюстрации, что крайне необходимо при создании электронных книг

Перед импортом файла надо подготовить его в соответствующем прило жении и записать в виде файла в текущий каталог работы Файл может иметь расширение.bmp (BitMap) Воспринимаются и файлы с расширением msc из прежних версий системы MathCAD

Для импорта файла с рисунком достаточно выполнить операцию Picture (Рисунок) — появится шаблон рисунка с единственным маленьким шабло ном в левом нижнем углу В нем надо записать имя файла и, отведя курсор мыши в сторону от рисунка, щелкнуть ее левой клавишей На рис 518 показано, как рисунок из файла Columbia msc с созданным с помощью системы AutoCAD изображением космического челнока встраивается в документ системы MathCAD

Рис. 5.18 Пример импорта графического изображения

Импортируемый рисунок можно, как и любой другой, перемещать с помощью мыши по экрану, растягивать его, выделять и помещать в буфер обмена и т. д. Заглядывая вперед, отметим, что можно перенести в текст документов и множество рисунков из электронного справочника системы. Это заметно облегчает подготовку в среде MathCAD хорошо иллюстрированных учебных программ.

Помимо импорта рисунков из файлов система MathCAD допускает копирование рисунков из буфера обмена системы Windows. Для этого надо ввести рисунок в этот буфер (например, используя графический редактор Windows Paint Brush или операции Copy либо Cut прикладных Windows-программ). Затем, перейдя к работе с системой MathCAD, нужно установить курсор на место верхнего левого угла будущего рисунка и выполнить операцию Paste в позиции Edit главного меню (или нажать клавишу F4).

5.13. Вставка текстовой области (Text Region...)

Текстовые области вставляются в документы MathCAD для создания текстовых комментариев. В MathCAD 7.0 PRO оставлена операция вставки расширяемой текстовой области — Text Region... (Текстовая область). Перед ее применением нужно установить курсор мыши (красный крест) в то место окна редактирования, откуда должен начинаться текст — это левый верхний угол будущей текстовой области. После этого исполняется данная операция и на месте курсора появляется прямоугольник (шаблон текстовой области) с текстовым маркером внутри него — см. рис. 5.19.

Рис. 5.19 Операции ввода текста и математических символов в текстовые области

Перед вводом русскоязычного текста рекомендуется выбрать подходящий шрифт. У многих русскоязычных (кириллических) шрифтов в названии имеется слово "Суг". Если в начале ввода выяснилось, что введена буква не русского алфавита, то при попытке ее стирания шаблон текстовой области исчезает и его придется выводить снова.

5.14. Вставка в текстовую область математических формул (Math Region...)

В текстовые области нередко надо вставлять математические формулы. Такие объекты не должны быть исполняемыми в отличие от формул в формульных блоках. Эти формулы в ряде случаев (например, при символьных операциях) могут модифицироваться.

Для вставки в текстовые блоки математических формул надо выполнить операцию Math Region... (Математическая область). Кстати, эта операция доступна только в том случае, когда текстовый маркер установлен в нужное место текстовой области. Тогда выполнение операции Math Region... приведет к появлению в текстовой области шаблона в виде маленького черного квадрата. В этом квадрате можно задавать математические формулы, в том числе используя наборные панели с математическими символами (см. пример на рис. 5.19).

5.15. Вставка линии разрыва страницы (Page Break)

Большие документы нередко занимают много страниц. Бывает крайне нежелательно, когда при печати таких документов какой-нибудь график или таблица обрываются линией раздела страниц. Недопустимы и ситуации, когда заголовок раздела оказывается на одной странице, а непосредственно сам раздел начинается на другой.

Для предотвращения таких ситуаций желательно прервать страницу в заданном месте. Для этого служит операция Page Break (Разрыв страницы), вставляющая в документ горизонтальную линию разрыва страницы. На рис. 5.19 эта линия показана внизу окна редактирования.

5.16. Вставка гиперссылки (Hyperlink)

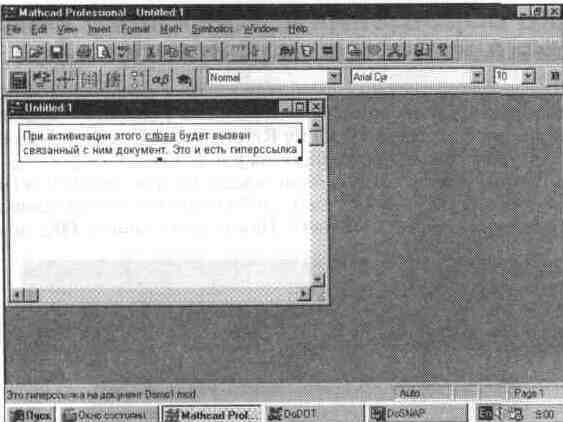
Гиперссылки — важный элемент создания сложных документов, обучающих программ и справочных систем. Напомним, что гиперссылка в системе MathCAD представляется подчеркнутым словом, при активизации которого вызывается связанный с ней документ (файл).

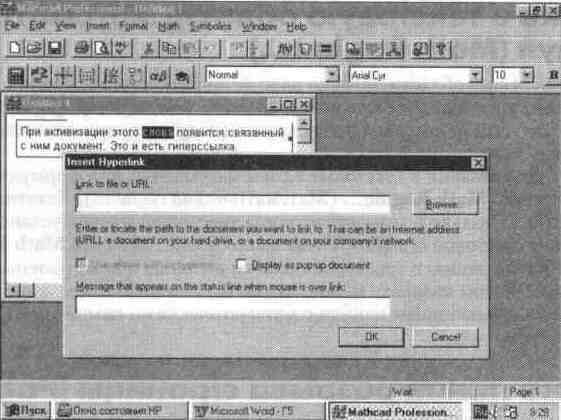
Для создания гиперссылки должен быть создан текстовый блок, в котором нужно выделить некоторый фрагмент текста, чаще всего какое-либо слово. Начало создания гиперссылки показано на рис. 5.20.

После этого надо выполнить операцию Hyperlink (Гиперссылка) с опцией New (Новая) для вывода диалогового окна задания гиперссылки Оно также показано на рис 5.20 под текстовым блоком В этом окне следует указать в верхнем свободном поле полное имя файла, который будет вызываться данной гиперссылкой В другом поле можно ввести текст сообщения, которое будет появляться в строке состояния (внизу экрана системы) при установке курсора мыши на гиперссылку.

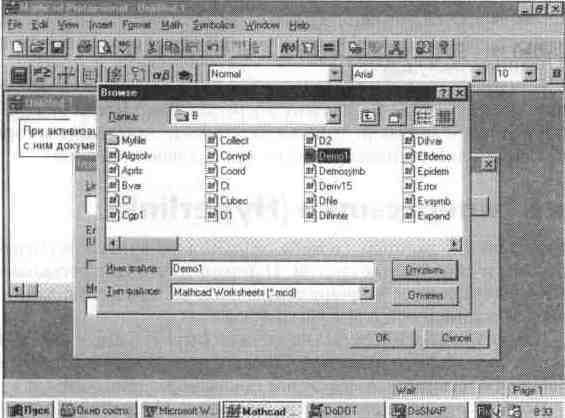
Обычно точное имя файла (с полным путем доступа к нему) запомнить трудно Поэтому, активизируя клавишу Browse (Обзор) окна задания гиперссылки, можно вызвать окно поиска файла — см. рис. 521.

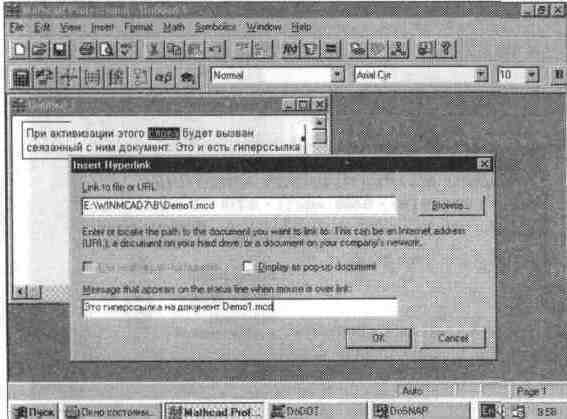
После нахождения файла его полное имя появляется в верхнем поле окна гиперссылки, теперь в нижнее поле можно ввести текст сообщения (см. рис. 5.22).

Рис. 5.20 Подготовка к заданию гиперссылки

Рис. 5.21 Поиск файла, который связывается с гипер-ссылкой

Для завершения создания гиперссылки достаточно нажать кнопку ОК окна создания гиперссылки. При отказе от ее создания надо нажать кнопку Cancel.

Если установить курсор мыши на гиперссылку, то в строке состояния (внизу экрана системы) появится сообщение, которое было задано ранее (оно видно на рис. 5.23). Такие сообщения очень полезны при большом числе ги-перссылок, поскольку позволяют судить об их назначении.

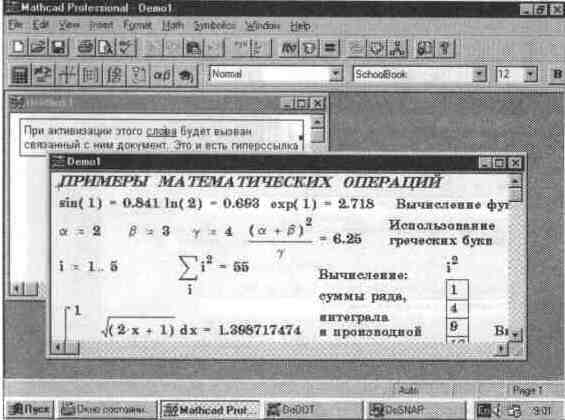
Для осуществления гиперссылки достаточно установить курсор мыши на подчеркнутое слово, гиперссылку, и быстро дважды щелкнуть левой клавишей мыши. Текстовое сообщение, в котором имеется гиперссылка, станет выделенным, и на экране появится вызываемый гиперссылкой документ — см. рис. 5.24.

Рис. 5.22 Завершение создания гиперссылки

Рис. 5.23 Вид экрана после задания гиперссылки

После ознакомления с вызываемым документом его можно закрыть. До этого возможно редактирование документа. Объектами гиперссылок Могут быть не только документы. Можно, к примеру, дать гиперссылку на рисунок, создаваемый графическим редактором, на электронную таблицу и т. д. Все это позволяет готовить вполне современные и удобные в применении документы не только расчетного, но и информационно-справочного и учебного характера.

Гиперссылку можно убрать с помощью опции Erase (Уничтожить), а также отредактировать, используя опцию Edit... (Редактировать), выводящую окно редактирования гиперссылки.

Рис. 5.24 Использование гиперссылки

5.17. Вставка обращения к заданному файлу активизацией кнопки (Reference...)

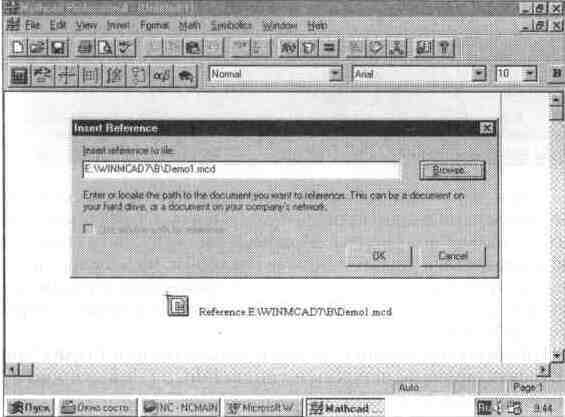
Есть еще один удобный способ обращения к заданным файлам путем создания ассоциированного с ними графического объекта — использование кнопок Для этого существует операция Reference... (Ссылка) Она выводит окно задания такой ссылки, показанное на рис 5 25

В этом окне надо либо явно указать полное имя файла (на рис 5 25 это относится к файлу Demo1 mcd), пибо найти его, воспользовавшись кнопкой вызова окна просмотра Browse Нажав далее кнопку ОК, можно вывести по

Рис. 5.25 Задание гиперссылки в виде кнопки, ассоциированной с файлом

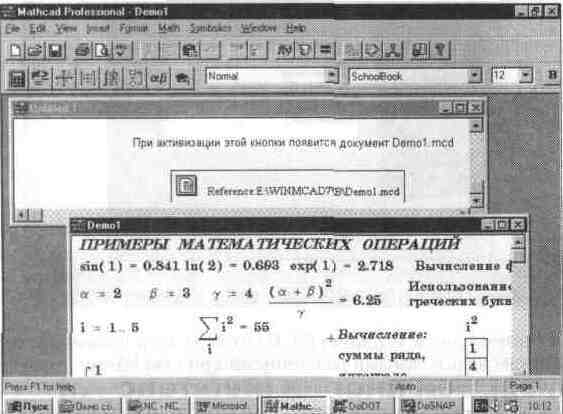
месту расположения курсора мыши кнопку гиперссылки с указанным после нее именем вызываемого ею файла (вид этой кнопки показан на рис. 5.25 под окном задания гиперссылки). Активизация кнопки ОК ведет к появлению окна с вызываемым документом (см. рис. 5.26).

Рис. 5.26 Использование гиперссылки в виде кнопки

Два вида гиперссылок, реализованных в системе MathCAD, расширяют возможности подготовки сложных документов, а возможности использования гиперссылок делают более разнообразными.

5.18. Связь с другими компонентами системы (Component...)

Одной из главных отличительных особенностей системы MathCAD 7.0 PRO является возможность подключения к ней других математических систем — компонентов и использование входящих в них средств и функций, что намного увеличивает возможности объединенной вычислительной системы.

Для подключения к MathCAD новых компонентов используется операция Component... (Компоненты), выводящая диалоговое окно с перечнем компонентов, с которыми можно общаться после установления связи с тем или иным компонентом. Это окно показано на рис. 5.27.

В этом окне можно выбрать одну из систем и подключить ее к MathCAD. После этого, нажав кнопку Finish (Конец), можно наблюдать загрузку системы. Работу с расширенной системой мы опишем позже, после более детального знакомства с собственными (и достаточно обширными) возможностями самой системы MathCAD.

5.19. Вставка объектов (Object...)

Вставка объектов — пожалуй, самая мощная возможность системы MathCAD. Впрочем, она присуща большинству серьезных приложений для операционных систем класса Windows 95. Благодаря этой возможности легко устанавливается связь с самыми различными приложениями этой операционной системы, в том числе с довольно далекими от математических систем, такими, например, как текстовый процессор Word или база данных Acess из офисного пакета Microsoft Office 95.

Рис. 5.27 Окно связи с другими компонентами системы MathCAD

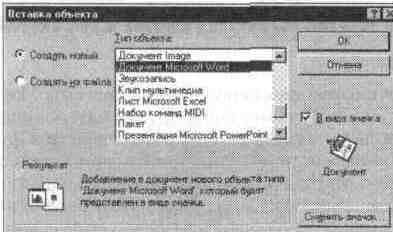
Для реализации вставки объектов из других приложений надо выполнить операцию Object... (Объект). Она выводит окно с перечнем приложений, с которыми может осуществляться объектная связь (см. рис. 5.28).

Рис. 5.28 Окно объектной связи с приложениями

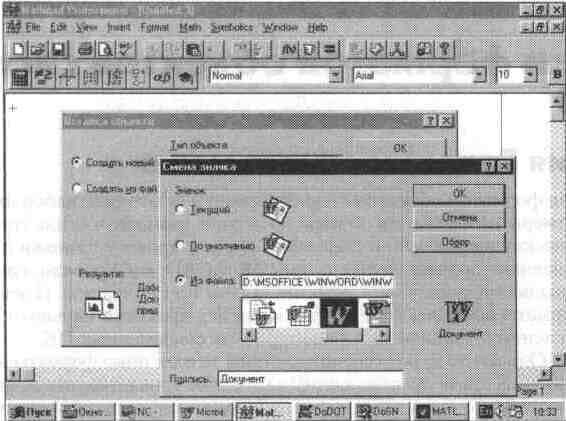
После выбора приложения для объектной связи с MathCAD на месте курсора мыши появляется пиктограмма с изображением объекта. Вид этой пиктограммы можно менять, если активизировать кнопку Смена значка... При этом появляется окно, в котором можно выбрать подходящий значок (пиктограмму), устраивающий пользователя (см. рис. 5.29).

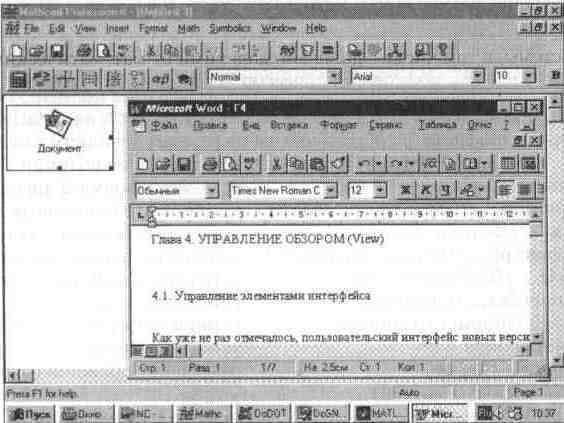
На рис. 5.30 показан случай, когда в качестве объекта для вставки используются документы текстового редактора Word 95 из пакета Microsoft Office 95. Пиктограмма этого объекта показана в левом верхнем углу окна редактирования текущего документа.

Рис. 5.29 Выбор значка для обозначения вставляемого объекта

Рис. 5.30 Установление объектной связи с текстовым редактором Word 95

Если активизировать значок-пиктограмму, то появится окно текстового редактора Word 95, которое также показано на рис. 5.30. В этом окне можно подготовить любой документ, и он в дальнейшем будет вызываться активизацией значка объекта.

Объекты для связи с MathCAD могут быть самыми разнообразными; это текстовые и графические данные, таблицы и записи из баз данных, музыкальные фрагменты, видеоклипы и т. д. По существу, этот способ связи позволяет свести воедино самые различные приложения и обеспечить между ними полноценный обмен данными.