Глава 8 Работа с символьным процессором

Глава 8 Работа с символьным процессором

8.1. Возможности символьного процессора (Symbolic)

Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, разумеется, если такое решение существует в принципе (что бывает далеко не всегда).

Ядро символьного процессора системы MathCAD — несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software [12, 18], у которой MathSoft (разработчик MathCAD) приобрела лицензию на его применение, благодаря чему MathCAD стала (начиная с версии 3.0) системой символьной математики.

Прямой доступ к большинству операций ядра (возможный в системе Maple V R3/R4), для пользователя MathCAD, к сожалению, закрыт. К примеру, библиотечный модуль Maple V содержит около 100 функций линейной алгебры, тогда как в модуле MathCAD 3.0 есть только три важнейшие функции из этого раздела. Многие функции и правила преобразования в ядре используются лишь для получения промежуточных преобразований.

Тем не менее это обстоятельство нельзя считать уж слишком большим недостатком системы MathCAD. Во-первых, потому, что ее назначение иное — прежде всего решение задач в численном виде, а во-вторых, потому, что система Maple V явно избыточна (в ее ядре около 2800 функций и правил преобразования) и ориентирована на пользователей с весьма далекими от средних потребностями в решении задач компьютерной алгебры (символьной математики) [12].

Введение в систему MathCAD символьных вычислений придает ей качественно новые возможности, которые отсутствовали у прежних версий системы [5—7]. Теоретические сведения об алгоритмах компьютерной алгебры можно найти в книге [19]. Куда важней, что символьные вычисления выполняются в конечном счете столь же просто (для пользователя), как, скажем, вычисление квадрата х.

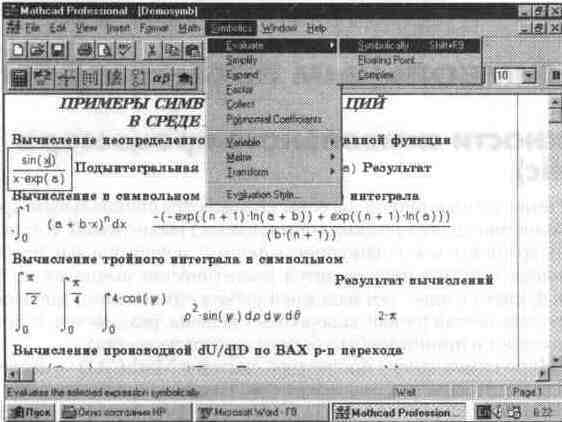
Операции, относящиеся к работе символьного процессора, содержатся в подменю позиции Symbolic (Символика) главного меню (см. рис. 8.1).

Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т е надо выделить выражение (правила выделения неоднократно описывались выше) Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция. Само выражение в таком случае не выделяется. ведь и так ясно, что если маркер ввода выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной

Рис. 8.1 Вид экрана системы с подменю позиции Symbolic главного меню

Символьные операции разбиты на пять характерных разделов Первыми идут наиболее часто используемые операции Они могут выполняться с выра жениями, содержащими комплексные числа или имеющими решения в комплексном виде

Операции с выделенными выражениями

К операциям с выделенными выражениями относятся следующие Evaluate (Вычислить) — преобразовать выражение с выбором вида преоб разований из подменю,

Simplify (Упростить) — упростить выделенное выражение с выполнением таких операций, как сокращение подобных слагае мых, приведение к общему знаменателю, использова ние основных тригонометрических тождеств и т д, Expand (Разложить — раскрыть выражение [например, для по степеням) (Х+ Y) (Х- Y) получаем X2- Y2}, Factor (Разложить — разложить число или выражение на множи-на множители) тели [например X2-Y2 даст (X+Y) (X-Y)], Collect (Разложить — собрать слагаемые, подобные выделенному по подвыражению) выражению, которое может быть отдельной переменной или функцией со своим аргументом (ре зультатом будет выражение, полиномиальное от носительно выбранного выражения),

Polynomial Coefficients — найти коэффициенты полинома по заданной

(Полиномиальные переменной, приближающего выражение,

коэффициенты) в котором эта переменная использована

Операции с выделенными переменными

К числу операций с выделенными переменными относятся

Solve (Решить — найти значения выделенной переменной,

относительно переменной) при которых содержащее ее выражение становится равным нулю (решить уравнение или неравенство относительно выделенной переменной);

Substitute (Заменить — заменить указанную переменную содержи-

переменную) мым буфера обмена;

Differentiate — дифференцировать все выражение, содержа-(Дифференцировать щее выделенную переменную, по отношению по переменной) к этой переменной (остальные переменные рассматриваются как константы);

Integrate (Интегрировать — интегрировать все выражение, содержащее

по переменной) выделенную переменную, по этой переменной;

Expand to Series... — найти несколько членов разложения выра-(Разложить в ряд) жения в ряд Тейлора относительно выделен ной переменной;

Convert to Partial Fraction — разложить на элементарные дроби выраже-(Разложить на элементарные ние, которое рассматривается как рацио-дроби) нальная дробь относительно выделенной пе ременной.

Операции с выделенными матрицами

Операции с выделенными матрицами представлены позицией подменю Matrix (Матричные операции), которая имеет свое подменю со следующими операциями:

Transpose (Транспонировать) — получить транспонированную матрицу;

Invert (Обратить) — создать обратную матрицу;

Determinant (Определитель) — вычислить детерминант (определитель) матрицы.

Операции преобразования

В MathCAD 7.0 PRO в позиции Symbol содержится раздел операций преобразования, создающий подменю со следующими возможностями:

Fourier Transform — выполнить прямое преобразование Фурье

(Преобразование Фурье) относительно выделенной переменной;

Inverse Fourier Transform — выполнить обратное преобразование

(Обратное преобразование Фурье относительно выделенной

Фурье) переменной;

Laplace Transform — выполнить прямое преобразование (Преобразование Лапласа) Лапласа относительно выделенной пере менной (результат — функция от пере менной s);

Inverse Laplace Transform — выполнить обратное преобразование (Обратное преобразование Лапласа относительно выделенной Лапласа) переменной (результат — функция от переменной t);

Z Transform (Z-преобразование) — выполнить прямое Z-преобразование вы ражения относительно выделенной пере менной (результат — функция от пере менной z);

Inverse Z Transform — выполнить обратное Z-преобразование (Обратное Z-преобразование) относительно выделенной переменной (результат — функция от переменной n)

Стиль эволюции

К стилю эволюции относится одна операция-

Evaluation Style... — задать вывод результата символьной операции под

(Стиль эволюции) основным выражением, рядом с ним или вместо него

В последующих разделах этой главы каждая из упомянутых выше операций будет рассмотрена более подробно с необходимыми примерами.

8.2. Выделение объектов символьных операций

Для проведения символьных операций нужно прежде всего выделить объект, над которым эти операции будут выполняться. Если объект отсутствует, доступа к соответствующим операциям в позиции Symbolic главного меню нет, а сами операции выделены затененным шрифтом. Объектом операции может быть самостоятельное математическое выражение, часть такого выражения или заданной пользователем функции, результат предшествующей операции и т д.

Напомним, что есть два вида выделения: пунктирными линиями и сплошными. Чтобы отметить объект пунктирной линией, достаточно установить на него курсор-крестик, нажать клавишу Ctrl или Shift и воспользоваться правой клавишей мыши.

Можно установить курсор около выбранного объекта и, нажав правую клавишу мыши, перемещать ее по столу При этом появляется пунктирный прямоугольник, который перемещением мыши можно расширять в различных направлениях. Как только этот прямоугольник захватывает один или несколько объектов, они оказываются также выделенными — обведенными пунктирной линией, отмечающей область, занимаемую объектом в окне.

Выделение пунктирной линией используется для перемещения объектов по окну. Для этого достаточно внутрь отмеченного объекта (выражения) поместить курсор мыши, нажать правую клавишу и, удерживая ее нажатой, перемещать мышь. При этом объект (или сразу несколько объектов) будет перемещаться по экрану и его можно оставить (отпустив клавишу мыши) на новом месте Напоминаем, что нажатие клавиши F3 ведет к переносу выражений в буфер обмена и стиранию их в окне. Нажатие клавиши F4 переносит выражения из буфера обмена на место, указанное курсором. Курсор можно перемещать как мышью, так и обычными клавишами управления им.

Для выполнения операций с символьным процессором нужно выделить объект (целое выражение или его часть) сплошными линиями, синими на экране цветного дисплея. Для выделения некоторой переменной в объекте нужно подвести к ее концу курсор мыши и нажать левую клавишу. Переменная будет отмечена жирной чертой (синей на экране цветного дисплея), расположенной сразу после переменной Перемещая курсор по полю объекта и нажимая левую клавишу повторно, можно выделить отдельные части выражения или выражение целиком.

Часть символьных операций производится указанием на объект как на выражение или его часть. Например, расширение или упрощение выражений требуют такого указания на объект Другие операции, такие, как вычисление производной или интеграла, требуют указания переменной, относительно которой производится операция, допустим, дифференцирования или интегрирования.

Если заданная операция невыполнима, система выводит в дополнительном окне сообщение об ошибке или просто повторяет выделенное выражение. Последнее означает, что операция задана корректно, но результат не может быть получен, например, если делается попытка разложить на множители объект, уже разложенный или не содержащий такого разложения в принципе.

При выполнении символьных операций иногда приходится сталкиваться с неприятной и трудной проблемой — "разбуханием" результатов, как промежуточных, так и конечных. Решения, которые хорошо известны профессиональному математику (и даже студенту), система обычно выдает с блеском — в виде, который описан в справочнике или учебнике. Примером может служить решение квадратного уравнения или вычисление простого неопределенного интеграла

Но даже незначительное усложнение задачи порою может породить очень сложное и громоздкое решение. Пример тому — решение кубического уравнения. В этом случае решение (по запросу системы) можно поместить в буфер обмена и использовать его для оценки пользователем (но не для дальнейших преобразований системой в автоматическом режиме).

Система MathCAD содержит пять типов символьных операций, выполняемых над объектами — выделенными математическими выражениями. При этом под математическим выражением подразумевается как полная математическая формула, так и функционально полная часть какой-либо формулы. Ниже представлено описание символьных операций над выражениями

8.3. Выполнение символьных вычислений (Evaluate Symbolically)

Символьная операция Evaluate Symbolically [Shift+F9] (Вычислить) обеспечивает работу с математическими выражениями, содержащими встроенные в систему функции и представленными в различном виде: полиномиальном, дробно-рациональном, в виде сумм и произведений, производных и интегралов и т. д. Операция стремится произвести все возможные численные вычисления и представить выражение в наиболее простом виде. Она возможна над матрицами с символьными элементами. Производные и определенные интегралы, символьные значения которых вычисляются, должны быть представлены в своей естественной форме.

Особо следует отметить возможность выполнения численных вычислений с повышенной точностью — 20 знаков после запятой. Для перехода в такой режим вычислений нужно числовые константы в вычисляемых объектах задавать с обязательным указанием десятичной точки, например 10.0 или 3.0, а не 10 или 3. Этот признак является указанием на проведение вычислений такого типа.

На рис. 8.2 показаны типовые примеры действия операции Evaluate Symbolically.

Здесь слева показаны исходные выражения, подвергаемые символьным преобразованиям, а справа — результат этих преобразований. Так представлены и другие примеры, приведенные в этой главе.

Рис. 8.2 Действие операции Evaluate Symbolically

Операция Evaluate Symbolically одна из самых мощных. Как видно на рис. 8.2, она позволяет в символьном виде вычислять суммы (и произведения) рядов, производные и неопределенные интегралы, выполнять символьные и численные операции с матрицами.

Эта операция содержит подменю со следующими командами:

Evaluate Symbolically [Shift+F9] — выполнить символьное вычисление (Вычислить в символах) выражения;

Floating Point Evaluation... — выполнить арифметические (С плавающей точкой) операции в выражении с результатом в форме числа с плавающей точкой;

Complex Evaluation — выполнить преобразование с пред-(В комплексном виде) ставлением в комплексном виде.

Команда Evaluate Symbolically тут наиболее важная. Назначение других команд очевидно: они нужны, если результат требуется получить в форме комплексного или действительного числа. К примеру, если вы хотите вместо числа л получить 3.141..., используйте команду Floating Point Evaluation. В режиме символьных вычислений результат может превосходить машинную бесконечность системы — см. пример на вычисление ехр( 1000.0) на рис. 7.2. При этом число точных значащих цифр результата практически не ограничено (или, точнее говоря, зависит от емкости ОЗУ).

8.4. Упрощение выражений (Simplify)

Символьная операция Simplify (Упростить) — одна из самых важных. Эта операция позволяет упрощать математические выражения, содержащие алгебраические и тригонометрические функции, а также выражения со степенными многочленами (полиномами).

Упрощение означает замену более сложных фрагментов выражений на более простые. Приоритет тут отдается простоте функций. К примеру, функция tan(x) считается более сложной, чем функции sin(x) и cos(.x). Поэтому tan(x) упрощается так, что получает представление через соотношение этих функций, что несколько неожиданно, так как в некоторых пакетах символьной математики, например Derive, ситуация иная: они заменяют отношение sin(x)/cos(x) функцией tan(x).

Эта команда открывает широкие возможности для упрощения сложных и плохо упорядоченных алгебраических выражений. На рис. 8.3 даны примеры применения операции Simplify.

Рис. 8.3 Действие операции Simplify

Два последних примера на приведенном рисунке показывают, как с помощью операции Simplify можно выполнять символьные вычисления производных и определенных интегралов. Результатом вычислений могут быть специальные математические функции (см. последний пример, в котором символьное значение интеграла дает результат, выраженный через интегральный синус). Вполне возможно вычисление производных высшего порядка. На рис. 8.4 показано последовательное применение операции Simplify для вычисления производных алгебраического выражения, от первой до пятой включительно.

Система MathCAD содержит встроенную функцию для вычисления значений определенных интегралов приближенным численным методом. Ею целесообразно пользоваться, когда нужно просто получить значение определенного интеграла в виде числа. Однако команда Simplify применительно к вычислениям определенных интегралов делает гораздо больше — она ищет аналитическое выражение для интеграла. Более того, она способна делать это и при вычислении кратных интегралов, пределы которых — функции. Наглядный пример этому дает рис. 8.5.

На рис. 8.6 показано применение операции Simplify для вычисления сумм и произведений символьных последовательностей. Результат операции, как и следовало ожидать, получается в символьной форме (если она существует).

Приведенные примеры могут создать впечатление, что MathCAD лихо справляется со всеми производными, интегралами, суммами и произведения-

Рис. 8.4 Вычисление производных алгебраического выражения с порядком от 1 до 5

Рис. 8.5 Вычисление двойных и тройных определенных интегралов

ми с помощью операции Simplify. К сожалению, это далеко не так. Нередко система не справляется с кажущимися простыми справочными примерами. Надо помнить, что символьный процессор системы MathCAD обладает заметно урезанной библиотекой функций и преобразований (в сравнении с библиотекой системы Maple V). Поэтому часто система не находит решение в замкнутом виде, хотя оно и приводится в справочнике. Тогда система повторяет введенное выражение или сообщает об ошибке.

Следует также отметить, что при выполнении командами меню Symbol символьных вычислений выражения необходимо указывать явно. Например, недопустимо вводить некоторую функцию пользователя F(x) и пытаться найти ее производные или интеграл. Это существенное ограничение, и котором надо всегда помнить. Однако оно преодолимо при выполнении вычислений с помощью функций системы SmartMath, которая описывается в дальнейшем; 

Рис. 8.6 Вычисление сумм и произведений символьных последовательностей

главное в том, что для вывода символьных вычислений в этом случае используется оператор —>.

В результате преобразований могут появляться специальные функции — как встроенные в систему (функции Бесселя, гамма-функция, интеграл вероятности и др.), так и ряд функций, дополнительно определенных при загрузке символьного процессора (интегральные синус и косинус, интегралы Френеля, эллиптические интегралы и др.) Последние нельзя использовать при создании математических выражений.

8.5. Расширение выражений (Expand)

Действие операции Expand (Разложить по степеням) в известном смысле противоположно действию операции Simplify. Подвергаемое преобразованию выражение расширяется с использованием известных (и введенных в символьное ядро) соотношений, например алгебраических разложений многочленов, произведений углов и т. д Разумеется, расширение происходит только в том случае, когда его результат однозначно возможен Иначе нельзя считать, что действие этой операции противоположно действию операции Simplify. К примеру, операция Simplify преобразует сумму квадратов синуса и косинуса в 1, тогда как обратное преобразование многозначно и потому в общем виде невыполнимо

При преобразовании выражений операция Expand Expression старается более простые функции представить через более сложные, свести алгебраические выражения, представленные в сжатом виде, к выражениям в развернутом виде и т д Примеры действия операции Expand Expression даны на рис. 8 7

Последний пример на этом рисунке показывает, что результатом операции может быть специальная математическая функция, которая считаегся более сложным выражением, чем порождающее ее выражение С виду, однако, выражения со специальными математическими функциями обычно выглядят гораздо проще, чем исходные выражения

Рис. 8.7 Действие операции Expand Expression

 

8.6. Разложение выражений (Factor)

Операция Factor Expression (Разложить на множители) используется для факторизации — разложения выражений или чисел на простые множители Она способствует выявлению математической сущности выражений, к примеру, наглядно выявляет представление полинома через его действительные корни, а в том случае, когда разложение части полинома содержит комплекс-

Рис. 8.8 Действие операции Factor Expression

но-сопряженные корни, порождающее их выражение представляется квадратичным трехчленом. Примеры действия этой операции даны на рис. 8.8.

В большинстве случаев (но не всегда) операция факторизации ведет к упрощению выражений. Термин факторизация не является общепризнанным в отечественной математической литературе, но мы его оставляем в связи с созвучностью с англоязычным именем этой операции.

8.7. Комплектование по выражениям (Collect)

Операция Collect (Разложить по подвыражению) обеспечивает замену указанного выражения выражением, скомплектованным по базису указанной переменной, если такое представление возможно. В противном случае появляется окно с сообщением о невозможности комплектования по указанному базису. Эта команда особенно удобна, когда заданное выражение есть функция ряда переменных и нужно представить его в виде функции заданной переменной, имеющей вид степенного многочлена. При этом другие переменные входят в сомножители указанной переменной, представленной в порядке уменьшения ее степени. На рис. 8.9 показаны примеры действия этой операции.

Рис. 8.9 Действие операции Collect

В том случае, когда комплектование по базису указанной переменной невозможно, система выдает сообщение об этом. Оно выводится в отдельном небольшом информационном окошке.

8.8. Вычисление коэффициентов полиномов (Polynomial Coefficients)

Операция Polynomial Coefficients (Полиномиальные коэффициенты), в ранних версиях MathCAD отсутствующая, служит для вычисления коэффициентов полинома. Операция применяется, если заданное выражение — полином

Рис. 8.10 Примеры применения операции Polynomial Coefficients

(степенной многочлен) или может быть представлено таковым относительно выделенной переменной На рис 810 показаны примеры применения этой операции

Результатом операции является вектор с коэффициентами полинома Операция полезна при решении задач полиномиальной аппроксимации и регрессии

8.9. Дифференцирование по заданной переменной (Differentiate)

Следующая группа символьных операций выполняется с выражениями, требующими указания переменной, по отношению к которой выполняется операция Для этого достаточно установить на переменной курсор ввода Само выражение при этом не указывается отдельно, поскольку указание в нем на переменную является одновременно и указанием на само выражение. Если выражение содержит другие переменные, то они рассматриваются как константы Изучим операции этой группы, начиная с операции дифференцирования

Нахождение символьного значения производной — одна из самых рас пространенных задач в аналитических вычислениях. Операция Differentiate (Дифференцировать по переменной) возвращает символьное значение производной выражения по той переменной, которая указана курсором Для вычисления производных высшего порядка (свыше 1) нужно повторить вычисление необходимое число раз На рис 811 показано применение операции дифференцирования

В трех последних примерах на рис 811 показано, что в выражениях, производная которых вычисляется, могут стоять и встроенные в систему специальные математические функции Они могут появляться и в результатах вычислений

Рис. 8.11 Примеры символьного дифференцирования

Особое внимание стоит обратить на последний пример. Попытка вычислить производную от функции Бесселя здесь ведет к тому, что результат направляется в буфер обмена, поскольку представлен в виде функций или действий, содержащихся в ядре символьных операций системы, но недоступных символьному процессору. Поэтому результат дифференцирования вызывается из буфера обмена командой Paste (Вставить). Такой результат нельзя использовать в других операциях прямо, но он вполне подходит для творческого осмысления пользователем. Тот и решает, полезен результат или нет

8.10. Интегрирование по заданной переменной (Integrate)

Другая не менее важная операция при символьных вычислениях — вычисление интегралов (или нахождение первообразных) для аналитически заданной функции. Для этого используется операция Integrate (Интегрировать по переменной). Она возвращает символьное значение неопределенного интеграла по указанной курсором ввода переменной. Выражение, в состав которого входит переменная, является подынтегральной функцией.

На рис. 8.12 показаны примеры символьного интегрирования по переменной х. Визуализация таких вычислений (как и описанных выше), прямо скажем, не велика если бы не поясняющие текстовые комментарии, то было бы совсем неясно, откуда берутся выражения в документе и резульгаты чего они представляют

Как и для операции дифференцирования, в состав исходных выражений и результатов символьного интегрирования могут входить встроенные в систему специальные математические функции. На это указывают два последних примера из приведенных на рис. 8.12.

Рис. 8.12 Примеры символьного интегрирования

8.11. Решение уравнения относительно заданной переменной (Solve)

Если задано некоторое выражение F(x) и отмечена переменная х, то операция Solve (Решить) возвращает символьные значения указанной переменной х, при которых F(x)==0. Это очень удобно для решения алгебраических уравнений, например квадратных и кубических, или для вычисления корней полинома. Рис. 8.13 содержит примеры решения квадратного уравнения и нахождения комплексных корней полинома четвертой степени.

Рис.8.13 Примеры решения уравнений

Ранее отмечалось, что усложнение уравнения, например переход от квадратного уравнения к кубическому, может вызвать и существенное усложнение результата. Тогда система представляет решение в более компактном виде (но без общепринятой математической символики) и предлагает занести его в буфер обмена.

С помощью операции Paste (Вставить) в позиции Edit (Правка) главного меню можно перенести решение в основное окно системы, но оно имеет уже тип текстового комментария, а не математического выражения, пригодного для дальнейших преобразований. Впрочем, часть его можно (опять-таки с помощью буфера обмена) ввести в формульные блоки для последующих преобразований и вычислений.

Более того, форма представления результата в таком случае отличается от принятой в системе MathCAD (например, в качестве знака деления используется косая черта, для возведения в степень — составной знак** и т. д.). Это сделано ради компактности представления результатов вычислений. Рис. 8.14 показывает результат решения кубического уравнения в символьном виде.

Рис. 8.14 Решение кубического уравнения в символьном виде

Последний пример наглядно иллюстрирует проблему "разбухания" результатов. Если при решении квадратного уравнения получены простые выражения, известные даже школьникам (рис. 8.13 — первый пример), то при увеличении порядка уравнения всего на единицу результат оказался представленным весьма громоздкими и малопригодными для анализа формулами. Хорошо еще, что существующими!

В случаях, подобных приведенному, пользователю надо реально оценить свои силы в упрощении решения. Это придется сделать вручную. При технических расчетах специалист нередко знает, какие из параметров решения несущественны и может отбросить их. Однако для строгих математических расчетов это не всегда возможно, поэтому даже громоздкий результат может быть весьма полезным с познавательной точки зрения.

8.12. Подстановка для заданной переменной (Substitute)

Операция Substitute (Подстановка) возвращает новое выражение, полученное путем подстановки на место указанной переменной некоторого другого выражения. Последнее должно быть подготовлено и скопировано (операциями Cut или Copy) в буфер обмена. Наряду с получением результата в символьном виде эта команда позволяет найти и числовые значения функции некоторой переменной путем замены ее на числовое значение. На рис. 8.15 представлены примеры операций с подстановкой.

Рис. 8.15 Примеры операций с подстановкой

Подстановки и замены переменных довольно часто встречаются в математических расчетах, что делает эту операцию весьма полезной. Кроме того, она дает возможность перейти от символьного представления результата к числовому.

8.13. Разложение в ряд Тейлора по заданной переменной (Expand to Series...)

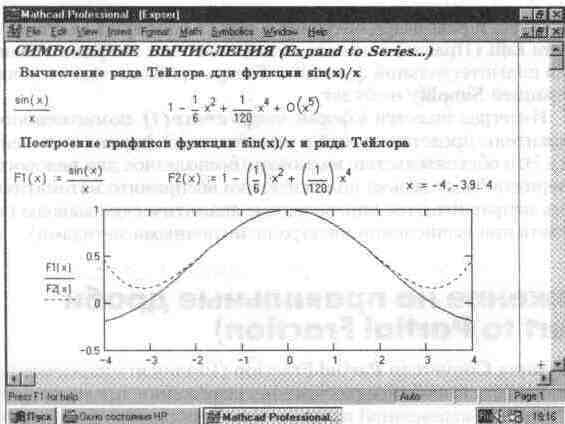
Операция Expand to Series... (Разложить в ряд) возвращает разложение в ряд Тейлора выражения относительно выделенной переменной с заданным по запросу числом членов ряда n (число определяется по степеням ряда). По умолчанию задано п=6. Разложение возможно для функции заданной переменной. В разложении указывается остаточная погрешность разложения. На рис. 8.16 представлено применение этой операции для разложения функции sin(x)/x. Минимальная погрешность получается при малых х (см. графическое представление функции и ее ряда).

Символьные операции нередко можно комбинировать для решения сложных задач. Рис. 8.17 показываег интересное решение одной из таких задач — вычисление определенного интеграла, который не берется в замкнутой форме.

Рис. 8.16 Пример на разложение функции в ряд Тейлора

Рис. 8.17 Взятие определенного интеграла в символьной форме с заменой подынтегральной функции ее разложением

Если пользователя (например, инженера) интересует просто числовое значение интеграла, надо лишь поставить после интеграла знак вывода = и значение интеграла будет вычислено адаптивным численным методом Симп-сона. Однако вычислить такой интеграл с помощью операции Simplify (Упростить) не удастся после долгих попыток система сообщит, что интеграл в замкнутой форме не берется.

Прием, который иллюстрирует рис. 8.17, заключается в замене подынтегральной функции ее разложением в ряд Тейлора. Вначале получим такое разложение с избытком — для 10 членов ряда (однако учтенных нечетных членов тут нет, такова специфика функции). Далее, выделив четыре первых реальных члена и используя операции Copy (Копировать) и Paste (Вставить) в позиции Edit (Правка) главного меню, поместим это разложение на место шаблона подынтегральной функции. Теперь проблем с вычислением интеграла операцией Simplify не будет

Интеграл получен в форме числа е=ехр(1), помноженного на дробный множитель, представленный в рациональной форме (отношения целых чисел) Это обстоятельство, возможно, бесполезное для рядового пользователя, наверняка будет весьма положительно воспринято математиком, поскольку здесь напрашиваются определенные аналитические выводы (которых нельзя сделать при вычислении интеграла численными методами)

8.14. Разложение на правильные дроби (Convert to Partial Fraction)

Операция Convert to Partial Fraction (Разложить на элементарные дроби) возвращает символьное разложение выражения, представленное относительно заданной переменной в виде суммы правильных целых дробей. На рис 8 18 даны примеры такого разложения

Рис. 8.18 Примеры разложения на дроби

Как видно из представленных примеров, применение этой операции в большинстве случаев делает результат более длинным, чем исходное выражение Однако он более нагляден и содействует выявлению математической сущности исходного выражения

8.15. Транспонирование матрицы (Transpose)

Символьный процессор системы MathCAD обеспечивает проведение в символьном виде трех наиболее распространенных матричных операций' транспонирование и обращение матриц, а также вычисление их детерминанта.

Эти операции в подменю Matrix обозначены так: Transpose (Транспонировать), Invert (Обратить) и Determinant (Найти определитель). Если элементы матрицы — числа, то выполняются соответствующие операции в числовой форме.

Транспонирование матрицы означает перестановку строк и столбцов. Оно реализуется операцией Transpose (Транспонировать). Подлежащая транспонированию матрица должна быть выделена.

8.1 б. Обращение матриц (Invert)

Обращение матриц означает создание такой матрицы А-1, для которой произведение ее на исходную матрицу А дает единичную матрицу, т. е. матрицу с диагональными элементами, равными 1, и остальными — нулевыми. Обращение допустимо для квадратных матриц с размером NxN, где N> 1 — число строк и столбцов матрицы. Такую же размерность имеет и обращенная матрица.

Обращение матриц — широко распространенная математическая задача. Существует множество программ на разных языках программирования, решающих эту задачу с той или иной степенью успеха. Для MathCAD это рутинная задача. На рис. 8.19 приведены примеры выполнения типовых матричных операций. Последняя из них — обращение матрицы в символьной форме с помощью операции Invert.

Рис. 8.19 Примеры матричных операций в символьной форме

При выполнении матричных операций в символьной форме проблема "разбухания" результатов становится весьма серьезной. Если, к примеру, для обратной матрицы с размером 2х2 или 3х3 еще можно получить ответ, размещающийся в окне документа, то для матриц большего размера это становится невозможным. Впрочем, большинство аналитических задач очень редко оперирует такими матрицами.

8.17. Функции преобразований Фурье, Лапласа и Z-преобразований

Для выполнения широко распространенных в технических и научных приложениях преобразований Фурье (Fourie и Inverse Fourie), Лапласа (Laplace и Inverse Laplace) и Z-преобразований (Z и Inverse Z) служат соответствующие операции в подменю позиции Symbolic главного меню

Для применения этих операций следует записать исходное выражение и отметить в нем переменную, относительно которой будет производиться преобразование Тогда указанные выше операции становятся доступными и выделяются четкими надписями

Не вдаваясь в суть перечисленных достаточно известных преобразований, приведем простейшие примеры их применения, они показаны на рис 8 20 Здесь даны примеры как прямого, так и обратного (Inverse) преобразования каждого типа

Рис. 8.20 Примеры применения функций преобразования Фурье, Лапласа и Z-преобразований

Не следует полагать, что для всех случаев результаты преобразования будут в точности совпадать со справочными и что результат двойного преобразования (вначале прямого, а затем обратного) приведет к первоначальной функции Указанные преобразования довольно сложны, и грамотное применение их требует соответствующих математических познаний Не случайно в ранние версии MathCAD (например, 3 0) они не были включены в виде команд

8.18. Установка стиля эволюции символьных выражений (Evolution Style...)

Последняя позиция подменю Symbolic — Evalution Style... — служит для установки стиля эволюции выражений, над которыми выполняются символьные операции Напомним, что под эволюцией математических выражений в данном случае подразумеваеюя изменение их вида в результате символьных преобразований.

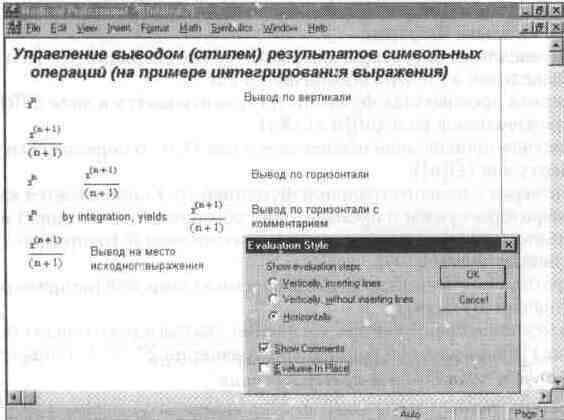
Данная операция выводит окно с установками стиля эволюции, показанное на рис. 8.21.

Рис. 8.21 Окно установки стиля эволюции

В этом окне можно установить три тина вывода результата символьных преобразований:

Vertically, inserting lines — расположение результата под основным

(Вертикально, включая линии) выражением с включением пустых линий,

Vertically, without inserting lines — расположение результата прямо под

(Вертикально, без линий) основным выражением;

Gorizontally (По горизонтали) — расположение результата рядом (по го ризонтали) с основным выражением.

Кроме того, установкой знака "птички" в прямоугольниках можно ввести еще две опции:

Show Comments — наблюдать комментарии;

(Просмотр комментариев)

Evaluate in Place (Замещать) — заместить исходное выражение резуль татом его символьного преобразования.

Все варианты стиля вывода результатов символьных операций представлены на рис. 8.21. В ряде случаев предпочтительно применение символьного оператора вывода —>, который делает символьные преобразования более наглядными.

8.19. Интерпретация результатов символьных операций в буфере обмена

Необходимо отметить, что не всегда результат символьных операций выводится в окно редактирования. Иногда он оказывается настолько громоздким, что MathCAD использует специальную компактную форму его представления и помещает его в буфер обмена. Уже оттуда его можно вызвать в текстовом формате в окно редактирования, нажав клавишу F4 или клавиши Shift+ Ins. To же самое можно сделать с помощью команды Copy (Копировать) в позиции Edit (Правка) главного меню.

Записи математических выражений в буфере обмена напоминают их записи на языке Фортран:

• справедливы операторы арифметических операций+, -,* и /;

• возведение в степень обозначается как**;

• первая производная функции f(x) записывается в виде diff(f(x),x), а п-я производная в виде diff(f(x),x$n);

• частная производная обозначается как D, п-го порядка (D,n) и по п-му аргументу как (D[n]);

• интеграл с подынтегральной функцией/^) записывается как int(f(x),x);

• операторы суммы и произведения обозначаются как sum() и product();

• композиция функций указывается символом @ [например, (exp@cos) (x) означает exp(sin(x))\,

• кратная композиция указывается символами @@ [например, (f(@@3) (x) означает f(f(f(x)))};

• замещение любого корня уравнения указывается записью RootOf (уравнение) [например, оба корня i и -г уравнения Z**2+1=0 представляются записью RootOf(Z**2+l)].

С помощью команды Save As... (Сохранить как) в позиции File папки обмена можно сохранить последнее содержимое буфера обмена в виде текстового файла. Это может быть полезным для осмысления и анализа полученного результата. В Windows 95 доступ к папке обмена обеспечивает приложение "Просмотр папки обмена", которое находится в папке "Стандартные" меню программ.

8.20. Применение преобразований Лапласа для

аналитического решения дифференциальных уравнений

Итак, если результаты символьных вычислений включают функции, не содержащиеся во входном языке системы, они помещаются в буфер обмена по запросу системы и могут быть вызваны оттуда командой Paste (Вставить). Тогда результаты имеют статус текстовых комментариев, т. е. в явном виде с ними дальнейшие действия проводить невозможно.

Однако это совсем не означает бесполезности таких результатов. Напротив, пользователь, владеющий приемами аналитических вычислений, может успешно использовать такие результаты для решения серьезных математических задач. Здесь мы остановимся на задаче получения аналитического решения для линейных дифференциальных уравнений. Сразу отметим, что системы компьютерной алгебры Mathematica 2.2.2 или Maple V R3/R4 легко решают подобные задачи встроенными средствами. Рассмотрим, как это можно сделать в системе MathCAD 6.0 PRO, таких средств не имеющей.

Для получения решения можно воспользоваться преобразованиями Лапласа. Это иллюстрирует рис. 8.22, на котором подробно показан процесс получения результата. Приходится вручную запускать прямое преобразование Лапласа, по его результатам составлять алгебраическое уравнение и после решения запускать обратное преобразование Лапласа — оно дает решение в виде временной зависимости

Рис. 8.22 Пример решения дифференциального уравнения второго порядка с применением преобразований Лапласа

На рис 8.23 приведено решение другого дифференциального уравнения Используется тот же метод решения, что и в предыдущем примере.

Оба примера наглядно показывают, что помещаемый в буфер обмена результат символьных операций может быть очень полезным и порой предоставлять возможности, которые нельзя получить прямым образом. Это расширяет области применения системы MathCAD

Рис. 8.23 Пример решения другого дифференциального уравнения