Главное меню
Вы здесь
17.1.3 Одномерный дисперсионный анализ с повторным измерением
17.1.3 Одномерный дисперсионный анализ с повторным измерением
Исследуем вопрос следующего характера: наблюдаются ли в течение четырёх моментов времени значимые изменения показаний теста на внимательность. При этом необходимо учесть влияние двух факторов: пола и возраста.
В общем, в нашем распоряжении имеется три фактора: пол с двумя категориями, возраст с тремя категориями и время с четырьмя категориями. Это приводит к необходимости выполнения трёхфакторного дисперсионного анализа, в котором третий фактор (время) является фактором с повторным измерением. Этот фактор будет представлен не при помощи отдельных групп испытуемых, а при помощи значений переменных ml-m4.
-
Откройте файл varana.sav.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)
-
Как уже было изложено в главе 13.4, отроется диалоговое окно Repeated Measures Define Factors(s) (Повторные измерения: Определение фактора(ов)).
-
Вместо установленного по умолчанию имени фактора factorl введите новое имя: zeit (время).
-
В поле Number of Levels (Количество слоев) введите значение 4. Щёлкните на Add (Добавить), и, если больше цет никаких факторов с повторными измерениями, покиньте диалоговое окно посредством нажатия кнопки Define (Определить).
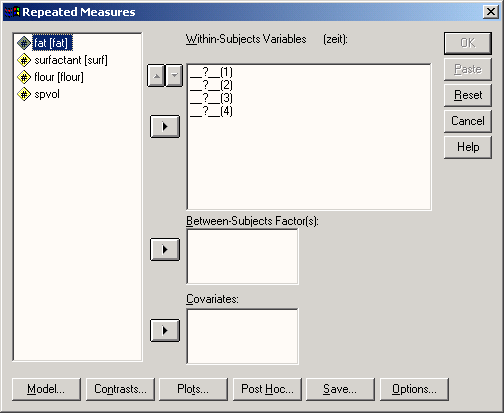
Появится диалоговое окно Repeated Measures (Повторные измерения) (см. рис. 17.7).
-
Здесь, в первую очередь, последовательно перенесите четыре переменные повторных измерений ml-m4 в поле для внутрисубъектных переменных (Within-Subjects Variables).
-
Затем, переменные geschl (пол) и alter (возраст) перенесите в поле для межсубъектных факторов (Between-Subjects Factor(s)).
-
В диалоговом окне Options (Опции) активируйте вывод средних для трёх факторов: geschl (пол), alter (возраст) и zeit (время), в поле отображаемых результатов (Display) активируйте вывод дескриптивных статистик и, помимо этого, сделайте запрос на тест однородности.
Рис. 17.7: Диалоговое окно Repeated Measures (Повторные измерения)
-
Начните расчёт нажатием ОК.
На экране появятся довольно обширные результаты расчёта. Их расшифровка может оказаться довольно проблематичной для новичка. Поэтому ниже будет рассмотрена только та часть результатов, которая является важной для поиска ответа на вопрос: какой из трёх факторов — пол, возраст или время, оказывает значимое влияние и какие взаимодействия между этими факторами являются значимыми.
Сначала даётся сводная таблица для внутрисубъектных (время) и межсубъектных (пол и возраст) факторов. Затем выводятся дескриптивные статистики (среднее значение, стандартное отклонение, количество наблюдений) для отдельных ячеек, то есть характеристики переменных ml-m4 отдельно для пола и возрастных групп. Вывод этих показателей в книге не приводится.
Далее следуют результаты расчёта для фактора "Zeit" ("Время") и для взаимодействий с этим фактором, в основу которых положен метод общей линейной модели. Для этого были определены различные тестовые величины, которые выводятся под наименованиями: "Pillai's Trace" (След Пиллая), "Wilks' Lambda" (Лямбда Уилкса), "Hotelling's Trace" (След Хоттелинга) и "Roy's Largest Root" (Максимальный характеристический корень по методу Роя). С помощью надлежащих преобразований по этим тестовым величинам восстанавливается рампределения значение F, по которому затем определяется значение р, приводимое в колонке "Значимость" (Sig). Следует отметить, что след Пиллая ("Pillai's Trace") является наиболее сильным и устойчивым (робастным) тестом.
Результаты первых трёх тестов являются практически идентичными. Обнаружено очень значимое влияние временного фактора, а вот взаимодействия других факторов со временем, напротив, оказались не значимыми.
Одни и те же расчёты, то есть проверка временного фактора и взаимодействий со временем, производятся также при помощи традиционного "классического" метода Фишера. Соответствующие результаты можно взять из строки "Предполагается сферичность" во второй из нижеследующих таблиц, которая наряду с ними содержит ещё три варианта проверок.
Multivariate Tests c (Многомерные тесты)
Effect (Эффект) | Value (Значе-ние) | F | Hypothesis df (Гипотеза df) | Error df (Ошибка df) | Sig. (Зна-чимость) | |
ZEIT (Время) | Pillai's Trace (След Лиллая) | ,955] | 133,367" | 3,000 | 19,000 | ,000 |
Wilks' Lambda (Лямбда Уилкса) | ,045 | 133,367" | 3,000 | 19,000 | ,000 | |
Hotelling's Trace (След Хоттелинга) | 21,058 | 133,367а | 3,000 | 19,000 | ,000 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | 21,058 | 133,367е | 3,000 | 19,000 | ,000 | |
ZEIT*GESCHL (Время'Пол) | Pillai's Trace (След Пиллая) | ,106 | ,752" | 3,000 | 19,000 | ,535 |
Wilks1 Lambda (Лямбда Уилкса) | ,894 | ,752а | 3,000 | 19,000 | ,535 | |
Hotelling's Trace (След Хоттелинга) | ,119 | ,752а | 3,000 | 19,000 | ,535 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,119 | ,752" | 3,000 | 19,000 | ,535 | |
ZEIT * ALTER (Время* Возраст) | Pillai's Trace (След Пиллая | ,293 | 1,145 | 6,000 | 40,000 | ,355 |
Лямбда Уилкса) | ,710 | 1,183а | 6,000 | 38,000 | ,336 | |
Hotelling's Trace (След Хоттелинга) | ,404 | 1,213 | 6,000 | 36,000 | ,322 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,394 | 2,625" | 3,000 | 20,000 | ,079 | |
ZEIT * GESCHL * ALTER (Время'Пол* Возраст) | Pillai's Trace (След Пиллая) | ,406 | 1,699 | 6,000 | 40,000 | ,146 |
Wilks1 Lambda (Лямбда Уилкса) | ,622 | 1,699а | 6,000 | 38,000 | ,148 | |
Hotelling's Trace (След Хоттелинга) | ,564 | 1,691 | 6,000 | 36,000 | ,151 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,468 | 3,118Ь | 3,000 | 20,000 | ,049 | |
a, b, с — см. след. стр. | ||||||
Tests of Within-Subjects Effects (Тест внутрисубъектных эффектов)
Measure: MEASURE_1 (Мера: MEASURE_1 )
Source Источник) | Type III Sum of Squares (Сумма квадратов III типа) | df | Чеап Square (Среднее значение квадрата) | F | Sig. (Значи-мость) | |
ZEIT Время) | Sphericity Assumed (Предполагается сферичность) | 185,661 | 3 | 61,887 | 83,028 | ,000 |
Greenhouse-Geisser (Гринхауз-"айссер) | 185,661 | 2,577 | 72,055 | 83,028 | ,000 | |
Huynh-Feldt (Гин-Фельд) | 185,661 | 3,000 | 61,887 | 83,028 | ,000 | |
Lower-bound (Нижний предел) | 185,661 | 1,000 | 185,661 | 83,028 | ,000 | |
ZEIT* GESCHL Время * Пол) | Sphericity Assumed (Предполагается сферичность) | 1,520 | 3 | ,507 | ,680 | ,568 |
Greenhouse-Geisser (Гринхауз-"айссер) | 1,520 | 2,577 | ,590 | ,680 | ,547 | |
Huynh-Feldt (Гин-Фельд1 | 1,520 | 3,000 | ,507 | ,680 | ,568 | |
.ower-bound (Нижний предел) | 1,520 | 1,000 | 1,520 | ,680 | ,419 | |
ZEIT* ALTER (Время * Возраст) | Sphericity Assumed ^Предполагается сферичность) | 4,190 | 6 | ,698 | ,937 | ,475 |
Greenhouse-Geisser (Гринхауз-Гайссер) | 4,190 | 5,153 | ,813 | ,937 | ,467 | |
Huynh-Feldt (Гин-Фельд) | 4,190 | 6,000 | ,698 | ,937 | ,475 | |
Lower-bound (Нижний предел) | 4,190 | 2,000 | 2,095 | ,937 | ,408 | |
ZEIT* GESCHL* ALTER Время * Пол* Зозраст) | Sphericity Assumed (Предполагается сферичность) | 6,557 | 6 | 1,093 | 1,466 | ,204 |
Greenhouse-Geisser (Гринхауз-Гайссер^ | 6,557 | 5,153 | 1,272 | 1,466 | ,215 | |
Huynh-Feldt (Гин-Фельд) | 6,557 | 6,000 | 1,093 | 1,466 | ,204 | |
Lower-bound (Нижний предел) | 6,557 | 2.00C | 3,278 | 1,466 | ,254 | |
Error (ZEIT) (Ошибка (Время)) | Sphericity Assumed (Предполагается сферичность) | 46,958 | 63 | ,745 |
|
|
Greenhouse-Geisser (Гринхауз-Гайссер) | 46,958 | 54,110 | ,868 |
|
| |
Huynh-Feldt (Гин-Фельд) | 46,95f | 63,000 | ,745 |
|
| |
Lower-bound (Нижний предел) | 46,958 | 21.00C | 2,236 |
|
| |
a Exact statistic (Точная статистика)
b The statistic is an upper bound on F that yields a lower bound on the significance level (Статистической характеристикой является верхний придел значения Е-распределе-ния, который указывает на нижний предел уровня значимости).
c Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол * Возраст )
Within Subjects Design: ZEIT (Компоновка внутри субъектов: Время)
Полученные результаты близки к результатам расчётов по общей линейной модели. Тест Левене на равенство дисперсий демонстрирует однородность дисперсии для моментов времени со второго по четвёртый и неоднородность дисперсии (р = 0,009) для первого момента (см. гл. 17.1.1).
Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)
F | df1 | df2 | Sig. (Значимость) | |
М1 | 4,177 | 5 | 21 | ,009 |
М2 | ,878 | 5 | 21 | ,513 |
МЗ | 1,751 | 5 | 21 | ,167 |
М4 | 2,022 | 5 | 21 | ,117 |
Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяется нулевая гипотеза о том, что дисперсия ошибки независимых переменных остаётся постоянной для всех групп). a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол * Возраст ) Within Subjects Design: ZEIT (Компоновка внутри субъектов: Время)
Далее идут расчёты для обоих факторов (пол и возраст), для которых не производятся повторные измерения, а также для их взаимодействия.
Tests of Between-Subjects Effects (Тест межсубъектных эффектов)
Measure: MEASURE_1 (Мера: MEASURE_1)
Transformed Variable: Average (Трансформированная переменная: Среднее значение)
Source (Источник) | Type III Sum of Squares (Сумма квадратов III типа) | Df | Mean Square (Среднее значение квадрата) | F | Sig. (Значимость) |
Intercept (Отрезок) | 25080,367 | 1 | 25080,367 | 2029,299 | ,000 |
GESCHL (Пол) | ,738 | 1 | ,738 | ,060 | ,809 |
ALTER (Возраст) | 667,147 | 2 | 333,573 | 26,990 | ,000 |
GESCHL * ALTER (Пол * Возраст) | 33,571 | 2 | 16,785 | 1,358 | ,279 |
Error (Ошибка) | 259,542 | 21 | 12,359 |
Получается незначимое влияние пола (р = 0,809), очень значимое влияние возраста (р < 0,001) и незначимое взаимодействие (р = 0,279). Под заголовком "Оцененные пределы средних" (Estimated Marginal Means) выводится информация о средних значениях и стандартных отклонениях для отдельных слоев факторов:
1. GESCHL (Пол)
| Measure: MEASURE_1 (Мера: MEASURE_1) | ||||
GESCHL (Пол) | Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
maennlich (Мужской) | 15,700 | ,460 | 14,743 | 16,657 |
weiblich (Женский) | 15,531 | ,519 | 14,452 | 16,609 |
2. ALTER (Возраст)
| Measure: MEASURE 1 (Мера: MEASURE 1) | ||||
ALTER (Возраст) | Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
bis 30 Jahre (До 30 лет) | 17,646 | ,671 | 16,250 | 19,042 |
31 - 50 Jahre (31 - 50 nejr) | 16,988 | ,590 | 15,761 | 18,214 |
ueber 50 Jahre (Свыше 50 лет) | 12,213 | ,532 | 11,106 | 13,319 |
3. ZEIT (Время)
| Measure: MEASURE_1 (Мера: MEASURE_1) | ||||
ZEIT (Время) | Mean (Среднее значение | Std. Error (Стандартная ошибка; | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
1 | 13,828 | ,307 | 13,190 | 14,466 |
2 | 14,964 | ,405 | 14,121 | 15,807 |
3 | 16,275 | ,386 | 15,472 | 17,078 |
4 | 17,394 | ,400 | 16,562 | 18,227 |
Для факторов, для которых не производятся повторные измерения (межсубъектные эффекты), можно вновь провести дополнительные тесты (Post Hoc), но, к сожалению, их нельзя применить для факторов, для которых производятся повторные измерения.