Урок 4. Операции математического анализа
Урок 4. Операции математического анализа
1. Операции математического анализа
Операции математического анализа
- Вычисление сумм
- Вычисление произведений
- Вычисление производных
- Вычисление интегралов
- Вычисление пределов функций
- Решение уравнений и систем уравнений
- Решение дифференциальных уравнений
- Поиск максимального и минимального чисел в списке
- Поиск максимума и минимума функции
- Решение задач линейного программирования
- Преобразования Лапласа
- Z-преобразования
В этом уроке описаны основные операции математического анализа, детали которых можно найти в любом справочнике по высшей математике. Эти операции чаще всего используются при проведении математических и научно-технических расчетов и потому описаны достаточно полно
2. Вычисление сумм
Вычисление сумм
Вычисление сумм в аналитическом виде
В числе операций математического анализа прежде всего надо отметить суммы
Сумма от i=min до imax по fi
В этих операциях индекс i принимает целочисленные значения от минимального (начального) imin до максимального (конечного) imax с шагом, равным +1.
Суммы и произведения легко вычисляются численными математическими системами, такие вычисления просто описываются на всех языках программирования. Однако важным достоинством систем символьной математики, включая Ма-thematica, является вычисление сумм и произведений в аналитическом виде (если это возможно) и при большом числе членов — вплоть до стремящегося к бесконечности.
Для вычисления сумм в системе Mathematica предусмотрена функция Sum, используемая в ряде форм:
- Sum [ f, {i, imax} ] — вычисляет сумму значений f при изменении индекса i от 1 до imax с шагом +1;
- Sum[f, {i, imin, imax}]—вычисляет сумму значений f при изменении индекса i от минимального значения i=imin до максимального i=imax с шагом +1;
- Sum[f, {i, imin, imax, di}]— вычисляет сумму значений f при изменении управляющей переменной вещественного типа от минимального значения i=imin до максимального i=imax с шагом di;
- Sum[f, {i, imin, imax}, {j, jmin, jmax},...] — вычисляет многократную сумму значений f при изменении индексов i от imin до imax с шагом +1, j от jmin до jmax с шагом +1 и т. д. (число индексов не ограничено).
Таким образом, эта функция обеспечивает расширенные возможности вычисления сумм — как при целочисленных, так и при вещественных значениях управляющих переменных, задающих циклы вычислений. Примеры использования функций суммирования:
Sum[i^2,{i,10}]
385
Sum[i*2,{i,l,10}]
385
Sum[i^2, {1,1,2,0.25}]
11.875
Sum[i*j, {i,1,10},{j, 2, 5}]
770
В последнем примере использована стандартная форма вывода — при ней функция суммирования представляется в виде оператора суммирования.
Обычно в математических системах недопустима перестановка imin и imax, хотя в математике известно школьное правило — от перестановки слагаемых сумма не изменяется. Рискнем проверить это:
Sum[i,{i, 1,100}]
5050
Sum[i, {1,100,1}]
0
Sum[i, {1,100, 1,-1}]
5050
Второй пример тут дал явно ошибочный результат, хотя третий с честью оправдал указанное правило.
Не применяйте установки параметров, противоречащие синтаксису записи той или иной функции — в частности, Sum. Это чревато возникновением серьезных ошибок.
Приведем еще ряд примеров выполнения операции суммирования:
Sum[ xn/n! , {n, 0, 8}]
1+X+X2/2 X3/6 X4/24 X5/120 X6/720 X7/5040 X8/40320
Sum[xn/n! , {n, 1, 9, 2}]
X+X3/3 X5/120 X7/5040 X9/362880
Sum[xi yi , {i, 1, 4},{j, 1, i}]
xy+ x2 у + x3 у + x4 у + x2:/2 + x3 у2 + x4y2 + x3 у3 + x4 у3 + x4y4
Sum[1/n*n , {n, 1, бесконечность}]
л2/6
Sum[i4 {i, 1, n}]
1/30n(1-n)(1+2n) (-l + 3n+3n2)
1/3(3 - 3 EulerGamma + 2 n + n3) - PolyGamma[0, 2 + n]
Из этих примеров видно, что Mathematica 3/4 обеспечивает возможность символьного вычисления сумм, в том числе с бесконечным пределом суммирования. Вычисляются даже суммы, выраженные через специальные математические функции (см. последний пример). При этом для вычисления сумм в символьном виде, в отличие от предшествующих версий Mathematica, уже не требуется загрузка специального пакета для расширенных (символьных) операций с суммами.
Вычисление сумм в численном виде
Для вычисления сумм в численном виде используются следующие функции:
- NSum[f, {i, imin, imax }]— возвращает численное значение суммы f [ i ] при i, изменяющемся от imin до imax с шагом +1;
- NSumff, {i, imin, imax, di }]— возвращает сумму численных значений функции f [i] при i, изменяющемся от imin до imax с шагом di;
- NSum[f, {i, imin, imax}, {j, jmin, j max },...]— выполняет многомерное суммирование. Функция NSum[... ] эквивалентна выражению N[Sum[...] ].
Особенностью этой функции является возможность использования ряда опций, управляющих вычислительным процессом. Одной из них является NSumTerms, задающая число членов, которые явно должны быть включены в сумму перед экстраполяцией. Вы можете просмотреть список опций, используя команду Options [NSum] .
Пример применения функции NSum представлен ниже:
NSum[1/i3, {i, 1, бесконечность}]
1.20206
Пример точного вычисления суммы (для сравнения) с помощью функции Sum:
truesum = Sum [1+k/ 2k k/ 3k{k, 1, 50}
1818632874295681087853745424762603034467 / 808281277464764060643139600456536293376
N[%]
2.25
Пример вычисления той же суммы с помощью функции NSum с опциями:
NSum [ 1+k/ 2 k -3k, {k, 1, 50}, Method -> SequenceLimit,
NSumTerms -> 2 , NSumExtraTerms -> 4 ] - truesum
0.0530365
При следующем наборе опций результат еще лучше:
NSum [ 1+k/ 2 k -3k, {k, 1, 50}, Method -> SequenceLimit, WorkingPrecision -> 30 , NSumTerms -> 2 ,
NSumExtraTerms -> 10, WynnDegree -> 4] - truesum
0.x10-26
Функция вычисления суммы NSum выполняется заметно быстрее, чем функция Sum, хотя на практике заметить это трудно — все приведенные выше примеры выполняются за доли секунды. Возвращаемый функцией NSum результат вещественный.
3. Вычисление произведений
Вычисление произведений
Вычисление произведений в аналитическом виде
Операции вычисления произведений
Произведение от i=imin до i=imax по fi представлены следующими функциями:
- Product [f, {i, imax}] — возвращает произведения значений f [i] для значений i, изменяющихся от 1 до imax;
- Product [f, {i, imin, imax}]—возвращает произведение значений f [ i ] при изменении i от imin до imax с шагом +1;
- Product[f, {i, imin, imax, di}] — возвращает произведение f [ i ] при i, меняющемся от значения imin до значения imax с шагом di;
- Product [f, {i, imin, imax}, {j, jmin, jmax},...] — вычисляет многократное произведение (произведение по нескольким переменным).
Примеры использования функций вычисления произведения.
| Ввод (In) | Вывод (Out) |
| Product [i,{i ,10}] | 3628800 |
| NProduct [k ^ 2,{k, 1,5}] | 14400. |
| NProduct[i ^ 2, {1,1,2,0. 2}] | 93.6405 |
| Product [Logfi], {±,2,5,0.5}] | 4.23201 Log[2] |
Следующий пример иллюстрирует вычисление произведения в символьном виде:
Произведение (x+i2) , где i=1...5
(1+х) (4 + х) (9 + х) (16 + х) (25 + х)
Об опасности перестановки сомножителей свидетельствуют следующие примеры: Product [i, i,l, 10] 3628800
Product [i,i, 10,1]
1
Product[i,i,10,l,-l]
3628800
Как и в случае вычисления суммы, средний пример явно ошибочен. Он просто недопустим с точки зрения синтаксиса данной функции.
Вычисление произведений в численном виде
Для вычисления численных значений произведения используются следующие функции:
- NProduct [f , {i, imax }]— возвращает численное значение произведения значений f [i] для значений i, изменяющихся от 1 до imax;
- NProduct [f, {i, imin, imax}] — возвращает численное значение произведения значений f [i] при изменении i от imin до imax с шагом +1;
- NProduct [f, {i, imin, imax, di }]— возвращает численное значение произведения значений f [i] при i, меняющемся от значения imin до значения imax с шагом di;
- NProduct[f, {i, imin, imax}, {j, jmin, j max },...]— вычисляет численное значение многократного произведения (произведение по нескольким переменным).
Эти функции применяются с теми же опциями, которые используются для функции Nsum, что позволяет управлять вычислительным процессом. Ознакомиться с опциями можно, выполнив команду Options [NProduct] . Ниже представлен пример на использование функции Nproduct. Сначала вычисляем точное значение произведения для использования в качестве эталона:
trueproduct = Product [ j/(1+j), { j , 1 , 50 } ]
1/ 51
Пример вычисления того же произведения с помощью функции NProduct — погрешность велика:
NProduct [ j/(1+j) , {j, I, 50},
Method -> SequenceLimit, NProductFactors -> 2 ,
NProductExtraFactors -> 4] - trueproduct
0.188235
В следующем примере опции подобраны лучше — погрешность мала:
NProduct[j/(1+j) , {j, 1, 50},
Method-» SequenceLimit, NProductFactors -> 50,
NProductExtraFactors ->4] - trueproduct
-1.38778 x 10-17
Применение функции NProduct оправдано высокой скоростью производимых ею вычислений. Однако, как показывают приведенные примеры, к такому применению надо относиться с осторожностью из-за возможности возникновения больших вычислительных погрешностей.
4. Вычисление производных
Вычисление производных
К числу наиболее часто используемых математических операций принадлежит вычисление производных функций как в аналитической, так и в символьной форме. Для этого используются следующие функции:
- D [ f, х ] — возвращает частную производную функции f по переменной х;
- D [f, {х, n}]— возвращает частную производную n-го порядка по х;
- D[f, xl, х2,...] — возвращает смешанную производную;
- Dt[f, х] — возвращает обобщенную производную функции f по переменной х;
- Dt [ f ] — возвращает полный дифференциал f.
Название функции из одной буквы — это явно исключение из правил. Оно выбрано осознанно, в силу массовости этой операции.
Для функции D существует опция NonConstants, которая позволяет задать список объектов, находящихся в неявной зависимости от переменных дифференцирования. По умолчанию этот список пустой. Для функции Dt имеется опция Constants, которая, наоборот, указывает символы, которые являются константами (по умолчанию их список также пуст). На практике применять данные опции приходится редко.
Существует еще одна функция, Derivative [nl, n2,...] [f ], — основная (общая) форма представления функции, полученной в результате nl-кратного дифференцирования функции f по первому аргументу, п2-кратного — по второму аргументу и т. д.
К примеру, Derivative [2] [х*у] возвращает (ху)", a Derivative [2, 3] [х*у] — соответственно, (ху) (2.3)
Следующие примеры показывают применение функции D для вычисления производной в аналитическом виде:
- Производная тригонометрической функции:
D[x*Sin[x],x]
xCos[x] + Sin[x]
- Производная экспоненциальной функции:
D[Exp[x/b],x]
ex/b/b
- Производная логарифмической функции:
D[Log[3*x/4],x]
1/x
- Производная степенного многочлена:
D[а*х^2+b*х+с,х]
b+ 2ах
- Пятая производная от х n :
D[х^n,{х,5}]
(-4 + n) (-3+n) (-2+n) (-1+n)nх -5+n
- Производная функции двух переменных:
D[(x^m)*y^n,x,y]
mnx -1+m y -1+n
- Производная функции Бесселя:
D[BesselJ[2,x] ,x]
1/2 (BesselJ[l, х] -BesselJ[3, x] )
- Производная ортогонального полинома Чебышева:
D[ChebyshevT[4,x],x]
-16x + 32x3
Следующие примеры иллюстрируют вычисление производных от первого до третьего порядка включительно для функции f [ х ], заданной пользователем.
| Ввод (In) | Вывод (Out) |
| f[x] :=х/(1+х ^ 2) | |
| D[f[x],{x,l}] | -2x 2 /(1+x 2 ) 2 +1/(1+x 2 ) |
| D[%,x] | -8x 3 /(1+x 2 ) 3 +6x/(1+x 2 ) 2 |
| D[f[x],{x,2}] | -8x 3 /(1+x 2 ) 3 +6x/(1+x 2 ) 2 |
| D[D[D[f[x],x],x],x] | -48x 4 /(1+x 2 ) 4 +48x 2 /(1+x 2 ) 3-6/(1+x 2 ) 2 |
| D[f[x],{x,3}] | -48x 4 /(1+x 2 ) 4 +48x 2 /(1+x 2 ) 3-6/(1+x 2 ) 2 |
Из предпоследнего примера видно, что для вычисления высших производных возможно последовательное применение функции D.
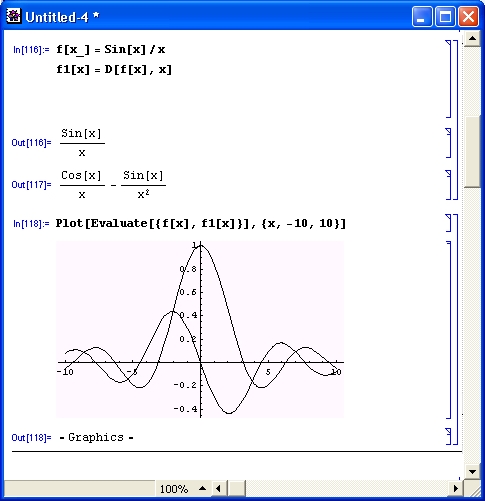
На рис. 4.1 показано построение графика функции Sin [x] /х, заданной как функция пользователя, и ее производной с помощью функции Plot.
Рис. 4.1. График функции Sin[x]/x и ее производной
В целом средства для символьного вычисления производных, имеющиеся в ядре системы Mathematica, охватывают практически все важные типы математических выражений. Они могут включать в себя как элементарные, так и специальные математические функции, что выгодно отличает систему Mathematica от некоторых простых систем символьной математики, таких как Derive.
Использование функции Dt демонстрируют примеры, приведенные ниже.
| Ввод (In) | Вывод (Out) |
| Dt[x*n,x] | x n (n/x +Dt[n, x] Log[x] ) |
| Dt[x*Sin[x] ,x] | xCos[x] + Sin[x] |
| Dt[Exp[x/b],x] | e x/b /b(1/b-xDt[b, x]/b 2 ) |
| Dt[a*x ^ 2+b*x+c,x] | b+ 2 ax + x 2 Dt[a, x] + xDt[b, x] + Dt[c, x] |
| Dt[x*n,{x,2}] | x n (n/x+Dt[n, x] Log[x] ) + x n (-n/x 2 2Dt[n, x] +Dt[n, {x/2}]Log[x]) |
| Dt[Log[3*x/4],x] | 1/x |
| Dt[BesselJ[2,x] ,x] | 1/2(BesselJ[l, x] -BesselJ[3, x] ) |
| Dt[ChebyshevT[4,x] ,x] | -16x + 32x 3 |
Обратите внимание на то, что порой результаты для одного и того же дифференцируемого выражения у функций D и Dt заметно различаются. Это вполне закономерно вытекает из различных определений данных функций.
gl4-1.jpg
5. Вычисление интегралов
Вычисление интегралов
Вычисление интегралов в символьном виде
Одна из важнейших операций — вычисление первообразных и определенных интегралов в символьном виде. Первообразная — это функция F(x), удовлетворяющая уравнению
f(x)dx = F(x) + C,
где С — постоянная интегрирования. А вычисление определенного интеграла с пределами — верхним b и нижним а — производится по формуле
f(X)dX = F(b)-F(a)
Заметим, что определенный интеграл может быть представлен как аналитическим, так « численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов — от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).
Для интегрирования в системе Mathematica используются следующие функции:
- Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х;
- Integrate [f, {x, xmin, xmax}] — возвращает значение определенного интеграла с пределами от x min до x max ;
- Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},...] —возвращает значение кратного интеграла с пределами от x min до x max по переменной х, от y min до y max по переменной у и т. д. (кратность реально не ограничена).
Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции:
Options[Integrate]
{Assumptions -> {}, GenerateConditions->Automatic,
PrincipalValue > False)
Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком «минус». Пределы могут задаваться как константами, так и функциями.
Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде. Это иллюстрируют примеры на вычисление неопределенных интегралов с алгебраическими подынтегральными функциями, представленные на рис. 4.2.
Здесь входная ячейка в первом примере представлена в формате ввода (Input-Form), а в остальных примерах — в стандартном формате (StandardForm). При записи интегралов последний предпочтителен ввиду большей наглядности, поскольку при этом знаки интеграла имеют естественный математический вид. Обратите внимание на проверку операции интегрирования с помощью дифференцирования в двух последних примерах.
На рис. 4.3 показано еще несколько примеров вычисления неопределенных интегралов. Нетрудно заметить, что интегралы от ряда алгебраических функций дают выражения с тригонометрическими функциями.
Другая группа примеров, представленная на рис. 4.4, показывает нахождение интегралов с тригонометрическими и гиперболическими подынтегральными функциями.
Последний пример показывает, что возможно вычисление списка определенных интегралов, если подынтегральные функции представлены также в виде списка.
Рис. 4.2. Примеры вычисления неопределенных интегралов (начало)
Рис. 4.3. Примеры вычисления неопределенных интегралов (продолжение)
Рис. 4.4. Примеры вычисления неопределенных интегралов (окончание)
Вычисление определенных интегралов
Следующая серия примеров (рис. 4.5) иллюстрирует вычисление определенных интегралов в символьном виде.
Рис. 4.5. Примеры вычисления определенных интегралов обычного вида
Приведенные на рис. 4.6 примеры показывают вычисление определенных интегралов с пределами-функциями.
Рис. 4.6. Примеры вычисления определенных интегралов с пределами-функциями
Системы Mathematica имеют самые обширные возможности вычисления интегралов. Ядро системы вобрало в себя формулы интегрирования из всех известных справочников и даже древних рукописей.
Mathematica способна вычислять даже кратные интегралы с фиксированными и переменными верхним или нижним пределами. Кратный, например двойной, интеграл с фиксированными пределами имеет вид:
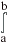
f(x,y)dxdy
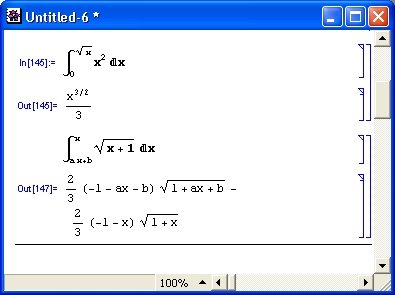
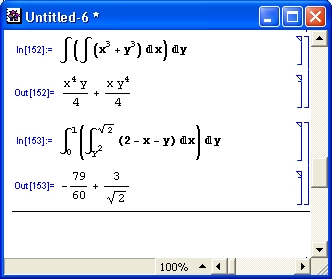
На рис. 4.7 представлено вычисление нескольких двойных определенных интегралов.
Рис. 4.7. Примеры вычисления двойных определенных интегралов
Следующий пример при двух форматах ввода показывает вычисление двойного неопределенного интеграла двойным применением функции Integrate:
Integrate!Integrate[x^3+y^3,x],y]
x4y/4+y4x/4
(
(x3 + y3) dx) dy
x4y/4+y4x/4
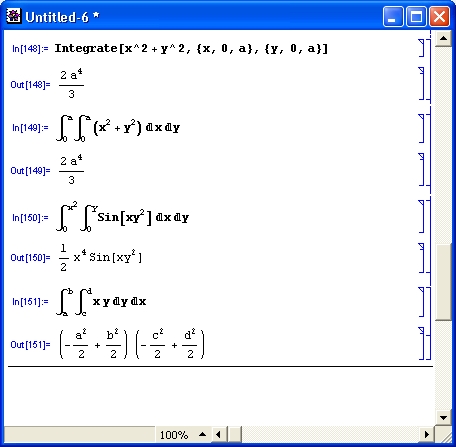
Другая серия примеров (рис. 4.8) показывает, как вычисляются двойные и тройные интегралы, пределы которых сами по себе являются функциями.
Рис. 4.8. Примеры вычисления кратных интегралов с пределами-функциями
Хотя вычисление двойного интеграла предусмотрено в синтаксисе функции Integrate, это не всегда дает результат. Как правило, вычисление кратных интегралов лучше производить, используя последовательное вычисление однократных интегралов, вложенных друг в друга. Это и показывают приведенные примеры.
Особые случаи вычисления интегралов
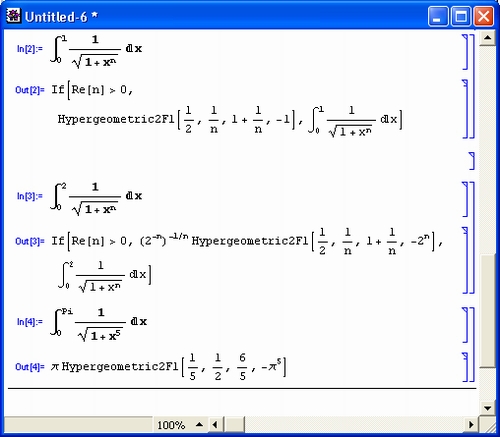
При вычислении сложных интегралов, например не имеющих представления через элементарные функции, система Mathematica 2 обращалась к своим пакетам расширений в попытке найти решение, которое может быть представлено через специальные математические функции. Mathematica 3/4 уже не акцентирует внимание пользователя на своих проблемах и, как правило, выдает результат интегрирования. Однако порой он может иметь довольно необычный вид (рис. 4.9).
Эти примеры наглядно показывают, что вычисление первообразных в системе может дать результаты, далекие от тривиального вычисления неопределенных интегралов, имеющихся в обычных справочниках по математике. Кстати, и при вычислении тривиальных интегралов результат может оказаться иным, чем в справочниках, из-за различных преобразований, примененных для получения конечных формул. Подчас могут потребоваться определенные усилия для получения результата в заданной форме. Как подынтегральное выражение, так и результаты вычислений могут содержать как элементарные, так и специальные математические функции.
Рис. 4.9. Примеры вычисления особых интегралов
В заключение надо отметить, что результаты символьного интегрирования в системах Mathematica 3 и Mathematica 4 нередко различаются. Более того, они могут различаться и в пределах одной версии Mathematica, так как ядро системы постоянно совершенствуется. Обычно более поздние версии дают более точные результаты вычислений особых интегралов, хотя подчас они и выглядят более сложными и даже необычными. Это говорит о необходимости вдумчиво относиться к получаемым результатам.
Для вычисления численных значений определенных интегралов используется функция NIntegrate [f, {x, xmin, xmax}], которая возвращает численное приближение интеграла от функции f по переменной х в пределах от x min до x max .
Она имеет ряд опций, которые можно получить, исполнив команду Options [Nlnteg-rate]. Описание этих опций дано в приложении. Приведем примеры численного интегрирования.
| Ввод (In) | Вывод (Out) |
| NIntegrate [Bessel J [l,x] ^ 3,{x,0,l}] | 0.0243409 |
| N[Sqrt [Pi] *Gamma [1/6] / (6*Gamma [2/3] ) ] | 1.21433 |
| NIntegrate [1/Sqrt [1-х^6] , {х , 0 , 1 } ] | 1.21433 |
| NIntegrate [E ^ -x*Cos [х] , {х, 0 , Infinity} ] | 0.5 |
| NIntegrate [х*у, {х,0,1} , {у,х,х ^ 2} , {z,x*y,x ^ 2*y ^ 3}] | 0.010582 |
| NIntegrate [l/(x*y) , {х,4,4 .4} , {у, 2, 2. 6}] | 0.025006 |
| NIntegrate [Sqrt[2*x+l] ,{x,0,l}] | 1.39872 |
Эти примеры показывают, что функция NIntegrate с успехом может применяться для вычисления как однократных, так и многократных определенных интегралов, в том числе с переменными пределами.
gl4-2.jpg

gl4-3.jpg

gl4-4.jpg

gl4-5.jpg

gl4-6.jpg
gl4-7.jpg
gl4-8.jpg
gl4-9.jpg
6. Вычисление пределов функций
Вычисление пределов функций
Многие функции при приближении аргумента к некоторому значению или к некоторой области значений стремятся к определенному пределу. Так, функция sin(x)/x при х, стремящемся к нулю (обозначим это как х—> 0), дает предел 1 в виде устранимой неопределенности 0/0.
Численные математические системы, равно как и большинство программ на обычных языках программирования, не воспринимают выражение 0/0 —> 1 как объективную реальность. Их защитный механизм настроен на примитивное правило — ничего нельзя делить на 0. Следовательно, вычисление sin(x)/x при х = 0 будет сопровождаться выдачей ошибки типа «Деление на 0». Конечно, в данном конкретном случае можно предусмотреть особый результат — выдать 1 при х = 0. Но это частный случай. В целом же подобные системы «не понимают» понятия предела.
Пределом некоторых функций может быть бесконечность, тогда как многие функции стремятся к конечному пределу при аргументе х, стремящемся к бесконечности. Система Mathematica не только численно находит пределы функций, заданных аналитически, но и позволяет найти предел в виде математического выражения.
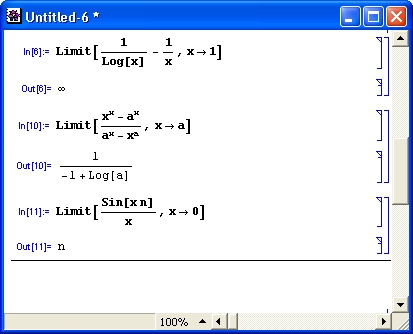
На рис. 4.10 представлены примеры применения функции Limit. Они показывают, что возможно вычисление пределов функций, устремляющихся к бесконечности, и вычисление пределов при переменной х, стремящейся в бесконечность. Вычисление пределов функций в аналитическом виде — важное достоинство систем символьной математики.
Рис. 4.10. Примеры вычисления пределов
При работе с функцией Limit используются следующие опции:
- Analytic — указывает, следует ли неопознанные функции интерпретировать как аналитические (значение по умолчанию — Automatic);
- Direction — указывает направление, в котором происходит приближение к пределу. Опция используется в виде Direction -> -1 (или +1), по умолчанию выбор остается за системой (Automatic). Значение +1 означает предел слева, а -1 — справа (казалось бы, должно быть наоборот, но задано именно так).
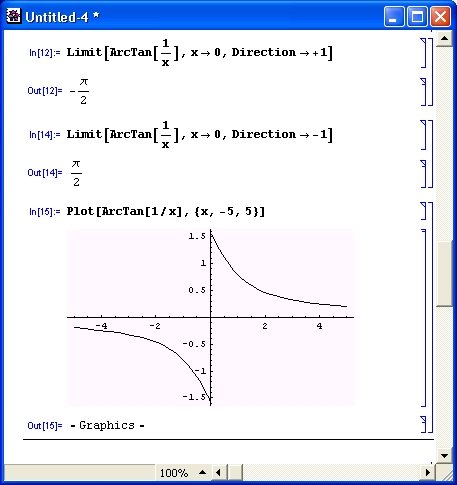
Применение данных опций поясняют примеры, показанные на рис. 4.11.
Рис. 4.11. Примеры вычисления пределов с применением опций
gl4-10.jpg
gl4-11.jpg
7. Уравнения и системы уравнений
Уравнения и системы уравнений
Многие математические задачи сводятся к решению в общем случае нелинейных уравнений вида f(x) = 0 или f(x) = expr.
В системе Mathematica они обозначаются как eqns (от слова equations — уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений.
Для решения уравнений (как одиночных, так и систем) в численном и символьном виде Mathematica имеет функцию Solve:
- Solve [eqns, vars] — предпринимает попытку решить уравнение или систему уравнений eqns относительно переменных vars;
- Solve [eqns, vars, elims] — пытается решать уравнения eqns по переменным vars, исключая переменные elims.
Входные параметры этой функции могут быть представлены списками или записаны выражениями через объединительный знак«&&». В eqns в качестве знака равенства используется знак «= =». Примеры применения функции Solve представлены на рис. 4.12.
Рис. 4.12. Примеры решения уравнений
Обратите внимание на то, что в определенных ситуациях система подсказывает тонкости решения, выдавая предупреждающие сообщения. Если такие ситуации не являются ошибками, препятствующими решению, то полученное решение выводится в ячейку вывода.
Решение систем нелинейных уравнений в символьном виде
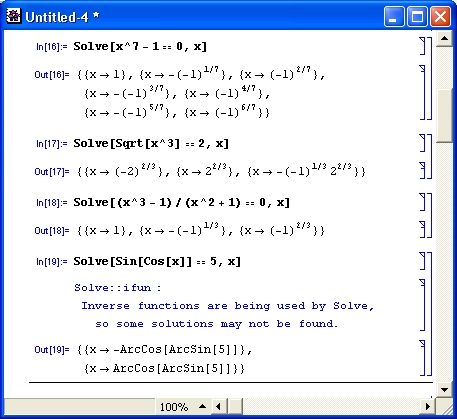
Приведенные на рис. 4.13 примеры показывают решение систем нелинейных уравнений с помощью функции Solve.
Достаточно характерен пример с применением функции N. Если убрать в нем функцию N, то будет получен чрезвычайно громоздкий, хотя и точный результат (проверьте это сами, поскольку размеры результата делают нецелесообразным его приведение в книге). Функция N осуществляет выполнение всех промежуточных вычислений, благодаря чему результат получается вполне обозримым и представленным в комплексных числах.
В последнем примере рис. 4.13 получен набор из пяти пар корней, определенных через функцию Root. Эта функция, в свою очередь, означает вычисление корней полиномиального уравнения пятой степени. Данный пример, как и ранее приводимые решения кубического уравнения, является наглядной иллюстрацией того, что простота нелинейных уравнений порой оказывается весьма обманчивой, а их решение порой приводит к весьма громоздким и сложным результатам. Тем не менее, возможность решения отдельных нелинейных уравнений и их систем в символьном виде трудно переоценить. К сожалению, далеко не все уравнения имеют такие решения — многие можно решать только в численном виде.
Рис. 4.13. Примеры решения систем нелинейных уравнений
Не следует полагать, что Mathematica всегда выдает верное решение систем нелинейных уравнений. На самом деле решение иногда бывает ошибочным. Поэтому в большинстве случаев стоит оформлять решение таким образом, чтобы обеспечить его проверку. Для этого рекомендуется отдельно задать систему уравнений и результат решения. Тогда проверка легко осуществляется с помощью подстановки. Два примера решения систем уравнений с проверкой решений показаны на рис. 4.14.
В первом примере решение кажется очевидным (равенства выполняются, например, при х=2 и у=3). Однако здесь Mathematica дает сразу три пары решений, и все они оказываются верны, поскольку после подстановки проверка всех равенств возвращает True.
А вот во втором примере проверка дала не совсем обычный результат, что связано с наличием в решении неопределенной переменной а. В таких случаях стоит попробовать упростить решение с помощью функции Simplify, что и показано на рис. 4.14.
Рис. 4.14. Примеры решения уравнений с проверкой
С функцией Solve можно использовать ряд опций. Их можно вывести командой Options [Solve]. Ниже описано их назначение:
- InverseFunctions — указывает, следует ли использовать обратные функции;
- MakeRules — указывает, должен ли результат быть представлен как объект AlgebraicRulesData;
- Method — устанавливает алгоритм, используемый для вычисления результата (возможны методы 1, 2 и 3);
- Mode — задает характер решения уравнения (возможны Generic, Modular и Rational);
- Sort — устанавливает, нужна ли сортировка результатов;
- Verif ySolutions — устанавливает, следует ли проводить проверку полученных решений и удаление посторонних решений;
- WorkingPrecision — устанавливает число цифр промежуточных вычислений (по умолчанию Infinity).
На рис. 4.15 приведены примеры применения функции Solve с опцией Inverse-Functions.
Обратите внимание на то, что последняя система уравнений при отсутствии опции InverseFunctions решается с предупреждением. Она вообще не решается, если эта опция задана как False, и гладко решается при InverseFunctions -> True.
Рис. 4.15. Примеры решения уравнений с опцией InverseFunction
То, насколько может влиять на решение опция Method, наглядно показывают примеры, представленные на рис. 4.16.
Рис. 4.16. Примеры решения уравнений разными методами
Множество примеров решения систем нелинейных уравнений в символьном виде можно найти в справочной системе Mathematica.
Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако их решение вполне возможно численными методами. Для численного решения систем нелинейных уравнений используется функция NSolve:
- NSolve [eqns, vars] — пытается численно решить одно уравнение или систему уравнений eqns относительно переменных vars;
- NSolve [eqns, vars, elims] — пытается численно решить уравнения eqns относительно vars, исключая переменные elims.
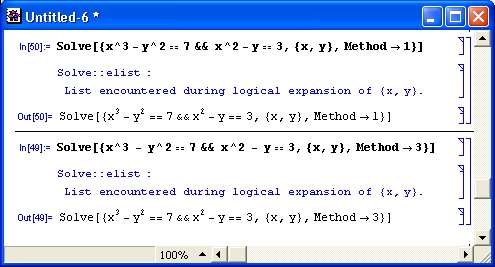
С этой функцией используется единственная опция WorkingPrecision, задающая число верных цифр результата — по умолчанию 16. На рис. 4.17 представлены примеры использования функции NSolve для численного решения уравнений.
Риc. 4.17. Примеры численного решения уравнений
Результаты решения с помощью функции NSolve также рекомендуется проверять с помощью подстановки, например, так:
е=2*х^2 + 5*х- 15 == х^3
-15 + 5х + 2х2 ==х3
r=NSolve[e,x]
{{х->-2.4734}, {х->2.2367-1.03038i},
{х->2.2367 + 1.03038i}}
е/.r
{True, True, True}
Нетрудно заметить, что в данном случае решение верно.
Для вычисления корней полиномиальных уравнений используется функция Roots:
Roots[lhs==rhs, var]
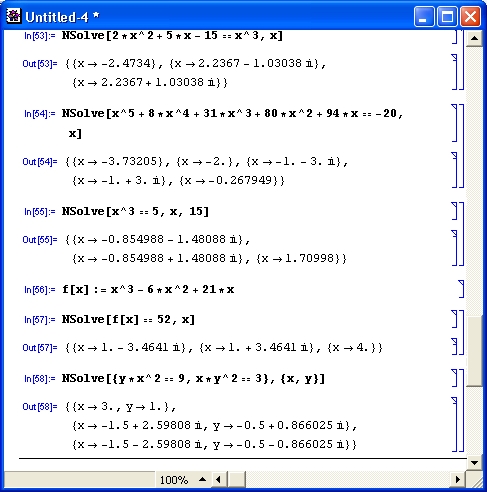
На рис. 4.18 представлены примеры применения функции Roots.
Рис. 4.18. Примеры использования функции Roots
Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:
e = x^2+3x==2
Зх + х2 == 2
N[Roots[e, x]]
х == -3.56155 | | х == 0.561553
r= {ToRules[%]}
{{х^-3.56155}, {х^ 0.561553}}
е/. r
{True, True}
Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.
При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:
Options[Roots]
{Cubics -> True, Eliminate -> False, EquatedTo-> Null,
Modulus -> 0, Multiplicity->1, Quar tics -> True, Using -> True}
Ниже они описаны подробно:
- Cubics — указывает, следует ли искать явные решения для неприводимых кубических уравнений;
- EquatedTo — задает выражение для замещения переменной в решении;
- Modulus — задает промежуточную факторизацию полинома;
- Multiplicity— устанавливает кратность каждого из корней в конечном результате;
- Quartics — задает точное решение квадратного уравнения и полинома четвертой степени;
- Using — указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.
Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.
Дополнительные функции для решения уравнений
Имеется также ряд дополнительных функций, которые используются описанными ранее функциями и также могут применяться при решении нелинейных уравнений:
- Auxiliary [v] — применяется модулем Solve для указания того, что переменная v должна использоваться функцией Roots для результирующих решений, но соответствующие значения v не должны быть включены в окончательный ответ;
- Eliminate [eqns, vars] — исключает переменные vars из системы уравнений eqns;
- FindRoot [Ihs == rhs, {x, x0}] — ищет численное решение уравнения Ihs == rhs, начиная с х = x0;
- MainSolve [eqns] — основная функция для преобразования системы уравнений. Ее вызывают Solve и Eliminate. Уравнения должны быть представлены в форме Ihs == rhs. Они могут объединяться с помощью && и | |. MainSolve возвращает False, если не существует решения уравнений, и возвращает True, если все значения переменных являются решениями. MainSolve перестраивает уравнения, применяя определенные директивы;
- MainSolve [eqns, vars, elim, rest] — пытается перестраивать уравнения eqns так, чтобы найти решения для переменных vars и исключить переменные elim. Список rest может включаться для указания порядка исключения любых остальных переменных;
- NRoots [lhs==rhs, var] — возвращает список численных приближений корней полиномиального уравнения;
- Residue [ехрr, {х, х0 } ] — ищет вычет ехрг в точке х = х0;
- SolveAlways [eqns, vars] — возвращает значения параметров, которые превращают уравнения eqns в тождества для всех значений переменных vars.
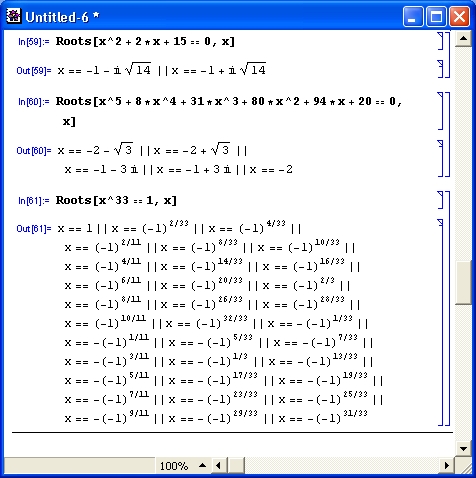
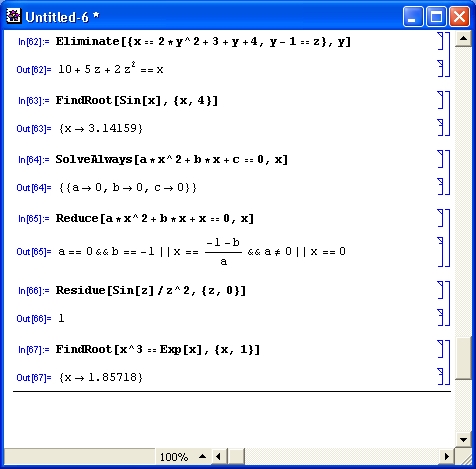
Примеры использования некоторых из этих функций показаны на рис. 4.19.
Рис. 4.19. Примеры применения дополнительных функций для решения уравнений
В целом надо отметить, что система Mathematica обладает обширными средствами для решения уравнений и их систем. Умение их применять — залог правильного и эффективного решения сложных математических задач, относящихся к классу решения уравнений.
Графическая иллюстрация и выбор метода решения уравнений
При рассмотрении приведенных выше примеров может сложиться благодушное впечатление о том, что решение нелинейных уравнений может производиться автоматически и без размышлений. Но это далеко не так — представленные выше примеры просто подобраны так, что они имеют решение с помощью соответствующих функций.
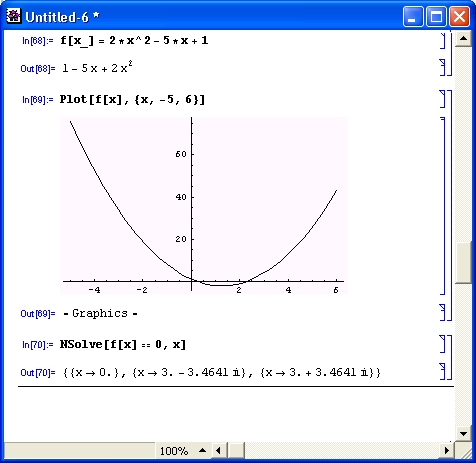
На самом деле порой даже простые уравнения могут не иметь решения. В сложных случаях очень полезна графическая визуализация решения. В качестве примера на рис. 4.20 показана визуализация вычисления корней квадратного уравнения. В данном случае график функции явно указывает на существование двух действительных корней при х, близких к 0.2 и 2.3. Функция Nsolve без труда находит оба корня.
Рис. 4.20. Визуализация решения квадратного уравнения для случая двух действительных корней
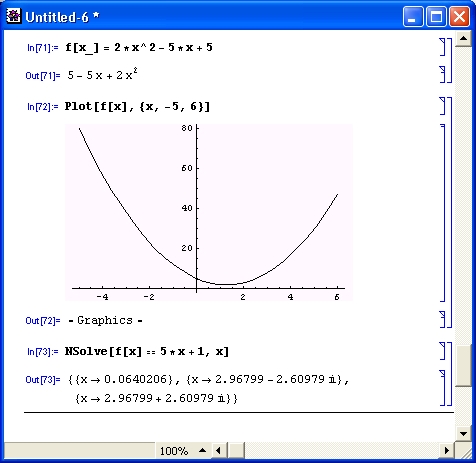
А вот на рис. 4.21 показан случай, когда из-за изменения последнего члена квадратичной функции ее график уже не пересекает ось х вообще. Это говорит о том, что решения в виде действительных корней нет. И в самом деле, NSolve находит корни как комплексно-сопряженные числа. Действительная часть найденных корней дает координату х для впадины кривой — параболы.
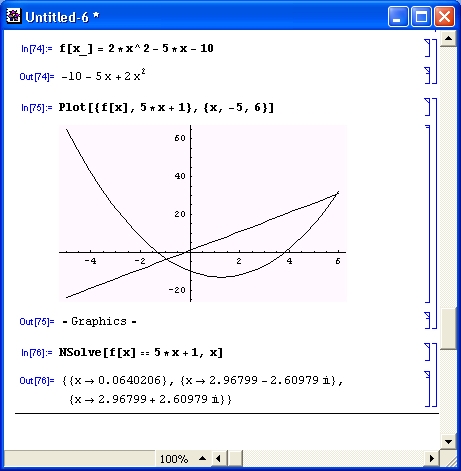
Если требуется решение равенства f1(х) = f 2 (x), то для графической визуализации решения можно построить графики функций f1(х) и f 2 (лг) — наличие точек их пересечения будет означать существование действительных корней. Этот случай иллюстрирует рис. 4.22. В данном случае проблем с решением нет, поскольку, по существу, решается квадратное уравнение.
Рис. 4.21. Визуализация решения квадратного уравнения для случая двух комплексных корней
Рис. 4.22. Пример визуализации решения уравнения вида f(x) = 5х + 1
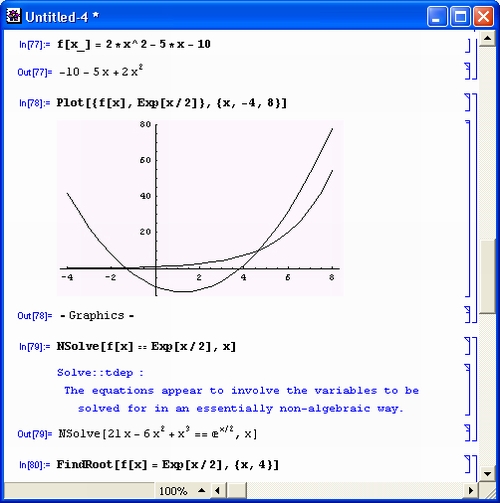
Но вот на рис. 4.23 показан случай решения уравнения f(x) = ехр(х/2). Графики функций ясно показывают, что парабола пересекается экспонентой в двух точках. Однако функция NSolve отказывается решать такое уравнение и выдает сообщение о том, что оно является трансцендентным.
Таким образом, в данном случае наличие графического решения говорит о необходимости смены функции, с помощью которой до сих пор решались уравнения. Подходящей в данном случае является функция FindRoot, которая отыскивает одно решение вблизи заданной начальной точки. Применив ее дважды, нетрудно получить оба корня данного уравнения.
Рис. 4.23. Пример решения уравнения вида f(x) = ехр(х/2)
Приведенные примеры далеко не исчерпывают проблему графической визуализации решения и выбора методов решения. Однако они иллюстрируют возможности системы Mathematica в этой области и заостряют внимание на потенциальных проблемах. Для реализации численных расчетов в системе Mathematica отобраны наилучшие и наиболее эффективные численные методы из описанных в литературе, в том числе в отечественной.
Получение сразу нескольких корней
Многие уравнения с тригонометрическими функциями могут иметь периодические или близкие к ним решения. К сожалению, функции Mathematica, вычисляющие корни уравнений, не способны в этом случае дать сразу несколько корней. Однако ситуация тут далеко не безнадежна — приведенный ниже пример наглядно показывает это.
Пусть требуется в интервале изменения х от 0 до 20 найти все решения уравнения
х sin(x) + х/2 - 1 = 0
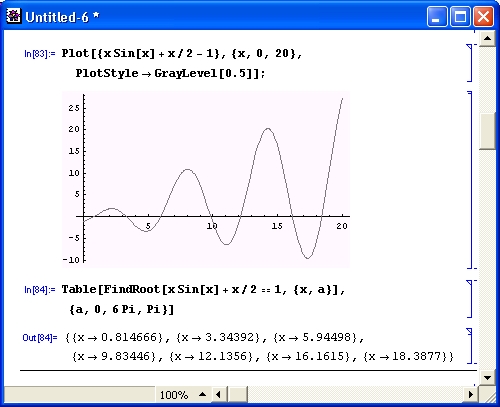
График функции, представляющей левую часть уравнения, показан на рис. 4.24. Хорошо видно, что он пересекает ось х семь раз, то есть имеет в интересующем нас диапазоне семь корней.
Рис. 4.24. График функции х sin(x) + х/2 - 1 и пример вычисления всех ее корней в интервале изменения х от 0 до 20
Колебательная составляющая функции обусловлена входящей в нее функцией sin(x), которая имеет нули в точках 0, n, 2n, Зn... Однако, как видно из рис. 4.24, эти значения лишь приближенные, ввиду влияния других членов уравнения.
Ключевая идея получения всех корней уравнения заключается в поиске нужных решений с помощью функции FindRoot, которой последовательно подставляются различные начальные приближения. Однако вместо уже испытанного приема — поиска корней поодиночке — можно воспользоваться «таблицей» решений, используя функцию Table. Решение, приведенное под графиком функции на рис. 4.24, наглядно иллюстрирует возможности этого приема — найдены (или, вернее, уточнены) все семь корней исходного уравнения.
Получение неизвестных в явном виде
Читатель, возможно, обратил внимание на то, что решения всех представленных выше примеров выглядят не совсем обычно — в виде списка подстановок. Это не позволяет использовать неизвестные в явном виде, например, для проверки решений или передачи найденных неизвестных в последующие вычислительные блоки. Однако от этого затруднения легко избавиться, если перед конструкций блока решения использовать выражение следующего вида:
{х,у,z,...}/.
Список переменных в этом выражении должен однозначно соответствовать списку неизвестных системы уравнений. Покажем этот прием в действии. Ниже приведено решение системы из трех нелинейных уравнений:
FindRoot[{x-2==9,y^2=16,x+y+z==10},{x,l.},{y,l.},{z,l.}]
(Х-> 3., у-> 4., z->3.} {x,y,z}
{X, у, 2}
Обратите внимание на то, что вывод списка {х, у, z } не дает полученных значений неизвестных. Это связано с тем, что переменные в блоке решения имеют ло-к(1лъный характер и за пределами блока их значения (в том числе неопределенные) сохранятся такими, какими они были до применения в блоке решения.
Теперь зададим решение в ином виде:
{x,y,z}/.FindRoot[{x*2==9, уА2==1б, x+y+z==10}, {x,l.}, {у,1.}, {z,l.}]
{3., 4., 3.}
Как видите, на сей раз решение получено в виде списка с числами — явными значениями неизвестных. Можно обозначить их как а, Ь и с, получить список {а, b, с} и даже использовать их отдельно:
{а,b,с}=%
(З.,4.,3.)
а,b,с
{З.,4.,3.}
а
3.
b
4.
с
3.
Теперь можно проверить решение данной системы:
{а^2, b^2,а+b+с}
{9., 16., 10.}
Полученный вектор правых частей системы совпадает с заданным, что свидетельствует о правильности решения. Разумеется, вместо нового списка { а , b , с } для вектора решения можно было использовать и вектор { х, у, z } .
gl4-12.jpg
gl4-13.jpg

gl4-14.jpg

gl4-15.jpg

gl4-16.jpg
gl4-17.jpg
gl4-18.jpg
gl4-19.jpg
gl4-20.jpg
gl4-21.jpg
gl4-22.jpg
gl4-23.jpg
gl4-24.jpg
8. Дифференциальные уравнения
Дифференциальные уравнения
Решение дифференциальных уравнений в символьном виде
Дифференциальными принято называть уравнения, в состав которых входят производные функции у(х), представляющей решение уравнения. Дифференциальные уравнения могут быть представлены в различной форме, например в общеизвестной форме Коши:
у'(х) = eqn=f(x,y).
Несколько дифференциальных уравнений образуют систему дифференциальных уравнений. Решение таких систем также возможно средствами Mathematica и подробно описано в ряде книг по использованию системы [65-71]. Дифференциальные уравнения и системы дифференциальных уравнений могут быть линейными и нелинейными. Для линейных уравнений обычно существуют решения в аналитическом виде. Нелинейные дифференциальные уравнения в общем случае аналитических решений не имеют, но могут решаться приближенными численными методами.
Дифференциальные уравнения широко используются в практике математических вычислений. Они являются основой при решении задач моделирования — особенно в динамике. Немногие математические системы имеют реализации численных методов решения систем дифференциальных уравнений. Но система Mathematica имеет средства как для символьного, так и для численного решения дифференциальных уравнений и их систем.
Для решения дифференциальных уравнений в символьном виде используются следующие средства:
- DSolve[eqn, y[x], х] — решает дифференциальное уравнение относительно функций у [ х ] с независимой переменной х;
- DSolve[{eqnl, eqn2,...}, {yl [xl,...],...}, {xl,...}]-решает систему дифференциальных уравнений.
У функции DSolve и ее численного варианта NDSolve есть пара опций, на которые следует обратить внимание:
- DSolveConstants — опция к DSolve, определяющая постоянные интегрирования, которые будут использованы в результате;
- StartingStepSize — опция к NDSolve, определяющая величину начального шага.
В решении дифференциальных уравнений встречаются постоянные интегрирования. По умолчанию они обозначаются как С [ i ].
Приведем примеры решения дифференциальных уравнений:
DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х], х]
{{у[х]->aх4/2+С[1]}}
DSolve[{yl' [х] == 2 х2, у2' [х] == 3 х}, {yl[х], у2[х]}, х]
{{yl[x] ->-2х3/3+C[1], у2[х] ->3х2/2+C[2]}}
DSo2ve{y'[x] +у[х] ==х, у[х], х}
{{у[х] -*-1+х + е-хС[1]}}
DSolve [у" [х] - у' [х] - 6 у [х] == 0, у [х] , х] {{У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]}}
DSolve [у" [х] + 4 у'[х] == 10 Sin [2 х] , у [х] , х]
{{У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]}}
DSolve[y'[x] == Sin[Ex] , y[x] , x]
{{y[x] ->C[1] +Sinlntegral[ex]}}
DSolvefz2 w"[z] +zw'[z] - (z2 + l)w[z] ==0, w[z], z]
{{w[z] ->BesselI[l, z] C[l] +BesselK[l, z] C[2] }}
Как нетрудно заметить, аналитические решения дифференциальных уравнений могут содержать не только элементарные, но и специальные математические функции, что заметно расширяет возможности применения системы Mathematica в решении задач динамического моделирования.
Решение дифференциальных уравнений в численном виде
Многие дифференциальные уравнения не имеют аналитических решений — например, нелинейные. Однако они могут с приемлемой точностью решаться численными методами. Для численного решения систем дифференциальных уравнений используется функция NDSolve:
- NDSolve [eqns, у, {x, xmin, xmax }]— ищет численное решение дифференциальных уравнений .eqns относительно функции у независимой переменной х в интервале от xmin до xmax;
- NDSolve [eqns, {yl, y2,...}, {x, xmin, xmax }]— ищет численные решения относительно функций yi.
MaxSteps — опция к NDSolve, которая определяет максимальное количество шагов.
Часто весьма желательно выводить результаты решения дифференциальных уравнений в графической форме. Рисунок 4.25 поясняет, как это делается при решении системы нелинейных дифференциальных уравнений, описывающих достаточно сложный колебательный процесс.
Нередко решение предпочитают представить на фазовой плоскости. Рисунок 4.26 иллюстрирует такую возможность. Более того, поскольку решается система из трех дифференциальных уравнений, фазовая траектория решения находится в трехмерном пространстве.
Простота задания решения и вывода его результатов в графической форме открывает широкие возможности применения системы для математического моделирования сложных явлений. При этом, в отличие от такого решения с помощью обычных языков высокого уровня (например, Фортран, Бейсик, Паскаль или С), не требуется составления каких-либо программ по реализации численных методов решения систем дифференциальных уравнений, таких как, скажем, метод Рунге— Кутта. Они представлены в виде уже готовых функций.
Рис. 4.25. Решение системы дифференциальных уравнений с выводом решения в виде графиков временных зависимостей
Рис. 4.26. Решение системы дифференциальных уравнений с выводом решения в форме кривых на фазовых плоскостях
gl4-25.jpg

gl4-26.jpg

9. Оптимизационные задачи
Оптимизационные задачи
Поиск максимального и минимального чисел в списке
В практике математических прикладных вычислений важная роль принадлежит оптимизационным задачам, например таким, как поиск минимальных и максимальных значений функций одной или нескольких переменных. Mathematica дает разнообразные возможности решения задач оптимизации — от поиска элементов списка с минимальным или максимальным значением до поиска локальных и даже глобальных минимумов функций, заданных аналитически.
Для поиска максимального и минимального значений ряда чисел, входящих в список, система Mathematica предоставляет следующие средства:
- Max [xl, х2,...]— возвращает наибольшее значение из xi;
- Max[{xl, x2,...}, {yl,...},...] — выбирает наибольший элемент из нескольких списков;
- Min[xl, x2,...] — возвращает наименьшее значение из xi;
- Min[{xl, x2,...}, {yl,...},...] — выбирает наименьший элемент из нескольких списков.
Следующие примеры показывают действие этих простых функций.
| Ввод (In) | Вывод(Out) |
| Мах[1,5,2,6.5,3,4] | 6.5 |
| Мах[{1,3,2},{4,5,6},{9,8,7}] | 9 |
| Min[1,5,2,6.5,-3,4] | -3 |
| Min[{1,3,2},{4,5,6},{9,8,7}] | 1 |
Поиск локального минимума аналитической функции
Если нужен поиск локального минимума некоторой аналитической функции, используется функция FindMinimum [ f, {х, х0 } ], которая выполняет поиск локального минимума функции f, начиная со значения х=х0, и возвращает его значение.
Для указания градиента минимизируемой функции используется опция Gradient.
Приведем примеры применения функции FindMinimum:
FindMinimum[-хЕхр[-2 х] , {х, 1}]
{-0.18394, {х^ 0.5}}
FindMinimum[-хЕхр[-2 х] , {х, 0.2, 6, 1}]
{-0.18394, {х^ 0.5}}
FindMinimum [-5 xExp[-x/2] (2 + Sin[3x]), {х, 1}]
{-7.17833, {х^ 0.783139}}
FindMinimum[-5xExp[- x/2] (2 + Sin[3 x]) , {x, 3}]
(-10.6299, {x^ 2.5805}}
FindMinimum[-5xExp[- x/2] (2+Sin[3x]), {x, 4}]
{-6.79134, {x^ 4.6179}}
FindMinimum[l00 (y-x2)2+ (1 -x)2, {x, 0}, {y, 0},
AccuracyGoal-»Automatic]
{9.90511X10-13, {x->l., y^ 0.999999}}
Эти примеры показывают, что выбирая разные начальные значения х, можно найти ряд минимумов функции f(x), разумеется, если таковые имеют место. Если необходимо разыскивать локальные максимумы, достаточно перед функцией поставить знак «минус» или умножить ее на -1.
Поиск глобального максимума и минимума аналитической функции
Следующие две функции служат для поиска глобального максимума и минимума аналитически заданной функции:
- ConstrainedMax [f, {inequalities}, {x, у,...}] — ищет глобальный максимум функции f в области, определяемой неравенствами inequalities. Полагается, что все переменные х, у... неотрицательны;
- ConstrainedMin [f, {inequalities}, {x, у,...}]— ищет глобальный минимум функции f в области, определяемой неравенствами inequalities. Все переменные х, у... полагаются неотрицательными.
Решение задач линейного программирования
Две последние функции решают типовые задачи линейного программирования. В дополнение к ним может использоваться функция
LinearProgramming[с, m, b]
которая ищет вектор х, минимизирующий величину с. х в соответствии с условиями m.x>=b и х>=0.
Рассмотрим типичный пример на линейное программирование. Пусть цех малого предприятия должен изготовить 100 изделий трех типов, причем не менее 20 штук каждого. На изготовление этих изделий уходит, соответственно, 4, 3,4 и 2 кг металла. Имеющийся в наличии запас материала — 700 кг. Спрашивается, сколько изделий xl, х2 и хЗ каждого типа надо выпустить для обеспечения максимальной стоимости продукции, если цена изделий равна, соответственно, 4, 3 и 2 рубля.
Ниже представлено решение этой задачи с помощью функции ConstrainedMax:
ConstrainedMax [
4 * xl + 3 * x2 + 2 * хЗ ,
{xl >= 20, x2 >= 20, хЗ >= 20,
4 * xl + 3 . 4 * x2 + 2 * x3 <= 340 ,
4 .75 * xl + 11 * x2 + 2 * x3 < = 700 ,
xl + x2 + x3 == 100},
{xl, x2, x3}]
{332., {xl^ 56^x2^ 20., x3^24.}}
После имени функции указывается максимизируемая целевая функция, затем перечисляются все ограничения и, наконец, задается список искомых переменных. Результатом вычислений является максимально достижимая стоимость продукции и список переменных, отражающих количество изделий каждого типа.
Задачи минимизации традиционно относятся к сложным задачам программирования — особенно при поиске глобального минимума. Наличие в ядре системы Mathematica их реализаций делает систему привлекательной для решения задач этого класса.
10. Преобразования Лапласа — LaplaceTransform
Преобразования Лапласа-LaplaceTransform
Преобразования Лапласа — важный вид интегральных преобразований. Они лежат в основе, например, символического метода расчета электрических цепей. В системе Mathematica 3 функции преобразования размещены в подпакете Laplace-Transform. Но в CKM Mathematica 4 эти функции стали встроенными.
Основными являются следующие функции этого класса:
- LaplaceTransform[expr, t, s] — возвращает результат прямого преобразования Лапласа для выражения expr [t] в виде функции переменной s;
- InverseLaplaceTransform[expr, s,t] — возвращает результат обратного преобразования Лапласа для выражения expr [s] в виде функции переменной t;
- LaplaceTransform [expr, {tl, t2,...}, {s1i, s2,...} ] — возвращает результат прямого преобразования Лапласа для выражения expr [ 11, t2,... ] в виде функции переменных {s1, s2,...};
- InverseLaplaceTransform [expr, {s1, s2,...}, {tl, t2,...} ] — возвращает результат обратного преобразования Лапласа для выражения expr [s1, s2,...] в виде функции переменных {tl, е2,...}.
Хотя имена переменных t и s можно выбирать произвольно, обычно t означает время, as — оператор Лапласа. Ниже представлено несколько примеров выполнения преобразования Лапласа:
<<Calculus'LaplaceTransfornT'
LaplaceTransform[Exp[-t]*Sin[t], t, s]
1+1/ (1 + s)2
InverseLaplaceTransform[%,s,t]
E-tSin[t]
LaplaceTransform[t^2 Exp[-x], {t,x}, {s,v}]
2/s3(1 + v)
Функции z-преобразований — ZTransform
Z-преобразования широко используются в теории автоматического регулирования. Поэтому в системе Mathematica 4 для осуществления z-преобразований в ядро включены следующие функции:
- ZTransform[expr, n, z] — возвращает результат прямого 2-преобразования для выражения ехрr, представленного как функция целочисленного аргумента n;
- InverseZTransform[expr, n, z] — возвращает результат обратного z-npeобразования для выражения ехрr, представленного как функция целочисленного аргумента п.
Приведем примеры выполнения z-преобразований:
ZTransform[Cos[n], n, z]
(1-cos(1)/z)/(1+1/z2-2Cos(1)/z)
InverseZTransform[%,s,t]
Cos[n]
ZTransform[n^2 а^n, n, z]
[-a(1+a/z)/(-1+a/z)3 z
InverseZTransf orm [%, z, n] // Together
ann2
Как и следовало ожидать, прямое, а затем обратное z-преобразование выражения ехрг восстанавливает его в исходном виде. В системе Mathematica 3 эти функции становятся доступными после исполнения команды «DiscreteMath' ZTransform' поскольку они входят не в ядро, а в пакет расширения дискретной математики.
11. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Вычислять суммы в аналитическом и численном видах.
- Вычислять произведения в аналитическом и численном видах.
- Вычислять производные.
- Вычислять интегралы в символьном и численном видах.
- Вычислять пределы функций.
- Решать в аналитическом и численном видах уравнения и системы уравнений.
- Осуществлять графическую иллюстрацию решения уравнений.
- Решать дифференциальные уравнения в символьном и численном видах.
- Искать максимальное и минимальное числа в списке.
- Искать локальный максимум и минимум аналитической функции.
- Решать задачи линейного программирования.
- Выполнять преобразования Лапласа и z-преобразования.

























