Самоучитель по Mathematica
Урок 1. Первое знакомство
Урок 1. Первое знакомство
1. Первое знакомство
Первое знакомство
- Зарождение и развитие систем компьютерной алгебры
- Математические системы Mathematica
- Структура систем Mathematica и их идеология
- Отражение Mathematica в сети Интернет
- Особенности систем компьютерной математики
- Математические системы в образовании и в науке
- Диалоге системой и ее входной язык
- Инсталляция и запуск
- Прямая работа с CD-ROM
- Отличительные особенности Mathematica 4
В наши дни многие уже путают компьютерную математику как науку о математических вычислениях и преобразованиях с помощью компьютеров с СКМ Маthematica, созданной фирмой Wolfram Research, Inc. Хотя это и знаменательно само по себе, во избежание такой путаницы мы начнем наш курс с рассказа о том, как зародилась компьютерная математика и как были созданы программные системы компьютерной математики различных классов. Здесь мы также опишем отражение системы Mathematica в мировой сети Интернет.
Для многих неискушенных в математике пользователей не совсем понятно, что делают СКМ, особенно те из них, которые выполняют символьные операции. Поэтому в этом уроке мы впервые познакомимся с особенностями различных систем и оценим их возможности, так сказать, в первом приближении. Некоторые из приведенных примеров лучше повторить в дальнейшем — после изучения основ работы с системой Mathematica. Впрочем, нетерпеливые учащиеся могут попробовать сделать это немедленно! Однако, чтобы запустить систему Mathematica 3 или 4 и начать работу с ней, надо вначале установить систему на жесткий диск вашего ПК. Об этом пойдет речь в конце данного урока.
2. Зарождение и развитие систем компьютерной алгебры
Зарождение и развитие систем компьютерной алгебры
У истоков рождения систем компьютерной алгебры
Эру создания компьютерной символьной математики принято отсчитывать с начала 60-х годов. Именно тогда в вычислительной технике возникла новая ветвь компьютерной математики, не совсем точно, но зато броско названная компьютерной алгеброй. Речь шла о возможности создания компьютерных систем, способных осуществлять типовые алгебраические преобразования: подстановки в выражениях, упрощение выражений, операции со степенными многочленами (полиномами), решение линейных и нелинейных уравнений и их систем, вычисление их корней и т. д. При этом предполагалась возможность получения аналитических (символьных) результатов везде, где это только возможно.
К сожалению, книги по этому направлению были способны лишь отпугнуть обычного читателя и пользователя компьютера от изучения возможностей компьютерной алгебры в силу перенасыщенности их узкоспециальным теоретическим материалом и весьма специфического языка описания. Материал таких книг, возможно, интересен математикам, занимающимся разработкой систем компьютерной алгебры, но отнюдь не основной массе их пользователей.
Большинство же пользователей заинтересовано в том, чтобы правильно выполнить конкретные аналитические преобразования, вычислить в символьном виде производную или первообразную заданной функции, разложить ее в ряд Тейлора или Фурье, провести аппроксимацию и т. д., а вовсе не в детальном и сложном математическом и логическом описании того, как это делается компьютером (или, точнее, его программистом). Здесь та же ситуация, что и с телевизором, радиоприемником или факсом: большинство из нас пользуются этими аппаратами, вовсе не интересуясь тем, как именно они выполняют свои довольно сложные функции.
Поняв эту истину, многие западные фирмы приступили к созданию компьютерных систем символьной математики, ориентированных на широкие круги пользователей, не являющихся профессионалами в компьютерной алгебре. Учитывая невероятно большую сложность автоматизации решения задач в аналитическом виде (число математических преобразований и соотношений весьма велико, и некоторые из них неоднозначны в истолковании), первые подобные системы удалось создать лишь для больших ЭВМ. Но затем появились и системы, доступные для мини-ЭВМ. Заметное развитие получили языки программирования для символьных вычислений Reduce, система muMath для малых ЭВМ, а в дальнейшем — интегрированные системы символьной математики для персональных компьютеров: Derive, MathCAD, Mathematica, Maple V и др.
В бывшем СССР большой вклад в развитие систем символьной математики внесла школа покойного академика Глушкова. В конце 70-х годов были созданы малые инженерные ЭВМ класса «Мир», способные выполнять аналитические вычисления даже на аппаратном уровне. Был разработан и успешно применялся язык символьных вычислений «Аналитик». Эти работы отчасти предвосхитили развитие систем символьной математики. К огромному сожалению, они появились слишком рано для своего времени и не соответствовали «генеральной линии» развития советской вычислительной техники в те годы. Уклон в сторону развития больших ЭВМ серии ЕС, навязанный в СССР компьютерными чиновниками, отодвинул компьютеры «Мир» на задний план, а затем этот класс компьютеров просто прекратил свое существование и развитие.
К сожалению, в отрыве от мировой науки и серьезных источников финансирования наши работы (за исключением некоторых теоретических) в области компьютерной алгебры оказались малоэффективными — отечественных систем компьютерной алгебры для персональных компьютеров, доведенных до серийного производства и мировой известности, так и не было создано (впрочем, как и конкурентоспособных ПК на нашей элементной базе). Зато множество наших специалистов — как математиков, так и программистов — эмигрировали на Запад и приняли участие, порой весьма серьезное, в разработке западных систем символьной математики. В том числе и систем класса Mathematica.
Стоимость серийных СКМ все еще чрезмерно велика для большинства наших пользователей. Поэтому не случайно, что (за редчайшим исключением) наши пользователи используют такие системы, распространяемые на CD-ROM сомнительного происхождения. Однако программные продукты на таких CD-ROM поступают без документации, а порой даже в неполном и неполноценном виде, что затрудняет их серьезное применение.
Книги, подобные этой, призваны помочь нашим пользователям эффективно использовать современные программные продукты. Хочется надеяться, что со временем это приведет к росту авторитета нашей науки и образования, повышению благосостояния ученых, педагогов и учащихся, которые, наконец, получат возможность приобретать вполне легальное программное обеспечение с полной документацией.
Системы символьной математики для персональных компьютеров
На Западе решающий скачок в компьютеризации общества произошел с началом массового производства и внедрения ПК. Долгое время их ограниченные возможности не позволяли реализовать на них серьезные системы символьной математики. Но к началу 90-х годов ситуация стала заметно меняться к лучшему. С одной стороны, аппаратные возможности ПК стали резко возрастать по мере быстрой смены поколений микропроцессоров. Тут надо помянуть добрым словом фирму Intel, отстаивающую честь «закона Мура» (одного из своих основателей) и каждый год удваивающую как степень интеграции своих процессоров, так и их производительность. В итоге по скорости счета и объему оперативного запоминающего устройства (ОЗУ) ПК стали обходить «большие» ЭВМ класса ЕС, а сейчас оставили их далеко позади. Это создало реальные предпосылки к развертыванию работ по разработке систем компьютерной алгебры. Впрочем, надо помнить, что разрыв в производительности между новейшими ПК и многопроцессорными суперЭВМ и в наши дни остается поразительно большим!
Многие СКМ пришли в мир ПК из мира больших ЭВМ, таких как суперкомпьютеры Cray (производятся и поныне фирмой Silicon Graphics). В итоге они стали доступными не только представителям научной элиты, вполне познавшим возможности таких систем, но и рядовым пользователям, которые испытывали граничащее с шоком восхищение от созерцания обширных возможностей этих новых систем. Перейти от него к реальному применению СКМ — этому и призвана помочь данная книга.
Среди разработчиков математических систем долгое время бытовало мнение о вторичной роли пользовательского интерфейса и главенствующем значении математических возможностей таких систем. В результате в прошлом пользовательский интерфейс многих математических систем отличался ущербной простотой и архаичностью.
С переводом таких систем на ПК с графическими операционными системами класса Windows с таким подходом пришлось решительно кончать. Более того, превосходная цветная графика высокого разрешения современных ПК, о которой пользователи ЭВМ класса ЕС не могли и мечтать, резко повысила не только роль графического представления данных вычислений, но и привела к слиянию пользовательского интерфейса математических систем с интерфейсом современных графических операционных систем, таких как Windows 3.1/3.11/95/98/NT/2000. Образцом для подражания повсеместно стал интерфейс пользователя массовых офисных программ — Microsoft Office 95/97/2000.
Наибольшую известность получили три класса систем символьной математики: созданная на базе языка искусственного интеллекта Mu Lisp малая система Derive, одна из самых мощных и поныне привлекательных систем Maple V (ядро написано на языке С) и системы Mathematica 1 и 2. Позже на базе ядра системы Maple V символьные вычисления были реализованы в популярных числовых системах Mathcad - версии Mathcad 3.0/4.0/5.0/Plus 5.0/6/0/Plus 6.0/7.0/Plus 7.0/8.0/ 8.0 PRO/2000 PRO/2000 Premium имеют изумительный пользовательский интерфейс и возможности, улучшающиеся от версии к версии. Блок символьной математики на базе ядра Maple V был добавлен и в одну из самых крупных матричных систем — MATLAB.
Система Derive [15,16] и поныне привлекательна своими невзыскательными требованиями к аппаратным ресурсам ПК — это единственная система, которая работает даже на ПК класса IBM PC XT без жесткого диска. Более того, при решении задач умеренной сложности она показала более высокое быстродействие и большую надежность решения, чем первые версии систем Maple V и Mathematica. Впрочем, системе Derive трудно конкурировать с этими системами всерьез — ни по обилию функций и правил аналитических преобразований, ни по возможностям машинной графики и удобству пользовательского интерфейса. Пока Derive обречена на достаточно важную роль учебных систем компьютерной алгебры начального уровня.
Хотя новейшая версия Derive 5 под Windows уже имеет современный интерфейс, он все же во многом уступает изысканному интерфейсу своих маститых конкурентов. А по возможности графической визуализации результатов вычислений Derive все еще далеко отстает от них. То же можно сказать и о новой системе символьной математики MuPAD 1.4.
Система Maple V— патриарх в семействе систем символьной математики. И поныне это весьма привлекательная система для математика-аналитика и научного работника. Даже в среде MS-DOS Maple V имеет неплохой интерфейс и превосходно организованную обширную базу данных помощи. Полнота ядра системы, хранящего более 2700 математических функций (у последней реализации Maple 6 их уже свыше 3000!) и правил их преобразования, вполне заслуживает восторга и большого уважения. Весьма привлекательное свойство этой системы — подробная встроенная помощь и множество примеров ко всем встроенным в нее функциям и прикладным пакетам. Эти примеры легко скопировать в окно редактирования системы и тут же решить.
Достойна восхищения и математическая графика системы Maple, в частности возможность изображения пересекающихся трехмерных фигур с функциональной окраской. Новейшие системы Maple V для Windows (реализации R5 и 6) по возможностям графики стоят на одном уровне с системами Mathematica 3/4. Считается, что они несколько превосходят системы Mathematica в части символьных преобразований, но такое превосходство на сегодня уже является весьма спорным.
К сожалению, фирма Waterloo Maple, Inc. (Канада) - разработчик системы Maple V — больше блистала математической проработкой своего проекта, чем уровнем его коммерческой реализации. В силу этого система Maple V была доступна в основном узкому кругу профессионалов. Сейчас эта фирма работает совместно с более преуспевающей в коммерции и проработке пользовательского интерфейса математических систем фирмой MathSoft, Inc. — создательницей весьма популярных и массовых систем для численных расчетов Mathcad, ставших международным стандартом для технических вычислений. Пока, однако, математические возможности этих систем в области компьютерной алгебры намного уступают системам Maple V, Mathematica 2 и даже малютке Derive (не говоря уже о реализациях Mathematica 3 и 4).
Появление новых версий Mathematica 3 и 4 вновь резко поднимает планку оценки качества систем компьютерной алгебры. Наступает новый этап интеграции математических систем как друг с другом, так и с современными текстовыми и табличными процессорами, такими как Word 95/97 и Excel 95/97 из офисных пакетов Microsoft Office 95/97 (на подходе и Office 2000).
Всяческих похвал заслуживают последние реализации матричных систем MAT-LAB 5.2/5.3, но это очень громоздкая система, последняя реализация которой — MATLAB 5.3.1 - занимает на жестком диске 1500 Мбайт памяти (даже Mathematica 4 требует на порядок меньше места). Система MATLAB создана фирмой Math Works (США).
Сейчас уже ясно, что конкурентоспособные отечественные системы символьной математики у нас, в силу известной экономической ситуации, в обозримом будущем не появятся. Это печальное положение делает особенно актуальным освоение нашими учеными, педагогами и учащимися новейших западных систем компьютерной алгебры. К таковым и относятся системы класса Mathematica — признанные мировые лидеры среди систем символьной математики, ориентированных на персональные компьютеры.
3. Математические системы Mathematica
Математические системы Mathematica
Системы класса Mathematica 2.x
В 80-е годы возможностями символьной математики увлекся защитивший докторскую диссертацию Стивен Вольфрам (Stephen Wolfram) из США (рис. 1.1). Его интересы были столь серьезны, что он основал фирму Wolfram Research, Inc., приступившую к созданию проекта престижной математической системы Mathe-
matica. Версия Mathematica 1.0 этой системы, появившаяся в 1988 г., уже устарела, и самой известной разработкой фирмы стала версия 2.0 системы Mathematica 2, появившаяся в 1991 г. и благополучно дожившая до наших дней. У нас она впервые стала известна благодаря обзорам.
Рис. 1.1. Страница Интернет-сайта фирмы StatSoft.
Цели нового проекта были достаточно амбициозными — разработка мощного и универсального ядра системы (Kernel), способного работать на различных компьютерных платформах, создание многофункционального языка программирования, ориентированного на математические приложения, подготовка современного пользовательского интерфейса и обширного набора прикладных пакетов и расширений системы (Packages), мощного языка программирования математических преобразований и вычислений. Система приобрела свойства адаптации и обучения новым математическим законам и закономерностям.
В разработках систем Mathematica, наряду с головной фирмой Wolfram Research, Inc., принимали участие ряд других фирм и сотни специалистов высокой квалификации (в том числе математики и программисты). Среди них есть и представители пользующейся уважением и «спросом» за рубежом математической школы России. Системы Mathematica являются одними из самых крупных программных систем, они реализуют самые эффективные алгоритмы вычислений и имеют множество новинок. К их числу относится механизм контекстов, исключающий появление в программах побочных эффектов.
Система Mathematica 2 всегда рассматривалась как мировой лидер среди компьютерных систем символьной математики для ПК, обеспечивающих не только возможности выполнения сложных численных расчетов с выводом их результатов в самом изысканном графическом виде, но и проведение особо трудоемких аналитических вычислений и преобразований. Версии системы под Windows имеют современный пользовательский интерфейс и позволяют готовить документы в форме Notebooks («записных книжек»). Они объединяют исходные данные, описание алгоритмов решения задач, программ и результатов решения в самой разнообразной форме (математические формулы, числа, векторы, матрицы, графики).
Mathematica 2 была задумана как система, максимально автоматизирующая труд научных работников и математиков-аналитиков. Она заслуживала изучения как типичный представитель элитных и высокоинтеллектуальных программных продуктов высшей степени сложности. Однако куда больший интерес она представляет как мощный и гибкий математический инструментарий, который может оказать неоценимую помощь большинству научных работников, преподавателей университетов и вузов, студентов и инженеров и даже школьников.
С самого начала большое внимание уделялось графике, в том числе динамической, и даже возможностям мультимедиа — воспроизведению динамических изображений и синтезу звуков с поддержкой звуковой платы (аудиоадаптера). Набор функций графики и меняющих их действие опций и директив весьма полон. Графика всегда была козырной картой систем Mathematica и обеспечивала им лидерство среди систем компьютерной математики.
Рождение столь мощной и сложной системы, как Mathematica 2, шло не без трудностей. Первые версии Mathematica 2 для MS-DOS имели примитивный пользовательский интерфейс, заметно уступающий интерфейсу конкурирующей системы Maple V 1.0 для MS-DOS. Однако фирма Wolfram быстро сумела оценить возможности графической оболочки Windows и одной из первых создала версию своей системы для Windows. В книге приведены многие десятки недостатков версии Mathematica 2, практически устраненных в последующих версиях.
Mathematica 2 — одна из самых крупных и изощренных математических программных систем своего времени (начала 90-х годов). На протяжении ряда лет эта система модернизировалась и улучшалась. Ее расширенная версия (Mathematica 2.2.2) для IBM-совместимых ПК класса 386/486/Pentium требует ОЗУ объемом не менее 8 Мбайт. Сейчас это вряд ли ограничивает применение системы — компьютеры класса Pentium II/III и даже Pentium MMX с таким объемом памяти и частотами работы процессоров от 166 до 450 МГц можно приобрести в России по цене порой менее $300. Множество подходящих для этой системы ПК есть в системе образования и в индивидуальном владении пользователей.
Если по части графических возможностей лидерство системы Mathematica 2 не вызывало особых споров, то в части выполнения аналитических преобразований и надежности работы система неоднократно подвергалась заслуженной критике. В частности, приводились данные не только об отказе системы выполнять некоторые типы символьных вычислений, но и даже о получении при этом явно неверных результатов. Однако такие нарекания относятся лишь к версиям системы 2.1 и ниже. При этом в справедливо указывалось, что недоработки системы обусловлены ее новизной, сложностью и обширными возможностями.
Раньше грубые просчеты пользователя могли привести к зависанию системы. Однако уже в версии 2.2.2 это было практически исключено. Кроме того, оно устраняется обычным для Windows способом — одновременным нажатием клавиш Ctrl+Alt+Del При этом работа с системой Mathematica может прерваться, но общего краха системы Windows обычно не происходит. Нажатие клавиши Enter возвращает нас в менеджер программ Windows.
Тем, кто слишком щепетильно относится к возможностям ошибок в символьных вычислениях, стоит напомнить, что от неверных результатов не застрахован даже самый талантливый математик-аналитик. За рубежом (но только не у нас!) такой специалист получает в месяц заработную плату, намного превосходящую стоимость среднего ПК вместе с установленной на нем системой Mathematica. Так что стоит подумать о том, какие средства вам нужны для решения ваших задач и сколько вы готовы за них заплатить!
Несмотря на отмеченные недоделки, система быстро заняла ведущие позиции на рынке математических систем. Особенно привлекательны были обширные графические возможности системы и реализация интерфейса типа Notebook («записная книжка»), позволяющего сочетать в пределах одного документа программы и команды с данными, представленными в формульном, текстовом, табличном и графическом видах. При этом система обеспечивала динамическую связь между ячейками документов в стиле электронных таблиц даже при решении символьных задач, что принципиально и выгодно отличало ее от других систем.
У разных фирм различны подходы к обозначению новых версий своих программных продуктов. MathSoft, Inc., к примеру, за какие-то пять лет породила добрый десяток новых версий популярной системы Mathcad — 3.0, 4.0, 5.0, Plus 5.0, 6.0, Plus 6.0, 7.0, Plus 7.0, 8.0, 8.0 PRO и даже Mathcad 2000 PRO/Premium. И почти каждый раз отмечала их новой цифрой, хотя революционными отличия этих версий друг от друга назвать трудно.
Фирма Wolfram Research, Inc. (разработчик систем Mathematica) явно относится к числу тех фирм, у которых малейший намек на изменение версии означает существенную ее переработку. В итоге версии Mathematica 3 и 4 на фоне более старых Mathematica 2.0, 2.1 и 2.2 выглядят кардинально новыми системами с новым превосходным пользовательским интерфейсом и обширными математическими возможностями.
В июле 1996 г. на бета-тестирование поступила система Mathematica 3. Вскоре (середина 1997 г.) она стала серийным продуктом, начались ее поставки на рынок. Был кардинально переработан пользовательский интерфейс системы, он вобрал в себя массу новинок — от раздельного вывода на экран деталей и панелей интерфейса до мощной и прекрасно реализованной справочной системы. Устранен недостаток предшествующих версий — небольшое число примеров в справочной системе. Все примеры стали «живыми» — их в любой момент можно переиначить на свой лад и перенести в свои документы.
Продолжая линию развития универсального ядра системы, фирма Wolfram обеспечила применение этой системы на целом ряде операционных систем — Windows 95, Windows NT, Macintosh, Power Macintosh, SunOS, Solaris, HP-UX, SGI, Linux и др. Это делает систему доступной самым различным категориям пользователей и позволяет распределять решение математических задач любой сложности по оптимальным для этого компьютерным платформам.
Для системы Mathematica 3 на массовой платформе Windows установлены следующие требования к аппаратной части:
- процессор Intel 80386 и выше;
- операционная система Windows 95 или Windows NT 3.51 и старше;
- дисковое пространство — минимальное 24 Мбайт, стандартное 83 Мбайт и максимальное около 120 Мбайт;
- запуск с жесткого диска или с CD-ROM;
- емкость ОЗУ — минимальная 8 Мбайт, желательная 16 Мбайт.
Система поставляется на CD-ROM в комплекте с электронным учебником и документацией. Возможен запуск системы прямо с компакт-диска, что экономит пространство на жестком диске, но замедляет файловые операции. Любопытно отметить, что большую часть памяти на дисках (жестком и CD-ROM) занимает справочная база данных системы.
Из других возможностей системы Mathematica 3 можно отметить:
- повышение эффективности численных методов, в частности, функций одномерной и многомерной интерполяции, решения дифференциальных уравнений, решения систем линейных уравнений и др.;
- введение адаптивного контроля за вычислениями численными методами;
- расширенный диапазон аналитических преобразований, в том числе для уравнений с частными производными;
- введение новой функции полного упрощения Full Simplify, способной упрощать выражения со специальными математическими функциями;
- расширение числа форматов файлов, в которых можно сохранять документы (в их числе популярные форматы файлов EPS, TIFF, GIF, HPML и др.);
- повышенное (полиграфическое) качество документов; О улучшенное использование памяти ОЗУ.
Благодаря этим и другим описанным выше возможностям сферы применения системы Mathematica 3 заметно расширились. Было создано свыше двух десятков профессиональных пакетов расширения системы.
Ожидалось, что, как и предшествующие реализации 1 и 2, система Mathematica 3 даст начало многолетнему марафону постепенного усовершенствования этой системы. Но вопреки этому фирма Wolfram совершила довольно неожиданный для нее шаг — не успели пользователи разобраться с многими новациями Mathematica 3, как в июне 1999 г. на рынок была выпущена новейшая реализация системы — Mathematica 4. При этом имеющиеся данные свидетельствуют о коренном пересмотре базовых концепций, заложенных в систему. Видимо, роль в этом сыграло приближение 2000 года.
Новая система получила развитие прежде всего как система для быстрых и объемных численных вычислений при сохранении всего ее могущества в области символьной математики. Значительно повышена скорость основных численных вычислений и операций с произвольной разрядностью. Улучшена плотность упаковки массивов, введен ряд новых встроенных функций. Повышена скорость работы пользовательского интерфейса, он стал более удобным. Чего стоит, к примеру, такая мелочь, как изменение цвета элементов выражений в ходе их ввода — это облегчает устранение ошибок при вводе сложных выражений.
Теперь уже окончательно ясно — разработчики системы продолжают интенсивно работать над ней и превратили Mathematica 4 в мощную универсальную СКМ. И первые данные о новой версии системы, которые читатель найдет в этой книге, ясно говорят о том, что разработчики систем этого класса отнюдь не намерены уступать первенство в создании наиболее сложных и продвинутых систем компьютерной алгебры. Возможности новой системы весьма впечатляют!
Важно отметить, что весьма обширные новые возможности Mathematica 4 относятся почти исключительно к количественным показателям системы и никоим образом не влияют на статический вид интерфейса систем (в сравнении с Mathematica 3) и на вид готовящихся документов-блокнотов (notebooks). Поэтому в дальнейшем мы под системой Mathematica будем иметь в виду одновременно обе версии — ставшую у нас хорошо известной Mathematica 3 и новейшую Mathematica 4. Указание на конкретную версию будет делаться только в том случае, если описываются ее специфические возможности. Многочисленные внутренние отличия системы Mathematica 4 от Mathematica 3 будут рассмотрены по ходу дела.
Работа с системами Mathematica 3 и Mathematica 4 происходит практически одинаково. Небольшое ускорение при ряде манипуляций с интерфейсом Mathematica 4 внешне не сказывается на такой работе. Поэтому, за редкими (и оговоренными) исключениями, все, что описано применительно к системе Mathematica 4, применимо и к Mathematica 3. Однако отличия ранних версий Mathematica 2.x от описанных в книге версий нового поколения достаточно серьезны, поэтому их пользователям описание пользовательского интерфейса Mathematica 3/4 не подходит, хотя набор операторов и функций ранних версий является сокращенным набором этих средств, описанных в данной книге.
gl1-1.jpg
4. Структура систем Mathematica и их идеология
Структура систем Mathematica и их идеология
Следует отметить, что скромные (в смысле аппаратных требований) версии системы Mathematica 2.2.2 по сей день производятся фирмой Wolfram и используются в основном в системе образования. Они продаются по ценам в несколько раз меньшим, чем последующие реализации 3 и 4. Сейчас версии системы для IBM-совместимых ПК Mathematica 2, 3 и 4 распространяются в России на оптических дисках. Это намного повышает их доступность, хотя нередки случаи поставки не вполне работоспособных систем на дисках сомнительного происхождения.
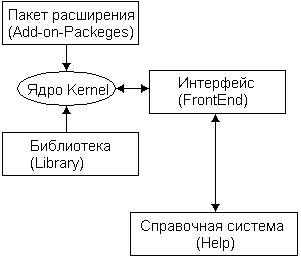
Общая структура систем Mathematica (всех версий) представлена на рис. 1.2.
Рис. 1.2. Структура системы Mathematica
Центральное место в системах класса Mathematica занимает машинно-независимое ядро математических операций — Kernel. Для ориентации системы на конкретную машинную платформу служит программный интерфейсный процессор Front End. Именно он определяет, какой вид имеет пользовательский интерфейс системы. В этой главе далее будет описан интерфейсный процессор для ПК с массовыми операционными системами Windows 95/98/NT. Разумеется, интерфейсные процессоры систем Mathematica для других платформ могут иметь свои нюансы, но особых различий с описанным интерфейсным процессором у них нет.
Любопытны данные об объеме ядра разных реализаций системы Mathematica, приведенные в книге Стивена Вольфрама:
| Система | Mathematica 1 | Mathematica 2 | Mathematica 3 | Mathematica 4 |
| Число строк на языке С | 150 000 | 350 000 | 600 000 | 800 000 |
Увеличение объема ядра в системе Mathematica 4 позволило перенести в ядро ряд функций из пакетов расширения. Ядро системы тщательно оптимизировано, что повысило скорость выполнения большинства команд.
Ядро сделано достаточно компактным с тем, чтобы любая функция из него вызывалась достаточно быстро. Для расширения набора функций служит библиотека (Library) и набор пакетов расширения (Add-on Packages). Пакеты расширений готовятся на собственном языке программирования систем Mathematica и являются главным средством расширения возможностей системы и их адаптации к решению конкретных классов задач пользователя. Кроме того, системы имеют встроенную электронную справочную систему — Help. Она содержит шесть электронных книг с «живыми» примерами, включая упомянутые во введении книги.
Ядро систем Mathematica 3/4 сделано независимым от компьютерной платформы, на которой может устанавливаться и работать система. Это гарантирует идентичность операторов и функций, используемых в системах Mathematica, устанавливаемых на разных ЭВМ — от ПК до суперкомпьютеров. Поэтому большая часть материалов данной книги, посвященных математическим возможностям и даже интерфейсу систем Mathematica 3/4, относится к компьютерам самого разного класса — от платформы Windows до Macintosh и UNIX.
Идеология систем Mathematica базируется на двух, казалось бы, взаимно исключающих друг друга положениях:
- решение большинства математических задач в системе может производиться в диалоговом режиме без традиционного программирования;
- входной язык общения системы является одним из самых мощных языков функционального программирования, ориентированных на решение различных задач (в том числе математических).
Противоречивость этих положений кажущаяся. На самом деле Mathematica — типичная система программирования с проблемно-ориентированным языком программирования сверхвысокого уровня . Его можно отнести к классу интерпретаторов. Как известно, языки такого типа последовательно анализируют (интерпретируют) каждое выражение и тут же исполняют его. Таким образом, работа с системой происходит явно в диалоговом режиме — пользователь задает системе задание, а она тут же выполняет его. Разумеется, Mathematica содержит достаточный набор управляющих структур для создания условных выражений, ветвления в программах, циклов и т. д.
На первый взгляд может показаться, что система ведет диалог на куда более примитивном уровне, чем хорошо известный язык программирования Бейсик (тоже относящийся к интерпретирующему типу). И в самом деле, работа с системой Mathematica напоминает работу с Бейсиком в режиме непосредственного исполнения команд — в ответ на каждый вопрос тут же следует результат вычислений. Более того, сохранился такой архаизм (впрочем, при необходимости отключаемый), как нумерация строк (ячеек).
Однако первое впечатление часто бывает обманчивым. Помимо того что Mathematica даже в ходе такого элементарного диалога предоставляет пользователю средства сверхвысокого уровня (например, аналитическое вычисление производных или интегралов, что Бейсику абсолютно недоступно), система имеет все возможности для создания практически любых управляющих структур , организации ввода/вывода, работы с системными функциями, обслуживания любых периферийных устройств и т. д. Другое дело, что рядовому пользователю эти средства программирования могут и не понадобиться — его вполне удовлетворят встроенные математические функции системы, поражающие своим обилием и многообразием даже опытных математиков.
Можно сказать, что для решения математических задач система содержит готовые рецепты почти на любой «вкус и цвет». Однако с помощью пакетов расширения (Add-ons) имеется возможность постоянно готовить новые «блюда», подстраивая «кухню» (то есть возможности) системы под запросы любого ее пользователя.
К идеологии систем Mathematica надо отнести и комплексную визуализацию всех этапов вычислений, начиная с легко понятного и естественного ввода текстов и формул и кончая наглядным выводом результатов в разнообразных формах представления. Особое место при этом играет полная визуализация результатов вычислений, включающая в себя построение огромного числа графиков самого различного вида, в том числе средства анимации изображений и синтеза звуков.
gl1-2.jpg
5. Знакомство с символьными вычислениями
Знакомство с символьными вычислениями
Особенности систем компьютерной математики
Недостатки численных расчетов
Большинство первых CKM (Eureka, Mercury, Excel, Lotus-123, Mathcad для MS-DOS, PC MATLAB и др.) предназначались для численных расчетов. Они как бы превращали компьютер в большой программируемый калькулятор, способный быстро и автоматически (по введенной программе) выполнять арифметические и логические операции над числами или массивами чисел. Их результат всегда конкретен — это или число, или набор чисел, представляющих таблицы, матрицы или точки графиков. Разумеется, компьютер позволяет выполнять такие вычисления с немыслимой ранее скоростью, педантичностью и даже точностью, выводя результаты в виде хорошо оформленных таблиц или графиков.
Однако результаты вычислений редко бывают абсолютно точными в математическом смысле: как правило, при операциях с вещественными числами происходит их округление, обусловленное принципиальным ограничением разрядной сетки компьютера при хранении чисел в памяти. Реализация большинства численных методов (например, решения нелинейных или дифференциальных уравнений) также базируется на заведомо приближенных алгоритмах. Часто из-за накопления погрешностей эти методы теряют вычислительную устойчивость и расходятся, давая неверные решения или даже ведя к полному краху работы вычислительной системы — вплоть до злополучного «зависания».
Условия, при которых это наступает, не всегда известны — их оценка довольно сложна в теоретическом отношении и трудоемка на практике. Поэтому рядовой пользователь, сталкиваясь с такой ситуацией, зачастую становится в тупик или, что намного хуже, неверно истолковывает явно ошибочные результаты вычислений, «любезно» предоставленные ему компьютером. Трудно подсчитать, сколько «открытий» на компьютере было отвергнуто из-за того, что наблюдаемые колебания, выбросы на графиках или асимптоты ошибочно вычисленных функций неверно истолковывались как новые физические закономерности моделируемых устройств и систем, тогда как на деле были лишь грубыми погрешностями численных методов решения вычислительных задач.
Многие ученые справедливо критиковали численные математические системы и программы реализации численных методов за частный характер получаемых с их помощью результатов. Они не давали возможности получить общие формулы, описывающие решение задач. Как правило, из результатов численных вычислений невозможно было сделать какие-либо общие теоретические, а подчас и практические выводы. Поэтому, прежде чем использовать такие системы в реализации серьезных научных проектов, приходилось прибегать к дорогой и недостаточно оперативной помощи математиков-аналитиков. Именно они решали нужные задачи в аналитическом виде и предлагали более или менее приемлемые методы их численного решения на компьютерах.
Понятие о символьных (аналитических) вычислениях
Символьные операции — это как раз то, что кардинально отличает систему Mathematica (и подобные ей символьные математические системы) от систем для выполнения численных расчетов. При символьных операциях, называемых также аналитическими, задания на вычисление составляются в виде символьных (формульных) выражений, и результаты вычислений также получаются в символьном виде. Численные результаты при этом являются частными случаями символьных.
Выражения, представленные в символьном виде, отличаются высокой степенью общности. К примеру, тождество sin(x) 2 + соs(x) 2 = 1 справедливо при любых значениях аргумента х. Если результат символьной операции равен, к примеру, sin(1), то он и будет выведен как sin(1) — конкретное вещественное число, приближенно представляющее или аппроксимирующее sin(1), вычисляться не будет, ибо носит частный характер.
Результат вычисления sin(х) 2 + cos(x) 2 можно проверить с помощью систем для численных расчетов, задав ряд конкретных значений х и вычислив сумму квадратов синуса и косинуса. Однако всякий раз мы будем получать частный результат, не имея никакой гарантии того, что он действительно справедлив при любом значении х. К тому же этот результат нередко может оказаться равным 0,9999999 или 1,0000001, так что лишь наша фантазия округляет его до точной единицы. Между тем это как раз то, что абсолютно недопустимо в действиях профессионала — математика-аналитика. Его приведет в ужас малейшее отличие указанного выражения от единицы! Ведь почтенные классики математики давно уже доказали, что этот результат равен в точности единице!
Так чему равна сумма квадратов синуса и косинуса?
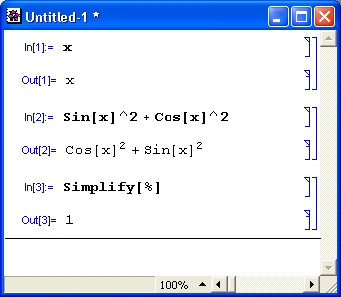
Попытка вычислить в общем виде выражение sin(x) 2 + соs(x) 2 с помощью численных математических систем или программ на обычных языках программирования к успеху не приведет. Вместо ожидаемого результата появится сообщение об ошибке вида: «Переменная х не определена!». Компьютер будет ждать ввода конкретного значения для х.Так будет независимо от того, запрограммировали вы вычисления на простеньком Бейсике или на языке профессионалов-программистов C++. И лишь системы символьной математики при вычислениях дадут долгожданное и абсолютно точное значение 1 (рис. 1. 3) .
Рис. 1.3. Система Mathematical вычисляет значение sin(x) 2 +cos(x) 2
Пока не стоит обращать внимание на то, как получен рис. 1.15 — это окно реально работающей системы Mathematica. Уже при рассмотрении простейшего примера, представленного на этом рисунке, можно сделать несколько характерных выводов. Прежде всего видно, что при выводе неопределенной переменной х мы получаем просто имя этой переменной. Функции sin(х) и cos(х) в системе Mathematica обозначаются как Sin [х] и Cos [х]. Само по себе выражение sin(х) 2 + cos(х) 2 просто повторяется, а для его вычисления используется функция Simplify (упростить), аргументом которой является знак %, означающий подстановку предшествующего выражения. Два знака % можно использовать для подстановки предшествующего предшествующему выражению и т. д. Для вычисления строки ввода надо нажимать клавиши Shift+Enter, нажатие же одной клавиши Enter просто переводит строку в области ввода, именуемой также ячейкой ввода.
Любопытно, что в начале запуска, сопровождаемого музыкальным звуком, Mathematica выводит чистое окно редактирования документа, в котором нет даже маркера ввода — характерной вертикальной черточки. Этот маркер появится, как только вы введете какой-то первый символ. После получения первого результата появляется и длинная горизонтальная черта, отделяющая выведенные ячейки от свободного поля окна редактирования под ними. Эта черта является признаком возможности ввода очередной ячейки. Ее можно перевести в уже созданную область документа, если вы захотите создать новую ячейку среди уже существующих ячеек ввода.
Обратите внимание на то, что система выделяет ячейки ввода определителем In [N], а ячейки вывода — определителем Out [N], где N — автоматически проставляемый номер строки. Кроме того, в левой части отображаются квадратные скобки с особыми признаками, которые будут описаны в позже. Далее мы, как правило, будем опускать определители ячеек и квадратные скобки и представлять документы в упрощенной и более компактной форме. Например, представленный на рис. 1.15 документ может быть записан в следующем виде:
х
x
Sin[х]^2+Соs[х]^2
Cos[x] 2 +Sin[x] 2
Simplify[%]
1
Здесь входные выражения задаются жирным прямым шрифтом, а выходные — прямым шрифтом обычной насыщенности, то есть именно так, как они выглядят при настройке системы по умолчанию. При этом выходные выражения имеют обычный (в терминах системы Mathematica — стандартный) вид, присущий математическим формулам. Все такие выражения в книге представлены путем копирования ячеек ввода и вывода в текст с помощью буфера обмена (Clipboard). Технология такого копирования и ее особенности будут описаны далее.
Ячейки нумеруются по мере их использования. При этом можно с конца документа вернуться к его началу или середине и, изменив содержимое ранее использованных ячеек, снова выполнить вычисления. При этом ячейки меняют номера. При загрузке файла ячейки перенумеруются в строго последовательном порядке. Таким образом, номера ячеек не являются жестко фиксированными, они представляют собой сугубо техническое средство, отражающее работу системы в текущем сеансе — сессии. Это говорит в пользу отказа от вывода определителей ячеек при записи большинства примеров.
Математические системы в образовании и в науке
Можно сказать, что даже самые мощные системы для численных расчетов являются полными «профанами» в символьной математике. Они начисто лишены даже задатков элементарного разума, что видно уже из приведенного примера — даже школьник знает, что сумма квадратов синуса и косинуса равна в точности единице при любом аргументе х. А что говорить о столь распространенных аналитических вычислениях, как упрощение сложных математических формул, осуществление подстановок, вычисление пределов, производных и первообразных функций, разложении их в ряды Тейлора и Фурье, вычислении корней многочленов с буквенными коэффициентами и т. д.?
Такая возможность действительно имеется, однако следует иметь в виду, что векторные графические объекты, скопированные из Mathematica через буфер обмена, не вполне корректно воспринимаются другими приложениями. При верстке данной книги это вызвало очень много проблем.
Трудно сказать, сколько слез пролито школьниками и их матерями по поводу неправильно сделанных математических преобразований на контрольных работах и экзаменах и сколько ребят восприняли математику как заклятого врага из-за первых неудач в ее изучении. Еще больший урон народному хозяйству (то бишь рынку) наносит неумение выпускников школ и вузов применять современные математические методы на практике, хотя именно это является конечной целью фундаментального математического образования. Многие студенты запоминают математические истины от силы на несколько дней во время экзаменов.
Как же найти выход из этого тупика? Одна из возможностей — применение достаточно универсальных СКМ, автоматизирующих большую часть математических вычислений. Такие системы позволяют пользователю — как студенту, так и научному работнику — быстро вспомнить полученные в вузе знания и легко использовать их на практике без этапа нудных и трудоемких рутинных вычислений и преобразований. А заодно и освоить новые для себя методы и разделы современной математики.
К сожалению, за пределами возможностей численных математических систем оказались обширные области математики, связанные с проведением аналитических расчетов — от простых подстановок и сокращений до аналитической обработки математических выражений и функций и обучения компьютера новым математическим закономерностям и соотношениям. Всей этой работой, относящейся в основном к разделам элементарной и высшей алгебры, и были вынуждены заниматься математики-аналитики.
Увы, в нашей системе образования недостаточное знакомство с современными СКМ характерно не только для студентов, но и для доцентов и профессоров вузов. Среди них хорошее владение СКМ скорее исключение, чем правило. Это серьезно препятствует решению ряда первостепенных проблем образования — повышению его фундаментальности и вхождению нашей образовательной системы в общемировую, где компьютерные системы символьной математики в последние годы нашли самое широкое применение.
Очевидно, что чем раньше пользователь ПК начнет знакомиться с СКМ, тем больше математических знаний он получит. Хотя, безусловно, желательно, чтобы такое использование шло под контролем опытного преподавателя.
К сожалению, у нас есть серьезная причина, препятствующая широкому применению СКМ в образовании, — слабость материально-технической базы школ, вузов, да и многих университетов. Классами с современными ПК многие наши образовательные учреждения не обладают. Тем не менее, это чисто техническая проблема, которая постепенно решается.
В новых стандартах образования роль СКМ наконец-то осознана всерьез. По ряду специальностей математического профиля предусмотрено изучение СКМ. Это делает книги, подобные данной, нужными для системы образования.
Разумны ли системы символьной математики?
Математика непрерывно развивается, и ни один самый способный ученик не в состоянии (и слава Богу!) вместить в извилины своего мозга все математические законы и правила, созданные за многовековую историю человечества. Сотни лет назад такие задачи, как решение квадратного уравнения в общем виде, были в числе труднейших математических задач, а сейчас их «щелкают» школьники. Даже многотомные справочники по математике не гарантируют полного описания всех ее возможностей. Так что нет ничего страшного в том, что в наш просвещенный век вычисление производных или первообразных функций в аналитическом виде берет на себя компьютер. И их применение внешне становится таким же простым, как таблица умножения.
Сейчас слова «компьютерный разум» обычно берут в кавычки, всячески подчеркивая, что компьютер сам по себе не способен дать принципиально новые результаты (то есть те, которые не были заранее заложены в него человеком, его создавшим). Для многих, что в целом справедливо, вопрос о том, разумна ли система символьной математики, подобен вопросу о том, разумен ли хороший и полный справочник по математике.
И все же применительно к современным системам символьной математики (и универсальным СКМ) такая аргументация, пожалуй, не вполне приемлема. Да, базовые формулы и правила символьных преобразований в математические системы компьютерной алгебры заложены их создателями. Поэтому принципиально новых научных данных система сама по себе вроде бы и не дает. Но разве не такова в целом и ситуация с обычным использованием математического аппарата любым математиком-аналитиком?
Между тем большинству конкретных пользователей системы символьной математики дают новые знания в виде далеко не очевидных для них математических и иных закономерностей. Результат сложных и многоэтапных рекуррентных символьных преобразований даже по известным правилам может быть действительно новым, то есть ранее не опубликованным, заранее не предсказуемым и далеко не очевидным. Этим системы символьной математики принципиально отличаются от обычных справочников по тем или иным формулам. Они дают сведения не только по жесткому набору формул, но и по тем аналитическим соотношениям, которые в такой набор не вошли.
Подобные результаты нередко могут подтолкнуть серьезного научного работника или педагога к открытию неизвестных закономерностей в исследуемых или изучаемых ими явлениях. К тому же современные системы компьютерной алгебры способны к расширению — в них можно вводить новые закономерности и связи (подчас самые смелые и безумные), а затем исследовать малоизвестные или вообще неизвестные результаты их действия, получаемые в результате сложных аналитических преобразований. Так что вполне допустимо считать такие системы в известной мере разумными и способными помочь пользователю в создании новых теоретических положений и даже научных теорий.
Немаловажный довод в пользу некоторой разумности современных систем символьной математики заключается в особом назначении примеров их применения, которых в справочной базе данных могут насчитываться тысячи. Здесь уместно упомянуть высказывание И . М. Гельфанда: «Теории приходят и уходят, а примеры остаются».
Во всех современных СКМ примеры применения «живые» — вы можете подыскать наиболее близкий к решаемой вами задаче пример и тут же перестроить его под свои нужды. Обычные книги и справочники такой возможности принципиально не дают. Обучение на примерах — один из самых эффективных методических приемов. Он широко используется в данной книге и составляет основу справочной базы данных систем Mathematica.
В свое время нас учили, что количество переходит в качество. Примеров этого в природе превеликое множество. Системы компьютерной математики по обилию встроенных в них функций, правил преобразования и конкретных примеров применения уже вышли за пределы, которые способен оценить индивидуальный пользователь, даже если он достаточно опытный математик. К примеру, ядро Mathematica 4 хранит данные о примерно 5 тысячах интегралов! Это говорит о том, что СКМ находятся уже на пороге того, что их количественные характеристики перерастут в качественные. Среди них может оказаться и разум СКМ — на сей раз без каких-либо оговорок.
Что дает компьютерная математика университетам и школам
В конечном счете, СКМ — не более чем удобный и мощный инструмент для учащегося, педагога, инженера или научного работника. Как его применять (в методическом, научном и практическом отношении), зависит уже от пользователя. Однако важно и ценно то, что системы символьной математики снимают у учащихся психологический барьер в реальном применении математики, особенно высшей.
Тем не менее, многие преподаватели математики опасаются приобщения своих учеников к работе с СКМ. Бывает, что некоторые преподаватели школ и вузов при подготовке массовых заданий по алгебре, тригонометрии и геометрии сами применяют СКМ — например, для подготовки заданий по курсам математики или физики. Но это становится еще одним наивным поводом ограждать учащихся от систем символьной математики и даже запрещать их в учебном процессе. Оно и понятно — ведь школьник или студент, имеющий компьютер с системой компьютерной алгебры, прощелкает все подобные примеры за считанные минуты. Между тем учащихся, столь виртуозно владеющих системами компьютерной математики, надо лишь всячески поощрять! Увы, пока их очень мало...
Надо учитывать, что эффективное применение систем компьютерной алгебры практически невозможно без четкого понимания основ элементарной и высшей математики. Невозможно оно и без творческого участия пользователя как в постановке решения задач, так и в контроле и отборе результатов их решения. В большинстве математических систем используются специальные опции и директивы, направляющие решение в нужное русло. В какое именно — должен определить пользователь, владеющий нужными для этого математическими понятиями. Кроме того, именно пользователю необходимо проверить полученные результаты и убедиться в их достоверности.
Среди части преподавателей вузов существует в корне неверное мнение о том, что не нужно изучать сами СКМ — достаточно использовать доморощенные обучающие программы. Среди таких программ и впрямь есть интересные разработки, но, как правило, они базируются на ядре той или иной символьной СКМ, причем нередко старых версий, применяемых с целью обойти лицензионные ограничения.
По большому счету, такие обучающие системы ничего нового в процесс математических вычислений не вносят. Современные универсальные СКМ намного мощнее подобных программ, имеют более совершенный и более удобный интерфейс пользователя, а главное — только они реально применяются на месте работы будущих специалистов. Поэтому изучение современных СКМ столь же необходимо, как изучение офисных программ, например, того же текстового редактора Word 95/97. Наиболее удобной формой для этого являются спецкурсы, хотя и в ряде обязательных курсов такое изучение предусмотрено новыми учебными программами Министерства образования РФ.
В наших экономических условиях особенно велика роль систем компьютерной математики как мощных электронных справочников. Число издаваемых обычным способом справочников по математике или физике (не говоря уже о инженерных дисциплинах) в последние годы катастрофически упало. Это повышает роль справочников электронных, тем более что справочные базы данных современных систем компьютерной математики обладают рядом очевидных достоинств:
- вмещают в себя объемы информации, эквивалентные порой десяткам книг;
- аккумулируют знания, полученные за многие тысячелетия развития математики;
- имеют безупречное оформление документов (цветные тексты и иллюстрации, всевозможные выделения, качественные иллюстрации и т. д.);
- имеют разную организацию оглавления (индексную, поиск по контексту и т. д.); О отличаются очень быстрым поиском нужной информации по ряду критериев;
- имеют «живые» примеры, которые можно изменять в ходе просмотра справочных данных;
- справочные материалы могут сопровождаться звуковыми и видеокомментариями;
- позволяют готовить высококачественные и наглядные уроки не только по любым разделам математики, но и по многим дисциплинам, базирующимся на применении математического аппарата;
- позволяют быстро размножить интересующие пользователя материалы;
- обладают возможностью обновления и пополнения из сети Интернет.
Современные СКМ следует рассматривать не только как электронные справочники нового поколения, но и как системы для самообучения и дистанционного обучения математике. Однако для этого они должны быть снабжены грамотно составленными (прежде всего в методическом отношении) электронными уроками или книгами. Здесь необъятный простор для творчески мыслящих педагогов! В то же время, при отсутствии таких уроков применение математических систем может иметь негативные последствия для образования — опасна подмена обучения основам математики обучением основам работы с математическими системами.
Многие виды вычислений, даже элементарных, довольно трудоемки. Например, построение трехмерной поверхности требует зачастую сотен однообразных вычислений, выполнять которые крайне муторно даже при применении калькуляторов. Современные СКМ (в том числе Mathematica) делают это за считанные секунды, а то и за доли секунды. К тому же они сразу же строят графики поверхностей с разнообразной функциональной окраской и позволяют интерактивно вращать их (Mathematica 4), добиваясь лучшей выразительности и лучшего обзора фигур.
Применение СКМ в образовании избавляет учащихся от массы рутинных вычислений и высвобождает их время для обдумывания алгоритмов решения задач, более обоснованной постановки их решения, многовариантного подхода и представления результатов в наиболее наглядной форме. Высвободившееся время можно использовать для более глубокого изучения математической или физической сущности решаемых задач и их решения различными методами. Таким образом, СКМ не только не лишают учащихся серьезных математических навыков, но, напротив, способны их расширить и углубить.
Немаловажным фактором является то, что новейшие СКМ относятся к самым серьезным программным продуктам, имеющим современный пользовательский интерфейс и мощные средства визуализации всех этапов работы — причем, в области математики более выразительные, чем те, которые дают текстовые процессоры класса Word 95/97. Так что, работая с ними, пользователь поневоле осваивает работу с компьютером и познаёт тонкости интерфейса современных программ.
Кроме того, современные СКМ позволяют готовить и распечатывать документы, затрачивая на это куда меньше времени, чем популярные у математиков системы ТеХ или LaTeX. Впрочем, Mathematica прекрасно сожительствует с ними и позволяет представлять данные в необходимом для этих систем формате. Mathematica 4 поддерживает новейший формат подготовки математических документов для Интернета — MathML.
Работать с современными СКМ просто, приятно и поучительно. Благодаря этому освоение систем Mathematica воспринимается учащимися с большим интересом, что служит побудительным мотивом к их внедрению в систему образования, причем не только высшего, но и среднего, и даже начального (последнему, как отмечалось, фирма Wolfram в последние годы уделяет большое внимание).
Диалог с системой и ее входной язык
Интересно отметить, что, родившись как программа для профессионалов, Mathematica в последние годы упорно позиционируется фирмой Wolfram как система, перспективная не только для высшего, но и для школьного образования. Диалог с системой идет по методу «задал вопрос — получил ответ». Не считая отдельных мелочей, такой диалог вполне понятен не только опытному математику, но и успевающему студенту и даже школьнику.
Впрочем, уже из приведенных простейших примеров видны определенные тонкости записи входных выражений, которые определяются совокупностью правил их ввода, то есть синтаксисом входного языка системы, или (более строго) языка программирования системы. Он будет рассмотрен по мере описания возможностей систем класса Mathematica. Обширные возможности этих систем в решении математических задач придают им функции не только суперкалькуляторов, но и мощных электронных справочников по математике и математическим расчетам.
Даже интуитивно ясно, что осуществление символьных операций — процесс намного более тонкий и сложный, чем реализация даже сложных численных расчетов. В какой-то степени он противен сущности вычислений, реализуемых в современных ЭВМ, — как известно, они работают с «голыми» цифрами и являются «числодробилками». Эти операции сложнее и обычных (довольно примитивных) строковых операций, используемых при обработке текстов. К тому же известно, что одни только таблицы производных, интегралов и формул преобразований занимают многие тома объемных книг. Поэтому высокая эффективность символьных операций реальна только при их реализации на современных высокопроизводительных ПК. Не случайно системы символьной математики получили серьезное развитие лишь в последний десяток лет.
Все сказанное ведет к необходимости символьного представления чисел и использования особых алгоритмов для выполнения операций с ними. Естественно, что реализация символьных операций вначале обеспечивалась за счет снижения эффективности численных расчетов. Тем более приятно, что в новейшей системе Mathematica 4 эта порочная тенденция была решительно остановлена — данная версия системы имеет не только превосходные возможности в части символьных вычислений, но и повышенную эффективность и скорость численных расчетов. Это выдвигает систему Mathematica 4 в число лучших универсальных систем компьютерной математики.
Операции с целыми числами
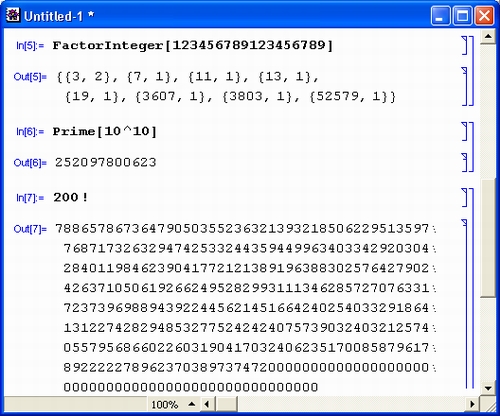
Продолжим знакомство с возможностями системы Mathematica 4 примерами работы с целыми числами. Несколько таких примеров приведено на рис. 1.4.
Рис. 1.4. Примеры целочисленных операций
Первая из приведенных операций дает разложение целого числа на простые множители с помощью функции Factorlnteger. Они представлены списками (в фигурных скобках) из двух чисел. Первое число — это множитель, а второе — число его повторений. В считанные секунды Mathematica 4 находит десятибиллионное простое число с помощью функции Prime. Другой характерный пример целочисленных операций — вычисление факториалов (вы можете запросто получить факториал 10 000, но ради сокращения места при описании примера в нем вычислено значение 200! Последний пример показывает отсутствие ошибок при работе с большими целыми числами — и это несмотря на то, что при его выполнении и впрямь дважды вычисляется факториал числа 10 000.
Операции с целыми числами выполняются абсолютно точно. При этом число цифр не ограничено (в разумных пределах).
Арифметика произвольной точности
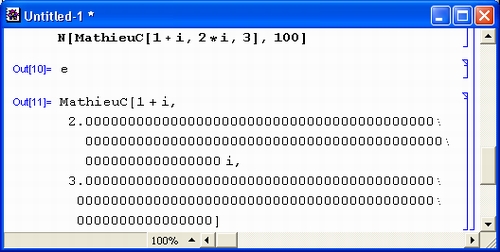
Арифметика произвольной точности — еще одна из областей применения систем символьной математики (рис. 1. 5).
Рис. 1.5. Примеры вычислений с большой точностью
Здесь использована одна из самых распространенных функций системы Mathematica — N[expr, n], дающая результат вычисления выражения ехр r с точностью до n знаков после десятичной точки. Константы я и е вычислены с 500 верными знаками, а новая функция Матье (MathieuC) — с точностью до 200 знаков. Однако в системе Mathematica n может достигать миллиона и более. Ограничения по разрядности чисел и их верхнему и нижнему пределам практически отсутствуют.
Примеры из математического анализа
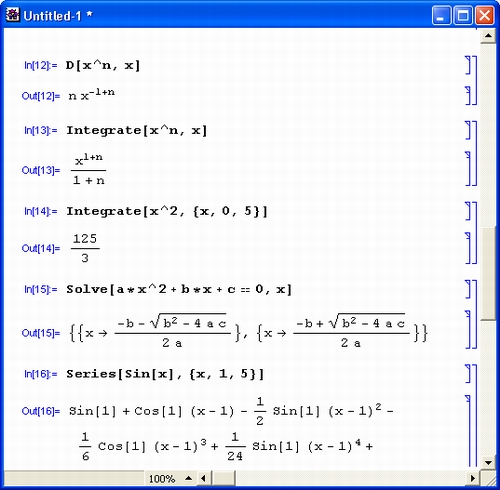
Разумеется, роль систем символьной математики далеко не исчерпывается приведенными выше примерами. Эти системы способны преобразовывать сложнейшие алгебраические выражения, находить аналитические решения сложных систем линейных, нелинейных и дифференциальных уравнений, манипулировать со степенными многочленами, вычислять производные и интегралы, анализировать функции, находить их пределы и т. д. Это видно уже из примеров, представленных на рис. 1.6 .
Рис. 1. 6 . Примеры вычислений из области математического анализа
В этих примерах функция D (как приятное исключение из правил, обозначенная одной буквой) вычисляет производную, функция Integrate — интеграл, функция Solve решает нелинейное уравнение (в данном случае квадратное), а функция Series разлагает выражение в ряд относительно заданной переменной и при заданных начальном значении переменной и максимальной степени ряда. В фигурных скобках задаются списки некоторых входных и выходных параметров (аргументов).
Системы символьной математики являются справочниками по многим специальным функциям. При этом они способны давать результаты вычислений в виде специальных функций, что демонстрируют следующие примеры:
Sum[1/k^9,{k,1,n}]
HarmonicNumber [n, 9]
Integrate [Log [x] *Exp [ -х^4 ], {x, 0, Infinity}]
-1/32*Gamma[ 1/4 ] ( 2 EulerGamma + л + Log[64] )
DSolve[y " [t] + y' [t] + y[t]/t = 0, y[t] , t]
{{y[t]->e^-tC[1]+e^-tC[2]Gamma[-1,-t]}}
Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и решения в аналитическом виде дифференциального уравнения. Соответствующие функции будут более подробно описаны в дальнейшем. Обратите внимание на то, что эти примеры даны прямо в тексте книги. Мы будем часто использовать такой прием для представления небольших примеров.
Чем дальше в лес, тем больше дров!
К сожалению, в математике нередко оказывается так, что результирующие выражения быстро нарастают по сложности при, казалось бы, незначительном усложнении или просто изменении условий задачи. Покажем это на примере решения одной из самых часто встречающихся задач — поиска в аналитическом виде корней алгебраического уравнения с целыми степенями членов.
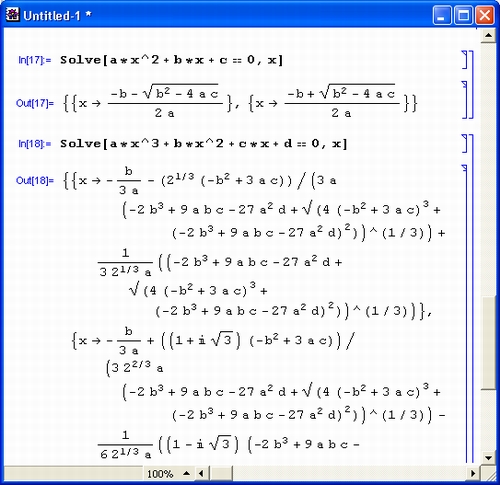
Многие из нас прекрасно помнят формулы для корней квадратного уравнения, которые нам давали еще в школе. Их в точности воспроизвела Mathematica в одном из примеров, приведенных в этом уроке чуть ранее. Это решение еще раз воспроизведено на рис. 1.7 (сверху).
Рис. 1.7. Система Mathematica решает квадратное и кубическое уравнения
Однако едва ли кто вспомнит по памяти формулы аналитического решения кубического уравнения общего вида. Зато система Mathematica играючи справляется с этой задачей с помощью функции Solve, что и показано во втором примере на рис. 1.19. Полученное выражение впечатляет даже студентов университетов, уже изучивших курс математики в полном объеме. Это блестящий пример эффективного представления справочной информации.
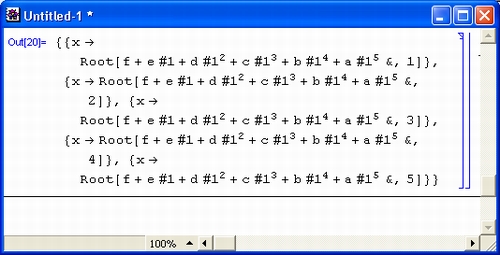
Можно пойти чуть дальше и убедиться в том, что Mathematica решает подобное уравнение даже четвертого порядка. Полученное при этом крайне громоздкое решение (в силу этого оно не приводится) заставит в задумчивости почесать затылок многих любителей математики. Но можно ли продолжать эти вычисления? Увы, классическая математика говорит, что нет! Подобные уравнения порядка выше четвертого современная математика в аналитическом виде не решает. Тем не менее, попытаемся вычислить корни алгебраического уравнения пятой степени в общем виде (рис. 1. 8 ).
Рис. 1.8 . Система Mathematica пытается решить алгебраическое уравнение пятой степени
А вот и сюрприз: Mathematica не только не отказалась решать эту задачу (при отказе она просто повторяет вводимое выражение), но даже подсказала путь ее решения с помощью пятикратного применения функции вычисления корней Root степенных многочленов.
В упомянутых примерах мы сталкиваемся с одной из серьезных проблем символьной математики — разбуханием результатов аналитических преобразований при порой незначительном усложнении решаемых задач. В данном случае это никоим образом не является недостатком систем компьютерной математики как таковых — просто так нарастает сложность решения данной математической задачи в соответствии с канонами абстрактной математики.
Однако нередко разбухание результатов кроется в сложности алгоритмов, особенно рекурсивных. Современные системы символьной математики способны осуществлять весьма глубокую рекурсию, и порой трудно даже предположить, к сколь громоздкому результату это в конечном счете приведет.
Научные работники и инженеры настолько привыкли к упрощению (порой весьма грубому, с точки зрения математиков), что громоздкие решения, получаемые с помощью систем символьной математики, способны их раздражать. Это в определенной мере препятствует применению систем символьной математики на практике и в наши дни.
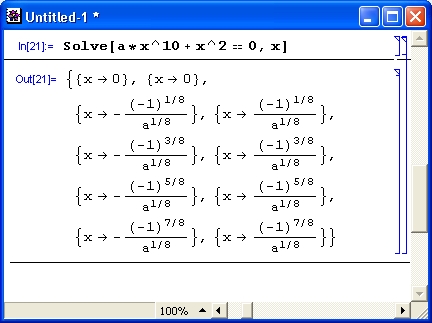
Однако для частных случаев нередко можно получить вполне сносные по виду решения. Вот пример решения неполного алгебраического уравнения десятой степени, при котором Mathematica благополучно возвращает все десять корней довольно простого вида (рис. 1.9 ).
Примеры такого рода можно встретить повсеместно. Есть множество нелинейных алгебраических или дифференциальных уравнений обманчиво простого вида, но имеющих сложнейшие решения или не имеющих их вовсе. Так что если система символьной математики не находит ответ, это зачастую не является признаком ее слабости — может быть, решения не существует вообще? Порой даже такой отрицательный результат избавляет пользователя от трудоемкого поиска несуществующих решений «в лоб» и направляет его на поиск обходных, порою весьма ценных и полезных методов решения.
Рис. 1.9 . Система Mathematical решает алгебраическое уравнение 10-й степени
Доверяй, но проверяй!
Ситуация с применением математических систем компьютерной алгебры осложняется тем, что они, как и люди-математики, могут давать результаты в различной форме и даже делать ошибки. Вынесенная в заголовок этого подраздела армейская поговорка как нельзя лучше характеризует правильные приемы работы с математическими системами. Если вы получили результат, который не ожидали, — не спешите считать его окончательным и тем более новым. Всегда желательно этот результат сначала проверить. Покажем, как это делается.
Пусть мы решили некоторое уравнение
eqns = х^3 - 3*х + 2 == 0
2-3х+х 3 == 0
и получили его корни
r = Solve[eqns, x]
{{х-> -2), {х^ 1}, {х-> 1}}
Для проверки решения можно использовать операцию подстановки в eqns списка корней г. Эта операция реализуется оператором / ., что иллюстрирует следующий пример:
eqns/.r
{True, True, True}
Результат этой операции — список из трех логических констант True (Истинно). Он означает, что решение верно. Кстати, с помощью этой подстановки можно получить истинный список корней:
х/.r
{-2, 1, 1}
Mathematica имеет и множество иных способов проверки полученных результатов. Но, к сожалению, очень редко встречаются ситуации, когда выданное Mathematica ошибочное или несуществующее решение при подобной проверке дает положительный результат. Как говорится, за что боролись, на то и напоролись! В таких особо каверзных случаях надо ориентироваться на свою интуицию, решение схожей тестовой задачи или решение с помощью других математических систем с иным ядром — например, Derive или Maple V.
Не стоит брезговать проверкой решений даже с помощью менее мощных систем — помните поговорки «Устами младенца глаголет истина!», «Пуля дура — штык молодец», «Мал золотник, да дорог!» и т. д.? Обращайтесь к описанным выше правилам проверки по мере освоения работы с системой Mathematica. При этом вам быстро станут понятными некоторые ее тонкости, которые пока остались «за бортом».
gl1-3.jpg
gl1-4.jpg
gl1-5.jpg
gl1-6.jpg
gl1-7.jpg
gl1-8.jpg
gl1-9.jpg
6. Установка систем и их особенности
Установка систем и их особенности
Инсталляция систем Mathematica 3
Объем инсталляционных файлов Mathematica 3 и 4 превышает 100 Мбайт. Поэтому поставляются системы на CD-ROM, а компьютер, на который они устанавливаются, должен иметь устройство чтения CD-ROM. Возможна и установка систем из локальной сети, но для большинства пользователей систем эта возможность существенного интереса не представляет и потому здесь не описывается. Кроме того, мы ограничимся описанием инсталляции систем, рассчитанных на работу в среде операционных систем Windows 95/98/NT.
Для установки системы Mathematica 3, по существу, нужен современный мультимедийный компьютер, оснащенный современной видеокартой, звуковой картой (совместимой с Sound Blaster фирмы Creative Labs), микрофоном и акустическими системами. ПК должен иметь процессор Pentium и емкость ОЗУ не менее 16 Мбайт (желательно даже 24 Мбайт и более). Минимальный объем файловой системы Mathematica 3/4 составляет 40 Мбайт, максимальный — 156 Мбайт (версии для Windows 95/98/NT с полной справочной системой).
Для инсталляции системы нужно прежде всего проверить соответствие аппаратных возможностей ПК требуемым. Только после этого можно начать инсталляцию запуском файла setup.exe (установка) с инсталляционного CD-ROM (часто это делается автоматически, если ПК настроен на самозапуск CD-ROM). Процесс инсталляции показан на рис. 1.10 на примере системы Mathematica 3.
В процессе инсталляции необходимые файлы с CD-ROM переносятся на жесткий диск, формируется файловая система пакета и создается папка под него. Практически сразу после инсталляции система готова к работе.
Рис. 1.10. Инсталлятор системы Mathematica 4
После инсталляции и первого запуска системы (из меню Пуск или активизацией ярлыка на рабочем столе) появляется окно регистрации, представленное на рис. 1.11. В нем надо заполнить все пункты. Номер лицензии указывается на конверте оптического диска, а вот для задания регистрационного номера может потребоваться запрос на фирму Wolfram Research — через Интернет или по обычной почте.
Рис. 1.11. Окно регистрации системы Mathematica4

Работа с CD-ROM системы Mathematica 4
Mathematica 4 также поставляется на CD-ROM. Поскольку данная книга посвящена детальному знакомству с системой Mathematica 4, мы рассмотрим работу с CD-ROM этой системы более подробно.
Самозапуск CD-ROM системы Mathematica 4 и выбор режима работы
CD-ROM системы Mathematica 4 рассчитан на автоматический запуск, для чего в его исходной директории имеется файл autorun.inf, считывание которого обеспечивает самозапуск CD-ROM. При этом появляется окно, показанное на рис. 1.12.
Рис. 1.12. Окно CD-ROM системы Mathematica 4
Из рисунка видно, что окно содержит меню выбора режима работы с CD-ROM:
- Install Mathematica to a hard disk — установка (инсталляция) системы на жесткий диск;
- Run Mathematica off the CD-ROM - запуск Mathematica 4 с CD-ROM;
- Run the Mathematica kernel off the CD-ROM — запуск ядра Mathematica 4 с CD-ROM;
- Browse the contents off the CD-ROM - просмотр CD-ROM;
- Register on the web — регистрация через Интернет.
Помимо обычной инсталляции системы на жесткий диск меню предусматривает работу с системой Mathematica 4 или с ядром системы непосредственно с CD-ROM. Это полезно, если работа с системой носит эпизодический характер или если на жестком диске ПК недостаточно места для установки системы Mathematica 4. Разумеется, комфортность и скорость работы с системой при ее установке на жесткий диск выше, чем при работе прямо с CD-ROM, особенно если используется устройство чтения с невысокой скоростью считывания. Впрочем, для современных CD-ROM с кратностью скоростей 32 и выше работа оказывается вполне сносной. В корневом каталоге CD-ROM содержатся три подкаталога:
- PC — подкаталоги и файлы для стандартной инсталляции и работы в среде операционной системы Windows 95/98/NT;
- PC_8_3 — подкаталоги и файлы для инсталляции системы в случае, если устройство чтения CD-ROM не поддерживает длинные имена файлов;
- UNIX — подкаталоги и файлы для инсталляции в среде операционной системы UNIX.
Подкаталог PC содержит обычные (не архивированные) файлы системы Mathematica 4. Они используются как для копирования на жесткий диск при обычной инсталляции системы, так и для прямой работы с CD-ROM. Если устройство чтения CD-ROM не поддерживает считывание длинных имен файлов, то для инсталляции системы на жесткий диск используются файлы из каталога PC_8_3, которые имеют до 8 символов в имени и до 3 символов в расширении. Подкаталог UNIX содержит файлы, необходимые для инсталляции системы на компьютерах платформы UNIX.
Установка Mathematica 4 на жесткий диск
Для серьезной работы с системой Mathematica 4 ее следует установить на жесткий диск компьютера. Перед этим надо проверить соответствие аппаратных требований реальным возможностям вашего ПК. Минимальные требования для установки системы Mathematica 4 следующие:
- IBM/Intel-совместимый компьютер с процессором класса не ниже 80386;
- операционная система Windows 95, 98 или NT;
- объем ОЗУ не менее 16 Мбайт, желательно 24 Мбайт при работе с Windows 95/ 98 и 32 Мбайт при работе с Windows NT;
- устройство чтения CD-ROM — для считывания инсталляционного диска;
- видеосистема класса SVGA;
- звуковая карта класса Sound Blaster для работы со звуком;
- все файлы системы Mathematica 4 занимают 156 Мбайт. Из них лишь 40 Мбайт приходится на минимальный вариант установки — файлы ядра (Kernel), интерфейсного процессора (Front end), библиотеки (Mathlink Libraries) и шрифты математических символов (Fonts). Дополнительно могут устанавливаться стандартные пакеты расширения (Standard Add-on Packages) и необходимые для связи с ними файлы инструментария (MathLmk Developer's Kit ) — 12 Мбайт. Куда больше занимает онлайновая документация справочной системы — The Mathematica Book, Reference Guide, Standard Add Package и Additional Documentation. Для ее установки нужно еще 104 Мбайт.
Для установки Mathematica 4 на жесткий диск надо активизировать кнопку с надписью Install Mathematica to a hard disk. Начнется подготовка инсталлятора системы. В ходе установки в особом каталоге создаются временные файлы, которые впоследствии автоматически уничтожаются. Однако для их установки на жестком диске необходимо иметь свободное пространство — около 200 Мбайт при полной установке системы.
После подготовки инсталлятора появляется обычное окно с вступительным сообщением. Нажав кнопку Next, можно перейти к следующему этапу инсталляции. При этом появляется окно регистрации системы (рис. 1.13). Обычно первые три поля из пяти бывают заполнены автоматически: это идентификационный номер MathID, имя компьютера и имя организации. Разумеется, вы можете их изменить. Номер лицензии обычно указывается на коробке, в которой поставляется система, и на конверте с текстами лицензионных материалов. А вот пароль дается фирмой Wolfram отдельно — по телефону, факсу, электронной почте или через Интернет (нелегальные способы получения пароля с помощью генератора номеров лицензии и пароля здесь не обсуждаются).
Рис. 1.13. Окно регистрации системы
Если все данные в окне регистрации введены, то нажатие кнопки Next обеспечивает продолжение установки системы на жесткий диск. Как обычно, в окне выбора режима инсталляции будет предложено три варианта — полный, минимальный и выборочный. Рекомендуется использовать выборочный, поскольку при этом можно прочесть наименования всех компонентов системы (рис. 1.14). Обратите внимание, что при полной установке системы она занимает на жестком диске около 170 Мбайт. Вы можете значительно уменьшить этот объем, отказавшись от установки пакетов расширений, документации и т. д. Минимальный объем памяти на диске при этом составит около 50 Мбайт. Но возможности системы будут заметно урезаны.
Рис. 1.14. Окно выбора устанавливаемых компонентов системы
Установив (или подтвердив) набор компонентов нажатием кнопки Next, можно перейти к следующему шагу установки — выбору имени системы в главном меню операционной системы Windows 95/98/NT. Окно, дающее возможность такого выбора, представлено на рис. 1.15.
Рис. 1.15. Окно выбора имени позиции системы в главном меню
Осуществив выбор имени позиции меню, можно нажатием кнопки Next завершить подготовку к инсталляции. Она подтверждается появлением окна, показанного на рис. 1.16. В этом окне приводится список всех компонентов системы, намеченных к установке на жесткий диск. Если вы обнаружили, что пропустили нужный вам компонент, еще не поздно сделать шаг назад, активизировав кнопку Back.
Рис 1.16. Окно подтверждения завершения подготовки к инсталляции
Нажав кнопку Next, мы переходим к инсталляции системы Mathematica 4 на жесткий диск. Картина работы инсталлятора представлена на рис. 1.17. Окна с краткими описаниями новшеств в верхнем левом углу окна инсталлятора время от времени меняются. Полезно просмотреть их содержание, благо на этом этапе инсталляции пользователю делать больше нечего. Индикатор прогресса (внизу справа) показывает ход инсталляции и имена текущих файлов, копируемых на жесткий диск. Общую информацию дают гистограммы, расположенные в левом нижнем углу окна инсталлятора.
Инсталляция заканчивается выводом окна завершения инсталляции (рис. 1.18). Фирма Wolfram рекомендует в случае появления проблем с инсталляцией прежде всего попытаться устранить факторы, препятствующие инсталляции. Для этого надо внимательно разобраться с сообщениями о причинах сбоя. Далее следует провести инсталляцию с помощью файлов поддиректории PC_8_3 CD-ROM. Если и это не помогает, то остается предпоследнее — обратиться в службу технической поддержки фирмы Wolfram. Или последнее — сменить компьютер!
Нажатие кнопки ОК в заключительном окне завершает процесс установки системы Mathematica и стирает временные файлы инсталлятора.
Рис. 1.17. Ход инсталляции системы Mathematica 4
Рис. 1.18. Окно с подтверждением успешно проведенной установки
После установки системы Mathematica 4 на жесткий диск в папке Программы главного меню операционной системы Windows появляется позиция с ярлыками системы Mathematica 4 (рис. 1.19).
Рис. 1.19. Система Mathematica 4 в главном меню Windows 98
Как видно из рис. 1.19 (нижняя позиция главного меню), система Mathematica 4 представлена тремя ярлыками:
- Mathematica 4 — запуск системы Mathematica 4;
- Mathematica 4 Kernel — запуск ядра системы Mathematica 4;
- Uninstall Mathematica 4 — удаление системы Mathematica 4.
Запуск Mathematica 4 выполняется, как обычно, активизацией позиции Mathematica 4 в главном меню программ. При этом появляются строка меню, чистое окно документа Untitled-1 и базовая панель ввода. Теперь можно начинать работу, как было описано ранее (рис. 1.20).
Пользовательский интерфейс создается одной из двух основных частей системы — интерфейсным процессором (Front-end); вторая основная часть — ядро системы (Kernel). После загрузки интерфейсного процессора появляется скромная панель главного меню системы и пустое окно редактирования документов. В нем можно начинать вычисления, что и показано на рис. 1.20.
Рис. 1.20. Начало работы с системой Mathematica 4
В правой части экрана видна одна из палитр системы — палитра ввода математических выражений. Она появляется по умолчанию при обычной инсталляции системы. Если этой палитры нет, то для ее вывода надо исполнить команду Basic-Input в подменю Palettes меню File. При этом запускается специальный файл, выводящий данную палитру. После этого она будет выводиться всякий раз при очередном запуске системы.
Палитру можно использовать для ввода спецзнаков и операторов, например возведения в степень, вычисления производной или интеграла и т. д. Примеры применения палитры тоже показаны на рис. 1.20. Обратите внимание, к примеру, на естественный вид интеграла в строке ввода 6. Шаблон интеграла вводится с помощью палитры Basiclnput и затем заполняется. Мы не будем описывать этот процесс подробно, поскольку он вполне естественен и легко осваивается даже начинающими пользователями.
В общем случае для получения естественной формы шаблона математического выражения в строках ввода надо изменить их обычный формат InputForm (форма ввода) на формат StandardForm (стандартная форма). Для этого выберите вариант InputForm в подменю Convert То (Преобразовать в...) меню Cell.
Можно отметить некоторые отличительные, но вовсе не принципиальные признаки работы именно с системой Mathematica 4. Над строкой меню дано полное название системы — «Mathematica 4». При вводе выражений используется цветная раскраска элементов — например, незакрытые скобки имеют красный цвет и меняют его на черный после ввода завершающих скобок. Это облегчает ввод сложных выражений и их редактирование в строках ввода. Более скромным (в стиле Microsoft Office 97) стало оформление кнопок. Но главное — даже на первый взгляд заметно ускорение работы с элементами пользовательского интерфейса.
Если вы намерены часто пользоваться системой Mathematica 3/4, позаботьтесь о том, чтобы создать ярлык системы на рабочем столе Windows 95/98/NT. В этом случае запуск системы предельно упрощается — надо установить курсор мыши на ярлык и дважды быстро щелкнуть левой кнопкой мыши (пользователи Windows 98 могут настроить систему на запуск программ однократным коротким нажатием левой кнопки мыши).
Если пользователь работает с системой Mathematica 4 эпизодически, он может воспользоваться прямой работой с CD-ROM. Для этого после самозапуска CD-ROM нужно активизировать кнопку Run Mathematica off the CD-ROM. Появится окно регистрации, уже описанное ранее. После ввода данных о регистрации работа с системой ничем не отличается от обычной (при запуске с жесткого диска). Заметно лишь замедление работы при манипуляциях с пользовательским интерфейсом и файлами.
Работа с ядром системы Mathematica 4
В Mathematica 4 предусмотрена прямая работа с ядром системы в режиме командной строки. Такая работа возможна как после активизации ярлыка Mathematica 4 Kernel в папке системы, так и после выбора команды Run the Mathematica kernel off the CD-ROM при самозапуске CD-ROM. При этом работа с ядром возможна даже в MS-DOS.
При пуске ядра указанными способами появляется окно, показанное на рис. 1.21, в полностью развернутом виде. Лишь сообщения сверху окна указывают на то, что работает новейшая версия системы — Mathematica 4. В остальном работа с ядром напоминает работу в текстовом режиме системы Mathematica 1.0. Даже графики в данном случае строятся текстовыми символами, что наверняка умилит почитателей ретро в области вычислений.
При всей примитивности прямой работы с ядром она имеет ряд достоинств:
- работа происходит быстро;
- удобно знакомиться с назначением функций системы;
- простой формат ввода и вывода облегчает копирование;
- возможна работа в MS-DOS;
- требуются минимальные ресурсы ПК.
Таким образом, прямая работа с ядром может быть полезна при освоении системы Mathematica.
Рис. 1.21. Пример прямой работы с ядром системы Mathematica 4
gl1-11.jpg
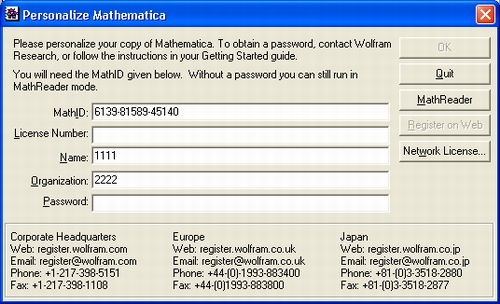
gl1-12.jpg

gl1-13.jpg
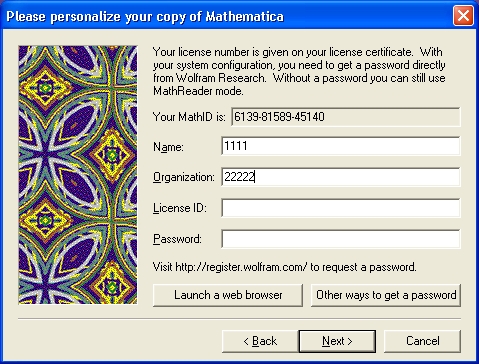
gl1-14.jpg
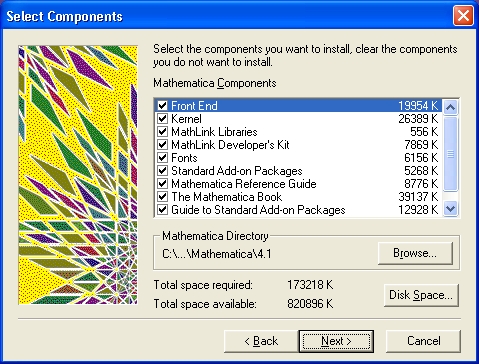
gl1-15.jpg
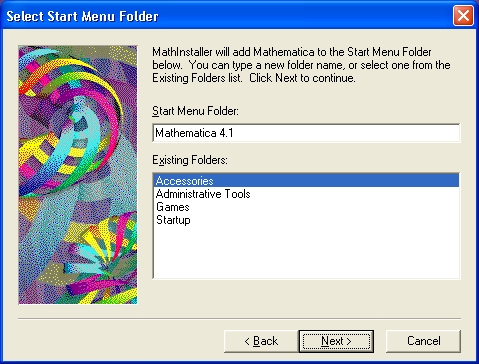
gl1-16.jpg
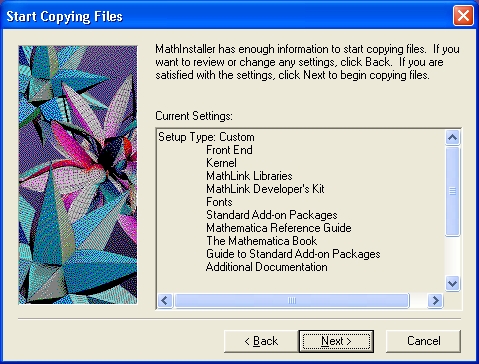
gl1-17.jpg
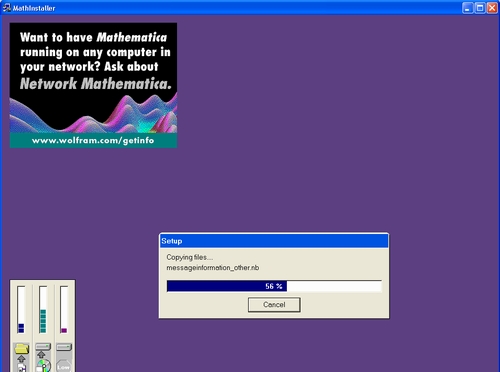
gl1-18.jpg
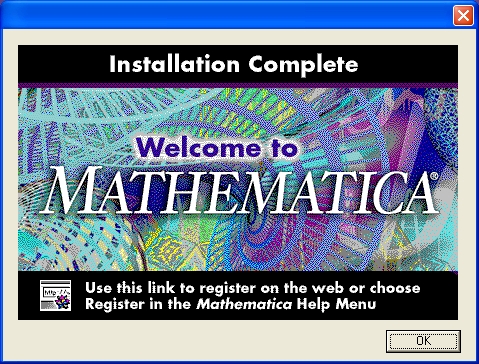
gl1-19.jpg
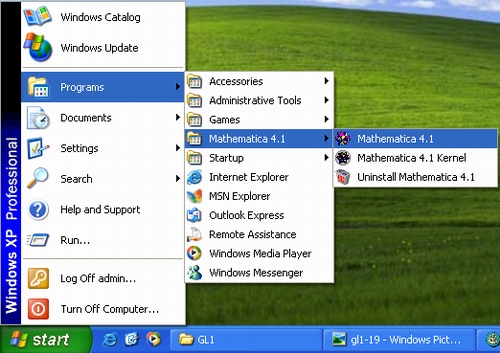
gl1-20.jpg
gl1-21.jpg
7. Отличительные особенности Mathematica 4
Отличительные особенности Mathematica 4
Ускорение численных расчетов и повышение их точности
Большинство пользователей с трудом уловят разницу между версиями Mathematiea 3 и Mathematica 4. Именно поэтому основной материал данной книги полностью относится к этим двум последним версиям. Тем не менее, различия между версиями есть, и достаточно серьезные.
Пожалуй, главной отличительной особенностью системы Mathematica 4 стало кардинальное ускорение численных расчетов. Традиционно системы символьной математики проигрывали численным системам, таким как MATLAB. До сих пор скорость вычислений в системе MATLAB в 5-10 раз превышала скорость вычислений, производимых системами символьной математики. Поэтому в системе Mathematica 4 были предприняты необычные для систем символьной математики и даже беспрецедентные меры по ускорению численных расчетов. Они перечислены ниже:
- Значительно ускорены все операции с матрицами, особенно большого размера.
- Существенно оптимизированы алгоритмы для выполнения вычислений с числами, содержащими вплоть до миллиона знаков.
- Ускорен ввод и вывод очень больших целых чисел.
- Полностью сохраняется точность при вводе и выводе приближенных действительных чисел.
- Обеспечивается свертка и корреляция массивов любой размерности.
- Применены новые оптимизированные алгоритмы для преобразований Фурье.
- Ускорены процедуры численного решения полиномиальных уравнений.
Рисунок 1.22. иллюстрирует некоторые простые вычисления в численном виде с фиксацией времени вычислений для систем Mathematica 3 и 4 (данные получены от разработчика).
Рис. 1.22. Сравнительные данные по скорости простых вычислений
Из примеров на рис. 1.34 видно, что скорость простых вычислений возросла в 5-10 раз.. В отдельных случаях скорость более сложных вычислений возрастала намного больше. Ниже приведены данные о выполнении некоторых операций над матрицей m большого размера (500x500).
|
Операция |
Mathematica 4 |
Mathematica 3 |
Отношение времен |
|
Sin [m] (m+ 1) 100 Min [m] |
0,13с 0,311 с 0,02с |
2,433 с 4,426 с 4,487 с |
18,7:1 14,23:1 224:1 |
Такое резкое ускорение скорости численных расчетов способно открыть для системы Mathematica 4 новые обширные сферы применения, например численное моделирование сложных систем, описываемых матричными алгебраическими и дифференциальными уравнениями.
Кардинально уменьшено и время обращения к памяти при записи и считывании массивов, а заодно существенно повышена плотность упаковки массивов для данных различного типа (за счет применения особой технологии упаковки массивов). Приведенные ниже сведения характеризуют это для версий Mathematica 4 и 3 для ряда типов данных — целых (Integers), вещественных (Reals) и комплексных (Complex Numbers).
|
Mathematica 4 |
Mathematica 3 |
|||
|
Тип данных |
Время, с |
Объем памяти |
Время, с |
Объем памяти |
| Integers | 0,24 | 400 056 | 0,43 | 2 000 024 |
| Reals | 0,231 | 800 056 | 0,611 | 2 000 024 |
|
Complex Numbers |
0,35 |
1 600 056 |
1,341 |
6 000 024 |
Уплотнение массивов означает, что Mathematica 4 при заданном объеме свободной памяти может решать более объемные и серьезные задачи, чем это смогла бы сделать предшествующая версия системы.
Указанные достоинства системы Mathematica 4 достигнуты за счет выбора и тщательной оптимизации алгоритмов численных вычислений:
- введена прямая поддержка следов матриц;
- изменены алгоритмы нахождения минимума (функция FindMinimum);
- реализован ускоренный вывод больших чисел — вплоть до миллионов цифр;
- введена новая технология упаковки больших массивов чисел;
- существенно уменьшена необходимость в повторных циклах;
- обеспечена абсолютная точность при целочисленных вычислениях;
- гарантирована заданная погрешность при вычислениях с вещественными числами;
- улучшено размещение переменных в памяти.
По умолчанию погрешность вычислений при целочисленных операциях в системе Mathematica 4 определена в 1 000 000 верных цифр. К примеру, чтобы выдать число n с миллионом верных знаков, системе Mathematica 4 понадобится чуть больше двух минут (разумеется, на современном компьютере)! В некоторых видах сложных целочисленных вычислений, используемых в технике кодирования информации, Mathematica 4 обеспечивает беспрецедентно малое время вычислений.
Улучшенные математические возможности
Математические возможности системы Mathematica 4 существенно пополнены и улучшены. В частности, обеспечены следующие возможности:
- прямая поддержка линейной алгебры разреженных матриц;
- экспериментальная поддержка кванторного исключения с использованием цилиндрического алгебраического разложения;
- экспериментальная поддержка символьной оптимизации;
- быстрая свертка и корреляция для массивов любого размера и размерности;
- новые улучшенные алгоритмы для преобразований Фурье (рис. 1.23);
- ускоренное вычисление полиномиальных уравнений;
- новые алгоритмы для функции минимизации FindMinimum;
- расширение возможностей матричных преобразований;
- алгебраическая вычислительная поддержка для функций символьных преобразований Simplify, FunctionExpand и связанных с ними других функций;
- расширение возможностей функций преобразования FullSimplify и FunctionExpand;
- упрощение полиномиальных и других неравенств;
- полная улучшенная поддержка символьных преобразований Лапласа и Фурье;
- расширенные возможности решения трансцендентных уравнений;
- ускоренное неоднократное дифференцирование;
- поддержка ряда новых специальных функций (Дирака, Струве, обобщенных логарифмов, двумерных гипергеометрических функций Аппеля, полилогарифмов Ньелсена, гармонических функций, различных констант и т. д.);
- новые оптимизированные методы для оценивания е, n и других констант с очень высокой точностью;
- полная поддержка для непрерывных дробей и периодических цифровых последовательностей ;
- прямая поддержка поразрядных операций.
Рис. 1.23. Пример выполнения преобразования Фурье в среде Mathematica 4
Из рис. 1.23. видно, что на преобразование Фурье массива 500x500 элементов Mathematica 4 затратила около 2 с. Для сравнения отметим, что Mathematica 3 выполнила ту же работу за 11 с, то есть ускорение преобразования Фурье оказывается более чем пятикратным.
Рисунок 1.24. иллюстрирует возможности выполнения интегральных преобразований Лапласа и Фурье в символьном виде.
Рис. 1.24. Примеры интегральных аналитических преобразований
Некоторые другие примеры использования, характерные для системы Mathematica 4, можно найти на Интернет-странице фирмы Wolfram.
Улучшенная поддержка средств графики и звука
Графика всегда была козырной картой систем Mathematica. В новой версии системы также реализованы многочисленные новые возможности. Отметим наиболее существенные из них:
- ускоренный вывод графических данных на дисплеи больших размеров;
- экспорт и импорт графики и звука во многих форматах (рис. 1.25);
- поддержка дискретного масштабирования уровней цвета;
- поддержка трехмерной динамической графики в реальном времени (только в среде Windows);
- ускоренная генерация и вывод на экран больших графиков;
- полностью согласованная поддержка безусловных опций.
Рис. 1.25. Форматы ввода и вывода изображений, поддерживаемые системой Mathematica 4
Всего Mathematica 4 поддерживает свыше 20 различных форматов файлов. Возможность импорта графического файла с высоким разрешением в формате TIFF и последующего преобразования файла в формат JPG иллюстрирует рис. 1.26.
Рис. 1.26. Пример импорта файла в одном формате и экспорта того же файла в другом формате
Средства графики Mathematica 4 позволяют использовать систему в качестве графического процессора, осуществляющего эффективные цифровые преобразования изображений, такие как стилизация (рис. 1.27), повышение и понижение контрастности и яркости, обработка цветов, фильтрация и т. д.
Рис. 1.27. Пример обработки изображения, показанного на рис. 1.26
Все это, разумеется, повышает шансы системы Mathematica 4 сохранить за собой роль мирового лидера среди систем компьютерной математики для ПК.
Вращение трехмерных графиков мышью
Следом за системами Maple V R5 и Mathcad 8 PRO Mathematica 4 приобрела возможность быстрого вращения произвольных трехмерных графиков. Пример реализации этой возможности представлен на рис. 1.28.
Данная возможность достигнута за счет существенного ускорения построения сложных трехмерных фигур с помощью команды, включенной в специальный файл и загружаемой как
<<RealTime3D`
Другая команда,
<<Default3D`
возвращает систему к стандартным возможностям трехмерной графики.
Из приведенных данных ясно, что возможности системы Mathematica 4 и скорость ее работы существенно повышены. Однако при этом сохранена практически полная совместимость по интерфейсу пользователя и базовому набору операторов и функций с предшествующей версией Mathematica 3. Так что из этой книги читатель получит достаточно полные сведения не только о новейшей версии Mathematica 4, но и о ее предшественнице — системе Mathematica 3. Значительная часть сведений и примеров полезны и пользователям версий Mathematica 2.x.
Рис. 1.28. Стоп- кадр документа, показывающего возможность вращения трехмерной фигуры в реальном времени
При выборе той или иной версии решающую роль играют финансовые соображения и аппаратные требования к компьютеру. Как уже отмечалось, новая версия Mathematica 4 для установки на компьютере с операционной системой Windows 95/98 требует объема ОЗУ 16/24 Мбайт и 40/156 Мбайт места на жестком диске (в числителе дробей минимальное значение, в знаменателе — рекомендуемое). В то же время, система Mathematica 2.2.2 требует емкости ОЗУ 8 Мбайт (версия 2.1 — даже 4 Мбайт), занимает на жестком диске 14 Мбайт и инсталлируется с 6 обычных гибких дисков.
Программирование и ядро системы
Средства программирования и ядра системы Mathematica дают ряд новых возможностей:
- функции NestWhile и NestWhileList, позволяющие обобщения функции FixedPoint;
- функции PadLeft и PadRight;
- поддержку перекрытия и расширения подсписков, генерируемых функцией Partition;
- функции ListConvolve и ListCorrelate;
- обобщение функций Take, Drop и связанных с ними функций до любой размерности и любых шагов по индексу;
- поддержку функции All для определения частей на определенных уровнях в выражениях;
- расширения в функции Mod для поддержки кириллических списков;
- контекст Developer, предоставляющий доступ к внутренним функциям системы;
- контекст Experimental, предоставляющий доступ к функциям, находящимся в стадии разработки.
Операции ввода и вывода в Mathematica 4 дают следующие новые возможности:
- оптимизированный разрыв строк для удобства ввода выражений и программ;
- динамический текстовый курсор, обеспечивающий визуальную непрерывность ввода;
- динамические цветные подсказки при вводе ограничивающих скобок;
- автоматическое замещение вводимых ключевых последовательностей специальными символами или другими объектами;
- новый альтернативный синтаксис для извлечения частей выражений и применения функций;
- внедрение ячеек в текст;
- существенно ускоренный вывод строковых выражений.
На уровне системного интерфейса в Mathematica 4 обеспечены:
- поточный вывод табличных данных;
- развитая поддержка преобразования ячеек в HTML;
- дополнительная поддержка вывода в формате ТеХ;
- ускорено взаимодействие с внешними программами через MathLink;
- поддержка дополнительных наборов символов, включая китайские и корейские;
- экспериментальная поддержка вывода на экран в режиме реального времени;
- экспериментальная поддержка удаленных файловых систем через MathLink;
- экспериментальная поддержка всплывающих кнопочных палитр.
gl1-22.jpg
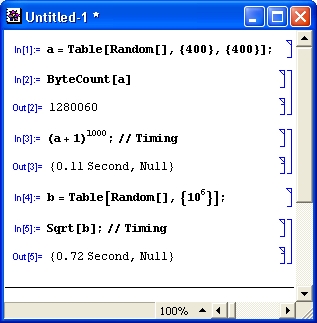
gl1-23.jpg
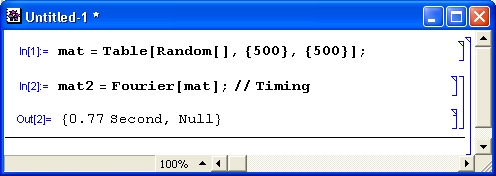
gl1-24.jpg
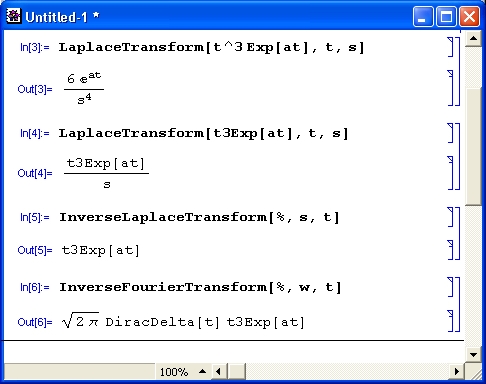
gl1-25.jpg
gl1-26.jpg
gl1-27.jpg
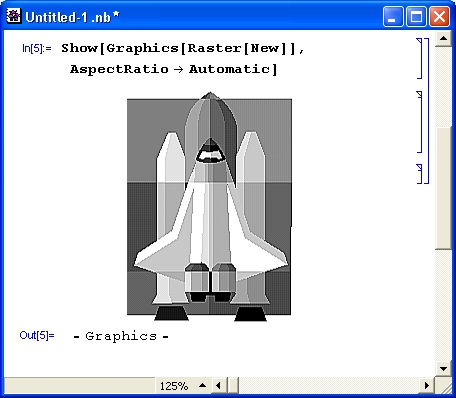
gl1-28.jpg
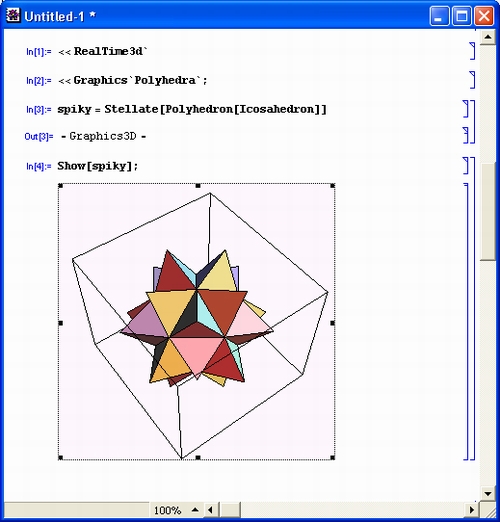
8. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Классифицировать системы компьютерной математики.
- Оценивать аппаратные ресурсы, нужные для работы с системами Mathematiса 3 и 4.
- Использовать Интернет-сайт фирмы Wolfram Research — разработчика систем Mathematica.
- Использовать некоторые средства диалога с системой.
- Выполнять проверку некоторых решений.
- Выполнять инсталляцию систем Mathematica 3 и 4.
- Запускать системы Mathematica 3 и 4.
- Выполнять прямые операции с ядром систем.
- Распознавать многочисленные отличительные особенности Mathematica 4.
Урок 2. Интерфейс системы
Урок 2. Интерфейс системы
1. Интерфейс системы
Интерфейс системы
- Строка меню и окно редактирования документов
- Палитры математических операторов и функций
- Понятие о документах в форме notebooks
- Особенности интерфейса Mathematica 4
- Основные виды файлов и пакеты расширения
- Работа с файлами
- Печать документов
- Основные понятия о документах и их стилях
- Понятие о ячейках документов
- Манипуляции с ячейками
- Вставка различных элементов
- Управление процессом вычислений
- Команды поиска и замены
- Управление расположением окон
- Справочная база данных
Прежние версий системы Mathematica имели довольно скромный стандартный интерфейс, характерный для приложений MS-DOS. Однако в версиях Mathematica 3/4 интерфейс был существенно переработан. В этом уроке подробно рассматривается интерфейс систем Mathematica 3/4. Освоение интерфейса не менее важно, чем освоение чисто математических возможностей системы, поскольку именно использование всех возможностей интерфейса позволяет готовить вполне современные документы, отличающиеся высоким качеством визуализации.
2. Строка меню и окно редактирования документов
Строка меню и окно редактирования документов
До сих пор разработчики пользовательского интерфейса математических систем по существу копировали стандартный интерфейс программ из комплекса Microsoft Office 95/97, в частности, самого популярного текстового процессора Word 95/97. Разработчики интерфейса пользователя систем Mathematica 3/4 отошли от этой традиции.
Нетрудно заметить, что пользовательский интерфейс систем Mathematica 3/4 реализует отдельный вывод своих элементов — окон (включая основное окно редактирования), панелей, палитр знаков и т. д. Это позволяет располагать их в любых местах экрана, что особенно удобно при работе с дисплеями, имеющими большой размер изображения — от 17 дюймов по диагонали и выше. При работе с дисплеями, имеющими небольшой экран (14 или 15 дюймов) и стандартном разрешении 640x480 пикселей раздельный вывод элементов интерфейса скорее неудобен, поскольку приходится тщательно располагать их в нужных местах и индивидуально подстраивать размеры отдельных окон и палитр. Однако после настройки элементы интерфейса выводятся в том виде, как это было задано.
Главное окно системы имеет крайне невзрачный вид, поскольку не содержит ничего, кроме строки заголовка и строки меню.
Справа и снизу большого окна редактирования находятся линейки прокрутки с характерными ползунками, управляемыми мышью. Они предназначены для скроллинга текстов больших документов, если последние не помещаются в видимой части окна. Положение ползунка приближенно указывает место в документе, которое в данный момент отображается на экране.
В самом низу в начале линейки прокрутки имеется строка состояния (Status bar) с информацией о текущем режиме работы. Эта информация (если она есть в данный момент) полезна для оперативного контроля в ходе работы с системой.
Главное меню системы (см. рис. 1.20, сверху) содержит следующие позиции:
- File — работа с файлами: создание нового файла, выбор файла из каталога, закрытие файла, запись текущего файла, запись файла с изменением имени, печать документа и завершение работы;
- Edit — основные операции редактирования (отмена операции, копирование выделенных участков документа в буфер с их удалением и без удаления, перенос выделенных участков, их стирание);
- Cell — работа с ячейками (объединение и разъединение ячеек, установка статуса ячейки, открытие и закрытие);
- Format — управление форматом документов;
- Input — задание элементов ввода (графиков, матриц, гиперссылок и т. д.);
- Kernel — управление ядром системы;
- Find — поиск заданных данных;
- Window — операции с окнами и их расположением;
- Help — управление справочной системой.
Часть команд может быть в данный момент невыполнима — например, нельзя вычислить значение выражения, если его самого нет в окне редактирования или если ячейка с ним не выделена. Названия таких команд выделяются характерным серым расплывчатым шрифтом. Четкий шрифт, напротив, характерен для тех команд, которые в данный момент могут исполняться. Управление главным меню самое обычное.
3. Палитры математических операторов и функций
Палитры математических операторов и функций
У многих программ интерфейс предусматривает вывод панелей с кнопками быстрого управления — уже привычными стали панели инструментов и панели форматирования. С одной стороны, эти панели упрощают работу, особенно для начинающих пользователей, но, с другой стороны, они загромождают экран.
Тогда как большинство фирм-разработчиков программ компьютерной математики пошло по пути уменьшения числа таких кнопок, Wolfram Research сделала решительный шаг и вообще отказалась от вывода инструментальной панели с подобными кнопками. Причина такого шага вполне очевидна — запомнить назначение множества кнопок по рисункам на них оказалось ничуть не проще, чем иметь дело с множеством имен команд в обычном меню. Однако все же надо признать, что некоторое количество кнопок быстрого управления стоило бы оставить.
Однако, сделав шаг назад, упомянутая фирма одновременно сделала два шага вперед — она ввела выбираемые пользователем и перемещаемые по экрану в любое место инструментальные палитры со множеством пиктограмм ввода математических символов, функций и команд управления системой. Они выводятся с помощью меню File | Palettes (Файл | Палитры). Если вывести все инструментальные палитры, то они едва умещаются в главном окне системы (рис. 2.1).
Рис. 2.1. Инструментальные палитры системы Mathematica 4
Палитры, предназначенные для ввода математических спецзнаков, намного упрощают работу по подготовке документов. Общее число специальных математических знаков (греческих и латинских букв, операторов, функций и команд), вводимых с помощью палитр, составляет около 700. Многие знаки имеют альтернативные варианты ввода с применением комбинаций клавиш — их можно найти в справочной базе данных системы.
Рисунок 2.1, однако, наглядно показывает, что целесообразно пользоваться не более чем 2-3 панелями одновременно. Для удаления ненужных панелей в правом верхнем углу каждой из них расположены маленькие кнопки со знаком х. Все панели максимально компактны и могут перетаскиваться мышью в наиболее удобное место экрана.
Если убрать все панели, то интерфейс системы на первый взгляд оказывается даже слишком простым — остается единственная панель с главным меню и висящее отдельно окно документа. Вокруг него можно разглядеть объекты рабочего стола операционной системы Windows 95/98 (при подготовке этой книги использовалась Windows 98). Если работа идет с несколькими документами, то можно увидеть несколько окон документов.

gl2-1.jpg
4. Понятие о документах в форме notebooks
Понятие о документах в форме notebooks
Как уже отмечалось, для выполнения простых арифметических операций достаточно набрать необходимое математическое выражение и нажать клавиши Shift и Enter одновременно (сама по себе клавиша Enter используется только для перевода строки внутри текущей строки ввода).
Нетрудно заметить, что вычисления в оболочке системы проходят так же, как при вычислениях на обычном калькуляторе. Однако прежде чем получить результат первого вычисления, даже столь простого, как вычисление 2 + 3, вам придется запастись терпением и дождаться, когда система загрузит свое ядро.

Отдельные ячейки с математическими выражениями и результатами их вычислений отмечаются в правой части главного окна редактирования характерными тонкими квадратными скобками синего цвета. Это наглядно показывает, к чему относятся математические выражения — к исходным данным или результатам. Кроме того, ячейки могут иметь различный статус, который отмечается соответствующими значками над квадратными скобками, — речь об этом более подробно пойдет ниже.
Изображение в окне редактирования очень напоминает записи аккуратного и педантичного инженера или ученого в записной книжке или на листке бумаги. В общем случае в окне видны поясняющие текстовые комментарии, числа, таблицы, математические выражения, формулы, графики различных типов. Мы будем называть эти записи документом — в оригинале они именуются словом notebook, которое с английского языка на русский переводится как «записная книжка» или «блокнот». Представление протокола работы с системой в такой форме считается наиболее целесообразным для математических систем.
Чтобы документ имел форму «блокнота», надо предпринять определенные операции по форматированию документа и приданию ему нужного вида. Прежде всего, каждый шаг вычислений следует снабжать поясняющими надписями. Их можно прямо вводить в строки ввода, но затем отформатировать с использованием текстового формата подходящего стиля. Для этого выделяется строка ввода с текстовой надписью (щелчком на скобке соответствующей ячейки). Пространство внутри скобки при этом затеняется (делается черным). Затем выполняется команда меню Format | Style | Text (Alt+7). Она задает текстовый формат надписи, который является неисполняемым.
С помощью других команд меню Format, которые мы рассмотрим в дальнейшем, можно задать надпись разным шрифтом, разным цветом с выделением фона и т. д. Как уже отмечалось, для ввода математического выражения по шаблону и для представления его в естественной математической форме используется стандартный формат ячеек ввода (StandardForm). Рисунок 2.2 показывает созданный таким образом простой «блокнот», в котором наряду с поясняющими текстовыми надписями заданы вычисление определенного интеграла, вычисление суммы квадратов чисел от 1 до и и построение графика с помощью графической функции Plot.
Рис. 2.2. Простейший документ в форме «блокнота»
В «блокнотах» желательно, чтобы форма представления математических выражений хотя бы напоминала общепринятую. В этом отношении документы системы Mathematica 3/4 все еще уступают документам систем Mathcad для Windows — последние содержат записи математических выражений (включающих знаки интегралов, сумм, произведений, греческие буквы и прочие спецзнаки) в их обычном начертании. Более того, формулы, текстовые комментарии и графики могут располагаться как угодно — например, вдоль строки могут располагаться формулы, графики и таблицы вывода. Зато Mathematica 3/4 позволяет задавать формы представления документов, принятые в таких мощных языках программирования, как Fortran, С и даже ТеХ (язык для программирования типографского набора сложных научных текстов).
Каждая надпись, математическое выражение или график занимают отдельную ячейку (cell). Ячейка может занимать одну или несколько строк и всегда выделена своей квадратной скобкой. Важным свойством ячеек систем Mathematica является возможность их эволюции (изменения) по всему документу. Этим осуществляется динамический обмен данными в ходе символьных преобразований — свойство, которое оказалось так и не реализованным в других символьных математических системах (за исключением, пожалуй, Maple V).
Теперь понятно, почему каждая ячейка занимает полную строку или ряд строк. Порой в ходе символьных преобразований, например при вычислении неопределенных интегралов, результат может иметь самые различные размеры. Разумеется, символьная система не может заранее знать, какой это будет результат и сколько строк он займет в ячейке. Поэтому размеры ячейки не фиксированы, и в нее нельзя помещать одновременно входные данные и результаты вычислений.
Честь и хвала разработчикам Mathcad, обошедшим эту проблему и создавшим интерфейс, способный готовить документы с произвольным расположением блоков. Однако об оборотной стороне медали — перекрытии блоков при увеличении их размеров — забывать в данном случае не стоит.
gl2-2.jpg
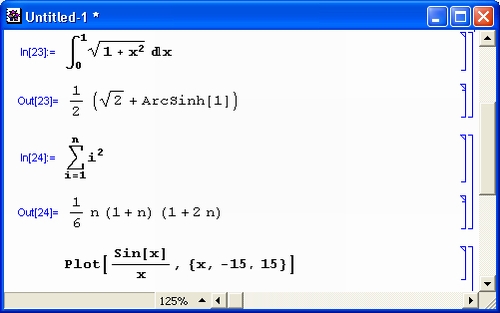
5. Особенности интерфейса Mathematica 4
Особенности интерфейса Mathematica 4
Интерфейс системы Mathematica 4 в целом повторяет интерфейс третьей версии, кратко описанный выше. Однако ряд внешне незаметных, но существенных новинок все же введен:
- улучшена плавная прокрутка больших документов;
- введен экспорт табличных данных;
- улучшены возможности создания документов в стиле Notebook;
- добавлена панель ввода шаблонов ЗD-фигур;
- расширена поддержка преобразований файлов в формат HTML;
- введена дополнительная команда для вывода в формате ТеХ;
- обеспечена поддержка дополнительных наборов символов, включая символы китайского и корейского языков;
- переработаны редакторы программ с цветной раскраской листингов;
- улучшены средства отладки программ;
- улучшена связь программных модулей.
Средства Mathematica 4 позволяют готовить документы в стиле Notebook на самом высоком полиграфическом уровне воспроизведения текстов, математических формул и графиков. Общий вид одного из таких документов, содержащего рисунок с высоким разрешением, представлен на рис. 2.3.
Рис. 2.3. Вид документа системы Mathematica 4 со встроенным рисунком
Размеры блокнота практически не ограничены, и он может быть распечатан во всей красе с помощью цветного струйного или лазерного принтера.

gl2-3.jpg
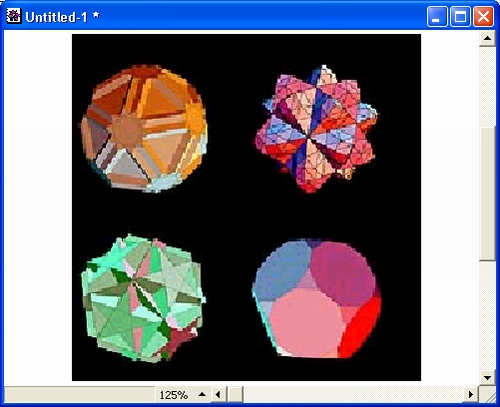
6. Работа с файлами
Работа с файлами
Файлы — важнейший компонент любой программной среды или любого приложения:. В этом разделе мы познакомимся с различными типами файлов, обычно называемыми их форматами. Основное внимание будет уделено файлам документов, которые создаются пользователями систем Mathematica.
Основные виды файлов и пакеты расширения
Файлы документов прежних версий системы Mathematica имели расширение .та (от слов Mathematical Applications — применения системы Mathematica), их можно загружать в окно редактирования для исполнения, дополнения или редактирования. При записи таких файлов система одновременно создает бинарные файлы с расширением .mb, хранящие битовый графический образ документа. Благодаря этому считывание файлов ранее подготовленных в системе документов происходит быстро, без включения в работу символьного процессора, так что текст с графиками сразу появляется на экране дисплея.
Однако бинарные файлы, особенно для документов со сложными графическими объектами, имеют большие размеры и хранить их на диске не всегда разумно. Поэтому такие файлы можно с диска стереть, но в этом случае все построения повторяются при загрузке файлов с включением в работу символьного процессора.
В версиях Mathematica 3/4 основным типом документов стали блокноты (notebooks). Им соответствуют файлы текстового формата с расширением .nb. Эти файлы могут редактироваться любым текстовым редактором, поддерживающим формат ASCII. Файлы содержат подробное описание документа с указаниями типов шрифтов, деталей оформления и местоположения различных объектов. Они завершаются довольно пространным описанием того, что собой представляет notebook. К сожалению, это ведет к значительному росту объема таких файлов — он значительно больше, чем у документов систем Mathcad. Зато файлы блокнотов весьма наглядны, и при необходимости в них может разобраться обычный пользователь.
Кроме того, система имеет ряд стандартных пакетов расширения (в оригинале — Add-Ons), расположенных в каталоге ADDONS:
- Algebra — работа с полиномами, алгебраическими неравенствами, Гамильтоно-вой алгеброй и т. д.
- Calculus — символьные вычисления производных, интегралов и пределов функций, прямое и обратное преобразования Фурье и Лапласа, решение систем нелинейных уравнений, реализация инвариантных методов, решение дифференциальных уравнений в частных производных, нахождение полных интегралов и дифференциальных инвариантов нелинейных уравнений, аппроксимация Паде, вычисление эллиптических интегралов и работах векторами.
- DiscreteMath — вычисления из области дискретной математики, комбинаторики, вычислительной геометрии и теории графов, решение рекуррентных и разностных уравнений, операции с целыми числами и т. д.
- Geometry — функции для выполнения геометрических расчетов, создания правильных прямоугольников и многогранников, вращения геометрических фигур в плоскости и в пространстве.
- Graphics — построение графиков специального вида, геометрических фигур и поверхностей, графиков параметрически и неявно заданных функций, представления функций комплексного переменного, отображение ортогональных проекций трехмерных фигур, имитация теней, средства оформления графиков.
- LinearAlgebra — решение задач линейной алгебры, дополнительные векторные и матричные операции, задание ортогональных векторных базисов и т. д.
- Miscellaneuos — задание единиц измерения физических величин, данные о химических элементах, физические константы, географические данные и все прочее, не вошедшее в другие категории.
- NumberTheory — функции теории чисел.
- NumericalMath — реализация важнейших численных методов, аппроксимация данных и аналитических функций полиномами, сплайнами и тригонометрическими рядами, численное интегрирование и дифференцирование, решение дифференциальных уравнений, вычисление корней нелинейных уравнений, нахождение вычетов и разложений в комплексной плоскости и т. д. .
- Statistics — статистические функции для непрерывных и дискретных распределений, реализация линейной и нелинейной регрессии, вычисление параметров ряда распределений (особенно нормального), функции сглаживания и подгонки данных и т. д.
- Utilities — дополнительные утилиты для работы с бинарными файлами и памятью компьютера, поддержки языков, работы с системами класса AutoCAD и т.д.
Пакеты расширения содержат множество (полторы сотни) библиотечных файлов с расширениями .m, в каждом из которых определен ряд новых функций системы. Число функций в одном пакете расширений лежит в пределах от нескольких функций до нескольких десятков, а общее число дополнительных функций и их вариантов достигает тысячи. С их помощью можно реализовывать новые алгоритмы решения математических задач и постоянно расширять возможности системы. Все библиотечные файлы подробно прокомментированы, что облегчает их использование пользователями, владеющими английским языком.
В версии Mathematica 4 число файлов в пакетах расширения несколько сокращено по сравнению с версией Mathematica 3. Часть таких файлов вообще являются «пустышками» — они оставлены ради сохранения полной совместимости с предшествующими версиями системы. Перенос части имеющихся в пакетах расширений функций и команд в тщательно оптимизированное ядро системы позволил существенно повысить скорость выполнения соответствующих операций.
Дальнейшее описание интерфейса и возможностей системы Mathematica в равной мере относится к третьей и четвертой версиям. В тех случаях, когда между ними есть видимые различия, они будут специально оговариваться.
Для работы с файлами служит меню File (рис. 2.4).
Рис. 2.4. Меню File
В этом меню содержатся следующие команды:
- New (Ctrl+N) — вывод окна нового документа;
- Open (Ctrl+0) — загрузка существующего документа;
- Close (Ctrl+F4) — закрытие текущего окна;
- Save (Ctrl+S) — запись документа с текущим именем;
- Save As (Shift+Ctrl+S) — запись документа с изменением имени;
- Save As Special — запись в специальных форматах;
- Open Special — открытие файлов в специальных форматах;
- Import — вставка содержимого файла в ячейку текущего документа;
- Send To — зарезервированная команда;
- Send Selection — зарезервированная команда;
- Palettes — вывод палитр математических спецзнаков, операторов и функций (см. выше раздел «Палитры математических операторов и функций»);
- Notebook — вывод списка документов, которые загружались ранее;
- Generate Palette from Selection — преобразует выделенные ячейки документа в палитру;
- Generate Notebook from Palette — преобразует палитру в документ;
- Printing Settings — установка параметров печати;
- Print (Ctrl+P) — печать текущего документа;
- Print Selection — печать выделенных ячеек;
- Exit (Alt+F4) — завершение работы с системой.
Следует отметить, что хотя библиотечные файлы расширений можно, как и файлы с расширением .mа, загружать в окно редактирования, как правило, это делается только при их подготовке и отладке. Указанные файлы обычно подгружаются в текущий документ без отображения их текстов с помощью специальных команд. Эти команды будут рассмотрены в дальнейшем.
Открытие окна нового документа — команда New
Команда New используется, когда нужно начать работу с новым документом. Эта команда полностью очищает экран, выводя запрос о том, нужно ли записать текущий документ, если он есть и модифицировался со времени последнего сохранения. Окно будущего документа получает имя Untitled-N (в версиях Mathematica 2.x имя было Newnb-N), где N — текущий номер документа. После исполнения этой команды можно начинать ввод документа с помощью клавиатуры и выполнять его редактирование. Важно отметить, что даже эта. команда не отменяет определений, сделанных в предшествующих исполненных документах и в ранее загруженных файлах пакетов расширений. Лишь полная перезагрузка системы отменяет эти определения.
Загрузка ранее созданных документов — команда Open
Загрузка файлов ранее созданных документов — одна из самых распространенных операций. Она реализуется командой Open, которая служит для загрузки ранее созданного документа с его поиском в файловой системе компьютера. Эта команда выводит диалоговое окно, типичное для Windows-приложений и предназначенное для удобного поиска файлов (рис. 2.5).
Рис. 2.5. Диалоговое окно выбора файлов
Кроме команды Open, которая загружает документ, открывая его в новом окне, в меню File. имеется еще команда Import, вставляющая содержимое указанного файла в текущий документ. Обе команды позволяют загружать файлы как основного формата notebook с расширением .nb, так и файлы ряда других форматов.
Запись документа с текущим именем — команда Save
Если документ создан с помощью команды New или открыт с помощью команды Open, то он обычно подвергается модификации и редактированию. После отладки документа его измененный вариант бывает нужно записать на магнитный диск — гибкий или жесткий. Для этого служат команды Save и Save As. Команда Save выполняет запись текущего документа без изменения его имени. Поэтому она выполняется быстро и без каких-то дополнительных действий. Запись идет в формате notebook.
Запись документа с заданным именем — команда Save As
Команда Save As позволяет изменить имя файла и поместить его в любую директорию любого диска. Эта команда вызывает появление диалогового окна, показанного на рис. 2.6.
Рис. 2.6. Окно сохранения файла документа
Помимо установок диска и нужной директории следует задать имя записываемого файла или подтвердить предлагаемое имя. Вводить расширение не обязательно — система сама позаботится об этом. Запись идет в формате notebook.
Операции с файлами в специальных форматах
Mathematica может записывать и считывать файлы, представленные в ряде специальных форматов. С помощью команды Save As Special можно записывать файлы в следующих форматах:
- Version 2 Notebook — формат блокнотов старой версии системы (.mа);
- Text — текстовый формат (.txt);
- Cell Expression — формат ячеек;
- Notebook Expression — формат выражений в блокнотах;
- Package Format —формат пакетов расширения (.m);,
- ТеХ — формат редакторов семейства ТеХ (.tex);
- HTML — формат гипертекстовой разметки (.htm).
Из специальных форматов файлов следует особо выделить два — ТеХ и HTML. Формат ТеХ используется весьма популярными у математиков редакторами математических текстов, насыщенных математическими знаками и формулами. Фактически, ТеХ представляет собой особый язык программирования, предназначенный для разметки математических выражений. Возможность работы систем Mathematica с данным форматом позволяет публиковать подготовленные в системах Mathematica документы в изданиях, ориентированных на математиков.
Формат HTML используется при подготовке страниц для Интернета. HTML — это язык гипертекстовых ссылок, позволяющих быстро переходить от одного документа к другому. Возможность работы Mathematica с этим форматом позволяет готовить документы, которые могут вставляться в.Интернет-страницы и немедленно, без какой то доработки, передаваться по сети — в том числе с помощью электронной почты. В последнее время формат HTML становится стандартным для подготовки электронных документов и книг, а также для создания высококачественных (в том числе обновляемых через Интернет) справочных систем.
Для загрузки файлов в специальных форматах служит команда Open Special. Эта команда открывает довольно простое окно, с помощью которого устанавливаются данные, необходимые для открытия файлов.
Преобразование документов в палитры и наоборот
Любую часть документа после выделения можно преобразовать в палитру. Для этого используется команда Generate Palette from Selection.
Палитра — это уменьшенное окно, похожее на окно документа, но имеющее в строке заголовка только имя и кнопку закрытия (у обычного окна кнопок в строке заголовка три). Палитру, как и документ, можно записывать на магнитные диски. Для преобразования палитры в документ используется команда Generate Notebook from Palette.
Установка параметров печати — подменю Printing Settings
Подготовленный документ обычно нуждается в печати. Многие предпочитают обдумывать и корректировать документы, используя их распечатки, не очень удачно именуемые «твердыми копиями». Нередко бывает нужна распечатка даже промежуточных версий документов.
Команда Printing Settings выводит подменю с тремя операциями. Первая — Page Setup — служит для установки параметров страниц при печати. Она выводит окно, показанное на рис. 2.7. Это окно операционной системы Windows 95/98 содержит типовые установки параметров страниц — их размер, ориентацию, способ подачи бумаги и размеры полей.
Рис. 2.7. Окно установки параметров страницы при печати документа
Вторая операция — Printing Options — служит для установки типовых опций пе чати. Их устанавливают в окне, показанном на рис. 2.8.
Рис. 2.8. Окно установки опций печати
Третья операция — Headers and Footers — служит для установки верхних и нижних колонтитулов (надписей сверху и снизу на каждой печатаемой странице). Эта операция выводит окно, показанное на рис. 2.9. В нем можно задать основные параметры колонтитулов и ввести соответствующие надписи.
Поскольку документы Mathematica могут иметь самые разнообразные средства выделений и цветной раскраски, то наиболее подходящим для печати документов в настоящее время является цветной струйный принтер. Сейчас можно приобрести высококачественные принтеры такого типа по цене от $150 до $300. Лазерные принтеры стоят примерно вдвое дороже и обеспечивают высококачественную монохромную печать. О цветных лазерных принтерах можно и не упоминать — их стоимость настолько велика, что пока они доступны только крупным фирмам.
Рис. 2.9. Окно задания колонтитулов
Mathematica для Windows не имеет своей собственной системы печати и использует стандартную систему печати операционных систем Windows 3.1/3.11/95/ 98/NT. При этом окна настройки печати задаются драйверами, установленными для применяемых принтеров. К примеру, Windows 98 поддерживает сотни типов принтеров десятков фирм. Для определенности ниже рассматриваются установки печати для широко распространенного цветного струйного принтера Epson Stylus Color 600, который при цене менее $300 обеспечивает высочайшее качество печати с разрешением до 1420 точек на дюйм при 16,7 миллионах цветовых оттенков. Этот принтер имеет два картриджа — для обычной черно-белой печати и для цветной печати (с тремя чернильницами, заполненными чернилами разных цветов).
Цветные принтеры поддерживают высококачественную цветную печать. Однако надо помнить, что не стоит увлекаться цветовыми выделениями и особенно цветным фоном в документах, так как при этом резко возрастает расход дорогих чернил. Кроме того, ярко раскрашенные документы выглядят аляповато и пестро. Им недостает серьезности. В конце концов, надо помнить, что документы с математическими расчетами и рисунки детишек в графических редакторах — вещи явно разные!
Как правило, превосходные по качеству документы дают и монохромные принтеры, особенно лазерные. Профессиональные монохромные принтеры обычно печатают текст документа в виде PostScript-графики. При этом полутона серого изображения воспроизводятся путем соответствующего выбора густоты точек и штриховых линий (наподобие печати фотографий в газетах).
В целом, можно сказать, что печать идет по известному принципу WYSIWYG — что видишь, то и будет напечатано. К сожалению, определенные отличия в том, что видно на экране дисплея и что напечатано принтером, все же могут быть. К примеру, знаки деления, видимые в виде горизонтальной черты на экране дисплея, в текстовом формате выглядят непрерывными, а принтерами часто печатаются пунктиром — это может привести к недоразумениям со знаками «минус». Случается и расхождение размеров шрифтов, способное нарушить правильность расположения частей формул по горизонтали. В таких случаях рекомендуется поэкспериментировать со стилями ячеек. Как правило, стили, основанные на графическом представлении данных, печатаются без искажений. Вообще же Mathematica имеет обширные возможности по стилевому оформлению документов и настройке качества печати под любой принтер.
Печать документов — команда Print
После настройки параметров можно осуществить собственно печать с помощью команды Print для всего документа или Print Selection для печати только выделенных ячеек. Команда Print открывает окно печати, показанное на рис. 2.10.
Рис. 2.10. Окно печати
В этом окне имеется поле Принтер с переключателем выбора принтера и кнопкой вывода окна его свойств. Интересна опция Печать в файл, с помощью которой данные печати направляются вместо принтера на диск. Поле Печатать позволяет установить номера страниц, которые будут распечатаны, или задать печать только выделенных ячеек. Поле Копии служит для установки числа копий и задания (если это нужно) разборки копий.
Для начала печати надо нажать кнопку ОК, кнопка Отмена позволяет отменить печать, а кнопка Справка — вывести справку о печати. При печати документа появляется (иногда кратковременно) окно принтера, демонстрирующее процесс печати. Это окно показано на рис. 2.11.
Рис. 2.11. Процесс печати
Окно принтера отображает не только нормальный ход печати, но и различные аварийные ситуации. Например, если принтер не включен, то на его изображении появится жирный красный крест. Отображаются и другие ситуации, например, заминание бумаги или ее отсутствие, окончание чернил в чернильнице, обрыв кабеля и т. д. Следует отметить, что разрешение современных принтеров при печати намного выше разрешения дисплея, поэтому качество отпечатанных документов (особенно их графической части) может быть заметно выше, чем при прямом просмотре на экране дисплея — например, у графиков практически отсутствуют зазубрины на кривых, хорошо видимые на экране.
Нажатие кнопки Свойства в окне (рис. 2.10) выводит окно настройки принтера. Вид этого окна зависит от применяемого для печати принтера и установленного для него драйвера. В связи с этим работа с данным окном подробно не рассматривается.
Команда Print Selection служит для печати набора выделенных ячеек. Обычно она также выводит окно печати, показанное на рис. 2.10. В этом окне, как отмечалось, можно выбрать нужный принтер из нескольких, если их драйверы были инсталлированы.
Завершение работы с системой — команда Exit
Команда Exit используется для окончания работы с системой Mathematica. Если все документы, с которыми пользователь работал (их может быть много), были записаны на диск, то при исполнении этой команды можно наблюдать последовательное закрытие окон с текстами документов. Если какой-то из документов не был записан после модификации, то команда Exit выведет запрос о необходимости записи.
В подменю Notebooks меню File содержится перечень файлов, с которыми в последнее время работал пользователь. Выбор любого из этих файлов ведет к его загрузке в новое окно редактирования. Это делает работу с системой более удобной, так как избавляет пользователя от поиска наиболее нужных файлов по дискам и директориям.
gl2-10.jpg
gl2-11.jpg
gl2-4.jpg
gl2-5.jpg
gl2-6.jpg
gl2-7.jpg
gl2-8.jpg
gl2-9.jpg
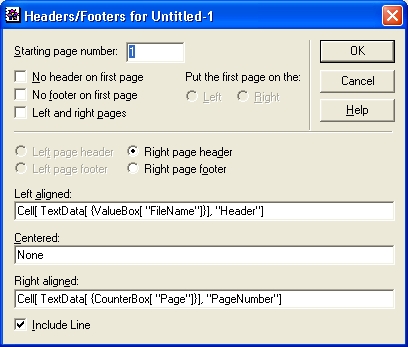
7. Редактирование документа
Редактирование документа
Под редактированием, строго говоря, подразумевается модификация уже готового документа. Однако мы в данном разделе рассмотрим не только редактирование, но и подготовку всего документа — начиная с этапов задания входных ячеек с текстовыми комментариями, исходными данными для вычислений и необходимыми расчетными формулами. В детали подготовки сложных документов (например, программ для пакетов расширения системы) мы пока вникать не будем.
Основные понятия о документах и их стилях
Вообще говоря, системы Mathematica 3/4 работают с «блокнотами» (Notebooks), которые могут содержать множество ячеек различного типа. Однако слово «блокнот» при частом его употреблении действует на нервы российскому читателю — в частности, так у нас уже привыкли называть миниатюрные компьютеры. Название «записная книжка» тоже не очень удачно, хотя бы из-за того, что содержит два слова. Поэтому мы будем пользоваться более распространенным понятием документа.
Документы Mathematica в общем случае содержат текстовые комментарии, ячейки с математическими выражениями в том или ином формате (в том числе вполне естественном для математиков) и результаты вычислений в различной форме, включая табличную, матричную или графическую. Таким образом, документы и впрямь содержат записи, очень напоминающие записи в записных книжках или блокнотах научных работников и инженеров (или конспекты старательных студентов).
Редактированием документа является всякое изменение текста комментариев, исходных данных и математических формул с целью придания документу более подходящего вида (стиля) или получения новых результатов. К редактированию относится и изменение формата графиков. Простейшие приемы редактирования настолько естественны, что не нуждаются в особых пояснениях — разумеется, если у пользователя есть хотя бы начальный опыт работы с Windows и встроенными в эту оболочку текстовыми редакторами Write и WordPad (либо с популярным редактором Word 95/97 ).
Для редактирования содержимого ячеек документов в них вводится текстовый курсор. Для этого курсор мыши устанавливается в нужное место ячейки и нажимается левая кнопка мыши — в этом месте и появляется текстовый курсор. Для редактирования используется обычный строчный редактор, который хорошо знаком даже начинающим пользователям, — именно с его помощью вводятся команды MS-DOS. В силу этого не будем описывать возможности этого редактора подробно. Напомним лишь, что они предусматривают перемещение маркера ввода, забой (удаление) символа слева (клавиша Backspace) или справа (клавиша Del) от курсора, установку режима вставки (клавиша Ins) и т. д.
В общем случае документы характеризуются стилем оформления. Под ним подразумевается совокупность параметров, характеризующих вид ячеек, — тип шрифта надписей и математических знаков, их размер и цвет, характер выравнивания надписей и т. д. Понятие стиля хорошо известно пользователям уже упомянутых текстовых редакторов. Стиль каждой ячейки можно задавать предварительно, а можно скорректировать после заполнения ячейки.
От выбора стиля документа во многом зависят его наглядность и эстетичность восприятия. Поэтому в Mathematica предусмотрены обширные возможности изменения стиля документов и их частей. Они сосредоточены в меню Format, содержащем многочисленные подменю. Однако обилие средств установки стиля порождает проблему совместимости стилей. Для ее решения используются специальные средства преобразования стилей. Для ячеек они сосредоточены в меню Cell
Выделения в документах и использование мыши
При редактировании документа курсор мыши приходится перемещать из одной ячейки в другую и обращаться к командам меню для выполнения тех или иных операций, например, для копирования содержимого ячейки в буфер, изменения шрифта и т. д. Следует учитывать, что вид курсора при этом меняется и позволяет оценивать его местонахождение. Рекомендуется понаблюдать за изменением формы курсора мыши при его перемещении в различных областях документов.
Важным моментом в работе с документами является выделение их элементов — ячеек ввода и вывода, их содержимого и т. д. Для выделения ячейки достаточно щелкнуть на ее правой скобке — скобка заполнится черным цветом, это и есть выделение ячейки. На рис. 2.12 показана выделенная ячейка вывода с числом. Если при этом нажать правую кнопку мыши, появится контекстно-зависимое меню, которое также показано на рис. 2.12, с раскрытым подменю Copy As, позволяющим скопировать содержимое выделенной ячейки в буфер обмена Windows (Clipboard; далее он будет именоваться просто буфером).
В другом случае (рис. 2.13) показан выделенный рисунок. Для выделения рисунка (графика) достаточно поместить курсор мыши в область рисунка и щелкнуть левой кнопкой мыши. Рисунок будет обведен рамкой с характерными прямоугольниками.? Перетаскивая их мышью, можно растягивать график в разные стороны и менять его размер. В этом случае также можно вывести контекстно-зависимое меню — оно тоже показано на рис. 2.13.
Рис. 2.12. Выделенная ячейка вывода и ее контекстно-зависимое меню
Рис. 2.13. Выделенный график и его контекстно-зависимое меню
Контекстно-зависимые меню, вызываемые с помощью правой кнопки мыши, очень удобны при профессиональной работе с системой Mathematica. Они дают полный перечень команд, которые можно использовать для выделенного объекта, не обращаясь к главному меню, — там они также есть, но разбросаны по разным местам.
Когда курсор мыши находится в пределах ячейки ввода или вывода, двойной щелчок вызывает выделение некоторой части этой ячейки. Это выделение можно расширять повторными щелчками. Можно расширять область выделения путем перетаскивания курсора при нажатой левой кнопке мыши.
Если курсор мыши находится в ячейке ввода, он используется для точного указания места, в котором должно начаться редактирование. После щелчка левой кнопкой мыши появится текстовый курсор в виде вертикальной черты. За пределами ячеек (то есть в областях меню, линеек и т. д.) курсор мыши имеет обычный вид наклонной стрелки.

Подготовка текстовых комментариев
Важной частью профессионально составленного документа являются текстовые комментарии. Без них документ через некоторое время становится непонятным даже его разработчику. Поэтому правилом хорошего тона является применение достаточно подробных текстовых комментариев.
Тестовые комментарии вводятся прямо в текущую строку ввода с использованием стандартных приемов строчного редактирования. Однако не следует завершать ввод нажатием комбинации клавиш Shift+Enter, так как это приведет к выводу комментария в строку вывода с возможными сообщениями об ошибках (рис. 2.14). Они обусловлены тем, что в текстовых комментариях обычно не придерживаются синтаксиса входного языка системы Mathematica, что и чревато появлением ошибок.
Чтобы отмеченная ситуация не повторялась, просто установите курсор мыши под строку ввода с комментарием, а затем щелкните левой кнопкой мыши — в новой строке ввода можно будет размещать новый комментарий или математические выражения для вычислений.
Часто в ходе редактирования приходится изменять текстовые комментарии, например заголовки в документах. Для этого достаточно выделить ту ячейку, в
которой находится надпись. Подведите курсор мыши к квадратной скобке в правом конце ячейки — курсор при этом превращается в стрелку с вертикальной линией. Указав стрелкой нужную ячейку, нажмите левую кнопку мыши. Скобка выделенной ячейки заполнится черным цветом.
Рис. 2.14. Примеры ввода текстовых комментариев
Далее можно выбрать тип оформления ячейки. Для установки стиля ячеек используется ряд команд, которые собраны в меню Format | Style. Эти команды более подробно будут рассмотрены далее. Пока же отметим, что обычные текстовые комментарии рекомендуется отформатировать стилем Text или SmallText (в этом случае ячейки ввода имеют статус текстовых ячеек, не дающих вывод).
К важной операции редактирования ячеек с текстами комментариев относится выравнивание текстов в пределах строки ввода. Для оперативного осуществления этой операции целесообразно вывести панель инструментов (ToolBar) и мерную линейку (Ruler). Соответствующие команды (Show ToolBar и Show Ruler) находятся в меню Format. На рис. 2.15 представлено окно документа с панелью инструментов, линейкой и примерами форматирования строки ввода с текстовыми комментариями. Для быстрого форматирования используются четыре кнопки с изображением соответствующего отформатированного текста.
Ряд расширенных возможностей редактирования представляют команды меню Edit. В основном эти операции связаны с обменом информацией между выделенной ячейкой или группой ячеек и специальным буфером.
Рис. 2.15. Различные типы выравнивания текстовых надписей
Основные операции редактирования сосредоточены в меню Edit. Рисунок 2.16 показывает вид экрана системы с открытыми меню Edit и двумя его подменю.
Как видно из рис. 2.16, в меню Edit сосредоточены следующие команды:
- Undo (Ctrl+Z) — отмена операции;
- Cut (Ctrl+X) — перенос содержимого ячейки в буфер;
- Copy (Ctrl+C) — копирование содержимого ячейки в буфер;
- Paste (Ctrl+V) — вставка информации из буфера без его очистки;
- Clear (Del) — уничтожение выделенной ячейки;
- Copy As — копирование содержимого ячейки в буфер в заданном формате;
- Paste As — вставка информации из буфера в заданном формате;
- Save Selection As — запись выделенных ячеек в специальных форматах;
- Select All (Ctrl+A) — выделение всех ячеек;
- Insert Object — вставка объектов;
- Motion — различные перемещения в текстовом блоке;
- Expression Input — ввод выражений в разных форматах;
- Make 2D (Shift+Ctrl+Y) — преобразование текстовой строки ввода в двумерный формат;
- Check Balance (Shift+Ctrl+B) — поиск пары скобок, окружающих место расположения текстового курсора;
- Check Spelling (Alt+;) — проверка орфографии;
- Preferences — вызов окна настроек системы.
Рис. 2.16. Меню Edit
Часть из этих команд дублирует описанные выше операции — в частности, операции по работе с буфером. Другие требуют некоторого пояснения. Так, команда Save Selection As служит для записи выделенных ячеек в файлы специальных форматов. Подменю с перечнем этих форматов показано на рис. 2.17.
Рис. 2.17. Подменю команды Save Selection As
Среди возможных вариантов здесь перечислены форматы различных ячеек, графических файлов и специальные форматы документов.
Команда Insert Object открывает окно вставки объектов, показанное на рис. 2.18. Это стандартное окно, имеющееся во всех приложениях операционной системы Windows 95/98/NT. В окне есть перечень приложений, которые могут экспортировать в Mathematica порожденные ими объекты. Это могут быть тексты, рисунки, документы различных программных систем и т. д. Такие объекты внедряются в ячейки Mathematica и могут редактироваться теми программами, которые их породили. Позже мы рассмотрим технологию вставки объектов более подробно.
Рис. 2.18. Окно вставки объектов
Для редактирования больших текстовых блоков служат команды подменю Motion. Это стандартные команды перемещения курсора по отдельным символам, словам и т. д. Следует отметить, что правильное их исполнение гарантируется только для англоязычных текстов. Эта группа команд применяется редко — чаще всего перемещение текстового курсора производится с помощью клавиатуры. Кроме того, работать с такими командами через меню не очень удобно.
Команда Expression Input открывает подменю с рядом команд, задающих вид ячеек. Если надо представлять и редактировать ячейки ввода как двумерные объекты, то следует использовать команду Make 2D. Практика, однако, показывает, что гораздо проще вводить содержимое ячеек в обычном текстовом формате, чем в двумерном. В этот формат легко перейти средствами изменения формата ячейки.
Как известно, операционные системы класса Windows имеют так называемый буфер обмена — в дальнейшем просто «буфер». Это специально организованная динамическая область памяти, в которую можно помещать информацию различного формата — например, текстовую или графическую. Буфер используется как для редактирования, так и для обмена информацией между различными приложениями. Буфер обладает определенным «интеллектом» и «понимает», какая именно информация (например, текстовая или графическая) в него помещается.
Команда Nut удаляет выделенную ячейку и помещает ее содержимое в буфер. Команда Сору делает то же самое, что и Cut, но без удаления выделенной ячейки. Команда Paste копирует содержимое буфера в место вставки, определяемое положением текстового курсора. При этом содержимое буфера сохраняется. Команда Paste and Discard, расположенная в подменю Paste As, переносит содержимое буфера на место, определяемое положением курсора, но при этом сам буфер очищается. Таким образом, в этом случае возможна только одна операция переноса. Ее применение разумно при перемещении больших объемов информации, поскольку позволяет сразу же высвободить память, занимаемую буфером. Команда Clear уничтожает выделенную ячейку без ее сохранения в буфере.
Хотя до сих пор речь шла о манипуляциях с одной ячейкой, они вполне возможны и с несколькими одновременно выделенными ячейками. При этом содержимое ячеек может быть любым — тексты, математические формулы или графики. Аналогично происходят манипуляции и с выделенными частями ячеек.
Применение этих команд очень удобно при подготовке сложных документов. Например, серию похожих надписей не стоит вводить целиком вручную. Гораздо удобнее одну из надписей поместить в буфер, выделив ее и задав команду Сору. Затем, используя команду Paste, можно поместить эту надпись в другие ячейки, а затем выполнить необходимые модификации. Важно отметить еще раз, что применение буфера возможно для обмена данными между системой Mathematica и другими приложениями.

gl2-12.jpg
gl2-13.jpg
gl2-14.jpg

gl2-15.jpg
gl2-16.jpg
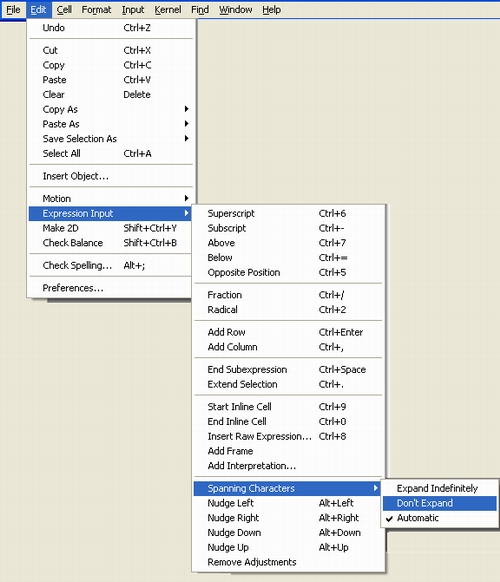
gl2-17.jpg
gl2-18.jpg
8. Работа с ячейками
Работа с ячейками
Итак, ячейки (Cells) являются основными объектами документов. Ячейки отличаются друг от друга статусом, то есть совокупностью свойств, определяющих тип ячейки и ее поведение в различных ситуациях. Важными понятиями, относящимися к ячейкам и отражающими особенности работы систем символьной математики, являются понятия оценивания (evaluation) и модификации содержимого ячеек.
К примеру, ячейки, содержащие текстовые надписи-комментарии, не оцениваются и не меняются в ходе пересчета документа. Ячейки ввода, напротив, оцениваются, их содержимое меняется, и они порождают ячейки вывода с разным содержимым — например, ячейка, выражение которой содержит функцию f [х], будет меняться в соответствии с изменением f [ х ]. Ячейки могут быть заблокированными от модификации, разблокированными и т. д. Итак, статус ячеек постоянно проверяется с помощью операции оценивания в ходе пересчета документа.
Статус ячеек можно распознать и без пересчета документа по ряду характерных признаков. Один из них — вид курсора мыши при его размещении в области ячеек — был описан выше. Другой признак — малозаметный опознавательный знак в верхней части квадратной скобки, обрамляющей ячейку. Отсутствие знака означает, что это обычная ячейка ввода. Знак «-» (короткая горизонтальная черточка) отмечает ячейку вывода со статусом Inactive. Заблокированная (закрытая) ячейка {Locked) помечается знаком «х», а инициализационная ячейка (Initialization) — знаком «т». Кроме того, меняющие свое содержимое ячейки отмечаются маленьким треугольником. О типе ячейки можно также судить по ее стилю, в частности по шрифту используемых в ней символов.
Для получения информации о стиле ячейки нужно поместить в нее текстовый курсор. Текущий стиль будет показан в списке стилей, имеющемся на панели форматирования (команда вывода этой панели на экран, как уже говорилось; расположена в меню Format). Для смены стиля ячейки просто выберите нужный вариант в списке. Это можно сделать и с помощью команд меню Format | Style.
В меню Cell (рис. 2.19) собраны команды для работы с ячейками. Как видно из рис. 2.19, это меню содержит следующие команды:
- Convert To — преобразование формата ячеек;
- Display As — установка формата отображения ячеек;
- Default Input Format Type — установка формата по умолчанию для ячеек ввода;
- Default Output Format Type — установка формата по умолчанию для ячеек вывода;
- Default Inline Format Type — установка формата по умолчанию для ячеек Inline;
- Cell Properties — установка свойств ячеек;
- Cell Grouping — группировка ячеек;
- Divide Cell (Shift+Ctrl+D) — разделение сгруппированных ячеек;
- Merge Cells (Shift+Ctrl+M) — объединение ячеек;
- Animate Selected Graphics (Ctrl+Y) — анимация выделенной ячейки с графиком;
- Play Sound — воспроизведение синтезированного звука;
- Rerender Graphics — построение графиков заново;
- Rerender And Save Graphics — построение графиков заново с последующей записью;
- Make Standard Size — установка стандартного размера ячейки;
- Allign Selected Graphics — выравнивание выделенных графиков;
- Cell Size Statistics — вывод статистики о размерах ячеек.
Далее эти команды описаны более подробно.
Рис. 2.19. Меню Cell
При вводе данных в ячейки ввода данные представляются в одном из форматов, заданных командой Default Input Format Type. Соответственно, в ячейках вывода результаты представляются в формате, установленном командой Default Output Format Type. Однако есть возможность изменить формат данных в ячейках с помощью команды преобразования форматов Convert To. Эта команда открывает подменю с перечнем всех возможных форматов (см. рис. 2.19). Текущий формат ячейки помечен галочкой. Для задания другого формата надо выбрать его в подменю, предварительно активизировав ячейку.
Как видно из рис. 2.19, возможна установка следующих форматов ячеек:
- InputForm (Shift+Ctrl+I) — формат ввода; О OutputForm — формат вывода; . ..
- StandardForm (Shift+Ctrl+N) — стандартный формат;
- TradidonalForm (Shift+Ctrl+T) — традиционный формат;
- PostScript — векторный графический формат PostScript;
- Bitmap — растровый формат изображений;
- Metafile — векторный графический формат Windows Metafile.
Из этих форматов (стоит их просмотреть, поскольку форматов множество) особо надо отметить стандартный формат, который позволяет отображать формулы в ячейках ввода в виде, наиболее приближенном к обычному, то есть с применением стандартных математических знаков для интегралов, сумм, произведений и т. д. Указанные форматы фигурируют и в других подменю меню Cell.
Подменю Cell Properties служит для установки свойств, то есть статуса ячеек. Это подменю содержит следующие команды:
- Cell Open — делает ячейку открытой или закрытой;
- Cell Editable — делает ячейку редактируемой или нередактируемой;
- Cell Edit Duplicate — делает ячейку заново создаваемой при попытке редактирования;
- Cell Evaluatable — делает ячейку оцениваемой или неоцениваемой;
- Cell Active — делает ячейку активной или неактивной;
- Initialization Cell — делает ячейку инициализационной или неинициализационной.
Установка свойств выделенной ячейки осуществляется выбором нужной команды в подменю Cell Properties. Одновременно может быть установлено несколько свойств. Для удаления свойства надо выбрать соответствующую команду еще раз.
Ячейка ввода и соответствующая ей ячейка вывода обрамляются не только своими удлиненными квадратными скобками справа, но и общей скобкой. Активизируя эту скобку двойным щелчком, можно скрывать и снова выводить на экран выходную ячейку. Скрывать последнюю полезно, если содержащийся в ней результат слишком громоздок.
Интересно отметить, что редактировать можно не только входные, но и выходные ячейки — например, вручную задавая более приемлемый вид результата. Однако для этого выходную ячейку надо сделать редактируемой, установив свойство Cell Editable. Редактируемая ячейка имеет символ «?» у своей обрамляющей скобки.
Ячейки могут быть оцениваемыми и исполняемыми или неоцениваемыми, что задается командой Cell Evaluatable. Только оцениваемые ячейки исполняются ядром системы и порождают выход. Неоцениваемые ячейки помечаются знаком «-» в обрамляющей их правой скобке.
Исполнение начинается, как только происходит оценивание статуса какой-либо ячейки. От пользователя зависит, какие ячейки и в каких сочетаниях оцениваются при пересчете всего документа. Можно выполнить, например, выделение ячеек так, чтобы они оценивались только совместно, но не индивидуально.
Ячейки также могут быть активными и неактивными. Изменение активности достигается командой Сеll Active. Активная ячейка помечается в скобке знаком «А» и обычно управляется кнопкой.
Наконец, ячейки могут быть инициализационными и нет, в зависимости от установки свойства Initialization Cell. Инициализационная ячейка помечается в скобке знаком «|» и автоматически исполняется при загрузке документа, содержащего такую ячейку (или ряд ячеек).
Команда Group Cells используется для объединения ряда ячеек в одну группу. Вначале нужно выделить объединяемые ячейки (рис. 2.20), а затем использовать команду объединения.
Рис. 2.20. Выделение ячеек документа перед их объединением
При этом выбранные ячейки обрамляются общей для них длинной квадратной скобкой (рис. 2.21). Активизация этой скобки позволяет управлять просмотром ячеек.
Сделав двойной щелчок на группирующей скобке, можно получить скрытый блок ячеек, в качестве названия которого выступает первая ячейка (рис. 2.22). Таким образом можно поочередно то открывать, то закрывать блок ячеек. Заметим, что закрытые ячейки по-прежнему оцениваются в соответствии с их статусом (свойствами).
Рис. 2.21. Документ после объединения ячеек в группу
Рис. 2.22. Документ со скрытым блоком ячеек
Команда Ungroup Cells разъединяет объединенные в группу ячейки. Если при этом в группе есть ячейки, объединенные в более мелкие подгруппы, то они сохраняются. Для деления ячейки на части используется команда Divide Cell, а для объединения двух ячеек — команда Merge Cells.
Чтобы иметь возможность воспользоваться командами объединения и разъединения ячеек, необходимо предварительно выбрать в подменю Cell Grouping команду Manual Grouping. По умолчанию в этом подменю выбран режим Automatic Grouping, при котором Mathematica сама управляет группировкой ячеек, базируясь на их стилях.
Команда Open All Subgroups открывает все выделенные группы и подгруппы ячеек, а команда Close All Subgroups закрывает все выделенные группы и подгруппы.
Действие команды Open/Close Group уже описывалось — она сокращает число ячеек в группе так, что видимой остается только первая ячейка — как правило, имеющая титульную надпись.
Таким образом, команды управления статусом и объединением ячеек позволяют создавать довольно сложные структуры электронных документов с многочисленными открывающимися и закрывающимися вложениями. Такие документы удобны для создания полноценных электронных уроков и даже электронных книг. С системой поставляется множество примеров таких уроков, с которыми стоит познакомиться.
В этой книге большинство примеров дается в самом простейшем виде — без объединения ячеек и создания структуры электронных документов. Это сводит к минимуму пояснения по примерам, которые даются, как правило, в текстах соответствующих разделов книги.
Работа с графическими и звуковыми возможностями
Система Mathematica обладает превосходными графическими возможностями — от построения двумерных и трехмерных графиков до синтеза сложных изображений (например цветных карт) и динамически изменяющихся поверхностей. Эти возможности задаются встроенными в ядро графическими функциями и дополняются средствами пакетов расширения.
Например, графическая функция
Plot[f[х],{х,xmin,xmax}]
строит, график произвольной математической функции f [ х ] одной переменной х при ее изменении от минимального значения xmin до максимального хтах.
Другая графическая функция,
Plot3D[f[x,y] , { {х, xmin, хтах}, {у, ymin, углах} } ]
строит график трехмерной поверхности для математической функции f [х,у] двух переменных, изменяющихся в указанных пределах. Примеры применения этих функций приводились ранее.
Каждая графическая функция в ответ на обращение к ней возвращает графический объект — тот или иной рисунок. Именно поэтому в системе Mathematica для построения графиков используются функции, а не операторы, как в большинстве языков программирования. Это говорит о том, что понятие функции в данной системе существенно расширено.
Возвращаемый графической функцией объект представлен ячейкой с соответствующим графиком. Ряд параметров такого объекта, такие как размеры графика, используемые цвета, толщина линий и т. д., задаются по умолчанию. Помимо указанных параметров в их список могут включаться специальные опции и директивы, расширяющие возможности графики. С их помощью можно управлять выводом координатных осей и текстовых надписей, менять размеры графика, строить графики типовых геометрических фигур и т. д. Эти возможности мы рассмотрим позднее.
В меню Cell можно найти ряд команд, относящихся только к ячейкам вывода с графическими и звуковыми объектами (см. рис. 2.19) — ранее, в версиях ниже Mathematica 3.0, они были расположены в меню Graph.
В общих чертах назначение этих команд очевидно. Например, исполнение команды анимации для документа, содержащего подготовленный для анимации график, вызывает появление внизу окна анимационного проигрывателя (рис. 2.23).
Рис. 2.23. Окно документа с проигрывателем анимационных рисунков
Демонстрация на уроках математики или физики демонстрационных анимационных картинок в среде Mathematica 3/4 производит не изгладимое впечатление. Однако при их описании в обычных книгах эффект от созерцания таких картинок исчезает, поскольку анимация при этом невозможна. Тем не менее, показ отдельных фаз анимации позволяет улучшить восприятие материала и в данном случае.
Мы рассмотрим эти команды более детально после описания графических и звуковых возможностей систем Mathematica.
Mathematica обладает обширными возможностями форматирования ячеек ввода и вывода. К этим возможностям относятся изменение размеров и цвета символов, выбор шрифтов, задание цвета фона и т. д.
Команды меню Format
Средства форматирования сосредоточены в меню Format (рис. 2.24).
Рис. 2.24. Меню Format и его подменю Style
В системах Mathematica 3/4 это меню содержит множество позиций, дающих практически неограниченные средства форматирования документов. Большинство из них обычному пользователю может никогда и не понадобиться — вполне достаточно установок, используемых по умолчанию. Однако при решении специфических задач, например при подготовке документов к полиграфическому изданию, наличие многочисленных средств форматирования становится далеко не лишним.
Изменение стиля документов
Команда Style открывает подменю стандартных стилей ячеек. Стилем ячеек называют совокупность параметров, задающих вид ячеек. Прежде всего это используемые наборы шрифтов, размеры символов, различные виды выделений и т. д.
На рис. 2.25 представлена серия ячеек ввода, отформатированная под все возможные стандартные стили. Стили существенно отличаются друг от друга, что позволяет легко распознавать их визуально. Самые распространенные из них — это текстовые ячейки разного стиля и ячейки ввода и вывода.
Рис. 2.25. Ячейки ввода, отформатированные разными стилями
Следующие две команды меню Format — это ScreenStyleEnvironment и PrintStyle-Environment Данные подменю служат для изменения текущего формата ячеек документа при его наблюдении на экране дисплея и при печати. Возможны следующие установки:
- Working — рабочий стиль (типичный);
- Presentation — презентационный (увеличенные размеры символов);
- Condensed — сжатый (уменьшенный размер символов);
- Ptintout — принтерный (оптимальный для печати).
Смысл глобальной замены стиля довольно очевиден. Можно порекомендовать читателю самостоятельно просмотреть различные документы после их форматирования тем или иным стилем.
Опции стилей и программ и их изменение
Команда-ShowExpression служит для управления показом выражений в стандартном и развернутом видах. Например, введем и исполним простое выражение при отключенном режиме ShowExpression:
2*Log[3]/Exp[5]
2Log[3]/Е5
Здесь вид ячеек стандартный. А теперь, выделив эти ячейки и исполнив команду ShowExpression (Shift+Ctrl+E), получим представление в развернутом формате:
Cell["2*Log[3]/Exp[5]", "Input",
CellLabel->"In[53]:="]
Cell[BoxData[
FractionBox[
RowBox["2", " ",
RowBox["Log", "[", "3", "]"]],
SuperscriptBox["E", "5"]]], "Output",
CellLabel->"Out[53]="]
Такой формат является внутренним в том смысле, что он характерен для внутреннего представления вывода на экран дисплея, принятого в языке программирования системы Mathematica. Словом, это типичная программа для вывода указанных выражений. Чем сложнее выражение, тем длиннее и непонятнее для непосвященных выглядит его развернутое представление во внутреннем формате.
Читатель, вероятно, догадался, что наглядность представления информации на экране дисплея и при печати в системе Mathematica достигается дорогой ценой — каждую «приятную мелочь» приходится программировать, используя при этом функции и команды встроенного языка системы. При этом часто используются опции — специальные указания, задающие объектам системы особые свойства. Опции обычно записываются в виде
Имя_0пции->3начение_0пции
Даже в приведенном простом примере программы используются две опции.
Поспешим успокоить рядового пользователя системы Mathematica — опции задаются по умолчанию настолько удачно, что можно вообще не вспоминать о них, работая с системой без программирования. Тем не менее, система позволяет контролировать и изменять опции, используемые в программах. Для этого служит специальный инспектор опций, запускаемый командой меню Format -> Option Inspector (Shift+Ctrl+0). Эта команда выводит окно инспектора опций (рис. 2.26).
Фактически, инспектор опций обеспечивает визуально-ориентированное изменение программ в части, касающейся установок опций. Окно инспектора не только дает представление о многочисленных опциях в программах, но и обеспечивает возможность их удобного изменения с целью решения особых задач представления информации. Еще раз отметим, что это нужно достаточно опытным пользователям и может не учитываться в начале работы с системой.
Рис. 2.26. Окно инспектора опций
Команда Remove Options убирает все опции, введенные пользователем, и восстанавливает исходное состояние системы — то, с которым и целесообразно работать в большинстве случаев.
Утонченное управление стилем документов
Целый ряд последующих команд служит для утонченного управления стилем документов:
- Style Sheet — выбор готовых описаний стилей документа из обширного стандартного набора;
- Edit Style Sheet — редактирование набора описаний стилей;
- Font — установка типа шрифта;
- Face — установка начертания символов (наклонное, полужирное, подчеркнутое);
- Size — установка размера символов;
- Text Color — установка цвета текста;
- Background Color — установка цвета фона;
- Chooze Font — вывод диалогового окна для задания сразу всех атрибутов шрифта;
- Text Alignment — установка типа выравнивания текста (по правому краю, по левому краю, по центру);
- TextJustification — установка выравнивания текста по ширине;
- Word Wrapping — установка разбивки текста на строки;
- Cell Dingbat — выбор маркеров ячеек из обширного списка (маркеры сохраняются при отключении номеров строк);
- Horizontal Lines — установка типа горизонтальной линии сверху или снизу ячейки.
Каждая из этих команд выводит подменю с обширным списком установок для выбора соответствующего параметра. Поскольку эти параметры достаточно очевидны, мы не будем их обсуждать более подробно.
Управление элементами окна документа
В новых версиях Mathematica 3/4 управление окном документа также производится с помощью меню Format. Для этого имеются четыре команды:
- Show Ruler — отображение мерной линейки;
- Show ToolBar — вывод на экран панели инструментов;
- Show Page Breaks — показ линий разрыва страниц;
- Magnitification — установка (в процентах) масштаба отображения документа.
Все эти команды влияют на вид окна документа. На рис. 2.27 показан вид окна документа с мерной линейкой и панелью инструментов при задании масштаба отображения 200 % вместо обычных 100 %.
Рис. 2.27. Окно документа с линейкой и панелью инструментов при масштабе отображения 200 %
Изменение стиля интерфейса полезно во многих случаях, например при демонстрации какого-либо документа системы Mathematica большой аудитории. В этом случае для увеличения полезной площади окна документа полезно убрать линейку и панель инструментов, а также увеличить размеры всех элементов документа.
gl2-19.jpg
gl2-20.jpg
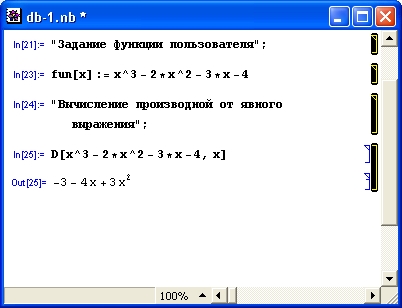
gl2-21.jpg
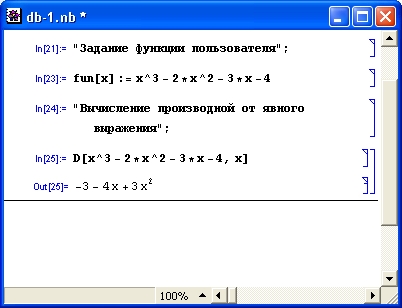
gl2-22.jpg
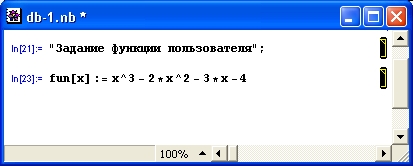
gl2-23.jpg
gl2-24.jpg
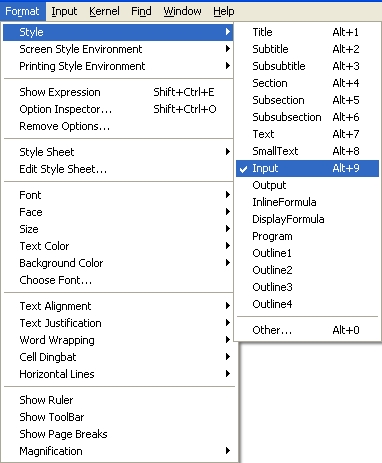
gl2-25.jpg
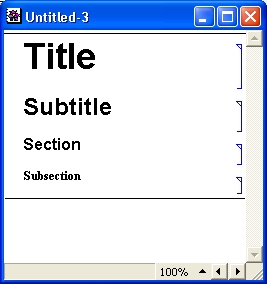
gl2-26.jpg
gl2-27.jpg

9. Ввод элементов документов
Ввод элементов документов
Чтобы начать любые вычисления, нужно ввести по крайней мере исходные данные для вычислений и математические выражения, по которым выполняются вычисления. Иными словами, нужно освоить ввод элементов в создаваемые пользователем документы. Это и описывается в данном разделе.
Меню Input (рис. 2.28) содержит целый ряд описанных ниже команд ввода. Следует отметить, что для некоторых из этих команд более принятым является термин Insert (вставка).
Рис. 2.28. Меню Input и его подменю Create Button
Ряд команд меню Input создан явно не без претензий на новизну, что на практике оборачивается усложнением их применения. За исключением вставок координат двумерных графиков, использования инспектора обзора трехмерных графиков и применения гиперссылок, остальные виды ввода обычный пользователь может и не использовать. Тем не менее, все они в той или иной мере описаны ниже.
Ввод координат двумерных графиков
Иногда бывает нужно знать координаты точек двумерных графиков. Например, это полезно при решении нелинейных уравнений с целью уточнения корней функции, график которой был построен. Mathematica имеет довольно своеобразную возможность определения координат произвольной точки графика и даже ряда точек. Они поясняются окном, которое выводится при исполнении команды Get Graphics Coordinates.
Для получения координат нужно прежде всего выделить двумерный график. Затем следует нажать и удерживать клавишу Ctrl и поместить курсор мыши вблизи нужной точки графика. При этом в левой части строки состояния появятся координаты точки. Можно повторить определение координат для ряда точек. Затем следует воспользоваться командой Сору для переноса координат точек в буфер, а затем, исполнив команду Paste, можно перенести список с координатами точек в текущую строку ввода. Это удобно делать, используя команды контекстно-зависимого меню, вызываемого правой кнопкой мыши. К примеру, координаты трех точек графика в строке ввода могут выглядеть так:
{{3.04804, 0.0165875}, {-8.21841, 0.73632},
{9.39226, 0.0165875}}
Этот способ не очень удобен, но зато позволяет получать списки координат ряда точек графика.
Выбор точки обзора трехмерных графиков
Команда 3D View Point Selector (Shift+Ctrl+V) служит для вывода селектора точки обзора трехмерных графиков (рис. 2.29). Это следует делать при наличии в документе трехмерного графика.
В этом окне имеется пространственное изображение куба, которое можно вращать с помощью мыши или путем перемещения ползунков прокрутки, задающих параметры просмотра и перспективы объекта (увы, сам объект при этом не виден). Для задания поворота рекомендуется окно с самой фигурой разместить рядом — на рис. 2.29 оно показано справа. В правой части окна вращения имеется ряд кнопок:
- Close Dialog — завершение диалога;
- Cancel — прекращение работы;
- Paste — перенос параметров точки обзора в окно документа;
- Defaults - возврат к принятым по умолчанию значениям параметров вращения и перспективы;
- Help — вызов справки.
Рис. 2.29. Трехмерный график (справа) и селектор точки обзора (слева)
Действие всех кнопок вполне очевидно. Поэтому остановимся на главном - нажатие кнопки Paste создает строку с опцией Viewpoint [ {х, у, z} ], которая вставляется в текущий документ в месте расположения текстового курсора В нашем случае текстовый курсор надо расположить в строке функции Show [gl g2 ] после запятой, установленной вслед за g2. Если теперь исполнить модифицированную функцию Show, то рисунок будет перестроен (рис. 2.30).
Подобное средство введено и в новую версию системы Mathematica 4 -оно реализуется пакетом расширения RealTime3D. Мы его уже рассматривали. Вращение SD-объектов мышью - очень удобное средство. Оно позволяет в считанные секунды найти наиболее удачное положение фигуры или ряда фигур в пространстве, при котором их особенности видны наиболее отчетливо.
Разумеется, такая процедура поворота фигуры в пространстве не очень удобна При очередном повороте надо будет отредактировать строку с функцией Show!
убрав из нее старую запись опции Viewpoint и вставив новую запись. Между тем, в ряде систем компьютерной математики (например в Maple V R5 и Mathcad 8) уже давно появилось новое мощное средство редактирования изображений ЗD-объектов — их вращение мышью в реальном масштабе времени.
Рис. 2.30. Пример разворота трехмерной фигуры
Изменение цветовой гаммы
Команда Color Selector выводит стандартное окно изменения цветовой гаммы, используемой при функциональной окраске графиков (рис. 2.31). Это типовое окно системы Windows 95/98. С его помощью можно создать дополнительные цвета и изменить гамму цветов линий рисунков и заливки.
Не рекомендуется пользоваться селектором цветов без особой на то надобности. Практика показывает, что исходные установки цветов выбраны очень тщательно, с учетом особенностей нашего зрения. Обычно после изменения установок цвета пользователь быстро осознает, что его цветовые «новации» лишь испортили цветовую гамму рисунков, и возвращается к исходной установке цветов.
Рис. 2.31. Окно селектора цветов
Команда Record Sound выводит окно программы Звукозапись, входящей в состав операционной системы Windows 95/98 (рис. 2.32). Звукозапись — это специальное приложение, позволяющее записывать звуки с микрофона и воспроизводить их с помощью звуковой карты компьютера. Органы управления программы по виду подобны применяемым у обычных магнитофонов, а потому не нуждаются в подробном описании.
Рис. 2.32. Интерфейс программы Звукозапись
Особенности работы со звуком будут описаны в дальнейшем. Отметим лишь, что Mathematica имеет возможность работы как с математическим синтезом звуковых сигналов, так и с реальными звуковыми сигналами речи и музыки, записываемыми в виде файлов с расширением .wav. Для такой записи и служит команда Record Sound.
Не стоит забывать, что для реализации возможностей записи и воспроизведения звуков компьютер должен быть оснащен звуковой платой, звуковыми колонками или наушниками и микрофоном. Желательно, чтобы эти средства были отлажены в среде Windows 95/98 до их использования системой Mathematica.
Иногда возникает необходимость вставить в документ ссылку на имя файла, в котором хранятся какие-либо данные. Команда Get File Path предоставляет удобный способ вставить в документ имя файла вместе с полным путем к нему. При выборе команды открывается стандартное окно загрузки файлов. После выбора нужного файла и щелчка на кнопке Open полное имя файла будет вставлено в документ в месте расположения текстового курсора.
Задание таблиц и матриц в системе Mathematica легко выполняется с помощью соответствующих функций. Однако команда Create Table/Matrix/Palette дает возможность сделать это и через главное меню. Она выводит окно задания таблиц, матриц и палитр, показанное на рис. 2.33 справа.
Рис. 2.33. Работа с окном Create Table/Matrix/Palette
Практика показывает, что таблицы и матрицы малых размеров проще вводить в виде списков в режиме ввода из командной строки. Только в том случае, когда вводимые элементы таблиц и матриц — громоздкие числа, их удобнее вводить с помощью окна Create Table/Matrix/Palette.
В левой части документа показаны примеры работы с данным окном. Оно выводит палитру матриц — по умолчанию из трех строк и трех столбцов. Возможны разные варианты представления матриц в строках ввода — с подчеркнутыми строками, обведенные рамкой, с кнопками ввода и без них. Но в любом случае исполнение строки ввода создает список, соответствующий введенной таблице или матрице. Если ввод не был завершен, то вместо элемента таблицы или матрицы выводится кнопка.
Ввод и редактирование кнопок
При создании сложных документов для диалогового режима работы с системой Mathematica иногда полезно создание кнопок. Оно выполняется командой Create Button. Она выводит подменю, содержащее небольшое число типов кнопок. Например, кнопка типа Evaluate Cell служит для создания ячейки, исполняющей вычисления. Она выглядит как прямоугольник:
2+3/4;
Обратите внимание на то, что записанное перед кнопкой выражение не вычисляется, поскольку строка завершается точкой с запятой. Если активизировать кнопку двойным щелчком, получим вместо кнопки знак «%» и выполнение вычислений:
%
11/4
Редактирование кнопок осуществляется по команде Edit Button. Она выводит окно редактирования кнопок, показанное на рис. 2.34. В этом окне содержатся перечень кнопок и окно с программой, создающей кнопку с нужными свойствами.
Рис. 2.34. Окно редактирования кнопок
Редактирование как внешнего вида кнопок, так и их назначения требует знания языка программирования системы Mothematica. Поэтому мы ограничимся приведенными выше сведениями о создании кнопок. Чаще всего пользователи обходятся без этой своеобразной возможности и вспоминают о ней лишь тогда, когда становятся способными составлять в среде Mathematica полноценные учебные программы.
Гиперссылка является объектом класса ButtonBox (кнопка), связанным с некоторым другим объектом, представленным файлом — например, каким-либо документом или рисунком. При активизации гиперссылки загружается связанный с ней объект.
Гиперссылка создается следующим образом. В строке ввода готовится некоторый текст, например фраза: «Просмотр документа dl.nb». Какое-либо слово или вся фраза выделяются с помощью мыши, затем исполняется команда Create Hyperlink (Создать гиперссылку). Открывается окно, показанное на рис. 2.35 в правой части экрана.
Рис. 2.35. Создание гиперссылки
Следующий этап заключается в установке связи гиперссылки с нужным файлом. Его полное имя можно прямо указать в верхнем поле над кнопкой Browse. Однако чаще всего пользователь не помнит полного имени файла. Тогда он может воспользоваться кнопкой обзора файловой системы Browse, которая выводит стандартное окно поиска файлов, показанное на рис. 2.35 слева. В этом окне надо найти нужный файл (в нашем случае это файл документа dl.nb) и нажать кнопку Открыть. Имя файла появится в поле окна Create Hyperlink, теперь для создания гиперссылки достаточно нажать кнопку ОК.
Выделенное слово (фраза) превратится в кнопку, подчеркнутую снизу чертой. Это и есть гиперссылка. Активизация гиперссылки вызовет немедленное появление документа, представленного (в нашем примере) файлом dl.nb (рис. 2.36).
Рис. 2.36. Пример использования гиперссылки
Гиперссылки обычно применяются для создания сложных документов с многочисленными перекрестными связями. На основе гиперссылок создаются документы, широко используемые во всемирной сети Интернет. Для записи таких документов целесообразно использовать формат файлов HTML.
Создание и ввод специальных объектов
Еще одна редко используемая возможность — создание объекта, которому присвоен номер. При этом номер генерируется автоматически. Для этого служит команда Create Automatic Numbering Object. Она открывает окно, показанное на рис. 2.37.
Рис. 2.37. Окно создания объекта с автоматической нумерацией
Как видно из рис. 2.37, окно содержит переключатель, выводящий обширный перечень возможных вариантов нумерованных объектов. В дальнейшем мы не будем пользоваться объектами данного типа, так что ограничимся приведенным выше описанием и предоставим читателю самому поэкспериментировать с такими объектами. Предоставим читателю самостоятельно разобраться и с еще одной редко используемой возможностью — вставкой объектов, отображающих значения опций системы Mathematica, с помощью команды Create Value Display Object. Эта команда также выводит окно для задания свойств таких объектов.
Вставки, связанные с ячейками
Для вставки содержимого предшествующих ячеек ввода и вывода служат команды Copy Input from Above и Copy Output from Above. Поясним это примерами. Введем в ячейку ввода выражение
1+2
Нажав клавиши Shift+Enter, получим строку вывода:
3
Теперь, исполнив команду Copy Input from Above, получим в новой строке ввода:
1+2
Исполнение этой ячейки даст такой же вывод:
3
То же самое, но в строке ввода, может быть получено с помощью команды Сору Output from Above:
3
Еще одна команда — Start New Cell Below — служит для вставки новых пустых ячеек ввода между уже имеющимися. Ячейка вставляется ниже положения текстового курсора, указывающего место вставки.
Вставка имен функций и списков их параметров
Запомнить около тысячи функций, входящих в ядро систем Mathematica, также как и правила их записи, довольно сложно. Для облегчения этого служат две заключительные команды меню Input
Первая из них работает, если вы ввели часть ключевого слова в строке ввода. Тогда исполнение команды Complete Selection (Ctrl+K) выводит список имен всех функций, которые начинаются с уже введенных символов. Рисунок 2.38 поясняет это на примере ввода слова «Plot».
Рис. 2.38. Пример исполнения команды Complete Selection
Следующая команда — Make Template — выдает список параметров функции, в имени которой установлен текстовый курсор. Например, если введено слово «Plot» и курсор стоит после него, то команда Make Template приведет к следующему изменению строки ввода:
Plot[f, {x, xmin, xmax}]
Теперь становится ясно, какие параметры имеет эта функция, и редактированием строки ввода можно ввести нужные конкретные значения этих параметров.
gl2-28.jpg
gl2-29.jpg
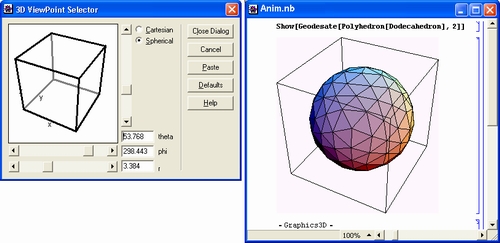
gl2-30.jpg
gl2-31.jpg
gl2-32.jpg
gl2-33.jpg
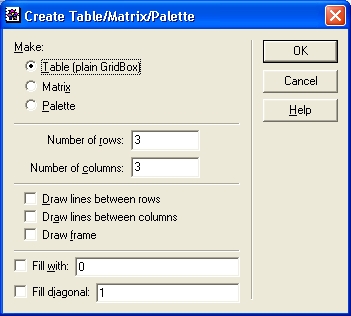
gl2-34.jpg
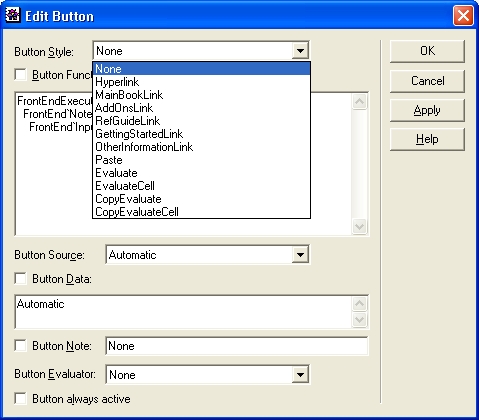
gl2-35.jpg
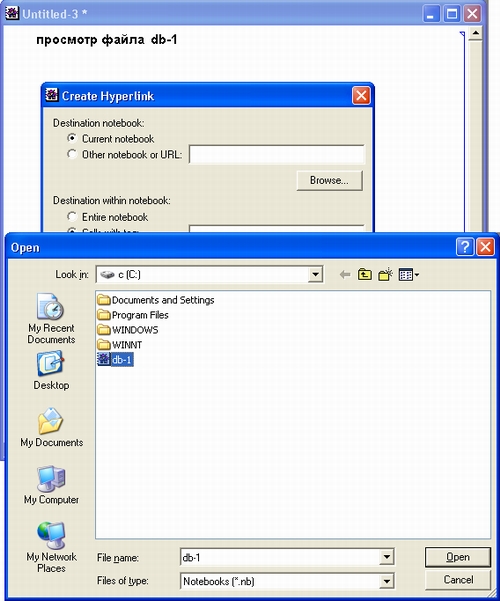
gl2-36.jpg
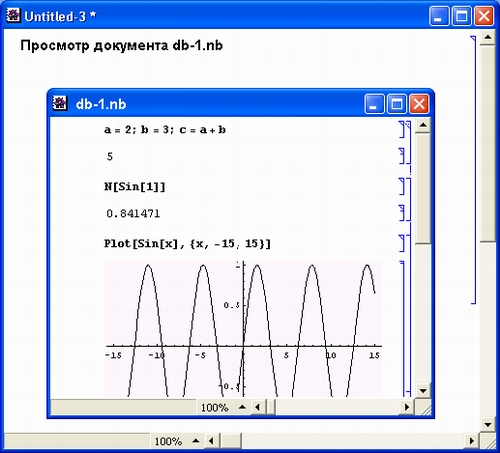
gl2-37.jpg
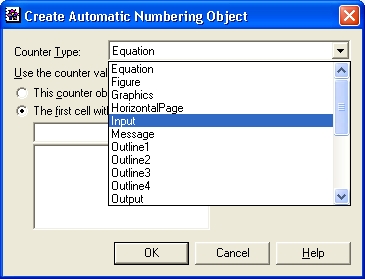
gl2-38.jpg
10. Управление работой ядра
Управление работой ядра
В этом небольшом разделе рассматриваются достаточно важные вопросы управления ядром систем Mathematica и, в конечном счете, процессом вычислений.
Меню Kernel служит для управления действиями, проводимыми ядром системы над ячейками загруженного документа. Внешний вид меню Kernel и его подменю Evaluation показан на рис. 2.39.
Рассмотрим команды этого подменю более подробно.
Управление процессом вычислений
Основные команды управления процессом вычислений сосредоточены в подменю Evalution меню Kernel:
- Evaluate Cells (Shift+Enter) — вычисление выделенных ячеек;
- Evaluate in Place (Shift+Ctrl+Enter) — вычисление выделенного выражения «на месте»;
- Evaluate Next Input (Shift+Enter на цифровом поле клавиатуры) — вычисление следующей строки ввода;
- Evaluate in Subsession — вычисление выделенных ячеек в параллельном интерактивном сеансе работы с ядром;
- Evaluate Notebook — вычисление всех ячеек документа;
- Evaluate Initialization — вычисление инициализационных ячеек;
- Enter Subsection — запуск диалогового сеанса работы с ядром;
- Exit Subsection — завершение диалогового сеанса работы с ядром.
Рис. 2.39. Меню Kernel и его подменю Evaluation
Данная группа команд управляет вычислением ячеек. Перед вычислением каждая ячейка оценивается по своим признакам. Команда Evaluate Cells оценивает все выделенные ячейки, вызывает их вычисление и помещает результат вычисления каждой ячейки сразу после нее. Это одна из наиболее распространенных команд. Следует помнить, что, казалось бы, естественное нажатие клавиши Enter вызывает лишь переход на новую строку, а не вычисление выделенных ячеек ввода. При управлении с клавиатуры вычисление выделенных ячеек происходит при одновременном нажатии клавиш Shift и Enter.
Особое внимание надо обратить на команду Evaluate in Place. Допустим, вы ввели в ячейку ввода, выражение
(2+3)/7
Выделите мышью выражение (2+3). Теперь, исполнив команду Evaluate in Place нажатием клавиш Ctrl+Shift+Enter, мы получим в строке ввода следующее:
5/7
Таким образом, выражение (2 + 3) было вычислено прямо в строке ввода, и на его месте появился результат — 5. Если теперь исполнить команду Evaluate Cells, то появится строка вывода с результатом:
5/7
Поскольку результат представлен дробно-рациональным числом, он повторяет выражение в строке ввода, но в ином формате — в формате вывода.
Команда Evaluate Next Input позволяет последовательно вычислить ряд ячеек, расположенных под выделенной ячейкой. Если текстовый курсор находится в ячейке ввода, данная команда вычисляет эту ячейку. В противном случае она перемещает выделение на следующую ячейку. Последующее использование команды ведет к исполнению этой ячейки, затем к выделению следующей ячейки, ее вычислению и т. д. Таким образом, можно последовательно вызывать вычисление ячеек документа, используя эту команду дважды для каждой ячейки.
Команда Evaluate Notebook вычисляет все ячейки введенного документа сверху вниз. Это особенно полезно, если результаты вычисления последующих ячеек зависят от результатов вычисления предыдущих. При этом все ячейки переоцениваются, то есть выполняются заново с учетом всех возможных изменений их содержимого. Это напоминает работу с электронными таблицами, когда смена численного значения в одной ячейке автоматически меняет содержание всех других ячеек, использующих данные из данной ячейки.
Команда Evaluate Initialization вычисляет все ячейки, помеченные как инициали-зационные, то есть имеющие символ «т» над квадратной скобкой, обрамляющей ячейку. О задании такого признака говорилось ранее в разделе «Манипуляции с ячейками». Ячейки с указанным признаком выполняются этой командой без их выделения.
Следующие две команды меню Kernel управляют процессом текущих вычислений:
- Interrupt (Alt+,) — прерывание вычислений;
- Abort (Alt+.) — полное прекращение вычислений.
Их действие вполне очевидно. Команда Interrupt служит для прерывания текущих вычислений. Эта команда при исполнении задает запрос о том, каким образом вы хотите прервать вычисления и сколько шагов вычислений надо еще сделать. Разумеется, можно и отменить прерывание. Команда Abort вызывает полное прекращение вычислений, так что их можно возобновить лишь с самого начала. Вместо результата выдается сообщение $Abort.
Полезно запомнить клавиатурные комбинации для этих команд, поскольку «зависание» системы из-за чрезмерно большого времени исполнения неудачного алгоритма (например, глубокой рекурсии) не редкость. Кстати, в процессе таких вычислений команды прерывания доступны и из меню.
Используйте команды Interrupt и Abort, если вы загнали систему в режим «вечных вычислений» — зацикливание. Это позволит вам благополучно выйти из этого режима, сохранив текущие данные и текущую программу (документ). Иные способы прерывания вычислений чреваты потерей текущих данных и документа.
Новые версии Mathematica приобрели возможность работы не только с установленным локальным ядром, но и с другими ядрами, ориентированными на какие-либо специфические классы вычислений. Это привело к появлению ряда новых команд:
- Start Kernel — запуск выбранного ядра;
- Quit Kernel — завершение работы выбранного ядра;
- Default Kernel — выбор ядра, используемого по умолчанию;
- Notebook's Kernel — выбор ядра для данного документа;
- Kernel Configuration Options — выводит окно установки свойств ядер.
Перечисленные команды позволяют, в частности, подключаться к ядру через сеть, запуская его на удаленной машине. Таким образом, интерфейсный процессор системы Mathematica, установленный на рабочей станции, может использовать для вычислений ядро, запущенное через сеть на мощном сервере.
Управление показом номеров ячеек
Номера строк ввода и вывода — причуда системы, унаследованная от старого доброго Бейсика. В принципе, нумерация строк при культурном программировании в системе Mathematica не нужна и даже вредна. В частности, нумерация не является строго последовательной и нарушается при изменении ячеек ввода в начале документа и повторном их вычислении после редактирования. К тому же в общем случае она меняется после записи и повторной загрузки документа.
Поэтому предусмотрена команда-переключатель Show In/Out Names. Она управляет показом или скрытием номеров строк. Если напротив этой команды в меню стоит галочка, то номера строк будут показаны в виде In [n] и Out [n]. При отсутствии галочки номера строк и слова In и Out не отображаются.
Во многих приводимых в книге примерах решения задач в среде Mathematica нумерация строк устранена, поскольку не несет никакой полезной информации. Ее целесообразно оставлять в тех случаях, когда надо комментировать ту или иную строку или когда исполнение документа предполагает иной порядок, чем последовательный сверху вниз.
Иногда желательно удалить все ячейки вывода, например для того, чтобы при объединении в группы они не превратились в элементы ячеек ввода. Для удаления всех ячеек вывода служит команда Delete All Output. Выбор этой команды приводит к удалению из текущего документа всех ячеек вывода.
Удаление всех ячеек вывода целесообразно, если конечный документ содержит управляющие структуры, меняющие последовательный порядок выполнения ячеек. После удаления ячеек вывода их можно восстановить, задав вычисление всего документа в целом.
gl2-39.jpg
11. Операции поиска и замены
Операции поиска и замены
Операции поиска и замены относятся к типовым операциям редактирования документов. Они, наряду с другими родственными операциями, собраны в меню Find. В этом небольшом разделе мы познакомимся с командами и операциями этого меню.
Меню Find содержит команды поиска и замены фрагментов текстов и выражений (рис. 2.40).
Эти операции характерны для любого текстового процессора, например Microsoft Word 95/97, и знакомы даже начинающим пользователям. Поэтому ограничимся их кратким описанием.
Рис. 2.40. Меню Find
Первая группа команд меню Find реализует типичные операции поиска и замены:
- Find (Ctrl+F) — поиск заданных строк вперед и назад (но без замены);
- Enter Selection (Ctrl+E) — ввод выделенной строки в окно поиска;
- Find Next (F3) — поиск по документу вперед;
- Find Previous (Shift+F3) — поиск по документу назад;
- Find in Cell Tags — поиск ячейки с заданной этикеткой (tag);
- Replace (Ctrl+R) — замена одной строки на заданную другую;
- Replace and Find Again (Shift+Ctrl+R) — выполнение замены с продолжением поиска;
- Replace All — выполнение замены по всему документу.
Эти операции выполняются с помощью окна поиска и замены, показанного на рис. 2.41. Оно имеет поля для задания искомой строки и строки замены.
Рис. 2.41. Пример поиска подстроки «4х» и ее замены на подстроку «6х»
В данном случае осуществлена замена члена в математическом выражении. Работа с окном поиска и замены вполне очевидна и не отличается от аналогичной операции в текстовых редакторах. Поэтому мы не будем вдаваться в ее подробности. Читателю рекомендуется самостоятельно поупражняться в операциях поиска и замены различных объектов в текстовых и формульных ячейках.
Обнаружение и открытие выделенных строк
Следующие три команды меню Find служат для работы с выделенными строками:
- Open Selected — открытие групп, содержащих выделенные строки;
- Scroll to Selection — прокрутка документа до выделенной строки;
- Go Back — возврат назад после использования гиперссылки.
Их действие также очевидно.
Особым признаком ячеек ввода могут быть их этикетки (tags) — короткие сообщения, характеризующие суть выполняемых ячейками действий и размещаемые сверху строки ввода. Этикетки вводятся для того, чтобы можно было одним разом вызвать на просмотр те ячейки, которые объединены какими-либо общими свойствами.
Признаком наличия у данного документа этикеток является их список, который появляется в подменю Cell Tags (Ячейки с этикетками) меню Find. Например, документ, представленный на рис. 2.42, имеет целый набор этикеток.
Рис. 2.42. Выбор этикетки
Если выбрать имя этикетки (например Euler), будут выделены все ячейки, помеченные данной этикеткой.
Команда Add/Remove Cell Tags (Ctrl+J) позволяет вставить этикетку в строку ввода, в которой ее нет, или удалить этикетку из строки, где она есть. Эта команда вызывает появление окна редактирования этикеток, показанного на рис. 2.43. Работа с этим окном вполне очевидна — кнопка Add добавляет этикетку, а кнопка Remove удаляет ее. Команда Cell Tags from In/Out Names позволяет создать для текущей ячейки этикетку на основе номера ячейки.
Последняя команда меню Find — Make Index — помещает в буфер все этикетки текущего документа. Перед этим она выводит окно, в котором можно указать признаки этикеток. Нажатие кнопки ОК помещает список этикеток в буфер, откуда его можно извлечь с помощью команды Paste. Рисунок 2.44 показывает окно команды Make Index и созданный список этикеток под ним.
Рис. 2.43. Окно редактирования этикеток
Рис. 2.44. Окно подготовки списка этикеток и результат вставки списка этикеток из буфера
gl2-40.jpg
gl2-41.jpg
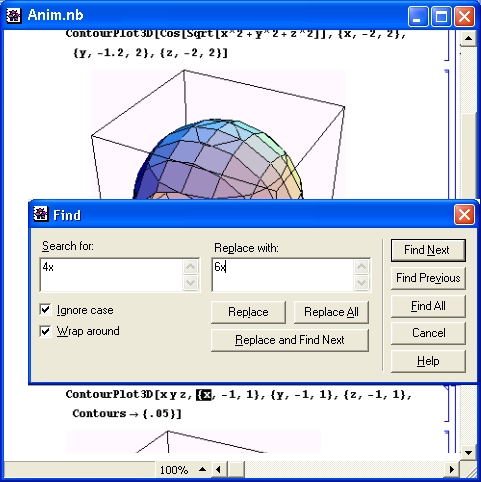
gl2-42.jpg
gl2-43.jpg
gl2-44.jpg
12. Работа с окнами и справкой
Работа с окнами и справкой
Как и большинство приложений Windows, Mathematica 3/4 является многооконной системой. Поэтому важно с самого начала работы с ней научиться управлять окнами системы. Система может работать с многими окнами документов, окнами интерфейса и справочной системы. Как это делается, описано в этом небольшом разделе.
Система Mathematica многооконная и может работать сразу с несколькими документами. По мере загрузки файлов их список появляется в нижней части меню Window (Окно). Само меню содержит следующие команды для работы с окнами:
- Stack Windows — каскадное расположение окон;
- Tile Windows Wide — расположение мозаикой по высоте;
- The Windows Tall — расположение мозаикой по ширине;
- Messages — управление выводом окна сообщений об ошибках.
За каждым загруженным документом закрепляется свое окно. Обычно в главном окне редактирования виден лишь последний документ. Однако меню Window позволяет управлять расположением окон, делая его наиболее приемлемым для пользователя.
Если выбрать команду Stack Windows, то окна будут расположены каскадом (рис. 2.45).
Рис. 2.45. Каскадное расположение окон документов
При каскадном расположении окон на переднем плане находится окно с текущим документом. Оно заслоняет другие окна, но так, что остаются видны их строки заголовка.
Заметим, что, как принято в операционной системе Windows 95/98, положением и размерами окон легко управлять, используя кнопки в строке заголовка окна.
Две другие команды — Tile Windows Wide и Tile Windows Tall — обеспечивают расположение окон мозаикой. Рисунок 2.46 показывает расположение окон мозаикой по высоте после исполнения команды Tile Windows Wide.
Рис. 2.46. Расположение окон после исполнения команды Tile Windows Wide
Ha рис. 2.47 показано расположение тех же окон после исполнения команды Tile Windows Tall.
Как видно из сравнения, рис. 2.46 и 2.47 различаются способом деления окон — по ширине или по высоте. Естественно, сохраняются все описанные выше возможности управления окнами — их расширения на весь экран, изменения размеров и местоположения.
Каждое окно можно минимизировать с помощью команды Свернуть (Minimize) системного меню окна или левой кнопки строки заголовка окна.
Рис. 2.47. Расположение окон после исполнения команды Tile Windows Tall
Работа с такой мощной системой, как Mathematica, была бы кошмаром, если бы постоянно приходилось заглядывать в огромные тома ее описания. К тому же эти системы обычно используются коллективно, и не у всех пользователей есть свободный доступ к документации в виде бережно хранимых дорогих и редких книг, поставляемых с системой. Поэтому в систему встроена довольно мощная справочная база данных. Хотя справочная база данных не заменяет руководства пользователя в виде обычной книги, она позволяет оперативно уточнить возможности системы Mathematica и выяснить синтаксис используемых функций, опций и директив, не отходя от компьютера.
Справочная база данных позволяет уточнить назначение любой функции, оператора или служебного слова системы и постепенно знакомиться с ее возможностями. Однако она не претендует на роль обучающей системы и неудобна для знакомства с системой.
Главный недостаток справочной базы данных состоит в том, что она требует для просмотра компьютер. Его не возьмешь с собой на дачу или на пляж, да и читать долго с экрана дисплея вредно для глаз и здоровья в целом. Компьютерная база данных настолько обширна и разветвлена, что ее трудно обозревать даже несмотря на гипертекстовую организацию.
В то же время, если вы уже сидите за компьютером, то пользоваться книгами не очень удобно. Куда проще тут же найти нужные сведения во встроенной в Mathematica справочной системе. К тому же, в отличие от книг, она содержит «живые» примеры, которые можно быстро приспособить к своим нуждам.
Таким образом, можно сделать вывод, что справочная база данных систем Mathematica ориентирована прежде всего на получение оперативной справки по той или иной функции или команде либо по некоторому элементу интерфейса. В общем, пока что книги и электронная справочная система прекрасно уживаются друг с другом.
Открытие справочной базы данных
Справочная база данных управляется командами, расположенными в меню Help (Справка).
Справочная система Mathematica, начиная с версии 3, переработана кардинально и построена в виде броузера справки. Его можно вызвать с помощью команды Help Browser (Shift+Fl). Почти аналогично действует команда Find Selection Function (F1), которая служит для поиска заданной функции.
Справочная база данных стала очень удобной и содержит все лучшее из интерфейса справочных систем других математических пакетов. В частности, заимствована система иерархического поиска нужных данных (рис. 2.48), применяемая в системах класса Maple V.
Рис. 2.48. Окно броузера справочной системы
В окне броузера справочной системы можно (активизацией соответствующей кнопки) выбрать следующие разделы справок:
- Built-in Functions — встроенные функции;
- Add-ons — пакеты расширений;
- The Mathematica Book — электронная версия книги «The Mathematica Book», написанной разработчиком системы Стивеном Вольфрамом;
- Getting Started/Demos — руководство для начинающих и примеры;
- Other Information — другая информация;
- Master Index — справка по индексу (алфавитный указатель).
На рис. 2.48 наглядно показан поиск данных о встроенной функции, вычисляющей синус угла х. При этом возможен как прямой поиск по имени функции (в нашем случае Sin), так и поиск по контексту. В окнах справочной системы можно просматривать также страницы электронных книг, поставляемых с системой. Справочная система имеет гипертекстовые ссылки (подчеркнутые слова синего цвета), что позволяет расширять знакомство с объектами системы.
Рис. 2.49. Пример замены примера в ячейке 1п[1] и его вычисления
Практически по каждой функции приведен ряд примеров, которые открываются при активизации гиперссылки в виде треугольника с надписью Further Examples (вначале примеры скрыты). Примеры являются «живыми» в том смысле, что, не выходя из справочной системы, можно перенабрать содержимое любой ячейки ввода и тут же, вычислив ячейку, получить новый результат. К примеру, на рис. 2.49 показано, как список синусов, заданный ранее (см. рис. 2.48) строкой ввода In , заменен на построение графика функции Sin [х] (а строка ввода получила номер In ).
Можно также, выделив ячейки примеров, перенести их содержимое в буфер командой Сору и затем разместить в текущем документе командой Paste. Такой пример можно редактировать и использовать для решения своих, близких к нему по сути задач.
Работа с электронным учебником
Для демонстрации возможностей системы служит электронный учебник Getting Started/Demos. На рис. 2.50 показан пример работы с ним — иллюстрируется построение документов в формате Notebook.
Электронный учебник содержит множество полезных применений системы Mathematica 4. Однако в целом он рассчитан на начальный уровень знакомства с системой. Учебник представляет материал по контексту.
Рис. 2.50. Пример работы с электронным учебником
В систему Mathematics встроен ряд дополнительных пакетов расширения (Add-ons), содержащих массу полезных новых функций. Они служат для расширения функциональных возможностей системы в таких областях, как алгебра, геометрия, приближенные вычисления, дискретная математика, теория чисел, математическая статистика, линейная алгебра и т. д.
Доступ к ним возможен объявлением соответствующего пакета. На рис. 2.51 показан раздел справки по применению одного из таких пакетов для прямого и обратного преобразований Фурье.
Рис. 2.51. Пример справки по преобразованию Фурье
Доступ к справке по пакетам расширения обеспечивается разделом Add-ons справочной системы. Фактически, справка повторяет материал книги от соответствующей версии системы [31,32].
Любой пример применения функции из пакета расширения также можно перенести в документ. Для этого нужно выделить соответствующую ячейку примера и с помощью команды Сору перенести ее в буфер промежуточного хранения. Затем с помощью команды Paste можно перенести содержимое буфера в документ. Для этого можно использовать и контекстно-зависимое меню, которое появляется при нажатии правой кнопки мыши.
Раздел справки The Mathematica Book — это электронный вариант книги Стивена Вольфрама по соответствующей версии системы. Рисунок 2.52 иллюстрирует работу с электронной книгой — открыт раздел со списком ряда определенных интегралов (видно лишь начало списка).
Рис. 2.52. Раздел электронной книги со списком определенных интегралов
С первого взгляда трудно уловить отличие электронной книги «The Mathematica Book» («Математическая книга») от справки по пакетам расширения системы. Однако эти различия есть и заключаются в следующем:
- книга содержит большой объем чисто справочной информации (формулы, графики, примеры вычислений и т. д.);
- книга является систематическим руководством по применению системы;
- книга использует как встроенные функции, так и дополнительные функции из пакетов расширения.
Галерея формул (Formula Gallery), показанная на рис. 2.52, представляет собой весьма полное собрание математических формул. Любую формулу можно выделить и поместить в буфер обмена для использования в документах. Таким образом, электронная книга в состоянии заменить обычный математический справочник. Приходится еще раз сожалеть, что как и вся справочная база данных, электронная книга написана на английском языке.
Интересна также галерея рисунков (Graphics Gallery) электронной книги, дающая представление о графических возможностях системы. Впрочем, эту галерею мы уже описывали в уроке 1. В электронной книге можно найти множество интересных и весьма эффектных примеров применения графики — например, построения карт или анимационных рисунков.
Электронная книга системы Mathematica являет собой наглядный пример развития электронных книг. Они характеризуются рядом новых качеств:
- красотой и наглядностью оформления;
- простотой поиска нужных сведений;
- возможностью применения действующих примеров;
- использованием гипертекстовых ссылок;
- применением наглядных средств анимации изображений;
- объединением с другими программными средствами;
- легкостью модификации.
При всех этих очевидных достоинствах совершенно ясно, что в ближайшие годы подобные электронные книги не заменят обычные, поскольку их стоимость неизмеримо выше, чем стоимость обычных книг, а удобства работы с электронными книгами нивелируются необходимостью многочасового сидения за экраном дисплея компьютера. К тому же обычные книги написаны на исконно русском и понятном нам языке, тогда как подавляющее большинство электронных книг остаются англоязычными.
Раздел Other Information (Другая информация) посвящен различным сведениям об интерфейсе системы Mathematica и данным по связи с ее разработчиком — фирмой Wolfram Research. На рис. 2.53 показана одна из страниц этого раздела, посвященная правилам ввода показателей степени.
В этом разделе справочной системы можно найти сведения обо всех командах главного меню системы, о правилах набора сложных выражений и об использовании в ячейках ввода записей математических выражений, предельно приближенных к естественной математической записи.
Работа с алфавитным указателем
Последний раздел справочной системы — алфавитный (или индексный) указатель Master Index. Если вы знаете, какую команду или функцию ищете, то достаточно указать ее в поле у кнопки Go То (Перейти к...) и нажать эту кнопку. Можно также воспользоваться системой поиска по начальным буквам искомого слова (рис. 2.54).
Риc. 2.53. Одна из страниц раздела Other Information справочной системы
Рис. 2.54. Пример работы с алфавитным указателем
Алфавитный указатель ценен тем, что в него входят все команды и функции, опции и примитивы, причем не только встроенные, но и входящие в состав пакетов расширений.
Помимо упомянутых команд меню Help имеет команды, повторяющие разделы справочной системы, и еще ряд команд:
- Why the Beep? — информация о причинах выдачи звукового сигнала;
- Registration — вывод формы регистрации (для легальных пользователей);
- About Mathematica — вывод окна с краткими сведениями о системе и фирме Wolfram (рис. 2.55);
- Rebuild Help Index — создание индексного указателя (обычно требуется сразу после первого запуска системы).
Рис. 2.55. Окно с данными о системе Mathematica 4
Справочная система Mathematica 3/4 во многим дублирует обычную документацию по системам в виде обычных книг. Как показывает практика, оба вида документации (электронная в виде справки и обычная) прекрасно уживаются друг с другом и занимают разные ниши. Так, электронной справкой можно пользоваться только сидя за компьютером. Обычные книги позволяют полнее охватить информацию и найти нужные сведения. Однако фирменные книги и электронная справка подготовлены на английском языке и не могут заменить обычные книги, особенно для русскоязычных пользователей.
Действие этих команд очевидно и не нуждается в особых пояснениях. Остается лишь отметить, что уверенное владение системой основано на освоении не только пользовательского интерфейса системы, но и многих ее команд и функций, а также на знании языка программирования системы.
gl2-45.jpg
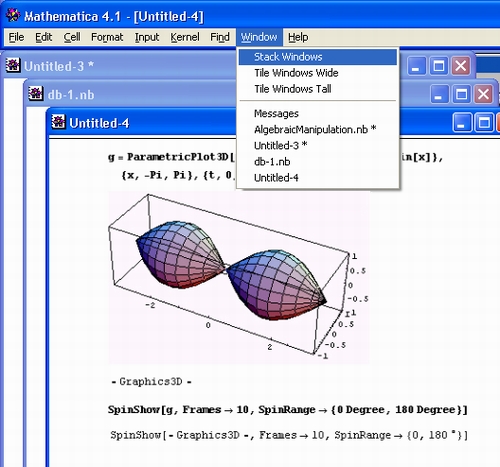
gl2-46.jpg
gl2-47.jpg
gl2-48.jpg
gl2-49.jpg
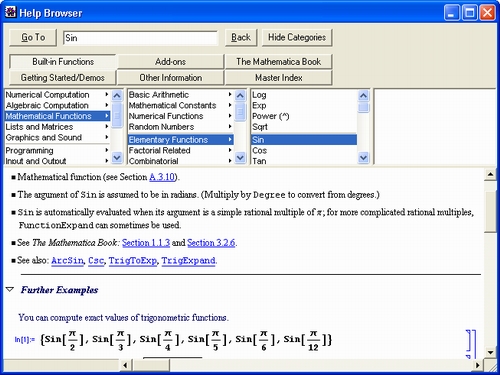
gl2-50.jpg
gl2-51.jpg
gl2-52.jpg
gl2-53.jpg
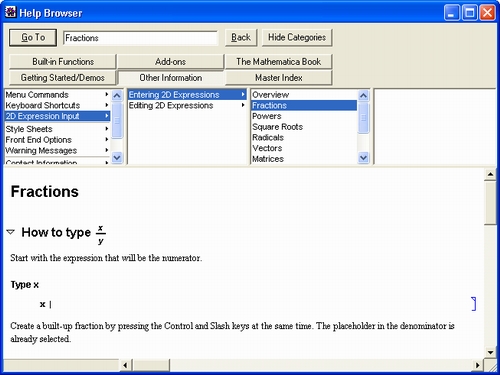
gl2-54.jpg
gl2-55.jpg
13. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Пользоваться строкой меню.
- Управлять окном редактирования документов.
- Работать с файлами.
- Создавать простые документы и осуществлять их редактирование.
- Работать с ячейками и форматировать их содержимое.
- Вставлять в ячейки различные объекты системы Mathematica.
- Управлять вычислением ячеек.
- Производить поиск и замену текста в документе.
- Управлять расположением окон.
- Пользоваться справочной системой.
Урок 3. Типы данных
Урок 3. Типы данных
1. Типы данных
Типы данных
- Основные классы данных
- Выражения
- Списки и массивы
- Объекты и идентификаторы
- Функции, опции, атрибуты и директивы
- Подстановки
- Функции линейной алгебры
С этого урока начинается серьезное освоение математических возможностей систем Mathematica 3 и 4. Мы изучим основные типы данных, операторов, функций и объектов, с которыми может работать система Mathematica 3/4, а попутно познакомимся и с некоторыми простыми операциями ввода данных и их обработки.
2. Основные классы данных
Основные классы данных
Mathematica оперирует с тремя основными классами данных:
- численными данными, представляющими числа различного вида;
- символьными данными, представляющими символы, тексты и математические выражения (формулы);
- списками — данными в виде множества однотипных или разнотипных данных.
Каждый из этих классов данных в свою очередь имеет ряд специальных, более частных типов данных. На них мы остановимся более подробно.
Двоичные числа, биты и байты
Минимальной единицей информации в компьютерной технике является двоичная единица — бит. Она имеет представление в виде 0 или 1, удобное для реализации простейшими электронными схемами с двумя состояниями электрического равновесия (например, триггерами или иными ячейками памяти). Многоразрядные двоичные числа представляют собой набор цифр 0 и 1, например, 100110 или 111001. Каждый старший разряд относительно предыдущего имеет весовой коэффициент, равный 2.
Именно с битами работает микропроцессор на нижнем уровне операций. Однако бит — слишком мелкая единица, не очень удобная в обращении. К тому же мы привыкли к куда более удобным и наглядным для нас элементам информации, таким как буквы, цифры, знаки арифметических операций, спецзнаки и символы псевдографики. В принципе, набор этих знаков, минимально необходимый для представления обычной текстовой и цифровой информации, содержит до 2 8 = 256 элементов. Каждый из них в компьютере представляется кодом от 0 до 255. Для задания таких кодов достаточно 8 бит (2^8=256), которые и образуют наиболее распространенную единицу представления информации — байт. 1024 байта образуют килобайт (Кбайт), 1024 Кбайт дают 1 Мбайт (мегабайт) и т. д.
Широко применяется общеизвестный стандарт кодирования текстовой информации ASCII (American Standard Code for Information Interchange).
Десятичные числа
К наиболее известным типам данных в математике относятся привычные нам десятичные числа (DECIMAL). Каждый разряд таких чисел имеет представление, заданное одной из арабских цифр — 0, 1, 2,..., 9. Весовой коэффициент старшего разряда относительно предшествующего равен 10. Количество цифр, представляющих число, может быть, в принципе, любым. Десятичные числа относятся к следующим основным типам.
| Обозначение | Тип чисел | Примеры задания | |
| Integer | Целочисленные | 123 | -345 |
| Rational | Рациональные | 123/567 | -23/67 |
| Real | Вещественные | 123. | -123.45610 ^ 6 |
| Complex | Комплексные | -3.5 + 0. | 56 I |
Десятичные числа наиболее распространены в научно-технических расчетах.
Целые числа
Целочисленные данные (Integer) — это целые числа, например 1, 2 или 123, которые представляются системой без погрешности и ограничения разрядности. Более того, арифметические операции над целыми числами система выполняет также без погрешностей и без ограничения числа цифр (рис. 3.1).
Рис. 3.1. Операции с целыми числами
Количество цифр, представляющих большое целое число, ограничено лишь его значением, но не какими-либо фиксированными форматами. Рациональные данные задаются отношением целых чисел, например 123/567, и также представляют результат точно. Поэтому система при символьных и численных расчетах всегда старается выдать результат в виде целых или рациональных чисел, там где это возможно:
1000000/3000000
1/3
(124-1)/(455+1)
41/152
Фактически целые числа произвольной разрядности в системах символьной математики представляются списками отдельных цифр. Особая организация списков повышает компактность представления больших целых чисел. Характерным примером работы с целыми числами большой разрядности является вычисление факториала n!=1*2*3*. . . *n. Примеры его вычисления уже приводились (см. рис. 1.16).
Числа с произвольным основанием
Для вычисления чисел с произвольным основанием используется конструкция
Основание^^Число
Число должно быть записано по правилам записи чисел с соответствующим основанием. Если основание больше 10, для обозначения значений чисел используются буквы от а до z. Наиболее известными из чисел с основанием системы счисления, превышающим 10, являются шестнадцатеричные числа (HEX — от слова hexagonal). Разряды таких чисел могут иметь следующие значения:
HEX 0123456789abCdef
DECIMAL 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Каждый более старший разряд имеет весовой коэффициент относительно предыдущего разряда, равный 16.
Примеры задания шестнадцатеричного и двоичного чисел:
16^^123abcde
305839326
2^^1010111
87
Для представления чисел с произвольным основанием n (до 32) используется функция BaseForm[expr, n], которая возвращает выражение ехрг в форме числа с основанием n, которое указывается как подстрочный индекс.
Примеры использования функции BaseForm:
BaseForm[87,2]
10101112
BaseForm[305839326,16]
123abcde16
В дальнейшем мы будем использовать только десятичные числа.
Вещественные числа
Численные данные могут быть представлены также десятичными вещественными числами, которые могут иметь различную форму, например 123.456, 1.23456 10^2,12345.6 10^-2 и т. д. В общем случае они содержат мантиссу с целой и дробной частями и порядок, вводимый как степень числа 10. Как правило, вещественные числа в системах символьной математики могут иметь мантиссу с любым, но конечным числом знаков. Пробел между мантиссой и порядком эквивалентен знаку умножения *:
23.456*10^100
2.345бх10^101
10^-100
1/
100000000000000000000000000000
0000000000000000000000000000
0000000000000000000000000000000000000000000
10.^-100
1.x 10^-100
Как принято в большинстве языков программирования, целая часть мантиссы отделяется от дробной части точкой, а не запятой.
Mathematica производит операции с числами изначально как с целыми. Однако установка значка разделительной точки означает, что число должно рассматриваться как вещественное. Например, 1 — целое число, но 1. — уже вещественное число. Для представления выражения ехрг в форме вещественного числа используется функция N [ехрг] или N [ехрг, число_цифр_результата].
Примеры:
1/3
1/3
1./3 .
0.333333
N[1/3]
0.333333
N[2*Pi,50]
6.283185307179586476925286766559005768394338
Вещественные числа всегда имеют некоторую погрешность представления результатов из-за неизбежного округления и существования так называемого машинного нуля — наименьшего числа, которое воспринимается как нуль. В терминах системы Mathematica говорят о приближении числовых данных как об их аппроксимации, хотя в отечественной литературе под аппроксимацией чаще подразумевают описание некоторой зависимости между данными достаточно приближенной аналитической зависимостью.
Mathematica имеет две системные переменные, позволяющие вывести максимально и минимально возможные значения чисел, с которыми оперирует система:
$MaxMachineNumber
1.79769х10^308
$MinMachineNumber
2.22507х 10^-308
Обратите внимание на то, что функция N [ехрr, m] позволяет получить число с практическим любым числом цифр результата m. Разработчики последней версии Mathematica 4 утверждают, что это верно при количестве цифр результата до одного миллиона, что с лихвой удовлетворяет требованиям подавляющего большинства расчетов и вычислений.
Функции IntegerPart [x] и FractionalPart [x] обеспечивают возврат целой и дробной частей вещественного числа х:
N[Pi]
3.14159
IntegerPart[Pi]
3
FractionalPart[Pi]
-3.+ Л
N[FractionalPart[Pi]]
0.141593
Еще одна функция RealDigits [x] возвращает список реальных цифр результата и число цифр целой части х:
RealDigits[N[2*Pi]]
{{6, 2, 8, 3, 1, 8, 5, 3, 0, 7, 1, 7, 9, 5, 8, 6}, 1}
Есть и множество других функций для работы с вещественными числами. Они будут рассмотрены в дальнейшем. В Mathematica 4 функция RealDigits имеет расширенные формы, например RealDigits [x, b, len, n]. Для получения цифр мантиссы введены функции MantissaExponent [x] и MantissaExpo-nent[x,b].
Комплексные числа
Многие математические операции базируются на понятии комплексных чисел. Они задаются в форме
z=Re(z)+I*Im(z)
или
z=Re(z)+i Im (z)
где знак I (i) — мнимая единица (квадратный корень из -1), Re (z) — действительная часть комплексного числа, a Im (z) — мнимая часть комплексного числа. Пример задания комплексного числа:
2 + I3
или
2 + 3*I
Мнимая часть задается умножением ее значения на символ мнимой единицы I. При этом знак умножения * можно указывать явно или заменить его пробелом — в последнем случае комплексное число выглядит более естественным. Функции Re [ z ] и Im [ z ] выделяют, соответственно, действительную и мнимую части комплексного числа z. Это иллюстрируют следующие примеры:
Re[3+2*1]
3
Im[3+2 I]
2
Большинство операторов и функций системы Mathematica работают с комплексными числами. Разумеется, это расширяет сферу применения системы и позволяет решать с ее помощью различные специальные задачи — например, относящиеся к теории функций комплексного аргумента. Комплексные числа широко используются в практике электро- и радиотехнических расчетов на переменном токе.
Символьные данные в общем случае могут быть отдельными символами (например a, b,..., z), строками (strings) и математическими выражениями ехрг (от expression — выражение), представленными в символьном виде.
Символьные строки задаются цепочкой символов в кавычках, например "sssss". В них используются следующие управляющие символы для строчных объектов:
- \n— новая строка (line feed);
- \ t — табуляция.
Это иллюстрируется следующими примерами:
"Hello my friend!"
Hello my friend!
"Hello\nmy\nfriend!"
Hello
my
friend!
"Hello\tmy\tfriend!"
Hello my friend;
Следует помнить, что управляющие символы не печатаются принтером и не отображаются дисплеем, а лишь заставляют эти устройства вывода выполнять определенные действия. Mathematica имеет множество функций для работы со строками, которые будут описаны в дальнейшем.
Выражения в системе Mathematica обычно ассоциируются с математическими формулами, как показано в следующей таблице.
| Запись на языке Mathematica | Обычная математическая запись |
| 2*Sin[x] | 2*sin(x) |
| 2 Sin[x] | 2*sin(x) |
| (а +b^2 + с^З) / (3*d - 4*e) | (a + b 2 +с 3 )/(3d-4е) |
| sqrt(2) | Кореннь из 2 |
| Integrate [Sin [x] , х] | Интеграл sin(x) dx |
Для записи математических выражений используются как операторы, так и функции. Их особенности будут рассмотрены несколько позже. А пока сразу отметим некоторые тонкости синтаксиса системы, используемого при записи арифметических операций:
- знак умножения может быть заменен пробелом;
- встроенные функции начинаются с большой буквы и обычно повторяют свое общепринятое математическое обозначение (за исключением тех, в названии которых есть греческие буквы — они воспроизводятся латинскими буквами по звучанию соответствующих греческих букв);
- круглые скобки () используются для выделения частей выражений и задания последовательности их вычисления;
- параметры функций задаются в квадратных скобках [ ];
- фигурные скобки {} используются при задании списков.
Новые системы Mathematica 3/4 обладают обширными возможностями по заданию форматов записи математических выражений при их выводе на экран или принтер, а также при вводе с клавиатуры. Они будут рассмотрены в дальнейшем.
Наиболее общим видом сложных данных в системе являются списки (lists). Списки представляют собой совокупности однотипных или разнотипных данных, сгруппированных с помощью фигурных скобок:
- { 1 , 2 , 3 } — список из трех целых чисел;
- { а , b , с } — список из трех символьных данных;
- {1, а, x^ 2} — список из разнотипных данных;
- {{a,b},{c,d}} — список, эквивалентный матрице
a b
c d
- {х^2+у^2, 2*Sin [x] } — список из двух математических выражений.
Как видно из этих примеров, элементы списков размещаются в фигурных скобках — открывающей { и закрывающей } . Списки могут быть с вложениями из списков — так получаются многоуровневые списки (двухуровневый список дает матрицу). Позже свойства и возможности списков будут рассмотрены детально. С помощью списков представляются множественные данные — массивы.
В общем случае система Mathematica оперирует с объектами. Под ними подразумеваются математические выражения (ехрг), символы (symbols), строки из символов (strings), упомянутые выше числа различного типа, константы, переменные, графические и звуковые объекты и т. д.
Каждый объект характеризуется своим именем — идентификатором. Это имя должно быть уникальным, то есть единственным. Существуют следующие правила задания имен:
- sssss — имя объекта, заданного пользователем;
- Sssss — имя объекта, входящего в ядро системы;
- $Sssss — имя системного объекта.
Итак, все объекты (например функции), включенные в ядро, имеют имена (идентификаторы), начинающиеся с большой буквы (например Plus, Sin или Cos). Идентификаторы относящихся к системе объектов начинаются со знака $. Заданные пользователем объекты следует именовать строчными (малыми) буквами. Разумеется, под символами s...s подразумеваются любые буквы и цифры (но не специальные символы, такие как +, -, * и т. д.).
Объекты (чаще всего это функции), встроенные в систему, принято называть внутренними или встроенными. Объекты, которые создает пользователь (в том числе используя внутренние объекты), называют внешними объектами. К ним, в частности, относятся процедуры и функции, составляемые пользователем, которые детально рассматриваются в дальнейшем.
Функции, опции, атрибуты и директивы
К важному типу объектов принадлежат функции — объекты, имеющие имя и список параметров, возвращающие некоторое значение в ответ на обращение к ним по имени с указанием списка конкретных (фактических) значений параметров. В системах Mathematica 2/3/4 встроенные функции задаются в виде
И дентификатор_Функции [ol, о2, o3, ...]
где ol, о2, оЗ... — объекты (параметры, опции, математические выражения и т. д.). Список входных параметров задается необычно — в квадратных скобках. В числе входных параметров могут быть специальные объекты — опции. Они задаются в виде
Имя_опции->3начение_опции
Значением опции обычно является то или иное слово. Например, в функции построения графиков
Plot [sin[x] , {x, 0,20} ,Axes->None]
опция Axes->None указывает на то, что отменяется вывод координатных осей (Axes). Функция Options [name] выводит для функции с идентификатором name список всех возможных для нее опций. Некоторые функции, например Sin, могут вообще не иметь опций, другие, такие как Solve, могут иметь целый «букет» опций:
Options [Sin]
Options [Solve]
{InverseFunctions -> Automatic, MakeRules -> False,
Method -> 3, Mode -> Generic, Sort -> True,
VerifySolutions -> Automatic, WorkingPrecision -> 00}
В последнем случае характер возвращаемого функцией результата может сильно зависеть от значений опций. Назначение каждой опции мы рассмотрим в дальнейшем. В этой главе они нам пока не понадобятся.
Каждый объект может характеризоваться некоторой совокупностью своих свойств и признаков, называемых атрибутами. Функция Attributes [name] возвращает список всех атрибутов функции с именем name, например:
Attributes [Sin]
{bistable, NumericFunction, Protected}
Attributes [Solve]
{Protected}
Как видите, для функции синуса характерны три атрибута:
- bistable — указывает на применимость в списках и таблицах;
- NumericFunction — указывает на отношение к числовым функциям;
- Protected — указывает на то, что слово Sin защищено от какой-либо модификации.
Кроме того, в Mathematica 2/3/4 имеется понятие функций-директив. Эти функции не возвращают значений, а указывают, как в дальнейшем будут выполняться функции, работа которых зависит от директив. Синтаксис функций-директив тот же, что и у обычных функций.
Применение опций и директив делает аппарат функций более гибким и мощным, поскольку позволяет задавать те или иные свойства функций и условия их выполнения. Это особенно важно при использовании функций в задачах графики и символьной математики.
Константы являются типовыми объектами системы, несущими заранее предопределенное численное или символьное значение. Это значение не должно меняться по ходу вычисления документа. К численным константам относятся любые числа, непосредственно используемые в математических выражениях или программных объектах, например процедурах и функциях. Так, числа 1 и 2 в выражении 2*Sin [ 1 ] являются численными константами. Константы-числа не имеют идентификаторов. Идентификатором, в сущности, является само число. Его представление и хранится в памяти.
Имеется также ряд именованных констант, которые можно рассматривать как функции без аргумента, возвращающие заранее заданное значение. Имена констант (и других объектов, например функций и переменных) представляются их идентификаторами — непрерывной строкой символов, отождествляемой с именем. В системе Mathematica большинство идентификаторов имеют естественный математический смысл и начинаются с большой буквы. Например, Е — это основание натурального логарифма.
Используются следующие встроенные именованные константы:
- Complexlnf inity — комплексная бесконечность, которая представляет величину с бесконечным модулем и неопределенной комплексной фазой.
- Degree — число радиан в одном градусе, которое имеет числовое значение Pi/180.
- Е- основание натурального логарифма с приближенным числовым значением 2 . 71828....
- EulerGamma — постоянная Эйлера с числовым значением 0.577216....
- GoldenRatio — константа со значением (l+Sqrt[5] ) /2, определяющая деление отрезка по правилу золотого сечения.
- I — представляет мнимую единицу Sqrt [-1].
- Infinity — «положительная» бесконечность (со знаком «минус» дает «отрицательную» бесконечность).
- Catalan — константа Каталана 0 . 915966....
- Pi — число, имеющее значение 3 .14159... и равное отношению длины окружности к ее диаметру.
Константы, имеющие значение, дают его в виде вещественного числа:
{N [Degree], N[E], N[Pi]}
{0.0174533, 2.71828, 3.14159}
{N[EulerGamma],N[GoldenRatio],N[Catalan]}
{0.577216, 1.61803, 0.915966}
Константы в описываемой системе используются вполне естественно, так что от дальнейшего их описания можно воздержаться.
Размерные величины
Mathematica позволяет оперировать с размерными величинами, которые широко используются в физических и химических расчетах. Размерные величины характеризуются не только численными значениями, но и единицами измерения, например Meter (метр), Second (секунда) и т. д. Последние могут стоять в числителе и в знаменателе выражений, представляющих размерные величины:
1 Meter
Meter
5Meter
5 Meter
0.5Second
0.5Second
Между значением размерной величины и единицей измерения знак умножения можно не ставить. Это видно из приведенных выше примеров.
Для облегчения ввода физических констант, представляющих собой размерные величины, в наборе файлов Mathematica можно найти файл PhysicalConstants.nb. При его загрузке появляется дополнительная палитра физических констант, показанная на рис. 3.2.
Для ввода констант достаточно активизировать соответствующую кнопку с нужной константой. Будут введено выражение, задающее константу. Ниже представлены примеры ввода первой и последней констант, содержащихся в палитре, представленных в стандартной форме:
2.99792458000000028'*^8 Meter/ Second
2.99792х108 Meter/ Second
6. 9599 x 108 Meter
6.9599xl08 Meter
Следует отметить, что без острой необходимости применять размерные величины не следует, поскольку они усложняют математические выражения и зачастую не позволяют выполнять с ними символьные преобразования. Рекомендуется нормировать выражения (формулы) так, чтобы результаты их вычисления имели безразмерный вид.
Рис. 3.2. Дополнительная палитра физических констант
Переменными в математике принято называть именованные объекты, которые могут принимать различные значения, находящиеся в определенном множестве допустимых значений. Подобно этому, переменными в системе Mathematica являются именованные объекты, способные в ходе выполнения документа неоднократно принимать различные значения — как численные, так и символьные. При этом символьные значения переменных, в отличие от обычных языков программирования, могут представлять собой как исполняемые математические выражения ехрг, так и некоторые обобщенные классы функций и объектов. Например, переменная может представлять графический объект, такой как изображение трехмерной поверхности, или звуковой объект, при активизации которого исполняется звук. Значением переменных могут быть также множественные объекты — списки.
Имена переменных называют их идентификаторами. Они должны быть уникальными, то есть не совпадать с именами директив, атрибутов, опций и функций в ядре системы. Имена переменных должны начинаться с буквы. Общеприняты, скажем, имена х и у для функциональной зависимости у (х) или представления графиков, f — для функций. Желательно назначать именам переменных смысловые значения, например xcoordinaate или ycoordinate для координат точки. Все сказанное об идентификаторах объектов справедливо и для идентификаторов переменных, поскольку переменные — распространенные виды объектов.
Особенности применения переменных
В отличие от переменных в математике, каждая переменная в системе Mathematica, как и в любой системе программирования, всегда отождествляется с некоторой физической областью памяти, в которой и хранится значение переменной. Для уменьшения объема памяти применяются различные способы компактного размещения информации. Надо помнить, что и имя переменной занимает определенную область памяти. Распределение памяти под переменные — динамическое. Это означает, что местоположение ячеек памяти и объем памяти под ту или иную переменную не фиксированы, а меняются в ходе выполнения задачи.
Заранее объявлять тип переменной не требуется. Он определяется операцией присваивания переменной некоторого значения. Такой подход упрощает построение программ и естественен при использовании переменных в обычной математической литературе.
Без особых на то указаний переменные в системе Mathematica являются глобальными. Это означает, что после определения переменной ее значение можно изменить в любом месте документа или программы. Переменная появляется как действующий объект только после ее первого определения или задания. Определения переменных выполняются с помощью операции присваивания, вводимой знаком равенства:
var = value
Здесь var — имя переменной, value — ее значение. Ниже представлены основные операции по присваиванию переменным значений:
- х = value — переменной х присваивается вычисленное значение value;
- х = у = value — вычисленное значение value присваивается переменным х и у;
- x:=value — присваивание переменной х невычисленного значения value;
- х =. — с переменной х снимается определение.
Примеры (комментарий ln[...] опущен):
- g = Plot[Sin[x],{x,0,20}] — переменной д присваивается значение в виде графического объекта;
- у = 1 + х ^ 2— переменной у присваивается символьное значение в виде математического выражения (1 + х ^ 2);
- z= {1, 2, х, a + b}— переменной z присваивается значение в виде списка, содержащего четыре элемента.
Различие в присваивании переменным значений с помощью знаков «=>> и <<:=» иллюстрируют следующие примеры:
а=12;
b=а
12
с:=а
с
12
а=15;
b
12
с
15
Как видите, после первоначальных присваиваний b=а и с: =а обе переменные, b и с, имеют значение 12. Однако после присваивания переменной а нового значения (15) переменная b, которой было присвоено вычисленное значение а, остается равной 12, а переменная с, которой было присвоено невычисленное значение а, становится равной 15.
Особо обратите внимание на то, что возможно снятие с переменной определения с помощью символов «=.» или функции Clear [var]. В символьной математике это очень полезная возможность, поскольку нередко переменные с одним и тем же именем в разных частях программы могут иметь разный смысл и представлять объекты, требующие значительных затрат памяти.
Более того, эти объекты сохраняются даже при использовании команды New при переходе к подготовке нового документа. Поэтому рекомендуется всякий раз удалять определения переменных, как только их использование завершается. Это предотвращает возникновение конфликтов между одноименными переменными и освобождает память.
Переменные могут быть локальными, то есть действующими только в пределах объекта, в котором они объявлены. Таким объектом может быть функция или процедура со списком входных параметров. Такие объекты мы рассмотрим позже.
Оценивание переменных и операции присваивания
Специфику математических выражений в системе Mathematica составляет возможность их оценивания и изменения в соответствии с заложенными в ядро системы правилами математических преобразований. В итоге после изменения значение выражения, которое присваивается переменной, может быть совсем иным, чем до оценивания. Поэтому в целом для определения переменных используют описанные ниже конструкции.
Основная функция Set [ Ihs, rhs ] имеет аналогичные по действию упрощенные операторы:
- Ihs = rhs — вычисляет правую часть rhs и присваивает ее значение левой части Ihs. С этого момента Ihs замещается на rhs всюду, где бы этот идентификатор ни появился;
- {11, 12, ...} = {rl, г2, ...} — вычисляет ri и назначает полученные результаты соответствующим 11.
Функция задержанного присваивания SetDelayed[lhs,rhs] может быть заменена аналогичным по действию оператором Ihs : =rhs, который назначает правой части rhs роль отложенного значения левой части Ihs. При этом rhs содержится в невычисленной форме. После этого, когда появляется идентификатор Ihs, он заменяется на значение rhs, вычисляемое каждый раз заново.
При задержанном (отложенном) присваивании вывода нет, тогда как при обычном немедленном присваивании lhs=rhs значение rhs вычисляется немедленно и результат выводится в строку вывода.
Функция присваивания верхнего уровня UpSet [Ihs, rhs] применяется в виде lhs A =rhs. При этом левой части Ihs присваивается значение правой части rhs, причем это значение связывается с символами, которые появляются на первом уровне вложенности в Ihs.
И, наконец, функцию отложенного присваивания верхнего уровня UpSetDelayed[lhs, rhs] может заменить оператор lbs^ :=rhs. При этом величина rhs выполняет роль отложенного значения Ihs, и связывается это присваивание с символами, которые появляются на первом уровне вложенности в Ihs.
Отметим еще одну важную конструкцию SetOptions [s, namel->valuel, name2->value2, . . . ], которая устанавливает для символа s указанные опции, определяемые по умолчанию.
Применение различных типов операций присваивания способствует большей гибкости системы. Различия между этими операциями на первый взгляд несущественны, но они принципиальны, и это станет понятно после более детального знакомства с символьными преобразованиями и приобретения практики работы с системой.
Имеются также системные переменные, значениями которых являются данные о системе и ее работе, например версия применяемой операционной системы, текущая дата, время в данный момент, машинная точность вычислений и т. д. Многие из таких переменных имеют отличительный знак $ перед своим именем. Такие переменные более подробно будут рассматриваться в дальнейшем.
gl3-1.jpg
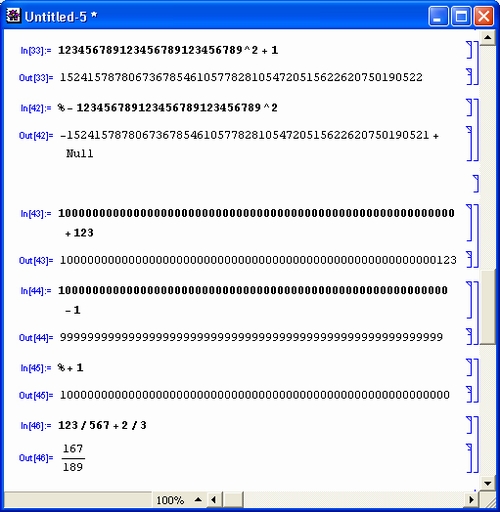
gl3-2.jpg
3. Операторы и функции
Операторы и функции
Операторы и функции являются основными кирпичиками в построении математических выражений, которые вычисляются или преобразуются системой Mathematica. Кроме того, это важнейшие элементы языка программирования системы. В данном разделе мы познакомимся с этими объектами.
Математические выражения в системе Mathematica записываются с помощью операторов и функций. Операторы (от слова operator — исполнитель) являются элементами записи математических выражений, указывающими на то, какие действия производятся над символьными или числовыми данными. Когда эти данные используются совместно с операторами, их называют операндами.
Выражения, составленные из операторов, операндов и функций, способны возвращать результат своего вычисления. К примеру, если вычисляется сумма 2+3, то знак «+» является оператором, числа 2 и 3 — операндами, а вся запись 2+3 — выражением. Сами по себе операторы не возвращают какого-либо значения.
Существуют общепринятые приоритеты выполнения операций, например, в первую очередь выполняются сложение и вычитание, затем умножение и деление и далее другие операции. С помощью круглых скобок можно изменять последовательность выполнения действий, например, в выражении (2+3) М вначале будет вычислено 2+3, а затем уже результат будет умножен на число 4. В сомнительных случаях применение скобок особенно желательно, например 2^2+3 даст 7, а 2^ (2 + 3) даст 32.
Ниже перечислены основные операторы для выполнения арифметических операций (х, у и z — операнды, задающие данные, над которыми выполняются вычисления):
x+y+z Сложение
x-y-z Вычитание
х*у*z или x у z Умножение
х/у Деление
х^у Возведение х в степень у
Expr //N Дает приближенное (с установленной точностью и формой) значение выражения ехрг

Как уже отмечалось, при выполнении вычислений особая роль принадлежит символам «%». Эти символы как сами по себе, так и в качестве аргументов функций используются для указания на применение результата предшествующих операций:
- % — возвращает результат последней операции;
- %% — возвращает результат предпоследней операции;
- %...% — возвращает результат операции, выполненной в строке, отстоящей от конца на число повторений символа «%»;
- %n — возвращает результат операции в строке n.
Нетрудно заметить, что применение этих символов облегчает выполнение последовательных вычислений.
Как уже отмечалось, для представления арифметических выражений ехрг в виде вещественного результата используется функция N[expr,m]. Можно также задать вычисление любого выражения в численном виде, используя выражение ехрг //N:
1/3+2/7
13/21
1/3+2/7 //N
0.619048
Таким образом, используя функцию N[expr,m] или вывод с помощью символов //N, можно организовать вычисления в режиме калькулятора, находясь в среде оболочки системы.
Если х имеет вещественное значение, то функция
MantissaExponent[x]
возвращает список, содержащий мантиссу и порядок приближенного вещественного числа х. Примеры:
123.456 10^10
1.23456 х1012
MantissaExponent[%]
{0.123456, 13}
Арифметические вычисления с повышенной точностью
Важное достоинство систем символьной математики — выполнение арифметических вычислений с произвольными разрядностью и точностью. Хотя на деле они ограничены объемом ОЗУ, но для современных компьютеров с объемом ОЗУ в единицы и десятки мегабайт вряд ли можно столкнуться со случаем, когда ограничения по разрядности и точности становятся существенными.
Следующие две функции, Rationalize [х] и Rationalize [x, dx], дают приближение для числа х в виде рациональных чисел. Вторая из этих функций задает приближение с заданной точностью dx.
Mathematica может работать с большими числами и выполнять определенные операции с очень высокой точностью. Примеры, приведенные на рис. 3.3, иллюстрируют эти возможности.
Как видно из примеров представления рациональных чисел, результат приближения зависит от заданной погрешности. Чем она меньше, тем большие значения целых чисел в числителе и знаменателе результата разыскивает система. Функция Rationalize открывает широкие возможности для разработки целочисленных алгоритмов вычислений, позволяя легко получать рациональные приближения для наиболее распространенных числовых констант — на рис. 3.3 примеры этого даны для числа 8.
Обратите внимание на последние два примера — вычисление факториала достаточно большого числа. Первый результат целочисленный: он занял целых три строки, но зато он точен. С помощью функции N [ехрг] результат всегда можно представить в виде большого вещественного числа — но приближенного. При этом может использоваться научная форма представления чисел — с мантиссой и порядком.
Рис. 3.3. Примеры представления чисел в разных формах
Укороченная форма записи арифметических операций
Спецификой систем Mathematica являются арифметические операторы с укороченной формой записи, объединяющие операцию присваивания с арифметической операцией. Эти довольно специфические операторы, хорошо известные пользователям языка С, представлены ниже вместе с соответствующими им функциями.
| Функция | Оператор | Назначение |
| Increment [i] | i++ | Увеличивает значение i на 1 после использования i в выражении |
| Decrement [i] | i -- | Уменьшает значение i на 1 после использования i в выражении |
| Preincrement [i] | ++i | Увеличивает значение i на 1 до использования i в выражении |
| PreDecrement [i] | --i | Уменьшает значение i на 1 до использования i в выражении |
| AddTo[x,d] | x += dx | Прибавляет dx к х и возвращает новое значение х |
| SubtractFrom[x,dx] | x -= dx | Отнимает dx от х и возвращает новое значение х _ |
| TimesBy [х, с] | X **= 'С | Умножает х на с и возвращает новое значение х |
| DivideBy [х, с] | X /= С | Делит х на с и возвращает новое значение х |
Применение укороченных операторов делает запись математических выражений более короткой, хотя наглядность их при этом несколько снижается. Ниже представлены примеры выполнения укороченных арифметических операций.
| Ввод (In) | Вывод (Out) |
| i=0 | 0 |
| ++i; ++i; ++i | 3 |
| i=0; i++; i++; i++ | 2 |
| i=5 | 5 |
| -- i | 4 |
| i=5 | 5 |
| i -- | 5 |
| i -- | 4 |
| x=5 | 5 |
| x+=0 . 5 | 5.5 |
| x-=0 . 5 | 5. |
| x*=2 | 10. |
| x/=5 | 2. |
Важнейшим объектом любой компьютерной математической системы является функция. Она отражает зависимость некоторой величины от одного или нескольких аргументов. Например, функция sin(x) дает зависимость синуса х от величины аргумента х при изменении последнего от -°° до +°°.
Признаком функции является возврат результата выполняемого ею действия. Характер результата будет зависеть от смысла функции, который нередко явно указывается ее именем — идентификатором. Например, функция Digitslnteger [n] возвращает число десятичных цифр десятичного целого числа. Это ясно из прямого перевода имени функции — слово Digitslnteger говорит о том, что она возвращает число цифр целого числа. Подобные смысловые имена задаются для большинства функций системы Mathematica и облегчают их запоминание.
Понятие функции в системе Mathematica существенно расширено — функции могут возвращать графические и даже звуковые объекты. Здесь мы, однако, остановимся на общепринятом в программировании понятии функций, возвращающих в ответ на обращения к ним численные или символьные значения.
Функции могут входить в состав математических выражений. Обычно они имеют один или несколько параметров, указываемых в квадратных скобках. Если параметров несколько, то в квадратных скобках указывается список параметров, разделенных запятыми. В общем случае параметрами могут быть списки. Наконец, в состав функций могут входить опции, указанные своим именем и (после знака ->) значением. Для обозначения положительной бесконечности используется символ Infinity. Целочисленные функции имеют в своем имени слово Integer.
В ядро систем Mathematica 3/4 входит множество встроенных функций, то есть функций, готовых к немедленному использованию без какого-либо предварительного объявления. Таких функций многие сотни. Среди них различные арифметические функции, тригонометрические и гиперболические функции, специальные математические функции и т. д. Мы рассмотрим их в дальнейшем.
Основные арифметические функции
Для выполнения арифметических действий в системах Mathematica 3/4 определены следующие арифметические функции:
- Divide [х, у] — возвращает результат деления х на у эквивалентно выражению х у ^ -1;
- Plus[x, у,...] — возвращает сумму элементов списка;
- PowerModta, b, n] — возвращает Mod[a ^ b, n]. Для b<0 возвращает инверсию остатка;
- Times [х, у,...] — возвращает произведение аргументов х*у*...;
- Mod [m, n] — возвращает остаток от деления m на п. Результат имеет такой же знак, как п.
Ниже представлены примеры применения арифметических функций.
| Ввод (In) | Вывод (Out) |
| Divide [1. ,3] | 0.333333 |
| Mod [123, 20] | 3 |
| Mod [123, -20] | -17 |
| Mod[-123,20] | 17 |
| Plus[2,3,4] | 9 |
| Times [2, 3,4] | 24 |
Для обмена значениями переменных х и у можно использовать выражение {х,у}={у,х}
Пример обмена переменных значениями:
а=1;b=2;
{а,b}={b,а};
{а,b}
{2, 1}
Следующие функции служат для приведения вещественных чисел к ближайшим целым по определенным правилам:
- Ceiling [х] — возвращает значение наименьшего целого числа, большего или равного х;
- Floor [х] — возвращает наибольшее целое число, не превышающее данного х;
- Quotient [n, m] — возвращает целое значение n/m, определяемое как Floor[n/m];
- Round [х] — округляет х до ближайшего целого.
Хотя аргументами этих функций указано значение х, под ним можно понимать список вещественных чисел. Следующие примеры поясняют это и наглядно иллюстрируют правила приведения к целым числам.
| Ввод (In) | Вывод (Out) |
| Ceiling [{-5. 9, -5..1, 5, 5.1, 5.9}] | {-5, -5, 5, б, 6} |
| Floor [{-5. 9, -5.1,, 5, 5.1, 5.9}] | {-6, -6, 5, 5, 5} |
| Round[{-5.9, -5.1,, 5, 5.1, 5.9}] | {-6, -5, 5, 5, 6} |
Ряд функций обеспечивает нахождение делителей целых чисел и наименьшего общего -кратного:
- Divisors [n] — возвращает список целочисленных делителей числа п;
- DivisorSigma [k, n] — возвращает сумму &-х степеней положительных делителей числа п;
- ExtendedGCD [n, m] — возвращает расширенный наибольший общий делитель целых чисел пит;
- GCD [nl,n2,...] — возвращает наибольший общий делитель целых чисел ni;
- LCM[nl, n2,...] — возвращает наименьшее общее кратное целых чисел ni.
Ниже представлены примеры применения этих функций.
| Ввод (In) | Вывод (Out) |
| LCM[124,12,6] | 372 |
| GCD [144, 12, 6] | 6 |
| Divisors [123] | {1,3,41,123} |
| DivisorSigma [17,3] | 129140164 |
| ExtendedGCD [144,12] | {12, {0,1}} |
К целочисленным функциям можно отнести также функции вычисления факториала и двойного факториала:
- Factorial [n] или n! — возвращает значение факториала числа n (n!=n* (n-1) *...*3*2*1, причем 0 !=1 и 1 !=1);
- Factorial2 [n] или n! ! — возвращает значение двойного факториала числа п, равное п* (n-2) * (n-4) *...«%»
Ниже представлены примеры вычисления факториалов.
| Ввод (In) | Вывод (Out) |
| Factorial [10] | 3628800 |
| 20! | 2432902008176640000 |
| 10!! | 3840 |
| 20!//N | 2.4329Х10 18 |
Mathematica способна вычислять факториалы больших чисел. Практически мгновенно (даже на компьютере с 486-м процессором) вычисляются значения до 1000!, хотя результат при этом занимает несколько страниц на экране дисплея. Можно вычислить даже 10000!, но для этого потребуется время до нескольких минут (зависит от типа компьютера). Обратите внимание на то, что управляющий символ //N за выражением дает вывод (аппроксимацию) в форме научной нотации.
Следующие функции служат для получения простых чисел и некоторых их характеристик:
- Prime [n] — возвращает п-е простое число. Например, Prime [5] возвращает пятое простое число — 11. Всего лишь доли секунды требуются системе для вычисления миллиардного простого числа: Рг1те[10 Л 9] дает 22801763489;
- PrimePi [x] — возвращает количество простых чисел, не превышающих х. Например, PrimePi [10] возвращает 4;
- Partitions? [n] — возвращает числор(п) неупорядоченных разбиений целого числа п. Например, Partitions? [10] возвращает 42;
- PartitionsQ [n] — возвращает q(n) — число разбиений с неравными частями для целого числа п. Например, PartitionsQ [15] возвращает 27.
Эти функции полезны при решении задач теории чисел.
Функции генерации случайных чисел
Для реализации статистических методов моделирования используются случайные числа. Система имеет генератор псевдослучайных чисел, доступ к которому обеспечивают следующие функции:
- Random [ ] — возвращает равномерно распределенное псевдослучайное число типа Real в интервале от 0 до 1;
- Random [type, range] — дает псевдослучайное число указанного типа type, лежащее в указанном интервале range. К возможным типам относятся Integer, Real и Complex. По умолчанию принят интервал от 0 до 1. Можно задать интервал явно в виде {min, max}; спецификация интервала в виде max эквивалентна {0, max};
- SeedRandom[n] — сбрасывает (устанавливает в начальное состояйие) генератор случайных чисел, используя целое п как начальное число;
- SeedRandom [ ] — устанавливает генератор, используя в качестве начального числа текущее время.
Хотя генерируемые числа не являются строго случайными, их количество в повторяющейся последовательности очень велико. Использование специальной установки начального состояния генератора, например по времени дня, делает повторение последовательности практически невозможным.
Для проверки равномерности распределения большого массива случайных чисел можно задать с их помощью случайные координаты и затем построить точки, соответствующие координатам (х, у). Рисунок 3.4 наглядно показывает, как это делается для массива из 10 000 случайных точек. О равномерности распределения случайных чисел говорит равномерность распределения плотности точек на графике.
Рис. 3.4. Графическая иллюстрация распределения точек со случайными координатами (х, у)
Возможно, читателю не сразу понятны графические средства, использованные в документе, показанном на рис. 3.4. Это не беда — в последующих уроках они будут описаны довольно подробно.
Функции выявления погрешностей и анализа структуры чисел
Следующие функции, опции и директивы используются, в основном, для выявления погрешностей вычислений и уточнения структуры чисел:
- Accuracy [х] — возвращает количество десятичных цифр справа от десятичной точки числа х;
- EvenQ [expr] — возвращает значение True, если expr есть четное число, и False — в противном случае;
- IntegerDigits [n] — возвращает список десятичных цифр целого числа n;
- IntegerDigits [n,b] — возвращает список цифр целого числа п в записи по основанию b;
- IntegerDigits [n, b, k] — возвращает список длиной k, содержащий самые младшие (наименьшие) значащие цифры в n;
- Precision [x] — возвращает количество точных знаков в числе х.
Поясним применение этих функций следующими примерами.
| Ввод (In) | Вывод(Out) |
| Accuracy [123 . 456] | 14 |
| EvenQ [2*3+2] | True |
| EvenQ [2*3+3] | False |
| IntegerDigits [12345] | {1, 2,3, 4, 5} |
| IntegerDigits [12345, 16] | {3, 0,3, 15} |
| IntegerDigits [12352 , 16] | {3, 0,4, 0} |
| IntegerDigits [12352 ,2] | {1,1,0,0,0,0,0,0,1,0,0,0,0,0,0} |
| Precision [123. 452] | 16 |
Функциями Accuracy и Precision возвращаются значения, установленные в последний раз или по умолчанию при первой загрузке системы.

Хотя в систему входят многие сотни встроенных функций (начиная от элементарных и кончая специальными математическими функциями и системными функциями), нередко требуется расширить ее вводом новых функций, действие которых задается пользователем. Такие функции принято называть функциями пользователя. Функции пользователя — простейшие программные объекты, необходимые даже в том случае, когда пользователь не желает углубляться в тонкости программирования системы. Их цель — расширение системы и ее обучение работе с новыми функциями.
Для задания, опознавания и уничтожения функций пользователя используются следующие конструкции:
- f (x_) := х^3 — отложенное задание функции пользователя с именем f;
- f (х_) = х^3 — немедленное задание функции пользователя с именем f;
- ?f — вывод информации о функции f;
- Clear [f] — уничтожение определения функции f.
В обозначениях вида х_ знак _ применяется для создания так называемых образцов, задающих локальные переменные в теле функции — в нашем примере это х. При этом в самом теле функции переменные обозначаются как обычно, без знака образца. Он лишь указывает на особый статус переменных в ограниченном пространстве программы — в теле функции. Так, если вместо х_ будет подставлено число 2, то f (2) будет возвращать 2 А 3. Вне тела функции значение переменной х не изменяется. Переменная х может быть и неопределенной: х_ определяет переменную х только для тела функции. Более подробно создание образцов будет описано в дальнейшем.
Mathematica позволяет записать введенные пользователем функции с их определениями на магнитный диск с помощью оператора
Save["filename", fl, f2, ...]
После этого функция пользователя становится внешней функцией. При этом для ввода таких функций в текущий документ (notebook) достаточно вызвать файл с именем filename:
<<filename
Рекомендуется создавать файлы с типовым расширением .т. Такие файлы входят в пакеты расширений системы. Имя файла нужно задавать по общепринятым для MS-DOS правилам, то есть при необходимости указывать логическое имя дисковода и путь к файлу, например, так:
<<D: \MAT\myfunc .m
Создание внешних функций по существу означает возможность расширения системы и ее адаптации к решению типовых задач конкретного пользователя. Как уже отмечалось, в систему входит мощная библиотека внешних расширений, и каждый пользователь может пополнить ее своими собственными библиотеками расширений.

Функции пользователя можно задавать и выводить на печать как на языке системы, так и на некоторых общепринятых языках программирования, например Fortran, С или ТеХ. Для этого существует ряд функций преобразования, в имена которых входит слово Form (форма) и название языка для записи функций. Основные из них — это CForm [expr], FortranForm [expr ] и TeXForm [expr]. С их помощью выражения можно преобразовать в форму, принятую для языков программирования С, Fortran и ТеХ. При преобразовании в форму языка ТеХ греческие буквы заменяются их латинскими именами, например alpha, Alpha, beta, Beta, gamma и т. д. К сожалению, в отличие от систем класса MathCAD и Maple V R3, вывод математических формул в их полностью естественном виде не предусмотрен, хотя многое для этого уже сделано.
Для преобразования формул и данных, записанных на языке системы Mathematica и хранящихся в текстовых файлах, в другие формы используются следующие функции:
- Splice ["file.rar"] — читает текстовый файл file.mx, интерпретирует его фрагменты, заключенные в ограничители <*...*>, и пишет текстовый файл file.*, в котором эти фрагменты преобразованы в формат, определяемый расширением х (с — С, f — Fortran, tex — ТеХ);
- Splice ["infile", "outfile"] — то же, но с раздельным заданием имен входного и выходного файлов.
Таким образом, система Mathematica может общаться с другими программами, написанными на языках программирования, получивших распространение в практике реализации математических расчетов. Этому во многом способствует возможность преобразования форматов данных и результатов вычислений в различную форму, характерную для используемой внешней системы. К примеру, если вы работаете с программами на языке Fortran, то следует использовать соответствующий формат представления данных и результатов вычислений.
Mathematica может общаться также с иными системами, например текстовыми редакторами. К примеру, для передачи содержимого каких-либо ячеек в текстовый редактор Write, входящий в оболочку Windows, достаточно выделить эти ячейки и поместить их в буфер обмена, используя команду Сору из меню Edit. После этого надо запустить текстовый редактор и с помощью команды Edit | Paste поместить в окно редактирования содержимое ячеек. Если оно символьное, то с помощью редактора можно записать полученный документ с расширением .txt, то есть в стандартном текстовом формате, с которым работает большинство DOS-приложений.
Логическими принято называть операции, отражающие чисто логическое соответствие между данными. В обиходном языке эти связи выражаются утверждениями типа «да» или «нет». Например, на вопрос «Сын вырос выше отца?» мы можем ответить «да» или «нет». В математике (да и в информатике) принято характеризовать логическое соответствие утверждениями True («Верно», «Истина» или «Да») и False («Неверно», «Ложь» или «Пет»). Слова True и False являются символьными константами, отражающими результаты логических операций и в системе Mathematica.
Для осуществления логических операций используются следующие логические операторы:
Равенство (например, а == b)
! = Неравенство
> Больше (например, b > а)
>= Больше или равно
< Меньше
<= Меньше или равно
Возможны следующие формы применения операторов сравнения:
а == b == с
а != b != с
х < у < z
и т. д.
Результатом вычисления этих выражений является выдача логических значений True или False. Это демонстрируют следующие примеры.
| Ввод (In) | Вывод (Out) |
| 2=2 | True |
| a=a | True |
| a=b | a == b |
| 2=3 | False |
| 2<3 | True |
| 2>3 | False |
| 2!=3 | True |
| 2+1==3==4-1 | True |
Основные логические функции над логическими данными р, q и т. д. задаются следующим образом:
Not[p] или !р Логическое отрицание
And[p, q,...] или р && q &&... Логическое умножение — операция «И»
Or[p,q,...] или р || q | |... Логическое сложение — операция «ИЛИ»
Приведем примеры применения логических операторов и функций.
| Ввод (In) | Вывод(Out) |
| And [True , True , True ] | True |
| True && True && False | False |
| Not [True] | False |
| Not [False] | True |
| Or [True, True, False] | False |
| 2==2 && 3==3 | True |
| True && True | True |
| And[l,l,0] | 11111 1 0 |
| And[l,l,0] | 1 && 1&& 0 |
Эти примеры показывают, что аргументами логических функций и операндами логических операций должны быть только логические константы True и False или выражения, значения которых представлены ими. Недопустимо использовать численные значения 1 и 0, отождествляя их с логической единицей и логическим нулем. Результатом задания операций с ними будет повтор задания — возможно, в укороченной форме.
Отметим еще ряд логических операторов и функций:
Equal[Ihs, rhs] Greater[х,у] или х > у Возвращает True, если Ihs и rhs тождественны
Greater[xl,x2,x3] или xl > х2 > хЗ Возвращает True, если х оказывается больше у, иначе возвращает False
GreaterEqual[х,у] или х >= у Возвращает True, если xi образуют строго убывающую последовательность, иначе возвращает False
GreaterEqual[xl,х2,хЗ] или xl>= х2 >= хЗ Возвращает True, если х больше или равно у, иначе возвращает False
Negative[х] NonNegative[х] Positive[х] Возвращает True, если xi образуют невозрастающую последовательность, иначе возвращает False
SameQtlhs,rhs] или Ihs === rhs Возвращает True, если х оказывается отрицательным числом, иначе возвращает False
Xor[el, e2,...] Возвращает True, если х — неотрицательное число, иначе возвращает False
Возвращает True, если х — положительное число, иначе возвращает False
Возвращает значение True, если выражение Ihs тождественно rhs, иначе False. В отличие от Equal, сравнивает форму представления операндов, а не их значения
Является логической функцией XOR (исключающее «ИЛИ»). Возвращает True, если нечетное количество из ei имеют значение True, а остальные False. Возвращает False, если четное количество ei имеют значение True, a остальные False
Ниже приводятся примеры использования этих функций.
| Ввод (In) | Вывод (Out) |
| Positive [2-3] | False |
| Equal [1+2, 4-1] | True |
| Equal [1+2, 2] | False |
| Greater [5, 4] | True |
| Greater [5, 4,3] | True |
| Greater [5, 4, 9] | False |
| Less [3,2+3] | True |
| Positive [2] | True |
| Negative [-2] | True |
| Neganbve[2] | False |
| NonNeganive [ -2 ] | False |
| NonNegative[2] | True |
| Xor[ True, True] | False |
| Xor [False , False] | False |
| Xor [True, False] | True |
Ряд дополнительных логических функций читатель найдет в приложении.
Функции комплексного аргумента
Элементарные функции в системе Mathematica могут иметь аргумент в виде действительного числа х или комплексного z. Аргументы указываются как параметры функций в квадратных скобках.
Прежде всего отметим функции для работы с комплексными числами z:
- Abs[z] — возвращает модуль комплексного числа z;
- Arg [ z ] — возвращает аргумент комплексного числа z;
- Conjugate [z] — возвращает комплексно-сопряженное с z число;
- Directedlnf inity [] — представляет бесконечную числовую величину с неопределенным направлением на комплексной плоскости;
- Directedlnfinity[z] — представляет бесконечную числовую величину, направление которой на комплексной плоскости определяется фазой комплексного аргумента z;
- Im [ z ] — возвращает мнимую часть комплексного числа z;
- Re [ z ] — возвращает вещественную часть числа z.
Далее приведены примеры операций с комплексными числами в непосредственном режиме.
| Ввод (In) | Вывод (Out) |
| z1 : =2+1*3; | |
| z2: =4+1*5; | |
| N[zl+z2] | 6. + 8.1 I |
| Re [2+1*3] | 2 |
| H[Im[z2]J | 5. |
| N[zl/z2] | 0.560976 + 0.0487805 I |
| N[Abs[zl*z2]] | 23.0868 |
| Con j ugate [ z 1 ] | 2-31 |
Если ввести N [ z 1 / 0 ], то система выдаст следующее сообщение:
N[zl/0]
Power::infy : Infinite expression 1/0 encountered.
Complexlnfinity
Итак, в этом случае система выдает сообщение об ошибке, но после него возвращает константу Complexlnfinity, означающую комплексную бесконечность.
Элементарные функции, надо полагать, хорошо известны читателю, взявшемуся за изучение Mathematica. Полный набор этих функций с их синтаксисом дан в приложении. Отметим, что в Mathematica имена элементарных функций записываются с большой буквы, а их аргументы задаются в квадратных скобках. Следующие примеры иллюстрируют сказанное.
| Ввод (In) | Вывод (Out) |
| Sqrt[2] | Sqrt[2] |
| Sqrt[2.] | 1.41421 |
| 2*Sin[l] | 2 Sin[l] |
| N[2*Sin[l]] | 1.68294 |
| Log[Exp[l]] | 1 |
| Simplif у [Sin [x] /Cos [x] ] | Tan[x] |
| ComplexExpand [ Sin [ a+b* I ] ] | Cos[b] Sin[a]+ I Cosfa] Sinh[b) |
Из этих примеров видно, что система знает и использует основные соотношения между элементарными функциями. В двух последних примерах используются символьные преобразования с применением функций Simplify (упрощение выражений) и ComplexExpand (расширение выражений с комплексным аргументом). Более подробно эти важные для символьных операций функции будут рассмотрены в дальнейшем.

gl3-3.jpg
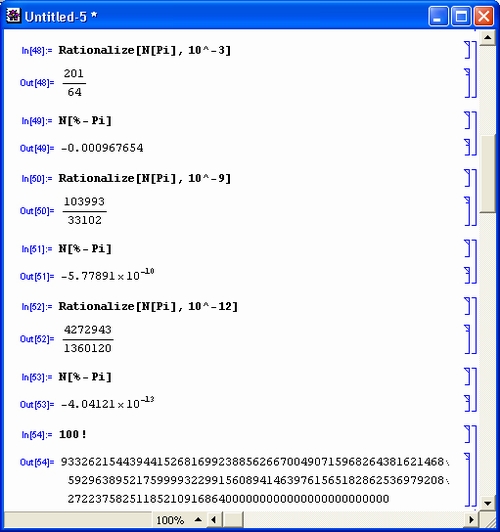
gl3-4.jpg
4. Работа с объектами
Работа с объектами
В этом разделе мы познакомимся с понятием объектов и научимся работать с ними. Объект — понятие обобщенное. Под ним может подразумеваться оператор или функция, рисунок (графический объект) и т. д. Объекты могут иметь ряд свойств, определяющих их назначение и поведение.
Различные объекты системы будут более подробно описаны в дальнейшем по мере знакомства с системой. Полный список объектов, заданных в ядре системы, легко получить, используя команду ? * (ниже приведены лишь начало и конец этого списка):
?*
Abort
AbortProtect
Above
Abs
AbsoluteDashing
AbsolutePointSize
$Version
$VersionNumber
Можно также получить список всех определений на заданную букву, используя команду ?S*, где S — любая буква латинского алфавита. Ниже дан пример вывода всех определений ядра на букву U:
?U*
UnAlias Unevaluated Update
Underflow Uninstall UpperCaseQ
Underoverscript Union UpSet
UnderoverscriptBox Unique UpSetDelayed
Underscript Unprotect Upvalues
UnderscriptBox UnsameQ Using
Unequal Unset
Аналогичные возможности предоставляет функция Names ["S"], например, Names ["А*"] дает список всех ключевых слов, начинающихся с символа «А». Наконец, командой ?Name можно вывести справку по любому определению с именем Name. Например, после выполнения команды
?Abs
Abs[z] gives the absolute
value of the real or complex number z.
становится ясно, что идентификатор Abs задает функцию Abs [ z ] для вычисления абсолютного значения комплексного числа.
С помощью выражения ?Name можно проверить, является имя объекта Name уникальным или оно уже использовано в системе:
?sin
Information::notfound : Symbol sin not found.
?Sin
Sin[z] gives the sine of z.
В первом случае ясно, что имя sin не использовано, а во втором случае мы видим, что имя Sin уже зарезервировано — это функция вычисления синуса. В задачу этой книги не входит описание всех без исключения определений ядра системы, так что указанные выше приемы весьма полезны, если вы обнаружили функцию, по которой нет информации.
Всякий объект перед использованием должен быть определен (задан). Внутренние объекты уже заданы в ядре. Объекты пользователя последний задает в текстах своих документов (notebooks).
Кроме того, некоторая совокупность новых внешних объектов может храниться в пакетах расширения, большой набор которых включен в поставку системы. Пользователь может и сам готовить пакеты расширений, обеспечивающие адаптацию системы к решению интересующего его класса задач. Пакеты расширений представлены файлами с расширением .т.
Оперативную помощь о назначении какой-либо функции или объекта в ходе работы с системой можно получить, используя следующие обращения:
- ? Name или Names [ "Name" ] — справка по заданному слову Name;
- ?? Name — расширенная справка по заданному слову Name;
- ?Аbс* — перечень всех определений, начинающихся с символов Abc;
- ©ptions [name] — получение информации об опциях объекта Name.
Примеры получения оперативной справки показаны на рис. 3.5.
Рис. 3.5. Примеры получения оперативной справки
Нетрудно заметить, что есть два уровня комментариев оперативной справки. Так, при обращении ?Sin получено лишь сообщение о назначении функции. Обращение ??Sin дает дополнительную информацию о признаках функции, именуемых ее атрибутами.
Многие встроенные функции защищены от модификации атрибутом Protected. К примеру, нельзя определить новую функцию Sin[x]=x A 2, причем вовсе не потому, что это определение абсурдно (далее мы покажем, что можно снять защиту и переопределить любую функцию даже самым абсурдным образом), а потому, что имя функции защищено указанием атрибута Protected (Защищенное). Позднее мы ознакомимся и с иными атрибутами — под ними подразумеваются определенные свойства объектов.
Средства диагностики и сообщения об ошибках
Средства диагностики органично входят во все программные модули системы Mathematica, созданные профессионально. Благодаря этому система обнаруживает неточные действия пользователя, например синтаксические ошибки при вводе идентификаторов функций и команд, неправильное использование типов данных, применение недопустимых операций (вроде злосчастного деления на ноль) и т. д. Всякий раз, когда ошибочное действие обнаружено, система выдает сообщение об ошибке в следующем виде:
Тип::Метка%Диагностика:Сообщение
Эти сообщения появляются в отдельных неактивных ячейках. Тип указывает на тип ошибки, например, General — ошибка общего вида, Syntax — синтаксическая ошибка, Arg — ошибка задания аргумента и т. д. Метка указывает место ошибки в списке ошибок данного типа, а Диагностика указывает (увы, не всегда...) на ошибочное выражение. Сообщение обычно раскрывает суть ошибки.
Допустим, мы пытаемся вычислить значение экспоненциальной функции, указав ошибочно аргумент 2,3 с разделительной запятой вместо точки. Вот как Mathematica отреагирует на такую попытку (рис. 3.6, первый пример).
Рис. 3.6. Примеры выполнения «ошибочных» операций
Итак, ясно, что произошла ошибка задания аргумента — функция Ехр должна иметь только один аргумент, а число 2,2 система воспринимает как два аргумента, разделенные запятой. Вот еще один пример — вроде бы ошибочно заданы круглые скобки в выражении N (Ехр (2) ). Mathematica 3 в этом случае дала бы два предупреждающих сообщения:
Syntax::bktwrn : "Ехр(2)" should probably be "Ехр[2]".
Syntax::bktwrn : "N(Exp(2)l" should probably be "N[Exp(2)]".
2ExpN
Однако Mathematica 4 в подобных случаях дает допустимую для данной системы форму представления введенного выражения. Тем не менее, надо отметить, что сообщения об ошибках системы Mathematica дают не только указания о самом по себе факте наличия ошибки, но и сообщают о том, что надо сделать для ее исправления.
Как видно из сведений о подготовке пакетов расширения, сообщения об ошибках и иные сообщения (в том числе информационные) заданы в их структуре. Насколько эти сообщения точны и как они предугадывают возможные ошибки — это уже зависит от опыта программиста, готовящего программные модули.
Включение и выключение сообщений об ошибках
Опытный пользователь нередко способен опознать ошибки и без слишком назойливых сообщений о них. Например, он может судить о своей промашке просто по отказу системы выполнить вычисление и по повтору выражения в строке вывода (см. примеры выше). Кроме того, часть сообщений носит предупреждающий характер и на первых порах может игнорироваться.
Для отключения сообщений об ошибках служит ключ
Off[Function::tag]
Например, отключим сообщение об ошибках у функции Ехр:
Off[Exp::argx]
Ехр[2,2]
Ехр[2,2]
Ехр[2]
Е2
N[Exp[2]]
7.38906
Для включения сообщения об ошибках используется ключ
On[Function::tag]
Например, для возобновления выдачи ошибок у функции Ехр надо исполнить команду
On[Exp::argx]
К сожалению, диагностика ошибок не способна опознать ошибки, имеющие формально правильный синтаксис. Чаще всего эти ошибки связаны с неверным описанием алгоритма вычислений. Например, если пользователь в математическом выражении вместо Sin [х] записал Cos [х], то эта грубая ошибка никак не будет распознана системой, поскольку синтаксически вызов функции Cos [х] записан безупречно. Часто пользователи путают идентификаторы переменных. Естественно, что ответственность за такие ситуации целиком лежит на пользователе — программисте.
Защита от модификации и ее отмена
Как уже отмечалось, объекты Mathematica имеют средства установки и снятия защиты от модификации. Для этого используются следующие функции-директивы:
- Protect [s1, s2,...] — устанавливает атрибут защиты от модификации Protected для перечисленных объектов si;
- Protect ["forml", "form2",...] — устанавливает атрибут защиты от модификации для всех объектов, имена которых сопоставимы с любым из указанных строковых шаблонов formi;
- Unprotect [s1, s2,...] — удаляет атрибут защиты от модификации Protected для объектов si, что делает возможной их модификацию;
- Unprotect ["form1", "form2",...] — снимает защиту всех объектов, имена которых текстуально (по буквам) сопоставимы с любым из указанных шаблонов formi.
Приведем наглядный пример модификации встроенной функции логарифма:
Log[7]=2
Set::write : Tag Log in Log[7] is Protected.
2
Итак, здесь предпринята попытка приписать логарифму числа 7 вовсе не свойственное ему значение 2. В ответ система выдала сообщение, что символ Log имеет атрибут Protected, то есть защищен от модификации. С помощью директивы Unprotect снимем защиту:
Unprotect[Log]
{Log}
Теперь выражение Log [ 7 ] можно модифицировать:
Log[7] =2
2
и использовать его уже в новом значении:
Log[7]=2
2
Log[7]+Log[3]
2 + Log[3]
Для отмены произведенной модификации и защиты символа Log от изменений выполните следующие действия:
Log[7]=.
Protect[Log]
{Log}
Теперь можно проверить, что присваивание Log [7] =2 не действует и функция Log работает как положено, возвращая значение In (7) =1. 94591:
Log[7]
Log[7]
N[Log[7]]
1.94591
Защита идентификаторов объектов от модификации является мощным средством контроля правильности вычислений. Эту защиту вряд ли стоит снимать подавляющему большинству пользователей. Тем не менее, возможность устранения защиты позволяет переименовать объект, например, при использовании с ним новых алгоритмов вычислений или при задании системе Mathematica каких-то новых свойств, не присущих ей изначально.
Важное значение в числовых и символьных преобразованиях имеют операции подстановки (rules). Их смысл заключается в замене одного объекта или его части другим объектом или частью другого объекта. Например, часто возникает необходимость вычислить значение математического выражения при замене некоторой переменной ее конкретным численным значением. Для этого достаточно вместо этой переменной подставить нужное численное значение.
Куда менее тривиальной является замена переменной ее символьным значением в виде математического выражения. При этом исходное выражение может в ходе решения задачи превратиться в совершенно новое выражение, поскольку после подстановки система может провести над исходным выражением достаточно сложные математические преобразования. Говорят, что в этом случае ячейка, содержащая выражение (а точнее — само выражение), оценивается и изменяется по ходу решения задачи. Операции подстановки обычно вводятся с помощью комбинации символов «/ .»:
- ехрг / . х -> value — в выражение ехрг вместо переменной х подставляется ее значение value;
- ехрг /. {х -> xvalue,. у -> yvalue} — в выражение ехрг вместо переменных х и у подставляются их значения xvalue и yvalue.
Примеры:
l+x^3/.x->l+z
1 + (1+ z)3
х^2+2*х+3/.х->2
11
Обратите внимание на то, что в результате подстановки в первом примере вместо переменной х оказалось математическое выражение (1 + z). Второй пример иллюстрирует подстановку на место переменной х ее численного значения.
В целом для операций подстановок используют следующие обозначения:
- Ihs -> rhs — прямая подстановка Ihs в rhs;
- Ihs :> rhs — отложенная подстановка (RuleDelayed), которая преобразует Ihs в rhs, вычисляя rhs не сразу, а только при использовании правила подстановки.
Ниже приведены еще два примера на использование операций подстановки:
р:=1+х^2+3*х^3
р/.х->1+у
1+ (1 + у)2+3 (1 + у)3
{f[1],f[2],f[3]}/.f[n_]->n^2
{1, 4, 9}
f[n_]:=n^2
f[4]+f[y]+f[x+y]
16+y2+(x+y)2
В первом примере подстановка произведена в математическое выражение, а во втором — в список.

gl3-5.jpg
gl3-6.jpg
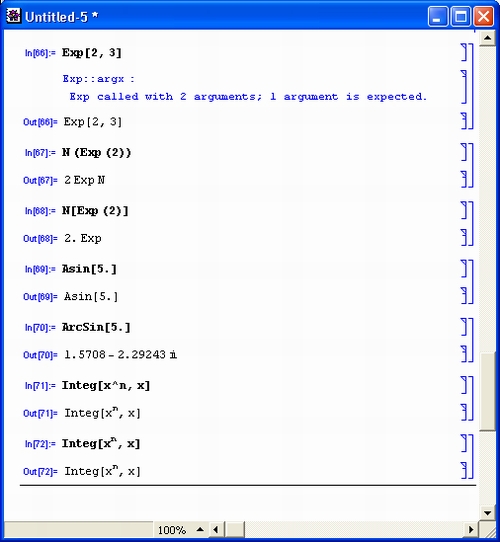
5. Работа со списками и массивами
Работа со списками и массивами
Списки относятся к данным множественного типа. Они имеют большое значение при обработке массивов данных и служат основой для создания векторов и матриц. В этом разделе мы познакомимся со свойствами списков, их созданием (генерацией) и использованием.
Часто математические или иные объекты содержат множество данных, которые желательно объединять под общим именем. Например, под объектом с именем М можно подразумевать квадратную матрицу размером 10x10 с общим числом элементов, равным 100. Человека с именем Victor, например, можно характеризовать целым списком разных данных — символьными фамилией, именем и отчеством, целочисленным годом рождения, вещественным ростом, объемом груди и т. д.
Для объединения данных могут использоваться списки (list). Mathematica имеет обширные возможности работы с объектами-списками, содержащими не только однотипные, но и разнотипные элементы. В частности, элементами списков могут быть числа, константы, переменные, выражения и даже сами списки. Списки используются для конструирования более частных типов данных — массивов, матриц и векторов [87].
На языке данной системы список — это совокупность произвольных данных, указанных в фигурных скобках, например: {1, 4, 2, 7, 9} или {а, Ь, с, d, e, sin[x], ln[y], "string"}
Возможно задание списков в списке, например, так:
{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}
Такой список представляет матрицу
1 2 3
4 5 6
7 8 9
Однако, чтобы вывести список в такой матричной форме, надо использовать после списка выражение //MatrixForm (рис. 3.7).
Рис. 3.7. Примеры задания и вывода матрицы
На рис. 3.7 показан еще один способ задания списка или матрицы — с помощью функции List:
- List [a, b, с,...] — создает список {а, b,, с,...};
- List [ {а,b, с,...}, {d,e, f,...}, {i, k, 1,...} ] — создает список — матрицу { {a,b, с,...}, {d,e, f,...}, {i, k, 1,...} }.
Списки можно составлять, непосредственно задавая объекты в соответствии с описанным синтаксисом. Однако можно и генерировать некоторые виды списков, таких как таблицы. Списки могут быть объектами присваивания переменным, например
V:={1, 2, 3, 4, 5}
Списки характеризуются размером, который представляет собой произведение числа элементов списков по каждому направлению (размерности). Например, одномерный список является вектором и характеризуется числом элементов по единственному направлению. При этом вектор может быть вектором-строкой или вектором-столбцом. Двумерный список представляет матрицу, имеющую m строк и n столбцов. Ее размер равен mxn. Если m=n, то матрица называется квадратной. Трехмерный список можно представить в виде параллелепипеда, содержащего mxnxp элементов. Списки большей размерности трудно наглядно представить, но они вполне возможны. Напомним, что имена векторов и матриц в данной книге обозначены жирными символами, например, V для вектора и М для матрицы.
Для генерации списков с элементами, являющимися вещественными и целыми числами или даже целыми выражениями, часто используется функция Table, создающая таблицу-список:
- Table [expr, {imax} ] — генерирует список, содержащий imax экземпляров выражения ехрг;
- Table [expr, {i, imax} ] — генерирует список значений ехрг при 1, изменяющемся от 1 до imax;
- Table [expr, {i, imin, imax}] — генерирует список значений ехрг при i, изменяющемся от imin до imax;
- Table [expr, {i, imin, imax, di} ] — использует шаг приращения i, равный di;
- Table[expr, {i, imin, imax}, {j, jmin, jmax},...] —возвращает вложенный список. Самым внешним является список по переменной i.
Ниже приводятся примеры использования функции Table (первая строка каждого примера — ввод, следующая — вывод).
| Пример | Комментарий |
| Table[i*j,{i,l,3},{j,l,3}] {{1, 2, 3), [2, 4, 6}, {3, 6, 9}} | Генерация матрицы размером |
|
Table[N[Exp[i]], {1,0, 2,0.5}] {1., 1.64872, 2.71828, 4.48169, 7.38906}
| Генерация пяти значений Е ^ 1 численном виде |
|
Table[Exp[i],{i,l,5}] {е, е 2 , е 3 , е 4 , е 5 }
| Генерация пяти значений Е ^ i (i=l, 2, 3,4 и 5) |
|
Table[Exp[i],{5}] {е i , е i , е i , е i , е i }
| Генерация пяти значений Е ^i |
Применяется также функция Range, которая предназначена для создания так называемых числовых списков, значения которых равномерно распределены в некотором заданном диапазоне:
- Range [imax] — генерирует список числовых элементов {1, 2, ..., imax};
- Range [imin, imax] — генерирует список числовых элементов {imin, ...,
- Range [imin, imax, di] — генерирует список числовых элементов от imin до imax с шагом di.
Примеры использования функции Range.
| Пример | Комментарий |
| Range [5] {1, 2, 3, 4, 5} | Генерация пяти целых чисел |
Range[0,2,0.5] {0, 0.5, 1.,1.5, 2.}
| Генерация чисел пяти вещественных |
Для выделения элементов списка list используются двойные квадратные скобки:
- list [ [i] ] — выделяет i-й элемент списка;
- list [ [ { i, j , --.}]] — выделяет i-й, j-й и т. д. элементы списка.
Ниже приведены примеры выделения элементов списков.
| Пример | Комментарий |
| 11:={1,2,3,4,5) | Задание исходного списка 11 |
| 11[[3]] | Выделение третьего элемента |
| 3 | |
| 11[[{1,2,5}]] | Выделение первого, второго и пятого элементов |
| (1, 2, 5} | |
| 12={{1,2,3},{4,5,6}} | Задание сдвоенного (двумерного) списка |
| {{1, 2, 3}, {4, 5, 6}} | |
| TableForm[12] | Вывод сдвоенного списка в табличной форме |
| 1 2 3 | |
| 4 5 6 | |
| L2[[2,3]] | Выделение элемента сдвоенного списка |
| 6 |
Для выделения заданного z'-ro элемента списка list используется также функция Part [list, i]. При i>0 отсчет номеров элементов идет с начала списка, а при i<0 — с его конца. Это правило поясняют следующие примеры:
L:={l,2,3,a,b,c}
{Part[L,2],Part[L,5],Part[L,6]}
{2, b, с}
{Part[L,-2],Part[L,-5],Part[L,2]}
{b, 2, 2}
Функция Part может использоваться для выбора заданного элемента выражения из списка. В этом случае вместо i надо указать три числа — номер выражения как элемента списка, уровень выражения и порядковый номер извлекаемого из
выражения объекта. Показанные на рис. 3.8 примеры иллюстрируют работу со списком, последним (четвертым) элементом которого является математическое выражение.
Рис. 3.8. Примеры выделения элементов выражения
Обратите внимание на то, что в последнем примере неверно задан уровень выражения — использованное выражение имеет только один (первый) уровень. Поэтому задание второго уровня вызывает появление сообщения об ошибке.
Функция Select используется для выделения элементов списка, удовлетворяющих заданному критерию:
- Select [list, crit] — выбирает все элементы ei списка list, для которых функция критерия crit [ei] имеет значение True;
- Select [list, crit, n] — выбирает первые п элементов, для которых critfei] есть True.
Ниже представлены примеры применения этой функции:
Select[{1,а,2,b,3,c},NumberQ]
{1, 2, 3}
Select[{l,a,2,b,3,c),NumberQ,2]
{1, 2}
Select[{l,a,2,b,3,c},PrimeQ]
{2, 3}
Для вывода элементов списка используются следующие функции:
- MatrixFormflist] — выводит список в форме массива (матрицы);
- TableForm [list] — выполняет вывод элементов списка list в виде таблицы.
С этими функциями используются следующие опции:
- TableAlignments — указывает, каким образом должно выравниваться содержимое списка в каждой размерности (слева, по центру или справа);
- TableDepth — устанавливает максимальное количество уровней, выводимых в табличном или матричном формате;
- TableDirections — указывает, как следует располагать последовательные (соседние) размерности — в виде строк или столбцов;
- TableHeadings — задает подписи (labels) для каждой размерности таблицы или матрицы;
- TableSpacing — устанавливает количество пробелов, которое следует оставлять между соседними строками или столбцами.
Обратите внимание на то, что эти опции используются как для функции TableForm, так и для функции MatrixForm, используемой для вывода матриц. Вообще, векторы и матрицы являются разновидностью списков. На рис. 3.9 поясняется использование функций MatrixForm и TableForm на примере вывода списка.
Рис. 3.9. Примеры вывода списка в матричной и табличной формах
Дополнительные возможности функции TableForm демонстрирует рис. 3.10. Здесь особенно полезно отметить возможность выравнивания данных в таблицах по левому и правому краям, а также по середине.
В большинстве случаев опции для функций MatrixForm и TableForm не используются. Точнее, они установлены по умолчанию. Проверить, какие опции использованы, можно, например, следующим образом:
Options[MatrixForm]
{TableAlignments -> Automatic, TableDepth-> со, TableDirections -> Column,
TableHeadings->None, TableSpacing-> Automatic}
Options[TableForm]
{TableAlignments -> Automatic, TableDepth ->бесконечность, TableDirections -> Column,
TableHeadings -» None, TableSpacing-> Automatic}
Рис. 3.10. Примеры вывода списка в табличной форме
Вывод можно сделать такой — Mathematica обладает обширными возможностями по части выделения элементов списков и представления списков на экране дисплея и в распечатках документов.
Функции выявления структуры списков
Списки относятся к данным сложной структуры. Поэтому при работе с ними возникает необходимость контроля за структурой, иначе применение списков может привести к грубым ошибкам, как явным, сопровождаемым выдачей сообщения об ошибке, так и неявным. Последние могут привести к серьезным просчетам.
Для выявления структуры списков используется ряд функций:
- Count [list, pattern] — возвращает количество элементов в списке list, которые соответствуют образцу pattern;
- Dimensions [list] — возвращает список размеров списка по каждой размерности;
- FreeQ [list, form] — возвращает True, если список list не содержит form;
- Length [list] — возвращает число элементов одномерного списка list или число размерностей в случае многомерного списка;
- MatrixQ [list ] — проверяет, является ли список матрицей, и дает True, если это так, и False в противном случае;
- MemberQ [list, form] — проверяет, есть ли form в списке, и возвращает True, если это так, и False в противном случае;
- Position [list, form] — возвращает номер позиции form в списке;
- TensorRank[list] — находит ранг списка, если он является тензором;
- VectorQ [list] — проверяет, является ли список вектором, и дает True, если это так, и False в противном случае.
Функции с буквой Q в конце имени являются тестирующими и возвращают логические значения True или False. Остальные функции возвращают численные значения соответствующего параметра списка.
Ниже даны примеры использования этих функций.
| Ввод (In) | Вывод(Out) |
| 11={1,2,3,4,1}; | |
| Length [11] | 5 |
| Dimensions [11] | {5} |
| MatrixQ [11] | False |
| TensorRank [ 11 ] | 1 |
| MemberQ[ll,l] | True |
| Count[ll,l] | 2 |
| FreeQ [11, 5] | True |
| Position [11,1] | {{1},{5}} |
| VectorQ [11] | True |
| M={{1, 2,3}, {4, 5, 6}} | |
| Length [M] | 2 |
| Dimensions [M] | {2,3} |
Система предоставляет пользователю свободу действий, производимых по результатам анализа структуры списков.
Списки можно представить в виде особой структуры данных — стека. Стек — это структура данных, напоминающая стопку тарелок в шкафу. При этом тарелки играют роль данных. Очередную тарелку можно положить только сверху (на вершину стека). На дне стека лежит первая помещенная в него тарелка. Стек подчиняется следующему правилу: последнее введенное значение извлекается первым, а первое введенное значение извлекается последним. Стек относится к системам хранения данных динамического типа, его размеры непрерывно меняются по ходу вычислений. Стек может быть пустым, если из него извлечены все данные.
Система Mathematica предоставляет широкие возможности для операций со стеками:
- Drop [list, n] — возвращает список list, из которого удалены первые п элементов;
- Drop [list, -n] — возвращает список list с отброшенными последними п элементами;
- Drop [list, {n}] — возвращает список list без n-го элемента;
- Drop [list, {m, n}] — возвращает список list с отброшенными элементами от m-го до п-го;
- Fold[f, x, list] — возвращает последний элемент из FoldList [f,x, list];
- Last [list] — возвращает последний элемент списка list;
- Rest [list] — возвращает список с уничтоженным первым элементом;
- Take [list, n] — возвращает первые п элементов списка list;
- Take [list, -n] — возвращает последние п элементов списка list;
- Take [list, {m, n}] — возвращает элементы списка с порядковыми номерами от m до п.
Следующие примеры поясняют работу со стеком.
| Ввод (In) | Вывод(Out) | |||||||
| Drop[{l | ,2 | ,3 | ,4 | ,5}, | 2] | {3, | 4, | 5} |
| Drop [ { 1 | ,2 | ,3 | ,4 | ,5}, | -2] | {1, | 2, | 3} |
| Drop [ { a | ,b | ,c | ,d | ,e>, | {2,4}] | (a, | e} | |
| Last[{l | ,2 | ,3 | ,4 | ,5}] | 5 | |||
| Rest[{l | ,2 | ,3 | ,4 | ,5}] | {2, | 3, | 4, 5} | |
| Take[{l | ,2 | ,3 | ,4 | ,5}, | 2] | (1, | 2} | |
| Take [ { 1 | ,2 | ,a | ,b | ,c}, | -2] | {b, | c} | |
| Take [ { 1 | ,2 | ,3 | ,4 | ,5}, | {2,4}] | {2, | 3, | 4} |
Тривиальная процедура общения со стеком (ввести/вывести данные) ограничивает возможности стековых операций. Из житейского опыта мы знаем, что, проявив настойчивость, можно вставить тарелку и в середину стопки. Mathematica предоставляет ряд расширенных возможностей для работы со списками, выходящих за рамки обычных стековых операций.
Так, например, для расширения списка путем включения в него новых элементов используются следующие функции:
- Append [list, element] — добавляет элемент в конец списка;
- PreoendTlist.element1 — добавляет элемент в начало списка:
- Insert [list, element, n] — вставляет элемент в позицию п (отсчет пози-ций.ведется с начала списка, а если число п отрицательное — то с конца). Данной функцией можно включать элемент в несколько позиций, указав каждую в фигурных скобках, взяв все перечисление в еще одни фигурные скобки и использовав его вместо п. При этом надо учитывать, что все позиции включаемых элементов определяются одновременно до начала расширения списка.
Следующие примеры иллюстрируют применение этих функций.
| Ввод (In) | Вывод(Out) | ||||
| 1={1,2,3} | (1, | 2, | 3} | ||
| Append[l,e] | (1, | 2, | 3, | e} | |
| Prepend[l,e] | {e, | 1, | 2, | 3} | |
| Insert[l,e,2] | {1, | e, | 2, | 3} | |
| L={1, 2, 3, 4 | , 5} | {1, | 2, | 3, | 4, 5} |
| Insert [L, e, | -5] | (1, | e, | 2, | 3, 4, 5} |
| Insert [L, e, | {{1},{5}}] | (e, | 1, | 2, | 3, 4, e, 5} |
Обратите внимание на то, что в данном случае элементы списка — числа, тогда как вставляемый элемент имеет символьное значение е.
Следует отметить, что описанные для стека функции Drop и Rest позволяют удалить из списка последний или первый элемент. Функция Delete [list, i] позволяет удалить из списка произвольный i-й элемент. Если i>0, то отсчет удаленного элемента идет с начала списка, а если i<0 — с конца:
L:={1,2,3,4,5}
{Delete[L,l],Delete[L,3],Delete[L,5]}
{{2, 3, 4, 5}, {1, 2, 4, 5}, {1, 2, 3, 4}}
{Delete[L,-2],Delete[L,-5]}
{{1, 2, 3, 5}, (2, 3, 4, 5}}
Delete[{l,2,3,{a,b,c},4,5},2]
{1, 3, {a, b, c}, 4, 5}
Если элементом списка является список, то он фигурирует как один элемент. Можно, однако, удалить избранный элемент из элемента списка, указав в фигурных скобках вместо i номер элемента списка во внешнем списке и номер удаляемого элемента во внутреннем списке. Это иллюстрируют следующие примеры:
Delete[(1,2,3,{а,Ь,с},4,5},{4,3}]
{1, 2, 3, {а, b}, 4, 5}
Delete[{1,2,3,{а, b, с},4,5},{4,1}]
{1, 2, 3, {b, с}, 4, 5}
Наконец, с помощью функции Delete можно удалить несколько элементов списка, указав каждый из них в фигурных скобках и оформив это указание также в фигурных скобках:
Delete [ {1,2,3, {a, b, c} , 4, 5}, {{2}, {4} ,{ 5}}]
{1, 3, 5}
Следует иметь в виду, что некоторые функции удаляют в списках определенные элементы. Этот вопрос будет рассмотрен ниже.
Изменение порядка расположения элементов в списке
Помимо добавления в список новых данных имеется возможность изменения порядка расположения элементов в списке. Она реализуется следующими операциями:
- Flatten [list] — выравнивает (превращает в одномерный) список по всем его уровням;
- Flatten [list, n] — выравнивает список по п его уровням;
- Flatten [list, n, h] — выравнивает выражения с заголовком h no n уровням;
- FlattenAt [list, n] — выравнивает подсписок, если он оказывается п-м элементом списка list. Если n отрицательно, позиция отсчитывается с конца;
- Sort [list] — сортирует элементы списка list в каноническом порядке;
- Sort[list,p] — сортирует согласно функции упорядочения р;
- Reverse [list] — возвращает список с обратным порядком расположения элементов;
- RotateLeft [list] — возвращает список после однократного поворота влево;
- RotateLeft [list, n] — возвращает список после n-кратного поворота влево;
- RotateRight [list] — возвращает список после однократного поворота вправо;
- RotateRight [list, n] — возвращает список после n-кратного поворота вправо;
- Transpose [list] — осуществляет транспозицию (смену строк и столбцов) для двумерного списка;
- Transpose [list, п] — осуществляет транспозицию n-мерного списка. Ниже приведен ряд примеров на использование этих функций.
| Ввод (In) | Вывод (Out) |
| 13={{1,2,3},{4,5,6},{7,8,9}}; | {1,2,3,4,5,6,7,8,9} |
| Flatten [13] | |
| FlattenAt[13,l] | {1,2,3,{4,5,6},{7,8,9}} |
| Sort[{l,5,3,4,2}] | {1,2,3,4,5} |
| Reverse[{l,2,3,4}] | {4,3,2,1} |
| RotateLeft[ {1,2,3,4,5}, 2] | {3,4,5,1,2} |
| RotateRight[{l,2,3,4,5} ,2] | {4,5,1,2,3} |
| 12={{a,b},{c,d}}; | |
| TableForm[12] | a b c d |
| TableFormf Transpose [12] ] | a c d b |
Изменение порядка расположения элементов в списке полезно при реализации некоторых алгоритмов. К примеру, сортировка списка ускоряет выполнение статистических расчетов и уменьшает их погрешности.
Комбинирование списков и работа с множествами
Иногда возникает необходимость комбинирования нескольких списков. Для этого используются следующие функции:
- Complement [list, listl, list2, ...] — возвращает список list с элементами, которые не содержатся ни в одном из списков listl, Iist2, ...;
- Intersection [listl, list2,...] (пересечение множеств) —возвращает упорядоченный список элементов, общих для всех списков listi;
- Join[list1, list2,... ] — объединяет списки в единую цепочку (выполняет конкатенацию). Join может применяться к любому множеству выражений, имеющих один заголовок;
- Union [listl, Iist2, ...] (объединение множеств) — удаляет повторяющиеся элементы списков и возвращает отсортированный список всех различающихся между собой элементов, принадлежащих любому из данных списков listi. Функция обеспечивает теоретико-множественное объединение списков;
- Union [list] — возвращает отсортированный вариант списка list, из которого удалены все повторяющиеся элементы.
Приведенные ниже примеры иллюстрируют применение функций комбинирования списков.
| Ввод (In) | Вывод (Out) | |
| Complement! {1, 2, 3,4, 5}, {1, а, 2}, {b, с, 5}] | {3, | 4} |
| 11={1,2,3,4,5}; | ||
| 12={а,b,3,4,с}; | ||
| Intersection [11 , 12] | {3, | 4} |
| Join [11, 12] | (1, | 2, 3, 4, 5, a, b, 3, 4, c} |
| Union[{l,2,4,3,2,7,3,5}] | {1, | 2, 3, 4, 5, 7}. |
| Union[{3,2},{!,4}] | (1, | 2, 3, 4} |
| Union[{a,b,c,a},{l,d,3}] | {1, | 3, a, b, c, d} |
Комбинирование списков позволяет создавать сложные структуры данных из более простых структур. Это может быть полезно при построении очередей, деревьев и иных структурных построений. Кроме того, приведенные функции обеспечивают основные операции со множествами. Функцию Union удобно использовать при решении нелинейных и алгебраических уравнений для удаления повторяющихся решений.
Ряд других функций этого урока перечислен в приложении. В целом можно сделать вывод, что обилие функций работы со списками позволяет решать практически любые задачи, в основе которых лежат манипуляции со списками, стеками и другими родственными типами данных.
gl3-10.jpg

gl3-7.jpg
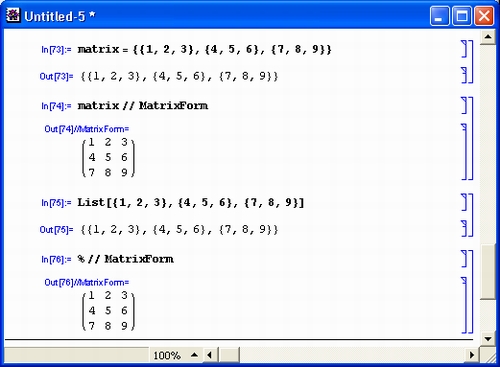
gl3-8.jpg
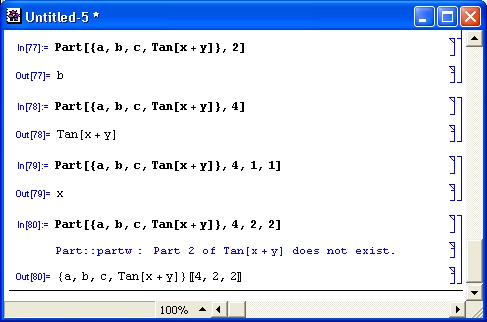
gl3-9.jpg
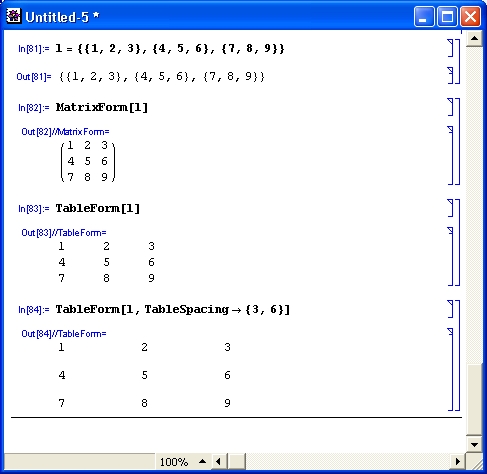
6. Операции линейной алгебры
Операции линейной алгебры
Линейная алгебра — один из фундаментальных разделов математики. Он во многом способствовал развитию методов вычислений. Средства линейной алгебры (преобразование матриц, решение систем линейных уравнений и т. д.) широко используются при решении задач механики, электро- и радиотехники и других отраслей науки и техники. В этом разделе мы познакомимся с основным набором средств системы Mathematica, предназначенных для решения задач линейной алгебры.
Совокупность данных образует массив (Array). Массивы могут быть одномерными (один список), двумерными и многомерными (два и более списка). Одномерные массивы в математике называют векторами, двумерные — матрицами. В общем случае массив характеризуется размерностью (числом измерений) и размером — произведением числа элементов по всем размерностям. Mathematica позволяет создавать многомерные массивы — число элементов в них ограничено лишь объемом памяти компьютера.
Для задания массивов используются следующие функции:
- Array [ f, n] — генерирует список длиной п с элементами f [ 1 ], f [ 2 ], ..., f[n];
- Array [f, {nl, n2, ...}] — генерирует массив размером n1x n2 x... в виде вложенных списков с элементами f [ i I, i2,...] (аргумент функции i k меняется от 1 до nk);
- Array[f, dims, origin] — генерирует список с размерностью dims, используя спецификацию индекса origin;
- Array [f, dims, origin, h] — использует заголовок h, а не List, для каждого уровня массива.
Далее приводятся примеры задания массивов и их вывода.
| Ввод (In)
| Вывод (Out) | ||||||||||
| Y : =Array [Exp , 4 ] Y | {e, | e 2 , | e 3 , | e 4 } | |||||||
| N[Y] |
|
| {2. | 71828, | 7. | 38906, | 20.0855, 54 | .5982} | |||
| Array[f,{3 | , | 3}] | {{f | [1, | 1], | f | [1, 2] | { | f[l, | 3]}, | {f[2, 1], f[2, 2], |
| {[2 | , 3] | }, | {f | [3, 1] | { | f[3, | 2], f | [3, 3] }} | |||
| Array [Sin, | 3 | ,0] | {0, | Sin | [1] | , Sin[2] | } | ||||
| Array [Sin, | 4 | ,l,Plus] | Sin | [1] | + Sin | [2] + | Sin[3] | + Sin | [4] | ||
| Array[f ,5, | 2 | ,2] | 2[f | [2], | f [ | 3] | , f[4] | { | f [5] | , f[6] | ] |
Основные понятия линейной алгебры
Массивы, в основном в виде векторов и матриц, широко применяются при решении задач линейной алгебры. Прежде чем перейти к рассмотрению возможностей Mathematica в части решения таких задач, рассмотрим краткие определения, относящиеся к линейной алгебре.
Матрица — прямоугольная двумерная таблица, содержащая m строк и п столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).
Квадратная матрица — матрица, у которой число строк m равно числу столбцов п. Пример квадратной матрицы размером 3x3:
1 2 3
4 5 6
7 8 9
Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.
Единичная матрица — это квадратная матрица, у которой диагональные элементов равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размером 4x4:
| 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| E | = | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Транспонированная матрица — квадратная матрица, у которой столбцы и строки меняются местами. Приведем простой пример.
Исходная матрица:
| a | b | c | ||
| A | = | d | e | f |
| i | k | l |
Транспонированная матрица:
| a | d | i | ||
| А т | = | b | e | k |
| c | f | l |
Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.
Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.
Диагональ матрицы — расположенные диагонально элементы А., матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:
| A | b | c | ||
| А | = | d | E | f |
| i | k | L |
Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия поддиагоналей (элементы d и k) и наддиагоналей (элементы b к f).
Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.
След матрицы — сумма диагональных элементов квадратной матрицы. Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением п элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:
detА = Сумма a1j(-1)j+1M1<j>
где M <J> — определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-то столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.
Матрица в целой степени — квадратная матрица в степени п (п — целое неотрицательное число), определяемая следующим образом: М° = Е, М 1 = М, М 2 = = М*М,..., Мn = М n-1 -М.
Идемпотентная матрица — матрица, отвечающая условию Р 2 = Р.
Инволютивная матрица — матрица, отвечающая условию I 2 = Е.
Симметрическая матрица — матрица, отвечающая условию А т = А.
Кососимметрическая матрица — матрица, отвечающая условию А т = -А.
Ортогональная матрица — матрица, отвечающая условию А т = А- 1 .
Комплексно-сопряженная матрица — матрица А , полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные.
Эрмитова матрица — матрица А, удовлетворяющая условию А = А .
Собственный вектор квадратной матрицы А — любой вектор х е V n , х не равно 0, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.
Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена — |А - g Е|.
Собственные значения матрицы — корни ее характеристического многочлена.
Норма — обобщенное понятие абсолютной величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||). I-норма матрицы А — число
Матричная форма записи системы линейных уравнений — выражение А-Х = В, где А — матрица коэффициентов системы, X — вектор неизвестных, и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А -1 В, где А- 1 — обратная матрица.
Следующая группа функций системы Mathematica позволяет осуществлять над векторами и матрицами основные операции, используемые в линейной алгебре:
- Cross [vl,v2, v3,...] — векторное произведение (может задаваться в виде v1*v2*v3*...);
- Det [m] — возвращает детерминант (определитель) квадратной матрицы m;
- DiagonalMatrix [list] — возвращает диагональную матрицу с главной диагональю, сформированной из элементов списка list, и нулевыми остальными элементами матрицы;
- Dot [a, b, с] — возвращает произведения векторов, матриц и тензоров. Операцию произведения можно задавать также в виде а. b. с;
- Eigensystem[m] — возвращает список {values, vectors} собственных значений и собственных векторов квадратной матрицы т;
- Eigenvalues [m] — возвращает список собственных значений квадратной матрицы m;
- Eigenvectors [m] — возвращает список собственных векторов квадратной матрицы m;
- IdentityMatrix [n] — возвращает единичную матрицу размером пхп (у нее диагональные элементы имеют значения 1, остальные 0);
- Inverse [m] — возвращает обратную матрицу для квадратной матрицы т, то есть матрицу m- 1 , которая, будучи умноженной на исходную матрицу, дает единичную матрицу;
- LinearSolve [m, b] — возвращает вектор х, представляющий собой решение матричного уравнения m. x==b, где m — матрица коэффициентов левой части системы линейных уравнений, х — вектор неизвестных и b — вектор свободных членов в правой части системы;
- Tr [list] — возвращает след матрицы или тензора (эта функция есть только у Mathematica 4);
- Transpose [m] — возвращает транспонированную матрицу, у которой столбцы и строки меняются местами в сравнении -с исходной матрицей m;
- RowReduce [m] — производит гауссовское исключение переменных, возвращая упрощенную форму матрицы m, полученную путем линейного комбинирования строк.
Следующие примеры иллюстрируют применение основных из этих функций.
| Ввод (In) | Вывод (Out) | |||
| A: =IdentityMatrix [3] | ||||
| А | {{1, | 0, | 0}, | {0, 1, 0}, {0, 0, 1}} |
| MatrixExp [A] | {{E, | 0, | 0}, | {0, E, 0}, {0, 0, E}} |
| MatrixQ [A] | True | |||
| MatrixPower [MatrixExp [A] , -1 . 5] | {{0. {0, | 22313, 0, 0}, {0, 0.22313, 0), 0, 0.22313}} | ||
| А+{{1,2,3},{4,5,6},{7,8,9}} | {{2, | 2, | 3}, | {4, 6, 6}, {7, 8, 10}} |
| m:={{1,2},{3,7}} | ||||
| Inverse [m] | {{7, | -2} | , ( | -3, 1}} |
| MatrixQ [m] | True | |||
| RowReduce [m] | {{1, | 0}, | {0 | , 1}} |
Вычисление детерминанта матрицы и функций, относящихся к собственным значениям, представлено на рис. 3.11.
Рис. 3.11. Вычисление детерминанта, собственных значений и векторов матрицы
Приведем еще несколько примеров:
m={{1,2},{3,7}}
{{1, 2}, {3, 7}}
Transpose[m]
{{1, 3), {2, 7}}
m//MatrixForm
1 2
3 7
Transpose[m]//MatrixForm
Inverse[m]//MatrixForm
7 -2
-3 1
В приложении указан ряд дополнительных матричных функций, применяемых реже, чем описанные выше функции.
Решение систем линейных уравнений
Приведем также примеры на решение систем линейных уравнений матричными методами. В первом из них решение выполняется в символьном виде на основании формулы X = А -1 В, где А — матрица коэффициентов системы линейных уравнений, В — вектор свободных членов. Для перемножения используется функция Dot, а для инвертирования матрицы — функция Inverse:
A:={{a,b},{c,d}}
B:={e,f}
X:=Dot[Inverse[A],B]
X
{-de/(bc+ad) -bf/(bc+ad)- ce/(bc+ad) -af/(bc+ad)}
Во втором примере для решения системы линейных уравнений используется функция LinearSolve:
LinearSolve[{{l,2},{3,4}},{7,9}]
{-5, 6}
Нередко, например в электротехнических расчетах, встречается необходимость решения систем линейных уравнений с комплексными элементами. Все описанные выше функции обеспечивают работу с комплексными числами. Следующий пример иллюстрирует решение системы линейных уравнений с комплексными данными:
А={ U+2I,2+3I},{3+4I,4+5I}}
{{1+21, 2 + 31}, {3 + 41, 4+ 51}}
В={21,3}
{21,3} X=LinearSolve[А,В]
{1/4-41, 11I/4}
Число матричных функций в системе Mathematica 3/4 ограничено разумным минимумом, позволяющим реализовать множество других, более сложных матричных функций и преобразований. Их можно найти в пакетах расширения системы, посвященных линейной алгебре.
gl3-11.jpg
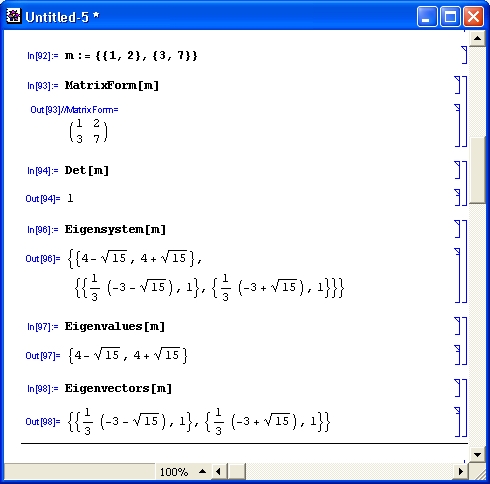
7. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Использовать основные классы данных системы Mathematica.
- Выполнять арифметические вычисления.
- Применять встроенные и пользовательские функции.
- Получать данные об объектах.
- Осуществлять подстановки.
- Работать со списками.
- Создавать массивы, векторы и матрицы.
- Пользоваться функциями линейной алгебры
Урок 4. Операции математического анализа
Урок 4. Операции математического анализа
1. Операции математического анализа
Операции математического анализа
- Вычисление сумм
- Вычисление произведений
- Вычисление производных
- Вычисление интегралов
- Вычисление пределов функций
- Решение уравнений и систем уравнений
- Решение дифференциальных уравнений
- Поиск максимального и минимального чисел в списке
- Поиск максимума и минимума функции
- Решение задач линейного программирования
- Преобразования Лапласа
- Z-преобразования
В этом уроке описаны основные операции математического анализа, детали которых можно найти в любом справочнике по высшей математике. Эти операции чаще всего используются при проведении математических и научно-технических расчетов и потому описаны достаточно полно
2. Вычисление сумм
Вычисление сумм
Вычисление сумм в аналитическом виде
В числе операций математического анализа прежде всего надо отметить суммы
Сумма от i=min до imax по fi
В этих операциях индекс i принимает целочисленные значения от минимального (начального) imin до максимального (конечного) imax с шагом, равным +1.
Суммы и произведения легко вычисляются численными математическими системами, такие вычисления просто описываются на всех языках программирования. Однако важным достоинством систем символьной математики, включая Ма-thematica, является вычисление сумм и произведений в аналитическом виде (если это возможно) и при большом числе членов — вплоть до стремящегося к бесконечности.
Для вычисления сумм в системе Mathematica предусмотрена функция Sum, используемая в ряде форм:
- Sum [ f, {i, imax} ] — вычисляет сумму значений f при изменении индекса i от 1 до imax с шагом +1;
- Sum[f, {i, imin, imax}]—вычисляет сумму значений f при изменении индекса i от минимального значения i=imin до максимального i=imax с шагом +1;
- Sum[f, {i, imin, imax, di}]— вычисляет сумму значений f при изменении управляющей переменной вещественного типа от минимального значения i=imin до максимального i=imax с шагом di;
- Sum[f, {i, imin, imax}, {j, jmin, jmax},...] — вычисляет многократную сумму значений f при изменении индексов i от imin до imax с шагом +1, j от jmin до jmax с шагом +1 и т. д. (число индексов не ограничено).
Таким образом, эта функция обеспечивает расширенные возможности вычисления сумм — как при целочисленных, так и при вещественных значениях управляющих переменных, задающих циклы вычислений. Примеры использования функций суммирования:
Sum[i^2,{i,10}]
385
Sum[i*2,{i,l,10}]
385
Sum[i^2, {1,1,2,0.25}]
11.875
Sum[i*j, {i,1,10},{j, 2, 5}]
770
В последнем примере использована стандартная форма вывода — при ней функция суммирования представляется в виде оператора суммирования.
Обычно в математических системах недопустима перестановка imin и imax, хотя в математике известно школьное правило — от перестановки слагаемых сумма не изменяется. Рискнем проверить это:
Sum[i,{i, 1,100}]
5050
Sum[i, {1,100,1}]
0
Sum[i, {1,100, 1,-1}]
5050
Второй пример тут дал явно ошибочный результат, хотя третий с честью оправдал указанное правило.
Не применяйте установки параметров, противоречащие синтаксису записи той или иной функции — в частности, Sum. Это чревато возникновением серьезных ошибок.
Приведем еще ряд примеров выполнения операции суммирования:
Sum[ xn/n! , {n, 0, 8}]
1+X+X2/2 X3/6 X4/24 X5/120 X6/720 X7/5040 X8/40320
Sum[xn/n! , {n, 1, 9, 2}]
X+X3/3 X5/120 X7/5040 X9/362880
Sum[xi yi , {i, 1, 4},{j, 1, i}]
xy+ x2 у + x3 у + x4 у + x2:/2 + x3 у2 + x4y2 + x3 у3 + x4 у3 + x4y4
Sum[1/n*n , {n, 1, бесконечность}]
л2/6
Sum[i4 {i, 1, n}]
1/30n(1-n)(1+2n) (-l + 3n+3n2)
1/3(3 - 3 EulerGamma + 2 n + n3) - PolyGamma[0, 2 + n]
Из этих примеров видно, что Mathematica 3/4 обеспечивает возможность символьного вычисления сумм, в том числе с бесконечным пределом суммирования. Вычисляются даже суммы, выраженные через специальные математические функции (см. последний пример). При этом для вычисления сумм в символьном виде, в отличие от предшествующих версий Mathematica, уже не требуется загрузка специального пакета для расширенных (символьных) операций с суммами.
Вычисление сумм в численном виде
Для вычисления сумм в численном виде используются следующие функции:
- NSum[f, {i, imin, imax }]— возвращает численное значение суммы f [ i ] при i, изменяющемся от imin до imax с шагом +1;
- NSumff, {i, imin, imax, di }]— возвращает сумму численных значений функции f [i] при i, изменяющемся от imin до imax с шагом di;
- NSum[f, {i, imin, imax}, {j, jmin, j max },...]— выполняет многомерное суммирование. Функция NSum[... ] эквивалентна выражению N[Sum[...] ].
Особенностью этой функции является возможность использования ряда опций, управляющих вычислительным процессом. Одной из них является NSumTerms, задающая число членов, которые явно должны быть включены в сумму перед экстраполяцией. Вы можете просмотреть список опций, используя команду Options [NSum] .
Пример применения функции NSum представлен ниже:
NSum[1/i3, {i, 1, бесконечность}]
1.20206
Пример точного вычисления суммы (для сравнения) с помощью функции Sum:
truesum = Sum [1+k/ 2k k/ 3k{k, 1, 50}
1818632874295681087853745424762603034467 / 808281277464764060643139600456536293376
N[%]
2.25
Пример вычисления той же суммы с помощью функции NSum с опциями:
NSum [ 1+k/ 2 k -3k, {k, 1, 50}, Method -> SequenceLimit,
NSumTerms -> 2 , NSumExtraTerms -> 4 ] - truesum
0.0530365
При следующем наборе опций результат еще лучше:
NSum [ 1+k/ 2 k -3k, {k, 1, 50}, Method -> SequenceLimit, WorkingPrecision -> 30 , NSumTerms -> 2 ,
NSumExtraTerms -> 10, WynnDegree -> 4] - truesum
0.x10-26
Функция вычисления суммы NSum выполняется заметно быстрее, чем функция Sum, хотя на практике заметить это трудно — все приведенные выше примеры выполняются за доли секунды. Возвращаемый функцией NSum результат вещественный.
3. Вычисление произведений
Вычисление произведений
Вычисление произведений в аналитическом виде
Операции вычисления произведений
Произведение от i=imin до i=imax по fi представлены следующими функциями:
- Product [f, {i, imax}] — возвращает произведения значений f [i] для значений i, изменяющихся от 1 до imax;
- Product [f, {i, imin, imax}]—возвращает произведение значений f [ i ] при изменении i от imin до imax с шагом +1;
- Product[f, {i, imin, imax, di}] — возвращает произведение f [ i ] при i, меняющемся от значения imin до значения imax с шагом di;
- Product [f, {i, imin, imax}, {j, jmin, jmax},...] — вычисляет многократное произведение (произведение по нескольким переменным).
Примеры использования функций вычисления произведения.
| Ввод (In) | Вывод (Out) |
| Product [i,{i ,10}] | 3628800 |
| NProduct [k ^ 2,{k, 1,5}] | 14400. |
| NProduct[i ^ 2, {1,1,2,0. 2}] | 93.6405 |
| Product [Logfi], {±,2,5,0.5}] | 4.23201 Log[2] |
Следующий пример иллюстрирует вычисление произведения в символьном виде:
Произведение (x+i2) , где i=1...5
(1+х) (4 + х) (9 + х) (16 + х) (25 + х)
Об опасности перестановки сомножителей свидетельствуют следующие примеры: Product [i, i,l, 10] 3628800
Product [i,i, 10,1]
1
Product[i,i,10,l,-l]
3628800
Как и в случае вычисления суммы, средний пример явно ошибочен. Он просто недопустим с точки зрения синтаксиса данной функции.
Вычисление произведений в численном виде
Для вычисления численных значений произведения используются следующие функции:
- NProduct [f , {i, imax }]— возвращает численное значение произведения значений f [i] для значений i, изменяющихся от 1 до imax;
- NProduct [f, {i, imin, imax}] — возвращает численное значение произведения значений f [i] при изменении i от imin до imax с шагом +1;
- NProduct [f, {i, imin, imax, di }]— возвращает численное значение произведения значений f [i] при i, меняющемся от значения imin до значения imax с шагом di;
- NProduct[f, {i, imin, imax}, {j, jmin, j max },...]— вычисляет численное значение многократного произведения (произведение по нескольким переменным).
Эти функции применяются с теми же опциями, которые используются для функции Nsum, что позволяет управлять вычислительным процессом. Ознакомиться с опциями можно, выполнив команду Options [NProduct] . Ниже представлен пример на использование функции Nproduct. Сначала вычисляем точное значение произведения для использования в качестве эталона:
trueproduct = Product [ j/(1+j), { j , 1 , 50 } ]
1/ 51
Пример вычисления того же произведения с помощью функции NProduct — погрешность велика:
NProduct [ j/(1+j) , {j, I, 50},
Method -> SequenceLimit, NProductFactors -> 2 ,
NProductExtraFactors -> 4] - trueproduct
0.188235
В следующем примере опции подобраны лучше — погрешность мала:
NProduct[j/(1+j) , {j, 1, 50},
Method-» SequenceLimit, NProductFactors -> 50,
NProductExtraFactors ->4] - trueproduct
-1.38778 x 10-17
Применение функции NProduct оправдано высокой скоростью производимых ею вычислений. Однако, как показывают приведенные примеры, к такому применению надо относиться с осторожностью из-за возможности возникновения больших вычислительных погрешностей.
4. Вычисление производных
Вычисление производных
К числу наиболее часто используемых математических операций принадлежит вычисление производных функций как в аналитической, так и в символьной форме. Для этого используются следующие функции:
- D [ f, х ] — возвращает частную производную функции f по переменной х;
- D [f, {х, n}]— возвращает частную производную n-го порядка по х;
- D[f, xl, х2,...] — возвращает смешанную производную;
- Dt[f, х] — возвращает обобщенную производную функции f по переменной х;
- Dt [ f ] — возвращает полный дифференциал f.
Название функции из одной буквы — это явно исключение из правил. Оно выбрано осознанно, в силу массовости этой операции.
Для функции D существует опция NonConstants, которая позволяет задать список объектов, находящихся в неявной зависимости от переменных дифференцирования. По умолчанию этот список пустой. Для функции Dt имеется опция Constants, которая, наоборот, указывает символы, которые являются константами (по умолчанию их список также пуст). На практике применять данные опции приходится редко.
Существует еще одна функция, Derivative [nl, n2,...] [f ], — основная (общая) форма представления функции, полученной в результате nl-кратного дифференцирования функции f по первому аргументу, п2-кратного — по второму аргументу и т. д.
К примеру, Derivative [2] [х*у] возвращает (ху)", a Derivative [2, 3] [х*у] — соответственно, (ху) (2.3)
Следующие примеры показывают применение функции D для вычисления производной в аналитическом виде:
- Производная тригонометрической функции:
D[x*Sin[x],x]
xCos[x] + Sin[x]
- Производная экспоненциальной функции:
D[Exp[x/b],x]
ex/b/b
- Производная логарифмической функции:
D[Log[3*x/4],x]
1/x
- Производная степенного многочлена:
D[а*х^2+b*х+с,х]
b+ 2ах
- Пятая производная от х n :
D[х^n,{х,5}]
(-4 + n) (-3+n) (-2+n) (-1+n)nх -5+n
- Производная функции двух переменных:
D[(x^m)*y^n,x,y]
mnx -1+m y -1+n
- Производная функции Бесселя:
D[BesselJ[2,x] ,x]
1/2 (BesselJ[l, х] -BesselJ[3, x] )
- Производная ортогонального полинома Чебышева:
D[ChebyshevT[4,x],x]
-16x + 32x3
Следующие примеры иллюстрируют вычисление производных от первого до третьего порядка включительно для функции f [ х ], заданной пользователем.
| Ввод (In) | Вывод (Out) |
| f[x] :=х/(1+х ^ 2) | |
| D[f[x],{x,l}] | -2x 2 /(1+x 2 ) 2 +1/(1+x 2 ) |
| D[%,x] | -8x 3 /(1+x 2 ) 3 +6x/(1+x 2 ) 2 |
| D[f[x],{x,2}] | -8x 3 /(1+x 2 ) 3 +6x/(1+x 2 ) 2 |
| D[D[D[f[x],x],x],x] | -48x 4 /(1+x 2 ) 4 +48x 2 /(1+x 2 ) 3-6/(1+x 2 ) 2 |
| D[f[x],{x,3}] | -48x 4 /(1+x 2 ) 4 +48x 2 /(1+x 2 ) 3-6/(1+x 2 ) 2 |
Из предпоследнего примера видно, что для вычисления высших производных возможно последовательное применение функции D.
На рис. 4.1 показано построение графика функции Sin [x] /х, заданной как функция пользователя, и ее производной с помощью функции Plot.
Рис. 4.1. График функции Sin[x]/x и ее производной
В целом средства для символьного вычисления производных, имеющиеся в ядре системы Mathematica, охватывают практически все важные типы математических выражений. Они могут включать в себя как элементарные, так и специальные математические функции, что выгодно отличает систему Mathematica от некоторых простых систем символьной математики, таких как Derive.
Использование функции Dt демонстрируют примеры, приведенные ниже.
| Ввод (In) | Вывод (Out) |
| Dt[x*n,x] | x n (n/x +Dt[n, x] Log[x] ) |
| Dt[x*Sin[x] ,x] | xCos[x] + Sin[x] |
| Dt[Exp[x/b],x] | e x/b /b(1/b-xDt[b, x]/b 2 ) |
| Dt[a*x ^ 2+b*x+c,x] | b+ 2 ax + x 2 Dt[a, x] + xDt[b, x] + Dt[c, x] |
| Dt[x*n,{x,2}] | x n (n/x+Dt[n, x] Log[x] ) + x n (-n/x 2 2Dt[n, x] +Dt[n, {x/2}]Log[x]) |
| Dt[Log[3*x/4],x] | 1/x |
| Dt[BesselJ[2,x] ,x] | 1/2(BesselJ[l, x] -BesselJ[3, x] ) |
| Dt[ChebyshevT[4,x] ,x] | -16x + 32x 3 |
Обратите внимание на то, что порой результаты для одного и того же дифференцируемого выражения у функций D и Dt заметно различаются. Это вполне закономерно вытекает из различных определений данных функций.
gl4-1.jpg
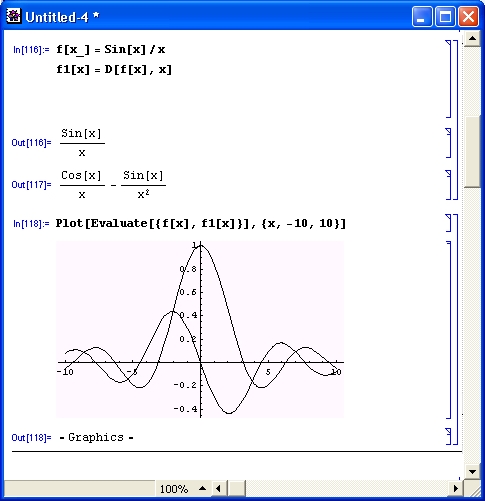
5. Вычисление интегралов
Вычисление интегралов
Вычисление интегралов в символьном виде
Одна из важнейших операций — вычисление первообразных и определенных интегралов в символьном виде. Первообразная — это функция F(x), удовлетворяющая уравнению
f(x)dx = F(x) + C,
где С — постоянная интегрирования. А вычисление определенного интеграла с пределами — верхним b и нижним а — производится по формуле
f(X)dX = F(b)-F(a)
Заметим, что определенный интеграл может быть представлен как аналитическим, так « численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов — от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).
Для интегрирования в системе Mathematica используются следующие функции:
- Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х;
- Integrate [f, {x, xmin, xmax}] — возвращает значение определенного интеграла с пределами от x min до x max ;
- Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},...] —возвращает значение кратного интеграла с пределами от x min до x max по переменной х, от y min до y max по переменной у и т. д. (кратность реально не ограничена).
Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции:
Options[Integrate]
{Assumptions -> {}, GenerateConditions->Automatic,
PrincipalValue > False)
Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком «минус». Пределы могут задаваться как константами, так и функциями.
Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде. Это иллюстрируют примеры на вычисление неопределенных интегралов с алгебраическими подынтегральными функциями, представленные на рис. 4.2.
Здесь входная ячейка в первом примере представлена в формате ввода (Input-Form), а в остальных примерах — в стандартном формате (StandardForm). При записи интегралов последний предпочтителен ввиду большей наглядности, поскольку при этом знаки интеграла имеют естественный математический вид. Обратите внимание на проверку операции интегрирования с помощью дифференцирования в двух последних примерах.
На рис. 4.3 показано еще несколько примеров вычисления неопределенных интегралов. Нетрудно заметить, что интегралы от ряда алгебраических функций дают выражения с тригонометрическими функциями.
Другая группа примеров, представленная на рис. 4.4, показывает нахождение интегралов с тригонометрическими и гиперболическими подынтегральными функциями.
Последний пример показывает, что возможно вычисление списка определенных интегралов, если подынтегральные функции представлены также в виде списка.
Рис. 4.2. Примеры вычисления неопределенных интегралов (начало)
Рис. 4.3. Примеры вычисления неопределенных интегралов (продолжение)
Рис. 4.4. Примеры вычисления неопределенных интегралов (окончание)
Вычисление определенных интегралов
Следующая серия примеров (рис. 4.5) иллюстрирует вычисление определенных интегралов в символьном виде.
Рис. 4.5. Примеры вычисления определенных интегралов обычного вида
Приведенные на рис. 4.6 примеры показывают вычисление определенных интегралов с пределами-функциями.
Рис. 4.6. Примеры вычисления определенных интегралов с пределами-функциями
Системы Mathematica имеют самые обширные возможности вычисления интегралов. Ядро системы вобрало в себя формулы интегрирования из всех известных справочников и даже древних рукописей.
Mathematica способна вычислять даже кратные интегралы с фиксированными и переменными верхним или нижним пределами. Кратный, например двойной, интеграл с фиксированными пределами имеет вид:
f(x,y)dxdy
На рис. 4.7 представлено вычисление нескольких двойных определенных интегралов.
Рис. 4.7. Примеры вычисления двойных определенных интегралов
Следующий пример при двух форматах ввода показывает вычисление двойного неопределенного интеграла двойным применением функции Integrate:
Integrate!Integrate[x^3+y^3,x],y]
x4y/4+y4x/4
(
(x3 + y3) dx) dy
x4y/4+y4x/4
Другая серия примеров (рис. 4.8) показывает, как вычисляются двойные и тройные интегралы, пределы которых сами по себе являются функциями.
Рис. 4.8. Примеры вычисления кратных интегралов с пределами-функциями
Хотя вычисление двойного интеграла предусмотрено в синтаксисе функции Integrate, это не всегда дает результат. Как правило, вычисление кратных интегралов лучше производить, используя последовательное вычисление однократных интегралов, вложенных друг в друга. Это и показывают приведенные примеры.
Особые случаи вычисления интегралов
При вычислении сложных интегралов, например не имеющих представления через элементарные функции, система Mathematica 2 обращалась к своим пакетам расширений в попытке найти решение, которое может быть представлено через специальные математические функции. Mathematica 3/4 уже не акцентирует внимание пользователя на своих проблемах и, как правило, выдает результат интегрирования. Однако порой он может иметь довольно необычный вид (рис. 4.9).
Эти примеры наглядно показывают, что вычисление первообразных в системе может дать результаты, далекие от тривиального вычисления неопределенных интегралов, имеющихся в обычных справочниках по математике. Кстати, и при вычислении тривиальных интегралов результат может оказаться иным, чем в справочниках, из-за различных преобразований, примененных для получения конечных формул. Подчас могут потребоваться определенные усилия для получения результата в заданной форме. Как подынтегральное выражение, так и результаты вычислений могут содержать как элементарные, так и специальные математические функции.
Рис. 4.9. Примеры вычисления особых интегралов
В заключение надо отметить, что результаты символьного интегрирования в системах Mathematica 3 и Mathematica 4 нередко различаются. Более того, они могут различаться и в пределах одной версии Mathematica, так как ядро системы постоянно совершенствуется. Обычно более поздние версии дают более точные результаты вычислений особых интегралов, хотя подчас они и выглядят более сложными и даже необычными. Это говорит о необходимости вдумчиво относиться к получаемым результатам.
Для вычисления численных значений определенных интегралов используется функция NIntegrate [f, {x, xmin, xmax}], которая возвращает численное приближение интеграла от функции f по переменной х в пределах от x min до x max .
Она имеет ряд опций, которые можно получить, исполнив команду Options [Nlnteg-rate]. Описание этих опций дано в приложении. Приведем примеры численного интегрирования.
| Ввод (In) | Вывод (Out) |
| NIntegrate [Bessel J [l,x] ^ 3,{x,0,l}] | 0.0243409 |
| N[Sqrt [Pi] *Gamma [1/6] / (6*Gamma [2/3] ) ] | 1.21433 |
| NIntegrate [1/Sqrt [1-х^6] , {х , 0 , 1 } ] | 1.21433 |
| NIntegrate [E ^ -x*Cos [х] , {х, 0 , Infinity} ] | 0.5 |
| NIntegrate [х*у, {х,0,1} , {у,х,х ^ 2} , {z,x*y,x ^ 2*y ^ 3}] | 0.010582 |
| NIntegrate [l/(x*y) , {х,4,4 .4} , {у, 2, 2. 6}] | 0.025006 |
| NIntegrate [Sqrt[2*x+l] ,{x,0,l}] | 1.39872 |
Эти примеры показывают, что функция NIntegrate с успехом может применяться для вычисления как однократных, так и многократных определенных интегралов, в том числе с переменными пределами.
gl4-2.jpg

gl4-3.jpg

gl4-4.jpg

gl4-5.jpg

gl4-6.jpg
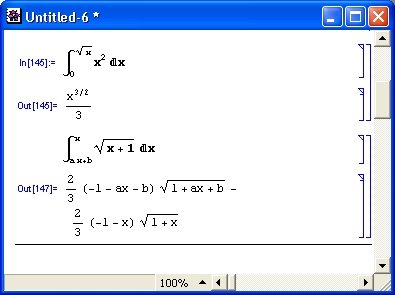
gl4-7.jpg
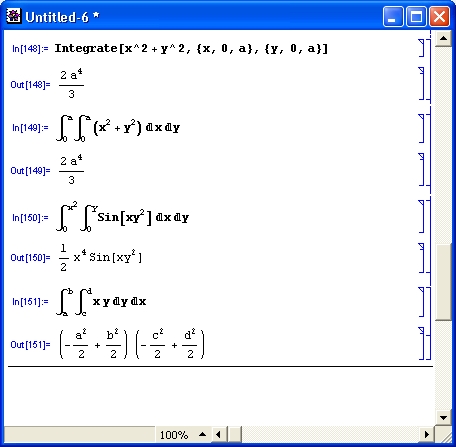
gl4-8.jpg
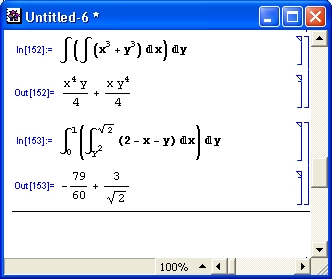
gl4-9.jpg
6. Вычисление пределов функций
Вычисление пределов функций
Многие функции при приближении аргумента к некоторому значению или к некоторой области значений стремятся к определенному пределу. Так, функция sin(x)/x при х, стремящемся к нулю (обозначим это как х—> 0), дает предел 1 в виде устранимой неопределенности 0/0.
Численные математические системы, равно как и большинство программ на обычных языках программирования, не воспринимают выражение 0/0 —> 1 как объективную реальность. Их защитный механизм настроен на примитивное правило — ничего нельзя делить на 0. Следовательно, вычисление sin(x)/x при х = 0 будет сопровождаться выдачей ошибки типа «Деление на 0». Конечно, в данном конкретном случае можно предусмотреть особый результат — выдать 1 при х = 0. Но это частный случай. В целом же подобные системы «не понимают» понятия предела.
Пределом некоторых функций может быть бесконечность, тогда как многие функции стремятся к конечному пределу при аргументе х, стремящемся к бесконечности. Система Mathematica не только численно находит пределы функций, заданных аналитически, но и позволяет найти предел в виде математического выражения.
На рис. 4.10 представлены примеры применения функции Limit. Они показывают, что возможно вычисление пределов функций, устремляющихся к бесконечности, и вычисление пределов при переменной х, стремящейся в бесконечность. Вычисление пределов функций в аналитическом виде — важное достоинство систем символьной математики.
Рис. 4.10. Примеры вычисления пределов
При работе с функцией Limit используются следующие опции:
- Analytic — указывает, следует ли неопознанные функции интерпретировать как аналитические (значение по умолчанию — Automatic);
- Direction — указывает направление, в котором происходит приближение к пределу. Опция используется в виде Direction -> -1 (или +1), по умолчанию выбор остается за системой (Automatic). Значение +1 означает предел слева, а -1 — справа (казалось бы, должно быть наоборот, но задано именно так).
Применение данных опций поясняют примеры, показанные на рис. 4.11.
Рис. 4.11. Примеры вычисления пределов с применением опций
gl4-10.jpg
gl4-11.jpg
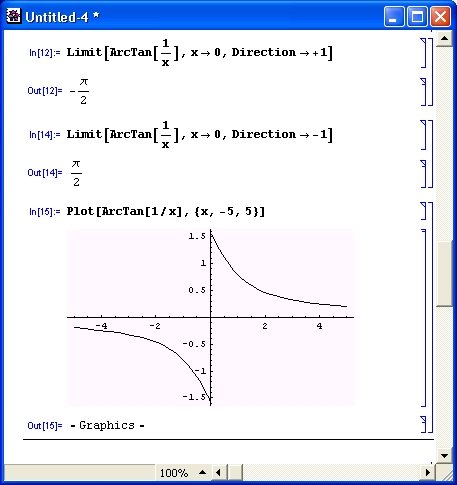
7. Уравнения и системы уравнений
Уравнения и системы уравнений
Многие математические задачи сводятся к решению в общем случае нелинейных уравнений вида f(x) = 0 или f(x) = expr.
В системе Mathematica они обозначаются как eqns (от слова equations — уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений.
Для решения уравнений (как одиночных, так и систем) в численном и символьном виде Mathematica имеет функцию Solve:
- Solve [eqns, vars] — предпринимает попытку решить уравнение или систему уравнений eqns относительно переменных vars;
- Solve [eqns, vars, elims] — пытается решать уравнения eqns по переменным vars, исключая переменные elims.
Входные параметры этой функции могут быть представлены списками или записаны выражениями через объединительный знак«&&». В eqns в качестве знака равенства используется знак «= =». Примеры применения функции Solve представлены на рис. 4.12.
Рис. 4.12. Примеры решения уравнений
Обратите внимание на то, что в определенных ситуациях система подсказывает тонкости решения, выдавая предупреждающие сообщения. Если такие ситуации не являются ошибками, препятствующими решению, то полученное решение выводится в ячейку вывода.
Решение систем нелинейных уравнений в символьном виде
Приведенные на рис. 4.13 примеры показывают решение систем нелинейных уравнений с помощью функции Solve.
Достаточно характерен пример с применением функции N. Если убрать в нем функцию N, то будет получен чрезвычайно громоздкий, хотя и точный результат (проверьте это сами, поскольку размеры результата делают нецелесообразным его приведение в книге). Функция N осуществляет выполнение всех промежуточных вычислений, благодаря чему результат получается вполне обозримым и представленным в комплексных числах.
В последнем примере рис. 4.13 получен набор из пяти пар корней, определенных через функцию Root. Эта функция, в свою очередь, означает вычисление корней полиномиального уравнения пятой степени. Данный пример, как и ранее приводимые решения кубического уравнения, является наглядной иллюстрацией того, что простота нелинейных уравнений порой оказывается весьма обманчивой, а их решение порой приводит к весьма громоздким и сложным результатам. Тем не менее, возможность решения отдельных нелинейных уравнений и их систем в символьном виде трудно переоценить. К сожалению, далеко не все уравнения имеют такие решения — многие можно решать только в численном виде.
Рис. 4.13. Примеры решения систем нелинейных уравнений
Не следует полагать, что Mathematica всегда выдает верное решение систем нелинейных уравнений. На самом деле решение иногда бывает ошибочным. Поэтому в большинстве случаев стоит оформлять решение таким образом, чтобы обеспечить его проверку. Для этого рекомендуется отдельно задать систему уравнений и результат решения. Тогда проверка легко осуществляется с помощью подстановки. Два примера решения систем уравнений с проверкой решений показаны на рис. 4.14.
В первом примере решение кажется очевидным (равенства выполняются, например, при х=2 и у=3). Однако здесь Mathematica дает сразу три пары решений, и все они оказываются верны, поскольку после подстановки проверка всех равенств возвращает True.
А вот во втором примере проверка дала не совсем обычный результат, что связано с наличием в решении неопределенной переменной а. В таких случаях стоит попробовать упростить решение с помощью функции Simplify, что и показано на рис. 4.14.
Рис. 4.14. Примеры решения уравнений с проверкой
С функцией Solve можно использовать ряд опций. Их можно вывести командой Options [Solve]. Ниже описано их назначение:
- InverseFunctions — указывает, следует ли использовать обратные функции;
- MakeRules — указывает, должен ли результат быть представлен как объект AlgebraicRulesData;
- Method — устанавливает алгоритм, используемый для вычисления результата (возможны методы 1, 2 и 3);
- Mode — задает характер решения уравнения (возможны Generic, Modular и Rational);
- Sort — устанавливает, нужна ли сортировка результатов;
- Verif ySolutions — устанавливает, следует ли проводить проверку полученных решений и удаление посторонних решений;
- WorkingPrecision — устанавливает число цифр промежуточных вычислений (по умолчанию Infinity).
На рис. 4.15 приведены примеры применения функции Solve с опцией Inverse-Functions.
Обратите внимание на то, что последняя система уравнений при отсутствии опции InverseFunctions решается с предупреждением. Она вообще не решается, если эта опция задана как False, и гладко решается при InverseFunctions -> True.
Рис. 4.15. Примеры решения уравнений с опцией InverseFunction
То, насколько может влиять на решение опция Method, наглядно показывают примеры, представленные на рис. 4.16.
Рис. 4.16. Примеры решения уравнений разными методами
Множество примеров решения систем нелинейных уравнений в символьном виде можно найти в справочной системе Mathematica.
Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако их решение вполне возможно численными методами. Для численного решения систем нелинейных уравнений используется функция NSolve:
- NSolve [eqns, vars] — пытается численно решить одно уравнение или систему уравнений eqns относительно переменных vars;
- NSolve [eqns, vars, elims] — пытается численно решить уравнения eqns относительно vars, исключая переменные elims.
С этой функцией используется единственная опция WorkingPrecision, задающая число верных цифр результата — по умолчанию 16. На рис. 4.17 представлены примеры использования функции NSolve для численного решения уравнений.
Риc. 4.17. Примеры численного решения уравнений
Результаты решения с помощью функции NSolve также рекомендуется проверять с помощью подстановки, например, так:
е=2*х^2 + 5*х- 15 == х^3
-15 + 5х + 2х2 ==х3
r=NSolve[e,x]
{{х->-2.4734}, {х->2.2367-1.03038i},
{х->2.2367 + 1.03038i}}
е/.r
{True, True, True}
Нетрудно заметить, что в данном случае решение верно.
Для вычисления корней полиномиальных уравнений используется функция Roots:
Roots[lhs==rhs, var]
На рис. 4.18 представлены примеры применения функции Roots.
Рис. 4.18. Примеры использования функции Roots
Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:
e = x^2+3x==2
Зх + х2 == 2
N[Roots[e, x]]
х == -3.56155 | | х == 0.561553
r= {ToRules[%]}
{{х^-3.56155}, {х^ 0.561553}}
е/. r
{True, True}
Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.
При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:
Options[Roots]
{Cubics -> True, Eliminate -> False, EquatedTo-> Null,
Modulus -> 0, Multiplicity->1, Quar tics -> True, Using -> True}
Ниже они описаны подробно:
- Cubics — указывает, следует ли искать явные решения для неприводимых кубических уравнений;
- EquatedTo — задает выражение для замещения переменной в решении;
- Modulus — задает промежуточную факторизацию полинома;
- Multiplicity— устанавливает кратность каждого из корней в конечном результате;
- Quartics — задает точное решение квадратного уравнения и полинома четвертой степени;
- Using — указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.
Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.
Дополнительные функции для решения уравнений
Имеется также ряд дополнительных функций, которые используются описанными ранее функциями и также могут применяться при решении нелинейных уравнений:
- Auxiliary [v] — применяется модулем Solve для указания того, что переменная v должна использоваться функцией Roots для результирующих решений, но соответствующие значения v не должны быть включены в окончательный ответ;
- Eliminate [eqns, vars] — исключает переменные vars из системы уравнений eqns;
- FindRoot [Ihs == rhs, {x, x0}] — ищет численное решение уравнения Ihs == rhs, начиная с х = x0;
- MainSolve [eqns] — основная функция для преобразования системы уравнений. Ее вызывают Solve и Eliminate. Уравнения должны быть представлены в форме Ihs == rhs. Они могут объединяться с помощью && и | |. MainSolve возвращает False, если не существует решения уравнений, и возвращает True, если все значения переменных являются решениями. MainSolve перестраивает уравнения, применяя определенные директивы;
- MainSolve [eqns, vars, elim, rest] — пытается перестраивать уравнения eqns так, чтобы найти решения для переменных vars и исключить переменные elim. Список rest может включаться для указания порядка исключения любых остальных переменных;
- NRoots [lhs==rhs, var] — возвращает список численных приближений корней полиномиального уравнения;
- Residue [ехрr, {х, х0 } ] — ищет вычет ехрг в точке х = х0;
- SolveAlways [eqns, vars] — возвращает значения параметров, которые превращают уравнения eqns в тождества для всех значений переменных vars.
Примеры использования некоторых из этих функций показаны на рис. 4.19.
Рис. 4.19. Примеры применения дополнительных функций для решения уравнений
В целом надо отметить, что система Mathematica обладает обширными средствами для решения уравнений и их систем. Умение их применять — залог правильного и эффективного решения сложных математических задач, относящихся к классу решения уравнений.
Графическая иллюстрация и выбор метода решения уравнений
При рассмотрении приведенных выше примеров может сложиться благодушное впечатление о том, что решение нелинейных уравнений может производиться автоматически и без размышлений. Но это далеко не так — представленные выше примеры просто подобраны так, что они имеют решение с помощью соответствующих функций.
На самом деле порой даже простые уравнения могут не иметь решения. В сложных случаях очень полезна графическая визуализация решения. В качестве примера на рис. 4.20 показана визуализация вычисления корней квадратного уравнения. В данном случае график функции явно указывает на существование двух действительных корней при х, близких к 0.2 и 2.3. Функция Nsolve без труда находит оба корня.
Рис. 4.20. Визуализация решения квадратного уравнения для случая двух действительных корней
А вот на рис. 4.21 показан случай, когда из-за изменения последнего члена квадратичной функции ее график уже не пересекает ось х вообще. Это говорит о том, что решения в виде действительных корней нет. И в самом деле, NSolve находит корни как комплексно-сопряженные числа. Действительная часть найденных корней дает координату х для впадины кривой — параболы.
Если требуется решение равенства f1(х) = f 2 (x), то для графической визуализации решения можно построить графики функций f1(х) и f 2 (лг) — наличие точек их пересечения будет означать существование действительных корней. Этот случай иллюстрирует рис. 4.22. В данном случае проблем с решением нет, поскольку, по существу, решается квадратное уравнение.
Рис. 4.21. Визуализация решения квадратного уравнения для случая двух комплексных корней
Рис. 4.22. Пример визуализации решения уравнения вида f(x) = 5х + 1
Но вот на рис. 4.23 показан случай решения уравнения f(x) = ехр(х/2). Графики функций ясно показывают, что парабола пересекается экспонентой в двух точках. Однако функция NSolve отказывается решать такое уравнение и выдает сообщение о том, что оно является трансцендентным.
Таким образом, в данном случае наличие графического решения говорит о необходимости смены функции, с помощью которой до сих пор решались уравнения. Подходящей в данном случае является функция FindRoot, которая отыскивает одно решение вблизи заданной начальной точки. Применив ее дважды, нетрудно получить оба корня данного уравнения.
Рис. 4.23. Пример решения уравнения вида f(x) = ехр(х/2)
Приведенные примеры далеко не исчерпывают проблему графической визуализации решения и выбора методов решения. Однако они иллюстрируют возможности системы Mathematica в этой области и заостряют внимание на потенциальных проблемах. Для реализации численных расчетов в системе Mathematica отобраны наилучшие и наиболее эффективные численные методы из описанных в литературе, в том числе в отечественной.
Получение сразу нескольких корней
Многие уравнения с тригонометрическими функциями могут иметь периодические или близкие к ним решения. К сожалению, функции Mathematica, вычисляющие корни уравнений, не способны в этом случае дать сразу несколько корней. Однако ситуация тут далеко не безнадежна — приведенный ниже пример наглядно показывает это.
Пусть требуется в интервале изменения х от 0 до 20 найти все решения уравнения
х sin(x) + х/2 - 1 = 0
График функции, представляющей левую часть уравнения, показан на рис. 4.24. Хорошо видно, что он пересекает ось х семь раз, то есть имеет в интересующем нас диапазоне семь корней.
Рис. 4.24. График функции х sin(x) + х/2 - 1 и пример вычисления всех ее корней в интервале изменения х от 0 до 20
Колебательная составляющая функции обусловлена входящей в нее функцией sin(x), которая имеет нули в точках 0, n, 2n, Зn... Однако, как видно из рис. 4.24, эти значения лишь приближенные, ввиду влияния других членов уравнения.
Ключевая идея получения всех корней уравнения заключается в поиске нужных решений с помощью функции FindRoot, которой последовательно подставляются различные начальные приближения. Однако вместо уже испытанного приема — поиска корней поодиночке — можно воспользоваться «таблицей» решений, используя функцию Table. Решение, приведенное под графиком функции на рис. 4.24, наглядно иллюстрирует возможности этого приема — найдены (или, вернее, уточнены) все семь корней исходного уравнения.
Получение неизвестных в явном виде
Читатель, возможно, обратил внимание на то, что решения всех представленных выше примеров выглядят не совсем обычно — в виде списка подстановок. Это не позволяет использовать неизвестные в явном виде, например, для проверки решений или передачи найденных неизвестных в последующие вычислительные блоки. Однако от этого затруднения легко избавиться, если перед конструкций блока решения использовать выражение следующего вида:
{х,у,z,...}/.
Список переменных в этом выражении должен однозначно соответствовать списку неизвестных системы уравнений. Покажем этот прием в действии. Ниже приведено решение системы из трех нелинейных уравнений:
FindRoot[{x-2==9,y^2=16,x+y+z==10},{x,l.},{y,l.},{z,l.}]
(Х-> 3., у-> 4., z->3.} {x,y,z}
{X, у, 2}
Обратите внимание на то, что вывод списка {х, у, z } не дает полученных значений неизвестных. Это связано с тем, что переменные в блоке решения имеют ло-к(1лъный характер и за пределами блока их значения (в том числе неопределенные) сохранятся такими, какими они были до применения в блоке решения.
Теперь зададим решение в ином виде:
{x,y,z}/.FindRoot[{x*2==9, уА2==1б, x+y+z==10}, {x,l.}, {у,1.}, {z,l.}]
{3., 4., 3.}
Как видите, на сей раз решение получено в виде списка с числами — явными значениями неизвестных. Можно обозначить их как а, Ь и с, получить список {а, b, с} и даже использовать их отдельно:
{а,b,с}=%
(З.,4.,3.)
а,b,с
{З.,4.,3.}
а
3.
b
4.
с
3.
Теперь можно проверить решение данной системы:
{а^2, b^2,а+b+с}
{9., 16., 10.}
Полученный вектор правых частей системы совпадает с заданным, что свидетельствует о правильности решения. Разумеется, вместо нового списка { а , b , с } для вектора решения можно было использовать и вектор { х, у, z } .
gl4-12.jpg
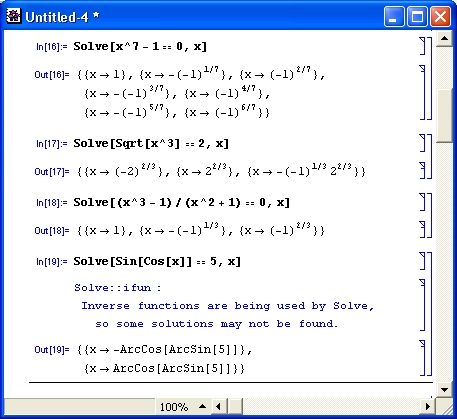
gl4-13.jpg

gl4-14.jpg

gl4-15.jpg

gl4-16.jpg
gl4-17.jpg
gl4-18.jpg
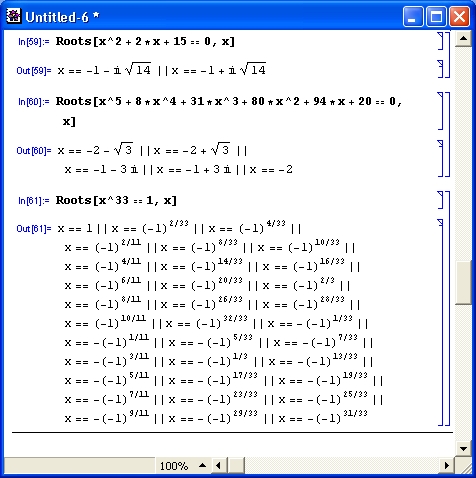
gl4-19.jpg
gl4-20.jpg
gl4-21.jpg
gl4-22.jpg
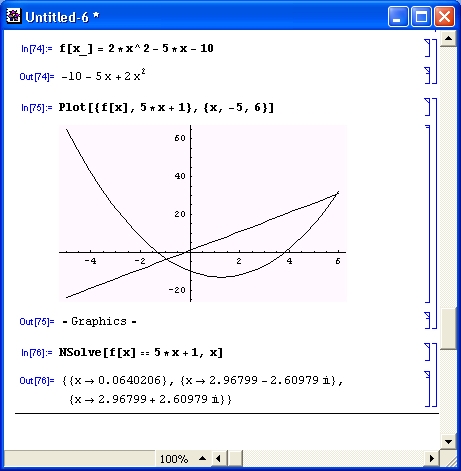
gl4-23.jpg
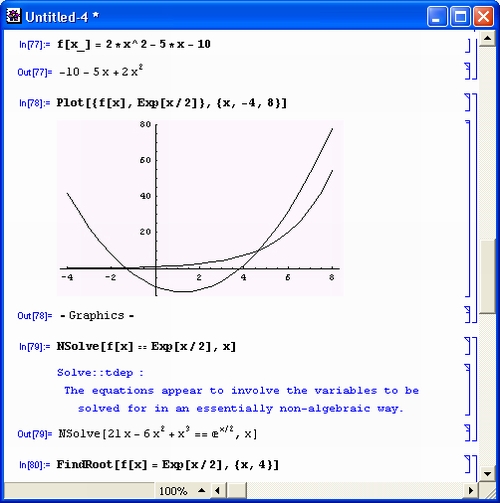
gl4-24.jpg
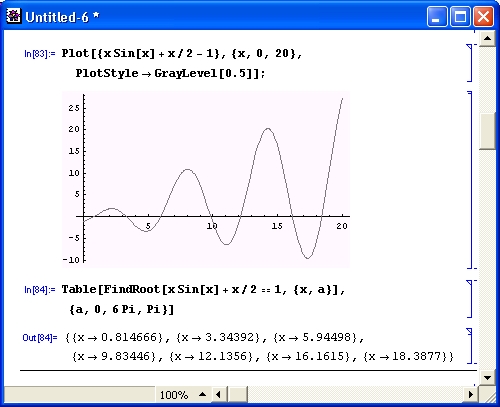
8. Дифференциальные уравнения
Дифференциальные уравнения
Решение дифференциальных уравнений в символьном виде
Дифференциальными принято называть уравнения, в состав которых входят производные функции у(х), представляющей решение уравнения. Дифференциальные уравнения могут быть представлены в различной форме, например в общеизвестной форме Коши:
у'(х) = eqn=f(x,y).
Несколько дифференциальных уравнений образуют систему дифференциальных уравнений. Решение таких систем также возможно средствами Mathematica и подробно описано в ряде книг по использованию системы [65-71]. Дифференциальные уравнения и системы дифференциальных уравнений могут быть линейными и нелинейными. Для линейных уравнений обычно существуют решения в аналитическом виде. Нелинейные дифференциальные уравнения в общем случае аналитических решений не имеют, но могут решаться приближенными численными методами.
Дифференциальные уравнения широко используются в практике математических вычислений. Они являются основой при решении задач моделирования — особенно в динамике. Немногие математические системы имеют реализации численных методов решения систем дифференциальных уравнений. Но система Mathematica имеет средства как для символьного, так и для численного решения дифференциальных уравнений и их систем.
Для решения дифференциальных уравнений в символьном виде используются следующие средства:
- DSolve[eqn, y[x], х] — решает дифференциальное уравнение относительно функций у [ х ] с независимой переменной х;
- DSolve[{eqnl, eqn2,...}, {yl [xl,...],...}, {xl,...}]-решает систему дифференциальных уравнений.
У функции DSolve и ее численного варианта NDSolve есть пара опций, на которые следует обратить внимание:
- DSolveConstants — опция к DSolve, определяющая постоянные интегрирования, которые будут использованы в результате;
- StartingStepSize — опция к NDSolve, определяющая величину начального шага.
В решении дифференциальных уравнений встречаются постоянные интегрирования. По умолчанию они обозначаются как С [ i ].
Приведем примеры решения дифференциальных уравнений:
DSolve [Derivative [1] [у] [х] ==2*а*х^3, у[х], х]
{{у[х]->aх4/2+С[1]}}
DSolve[{yl' [х] == 2 х2, у2' [х] == 3 х}, {yl[х], у2[х]}, х]
{{yl[x] ->-2х3/3+C[1], у2[х] ->3х2/2+C[2]}}
DSo2ve{y'[x] +у[х] ==х, у[х], х}
{{у[х] -*-1+х + е-хС[1]}}
DSolve [у" [х] - у' [х] - 6 у [х] == 0, у [х] , х] {{У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]}}
DSolve [у" [х] + 4 у'[х] == 10 Sin [2 х] , у [х] , х]
{{У[х] ->| е-4хС[1] + С[2] -Cos[2x] -|sin[2x]}}
DSolve[y'[x] == Sin[Ex] , y[x] , x]
{{y[x] ->C[1] +Sinlntegral[ex]}}
DSolvefz2 w"[z] +zw'[z] - (z2 + l)w[z] ==0, w[z], z]
{{w[z] ->BesselI[l, z] C[l] +BesselK[l, z] C[2] }}
Как нетрудно заметить, аналитические решения дифференциальных уравнений могут содержать не только элементарные, но и специальные математические функции, что заметно расширяет возможности применения системы Mathematica в решении задач динамического моделирования.
Решение дифференциальных уравнений в численном виде
Многие дифференциальные уравнения не имеют аналитических решений — например, нелинейные. Однако они могут с приемлемой точностью решаться численными методами. Для численного решения систем дифференциальных уравнений используется функция NDSolve:
- NDSolve [eqns, у, {x, xmin, xmax }]— ищет численное решение дифференциальных уравнений .eqns относительно функции у независимой переменной х в интервале от xmin до xmax;
- NDSolve [eqns, {yl, y2,...}, {x, xmin, xmax }]— ищет численные решения относительно функций yi.
MaxSteps — опция к NDSolve, которая определяет максимальное количество шагов.
Часто весьма желательно выводить результаты решения дифференциальных уравнений в графической форме. Рисунок 4.25 поясняет, как это делается при решении системы нелинейных дифференциальных уравнений, описывающих достаточно сложный колебательный процесс.
Нередко решение предпочитают представить на фазовой плоскости. Рисунок 4.26 иллюстрирует такую возможность. Более того, поскольку решается система из трех дифференциальных уравнений, фазовая траектория решения находится в трехмерном пространстве.
Простота задания решения и вывода его результатов в графической форме открывает широкие возможности применения системы для математического моделирования сложных явлений. При этом, в отличие от такого решения с помощью обычных языков высокого уровня (например, Фортран, Бейсик, Паскаль или С), не требуется составления каких-либо программ по реализации численных методов решения систем дифференциальных уравнений, таких как, скажем, метод Рунге— Кутта. Они представлены в виде уже готовых функций.
Рис. 4.25. Решение системы дифференциальных уравнений с выводом решения в виде графиков временных зависимостей
Рис. 4.26. Решение системы дифференциальных уравнений с выводом решения в форме кривых на фазовых плоскостях
gl4-25.jpg

gl4-26.jpg

9. Оптимизационные задачи
Оптимизационные задачи
Поиск максимального и минимального чисел в списке
В практике математических прикладных вычислений важная роль принадлежит оптимизационным задачам, например таким, как поиск минимальных и максимальных значений функций одной или нескольких переменных. Mathematica дает разнообразные возможности решения задач оптимизации — от поиска элементов списка с минимальным или максимальным значением до поиска локальных и даже глобальных минимумов функций, заданных аналитически.
Для поиска максимального и минимального значений ряда чисел, входящих в список, система Mathematica предоставляет следующие средства:
- Max [xl, х2,...]— возвращает наибольшее значение из xi;
- Max[{xl, x2,...}, {yl,...},...] — выбирает наибольший элемент из нескольких списков;
- Min[xl, x2,...] — возвращает наименьшее значение из xi;
- Min[{xl, x2,...}, {yl,...},...] — выбирает наименьший элемент из нескольких списков.
Следующие примеры показывают действие этих простых функций.
| Ввод (In) | Вывод(Out) |
| Мах[1,5,2,6.5,3,4] | 6.5 |
| Мах[{1,3,2},{4,5,6},{9,8,7}] | 9 |
| Min[1,5,2,6.5,-3,4] | -3 |
| Min[{1,3,2},{4,5,6},{9,8,7}] | 1 |
Поиск локального минимума аналитической функции
Если нужен поиск локального минимума некоторой аналитической функции, используется функция FindMinimum [ f, {х, х0 } ], которая выполняет поиск локального минимума функции f, начиная со значения х=х0, и возвращает его значение.
Для указания градиента минимизируемой функции используется опция Gradient.
Приведем примеры применения функции FindMinimum:
FindMinimum[-хЕхр[-2 х] , {х, 1}]
{-0.18394, {х^ 0.5}}
FindMinimum[-хЕхр[-2 х] , {х, 0.2, 6, 1}]
{-0.18394, {х^ 0.5}}
FindMinimum [-5 xExp[-x/2] (2 + Sin[3x]), {х, 1}]
{-7.17833, {х^ 0.783139}}
FindMinimum[-5xExp[- x/2] (2 + Sin[3 x]) , {x, 3}]
(-10.6299, {x^ 2.5805}}
FindMinimum[-5xExp[- x/2] (2+Sin[3x]), {x, 4}]
{-6.79134, {x^ 4.6179}}
FindMinimum[l00 (y-x2)2+ (1 -x)2, {x, 0}, {y, 0},
AccuracyGoal-»Automatic]
{9.90511X10-13, {x->l., y^ 0.999999}}
Эти примеры показывают, что выбирая разные начальные значения х, можно найти ряд минимумов функции f(x), разумеется, если таковые имеют место. Если необходимо разыскивать локальные максимумы, достаточно перед функцией поставить знак «минус» или умножить ее на -1.
Поиск глобального максимума и минимума аналитической функции
Следующие две функции служат для поиска глобального максимума и минимума аналитически заданной функции:
- ConstrainedMax [f, {inequalities}, {x, у,...}] — ищет глобальный максимум функции f в области, определяемой неравенствами inequalities. Полагается, что все переменные х, у... неотрицательны;
- ConstrainedMin [f, {inequalities}, {x, у,...}]— ищет глобальный минимум функции f в области, определяемой неравенствами inequalities. Все переменные х, у... полагаются неотрицательными.
Решение задач линейного программирования
Две последние функции решают типовые задачи линейного программирования. В дополнение к ним может использоваться функция
LinearProgramming[с, m, b]
которая ищет вектор х, минимизирующий величину с. х в соответствии с условиями m.x>=b и х>=0.
Рассмотрим типичный пример на линейное программирование. Пусть цех малого предприятия должен изготовить 100 изделий трех типов, причем не менее 20 штук каждого. На изготовление этих изделий уходит, соответственно, 4, 3,4 и 2 кг металла. Имеющийся в наличии запас материала — 700 кг. Спрашивается, сколько изделий xl, х2 и хЗ каждого типа надо выпустить для обеспечения максимальной стоимости продукции, если цена изделий равна, соответственно, 4, 3 и 2 рубля.
Ниже представлено решение этой задачи с помощью функции ConstrainedMax:
ConstrainedMax [
4 * xl + 3 * x2 + 2 * хЗ ,
{xl >= 20, x2 >= 20, хЗ >= 20,
4 * xl + 3 . 4 * x2 + 2 * x3 <= 340 ,
4 .75 * xl + 11 * x2 + 2 * x3 < = 700 ,
xl + x2 + x3 == 100},
{xl, x2, x3}]
{332., {xl^ 56^x2^ 20., x3^24.}}
После имени функции указывается максимизируемая целевая функция, затем перечисляются все ограничения и, наконец, задается список искомых переменных. Результатом вычислений является максимально достижимая стоимость продукции и список переменных, отражающих количество изделий каждого типа.
Задачи минимизации традиционно относятся к сложным задачам программирования — особенно при поиске глобального минимума. Наличие в ядре системы Mathematica их реализаций делает систему привлекательной для решения задач этого класса.
10. Преобразования Лапласа — LaplaceTransform
Преобразования Лапласа-LaplaceTransform
Преобразования Лапласа — важный вид интегральных преобразований. Они лежат в основе, например, символического метода расчета электрических цепей. В системе Mathematica 3 функции преобразования размещены в подпакете Laplace-Transform. Но в CKM Mathematica 4 эти функции стали встроенными.
Основными являются следующие функции этого класса:
- LaplaceTransform[expr, t, s] — возвращает результат прямого преобразования Лапласа для выражения expr [t] в виде функции переменной s;
- InverseLaplaceTransform[expr, s,t] — возвращает результат обратного преобразования Лапласа для выражения expr [s] в виде функции переменной t;
- LaplaceTransform [expr, {tl, t2,...}, {s1i, s2,...} ] — возвращает результат прямого преобразования Лапласа для выражения expr [ 11, t2,... ] в виде функции переменных {s1, s2,...};
- InverseLaplaceTransform [expr, {s1, s2,...}, {tl, t2,...} ] — возвращает результат обратного преобразования Лапласа для выражения expr [s1, s2,...] в виде функции переменных {tl, е2,...}.
Хотя имена переменных t и s можно выбирать произвольно, обычно t означает время, as — оператор Лапласа. Ниже представлено несколько примеров выполнения преобразования Лапласа:
<<Calculus'LaplaceTransfornT'
LaplaceTransform[Exp[-t]*Sin[t], t, s]
1+1/ (1 + s)2
InverseLaplaceTransform[%,s,t]
E-tSin[t]
LaplaceTransform[t^2 Exp[-x], {t,x}, {s,v}]
2/s3(1 + v)
Функции z-преобразований — ZTransform
Z-преобразования широко используются в теории автоматического регулирования. Поэтому в системе Mathematica 4 для осуществления z-преобразований в ядро включены следующие функции:
- ZTransform[expr, n, z] — возвращает результат прямого 2-преобразования для выражения ехрr, представленного как функция целочисленного аргумента n;
- InverseZTransform[expr, n, z] — возвращает результат обратного z-npeобразования для выражения ехрr, представленного как функция целочисленного аргумента п.
Приведем примеры выполнения z-преобразований:
ZTransform[Cos[n], n, z]
(1-cos(1)/z)/(1+1/z2-2Cos(1)/z)
InverseZTransform[%,s,t]
Cos[n]
ZTransform[n^2 а^n, n, z]
[-a(1+a/z)/(-1+a/z)3 z
InverseZTransf orm [%, z, n] // Together
ann2
Как и следовало ожидать, прямое, а затем обратное z-преобразование выражения ехрг восстанавливает его в исходном виде. В системе Mathematica 3 эти функции становятся доступными после исполнения команды «DiscreteMath' ZTransform' поскольку они входят не в ядро, а в пакет расширения дискретной математики.
11. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Вычислять суммы в аналитическом и численном видах.
- Вычислять произведения в аналитическом и численном видах.
- Вычислять производные.
- Вычислять интегралы в символьном и численном видах.
- Вычислять пределы функций.
- Решать в аналитическом и численном видах уравнения и системы уравнений.
- Осуществлять графическую иллюстрацию решения уравнений.
- Решать дифференциальные уравнения в символьном и численном видах.
- Искать максимальное и минимальное числа в списке.
- Искать локальный максимум и минимум аналитической функции.
- Решать задачи линейного программирования.
- Выполнять преобразования Лапласа и z-преобразования.
Урок 5. Представление и обработка данных
Урок 5. Представление и обработка данных
1. Представление и обработка данных
Представление и обработка данных
- Разложение функций в ряды Тейлора и Маклорена
- Удаление члена с остаточной погрешностью ряда
- Графическая визуализация разложения в ряд
- Прямое и обратное дискретные преобразования Фурье
- Спектральный анализ на основе преобразования Фурье
- Фильтрация сигналов на основе преобразований Фурье
- Полиномиальная интерполяция и аппроксимация
- Регрессия и визуализация ее результатов
- Спектральный анализ таблично заданных сигналов с интерполяцией
- Моделирование нелинейных цепей с применением интерполяции
Представление и обработка данных — еще один класс математических задач, имеющих явно практическую направленность. В этом уроке мы рассмотрим ряд средств решения этих задач — начиная с общеизвестного разложения аналитических функций в ряды Тейлора и Маклорена и кончая различными видами аппроксимации, интерполяции и регрессии. Будут также затронуты прикладные вопросы применения интерполяции при спектральном анализе сигналов и моделировании нелинейных электрических и электронных цепей.
2. Разложение функций в ряды
Разложение функций в ряды
Разложение функций в ряды Тейлора и Маклорена
Одна из широко распространенных математических задач представления данных — разложение заданной аналитической функции в степенной ряд Тейлора относительно некоторой узловой точки с абсциссой хО. Такой ряд нередко проще самой функции (в том смысле, что не требует вычисления даже элементарных функций и вычисляется с помощью только арифметических операций) и дает единообразное представление для разлагаемых функций в виде обычных степенных многочленов.
Большинство достаточно гладких функций, не имеющих разрывов в области р"аз-ложения, довольно точно воспроизводятся рядом Тейлора. Как правило, такие разложения достаточно просты в окрестностях узловой точки разложения.
Для разложения в ряд используются следующие функции системы Mathematical
- Series[f, {х, х0, п}]— выполняет разложение в степенной ряд функции f в окрестности точки х=х0 по степеням (х-х0) ^ n;
- Series [f, {х, х0, nх}, {у, у0, nу}] — последовательно ищет разложения в ряд сначала по переменной у, затем по х;
- SeriesCoef ficient [s,n] — возвращает коэффициент при переменной n-й степени ряда s;
- SeriesData [х, х0, {а0, al,...}, nmin, nmax, den] —представляет степенной ряд от переменной х в окрестности точки х0. Величины ai являются коэффициентами степенного ряда. Показатели степеней (х-х0) представлены величинами nmin/den, (nmin+1) /den, ..., nmax/den.
Суть разложения функции в степенной ряд хорошо видна из разложения обобщенной функции/(д:), представленного на рис. 5.1 (выходные ячейки имеют стандартный формат).
Рис. 5.1. Разложение в ряд обобщенной функции f(x)
В первом примере разложение идет относительно исходной точки х0=0, что соответствует упрощенному ряду Тейлора, часто называемому рядом Маклорена. Во втором случае разложение идет относительно исходной точки х0, отличной от нуля. Обычно такое разложение сложнее и дает большую остаточную погрешность.
В соответствии с принятой математической символикой эта погрешность обозначается как О [x] i с показателем степени, указывающим на порядок погрешности. Следует отметить, что разложение в ряд использует особый формат вывода, частью которого и является член остаточной погрешности. На рис. 5.2 показано разложение в ряд Тейлора для нескольких функций, причем вывод дан в стандартной форме.
Рис. 5.2. Примеры представления функций рядами
Нетрудно заметить, что не все функции разлагаются в ряд Тейлора системой . Mathematica. Например, не имеют разложения логарифм и квадратный корень — они возвращаются в исходном виде. А разложение факториала представлено через гамма- и полигамма-функции.
Удаление члена с остаточной погрешностью ряда
Из-за особого формата результаты разложения в ряд нельзя явно использовать для расчетов (например, для построения графика функции по данным ее разложения в ряд). Для устранения остаточного члена и получения приемлемых для расчетов выражений можно использовать функции Collect и Normal. Ниже показаны примеры применения этих функций:
Series[Sin[x],{х,0,7}]
x-x3/6+x5/120 -x7/5040+0[Xl 8
Collect[%,x]
x-x3/6+x5/120 -x7/5040
Normal[Series[Sin[x*y],{х,0,3},{у,0,3}] ]
xy-х3 у3/6
f [х_, у ] =xy-х3 у3/6
xy-х3 у3/6
f[0.1,0.2]
0.0199987
В данном случае результат представлен в формате стандартного вывода. Его можно использовать для создания функций пользователя, например, путем переноса через буфер обмена в правую часть такой функции. Это и показано в конце приведенных выше примеров. Разумеется, можно задать функцию пользователя и напрямую:
F[x_, у_] = Normal [Series [Sin[x* у] , {х, 0, 3), {у, 0, 3}]
xy-х3 у3/6
F[0.1, 0.2]
0.0199987
В Mathematica 3/4 преобразование результатов разложения в ряд в стандартные расчетные выражения несколько упрощено. Это позволяет ограничиться описанными выше (но вовсе не единственными) приемами.
Графическая визуализация разложения в ряд
Погрешность разложения в ряд возрастает с ростом отклонения от узловой точки. При больших отклонениях даже качественное описание функции может резко нарушаться — например, монотонно возрастающая функция при вычислении по разложению в ряд может убывать или даже стремиться к бесконечности. Для оценки того, насколько и в какой окрестности исходной точки разложение в ряд адекватно разлагаемой функции, полезно построить на одном рисунке график исходной функции и график выражения, соответствующего полученному ряду (без остаточной погрешности). Другими словами, нужна графическая визуализация разложения в ряд.
Пример графической визуализации разложения в ряд представлен на рис. 5.3. На нем, кстати, использовано описанное выше применение функции Collect для получения результата разложения в обычной форме, допускающей вычисления.
Рис. 5.3. Представление синусоидальной функции рядом Тейлора с графической иллюстрацией его точности
На рис. 5.3 представлены график синусоиды, построенной по аналитическому выражению, и график ее разложения в ряд Тейлора в окрестности точки х 0 =2. Хорошо заметно расхождение за пределами области, примыкающей к оперной точке функции. Как отмечалось, погрешность уменьшается, если х0=0 (ряд Маклорена). К сожалению, при большом числе членов ряда его поведение становится трудно предсказуемым, и погрешность приближения катастрофически нарастает.
gl5-1.jpg
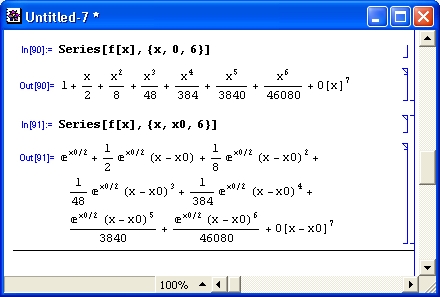
gl5-2.jpg

gl5-3.jpg
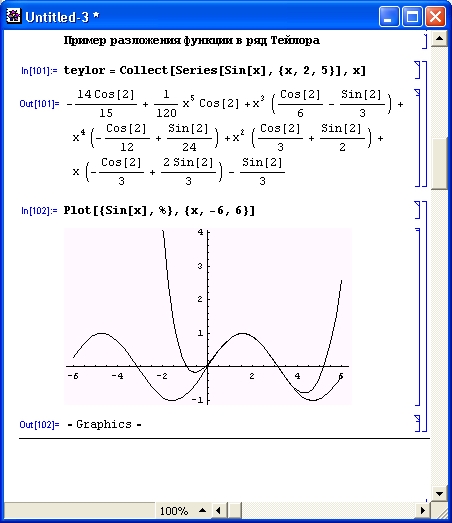
3. Преобразования Фурье
Преобразования Фурье
Основные понятия о спектральном анализе и синтезе
Спектральный подход (метод) лежит в основе целых направлений науки и техники. Достаточно отметить, что он плодотворно используется в технике электро- и радиосвязи, где разделение частот модулированных сигналов базируется на различии их спектров. Спектральный подход также широко используется для создания аналоговых и цифровых фильтров и для оценивания искажений сигналов в ходе их преобразования, например усиления реальными усилителями.
Схема применения спектрального подхода достаточно проста. Сигнал вначале представляется совокупностью гармонических составляющих — гармоник ~ в виде тригонометрического ряда Фурье. Для точного представления сигнала требуется бесконечное число гармоник, но на практике оно всегда ограничено. Такое ограничение порождает волнообразный характер изменения сигнала и появление выбросов, что известно под названием эффекта Гиббса.
Получение сигнала в виде суммы гармонических составляющих получило название спектрального анализа. Суммирование гармоник сигнала и его приближенное представление во временной области называется гармоническим синтезом сигнала.
Итак, спектральный подход заключается в следующем. Вначале получают достаточно представительный (с большим числом гармоник) спектр заданного сигнала. Довольно часто используют тестовые сигналы в виде прямоугольных, треугольных, пилообразных и других импульсов. Для моделирования таких сигналов можно использовать различные функции, например, Sign [Sin [t] ] позволяет получить симметричные прямоугольные импульсы (меандр), а Abs [Sin [t] ] моделирует результат двухполупериодного выпрямления синусоидального напряжения. Для получения разрывных сигналов можно использовать функции с условиями сравнения, например функцию If (на рис. 5.4 даны примеры имитации с помощью этой функции импульсов прямоугольной и пилообразной формы).
Для многих частных видов сигналов (а к ним относится большинство тестовых сигналов) разложения в ряд Фурье хорошо известны и приводятся в любом математическом справочнике (иногда в несколько разных формах). Это позволяет сразу получить нужное число гармоник сигнала и, что особенно важно, проверить, насколько адекватно синтезируемый сигнал описывает реальный сигнал.
На рис. 5.5 показан пример прямого синтеза разнополярных коротких прямоугольных импульсов. Используется известное разложение их в ряд, причем графики построены для 5 и 20 гармоник. Нетрудно заметить, что даже при двадцати гармониках представление такого сигнала гармоническим рядом не очень точно — отчетливо наблюдаются колебания и выбросы, то есть эффект Гиббса.
Рис. 5.4. Имитация импульсов прямоугольной и пилообразной формы с помощью функции If
Рис. 5.5. Гармонический синтез коротких разнополярных прямоугольных импульсов
Еще один подобный пример — синтез разнополярных треугольных импульсов — представлен на рис. 5.6. Здесь также используется известное выражение для ряда
Фурье. Графики построены для 3 и 20 гармоник. Нетрудно заметить, что гармонический синтез для этого сигнала дает гораздо лучшие результаты — даже три гармоники неплохо воспроизводят сигнал. Это связано с тем, что данный сигнал не имеет разрывов — для него характерны лишь точки резких перегибов временной зависимости.
Рис. 5.6. Гармонический синтез симметричных треугольных импульсов
В целом надо отметить, что чем плавнее временная зависимость сигнала, тем меньше проявляются отмеченные выше искажения и слабее заметен эффект Гиббса.
Итак, в результате гармонического анализа сигнала (или его прямого гармонического синтеза) сигнал получается в виде совокупности гармонических сигналов — гармоник. В общем случае каждая гармоника имеет свою амплитуду и фазу, и для их получения в общем случае можно использовать прямое преобразование Фурье (см. ниже).
Полученный спектр сигнала можно подвергать различным преобразованиям, например частотной фильтрации. Полученный после этого измененный спектр гармоник используется (путем гармонического синтеза) для воссоздания искаженного (например, после фильтрации) сигнала.
Простота спектрального подхода обманчива, поскольку он требует довольно громоздких вычислений. Для быстрого их выполнения были созданы различные ускоренные методы спектрального анализа и синтеза — например, метод быстрого преобразования Фурье (БПФ). Но лишь с появлением СКМ класса Mathematica (и ей подобных) спектральный подход превращается в «рабочую лошадку», обеспечивая наглядное и достаточно быстрое решение задач спектрального анализа и синтеза.
Прямое и обратное преобразования Фурье
Для представления временных зависимостей (сигналов) в виде набора гармоник в общем случае (и в системе Mathematica) используется прямое дискретное преобразование Фурье (ДПФ), а для обратного преобразования спектра во временную зависимость — обратное дискретное преобразование Фурье. Математические основы этих преобразований хорошо известны и описаны в соответствующей литературе. В Mathematica 4 имеются следующие основные функции для осуществления дискретного преобразования Фурье:
- Fourier [list] — осуществляет дискретное преобразование Фурье для списка list комплексных чисел;
- InverseFourier [list] — осуществляет дискретное обратное преобразование Фурье списка list комплексных чисел.
Параметром list этих функций в общем случае является список, содержащий комплексные числа. Последовательное применение прямого и обратного преобразований Фурье должно приводить к результату, совпадающему с исходными данными (в пределах малой погрешности). Это хорошо подтверждает следующий пример:
DF:=Fourier[{1,1,0,0}]
DF
{1. + 0.I, 0.5+0.51, 0. + 0.I, 0.5-0.51}
IF:=InverseFourier[DF]
IF
{1.+ 0. I, 1. + 2.77556х10-171, 0. + 0. I, 0. -2.77556x 10-17I}
Разумеется, этот пример носит исключительно тестовый характер. Используя множество возможностей работы с комплексными числами, можно решать различные задачи спектрального анализа и синтеза сигналов различной формы.
Применение описанных функций имеет некоторые тонкости. Прежде всего надо отметить, что отсчет элементов векторов начинается не с нуля, а с единицы. Поэтому нулевая гармоника (в электро- и радиотехнике ее называют постоянной составляющей разлагаемой в ряд Фурье зависимости) соответствует индексу 1, первая гармоника — индексу 2 и т. д. Таким образом, имеет место смещение нумерации индексов на единицу.
Согласно теореме отсчетов, именуемой также теоремой Котельникова, если функция имеет N отсчетов, то максимальное число гармоник спектрального разложения равно N/2. Между тем, функция Fourier в системе Mathematica дает все N элементов создаваемого ею вектора. При этом на спектрограмме «лишние» гармоники на деле просто образуют зеркальное отображение реально возможных N/2 гармоник. Именно поэтому двойное (прямое и обратное) преобразование Фурье в системе Mathematica 3/4 почти идеально точно восстанавливает исходный вектор.
Еще одна тонкость связана с необычным представлением нулевых мнимых частей элементов векторов, получаемых в ходе преобразований. Они записываются в виде 0.1. Для их устранения может использоваться функция Chop [V].
Для лучшего понимания особенностей спектрального анализа и синтеза рекоменду.ется внимательно ознакомиться с формулами преобразований Фурье, которые можно найти в справочной системе, благо эти формулы вполне понятны даже тем, кто не силен в английском языке. В литературе подобные формулы встречаются в нескольких различных видах, что порождает некоторые трудности в интерпретации и нормировке результатов спектрального анализа и синтеза. Поэтому полезно познакомиться с дополнительными и вполне конкретными примерами, приведенным ниже.
Спектральный анализ на основе прямого преобразования Фурье
Итак, прямое преобразование Фурье означает перевод временного представления сигнала в частотное. Другими словами, оно позволяет получить частотный спектр сигнала, представленного отсчетами его временной зависимости. Нередко это является конечной целью спектрального анализа.
На рис. 5.7 представлен пример спектрального анализа простого сигнала — треугольного импульса, заданного с помощью функции If. Затем с помощью функции Fourier прямого преобразования Фурье получены в явном виде векторы амплитуд Мg и фаз Аg гармоник этого сигнала.
Рис. 5.7. Спектральный анализ пилообразного импульса на основе прямого преобразования Фурье
На рис. 5.8 представлено продолжение документа, показанного на рис. 5.7. Здесь с помощью графиков лестничного типа, подчеркивающих дискретность гармоник, построены спектрограммы амплитуд и фаз гармоник пилообразного импульса. Хорошо видно симметричное отражение линий спектра относительно восьмой гармоники — в нашем случае имелось 16 отсчетов сигнала. Это значит, что амплитуда и фаза девятой гармоники те же, что у седьмой гармоники, у десятой — те же, что у шестой, и т. д.
Рис. 5.8. Спектрограммы амплитуд и фаз гармоник пилообразного импульса
Теперь рассмотрим более сложный случай — получение спектра сложного сигнала (рис. 5.9). :
Рис. 5.9. Получение спектра сложного сигнала с помощью прямого преобразования Фурье
В начале этого рисунка показано формирование синусоидального сигнала с частотой 50 Гц, на который наложена значительная по амплитуде шумовая составляющая. Она создается добавлением к отсчетам сигнала случайных величин, созданных генератором случайных чисел.
Во второй части рисунка показан график частотных отсчетов, полученных после прямого преобразования Фурье. На нем отчетливо виден пик в районе частоты 50 Гц (поскольку первый элемент результирующего списка соответствует нулевой частоте, этот пик возникает на 51-м элементе списка). Однако помимо него существует еще один пик на частоте 256 - 50 = 206 Гц. Он связан с отмеченным ранее свойством симметрии спектра вещественного сигнала.
Фильтрация сигналов на основе преобразований Фурье
Преобразование Фурье является теоретической основой фильтрации сложных сигналов. Мы рассмотрим комплексный пример на фильтрацию сигнала, представляющего собой функцию Бесселя первого рода третьего порядка. Рисунок 5.10 показывает верхнюю часть документа, демонстрирующую создание исходного сигнала и описание частотного фильтра.
Рис. 5.10. Часть документа, показывающая создание сигнала и синтез фильтра для него
Как и в ранее рассмотренном примере, сигнал формируется как сумма чистого сигнала со случайной составляющей, моделирующей шум. Выбранная форма сигнала напоминает затухающую синусоиду. Уровень шумов выбран достаточно большим, так что форма чистого сигнала с трудом угадывается на фоне шумов (верхний график). Далее показаны синтез цифрового частотного фильтра и его амплитудно-частотная характеристика (АЧХ). График АЧХ показан в нижней части рис. 5.10.
На рис. 5.11 показан процесс фильтрации. Он сводится к уточнению модели фильтра (сдвигу АЧХ в область более низких частот и созданию зеркального отражения спектра), проведению прямого преобразования Фурье, выделению фильтром соответствующих составляющих сигнала и, наконец, выполнению обратного преобразования Фурье. Оба преобразования и фильтрация осуществляются в одном выражении (строка с переменной conv). При этом векторы прямых преобразований Фурье для сигнала и для отсчетов частотной характеристики фильтра перемножаются. Обратное преобразование Фурье переводит результат фильтрации во временную область. Полученный в результате фильтрации сигнал практически очищен от шума. Это подтверждает график выходного сигнала, представленный в нижней части рис. 5.11.
Рис. 5.11. Часть документа, показывающего фильтрацию сигнала и построение графика сигнала, очищенного от шума
Эти примеры показывают высокую эффективность средств Mathematica 3/4 в решении задач спектрального анализа, синтеза сигналов, их фильтрации и иных преобразований. Важно отметить, что в новейшей версии Mathematica 4 использованы ускоренные алгоритмы преобразований Фурье, повышающие скорость выполнения описанных операций в несколько раз. Это открывает возможность решения серьезных задач обработки сигналов, представленных многими тысячами отсчетов. Другими словами — сигналов, реально применяемых в технике связи.
Функции пакета — FourierTransform
Подпакет FourierTransform пакета Calculus в версии Mathematics 3 служит для осуществления расширенных преобразований Фурье. Он вызывается командой
<<Calculus` FourierTransform`
Ввиду важности этих преобразований в системе Mathematica 4 их функции были размещены уже в ядре системы. Это следующие функции:
- FourierTransform [expr, t, w] — возвращает результат прямого преобразования Фурье над выражением expr [t], выраженного через переменную w;
- InverseFourierTransform[expr, w, t] — возвращает результат обратного преобразования Фурье над выражением expr[w], выраженного через переменную t;
- FourierCosTransform[expr, t, w] — возвращает результат косинусного преобразования Фурье над выражением expr [t ], выраженного через переменную w;
- FourierSinTransform[expr, t, w] — возвращает результат синусного преобразования Фурье над выражением expr [t], выраженного через переменную w;
- FourierTransform [expr, {tl,t2}, {wl, w2 } ] — возвращает результат прямого преобразования Фурье над выражением expr [ tl, t2,...], выраженного через переменные {wl, w2,-...};
- InverseFourierTransformtexpr, {tl,t2}, {wl,w2} ]'— возвращает результат обратного преобразования Фурье над выражением expr [ wl, wl,...], выраженного через переменные {tl, t2,...}.,
Примеры осуществления прямого и обратного преобразований Фурье представлены ниже:
FourierTransform[Sin[t]*t:2, t, w]
-Iл(DiracDelta"[l - w] - DiracDelta" [1 + w])
InverseFourierTransform[%, w, t]
t2Sin[t]
FourierCosTransform[Sin[t]*t:2, t, w]
-8w2/(1-w2)3-2/(1-w2)2
FourierSinTransform[Cos[a*t], t, w]
-w/(a2-w2)
FourierTransform[tl^2 Exp[-a t2] UnitStep[tl, t2],
{tl, t2}, {wl, w2}]
-2I/w13-лDiracDelta''[w1]/a-IW2
InverseFourierTransformtwl/(l-b*w2), {wl, w2}, {tl, t2}]
Для реализации спектрального анализа и синтеза имеются следующие функции:
- FourierExpSeries [expr, {x, xmin, xmax), n] — возвращает разложение expr [х] в экспоненциальный ряд Фурье с n членами на отрезке {xmin, xmax};
- FourierExpSeriesCoef f icient [expr, {x, xmin, xmax} ,n] —возвращает коэффициенты разложения expr [x] в экспоненциальный ряд Фурье с n членами на отрезке {xmin, xmax};
- FourierTrigSeries [expr, {x, xmin, xmax}, n] — возвращает разложение expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax};
- FourierSinSeriesCoef f icient [expr, {x, xmin, xmax}, n] —возвращает синусные коэффициенты разложения expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin,xmax};
- FourierCosSeriesCoef f icient [expr, {x, xmin, xmax}, n] —возвращает косинусные коэффициенты разложения expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax}.
Рисунок 5.12 иллюстрирует создание пилообразного сигнала, его разложение в тригонометрический ряд Фурье с п = 4, графическое воспроизведение сигнала и его представление суммой из четырех гармоник (на рисунке оставлены только совмещенные графики). Таким образом, последняя операция демонстрирует проведение синтеза пилообразного сигнала по четырем гармоникам.
Рис. 5.12. Создание пилообразного сигнала, его разложение в тригонометрический ряд Фурье и синтез сигнала по четырем гармоникам
Помимо указанных функций существует целая группа функций для численных операций, связанных с разложением в ряд Фурье. Все они имеют в начале имени букву N, например:
- NFourierTrigSeries [expr, {x, xmin,xmax}, n] — возвращает разложение expr t x ] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax} в численном виде.
Предоставляем читателю опробовать эти функции самостоятельно.
gl5-10.jpg
gl5-11.jpg
gl5-12.jpg
gl5-4.jpg
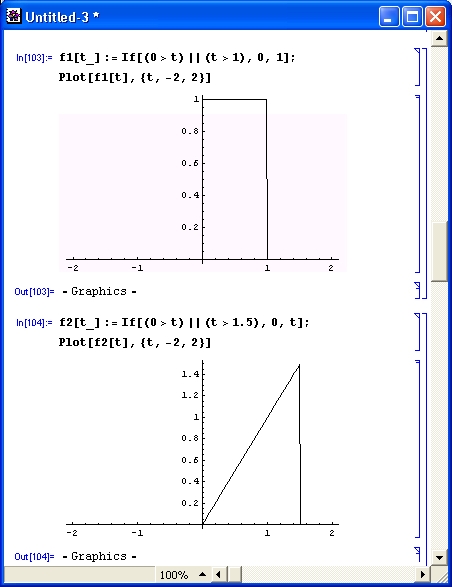
gl5-5.jpg
gl5-6.jpg
gl5-7.jpg

gl5-8.jpg
gl5-9.jpg
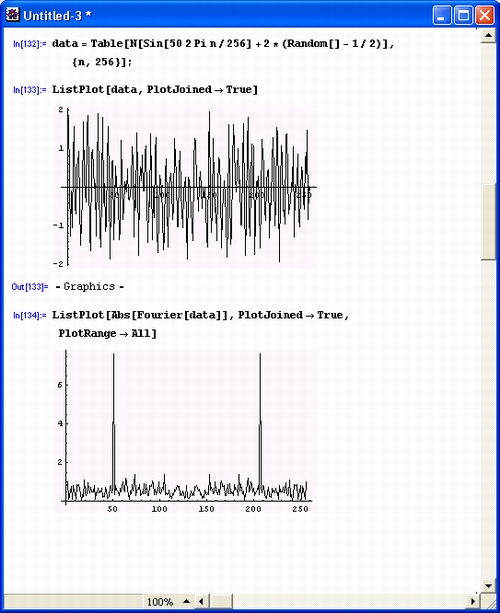
4. Интерполяция, аппроксимация и регрессия
Интерполяция, аппроксимация и регрессия
Нередко исходные данные при решении математических задач представлены рядом точек произвольной зависимости вида у(х). Сама по себе эта зависимость может быть неизвестной. Для вычисления промежуточных значений функции используется аппарат интерполяции. При нем истинная функция заменяется аппроксимирующей функцией, которая в узловых точках дает точные значения ординат и позволяет вычислить значения интерполируемой функции в промежуточных точках.
Полиномиальная интерполяция и аппроксимация
Для решения задач интерполяции и аппроксимации функций, заданных рядом узловых точек, в Mathematica используются следующие функции:
- InterpolatingFunctionfrange, table] — возвращает интерполирующую функцию, позволяющую вычислять промежуточные значения в заданном диапазоне range для таблицы table;
- InterpolatingPolynomial [data, var] — возвращает полином (степенной многочлен) по переменной var, значения которого в узловых точках точно совпадают с данными из списка data. Он может иметь форму { {xl, f1}, {х2, f2},...} или {fl, f2,...} (во втором случае xi принимают значения 1, 2,...). Вместо fi может быть список {fi, dfi, ddfi,...}, указывающий значения производных в точках xi;
- Interpolation [data] — конструирует объект InterpolatingFunction.
InterpolationOrder — опция функции Interpolation, указывающая степень подходящего полинома. При ее значении, равном 1, осуществляется кусочно-линейная интерполяция. Целое значение, большее единицы, задает степень глобальной полиномиальной интерполяции.
Применение основной функции Interpolation поясняет следующий пример:
data = ТаЫе[{х, х^2 + 1}, {х, 1, 5}]
{{1, 2}, {2, 5}, {3, 10}, {4, 17}, {5, 26}}
funi = Interpolation[data]
InterpolatingFunctionf{{1, 5}}, 0]
{funi [1.5], funi[3], funi[4.5]}
{3.25, 10, 21.25}
Таким образом, на заданном отрезке изменения х функция Interpolation позволяет найти любое промежуточное значение функции funi [x], в том числе значения в узловых точках.
Теперь рассмотрим часто используемую полиномиальную аппроксимацию, при которой ищется полином, график которого точно проходит через узловые точки данных.
Степень интерполирующего (и аппроксимирующего) полинома всегда на 1 меньше числа узловых точек интерполяции или аппроксимации. Аппроксимация отличается от интерполяции тем, что предполагает получение аппроксимирующей функции в явном виде. При полиномиальной аппроксимации такой функцией является степенной многочлен.
Пример на рис. 5.13 иллюстрирует технику проведения полиномиальной аппроксимации с применением интерполирующего степенного многочлена.
Рис. 5.13. Полиномиальная аппроксимация таблично заданных данных
Как и следовало ожидать, степень аппроксимирующего многочлена оказалась равной трем, поскольку было задано четыре пары данных. На рис. 5.13 представлено также сравнение результата полиномиальной аппроксимации с исходными данными. Исходные данные представлены на графике в виде точек, а зависимость, представленная аппроксимирующим полиномом, выведена сплошной линией.
В узлах интерполяции значения интерполирующего многочлена точно совпадают со значениями исходных данных. Однако это не гарантирует малую погрешность за пределами узловых точек (особенно при экстраполяции функций). Чем больше пар данных и чем выше степень аппроксимирующего многочлена, тем выше погрешность аппроксимации. Обычно аппроксимация при степени многочлена выше 8-10 не применяется из-за резкого возрастания погрешности. При большом числе пар исходных данных более полезной на практике является регрессия.
Регрессия и визуализация ее результатов
Еще один широко используемый вид аппроксимации — регрессия. Она заключается в нахождении параметров некоторой функции регрессии, при которой график этой функции проходит в «облаке» узловых точек, обеспечивая наименьшую среднеквадратичную погрешность их представления. В отличие от интерполяции, при регрессии найденная функция не дает точного значения ординат в узловых точках — она просто минимизирует погрешность вычислений в этих точках.
Для решения задач регрессии используется функция ядра
Fit: Fit[data, funs, vars]
Эта функция ищет приближение для списка данных data методом наименьших квадратов в виде линейной комбинации функций funs переменных vars. Данные data могут иметь форму {{xl, yl,..., f1}, {х2, у2,..., f2 },...}, где число координат х, у,... равно числу переменных в списке vars. Также данные data могут быть представлены в форме {f 1, f 2, =..} с одной координатой, принимающей значения 1, 2... Аргумент funs может быть любым списком функций, которые зависят только от объектов vars.
Следующие примеры показывают приближение исходных данных степенным полиномом и линейной комбинацией двух функций:
Fit[{{0, 0.9}, {2, 8.099999999999999), {3, 17}, {4, 33}}, {а, х, х2}, х]
0. 997273-1.40864 х+2.33409 х2
Fit[{{0, 0.9}, {2, 8.099999999999999}, {3, 17}}, {х2, Ехр[х], х} , х]
0.9ех + 2.89276х- 1.08392 х2
Здесь в первом примере выполняется полиномиальная регрессия со степенью полинома, равной 2. Максимальная степень на 1 меньше числа пар исходной зависимости (в нашем случае их 4) — при такой степени регрессия вырождается в обычную полиномиальную аппроксимацию, которая рассматривалась ранее.
Рисунок 5.14 показывает несколько иной путь проведения полиномиальной аппроксимации — исходные данные заданы объектом-списком data.
В конце документа рис. 5.14 показано построение графика аппроксимирующего полинома второй степени и точек исходных данных. Заметно, что при регрессии график полинома проходит в середине «облака» исходных точек и не укладывается на них точно.
В уроке 12 будут рассмотрены дополнительные функции для проведения регрессии. Они входят в различные пакеты расширения системы Mathematica 3/4.
Рис. 5.14. Полиномиальная регрессия с графическим выводом
gl5-13.jpg
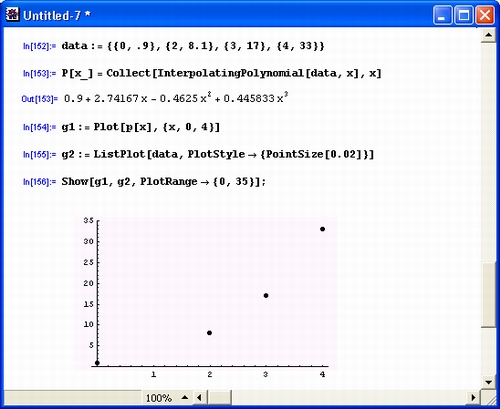
gl5-14.jpg
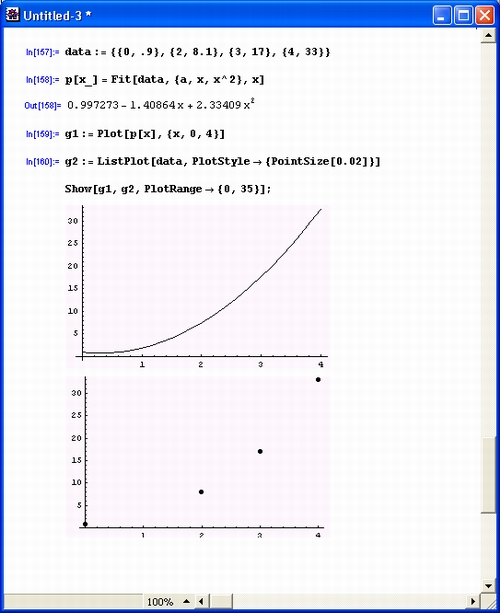
5. Спектральный анализ с линейной интерполяцией сигнала
Спектральный анализ с линейной интерполяцией сигнала
Как уже отмечалось, одной из проблем точного представления сигналов при гармоническом синтезе является ограничение числа гармоник, связанное с конечностью числа отсчетов сигнала. К примеру, если вещественный сигнал задан 20 отсчетами, то максимальное число гармоник будет всего 10, что недостаточно для хорошего представления большинства реальных сигналов.
Ниже описан путь преодоления этого ограничения. Он основан на интерполяции сигнала, что позволяет при ограниченном числе его отсчетов (выборок) использовать любое число дополнительных отсчетов. Разумеется, при этом строится спектр интерполированного сигнала, но он может представлять реальный сигнал гораздо лучше, чем просто ограниченный N/2 гармониками спектр сигнала с малым числом выборок.
Еще одна проблема при спектральном анализе связана с необходимостью нормировки коэффициентов Фурье. Их расчет по аналитическим формулам не является достаточно эффективным — уже давно доказано, что если сигнал представлен отдельными выборками, то единственно обоснованным методом вычисления интегралов (коэффициентов) Фурье является простейший метод прямоугольников. Это обстоятельство также учтено в описанном ниже документе (вполне законченном «блокноте» системы Mathematica).
Пусть сигнал задан N отсчетами. На рис. 5.15 показан пример задания достаточно сложного сигнала путем формирования вектора его ординат Yi (индекс i от 1 до 20). Пусть сигнал задан на периоде Т = 4*10^-6 с, что соответствует частоте f 1 основной гармоники сигнала, равной 250 кГц. Рисунок 5.15 поясняет технику нормировки сигнала и построения его графика с реальной шкалой времени (то есть на отрезке времени от 0 до Т).
Рис. 5.15. Задание сигнала, его кусочно-линейная интерполяция и построение графика временной зависимости
При построении графика сигнала и его временной зависимости использована наиболее широко применяемая на практике техника кусочно-линейной интерполяции. Однако изменением значения опции InterpolationOrder можно выполнить и глобальную полиномиальную аппроксимацию сигнала, которая может быть предпочтительна для гладких сигналов.
Рисунок 5.16 показывает раздел документа с расчетом коэффициентов косинусных и синусных коэффициентов Фурье методом прямоугольников. В расчете есть небольшая тонкость, иногда ускоряющая вычисления, — нулевые отсчеты не обрабатываются. Показанные на рис. 5.16 соотношения хорошо знакомы специалистам, применяющим инженерные методы спектрального анализа и синтеза.
На рис. 5.17 крупным планом показано построение спектрограммы амплитуд гармоник заданного сигнала. Дабы подчеркнуть дискретность гармоник, амплитуда каждой из них показана точкой, около которой стоит номер гармоники. Для этого пришлось использовать графическую функцию LabelListPlot из пакета расширения Graphics. Нетрудно заметить, что амплитуды гармоник быстро убывают по мере роста их номера. Однако, поскольку суммируется множество гармоник, это не является основанием для слишком поспешного отбрасывания высших гармоник.
Рис. 5.16. Вычисление коэффициентов Фурье, амплитуд и фаз гармоник
Рис. 5.17. Спектрограмма амплитуд гармоник
Рисунок 5.18 представляет спектрограмму фаз гармоник. Фазы гармоник также имеют дискретные значения и показаны точками с номерами. Значение фазового сдвига лежит в пределах от -л до л.
Теперь, получив набор гармоник заданного сигнала, можно приступить к его гapмоническому синтезу. Он представлен на рис. 5.19 сверху. Здесь также применен прием, иногда ускоряющий вычисления, — гармоники с нулевой амплитудой из формулы синтеза устраняются.
Рис. 5.18. Спектрограмма фаз гармоник
Рис. 5.19. Гармонический синтез сигнала и сравнение его результатов с временной зависимостью интерполированного сигнала
Самый «волнующий» момент представлен во второй части рис. 5.19 — здесь показано сравнение результата гармонического синтеза сигнала с его временной зависимостью (интерполированной). Чтобы исходный и синтезированный сигналы не сливались, синтезированный сигнал намеренно немного сдвинут вправо и вверх. Нетрудно заметить, что несмотря на сложный характер сигнала его гармонический (спектральный) синтез в данном случае дает превосходные результаты уже при использовании 51 гармоники (включая нулевую). Если убрать отмеченный выше сдвиг, то сигналы практически сливаются.
Рисунок 5.20 показывает задание амплитудно-частотной и фазо-частотной (ФЧХ) характеристик некоего фильтра, ослабляющего высокие частоты и вносящего фазовый сдвиг, пропорциональный частоте сигнала. В нижней части рисунка построены эти характеристики. Заметим, что здесь АЧХ и ФЧХ заданы без «хитростей», присущих решению аналогичной задачи с применением встроенных функций дискретного преобразования Фурье. Они задаются в явном виде как функции от частоты.
Рис. 5.20. Амплитудно-частотная и фазочастотная характеристики фильтра
Рисунок 5.21 показывает, как влияет на форму сигнала его прохождение через фильтрующую цепь. Для оценки этого используется формула синтеза гармоник. Однако отличные от нуля амплитуды гармоник умножаются на модуль коэффициента передачи (АЧХ) фильтра, а к фазе каждой гармоники добавляется фазовый сдвиг, вносимый фильтром (ФЧХ). Таким образом, в процессе синтеза временной зависимости сигнала учитываются амплитудно-частотные и фазо-частотные искажения сигнала фильтром.
Рис. 5.21. Сравнение исходной временной зависимости сигнала и сигнала на выходе фильтрующей цепи
Рассмотренный документ является хорошей иллюстрацией применения системы Mathematica для решения нестандартных задач и реализации альтернативных методов их решения. В частности, в данном случае спектральный анализ и синтез велись по типичной для инженерных расчетов методике и без использования встроенных функций преобразования Фурье.
gl5-15.jpg

gl5-16.jpg
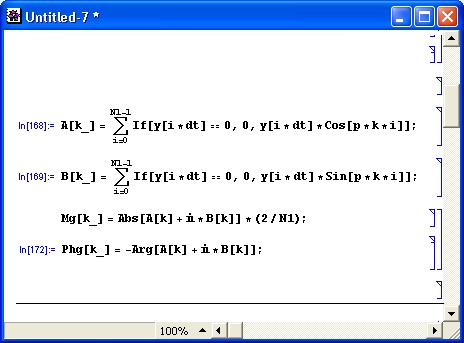
gl5-17.jpg
gl5-18.jpg
gl5-19.jpg
gl5-20.jpg
gl5-21.jpg
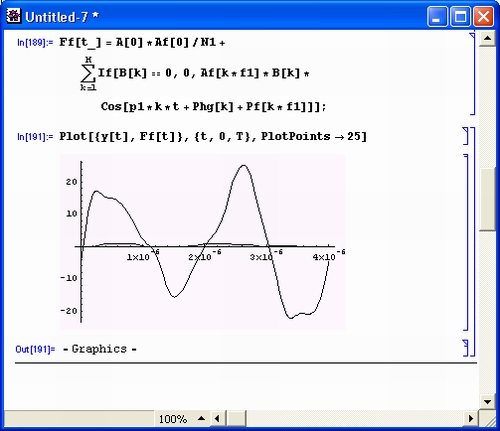
6. Моделирование нелинейных цепей с применением интерполяции
Моделирование нелинейных цепей с применением интерполяции
Интерполяция может быть очень полезной при решении задач моделирования нелинейных цепей как с обычными (например, электронные лампы и транзисторы), так и с «необычными» активными приборами, например туннельными диодами или лавинными транзисторами.
Одна из проблем такого моделирования — задание нелинейных вольт-амперных характеристик (ВАХ) активного прибора. Mathematica позволяет задать такие ВАХ, используя различные виды интерполяции и аппроксимации — от кусочно-линейной до полиномиальной или сплайновой. Рисунок 5.22 демонстрирует простое табличное задание N-образной ВАХ туннельного диода с полиномиальной интерполяцией (используется полином четвертой степени). Обратите внимание на применение импортируемого рисунка — схемы цепи. Он готовился отдельно в графическом редакторе.
Рис. 5.22. Начало документа, позволяющего моделировать схему на туннельном диоде
Рисунок 5.23 показывает часть документа, в которой выполнено математическое моделирование поведения схемы с момента ее включения. Для моделирования используется известная система из двух нелинейных дифференциальных уравнений, решаемая с помощью встроенной функции NDSolve (эта система записана первой в списке параметров данной функции). Полученные в результате моделирования временные зависимости напряжения на туннельном диоде и тока во внешней цепи показаны ниже. Они свидетельствуют о возникновении в цепи стационарных и почти синусоидальных колебаний. Таким образом, цепь выполняет функции генератора высокочастотных колебаний
Рис. 5.23. Моделирование возникновения и установления синусоидальных колебаний в схеме на туннельном диоде
Поведение схемы очень наглядно характеризует фазовый портрет колебаний, представленный на рис. 5.24 и построенный на фоне интерполированной ВАХ туннельного диода и линии нагрузки резистора Rs, задающей положение рабочей точки на падающем участке ВАХ. В этом случае туннельный диод вносит во внешнюю цепь отрицательную дифференциальную проводимость, что и ведет к возможности возникновения гармонических или релаксационных колебаний (уменьшив С или увеличив L, вы можете посмотреть, как происходит переход к релаксационным колебаниям).
Рис. 5.24. Фазовый портрет колебаний в схеме с туннельным диодом для случая почти гармонических колебаний
Если задать вместо постоянного напряжения Es некоторый импульсный сигнал, то можно смоделировать множество других режимов работы цепи, например генерацию ждущих колебаний, нелинейное усиление, триггерный режим и т. д. Рисунок 5.25 показывает задание e(t) в виде постоянного напряжения Es, на которое наложены положительный и отрицательный запускающие импульсы.
Если линия нагрузки резистора Rs пересекает ВАХ туннельного диода в трех точках (две из них расположены на восходящих участках ВАХ), то будет наблюдаться триггерный режим с раздельным запуском. Этот случай показан на рис. 5.26, где построены временные зависимости напряжения и тока в триггере на туннельном диоде.
Риc. 5.25. Задание временной зависимости e(t), обеспечивающей триггерный режим работы схемы с туннельным диодом
Риc. 5.26. Моделирование триггерного режима работы схемы с туннельным диодом
Фазовый портрет колебаний для этого случая представлен на рис. 5.27. Он дает хорошее представление о сложности физических процессов даже в такой, казалось бы, простой схеме, которая представлена на рис. 5.22.
Риc. 5.27. Фазовый портрет, иллюстрирующий работу схемы с туннельным диодом в триггерном режиме
Если собрать приведенные на рис. 5.22-5.27 фрагменты воедино, вы получите еще один полностью завершенный «блокнот», прекрасно иллюстрирующий решение одной из реальных научно-технических задач. Вы можете дополнить его анализом ряда других режимов работы схемы, причем не обязательно на туннельном диоде, а на любом приборе с нелинейной В АХ вида I(U). Для этого достаточно просто сменить вектор с табличными данными опорных точек ВАХ, полученных, например, в эксперименте, и использовать иные параметры схемы.
gl5-22.jpg

gl5-23.jpg
gl5-24.jpg
gl5-25.jpg
gl5-26.jpg
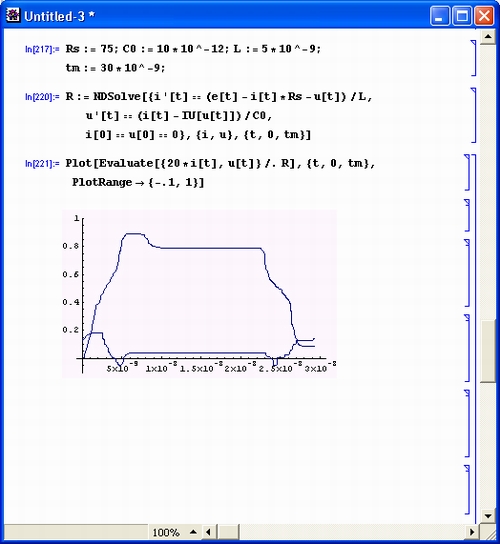
gl5-27.jpg
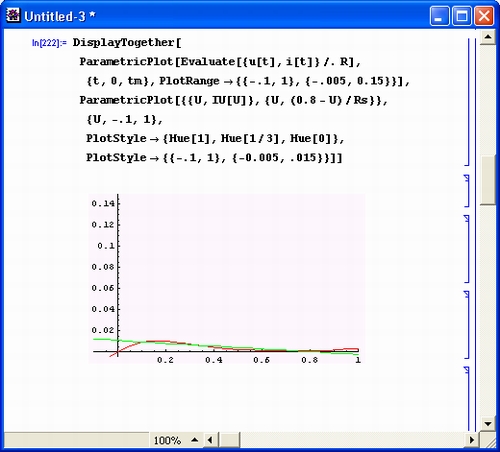
7. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Находить разложения заданных функций и выражений в ряды Тейлора и Маклорена.
- Удалять член с остаточной погрешностью ряда.
- Представлять разложение в ряд графически.
- Осуществлять прямое и обратное дискретные преобразования Фурье.
- Выполнять спектральный анализ на основе преобразования Фурье.
- Осуществлять фильтрацию сигналов на основе преобразования Фурье.
- Выполнять полиномиальную интерполяцию и аппроксимацию.
- Осуществлять регрессию и визуализацию ее результатов.
- Выполнять спектральный анализ таблично заданных сложных сигналов с интерполяцией их временных зависимостей.
- Выполнять моделирование схем на приборах с N-образными ВАХ, используя при этом их интерполяцию.
Урок 6. Специальные математические функции
Урок 6. Специальные математические функции
1. Специальные математические функции
Специальные математические функци
Специальные математические функции являются решениями линейных дифференциальных уравнений специального вида или представлениями особых интегралов, которые не могут быть выражены через элементарные функции. Здесь не приводятся определения специальных математических функций ввиду их общеизвестности и наличия соответствующей информации в справочной базе данных систем Matheraatica.
К сожалению, входной язык общения с системами Mathematica 3/4 не предусматривает использования греческих букв для имен специальных функций (хотя палитра с такими буквами есть), и их имена задаются английскими словами. Специальные математические функции удобно подразделять на несколько групп, представленных ниже.
2. Ортогональные многочлены
Ортогональные многочлены
Одними из широко распространенных специальных функций являются ортогональные многочлены (полиномы). Mathematica имеет следующие функции, возвращающие значения ортогональных многочленов:
- ChebyshevT [n, х] — полином Чебышева п-й степени первого рода;
- CyebyshevU [n, x] — полином Чебышева п-йстепени второго рода;
- HermiteH[n, х] — полином Эрмита п-йстепени;
- JacobiP[n, a, b, х] — полином Якоби п-й степени;
- 'GegenbauerC [n, m, х] — полином Гегенбауэра;
- LaguerreL[n, х] — полином Лагерра n-й степени;
- LaguerreL[n, а, х] — обобщенный полином Лагерра п-й степени;
- LegendreP [n, х] — полином Лежандра n-й степени;
- LegendreP [n, m, x] — присоединенный полином Лежандра;
- LegendreQ [n, z] — функция Лежандра второго рода n-го порядка;
- LegendreQ [n, m, z] — присоединенная функция Лежандра второго рода.
LegendreType — опция для функций LegendreP и LegendreQ; она указывает выборы разрывов кривой для функций Лежандра на комплексной плоскости.
Все ортогональные полиномы имеют простые рекуррентные представления. Поэтому приведенные выше функции вычисляются по ним довольно быстро и точно. Они находят широкое применение в технике интерполяции и аппроксимации функций.
Следующие примеры иллюстрируют работу с ортогональными многочленами.
| Ввод (In) | Вывод (Out) |
| ChebyshevT [ 8, х] | 1 - 32 x 2 + 160 x 4 - 256 x 6 + 128 x 8 |
| ChebyshevT [5, 0.2] | 0.84512 |
| ChebyshevU [3,0. 15] | -0.573 |
| HermiteH[4,3] | 876 |
| JacobiP[3,l,2,0.2] | -0.256 |
| GegenbauerC [ 3 , 1 , x] | -4 x + 8 x 3 |
| N [LaguerreL [3,x]] | 0.166667 (6. -18. x+ 9. x 2 - 1. X 3 ) |
| LegendreP [ 5 , x ] | 15 x /6-35 x 3 /4+63 x 5 /8 |
| LegendreQ[2,0.2] | -0.389202 |
Важно отметить, что при указании конкретного значения параметра п и символьном значении параметра х функции этой группы возвращают присущие им представления через степенные многочлены с соответствующими коэффициентами.
На рис. 6.1 показаны графики ортогональных полиномов Чебышева ChebyshevT и ChebyshevU. Для этих полиномов характерно изменение от -1 до +1 при \х\<1, причем при высоком порядке полиномов графики функций имеют колебательный характер.
Рис. 6.1. Графики ортогональных полиномов Чебышева ChebyshevT (сверху) и ChebyshevU (снизу)
Графики функций полиномов Лагерра LaguerreL и Лежандра LegendreP показаны на рис. 6.2. Они дают представление о поведении этих функций.
Рис. 6.2. Графики ортогональных полиномов Лагерра LaguerreL и Лежандра LegendreP (снизу)
На рис. 6.3 представлены графики полиномов Лежандра LegendreQ.
Рис. 6.3. Графики функций Лежандра LegendreQ (сверху) и полиномов Гегенбауэра GegenbauerC (снизу)
gl6-1.jpg
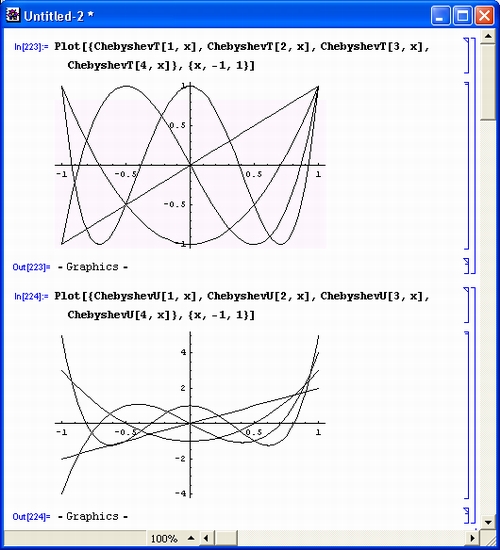
gl6-2.jpg
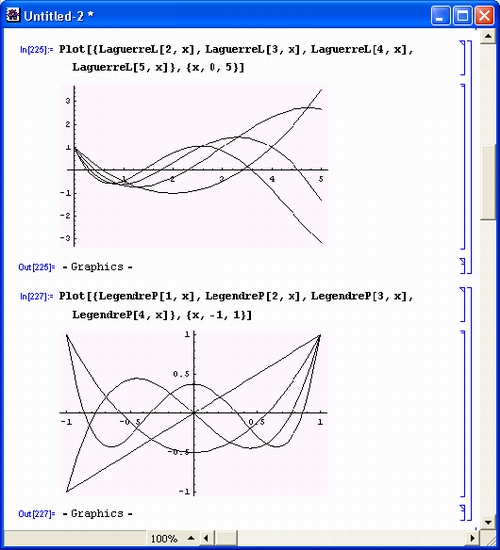
gl6-3.jpg
3. Интегральные показательные и родственные им функции
Интегральные показательные и родственные им функции
К другой известной группе специальных функций относятся интегральные показательные и родственные им функции:
- Coshlntegralfx] — гиперболический интегральный косинус;
- Coslntegral [х] — интегральный косинус С1(х);
- Erf [z] — функция ошибок (интеграл вероятности);
- Erf[z0, zl] — обобщенная функция ошибок erf (zl)-erf (z0);
- Erf с [z] — дополняющая функция ошибок 1-erf (z);
- Erfi [z] — мнимое значение функции ошибок erf (iz) /i;
- ExplntegralE [n, z] — интегральная показательная функция Е(п,z);
- ExplntegralEi[z] — интегральная показательная функция Ei(z);
- Loglntegral [z] — интегральный логарифм li(z);
- Sinhlntegral [x] — интегральный гиперболический синус;
- Sinlntegral [х] — интегральный синус 81(лг).
Ниже представлены примеры применения этих функций.
| Ввод (In) | Вывод (Out) |
| Coshlntegral[1.] | 0.837867 |
| Coslntegral [1 . ] | 0.337404 |
| Erf[l.] | 0.842701 |
| Erf [2. +1*3.] | -20.8295 + 8.68732 I |
| Erf[2.,3.] | 0.00465564 |
| Erfc[l.] | 0.157299 |
| Erfi[l.] | 1.65043 |
| ExplntegralE [3,1.] | 0.109692 |
| ExpIntegralEi [1 . ] | 1.89512 |
| Loglntegral [2 . +3 . *I ] | 2.3374 + 2.51301 I |
| Sinhlntegral [1 . ] | 1.05725 |
| Sinlntegral [1 . ] | 0.946083 |
На рис. 6.4 представлены графики ряда интегральных показательных функций, дающие представление об их поведении при вещественном аргументе.
Следует обратить внимание на то, что большая часть этих функций может иметь комплексный аргумент. Для получения численных значений функций нужно задавать аргумент в форме вещественного числа или 1 комплексного числа с вещественными действительной и мнимой частями.
Рис. 6.4. Графики интегральных показательных функций
gl6-4.jpg
4. Гамма- и полигамма-функции
Гамма- и полигамма-функции
Широко используются гамма-функция и относящиеся к ней родственные функции:
- Gamma [ а ] — эйлерова гамма-функция;
- Gamma [ a, z] — неполная гамма-функция;
- Gamma [a, z 0, z 1 ] — обобщенная неполная гамма-функция Gamma (а, z 0) -Gamma(a,zl);
- GammaRegularized[a, z] — регуляризованная неполная гамма-функция
- (а,2)=Gamma(а,z)/Gamma(a);
- GammaRegularized[a, z0, zl] — обобщенная неполная гамма-функция Q(a,z0)-Q(a, zl);
- LogGamma [ z ] — логарифм эйлеровой гамма-функции;
- Pol у Gamma [ z ] — дигамма-функция \|/(z);
- Pol у Gamma [n, z] — n-я производная от дигамма-функции.
Приведем примеры вычисления этих функций.
| Ввод (In) | Вывод (Out) |
| Gamma[l,2.+3.*I] | -0.133981- 0,.0190985 I |
| Gamma [0.5] | 1.77245 |
| Gaitima [1,2. , 3 . ] | 0.0855482 |
| GammaRegularized [ 1 , 2 . +3 . I , 4 . +6 . *I ] | -0.139176- 0.0366618 I |
| LogGamma [0.5] | 0.572365 |
| LogGarama [ 2 . +3 . * I ] | -2.09285 + 2.3024 I |
| PolyGamma[l] | -EulerGamma |
| PolyGamma [ 1 . ] | -0.577216 |
| PolyGarama [2 . +3 . *I] | 1.20798 + 1.10413 I |
Как видно из этих примеров, данный класс функций (как и многие другие) определен в общем случае для комплексного значения аргумента.
На рис. 6.5 представлены графики эйлеровой гамма-функции и неполной гамма-функции при вещественном аргументе. Поведение эйлеровой гамма-функции довольно сложно, особенно при отрицательных значениях аргумента — наблюдаются характерные разрывы функции с ее уходом в положительную и отрицательную бесконечность.
Рис. 6.5. Графики эйлеровой гамма-функции (сверху) и неполной гамма-функции (снизу)
Поведение эйлеровой гамма-функции в комплексной плоскости довольно интересно. На рис. 6.6 показан контурный график этой функции, отражающий ее поведение на комплексной плоскости в ограниченной области изменения действительной и мнимой частей аргумента.
Рис. 6.6. Контурный график эйлеровой гамма-функции на комплексной плоскости
Графики других гамма-функций пользователь может' построить и просмотреть самостоятельно.
gl6-5.jpg
gl6-6.jpg
5. Функции Бесселя
Функции Бесселя
Функции Бесселя, являющиеся решениями линейных дифференциальных уравнений вида z 2 y" + zy'+ (z 2 - п 2 )у = 0, широко используются в анализе и моделировании волновых процессов. В системе Mathematica к этому классу относятся следующие функции:
- Bessell[n, z] — модифицированная функция Бесселя первого рода I(n, z);
- BesselJ[n, z] — функция Бесселя первого рода J(и, z);
- BesselK[n, z] — модифицированная функция Бесселя второго рода К(п, z);
- BesselY[n, z] — функция Бесселя второго рода Y(n, z).
Соотношения между этими функциями хорошо известны. Следующие примеры показывают вычисление функций Бесселя.
| Ввод (In) | Вывод (Out) |
| Bessell[0,l.] | 1.26607 |
| Bessell[3,l.] | 0.0221684 |
| Bessell[l,2.+3.*I] | -1.26098 + 0.780149 I |
| Bessell[2,2.+3.*I] | 1.25767 + 2.31877 I |
| BesselK[2,2.+3.*I] | -0.0915555 + 0.0798916 I |
| BesselY[2,2.+3.*I] | -2.3443 + 1.27581 I |
| BesselY[2,2.+3.*I] | |
| N[BesselJ[l,0.5]] | 0.242268 |
| N[BesselJ[l, 2+1*3]] | 3.78068- 0.812781 I |
Приведем также пример на вычисление производной от функции Бесселя:
D[BesselJ[l, x], (х, 2}]
1/2 (-BesselJ[l, x] +
1/2 (-BesselJ[l, x] +BesselJ[3, x]) )
Нетрудно заметить, что результат в данном случае также представлен через функции Бесселя.
В другом примере — вычислении интеграла от функции Бесселя — результат выражается через гипергеометрическую функцию:
Integrate[BesselJ[2,x],x]
1/24 x3 HypergeometricPFQ [ { 2/3 }, { 5/2,3}, -x2/4]
На рис. 6.7 показаны графики функций Бесселя Bessell и BesselJ первых четырех порядков.
Рис. 6.7. Графики функций Бесселя Bessell (сверху) и Bessell (снизу) первых четырех порядков
Графики других функций Бесселя вы можете получить самостоятельно. Они представляют меньший интерес, чем графики, приведенные на рис. 6.7.
gl6-7.jpg
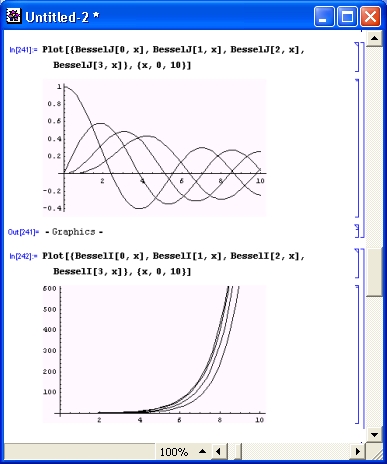
6. Гипергеометрические функции. Эллиптические интегралы и интегральные функции
Гипергеометрические функции
Класс гипергеометрических функций в системе Mathematica представлен следующими встроенными в ядро функциями:
- HypergeometricU [a, b, z] — конфлюэнтная (вырожденная) гипергеометрическая функция U(a, b, z);
- Hypergeometric0Fl [a, z] — гипергеометрическая функция 0 F 1 , (; a; z);
- HypergeometriclFl [а, b, z] — вырожденная гипергеометрическая функция Куммера 2 F 1 (a; b; z);
- Hypergeometric2Fl [a, b, с, z] — гипергеометрическая функция F 1 (a, b; c, z). Следующие примеры показывают вычисления гипергеометрических функций.
| Ввод (In) | Вывод (Out) |
| HypergeometricOFl [2 . , 1 . ] | 1.59064 |
| HypergeometricOFl [2 . , 2 . +3 . *I] | 1.22457 + 2.31372 I |
| HypergeometriclFl [1 . , 2 . , 2 . +3 . *I] | -1.03861 + 2.07929 I |
| Hypergeometric2Fl[l. ,2. ,3. ,2.+3.*I] | 0.0291956 + 0.513051 I |
На рис. 6.8 представлены графики ряда гипергеометрических функций, перечисленных выше.
Рис. 6.8. Графики гипергеометрических функций
Следует отметить, что число этих функций в ядре новых версий даже несколько сокращено по сравнению с предшествующими версиями. Убраны довольно редко используемые функции, в имени которых имеется слово Regularized.
Эллиптические интегралы и интегральные функции
В ядро системы Mathematica входят эллиптические функции и функции вычисления эллиптических интегралов:
- EllipticE [m] — полный эллиптический интеграл Е(т);
- EllipticE [phi, m] — эллиптический интеграл второго рода Е(Ф\т);
- EllipticExp [u, {a, b}] — обобщенный экспоненциал, связанный с эллиптической кривой у 2 = х 3 + ах 2 + bx,
- EllipticExpPrime [и, {а, Ь}] — производная по первому аргументу EllipticExp[u, {a, b}];
- Elliptic? [phi, m] — эллиптический интеграл первого рода Р(Ф\т);
- EllipticK[m] — полный эллиптический интеграл первого рода К(т)\
- EllipticLog [ {х, у}, {а, Ь}] — обобщенный логарифм, связанный ц эллиптической кривой у 2 = л 3 + а х 2 + b т,
- EllipticNomeQ [m] — возвращает значение q = Exp[-PiEllipticK[l - m]/EllipticK[m]];
- Elliptic?! [n, phi, m] — эллиптический интеграл третьего рода П(и; Ф\т);
- Elliptic?! [n, m] — полный эллиптический интеграл П(п|т);
- EllipticTheta [i, z, q] — эллиптическая тета-функция &.(z, q), где i = i, 2, 3 или 4;
- EllipticThetaC [u, m] — эллиптическая тета-функция Невилла $ с (и, т);
- EllipticThetaD [u, m] — эллиптическая тета-функция Невилла $ d (u, m);
- EllipticThetaN [u, m] — эллиптическая тета-функция Невилла $ п (и, m ) ;
- EllipticThetaPrime [i, z, q] — производная по второму аргументу эллиптической тета-функции в .(z, q), где i= I, 2, 3 или 4;
- EllipticThetaS [u, m] — эллиптическая тета-функция Невилла u s (w, т);
- FresnelCfx] — интеграл Френеля С(х),
- FresnelS[x] — интеграл Френеля S(x);
- InverseJacobi** [v, m] — обратная эллиптическая функция Якоби с обобщенным названием **. Возможны следующие наименования для **: CD , CN, CS, DC, DN, DS, NC, ND, NS, SC, SD И SN;
- JacobiAmplitude [u, m] — амплитуда для эллиптических функций Якоби;
- Jacobian — опция для FindRoot; может применяться для указания якобиана системы функций, для которых ищется корень;
- Jacob!** [u, m] — эллиптическая функция Якоби с обобщенным именем **, которое может принимать значения CD, CN, CS, DC, DN, DS, NC, ND, NS, SC, SD и SN;
- JacobiSymbol [n, m] — символ Якоби от n и in;
- JacobiZeta [phi, m] — дзета-функция Якоби Z(Ф|m);
- WeierstrassP [u, g2, g3] — эллиптическая функция Вейерштрасса Р,
- WeierstrassPPrime [u, g2, g3] — производная эллиптической функции Вейерштрасса Р'по переменной и.
Приведем примеры использования некоторых из этих функций.
| Ввод (In) | Вывод (Out) |
| EllipticE[0.1] | 1.53076 |
| EllipticE[Pi,0.1] | 3.06152 |
| EllipticF [Pi/2 ,0.1] | 1.61244 |
| EllipticPi[Pi,0.1] | -0.0266412- 1.09088 I |
| EllipticK[0.l] | 1.61244 |
| FresnelC[1.0] | 0.779893 |
| FresnelSfl.0] | 0.438259 |
| JacobiCD[l,0.2] | 0.605887 |
| JacobiZeta [ Pi , 0 . 5] | 0 |
| WeierstrassPPrime [1. ,2. ,3.] | -1.31741 |
Эллиптические функции (интегралы) широко используются в оптических расчетах и в астрофизике. На рис. 6.9 показаны графики некоторых эллиптических функций.
Рисунок 6.10 показывает построение контурного графика на комплексной плоскости с параметрическим заданием функций, выраженных через функцию Якоби и эллиптические интегралы. Нетрудно заметить, что график описывает довольно сложную и специфическую поверхность, содержащую периодические пики и впадины.
Читателю рекомендуется просмотреть ряд других примеров на использование функций данного раздела (например, в справочной базе данных системы Mathematica).
Рис. 6.9. Графики некоторых эллиптических функций
Рис. 6.10. Контурный график с параметрическим заданием комбинированной функции, содержащей функцию Якоби и эллиптические интегралы
gl6-10.jpg
gl6-8.jpg
gl6-9.jpg
7. Функции Эйри
Функции Эйри
Функции Эйри представляют собой независимые решения линейного дифференциального уравнения w"- zw = 0. В Mathematica эти функции представлены следующим набором:
- AiryAi [z] — возвращает значение функции Эйри Ai(z);
- AiryAiPrime [ z ] — возвращает значение производной функции Эйри Ai '(z);
- AiryBi [z] — возвращает значение функции Эйри Bi(z);
- AiryBiPrime [z] — возвращает производную функции Эйри Bi'(z).
Ниже представлены примеры на вычисление функций Эйри.
| Ввод (In) | Вывод (Out) |
| AiryAi [2. +3.*I] | 0.00810446 + 0.131178 I |
| AiryAi[l.] | 0.135292 |
| AiryBi [2. +3.*I] | -0.396368 - 0.569731 I |
| AiryBiPrime [2 . +3 . *I] | 0.349458 - 1.10533 I |
С функциями Эйри связаны многие специальные математические функции. Эта связь проявляется и при выполнении различных математических операций над функциями Эйри:
D[AiryAi[x],х]
AiryAiPrime[x]
Integrate[AiryBi[x],x]
{xGamma[1/3 ] HypergeometricPFQ[{1/3 }, {2/3,4/3}, x3/9]} /{3 31/6 Gamma [ 2/3 ] Gamma [ 5/3 ]}
{ x2Gamma[1/3 ] HypergeometricPFQ[{1/3 }, {2/3,4/3}, x3/9]} /{3 35/6 Gamma [ 4/3 ] Gamma [ 5/3 ]}
Series[AiryBi[x],{x,0,5}]
{1 /31/6xGamma[2/3]}+ {31/6x /Gamma[1/3]}+ {x3 /631/6Gamma[2/3]}+{x4 /435/6Gamma[1/3]}+O[x]6
Графики функций, Эйри представлены на рис. 6.11.
Нетрудно заметить, что при х < 0 они имеют колебательный характер.
Рис. 6.11. Графики функций Эйри (сверху) и их производных (снизу)
Бета-функция и родственные ей функции
Класс бета-функций, имеющих специальное интегральное представление, в Mathematica представлен следующим набором:
- Beta [а, b] — эйлерова бета-функция В(a, b);
- Beta[z, а, b] — неполная бета-функция;
- Beta[z0, zl, a, b] — обобщенная неполная бета-функция Beta [z1, a, b] - Beta[z0, а, b];
- BetaRegularized [z, a> b] — регуляризированная неполная бета-функция I(z,a,b) = Betafz, a, b]/Beta[a, b];
- BetaRegularized [z0, zl, a, b]—регуляризированная обобщенная неполная бета-функция I(z1l,a,b) - I(z0, a, b).
Поимепы на вычисление этих функций представлены ниже.
| Ввод (In) | Вывод (Out) |
| Beta[l.,2.] | 0.5 |
| Beta[l.,2.,3.] | 0.0833333 |
| Beta[2.+3.*I,4.+6.*I,l,2] | 4. - 12. I |
| BetaRegulari zed [0.1,1,2] | 0.19 |
gl6-11.jpg
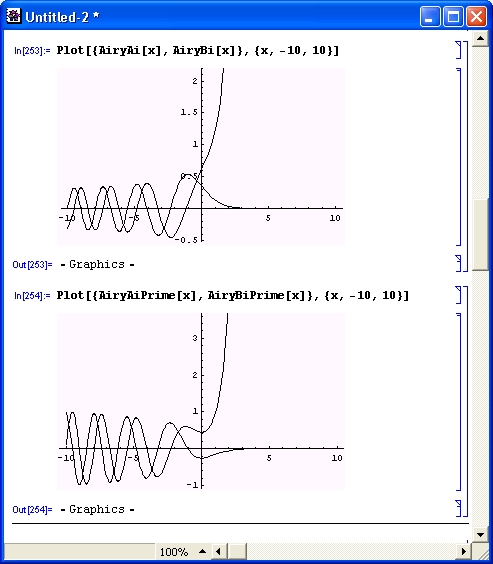
8. Специальные числа и полиномы
Специальные числа и полиномы
Для вычисления специальных чисел и полиномов служит следующая группа функций:
- BernoulliB [n] — n-е число Бернулли;
- BernoulliB [n, х] — полином Бернулли n-й степени;
- Binomial [n, m] — биномиальный коэффициент;
- Cyclotomic [n, х] — циклотомический полином порядка п по переменной х;
- EulerE[n] — n-е число Эйлера;
- EulerE[n, х] — n-й полином Эйлера;
- EulerPhi [n] — эйлерова функция сумм ф(n) — количество положительных целых чисел, не превосходящих п и взаимно простых с и;
- Fibonacci [n] — n-е число Фибоначчи;
- Fibonacci [n, х] — полином Фибоначчи F n (x);
- Multinomial [n1, n2, . . . ] — мультиномиальный коэффициент (n! + n2 + . . .) !/(n1! n2! ...);
- NBernoulliB [n] — численное значение n-го числа Бернулли;
- NBernoulliB [n, d] — n-е число Бернулли с n?-цифровой точностью представления;
- Pochhammer [а, n] — символ Похгамера;
- StirlingSl [n, m] — число Стирлинга первого рода;
- StirlingS2 [n, m] — число Стирлинга второго рода.
Ниже представлены примеры вычисления данных функций.
| Ввод (In) | Вывод (Out) |
| N [BernoulliB [2]] | 0.166667 |
| BernoulliB [2, 0.1] | 0.0766667 |
| Binomial [6, 4] | 15 |
| Cyclotomic [ 5, х] | 1 + x + x 2 + x 3 + x 4 |
| Cyclotomic [5,0.2] | 1.2496 |
| EulerE[2] | -1 |
| EulerE[2,0.1] | -0.09 |
| EulerPhi [2] | 1 |
| Fibonacci [10] | 55 |
| Fibonacci [ 6 , x] | 3 x + 4 x 3 + x 5 |
| Pochhammer [1,3] | 6 |
| StirlingSl [8, 4] | 6769 |
На рис. 6.12 показаны графики полиномов Бернулли и циклотомического полинома различных порядков.
Рис. 6.12. Графики полиномов Бернулли (сверху) и циклотомических полиномов (снизу)
Обратите внимание на то, что здесь использована функция Plot, модифицированная пакетом расширения plot.m, который будет описан в уроке 10. Эта функция позволяет автоматически строить графики ряда функций с линиями разного стиля, что облегчает их распознавание.
На рис. 6.13 представлены графики полиномов Эйлера EulerE разного порядка п.
Помимо описанных выше, в ядро системы входит также ряд других, менее распространенных функций. Они описаны в приложении.

Рис. 6.13. Графики полиномов Эйлера разного порядка
gl6-12.jpg
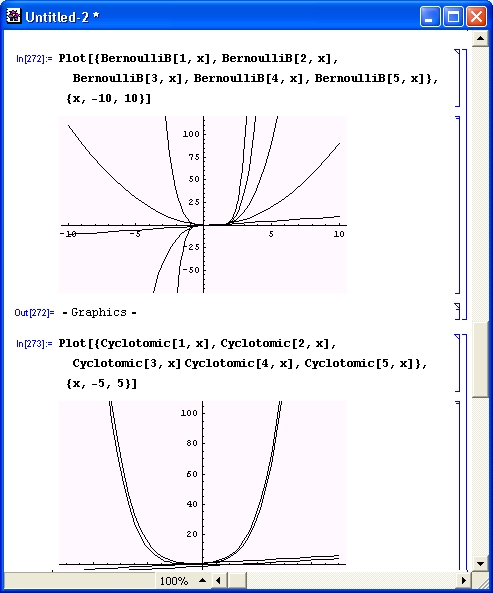
gl6-13.jpg
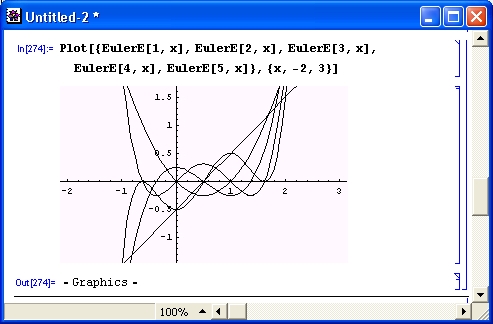
9. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Вычислять ортогональные многочлены.
- Вычислять интегральные показательные и родственные им функции.
- Вычислять гамма- и полигамма-функции.
- Работать с функциями Бесселя разного рода и порядка.
- Вычислять гипергеометрические функции.
- Вычислять эллиптические интегралы и интегральные функции.
- Вычислять функции Эйри.
- Вычислять бета-функцию и родственные ей функции.
- Использовать специальные числа и полиномы.
Урок 7. Работа с периферийными устройствами
Урок 7. Работа с периферийными устройствами
1. Работа с периферийными устройствами
Работа с периферийными устройствами
- Функции ввода/вывода
- Работа со строками
- Потоки и файлы
- Запись определений
- Системные функции
Если пользователь использует систему Mathematica для выполнения чисто математических расчетов, то он может ничего не знать о подавляющем большинстве описанных в этом уроке функций. Их основное назначение — незаметная поддержка работы с периферийными устройствами ввода/вывода. Однако все функции этого урока открыты для опытных пользователей, стремящихся использовать систему в составе программных комплексов. Здесь рассматривается только часть функций для работы с периферийными устройствами — даны те из них, которые используются достаточно часто. Многие функции этой группы перечислены в приложении.
Ввод/вывод в системе Mathematica организован с помощью интерфейсного процессора (FrontEnd) настолько естественно, что у большинства пользователей едва ли появится искушение изменять формы ввода/вывода по сравнению с установленными по умолчанию. Тем не менее, это возможно с помощью обширного набора команд, имеющихся в меню системы.
Более того, система предоставляет пользователю обширные возможности по организации ввода/вывода и различных форм диалога с помощью соответствующих функций, команд, директив и опций. Эти средства входят в язык программирования систем Mathematica и нередко используются для подготовки серьезных документов (например, обучающих и тестирующих программ), а также для создания пакетов расширения.
Прежде всего отметим функции ввода/вывода, позволяющие организовать диалог с системой в стиле, подобном тому, что используется при программировании на Бейсике. Основные функции для этого следующие:
- Input [ ] — останавливает работу системы и возвращает значение выражения, которое будет введено в появившемся диалоговом окне (служит для организации диалогового ввода);
- Input [ "prompt" ] — то же, что и предыдущая функция, но с выводом в диалоговое окно комментария prompt;
- InputString [ ] — выполняет интерактивное чтение в символьную строку;
- InputString [ "prompt" ] — то же, но с выводом в диалоговое окно комментария prompt;
- StylePrint [ехрr] — создает в текущем документе новую ячейку со стилем по умолчанию и заносит в нее выражение ехрг;
- StylePrint[expr,"style"] — создает в текущем документе новую ячейку со стилем style и заносит в нее выражение ехрr;
- Print [expr] — выводит на экран дисплея значение выражения ехрг; совместно с Input может использоваться для организации диалога;
- Print ["prompt", expr] — выводит на экран дисплея текстовый комментарий, указанный в кавычках, и следом — значение выражения ехрr.
Этих функций достаточно для организации простейшего диалога с программой.
На рис. 7.1 показан простейший пример организации диалога в стиле, принятом в языке Бейсик. В данном случае вычисляется длина окружности с запросом радиуса R.
Рис. 7.1. Пример организации диалога
При вычислении документа, приведенного на рис. 7.1, вначале исполняется функция Input. Это ведет к появлению диалогового окна в центре экрана — на рис. 7.1 оно несколько смещено вниз, чтобы не загораживать содержимое ячейки документа. В окне виден запрос, который указан в кавычках как параметр функции Input. После ввода нужного значения (в нашем примере это радиус окружности) и нажатия клавиши Enter или щелчка на кнопке ОК диалогового окна функция Input возвращает введенное значение, и оно присваивается переменной Р.. После этого функция Print выводит на экран вычисленное значение длины окружности с кратким комментарием (рис. 7.2).
Рис. 7.2. Документ рис. 7.1 по окончании диалога
Разумеется, для данного примера нет никакого смысла организовывать диалог в такой форме, поскольку однократное вычисление длины окружности проще задать прямо в тексте документа без запроса радиуса — просто указав R = 10. Однако при составлении сложных программ, например ориентированных на многократные вычисления с различными данными по скрытым формулам, такая возможность организации диалога очень полезна. Ее можно использовать и при составлении обучающих программ на базе системы Mathematica.
К сожалению, комментарий, отображаемый в окне функции ввода Input, возможен только на английском языке — при вводе символов кириллицы вместо обычных надписей выводятся коды (в то же время функция Print исправно выводит комментарии на русском языке). Это связано с выбором для данного окна шрифта, не содержащего символов кириллицы.
gl7-1.jpg
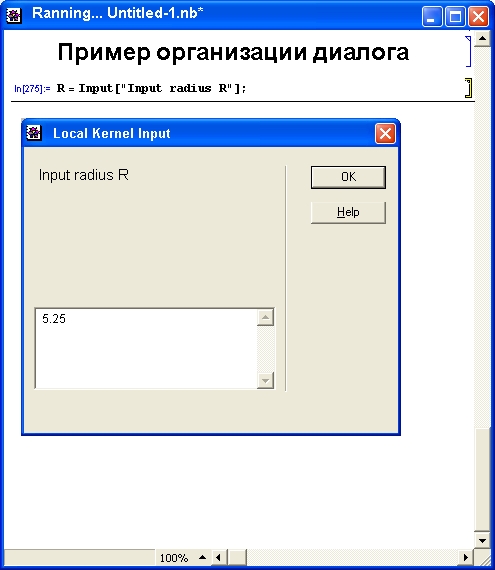
gl7-2.jpg
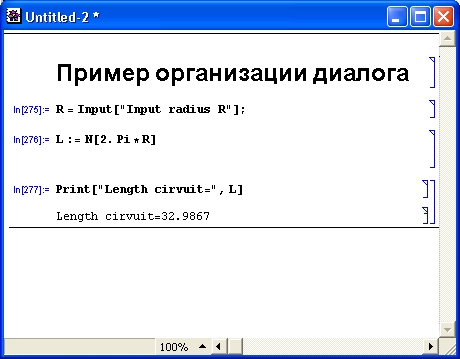
2. Функции задания формата вывода
Функции задания формата вывода
Далее отметим функции, меняющие формат представления выражений. Все они имеют в своем названии слово Form (форма). Таких функций довольно много, и их полный список вы найдете в приложении. Отметим лишь несколько наиболее часто используемых функций этого рода:
- AccountingForm [ехрг] — выполняет вывод всех чисел, содержащихся в выражении ехрr, в бухгалтерской форме представления;
- CForm[expr] — выполняет вывод expr в форме, принятой для языка С;
- EngineeringForm [expr ] — дает вывод, представляя все вещественные числа в выражении expr в инженерной форме (это означает, что порядок чисел равен нулю или кратен трем);
- FortranForm[expr] — выводит expr в форме, принятой для языка Фортран;
- FullForm [expr] — выводит полную форму выражения expr без использования специального синтаксиса;
- InputForm[expr] — выводит expr во входной форме;
- NumberForm[expr, n] — выполняет вывод expr с вещественными числами, представленными с точностью до n цифр;
- OutputForm [expr] — выполняет вывод expr в стандартной выходной форме системы Mathematica;
- ScientificForm [expr] — выполняет вывод, представляя все вещественные числа в выражении expr в научном формате;
- TeXFormfexpr] — выводит expr в форме, принятой для языка ТеХ, ориентированного на верстку текстов с математическими формулами;
- TextForm[expr] — выполняет вывод expr в обычном текстовом формате;
- TreeForm [expr] — выполняет вывод expr с показом разных уровней выражения.
В большинстве своем действие этих функций вполне очевидно. Если это не так, то смело экспериментируйте с ними. Следующие примеры дают представление об использовании различных форм вывода в системе.
| Ввод (In) | Вывод (Out) |
| Accounting [30*10^15] | Accounting [30000000000000000] |
| BaseForm [55434, 16] | d88a 16 |
| CForm[x ^ 2+3*x+x] | 4*x + Power (x, 2) |
| ColumnForm [ { а , b , с ) ] | a b с |
| EngineeringForm[N[12*10 A 29] ] | 1.2xl0 30 |
| Format [Exp [x ^ 2 ] /а] | e x 2 /a |
| FortranForm[Exp[x] ^ 2/а] | E**(2*x)/a |
| HoldForm[Exp[x] ^ 2/а] | e 2x /a |
| NumberForm[N[Exp[2]] ,15] | 7.38905609893065 |
| OutputForm [Exp [x]^2/a] | e 2x /a |
| TeXForm[Exp [x]^2/a] | \frac{e^{2\,x}}{a} |
| Scientif icForm[12*10 ^ 5] | 1200000 |
Приведем еще несколько примеров использования различных форм вывода (здесь содержимое ячеек вывода дано под содержимым ячеек ввода):
FullForm[Exp[x]^2/а]
Times[Power[a, -1, Power[E, Times[2, х]]]
TreeForm[Exp[x]^2/а]
Times[ , ] Power[a, -1] Power[E, | ]
Times[2, x]
PaddedForm[(х^З+2*х^2+3*х-1)/ (x-1) ,3]
(2 3 -l+3x+2x +x)/(-1 + x)
PrecedenceForm[12*b/c,5]
a + 12 b/c
SequenceForm[Exp[x]^2/a]
E^2 x/a
TableForm[{{"x","y"},{l,2},{3,4},{5,6}}]
x у
1 2
3 4
5 6
Prefix[f[x^2]]
2
f@ (x )
Unevaluated[Exp[х^(a/b)]/x/a]
a/b
Exp[x ] Unevaluated[Exp[x^a/b]/x a]
3. Удаление введенных в ходе сессии определений
Удаление введенных в ходе сессии определений
Мы уже не раз отмечали возможность уничтожения введенных в ходе сессии определений. Приведем в систематизированной форме функции, используемые для этого:
- Clear [symbol1, symbol2,...] — стирает значения и определения для указанных символов (идентификаторов);
- Clear ["pattern1", "pattern2",...] — стирает значения и определения для всех символов, чьи имена подходят под любой из указанных строковых шаблонов;
- ClearAll [symboll, symbo!2,...] — стирает все значения, определения, атрибуты, сообщения и значения, принятые по умолчанию, связанные с указанными символами;
- ClearAll ["patternl", "pattern2",...] — стирает все символы, чьи имена буквально подходят к одному из указанных строковых образцов;
- ClearAttributes [s, attr] — удаляет attr из списка атрибутов символа s.
Применение большинства этих функций полезно разработчику серьезных приложений для систем Mathematica, например новых пакетов расширений и применений системы. В то же врем-я, для большинства пользователей вполне достаточно возможностей, предоставляемых системой по умолчанию — средств диалога с ее оболочкой и функций Input и Print.
Хотя Mathematica ориентирована на математические приложения, в ней достаточно полно представлены функции для работы со строками (strings). Они могут потребоваться как для организации вывода текстовых сообщений (например надписей на графиках), так и для организации текстового диалога при разработке пакетов расширений и приложений системы. К тому же надо постоянно помнить, что Mathematica — система символьной математики, так что символьным преобразованиям, как сугубо математическим, так и общепринятым, в ней, естественно, уделено много внимания.
Многие функции для работы со строками выполняют общепринятые преобразования, имеющиеся в большинстве языков программирования высокого уровня. Строкой является произвольная цепочка символов, заключенная в кавычки, например "String". Ниже представлены некоторые функции для работы со строками:
- StringByteCount ["string"] — возвращает полное число байтов, используемых для хранения символов в строке "string";
- StringDrop ["string", {m, n}] — возвращает строку "string", удалив в ней символы от m до п;
- StringJoin["sl", "s2",...] или StringJoin [ { "s1", "s2",...}]-формирует строку, содержащую конкатенацию (объединение) указанных строк "s1";
- Stringlnsert ["string1", "string2",M] — вставляет строку "string2" в строку "string1", начиная с позиции М от начала этой строки (при отри-, цательном М позиция отсчитывается от конца указанной строки);
- StringLength ["string" ] — возвращает число символов в строке;
- StringReplace["string", "s1 -> "spl"] или StringReplace["string", {"s1" -> "spl", "s2" -> "sp2",...}] — замещает "s1" на "spi" всякий раз, когда они появляются как подстроки "string";
- StringReverse ["string"] — меняет порядок символов в строке "string" на противоположный;
- StringPosition["string", "sub"] — возвращает список с позициями строки "sub" в строке "string" (дополнительные формы см. в справочной системе);
- StringTake ["string", n] — возвращает строку, состоящую из первых п символов строки "string";
- StringTake ["string", -n] — возвращает последние п символов из строки "string";
- StringTake ["string", {n}] — возвращает n-й символ в строке "string";
- StringTake ["string", {m, n}] — возвращает строку из символов, расположенных в позициях от m до п строки "string".
Эти функции хорошо известны программистам, работающим с современными языками программирования. Большое число дополнительных функций для работы со строками можно найти в приложении. Обилие таких функций в языке программирования системы Mathematica указывает на его универсальный характер и обширные возможности в решении даже на первый взгляд далеких от математики задач. Ниже приведены примеры действия ряда функций работы со строками.
| Ввод (In) | Вывод (Out) |
| StringByteCount [ "Hello ! " ] | 6 |
| StringDrop ["Hello my friend!", 6] | my friend! |
| StringDrop ["Hello my friend! ", -10] | Hello |
| StringDrop ["Hello my friend! ", {7}] | Hello у friend! |
| StringDrop [ "Hello my friend ! " , { 6 , 8 } ] | Hello friend! |
| Stringlnsert ["Hello friend!"," my", 6] | Hello my friend! |
| StringJoin ["Hello"," my "]<>"friend!" | Hello my friend! |
| StringLength [ "Hello" ] | 5 |
| StringPosition[ "Hello my friend! ", "e"] | {{2, 2}, {13, 13}} |
| StringReplace["Hilo" , "i"->"el"] | Hello |
| StringReverse [ "Hello ! " ] | !olleH |
| StringTakef "Hello my friend!", 6] | Hello |
| StringTake[ "Hello my friend!", -8] | friend! |
| StringTake [ "Hello my friend ! " , { 7 , 9 } ] | my |
Отметим еще несколько функций, относящихся к работе с символами и строками:
- FromCharacterCode [n] — возвращает строку, состоящую из одного символа с кодом n;
- FromCharacterCode [ {n1, n2,...}] — возвращает строку, состоящую из последовательности символов с кодами ni;
- Characters ["string"] — возвращает список целочисленных кодов, соответствующих символам строки "string";
- ToLowerCase ["string"] — производит строку, в которой все буквы преобразованы в нижний регистр;
- ToString [expr] — возвращает строку, соответствующую форме вывода выражения ехрг. Опции устанавливают ширину линии, тип формата и т. д.;
- ToUpperCase [ "string" ] — вырабатывает строку, в которой все буквы преобразованы в верхний регистр;
- Unique [ ] — создает новый символ с именем в форме $nnn (nnn — уникальный порядковый номер);
- Unique [х] — создает новый символ с именем в форме x$nnn (nnn — уникальный порядковый номер);
- Unique [ {х, у,...}]— создает список новых символов с уникальными именами;
- Unique [ "ххх" ] — создает новый символ с именем в форме xxxnnn (nnn — уникальный порядковый номер);
- Unique [name, {attrl, attr2,...}] — создает символ с указанными атрибутами attri;
- UpperCaseQ [string] — возвращает True, если все символы строки string являются прописными буквами (верхнего регистра), иначе возвращает False.
Примеры, приведенные ниже, показывают работу с этими функциями.
| Ввод (In) | Вывод (Out) |
| ToCharacterCode [ "Hello ! " ] | {72,101,108,108,111,33} |
| FromCharacterCode [ {72 , 101 , 108 , 108 , 111 , 33} ] | Hello! |
| ToExpression [ "2+3*4 " ] | 14 |
| ToLowerCase [ "HeLLo ! " ] | hello! |
| ToUpperCase [ "Hello" ] | HELLO |
| Ввод (In) | Вывод (Out) |
| x:=ToString[2+3*4] | |
| X | 14 |
| Unique [ ] | $1 |
| Unique [xyz] | xyz$2 |
| Unique [xyz] | xyz$3 |
| UpperCaseQ [ "Hello" ] | False |
| UpperCaseQ [ "HELLO" ] | True |
4. Потоки и файлы
Потоки и файлы
Система Mathematica имеет развитые средства для работы с потоками (streams) и файлами (files). Под потоком подразумевается непрерывная последовательность данных, циркулирующих внутри компьютера. Обмен потоками происходит практически непрерывно, например, при вводе поток ввода поступает от клавиатуры в компьютер, при печати поток данных поступает от компьютера в принтер через порт принтера и т. д.
Файлом является упорядоченная структура данных, имеющая имя и хранящаяся на каком-либо носителе, чаще всего на магнитном диске. Файлы могут иметь различные форматы и различный тип доступа к хранимой на них информации. Наиболее распространенные в системе Mathematica файлы документов являются файлами с последовательным доступом и имеют текстовый формат.
Последовательный доступ означает, что информация из открытого файла может быть считана строго последовательно от его начала до конца, отмеченного специальной меткой. Это напоминает считывание с магнитофонной кассеты. Текстовый формат означает, что все данные записаны в виде ASCII-кодов. Следовательно, прочесть такой файл можно с помощью любого текстового редактора, работающего с текстами в виде ASCII-кодов.
Потоки и файлы имеют много общего: имена, определенную структуру, необходимость открытия перед использованием и закрытия после использования. Однако если с файлами пользователь сталкивается уже в начале работы с системой (нужно вызвать файл с демонстрационным документом или сохранить его, а затем вызвать другой файл), то с понятием потока при работе с системой сталкиваться практически не приходится, хотя помимо нашей воли потоки данных постоянно текут между компьютером и его периферийным оборудованием.
Прежде чем рассматривать весьма обширные возможности системы по работе с файлами в целом, отметим упрощенный прием вызова файла с помощью двойного символа «<<»:
<<filename
Эта команда считывает файл с указанным именем filename и заносит в память компьютера содержащиеся в нем определения. Имя файла надо указывать полностью, то есть вместе с расширением. Исключением является случай, когда файл находится в основном каталоге системы. Эта команда эквивалентна функции
Get["filename", key]
Для записи объекта (переменной, массива, списка и т. д.) в файл служат упрощенные команды:
- expr >> filename — передает значение ехрг в файл с заданным именем;
- ехрг >>> filename — добавляет ехрг в конец файла с заданным именем.
Указанные команды по существу есть укороченные (и потому более удобные) формы следующих функций:
- Get ["filename", "key"] — читает файл, который закодирован функцией Encode с использованием ключа "key";
- GetContext [ "context' " ] — загружает файл с заданным контекстом;
- Put[exprl, expr2, ..., "filename"] — записывает последовательность выражений expri в файл с именем filename;
- PutAppend[expr1, expr2, ..., "filename"] — присоединяет последовательность выражений expri к файлу с именем filename.
Еще одна упрощенная функция — ! ! filename — выводит содержимое файла с заданным именем.
Следующие примеры показывают запись списка в файл C:\ma.vat, его считывание, затем добавление в файл еще одного списка и контроль контекста файла:
{{l,2,3},{4,5,6},{a,b,c}}>>C:\ma.val
<<С: \ma. val
{{1, 2, 3}, {4, 5, б), {а, b, с}} {d,e,f}>>>C: \ma.val
<<С: \та. val
{d, e, f}
!!С:\mа.val
1, 2, 3, 4, 5, б, а, b, с d, e, f
Такая форма вызова особенно удобна для вызова файлов пакетов расширений и применений системы. Имя файла указывается по правилам, принятым в MS-DOS. Файлы пакетов применений имеют расширение .т. Мы уже приводили примеры использования определений, содержащихся в файлах пакетов расширения системы.
Имеется еще ряд функций для работы с файлами:
- ReadList ["filename" ] — читает все оставшиеся в файле "filename" выражения и возвращает их в виде списка;
- ReadList ["filename", type] — читает из файла "filename" объекты указанного типа type до конца файла. Возвращает список считанных объектов;
- ReadList ["filename", {typel, type2,...}] — читает объекты указанных типов type1 до конца файла filename;
- ReadList [ "filename", types, n] — читает только первые п объектов указанных типов types из файла filename;
- Save ["filename", x1, x2,...] — создает файл с заданным именем filename, содержащий значения переменных x1, х2, ...;
- ! command — исполняет заданную команду операционной системы.
Допустим, что в любом текстовом редакторе создан файл с полным именем C:\datas.txt в ASCII-формате, содержащий просто шесть чисел с разделительными пробелами, размещенные в двух строках и представляющие массив 2x3 элемента:
1 11.2 34.5
2. 3.4 56
Тогда о структуре файла можно судить, используя команду
!!С:\datas.txt
1 1.2 34.5 2. 3.4 56.
Нетрудно заметить, что структура файла соответствует структуре массива. Однако считывание файла командой «name дает следующий результат:
<<С: \datas. txt
380.8
Результат представляет вычисленное выражение второй строки файла. Считывание функцией ReadList без дополнительного аргумента также дает ошибочный результат:
ReadList["С:\datas.txt"]
{41.4, 380.8}
Нетрудно подметить, что функция восприняла каждую строку содержимого файла как результат перемножения трех чисел (пробел на языке Mathematica означает умножение). С дополнительным параметром Number все числа считываются верно:
ReadList["С:\datas.txt", Number]
{1, 1.2, 34.5, 2., 3.4, 56.}
Однако мы получили одномерный список — данные просто считываются построчно. Применение дополнительного параметра в виде {Number, Number} дает следующий результат:
ReadList["С:.txt", {Number, Number}]
{{1, 1.2), {34.5, 2.}, {3.4, 56.}}
Правильный результат можно получить, используя опцию RecordList->True: .
ReadList["C:.txt",Number,RecordLists-XTrue]
{{1, 1.2, 34.5), {2., 3.4, 56.}}
Для загрузки файлов пакетов расширений (Add-On) используются функции, позволяющие задать контекст файлов (подробнее о контекстах речь пойдет в уроке 10):
- Needs ["context' ", "filename"] — загружает файл, если указанный контекст отсутствует в списке загруженных;
- Needs [ "context s " ] — загружает файл, имя которого определяется с помощью функции ContextToFilename [ "context ч " ], если указанный контекст отсутствует в списке загруженных.
Загрузка файлов с указанием их контекстов позволяет избежать конфликтов между разными пакетами расширения, используемыми одновременно (см. более подробно урок 10).
5. Использование файлов других языков программирования
Использование файлов других языков программирования
Из функций для работы с файлами особо надо отметить следующую функцию-директиву:
- Splice [ "file .mx" ] — вставляет в файлы на других языках программирования вычисленные выражения системы Mathematica, которые должны быть записаны в скобках вида <* и *>;
- Splice ["infile", "outfile"] — читает файл infile, интерпретирует фрагменты, содержащиеся между скобками <* и *>, и записывает результат в файл outfile.
Эта возможность особенно существенна при использовании программ на языках программирования С (расширение .me), Fortran (расширение .mf) и ТеХ (расширение .mtex), для форматов которых Mathematica имеет средства конвертирования выражений (CForm, FortranForm и TexForm соответственно). Таким образом, имеется возможность экспорта выражений системы Mathematica в программы, составленные на этих языках.
Поясним применение функции-директивы Splice. Пусть имеется экспортированная программа на языке С, которая должна рассчитывать численное значение некоторого интеграла, и мы хотим получить формулу для этого интеграла средствами системы Mathematica. Допустим, она представлена файлом demo.me. Его можно просмотреть следующим образом:
!!demo.me
#include "mdefs.h"
double f(x)
double x;
{
double y;
у = <* Integrate[Sin[x]^5, x] *> ;
return (2*y- 1) ;
}
После исполнения функции Splice ["demo.me"] программа будет записана в файл demo.с, в котором выражение в скобках <*...*> заменено вычисленным значением интеграла (в форме CForm). Файл при этом будет выглядеть так:
!!demo.с
#include "mdefs.h" double f(x) double x;
{
double y;
у = -5*Cos(x)/8 + 5*Cos(3*x)/48- Cos(5*x)/80 ;
return (2*y- 1) ;
}
Из простых функций, обеспечивающих создание файлов с заданными определениями, надо отметить также функцию Save:
Save ["filename", symb1, symb2,...]
Она добавляет определения символов symbi к файлу filename (возможны упрощенные формы Save).
Приведем пример ее использования:
f[x_] = Sin[x] + y
у+ Sin[x]
у=а
а
Save["demol",f]
!!demol
f[x_] = у + Sin[x]
у = а
6. Другие функции для работы с файлами
Другие функции для работы с файлами
В целом средства системы Mathematica обеспечивают возможности работы с различными файлами, присущие MS-DOS, без выхода из среды системы. Относящиеся к этой группе функции даны в приложении. Для этих функций характерно, что в момент выполнения они не дают видимого эффекта. К таким функциям относятся функции копирования директорий и файлов, смены их имен, удаления и т. д. Они хорошо известны пользователям MS-DOS и могут выполняться из среды Mathematica.
Рассматривая обширный список файловых и поточных операций, можно поневоле сделать вывод об их избыточности. Но здесь действует простое правило: не хочешь применять эти функции — не применяй! Они рассчитаны на пользователя, всерьез занимающегося стыковкой систем Mathematica с другими программными системами.
Важное место занимают функции, дающие информацию о директориях, файлах и потоках. К ним относятся следующие функции:
- Directory [ ] — возвращает текущий рабочий каталог;
- DirectoryStack [ ] — возвращает содержимое стека каталогов, которое представляет последовательность используемых в текущем сеансе каталогов;
- $Display— возвращает список файлов и каналов (pipes— канал или абстрактный файл), используемый функцией вывода $DisplayFunction по умолчанию;
- FileByteCount ["filename"] — возвращает количество байтов в файле;
- FileDate ["filename"] — возвращает дату и время последней модификации файла в виде списка;
- Filelnformation ["filename"] — возвращает информацию о файле;
- FileNames [ ] — приводит список всех файлов в текущем рабочем каталоге;
- FileNames [" form" ] — перечисляет все файлы в текущем рабочем каталоге, чьи имена совпадают с шаблоном form;
- FileNames [{ "forml", "form2",...} ] — перечисляет все файлы, чьи имена соответствуют любому из шаблонов formi;
- FileNames [forms, {"dirl", "dir2",...} ] — перечисляет файлы с именами, соответствующими шаблонам forms, в любом из указанных каталогов diri;
- FileType ["filename"] — возвращает тип файла: File, Directory или None (если указанного файла не существует);
- $HomeDirectory — дает имя «домашней» директории пользователя;
- $Output — дает список файлов и каналов, в которые направляется стандартный вывод системы Mathematica;
- ParentDirectory [ ] — возвращает имя родительского каталога для текущего рабочего каталога;
- ParentDirectory ["dir"] — возвращает имя родительского каталога для каталога dir;
- $ Path — дает список каталогов для просмотра при попытке поиска внешнего файла;
- StreamPosition [stream] — возвращает целое число, которое указывает позицию текущей точки в открытом потоке stream;
- Streams [ ] — возвращает список всех потоков, открытых в данный момент;
- Streams ["name" ] — перечисляет только потоки с указанным именем name.
Приведенные ниже примеры иллюстрируют использование большинства из этих достаточно простых функций:
Directory[]
C:\PROGRAM FILES\WOLFRAM RESEARCH\MATHEMATICA\4.0
DirectoryStack[]
{} / $Display
stdout
FileByteCount["C:.val"]
46
FileDatef'C: .val"]
{1999, 8, 3, 16, 4, 44}
FileInformation["C:.val"]
{File->C:\ma.val, FileType->File, Date -> 3142685084, ByteCount ->46}
Filenames[]
{Examples, FILES, MATHEMATICA.EXE,
MATH.EXE, MATHINSTALLER.EXE, MATHKERNEL.EXE}
FileType["C:.val"]
File HomeDirectory[]
c:\ $0utput
{OutputStream[stdout, 1]}
ParentDirectory[]
С: \m3 Streams[]
{OutputStream[stdout, 1],
OutputStream[stderr, 2]}
Высказанное выше соображение об избыточности набора операций вполне применимо и для этих функций.
Для управления системой в процессе вычислений служат системные директивы и функции. Некоторые из них широко используются при программировании решения прикладных задач, другие служат в основном для контроля над системой.
Имена многих, вспомогательных с точки зрения конечного пользователя, системных функций начинаются с символа $. Ниже описаны основные системные функции.
Ряд системных функций служит для получения информации о времени и текущей дате:
- AbsoluteTime[ ] — возвращает полное количество секунд, прошедших с момента 1 января 1900 г.;
- $CreationDate — возвращает дату и время создания используемой версии системного ядра Mathematical
- Date [ ] — возвращает текущее значение даты и времени в виде {год, месяц, день, час, минута, секунда};
- FromDate [date] — превращает дату date вида {год, месяц, день, час, минута, секунда} в число секунд, прошедших с 1 января 1900 г.;
- TimeUsedt ] — возвращает полное количество секунд процессорного времени, использованного на данный момент в текущем сеансе Mathematical
- $TimeUnit — возвращает минимальный временной интервал в секундах, который можно зарегистрировать в вашей компьютерной системе;
- TimeZone [ ] — возвращает часовой пояс, установленный для вашей компьютерной системы;
- Timing [ехрг] — вычисляет ехрг и возвращает список, состоящий из значения затраченного времени и результата вычислений;
- ToDate [time] — преобразует абсолютное время в секундах, прошедшее с 1 января 1900 г., в дату вида {год, месяц, день, час, минута, секунда}.
Следующие примеры иллюстрируют применение некоторых из этих функций.
| Ввод (In) | Вывод (Out) |
| AbsoluteTime [ ] | 2967708137 |
| Date[] | {2000, 7, 16,11, 23, 8} |
| FromDate [ {2000 ,7,15,4,51,30}] | 3172625490 |
| SessionTime[] | 8171.1 |
| TimeUsedf] | 69.57 |
Их действие вполне очевидно и не требует комментариев.
7. Общесистемные функции
Общесистемные функции
Ниже представлены функции общесистемного характера:
- $Aborted — возвращает сообщение о прекращении вычислений при их прерывании функцией Abort [ ];
- AbortProtect [ехрг] — вычисляет ехрг, запоминая все попытки прерывания, но не выполняя их до тех пор, пока не будет завершено вычисление либо пока не будет вызвана процедура CheckAbort;
- Accuracy [x] — указывает число цифр в числе х после десятичной точки, которое используется при вычислениях;
- ByteCount [expr] — возвращает число байт, которое используется для представления выражения ехрг;
- Environment [ "var" ] — возвращает значение переменной окружения операционной системы с именем "var";
- $ Line — глобальная переменная, указывающая номер текущей строки ввода;
- $MachineEpsilon — возвращает машинную точность представления — наименьшее число, которое, будучи прибавленным к 1.0, даст результат, отличный от 1.0;
- $MachineID — строка, которая возвращает, если возможно, уникальный код идентификации применяемого компьютера;
- $MachineName — строка, возвращающая имя, которое присвоено используемому компьютеру, если такое имя определено;
- $MachinePrecision — возвращает количество десятичных знаков точности представления чисел;
- $MachineType — строка, возвращающая общий тип компьютера, на котором запущена система Mathematical
- $MinMachineNumber — наибольшее машинно-представимое число, которое может применять данная компьютерная система;
- $MaxNumber — возвращает наибольшее из представимых в системе Mathe-matica чисел;
- $MinMachineNumber — наименьшее положительное машинно-представимое число, которое может применять данная компьютерная система;
- $MinNumber — возвращает наименьшее (положительное) представимое в системе Mathematica число;
- $OperatingSystem — строка, дающая тип операционной системы, под управлением которой работает Mathematica;
- Pause [n] — выдерживает паузу не менее п секунд;
- $ReleaseNumber — целое число, которое дает младший номер версии ядра данной системы Mathematica;
- $Remote — имеет значение True, если Mathematica применяется в дистанционном режиме или с программным препроцессором, иначе — значение False;
- $SessionID — уникальный номер, который присвоен данному сеансу системы Mathematica;
- SessionTime[ ] — возвращает полное число секунд реального времени, прошедшего с момента начала вашего сеанса работы в системе Mathematica; -
- $System — представляет собой строку с указанием типа используемой компьютерной системы;
- $Version — символьная строка, которая представляет используемую версию системы Mathematica;
- $VersionNumber — вещественное число, которое дает полный номер текущей версии системного ядра Mathematica.
Ниже приведены примеры использования ряда общесистемных функций.
| Ввод (In) | Вывод (Out) |
| Accuracy [12. 34] | 15 |
| ByteCount [Exp [x] A 2/a] | 120 |
| $Version | 4.0 for Microsoft Windows (April 21, 1999) |
| $ System | Microsoft Windows |
| $Path | {C:\Program FilesXCommon Files\Mathematica\ 4.0\Kernel, C:\Program FilesXCommon Files\ Mathematical . 0\AddOns\Autoload, ... } |
| $OperatingSystem | Windows 9 5 |
| $MachineEpsilon | 2.22045xl0 -16 |
| $MaxMachineNumber | 1.79769xl0 308 |
| $MinMachineNumber | 2.22507x10 -308 |
| $MachinePrecision | 16 |
| $Packages | {Global 4 , System 4 } |
Приведенные примеры показывают, что благодаря системным функциям можно извлечь достаточно полную информацию о текущих параметрах системы и использовать ее для создания специальных алгоритмов вычислений (например, для генерации последовательности псевдослучайных чисел со случайной базой, заданной системным временем) или организации развитого диалога с системой.
В этом уроке мы научились:
- Использовать функции ввода/вывода.
- Работать со строками.
- Использовать функции потоков и файлов.
- Использовать файлы других языков программирования.
- Работать с системными функциями.
Урок 8. Графика и звук
Урок 8. Графика и звук
1. Графика и звук
Графика и звук
- Двумерные и трехмерные графики
- Опции графических функций
- Графические директивы
- Построение графиков лоточкам
- Получение информации о графических объектах
- Перестройка и комбинирование графиков
- Примитивы двумерной и трехмерной графики
- Импорт графических изображений
- Вставка объектов
- Синтез звуков
Графика, как важнейшее средство визуализации вычислений, всегда была козырной картой системы Mathematica и во многом способствовала ее высокой репутации как мирового лидера среди систем компьютерной математики. Обширные графические возможности достигаются при небольшом числе встроенных функций графики за счет их модификации с помощью опций и директив. Благодаря этому Mathematica позволяет строить практически любые виды графиков. Для просмотра и изменения опций графика можно (выделив ячейку с графиком) воспользоваться описанным ранее инспектором опций, в котором есть соответствующий раздел. Однако в этом уроке мы инспектором опций пользоваться не будем — все необходимые опции будут вводиться в соответствующие функции так, как это принято делать при программировании задач графики.
2. Двумерная графика
Двумерная графика
Концептуально графики в системе Mathematica являются графическими объектами, которые создаются (возвращаются) соответствующими графическими функциями. Их немного, около десятка, и они охватывают построение практически всех типов математических графиков. Как уже отмечалось, достигается это за счет применения опций и директив.
Поскольку графики являются объектами, то они могут быть значениями переменных. Поэтому Mathematica допускает следующие конструкции:
- Plot[Sin[x],{x,0,20}] — построение графика синусоиды;
- g:=Plot [Sin [x], {х, 0, 20} ] — задание объекта — графика синусоиды — с отложенным выводом;
- g=Plot [Sin [x], {х, 0, 20} ] — задание объекта — графика синусоиды — с немедленным выводом.
Начнем рассмотрение графических возможностей системы с построения простейших графиков функций одной переменной вида у =f(x) или просто f(x). График таких функций строится на плоскости, то есть в двумерном пространстве. При этом используется прямоугольная (декартова) система координат. График представляет собой геометрическое положение точек (х, у) при изменении независимой переменной (абсциссы) в заданных пределах, например от минимального значения xmin до максимального хтах с шагом dx. По умолчанию строятся и линии координатной системы.
Для построения двумерных графиков функций вида f(x) используется встроенная в ядро функция Plot:
- Plot [f, {x, xmin, xmax}] — возвращает объект, представляющий собой график функции f аргумента х в интервале от xmin до xmax;
- Plot[{f1, f2,...}, {x, xmin, xmax}]— возвращает объект в виде графиков ряда функций fi.
Функция Plot используется для построения одной или нескольких линий, дающих графическое представление для указанных функций f, f1, f2 и т. д. На рис. 8.1 показано построение графика функции sin(x)/x без использования каких-либо опций (точнее, с набором опций по умолчанию).
Рис. 8.1. Построение двумерного графика
Тут виден как раз тот случай, когда масштаб графика по вертикали выбран системой неудачно — часть графика сверху просто отсекается. В большинстве же случаев применение функции Plot позволяет получить вполне «удобоваримый» график.
По мере усложнения задач, решаемых пользователем, его рано или поздно перестанут устраивать графики, получаемые при автоматическом выборе их стиля и иных параметров. Для точной настройки графиков Mathematica использует специальные опции графических функций Для вывода их списка надо использовать команду Options [Plot]. Полный список опций дан в приложении.
Опции внутри.графических функций задаются своим именем name и значением value в виде
name -> value
Наиболее распространённые символьные значения опций:
- Automatic — используется автоматический выбор;
- None — опция не используется;
- All — используется в любом случае;
- True — используется;
- False — не используется.
Многие опции могут иметь числовые значения. В сомнительных случаях рекомендуется уточнять форму записи опций и их значений по оперативной справочной смстеме. Рассмотрим примеры применения опций двумерной графики.
Мы уже отметили неудачный выбор масштаба в случае, представленном на рис. 8.1. Очевидно, этот недостаток графика легко исправить, введя коррекцию масштаба по оси у. Это и сделано в примере, показанном на рис. 8.2. Для изменения масштаба использована опция PlotRange->{ -.25,1.2}. Нетрудно догадаться, что эта опция задает пределы отображения графика по вертикали от -0.25 до 1.2.
Рис. 8.2. График функции sin(x)/x с масштабом, дающим его отображение в полном виде
По умолчанию система строит графики, не указывая надписей ни по осям координат (кроме букв х и г/), ни в верхней части графика. Такая надпись на графике по центру сверху называется титульной. Рисунок 8.3 показывает построение графика с надписями у координатных осей. Для создания таких надписей используется опция Axes Label. После нее указывается список, содержащий две надписи — одну для оси х, вторую — для оси у. Надписи указываются в кавычках. Таким образом, задание опции выглядит следующим образом: AxesLabel-> {"X value","f(x)}.
Рис. 8.3. График с надписями по координатным осям
С помощью опции Axes со значением None можно убрать с графика отображение осей. Вид получающегося при этом графика показан на рис. 8.4. При его построении, кроме удаления осей, использована опция PlotLabel для вывода указанной в качестве ее значения титульной надписи.
Рис. 8.4. График без координатных осей, но с титульной надписью
Часто возникает необходимость построения на одном рисунке нескольких графиков одной и той же функции, но при разных значениях какого-либо параметра — например, порядка специальных математических функций. В этом случае они могут быть заданы в табличной форме. Рисунок 8.5 дает пример построения пяти графиков функций Бесссля.
Рисунок 8.5 иллюстрирует недостаток одновременного представления нескольких графиков, создаваемого по умолчанию, — все графики построены одинаковыми линиями, и не сразу ясно, какой график к какой функции относится. Рисунок 8.6 показывает возможности управления стилем линий (густотой черного цвета) графиков с помощью опции PlotStyle. Если желательно выделение линий разными цветами, удобно использовать в качестве значения опции PlotStyle список вида {Hue [cl] , Hue [с2] ,...}, где параметры c1, с2, ... выбираются от 0 до 1 и задают цвет соответствующей кривой.
Рис. 8.5. Семейство функций Бесселя на одном графике
Риc. 8.6. Построение графиков линиями разного стиля
Применение других опций позволяет задавать массу свойств графиков, например цвет линий и фона, вывод различных надписей и т. д. Помимо представленных примеров, полезно просмотреть и множество примеров построения двумерных графиков, приведенных в справочной системе Mathematica.
Еще одним важным средством настройки графиков являются графические директивы. Синтаксис их подобен синтаксису функций. Однако директивы не возвращают объектов, а лишь влияют на их характеристики. Используются следующие основные директивы двумерной графики:
- AbsoluteDashing [ {dl, d2,...}]— задает построение последующих линией пунктиром со смежными (последовательными) сегментами, имеющими абсолютные длины dl, d2, ... (повторяемые циклически). Значения длины di задаются в пикселях;
- AbsolutePointSize [d] — задает построение последующих точек графика в виде кружков с диаметром d (в пикселях);
- AbsoluteThickness [d] — задает абсолютное значение толщины (в пикселях) для последующих рисуемых линий;
- Dashing [{rl, r2,...}] — задает построение последующих линий пунктиром с последовательными сегментами длиной rl, г2, ..., повторяемыми циклически, причем ri задается как доля полной ширины графика;
- PointSize [d] — задает вывод последующих точек графика в виде кружков с относительным диаметром d, заданным как доля общей ширины графика;
- Thickness [r] — устанавливает для всех последующих линий толщину г, заданную как доля полной ширины графика.
Рисунок 8.7 показывает построение графика функции Бесселя в виде пунктирной линии. Она задается с помощью графической директивы Dashing.
Риc. 8.7. Построение графика функции Бесселя с применением графической директивы Dashing
Применение графических директив совместно с опциями позволяет создавать графики самого различного вида, вполне удовлетворяющие как строгим требованиям, так и различным «извращениям» в их оформлении.
Построение графика по точкам — функция List Plot
Часто возникает необходимость построения графика по точкам. Это обеспечивает встроенная в ядро графическая функция ListPlot:
- ListPlot [ {yl, у2,...}]— выводит график списка величин. Координаты х принимают значения 1, 2, ...;
- ListPlot [{{x1, y1}, {х2, у2 },...}]—выводит график списка величин с указанными х- иy-координатами.
В простейшем случае (рис. 8.8) эта функция сама задает значения координаты х= 0, 1, 2, 3, ... и строит на графике точки с координатами (х, у), выбирая у последовательно из списка координат.
Рис. 8.8. Построение графика по точкам
Можно заметить характерный недостаток построений — точки (особенно при небольшом размере) имеют вид, заметно отличающийся от идеального круга. Функция ListPlot, особенно в ее второй форме (с заданными координатами х и г/), удобна для вывода на график экспериментальных точек.
Получение информации о графических объектах
Порой некоторые детали построения графиков оказываются для пользователя неожиданными и не вполне понятными. Причина этого кроется во множестве опций, которые могут использоваться в графиках, причем в самых различных сочетаниях. Поэтому полезно знать, как можно получить информацию о свойствах графических объектов. Порой небольшая модификация опций (например, замена цвета линий или фона) делает график полностью удовлетворяющим требованиям пользователя. Информацию об опциях графического объекта g дают следующие функции:
- FullAxes [g] — возвращает список опций координатных осей;
- Options [g] — возвращает упрощенный список опций;
- FullOptions [g] — возвращает полный список опций;
- InputForm[g] — возвращает информацию о графике (включая таблицу точек).
Пусть задан графический объект g: g:=Plot[Sin[x],{х,-10,10}]
Ниже представлено получение упрощенного списка опций этого графического объекта:
Options[g]
{PlotRange -> Automatic, AspectRatio ->1/GoldenRatio,
DisplayFunction :> $DisplayFunction, ColorOutput -> Automatic, Axes -> Automatic, AxesOrigin -> Automatic, PlotLabel -> None, AxesLabel -> None, Ticks -> Automatic, GridLines -> None, Prolog -> {}, Epilog -> {}, AxesStyle -> Automatic, Background -> Automatic, DefaultColor -> Automatic, DefaultFont :> $DefaultFont, RotateLabel -> True, Frame -> False, FrameStyle -> Automatic, FrameTicks -> Automatic!, FrameLabel -> None, PlotRegion -> Automatic, ImageSize -> Automatic, TextStyle :> $TextStyle, FormatType :> $FormatType}
Для получения полного списка опций вместе с их значениями можно использовать функцию FullOptions. Аналогично можно получить и иные данные — они не приводятся ввиду громоздкости выводимой информации. Анализ графиков с применением этих функций может оказаться весьма полезным при построении и редактировании сложных графиков.
Функции FullOptions и Options можно также использовать в следующем виде:
- Options [g, option] — возвращает значение указанной опции option;
- FullOptions [g, option] — возвращает значение указанной опции option.
В этом случае можно получить информацию по отдельной опции.
Перестроение и комбинирование графиков
При построении графиков часто требуется изменение их вида и тех или иных параметров и опций. Этого можно достичь повторением вычислений, но при этом скорость работы с системой заметно снижается. Для ее повышения удобно использовать специальные функции перестроения и вывода графиков, учитывающие, что узловые точки уже рассчитаны и большая часть опций уже задана. В этом случае удобно использовать следующую функцию-директиву:
- Show [plot] — построение графика;
- Show [plot, option -> value] — построение графика с заданной опцией;
- Show[plotl, plot2,...] — построение нескольких графиков с наложением их друг на друга.
Директива Show полезна также и в том случае, когда желательно, не трогая исходные графики, просмотреть их при иных параметрах. Соответствующие опции, меняющие параметры графиков, можно включить в состав директивы Show. Другое полезное применение директивы — объединение на одном графике нескольких графиков различных функций или объединение экспериментальных точек и графика теоретической зависимости. Для этого также удобна функция Display-Together, которая будет описана при описании пакета расширения Graphics в уроке 14. В отличие от функции Show, она позволяет объединять графики без предварительного построения каждого из них.
Рисунок 8.9 показывает создание двух графических объектов g1 и g2 с отложенным выводом, а затем построение графиков функций и применение директивы Show для создания объединенного графика. В этом случае директива Show вначале строит исходные графики отдельно, а затем создает объединенный график. В приведенных ниже примерах оставлен только объединенный график, другие удалены командой меню Edit > Clear.
Рис. 8.9. Построение двух графических объектов и их объединение
Разумеется, при использовании директивы Show надо побеспокоиться о выравнивании масштабов графиков, налагаемых друг на друга. Полезно особо обратить внимание на возможность присваивания графиков функций переменным (в нашем примере — g1 и g2) в качестве значений. Такие переменные становятся графическими объектами, используемыми директивой Show для вывода на экран дисплея.
Директива Show часто применяется, когда надо построить на одном графике кривую некоторой функции и представляющие ее узловые точки (например, при построении кривых регрессии в облаке точек исходных данных).
Примитивами двумерной графики называют дополнительные указания, вводимые в функцию Graphics [primitives, options], которая позволяет выводить различные примитивные фигуры без задания математических выражений, описывающих эти фигуры. Примитивы могут выполнять и иные действия. Они заметно увеличивают число типов графиков, которые способна строить система Mathematica. Имеются примитивы для построения окружностей, эллипсов, кругов, овалов, линий и полигонов, прямоугольников и текстов. Полное описание примитивов дано в разделе приложения, посвященном данному уроку. Примитивы задаются подобно графическим функциям, например, Circle[{x, у}, r] строит окружность с радиусом г и центром в точке {х, у}.
Рисунок 8.10 показывает применение функции Graphics для построения одновременно трех графических объектов: отрезка прямой, заданного координатами его концевых точек, окружности с центром (0, 0) и радиусом 0.8 и текстовой надписи «Привет!». Каждый объект задан своим примитивом. Из-за искажения масштаба дисплеем компьютера окружность выглядит как эллипс.
Рис. 8.10. Построение трех графических объектов с помощью примитивов двумерной графики
На другом рисунке (рис. 8.11) представлено построение пятиугольника, заданного координатами его вершин.
Приведенные примеры поясняют технику применения графических примитивов. Но они, разумеется, не исчерпывают всех возможностей этого метода построения геометрических фигур и объектов. Все указанные примитивы используются при построении как двумерных, так и трехмерных графиков.
Рис. 8.11. Построение пятиугольника
Графики функций, заданных в параметрической форме
Построение графиков в полярной системе координат возможно двумя способами. Первый способ основан на использовании обычной декартовой системы координат. Координаты каждой точки при этом задаются в параметрическом виде: x = f x (t) и у = f y (t), где независимая переменная t меняется от минимального значения £ min до максимального t mах с шагом dt. Особенно удобно применение таких функций для построения замкнутых линий, таких как окружности, эллипсы, циклоиды и т. д. Например, окружность радиусом R может быть задана в следующей параметрической форме: х = R cos(t) и у = R sin(t), если t меняется от 0 до 2п. В общем случае радиус также может быть функцией параметра t.
Для построения параметрически заданных функций используются следующие графические средства:
- ParametricPlot [ {fx, fy}, {t, tmin, tmax} ]—строит параметрический график с координатами f х и f у (соответствующими х и у), получаемыми как функции от t;
- ParametricPlot [{{fx, fy}, {gx, gy},...}, {t, tmin, tmax}] —строит графики нескольких параметрических кривых.
Функции f x, f у и т. д. могут быть как непосредственно вписаны в список параметров, так и определены как функции пользователя.
Рисунок 8.12 показывает построение параметрически заданной фигуры Лиссажу. Она задается функциями синуса и косинуса с постоянным параметром R и аргументами, кратными t. Эти фигуры наблюдаются на экране электронного осциллографа, когда на его входы X и Y подаются синусоидальные сигналы с кратными частотами.
Рис. 8.12. Построение фигуры Лиссажу
На одном графике можно строить две и более фигур с заданными параметрически уравнениями. На рис. 8.13 показан пример такого построения — строятся две фигуры Лиссажу, причем одна из них является окружностью. Больше двух фигур строить нерационально, так как на черно-белом графике их трудно различить.
Теперь рассмотрим второй способ построения графиков в полярной системе координат (рис. 8.14). Здесь каждая точка является концом радиус-вектора R(t), причем угол t меняется от 0 до 2я. На рис. 8.14 функция R(t) задана как функция пользователя R[t_] с использованием образца t_ для задания локальной переменной t в теле функции.
Изменение параметра R позволяет заметно увеличить число отображаемых функций — фактически, их бесконечно много. Помимо описанной фигуры на рис. 8.14 дополнительно построена линия окружности единичного радиуса. Чтобы она имела правильные пропорции на экране, задана опция AspectRatio->l.
Рис. 8.13. Построение на одном графике двух фигур Лиссажу
Рис. 8.14. Построение графика функции в полярной системе координат
gl8-1.jpg
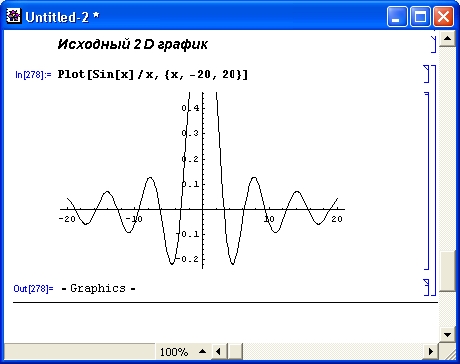
gl8-10.jpg
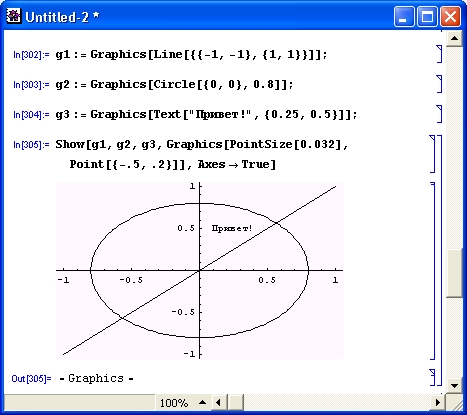
gl8-11.jpg
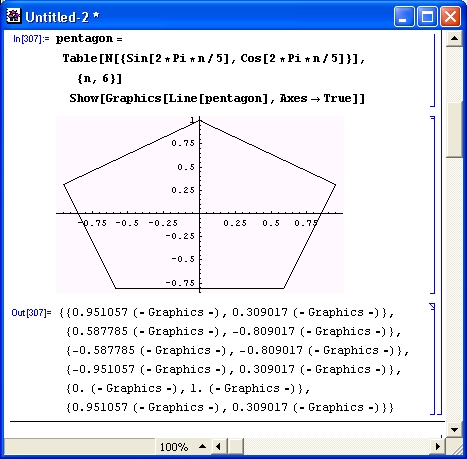
gl8-12.jpg
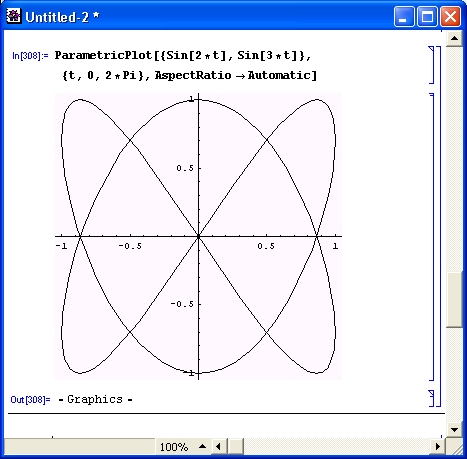
gl8-13.jpg
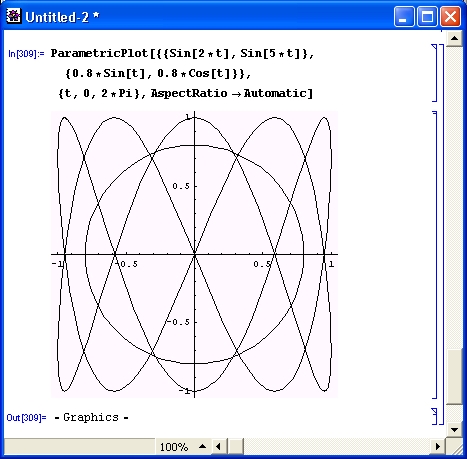
gl8-14.jpg
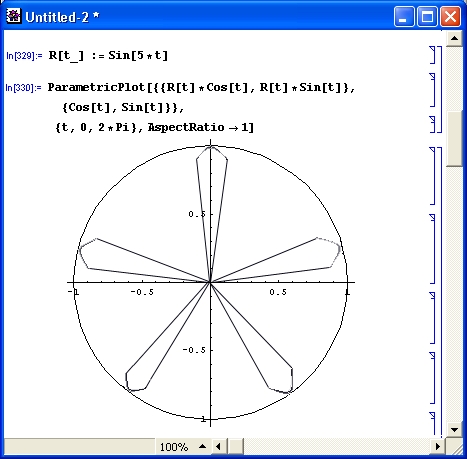
gl8-2.jpg
gl8-3.jpg
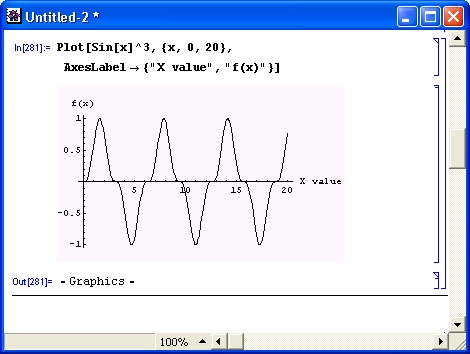
gl8-4.jpg
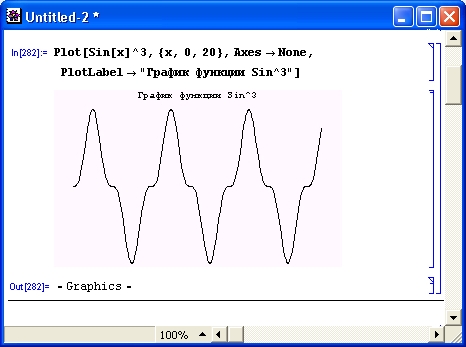
gl8-5.jpg
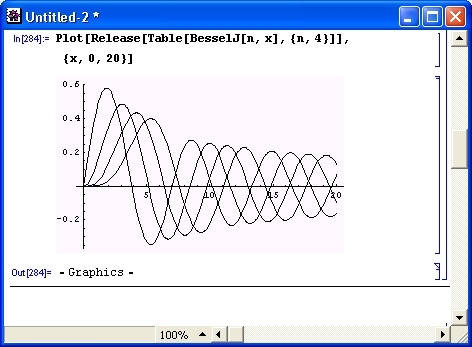
gl8-6.jpg
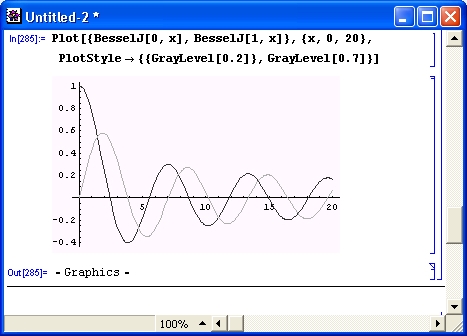
gl8-7.jpg
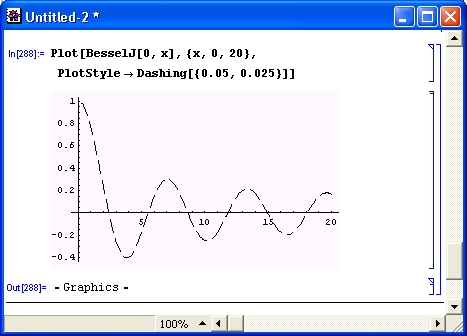
gl8-8.jpg
gl8-9.jpg
3. Трехмерная графика
Трехмерная графика
Трехмерная графика, называемая также ЗD-графикой, представляет в аксонометрической проекции объемное изображение поверхностей или фигур, которые описываются либо функциями двух переменных, либо параметрически заданными координатами объектов. В данном разделе описаны многие способы построения трехмерных графиков, начиная от простых контурных графиков и кончая графиками поверхностей и фигур с функциональной окраской.
Контурные графики, или графики линий равных высот, используются для отображения поверхностей на плоскости. Они удобны для выявления всех экстремумов функций в пределах области графика. Такие графики являются линиями пересечения поверхности с секущими горизонтальными плоскостями, расположенными параллельно друг под другом. Они часто используются в картографии.
Основными функциями и директивами для построения контурных графиков являются следующие:
- ContourPlot[f,{x, xmin, xmax}, {у, ymin, ymax}] — порождает контурный график f как функции от х и у;
- ContourGraphics [array] — представляет контурный график массива array;
- ListContourPlot[array] — формирует контурный график из массива величин высот.
Этих функций достаточно для построения практически любых монохромных графиков такого типа.
Для управления возможностями графической функции ContourPlot используются опции, полный список которых выводит команда Options [ContourGraphics ]. Помимо уже рассмотренных ранее опций используются следующие:
- ColorFunction — задает окраску областей между линиями;
- Contours — задает число контурных линий;
- ContourLines — задает прорисовку явных (explicit) контурных линий;
- ContourShading — задает затенение областей между контурными линиями;
- ContourSmoothing — задает сглаживание контурных линий;
- ContourStyle — задает стиль рисуемых линий для контурных графиков;
- MeshRange — задает области изменения х- и y-координат.
Рисунок 8.15 показывает построение контурного графика с окраской промежуточных областей между линиями. Окраска обеспечивается опцией ColorFunction-> Hue. Опция ContourSmoothing -> True задает сглаживание контурных линий.
Рис. 8.15. Контурный график поверхности sin(x у) с закраской областей между линиями равного уровня оттенками серого цвета
Следующий пример (рис. 8.16) иллюстрирует эффективность применения опции ContourShading. Если задать ее значение равным False, то заполнение пространства между линиями будет отсутствовать. Таким образом, в данном случае строятся только линии равного уровня.
Рис. 8.16. Контурный график, представленный только линиями равного уровня
Иногда график оказывается более наглядным, если убрать построение контурных линий, но оставить закраску областей между линиями. Такой вариант графика более предпочтителен, если нужно наблюдать качественную картину. Для построения такого графика надо использовать опцию ContourLine->False (рис. 8.17).
Рис. 8.17. Контурный график без пиний равного уровня
В данном случае используется вариант монохромной окраски областей между линиями (PostScript). Он может оказаться предпочтителен, например, если предполагается печать графика монохромным принтером.
Функцией двух переменных f(x, у) может описываться плотность некоторой среды. Для построения графиков плотности используются следующие графические функции:
- DensityGraphics [array] — является представлением графика плотности;
- DensityPlot[f, {х, xmin, xmax}, {у, ymin, ymax}] — строит график плотности f как функции от х и у;
- ListDensityPlot [array] — формирует график плотности из массива величин высот.
С этими функциями используется множество (в основном уже рассмотренных) опций. Их перечень можно получить с помощью функции Options.
Внешне график плотности похож на контурный график. Однако для него характерно выделение элементарных участков (с равной плотностью) в форме квадратиков (рис. 8.18).
Рис. 8.18. График плотности
График плотности (рис. 8.18) также дан в режиме PostScript. Цветная функциональная раскраска таких графиков тоже возможна (см. опции, указанные выше для контурных графиков).
Построение графиков поверхностей — функция Plot 3D
Функция двух переменных z = f(x, у) образует в пространстве некоторую трехмерную поверхность или фигуру. Для их построения приходится использовать координатную систему с тремя осями координат: х, у и z. Поскольку экран дисплея плоский, то на самом деле объемность фигур лишь имитируется — используется хорошо известный способ наглядного представления трехмерных фигур с помощью аксонометрической проекции.
Вместо построения всех точек фигуры обычно строится ее каркасная модель, содержащая линии разреза фигуры по взаимно перпендикулярным плоскостям. В результате фигура представляется в виде совокупности множества криволинейных четырехугольников. Для придания фигуре большей естественности используются алгоритм удаления невидимых линий каркаса и функциональная закраска четырехугольников с целью имитации бокового освещения фигуры.
Для построения графиков трехмерных поверхностей используется основная графическая функция Plot 3D:
- Plot3D[f, {x, xmin, xmax), {у, ymin, ymax}] — строит трехмерный график функции f переменных х и у;
- Plot3D[{f, s}, {x, xmin, xmax}, {y, ymin, ymax}] — строит трехмерный график, в котором высоту поверхности определяет параметр f, а затенение — параметр s.
На рис. 8.19 показан пример построения поверхности, описываемой функцией двух переменных cos(x у) при х и у, меняющихся от -3 до 3. Поверхность строится в виде каркаса с прямоугольными ячейками с использованием функциональной окраски. Все опции заданы по умолчанию.
Рис. 8.19. Пример построения поверхности cos(xy) функцией Plot3D с опциями по умолчанию
Этот график будем считать исходным для демонстрации его модификаций, получаемых путем изменения опций.
Опции и директивы трехмерной графики
Для модификации трехмерных графиков могут использоваться многочисленные опции и директивы, список которых дан в приложении. Их применение позволяет строить большое число графиков различных типов даже при задании одной и той же поверхности. В качестве примера рассмотрим отдельные кадры документа, демонстрирующего влияние опций на вид трехмерной математической поверхности.
На рис. 8.20 показана исходная поверхность (см. рис. 8.19), построенная с применением опции PlotPoint->50. Это означает, что поверхность по каждой оси делится на 50 частей (в исходном графике по умолчанию используется деление на 10 частей). Масштаб по вертикали задается автоматически, с тем чтобы все высоты поверхности не ограничивались.
На рис. 8.21 показана та же поверхность, полученная с применением опции PlotRange-> {0, 0.5}, срезающей верхнюю часть поверхности (точки с ординатами выше 0.5). График поверхности при этом существенно меняется (сравните с рис. 8.20).
Рис. 8.20. Поверхность рис. 8.19 с большим числом ячеек
Рис. 8.21. Математическая поверхность с отсеченной верхней частью
Опция Boxed -> False удаляет ограничивающие рамки, образующие «ящик», в который вписывается построенная трехмерная поверхность (рис. 8.22). Остаются лишь координатные оси.
Опция Viewpoint позволяет включить при построении отображение перспективы и изменять углы, под которыми рассматривается фигура. Рисунок 8.23 иллюстрирует применение этой опции.
Рис. 8.22. Построение трехмерной поверхности без ограничительного «ящика»
Рис. 8.23. Математическая поверхность, построенная с учетом перспективы
Опция Mesh -> False позволяет удалить линии каркаса фигуры. Нередко это придает фигуре более естественный вид (рис. 8.24) — обычно мы наблюдаем такие фигуры без линий каркаса.
В ряде случаев, напротив, именно линии каркаса несут важную информацию. Система строит каркас трехмерных поверхностей двумя способами — с использованием и без использования алгоритма удаления невидимых линий. Рисунок 8.25 показывает результат построения при использовании алгоритма удаления невидимых линий. Нетрудно заметить, что в этом случае поверхность выглядит достаточно эстетично даже без применения функциональной закраски.
Рис. 8.24. Математическая поверхность с удаленными линиями каркаса
Рис. 8.25. Построение каркаса математической поверхности с использованием алгоритма удаления невидимых линий
На рис. 8.26 показано построение каркаса без удаления невидимых линий. Такой вид математическая поверхность имеет, если представить ее построенной из тонких проволочек, висящих в пространстве. Это дает дополнительную информацию о пространственной фигуре, но эстетически она выглядит хуже, чем фигура, построенная с применением алгоритма удаления невидимых линий каркаса.
Таким образом, как и ранее, применение опций позволяет легко управлять характером и типом графиков, придавая им вид, удобный для заданного применения. На рис. 8.27 показан пример построения трехмерного графика с применением одновременно нескольких опций.
Риc. 8.26. Построение каркаса математической поверхности без использования алгоритма удаления невидимых линий
Риc. 8.27. Пример построения трехмерного графика с несколькими опциями
Приведенные примеры самым наглядным образом показывают, насколько легко модифицируются графики с помощью различных опций. Разумеется, есть множество возможностей для иных модификаций, которые пользователь может опробовать самостоятельно.
В разделе приложения, посвященном данному уроку, указан ряд дополнительных директив и опций трехмерной графики. С их помощью можно расширить возможности построения графиков. Читателю рекомендуется самостоятельно построить графики ряда поверхностей с использованием различных опций.
Графическая функция ListPlot3D
Часто трехмерная поверхность задается массивом своих высот (аппликат). Для построения графика в этом случае используется графическая функция ListPlotSD:
- ListPlot3D [array] — строит трехмерный график поверхности, представленной массивом значений высот;
- ListPlot3D [array, shades] — строит график так, что каждый элемент поверхности штрихуется (затеняется) согласно спецификации shades.
Plot Joined — дополнительная опция для ListPlot, указывающая, следует ли соединять линией точки, нанесенные на график.
Пример применения функции ListPlotSD показан на рис. 8.28. График построен по данным таблицы tS, формирующей значения аппликат поверхности, которая описывается функцией cos(xy).
Рис. 8.28. Пример применения функции ListPlotSD

Командой Options [ListPlot3D] можно вывести полный список опций данной функции, чтобы использовать их для модификации графиков, которые строит эта функция.
gl8-15.jpg
gl8-16.jpg
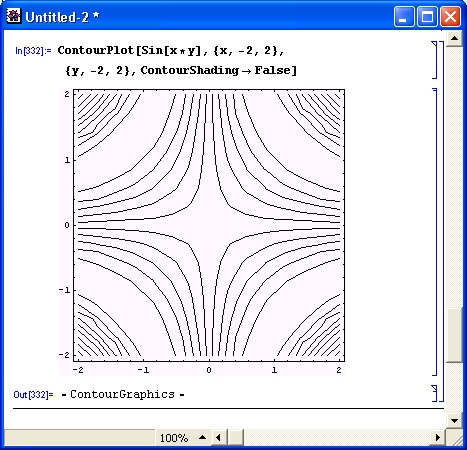
gl8-17.jpg
gl8-18.jpg
gl8-19.jpg
gl8-20.jpg
gl8-21.jpg
gl8-22.jpg
gl8-23.jpg
gl8-24.jpg
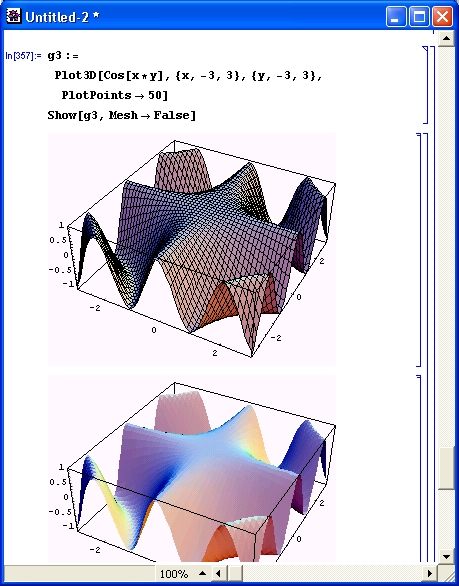
gl8-25.jpg
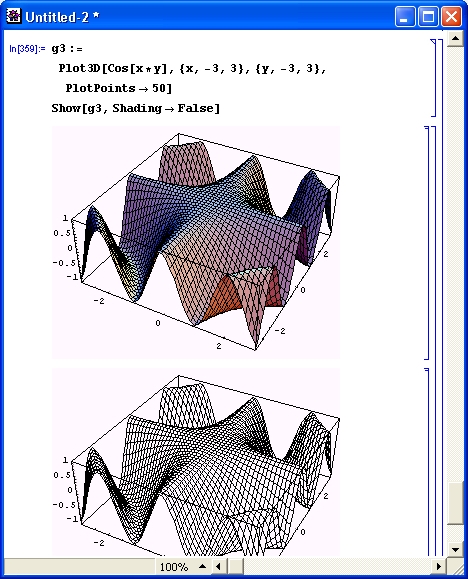
gl8-26.jpg
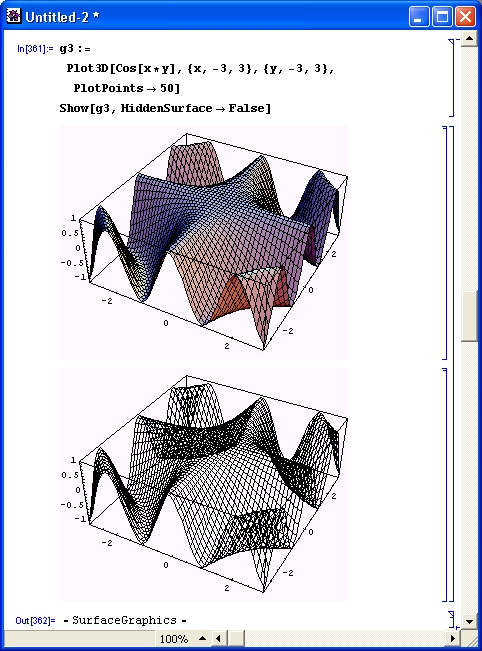
gl8-27.jpg
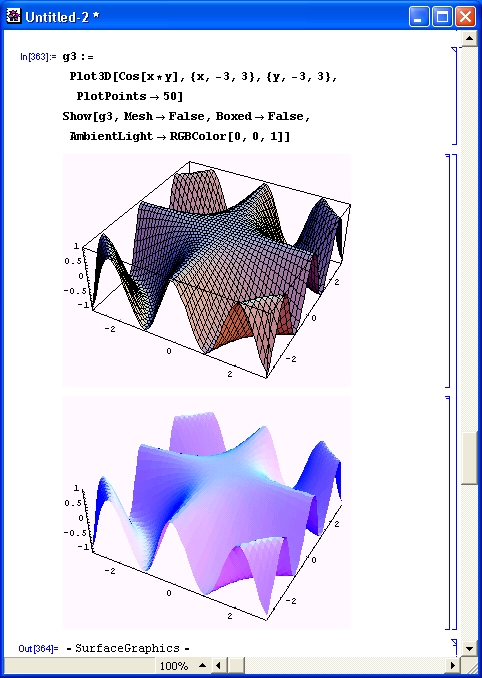
gl8-28.jpg
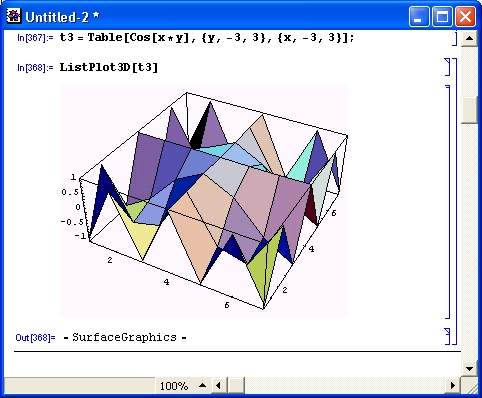
4. Специальные средства визуализации и звука
Специальные средства визуализации и звука
Системы Mathematica содержат множество средств, повышающих наглядность представления (визуализации) результатов вычислений — как простых, так и сложных. К ним можно отнести особые виды трехмерной графики, используемые при параметрическом задании поверхностей, в том числе пересекающихся в пространстве, а также графики объемных фигур — полиэдров. Возможности визуализации расширяются при использовании импортируемых рисунков и вставки графических объектов. К специфическим приемам визуализации относится и применение звуковых объектов, способных генерировать и воспроизводить звуки при наличии в компьютере звуковой карты.
Параметрическая трехмерная графика
Особый шик построениям трехмерных фигур и поверхностей придает функция ParametricPlot3D, в которой предусмотрено параметрическое задание всех трех функций, описывающих координаты точек. Каждая из функций, задающих координаты точек, является функцией двух переменных.
Функция ParametricPlot3D используется в следующих видах:
- PararnetricPlot3D[ {fx, fy, fz}, {t, tmin, tmax}, {u, umin, umax} ] — строит трехмерную поверхность, параметризованную по t и u;
- ParametricPlot3D[{fx, fy, fz}, {t, tmin, tmax}] — создает трехмерную пространственную кривую, параметризованную переменной t, которая изменяется от tmin до tmax;
- ParametricPlot3D[ { fx, fy, fz, s},...] — выполняет затенение графика в соответствии с цветовой спецификацией s;
- ParametricPlot3D[ { {fx, fy, fz}, {gx, gy, gz},...},...] — строит несколько объектов вместе.
Эта функция имеет множество опций, которые можно вывести с помощью команды Options [ParametricPlotSD]. Большая часть из них уже рассматривалась ранее. При этом даже при использовании только опций, заданных по умолчанию, можно получить любопытные построения. На рис. 8.29 показан простой пример применения функции ParametricPlot3D для построения замкнутой линии, расположенной в пространстве. Это, так сказать, объемный вариант, фигур Лиссажу, построение которых было описано ранее.
Параметрическое задание функций позволяет легко строить сложные пространственные фигуры, визуально весьма напоминающие реальные объекты. Покажем это на трех характерных примерах.
Рис. 8.29. Построение пространственной кривой, заданной в параметрической форме
Первым примером может служить фигура «рог изобилия», показанная на рис. 8.30. По существу, это раскручивающаяся объемная спираль, диаметр которой постепенно нарастает.
Рис. 8.30. Построение фигуры «рог»
Другой пример — объемное кольцо с сечением, напоминающим знак бесконечности (бесконечность). Результат построения показан на рис. 8.31. Обратите внимание на интересный эффект — из кольца удален сектор, что позволяет рассмотреть его внутреннее строение. Все, что потребовалось для создания этого эффекта, — это задать верхний предел изменения переменной t равным 2л - 0.6. Если сделать этот предел равным 2л, то кольцо станет непрерывным.
Рис. 8.31. Построение кольца с удаленным сектором
Рис. 8.32. Построение сферы с удаленным сегментом
Третий пример такого рода — построение объемной сферы. Этот пример показан на рис. 8.32. Здесь также использован прием изменения значений переменной t для получения выреза сегмента сферы. Опять-таки, задав изменение t от 0 до 2л, можно получить построение всей сферы без выреза.
Любопытно отметить, что описанные приемы создания вырезов в объемных фигурах позволяют наблюдать внутреннюю часть фигур, которая обычно (без вырезов) не видна. Это делает описанный прием построения фигур с вырезом достаточно продуктивным.
Построение фигур, пересекающихся в пространстве
Пожалуй, наиболее впечатляющими являются построения трехмерных фигур, пересекающихся в пространстве. Для этого достаточно представить каждую фигуру в виде графического объекта, а затем с помощью директивы Show вывести их на одном графике. При этом Mathematica автоматически рассчитывает линии пересечения фигур и строит график так, чтобы заслоненные ячейки фигур не были видны.
Проиллюстрируем это на примере. На рис. 8.33 показано задание и построение одного графического объекта gl — объемной спирали, полученной сворачиванием ленты.
Рис. 8.33. Построение объекта gl — объемной спирали
Второй объект, построение которого представлено на рис. 8.34, — это объемное кольцо. Его построение было описано выше. В конце части документа, показанного на рис. 8.34, задана функция Show для вывода объектов на одном графике.
Рис. 8.34. Построение объекта g2 — объемного кольца с удаленным сегментом
Рисунок 8.35 демонстрирует комбинированный график, построенный функцией Show. Он показывает кольцо, через отверстие которого проходит объемная спираль. Вырез в кольце показывает, как спираль проходит внутри кольца.
Рис. 8.35. Построение комбинированного объекта — спираль проходит внутри кольца
Графики такого типа дают большие возможности визуализации трехмерных поверхностей и фигур.
Функция Graphics3D, ее опции и примитивы
Наряду с построением графиков поверхностей, заданных аналитическими выражениями, имеется возможность создания графиков из различных элементарных геометрических объектов, называемых примитивами. Они включаются в список параметров функции Graphics3D [primitives, options] и позволяют строить в пространстве различные простые фигуры. Помимо примитивов двумерной графики могут использоваться примитивы трехмерной графики, приведенные в приложении.
Функция Graphics3D со своими примитивами может использоваться для построения в пространстве различных объектов, например точек, кубиков или многоугольников.
Рисунок 8.36 показывает два варианта размещения случайных точек в пространстве. Для генерации координат точек используется функция Random [ ], возвращающая случайные числа, распределенные по равномерному закону.
Рис. 8.36. Построение случайных точек в пространстве
Поскольку ограничительный «ящик» не удален, создается впечатление о построении точек внутри куба.
На рис. 8.37 показано построение в пространстве ряда небольших кубиков. Для этого используется примитив Cuboid, повторенный 7 раз. Для воспроизведения набора кубиков, перечисленных в функции GraphicsSD, применяется функция-директива Show.
Нетрудно заметить, что и здесь неплохо работают встроенные алгоритмы удаления невидимых линий. Это дает довольно реалистическое изображение объектов в пространстве.
Рис. 8.37. Построение нескольких кубиков в пространстве
Еще более наглядное представление об этом алгоритме дает рис. 8.38. На нем показано построение в пространстве ряда плоских многоугольников, частично проникающих друг в друга. Нетрудно заметить, что и здесь алгоритм удаления невидимых поверхностей работает превосходно.
Рис. 8.38. Построение взаимно пересекающихся плоских многоугольников в пространстве
Здесь каждый из многоугольников формируется с помощью функции пользователя randpoly [n_], в теле которой используется примитив Polygon. Эта функция формирует случайные многоугольники, выводимые затем функцией-директивой Show.
Язык программирования системы Mathematica позволят создавать средства визуального программирования графических задач. Примером таких средств является приложение Polyhedron Explorer, предназначенное для создания множества объемных фигур класса полиэдров. Это приложение (вместе с системой Mathematica, разумеется) вполне может заменить множество бумажных объемных фигур, которые можно еще встретить в кабинетах математики школ и вузов. Его можно получить по Интернету с файлового сервера фирмы Wolfram Research.
При загрузке этого приложения (как обычного документа) создается панель с окном просмотра фигуры и пультом с множеством кнопок, с помощью которых легко выбрать подходящую фигуру и наблюдать ее в окне просмотра (рис. 8.39).
Рис. 8.39. Работа с приложением PolyhedronExplorer
Обратите внимание на кнопки внизу панели пульта (см. рис. 8.39). Стоит нажать кнопку Paste Code, как фрагмент программы, рисующий выбранную фигуру, будет вставлен в окно редактирования документов — оно видно на рис. 8.39 слева.
Теперь достаточно выполнить этот фрагмент программы, как в строке вывода появится соответствующая фигура. Добавляя те или опции, можно получить нужные изменения ее вида.
В состав примеров системы Mathematica входит немало и других иллюстраций реализации объектно-ориентированного программирования: палитры физических констант и химических элементов (таблица Менделеева), палитры дополнительных функций и т. д. Элементы такого программирования просматриваются и при работе с селектором положения трехмерных графиков (вставка опций с указанием о положении графика).
Импорт графических изображений
Несмотря на обширные возможности встроенных в ядро системы Mathematica графических функций, примитивов и опций, они не способны охватить все многообразие графических приложений в математике. Поэтому предусмотрен импорт рисунков, созданных в различных графических системах или в документах самой системы Mathematica.
Описанное выше приложение PolyhedronExplorer позволяет импортировать выбранную фигуру в документ. Для этого достаточно нажать кнопку Paste Graphic. Этот процесс иллюстрирует рис. 8.40.
Рис. 8.40. Пример импорта рисунка из приложения PolyhedronExplorer в документ системы Mathematica
Возможен также импорт изображения с использованием буфера обмена. Нужное -изображение, открытое в каком-либо приложении (например, в графическом редакторе), нужно выделить и поместить в буфер командой Сору или Cut. Затем надо перейти к работе с системой Mathematica. Установив текстовый курсор в нужное место, достаточно исполнить команду меню Edit -> Paste. Если при импорте изображения надо очистить буфер, следует использовать команду Edit -> Paste As -> Paste and Discard.
Импортированное изображение размещается в ячейке вывода, и с ним возможны все манипуляции, характерные для рисунков в ячейках вывода. Так, их можно растягивать или сжимать, а также перемещать в пределах ячейки. Этот способ импорта изображений полезен для создания средствами системы Mathematica электронных книг, уроков и статей.
Вставка графических и иных объектов
Более широкие возможности предоставляет вставка объектов. Как уже отмечалось в уроке 2, она реализуется командой Insert Object из меню Edit. Эта команда открывает окно со списком возможных приложений, которые могут экспортировать объекты в систему Mathematica.
Если, к примеру, выбрать в качестве объекта рисунок графического редактора Paint, то на экране появится окно редактора (рис. 8.41). Теперь в этом редакторе можно создавать любые изображения, например, вроде рожицы, квадрата и эллипса, представленных в окне редактора на рис. 8.41.
Если теперь закрыть окно редактора, то созданный рисунок появится в ячейке вывода документа системы Mathematica (рис. 8.42). Его можно выделять, растягивать в разных направлениях, перемещать и т. д.
Вставка объекта отличается от импорта рисунков (или текстов) одним принципиально важным обстоятельством — объект может редактироваться с автоматическим вызовом приложения, в котором он был создан. Для редактирования объекта, например нашего рисунка, достаточно сделать на нем двойной щелчок. Произойдет загрузка графического редактора, и мы увидим картину, подобную приведенной на рис. 8.41, — в нашем распоряжении будет окно редактора с рисунком, который можно произвольно изменять. После закрытия окна редактора новый рисунок появится в месте вставки.
Разумеется, объектами вставки могут быть не только рисунки, но также тексты и документы других систем. Интересно оценить, насколько Mathematica восприимчива к другим математическим системам. Увы, эта «высокопоставленная мадам» очень критична к своим возможным партнерам или соперницам. Так, она не воспринимает системы Maple V и MATLAB, которые способны соперничать с ней по своим возможностям и скорости работы. Не понимает система и такую «мелочь», как системы начального уровня Derive и MuPAD.
Зато Mathematica сравнительно благосклонно относится к системе Mathcad, известной своим бесподобным интерфейсом и, главное, возможностями задания в документах сложных формул в их вполне естественном виде. Рисунок 8.43 показывает подготовку в Mathcad графика трех функций и вычисление определенного интеграла.
Рис. 8.41. Подготовка объекта в среде графического редактора Paint, вызванного из документа системы Mathematica
Риc. 8.42. Пример вставленного объекта, созданного в среде графического редактора Paint
Рис. 8.43 .Подготовка в Mathcad графика функций и вычисление определенного интеграла
Увы, Mathematica не способна воспринимать документ Mathcad целиком, если в нем больше одного блока, ибо каждый блок воспринимается как отдельный объект. Поэтому приходится располагать блоки Mathcad (поочередно выделяя их) в отдельных ячейках системы Mathematica, что и показано на рис. 8.44.
Рис. 8.44. Документ системы Mathematica с двумя объектами из документа Mathcad
Из этого следует, что Mathematica реализует полноценную объектную связь еще далеко не со всеми программами. И, по всей видимости, это сделано разработчиками намеренно. Не случайно пары «Mathematica — Word» и «Mathematica — Excel» поставляются фирмой Wolfram как самостоятельные программные продукты.
Mathematica, в отличие от других систем компьютерной математики, имеет средства для синтеза звука. Сопровождение звуком описания некоторых математических закономерностей (например, биений, развития взрывных процессов и т. д.) делает это описание более понятным и естественным. Особенно удобна эта возможность в теоретической акустике и в технике аналоговой и цифровой обработки акустических сигналов. Таким образом, при более серьезном рассмотрении можно найти немало прикладных задач, где звуковое сопровождение их решения полезно и является важной составляющей общего описания результатов решения.
Возможности синтеза звука становятся доступными, если компьютер оборудован звуковой картой класса Sound Blaster фирмы Creative Labs или совместимой с ней. К карте должна быть подключена стереофоническая акустическая система для воспроизведения звуков. Возможен синтез как монофонических, так и стереофонических звуков.
С синтезируемым звуком связан некоторый графический образ — ячейка. Этот графический образ имеет вид осциллограмм звуковых сигналов по обоим стереоканалам. Если такая ячейка выделена, то возможен запуск воспроизведения звука с помощью главного меню, как описывалось в уроке 2.
Для синтеза звуков в системе Mathematica используются следующие функции:
- ListPlay [ {a1l, a2,...}] — проигрывает звук с амплитудой, заданной последовательностью уровней ai;
- Play[f, {t, tmin, tmax}] — воспроизводит звук с амплитудой, заданной f как функцией от времени t в секундах между значениями tmin и tmax;
- PlayRange — опция для Play и родственных функций, указывающая, какой диапазон уровней звуковых амплитуд должен использоваться;
- SampleDepth — опция для звуковых примитивов, устанавливающая количество бит для кодирования уровней амплитуды звуковых сигналов;
- SampledSoundFunction [f, n, r] — звуковой примитив; воспроизводит звук с частотой дискретизации г герц; значения дискретных отсчетов генерируются применением функции f к последовательным целым от 1 до л;
- SampledSoundList [ {al, а2,...},r] — звуковой примитив, воспроизводящий звук, амплитуда которого имеет уровни ai с дискретностью г раз в секунду;
- SampleRate — опция для звуковых примитивов, устанавливающая частоту дискретизации звука в герцах;
- Sound [primitives] — представляет звук;
- $SoundDisplayFunction — возвращает значение по умолчанию для опции Display Function в звуковых функциях.
Некоторые из указанных функций напоминают графические функции, и это не случайно. Идеология применения этих функций та же, что при использовании функций графики. Звуковые объекты имеют много схожего с графическими объектами, их можно наряду с последними включать в различные функции-директивы. Таким образом, единство работы со звуком и графикой обеспечено специально.
Рисунок 8.45 показывает использование функции Sound для создания звукового объекта. Графически этот объект представляет собой сдвоенную «осциллограмму» звука. Слово «осциллограмма» не случайно взято в кавычки — на самом деле речь идет лишь о некотором графическом представлении звуковых сигналов, отдаленно напоминающем осциллограмму. К тому же вид этого отображения сильно зависит от компьютерной платформы, на которой установлена система Mathe-matica и даже от применяемых в компьютере видеосредств.
Рис. 8.45. Создание звукового объекта
Принятый в системе способ синтеза звуков имеет определенные недостатки. Звуковые средства слишком привязаны к математике — для задания звука надо описать звуковые колебания математической формулой. Наконец, надо отметить, что графическая интерпретация звукового объекта не всегда понятна — например, неясно, что нового дает нижняя осциллограмма при синтезе монофонического звука.
Использование звуковых объектов сильно увеличивает объем файлов документов. Да и скорость синтеза звуков даже по простым выражениям оставляет желать лучшего.
В этом уроке мы научились:
- Строить двумерные и трехмерные графики различного вида.
- Использовать опции графических функций для форматирования графиков.
- Применять графические директивы.
- Строить графики по точкам.
- Использовать графические примитивы.
- Вставлять в документы графические и иные объекты.
- Осуществлять синтез звуков.
gl8-29.jpg
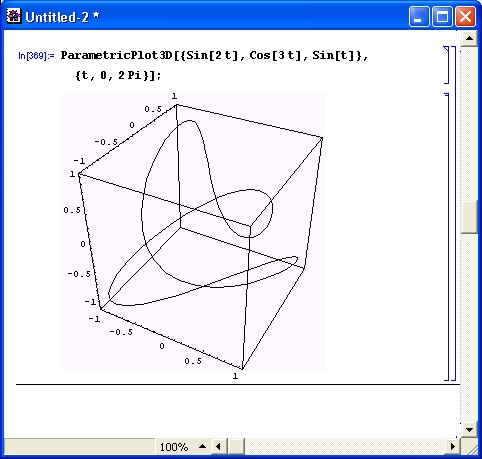
gl8-30.jpg
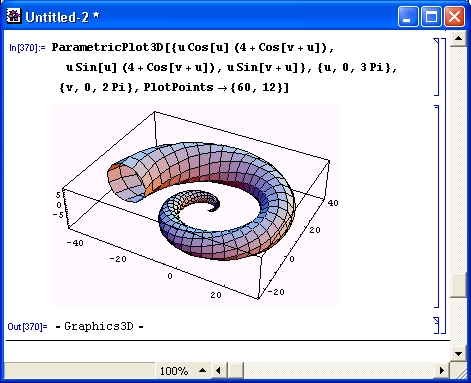
gl8-31.jpg
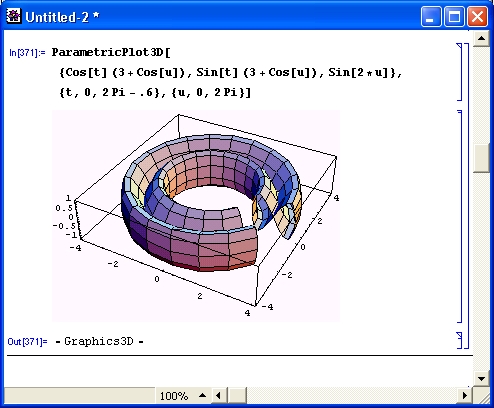
gl8-32.jpg
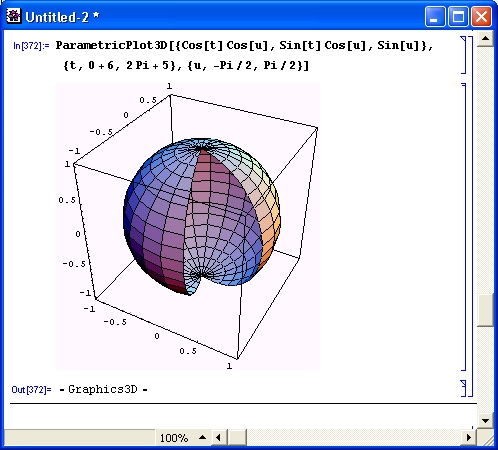
gl8-33.jpg
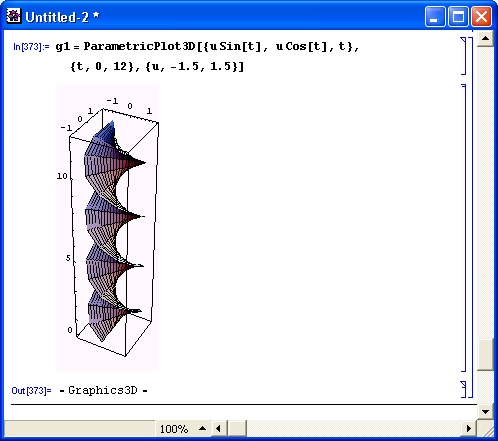
gl8-34.jpg
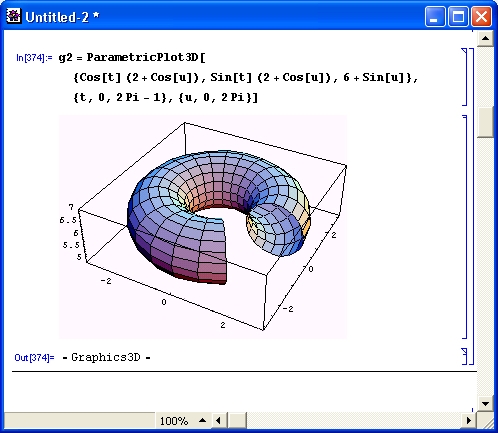
gl8-35.jpg
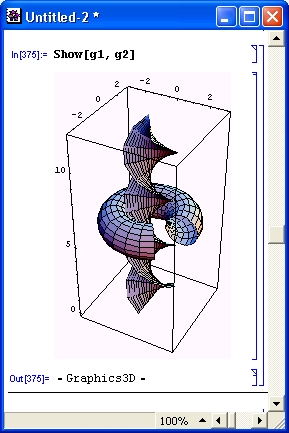
gl8-36.jpg
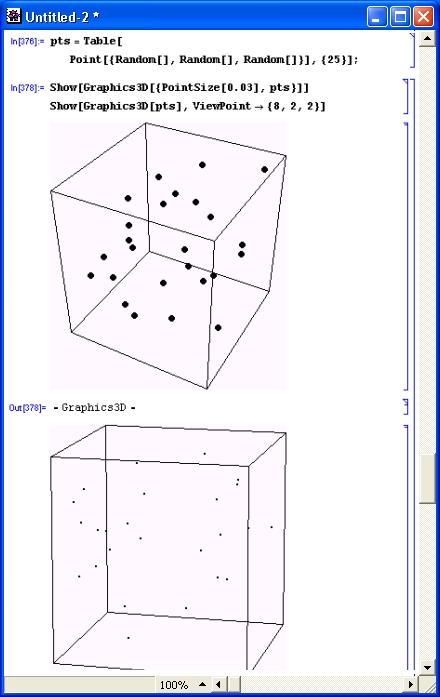
gl8-37.jpg
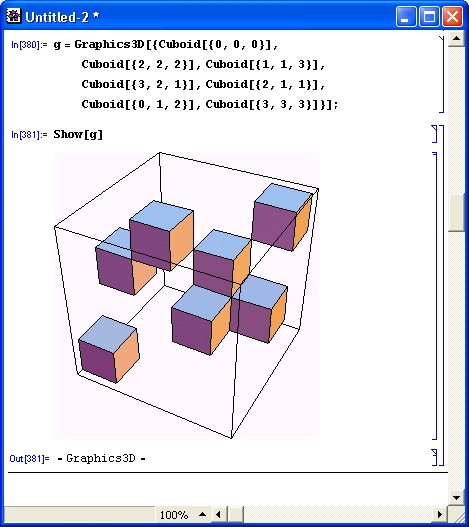
gl8-38.jpg
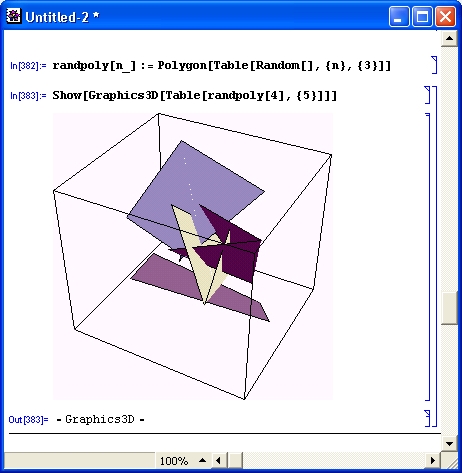
gl8-39.jpg
gl8-40.jpg
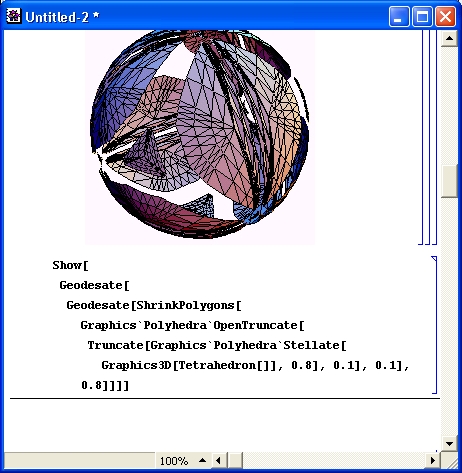
gl8-41.jpg
gl8-42.jpg
gl8-43.jpg
gl8-44.jpg
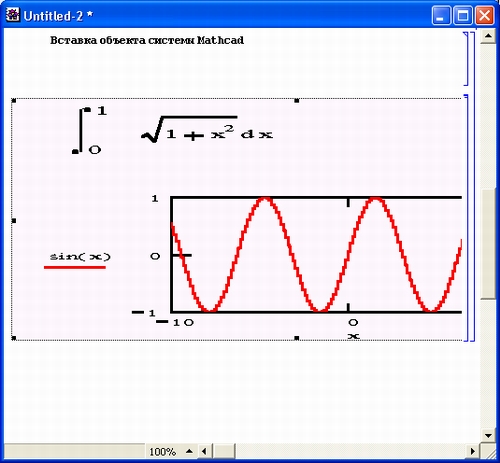
gl8-45.jpg
Урок 9. Компьютерная алгебра
Урок 9. Компьютерная алгебра
1. Компьютерная алгебра
Компьютерная алгебра
- Работа с выражениями
- Выделения и подстановки в функциях
- Рекурсивные функции
- Инверсные функции
- Задание математических отношений
- Упрощение выражений
- Раскрытие и расширение выражений
- Функции преобразования тригонометрических выражений
- Основные операции над полиномами
- Функции для расширенных операций с выражениями
Математические выражения — основа описания алгоритмов вычислений. Фактически, вся символьная математика основана на тех или иных видах преобразований выражений. Такие преобразования и описаны в данном уроке.
2. Работа с выражениями
Работа с выражениями
Одним из важнейших понятий системы Mathematica является математическое выражение, или просто выражение — ехрг (от английского слова expression). Работа с математическими выражениями в символьном виде — основа основ символьной математики.
Выражение может быть представлено в общепринятом виде (как математическая формула или ее часть) с помощью операторов, например, а* (х + у + z) или х ^ у, оно может задавать и некоторую функцию f [х, у,...] или их комбинацию. Наряду с такой формой существует так называемая полная форма представления выражений, при которой основные арифметические операции задаются не операторами, а только соответствующими функциями. Ее примеры даны ниже.
| Выражение ехрг | Полная форма ехрг | Комментарий |
| х + у + z | Plus [х, у, z] | Сложение |
| х у z | Times [x, у, z] | Умножение |
| х^n | Power [x,n] | Возведение в степень |
| {a,b,c} | List [a,b, c] | Создание списка |
| a->b | Rule [a,b] | Подстановка |
| a=b | Set [a,b] | Присваивание |
Для вывода выражения ехрг в полной форме используется функция FullForm [ехрг ]. Примеры перевода выражений в полную форму:
1+х^2+(у+г)^2+2
3 + х2 + (y+z)2
FullForm[%]
Plus[3, Power[x, 2], Power[Plus[у, z] , 2]]
Integrate[a*Sin[b*x]*Exp[-c*x],x]
a [(be-cxCos[bx])/{-ib + c) (ib + c)-( ce+cxSin[bx]) \(-ib + c) (ib + c) ]
FullForm[%]
Times[a, Plus[Times[-1, b, Power[Plus[Times[Complex[0, -1], b], c] , -1], Power[Plus[Times[Complex[0, 1], b], c] , -1], Power[E, Times[-l, c, x] ] , Cos[Times[b, x] ] ] , Times[-1, c, Power[Plus[Times[Complex[0, -1], b] , c], -1] , Power[Plus[Times[Complex[0, 1] , b], c] , -1] , Power[E, Times[-1, c, x] ] , Sin[Times[b, x]]]]]
Для определения типа выражения служит функция Head [ехрr ]. Применительно к числовым выражениям она возвращает тип результата, как показано в приводимых ниже примерах.
| Ввод (In) |
Вывод (Out) |
| 1+2+3 | 6 |
| Head[%] | Integer |
| Head[123/12345] | Rational |
| Head[2*0.25] | Real |
Следующие примеры поясняют действие функции Head для символьных выражений:
- Head[f [x,y, z] — возвращает f;
- Head[a+b+c] — возвращает Plus;
- Head[x ^ n] — возвращает Power;
- Head[ {a, b, с} ] — возвращает List.
Другая пара примеров показывает применение Head в списках с разнородными выражениями:
{Head[l + 2], Head[аЬ] , Head[ 5/7], Headfl + 3i], Head[e2]}
{Integer, Times, Rational, Complex, Power}
Head/@{l, 1/3, 2.1, 2 + 3i, x, f [x] , {1, 2, 3}, a+b, a/b}
{Integer, Rational, Real, Complex, Symbol, f, List, Plus, Times}
Обратите внимание на второй пример — в нем функция Head применяется к каждому выражению списка, что дает более компактную запись.
Основные формы записи выражений
Возможны четыре основные формы записи выражений:
- f [х, у] — стандартная форма для f [х, у];
- f @ х — префиксная форма для f [ х ];
- х / / f — постфиксная форма для f [ х ];
- х ~ f ~ у — инфиксная форма для f [ х, у ].
Далее приведены примеры применения этих форм.
| Ввод (In) | Вывод (Out) |
| F[x_] = 2*х^2 | 2X 2 |
| F[a] | 2a 2 |
| a//F | 2 a 2 |
| f [x_, y_] = х^ 2 + у^2 | y 2 +x 2 |
| f[a,b] | a 2 +b 2 |
| a-f-b | a 2 + b 2 |
Можно использовать ту или иную форму выражений в зависимости от класса решаемых математических задач.
Части выражений и работа с ними
Сложные выражения состоят из частей, которые могут интерпретироваться различным образом.
| Тип части | Зависимость | Пример |
| Function | От аргументов или параметров | Ехр[х], f [х,у] |
| Command | От аргументов или параметров | Expand [ (х-1) ^2] |
| Operator | От операндов | x + y+z, a = b |
| Head | От элементов | {a,b,c} |
| Object type | От контекста | RGBColor [r,g,b] |
Работа с частями выражений напоминает работу со списками. Для выделения любой заданной части выражения используются функция Part или двойные квадратные скобки;
- Part [expr, n] или expr [ [n] ] — выделяет п-ю часть выражения, начиная с начала;
- expr [ [-n] ] — выделяет п-ю часть выражения, начиная с конца;
- expr [ [nl,n2,...] ] — выделяет части выражения и показывает их в форме дерева;
- expr [[{nl, n2,...}]] — дает комбинацию нескольких частей выражения. Приведем примеры использования этих средств.
| Ввод (In) | Вывод (Out) |
| f :=а + b*х^2 + с*х^3 | |
|
Part[f, 3] |
ex 3 |
| Part[f, 2] | bx 2 |
| f[[1]] | a |
| f[[3]] | ex 3 |
| f[[-1]] | ex 3 |
Нередко выражения рассматриваются как возможные значения переменных. В этом случае используются операторы присваивания переменным заданных значений. Mathematica имеет два типа присваивания — с помощью символов «: =» и с помощью символа «=». Они различаются временем вычисления выражения, следующего за этими символами. Знак «: =» используется для задержки присваивания до вычисления правой части, например:
f[x_] := % + 2 х
Вывода здесь нет. Продолжим наш эксперимент: 1 + у^2
1 + y2
g[х_] = % + 2 х
1 + 2 х + у2
Теперь вывод есть, так как % (ссылка на предыдущий результат) определена в виде выражения 1 + у^2 и при задании [х_] использован оператор немедленного присваивания. Далее:
2 + z
2 + z
{f[a],g[a]>
{2 + 2a+z, 1 + 2 а + у2}
Следующие функции возвращают особые части выражения:
- Denominator [expr] — возвращает знаменатель выражения ехрг;
- First[expr] — возвращает первый элемент из ехрг;
- Last[expr] — возвращает последний элемент из ехрг;
- Rest [expr] — возвращает ехрг с удаленным первым элементом.
Ниже приводятся примеры применения этих функций.
| Ввод (In) | Вывод (Out) |
| Denominator [ (х + 1) / (х ^ 2 + 2*х + 3) ] | 3+ 2х+ х^2 |
| ехрг = а * b + с - d | ab+ с- d |
| First [expr] | ab |
| Last [expr] | -d |
| Rest [expr] | c-d |
Работа с выражениями, умение их преобразовывать и выделять нужные фрагменты является важнейшей частью культуры символьных преобразований.
Иногда возникает необходимость в удалении части выражения. Для этого используются следующие функции:
- Delete [expr, n] — удаляет элемент в позиции п в выражении ехрг. Если п отрицательно, позиция отсчитывается с конца;
- Deletefexpr, (i, j,...}] — стирает часть выражения в позиции {i, j ,...};
- Delete [expr, {{i1, j1,...}, {i2, j2,...},...}] — удаляет части выражения в нескольких указанных позициях;
- DeleteCases [expr, pattern] — удаляет все элементы выражения expr, которые совпадают с образцом pattern;
- DeleteCases[expr, pattern, levspec] — удаляет все части выражения ехрг на уровнях, указанных levspec и соответствующих образцу pattern.
Следующие примеры иллюстрируют применение этих функций.
| Ввод (In) | Вывод (Out) |
| ехрr = а * b + с - d | ab + с - d |
| Delete [expr, 1] | c-d |
| Delete [expr, 3] | ab+ с |
| Delete [expr, {{!}, {3}}] | с |
| DeleteCases [expr, а*b] | c-d |
| DeleteCases [expr, с, 1] | ab-d |
Обратите внимание на то, что в общем случае выражения могут быть многоуровневыми. Уровень задается спецификацией levspec.
Другие манипуляции с выражениями
В процессе преобразования выражений с ними возможны и иные манипуляции. Наиболее важные из них выполняются следующими функциями:
- Append [expr, elem] — возвращает ехрг с дополнением elem;
- AppendTo [s, elem] — добавляет elem к значению s и присваивает s новое значение;
- Apply [f, expr, levelspec] — возвращает ехрг, замещая заголовки в тех частях ехрг, которые указаны спецификацией уровня levelspec;
- Cancel [expr] — возвращает ехрг с сокращением общих множителей числителя и знаменателя;
- Cases [expr, pattern, levelspec] — возвращает список всех частей выражения expr на уровнях, указанных спецификацией levelspec, которые соответствуют шаблону pattern;
- Chop [expr] — присваивает значение 0 тем приближенным вещественным числам в выражении expr, абсолютные величины которых меньше 10 -10 ;
- Chop [expr, tol ] — присваивает значение 0 тем приближенным вещественным числам в выражении expr, абсолютные величины которых меньше tol;
- Replace [expr, rules] — возвращает expr с подстановкой, заданной правилом или списком правил rules;
- ReplaceAll — используется в виде expr /. rules и возвращает expr с подстановками, заданными правилом или списком правил rules;
- ReplacePart [expr, new, n] — возвращает выражение, в котором п-я часть expr заменена на new;
- ReplacePart [expr, new, {i, j,...}] — заменяет на new часть в позиции {i, j,...};
- ReplacePart [expr, new, {{il, jl,...}, {i2, j 2 ,...},...}] — заменяет на new части в нескольких позициях выражения;
- ReplaceRepeated — применяется в виде expr //. rules и неоднократно выполняет замещения до тех пор, пока expr не перестанет изменяться.
Действие этих функций достаточно очевидно и поясняется следующими примерами.
| Ввод (In) | Вывод (Out) |
| Append [a + с, b] | a+ b+ с |
| х = {а, b, с} | {a, b, c} |
| AppendTo [ х , 15 ] | {a, b, c, 15} |
| x | {a, b, c, 15} |
| Apply[f, а А 2 + b ^ 2, 2] | f[a, 2] +f[b, 2] |
| Cancel [(z-1) ^ 2/ (z - 1) ] | -1 + Z |
| Cases[{a, 3.5, 2, 5, "HELLO"}, _Integer] | {2, 5} |
| Exp[N[-лI]] | -1. - 1. 22461 x 10 -16 I |
| Chop[%] | -1. |
| Ехр[N[-лI]] | -1. - 1. 22461 x10 16 I |
| Chop[%, 1*10^-10] | -1. |
| Replace[s ^ 2, s ^ 2 -> a] | a |
| s^2 /. s -> a | a 2 |
Заинтересованному в таких манипуляциях читателю рекомендуется просмотреть множество примеров, имеющихся в справочной системе Mathematica, и, разумеется, попробовать свои собственные примеры.
При создании программного обеспечения на языке Mathematica, а иногда и в ходе диалоговой работы с системой необходим контроль за некоторыми свойствами выражений. Следующие функции обеспечивают такой контроль:
- AtomQ [expr] — возвращает True, если выражение ехрг не может быть разложено на подвыражения и является атомарным, и возвращает False в противном случае;
- FreeQ [expr, form] — возвращает значение True, если в выражении ехрr отсутствует подвыражение, совпадающее с form, в противном случае возвращает False;
- FreeQ[expr, form, levelspec] — тестирует только части выражения на уровнях, указанных levelspec.
Следующие примеры показывают действие этих функций.
| Ввод (In) | Вывод (Out) |
| AtomQ [{a | False |
| AtomQ[2+3/4] | True |
| AtomQ [Sin] | True |
| FreeQ[a*x^b,a] | False |
| FreeQ [ a*x ^ b+c , 1 ] | True |
| FreeQ [a*x^b+c, 1,1] | True |
| FreeQ[a*x^b+c,b,2]}] | True |
Приложение имени функции к выражению или его части
Функции в системе Mathematica характеризуются именем (обобщенно — f) и выражением ехрг, задающим функциональную зависимость. Обычно функция в ответ на обращение к ней возвращает значение выражения — численное или символьное. Однако в системе Mathematica понятие функции значительно расширено, и она может возвращать любой объект, в том числе графический или звуковой. Можно сказать, что входной язык общения с системой Mathematica основан на принципах функционального программирования с применением полных форм представления выражений.
Следующие функции позволяют прикладывать имя функции к выражению или к частям выражения:
- Apply [f, expr] — замещает заголовок выражения ехрг на f;
- Nest [f, expr, n] — возвращает выражение, полученное и-кратным применением f к ехрг;
- Map [f, expr] — применяет f к каждому элементу на первом уровне в ехрr;
- Map[f, expr, levelspec] — применяет f к частям ехрг, указанным с помощью levelspec;
- MapAll [f, expr] — применяет f ко всем частям выражения ехрг.
Приведем примеры действия этих функций.
| Ввод (In) | Вывод (Out) |
| Apply [f, {a, b, x}] | f [a, b, x] |
| Nest[f , x, 3] | f[f[f[x]]] |
| s[x_, y_, z_] := x + y + b | |
| N[Apply[s, {1, 2, a}]] | 3. + b |
| Map[f, {а, Ь, с}] | {f[a], f[b], f[c]} |
| MapAll [f, a*x + b] | f[f[b] + f[f[a] f[x]]] |
| MapAll [f, {а, Ь, с}] | f[{f[a], f[b] , f[c]}] |
Из описания указанных функций вытекает, что они наряду с полной формой могут задаваться укороченной формой.
| Укороченная форма | Полная форма |
| f @ ехрг | f [expr] |
| f @@ ехрг | Apply [f, expr] |
| f /@ ехрг | Map[f, expr] |
| f //@ ехрг | MapAll [f, expr] |
Смысл укороченных выражений очевиден. Приведем несколько примеров их использования.
| Ввод (In) |
Вывод (Out) |
| f@{a, b, с} | f[{a, b, c}] |
| f@@{a, b, c} | f [a, b, c] |
| f /@{a, b, c} | {f[a], f[b], f[c]} |
| f//@{a, b, x} | f[{f[a], f[b], f[x]}] |
Укороченная форма функций может оказаться полезной для сокращения записи алгоритмов и программ.
Выделения и подстановки в функциях
Функция Slot[n], или, в укороченной форме, #n, представляет n-й аргумент функции. Это иллюстрируют следующие примеры.
| Ввод (In) | Вывод (Out) |
| (5* Slot [1] + Slot [2] *Slot[3] A 2) &[a, b, с] | 5a+bc 2 |
| #1 A #2 S[a, b] | a b |
Объект # эквивалентен #1, a #0 — заголовку абстрактной функции. Таким образом, F[#.#2]&F[a,b] эквивалентно F[a,b].
Функция SlotSequence [n], или, в укороченной форме, ##n, где п = 1, 2, ..., представляет порядок применения формальных аргументов к абстрактной функции. Таким образом, объект ##n определяет последовательность аргументов, начиная с n-го.
| Ввод (In) | Вывод (Out) |
| (Times[5, ##2] +Times[##2, ##3 A 2]) &[а, b, с] | Sbobc 3 |
Представленные средства обеспечивают работу с функциями на абстрактном уровне.
Интересные возможности связаны с использованием подстановок при определении функций. Система допускает использование подстановок в виде f [x] = value и f[x_] = value.
Поясним это несколькими примерами.
| Ввод (In) | Вывод (Out) |
| f[x] =u | u |
| f[x] +f[y] | u+f ty] |
| f [x_] = х^2 | x 2 |
| f[x] +f[y] | u+y 2 |
| Clear [f] | |
| f[x]+f[y] | f [x] + f [y] |
Как нетрудно заметить из этих примеров, подстановки в функциях могут существенно изменить исходную функциональную зависимость. А потому важной областью их применения является модификация функций.
Использование подстановок при определении функций позволяет легко реализовывать рекуррентные алгоритмы, то есть алгоритмы, при которых очередной шаг вычислений основан на определенном преобразовании предшествующих шагов. Примером может служить задание функции вычисления факториала fact [n], представленное ниже.
| Операция | Комментарий |
| fact[n_] :=n*fact[n-l] | Задана рекурсивная функция факториала |
| fact[l]=l | Выполнена инициализация функции |
| 1 | |
| fact[3] | Вычислено значение 3! |
| 6 | |
| fact[10] | Вычислено значение 10! |
| 3628800 | |
| ?fact[l] | Выполнена проверка определения функции |
| Global ' fact | |
| fact[l] = 1 | |
| fact[n_] :=nfact[n-l] |
Обратите внимание на использование знака вопроса перед именем функции в конце примера, показанного выше. Оно позволяет вывести текст декларации (определения) функции. После объявления функция может быть использована в последующих ячейках документа.
Дополнительные примеры работы с функциями
Приведем еще ряд примеров действия функций Apply, Map и Nest.
| Ввод (In) | Вывод (Out) |
| Nest[f ,x,3] | f [f[f [X]]] |
| Apply[f,{a,b,c}] | f[a, b, c] |
| s [x_,y_, z_] : =х+у+b | |
| N[Apply[s,{l,2,a}]] | 3. + b |
| Map[f,{a,b,c}] | {f [a], f [b], f [c] } |
| N[Map[Exp, {1,2,3}]] | {2.71828, 7.38906, 20.0855} |
| Map[f ,1+2+c] | f[3] + f[c] |
| m={{a,b},{c,d}} | {{a, b}, {c, d}} |
| Map[f,m] | {f [{a, b}], f [{c, d}] } |
| take2[list_] :=Take[list,2] | |
| Map[take2,{{a,b,c},{c,a,b),{c,c,a}}] | {{a, b}, {c, a}, {c, c}} |
Большинство описанных операций для работы с функциями могут использоваться и при работе со списками. Порой это резко упрощает запись алгоритмов вы-числений для данных, представленных списками, поскольку дает общее определение функций для произвольного числа их параметров. Примерами могут служить определения следующих статистических функций.
Вычисление среднего для элементов списка:
Mean[list_] := Apply[Plus, list] / Length[list] /;
VectorQ[list] && Length[list] > 0
General: :spell! : Possible spelling error: new
symbol name "list" is similar to existing symbol "List".
Вычисление среднего геометрического для списка:
GeometricMean[list_] : = Apply
[Times, list"4 (I/Length [list])] /;
VectorQ[list] && Length[list] > 0
Вычисление гармонического среднего для списка:
HarmonicMean[list_] := Length[list]
/ Apply[Plus, I/list] /;
VectorQ[list] && Length[list] > 0
Обратите внимание на то, что при задании первой функции Mathematica предупреждает о том, что введенный идентификатор list подозрительно напоминает зарезервированный идентификатор List. Все приведенные выше функции не имеют смысла, если список пустой. Поэтому в них введен контроль за такой ситуацией.
Теперь можно выполнить расчеты по этим формулам.
| Ввод (In) | Вывод (Out) |
| data={l,2,3,4} | {1, 2, 3, 4} |
| Mean [data] | 5/2 |
| GeometricMean [data] | 2 3/4 3 l/4 |
| N[%] | 2.21336 |
| HarmonicMean [data] | 48/25 |
Большое число операций для работы с функциями полезно при организации функционального программирования, а также при создании пакетов расширения системы для выполнения символьных преобразований и расчетов. Разумеется, это разумно делать профессионалам-математикам, а не обычным пользователям. Последних, скорее всего, более чем удовлетворит уже имеющийся в системе набор таких операций и функций.
Инверсными функциями называют функции, полученные в результате обращения заданных функций. Например, для функции Sin [x] инверсной будет ArcSin [х] и т. д. Следующие функции обеспечивают представление инверсных функций:
- InverseFunction [f ] — представляет функцию, обратную для f, то есть определенную таким образом, что InverseFunction [f ] [у] возвращает значение х, для которого f [х] равно у. Для функции нескольких переменных InverseFunction [ f ] представляет обращение по первому аргументу;
- InverseFunction [f, n] — представляет обращение по п-му аргументу;
- InverseFunction [f, n, tot] — представляет обращение по п-му аргументу, когда имеется всего tot аргументов.
Следующие примеры иллюстрируют работу с этими функциями.
| Ввод (In) | Вывод (Out) |
| InverseFunction [Sin] | ArcSin |
| %[х] | ArcSin[x] |
| Composition [ f , g , h] | Ccrrposition[f , g, h] |
| InverseFunction [Composition [% , q] ] | Corpositiont [q- 1 , h- 1 , g- 1 ,f- 1] |
Обратите внимание на то, что в этих примерах фигурируют заголовки функций — например, для получения инверсной функции от Sin [х] следует использовать
Sin в качестве аргумента f функции InverseFunction [f].
Задание математических отношений
Символьные преобразования- при всей их кажущейся таинственности осуществляются по определенным, хотя и весьма многочисленным, а потому для нас запутанным, правилам. Основные из них давно известны из математики и описаны в многочисленных справочниках и монографиях. Они записаны в ядре системы и вызываются из него при создании условий, необходимых для выполнения того или иного преобразования. Если этих условий нет, исходное выражение просто повторяется. А если обнаружена явная ошибка в преобразованиях, то о ее сути выводится соответствующее сообщение. При ситуациях, лишь близких к ошибочным, выводится предупреждающее сообщение, и вычисления продолжаются.
Однако математика и использующие ее науки непрерывно развиваются. Появляются все новые и новые правила преобразований. Пользователь-математик может пожелать изменить встроенные правила преобразований — например, для создания новых разделов математики, базирующихся на каких-либо новых представлениях. Блестящий пример этого — теория относительности Эйнштейна.
Таким образом, возникает необходимость расширения математических символьных систем и обучения их новым правилам математических преобразований. Система Mathematica имеет и такие возможности. Поясним на простых примерах, как это делается.
В математике можно найти множество примеров математических отношений. Например, хорошо известно такое отношение для логарифма и экспоненциальной функции:
log(exp(x)) = х.
Не обременяя себя поиском действительно новых закономерностей (порой на это может не хватить жизни, да и везет не каждому ученому), зададим приведенную закономерность для введенных по-новому функций log и ехр. Центральным моментом тут является введение новых имен функций, которые начинаются с малых букв, а не с больших, как у встроенных функций Log и Ехр. Поэтому система воспринимает log и ехр как новые функции.
Итак, вводим «новую» закономерность следующим образом:
log[exp[x_]] :=x
General::spelll : Possible spelling error:
new symbol name "log" is similar to existing symbol "Log".
General::spelll : Possible spelling error:
new symbol name "exp" is similar to existing symbol "Exp".
Система на всякий случай сообщает о рискованности эксперимента — символы log и ехр похожи на зарезервированные имена функций Log и Ехр. Проигнорировав это предупреждение, проверим введенную закономерность в работе.
| Ввод (In) | Вывод (Out) |
| log [exp [15]] | 15 |
| 1оg[ехр[у^2+1]] | 1+y 2 |
Итак, наша «новая» закономерность работает. Можно ввести, скажем, и такое известное отношение:
log[x_^n_] :=n*log[x]
Проверим, какие отношения заданы нами для функции log:
?log
Global' log
log[exp[x_] ] : = x
log[x_n-] := n log[x]
Проверим введенные правила, например, так:
5lоg[[1+х]^5]
5lоg[1+х]
Рассмотрим еще пару примеров задания «новых» математических правил. В первом примере задано правило — логарифм произведения равен сумме логарифмов сомножителей:
log[x_*y_] := log[x] +log[y]
Любопытно, что эта закономерность действует при любом числе сомножителей:
log[a*b*c*d*e]
log [a] + log[b] + log[c] + log[d] + log[e]
Второй пример иллюстрирует задание объекта, ассоциированного со списком:
а /: а[х_] +а[у_] :=а[х + у]
а[х] + а[у] +a[z]
а[х+ у+ z]
Введенные здесь обозначения х_, у_ и n_ представляют собой образцы, на место которых могут подставляться произвольные выражения. Позже мы обсудим применение образцов более детально.
Описанные выше примеры наглядно демонстрируют возможности выполнения так называемого математического программирования, в основе которого лежит задание определенных математических соотношений между математическими понятиями, прежде всего такими, как функции.
3. Функции компьютерной алгебры
Функции компьютерной алгебры
Системы компьютерной алгебры имеют несколько характерных для них функций, выполняющих достаточно сложные преобразования выражений. Эти функции имеют вполне установившиеся названия (Simplify, Expand, Collect, Factor и т. д.) и встречаются практически во всех системах символьной математики. Настало время детально познакомиться с ними, что и делается в данном разделе.
Упрощение выражений — функция Simplify
Упрощение математических выражений — одна из самых важных задач символьной математики. Частенько невероятно сложное математическое выражение, пугающее новичков своим грозным видом, является просто нулем или единицей либо сводится к простому выражению после ряда вполне заурядных (хотя, порою, и довольно сложных) преобразований. Качество выполнения операции упрощения во многом определяется мощью ядра математической системы, поскольку зависит от числа заложенных в него функций и правил преобразования выражений.
С точки зрения простоты выражений они делятся на недостаточно простые и достаточно простые выражения. Недостаточно простые выражения таят в себе всевозможные «излишества»: сокращаемые общие члены, лишние переменные и функции, полиномы со степенями, допускающими понижение, и т. д. Это затрудняет качественный анализ выражений и может даже приводить к неоднозначным и даже неверным результатам.
Mathematica всегда старается упростить то или иное выражение, если для этого не требуется каких-либо особых средств. Например, сложные выражения, содержащие элементарные или специальные функции, превращаются в более простые выражения — в том лишь смысле, что они состоят из более простых функций. Следующие примеры иллюстрируют это.
| Ввод (In) | Вывод (Out) |
| (Csc[x] Tan[w]) / (Cot[x] Sec[w]) | Sec[x] Sin[w] |
| BesselY[5/2, Е] | SQRT(2/л)(Cos[E]-[3Cos[E]+3Sin[E]]/SQRT(E)) |
Однако так бывает далеко не всегда, и для проведения необходимых преобразований используются различные функции, описанные ниже.
Для упрощения выражений используется функция Simplify [ехрг]. Она исполняет последовательность алгебраических преобразований над выражением ехрг и возвращает простейшую из найденных форм (обычно это бывает нормальная форма выражения).
Функция Simplify работает с самыми различными математическими выражениями: многочленами, рациональными выражениями (состоящими из полиномов и их отношений), расширенными рациональными выражениями (имеющими дробные степени переменных), элементарными и специальными функциями, алгебраическими и тригонометрическими выражениями и т. д. Обычно она приводит выражения к нормальному виду, что автоматически означает и приведение к виду достаточно простых выражений.
Приведем наиболее характерные результаты действия функции Simplify.
| Ввод (In) | Вывод (Out) |
| Комбинирование числовых подвыражений Simplify [6 х 2] | 12 х |
| Приведение подобных множителей у произведений Simplify[x ^ 3 у х ^ 5] | х 8 у |
| Приведение подобных членов суммы Simplify[x + 12 + 4 х] | 5 х + 12 |
| Упрощение тождеств, содержащих 0 или 1 Simplify [2+0] Simplify[l*x] | 2 х |
| Распределение целочисленных показателей степени в произведениях Simplify[(5 х ^ 2 у ^ 3) ^ 2] | 5 х 4 у 5 |
| Приведение общих знаменателей к выражениям с пониженной степенью или с исключением сокращаемых переменных Simplify [2 х / (х ^ 2- 1) - 1/(х + 1) ] | 1/(х + 1) |
| Разложение полиномов и понижение степени выражений Simplify[(x + 1) ^ 2-х ^ 2] | 2 х + 1 |
| Сокращение на наибольший полиномиальный делитель ; Simplify [ (х ^ 2 - 2 х у + у ^ 2 ) / (х ^ 2 - у ^ 2 ) ] | (х -у)/(х + у) |
Следующие примеры дополнительно поясняют применение функции Simplify.
| Ввод (In) | Вывод (Out) |
| Simplify[a*a - 2*а*b + b^2] | (a-b) 2 |
| Simplify [Exp [х] ^2/х] | E 2x /X |
| Sirnplif у [Sin [x-y] H-Sin [х+у] ] | 2Cos[y] Sin[x] |
| Simplif у [Ехр [х] *Ехр [у] /Exp [z] ] | E x+y-z |
| Simplify [Exp [z*Log [b] ] ] | b z |
| Simplify [Log [x/y] ] | Log[x/y] |
| А := (Cos[4*x] - 4*Cos[2*x] +3)/ (4*Cos[2*x] + Cos[4*x] + 3) | |
| Simplify [A] | Tan[x] 4 |
| Simplify[6*Log[10] ] | 6Log[10] |
| Simplify[6 Log[10], Complexity Function -> LeafCount] | Log[ 1000000] |
Операция Simplify часто выполняется по умолчанию. Например, это обычно происходит при вычислении выражений, примеры чего приводились выше. Несомненно, это одна из наиболее важных и часто применяемых операций компьютерной алгебры.
Вообще говоря, понятие упрощения математических выражений не является однозначным. К примеру, некоторые пакеты символьной математики упрощают sin(x)/cos(x) к единой математической функции tan(x), тогда как другие упрощают tan(x) к sin(.r)/cos(.r), считая, что функции sin(x) и cos(.r) более простые, чем функция tan(.r). Эта неоднозначность часто путает неопытных пользователей, пытающихся проверить символьные системы примерами из справочников, — вполне возможно, что авторы их придерживались несколько иного подхода к упрощению выражений, чем разработчики той или иной математической системы.
Функция полного упрощения FullSimplify
Функция FullSimplify, область применения которой в Mathematica 4 заметно расширена, обладает заметно большими возможностями, чем функция Simplify. В частности, она обеспечивает упрощение выражений, содержащих специальные математические функции:
Simplify [Gamma [х] *х* (х+1) * (х+2) * (х+n) ]
х(1+х) (2 + х) (n+x) Garrma[x]
FullSimplify [Gamma [х] *х* (х+1) * (х+2) * (х+n) ]
(п+ х) Garrma[3 + х]
Simplify[Tan[x] , ComplexityFunction-> (Count[{#l}, _Tan, \ [Infinity]]*;)]
Tan[x]
FullSimplify [Tan [x] , ComplexityFunction -> (Count[{#l}, _Tan,
\ [Infinity]] &)]
Как видно из этих примеров, функция FullSimplify обеспечивает упрощение даже в том случае, когда функция Simplify пасует. Неплохо упрощаются тригонометрические функции, особенно при использовании опции Complexity-Function, подсказывающей путь упрощения.
В то же время нельзя не отметить, что теоретический фундамент упрощения выражений находится лишь в начале своего возведения, так что не стоит удивляться, если отдельные выражения не будут упрощаться — даже в том случае, когда это в принципе возможно. Более того, с позиций истинного математика функции Simplify и FullSimplify делают не совсем понятно что. Тем не менее, часто эти функции позволяют получить вполне приемлемую, хотя вовсе не единственную и не самую простую форму упрощаемого выражения.
Раскрытие и расширение выражений — функции класса Expand
Расширение, или раскрытие, выражений — еще одна типовая операция компьютерной алгебры. По смыслу она противоположна упрощению выражений. Часто компактная форма представления выражений обусловлена определенными операциями по их упрощению. Существует множество выражений, для которых эти правила известны. Например, мы знаем, что выражение
(а -b)2 = (а - b) (а - b)
можно представить как
a2-2ab + b2
Разумеется, такое соответствие существует далеко не всегда. К примеру, выражение в виде числа 1 вовсе не является представлением только выражения sin(X) 2 + cos(x) 2 .
Ниже представлены основные функции, производящие раскрытие и расширение выражений:
- ComplexExpand[expr] — раскрывает ехрг, полагая все переменные вещественными;
- ComplexExpand [expr, {x1, х2,...}] — раскрывает ехрг, считая переменные xi комплексными;
- FunctionExpand [expr] — раскрывает выражения ехрг, содержащие специальные функции;
- Expand [ехрг ] — раскрывает произведения и положительные целые степени в ехрг;
- Expand [expr, patt] — выполняет расширение только для тех элементов ехрг, которые содержат соответствующие шаблону patt члены;
- Exp_andAll [expr] — раскрывает все произведения и целочисленные степени в любой части ехрг;
- ExpandAll [expr, patt] — исключает из операции расширения те части ехрг, которые не содержат соответствующие шаблону patt члены;
- ExpandDenominator [expr] — раскрывает произведение и степени, которые присутствуют в выражении ехрг в роли знаменателей;
- ExpandNumerator [expr] — раскрывает произведения и степени в числителе выражения ехрг;
- PowerExpand[expr] — раскрывает вложенные степени, степени произведений, логарифмы от степеней и логарифмы от произведений. Осторожно используйте PowerExpand, так как эта функция не реагирует на разрывный характер выражения ехрг.
Приведем примеры операций расширения выражений с помощью функции Expand:
Expand[(х - а)*(х - b)*(х - с)]
-abc+ abx + acx+bcx-ax2- bx2-cx2 + x3
Simplify[%]
-(а-х) (-b+х) (-с + х)
Expand!(Sin[x]+Cos[x])/(Cos[x]*Sin[x])]
Csc[x] + Secfx]
Simplify[%]
Sirrplfy[Csc[x] + Sec[x] ]
Expand[2*Cos[x]^2,Trig-> True]
2Cos[x]2
Simplify[%]
l+Cos[2x]
Expand[Sin[x]^2+Cos[x]^2]
Cos[y]2+Sin[x]2
Expand[Sin[x]^2+Cos[x]^2,Trig-> True]
1- Cos[x]2/2 +Cos [у]2/2 +Sin[x]2/2 -Sin[y]2/2
Simplify[%]
1/2 (2-Cos[2x] + Cos[2y])
В этих примерах полезно обратить внимание на то, что далеко не всегда последовательное применение функций Expand и Simplify дает исходное выражение. Гораздо чаще получается новое выражение, порой представляющее ценность. При операциях с тригонометрическими выражениями нередко нужно использовать опцию Trig->True, намечая тригонометрический путь решения. В противном случае может быть просто выдан отказ от выполнения операции Expand с заданным выражением, которое будет просто повторено в ячейке вывода.
Приведем примеры использования других функций расширения выражений:
ExpandAll[Sin[2*Cos[x]], Trig -> True]
Cos [Cos [x] + ISin[x] ] Sin[Cos[x] - ISin[x] ] +
Cos [Costx] - ISintx] ] Sin[Cos[x] + ISin[x] ] Simplify[%]
Sin [ 2 Cos [x]]
ExpandNumerator[(1 + x)^2/х]
1 + 2 x + x2/x
ExpandDenominator[(1 - x)^2/(l + x)^2]
(1-х)2/1 + 2 x + x2
ComplexExpand[Sin[a + I*b]]
Cosh[b] Sin [a] + I Cos [a] Sirihfb]
ComplexExpand[ (a. + b I) / (x + d I) ]
-lad/Abs[Id+x]2+bd/Abs[Id+x]2 + ax/Abs[Id + x]2 +Ibx/Abs[Id+x]2
Simplify[%]
(-Ia + b) (d + Ix)/^bstld+x]2
PowerExpand[Sqrt[a^2*b*c]]
aSQRT(b)SQRT(c)
FunctionExpand[Gamma[4, x]]
E-xx3+ 3 (Fxx2+ 2 (E-x+ E-xx))
FunctionExpand[Beta[4, 2 + x]]
6/(2 + x) (3+x) (4 + x) (5 + x)
FunctionExpand[Zeta[3, 2 + x] ]
Разумеется, этими примерами далеко не исчерпываются возможности данной группы функций. Рекомендуется опробовать примеры из справочной системы данных Mathemaca и свои собственные примеры.
К операциям, расширяющим выражения, относится также функция Collect:
- Collect[expr, x]— выполняет приведение общих членов выражения по степеням переменной х;
- Collect [expr, {x1, x2, ...}]— выполняет приведение общих членов выражения по степеням переменных xl, х2, ...
Эта операция особенно полезна, если результат можно представить в виде степенных многочленов. Проиллюстрируем это следующими примерами.
| Ввод (In) | Вывод (Out) |
| Collect [%, x] | -5x+5x 2 -x 3 + x 4 |
| expr = (5 + x ^ 2) * (x- 1) *x | (-1 + x) x(5 + x 2 ) |
| Collect [a *x ^ 2 +b*x*y+c*y+d*y ^ 2, y] | ax + (c+ bx) y+ dy 2 |
| Collect [a *x ^ 2+b*x*y + c*y+d*y ^ 2, x] | ax + cy+ bxy+ dy 2 |
| Collect[ (x - 1) * (x - 2) * (х^2 - 9) , x] | -18-27х-7х 2 -Зх 3 + х 4 |
Следующий пример показывает применение функции Collect к выражению с двумя переменными:
Collect[(х-1)*(у-3)*(х-2)*(у-2)*(х-1),у,х]
-12.+ 30х-24х2+ 6х3 + (10-25х + 20Х2- Sx3) y+
(-2+ 5х-4х2 + х3) у2
Разумеется, как и в случае упрощения выражений, их расширение не является однозначной операцией и предполагает наличие определенных условностей. Опытный пользователь, используя опции функций, обычно без труда может получить результат в нужной форме.
Функции преобразования тригонометрических выражений
Хотя представленные выше функции иногда применимы для тригонометрических выражений, для последних есть ряд специальных функций, дающих более надежные результаты в ходе преобразований тригонометрических функций. В названии этой группы функций имеется слово Trig. Начнем с функции Trig-Expand [expr ], которая обеспечивает расширение выражения ехрг, содержащего тригонометрические и гиперболические функции. Представленные ниже примеры иллюстрируют работу этой функции:
TrigExpandfSin[а+b]]
Cos[b] Sin[a] +Cos[a] Sin[b]
TrigExpand[Cos[3*x]] TrigExpand[Cos[3*x]]
Cos[x]3-3Cos[x] Sin[x]2
TrigExpand[Sinh[2^x]]
2Cosh[x] Sinh[x]
TrigExpand[Sin[Cos[Tan[x]^2]]]
Cos[1/2Cos[Tan[x]2] + 1/2ISin[Tan[x]2]
Sin[1/2Cos[Tan[x]2] - 1/2ISin[Tan[x]2]
Cos[1/2Cos[Tan[x]2] - 1/2ISin[Tan[x]2]
Sin[1/2Cos[Tan[x]2] + 1/2ISin[Tan[x]2]
TrigExpand[Sin[2*x]-Cos[3*x]^2]
1/2 Cos[x]6/2+2Cos[x] Sin[x] + 15/2Cos[x]4Sin[x]2
15/2Cos[x]2/Sin[x]4+Sin[x]6 /2
TrigExpand[Sin[2 ArcCoth[t]]]
2 Cos [ArcCoth[ t] ] Sin[ArcCoth[ t] ]
Следующие две функции обеспечивают взаимные преобразования экспоненциальных и тригонометрических выражений:
- TrigToExp [expr] — преобразует тригонометрические выражения к экспоненциальному виду;
- ExpToTrig [expr] — преобразует экспоненциальные выражения в тригонометрические.
Примеры применения этих функций:
TrigToExp[Cos[z]]
1/2( EIz+EIz)
ExpToTrig [ % ]
Cos [ z]
f := Sinh[z] + Cosh[z] TrigToExp[f]
Ez
ExpToTrig[%]
Cosh[z] + Sinh[z]
TrigToExp[Sin[x]/Cos[y]]
I (E-IX- EIX)/(E-IX+ EIX)
ExpToTrig[%]
Sec[y] Sin[x]
Приведем еще две функции:
- TrigFactor [expr] — раскладывает на простые множители тригонометрическое выражение ехрr;
- TrigFactorList [expr] — раскладывает тригонометрическое выражение ехрг на списки с термами выражения.
Следующие примеры показывают применение этих функций:
expr = TrigExpand[Sin[a + b]^3]
3/4Cos[b] Sinfa] - 3/4 Cos [a]2 Cos [b]3 Sin [a] +
1/4 Cos[b]3Sin[a]3 + 3/4 Cos[a] Sin[b]-
3/4Cos[a]3Cos[b]2Sin[b] +9/4 Cos[a] Cos[b]2Sin[a]2 Sin[b] +
9/4 Cos[apCos[b] Sin [a] Sin[a]2-3/4 Cos[b] Sin[a]-3 Sin[b]2 +
1/4Cos[a]3Sin[b]3-3/4 Cos[a] Sin[a]2Sin[b]3
TrigFactor[expr]
Sin[a+b]3
TrigFactorList[expr]
{{1, 1}, {Sin[a+b] , 3}}
TrigExpand[Cosh[Sin[x*y]]]
Cos[1/2 Cos[xy] - 1/2 ISin[xy]] Cos[1/2 Cos[xy] + 1/2 ISin[xy]]
Sin[1/2Cos[xy] -1/2 ISin[xy]] Sin[1/2 Cos[xy] + 1/2 ISin[xy]]
TrigFactorList[%]
{{1, 1}, {Cosh[Sin[xy]], 1}}
Наконец, функция TrigReduce [expr] упрощает выражения с произведениями тригонометрических функций.
Примеры применения этой функции:
TrigReduce[2*Sin[x]*Cos[у]]
Sin[x- у] + Sin[x + y]
TrigReduce[Cosh[x]*Tanh[x]]
Sinh[x]
TrigReduce[Sin[x]^2 + Cos[x]^2]
1
TrigReduce[Sin[x]*Cos[x]]
1/2 Sin[2x]
TrigReduce[Sinh[x/y]^3]
1/4 (-3Sinh[x/y] + Sinh[3x/y])
Применение рассмотренных функций расширяет круг задач, решаемых с применением символьных преобразований.
Основные операции над полиномами
Полиномом называют выражение, состоящее из нескольких частей одного вида. В западной математической литературе к ним часто относят степенной многочлен вида
Р(х) = а0 + а1х + а2 х2 + а3 х3 + ... + аnхn.
Хотя термин «полином» не очень прижился в отечественной математической литературе, мы оставляем его ввиду краткости и ради лучшего понимания синтаксиса функций системы, поскольку слова poly и Polynomial входят в параметры и имена многих функций. При этом полиномы мы будем кратко обозначать как poly или pi (здесь i — индекс или порядковый номер полинома).
Над полиномами можно выполнять обычные арифметические операции: сложение, вычитание, умножение и деление. Это иллюстрируют следующие примеры (здесь р! и р2 — полиномы от одной переменной х):
р1 := х^3 + 2*х^2 + 3*х + 4
р2 := х^2 - 1
р1 + р2
3+3х+3х2+х3
р1 - p2
5+3х+х2+х3
Expand[pl*p2]
-4- 3х + 2х2 + 2х3 + 2х4 + х5
pl/p2
[4 + Зх+2х2 + х3]/[-1 + х2]
Simplify[(х^5 + 2*х^4 + 2*х^3 + 2*х^2 - 3*х - 4)/(х^2 - 1)]
4+3х+2х2+х3
Если ситуация со сложением и вычитанием полиномов достаточно очевидна, то с умножением и делением результат часто повторяет задание. Для получения результата умножения полиномов в обычной форме следует использовать функцию расширения символьных выражений Expand.
Если один полином делится на другой (это бывает далеко не всегда), то для получения результата надо использовать функцию Simplify. В общем случае при делении полиномов может оставаться остаток. Функция, обеспечивающая деление полиномов и вычисляющая остаток, описана ниже.
Разложение полиномов — функции класса Factor
Разложение чисел, математических выражений и особенно полиномов на простые , множители является столь же распространенной операцией, что и функции Simplify, Collect и Expand. Имеется целый ряд функций, в названии которых есть слово Factor и которые решают указанные задачи:
- Factor [poly] — выполняет разложение полинома над целыми числами;
- Factor [poly, Modulus->p] — выполняет разложение полинома по модулю простого числа р;
- Factorlnteger [n] — возвращает список простых множителей целого числа п вместе с их показателями степеней. Опция FactorComplete позволяет указать, следует ли выполнять полное разложение;
- FactorList [poly] — возвращает список множителей полинома с их показателями степени. Опция Modulus->p позволяет представить множители полинома по модулю простого числа р;
- FactorSquareFree [poly] — записывает полином в виде произведения множителей, свободных от квадратов. Опция Modulus->p позволяет представить разложение полинома по модулю простого числа р;
- FactorSquareFreeList [poly] — возвращает список множителей полинома, свободных от квадратов, вместе с показателями степени. Может использоваться опция Modulus->р;
- FactorTerms [poly] — извлекает полный (общий) числовой множитель в poly;
- FactorTermsList [poly] — возвращает лист всех общих числовых множителей полинома poly.
Далее представлен ряд примеров применения этих функций.
| Ввод (In) | Вывод (Out) |
| Factor [x ^ 3 - 6*x ^ 2 + 11*х - 6] Factor[x ^ 3 - 6*х ^ 2 + 21*х - 52] | (-3 + x) (-2+x) (-1 + x) (-4 + x) (13-2X+X 2 ) |
| Factor [х А 5 + 8*х ^ 4 + 31*х ^ 3 + 80*х ^ 2 + 94*х + 20, Modulus -> 3] | (1+x) 2 (2+x) 3 |
| FactorList[x A 4 - 1, Modulus -> 2] FactorSquareFree [ (x ^ 2 + 1)*(х ^ 4 - 1) ] | {{1, 1}, {1 + x, 4}} (-1+x 2 ) (1 + x 2 ) 2 |
| FactorSguareFree [ (x ^ 2 + l)*(x ^ 4 - 1) , Modulus -> 2] | (1+x) 6 |
| FactorSquareFreeListt (x ^ 2 +1)* | |
| (x A 4 - 1) , Modulus -> 2] FactorTerms[2*x ^ 2 + 4*x + 6] FactorTermsList[2*x ^ 2 + 4*x + 6] | {{1, 1), {1 + x, 6}} 2 (3+ 2x+ x 2 ) {2, 3 + 2X+X 2 } |
| Factorlnteger [123456789] | {{3, 2), {3607, 1}, {3803, 1}} |
| FactorList[x ^ 4 - 1] | {{!,.!}, {-1 + x, 1}, {1+x, 1}, {1+x 2 , 1}} |
| FactorSquareFreeListt (x ^ 2 +1)* (x ^ 4 - 1) ] | {{1, 1}, {-1+x 2 , 1}, {1 + x 2 , 2}} |
Обычно функция Factor выявляет внутреннюю суть полинома, раскладывая его на множители, содержащие корни полинома. Однако в ряде случаев корни полинома удобнее получать в явном виде с помощью уже рассмотренной функции Roots.
Функция Factor может работать и с тригонометрическими выражениями, поскольку многие из них подчиняются правилам преобразований, присущим полиномам. При этом тригонометрический путь решения задается опцией Trig->True. Это иллюстрируют следующие примеры.
| Ввод (In) | Вывод (Out) |
| Factor [Csc[x] + Sec[x], Trig -> True] | Csc[x] Sec[x] (Cos[x]+ Sin[x] ) |
| Factor [ Sin [3*x] , Trig -> True] | (1+ 2Cos[2x]) Sin[x] |
Функции для работы с полиномами
Для работы с полиномами имеется множество функций, по большей части достаточно очевидных для знакомого с математикой пользователя:
- Decompose [poly, x] — выполняет разложение полинома, если это возможно, на более простые полиномиальные множители;
- GroebnerBasis [ {polyl, poly2,...}, {xl, х2,...}]—возвращает список полиномов, которые образуют базис Гробнера для идеала, порожденного полиномами polyi;
- Polynomial-Division [p, q, x] — возвращает список частного и остатка, полученных делением полиномов р и q от х;
- PolynomialGCD [polyl, poly2,...] — возвращает наибольший общий делитель ряда полиномов polyl, poly2, ... С опцией Modulus->p функция возвращает наибольший общий делитель по модулю простого числа р;
- PolynomialLCM[polyl, poly2,...] — возвращает наименьшее общее кратное полиномов polyl, poly2, ... С опцией Modulus->p функция возвращает наименьшее общее кратное по модулю простого числа р;
- PolynomialMod [poly, m] — возвращает полином poly, приведенный по модулю m;
- PolynomialMod [poly, {ml, m2,...}] — выполняет приведение по модулю всех mi;
- PolynomialQ [expr, var] — возвращает значение True, если expr является полиномом от var, иначе возвращает False;
- PolynomialQ [expr, {varl,...}] — проверяет, является ли expr полиномом от vari;
- PolynomialQuotient [р, q, х] — возвращает частное от деления р и q как полиномов от х, игнорируя какой-либо остаток;
- PolynomialRemainder [р, q, х] — возвращает остаток от деления р на q как полиномов от х;
- Resultant [polyl, poly2, var] — вычисляет результант полиномов polyl и poly2 по переменной var. С опцией Modulus->p функция вычисляет результант по модулю простого числа р.
Итак, работа с этими функциями, по существу, сводит операции с таким сложным видом символьных данных, как многочлены, к типовым алгебраическим операциям над обычными символьными переменными. Следующие примеры поясняют работу с полиномами:
Р[х] := а*х^3 + b*х^2 + с*х + d
Q[x] := е*х^2 - f*x - 1
Null2
Collect[P[x] + Q[x], x]
-1 + d+ (c- f) x+ (b+e) x^ax3
Collect[P[x]*Q[x], x]
-d+ (-c-df) x+ (-b+de- cf) x2* (-a+ ce-bf) x3 +
(be-af) x4+aex5
{PolynomialQ[P[x]], PolynomialQ[Q[x]]}
{True, True}
PolynomialQ[Sin[x], x]
False
PolynomialQ[P[x] + Q[x]]
True
Decompose[P[x], х]
{d+ cx+ bх2 + ах3}
PolynomialQuotient[P[x], Q[x], x]
b/e+af/e2+ax/e
PolynomialRemainder[Q[x], Р[х], х]
-1-fx+ex2
CoefficientList[P[x], x]
{d, с, b, a}
Decompose[х^6 + х + 1 - х^3 + 2*х^5, х]
{1+х-х3+2х5 + х6}
PolynomialGCD[Р[х], Q[х]]
1
PolynomialLCM[P[x], Q[x]]
Р[х] Q[x]
PolynomialQuotient[3*x^3 - 2*х^2 + х, х^2 - х + 1, х]
1+Зх
PolynomialRemainder[3*х^3 - 2*х^2 + х, х^2 - х + 1, х]
-1-х
Reduce[а*х^2 + b*х + с == 0, х]
Полиномы широко используются в математических расчетах. Поэтому обилие функций по работе с ними облегчает проведение сложных вычислений и позволяет представлять результаты в достаточно простой и удобной форме. Если бы системы компьютерной алгебры работали только с одними полиномами, то и в этом случае они вполне оправдали бы себя в глазах многих математиков.
Функции для расширенных операций с выражениями
Выше была описана сравнительно немногочисленная группа функций для работы с выражениями — их упрощения, расширения, выделения множителей и т. д. Эти функции способны решать большинство повседневных задач, связанных с аналитическими преобразованиями выражений. Однако система Mathematica имеет гораздо более полный набор функций для работы с выражениями. Они приведены в приложении.
К сожалению, объем книги не позволяет привести примеры использования всех этих функций, да и вряд ли они будут интересны всем читателям. Поэтому приведем лишь отдельные примеры работы с некоторыми из этих функций:
- Apart [expr] — переписывает рациональное выражение expr в виде суммы членов с минимальными знаменателями;
- Apart [expr, var] — аналогична Apart [expr], но все переменные, кроме var, интерпретируются как константы.
Примеры использования функции Apart:
Apart[(x^4 + 1)/(х^2 - 1)]
1+-1/(1+X)+X2-1/(1 + х )
Apart[(х^3 - у^3 - 1)/(х^2 - у), у]
Две уже знакомые нам функции выделяют знаменатель и числитель выражения в виде дроби:
Denominator[(х^2 - х - 1)/(х - 1)]
-1 + х
Numerator[(х^2 - х - 1)/(х - 1)]
-1-х + х2
Следующие функции позволяют судить о размерности выражений:
- Depth [expr ] — возвращает значение, на единицу превышающее максимальное число индексов, требуемых для указания любой части выражения expr;
- Dimensions [expr] — возвращает список размерностей выражения expr;
- Dimensions [expr, n] — возвращает список размерностей expr до уровня n. Примеры применения этих функций:
Depth[х^3 + х^2 + х + 1]
3
Dimensions[х^3 - 2*х^2 + 1]
{3}.
Функция Evaluate [expr] вычисляет выражение expr безусловно, то есть даже если оно оказывается аргументом функции, чьи атрибуты определяют его невычисляемым:
Evaluate[1 + 1 + Sin[l]]
2+Sin[l]
Обилие функций для работы с математическими выражениями позволяет решать с помощью системы Mathernatica самые серьезные задачи символьной математики (компьютерной алгебры). Разумеется, для этого требуется время на полное освоение системы и серьезный опыт практического ее использования. Он приходит лишь спустя год-два постоянной и интенсивной работы, поэтому не упускайте возможности потренироваться в работе с системой Mathematica.
4. Что нового мы узнали?
Что нового мы узнали
В этом уроке мы научились:
- Записывать выражения в разной форме.
- Работать с частями выражений.
- Осуществлять выделения и подстановки в функциях.
- Работать с рекурсивными функциями.
- Задавать инверсные функции.
- Задавать математические отношения.
- Упрощать, раскрывать и расширять выражения.
- Преобразовывать тригонометрические выражения.
- Работать с полиномами.
Урок 10. Основы программирования
Урок 10. Основы программирования
1. Основы программирования
Основы программирования
- Методы программирования
- Образцы (patterns) и их применение
- Функции пользователя
- Функции FixedPoint и Catch
- Реализация рекурсивных и рекуррентных алгоритмов
- Использование процедур
- Организация циклов
- Условные выражения и безусловные переходы
- Контексты
- Подготовка пакетов расширений
- Средства визуального программирования
- Отладка и трассировка программ
Ранее не раз говорилось, что Mathematica, в сущности, является диалоговым языком программирования сверхвысокого уровня. Однако мы еще не поднимались (или не опускались) до уровня подготовки программ в среде Mathematica 3/4. Между тем, Mathematica и впрямь имеет программные средства, ничем не уступающие таковым для современных языков программирования, а в области подготовки программ для математических преобразований и вычислений намного их превосходящие. В этом уроке мы, наконец, изучим систему Mathematica как язык программирования.
2. Методы программирования
Методы программирования
Такие мощные системы, как Mathematica, предназначены, в основном, для решения математических задач без их программирования большинством пользователей. Однако это вовсе не означает, что Mathematica не является языком (или системой) программирования и не позволяет при необходимости программировать решение простых или сложных задач, для которых имеющихся встроенных функций и даже пакетов расширений оказывается недостаточно или которые требуют для реализации своих алгоритмов применения типовых программных средств, присущих обычным языкам программирования. Все обстоит совсем иначе.
Фактически, основой системы Mathematica является проблемно-ориентированный на математические расчеты язык программирования сверхвысокого уровня. По своим возможностям этот язык намного превосходит обычные универсальные языки программирования, такие как Фортран, Бейсик, Паскаль или С.
Важно подчеркнуть, что здесь речь идет о языке программирования системы Mathematica, а не о языке реализации самой системы. Языком реализации является универсальный язык программирования C++, показавший свою высокую эффективность в качестве языка системного программирования.
Как и всякий язык программирования, входной язык системы Mathematica содержит операторы, функции и управляющие стриктуры. Основные операторы и функции этого языка и относящиеся к ним опции мы фактически уже рассмотрели. Набор описанных ранее типовых операторов и функций характерен для большинства современных языков программирования. Мощь системы Mathematica как средства программирования решения математических задач обусловлена необычно большим (в сравнении с обычными языками программирования) набором функций, среди которых немало таких, которые реализуют сложные и практически полезные математические преобразования и современные вычислительные методы (как численные, так и аналитические).
Число этих функций только в ядре и библиотеках приближается к тысяче. Среди них такие операции, как символьное и численное дифференцирование и интегрирование, вычисление пределов функций, вычисление специальных математических функций и т. д. — словом, реализации именно тех средств, для создания которых на обычных языках программирования приходится составлять отдельные, подчас довольно сложные программы. Почти столько же новых функций (или модернизированных старых) содержат пакеты расширения (Add-on Packages).
Язык программирования системы Mathematica трудно отнести к какому-либо конкретному типу. Можно разве что сказать, что он является типичным интерпретатором и не предназначен для создания исполняемых файлов. Впрочем, для отдельных выражений этот язык может осуществлять компиляцию с помощью функции Compile, что полезно при необходимости увеличения скорости счета.
Этот язык вобрал в себя лучшие средства ряда поколений языков программирования, таких как Бейсик, Фортран, Паскаль и С. Благодаря этому он позволяет легко реализовывать все известные типы (концепции) программирования: функциональное, структурное, объектно-ориентированное, математическое, логическое, рекурсивное и т. д. К примеру, вычисление таких функций, как факториал, в Mathematica можно запрограммировать в виде функции пользователя целым рядом способов:
f[n_] =n!
f[n_] =Gamma[n-l]
f [n_] =n*f [n-1] ;f [0]=l;f [1]=1;
f[n_] =Product[i/i,n]
f [n_] =Module[t=l,Do[t=t*i,i,n] ;t]
f [n_] =Module [ { t=l } , For [ i=l , i<=n , i++ , t*=i ] ; t]
f[n_] =Fold [Times,1, Range [n] ]
Все их можно проверить с помощью следующего теста:
{f[0],f[1],f[5],f[10]}
{1, 1, 120, 3628800}
Как отмечалось, внутреннее представление всех вычислений базируется на применении полных форм выражений, представленных функциями. И вообще, функциям в системе Mathematica принадлежит решающая роль. Таким образом, Mathematica. фактически, изначально реализует функциональный метод программирования — один из самых эффективных и надежных. А обилие логических операторов и функций позволяет полноценно реализовать и логический метод программирования. Множество операций преобразования выражений и функций позволяют осуществлять программирование на основе правил преобразования.
Надо также отметить, что язык системы позволяет разбивать программы на отдельные модули (блоки) и хранить эти модули в тексте документа или на диске Возможно создание полностью самостоятельных блоков — именованных процедур и функций с локальными переменными. Все это наряду с типовыми управляющими структурами позволяет реализовать структурное и модульное программирование.
Столь же естественно язык системы реализует объектно-ориентированное программирование. Оно базируется прежде всего на обобщенном понятии объекта и возможности создания множества связанных друг с другом объектов. В системе Mathematica каждая ячейка документа является объектом и порождается другими, предшествующими объектами. При этом содержанием объектов могут быть математические выражения, входные и выходные данные, графики и рисунки, звуки и т. д.
С понятием объекта тесно связаны три основных свойства, перечисленные ниже:
- инкапсуляция — объединение в одном объекте как данных, так и методов их обработки;
- наследование — означает, что каждый объект, производный от других объектов, наследует их свойства;
- полиформизм — свойство, позволяющее передать ряду объектов сообщение, которое будет обрабатываться каждым объектом в соответствии с его индивидуальными особенностями.
Приведенный ниже пример объектно-ориентированного программирования дает три определения, ассоциированные с объектом h:
h/ : h [x_] +h [y_] : =hplus [х , у]
h/:p[h[x_],x]:=hp[x]
h/:f_[h[x_]] :=fh[f,x]
В принципе, язык программирования системы Mathematica специально создан для реализации любого из перечисленных подходов к программированию, а также ряда других — например, рекуррентного программирования, при котором очередной шаг вычислений базируется на данных, полученных на предыдущих шагах. Наглядным примером этого может служить вычисление факториала рекуррентным методом. Возможно также создание рекурсивных функций (с обращением к самим себе) и, соответственно, использование рекурсивного программирования. Оно, кстати, играет большую роль в осуществлении символьных преобразований.
Средства языка Mathematica позволяют осуществить и визуально-ориентированное программирование. Его смысл заключается в автоматической генерации программных модулей путем визуального выбора интуитивно понятного объекта — чаще всего путем щелчка на кнопке. Mathematica позволяет создавать палитры и панели с различными кнопками, позволяющими управлять программой или вводить новые программные объекты. Однако визуально-ориентированное программирование не является основным. В основном оно ориентировано на создание палитр пользователя с нужными ему функциями.
Поскольку алфавит языка программирования системы и набор операторов и функций уже были рассмотрены ранее, в этой главе нам остается рассмотреть лишь специфические средства языка и его управляющие структуры.
3. Образцы и их применение
Образцы и их применение
Образцы (patterns) в системе Mathematica служат для задания выражений различных классов и придания переменным особых свойств, необходимых для создания специальных программных конструкций, таких как функции пользователя и процедуры. Это необычайно гибкое и мощное средство обобщенного представления математических выражений, используемое при любом подходе к программированию.
Признаком образца являются знаки подчеркивания «_» (от одного до трех). Они обычно выглядят слитно, так что надо внимательно следить за общей длиной символов образцов. Наиболее распространенное применение образцов — указание на локальный характер переменных при задании функций пользователя. Например, функция
fsc[x_,y_]:= х * Sin[y] + у * Cos[х] + z
в списке параметров содержит два образца, х_ и у_. В правой части этого выражения переменные х и у, связанные с образцами х_ и у_, становятся локальными переменными, тогда как переменная z будет глобальной переменной. Обратите особое внимание на то, что символы образцов используются только в списках параметров — в правой части выражений они уже не применяются.
Образцами можно задавать некоторые общие свойства функций. Например, запись
f[х_,х_] := р[х]
означает, что функция f двух идентичных аргументов становится тождественной функции р [ х ]. Следовательно, вызов функции
f[a,a] + f[а,b]
даст выход в виде
f[а,b] + р[а]
а при вызове
f[a^2- 1, a^2- 1]
будет получен результат
р[-1 + а^2]
Примеры применения образцов для задания функции вычисления факториала приводились выше. В образце можно указывать его тип данных:
- x_Integer — образец целочисленный;
- x_Real — образец с действительным значением;
- x_Complex — образец с комплексным значением;
- x_h — образец с заголовком h (от слова head — голова).
Задание типов данных с помощью образцов делает программы более строгими и наглядными и позволяет избежать ошибок, связанных с несоответствием типов.
В системе Mathematica используются следующие типы образцов.
| Обозначение | Назначение образца |
| - | Любое выражение |
| x_ | Любое выражение, представленное именем х |
| : : pattern | Образец, представленный именем х |
| pattern ? test | Возвращает True, когда test применен к значению образца |
| _h | Любое выражение с заголовком h |
| x_h | Любое выражение с заголовком h, представленное именем х |
| - | Любая последовательность с одним и более выражений |
| - | Любая последовательность с нулем или более выражений |
| :x_< ИЛИ х__ | Последовательности выражений, представленные именем х |
| _h или h__ | Последовательности выражений, каждое с заголовком h |
| x _ h или х__h | Последовательности выражений с заголовком h, представленные именем х |
| x_ :v | Выражение с определенным значением v |
| x_h:v | Выражение с заголовком h и определенным значением v |
| x_. | Выражение с глобально заданным значением по умолчанию |
| Optional [x h] | Выражение с заголовком h и с глобально заданным значением |
| по умолчанию | |
| Pattern. . | Образец, повторяемый один или более раз |
| Pattern. . . | Образец, повторяемый ноль или более раз |
Еще раз отметим, что символ «_» в образцах может иметь одинарную, двойную или тройную длину. Надо следить за правильностью его применения, поскольку эти варианты различаются по смыслу. Образцы широко применяются при задании функций пользователя и в пакетах расширения системы.
4. Функции пользователя
Функции пользователя
Понятие функции ассоциируется с обязательным возвратом некоторого значения в ответ на обращение к функции по ее имени с указанием аргументов (параметров) в квадратных скобках. Возврат функциями некоторых значений позволяет применять их наряду с операторами для составления математических выражений.
Функции подразделяются на встроенные в ядро системы внутренние функции и функции, заданные пользователем. Примером первых могут быть Sin[x], Bessell [n, x] и т.д. Mathematica содержит множество таких функций, охватывающих практически все широко распространенные элементарные и специальные математические функции. Есть и возможность создания функций со специальными свойствами — чистых (pure functions) и анонимных функций.
Суть функционального программирования заключается в использовании в ходе решения задач только функций. При этом возможно неоднократное вложение функций друг в друга и применение функций различного вида. В ряде случаев, особенно в процессе символьных преобразований, происходит взаимная рекурсия множества функций, сопровождаемая почти неограниченным углублением рекурсии и нарастанием сложности обрабатываемых системой выражений.
Встроенные стандартные функции и их типовые применения уже были описаны в предшествующих уроках. Так что далее мы рассмотрим только задание функций особого вида, создаваемых пользователем или используемых в управляющих структурах программ.
Хотя в системах Mathematica имеется около тысячи встроенных функций, любому пользователю рано или поздно может потребоваться создание какой-либо своей функции. Кажется естественным задать ее по правилам, принятым во многих языках программирования. Например, функцию для возведения х в степень п можно было бы определить так:
powerxn[x, n] := x^n
Однако такая функция отказывается работать:
{powerxn[2, 3], powerxn[a, b]}
{powerxn[2, 3] , powerxn[a, b]}
Причина этого кроется в том, что в системе Mathematica символы х и n являются обычными символами, не наделенными особыми свойствами. Будучи использованными в качестве параметров функции, они не способны воспринимать формальные параметры [2,3] или [ а, b ]. Так что вычислить нашу ущербную функцию можно лишь при предварительном присваивании х иn нужных значений:
х := 2; n := 3; powerxn[x, n]
8
Разумеется, заданная таким образом функция является неполноценной. Для того чтобы функция пользователя нормально воспринимала переданные ей аргументы, в списке параметров надо использовать образцы в виде переменных, но имеющие после своих имен символы подчеркивания. Образцы способны быть формальными параметрами функций и воспринимать значения фактических параметров (в нашем случае значений 2 и 3). Таким образом, правильной будет запись функции пользователя в виде
powerxn[x_, n_] := х^n
Теперь вычисление по заданной функции пользователя пройдет гладко, причем как в численном, так и в символьном виде:
{powerxn[2, 3], powerxn[z, у], powerxn[x, n]}
{8, zy, 8}
Заметим, что для уничтожения определения заданной функции можно использовать команду-функцию Clear [Name_f unction], где Name_f unction — имя функции.
Можно также задать функцию пользователя, содержащую несколько выражений, заключив их в круглые скобки:
f[x_] := (t = (1 + х)^2; t = Expand[t])
Переменные списка параметров, после имен которых стоит знак «_», являются локальными в теле функции или процедуры. На их место подставляются фактические значения соответствующих параметров, например:
f [а + b]
1+2а+а2+2b+2ab+b2
t
1+2а+а2+2b+2ab+b2
Обратите внимание на то, что переменная t в функции f является глобальной. Это поясняет результат последней операции. Применение глобальных переменных . в теле функции вполне возможно, но создает так называемый побочный эффект — в данном случае меняет значение глобальной переменной t. Для устранения побочных эффектов надо использовать образцы и другие специальные способы задания функций, описанные ниже. Итак, можно сформулировать ряд правил для задания функций пользователя:
- такая функция имеет идентификатор — имя, которое должно быть уникальным и достаточно понятным;
- в списке параметров функции, размещенном в квадратных скобках после идентификатора, должны использоваться образцы переменных, а не просто переменные;
- может использоваться отложенное (: =) или немедленное (=) присваивание;
- тело функции может содержать несколько выражений, заключенных в круглые скобки, при этом возвращается значение последнего выражения;
- переменные образцов в списке параметров являются локальными и действуют только в пределах тела функции;
- в теле функции могут использоваться глобальные переменные, но при этом возможны побочные эффекты;
- возможно обращение к функции из тела этой же функции (рекурсия).
Параметрами функций могут быть списки при условии допустимости их комбинации. Например, допустимо задать х списком, an — переменной или числом:
powerxn[{l, 2, 3, 4, 5}, z]
{1, 2Z, 3Z, 4Z, 5Z}
powerxn[{l, 2, 3, 4, 5}, 2]
{1, 4, 9, 16, 25}
После своего задания функции пользователя могут использоваться по тем же правилам, что и встроенные функции.
Иногда может потребоваться создание функции, не имеющей имени (например, если функция будет использоваться только один раз, сразу же после ее создания). Эта функция представляется только выражением без идентификатора, отсюда и ее название — чистая функция (pure function). Для создания такого объекта служит встроенная функция Function, используемая в одном из следующих вариантов:
- Function [body] — создает чистую функцию с телом body;
- Function [ {х}, body ] — создает чистую функцию параметра х с телом body;
- Function [ {xl, х2,...} ,body] — создает чистую функцию ряда параметров x1, х2, ... с телом body.
Для вычисления созданной таких образом функции после нее задается список параметров в квадратных скобках. Например, взятую ранее в качестве примера функцию возведения в степень можно задать и использовать следующим образом:
Function[{x, n}, x^n]
Function! {х, п), xn]
%[2, 3]
8
Чистую функцию можно легко превратить в обычную функцию пользователя, что показывает следующий пример:
fun=Function[{x,n},х^n]
Function[ {х, n}, хn]
{fun[2,3],fun{z,y}}
{8, zy }
Предельно компактную форму задания имеют так называемые анонимные функции. Они не имеют ни названия, ни обычного определения и задаются только выражениями специального вида. В этом выражении вместо переменных используют обозначения # (для одной переменной) или #1, #2, ... (для ряда переменных). Завершается тело функции символом «&». Если надо вычислить функцию, то после ее записи в квадратных скобках указывается список фактических параметров.
Для нашего примера анонимная функция выглядит так:
#1^#2 &[2, 3]
8
#1^#2 &[у, z]
y^z
С помощью анонимных функций нетрудно создавать обычные функции пользователя:
f[x_, y_] = #1^#2 &[х, у]
хy
f[2, 3]
8
Несмотря на то что применение анонимных функций открывает возможности компактного задания многих функций, эта форма едва ли интересна для большинства читателей — они наверняка предпочтут пусть немного более длинное, но значительно более очевидное задание функций другими способами.
5. Суперпозиция функций
Суперпозиция функций
При функциональном программировании часто используется суперпозиция функций. Для ее реализации используются следующие функции:
- Nest [expr, x, n] — n раз применяет выражение (функцию) ехрг к заданному аргументу х,
- NestList [f, x, n] — возвращает список результатов (п+1)-кратного применения функции f к заданному аргументу х;
- Fold[f, x, list] — дает последний элемент в FoldList [f, x, list];
- FoldList [f, x, {a,b,...} ] — возвращает список {x,f [x,a],f [f [x,a],b],...};
- ComposeList [ { f , f ,...}, x] — генерирует список в форме {х,а[х] ,а[а[х] ],...}.
Примеры, иллюстрирующие действие этих функций, представлены ниже:
Nest[f, x, 5]
f[f[f[f[f[x]]]]]
Nest[Exp[x], x, 5]
Ех[Ех[Ех[Ех[Ех[х]]]]]
NestList[f, x, 3]
{x, f[x], f[f[x]], f[f[f[x]]]}
Fold[f, x, (-1, 2, 3}]
f[f[f[x, 1], 2], 3]
FoldList[f, x, {1, 2, 3}]
{x, f[x, 1], f[f[x, 1], 2], f[f[f{x, 1], 2], 3]}
ComposeList[{Exp, Ln, Sin), x]
{x, Ex, Ln[Ex] , SinlLn[Ex]] ]}
В функциональном программировании вместо циклов, описываемых далее, может использоваться следующая функция:
- FixedPoint [ f, expr ] — вычисляет expr и применяет к нему f, пока результат не перестанет изменяться;
- FixedPoint [ f, expr, SameTest->comp] — вычисляет expr и применяет к нему f, пока два последовательных результата не дадут True в тесте SameTest.
Пример применения функции FixedPoint:
FixedPoint[Function[t, Print[t]; Floor[t/2]], 27]
27
13
6
3
1
0
0
Последний результат (ноль) выводится в отдельной (нумерованной) ячейке вывода и означает завершение процесса итераций — деления t на 2.
Следующий пример показывает, как можно создать цепную дробь с помощью функции Nest:
Nest[ Functiontt, 1/(1+t)], у, 3 ]
1/(1/(1/((1+y)+1)+1)+1)
Еще одна функция такого рода — это Catch:
- Catch [expr] — вычисляет expr, пока не встретится Throw [value], затем возвращает value;
- Catch [expr, form] — вычисляет expr, пока не встретится Throw [value, tag], затем возвращает value;
- Catch [expr, form, f] — возвращает f [value, tag] вместо value. Ниже представлены некоторые конструкции циклов с оператором Catch:
Catch[ x, a, f ]
х
Catch[ Throw[ x, у ], у, fun ]
fun[x, у]
Catch[ NestList[l/(# + 1)&, -3, 5] ]
{-3,-1/2, 2, 1/3, 3/4, 4/7}
Catch[ NestList[l/(# + 1)&, -3., 5] ]
{-3., -0.5, 2., 0.333333, 0.75, 0.571429}
Catch[Do[Print[i]; If[i > 4, Throw[i+2]], i, 10]]
1
2
3
4
5
7
Реализация рекурсивных и рекуррентных алгоритмов
Рассмотрим несколько простых примеров, выявляющих суть функционального программирования. Вначале это будет пример, в котором задана функция sen [х, n], вычисляющая сумму синуса в степени n и косинуса в степени n:
scn[x_, n_] := Sin[x]^n + Cos[х]^n
scn[l, 2]
1
scn[x, 2]
1
scn[x, n]
Cos[x]n+ Sin[x]n
В этом простейшем примере результат вычислений есть возвращаемое функцией sen значение — численное или символьное. В свою очередь, функция sen в своем теле имеет встроенные функции синуса и косинуса.
Важное место в решении многих математических задач занимают реализации рекурсивных и рекуррентных алгоритмов. Напомним, что рекурсия означает обращение функции к самой себе внутри ее тела, а рекуррентность — получение результата на данном шаге по результатам вычислений на предшествующих шагах.
Рассмотрим, как это делается, с помощью описанных выше функций. Классический пример реализации рекурсивного алгоритма — вычисление факториала путем задания функции, в теле которой есть обращение к ней же самой:
f[n_] :=n*f[n-1];f[0]=l;f[1]=1;
Полезно, однако, обратить внимание на возможность явного задания результата для конкретных значений аргумента: f [ 0 ] =1 и f [ 1 ] =1. Так что рекурсия реализуется, начиная с n=2 и выше, в соответствии с классическим определением факториала.
Для реализации рекуррентных алгоритмов в Mathematica имеется ряд функций, таких как Nest или FixedPoint. В следующих примерах показано вычисление
квадратного корня из числа 5 по известному алгоритму Ньютона, записанному в виде функции newtonS:
newtonS [x_] := N[ 1/2 ( х + 5/х )]
Nest[newton5, 1.0, 5]
2.23607
NestList [newtonS, 1.0, 5]
{1., 3., 2.33333, 2.2381, 2.23607, 2.23607}
FixedPoint [newtonS, 1.0]
2.23607
FixedPointList [newtonS, 1.0]
{1., 3., 2.33333, 2.2381, 2.23607, 2.23607, 2.23607, 2.23607}
FixedPointList [newtonS, 1.0, SameTest -> (Abs[#l- #2] < 10.A-4 &)]
{1., 3., 2.33333, 2.2381, 2.23607, 2.23607}
Обратите внимание на то, что функции Nest и FixedPoint дают единственный конечный результат, тогда как функции NestList и FixedPointList возвращают еще и все промежуточные результаты итераций. Последний пример иллюстрирует остановку вычислений по заданной погрешности, равной 10 -4 .
Далее зададим функцию, реализующую алгоритм Ньютона для нахождения корня произвольного выражения f(x) при начальном значении х 0 = а, по следующим формулам:
x0=a;
xn=xn-1-f(xn-1)/f'(xn-1)
Эту функцию можно записать следующим образом:
newtoniter[f_, x0_, n_] :=Nest[(# - f [#]/f'[#]) &, N[x0] , n]
Тогда вычисления корня из выражения е^x - 2 с начальным приближением х 0 = 0.5 при числе итераций n можно организовать с помощью функций Nest и NestList:
newtoniter [Function [ {х} , Ехр[х] - 2.0], 0.5, 5]
0.693147
newtoniter [Function [ {х }, Ехр[х] - 2.0], 0.5, #] & /@ Range [5]
{0.713061, 0.693344, 0.693147, 0.693147, 0.693147}
newtoniterl[f_,x0_,n_] := NestList[ (#-f [#] /f ' [#] ) &,N[x0] , n]
newtoniterl [Function [{x} , Exp[x] - 2.0], 0.5, 5]
{0.5, 0.713061, 0.693344, 0.693147, 0.693147, 0.693147}
В первом случае возвращается только окончательный результат, а в других — еще и все промежуточные. Функция FixedPoint позволяет осуществлять итерации
до тех пор, пока результат не перестанет изменяться (с машинной точностью). Это иллюстрирует следующий пример:
newtonfp[f_, х0_] := FixedPoint[ (# - f [#]/f'[#]) &, N[xO]]
newtonfp[Function[{x} , Exp[x] - 2.0], 0.5]
0.693147
Более сложные примеры функционального программирования мы рассмотрим позже, при описании создания пакетов расширения систем Mathematica.
6. Пример программирования графической задачи
Пример программирования графической задачи
Графические задачи составляют значительную часть задач, решаемых с помощью Mathematica. С точки зрения программирования эти задачи не имеют особой специфики. Большая часть из них сводится к заданию функции, описывающей график, и применению одной из многочисленных графических функций системы с соответствующими опциями и директивами.
На рис. 10.1 показано задание функции GrayCode и ее графическое представление, полученное с помощью встроенной функции ListPlot.
Рис. 10.1. Задание функции GrayCode и ее графическое представление на плоскости
В качестве следующего примера рассмотрим задачу на построение сложного графика функции Мандельброта. Пример задания соответствующей функции MandelbrotFunction и применения графической функции DensityPlot для наглядного визуального представления функции MandelbrotFunction на комплексной плоскости представлен на рис. 10.2.
Еще более сложную и любопытную задачу демонстрирует рис. 10.3. Здесь задана функция JuliaFunction, которая представляет одну из моделей деления клеток. На этом же рисунке показано построение множества графиков, дающих прекрасное визуальное представление данной функции.
Рис. 10.2. Пример задания функции MandelbrotFunction и построения ее графика плотности
Разумеется, приведенные примеры далеко не исчерпывают всего многообразия графических возможностей языка программирования систем Mathematica.
Рис. 10.3. Задание функции JuliaFunction и ее графическое представление
gl10-1.jpg
gl10-2.jpg
gl10-3.jpg
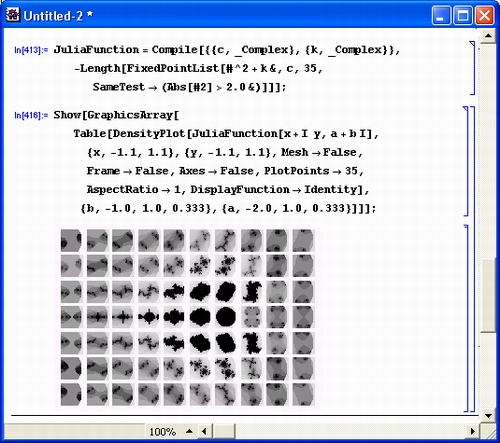
7. Использование процедур
Использование процедур
В основе процедурного программирования лежит понятие процедуры и типовых средств управления — циклов, условных и безусловных выражений и т. д. Процедурный подход — самый распространенный в программировании, и разработчики Mathematica были вынуждены обеспечить его полную поддержку. Однако программирование систем Mathematica и в этом случае остается функциональным, поскольку элементы процедурного программирования существуют в конечном счете в виде функций.
Процедуры являются полностью самостоятельными программными модулями, которые задаются своими именами и отождествляются с выполнением некоторой последовательности операций. Они могут быть заданы в одной строке с использованием в качестве разделителя символа «;» (точка с запятой). Вот пример задания однострочной процедуры, отождествленной с именем г:
r = (1 + х)^2; r= Expand[г]; r - 1
2Х+Х2
Обратите внимание на то, что в теле процедуры символ г используется как вспомогательная переменная. Эта процедура возвращает символьное выражение
Expand[ (1+х)^2] - 1.
В общем случае в теле процедуры могут находиться произвольные выражения, разумеется, с синтаксисом, присущим языку программирования системы. Процедура может не возвращать никаких значений, а просто выполнять определенный комплекс операций. Область записи подобных элементарных процедур ограничена ячейкой (строкой) ввода.
Для задания процедуры со списком локальных переменных {а, b,...} и телом ргос может использоваться функция Module [ {а, b,...} ,ргос]. С применением этой функции мы столкнемся позже.
Для создания полноценных процедур и функций, которые могут располагаться в любом числе строк, может использоваться базовая структура — блок:
- Block [{x, у,...}, procedure] — задание процедуры с декларацией списка локальных переменных х, у,...;
- Block[{x = х0, у=у0,...}, procedure] — задание процедуры с декларацией списка переменных х, у,... с заданными начальными значениями.
Пример использования базовой структуры:
g[x_] := Block[{u}, u = (1 + х)^2; u = Expand[u] ] g[а + b]
l+2a+a2+2b+2ab+b2
u
u
u = 123456; g[2]
9
u
123456
Обратите внимание: последние действия показывают, что переменная и, введенная в тело базовой структуры, является действительно локальной переменной, и присвоение ей символьного выражения (1 + х) ^ 2 в теле блока игнорируется вне этого блока. Если переменная и до применения в функции была не определена, то она так и остается неопределенной. А если она имела до этого некоторое значение (в нашем случае — 123 456), то и по выходе из процедуры она будет иметь это значение.
Многие задачи в системе Mathematica решаются с использованием линейных алгоритмов и программ. Они могут быть представлены непрерывной цепочкой выражений, выполняемых последовательно от начала до конца.
Однако в большинстве случаев серьезные вычисления базируются на использовании циклических и разветвленных алгоритмов и программ. При этом, в зависимости от промежуточных или исходных данных, вычисления могут идти по разным ветвям программы, циклически повторяться и т. д. Для реализации разветвленных программ язык программирования должен содержать управляющие структуры, то есть специальные конструкции языка, реализующие в программах ветвление. Они используются при различных методах программирования, в том числе при процедурном и функциональном программировании.
Циклы типа Do
К важнейшим управляющим структурам в языках программирования относятся циклы. С их помощью осуществляется циклическое исполнение некоторого выражения ехрr заданное число раз. Это число нередко определяется значением некоторой управляющей переменной (например, i, j и т. д.), меняющейся либо с шагом +1, либо от начального значения imin до конечного значения imax с шагом di. Циклы могут быть одинарными или множественными — вложенными друг в друга. Последние используют ряд управляющих переменных. Такого рода циклы организуются с помощью функции Do: О Do [expr, {imax} ] — выполняет imax раз вычисление ехрг; О Do [expr, {i, imax}] — вычисляет ехрг с переменной i, последовательно принимающей значения от 1 до imax (с шагом 1);
- Do [expr, {i, imin, imax} ]—вычисляет ехрr с переменной i, последовательно принимающей значения от imin до imax с шагом 1;
- Do [expr, {i, imin, imax, di}] — вычисляет ехрг с переменной i, последовательно принимающей значения от 1 до imax с шагом di;
- Do [expr, {i, imin, imax}, {j, jmin, j max},...] — вычисляет expr, организуя ряд вложенных циклов с управляющими переменными j, i и т. д.
Примеры организации цикла Do и его исполнения представлены ниже:
Do[Print["hello"], {5}]
hello
hello
hello
hello
hello
Do[Print[i], {i, 3}]
1
2
3
Do[Print[i], {i, 5, 8}]
5
6
7
8
Do[Print[i], {i, 0 , 1, 0.25}]
0
0.25
0.5
0.75
1.
Нетрудно убедиться в том, что переменная i в теле цикла (итератор) является локальной и по выходе из цикла ее значение остается тем же, что было до входа:
i=2
2
Do[Print[i], i, 1, 5]
1
2
3
4
5
1
2
Вся программа с циклом является содержанием одной ячейки, и ее листинг охвачен квадратной скобкой. Для иллюстрации вывода здесь использована команда Print в теле цикла. Нетрудно заметить, что управляющая переменная цикла может принимать как целочисленные, так и вещественные значения. Возможность организации цикла в цикле иллюстрируется следующим примером:
Do [Do [Print [i, " ", j, " ", i + j], {j, 1, 3}], {i, 1, 3}];
1 1 2
1 2 3
1 3 4
2 1 3
2 2 4
2 3 5
3 1 4
3 2 5
3 3 6
Здесь используются два цикла с управляющими переменными i и j. Командой Print выводятся значения переменных i и j, а также их суммы i+j.
Следующий пример показывает применение цикла Do для задания функции, вычисляющей п-е число Фибоначчи:
fibonacci[(n_Integer)?Positive] :=
Module[fnl = 1, fn2 =0,
Do[fnl, fn2 = fnl + fn2, fnl, n- 1] ; fnl]
fibonacci[10]
55
fibonacci[100]
354224848179261915075
fibonacci[-10]
fibonacci[-10]
Обратите внимание на применение в этом примере функции Module. Она создает программный модуль с локальными переменными (в нашем случае fnl и fп2), в котором организовано рекуррентное вычисление чисел Фибоначчи.
Наконец, последний пример показывает применение цикла Do для создания цепной дроби:
х = у; Do[x = 1/(1 + k х), {k, 2, 8, 2}]; х
Циклы типа For
Другой вид цикла — цикл For — реализуется одноименной функцией:
For[start, test, incr, body]
В ней сначала один раз вычисляется выражение start, а затем поочередно вычисляются выражения body и incr до тех пор, пока условие test не перестанет давать логическое значение True. Когда это случится, то есть когда test даст False, цикл заканчивается.
Следующий пример показывает создание простой программы с циклом For и результат ее выполнения:
Print["i x"]
For [x=0; i=0, i < 4, i++
[x += 5*i, Print[i, " ", x]]]
i x
15 ,
2 15
3 30
4 50
Return[x]
Return[50]
Программа, приведенная выше, позволяет наблюдать за изменением значений управляющей переменной цикла i и переменной х, получающей за каждый цикл приращение, равное 5*i. В конце документа показан пример на использование функции возврата значений Return [x]. В цикле For не предусмотрено задание локальных переменных, так что надо следить за назначением переменных — при использовании глобальных переменных неизбежны побочные эффекты.
Циклы типа While
Итак, функция For позволяет создавать циклы, которые завершаются при выполнении (эволюции) какого-либо условия. Такие циклы можно организовать и с помощью функции While [test, expr], которая выполняет expr до тех пор, пока test не перестанет давать логическое значение True.
Ниже дан практический пример организации и использования цикла While:
i := 1; х := 1; Print["i x"] ;
While[i < 5, i += 1; x += 2*i; Print[i, " ", N[x]]]
i x
2 5.
3 11.
4 19.
5 29.
Return[x]
Return[29]
Циклы типа While, в принципе, могут заменить другие, рассмотренные выше, типы циклов. Однако это усложняет запись и понимание программ. Аппарат локальных переменных в этом типе циклов не используется.
Директивы-функции прерывания и продолжения циклов
В указанных типах циклов и в иных управляющих структурах можно использовать следующие директивы-функции:
- Abort [ ] — вызывает прекращение вычислений с сообщением $ Aborted;
- Break [ ] — выполняет выход из тела цикла или уровня вложенности программы, содержащего данный оператор (циклы типа Do, For и While или тело оператора-переключателя Switch). Оператор возвращает Null-значение (без генерации секции выхода);
- Continue [ ] — задает переход на следующий шаг текущего цикла Do, For или While;
- Interrupt [ ] — прерывает вычисления с возможностью их возобновления;
- Return [ ] — прерывает выполнение с возвратом значения Null;
- Return [expr] — прерывает выполнение с выводом значения выражения ехрr;
- Throw [value] — задает прекращение выполнения цикла Catch, если в ходе эволюции ехрг встречается значение value (см. примеры выше).
На рис. 10.4 представлено применение директив Abort [ ] и Interrupt [ ] в середине набора команд. Нетрудно заметить, что директива Abort [ ] просто прерывает выполнение цепочки команд и выводит сообщение $ Aborted. А вот директива Interrupt [ ] выводит диалоговое окно, с помощью которого можно либо прервать вычисления, либо продолжить их.
Рис. 10.4. Действие директив Abort[] и lnterrupt[]
Если продолжить вычисления (нажав кнопку Continue Evaluation), то вывод выражений командами Print будет продолжен, что видно из рис. 10.5.
Условные выражения и безусловные переходы
Для подготовки полноценных программ помимо средств организации циклов необходимы и средства для создания разветвляющихся программ произвольной структуры. Обычно они реализуются с помощью условных выражений, позволяющих в зависимости от выполнения или невыполнения некоторого условия (condition) выполнять те или иные фрагменты программ.
Рис. 10..5. Продолжение вычислений после команды Interrupt[]
Функция IF
Как у большинства языков программирования, условные выражения задаются с помощью оператора или функции IF. Система Mathematica имеет функцию If, формы которой представлены ниже:
- If [condition, t, f] — возвращает t, если результатом вычисления condition является True, и f, если результат равен False;
- If [condition, t, f, u ]—то же, но дает и, если в результате вычисления condition не было получено ни True, ни False.
Следующий пример показывает создание программной процедуры с циклом Do, выход из которой реализуется с помощью функции I f и директивы прерывания Aborted! ]:
х := 1; Print["i x"];
Do[{If [i == 5, Abort[], None],
i += 1; x += 2*i; Print[i, " ", N[x]]},
{i, 1, 100}]
i x
2 5
3 11.
4 19.
5 29.
$Aborted
Return[x]
Return[1]
Тот же пример, но с применением директивы выхода из цикла Break [] в функции If показан ниже:
х := 1; Print["i x"];
Do[{If [i == 5, Break[], None],
i += 1; x += 2*i; Print[i, " ", N[x]]},
{i, 1, 100}]
i x
2 5.
3 11.
4 19.
5 29.
Return[x]
Return[29]
В данном случае никаких специальных сообщений о выходе из цикла не выдается. Функция If обеспечивает ветвление максимум по двум ветвям программы. Для ветвления по многим направлениям можно использовать древовидные структуры программ с множеством функций If. Однако это усложняет исходный текст программы.
Функции-переключатели
Для организации ветвления по многим направлениям в современных языках программирования используются операторы-переключатели. В системе Mathematica множественное ветвление организовано с помощью функций Which и Switch:
- Which [testl, valuel, test2, value2,...] — вычисляет в порядке следования каждый из testi, сразу возвращая именно ту величину из valuei, которая относится к первому testi, давшему True;
- Switch [expr, forml, valuel, form2, value2,...] — вычисляет селектор expr, затем сравнивает его последовательно с каждой из меток f ormi, вычисляя и возвращая то valuei, которое соответствует первому совпадению.
Приведем примеры работы функции which:
Whichtl == 2,1,2== 2, 2, 3 == 3, 3]
2
Which[l == 2, x, 2 == 2, у, 3 == 3, z]
y
Следующие примеры иллюстрируют работу функции Switch:
Switch[1, 1, а, 2, b, 3, с]
а
Switch[2, 1, а, 2, b, 3, с]
b
Switch[3, 1, а, 2, b, 3, с]
с
Switch[8, 1, а, 2, b, 3, с]
Switch[8,
1, а,
2, b,
3, с]
Обратите внимание на последний пример — при неверном задании первого параметра (селектора) просто повторяется запись функции.
Следующий пример показывает возможность выбора с применением вещественных значений селектора и меток:
Switch[8., 1.5, а, 2.5, b, 8., с]
с
Switch[1.5, 1.5, а, 2.5, b, 8., с]
а
Switch[8, 1.5, а, 2.5, b, 8., с]
Switch[8,
1.5, а,
2.5, b,
8., с]
Опять-таки, обратите внимание на последний пример — здесь использован селектор в виде целого числа 8, тогда как метка выбора — вещественное число 8. Выбор при этом не происходит, поскольку целочисленное значение 8 не является тождественным вещественной восьмерке.
Безусловные переходы
В целом, условные выражения в языке программирования системы Mathematica позволяют реализовать любой вид ветвления в программах. Однако иногда бывает полезно без лишних раздумий указать в программе явный переход к какой-либо ее части. Для этого используется оператор безусловного перехода Goto [tag]. который дает переход к тому месту программы, которое отмечено меткой Label [tag]. Возможны также формы Goto [expr] и Label [expr], где ехрr — вычисляемое выражение.
Применение оператора Goto иллюстрирует следующий пример:
(q = 2; Label[start]; Print[q]; q += 2;
If[q < 7, Goto[start]])
2
4
6
Здесь с помощью оператора Goto [start] организован цикл с возвратом на метку Label [start], действующий до тех пор, пока значение q меньше 7. При этом q меняется от начального значения 2 с шагом 2, причем добавление 2 к текущему значению q осуществляется укороченным оператором сложения q+=2.
Интересной особенностью языка программирования Mathematica является возможность создания переходов по значению вычисляемого выражения. Например, Goto [2+3] дает переход к метке Label [5] или даже Label [1+4], что видно из следующего примера:
Goto[2 + 3];
Print["ааааа"];
Label[1 + 4];
Print["bbbbb"]
bbbbb
Переходы, задаваемые выражениями, и метки, меняющие свой идентификатор, редко встречаются в обычных языках программирования, хотя они обеспечивают новые обширные и довольно необычные возможности по созданию программ с различными ветвлениями.
Для языка программирования системы Mathematica, ориентированного на безупречное и строгое структурное программирование, введение оператора Goto может расцениваться как отступничество от основополагающих идей структурного программирования. Поэтому на применение этого оператора в методах структурного программирования наложено табу. Тем не менее, этот оператор есть, а применять его или нет — дело пользователя.
gl10-4.jpg
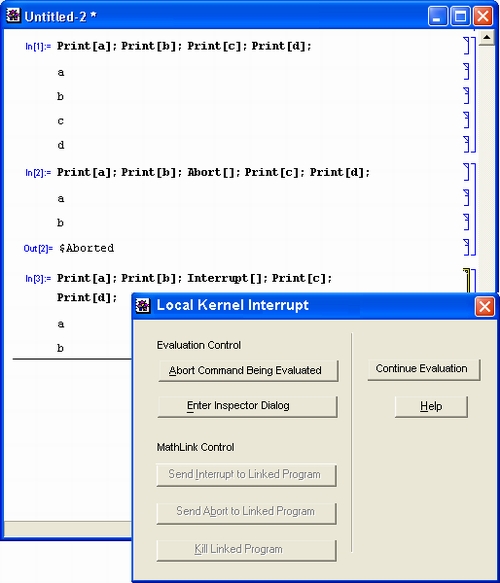
gl10-5.jpg
8. Проблемы совместимости
Проблемы совместимости
Мы уже не раз обращали внимание на то, что при создании документов нередки конфликты между переменными, назначаемыми пользователем, и переменными, входящими в программы ядра, между функциями пользователя и встроенными функциями, между их заголовками и т. д. Ситуация усложняется при использовании пакетов расширения, поскольку в них широко используются переменные и различные функции, причем нередко обозначенные так же, как и встроенные функции.
Особенно коварны побочные эффекты в конструкциях, содержащих вспомогательные переменные, — например, в итерационных циклах, функциях вычисления суммы и произведения и т. п. Они содержат переменные-итераторы i,. j, k и т. д. Обычно избежать конфликтов можно с помощью механизма локализации итераторов. Вернемся к уже обсуждавшимся примерам. Возьмем пример с вычислением суммы:
i=2
2
Sum[i,{i,l,4}]
10
i
2
Ясно, что сумма вычисляется с применением цикла с заданным числом повторений. В его конце итератор i получает значение 4. Но глобальная переменная с тем же именем имеет значение 1=2, которое она получила до вычисления суммы с помощью функции Sum. В данном случае это достигнуто за счет того, что в теле функции переменная-итератор является локальной.
Нетрудно убедиться, что проблемы со статусом переменных возможны и в, казалось бы, изученных функциях суммирования и перемножения. На это явно указывает следующий пример:
func[x_] :=Sum[x^i, {i,4} ] {func[y] ,func[i] }
(У +У2+ У3+У4, 30}
i
2
Результат вычисления func [у] вполне понятен, тогда как вычисление func [i] носит явно обескураживающий характер. Причина его в том, что вместо символьного значения i в данном случае оказались использованы численные значения итератора i. А в этом случае функция Sum просто вычисляет численные значения. Говорят, что она работает по контексту]
А теперь рассмотрим пример с циклом For:
For [ i=l , i<=4 , i++ , Print [ i ] ]
1
2
3
4
i
5 .
На этот раз переменная i изменила свое значение в конце цикла с 2 на 5. Это говорит о том, что пользователю-программисту надо очень внимательно относиться к статусу переменных во всех итерационных, да и других программах.
Разумеется, Mathematica содержит средства для избежания подобного смешения ролей переменных. Одно из них — применение конструкции Module:
i=2
2
Module[{i},For[i=l,i<=4,i++,Print[i]]]
1
2
3
4
i
2
На этот раз захвата итератором глобальной переменной i удалось избежать. Однако этот пример носит не более чем частный характер. Вообще говоря, если переменная-итератор задается в теле функции, то она будет локальной, а если она задается за пределами функций, то глобальной.
Для разрешения подобных противоречий в системе Mathematica введен особый механизм контекстов. Напомним, что под контекстом подразумевается некоторое разъяснение характера связанных с контекстом объектов. Другими словами, это означает, что с каждым объектом системы Mathematica (например, с переменными или функциями) связан некоторый контекст. Чисто внешне контекст задается в виде Имя_контекста (обратный апостроф в конце имени и есть признак контекста).
Итак, контекст фактически является некоторым признаком объекта. Каждый объект системы Mathematica имеет свой контекст, который записывается перед именем объекта (знак «'» при этом является разделителем). Обычно он не виден, но существует. Объекты с одинаковыми именами могут иметь разные контексты и действовать по-разному — то есть по контексту. Пользователям полезно усвоить такую аналогию: контексты — это как бы разные папки со своими именами, куда могут помещаться одноименные файлы-объекты.
С другой стороны, один и тот же контекст может принадлежать разным объектам. Например, все системные переменные и встроенные функции имеют контекст System', то есть они относятся к системным объектам, а все символы, вводимые в начале работы с системой, имеют контекст Global (глобальные).
В системе Mathematica есть средства для визуализации контекстов. Прежде всего это функция Context:
Context[Tan]
System'
Context[E]
System'
Context/@Cos,Pi,Abort
{System', System' , System'}
Текущее значение контекста определяет системная переменная $Context или функция Context [ ]:
{$Context,Context[]}
{Global', Global'}
В начале сеанса работы по умолчанию действует контекст Global ~, что означает глобальный статус вводимых символов:
Context/@{q,r,w}
{Global', Global', Global'}
Однако контекст может быть заменен на любой нужный пользователю просто указанием его перед соответствующим символом или словом:
{new'q, new' w,Global'r}
{new'q, new'w, r}
Context/@{new' q,new' w,Global' r}
{new', new', Global4}
Обратите внимание на то, что символы new 4 q и new' w имеют новый контекст new s и отображаются вместе с ним (но контекст указан перед символом). А вот символ Global ~ r отображается лишь своим кратким именем. Причина этого в том, что текущий контекст есть Global 4 , а контекст new 4 отсутствует в списке контекстов (context path). Что касается символов q, r и z, то сами по себе (без новой контекстной приставки) они по-прежнему имеют контекст "Global:
Context/@{q,r,w}
{Global 4 , Global 4 , Global 4 }
Для вывода списка контекстов используется переменная $ContextPath:
$ContextPath
{Graphics 4 Animation 4 , Global 4 , System 4 }
С помощью функции Prepend можно добавить в список новый контекст, например new":
$ContextPath=Prepend[$ContextPath,"new4"]
{new', Graphics' Animation', Global', System'}
Теперь функция Context возвращает только контексты символов new'q, new'w и Global' r:
Context/@{new'q,new'w,Global'r}
{new', new', Global'}
С помощью функции Begin можно изменить текущий контекст на заданный, например Global' на new':
Begin["new''"]
new'q=5;
{q,Context[q]} {5, new'}
Теперь легко разобраться, как интерпретируются символы с разными контекстами. Любой символ, вводимый без контекстной приставки, то есть своим коротким именем, интерпретируется и выводится с этим именем, если его контекст является текущим. Если символ вводится полным именем, то проверяется, есть ли его контекст в списке $ContextPath. Если он есть, то к символу добавляется самый левый контекст из имеющихся в списке. Таким образом, по мере ввода новых контекстов, имена которых совпадают со старыми, происходит вытеснение новыми контекстами старых. Другими словами, это позволяет обновить уже имеющиеся определения, сохранив их на случай отмены старых контекстов.
Этот принципиально важный механизм модификации объектов играет решающую роль в создании пакетов расширений. В них часто уже имеющиеся функции (со старыми контекстами) заменяются новыми, одноименными с ними, но имеющими иные контексты.
Получение списков определений с контекстами
Для получения списка всех определений с заданным контекстом можно использовать функции Names [ "Context' S" ], где S — шаблон, определяющий интересующие нас имена. Например, для получения всех определений с контекстом System' можно использовать функцию Names ["System' *]. Поскольку этот список довольно большой, ограничимся примером вывода всех определений с контекстом System", начинающихся с буквы U:
Names["System'U*"]
{UnAlias, Underflow, Underoverscript, UnderoverscriptBox, UnderoverscriptBoxOptions, Underscript, UnderscriptBox, UnderscriptBoxOptions, UndocumentedTestFEParserPacket, UndocumentedTestGetSelectionPacket, Unequal, Unevaluated, Uninstall, Union, Unique, UnitStep, Unprotect, UnsameQ, Unset, Up, Update, UpperCaseQ, UpSet, UpSetDelayed, Upvalues, URL, Using)
Функция Names [ ] без параметра выводит полный список всех определений как из ядра, так и из пакетов расширений с указанием их контекстов. Таким образом, данная функция дает самую полную информацию об определениях (функциях, константах и т. д.), которые содержит текущая версия системы Mathematica.
9. Подготовка пакетов расширений системы Mathematica
Подготовка пакетов расширений системы Mathematica
Мощным средством расширения возможностей системы Mathematica является подготовка пакетов расширений. Пакеты расширений позволяют создавать новые процедуры и функции и хранить их на диске в виде файлов с расширением . m. После считывания такого пакета с диска все входящие в него определения функций становятся доступными для использования в соответствии с правилами, принятыми для встроенных функций. Текст пакета расширения не выводится после его вызова, чтобы не загромождать документ вспомогательными описаниями. В сущности, пакеты расширения — это просто наборы программ на языке программирования системы Mathematica, подобранные по определенной тематике.
Типовая структура пакетов расширения
Структура пакета расширений (программы) в минимальном виде выглядит следующим образом:
(* Вводный комментарий *)
BeginPackage["Имя_пакета' "]
Mean::usage = "Имя функции[Параметры] Текстовый комментарий"
Begin[" 'Private' "] Unprotected[Список_имен] Определения новых функций
End[ ]
Установка атрибутов защиты EndPackage[ ] (* Завершающий комментарий *)
Особая структура пакетов расширений связана с реализацией описанной выше идеологии контекстов. Пакет открывается необязательным текстовым комментарием, который обрамляется двойными символами « (*» и «*) ». Он может быть как однострочным, так и многострочным. Обычно вводный комментарий включает в себя имя пакета, наименование фирмы и автора — создателей пакета, историю развития, дату создания и т. д. Если вы программируете для себя, можете на первых порах опустить все эти комментарии. Но не забудьте их ввести после отладки пакета, как того требуют культура и дисциплина программирования.
Затем пакет открывается словом BeginPackage. Это слово дается с квадратными скобками, в которых указывается контекст (см. выше) пакета. Обратите внимание на то, что после имени пакета должен стоять апостроф или цепочка символов, обрамленная апострофами. Имя пакета не должно совпадать ни с одним из известных, то есть быть уникальным.
Эта команда изменяет список контекстов, и он принимает вид
{Имя_пакета',System'}.
Таким образом, на первом месте списка контекстов оказывается имя пакета, а на втором — контекст System'. Теперь любой вводимый и не встроенный символ приобретает контекстную приставку с именем данного пакета.
Обратите внимание на то, что контекст System' сохранился в новом списке контекстов, но стал вторым. Это значит, что если вы вводите слова и символы, встроенные в систему, то они будут замещены новыми определениями. К примеру, если вы решили вычислять функцию Sin [x] по новому и ценному для вас алгоритму, то ему будет отдаваться предпочтение при каждом использовании этой функции до тех пор, пока вы работаете с данным пакетом расширения. Однако, как только вы перестанете работать с пакетом, восстановится роль встроенной функции Sin[x].
Следующий блок пакета — сообщения о назначении функций. Эти сообщения выводятся, если после загрузки пакета задать вопросительный знак с последующим именем функции. Эти сообщения не обязательны, но они обеспечивают единство диалога с системой и, безусловно, нужны при профессиональной подготовке пакета. Обычно в этих сообщениях кратко указываются синтаксические правила использования функций и назначение их параметров, указываемых в квадратных скобках.
Затем следует главная часть пакета — определения новых функций. Она открывается определением Begin [" ' Private ' "]. Оно, не меняя список контекстов, устанавливает новый текущий контекст Имя_пакета' Private'. Он присваивается всем ранее не встречавшимся символам. Имя Private принято в пакетах расширения системы Mathematica, хотя, в принципе, может быть любым другим именем. После него следуют сами определения, в которых могут использоваться любые средства, включенные в ядро системы.
В некоторых случаях имена функций могут повторять ранее определенные в ядре системы. Это полезно, если пользователь считает, что введенное им определение уже известной функции более точно или более универсально, чем использованное в системе. В таких случаях перед новым применением идентификатора надо позаботиться о снятии с него защиты с помощью функции Unprotect. Именно эта часть и определяет существо пакета и его ценность.
Завершается эта часть определением End [ ]. При этом восстанавливается контекст, который был до определения Begin [" ' Private' " ], то есть контекст с именем пакета. После этого идет необязательная часть с указанием атрибутов защиты. Пакет завершается определением EndPackage [ ], которое восстанавливает контекст, бывший текущим до загрузки пакета (например Global' 4 ), a контекст Имя_пакета 4 помещает в начало прежнего списка контекстов..
Контексты в системах Mathematica 3 и 4 идентичны — иначе и быть не может, поскольку всякая старшая версия системы должна обеспечивать совместимость с предшествующей версией. Впрочем, в Mathematica 4 включены два новых контекста, Developer 4 и Experimental 4 .
Необязательный заключительный комментарий чаще всего дает список тестовых примеров. Он особенно желателен, если пакет содержит определения не вполне очевидных функций. Не забывайте, что этот комментарий не выводится и не исполняется — он нужен лишь на этапе знакомства с пакетом. Разумеется, такое знакомство необходимо при каждой серьезной попытке применения того или иного пакета расширения или применения системы.
В принципе, текстовые комментарии могут вводиться на русском языке. Однако при этом возникают определенные трудности. При выводе комментариев на экран дисплея при работе с оболочкой системы Mathematica могут наблюдаться несоответствия между шрифтами, установленными при вводе комментариев и при их выводе. Поэтому лучше использовать комментарии на английском языке, тем более что комментарии ко всем встроенным функциям и к поставляемым расширениям системы даны, естественно, на английском языке.
Средства создания пакетов расширений
Для создания пакетов расширений в общем случае используются следующие средства системы:
- Begin ["context'"] — устанавливает текущий контекст;
- BeginPackage ["context'"] — делает context единственным активным контекстом. Возможна также форма BeginPackage [ "context" ", { "needl' ", "need2'",...}];'
- Return [ ] — возвращает Null;
- End [ ] — возвращает текущий контекст и переходит к предыдущему;
- EndAdd [ ] — возвращает текущий контекст и переходит к предыдущему, предварительно добавляя текущий контекст к списку контекстов $Context-Path;
- EndPackage [ ] — восстанавливает $Context и $ContextPath в их значениях до предшествующего BeginPackage и добавляет текущий контекст к списку $ContextPath;
- Exit [ ] — завершает сеанс работы Mathematica;
- Goto [tag] —просматривает текущее составное выражение в поиске Label [tag] и передает управление в эту точку;
- Interrupt [ ] — производит прерывание в теле вычислений;
- Label [tag] — представляет точку в составном выражении, в которую управление передается директивой Goto;
- Quit [ ] — завершает сеанс работы Mathematica.
Приведем пример простого фрагмента программы, дающего определение новой функции ExpandBoth с помощью некоторых из представленных средств:
(* :Title: ExpandBoth *)
(* :Context: ProgramminglnMathematica'ExpandBoth" *)
(* : Author: Roman E. Maeder *)
ExpandBoth: : usage = "ExpandBoth [e] expands all numerators and denominators in e."
Begin ["' Private1"]
ExpandBoth [x_Plus] := ExpandBoth /@ x
ExpandBoth [x_] := Expand [ Numerator [x] ] / Expand [ Denominator [x] ]
End [ ] Null
Этот пример настолько прост, что читателю будет нетрудно разобраться с его сутью — расширением выражения по числителю и знаменателю. Ниже представлен сеанс работы с этим пакетом, файл которого expboth.m размещен в каталоге mypack, включенном в общий каталог пакетов расширений:
<<mypack\expboth.m
?ExpandBoth
ExpandBoth [e] expands all numerators and denominators in e.
ExpandBoth [124 /12]
31/3
ExpandBoth [1234/12]
617/6
Мы вернемся к рассмотрению построения пакетов расширений после более детального рассмотрения некоторых деталей этого процесса.
Текстовые сообщения и комментарии
Ценность многих программ на любом языке программирования нередко сводится к нулю из-за отсутствия подробных текстовых комментариев. Из-за этого даже сами разработчики программ через месяц-другой перестают понимать собственные творения. А что говорить о пользователях, рискующих применить такие программы?
Для создания текстовых комментариев различного назначения (как выводимых, так и не выводимых на экран в ходе работы с пакетом) в языке программирования системы Mathematica используются следующие средства:
- (* Comment *) — задание не выводимого на экран текстового комментария, как однострочного, так и многострочного, в любом месте пакета;
- Message [symbol: : tag] — вывод сообщения symbol::tag, если только вывод сообщений не отключен;
- Message [symbol: :tag, e1, e2,...] — выводит сообщение, вставляя значения ei по мере необходимости;
- $MessageList — глобальная переменная, возвращающая список имен сообщений, вырабатываемых во время вычисления текущей входной строки. Имя каждого сообщения заключено в HoldForm [ ]. $MessageList сохраняется в MessageList [n] и переустанавливается в { } после того, как произведена п-я выходная строка;
- MessageList [n] — глобальный объект, который является списком имен (сообщений), которые вырабатываются в процессе обработки п-й входной строки;
- MessageName, применяется в виде symbol: : tag или MessageName [symbol, "tag" ] — имя для сообщения;
- $MessagePrePrint — глобальная переменная, чье значение, если установлено, применяется к выражениям перед тем, как они помещаются в текст сообщений;
- $Messages — возвращает список файлов и каналов, в которые направляется вывод сообщений;
- Messages [symbol] — возвращает все сообщения, присвоенные данному символу symbol.
Следует отметить, что широкое применение комментариев обычно является признаком культуры программирования. Это особенно важно для математических систем, реализующих вычисления по сложным и подчас малопонятным для неспециалистов алгоритмам. Без подробных комментариев пакеты расширений и применений теряют свою практическую полезность и превращаются в ребусы — увы, куда менее интересные, чем те, которые публикуются в газетах и журналах.
Защита идентификаторов от модификации
Атрибут защиты Protected
Как уже отмечалось, система Mathematica позволяет вводить константы, переменные и функции со своими именами — идентификаторами. Между функциями можно задавать различные отношения, в том числе и те, которые не соответствуют правилам, заданным в ядре системы.
Идентификаторы должны быть уникальными, то есть не совпадать с именами встроенных функций, директив, опций, переменных и констант. Однако как быть, если нужно задать новое отношение для уже имеющихся встроенных функций или изменить их определения?
Для решения таких вопросов в систему введена защита идентификаторов от модификации, которая при необходимости может сниматься. Все встроенные в ядро именованные объекты языка программирования системы являются защищенными по умолчанию. Они имеют соответствующий признак — атрибут Protected (защищенный).
Установка и снятие атрибута защиты
Для управления средствами защиты от модификации используются следующие директивы:
- Protect [s1, s2,...] — устанавливает атрибут защиты от модификации (Protected) для перечисленных символов si;
- Protect [\"forml\", \"form2\",...] — устанавливает атрибут защиты от модификации для всех символов, имена которых сопоставимы с любым из указанных строковых шаблонов f ormi;
- Unprotect [s1, s2,...] — удаляет атрибут защиты от модификации (Protected) для символов si, что делает возможной их модификацию;
- Unprotect [\"forml\", \"form2\",...] — снимает защиту всех символов, имена которых текстуально (по буквам) сопоставимы с любым из указанных formi.
Дополнительные функции защиты
Следующие атрибуты и директивы также используются при управлении модификацией:
- NProtectedAll — атрибут, устанавливающий, что ни один из аргументов функции не будет модифицирован при применении N [ ];
- NProtectedFirst — атрибут, указывающий, что первый аргумент функции не будет модифицирован применением N [ ];
- NProtectedRest — атрибут, устанавливающий, что все аргументы после первого аргумента функции не будут модифицированы применением N [ ].
Мы уже рассматривали модификацию функций, в частности снятие и назначение атрибутов защиты. Отметим лишь, что из последующих примеров будет ясно, что эти операции широко применяются в пакетах расширений.
Примеры подготовки пакетов расширений
Наиболее сложным моментом работы с системой Mathematica является разработка пакетов расширения профессионального качества. Именно такие пакеты позволяют приспособить всю мощь системы к решению тех задач, которые полезны конкретному пользователю.
Начать работу с системой можно за несколько часов. Реальное ее освоение потребует нескольких месяцев упорной работы. А подготовка серьезных пакетов, решающих достаточно сложные задачи, может занять и несколько лет. Для облегчения этого процесса рассмотрим основные приемы подготовки пакетов расширений. Напоминаем, что пакеты можно готовить как в оболочке системы (их затем следует записать на диск как файлы с расширением .т), так и с помощью .внешних текстовых редакторов.
В этом разделе представлено несколько примеров построения пакетов расширений системы Mathematica (версии не ниже 3.0), взятых из книги [34], а точнее, из примеров этой книги, включенных в справочную базу данных систем Mathematica. Из примеров удалена большая часть текстовых комментариев, сделанных на английском языке.
Пакет проверки выражений на их алгебраичность
Следующий пакет содержит определение функции AlgExpQ [expr], которая позволяет выяснить, является ли выражение ехрг алгебраическим.
(* :Title: AlgExp *)
(* :Context: Pro gra mminglnMathematica4AlgExp4 *) BeginPackage["ProgramminglnMathematica ' AlgExp '"]
AlgExpQ::usage = "AlgExpQ[expr] returns true if expr is an algebraic expression."
Begin["'Privateч"] SetAttributes[AlgExpQ, bistable]
AlgExpQ[ _Integer ] = True
AlgExpQ[ _Rational ] = True
AlgExpQ[ c_Complex ] := AlgExpQ[Re[c]] && AlgExpQ[Im[c]]
AlgExpQ[ _Symbol ] = True
AlgExpQ[ a_ + b_ ] := AlgExpQ[a] && AlgExpQ[b]
AlgExpQ[ a_ * b_ ] := AlgExpQ[a] && AlgExpQ[b]
AlgExpQ[ a_ ^ b_Integer ] := AlgExpQ[a]
AlgExpQ[ a_ ^ b_Rational ] := AlgExpQ[a]
AlgExpQ[_] = False End[]
EndPackage[]
Если выражение является алгебраическим, то функция AlgExpQ возвращает логическое значение True, иначе она возвращает значение False:
<<mypack\algexp.m
? AlgExpQ
AlgExpQ[expr] returns true
if expr is an algebraic expression.
AlgExpQ [a * x ^ 2 + b * x + c]
True
AlgExpQ[Sqrt[x]]
True
AlgExpQ["x^2+l"]
False
AlgExpQ[1] True AlgExpQ[1.0]
False
Пакет реализации метода Рунге—Кутта
Теперь рассмотрим, как выглядит пакет расширения, решающий систему дифференциальных уравнений хорошо известным численным методом Рунге—Кутта четвертого порядка. Ниже представлена распечатка данного пакета.
(* :Title: RungeKutta *)
(* iContext: ProgramminglnMathematica'RungeKutta' *)
BeginPackage["ProgramminglnMathematica'RungeKutta'"]
RKSolve::usage =
"RKSolve[{el,e2,..}, {yl,y2,..}, {al,a2,..}, {tl, dt}] numerically integrates the ei as functions of the yi with inital values ai.The integration proceeds in steps of dt from 0 to tl.
RKSolve[{el, e2,..},{yl,y2,..},{al,a2,..},{t,t0,tl, dt} ] integrates a time-dependent system from t0 to tl."
Begin["'Private'"]
RKStep[f_, y_, y0_, dt_] :=
Module [{ kl, k2, k3, k4 }, kl = dt N[ f /. Thread[y -> yO] ];
k2 = dt N[ f /. Thread[y -> y0 + kl/2] ];
k3 = dt N[ f /. Thread [y -> yO + k2/2] ] ;
k4 = dt N[ f /. Thread [y -> yO + k3] ] ;
y0 + (kl + 2 k2 + 2 k3 + k4)/6
RKSolve[f_List, y_List, y0_List, {tl_, dt_}] :=
NestList[ RKStepff, y, #, N[dt]]&, N[y0], Round [N [ tl /dt ]] ] /;
Length [f] == Length [y] == Length [y0]
RKSolve [f_List, y_List, y0_List, {t_, t0_, tl_, dt_}] := Module f { res } ,
res = RKSolve [ Append[f, 1], Append[y, t] , Append[y0, t0], {tl-t0, dt} ] ;
Drop[#, -1]& /@ res /;
Length [f] == Length [y] == Length [y0]
End[]
Protect [ RKSolve ]
EndPackage[]
Знающие реализацию этого метода обратят внимание на естественность записи общеизвестных математических операций. Пакет содержит определения двух функций: основной (RKSolve) и вспомогательной (RKStep). Последняя содержит вычисление решения на очередном шаге алгоритма по результатам вычислений на предшествующем шаге. Используется подстановка для переменной х и вычисление решения на очередном шаге по известной формуле Рунге— Кутта четвертого порядка точности.
Теперь рассмотрим, как можно использовать такой пакет, создать который можно в любом текстовом редакторе, например в редакторе NotePad, входящем в состав Windows 95/98. Для удобства работы можно поместить файл этого пакета rk4.m в папку Mypack, расположенную в папке со стандартными пакетами. В этом случае вызов пакета и проверка его загрузки осуществляются следующим образом:
<< mypack\rk4.m
?RKSolve
RKSolve [ {el, e2, ..}, {yl,y2,..}, {al,a2,..}, {tl, dt}] numerically integrates the ei as functions of the yi with inital values ai.The integration proceeds in steps of dt from 0 to tl. RKSolve [ {el, e2, ..}, {yl,y2,..}, {al,a2,..}, {t, t0, tl, dt}] integrates a time-dependent system from t0 to tl .
Итак, при обращении ?RKSolve выводится информация о формате применения функции RKSolve. Она задана на английском языке. Можно записать эту информации и на русском языке, однако при этом возможна нестыковка наборов шрифтов. Поэтому рекомендуется подобную информацию давать на английском языке. В нашем случае решается система дифференциальных уравнений первого порядка в форме Коши, заданная правыми частями {el, е2,...} с переменными {yl, у2,...} и их начальными значениями {al, а2,...} в интервале времени от 0 до .1 при фиксированном шаге dt. Во второй форме записи функции время t может меняться от tO до tl с шагом dt.
Приведенный ниже пример демонстрирует, как этот пакет используется на практике для решения системы дифференциальных уравнений y' = t*y + z и z' = t + y*z при начальных значениях у = z = 1 и t, меняющемся от 1 до 1.5 с шагом 0.1:
RKSolve[{t*y + z, t + y*z}, {у, z}, {1, 1}, {t, 1, 1.5, 0.1}]
{{!., 1.}, {1.22754, 1.22844), {1.52241, 1.53202),
{1.90912, 1.95373}, {2.42456, 2.57444), {3.12741, 3.55937}}
Решение представлено списком значений {yi, zi}, определяющим зависимости y(t) и z(t). Этот пример хорошо иллюстрирует реализацию популярного численного метода для решения систем дифференциальных уравнений.
Пакет символьных преобразований тригонометрических функций
Следующий пакет служит для демонстрации символьных преобразований тригонометрических функций синуса и косинуса.
(* :Title: TrigDefine *)
(* :Context: ProgramminglnMathematica'TrigDefine" *)
BeginPackage["ProgramminglnMathematica' TrigDefine'"]
TrigDefine::usage = "TrigDefine.m defines global rules for putting products of trigonometric functions into normal form."
Begin["'Private'"] (* set the private context *)
(* unprotect any system functions for which rules will be defined *)
protected = Unprotect[ Sin, Cos ] (* linearization *) Sin/: Sin[x_] Cos[y_] := Sin[x+y]/2 + Sin[x-y]/2
Sin/: Sin[x_] Sin[y_] := Cos[x-y]/2 - Cos[x+y]/2 Cos/: Cos[x_] Cos[y_] := Cos[x+y]/2 + Cos[x-y]/2
Sin/: Sin[x_]An_Integer?Positive :=
Expandt (1/2- Cos[2x]/2) Sin [x]^(n-2) ]
Cos/: Cos[x_]An_Integer?Positive :=
Expand[(l/2 + Cos[2x]/2) Cos[x]^(n-2)]
Protect[ Evaluate[protected]](* restore protection of system symbols *)
End[] (* end the private context *) EndPackage[] (* end the package context *)
Данный пакет задает преобразования для произведений sin(x) cos(x), sin(x) sin(y) и cos(x) cos(y), а также для sin(x) n и cos(x) n . Следующие примеры наглядно показывают работу с этим пакетом:
<< mypack\trigdefine.m
?Sin
Sin[z] gives the sine of z. Sin[a]*Cos[b]
1/2Sin[a-b] + 1/2 Sin[a+b]
Sin[a]*Sin[b]
1/2Cos[a-b] - 1/2Cos[a+b]
Cos[a]*Cos[b]
1/2 Costa-b] + 1/2Cos[a+b]
Sin[x]^2
1/2-1/2 Cos[2x]
Cos[x]^3
Sec[x]/4 +1/2Cos[2x] Sec[x] + 1/4(1/2 + 1/2 Cos[4x]) Sec[x]
Sin[x]^n
Sin[x]n
Данный пример — наглядная иллюстрация программирования символьных вычислений.
Пакет вычисления функций комплексного переменного
Еще один пакет расширений для вычисления функций комплексного переменного (блок пакетов ALGEBRA) представлен распечаткой, приведенной ниже.
(* :Title: Relm *)
(* :Authors: Roman Maeder and Martin Buchholz *) BeginPackage [ "Algebra 'RelrrT "]
RealValued::usage = "RealValued[f] declares f to be a real-valued function
(for real-valued arguments)."
SBegin["'Private'"]
protected = Unprotect[Re, Im, Abs, Conjugate, Arg] (* test for "reality", excluding numbers *)
realQ[x_] /; !NumberQ[x] := Im[x] == 0 imagQ[x_] /; !NumberQ[x] := Re[x] == 0
(* fundamental rules *)
Re[x_] := x /; realQ[x] Arg[x_] := 0 /; Positive[x] Arg[x_J :=Pi /; Negative[x] Conjugate[x_] := x /; realQ[x] Conjugate[x_] := -x /; imagQ[x]
(* there must not be a rule for Im[x] in terms of Re[x] !! *) (* things known to be real *)
Im[Re[_]] := 0 Im[Im[_]] := 0 Im[Abs[_]] := 0 Im[Arg[_]] := 0 Im[x_?Positive] = 0 Im[x_?Negative] = 0
Im[x_ ^ y_] := 0,/; Positive[x] && Im[y] == 0 Im[Log[r ?Positive]] := 0
(*' arithmetic *)
Re[x_Plus] := Re /@ x Im[x_Plus] := Im /@ x
Re[x_ y_Plus] := Re[Expand[x y]] Im[x_ y_Plus] := Im[Expand[x y]]
Re[x_ y_] := Re[x] Re[y]— Im[x] Im[y] Im[x_ y_] := Re[x] Im[y] + Im[x] Re[y]
(* products *)
Re[(x_?Positive y_) ^k_] := Re[x^k y^k] Im[(x_?Positive y_)^k_] := Im[x^k yAk]
(* nested powers *)
Re[(x_?Positive ^ y_ /; Im[x]==0)^k_] := Re[x^(y k)] Im[(x_?Positive ^ y_ /; Im[x]==0)"kj := Im[хл(у k)]
Re[ l/x_ ] := Re[x] / (Re[x]^2 + Im[х]^2) Im[ l/x_ ] := -Im[x] / (Re[x]"2 + Im[x]A2)
Im[x_^2] := 2 Re[x] Im[x]
Re[ x_^n_Integer ] := Block[{a, b},
a = Round[n/2]; b = n-a;
Re[x^a] Re[x^b] - Im[х^а] 1т[х^b] ]
Im[ x_^n_Integer ] :=Block[{a, b}, a = Round[n/2]; b = n-a; Re[x^a] Im[х^b] + Im[х^a] Re[x^b] ]
Re[x_IntegerAn_Rational] := 0 /; IntegerQ[2n] && Negative[x]
Im[x_IntegerAn_Rational] :=
(-х)лп (-1)л((Numerator[n]-l)/2 /; IntegerQ[2n] && Negative[x]
(* functions *)
Re[Log[r_?Negative]] := Log[-r] Im[Log[r_?Negative]] := Pi Re[Log[z_]] := Log[Abs[z]] /; realQ[z] Re[Log[z_]] := (1/2) Log[Re[z]^2 + Im[z]^2] Im[Log[z_]] := Arg[z]
Re[Log[a_ b_]] := Re[Log[a] + Log[b]]
Im[Log[a_ b_]] := Im[Log[a] + Log[b]]
Re[Log[a_^c_]] := Re[c Log[a]]
Im[Log[a_^c_]] := Im[c Log[a]]
Ке[Е^х_] :=Cos[Im[x]] Exp[Re[x]] Im[Е^х_] := Sin[Im[x]] Exp[Re[x]]
Re[Sin[x_]] := Sin[Re[x]] Cosh[Im[x]] Im[Sin[x_]] :=Cos[Re[x]] Sinh[Im[x]]
Re[Cos[x_]] := Cos[Re[x]] Cosh[Im[x]] Im[Cos[x_]] := -Sin[Re[x]] Sinh[Im[x]]
Re[Sinh[x_]] := Sinh[Re[x]] Cos[Im[x]] Im[Sinh[x_J] := Cosh[Re[x]] Sin[Im[x]]
Re[Cosh[x_]] := Cosh[Re[x]] Cos[Im[x]] Im[Cosh[x_]] := Sinh[Re[x]] Sin[Im[x]]
(* conjugates *)
Re[Conjugate[z_]] := Re[z] Im[Conjugate[z_]] :=
Conjugate[x_Plus]:= Conjugate /@ x Conjugate[x_Times]:= Conjugate /@ x Conjugate[x_^n_Integer]:= Conjugate[x]An Conjugate[Conjugate[x_]]:= x
(* real-valued rules *)
Attributes[RealValued] = {Listable, HoldAll} Attributes[RealValuedQ] = {HoldFirst}
RealValued[f_Symbol] := (f/: RealValuedQ[f] = True; f) RealValued[f ] := RealValued /@ {f}
Im[ (_?RealValuedQ) [_? (Im[#J ==0&)...] ] := 0
(* define built-in function to be real-valued *)
DoRules[flist_] := Block[{protected},
protected = Unprotect[flist];
RealValued[flist];
Protect[Evaluate[protected]]
]
DoRules[{Sin, Cos, Tan, ArcSin, ArcCos, ArcTan, ArcCot, Sinh, Cosh, Tanh, ArcSinh, ArcCosh, ArcTanh, Floor, Ceiling, Round, Sign, Factorial}]
Protect[Evaluate[protected]]
End[]
Protect[RealValued]
EndPackage[]
Как нетрудно заметить, в этом пакете задано вычисление действительной и мнимой частей для ряда тригонометрических, гиперболических и числовых функций.
Пакет расширения графики
Следующий пример иллюстрирует подготовку графического пакета расширения, который строит графики ряда функций с автоматической установкой стиля линий каждой кривой.
(* :Title: Plot *)
(* :Context: ProgramminglnMathematica"Plot" *)
BeginPackage["ProgramminglnMathematica4 Plot4"]
Plot::usage = Plot::usage <> " If several functions are plotted, different plot styles are chosen automatically."
Begin["'Private'"] protected = Unprotect[Plot]
$PlotActive = True
Plot[f_List, args__]/; $PlotActive := Block[{$PlotActive = False},
With[{styles = NestList[nextStyle, firstStyle, Length[Unevaluated[f]]-1]}, Plot[f, args, PlotStyle -> styles] ] ]
(* style definitions *)
unit = 1/100 max = 5
firstStyle = Dashing[{}]
nextStyle[Dashing[{alpha__, x_, y_, omega__}]] /; x > у + unit :=
Dashing[{alpha, x, у + unit, omega}] nextStyle[Dashing[l_List]] :=
Dashing[Prepend[Table[unit, {Length[1] +1}], max unit]]
Protect! Evaluate[protected] ]
End[]
EndPackage[]
Рисунок 10.6 показывает применение данного пакета.
Пакеты-пустышки
Разумеется, эти примеры не исчерпывают всего разнообразия пакетов расширений. В сущности, они не дают ничего нового, поскольку приведенные листинги являются просто упрощением гораздо более полных и мощных пакетов, уже входящих в систему. В Mathematica 3 и 4 многие функции из пакетов расширения перекочевали в ядро системы, что позволило существенно ускорить вычисления. Поэтому в пакетах расширения можно встретить определения-пустышки, просто сообщающие об этом и не содержащие новых определений функций. Примером такого рода является модуль countroot.m, листинг которого приведен ниже.
Рис. 10.6. Пример применения функции Plot из пакета расширения plot.m (* :Name: Algebra"CountRoots' *)
(* :Copyright: Copyright 1994-1996, Wolfram Research, Inc.*)
(* :Summary:All CountRoots functionality is now provided by Algebra'Rootlsolation". The package Algebra'CountRoots" is obsolete.
*)
Needs["Algebraч Rootlsolation'" ]
CountRoots::obslt =
"All CountRoots functionality is now provided by
Algebra'Rootlsolation'.
The package Algebra'CountRoots" is obsolete."
Message[CountRoots::obslt]
Надо прямо сказать, что в области математики пользователь средней квалификации едва ли может придумать что-либо такое, что еще не включено в ядро или в пакеты расширений системы. Разумно готовить такие пакеты лишь для тех специальных областей применения математики, с которыми работает пользователь, — например в области физики, химии, механики, электротехники и радиотехники и т. д. Однако более вероятно, что пользователь предпочтет готовить не пакеты расширений, а пакеты применений.
Пакеты применений — это группы документов с программами, предназначенные для решения определенного класса математических или научно-технических проблем и задач. В отличие от пакетов расширения, в документах пакетов применений обычно дается подробно комментируемое описание всех основных алгоритмов решения задач. При этом комментарий, как правило, выводится на экран дисплея.
Довольно часто в пакетах применений используется прием объединения ряда ячеек в одну с общим текстовым заголовком. Это особенно полезно для организации вспомогательных и промежуточных вычислений, ячейки которых загромождают экран и лишают текст документа наглядности. Данный прием скрывает такие вычисления, но позволяет в любой момент вывести их на экран дисплея при активизации маленького прямоугольника, отмечающего такие совмещенные ячейки. Тексты документов, поставляемых с системой, являются прекрасными образцами использования этого приема.
Документы пакетов применения — это конечный продукт практического использования системы Mathematica. Поэтому они могут включать в себя все ранее описанные средства системы. Как уже неоднократно отмечалось, документы записываются на диск в виде файлов с расширением .т (в ранних версиях Mathematica — .та), а их полный битовый образ (включающий рисунки) сохраняется во вспомогательных файлах с расширением .mb. При большом числе сложных рисунков в документе эти файлы могут быть весьма большими — сотни килобайт и даже единицы мегабайт.
gl10-6.jpg
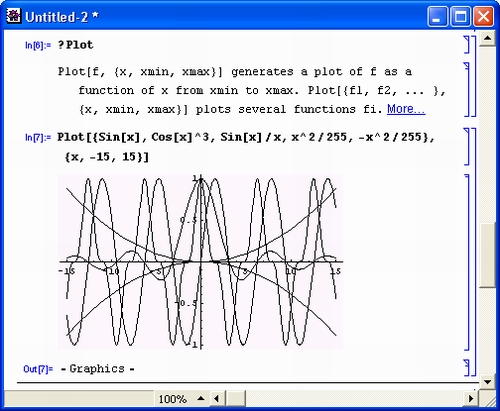
10. Создание средств визуального программирования
Создание средств визуального программирования
Что такое визуально-ориентированное программирование
Под визуально-ориентированным программированием обычно понимается автоматическая генерация кодов программ на некотором языке программирования при активизации различных графических объектов — чаще всего кнопок с наглядным изображением программируемых действий или с надписями, указывающими на-такие действия.
Mathematica изначально реализует визуально-ориентированное программирование с помощью палитр, содержащих математические операторы и символы. Однако язык программирования системы поддерживает возможность создания таких панелей для произвольных программных модулей. Целый ряд документов, готовящих средства визуально-ориентированного программирования, включен в справочную систему и дает наглядное представление о технике программирования в этой области.
Пример создания палитры функций
С помощью директивы Notebook [...] можно создать документ-«блокнот». Ниже представлен такой документ, создающий палитру из нескольких простых функций.
Notebook[{
Cell[BoxData[GridBox[{{
ButtonBox[\(Create\ a\ New\ Notebook\), ButtonFunction:>CompoundExpression[ Needs[ "Graphics"Graphics*"] , Needs[ "Graphics'Colors' "], Clear[ targetNB], Set[ targetNB,
NotebookCreate[ ] ] ] , ButtonEvaluator->Automatic]}, {ButtonBox[\(f[x_] := \)]},
{ButtonBox[\(Apply\ DefinitionX),
ButtonFunction:>CompoundExpression[ NotebookWrite[ targetNB, Cell[
BoxData[
FractionBox[ RowBox[ {
RowBox[ {"f", "[", "x", "]"}]/ "-", RowBox[ {"f", "[", "a", "]"}]}], RowBox[ {"x", "-", "a"}]]],
"Input"], All],
SelectionEvaluateCreateCell[ targetNB]], ButtonEvaluator->Automatic]},
{ButtonBox[\(Cancel[\[SelectionPlaceholder]]\)]}, {ButtonBox[\(Limit[\[SelectionPlaceholder] , x -> a]\)]}, {ButtonBox[\(DisplayX TogetherX),
ButtonFunction:>CompoundExpression[ NotebookWrite[ targetNB, Cell[
BoxData[
RowBox [ {
RowBox[ {"DisplayTogether", "[", "\n", "\t'V
RowBox[ {RowBox[ {"Plot", "[",
RowBox[ {RowBox[ {"f", "[", "x", "]"}], ",",
RowBox[ {"{", RowBox[ {"x", ",",
RowBox[ {"-", "5"}], ",", "5"}], "}"}],",",
RowBox[ {"PlotStyle", "->",
RowBox[ {"{", "Orange", "}"}]}]}], "]"]],
RowBox[ {"Plot", "[",
RowBox[ {"\[Placeholder]", ",",
RowBox[ {"{",
RowBox[ {"a", ",",
D/-M7i2^vr ;» "» "5"}] " , " , "5"}] '} " } ] , " , " KOWBOX [1~л -3)J, ,, Э ] \ , s ) J , ,,
RowBox[ {"PlotStyle", "->", RowBox [ {"{", "Violet", "}"}]}]}], "]"}]}']/ "]"}], ";"}]], "Input"], All]], ButtonEvaluator->Automatic]}}, RowSpacings->0, ColumnSpacings->0, GridDefaultElement:>ButtonBox[ "\\[Placeholder]"]]],
NotebookDefault,
CellMargins->{{Inherited, Inherited}, {5, Inherited}}, Evaluatable->True,
CellGroupingRules->"InputGrouping", PageBreakAbove->True, PageBreakWithin->False, GroupPageBreakWithin->False, CellLabelMargins->{{11, Inherited},
{Inherited, Inherited}},
DefaultFormatType->DefaultInputFormatType, LineSpacing->{!.25, 0}, AutoItalicWords->{}, FormatType->InputForm, ScriptMinSize->9, ShowStringCharacters->True, NumberMarks->True, Counterlncrements->"lnput", StyleMenuListing->None, FontFamily->"Courier", FontWeight->"Bold"]},
FrontEndVersion->"Microsoft Windows 3.0", ScreenRectangle->{{0, 800}, {0, 544}},
Editable->False, WindowToolbars->{},PageWidth->358 WindowSize->{151, 105}, WindowMargins->{{291, Automatic} Automatic, 19}},
WindowFrame->"Palette", WindowElements->{},
WindowFrameElements->"CloseBox",
WindowClickSelect->False,
ScrollingOptions->{"PagewiseScrolling"->True}, ShowCellBracket->False, CellMargins->{{0, 0}/ {Inherited, 0}}, Active->True, CellOpen->True, ShowCellLabel->False, ShowCellTags->False, ImageMargins->{{0, Inherited}, {Inherited! 0}}, Magnification->l]
Справа показано окно, в котором выполнены операции, шаблоны которых выводит созданная палитра функций. Это окно создается если нажать кнопку Create New Notebook (Создать новый документ)
Рис. 10.7. Работа с созданной палитрой функций
Созданная чисто демонстрационная палитра позволяет вводить в окно документа шаблоны нескольких операций. Например, если нажать кнопку f[x ]:= то шаблон этой операми (задание функции пользователя) Аналогично можно ввести в документ шаблоны и для ряда операций.
К сожалению, даже из приведенного простейшего примера видно, что программы, создающие визуально-ориентированные инструментальные средства, достаточно громоздки. Они используют целый ряд функций, не имеющих никакого отношения к математическим вычислениям и служащих лишь для создания элементов пользовательского интерфейса. Объем данной книги не позволяет описать эти функции более подробно. Читателю рекомендуется просмотреть функции, вошедшие в приведенный пример, и изучить ряд других примеров на создание элементов пользовательского интерфейса.
Среди этих примеров стоит отметить построение в виде палитры элементов периодической системы Менделеева (рис. 10.8). Активизация любой кнопки с именем химического элемента заносит в строку ввода текущего документа данные об этом элементе.
Рис. 10.8. Палитра периодической системы Менделеева и ее применение
gl10-7.jpg
gl10-8.jpg
11. Отладка и трассировка программ
Отладка и трассировка программ
Отладка программ, за исключением самых простейших, дело далеко не простое. Начальный опыт программирования на любом языке приходит спустя годы практической работы с ним. Эти сроки намного сокращаются, если пользователь всерьез знаком хотя бы с одним, а лучше с несколькими языками программирования.
Но даже такой пользователь нуждается в специальных средствах диагностики и контроля программ. Чем их больше, тем совершеннее система программирования. При этом пользователь-программист должен заботиться и о том, чтобы такие средства входили в программные модули, которые создает он сам.
Некоторые правила культурного программирования
Выше мы описали множество методов программирования на языке системы Mathematica. Попробуем сформулировать некоторые общие правила так называемого культурного программирования с учетом специфики систем Mathematica, позволяющие создавать надежные и эффективные программные средства:
- Тщательно продумайте алгоритм решения задачи. Порой выбор лучшего алгоритма позволяет кардинально повысить скорость вычислений и упростить программу (впрочем, одновременно это достигается далеко не всегда).
- Используйте прежде всего возможности функционального программирования — из него родились основы языка программирования систем Mathematica.
- Разделяйте задачу на малые части и оформляйте их в виде законченных программных модулей — прежде всего функций.
- Pie скупитесь на программные комментарии — чем их больше, тем понятнее программа и тем больше шансов, что она заинтересует пользователей и будет долго жить. Учтите, что ясность программы в большинстве случаев важнее скорости ее работы.
- Тщательно готовьте сообщения об ошибках и диагностические сообщения, а также наименования программных модулей и описания их назначения.
- Тщательно производите диагностику программных модулей, в том числе с самыми безумными значениями и типами параметров — хорошо спроектированный модуль должен диагностировать любые виды ошибочных ситуаций и реагировать на них адекватным образом.
- Используйте имена переменных и констант в стиле, принятом в Mathematica, и обязательно с использованием понятных по смыслу обозначений. По мере возможности не используйте в именах зарегистрированные идентификаторы команд и функций.
- Заменяйте циклы функциями обработки списков, например функциями суммирования и произведения. Применяйте эффективные варианты упрощенных операторов и функций.
- В максимальной степени используйте функции ядра системы. Обращайтесь к пакетам расширений только в том случае, когда это действительно необходимо.
- Проводите тщательное тестирование своих модулей, в том числе с выполнением их трассировки. Помните, что нет программы, которую нельзя хоть чуть-чуть, но улучшить и сократить. Однако при этом цените затраченное на это время!
- По мере возможности используйте готовые апробированные программные модули — изобретать велосипед и делать то, что уже сделано, неразумно.
- Обращайте особое внимание на реализацию механизма контекстов, позволяющего избежать грубых ошибок при модернизации различных объектов программ, прежде всего наборов функций.
- Не слишком оригинальничайте! Не применяйте программные трюки и недокументированные приемы программирования. Такие программы в момент создания могут выглядеть удивительно эффектными и потрясающе оригинальными, но вполне возможно, что в следующей версии системы они перестанут работать вообще, поскольку разработчики обычно стараются исключить любые недокументированные трюки в своих программах.
Применение этих рекомендаций на практике позволит вам создавать программы, которые нужны не только вам, но и многим пользователям системы Mathematica. Только такие программы могут быть размещены в Интернете и, вполне возможно, войти в пакеты расширения и электронные книги системы Mathematica.
Трассировка программных модулей
В практике подготовки и отладки программ важное значение имеет наличие специальных средств отладки программ по шагам — средств трассировки. Mathematica имеет ряд функций для осуществления трассировки своих программных конструкций.
Функция Trace [ехрг] позволяет выполнить трассировку выражения ехрг. Возьмем простой пример — вычисление выражения 2 (3 + 4) 2 /5:
Trace[2 (3 + 4)^2 / 5]
{{{{3+4, 7 },7^2,49}, {1/5,1/5}, 49/5, 49/5}, 249/5, 98/5}
Результат трассировки представлен вложенными списками, имеющими два элемента — вычисляемое выражение и результат вычислений. В частности, для приведенного примера отчетливо видно, что вначале вычисляется выражение в круглых скобках (3 + 4) и получается результат 7, который затем возводится в квадрат — получается число 49. Затем вызывается явно не записанная единица для деления на 5, потом 49 умножается на 1/5 и, наконец, 49/5 умножается на 2 и получается конечный результат. Отсюда ясно, что даже равноценные операции умножения и деления Mathematica разделяет по приоритету — деление выполняется перед умножением! Символьные операции также могут трассироваться:
Trace[а*а/(b*b)]
{{ {{bb,b^2}, 1/b^2, 1/b^2}, aa/b^2, a^2/b^2}
Можно выполнить и трассировку рекуррентных вычислений. Ниже представлен пример трассировки вычисления чисел Фибоначчи:
fib[n_] := fib[n - 1] + fib[n - 2]
fib[0] = fib[l] = 1
1
Trace[fib[5], fib[n_] -> n]
{5, {4, {3, {2, {!}, {0}}, {!}}, {2, {1}, {0}}},
{3, {2, {!}, {0}}, {!}}}
Trace[fib[3]]
{fib[3], fib[3-l] + fib[3-2] ,
{{3- 1, 2}, fib[2] , fib[2-l] + fib[2- 2] , {{2-1, 1}, fibtl], 11, {{2-2, 0}, fib[0] , 1}, 1+1, 2},
{{3-2, 1}, fib[l], 1}, 2+1, 3}
Функция TracePrint [expr] дает распечатку последовательности действий при вычислении выражения ехрг:
TracePrint[a*b/c]
ab/c
Times а b _1 с
Power
1/c
ab/с
Помимо указанных примеров выполнения трассировки и отладки возможны и иные их варианты, осуществляемые с помощью ряда функций. Эти функции представлены в приложении. Надо, однако, отметить, что применение этих функций на современном уровне программирования ограничено — в подобной трассировке особой необходимости нет, поскольку система выдачи диагностических сообщений позволяет выполнять отладку более удобными средствами.
В этом уроке мы научились:
- Работать с образцами.
- Создавать функции.
- Использовать функции FixedPoint и Catch.
- Реализовывать рекурсивные и рекуррентные алгоритмы.
- Использовать процедуры.
- Создавать циклы различного типа.
- Использовать условные выражения и безусловные переходы.
- Работать с контекстами.
- Готовить пакеты расширений системы Mathematica.
- Создавать простейшие средства визуального программирования.
- Использовать средства отладки и трассировки программ.
Урок 11. Математические пакеты расширения
Урок 11. Математические пакеты расширения
1. Математические пакеты расширения
Математические пакеты расширения
- Пакет алгебраических функций Algebra
- Пакет вычислительных функций Calculus
- Пакет дискретной математики DiscreteMath
- Геометрические расчеты — пакет Geometry
- Линейная алгебра — пакет LinearAlgebra
- Расширение в теории чисел — пакет NumberTheory
- Численные расчеты — пакет NumericalMath
Начиная с этого урока, мы переходим к изучению стандартных пакетов расширения (Standard Add-on Packages), которые встроены в системы Mathematica 3/4. Они не требуют отдельной инсталляции, но перед использованием их средств пакеты надо объявлять. Стандартные пакеты расширений содержат примерно столько же дополнительных средств, сколько их содержится в ядре, — то есть тоже порядка тысячи. Применение пакетов расширения особенно эффективно, если оно производится достаточно опытными пользователями.
Общие замечания по пакетам расширения
Пакеты расширения системы Mathematica (Add-ons) являются наборами файлов с расширением .т, написанными на языке программирования системы и объединенными под именами соответствующих пакетов. Пакеты добавляют в систему ряд функций, которые отсутствуют в ядре системы. Они могут модифицироваться и создаваться пользователями, что обеспечивает легкую адаптацию системы под задачи конкретного пользователя.
Применение пакетов имеет три основные особенности:
- необходимо предварительно объявлять загрузку пакета или отдельных его частей — подпакетов или функций;
- скорость вычислений для функций пакетов несколько ниже, чем для функций ядра;
- модификация функций пакетов пользователем может нарушить программную совместимость, что не позволит работать с ними в стандартной системе Mathematica и затруднит обмен документами.
В системе Mathematica 3 (и особенно в Mathematica 4) проведена тщательная оптимизация ядра, что позволило перенести часть апробированных функций из пакетов расширений в ядро системы и тем самым существенно повысить скорость их выполнения. Однако пакеты расширения по-прежнему относятся к важным средствам дополнения и модернизации системы. Некоторые функции вызываются из пакетов автоматически — они описаны ранее как средства ядра системы Mathematica 4.
Следует отметить, что систематизация пакетов расширения по содержащимся в них функциям не доведена до совершенства. Например, функции регрессии разбросаны по ряду пакетов расширения. По мере возможности этот недостаток в данной книге устранен.
2. Пакет алгебраических функций Algebra
Пакет алгебраических функций Algebra
Пакет расширения Algebra содержит ряд новых функций для работы с неравенствами, ограниченными полями и полиномами. Для доступа сразу ко всем функциям пакета используется команда «Algebra`.
Загрузка отдельных функций показана в примерах использования этого пакета, описанных ниже.
До сих пор мы сталкивались с решениями уравнений, представленных равенствами. Пакет Algebra дает важное дополнение в виде функций, обеспечивающих работу с неравенствами. Прежде всего это функция SemialgebraicCompo-nents [ineqs, vars], которая определят комплект решений неравенств ineqs по переменной vars.
Приведенные ниже примеры иллюстрируют работу данной функции:
<<Algebra`Algebraiclnequalities`
SemialgebraicComponents[{х (х^2 - 1) (х^3 - 2) > 1}, х]
{-3, 3}
SemialgebraicComponents[{х + у ^ 2 < 5, х/у > 1}, {х, у}]
SanialgebraicCarpanents[(x+у 2 < 5, — x/y>1}, {х, у}]
SemialgebraicComponents[{х ^ 2 + у ^ 2 < 5, х у > 0}, {х, у}]
{{-3/16,-3/16},{3/16,3/16}}
SemialgebraicComponents[{x ^ 2 + y ^ 2/4 + z ^ 2/9 > 1, х ^ 2 + (у - 1) ^ 2 + (2- 2) ^ 2 < 0}, {х, у, z}]
{}
Для решения неравенства служит функция InequalitySolve [expr, var], которая решает неравенство ехрг относительно переменной var.
Следующие примеры иллюстрируют применение данной функции:
<<Algebra` InequalitySolve`
InequalitySolve [х (х^2- 5) (х^2- 6) > 0, х]
-sqrt(6) <х<-sqrt(5) | | 0<х<sqrt(6)| | х>7sqrt(6)
InequalitySolve[x^2/Abs[х- 2] >= 0 && 1/х < х + 1, х]
-1/2(1-sqrt(5)<x<0| | 1/2(-1+sqrt(5)<x<2| | x>2
Функции для представления комплексных данных — Relm
Подпакет Relm обеспечивает переназначение функций комплексной переменно!! для более корректной их работы:
<<Algebra`ReIm`
Re[l/x+l/y]
Re[x]/(Im[x]2+Re[x]2 )+ Re[y]/( Iim[y]2+Re[y]2)
Re[(z + I)^3 + Exp[I z]]
E[mz] Cos[Re[z]] -2 (1+ Im[z])2Re[z] +
Re[z] (-(1+ Im[z])2+Re[z]2)
Im[x] ^= 0; RealValued[f, g]
{f, g)
Im[l/(l- I f[x] g[x])]
f [x] g[x]/(1+ f[x]2g[x]2 )
Im[Sin[a]]
Cos[Re[a]] Sinh[Tm[a]]
Операции в конечных полях — FiniteFields
Поле является алгебраическим понятием, которое может быть определено как множество, имеющее не менее двух элементов, над которыми заданы две бинарные ассоциативные и коммутативные операции — сложения и умножения. Кроме того, для существования поля нужны два особых элемента — нуль 0, задающий правило сложения а + 0 = а, и единица 1 для задания правила умножения а*1 = 1. Определено также понятие противоположного элемента -а, такого что а + (-а) = 0, и обратного элемента а-- 1 , такого что a- 1 а = 1. Поле характеризуется размером р и целым положительным целым d, называемым степенью расширения.
Пакет задает набор функций GF[p] [{k}], GF[p,l] [{k}], GF[p, {0,1}] [{k}], GF[p,d] HGF[p,ilist] [elist], действие которых иллюстрируют следующие примеры:
<<Algebra` FiniteFields`
GF[7][4] + GF[7][6]
{3}7
GF[3,4][1,2,1] GF[3,4][2,2,2,0]
{1, 1, 2, 0}3 GF[5,1][1] + GF[3,4][1,1,1]
{1, 1, 1, 0}3+ (1)5
Вряд ли подробное их описание заинтересует большинство читателей. Специалистов по полям не затруднит более детальное знакомство с этими функциями в разделе Add-ons справочной базы данных. Там же можно найти описание ряда других функций, относящихся к теории конечных полей.
Оценка интервалов изоляции корней полиномов — Rootlsolation
Следующие функции подпакета Rootlsotation позволяют оценивать интервалы изоляции для действительных и комплексных корней полиномов:
- CountRoots [poly, {x,ml,m2} ] — возвращает число корней полинома poly от переменной х в комплексном интервале {ml, m2 };
- RealRootsIntervals [poly] — возвращает разделенный интервал изоляции для вещественных корней полинома poly;
- RealRootsIntervals [polyl,poly2,...] — возвращает разделенные интервалы изоляции для вещественных корней нескольких полиномов;
- ComplexRootsIntervals [poly] — возвращает разделенный интервал изоляции для комплексных корней полинома;
- ComplexlRootsIntervals [polyl, poly2,...] — возвращает разделенные интервалы изоляции для комплексных корней нескольких полиномов;
- Contractlnterval [a,n] — возвращает интервал изоляции для числа а с точностью, задаваемой числом знаков результата п.
Применение этих функций поясняют следующие примеры:
<<Algebra`Rootlsolation`
f = (x^2- 1) (х^2- 3) (х^2- 5); CountRoots [f, {x, 1, 2}]
1
CountRoots[(х^2+2) х^4, {х, -I, 2 I}]
5
CountRoots[х^21- 1, {х, 0, 5 + 10*1}]
5
RealRootlntervals[f]
{{-4, -2}, {-2,.-1}, {-1, -1}, {1, 1}, {1, 2}, {2, 4}}
ComplexRootlntervals[f+5]
{{-1, 0}, {0, 1}, {-7-71, -7/4}, {-7, -7/4 + 7I},
{-7/4, -7I + 7/2}, {-7/4, -7/2 + 7I}}
ComplexRootlntervals[x^3, x^5+l]
{{{-2, 0}, {0, 0),
{-3-31, 0}, {-3, 31}, {-31, 3), {0, 3+31}}, {2, 1, 2, 2, 2, 2}}
Contractlnterval[Root[x^7- 1, 5], 5]
{ 58333/262144 + 511143I/ 524288+ 116665/524288+ 63893I/65536}
N[%]
{-0.222523+ 0.9749281, -0.222521 + 0.974931}
Если конечные поля — понятие достаточно экзотическое, то полиномы встреча- ются сплошь и рядом во многих математических и научно-технических расчетах. В пакете расширения Algebra определен ряд новых операций над полиномами. Начнем их рассмотрение с функции PolynomialExtendedGCD:
- PolynomialExtendedGCD [polyl, poly2 ] — возвращает наибольший общий делитель двух полиномов;
- PolynomialExtendedGCD[polyl,poly2,Modulus->p] —возвращает наи- больший общий делитель двух полиномов по модулю р.
Примеры применения этой функции приведены ниже:
<<Algebra"PolynomialExtendedGCD
PolynomialExtendedGCDlxл2 + 3 х + 2, Expand[(x + 1)(х + 2)], Modulus->7]
{2+ Зх+х2, (0, 1}}
PolynomialExtendedGCD[
Expand[ ((12+1) z^2 + 5 z + I) (I z + 3)], Expand[ ((9+1) z + (3+1)) ((31) z +9)]]
{-31+z,
{- 2261/3341+ 710I/3341( 35/3341- 3951/10023)+ (5959/20046- 20531/20046)z}}
Далее следует функция PolynomialPowerMod [polyl, n, (poly2, р} ], которая является существенно ускоренной версией функции PolynomialMod.
- степени ускорения свидетельствует следующий пример:
<<Algebra`PolynomialPowerMod`
Timing[PolynomialPowerMod[1 + х, 200, х^З + x^2 + 1, Prime[4750]]][[1]], Timing [ PolynomialMod [ (1 + x)^200, x^ + х^2 + 1, Prime [4750] ]][[1]]
{0. Second, 2.37 Second)
В данном случае вычисления по функции PolynomialPowerMod оказались вы- полненными менее чем за 0.01 с, что дает нулевой результат.
Еще одна функция в трех ее модификациях работает с симметричными полиномами:
- SymmetricReduction [ {xl,...,xn}, k] — возвращает симметричный полином степени k по переменным {х1,..., хn);
- SymmetricReduction [f, {xl,...,xn}] — возвращает часть полинома {p,q} по переменным {х1,...,хп}, где f=p+q, причем р есть симметричная часть, q — остаток;
- SymmetricReduction [f, {xl,...,xn}, {s1,..., sn} ] — возвращает часть полинома (p,q) попеременным {xl, ...,xn}, где элементарный симметричный полином представляет список {s1,..., sn}.
Следующий пример поясняет создание симметричного полинома 4-й степени по переменным {х,у, z,w,t}:
<<Algebra` SymmetricPolynomials`
SyiranetricPolynomial[{x, y, z, w, t}, 4]
twxy+ twxz+ twyz+txyz+wxyz
Действие других функций поясняют следующие примеры:
SynraetricReduction[(х + у)^2 + (х + z)^2 + (z + у)^2, {х, у, z}]
{2 (х+у+ z)2- 2 (xy+xz+yz), 0}
SymmetricReduction[х^5 + у^5 + z^4, {х, у, z}, {s1, s2, s3}]
{s15- 5s13s2 + 5s1s22+ 5sl2s3- 5s2s3, z4-z5}
Преобразование полиномов в схему Горнера — Horner
Подпакет Horner в системе Mathematica 4 реализует хорошо известную схему вычисления полиномов — схему Горнера. При ней операции возведения в степень заменяются операциями умножения. Для этого служит функция Horner:
- Horner [poly] — устанавливает полином poly в форму Горнера;
- Horner [poly, vars] — устанавливает полином ряда переменных vars в форму Горнера.
Примеры преобразования полиномов в схему Горнера:
<<NumericalMath`Horner`
Horner[ 11 х^3 -4 х^2 + 7 х + 2 ]
2+ х (7 + х (-4 + 11х))
Horner[ а х^3 + bх^2 + с х + d, х ]
d+ х (с + х (b + ах))
Horner[ х^(1/3) + х + х^(3/2) ]
Схема Горнера может использоваться и для отношения полиномов:
Horner [polyl/poly2] и Horner [polyl/poly2, varsl,vars2] .
Эти функции можно использовать для улучшенного представления аппроксимации Паде, что демонстрирует следующий пример:
<<Calculus ` Fade`
approx = Padef Exp[Log[x] -х] , {х, 0, 3, 2}]]
Horner[ approx ]
Переход к схеме Горнера дает ряд преимуществ перед обычным вычислением полиномов: уменьшается время вычислений, повышается их точность, уменьшается вероятность расхождения численных методов, в которых используются полиномы. В системе Mathematica 3 подпакет Corner находился в пакете расширения NumberMath, что было не вполне логично.
3. Пакет вычислительных функций Calculus
Пакет вычислительных функций Calculus
Пакет расширения Calculus содержит представительный набор функций для решения дифференциальных уравнений, задания функций единичного скачка и импульса, выполнения операций с векторами, преобразований Фурье и Лапласа, выполнения спектрального анализа и синтеза, расширенного вычисления пределов и проведения аппроксимаций аналитических функций. Для открытия пакета используется команда Calculus`
Решение дифференциальных уравнений — DSolvelntegrals
Многие нелинейные дифференциальные уравнения не имеют общего решения. В под-пакете DSolvelntegrals определены функции, позволяющие найти решения в форме полного интеграла:
- Completelntegral [eqn, u [х, у,...], {х, у...} ] — создает полный интеграл для дифференциального уравнения, касательного к и [х, у,...];
- Differential Invariants [ {eqnsl, eqns2,...}, {u [х] , v [х] ,...}, х} — возвращает список дифференциальных инвариантов для простых переменных {u[x] ,v[x] ,...} и х;
- Differential Invariants [ {eqnsl, eqns2,...}, {u, v,...}, х} — возвращает список дифференциальных инвариантов для простых переменных {u, v,...} и х;
Применение этих функций поясняют следующие примеры:
<<Calculus`DSolvelntegrals`
Completelntegral[
Derivative[0, 1][u][х, у] == (u[x, у] +
x^2*Derivative[l, 0][u][x, y]^2)/y, u[x,y], {х,у}]
Completelntegral[-u[x, у] +
(2 + y)*Derivative[0, 1][u] [x, y] +
x*Derivative[l, 0][u][x, y] + 3*Derivative[l, 0][u][x, y]^2 == 0,
u[x,y], {x,y}, IntegralConstants->F]
Differentiallnvariants[
{U`[X] == -(U[X] (U[X] +V[X])),
V`-[x] == V[x] (u[x] +V[x])},{u, v}, x]
Дельта-функция Дирака — DiracDelta
В подпакете DiracDelta системы Mathematica 3 задано определение двух полезных функций Дирака:
- UnitStep [х] — возвращает функцию с единичным скачком при х = 0 (дает значение 0 при х < 0 и 1 при х > 1);
- DiracDelta [x] — возвращает дельта-функцию Дирака, которая является импульсом с единичной площадью, бесконечно малой шириной в точке х = 0 и бесконечно большой амплитудой.
Рисунок 11.1 поясняет применение этих функций. Функция UnitStep имеет простую графическую иллюстрацию, тогда как построение графика функции DiracDelta в принципе невозможно — эта функция представляет собой линию бесконечно большой высоты в точке х - 0. Обратите внимание на то, что интеграл от функции Дирака при интегрировании от -°° до +°° равен 1.
Рис. 11.1. Робота с функцией единичного скачка и дельта-функцией Дирака
Обе описанные функции широко применяются при решении задач автоматического регулирования и при математическом моделировании систем и устройств. Поэтому в системе Mathematica 4 они перешли в разряд встроенных функций.
Улучшенное вычисление пределов — Limit
Подпакет Limit не создает новых функций. Он просто переопределяет встроенную функцию Limit, так что ограничимся примерами его применения:
<<Calculus` Limit`
Limit[Е^х^х/ Е^х^(2 х), x->Infinity]
0
Limit [Е^х^х— Е^х^ (2 х) , x->Infinity]
-бесконечность
Limit[E:x ExpIntegralE[2, ArcTan[E^x]- Pi/2] -E^x- x, x->Infinity]
1 - EulerGamma - I л
Limit[Zeta[l+x, v] - 1/x, x->0]
-PolyGamma[0, v] ,
Limit[x^0 PolyGamma[2,x], x->Infinity] .
0
Limit[x^2 PolyGamma[2,x], x->Infinity]
-1
Limit[x^3 PolyGamma[2,x], x->Infinity]
-бесконечность
Работа скорректированной функции наиболее эффективна при вычислении пределов от выражений, содержащих специальные математические функции, и пределов при х, стремящемся к бесконечности.
Рациональная аппроксимация аналитических функций — Fade
Полиномиальная аппроксимация и обычное разложение функций в ряд Тейлора нередко дают слишком большую погрешность. Уменьшение ее возможно при представлении аппроксимирующей функции в виде отношения двух полиномов разной степени. В подпакете Fade определены две функции для рациональной аппроксимации Паде:
- Pade[f, {x,x0,m,k}] — возвращает выражение для аппроксимации Паде функции f(x) в окрестностях точки х0 в виде отношения двух полиномов степеней m и k;
- EconomizedRationalApproximation [f, {х, {xmin, xmax}, m, k} ] —возвращает выражение для осуществления экономичной рациональной аппроксимации функции f(x) в интервале {xmin, xmax} в виде отношения двух полиномов степеней m и k.
Аппроксимация Паде является расширением полиномиальной аппроксимации, обеспечивающим повышенную точность представления функции. На рис. 11.2 представлен пример выполнения аппроксимации Паде с построением графика исходной функции (темная линия) и аппроксимирующей функции (более светлая линия).
Рис. 11.2. Пример, осуществления аппроксимации Паде
Пример осуществления экономичной рациональной аппроксимации показан на рис. 11.3. Здесь также дана визуализация аппроксимации в виде наложенных друг на друга графиков исходной и аппроксимирующей функций.
Рис. 11.3. Пример осуществления экономичной рациональной аппроксимации
Экономичная рациональная аппроксимация обычно позволяет получить приемлемую погрешность при меньшей степени полиномов числителя и знаменателя аппроксимирующей функции. В ограниченной области {xmin, xmax} эта аппроксимация нередко позволяет получить погрешность менее сотых долей процента (рис. 11.4). На этом рисунке показан график погрешности в виде разности между значениями аппроксимирующей и аппроксимируемой функций.
Рис. 11.4. Пример осуществления экономичной рациональной аппроксимации с построением графика погрешности
Несмотря на обширные возможности выбора средств аппроксимации, все же надо отметить, что они уступают таковым у конкурента системы Mathematica — Maple V R4/R5, где функций для осуществления аппроксимации больше.
Векторный анализ —VectorAnalysis
Подпакет VectorAnalysis содержит множество функций, используемых при выполнении векторного анализа. Здесь надо иметь в виду, что речь идет не о векторах как представителях одномерных массивов, которые рассматривались ранее. В данном случае вектор — это направленный отрезок прямой в пространстве, заданном той или иной системой координат.
Системы координат и их преобразования
Заметная часть функций подпакета VectorAnalysis относится к заданию и преобразованию координат:
- Coordinates [ ] — возвращает имена переменных текущей системы координат;
- Coordinates [coordsys] — возвращает имена переменных системы координат coordsys;
- SetCoordinates [coordsys] — устанавливает систему координат coordsys с текущими переменными;
- Coordinates [coordsys, {vars}] — устанавливает систему координат coordsys с переменными, заданными списком {vars }.
Ниже даны названия систем координат и соответствующие им представления.
| Наименование | Представление |
| Прямоугольные | Cartesian [х, у, z] |
| Цилиндрические | Cylindrical [r, theta, z] |
| Сферические | Spherical [r, theta, phi] |
| Параболические цилиндрические | ParabolicCylindrical [u, v, z] |
| Параболические | Paraboloidal [u, v, phi] |
| Эллиптические цилиндрические | EllipticCylindrical [u, v, z, a] |
| Вытянутые сфероидальные | ProlateSpheroidal [xi, eta, phi, a] |
| Сплющенные сфероидальные | OblateSpheroidal [xi, eta, phi, a] |
| Биполярные | Bipolar[u, v, z, a] |
| Бисферические | Bispherical [u, v, phi, a] |
| Тороидальные | Toroidal [u, v, phi, a] |
| Конические | Conical [lambda, mu, nu, a, b] |
| Конфокальные эллипсоидальные | ConfocalEllipsoidal [lambda, rnu, nu, a, b, c] |
| Конфокальные параболические | ConfocalParaboloidal [lambda, mu, nu, a, bj |
Например, параболическую систему координат можно задать следующим образом:
SetCoordinates[Paraboloidal[x, у, z] ]
Paraboloidal [x, у, z]
{CoordinateSystem, Coordinates[]}
{Paraboloidal, {x, y, z}}
Ряд функций служит для контроля и установки параметров систем координат:
- CoordinateRanges [ ] — возвращает пределы изменения переменных текущей координатной системы;
- Parameters [ ] — возвращает параметры текущей координатной системы;
- ParametersRanges [ ] — возвращает пределы изменения параметров текущей координатной системы;
- CoordinateRanges [coordsys] — возвращает пределы изменения переменных координатной системы coordsys;
- Parameters [coordsys] — возвращает параметры координатной системы coordsys;
- ParametersRanges [coordsys] — возвращает пределы изменения параметров координатной системы coordsys;
- SetCoordinates [coordsys, {vars,param} ] — устанавливает параметры текущей координатной системы как параметры coordsys с переменными vars и параметрами param.
Ниже представлены примеры применения этих функций:
CoordinateRanges[]
{0<Х<бесконечности,0<Y<бесконечность,-л<Z<=л}
Parameters[]
{}
ParameterRanges[ ]
Coordinates[Conical], CoordinateRanges[Conical]
{{Llanibda, Мmu, Nnu}, {-бесконечность< Llambda< бесконечность, l< Mmu2 < 4, Nnu2< 1}}
Parameters[Bipolar],ParameterRanges[Bipolar]
{{1}, 0< #1<бесконечность}
Для преобразования координат служат следующие функции:
- CoordinatesToCartesian [pt] — преобразование текущих координат в декартовы;
- CoordinatesToCartesian [pt, coordsys] — преобразование координат coordsys в декартовы;
- CoordinatesFromCartesian [pt] — преобразование из декартовых координат в текущие;
- CoordinatesFromCartesian [pt, coordsys] — преобразование из декартовых координат в координаты coordsys.
Эти примеры демонстрируют преобразования координат:
CoordinatesToCartesian[{I, Pi/3, Pi/3}, Spherical]
CoordinatesToCartesian [u, v, phi}, Bipolar]
CoordinatesFromCartesian [ {x, y, z} , Bipolar]
{-2Im[ArcCoth[x+ Iy]] , 2Re[ArcCoth[x+ Iy] ] , z}
Функции векторного анализа
Помимо функций для задания и преобразования систем координат подпакет Vector An a lysis содержит ряд функций собственно векторного анализа:
- DotProduct [vl, v2] — возвращает скалярное произведение векторов vl и v2, заданных в текущей системе координат;
- CrossProduct [vl,v2] — возвращает векторное произведение векторов vl и v2, заданных в текущей системе координат;
- ScalarTripleProduct [vl, v2, v3 ] — возвращает тройное скалярное произведение для векторов vl, v2 и v3, заданных в текущей системе координат;
- DotProduct [vl, vl, coordsys ] — возвращает скалярное произведение векторов vl и v2, заданных в системе координат coordsys;
- CrossProduct [vl, v2, coordsys] — возвращает векторное произведение векторов vl и v2, заданных в системе координат coordsys.
Примеры выполнения этих операций представлены ниже:
SetCoordinates[ParabolicCylindrical[ ]]
ParabolicCylindrical[Uu, W, Zz]
DotProduct[{1.2, 1.1, 0}, {5.4, -2, 1.2}]
-12.8093
CrossProduct[{1.2, 1.1, 0}, {5.4, -2, 1.2}]
{-1.78157, 0.0774597, -17.8476}
ScalarTripleProduct[{1, 0, 1}, {1, 1, 0}, {0, 1, 1}, Cartesian]
2
Для вычисления производной дуги служат функции:
- ArcLengthFactor [ { fx, f у, f z}, t] — дает дифференциал длины дуги, заданной параметрически с параметром t в текущей системе координат;
- ArcLengthFactor [ {fx, f у, fz}, t, coordsys] — дает дифференциал длины дуги, заданной параметрически с параметром t в системе координат coordsys
Примеры вычисления дифференциалов и длин дуг с помощью этих функций:
param = {Cos[t], Sin[t], t}
{Cos[t], Sin[t], t}
ArcLengthFactor[ param, t, Cartesian] //Simplify
корень из 2
f[x_, y_, z_] := x^2 y^2 z
Integrate[ f[param] ArcLengthFactor[
param, t, Cartesian], {t, 0, 2 Pi}] // Simplify
Ряд функций служит для создания матрицы Якоби (матрицы частных производных) и вычисления относящихся к ней понятий:
- JacobianMatrix [ ] — возвращает матрицу Якоби, определенную в текущих координатах;
- JacobianMatrix [pt] — возвращает матрицу Якоби в точке pt и в текущих координатах;
- JacobianMatrix [coordsys] — возвращает матрицу Якоби, определеннук в системе координат coordsys;
- JacobianMatrix [pt, coordsys] — возвращает матрицу Якоби в точке pt, определенную в системе координат coordsys;
- JacobianDeterminant [], JacobianDeterminant [pt] и т. д. — вычисление детерминанта матрицы Якоби при указанных выше определениях;
- ScaleFactor [ ], ScaleFactor [pt] и т. д. — вычисление масштабного фактора при указанных выше определениях.
Применение этих функций поясняют следующие примеры:
JacobianMatrix[Cartesian[x, у, z]]
{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}
JacobianMatrix[Spherical[r, t, p] ]
{{Cos[p] Sin[t] , rCos[p] Cos[t] ,-rSin[p] Sin[t]},
{Sin[p] Sin[t] , rCos[t] Sin[p] , rCos[p] Sin[t]},
{Cos[t] , -rSin[t], 0}}
JacobianDeterminant[Spherical[r, t, p] ]
r^2Sin[t]
Integrate[r^2 JacobianDeterminant[ Spherical[r, theta, phi]],
{r, 0, 2}, {theta, 0, Pi}, {phi, -Pi, Pi}]
128n/5
Следующие функции определяют ряд характеристик векторного поля:
- Div[f] — возвращает дивергенцию векторного поля f в текущей системе координат;
- Curl [f ] — возвращает вихрь (ротор) векторного поля f в текущей системе координат;
- Grad[f ] — возвращает градиент векторного поля f в текущей системе координат;
- Laplasian [f] — возвращает лапласиан векторного поля f в текущей системе координат;
- Вiharmonic [f] — возвращает лапласиан лапласиана векторного поля f в текущей системе координат;
- Div [f, coordsys], Curl [f, coordsys] и т. д. — указанные выше функции в системе координат coordsys.
Приведем примеры использования этих функций:
Laplacian[x*y^2*z^3,ProlateSpheroidal[х, у, z]]
(Csc[y] Csch[x] (y2z3Cosh[x] Sin [у] +
2xyz3Cos[y] Sirih[x] +2xz3Sin[y] Sinh[x] +
6xy2zCsc[y] Csch[x] (Sin[y]2+ Sinh[x]2))) /
(Sin[y]2+Sinh[x]2)
Grad[x^2 y^3 z^4,ProlateSpheroidal[x, у, z]]
Вариационные методы —VariationalMethods
Подпакет VariationaLMethods содержит функции для реализации вариационных методов. Напомним, что вариационные методы заменяют минимизацию функционала, заданного на некотором бесконечномерном линейном пространстве, задачами его минимизации на последовательности конечномерных подпространств. Функционал в системе Mathematica задается следующим образом:
F=
f[u[x], u'(x),x]dx
В данный подпакет включены следующие функции:
- VariationalD [f, u [х] , х] — дает первую вариационную производную для функционала f одной переменной х;
- VariationalD [f, u [х, у,...] , {х, у,...} ] — дает первую вариационную производную для функционала ряда переменных;
- VariationalD [f, {u [х, у,...], v [х, у],...}, {х, у,...} ] — дает список первых вариационных производных для функционала ряда переменных;
- EulerEquations [f, u [х] , х] — дает равенство Эйлера при f с одной переменной;
- EulerEquations [f, u [х, у,...], {х, у,...} ] — дает равенство Эйлера при f с рядом переменных;
- EulerEquations [f, {u [х, у,...] , v [х, у,...],...}, {х, у,...} ] — дает список с равенствами Эйлера при f с рядом переменных;
- Firstlntegral [ f, u [х] , х] — дает первый интеграл с f, определенной для одной переменной х;
- Firstlntegral [f, {u [х, у,...] ,v [х, у,...],...}, {х, у,...} ] — дает первый интеграл при f с рядом переменных;
- Firstlntegral[u] — дает первый интеграл, ассоциированный с переменной и.
Применение данных функций поясняют следующие примеры:
<<Calculus `VariationalMethods`
VariationalD[y[x] Sin[l+y'[x]], y[x], x]
-Cost 1 +У [x]] y'[x] + Sin[l + y'[x]] d+y[x] y'[x])
EulerEquations[ m1^2 theta1[t]^2/2+m g 1 Cos[theta[t]], theta[t], t]
-Im(gSin[theta[t]] + 1 theta''[ t]) == 0
Firstlntegrals[m(r'[t]^2+r[t]^2 phi'[t]^2)/ 2-U[r], r[t],phi[t], t]
{Firstlntegral[phi] ->-mr[ t]2 phi' [ t] , Firstlntegral[t] -> 1/2 (2U[r] + m (r[t]2phi'[t]2 + r^t]2)) }
Помимо указанных функций подпакет содержит функцию VariationalBound для представления границ и значений функционала. Ввиду громоздкости записи параметров этой функции ограничимся примерами ее применения:
VariationalBound[(-u[r] D[r^2 u'[r],r]/r^2-2u[r]^2/r)r^2,
u[r]^2 r^2,u[r], r,0,Infinity,(a-r)E^(-b r),a,b]
{-0.25, (a-> 2., b-> 0.5}}
VariationalBound[-u[x,у](D[u[x,y],x,2]+
D[u[x,y],y,2]) -2u[x,y],u[x,y],x,-a,a,y,-a,a,
(x^2-a^2)(y^2-a^2)(al+a2(x^2+y^2)),al,a2]
С полными возможностями этой функции можно ознакомиться по справочной базе данных (раздел Add-ons).
gl11-1.jpg
gl11-2.jpg
gl11-3.jpg

gl11-4.jpg
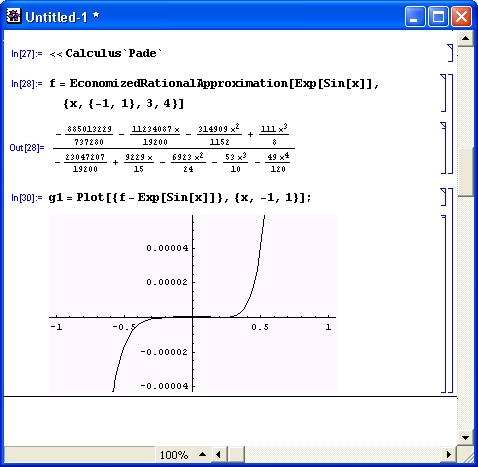
4. Пакет дискретной математики DiscreteMath
Пакет дискретной математики DiscreteMath
Пакет DiscreteMath задает набор функций дискретной математики. Это прежде всего функции комбинаторики и работы с графами (более 230 функций). Мы вынуждены рассмотреть их только выборочно.
Комбинаторика и ее функции — Combinatorica и CombinatorialFunctions
Несколько функций комбинаторики (Factorial, Factorial2, Binomial, Multinomial, Pochhammer и Fibonacci) могут использоваться без загрузки пакетов расширения. Рисунок 11.5 демонстрирует работу подпакета Combinatorial-Functions (функции комбинаторики). Определения функций этого пакета есть в справочной базе данных.
Рис. 11.5. Примеры работы с подпакетом функций комбинаторики
Подпакет Combinatorica задает определение ряда функций комбинаторики и теории графов. Ниже представлены имена функций комбинаторики.
| Функции перестановок и сочетаний | |
| Backtrack | BinarySearch |
| Binary Subsets | DerangementQ |
| Derangements | Distinct Permutations |
| EquivalenceClasses | EquivalenceRelationQ |
| Equivalences | Eulerian |
| FromCycles | FromlnversionVector |
| GrayCode | HeapSort |
| Heapify | HideCycles |
| Index | InversePermutation |
| Inversions | InvolutionQ |
| Josephus | Ksubsets |
| Lexicographic Permutations | LexicographicSubsets |
| MinimumChangePermutations | MultiplicationTable |
| NextKSubset | Next Permutation |
| NextSubset | NthPermutation |
| NthSubset | NumberOf Derangements |
| NumberOf Involutions | NumberOf Permu tat ion sByCycles |
| PermutationGroupQ | PermutationQ |
| Permute | Polya |
| RandomHeap | RandomKSubset |
| RandomPermutation | RandomPermutationl |
| RandomPermutation2 | RandomSubset |
| RankPermutation | RankSubset |
| RevealCycles | Runs |
| SamenessRelation | SelectionSort |
| SignaturePermutation | StirlingFirst |
| StirlingSecond | Strings |
| Subsets | ToCycles |
| ToInversionVector | TransitiveQ |
Следует отметить, что ввиду обилия функций даже в справочной системе даны примеры лишь для избранных функций. Для ознакомления с назначением конкретной функции достаточно исполнить команду ?Имя_функции, например:
<<DiscreteMath`Combinatorica`
?Permute
Permute[l, p] permutes list 1 according to permutation p.
?KSubsets
KSubsets[l, k] gives all subsets of set 1 containing exactly k
elements, ordered lexicographically.
KSubsets[{l, 2, 3, 4, 5}, 2]
{{1, 2}, {1, 3), {1, 4}, {1, 5}, {2, 3), {2, 4}, {2, 5}, {3, 4}, {3, 5}, (4, 5}}
<< DiscreteMath`Combinatorica`
MinimumChangePermutations[{1,2,3}]
{{1, 2, 3}, {2, 1, 3}, {3, 1, 2}, {1, 3, 2}, {2, 3, 1}, {3, 2, 1}}
Map[RankPermutation, Permutations[{1,2,3,4}]]
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23}
InversePermutation[{4,8,5,2,1,3,7,6}]
(5, 4, 6, 1, 3, 8, 7, 2}
Polya[Table[ RotateRight[Range[8],i], {i,8}], m]
1/8 (4m+2m2 +m4 +m8)
Table[NthSubset[n,a,b,c,d], {n,0,15}]
{{}, {a}, {b}, {a, b}, {c}, {a, c}, {b, c}, {a, b, c}, {d}, (a, d}, {b, d}, {a, b, d}, {c, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}
Вторая группа функций комбинаторики представлена следующими функциями.
| Функции разделения, композиции и картин Янга | |
| CatalanNumber | Compositions |
| ConstructTableau | DeleteFromTableau |
| DurfeeSquare | EncroachingListSet |
| FerrersDiagram | FirstLexicographicTableau |
| . Insert IntoTableau | LastLexicographicTableau |
| Longest IncreasingSubsequence | NextComposition |
| Next Part it ion | NextTableau |
| NumberOf Compos it ions | NumberOf Partitions |
| NumberOf Tableaux | PartitionQ |
| Partitions | RandomComposition |
| RandomPartition | RandomTableau |
| TableauClasses | TableauQ |
| TableauxToPermutation | Tableaux |
| TransposePartition | TransposeTableau |
Ha рис. 11.6 показано несколько примеров работы с некоторыми из этих функций.
Рис. 11.6. Примеры работы с функциями разделения, композиции и картин Янга
Этих примеров достаточно, чтобы заинтересованный читатель по их образцу и подобию изучил свойства и возможности нужных ему функций комбинаторики.
Mathematica имеет самые обширные возможности решения задач, связанных с графами. Задание графов и манипуляции с ними также включены в пакет комбинаторики. Они представлены четырьмя группами функций.
| Представление графов | ||
| AddEdge | AddVertex | Breadth'FirstTraversal |
| ChangeEdges | ChangeVertices | CircularVertices |
| CompleteQ | Contract | DeleteEdge |
| DeieteVertex | DepthFirstTr aversal | Diameter |
| DilateVertices | Distribution | Eccentricity |
| Edges | EmptyQ | FromAd j acencyLists |
| FromOrderedPairs | FromUnorderedPairs | GraphCenter |
| GraphComplement | InduceSubgraph | M |
| MakeSimple | MakeUndirected | Normal! zeVerticesPointsAndLines |
| Pseudograph | RadialEmbedding | Radius |
| RankGraph | RankedEmbedding | ReadGraph |
| RemoveSelf Loops | RootedEmbedding | RotateVertices |
| ShakeGraph | ShowGraph | ShowLabe 1 edGr aph |
| SimpleQ | Spectrum | SpringErrbedding |
| ToAdjacencyLists | ToOrderedPairs | ToUnorderedPairs |
| TranslateVertices | UndirectedQ | UnweightedQ |
| Vertices | WriteGraph | |
Одной из самых важных функций этой группы является функция ShowGraph (показать граф). Она обеспечивает визуальное представление графа, заданного аргументом функции. Покажем работу избранных функций этой группы на нескольких примерах.
На рис. 11.7 показано построение полного графа и его таблицы. Параметром графа является число 6, характеризующее число узловых точек графа, соединенных друг с другом.
Изменяя значение параметра графа, можно получить множество других графов. На рис. 11.8 показан вид двух разных графов. Верхний граф — многолучевая звезда с добавленным отрезком, полученная с помощью функции AddEdge. Первый аргумент задает исходный граф (в нашем случае — звезду с 11 узлами), а второй — соединяемые отрезком прямой точки. Нижний рисунок иллюстрирует построение подграфа.
Еще пара графов представлена на рис. 11.9. Этот рисунок иллюстрирует применение функций Contract и GridGraph. Последняя из них строит сеточный граф.
Рис. 11.7. Пример построения полного графа и его таблицы
Рис. 11.8. Построение графа звезды и подграфа
Рис. 11.9. Примеры построения графов с помощью функций Contractn GridGraph
Приведенный выше набор функций позволяет строить практически любые виды графов и обеспечивает высокую степень их визуализации.
| Создание графов | ||
| CartesianProduct | CirculantGraph | CodeToLabeledTree |
| CompleteGraph | Cycle | DegreeSequence |
| EmptyGraph | ExactRandomGraph | ExpandGraph |
| Functional-Graph | GraphDif ference | Graphlnter section |
| GraphJoin | GraphPower | GraphProduct |
| GraphSum | GraphUnion | GraphicQ |
| GridGraph | Hypercube | IncidenceMatrix |
| IntervalGraph | LabeledTreeToCode | LineGraph |
| MakeGraph | NthPair | Path |
| RandomGraph | RandomTree | RandomVertices |
| RealizeDegreeSequence | RegularGraph | RegularQ |
| Turan | Wheel | - |
Рисунок 11.10 показывает применение функций GraphUnion (верхний график) и GraphProduct (нижний график).
Рис. 11.10. Создание графов с помощью функций GraphUnion и GraphProduct С действием других функций нетрудно ознакомиться самостоятельно.
| Свойства графов | ||
| ArticulationVertices | Automorphisms | Bi Connected Components |
| BiconnectedQ | BipartiteQ | Bridges |
| ChromaticNumber | Chromatic Polynomial | CliqueQ |
| Connected Components | ConnectedQ | DeBruijnSequence |
| DeleteCycle | EdgeChromatic Number | EdgeColoring |
| EdgeConnectivity | Element | EulerianCycle |
| EulerianQ | ExtractCycles | FindCycle |
| Girth | GraphPower | HamiltonianCycle |
| HamiltonianQ | Harary | HasseDiagram |
| IdenticalQ | Independent SetQ | IsomorphicQ |
| Isomorphism | IsomorphismQ | MaximumClique |
| Maximum lndependentSet | Minimum VertexCover | OrientGraph |
| PartialOrderQ | PerfectQ | SelfComplementaryQ |
| StronglyConnected Components | TopologicalSort | TransitiveClosure |
| TransitiveReduction | TravelingSalesman | TravelingSalesman Bounds |
| TreeQ | Trianglelnequality | TwoColoring |
| VertexColoring | VertexConnectivity | VertexCoverQ |
| WeaklyConnected Components | ||
Рисунок 11.11 (сверху) показывает применение функции OrientGraph для построения ориентированного графа, который представляется стрелками. Там же (снизу) показано применение функции ShowLabeledGraph для построения графа с маркированными числами вершинами. Напомним, что функция ShowGraph позволяет наблюдать графы без маркировки вершин.
Рис. 11.11. Построение графов — ориентированного (сверху) и с маркированными вершинами (снизу)
Построение широко используемой в теории графов диаграммы Хассе (Hasse) иллюстрирует рис. 11.12.
| Алгоритмическая теория графов | ||
| AllPairsShor test Path | BipartiteMatchin | Cofactor |
| Dijkstra | FindSet | GraphPower |
| InitializeUnionFind | Maxima IMatching | MaximumAntichain |
| MaximumSpanningTree | MinimumChainPartition | MinimumSpanningTree |
| NetworkFlowEdges | Networks' low | NumberOfSpanningTrees |
| PathConditionGraph | PlanarQ | Shortest PathSpanningTree |
| ShortestPath | StableMarriage | UnionSet |
Рисунок 11.13 показывает действие функции MinimumSpanningTree с выводом графа с метками узловых точек.
Риc. 11.12. Построение диаграммы Хассе
Риc. 11.13. Пример применения функции MinimumSpanningTree
В целом следует отметить, что набор функций в области создания, визуализации и теории графов весьма представителен, так что специалисты в области графов могут найти в этом наборе как типовые, так и уникальные средства.
Функции вычислительной геометрии — ComputationalGeometry
В подпакете ComputationalGeometry заданы следующие функции, относящиеся к геометрическим поверхностям:
- ConvexHull [ { {xl, yl...}, {х2, у2,...},...] — вычисляет выпуклость оболочки в точках плоскости;
- DelaunayTriangulation[ {{xl,yl...}, {х2, у2,...},...] — вычисляет триангуляцию Делоне (разбивку на выпуклые треугольники) в точках плоскости;
- DelaunayTriangulationQ [ {{xl, yl...}, {х2, у2,...},...}, trival] — тестирует триангуляцию Делоне в точках плоскости; ,
- DiagramPlot [ {{xl, yl...}, {х2, у2,...},...] — построение диаграммы по заданным точкам (после списка параметров возможны спецификации в виде списков diagvert, diagval);
- PlanarGraphPlot [{ {xl, yl...}, {x2, y2,...},...] — построение планарного графа по заданным точкам (после списка параметров возможна спецификация в виде списка indexlist или vals);
- TriangularSurfacePlot [ {{xl,yl, zl}, {x2,y2, z2 },...] — строит поверхность из треугольников по заданным точкам;
- VoronoiDiagramm[ {{xl, yl...}, {х2, у2,...},...] — вычисляет данные для построения диаграммы Вороного.
Примеры применения этих функций приведены ниже:
<<DiscreteMath`ComputationalGeometry`
ConvexHull[{{0,2}, {1,1}, {0,0}, {2,0}, {1,2}}]
{4, 5, 1, 3}
delval = (DelaunayTriangulation[{{l,2J, {0,3}, {1,1}}]) // Short[#,2]&
{{1, {2, 3}}, {2, {3, 1}}, {3, {1, 2}}}
VoronoiDiagram[{{l,2}, {0,3}, {1,1}}]
{{{-0.50000000000000, 1.5000000000000},
Ray [{- 0.50000000000000, 1.5000000000000},
{1.5000000000000, 3.5000000000000}],
Ray [ {- 0.50000000000000, 1.5000000000000},
{2.0000000000000,1.50000000000000}],
Ray[ {- 0.50000000000000, 1.5000000000000},
{-2.5000000000000, 0.50000000000000} ]},
{{1, {1, 3, 2}}, {2, {1, 2, 4}}, {3, {1, 4, 3}}}}
Рисунок 11.14 показывает задание на плоскости массива точек data2D, построение планарного графа и его выпуклой огибающей с помощью функции Convex-Hull.
Рис. 11.14. Пример построения планарного графа и его выпуклой огибающей Выполнение триангуляции Делоне иллюстрирует рис. 11.15.
Рис. 11.15. Выполнение триангуляции Делоне
Наконец, на рис. 11.16 показаны результаты действия еще двух функций — построение диаграммы и триангуляция в пространстве.
Рис. 11.16. Построение диаграммы (сверху) и триангуляция в пространстве (снизу)
Дискретные функции единичного скачка и импульса — KroneckerDelta
В подпакете KroneckerDelta системы Mathematica 3 заданы дискретные функции единичного скачка и единичного импульса:
- DiscreteStep [n] — возвращает единичный скачок при целом n=0;
- DiscreteStep [n1, n2,...] — функция многомерного единичного скачка;
- KroneckerDelta [n] — возвращает 1 при целом n=0 и 0 во всех других случаях;
- KroneckerDelta [n1, n2,...] — многомерная функция Кронекера.
Примеры использования этих функций в одномерном варианте представлены ниже:
<<DiscreteMath` KroneckerDelta`
Table[DiscreteStep[n], {n, -3, 3}]
{0, 0, 0, 1, 1, 1, 1}
Table[DiscreteStep[n], {n, -3, 3, 1/2}]
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1}
Table[KroneckerDelta[n], {n, -2, 2, 1/2}]
{0, 0, 0, 0, 1, 0, 0, 0, 0}
Sum[KroneckerDelta[n— a]f[n], {n, -Infinity, Infinity}]
f[a]
Sum[( (KroneckerDelta[n]— KroneckerDelta[n-1]) -
(KroneckerDelta[n-1]— KroneckerDelta[n-2]) ) f[n], {n, -Infinity, Infinity}]
f[0]-2f[l] +f[2]
Рисунок 11.17 иллюстрирует применение функции единичного скачка в двумерном случае.
Рис. 11.17. Пример применения функции скачка в двумерном случае
В системе Mathematica 4 функция KroneckerDelta стала встроенной. В данный подпакет входят еще две функции:
- SimplifyDiscreteStep [ехрr] — упрощение выражения ехрг с функциями дискретного скачка;
- SimplifyKroneckerDelta [ехрг] — упрощение выражения ехрг с дельта-функцией Кронекера.
Действие этих функций демонстрируют следующие примеры:
DiscreteStep[n - 1] (KroneckerDelta[n - 2] + DiscreteStep[n, m] DiscreteStep[m - 1]) // SimplifyDiscreteStep
DiscreteStep[-1+m]
DiscreteStep[-l+m] + KroneckerDelta[-2+n]
(f[n] + KroneckerDelta[n]) DiscreteStep[n-l] // SimplifyKroneckerDelta
DiscreteStep [ -1 + n] f [ n]
Дискретные перестановки — Permutations
В подпакете Permutations определен ряд функций дискретных перестановок:
- RandomPermutation [n] — случайные перестановки из n элементов;
- Ordering [list] — дает перестановки в установленном списком list порядке;
- ToCycles [perm] — дает циклическую декомпозицию для списка list;
- FromCycles [ {cicl, cic2,...}] — возвращает перестановки из циклических декомпозиций cic1, cic2, ...;
- PermutationQ [list] — возвращает True, если список list представляет перестановки, и False в ином случае.
Работа функций поясняется следующими примерами:
<<DiscreteMath`Permutations`
RandomPermutation[16]
{16, 12, 11, 5, 3, 4, 9, 14, 2, 8, 15, I, 13, 7, 10, 6}
ToCycles[%]
{{16, 6, 4, 5, 3, 11, 15, 10, 8, 14, 7, 9, 2, 12, 1}, {13}}
FromCycles[%]
{16, 12, 11, 5, 3, 4, 9, 14, 2, 8, 15, 1, 13, 7, 10, 6}
Ordering[%]
{12, 9, 5, 6, 4, 16, 14, 10, 7, 15, 3, 2, 13, 8, 11, 1}
Решение рекуррентных разностных уравнений — RSolve
Для решения рекуррентных разностных уравнений в подпакет RSolve введены следующие функции:
- RSolve [eqn, a [n] , n] — решает рекуррентное уравнение для а [n];
- RSolve [eqn, a, n] — решает рекуррентное уравнение для функции а;
- RSolvet {eqnl, eqn2,...}, {al, a2,...},n] — решает систему рекуррентных уравнений, представленных списками.
Ниже представлены примеры применения данных функций:
<<DiscreteMath` RSolve`
RSolve[a[n+l] == 2 a[n], a[n], n]
{{a[n] -> 2nC[l]}}
RSolve[a[n] == a[n-l] + a[n-2], a[0] == a[l] == 1, a[n], n]
RSolve[ a[0] == a[l] == 2,
(n+1) (n+2) a[n+2]- 2 (n+1) a[n+l]- 3 a[n] == 0, a[n], n]
Подпакет Tree содержит функции создания и применения древовидных структур, именуемых деревьями. Вот эти функции:
- MakeTree [list] — создает дерево по информации, представленной в списке list;
- TreeFind [tree, x] — возвращает позицию наименьшего элемента, превосходящего х в списке list, представляющем дерево.
Действие этих функций поясняют следующие примеры:
<<DiscreteMath` Tree`
MakeTree[{el, e2, е3, е4}]
{{e2, 2), {{el, 1}, {}, {}}, {{e3, 3}, {}, {{e4, 4}, {}, {}}}}
tree = MakeTree[{8.5, 1.2, 9.1, 3.4, 5., 7.6 ,6.4}]
{{6.4, 4}, {{3.4, 2}, {{1.2, 1}, {}, {}}, {{5., 3}, {}, {}}},
{{8.5, 6}, {{7.6, 5}, {}, {}}, {{9.1, 7}, {},{}}}}
TreeFind[tree, 1.2]
1 . .
TreeFind[tree, 1]
0
Для визуализации деревьев служат следующие функции:
- TreePlot [tree] — строит график дерева tree;
- ExprPlot [expr] — строит график, представляющий ехрг в виде дерева.
Примеры построения графиков деревьев представлены на рис. 11.18. Верхнп; график построен по данным дерева tree, определенного в приведенных выи: примерах, а нижний — по данным случайного дерева.
Построение графиков деревьев по выражению ехрг с помощью функции ExprPlot демонстрирует рис. 11.19.
Рис. 11.18. Примеры визуализации деревьев
Рис. 11.19 . Построение графиков деревьев с помощью функции ExprPlot
gl11-10.jpg

gl11-11.jpg
gl11-12.jpg
gl11-13.jpg
gl11-14.jpg
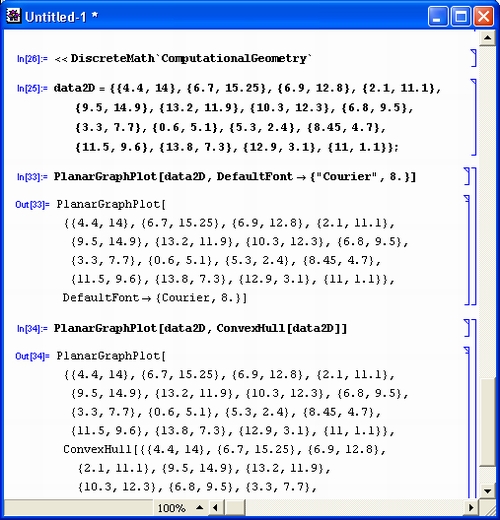
gl11-15.jpg
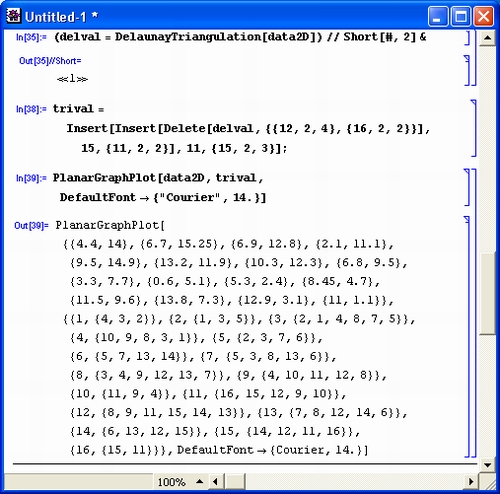
gl11-16.jpg
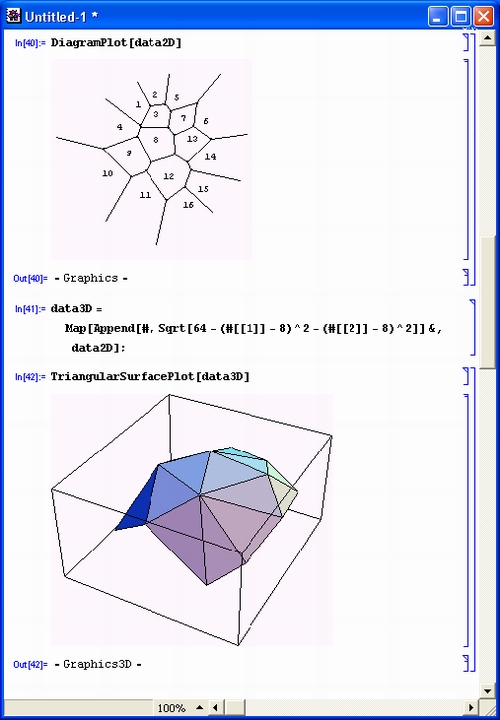
gl11-17.jpg
gl11-18.jpg

gl11-19.jpg
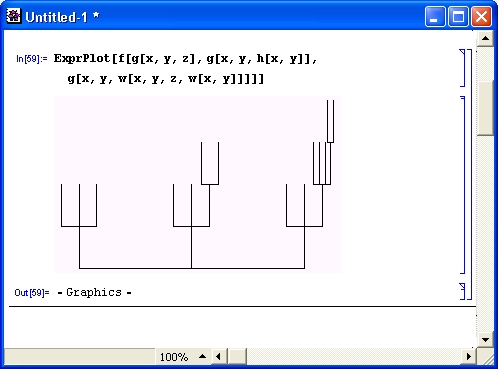
gl11-5.jpg
gl11-6.jpg

gl11-7.jpg
gl11-8.jpg
gl11-9.jpg
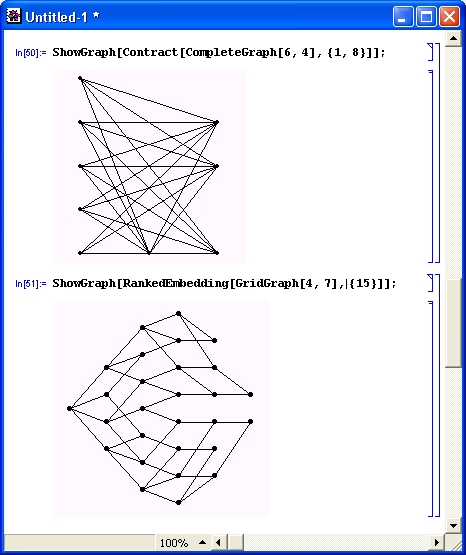
5. Геометрические расчеты — пакет Geometry
Геометрические расчеты — пакет Geometry
В этом разделе описан пакет Geometry, содержащий ряд функций, полезных при выполнении геометрических расчетов. В основном это функции, относящиеся к построению регулярных полигонов на плоскости и полиэдров в пространстве. Кроме того, в пакете есть функции, задающие вращение фигур на плоскости и в пространстве.
Характеристики регулярных полигонов и полиэдров — Polytopes
Подпакет Polytopes содержит ряд функций для регулярных полигонов (многоугольников):
- NumberOfVertices [р] — число вершин углов полигона;
- NumberOfEdges [p] — число сторон полигона;
- NumberOf Faces [p] — число граней полигона;
- Vertices [р] — список координат вершин углов полигона;
- Area [р] — площадь полигона при длине каждой стороны, равной 1;
- InscribeciRadius [р]— радиус вписанной в полигон окружности;
- CircumscribedRadius [р] — радиус описывающей полигон окружности.
В этих функциях наименование полигона р может быть следующим (в скобках дано число сторон):
Digon (2)
Triangle (3)
Square (4)
Pentagon (5)
Hexagon (6)
Heptagon (7)
Octagon (8)
Nonagon (9)
Decagon (10,)
Undecagon (11)
Dodecagon (12)
На рис. 11.20 показаны примеры применения некоторых из этих функций и построение крупными точками вершин полигона — Пентагона (пятиугольника).
Для объемных фигур — полиэдров — имеются следующие функции:
- NumberOfVertices [р] — число вершин углов полиэдра;
- NumberOfEdges [р] — число сторон полиэдра;
- NumberOf Faces [р] — число граней полиэдра;
- Vertices [p] — список координат вершин углов полиэдра;
- Area [p] — площадь полиэдра при длине каждой стороны, равной 1;
- InscribedRadius [р] — радиус вписанной в полиэдр окружности;
- CircumscribedRadius [р] — радиус окружности, описывающей полиэдр;
- Volume [p] — объем полиэдра;
- Dual[p] — дуальный полиэдр;
- Schlafli[p] — символ полиэдра.
Рис. 11.20. Примеры работы с функциями полигонов
Здесь наименование полиэдра может быть следующим:
Tetrahedron (4)
Cube (6)
Octahedron (8)
Didecahedron (12)
Icosahedron (20)
Примеры применения функций полиэдров представлены ниже:
Volume[Octahedron]
(Корень из 2) /3
Vertices [Octahedron]
{{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0},
{0, 0, -1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}}
Dual [Octahedron]
Cube
InscribedRadius [Octahedron]
1/(Корень из 6)
GircumscribedRadius [Octahedron]
1/(Корень из 2)
Вращение фигур на плоскости и в пространстве — Rotations
Для задания поворота плоских фигур на заданный угол в подпакете Rotations заданы следующие функции:
- RotationMatrix2D[theta] — дает матрицу для поворота на угол theta в двух измерениях;
- Rotate2D [vec, theta] — поворачивает вектор vec по часовой стрелке на угол theta;
- Rotate2D[vec,theta,{x,y}] — поворачивает вектор vec по часовой стрелке на угол theta относительно точки с координатами {х, у}.
Рисунок 11.21 иллюстрирует работу с этими функциями.
Рис. 11.21. Работа с функциями поворота
Аналогичные функции существуют и для поворота трехмерных фигур:
- RotationMatrix3D [psi, theta,phi] — дает матрицу поворота на заданные углы в трехмерном пространстве;
- Rotate3D [vec, psi, theta, phi] — поворачивает вектор vec на заданные углы в трехмерном пространстве;
- Rotate3D [vec, psi, theta, phi,{x,y,z}]— поворачивает вектор vec на заданные углы в трехмерном пространстве относительно точки с координатами {х,у, z}.
Приведем пример вычисления матрицы трехмерного поворота:
RotationMatrix3D[Pi, Pi/2, Pi/6]
{{-(Корень из 3)/2,0,1/2 }},{1/2,0,(Корень из 3)/2},{ 0,1,0,}}
gl11-20.jpg

gl11-21.jpg
6. Линейная алгебра — пакет LinearAlgebra
Линейная алгебра— пакет LinearAlgebra
Пакет расширения LinearAlgebra добавляет ряд новых функций, полезных при решении сложных задач линейной алгебры.
Декомпозиция Холесского — Cholesky
Подпакет Cholesky содержит единственную функцию HoleskyDecomposition [m], которая вычисляет декомпозицию (факторизацию, разложение) Холесского для симметричной положительно определенной матрицы т.
Примеры выполнения декомпозиции Холесского даны ниже:
<<LinearAlgebra`Cholesky`
hil = Tablet l/(i + j - 1) , {i, 1, 4}, {j, 1, 4}]
Eigenvalues[ N[hil] ]
{1.50021, 0.169141, 0.00673827, 0.0000967023}
u = CholeskyDecomposition[hil]
MatrixForm[Transpose[u] . u]
Метод исключения Гаусса — GaussianElimination
Следующие функции обеспечивают реализацию метода исключения Гаусса при решении линейного уравнения вида А-x =b:
- LUFactor [m] — возвращает LU-декомпозицию матрицы m;
- LUSolve [lu, b] — решает систему линейных уравнений с матрицей коэффициентов lu и вектором свободных членов b методом исключения переменных Гаусса;
- LU [a, pivots] — создает объект, используемый в LUSolve. Применение этих функций поясняют примеры, показанные ниже:
<<LinearAlgebra`GaussianElimination`
MatrixForm[a = {{1, 2, 3}, {4, 5, 6}, {-1, 5, -5}}]
lu = LUFactor[a]
b = {10, -3, 12}
{10, -3, 12}
LUSolve[lu, b]
Метод исключения Гаусса является хорошо апробированным методом решения систем линейных уравнений, что делает реализацию описанных функций полезным дополнением к встроенным функциям линейной алгебры.
Операции с матрицами — MatrixManipulation
Подпакет MatrixManipulation добавляет к матричным функциям ядра системы Ма-thematica ряд новых функций. Начнем с функций объединения матриц:
- AppendColumns [ml,m2,...] — объединяет по столбцам матрицы ml,m2,...;
- AppendRows [ml,m2,...] — объединяет по строкам матрицы ml,m2,...;
- BlockMatrix [blocks] — объединяет по строкам и столбцам блоки blocks, создавая новую матрицу.
Данные операции с матрицами иллюстрируют следующие примеры:
<< LinearAlgebra`MatrixManipulation`
a = {{a11, a12}, {a21, a22}}; MatrixFormfa]
b = {{b11, b12}, {b21, b22}}; MatrixForm[b]
MatrixForm[AppendColumns[a, b] ]
AppendRows[a, b] //MatrixForm
BlockMatrix[{{a, b}, {b, {{0, 0}, {0, 0}}}}] //MatrixForm
Следующая группа функций вставляет или удаляет столбцы или строки матриц:
- TakeRows [mat, n] — вставляет в матрицу mat n-ю строку;
- TakeRows [mat, -n] — удаляет из матрицы mat п-ю строку;
- TakeRows [mat, {m,n} ] — вставляет в матрицу mat строки от m до n;
- TakeColumns [mat, n] — вставляет в матрицу mat п-й столбец;
- TakeColumns [mat, -n] — удаляет из матрицы mat п-й столбец;
- TakeColumns [mat, {m, n} ] — вставляет в матрицу mat столбцы от m до п.
Действие функции иллюстрируется следующими примерами:
mat = Array[m, 3, 4]; MatrixForm[mat]
m[l, 1] m[l, 2] m[l, 3] m[l, 4]
m[2, 1] m[2, 2] m[2, 3] m[2, 4]
m[3, 1] m[3, 2] m[3, 3] m[3, 4]
TakeRows[mat, -2] //MatrixForm
m[2, 1] m[2, 2] m[2, 3] m[2, 4]
m[3, 1] m[3, 2] m[3, 3] m[3, 4]
TakeColumns[mat, {2,3}] //MatrixForm
m[l, 2] m[l, 3] )
m[2, 2] m[2, 3]
m[3, 2] m[3, 3]
TakeMatrix[mat, {2, 3}, {3, 4}] //MatrixForm
m[2, 3] m[2, 4]
m[3, 3] m[3, 4]
SubMatrix[mat, {2, 3}, {2, 2}] //MatrixForm
m[2, 3] m[2, 4]
m[3, 3] m[3, 4]
Следующая группа функций служит для задания матриц специального вида:
- UpperDiagonalMatrix [f, n] — формирует наддиагональную матрицу размером пхп;
- LowerDiagonalMatrix [f, n] — формирует поддиагональную матрицу размером пхп;
- ZeroMatrix [n] — формирует квадратную нулевую матрицу размером пхп;
- ZeroMatrix [m, n] — формирует нулевую матрицу размером тхп;
- HilbertMatrix [n] — формирует квадратную матрицу Гильберта размером пхп;
- HilbertMatrix [m, n] — формирует матрицу Гильберта размером тхп;
- HankelMatrix [n] — формирует квадратную матрицу Ганкеля размером пхп;
- HankelMatrix [m, n] — формирует матрицу Ганкеля размером тхп.
Примеры задания матриц разного типа приведены ниже:
UpperDiagonalMatrix[f, 3] //MatrixForm
LowerDiagonalMatrix[#1 + #2 &, 4] //MatrixForm
HilbertMatrix[2, 4] //MatrixForm
HankelMatrix[{w, x, y, z}] //MatrixForm
Наконец, в подпакет входит еще одна функция, LinearEquationsToMatri-ces [eqns, vars], которая из записи линейного уравнения eqns с переменными vars формирует расширенную матрицу, содержащую матрицу коэффициентов левой части уравнения и вектор свободных членов.
Пример применения данной функции:
LinearEquationsToMatrices[
а[1,1]*х + а[1,2]*у == с[1],
а[2,1]*х + а[2,2]*у == с[2], х, у]
{{{{{a11, a12), {а21, а22}}[1, 1],
{{a11, a12), {a21, а22}}[1, 2]}, {{{a11, a12}, {a21, a22}}[2, 1],
{{a11, a12), {a21, a22}} [2, 2]}}, {c[l],c[2]}}
Ортогонализация и нормализация — Ortogonalization
В подпакете ортогонализации Ortogonalization имеются следующие функции:
- GramSchmidt [ {vl, v2,...} ] — создает ортогональное множество на основе списка векторов v1, v2, ...;
- Normalize [vect] — возвращает нормированный вектор vect;
- Projection [vectl, vect2] — дает ортогональную проекцию вектора vl на вектор v2.
В этих функциях после аргументов допустимы опции InnerProduct->exprn Normalized->False (отказ от нормировки). Примеры работы с функциями ортогонализации представлены ниже:
<<LinearAlgebra`Orthogonalization`
{wl, w2, w3} = GramSchmidt[ {{1,3,2}, {2,4,3}, {2,4,6}}]
{ wl . w2, w2 . w3, wl . w3, wl . wl, w2 . w2, w3 . w3}
{0, 0, 0, 1, 1, 1}
GramSchmidt[{1, x, x^2, x^3, x^4}, InnerProduct -> (Integrate[#l #2,{x,-l,l}]&)] //Simplify
Normalize[LegendreP[2,x], InnerProduct ->(Integrate[#l #2,{x,-l,l}]&)]
{wl, w2} = GramSchmidt[{{3,4,3}, {2,3,6}}, Normalized -> False]
{wl . wl, wl . w2}
{34, 0}
Решение линейных уравнений с трехдиагональной матрицей —Tridiagonal
При решении линейных уравнений часто встречаются матрицы особой формы — трехдиагональные. Подпакет Tridiagonal имеет функцию для решения линейных уравнений с такой матрицей:
- TridiagonalSolve [a,b, с, г] — решение системы линейных уравнений с трехдиагональной матрицей m. х==г (диагонали представлены векторами а, b и с, вектор свободных членов — г).
Пример применения данной функции:
<<LinearAlgebra` Tridiagonal`
{а, b, с} = {{1, 2, 3}, {4, 5, б, 7}, {10, 9, 8}}
{{1, 2, 3}, {4, 5, 6, 7}, {10, 9, 8}}
m = Table[Switch[ j-i, -1, a[[j]], 0, b[[jj], 1, c[[j-l]], _, 0], {i, 4}, {j, 4}]//MatrixForm
TridiagonalSolve[a, b, c, {8, 3, 4, 5}

7. Расширение в теории чисел — пакет NumberTheory
Расширение в теории чисел
Мы уже описывали уникальные возможности систем Mathematica 3/4 в области обработки чисел и численных вычислений. Эти возможности существенно расширяет пакет NumberTheory, содержащий функции, реализующие алгоритмы теории чисел. Данный раздел посвящен знакомству с этим пакетом.
Цепные дроби — ContinuedFractions
Следующие функции подпакста ContinuedFractions служат для представления чисел в виде цепных дробей или для формирования цепной дроби из списков:
- ContinuedFraction [х] — возвращает цепную дробь для рационального числа х;
- ContinuedFraction [х, n] — возвращает цепную дробь для числа х с числом членов п;
- ContinuedFractionForm [{а0, al,...}] — создает цепную дробь из списка {a0,al,...};
- Normal [ContinuedFractionForm[ {а0, al,...}]] — представление в нормальной форме.
Примеры разложения чисел на цепные дроби:
<<NumberTheory`
ContinuedFractionss ContinuedFraction[123/1234]//ContinuedFractionForm
ContinuedFraction[Sqrt[5], 10]//ContinuedFractionForm 2,
ContinuedFraction[GoldenRatio, 6 ] //ContinuedFractionForm
Table[ Normal[ContinuedFractionForm[Table[1, {n}]]], {n, 9}]
%- N[GoldenRatio]
{-0.618034, 0.381966, -0.118034, 0.0486327,
-0.018034, 0.00696601, -0.00264937, 0.00101363,-0.00038693}
В подпакете имеются также следующие функции:
- ToPeriodicForm[x] — дает десятичное представление для рациональнЪго числа 0 < х < 1;
- ToPeriodicForm [х, b] — дает представление рационального числа х числом с основанием b;
- PeriodicForm[ {а0,...}, {am,...}] — дает периодическую форму представления списков;
- PeriodicForm[ {а0,...}, {am,...},b] — дает периодическую форму представления списков с основанием b;
- Normal [ PeriodicForm [{а0,...}, {am,...}]] — преобразование в нормальную форму;
- Normal [PeriodicForm[ {а0,...}, {am,...} ,b] ] — преобразование в нормальную форму с основанием b.
Ниже представлены примеры применения этих функций:
ToPeriodicForm[ 1/50 ]
0.02
ToPeriodicForm[ 1/23 ]
0.0434782608695652173913
PeriodicForm[1,2,3,4]
0.1234
RealDigits[ N[ 1/23, 25 ] ]
{{4, 3, 4, 7, 8, 2, 6,
0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3, 0, 4, 3, 5},
-1}
ToPeriodicForm[ 1/20, 2 ]
0.000011 ToPeriodicForm[ 1/127 ]
0.007874015748631496062992l2598425l968503937
Normal[%]
1/127
В системе Mathematica 4 функция ContinuedFraction стала встроенной. Имеется также встроенная функция FromContinuedFraction [list], которая строит цепную дробь по элементам списка list.
Улучшенное разложение на простые множители — FactorlntegerECM
Алгоритм разложения чисел на простые множители, реализованный в ядре Mathematiica 3, способен за 3 часа (на рабочих станциях) разлагать числа, имеющие до 18 цифр. Улучшенный алгоритм в подпакете FactorlntegerECM позволяет увеличить максимальное число цифр до 40. Реализуется разложение следующей функцией:
- FactorIntegerECM[n] — возвращает один из делителей числа п. Возможны опции FactorSize->q, CurveNumber->b и CurveCountLimit->c.
Примеры применения этой функции:
<<NumberTheory`FactorlntegerECM`
FactorIntegerECM[123456789]
34227
3*5*7*9
945
FactorlntegerECM[945]
189
Функции теории чисел — NumberTheory Functions
В подпакете NumberTheoryFunctions имеется ряд функций, относящихся к теории чисел:
- SquareFreeQ[n] — дает True, если п не имеет квадратичного фактора, и False в ином случае;
- NextPrime [n] — дает наименьшее простое число, превосходящее п;
- ChineseRemainderTheorem[listl, Iist2.] — дает наименьшее неотрицательное целое г, такое что Mod [r, Iist2] ==list1;
- SqrtMod [d, n] — дает квадратный корень из (d mod п) для нечетного n;
- PrimitiveRoot [n] — дает примитивный корень п;
- QuadraticRepresentation [d, n] — дает решение {х,у} для уравнения х 2 + (d у) 2 ==п для нечетного п и положительного d;
- ClassList[d] — дает список неэквивалентных квадратичных форм дискриминанта d для отрицательного и свободного от квадратов целого d вида 4n+1;
- ClassNumber [d] — дает список неэквивалентных квадратичных форм дискриминанта d;
- SumOf Squares [d, n] — дает число представлений целого числа п в виде суммы d квадратов;
- SumOf SquaresRepresentations [d, n] — дает список представлений целого числа п в виде суммы d квадратов, игнорируя порядок и знаки.
Примеры применения данных функций приведены ниже:
<<NumberTheory`NumberTheoryFunctions`
SquareFreeQ[2*3*5*7]
True SquareFreeQ[50]
False
NextPrime[1000000]
1000003
ChineseRemainderTheorem[{0, 1, 2}, {4, 9,
244
ChineseRemainderTheorem[Range[16], Prime[Range[16]]]
20037783573808880093
SqrtMod[3, 11]
5
SqrtMod[2, 10^64 +57]
876504467496681643735926111996
54610040103361197677707490912
2865
PrimitiveRoot[7]
3
QuadraticRepresentation[l, 13]
{3,. 2}
ClassList[-19]
{{1, 1, 5}}
ClassNumber[-10099]
25
SumOfSquaresRepresentations[3, 100]
{{0, 0, 10}, (0, 6, 8}}
Работа с простыми числами-PrimeQ
В подпакете PrimeQ в дополнение к функции ядра PrimeQ [n] имеется ряд функций для работы с простыми числами:
- ProvablePrimeQ [n] — возвращает True, если п проверено на простоту, и False в ином случае;
- PrimeQCertif icate [n] — возвращает сертификат о том, что n— простое или композитное число;
- ProvablePrimeQ [n, Certif icate->True] — возвращает сертификат, который может использоваться для проверки чисел на простоту;
- PrimeQCertif icateCheck [check, n] — проверяет, удостоверяет ли сертификат check простоту или композитность п.
Следующие примеры показывают работу с простыми числами:
<<NumberTheory` PrimeQ`
PrimeQ[127]
True
ProvablePrimeQ[127]
True
PrimeQCertificate[127]
{127, 3, {2, {3, 2, {2}.}, {7, 3, {2, {3, 2, {2}}}}}}
ProvablePrimeQ[127, Certificate->True]
(True, {127, 3, {2, {3, 2, {2}}, {7, 3, {2, {3, 2, {2}}}}}}}
PrimeQCertificate[3511, SmallPrime -> 1000]
{{CertificatePrime -> 3511,
CertificatePoint->PointEC[2, 2467, 1447, 2135, 3511], Certif icateK-> 32, Certif icateM -> 3424,
CertificateNextPrime -*107, CertificateDiscriminant -> -7},
107, 2, {2, {53, 2, {2, {13, 2, {2, {3, 2, {2}}}}}}}}
Вычисление примитивных элементов — Primitive Element
Подпакет PrimitiveElement содержит всего одну функцию для вычисления примитивных элементов множественного алгебраического выражения:
- PrimitiveElement [z, {а1„а2,...} ] — возвращает список {b, { f1, f2,...}}, где b — примитивный элемент расширения рациональных алгебраических чисел al, а2,... и f1, f 2,... — полином переменной z, представляющей al, a2, ... как термы примитивного элемента.
Ее действие видно из следующего примера:
<<NumberTheory`PrimitiveElement`
PrimitiveElement[z, {Sqrt[2], Sqrt[3]}]
RootReduce[%[[2]] /. z -> %[[1]]]
Создание рядов Рамануджанат-Дирихле — Ramanujan
В подпакете Ramanujan определены следующие функции:
- RamanujanTau [n] — n-й коэффициент ряда Рамануджана т-Дирйхле (т n );
- RamanujanTauGeneratingFunction [z] — производящая функция ряда Рамануджана т-Дирихле;
- RamanujanTauDirichletSeries [s] — ряд Рамануджана т-Дирихле f(s);
- RamanujanTauTheta [t] — функция Рамануджана т-Дирихле o(t)
- RamanujanTauZ [t] — функция Рамануджана т-Дирихле z(t).
Это довольно редкие функции, представляющие интерес для специалистов в теории чисел. Достаточно подробные их определения даны в справочной базе данных. Ограничимся приведением примеров их использования:
<<NumberTheory`Ramanujan`
RamanujanTau[5]
4830
Sum[RamanujanTau[n] z^n, {n, 5}]
z - 24 z2 + 252 z3 - 1472 z4 + 4830 z5
RamanujanTauGeneratingFunction[. 1]
0.00610209
RamanuJanTauGeneratingFunction[.99]
4.10287803703 x -1673
RamanujanTauDirichletSeries[6 + 9.221]
0.00040309-0.002390131
z = RamanujanTauZ[9.22]
0.00242388
theta = RamanujanTauTheta[9.22]
1.40372043366323 z Exp[-I theta]
0.00040309 - 0.00239013 I
Рационализация чисел — Rationalize
Подпакет Rationalize расширяет возможности представления чисел в рациональном виде. Он содержит определения следующих функций:
- ProjectiveRationalize [ {х0, xl,..., хn} ] — возвращает список целых чисел, дающих рациональные представления для чисел заданного списка;
- ProjectiveRationalize [ {х0, xl,..., хn} ,ргес] — возвращает список целых чисел, дающих рациональные представления с погрешностью не более 10- рreк
- Af f ineRationalize [ {х0, xl,..., хn} ] — возвращает список рациональных приближений для чисел заданного списка;
- Aff ineRationalize [ {х0, xl,..., xn} ,prec] — возвращает список рациональных приближений для чисел заданного списка, вычисленных с погрешностью не более 10- ргес .
Встроенная в ядро функция Rationalize дает рациональное представление для одиночных вещественных чисел. Приведенные функции выполняют рационализацию для списков чисел. Примеры их применения представлены ниже:
<<NumberTheory` Rationalize`
Rationalize[N[3 Pi], 6]/ Rationalize[N[11 Pi], 6]
9/35
ProjectiveRationalize[{N[3 Pi], N[11 Pi]}]
{3, 11}
AffineRationalize[{N[3 Pi], N[11 Pi]}, 6]
{1065/113, 3905/113 }
Нахождение полинома, дающего заданный корень — Recognize
Подпакет Recognize содержит определение одноименной с ним функции в двух формах:
- Recognize [x,n,t] — находит полином переменной t степени, большей п, такой, что х является его корнем;
- Recognize [х, n, t, k] — находит полином переменной t степени, большей п, такой, что х является его корнем, и со штрафным весовым коэффициентом k, предназначенным для подавления генерации полиномов высших степеней.
Действие этой функции поясняют следующие примеры:
<<NumberTheory`Recognize`
NSolve[2 x^3- x + 5 == 0]
{{x->-1.4797}, {x-> 0.739852-1.068711}-,
{x->0.739852+ 1.068711}}
sol = First[x /. %]
-1.4797
Recognize[sol, 3, t]
5-t+2t3
Recognize[sol, 2, t]
-225599 - 1464961 + 4032 t2
Recognize[N[Sqrt[3^(2/5)]], 5, t]
-3+t5
Recognize[N[Sqrt[3A(2/5)]], 5, t, 10]
-14625 + 11193 t + 328 t2 + 8813 + t4
Подпакет SiegelTheta содержит еще одну редкую функцию:
- SiegelTheta [z, s] — возвращает значение тета-функции Зигеля Q(Z, s).
Примеры вычисления этой функции даны ниже:
<< NumberTheory` SiegelTheta`
SiegelTheta[{1+1,2+1}, {2+1,-1+41}, {1.2, 2.3+.3I}]
0.973715-0.0002970481
Sum[E^(Pi I {tl,t2}.{ {1+1,2+1}, {2+1, -1+41} }.{tl,,t2} +
2 Pi I {tl,t2}.{l.2,2.3+.31}), {tl,-10,10>, {t2,-10,10}]
0.973715 - 0.000297048 I
В заключительной части этого примера дано вычисление тета-функции Зигеля по ее исходному определению.
8. Численные расчеты — пакет NumericalMath
Численные расчеты — пакет NumericalMath
Пакет расширения NumericalMath содержит множество полезных функций для тех, кто имеет дело с численными расчетами. В их числе функции для выполнения высокоточных аппроксимаций рациональными функциями, численного интегрирования и дифференцирования, вычисления пределов функций, решения уравнений, разложения в ряд и т. д. Ниже описано подавляющее большинство функций этого расширения. Исключены лишь отдельные функции, представляющие ограниченный интерес и несложные для самостоятельного изучения (в подпаке-mах Butcher, Microscope и ComputerArithmetic).
Аппроксимация аналитических функций — Approximations
Подпакет Approximations содержит ряд функций для улучшенной рациональной аппроксимации аналитических функций. Для рациональной интерполяции и аппроксимации функций по заданным значениям абсцисс служит следующая функция:
- Rationallnterpolation [f, {x,m, k}, {x 1 , x 2 , ...,.x m+k+1 } ] — возвращает аппроксимирующее функцию f выражение в виде отношения полиномов а степенью полинома числителя m и знаменателя k в абсциссах, заданных списком {x l ,x 2 ,...,x m+jt+1 }.
Пример применения этой функции:
<<NumericalMath `Approximations`
ril = Rationallnterpolation[ Exp[x], {х, 2, 4}, {0, 1/3, 2/3, 1, 4/3, 5/3, 2}]
Построим график погрешности аппроксимации, то есть график разности функ ии ril и Ехр [х] — он представлен на рис. 11.22.
Нетрудно заметить, что если в центральной части области аппроксимации погрешность мала (менее 5-10- 7 ), то у правого края она резко возрастает.
Представленная функция может использоваться и в иной форме:
Rationallnterpolation[f,{х, m, k},{x, xmin, xmax}]
Рис. 11.22. График погрешности рациональной аппроксимации экспоненциальной функции
В данном случае выбор абсцисс осуществляется автоматически в интервале от xmin до mах. В отличие от первого случая, когда абсциссы могли быть расположены неравномерно, в данном случае расположение их будет равномерным. Приведем пример аппроксимации функции синуса в интервале от n до n:
ri2 = RationalInterpolation[Sin[x],{x,3,4},{x,-Pi,Pi}]
Интересно оценить погрешность аппроксимации. Для этого достаточно построить график разности аппроксимирующей и аппроксимируемой функций. Это построение представлено на рис. 11.23. Любопытно, что хотя максимальная погрешность и значительна, резких выбросов погрешности в данном случае нет.
Рис. 11.23. График погрешности аппроксимации синусоидальной функции
При рациональной аппроксимации можно задать опции WorkingPrecision и Bias со значениями по умолчанию $MachinePrecision и 0 соответственно. Опция Bias обеспечивает автоматическую расстановку узлов интерполяции. При Bias->0 обеспечивается симметрирование выбросов погрешности, дающее наименьшее ее значение в пиках. Ниже приведен пример интерполяции (аппроксимации) экспоненциальной функции в интервале изменения х от 0 до 2:
ri3 = RationalInterpolation[Exp[x],{x,2,4},{x,0,2},Bias->.25]
Построение графика погрешности (рис. 11.24) показывает, что правильным выбором центра интерполяции можно существенно уменьшить ее погрешность. Теперь большая погрешность наблюдается в левой части графика. Однако резкого выброса погрешности в данном случае нет.
Рис. 11.24. Погрешность аппроксимации экспоненты при выборе опции Bias->.25
Из приведенных примеров ясно, что рациональная аппроксимация способна дать существенное уменьшение погрешности при некотором оптимальном расположении узлов аппроксимации и выравнивании погрешностей по абсолютной величине в точках минимумов и максимумов кривой погрешности. Это лежит в основе так называемой минимаксной аппроксимации. Она реализуется следующей функцией:
- MiniMaxApproximation[f,{x,{xmin,xmax},m,k}] — возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax:
- MiniMaxApproximation [f, approx, {x, {xmin, xmax} ,m, k} ] —возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax с возможностью выбора метода аппроксимации approx.
Эта аппроксимация использует итерационный алгоритм вычислений. Они начинаются с первого шага, на котором используется функция Rational Interpolation. Затем аппроксимация последовательно улучшается применением алгоритма Ремеза, лежащего в основе этого вида аппроксимации.
Функция MiniMaxApproximation возвращает два списка — первый с координатами абсцисс, при которых наблюдается максимальная погрешность, второй содержит рациональную функцию аппроксимации. Ниже представлен пример аппроксимации экспоненциальной функции:
mmlist = MiniMaxApproximation[Ехр[х], {х, {0, 2}, 2, 4}]
Выделим формулу аппроксимации:
mmfunc = mmlist[[2, 1]]
Теперь можно построить график погрешности аппроксимации (рис. 11.25).
Рис. 11.25. График погрешности при минимаксной аппроксимации экспоненциальной функции
Следует отметить, что малость абсолютной ошибки для ряда функций (например, тригонометрических) может приводить к большим относительным погрешностям в точках, где функции имеют нулевые значения. Это может привести к отказу от выполнения аппроксимации вследствие исчерпания числа итераций (опция Maxlterations по умолчанию имеет значение 20). Такой случай наблюдается, например, при исполнении следующей команды:
MiniMaxApproximation[Cos[x], {х, {1, 2}, 2, 4}]
Делением функции на (x-Pi/2) можно исключить эту ситуацию:
MiniMaxApproximation[Cos[x]/(x-Pi/2),{*,{1!,2},2,4}] [[2,1]]
График погрешности для этого примера представлен на рис. 11.26. Обратите внимание на то, что в этом примере погрешность аппроксимации не превышает (б...7)-10- 10 .
В приложении дан список функций общей рациональной интерполяции (аппроксимации) для аналитических зависимостей, заданных параметрически. Примеры применения этого довольно редкого вида аппроксимации можно найти в справочной базе данных системы Mathematica. Там же можно найти дополнительные соображения по уменьшению погрешности аппроксимации.
Рис. 11.26. График погрешности при минимаксной аппроксимации функции косинуса
Нули функций Бесселя — BesselZeros
В подпакете BesselZeros определены функции, дающие список аргументов функций Бесселя в их первых п нулевых точках: BesselJZeros [mu, n], Bessel-YZeros[mu,n], BesselJPrimeZeros[mu,n], BesselYPrimeZeros[mu,n] и др. Ввиду редкого использования функций этого класса ограничимся парой примеров их применения:
<<NumericalMath`BesselZeros`
BesselJZeros[0, 5]
{2.40483, 5.52008, 8.65373, 11.7915, 14.9309}
BesselJYJYZeros[2, 6/5, 3, WorkingPrecision -> 20]
{15.806622444176579073, 31.46556009153683, 47.1570167108650315}
Поиск корней уравнений с интерполяцией — InterpolateRoot
Подпакет InterpolateRoot дает средства для ускоренного и более точного поиска корней уравнений по сравнению с соответствующими функциями ядра. Достигается это за счет применения интерполяции функции, корни которой ищутся. Под-пакет задает функцию InterpolateRoot [f, {х, a, b} ], которая находит корень функции f в интервале х от а до b. Вместо функции f можно задавать уравнение eqn. Возможны опции AccuracyGoal->Automatic, Maxlterations->15, WorkingPrecision->$MachinePrecision и ShowProgress->False (указаны принятые по умолчанию значения).
Примеры применения данной функции (n — число итераций):
<<NumericalMath` InterpolateRoot`
n = 0; FindRoot[n++; Exp[x] == 2, {x, 0, 1},
WorkingPrecision -> 100, AccuracyGoal -> 95]
{x->
0.693147180559945309417232121458176568075500134360255 2541206800094933936219696947156058633269964186876}
n
17
n = 0; f[x_] := (n++; Exp[x]-2) /; NumberQ[x]
InterpolateRoot[f[x], {x, 0, 1), WorkingPrecision -> 100,
AccuracyGoal -> 95]; n 10
InterpolateRoot[Exp[x] ==2, {x, 0, 1},ShowProgress -> True,
WorkingPrecision -> 40]
{0, 0.58197670686932642439}
{21, 0, -0.12246396352039524100}
{1, 0.7019353037882764014443370764853594873432}
{21, 20, 0.0130121629575404389120930392554}
{3,0.6932065772065263165289985793736618546663}
{21, 20, 0.000062480788747713548804773113708}
{6, 0.6931471932603933841618726058237307884661}
{21, 20, 1.26443483693584888038460396742xHT8}
{12, 0.693147180559945119457822446
95590259222308309027205042483074}
{40, 20, -1.89953767048152086910014102216x 10-16}
{24, 0.6931471805599453094172321214
5786257157118117337249076750141}
Реализация интервальных методов —IntervalRoots
Иногда важно не найти приближенное значение корня, а уточнить интервал, в котором он находится. В подпакете IntervalRoots для этого используется ряд известных методов, реализованных следующими функциями:
- IntervalBisection [f ,x, int, eps] — находит корень функции f(x) путем уточнения исходного интервала int с заданной погрешностью eps методом половинного деления;
- IntervalSecant [f ,x, int, eps] — находит корень функции f(x) путем уточнения исходного интервала int с заданной погрешностью eps методом секущей;
- IntervalNewton [ f, x, int, eps ] — находит корень функции/(x) путем уточнения исходного интервала int с заданной погрешностью eps методом Ньютона (касательной).
Во всех функциях можно опциями задать максимальное число рекурсий (Max-Recursion) и погрешность (WorkingPrecision). Примеры применения этих функций даны ниже:
<<NumericalMath`IntervalRoots`
IntervalBisection[Sin[x], x, Interval[{2., 8.}], .1]
Interval[{3.125, 3.218750000000001}, {6.218750000000003, 6.312500000000006}]
IntervalBisection[Sin[x], x, Interval[{2., 8.}], .01]
Interval[{3.125, 3.17188}, {6.26563, 6.3125}]
IntervalBisection[Sin[x], x, Interval[{2., 8.}], .01, MaxRecursion -> 10]
Interval[{3.13672, 3.14258}, {6.27734, 6.2832}]
IntervalSecant[Sin[x], x, Interval[{2., 8.}], .01]
Interval[{3.14159, 3.1416}, {6.28316, 6.28321}]
IntervalSecant[Sin[x], x, Interval[{2., 8.}], .01]
Interval[{3.14159, 3.1416}, {6.28316, 6.28321}]
IntervalBisection[Sin[x], x,
Interval[{2, 8}], .1, WorkingPrecision -> Infinity]
Табличное численное интегрирование — Listlntegrate
Встроенная в ядро функция NIntegrate вычисляет определенные интегралы при известной подынтегральной функции. Однако нередко, например при экспериментах, такая функция задается таблицей или списком значений. В подпакете List-Integrate имеются функции для решения этой задачи — табличного интегрирования:
- Listlntegrate [ {yl, y2,..., yn} ,h] — возвращает численное значение интеграла для функции, заданной списком ординат yi при заданном шаге h по х;
- Listlntegrate [ {yl, y2,..., yn}, h, k] — возвращает численное значение интеграла для функции, заданной списком ординат yi при заданном шаге h по х, используя k точек каждого подинтервала;
- Listlntegrate [ {{xl, yl}, {х2, у2 },..., {хп, уп}}, k] — возвращает численное значение интеграла для функции, заданной списком координат {х.., у.}. используя k точек для каждого подынтервала.
Примеры применения данной функции:
<<NumericalMath`Listlntegrate`
data = Tablet n^2, {n, 0, 7}]
{0, 1, 4, 9, 16, 25, 36, 49}
ListIntegrate[data, 1]
343/3
Listlntegrate[{{0,0},{1,1},{2,4},{5,25},{7,49}},2] 241/2
При проведении интегрирования для данных, заданных таблично, можно использовать интерполяцию:
арр = Listlnterpolation[data,{{0,7}}] Integrate[app[x],{x,0,7}]
343/3
Integrate[Interpolation[{{0,0},{1,1},{2,4}, {5,25}, {7,49}},
InterpolationOrder->l][x],{x,0,7}]
241/2
Численное вычисление пределов — NLimit
В подпакете N limit определена функция
Nlimit[expr,х->х0]
для численного вычисления пределов выражений ехрг (см. примеры ниже):
<<NumericalMath` NLimit`
NLimit[Zeta[s] - l/(s-l), s->l]
0.577216
N[EulerGamma]
0.577216
С помощью команды Options [NLimit] можно просмотреть опции, которые используются функцией NLimit по умолчанию. В этом подпакете задано также вычисление бесконечных сумм Эйлера EulerSum[f, { i, imin, Infinity} ]. Например:
EulerSum[(-l)^k/(2k + 1) , {k, 0, Infinity}]
0.785398
EulerSumt(-1)^k/(2k +1), {k, 0, Infinity},
WorkingPrecision->40, Terms->30, ExtraTerms->30]
0.78539816339744830961566084579130322540
%- N[Pi/4, 40]
-2.857249565x 10-29
Имеется также функция вычисления производной в численном виде:
- ND [ f, х, хО] — вычисляет первую производную f(x) в точке х0;
- ND[f, {x,n} ,х0] — вычисляет п-ю производную f(X) в точке х0. Пример вычисления производной:
ND[Exp[Sin[x]], х, 2]
-1.03312
Options[ND]
{WorkingPrecision-> 16, Scale-> 1, Terms-> 7, Method-> EulerSum]
В некоторых случаях вычисления могут быть ошибочными. Тогда следует использовать опции — особенно опцию выбора метода Method. Помимо метода по умолчанию (EulerSum) можно использовать NIntegrate (метод интегрирования по формуле Коши).
Численное вычисление остатка — N Residue
В подпакете NResidue имеется функция вычисления остатка NResidue [expr, {x, x0} ] в точке х=х0:
<<NumericalMath` NResidue`
NResidue[1/z, {z, 0}]
1. + 6.35614x 10-18 I
Residue[f, {z, 1.7}]
0
NResidue[f, {z, 1.7}]
0.259067 - 1.9353xl0-17I
l/((z+.2+.5 I)(z+.2-.5 I)) /. z -> 1.7
0.259067 + 0. I
Options[NResidue]
Обратите внимание на возможные опции для этой функции в последнем примере.
Численное разложение в ряд — NSeries
Подпакет NSeries вводит функцию NSeries [f, {x,xO,n}], которая дает численный ряд, аппроксимирующий функцию f(x) в окрестности точки х = х 0 , включая термы от (х -х 0 ) -n до (х - х 0 ) п .
Примеры применения данной функции:
<<NumericalMath`NSeries`
NSeries[Sin[х], {х, -2, 2}]
Rationalize[Chop[%]]
Rationalize[Chop[NSeries[Log[x], {x, 1, 5}, Radius -> 1/8]]]
Rationalize[Chop[NSeries[Exp[x], {x, 0, 5},
WorkingPrecision -> 40, Radius -> 1/8]]]
Rationalize[Chop[NSeries[Exp[x], {x, 0, 5}, Radius -> 4]]]
Chop[NSeries[Zeta[s], {s, 1, 3}]]
Вычисление коэффициентов формулы интегрирования Ньютона—Котесса — NewtonCotes
Функция NIntegrate, имеющаяся в ядре системы Mathematica, реализует метод интегрирования Гаусса—Кронрода. Еще одним известным методом интегрирования является метод Ньютона—Котесса, сводящий интегрирование к вычислению взвешенных ординат функции в равномерно расположенных точках оси абсцисс. Для реализации метода используются следующие функции:
- NewtonCotesWeights [n, a, b] — возвращает список весовых коэффициентов и абсцисс узловых точек {wi, xi} для квадратуры Ньютона—Котесса на интервале от а до b;
- NewtonCotesError [n, f, a, b] — возвращает погрешность формулы Ньютона—Котесса для заданной функции f.
Примеры применения этих функций представлены ниже:
<<NumericalMath` NewtonCotes`
NewtonCotesWeights[5, 0, 10]
NewtonCotesError[5, f, 0, 10]
NewtonCotesError[5, f, a, a+h]
NewtonCotesWeights[5, -0, 10, QuadratureType -> Open]
NewtonCotesError[5, f, 0, 10, QuadratureType -> Open]
Обратите внимание на то, что приведенные формулы готовят данные для численного интегрирования методом Ньютона—Котесса, но не выполняют самого интегрирования.
В этом уроке мы научились:
- Пользоваться алгебраическими функциями пакета Algebra.
- Применять вычислительные функции пакета Calculus.
- Работать с функциями дискретной математики из пакета DiscreteMath.
- Производить геометрические расчеты с помощью пакета Geometry.
- Выполнять алгебраические вычисления с помощью пакета LinearAlgebra.
- Пользоваться расширенными функциями теории чисел из пакета NumberTheory.
- Осуществлять численные расчеты с помощью пакета NumericalMath.
gl11-22.jpg
gl11-23.jpg
gl11-24.jpg
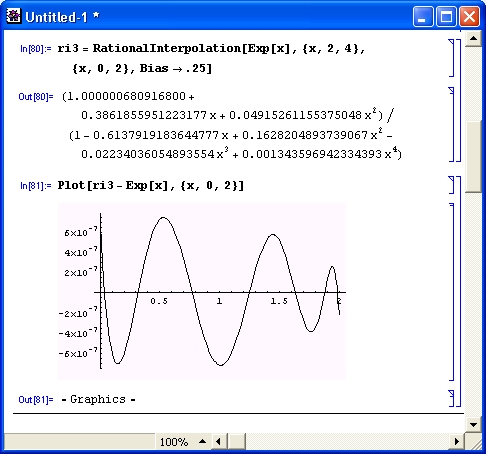
gl11-25.jpg
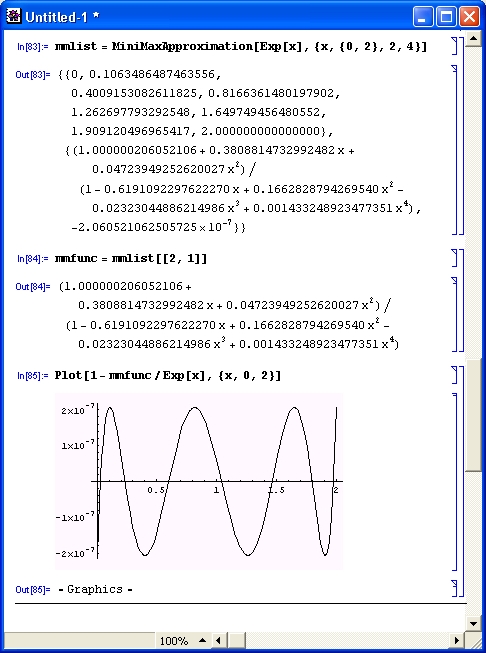
gl11-26.jpg
Урок 12. Статистические расчеты
Урок 12. Статистические расчеты
1. Статистические расчеты
Статистические расчеты
- Статистические расчеты — пакет Statistics
- Построение гистограмм
- Статистика распределен и и
- Статистическая обработка данных
- Сглаживание данных
- Регрессия различного вида
В ядре системы Mathematica практически нет статистических функций. Зато пакет расширения Statistics дает сотни функций, охватывающих практически все разделы теоретической и прикладной статистики. Тем не менее, вопрос о привлечении универсальных математических систем к выполнению серьезных математических расчетов является спорным из-за существования множества специальных статистических компьютерных систем, таких как Statistica, StatGraphics и т. д.
Большинство специализированных статистических программ предлагают специальный интерфейс, базирующийся на обработке табличных данных большого объема, реализуют многовариантный расчет необходимых статистических параметров (например, регрессию сразу по десяткам формул) и отсев заведомо ошибочных данных. Поэтому при статистических расчетах применение подобных программ предпочтительно.
2. Статистические расчеты— пакет Statistics
Статистические расчеты— пакет Statistics
Учитывая ограниченный объем книги и приведенные выше обстоятельства, данный раздел не содержит исчерпывающего описания всех сотен функций расширения Statiatics, а лишь дает обзор этого пакета с описанием наиболее часто используемых средств статистики, относящихся к обработке данных. Это не слишком снижает ценность описания, поскольку функции статистики по большей части просты и имеют вполне очевидные (для специалистов) имена.
Пакет расширения Statistics содержит следующие подпакеты:
- Confidencelntervals — функции доверительных интервалов;
- ContinuousDistributions — функции непрерывных распределений;
- DataManipulation — манипуляции с данными;
- DataSmoothing — сглаживание данных;
- DescriptiveStatistics — статистика распределений;
- DiscreteDistributions — функции дискретных распределений;
- HypothesisTests — проверка статистических гипотез;
- LinearRegression — линейная регрессия;
- MultiDescriptiveStatistics — статистика многомерных распределений;
- MultinormalDistribution — функции многомерных нормальных распределений;
- NonlinearFit — нелинейная регрессия;
- NormalDistribution — функции нормального распределения;
- Common — данные общего характера.
Как и ранее, для работы каждого из подпакетов требуется его загрузка в память компьютера с помощью команды
<<Statistics`Имя_подпакета`
Имена подпакетов расширения статистики приведены выше.
Манипуляции с данными — DataManipulation
Статистические данные обычно бывают представлены в виде списков — как одномерных, так и двумерных (таблиц и матриц) и даже многомерных. Большая часть функций, обеспечивающих манипуляции с данными, сосредоточена в подпакете DataManipulation.
Данные могут вводиться в строках ввода или считываться из файлов с помощью функции ReadList. Для манипуляций с данными могут использоваться многие функции ядра системы, описанные ранее, — в частности, все функции обработки списков. Подпакет DataManipulation дает ряд удобных функций. Ниже представлена первая группа таких функций:
- Column [data, n] — возвращает n-й столбец списка data;
- Column [data, {nl, n2,...}] — возвращает список из столбцов ni списка данных;
- ColumnTake [data, spec] — возвращает столбцы списка data с данной спецификацией spec;
- ColumnDrop [data, spec] — удаляет столбцы списка data с данной спецификацией spec;
- Column Jo in [datal, data2,...] — объединяет столбцы списков datai;
- RowJoin [datal, data2,...] — объединяет строки списков datai;
- DropNonNumeric [data] — удаляет из списка data нечисловые элементы;
- DropNonNumericColumnfdata] — удаляет из списка data столбцы с нечисловыми элементами.
Примеры применения этих функций:
<<Statistics`DataManipulation `
data = {{а, 3}, {b, 6}, {с, 4}, {d, i},
{e, 5}, {i 4}}
{{a, 3}, {b, 6}, {c, 4}, {d, i}, {e, 5), {f, 4}}
col2 = Column[data, 2]
{3, 6, 4/i, 5, 4}
newdata = DropNonNumeric[col2]
{3, 6, 4, 5, 4}
Полезны также следующие функции подпакета:
- BooleanSelect [list, sel] — удаляет из list элементы, которые дают True при тестировании выражения sel;
- TakeWhile [list,pred] — удаляет из list все элементы, начиная с того, для которого pred дает True;
- LengthWhile [list,pred] — возвращает число элементов, которые были удалены после того, как pred дало значение True (отсчет с начала списка).
Примеры применения этих функций:
TakeWhile[col2, NumberQ]
(3,6, 4}
LengthWhile[col2, NumberQ]
3
Ряд функций служит для подготовки данных с целью построения гистограмм:
- Frequencies [list] — готовит данные для представления частотной гистограммы;
- QuantileForm[list] — дает отсортированные данные для представления квантилей;
- CumulativeSums [list] — дает кумулятивное суммирование данных списка.
Пример построения гистограммы по данным списка из двойных элементов с помощью функции Frequencies дан на рис. 12.1. Для построения графика при этом использована функция BarChart из пакета расширения Graphics.
Рис. 12.1. Пример построения гистограммы по данным функции Frequencies
Для подготовки гистограмм могут использоваться и следующие функции:
BinCounts[data,{min,max,dx}]
RangeCounts [data, {cl, c2,...} ]
CategoryCounts [data, {el, e2,...} ]
BinLists[data,{min,max,dx}]
RangeLists [data, {cl,c2,...} ]
CategoryLists [data, {el, e2,...} ]
С примерами их работы можно ознакомиться по справочной системе Mathenatica, содержащей полное описание данного подпакета.
Статистика распределений — DescriptiveStatistics
В подпакете DescriptiveStatistics сосредоточены наиболее важные функции по статистике распределений:
- CentralMoment (data, r) — возвращает центральный момент данных data порядка r;
- Mean [data] — возвращает среднее значение данных data;
- MeanDeviation [data] — возвращает среднее отклонение данных;
- Median [data] — возвращает центральное значение (медиану) данных;
- MedianDeviation [data] — возвращает абсолютное отклонение (от медианы) данных;
- Skewness [data] — возвращает коэффициент асимметрии данных;
- StandardDeviation [data] — возвращает стандартное отклонение данных;
- GeometricMean [data] — возвращает геометрическое среднее данных;
- HarmonicMean [data] — возвращает гармоническое среднее данных;
- RootMeanSquare [data] — возвращает среднеквадратичное значение данных;
- Quantile [data, q] — возвращает q-й квантиль;
- InterpolatingQuantile [data, q] — возвращает q-й квантиль, используя при вычислениях интерполяцию данных;
- VarianceData [data] — возвращает среднеквадратичное отклонение данных.
Мы не приводим определений этих функций, поскольку при символьных данных data их легко получить именно в том виде, который реализован в системе Mathematica:
ds={xl,x2,x3} {xl, x2, хЗ}
Mean[ds]
1/3 *(xl + x2 + x3)
MeanDeviation[ds]
1/3 (Abs[xl + — (-xl-x2-x3)] +
Abs[x2+ 1/3 (-xl-x2-x3) + Abs 1/3[-xl-x2-x3) +хЗ])
Median[ds]
x2
Variancefds]
1/2((x1+1/3(-xl + x2 - x3))2 + (x2 + 1/3 (-xl-x2-x3))2 + (— (-xl-x2-x3) + x3)2)
Skewness[ds]
(SQRT(3) ( (xl 4- -1 (-xl - x2 - x3))3 +
(x2+1/3 (-xl-x2-x3))3 + (1/3 (-xl -x2- x3) + x3))2 /
(x2+ 1/3 (-xl-x2-x3))2 +(1/3 (-xl-x2-x3) +х3)2 )^(3/2)
Следующие примеры поясняют действие этих функций при обработке численных данных:
<<Statistics'DescriptiveStatis tics'
data:={10.1,9.6,11,8.2,7.5,12,8.6,9}
CentralMoment[data,2]
1.9525
Mean[data]
9.5
MeanDeviation[data]
1.175
Median[data]
9.3
MedianDeviation[data]
0.95
Skewness[data]
0.374139
StandardDeviation[data]
1.4938
GeometricMean[data]
9.39935
HarmonicMean[data]
9.30131
RootMeanSquare[data]
9.60221
Quantile[data,1]
12
InterpolatingQuantile[data,1]
InterpolatingQuantile[
{10.1, 9.6, 11, 8.2, 7.5, 12, 8.6, 9), 1]
Variance[data]
2.23143
С рядом других, менее распространенных функций этого подпакета можно ознакомиться с помощью справочной системы. Там же даны примеры их применения.
Сглаживание данных — DataSmoothing
В подпакете DataSmoothing определены функции для сглаживания данных, имеющих большой случайный разброс. К таким данным обычно относятся результаты ряда физических экспериментов, например по энергии элементарных частиц, или сигналы, поступающие из космоса. Для того чтобы отсеять информацию из таких данных с большим уровнем шумов и применяется процедура сглаживания. Она может быть линейной (например, усреднение по ряду точек) или нелинейной.
Определены следующие функции сглаживания:
- MovingAverage [data, r] — сглаживание данных data методом усреднения для г точек;
- MovingMedian [data, r] — сглаживание данных data по медиане для г точек (опция RepeatedSmoothing->True используется для повторного сглаживания);
- LinearFilter [data, {c0, cl,..., сr-1} ] — линейная фильтрация (сj— весовые множители);
- ExponentialSmoothing [data, a] — экспоненциальное (нелинейное) сглаживание, параметр а задает степень сглаживания.
Ниже представлены результаты сглаживания символьных данных, выявляющие соотношения, используемые при сглаживании:
ds : = {xl, х2 , хЗ , х4 , х5}
MovingAverage[ds,3]
{1/3* (xl + x2 + x3), — (х2 + хЗ + х4), — (хЗ + х4 + х5)}
MovingMedian[ds,3]
{х2, хЗ, х4}
ExponentialSmoothing[ds, 0.2]
{xl, xl + 0.2 (-xl + x2) , xl+0.2 (-xl + x2) +0.2 (-xl-0.2 (-xl + x2) + x3) , xl+0.2(-xl+x2)+0.2 (-xl-0.2 (-xl + x2) +x3) +
0.2 (-xl-0.2 (-xl+x2) - 0.2 (-xl- 0.2 (-xl + x2) + x3) + x4) , xl+0.2(-xl + x2) +0.2(-xl-0.2(-xl + x2) +x3) + 0.2 (-xl- 0.2 (-xl+x2) -0.2(-xl-0.2(-xl + x2) + x3) + x4) + 0.2 (-xl- 0.2 (-xl+x2) - 0.2 (-xl- 0.2 (-xl+x2) + x3) -
0.2 (-xl-0.2 (-xl+x2) -0.2 (-xl-0.2 (-xl + x2) + x3) + x4) + x5)}
Применение сглаживания усреднением иллюстрирует рис. 12.2. На нем задан массив (таблица) из 500 случайных точек с равномерным распределением и создан графический объект из этих точек в виде кружков малого диаметра. Затем выполнена операция сглаживания (по 12 смежным точкам) и создан графический объект сглаженных точек в виде кружков большего диаметра. Для сопоставления оба объекта построены на одном графике функцией Show.
Рис. 12.2. Пример линейного сглаживания данных из 500 точек
Нетрудно заметить, что сглаженные точки группируются вокруг среднего значения, равного 0.5, тогда как исходные точки разбросаны практически равномерно по всему полю рисунка. Эффективность нелинейного (экспоненциального) сглаживания демонстрирует рис. 12.3. Показанный на этом рисунке документ построен по тому же принципу, что и документ рис. 12.2.
Остальные функции сглаживания можно использовать аналогичным образом. Выбор метода сглаживания зависит от решаемых пользователем задач и остается за ним.
Рис. 12.3. Пример экспоненциального сглаживания
Другие подпакеты расширения Statistics
Подпакет NormalDistribution содержит хорошо известные функции нормального распределения вероятностей и родственные им функции следующих распределений:
- NormalDistribution [mu, sigma] — нормальное распределение;
- StudentTDistribution [r] — T-распределение Стьюдента;
- ChiSquareDistribution [r] — X 2 -распределение;
- FRatioDistribution [rl, r2] — F-распределение.
Для этих и многих других непрерывных распределений заданы также функции плотности распределения, среднего значения, среднеквадратичного отклонения, стандартного отклонения, вычисления коэффициента асимметрии и т. д. Целый ряд таких функций задан и в подпакете ContinuousDistributions для ряда функций непрерывного распределения. Мы не приводим их, поскольку они подобны функциям обработки списков, описанным выше.
Рисунок 12.4 иллюстрирует получение выражения для плотности нормального распределения pdf и получение графика плотности этого распределения со смещенной вершиной.
Подпакет DiscreteDistributions содержит подобные функции для дискретного распределения вероятностей (Пуассона, биномиального, гипергеометрического и иных распределений). Таким образом, три упомянутых подпакета охватывают практически все имеющие применение законы распределения. Функции для оценки доверительных интервалов сосредоточены в подпакете Confidencelntervals.
Рис. 12.4. Пример работы с функцией нормального распределения
В подпакете HypothesisTests сосредоточено сравнительно небольшое число хорошо известных функций для выполнения тестов проверки статистических гипотез. Загрузка пакета и проведение теста на среднее значение показаны ниже:
<<Statistics` HypothesisTests`
datal = {34, 37, 44, 31, 41, 42, 38, 45, 42, 38};
MeanTest[datal, 34, KnownVariance -> 8]
QneSidedPValue -> 3.05394 x 10-9 ...
У специалистов в области статистики интерес вызовут подпакеты MultiDescriptive-Statistics и MultinormalDistribution с многочисленными функциями многомерных распределений. Они позволяют оценивать статистические характеристики объектов, описываемых функциями нескольких переменных. Рисунок 12.5 поясняет загрузку подпакета MultinormalDistribution, получение выражения для плотности нормального распределения по двум переменным xl и х2 и получение трехмерного графика для плотности такого распределения.
Подпакет Common используется остальными подпакетами пакет Statistics.
Рис. 12.5. Получение аналитического выражения и графика нормального распределения по двум переменным
gl12-1.jpg

gl12-2.jpg
gl12-3.jpg
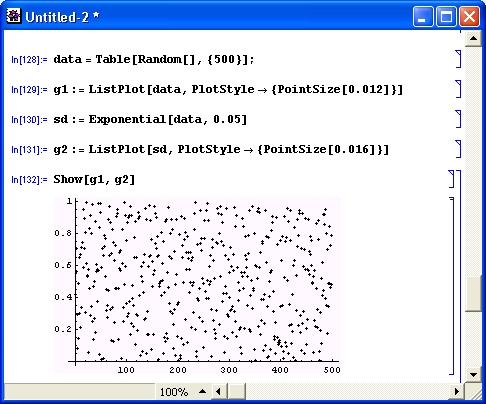
gl12-4.jpg
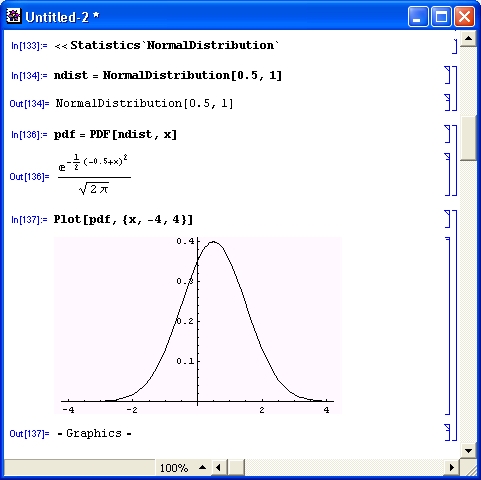
gl12-5.jpg
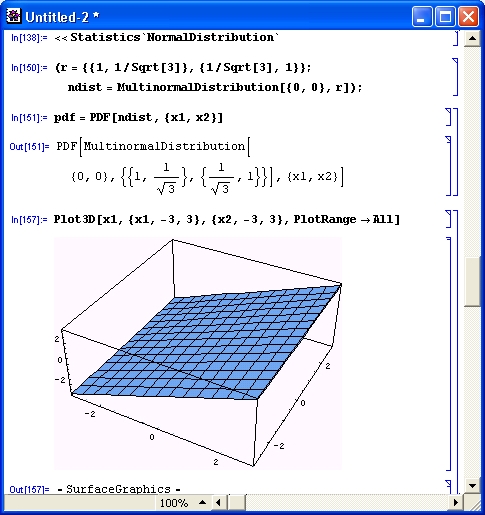
3. Регрессия
Регрессия
Линейная регрессия общего вида — LinearRegression
В подпакете LinearRegression имеются расширенные функции для проведения линейной регрессии общего вида — в дополнение к включенной в ядро функции Fit. Прежде всего это функция Regress:
- Regress [data, { I, х, х^2 }, х] — осуществляет регрессию данных data, используя квадратичную модель;
- Regress [data, {I, x1, x2, xlx2 }, {x1, x2 }] — осуществляет регрессию, используя в ходе итераций зависимость между переменными x 1 и х 2 ;
- Regress [data, {f 1, f2,...}, vars] — осуществляет регрессию, используя модель линейной регрессии общего вида с уравнением регрессии, представляющим линейную комбинацию функций f i от переменных vars.
Данные могут быть представлены списком ординат {у1,у2,...} или списком
{{xll,xl2,...,yl}, {х21,х22,...,у2},...}.
Ниже приведены примеры использования функции Regress:
<<Statistics`LinearRegression`
data={{1,1.9},{2,2.95},{3,4.3},{4,4.8},{5,5}}
{{1, 1.9}, {2, 2.95}, {3, 4.3}, {4, 4.8}, (5, 5}}
(regress = Regress[data, {l,x, x^2}, x] Chop[regress, 10^(-6)])
[Parameter-Table->
| Estimate | SE | TStat | PValue | |
| 1 | 0.1 | 0.421613 | 0.237185 | 0.834595 |
| x | 1.89786 | 0.321297 | 5.90687 | 0.0274845' |
| X 2 | -0.182143 | 0.0525376 | -3.4669 | 0.0740731 |
RSquared->0.988994, AdjustedRSquared ->0.977988,
EstimatedVariance -> 0.0386429, ANOVATable ->
| Model | DF 2 | SumOfSq 6.94471 | MeanSq 3.47236 | FRatio 89.8577 | PValue 0.0110062, |
| Error | 2 | 0.0772857 | 0.0386429 | ||
| Total | 4 | 7.022 |
func = Fit[data, {l,x,.x^2}, x]
0.1 +1.89786x-0.182143x2
Options[Regress]
{RegressionReport -> SurnmaryReport, IncludeConstant -» True, BasisNames->Automatic, Weights->Automatic, Tolerance->Automatic, ConfidenceLevel->0.95}
На рис. 12.6 показан еще один пример проведения регрессии, сопровождаемой графической визуализацией с помощью функции MultipleListPlot.
Риc. 12.6. Пример проведения регрессии с графической визуализацией
Пакет линейной регрессии содержит и ряд иных функций, с которыми можно ознакомиться с помощью справочной базы данных системы Mathematica. Напоминаем еще раз, что сама функция при линейной регрессии может быть нелинейна, она является линейной только относительно искомых коэффициентов регрессии.
Нелинейная регрессия — NonlinearFit
В подпакете NonlinearFit содержатся функции для выполнения нелинейной регрессии общего вида:
- NonlinearFit[data,model,variables,parameters] — выполняет регрессию по заданной модели (формуле) model с переменными variables и параметрами parameters для заданных данных data;
- NonlinearRegress[data,model,variables,parameters] —выполняет регрессию по заданной модели (формуле) model с переменными variables и параметрами parameters для заданных данных data с выдачей списка диагностики.
Данные могут быть представлены списком ординат {у1,у2,...} или списком {{x11,x12,..., yl}, {х21, х22,..., у2},...}. В ходе регрессии минимизируются заданные параметры, так что заданная модель регрессии приближает данные с минимальной среднеквадратичной погрешностью.
На рис. 12.7 показан пример выполнения логарифмической регрессии. При ней модель представлена выражением a*Log[b*x]. Результатом действия функции NonlinearFit является уравнение регрессии в виде этой модели с найденными значениями параметров а и Ь. Представлена также визуализация регрессии в виде графика функции-модели и исходных точек. Следует отметить, что реализация нелинейной регрессии разными методами может давать заметно различающиеся результаты, так что представленные результаты не являются абсолютно строгими.
Рис. 12.7. Пример логарифмической регрессии
Применение функции NonlinearRegress иллюстрирует следующий пример:
NonlinearRegress [data, a*Log[b*x] ,{x},{a,b}]
{BestFitParameters -> {a -> 0.665503, b -4 4. 11893},
ParameterCITable ->
Estimate Asymptotic SE CI
a 0.665503 0.0504167 {0.525524, 0.805482},
b 4.11893 0.806289 {1.88031, 6.35754}
EstimatedVariance -> 0 . 00558058,
DF SumOfSq MeanSq
Model 2 17.7425 8.87126
ANOVATable ->
Error 4 '0.0223223 0.00558058,
Uncorrected Total 6 17.7648
Corrected Total 5 0.994689
1. -0.972212 AsymptoticCorrelationMatrix ->
Curvature
Max Intrinsic 2 . 94314 x lO'16,
FitCurvatureTable -» }
Max Parameter-Effects 2.07792
95. % Confidence Region 0.379478
Как нетрудно заметить, в данном случае выдается отчет о проведении регрессии. Более детальные данные об опциях и обозначениях в отчетах нелинейной регрессии можно найти в справочной базе данных.
Полиномиальная регрессия — PolynomialFit
К сожалению, средства регрессии в Mathematica разбросаны по разным пакетам. Так, в подпакете PolynomialFit пакета NumericalMath определена функция для полиномиальной регрессии:
- PolynomialFit [data, n] — возвращает полином степени п, обеспечивающий наилучшее среднеквадратичное приближение для данных, представленных параметром data. Если data является списком ординат функции, то абсциссы формируются автоматически с шагом 1. Если data является списком координат {xi,yi}, то полином наилучшим образом приближает зависимости
Ниже представлен пример применения функции полиномиальной аппроксимации
<<NumericalMath`PolynomialFit`
р = PolynomialFit[{l,3.9,4.1,8.9,16,24.5,37,50},3]
FittingPolyncmial [ <> , 3]
p[5]
15.8727
Expand[p[x]]
2.35-1.44066x+0.659848x2 +0.0338384x3
Другой пример с построением графиков исходных точек и аппроксимирующего полинома дан на рис. 12.8.
Рис. 12.8. Графики точек исходной зависимости и аппроксимирующего полинома
Нетрудно заметить, что точки исходной зависимости неплохо (но не точно) укладываются на график полинома.
Сплайны представляют собой набор полиномов невысокой степени, последовательно применяемых к наборам точек аппроксимирующей функции. Чаще всего используется кубическая сплайновая аппроксимация, при которой коэффициенты полиномов выбираются из условий равенства в стыкуемых точках не только значений функции, но также первой и второй производных. Это придает графику сплайна вид плавной кривой, точно проходящей через узловые точки и напоминающей изгибы гибкой линейки (spline в переводе — гибкая линейка).
Подпакет SplineFit пакета NumericalMath содержит функцию для проведения сплайн- регрессии, при которой сплайн-функция проходит максимально близко к аппроксимируемым точкам в смысле наилучшего среднеквадратичного приближения. Для этого используется функция SplineFit [data, type], которая возвращает сплайн функцию для данных data, используя сплайн-аппроксимацию типа type — по умолчанию это кубический сплайн Cube (другие типы — Bezier и CompositeBezier).
Рисунок 12.9 показывает пример сплайн- регрессии для обычной зависимости у(х), представленной пятью парами точек. На нем построены также графики аппроксимирующей функции и исходных точек.
Рис. 12.9. Пример сплайн- регрессии для зависимости у(х), заданной списком координат своих узловых точек
Рис. 12.10. Пример сплайн-интерполяции параметрически заданной функции
Специфика сплайн- регрессии по функции SplineFit заключается в преобразовании значений как xi, так и yi. Это позволяет представлять сплайнами в общем виде параметрически заданные функции, что поясняет рис. 12.10.
Тригонометрическая регрессия — TrigFit
Многие выражения содержат периодические тригонометрические функции, например sin(X) или cos(X). Помимо обычного спектрального представления выражений, подпакет TrigFit пакета NumericalMath имеет функции для тригонометрической регрессии:
- TrigFit [data, n, x] — дает тригонометрическую регрессию для данных data с использованием косинусов и синусов вплоть до cos(n x) и sin(n x) и с периодом 2л;
- TrigFit [data, n, {x,L}] — дает тригонометрическую регрессию для данных data с использованием косинусов и синусов вплоть до cos(2лuc/L) и sm(2лnx/L) и с периодом I;
- TrigFit [data, n, {x, x0, xl} ] — дает тригонометрическую регрессию для данных data с использованием косинусов и синусов вплоть до cos(2лn(x - х 0 )/ (x-x0)) и sin(2лn(x-x 0 )/(x 1 -x 0 )) и с периодом (x1-x0).
Примеры выполнения тригонометрической регрессии даны ниже:
<<Numerical Math'TrigFit'
data = Table[l+2Sin[x]+3Cos[2x],{x, 0, 2Pi-2Pi/7, 2Pi/7}];
TrigFit[data, 0, x]
1.
TrigFit[data, 1, {x, L}]
l.+ 0.Cos 2[лx/L]+ 2. Sin [2лx/L]
Fit[Transpose!{Range[0, 2Pi-2Pi/7, 2Pi/7], data}],
{1, Cos[x], Sin[x]}, x]
1. - 4.996xl(T16Cos[x] + 2. Sin[x]
TrigFit[data, 3, {x, x0, xl}];
Chop[%]
l. + 3.Cos [4л (x-x0)/(-x0+x1)]+2. Sin [2л (x-x0)/(-x0+x1)]
В этом уроке мы научились:
- Вычислять ортогональные многочлены.
- Выполнять статистические расчеты с помощью пакета Statistics.
- Строить гистограммы.
- Вычислять статистики распределений.
- Использовать статистическую обработку данных.
- Сглаживать данные.
- Выполнять регрессию различного вида.
gl12-10.jpg

gl12-6.jpg
gl12-7.jpg
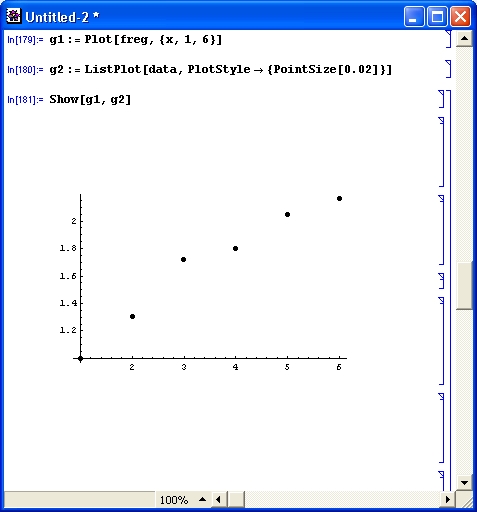
gl12-8.jpg
gl12-9.jpg
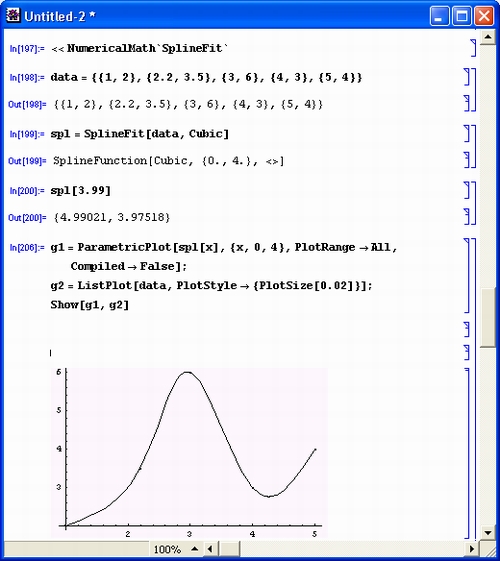
Урок 13. Полезные функции
Урок 13. Полезные функции
1. Полезные функции
Полезные функции
- Синтез звуков — Audio
- Синтез музыкальных звуков — Music
- Функции времени и дат — Calendar
- Географические и картографические данные — World Data
- Физические константы и размерные величины — PhysicalConstants
- Данные о химических элементах — ChemicalElements
- Задание данных только вещественного типа — RealOnly
- Работа с бинарными файлами — BinaryFiles
- Запись графических объектов в файл формата DXF
- Фильтрация опций — FiltersOptions
- Уплотнение памяти — MemoryConserve
- Работа с пакетами расширений — Package
- Показ времени операций — ShowTime
Пакет расширения Miscellaneous
Слово Miscellaneous в переводе на русский язык означает «всякая всячина». Большинство функций этого пакета, на первый взгляд, не имеет прямого отношения к математическим расчетам. Однако как сказать! Этот пакет представляет систему Mathematica в особом свете — как систему, имеющую далеко не стандартные средства синтеза звука и графического представления информации самого общего вида. Физики, химики, географы и даже музыканты могут найти в этом пакете средства, полезные им при обработке на компьютере информации произвольного вида.
Подпакет Audio служит для генерации стандартных звуковых сигналов разной формы, частоты и длительности, модуляции сигналов по амплитуде и по частоте и считывания звуковых файлов с дисков. Для создания звуковых объектов служит функция Waveform:
- Waveform [type, freq, dur] — создает звуковой сигнал формы type с частотой freq (в герцах) и длительностью dur (в секундах). Возможны следующие формы сигнала: Sinusoid — синусоидальный, Triangle — треугольный, Square — прямоугольный и Sawtooth — пилообразный;
- Waveform [type, freq, dur, Overtones->n] — создает звуковой сигнал формы type с частотой freq (в герцах) и длительностью dur (в секундах), имеющий п гармоник.
Приведенный на рис. 13.1 пример дает генерацию прямоугольного сигнала частотой 1000 Гц и длительностью 0.5 с. Следует обратить внимание.на то, что созданный звуковой объект проигрывается и показывается после команды Show.
Звуковой объект, как отмечалось, ассоциируется с графическим объектом. К сожалению, явной связи между осциллограммой звукового сигнала и его графическим образом нет. Более того, вид графического объекта сильно зависит от компьютерной платформы, на которой установлена система Mathematica. Так что графический звуковой объект — это просто некий условный графический образ звукового сигнала.
Рисунок 13.2 показывает генерацию прямоугольного сигнала с двумя гармониками. Здесь используется опция Overtones->2. Ее нельзя применять к синусоидальному сигналу, поскольку он принципиально не имеет гармоник.
Рис. 13.1. Создание и просмотр звукового объекта — синусоидального сигнала
Рис. 13.2. Генерация прямоугольного сигнала с двумя гармониками
Когда указана опция Overtones, функция Waveform использует ряд Фурье для создания высших гармоник, обогащающих тембр звука. При этом возможно изменение числа гармоник. Возможно также создание сигнала с заданными номерами и амплитудами гармоник. Для этого служит функция ListWaveform:
- ListWaveform[ { {nl, al}, {n2, a2 },...}, freq, dir] — создает звуковой объект с частотой основной гармоники f req и длительностью dir, содержащий дополнительные частоты с кратностями ni и амплитудами ai.
На рис. 13.3 представлен пример создания звукового объекта сложного типа, содержащего ряд частотных составляющих. Данные представлены списком partial-List. С помощью функции Table подготовлен объект, содержащий шесть звуковых подобъектов.
Рис. 13.3. Генерация многочастотного сигнала
Для создания звуковых объектов, порождающих звук с амплитудной и частотной модуляцией, служат следующие функции:
- AmplitudeModulation [f c , f m ,m t ,dur] — создает амплитудно-модулирован-ный синусоидальный сигнал с несущей частотой f c , частотой модуляции f m , коэффициентом модуляции m. и длительностью dur. Опция RingModula-tion->True позволяет получить амплитудную модуляцию с подавленной несущей;
- FrequencyModulation [f c , {{f m ,pd}, dur] — создает частотно-модулированный синусоидальный сигнал с несущей частотой f c , модулированный по частоте сигналом с частотой модуляции f m , с девиацией частоты pd (в герцах) и длительностью dur.
Рисунок 13.4 демонстрирует создание звукового объекта с амплитудной и частотной модуляцией. Обратите внимание на то, что объект показывается сразу, поскольку в состав его выражения включена команда //Show.
Для создания сложных сигналов с частотной модуляцией функция Frequency-Modulation используется в следующем виде:
- FrequencyModulation [fc, {{f l,pdl}, (f2,pd2 },...}, dur] — создает частотно-модулированный синусоидальный сигнал длительностью dur с несущей частотой f с и каскадом частот модуляции fmi с девиациями pdi. Опция ModulationType->Parallel создает сигнал, независимо промодулированнып всеми указанными частотами, а опция ModulationType->Cascade включает режим, при котором перечисленные частоты последовательно модулируют друг друга.
Рисунок 13.5 показывает создание и воспроизведение композитного звуковок сигнала. Он представлен списком объектов {s 1, s 2, s 3}.
Рис. 13.4. Генерация звуковых объектов с амплитудной (сверху) и частотной (снизу) модуляцией
Рис. 13.5. Генерация композитного звукового сигнала
Для считывания звуковых файлов с магнитного диска служит функция Read-Soundfile:
- ReadSoundf ile [ "soundfile" ] — опознает файлы разного формата и конвертирует их в список, содержащий целые числа в диапазоне от -32 768 до +32 767. Опция PrintHeader->True позволяет вывести отчет о звуковом файле. Поддерживаются следующие форматы звуковых файлов: NeXT/Sun, WAVE и AIFF.
Разумеется, считываемый звуковой файл должен быть расположён в текущей директории или его имя должно точно указывать местоположение файла. Файлы отображаются соответствующим графическим образом (как описывалось выше).
Синтез музыкальных звуков — Music
Подпакет Music как бы продолжает рассмотренный ранее подпакет поддержки звуковых возможностей системы Mathematica. Он задает функцию последовательного воспроизведения списка, содержащего отдельные звуки:
- Scale [ilist, freq, dur] — генерирует звуковой объект, представленный данными списка ilist музыкальных интервалов, с частотой freq и длительностью dur.
Пример воспроизведения мажорной гаммы (поставляемая с системой мелодия JustMajor) представлен на рис. 13.6. Помимо фрагмента JustMajor имеется еще 11 фрагментов, которые поставляются с системой Mathematica (QuarterTone, Mean-Major, MeanMinor, SixthTone, JustMinor и т. д.). Все они могут воспроизводиться функцией Scale.
Рис. 13.6. Пример воспроизведения музыкального фрагмента
Кроме того, есть ряд функций преобразования:
- HertzToCents [f list] — преобразует список частот (в герцах) в список музыкальных интервалов (в центах);
- CentsToHertz [ilist] — преобразует список музыкальных интервалов (в центах) в список частот (в герцах), начиная с частоты 440 Гц;
- CentsToHertz [ilist, f ] — преобразует список музыкальных интервалов (в центах) в список частот (в герцах), начиная с заданной частоты f.
Примеры преобразования даны ниже:
<<Miscellaneous`Music`
HertzToCents[{400, 450, 525}]
{203.91, 266.871}
alist = Tablet N[440 2^(i/12)], {i, 0, 12}]
{440,., 466.164, 493.883, 523.251, 554.365, 587.33, 622.254,
659.255, 698.456/739.989, 783.991, 830.609, 880.}
HertzToCents[alist]
{100., 100., 100., 100., 100., 100., 100., 100., 100., 100., 100., 100.}
CentsToHertz[{0, 600}]
{440., 622.254}
Описанные возможности синтеза музыки являются скорее данью моде на мультимедиа, чем нужными на практике. Так, время подготовки музыкального объекта довольно значительно (до десятка секунд на компьютере с процессором Pentium II 350). Так что они годятся только для создания простейших музыкальных звуков, которыми можно сопровождать некоторые учебные программы.
Функции времени и дат — Calendar
В пакете расширений Miscellaneous есть ряд подпакетов, содержащих функции времени и даты. Так, в подпакете Calendar сосредоточены вычисления, относящиеся к календарным датам:
- DayOfWeek [ {year, month, day} ] — вычисляет день недели по заданным году, месяцу и числу;
- DaysBetween[{yearl,monthl,dayl},{year2, month2, day2} — вычисляет число суток между двумя датами:
- DaysPlus [ {year, month, day}, n] — дает дату и-го дня после заданной даты.
Во всех этих функциях возможна опция Calendar->cal. Имеется также функция смены календаря:
- CalendarChange [ {year, month, day}, call, cal2] — преобразует заданную дату из одного календаря в другой.
Примеры вычислений с датами:
<<Miscellaneous` Calendar`
DayOfWeek{[1988, 6, 23}]
DaysBetween[{1900, 1, 1}, {1901, 1,1}]
365
DaysPlus[{1900, 1, 1}, 366]
{1901, 1, 2}
DaysBetween[{1900, 1, 1},{1901, 1, 1},Calendar -> Julian]
366
Calendar-Change[{1992, 2, 29}, Gregorian, Julian]
{1992, 2, 16}
CalendarChange[{1992, 2, 29}, Gregorian, Islamic]
{1412, 8, 25}
CalendarChange[{1,1,1}, Islamic, Julian]
{622, 7, 16}
Города и расстояния — CityData и Geodesy
В подпакете CityData можно найти функции, позволяющие найти координаты большинства крупных городов мира: CityData [city, datatype], CityData [city] иCityData[datatype]. Например:
<<Miscellaneous`CityData`
CityData["Montreal",
CityPosition]
{{45, 30}, {-73, -36}}
CityData["Washington"]
{{CityPosition, {{38, 53, 42}, {-77, -2, -12}}}}
Координаты (широта и долгота) выдаются в формате {градусы, минуты} или {градусы, минуты, секунды}.
В этом же подпакете есть функции для вычисления расстояний между городами:
- CityDistance [ "cityl", "pity"] — возвращает расстояние между двумя указанными городами;
- CityDistance["cityl","city",CityDistanceMethod->Method] — возвращает расстояние между двумя указанными городами со спецификацией метода вычислений (по умолчанию используется функция SphericalDistance из подпакета Geodesy).
Пример вычисления расстояния между городами дан ниже:
CityDistance["Washington", "Montreal"]//N
786.915
Базу данных можно расширять, добавляя в нее информацию о новых городах:
CityPosition[{"Champaign", "USA", "IL"}] = {{40, 7, 5},
{-88, -14, -48}};
Убедимся, что информация действительно добавлена:
CityData["Champaign", CityPosition]
{{40, 7, 5}, {-88, -14, -48}}
Для добавления новых полей в базу данных можно использовать функцию AppendTc (см. урок 9). Например, добавим поле для хранения информации о населении:
AppendTo[$CityFields, CityPopulation]
Теперь введем в базу данных информацию о населении Вашингтона:
CityPopulation[{"Washington", "USA", "DC"}] = 638000;
Проверим результат, запросив всю имеющуюся в базе информацию об этом городе:
CityData["Washington"]
{{CityPosition, {{38, 53, 42}, {-77, -2, -12}}},
{CityPopulation, 638000}}
Как видите, результат теперь включает новую информационную категорию —
CityPopulation.
В подпакете Geodesy есть функции, вычисляющие расстояние между двумя точками с учетом выпуклости Земли:
- SphericalDistance [posl,pos2] — вычисляет расстояние между двумя точками в предположении, что Земля — идеальный шар (сфера);
- SpheroidalDistance [posl,pos2] — вычисляет расстояние между двумя точками в предположении, что Земля — приплюснутый шар (сфероид).
Примеры вычислений по этим функциям представлены ниже:
SphericalDistance[{0, 0}, {45,-45}] //N
6671.7
SpheroidalDistance[{0, 0}, {45, 45}] //N
6662.47 % - %%
-9.23014
Географические и картографические данные — WortdData, WorldNames и WorldPlot
В пакете Miscellaneous имеется база данных по странам мира. Доступ к ней открывает подпакет WorldData. Для этого имеется функция WorldData [ "Страна" ], возвращающая список координат конечных отрезков прямых, которые задают контурный график — карту заданной страны. Например, данные по Азербайджану можно получить следующим образом:
<<Miscellaneous` WorldData`
WorldData["Azerbaijan"]
{{{2378, 2689}, {2374, 2770}, {2344, 2806}, {2330, 2770}, {2378, 2689}}, {{2361, 2849}, {2419, 2781}, {2472, 2701}, {2445, 2823}, {2509, 2778}, {2473, 2871}, {2510, 2915}, {2414, 3024}, {2307, 2933}, {2376, 2888}, {2361, 2849}}}
Попробуйте сами найти данные по России (Russia) — мы их не приводим ввиду громоздкости списка, что вполне естественно, поскольку Россия — крупнейшая страна мира и имеет самую длинную границу (контурную линию) с многочисленными изломами.
В подпакете WorldNames имеется список стран, систематизированный по континентам: Africa, Asia, Europa, MiddleEa.st, NorthAmerica, Oceania, South-America и World (весь мир). Например, так можно узнать, какие страны расположены в Океании:
<<Miscellaneous`WorldNames`
Oceania // InputForm
{"Indonesia", "Papua New Guinea", "Fiji", "Australia", "New Zealand")
Наиболее эффектными являются возможности подпакета WorldPlot, функции которого позволяют строить карты любой страны или всего мира:
- WorldPlot [countrylist] — построение карты страны по списку ее данных;
- WorldPlot [countrylist, RandomColors] — построение карты страны по списку ее данных с раскраской случайными цветами;
- WorldPlot [countrylist, RandomGrays] — построение карты страны по списку ее данных с раскраской случайными оттенками серого цвета;
- WorldPlot [ {countrylist, colorfunc} ] — построение карты страны по списку ее данных с раскраской по функции colorfunc;
- WorldPlot [ {countrylist, colorlist) ] — построение карты страны по списку ее данных с раскраской по списку colorlist.
На рис. 13.7 показано построение контурной карты России (верхний рисунок) и цветной карты мира. Раскраска достигается применением директивы RandomColors.
Рис. 13.7. Контурная карта России и цветная карта мира
Следующий рисунок (рис. 13.8) показывает возможность композиционного изображения картографических изображений. На нем построена карта Америки и особо выделены (более темным цветом) территории Канады и Мексики. Здесь для цветовых выделений использована директива GrayLevel, позволяющая задавать степень густоты серого цвета.
Рис. 13.8. Карта Америки с выделенными Канадой и Мексикой
Карты могут строиться в различных проекциях: Albers, Equirectangular, LambertAzimuthal, LambertCylindrical, Mercator, Mollweide, Orthographic и Sinusoidal. Для этого используется опция WorldProjection-> Имя_проекции.
На рис. 13.9 представлена цветная карта всего мира, построенная в синусоидальной проекции. Такая проекция удобна для общего обозрения всей поверхности земного шара при взгляде с экватора (сравните рис. 13.9 с рис. 13.7).
Рис. 13.9. Вид на земной шар при синусоидальной проекции
Выбор вида проекции способен преобразовать вид изображения. Для иллюстрации этого на рис. 13.10 представлена карта мира в иной проекции — азимутальной проекции Ламберта (LambertAzimuthal). В таком виде получается прекрасный вид на Землю со стороны Северного полюса.
Рис. 13.10. Вид но земной шор со стороны Северного полюса при азимутальной проекции Ламберта
Еще один пример (с цилиндрической проекцией Ламберта) представлен на рис. 13.11. Здесь показана карта Африки. Цилиндрическая проекция в некоторых случаях позволяет визуально уменьшить геометрические искажения границ, обусловленные сферической поверхностью Земли. Обратите также внимание на технику окраски самого континента, фона и рамки.
Рис. 13.11. Контурная карта Африки в цилиндрической проекции
В подпакет World Plot включены функции преобразования углов:
- ToMinutes [deg] — преобразует градусы в минуты;
- ToMinutes [ {deg,min} ] — преобразует градусы и минуты в минуты с долями;
- ToMinutes [ {deg,min, sec} ] — преобразует градусы, минуты и секунды в минуты с долями.
Примеры преобразований представлены ниже:
ToMinutes [1]
60
ToMinutes [{1,20}]
80
ToMinutes [{1,20,10}]
481/6
N[%]
80.1667
Физические константы и размерные величины — PhysicalConstants
В подпакете PhysicalConstants определено несколько десятков наиболее употребительных физических констант. Они представлены как размерные величины, то есть помимо своего численного значения имеют единицы измерения. Физические константы вводятся своими полными символьными именами, например, как показано в следующей таблице.
|
Ввод и вывод |
Комментарий |
|
<<Miscellaneous " PhysicalConstants " SpeedOfLight 299792458 Meter/Second |
Загрузка подпакета Скорость света |
|
Second SpeedOfLight AgeOfUniverse 1. 40902 xl0 26 Meter |
Выражение с константами |
| ElectronMass
9 . 10939 x 10- 31 Kilogram |
Масса электрона |
|
AccelerationDueToGravity 9. 80665 Meter/Second 2 |
Ускорение свободного падения |
Полные списки физических констант приведены в справочной базе данных по подпакету PhysicalConstants.
Для выполнения физических, химических и иных расчетов в Mathematica предусмотрена возможность работы с размерными переменными. Для этого база данных системы содержит символьные имена практически для всех единиц измерения (времени, массы, расстояния, температуры и т. д.). Данные о них можно найти в справочной базе данных подпакета Units. Там же имеются функции для перевода единиц измерении из одной системы размерных единиц в другую.
Начнем с функции Convert [old, newunits], которая осуществляет преобразование одних единиц в другие. Например:
<<Miscellaneous`Units`
Convert[12 Meter/Second, Mile/Hour]
26. 8432 Mile / Hour
Convert[3 Kilo Meter / Hour, Inch / Minute]
1968. 5 Inch / Minute
Для преобразования температуры служит функция ConvertTemperature [temp, oldutits, newunits], производящая преобразование температуры из одних единиц в другие. Возможные единицы измерения температуры следующие: Celsius (шкала Цельсия), Centigrade (то же самое), Fahrenheit (шкала Фаренгейта), Kelvin (шкала Кельвина) и Rankine (шкала Ренкина).
Пример преобразования температуры:
ConvertTemperature[20, Fahrenheit, Centigrade]
-6.66667
Наконец, имеются три широкопрофильные функции преобразования в различные системы единиц:
- SI [ехрr] — преобразует ехрг в Международную систему единиц SI;
- MKS [ехрr] — преобразует ехрг в систему единиц МКС (метр/килограмм секунда);
- CGS [ехрr] — преобразует ехрг в систему единиц СГС (сантиметр/грамм секунда).
Пример преобразования дан ниже:
SI[3 Atmosphere]
303975. Pascal
?Pascal
Pascal is the derived SI unit of pressure.
Помимо возможности задания физических констант в пакете расширения Miscellaneous системы Mathematica 4 имеются три дополнительных подпакета: Standard-Atmosphere (данные об атмосфере), ResonanceAbsorptionLines (построение резонансных линий поглощения) и BlackBodyRadiation (излучение абсолютно черного тела).
Ввиду узкой направленности входящих в них функций эти подпакеты подробно не описываются. С ними несложно познакомиться по справочной базе данных системы Mathematica 4 (раздел Add-ons).
Данные о химических элементах — ChemicalElements
В подпакете ChemicalElements имеется ряд функций, позволяющих выявить свойства химических элементов. Начнем с функции без параметров Elements, выводящей список всех химических элементов (он полезен для знакомства с англоязычными наименованиями элементов):
<<Miscellaneous` ChemicalElements`
Elements
{Hydrogen, Helium, Lithium, Beryllium, Boron, Carbon, Nitrogen, Oxygen, Fluorine, Neon, Sodium, Magnesium, Aluminium, Silicon, Phosphorus, Sulfur, Chlorine, Argon, Potassium, Calcium, Scandium, Titanium, Vanadium, Chromium, Manganese, Iron, Cobalt, Nickel, Copper, Zinc, Gallium, Germanium, Arsenic, Selenium, Bromine, Krypton, Rubidium, Strontium, Yttrium, Zirconium, Niobium, Molybdenum', Technetium, Ruthenium, Rhodium, Palladium, Silver, Cadmium, Indium, Tin, Antimony, Tellurium, Iodine, Xenon, Caesium, Barium, Lanthanum, Cerium, Praseodymium, Neodymium, Promethium, Samarium, Europium, Gadolinium, Terbium, Dysprosium, Holmium, Erbium, Thulium, Ytterbium, Lutetium, Hafnium, Tantalum, Tungsten, Rhenium, Osmium, Iridium, Platinum, Gold, Mercury, Thallium, Lead, Bismuth, Polonium, Astatine, Radon, Francium, Radium, Actinium, Thorium, Protactinium, Uranium, Neptunium, Plutonium, Americium, Curium, Berkelium, Californium, Einsteinium, Fermium, Mendelevium, Nobelium, Lawrencium, Rutherfofdium, Dubnium, Seaborgium, Bohrium, Hassium, Meitnerium, Ununnilium, Unununium, Ununbium}
Для выявления свойств элементов служат следующие функции:
- Abbreviation [element] — возвращает стандартную аббревиатуру элемента;
- AtomicNumber [element] — возвращает атомный номер элемента;
- AtomicWeight [element] — возвращает атомный вес элемента;
-
Stablelsotopes [element] — возвращает список стабильных изотопов элемента.
<<Miscellaneous`ChemicalElements`
Abbreviation[Wolfram]
W
AtomicNumber[Wolfram]
74
AtomicWeight[Wolfram]
183.85
Stablelsotopes[Wolfram]
{180, 182, 183, 184, 186}
Off[AtomicWeight::unstable]
Рисунок 13.12 графически показывает отношение атомного веса к атомному номеру для разных элементов.
Рис. 13.12. График отношения атомного веса к атомному номеру химических элементов
Полезны также функции, возвращающие значения величин, определяющих физические свойства элементов:
- MeltingPoint [element] — температура в точке плавления (здесь и далее в Кельвинах);
- BoilingPoint [element] — температура в точке кипения;
- HeatOf Fusion [element] — теплота плавления (килоджоуль/моль);
- HeatOfVaporization [element] — теплота парообразования (килоджоуль/моль):
- Density [element] — плотность в килограммах на кубический метр (при 298 К);
- TermalConductivity [element] — теплопроводность элемента;
- ElectronConf iguration [element] — конфигурация электронов в виде списка;
- ElectronConf igurationFormat [element] — конфигурация электронов Б стандартной форме записи.
Используемая в размерных значениях этих функций величина «моль» является мерой количества вещества, численно равной 6.0221367х10 23 молекул вещества. Определим свойства элемента — вольфрама (чувствуете намек на фамилию создателя системы Mathematica?):
MeltingPoint[Wolfram]
3680. Kelvin
BoilingPoint[Wolfram]
5930.Kelvin
HeatOfFusion[Wolfram]
35.2 Joule Kilo/Mole
HeatOfVaporization[Wolfram]
824.2 Joule Kilo / Mole
Density[Wolfram]
19300. Kilogram / Meter3
ThermalConductivity[Wolfram]
174. Watt /Kelvin Meter
ElectronConfiguration[Wolfram]
{{2}, {2, 6}, {2, 6, 10}, {2, 6, 10, 14}, {2, 6, 4}, {2}}
ElectronConfigurationFormat[Wolfram]
1s2 2s22p6 3s23p63d10 4s24p64d104f14 5s25p65d4 6s2
Вольфрам — один из самых тугоплавких элементов в природе. Недаром из него делают нити для ламп накаливания.
Задание данных только вещественного типа — RealOnly
В ряде случаев (как при вычислениях, так и при построении графиков) Mathematica сообщает о наличии у функций особых значений. Это хорошо иллюстрирует рис. 13.13, на котором предпринята попытка построения графика, казалось бы, простой функции х^ (1/3). Нетрудно заметить, что график в отрицательной области значений х не построен и перед построением неполного графика выдан целый букет предупреждающих сообщений.
Причина этой частичной неудачи в том, что в некоторых точках данная функция дает комплексные значения. Например:
(-8.0) ^ (1/3)
1. + 1.732051
Подпакет ReaLOnly не вводит никаких новых функций. Он просто превращает данные последующих вычислений в чисто вещественные. Так что после его загрузки построение графика указанной функции проходит без каких-либо проблем (рис. 13.14).
Рис. 13.13. Попытка построения графика функции х^(1/3)
Рис. 13.14. Построение графика функции х^(1/3) после загрузки подпа.кета RealOnly
Разумеется, подобное свойство нужно далеко не всегда и при неумелом его применении способно привести к ошибочным результатам. Тем не менее, есть случаи (см. приведенный пример), когда оно полезно.
gl13-1.jpg

gl13-10.jpg
gl13-11.jpg
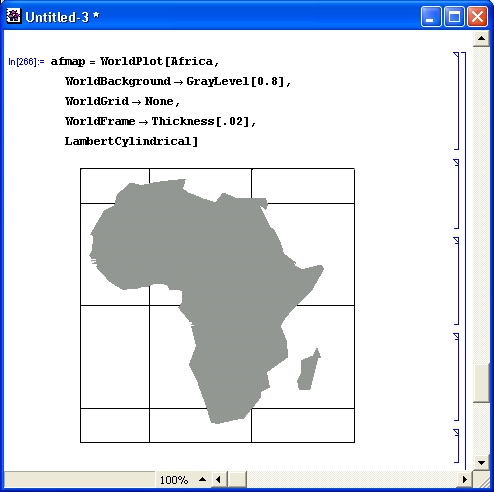
gl13-12.jpg
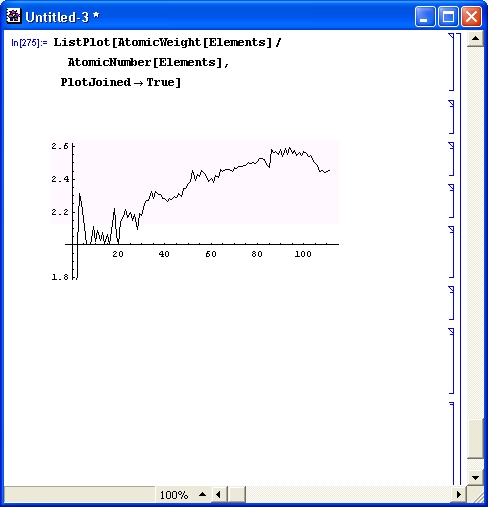
gl13-13.jpg
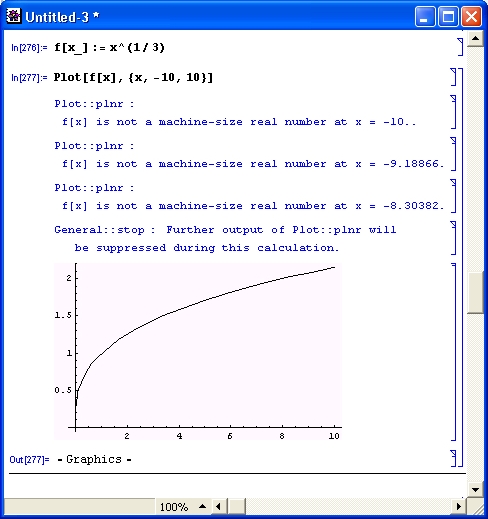
gl13-14.jpg
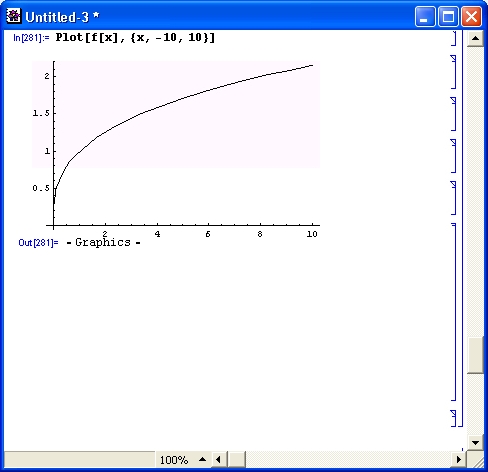
gl13-2.jpg
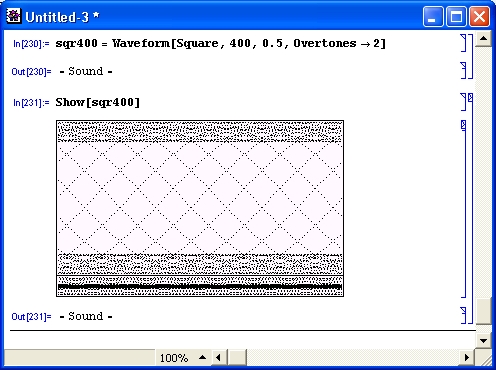
gl13-3.jpg
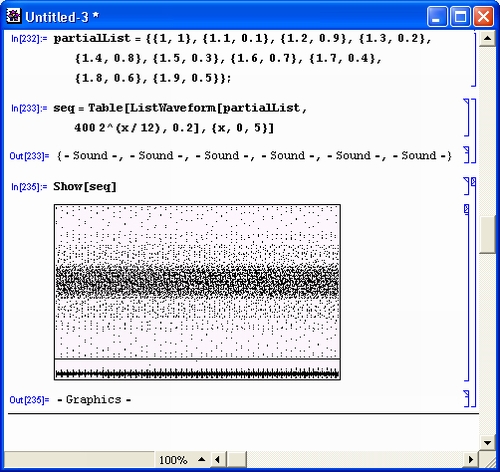
gl13-4.jpg

gl13-5.jpg
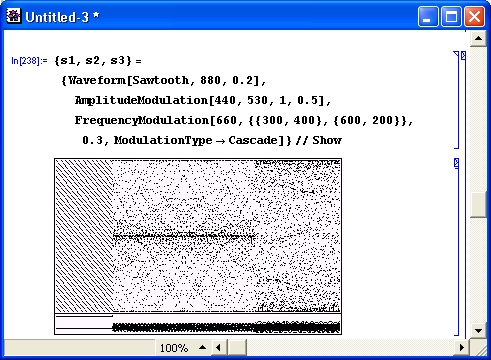
gl13-6.jpg
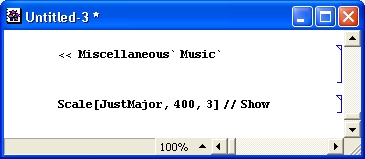
gl13-7.jpg
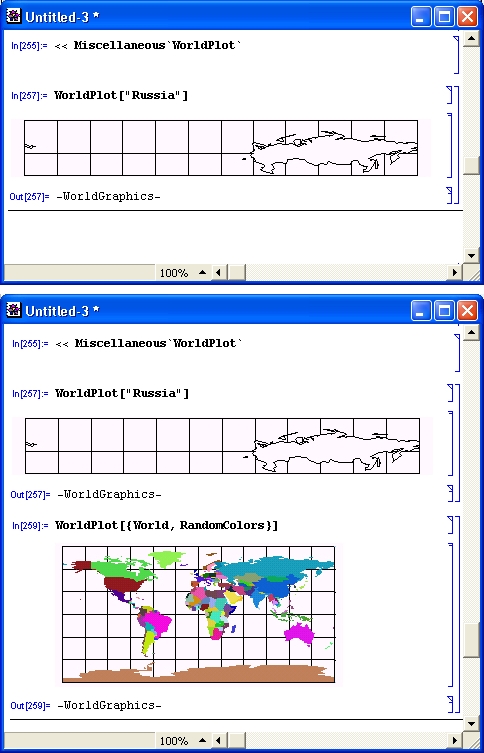
gl13-8.jpg
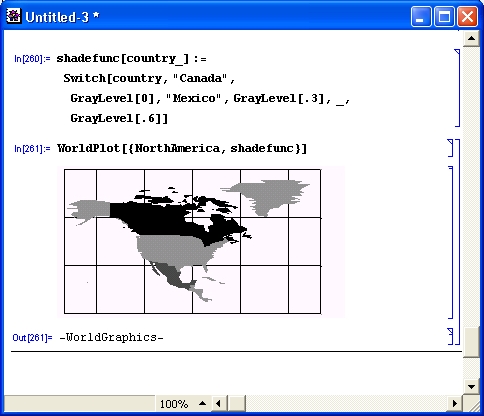
gl13-9.jpg
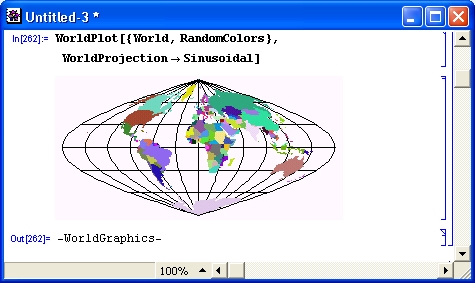
2. Пакет расширения с утилитами — Utilities
Пакет расширения с утилитами— Utilities
Утилитами принято называть небольшие программы, в основном вспомогательного назначения. Они предназначены чаще всего для работы с файлами и памятью компьютера. Ряд таких утилит включен в пакет расширения Utilities, знакомству с которым и посвящен данный небольшой раздел.
Работа с бинарными файлами — BinaryFiles
В подпакете BinaryFiles имеются типовые функции для работы с бинарными файлами:
- OpenReadBinary [ "filename" ] — открытие файла для считывания бинарных данных;
- OpenWriteBinary["filename"] — открытие файла для записи бинарных данных;
- OpenAppendBinary ["filename"] — открытие файла для добавления данных в конец;
- ReadBinary [stream, type] — считывает бинарные данные из потока;
- ReadBinary [ stream, expr ] — считывает из потока бинарные данные, типы которых определяются выражением ехрг.
Функции
ReadListBinary[filename,type]
ReadListBinary[stream,type, n]
ReadListBinary[stream,type]
оперируют с данными в виде списков, а функция WriteBinary [stream, data] записывает данные в поток в бинарной форме. Примеры применения этих функций представлены ниже:
<< Utilities`BinaryFiles`
data = N[Table[10^n, {n, -10, 10}]]
{l.x l10-10, 1.x 10-9, 1.x 10-8, 1.x 10-7, 1.x 10-6, 0.00001, 0.0001, 0.001, 0.01, 0.1, 1., 10., 100.-, 1000., 10000., 100000., 1.x 106, 1.x 107, 1.x 108, 1.x 109, 1.x 1010}
stream = OpenWriteBinary["binarytest"]
OutputStream["binarytest" , 4]
WriteBinary[stream, data]
Close[stream]
binarytest
ReadListBinary["binarytest", Double]
{1.х10-10, 1. xlO-9, 1. x10-8, 1.x 10-7, 1.x 10-6, 0.00001, 0.0001, 0.001, 0.01, 0.1, 1., 10., 100., 1000., 10000., 100000., 1.x 106, 1.x 107, l.xl08, 1.x 109, 1.x 1010}
ReadListBinary["binarytest", Signedlntl6, 5]
{15835, 31967,-9769, -16965, 15889}
Для конвертирования выражений ехрг в байтовый формат служат функции ТоBytes[expr] и ToBytes[expr, type].
Например:
ToBytes[-34.3421435]
{192, 65, 43, 203, 91, 128, 0, 0}
ToBytes[-34.3421435, CString]
{45, 51, 52, 46, 51, 52, 50, 49, 52, 51, 53, 0}
Запись графических объектов в файл формата DXF
В широко распространенных графических системах AutoCAD используется формат файлов DXF. Подпакет DXF позволяет записывать графические объекты Mathematica в этом формате с помощью функции WriteDXF["filename", graphics].
Здесь filename — имя файла, a graphics — имя предварительно созданного графического объекта. Применение данной функции вполне очевидно.
Фильтрация опций — FilterOptions
В ряде случаев возникает необходимость в передаче опций из одной функции в другую. При этом передавать нужно не- все опции, а только те из них, которые имеют смысл для вызываемой функции. В подпакете FilterOptions имеется функция, позволяющая фильтровать опции:
- FilterOptions [symbol, optl, opt2,...] — возвращает набор опций, применимых к объекту symbol.
Риc. 13.15. Пример применения подпакета FilterOptions
Рисунок 13.15 поясняет применение опции фильтрации для создания графической функции Plotlntegrate, строящей график интеграла от заданной функции. Показан также пример построения графика интеграла от функции Cos [x] в интервале от 0 до 2п. Как и следовало ожидать, график функции очень близок к синусоиде.
Вы можете опробовать действие этой графической функции и на других примерах (желательно, чтобы интегрируемая функция не имела особенностей в пределах области построения графика).
Уплотнение памяти — MemoryConserve
Подпакет MemoryConserve в дополнение к имеющейся в ядре функции освобождения памяти Share [ ] содержит две директивы управления памятью:
- On [MemoryConserve] — включает автоматическое сжатие занимаемой системой памяти;
- Off [MemoryConserve] — отключает автоматическое сжатие памяти. Ниже демонстрируется применение этого подпакета:
<<Utilities 'MemoryConserve' $MemoryIncrement
100000
ТаЫе[ ToString[0], {2^15} ] ;
Length[ % ]
MemoryConserve::start : Running Share[] to conserve memory. MemoryConserve::end : Finished running Share[];
929200 bytes of memory freed.
32768
Off[ MemoryConserve ]
On[ MemoryConserve ]
Данная утилита полезна лишь при использовании системы Mathematica на компьютерах с малым объемом оперативной памяти.
Работа с пакетами расширений — Package
В подпакете Package имеется несколько функций, полезных при работе с пакетами расширения:
- FindPackages [path] — возвращает список файлов с расширением .m, имеющихся в каталоге path. Опция FullPath->True дает возврат полных (вместе с путем) имен файлов;
- FindPackages [path, pattern] — возвращает список файлов с расширением .m, имеющихся в каталоге path и удовлетворяющих заданному образцу pattern;
- Annotation [package] — возвращает список ключевых слов, содержащихся в аннотации пакета;
- Annotation [package, keyword] — возвращает текст аннотации пакета, связанной с ключевым словом keyword.
Примеры работы с этими функциями:
<<Utilities' Package'
FindPackages[$Path, "*ca"]
{{}, {}, {}, {DiscreteMath'Combinatorica'}, {}}
FindPackages[$Path, "*ca",
FullPath -> True]
{{},(},{},
{/usr/local/mathematica/AddOns/StandardPackages/ DiscreteMath/Combinatorica.m}, {}}
Annotation["Utilities' Package'"]
{Title, Context, Author, Summary, Package Version, Mathematica Version, Copyright, History, Keywords, Limitations, Discussion}
Annotation["Utilities'Package'", "Mathematica Version"]
{(* :Mathematica Version: 4.0 *)}
Показ времени операций — ShowTime
В подпакете ShowTime собраны средства для осуществления контроля за временем выполнения различных операций:
- ShowTime [expr] — выводит время выполнения операции ехрr;
- On [ShowTime] — включает вывод времени исполнения последовательности операций;
- Off [ShowTime] — выключает вывод времени исполнения последовательности операций.
Следующие примеры иллюстрируют применение этих средств:
<<Utilities'ShowTime'
NIntegrate[x Exp[-x] Sin[x], {x, 0, Infinity}]
0.05 Second
0.5
Off[ShowTime]
0. Second
ShowTime[Sum[1/n, {n, I, 999}]];
0.11 Second
Контроль за временем исполнения операций — важная часть отладки высокоэффективных программ и программных модулей.

В этом уроке мы научились:
- Синтезировать звуки.
- Использовать функции времени и дат.
- Работать с географическими и картографическими данными.
- Вводить физические константы и размерные величины.
- Получать данные о химических элементах.
- Задавать данные только вещественного типа.
- Работать с бинарными файлами.
- Записывать графические объекты в файл формата DXF.
- Применять фильтрацию опций.
- Выполнять уплотнение памяти.
- Выводить данные о времени выполнения операций.
gl13-15.jpg
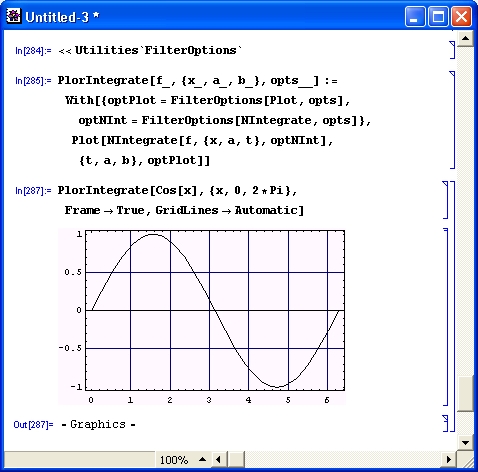
Урок 14. Расширения графики— пакет Graphics
Урок 14. Расширения графики— пакет Graphics
1. Расширения графики— пакет Graphics
Расширения графики— пакет Graphics
- Анимация графиков различного типа
- Использование цвета
- Построение стрелок
- Графики комплекснозначных функций
- Построение объемных контурных графиков
- Построение графиков с окраской внутренних областей
- Графики специальных типов
- Специальные типы трехмерных графиков
- Построение графиков неявных функций
- Вывод обозначений кривых
- Построение трехмерных параметрических графиков
- Представление полей на плоскости и в пространстве
- Трехмерные графические объекты
Пакет расширения Graphics дает множество средств для построения графиков самого изысканного вида. Он является прекрасным инструментом для визуализации задач, допускающих представление результатов в графической форме. Объем материала данного пакета намного выходит за пределы одного урока, поскольку предполагает отбор нужного материала для изучения того или иного вида графики.
Анимация графиков различного типа — Animation
Фактически, техника анимации (оживления) графиков уже была описана. Напомним, что она сводится к подготовке отдельных кадров анимационного рисунка, которые специфицируются особой изменяющейся переменной t. Это не обязательно время, возможно, что t задает размеры изображения, его положение или иную характеристику. Естественно, что имя переменной можно выбирать произвольно.
Подпакет Animation подключается автоматически и в ряде случаев не требует загрузки (хотя на всякий случай его лучше загрузить при использовании средств анимации). Пакет задает две важнейшие функции:
- Animate [grcom, {t, tmin, tmax, dt] — задает построение серии графических объектов grcom при изменении параметра t от tmin до tmax с шагом dt;
- ShowAnimation [ {p1,p2, р3,...} ] — дает анимацию последовательным воспроизведением ранее подготовленных объектов p1, р2, рЗ, ...
Рисунок 14.1 показывает пример подготовки к анимации простого графика — функции n*Sin [х] /х при n, меняющемся от 0.1 до 1 с шагом 0.1. Таким образом демонстрируется изменение данной функции по высоте (амплитуде).
При задании анимации есть небольшая проблема — Mathematica автоматически меняет масштаб с тем, чтобы график был наиболее представительным. Но для анимации это недопустимо, поэтому опцией PlotRange задан фиксированный масштаб для всех кадров анимации. Выполнив показанные на рис. 14.1 команды, можно наблюдать построение всех кадров — для n = 0.1,0.2,0.3,..., 1. 0. Первые три кадра анимации видны на рис. 14.1 снизу.
Теперь для наблюдения анимации достаточно двойным щелчком выделить первый рисунок. Будет видна быстрая смена кадров. Остановить анимацию и снова запустить ее можно нажатием клавиш Ctrl+Y. При выполнении анимации внизу окна документа появляются кнопки анимационного проигрывателя (рис. 14.2).
Рис. 14.1. Демонстрация графика функции n*Sin[x]/x, меняющейся по высоте
Рис. 14.2. Стоп-кадр анимации графика функции n*Sin[x]/x
Проигрыватель имеет мнемонику кнопок, подобную мнемонике бытовых проигрывателей видеодисков. Есть кнопки пуска и остановки, реверса проигрывания, замедления и ускорения проигрывания. Последние особенно важны, поскольку на современных компьютерах анимация рисунков происходит слишком быстро и лишь ее замедление позволяет обеспечить хорошую визуализацию данного процесса. Число кадров анимации не должно быть меньше 8-10, иначе вместо плавного движения будут видны резкие скачки изображения.
Следующий пример иллюстрирует анимацию графика с параметрическим заданием функции:
ShowAnimation[Table[ Graphics[Line[{{0 0},
{Cos[t], Sin[t]}}], PlotRange -> {{-1, 1}, {-1, 1}}],
{t, 0, 2Pi, Pi/8}]]
Запустив этот фрагмент программы, вы увидите построение отрезка прямой, вращающегося вокруг одного неподвижного конца. Здесь для анимации вначале строится набор кадров, а затем используется функция ShowAnimation.
Аналогичным образом осуществляется анимация трехмерных графиков поверхностей или фигур. Рисунок 14.3 показывает начало подготовки к анимации сложной поверхности, описываемой функцией Бесселя, аргумент которой меняется от кадра к кадру.
Рис. 14.3. Подготовка к анимации сложной трехмерной поверхности
Обратите внимание на применение функций Show и Graph!csArray для построения на одном графике сразу всех кадров (фаз) анимации. Порой этот набор кадров даже важней, чем анимация, длящаяся доли секунд или несколько секунд.
Рисунок 14.4 иллюстрирует следующий шаг анимации — исполнение функции ShowAnimation. Как и для предшествующих примеров, она строит последовательно все рисунки — кадры анимации.
Рис. 14.4. Подготовка кадров анимации сложной трехмерной поверхности
Запуск анимации выполняется, как уже было описано (рис. 14.5). При этом наблюдаются характерные колебания поверхности — пик ее проваливается вниз, образуя впадину, а затем снова выходит вверх. Внизу графика видны кнопки анимационного проигрывателя, работа с которым также была описана выше.
Для упрощения анимации сложных графиков в подпакете Animations задан ряд специализированных функций, которые приведены в приложении. Рисунок 14.6 поясняет задание анимации и построение начального кадра для параметрически заданной раскручивающейся спирали — используется функция MovieParametricPlot. Запустив начальный кадр, можно наблюдать раскручивание спирали.
Рис. 14.5. Один из стоп-кадров анимации сложной трехмерной поверхности
Рис. 14.6. Построение раскручивающейся спирали
Еще один пример построения сложной вращающейся в пространстве фигуры, напоминающей гантель, показан на рис. 14.7. В данном случае трехмерная фигура задана в параметрической форме, а для последующей ее анимации используется функция SpinShow.
Последние примеры даны в упрощенной форме — без окна с проигрывателем. Разумеется, кнопки проигрывателя появляются при реальном пуске анимации.
Рис. 14.7. Построение вращающейся в пространстве фигуры — «гантели»
gl14-1.jpg
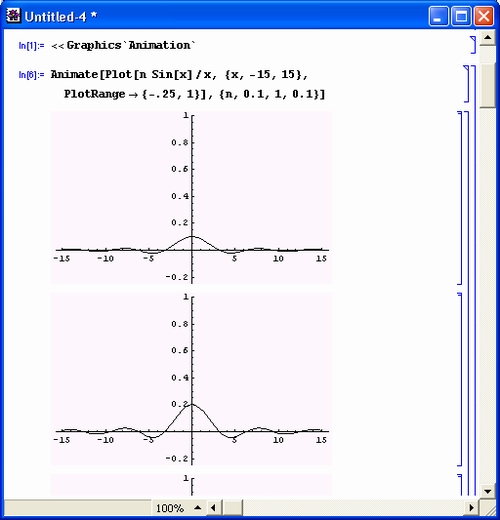
gl14-2.jpg
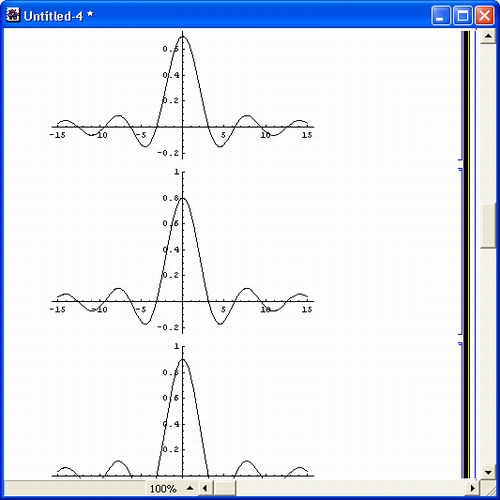
gl14-3.jpg
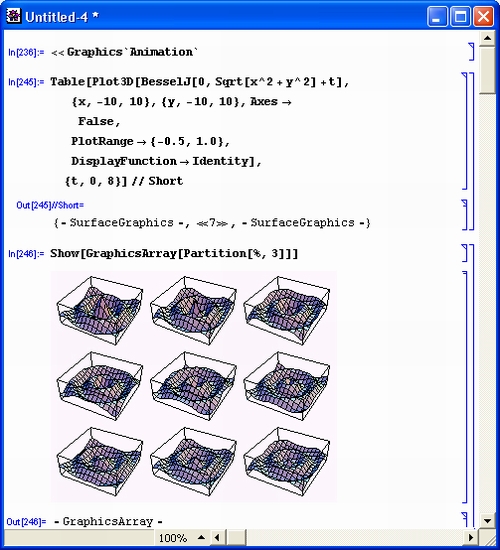
gl14-4.jpg
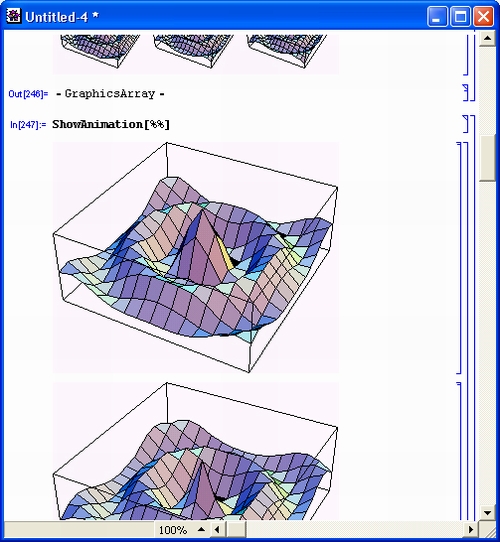
gl14-5.jpg
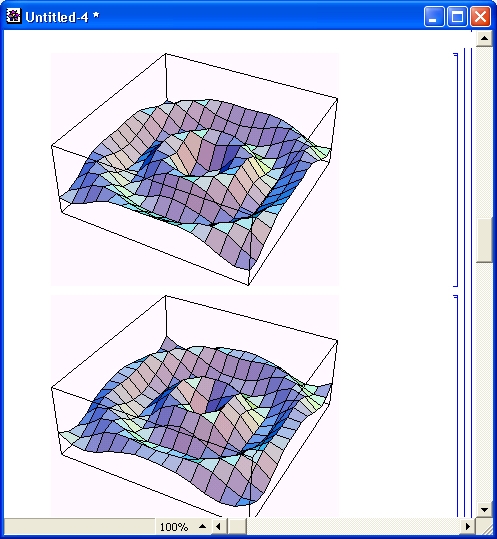
gl14-6.jpg
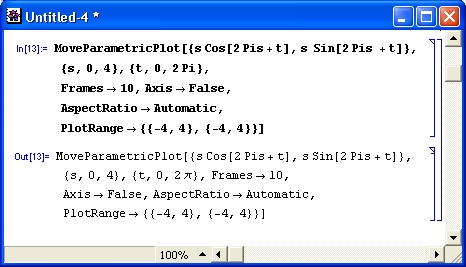
gl14-7.jpg
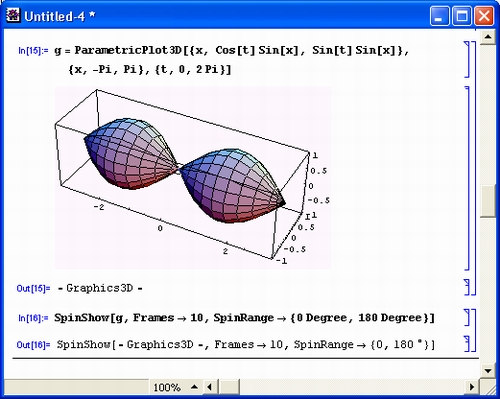
2. Установка аргумента цвета — ArgColor
Установка аргумента цвета — ArgColor
При построении графиков в полярной системе координат полезно использовать цвет, зависящий от фазы комплексного числа. Для этого в подпакете ArgColor служат следующие функции:
- ArgColor [z] — дает цвет, определяемый фазой комплексного аргумента z;
- ArgShade [ z ] — дает уровень серого цвета, определяемый фазой комплексного аргумента z.
Рис. 14.8. Построение кругов, расположенных по окружности, с разной степенью окраски серыми полутонами
Действие функции ArgShade иллюстрирует показанный на рис. 14.8 пример. Он строит 12 расположенных по окружности кругов с разной степенью окраски (от белого до черного) с помощью функции ArgShade.
Заменив в этом программном модуле функцию ArgShade на ArgColor, вы сможете наблюдать окраску кругов разными цветами.
Установка цветовой системы — Colors
Обычно цвета задаются в цветовой системе RGB (Red-Green-Blue). В подпакете Colors содержатся функции установки цвета, заданного в других известных цветовых системах:
- CMYColor [с, m, у] — установка цвета по системе CMY (Cyan-Magenta-Yellow);
- YIQColor[y,i,q] — установка цвета по системе YIQ (используется в телевизионном стандарте NTSC);
- HLSColor [h, I, s ] — установка цвета по системе HLS (Hue-Lightness-Saturation);
- AllColors — переменная-функция, выводящая список установленных цветов.
Примеры применения функций даны ниже:
<<Graphics" Colors"
RGBColor[0.5, -O.I, 0.2]
RGBColor[0.53, 0.4, 0.957]
RGBColor[0.5, -0.1, 0.2]
RGBColor[0.53, 0.4, 0.957]
Orange
RGBColor[l., 0.5, 0.]
Кроме этого в подпакете имеется внушительная таблица англоязычных наименований разных цветов и цветовых оттенков — она выводится функцией AllColors. Их можно использовать для задания в качестве аргумента у функций, управляющих цветами. Например, шоколадный цвет можно задать следующим образом:
Chocolate
RGBColor[0.823496, 0.411802, 0.117603]
Подпакет Arrow служит для построения стрелок на двумерных графиках (или самих по себе). Для этого предназначена функция Arrow [start, finish, opts], которая строит стрелку по координатам ее начала start и конца finish. Рекомендуется просмотреть список опций этой функции.
Рисунок 14.9 показывает построение множества стрелок, острия которых находятся на спирали. Для этого координаты стрелок задаются в параметрическом виде.
Рис. 14.9. Построение множества стрелок с остриями, расположенными по спирали
Другой пример, представленный на рис. 14.10, иллюстрирует построение двуна-равленной стрелки, опирающейся на иглу, стоящую на кресте, — получается своеобразная модель компаса.
Рис. 14.10. Построение двунаправленной стрелки, опирающейся на иглу
Построение стрелок оживляет многие типы графиков. Их можно использовать, к примеру, для указания особых точек на графиках.
Графики комплексных функций — ComplexMap
Подпакет ComplexMap задает функции для построения графиков комплексных функций комплексной переменной путем демонстрации преобразования координатных линий:
- CartesianMap [f, {xmin,xmax}, {ymin,ymax}] — строит изображение декартовых координатных линий после их преобразования функцией f;
- PolarMap[f, {rmin,rmax}, {thetamin, thetamax} ] — строит изображение координатных линий полярной системы после их преобразования функцией f.
Действие этих довольно простых функций иллюстрирует рис. 14.11.
Рис. 14.11. Построение неискаженной декартовой координатной сетки (сверху) и полярной координатной сетки, искаженной воздействием функции Sqrt (снизу)
gl14-10.jpg
gl14-11.jpg
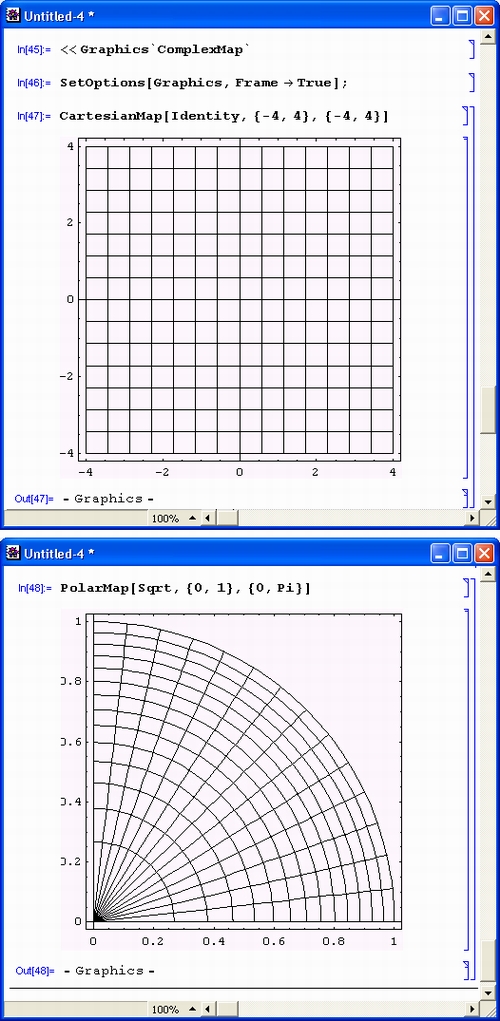
gl14-8.jpg
gl14-9.jpg
3. Построение объемных контурных графиков — ContourPlot3D
Построение объемных контурных графиков — ContourPlot3D
В подпакете ContourPlotSD заданы две функции, которые строят контурные объемные графики. Напоминаем, что функции ядра ContourPlot и ListContourPlot строят только двумерные графики этого типа. Для построения объемных контурных графиков надо использовать следующие функции:
- ContourPlotSD[f,{x,xmin,xmax},{у,ymin,углах),{z,zmin,zmax)] — строит трехмерный контурный график функции f трех переменных: х, у и z;
- ListContourPlot3D[f, { fill, f 112,...}, { f 121, f 122,...},...},...}] -строит контурный график по данным трехмерного массива значений f .
На рис. 14.12 показано построение сферы с отверстием с помощью первой из этих функций.
Обратите внимание на то, что никаких усилий по созданию в сфере отверстия не требуется, Оно получено просто усечением ограничительного «ящика», в котором размещается сфера. Для этого пределы по оси у заданы как {-1.2,2}, тогда как по остальным осям используются пределы {-2,2}.
Рис. 14.12. Построение сферы с отверстием
Интересные возможности открывает опция Contours, которая позволяет как бы раздвинуть в пространстве части трехмерной поверхности. Рисунок 14.13 демонстрирует ее действие.
Риc. 14.13. Построение частей сферы в пространстве
Вторая функция— ListContourPlot3D — позволяет строить ряд фигур или поверхностей в пространстве. Пример такого построения дан на рис. 14.14. Масштабы осей подобраны так, чтобы фигура была несколько обрезана справа, что создает изображение отверстия во внутренней яйцеобразной фигуре.
Рис. 14.14. Построение яйцо, вложенного в параболы
Как видно из этих примеров, применение описанных функций позволяет упростить построение трехмерных поверхностей и добиться интересных эффектов.
Построение графиков с окраской внутренних областей — FilledPlot
Многие графики сильно выигрывают при их построении с закраской. Например, чтобы проиллюстрировать значение определенного интеграла от какой-то функции f(x), достаточно просто закрасить ее график в диапазоне изменения х от нижнего предела интегрирования а до верхнего b. Для построения подобных графиков в подпакете FilledPlot имеется ряд полезных функций.
Начнем их описание с основных:
- FilledPlot [f, {х, xmin, xmax} ] — строит график функции/(x) с окраской площадей, образованных линией функции и горизонтальной осью х. По умолчанию действуют опции Fills->Automatic и Curves->Back (то есть кривые строятся на заднем плане, при значении Front построение фигур производится на переднем плане);
- FilledPlot [{ fl, f2,...}, {х, xmin, xmax} ] — строит графики функций с выделением областей между ними разной окраской (цвет задается автоматически).
Поясним применение этих функций рядом примеров. Перед этим надо не забыть загрузить подпакет командой
<< Graphics`FilledPlot`
На рис. 14.15 показано построение смещенной по оси у экспоненты с закраской области между линией экспоненты и горизонтальной осью х.
Рис. 14.15. Построение экспоненты с закраской областей между ней и осью абсцисс
Действие функции FilledPlot при построении графиков трех функций показано на рис. 14.16. Здесь использована опция Curves->Front, выводящая построение кривых на первый план, благодаря чему отчетливо видны разделительные линии перекрывающихся областей.
Рис. 14.16. Построение трех кривых с закраской областей между ними и осью абсцисс
Еще один пример построения графиков трех фигур показан на рис. 14.17. Здесь для закраски областей между фигурами и осью абсцисс использована опция Fills и директива GrayLevel (окраска серым цветом заданной плотности).
Рисунок 14.18 иллюстрирует закраску областей совместного применения двух функций, одна из которых — корень квадратный из х - 1 — определена только для И > 1. Именно эта область и закрашена.
Рис. 14.17. Построение трех кривых с закраской серым цветом
Рис. 14.18. Пример закраски области совместного действия двух функций
Имеется также ряд специальных функций для построения кривых с окраской образуемых ими областей:
- FilledListPlot [ {yl, у2,...} ] —строит графики с окраской, меняющейся между кривыми {1, y1}, {2, у2 } и осью абсцисс х;
- FilledListPlot [ {{xl, yl}, {х2, у2},...}] — строит графики ряда кривых с окраской, заданной {xi,yi} и осью абсцисс х;
- FilledListPlot [datal, data2,...}] — строит графики ряда кривых с закраской областей, специфицированных данными datai.
Применение функции FilledListPlot показано на рис. 14.19.
Иногда важное значение может иметь опция AxesFront->Значение. При значении этой опции False область закраски закрывает соответствующую часть осей, а при значении True оси выводятся поверх закраски. Сам по себе вывод осей задастся опцией Axes->True. При Axes->False они вообще не выводятся. Рисунок 14.20 поясняет вывод осей и их построение поверх закращениой области.
В данном случае область окраски ограничена треугольником, который строится как полигон. Если установить опцию AxesFront->False, то часть осей (внутри треугольника) будет не видна.
Рис. 14.19. Пример применения функции FilledListPlot
Рис. 14.20. Пример вывода осей поверх закрашенной области
Графики специальных типов — Graphics
Подпакет Graphics задает ряд функций для построения специальных графиков, например с логарифмическими и полулогарифмическими масштабами, с нанесенными на кривые точками, графиков в виде гистограмм и т. д. Такие графики широко применяются для визуализации не только математических и физических, но также финансовых и экономических расчетов. К примеру, функция Log-Plot [f, {х,xmin,xmax}] строит линейно-логарифмический график/(x) при изменении х от xmin до xmax. Список таких функций дан в приложении.
Ввиду очевидности этих функций ограничимся одним примером — построением экспоненциальной функции в полулогарифмическом масштабе (по оси у масштаб логарифмический, а по оси х~ линейный). Как видно из рис. 14.21, график вырождается в прямую линию.
Для построения графиков в полярной системе координат заданы следующие функции:
- PolarPlotff, {t, tmin, tmax} ] — строит график функции в полярной системе координат как положение конца радиус-вектора f при изменении угла t от tmin до tmax;
- PolarPlot [ { f 1, f 2,...}]- строит графики ряда функций f 1, f 2,... в полярной системе координат;
- PolarListPlot [ {rl, r2,...} ] — строит график списка радиусов ri, равномерно изменяя угловую координату.
Рис. 14.21. Построение графика экспоненты в полулогарифмическом масштабе
Построение графика трех функций в полярной системе координат с помощью функции PolarPlot представлено на рис. 14.22.
Рис. 14.22. Построение графиков трех функций в полярной системе координат
В ряде случаев удобно представление данных в виде столбцовых и круговых диаграмм. Для построения столбцовых диаграмм служат функции, описанные ниже:
- BarChart [datalistl,datalist2,...] — строит столбцовую диаграмму по данным списков, располагая столбцы рядом и обеспечивая их автоматическую закраску цветом (рис. 14.23).
Здесь любопытно отметить, что списки данных могут иметь разную длину. Число столбцов задается большим списком. Отсутствующие данные у спис-
ков меньшей длины считаются нулевыми, и для них столбцы не строятся. Данные, представленные отрицательными числами, строятся как столбцы, обращенные вниз.
Рис. 14.23. Построение столбцовых диаграмм для двух списков данных с расположением столбцов друг рядом с другом
- StackedBarChart [datalist1, datalist2,...] — строит столбцовую диаграмму, располагая столбцы одних данных над столбцами других данных (рис. 14.24) с автоматическим выбором цветов для каждого набора данных.
Рис. 14.24. Построение столбцовых диаграмм со столбцами, расположенными друг над другом
В этой столбцовой диаграмме вначале строятся столбцы, представляющие данные для первого списка, над ними надстраиваются столбцы новых данных, так что общая высота столбцов пропорциональна сумме численных значений i-x элементов списков.
- PercentileBarChart [datalistl, datalist2,...] — строит столбцовую диаграмму, отображающую нормированные данные в процентах (рис. 14.25).
Здесь построение идет так же, как в предыдущем случае. Однако высоты столбцов указываются в процентах и нормируются — за 100 % принимается максимальная высота столбцов выше горизонтальной оси, а за -100 % — максимальная высота столбца ниже горизонтальной оси.
- GeneralizedBarChart [datalistl, datalist2,...] — строит столбцовую диаграмму с заданной высотой и шириной столбцов (рис. 14.26).
Рис. 14.25. Построение столбцовых диаграмм с процентным отсчетом
Рис. 14.26. Построение столбцовых диаграмм с произвольной шириной столбцов
В этом случае имеется возможность указать в списках данных позицию по оси х, высоту столбца и его ширину. Ширина задается в относительных единицах: при ширине, равной 1, столбцы сливаются (но выделяются цветом), при величине меньше 1 они разделяются пустыми промежутками, а при величине, большей 1, столбцы перекрываются.
Все указанные функции имеют опции, существенно влияющие на вид диаграмм. Рекомендуется просмотреть их с помощью функции Options. Ограничимся тремя наглядными примерами на применение опций. Рисунок 14.27 показывает построение столбцовой диаграммы с горизонтальным расположением столбцов и произвольным выбором цвета для каждого набора.
На рис. 14.28 построена диаграмма для одного комплекта данных. Но выбор цвета каждого из столбцов задается с помощью условного оператора. На рис. 14.29 показан наиболее сложный пример построения столбцовых диаграмм. Наряду с цветовыми эффектами задается обвод пунктирной линией столбцов одного из комплектов данных и, главное, — вывод надписей (названий месяцев) под наборами столбцов. Обратите внимание на то, что надписи могут быть на русском языке.
Рис. 14.27. Построение столбцовой диаграммы с горизонтально расположенными столбцами и произвольным выбором цвета для каждого набора данных
Рис. 14.28. Столбцовая диаграмма с выбором цвета столбцов по условию
Рис. 14.29. Комплексное построение столбцовых диаграмм
Следующая функция позволяет стоить круговые диаграммы. Они наиболее удобны, когда оцениваются относительные величины, при этом сумма данных соответствует площади круга:
- PieChart [data] — строит круговые диаграммы по данным data (рис. 14.30). Тип диаграммы задается опциями, список которых и значения по умолчанию можно получить командой Options [PieChart]. Одна из опций— PieExploded — позволяет отделить заданный сектор от диаграммы, что порой повышает наглядность представления данных.
Рис. 14.30. Построение набора круговых диаграмм Здесь использована также одна из следующих функций:
- DisplayTogether [plotl,plot2,..., opts] — строит комбинированный графический объект, объединяя графики ploti в общих координатных осях;
- DisplayTogetherArray [plotl,plot2,..., opts] — строит комбинированный графический объект, выводя графики ploti в виде массива.
На рис. 14.31 показано построение круговой диаграммы с применением окраски чередующихся секторов оттенками серого цвета.
Рис. 14.31. Построение круговой диаграммы с раскраской чередующихся секторов оттенками серого цвета
Еще одну возможность разнообразить круговые диаграммы иллюстрирует рис. 14.32. Здесь показано, что в секторы можно заносить небольшие надписи, например имена людей, даты и т. д.
Рис. 14.32. Построение круговой диаграммы с надписями внутри секторов
Функция DisplayTogether позволяет объединять графики разного типа. На рис. 14.33 показано построение графика экспериментальных точек и линий линейной и параболической регрессии.
Рис. 14.33. Совместное построение исходных точек данных и линий линейной и параболической регрессии
Применение функции DisplayTogetherArray для построения трех круговых диаграмм с номерами секторов показано на рис. 14.34. Это те же диаграммы, что и на рис. 14.30, но аргумент функции DisplayTogetherArray на сей раз представляет собой не одномерный, а двумерный массив (в первой строке два графика, во второй — один).
Рис. 14.34. Построение трех круговых диаграмм с номерами секторов
Иногда нужно использовать в качестве точек графика цифры. Это реализует следующая функция, имеющая три формы:
- TextListPlot [ {y1, у2,...} ] — построение точек с ординатами yi и абсциссами 1, 2, ... с представлением их числами 1, 2, ... (рис. 14.35);
- TextListPlot [ {{xl, yl}, {х2, у2},...} ] — построение точек с координатами {xi, yi} и представлением их числами 1, 2, ...;
- TextListPlot [ {{xl, yl, exprl), {x2,y2,expr2 },...}] — построение точек с координатами {xi, yi} и представлением их числами, заданными выражениями expri.
Рис. 14.35. Построение графика сточками, представленными цифрами
Еще одна функция, также имеющая три формы, дает тот же результат, но дополнительно строит и сами точки:
LabelListPlot [ {yl, у2,...} ] LabelListPlot [{ {xl,yl}, {х2,у2 },...}] LabelListPlot [{ {x1, y1, expr1}, {х2, у2, expr2 },...}]
Наконец, есть еще одна функция:
- ErrorListPlot [{{yl, dl}, {y2, d2 },...}] — построение графика точек yi с зонами ошибок di (рис. 14.36).
Рис. 14.36. График с точками и зонами ошибок
Таким образом, подпакет Graphics обеспечивает построение наиболее распространенных типов графиков, используемых в научно-технической и финансово-экономической литературе.
gl14-12.jpg
gl14-13.jpg
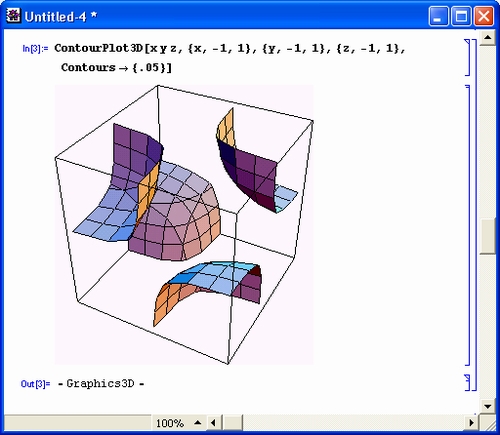
gl14-14.jpg
gl14-15.jpg
gl14-16.jpg
gl14-17.jpg
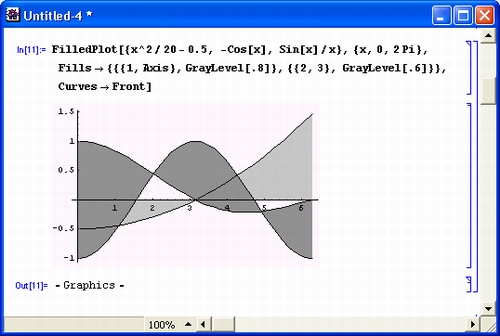
gl14-18.jpg
gl14-19.jpg
gl14-20.jpg
gl14-21.jpg
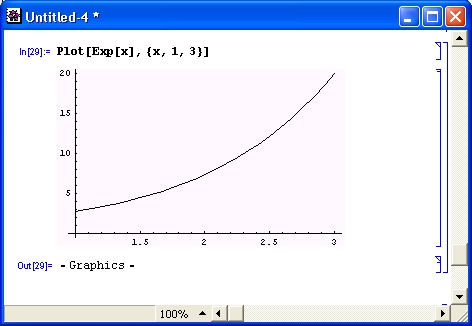
gl14-22.jpg
gl14-23.jpg
gl14-24.jpg
gl14-25.jpg
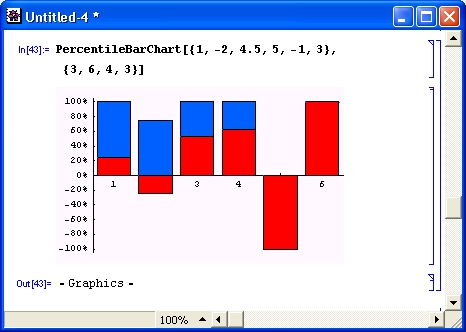
gl14-26.jpg
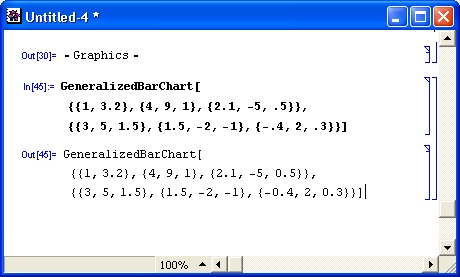
gl14-27.jpg
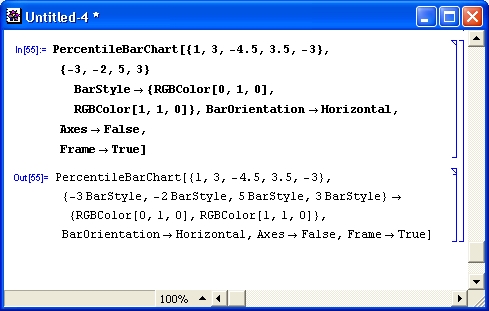
gl14-28.jpg
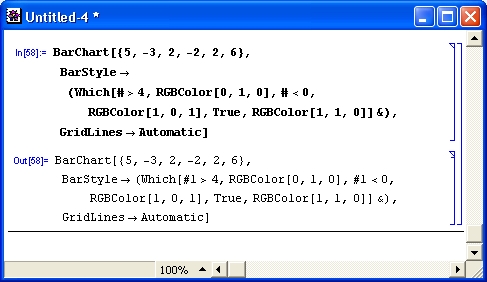
gl14-29.jpg
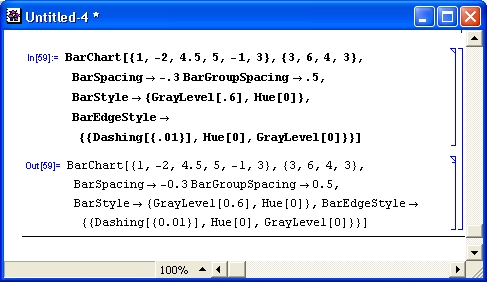
gl14-30.jpg
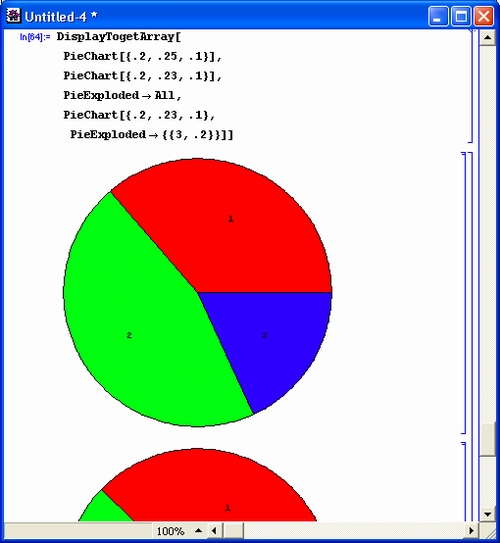
gl14-31.jpg
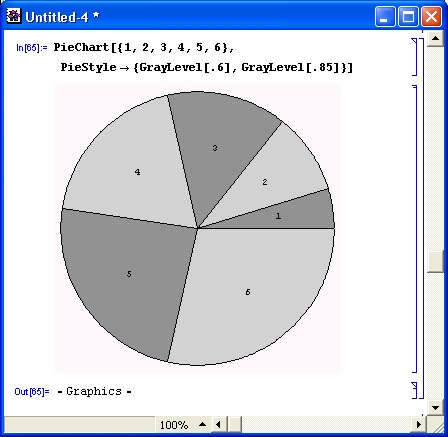
gl14-32.jpg
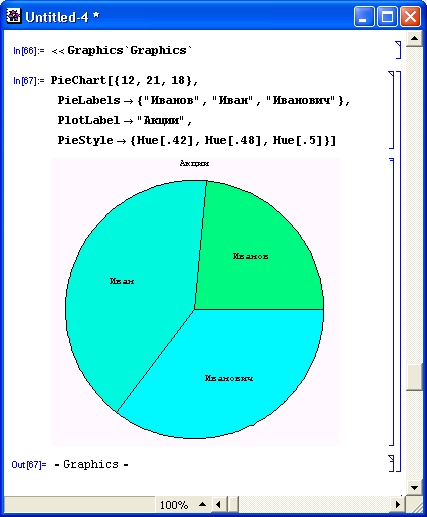
gl14-33.jpg
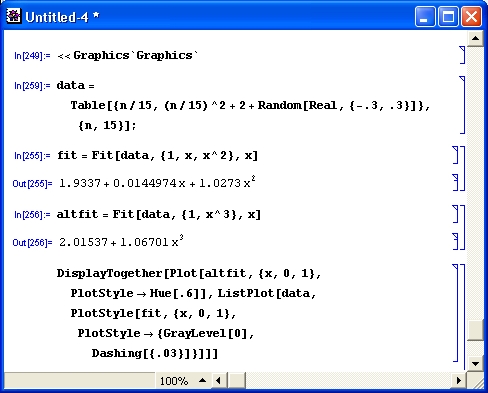
gl14-34.jpg
gl14-35.jpg
gl14-36.jpg
4. Специальные типы трехмерных графиков — Graphics3D
Специальные типы трехмерных графиков— Graphics3D
В подпакете Graphics3D, загружаемом командой
<<Graphics`Graphics 3D`
имеется ряд программ для простого построения трехмерных графиков. Они описаны ниже с примерами:
- BarChart3D[ {{ zll, z!2,...},{z21, z22 },...} ] — строит трехмерную столбцовую диаграмму по наборам данных высот столбцов z 11 , z п , ... (рис. 14.37);
- BarChart3D[ {{{zll, stylell}, {z21, style21},...} ] — строит трехмерную столбцовую диаграмму по наборам данных высот столбцов z u , z vl , ... с указанием спецификации стиля для каждого столбца.
Нетрудно заметить, что функция BarChartSD автоматически задает стиль и цвет построения столбцов диаграммы. Эта функция имеет массу опций, с помощью которых можно менять вид диаграммы (рис. 14.38). Как обычно, перечень опций можно вывести с помощью команды Options [BarChart3D].
Рис. 14.37. Построение трехмерной столбцовой диаграммы
Рис. 14.38. Вариант диаграммы с черно-белой раскраской
- Scatter Plot 3D [{ {x1, yl, zl}, {х2, у2, z2 },...}] — строит точки в пространстве по их заданным координатам. При использовании опции Plot-Joined->True точки соединяются отрезками прямых, и строится линия в пространстве (рис. 14.39).
Рис. 14.39. Построение пространственной кривой по точкам
Обратите внимание на то, что список точек формируется с помощью функции Table. Это возможно, когда построение делается для аналитически заданной функции, описывающей трехмерную поверхность.
- ListSurfacePlot3D[{ { {x11, y11, zll}, {x12, y12, z13},...} } }] - строит трехмерную поверхность по координатам ее точек-(рис. 14.40).
Рис. 14.40. Построение трехмерной поверхности по координатам ее точек
Здесь список координат точек также задаются функцией Table. Выбором диапазона изменения значений переменных х, у и z можно добиться различных эффектов, например изображения только части сферы (на рис. 14.40, к примеру, показано построение полусферы).
Следующие функции дают построения с проекциями:
- ShadowPlot3D [f, {х, xmin, xmax}, {у, ymin, углах} ] — строит график поверхности f(z, y) с ее проекцией на опорную плоскость (рис. 14.41);
- ListShadowPlot3D[{{ {xll, yll, zll}, {x!2, y!2, z!3},...}} }] -строит график поверхности z(x, у) с ее проекцией на опорную плоскость по координатам точек поверхности.
Рис. 14.41. Построение графика трехмерной поверхности и ее проекции на опорную плоскость
Еще один простой и эффектный пример применения функции ShadowPlot3D показан на рис. 14.42. Здесь изображение поверхности — пика — проецируется на верхнюю плоскость, что дает наглядное представление о построенной фигуре.
Рис. 14.42. Построение фигуры — пика — и ее проекции на верхнюю плоскость
С помощью функции Shadow [go], где до — графический объект, представляющий трехмерную фигуру, можно построить и более сложные рисунки — например, график объемной фигуры и сразу всех трех ее проекций на взаимно перпендикулярные плоскости. Такое построение иллюстрируется документом, показанным на рис. 14.43.
С функцией Shadow можно использовать различные опции. Отметим наиболее существенные — XShadow, YShadow и ZShadow. Например, задав Zshadow-> False, можно удалить одну из проекций, плоскость которой перпендикулярна оси z.
Для получения проекций на заданную плоскость, расположенную в пространстве, служат следующие функции:
- Project [g,pt] — дает проекцию объекта g на плоскость, нормаль которой задана списком из трех элементов pt. Например, список {1,1,0} даст проекцию на диагональную плоскость;
- Project[g, {e1,e2},pt] — дает проекцию объекта g в плоскости, определенной векторами {el,e2}, выходящими из точки с координатами pt (рис. 14.44);
- Project[g, {e1, e2 } ,pt, origin] — то же, но направление проецирования определяется точками pt и origin.
В конце подпакета определена функция StackGraphics [ {gl, g2,...}], которая строит двумерные графические объекты, располагая их каскадно, то есть разнося в пространстве по третьей координате (рис. 14.45).
Рис. 14.43. Построение объемной фигуры и всех трех ее проекций
Рис. 14.44. Пример построения проекции но заданной плоскости
Обратите внимание на то, что здесь каждая синусоида расположена на своей плоскости.
Рис. 14.45. Пример построения трех синусоид, расположенных каскадно
Построение графиков неявных функций — ImplicitPlot
Подпакет ImplicitPlot задает три варианта функции для построения графиков неявно заданных функций:
- ImplicitPlot [eqn, {x, xmin, xmax} ] — построение функции, неявно заданной уравнением eqn, при х, меняющемся от xmin до xmax;
- ImplicitPlot [eqn, {x, xmin,ml,m2,..., xmax} ] — построение функции, неявно заданной уравнением eqn, при х, меняющемся от xmin до xmax с исключением точек m1, m2, ...;
- ImplicitPlot [ {eqnl, eqn2,...}, ranges, options] — построение функций, неявно заданных уравнениями eqni, при х, меняющемся в пределах ranges и при задании опций options.
Примером может быть функция х 2 + k у 2 = r 2 , задающая построение эллипса. На рис. 14.46 показано такое построение.
Вторая форма задания функции иллюстрируется рис. 14.47. Здесь строится сразу целое семейство эллипсов.
И, наконец, на рис. 14.48 показано применение третьей формы функции ImplicitPlot с использованием опции PlotStyle и директивы Dashing.
Рис. 14.46. Построение эллипса по неявному выражению
Рис. 14.47. Построение семейства эллипсов по их уравнениям
Рис. 14.48. Пример применения функции ImplicitPlot с опцией PlotStyle
gl14-37.jpg
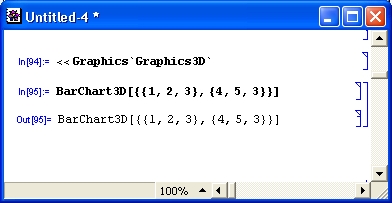
gl14-38.jpg
gl14-39.jpg
gl14-40.jpg
gl14-41.jpg
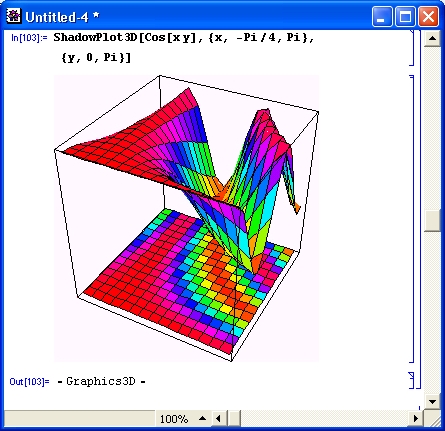
gl14-42.jpg
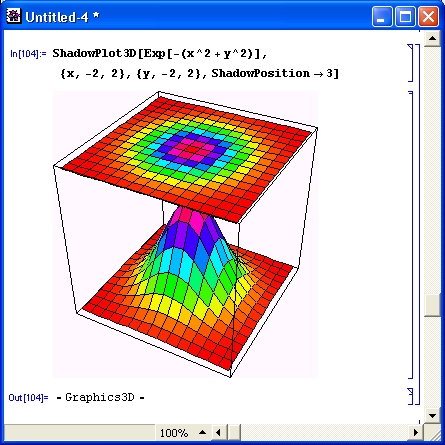
gl14-43.jpg
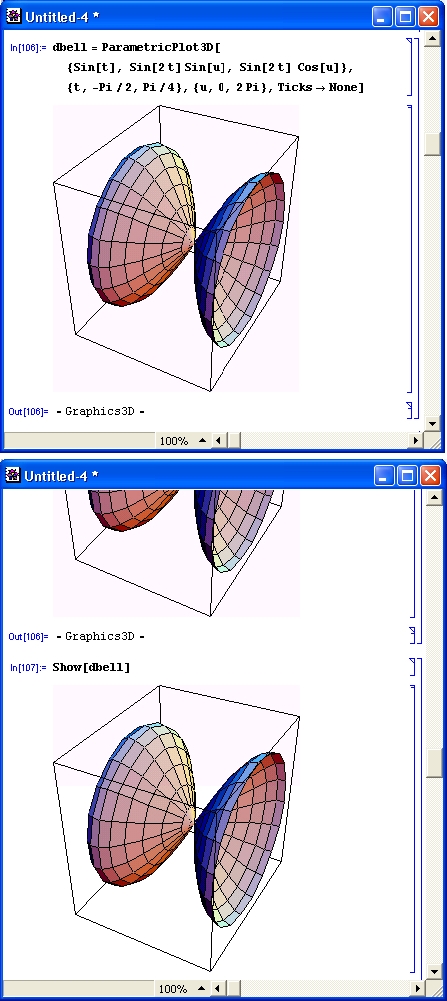
gl14-44.jpg
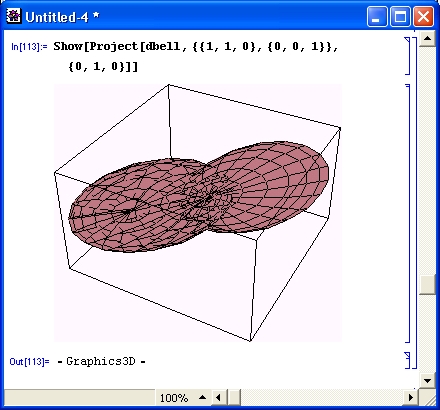
gl14-45.jpg
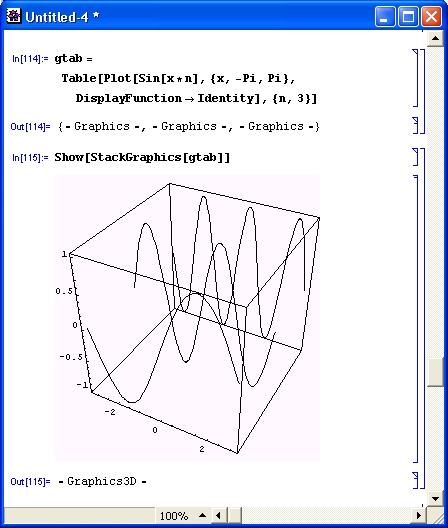
gl14-46.jpg
gl14-47.jpg
gl14-48.jpg
5. Вывод обозначений кривых — Legend
Вывод обозначений кривых— Legend
Наглядность графиков, особенно имеющих несколько кривых, повышается при выводе обозначений кривых — так называемой легенды. В подпакете Legend для этого имеются следующие средства:
- PlotLegend->{textl,text2,...} — опция для функции Plot, устанавливающая легенду в виде последовательных текстовых надписей (рис. 14.49);
- ShowLegend [graphic, legendl, Iegend2,...] — добавляет легенду в имеющийся график graphic;
- {{{boxl, textl},...}, opts} — спецификация легенды с цветными примитивами или графиками для рамок boxi с текстами texti;
- {colorfunction, n, ninstring,maxstring, opts} — спецификация легенды с n рамками, указанием цветовой спецификации и строк, размещаемых в рамках.
Рис. 14.49. Пример построения графиков двух функций с выводом легенды
Обратите внимание на то, что среди многочисленных опций функции Plot имеется ряд, относящихся к параметрам легенды: LegendPosition-> {-1,1} — установка позиции легенды, LegendSize->Automatic — установка размера легенды, LegendShadow->Automatic — установка тени для рамки легенды, Legend-Orientation->Vertical — ориентация рамки легенды, LegendLabel->None — заголовок легенды и LegendTextDirection->Automatic — направление текста. С помощью этих опций можно существенно влиять на вид легенды.
На рис. 14.50 показано построение графика плотности с применением функции ShowLegend для вывода легенды в виде таблицы плотностей. Обратите внимание на применение опции LegendPosition для вывода легенды справа от графика.
Рис. 14.50. Построение графика плотности с легендой
Для иллюстрации эффективности применения опций функции Plot, влияющих на вид легенды, рассмотрим еще один пример, представленный на рис. 14.51.
Рис. 14.51. Пример построения графика двух функций с легендой и установкой ряда ее опций
В заключение отметим еще две функции подпакета Legend:
- Legend [legendargs, opts] — создает графический примитив для задания индивидуальной легенды;
- ShadowBox [pos, size, opts] — создает графический примитив в виде рамки для легенды.
К примеру, показанный ниже вызов функции ShadowBox создает графический примитив в виде пустой рамки с тенью:
ShadowBox[{0, 0}, {1, 1},ShadowBackground -> GrayLevel[.8]]
{GrayLevel[0.8], Rectangle[{0.1, -0.1), {1.1, 0.9}], GrayLevel[l], Rectangle[{0, 0}, {1, 1}], Thickness[0.001], GrayLevel[0], Line[{{0, 0), {1, 0), {1, 1}, {0, 1), {0, 0}}]} Для просмотра полученной рамки можно использовать команду Show[Graphics[%]]
Применение функции Graphics здесь связано с тем, что ShadowBox порождает графический примитив, а не законченный графический объект.
Построение графиков с множеством объектов — MultipleListPlot
В подпакете MultipleListPlot содержится расширенный вариант встроенной функции ListPlot:
- MultipleListPlot [listl, Iist2,...] — строит множество графических объектов по данным списков. Списки могут быть представлены ординатами у, координатами точек {х,у), в виде {point, ErrorBar [ {negerr,poserr} ] } и т.д.
Рис. 14.52. Создание трех списков значений функций и их построение
Рисунок 14.52 иллюстрирует создание трех списков — 11, 12 и 13 — для трех функций и вывод их графиков в виде различных маленьких фигур.
Особое значение имеет опция Plot Joined. Если она используется в виде Plot-Joined->True, то это означает соединение точек на графиках отрезками линий разного стиля, выбираемого автоматически (рис. 14.53).
Рис. 14.53. Графики трех функций, построенные линиями, соединяющими их точки
Эта опция может быть представлена и со значением в виде списка. Например, ее применение в виде PlotJoined->{True, False, False} означает, что точки первой кривой соединяются линиями, тогда как точки второй и третьей кривых линиями не соединяются. Рисунок 14.54 поясняет этот способ построения графиков.
Рис. 14.54. Построение трех графиков, только у одного из которых точки соединены линиями
Функция MultipleListPlot может использовать в списках указания на построение точки с зоной погрешности (ErrorBar). Этот случай иллюстрирует рис. 14.55.
Более интересный случай построения точек с двумерными зонами погрешности в виде окружностей или эллипсов демонстрирует рис. 14.56.
Рис. 14.55. Построение точек с одномерными зонами погрешности
Рис. 14.56. Построение точек с двумерными зонами погрешности
- Следующие функции служат для вывода символов в качестве точек:
- PlotSymbol [type] — задает тип символа (возможные значения: Box, Diamond, Star или Triangle). Возможно применение опции_ Filled-> False;
- PlotSymbol [type, size] — задает тип символа и его размер size;
- MakeSymbol [primitives] — задает вывод символа, создаваемого графическим примитивом.
Рисунок 14.57 показывает построение точек с применением графических примитивов. Этот путь позволяет обозначать точки графиков практически любыми фигурами.
Рис. 14.57. Построение точек с применением графических примитивов
Для создания примитивов в виде правильных многоугольников (полигонов) используется директива RegularPolygon:
- RegularPolygon [n] — правильный «-угольный полигон;
- RegularPolygon [n, rad] — правильный и-угольный полигон с заданным радиусом описанной окружности rad;
- RegularPolygon [n, rad, ctr] — то же с заданным центром ctr;
- RegularPolygon [n, rad, ctr, tilt] — то же с углом поворота фигуры на tilt градусов;
- RegularPolygon [n, rad, ctr, titl, k] — соединение линиями через k вершин.
Рисунок 14.58 показывает построение полигона — семиугольника с радиусом 3, центром в точке {0, 0}, углом поворота 20° и соединением через 3 вершины (попробуйте задать этот параметр другим целым числом и убедитесь, насколько меняется форма фигуры).
Директивы Dashing[ {Dot, Dash, LongDash,...} ] и AbsoluteDashing[ {Dot,...} ] служат для спецификации типа линий графиков. На рис. 14.59 представлены примеры такой спецификации и построения отрезков прямой линиями разных типов.
Применение функций подпакета MultipleListPlot наиболее ценно при визуализации математических расчетов, где преобладают графики тех типов, которые создаются этими функциями.
Рис. 14.58. Построение полигона
Рис. 14.59. Примеры построения отрезков прямых разными стилями
gl14-49.jpg
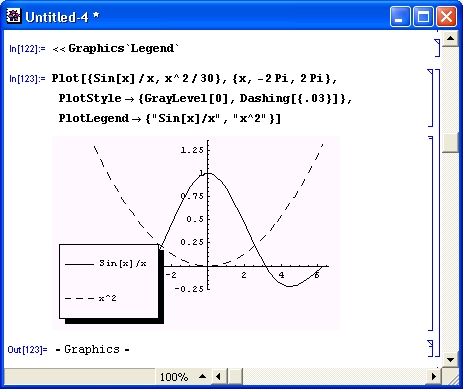
gl14-50.jpg
gl14-51.jpg
gl14-52.jpg
gl14-53.jpg
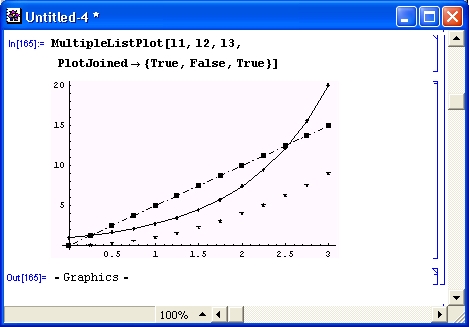
gl14-54.jpg
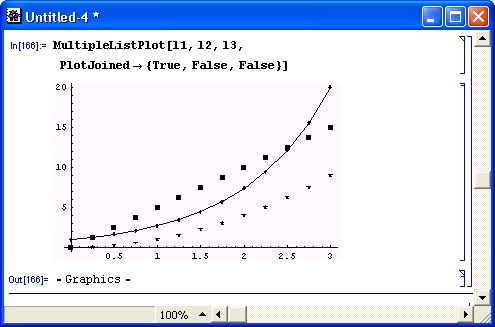
gl14-55.jpg
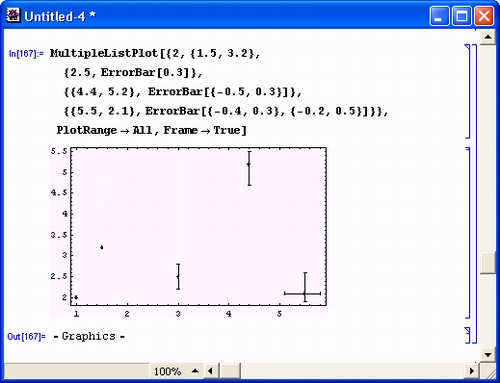
gl14-56.jpg
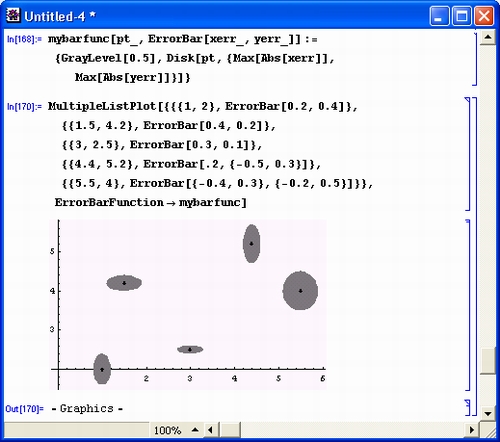
gl14-57.jpg
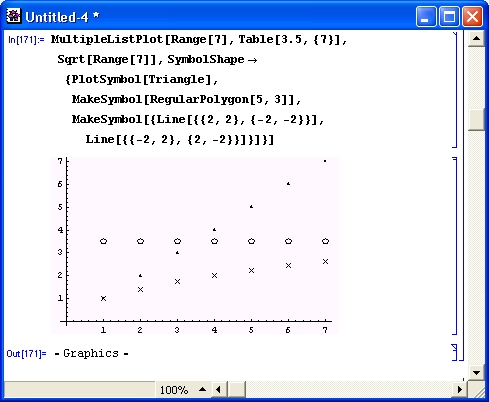
gl14-58.jpg
gl14-59.jpg
6. Построение 3D-параметрических графиков — ParametricPlot3D
Построение 3D-параметрических графиков — ParametricPlot3D
Трехмерные графики с параметрически заданными функциями, описывающими положение их точек, относятся к числу наиболее сложных, но в то же время весьма эффектных. В подпакете ParametricPlotSD определены функции, упрощающие подготовку таких графиков:
- ParametricPlot3D[{fx,fy,fz},{u,u0,ul,du},{v,c0,vl,dv}] — строит трехмерную поверхность, заданную параметрически функциями f x, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv (рис. 14.60);
- PointParametricPlot3D[ { fx, f у, f z},{u,u0,ul,du}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от одной переменной и с заданным диапазоном изменения и приращением du;
- PointParametricPlot3D[{fx,fy,fz},{u,u0,ul,du),{v,c0,vl,dv}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv.
Рис. 14.60. Пример построения сферы с вырезом с помощью функции ParametricPlot3D
Обратите внимание на то, что выбором диапазона изменения углов можно получить вырез сферы. Окраска поверхности осуществляется автоматически.
На рис. 14.61 показан пример применения функции PointParametricPlotSD. Здесь сфера построена отдельными точками.
Для построения трехмерных поверхностей в сферической и цилиндрической системах координат служат следующие функции:
- SphericalPlot3D[r, {t, trnin, tmax}, {p,pmin,pmax} ] — построение графика в сферической системе координат;
- CylindricalPlot3D[z,{t,tmin,tmax},{p,pmin,pmax}] — построение графика в цилиндрической системе координат.
На рис. 14.62 показано построение усеченной сверху сферы с помощью функции SphericalPlot3D. Нетрудно заметить, что применение данной функции — самый простой способ построения сферы. Это естественно, поскольку система координат сферическая.
Риc. 14.61. Пример построения сферы точками
Рис. 14.62. Пример построения сферы с помощью функции SphericolPlot3D
Пример построения поверхности, напоминающей по виду «тарелку» спутниковой антенны, в цилиндрической системе координат дан на рис. 14.63.
С помощью опции Viewpoint можно изменять положение точки, с которой рассматривается фигура. Это существенно меняет ее вид (рис. 14.64).
Еще раз напоминаем, что интерфейс Mathematica предусматривает изменение точки просмотра уже построенной фигуры. При этом Mathematica 4 позволяет вращать фигуру мышью. Рекомендуется просмотреть список опций данных функций, позволяющих в широких пределах менять вид и стиль построения графиков.
Рис. 14.63. Пример построения поверхности в цилиндрической системе координат
Рис. 14.64. Пример построения фигуры, видимой из заданной точки просмотра
Представление полей на плоскости — PlotField
В подпакете PlotField имеются функции, позволяющие строить стрелками графики полей:
- PlotVectorField[ {fx, f у}, {x, xmin, xmax), {y, ymin, ymax} ] —строит плоскость из векторов (стрелок), ограниченную пределами изменения х и у;
- PlotGradientField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) градиента функции f, ограниченную пределами изменения х и у;
- PlotHamiltonianField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) гамильтониана функции f, ограниченную пределами изменения х и у;
- PlotPolyaField[f, {х,xmin,xmax}, {у, ymin, ymax} ] — представляет график комплексной функции f(x, у).
Рисунок 14.65 показывает применение функции PlotVectorField для построения векторного поля согласно параметрически заданной на плоскости функции.
Риc. 14.65. График векторного поля на плоскости
Еще один пример (рис. 14.66), иллюстрирует построение градиента поля с помощью функции PlotGradientField. Применение функции PlotHamiltonianField демонстрирует рис. 14.67.
Указанные функции имеют множество опций. Отметим основные из них (в качестве значений приведены значения по умолчанию):
- ScaleFactor->Automatic — устанавливает размер векторов (стрелок);
- ScaleFunction->None — устанавливает функцию, вычисляющую размер стрелок;
- MaxArrowLenght->None — устанавливает ограничение длины стрелок;
- ColorFunction->None — задает функцию цвета;
- PlotPoints->15 — задает число точек по координатам для построения стрелок.
Рис. 14.66. График градиента поля
Риc. 14.67. Пример применения функции PlotHamiltonianField
Пример построения сложного графика с применением шестнадцати узловых точек по каждому направлению и использованием опции ScaleFunction показан на рис. 14.68.
Работу функции PlotPolyaField поясняет рис. 14.69. Обратите внимание на то, что функция в данном случае комплексная.
Рис. 14.68. Пример графика поля с применением нескольких опций
Рис. 14.69. Пример графика поля для комплексной функции
Применение опций позволяет строить самые разнообразные графики различных полей — тепловых, гравитационных, электрических и др.
В подпакете PlotField есть еще одна функция, представляемая в двух формах:
- ListPlotVectorField [ {{vect 11, vect12,...},{vect21, vect22,...},...} ] — строит график векторного поля прямоугольного массива векторов vect xy ;
- ListPlotVectorField [{{pt1, vect1,...}, (pt2,vect2,...},...}] —строит график векторного поля по списку векторов vect xy , расположенных в точках pti.
Применение этой функции поясняет график, представленный на рис. 14.70.
Рис. 14.70. Пример построения графика векторного поля с помощью функции ListPlotVectorField
Приведенных примеров вполне достаточно, чтобы судить о возможностях подпа-кета PlotField. В справочной базе данных можно найти другие примеры построения графиков векторных полей.
Представление полей в пространстве — PlotField3D
Для представления векторных полей в пространстве служат функции подпакета PlotField3D:
- PlotVectorField3D[{fx,fy,fz},{x,xmin,xmax},{y,ymin, ymax}, {z, zmin, zmax} ] — строит график векторного поля параметрически заданной трехмерной фигуры;
- PlotGradientField3D[{fx,fy,fz},{x,xmin,xmax},{y,ymin,ymax}, {z, zmin, zmax} ] — строит график градиента векторного поля параметрически заданной трехмерной фигуры.
Эти функции подобны описанным в предшествующем разделе, но используются для построения векторных полей не на плоскости, а в пространстве. Рисунок 14.71 показывает пример такого построения.
Как видно из рис. 14.71, векторное поле строится отрезками прямых, а не стрелками. Последнее связано с тем, что по умолчанию задана опция VectorHeads-> False. Изменив ее на VectorHeads->True, можно получить представление векторного поля направленными стрелками. Кроме того, используя опцию Plot-Points->n, можно получить заданное число стрелок п по всем направлениям графика. Все это учтено на графике, представленном на рис. 14.72.
Рис. 14.71. Пример построения графика векторного поля в пространстве отрезками прямых
Рис. 14.72. Пример построения графика градиента поля направленными стрелками
В подпакете PlotFieldSD имеется еще одна функция:
- ListPlotVectorField3D[{ {ptl, vectl}, {pt2, vect2 },...} ] -строит график векторного поля в пространстве по данным векторов vecti, расположенных в точках pti.
Рисунок 14.73 поясняет применение этой функции.
Рис. 14.73. Пример построения графика векторного поля функцией ListPlotVectorReld3D
Нетрудно заметить, что при большом числе векторов в пространстве графики этого типа теряют наглядность. Рекомендуется тщательно отлаживать их, используя весь набор опций (как его получить, описывалось неоднократно).
gl14-60.jpg
gl14-61.jpg
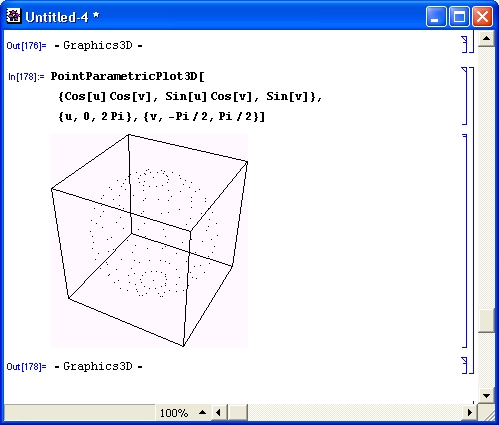
gl14-62.jpg
gl14-63.jpg
gl14-64.jpg
gl14-65.jpg
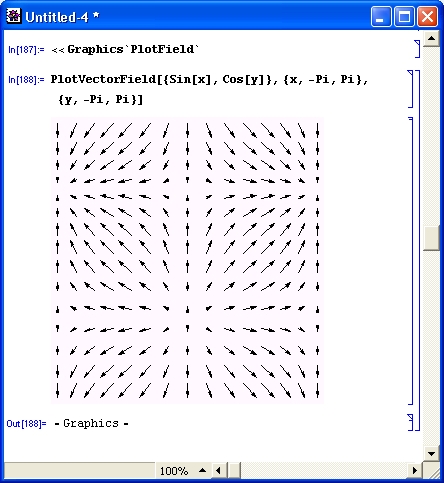
gl14-66.jpg
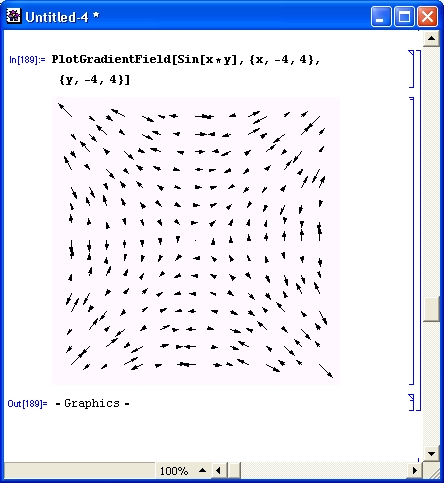
gl14-67.jpg
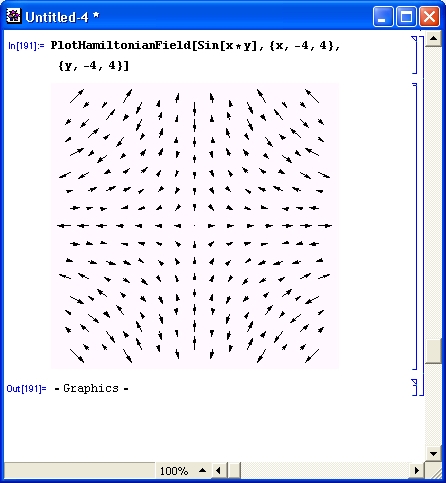
gl14-68.jpg
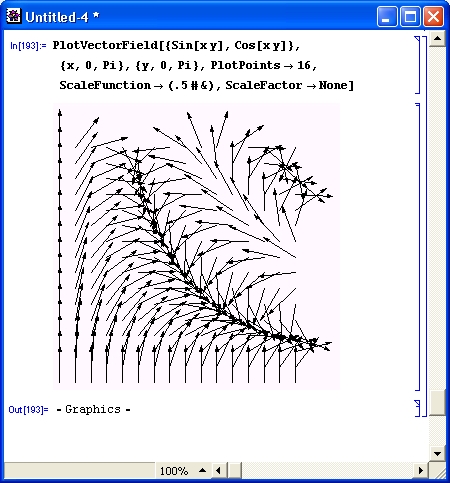
gl14-69.jpg
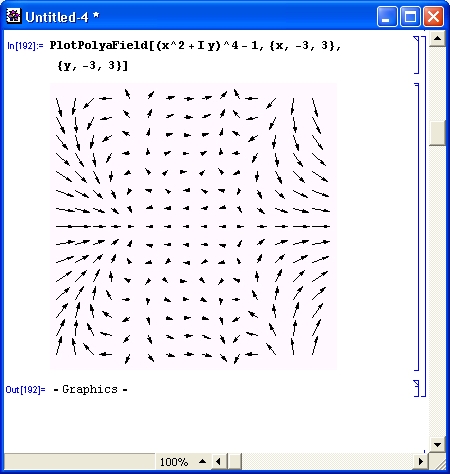
gl14-70.jpg
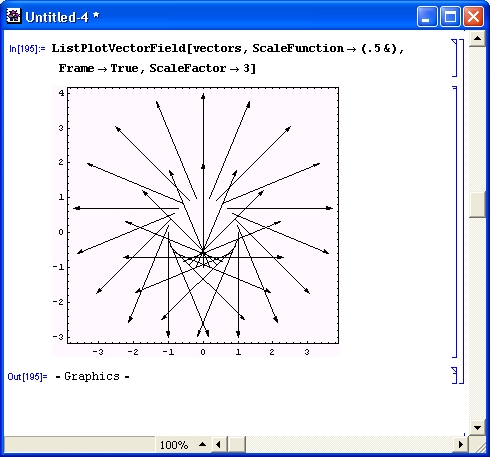
gl14-71.jpg
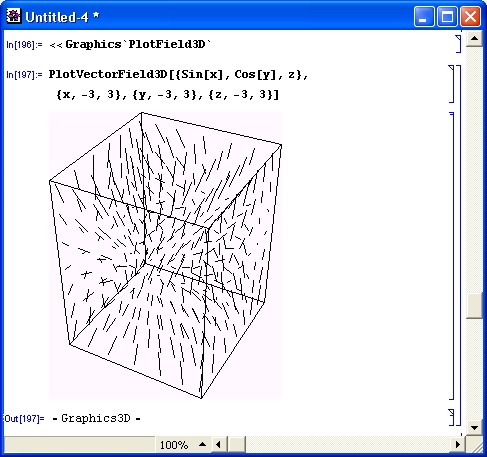
gl14-72.jpg
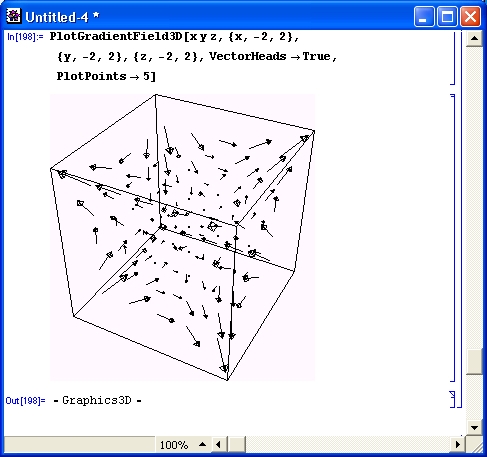
gl14-73.jpg
7. Построение полиэдров — Polyhedra
Построение полиэдров — Polyhedra
Подпакет Polyhedra служит для создания регулярных пространственных фигур — полиэдров. Они задаются как графические примитивы и выводятся функцией Show:
- Show [Polyhedron [polyname] ] — строит полиэдр с именем polyname в центре графика;
- Show[Polyhedron[polyname,{х,у,z},scale]] — строит полиэдр с именем polyname с центром в точке {х, у, z} и параметром масштаба scale.
Возможно задание следующих имен полиэдров: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron, Hexahedron, GreatDodecahedron, Small-StellatedDodecahedron, GreatStellatedDodecahedron и Greatlcosa-hedron. Пример построения полиэдра Icosahedron показан на рис. 14.74.
Рис. 14.74. Построение полиэдра Icosahedron
Возможность вывода с помощью функции Show двух полиэдров иллюстрирует рис. 14.75.
Рис. 14.75. Вывод функцией Show двух полиэдров
Для вывода полиэдров служит также ряд описанных ниже функций. Так, для построения звездчатых форм полиэдров предназначена функция Stellate:
- Show [Stellate [Polyhedron [polyname] ] — построение звездчатых форм полиэдров;
- Show[Stellate[Polyhedron[polyname], ratio] — построение звездчатых форм полиэдров с заданным отношением радиусов описанной и вписанной сфер ratio.
Рисунок 14.76 показывает построение звездообразного (или игольчатого) полиэдра. Представленная фигура напоминает некоторых морских животных — ежей и звезд.
Рис. 14.76. Построение звездчатой формы полиэдра
Полиэдры, применяемые в геодезии, можно получить с помощью следующей функции:
- Show [Geodesate [Polyhedron [polyname], n] — построение полиэдра с вершинами, лежащими на сфере, представляющего собой результат я-кратно-го разбиения на треугольники граней полиэдра polyname;
- Show [Geodesate [Polyhedron [polyname] , n, {x, y, z}, radius] —построение полиэдра с вершинами, лежащими на сфере с заданным положением центра {x,y,z} и радиусом radius, представляющего собой результат п-кратного разбиения на треугольники граней полиэдра polyname.
Рисунок 14.77 показывает применение этой функции.
Для построения усеченных полиэдров предназначены следующие функции:
- Show [Truncate [Polyhedron [polyname] ] ] — построение усеченных полиэдров;
- Show [Truncate [Polyhedron [polyname], ratio] — построение усеченных полиэдров с заданным коэффициентом усечения ratio (от 0 до 0.5);
- Show[OpenTruncate[Polyhedron[polyname]]] — построение полиэдров с открытым усечением;
- Show[OpenTruncate[Polyhedron[polyname], ratio] — построение полиэдров с открытым усечением и заданным коэффициентом усечения ratio (от 0 до 0.5).
Рис. 14.77. Построение полиэдра в виде сферы
Рисунок 14.78 показывает построение усеченного полиэдра Усечение сделано так, будто полиэдр заполнен материалом. Поэтому усеченные области выглядят как дополнительные грани. Параметр ratio, задающий степень усечения, может иметь значения от 0 до 0.5 (в ином случае выводятся сообщения об ошибке в задании параметра).
Рис. 14.78. Построение усеченного полиэдра
Усечение может быть открытым — такой вариант реализуется функцией со словом Open в имени. В этом случае фигура выглядит так, будто она склеена из тонкого картона (рис. 14.79). При этом в местах усечения фигура прозрачна.
Рис. 14.79. Построение усеченного полиэдра с открытыми местами усечения
В заключение этого раздела отметим следующие функции:
- First [Polyhedron [polyname] ] — возвращает список полигонов для указанного полиэдра;
- Vertices [polyname] — возвращает список координат вершин полиэдра;
- Faces [polyname] — возвращает список вершин, ассоциированных с каждой гранью.
Они ничего не строят, а лишь возвращают специфические параметры полиэдров. Примеры применения этих функций представлены ниже:
First[ Polyhedron[ Octahedron ]]
{Polygon[{{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0}}],
Polygon[{{0, 0, 1.41421}, {0, 1.41421, 0}, {-1.41421, 0, 0}}],
Polygon[{{0, 0, 1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}}],
Polygon[{{0, 0, 1.41421}, {0, -1.41421, 0}, {1.41421, 0, 0}}],
Polygon[{{1.41421, 0, 0}, {0, -1.41421, 0}, {0, 0, -1.41421}}],
Polygon[ {{1.41421, 0, 0}, {0, 0, -1.41421}, {0, 1.41421, 0}}],
Polygon[{{0, 0, -1.41421}, {0, -1.41421, 0}, {-1.41421, 0, 0}}],
Polygon[{{0, 1.41421, 0}, {0, 0, -1.41421}, {-1.41421, 0, 0}}]}
Vertices[ Octahedron ]
{{0, 0, 1.41421}, {1.41421, 0, 0},
{0, 1.41421, 0}, {0, 0, -1.41421},
{-1.41421, 0, 0}, {0, -1.41421, 0}}
Faces[ Octahedron ]
{{1, 2, 3}, {1, 3, 5}, {1, 5, 6},
{1, 6, 2}, {2, б, 4}, {2, 4, 3}, {4, б, 5}, {3,4,5}}
Приведенные выше функции можно использовать на занятиях по стереометрии, где полученные с их помощью фигуры могут прекрасно иллюстрировать теоретические положения курса.
Создание графических форм — Shapes
Нередко желательно придать трехмерным объектам определенную форму, например кольца или бублика. Некоторые возможности для этого дают функции под-пакета Shapes. Основной из них является функция Show [Graphics3D [shape] ], которая производит отображение формы со спецификацией shape.
С ней могут использоваться графические примитивы:
- Cone [r, h, n] — конус с основанием радиуса r и высотой h на основе n-сто-роннего полигона;
- Cylinder [r, h, n] — цилиндр радиуса r и высотой h на основе и-стороннего полигона;
- Torus[rl,r2,n,m] — объемное кольцо с внешним и внутренним радиусами rl и г 2 и числом сторон каркаса n и m;
- Sphere [r, n,m] — сфера радиуса г, составленная из многоугольников с параметрами n и m и числом сторон п(т - 2) + 2;
- MoebiusStrip [rl, r2, n] — кольцо Мебиуса с радиусами rl и r2, построенное на основе полигона с 2n сторонами;
- Helix[r,h,m,n] — плоская спираль радиусом г и высотой h c m витками на основе поверхности, разбитой на nxm четырехугольников;
- DoubleHelix[r,h,m,n] — плоская двойная спираль радиусом r и высотой h с m витками на основе поверхности, разбитой на nxm четырехугольников.
Возможно указание фигур без параметров. Это означает, что они выбираются по умолчанию следующими:
Соnе[1, 1, 20]
Cylinder[1, 1, 20]
Helix[l, 0.5, 2, 20]
DoubleHelix[l, 0.5, 2, 20]
MoebiusStrip[1, 0.5, 20]
Sphere[l, 20, 15]
Torus[l, 0.5, 20, 10]
На рис. 14.80 показан пример построения фигуры DoubleHelix без указания ее параметров с помощью функций Show и GraphicsSD.
Рисунок 14.81 показывает построение другой фигуры — кольца Мебиуса с указанием параметров фигуры. Обратите внимание на то, что в обоих случаях автоматически обеспечивается функциональная окраска фигур, облегчающая их восприятие.
Рис. 14.80. Пример построения фигуры без указания параметров
Рис. 14.81. Построение кольца Мебиуса
Для преобразования графических объектов в подпакете Shapes имеются следующие функции:
- RotateShape [g,phi, theta,psi] — поворот графического объекта на углы phi, theta и psi;
- TranslateShape [g, {х, у, z} ] — сдвиг графического объекта на расстояния {х,у, z};
- Af fineShape [g, {scalel, svale2, scaleS} ] — умножение всех координат объекта g на указанные множители.
Рисунок 14.82 иллюстрирует осуществление вращения для кольца Мебиуса. Эффект вращения хорошо заметен, если сравнить положения фигуры на рис. 14.81 и 14.82.
Рис. 14.82. Кольцо Мебиуса после поворота
Функции Show и Graphics3D позволяют строить трехмерные фигуры, которые пересекаются в пространстве. Пример такого построения приведен на рис. 14.83. Нетрудно заметить, что линии пересечения строятся с точностью до одной ячейки — полигона. Поэтому для получения качественных фигур надо увеличивать число полигонов, из которых фигуры синтезируются. Это, однако, увеличивает время построения фигур — оно становится заметным даже при работе на современных компьютерах с процессорами Pentium II и Pentium III.
Рис. 14.83. Фигуры, пересекающиеся в пространстве
В заключение этого раздела отметим, что функция WireFrame [g] дает «каркас» графического объекта, то есть делает все его грани прозрачными. Применение этой функции иллюстрирует пример, показанный на рис. 14.84.
Рис. 14.84. Пример применения функции WireFrame для построения каркаса сферы
gl14-74.jpg
gl14-75.jpg
gl14-76.jpg
gl14-77.jpg
gl14-78.jpg
gl14-79.jpg
gl14-80.jpg
gl14-81.jpg
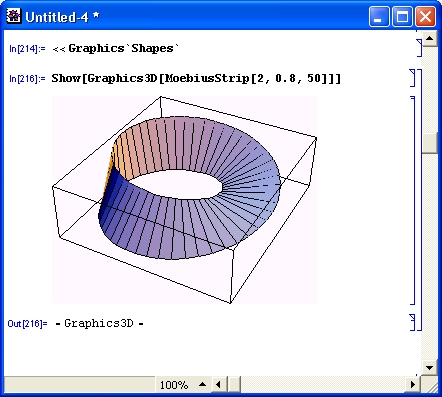
gl14-82.jpg
gl14-83.jpg
gl14-84.jpg
8. Примитивы, использующие сплайны — Spline
Примитивы, использующие сплайны — Spline
Подпакет Spline вместе с уже описанным подпакетом NumericalMath'SplineFit' (сплайновая регрессия) обеспечивает представление данных с помощью сплайна. В подпакете Spline определена единственная функция Spline [points, type], которая создает графический примитив, представляющий сплайн-кривую типа type (Cubic, Bezier или CompoziteBezier — см. описание подпакета NumericalMath'SplineFit').
Среди ее опций важно отметить следующие (как и ранее, приведены значения, используемые по умолчанию): SplineDots->None, SplinePoints->25, Max-Bend->10.0 и SplineDivision->20.0.
Рисунок 14.85 показывает задание массива из пяти точек на плоскости и соединение их отрезками прямых и кубическими сплайн-функциями. Хорошо видна аналогия сплайна с гибкой линейкой.
Сплайн-функции в данном случае применяются в порядке задания точек в списке pts. В этом случае возможно создание замкнутых линий (рис. 14.85 является наглядным примером этого).
Следует отметить, что хотя сплайн-аппроксимация дает хорошие результаты при умеренном числе точек, при малом их числе и неудачном выборе типа сплайнов результат может оказаться неудовлетворительным. Рисунок 14.86 иллюстрирует такую ситуацию.
Рисунок 14.87 показывает возможность построения сплайн-функции вместе с точками, через которые она проходит.
Рис. 14.85. Пример интерполяции пяти точек отрезками прямой и сплайнами
Рис. 14.86. Пример срыва сплайн-интерполяции точек
Рис. 14.87. Построение исходных точек и проходящей через них сплайн-функции
Создание поверхностей вращения — SurfaceOfRevolution
Одна из задач компьютерной графики — создание поверхностей вращения. Средства для этого дает подпакет SurfaceOfRevolution. Они представлены следующими функциями:
- SurfaceOfRevolution [f, {x, xmin, xmax} ] — строит поверхность, образованную вращением кривой, описанной функцией f, при изменении х от xmin до xmax, в плоскости ху;
- SurfaceOfRevolution [{fx, f у}, {t, tmin, tmax} ] — строит поверхность, образованную вращением кривой, описываемой параметрически заданной на плоскости функцией {f x, f у}, в плоскости xz при изменении параметра t от tmin до tmax;
- SurfaceOfRevolution[{fx,fy,fz},{t,tmin,tmax}] — строит поверхность, образованную вращением кривой, описываемой параметрически заданной в пространстве функцией {fx, fy, fz}, в плоскости xz при изменении параметра t от tmin до tmax;
- SurfaceOfRevolution[f,{{x,xmin,xmax},{theta,thetamin,thetamax}}] — строит поверхность вращения кривой, описываемой функцией f, при угле theta, меняющимся от thetamin до thetamax.
Рисунок 14.88 дает простой пример построения поверхности, образованной линией cos(x) при изменении х от 0 до 4л, вращающейся вокруг оси xz. Построение задано функцией SurfaceOfRevolution [f, {x, xmin, xmax} ]. В этом случае линия вращается в пределах угла от 0 до 2-я, поэтому поверхность получается круговой.
Рис. 14.88. Фигура, образованная вращением линии cos(x)
Следующий пример показывает ту же фигуру (рис. 14.89) в другом положении. Это достигается сменой угла обзора с помощью опции viewVertical.
Рис. 14.89. Фигура рис. 14.88 в другом положении
Пример применения функции SurfaceOfRevolutibn [ {fx, fy}, {t, tmin, tmax) ] представлен на рис. 14.90. Формируется этакое декоративное яйцо на подставке. Заменив в определении функции Cos [u] на Sin [u], можно получить изображение рюмки.
Рис. 14.90. Построение декоративного яйца на подставке
Рисунок 14.91 демонстрирует возможность построения объемной фигуры с вырезами. Все, что для этого надо, — удачно выбрать диапазон изменения угла вращения. Если он будет от 0 до 2л, то фигура будет сплошной, не содержащей вырезов.
Рис. 14.91. Построение яйца с вырезом
Для управления положением оси вращения служат следующие опции:
- RevolutionAxis->{x, z } — задает поворот вокруг оси, соединяющей начало координат с точкой {х, z} в плоскости xz\
- RevolutionAxis-> {х, у, z} — задает поворот вокруг оси, соединяющей начало координат с точкой {х, у, z}.
Рисунок 14.92 иллюстрирует применение опции RevolutionAxis->{x, у, z }.
Следующая функция позволяет построить фигуру вращения, образующая линия которой задается массивом точек:
- ListSurfaceOfRevolution [ {point1,point2,...} ] — создает поверхность вращения, заданную массивом точек pointl, point2, ...;
- ListSurfaceOfRevolution[{point1,point2,...}, {theta,thetamin,thetamax}] — создает поверхность вращения, заданную массивом точек, при угле вращения theta от thetamin до thetamax.
Рисунок 14.93 показывает задание массива точек с помощью функции Table и фигуру вращения, полученную при использовании функции ListSurfaceOf-Revolution во второй форме.
Рис. 14.92. Управление положением оси вращения
Рис. 14.93. Пример построения фигуры вращения с образующей, заданной массивом точек
Что еще есть в пакете расширения Graphics
Помимо уже рассмотренных подпакетов пакет расширения Graphics содержит подпакеты ThreeScript и Common. Подпакет ThreeScript содержит функцию преобразования трехмерных графических объектов в программный код формата 3-Script, например:
<<Graphics 'ThreeScript'
obj = Graphics3D[Polygon[0,0,0, 0,1,0, 0,1,1]]
• GraphicsSD •
ThreeScript[ "object.ts", obj]
object.ts
!!object.ts
% Graphics3D objects
boundingbox
0 0 0
0 1 1
viewpoint
1.3 -2.399999999999999 2.
ambientlight
000
lightsources
1. 0. 1.
1 0 0
1. 1. 1.
0 1 0
0. 1. 1.
0 0 1
polygon
0 0 0
0 1 0
0 1 1
Подпакет Common содержит просто перечень системных символов (точнее, слов), которые приняты во всех подпакетах пакета Graphics. Вот этот список: Horizontal, MaxArrowLength, ScaleFactor, ScaleFunction и Vertical.
В этом уроке мы научились:
- Выполнять анимацию графиков различного типа.
- Управлять цветами графиков.
- Строить стрелки на графиках.
- Строить графики комплекснозначных функций.
- Строить объемные контурные графики.
- Строить графики с окраской внутренних областей.
- Строить графики специальных типов.
- Строить графики неявных функций.
- Выводить обозначения кривых — легенды.
- Строить графики с множеством объектов.
- Строить параметрические трехмерные графики.
- Представлять поля на плоскости и в пространстве.
- Строить объемные многогранники — полиэдры.
- Создавать графические формы.
- Работать с примитивами, использующими сплайны.
- Создавать поверхности вращения.
gl14-85.jpg
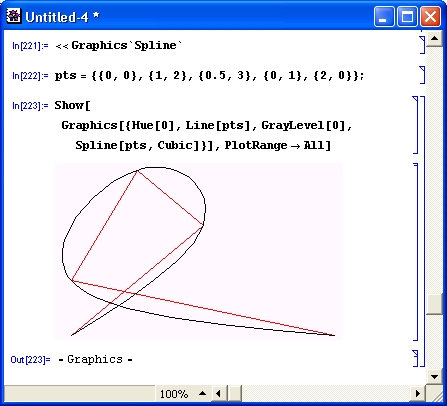
gl14-86.jpg
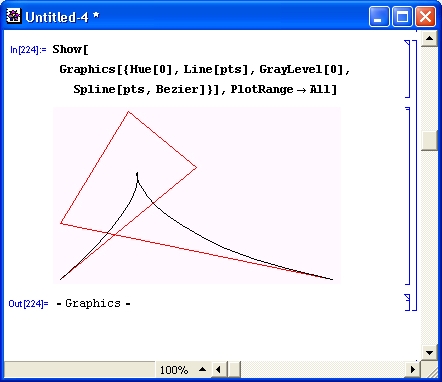
gl14-87.jpg
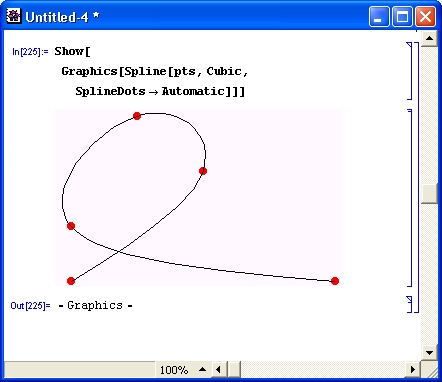
gl14-88.jpg
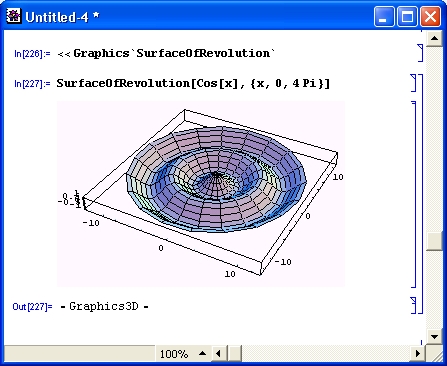
gl14-89.jpg
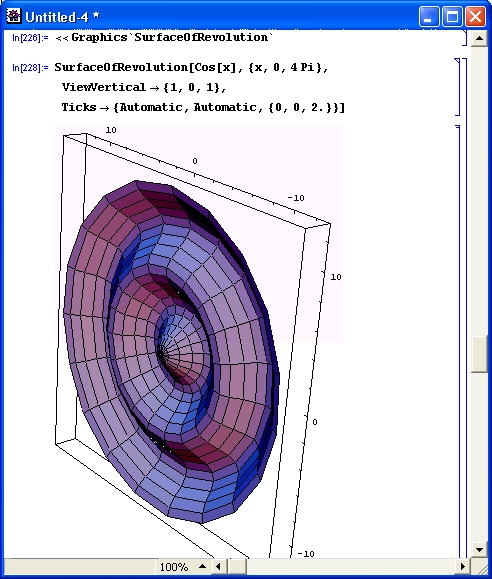
gl14-90.jpg
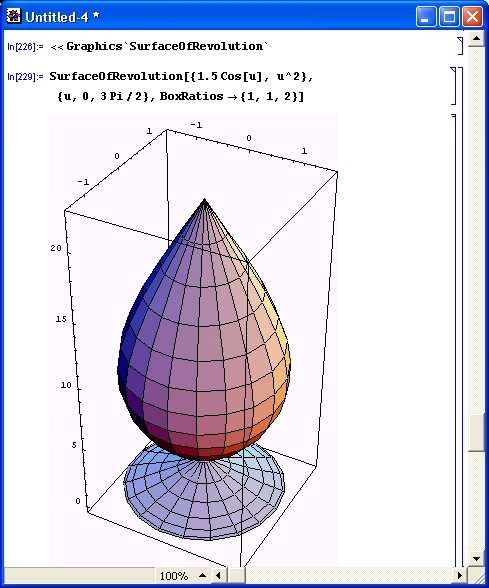
gl14-91.jpg
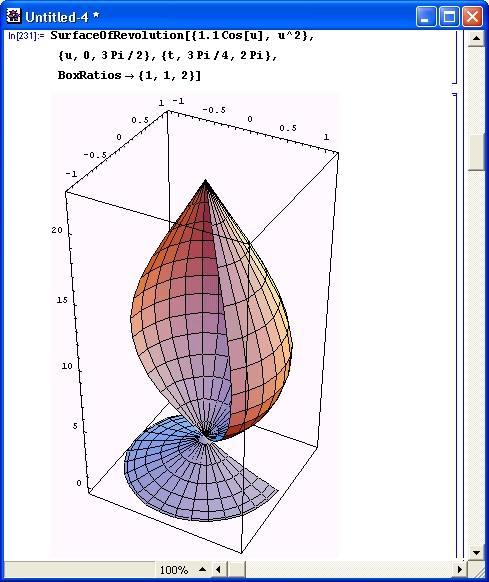
gl14-92.jpg
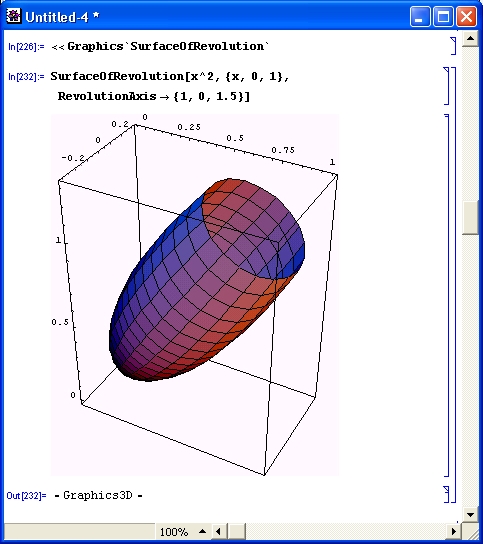
gl14-93.jpg
Приложение. Данные по дополнительным функциям Mathematica
Приложение. Данные по дополнительным функциям Mathematica 4
1. Данные по дополнительным функциям Mathematica 4, К уроку 3
Данные по дополнительным функциям Mathematica 4
В этом приложении даны некоторые дополнительные функции систем Mathematica 3/4 и (иногда) примеры их применения. В основном это редко используемые функции, и они приведены для того, чтобы пользователь имел достаточно полную информацию по большинству из примерно 1000 функций, встроенных в ядро систем, и по ряду функций пакетов применения. Функции классифицированы по урокам, в которых описаны базовые функции близкого назначения.
Дополнительные логические функции
- DigitQtstring] — вырабатывает значение True, если все символы строки string являются цифрами от 0 до 9, иначе возвращает False.
- Identity [ехрг] — возвращает ехрг (операция тождественности).
- Implies [p, q] — представляет логическую импликацию р => q.
- IntegerQ [ехрг] — возвращает True, если ехрг является целым числом, иначе False.
- LetterQ [string] — вырабатывает True, если все символы строки string являются буквами, иначе False.
- ListQ [ехрг] — возвращает True, если ехрг является списком, иначе False.
- LowerCaseQ [string] — вырабатывает значение True, если все символы в строке являются строчными буквами (буквами нижнего регистра), иначе False.
- MachineNumberQ[х] — возвращает True, если х является числом в машинном формате с плавающей точкой, иначе возвращает False.
- MatchQ[expr, form] — возвращает True, если модель (образец) form соответствует ехрг, и возвращает False в противном случае.
- NumberQ [ехрг] — возвращает True, если ехрг является числом, иначе False.
- OddQ[expr] — возвращает True, если ехрг нечетное целое, иначе False.
- OptionQ[e] — возвращает True, если е может считаться опцией или списком опций, иначе False.
- PrimeQ [ехрг] — дает True, если ехрг является простым числом, иначе дает False.
- TrueQfexpr] — возвращает True, если expr имеет значение True, иначе возвращает False.
- UnsameQ — применяется в виде: Ihs =1 = rhs; возвращает True, если выражение Ihs не тождественно (не идентично) rhs, в противном случае возвращает False.
- ValueQ [expr] — возвращает True, если было определено значение для ехрг, иначе возвращает False.
- VectorQ [expr] — возвращает True, если expr является списком, но ни один из его элементов, в то же время, сам не является списком, иначе возвращает False.
- VectorQ [expr, test] — возвращает True, только если test, будучи применен к каждому элементу ехрr, дает True.
В систему Mathematica 4 помимо указанных выше функций дополнительно включены побитовые логические функции: BitAnd [n1, n2,...], BitOr [n1, n2,...], BitXor [n1, n2,...] и BitNot[n]. Их действие вполне очевидно.
- Abs [ z ] — возвращает абсолютное значение для действительного числа и модуль для комплексного z.
- ArcCos [z] — возвращает арккосинус комплексного числа z.
- ArcCoshfz] — возвращает значение обратного гиперболического косинуса комплексного аргумента z.
- ArcCot [ z ] — возвращает значение арккотангенса комплексного аргумента z.
- ArcCoth [ z ] — возвращает обратный гиперболический котангенс комплексного аргумента z.
- ArcCsc [ z ] — возвращает арккосеканс комплексного аргумента z.
- ArcCsch [z] — возвращает обратный гиперболический косеканс комплексного аргумента z.
- ArcSecfz] — возвращает арксеканс комплексного аргумента z.
- ArcSech [z] — возвращает обратный гиперболический секанс комплексного аргумента z.
- ArcSin [ z ] — возвращает арксинус комплексного аргумента z.
- ArcSinhfz] — возвращает обратный гиперболический синус комплексного аргумента z.
- ArcTan [z] — возвращает арктангенс аргумента z.
- ArcTan [х, у] — возвращает арктангенс отношения у/х вещественных х и у для квадранта, в котором лежит точка (х, у).
- ArcTanh [ z ] — возвращает обратный гиперболический тангенс комплексного аргумента z.
- Cos [z] — возвращает косинус аргумента z.
- Cosh[z] — возвращает гиперболический косинус аргумента z.
- Cot [ z ] — возвращает значение котангенса аргумента z.
- Coth [ z ] — возвращает гиперболический котангенс аргумента z.
- Csc [z] — возвращает значение косеканса z.
- Csch[z] — возвращает гиперболический косеканс z.
- Ехр [ z ] — возвращает значение exp(z).
- Log [ z ] — возвращает натуральный логарифм аргумента z (логарифм по основанию Е).
- Log [b, z] — возвращает логарифм по основанию b.
- Sec [ z ] — возвращает секанс аргумента z.
- Sech[z] — возвращает гиперболический секанс z.
- Sign [х] — возвращает -1, 0 или 1, если аргумент х, соответственно, отрицательный, нулевой или положительный.
- Sign [z] — возвращает отношение z/Abs [z] для комплексного числа z.
- sin [z] — возвращает синус аргумента z.
- Sinh[z] — возвращает гиперболический синус z.
- Sqrt [z] — возвращает корень квадратный из аргумента z.
- Tan [ z ] — возвращает тангенс аргумента z.
- Tanh[z] — возвращает гиперболический тангенс z.
Дополнительные функции для работы со списками
- Accumulate [f, g [el, e2,...]] —возвращает g[el,f [el,e2] , f'[f [el,e2] ,e3 ],...].
- Cases [{el, e2,...}, pattern] — возвращает список тех ei, которые соответствуют заданному шаблону pattern.
- Cases [ {el,...}, pattern -> rhs] или Cases [ {el,...}, pattern :> rhs] — возвращает список значений rhs, соответствующих тем ei, которые подходят под шаблон pattern.
- CoefficientList [poly, var] — возвращает список коэффициентов перед степенями переменной var в полиноме poly, начиная со степени 0.
- CoefficientList [poly, {varl, var2,...}] — возвращает матрицу коэффициентов vari.
- $CommandLine — список строк, возвращающий элементы командной строки, с помощью которой была вызвана Mathematica.
- Compose [а, b, с, d] — возвращает а [b [с [d] ]].
- ComposeList [ {f I, f2,...}, х] — формирует список формы {x,fl[x],
- ComposeSeries [s, t, u,...] — объединяет степенные ряды, подставляя в ряд s ряд t, затем ряд и и т. д. Ряды (исключение для первого элемента) должны начинаться положительной степенью переменной.
- Composition [f1, f2, f3,...] — представляет композицию функций fl, f2, f 3, ...
- FoldList[f, x, {a, b,...}]—возвращает {x, f [x, a] , f [f [x, a] ,b],...}.
- HeadCompose [a, b, c, d] — возвращает a [b] [c] [d].
- bistable — атрибут, который может назначаться символу f для указания того, что если функция f получит аргумент (аргументы) в виде списка, то и результатом будет являться список.
- MemberQ [list, form, levelspec] — тестирует все части списка list, определяемые спецификацией уровня levelspec.
- Partition [list,n] — разбивает список list на неперекрывающиеся части длиной п. Если количество элементов в списке не делится нацело на п, то последние k (k < п) элементов удаляются.
- Partition [list, n, d] — как и предшествующая функция, дает разбиение списка, но со сдвигом между соседними подсписками, равным d. При d<n подсписки перекрываются.
- Permutations [list] — генерирует список всех возможных перестановок элементов в списке list.
- Position [expr, pattern] — возвращает список позиций в ехрг, в которых размещаются объекты, сопоставимые с указанным шаблоном pattern.
- Position [expr, pattern, levspec] — выполняет поиск только объектов, находящихся на уровнях, указываемых levspec.
- RealDigits [x] — возвращает список цифр в приближенном вещественном числе х вместе с количеством цифр слева от десятичной точки, присутствующих в научной записи числа.
- RealDigits [x,b] — возвращает список цифр числа х по основанию Ь.
- Signature [list] — дает сигнатуру перестановки, необходимой для размещения элементов списка list в каноническом порядке.
- SingularValues [m] — возвращает особое значение декомпозиции для чис-ловой матрицы т. Результатом будет список {u, w, v}, где w — список ненулевых особых значений, а исходная матрица m может быть записана как Соп-jugate[Transpose[u]].DiagonalMatrix[w].v.
- SequenceLimit [list] — возвращает по эпсилон-алгоритму Винна аппроксимацию предела последовательности, первые несколько членов которой зада-. ны в виде списка list. Этот алгоритм может давать конечные значения для расходящихся последовательностей.
- SubValues [f ] — возвращает список правил преобразования, относящихся ко всем подзначениям (значениям для f [х,...][...] и т.д.), определенным для символа f.
- $SuppressInputFormHeads — представляет собой список заголовков тех выражений, чьи Input Form не должны автоматически пересылаться в программный препроцессор.
Функции расширения списков нулями
PadLeft[list] PadLeft[list,n]
PadLeft[list,f,n] PadRight[list]
PadRight[list,n]
PadRightLeft[list,n]
Примеры их применения:
- PadLeft [ {a,b, с}, 6] — возвращает список {0, 0, 0, a,b, с}.
- PadRight [ {a,b, с}, 6] — возвращает список {а,b, с, 0, 0,0}.
Дополнительные матричные функции
- MatrixExp [m] — возвращает экспоненциал матрицы m.
- MatrixPower [m, n] — возвращает п-ю степень матрицы m.
- MatrixQ [ехрг] — возвращает True, если ехрг является списком списков, который может представлять матрицу, иначе возвращает False.
- MatrixQ [expr, test] — возвращает True, только если test дает True в применении к каждому элементу матрицы в ехрг.
- Minors [m, k] — возвращает матрицу, составленную из определителей всех kxk субматриц m.
- NullSpace [m] — возвращает список векторов, которые формируют базис для нулевого пространства матрицы m
- Pivoting — опция, относящаяся к функциям декомпозиции матрицы; указывает, что должен выполняться поворот столбца. Результат имеет форму {Q, R, Р}, где Р — матрица перестановок, такая что имеет место соотношение M.P=Conjugate [Transpose [Q] ] .R, где М— начальная (исходная) матрица.
- Pseudolnverse [m] — ищет псевдообратную матрицу для прямоугольной матрицыm.
- QRDecomposition [m] — возвращает QR-разложение (декомпозицию) для числовой матрицы m. Результат представляет собой список {q, r), где q — ортогональная матрица, r — верхняя треугольная матрица.
- ZeroTest — опция для LinearSolve и других линейных алгебраических функций; дает функцию для применения ее к сочетаниям (комбинациям) из матричных элементов с целью определения, следует ли полагать их равными нулю.
2. К уроку 4
К уроку 4
Опции численного интегрирования
- AccuracyGoal — указывает число цифр, задающих точность промежуточных результатов.
- Compiled — указывает на возможность компиляции функции.
- GaussPoints — устанавливает количество точек в гауссовой части квадратуры Гаусса—Кронрода.
- MaxPoint — задает максимальное число точек при интегрировании.
- MaxRecursion — задает максимальную глубину рекурсии.
- Method -> DoubleExponential — назначает для использования алгоритм двойной экспоненциальной сходимости.
- Method -> MultiDimensional — назначает для использования многомерный алгоритм. Имеет смысл только для интегрирования кратных интегралов.
- Method -> GaussKronrod — выбирает для использования адаптивную квадратуру Гаусса—Кронрода. При многомерном интегрировании GaussKronrod обращается к декартову произведению одномерных квадратурных формул Гаусса—Кронрода.
- Method -> Trapezoidal — назначает для решения рекурсивный метод трапеций. Он особенно успешен, если подынтегральная функция периодична и интервал интегрирования составляет точно один период. Для многомерного интегрирования данный метод обращается к декартову произведению одномерных правил трапеций.
- MinRecursion — задает минимальную глубину рекурсии.
- PrecisionGoal — задает погрешность вычислений.
- SingularityDepth — указывает, насколько глубокая рекурсия допустима перед тем, как начинается изменение переменной на границах интервала интегрирования.
3. К уроку 6
К уроку 6
Дополнительные специальные функции
- ArithmeticGeometricMean [а, b] — арифметико-геометрическое среднее значение аргументов а иb.
- IncludeSingularTerm — опция для LerchPhi и Zeta, определяющая, следует ли включать члены вида (k+a) A -s при k + а == 0.
- InverseErf [s] — инверсная функция ошибок.
- InverseErfс [s] — инверсная дополнительная функция ошибок.
- InverseGammaRegularized[a, s] — инверснаярегуляризированнаянеполная гамма-функция.
- InverseBetaRegularized[s,a,b] — инверсная регуляризированная неполная бета-функция.
- InverseSeries [s] — берет ряд s, порождаемый директивой Series, и возвращает ряд для функции, обратной по отношению к функции, представленной рядом s.
- InverseSeries [s, у] — обратный ряд по переменной у.
- InverseWeierstrassP [ {Р, Р'}, g2, gЗ ]— возвращает величину и, такую что P=WeierstrassP[и, д2, дЗ] иP'=WeierstrassPPrirne[и, д2, дЗ]. Следует заметить, что Р и Р' не являются независимыми.
- JordanDecomposition[A] — возвращает список {S,J}, такой что A=S.J. Inverse [S] и J является канонической формой Жордана для матрицы А.
- LerchPhi[z, s, a] — трансцендентная функция Лерча Ф(г, s, a).
- MathieuC[a, q, z] и MathieuS [a, q, z] — функции Матье.
- MathieuCPrime [a, q, z] и MathieuSPrime [a, q, z] —производные от функций Матье.
- MathieuCharacteristic** [r, q] — характеристическая функция Матье (** может иметь значения А, В и Exponent).
- MeijerG[{{a 1 ,...,a /] },{a ji+1 ,...,a p }}, {{bl,...,bm}, {b m+1 ,...,b q }}, z] - G-функция Мейджера.
- MoebiusMu [n] — значение функции Мебиуса ц(и).
- PolyLogtn, z] — п-я полилогарифмическая функция от z.
- RiemannSiegelTheta [t] — аналитическая функция g(E), удовлетворяющая уравнению RiemannSiegelZ[t] = Exp[I RiemannSiegelTheta[t]] Zeta[l/2 + I t]. Аргумент t не обязательно должен быть вещественным, но если является таковым, тогда RiemannSiegelTheta[t]] = Im[LogGamma[1/4 + I t/2]]-- t Log[Pi]/2.
- RiemannSiegelZ [t] — возвращает значение Exp[I RiemannSiegelTheta[t]] Zeta[l/2 + I t].
- SphericalHarmonicY [1, m, theta, phi] — сферическая гармоника уде, Ф ).
- Zeta[s] — дзета-функция Римана (s).
- Zeta[s, а]— возвращает значение обобщенной дзета-функции Римана.
Ниже даны примеры использования некоторых из этих функций.
| Ввод (In) | Вывод (Out) |
| LerchPhi[2.+3.*I,l,2] | 0.0145978+ 0.256525 I .. |
| InverseErf [0 . 1] | 0.088856 |
| InverseErf с [0.1] | 1.16309 |
| InverseGammaRegularized[l, 0.5] | 0.693147 |
| InverseBetaRegularized[0.5, 1, 2] | 0.292893 |
| MathieuC[l,2,0.1] | 0.196600+0.879889 I |
| MathieuS[l,2,0.1] | 0.133005- 0.0297195 I |
| MathieuCharacteristicAfl . 5,2.] | 2.85238 |
| Mei jerG[ { {1, 1), {)},{{!) Л 0}),x] | Log[l+x] |
| MoebiusMu[3] | -1 |
| NBernoulliB[2] | 0.166667 |
| NBernoulliB[l,5] | -0.5 |
| PolyLog[2,2.+3.*I] | -0.280988 + 3.01725 I |
| RiemannSiegelTheta [1 . ] | -1.76755 |
| RiemannSiegelZ [1 . ] | -0.736305 |
| SphericalHarmonicY [ 0 . 1 , 0 . 5 , Pi/3 , Pi/2 ] | 0.195671 + 0.195671 I |
| Zeta[0.1] | -0.603038 |
| Zeta[0.1,0.5] | -0.0432821 |
В Mathematica 4 добавлены новые встроенные функции struveH [n, z ] и StruveL [n, z ], вычисляющие функции Струве порядка n для комплексного аргумента z.
4. К уроку 7
К уроку 7
- CForm[expr] — выполняет вывод ехрг в форме, принятой для языка С.
- ColonForm[a,b] — выводит в виде а:b.
- ColumnForm[ {el, e2,...} ] — дает вывод в виде столбца с el над е2 и т.д.
- ColumnForm[list, horiz] — при выводе дает горизонтальное выравнивание каждого элемента.
- ColumnForm[list, horiz, vert] — при выводе дает как горизонтальное, так и вертикальное выравнивание всего столбца.
- FontForm[expr, {"font", size}] — устанавливает шрифт "font" и размер size, с которыми выводится выражение ехрг.
- Format [ехрг] — выводит ехрг в форматированном виде.
- Format [expr, type] — возвращает формат для указанного типа type.
- InputForm[expr] — выводит ехрг во входной форме.
- NumberForm[expr, n] — выполняет вывод приближенного представления вещественного значения ехрr с точностью до n цифр.
- OutputForm[expr] — выполняет вывод ехрr в стандартной выходной форме системы Mathematica.
- PaddedForm[expr, n] — выводит все числа ехрr, заполняя оставшиеся места так, чтобы каждое число содержало n знаков.
- PaddedForm[expr, {n, f} ]—выводит ехрг с приближенными вещественными числами, имеющими ровно f цифр справа от десятичной точки.
- PrecedenceForm[expr, prec] — выводит выражение ехрг, заключенное в скобки так, как если бы оно содержало оператор с приоритетом ргес.
- Prefix [f [ехрг] ] — выводит функцию f [ехрг] в префиксной форме: f @ ехрг.
- Prefix [f [ехрг] , h] — выводит функцию f [ехрг] с заголовком h, то есть как hexpr.
- $ Print Forms — является списком базисных форм вывода. Он автоматически обновляется при создании описаний Format, использующих новые формы вывода.
- TextForm[expr] — выполняет вывод ехрг в обычном текстовом формате.
- Unevaluated [ехрr] — представляет невычисляемую форму выражения ехрг, когда оно используется как аргумент функции.
Для функции Number Form и родственных функций используется ряд опций:
- DigitBlock — указывает максимальную длину групп разрядов при использовании разделителей.
- FormatType — указывает тип формата по умолчанию при выводе выражений.
- NumberFormat — указывает, как мантисса, основание и порядок должны быть скомпонованы в конечную форму вывода.
- NumberPadding — задает символы, которые будут использоваться для заполнения с левой и правой сторон числа.
- NumberPoint— задает строку для использования в качестве десятичной точки.
- NumberSeparator — задает строку для вставки между группами разрядов.
- Right — используется для указания правостороннего выравнивания в таких формах вывода, как ColumnForm и TableForm.
Дополнительные функции и опции ввода/вывода
- Attributes [symbol] — возвращает список атрибутов символа symbol.
- Bastchlnput — возвращает True, если ввод в текущем сеансе работы производится непосредственно в ядро системы в пакетном режиме, и False в противном случае.
- $BatchOutput — возвращает True, если вывод в текущем сеансеработы пересылается в пакетном режиме и пригоден для чтения другими программами, и False в ином случае.
- Characters ["string"] — возвращает список символов в строке.
- Dialog[ ]— инициирует диалог (часто используется совместно с функцией Return).
- Dialog [ехрг] — инициирует диалог с использованием ехрг как текущего значения.
- Dialoglndent [d] — возвращает величину отступа для строк ввода и вывода, которая используется в диалогах с глубиной вложенности d.
- FullDefinition [s1, s2,...] — выводит определения, присвоенные символам si и всем символам, от которых данные символы зависят.
- Information [symbol] — выводит информацию о символе symbol.
- $ Input — глобальная переменная, значением которой является имя потока, из которого Mathematica в данный момент ожидает поступления входной информации.
- $ Language — является списком строк, которые дают названия языков, используемых для сообщений.
- Normal [ехрг] — преобразует ехрг из ряда специальных форм в нормальное выражение.
- Out [n] — глобальный объект, соответствующий выводу, произведенному в и-й выходной строке (ячейке).
- % — возвращает последний произведенный результат.
- % % — возвращает предпоследний результат.
- %%...% (k раз) — возвращает k-й предшествующий результат.
- %k — возвращает результат из k-й выходной строки (абсолютная адресация).
- Shallow [ехрг] — выводит первые четыре уровня ехрг, за исключением частей ехрг, длина которых превышает 10. Остальные части выводятся в структурной (скелетной) форме.
- Shallow [expr, depth] — выводит части выражения ехрг до указанной глубины depth. Остальные части выводятся в структурной (скелетной) форме.
- Shallow [expr, {depth, length}] — возвращает в структурной (скелетной) форме также и те части, длины которых выше указанного предела length.
- Shallow[expr, {depth, length}, form] — использует скелетную форму для любых частей выражения, сопоставимых с указанным шаблоном form.
- Short [expr] — выводит краткую форму ехрг, не превышающую длину одной строки.
- Short [expr, n] — выводит ехрг в форме длиной около n строк.
- SpaceFormfn] — выводит n пробелов.
Некоторые из этих функций используют приведенные ниже опции:
- Above — опция, используемая для установки выравнивания в таких формах вывода, как ColumnForm и TableForm.
- Bottom— является возможным значением опции TableAlignments для TableForm.
- Below — используется для указания выравнивания в таких формах вывода, как ColumnForm и TableForm.
- Center — устанавливает выравнивание в таких формах вывода, как Column-Form и TableForm.
- DialogProlog — опция для Dialog, которая позволяет вычислить выражение до начала диалога.
- DialogSymbols — опция для Dialog, которая возвращает список символов, чьи значения будут локализованы в диалоге.
- Heads — опция для функций, которые используют спецификации уровня, указывающая, следует ли включать заголовки выражений.
- IgnoreCase — опция для функций манипулирования строками и функций поиска, которая указывает, следует ли считать прописные и строчные буквы эквивалентными.
- SignPadding — опция для NumberForm и родственных функций, указывающая, что заполнитель (если он используется) должен размещаться после знака числа.
Приведем примеры использования этих форм вывода.
| Ввод (In) | Вывод (Out) |
| Dialog [] ^n Return [a+b+c] | (a+b+c) n |
| Dialog []*y Return [x] | xy |
| Shallow [Exp [х ^ (a/b) ] /x/a] | e Power[ /ax |
| Short [Exp [х ^ (a/b) ] /x/a, 1] | e x^a/b /ax |
В этих примерах надо обратить особое внимание на применение функции Dialog. При ее начальном вызове строка вывода не формируется. Она появляется после исполнения ячейки ввода с функцией Return, причем ячейки ввода в пределах тела диалога нумеруются так: (Dialog) In[n]:=.
Функции для работы со строками
- $StringConversion — возвращает установочное значение по умолчанию для опции StringConversion в выходных функциях (функциях вывода).
- StringConversion — опция для функций вывода (выходных функций), которая устанавливает, каким образом должны быть выведены строки, содержащие специальные символы.
- StringDrop ["string", n] — возвращает строку "string", отбрасывая первые n ее символов.
- StringDrop ["string", -n] — возвращает строку "string", отбрасывая последние n символов.
- StringDrop ["string", {n} ] — возвращает строку "string", удалив n-й символ.
- StringForm["controlstring", exprl,...] — выводит текст контрольной (управляющей) строки controlstring с внедрением в нее печатных форм expri.
- Stringlnsert ["string", "snew", n] — формирует новую строку, помещая "snew" внутрь строки "string", начиная с позиции п.
- Stringlnsert ["string", "snew", -n] — делает вставку, отсчитывая позицию n с конца "string".
- StringJoin (объединение строк) — применяется в виде "s1"<>"s2"<>...
- StringMatchQ [ "string", "pattern" ] — вырабатывает True, если "string" сопоставим с указанным строковым шаблоном, и False — в противном случае.
- $StringOrder — дает порядок символов для использования в строках сортировки и символьных именах.
- StringPosition ["string", "sub"] — возвращает список начальных и конечных символьных позиций, в которых "sub" появляется как подстрока строки "string".
- StringPosition ["string", "sub", k] — возвращает только первые k вхождений "sub".
- StringPosition ["string", {"subl", "sub2",...}] — возвращает позиции всех "subi".
- StringQ [expr] — возвращает True, если ехрг является символьной строкой, иначе дает False.
- StringSkeleton [n] — представляет последовательность из n пропущенных символов в строке, выведенной с помощью Short.
Стандартные функции для работы с файлами и директориями
- CopyDirectory ["dirl", "dir2"] — копирует директорию dirl в dir2.
- CopyFile["filel", "file2"] — копирует файл filel в file2.
- CreateDirectory ["dir"] — создает директорию.
- DeleteDirectory [ "dir" ] — удаляет указанную директорию. Опция DeleteContents позволяет указать, следует ли удалять непустую директорию.
- DeleteFile ["filename"] — удаляет файл filename.
- DeleteFile [ {"file1", "file2",...} ]—удаляет список файлов.
- Display [channel, graphics] — направляет графический объект graphics или звук в указанный выходной канал channel.
- $DumpSupported — имеет значение True, если Dump может использоваться в данной версии системы Mathematica, и False в противном случае.
- Encode ["source", "dest"] — пишет закодированную версию файла source в файл dest. Вызов «dest декодирует файл перед чтением его содержимого.
- Encode ["source", "dest", "key"] — производит закодированный файл, который нужно считывать, используя Get [ "dest", "key" ].
- FileNames [forms, dirs, n] — возвращает список файлов в поддиректориях вплоть до уровня п.
- InputStream["name", n] — объект, представляющий входной поток для таких функций, как Read и Find.
- OutputStream [ "name", n] — объект, представляющий выходной поток для функций типа Write.
- $PathnameSeparator — строка, выполняющая роль разделителя имен каталогов и файлов в указателях пути, используемых данной операционной системой.
- PageHeight — опция для потоков вывода, которая указывает количество строк текста, выводимых между разрывами страниц.
- PageWidth — опция, которая может устанавливаться для выходных потоков, указывая ширину строки выводимого текста.
- Read [stream] — читает одно выражение из входного потока stream и возвращает это выражение.
- Read[stream, type] — читает один объект указанного типа type из входного потока stream.
- Read [stream, {typel, type2,...}] — читает последовательность объектов указанных типов typei из входного потока stream.
- RenameDirectory ["dirl", "dir2"] — переименовывает каталог dir1 в dir2.
- RenameFile ["filel", "file2"] — переименовывает файл с именем filel в файл с именем f ile2.
- ResetDirectory [ ] — сбрасывает (восстанавливает) имя текущего рабочего каталога в его предыдущее значение.
- ResetMedium["file", options] — сбрасывает (восстанавливает) опции, связанные с файлом file, который уже открыт.
- ResetMedium[options] — сбрасывает опции для стандартного вывода.
- SetDirectory ["dir"] — устанавливает текущий рабочий каталог.
- SetFileDate ["filename"] — устанавливает датой модификации файла текущую дату.
- SetFileDate [ "filename", date] — устанавливает датой модификации указанную дату date. Дата должна быть представлена в формате функции Date: {год, месяц, день, час, минута, секунда}.
- SetOptions [stream,...] или SetOptions [ "name",...] — устанавливает опции, связанные с указанным потоком stream.
- Socket — возможное значение, возвращаемое FileType и родственными функциями.
- StringToStream["string"] — открывает входной поток для чтения из строки.
Мы не приводим примеров использования этих функций ввиду очевидности их действия и отсутствия прямого отображения результата.
Функции поиска записей в файлах
- Find [stream, "text"] — ищет первую запись во входном потоке stream, которая содержит указанную строку.
- Find[stream, {"textl", "text2",...} ] — ищет первую запись, в кото-рой содержится любая из указанных строк.
- FindList ["filename", "text"] — возвращает список всех записей в файле filename, которые содержат указанную строку.
- FindList ["filename", {"textl", "text2",...} ] - дает список всех записей, содержащих любую из указанных строк.
- FindList [{ "filename1",...}, text] — возвращает список записей, содержащих указанные строки, в любом из данных файлов.
- FindList [files, text, n] — возвращает только первые п найденных записей.
Это достаточно редкие в применении функции, так что заинтересованный пользователь может опробовать их самостоятельно.
Функции открытия и закрытия файлов и потоков
- Close [stream] — закрывает поток stream.
- EndOfFile — символ, возвращаемый командой Read при достижении ею конца файла.
- $lgnoreEOF — указывает, должна ли Mathematica завершать работу, получив признак конца файла на входе.
- OpenAppend["filename"] — открывает файл для подсоединения (конкатенации — присоединения в конец) к нему вывода и возвращает объект OutputStream.
- OpenRead [ "filename" ] — открывает файл для чтения данных и возвращает объект InputStream.
- OpenTemporary [ ] — открывает временный файл, в который может записываться вывод, и возвращает объект OutputStream.
- OpenWrite ["filename" ] — открывает файл для записи в него вывода и возвращает объект OutputStream.
- TextRendering — опция, которая указывает, каким образом должен воспроизводиться текст в данном выходном файле.
5. К уроку 8
К уроку 8
Ниже дан список опций, при этом знаком «*» отмечены опции, применяемые как для двумерной, так и для трехмерной графики:
- *AspectRatio — задает пропорцию графика — отношение высоты к ширине (значение по умолчанию, 1/GoldenRatio, задает отношение по правилу золотого сечения — около 1.618).
- *Axes — задает прорисовку координатных осей (False — осей нет, True — строятся обе оси, а список {Boolean, Boolean} задает построение осей раздельно).
- *AxesLabel — задает вывод меток для осей в виде {"stringX", "stringY"}
- * AxesOrigin — задает начало отсчета для осей (указывает точку пересечения осей).
- *AxesStyle — задает стиль вывода осей с помощью ряда директив.
- *Background — задает цвет фона в одной из трех цветовых систем.
- *ColorOutput — задает цвет построений в одной из трех цветовых систем.
- *DefaultFont — задает шрифт для текста в графиках.
- Frame — задает прорисовку рамки вокруг графика при значении True и ее отсутствие при False.
- FrameLabel — задает надписи на гранях рамки (FrameLabel -> { "Text1", "Text2", "Text3", "Text4" }, причем построение идет по часовой стрелке, начиная с нижней надписи).
- FrameStyle — задает стиль граней рамки с помощью ряда директив.
- FrameTicks — задает прорисовку штриховых меток для граней рамки.
- GridLines — задает прорисовку линий сетки.
- *PlotLabel — задает вывод титульной надписи (PlotLabel->"Text").
- *PlotRange — задает масштаб построения в относительных единицах.
- *PlotRegion — задает область построения в относительных единицах.
- RptateLabel — задает разворот символьных меток на вертикальных осях фрейма с тем, чтобы они стали вертикальными.
- *Ticks — устанавливает штриховые метки для осей. Кроме того, имеется ряд характерных для функции Plot дополнительных опций:
- Compiled — задает компиляцию функции перед выводом.
- MaxBend — задает максимальный угол излома между сегментами кривой.
- PlotDivision — задает количество делений при построении гладкой кривой.
- PlotPoints — задает число точек выборки, участвующих в построении.
- PlotStyle — задает стиль линий или точек графика.
Графические примитивы функции Graphics
- Circle[{x, у}, r]— строит окружность с радиусом г и центром в точке {х, у}.
- Circle [{х, у), {rх, rу) ] — строит эллипс с центром {х,у} и полуосями гх и гу.
- Circle[{x, у}, r, {thetal, theta2 }]— представляет дугу окружности радиусом г с центром {х, у} и углами концевых точек thetal и theta2.
- Disk[{x, у), r]— является примитивом двумерной графики, представляющим закрашенный круг радиусом г с центром в точке {х, у}.
- Disk [ {х, у}, {rх, rу} ] — строит закрашенный овал с полуосями rх и rу и центром {х, у}.
- Disk[{x, у}, r, {thetal, theta2}]—строит сегмент круга радиусом г с центром {х, у} и углами концевых точек thetal и theta2.
- Line [ {pt1 pt2,...} ] — строит линию, соединяющую последовательность точек.
- Point[{x,y}] — строит точку с координатами х и у.
- Polygon [{x1, y1},{х2, у2},...] — построение полигона с закраской.
- PostScript [ "string" ] — построение объекта, заданного на языке PostScript.
- Rectangle [ {xmin, ymin}, {xmax, ymax}]—строит закрашенный прямоугольник, ориентированный параллельно осям и намеченный координатами противолежащих углов.
- Rectangle [ {xmin, ymin}, {xmax, ymax}, graphics] — строит закрашенный прямоугольник, заполненный в соответствии с указаниями в функции graphics и заданный координатами противолежащих углов.
- Raster [{{all, a 12,...},...}] — строит прямоугольный массив ячеек яркости.
- RasterArray [ {{gll, g!2,...},...}] — строит прямоугольный массив ячеек, окрашенных в соответствии с графическими директивами gij.
- Text[expr, coords] — выводит текст, соответствующий печатной форме выражения ехрг, центрированный в точке с указанными координатами coords.
- AmbientLight — задает директиву фоновой подсветки сцены.
- AxesEdge — определяет, на каких гранях ограничительного параллелепипеда («ящика») должны выводиться оси.
- Boxed — указывает, надо ли рисовать контуры (ребра, грани) ограничительного параллелепипеда в трехмерном изображении.
- BoxRatios — задает значение отношений длин сторон для ограничительного параллелепипеда трехмерного изображения.
- BoxStyle — задает прорисовку ограничительного параллелепипеда.
- Background — задает цвет фона.
- ClipFill — определяет, как должны выводиться отсекаемые части поверхности.
- ColorFunction — определяет функцию, используемую для функциональной окраски.
- ColorOutput — задает тип производимого цветового вывода.
- Def aultFont — возвращает шрифт по умолчанию для текста в графике.
- DefaultColor — задает цвет по умолчанию для линий, точек и т. д.
- $DisplayFunction — задает значение по умолчанию для опции Display-Function в графических функциях.
- DisplayFunction — определяет функцию, которая применяется к графическим и звуковым примитивам для их отображения.
- Epilog — опция для графических функций, дающая список графических примитивов, которые должны воспроизводиться после воспроизведения главной части графики.
- FaceGrids — опция для функций трехмерной графики; устанавливает вывод линий сетки на гранях (лицевых сторонах) ограничительного параллелепипеда.
- HiddenSurf асе — определяет, нужно или нет удалять невидимые линии каркаса.
- Lighting — указывает, следует ли моделировать освещение в трехмерных изображениях.
- LightSources — опция для Graphics3D и родственных функций, которая устанавливает возможности (свойства) точечных источников света для моделируемого освещения.
- Mesh — указывает, следует ли прорисовывать явно заданную х-у-сетку.
- MeshRange — устанавливает диапазон (область изменения) х- и y-координат, которые соответствуют массиву заданных величин z.
- MeshStyle — задает стиль вывода линий сетки.
- SphericalRegion — указывает, следует ли конечный образ масштабировать так, чтобы сфера, рисуемая вокруг трехмерного ограничительного параллеле-пипеда, вписывалась в область отображения.
- Polygonlntersections — опция для Graphics3D, которая определяет, следует ли пересекающиеся многоугольники оставлять без изменения.
- Prolog — опция для графических функций, дающая список графических примитивов, которые визуализируются до вывода главной части графики.
- RenderAll — опция для Graphics3D, которая указывает, должен ли код PostScript генерироваться для всех многоугольников (включая невидимые).
- Shading — опция для Surf aceGraphics, указывающая, следует ли выполнять затенение поверхностей.
- ToColor [color, form] — превращает color в form; если form представляет собой функцию GrayLevel, RGBColor или CMYKColor, то color превращается в нее. В противном случае вычисляется form [color] — ожидается, что результат будет допустимой цветовой директивой.
- ViewCenter — задает масштабные координаты точки, оказывающейся в центре области отображения в окончательном графике.
- Viewpoint — меняет точку пространства, из которой рассматривается объект.
- ViewVertical — устанавливает, какое направление в относительных координатах должно быть вертикальным в окончательном образе.
Дополнительные директивы и функции трехмерной графики
- CMYKColor [cyan, magenta, yellow, black] — устанавливает составляющие цвета.
- EdgeForm [g] — указывает, что грани многоугольников должны быть нарисованы с применением графической директивы или списка директив.
- FaceForm [gf, gb] — указывает, что передние грани (лицевые поверхности) многоугольников должны выводиться с применением графического примитива gf, a задние грани (невидимые поверхности) — посредством gb.
- FullAxes [graphics] — возвращает опции осей графического объекта.
- FullGraphics [g] — берет графический объект и производит новый, в котором объекты, определяемые графическими опциями, даются как явные (точные) списки графических примитивов.
- FullOptions [expr] — возвращает полные установки опций, которые явно определены в выражении типа графического объекта.
- Hue [h] — указывает, что графические объекты, которые последуют, должны будут по возможности отображаться в цвете h.
- Hue [h, s, b] — определяет цвета в значениях оттенка h, насыщенности s и яркости b.
- LineForm[g] — устанавливает, что вывод линий следует выполнять с применением графической директивы g или списка графических директив g.
- PointForm [g] — указывает, что вывод точек следует выполнять с применением графической директивы g.
- PointSize[r] — указывает, что точки при последующем выводе должны изображаться по возможности в виде кругов радиусом г (доля от общей ширины графика).
- RGBColor [red, green, blue] — указывает, что последующие графические объекты должны отображаться заданной совокупностью цветов. Значения red (красный), green (зеленый) и blue (синий) указываются в относительных единицах — от 0 до 1.
- SurfaceColor [dcol] — устанавливает, что последующие многоугольники должны действовать как рассеивающие (диффузные) отражатели света с заданным цветом dcol.
- SurfaceColor [dcol, scol]—указывает, что в последующих многоугольниках должен содержаться компонент зеркального отражения с цветом, заданным scol.
- SurfaceColor [dcol, scol, n] — указывает, что отражение должно происходить с показателем зеркального отражения п.
- Cuboid [ {xmin, ymin, zmin} ] — представляет единичный куб, ориентированный параллельно осям.
- CellArray [ { {all, a12,...},...}] — представляет прямоугольный массив элементов яркости.
- Cuboid [ {xmin, ymin, zmin}, {xmax, ymax, zmax}] — представляет прямоугольный параллелепипед, заданный координатами противоположных вершин.
- PostScript ["string1", "string2",...] — графический примитив, задающий построение графика по кодам языка PostScript.
- SurfaceGraphics [array, shades] — представляет поверхность, части которой затеняются согласно массиву shades.
- SurfaceGraphics [array] — представляет трехмерный график поверхности, для которого значения высоты каждой точки на сетке заданы элементами массива.
- SurfaceGraphics [array, shades] — представляет поверхность, части которой затеняются согласно массиву shades.
- SurfaceGraphics [array] — представляет трехмерный график поверхности, для которого значения высоты каждой точки на сетке заданы элементами массива.
6. К уроку 9
К уроку 9
Дополнительные функции для работы с выражениями
- Catch [expr] — возвращает аргумент первого Throw, генерируемого при вычислении ехрr.
- Check!;expr, failexpr] — вычисляет ехрг и возвращает его результат, если только в процессе вычислений не вырабатывались сообщения, иначе вычисляет и возвращает failexpr.
- Check[expr, failexpr, s1: :t1, s2 : :t2,...] — выполняет контроль только для указанных сообщений.
- CheckAbort [expr, failexpr] — вычисляет expr, возвращая failexpr в случае прерывания.
- Coefficient [expr, form] — возвращает коэффициент перед form в полиномиальном выражении expr.
- Coefficient [expr, form, n] — возвращает коэффициент перед f о гт л п в выражении expr.
- CompoundExpression — применяется в виде exprl; expr2;... и вычисляет expri по очереди, возвращая последнее как результат . .
- Edit [expr__] — предоставляет возможность редактирования выражения expr.
- Exponent [expr, form] — возвращает максимальную степень, с которой form присутствует в expr.
- Exponent [expr, form, h]— применяет h к множеству показателей степеней (экспонент), с которыми form обнаруживается в выражении expr.
- FlattenAt [expr, {i, j,...}] — выравнивает часть выражения expr на позиции {i, j ,...}.
- FlattenAt [expr, {{il, jl,...}, {i2, j 2,...},...}]—выравнивает части выражения expr в нескольких позициях.
- HeldPart [expr, pos] — извлекает (удаляет) часть или несколько частей, указанных при помощи pos, и помещает их в Hold.
- Hold [expr] — содержит expr в невычисленном виде.
- HoldFormfexpr] — выводит выражение expr, сохраняя при этом его в невычисленной форме.
- LeafCount [expr] — возвращает общее (полное) число неделимых подвыражений в expr.
- Length [expr] — возвращает число элементов в expr.
- Level [expr, levelspec] — возвращает список всех подвыражений выражения expr на уровнях, указанных параметром levelspec.
- Level [expr, levelspec, f ]—относит f к списку подвыражений.
- Literal [expr] — является эквивалентом expr в смысле совпадения формы, но содержит expr в непреобразованном виде.
- LogicalExpand[expr] — выполняет расширение выражений, содержащих логические связи, такие как & & и | |.
- Map At [f, expr, n] — применяет f к элементу на позиции n в выражении expr. Если n отрицательно, позиция отсчитывается с конца.
- MapAt[f, expr, {i, j,...}] — применяет f к частям expr на позиции {i, j,...}.
- MapAt[f, expr, {{il, jl,...}, {12, j2,...},...}]— применяет f к частям expr в ряде позиций.
- Maplndexed [f, expr] — применяет f к элементам ехрг, возвращая спецификацию части каждого элемента в качестве второго аргумента в f.
- Maplndexed [f, expr, levspec] — применяет f ко всем частям ехрг на уровнях, указанных с помощью levspec.
- Order [expr1, expr2] — возвращает 1, если exprl предшествует ехрг2 в канонической последовательности, и дает -1, если exprl стоит после ехрг2 в каноническом порядке. Результатом будет 0, если exprl тождественно ехрг2.
- Postfix[f[expr]] — дает вывод функции f [ехрг], заданной по умолчанию в постфиксной форме: expr // f.
- Postf ix [f [expr] , h] — дает вывод в виде exprh.
- Prepend[expr, elem] — возвращает ехрг, к которому предварительно добавлен el em.
- Print [exprl, expr2,...] — выводит на экран дисплея выражения expri и затем дает перевод строки. Может использоваться для создания диалога.
- Return [ехрr] — возвращает из функции величину ехрг.
- Run[expr1, expr2,...] — создает выходную форму выражений expri, разделенных пробелами, и выполняет ее как внешнюю команду операционной системы.
- RunThrough ["command", expr] — выполняет внешнюю команду, передавая ей в качестве аргумента результат вычисления ехрг, а затем интерпретирует вывод, производимый командой, и возвращает его в качестве результата.
- Scan [f, expr] — вычисляет f, применяемую к каждому элементу ехрг по очереди.
- Scan[f, expr, levelspec] — применяет f к частям выражения ехрг, указанным с помощью levelspec.
- SequenceForm[exprl, expr2,...] — выводит в виде текстовой конкатенации (объединения) печатные формы выражений expri.
- SetAccuracy[ехрг, n] — дает вариант ехрг, в котором все числа представлены с п цифр после десятичной точки.
- SetPrecision [ехрг, n] — вырабатывает вариант ехрг, в котором все числа установлены с точностью представления п значащих цифр.
- Share [expr] — меняет способ внутреннего хранения выражения ехрг, что минимизирует объем используемой памяти.
- Through [expr, h] — выполняет преобразование всюду, где h появляется в заголовке выражения ехрг.
- Together [ехрr] — приводит члены суммы к общему знаменателю и сокращает множители в полученном результате.
- Variables [ехрr] — возвращает список всех независимых переменных в выражении.
- With[{x = х0, у = у0,...}, ехрг] — указывает, что в случае обнаружения в выражении ехрг символов х, у, ... они должны быть заменены на х0, у0 и т. д.
- Write [channel, exprl, expr2,...] — записывает в указанный выходной канал channel последовательно (один за другим) выражения expri, завершаемые переводом строки.
- WriteString [channel, exprl, expr2,...]—превращает expri в строки символов, а затем последовательно записывает их в указанный выходной канал channel.
7. К уроку 10
К уроку 10
Функции трассировки и отладки программ
- Off [s] — отключает сообщения трассировки, связанные с символом s.
- Off [m1, m2,...] — отключает несколько сообщений.
- Off[ ] — отключает все сообщения трассировки.
- On [s] — включает трассировку для символа s.
- On [m1, m2,...] — включает ряд сообщений.
- On [ ] — включает трассировку для всех символов.
- Trace [ехрг] — генерирует список всех выражений, используемых при вычислении ехрг.
- Trace[expr, form] —включает в список только те выражения, которые сопоставимы с form.
- Trace [ехрr, s] — включает в список все вычисления, которые используют правила преобразования, связанные с символом s.
- TraceDialog [ехрг] — инициирует диалог для каждого выражения, используемого при вычислении ехрr (на каждом шаге продолжение диалога осуществляется исполнением команды Return []).
- TraceDialog [expr, form] — инициирует диалог только для выражений, сопоставимых с form.
- TraceDialog [expr, s] — инициирует диалоги только для выражений, при вычислении которых используются правила преобразований, связанные с символом S.
- TraceLevel [ ] — всякий раз, когда вычисляется Trace [ ] или родственная функция, TraceLevel [ ] возвращает тот уровень ее выхода, который в данный момент заполняется.
- TracePrint [ехрr] — выводит (печатает) все выражения, используемые в процессе вычисления ехрг.
- TracePrint [expr, form] — включает в операцию только те выражения, которые совпадают с form.
- TracePrint [expr, s] — включает в вывод все вычисления, которые применяют правила преобразования, связанные с указанным символом s.
- TraceScan[f, expr] — применяет f ко всем выражениям, используемым при вычислении ехрr,
- TraceScan[f, expr, form] — включает только те выражения, которые сопоставимы с form.
- TraceScan [f, expr, s] — включает все вычисления, которые применяют правила преобразования, связанные с символом s.
- TraceScan [f, expr, form, fp] — применяет f до вычисления, a fp после вычисления к выражениям, используемым при вычислении ехрr.
С этими функциями могут использоваться следующие основные опции и относящиеся к ним значения:
- TraceForward — указывает, следует ли включать в вычислительную цепочку более поздние (последующие) выражения, которые содержат искомую форму шаблона.
- Tracelnternal — имея значения True или False, указывает, следует ли трассировать вычисления выражений, генерируемые внутри Mathematica. Вспомогательная установка Automatic трассирует выбранное множество внутренний вычислений, включая сообщения и установки или отмены установок видимых символов.
- $TraceOff — является значением активной в данный момент опции Trace-Off, относящейся к Trace и родственным функциям. В течение трассировки она может быть переустановлена для изменения множества выражений, в которых трассировка заблокирована.
- TraceOf f — отключает трассировку.
- $ТгасеОn — является значением активной в данный момент опции ТгасеОn, относящейся к функции Trace и родственным функциям. Она может быть переустановлена в процессе трассировки для изменения множества выражений, в которых трассировка произойдет.
- ТгасеОп — включает трассировку.
- TraceOriginal — указывает, следует ли проверять форму каждого выражения перед вычислением его заголовка и аргументов.
- $TracePattern — активный в данный момент параметр-шаблон, относящийся к Trace и родственным функциям. Он может быть переустановлен в процессе трассировки для изменения множества записываемых или выводимых выражений.
- $TracePostAction — активный в данный момент четвертый параметр функции TraceScan (или эквивалент в родственных функциях). Он может быть переустановлен во время трассировки для изменения операции, применяемой после того, как перехваченные выражения вычислены.
- $TracePreAction — активный в данный момент первый аргумент функции TraceScan (или эквивалент в родственных функциях). Он может быть переустановлен во время трассировки для изменения действия, предпринимаемого перед тем, как перехваченные выражения будут вычислены.
8. К уроку 11
К уроку 11
Функции общей рациональной интерполяции
- GeneralRationalInterpolation[{f x , f y }, {t,m, k}, {t 1 , t 2 ,..., t n+A+1 } ] -дает рациональную интерполяцию параметрически заданной функции для списка значений параметра t.
- GeneralRationallnterpolation[{f x , f y },{t,m,k}, {t,tmin,tmax}] — дает рациональную интерполяцию параметрически заданной функции при автоматическом выборе значений параметра t.
С помощью других функций можно осуществить общую минимаксную интерполяцию, обычно обеспечивающую минимальную погрешность:
- GeneralMiniMaxInterpolation[{± х , f y ],{t, (tmin,tmax},m,k},x] — дает рациональную минимаксную интерполяцию параметрически заданной функции с параметром t.
- GeneralMiniMaxInterpolation[{f x , f },approx,(t,(tmin,tmax},m,k},x] — дает рациональную минимаксную интерполяцию параметрически заданной функции для списка значений параметра t с указанием метода аппроксимации арргох.
- GeneralMiniMaxInterpolation[{f x , f ,g},{t, (tmin,tmax},m,k},x] — дает рациональную минимаксную интерполяцию параметрически заданной функции при автоматическом выборе значений параметра t, используя вычисление ошибки с помощью функции g(t) .
Функции создания анимационной графики
- MoviePlot[f[x,t],{x,xmin,xmax},{t,tmin,tmax}] — дает анимацию графика Plot[f[x,t],{x,xmin,xmax}].
- MoviePlot3D[f[x,y,t],{x,xmin,xmax},{y,ymin,ymax},{t,tmin,tmax}] — дает анимацию трехмерного графика.
- MovieDensityPlot[f[x,y,t],{x,xmin,xmax},{y,ymin,ymax},{t,tmin, tmax} ] — дает анимацию трехмерного графика плотности.
- MovieContourPlot[f[x,у,t],{x,xmin,xmax}, {y, ymin,ymax},{t, tmin, tmax} ] — дает анимацию контурного графика.
- MovieParamenticPlot[{f[s,t},{g[s,t)}],{s,smin,smax},{t,tmin, tmax} ] — дает анимацию параметрического графика.
- SpinShow [graphics] — дает вращение графического объекта. Эта функция имеет ряд опций, которые можно просмотреть командой Options [SpinShow].
Функции для построения графиков в логарифмическом масштабе
- LogPlotff, {x,xmin,xmax} ] — строит линейно-логарифмический график f(x) при изменении х от xmin до хтах.
- LogLinearPlot [f, {х, xmin, хтах} ] — строит логарифмически-линейный график f(x).
- LogLogPlot [f, {х, xmin, xmax} ] — строит логарифмический (по обеим осям) график f(x).
- LogListPlot [{{xl, yl}, {х2, у2},...}] — строит линейно-логарифмический график точек.
- LogLinearListPlot [ {{xl, yl}, {х2, у2},...}] — строит логарифмически-линейный график точек.
- LogLogListPlot [{{xl, у 1},{х2, у2},...}] — строит логарифмический (по обеим осям) график точек.
Функции LogListPlot [ {yl, y2,...}], LogLinearListPlot [{ yl, y2,...}] и LogLogListPlot [ {yl, y2,...} ] дают те же построения, что и предшествующие функции, с той разницей, что ординаты абдцисс точек х равны 1, 2, 3 и т. д. Это иногда упрощает задание графиков.





































































































































































































































































































































































