Главное меню
Вы здесь
11. Анализ попадания точек внутрь полигона
Анализ попадания точек внутрь полигона
Функция Inpolygon используется для анализа того, попадают ли заданные точки внутрь полигона:
-
IN=inpolygon(X,Y.xv.yv) — возвращает матрицу IN того же размера, что X и Y. Каждый элемент матрицы IN принимает одно из значений — 1, 0.5 или 0 — в зависимости от того, находится ли точка с координатами (X(p,q),Y(p,q)) внутри полигона, вершины которого определяются векторами xv и yv:
-
IN(p,q) = 1 — если то.чка (X(p.q) ,Y(p,q)) лежит внутри полигона;
-
IN(p,q) = 0.5 — если точка (X(p,q) ,Y(p,q)) лежит на границе полигона;
-
IN(p.q) = 0 — если точка (X(p.q),Y(p,q)) лежит вне полигона. Пример:
-
» L = linspace(0.2*pi,8);
» yv = sin(L)';
» xv= cos(L)';
» x= randn(100,1); у = randn(100,1);
» IN = inpolygon(x,y,xv,yv);
» plot(xv,yv,'k',x(IN),y(IN),'r*',x(~IN),y(~IN),'b*')
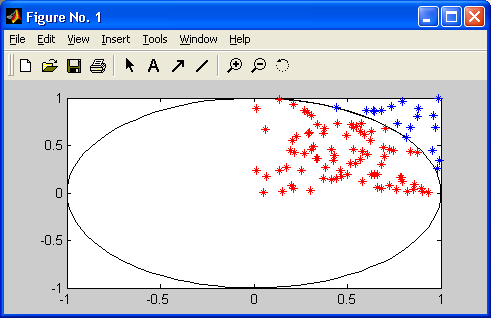
Построенные в этом примере массив точек и полигон представлены на рис. 17.4.
Рис. 17.4. Пример применения функции inpolygon
Точки, попавшие внутрь полигона, обозначены символом звездочки, а точки вне полигона обозначены кружками.