7. Создание массивов со случайными элементами

Создание массивов со случайными элементами

• р = randperm(n) — возвращает случайные перестановки целых чисел 1:n в векторе-строке. Пример:

» randperm(6) 

ans =

243651

Функция rand генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке (0, 1):

• rand(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;

•  rand(m.n) или rand([m п]) — возвращают матрицу размера mxn;

• rand(m.n,p....) или rand([m n р...]) — возвращает многомерный массив;

• rand(size(A)) — возвращает массив того же размера и размерности, что и А, с элементами, распределенными по равномерному закону;

• rand (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет равномерный закон распределения;

• rand(' state') — возвращает вектор с 35 элементами, содержащий текущее состояние генератора случайных чисел с равномерным распределением. Для изменения состояния генератора можно применять следующие формы этой функции:

  • rand('state' .s) — устанавливает состояние в s;

  • rand( 'state' ,0) — сбрасывает генератор в начальное состояние;

  • rand( 'state'. j) — для целых j, устанавливает генератор в j-е состояние;

  • rand( 'state' ,sum(100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.

Пример: 

» Y=rand(4,3)

Y=

0.9501     0.8913     0.8214

0.2311     0.7621     0.4447

0.6068     0.4565     0.6154

0.4860     0.0185     0.7919

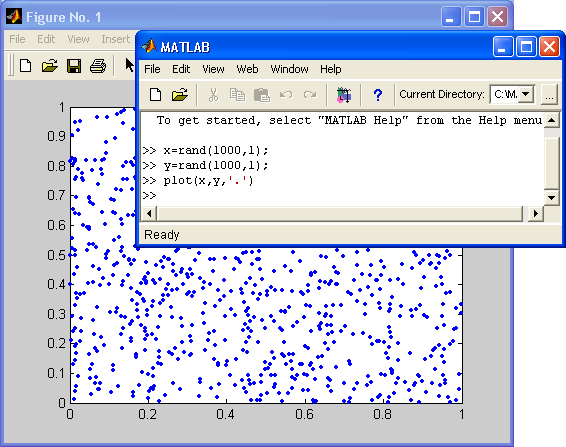
Проверить равномерность распределения случайных чисел можно, построив большое число точек на плоскости со случайными координатами. Это делается с помощью следующих команд:

» X=rand(1000,1);

 » Y=rand(1000,1);

 » plot(X,Y,'.')

Полученный при этом график показан на рис. 10.1. Нетрудно заметить, что точки довольно равномерно распределены на плоскости, так что нет оснований не доверять заданному закону распределения координат точек.

Рис. 10.1. Случайные точки с равномерным распределением координат на плоскости

Функция randn генерирует массив со случайными элементами, распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 1:

• randn(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;

•  randn(m.n) или randn([m n]) — возвращают матрицу размера mxn;

• randn(m,n,p,...) или randn([m n р...]) — возвращает массив с элементами, значения которых распределены по нормальному закону;

• randn(size(A)) — возвращает массив того же размера, что и А, с элементами, распределенными по нормальному закону;

• randn (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет нормальное распределение;

• randn( 'state') — возвращает двухэлементный вектор, включающий текущее состояние нормального генератора. Для изменения состояния генератора можно применять следующие формы этой функции:
  

  • randn('state',s) — устанавливает состояние в s;

  • randn('state' ,0) — сбрасывает генератор в начальное состояние;

  • randn('state', j) — для целых j устанавливает генератор в J-e состояние;

  • randn('state', sum( 100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.

Пример:

>>Y=randn(4.3)

Y =

-0.4326    -1.1465     0.3273

-1.6656     1.1909     0.1746 

0.1253     1.1892     -0.1867 

0.2877     -0.0376     0.7258

Проверить распределение случайных чисел по нормальному закону можно, построив гистограмму распределения большого количества чисел. Например, следующие команды

» Y=randn(10000,1); 

» hist(Y,100)

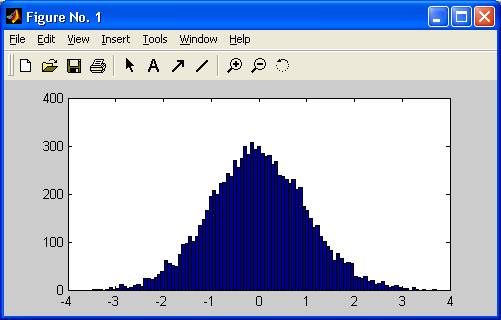
строят гистограмму (рис. 10.2) из 100 столбцов для 10 000 случайных чисел с нормальным распределением.

Рис. 10.2. Гистограмма для 10 000 нормально распределенных чисел в 100 интервалах

Из рисунка видно, что огибающая гистограммы действительно близка к нормальному закону распределения.

В пакете расширения Statistics Toolbox можно найти множество статистических функций, в том числе для генерации случайных чисел с различными законами распределения и определения их статистических характеристик.