Главное меню
Вы здесь
14. Написание программ в системе Mathematica
Язык программирования высокого уровня системы Mathematica позволяет Вам писать сложные программы быстрее, чем когда-либо прежде.
Даже состоящая всего из одной строки программа системы Mathematica может выполнять сложные операции.
Эта программа моделирует одномерное случайное блуждание.
RandomWalk[n_]:=NestList[(#+(-1) ^Random[Integer])&,0,n]
|
График, демонстрирующий первые 200 шагов случайного блуждания.
ListPlot[RandomWalk[200],PlotJoined->True];
|
Ясность программ системы Mathematica позволяет легко модифицировать их для более общих случаев.
Эта программа моделирует случайное блуждание в пространстве размерности d.
RandomWalk[n_,d_]:=NestList[(#+(-1) ^Table[Random[Integer],{d}])&,Table[0,{d}],n] |
График трехмерного случайного блуждания.
Show[Graphics3D[Line[RandomWalk[1000,3]]]];
|
Богатство языка программирования системы Mathematica делает простой реализацию сложнейших алгоритмов.
Это программа для моделирования одного шага эволюции клеточной системы.
LifeStep[a_List] := MapThread[If[(#1 == 1 && #2 == 4) || #2 == 3, 1, 0]&, {a, Sum[RotateLeft[a, {i, j}], {i, -1, 1}, {j, -1, 1}]}, 2] |
А это пример оптимизированной программы, которая оперирует со списками живых клеток.
LifeStep[list_] := With[{u=Split[Sort[Flatten[Outer[Plus,list,N9,1] ,1]]]}, Union[Cases[u,{x_,_,_}->x], Intersection[Cases [u,{x_,_,_,_}->x],list]]]N9=Flatten[Array[List,{3, 3},-1], 1] ; |
Система Mathematica позволяет легко создавать программы, состоящие из нескольких компонент.
Здесь приведены составляющие программы, моделирующей поведение клеточных систем
CenterList[n_Integer]:=ReplacePart[Table[0, {n}], 1, Ceiling[n/2]]ElementaryRule [num_Integer] := IntegerDigits[num, 2, 8] CAStep[rule_List, a_List] :=rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]] CAEvolveList[rule_List, init_List, t_Integer] :=NestList[CAStep[rule, #]&, init, t] CAGraphics[history_List] :=Graphics[Raster[1 - Reverse[history]], AspectRatio -> Automatic] |
Пример работы программы.
Show[CAGraphics[ CAEvolveList[ElementaryRule[30], CenterList[101], 50]] ];
|
Mathematica имеет компилятор для оптимизации программ, которые работают со списками и числами.
CAStep = Compile[{{rule, _Integer, 1}, {a, _Integer,1}}, rule[[ 8 - (RotateLeft[a] + 2 (a + 2 RotateRight[a])) ]]] |
Программы системы Mathematica зачастую являются прямой трансляцией теоретических положений справочной литературы.
Здесь вводятся необходимые определения для расчета импеданса электрической цепи.
Использование данных выше определений.
![[Graphics:wrgr21.gif]](/files/images/soft/book14/programs//wrgr21.gif) |
Пример электрической схемы, заданной при помощи символической спецификации.
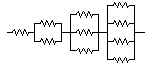 |
Программы в системе Mathematica предоставляют беспрецедентно ясные способы записи алгоритма.
Обе эти программы аппроксимируют Золотое Сечение с точностью до k знаков.
{1.6180339887498948482,1.6180339887498948482, 1.6180339887498948482} |
В программах системы Mathematica возможно уникальное соединение математической и вычислительной систем обозначений.
Эта программа соответствует недавно открытой приближенной формуле для нахождения количества простых чисел, меньших заданного числа.
Сравнение приближенного результата с точным значением, полученным с помощью встроенной функции PrimePi.
{168, 168} |
Программа в системе Mathematica может одновременно состоять из блоков, выполняющих численные, символические и графические операции. Ниже в качестве примера приведена короткая программа для работы с одной сложной квантовой моделью.
Это программа, отвечающая модели Kohmoto для спектра энергии квантовой частицы в одномерном квазипериодическом потенциале.
FareySequence[q_]:=Apply[Union,Array[Range[#-1]/#&,q]]
|
Пример работы программы.
Show[Graphics[SpectrumData /@ FareySequence[20]]] -Graphics- |
