Главное меню
Вы здесь
8. Специальные числа и полиномы
Специальные числа и полиномы
Для вычисления специальных чисел и полиномов служит следующая группа функций:
- BernoulliB [n] — n-е число Бернулли;
- BernoulliB [n, х] — полином Бернулли n-й степени;
- Binomial [n, m] — биномиальный коэффициент;
- Cyclotomic [n, х] — циклотомический полином порядка п по переменной х;
- EulerE[n] — n-е число Эйлера;
- EulerE[n, х] — n-й полином Эйлера;
- EulerPhi [n] — эйлерова функция сумм ф(n) — количество положительных целых чисел, не превосходящих п и взаимно простых с и;
- Fibonacci [n] — n-е число Фибоначчи;
- Fibonacci [n, х] — полином Фибоначчи F n (x);
- Multinomial [n1, n2, . . . ] — мультиномиальный коэффициент (n! + n2 + . . .) !/(n1! n2! ...);
- NBernoulliB [n] — численное значение n-го числа Бернулли;
- NBernoulliB [n, d] — n-е число Бернулли с n?-цифровой точностью представления;
- Pochhammer [а, n] — символ Похгамера;
- StirlingSl [n, m] — число Стирлинга первого рода;
- StirlingS2 [n, m] — число Стирлинга второго рода.
Ниже представлены примеры вычисления данных функций.
| Ввод (In) | Вывод (Out) |
| N [BernoulliB [2]] | 0.166667 |
| BernoulliB [2, 0.1] | 0.0766667 |
| Binomial [6, 4] | 15 |
| Cyclotomic [ 5, х] | 1 + x + x 2 + x 3 + x 4 |
| Cyclotomic [5,0.2] | 1.2496 |
| EulerE[2] | -1 |
| EulerE[2,0.1] | -0.09 |
| EulerPhi [2] | 1 |
| Fibonacci [10] | 55 |
| Fibonacci [ 6 , x] | 3 x + 4 x 3 + x 5 |
| Pochhammer [1,3] | 6 |
| StirlingSl [8, 4] | 6769 |
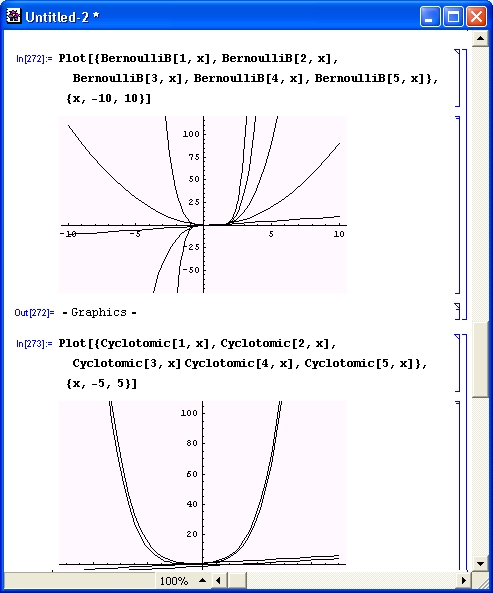
На рис. 6.12 показаны графики полиномов Бернулли и циклотомического полинома различных порядков.
Рис. 6.12. Графики полиномов Бернулли (сверху) и циклотомических полиномов (снизу)
Обратите внимание на то, что здесь использована функция Plot, модифицированная пакетом расширения plot.m, который будет описан в уроке 10. Эта функция позволяет автоматически строить графики ряда функций с линиями разного стиля, что облегчает их распознавание.
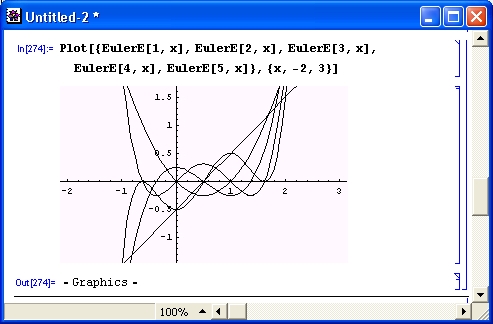
На рис. 6.13 представлены графики полиномов Эйлера EulerE разного порядка п.
Помимо описанных выше, в ядро системы входит также ряд других, менее распространенных функций. Они описаны в приложении.
По числу встроенных специальных математических функций Mathemafica заметно превосходит другие системы компьютерной математики. При этом все такие функции могут участвовать в символьных преобразованиях. Это делает системы Mathematica предпочтительными при решении задач, в которых часто встречаются специальные математические функции. В то же время надо отметить, что многие специальные функции системами Mathemafica вычисляются только для целого порядка.
Рис. 6.13. Графики полиномов Эйлера разного порядка