Главное меню
Вы здесь
2. Основные классы данных
Основные классы данных
Mathematica оперирует с тремя основными классами данных:
- численными данными, представляющими числа различного вида;
- символьными данными, представляющими символы, тексты и математические выражения (формулы);
- списками — данными в виде множества однотипных или разнотипных данных.
Каждый из этих классов данных в свою очередь имеет ряд специальных, более частных типов данных. На них мы остановимся более подробно.
Двоичные числа, биты и байты
Минимальной единицей информации в компьютерной технике является двоичная единица — бит. Она имеет представление в виде 0 или 1, удобное для реализации простейшими электронными схемами с двумя состояниями электрического равновесия (например, триггерами или иными ячейками памяти). Многоразрядные двоичные числа представляют собой набор цифр 0 и 1, например, 100110 или 111001. Каждый старший разряд относительно предыдущего имеет весовой коэффициент, равный 2.
Именно с битами работает микропроцессор на нижнем уровне операций. Однако бит — слишком мелкая единица, не очень удобная в обращении. К тому же мы привыкли к куда более удобным и наглядным для нас элементам информации, таким как буквы, цифры, знаки арифметических операций, спецзнаки и символы псевдографики. В принципе, набор этих знаков, минимально необходимый для представления обычной текстовой и цифровой информации, содержит до 2 8 = 256 элементов. Каждый из них в компьютере представляется кодом от 0 до 255. Для задания таких кодов достаточно 8 бит (2^8=256), которые и образуют наиболее распространенную единицу представления информации — байт. 1024 байта образуют килобайт (Кбайт), 1024 Кбайт дают 1 Мбайт (мегабайт) и т. д.
Широко применяется общеизвестный стандарт кодирования текстовой информации ASCII (American Standard Code for Information Interchange).
Десятичные числа
К наиболее известным типам данных в математике относятся привычные нам десятичные числа (DECIMAL). Каждый разряд таких чисел имеет представление, заданное одной из арабских цифр — 0, 1, 2,..., 9. Весовой коэффициент старшего разряда относительно предшествующего равен 10. Количество цифр, представляющих число, может быть, в принципе, любым. Десятичные числа относятся к следующим основным типам.
| Обозначение | Тип чисел | Примеры задания | |
| Integer | Целочисленные | 123 | -345 |
| Rational | Рациональные | 123/567 | -23/67 |
| Real | Вещественные | 123. | -123.45610 ^ 6 |
| Complex | Комплексные | -3.5 + 0. | 56 I |
Десятичные числа наиболее распространены в научно-технических расчетах.
Целые числа
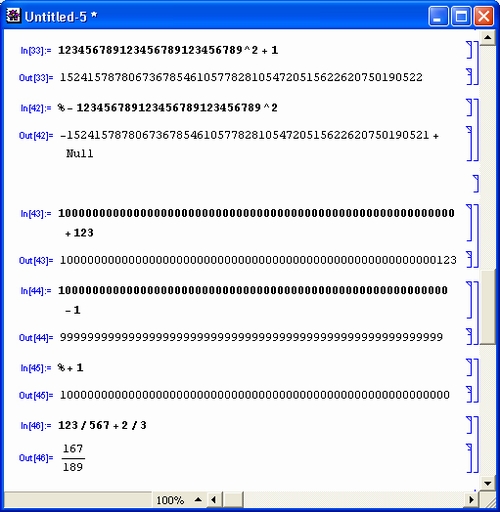
Целочисленные данные (Integer) — это целые числа, например 1, 2 или 123, которые представляются системой без погрешности и ограничения разрядности. Более того, арифметические операции над целыми числами система выполняет также без погрешностей и без ограничения числа цифр (рис. 3.1).
Рис. 3.1. Операции с целыми числами
Количество цифр, представляющих большое целое число, ограничено лишь его значением, но не какими-либо фиксированными форматами. Рациональные данные задаются отношением целых чисел, например 123/567, и также представляют результат точно. Поэтому система при символьных и численных расчетах всегда старается выдать результат в виде целых или рациональных чисел, там где это возможно:
1000000/3000000
1/3
(124-1)/(455+1)
41/152
Фактически целые числа произвольной разрядности в системах символьной математики представляются списками отдельных цифр. Особая организация списков повышает компактность представления больших целых чисел. Характерным примером работы с целыми числами большой разрядности является вычисление факториала n!=1*2*3*. . . *n. Примеры его вычисления уже приводились (см. рис. 1.16).
Числа с произвольным основанием
Для вычисления чисел с произвольным основанием используется конструкция
Основание^^Число
Число должно быть записано по правилам записи чисел с соответствующим основанием. Если основание больше 10, для обозначения значений чисел используются буквы от а до z. Наиболее известными из чисел с основанием системы счисления, превышающим 10, являются шестнадцатеричные числа (HEX — от слова hexagonal). Разряды таких чисел могут иметь следующие значения:
HEX 0123456789abCdef
DECIMAL 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Каждый более старший разряд имеет весовой коэффициент относительно предыдущего разряда, равный 16.
Примеры задания шестнадцатеричного и двоичного чисел:
16^^123abcde
305839326
2^^1010111
87
Для представления чисел с произвольным основанием n (до 32) используется функция BaseForm[expr, n], которая возвращает выражение ехрг в форме числа с основанием n, которое указывается как подстрочный индекс.
Примеры использования функции BaseForm:
BaseForm[87,2]
10101112
BaseForm[305839326,16]
123abcde16
В дальнейшем мы будем использовать только десятичные числа.
Вещественные числа
Численные данные могут быть представлены также десятичными вещественными числами, которые могут иметь различную форму, например 123.456, 1.23456 10^2,12345.6 10^-2 и т. д. В общем случае они содержат мантиссу с целой и дробной частями и порядок, вводимый как степень числа 10. Как правило, вещественные числа в системах символьной математики могут иметь мантиссу с любым, но конечным числом знаков. Пробел между мантиссой и порядком эквивалентен знаку умножения *:
23.456*10^100
2.345бх10^101
10^-100
1/
100000000000000000000000000000
0000000000000000000000000000
0000000000000000000000000000000000000000000
10.^-100
1.x 10^-100
Как принято в большинстве языков программирования, целая часть мантиссы отделяется от дробной части точкой, а не запятой.
Mathematica производит операции с числами изначально как с целыми. Однако установка значка разделительной точки означает, что число должно рассматриваться как вещественное. Например, 1 — целое число, но 1. — уже вещественное число. Для представления выражения ехрг в форме вещественного числа используется функция N [ехрг] или N [ехрг, число_цифр_результата].
Примеры:
1/3
1/3
1./3 .
0.333333
N[1/3]
0.333333
N[2*Pi,50]
6.283185307179586476925286766559005768394338
Вещественные числа всегда имеют некоторую погрешность представления результатов из-за неизбежного округления и существования так называемого машинного нуля — наименьшего числа, которое воспринимается как нуль. В терминах системы Mathematica говорят о приближении числовых данных как об их аппроксимации, хотя в отечественной литературе под аппроксимацией чаще подразумевают описание некоторой зависимости между данными достаточно приближенной аналитической зависимостью.
Mathematica имеет две системные переменные, позволяющие вывести максимально и минимально возможные значения чисел, с которыми оперирует система:
$MaxMachineNumber
1.79769х10^308
$MinMachineNumber
2.22507х 10^-308
Обратите внимание на то, что функция N [ехрr, m] позволяет получить число с практическим любым числом цифр результата m. Разработчики последней версии Mathematica 4 утверждают, что это верно при количестве цифр результата до одного миллиона, что с лихвой удовлетворяет требованиям подавляющего большинства расчетов и вычислений.
Функции IntegerPart [x] и FractionalPart [x] обеспечивают возврат целой и дробной частей вещественного числа х:
N[Pi]
3.14159
IntegerPart[Pi]
3
FractionalPart[Pi]
-3.+ Л
N[FractionalPart[Pi]]
0.141593
Еще одна функция RealDigits [x] возвращает список реальных цифр результата и число цифр целой части х:
RealDigits[N[2*Pi]]
{{6, 2, 8, 3, 1, 8, 5, 3, 0, 7, 1, 7, 9, 5, 8, 6}, 1}
Есть и множество других функций для работы с вещественными числами. Они будут рассмотрены в дальнейшем. В Mathematica 4 функция RealDigits имеет расширенные формы, например RealDigits [x, b, len, n]. Для получения цифр мантиссы введены функции MantissaExponent [x] и MantissaExpo-nent[x,b].
Комплексные числа
Многие математические операции базируются на понятии комплексных чисел. Они задаются в форме
z=Re(z)+I*Im(z)
или
z=Re(z)+i Im (z)
где знак I (i) — мнимая единица (квадратный корень из -1), Re (z) — действительная часть комплексного числа, a Im (z) — мнимая часть комплексного числа. Пример задания комплексного числа:
2 + I3
или
2 + 3*I
Мнимая часть задается умножением ее значения на символ мнимой единицы I. При этом знак умножения * можно указывать явно или заменить его пробелом — в последнем случае комплексное число выглядит более естественным. Функции Re [ z ] и Im [ z ] выделяют, соответственно, действительную и мнимую части комплексного числа z. Это иллюстрируют следующие примеры:
Re[3+2*1]
3
Im[3+2 I]
2
Большинство операторов и функций системы Mathematica работают с комплексными числами. Разумеется, это расширяет сферу применения системы и позволяет решать с ее помощью различные специальные задачи — например, относящиеся к теории функций комплексного аргумента. Комплексные числа широко используются в практике электро- и радиотехнических расчетов на переменном токе.
Символьные данные в общем случае могут быть отдельными символами (например a, b,..., z), строками (strings) и математическими выражениями ехрг (от expression — выражение), представленными в символьном виде.
Символьные строки задаются цепочкой символов в кавычках, например "sssss". В них используются следующие управляющие символы для строчных объектов:
- \n— новая строка (line feed);
- \ t — табуляция.
Это иллюстрируется следующими примерами:
"Hello my friend!"
Hello my friend!
"Hello\nmy\nfriend!"
Hello
my
friend!
"Hello\tmy\tfriend!"
Hello my friend;
Следует помнить, что управляющие символы не печатаются принтером и не отображаются дисплеем, а лишь заставляют эти устройства вывода выполнять определенные действия. Mathematica имеет множество функций для работы со строками, которые будут описаны в дальнейшем.
Выражения в системе Mathematica обычно ассоциируются с математическими формулами, как показано в следующей таблице.
| Запись на языке Mathematica | Обычная математическая запись |
| 2*Sin[x] | 2*sin(x) |
| 2 Sin[x] | 2*sin(x) |
| (а +b^2 + с^З) / (3*d - 4*e) | (a + b 2 +с 3 )/(3d-4е) |
| sqrt(2) | Кореннь из 2 |
| Integrate [Sin [x] , х] | Интеграл sin(x) dx |
Для записи математических выражений используются как операторы, так и функции. Их особенности будут рассмотрены несколько позже. А пока сразу отметим некоторые тонкости синтаксиса системы, используемого при записи арифметических операций:
- знак умножения может быть заменен пробелом;
- встроенные функции начинаются с большой буквы и обычно повторяют свое общепринятое математическое обозначение (за исключением тех, в названии которых есть греческие буквы — они воспроизводятся латинскими буквами по звучанию соответствующих греческих букв);
- круглые скобки () используются для выделения частей выражений и задания последовательности их вычисления;
- параметры функций задаются в квадратных скобках [ ];
- фигурные скобки {} используются при задании списков.
Новые системы Mathematica 3/4 обладают обширными возможностями по заданию форматов записи математических выражений при их выводе на экран или принтер, а также при вводе с клавиатуры. Они будут рассмотрены в дальнейшем.
Наиболее общим видом сложных данных в системе являются списки (lists). Списки представляют собой совокупности однотипных или разнотипных данных, сгруппированных с помощью фигурных скобок:
- { 1 , 2 , 3 } — список из трех целых чисел;
- { а , b , с } — список из трех символьных данных;
- {1, а, x^ 2} — список из разнотипных данных;
- {{a,b},{c,d}} — список, эквивалентный матрице
a b
c d
- {х^2+у^2, 2*Sin [x] } — список из двух математических выражений.
Как видно из этих примеров, элементы списков размещаются в фигурных скобках — открывающей { и закрывающей } . Списки могут быть с вложениями из списков — так получаются многоуровневые списки (двухуровневый список дает матрицу). Позже свойства и возможности списков будут рассмотрены детально. С помощью списков представляются множественные данные — массивы.
В общем случае система Mathematica оперирует с объектами. Под ними подразумеваются математические выражения (ехрг), символы (symbols), строки из символов (strings), упомянутые выше числа различного типа, константы, переменные, графические и звуковые объекты и т. д.
Каждый объект характеризуется своим именем — идентификатором. Это имя должно быть уникальным, то есть единственным. Существуют следующие правила задания имен:
- sssss — имя объекта, заданного пользователем;
- Sssss — имя объекта, входящего в ядро системы;
- $Sssss — имя системного объекта.
Итак, все объекты (например функции), включенные в ядро, имеют имена (идентификаторы), начинающиеся с большой буквы (например Plus, Sin или Cos). Идентификаторы относящихся к системе объектов начинаются со знака $. Заданные пользователем объекты следует именовать строчными (малыми) буквами. Разумеется, под символами s...s подразумеваются любые буквы и цифры (но не специальные символы, такие как +, -, * и т. д.).
Объекты (чаще всего это функции), встроенные в систему, принято называть внутренними или встроенными. Объекты, которые создает пользователь (в том числе используя внутренние объекты), называют внешними объектами. К ним, в частности, относятся процедуры и функции, составляемые пользователем, которые детально рассматриваются в дальнейшем.
Функции, опции, атрибуты и директивы
К важному типу объектов принадлежат функции — объекты, имеющие имя и список параметров, возвращающие некоторое значение в ответ на обращение к ним по имени с указанием списка конкретных (фактических) значений параметров. В системах Mathematica 2/3/4 встроенные функции задаются в виде
И дентификатор_Функции [ol, о2, o3, ...]
где ol, о2, оЗ... — объекты (параметры, опции, математические выражения и т. д.). Список входных параметров задается необычно — в квадратных скобках. В числе входных параметров могут быть специальные объекты — опции. Они задаются в виде
Имя_опции->3начение_опции
Значением опции обычно является то или иное слово. Например, в функции построения графиков
Plot [sin[x] , {x, 0,20} ,Axes->None]
опция Axes->None указывает на то, что отменяется вывод координатных осей (Axes). Функция Options [name] выводит для функции с идентификатором name список всех возможных для нее опций. Некоторые функции, например Sin, могут вообще не иметь опций, другие, такие как Solve, могут иметь целый «букет» опций:
Options [Sin]
Options [Solve]
{InverseFunctions -> Automatic, MakeRules -> False,
Method -> 3, Mode -> Generic, Sort -> True,
VerifySolutions -> Automatic, WorkingPrecision -> 00}
В последнем случае характер возвращаемого функцией результата может сильно зависеть от значений опций. Назначение каждой опции мы рассмотрим в дальнейшем. В этой главе они нам пока не понадобятся.
Каждый объект может характеризоваться некоторой совокупностью своих свойств и признаков, называемых атрибутами. Функция Attributes [name] возвращает список всех атрибутов функции с именем name, например:
Attributes [Sin]
{bistable, NumericFunction, Protected}
Attributes [Solve]
{Protected}
Как видите, для функции синуса характерны три атрибута:
- bistable — указывает на применимость в списках и таблицах;
- NumericFunction — указывает на отношение к числовым функциям;
- Protected — указывает на то, что слово Sin защищено от какой-либо модификации.
Кроме того, в Mathematica 2/3/4 имеется понятие функций-директив. Эти функции не возвращают значений, а указывают, как в дальнейшем будут выполняться функции, работа которых зависит от директив. Синтаксис функций-директив тот же, что и у обычных функций.
Применение опций и директив делает аппарат функций более гибким и мощным, поскольку позволяет задавать те или иные свойства функций и условия их выполнения. Это особенно важно при использовании функций в задачах графики и символьной математики.
Константы являются типовыми объектами системы, несущими заранее предопределенное численное или символьное значение. Это значение не должно меняться по ходу вычисления документа. К численным константам относятся любые числа, непосредственно используемые в математических выражениях или программных объектах, например процедурах и функциях. Так, числа 1 и 2 в выражении 2*Sin [ 1 ] являются численными константами. Константы-числа не имеют идентификаторов. Идентификатором, в сущности, является само число. Его представление и хранится в памяти.
Имеется также ряд именованных констант, которые можно рассматривать как функции без аргумента, возвращающие заранее заданное значение. Имена констант (и других объектов, например функций и переменных) представляются их идентификаторами — непрерывной строкой символов, отождествляемой с именем. В системе Mathematica большинство идентификаторов имеют естественный математический смысл и начинаются с большой буквы. Например, Е — это основание натурального логарифма.
Используются следующие встроенные именованные константы:
- Complexlnf inity — комплексная бесконечность, которая представляет величину с бесконечным модулем и неопределенной комплексной фазой.
- Degree — число радиан в одном градусе, которое имеет числовое значение Pi/180.
- Е- основание натурального логарифма с приближенным числовым значением 2 . 71828....
- EulerGamma — постоянная Эйлера с числовым значением 0.577216....
- GoldenRatio — константа со значением (l+Sqrt[5] ) /2, определяющая деление отрезка по правилу золотого сечения.
- I — представляет мнимую единицу Sqrt [-1].
- Infinity — «положительная» бесконечность (со знаком «минус» дает «отрицательную» бесконечность).
- Catalan — константа Каталана 0 . 915966....
- Pi — число, имеющее значение 3 .14159... и равное отношению длины окружности к ее диаметру.
Константы, имеющие значение, дают его в виде вещественного числа:
{N [Degree], N[E], N[Pi]}
{0.0174533, 2.71828, 3.14159}
{N[EulerGamma],N[GoldenRatio],N[Catalan]}
{0.577216, 1.61803, 0.915966}
Константы в описываемой системе используются вполне естественно, так что от дальнейшего их описания можно воздержаться.
Размерные величины
Mathematica позволяет оперировать с размерными величинами, которые широко используются в физических и химических расчетах. Размерные величины характеризуются не только численными значениями, но и единицами измерения, например Meter (метр), Second (секунда) и т. д. Последние могут стоять в числителе и в знаменателе выражений, представляющих размерные величины:
1 Meter
Meter
5Meter
5 Meter
0.5Second
0.5Second
Между значением размерной величины и единицей измерения знак умножения можно не ставить. Это видно из приведенных выше примеров.
Для облегчения ввода физических констант, представляющих собой размерные величины, в наборе файлов Mathematica можно найти файл PhysicalConstants.nb. При его загрузке появляется дополнительная палитра физических констант, показанная на рис. 3.2.
Для ввода констант достаточно активизировать соответствующую кнопку с нужной константой. Будут введено выражение, задающее константу. Ниже представлены примеры ввода первой и последней констант, содержащихся в палитре, представленных в стандартной форме:
2.99792458000000028'*^8 Meter/ Second
2.99792х108 Meter/ Second
6. 9599 x 108 Meter
6.9599xl08 Meter
Следует отметить, что без острой необходимости применять размерные величины не следует, поскольку они усложняют математические выражения и зачастую не позволяют выполнять с ними символьные преобразования. Рекомендуется нормировать выражения (формулы) так, чтобы результаты их вычисления имели безразмерный вид.
Рис. 3.2. Дополнительная палитра физических констант
Переменными в математике принято называть именованные объекты, которые могут принимать различные значения, находящиеся в определенном множестве допустимых значений. Подобно этому, переменными в системе Mathematica являются именованные объекты, способные в ходе выполнения документа неоднократно принимать различные значения — как численные, так и символьные. При этом символьные значения переменных, в отличие от обычных языков программирования, могут представлять собой как исполняемые математические выражения ехрг, так и некоторые обобщенные классы функций и объектов. Например, переменная может представлять графический объект, такой как изображение трехмерной поверхности, или звуковой объект, при активизации которого исполняется звук. Значением переменных могут быть также множественные объекты — списки.
Имена переменных называют их идентификаторами. Они должны быть уникальными, то есть не совпадать с именами директив, атрибутов, опций и функций в ядре системы. Имена переменных должны начинаться с буквы. Общеприняты, скажем, имена х и у для функциональной зависимости у (х) или представления графиков, f — для функций. Желательно назначать именам переменных смысловые значения, например xcoordinaate или ycoordinate для координат точки. Все сказанное об идентификаторах объектов справедливо и для идентификаторов переменных, поскольку переменные — распространенные виды объектов.
Особенности применения переменных
В отличие от переменных в математике, каждая переменная в системе Mathematica, как и в любой системе программирования, всегда отождествляется с некоторой физической областью памяти, в которой и хранится значение переменной. Для уменьшения объема памяти применяются различные способы компактного размещения информации. Надо помнить, что и имя переменной занимает определенную область памяти. Распределение памяти под переменные — динамическое. Это означает, что местоположение ячеек памяти и объем памяти под ту или иную переменную не фиксированы, а меняются в ходе выполнения задачи.
Заранее объявлять тип переменной не требуется. Он определяется операцией присваивания переменной некоторого значения. Такой подход упрощает построение программ и естественен при использовании переменных в обычной математической литературе.
Без особых на то указаний переменные в системе Mathematica являются глобальными. Это означает, что после определения переменной ее значение можно изменить в любом месте документа или программы. Переменная появляется как действующий объект только после ее первого определения или задания. Определения переменных выполняются с помощью операции присваивания, вводимой знаком равенства:
var = value
Здесь var — имя переменной, value — ее значение. Ниже представлены основные операции по присваиванию переменным значений:
- х = value — переменной х присваивается вычисленное значение value;
- х = у = value — вычисленное значение value присваивается переменным х и у;
- x:=value — присваивание переменной х невычисленного значения value;
- х =. — с переменной х снимается определение.
Примеры (комментарий ln[...] опущен):
- g = Plot[Sin[x],{x,0,20}] — переменной д присваивается значение в виде графического объекта;
- у = 1 + х ^ 2— переменной у присваивается символьное значение в виде математического выражения (1 + х ^ 2);
- z= {1, 2, х, a + b}— переменной z присваивается значение в виде списка, содержащего четыре элемента.
Различие в присваивании переменным значений с помощью знаков «=>> и <<:=» иллюстрируют следующие примеры:
а=12;
b=а
12
с:=а
с
12
а=15;
b
12
с
15
Как видите, после первоначальных присваиваний b=а и с: =а обе переменные, b и с, имеют значение 12. Однако после присваивания переменной а нового значения (15) переменная b, которой было присвоено вычисленное значение а, остается равной 12, а переменная с, которой было присвоено невычисленное значение а, становится равной 15.
Особо обратите внимание на то, что возможно снятие с переменной определения с помощью символов «=.» или функции Clear [var]. В символьной математике это очень полезная возможность, поскольку нередко переменные с одним и тем же именем в разных частях программы могут иметь разный смысл и представлять объекты, требующие значительных затрат памяти.
Более того, эти объекты сохраняются даже при использовании команды New при переходе к подготовке нового документа. Поэтому рекомендуется всякий раз удалять определения переменных, как только их использование завершается. Это предотвращает возникновение конфликтов между одноименными переменными и освобождает память.
Переменные могут быть локальными, то есть действующими только в пределах объекта, в котором они объявлены. Таким объектом может быть функция или процедура со списком входных параметров. Такие объекты мы рассмотрим позже.
Оценивание переменных и операции присваивания
Специфику математических выражений в системе Mathematica составляет возможность их оценивания и изменения в соответствии с заложенными в ядро системы правилами математических преобразований. В итоге после изменения значение выражения, которое присваивается переменной, может быть совсем иным, чем до оценивания. Поэтому в целом для определения переменных используют описанные ниже конструкции.
Основная функция Set [ Ihs, rhs ] имеет аналогичные по действию упрощенные операторы:
- Ihs = rhs — вычисляет правую часть rhs и присваивает ее значение левой части Ihs. С этого момента Ihs замещается на rhs всюду, где бы этот идентификатор ни появился;
- {11, 12, ...} = {rl, г2, ...} — вычисляет ri и назначает полученные результаты соответствующим 11.
Функция задержанного присваивания SetDelayed[lhs,rhs] может быть заменена аналогичным по действию оператором Ihs : =rhs, который назначает правой части rhs роль отложенного значения левой части Ihs. При этом rhs содержится в невычисленной форме. После этого, когда появляется идентификатор Ihs, он заменяется на значение rhs, вычисляемое каждый раз заново.
При задержанном (отложенном) присваивании вывода нет, тогда как при обычном немедленном присваивании lhs=rhs значение rhs вычисляется немедленно и результат выводится в строку вывода.
Функция присваивания верхнего уровня UpSet [Ihs, rhs] применяется в виде lhs A =rhs. При этом левой части Ihs присваивается значение правой части rhs, причем это значение связывается с символами, которые появляются на первом уровне вложенности в Ihs.
И, наконец, функцию отложенного присваивания верхнего уровня UpSetDelayed[lhs, rhs] может заменить оператор lbs^ :=rhs. При этом величина rhs выполняет роль отложенного значения Ihs, и связывается это присваивание с символами, которые появляются на первом уровне вложенности в Ihs.
Отметим еще одну важную конструкцию SetOptions [s, namel->valuel, name2->value2, . . . ], которая устанавливает для символа s указанные опции, определяемые по умолчанию.
Применение различных типов операций присваивания способствует большей гибкости системы. Различия между этими операциями на первый взгляд несущественны, но они принципиальны, и это станет понятно после более детального знакомства с символьными преобразованиями и приобретения практики работы с системой.
Имеются также системные переменные, значениями которых являются данные о системе и ее работе, например версия применяемой операционной системы, текущая дата, время в данный момент, машинная точность вычислений и т. д. Многие из таких переменных имеют отличительный знак $ перед своим именем. Такие переменные более подробно будут рассматриваться в дальнейшем.