Главное меню
Вы здесь
3. Операторы и функции
Операторы и функции
Операторы и функции являются основными кирпичиками в построении математических выражений, которые вычисляются или преобразуются системой Mathematica. Кроме того, это важнейшие элементы языка программирования системы. В данном разделе мы познакомимся с этими объектами.
Математические выражения в системе Mathematica записываются с помощью операторов и функций. Операторы (от слова operator — исполнитель) являются элементами записи математических выражений, указывающими на то, какие действия производятся над символьными или числовыми данными. Когда эти данные используются совместно с операторами, их называют операндами.
Выражения, составленные из операторов, операндов и функций, способны возвращать результат своего вычисления. К примеру, если вычисляется сумма 2+3, то знак «+» является оператором, числа 2 и 3 — операндами, а вся запись 2+3 — выражением. Сами по себе операторы не возвращают какого-либо значения.
Существуют общепринятые приоритеты выполнения операций, например, в первую очередь выполняются сложение и вычитание, затем умножение и деление и далее другие операции. С помощью круглых скобок можно изменять последовательность выполнения действий, например, в выражении (2+3) М вначале будет вычислено 2+3, а затем уже результат будет умножен на число 4. В сомнительных случаях применение скобок особенно желательно, например 2^2+3 даст 7, а 2^ (2 + 3) даст 32.
Ниже перечислены основные операторы для выполнения арифметических операций (х, у и z — операнды, задающие данные, над которыми выполняются вычисления):
x+y+z Сложение
x-y-z Вычитание
х*у*z или x у z Умножение
х/у Деление
х^у Возведение х в степень у
Expr //N Дает приближенное (с установленной точностью и формой) значение выражения ехрг

Как уже отмечалось, при выполнении вычислений особая роль принадлежит символам «%». Эти символы как сами по себе, так и в качестве аргументов функций используются для указания на применение результата предшествующих операций:
- % — возвращает результат последней операции;
- %% — возвращает результат предпоследней операции;
- %...% — возвращает результат операции, выполненной в строке, отстоящей от конца на число повторений символа «%»;
- %n — возвращает результат операции в строке n.
Нетрудно заметить, что применение этих символов облегчает выполнение последовательных вычислений.
Как уже отмечалось, для представления арифметических выражений ехрг в виде вещественного результата используется функция N[expr,m]. Можно также задать вычисление любого выражения в численном виде, используя выражение ехрг //N:
1/3+2/7
13/21
1/3+2/7 //N
0.619048
Таким образом, используя функцию N[expr,m] или вывод с помощью символов //N, можно организовать вычисления в режиме калькулятора, находясь в среде оболочки системы.
Если х имеет вещественное значение, то функция
MantissaExponent[x]
возвращает список, содержащий мантиссу и порядок приближенного вещественного числа х. Примеры:
123.456 10^10
1.23456 х1012
MantissaExponent[%]
{0.123456, 13}
Арифметические вычисления с повышенной точностью
Важное достоинство систем символьной математики — выполнение арифметических вычислений с произвольными разрядностью и точностью. Хотя на деле они ограничены объемом ОЗУ, но для современных компьютеров с объемом ОЗУ в единицы и десятки мегабайт вряд ли можно столкнуться со случаем, когда ограничения по разрядности и точности становятся существенными.
Следующие две функции, Rationalize [х] и Rationalize [x, dx], дают приближение для числа х в виде рациональных чисел. Вторая из этих функций задает приближение с заданной точностью dx.
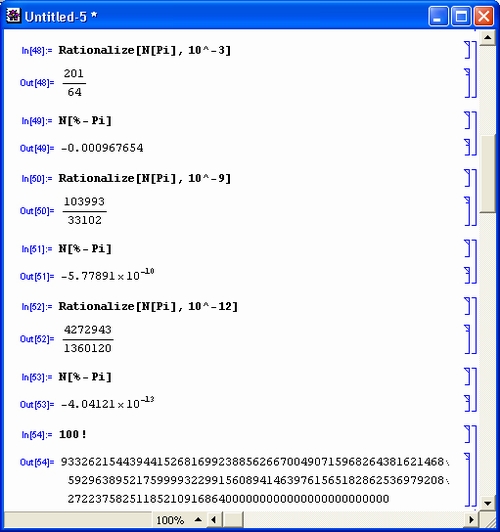
Mathematica может работать с большими числами и выполнять определенные операции с очень высокой точностью. Примеры, приведенные на рис. 3.3, иллюстрируют эти возможности.
Как видно из примеров представления рациональных чисел, результат приближения зависит от заданной погрешности. Чем она меньше, тем большие значения целых чисел в числителе и знаменателе результата разыскивает система. Функция Rationalize открывает широкие возможности для разработки целочисленных алгоритмов вычислений, позволяя легко получать рациональные приближения для наиболее распространенных числовых констант — на рис. 3.3 примеры этого даны для числа 8.
Обратите внимание на последние два примера — вычисление факториала достаточно большого числа. Первый результат целочисленный: он занял целых три строки, но зато он точен. С помощью функции N [ехрг] результат всегда можно представить в виде большого вещественного числа — но приближенного. При этом может использоваться научная форма представления чисел — с мантиссой и порядком.
Рис. 3.3. Примеры представления чисел в разных формах
Укороченная форма записи арифметических операций
Спецификой систем Mathematica являются арифметические операторы с укороченной формой записи, объединяющие операцию присваивания с арифметической операцией. Эти довольно специфические операторы, хорошо известные пользователям языка С, представлены ниже вместе с соответствующими им функциями.
| Функция | Оператор | Назначение |
| Increment [i] | i++ | Увеличивает значение i на 1 после использования i в выражении |
| Decrement [i] | i -- | Уменьшает значение i на 1 после использования i в выражении |
| Preincrement [i] | ++i | Увеличивает значение i на 1 до использования i в выражении |
| PreDecrement [i] | --i | Уменьшает значение i на 1 до использования i в выражении |
| AddTo[x,d] | x += dx | Прибавляет dx к х и возвращает новое значение х |
| SubtractFrom[x,dx] | x -= dx | Отнимает dx от х и возвращает новое значение х _ |
| TimesBy [х, с] | X **= 'С | Умножает х на с и возвращает новое значение х |
| DivideBy [х, с] | X /= С | Делит х на с и возвращает новое значение х |
Применение укороченных операторов делает запись математических выражений более короткой, хотя наглядность их при этом несколько снижается. Ниже представлены примеры выполнения укороченных арифметических операций.
| Ввод (In) | Вывод (Out) |
| i=0 | 0 |
| ++i; ++i; ++i | 3 |
| i=0; i++; i++; i++ | 2 |
| i=5 | 5 |
| -- i | 4 |
| i=5 | 5 |
| i -- | 5 |
| i -- | 4 |
| x=5 | 5 |
| x+=0 . 5 | 5.5 |
| x-=0 . 5 | 5. |
| x*=2 | 10. |
| x/=5 | 2. |
Важнейшим объектом любой компьютерной математической системы является функция. Она отражает зависимость некоторой величины от одного или нескольких аргументов. Например, функция sin(x) дает зависимость синуса х от величины аргумента х при изменении последнего от -°° до +°°.
Признаком функции является возврат результата выполняемого ею действия. Характер результата будет зависеть от смысла функции, который нередко явно указывается ее именем — идентификатором. Например, функция Digitslnteger [n] возвращает число десятичных цифр десятичного целого числа. Это ясно из прямого перевода имени функции — слово Digitslnteger говорит о том, что она возвращает число цифр целого числа. Подобные смысловые имена задаются для большинства функций системы Mathematica и облегчают их запоминание.
Понятие функции в системе Mathematica существенно расширено — функции могут возвращать графические и даже звуковые объекты. Здесь мы, однако, остановимся на общепринятом в программировании понятии функций, возвращающих в ответ на обращения к ним численные или символьные значения.
Функции могут входить в состав математических выражений. Обычно они имеют один или несколько параметров, указываемых в квадратных скобках. Если параметров несколько, то в квадратных скобках указывается список параметров, разделенных запятыми. В общем случае параметрами могут быть списки. Наконец, в состав функций могут входить опции, указанные своим именем и (после знака ->) значением. Для обозначения положительной бесконечности используется символ Infinity. Целочисленные функции имеют в своем имени слово Integer.
В ядро систем Mathematica 3/4 входит множество встроенных функций, то есть функций, готовых к немедленному использованию без какого-либо предварительного объявления. Таких функций многие сотни. Среди них различные арифметические функции, тригонометрические и гиперболические функции, специальные математические функции и т. д. Мы рассмотрим их в дальнейшем.
Основные арифметические функции
Для выполнения арифметических действий в системах Mathematica 3/4 определены следующие арифметические функции:
- Divide [х, у] — возвращает результат деления х на у эквивалентно выражению х у ^ -1;
- Plus[x, у,...] — возвращает сумму элементов списка;
- PowerModta, b, n] — возвращает Mod[a ^ b, n]. Для b<0 возвращает инверсию остатка;
- Times [х, у,...] — возвращает произведение аргументов х*у*...;
- Mod [m, n] — возвращает остаток от деления m на п. Результат имеет такой же знак, как п.
Ниже представлены примеры применения арифметических функций.
| Ввод (In) | Вывод (Out) |
| Divide [1. ,3] | 0.333333 |
| Mod [123, 20] | 3 |
| Mod [123, -20] | -17 |
| Mod[-123,20] | 17 |
| Plus[2,3,4] | 9 |
| Times [2, 3,4] | 24 |
Для обмена значениями переменных х и у можно использовать выражение {х,у}={у,х}
Пример обмена переменных значениями:
а=1;b=2;
{а,b}={b,а};
{а,b}
{2, 1}
Следующие функции служат для приведения вещественных чисел к ближайшим целым по определенным правилам:
- Ceiling [х] — возвращает значение наименьшего целого числа, большего или равного х;
- Floor [х] — возвращает наибольшее целое число, не превышающее данного х;
- Quotient [n, m] — возвращает целое значение n/m, определяемое как Floor[n/m];
- Round [х] — округляет х до ближайшего целого.
Хотя аргументами этих функций указано значение х, под ним можно понимать список вещественных чисел. Следующие примеры поясняют это и наглядно иллюстрируют правила приведения к целым числам.
| Ввод (In) | Вывод (Out) |
| Ceiling [{-5. 9, -5..1, 5, 5.1, 5.9}] | {-5, -5, 5, б, 6} |
| Floor [{-5. 9, -5.1,, 5, 5.1, 5.9}] | {-6, -6, 5, 5, 5} |
| Round[{-5.9, -5.1,, 5, 5.1, 5.9}] | {-6, -5, 5, 5, 6} |
Ряд функций обеспечивает нахождение делителей целых чисел и наименьшего общего -кратного:
- Divisors [n] — возвращает список целочисленных делителей числа п;
- DivisorSigma [k, n] — возвращает сумму &-х степеней положительных делителей числа п;
- ExtendedGCD [n, m] — возвращает расширенный наибольший общий делитель целых чисел пит;
- GCD [nl,n2,...] — возвращает наибольший общий делитель целых чисел ni;
- LCM[nl, n2,...] — возвращает наименьшее общее кратное целых чисел ni.
Ниже представлены примеры применения этих функций.
| Ввод (In) | Вывод (Out) |
| LCM[124,12,6] | 372 |
| GCD [144, 12, 6] | 6 |
| Divisors [123] | {1,3,41,123} |
| DivisorSigma [17,3] | 129140164 |
| ExtendedGCD [144,12] | {12, {0,1}} |
К целочисленным функциям можно отнести также функции вычисления факториала и двойного факториала:
- Factorial [n] или n! — возвращает значение факториала числа n (n!=n* (n-1) *...*3*2*1, причем 0 !=1 и 1 !=1);
- Factorial2 [n] или n! ! — возвращает значение двойного факториала числа п, равное п* (n-2) * (n-4) *...«%»
Ниже представлены примеры вычисления факториалов.
| Ввод (In) | Вывод (Out) |
| Factorial [10] | 3628800 |
| 20! | 2432902008176640000 |
| 10!! | 3840 |
| 20!//N | 2.4329Х10 18 |
Mathematica способна вычислять факториалы больших чисел. Практически мгновенно (даже на компьютере с 486-м процессором) вычисляются значения до 1000!, хотя результат при этом занимает несколько страниц на экране дисплея. Можно вычислить даже 10000!, но для этого потребуется время до нескольких минут (зависит от типа компьютера). Обратите внимание на то, что управляющий символ //N за выражением дает вывод (аппроксимацию) в форме научной нотации.
Следующие функции служат для получения простых чисел и некоторых их характеристик:
- Prime [n] — возвращает п-е простое число. Например, Prime [5] возвращает пятое простое число — 11. Всего лишь доли секунды требуются системе для вычисления миллиардного простого числа: Рг1те[10 Л 9] дает 22801763489;
- PrimePi [x] — возвращает количество простых чисел, не превышающих х. Например, PrimePi [10] возвращает 4;
- Partitions? [n] — возвращает числор(п) неупорядоченных разбиений целого числа п. Например, Partitions? [10] возвращает 42;
- PartitionsQ [n] — возвращает q(n) — число разбиений с неравными частями для целого числа п. Например, PartitionsQ [15] возвращает 27.
Эти функции полезны при решении задач теории чисел.
Функции генерации случайных чисел
Для реализации статистических методов моделирования используются случайные числа. Система имеет генератор псевдослучайных чисел, доступ к которому обеспечивают следующие функции:
- Random [ ] — возвращает равномерно распределенное псевдослучайное число типа Real в интервале от 0 до 1;
- Random [type, range] — дает псевдослучайное число указанного типа type, лежащее в указанном интервале range. К возможным типам относятся Integer, Real и Complex. По умолчанию принят интервал от 0 до 1. Можно задать интервал явно в виде {min, max}; спецификация интервала в виде max эквивалентна {0, max};
- SeedRandom[n] — сбрасывает (устанавливает в начальное состояйие) генератор случайных чисел, используя целое п как начальное число;
- SeedRandom [ ] — устанавливает генератор, используя в качестве начального числа текущее время.
Хотя генерируемые числа не являются строго случайными, их количество в повторяющейся последовательности очень велико. Использование специальной установки начального состояния генератора, например по времени дня, делает повторение последовательности практически невозможным.
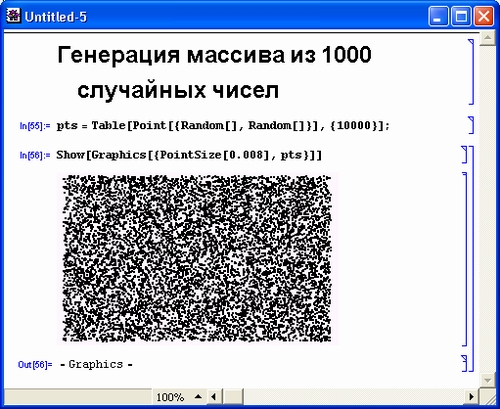
Для проверки равномерности распределения большого массива случайных чисел можно задать с их помощью случайные координаты и затем построить точки, соответствующие координатам (х, у). Рисунок 3.4 наглядно показывает, как это делается для массива из 10 000 случайных точек. О равномерности распределения случайных чисел говорит равномерность распределения плотности точек на графике.
Рис. 3.4. Графическая иллюстрация распределения точек со случайными координатами (х, у)
Возможно, читателю не сразу понятны графические средства, использованные в документе, показанном на рис. 3.4. Это не беда — в последующих уроках они будут описаны довольно подробно.
Функции выявления погрешностей и анализа структуры чисел
Следующие функции, опции и директивы используются, в основном, для выявления погрешностей вычислений и уточнения структуры чисел:
- Accuracy [х] — возвращает количество десятичных цифр справа от десятичной точки числа х;
- EvenQ [expr] — возвращает значение True, если expr есть четное число, и False — в противном случае;
- IntegerDigits [n] — возвращает список десятичных цифр целого числа n;
- IntegerDigits [n,b] — возвращает список цифр целого числа п в записи по основанию b;
- IntegerDigits [n, b, k] — возвращает список длиной k, содержащий самые младшие (наименьшие) значащие цифры в n;
- Precision [x] — возвращает количество точных знаков в числе х.
Поясним применение этих функций следующими примерами.
| Ввод (In) | Вывод(Out) |
| Accuracy [123 . 456] | 14 |
| EvenQ [2*3+2] | True |
| EvenQ [2*3+3] | False |
| IntegerDigits [12345] | {1, 2,3, 4, 5} |
| IntegerDigits [12345, 16] | {3, 0,3, 15} |
| IntegerDigits [12352 , 16] | {3, 0,4, 0} |
| IntegerDigits [12352 ,2] | {1,1,0,0,0,0,0,0,1,0,0,0,0,0,0} |
| Precision [123. 452] | 16 |
Функциями Accuracy и Precision возвращаются значения, установленные в последний раз или по умолчанию при первой загрузке системы.

Хотя в систему входят многие сотни встроенных функций (начиная от элементарных и кончая специальными математическими функциями и системными функциями), нередко требуется расширить ее вводом новых функций, действие которых задается пользователем. Такие функции принято называть функциями пользователя. Функции пользователя — простейшие программные объекты, необходимые даже в том случае, когда пользователь не желает углубляться в тонкости программирования системы. Их цель — расширение системы и ее обучение работе с новыми функциями.
Для задания, опознавания и уничтожения функций пользователя используются следующие конструкции:
- f (x_) := х^3 — отложенное задание функции пользователя с именем f;
- f (х_) = х^3 — немедленное задание функции пользователя с именем f;
- ?f — вывод информации о функции f;
- Clear [f] — уничтожение определения функции f.
В обозначениях вида х_ знак _ применяется для создания так называемых образцов, задающих локальные переменные в теле функции — в нашем примере это х. При этом в самом теле функции переменные обозначаются как обычно, без знака образца. Он лишь указывает на особый статус переменных в ограниченном пространстве программы — в теле функции. Так, если вместо х_ будет подставлено число 2, то f (2) будет возвращать 2 А 3. Вне тела функции значение переменной х не изменяется. Переменная х может быть и неопределенной: х_ определяет переменную х только для тела функции. Более подробно создание образцов будет описано в дальнейшем.
Mathematica позволяет записать введенные пользователем функции с их определениями на магнитный диск с помощью оператора
Save["filename", fl, f2, ...]
После этого функция пользователя становится внешней функцией. При этом для ввода таких функций в текущий документ (notebook) достаточно вызвать файл с именем filename:
<<filename
Рекомендуется создавать файлы с типовым расширением .т. Такие файлы входят в пакеты расширений системы. Имя файла нужно задавать по общепринятым для MS-DOS правилам, то есть при необходимости указывать логическое имя дисковода и путь к файлу, например, так:
<<D: \MAT\myfunc .m
Создание внешних функций по существу означает возможность расширения системы и ее адаптации к решению типовых задач конкретного пользователя. Как уже отмечалось, в систему входит мощная библиотека внешних расширений, и каждый пользователь может пополнить ее своими собственными библиотеками расширений.

Функции пользователя можно задавать и выводить на печать как на языке системы, так и на некоторых общепринятых языках программирования, например Fortran, С или ТеХ. Для этого существует ряд функций преобразования, в имена которых входит слово Form (форма) и название языка для записи функций. Основные из них — это CForm [expr], FortranForm [expr ] и TeXForm [expr]. С их помощью выражения можно преобразовать в форму, принятую для языков программирования С, Fortran и ТеХ. При преобразовании в форму языка ТеХ греческие буквы заменяются их латинскими именами, например alpha, Alpha, beta, Beta, gamma и т. д. К сожалению, в отличие от систем класса MathCAD и Maple V R3, вывод математических формул в их полностью естественном виде не предусмотрен, хотя многое для этого уже сделано.
Для преобразования формул и данных, записанных на языке системы Mathematica и хранящихся в текстовых файлах, в другие формы используются следующие функции:
- Splice ["file.rar"] — читает текстовый файл file.mx, интерпретирует его фрагменты, заключенные в ограничители <*...*>, и пишет текстовый файл file.*, в котором эти фрагменты преобразованы в формат, определяемый расширением х (с — С, f — Fortran, tex — ТеХ);
- Splice ["infile", "outfile"] — то же, но с раздельным заданием имен входного и выходного файлов.
Таким образом, система Mathematica может общаться с другими программами, написанными на языках программирования, получивших распространение в практике реализации математических расчетов. Этому во многом способствует возможность преобразования форматов данных и результатов вычислений в различную форму, характерную для используемой внешней системы. К примеру, если вы работаете с программами на языке Fortran, то следует использовать соответствующий формат представления данных и результатов вычислений.
Mathematica может общаться также с иными системами, например текстовыми редакторами. К примеру, для передачи содержимого каких-либо ячеек в текстовый редактор Write, входящий в оболочку Windows, достаточно выделить эти ячейки и поместить их в буфер обмена, используя команду Сору из меню Edit. После этого надо запустить текстовый редактор и с помощью команды Edit | Paste поместить в окно редактирования содержимое ячеек. Если оно символьное, то с помощью редактора можно записать полученный документ с расширением .txt, то есть в стандартном текстовом формате, с которым работает большинство DOS-приложений.
Логическими принято называть операции, отражающие чисто логическое соответствие между данными. В обиходном языке эти связи выражаются утверждениями типа «да» или «нет». Например, на вопрос «Сын вырос выше отца?» мы можем ответить «да» или «нет». В математике (да и в информатике) принято характеризовать логическое соответствие утверждениями True («Верно», «Истина» или «Да») и False («Неверно», «Ложь» или «Пет»). Слова True и False являются символьными константами, отражающими результаты логических операций и в системе Mathematica.
Для осуществления логических операций используются следующие логические операторы:
Равенство (например, а == b)
! = Неравенство
> Больше (например, b > а)
>= Больше или равно
< Меньше
<= Меньше или равно
Возможны следующие формы применения операторов сравнения:
а == b == с
а != b != с
х < у < z
и т. д.
Результатом вычисления этих выражений является выдача логических значений True или False. Это демонстрируют следующие примеры.
| Ввод (In) | Вывод (Out) |
| 2=2 | True |
| a=a | True |
| a=b | a == b |
| 2=3 | False |
| 2<3 | True |
| 2>3 | False |
| 2!=3 | True |
| 2+1==3==4-1 | True |
Основные логические функции над логическими данными р, q и т. д. задаются следующим образом:
Not[p] или !р Логическое отрицание
And[p, q,...] или р && q &&... Логическое умножение — операция «И»
Or[p,q,...] или р || q | |... Логическое сложение — операция «ИЛИ»
Приведем примеры применения логических операторов и функций.
| Ввод (In) | Вывод(Out) |
| And [True , True , True ] | True |
| True && True && False | False |
| Not [True] | False |
| Not [False] | True |
| Or [True, True, False] | False |
| 2==2 && 3==3 | True |
| True && True | True |
| And[l,l,0] | 11111 1 0 |
| And[l,l,0] | 1 && 1&& 0 |
Эти примеры показывают, что аргументами логических функций и операндами логических операций должны быть только логические константы True и False или выражения, значения которых представлены ими. Недопустимо использовать численные значения 1 и 0, отождествляя их с логической единицей и логическим нулем. Результатом задания операций с ними будет повтор задания — возможно, в укороченной форме.
Отметим еще ряд логических операторов и функций:
Equal[Ihs, rhs] Greater[х,у] или х > у Возвращает True, если Ihs и rhs тождественны
Greater[xl,x2,x3] или xl > х2 > хЗ Возвращает True, если х оказывается больше у, иначе возвращает False
GreaterEqual[х,у] или х >= у Возвращает True, если xi образуют строго убывающую последовательность, иначе возвращает False
GreaterEqual[xl,х2,хЗ] или xl>= х2 >= хЗ Возвращает True, если х больше или равно у, иначе возвращает False
Negative[х] NonNegative[х] Positive[х] Возвращает True, если xi образуют невозрастающую последовательность, иначе возвращает False
SameQtlhs,rhs] или Ihs === rhs Возвращает True, если х оказывается отрицательным числом, иначе возвращает False
Xor[el, e2,...] Возвращает True, если х — неотрицательное число, иначе возвращает False
Возвращает True, если х — положительное число, иначе возвращает False
Возвращает значение True, если выражение Ihs тождественно rhs, иначе False. В отличие от Equal, сравнивает форму представления операндов, а не их значения
Является логической функцией XOR (исключающее «ИЛИ»). Возвращает True, если нечетное количество из ei имеют значение True, а остальные False. Возвращает False, если четное количество ei имеют значение True, a остальные False
Ниже приводятся примеры использования этих функций.
| Ввод (In) | Вывод (Out) |
| Positive [2-3] | False |
| Equal [1+2, 4-1] | True |
| Equal [1+2, 2] | False |
| Greater [5, 4] | True |
| Greater [5, 4,3] | True |
| Greater [5, 4, 9] | False |
| Less [3,2+3] | True |
| Positive [2] | True |
| Negative [-2] | True |
| Neganbve[2] | False |
| NonNeganive [ -2 ] | False |
| NonNegative[2] | True |
| Xor[ True, True] | False |
| Xor [False , False] | False |
| Xor [True, False] | True |
Ряд дополнительных логических функций читатель найдет в приложении.
Функции комплексного аргумента
Элементарные функции в системе Mathematica могут иметь аргумент в виде действительного числа х или комплексного z. Аргументы указываются как параметры функций в квадратных скобках.
Прежде всего отметим функции для работы с комплексными числами z:
- Abs[z] — возвращает модуль комплексного числа z;
- Arg [ z ] — возвращает аргумент комплексного числа z;
- Conjugate [z] — возвращает комплексно-сопряженное с z число;
- Directedlnf inity [] — представляет бесконечную числовую величину с неопределенным направлением на комплексной плоскости;
- Directedlnfinity[z] — представляет бесконечную числовую величину, направление которой на комплексной плоскости определяется фазой комплексного аргумента z;
- Im [ z ] — возвращает мнимую часть комплексного числа z;
- Re [ z ] — возвращает вещественную часть числа z.
Далее приведены примеры операций с комплексными числами в непосредственном режиме.
| Ввод (In) | Вывод (Out) |
| z1 : =2+1*3; | |
| z2: =4+1*5; | |
| N[zl+z2] | 6. + 8.1 I |
| Re [2+1*3] | 2 |
| H[Im[z2]J | 5. |
| N[zl/z2] | 0.560976 + 0.0487805 I |
| N[Abs[zl*z2]] | 23.0868 |
| Con j ugate [ z 1 ] | 2-31 |
Если ввести N [ z 1 / 0 ], то система выдаст следующее сообщение:
N[zl/0]
Power::infy : Infinite expression 1/0 encountered.
Complexlnfinity
Итак, в этом случае система выдает сообщение об ошибке, но после него возвращает константу Complexlnfinity, означающую комплексную бесконечность.
Элементарные функции, надо полагать, хорошо известны читателю, взявшемуся за изучение Mathematica. Полный набор этих функций с их синтаксисом дан в приложении. Отметим, что в Mathematica имена элементарных функций записываются с большой буквы, а их аргументы задаются в квадратных скобках. Следующие примеры иллюстрируют сказанное.
| Ввод (In) | Вывод (Out) |
| Sqrt[2] | Sqrt[2] |
| Sqrt[2.] | 1.41421 |
| 2*Sin[l] | 2 Sin[l] |
| N[2*Sin[l]] | 1.68294 |
| Log[Exp[l]] | 1 |
| Simplif у [Sin [x] /Cos [x] ] | Tan[x] |
| ComplexExpand [ Sin [ a+b* I ] ] | Cos[b] Sin[a]+ I Cosfa] Sinh[b) |
Из этих примеров видно, что система знает и использует основные соотношения между элементарными функциями. В двух последних примерах используются символьные преобразования с применением функций Simplify (упрощение выражений) и ComplexExpand (расширение выражений с комплексным аргументом). Более подробно эти важные для символьных операций функции будут рассмотрены в дальнейшем.