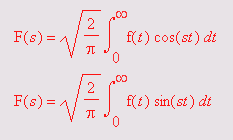Самоучитель по Maple
Самоучитель по Maple
Предисловие
Предисловие
Автор данной книги, как и многие почитатели компьютерных вычислений, прошел долгий путь их реализации: от программируемых микрокалькуляторов до работы на малых и персональных ЭВМ, использующих универсальные языки программирования высокого уровня. Это нашло отражение в его ранних книгах [1-3]. Совсем недавно пользователь ЭВМ, решая даже простые численные задачи, был вынужден осваивать основы программирования и готовить кустарные программы, вряд ли нужные кому-либо еще, кроме их создателя. Между тем возможности компьютеров постоянно росли. Сейчас персональный компьютер (ПК) с микропроцессором класса Pentium II, III или 4 намного превосходит по своим возможностям первые ЭВМ, занимавшие целые комнаты и залы. А скорость вычислений нынешних ПК в сотни раз превосходит скорость вычислений легендарных IBM PC XT и AT (первых ПК) и вплотную приближается к скорости вычислений суперЭВМ недавнего прошлого.
В связи с этим стал меняться взгляд на назначение компьютера. На первое место вышло применение их для работы с текстовыми процессорами (например, Microsoft Word) и прикладными программными системами для автоматизации офисной деятельности. Увы, при этом многие пользователи стали забывать о том, что ЭВМ изначально создавались для вычислений, а вовсе не для замены ими популярной, но ставшей неудобной пишущей машинки. Развитие мультимедиа привело к бурному применению компьютеров в роли игровых автоматов. В результате главный стимул развития «электронного помощника» создается отнюдь не высокоинтеллектуальными задачами.
Однако времена меняются и вечные ценности, к коим принадлежат разум и образование, вновь возвращаются. В последние годы во всем мире существенно возрос интерес к серьезному применению ПК, в том числе в области математических расчетов. Этому в большой степени способствовала разработка специальных компьютерных математических программных систем, резко снизивших потребность в написании собственных программ при решении математических задач. Первое поколение таких систем [4-10] было ориентировано на операционную систему MS-DOS и появилось, казалось бы, совсем недавно — в начале 90-х гг. Так или иначе, но компьютерный мир вновь заговорил об «искусственном интеллекте», понимая под этим способность электронной машины выдавать нетривиальные решения и обучаться решению новых задач. Интерес к компьютерному моделированию в самых широких областях заметно возрос после шахматных баталий между суперкомпьютером фирмы IBM и бывшим чемпионом мира по шахматам Гарри Каспаровым. Как известно, они завершились триумфальной победой машины — или, точнее говоря, коллективного разума тех, кто создал ее и ее программное обеспечение.
В последние годы показателем интеллектуальной мощи компьютеров, в том числе и персональных, стали уже не программы для игры в шахматы, а новейшие программные системы символьной математики или компьютерной алгебры [17-38]. Созданные для проведения символьных преобразований математических выражений, эти системы были доведены до уровня, позволяющего резко облегчить, а подчас и заменить, труд самой почитаемой научной элиты мира — математиков: теоретиков и аналитиков. Уже появились открытия, сделанные с помощью таких систем — но не ими самими! Вряд ли есть хоть один действительно серьезный научный проект, связанный с математикой, где они не применялись бы в деле.
Системы символьной математики долгое время были ориентированы на большие компьютеры, С появлением ПК класса IBM PC и Macintosh и с ростом их возможностей эти системы были переработаны под них и доведены до уровня массовых серийных программных систем. Сейчас системы символьной математики (или компьютерной алгебры) выпускаются самого разного «калибра» — от рассчитанной «на всех» системы Mathcad [11-21], поразительно компактной, быстрой и удобной для простых символьных вычислений системы Derive [22-24] и до компьютерных монстров Mathematica [26-28], MATLAB [29-31] и Maple [32-38], имеющих тысячи встроенных и библиотечных функций и изумительные возможности графической визуализации вычислений:
Все эти системы работают на персональных компьютерах, оснащенных популярными операционными системами класса Windows 95/98/NT/2000. Но не только на них — есть версии под операционные системы Linux, Unix, Mac и др. Они давно знакомы пользователям больших компьютеров и даже суперкомпьютеров.
К среднему уровню таких систем относятся интенсивно развиваемые системы класса Mathcad," имеющие (в дополнение к прекрасным средствам числовых вычислений) приобретенное по лицензии у фирмы Waterloo Maple Inc. (создателя систем Maple) ядро символьных вычислений. Ядро системы Maple используется и в другой маститой системе — MATLAB, придавая ей необычные для нее возможности символьной математики.
В данной книге впервые дается достаточно полное описание одной из самых мощных и интеллектуальных систем компьютерной алгебры — Maple под Windows, ее последней реализации — Maple 7. Эта система была создана группой ученых, занимающихся символьными вычислениями (The Symbolic Group), организованной Кейтом Геддом (Keith Geddes) и Гастоном Гонэ (Gaston Gonnet) в 1980 году в университете Waterloo, Канада. Вначале она была реализована на больших компьютерах и прошла долгий путь апробации, вобрав в свое ядро и библиотеки большую часть математических функций и правил их преобразований, выработанных математикой за столетия развития. Есть реализации программы на платформах ПК Macintosh, Unix, Sun и др.
Системам класса Maple посвящены сотни книг. Отметим лишь некоторые из них [39-56], изданные за рубежом. Достаточно полный список (около 400 наименований) книг по системам Maple можно найти на сайте разработчика этой системы — компании Waterloo Maple Software (www.maplesoft.com). Однако книг по системе Maple 7 (за исключением фирменных руководств по ней) на момент сдачи рукописи данной книги в этом списке не было.
Вряд ли эта мощная математическая система, разделяющая претензии на мировое лидерство с системами Mathematica фирмы Wolfram Research Inc., нужна секретарше или даже директору небольшой коммерческой фирмы. Но, несомненно, любая серьезная научная лаборатория или кафедра вуза должны располагать подобной системой, если они всерьез заинтересованы в автоматизации выполнения математических расчетов любой степени сложности. Несмотря на свою направленность на серьезные математические вычисления, системы класса Maple необходимы довольно широкой категории пользователей: студентам и преподавателям вузов, инженерам, аспирантам, научным работникам и даже учащимся математических классов общеобразовательных и специальных школ. Все они найдут в Maple многочисленные достойные возможности для применения.
По мнению автора данной книги, сравнение системы Maple 7 с лидером среди систем компьютерной математики — системой Mathematica 4.1 — непродуктивно. У каждой программы есть свои достоинства и недостатки. А главное — у них есть свои приверженцы, которых бесполезно убеждать, что иная система в чем-то лучше. Это все равно, что сравнивать великих исполнителей джазовой и рок-музыки Луи Амстронга и Би Би Кинга. Все, кто всерьез применяют системы компьютерной математики, должны работать с несколькими системами, ибо только это гарантирует высокий уровень надежности сложных вычислений.
И все же надо отметить, что интерфейс Maple 7 более интуитивно понятен, чем у строгой Mathematica 4.1. Maple 7 на первый взгляд имеет несколько менее мощную графику, но простота управления параметрами и легкость подготовки графических процедур часто позволяет визуализировать решения математических задач с меньшими усилиями, чем при использовании системы Mathematica 4.1. Обе системы в последних реализациях сделали качественный скачок в направлении эффективности решения задач в численном виде, в частности за счет повышения скорости выполнения матричных операций.
Особенно эффективно использование Maple при обучении математике. Высочайший «интеллект» этой системы символьной математики объединяется в ней с прекрасными средствами математического численного моделирования и просто потрясающими возможностями графической визуализации решений. Применение таких систем, как Maple, возможно при преподавании и самообразовании от самых основ до вершин математики.
Практика (да и личный опыт автора) показывает, что самым трудным является первый этап освоения системы. Первое знакомство с программой многих пользователей просто подавляет — убедившись в невероятном множестве возможностей системы и не имея ее систематизированного описания (а оно поставляется в виде трех книг приличного размера, включая книги учебного характера [39, 40]), многие пользователи помещают систему в архив, где она «пылится» без дела.
Эта книга впервые основательно знакомит читателя с новейшей версией системы Maple — Maple 7 в форме подробного учебного курса. Книга написана на основе ранее изданного учебного курса по системе Maple 6 [37], существенно переработанного и дополненного. Среди новых материалов, появившихся в книге, следует отметить:
- полное описание инсталляции системы Maple 7;
- улучшенное описание интерфейса;
- обновление материала по информационной поддержке системы, в том числе через Интернет;
- адаптация примеров и рисунков к новой версии Maple 7;
- устранение замеченных в предыдущем издании [37] неточностей и опечаток;
- впервые представленное описание целого ряда новых встроенных математических пакетов системы (CurveFitting, LinearFunctionalSystems, PolynomialTools, OrthogonalSeries, RandomTools и др.);
- описание расширенной поддержки Интернета и встроенного пакета XMLTools, который ее обеспечивает;
- впервые приведенное описание новейших средств поддержки стандарта MathML и пакета MathML;
- описание многочисленных новинок системы Maple 7 в области реализации вычислений и их графической визуализации;
- десятки новых примеров применения Maple 7.
Основное внимание в книге уделено обучению основам и приемам эффективной работы с системой Maple 7. На роль всеобъемлющего справочного руководства книга не претендует, хотя во многих случаях способна выполнять роль справочника или руководства пользователя Maple 7. Хотя эта книга одна из самых обширных среди русскоязычных книг, посвященных системе Maple, автор был вынужден ограничить описание ряда важных возможностей программы. Основной акцент в книге сделан на описание возможностей системы в области математических расчетов и интерфейса пользователя. Менее подробно, а порой просто не описаны средства расширения системы и пакеты узкоспециального назначения (электронная база данных по системе Maple 7 дает полное представление о всех свыше 3000 операторов и функций этой системы, большинство из которых используется крайне редко).
Хотя книга посвящена версии Maple 7, большинство материала может использоваться и пользователями предшествующей версии Maple 6. В частности, это достигнуто выделением новых возможностей Maple 7 в отдельные разделы книги. Остальные разделы книги без каких-либо ограничений могут быть отнесены к наиболее распространенной версии Maple — Maple 6.
Структура книги
Книга содержит 17 уроков и составлена так, что эти уроки постепенно знакомят читателя с возможностями системы. Уже после прохождения урока 1 вы сможете начать осмысленно и плодотворно работать с системой. Этот урок является как бы ознакомительным курсом по работе с системой Maple 7. Он может быть полезен как для быстрого самостоятельного освоения системы не слишком требовательным пользователем, так и как основа вводного курса по системе в вузах и школах, где для основательного изучения Maple 7 не предусмотрено достаточного количества учебных часов. Кроме того, этот урок знакомит читателя с основами интерфейса пользователя и правилами работы с панелями инструментов и форматирования выражений. По сравнению с учебным курсом по системе Maple 6 [37] этот урок существенно переработан и дополнен. В частности, подробно описана инсталляция системы Maple 7 и аппаратные требования для работы с ней. Последующие уроки расширяют заведенное знакомство и постепенно готовят читателя к серьезной самостоятельной работе практически без применения какой-либо иной документации, кроме встроенной в систему справочной базы данных. Урок 2 посвящен знакомству с мощной справочной базой данных системы Maple 7 и информационной поддержкой этой системы в Интернете. Данные разделы намеренно вынесены в начало книги, поскольку успех освоения системы Maple 7 до профессионального уровня требует обучения работе со справочной базой данных. В уроке 3 описаны основные приемы работы с файлами документов, которые готовятся в Maple 7. Урок 4 дает систематизированное описание интерфейса, хотя и без многих подробностей, известных всем пользователям операционных систем класса Windows 95/98/NT/2000.
Остальные уроки посвящены базовым математическим возможностям системы Maple 7 и основам практической работы в ней. В уроке 5 описаны основные типы данных системы, а в уроке 6 — основные виды встроенных операторов и функций. Урок 7 посвящен основам программирования в среде Maple 7. Читатель должен понимать, что все описанные и в других главах команды системы Maple 7 являются одновременно и командами ее языка программирования. Именно это позволяет считать язык программирования Maple 7 языком программирования сверхвысокого уровня, проблемно ориентированным на математические расчеты. Урок 8 является одним из наиболее важных. Он посвящен решению типовых задач математического анализа, таких как вычисление сумм и произведений последовательностей, производных и интегралов, разложений функций в ряд и т. д. При этом особое внимание уделяется технике аналитических вычислений, где возможности системы Maple 7 вызывают особый интерес. Но и техника численных расчетов рассмотрена достаточно детально, в частности арифметика высокой точности. Работа с функциями и степенными многочленами (полиномами) описана в уроке 9. Урок 10 посвящен изучению главной «козырной карты» системы Maple 7 — ее возможностям в области символьной математики. Здесь описано много тонкостей работы с математическими выражениями и другими объектами системы, позволяющими выполнять множество математических преобразований и подстановок.
Два больших урока — уроки 11 и 12 — посвящены графическим возможностям системы. При этом урок 11 описывает обычные графические средства, а в уроке 12 дается описание расширенных средств, позволяющих эффективно решать задачи визуализации решений математических проблем — вплоть до подготовки графиков с элементами анимации.
Учитывая огромную роль дифференциальных уравнений в решении ряда математических, физических и технических задач, работе с ними посвящен отдельный урок 13. Наряду с решением одиночных дифференциальных уравнений первого и второго порядка рассматривается решение систем линейных и нелинейных дифференциальных уравнений как аналитическими, так и численными методами. Большое внимание уделено графической визуализации решений и построению наглядных фазовых портретов решения. В уроке отражены новые возможности Maple 7 в решении дифференциальных уравнений.
В уроке 14 рассмотрены важнейшие пакеты системы Maple 7 математической направленности. Эти пакеты поставляются вместе с системой, и применение функций из них столь же важно, как и применение средств ядра системы. Описанные в уроке 14 пакеты рассмотрены достаточно полно.
В отдельный урок 15 вынесены широко используемые на практике средства решения задач линейной алгебры. Это операции с векторами и матрицами, различные их преобразования и техника решения систем линейных уравнений. Здесь описаны такие важные пакеты, как linalg (стандартные средства линейной алгебры) и LinearAlgebra. В последний пакет входят новые средства линейной алгебры повышенной эффективности на основе алгоритмов, заимстованных из знакомого математикам пакета программ NAG (Numbering Algorithms Group). Впервые описан новый пакет анализа линейных функциональных систем LinearFunctionalSystems, появившийся в версии Maple 7.
Остальные пакеты, относящиеся к сравнительно узким областям математики и п-редставляющие ограниченный интерес для большинства читателей, рассмотрены обзорно или в виде аннотации в уроке 16. К сожалению, материал по всем пакетам расширения Maple 7 настолько обширен, что его невозможно отразить в одной книге (тем более в форме учебного курса). Тем не менее в отличие от учебного курса по системе Maple 6 [37] этот урок существенно расширен и в нем впервые описан ряд новых пакетов системы Maple, в частности пакеты PolymomialTools, OrthogonalSeries, RandomTools, MathML и XMLTools.
Последний урок 17 описывает законченное решение ряда конкретных и интересных задач из области математики, физики и радиоэлектроники. Таким образом, читатель получает возможность познакомиться с широким спектром применения системы Maple 7 — от примеров простых расчетов и вычислений (таких в книге тысячи) до решения конкретных научных и технических проблем. Материал книги иллюстрируется многими сотнями копий экрана как в виде отдельных рисунков, так и фрагментов вычислений и программных процедур в тексте книги. Они дают наглядное представление о реальном диалоге с системой и о форматах ввода и вывода.
Большинство примеров в книге оригинальны и отражают взгляд автора на методологию изучения системы Maple. В то же время в книге использованы и лучшие (и наиболее поучительные) примеры, которые приведены в обширной библиотеке процедур, составленных пользователями систем Maple разных реализаций со всего мира, и примеры из ряда учебников по системе — в том числе новейших электронных (таких; как Power Tools), размещенных в Интернете. Все заимствованные примеры также специально адаптированы применительно к новейшей версии системе Maple 7, описанной в книге.
Урок 1. Первое знакомство с системой Maple
1. Краткая характеристика систем класса Maple
Урок 1.
Первое знакомство с системой Maple 7
Краткая характеристика систем класса Maple
Назначение и место систем Maple
Maple — система компьютерной математики, рассчитанная на широкий круг пользователей. До недавнего времени ее называли системой компьютерной алгебры, Ито указывало на особую роль символьных вычислений и преобразований, которые способна осуществлять эта система. Но такое название сужает сферу применения системы. На самом деле она уже способна выполнять быстро и эффективно не только символьные, но и численные расчеты, причем сочетает это с превосходными средствами графической визуализации и подготовки электронных документов.
Казалось бы, нелепо называть такую мощную систему, как Maple 7 математической системой «для всех». Однако по мере ее распространения она становится полезной для многих пользователей ПК, вынужденных в силу обстоятельств (работа, учеба, хобби) заниматься математическими вычислениями и всем, что с ними связано. А все это простирается от решения учебных задач в вузах до моделирования сложных физических объектов, систем и устройств, и даже создания художественной графики (например, фракталов).
Для наших читателей (в том числе и для математиков-профессионалов) возможности систем символьной математики, реализованных на массовых ПК класса IBM PC, порой являются полной неожиданностью и вызывают вполне заслуженное удивление и восхищение, но иногда и резкое отрицание. Впрочем, последнее характерно скорее для тех, кто с системой Maple просто не работал и относится к ней, как дама из анекдота о паровозе — увидев паровоз впервые, она воскликнула: «Не может быть, что он едет без лошадей!» Maple — тщательно и всесторонне продуманная система компьютерной математики. Она с равным успехом может использоваться как для простых, так и для самых сложных вычислений и выкладок. Заслуженной популярностью системы Maple (всех версий) пользуются в университетах — свыше 300 самых крупных университетов мира (включая и наш МГУ) взяли эту систему на вооружение. А число только зарегистрированных пользователей системы уже давно превысило один миллион. Ядро системы Maple используется в ряде других математических систем, например в MATLAB и Mathcad, для реализации в них символьных вычислений.
Добавьте к этому куда большее число незарегистрированных пользователей — ведь система записана на многих компакт-дисках, лихо продаваемых в России по вполне доступным ценам. Если учесть все это, то оказывается, что популярность системы Maple ничуть не ниже, а то и выше, чем у гораздо более простых систем, таких как Derive и Mathcad. Вот и решайте, какая из систем и впрямь рассчитана на всех!
Maple — типичная интегрированная система. Она объединяет в себе:
- мощный язык программирования (он же язык для интерактивного общения с системой);
- редактор для подготовки и редактирования документов и программ;
- современный многооконный пользовательский интерфейс с возможностью работы в диалоговом режиме;
- мощную справочную систему со многими тысячами примеров;
- ядро алгоритмов и правил преобразования математических выражений;
- численный и символьный процессоры;
- систему диагностики;
- библиотеки встроенных и дополнительных функций;
- пакеты функций сторонних производителей и поддержку некоторых других языков программирования и программ.
Ко всем этим средствам имеется полный доступ прямо из программы. Maple — одна из самых мощных и «разумных» интегрированных систем символьной математики, созданная фирмой Waterloo Maple, Inc. (Канада).
Во многих обзорах систем компьютерной алгебры Maple справедливо считается одним из первых кандидатов на роль лидера среди них. Это лидерство она завоевывает в честной конкурентной борьбе с другой замечательной математической системой — Mathematica 4.1. Каждая из данных двух систем имеет свои особенности, но в целом эти две лидирующие системы практически равноценны. Однако надо отметить, что появление новейшей версии Maple 7 означает очередной виток в соревновании этих систем за место лидера мирового рынка. Причем виток на этот раз раньше сделала система Maple 7.
Система Maple прошла долгий путь развития и апробации. Она реализована на больших ЭВМ, рабочих станциях Sun, ПК, работающих с операционной системой Unix, ПК класса IBM PC, Macintosh и др. Все это самым положительным образом повлияло на ее отработку и надежность (в смысле высокой вероятности правильности решений и отсутствия сбоев в работе). Не случайно ядро системы Maple V используется целым рядом других мощных систем компьютерной математики, например системами класса Mathcad и MATLAB. А совсем недавно упрощенная версия Maple для операционной системы Windows СЕ стала использоваться в миниатюрных компьютерах фирмы Casio — Cassiopeia.
2. Версии систем класса Maple.
Версии систем класса Maple
Известен ряд версий системы Maple, называемых реализациями. Одной из самых известных реализаций является реализация Maple V R5. В ней появилась возможность работы с электронными таблицами, несколько улучшен интерфейс пользователя (введены палитры для ввода математических символов и расширены возможности управления мышью), стала возможной запись файлов в формате HTML и введена возможность обмена объектами между документами методом перетаскивания (Drag and Drop).
Основное достоинство предшествующей версии Maple 6 — это существенное ускорение вычислений с большими матрицами, достигнутое применением алгоритмов матричных вычислений известного пакета NAG (Numbering Algorithms Group). Хотя данная книга посвящена новейшей реализации системы Maple 7, ее основной материал будет полезен и пользователя реализации Maple 6.
Новейшая версия систем Maple — Maple 7 появилась 21 июня 2001 г. Корпорация Waterloo Maple оценивает ее появление как новый виток в борьбе за мировое лидерство в области автоматизации математических вычислений — как численных, так и, в особенности, символьных. Являясь одними из лучших и надежных систем компьютерной математики, Maple 6 и Maple 7 становятся мировым стандартом в области математических вычислений.
3. Об ошибках в символьных вычислениях
Об ошибках в символьных вычислениях
На многих пользователей систем символьной математики удручающее впечатление может произвести наличие хотя и редких, но ошибочных решений. В самом деле, мы немедленно стерли бы с жесткого диска табличный процессор, давший ошибку в бухгалтерских расчетах, и перестали бы доверять системе проверки орфографии, дающей ошибки при проверке. Впрочем, последнее случается сплошь и рядом — пока нет таких систем, которые корректно проверяли бы орфографию и грамматику. Тот же текстовый процессор Word 97/2000 постоянно ошибается при проверке орфографии текстов, в чем автор не раз убеждался, готовя с его помощью большие книги.
У систем компьютерной алгебры нет проблем с обработкой естественного языка — математика полностью формализованная наука. Однако в них много своих условностей и неоднозначностей, которые здесь как бы заранее запрограммированы. К примеру, что считать более простым выражением: tan(x) или sin(x)/cos(x)? Система Derive полагает более простым выражением tan(x) и преобразует к нему выражение sin(x)/cos(x). А вот система Maple V ничуть не менее справедливо считает, что функции sin(x) и cos(x) математически более простые, чем tan(.r), и вообще — tan(x), по сути, не самостоятельная функция, a sin(x)/cos(x). Поэтому Maple V везде вместоtm(x) будет выводить sin(x)/cos(x).
Представьте себе, что таких условностей десятки и вы ничего об этом не знаете. Поэтому не стоит удивляться, что символьное значение какой-либо производной или интеграла может заметно отличаться по виду от приводимого в том справочнике, из которого взято исходное выражение для проверки правильности работы системы. Часто, чтобы получить результат в необходимом виде, необходимо приложить определенные усилия либо дать конкретные указания системе о типе преобразований в ходе вычислений. Указания реализуются в виде параметров к командам и функциям системы.
По образному выражению автора обзора [40], решение задач в символьном виде напоминает переход через поле, густо напичканное минами. Удивительно не то, что системы символьной математики могут ошибаться и «взрываться», а то, что число этих ошибок мало и уже на нынешнем этапе развития таких систем это не мешает их серьезному практическому применению. Стоит еще раз подчеркнуть, что Maple в этом отношении является одной из лучших систем, реализованных на ПК класса IBM PC и Macintosh с достаточно умеренными техническими характеристиками. Кстати говоря, для ПК Macintosh последней реализацией пока что является Maple V R4.
Один знакомый автор любил говорить, что компьютеры делают умных людей умнее, а глупых — глупее. Пожалуй, это более чем справедливо для людей, сидящих у ПК с установленной на нем системой символьной математики. Лишь те, кто понимают суть математических вычислений и имеют должную математическую интуицию и подготовку, могут получить от таких систем самые серьезные и даже новые результаты. Те же, кто думает, что системы символьной математики заменят им математические знания, глубоко ошибаются и могут получить красочно выглядящие, но абсолютно неверные и даже псевдонаучные результаты!
Однако вряд ли следует утрировать вероятность выдачи системами символьной математики ошибочных результатов — даже самые опытные математики-аналитики тоже могут ошибаться в своих вычислениях. В разработке таких систем, как Maple или Mathematica принимают участие крупные математические школы всего мира! Эти системы — кладезь математических понятий, сведений и знаний. Они способны заменить самые серьезные справочники по математическим вычислениям в любой области науки, техники и образования. Кроме того, они имеют множество средств для проверки корректности выполняемых вычислений, например путем подстановки полученных результатов в исходные выражения.
Кстати, одно из самых действенных приемов проверки таких средств — решение задачи одновременно на нескольких системах символьной математики. Не случайно уже сейчас можно заметить тенденцию к объединению математических систем. Эта новая и безусловно прогрессивная тенденция в ближайшее время приведет к созданию автоматизированных рабочих мест математиков и ученых других близких специальностей. Разработки таких рабочих мест (разумеется, компьютер на них — главный инструмент), в том числе с использованием систем Maple, уже появились и о них немного говорится в заключении. В добавление к сказанному надо отметить, что Maple 7 — одна из самых надежных систем компьютерной математики. Надежных прежде всего в смысле высокой достоверности получения правильных результатов при сложных символьных вычислениях. Эта первая система компьютерной математики, успешно прошедшая полное тестирование на задачах повышенной сложности, предлагаемых для оценки качества подобных систем.
4. Ядро и пакеты Maple 7
Ядро и пакеты Maple 7
Основой для работы с символьными преобразованиями в Maple является ядро системы. Оно содержит сотни базовых функций и алгоритмов символьных преобразований. В новых реализациях объем ядра достигает 6-7 Мбайт. Имеется также основная библиотека операторов, команд и функций. Многие встроенные в нее функции, как и функции ядра, могут использоваться без какого-либо объявления, другие нуждаются в объявлении. Кроме того, имеется ряд подключаемых пакетов (packages).
Дополнительные функции из пакетов могут применяться после объявления подключения пакета с помощью команды with(name), где name — имя применяемого пакета. Общее число функций, с учетом встроенных в ядро и размещенных в пакетах в системе Maple V R4 приближается к 2500, в реализации R5 — к 2700, а в Maple бив Maple 7 оно уже превышает 3000. Это означает, что большинство задач может решаться в режиме прямого диалога с системой без использования каких-либо средств программирования.
5. Языки системы Maple 7
Языки системы Maple 7
Maple способна решить огромное число задач вообще без какого-либо программирования в общепринятом смысле этого понятия. Достаточно лишь описать алгоритм решения задачи и разбить его на отдельные вопросы, на которые система Maple способна дать ответы. Более того, есть тысячи задач, алгоритмы решения которых уже реализованы в виде функций и команд системы. Тем не менее это вовсе не означает, что в Maple нельзя программировать. На самом деле Maple поддерживает три собственных языка: входной, реализации и программирования.
Maple имеет входной язык сверхвысокого уровня, ориентированный на решение математических задач практически любой сложности. Он служит для задания системе вопросов или, говоря иначе, задания входных данных для последующей их обработки. Это язык интерпретирующего типа и по своей идеологии напоминает добрый старый Бейсик. И такое сходство вовсе не недостаток, а огромное достоинство — ведь именно с Бейсика начался подлинный диалог пользователя напрямую с компьютером! Входной язык имеет большое число заранее определенных математических и графических функций, а также обширную библиотеку, подключаемую по мере необходимости.
Имеет Maple и свой язык процедурного программирования — Maple-язык. Этот язык имеет вполне традиционные средства структурирования программ: операторы циклов, операторы условных и безусловных переходов, операторы сравнения, логические операторы, команды управления внешними устройствами, функции пользователя, процедуры и т. д. Он также включает в себя все команды и функции входного языка, ему доступны все специальные операторы и функции. Многие из них являются весьма серьезными программами, например символьное дифференцирование, интегрирование, разложение в ряд Тейлора, построение сложных трехмерных графиков и т. д.
Не следует путать входной язык и язык программирования системы (Maple-язык) с языком ее реализации. Им является один из самых лучших и мощных универсальных языков программирования — Си. На нем написано ядро системы, содержащее тщательно оптимизированные процедуры. Большинство же функций, которые содержатся в пакетах, написаны на Maple-языке, благодаря чему их можно модифицировать и даже писать свои собственные библиотеки. По разным оценкам, лишь от 5 до 10 % средств Maple создано на языке реализации — все остальное написано на Maple-языке. Таким образом, система имеет развитые возможности для расширения и адаптации к задачам пользователя. Для подготовки программ на языке Maple могут использоваться внешние редакторы, но система имеет и свой встроенный редактор, вполне удовлетворяющий требованиям большинства пользователей. Он открывается командами New и Open в меню File. Этот редактор можно использовать для редактирования файлов программ или математических выражений. Версии Maple для MS-DOS имеют свой редактор программ и отладчик с функциями проверки синтаксиса. После версии Maple V для Windows необходимость в этих средствах практически отпала.
Синтаксис структурных операторов языка Maple напоминает смесь Бейсика и Паскаля. Это облегчает знакомство с ним тем, кто имеет хотя бы начальный опыт программирования на этих языках. По близким к Бейсику правилам (и при помощи общепринятых математических сокращений) выполняется и ввод математических выражений в диалоговом режиме работы с системой.
6. Ориентация систем Maple
Ориентация систем Maple
Вообще говоря, системы Maple ориентированы на решение сложных задач, хотя и решение в них простых задач вполне возможно и уместно. Возможно, для решения таких задач вполне подойдет весьма простая, быстрая и надежная система Derive или система Mathcad, в которую (начиная с версии 3.0 под Windows) включен приобретенный по лицензии фирмы Waterloo Maple упрощенный символьный процессор Maple. Однако по числу доступных пользователю математических функций эти скромные системы не идут ни в какое сравнение с патриархом символьной математики — системой Maple.
Система Maple 7 может с успехом применяться для решения самых серьезных математических задач аэродинамики, теории поля, теплопроводности и диффузии, теоретической механики и др. Решение таких задач нередко является многолетним трудом элитных научных коллективов.
Впрочем, поскольку система может быть установлена на любом современном ПК, ее можно (да и нужно) применять как можно чаще и по любому поводу. Это способствует как приобретению практических навыков работы с Maple, так и росту математических познаний тех, кто с ней работает.
7. Возможности предшествующей версии Maple 6
Возможности предшествующей версии Maple 6
Перечислим основные возможности предшествующей версии системы Maple 6.
Интерфейс:
- работа со многими окнами;
- вывод графиков в отдельных окнах или в окне документа;
- представление выходных и входных данных в виде естественных математических формул;
- задание текстовых комментариев различными шрифтами;
- возможность использования гиперссылок и подготовки электронных документов;
- удобное управление с помощью клавиатуры через главное меню и инструментальную панель;
- управление с помощью мыши.
Символьные и численные вычисления:
- дифференцирование функций;
- численное и аналитическое интегрирование;
- вычисление пределов функций;
- разложение функций в ряды;
- вычисление сумм и произведений;
- интегральные преобразования Лапласа, Фурье и др.;
- дискретные Z-преобразования;
- прямое и обратное быстрое преобразование Фурье;
- работа с кусочно-заданными функциями.
Работа с уравнениями в численном и символьном виде:
- решение систем линейных и нелинейных уравнений;
- решение систем дифференциальных уравнений;
- символьное вычисление рядов;
- работа с рекуррентными функциями;
- решение трансцендентных уравнений;
- решение систем с неравенствами.
Работа с функциями:
- вычисление значений всех элементарных функций;
- вычисление значений большинства специальных математических функций;
- пересчет координат точек между различными координатными системами;
- задание функций пользователя.
Линейная алгебра:
- свыше ста операций с векторами и матрицами;
- решение систем линейных уравнений;
- формирование специальных матриц и их преобразования;
- вычисление собственных значений и собственных векторов матриц;
- поддержка быстрых векторных и матричных алгоритмов пакета программ NAG.
Графическая визуализация результатов вычислений:
- построение графиков многих функций;
- различные типы осей (с линейным и логарифмическим масштабом);
- графики функций в декартовой и полярной системах координат;
- специальные виды графиков (точки массивов, векторные графики, диаграммы уровней и др.);
- системы координат, определяемые пользователем;
- графики, представляющие решения дифференциальных уравнений;
- графики трехмерных поверхностей с функциональной закраской;
- построение пересекающихся в пространстве объектов;
- задание пользователем окраски графиков;
- импорт графиков из других пакетов и программных систем;
- анимация графиков;
- создание и проигрывание анимационных файлов.
Программирование:
- встроенный язык процедурного программирования;
- простой и типичный синтаксис языка программирования;
- обширный набор типов данных;
- типы данных, задаваемых пользователем;
- средства отладки программ;
- мощные библиотеки функций;
- задание внешних функций и процедур;
- поддержка языков программирования С и Fortran;
- возможность записи формул в формате LaTeX.
8. Новые возможности системы Maple 7
Новые возможности системы Maple 7
Система Maple 7 приобрела ряд новых возможностей. Кратко отметим их:
- расширенная поддержка численных алгоритмов пакета программ NAG, в том числе при решении численных задач математического анализа (например, вычисление определенных интегралов в Maple 7 ускорено в 20-40 раз в сравнении с Maple 6) и при решении дифференциальных уравнений;
- новый обучающий курс User's Tour, встроенный в ее справку;
- существенно переработанные и обновленные пакеты функций;
- ускоренные алгоритмы целочисленных вычислений (например, факториал числа 25000 вычисляется более чем на порядок быстрее, чем системой Maple 6);
- обширный набор новых алгоритмов решения дифференциальных уравнений, обеспечивающий дополнительную эффективность решения задач в области моделирования физических явлений и устройств;
- выполненное впервые 100% успешное испытание при решении специальных тестовых задач, что является высшим достижением на рынке средств компьютерной математики;
- усовершенствованные и новые алгоритмы реализации многих численных методов решения задач;
- новые встроенные пакеты аппроксимации кривых CurveFitting, внешних вычислений ExternalCalling, решения линейных функциональных систем LinearFunctionalSystem, ортогональных рядов OrthogonalSeries, работы с полиномами PolynomialTools, решения уравнений SolveTools и поддержки вычислений с размерными величинами Units;
- новый пакет для поддержки языка XML;
- поддержка новейшего стандарта записи математической информации — языка MathML 2.0;
- улучшение пользовательского интерфейса, в частности введение новой палитры ввода шаблонов векторов;
- поддержка протокола TCP/IP, обеспечивающего динамический удаленный доступ к данным, например, для финансового анализа в реальном масштабе времени или данных о погоде;
- дополнительные пакеты (Maple PowerTools™), доступные через Интернет, поддерживающие анализ методом конечных элементов (РЕМ), нелинейную оптимизацию и статистику, а также три новых пакета: вычисления для новичков, теоретическая физика и программирование;
- возможность работы с курсом университетского математического образования, загружаемого через Интернет.
В сочетании с сохраненными возможностями предшествующей версии системы это дает новой версии Maple 7 обширные возможности в эффективном решении широкого класса математических и научно-технических задач, а также задач в области образования.
9. Установка системы Maple 7 на ПК
Установка системы Maple 7 на ПК
В этой книге рассматривается реализация системы Maple 7, требующая:
- процессор — Pentium 150 МГц и выше;
- оперативная память — не менее 16 Мбайт (рекомендуется 32 Мбайта и выше);
- место на жестком диске — около 80 Мбайт (120 Мбайт для сетевой версии).
- бширная библиотека пользователя, поставляемая с предшествующими версиями системы Maple V, с новыми версиями Maple 6 и Maple 7 пока не поставляется, поскольку требует серьезной переработки. Достаточно отметить, что использование в новых версиях системы оператора % для вызова последнего результата (вместо применяемого ранее оператора кавычек) делает неработоспособными большинство программ этой библиотеки. Также в новой версии изменен синтаксис некоторых функций.
10. Установка системы Maple 7
Установка системы Maple 7
Установка системы производится обычно с компакт-диска. Обычно компакт-диск с инсталляционной версией Maple 7 стартует автоматически. При этом появляется окно Мастера установки со шкалой выполнения предварительной подготовки, показанное на рис. 1.1.
Затем Мастер автоматически переходит к окну, в котором просит ввести серийный номер программного продукта, который имеется в документации к системе или указан на конверте с компакт-диском.
Для продолжения установки следует щелкнуть на кнопке Next. Это приводит к появлению следующего окна и т. д. В каждом окне после указания необходимых данных нужно нажать кнопку Next или Yes. Работа с остальными окнами мастера установки описана ниже.
Рис. 1.2. Окно с приглашением к установке системы Maple 7
На рис. 1.3 показано следующее окно Мастера, которое служит для задания папки, в которой будут установлены файлы Maple 7. Вы можете оставить предлагаемую по умолчанию папку, а можете ввести любую другую.
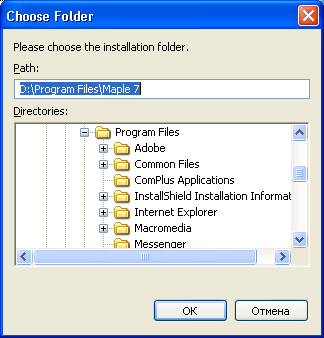
Если папка, заданная по умолчанию в поле Destination Folder вас не устраивает, то вы можете определить другую. Для этого щелкните на кнопке Browser. Появится стандартное окно Choose Folder, показанное на рис. 1.4. В этом окне можно задать желаемую папку, либо явно указав ее имя в поле Path, либо выбрав существующую в дереве Directories.
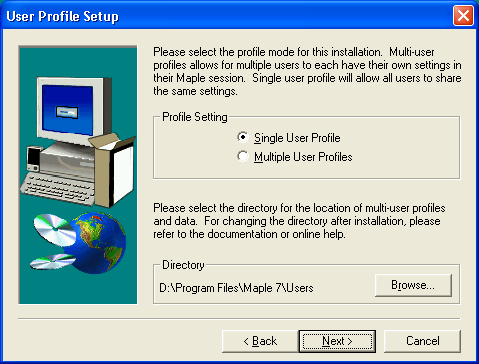
Система Maple 7 может быть установлена как для индивидуального пользователя, так и для многих пользователей (сетевой вариант). Данный выбор можно осуществить в следующем окне Мастера установки, показанном на рис. 1.5. В этом окне надо задать вариант установки, щелкнув в соответствующем положении переключателя. Здесь же можно уточнить директорию (по умолчанию Users) для хранения файлов пользователей.
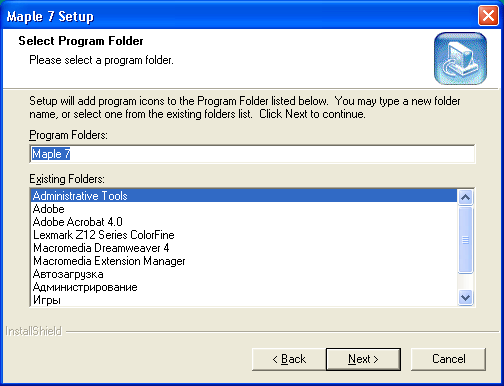
Следующий этап установки — определение имени ярлыка, активизацией которого в дальнейшем будет запускаться система. Для этого служит окно Мастера установки, показанное на рис. 1.6. В этом окне можно оставить имя ярлыка Maple 7, предлагаемое по умолчанию, ввести вместо него другое или выбрать имя из списка, представленного в нижней части окна. Разумно согласиться с предложенным Мастером именем.
Рис. 1.3. Окно задания папки для размещения файлов системы Maple 7
Рис. 1.4. Задание имени папки для размещения файлов системы Maple 7
Рис. 1.5. Выбор установки системы Maple 7 для одного пользователя или для многих пользователей
Рис. 1.6. Выбор ярлыка для запуска системы Maple 7
На этом предварительная часть установки завершается, и нажатием кнопки Next в окне рис. 1.6 можно перейти к этапу копирования файлов в намеченную папку (учтите, что часть файлов копируется и в папки с операционной системой Windows, установленной на вашем ПК). В процессе копирования файлов окно Мастера установки сменяется информационными окнами, которые сообщают о возможностях Maple 7. Одно из таких окон представлено на рис. 1.7. Кроме того, на экране будет отображаться окно с индикатором процесса копирования файлов, который позволяет судить о том, какая часть работы уже проделана, а также какие файлы копируются в данный момент.
Рис. 1.7. Информационное окно и индикатор процесса копирования файлов
В процессе копирования файлов могут быть ситуации, когда встречается файл с таким же именем, что и копируемый. В этом случае Мастер установки сообщит вам об этом с помощью соответствующего сообщения. Чаще всего такая ситуация встречается, если Maple 7 устанавливается поверх прежней версии системы Maple. Если пользователь твердо намерен установить новую версию системы, то рекомендуется предварительно удалить предшествующую версию (с помощью соответствующих программ и средств, разумеется). В противном случае придется решать, какой файл будет занимать место на диске — останется старый или его заменит новый (естественно, рекомендуется установить новый файл).
По завершении копирования файлов появляется окно Мастера с запросом о том, надо ли помещать ярлык запуска системы на рабочий стол, изображенное на рис. 1.8.
Рис. 1.8. Запрос о размещении ярлыка запуска Maple 7 на рабочий стол
Рис. 1.9. Окно Мастера установки с сообщением о ее завершении
Вы можете отказаться от такого размещения и запускать Maple 7 из меню Пуск или из Проводника. Но, если вы намерены работать с Maple 7 часто, то рекомендуется поместить ярлык на рабочий стол Windows.
Установка завершается вывбдом окна Мастера установки, в котором сообщается о ее успешном завершении. Данное окно представлено на рис. 1.9.
В этом окне достаточно нажать кнопку Finish для завершения установки. Maple 7 будет установлена на вашем компьютере и готова к работе.
Проблемы, связанные с установкой и возможными конфликтами, описаны в файле readme.txt, который рекомендуется просмотреть перед инсталляцией системы. К сожалению, он подготовлен па английском языке, как и вся встроенная в Maple 7 документация.
1.gif
2.gif
3.gif
4.gif
5.gif
6.gif
7.gif
8.gif

9.gif

11. Запуск системы
Запуск системы
Запуск Maple 7 производится, как обычно, из меню Пуск (рис. 1.10). Найдя строчку Maple 7, необходимо открыть подменю и щелкнуть на команде Maple 7 (рис. 1.10).
Рис. 1.10. Запуск Maple 7 из меню Пуск
Возможен также запуск с помощью ярлыка, помещенного на рабочий стол. В любом случае, вначале на некоторое время появляется красочное окно-заставка, показанное в центре рис. 1.1. После этого появляется рабочее окно системы, изображенное на рис. 1.11.
Рис. 1.11. Окно системы Maple 7
10.gif

11.gif

12. Интерфейс системы Maple 7
Интерфейс системы Maple 7
Долгое время системы Maple имели довольно архаичный (хотя и неплохой) пользовательский интерфейс, ориентированный на операционную систему MS-DOS. Но затем версия Maple V R3, далее Maple V R4, Maple V R5 и, наконец, Maple 6 и Maple 7 приобрели вполне современный графический пользовательский интерфейс, характерный для приложений операционных систем Windows. Это намного повысило удобство работы с Maple и обеспечило интеграцию со многими другими программными продуктами.
Как у всех приложений под Windows интерфейс Maple 7 имеет ряд характерных элементов, видимых на рис. 1.11 и перечисленных ниже:
- строка заголовка (сверху);
- строка главного меню;
- главная панель инструментов;
- контекстная панель инструментов, вид которой зависит от режима работы с Maple 7;
- окно ввода и редактирования документов; О строка состояния (в самом низу окна).
Пользовательский интерфейс Maple 7 позволяет готовить документы, содержащие одновременно текстовые комментарии, команды входного языка (с возможным преобразованием их в естественную математическую форму), результаты вычислений в виде обычных математических формул и графические данные. Это обеспечивает понятное представление исходных данных и результатов вычислений, а также удобство их повторного использования.
В основе пользовательского интерфейса Maple 7 лежит графический многооконный интерфейс операционной системы Windows. Управление системой Maple 7 возможно с помощью главного меню, панелей инструментов и палитр, а также «горячих» клавиш. Поддерживаются также многие возможности мыши, присущие приложениям под Windows.
Важно отметить и прекрасно реализованную справочную систему Maple 7. Преодолев первые трудности общения с системой, пользователь быстро осваивает систему справки, которая позволяет без какой-либо бумажной документации получить исчерпывающую информацию о любом операторе, функции или пакете (разумеется, на английском языке). На каждой странице справки нахддит-ся по несколько примеров, причем их можно скопировать и перенести в редйк-тор или в окно исполняемых документов системы. Это способствует быстрому обучению пользователя. Подробное описание справочной системы Maple 7 дано в уроке 2.
Пользователь Maple 7 (как и ряда других математических систем) работает с документами, которые являются одновременно описаниями алгоритмов решения задач, программами и результатами их исполнения. Все данные команды и результаты размещаются в соответствующих ячейках. Графические построения выполняются как в ячейках документа, так и в отдельных окнах, и имеют свои меню для оперативного управления параметрами.
13. Меню системы Maple 7
Меню системы Maple 7
Наиболее полные возможности управления предоставляет главное меню системы Maple 7. Оно, как обычно, расположено непосредственно под строкой заголовка. Меню предоставляет доступ к основным операциям и параметрам пользовательского интерфейса системы. Ниже дан перечень меню, доступных при наличии открытого документа:
- File — работа с файлами и печатью документов;
- Edit — команды редактирование документа и операции с буфером обмена;
- View — управление видом пользовательского интерфейса;
- Insert — операции вставки;
- Format — операции задания форматов;
- Spreadsheet — операции задания таблиц;
- Options — задание параметров;
- Window — управление окнами;
- Help — работа со справочной системой.
Главное меню Maple 7 является контекстно-зависимым. Это означает, что его вид может меняться в зависимости от текущего состояния (контекста) системы. Например, если все документы закрыты, то главное меню содержит только три заголовка меню: File, Options и Help. При этом место для окон документов пусто и окрашено в серый цвет. Вид меню также меняется в зависимости от того, какие объекты в документе выделены. Более подробно работу с меню системы Maple 7 мы рассмотрим позже, начиная с урока 3.
14. Палитры ввода математических символов
Палитры ввода математических символов
Полезно сразу обратить внимание на возможность модификации интерфейса системы Maple 7 с помощью команд меню View. В этом меню (оно показано на рис. 1.11 в открытом состоянии) можно увидеть список палитр Palettes, предназначенных для ввода математических знаков. Установив флажки соответствующих палитр, можно вывести их на экран и переместить в любое место. Все четыре палитры математических символов представлены на рис. 1.11. При этом палитра VECTOR введена в Maple 7 впервые.
Назначение знаков в палитрах очевидно из их названий:
SYMBOL — ввод отдельных символов (греческих букв и некоторых математических знаков);
EXPRESSION — ввод шаблонов математических операторов и операций;
MATRIX — ввод шаблонов матриц разных размеров;
VECTOR — ввод шаблонов векторов разных размеров и типов (векторы-столбцы или векторы-строки).
Следует отметить, что не всегда введенный на палитре символ буквально повторяет представленный на кнопке. Например, вместо символа а может быть введено слово alpha. Так происходит, если установлен действующий по умолчанию Maple-режим представления символов. Палитра ввода векторов введена в Maple 7 впервые, что сделало ввод векторов более удобным.
15. Всплывающие подсказки
Всплывающие подсказки
Еще один важный и полезный элемент интерфейса — всплывающие подсказки. Они появляются, если навести курсор мыши на тот или иной элемент интерфейса. На рис. 1.11 показана одна из всплывающих подсказок. Подсказки имеют вид облачка, которое вытекает из указанного элемента интерфейса. Особенно удобны подсказки для пояснения назначения кнопок палитр и панелей инструментов. В дальнейшем мы будем неоднократно приводить примеры всплывающих подсказок при работе с интерфейсом.
16. Основы работы с Maple 7 в диалоговом режиме
Основы работы с Maple 7 в диалоговом режиме
После загрузки и запуска системы можно начать диалог с ней, используя ее операторы и функции (с параметрами) для создания и вычисления математических выражений.
ВНИМАНИЕ
Во избежании грубых ошибок при исполнении того или иного примера рекомендуется перед этим исполнить команду restart которая снимает определения со всех использованных ранее переменных и позволяет начать вычисления «с чистого листа».
На рис. 1.12 представлен реальный диалог с системой (в виде копии экрана) при решении простейших арифметических задач и построении графика функции sin(x)/x.
Рис. 1.12. Начало диалога с системой Maple 7
Уже из этого простого примера видны особенности диалога с Maple и синтаксиса ее входного языка, то есть языка, на котором системе задаются вопросы. Диалог идет в стиле: «задал вопрос, получил ответ». Вопросы и ответы занимают отдельные блоки, выделяемые в левой части квадратными скобками. Длина квадратных скобок зависит от размера выражений — исходных (вопроса) и результатов вычислений (ответов на вопросы). Знак > является знаком приглашения к заданию вопроса. Мигающая вертикальная черта | — маркер ввода (курсор).
Ввод выражений (вопросов) задается по правилам, давно принятым для строчных редакторов. Они хорошо известны, и мы не будем на них останавливаться подробно. Отметим лишь, что клавиша Ins позволяет задавать два основных режима ввода — замены и вставки. В режиме замены вводимый символ заменяет существующий символ, который отмечен маркером ввода. А в режиме вставки новый символ вставляется в текст, не уничтожая имеющиеся символы.
Перемещение маркера ввода осуществляется клавишами перемещения курсора <- и -> Клавиша Backspace стирает символ слева от маркера ввода, а клавиша Del — справа от маркера ввода. Для ввода любого символа надо нажать соответствующую клавишу. Клавиша Shift включает верхний регистр для ввода заглавных (прописных) букв, а клавиша Caps Lock переключает верхний и нижний регистры клавиш с буквами (они меняются местами).
Знак фиксации конца выражения : (точка с запятой) указывает, что результат его вычисления должен быть выведен на экран, а знак : (двоеточие) отменяет вывод и может использоваться как знак разделителя при записи нескольких выражений в одной строке. Клавиши перемещения курсора позволяют передвигаться по ранее введенным строкам на экране.
12.gif

17. Понятие о функциях и операторах
Понятие о функциях и операторах
Важным понятием системы Maple 7 (да и математики вообще) является понятие функции. Функция возвращает результат некоторого преобразования исходных данных — параметров функции. Maple 7 имеет множество встроенных функций, включенных в его ядро и в пакеты.
Функция в выражениях задается вводом ее имени и списка параметров функции (одного или нескольких), заключенного в круглые скобки, например sqrt(2) задает функцию вычисления квадратного корня с параметром 2 (численной константой). Основным признаком функции является возврат значения в ответ на обращение к ней по имени (идентификатору) с указанием списка параметров функции. Например:
Обратите внимание на особую роль десятичной точки — здесь она служит указанием к выполнению вычисления значения sin( 1.0) (или, что то же самое, sin( 1.)). А вот синус целочисленного аргумента 1 не вычисляется — считается, что вычисленное значение менее ценно, чем точное значение sin(1).
В данном случае надо понимать, что Maple предпочитает иметь с дело точными значениями функций. Логично, что точное значение синуса от 1 записывается в виде sin(f). — Прим. ред.
Ради единства терминологии мы будем пользоваться расширительным понятием функции, относя к нему и те объекты, которые в некоторых языках программирования именуют процедурами или командами. Например, слова plot и plot3d мы также будем называть функциями, которые возвращают графики аргументов. Под командами же мы будем подразумевать прежде всего команды, содержащиеся в меню. Помимо функций в математических системах для записи математических выражений используются специальные знаки — операторы. К примеру, вычисление квадратного корня часто записывается с помощью его специального знака — V. Достаточно хорошо известны операторы сложения +, вычитания -, умножения *, деления / и некоторые другие. Операторы обычно используются с операндами в виде констант или переменных, например в записи 2* (3+4) числа 2, 3 и 4 — это операнды, а знаки * и + — операторы. Скобки используются для изменения порядка выполнения операций. Так, без них 2*3+4=10, тогда как 2*(3+4)=14, поскольку вначале вычисляется выражение в скобках. Пожалуй, самым распространенным оператором является оператор присваивания ':=. Он используется для задания переменным конкретных значений, например:
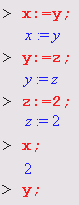
Этот простой пример наглядно иллюстрирует эволюцию переменных и особую роль оператора присваивания в системе Maple. В частности, в этом примере переменные х, у и z взаимосвязаны с помощью операций присваивания. Поэтому задание значения 2 переменной z приводит к тому, что и переменные у и х принимают то же значение.
Другой распространенный оператор — оператор равенства = — используется для задания равенств и логических условий (например, а=b), указания областей изменения переменных (например, 1=1..5 означает формирование диапазона изменения i от 1 до 5) и определения значений параметров в функциях и командах (например, color=b1ack для задания черного цвета у линий графиков).
Операторы сами по себе результат не возвращают. Но они, наряду с функциями и своими параметрами (операндами), позволяют конструировать математические выражения, которые при их вычислении также возвращают результат. В силу этого математические выражения, содержащие операторы и операнды, могут быть параметрами функций. Выражения в Maple бывают очень простыми (например, имена переменных х и у или константы 1 и 2), а могут содержать многие тысячи знаков. С позиции канонов символьной математики квадратный корень из двух уже является основным результатом вычислений. Поэтому такая функция обычно не вычисляется в численном виде, а выводится в естественном виде с применением знака квадратного корня V. Для вычисления в привычном виде (в виде десятичного числа с мантиссой и порядком) надо воспользоваться функцией evalf(sqrt(2)) — эта функция обеспечивает вычисление символьного выражения, заданного ее параметром (числом 2).
13.gif

18. Обработка и индикация ошибок
Обработка и индикация ошибок
При работе с системой Maple 7 надо строго придерживаться правил корректного ввода выражений и иных объектов Maple-языка, называемых синтаксисом языка. Однако, как гласит русская пословица, не ошибается только тот, кто ничего не делает. Даже у опытного пользователя возможны ошибки в ходе ввода выражений и задания алгоритмов вычислений.
Алгоритмические, но синтаксически корректные ошибки часто могут не распознаваться системой. Например, если в выражении a*sin(x) вы вместо аргумента х взяли аргумент b, то есть записали a*sin(b), то такую ошибку Maple 7 распознать не может, ибо синтаксически как a*sin(x), так и a*sin(b) абсолютно корректны. Если вы перепутаете синус с косинусом и запишете a*cos(x), то такая ошибка также не будет распознана.
ПРИМЕЧАНИЕ
Ошибки в записи выражений, описывающих те или иные алгоритмы вычислений, не нарушающие синтаксическую корректность, системой Maple 7 не распознаются. Контроль за такими ошибками целиком лежит на пользователе.
Приведем еще один характерный пример ошибки, которую Maple 7 не может распознать. Вводя выражение X/Y*Z, мы можем предположить, что это означает X/(Y*Z). Однако в Maple 7 приоритет операций деления и умножения одинаков. Поэтому Maple 7 вначале делит X на Y, а затем полученный результат умножает на Z:
Ошибки такого рода называют семантическими. Если бы мы не проверили вывод с помощью оператора вычисления предыдущего выражения (%), то эта ошибка осталась бы нераспознанной. Выявление и устранение семантических ошибок выполняется на этапе отладки вычислений и программ.
ПРИМЕЧАНИЕ
Используйте блокировку вычислений с помощью знака двоеточия только в том случае, когда вы абсолютно уверены в правильности записи выражения. Иначе вы можете не заметить вкравшейся в вычисления серьезной ошибки.
В нашем примере мы получили бы верный результат, заключив выражение Y*X в круглые скобки. Как обычно, они предназначены для задания явного приоритета выполнения операций — в нашем случае вначале будет вычислено выражение в скобках (Y*Z), а затем уже X будет поделено на это выражение:
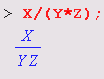
Но вернемся к ситуации с синтаксическими ошибками, которые система Maple 7 распознает с помощью встроенного в нее синтаксического анализатора. Например, если вы задали неправильное имя функции, то это будет опознано синтаксическим анализатором и вычисления не будут выполняться. Maple 7 просто повторит выражение в строке вывода:
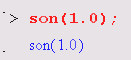
В этом примере вместо имени функции sin введено ошибочное имя son. Maple воспринимает его как некую введенную пользователем функциональную зависимость и потому просто повторяет запись и не выводит сообщение об ошибке. А вот другая ситуация — имя функции sin введено верно, но вместо десятичной точки при задании вещественного числа 1.0 использована запятая:

В данном случае Maple 7 «знает», что работа идет с его встроенной функцией синуса, которая должна иметь единственный аргумент. Задание (1,0) означает, что растяпа-пользователь ввел вместо вещественного числа два целочисленных числа, разделенных запятой. Этого синтаксический анализатор Maple 7 стерпеть уже не смог, и он отреагировал выдачей сообщения об ошибке (на экране дисплея оно имеет малиновый цвет). Исправьте ошибку, и синус единицы будет благополучно вычислен:

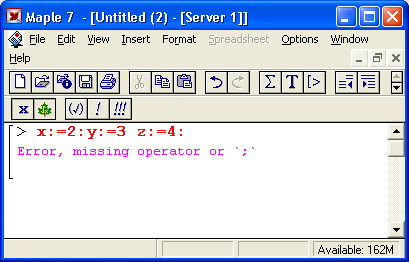
А вот еще одна типичная ситуация — в последовательности выражений опущен знак-разделитель (двоеточие или точка с запятой):
Тут Maple 7 не только реагирует на ошибку, но и пытается подсказать, что именно пропущено. Более того, маркер ввода в виде мигающей вертикальной черточки будет помещен на место ошибки и вы сможете тут же устранить ошибку. Правда, подсказки не всегда точны — в нашем случае явно пропущен разделитель в виде двоеточия, a Maple 7 сообщает о пропуске точки с запятой. Впрочем, откуда системе знать, хотим мы вывести результат операции Y:=4 сразу (для этого нужен разделитель в виде точки с запятой) или откладываем на потом (с помощью символа двоеточия).
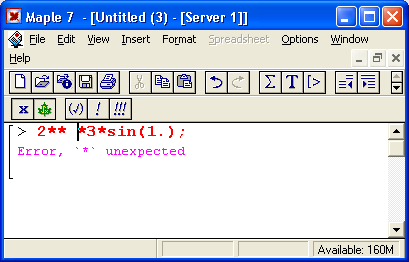
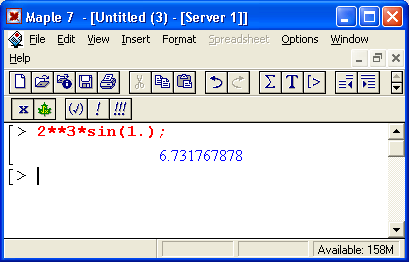
Вот еще один пример характерной ошибки — три знака * подряд:
Здесь Maple 7 подсказывает, что один оператор * надо убрать — два знака * подряд означают вполне законный вариант оператора — возведение в степень. При этом маркер ввода вновь указывает место ошибки. Проанализируйте следующие простые примеры:
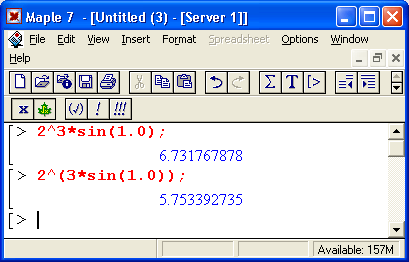
В этом примере Maple 7 вначале вычисляет функцию синуса, затем производит возведение в степень и лишь потом операцию умножения. Впрочем, такой приоритет операций принят практически во всех системах компьютерной математики и в языках программирования.
Некоторые пользователи версии системы Maple V R5 наблюдали, что русская буква «я» в конце программного комментария (он вводится после символа #) вела к зависанию программы, что требовало ее перезагрузки. В Maple 7 этот недостаток устранен:
> #Буква "я" в конце комментария уже не вызывает зависания
>
Позже, при описании программирования в Maple 7, мы опишем более развитые средства контроля над допускаемыми пользователем ошибками. Пока же ограничимся приведенными 'Выше сведениями, полезными уже в начале диалога с системой.
15.gif

20.gif
21.gif
22.gif
23.gif
19. Управление с помощью мыши
Управление с помощью мыши
Для управления состоянием ячеек можно использовать контекстное меню, появляющееся при нажатии правой кнопки мыши. Если установить указатель мыши на входной ячейке, то это меню будет содержать три команды:
- Standard Math — включает и выключает показ входных выражений в естественной математической форме;
- Maple Input — управляет видом ячейки ввода (математический/текстовый);
- Execute — включает выполнение ячейки.
Также в зависимости от состояния буфера обмена и наличия выделения в контекстном меню могут присутствовать команды Cut, Copy и Paste.
Левая кнопка мыши может использоваться для передачи фокуса управления или переноса маркера ввода, а также выделения частей документа.
20. Примеры задания функции пользователя и построения ее графика
Примеры задания функции пользователя и построения ее графика
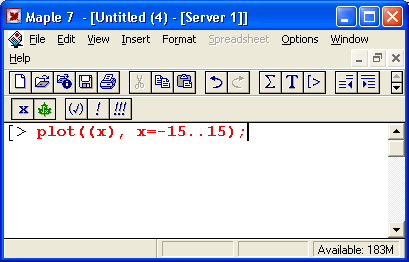
На рис. 1.12 показано, как задается функция пользователя f(x) с одним параметром х. Нетрудно заметить, что параметр указывается в скобках после имени функции а для записи выражения функции используется знак присваивания := (двоеточие со знаком равенства). Для построения графика функции f (х) используется функция plot в форме:
Нетрудно заметить, что при наличии нескольких параметров функции (в нашем случае их два) они разделяются запятыми. Выражение х=-15. .15 задает, во-первых, указание, относительно какой переменной строится график, а во-вторых, говорит, в какой области значений меняются значения этой переменной — в нашем случае от -15 до +15. Шаг изменения переменной выбирается автоматически в зависимости от размеров и вида графика.
24.gif
21. Пример построения трехмерного графика поверхности
Пример построения трехмерного графика поверхности
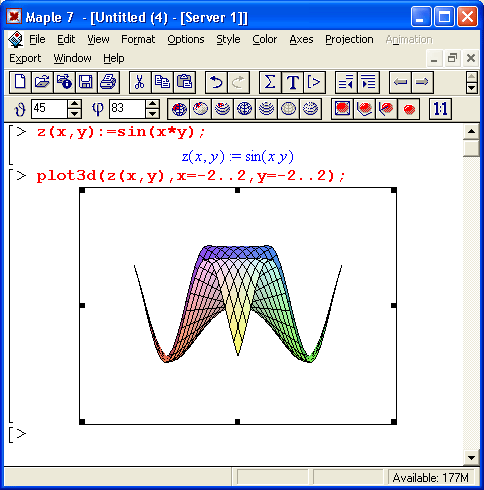
Столь же просто, как и график обычной функции в декартовой системе координат, можно построить график трехмерной поверхности. Это показано на примере рис. 1.13. В данном случае задана функция двух переменных z(x,y) :=sin(x*y) и ее график строится с использованием графической функции plot3d. Правила задания пределов изменения переменных х и у соответствуют описанным выше.
Рис. 1.13. Построение графика трехмерной поверхности
Возможно, многих читателей вполне удовлетворят уже описанные возможности, но сила системы Maple 7 прежде всего в возможности выполнения аналитических (символьных) вычислений. Поэтому мы перейдем к обсуждению некоторых из них.
25.gif
22. Управление формой представления документа
Управление формой представления документа
Форматы математических выражений
Приведенные выше примеры реализуют обычную форму представления документа. В нем имеются текстовые комментарии (для их ввода надо нажать клавишу F5), сформулированные на Maple-языке задания на вычисления, результаты вычислений в виде обычных математических формул и, там где это указано, графики.
Эта выстраданная форма представления документов является компромиссом между наглядностью и простотой ввода исходных данных. Может показаться, что в этом отношении намного дальше продвинулись системы класса Mathcad — у них исходные данные и описание алгоритмов вычислений давно задаются в виде естественных математических символов и формул. За исключением, правда, функций символьных вычислений, пока не имеющих общепринятых специальных математических символов и вводимых путем указания их имен.
Однако это достоинство кажется явным лишь на первый взгляд. Ввод сложных формул довольно трудоемок и требует специфических навыков, отсутствующих даже у самых опытных пользователей. В Mathcad эту проблему решили созданием панелей (палитр) с полным набором всех математических символов и шаблонов для представления сложных формул, таких как интегралы, суммы и произведения рядов, производные и т. д. Однако, хотя при этом их ввод и становится более простым, легким его не назовешь, а монотонность операций нервирует многих пользователей.
В Maple 7 ввод исходных данных производится привычными для языков программирования средствами — с помощью функций и операторов, задаваемых в командной строке. Зато результаты вычислений получаются по умолчанию в виде обычных формул (хотя есть возможность их представления в другом виде, например принятом в редакторе LaTeX или языках программирования Fortran и С). Тем не менее вид документа с таким специфическим заданием формул может озадачить математика и любого пользователя, не слишком знакомого с основами программирования. В целом он отрицательно сказывается на восприятии документов.
23. Представление входных выражений в математической форме
Представление входных выражений в математической форме
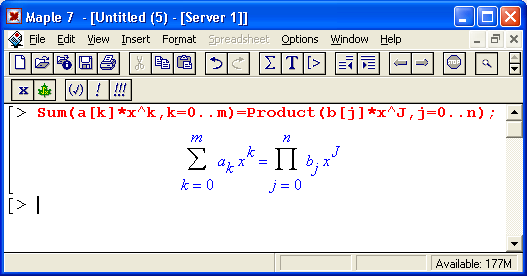
Для устранения подобного недостатка (а скорее, противоречия) Maple 7 предлагает ряд средств. Во-первых, это текстовые комментарии, в которые можно вводить формулы. Во-вторых, это инертные функции, которые не вычисляются, но дают вывод на экран в естественной математической форме (рис. 1.14). И в-третьих, это возможность быстрого преобразования строковых выражений ввода в естественные математические формулы.
Об инертных функциях мы поговорим позже более подробно. Отметим лишь, что имена таких функций начинаются с большой буквы и функции выводят математическое выражение в естественной математической нотации. С помощью ряда функций, например evalf, можно вычислить математическое выражение, полученное инертной функцией. На рис. 1.14 внизу дан пример такого вычисления для предела функции sin(x)/x.
Рис. 1.14. Примеры применения инертных функций
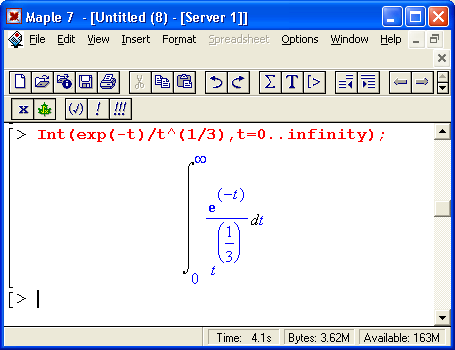
Теперь остановимся на преобразовании исполняемых выражений ввода на Maple-языке в обычные математические формулы. Для этого достаточно, выделив входное выражение, нажать первую кнопку контекстной панели — соответствующее выражение тут же приобретет вид обычной математической формулы. На рис, 1.15 показаны примеры вычислений интеграла при его задании в строках ввода в виде текстового выражения и в обычной математической нотации.
Таким образом, всегда можно получить формульное представление входных выражений. Более того, другой кнопкой их можно превратить в инертную форму, тогда выражение перестает вычисляться и становится, по существу, обычным комментарием.
Следует, однако, учитывать, что представление входных выражений в виде формул обычно занимает заметно больше места на экране и в документе, чем описание выражения на Maple-языке, поэтому оно используется довольно редко. Кроме того, далеко не всякое входное выражение может быть представлено в виде математической формулы — многие функции ядра и библиотек Maple 7попросту не имеют общепринятых обозначений в виде специальных математических знаков.
Рис. 1.15. Примеры вычислений интеграла при его задании в текстовой и математической нотации
26.gif
27.gif
24. Символьные вычисления
Символьные вычисления
Простой пример символьных вычислений
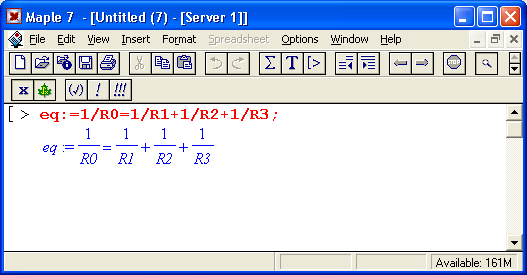
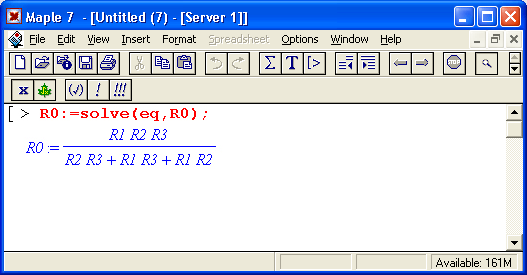
Maple 7 открывает обширные возможности выполнения символьных (аналитических) вычислений. Начнем с простого примера — требуется найти сопротивление трех параллельно включенных резисторов R1, R2 и R3 произвольной величины. Из курса электротехники известно, что можно задать следующее равенство, определяющее суммарное сопротивление R0:
Теперь достаточно использовать функцию решения уравнений solve, чтобы найти значение R0 в общей аналитической форме:
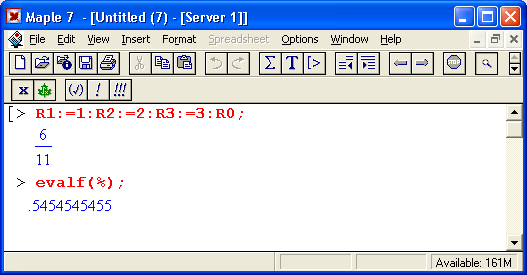
Нетрудно проверить, что результат может быть получен и в численном виде для конкретных значений R1, R2 и R3: > Rl:=a.:R2:-2:R3:=3:RO:
28.gif
29.gif
30.gif
25. Типовые символьные вычисления
Типовые символьные вычисления
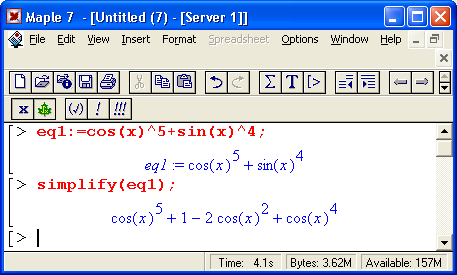
На рис. 1.16 показано несколько примеров выполнения символьных вычислений математического характера: преобразование тригонометрического выражения с помощью функции упрощения simplify, вычисление суммы ряда функцией sum и вычисление неопределенного интеграла функцией int.
Рис. 1.16. Примеры символьных вычислений
Обратите внимание на результат выполнения последнего примера. Он выделен. Выделение можно осуществить протаскиванием указателя мыши с нажатой левой кнопкой.
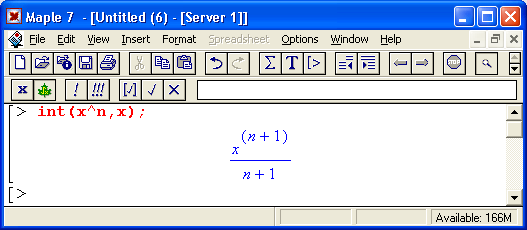
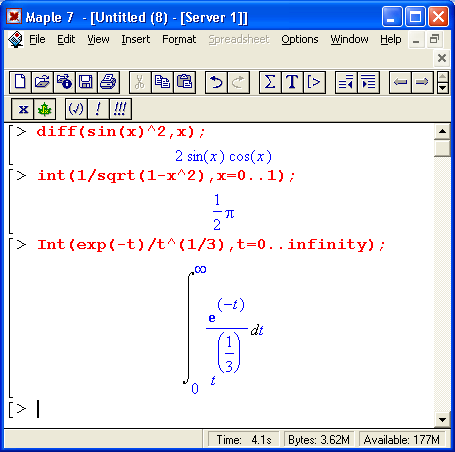
Вычисления производных и интегралов в .символьном виде, пожалуй, являются наиболее характерными областями применения систем символьной математики. На рис. 1.17 показаны примеры таких вычислений с применением функции dif для вычисления производной и int для вычисления определенных интегралов.
Рис. 1.17. Примеры вычисления производной и интегралов
Обратите внимание на функцию Int — инертную форму функции int. Как уже отмечалось, инертная форма служит для вывода записи интеграла в естественной математической форме, но с отложенным «на потом» выводом результата вычислений. Как отмечалось, это один из путей наглядного представления входных выражений. Все инертные функции имеют имена, начинающиеся с большой буквы, тогда как обычные функции имеют имена, начинающиеся с маленькой буквы.
На другом рисунке (рис. 1.18) показано вычисление интеграла, который не имеет представления через функции системы Maple 7, но может быть вычислен ею в численном виде.
Рис. 1.18. Численное вычисление значения интеграла, не имеющего аналитического представления
31.gif
32.gif
33.gif
26. Разбухание результатов символьных вычислений
Разбухание результатов символьных вычислений
Одной из проблем систем компьютерной алгебры является «разбухание» результатов — как оконечных, так и промежуточных. Связано это с тем, что аналитическое представление порою может оказаться весьма громоздким даже для простых задач — пожалуй, это главная причина прохладного отношения к аналитическим вычислениям со стороны инженеров, особенно практиков. К примеру, численное решение кубического уравнения не вызовет трудностей даже на калькуляторе [1], тогда как системы символьной математики выдают его в виде формул, едва помещающихся на экране. Это и иллюстрирует рис. 1.19, на котором показано решение квадратного уравнения (его знает каждый мало-мальски преуспевающий в учебе школьник) и решение кубического уравнения (оно вызывает бурный восторг или легкий шок — в зависимости от отношения учащегося к математике).
Щепетильность системы в ее стремлении выдать полный и математически предельно точный результат, безусловно, очень важна для математиков. Но для многих прикладных задач, с которыми имеют дело инженеры и техники, она оборачивается неудобствами. Инженеры часто прекрасно знают, какие из членов математических формул можно преспокойно отбросить, тогда как для математика-теоретика или аналитика такое действо — типичное кощунство. Порою системы компьютерной алгебры выдают настолько «заумный» и огромный результат, что его упрощение может занять куда больше времени, чем получение более простого результата с заранее выполненными упрощениями. Впрочем, каждому свое! И Maple имеет множество функций, обеспечивающих преобразование результатов в ту или иную форму.
Рис. 1.19. Решение квадратного и кубического уравнений в символьной форме
34.gif

27. Пример решения системы линейных уравнений
Пример решения системы линейных уравнений
Приведем еще один характерный пример — решение системы линейных уравнений с помощью функции solve (рис. 1.20). Обратите внимание на форму задания уравнений и выдачи результатов и поразительную естественность решения задачи. Значение переменной z на рис. 1.20 выделено, где видно, что Maple отображает его поле под панелью инструментов.
Слова solve, diff и int с их аргументами являются именами встроенных в систему функций, возвращающих символьные значения результатов. Нормальному пользователю может стать дурно, если вспомнить, что таких функций с их вариантами система Maple 7 имеет около трех тысяч! Да к тому же многие функции (та же solve для решения уравнений) подчас могут применяться во многих случаях и имеют массу параметров и директив для уточнения направлений решения и расширения областей применения.
Рис. 1.20. Решение системы из пяти линейных уравнений
В утешение можно отметить три важных обстоятельства:
- мало кто на практике использует из всей этой массы функций более чем несколько десятков;
- названия и формы представления многих функций интуитивно предсказуемы;
- наконец, система имеет превосходную справочную базу данных, с помощью которой при определенном терпении (и непременном желании) можно разобраться с синтаксисом любой функции.
Необходимые функции и правила их преобразования система черпает в библиотеке размером около 40 Мбайт (она содержит файлы maple.hdb, maple.lib, maple.ind и maple.cmd). Это иногда занимает заметное время, особенно при первом использовании определенной группы операторов (например, тригонометрических). При повторном использовании этой группы система заметно убыстряется, так как использует уже загруженные средства.
35.gif

28. Повышение эффективности работы с системой
Повышение эффективности работы с системой
Пока что мы при проведении вычислений пользовались лишь простейшими средствами управления системой — вводом выражений и текстовых надписей с клавиатуры. Теперь пора расширить представления о работе с Maple. Прежде чем начать работать с ее меню, надо отметить, что для многих (особенно начинающих) пользователей оказывается удобнее использовать кнопки, расположенные на панелях инструментов, которые находятся прямо под строкой меню.
На рис. 1.21 показано назначение кнопок панели инструментов (Tool Bar). Эти кнопки дублируют наиболее важные операции главного меню и имеют наглядные и типовые для Windows-приложений обозначения. Назначение кнопок и других деталей интерфейса также показаны на рис. 1.21.
Рис. 1.21. Панель инструментов
При необходимости панели инструментов можно убрать с помощью команд меню View (см. рис. 1.11). Если графика выводится в отдельное окно, там имеется своя панель инструментов, которая будет описана ниже.
36.gif
29. Работа с контекстной панелью
Работа с контекстной панелью
Другое полезное средство для облегчения работы по форматированию текстов, заданию параметров входных математических выражений и графиков — контекстная панель инструментов. Как следует из названия, контекстная панель Context Bar является контекстно-зависимой — ее содержание зависит от текущего положения маркера ввода или выделения.
Контекстная панель содержит следующие элементы при вводе текста комментария (рис. 1.22):
- списки для задания стиля, шрифта и размера символов, кнопки для придания полужирного (Bold), наклонного (Italic) и подчеркнутого (Underline) начертания;
- кнопки для выравнивания текста;
- кнопку команды исполнения всего документа.
Рис. 1.22. Контекстная панель инструментов для текста комментария
На рис. 1.15 была показана контекстная панель в случае, когда маркер ввода находится в строке ввода. Там же поясняется назначение кнопок панели для данного случая. Особо остановимся на кнопке со значком (V), которая обеспечивает проверку синтаксиса вводимого выражения до того, как оно завершено символами двоеточия или точки с запятой.
Поясним на примере. Допустим, мы ввели ошибочное выражение для интеграла, забыв указать показатель степени в подынтегральном выражении x^n:
> int(x^,x)
Если нажать кнопку автокоррекции, оно примет вид:
> int(x^ %? ,х)
Maple явно указывает на необходимость ввода показателя степени — в нашем случае переменной n.
А вот другой пример — мы забыли ввести закрывающую скобку в выражение:
> int(x*n ,x
Если теперь нажать кнопку автокоррекции, то вставка скобки произойдет автоматически:
> int(x^n ,x)
Таким образом, данная кнопка может быть полезна для оперативного контроля синтаксиса и исправления грубых ошибок при вводе выражений в формате Maple Input. Однако необходимо делать это до их исполнения.
Заметим, что пока формула является входным выражением в математической форме, она может редактироваться — но не сама по себе, а в виде текстового выражения, отображающегося в поле редактирования на контекстной панели. При этом изменение записи выражения в поле редактирования немедленно влечет соответствующее изменение вводимой формулы. Это тоже довольно удобное средство, имеющее свои преимущества перед прямым редактированием формулы — в MathCAD, например, прямое редактирование формул требует определенных навыков и усваивается довольно туго.
Рис. 1.23. Контекстная панель инструментов для выражений, представленных в математической нотации
Рисунок 1.23 показывает назначение кнопок контекстной панели при установке маркера ввода в строку, содержащую входное выражение в математической нотации. Нетрудно заметить, что в этом случае контекстная панель несколько изменяется — в частности, в ней появляется поле ввода, в котором выведено выделенное выражение на Maple-языке. Такой же вид контекстной панели будет, если выделено выражение или его часть в строке вывода.
37.gif
38.gif
30. Контекстная панель инструментов для двумерных графиков
Контекстная панель инструментов для двумерных графиков
Двумерные графики строятся с заданием ряда параметров, определяющих общий стиль графика. Эти параметры задают цвет и стиль линий графика, вывод координатных осей и т. д. Все параметры имеют значение по умолчанию — они и определяют вид графика, при формировании которого параметры не указаны.
Однако ряд параметров можно изменять, щелкая на соответствующих кнопках контекстной панели. На рис. 1.24 показано назначение кнопок контекстной панели инструментов для редактирования параметров двумерных графиков. Такая панель появляется, если двумерный график выделен или на нем находится маркер ввода.
Рис. 1.24. Контекстная панель инструментов для двумерного графика
Действие большинства кнопок этой формы контекстной панели достаточно очевидно, и вы легко сможете опробовать эти кнопки в работе. Так, график на рис. 1.18 построен точками при нажатии кнопки, задающей стиль Point style. Кроме того, в функции plot построения графика явно использована опция co1or=blue, которая задает синий цвет точек графика.
Полезно отметить, что в левой части контекстной панели есть поле с координатами текущей выделенной точки графика. Чтобы выделить точку, надо подвести к ней указатель мыши и щелкнуть левой ее кнопкой.
При построении контурных графиков и графиков плотности имеется возможность заливки их областей между линиями уровня с выводом линии сетки, на которой рассчитываются линии уровня, и без вывода линий сетки.
39.gif
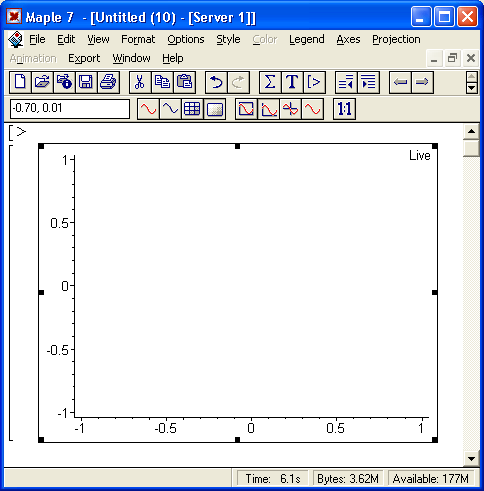
31. Контекстная панель инструментов для трехмерных графиков
Контекстная панель инструментов для трехмерных графиков
Свой вид контекстной панели имеют и трехмерные графики. Назначение ее элементов представлено на рис.-1.25.
Рис. 1.25. Контекстная панель инструментов для трехмерных графиков
С помощью контекстной панели трехмерных графиков можно задать 7 стилей построения трехмерных графиков и 4 стиля вывода координатных осей. Возможны следующие стили трехмерных графиков (группа из семи кнопок в середине панели): функциональная окраска с видимыми линиями каркаса, функциональная окраска без линий каркаса, функциональная окраска с контурными линиями, цветной каркас с видимыми линиями, цветные контурные линии, цветной каркас со всеми (в том числе невидимыми) линиями и поверхность, построенная точками.
Два расположенных слева счетчика позволяют задавать нужный угол обзора, причем Maple сразу же отражает заданный поворот построенной фигуры. Ее также можно вращать мышью, поместив указатель в область графика и держа нажатой левую кнопку. При этом счетчики будут отображать изменяющиеся при перемещении мыши углы обзора. Это очень удобное средство для наблюдения за деталями трехмерных поверхностей и фигур, которые строит функция plot3d.
40.gif
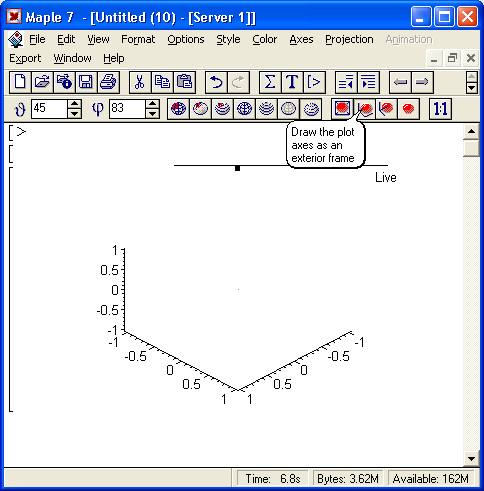
32. Строка состояния
Строка состояния
При работе с Maple полезно следить за информацией в строке состояния системы, расположенной внизу экрана. В ней появляются надписи, поясняющие исполняемые операции. Кроме того, в полях на правой части выводится текущее время, объем используемой оперативной памяти и объем доступной памяти на жестком диске, на котором установлена система.
Хотя панели инструментов и строка состояния удобны для быстрого управления системой, они обладают одним существенным недостатком — занимают часть полезной площади экрана. Однако в меню View имеются команды, позволяющие убрать с экрана любые из этих элементов. Действие этих команд вы можете заметить, если внимательно присмотритесь к предыдущим рисункам.
33. Горячие клавиши системы
Горячие клавиши системы
Для открытия меню можно использовать одновременное нажатие клавиши Alt и клавиши, которая подчеркнута в названии меню. Вызов команды при одновременном нажатии нескольких клавиш получило название «горячих» клавиш управления (Hot Keys).
Таблица 1.1. Горячие клавиши для открытия меню
|
Edit |
Alt+E |
|
File |
Alt+F |
|
Format |
Alt+R |
|
Help |
Alt+H |
|
Insert |
-> Alt+I |
|
Options |
Alt+0 |
|
View |
Alt+V |
|
Spreadsheet |
Alt+S |
|
Window |
Alt+W |
«Горячие» клавиши присвоены и многим другим, наиболее распространенным операциям. Они облегчают и ускоряют (наряду с кнопками панелей инструментов) быстрое управление программой. Ниже в таблицах приведен список наиболее используемых «горячих» клавиш, разбитых на ряд категорий.
Таблица 1.2. Горячие клавиши для задания начертания символов и режимов ввода текста
|
Полужирное начертание |
Ctrl+B |
|
Курсивное начертание |
Ctrl+I |
|
Подчеркнутое начертание |
Ctrl+U |
|
Включение/выключение ввода текста |
F5 |
|
Установка режима ввода (Input Mode) |
Ctrt+M |
|
Задание режима ввода текста (Text Input Mode) |
Ctrl+T |
Таблица 1.3. Горячие клавиши для операций выделения
|
Выделение символа слева |
Shift*- |
|
Выделение символа справа |
Shift*» |
|
Выделение строки вверх |
Shift+- |
|
Выделение строки вниз |
Shift+? |
|
Выделение от маркера ввода до начала строки |
Shift+Home |
|
Выделение от маркера ввода до конца строки |
Shift+End |
|
Выделение от маркера ввода и до начала документа |
Shift+PgUp |
|
Выделение от маркера ввода и до конца документа |
Shift+PgDn |
Таблица 1.4. Горячие клавиши операций удаления, копирования и вставки
|
Выделить все |
Ctrl+A |
|
Копирование выделения в буфер |
Ctrl+C |
|
Перенос выделения из документа в буфер |
Ctrl+X |
|
Вставка содержимого буфера в документ |
Ctrl+V |
|
Удаление строки ввода (параграфа) |
Ctrl+Delete |
|
Закрытие выделенной секции |
Ctrl*. |
|
Поиск |
Ctrl+F |
|
Вставка параграфа после маркера |
Shift+Ctrl+J |
|
Вставка параграфа до маркера |
Shift+Ctrl+K |
|
Восстановление закрытых секций |
Ctrl+, |
|
Вставка исполняемой группы после маркера |
Ctrl+0 |
|
Вставка исполняемой группы до маркера |
Ctrl+K |
|
Вставка конца страницы |
Ctrl+Enter |
|
Вставка выражения в стандартной математической форме |
Ctrl+R |
|
Вставка выражения в форме Standart Math Input |
Ctrl+G |
Таблица 1.5. Горячие клавиши переходов по документу
|
Переход к началу строки |
Ноте |
|
Переход в конец документа |
Ctrl+End |
|
Переход к концу строки |
End |
|
Переход в начало документа |
Ctrl+Home |
|
Создание новой строки |
Shift+Enter |
|
Переход к следующей строке ввода |
Tab |
|
Переход к предыдущей строке ввода |
Shift+Tab |
|
Переход к справке по контексту |
CtrU-Fl или-Fl |
|
Переход на предшествующий уровень вложенности секций |
Ctrl+UpArrow |
Таблица 1.6. Горячие клавиши команд для работы с файлами
|
Создание нового документа |
Ctrl+N |
|
Открытие документа |
Ctrl+0 |
|
Сохранение документа |
Ctrl+S |
|
Печать документа |
Ctrl+P |
|
Закрытие активного окна (документа) |
Ctrl+F4 |
|
Завершение работы с Maple |
Alt+F4 |
Таблица 1.7. Горячие клавиши команд просмотра документа
|
Перерисовка экрана (Redraw Screen) |
Ctrl+L |
|
Просмотр групп ячеек (Show Group Ranges) |
F9 |
|
Показ секций (Show Section Ranges) |
Shift+F9 |
|
Разделение строки на две части "(Split Group) |
F3 |
|
Объединение смежных строк (Join Group) |
F4 |
|
Разделение секции на две части (Split Section) |
Shift F3 |
|
Объединение смежных секций (Join Section) |
Shift F4 |
|
Отмена предшествующей операции (Undo) |
Ctrl+Z |
Таблица 1.8. Горячие клавиши установки масштаба (Zoom Factor)
|
50% |
Ctrl+1 |
|
100% |
Ctrl+2 |
|
150% |
Ctrl+3 |
|
200% |
Ctrl+4 |
|
300% |
Ctrl+5 |
|
400% |
Ctrl+6 |
Разумеется, можно успешно работать с системой, вообще ничего не зная про «горячие» клавиши. Многие так и делают! Однако быстрая и профессиональная работа в Maple 7 невозможна без использования этих клавиш, поскольку они существенно экономят время пользователя.
При работе с русифицированной версией Windows латинские буквы в обозначениях «горячих» клавиш нередко заменяются русскими буквами, не несущими никакой смысловой связи с выполняемой операцией. В этом случае полезно знать, что соответствующая латинская буква (или иной знак) и указанная в меню русская находятся на одной клавише (например, комбинация клавиш для сохранения документа (Ctrl+S) может быть показана как Ctrl+ы).
34. Доступ к справкам и примерам
Доступ к справкам и примерам
В меню Help системы Maple 7 сосредоточены средства доступа к справке по всем функциям системы. Детально работу со справочной базой данных Maple 7 мы рассмотрим в следующей главе. Здесь лишь отметим, что справку по любой функции можно получить, просто установив на ее имени маркер ввода и нажав клавишу F1. На рис. 1.26 показано окно с началом справки по функции cos(x).
Рис. 1.26. Пример справки по функции косинуса
Как видно из рис. 1.26, окно справки содержит пятиступенчатый контекстный указатель, позволяющий последовательно отыскивать нужный раздел справки. Когда справка запрашивается по конкретной теме (функции), то сразу появляется посвященный ей раздел, точнее начало этого раздела.
Примеры из справочной системы можно модифицировать, для этого их нужно скопировать в буфер и перенести в окно документа Maple 7 (см. следующую главу). Также в Maple 7 есть специальный раздел справки, дающий доступ к примерам и без их копирования. Для осуществления такого доступа в окне справки достаточно выбрать тему ExampleWorksheets в первом же разделе контекстного указателя. Откроется окно (теперь уже документа) с индексным каталогом примеров (рис. 1.27).
Каталог примеров дает доступ к огромному числу примеров применения Maple 7. Просмотр одного из них (вычисление эллиптических интегралов) показан на рис. 1.27 справа. Рисунок 1.27 иллюстрирует также технику работы с двумя окнами документов.
Рис. 1.27. Работа с каталогом примеров
В этой книге использованы некоторые наиболее интересные примеры из справочной базы данных системы Maple 7. Однако большинство примеров книги не повторяет помещенные в справку Maple, носит оригинальный характер и отражает результаты исследования возможностей системы Maple 7 автора. В связи с этим читателю рекомендуется просмотреть не только примеры в данной книге, но и примеры, представленные в справочной системе по интересующим читателя функциям.
41.gif
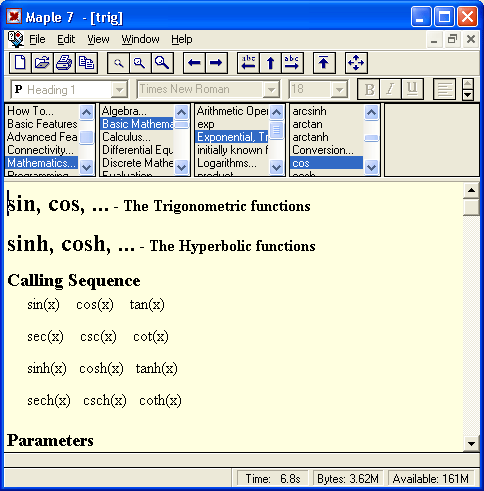
42.gif
35. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Устанавливать Maple 7.
- Отличать языки системы — входной, реализации и программирования.
- Загружать систему и работать с ней в режиме диалога.
- Выполнять простые вычисления.
- Строить простые графики.
- Пользоваться кнопками быстрого управления системой.
- Обращаться к справкам и примерам применения системы Maple 7.
Урок 2. Информационная поддержка Maple
1. Работа со справочной системой
Урок 2.
Информационная поддержка Maple
Справочной системе Maple 7 принадлежит исключительная роль — только в ней можно найти полную информацию обо всех почти трех тысячах функций Maple 7. Использование англоязычной справочной системы может быть полезно и для тех, кто и «двух слов по-английски связать не может», поскольку в ней приведен синтаксис функций и операторов, а также многочисленные примеры их применения — по самым скромным подсчетам их свыше десяти тысяч. К сожалению, справочная система Maple 7 очень громоздка. Но это нельзя считать недостатком справочной системы, поскольку просто велик объем входящего в нее материала. В справочной системе имеются все присущие современным базам данных возможности для быстрого поиска нужной информации и даже для ее структурирования и пополнения.
Основные команды по работе со справочной системой Maple 7 сосредоточены в меню Help, показанном на рис. 2.1.
Рис. 2.1. Меню Help справочной системы Maple 7
Оно содержит команды, объединенные в несколько групп. В первую группу входят следующие команды:
- Introduction — показ начального раздела справки (введения);
- Help on Context — вывод оперативной справки по контексту;
- New User's Tours — запуск обучающей системы;
- What's New — описание новых возможностей системы;
- Using Help — описание правил использования справочной системы;
- Glossary — вывод указателя терминов.
Второй раздел меню содержит команды:
- Topic Search — предметный поиск по заданному образцу;
- Full Text Search — предметный поиск с полным обзором текста справки;
- History — вывод истории поиска.
В третьем разделе имеются две команды для работы с базой данных:
- Save to Database — запись данных в базу данных;
- Remove Topic — восстановление базы данных предметного поиска путем удаления дополнительных данных;
Остальные разделы представлены следующими командами:
- Balloon Help — включение всплывающих подсказок;
- Register Maple 7 — регистрация Maple 7;
- About Maple 7 — вывод окна с информацией о Maple 7.
Рассмотрим детально работу справочной системы Maple 7. Следует отметить, что ценность справочной системы для наших читателей намного снижается из-за того, что она написана на английском языке. Учитывая громоздкость справочной системы и необходимость в наличии компьютера для ее использования, для знакомства с системой Maple 7 более подходят обычные книги, тогда как справочную систему следует применять при необходимости ознакомиться с тонкими деталями применения тех или иных операторов, функций и иных средств Maple 7.
1.gif

2. Просмотр введения
Просмотр введения
Команда Introduction в меню справки запускает справочную систему на странице введения (рис. 2.2).
В введении определено назначение Maple 7 как системы компьютерной алгебры и дается ссылка на сайт фирмы — разработчика системы (www.maplesoft.com). Щелкнув на гиперссылке, вы перейдете на начальную страницу web-сервера фирмы. На странице введения имеются также гиперссылки на обучающий курс (New User's Tour), на страницы с обзором новых возможностей Maple 7 и справки по различным элементам интерфейса.
Рис. 2.2. Окно справочной системы с введением
Обратите внимание на оригинальный подход к представлению пути нужной справки. Для его определения служат 5 окон-списков. На рис. 2.2 используется только одно окно, а остальные 4 пока пусты. Выбирая последовательно по элементу из каждого списка, вы сможете достигнуть требуемой справочной информации. Подробнее навигация по справочной системе будет описана позже.
2.gif
3. Оперативная справка по контексту
Оперативная справка по контексту
Оперативная справка по контексту — сравнительно новая возможность справочных систем. Она особенно удобна при разборе примеров, содержащих незнакомые пользователю функции и иные объекты системы Maple. Полезна она и в том случае, когда пользователь знаком с применяемым объектом, но хотел бы уточнить его свойства и синтаксис.
Для получения оперативной справки по контексту достаточно установить курсор на соответствующий объект, например на имя какой-либо функции, и открыть меню Help. В нем можно обнаружить, что операция Help on Context модифицируется и приобретает вид Help on "...", где на месте многоточия стоит слово, на котором остановился курсор. На рис. 2.1 таким словом является имя функции, вычисляющей синус, — sin.
Допустим, что в тексте документа в строке ввода есть функция sin(x). Если теперь выполнить команду Help on "..." — тут же появится окно со справкой о функции синуса. Существуют и горячие клавиши для этой команды — Ctrl+Fl (или просто F1). Пример справки по функции sin представлен на рис. 2.3.
Рис. 2.3. Пример справки по функции sin
Как видно из рис. 2.3, справка по контексту позволяет судить о назначении функции, синтаксических правилах ее задания и примерах применения. Реализована она по единым правилам справочной системы и содержит открываемые разделы и гипертекстовые ссылки.
В этом примере уже хорошо видна техника использования окон в верхней части справки для уточнения необходимого раздела. Так, обнаруженная функция cos (кстати не sin, это любопытное свойство справки Maple — наличие «союзных» разделов) находится уже в четвертном окне. Последовательность доступа к ней следующая: Mathematics-Basic Mathematics-Exponential, Trig and Hyperbolic-cos. Очевидно, что функция cos найдена потому, что она выступает в паре с функцией sin, — на странице справки приведены примеры и к той, и к другой функции. Учитывая огромное число функций системы Maple 7 и соответственно разделов справки, подобный способ поиска информации представляется очень удобным. Он, кстати, стал использоваться и в Mathematica 3/4 — ближайшем конкуренте Maple.
3.gif
4. Обучающий курс New User's Tour
Обучающий курс New User's Tour
Команда New User's Tour открывает окно курса по обучению основам пользования Maple, показанное на рис. 2.4.
Рис. 2.4. Окно курса обучения основам Maple
В конце страницы (рис. 2.4) имеется гиперссылка Click here to begin the New User's Tour. Она открывает окно обучающего курса по Maple с перечнем ее разделов, представленное на рис. 2.5. Наименования разделов являются гиперссылками. Как видно из рис. 2.5, обучающий курс имеет следующие разделы:
- (1) Working Through the New User's Tour — обучение работе с курсом;
- (2) The Worksheet Environment — создание документов;
- (3) Numerical Calculations — численные вычисления;
- (4) Algebraic Computations — алгебраические преобразования;
- (5) Graphics — графики;
- (6) Calculus — вычисления;
- (7) Differential Equations — дифференциальные уравнения;
- (8) Linear Algebra — линейная алгебра;
- (9) Finance and Statistics — финансы и статистика;
- (10) Programming — программирование;
- (11) Online Help — помощь через Интернет;
- (12) Summary — заключение.
Активизация любой из этих гиперссылок приводит к выводу соответствующего раздела обучающего курса. На рис. 2.6 представлено начало раздела 3, посвященного численным вычислениям.
Рис. 2.5. Окно с перечнем разделов обучающего курса
Рис.2.6. Начало раздела обучающего курса по численным вычислениям
Основные достоинства обучающего курса в том, что он (в отличие от справочной базы данных) дает обычное описание работы с системой Maple 7 с «живыми» примерами, которые не надо копировать в документы. Фактически обучающая система является просто набором документов системы. Вначале примеры даны без ячеек вывода, которые появляются после исполнения команды Edit> Execute> Worksheet. Это иллюстрирует рис. 2.7.
Рис. 2.7. Начало раздела обучающей системы по численным вычислениям после исполнения команды Edit> Execute > Worksheet
Пользователь может модифицировать любой пример и немедленно получить новые результаты (попробуйте, например, заменить вычисление 200! на 100! или 500!). К сожалению, написан обучающий курс на английском языке и в отличие от обычной книги для работы с ним нужен компьютер.
4.gif
5.gif
6.gif
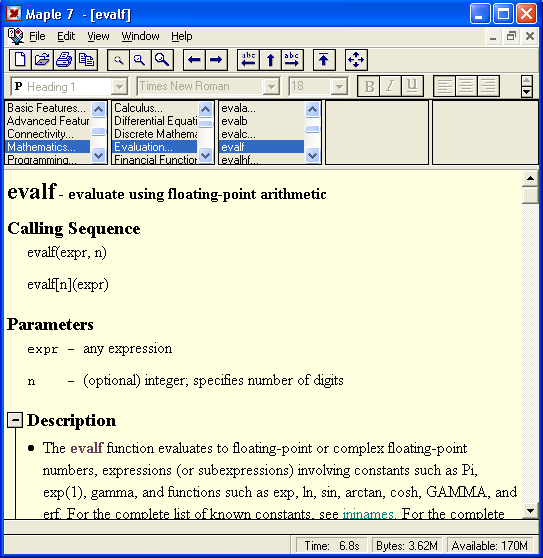
7.gif
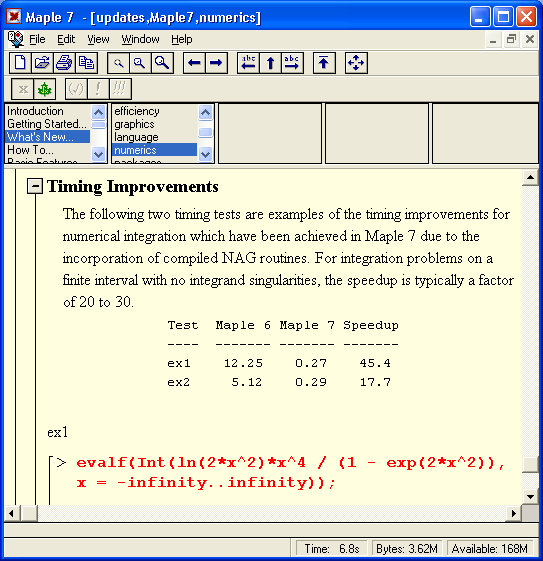
5. Новые возможности Maple 7
Новые возможности Maple 7
Пользователи, знакомые с предшествующими версиями системы Maple, обычно хотят узнать, что нового введено в последней версии. Однако, как у нас говорят, «лучшее — враг хорошего» — при большом числе новых возможностей (и особенно при модификации старых возможностей) появляется несовместимость между документами для старых и новых версий системы. Несмотря на меры, предпринятые по предотвращению такой несовместимости, ее проявление вполне возможно, в частности документы, созданные в Maple 7, уже нельзя использовать в предшествующих версиях из-за различий в их внутренних форматах.
Выполнение команды What's New открывает окно с описанием новых возможностей Maple 7. Оно показано на рис. 2.8.
Рис. 2.8. Окно справки с описанием новых возможностей системы Maple 7
С помощью гиперссылок на этой странице можно получить достаточно подробное описание всех появившихся в Maple 7 возможностей. Мы уже отмечали их в уроке 1.
8.gif
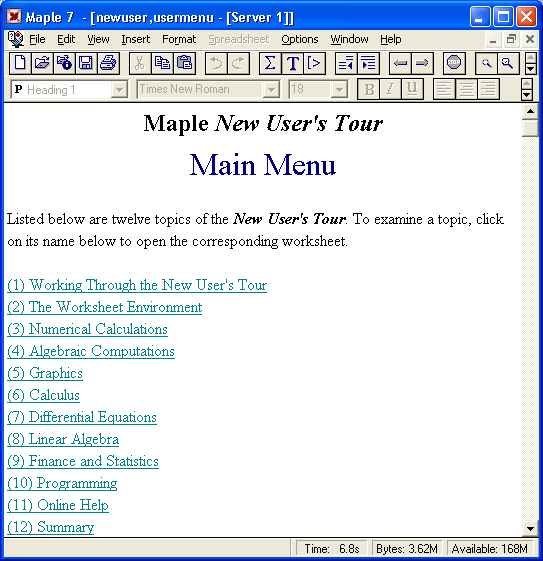
6. Правила работы со справочной системой
Правила работы со справочной системой
Справочная система Maple 7, по существу, является мощной базой данных с обширными возможностями поиска нужной информации и многочисленными примерами применения Maple 7. Работа с такой системой может вызвать затруднения у начинающих пользователей, поэтому в состав справочной системы включено описание правил ее использования. При исполнении команды Using Help появляется страница с перечнем разделов описания справочной системы (рис. 2.9).
Рис. 2.9. Окно с перечнем разделов описания справочной системы
Мы не будем подробно описывать содержание страницы и гиперссылок, поскольку весь материал данного урока и является, по существу, таким описанием.
9.gif
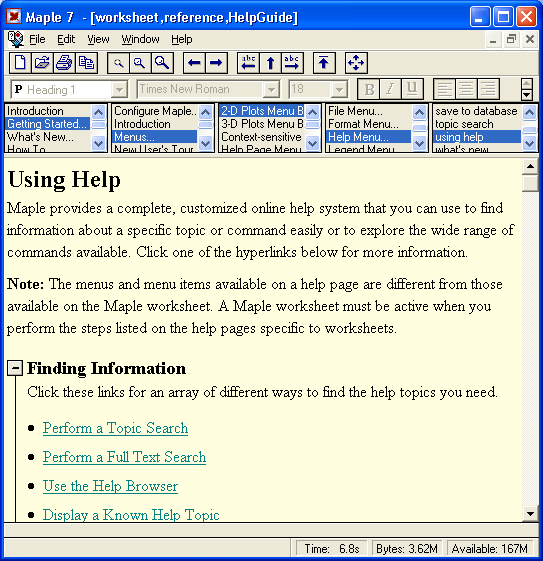
7. Предметный поиск
Предметный поиск
Команда Topic Search (предметный поиск) — одна из самых мощных функций справки. Она выводит окно поиска (рис. 2.10), содержащее в верхней части поле для ввода образца. Образцом может быть слово (например, имя функции) или даже часть слова. В окне под этим полем появляется список всех объектов Maple 7, в индекс которых входит заданный образец (рис. 2.10).
Теперь остается из заданного списка слов выбрать нужное, что приведет к появлению окна справки с информацией по данному слову. Иногда индекс по данному слову будет иметь несколько ссылок, на появившейся странице вам придется уточнить, справку по какому объекту вы хотите получить. Окно предметного поиска в правой части имеет четыре кнопки со следующим назначением:
- Search — поиск по образцу;
- Apply — вывод окна выбранного раздела справки при сохранении окна поиска;
- ОК — окончание поиска (выводится окно с выбранным разделом и исчезает окно поиска);
- Cancel — закрытие окна поиска.
Кроме того, имеется возможность задания двух параметров:
- Same Window — вывод в то же окно (если окно не открыто на полный экран);
- Auto-Search — автоматический поиск по образцу по мере ввода последнего.
Заметим, что если установлен флажок Auto-Search, то кнопка Search становится недоступна, поскольку отпадает необходимость в ней.
8. Предметный поиск с полным обзором текста справки
Предметный поиск с полным обзором текста справки
Предметный поиск с полным обзором текста справки (Full Text Search) — еще один эффективный метод получения справочной информации. Он напоминает ранее рассмотренный, но вхождение заданного образца ищется во всем тексте справочной системы, а не только по индексу, составленному создателями Maple. При этом выводится окно, подобное показанному на рис. 2.11. Обратите внимание на то, что в большом Поле этого окна указано существенно больше разделов справки, чем при поиске по индексу — очевидно, что большинство из них будет случайным упоминанием данного образца.
Рис. 2.10. Окно предметного поиска
Рис. 2.11. Окно предметного поиска с полным обзором текста справки
В этом окне используются те же кнопки управления, что и для окна поиска справки по образцу. Флажок Goodness of Match включает вывод статистики повторяемости образца в текстах разделов справочной системы.
10.gif
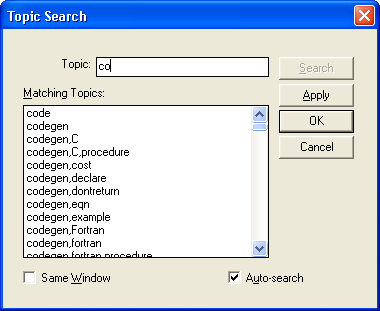
11.gif
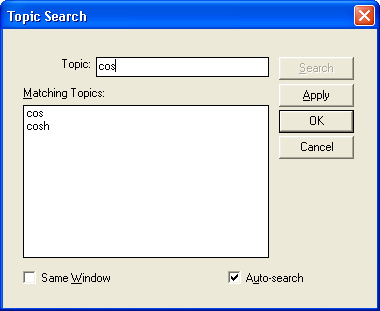
9. История работы со справкой
История работы со справкой
Было замечено, что пользователь, занятый решением определенного класса задач, обычно неоднократно возвращается к ранее просмотренным разделам справочной системы. Чтобы не искать их всякий раз заново, справочная система хранит список разделов, просмотренных в данном сеансе работы. Он выводится операцией History (рис. 2.12).
Достаточно найти в этом окне нужный раздел справки и нажать кнопку ОК, чтобы вывести его на экран. Кнопка Apply позволяет просматривать каждый новый раздел в своем окне.
Рис. 2.12. Список ранее просмотренных разделов справки
12.gif
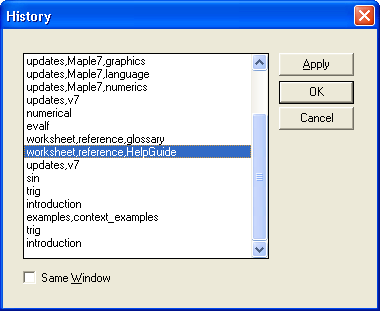
10. Модернизация справочной базы данных
Модернизация справочной базы данных
В справочной базе данных предусмотрена возможность ее расширения путем записи текущего документа, составленного пользователем, в указанный раздел. При выполнении операции Save to Database выводится специальное окно, в котором надо указать соответствующие данные о модернизируемом разделе справки. Вид окна представлен на рис. 2.13.
Ограничимся этим указанием, учитывая, что для нашего пользователя модернизация англоязычной справочной базы данных явно отдает экзотикой.
11. Удаление разделов базы данных
Удаление разделов базы данных
Для удаления разделов базы данных служит команда Remove Topic. Она выводит окно, показанное на рис. 2.14.
Обратите внимание, что модернизации в обоих случаях подвергается один и тот же файл базы данных maple.hdb.
Рис. 2.13. Окно дополнения базы данных
Рис. 2.14. Окно удаления разделов справочной базы данных
13.gif
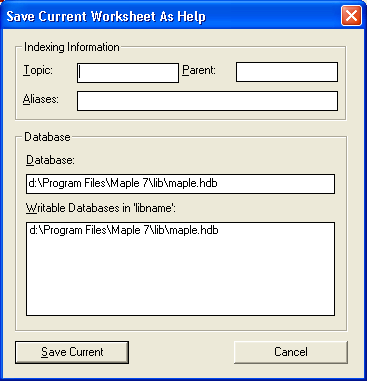
14.gif
12. Включение всплывающих подсказок
Включение всплывающих подсказок
На первом этапе знакомства с пользовательским интерфейсом системы Maple 7 удобно использовать всплывающие подсказки. Они вводятся при установке флажка Balloon Help. Для получения подсказки по какому-либо объекту достаточно задержать на пару секунд указатель мыши на этом объекте. Пример вывода всплывающей подсказки показан на рис. 2.1 — она указывает на назначение команды меню Help — Help on "sin".
13. Регистрация системы
Регистрация системы
Команда Register Maple 7 меню справочной системы открывает окно регистрации системы Maple 7. Это окно позволяет вызвать браузер Интернета, с помощью которого выполняется регистрация.
14. Вывод окна с информацией о системе
Вывод окна с информацией о системе
Последняя команда меню Help — About Maple 7 — выводит окно с информацией о версии Maple 7 (рис. 2.15). В этом окне содержатся данные, необходимые для регистрации системы Maple 7 (номера лицензии и самого продукта), а также данные о времени выпуска системы.
Рис. 2.15. Окно с данными о системе Maple 7
Обратите внимание, что данный продукт датирован концом мая 2001 г. Как уже отмечалось в уроке 1, официально он выпущен на рынок 21 июня 2001 г.
16.gif

15. Что нового мы узнали?
Что нового мы узнали ?
В этом уроке мы научились:
- Использовать контекстную справку.
- Работать со справочной системой.
Урок 3. Работа с файлами и документами
1. Операции с файлами
Урок 3.
Работа с файлами и документами
Система Maple работает с документами в стиле notebooks («блокноты» или «записные книжки»). Как было показано в уроке 1, документы содержат текстовые и формульные блоки, результаты вычислений, графики разного типа и другие компоненты. Документы могут готовиться с нуля или существовать в готовом виде — подготовленные кем-то ранее. Хранятся документы на внешних устройствах памяти в виде файлов. Файлом называют имеющую имя упорядоченную совокупность данных, размещенную на том или ином носителе — обычно на жестком, гибком или компакт-диске.
В Maple 7 используются файлы различных форматов, который указывается расширением файла (знак * означает произвольное имя файла):
- *.ms — файлы документов для систем с графическим интерфейсом (Windows/ Macintosh);
- *.msw — файлы документов (Worksheets);
- *.txt — текстовые файлы (включая формат Maple-текст);
- *.tex — файлы в формате LaTeX;
- *.ind и *.lib — файлы библиотек;
- *.т — файлы внутреннего Maple-языка.
Файлы документов содержат все необходимые данные для правильного отображения содержимого документа в окне редактирования с указаниями координат расположения блоков, фактического содержания и характера выполняемых операций, форматов предоставления информации и т. д. [Таким образом, файл содержит кроме текста, отображаемого на рабочем листе, специальные команды, адресованные Maple, аналогично файлам HTML, имеющим теги, предназначенные для интерпретации браузером.
Предусмотрена возможность записи документов и в особом формате LaTeX, предназначенном для создания книг и статей по математике. Текстовые файлы (с расширением .txt) можно просматривать и редактировать текстовыми редакторами, работающими с ASCII-кодировкой.
Важно отметить, что даже при записи документов со сложными рисунками используется не прямая запись их растровой или векторной копии, а сохранение данных для построения графиков. Поэтому размеры файлов Maple 7 невелики и их легко передавать по современным средствам телекоммуникаций, например по сети Интернет. Они требуют небольшого свободного пространства на дисках для записи. Тем не менее, чем сложнее график, содержащийся в документе, тем больше объем памяти, необходимой для хранения файла. Помимо обычных операций по работе с файлами (запись „а диск и загрузка с диска) предусмотрены возможности распечатки документов принтерами различного типа.
2. Меню File
Меню File
Меню File содержит основные операции для работы с файлами документов (рис, 3.1).
Рис. 3.1. Меню File и пустое окно нового документа
Меню содержит ряд операций, разбитых на группы. В первую группу входят следующие операции по работе с документами (в скобках приведены горячие клавиши):
- New (Ctrl+N) - создать новый документ;
- Open (Ctrl+0) - открыть существующий документ;
- Open URL - открыть URL-адрес;
- Save (Ctrl+S) - сохранить активный документ;
- Save As — сохранить активный документ под новым именем;
- Export As — экспортировать файл;
- Close (Ctrl+F4) — закрыть окно активного документа;
- Save Settings — запись конфигурации (установок) Maple;
- AutoSave Settings — автоматическая запись конфигурации.
Вторая группа команд относится к печати документов:
- Print Preview — предварительный просмотр документа перед печатью;
- Print (Ctrl+P) — печать документа;
- Printer Setup — установка параметров принтера.
Вторая из этих команд позволяет распечатать весь текст документа с комментариями, математическими формулами, таблицами и графиками. Печать производится принтерами в графическом режиме, поэтому и не очень быстро. Зато печатаются все шрифты и математические спецзнаки. Можно напечатать и отдельные части документа.
После этой группы команд имеется список документов (файлов с расширением .ms), которые были загружены в систему в предшествующие сеансы работы. Выбрав в этом списке название одного из файлов, можно быстро загрузить его, не тратя времени на открытие файла через команду Open. Последняя группа представлена единственной командой:
- Exit (Alt+F4) - выйти из Maple 7.
ПРИМЕЧАНИЕ
Если вы работаете в русифицированной версии Windows, то горячие клавиши могут содержать вместо латинских букв русские эквиваленты. Например, команда New имеет горячие клавиши Ctrl+N, тогда как в меню они могут быть обозначены как Ctrl+T (см. рис. 3.1). На самом деле, как обозначать клавишу: русской буквой или латинской — дело вкуса.
1.gif
3. Создание нового документа
Создание нового документа
Вернемся к широко используемым операциям первой группы и рассмотрим их более подробно. Заметим, что к некоторым из них можно быстро обратиться с помощью «горячих» клавиш (они указаны в скобках после названия команды). Команда New используется для создания нового документа. Она открывает новое пустое окно редактирования и переводит Maple в режим редактирования (рис. 3.1).
При создании нового документа в его начале появляется ячейка со знаком приглашения >, после которой виден мигающий маркер ввода в виде вертикальной черты |. Ячейка ввода обрамляется открывающей квадратной скобкой. Созданный документ приобретает имя Untitled (N) (в вольном переводе — «Безымянный под номером N», где N — целое число). Следуя приглашению программы, можно приступать к работе в Maple.
Операция New дублируется кнопкой со значком в виде чистого листа, размещенной на панели инструментов. Разумеется, нажать ее вы сможете, только если панель инструментов выведена на экран.
4. Открытие документа
Открытие документа
Команда Open служит для открытия созданного ранее документа. Вначале открывается диалоговое окно выбора файла (рис. 3.2). Для быстрого доступа к команде служит значок в виде открывающейся папки на панели инструментов.
Рис. 3.2. Окно открытия документа
В окне Открытие файла вам нужно найти нужный файл, а затем дважды щелкнуть на его имени или на кнопке ОК. Данное окно — пример единых диалоговых окон для всех приложений Windows.
Maple 7 — далеко не первая из версий системы компьютерной алгебры. Каждая очередная версия может иметь модифицированные элементы Maple-языка. Поэтому иногда возникает проблема частичной несовместимости документов, подготовленных в разных версиях системы Maple. Разработчики системы по мере возможностей учли это и предусмотрели автоматическое определение версии Maple, в которой был создан документ. Если выбранный документ был сохранен в старой версии программы, то перед его загрузкой появляется окно, представленное на рис. 3.3.
Рис. 3.3. Окно с предупреждением о загрузке документа другой версии Maple
Нажмите кнопку ОК, и документ будет открыт. Не следует думать, что загруженный документ старой версии Maple непременно будет полностью работоспособен. К сожалению, это не так — некоторые документы требуют коррекции, прежде чем Maple 7 сможет их исполнить.
ПРИМЕЧАНИЕ
Вас не должно удивлять появление в отдельных случаях элементов интерфейса с русскоязычными надписями — например, окно открытия файла (рис. 3.2). Они обусловлены тем, что Maple использует некоторые типовые элементы интерфейса операционной системы Windows. И если последняя русифицирована, то вполне возможно появление элементов интерфейса с русскоязычными надписями.
После загрузки документа его содержимое появляется в новом окне (см., например, рис. 1.16 или 1.17) и можно приступать к работе с ним. Во многих системах открытие нового окна командой New или Орел отменяет все предыдущие действия (значения переменных, функции и т. д.). Но в Maple 7 это не так — поскольку система предполагает совместную работу в нескольких окнах, каждое новое окно будет «знать» о происходившем в других окнах. Если же вы хотите начать с нуля в новом окне — исполните в нем команду restart. Maple 7 позволяет работать и с документами, представленными в HTML формате и имеющими URL-адрес. Для загрузки таких документов служит команда Open URL. Она открывает простое окно с полем для ввода URL-адреса. Работа с ним очевидна.
2.gif
3.gif
5. Сохранение документа
Сохранение документа
Команда Save записывает содержимое активного в данный момент окна в виде файла на диск с использованием его текущего имени. Исключением будут документы, созданные командой New и не переименованные, тогда действие команды будет аналогично выполнению команды Save as, обсуждаемой ниже. Следует с осторожностью пользоваться командой Save в том случае, когда вы модернизируете какой-либо документ, но желаете сохранить оригинал в неизмененном виде, ведь содержимое модернизированного файла будет записано «поверх» оригинала. Чтобы этого не произошло, для сохранения файла следует воспользоваться командой Save as, описанной в следующем разделе. При подготовке сложных документов рекомендуется периодически (в некоторых ситуациях довольно часто) давать команду Save, сохраняя сделанные изменения. Это позволяет избежать потери хотя бы части проделанной работы в случае сбоя компьютера. (Не важно, чем будет вызвано выключение или зависание компьютера — халтурной работой электрика или программиста или шалостью вашего ребенка — если вы лишний раз сохраните файл, вам придется меньше сил потратить на его восстановление.) Выполнение команды Save не приводит к выдаче сообщений и окон (кроме уже упомянутого исключения), и поэтому ее не обременительно дать лишний раз, особенно если вы запомните «горячие» клавиши для нее — Ctrl+S.
6. Запись документа на диск с переименованием
Запись документа на диск с переименованием
Команда Save As отличается от предыдущей тем, что перед записью файла на диск в появившемся диалоговом окне вы можете изменить имя файла (рис. 3.4).
Таким образом можно сохранить доработанный документ и в то же время оставить неизменным оригинал.
Рис. 3.4. Диалоговое окно для записи файла с указанием его имени
В списке Папка нужно найти папку, в которую вы хотите поместить файл, а в поле Имя файла вам нужно указать новое имя. Впрочем, не обязательно новое — если вы выберете другую папку, то можете сохранить и ее старым именем — оригинал не пострадает. , Maple позволяет сохранить файл в следующих форматах (список внизу окна):
- Maple Worksheet (*.rnws/*.ms) — файлы формата Maple 7;
- Maple Text (*.txt) — файлы в формате текста Maple;
- HTML Source (*.html) — файлы в формате HTML;
- Text (*.txt) — файлы в текстовом формате;
- LaTeX Source (*.tex) — файлы в формате LaTeX.
Формат HTML — новый для Maple формат, позволяющий записывать файлы документов в виде web-страниц. .
Команда Save as особенно полезна при доработке и модификации файлов, например входящих в комплект поставки системы, когда надо сохранить оригинальные файлы в неприкосновенности. Для этого достаточно записать измененные файлы под новыми именами.
4.gif
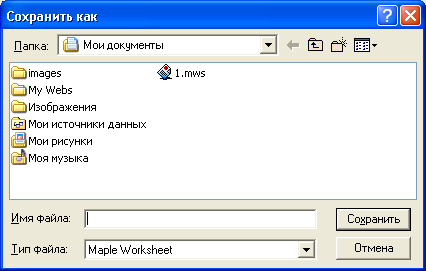
7. Экспорт файлов.
Экспорт файлов
Maple 7 имеет возможность экспорта файлов в различные форматы. Команда Export As открывает подменю, содержащее форматы, запись в которых поддерживает Maple После выбора нужного формата в подменю появляется окно, аналогичное окну для сохранения файла.
Maple экспортирует файлы в следующие форматы:
- Maple Text (*.txt);
- HTML (*.html);
- HTML with MathML (*.html);
- Plain Text (*.txt);
- Rich Text Format (*.rtf);
- LaTeX (*.tex).
Графики Maple может записывать в следующих форматах: DFX, EPS, GIF, JPEG, POV, WMF и BMP.
8. Закрытие документа
Закрытие документа
Команда Close закрывает окно вместе с текущим документом, и система переходит к работе со следующим окном (либо к пустому серому окну, если был закрыт последний документ).
Если закрываемый документ подвергался модификации, то система спросит, надо ли сохранять изменения (рис. 3.5).
Рис. 3.5. Диалоговое окно, появляющееся при закрытии модифицированного документа
Следует помнить, что каждое окно, будучи сложным графическим объектом, занимает определенный и вовсе не малый объем памяти. Поэтому команда Close является эффективным средством освобождения оперативной памяти, особенно когда закрывается большой документ. Однако надо помнить, что бывшие в нем определения (например, значения переменных, введенные функции пользователя и т. д.) сохраняются в памяти, даже когда документ закрыт, естественно, пока вы не дадите команду restart.
Быстро закрыть документ можно, нажав клавиши Ctrl+F4.
5.gif
9. Запись настроек программы
Запись настроек программы
Для записи сделанных настроек Maple в меню File предусмотрены две команды: Save Settings и Auto Save Settings. Последняя команда — это флажок, при установке которого новая настройки Maple будут записываться автоматически при завершении работы.
10. Выход из системы
Выход из системы
Команда Exit служит для выхода из Maple. Тогда при использовании операции Exit можно наблюдать последовательное исчезновение окон документов. Если пользователь забыл записать какой-либо документ на диск, система сообщит об этом, выдав запрос. Нужно ответить Yes (Да), если документ нужно сохранить, и No (Нет), если сохранение не требуется. Однако стоит сохранить документы, подвергавшиеся редактированию и модификации, заранее — вдруг вы по ошибке нажмете не ту кнопку.
Не следует применять команду Exit, если вам необходимо временно переключиться в окно другой программы, так как повторная загрузка Maple занимает много времени.
11. Печать документов
Печать документов
Команда Print служит для печати документа. Она имеет кнопку с изображением принтера на панели инструментов для быстрого доступа.
После того как отдана команда Print, появляется диалоговое окно, показанное на рис. 3.6, — стандартное окно печати в Windows.
Рис. 3.6. Окно печати
Нажатие кнопки Свойства в окне печати открывает окно свойств выбранного принтера. Вид окна зависит от типа принтера, функции его элементов достаточно очевидны, поэтому мы воздержимся от обсуждения работы с ним.
Таким образом, в списке вверху окна печати прежде всего следует установить принтер. Можно просто оставить установленный по умолчанию. В диалоговом окне также можно указать диапазон страниц для печати и число копий, а также установить флажок для разбора страниц по копиям. В целом диалог с компьютером при осуществлении операции печати прост и нагляден.
6.gif
12. Предварительный просмотр страниц
Предварительный просмотр страниц
Даже одна страница документа может не поместиться на экране монитора. Поэтому перед печатью полезно просмотреть расположение элементов документа на странице. Для этого служит команда Print Preview, которая выводит окно' с изображением текущей страницы (рис. 3.7).
Рис. 3.7. Предварительный просмотр страницы, предназначенной для печати
У окна просмотра имеется ряд элементов управления. Прежде всего это полосы прокрутки для перемещения изображения документа в окне просмотра. Кроме того, имеется ряд кнопок, назначение которых указано ниже:
- Print — печать просматриваемого документа;
- Prev. Page — просмотр предыдущей страницы многостраничного документа;
- Next Page — просмотр следующей страницы многостраничного документа;
- Sngl. Page — просмотр одной полной страницы;
- Dbl. Page — просмотр двух полных страниц;
- 100% — установка масштаба в 100 %;
- Zoom In и Zoom Out — увеличение и уменьшение масштаба;
- Done — завершение работы с окном предварительного просмотра.
Использование команды Print Preview может сэкономить не один лист читой бумаги и картридж краски.
7.gif
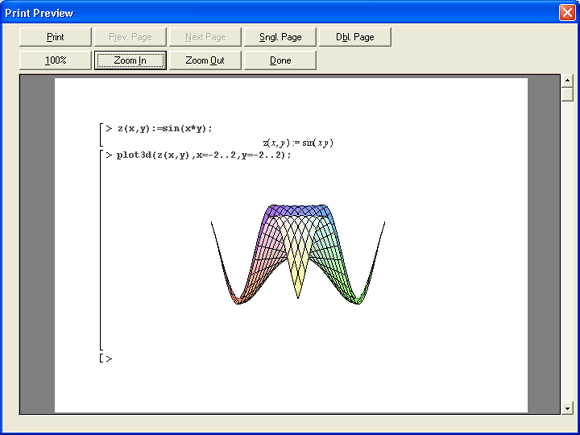
13. Установка параметров принтера
Установка параметров принтера
Печать документов — одна из основных функций любой среды подготовки документов. В общем случае она предполагает установку параметров принтера. Для этого служит команда Printer Setup, приводящая к открытию диалогового окна, показанного на рис. 3.8.
Рис. 3.8. Диалоговое окно настройки параметров принтера
Следует отметить, что вид этого окна будет варьироваться в зависимости от принтера и может существенно отличаться от приведенного на рисунке. Однако большинство параметров, которые требуют пользовательского вмешательства, очевидны.
8.gif
14. Редактирование документов
Редактирование документов
Как видно из рис. 3.9, меню Edit содержит различные операции редактирования. Они делятся на ряд групп. Первая группа содержит следующие операции:
- Undo (Ctrl+Z) — отменить последнюю операцию редактирования;
- Redo (Ctrl+Y) — восстановить последнюю отмененную операцию;
- Cut (Ctrl+X) — переместить выделенный фрагмент в буфер обмена;
- Copy (Ctrl+C) — скопировать выделенный фрагмент в буфер обмена;
- Copy As Maple Text — копирование выделения в буфер обмена в формате Maple-текста;
- Paste (Ctrl+V) — вставить содержимое буфера обмена в документ;
- Paste Maple Text — вставить данные из буфера обмена в формате Maple-текста;
- Delete Paragraph (Ctrl+Del) - удаление параграфа (строки);
- Select All (Ctrl+A) — выделение всех объектов документа.
Рис. 3.9. Меню Edit
Операции первой группы используют буфер обмена (Clipboard). Так называется специально организованная и динамически изменяющаяся область памяти в операционной системе Windows. В нее могут помещаться различные (обычно предварительно выделенные) объекты, документы и даже файлы. Буфер можно использовать для обмена объектами как в пределах текущего документа, так и между различными документами и даже приложениями.
ПРИМЕЧАНИЕ
Очень часто некоторые операции меню Edit будут недоступны — они отображены серым шрифтом это означает, что в данный момент не существует объекта, к которому может быть применена команда. Однако в демо-версии Maple команды копирования и вставки будут недоступны всегда — таково ограничение создателей.
Несколько следующих групп представлены одной операцией:
- Find (Ctrl+F5) — выводит окно поиска заданной строки и ее замены на другую строку;
- Hyperlinks — редактирование гиперссылок;
- Object — редактирование объекта;
- Unit Converter — перевод между различными единицами измерения;
- Complete Command — подсказка для завершения текущей незаконченной команды Maple-языка;
- Entry Mode (F5) — переключение режима ввода.
Последняя команда позволяет менять режим строк ввода — они могут содержать математические выражения или неисполняемые текстовые комментарии. Именно благодаря текстовым комментариям документы Maple 7 приобретают достаточно наглядный вид. Наглядность документов дополнительно повышается благодаря возможности представления результатов вычислений (а иногда и вводимых выражений) в естественной математической форме. Восьмая группа команд открывает подменю, содержащие команды с ячейками и секциями документа:
- Split or Join — разделение или объединение объектов;
- Execute — исполнение выделенных или всех строк документа;
- Remove Output — удаление вывода для выделенных или всех строк документа.
Команды подменю Split or Join позволяют легко модифицировать вид документов путем разделения и объединения строк и секций.
9.gif

15. Отмена последней операции
Отмена последней операции
Команда Undo Delete служит для отмены последней операции редактирования. Она позволяет удалить до 5 последних операций. Если вы случайно удалили нужный текст — вам придет на помощь команда Undo. В меню, а также во всплывающей подсказке указывается название последней операции редактирования — той, которую вы собрались отменить.
16. Восстановление отмененной операции
Восстановление отмененной операции
Команда Redo позволяет вернуть отмененную операцию, если в этом возникает необходимость. Действие этой команды, естественно, тоже распространяется не более чем на пять операций. Команды Undo и Redo имеют кнопки (с изображением стрелок) на панели инструментов для быстрого доступа к себе.
17. Перенос объекта в буфер обмена
Перенос объекта в буфер обмена
Команда Cut копирует выделенный объект в буфер обмена и удаляет его из документа. Выделить объект или группу объектов можно, обведя его мышью при нажатой левой кнопке. Можно также использовать клавиши перемещения курсора при нажатой клавише Shift. Выделенный фрагмент отмечается черным фоном и инверсией цвета входящих в него символов (на рис. 3.9 выделена первая строка).
Графические объекты не инвертируют свои цвета при выделении, к тому же их можно вырезать и копировать, когда на них находится маркер ввода. Вырезанный командой Cut объект поступает в буфер обмена, а его изображение в окне редактирования исчезает. Эта команда выполняется также комбинациями клавиш Shift+Del и Ctrl+X (в зависимости от настроек операционной системы). На рис. 3.10 показан результат выполнения команды Cut — видно исчезновение выделенного на предыдущем рисунке фрагмента в документе.
Рис. 3.10. Документ с рис. 3.9 после выполнения команды Cut
Щелчок левой кнопкой мыши за пределами выделенных объектов снимает все выделения.
10.gif
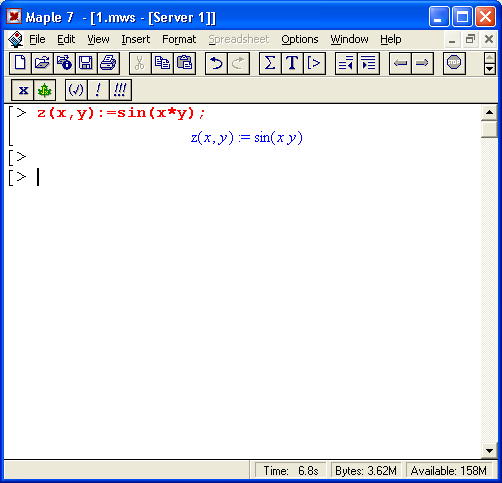
18. Копирование объекта в буфер
Копирование объекта в буфер
Команада Сору аналогична Cut, но с одним существенным отличием — выделенный объект (или блок объектов) не удаляется в окне редактирования. Эта команда обычно используется в том случае, когда нужно перенести заданный объект в другое место, сохранив при этом оригинал, — продублировать объект. Особенно полезна операция Сору при составлении документа из частей других документов, в том числе страниц справочной системы Maple (рис. 3.11). Переключаясь между окнами с помощью команд Сору и Paste, описанных ниже, можно с легкостью составить достаточно большой документ, не написав ни строки.
Рис. 3.11. Пример переноса выделенной в одном документе строки в окно другого документа
В данном случае титульная надпись, удаленная командой Cut, перенесена в другой, пустой, документ.
11.gif
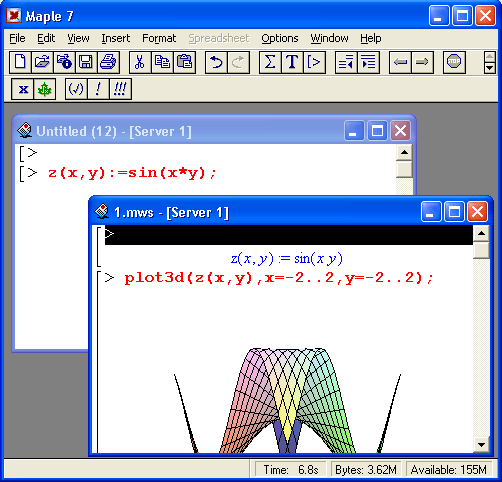
19. Перенос и копирование объектов перетаскиванием
Перенос и копирование объектов перетаскиванием
В Maple 7 имеется возможность переноса объектов из одного окна в другое методом перетаскивания (Drag and Drop). Для этого на группу выделенных объектов надо навести указатель мыши и при нажатой левой кнопке начать перенос объектов в новое место или новое окно. Отпустив левую кнопку мыши, можно наблюдать перенос объектов на новое место. Если все время держать нажатой клавишу Ctrl, то переносимый блок объектов будет сохранен и на старом месте.
20. Копирование в буфер обмена в формате Maple-текста
Копирование в буфер обмена в формате Maple-текста
Команда Copy As Maple Text используется в тех случаях, когда необходимо, чтобы скопированная в буфер информация была представлена в текстовом формате. При этом в буфер копируются выражения как из строк ввода, так и строк вывода — все в текстовом формате. Используя в этом случае команду Paste можно вывести из буфера все выражения как из входных, так и из выходных строк в текстовом формате (рис. 3.12).
Рис. 3.12. Пример использования операций Copy as Maple Text и Paste
Обратите внимание, что графическое представление интеграла в строке вывода превратилось в его отображение в текстовом формате. То же имеет место в отношении представления производных, сумм, произведений и т. д. Обратите также внимание на то, что текстовый комментарий в данном случае выводится стандартным шрифтом. Атрибуты (признаки) стиля, цвета и размера символов теряются.
12.gif
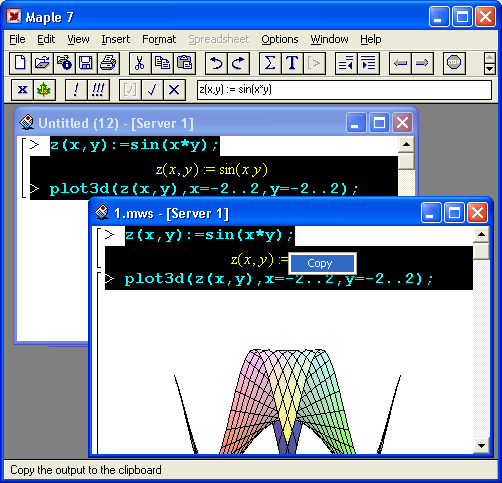
21. Вставка из буфера обмена в документ
Вставка из буфера обмена в документ
Команда Paste копирует содержимое буфера обмена, помещенное туда командами Сору или Cut, в место, указанное маркером ввода. При этом сохраняются форматы всех объектов документа, если они были скопированы (рис. 3.13).
Как видно из рис. 3.13, возможно применение этой операции не только в пределах окна одного документа, но и при переносе данных из одного окна в другое.
Надо отметить, что при копировании в буфер обмена математической формулы из ячейки вывода и вставке ее в строку ввода формат формулы меняется — она автоматически превращается в текстовое выражение. Это иллюстрирует рис. 3.14.
Рис. 3.13. Пример использования операций Сору и Paste
Рис. 3.14. Пример копирования формулы из ячейки вывода одного документа в ячейку ввода другого документа
Различные варианты преобразования форматов при использовании операций копирования и вставки надо учитывать при подготовке сложных документов.
13.gif
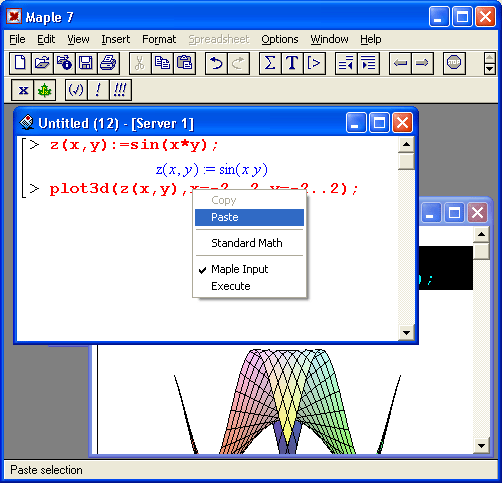
14.gif
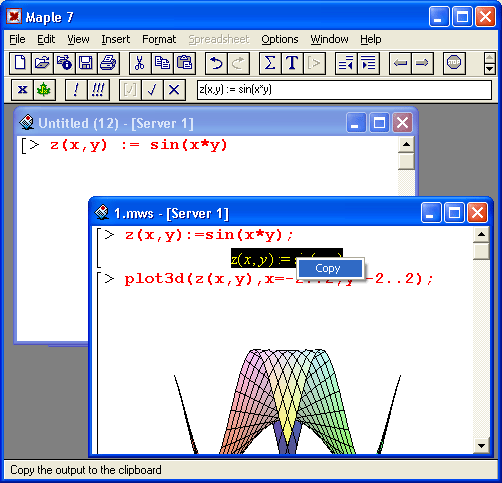
22. Вставка из буфера обмена в формате Maple-текста
Вставка из буфера обмена в формате Maple-текста
Операция Paste As Maple Text служит для вставки данных из буфера обмена с одновременным их преобразованием в текстовый формат.
Если данные в буфер обмена поступили в результате выполнения операции Сору as Maple Text, то при операции Paste Maple Text в документ будут скопированы только данные из строк ввода в формате Maple-текста. Это показано на рис. 3.15.
Рис. 3.15. Пример использования операций Copy as Maple Text и Paste Maple Text
Любопытно сравнить две пары операций, действие которых демонстрируют рис. 3.12 и 3.15.
15.gif
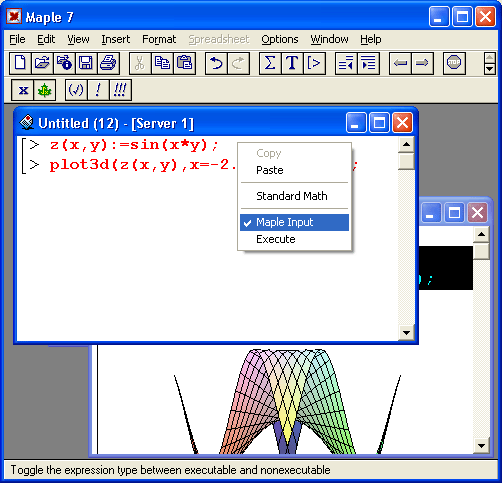
23. Уничтожение выделенного абзаца
Уничтожение выделенного абзаца
Команда Delete Paragraph служит для уничтожения блока ввода, на котором расположен курсор. При этом в буфер обмена удаленный текст не заносится. В отличие от операции вырезания Cut ее применение не загружает буфер и предотвращает нехватку оперативной памяти. Если вы случайно удалите нужную строку — есть время спохватиться — дайте команду Undo.
24. Выделение всех объектов
Выделение всех объектов
Команда Select All выделяет все объекты документа. Это полезно, например, для вставки всего документа в другой документ.
25. Поиск подстроки и ее замена
Поиск подстроки и ее замена
Команда Find служит для поиска указанного фрагмента в тексте документа. Она открывает окно Find, в котором можно указать искомую фрагмент-подстроку (рис. 3.16). При нажатии кнопки Next будет производиться поиск следующего вхождения (ниже по тексту), а при использовании Previous — предыдущего. Если искомое слово не найдется, выводится окно с сообщением (слева на рис. 3.17).
Рис. 3.16. Поиск заданного фрагмента текста
При обнаружении указанного фрагмента он выделяется, и маркер ввода устанавливается в начало найденной подстроки. После этого можно приступить к ее редактированию.
С помощью команды Find возможна также замена подстроки. Для этого надо указать текст замены в нижнем поле окна. Чтобы заменить найденную подстроку, надо нажать кнопку Change, чтобы заменить все подстроки, — Change All.
Рис. 3.17. Пример замены одной подстроки другой
16.gif
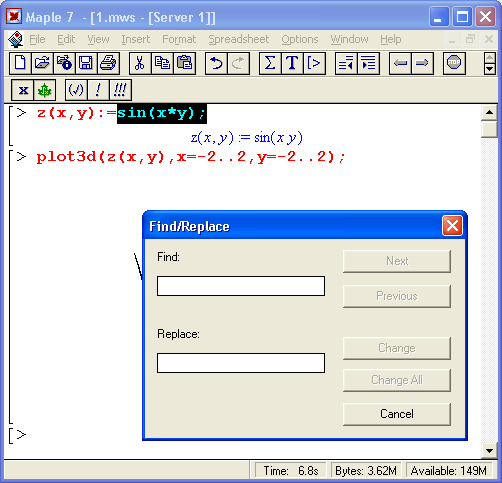
17.gif
26. Включение и выключение режима ввода текста
Включение и выключение режима ввода текста
Maple 7 позволяет вводить в ячейки текст комментариев и исполняемые математические выражения (для того чтобы ввести в одну ячейку комментарий и функцию Maple, надо воспользоваться командами меню Insert). Операция Input mode служит для переключения между режимами ввода. Горячая клавиша команды — F5. Если режим ввода текста комментария включен, приглашение в виде знака > исчезает. Если этот режим отменен, то можно вводить исполняемые математические выражения, придерживаясь синтаксиса языка Maple.
27. Операции разделения и объединения объектов
Операции разделения и объединения объектов
Команда Split or Join служит для разделения или объединения объектов документа, она открывает подменю со следующими операциями:
- Split Execution Group (F3) — разделение строки на две;
- Join Execution Group (F4) — соединение смежных строк;
- Split Section (Shift+F3) — разделение секции на две;
- Join Section (Shift+F4) — объединение смежных секций.
28. Исполнение выделенных ячеек или всего документа
Исполнение выделенных ячеек или всего документа
Команда Execute служит для запуска вычислений во всех выделенных ячейках или во всех ячейках документа. Соответственно она имеет подменю с двумя командами:
- Selection — исполнение выделенных ячеек;
- Worksheet — исполнение ячеек по всему документу.
Заметим, что альтернативой является нажатие клавиши Enter для каждой исполняемой строки документа, что при больших документах довольно нудное занятие.
29. Удаление ячеек вывода
Удаление ячеек вывода
Команда Remove Output служит для удаления из документа всех ячеек вывода. Это полезно для редактирования ячеек ввода, поскольку объем документа при этом заметно сокращается. Она открывает подменю с двумя командами:
- From Selection — удаление вывода только для выделенных ячеек;
- From Worksheet — удаление вывода для всего документа.
Рассмотрим, к примеру, документ, который был представлен на рис. 3.16. После выполнения для него команды Remove Output From Worksheet документ принимает вид, показанный на рис. 3.18.
Заметим, что документ с рис. 3.18 можно вернуть к исходному виду, выполнив команду Execute Worksheet, описанную выше. Однако в данном конкретном случае исполнение команды value(") даст сообщение об ошибке, поскольку в версиях Maple 6 и 7 данная команда должна быть записана в виде valueU).
Рис. 3.18. Документ после удаления всех ячеек вывода
18.gif
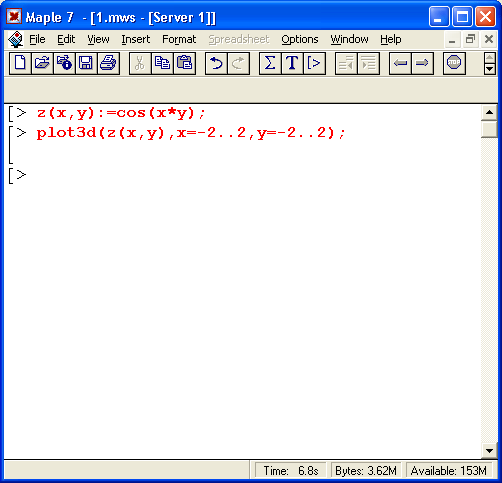
30. Операции вставки
Операции вставки
Документ системы Maple 7 состоит из различных объектов — текстовых областей, областей ввода, ячеек, абзацев, секций, подсекций и т. д. Некоторые из них формируются автоматически по мере ввода и исполнения документа. Но, кроме того, в меню Insert (рис. 3.19) сосредоточены основные команды по обеспечению вставки различных объектов в редактируемый документ. Это позволяет быстро модифицировать документ и добиться его большей выразительности.
Рис. 3.19. Меню Insert
Следует отметить, что меню Insert является контекстно-зависимым. К примеру, оно исчезает, если выделен график.
Меню вставки разделено на две группы. В первой группе содержатся следующие команды:
- Text (Ctrl+T) — ввод текста;
- Standard Math (Ctrl+R) — ввод неисполняемых математических выражений;
- Maple Input (Ctrl+M) — ввод исполняемых выражений в Maple-формате;
- Standard Math Input (Ctrl+G) — ввод выражений в математической форме в строку ввода.
Во второй группе содержатся следующие команды:
- Execution Group — вставка исполняемой ячейки до или после маркера ввода;
- Plot — вставка пустого шаблона двумерного или трехмерного графика;
- Spreadsheet — вставка электронной таблицы;
- Paragraph — вставка текстовой области (абзаца);
- Section — вставка кнопки секции;
- Subsection — вставка кнопки подсекции;
- HyperLink — вставка гиперссылки;
- Object — вставка связанного или внедренного объекта;
- Page Break — вставка разрыва страниц.
Перейдем к более подробному рассмотрению этих команд.
19.gif
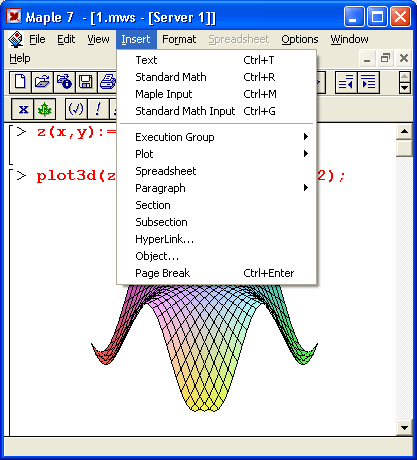
31. Ввод текста
Ввод текста
Команда Text приводит к исчезновению знака приглашения , после чего можно сразу же начинать ввод текста комментария. Данная команда позволяет формировать ячейку, содержащую текст комментария и исполняемые функции.
32. Ввод выражений в стандартной форме
Ввод выражений в стандартной форме
Команда Standard Math выводит в строке ввода вопросительный знак. После этого в поле ввода строки форматирования можно начинать ввод неисполняемого математического выражения (рис. 3.20).
Рис. 3.20. Ввод математического выражения по команде Standard Math
По завершении ввода надо нажать клавишу Enter, и выражение появится в строке ввода (рис. 3.21). При этом выражение будет выделено.
Рис. 3.21. Завершение ввода по команде Standard Math
20.gif
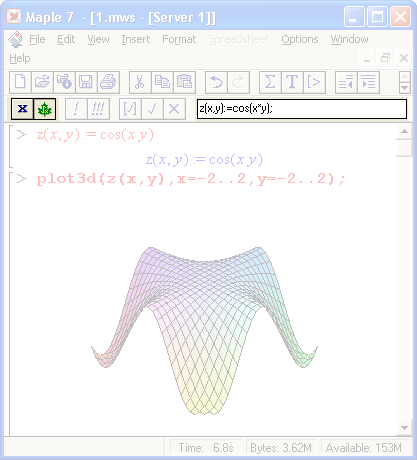
21.gif
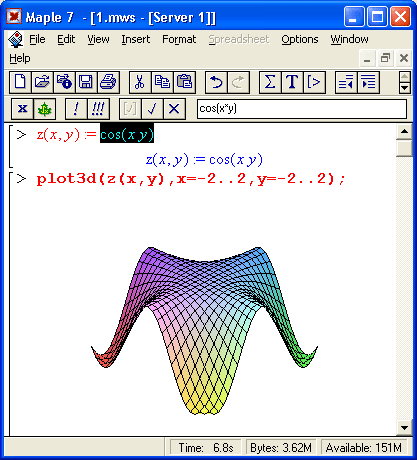
33. Ввод выражений
Ввод выражений
Команда Maple Input в меню Insert превращает текущую строку в строку ввода исполняемых математических выражений. В начале строки появляется приглашение ко вводу в виде значка , после чего можно начинать ввод выражения. Кнопка со знаком х в начале контекстной панели позволяет представить вводимое выражение в естественной математической форме, если таковая возможна. В таком случае ввод выражения осуществляется в поле на контекстной панели инструментов.
34. Ввод математических выражений
Ввод математических выражений
Команда Standard Math Input выводит новую строку ввода со знаком вопроса в ней. После этого ввод начинается в поле ввода строки форматирования. По завершении ввода нажимается клавиша Enter и введенное выражение появляется в строке ввода (обычно с выделенной последней частью).
35. Вставка исполняемых ячеек до и после курсора
Вставка исполняемых ячеек до и после курсора
Команда Execution Group обеспечивает вывод подменю с двумя командами:
- Before Cursor (Ctrl+K) — вставка исполняемых ячеек ввода до курсора;
- After Cursor (Ctrl+J) — вставка исполняемых ячеек ввода после курсора.
Напоминаем, что признаком исполняемых ячеек является знак приглашения . Данные команды позволяют ввести в любом месте документа новые входные ячейки, что часто бывает нужно при модификации документов.
36. Электронные-таблицы
Электронные таблицы
Электронные таблицы были впервые введены в реализацию Maple V R5. В системе Maple 7 для вставки электронных таблиц используется команда Insert Spreadsheet. Она выводит шаблон пустой таблицы, показанный на рис. 3.22. Как видно из рис. 3.22, электронная таблица представляет собой двумерный массив ячеек, имеющих адресацию по строкам и столбцам. Номера строк задаются цифрами, а номера столбцов — латинскими буквами. Верхняя левая ячейка имеет адрес А1, где А - номер столбца и 1 - номер строки. Если одиночные буквы в номерах столбцов заканчиваются, происходит переход на двухбуквенные адреса (АА, АВ, АС и т. д.). Такая адресация используется в функциях обработки табличных данных.
Рис. 3.22. Вставка шаблона электронной таблицы
По команде Insert Spreadsheet вставляется пустая электронная таблица, во всех ячейках которой нет никаких данных. Однако помимо заполнения таблицы с помощью соответствующих операций можно провести заполнение вручную. Для этого достаточно мышью выделить ячейку, щелкнув в ней левой кнопкой. Ячейка обводится черным контуром (ячейка А1 на рис. 3.22), и появляется контекстное меню с полем для ввода выражения. Во время ввода выражения ячейка покрывается серой сеточкой. Если после набора выражения нажать клавишу Enter, то числовое значение выражения будет помещено в ячейку А1 таблицы. К примеру, на рис. 3.23 показано введенное выражение 2+3. Однако в поле редактирования сохраняется исходное выражение (рис. 3.23).
Если маркер ввода находится в одной из ячеек электронной таблицы, становится доступным меню Spreadsheet (рис. 3.23).
22.gif
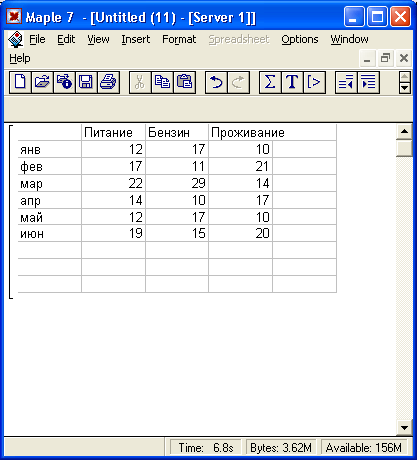
37. Меню Spreadsheet
Меню Spreadsheet
Для работы с таблицами в Maple 7 появилось отдельное меню Spreadsheet (рис. 3.23). Оно содержит набор команд, обеспечивающих работу с табличными данными:
- Evaluate Selection — вычисление выражения в выделенной ячейке;
- Evaluate Spreadsheet — вычисление выражений по всем ячейкам таблицы;
Рис. 3.23. Шаблон электронной таблицы и меню Spreadsheet
- Row — работа со строками (вставка, удаление и т. д.);
- Column — работа со столбцами (вставка, удаление и т. д.);
- Fill — автоматическое заполнение ячеек;
- Import data — импорт данных из других программ (например, из MATLAB);
- Export data — экспорт данных в другие программы;
- Properties — просмотр свойств ячеек;
- Show Border — управление показом обрамления таблицы;
- Resize to Grid — изменение размеров видимой таблицы с обрезанными ячейками до размера таблицы с целыми ячейками (дополнение идет по линиям раздела ячеек).
Если таблица активизирована (курсор находится внутри таблицы), то нажатие правой клавиши мыши вызовет появление контекстного меню. Его вид аналогичен виду описанного выше меню Spreadsheet.
Возможности Maple 7 в обработке табличных данных намного превосходят возможности обычных табличных процессоров. В частности, наряду с текстовыми и численными данными электронные таблицы Maple 7 могут работать с символьными данными — формулами.
23.gif
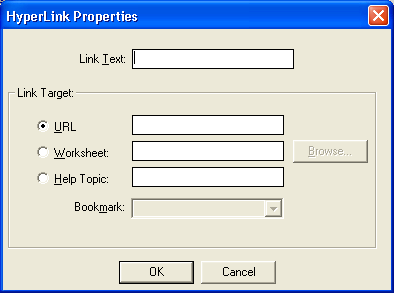
38. Работа с электронными таблицами
Работа с электронными таблицами
Для ввода данных в ячейку таблицы достаточно щелкнуть на ней мышью. После этого можно вводить нужные данные в поле ввода контекстной панели (она видна на рис. 3.22 и 3.23 под панелью инструментов). Контекстная панель в режиме редактирования таблиц имеет четыре кнопки. Их назначение (слева направо) следующее:
- Fill a range of cells — автоматическое заполнение ячеек таблицы;
- Evaluate all stale cells in the spreadsheet — исполнение всех ячеек таблицы;
- Accept the input and evaluate it — ввод напечатанных данных и их исполнение;
- Restore input to the previous value — восстановление предшествующего значения ячейки.
Основным способом ввода данных является активизация ячейки таблицы мышью и ввод данных (объектов) в поле ввода контекстной панели. Нажатие третьей кнопки (Accept the input and evaluate it) или нажатие клавиши Enter приводит к вводу данных в ячейку и их исполнению.
Имеется ряд возможностей для автоматического заполнения ячеек таблицы. Например, можно заполнить ряд ячеек, примыкающих к заданной ячейке, предварительно наметив направление заполнения. Для этого курсор помещается в заданную ячейку, а затем мышь перемещается в нужном направлении при нажатой левой кнопке. На рис. 3.24 показан случай, когда в заданную ячейку А1 помещено число 2 и затем мышью выделены первые ячейки столбца А. Теперь, нажав первую кнопку (Fill a range of cells) на контекстной панели форматирования (или исполнив команду Spreadsheet Fill Down в меню), можно вывести окно автоматического заполнения ячеек таблицы — Fill. Это окно также показано на рис. 3.24. В этом окне можно задать направление заполнения (обычно по умолчанию задано уже направление заполнения при выделении ячеек) и указать шаг изменения аргумента и значение, которого он не должен превышать. Например, на рис. 3.24 заданы шаг 3 и конечное значение 21. Нажав кнопку ОК, можно увидеть автоматическое заполнение таблицы. При этом она принимает вид, показанный на рис. 3,25.
В ячейки таблиц можно вносить различные математические формулы в соответствии с синтаксисом языка Maple 7. При этом возможно сослаться на любую другую ячейку. Такая ссылка указывается значком тильда (-) перед адресом ячейки. Так, обозначение ~А1 означает, что будут подставлены данные из ячейки А1.
В качестве примера составим таблицу значений n, интеграла int(x^n.x) и производной diff (x^n, x) для n = 1.. 9. В готовом виде эта таблица представлена на рис. 3.26.
Подготовка такой таблицы проходит в три этапа. Вначале формируется первый столбец вводом в ячейку А1 имени переменной n, а в ячейку А2 — значения 1. После этого выделяются ячейки от А2 до А10 и с применением автоматического заполнения они заполняются числами от 1 до 9.
Рис. 3.24. Подготовка к автоматическому заполнению ячеек под заданной ячейкой
Рис. 3.25. Электронная таблица с рис. 3.24 после автоматического заполнения ячеек первого столбца
Рис. 3.26. Электронная таблица с символьными данными
Затем во втором столбце в ячейку В1 вводится инертная формула Int(x^-Al.x), a в ячейку В2 — исполняемая формула int(x*~A2.x). После этого выделяются ячейки от В2 до В10 и исполняется команда Spreadsheet Fill Down. В результате формируется столбец с символьными значениями интегралов. Аналогично (третий этап) задается формирование столбца с символьными значениями производной от x^n (рекомендуем сделать это самостоятельно для закрепления навыков работы с электронными таблицами в среде Maple 7).
ПРИМЕЧАНИЕ
Выше описаны лишь основы работы с электронными таблицами в среде Maple 7. Для более полного знакомства с техникой применения электронных таблиц нужно обратиться к справочной системе Maple 7.
24.gif
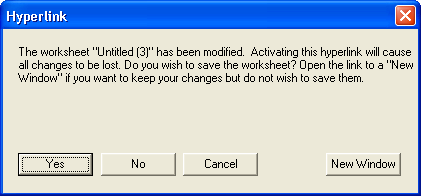
25.gif
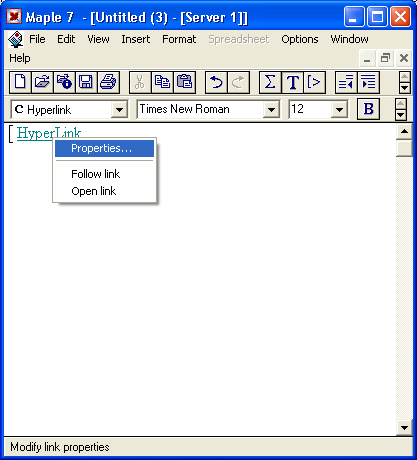
26.gif
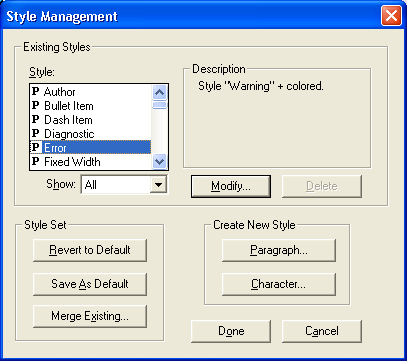
39. Вставка текстовой области
Вставка текстовой области
Для вставки строки текстовой области служит операция Paragraph. Она создает строку без приглашения >, в которую можно вводить текст. Единственным отличием этой команды от команды Text является то, что она вставляет новую строку, не меняя статуса имеющихся строк. При вводе длинных текстов число строк ввода автоматически увеличивается.
40. Вставка кнопки секции.
Вставка кнопки секции
Команда Section служит для установки кнопки, указывающей начало секции (см. рис. 2.6 с такой кнопкой) и служащей для открытия/закрытия секции. Секция может состоять из различных объектов: текстовых комментариев, строк ввода, строк вывода, графиков и других секций (подсекций).
Как и в операционной системе Windows, значок *+» указывает на закрытую секцию, значок «-» — на открытую. Секции предоставляют дополнительную свободу управления документом.
41. Вставка кнопки подсекции
Вставка кнопки подсекции
Подсекцией называют секцию, размещенную внутри другой секции. Создавая подсекции, можно строить документы со сложной древообразной структурой, напоминающей разделы книги с хорошей рубрикацией. Это может оказать большую помощь в создании электронных вариантов книг и обучающих программ в среде Maple 7.
Команда Subsection создает кнопку секции внутри уже созданной секции. Все, сказанное о секциях, распространяется и на подсекции!
42. Вставка гиперссылки
Вставка гиперссылки
Еще одна возможность сделать документы более удобными в работе заключается в создании гиперссылок. Гиперссылка — это текстовая надпись, подчеркнутая снизу, при щелчке на которой Maple перейдет к сопоставленному с ней объекту. Гиперссылку можно связать со следующими объектами:
- с файлом любого документа (Worksheet:);
- с заданной страницей справочной системы (Help Topic:);
- со страницей в Интернете (URL:).
Для создания гиперссылки надо установить на место будущей ссылки маркер ввода и выполнить операцию HyperLink. При этом появится окно связывания гиперссылки с объектом, показанное на рис. 3.27.
В окне надо задать заголовок гиперссылки (в виде короткой текстовой надписи) и выбрать одно из трех положений переключателя, перечисленных выше. Если вы намерены сослаться на документ, то следует использовать кнопку просмотра Browse для поиска нужного файла. Появляющееся окно показано на рис. 3.27 справа.
Как уже говорилось, гиперссылка выглядит как надпись, подчеркнутая снизу. Активизируя ее, можно вызвать объект, связанный с ней, — в нашем случае другой документ, файл которого находится на жестком диске. Использование гиперссылки на другой документ в Maple 7 реализовано не очень удачно. Дело в том, что в этом случае исходный документ по умолчанию закрывается. Если последние изменения в нем не были сохранены, то появляется окно с предупреждением об этом.1 Оно показано на рис. 3.28.
Можно избежать закрытия документа, щелкнув на кнопке New Window; Maple предоставит открывающемуся документу новое окно. Это иллюстрирует рис. 3.29. В нем также показано контекстное меню гиперссылки. Это меню содержит три команды:
- Properties — вывод окна свойств гиперссылки (рис. 3.27, слева);
- Follow link — смена документа с гиперссылкой на указанный в ней документ;
- Open link — открытие отдельного окна для открываемого документа (рис. 3.29).
Рис. 3.27. Пример создания гиперссылки
Рис. 3.28. Окно с предупреждением о закрытии документа при переходе по гиперссылке и необходимости сохранения изменений
Рис. 3.29. Результат активизации гиперссылки
Гиперссылки позволяют создавать сложные структуры документов, содержащие множество объектов, вызываемых в произвольном порядке. Например, для возврата в исходный документ можно организовать обратную гиперссылку в вызываемом документе. Лучшим примером такого применения гиперссылок является справочная система Maple 7. Гиперссылки также широко используются при создании web-страниц. Maple 7 позволяет сохранять документы в виде web-страниц (формат HTML), которые без каких-либо преобразований можно публиковать в сети Интернет.
Весьма привлекательной кажется возможность организации гиперссылок на разделы справочной системы. Она позволяет создавать учебные программы со ссылками на справки системы Maple 7.
23.gif
24.gif
25.gif
43. Операции форматирования
Операции форматирования
Операции форматирования служат для придания отдельным объектам и документу в целом определенного стиля путем изменения как общего вида объектов, так и ряда их частных характеристик, например цвета и размера надписей, выбранного набора шрифтов и т. д. При этом возможна подстройка под вкус любого пользователя и подготовка документов высокого полиграфического качества. Стиль является центральным понятием для современных документов, будь то документы текстового процессора класса Word или системы символьной математики Maple 7.
Команды форматирования в меню Format разбиты на шесть подгрупп. В первой подгруппе содержатся две команды:
- Styles — установка стилей для всех объектов;
- Page Numbers — задание параметров нумерации страниц.
Во второй подгруппе имеются три наиболее распространенные команды изменения начертания надписей:
- Italic (Ctrl+I) — задание курсивного начертания;
- Bold (Ctrl+B) — задание полужирного начертания;
- Underline (Ctrl+U) — задание подчеркнутого начертания.
Заметим, что все они дублируются кнопками на панели инструментов и горячими клавишами. При редактировании документов использование кнопок и горячих клавиш более удобно.
В третью группу попали команды выравнивания текста:
- Left Justify — по левому краю;
- Center — по центру;
- Right Justify — по правому краю.
В четвертой группе находятся следующие команды:
- Paragraph — форматирование абзаца;
- Character — форматирование символов. И наконец, в пятой группе имеются еще две команды:
- Indent (Ctrl+.) — внедрение текущей строки в секцию;
- Outdent (Ctrl+,) — выведение текущей строки из секции.
В последнюю группу попала еще одна команда, не имеющая непосредственного отношения к форматированию символов:
- Convert to — перевод из одной метрической системы в другую.
Рассмотрим применение команд форматирования.
44. Установка стилей.
Установка стилей
Команда Styles является основной, поскольку позволяет задать стиль текста — определенный набор значений доступных параметров: размещение на странице, выравнивание, шрифт, начертание, цвет, размер и т. д. Единство стилей документов важно при включении их в отчеты, курсовые и дипломные проекты, диссертации и иные документы. Придерживаться определенных стилей — это правило хорошего тона при работе как с текстовыми процессорами, так и с математическими системами. Именно поэтому ориентация на определенный стиль подготовки документов стала неотъемлемой частью пользовательского интерфейса системы Maple 7.
Операция Styles выводит диалоговое окно Style Management, в котором можно как изменить уже существующий стиль, так и создать новый (рис. 3.30).
Рис. 3.30. Окно задания и модернизации стилей
В большинстве случаев пользователя Maple 7 вполне удовлетворят стили, заданные по умолчанию. Более того, надо помнить, что задание своего стиля неизбежно означает повышение риска несовместимости при обмене документами Maple 7. Поэтому без особой на то необходимости изменять стандартный стиль не рекомендуется.
Однако бывают принципиальные обстоятельства, когда изменение стиля необходимо. Например, при выводе титульных надписей для графиков Maple 7 используют стандартный англоязычный шрифт Courier New. При вводе русскоязычных надписей Maple 7 воспринимает их вывод как ошибку, поскольку набор символов при вводе не соответствует набору символов, заданному в стиле. Таким образом, для организации вывода русскоязычных надписей необходимо сменить набор символов (шрифт), то есть изменить стиль. Покажем, как это делается. Вначале в списке стилей надо выбрать наименование Title, после чего нажать кнопку Modify. Появится окно Paragraph Style с параметрами стиля Title (рис. 3.31).
В этом окне надо нажать кнопку Font. Появится новое окно (оно также показано на рис. 3.31) для выбора шрифта. В нашем случае достаточно заменить шрифт по умолчанию Courier New на шрифт Courier New Cyr. Он содержит символы кириллицы, то есть буквы русского языка. После этого задание титульных надписей для графиков на русском языке перестает быть проблемой.
Рис. 3.31. Окна установки параметров абзацного стиля для абзаца и для выбора шрифта
Разумеется, в понятие стиля входит не только шрифт, но и размер, начертание, цвет и т. д. Все это можно настраивать, используя описанные выше окна. При необходимости изменения стиля можно записать его в специальный файл, используя кнопку Save As Default. При этом измененный стиль становится принятым по умолчанию. Кнопка Revert As Default позволяет вернуться к типовым стилям, которые заданы разработчиками системы. Если стили подверглись небольшим изменениям, то можно сохранить их с помощью кнопки Merge Existing.
26.gif
27.gif
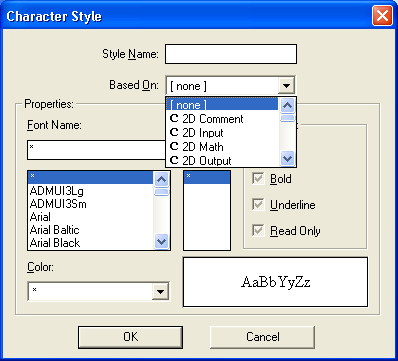
45. Форматирование абзацев
Форматирование абзацев
Для форматирования абзацев служит команда Paragraph. Она сразу выводит окно установки параметров абзаца. Это окно было показано на рис. 3.31. Правила работы с этим окном уже были описаны выше, так что нет смысла их повторять.
46. Форматирование символов
Форматирование символов
Команда Character открывает окно задания стиля символов: шрифта, размера, начертания и цвета.
47. Операция внедрения ячеек в секцию
Операция внедрения ячеек в секцию
Ранее описывалась операция вставки кнопки секции. При выполнения вставки сама секция еще пуста и ее надо заполнять. Команда Indent (или комбинация клавиш Ctrl+.) позволяет оформить в виде секции уже введенные ячейки. На рис. 3.32 показано такое оформление для ячейки документа с вычислением интеграла. Кнопка при этом имеет знак «минус», что указывает на ее открытое состояние.
Рис. 3.32. Применение операции Indent для одной из ячеек документа
Если щелкнуть на кнопке со знаком «минус», то секция свернется и вместо нее останется только кнопка со знаком «плюс» (рис. 3.33).
28.gif
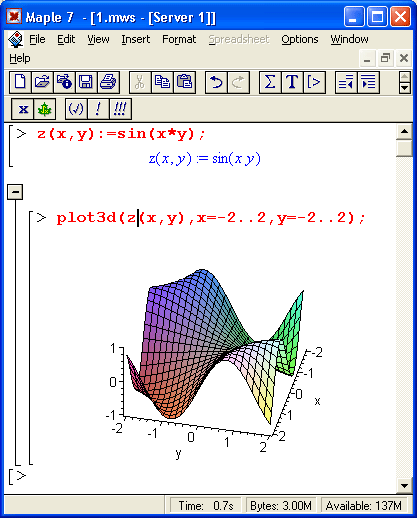
48. Операция выведения ячеек из секции
29.gif
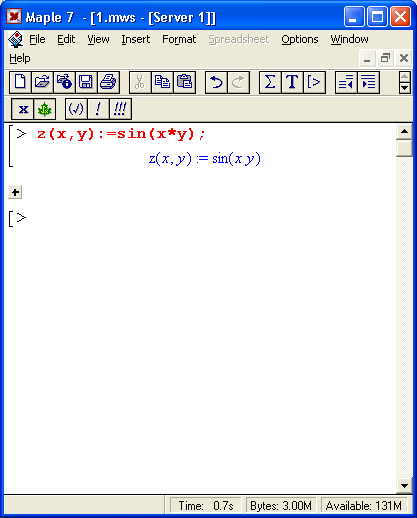
49. Работа с объектами
Работа с объектами
Хотя данная книга посвящена одной Maple 7, надо особо отметить, что эта программа способна взаимодействовать с рядом других программ, например с текстовым процессором Word, табличным процессорам Excel и даже с другими системами компьютерной математики, например, MATLAB. Это может быть копирование через буфер обмена или связь с применением механизма OLE. В роли объектов могут выступать ячейки из данного или других документов, текстовые фрагменты и файлы, рисунки в различных форматах и т. д. Работа с объектами существенно расширяет возможности пользователя по части создания полноценных и удобных в работе документов.
50. Вставка объектов
Вставка объектов
Для организации вставки объекта используется команда Insert > Object. Она выводит окно со списком тех приложений, с которыми возможна связь с применением механизма OLE. Это окно показано на рис. 3.34. Maple 7 использует стандартное окно вставки объектов из операционной системы Windows, поэтому если она русифицирована, то окно имеет русскоязычные надписи.
Рис. 3.34. Окно вставки объекта
Если оставить переключатель в первом положении, то объект может быть создан заново с помощью подходящего приложения, например редактора Paint. Этот процесс показан на рис. 3.35.
Рис. 3.35. Подготовка объекта в графическом редакторе PhotoShop
После того как объект готов, достаточно выйти из приложения, в котором он создавался, — в нашем случае из редактора Paint. Для этого в меню редактора имеется команда File > Exit. Окно Paint исчезнет, а сам объект появится в той ячейке Maple 7 (рис. 3.36), в которой был установлен маркер ввода в момент дачи команды вставки объекта.
Рис. 3.36. Пример документа со вставленным объектом-рисунком
Вместо рисунка (или другого объекта) можно поместить в документе Maple 7 значок — гипермедиа-ссылку. Для этого в окне на рис. 3.34 надо установить флажок В виде значка. Щелчок на вставленном в документ значке вызовет появление объекта. Этот способ удобен, когда объекты, например рисунки, имеют большой размер и их постоянное присутствие на экране нецелесообразно.
Необязательно каждый раз создавать объект с нуля — можно загрузить его из файла, в этом случае следует установить положение переключателя Создать из файла. Для поиска нужного файла пригодится кнопка Обзор. После выбора файла надо решить, какой вид будет иметь значок связи с файлом — вид стандартного значка или уменьшенной копии изображения.
30.gif
31.gif
32.gif
51. Редактирование вставленного объекта
Редактирование вставленного объекта
Если объект выделен (как обычно, щелчком мыши), то команда Edit > Object становится активной и может даже модифицироваться в зависимости от вида объекта, с которым установлена связь. Например, если объектом является .рсх-файл, то эта строка меню открывает подменю с тремя командами:
- Edit — редактировать объект;
- Open — открыть приложение, связанное с объектом;
- Print — распечатать объект.
Редактирование объекта производится в среде того приложения, с которым объект связан. Естественно, что изменение файла повлечет за собой отражение в документе его измененного варианта. Следует отметить, что в некоторых копиях программы Maple 7 операция Object не работает. Однако сохраняется возможность редактирования объекта в создавшей его программе после двойного щелчка на нем.
52. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Создавать новый документ.
- .Загружать ранее созданные документы.
- Работать с файлами документов.
- Редактировать документы.
- Печатать документы.
- Осуществлять операции вставки.
- Выполнять операции форматирования.
- Вставлять в Maple 7 объекты, созданные другими программами.
- Работать с объектами.
Урок 4. Управление интерфейсом пользователя
1. Управление видом интерфейса и документа
Урок 4.
Управление интерфейсом пользователя
Для управления видом интерфейса и документа служит меню View. Оно содержит ряд флажков и несколько команд управления общим видом программы (рис. 4.1). Установленные флажки, управляющие показом элементов интерфейса, распространяют свое действие на все открытые документы. При выходе из системы (командой Exit) все установки сохраняются, так что при новом запуске системы внешний вид интерфейса будет определяться именно ими.
Рис. 4.1. Меню View
Команды меню View разбиты на несколько групп. Первая группа содержит флажки, относящиеся к управлению показом главной и контекстной панелей инструментов, а также строки состояния системы:
- Toolbar — управление показом панели инструментов;
- Context Bar — управление показом контекстной панели;
- Status Line — управление показом строки состояния.
Вторая группа задает показ палитр и представлена одной командой, открывающей подменю управления показом палитр Palettes, содержащей флажки:
- Symbol Palette — палитра символов;
- Expression Palette — палитра выражений;
- Matrix Palette — палитра шаблонов матриц;
- Vector Palette — палитра шаблонов векторов.
И команды:
- Show All Palettes — показать все палитры;
- Hide All Palettes — скрыть все палитры.
Третья группа в меню View задает масштаб отображения документа на экране и установку закладок (bookmarks):
- Zoom Factor — задание масштаба просмотра документа;
- Bookmarks — установка закладок.
Четвертая группа обеспечивает переходы по гиперссылкам:
- Back — переход обратно по последней пройденной гиперссылке;
- Forward — команда, обратная команде Back.
Данные команды аналогичны командам браузера и управляются историей переходов по гиперссылкам. Поэтому, если вы не использовали ни одной гиперссылки, данные команды будут недоступны. В основном данные команды и соответствующие кнопки панели инструментов необходимы при работе со справкой Maple.
Пятая группа представлена командой Hide content, открывающей подменю скрытия элементов документа:
- Hide Spreadsheets — скрыть электронные таблицы;
- Hide Input — скрыть ввод;
- Hide Output — скрыть вывод;
- Hide Graphics — скрыть графические объекты
Шестая группа параметров управляет показом некоторых объектов документа:
- Show Invisible Characters — показ непечатаемых символов;
- Show Section Ranges (Shift+F9) — показ областей секций;
- Show Group Ranges — показ областей групп;
- Show OLE type — показ объектов OLE.
В седьмой группе содержатся следующие команды:
- Expand All Sections — раскрыть все секции;
- Collapse All Sections — свернуть все секции.
Действие всех перечисленных команд более подробно описано ниже. Рекомендуется поэкспериментировать с командами — когда вы уясните их действие, вы сможете настроить интерфейс Maple на свой вкус.
1.gif
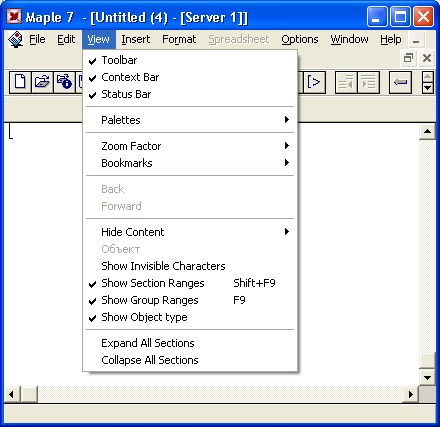
2. Управление показом панели инструментов (Toolbar)
Управление показом панели инструментов (Toolbar)
Панель инструментов (Toolbar) служит для быстрого управления системой без обращения к командам меню. Она позволяет вызывать наиболее часто используемые команды нажатием кнопки. Назначение всех кнопок этой панели было описано выше и представлено на рис. 1.21.
Несмотря на удобства, предоставляемые панелью инструментов, в ряде случаев она не нужна. Например, для ввода исходных данных и их редактирования достаточно иметь на экране только контекстную панель. Панель инструментов полезна при общей отладке документов, открытии нового документа, загрузке имеющегося документа, записи документа на диск, печати документа и т. д. В ряде случаев она просто занимает часть места, нужного для лучшего обзора документа.
Флажок Toolbar управляет показом панели инструментов.
3. Управление показом контекстной панели
Управление показом контекстной панели
Панель Context Bar служит для размещения кнопок быстрого доступа к операциям с текущим объектом.
Флажок Context Bar задает отображение контекстной панели на экране. Поскольку панель форматирования весьма удобна для оперативной работы, единственным мотивом временного ее удаления является необходимость высвободить больше , места на экране монитора для работы с документом.
4. Управление показом строки состояния
Управление показом строки состояния
Строка состояния внизу экрана, как отмечалось, выводит контекстно-зависимую информацию о состоянии программы в данный момент времени. В ряде случаев ее можно считать элементом контекстно-зависимой справки. Флажок Status Bar служит для управления показом строки состояния.
5. Вывод палитр математических символов
Вывод палитр математических символов
Палитры математических символов, впервые введенные в версии Maple V R5, являются очень удобным средством для облегчения набора математических выражений начинающим пользователям. Они выводятся на экран командой Palettes и показаны на рис. 1.11. Всего имеются четыре палитры:
- Symbol — палитра ввода греческих символов и констант;
- Expression — палитра ввода операторов и выражений;
- Matrix — палитра ввода матриц;
- Vector - новая (для Maple 7) палитра ввода векторов.
Ввод осуществляется на место маркера ввода. Щелчок на кнопке палитры — символ или его аналог окажется в точке ввода. Параметры, которые необходимо указать, при математической нотации выражений имеют вид вопросительного знака, а при Maple-нотации — %?.
Итак, в строке ввода введенный оператор или символ не обязательно повторит оператор или символ палитры. Это хорошо видно из рис. 4.2, на котором показан ввод с помощью палитры выражений шаблона определенного интеграла и его последовательное заполнение. Для наглядности заполнение каждого параметра дано в новой строке ввода.
Рис. 4.2. Пример ввода шаблона определенного интеграла из палитры выражений
2.gif
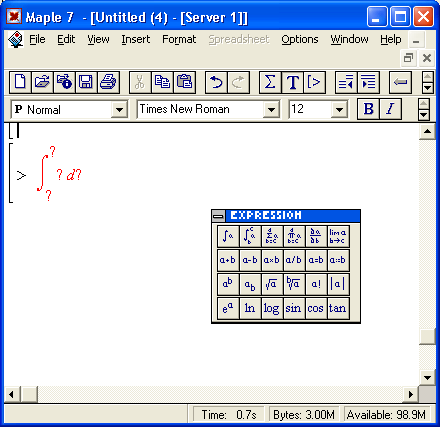
6. Установка масштаба отображения документа
Установка масштаба отображения документа
Команда Zoom Factor задает масштаб отображения текущего документа. Он задается в процентах относительно масштаба просмотра, заданного по умолчанию, — он принят за 100 %. Команда выводит подменю с перечнем возможных масштабов просмотра. На рис. 4.3 показано, как будет выглядеть документ при установке масштаба просмотра в 150 %. На этом рисунке показано подменю выбора масштаба в открытом виде.
Нетрудно заметить, что все символы документа увеличились при этом в размерах в полтора раза. Эта возможность, безусловно, полезна для пользователей с ослабленным зрением или для учителей, желающих показать примеры решения задач в среде Maple крупным планом для группы учащихся.
Рис. 4.3. Вид документа при масштабе просмотра в 150 %
3.gif
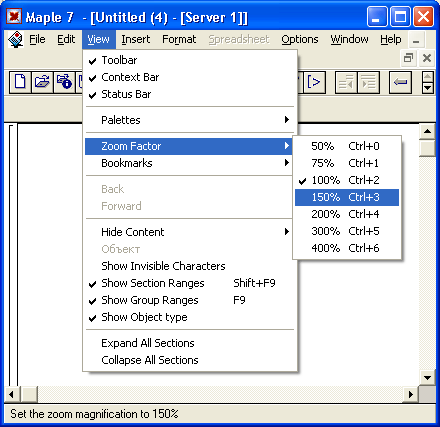
7. Установка закладок
Установка закладок
При работе с большими документами, как и при чтении книг, полезно устанавливать специальные маркеры — закладки. Для установки такой закладки достаточно поместить в нужное место документа маркер ввода и выполнить команду View > Bookmarks > Edit Bookmarks. Она выводит окно добавления и модификации закладки (рис. 4.4). Кнопка ОК вводит новую закладку, а кнопка Cancel позволяет отказаться от выполнения данной операции.
Если теперь вновь посмотреть подменю Bookmarks, в нем появится строка с созданной закладкой (рис. 4.5).
В нашем случае в списке представлены две ранее созданные закладки с именами «Это определенный интеграл» и «А это значение определенного интеграла».
При переходе по закладке строка, в которой установлена закладка, размещается в верхней части окна редактирования и маркер ввода устанавливается в место, которое определено закладкой. Таким образом, закладки — эффективное средство для быстрого перехода в отмеченные места документа. Однако надо помнить, что в отличие от закладок в книгах закладки в документах Maple 7 не видны — они имеются лишь в списке закладок, открываемом командой Bookmarks (рис. 4.5). Удалить созданную закладку не так-то просто: вам нужно перейти по закладке, дать команду View > Bookmarks > Edit Bookmarks и удалить текст в поле имени. Теперь нажатие кнопки ОК приведет к окну с предупреждением об удалении закладки. Нажмите ОК в обоих окнах — и закладка исчезнет.
Рис. 4.4. Пример создания и редактирования закладки
Рис. 4.5. Просмотр закладок
4.gif
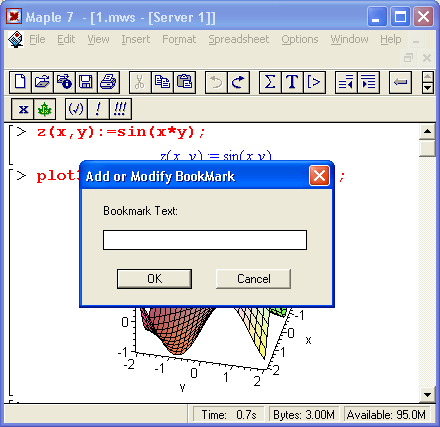
5.gif
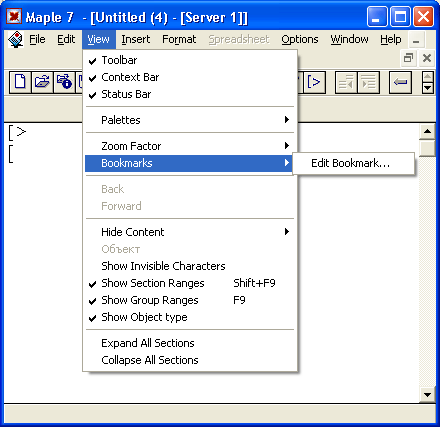
8. Управление показом компонентов документа
Управление показом компонентов документа
Документы Maple 7 состоят из ряда основных элементов. Это ячейки (строки) ввода и вывода, графики и электронные таблицы. При подготовке различных электронных книг, учебников и статей возникает необходимость скрыть тот или иной компонент документа. Например, педагог может захотеть скрыть от учащихся строки ввода, чтобы они могли мысленно представить функции, отображаемые показанными в документе графиками. Или, наоборот, скрыть графики, чтобы учащиеся назвали их особенности исходя из записи функций. Все эти возможности и обеспечивает команда View > Hide Content.
Для примера на рис. 4.6 показан документ, у которого скрыты все строки ввода и оставлены только строки вывода.
Рис. 4.6. Документ со скрытыми ячейками ввода
Разумеется, можно вернуть показ строк ввода, просто повторно дав эту команду Hide Input в подменю команды View > Hide Content > Hide Input (рис. 4.6). Co скрытием других компонентов документов читатель может разобраться самостоятельно.
6.gif
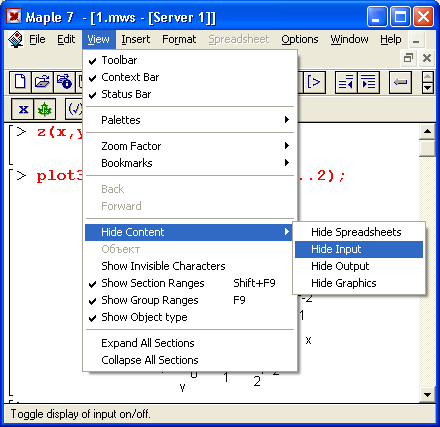
9. Управление показом непечатаемых символов.
Управление показом непечатаемых символов
В любом документе незримо присутствуют различные непечатаемые символы, например управляющие символы перевода строки или пробелы. Это хорошо известно читателям, работающим с текстовым процессором Word. Иногда полезно вывести эти символы — например, если вам неясно, сколько пробелов стоит между какими-то словами.
Для вывода непечатаемых символов служит команда-флажок Show Invisible Characters (рис. 4.7). Ее можно также дать, нажав кнопку на панели инструментов с изображением управляющего символа перевода строки — «fl». Этот символ, кстати, и является одним из наиболее часто встречающихся управляющих непечатаемых символов.
Рис. 4.7. Вид документа с выводом непечатаемых управляющих символов
Помимо символа перевода строки вы увидите множество символов пробела в виде точки на середине строки. По числу точек между словами можно судить о том, сколько пробелов установлено между ними. Проявятся также табуляции и другие управляющие операции, встречающиеся в документах Maple 7.
7.gif
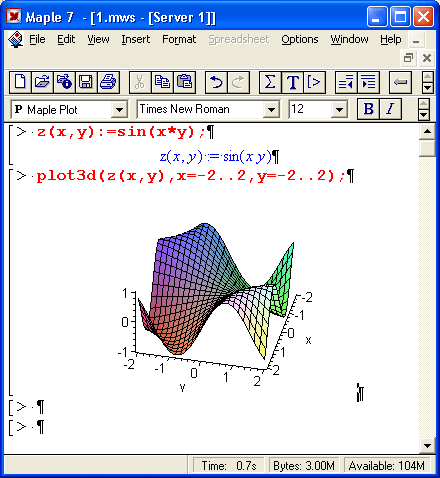
10. Управление показом областей секций
Управление показом областей секций
Понятие о секциях и подсекциях
Как уже отмечалось, документ Maple 7 состоит из отдельных ячеек (в оригинале — групп, groups). Они выделяются слева длинными тонкими квадратными скобками. Есть еще один способ выделения ячеек — объединение их в секции. Секция начинается с кнопки со знаком «плюс» или «минус» (рис. 4.8), управляющей ее состоянием: открытым или закрытым.
Рис. 4.8. Пример документа с открытой секцией и закрытой подсекцией
Для создания секции или подсекции необходимо дать команду Insert > Section (или Insert > Subsection), что указано на рис. 4.8. Секция выделяется вертикальной одиночной линией, а подсекция — двойной линией.
Секции и подсекции выгодно отличаются от ячеек тем, что они могут быть при необходимости закрыты и представлены только кнопкой со знаком «плюс». Таким образом, в секции удобно помещать различные вспомогательные вычисления, которые не стоит обозревать постоянно. Хотите посмотреть на них — нажмите кнопку, и содержимое секции появится под ней с выделением вертикальной чертой (рис. 4.9).
Секции весьма удобно применять и для подготовки документов в форме электронных книг. В этом случае секции снабжаются текстовыми заголовками и, по существу, являются главами книги, а подсекции — параграфами. Этот способ представления документов нашел широкое применение в сети Интернет, где он (наряду с гипертекстовыми и гипермедиа-ссылками) используется при создании web-страниц. Версия Maple 7 позволяет готовить и сохранять на диске документы в формате HTML, что позволяет напрямую готовить web-страницы.
Рис. 4.9. Пример документа с рис. 4.8 с открытой подсекцией
8.gif
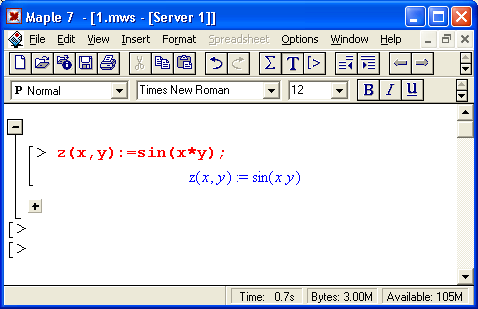
9.gif
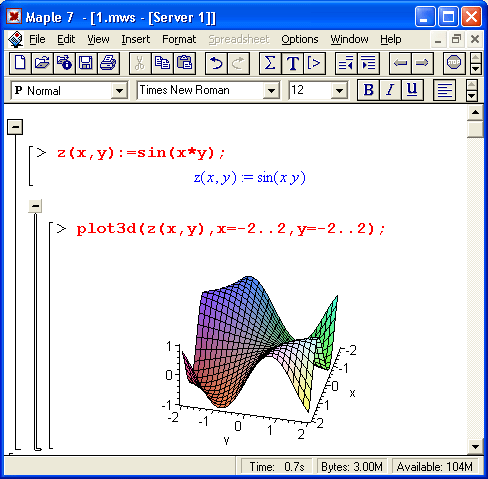
11. Управление показом областей секций
Управление показом областей секций
Итак, обычно секции и подсекции выделяются вертикальными линиями, заканчивающимися короткими горизонтальными штрихами. Это позволяет судить о размерах области экрана, представляющей секцию, особенно если секция большая и целиком не помещается на экране.
Тем не менее в окончательно отлаженном документе необходимость в применении линии показа области секции или подсекции отпадает. С помощью флажка Show Section Ranges можно управлять показом линий выделения областей секций и подсекций. Если этот флажок установлен, то линии показа областей секций и подсекций видны, как на рис. 4.9. Если его снять, то эти линии исчезнут (рис. 4.10).
Обратите внимание, что линии выделения групп (ячеек) остаются.
Рис. 4.10. Вид документа с рис. 4.9 при снятии показа областей секции и подсекции
10.gif
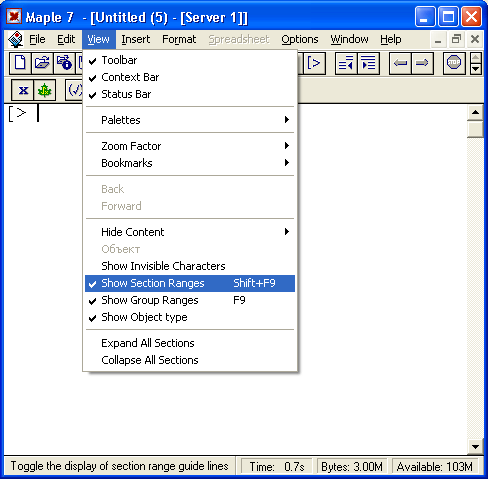
12. Управление показом областей ячеек (Show Group Ranges)
Управление показом областей ячеек (Show Group Ranges)
Команда Show Group Ranges служит для управления показом областей ячеек (групп), то есть длинных квадратных скобок, обрамляющих ячейки слева. Если флажок установлен, то линии показа областей ячеек видны. Если его снять, то эти линии исчезают, как показано на рис. 4.11, где убраны линии выделения как секции и подсекции, так и ячеек.
Убирать линии показа областей ячеек целесообразно, если документ уже отлажен. В таком документе необходимость показа областей выделения ячеек, секций и подсекций отсутствует, хотя иногда их разумно оставлять, так как они способствуют систематизации содержимого документов.
13. Закрытие всех секций
Закрытие всех секций
Все секции и подсекции документа можно закрыть командой Collapse All Sections. К примеру, если применить ее к документу, показанному на рис. 4.9, то документ примет вид, показанный на рис. 4.12.
Рис. 4.11. Документ с рис. 4.10 после удаления линий показа областей ячеек
Рис. 4.12. Документ с рис. 4.9 при закрытии всех секций
Документ с закрытыми секциями (и подсекциями) занимает на экране (и при распечатке принтером) минимальное место. При этом, естественно, содержимого секций и подсекций не видно.
11.gif
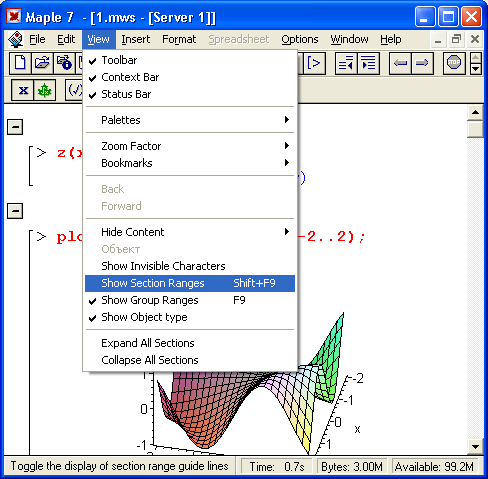
12.gif
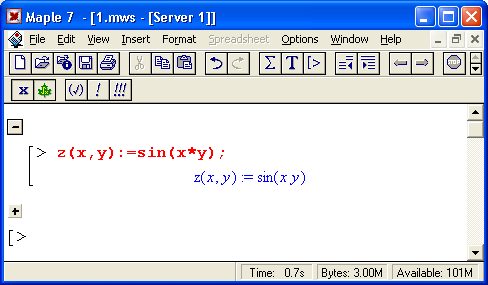
14. Раскрытие всех секций
Раскрытие всех секций
Для раскрытия всех секций служит команда Expand All Sections. Она открывает и все подсекции. К примеру, если применить эту операцию к документу, показанному на рис. 4.12, то он вернется к исходному виду (рис. 4.9).
Таким образом, Maple 7 имеет достаточно простые, но в то же время полные средства по управлению видом пользовательского интерфейса (окна) системы и видом имеющегося в нем документа. Это позволяет пользователю настраивать интерфейс и вид документа в соответствии со своими привычками, обеспечивая комфортную работу с программой.
15. Работа с параметрами Maple 7
Работа с параметрами Maple 7
Помимо ряда уже рассмотренных команд в меню Options сосредоточены средства для установки некоторых глобальных параметров ввода и вывода документов. Их число в Maple 7 существенно увеличено.
Первая группа команд содержит две команды:
- Replace Output — управляет характером вывода;,
- Insert Mode — устанавливает режим вставки при вводе.
Во второй группе всего одна команда Browser — задание броузера для перехода по URL.
Третья группа также представлена одной командой:
- Export — параметры экспорта документов.
Четвертая группа содержит 6 команд:
- Input Display — управление показом выражений в строке ввода;
- Output Display — управление показом результатов вычислений;
- Assumed Variables — контроль за предполагаемыми переменными;
- Plot Display — управление отображением графиков;
- Display 2D-legends — управление показом подписей обозначений двумерной графики;
- Print Quality — управление качеством печати.
Пятая и шестая группы содержат по одной команде:
- Palette Size — управление размером палитр;
- AutoSave — управление автоматическим сохранением документа.
С помощью этих параметров можно настроить систему на наиболее приемлемые формы вывода результатов вычислений без задания специальных команд в документе. Однако последние могут отменять параметры, заданные с помощью меню.
16. Управление выводом
Управление выводом
Команда Replace Output задает вывод результатов вычислений, заданных в ячейке, в одно и тоже место. Это означает, что если входные данные меняются, то при установленном флажке каждый последующий результат будет замещать предыдущий. Если же флажок снят, то каждый новый результат будет помещаться в новое место, то есть в документе будут выведены подряд (сверху вниз) все результаты вычислений.
Поясним на примере. Допустим, в какой-то строке ввода мы задаем вычисляемое выражение
2+3:
> 2+3; 5
Результат (в данном случае в Maple-нотации) появляется снизу. Теперь в той же строке ввода вычислим 3+4, а затем 4+5. Получим:
> 4+5; 9
Мы заметим, что результат появится на месте прежнего, и в конечном счете мы будем иметь в качестве результата число 9. Теперь снимем флажок Replace Output и проделаем все те же вычисления в новой строке ввода. Получим следующее:
> 4+5; 5
7
9
Здесь видны уже три ячейки вывода. Не следует следует устанавливать флажок Replace Output в том случае, когда желательно знать суть промежуточных преобразований и самих исходных выражений, поскольку они (а возможно, и предшествующие результаты преобразований) при ее использовании исчезают.
17. Установка режима вставки новой ячейки
Установка режима вставки новой ячейки
Этот флажок, будучи установленным, обеспечивает при нажатии клавиши Enter ввод новой пустой ячейки. Если флажок снят, то такая вставка не осуществляется.
Если работа с системой происходит в форме простейшего диалога, по типу «задать вопрос — получить ответ», то рекомендуется установить режим вставки 'новой ячейки. При этом по окончании вычислений в последней ячейке тут же появляется новая пустая ячейка для последующих вычислений.
18. Задание браузера
Задание браузера
Для открытия документов web-страниц (по URL-адресу) Maple 7 использует какой-либо из установленных на компьютере браузеров Интернета. Для этого необходимо указать путь к браузеру с помощью команды Browser. Она открывает окно, показанное на рис. 4.13.
Рис. 4.13. Окно задания браузера Интернета
В этом окне можно установить флажок Use System Default (использовать браузер, заданный в операционной системе по умолчанию). В противном случае путь к браузеру надо указать явно, введя его в поле или отыскав его с помощью кнопки Browse.
13.gif
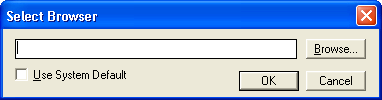
19. Параметры экспорта документов
14.gif
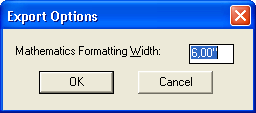
20. Установка параметров представления строк ввода
Установка параметров представления строк ввода
Команда Input Display выводит подменю, позволяющее выбрать режим представления выражений в строке ввода:
- Maple Notation — ввод выражений в Maple-нотации (в строку);
- Standard Math Notation — ввод выражений в обычном математическом виде (его признаком является появление вопросительного знака в строке ввода).
В качестве примера ниже даны две формы задания ввода двойного интеграла с помощью палитры выражений:
Верхняя строка соответствует Maple-нотации, а нижняя — стандартной математической нотации.
15.gif
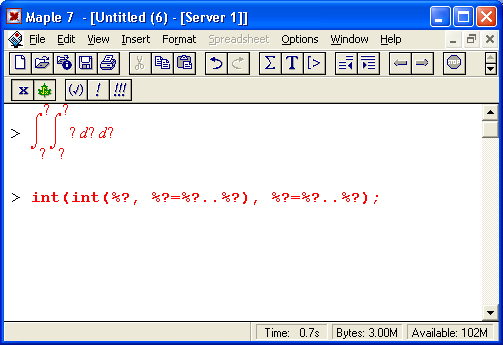
21. Установка параметров вывода
Установка параметров вывода
Команда Output Display раскрывает подменю, имеющее четыре команды, влияющие на вид результатов вычислений — вывода:
- Maple Notation — вывод в одну строку (как в Maple-языке);
- Character Notation t- вывод в виде формулы, набранной из знаков на разных строках;
- Typeset Notation — вывод в печатной форме без возможности редактирования;
- Standard Math Notation — вывод в виде обычной математической формулы.
Рисунок 4.15 наглядно иллюстрирует эти формы вывода. Последняя форма наиболее наглядна и задается по умолчанию.
Рис. 4.15. Демонстрация вывода в различных формах
Первая форма наиболее компактна, но менее всего наглядна. Вторая форма имитирует построение формул с помощью отдельных знаков, расположенных на разных уровнях (строках). Эти две формы позволяют использовать Maple даже в том случае, когда имеются устройства вывода (дисплеи и принтеры), работающие только в текстовых режимах. Третья форма дает вывод в виде обычных математических формул, но без возможности их редактирования.
Четвертая форма позволяет представить результат вывода, там, где это возможно, в виде обычных математических формул с применением типовых математических знаков — интегралов, производных, сумм, произведений, квадратных корней и т. д. В большинстве случаев именно эта форма вывода является наиболее наглядной. Она подобна третьей форме, но допускает редактирование выражений. Как отмечалось, нажатием кнопки с символом «х» в панели инструментов документа можно попытаться и вводимое выражение представить в виде обычной математической формулы. Однако это не всегда удается, поскольку далеко не все однострочные функции системы Maple 7 можно представить таким образом.
16.gif
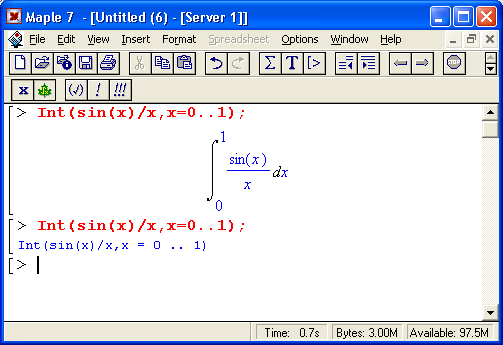
22. Контроль за предполагаемыми переменными (Assumed Variables)
Контроль за предполагаемыми переменными (Assumed Variables)
На переменные в Maple 7 могут быть наложены различные условия. Для этого используется специальная функция assume. Например, если переменная х может принимать только положительные значения, то для этого достаточно исполнить команду assume(x>0). Будем называть такие переменные предполагаемыми, поскольку предполагается, что они имеют какие-то дополнительные ограничения, помимо накладываемых на них типом.
В подменю Assume Variables меню Options имеются три команды, управляющие контролем признаков предполагаемых переменных:
- Trailing Tildes — включает маркировку предполагаемых переменных знаком тильды (-);
- No Annotation — включает параметр «без аннотаций», то есть запрещает вывод аннотации;
- Phrase — включает параметр вывода комментариев для предполагаемых переменных. ;
Предполагаемые переменные при выводе обычно обозначаются значком тильды (-) после их имени. Этот знак отображается при установки флажка Trailing Tildes (по умолчанию она включена). Однако с помощью флажка No Annotation можно отключить как это обозначение, так и короткий текстовый комментарий, который сопровождает предполагаемые переменные. Наконец, флажок Phrase включает вывод текстовых комментариев. Рисунок 4.16 наглядно иллюстрирует применение этих параметров.
Благодаря применению предполагаемых переменных облегчается реализация ряда алгоритмов, критичных к выбору переменных. Например, если использовать вычисление квадратного корня без привлечения понятия о комплексных числах, то на численные значения переменных надо наложить условие их положительности. Контроль за статусом таких переменных и дают описанные параметры.
Рис. 4.16. Применение параметров контроля предполагаемых переменных
17.gif

23. Управление показом графиков
Управление показом графиков
Графические результаты могут быть представлены прямо в документе в ячейках вывода или в отдельных окнах. Это обеспечивается двумя командами подменю Plot Display:
- Inline — вывод графиков в ячейках вывода;
- Window — вывод графиков в отдельных окнах.
На рис. 4.17 показан пример вывода двух графиков — один выводится с применением Inline в ячейку документа (сразу после ввода), а другой с применением Window в отдельное окно. Какой из этих двух вариантов предпочтительнее, зависит от привычек пользователя.
Следует отметить, что из всех окон (документов или графиков) в данный момент активным может быть только одно окно. Если это окно графическое, то для него выводится своя контекстная панель инструментов, позволяющая менять вид графика и некоторые параметры, используемые при его построении. Кстати говоря, запись заданного документа на диск возможна только при активном окне этого документа.
Рис. 4.17. Пример построения двух графиков с выводом одного из них в отдельное окно
Следует отметить, что из всех окон (документов или графиков) в данный момент активным может быть только одно окно. Если это окно графическое, то для него выводится своя контекстная панель инструментов, позволяющая менять вид графика и некоторые параметры, используемые при его построении. Кстати говоря, запись заданного документа на диск возможна только при активном окне этого документа.
18a.gif
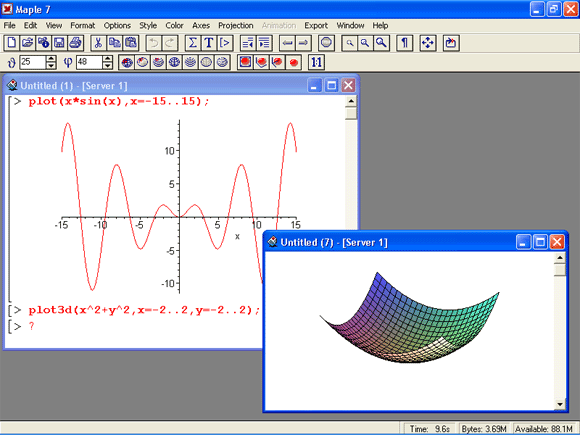
24. Управление построением двумерных графиков
Управление построением двумерных графиков
Двумерные графики обычно строятся с применением функции plot. На рис. 4.18 (и на рис. 1.24 с графиком в документе) представлено назначение кнопок контекстной панели инструментов двумерной графики. Кнопки обозначены номерами под ними, а в окне документа дано их краткое назначение.
Панель инструментов графиков появляется только при активном окне графики или при выделении графика в ячейке документа.
Рис.4.18. Окно двумерного графика и его панель инструментов
19.gif
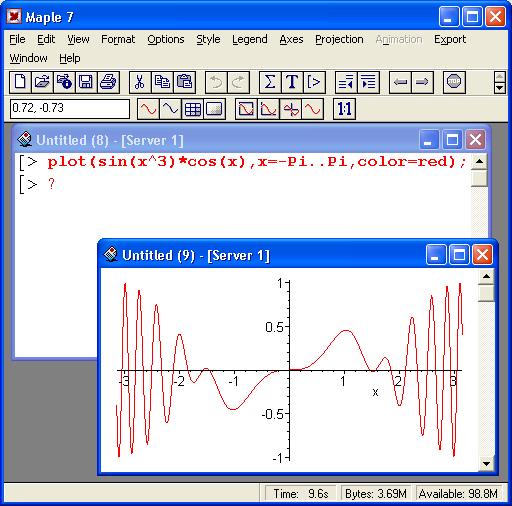
25. Управление построением трехмерных графиков
Управление построением трехмерных графиков
Трехмерные графики имеют свою контекстную панель инструментов (рис. 4.19; см. также рис. 1.25 с графиком в документе), с кнопками задания наиболее распространенных параметров для построения трехмерных графиков. Следует отметить, что панели инструментов графических окон дают доступ лишь к части параметров графиков. Более подробно состав и назначение параметров будут рассмотрены в дальнейшем при описании средств создания графиков. -Читателю настоятельно рекомендуется опробовать действие кнопок управления различными форматами графиков, что позволит быстрее освоить огромные возможности Maple 7 в создании цветных и монохромных графиков.
26. Работа с окнами
Работа с окнами
При серьезной работе в среде Maple 7 пользователь нередко вынужден работать одновременно с несколькими документами. Удобства такой работы зависят от того, как окна расположены в пределах экрана. Maple 7 дает возможность расположить их любым стандартным способом.
Основные команды по установке расположения окон сосредоточены в меню Window (рис. 4.20).
Рис. 4.20. Меню Window
Это меню содержит следующие команды:
- Cascade — каскадное расположение окон;
- Tile — расположение окон мозаикой;
- Horizontal — расположение окон по горизонтали;
- Vertical — расположение окон по вертикали;
- Arrange Icons - упорядочение расположения икон;
- Close All — закрытие всех окон документов;
- Close All Help - закрытие всех окон справочной системы.
20.gif
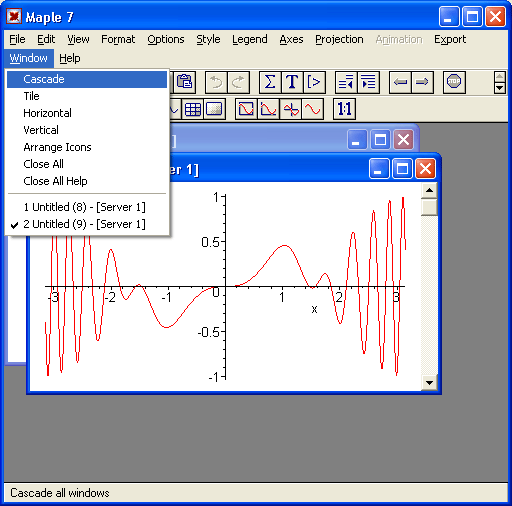
27. Каскадное расположение окон
21.gif
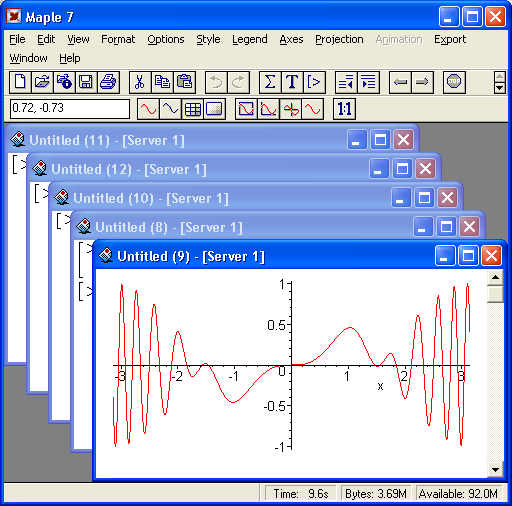
28. Расположение окон мозаикой
Расположение окон мозаикой
При выполнении команды Tile устанавливается расположение окон мозаикой показанное на рис. 4.22. При этом окна не перекрываются, имеют примерно одинаковый размер. К сожалению, при большом числе окон область просмотра оказывается настолько мала, что работать с документами при таком расположении окон становится неудобно.
Расположение окон мозаикой достаточно удобно при работе с двумя (или на большом экране тремя) окнами. Оно может быть полезно, например, при переносе содержимого отдельных ячеек с одного документа в другой путем перетаскивания. Можно также копировать объекты в одном окне, а затем, переключившись в другое окно, вставлять содержимое буфера обмена в нужную ячейку, используя команду Paste.
Рис. 4.22. Расположение окон мозаикой
22.gif
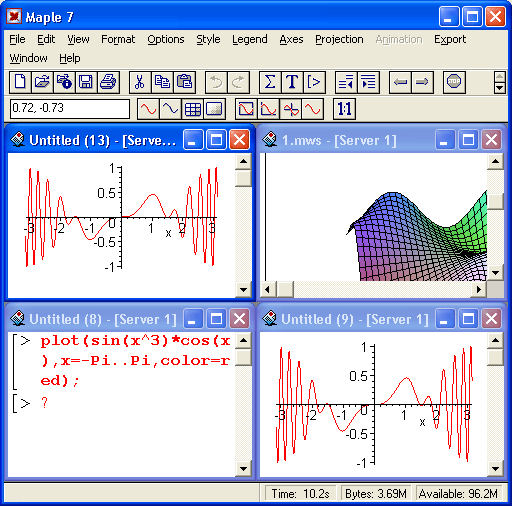
29. Горизонтальное расположение окон
Горизонтальное расположение окон
При использовании команды Horizontal окна оказываются расположенными на экране в виде горизонтальных полос (рис. 4.23). Этот вариант расположения окон, как и каскадное расположение, дает обзор заголовков документов, если область просмотра каждого документа расположена сверху окна. Последнее условие может нарушаться при перемещении окон документов.
30. Вертикальное расположение окон (Vertical).
Вертикальное расположение окон (Vertical)
Команда Vertical задает расположение окон в виде вертикальных полос (рис. 4.24). Такое расположение окон удобно, если содержимое ячеек документов представлено короткими выражениями.
Следует отметить, что описанным командам подчиняются только развернутые в данный момент окна — расположение вновь открытого или развернутого окна не зависит от данных до этого команд.
Рис. 4.23. Горизонтальное расположение окон
Рис. 4.24. Вертикальное расположение окон
23.gif
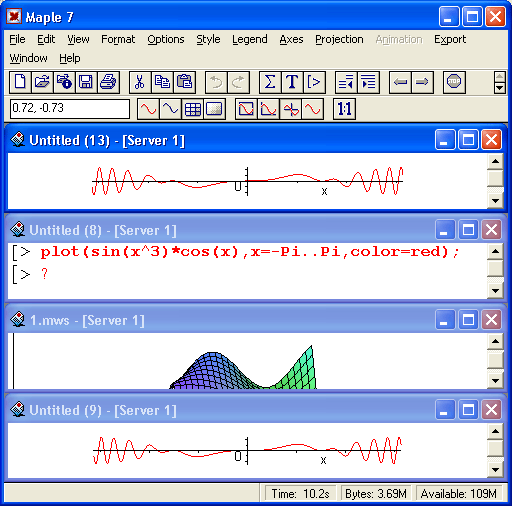
24.gif
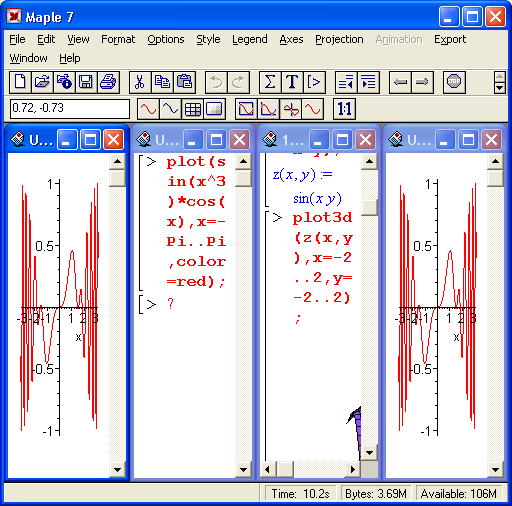
31. Приведение в порядок значков свернутых окон
Приведение в порядок значков свернутых окон
Свернутые окна представлены значками. Они могут перемещаться мышью по всему пространству экрана, поэтому иногда значки оказываются хаотично разбросанными (рис. 4.25).
Рис. 4.25. Хаотическое расположение значков свернутых окон
Для наведения порядка с расположением значков можно, разумеется, переместить каждый из них в удобное место. Но это довольно утомительное занятие. Лучше воспользоваться специальной командой Arrange Icons, которая автоматически наводит порядок в расположении значков свернутых окон, аккуратно располагая их снизу экрана. Действие этой команды показано на рис. 4.26. Как и окно, каждый значок имеет строку заголовка с четырьмя маленькими кнопками. Первая из них открывает меню управления, а три другие используются соответственно для восстановления размера, развертывания на весь экран и закрытия окна.
25.gif
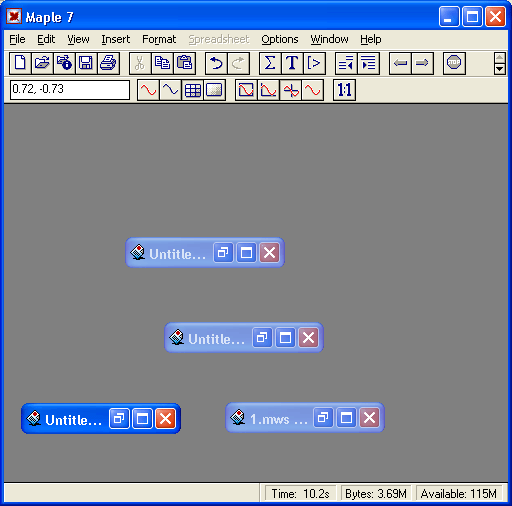
32. Закрытие всех окон одновременно
Закрытие всех окон одновременно
Команда Close All служит для закрытия всех окон одновременно. Эта команда будет выполнена сразу только в том случае, когда все документы не модифицировались или были записаны на диск после внесения исправлений. Если какой-либо документ был изменен, но еще не сохранен, то в центре экрана появится предупреждающее сообщение об этом (рис. 4,27).
Рис. 4.26. Вид экрана после выполнения команды Arrange Icons
Рис. 4.27. Окно, предупреждающие о том, что закрываемый документ был изменен
Разумеется, такое окно будет появляться столько раз, сколько имеется модифицированных документов.
26.gif
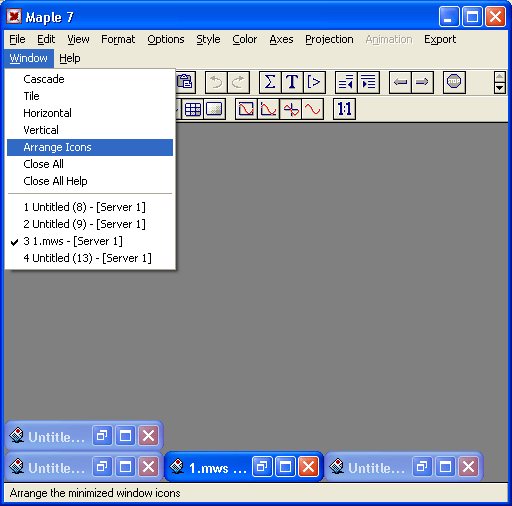
27.gif

33. Закрытие всех окон справочной системы
Закрытие всех окон справочной системы
В Maple 7 использована многооконная справочная система с гипертекстовыми ссылками. Поэтому при работе с ней экран системы довольно быстро оказывается забитым окнами справочной системы. Разумеется, их можно последовательно закрывать одно за другим, но это очень неудобно и долго. Команда Close All Help обеспечивает закрытие разом всех окон справочной системы, что позволяет продолжить работу с текущим документом. На окна загруженных документов операция Close All Help влияния не оказывает.
34. Список открытых документов
Список открытых документов
Заканчивая рассмотрение меню Window, надо отметить, что оно завершается списком всех открытых в Maple 7 документов и соответственно окон (рис. 4.26). Щелкнув на той или иной строке этого списка, можно открыть соответствующее окно и сделать его активным.
35. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Изменять вид интерфейса и документа.
- Выводить и скрывать палитры математических знаков.
- Управлять показом непечатаемых символов.
- Изменять статус ячеек документа.
- Устанавливать параметры Maple 7.
- Работать с окнами документов.
- Просматривать список открытых документов.
Урок 5. Типы данных системы Maple
1. Maple-язык и его синтаксис
Урок 5.
Типы данных системы Maple 7
Язык Maple (или Maple-язык) является одновременно входным языком общения с Maple 7 и языком ее программирования. Входящие в него средства (прежде всего операторы и функции) подобраны настолько полно и удачно, что при решении подавляющего большинства типовых математических задач от пользователя не требуется знаний даже основ программирования. Для решения нужной задачи обычно достаточно составить алгоритм и подобрать набор нужных для его реализации функций и иных средств Maple-языка.
В то же время Maple-язык — один из самых мощных языков программирования математических задач, содержащий почти 3000 операторов, команд и функций, входящих в ядро, основную библиотеку и пакеты функций Maple 7. При этом относящаяся к традиционному программированию часть Maple-языка реализована с помощью довольно скромного набора специальных знаков и зарезервированных слов.
Большинство функций Maple 7 (в частности, все, входящие в пакеты) написаны на этом языке. Поэтому знание этого языка является определяющим в серьезном изучении Maple. Ниже Maple-язык описывается как типичный язык программирования.
Алфавит Maple-языка содержит 26 малых латинских букв (от а до z), 26 больших латинских букв (от А до Z), 10 арабских цифр (от 0 до 9) и 32 специальных символа (арифметические операторы +, -, *, /, знак возведения в степень ж и др.). Все они будут рассмотрены в данной главе. Имеется пять пар альтернативных символов (означающих одно и тоже):
"и** [ и (| ] и |) { и (* } и *)
К специальным одиночным и составным знакам относятся элементы синтаксиса языка:
- % — системная переменная, хранящая результат предшествующей операции;
- : — фиксатор выражения, предотвращающий вывод результата вычисления в ячейку вывода;
- ; — фиксатор выражения, дающий вывод результата вычисления в ячейку вывода;
- # — указатель программного комментария;
- " — ограничитель строки (например, 'string');
- := — оператор присваивания (например, х:=5);
- : ; — пустой оператор;
- :: — указатель типа переменной (например, n::integer или z: -.complex);
- \ — знак обратного деления, который имеет множественные значения в зависимости от контекста (см. справку по этому знаку - backslash).
Комментарии в программе, не выводимые в ячейки вывода, задаются после символа #. В них допустимо использовать все символы кодовых таблиц, что важно при вводе русскоязычных комментариев, использующих символы кириллицы. Применение последних для идентификаторов (имен) объектов недопустимо.
2. Зарезервированные слова
Зарезервированные слова
Зарезервированные слова используются для создания условных выражений, циклов, процедур и управляющих команд. Список 42 зарезервированных слов Maple 7 дан ниже.
|
and |
break |
by |
catch |
description |
|
do |
done |
el if |
else |
end |
|
error |
export |
fi |
finally |
for |
|
from |
global |
if |
in |
intersect |
|
local |
minus |
mod |
module |
next |
|
not |
od |
option |
options |
or |
|
proc |
quit |
read |
return |
save |
|
stop |
then |
to |
try |
union |
|
use |
while |
|
|
|
Совокупность правил, по которым записываются определения всех объектов Maple-языка, называется его синтаксисом. Некоторые особенности синтаксиса полезно знать уже в начале освоения Maple. Например, то что знак - (минус) имеет двойное значение. Применительно к одному числу, переменной или выражению он меняет их знак. Однако два знака минус подряд (например, в записи --3) задавать нельзя. Другое назначение знака минус — создание операции вычитания, например 5-2 или а-b. Соответственно двойное назначение имеет и знак •+, причем число без знака считается положительным, так что +5=5.
При вводе действительных чисел с порядком для указания порядка используется символ * (например, 2*1(Г100 или 2*1(Г-100). Для возведения числа в степень наряду с оператором *• можно использовать и составной оператор ** (две звездочки подряд). Для изменения общепринятого приоритета вычислений используются круглые скобки, в них же задаются параметры функций и процедур. Более подробно синтаксис Maple-языка рассматривается ниже.
Некоторые операторы представлены двумя символами — например, оператор присваивания переменным их значения := содержит двоеточие и знак равенства. В таких операторах между символами недопустим знак пробела. Однако его можно использовать между отдельными частями выражений — так, (а+b)/с эквивалентно (а + b) / с.
По набору операторов и функций Maple-язык намного превосходит любой универсальный язык программирования. Это позволяет наряду с обычными программными конструкциями задавать множество специальных конструкций, подчас резко упрощающих запись математических выражений. К примеру, возможна работа со списками имен функций. Язык Maple имеет множество операций над символьными выражениями и гибкий аппарат создания и преобразования типов данных и результатов вычислений.
Для большинства пользователей возможности языка Maple кажутся явно избыточными, и большинство наиболее распространенных операций в нем реализуется несколькими способами. Однако каждый пользователь волен выбирать из множества возможностей именно те, которые ему необходимы в конкретной предметной области. Поскольку таких областей превеликое множество, то обширные возможности Maple лишними не являются.
3. Выражения и основы работы с ними
Выражения и основы работы с ними
Фактически Maple 7 — это система для манипулирования математическими выражениями.
Выражение в системе Maple — это объект, вполне соответствующий сути обычного математического выражения. Оно может содержать операторы, операнды и функции с параметрами. В этом уроке выражения записываются на Maple-языке без использования специальных средств для их представления в естественном математическом виде. Благодаря этому запись выражений и приводимых примеров одинаково пригодна для любой реализации системы Maple — даже под MS-DOS. Такая запись получается наиболее короткой, ее можно выводить и распечатывать без применения графических средств. Кроме того, она соответствует виду, принятому в справочной системе Maple.
Однако пользовательский интерфейс системы Maple 7 для Windows позволяет представлять как вводимые, так и выводимые выражения в самых различных формах, в том числе в естественном математическом виде — примеры этого многократно приводились и будут приводиться в дальнейшем. Maple 7 имеет многочисленные функции преобразования форматов, позволяющие менять форму представления данных.
Выражения в Maple могут оцениваться и изменяться в соответствии с заданными математическими законами и правилами преобразований. Например, функция упрощения выражений simplify способна упрощать многие математические выражения, записанные в качестве ее параметра (в круглых скобках):
Символьные преобразования и вычисления математических выражений более подробно будут рассмотрены в следующем уроке.
Для выполнения любых математических операций необходимо обеспечить ввод в систему исходных данных — в общем случае математических выражений. Для ввода их и текстовых комментариев служат два соответствующих типа строк ввода. Переключение типа текущей строки ввода осуществляется клавишей F5. Строка ввода математических выражений имеет отличительный символ >, а строка ввода текстов такого признака не имеет.
В строке ввода может располагаться несколько выражений. Фиксаторами (указанием, что выражение окончено) их могут быть символы ; (точка с запятой) и : (двоеточие). Символ «:» фиксирует выражение и задает вывод результатов его вычисления. А символ «:» фиксирует выражение и блокирует вывод результатов его вычисления. Фиксаторы выполняют также функцию разделителей выражений, если в одной строке их несколько.
Ввод выражения оканчивается нажатием клавиши Enter. При этом маркер ввода (жирная мигающая вертикальная черта) может быть в любой позиции строки. Если надо перенести ввод на новую строку, следует нажимать клавиши Shift и Enter совместно. С помощью одного, двух или трех знаков % (в реализациях до Maple V R5 это был знак прямых кавычек ") можно вызывать первое, второе или третье выражение с конца сессии:
Особая роль при вводе выражений принадлежит знакам прямого апострофа (одиночного ' или двойного ''). Заключенное в такие знаки выражение освобождается от одной пары (закрывающего и открывающего знаков '):
Некоторые другие возможности обрамления выражений апострофами мы рассмотрим позже. Наиболее важная из них — временная отмена выполненного ранее присваивания переменным конкретных значений.
Для завершения работы с текущим документом достаточно исполнить команду quit, done или stop, набранную в строке ввода (со знаком ; в конце).
1.gif

2.gif
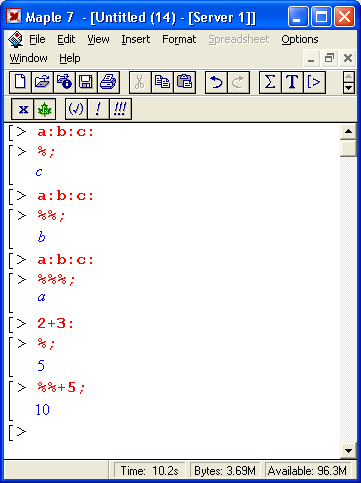
3.gif
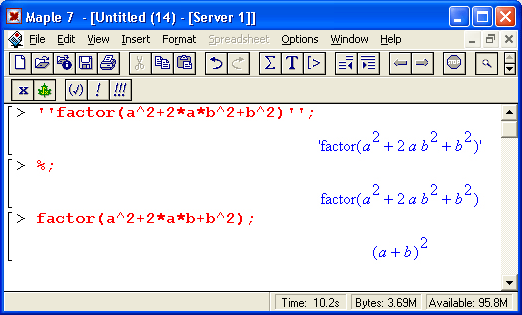
4. Оценивание выражений
Оценивание выражений
Встречая выражение, Maple 7 оценивает его, то есть устанавливает возможность его вычисления. Если выражение — скалярная переменная, то ее значение будет выведено в ячейке вывода. Для переменных более сложных типов выводится не их значение, а просто повторяется имя переменной. Просто повторяются также имена неопределенных переменных.
Для оценивания выражений различного типа существует группа функций, основные из которых перечислены ниже:
- eval (array) — возвращает вычисленное содержимое массива array;
- evalf(expr, n) — вычисляет ехрr и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки;
- eval hf(ехрг) — вычисляет ехрг и возвращает вычисленное значение с точностью, присущей оборудованию данного компьютера;
- evalf(int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла int(f,x=a. .b);
- evalf(Int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла, заданного инертной функцией Int(f,x=a. .b);
- evalf(Int(f. x=a..b, digits, flag)) — аналогично предыдущему, но возвращает значение интеграла с заданным параметром digits числом цифр после десятичной точки и со спецификацией метода вычислений flag;
- evalm(mexpr) — вычисляет значение матричного выражения mexpr и возвращает его;
- evalb(bexpr) — вычисляет и возвращает значения логических условий;
- evalc(cexpr) — вычисляет значение комплексного выражения;
- evalr (ехрr, ampl) — оценивает и возвращает значения интервальных выражений (функция должна вызываться из библиотеки);
- shake(expr, ampl) — вычисляет интервальное выражение.
Для функции evalf параметр n является необязательным, при его отсутствии полагается n=10, то есть вещественные числа выводятся с мантиссой, имеющей десять цифр после десятичной запятой.
В выражении ехрr могут использоваться константы, например Pi, exp(l), и функции, такие как ехр, 1 n, arctan, cosh, GAMMA и erf. В матричном выражении mexpr для функции evalr могут использоваться операнды в виде матриц и матричные операторы &*, +, - и ^. В комплексных выражениях mexpr наряду с комплексными операндами вида (а + I*b) могут использоваться многие обычные математические функции:
|
sin |
cos |
tan |
CSC |
sec |
cot |
|
sinh |
cosh |
tanh |
csch |
sech |
coth |
|
arcsin |
arccos |
arctan |
arccsc |
arcsec |
arccot |
|
arcsinh |
arccosh |
arctanh |
arccsch |
arcsech |
arccoth |
|
exp |
In |
•sqrt |
* |
abs |
conjugate |
|
polar |
argument |
signura |
csgn |
Re |
Im |
|
Ei |
LambertW |
dilog |
surd |
|
|
Примеры применения функций оценивания даны ниже:
В дальнейшем мы многократно будем применять функции оценивания для демонстрации тех или иных вычислений.
4.gif
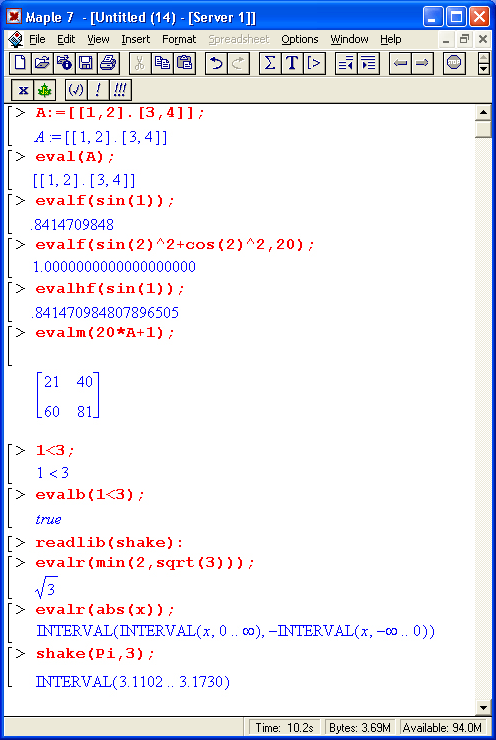
5. Последовательности выражений.
Последовательности выражений
Maple 7 может работать не только с одиночными выражениями, но и с последовательностями выражений. Последовательность выражений — это ряд выражений, разделенных запятыми и завершенных фиксатором:
Для автоматического формирования последовательности выражений применим специальный оператор $, после которого можно указать число выражений или задать диапазон формирования выражений:
Для создания последовательностей выражений можно использовать также функцию seq:
5.gif
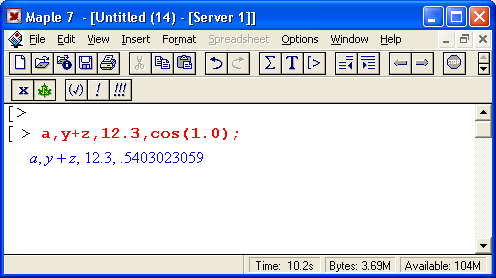
6.gif

7.gif

6. Вывод выражений
Вывод выражений
При выполнении порой даже простых операций результаты получаются чрезвычайно громоздкими. Для повышения наглядности выражений Maple 7 выводит их с выделением общих частей выражений и с присваиванием им соответствующих меток. Метки представлены символами #N, где N — номер метки. Помимо меток при выводе результатов вычислений могут появляться и другие специальные объекты вывода, например корни RootOf, члены вида О(х"), учитывающие погрешность при разложении функций в ряд, и обозначения различных специальных функций, таких как интегральный синус, гамма-функция и др. Примеры такого вывода приведены ниже:
Часто встречаются также знаки ~ для отметки предполагаемых переменных, постоянные интегрирования и другие специальные обозначения. По мере упоминания в тексте таких объектов вывода они будут описаны.
8.gif
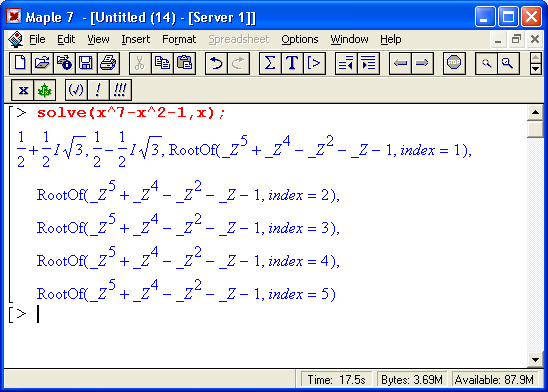
9.gif
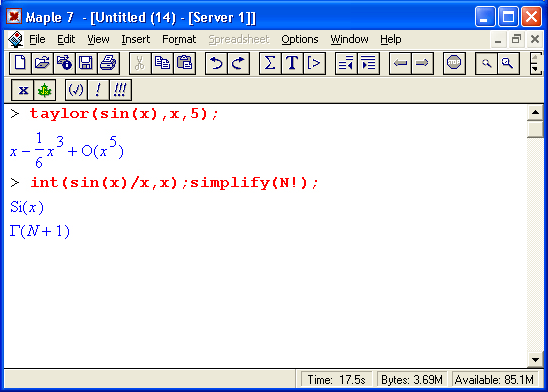
7. Простые типы данных
Простые типы данных
Maple 7 работает с числами следующего типа: целыми (О, 1, 123, -456 и т. д.), рациональными в виде отношения целых чисел (7/9, -123/127 и т. д.), вещественными с мантиссой и порядком (1.23Е5, 123.4567Е-10). Признаком вещественного числа является десятичная точка (запятая). Примеры простых операций с числами приведены ниже:
Как видно из этих примеров, ввод и вывод чисел имеет следующие особенности:
- для отделения целой части мантиссы от дробной используется разделительная точка;
- нулевая мантисса не отображается (число начинается с разделительной точки);
- мантисса отделятся от порядка пробелом, который рассматривается как знак умножения;
- мнимая часть комплексных чисел задается умножением ее на символ мнимой единицы I (квадратный корень из -1).
Десятичная точка в числах имеет особый статус — указание ее в любом месте числа, даже в конце, делает число вещественным и ведет к переводу вычислений в режим работы с вещественными числами. При этом количеством выводимых после десятичной точки цифр можно управлять, задавая значение системной переменной окружения Digits:
Для работы с числами Maple 7 имеет множество функций. Они будут рассмотрены в дальнейшем. На комплексной плоскости числа задаются координатами точек (х, у) (рис. 5.1).
Рис. 5.1. Представление обычных и комплексных чисел на плоскости
Для представления чисел на рис. 5.1 используется функция pointplot(list), где list — список координат точек. Эта функция становится доступной при подключении пакета plots командой with(plots). Кроме того, использована функция вывода ряда графических объектов на один график — display (см. далее описание представления комплексных чисел).
С помощью функции convert Maple 7 может преобразовывать числа с различным основанием (от 2 до 36, в том числе бинарные и шестнадцатеричные) в десятичные числа:
При символьных вычислениях Maple 7 реализует точную арифметику. Это значит, что результат может быть получен с любым числом цифр. Однако надо помнить, что идеально точные численные вычисления выполняются только в случае целочисленных операций, например таких, как приведены ниже:
10.gif
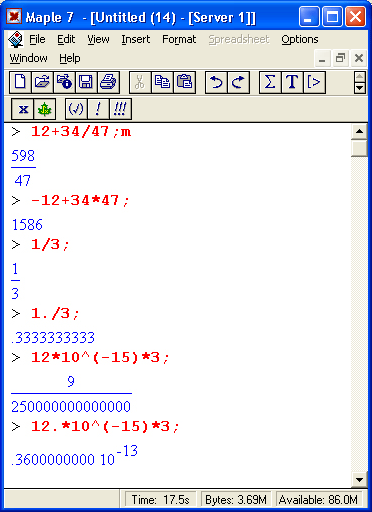
11.gif
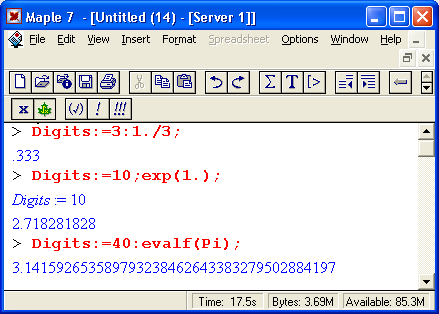
12.gif
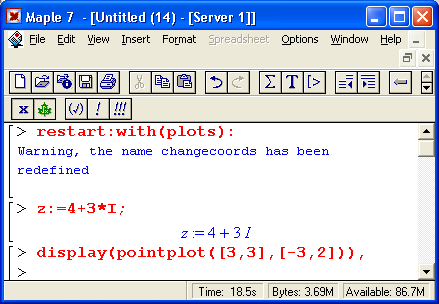
13.gif
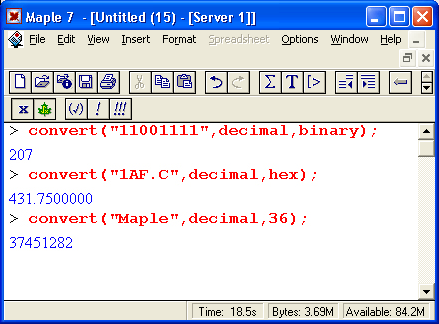
14.gif
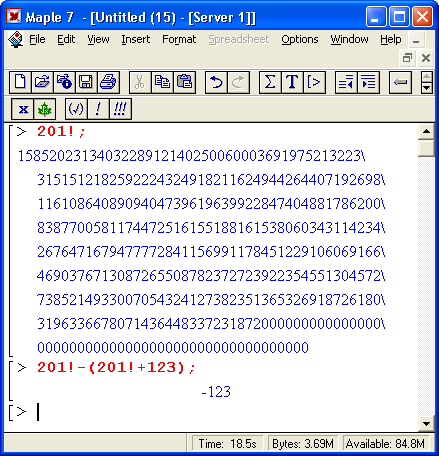
8. Комплексные числа
Комплексные числа
Maple 7, естественно, может работать с комплексными числами. Мнимая единица в комплексном числе (корень квадратный из -1) обозначается как I. Функции Re(x) и Im(x) возвращают действительную и мнимую части комплексных чисел. Примеры задания комплексного числа и вывода его действительной и мнимой частей представлены ниже:
Комплексные числа обычно представляют на так называемой комплексной плоскости, у точек которой координата х задает действительную часть комплексного числа, а у (мнимая ось) показывает мнимую часть такого числа. На рис. 5.1 показано задание в виде радиус-векторов комплексного числа z = 4+3I, -z и комплексно-сопряженного числа 4-3I.
Окружность радиуса abs(z)=sqrt(a2 + b2) представляет абсолютное значение комплексного числа z=a+b*I. Она является геометрическим множеством комплексных чисел, образованных концом вращающегося радиус-вектора числа z вокруг его начала в точке (0, 0) комплексной плоскости. Позже мы рассмотрим ряд функций для работы с комплексными числами.
15.gif

9. Контроль за числами
Контроль за числами
Числа могут служить объектами ввода, вывода и константами, входящими в математические выражения. Функция type(x, numeric) позволяет выяснить, является ли х числом. Если является, то она возвращает логическое значение true (истина), а если нет, то false (ложь). Например:
Функции type(x, integer), type(x, rational) и type(x, fraction) можно использовать для проверки того, имеет ли х значение соответственно целого числа, рационального числа или простой дроби:
16.gif
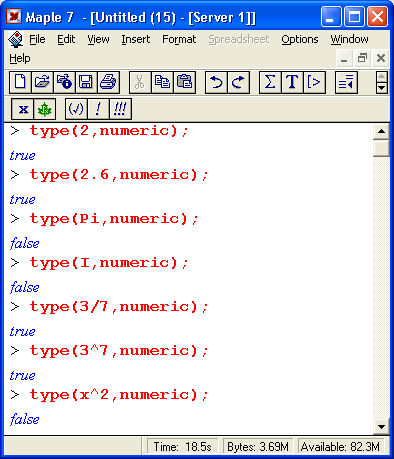
17.gif
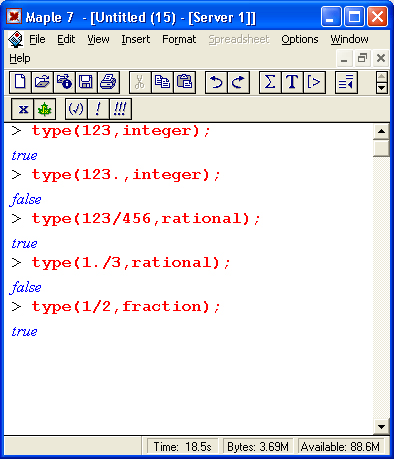
18.gif
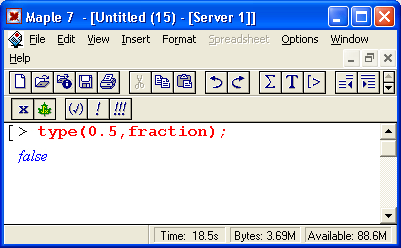
10. Преобразования чисел с разным основанием
Преобразования чисел с разным основанием
В Maple возможна работа с числами, имеющими различное основание (base), в частности с двоичными числами (основание 2 — binary), восьмеричными (основание 8 — octal) и шестнадцатеричными (основание 16 — hex). Функция convert позволяет легко преобразовывать форматы чисел:
Помимо приведенных вариантов функция convert имеет еще ряд других форм. С ними можно познакомиться с помощью справки по этой мощной функции. В дальнейшем будет приведен ряд других применений этой функции.
19.gif

11. Данные множественного типа.
Данные множественного типа
Любые выражения могут включаться также в наборы. Такие наборы в виде множеств создаются с помощью фигурных скобок { }:
Отличительная черта множеств — автоматическое устранение из них повторяющихся по значению элементов. Кроме того, Maple 7 расставляет элементы множеств в определенном порядке — числа в порядке увеличения значения, а символы и строки в алфавитном порядке. Для множеств нет строгого математического определения, и мы будем считать их наборами, удовлетворяющими перечисленным выше признакам.
20.gif
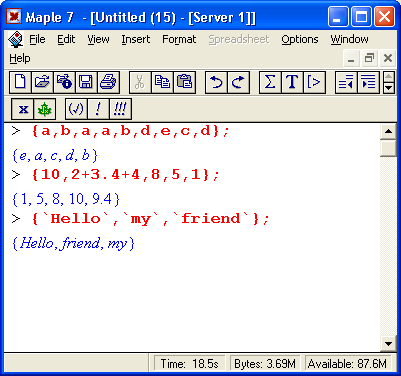
12. Списки выражений
Списки выражений
Для создания упорядоченных наборов — списков — служат квадратные скобки [ ]:
> [10,2+3.4+4,8,5,1]: [10,5,8,8,5,1]
Как нетрудно заметить, элементы списков преобразуются и выводятся строго в том порядке, в каком они были заданы. Списки широко применяются для задания векторов и матриц.
В ряде случаев, например при подготовке данных для двумерных графиков, возникает необходимость в подготовке парных списков — скажем, координат точек (х, у) графика. Для этого можно использовать функцию zip(f, u, v) или zip(f, u, v, d). Здесь f — бинарная функция, u, v — списки или векторы, d — необязательное значение. Примеры применения функции zip даны ниже:
Рисунок 5.2 показывает применение этих средств для построения точек, представляющих множество действительных чисел на плоскости. Для этого использована функция pointplot из пакета plots.
21.gif
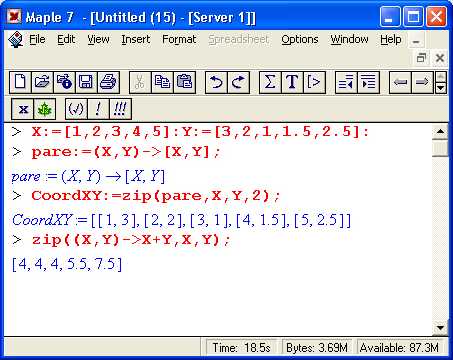
13. Массивы, векторы и матрицы
Массивы, векторы и матрицы
Как отмечалось, важным типом данных являются списки (lists). Они создаются с помощью квадратных скобок, например:
- [1,2,3,4] — список из четырех целых чисел;
- [1. ,2.34,5] — список из двух вещественных и одного целого числа;
- [а,b.'Привет'] — список из двух символов (переменных) и строковой константы;
- [sin(x), 2*cos(x) ,a^2-b] — список из трех математических выражений.
Для создания векторов (одномерных массивов) и матриц (двумерных массивов) служит функция array. Обычно она используется в следующих формах:
- аrrау[а. .b,sl] — возвращает вектор с индексами от а до b и значениями в одномерном списке si;
- аrrау[а. .b,c. .d,s2] — возвращает матрицу с номерами строк от а до b, номерами столбцов от с до d и значениями в двумерном списке s2.
Рис. 5.2. Представление множества чисел на плоскости
Двумерные списки часто путают с матрицами. Следует помнить, что векторы и матрицы создаются с помощью функции array и являются отдельным типом данных. Элементами векторов и массивов могут быть константы, переменные, выражения, списки и иные объекты. Эти элементы являются индексированными переменными и их положение указывается индексами. Имеется множество функций для работы со списками, массивами и матрицами. Они будут рассмотрены в дальнейшем. В принципе, размерность массивов, создаваемых списками, не ограничена и массивы могут быть многомерными.
22.gif
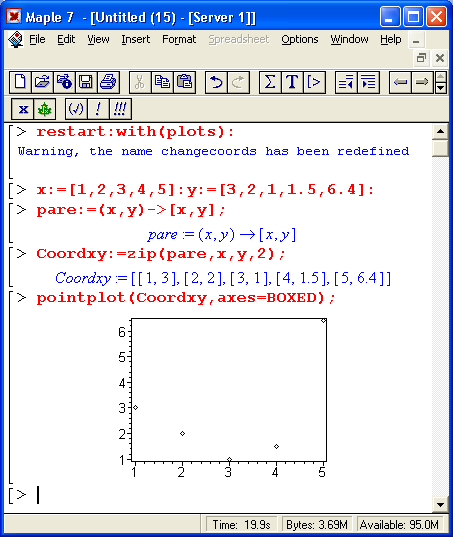
14. Таблицы
Таблицы
Еще одним важным типом множественных данных являются таблицы. Они задают данные с произвольной индексацией. Для создания таблиц служит функция table, которая при вызове в простейшем виде table[] создает шаблон пустой таблицы:
Пустая таблица резервирует память под данные. Когда параметром функции table является список выражений, он выводится в естественном порядке расположения элементов таблицы, но с произвольным порядком индексации:
В конце приведенных примеров показано, как можно выделить отдельные компоненты таблицы и вывести значения и индексы таблицы с помощью функций entries и indices. Следующие примеры показывают, что таблицу можно использовать для выполнения математических преобразований:
Следует внимательно присмотреться к этим примерам — они демонстрируют замену функции косинуса на отрицательный синус и синуса на косинус.
23.gif
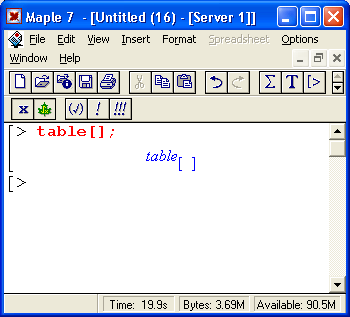
24.gif
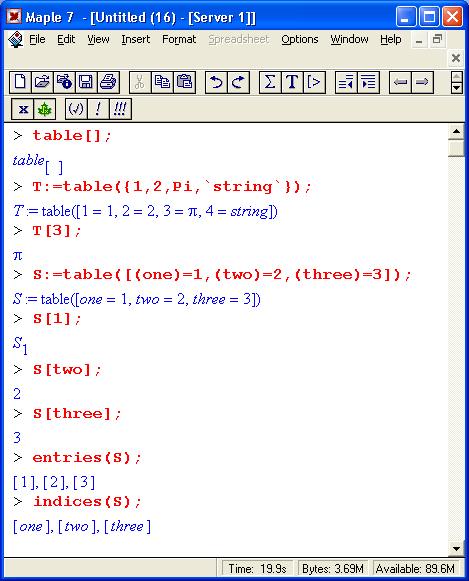
25.gif

15. Строки и комментарии
Строки и комментарии
Строки как тип данных — это просто цепочки символов. Они обычно используются для создания текстовых комментариев. Строки должны каким-либо образом выделяться, чтобы Maple не отождествляла их с именами констант и переменных. Для этого строки-комментарии имеют внутренний разделительный признак, который устанавливается при их вводе (нажатием клавиши F5, которое приводит к исчезновению знака >).
В других случаях последовательность символов рассматривается как строка, если она заключена в обратные апострофы, то есть в знаки '. Два апострофа подряд формируют апостроф как знак символьной строки, например `abc``def ` дает строку abc`def. Любое математическое выражение может входить в строку, разумеется, оно при этом не выполняется:
> '2+2 не всегда "четыре"';
2+2 не всегда 'четыре'
16. Неисполняемые программные комментарии
Неисполняемые программные комментарии
Часто возникает необходимость в задании программных комментариев. Любой текст после знака # рассматривается как невыводимый (неисполняемый) программный комментарий — даже если это математическое выражение. При этом он не вычисляется. Например:
> 2+3;#Это прииер. А это выражение не вычисляется: 4+5
.5
Комментарии полезны в программах на Maple-языке и обычно используются для объяснения особенностей реализованных алгоритмов.
17. Константы
Константы
Константы - это простейшие именованные объекты, несущие заранее предопределенные значения. Их имена (идентификаторы) также заранее определены и не могут меняться. Подробную информацию о константах можно найти, исполнив команду ?constant.
Обычные числовые константы не имеют имени и представлены просто числами, типы которых были указаны выше. Можно считать, что именем такой константы является само ее значение. Например, в выражении 2*sin(1.25) числа 2 и 1.25 являются числовыми константами. При этом указание десятичной точки делает константу действительным числом — например, 2 — это целочисленная константа, а 2., 2.0 или 1.25 — это уже действительные константы.
18. Строковые константы
Строковые константы
Строковыми константами являются произвольные цепочки символов, заключенные в обратные апострофы, например 'Hello', 'Привет', 'My number' и т. д. Числа, заключенные в апострофы, например '123456', также становятся строковыми константами, которые нельзя использовать в арифметических выражениях. Строковые константы представляют значения строковых переменных. В них можно использовать символы кириллицы при условии, что соответствующий шрифт имеется.
19. Встроенные в Ядро константы
Встроенные в ядро константы
Есть также ряд констант, которые правильнее считать заведомо определенными глобальными переменными:
- false — логическое значение «ложно»;
- gamma — константа Эйлера, равная 0.5772156649...;
- infinity — положительная бесконечность (отрицательная задается как infinity);
- true — логическое значение «истинно»;
- Catalan — константа Каталана, равная 0.915965594...;
- FAIL — специальная константа (см. справку, выдаваемую по команде ?FAIL);
- I — мнимая единица (квадратный корень из -1);
- Pi — представляет константу = 3.141...
Любопытно, что в этот список не входит основание натурального логарифма — число е. В качестве этой константы рекомендуется использовать ехр(1). Она отображается как жирная прямая буква Е. A exp(l.0) выводит 2.71828... (что и следовало ожидать).
20. Идентификация констант.
26.gif
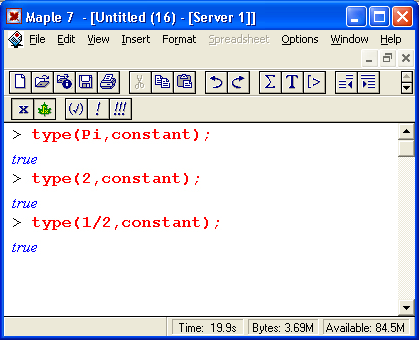
27.gif
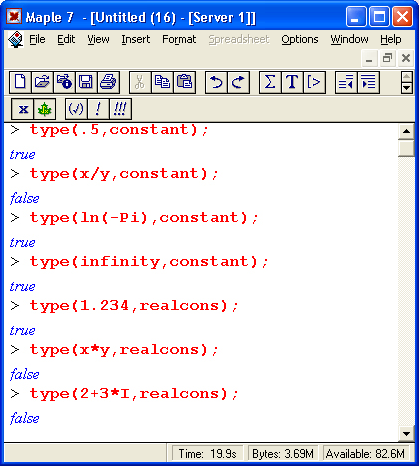
21. Защита идентификаторов констант
Защита идентификаторов констант
Имена встроенных констант (как и имена функций) защищены специальным атрибутом protected. Поэтому (без его снятия) константам нельзя присваивать какие-либо значения:
Стоит упомянуть о такой экзотической возможности, как задание в Maple 7 собственных констант путем описания алгоритма генерации входящих в константу цифр (это позволяет получать в представлении константы любое число цифр). Большинство пользователей довольствуется применением вместо таких констант обычных переменных подходящего типа. Зато истинные математики соревнуются друг с другом в создании все новых и новых констант и алгоритмов их вычислений. Примеры этого творчества можно найти на сайте фирмы Wateloo Maple.
28.gif
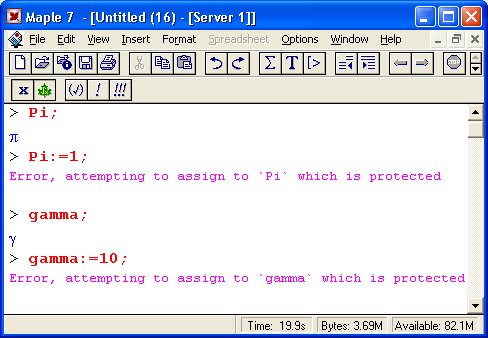
22. Переменные
Переменные
Как следует из самого названия, переменные — это объекты, значения которых могут меняться по ходу выполнения документа. Пока мы рассматриваем лишь глобальные переменные, доступные для модификации значений в любом месте документа. Тип переменной в системе Maple 7 определяется присвоенным ей значением — это могут быть целочисленные (integer), рациональные (rational), вещественные (real), комплексные (complex) или строчные (string) переменные и т. д. Переменные могут также быть символьного типа (их значением является математическое выражение) или типа списка (см. далее). Для явного указания типа переменных используется конструкция:
name::type
где name — имя (идентификатор) переменной, type — тип переменной, например целочисленный (integer), вещественный с плавающей точкой (float), с неотрицательным значением (nonneg), комплексный (complex) и т. д.
23. Идентификаторы (имена) переменных
Идентификаторы (имена) переменных
Переменные задаются своим именем — идентификатором, который должен начинаться с буквы и быть уникальным. Это значит, что ключевые слова языка Maple нельзя использовать в качестве имен переменных. Хотя имена ряда команд и функций можно использовать в качестве идентификаторов переменных, делать это крайне нежелательно. Ограничений на длину идентификатора практически нет — точнее, она не должна превышать 524 275 символов! Так что сложностей с подбором идентификаторов для переменных у вас не будет.
Имена переменных могут содержать одну букву (например, х, Y или Z) либо ряд букв (Xmin или Хmах). В любом случае имя переменной надо начинать с буквы. Некоторые символы, например знак _, могут использоваться в именах (например, Var_l, Var_2). Нельзя, однако, вводить в имена переменных знаки, обозначающие операторы, — например, а/b или а-b будет истолковано как деление а на b или вычитание из переменной а переменной b.
Имена могут задаваться в обратных апострофах. При этом они просто тождественны именам без апострофов:
Строчные и прописные буквы в идентификаторах различаются, так что Varl и varl — это разные переменные.
Для проверки предполагаемого имени на уникальность достаточно выполнить команду ?name, где name — выбранное имя. Если при этом откроется окно справки с этим именем, значит, оно уже использовано в Maple. Лучше воздержаться от его применения, так как связанная с этим именем команда или функция перестает работать, как только это имя закрепляется за какой-либо переменной.
29.gif
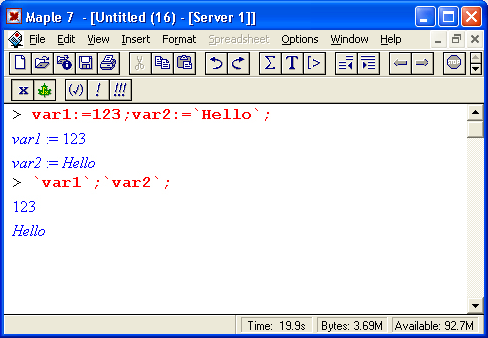
24. Присваивание переменным значений
Присваивание переменным значений
Поскольку Maple 7 прежде всего система символьной математики, то по умолчанию любые переменные рассматриваются как объекты символьного типа. Благодаря этому такие переменные могут фигурировать в математических выражениях (таких, как sia(x)/x) без их предварительного объявления. В отличие от обычных языков программирования такое использование переменных не влечет за собой появления сообщений об ошибках и является более естественным. Для присваивания переменным конкретных значений используется комбинированный символ присваивания «:=», например:
- n:=1 — переменной n присваивается, целочисленное значение 1;
- х:=123.456 - переменной х присваивается вещественное значение 123.456;
- у:=17/19 — переменной у присваивается рациональное значение 17/18;
- name:='Piter' — переменной name присваивается строковое значение "Piter";
- expr:=2*Pi/3 — переменной ехрг присваивается значение выражения 2л/3;
- V:=[1.2,3] - переменной V присваивается значение списка чисел [1,2,3];
- М:=[[1,2.3].[4,5.б]] - переменной М присваивается значение двумерного массива;
- f :=х->х^2 - переменной f присваивается значение функции пользователя f(x)=x^2.
Правая часть выражения присваивания определяет тип переменной. Например, она может быть целочисленной, действительной, строковой, индексированной (элемент массива) и т. д.
25. Отмена операции присваивания и команда restart
Отмена операции присваивания и команда restart
Переменная, имеющая какое-либо значение, занимает в памяти намного больше места, чем неопределенная переменная. У последней место в памяти занимают только символы идентификатора. Поэтому нередко целесообразно отменить присваивание у тех переменных, которые в дальнейшем можно не использовать. Это может понадобиться и в том случае, когда какую-либо переменную с численным или иным значением нужно использовать просто как неопределенную переменную. Рассмотрим следующий пример:
Здесь не удалось вычислить интеграл с подынтегральной функцией х"2 из-за того, что переменная х уже определена ранее как целочисленная переменная со значением 10, тогда как для вычисления интеграла она должна быть необъявленной или строковой (убедитесь в этом сами).
Для отмены присваивания надо использовать следующее выражение:
Итак, заключение имени переменной в прямые апострофы ликвидирует присваивание. Так что запись х:='х' означает, что переменной х возвращается статус неопределенной переменной. Теперь можно вычислить интеграл:
Можно сделать переменную х неопределенной и с помощью выражения вида x:=evaln(x). Это поясняет следующий пример:
Для отмены присваивания значений разом всем переменным (и введенным функциям пользователя) можно использовать команду restart. Следующий пример поясняет ее применение:
Следует отметить, что команда restart отменяет все предшествующие определения, что иногда чревато осложнениями. Применяйте ее только тогда, когда вы уверены, что предшествующая заданной часть документа (или даже ряда документов) действительно не важна.
Важно отметить, что Maple сохраняет в памяти все определения и присваивания, которые были сделаны во всех загруженных в систему документах. Поэтому результаты вычислений в текущем документе могут зависеть от определений в других документах. Команда restart позволяет исключить эту зависимость.
30.gif
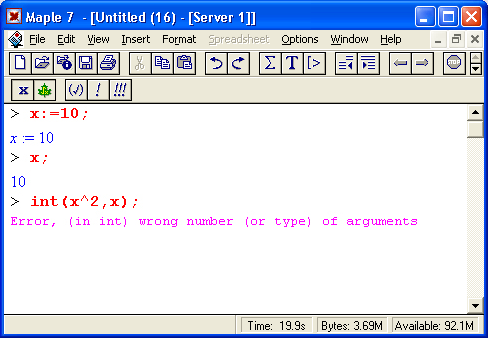
31.gif
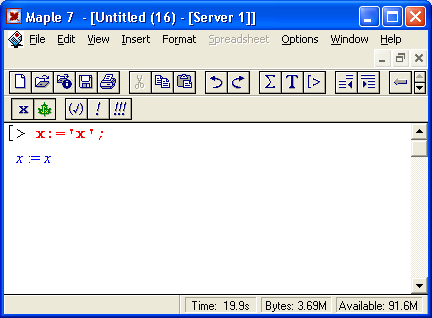
32.gif
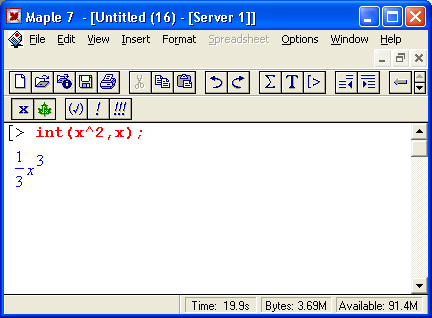
33.gif
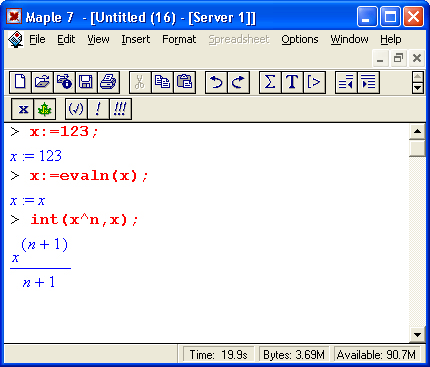
34.gif
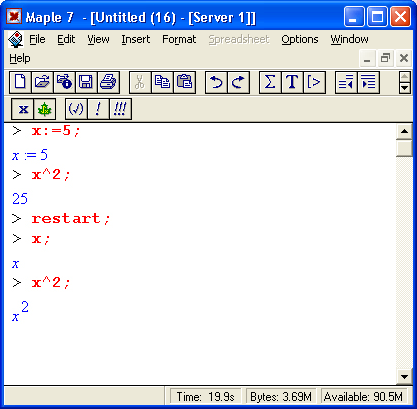
26. Придание переменным статуса предполагаемых
Придание переменным статуса предполагаемых
В большинстве расчетов пользователей Maple вполне удовлетворяет статус переменных, соответствующий присвоенным им значениям. Однако серьезные расчеты предполагают, что переменные могут иметь определенные ограничения — например, они не должны принимать отрицательных значений при обычном вычислении квадратного корня или логарифма числа.
Для придания переменным статуса предполагаемых используется функция assume: assume(x.prop): где х — переменная, имя или выражение, prop — свойство. Следующие примеры показывают применение функции assume:
Обратите внимание, что в этом примере переменная х помечена как положительная и при выводе сопровождается знаком тильды -, как бы предупреждающим нас о ее особом статусе. Это не означает, что она не может принять отрицательное значение. Однако с помощью функции is можно убедиться в ее особом статусе и при необходимости программным путем исключить вычисления для х <0. Кроме того, о свойствах переменной можно узнать с помощью функции about (name).
Иногда к уже имеющимся признакам надо добавить новые. Для этого используется функция additionally:
В этом примере переменной а вначале задан признак положительности, а затем а<=0. Оба признака удовлетворяются только при a= 0, что и подтверждает вывод информации о статусе этой переменной функцией about (а).
Предполагаемую переменную можно также изменить путем присваивания ей нового значения, противоречащего ее статусу:
Для отмены переменным статуса предполагаемых используются те же приемы, что и при отмене присвоенного значения. Например, запись х:=' х' отменяет статус предполагаемой для переменной х.
35.gif
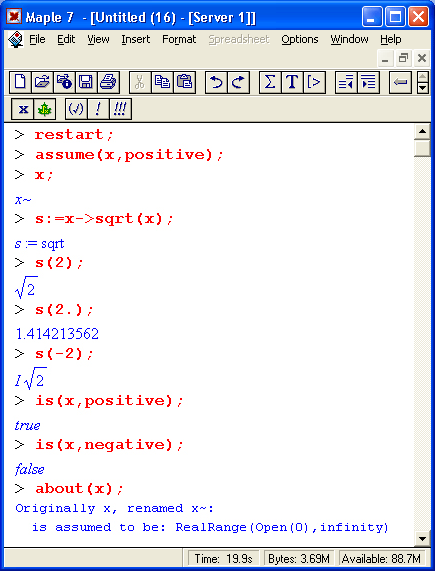
36.gif

37.gif
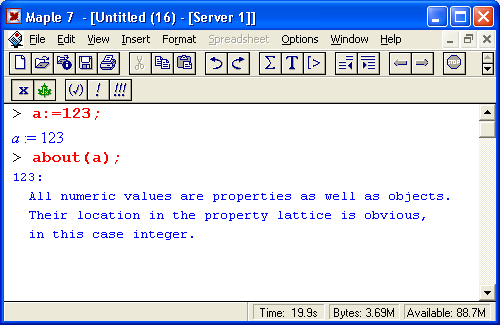
27. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Использовать Maple-язык и его синтаксис.
- Работать с выражениями.
- Задавать простые типы данных.
- Задавать данные множественного типа.
- Задавать данные строкового типа.
- Писать программные комментарии.
- Задавать переменные и определять их тип.
- Использовать константы различного типа.
Урок 6. Встроенные операторы и функции
1. Операторы и операнды
Урок 6.
Встроенные операторы и функции .
Операторы во входном языке и языке программирования Maple служат для конструирования выражений. Формально операторы представлены своими идентификаторами в виде специальных математических знаков, слов и иных имен. Операторы, как это вытекает из их названия, обеспечивают определенные операции над данными, представленными операндами.
Имеется пять основных типов операторов:
- binary — бинарные операторы (двумя операндами);
- unary — унарные операторы (с одним операндом);
- nullary — нульарные операторы (без операнда — это одна, две и три пары кавычек);
- precedence — операторы старшинства (включая логические операторы);
- functional — функциональные операторы.
Для просмотра операторов и их свойств можно использовать следующие команды:
> ?operators[binary];
> ?operators[unary];
> ToperatorsCnullary];
> ?operators[precedence];
> ?operators[functional]:
А для изучения примеров применения операторов нужно задать и исполнить команду:
> ?operators[examples];
Команда:
> Tdefine:
позволяет ознакомиться с функций define. С ее помощью можно определять новые операторы.
2. Бинарные (инфиксные) операторы
Бинарные (инфиксные) операторы
Бинарные (инфиксные) операторы используются с двумя операндами, обычно размещаемыми по обе стороны от оператора. В ядро Maple 7 включено около трех десятков бинарных операторов. Основные из них перечислены в табл. 6.1.
Tаблица 6.1. Бинарные операторы
|
Обозначение |
Оператор |
|
+ |
Сложение |
|
- |
Вычитание |
|
* |
Умножение |
|
/ |
Деление |
|
** или ^ |
Возведение в степень |
|
mod |
Остаток от деления |
|
$ |
Оператор последовательности |
|
. |
Разделительная точка |
|
@ |
Оператор композиции |
|
@@ |
Повторение композиции |
|
, |
Разделитель выражений |
|
:= |
Присваивание |
|
. .. |
Задание интервала |
|
/ |
Разделитель выражений |
|
&* |
Некоммутативное умножение |
|
&<string> |
Нейтральный оператор |
|
|| |
Конкатенация (объединение) |
Примеры использования бинарных операторов:
Оператор композиции @@ может использоваться для создания сложных функций, содержащих цепные дроби:
А вот еще один пример применения этого оператора для составления цепного радикала и вычисления ряда таких цепочек в цикле:
1.gif
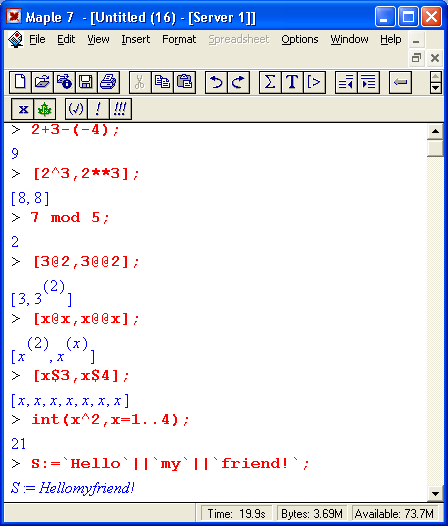
2.gif
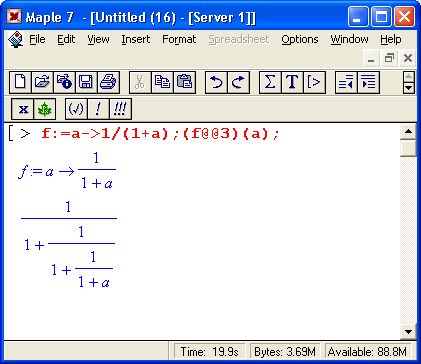
3.gif
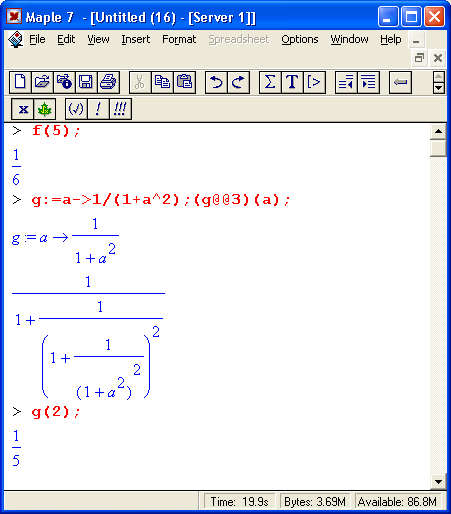
4.gif
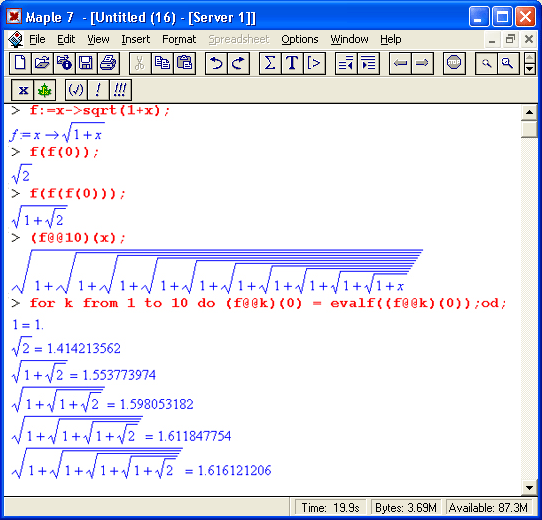
3. Операторы объединения, пересечения и исключения для множеств
Операторы объединения, пересечения и исключения для множеств
Для данных типа «множество» определены следующие бинарные операторы:
- union — включает первый операнд (множество) во второй;
- intersect — создает множество, содержащее общие для операндов элементы;
- minus — исключает из первого операнда элементы второго операнда.
В любом случае, в результирующем множестве устраняются повторяющиеся элементы. Действие этих операторов поясняют следующие примеры:
Напоминаем, что эти операторы заданы ключевыми словами. Обратите внимание на то, что в Maple 7 результат применения оператора union представлен членами, расположенными в довольно произвольном порядке.
5.gif
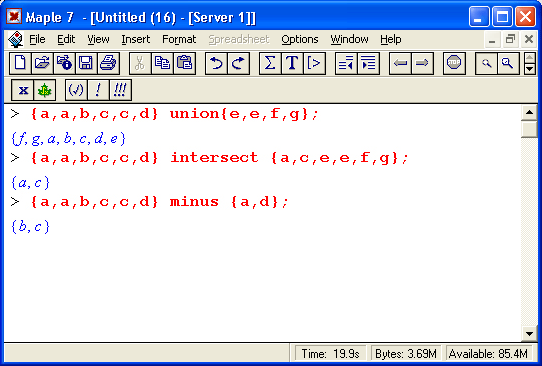
4. Унарные арифметические операторы
Унарные арифметические операторы
Унарные операторы используются с одним операндом. Они могут быть префиксными, если оператор стоит перед операндом, и постфиксными, если он стоит после операнда. К унарным относятся семь операторов, приведенных в табл. 6.2.
Таблица 6.2. Унарные операторы
|
Обозначение |
Оператор |
|
+ |
Унарный плюс (префикс) |
|
- |
Унарный минус (префикс) |
|
; |
Факториал (постфикс) |
|
. |
Десятичная точка (префикс или постфикс) |
|
$ |
Последовательность (префикс) |
| not |
Логическое отрицание (префикс) |
| &string |
Метка (префикс) |
Примеры применения унарных операторов:
6.gif
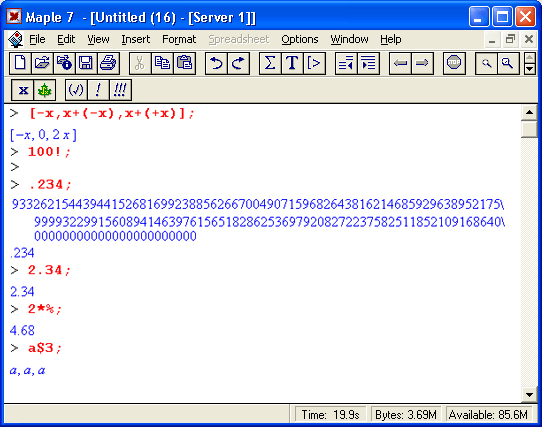
5. Оператор % и команда history
Оператор % и команда history
Мы уже неоднократно отмечали, что оператор % обеспечивает подстановку в строку ввода (или в выражение) последнего результата операции, Х% — предпоследнего и %%% — третьего с конца. Есть еще одна иногда полезная возможность проследить за ходом частных вычислений внутри документа — применение команды-функции history. В Maple V R5 это была библиотечная функция, которая требовала вызова из библиотеки. В Maple 7 такого вызова уже не требуется. Функция history (ехрr) или history() создает список переменных вида от, где индекс f = 1, 2, 3.... Этим переменным можно присваивать значения в диалоговом режиме и отслеживать результаты вычислений. Команда off;, вводимая после использования данной функции, завершает работу с ней. Ниже представлен диалог с применением функции history:
К сожалению, полученный результат и значения глобальных переменных 01 после завершения работы с данной функцией становятся недоступными, так что практической пользы от ее применения не так уж много. Разумеется, внутри блока history вы можете присвоить результат другой переменной и он сохранится (попробуйте это сделать сами). При каждом очередном применении функции history нумерация переменных 0i начинается с начала, так что какой-либо преемственности при использовании этой функции нет.
Функция history может применяться в качестве средства начальной отладки вычислений. Внутри фрагмента программы, заданного функцией history, можно задавать построения графиков. Например, при исполнении фрагмента программы:
будет построен график синусоиды. В целом работа с функцией history отличается не слишком высокой стабильностью, так что возможности этой функции пока остаются не слишком востребованными.
7.gif
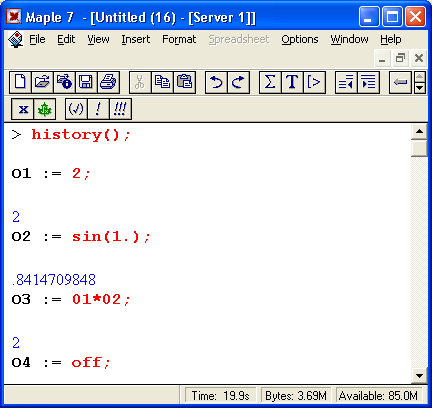
8.gif
10.gif
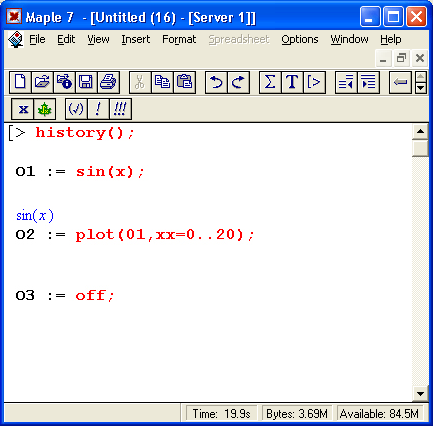
6. Логические операторы
Логические операторы
Логические (или булевы) операторы указывают на логическую связь величин (или выражений). Прежде всего они представлены рядом бинарных операторов, приведенных в табл. 6.3.
Таблица 6.З. Бинарные логические операторы
|
Обозначение |
Оператор |
|
< |
Меньше |
|
<» |
Меньше или равно |
|
> |
Больше |
|
>= |
Большее или равно |
|
- |
Равно |
|
О |
Не равно |
|
and |
Логическое «и» |
|
or |
Логическое «или» |
Конструкции с этими операторами, такие как х=у, возвращают логическое значение — константу true, если условие выполняется, и false, если оно не выполняется. Кроме того, к логическим операторам относится унарный оператор not — он представляет логическое «нет». Для возврата логических значений выражений с этими операторами используется функция evalb(условие), например:
Логические операторы часто используются в управляющих структурах программ, составленных на языке программирования Maple. Такое их применение мы рассмотрим позже.
11.gif
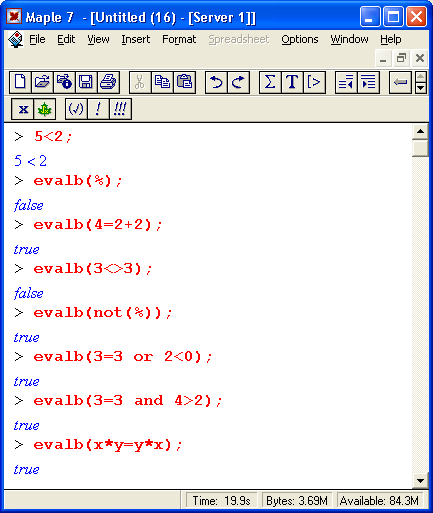
7. Специальные типы операторов
Специальные типы операторов
Операторы в Maple описывают операции по преобразованию данных, в частности выражений. Последние, в свою очередь, можно отнести к данным абстрактного типа. Могут быть описаны следующие типы операторов:
- неопределенные (f);
- нейтральные (&);
- процедурные;
- функциональные;
- композиционные (@).
Оператор относится к неопределенным, если он не был заранее определен. Такой оператор не выполняет никаких действий и просто повторяется в строке вывода:
> restar:f(1,2,а):
f(l,2,a)
Композиционные операторы (на базе знака @) мы уже применяли. Другие типы операторов рассмотрены ниже.
8. Функциональные операторы
Функциональные операторы
Функциональные операторы Maple-языка являются альтернативами функций и записываются в двух формах.
|
Нотация |
Запись оператора |
|
«arrow» (стрелочная) |
vars -> result |
|
«angle bracket» (в угловых скобках) |
<result | vars> |
Данные операторы могут использоваться для реализации подстановок. Например, запись х -> х^2 означает подстановку х*2 на место переменной х. Возможны и такие подстановки в множественной форме:
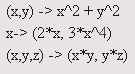
Функциональный оператор в Maple 7 часто используется для задания функций пользователя, которое будет рассмотрено несколько позднее.
9. Нейтральные операторы, определяемые пользователем
Нейтральные операторы, определяемые пользователем
Для создания нейтральных (задаваемых пользователем и в момент задания неисполняемых) операторов, определяемых пользователем, служит знак амперсанда — &. Синтаксис нейтрального оператора следующий:
&name
Имя оператора строится по правилам задания допустимых идентификаторов. Также в качестве имени может быть использована последовательность (один и более) специальных символов. В последовательности специальных символов не должно быть букв, цифр, подчеркивания, а также следующих символов:
& | () {} [] :: '' # <перевод строки> <пробел>
Максимальная длина имени — 495 символов. Нейтральные операторы могут быть унарными и бинарными. Примеры задания бинарного нейтрального оператора приведены ниже:
13.gif
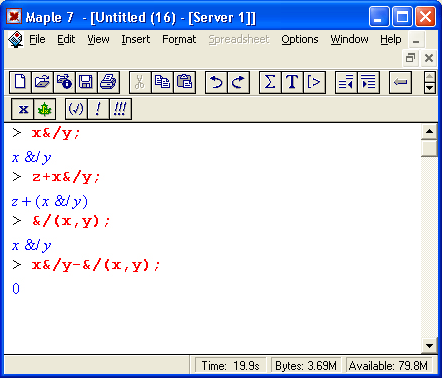
10. Определение операторов с помощью оператора define
Определение операторов с помощью оператора define
Большие возможности для создания операторов с заданными свойствами предоставляет специальный оператор define. Он записывается в следующей форме:
define(oper, property1, property2. ._)
Здесь ореr — имя определяемого оператора, property!, property2 и т. д. — наименования свойств. В принципе, оператор define позволяет создавать операторы с новыми свойствами, которые отсутствуют у операторов и функций, встроенных в систему.
Могут быть указаны следующие свойства операторов:
- unary — унарный оператор;
- binary — бинарный оператор;
- diff — дифференциальный оператор;
- linear — линейный оператор;
- multilinear — множественный линейный оператор;
- flat — ассоциативный оператор, для которого f(x/(y,z)) = f(f(x,y),z) = f(x,y,z);
- orderless — коммутативный симметричный оператор, такой что f(x,y) = f(y,x),
- antisymmetric — асимметричный оператор, такой что f(x,y) = -f(y,xc);
- zero — нулевой оператор (например, V:=Vector(5,shape=zero) задает вектор с 5 нулевыми элементами);
- identity — единичный оператор (например, M:=Matrix(3,3,shape=identity) задает единичную матрицу).
Следующий пример задает линейный оператор L:
Для задания некоторых свойств операторов можно использовать уравнения и соотношения вида f(x)=value. Чтобы свойство выполнялось для всех аргументов (или некоторого класса аргументов), используется описание forall. Так, приведенный ниже пример задает оператор F, который вычисляет n-е число Фибоначчи (n > 2):
Обратите внимание на то, что соотношения fib(0)=l и fib(l)=l задают начальные значения целочисленного массива чисел Фибоначчи, которые нужны для реализации обычного итерационного алгоритма их нахождения, — напоминаем, что очередное число Фибоначчи равно сумме двух предшествующих чисел Фибоначчи.
Последний пример иллюстрирует применение системной функции time для определения времени, затраченного на вычисление значения функции fib(20). Это время задается в секундах. Нетрудно заметить, что даже для ПК с процессором Pentium II 350 МГц это время оказалось довольно значительным (более 3 с), поскольку каждое новое число Фибоначчи вычисляется заново.
14.gif
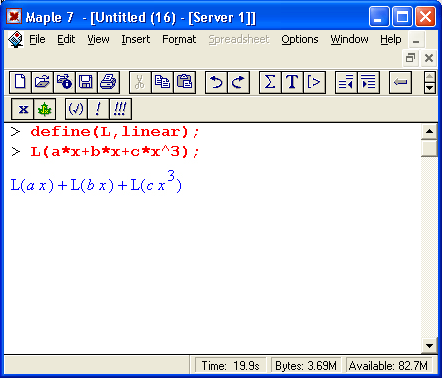
15.gif
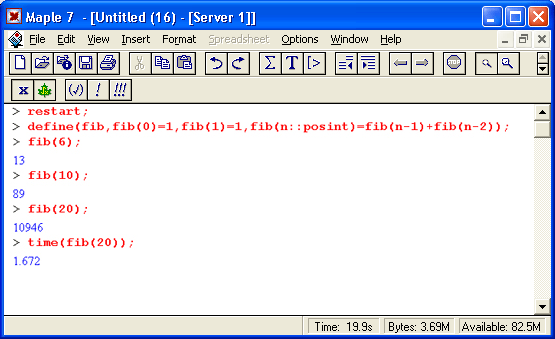
11. Математические функции
Математические функции
Maple 7 имеет полный набор элементарных математических функций. Все они, кроме арктангенса двух аргументов, имеют один аргумент х, например sin(x). Он может быть целым, рациональным, дробно-рациональным, вещественным или комплексным числом. В ответ на обращение к ним элементарные функции возвращают соответствующее значение. Поэтому они могут быть включены в математические выражения. Все описанные здесь функции называются встроенными, поскольку они реализованы в ядре системы.
Как правило, если аргументом функции является фундаментальная константа, целое или рациональное число, то функция выводится с таким аргументом без получения результата в форме действительного числа с плавающей точкой. Например:
Нетрудно заметить, что есть и исключения из этого правила — например, на экране монитора ехр(1) будет выведено как константа е, а значение функции arcsin( 2) все же вычислено и результат получен как 1/6 от константы Pi. Вообще говоря, если результат выражается через фундаментальную математическую константу, то он будет вычислен и представлен ею. В противном случае функция с целочисленным и рациональным аргументом или с константой просто повторяется в строке вывода в установленном для этой строки формате.
Для получения подробной информации о некоторой произвольной функции <f> достаточно задать команду:
?<f>
Ввиду общеизвестности элементарных функций мы не будем обсуждать ни их свойства, ни допустимые для них пределы изменения аргумента.
16.gif
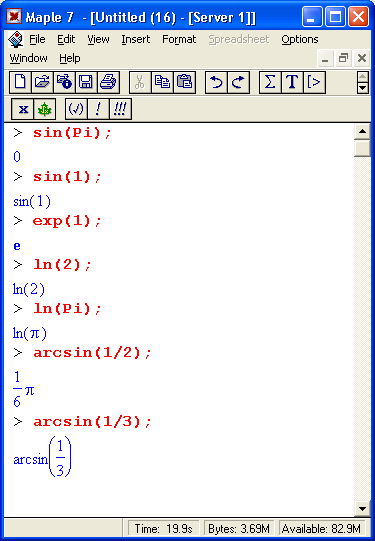
12. Некоторые целочисленные функции и факториал
Некоторые целочисленные функции и факториал
Ниже представлены наиболее распространенные целочисленные функции Maple 7, используемые в теории чисел:
- factorial (n) — функция вычисления факториала (альтернатива — оператор !);
- iquo(a.b) — целочисленное деление а на b;
- irem(a,b) — остаток от деления а на b;
- igcd(a b) — наибольший общий делитель;
- lcm(a,b) — наименьшее общее кратное.
Примеры применения:
В последних двух примерах применения оператора факториала полезно обратить внимание, что запись n!! означает лишь (n!)!, а не n!! = 2*4*6*..., то есть произведение четных целых чисел. Действие других функций очевидно.
17.gif
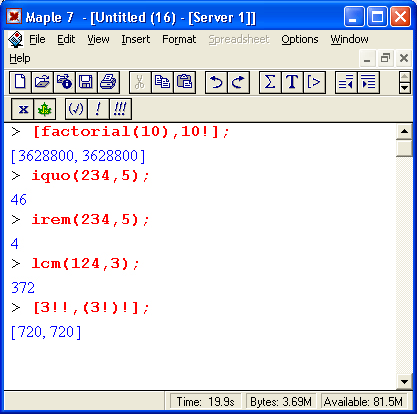
13. Тригонометрические функции
Тригонометрические функции
В ядре Maple определены следующие тригонометрические функции:
- sin — синус;
- cos — косинус;
- tan — тангенс;
- sec — секанс;
- csc — косеканс;
- cot — котангенс.
Все эти функции являются периодическими (с периодом 2л, кроме тангенса и котангенса, у которых период равен л) и определены для действительного и комплексного аргументов. Примеры вычислений:
Многие свойства тригонометрических функций можно оценить, рассматривая их графики. Для построения таких графиков можно использовать функцию pi ot. На рис. 6.1 сверху показаны графики ряда тригонометрических функций.
Рис. 6.1. Графики ряда тригонометрических и обратных тригонометрических функций
Из графиков тригонометрических функций (рис. 6.1, сверху) хорошо видна их периодичность. Функция тангенса имеет разрывы, и ее значение в этих точках в пределе равно бесконечности. Поэтому для наглядного ее представления вместе с функциями синуса и косинуса (их экстремальные значения по модулю равны 1) приходится вводить ограничения на масштаб графика по оси у.
ПРИМЕЧАНИЕ
Обратите внимание на параметр color=black в функции построения графиков plot. Он задает построение всех графиков черным цветом, что сделано для более четкой печати их в книге. Если убрать этот параметр, то графики разных функций будут строиться с использованием разных цветов, что облегчит их различение. Другие способы выделения отдельных кривых будут описаны в дальнейшем при описании графических возможностей системы Maple 7.
18.gif
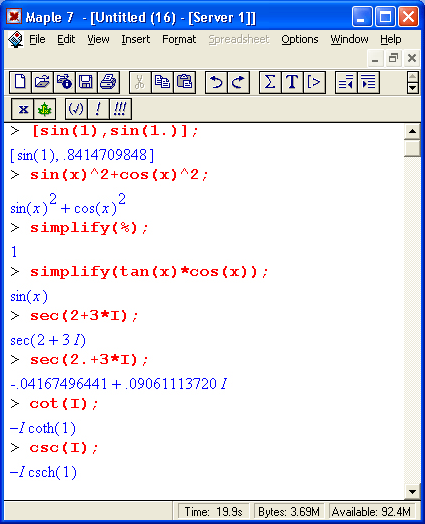
45.gif
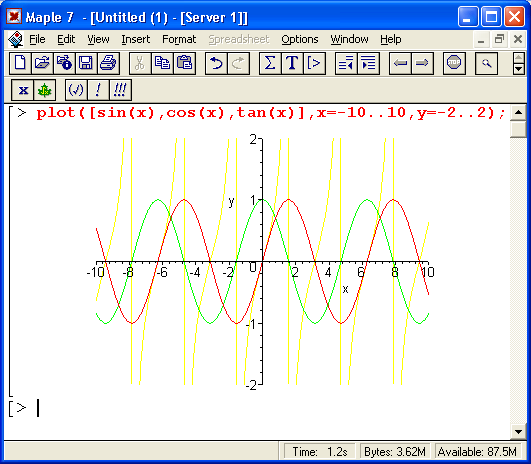
14. Обратные тригонометрические функции
Обратные тригонометрические функции
К обратным тригонометрическим относятся следующие функции:
- arcsin — арксинус;
- arccos — арккосинус;
- arctan — арктангенс;
- arcsec — арксеканс;
- arccsc — арккосеканс;
- arccot — арккотангенс.
Примеры вычислений:
К этому классу функций принадлежит еще одна полезная функция: arctan(y.x) = argument(x+I*y)
Она возвращает угол радиус-вектора в интервале от -Pi до Pi при координатах конца радиус-вектора х и у (см. пример ниже):
Графики ряда обратных тригонометрических функций показаны на рис. 6.1.
20.gif
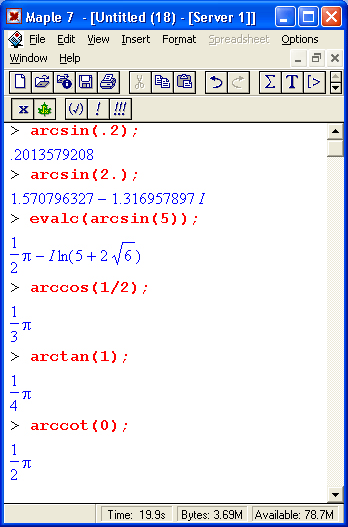
21.gif
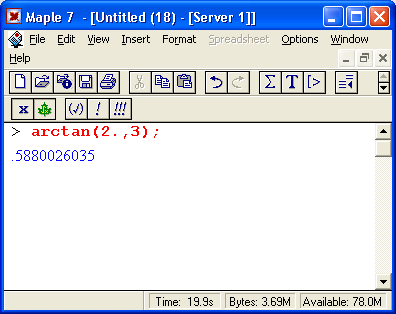
15. Гиперболические функции
Гиперболические функции
Гиперболические функции представлены следующим набором:
- sinh — гиперболический синус;
- cosh — гиперболический косинус;
- tanh — гиперболический тангенс;
- sech — гиперболический секанс;
- csch — гиперболический косеканс;
- coth — гиперболический котангенс.
Примеры применения гиперболических функций представлены ниже:
На рис. 6.2 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций.
Рис. 6.2. Графики основных гиперболических и обратных гиперболических функций
ПРИМЕЧАНИЕ
В отличие от тригонометрических гиперболические функции не являются периодическими. Функция гиперболического тангенса имеет симметричную кривую с характерными ограничениями. Поэтому она широко используется для моделирования передаточных характеристик нелинейных систем с ограничением выходного параметра при больших значениях входного параметра.
22.gif
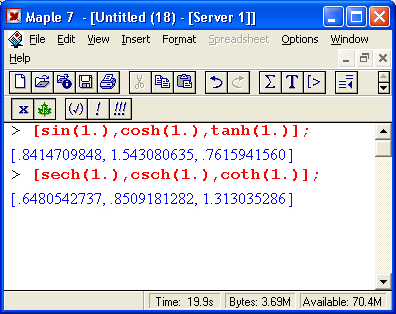
47.gif
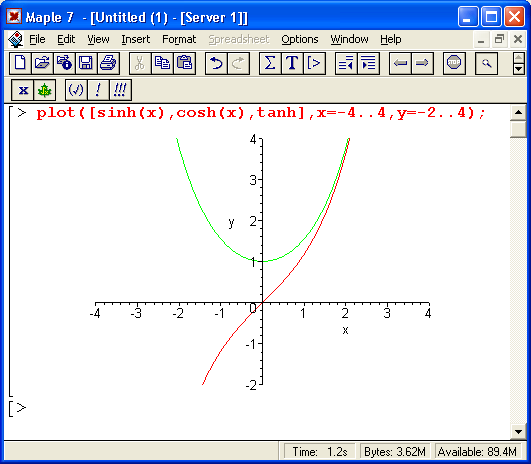
16. Обратные гиперболические функции
Обратные гиперболические функции
Как и тригонометрические функции, гиперболические имеют свои обратные функции:
- arcsinh — гиперболический арксинус;
- arccosh — гиперболический арккосинус;
- arctanh — гиперболический арктангенс;
- arcsech — гиперболический арксеканс:
- arccsch — гиперболический арккосеканс:
- arccoth — гиперболический арккотангенс.
Примеры применения:
Графики обратных гиперболических синуса, косинуса и тангенса представлены на рис. 6.2 снизу.
23.gif
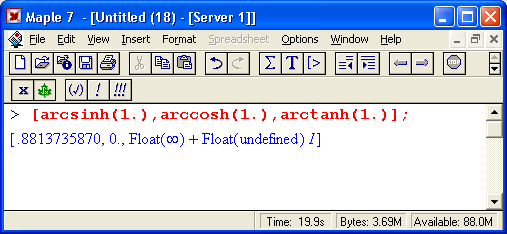
17. Степенные и логарифмические функции
Степенные и логарифмические функции
К степенным и логарифмическим относятся следующие функции системы Maple 7:
- ехр — экспоненциальная функция;
- ilog10 — целочисленный логарифм по основанию 10 (возвращает целую часть от логарифма по основанию 10);
- ilog — целочисленный логарифм (библиотечная функция, возвращающая
- целую часть от натурального логарифма);
- n — натуральный логарифм;
- log — логарифм по заданному основанию (библиотечная функция);
- log10 — логарифм по основанию 10;
- sqrt — квадратный корень.
Примеры применения:
Графики ряда алгебраических функций показаны на рис. 6.3.
Рис. 6.З. Графики ряда алгебраических функций
На рис. 6.3 показаны также графики синусоиды с экспоненциально падающей и нарастающей амплитудой. Читателю рекомендуется попробовать свои силы в построении графиков комбинаций различных функций.
24.gif
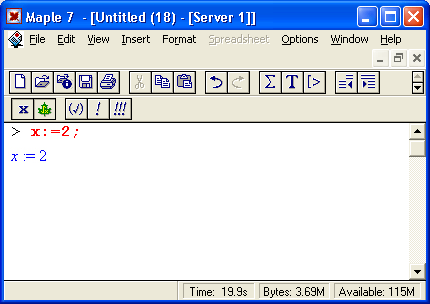
26.gif
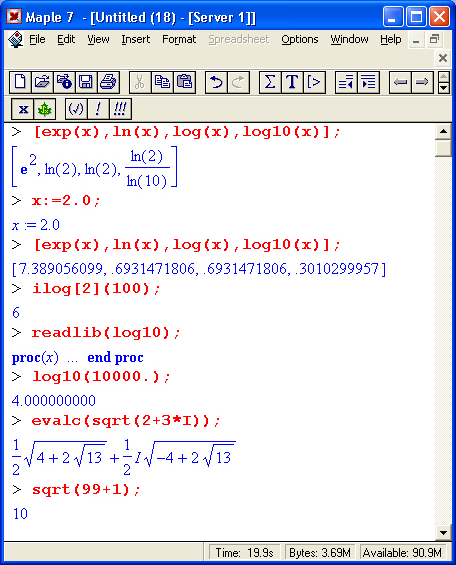
49.gif
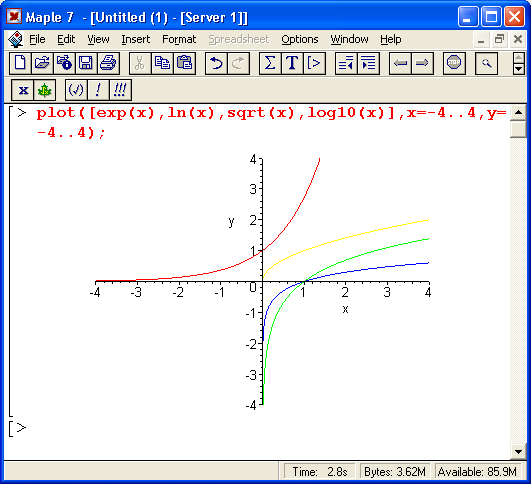
18. Функции с элементами сравнения
Функции с элементами сравнения
В алгоритме вычисления ряда функций заложено сравнение результата с некоторым опорным значением. К таким функциям относятся:
- abs — абсолютное значение числа;
- ceil — наименьшее целое, большее или равное аргументу;
- floor — наибольшее целое, меньшее или равное аргументу;
- frac — дробная часть числа;
- trunc — целое, округленное в направлении нуля;
- round — округленное значение числа;
- signum (х) — знак х (-1 при х < 0, 0 при х = 0 и +1 при х > 0).
Для комплексного аргумента х эти функции определяются следующим образом:
- tranc(x) = trunc(Re(*)) + I*trunc(IM(x));
- round(x) = round(Re(.r)) + I*round(Im(x));
- frac(x) - frac(Re(*)) + I*hac(Im(x)).
Для введения определения значения floor(x) от комплексного аргумента прежде всего запишем а = Re(x) - fооr(Re(x)) и b = Im(x) - floor(Im(x)). Тогда flооr(x) = floor(Re(x)) + I*floor(Im(x)) + X, где
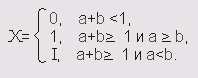
Наконец, функция ceil для комплексного аргумента определяется следующим образом:
cell(x) = -fооr(-х)
Примеры применения:
28.gif
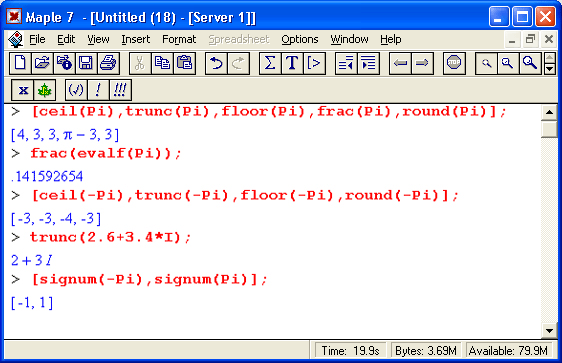
19. Функции комплексного аргумента
Функции комплексного аргумента
Для комплексных чисел и данных, помимо упомянутых в предшествующем разделе, определен следующий ряд базовых функций:
- argument — аргумент комплексного числа; 1
- conjugate — комплексно-сопряженное число;
- Im — мнимая часть комплексного числа;
- Re — действительная часть комплексного числа;
- роlаг — полярное представление комплексного числа (библиотечная функция).
Примеры применения:
29.gif
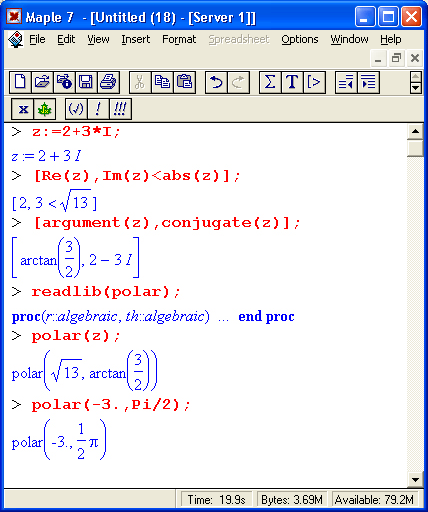
20. Специальные математические функции
Специальные математические функции
Специальные математические функции обычно являются решениями линейных дифференциальных уравнений различного типа и выражаются в виде интегралов, не представимых через элементарные функции. Maple 7 имеет практически полный набор таких функций. Их представления можно найти в справочной литературе, а также в справочной базе данных Maple. В связи с этим ограничимся приведением названий наиболее важных специальных функций:
- AiryAi (Bi) — функции Эйри;
- AngerJ — функция Ангера;
- bernoulli — числа и полиномы Бернулли;
- Bessel I (J, К, Y) — функции Бесселя разного рода;
- Beta — бета-функция;
- binomial — биноминальные коэффициенты;
- Chi — интегральный гиперболический косинус;
- Ci — интегральный косинус;
- csgn — комплексная сигнум-функция;
- dilog — дйлогарифм;
- Dirac — дельта-функция Дирака;
- Ei — экспоненциальный интеграл;
- EllipticCE (CK, CPi, E, F, К, Modulus, Nome, Pi) — эллиптические интегралы;
- erf — функция ошибок;
- erfc — дополнительная функция ошибок;
- euler — числа и полиномы Эйлера;
- FresnelC (f, g, S) — интегралы Френеля;
- GAMMA — гамма-функция;
- GaussAGM — арифметико-геометрическое среднее Гаусса;
- HankelHl (H2) — функции Ганкеля;
- harmonic — частичная сумма серии гармоник;
- Heaviside — функция Хевисайда;
- JacobiAM (CN, CD, CS, ON, DC, DS, NC, NO, NS, SC, SO, SN) - эллиптические функции Якоби;
- JacobiThetal (2, 3, 4) — дзета-функции Якоби;
- JacobiZeta — зет:функция Якоби;
- KelvinBer (Bei, Her, Hei, Ker, Kei) — функции Кельвина;
- Li — логарифмический интеграл;
- 1nGAMMA — логарифмическая гамма-функция;
- MeijerG — G-функция Мейджера;
- pochhammer — символ Похгамера;
- polylog — полилогарифмическая функция;
- Psi — дигамма-функция;
- Shi — интегральный гиперболический синус;
- Si — интегральный синус;
- Ssi — синусный интеграл смещения;
- StruveH (L) — функции Струве;
- surd — неглавная корневая функция;
- LambertW — W-функция Ламберта;
- WeberE — Е-функция Вебера;
- WeierstrassP — Р-функция Вейерштрасса;
- WeierstrassPPrime — производная Р-функции Вейерштрасса;
- WeierstrassZeta — зета-функция Вейерштрасса;
- WeierstrassSigma — сигма-функция Вейерштрасса;
- Zeta — зета-функция Римана и Гурвица.
Ввиду большого числа специальных функций и наличия множества примеров их вычисления в справочной системе Maple 7 ограничимся несколькими примерами вычисления наиболее распространенных специальных функций. По их подобию читатель может опробовать в работе и другие специальные функции.
На рис. 6.4 даны примеры применения ряда специальных функций. Обратите особое внимание на первый пример. Он показывает, как средствами системы Maple 7 задается определение функций Бесселя. Показано, что функции Бесселя являются решениями заданного на рис. 6.4 дифференциального уравнения второго порядка. Maple 7 способна вычислять производные и интегралы от специальных функций.
Рис. 6.4. Примеры применения специальных функций
Еще несколько примеров работы со специальными функциями представлены на рис.6.5. Как видно из приведенных примеров, на экране монитора можно получить математически ориентированное представление специальных функций, обычно более предпочтительное, чем представление на Maple-языке или в текстовом формате. Записи функций при этом выглядят как в обычной математической литературе.
Рис. 6.5. Примеры работы со специальными математическими функциями
На рис. 6.5 показаны примеры разложения специальных функций в ряды и применения функции convert для их преобразования.
Много информации о поведении специальных функций дает построение их графиков. На рис. 6.6 показано построение семейства графиков функций Бесселя BesselJ разного порядка и гамма-функции. Эти функции относятся к числу наиболее известных. Если читателя интересуют те или иные специальные функции, следует прежде всего построить и изучить их графики.
Подробное описание специальных функций можно найти в справочниках [43-45] и в справочной базе данных Maple 7.
Рис. 6.6. Графики функций Бесселя и гамма-функции
30.gif
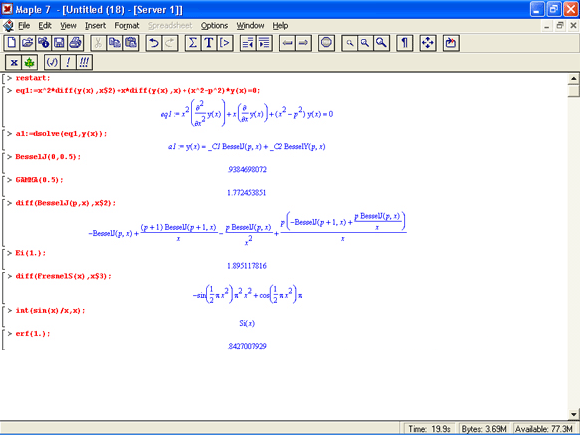
31.gif
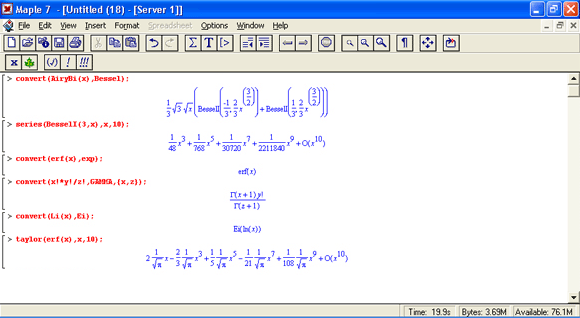
50.gif
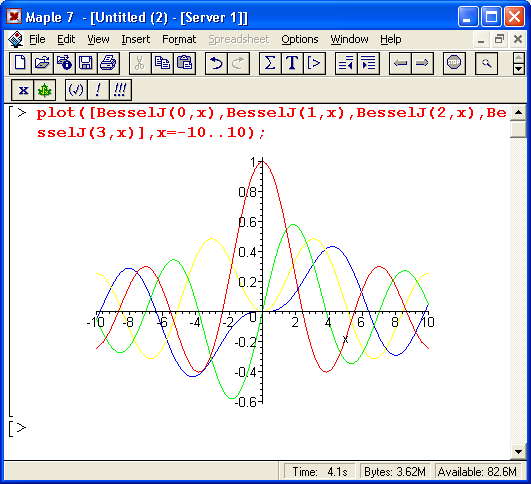
21. Функции для работы с векторами и матрицами
Функции для работы с векторами и матрицами
Элементы векторов и матриц являются индексированными переменными, то есть место каждого элемента вектора определяется его индексом, а у матрицы — двумя индексами. Обычно их обобщенно обозначают как i (номер строки матрицы или порядковый номер элемента вектора) iij (номер столбца матрицы). Допустимы операции вызова нужного элемента и присваивания ему нового значения:
V[1] — вызов i-го элемента вектора V;
M[i, j] — вызов элемента матрицы М, расположенного на г-н строке в j-ы столбце;
V[i]:=x — присваивание нового значения х i-му элементу вектора V;
M[i,j]:=x — присваивание нового значения х элементу матрицы М.
22. Преобразование списков в векторы и матрицы
Преобразование списков в векторы и матрицы
Прежде всего надо обратить внимание на то, что векторы и матрицы хотя и похожи на списки, но не полностью отождествляются с ними. В этом можно убедиться с помощью следующих примеров, в которых функция type используется для контроля типов множественных объектов (векторов и матриц):
Однако, используя функцию преобразования данных convert, можно преобразовывать одномерные списки в векторы, а двумерные — в матрицы. Функция type используется в следующих формах:
- type(V, vector) — тестирует аргумент V и возвращает true, если V — вектор, и false в ином случае;
- type(M,matrix) — тестирует аргумент М и возвращает true, если М — матрица, и false в ином случае.
Здесь параметры vector и matrix используются для указания того, какой тип объекта проверяется.
ПРИМЕЧАНИЕ
Обратите внимание на то, что матрицы отображаются иначе, чем двумерные списки, без двойных квадратных скобок. Отображение вектора подобно отображению одномерного списка, поэтому здесь особенно важен контроль типов данных.
32.gif
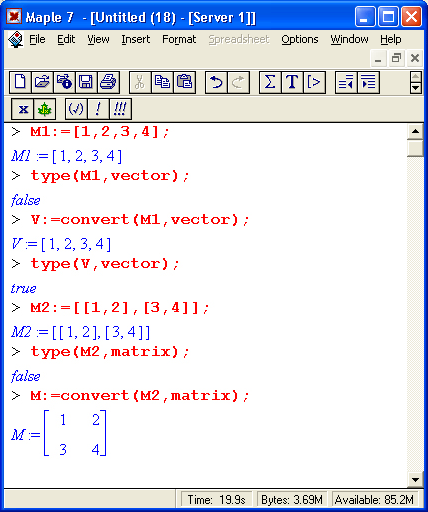
23. Операции с векторами
Операции с векторами
Важное достоинство систем компьютерной алгебры, к которым относится и Maple 7, заключается в возможности выполнения аналитических (символьных) операций над векторами и матрицами.
Приведем примеры операций над векторами:
В этих примерах используется функция evalm(M), осуществляющая вычисление матрицы или вектора М.
ПРИМЕЧАНИЕ
Рекомендуется перед проведением символьных операций с векторами и матрицами очистить память от предшествующих определений с помощью команды restart. Если какие-то элементы векторов или матриц были ранее определены, это может привести к очень сильным искажениям вида конечных результатов. Очистка памяти устраняет возможность ошибок такого рода.
33.gif
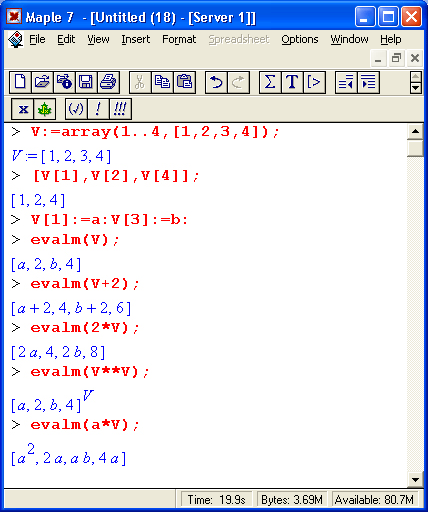
24. Операции над матрицами с численными элементами
Операции над матрицами с численными элементами
Над матрицами с численными элементами можно выполнять разнообразные операции. Ниже приведены основные из них:
ПРИМЕЧАНИЕ
Рекомендуется внимательно изучить эти примеры и попробовать свои силы в реализации простых матричных операций. Мы вернемся к гораздо более серьезному описанию матричных операций и функций в дальнейшем.
34.gif
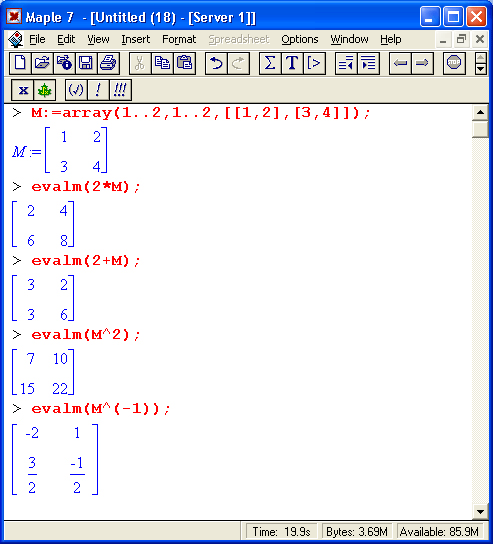
35.gif
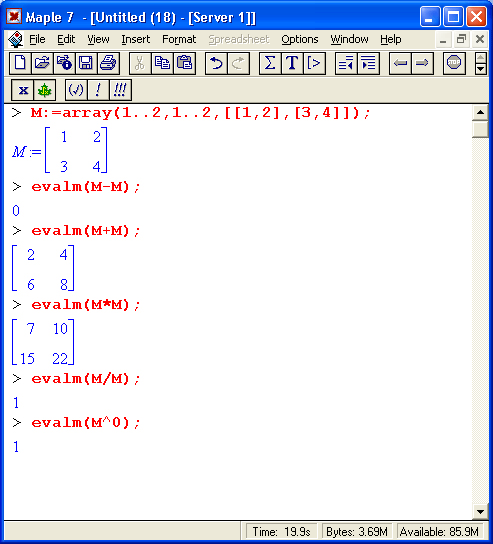
25. Символьные операции с матрицами
Символьные операции с матрицами
Ниже представлены примеры символьных операций, осуществляемых над квадратными матрицами одного размера:
Приведем еще ряд примеров выполнения символьных операций с одной матрицей:
Среди других функций для работы с матрицами полезно обратить внимание на функцию mар, которая применяет заданную операцию (например, функции дифференцирования diff и интегрирования int) к каждому элементу матрицы. Примеры такого рода даны ниже:
В результате возвращаются матрицы, каждый элемент которых представлен производной или интегралом. Аналогично можно выполнять над матрицами и другие достаточно сложные преобразования.
В дальнейшем мы продолжим изучение матричных функций и операций, включенных в пакеты Maple 7.
36.gif
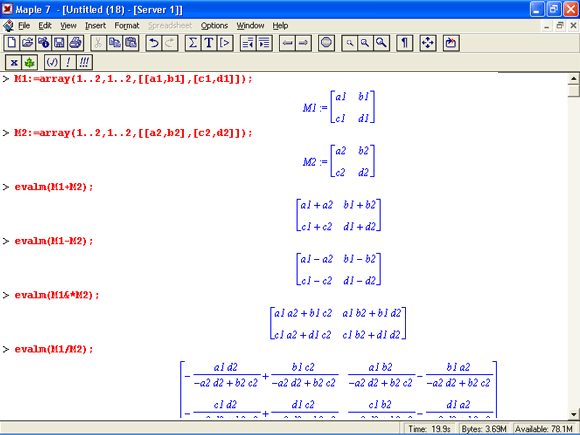
37.gif
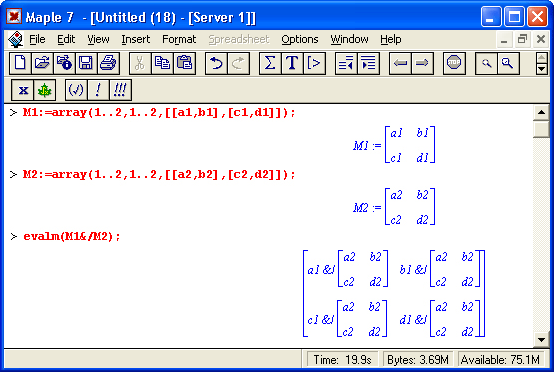
38.gif
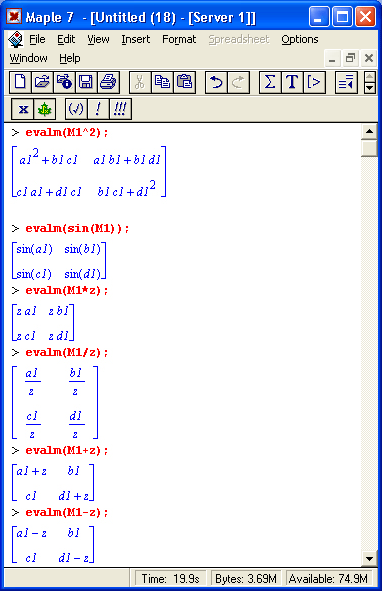
39.gif
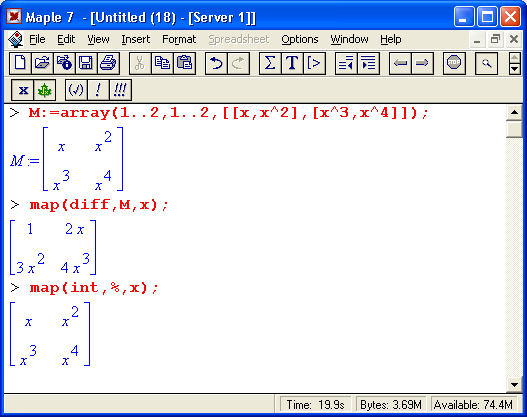
40.gif
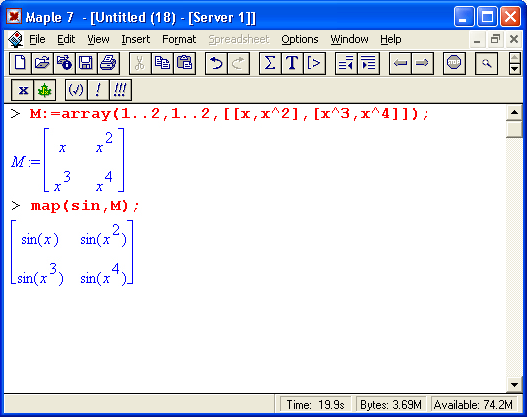
26. Функции для работы со строковыми данными
Функции для работы со строковыми данными
Контроль типа строковых данных
Напоминаем, что строковые данные представляются совокупностью любых символов в обратных апострофах, например *Привет* или `2+2`. Для контроля объектов на принадлежность к строковым данным служит функция type с параметром string:
Из приведенных примеров видно, что контроль строкового типа осуществляется не очень строго, — в частности, единичные символы рассматриваются как строковые и без заключения их в апострофы. В строках могут быть символы кириллицы, но гарантии в правильности обработки таких символов нет — надо мириться с тем, что Maple — англоязычная программа и ее возможности в поддержке других языков ограниченны.
41.gif
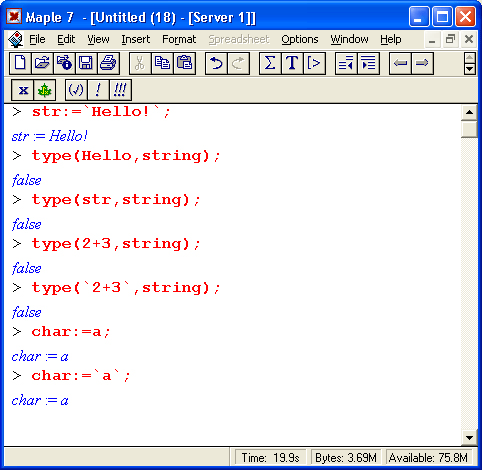
27. Интерактивный ввод строк
Интерактивный ввод строк
Для интерактивного ввода строк можно использовать функцию readline(filename), задав в качестве имени файла terminal или опустив имя файла. В этом случае ввод строки осуществляется с клавиатуры компьютера:
> s:=read1ine();
> Привет мой друг!
s:="Привет мой друг!"
ПРИМЕЧАНИЕ
Полезно обратить внимание на то, что запрос в ходе интерактивного ввода может быть сделан на русском языке (если установленный для запросов шрифт имеет символы кириллицы). Нужно также, чтобы и шрифт строки вывода содержал кириллицу, иначе в строке вывода будет типичная «абракадабра» — смесь непонятных символов.
28. Обработка строк
Обработка строк
Имеется ряд функций для работы со строками. Из них наиболее важны следующие:
- lenght(str) — возвращает число символов, содержащихся в строке str;
- substring(str,a. .b) — возвращает подстроку строки str от а-го символа до b-го;
- cat(strl,str2....) — возвращает строку, полученную объединением строк strl, str2,... (альтернатива — оператор конкатенации в виде точки .);
- SearchText(s.str) — производит поиск подстроки s в строке str и при его успехе возвращает номер позиции s в строке str (при отсутствии s в str функция возвращает 0).
Примеры применения этих функций (в виде продолжения ранее приведенных примеров) представлены ниже:
Эти функции дают достаточно средств для обработки данных строкового типа, которые можно применять не только для создания текстовых комментариев, но и для управления вычислительным процессом в программах.
42.gif
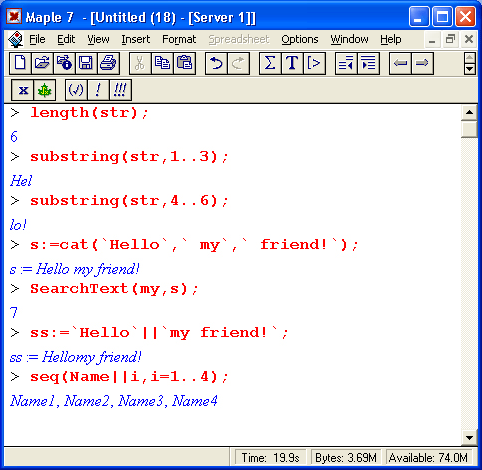
29. Преобразование строки в математическое выражение
Преобразование строки в математическое выражение
Часто возникает необходимость в интерактивном вводе математических выражений. Для ввода с запросом выражения используется функция readstat(promt), где promt — строка с текстовым комментарием. Пример ее применения дан ниже:
Альтернативой может стать ввод строкового выражения с последующим преобразованием его в математическое выражение с помощью функции parse:
Обратите внимание на то, что функция evaln не смогла вычислить строковое выражение `2+3` поскольку оно не является числовым типом данных. Однако функция parse преобразовала это выражение в числовое, что и привело к его вычислению.
43.gif
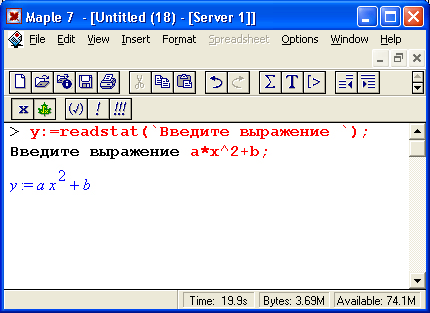
44.gif
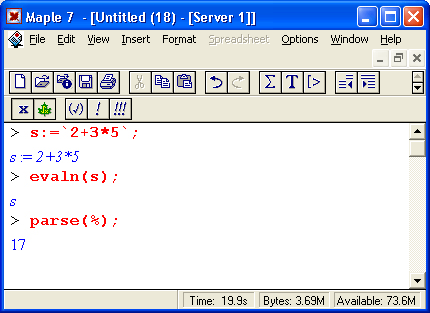
30. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Использовать операторы и операнды.
- Применять различные математические функции.
- Использовать операторы и функции для работы с векторами и матрицами.
- Использовать функции для работы со строковыми данными.
Урок 7. Типовые средства программирования
1. Функции пользователя
Урок 7.
Типовые средства программирования.
Упрощенные функции пользователя
Хотя ядро Maple 7, библиотека и пакеты содержат свыше 3000 функций, всегда может оказаться, что именно нужной пользователю (и порою довольно простой) функции все же нет. Тогда возникает необходимость в создании собственной функции, именуемой функцией пользователя. Начнем описание с обычных функций пользователя, задающих некоторую зависимость от одной или ряда переменных в явном виде.
Основным средством расширения Maple-языка являются модули — процедуры. Однако на первый взгляд они довольно сложны. Есть и более простые способы задания функций пользователя. Один из таких способов заключается просто в присваивании введенной функции (в виде выражения) некоторой переменной: Name:-выражение
Этот прием фактически означает просто операцию присваивания. Следующие примеры иллюстрируют технику работы с такими функциями:
Заданный таким образом объект все же не является полноценной функцией пользователя, и прежде всего потому, что в нем используются только глобальные переменные (х и у) и нет объявленного списка параметров, от которых зависит значение функции. При этом значения переменных функции приходится заведомо задавать отдельно, используя операции присваивания. Подобные конструкции нельзя ввести в библиотеки Maple 7.
1.gif
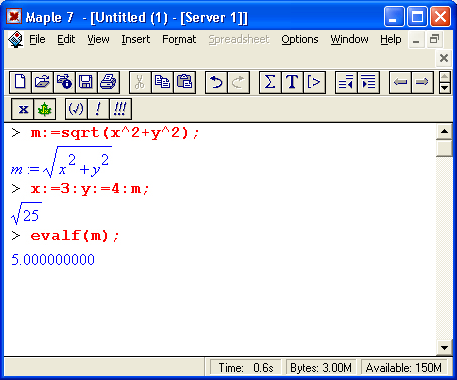
2. Основной способ задания функции пользователя
Основной способ задания функции пользователя
Более гибкий способ задания полноценных функций пользователя базируется на применении функционального оператора. При этом используется следующая конструкция:
name:=(x,y,...)->expr
После этого вызов функции осуществляется в виде name(x.y,...), где (х.у,...) — список формальных параметров функции пользователя с именем name. Переменные, указанные в списке формальных параметров, являются локальными. При подстановке на их место фактических параметров они сохраняют их значения только в теле функции (ехрr). За пределами этой функции переменные с этими . именами оказываются либо неопределенными, либо сохраняют ранее присвоенные им значения. Следующие примеры иллюстрируют сказанное:
Нетрудно заметить, что при вычислении функции m(х.у) переменные х и у имели значения 3 и 4, однако за пределами функции они сохраняют нулевые значения, заданные им перед введением определения функции пользователя. Еще один способ задания функции пользователя базируется на применении функции unapply: name:=unapply(expr.varl.var2,...) Ниже даны примеры такого задания функции пользователя:
Последний пример показывает возможность проведения символьных операций с функцией пользователя.
2.gif
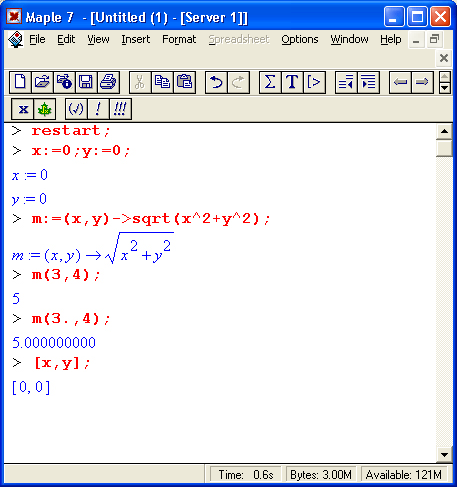
3.gif
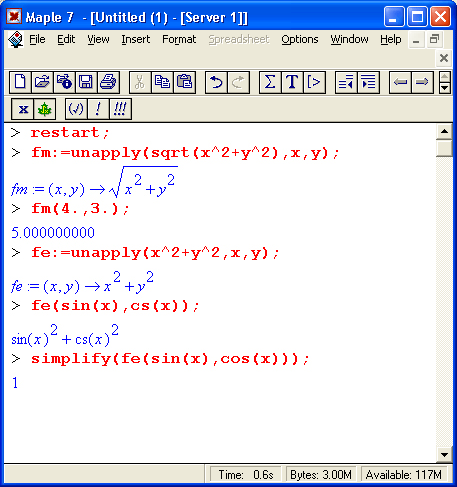
3. Графическая визуализация результатов выполнения функций пользователя
Графическая визуализация результатов выполнения функций пользователя
В ряде случаев весьма желательна визуализация результатов выполнения функций пользователя. Порой она может давать неожиданный результат. На рис. 7.1 представлены примеры задания двух функций пользователя от двух переменных и построение их графиков с помощью функции plot3d.
а
Рис. 7.1. Примеры задания функций пользователя двух переменных с построением их графиков
ВНИМАНИЕ
При задании функций пользователя рекомендуется просмотреть их графики в нужном — диапазоне изменения аргументов. К сожалению, наглядными являются только графики функций одной и двух переменных.
4.gif
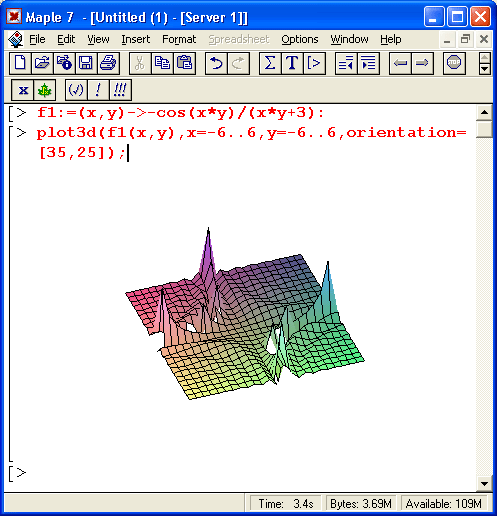
5.gif
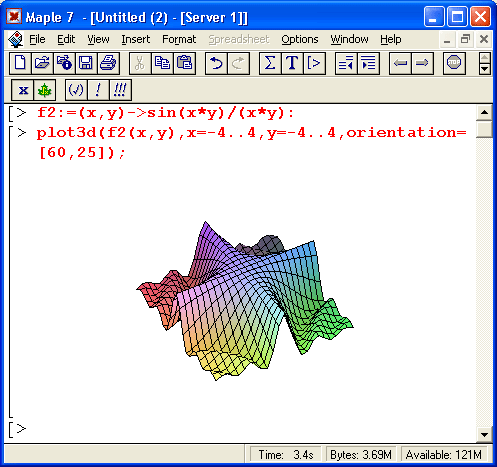
4. Импликативные функции
Импликативные функции
Другой важный класс функций, которые нередко приходится задавать, — импликативные функции, в которых связь между переменными задана неявно, в виде какого-либо выражения. Самый характерный пример такой функции — это выражение для задания окружности радиуса r: х^2 + у^2 = r^2.
Итак, импликативные функции записываются как уравнения. Соответственно их можно решать с помощью функции solve. Следующие примеры иллюстрируют задание уравнения окружности в общем и в частном (численном) виде:
Для графической визуализации импликативных функций служит функция implicitplot пакета plots. На рис. 7.2 представлено задание двух импликативных функций и построение их графиков.
Рис. 7.2. Задание двух импликативных функций и построение их графиков
В данном случае задано построение двух эллипсов. Верхний — это окружность, сплюснутая по вертикали, а второй — наклонный эллипс.
6.gif
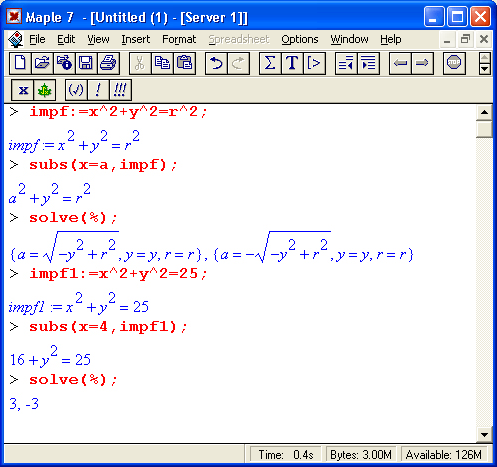
23.gif
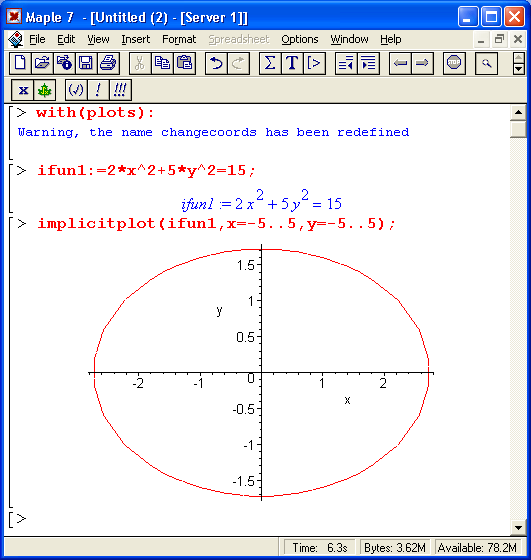
5. Условные выражения
Условные выражения
Для подготовки разветвляющихся программ в Maple-язык программирования включен оператор if, позволяющий создавать следующую конструкцию:
if <Условие сравнения? then <Элементы>
|elif «Условие сравнения> then <Элементы>|
|e1se <Элементы>|
fi:
В вертикальных чертах | | указаны необязательные элементы данной конструкции. Следующих два вида условных выражений чаще всего используются на практике:
- if <Условие> then <Элементы 1> fi — если Условие выполняется, то исполняются Элементы 1, иначе ничего не выполняется;
- if <Условие> then <Элененты 1> else <Элененты 2> fi — если Условие выполняется, то исполняются Элементы 1, иначе исполняются Элементы 2.
В задании условий используются любые логические конструкции со знаками сравнения (<, <=, >, >=, =, <>) и логические операторы and, or и not, конструкции с которыми возвращают логические значения true и false. Рассмотрим следующий простой пример:
> х:-5:
> if x<0 then print('Negative') fi;
Negative
> x:-l: > if x<0 then print('Negative') fi;
В этом примере анализируется значение х. Если оно отрицательно, то с помощью функции вывода print на экран выводится сообщение «Negative». А вот если х неотрицательно, то не выводится никакого сообщения. В другом примере если х неотрицательно, то выводится сообщение «Positive»:
> х.— 5:
> if x<0 then print('Negative') else print('Positive') fi;
Negative > x:-l:
> if x<0 then printСNegative") else printC'Positive') fi;
Positive
Приведем еще один пример, показывающий особую форму задания конструкции if-then-else-fi:
> х:=-5:
> 'if (x<0, printCNegative').print('Positive'));
Negative
> х:=1:
> *1f (х<0. print("Negative'),printrPositive'));
Positive
В этой конструкции вида 'if '(Условие. Выражение1, Выражение2)
если Условие выполнятся, то будет исполнено Выражение!, в противном случае будет исполнено Выражение2. Ввиду компактности записи такая форма условного выражения нередко бывает предпочтительна, хотя она и менее наглядна. На рис. 7.3 представлено применение данной конструкции для моделирования трех типов сигналов.
а
б
Рис. 7.3. Применение конструкции с функцией if для моделирования сигналов
К сожалению, функции на базе конструкции if не всегда корректно обрабатываются функциями символьной математики. Поэтому надо тщательно контролировать полученные в этом случае результаты.
7.gif
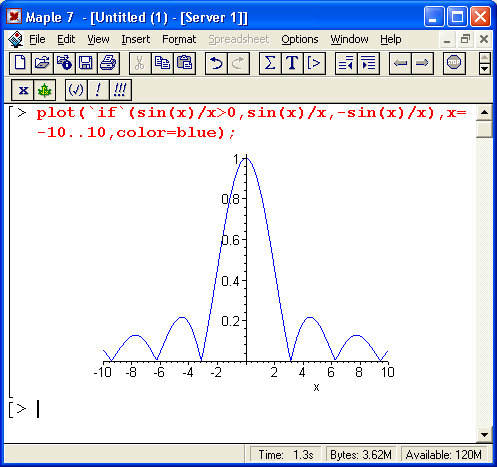
8.gif
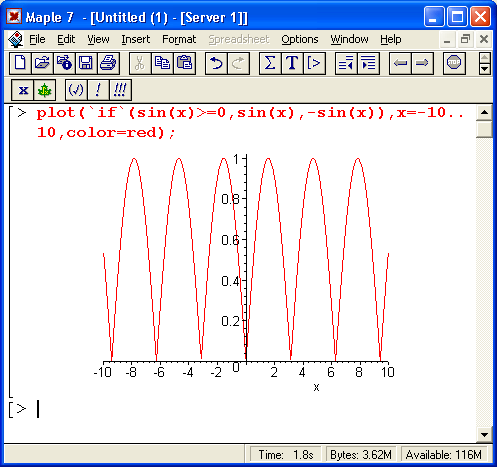
9.gif
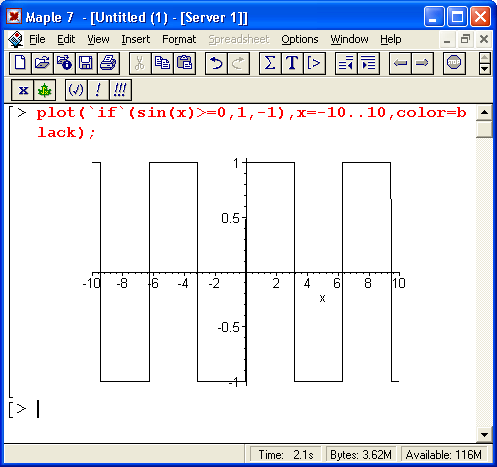
6. Циклы for и while
Циклы for и while
Зачастую необходимо циклическое повторение выполнения выражения заданное число раз или до тех пор, пока выполняется определенное условие. Maple 7 имеет обобщенную конструкцию цикла, которая задается следующим образом:
| for <name>| |from <exprl>| |to <expr3>| |by <expr2>| (while <expr4>| do Statement sequence> od;
Здесь name — имя управляющей переменной цикла, exprl, ехрr2 и ехрrЗ — выражения, задающие начальное значение, конечное значение и шаг изменения переменной name, ехрr4 — выражение, задающее условие, пока цикл (набор объектов между словами do и od) будет выполняться.
В ходе выполнения цикла управляющая переменная меняется от значения exprl до значения ехрr2 с шагом, заданным ехрrЗ. Если блок by <ехрr2> отсутствует, то управляющая переменная будет меняться с шагом +1 при ехргКехрг2. Это наглядно поясняет следующий пример:
> for i front 1 to 5 do printd) od;
1
2
3
4
5
В нем выводятся значения переменной i в ходе выполнения цикла. Нетрудно заметить, что она и впрямь меняется от значения 1 до значения 5 с шагом +1. Следующий пример показывает, что границы изменения управляющей переменной можно задать арифметическими выражениями:
> for i from 7/(2+5) to 2+3 do printd) od:
1
2
3
4
5
А еще один пример показывает задание цикла, у которого переменная цикла меняется от значения 1 до 10 с шагом 2:
> for i from 1 to 10 by 2 do printd) od: 1 3 5 7 9
8 этом случае выводятся нечетные числа от 1 до 9. Шаг может быть и отрицательным:
> for i from 9 to 1 by -2 do print(i) od:
9
7
5
3
1
Следует отметить, что если exprl>expr2 задать заведомо невыполнимое условие, например, ехрr1>ехрг2 и положительное значение шага, то цикл выполняться не будет. Цикл можно прервать с помощью дополнительного блока while <ехрr4>. Цикл с таким блоком выполняется до конца или до тех пор, пока условие ехрг4 истинно.
> for i from 1 to 10 by 2 while i<6 do print(i) od:
1
3
5
Таким образом, конструкция цикла в Maple-языке программирования вобрала в себя основные конструкции циклов for и while. Есть еще одна, более специфическая конструкция цикла:
|for <name>| |in <exprl>| |whi1e <expr2>| do statement sequence> od:
Здесь exprl задает список значений, которые будет принимать управляющая переменная name. Цикл будет выполняться, пока не будет исчерпан список и пока выполняется условие, заданное выражением ехрг2. Следующий пример иллюстрирует сказанное:
> for i in [1.2,5,-1.7.12] do print(i) od;
1
2 5 -1 7
12 > for i in [1,2.5.-1,7.12] while i>0 do print(i) od:
1
2 5
В цикле этого вида управляющая переменная может меняться произвольно. Циклы могут быть вложенными. Это иллюстрирует следующий пример, создающий единичную матрицу на базе заданного массива М:
Этот пример имеет не более чем познавательное значение, поскольку для создания такой матрицы Maple 7 имеет функцию identity, с помощью которой функция array позволяет сразу создать единичную матрицу:
В заключение отметим, что возможна упрощенная частная конструкция цикла типа while:
while expr do statseq od:
Здесь выражения statseq выполняются, пока выполняется логическое условие ехрr. Пример такого цикла:
> n:=1:
n:=1 .
> while n<16 do n:»2*n od;
n:=2
n := 4
n := 8
n :=16
В этом примере идет удвоение числа n с начальным значением n = 1 до тех пор, пока значение n меньше 16.
10.gif
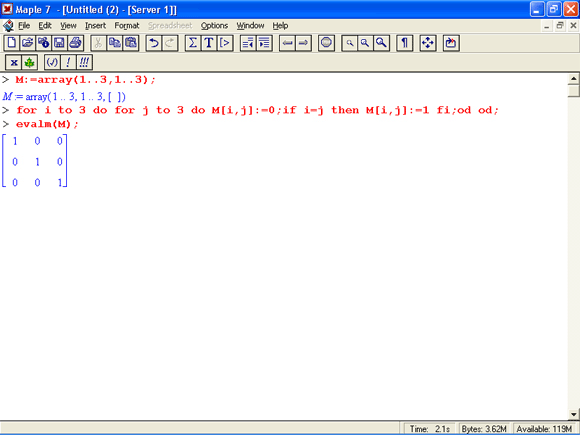
11.gif
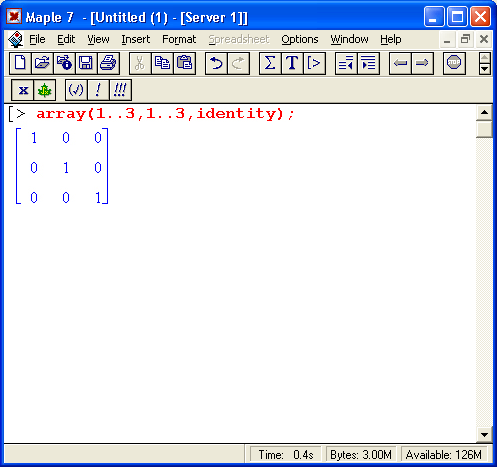
7. Операторы пропуска и прерывания
Операторы пропуска и прерывания
Иногда бывает нужным пропустить определенное значение переменной цикла. Для этого используется оператор next (следующий). Приведенный ниже пример иллюстрирует применение оператора next в составе выражения if-fi для исключения вывода значения i = -2:
> for 1 in [1,2.3.-2.4] do if i--2 then next else print(i) fi od:
1
2 .3
4
Другой оператор — break — прерывает выполнение фрагмента программы (или цикла). Его действие поясняет слегка модифицированный предшествующий пример:
> for i in [1.2.3.-2,4] do if i=2 then break else print(i) fi od:
1
2
3
В данном случае при значении i = -2 произошло полное прекращение выполнения цикла. Поэтому следующее значение 4 переменной z присвоено не было и это значение на печать не попало.
Любой из операторов quit, done или stop обеспечивает также прерывание выполнения текущей программы (в частности, цикла), но при этом окно текущего документа закрывается.
8. Процедуры и процедуры-функции
Процедуры и процедуры-функции
Процедурой называют модуль программы, имеющий самостоятельное значение и выполняющий одну или несколько операций, обычно достаточно сложных и отличных от операций, выполняемых встроенными операторами и функциями.
Процедуры являются важнейшим элементом структурного программирования и служат средством расширения возможностей системы Maple 7 пользователем. Каждая процедура имеет свое уникальное имя и список параметров (он может быть пустым). Процедуры вызываются так же, как встроенные функции, — указанием их имени со списком фактических параметров. При этом просто процедуры обычно не возвращают каких-либо значений после своего исполнения, хотя могут присваивать значения входящим в них переменным. Процедуры-функции в ответ на обращение к ним возвращают некоторое значение. Они как бы являются новыми функциями, задаваемыми пользователем. Описанные ранее функции пользователя фактически являются процедурами-функциями с несколько упрощенной структурой. Простейшая форма задания процедуры следующая:
name :=ргос(Параметры)
Тело процедуры
end;
Параметры процедуры задаются перечислением имен переменных, например ргос(х) или proc(x.y.z). С помощью знака :: после имени переменной можно определить ее тип, например в объявлении prog(n::Integer) объявляется, что переменная п является целочисленной. При вызове процедуры выражением вида:
name(Фактические_параметры)
фактические параметры подставляются на место формальных. Несоответствие фактических параметров типу заданных переменных ведет к сообщению об ошибке и к отказу от выполнения процедуры.
В качестве примера ниже приведена процедура вычисления модуля комплексного числа г — в данном случае это единственный параметр процедуры:
ПРИМЕЧАНИЕ
После ввода заголовка процедуры под строкой ввода появляется сообщение: «Warning, premature end of input». Оно указывает на то, что ввод листинга процедуры не закончен и должен быть продолжен до тех пор, пока не будет введено завершающее слово end листинга процедуры. Если после этого слова поставить символ точки с запятой, то листинг процедуры будет выведен на экран дисплея.
Теперь для вычисления модуля достаточно задать обращение к процедуре modc(z), указав вместо z конкретное комплексное число:
> modc(3.+I*4.); 5.000000000
Нетрудно заметить, что при знаке : после завершающего слова end текст процедуры повторяется в строке вывода (в общем случае в несколько ином виде). Если это повторение не нужно, после слова end надо поставить знак двоеточия. Обратите также внимание на то, что для обозначения действительной и мнимой частей процедуры в ее тексте появились готические буквы.
12.gif
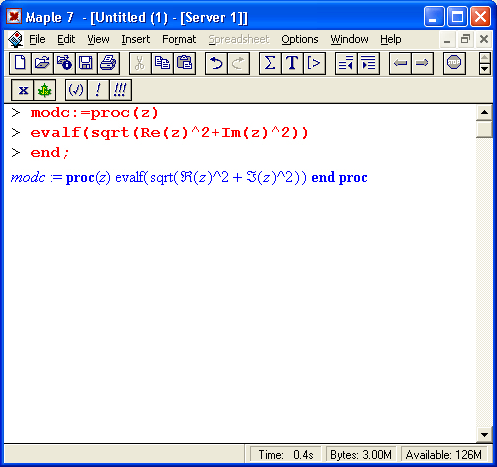
9. Оператор возврата значения RETURN
Оператор возврата значения RETURN
Как отмечалось, процедуры, которые возвращают значение результата в ответ на обращение к ним, во многом тождественны функциям. Будем называть их процедурами-функциями. Обычно процедура возвращает значение последнего выражения в ее теле или выражения, намеченного к возврату специальным оператором RETURN:
Параметром оператора RETURN может быть любое выражение. В Maple не принято выделять процедуры-функции в какой-то отдельный класс. Действует правило — если не использован оператор RETURN, процедура возвращает значение последнего выражения в ее теле. Для устранения выдачи значений выражений внутри процедуры-функции после них просто надо установить знак двоеточия.
13.gif
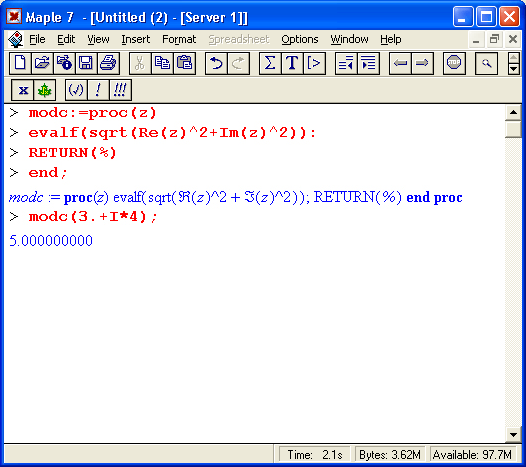
10. Статус переменных в процедурах и циклах
Статус переменных в процедурах и циклах
Переменные, которые указываются в списке параметров (например, г, в нашем случае), внутри процедуры являются локальными. Это означает, что изменение их значений происходит лишь в теле процедуры, то есть локально. За пределами тела процедуры эти переменные имеют то значение, которое у них было до использования процедуры. Это хорошо поясняет следующий пример:
> restart:z:=l;
z :=
> modc:=proc(z)
> evalf(sqrt(Re(z)"2+Im(z)"2));
> end;
mode := proc(z) evalf(sqrt(<R(z)A2 + 3(z)A2)) endproc > modc(3.+I*4.):
5.000000000
> z;
1
Нетрудно заметить, что внутри процедуры 2 = 3 + I*4, тогда как вне ее значение z= 1, Таким образом, имена переменных в списке параметров процедуры могут совпадать с именами глобальных переменных, используемых за пределами процедуры.
Переменные, которым впервые присваивается значение в процедуре, также относятся к локальным. Кроме того, переменные, применяемые для организации циклов, являются локальными. Все остальные переменные — глобальные.
11. Объявления переменных локальными с помощью оператора local
Объявления переменных локальными с помощью оператора local
Если в теле процедуры имеются операции присваивания для ранее определенных (глобальных) переменных, то изменение их значений в ходе выполнения процедуры создает так называемый побочный эффект. Он способен существенно изменить алгоритм решения сложных задач и, как правило, недопустим. Поэтому Maple-язык программирования имеет встроенные средства для исключения побочных эффектов. Встречая такие операции присваивания, Maple-язык корректирует текст процедуры и вставляет в нее объявление переменных локальными с помощью ключевого слова local и выдает предупреждающую надпись о подобном применении:
> restart:m:=0;
m := 0
> modc:=proc(z)
> m:=evalf(sqrt(Re(zr2+Im(zr2)):RETURN(m)
> end:
Warning, 'm' is implicitly declared local to procedure 'mode'
mode := proc (z) local т; т := evalf(sqrt(9*(z)A2 + 3(z)A2)); RETURN(m) end proc
> modc(3.+I*4.): 5.000000000
> m;
0
Обратите внимание на то, что в тело процедуры было автоматически вставлено определение local m, задающее локальный статус переменной т. Оператором print можно вывести текст процедуры:
> print(modc);
proc(z) local m; m := evalf(sqrt(R(z)^2 + J(z)^2)); RETURN(m) endproc
12. Объявления переменных глобальными с помощью слова global
Объявления переменных глобальными с помощью слова global
Говорят, что запретный плод сладок! Что бы ни говорили о нежелательности - работы с глобальными переменными, бывает, что их применение желательно или даже необходимо. Чтобы сделать переменные внутри процедуры глобальными, достаточно объявить их с помощью ключевого слова global, после которого перечисляются идентификаторы переменных.
Следующий пример поясняет применение оператора global в процедуре:
> а:=1;b:=1:
а := 1
b := 1
> fg:=proc(x,y)
> global a,b;
> a:-x^2:b:=y^2:
> RETURN(sqrt(a+b));
> end;
fg := proc (x, y) global a, b; a := x^2; b := y^2; RETURN( sqrt( a + b)) end proc
> fg(3.4):
5 > [a.b]:
[9,16]
В примере переменным а и b вначале присвоены значения 1. Поскольку они в процедуре объявлены глобальными, то внутри процедуры они принимают новые значения х2 и у2. В результате при выходе из процедуры они имеют уже новые значения. Это и есть побочный эффект при исполнении данной процедуры. Если пользователь не знает (или не помнит), что та или иная процедура имеет побочный эффект, то он рискует получить самые неожиданные (и неверные) результаты своих вычислений.
ПРИМЕЧАНИЕ
Следует отметить, что нельзя делать глобальными переменные, указанные в списке параметров процедуры, поскольку они уже фактически объявлены локальными. Такая попытка приведет к появлению сообщения об ошибке следующего вида «Error, argument and global'x' have the same name». При этом соответствующие переменные останутся локальными.
13. Функция вывода сообщений об ошибках ERROR
Функция вывода сообщений об ошибках ERROR
При профессиональной подготовке процедур пользователь должен предусмотреть их поведение при возможных ошибках. Например, если он готовит процедуру или функцию, вычисляющую квадратный корень из действительных чисел, то надо учесть, что такой корень нельзя извлекать из отрицательных чисел (будем, исключительно в учебных целях, считать, что комплексные числа в данном примере недопустимы).
Для контроля за типом данных обычно используются различные функции оценки и тестирования. При выявлении ими ошибки, как правило, предусматривается вывод соответствующего сообщения. Для этого используется функция ERROR:
ERROR(expr_1. expr_2. ...)
где ехрr_1, ... - ряд выражений (возможно, пустой). Наиболее часто ERROR выводит просто строковое сообщение об ошибке, например ERROR (`strings'). Полное сообщение об ошибке имеет вид:
Error, (in name) string. ...
Приведем пример процедуры, в которой предусмотрен вывод сообщения об ошибке при задании переменной х < 0:
> f := ргос (х) if x<0 then error "invalid variable x: XI". x else x*(l/2) end if end proc; f:= proc (x) if x < 0 then error "invalid variable x: %1" x else sqrt(x) end if end proc
> f(3.): 1.732050808
> f(-3.);
Error, (in f) invalid variable x: -3.
> lasterror;
"invalid variable x: %1" -3.
> lastexception;
f, "invalid variable x: %1", -3.
Эта процедура вычисляет квадратный корень из числа х. При х < 0 выводится заданное сообщение об ошибке. Еще раз обращаем внимание читателя на учебный характер данного примера, .поскольку вычисление квадратного корня (в том числе из комплексных и отрицательных действительных чисел) реализовано встроенной функцией sqrt.
14. Ключи в процедурах
Ключи в процедурах
В объявление процедуры можно включить ключевые слова, вводимые словом
options opseq
Иногда их называют расширяющими ключами. Предусмотрены следующие ключи:
- arrow — определят процедуру -оператор в нотации ->;
- bulltin — определяет функцию как встроенную;
- call_external — задает обращение к внешним программным модулям;
- copyright — защищает процедуру от копирования;
- inline — определяет процедуру как подчиненную (возможно, не для всех процедур - см. справку);
- load=memberName — загружает нужный для определений процедуры модуль (см. также опцию unload и детали в справке);
- operator — объявляет процедуру — функциональный оператор;
- system — определяет процедуру как системную,
- remember — определяет таблицу памяти для процедуры;
- trace — задает трассировку процедуры;
- unl oacNnemberName — выгружает нужный для определения процедуры модуль (см. опцию load).
Ключ remember
Ключ remember обеспечивает занесение результатов обращений к процедуре в таблицу памяти, которая используется при исполнении процедуры. Функция ор позволяет вывести таблицу:
> f:=proc(x) options remember; х^3 end:
> f(2):
8
> f(3):
27
> op(4,eval(f)): table([2 = 8, 3 = 27]) ,
Ключ remember особенно полезен при реализации итерационных процедур. К примеру, в приведенной ниже процедуре (без использования ключа remember) время вычисления n-го числа Фибоначчи растет пропорционально квадрату n:
> f:=proc(n) if n<2 then n else f(n-l)+f(n-2) fi end;
f:=proc(w)if n <2 then и else f(n - l) + ft>-2)endif endproc
> time(f(30)): 27.400
> f(30): 832040
Вычисление f(30) по этой процедуре на ПК с процессором Pentium II 350 МГц занимает около 30 с — см. контроль этого времени с помощью функции time (результат в секундах).
Стоит добавить в процедуру ключ remember, и время вычислений резко уменьшится:
> restart;
> fe:-proc(n) options remember: if n<2 then n else fe(n-l)+fe(n-2) fi end:
> fe(30);
832040
> time(fe(30));
0.
При этом вычисление fe(30) происходит практически мгновенно, так как все промежуточные результаты в первом случае вычисляются заново, а во втором они берутся из таблицы. Однако это справедливо лишь тогда, когда к процедуре было хотя бы однократное обращение. Обратите внимание на то, что данные процедуры являются рекурсивными — в их теле имеется обращение к самим себе.
Ключ builtin
Ключ builtin придает процедуре статус встроенной. Он должен использоваться всегда первым. С помощью функции eval(name) можно проверить, является ли функция с именем name встроенной:
> eval(type);
proc() option builtin; 268 end proc
> eval(print);
proc() option builtin; 229 end proc
Числа в теле процедур указывают системные номера функций. Следует отметить, что в новой версии Maple 7 они существенно отличаются от принятых в предшествующих версиях.
Ключ system
Этот ключ придает процедуре статус системной. У таких процедур таблица памяти может быть удалена. У обычных процедур таблица памяти не удаляется и входит в так называемый «мусорный ящик» (garbage collector).
Ключи operator и arrow
Эта пара ключей задает процедуре статус оператора в «стрелочной» нотации (->). Это достаточно пояснить следующими примерами:
Ключ trace
Ключ trace задает вывод отладочной информации:
> о:=ргос(х,у) option trace, arrow; x-sqrt(y) end:
о := proc (x, y) option trace, arrow, x - sqrt(y) end proc
> o(4,2.);
{--> enter o, args = 4,2.
2.585786438
<-- exit о (now at top level) = 2.585786438}
2.585786438
Ключ copyright
Этот ключ защищает тело процедуры от просмотра. Это поясняют следующие два примера:
> o:=proc(x,y) x-sqrt(y) end:
о := proc (x, у) х- sqii(y) end proc
> oo:=proc(x.y) option Copyright; x-sqrt(y) end;
oo := proc(x,y) ... endproc
> oo(4.2);
2.585786438
Нетрудно заметить, что во втором примере тело процедуры уже не просматривается. Для отмены защиты от просмотра можно использовать оператор interfасе(verboseproc=2).
14.gif
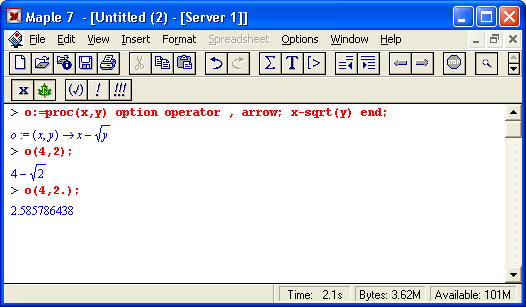
15. Общая форма задания процедуры
Общая форма задания процедуры
Выше мы рассмотрели основные частные формы задания процедур. Все они могут быть объединены в общую форму задания процедуры:
name:-proc(<argseq>) # объявление процедуры
local<nseq>; # объявление локальных переменных
g1oba1<nseq>; # объявление глобальных переменных
options<nseq>; # объявление расширяющих ключей
description<stringseq>; # объявление комментарий
<stateq> # выражения - тело процедуры
end; (или end:) # объявление конца процедуры
Эта форма охватывает все описанные выше частные формы и позволяет готовить самые сложные и надежно работающие процедуры.
16. Средства контроля и отладки процедур
Средства контроля и отладки процедур
Большая часть функций и операторов системы Maple 7 реализована в виде процедур, написанных на Maple-языке программирования. Благодаря возможности их просмотра пользователь получает неисчерпаемый источник примеров программирования на этом языке. Кроме того, пользователь может создавать свои собственные процедуры.
Для контроля и отладки процедур прежде всего надо уметь вывести их текст. Для этого служит функция:
print(name);
где name — имя процедуры.
Однако перед тем, как использовать эту функцию, надо исполнить команду:
> interfасе(verboseproc=2,prettyprint-l.version);
Maple Worksheet Interface, Maple 7, IBM INTEL NT, May 28 2001 Build ID 96223
Ее смысл будет пояснен ниже. Пока же отметим, что эта команда обеспечивает полный вывод текста процедур библиотеки. Встроенные в ядро процедуры, написанные не на Maple-языке, в полном тексте не представляются. Поясним это следующими примерами:
> print(evalf);
proc() option builtin, remember; 167 end proc
> print(erf);
proc(x::algebraic)
local Re_x, Im_x, sr, si, xr, xi;
option ' Copyright (c) 1994 by the University of Waterloo. All rights reserved`.;
if nargs <> 1 then error "expecting 1 argument, got %1", nargs
elif type(x, 'complex(float)') then evalf('erf (x)) elif x = 0 then 0 elif type(x, 'infinity') then
if type(x, {'cxjnfinity', 'undefined'}) thenundefined + undefined*!
elif type(Re(x), 'infinity') then CopySign(l, Re(x))
elif type(x, 'imaginary') then x
else infinity + infinity*I
end if
elif type(x, 'undefined') then x*undefined elif type(x, 'complex(numeric)')
then
if csgn(x) = -1 then -erf(-x) else 'erf'(x)
end if elif type(x, '*')
and type(op(l, x), 'complex(numeric)')
and csgn(op(l, x)) = -1 then -erf(-x) elif type(x, ' +')
and traperror(sign(x)) = -1 then -erfC-x)
else erf(x) := 'erf'(x) end if end proc
Здесь вначале выполнен вывод сокращенного листинга встроенной в ядро процедуры evalf, а затем выведен полный листинг процедуры вычисления функции ошибок erf. Эта функция имеет довольно короткую процедуру — многие важные функции и операторы задаются гораздо более сложными и большими процедурами.
Но вернемся к функции interface. Эта функция служит для управления выводом и задается в виде: interface( arg1. arg2, ... ) где аргументы задаются в виде равенств вида name=va1ue и слов-указателей:
|
ansi |
autoassign |
echo |
error-break |
errorcursor |
|
imaginaryunit |
indentamount |
labelling |
label width |
latexwidth |
|
"longdelim |
patchl evel |
plotdevice |
plqtoptions |
plotoutput |
|
postplot |
preplot |
prettyprint |
prompt |
quiet |
|
rtablesize |
screenheight |
screenwidth |
showassuraed |
verboseproc |
|
version |
warnl evel |
|
|
|
К сожалению, объем и характер данной книги не позволяют остановиться на всех вариантах использования этой очень мощной функции, тем более что в ней может использоваться множество аргументов. Мы рассмотрим только некоторые, наиболее важные возможности.
Указание verboseproc=n задает степень детальности вывода листинга процедур. При n=0 текст не выводится, при n=1 выводится текст только заданных пользователем процедур, а при n=2 — всех процедур на Maple-языке. Пример этого был дан выше. Указание prettyprint=0 или 1 управляет выводом стандартных сообщений. Указание plotdevice=string управляет выводом графики, например plotdevice=gif указывает на то, что запись графиков в виде файлов будет происходить в формате .gif.
Одним из основных средств отладки процедур является функция трассировки trace(name). Детальность ее работы задается системной переменной printlevel (уровень вывода). При printlevel :=n (значение n = 1 по умолчанию) выводится результат только непосредственно исполняемой функции или оператора. Для вывода информации о выполнении k-ro уровня вложенности надо использовать значение этой переменной от 5*k до 5*(k+i). Так, при п от 1 до 5 выводятся результаты трассировки первого уровня, при и от 6 до 10 — второго и т. д. Максимальное значение п = 100 обеспечивает трассировку по всем уровням вложенности процедуры name. Следующий пример показывает осуществление трассировки для функции int(x^n,x):
Действие функции трассировки отменяется командой untrace:
При отладке алгоритмов выполнения вычислений надо тщательно следить за сообщениями об ошибках. Для этого в Maple предусмотрены функция traceerr и системная переменная lasterr, в которой сохраняется последнее сообщение об ошибке. При каждом обращении к tracerr переменная lasterr очищается:
> 2/0;
Error, numeric exeption:division by zero
> 2/4;
1/2
> 2/.3;
6.666666667
> lasterror:
"division by zero"
> traperror(3/4);
3/4
> lasterror;
lasterror
> traperror(5/0);
Error, numeric exeption:division by zero
> lasterror:
"numeric exeption:division by zero"
Этот пример показывает, как может быть проведено отслеживание ошибок в ходе вычислений. Вообще говоря, пользователь системы Maple 7 редко привлекает описанные средства, поскольку проще отладить вычислительный алгоритм прежде, чем на его основе будет составлена процедура. При правильном построении процедур ошибочные ситуации заведомо предусматриваются и должным образом обрабатываются.
15.gif
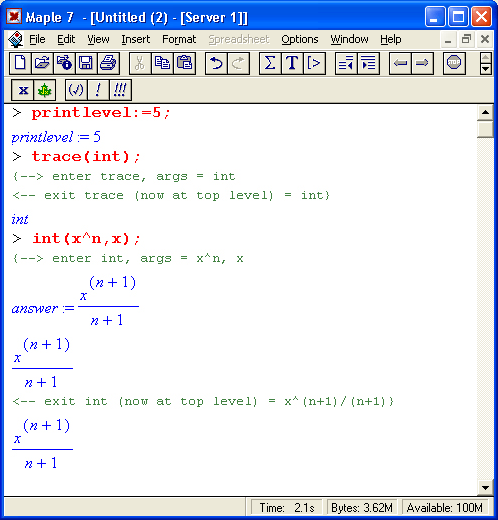
16.gif
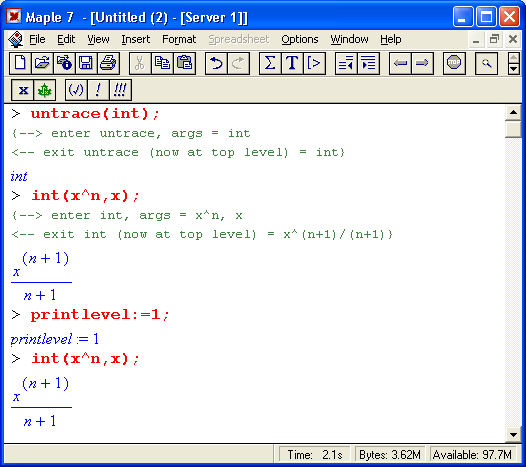
17. Работа с отладчиком программ
Работа с отладчиком программ
В большинстве случаев составители программ (процедур) редко прибегают к пошаговой их отладке. Средства общей диагностики Maple 7 развиты настолько хорошо, что позволяют выявлять грубые ошибки в процедурах при их выполнении. Иногда, правда, для этого приходится неоднократно «прогонять» процедуру, пока она не начнет работать как задумано. Тем не менее для отладки процедур служит специальный интерактивный отладчик (debugger). Опишем, как его запустить и как с ним работать.
Допустим, мы составили некоторую процедуру demo, вычисляющую сумму квадратов чисел (1^2+2^2+...+n^2):
> demo:=proc(n::integer) local y,i:
> y:=0:
> for i to n do y:=y+i^2 od
> end;
demo := proc (n::integer) local y, i; у := 0;
for i to n do у := у + i^2 end do end proc
> demo(3):
14
Чтобы включить отладчик в работу, надо исполнить команду stopat:
> stopat(demo);
[demo]
> demo(3);
demo:
1* y:=0;
DBG>
Признаком, указывающим на работу отладчика, является изменение приглашения к вводу со знака > на DBG> (как нетрудно догадаться, DB6 означает debugger). Теперь, подавая команды next (следующий), step (шаг) и stop (остановка), можно проследить выполнение процедуры:
DBG> next
0
demo:
2 for i to n do
end do
DB6> step
0
demo:
3 y:=y+i^2
DBG> Step
1
demo:
3 y:=y+i^2
DB6> step
5
demo:
3 y:=y+iA2
DBG> step
14
В последнем случае процедура по шагам дошла до конца вычислений; на этом работа отладчика завершается сама собой.
Можно также вывести листинг процедуры с помощью команды showstat:
> showstat(demo):
demo :=proc(n::integer)
local у, i;
1* y:=0;
2 for i to n do
3 y:=y+i^2
end do end proc
Обратите внимание, что в этом листинге строки вычисляемых элементов пронумерованы. Это сделано для облегчения разбора работы процедуры.
В общем случае отладчик выключается при выполнении команд stopat, stopwhen или stoperr. Если используется команда stopat, то вывод на экран соответствует исполнению последней выполненной команды. Для отмены этой команды используется команда unstopat.
Команда stopwhen позволяет установить точку наблюдения за указанной в команде переменной. Отменить ее можно командой unstopwhen. Команда stoperror позволяет задать остановку при появлении определенной ошибки. Для отмены этой команды используется команда unstoperror.
Команда cont используется для продолжения работы до следующей точки прерывания, установленной указанными выше командами, или до конца процедуры. Для прерывания отладки можно использовать команду quit. После команды stop можно вычислить любое Maple-выражение.
В действительности команд отладчика намного больше и их функции более развиты, чем это описано выше. Пользователи, заинтересованные в серьезной работе с отладчиком (скорее всего, их немного), могут просмотреть его подробное описание. Для этого в разделе справочной системы Context найдите раздел Programming, а в нем — раздел Debugging.
18. Операции ввода и вывода
Операции ввода и вывода
Считывание и запись программных модулей
В уроке 2 рассматривалась работа с файлами документов. Вводимые в текущий документ программные модули хранятся вместе с ним, так что при отказе от загрузки какого-либо документа все его программные блоки не могут использоваться в других документах. Кроме того, порой неудобно загружать объемный документ ради использования одного или нескольких модулей, например процедур. Поэтому в Maple 7 введены средства, позволяющие записывать нужные модули (в том числе результаты вычислений) на диск и считывать их в случае необходимости.
Для записи на диск используется оператор save:
- save filename — запись всех определений текущего файла под именем filename;
- save name_l, name_2, .... name_k, filename — запись избранных модулей с именами name_l, name_2, ..., name_k под именем filename.
Считывание имеющегося на диске файла filename осуществляется оператором read:
read <filename>
При считывании все имеющиеся в файле определения становятся доступными для рабочих документов Maple. При записи файлов отдельных определений используется специальный внутренний Maple-формат файлов. Для загрузки файлов типа *.m из стандартной библиотеки используется функция readlib. А для записи файлов в качестве библиотечных достаточно в имени filename оператора save указать расширение .т. Разумеется, можно считывать такие файлы и оператором read, указав в имени файла расширение .m:
> save my_proc,4myJib.nT: # запись файла пу_ргос и
> # библиотечного файла my_lib.m:
> load 'myjlib.m': # считывание библиотечного файла
> # myjib.m.
19. Создание своей библиотеки процедур
Создание своей библиотеки процедур
Если приведенные выше примеры составления процедур кажутся вам простыми, значит, вы неплохо знаете программирование и, скорее всего, уже имеете несколько полезных процедур, которые вы хотели бы сохранить — если не для потомков, то хотя бы для своей повседневной, работы. Сделать это в Maple 7 довольно просто.
Прежде всего надо определить имя своей библиотеки, например mylib, и создать для нее на диске каталог (папку) с заданным именем. Процедуры в Maple 7 ассоциируются с таблицами. Поэтому вначале надо задать таблицу-пустышку под будущие процедуры:
> restart;
> mylib:=tab1e():
mylib := table([])
Теперь надо ввести свои библиотечные процедуры. Они задаются с двойным именем — вначале указывается имя библиотеки, а затем в квадратных скобках имя процедуры. Для примера зададим три простые процедуры с именами fl, f2 и f3:
> mylib[fl]:=proc(x: Anything) sin(x)+cos(x) end:
> mylib[f2]:=proc(x:anything) sin(x)^2+cos(x)^2 end:
> mylib[f3]:=proc(x::anything) if x=0 then 1 else sin(x)/x fi end:
Рекомендуется тщательно проверить работу процедур, прежде чем записывать их на диск. Ограничимся, скажем, такими контрольными примерами:
Можно построить графики введенных процедур-функций. Они представлены на рис. 7,4.
Рис. 7.4. Построение графиков процедур-функций f1, f2 и f3
С помощью функции with можно убедиться, что библиотека mylib действительно содержит только что введенные в нее процедуры. Их список должен появиться при обращении with (mylib):
> with(mylib);
[f1,f2,f3]
Теперь надо записать эту библиотеку под своим именем на диск с помощью команды save:
> save(mylib,`c:/ mylib.m);
Обратите особое внимание на правильное задание полного имени файла. Обычно применяемый для указания пути знак \ в строках Maple-языка используется как знак продолжения строки. Поэтому надо использовать либо двойной знак \\, либо знак /. В нашем примере файл записан в корень диска С. Лучше поместить библиотечный файл в другую папку (например, в библиотеку, уже имеющуюся в составе системы), указан полный путь до нее.
После всего этого надо убедиться в том, что библиотечный файл записан. После этого можно сразу и считать его. Для этого вначале следует командой restart устранить ранее введенные определения процедур:
> restart;
С помощью команды with можно убедиться в том, что этих определений уже нет:
> with(mylib):
Error, (in pacman:-pexports) mylib is not a package
После этого командой read надо загрузить библиотечный файл:
> read('c:/mylib.m');
Имя файла надо указывать по правилам, указанным для команды save. Если все выполнено пунктуально, то команда with должна показать наличие в вашей библиотеке списка процедур fl, f2 и f3:
> with(mylib):
[f1. f2. f3]
И наконец, можно вновь опробовать работу процедур, которые теперь введены из загруженной библиотеки:
> fl(x):
sin(x) + cos(x) > simplify(f2(y});
1 > f3(0):
1 > f3(1.);
.8414709848
Описанный выше способ создания своей библиотеки вполне устроит большинство пользователей. Однако есть более сложный и более «продвинутый» способ ввода своей библиотеки в состав уже имеющейся. Для реализации этого Maple 7 имеет следующие операции записи в библиотеку процедур si, s2, ... и считывания их из файлов filel, file2, ...:
savelib(s1. s2, .... sn, filename)
readlib(f. file1. file2. ...)
С помощью специального оператора makehelp можно задать стандартное справочное описание новых процедур:
makehelp(n.f.b).
где n — название темы, f — имя текстового файла, содержащего текст справки (файл готовится как документ Maple) и b — имя библиотеки. Системная переменная libname хранит имя директории библиотечных файлов. Для регистрации созданной справки надо исполнить команду вида:
libname:-libname. '/mylib":
С деталями применения этих операторов можно ознакомиться в справочной системе.
К созданию своих библиотечных процедур надо относиться достаточно осторожно. Их применение лишает ваши Maple-программы совместимости со стандартной версией Maple 7. Если вы используете одну-две процедуры, проще поместить их в те документы, в которых они действительно нужны. Иначе вы будете вынуждены к каждой своей программе прикладывать еще и библиотеку процедур. Она нередко оказывается большей по размеру, чем файл самого документа. Не всегда практично прицеплять маленький файл документа к большой библиотеке, большинство процедур которой, скорее всего, для данного документа попросту не нужны. Особенно рискованно изменять стандартную библиотеку Maple 7.
Впрочем, идти на это или нет — дело каждого пользователя. Разумеется, если вы готовы создать серьезную библиотеку своих процедур, то ее надо записать и тщательно хранить. С Maple 7 поставляется множество библиотек полезных процедур, составленных пользователями со всего мира, так что и вы можете пополнить ее своими творениями (см. урок 14).
17.gif
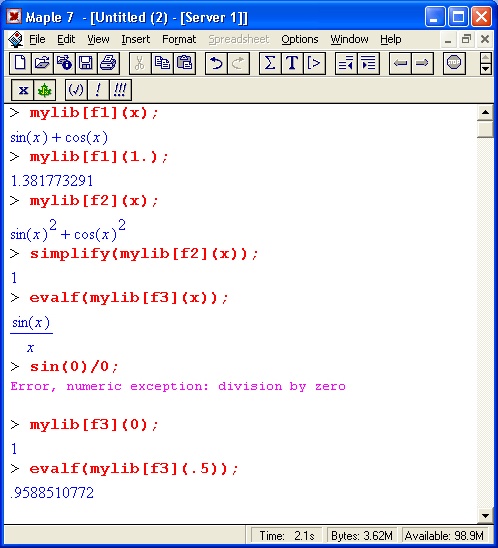
24.gif
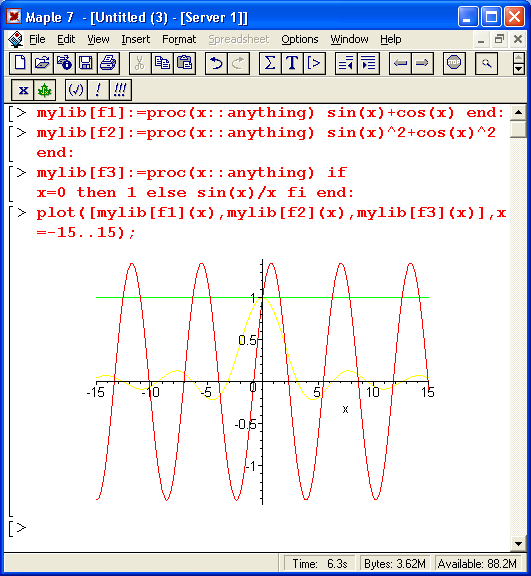
20. Запись и считывание данных
Запись и считывание данных
Обширные возможности Maple 7 делают привлекательным применение этой программы для автоматической обработки данных, поступающих от каких-либо экспериментальных установок. Для этого установки снабжаются интерфейсными платами (например, аналого-цифровыми преобразователями) и необходимым программным обеспечением. Возможна и передача данных, полученных с помощью Maple 7, в экспериментальные установки.
Обмен информацией между Maple 7 и внешней средой (к ней, кстати, относятся и другие программы) чаще всего осуществляется через файлы текстового формата, поскольку именно с такими файлами могут работать практически все программы. Для записи данных в файл служит оператор writedata:
writedata[APPEND](fileID. data)
writedata[APPEND](fileID, data, format)
writedata[APPEND](filelD, data, format, default)
Здесь filelD — имя или дескриптор файла данных, data — список, вектор или матрица данных, format — спецификация формата данных (integer, float или string), default — процедура, задающая запись нечисловых данных, например:
writedata(F.A.float.proc(f.x) fprintf(f/CMPLX(%g,%g)',Re(x).Im(x)) end):
Необязательный указатель APPEND используется, если данные должны дописываться в уже созданный файл. Считывание из файла filename обеспечивает функция readdata:
readdata(filelID. n)
readdata(fileID, format, n)
readdata(fileID. format)
Здесь n — целое положительное число, задающее число считываемых столбцов. Ниже представлены примеры этих операций:
Maple 7 имеет также типичные файловые операции:
- writeto — запись в файл;
- appendto — добавление к файлу;
- open — открытие файла;
- close — закрытие файла;
- write — запись в открытый файл;
- save — запись выражений в файл;
- read — считывание из файла.
Их реализация, однако, зависит от платформы, на которой установлена система, и от ее настройки.
19.gif
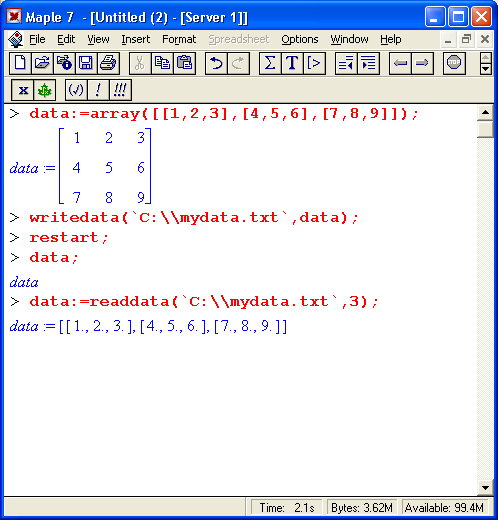
21. Вывод в специальных форматах
Вывод в специальных форматах
Maple 7 имеет ряд средств для общения с другими программами. Часть из них, в основном относящаяся к обмену через файлы, уже была описана. Однако Maple 7 способна генерировать коды для прямого их включения в такие программы, причем не только математические.
Для подготовки математических статей и книг широкое распространение получили редакторы ТеХ и LaTeX. Для подготовки выражений или файлов в их формате служит функция:
latex(expr.filename)
Параметр filename не обязателен, если достаточно получить нужное выражение в ячейке вывода Maple 7:
> latex(a*x^2+b*x+c):
а{х}^{2}+bх+с
> latex(diff(xAn.x$2));
{\frac {{х}^{n}{n}^{2}}{{х}^{2}}{\frас {{х}^{n}n}{{х}^{2}}}
22. Генерация кодов на языке Фортран
Генерация кодов на языке Фортран
Язык Фортран вот уже многие десятилетия используется для программирования вычислительных задач. Накоплены обширные библиотеки решения таких задач на Фортране. Почитателей этого языка Maple 7 порадует тем, что она позволяет готовить коды для программ на Фортране. Для этого вначале надо загрузить библиотечную функцию:
> with(codegen.fortran);
[fortran ]
После этого может использоваться функция fortran:
fortran(expr.filename=str.optimized)
Два последних параметра не обязательны при выводе выражения ехрr в форме, присущей языку Фортран:
> fortran(a*x*2+b*x+c);
t0 = a*x**2+b*x+c
> fortran(diff(x"n,x$2));
t0 = x**n*n**2/x**2-x**n*n/x**2
Параметр optimize позволяет генерировать оптимизированные коды:
> fortran(a*x*2+b*x+c.optimized);
t1 = x**2 t4 = a*tl+b*x+c
При этом вычислительный процесс строится так, чтобы минимизировать число арифметических операций.
23. Генерация кодов на языке С
Генерация кодов на языке С
Язык С (Си) также широко используется для решения вычислительных задач. Достаточно отметить, что сама система Maple 7 создана на языке С.
Для генерации кодов на языке С вначале надо подключить соответствующую функцию:
> with(codegen.C); [С]
Затем можно использовать функцию С:
С(ехрг.folename=str.optimi zed)
Эта функция используется по аналогии с функцией fortran, что и показывают приведенные ниже примеры:
> C(d1ff(x4>,x$2));
t0 = pow(x,1.0*b)*b*b/(x*x)-pow(x,1.0*b)*b/(x*x);
> C(diff(xAb,x$2),optimized);
tl = pow(x,1.0*b);
t2 = b*b;
t4 = x*x;
t5 = l/t4; '
t9 = tl*t2*t5-tl*b*t5;
Обширные возможности преобразования выражений в различные формы предоставляет функция convert. А функция interface позволяет управлять выводом. К сожалению, объем книги не позволяет рассмотреть все многочисленные варианты применения этих функций.
24. Дополнительные возможности Maple-языка
Дополнительные возможности Maple-языка
В большинстве случаев Maple-язык использует достаточно длинные идентификаторы для своих определений, например функций. Однако с помощью функции al i as можно изменить любое определение на другое, если оно кажется пользователю более удобным. Функция alias записывается в виде:
alias(e1. е2. .... еN)
где e1, e2, ..., eN — ноль или более равенств.
Эта функция возвращает список переназначений и осуществляет сами переназначения. Например, для замены имени функции BesselJ на более короткое имя BJ достаточно параметром функции alias записать BJ=BesselJ:
> alias(BJ-BesseU):
BJ,Fx
> [BJ(0.1.),Besse1J(0,1.)]:
[.7651976866, .7651976866]
Можно также переназначить функцию пользователя:
Для отмены переназначения, например BJ, используется та же функция alias с повтором переназначения:
> a1ias(B>BJ): Fx
> BJ(0,1.); BJ(0,1.)
Обратите внимание на то, что BJ исчезло из списка переназначений и функция BJ(0,1.) уже не вычисляется, поскольку ее больше нет.
20.gif
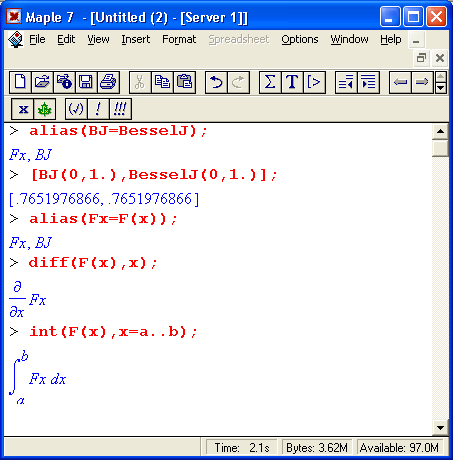
25. Модули.
Модули
Модули придают языку программирования Maple 7 некоторые свойства языков объектно-ориентированного программирования. Они служат для реализации абстрактного типа данных на основе инкапсуляции — объединения данных и процедур их обработки. Модули задаются ключевым словом module с пустыми скобками () и завершаются словами end module или просто end:
name := module()
export eseq; local Iseq; global gseq:
option optseq: description desc:
Тело модуля
end module (или просто end)
Хотя структура модуля во многом напоминает структуру процедуры, включая объявление локальных и глобальных переменных, параметров и описаний, между ними есть существенная разница:
- модуль не имеет списка входных параметров; О в модуле могут размещаться данные;
- модули могут использоваться для создания пакетов процедур, доступ к которым обеспечивается командой with;
- модули имеют свойства в виде локальных переменных и методы в виде процедур интерфейса модулей;
- реализация абстрактных типов данных с помощью модулей скрыта от пользователя;
- модули могут содержать оператор export eseq, объявляющий экспортируемые переменные модуля;
- для доступа к экспортируемым переменным модуля может использоваться специальный оператор «:-» (двоеточие и минус);
- модули и процедуры могут вкладываться друг в друга без ограничения уровня вложенности;
- модули могут иметь специальные конструкторы объектов.
Следующий пример демонстрирует создание модуля pt, в котором заданы две операции (сложения plus и умножения times) и показан доступ к ним:
> pt:= module()
export plus, times;
plus := (a.b) -> a + b;
times := (a.b) -> a * b: end module:
pt := module () export plus, times; end module
> pt:-p1us(3,5);
8
> pt:=times(3,7);
21
Детальную информацию о модулях и о конструкторах объектов можно найти в справках по ним. Некоторые пакеты Maple 7 (в основном сравнительно новые) реализованы уже не в виде процедур, а в виде модулей (например, в виде модуля сделан пакет LinearAlgebra). В простейшем виде модули могут использоваться всеми пользователями системы Maple 7, но их серьезное применение (например, с целью создания полноценных пакетов Maple 7) требует серьезного знакомства с техникой объектно-ориентированного программирования. Такое знакомство выходит за рамки данной книги.
26. Макросы
Макросы
Макрос — это макрокоманда, короткая запись длинных определений. По сравнению с переназначениями макросы более гибки и могут использоваться для сокращения операций загрузки новых определений из библиотеки и пакетов. Макросы создаются с помощью функции macro:
macrc(e1, e2, .... en)
где el, е2, ....,, en — ноль или более равенств.
В следующем примере функция numbperm с помощью макроса заменена на пр:
> numbperm([l,2,3,4]);
24
> macro(np=numbperm(V));
nр
> V:=[1.2.3.4]:
F:=[l,2,3,4]
> np(V);
24
Макросы могут быть использованы для конструирования выражений из их макроопределений.
27. Внешние вызовы
Внешние вызовы
Maple 7 имеет команду system(string), с помощью которой можно исполнить любую команду MS-DOS, записанную в виде строки string. Например, для форматирования гибкого диска из среды Maple 7 можно использовать стандартную команду MS-DOS:
> system(`format a:`);
На экране появится окно MS-DOS с начальным диалогом форматирования диска А. Это окно показано на рис. 7.5.
При работе в операционной системе Windows эта возможность практически бесполезна, поскольку форматирование диска с большими удобствами можно выполнить средствами Windows.
Внешние вызовы командой system куда более полезны для MS-DOS-реализаций Maple, которые кое-где используются и по сей день. Но поскольку данная книга посвящена самым современным Windows-реализациям системы Maple 7, более подробное рассмотрение операций внешних вызовов не имеет особого смысла.
Рис. 7.5. Результат выполнения команды форматирования гибкого диска
21.gif
28. Вызов внешних процедур, написанных на языке С
Вызов внешних процедур, написанных на языке С
Maple 7 имеет средства для вызова внешних откомпилированных процедур, написанных на языке С. Такая необходимость для подавляющего числа пользователей Maple 7 вызывает большие сомнения в силу следующих причин:
- вся идеология системы Maple 7 основана на максимальном исключении программирования на других языках, помимо Maple-языка;
- язык С сложен для большинства пользователей Maple 7, которых трудно отнести к «путным» программистам;
- отладка комплекса Maple 7 + компилятор С (например, фирмы Microsoft) вряд ли под силу обычным пользователям, тем более что на практике такой комплекс реально не работает без кропотливой отладки.
Учитывая сказанное, мы отметим лишь, что для использования внешних процедур (например, остро нужных пользователю или более быстрых, чем аналогичные процедуры Maple) используется специальная команды define_external, которая генерирует две интерфейсные программы — на языке С и на языке Maple соответственно. Программа на языке С компилируется вместе с внешней процедурой, которая будет использоваться. Результирующий код создает динамически подключаемую бублиотеку DLL. В свою очередь, программа на языке Maple служит как интерфейсная для организации взаимодействия с вызываемой внешней процедурой. Более подробное описание возможностей работы с внешними процедурами можно найти в справке по ним.
29. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Задавать функции пользователя.
- Использовать условные операторы.
- Применять циклы for и while.
- Использовать операторы пропуска и прерывания.
- Задавать процедуры, и процедуры-функции.
- Использовать средства контроля и отладки процедур.
- Работать с отладчиком программ.
- Применять операции ввода и вывода.
- Осуществлять вывод в специальных форматах.
- Использовать дополнительные возможности Maple-языка.
Урок 8. Математический анализ
1. Вычисление сумм последовательностей
Урок 8.
Математический анализ.
Основные формулы для вычисления сумм последовательностей
Применение систем символьной математики особенно эффективно при решении задач математического анализа. Maple 7 обладает богатейшей базой данных по формулам математического анализа и может полноценно заменять тома книг со справочными данными. При этом важно, что Maple не только «знает» многие формулы, но и может успешно использовать их при решении достаточно сложных задач в аналитическом (символьном) виде.
Начнем рассмотрение таких операций с вычисления сумм последовательностей. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, то есть выражения:
является достаточно распространенной операцией математического анализа. Для вычисляемой и инертной форм сумм последовательностей служат следующие функции:
sum(f.k): sum(f,k=m..n); sum(f,k=alpha):
Sum(f.k); Sum(f,k=m..n); Sum(f,k=a1pha);
Здесь f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение n может быть равно бесконечности. В этом случае для n используется обозначение ? или infinity.
Допустимо (а зачастую рекомендуется с целью исключения преждевременной оценки суммы) заключение f и k в прямые кавычки, например sum('f', 'k'=m. .n). Это сделано во всех примерах справочной системы Maple 7, относящихся к функции sum. Мы, однако, отказываемся от этого в тех случаях, когда результат идентичен при заключении f и k в кавычки и без такового. Во избежание путаницы, связанной с этой тонкостью синтаксиса функции sum, рекомендуется все примеры проверять после команды restart, убирающей предыдущие определения f и k.
1.gif
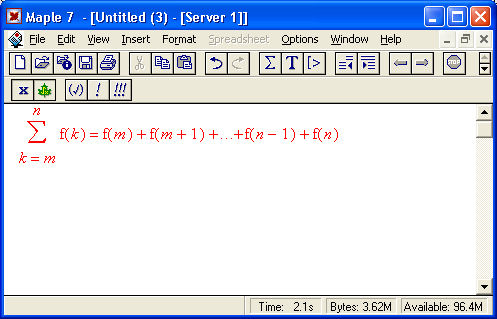
2. Последовательности с заданным числом членов
Последовательности с заданным числом членов
Простейшими являются суммы последовательностей с фиксированным числом членов. Ниже даны примеры применения этих функций:
Обратите внимание, что во втором примере система отказалась от вычисления, а в третьем даже выдала сообщение об ошибке, связанной с тем, что переменной k перед вычислением сумм было присвоено численное значение 2. После заключения выражения и переменной индекса k в прямые кавычки ошибка исчезла, поскольку такая операция означает, что переменной придается неопределенное значение.
2.gif
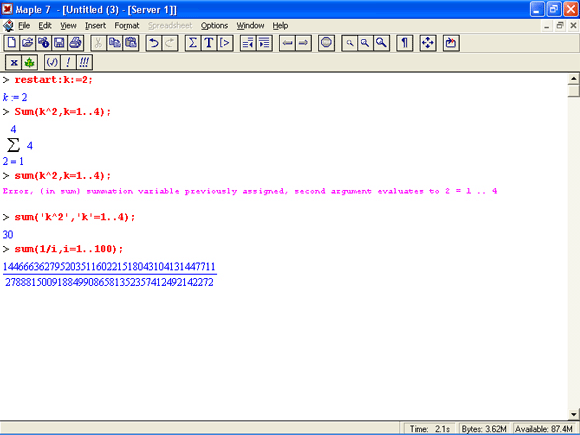
3. Суммы с заданным пределом
Суммы с заданным пределом
Особый класс образуют последовательности, у которых предел задается в общем виде значением переменной. Ниже представлен ряд последовательностей, у которых предел задается как 0.. n или 1.. n:
Такого рода последовательности, как видно из приведенных примеров, нередко имеют аналитические выражения для своего значения. Его вычисление намного проще, чем формирование заданной последовательности с прямым суммированием ее членов. Некоторые из таких сумм выражаются через специальные математические функции.
3.gif

4. Суммы бесконечных последовательностей
4.gif
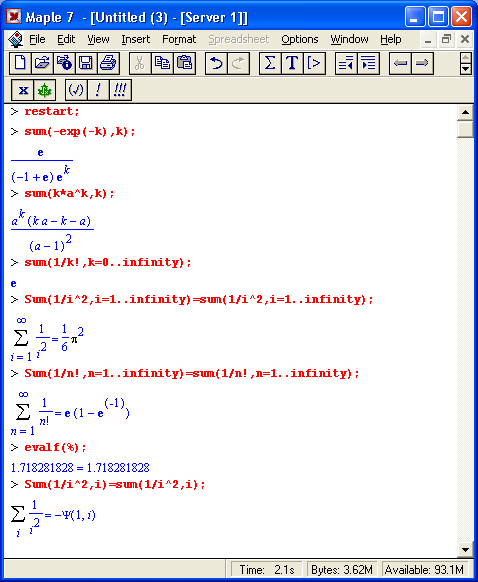
5. Сумма от перемены мест слагаемых меняется!
Сумма от перемены мест слагаемых меняется!
Даже школьники хорошо знают, что от перестановки слагаемых сумма не изменяется. Однако Maple 7 (кстати, как и большинство других систем компьютерной математики) при вычислении сумм, увы, этому правилу не следует. Приведенные ниже примеры наглядно показывают этот просчет системы:
ВНИМАНИЕ
При вычислении сумм последовательностей надо строго соблюдать прямой (нарастающий) порядок задания значений индексной переменной суммы. Нарушение этого порядка чревато грубыми ошибками.
6.gif

7.gif
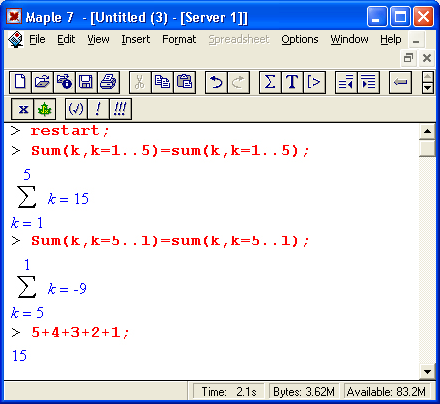
6. Двойные суммы
Двойные суммы
Могут встречаться множественные суммы по типу «сумма в сумме». Ограничимся приведением примера двойной суммы, имеющей аналитическое значение:
При конкретном значении N такую сумму нетрудно вычислить подстановкой:
> subs( N = 100, %);
8670850
Как видно из приведенных примеров, средства вычисления сумм последовательностей Maple 7 позволяют получать как численные, так и аналитические значения сумм, в том числе представляемые специальными математическими функциями.
8.gif
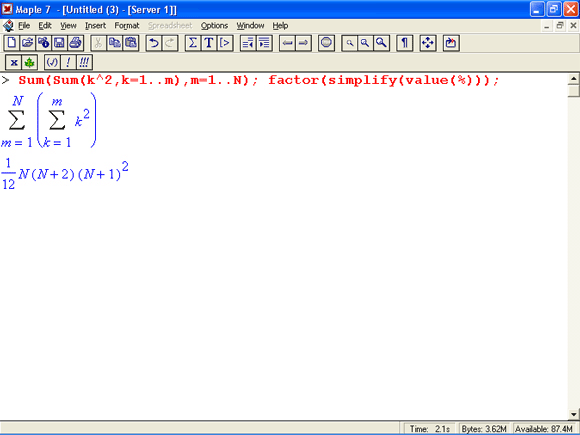
7. Вычисление произведений членов последовательностей
Вычисление произведений членов последовательностей
Основные формулы для произведения членов последовательностей
Аналогичным образом для произведений членов f(i) некоторой последовательности, например вида:
используются следующие функции:
product(f,k); product(f,k=m..n): product (f,k=alpha):
Product(f,k); Product(f,k=m..n): Product(f,k=alpha).
Обозначения параметров этих функций и их назначение соответствуют приведенным для функций вычисления сумм. Это относится, в частности, и к применению одиночных кавычек для f и k.
9.gif
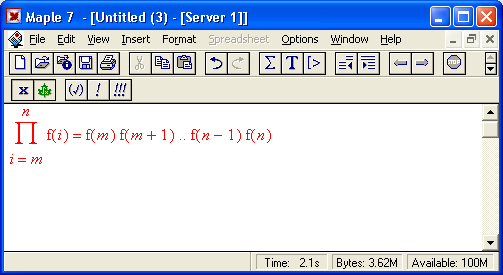
8. Примеры вычисления произведений членов последовательностей
Примеры вычисления произведений членов последовательностей
Примеры применения функций вычисления произведений даны ниже:
Как и в случае вычисления сумм, вычисление произведений возможно как в численной, так и в аналитической форме — разумеется, если таковая существует. Это показывает следующий пример:
Нетрудно понять, что при i, стремящемся к бесконечности, перемножаемые члены последовательности стремятся к нулю, а потому к нулю стремится и их произведение. Вопросы доказательства подобных утверждений находятся за рамками данного учебного курса, ибо он посвящен не математике как таковой, а конкретной программе для математики — Maple 7.
10.gif
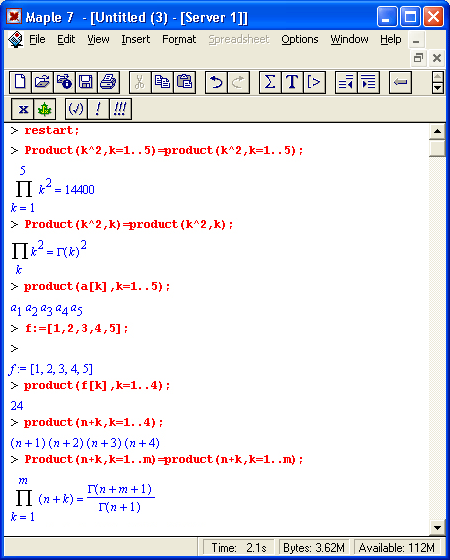
11.gif
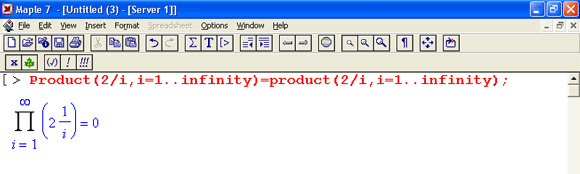
9. От перемены места сомножителей произведение меняется!
От перемены места сомножителей произведение меняется!
Хотя произведение не зависит от порядка расположения сомножителей, их перестановка в Maple 7 недопустима. Это иллюстрируют следующие примеры:
ВНИМАНИЕ
При вычислении произведений надо строго соблюдать прямой (нарастающий) поря-— док задания значений индексной переменной произведения. Нарушение этого порядка чревато грубыми ошибками.
12.gif

10. Вычисление производных
Вычисление производных
Функции дифференцирования выражений diff и Diff
Вычисление производных функций fn(x) = dfn(x)/dxn n-го порядка — одна из самых распространенных задач математического анализа. Для ее реализации Maple 7 имеет следующие основные функции:
diff(a., xl, х2, .... xn) diff(a, [xl, х2, .... хn])
Diff(a, xl, x2, .... xn) Diff(a, [xl, x2, .... хn])
Здесь а — дифференцируемое алгебраическое выражение, властности функция f(xl. x2, .... хn) ряда переменных, по которым производится дифференцирование. Функция Diff является инертной формой вычисляемой функции diff и может использоваться для естественного воспроизведения производных в документах. Первая из этих функций (в вычисляемой и в инертной форме) вычисляет частные производные для выражения а по переменным xl, х2, ..., .хn. В простейшем случае diff(f(x),x) вычисляет первую производную функции f(x) по переменной х. При n, большем 1, вычисления производных выполняются рекурсивно, например diff (f (х), х, у) эквивалентно diff(diff (f(x), х), у). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff (f(x) ,x$4) вычисляет производную 4-го порядка и эквивалентно записи diff (f (х) ,х,х,х.х). A diff (g(x,y) ,x$2,y$3) эквивалентно diff(g(x,y),x,x.y,y,y) ;
Примеры вычисления производных:
Как видно из приведенных примеров, функции вычисления производных могут использоваться с параметрами, заданными списками. Приведенные ниже примеры показывают эти возможности и иллюстрируют дифференцирование функции пользователя для двух переменных:
Получаемые в результате дифференцирования выражения могут входить в другие выражения. Можно задавать их как функции пользователя и строить графики производных.
13.gif
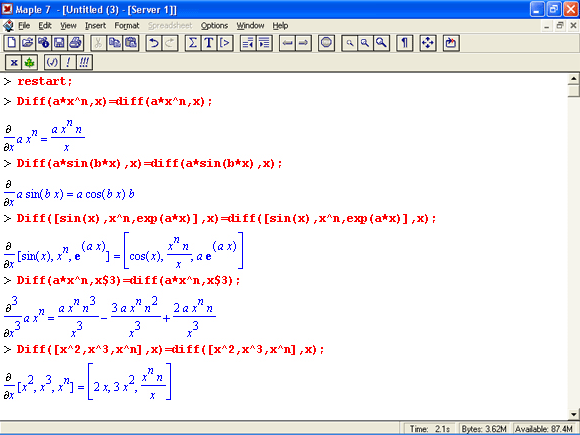
14.gif
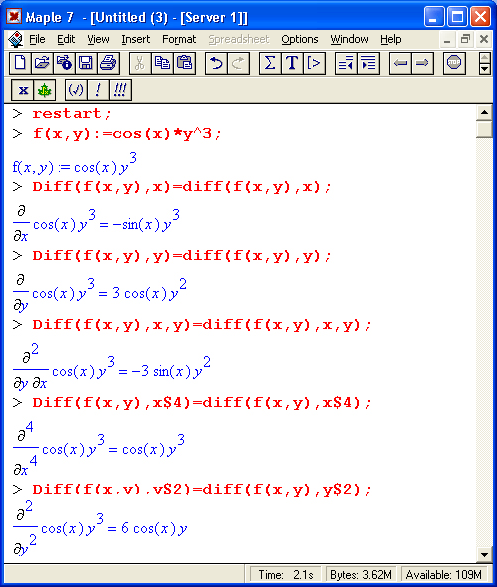
15.gif
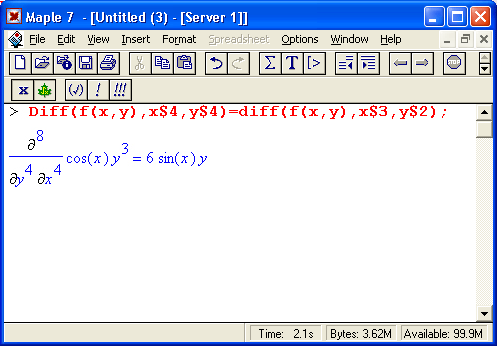
11. Дифференциальный оператор D
Дифференциальный оператор D
Для создания функций с производными может также использоваться дифференциальный оператор D. Порою он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор можно записывать в следующих формах: D(f) или D[i](f), где параметр f — выражение или имя функции, i — положительное целое число, выражение или последовательность. Оператор D(f) просто вычисляет имя производной от f, поскольку в этой форме он эквивалентен unnaplyCdiff (f (х) ,х) ,х). В форме D(f) (х) этот оператор подобен diff (f (x) ,x).
Приведем примеры дифференцирования функций, заданных только именами, и функций с одним параметром:
Следующий пример показывает дифференцирование функции пользователя fun с применением дифференциального оператора D и функции diff:
Дифференциальный оператор можно применять и для дифференцирования функций нескольких переменных по заданной переменной:
Пример применения дифференциального оператора для функции f, заданной программным объектом-процедурой, представлен ниже:
Этот пример показывает реализацию схемы Горнера для полинома b степени n от переменной х. При этом применение оператора дифференцирования возвращает процедуру. Ряд интересных возможностей по вычислению производных предоставляет пакет расширения student.
16.gif
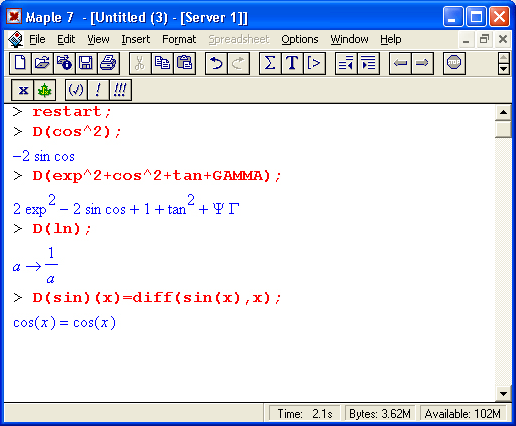
17.gif

18.gif
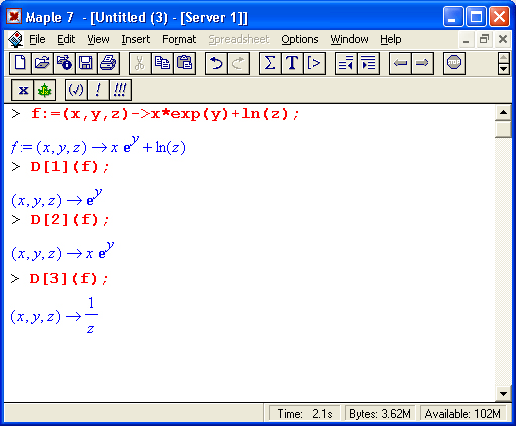
19.gif
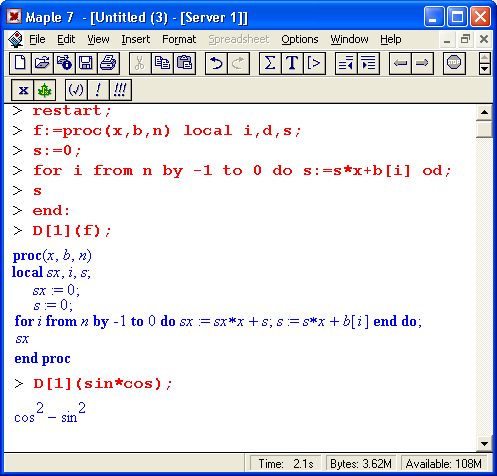
12. Вычисление интегралов
Вычисление интегралов
Вычисление неопределенных интегралов
Вычисление неопределенного интеграла обычно заключается в нахождении первообразной функции. Это одна из широко распространенных операций математического анализа.
Для вычисления неопределенных и определенных интегралов Maple V предоставляет следующие функции:
int(f.x); int(f.x=a..b); int(f.x=a..b,continuous):
Int(f.x); Int(f,x=a..b): Int(f,x=a..b,continuous):
Здесь f — подынтегральная функция, х — переменная, по которой выполняются вычисления, а и b — нижний и верхний пределы интегрирования, continuous — необязательное дополнительное условие.
Maple 7 старается найти аналитическое значение интеграла с заданной подынтегральной функцией, Если это не удается (например, для «не берущихся» интегралов), то возвращается исходная запись интеграла. Для вычисления определенного интеграла надо использовать функцию evalf(int(f ,х=а. .b)). Ниже приведены примеры вычисления интегралов:
Обратите внимание, что в аналитическом представлении неопределенных интегралов отсутствует произвольная постоянная С. Не следует забывать о ее существовании. Для вычисления кратных интегралов (двойных, тройных и т. д.) следует применять функцию int (или Int) внутри такой же функции, делая это столько раз, сколько нужно. В отличие от функции дифференцирования для функции интегрирования нельзя задавать подынтегральные функции в виде списка или множества. Возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов:
ПРИМЕЧАНИЕ
Maple 7 успешно берет большинство справочных интегралов. Но не всегда форма представления интеграла совпадает с приведенной в справочнике. Иногда требуется доводка ее до нужной формы, а иногда Maple 7 упорно дает иное выражение (в большинстве случаев правильное). Тем не менее следует помнить, что всегда может найтись интеграл, который окажется «не по зубам» и Maple 7.
20.gif
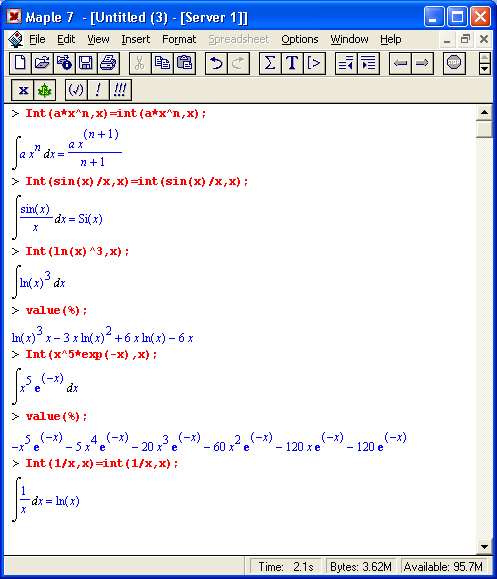
21.gif
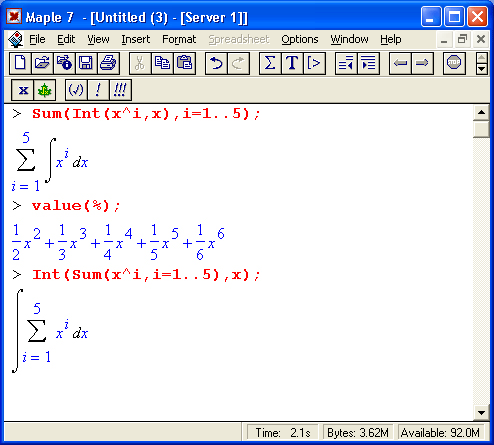
22.gif
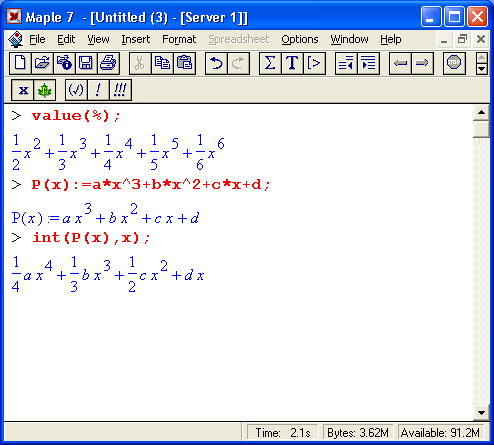
13. Конвертирование и преобразование интегралов
Конвертирование и преобразование интегралов
В некоторых случаях Maple 7 не может вычислить интеграл. Тогда она просто повторяет его. С помощью функций taylor и convert можно попытаться получить аналитическое решение в виде полинома умеренной степени, что демонстрирует следующий характерный пример:
Естественно, что в этом случае решение является приближенным, но оно все же есть и с ним можно работать, например построить график функции, представляющей данный интеграл.
Система Maple непрерывно совершенствуется. Например, в Maple V R4 интеграл с подынтегральной функцией ехр(x^4) не брался, а система Maple 7 с легкостью берет его:
Хотя полученный результат, выраженный через гамма- функцию, нельзя назвать очень простым, но он существует и с ним также можно работать. Например, можно попытаться несколько упростить его, используя функцию simplify:
Разумеется, существует также множество иных возможностей и приемов для выполнения операции интегрирования. В дальнейшем мы неоднократно будем рассматривать и другие, более специфические функции для осуществления интегрирования и вычисления интегральных преобразований. В частности, ряд средств вычисления интегралов реализован в пакете student.
23.gif
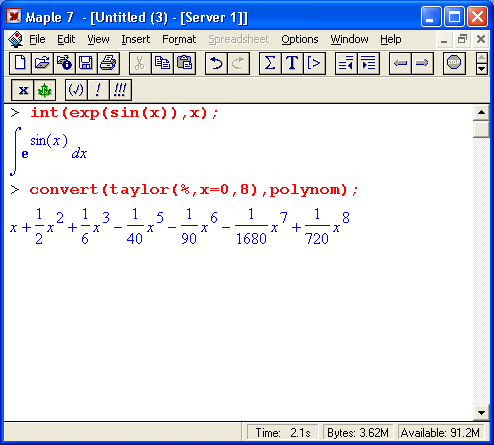
24.gif
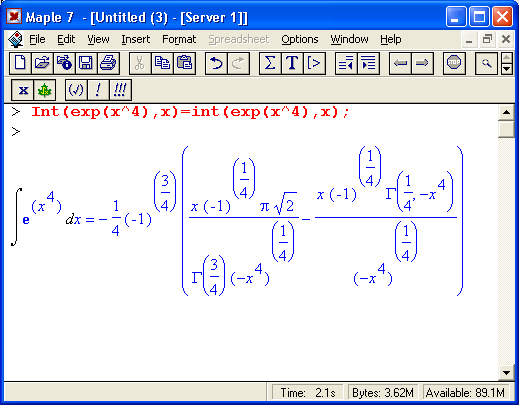
25.gif
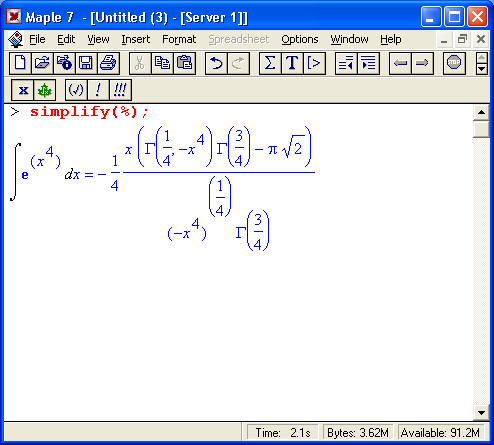
14. Вычисление определенных интегралов
Вычисление определенных интегралов
Другой важной операцией является нахождение в аналитической или численной форме определенного интеграла:
Определенный интеграл удобно трактовать как площадь, ограниченную кривой f(x), осью абсцисс и вертикалями с координатами, равными а и b. При этом площадь ниже оси абсцисс считается отрицательной. Таким образом, значение определенного интеграла — это число или вычисляемое выражение.
Для вычисления определенных интегралов используются те же функции int и Int, в которых надо указать пределы интегрирования, например х=а.. b, если интегрируется функция переменной х. Это поясняется приведенными ниже примерами:
Как видно из этих примеров, среди значений пределов может быть бесконечность, обозначаемая как infinity.
26.gif

27.gif
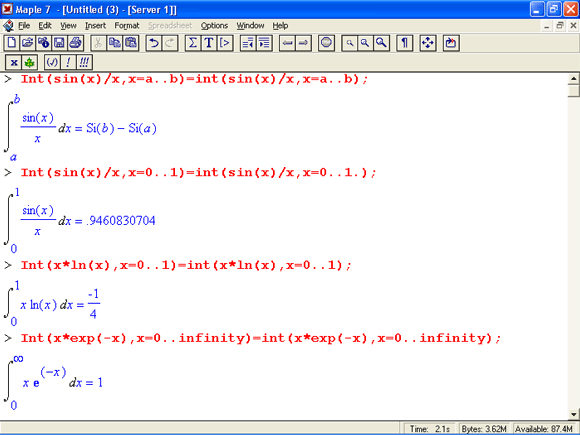
28.gif
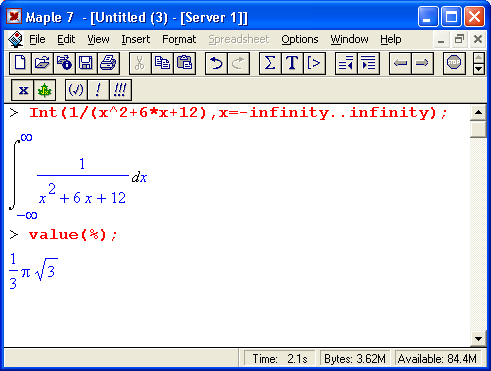
15. Каверзные интегралы и визуализация результатов интегрирования
Каверзные интегралы и визуализация результатов интегрирования
Выше мы уже сталкивались с примерами вычисления «каверзных» интегралов. Немного продолжим эту важную тему и заодно рассмотрим приемы визуализации вычислений, облегчающие понимание их сущности.
В Соросовском образовательном журнале (№ 6, 2000, с. 110) приводятся не совсем удачные примеры вычислений определенного интеграла с применением системы Mathematica, при которых якобы встречаются настолько большие трудности, что они не под силу любому калькулятору или компьютеру. При некоторых попытках вычисления этого интеграла он давал нулевое значение. Но Maple 7 (кстати, как и Mathematica 4) с легкостью берет этот интеграл и позволяет сразу и без какой-либо настройки вычислить для него как точное, так и приближенное значение:
Хотя первое из решений является самым кратким и, скорее всего, единственным точным решением, оно может и должно насторожить опытного пользователя. Дело в том, что в полученном выражении фигурируют большие числа, и потому для правильного приближенного решения (в виде вещественного числа в научной нотации) нужно заведомо использовать аппарат точной арифметики и ни в коем случае не полагаться на погрешность, заданную по умолчанию, — вот в чем основная ошибка в упомянутой статье.
Именно поэтому левая и правая части приближенного решения (выполненного с точностью до 30 цифр) заметно различаются. Знак равенства между ними вызывает чувство протеста у истинных математиков. На самом деле, не надо забывать, что знак равенства здесь был введен просто как текстовый комментарий, — вы можете попробовать сами заменить его на более приемлемый здесь знак приближенного равенства. Любопытно, что предшествующая версия Maple 6 при задании погрешности по умолчанию вычисляла значение этого интеграла также как 0, тогда как Maple 7 «поумнела» уже настолько, что дает значение 0.01835046770 даже в этом случае.
При таких условиях многие читатели могут сомневаться в корректности конечного результата. Между тем Maple 7 позволяет наглядно проиллюстрировать характер промежуточных вычислений подобных интегралов. Например, для этого можно вычислить неопределенный интеграл подобного вида:
Нетрудно заметить, что решение распадается на множество слагаемых, соответствующих общеизвестному интегрированию по частям. В каждом слагаемом имеются большие числа, и потому принципиально необходимо применение арифметики высокой точности (или разрядности). Maple 7 такими средствами, причем превосходными, обладает.
Продолжим изучение данного «каверзного» интеграла. Опробуем силы Maple 7 на интеграле более общего вида, где конкретный показатель степени заменен на обобщенный —п. Здесь нас ожидает приятный сюрприз — Maple 7 с легкостью выдает аналитическое решение для данного определенного интеграла:
Однако радоваться несколько преждевременно. Многие ли математики знают, что это за специальная функция — WhittakerM? Студенты, любящие подшучивать над своим профессором, могут попробовать спросить у него об этом. Скорее всего, профессор стушуется, а потом будет долго копаться в литературе, прежде чем найдет ее определение и сможет разъяснить, что это такое. Но хуже другое — Maple 7 при конкретном n = 20 дает грубо неверное решение — 0 (почему — уже объяснялось). Забавно, что при этом сама по себе функция WhittakerM вычисляется для n = 20 без проблем:
> WhittakerM(10,10.5.1);
6353509348
А теперь присмотритесь к новому результату вычисления злополучного интеграла. Оказывается, он уже не содержит больших чисел, свойственных прямому решению! Зная значение WhittakerM с погрешностью по умолчанию, можно уверенно вычислить приближенное численное значение интеграла с тойже погрешностью, уже не прибегая к арифметике высокой точности:
> (exp(-.5)*WihittakerM(10,10.5.1))/21;
01835046770
Итак, мы вычислили нужный интеграл несколькими разными способами. В этом и проявляется могущество современной математики, достойно представленной такими системами, как Maple 7. Заинтересованный читатель может попытаться найти еще ряд методов решения данного интеграла и преуспеть в этом! Мы же как торжество Maple 7 приведем график зависимости значений данного интеграла от показателя степени n при его изменении от 0 до 50 (рис. 8.1). Надо ли говорить о том, что полученный результат имеет куда более важное значение, чем вычисление нашего злополучного интеграла при конкретном n = 20? А плавный ход графика показывает, что в вычислении данного интеграла нет никаких признаков неустойчивости решения при изменении n, если соблюдать правило выбора погрешности вычислений.
Наличие у функции особых (сингулярных) точек нередко затрудняет выполнение с ней ряда операций, таких как численное интегрирование. В этом случае могут помочь соответствующие параметры. Например, вычисление следующего интеграла дает явно неудобное выражение в виде набора значений, разных для разных интервалов измененияа:
б
Рис. 8.1. Значение интеграла от х^n*ехр(-х) как функция n
Увы, попытка вычислить по этому выражению значение интеграла не всегда дает корректный результат. Например, при х от -2 до 0 получаются бесконечные значения. Да и график зависимости значения интеграла от параметра a имеет подозрительный вид (рис. 8.2). Это как раз тот случай, когда с ходу доверяться результатам Maple 7 рискованно.
В данном случае приходится констатировать давно известный факт — системы компьютерной математики (и Maple 7 в их числе) не всесильны и всегда можно найти интегралы даже с обманчиво простым внешним видом, которые поставят систему в тупик или дадут неверные результаты в той или иной области изменения аргументов. Особенно, опасны интегралы от кусочных функций с разрывами и интегралы, представляемые такими функциями. Именно к ним и относится обсуждаемый сейчас интеграл. Не меньше проблем вызывают интегралы от функций, области определения которых заданы некорректно или просто не изучены.
Между тем ситуация вовсе не является безнадежной. Надо просто знать, что предпринять, чтобы подсказать системе правильный путь решения. Например, в нашем случае, применив параметр continuous (в апострофах), можно получить куда более простое выражение:
б
Рис. 8.2. Построение графика зависимости значений интеграла с подынтегральной функцией 1/(х+а)^2 от параметра а
Рисунок 8.3 показывает это решение с двумя важными дополнениями — оно представляется функцией пользователя, а ее график строится при изменении а от -10 до 10.
Приведем еще один пример «каверзного» интеграла довольно простого вида:
> int(l/x^3,x=-1..2);
undefined
Этот интеграл вообще не берется функцией int без указания параметров (в строке вывода сообщается об этом). Но введение параметра CauchyPrinci pal Value позволяет получить значение интеграла:
Возьмем еще один наглядный пример — вычисление интеграла от синусоидальной функции при произвольно больших пределах, но кратных 2я! Очевидно, что при этом (учитывая равность площадей положительной и отрицательной полуволн синусоиды) значение интеграла будет равно 0. Например:
> int(sin(x),x-1000*pi..l000*pi);
0
Рис. 8.3. Зависимость значения интеграла с подынтегральной функцией 1/(х+а)^2 и пределами от 0 до 2 от параметра а
Однако распространение этого правила на бесконечные пределы интегрирования является грубейшей ошибкой. Интеграл такого рода уже не берется (или говорят, что он не сходится), и Maple 7 дает соответствующий результат:
> int(sin(x),x=-infinity..infinity);
undefined
Во многих областях техники часто употребляются выражения «затухающая синусоида» или «нарастающая синусоида». Иногда говорят и о «синусоиде с уменьшающейся или возрастающей амплитудой». Бесполезно утверждать, что эти названия принципиально ошибочны — в рамках допущений, принятых в технических расчетах, такие утверждения весьма наглядны и эта, в частных случаях вполне оправданная, наглядность с позиций математики идет в ущерб точности фундаментальных определений.
Возьмем, к примеру, широко распространенную функцию: y(t) = exp(-t)sin(2*Pi*t). Построим ее график и вычислим определенный интеграл от этой функции с пределами от 0 до oo (рис. 8.4).
С первого взгляда на график видно, что Каждая положительная полуволна функции (затухающей «синусоиды») явно больше последующей отрицательной полуволны. К тому же осцилляции функции быстро затухают и через десяток-другой периодов значение функции становится исчезающе малым. Вот почему Maple 7 уверенно вычисляет интеграл с такой подынтегральной функцией. Ее свойство — неопределенность при t->oo исчезает.
Рис. 8.4. График «затухающей синусоиды» и интеграл от нее с пределами от 0 до бесконечности
Однако называть такую функцию «затухающей синусоидой», безусловно, неточно. Умножение sin(2pt) на множитель, зависящий от времени t, лишает функцию главного свойства синусоиды — ее строгой симметрии. Так что exp(-t)sin(2pt) — это совсем новая функция со своими отличительными свойствами. Главные из них — несимметрия при малых t и исчезающе малые значения при больших t. Ни тем, ни другим свойством обычная синусоида не обладает. А теперь возьмем антипод этой функции — «синусоиду с экспоненциально нарастающей до стационарного значения 1 амплитудой». Такая функция записывается следующим образом:
Y(t) = (1 - exp(-t)) sin(2*Pi*t).
Ее график и попытки вычисления интеграла с такой подынтегральной функцией приведены на рис. 8.5.
Обратите внимание на то, что здесь прямое вычисление интеграла к успеху не привело, хотя из графика функции видно, что каждая положительная полуволна в близкой к t = 0 области явно больше по амплитуде, чем последующая отрицательная полуволна. Однако в отличие от предыдущей функции при больших значениях аргумента данная функция вырождается в обычную синусоиду с неизменной (и равной 1) амплитудой. Вот почему трудяга Maple 7 честно отказывается вычислять интеграл от такой коварной функции.
Рис. 8.5. График «экспоненциально нарастающей синусоиды» и интеграл от нее с пределами от 0 до бесконечности
На этом примере очень четко отслеживается разница в мышлении инженера и математика. Инженер скажет, что интеграл с такой функций должен быть, поскольку вначале положительные площади явно меньше отрицательных, а в дальней области они выравниваются, и потому площадь каждого «периода» функции становится примерно нулевой. По-своему инженер прав — если его не интересует точное определение подынтегральной области в заоблачных высотах бесконечности, то мы должны получить то же значение интеграла, что в предшествующем примере, но со знаком «минус». И в самом деле (см. рис. 8.5), интегрируя в пределах от 0 до100п, мы получаем именно это значение (опять-таки в пределах погрешности по умолчанию).
И все же прав здесь математик — переход от интегрирования с конечным (да еще и кратным 2тс) пределом к интегрированию с бесконечным пределом — далеко не простая операция. Она требует учета поведения функции при значении аргумента, стремящегося к бесконечности, а тут говорить о нулевой алгебраической площади синусоиды некорректно, ибо никакой кратности величине 2л у бесконечности нет! Остается лишь радоваться тому, что система Maple 7 может примирить математиков и инженеров, дав им в руки средства, позволяющие решать подобные задачи с приближениями, приемлемыми для тех или иных категорий пользователей.
Мы подробно рассмотрели этот класс задач потому, что многие важные интегральные преобразования (например, преобразование Фурье) оперируют с подобными подынтегральными функциями и надо тщательно разбираться в областях их применения.
ПРИМЕЧАНИЕ
Приведенные выше примеры показывают, что интегрирование является гораздо более тонким делом, чем это кажется на первый взгляд. Тут уместно напомнить, что и студент вуза, и профессор математики университета должны очень внимательно исследовать возможности вычисления интегралов того или иного типа разными математическими системами. Иными словами, применять системы компьютерной математики должны только пользователи, обладающие не столько учеными званиями и степенями, сколько культурой выполнения математических вычислений.
29.gif
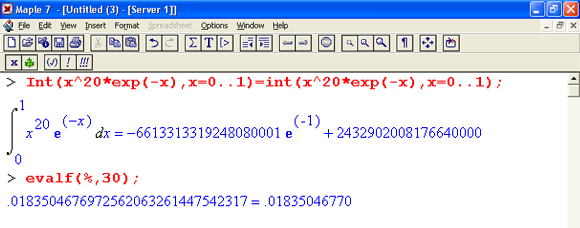
30.gif
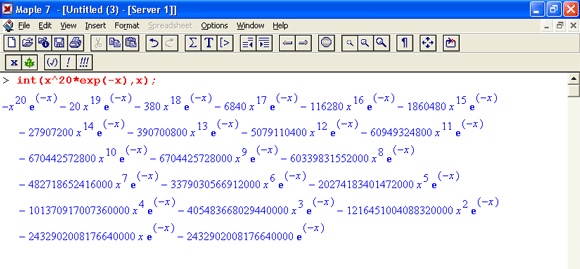
31.gif
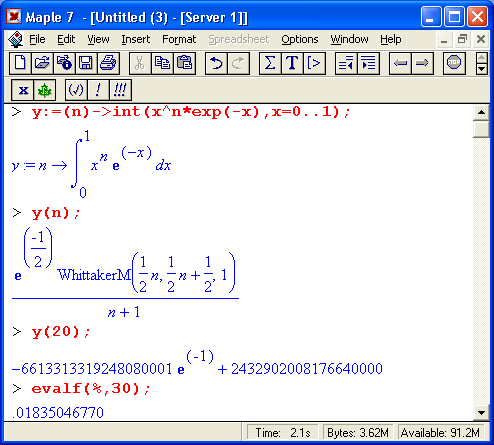
32.gif
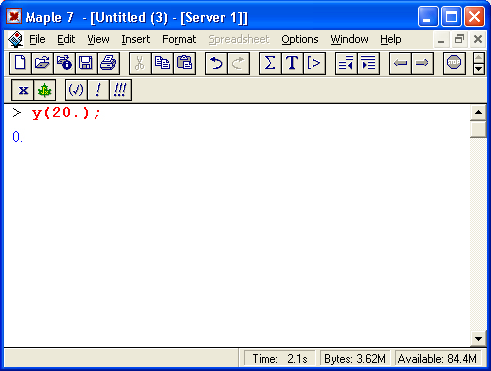
33.gif
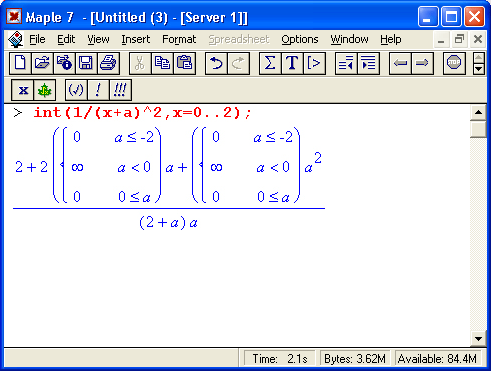
35.gif
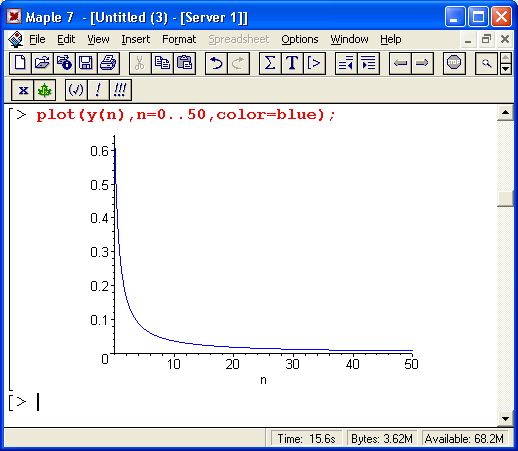
36.gif
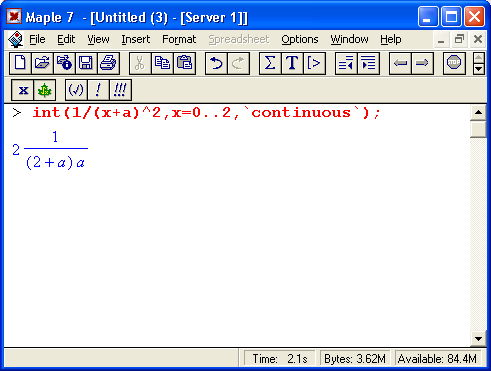
38.gif
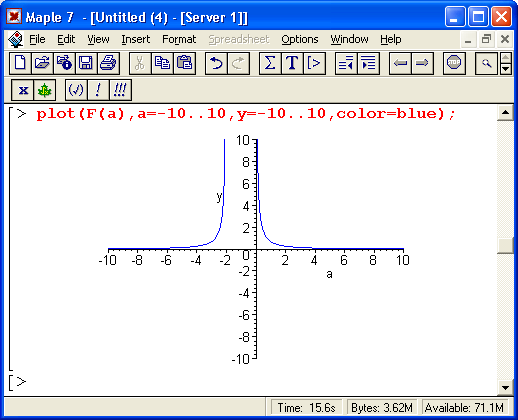
39.gif
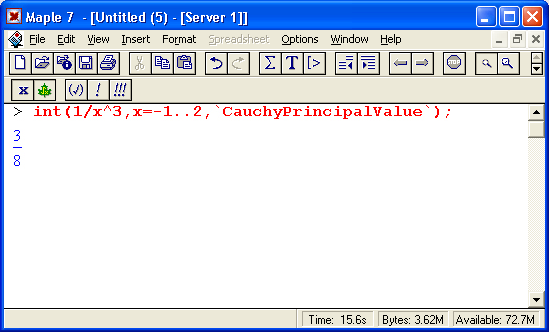
40.gif
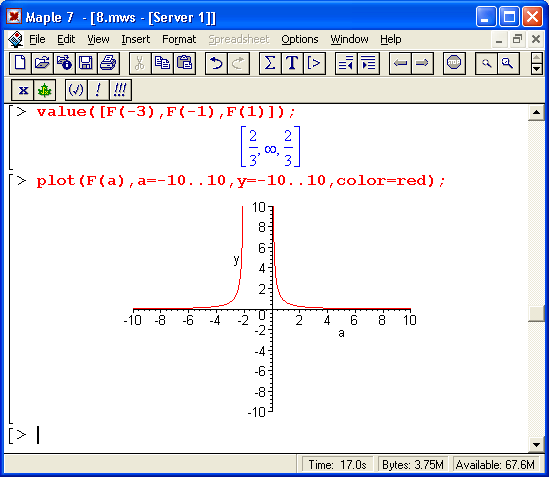
78.gif
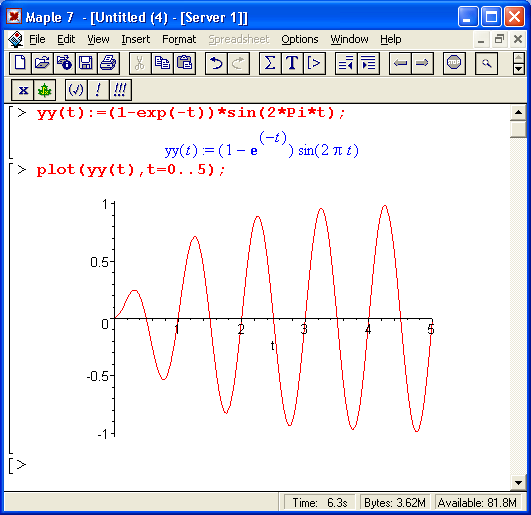
79.gif
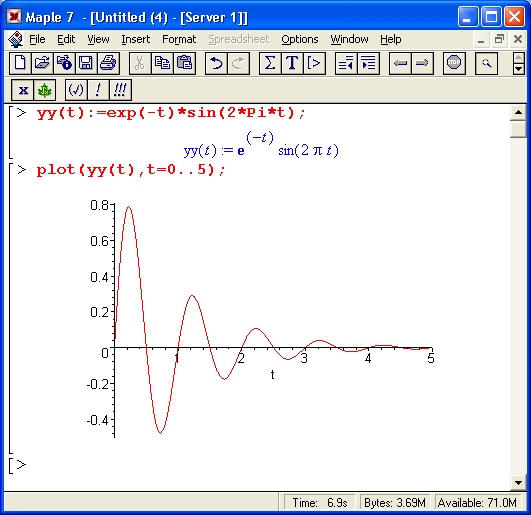
16. Интегралы с переменными пределами интегрирования
Интегралы с переменными пределами интегрирования
К интересному классу интегралов относятся определенные интегралы с переменными пределами интегрирования. Если обычный определенный интеграл представлен числом (или площадью в геометрической интерпретации), то интегралы с переменными пределами являются функциями этих пределов.
На рис. 8.6 показано два примера задания простых определенных интегралов с переменным верхним пределом (сверху) и обоими пределами интегрирования (снизу).
Рис.8.6. Примеры интегралов с переменными пределами интегрирования
На этом рисунке построены также графики подынтегральной функции (это наклонная прямая) и функции, которую задает интеграл.
80.gif
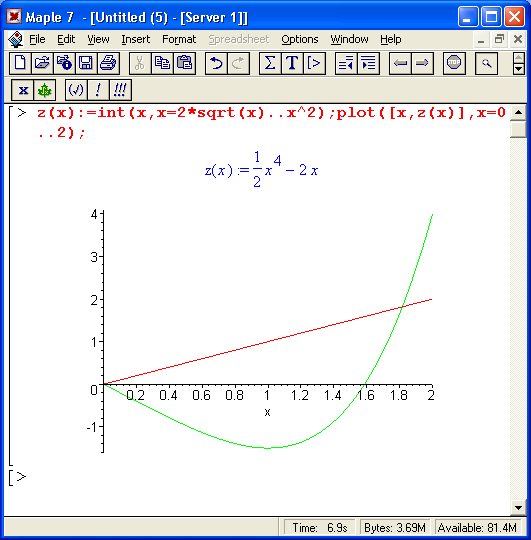
17. Вычисление кратных интегралов
Вычисление кратных интегралов
Функции int и Int могут использоваться для вычисления кратных интегралов, например двойных и тройных. Для этого функции записываются многократно:
Обратите внимание на нечеткую работу функции evalf в последнем примере. Эта функция уверенно выдает значение evalf (Pi) в форме вещественного числа с плавающей точкой, но отказывается вычислить значение интеграла, в которое входит число Pi. Этот пример говорит о том, что отдельные недостатки у Maple 7 все же есть, как и поводы для ее дальнейшего совершенствования.
Описанная возможность вычисления кратных интегралов функциями Int и int не является вполне законной. В пакете расширения student имеются дополнительные функции интегрирования, которые дополняют уже описанные возможности. В частности, в этом пакете есть функции для вычисления двойных и тройных интегралов.
44.gif
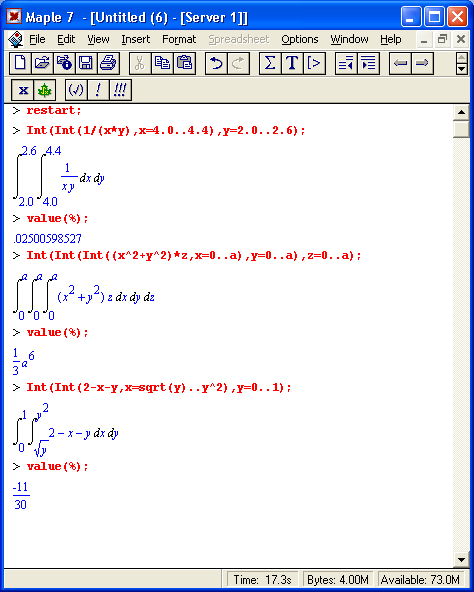
18. Вычисление пределов функций
Вычисление пределов функций
Для вычисления пределов функции f в точке х =а используются следующие функции:
limit(f,x=a); limit(f,x=a.dir);
Limit(f.x=a); Limit(f.x-a.dir);
Здесь f - алгебраическое выражение, х - имя переменной, dir - параметр, указывающий на направление поиска предела (left — слева, right — справа, real — в области вещественных значений, complex — в области комплексных значений). Значением а может быть бесконечность (как положительная, так и отрицательная). Примеры применения этих функций для вычисления пределов в точке приведены ниже:
Обратите внимание на то, что в первом примере фактически дано обозначение предела в самом общем виде. Рисунок 8.7 показывает вычисление пределов функции tan(x) в точке х=n/2, а также слева и справа от нее. Для указания направления используются опции right (справа) и left (слева). Видно, что в самой точке предел не определен (значение undefined), а пределы справа и слева уходят в бесконечность.
Рис. 8.7. Пример вычисления пределов функции tan(x) и построение ее графика
Показанный на рис. 8.7 график функции tan(x) наглядно подтверждает существование пределов справа и слева от точки х = П/2 и отсутствие их в самой этой точке, где функция испытывает разрыв от значения +oo до -oo.
45.gif
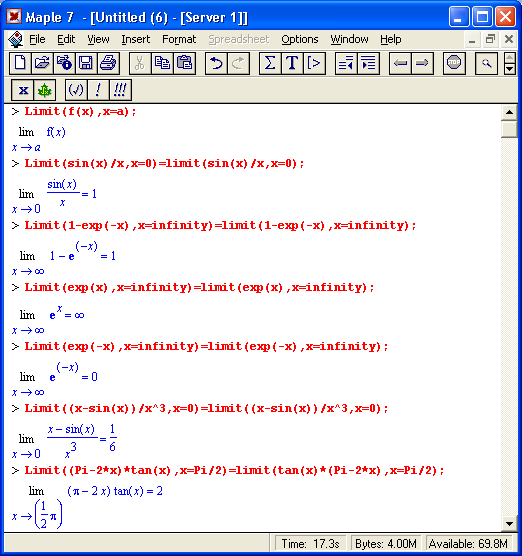
81.gif
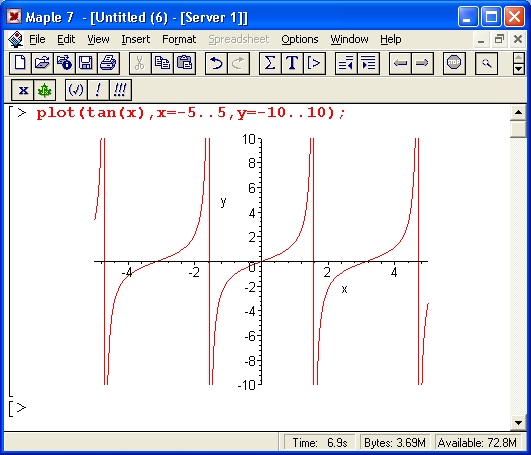
19. Разложение функций в ряды
Разложение функций в ряды
Огромное разнообразие функций давно заставляло математиков задумываться над возможностями их приближенного, но единообразного представления. К таким представлениям относятся различные ряды, сходящиеся к значениям функций в окрестности заданной точки. Для разложения функции или выражения ехрr в обычный степенной ряд служат функции series(ехрr, eqn) и series(expr, eqn, n). Здесь ехрr — разлагаемое выражение, eqn — условие (например, в виде х=а) или имя переменной (например, х) и n — необязательное и неотрицательное целое число, задающее число членов ряда (при его отсутствии оно по умолчанию берется равным 6, но может переустанавливаться системной переменной Order). Если в качестве eqn задано имя переменной, то это соответствует разложению по этой переменной в области точки с ее нулевым значением. Задав eqn в виде х=х0, можно получить разложение по переменной х в окрестности точки х = х0.
Разложение получается в форме степенного многочлена, коэффициенты которого задаются рациональными числами. Остаточная погрешность задается членом вида 0(х)^n. При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert. Ниже представлены примеры разложения различных выражений в ряд:
Здесь видно, что член, обозначающий погрешность, отсутствует в тех разложениях, которые точны, например, в разложениях степенных многочленов. Для визуализации приближения рядами заданных аналитических зависимостей очень полезно построить на одном графике кривые аналитической зависимости и разложения в ряд. Мы это покажем чуть позже на примере ряда Тейлора.
47.gif
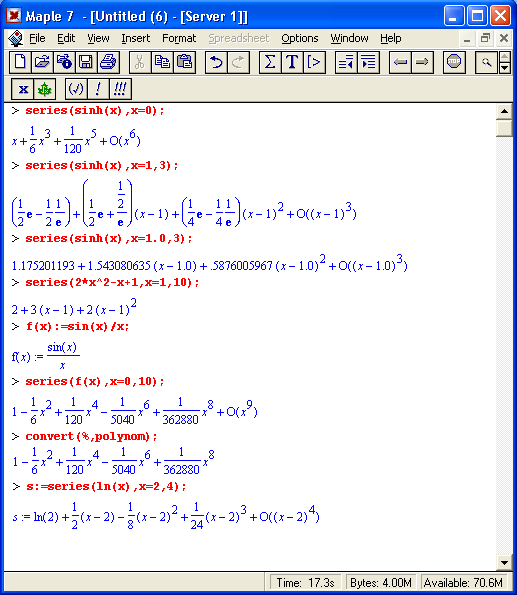
20. Разложение в ряды Тейлора и Маклорена
Разложение в ряды Тейлора и Маклорена
Для разложения в ряд Тейлора используется функция taylor(expr, eq/nm, n). Здесь ехрr — разлагаемое в ряд выражение, eq/nm — равенство (в виде х=а) или имя переменной (например, х), n — необязательный параметр, указывающий на порядок разложения и представленный целым положительным числом (при отсутствии указания порядка он по умолчанию принимается равным 6). При задании eq/nm в виде х=а разложение производится относительно точки х =а. При указании eq/nm в виде просто имени переменной разложение ищется в окрестности нулевой точки, то есть фактически вычисляется ряд Маклорена.
Ниже представлены примеры применения функции taylor:
Не все выражения (функции) имеют разложение в ряд Тейлора. Ниже дан пример такого рода:
> taylor(l/x+x^2,x,5):
Error, does not have a taylor expansion, try seriesQ
> series(l/x+x^2,x,10);
je-4*2
> taylor(l/x+x*2,x=l,5);
2 +x - 1 + 2(x - 1f - (x - 1 )3 +(x - 1 )4 +O((x- 1 )5)
Здесь Maple 7 отказалась от вычисления ряда Тейлора в окрестности точки х = 0 (по умолчанию) и предложил воспользоваться функцией series. Однако эта функция просто повторяет исходное разложение. В то же время в окрестности точки х = 1 ряд Тейлора вычисляется.
Для разложения в ряд Тейлора функций нескольких переменных используется библиотечная функция mtaylor:
mtaylor(f. v)
mtaylorCf. v. n)
mtaylor(f. v, n, w)
Здесь f — алгебраическое выражение, v — список имен или равенств, n — необязательное число, задающее порядок разложения, w — необязательный список целых чисел, задающих «вес» каждой из переменных списка v. Эта функция должна вызываться из библиотеки Maple 7 с помощью команды readlib:
Для получения только коэффициента при k=м члене ряда Тейлора можно использовать функцию coeftayl (expr,var,k). Если ехрr — функция нескольких переменных, то k должен задаваться списком порядков коэффициентов.
48.gif
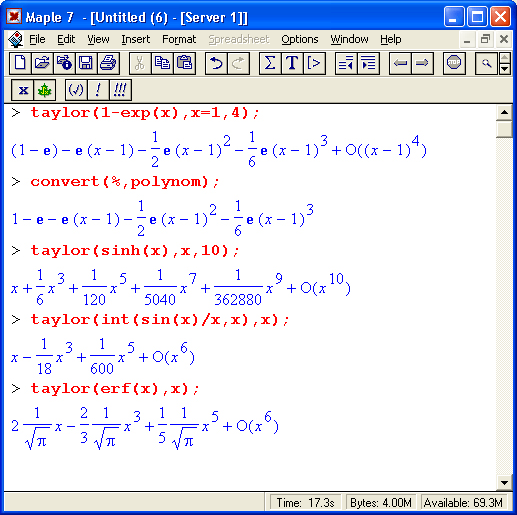
49.gif
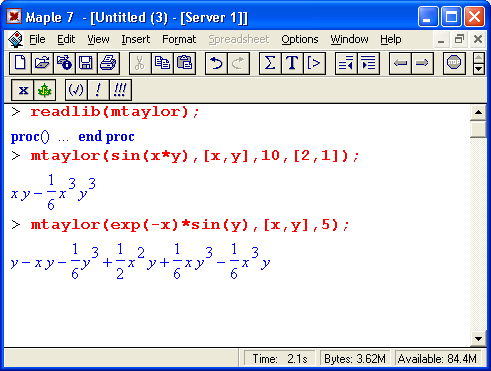
21. Пример документа — разложение синуса в ряд
Пример документа — разложение синуса в ряд
Полезно сочетать разложение выражений (функций) в ряд Тейлора с графической визуализацией такого разложения. Рассмотрим документ, в котором наглядно показаны возможности представления функции рядами Тейлора и Маклорена. На рис. 8.8 показана первая часть документа. Она дает пример разложения в ряд Тейлора функции sin(x) с построением ее графика и графика по разложению в ряд. Поскольку выбрано разложение относительно точки х = 0, то полученный ряд является рядом Маклорена. Это хороший пример визуализации результатов математических вычислений — здесь наглядно видно, что при малых значениях х график ряда практически повторяет разлагаемую функцию, но затем начинает сильно от нее отходить.
Обратите внимание, несмотря на то что мы задали шестой порядок ряда, последний член имеет только пятый порядок. Это связано со спецификой данного разложения — в нем просто отсутствуют члены четного порядка. Можно буквально в считанные секунды попробовать изменить число членов ряда или диапазон изменения переменной х, что и показано на рис. 8.9 (вторая часть документа). При этом легко убедиться в том, что при больших х поведение ряда не имеет ничего общего с поведением разлагаемой в ряд функции, в частности нет и намека на периодичность разложения, которая присуща тригонометрической функции sin(x).
В заключительной (третьей) части этого документа (рис. 8.10) представлено уже истинное разложение синуса в ряд Тейлора в окрестности смещенной от нуля точки х = 1. При смещении точки, относительно которой ведется разложение, выражение для ряда Тейлора существенно изменяется. В нем, во-первых, появляются члены четных степеней, а во-вторых, фигурирует аргумент вида (х- 1)n. Нетрудно заметить, что даже при представлении такой «простой» функции, как sin(x), приемлемая погрешность представления одного периода достигается при числе членов ряда Тейлора порядка 10 и более. Однако существенное повышение порядка ряда нецелесообразно из-за резкого возрастания вычислительных погрешностей. Кроме того, серьезным недостатком аппроксимации рядом Тейлора является непредсказуемое поведение полинома вдали от точки, относительно которой задается представление. Это хорошо видно на всех трех приведенных примерах.
Рис. 8.8. Разложение функции sin(x) в ряд Маклорена 6-го порядка и построение ее графика
Рис. 8.9. Разложение функции sin(x) в ряд Маклорена 12-го порядка и построение ее графика
a
Рис. 8.10. Разложение функции sin(x) в ряд Тейлора 12-го порядка относительно точки х = 1 и построение ее графика
Помимо указанных выше разложений в ряд Maple 7 имеет множество функций для иных разложений. Например, в пакете numapprox имеется функция laurent(expr,var,n), позволяющая получить разложение в ряд Лорана, функция chebyshev(expr, eq/nm, eps) дает разложение в форме полиномов Чебышева и т. д.
64.gif
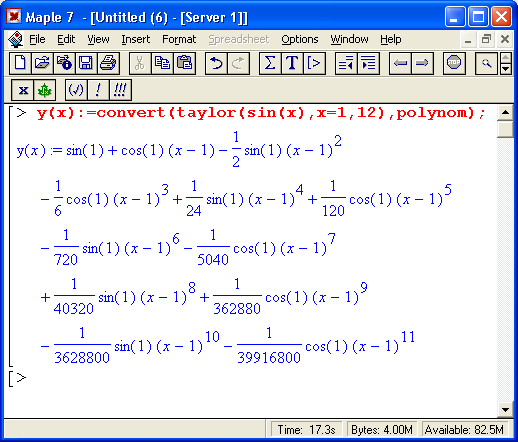
65.gif
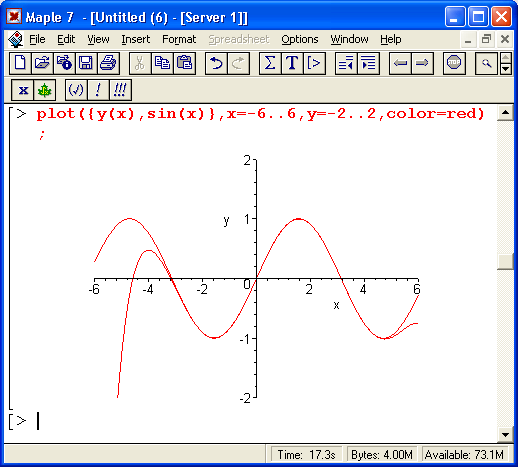
66.gif
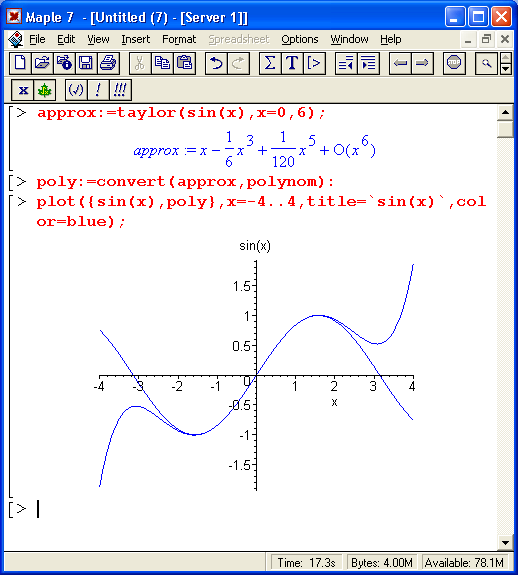
82.gif
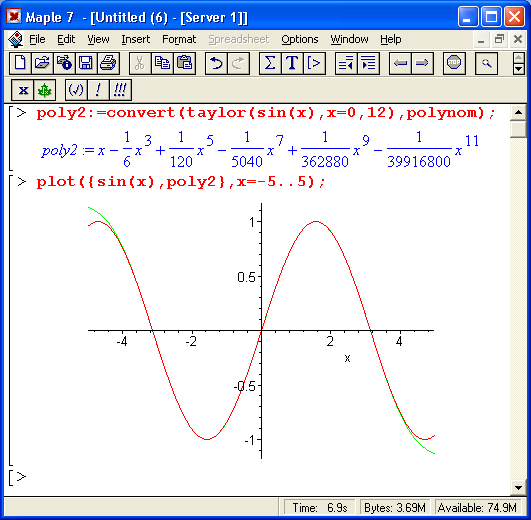
22. Решение уравнений и неравенств
Решение уравнений и неравенств
Решение линейных и нелинейных уравнений и неравенств — еще одна важная область математического анализа. Maple 7 имеет мощные средства для такого решения. Так, для решения линейных и нелинейных уравнений в аналитическом виде используется достаточно универсальная и гибкая функция solve(eqn, var) или so1ve({eqnl,eqn2,.. .}.{varl,var2,...}), где eqn — уравнение, содержащее функцию ряда переменных, var — переменная, по которой ищется решение, Если при записи eqn не используются знак равенства или знаки отношения, считается, что solve ищет корни уравнения eqn=0.
Характер решений можно изменить с помощью глобальных переменных:
- _SolutionsMayBeLost — при значении true дает решение, которое при обычном применении функции solve возвращает значения NULL;
- _MaxSols — задает максимальное число решений;
- _EnvAll Solutions — при значении true задает выдачу всех решений.
В решениях могут встречаться следующие обозначения:
- _NN — указывает на неотрицательные решения;
- _В — указывает на решения в бинарной форме;
- _Z — указывает на то, что решение содержит целые числа;
- %N — при текстовом формате вывода задает общие члены решения и обеспечивает более компактную форму его представления.
В форме solve[subtopic] возможны параметры subtopic функции solve следующих типов:
floats functions identity ineq linear
radical scalar series system
При решении систем уравнений они и список переменных задаются как множества, то есть в фигурных скобках. При этом и результат решения получается в виде множества. Чтобы преобразовать его к обычному решению, нужно использовать функцию assign, которая обеспечивает присваивание переменным значений, взятых из множества.
Функция solve старается дать решение в аналитическом виде. Это не означает, что ее нельзя использовать для получения корней уравнений в численном виде. Просто для этого придется использовать функции evalf или convert. Если результат решения представлен через функцию RootOf, то зачастую можно получить все корни с помощью функции all values.
23. Решение одиночных нелинейных уравнений
Решение одиночных нелинейных уравнений
Решение одиночных нелинейных уравнений вида f(x) = 0 легко обеспечивается функций solve(f,(x),x). Это демонстрируют следующие примеры:
Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной:
В частности, это позволяет легко проверить решение (даже если оно не одно, как в приведенном примере) подстановкой (subs):
Сводящиеся к одному уравнению равенства вида f1(x)=fl(x) также решаются функцией solve(fl(x)=f2(x),x):
Обратите внимание в этих примерах на эффективность применения функции evalf, позволяющей получить решения, выраженные через функцию RootOf, в явном виде.
50.gif
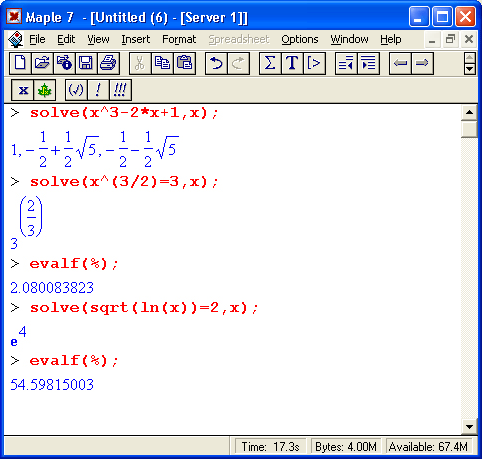
51.gif
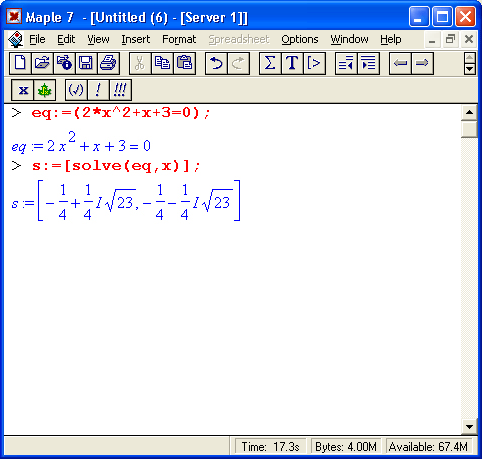
52.gif
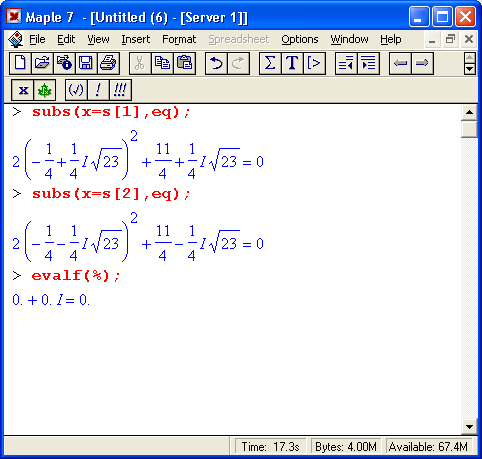
53.gif
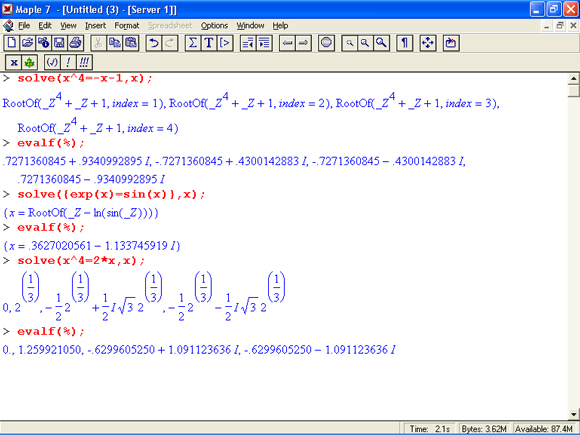
24. Решение тригонометрических уравнений
Решение тригонометрических уравнений
Функция solve может использоваться для решения тригонометрических уравнений:
Однако из приведенных примеров видно, что при этом найдено только одно (главное) решение. Периодичность тригонометрических функций и связанная с этим множественность решений оказались проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду:
> _EnvAllSolutions:=true;
EnvAllSolutions := true
Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить следующее:
На рис. 8.11 показан более сложный случай решения нелинейного уравнения вида f1(x)=f2(x). где f1(х) = sin(x) и f2(x) = cos(x) - 1. Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней.
В решениях встречаются переменные _В1- и _Z1~, означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже:
Рис. 8.11. Пример решения уравнения, имеющего периодические решения
54.gif
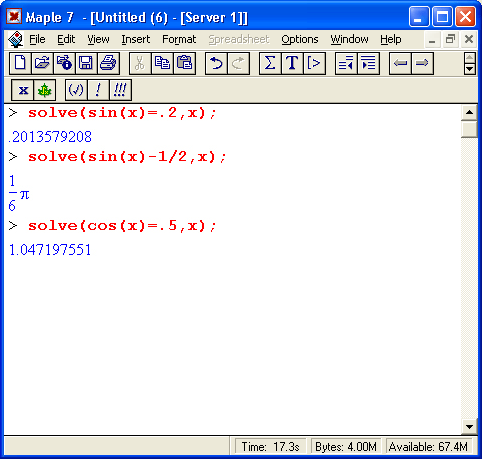
55.gif
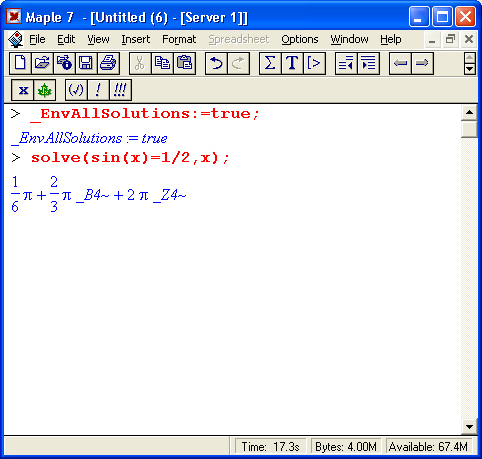
56.gif
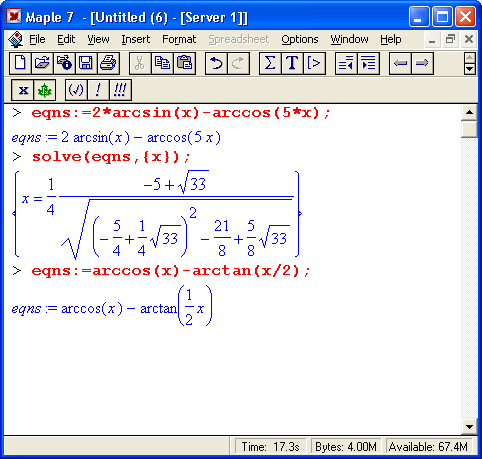
57.gif
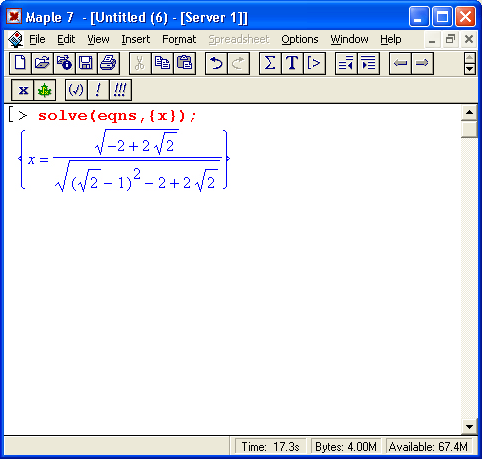
67.gif
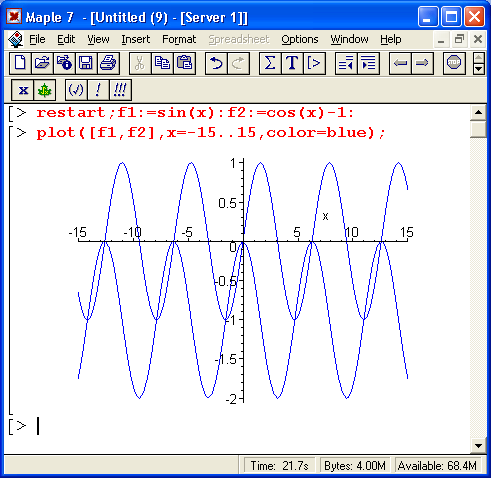
25. Решение систем линейных уравнений.
Решение систем линейных уравнений
Для решения систем линейных уравнений созданы мощные матричные методы, которые будут описаны отдельно. Однако функция solve также может с успехом решать системы линейных уравнений. Такое решение в силу простоты записи функции может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств (см. приведенные ниже примеры).
Рисунок 8.12 дает два примера решения систем из двух линейных уравнений. В первом примере функция solve возвращает решение в виде значений неизвестных х и у, а во втором отказывается это делать.
В чем дело? Оказывается, в том, что во втором случае система просто не имеет решения. Импликативная графика пакета расширения plots дает прекрасную возможность проиллюстрировать решение. Так, нетрудно заметить, что в первом случае геометрическая трактовка решения сводится к нахождению точки пересечения двух прямых, отображающих два уравнения. При этом имеется единственное решение, дающее значения х и у.
Рис. 8.12. Примеры решения системы из двух линейных уравнений с графической иллюстрацией
Во втором случае решения и впрямь нет, ибо уравнения задают параллельно расположенные прямые, которые никогда не пересекаются. Рекомендуем читателю самостоятельно проверить и третий случай — бесконечного множества решений. Он имеет место, если оба уравнения описывают одну и ту же зависимость и их графики сливаются в одну прямую.
Решение систем из трех линейных уравнений также имеет наглядную геометрическую интерпретацию — в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Для наглядности желательно представить и линии пересечения плоскостей. Это позволяет сделать функция импликативной трехмерной графики tmplicitplotSd, что и показано на рис. 8.13. Для объединения графиков площадей использована функция display.
Некоторые проблемы с решением систем из трех линейных уравнений иллюстрируют примеры, приведенные на рис. 8.14, В первом примере решения вообще нет. График показывает, в чем дело, — линии пересечения плоскостей идут параллельно и нигде не пересекаются. Во втором примере все три плоскости пересекаются по одной линии.
Рис. 8.13. Пример решения системы из трех линейных уравнений с графической иллюстрацией решения
Рис. 8.14. Графическая иллюстрация особых случаев решения системы из трех линейных уравнений
Следующий пример показывает решение системы из четырех линейных уравнений:
Эта система имеет решение, но его простая графическая иллюстрация уже невозможна.
Случай решения неполной системы уравнений (уравнений — 3, а неизвестных — 4) иллюстрирует следующий пример:
Как видно из приведенных примеров, функция solve неплохо справляется с решением систем линейных уравнений.
58.gif
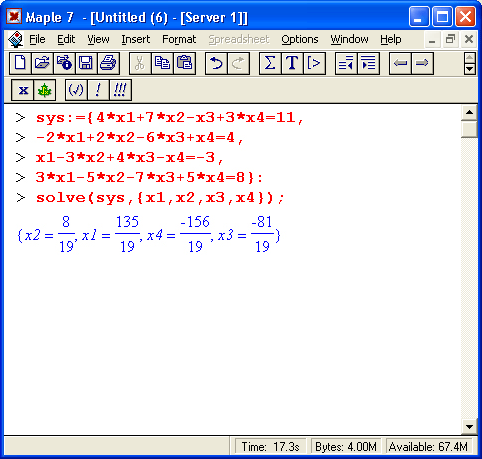
59.gif
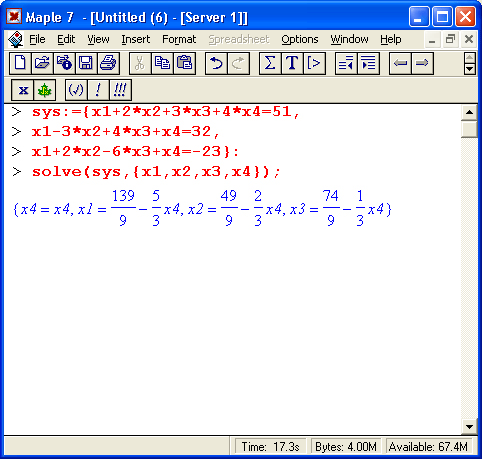
83.gif
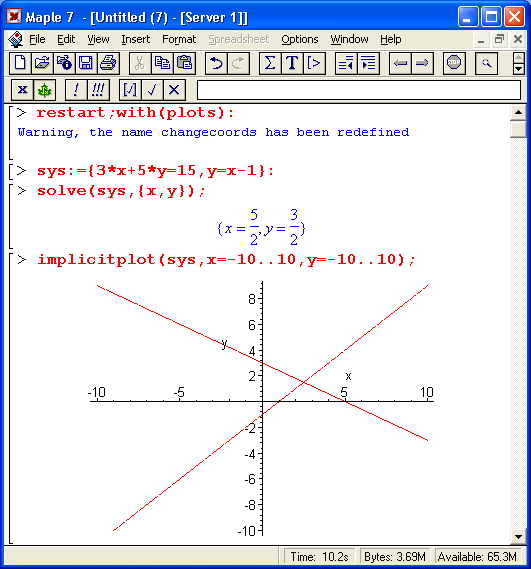
84.gif

85.gif
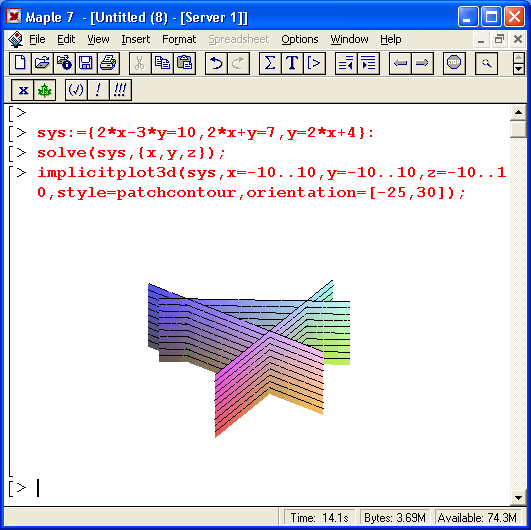
26. Решение систем нелинейных и трансцендентных уравнений
Решение систем нелинейных и трансцендентных уравнений
Функция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств. Ниже приведены примеры решения уравнений:
В этих примерах хорошо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятие определения переменных с помощью заключения их в прямые апострофы.
60.gif
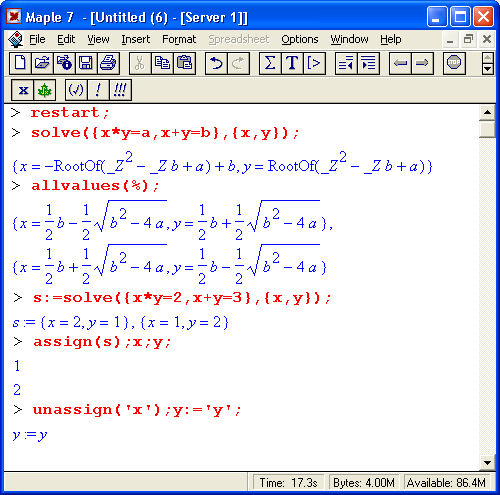
27. Функция RootOf.
Функция RootOf
В решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде RootOf(ехрr) или RootOf(ехрr, х), где ехрr — алгебраическое выражение или равенство, х — имя переменной, относительно которой ищется решение. Если х не указана, ищется универсальное решение по переменной _Z. Когда ехрr задано не в виде равенства, решается уравнение ехрr=0. Для получения решений вида RootOf в явном виде может использоваться функция all values. Примеры применения функции RootOf:
Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений.
61.gif
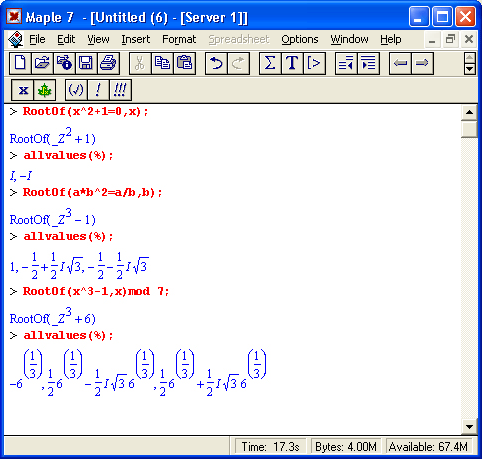
28. Решение уравнений со специальными функциями
62.gif
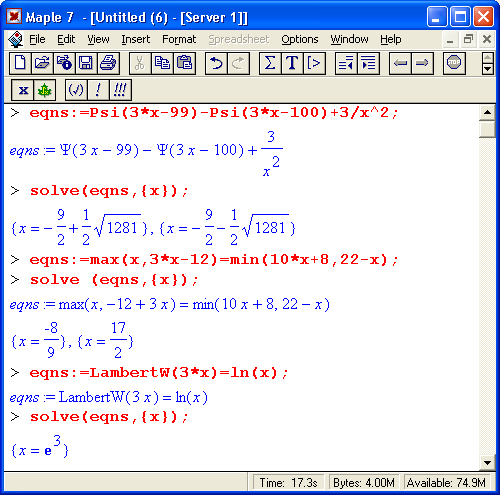
29. Решение неравенств
Решение неравенств
Неравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например: > (больше), < (меньше) и т. д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 8.15 примеры поясняют технику решения неравенств.
Из приведенных примеров очевидна форма решений — представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство, — это позволяет наглядно убедиться в правильности решения. Приведем еще несколько примеров решения неравенств в аналитической форме:
б
Рис. 8.15. Примеры, иллюстрирующие решение неравенств
В последних примерах показано решение систем неравенств." При этом выдаются области определения нескольких переменных.
63.gif
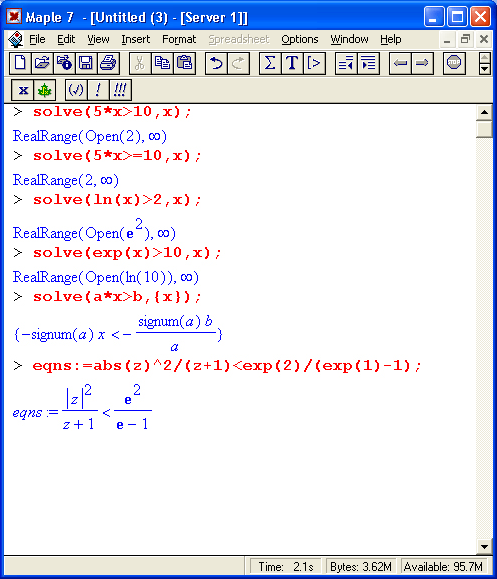
68.gif
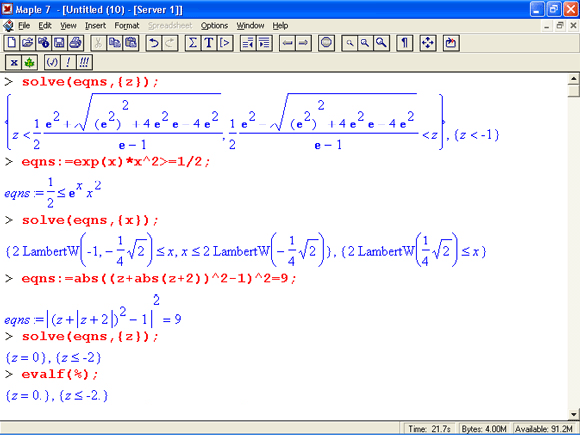
69.gif
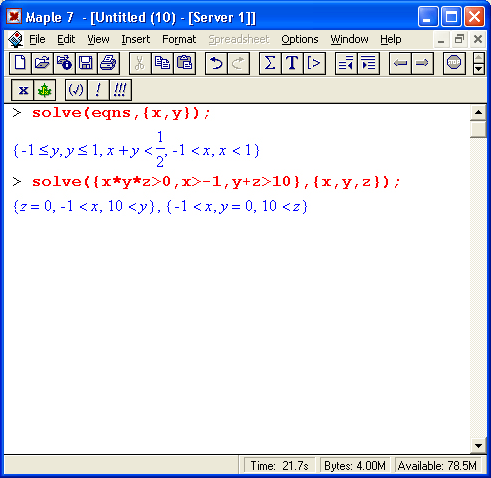
77.gif
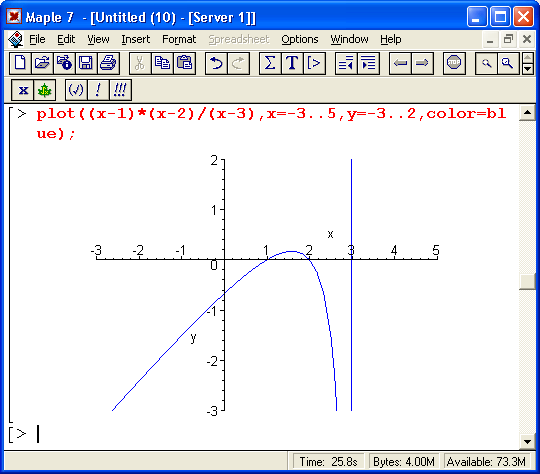
30. Решение функциональных уравнений
70.gif
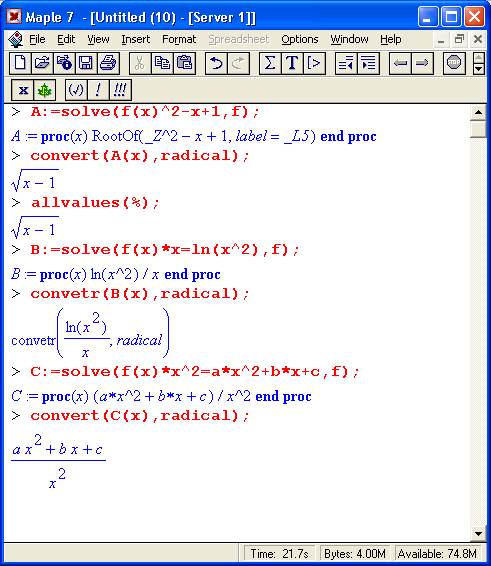
31. Решение уравнений с линейными операторами
71.gif
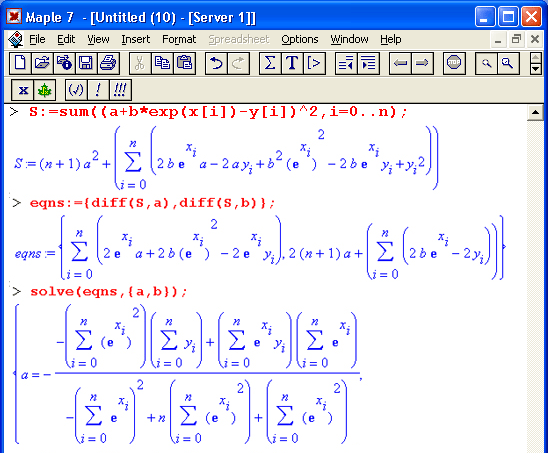
32. Решение в численном виде — функция fsolve
Решение в численном виде — функция fsolve
Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию:
fsolve( eqns. vars. options )
Эта функция может быть использована со следующими параметрами:
- complex — находит один или все корни полинома в комплексной форме;
- full digits — задает вычисления для полного числа цифр, заданного функцией Digits;
- maxsols=n — задает нахождение только n корней;
- interval — задается в виде а. .b или х=а. .b, или (х=а. .b, y=c. .d, ...} и обеспечивает поиск корней в указанном интервале.
Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры:
Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и д.
Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2:
> so1ve(erf(x)=l/2,x);
RootOf(2erf(_Z)-l)
> fsolve(erf(x)=l/2);
.4769362762
Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve находит обычное приближенное решение.
72.gif
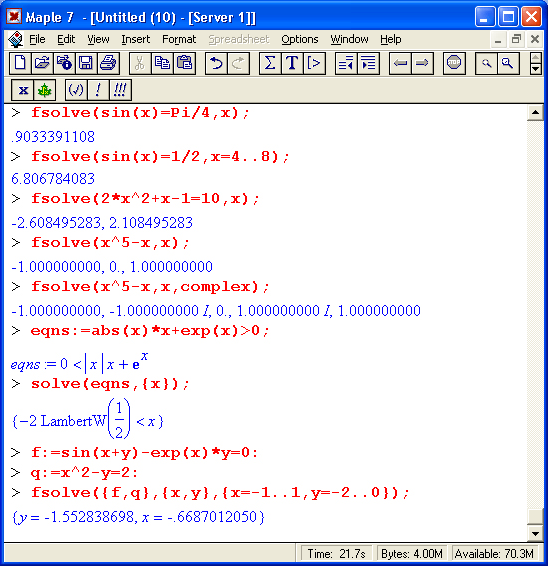
33. Решение рекуррентных уравнений — rsolve
Решение рекуррентных уравнений — rsolve
Функция solve имеет ряд родственных функций. Одну из таких функций — fsolve — мы рассмотрели выше. В справочной системе Maple 7 можно найти ряд и других функций, например rsolve для решения рекуррентных уравнений, isolve для решения целочисленных уравнений, msolve для решения по модулю m и т. д. Здесь мы рассмотрим решение уравнений важного класса — рекуррентных. Напомним, что это такие уравнения, у которых заданный шаг решения находится по одному или нескольким предшествующим шагам.
Для решения рекуррентных уравнений используется функция rsolve:
rsolve(eqns, fens) ,
rsolve(eqris. fens, 'genfunc'(z))
rsolve(eqns, fens, 'makeproc')
Здесь eqns — одиночное уравнение или система уравнений, fens — функция, имя функции или множество имен функций, z — имя, генерирующее функциональную переменную.
Ниже представлены примеры применения функции rsolve:
А теперь приведем результат вычисления функцией rsolve n-го числа Фибоначчи. Оно задается следующим выражением:
> eql :- (f(n+2) = f(rn-l) + f(n) . f(0) - 1 . f(l) - 1}:
eql~{f(n+2) = f(n + \) + f(n),f(0)=\,f(l)=l}
В нем задана рекуррентная формула для числа Фибоначчи — каждое новое число равно сумме двух предыдущих чисел, причем нулевое и первое числа равны 1. С помощью функции rsolve можно получить поистине ошеломляющий результат:
Числа Фибоначчи — целые числа. Поэтому представленный результат выглядит как весьма сомнительный. Но на самом деле он точный и с его помощью можно получить числа Фибоначчи. Ниже показан процесс получения чисел Фибоначчи для n = 5, 7, 10 и 20:
> [normal(subs(n=5,al).expanded).normal(subs(n-7.al).expanded).
normal(subs(n=10,al),expanded),normal(subs(n=20.al),expanded)];
[8,21,89,10946]
73.gif
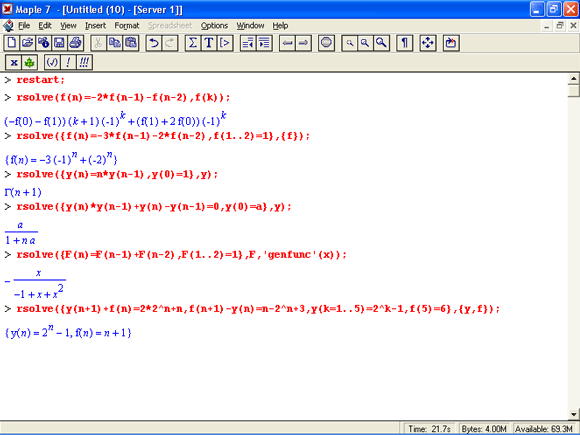
74.gif
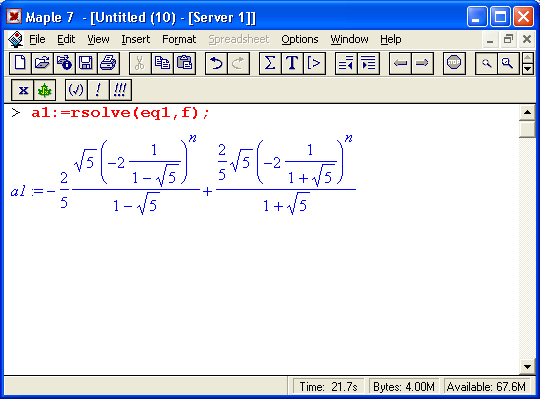
34. Решение уравнений в целочисленном виде — isotve
Решение уравнений в целочисленном виде — isolve
Иногда бывает нужен результат в форме только целых чисел. Для этого используется функция isolve(eqns, vans), дающая решение в виде целых чисел. Приведем примеры ее применения:
> iso1ve({2*x-5=3*y}):
{x = 4 + 3_Zl,y=\ + 2_Z1]
> iso1ve(y^4-z^2*y^2-3*x*z*y*2-x^3*z);
Во втором из приведенных примеров в выводе появилась вспомогательная переменная %1, которая упрощает запись результата при текстовом формате его вывода (Character Notation). Напоминаем, что в стандартной математической нотации вспомогательная переменная вида %N не формируется. В этом случае упомянутый пример будет выглядеть следующим образом:
Результат вычислений одинаков при любом формате вывода, но иногда вывод в текстовом формате с выделением вспомогательных переменных имеет преимущество, поскольку выглядит более компактным.
75.gif
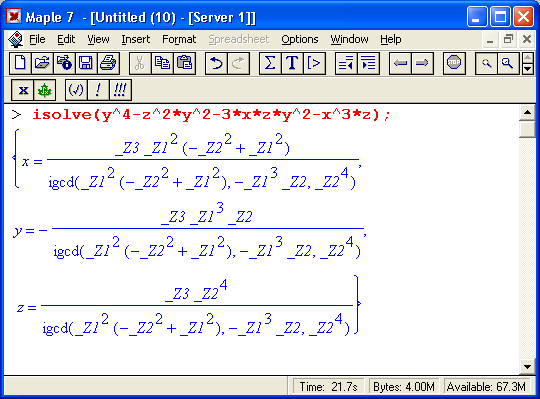
35. Функция msolve.
Функция msolve
Функция msolve(eqns,vars.m) или msolve(eqns,m) обеспечивает решение вида Z mod m (то есть при подстановке решения левая часть4 при делении нат дает остаток, равный правой части уравнения). При отсутствии решения возвращается объект NULL (пустой список).
Ниже даны примеры использования функции msolve:
> mso1ve({3*x-4*y=l,7*x+y=2}.12);
{у = 5,х=3}
> msolve(2^i=3.19);
{(=13 + 18_Z7~}
> mso1ve(8*j-2,x,17);
{/ = 3 + 8*}
На этом мы завершаем рассмотрение функций для решения уравнений, неравенств и систем с ними.
36. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Вычислять суммы членов последовательностей.
- Вычислять произведения членов последовательностей.
- Вычислять производные.
- Вычислять интегралы.
- Разлагать функции в ряды.
- Решать уравнения и неравенства.
Урок 10. Символьные (аналитические) операции
1. Основные операции с выражениями
Урок 10.
Символьные (аналитические) операции
Выражения (ехрr) или уравнения (eqn) обычно используются как сами по себе, так и в виде равенств или неравенств. В последнем случае объекты с выражениями имеют левую и правую части. Для простейших манипуляций с выражениями полезны следующие функции:
- cost (а) — возвращает число сложений и умножений в выражении а (функция пакета codegen);
- Ihs(eqn) — выделяет левую часть eqn;
- rhs(eqn) — выделяет правую часть eqn;
- normal (ехрr) — дает нормализацию (сокращение) ехрr в виде дроби;
- numer(expr) — выделяет числитель ехрr;
- Оdenom(expr) — выделяет знаменатель ехрr.
Ввиду очевидности действия этих функций ограничимся наглядными примерами их применения:
ПРИМЕЧАНИЕ
Обратите внимание на то, что в предшествующих версиях Maple загрузка библиотеч ной функции cost выполнялась иначе — командой readlib(cost). Это обстоятельство может служить причиной неверной работы документов, созданных в старых версиях Maple, в среде описываемой версии Maple 7.
1.gif
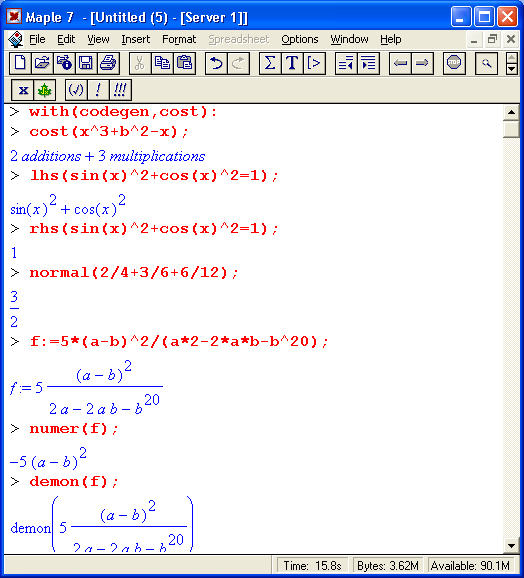
2. Работа с уровнями вложенности выражений
Работа с уровнями вложенности выражений
В общем случае выражения могут быть многоуровневыми и содержать объекты, расположенные на разных уровнях вложенности. Приведем две функции для оценки уровней выражений и списков:
- nops(expr) — возвращает число объектов первого уровня (операндов) в выражении ехрr;
- ор(ехрr) — возвращает список объектов первого уровня в выражении ехрr;
- ор(n.ехрr) — возвращает n-й объект первого уровня в выражении ехрr.
Ниже представлены примеры применения этих функций:
Рекомендуется просмотреть и более сложные примеры на применение этих функций в справке.
2.gif
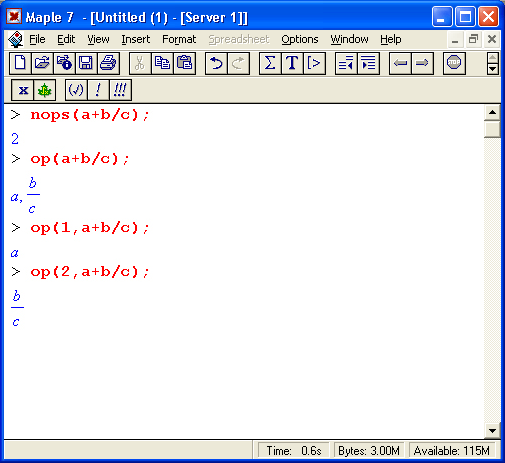
3. Преобразование выражений в тождественные формы
Преобразование выражений в тождественные формы
Многие математические выражения имеют различные тождественные формы. Порою преобразование выражения из одной формы в другую позволяет получить результат, более удобный для последующих вычислений. Кроме того, различные функции Maple 7 работают с разными формами выражений и разными типами данных. Поэтому большое значение имеет целенаправленное преобразование выражений и данных.
Основной функцией для такого преобразования является функция convert:
convert(expr. form, аrgЗ. ...)
Здесь ехрr — любое выражение, form — наименование формы, аrg3, ... — необязательные дополнительные аргументы.
convert — простая и вместе с тем очень мощная функция. Ее мощь заключается в возможности задания множества параметров. Их полный перечень (76 штук!) можно найти в справке по функции convert. Многие из этих параметров очевидны с первого взгляда, поскольку повторяют наименования типов чисел, данных или функций. Например, опции binary, decimal, hex и octal преобразуют заданные числа в их двоичное, десятичное, шестнадцатеричное и восьмеричное представление. Параметр vector задает преобразование списка в вектор (напоминаем, что список и вектор — разные типы данных), а параметр matrix — в матрицу. Приведем примеры применения функции convert:
Из этих примеров (их список читатель может пополнить самостоятельно) следует, что функция преобразования convert является одной из самых мощных функций Maple. С ее помощью можно получить множество различных форм одного и того же выражения.
3.gif
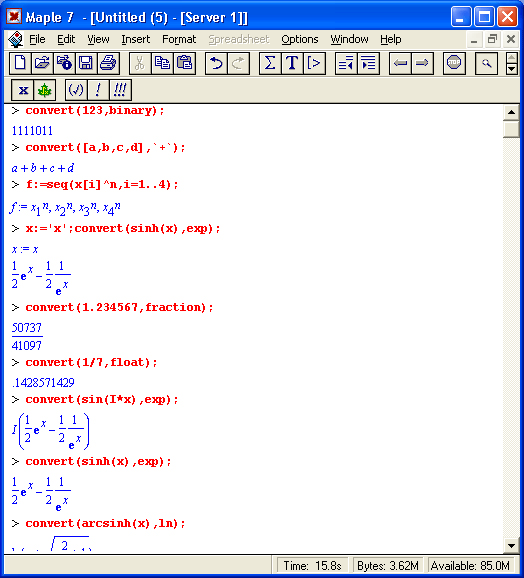
4.gif
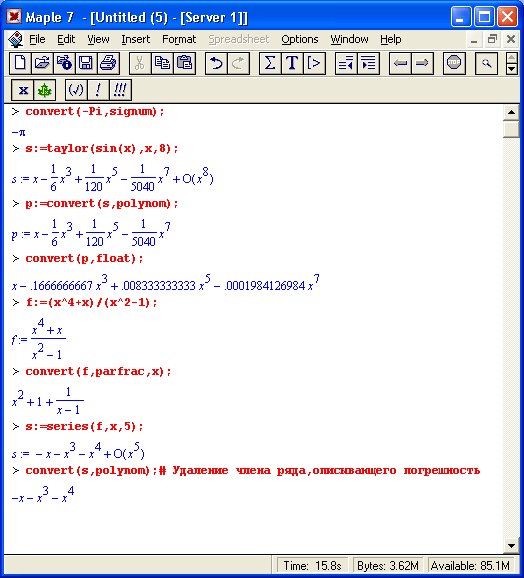
4. Преобразование выражений
Преобразование выражений
Еще одним мощным средством преобразования выражений является функция combine. Она обеспечивает объединение показателей степенных функций и преобразование тригонометрических и некоторых иных функций. Эта функция -может записываться в трех формах:
combine(f)
combinef(, n)
combine(f. n. optl. opt2. ...)
Здесь f — любое выражение, множество или список выражений; n — имя, список или множество имен; optl, opt2, ... — имена параметров. Во втором аргументе можно использовать следующие функции:
|
@@ |
abs |
arctan |
conjugate |
exp |
|
In |
piecewise |
polylog |
power |
product |
|
Ps |
radical |
range |
signum |
trig |
Примеры применения функции combine представлены ниже:
Эти примеры далеко не исчерпывают возможностей функции combine в преобразовании выражений. Рекомендуется обзорно просмотреть примеры применения функции combine с разными параметрами, приведенные в справочной системе Maple 7.
5.gif
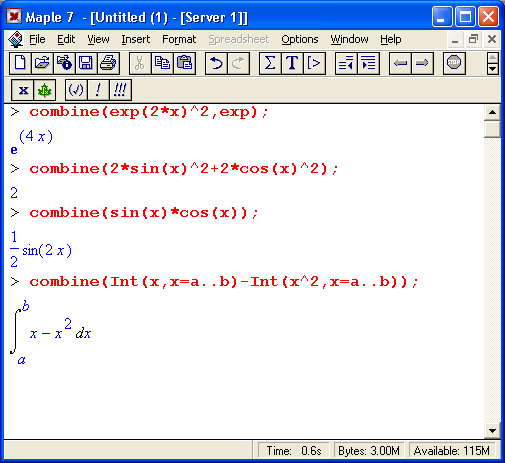
5. Контроль за типами объектов
Контроль за типами объектов
Выражения и их части в Maple 7 рассматриваются как объекты. В ходе манипуляций с ними важное значение имеет контроль за типом объектов. Одной из основных функций, обеспечивающих такой контроль, является функция whattype(object), возвращающая тип объекта, например string, integer, float, fraction, function и т. д. Могут также возвращаться данные об операторах. Примеры применения этой функции даны ниже:
> whattype(2+3);
integer
> whattype(Pi):
symbol
> whattype(123./5)
float
> whattype(l/3i:
fraction
> whattype(sin(x));
function
> whattype([1.2.3,a,b,c])
;list
> whattype(a+b+c);
+
> whattype(a*b/c):
*
> whattype(a'b):
^
> whattype(H-2+3=4);
=
С помощью функции type(object.t) можно выяснить, относится ли указанный объект к соответствующему типу t, например:
> type(2+3,integer):
true
> type(s1n(x).function);
true
> typeChello,string);
false
> type("hello",string);
true
> typed/3.fraction):
true
При успешном соответствии типа объекта указанному (второй параметр) функция type возвращает логическое значение true, в противном случае — false.
Для более детального анализа объектов может использоваться функция hastype(expr. t), где ехрr — любое выражение и t — наименование типа подобъекта.
Эта функция возвращает логическое значение true, если подобъект указанного типа содержится в выражении ехрr. Примеры применения этой функции даны ниже:
> hastype(2+3,integer);
true
> hastype(2+3/4.integer):
false
> hastype(2*sin(x).function);
true
> hastype(a+b-c/d,'+'):
true
Еще одна функция — has(f.x) — возвращает логическое значение true, если подобъект х содержится в объекте f, и false в ином случае:
> has(2*sin(x),2);
true
> has(2*sin(x).V);
false
> has(2*sin(x),3-l);
true
Следует отметить, что соответствие подобъекта выражения указанному подобъекту понимается в математическом смысле. Так, в последнем примере подобъект «3 - 1», если понимать его буквально, в выражении 2*sin(r) не содержится, но Maple-язык учитывает соответствие 3 - 1 = 2, и потому функция has в последнем примере возвращает true.
6. Подстановки
Подстановки
Функциональные преобразования подвыражений
Нередко бывает необходимо заменить некоторое подвыражение в заданном выражении на функцию от этого подвыражения. Для этого можно воснользоваться функцией applyop:
- applyop(f, i, е) — применяет функцию f к i-му подвыражению выражения е
- applyop(f, i, е. ..., xk, ...) — применяет функцию f к i'-му подвыражении выражения е с передачей необязательных дополнительных аргументов xk.
Ниже даны примеры применения этой функции:
6.gif
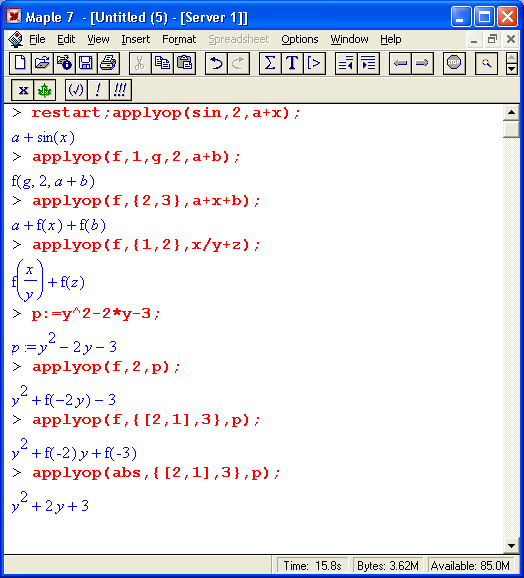
7. Функциональные преобразования элементов списков
Функциональные преобразования элементов списков
Еще две функции, реализующие операции подстановки, указаны ниже:
map(fcn, expr. arg2. .... argn)
map2(fcn, argl, expr. arg3, .... argn)
Здесь fen — процедура или имя, expr — любое выражение, argi — необязательные дополнительные аргументы для fen.
Первая из этих функций позволяет приложить fen к операндам выражения ехрr. Приведенные далее примеры иллюстрируют использование функции mар.
Из этих примеров нетрудно заметить, что если второй параметр функции mар — список, то функция (первый параметр) прикладывается к каждому элементу списка, так что возвращается также список. Из последнего примера видно, что если за вторым параметром идет перечисление аргументов, то они включаются в список параметров функции.
Функция mар2 отличается иным расположением параметров. Ее действие наглядно поясняют следующие примеры:
7.gif
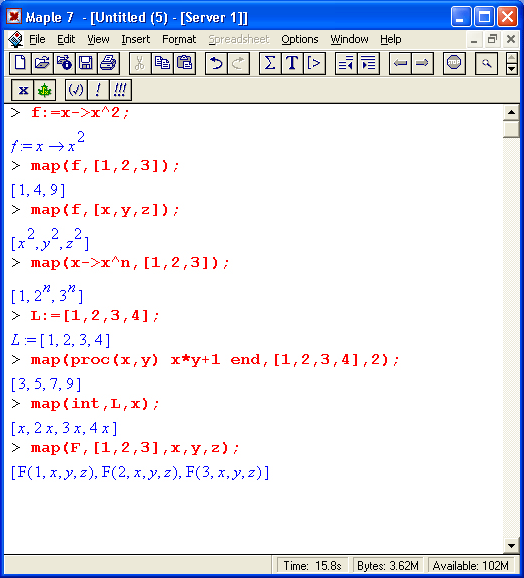
8.gif
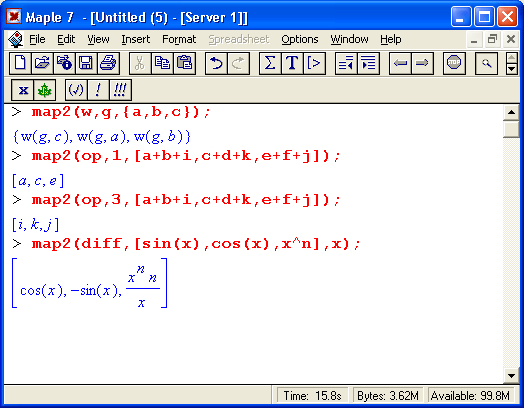
8. Подстановки с помощью функций add, mul и seq
9.gif
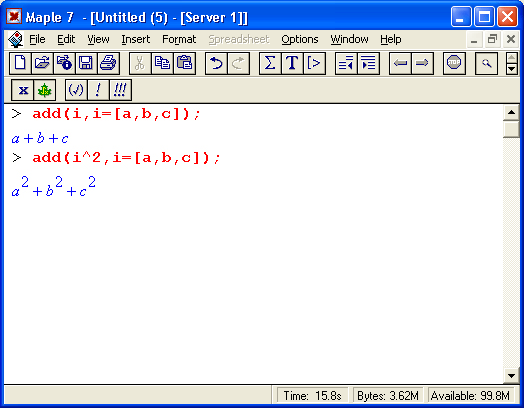
10.gif
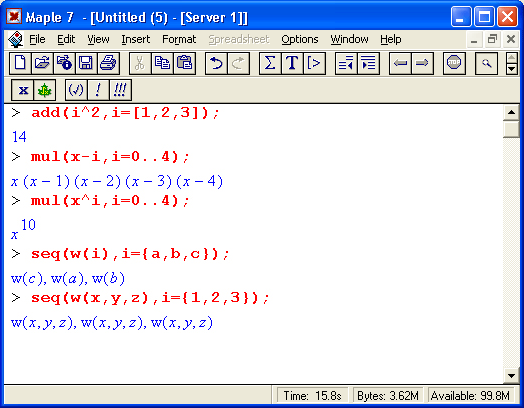
9. Подстановки с помощью функций subs и subsop
Подстановки с помощью функций subs и subsop
Подстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной ее численным значением. Основные операции подстановки выполняют следующие функции: .,
- subs(x=a.e) — в выражении е заменяет подвыражение х на подвыражение а;
- subs(sl,...,sn,e) — в выражении е заменяет одни подвыражения на другие, выбирая их из списков si, ..., sn вида х=а;
- subsop(eql, eq2, .... eqi, ...eqn, e) — в выражении е заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni — номер операнда, ei — выражение для замены.
Все эти функции возвращают измененное после подстановки выражение. Ниже показаны примеры применения функций подстановок:
Следует обратить внимание на то, что результат подстановок, полученный с помощью функции subop, порой может не совпадать с ожидаемым. Поэтому полезно контролировать получаемые в результате подстановок выражения на их корректность.
Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки:
Здесь задана система из трех нелинейных уравнений, которая затем решена функцией solve. В конце примера с помощью функции подстановки выполнена проверка правильности решения. Оно верно, поскольку у всех уравнений значение левой части совпадает со значением правой части.
11.gif
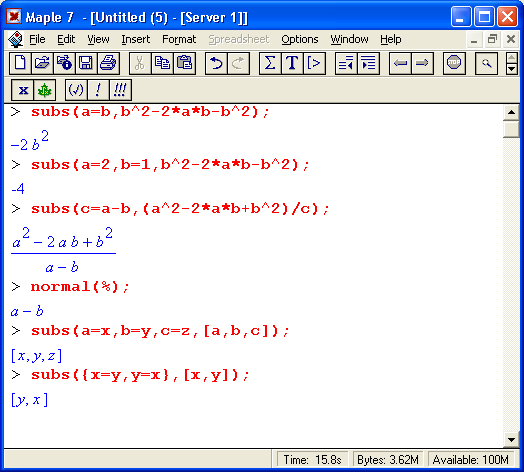
12.gif

13.gif
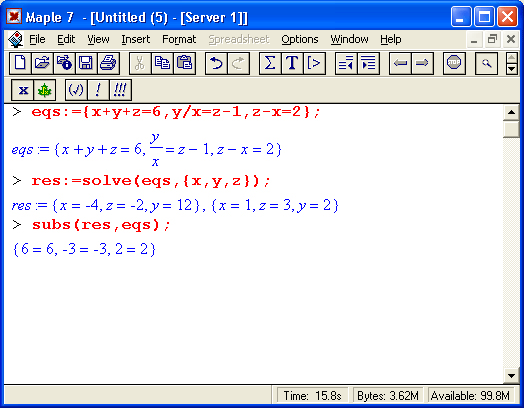
10. Функции сортировки и селекции
Функции сортировки и селекции
Сортировка и селекция выражений широко используются в практике символьных преобразований. Для выполнения сортировки служит функция sort, применяемая в одной из следующих форм:
sort(L) sort(L. F) sort(A) sort(A. V)
Здесь L — список сортируемых значений, F — необязательная булева процедура с двумя аргументами, А — алгебраическое выражение, V — необязательные дополнительные переменные.
ПРИМЕЧАНИЕ
Вы можете проверить, что функция sort в Maple 7 способна сортировать буквы и даже слова русского языка.
Если функция сортировки меняет порядок расположения членов в выражении (или порядок расположения выражений), то другая функция — select — служит для выделения требуемого выражения:
select(f, e)
select(f, е. Ы. ..., bn)
Как бы обратной ей по действию служит функция remove, устраняющая заданные выражения:
remove(f, e)
remove(f, е, b1.... bn)
В этих функциях f — процедура, возвращающая логическое значение, е — список, множество, сумма, произведение или функция, b1, ..., bn — необязательные дополнительные аргументы.
Далее даны примеры применения этих функций.
Maple имеет также оператор селекции А[ехрr]. Его действие поясняют следующие примеры:
14.gif
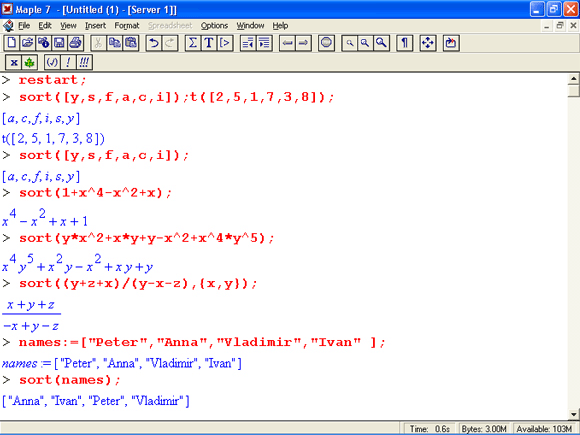
15.gif
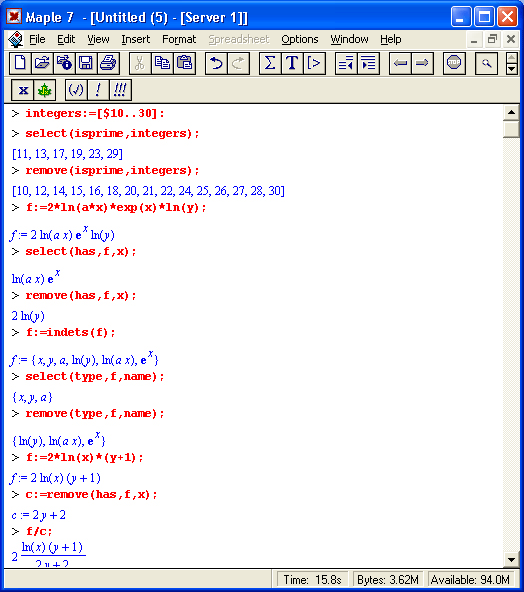
16.gif
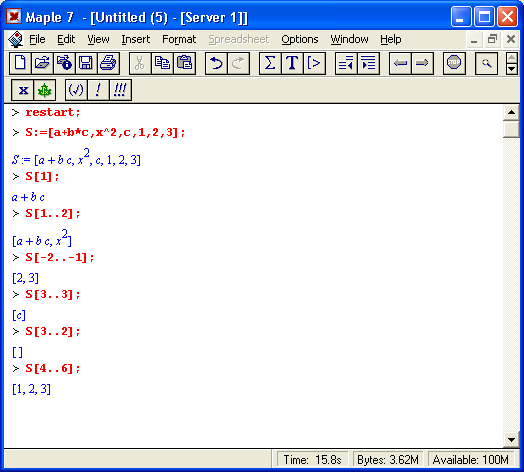
17.gif
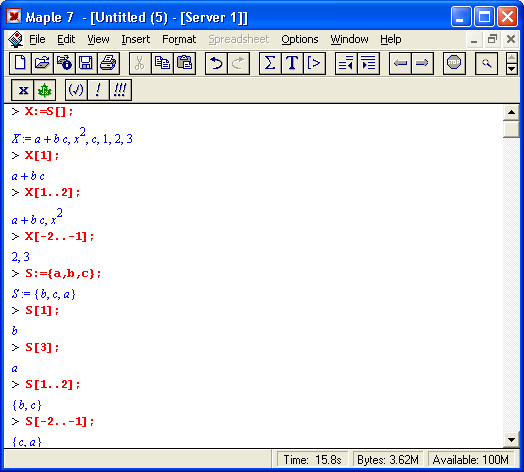
11. Упрощение выражений
Упрощение выражений
Функция simplify — одна из самых мощных в системах символьной математики. Она предназначена для упрощения математических выражений. «Все гениальное просто», — любим мы повторять, хотя это далеко не всегда так. Тем не менее стремление представить многие математические выражения в наиболее простом виде поощряется в большинстве вычислений и нередко составляет их цель. В системе Maple 7 функция упрощения используется в следующем виде:
- simplify(expr) — возвращает упрощенное выражение ехрr или повторяет его, если упрощение в рамках правил Maple 7 невозможно;
- simplify(expr, nl, n2, ...) —возвращает упрощенное выражение ехрr с учетом параметров с именами nl, n2, ... (в том числе заданных списком или множеством);
- simplify(ехрг,assume=prop) — возвращает упрощенное выражение ехpr с учетом всех условий.
Функция simplify — многоцелевая. Она обеспечивает упрощение математических выражений, выполняя следующие типовые действия (для простоты обозначим их как ->):
- комбинируя цифровые подвыражения (3*х*5->15*х, 10*х/5->2*х);
- приводя подобные множители в произведениях (х^3*а*х->а*х^4);
- приводя подобные члены в суммах (5*х+2+3*х->8*х+2);
- используя тождества, содержащие ноль (а+0->а, х-0->х);
- используя тождества, содержащие единицу (1*х->х);
- распределяя целочисленные показатели степени в произведениях ((3*x*y^3)^2 ->9*х^2*у^6);
- сокращая ехрr на наибольший общий полиномиальный или иной множитель;
- понижая степень полиномов там, где это возможно;
- используя преобразования, способные упростить выражения.
Несмотря на свою гибкость, функция simplify не всегда способна выполнить возможные упрощения. В этом случае ей надо подсказать, в какой области ищутся упрощения и где можно найти соответствующие упрощающие преобразования.
С этой целью в функцию simplify можно включать дополнительные параметры.
В качестве параметров могут задаваться имена специальных математических функций и указания на область действия упрощений: Bessell, BesselJ, BesselK, BesselY, Ei, GAMMA, RootOf, LambertW, dilog, exp, In, sqrt, polylog, pg, pochhammer, trig (для всех тригонометрических функций), hypergeom, radical, power и atsign (для операторов). Полезен также параметр symbolic, явно указывающий на проведение символьных преобразований.
Возможно также применение функции simplify в форме simplify[<name>], где <name> — одно из следующих указаний: atsign, GAMMA, hypergeom, power, radical, RootOf, , sqrt, trig. Ниже даны примеры применения функции Simplifу:
Действие функции simplify существенно зависит от областей определения переменных. В следующем примере упрощение выражения не произошло, поскольку результат этой операции неоднозначен:
Однако, определив переменные как реальные или положительные, можно легко добиться желаемого упрощения:
Читателю настоятельно рекомендуется просмотреть все разделы справочной системы, относящиеся к примерам применения функции simplify (в том числе с другими функциями символьных преобразований), поскольку их число очень велико и эти примеры наглядно демонстрируют необходимость правильного применения разнообразных параметров для придания упрощениям нужного характера. Если функция simplify не способна выполнить упрощение выражения ехрr, то она просто его повторяет. Это сигнал к применению опций.
18.gif
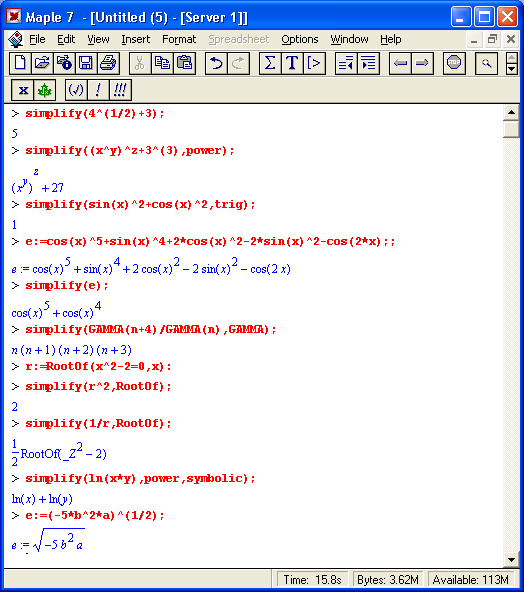
19.gif
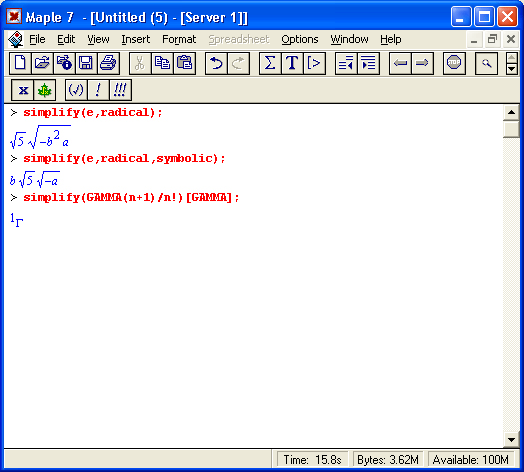
20.gif
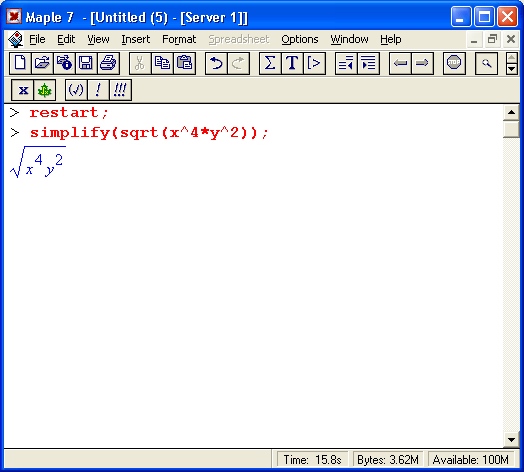
21.gif
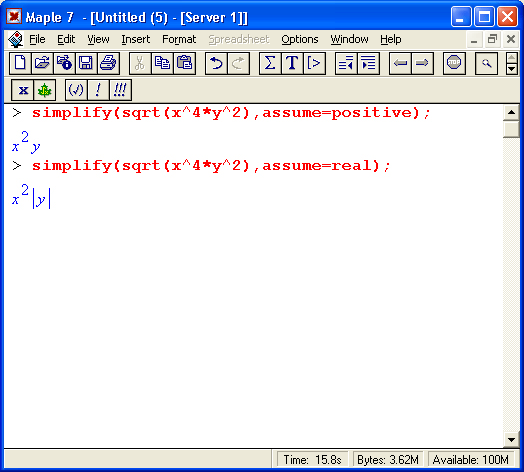
12. Расширение выражений
Расширение выражений
Даже в жизни мы говорим: «не все так просто». Порою упрощенное выражение скрывает его особенности, знание которых является желательным. Функция expand «расширяет» выражение ехрr и записывается в виде:
expanc(expr, expr1, ехрг2, .... ехрrn)
где ехрr — расширяемое выражение, exprl, ехрг2, ..., ехрrn — необязательные подвыражения — опции. Имеется также инертная форма данной функции — Expand (ехрr). Кроме того, возможно применение операторной конструкции frontend(expans,[expr]).
Функция expand раскладывает рациональные выражения на простые дроби, полиномы на полиномиальные разложения, она способна раскрыть многие математические функции, такие как sin, cos, tan, sinh, cosh, tanh, det, erf, exp, factorial, GAMMA, In, max, min, Psi, binomial, sum, product, int, limit, bernoulli, euler, abs, signum, pochhammer, polylog, BesselJ, BesselY, Bessell, BesselK, AngerJ, Beta, Hankel, Kelvin, Struve, WeberE и функция piecewise. С помощью дополнительных аргументов expr1, ехрr2, ..., exprh можно задать расширение отдельных фрагментов в ехрr.
Примеры применения функции expand приведены ниже:
22.gif
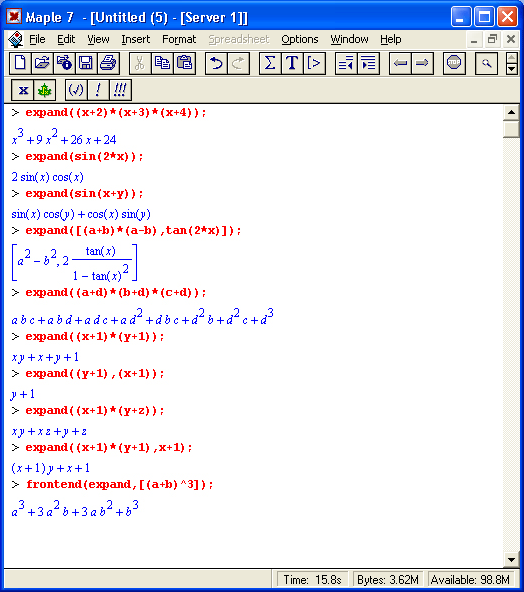
13. Факторизация выражений.
Факторизация выражений
Разложение целых и рациональных чисел
Для разложения целых или рациональных чисел на множители в виде простых чисел служит функция:
ifactor(n)
или
ifactor(n,method)
где n — число, method — параметр, задающий метод разложения. Другая библиотечная функция, if actors(n), возвращает результат разложения в форме вложенных списков:
23.gif

24.gif
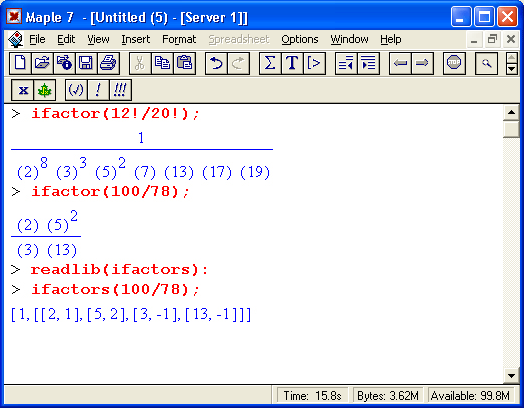
14. Разложение выражений (факторизация)
Разложение выражений (факторизация)
Для алгебраических выражений функция факторизации записывается в вычисляемой и не вычисляемой (инертной) формах:
factor(a) Factor(a)
factpr(a.K) Factor(а.К)
Здесь а — полином с несколькими переменными, К — необязательное алгебраическое расширение. Для получения результата от инертной формы функции факторизации надо использовать функции вычисления evala или evalgf.
Главная цель факторизации это нахождение максимального числа независимых сомножителей выражения, линейных по заданным переменным с коэффициентами наиболее простой формы. Ниже представлены примеры применения функции factor:
25.gif
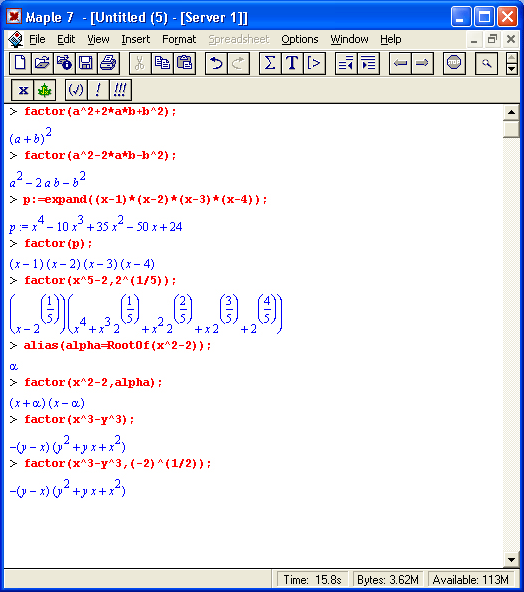
26.gif
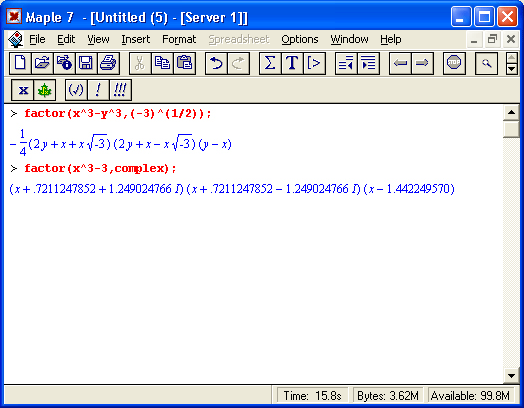
15. Комплектование по степеням
Комплектование по степеням
Еще одна функция общего назначения — collect — служит для комплектования выражения ехрr по степеням указанного фрагмента х (в том числе множества либо списка). Она задается в одной из следующих форм:
collect(a. x)
collect(a. x. form, func)
Во второй форме этой функции дополнительно задаются параметры form (форма) и func (функция или процедура). Параметр form может иметь два значения- recursive (рекурсивная форма) и distributed (дистрибутивная форма). Параметр func позволяет задать имя функции, по которой будет идти комплектование ехрr. Примеры применения функции collect представлены ниже:
27.gif
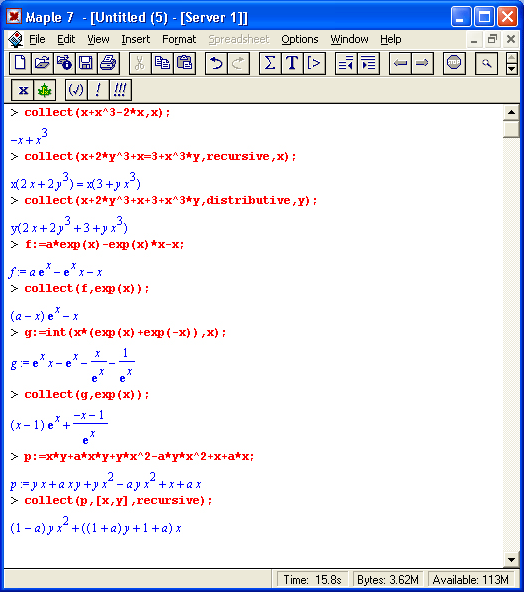
28.gif
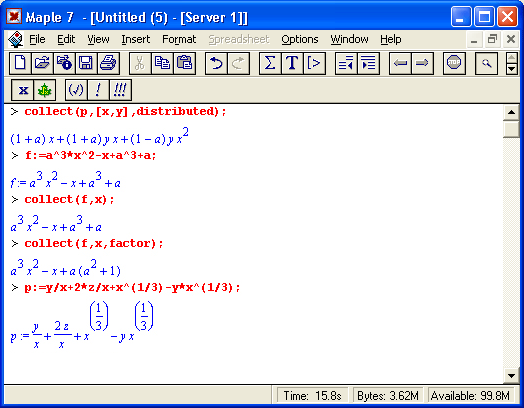
16. Программирование символьных операций
Программирование символьных операций
Реализация итераций Ньютона в символьном виде
Найти достаточно простую и наглядную задачу, решение которой отсутствует в системе Maple 7, не очень просто. Поэтому для демонстрации решения задачи с применением аналитических методов воспользуемся примером, ставшим классическим, — реализуем итерационный метод Ньютона при решении нелинейного уравнения вида f(x) - 0.
Как известно, метод Ньютона сводится к итерационным вычислениям по следующей формуле:
xi+1=x1+f(x1)/f'(x1);
Реализующая его процедура выглядит довольно просто:
Для получения итерационной формулы в аналитическом виде здесь используется функция unapply. Теперь, если задать решаемое уравнение, то можно получить искомое аналитическое выражение:
Далее, задав начальное приближение для х в виде х = х0, можно получить результаты вычислений для ряда итераций:
Нетрудно заметить, что, испытав скачок в начале решения, значениях довольно быстро сходятся к конечному результату, дающему корень заданной функции. Последние три итерации дают одно и то же значение х. Заметим, что этот метод дает только одно решение, даже если корней несколько. Вычислить другие корни в таком случае можно, изменив начальное условие.
Можно попробовать с помощью полученной процедуры получить решение и для другой функции:
Здесь итерационная формула имеет (и вполне естественно) уже другой вид, но сходимость к корню также обеспечивается за несколько итераций. ;
Возможна и иная форма задания итерационной процедуры с применением оператора дифференцирования D и заданием исходной функции также в виде процедуры:
Вообще говоря, в программных процедурах можно использовать любые операторы и функции, присущие Maple-языку, в том числе и те, которые реализуют символьные вычисления. Это открывает широкий простор для разработки новых процедур и функций, обеспечивающих выполнение символьных операций.
29.gif
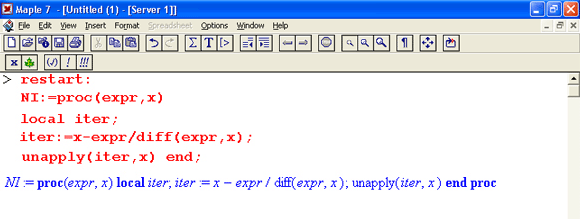
30.gif
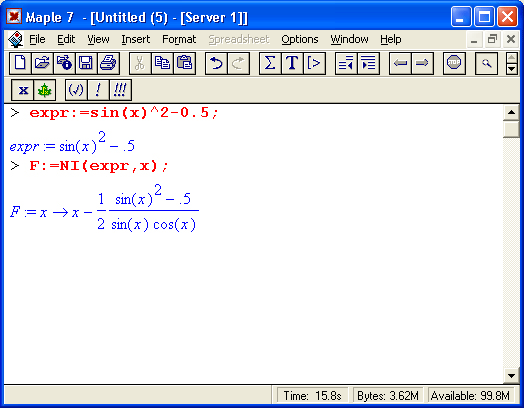
31.gif
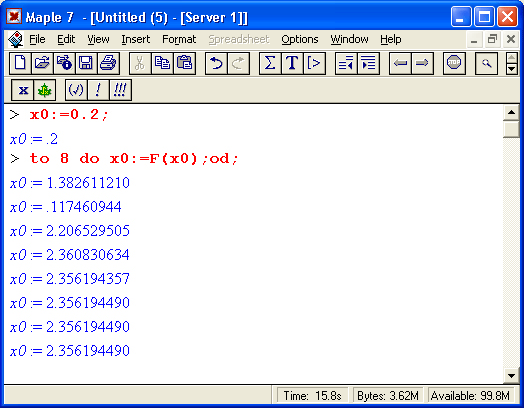
32.gif
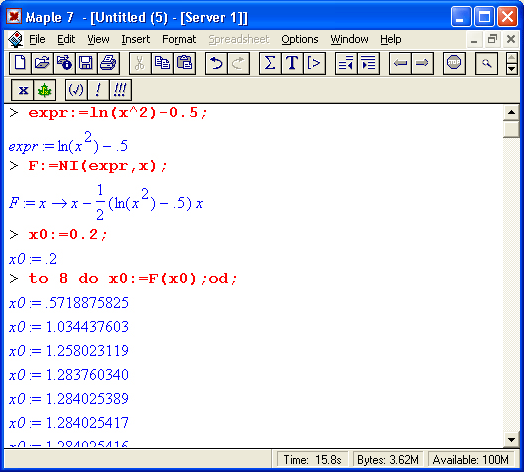
33.gif
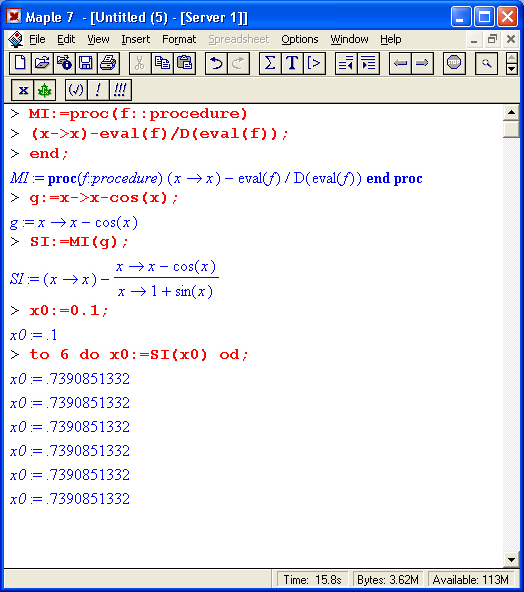
17. Вычисление интеграла по известной формуле
Вычисление интеграла по известной формуле
Рассмотрим следующий пример:
Прежние версии системы Maple не брали этот интеграл, поскольку он не имеет аналитического представления через обычные функции. Maple 7 блестяще вычисляет этот «крепкий орешек», но полученное выражение довольно сложно.
Из математики известно, что такой интеграл может быть представлен в следующем виде:
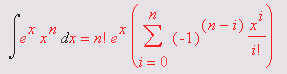
Используя эту формулу, мы можем создать простую процедуру для численного и аналитического вычисления данного интеграла:
Результат в аналитическом виде довольно прост для данного интеграла с конкретным значением т. Более того, мы получили несколько иной результат и дляп в общем случае. Но точен ли он? Для ответа на этот вопрос продифференцируем полученное выражение:
Результат дифференцирования выглядит куда сложнее, чем вычисленный интеграл. Однако с помощью функции simplify он упрощается к подынтегральной функции:
Это говорит о том, что задача вычисления заданного интеграла в аналитической форме действительно решена. А что касается громоздкости результатов, так ведь системы, подобные Maple 7, для того и созданы, чтобы облегчить нам работу с громоздкими вычислениями — в том числе аналитическими.
34.gif
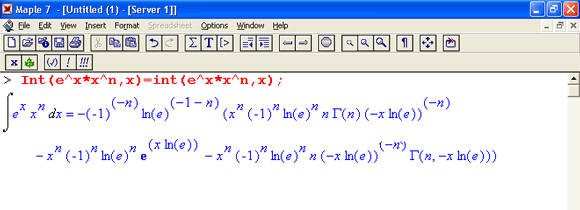
36.gif
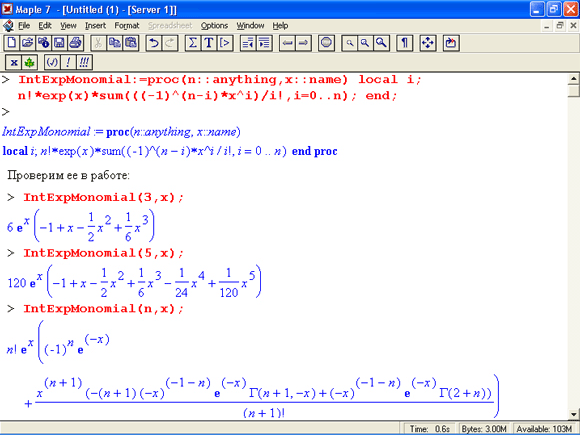
37.gif
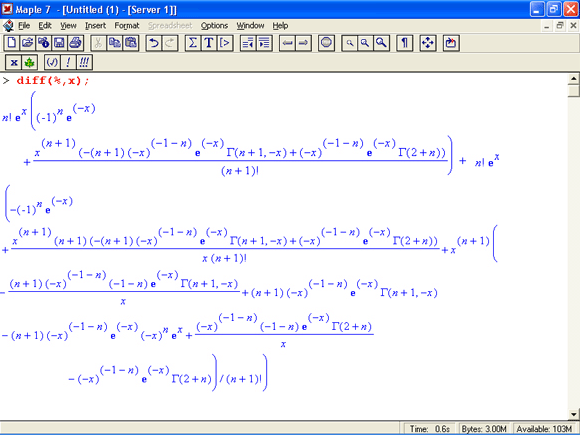
38.gif
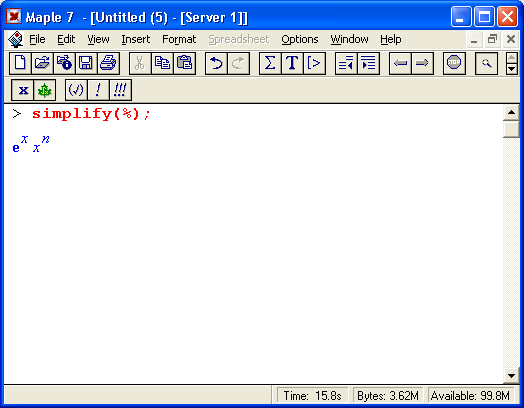
18. Вложенные процедуры и интегрирование по частям
Вложенные процедуры и интегрирование по частям
Теперь мы подошли к важному моменту, о котором читатель наверняка уже давно догадался — в составляемых пользователем процедурах можно использовать ранее составленные им (или кем-то еще) другие процедуры! Таким образом, Maple-язык позволяет реализовать процедуры, вложенные друг в друга. Для иллюстрации применения вложенных процедур рассмотрим операцию интегрирования по частям. Пусть нам надо вычислить интеграл:
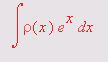
где р(х) — выражение, представляющее полином.
Приведенный ниже пример подготовлен в реализации Maple 7 [38]. Вначале подготовим процедуру IntExpMonomialR, реализующую вычисление уже рассмотренного ранее интеграла, но рекурсивным способом:
Теперь составим процедуру для вычисления по частям нашего интеграла:
В этой процедуре имеется обращение к ранее составленной процедуре IntExpMonomialR. Обратите внимание на то, что в процедуре введено предупреждение об определенных проблемах, связанных с использованием функции degree (сообщение начинается с символов ###). Тем не менее процедура работает, в чем убеждают по крайней мере следующие примеры:
В заключение остается отметить, что данный пример в Maple V R4 дает неточный результат, хотя никаких сообщений об ошибках не выводится.
40.gif
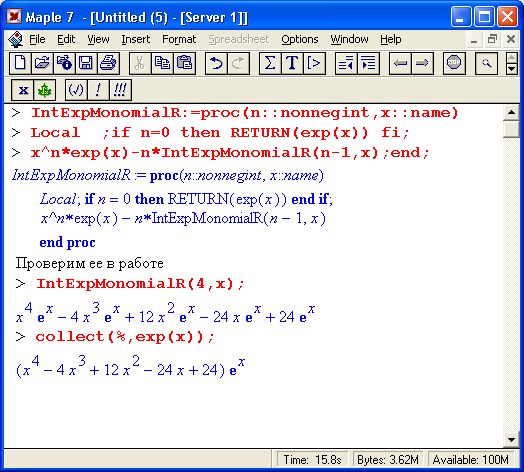
41.gif
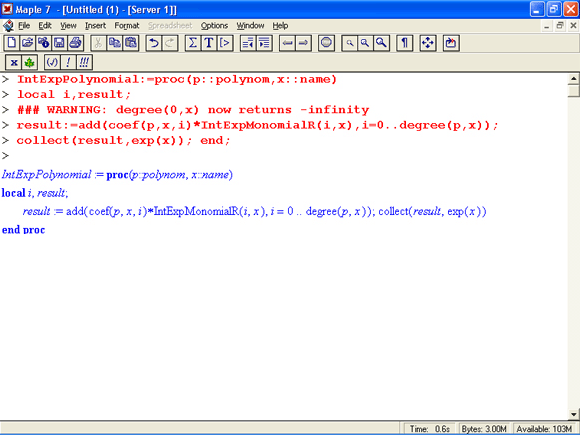
42.gif
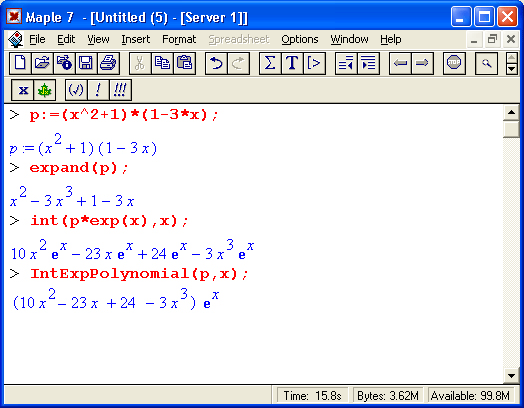
19. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Осуществлять основные операции с выражениями.
- Выполнять приложения и подстановки.
- Упрощать и расширять выражения.
- Осуществлять факторизацию выражений.
- Выполнять комплектование выражений по степеням.
- Программировать некоторые символьные операции.
Урок 11. Типовые средства построения графиков
1. Введение в построение двумерных графиков
Урок 11.
Типовые средства построения графиков
Основные возможности двумерной графики
Maple 7 реализует все мыслимые (и даже «немыслимые») варианты математических графиков. Строятся как графики простых функций в декартовой и полярной системах координат, так и графики, показывающие реалистические образы сложных, пересекающихся в пространстве фигур с их функциональной окраской. Возможны наглядные графические иллюстрации решений самых разнообразных уравнений, включая системы дифференциальных уравнений.
В само ядро Maple 7 встроено ограниченное число функций построения графиков. Это прежде всего функция для построения двумерных графиков plot и функция для построения трехмерных графиков plotSd. Они позволяют строить графики наиболее распространенных типов. Для построения специальных графиков (например, векторных полей градиентов, решения дифференциальных уравнений, построения фазовых портретов и т. д.) в пакеты системы Maple 7 включено большое число различных графических функций. Для их вызова необходимы соответствующие указания.
Вообще говоря, средства для построения графиков в большинстве языков программирования принято считать графическими процедурами, или операторами. Однако мы сохраним за ними наименование функций, в силу двух принципиально важных свойств:
О графические средства Maple V возвращают некоторые графические объекты, которые размещаются в окне документа — в строке вывода или в отдельном графическом объекте;
О эти объекты можно использовать в качестве значений переменных, то есть переменным можно присваивать значения графических объектов и выполнять над ними соответствующие операции (например, с помощью функции show выводить на экран несколько графиков).
Графические функции заданы таким образом, что обеспечивают построение типовых графиков без какой-либо особой подготовки. Для этого нужно лишь указать функцию, график которой строится, и пределы изменения независимых переменных. Однако с помощью дополнительных необязательных параметров можно существенно изменить вид графиков — например, настроить стиль и цвет линий, вывести титульную надпись, изменить вид координатных осей и т. д.
2. Основная функция построения двумерных графиков — plot
Основная функция построения двумерных графиков plot
В математике широко используются зависимости вида y(x) или у(х). Их графики строятся на плоскости в виде ряда точек y1(x1), обычно соединяемых отрезками прямых. Таким образом, используется кусочно-линейная интерполяция двумерных графиков. Если число точек графика достаточно велико (десятки или сотни), то приближенность построения не очень заметна.
Для построения двумерных графиков служит функция plot. Она задается в виде:
plot(f, h, v)
plot(f, h, v, о)
где f — визуализируемая функция (или функции), h — переменная с указанием области ее изменения, v — необязательная переменная с указанием области изменения, о — параметр или набор параметров, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т. д.).
Самыми простыми формами задания этой функции являются следующие:
- plot(f ,xrnin,xmax) — построение графика функции f, заданной только своим именем;
- plot(f(x),x=xmin,xmax) — построение графика функции f(x),
Диапазон изменения независимой переменной х задается как xmin. xmax, где xmin и xmax — минимальное и максимальное значение х, .. (две точки) — составной символ, указывающий на изменение независимой переменной. Разумеется, имя х здесь дано условно — независимая переменная может иметь любое допустимое имя.
Помимо построения самой кривой у(х) или f(x) необходимо задать ряд других свойств графиков, например вывод координатных осей, тип и цвет линий графика и др. Это достигается применением параметров графика — специальных указаний для Maple. Графики обычно (хотя и не всегда) строятся сразу в достаточно приемлемом виде. Это достигается тем, что многие параметры задаются по умолчанию и пользователь, по крайней мере начинающий, может о них ничего не знать. Однако язык общения и программирования Maple 7 позволяет задавать управляющие параметры и в явном виде.
Для двумерного графика возможны следующие параметры:
- adaptive — включение адаптивного алгоритма построения графиков (детали см. ниже);
- axes — вывод различных типов координат (axes=NORMAL — обычные оси, выводятся по умолчанию, axes=BOXES — график заключается в рамку с осями-шкалами, axes=FRAME — оси в виде перекрещенных линий, axes=NONE — оси не выводятся);
- axes font — задание шрифтов для подписи делений на координатных осях (см. также параметр font);
- color — задает цвет кривых (см. далее);
- coords — задание типа координатной системы (см. далее);
- discont — задает построение непрерывного графика (значения true или false);
- filled — при filled=true задает окраску цветом, заданным параметром color, для области, ограниченной построенной линией и горизонтальной координатной осью х;
- font — задание шрифта в виде [семейство, стиль, размер];
- labels — задание надписей по координатным осям в виде [X, Y], где X и Y — надписи по осям х и у графика;
- label directions — задает направление надписей по осям [X, Y], где X и Y может иметь строковые значения HORISONTAL (горизонтально) и VERTICAL (вертикально);
- label font — задает тип шрифта подписей (см. font);
- legend — задает вывод легенды (обозначения кривых);
- linestyle — задание стиля линий (1 — сплошная, 2 — точками, 3 — пунктиром и 4 — штрихпунктиром);
- numpoints — задает минимальное количество точек на графике (по умолчанию numpoints=49);
- resolutions — задает горизонтальное разрешение устройства вывода (по умолчанию resolutions=200, параметр используется при отключенном адаптивном методе построения графиков);
- sample — задает список параметров для предварительного представления кривых;
- scaling — задает масштаб графика: CONSTRAINED (сжатый) или UNCONSTRAINED (несжатый — по умолчанию);
- size.— задает размер шрифта в пунктах;
- style — задает стиль построения графика (POINT — точечный, LINE — линиями);
- symbol — задает вид символа для точек графика (возможны значения BOX — прямоугольник, CROSS — крест, CIRCLE — окружность, POINT — точка, DIAMOND — ромб);
- symbol size — установка размеров символов для точек графика (в пунктах, по умолчанию 10);
- title — задает построение заголовка графика (title="string", где string — строка);
- titlefont — определяет шрифт для заголовка (см. font);
- thickness — определяет толщину линий графиков (О, 1, 2, 3, значение по умолчанию — 0);
- view=[A, В] — определяет максимальные и минимальные координаты, в пределах которых график будет отображаться на экране, А = [xmin. .xmax], B=[ymin. .ymax] (по умолчанию отображается вся кривая);
- xtickmarks — задает минимальное число отметок по оси x,
- ytickmarks — задает минимальное число отметок по оси у.
В основном задание параметров особых трудностей не вызывает, за исключением задания титульной надписи с выбором шрифтов по умолчанию — в этом случае не всегда поддерживается вывод символов кириллицы (русского языка). Подбором подходящего шрифта эту проблему удается решить. Модификация графиков с помощью управляющих параметров подробно рассматривается ниже.
Специальный параметр adaptive задает работу специального адаптивного алгоритма для построения графиков наилучшего вида. При этом Maple автоматически учитывает кривизну изменения графика и увеличивает число отрезков прямых в тех частях графиков, где их ход заметно отличается от интерполирующей прямой. При задании adaptive=false адаптивный алгоритм построения графиков отключается, а при adaptive=true включается (значение по умолчанию).
3. Задание координатных систем двумерных графиков
Задание координатных систем двумерных графиков
В версии Maple 7 параметр coords задает 15 типов координатных систем для двумерных графиков. По умолчанию используется прямоугольная (декартова) система координат (coords=cartesian). При использовании других координатных систем координаты точек для них(и, v) преобразуются в координаты (х, у) как (n, v) —> (х, у). Ниже приведены наименования систем координат (значений параметра coords) и соответствующие формулы преобразования.
|
bipolar: |
x = sinh(v)/(cosh(v)-cos(u)) у - sin(u)/(cosh(v)-cos(u)) |
|
cardioid: |
x = l/2*(u^2-v^2)/(u^2+v^2)^2 у = u*v/(u^2+v^2)^2 |
|
cartesian: |
x = u У = v |
|
cassinian: |
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) + exp(u)*cos(v)+1^(l/2) у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(1/2) -exp(u)*cos(v)-1)^(l/2)] |
|
elliptic: |
x = cosh(u)*cos(v) у = sinh(u)*sin(v) |
|
hyperbolic: |
x = ((u^2+v^2)^(l/2)+u)^(l/2) у = ((u^2+v~2)^(l/2)-u)^(l/2) |
|
invcassinian: |
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) + exp(u)*cos(v)+1)^(1/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(l/2) у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) -exp(u)*cos(v)-l)^(l/2)/(exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) |
|
invelliptic: |
x = a*cosh(u)*cos(v)/(cosh(u)*2-sin(v)*2) у = a*sinh(u)*sin(v)/(cosh(u)^2-sin(vr2) |
|
logarithmic: |
x = a/Pi*ln(u^2+v^2) у = 2*a/Pi*arctan(v/u) |
|
logcosh: |
x = a/Pi*ln(cosh(ur2-sin(vr2) у =2*a/Pi*arctan(tanh(u)*tan(v)) |
|
maxwell : |
x - a/Pi*(u+l+exp(u)*cos(v)) у = a/Pi*(v+exp(u)*sin(v)) |
|
parabolic: |
x = (u^2-v^2)/2 • у - u*v |
|
polar: |
x = u*cos(v) у = u*sin(v) |
|
rose: |
x = ((u^2+v^2)^(l/2)+u)^(l/2)/(u^2+v^2)^(l/2) у - ((u^2+v^(1/2)+u)^(1/2)/(u^2+v^2)^(1/2) |
|
tangent: |
x = u/(u^2+v^2) у =v/(u^2+v^2) |
4. Управление стилем и цветом линий двумерных графиков
Управление стилем и цветом линий двумерных графиков
Maple 7 позволяет воспроизводить на одном графике множество кривых. При этом возникает необходимость как-то идентифицировать их. Для этого можно использовать построение линий разными стилями, разными цветами и с разной толщиной. Набор средств выделения кривых позволяет уверенно различать их как на экране цветного дисплея и в распечатках, сделанных цветным струйным принтером, так и при печати монохромными принтерами. Параметр style — позволяет задавать следующие стили для линий графиков:
- POINT или point — график выводится по точкам;
- LINE или line — график выводится линией.
Если задано построение графика точками, то параметр symbol позволяет представить точки в виде различных символов, например прямоугольников, крестов, окружностей или ромбов.
Другой параметр — color — позволяет использовать обширный набор цветов линий графиков:
|
aquamarine |
black |
blue |
navy |
coral |
|
cyan |
brown |
gold |
green |
gray |
|
grey |
khaki |
magenta |
maroon |
orange |
|
pink |
plum |
red |
sienna |
tan |
|
turquoise |
violet |
wheat |
white |
yellow |
Различные цветовые оттенки получаются благодаря использованию RGB-комбинаций базовых цветов: red — красный, gray — зеленый, bluе — синий. Приведем перевод ряда других составных цветов: black — черный, white — белый, khaki — цвет «хаки», gold — золотистый, orange — оранжевый, violet — фиолетовый, yellow — желтый и т. д. Перевод цветов некоторых оттенков на русский язык не всегда однозначен и потому не приводится. Средства управления стилем графиков дают возможность легко выделять различные кривые на одном рисунке, даже если для выделения не используются цвета.
5. Основные типы двумерных графиков
Основные типы двумерных графиков
При построении графика одной функции она записывается в явном виде на месте шаблона f. Примеры построения графика одной функции представлены на рис. 11.1. Обратите внимание на то, что график функции sin(x)/x строится без характерного провала в точке х = 0, который наблюдается при построении графиков этой функции многими программами. Он связан с используемым в них правилом — функция задается равной нулю, если ее числитель равен нулю. Данная функция в этой точке дает устранимую неопределенность 0/0->1, что и учитывает графический процессор системы Maple 7.
Рис. 11.1. Примеры построения графиков одной функции
При построении графиков одной функции могут быть введены описание диапазонов и различные параметры, например: для задания цвета кривой, толщины линии, которой строится график функции, и др. К примеру, запись в списке параметров color=black задает вывод кривых черным цветом, а запись thikness=2 задает во втором примере рис. 11.1 построение графика линией, удвоенной по сравнению с обычной толщиной. Кстати говоря, запись color=red дает красный цвет, color=green — зеленый цвет, color=blue — синий цвет и т. д. При черно-белой печати цвета представляются оттенками серого цвета.
1.gif
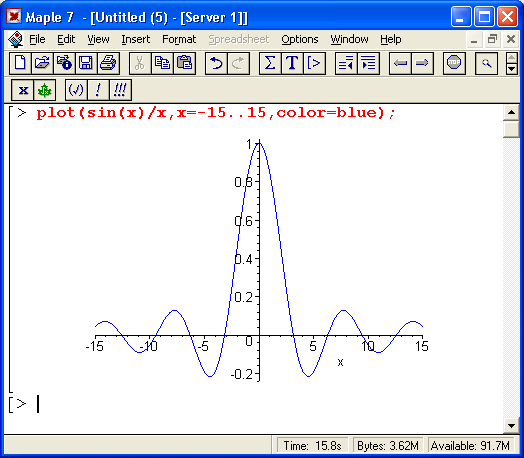
2.gif
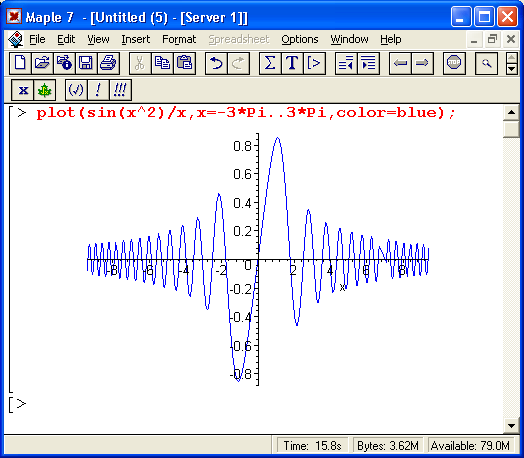
6. Управление диапазоном изменения переменной и значения функции
Управление диапазоном изменения переменной и значения функции
Для управления отображаемой на графике области служит задание диапазонов принимаемых значений для переменной и функции. В ряде случаев их можно не применять, тогда Maple автоматически задает приемлемые диапазоны. Однако их явное указание позволяет управлять областью графика вручную. Иногда соответствующее задание диапазонов случайно или целенаправленно ведет к отсечению части графика — например, на рис. 11.2 в первом примере отсечена верхняя часть графика.
Рис. 11.2. Построение графиков функции с явным указанием масштаба
Правильный выбор диапазонов повышает представительность графиков функций. Рекомендуется вначале пробовать строить графики с автоматическим выбором диапазонов, а уже затем указывать их вручную.
3.gif
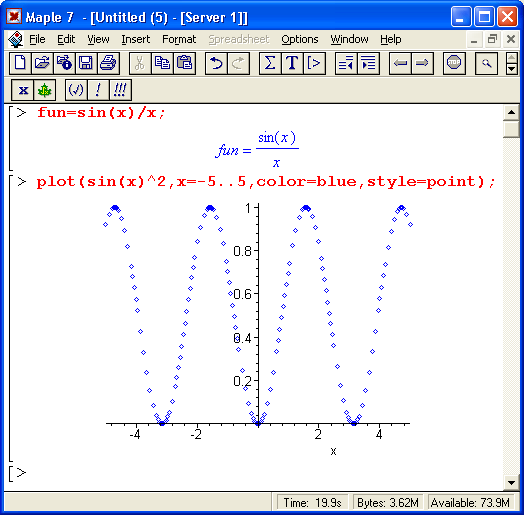
4.gif
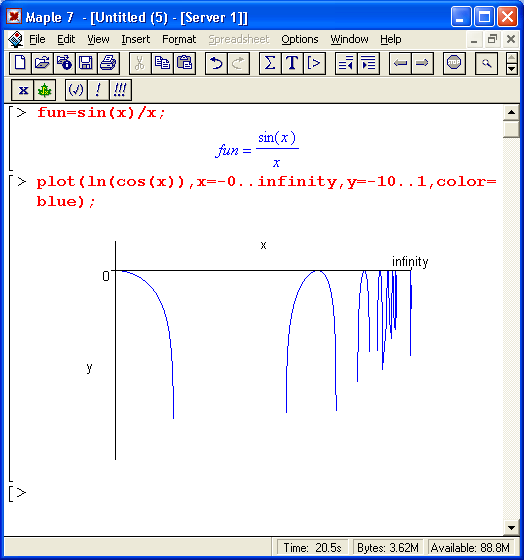
7. Графики функций в неограниченном диапазоне
Графики функций в неограниченном диапазоне
Изредка встречаются графики функций f(x), которые надо построить при изменении значениях от нуля до бесконечности или даже от минус бесконечности до плюс бесконечности. Бесконечность в таких случаях задается как особая константа infinity. В этом случае переменной х, устремляющейся в бесконечность, откладывается значение аrctan(x). Рисунок 11.2 (второй пример) иллюстрирует сказанное.
8. Графики функций с разрывами
Графики функций с разрывами
Некоторые функции, например tan(x), имеют при определенных значениях х разрывы, причем случается, что значения функции в этом месте устремляются в бесконечность. Функция tan(x), к примеру, в точках разрывов устремляется к +? и -?. Построение графиков таких функций нередко дает плохо предсказуемые результаты. Графический процессор Maple 7 не всегда в состоянии определить оптимальный диапазон по оси ординат, а график функции выглядит весьма непредставительно, если не сказать безобразно (рис. 11.3, первый пример).
Рис. 11.3. Построение графиков функций с разрывами
Среди аргументов функции plot есть специальный параметр discont. Если задать его значение равным true, то качество графиков существенно улучшается, см. второй пример на рис. 11.3. Улучшение достигается разбиением графика на несколько участков, на которых функция непрерывна, и более тщательным контролем за отображаемым диапазоном. При discont=false данный параметр отключен и строятся обычные графики.
ПРИМЕЧАНИЕ
Следует отметить, что вид графика можно улучшить, просто задав диапазон по оси у например введя в параметры функции запись у=-10..10). При этом в точках разрыва могут появиться вертикальные линии. Иногда это бывает полезно.
5.gif
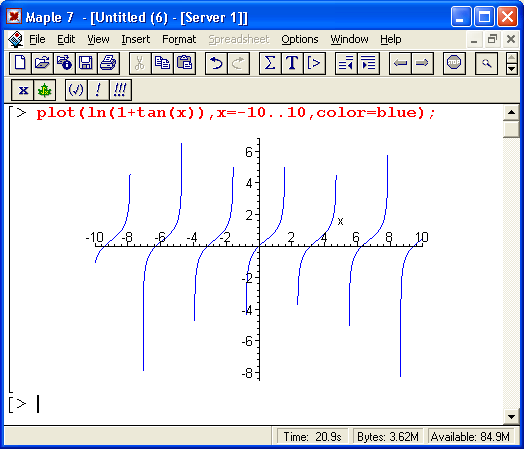
6.gif
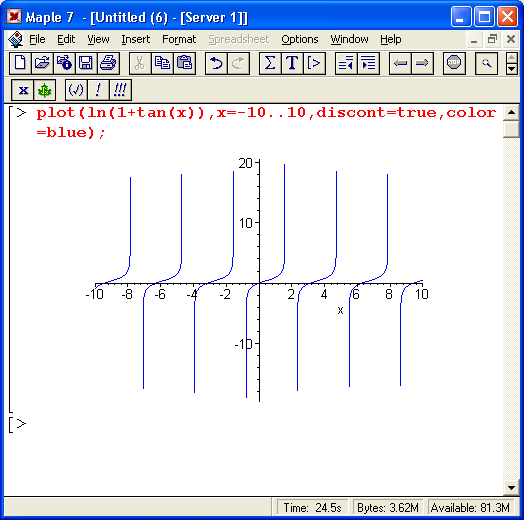
9. Графики нескольких функций на одном рисунке
Графики нескольких функций на одном рисунке
Важное значение имеет возможность построения на одном рисунке графиков нескольких функций. В простейшем случае (рис. 11.4, первый пример) для построения таких графиков достаточно перечислить нужные функции и установить для них общие интервалы изменения.
Рис. 11.4. Графики трех функций на одном рисунке
Обычно графики разных функций автоматически строятся разными цветами. Но это не всегда удовлетворяет пользователя — например, при распечатке графиков монохромным принтером некоторые кривые могут выглядеть слишком блеклыми или даже не пропечататься вообще. Используя списки параметров color (цвет линий) и style (стиль линий), можно добиться выразительного выделения кривых — это показывает второй пример на рис. 11.4 для случая, когда линии графиков выделяются стилем. Однако если кривые задаются разным цветом, то при черно-белой печати они могут перестать различаться.
На рис. 11.5 показан еще один пример такого рода. Здесь построен график функции sin(x)/x и график ее полиномиальной аппроксимации. Она выполняется настолько просто, что соответствующие функции записаны прямо в списке параметров функции plot.
Рис. 11.5. График функции sin(x)/x и ее полиномиальной аппроксимации
В данном случае сама функция построена сплошной линией, а график полинома точками — ромбами. Хорошо видно, что при малых х аппроксимация дает высокую точность, но затем с ростом х ее погрешность резко возрастает.
Рисунок 11.6 показывает построение нескольких любопытных функций, полученных с помощью комбинаций элементарных функций. Такие комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной.
Рис. 11.6. Построение графиков нескольких любопытных функций
В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к значению каждой функции некоторой константы.
8.gif
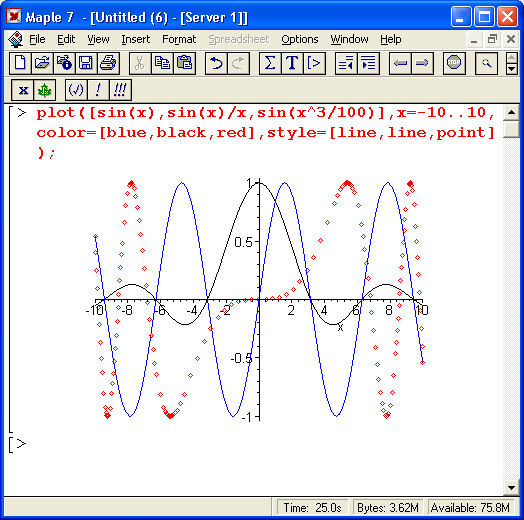
9.gif
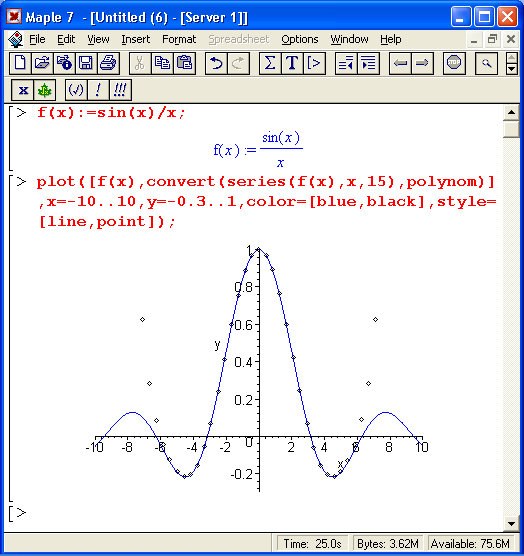
10.gif
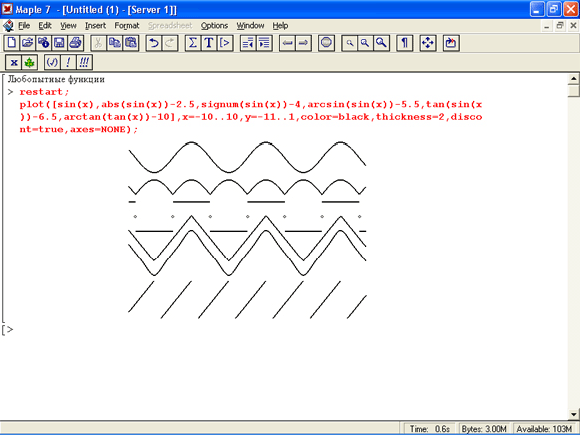
10. Графики функций, построенные точками
Графики функций, построенные точками
Показанный на рис. 11.5 график полинома, построенный ромбиками, не означает, что полином представлен отдельными точками. В данном случае просто выбран стиль линии в виде точек. Однако часто возникает необходимость построения графиков функций, которые представлены просто совокупностями точек. Такая совокупность может быть создана искусственно, как на рис. 11.7, либо просто задаваться списком координат х и значений функции.
В данном случае переменная Р имеет вид списка, в котором попарно перечислены координаты точек функции sin(x). В этом нетрудно убедиться, заменив знак «:» после выражения, задающего Р, на знак «;». Далее по списку Р построен график точек в виде крестиков, которые отображают отдельные значения функции sin(x).
На рис. 11.8 показано построение графиков функций по точкам при явном задании функции списком координат ее отдельных точек. В первом примере эти точки соединяются отрезками прямых, так что получается кусочно-линейный график. Видно также, что указание типа точек после указания стиля линии игнорируется (а жаль, было бы неплохо, чтобы наряду с кусочно-линейной линией графика строились и выделенные окружностями точки).
Рис. 11.7. Формирование списка отдельных точек функции и их построение на графике
Рис. 11.8. Построение графика функции, явно заданной отдельными точками
Во втором примере рис. 11.8 показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками. Читателю предлагается самостоятельно совместить оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.
11.gif
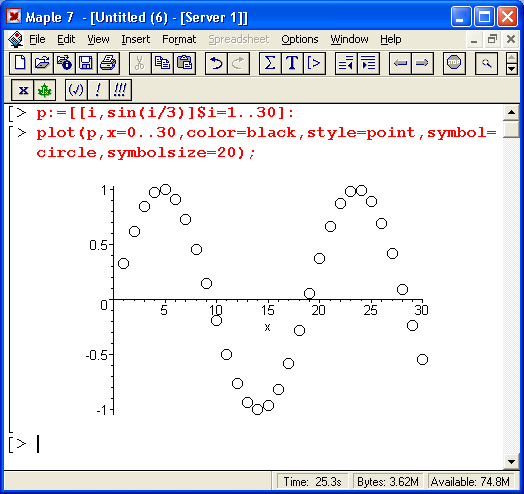
12.gif
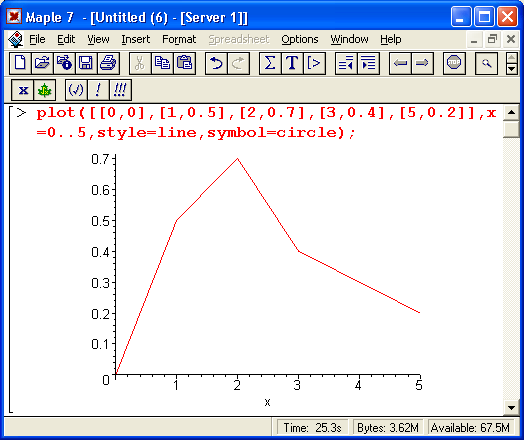
11. Графики функций, заданных своими именами
Графики функций, заданных своими именами
Способность Maple 7 к упрощению работы пользователя просто поразительна — жаль только, что многие возможности этого становятся ясными после основательного изучения программы, на что уходят, увы, не дни, а месяцы, а то и годы. Применительно к графикам одной из таких возможностей является построение графиков функций, заданных только их функциональными именами — даже без указания параметров в круглых скобках. Такую возможность наглядно демонстрирует рис. 11.9.
Рис. 11.9. Построение графиков четырех функций, заданных только их именами
Этот пример показывает, что возможно построение графиков функций даже без указания в команде plot диапазонов. При этом диапазон по горизонтальной оси устанавливается равным по умолчанию -10.. 10, а по вертикальной оси выбирается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной (условно х).
14.gif
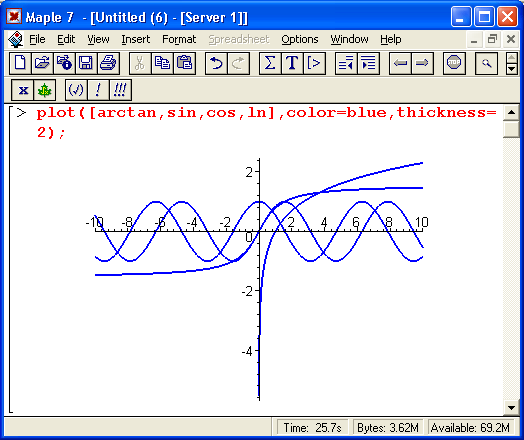
12. Графики функций с ординатами, заданными вектором
Графики функций с ординатами, заданными вектором
Часто возникает необходимость построения графика точек, ординаты которых являются элементами некоторого вектора. Обычно при этом предполагается равномерное расположение точек по горизонтальной оси. Пример построения такого графика дан на рис. 11.10.
Рис. 11.10. Построение графика точек с ординатами, заданными элементами вектора
Из этого примера нетрудно заметить, что данная задача решается составлением списка парных значений координат исходных точек — к значениям ординат точек, взятых из вектора, добавляются значения абсцисс. Они задаются чисто условно, поскольку никакой информации об абсциссах точек в исходном векторе нет, так что фактически строится график зависимости ординат точек от их порядкового номера n.
45.gif
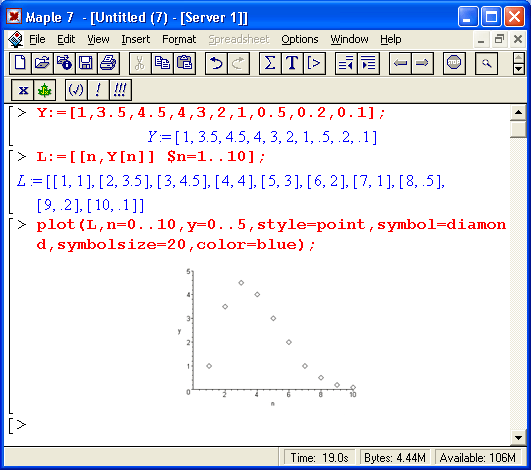
13. Графики функций, заданных процедурами
Графики функций, заданных процедурами
Некоторые виды функций, например кусочные, удобно задавать процедурами. Построение графиков функций, заданных процедурами, не вызывает никаких трудностей и иллюстрируется рис. 11.11.
Рис. 11.11. Построение графика функций, заданных процедурами
Здесь, пожалуй, полезно обратить внимание на то, что в функции plot указывается имя процедуры без списка ее параметров.
46.gif
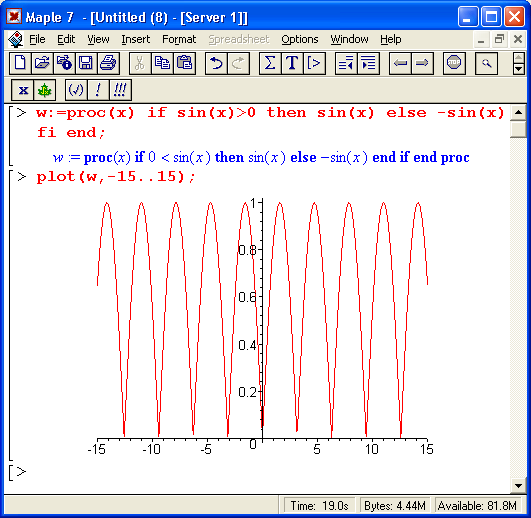
14. Графики функций, заданных функциональными операторами
Графики функций, заданных функциональными операторами
Еще одна «экзотическая» возможность функции plot — построение графиков функций, заданных функциональными операторами. Она иллюстрируется рис. 11.12.
Имена функций (без указания списка параметров в круглых скобках) тоже, по существу, являются функциональными операторами. Так что они также могут использоваться при построении графиков упрощенными способами.
15. Графики функций, заданных параметрически
Графики функций, заданных параметрически
В ряде случаев для задания функциональных зависимостей используются заданные параметрически уравнения, например х = f1(t) и у =f2(t) при изменении переменной t в некоторых пределах. Точки(х, у) наносятся на график в декартовой системе координат и соединяются отрезками прямых. Для этого используется функция plot в следующей форме:
Рис. 11.12. Построение графиков функции, заданной функциональными операторами
plot([fl(t),f2(t),t-tmin..tmax].h,v.p)
Если функции f1(£) и f2(0 содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t обычно задается равным 0. .2*Pi или -Pi..Pi. К примеру, если задать в качестве функций f1(t) и f2(t) функции sin(t) и cos(t), то будет получен график окружности. Рисунок 11.13 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.
Задание диапазонов для изменений h и v, а также параметров р не обязательно. Но, как и ранее, они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.
48.gif
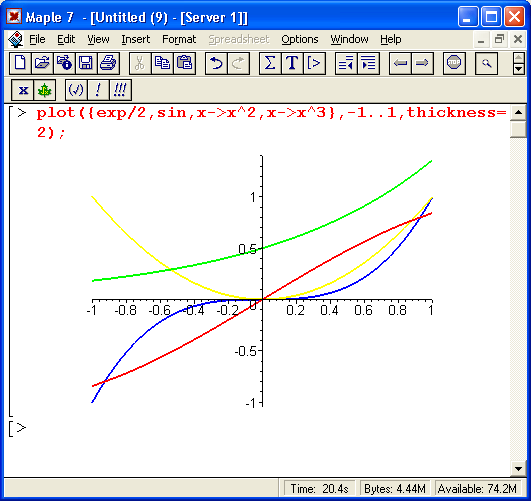
16. Графики функций в полярной системе координат
Графики функций в полярной системе координат
Графики в полярной системе координат представляют собой линии, которые описывают конец радиус- вектора r(t) при изменении угла t в определенных пределах — от t до t . Построение таких графиков также производится функцией plot, которая для этого записывается в следующем виде:
Рис. 11.13. Построение функций, заданных параметрически
plot([r(t),theta(t),t=tmin..tnrax],h,v,p,coords-polar)
Здесь существенным моментом является задание полярной системы координат параметром coords=polar. Рисунок 11.14 дает примеры построения графиков функций в полярной системе координат.
Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.
18.gif
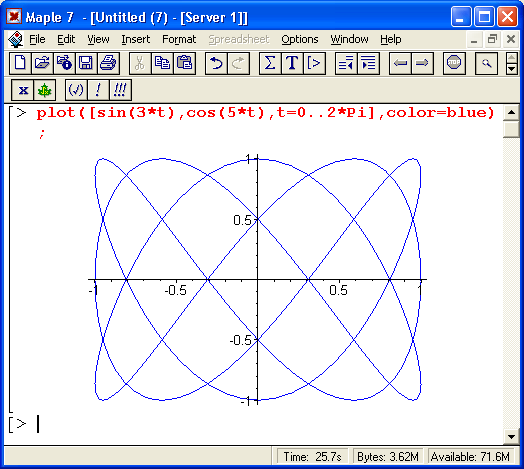
17. Построение трехмерных графиков
Построение трехмерных графиков
Особенности применения функции plot3d
Трехмерными называют графики, отображающие функции двух переменных z(х,у). Каждая точка zi таких графиков является высотой (аппликатой) точки, лежащей в плоскости XY и представленной координатами (х,у). Поскольку экран монитора компьютера в первом приближении является плоским, то на деле трехмерные графики представляют собой специальные проекции объемных объектов.
Рис. 11.14. Построение графиков функций в полярной системе координат
Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию pi ot3d. Она может использоваться в следующих форматах:
plot3d(exprl. x=a..b. y=c..d,p)
plot3d(f, a..b. c..d.p)
plot3d([exprf.exprg.exprh]. s=a..b, t=c..d.p)
plot3d([f.g.h]. a..b, c..d,p)
В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах записи f, g и h — функции; exprl — выражение, отражающее зависимость от -х и у; exprf, exprg и exprh — выражения, задающие поверхность параметрически; s, t, а и b — числовые константы действительного типа; end — числовые константы или выражения действительного типа; х, у, s и t — имена независимых переменных; р — управляющие параметры.
20.gif
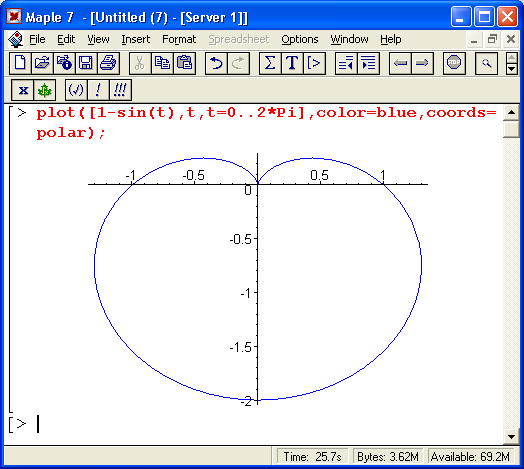
18. Параметры функции plot3d
Параметры функции plot3d
С помощью параметров р можно в широких пределах управлять видом трехмерных графиков, выводя или убирая линии каркасной сетки, вводя функциональную окраску поверхностей, меняя угол их обзора и параметры освещения, изменяя вид координатных осей и т. д. Следующие параметры функции p1ot3d задаются аналогично их заданию для функции plot:
axesfont font color coords font ,
labelfont linestyle numpoints scaling style
symbol t hickness title titlefont
Однако функция plot3d имеет ряд дополнительных специфических параметров:
- ambientl light=[r,g,b] — задает интенсивность красного (r), зеленого (g) и синего (b) цветов подстветки в относительных единицах (от 0 до 1);
- axes=f — задает вид координатных осей (BOXED, NORMAL, FRAME и NONE, по умолчанию NONE);
- grid=[m,n] — задает число линий каркаса поверхности;
- gridstyle=x — задает стиль линий каркаса х ('rectangular' или 'triangular');
- 1abels=[x,y,z] — задает надписи по осям (х, у и z — строки, по умолчанию пустые);
- 1ight=[phi ,theta,r,g,b] — задает углы, под которыми расположен источник освещения поверхности и интенсивности составляющих цвета (г, g и Ь);
- lightmodel=x — задает схему освещения (соответственно 'none', 'lightl', 'light2', 'lights1 и 'light4');
- orientat1on=[theta,phi]— задает углы ориентации поверхности (по умолчанию 45°);
- projections — задает перспективу при обзоре поверхности (г может быть числом 0 или 1, задающим включение или выключение перспективы, а также одной из строк 'FISHEYE', 'NORMAL' или 'ORTHOGONAL' (это соответствует численным значениям г, равным 0, 0,5 или 1, причем по умолчанию задано projection=ORTHOGONAL));
- shading=s — задает направления, по которым меняется цвет функциональной окраски (значения s могут быть XYZ, XY, Z, ZGREYSCALE, ZHUE, NONE);
- tickmarks=[1 ,n,m] — задает характер маркировки по осямх, у и z (числа 1, n и m имеют значения не менее 1);
- view=zmin. .zmax или view=[xmin. .xmax, ymin. .ymax, zmin..zmax] — задает минимальные и максимальные координаты поверхности для ее видимых участков.
19. Выбор и пересчет координат трехмерных графиков
Выбор и пересчет координат трехмерных графиков
Для трехмерных графиков возможно задание 31 типа координатных систем с помощью параметра сооrds= Тип _ координатной _ системы. Поскольку на экране монитора поверхность отображается только в прямоугольной системе координат и характеризуется координатами х, у и z, то для представления поверхности, заданной в иной системе координат с координатами u, v и w, используются известные [46, 47] формулы для преобразования (u, v, w) --> (х, у, z). Ниже перечислены типы трехмерных координатных систем и соответствующие формулы преобразования.
bipolar-cylindrical:
х = a*sinh(v)/(cosh(v)-cos'(u))
у = a*sin(u)/(cosh(v)-cos(u))
z = w
bispherical:
x = sin(u)*cos(w)/d
у = sin(u)*sin(w)/d
z = sinh(v)/d где d - cosh(v) - cos(u)
cardioidal:
x = u*v*cos(w)/(u^2+v^2)^2
у -=u*v*sin(w)/(u^2+v^2)^2
z = (u^2-v^2)/2/(u^2+v^2)^2
cardioidcylindrical:
x = (u^2-v^2)/2/(u^2+v^2)^2
у - u*v/(u^2+v^2)^2
z =w
casscylindhcal:
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2)+exp(u)*cos(v)+l)^(l/2)
у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2)-exp(u)*cos(v)-l)^(l/2)
z =w
confocalellip:
x = ((a^2-u)*(a^2-v)*(a^2-w)/(a^2-b^2)/(a^2-c^2))^(l/2)
у = ((b^2-u)*(b^2-v)*(b^2-w)/(b^2-a^2)/(b^2-c^2))^(l/2)
z = ((c^2-u)*(c^2-v)*(c^2-w)/(c^2-a^2)/(c^2-b^2))^(l/2)
confocalparab:
x = ((a^2-u)*(a^2-v)*(a^2-w)/(b^2-a^2)^(l/2)
у = ((b^2-u)*(b^2-v)*(b^2-w)/(b^2-a^2))^(l/2)
z = (a^2+b^2-u-v-w)/2
conical:
x = u*v*w/(a*b)
у = u/b*((v^2 - b^2)*(b^2-w^2)/(a^2-b^2))^(l/2)
z= u/a*((a^2 - v^2)*(a^2 - w^2)/(a^2-b^2))6(l/2)
cylindrical:
x = u*cos(y)
у = u*sin(y)
z = w
ellcylindrical:
x =a*cosh(u)*cos(v)
у = a*sinh(u)*sin(v)
z = w
ellipsoidal:
x = u*v*w/a/b
у = ((u^2-b^2)*(u^2-b^2)*(b^2-w^2)/(а^2-b^2)^(1/2)/b
z = ((u^2-a^2)*(a^2-v^2)*(a^2-w^2)/(a^2-b^2)^(l/2)/a
hypercylindrical:
x = ((u^2+v^2)^(l/2)-ni)^(l/2)
у = ((u^2+v^2)^(l/2)-u)^(l/2)
z = w
invcasscylindrical:
x = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+l)^(l/2) +
exp(u)*cos(v)+1)^(l/2)/(exp(2*u)+2*exp(u)*cos(v)+1)^(l/2)
у = a*2^(l/2)/2*((exp(2*u)+2*exp(u)*cos(v)+1)^(l/2) -
exp(u)*cos(v)-1)^(l/2)/(exp(2*u)+2*exp(u)*cos(v)-1)^(l/2)
z = w
invellcylindrical:
x = a*cosh(u)*cos(v)/(cosh(u)^2-sin(v)^2)
у = a*sinh(u)*sin(v)/(cosh(u)^2-sin(v)^2)
z = w
invoblspheroidal:
x = a*cosh(u)*sin(v)*cos(w)/(cosh(u)^2-cos(v)^2)
у = a*cosh(u)*sin(v)*sin(w)/(cosh(u)^2-cos(v)^2)
z = a*sinh(u)*cos(v)/(cosh(u)^2-cos(v)^2)
invprospheroldal:
x = a*s1nh(u)*sin(v)*cos(w)/(cosh(u)^2-sin(v)^2)
у = a*sinh(u)*sin(v)*sin(w)/(cosh(u)^2-sin(v)^2)
z = a*cosh(u)*cos(v)/(cosh(u)^2-s1n(v)^2)
logcyllndrical:
x = a/Pi*ln(u^2+v^2)
у = 2*a/Pi*arctan(v/u)
z = w
logcoshcylindrical:
x = a/Pi*ln(cosh(u^2-sin(v)^2)
у = 2*a/Pi*arctan(tanh(u)*tan(v))
z = w
maxwell cylindrical:
x = a/P1*(u+l+exp(u)*cos(v))
у = a/Pi*(v+exp(u)*sin(v))
z = w
oblatespheroidal:
x = a*cosh(u)*s1n(v)*cos(w)
у = a*cosh(u)*sin(v)*sin(w)
z = a*s1nh(u)*cos(v)
parabololdal:
x = u*v*cos(w)
у = u*v*sin(w)
z = (u^2 - v^2)/2
paraboloidal2:
x = 2*((u-a)*(a-v)*(a-w)/(a-b)^(l/2)
у = 2*((u-b)*(b-v)*(b-w)/(a-b))^(l/2)
z = u+v+w-a-b
paracylindrical:
x = (iT2 - v*2)/2
у =u*v
z = w
prolatespheroidal:
x = a*sinh(u)*sin(v)*cos(w)
y=a*s1nh(u)*sin(v)*sin(w)
z=a*cosh(u)*cos(v)
rectangular:
x = u
у = v
z = w
rosecylindrlcal:
х =((u^2+v^2)^(l/2)-Hi)^(l/2)/(u^2+v^2)^(l/2)
у = ((u^2+v^2)^(l/2)-u)^(l/2)/(u^2+v^2)^(l/2)
z =w
sixsphere:
x = u/(u^2+v^2+w^2)
у = v/(u^2+v^2+w^2)
z = w/(u^2+v^2+w^2)
spherical:
x = u*cos(v)*sin(w)
у = u*sin(v)*sin(w)
z = u*cos(w)
tangentcylindrical:
x = u/(u^2+v^2) '
у = v/(u^2+v^2)
z = w
tangentsphere:
x = u*cos(w)/(u^2+v^2)
у = u*sin(w)/(u^2+v^2)
z = v/(u^2+v^2)
toroidal:
x = a*sinh(v)*cos(w)/d
у = a*sinh(v)*sin(w)/d
z = a*sin(u)/d где d = cosh(v) - cos(u)
Эти формулы полезно знать, поскольку в литературе встречаются несколько отличные формулы пересчета. Вид графиков трехмерных поверхностей очень сильно различается в разных координатных системах. По умолчанию трехмерные графики строятся в прямоугольной системе координат — rectangular.
20. Построение поверхностей
Построение поверхностей
Построение поверхностей с разными стилями
На рис. 11.15 показано два примера простейших построений графиков трехмерной поверхности. По умолчанию в Maple 7 строится поверхность с функциональной окраской и стилем style=patch (верхний рисунок). Функциональная окраска делает рисунки более информативными, но, увы, на рисунках в книге она превращается в окраску оттенками серого цвета.
Параметр style=hidden строит каркасную поверхность с функциональной окраской тонких линий каркаса и удалением невидимых линий. Чтобы график выглядел более четким, построение во втором примере задано линиями/черного цвета с помощью параметра color=black (см. нижний рисунок на рис. (11.15).
Помимо значения patch для построения трехмерных поверхностей можно задавать ряд других стилей: point — точками, contour — контурными линиями, line — линиями, hidden — линиями каркаса с удалением невидимых линий, wireframe — линиями каркаса со всеми видимыми линиями, patchnogrid — с раскраской, но без линий каркаса, patchcontour — раскраска с линиями равного уровня.
Рис. 11.15. Примеры простейшего построения трехмерных поверхностей
Цвет трехмерного графика может задаваться (как и для двумерного) параметром соlог=с, где с — цвет (оттенки цвета перечислялись ранее). Возможно еще два алгоритма задания цвета:
- HUE — алгоритм с заданием цвета в виде color=f(x,y);
- RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения ехрrr, ехрrg и exprb задают относительную значимость (от 0 до 1) основных цветов (красного — ехрrr, зеленого — ехрrg и синего — exprb).
Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.
22.gif
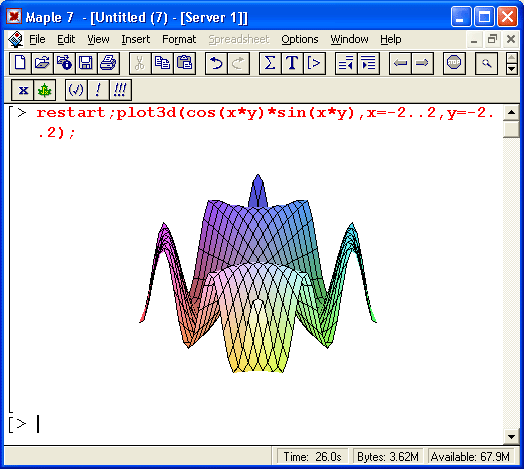
21. Построение фигур в различных системах координат
Построение фигур в различных системах координат
Как отмечалось, вид графика трехмерной поверхности существенно зависит от выбора координатной системы. Рисунок 11.16 показывает пример построения нелинейного конуса в цилиндрической системе координат. Для задания такой системы координат используется параметр coords=cylindrical.
Рис. 11.16. Нелинейная цилиндрическая поверхность
При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи (кстати, сделанной на русском языке).
Приведем еще один пример построения трехмерной поверхности — на этот раз . в сферической системе координат (рис. 11.17). Здесь функция задана вообще элементарно просто — в виде числа 1. Но, поскольку выбрана сферическая система координат, в результате строится поверхность шара единичного радиуса.
О том, насколько необычным может быть график той или иной функции в различных системах координат, свидетельствует рис. 11.18. На нем показан график параметрически заданной функции от одной координаты t = sin(t3), построенный в сферической системе координат.
Кстати, рис. 11.18 иллюстрирует возможность одновременного наблюдения нескольких окон. В одном окне задано построение графика, а в другом построен сам график. При построении графика в отдельном окне появляется панель форматирования графика. С помощью ее довольно наглядных кнопок можно легко скорректировать вспомогательные параметры графика (окраску, наличие линий каркаса, ориентацию и др.).
Рис. 11.17. Построение шарообразной поверхности в сферической системе координат
Рис. 11.18. График еще одной поверхности в сферической системе координат
24.gif
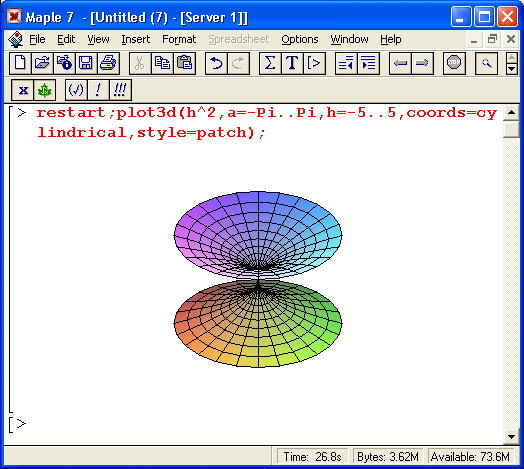
25.gif
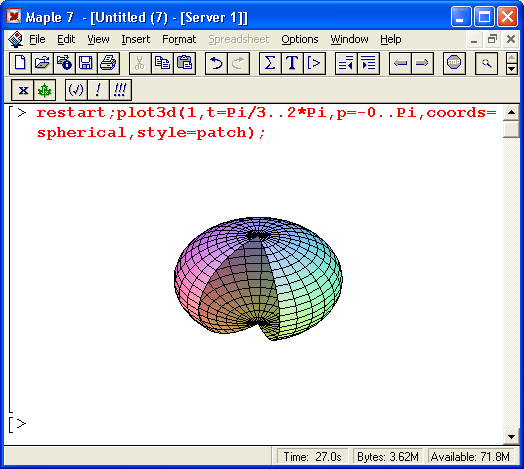
26.gif
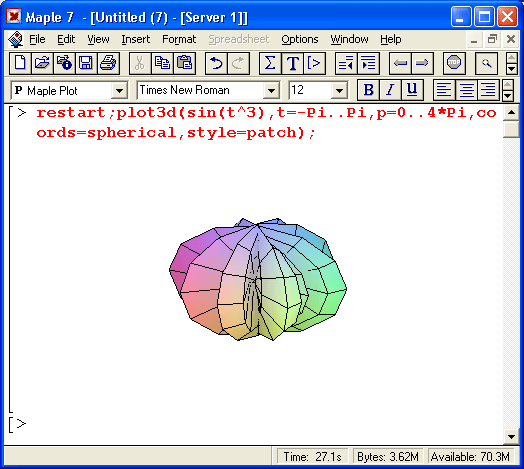
22. 3D-графики параметрически заданных поверхностей
3d- графики параметрически заданных поверхностей
На рис. 11.19 показано построение поверхности при полном ее параметрическом задании. В этом случае поверхность задается тремя формулами, содержащимися в списке.
Рис. 11.19. График трехмерной поверхности при полном параметрическом ее задании
В данном случае функциональная окраска задана из меню, поэтому в состав функции соответствующий параметр не введен. Обратите внимание на технику удаления частей фигуры путем задания соответствующего диапазона изменения параметров t и n.
Следующий пример показывает построение простого тороида — цилиндра, свернутого в кольцо (рис. 11.20). Здесь также использован прием удаления части фигуры, что делает ее представление более наглядным и красочным. Кроме того, введены параметры, задающие функциональную окраску.
Тор на рис. 11.20 выглядит, как произведение искусства. Он дает полное и наглядное представление об этой фигуре.
49.gif
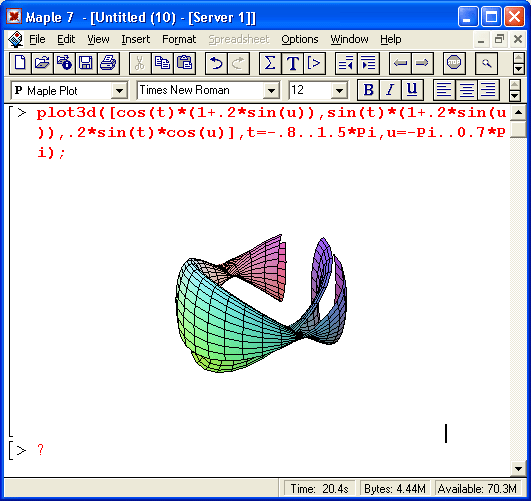
23. Масштабирование трехмерных фигур и изменение углов их обзора
Масштабирование трехмерных фигур и изменение углов их обзора
Полезно обратить внимание на параметр масштаба scalling=constrained, явно введенный в документ рис. 11.20. Его можно было бы и не вводить, поскольку этот параметр задается по умолчанию. Он выравнивает масштабы представления фигуры по осям координат, обычно используется по умолчанию и позволяет снизить до минимума геометрические искажения фигур — тор, например, при этом виден как круглая труба, свернутая в кольцо. У таких графиков есть специфический недостаток — они занимают малую часть окна вывода.
Рис. 11.20. Тор с функциональной окраской поверхности
Задание параметра scaling=unconstrained означает отказ от равного масштаба по осям. График при этом увеличивается в размерах, но становятся заметны его искажения по осям координат. В итоге тор превращается в толстую сплющенную трубу с эллиптическим сечением (рис. 11.21).
Весьма важным является учет углов, под которыми наблюдается трехмерная поверхность или объект. К примеру, построение рис. 11.21 неудачно в том плане, что оно не показывает наличия у тора дырки. В общем, как в поговорке: «кому бублик, а кому дырка от бублика» — ведь бублик и есть материально реализованный тор. Простейший и очень удобный способ изменить угол обзора заключается во вращении фигуры на рисунке мышью при нажатой левой кнопке. При этом можно повернуть фигуру так, что ее геометрические особенности будут видны (рис. 11.22).
В Maple есть способ явно задать углы обзора с помощью параметра orientation=[theta, phi], где theta и phi — углы, через которые задаются параметрические уравнения трехмерной фигуры или поверхности. Рисунок 11.23 дает пример такого задания фигуры, которую можно назвать «квадратным» тором. Обратите внимание, что значения заданных углов обзора повторяются в полях углов на контекстной панели инструментов. Разумеется, последние будут меняться, если начать вращать фигуру на рисунке мышью.
Рис. 11.21. Тор, построенный с применением значения параметра seating-unconstrained
Рис. 11.22. Тор с рис. 11.21 после поворота мышью демонстрирует, что он и впрямь имеет дырку
Рис. 11.23. «Квадратный» тор, представленный под заданными углами обзора
50.gif
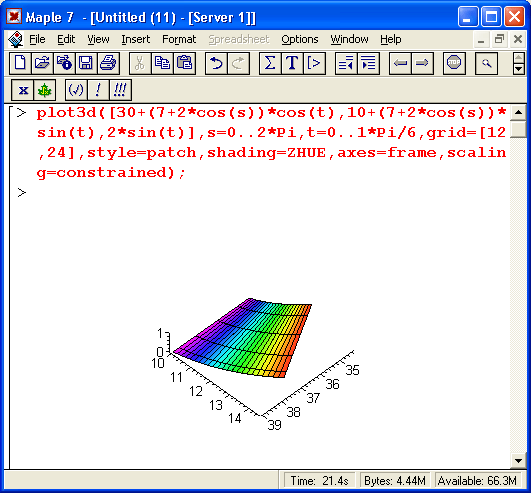
51.gif
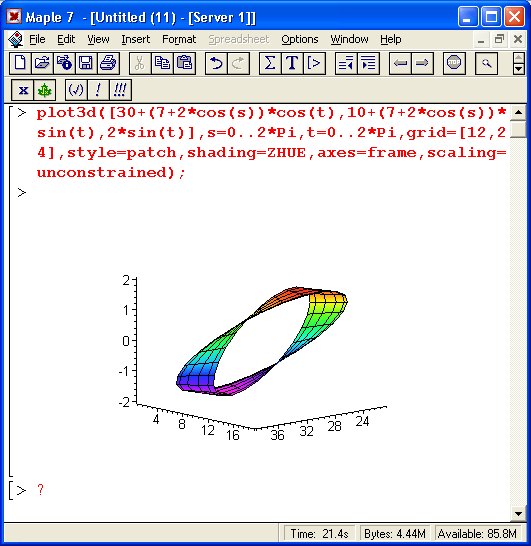
52.gif
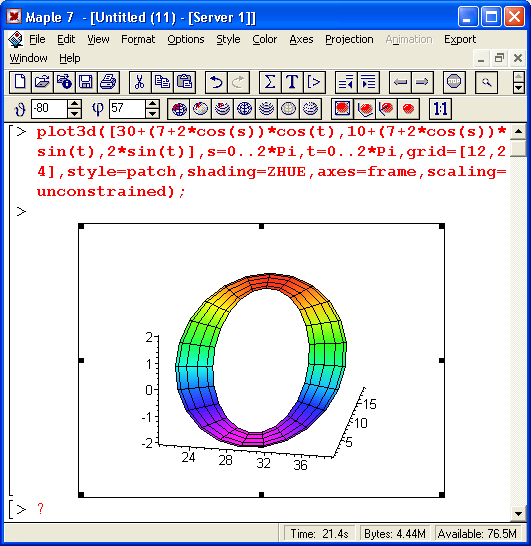
53.gif
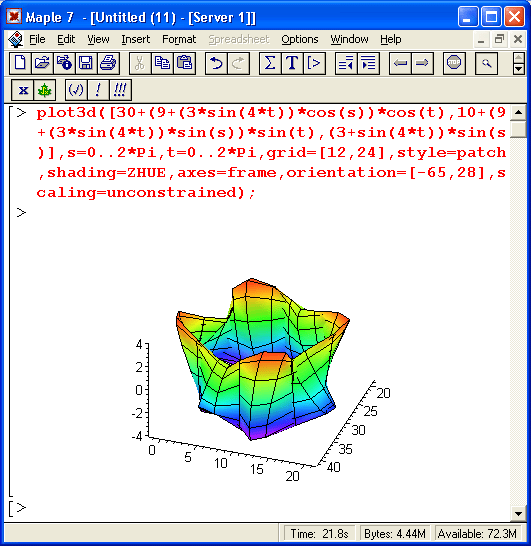
24. Занимательные фигуры — трехмерные графики
Занимательные фигуры — трехмерные графики
Параметрическое задание уравнений поверхности открывает почти неисчерпаемые возможности построения занимательных и сложных фигур самого различного вида. Приведем пару построений такого рода.
На рис. 11.24 показан тор, сечение которого имеет вид сплюснутой шестиконечной звезды. Вырез в фигуре дает прекрасный обзор ее внутренней поверхности, а цветная функциональная окраска и линии сетки, построенные с применением алгоритма удаления невидимых линий, дают весьма реалистичный вид фигуры. Замените параметр scaling=unconstrained на scaling=constrained, и вы получите тор с неискаженным сечением.
На рис. 11.25 показан еще один тор. На этот раз он круглого сечения, но сверху и снизу имеет вид пятиконечной звезды.
ПРИМЕЧАНИЕ
В приведенных на рис. 11.19-11.25 программах построения различных поверхностей — и трехмерных фигур имеется ряд характерных констант и математических выражений, определяющих как вид фигур, так и их размеры и положение. Рекомендуется тщательно проанализировать эти примеры и попробовать их в работе с несколько измененными теми или иными данными. Полезно построить ряд подобных примеров самостоятельно. Все это будет способствовать привитию учащимся специального геометрического стиля мышления, при котором геометрические особенности фигур связываются с их расчетным описанием.
Рис. 11.24. Тор с сечением в виде шестиконечной звезды
Рис. 11.25. Тор круглого сечения в виде пятиконечной звезды
54.gif
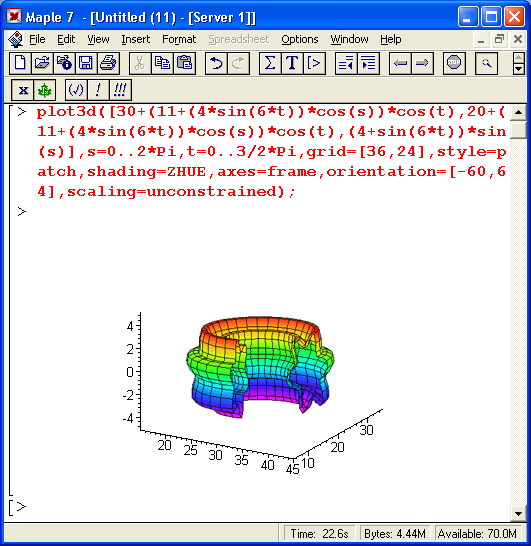
55.gif
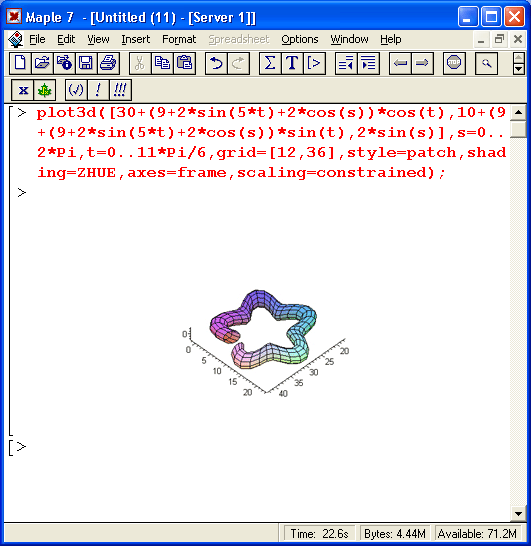
25. Быстрое построение графиков
Быстрое построение графиков
Двумерная быстрая графика — smartplot
В последние реализации системы Maple (5, 6 и 7) введены новые функции быстрого построения графиков. Функция smartplot(f) предназначена для создания двумерных графиков. Параметр f может задаваться в виде одиночного выражения или набора выражений, разделяемых запятыми. Задание управляющих парамтеров в этих графических функциях не предусмотрено; таким образом, их можно считать первичными, или черновыми. Для функции построения двумерного графика по умолчанию задан диапазон изменения аргумента -10.. 10. Рисунок 11.26 иллюстрирует применение функции smartplot для построения трех (верхний пример) и двух (нижний пример) графиков функций на одном рисунке.
Рис. 11.26. Построение графиков с помощью функции smartplot
Обратите внимание на второй пример применения функции smartplot. Здесь график выражения 5sin(y)/y построен относительно вертикальной оси. Поэтому он развернут на 90° относительно графика, построенного обычным образом.
ПРИМЕЧАНИЕ
На графиках, построенных командой smartplot(x), присутствует надпись «Live», что — видно на рис. 11.26.
34.gif
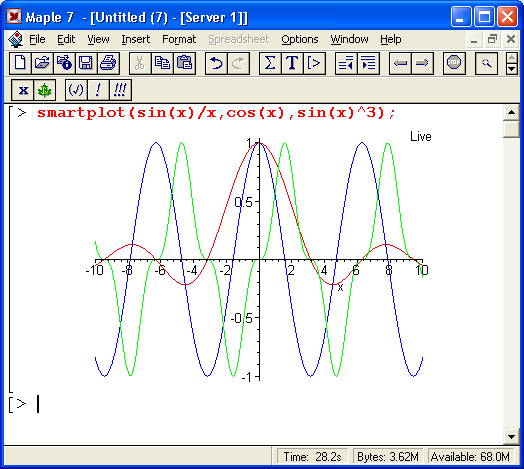
26. Быстрое построение трехмерных графиков smartplot3d
Быстрое построение трехмерных графиков smartplot3d
Быстрое (не в смысле ускорения самого построения, а лишь в смысле более быстрого задания построения графиков) построение трехмерных графиков обеспечивает функция smartplot3d Для этой функции задан диапазон изменения обоих аргументов -5..5. Рисунок 11.27 поясняет применение функции smartplot3d.
Рис. 11.27. Примеры применения функции smartplot3d
Как видно из второго примера, представленного на рис. 11.27, функция smartplot3d обеспечивает построение не только отдельных поверхностей, но и ряда Пересе, кающихся поверхностей. При этом линии пересечения поверхностей строятся вполне корректно.
36.gif
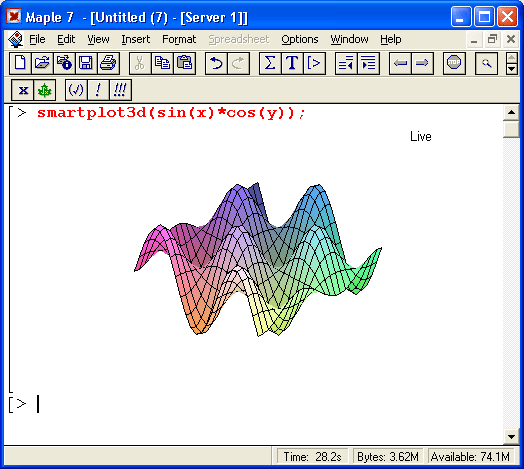
27. Специальные приемы построения трехмерных графиков
Специальные приемы построения трехмерных графиков
Трехмерный график как графический объект
Принадлежность функций plot и plot3d к функциям (в ряде книг их именуют операторами, командами или процедурами) наглядно выявляется при создании графических объектов. Графический объект — это, в сущности, обычная переменная, которой присваивается значение графической функции. После этого такая переменная, будучи вызванной, производит построение соответствующего графика. Пример этого дан на рис. 11.28.
Рис. 11.28. Пример задания и вывода трехмерного графика — графического объекта
В данном случае строится лента Мебиуса, свойства которой (например, плавный переход с одной стороны ленты на другую) уже много веков будоражат воображение людей.
Поскольку можно говорить, что вызов переменной возвращает графический объект, то это дает повод считать plot и plot3d графическими функциями.
38.gif
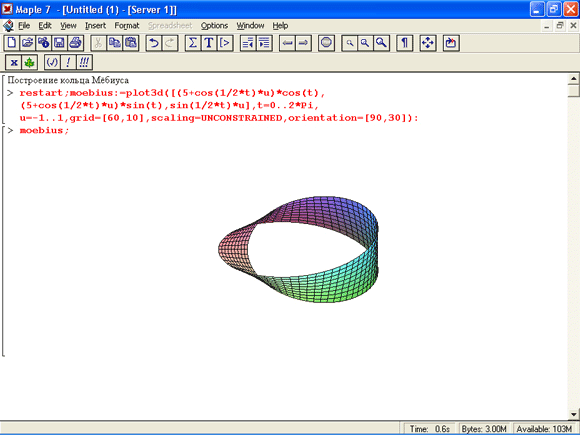
28. Задание трехмерных графиков в виде процедур
Задание трехмерных графиков в виде процедур
Язык программирования Maple 7 допускает применение в процедурах любых внутренних функций, в том числе графических. Пример такого применения дает рис. 11.29.
Рис. 11.29. Пример создания и применения процедуры трехмерной графики
Этот пример показывает еще один способ задания и построения кольца Мебиуса. Практически любые графические построения можно оформлять в виде процедур и использовать такие процедуры в своих документах.
39.gif
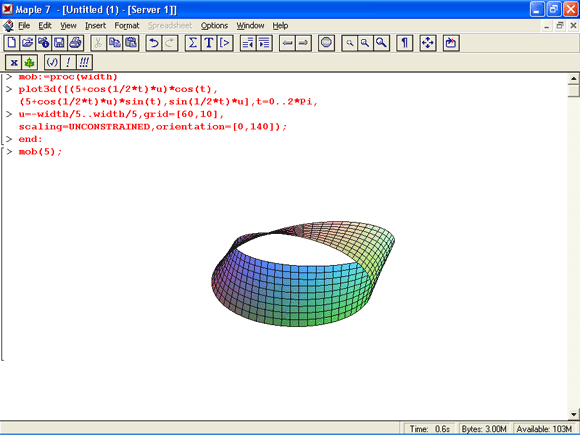
29. Построение ряда трехмерных фигур на одном графике
Построение ряда трехмерных фигур на одном графике
Функция plot3d позволяет строить одновременно несколько фигур, пересекающихся в пространстве. Для этого достаточно вместо описания одной поверхности задать список описаний ряда поверхностей. При этом функция plot3d обладает уникальной возможностью — автоматически вычисляет точки пересечения фигур и показывает только видимые части поверхностей. Это создает изображения, выглядящие вполне естественно. Пример такого построения для двух функций показан на рис. 11.30.
Рис. 11.30. Пример построения двух трехмерных фигур, пересекающихся в пространстве
40.gif
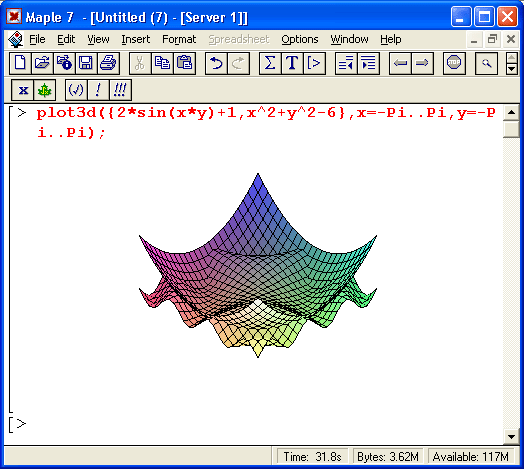
30. Двумерные и трехмерные графические структуры
Двумерные и трехмерные графические структуры
Понятие о графических структурах
Функции PLOT и PLOT3D (с именами, набранными большими буквами) позволяют создавать графические структуры, содержащие ряд графических объектов si, s2, s3 и т. д. Каждый объект может представлять собой точку или фигуру, полигон, надпись и т. д., позиционированную с высокой точностью в заданной системе координат. Координатные оси также относятся к графическим объектам. Важно отметить, что функции PLOT и PLOT3D одновременно являются данными, описывающими графики. Их можно записывать в виде файлов и (после открытия файлов) представлять в виде графиков. Особые свойства этих функций подчеркиваются их записью прописными буквами.
31. Графические структуры двумерной графики
Графические структуры двумерной графики
Графическая структура двумерной графики задается в виде:
PLOT(s1, s2, s3....,0);
где si, s2, s3 ... — графические объекты (или элементарные структуры — примитивы), о — общие для структуры параметры.
Основными объектами являются:
- POINTS([xl,yl],[x2,y2],...[xn,yn]) — построение точек, заданных их координатами;
- CURVES([[xll,yll],...[xln,yln]], [[х21,у21],...[х2п,у2п]],... [[xml,yml]....[xmn.ymn]]) -построение кривых по точкам;
- POLYGONS([[xll,yll]....[xln,yln]], [x2l.y2ll]....[x21n,y21n]].... [[xml,yml]....[xmn.ynm]]) -построение замкнутой области-полигона (многоугольника, так как последняя точка должна совпадать с первой);
- ТЕХТ([х, у], 'string', horizontal .vertical) — вывод текстовой надписи 'string4, позиционированной в точке с координатами [х.у], с горизонтальной или вертикальной ориентацией. Параметр horizontal может иметь значение ALIGNLEFT или ALIGNRIGHT, указывающие, в какую сторону (влево или вправо) идет надпись. Аналогично параметр vertical может иметь значение ALIGNABOVE или ALIGNBELOW, указывающее в каком направлении (вверх или вниз) идет надпись.
При задании графических объектов (структур) si, s2, s3 и т. д. можно использовать описанные выше параметры и параметры, например, для задания стиля построения - STYLE (POINT, LINE/PATCH, PATCHNOGRID); толщины линий, - THICKNESS (кроме координатных осей); символа, которым строятся точки кривых — SYMBOL (BOX, CROSS, CIRCLE, POINT, DIAMOND и DEFAULT); стиля линий - LINESTYLE; цвета -COLOR (например, COLOR(HUE.O) для закраски непрерывной области), типа шрифта — FONT; вывода титульной надписи — TITLE (string); имени объекта — NAME (string); стиля координатных осей - AXESSTYLE (BOX, FRAME, NORMAL, NONE или DEFAULT) и т. д.
Следует отметить, что параметры в графических структурах задаются несколько иначе — с помощью круглых скобок. Например, для задания шрифта TIMES ROMAN с размером символов 16 пунктов надо записать FONT(TIMES,ROMAN, 16), для задания стиля координатных осей в виде прямоугольника — AXESSTYLE (BOX) и т. д.
На рис. 11.31 показан пример графических построений при использовании основных структур двумерной графики.
Как видно из этого примера, графическая двумерная структура позволяет задавать практически любые двумерные графики и текстовые надписи в пределах одного рисунка.
Рис. 11.31. Пример использования двумерных структур
41.gif
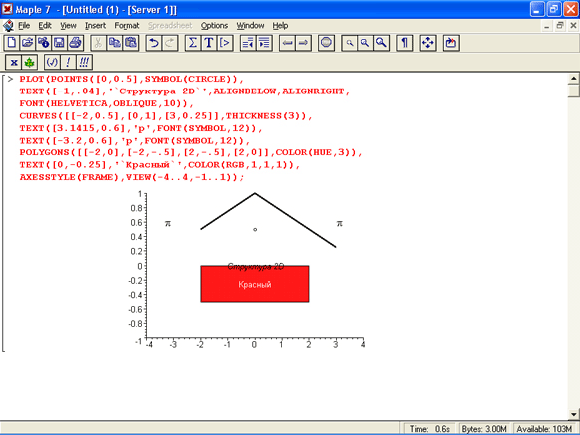
32. Графические структуры трехмерной графики
Графические структуры трехмерной графики
Графические структуры трехмерной графики строятся функцией PLOT3D:
PLOT3D(s1,s2,s3.....o)
В качестве элементарных графических структур можно использовать уже описанные выше объекты POINTS, CURVES, POLYGONS и TEXT — разумеется, с добавлением в списки параметров третьей координаты. Пример такого построения дан на рис. 11.32.
Кроме того, могут использоваться некоторые специальные трехмерные структуры. Одна из них — структура GRID:
- GRID(a. .b,c..d.listlist) — задание поверхности над участком координатной плоскости, ограниченной отрезками[а, b] и[с, d], по данным, заданным переменной-списком listlist:=[[z11,...z1n],[z21,...z2n],...[z1m...zmn]] с размерностью n?m. Заметим, что эта переменная задает координату z для равноотстоящих точек поверхности.
На рис. 11.33 показан пример создания структуры трехмерной графики на базе GRID. Изображение .представляет собой линии, соединяющие заданные точки.
Еще один тип трехмерной графической структуры — это MESH:
- MESH(listlist) — задание трехмерной поверхности по данным списочной переменной list! 1st, содержащей полные координаты всех точек поверхности (возможно задание последней при неравномерной сетке).
Рис. 11.32. Пример создания структуры трехмерной графики
Рис. 11.33. Пример задания графической структуры типа GRID
Обычная форма задания этой структуры следующая:
MESH([[[x11,y11,z11]....[x1n,y1n,z1n]]. [[x21,y21,z21]....[x2n,y2n,z2n]]. ...[[xm1,ym1,zm1]...[xmn,ymn,zmn]]])
Пример задания такой структуры представлен на рис. 11.34.
Рис. 11.34. Пример задания графической структуры типа MESH
Описанные структуры могут использоваться и в программных модулях. Много таких примеров описано в книгах, поставляемых с системой Maple 7.
42.gif
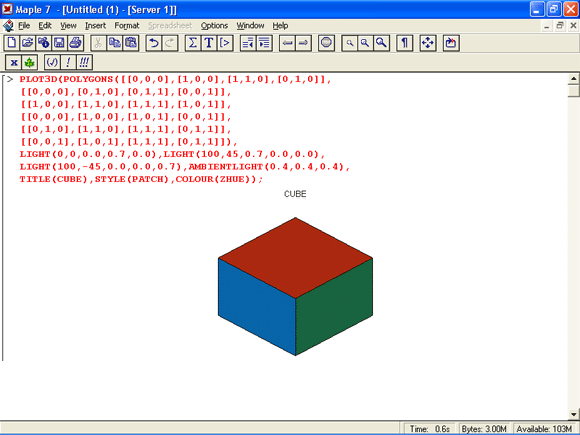
43.gif

44.gif
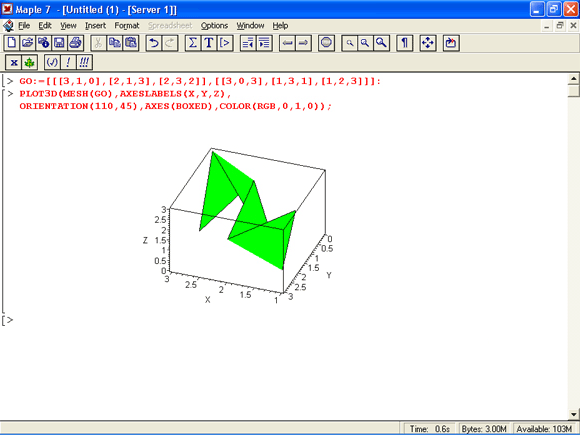
33. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Использовать основную функцию построения двумерных графиков — plot.
- Задавать координатные системы двумерных графиков.
- Управлять цветом и стилем двумерных графиков.
- Использовать основные типы двумерных графиков.
- Строить трехмерные графики.
- Строить различные поверхности.
- Выполнять быстрые (черновые) построения.
- Использовать специальные приемы для построения трехмерных графиков.
- Задавать графические структуры двумерной и трехмерной графики.
Урок 12. Расширенные средства графики
1. Пакет plots
Урок 12.
Расширенные средства графики
Общая характеристика пакета plots
Пакет plots содержит почти полсотни графических функций, существенно расширяющих возможности построения двумерных и трехмерных графиков в Maple 7:
> with(plots);
[animate, animate3d, animatecurve, changecoords, complexplot, complexplotSd, conformal, contourplot, contourplotSd, coordplot, coordplotld, cylinderplot, densityplot, display, displayed, fteldplot,fieldplot3d, gradplot, gmdplotSd, implicitplot, implicitplot3d, inequal, listcontplot, HslcontplotSd, listdensityplot, listplot, Iistplot3d, loglogplot, logplot, matrixplot, odeplot>pareto,pointplot, pointplotSd, polarplot, polygonplot, polygonplotSd, palyhedrajsupported, polyhedraplot, replot, rootlocus, semilogplot, setoptions, setoptionsSd, spacecurve, sparsematrixplot, sphereplot, surfdata, textplot, textplotSd, tubeplot]
Ввиду важности этого пакета отметим назначение всех его функций:
- animate — создает анимацию двумерных графиков функций;
- animate3d — создает анимацию трехмерных графиков функций;
- animatecurve — создает анимацию кривых;
- changecoords — смена системы координат;
- complexplot — построение двумерного графика на комплексной плоскости;
- complexplot3d — построение трехмерного графика в комплексном пространстве;
- conformal — конформный график комплексной функции;
- contourplot — построение контурного графика;
- contourplot3d — построение трехмерного контурного графика;
- coordplot — построение координатной системы двумерных графиков;
- coordplot3d — построение координатной системы трехмерных графиков;
- cylinderplot — построение графика поверхности в цилиндрических координатах;
- densityplot — построение двумерного графика плотности;
- display — построение графика для списка графических объектов;
- display3d — построение графика для списка трехмерных графических объектов;
- fieldplot — построение графика двумерного векторного поля;
- fieldplot3d — построение графика трехмерного векторного поля;
- gradplot — построение графика двумерного векторного поля градиента;
- gradplot3d — построение графика трехмерного векторного поля градиента;
- implicitplot — построение двумерного графика неявной функции;
- implicitp1ot3d — построение трехмерного графика неявной функции;
- inequal — построение графика решения системы неравенств;
- listcontplot — построение двумерного контурного графика для сетки значений;
- Iistcontplot3d — построение трехмерного контурного графика для сетки значений;
- listdensityplot — построение двумерного графика плотности для сетки значений;
- listplot — построение двумерного графика для списка значений;
- listplot3d — построение трехмерного графика для списка значений;
- loglogplot — построение логарифмического двумерного графика функции;
- logplot — построение полулогарифмического двумерного графика функции;
- matrixplot — построение трехмерного графика со значениями Z, определенными матрицей;
- odeplot — построение двумерного или трехмерного графика решения дифференциальных уравнений;
- pareto — построение диаграммы (гистограммы и графика);
- pointplot — построение точками двумерного графика;
- poi ntplot3d — построение точками трехмерного графика;
- polarplot — построение графика двумерной кривой в полярной системе координат;
- polygonplot — построение графика одного или нескольких многоугольников;
- polygonplot3d — построение одного или нескольких многоугольников;
- polyhedraplot — построение трехмерного многогранника;
- replot — перестроение графика заново;
- rootlocus — построение графика корней уравнения с комплексными неизвестными;
- semilogplot — построение графика функции с логарифмическим масштабом по оси абсцисс;
- setoptions — установка параметров по умолчанию для двумерных графиков;
- setoptions3d — установка параметров по умолчанию для трехмерных графиков;
- spaeecurve — построение трехмерных кривых;
- sparsematrixplot — построение двумерного графика отличных от нуля значений матрицы;
- sphereplot — построение графика трехмерной поверхности в сферических координатах;
- surfdata — построение трехмерного графика поверхности по численным данным;
- textplot — вывод текста на заданное место двумерного графика;
- textplot3d — вывод текста на заданное место трехмерного графика;
- tubeplot — построение трехмерного графика типа «трубы».
Среди этих функций надо отметить прежде всего средства построения графиков ряда новых типов (например, в виде линий равного уровня, векторных полей и т. д.), а также средства объединения различных графиков в один. Особый интерес представляют две первые функции, обеспечивающие анимацию как двумерных (animate), так и трехмерных графиков (animate3d). Этот пакет вполне заслуживает описания в отдельной книге. Но, учитывая ограниченный объем данной книги, мы рассмотрим лишь несколько характерных примеров его применения. Заметим, что для использования приведенных функций нужен вызов пакета, например командой with(plots).
2. Построение графиков функций в двумерной полярной системе координат
Построение графиков функций в двумерной полярной системе координат
В пакете plots есть функция для построения графиков в полярной системе координат. Она имеет вид polarplot(L,o), где L — объекты для задания функции, график которой строится, и о — необязательные параметры. На рис. 12.1, сверху, представлен пример построения графика с помощью функции polarplot. В данном случае для большей выразительности опущено построение координатных осей, а график выведен линией удвоенной толщины. График очень напоминает лист клена, весьма почитаемого в Канаде и ставшего эмблемой Maple.
3. Построение двумерных графиков типа implidtplot
Построение двумерных графиков типа implicitplot
В математике часто встречается особый тип задания геометрических фигур, при котором переменные х и у связаны неявной зависимостью. Например, окружность задается выражением х2 + у2 =R2, где R — радиус окружности. Для задания двумерного графика такого вида служит функция импликативной графики:
implicitplot(eqn,x=a..b,y=c..d,options)
Пример построения окружности с помощью этой функции показан на рис. 12.1, снизу. Чуть ниже мы рассмотрим подобную функцию и для трехмерного графика.
Рис. 12.1. Графики, построенные с помощью функций polarptot и impticitplot
1.gif
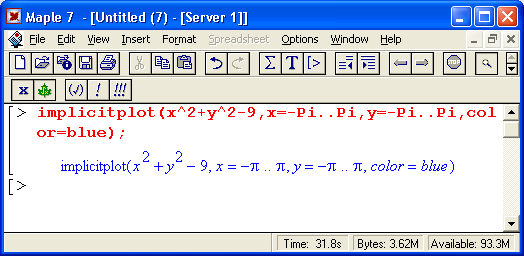
4. Построение графиков линиями равного уровня
Построение графиков линиями равного уровня
Графики, построенные с помощью линий равного уровня (их также называют контурными графиками), часто используются в картографии. Эти графики получаются, если мысленно провести через трехмерную поверхность ряд равноотстоящих плоскостей, параллельных плоскости, образованной осями X иY графика. Линии равных высот образуются в результате пересечения этих плоскостей с трехмерной поверхностью.
Для построения таких графиков используется функция contourplot, которая может использоваться в нескольких форматах:
contourplot(exprl,x=a..b,y=c..d)
contourplot(f,a..b,c..d)
contourplot([exprf ,exprg,exprh ] S=a. .b,t=c. .d)
contourplot([f.g.h ],a..b,c..d)
contourp1ot3d(exprl,x=a..b,y=c. .d)
contourplot3d(f,a..b,c..d)
contourplot3d([exprf,exprg,exprh],s=a..b,t=c,.d)
contourplot3d([f.g.h ],a..b,c..d)
Здесь f, g и h — функции; exprl — выражение, описывающее зависимость высоты поверхности от координат х и у; exprf, exprg и exprh — выражения, зависящие от s и t, описывающие поверхность в параметрической форме; а и b — константы вещественного типа; end — константы или выражения вещественного типа; х, у, s и t — имена независимых переменных.
На рис. 12.2 показано построение графика линиями равного уровня для одной функции. Параметр filled=true обеспечивает автоматическую функциональную окраску замкнутых фигур, образованных линиями равного уровня. Порою это придает графику большую выразительность, чем при построении только линий равного уровня.
Рис. 12.2. Пример построения графика функции линиями равного уровня
Обратите внимание на то, что данная функция по умолчанию строит легенду — она видна под графиком в виде линий с надписями. К сожалению, в данном варианте окраски сами контурные линии получаются черными и их невозможно отличить. Однако если убрать параметр filled=true, то контурные линии (и линии легенды) будут иметь разный цвет и легко различаться.
Функция contourplot позволяет строить и графики ряда функций. Пример такого построения показан на рис. 12.3. Множество окружностей на этом рисунке создается четырьмя поверхностями, заданными функциями cl, с2, сЗ и с4.
Рис. 12.3. Пример построения графиков многих функций линиями равного уровня
ВНИМАНИЕ
Обратите внимание, что на многих графиках Maple 7 по умолчанию вписывает легенду,то есть список линий с обозначениями. Иногда (как, например, на рис. 12.3) этот список оказывается просто некстати. Легенду можно убрать, расширив заодно место для графика, сняв флажок Show Legend в меню Legend, которое появляется при двойном щелчке на графике (это меню видно на рис. 12.3). То же самое можно сделать с помощью той же команды в контекстном меню. Заодно запомните, что легенду можно редактировать, выполнив команду Edit Legend.
Следует отметить, что хотя графики в виде линий равного уровня выглядят не так эстетично и естественно, как обычные графики трехмерных поверхностей (ибо требуют осмысления результатов), у них есть один существенный плюс - экстремумы функций на таких графиках выявляются порой более четко, чем на обычных графиках. Например, небольшая возвышенность или впадина за большой «горой» на обычном графике может оказаться невидимой, поскольку заслоняется «горой». На графике линий равного уровня этого эффекта нет. Однако выразительность таких графиков сильно зависит от числа контурных линий.
2.gif
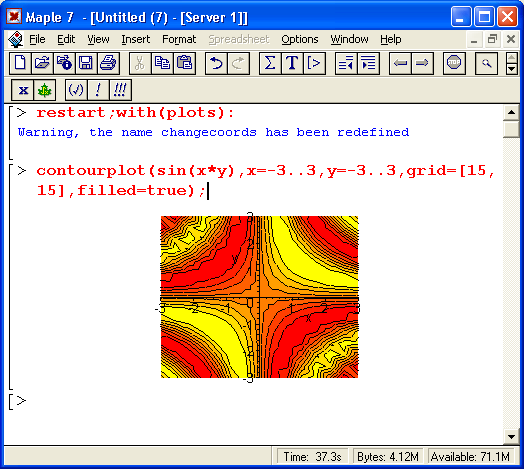
26.gif

5. График плотности
График плотности
Иногда поверхности отображаются на плоскости как графики плотности окраски — чем выше высота поверхности, тем плотнее (темнее) окраска. Такой вид графиков создается функцией densityplot. Она может записываться в двух форматах:
densityplot(exprl.x=a..b,y=c..d)
densityplot(f,a..b,c..d)
где назначение параметров соответствует указанному выше для функции contourplot. На рис. 12.4 (верхняя часть) дан пример построения графика такого типа. Нетрудно заметить, что в плоскости XY график разбит на квадраты, плотность окраски которых различна. В нашем случае плотность окраски задается оттенками серого цвета.
Рис. 12.4. Графики плотности и поля векторов
Обычно графики такого типа не очень выразительны, но имеют свои области применения. К примеру, оттенки окраски полупрозрачной жидкости могут указывать на рельеф поверхности дна емкости, в которой находится эта жидкость.
6. Двумерный график векторного поля
Двумерный график векторного поля
Еще один распространенный способ представления трехмерных поверхностей —-графики полей векторов. Они часто применяются для отображения полей, например электрических зарядов. Особенность таких графиков в том, что для их построения используют стрелки, направление которых соответствует направлению изменения градиента поля, а длина — значению градиента. Так что термин «поле векторов» надо понимать в смысле, что поле графика заполнено векторами.
Для построения таких графиков в двумерной системе координат используется функция fieldplot:
fieldplot(f, r1, r2)
fieldplot(f, r1, r2. ...)
где f — вектор или множество векторов, задающих построение; r1 и r2 — пределы.
На рис. 12.4 в нижней части документа показан вид одного из таких графиков. Следует отметить, что для получения достаточного числа отчетливо видных стрелок надо поработать с форматированием графиков. Иначе графики этого типа могут оказаться не очень представительными. Так, слишком короткие стрелки превращаются в черточки и даже точки, не имеющие острия, что лишает графики наглядности.
Несколько позже мы рассмотрим построение на одном рисунке графиков плотности и векторного поля, а также создание более наглядных толстых стрелок.
7. Трехмерный график типа implidtplot3d
Трехмерный график типа implicitplot3d
Трехмерные поверхности также могут задаваться уравнениями неявного вида. В этом случае для построения их графиков используется функция implicitplot3d:
implicitplot3d(exprl,x=a..b,y=c.,d,z=p..q,<options>)
implicitplot3d(f,a..b,c..d,p..q,<options>)
На рис. 12.5 показаны два примера построения объемных фигур с помощью функции implicitplot3d.
Эти примеры хорошо иллюстрируют технику применения функции implicitplot3d. С ее помощью можно строить весьма своеобразные фигуры, что, впрочем, видно и из приведенных примеров. Для наглядности фигур на рис. 12.5 они несколько развернуты в пространстве с помощью мыши.
8. Графики в разных системах координат
Графики в разных системах координат
В пакете plots имеется множество функций для построения графиков в различных системах координат. Объем книги не позволяет воспроизвести примеры всех видов таких графиков, ибо их многие сотни. Да это и не надо — во встроенных в справочную систему примерах можно найти все нужные сведения. Так что ограничимся лишь парой примеров применения функции tubeplot(C, options), позволяющей строить весьма наглядные фигуры в пространстве, напоминающие трубы или иные объекты, образованные фигурами вращения.
Рис. 12.5. Примеры применения функции implidtplot3d
На рис. 12.6 показана одна из таких фигур. Она поразительно напоминает раковину улитки. Функциональная окраска достигнута доработкой графика с помощью панели форматирования.
Эта функция может использоваться и для построения ряда трубчатых объектов в пространстве. При этом автоматически задается алгоритм удаления невидимых линий даже для достаточно сложных фигур. Это наглядно иллюстрирует пример на рис. 12.7, показывающий фигуру «цепи». Не правда ли, реалистичность этой фигуры поражает воображение?
Можно долго размышлять о том, как те или иные математические закономерности описывают предметы реального мира, положенные в основу тех или иных геометрических объектов, или, возможно, о гениальности людей, сумевших найти такие закономерности для многих из таких объектов. В наше время Maple 7 открывает огромные возможности для таких людей.
6.gif
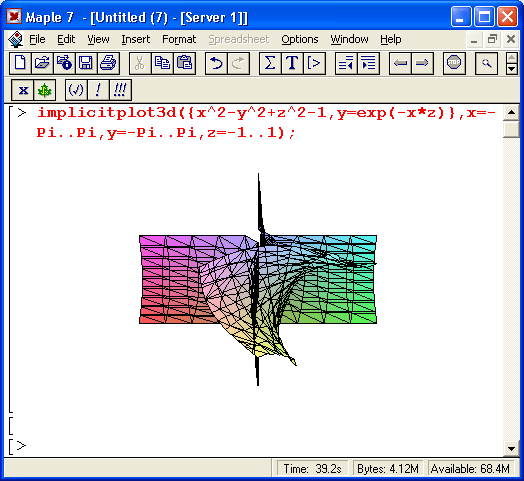
9. Графики типа трехмерного поля из векторов
Графики типа трехмерного поля из векторов
Наглядность ряда графиков можно существенно увеличить, строя их в трехмерном представлении. Например, для такого построения графиков полей из векторов можно использовать графическую функцию fieldplot3d. В отличие от функции fieldplot она строит стрелки как бы в трехмерном пространстве (рис. 12.8).
Рис. 12.6. Построение графика- «улитки»
Рис. 12.7. Фигура «цепи», построенная с применением функции tubeplot
Рис. 12.8. Построение поля в трехмерном пространстве с помощью векторов
Все сказанное об особенностях таких двумерных графиков остается справедливым и для графиков трехмерных. В частности, для обеспечения достаточной наглядности нужно тщательно отлаживать форматы представления таких графиков.
9.gif
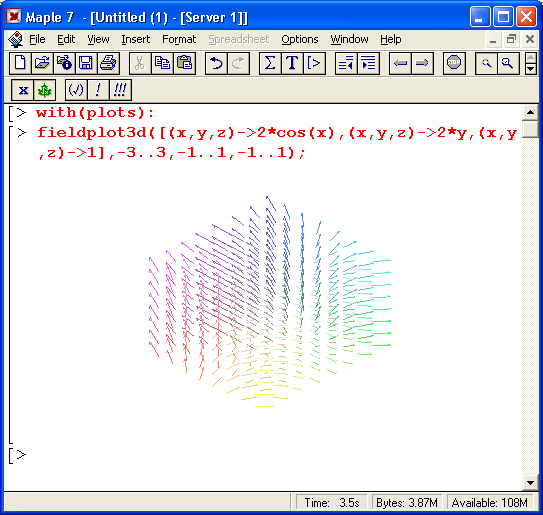
27.gif
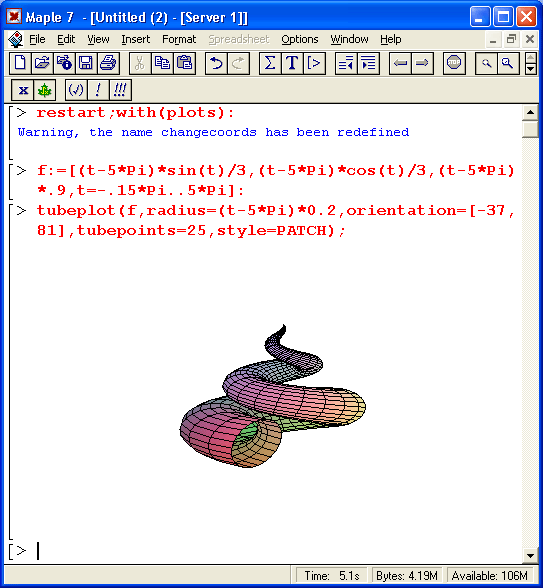
28.gif
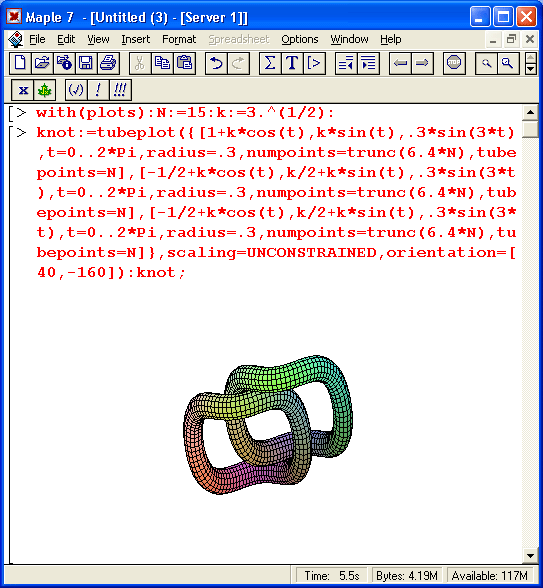
10. Контурные трехмерные графики
Контурные трехмерные графики
В отличие от векторных графиков контурные графики поверхностей, наложенные на сами эти поверхности, нередко повышают восприимчивость таких поверхностей — подобно изображению линий каркаса. Для одновременного построения поверхности и контурных линий на них служит функция contourplot3d. Пример ее применения показан на рис. 12.9.
Для повышения наглядности этот график доработан с помощью контекстной панели инструментов графиков. В частности, включена функциональная окраска и подобраны углы обзора фигуры, при которых отчетливо видны ее впадина и пик.
Рис. 12.9. График поверхности с контурными линиями
10.gif
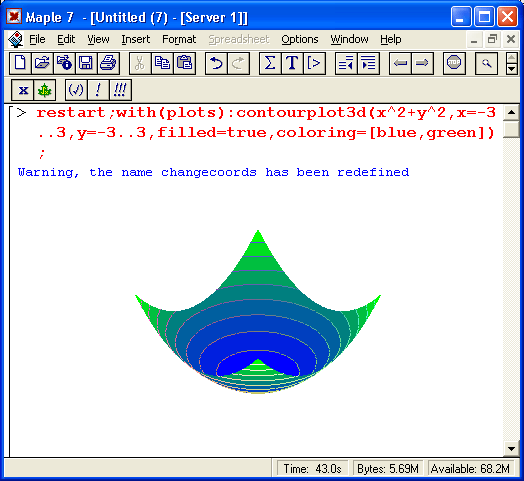
11. Техника визуализации сложных пространственных фигур
Техника визуализации сложных пространственных фигур
Приведенные выше достаточно простые примеры дают представление о высоком качестве визуализации геометрических фигур с помощью пакета plots. Здесь мы рассмотрим еще несколько примеров визуализации трехмерных фигур. Многие видели катушки индуктивности, у которых провод того или иного диаметра намотан на тороидальный магнитный сердечник. Некую математическую абстракцию такой катушки иллюстрирует рис. 12.10.
В документе рис. 12.10 для функции tubeplot использовано довольно большое число параметров. Не всегда их действие очевидно. Поэтому на рис. 12.11 показано построение трех взаимно пересекающихся торов с разными наборами параметров. Этот рисунок дает также наглядное представление о возможности построения нескольких графических объектов (представленных функциями pi, р2 и рЗ) с помощью функции tubeplot.
Рис. 12.10. Тор с обмоткой — толстой спиралью
Рис. 12.11. Три пересекающихся тора с разными стилями построения
Наконец, на рис. 12.12 показано построение тора с тонкой обмоткой. Рекомендуется внимательно посмотреть на запись функции tubeplot в этом примере и в примере, показанном на рис. 12.11. Можно также поэкспериментировать с управляющими параметрами графика, от которых сильно зависят его представительность и наглядность.
Рис. 12.12. Тор с тонкой обмоткой
В ряде случаев наглядно представленные фигуры можно строить путем объединения однотипных фигур. Пример графика подобного рода представлен на рис. 12.13. Здесь готовится список графических объектов s, смещенных по вертикали. С помощью функции display они воспроизводятся на одном графике, что повышает реалистичность изображения.
Последний пример имеет еще одну важную особенность — он иллюстрирует задание графической процедуры, в теле которой используются функции пакета plots. Параметр п этой процедуры задает число элементарных фигур, из которых строится полная фигура. Таким образом, высотой фигуры (или шириной «шины») можно управлять. Возможность задания практически любых графических процедур средствами Maple-языка существенно расширяет возможности Maple.
Наглядность таких графиков, как графики плотности и векторных полей может быть улучшена их совместным применением. Такой пример показан на рис. 12.14.
Рис. 12.13. Построение фигуры, напоминающей шину автомобиля
Рис. 12.14. Пример совместного применения графиков плотности и векторного поля
Этот пример иллюстрирует использование «жирных*- стрелок .для обозначения векторного поля. Наглядность графика повышается благодаря наложению стрелок на график плотности, который лучше, чем собственно стрелки, дает представление о плавности изменения высоты поверхности, заданной функцией.
25.gif
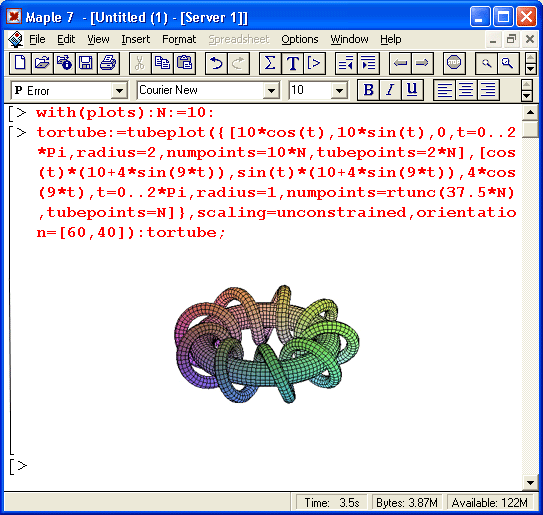
34.gif
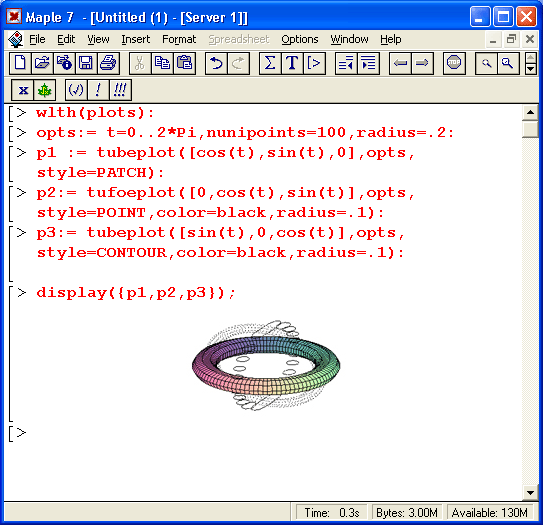
35.gif
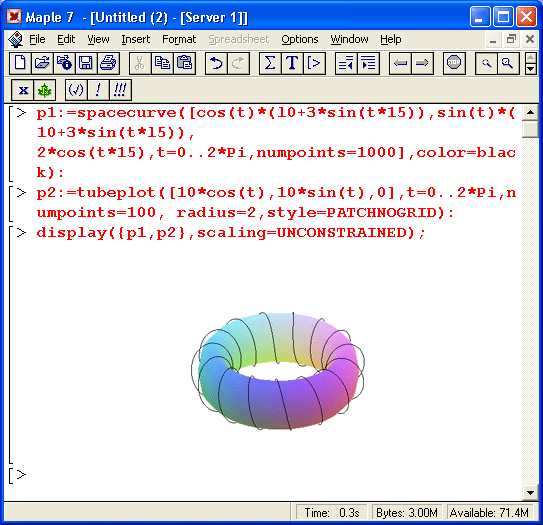
36.gif
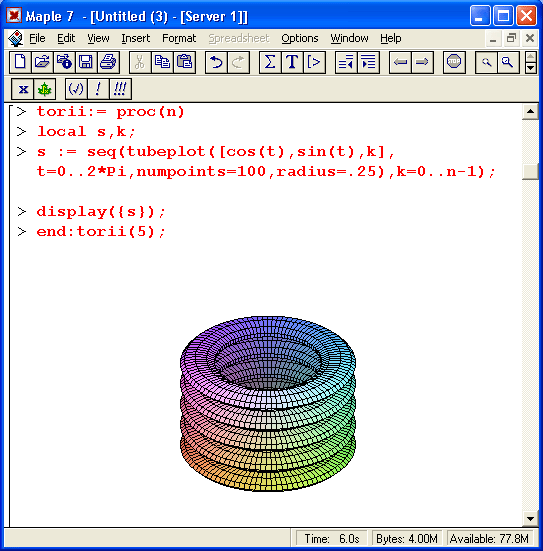
37.gif
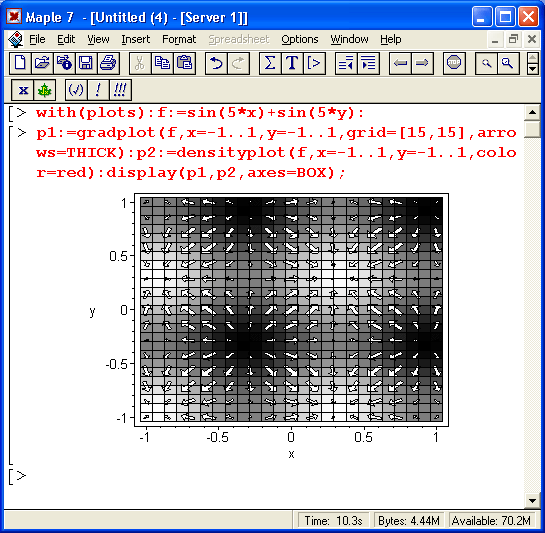
12. Техника анимирования графиков
Техника анимирования графиков
Визуализация графических построений и результатов моделирования различных объектов и явлений существенно повышается при использовании средств «оживления» "(анимации) изображений. Пакет plots имеет две простые функции для создания анимированных графиков.
Первая из этих функций служит для создания анимации графиков, представляющих функцию одной переменной F(x):
animatecurve(F, r, ...)
Эта функция просто позволяет наблюдать медленное построение графика. Формат ее применения подобен используемому в функции plot. При вызове данной функции вначале строится пустой шаблон графика. Если активизировать шаблон мышью, то в строке главного меню появляется меню Animation. Меню Animation содержит команды управления анимацией. Такое же подменю появляется и в контекстном (рис. 12.15). Указанное подменю содержит следующие команды анимации:
- Play — запуск построения графика;
- Next — выполнение следующего шага анимации;
- Backward/Forward — переключение направления анимации (назад/вперед);
- Faster — ускорение анимации;
- Slower — замедление анимации;
- Continiuus/Singlecycle — цикличность анимации.
При исполнении команды Play происходит построение кривой (или нескольких кривых). В зависимости от выбора команд Faster или Slower построение идет быстро или медленно. Команда Next выполняет один шаг анимации -построение очередного фрагмента кривой. Переключатель Backward/Forward позволяет задать направление построения кривой - от начала к концу или от конца к началу. Построение может быть непрерывным или циклическим в зависимости от состояния позиции Continiuus/Singlecycle в подменю управления анимацией. При циклической анимации число циклов задается параметром frames=n.
Рис. 12.15. Пример анимационного построения графика функцией animatecurve
11.gif
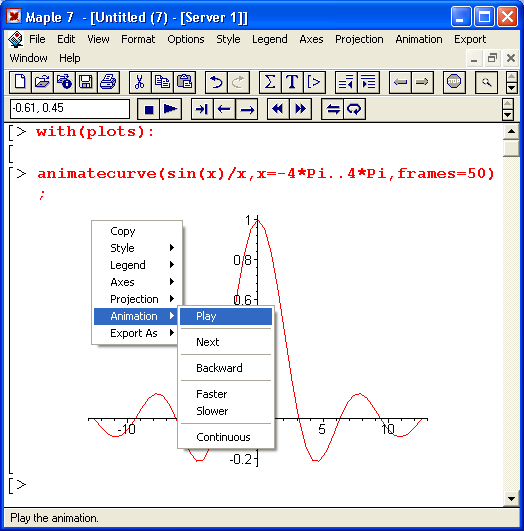
13. Проигрыватель анимированной графики
Проигрыватель анимированной графики
При включенном выводе панели форматирования во время анимации она приобретает вид панели проигрывателя клипов (рис. 12.15). Эта панель имеет кнопки управления с обозначениями, принятыми у современных магнитофонов:
1. Поле координат перемещающейся точки графика.
2. Остановка анимации.
3. Пуск анимации.
4. Переход к следующему кадру (фрейму).
5. Установка направления анимации от конца в начало.
6. Установка направления анимации из начала в конец (по умолчанию).
7. Уменьшение времени шага анимации.
8. Увеличение времени шага анимации.
9. Установка одиночного цикла анимации.
10. Установка серии циклов анимации.
Итак, кнопки проигрывателя, по существу, повторяют команды подменю управления анимацией.
Нажав кнопку пуска (с треугольником, острием обращенным вправо), можно наблюдать изменение вида кривой для функции sin(x)/(x). Другие кнопки управляют характером анимации. Проигрыватель дает удобные средства для демонстрации анимации, например, во время занятий со школьниками или студентами.
14. Построение двумерных анимированных графиков
Построение двумерных анимированных графиков
Более обширные возможности анимации двумерных графиков обеспечивает функция animate:
ammate(F, х, t)
animate(F,x, t, о)
В ней параметр х задает пределы изменения переменной х, а параметр t — пределы изменения дополнительной переменной t. Суть анимации при использовании данной функции заключается в построении серии кадров (как в мультфильме), причем каждый кадр связан со значением изменяемой во времени переменной t. Если надо явно задать число кадров анимации N, то в качестве о следует использовать frame=N.
Рисунок 12.16 показывает применение функции animate.
Рис. 12.16. Анимация функции sin(i*x)/(i*x) на фоне неподвижной синусоиды
В документе рис. 12.16 строятся две функции — не создающая анимации функция sin(x) и создающая анимацию функция sin(i*x)/(i*x), причем в качестве переменной t задана переменная i. Именно ее изменение и создает эффект анимации. Проигрыватель анимационных клипов и меню, описанные выше, могут использоваться для управления и этим видом анимации. Обратите внимание на вызов графических функций в этом примере командой with и на синтаксис записи этих функций.
К сожалению, картинки в книгах всегда неподвижны и воспроизвести эффект анимации невозможно. Можно лишь представить несколько текущих кадров анимации. Представленная на рис. 12.16 картина соответствует последнему кадру анимации.
Еще один пример анимации представлен на рис. 12.17. Этот документ показывает кадр анимированного процесса улучшения приближения синусоидальной функции рядом с различным числом членов (и порядком последнего члена ряда). Результирующая картина, изображенная на рис. 12.17, показывает как приближаемую синусоидальную функцию, так и графики всех рядов, которые последовательно выводятся в ходе анимации.
Рис. 12.17. Анимационная демонстрация приближения синусоиды рядом с меняющимся числом членов
Анимация графиков может найти самое широкое применение при создании учебных материалов. С ее помощью можно акцентировать внимание на отдельных параметрах графиков и образующих их функций и наглядно иллюстрировать характер их изменений.
12.gif

39.gif
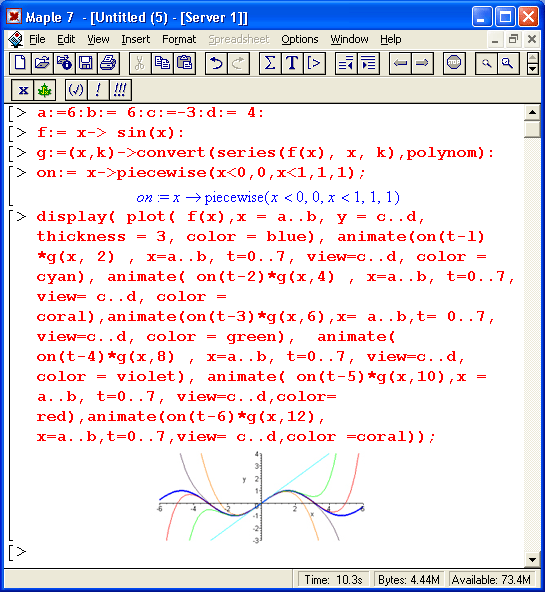
15. Построение трехмерных анимационных графиков
Построение трехмерных анимационных графиков
Аналогичным образом может осуществляться и анимирование трехмерных фигур. Для этого используется функция animate3d:
animate3d(F,x, y,t,o)
Здесь F — описание функции (или функций); х, у и t — диапазоны изменения переменных х, у и t Для задания числа кадров N надо использовать необязательный параметр о в виде frame=N.
На рис. 12.18 показано построение анимированного графика. После задания функции, график которой строится, необходимо выделить график и запустить проигрыватель, как это описывалось для анимации двумерных графиков.
Рис. 12.18. Подготовка трехмерного анимационного графика
На рис. 12.18 показано также контекстное меню поля выделенного графика. Нетрудно заметить, что с помощью этого меню (и содержащихся в нем подменю) можно получить доступ к параметрам трехмерной графики и выполнить необходимые операции форматирования, такие как включение цветовой окраски, выбор ориентации фигуры и т. д.
Назначение параметров, как и средств управления проигрывателем анимационных клипов, было описано выше.
13.gif
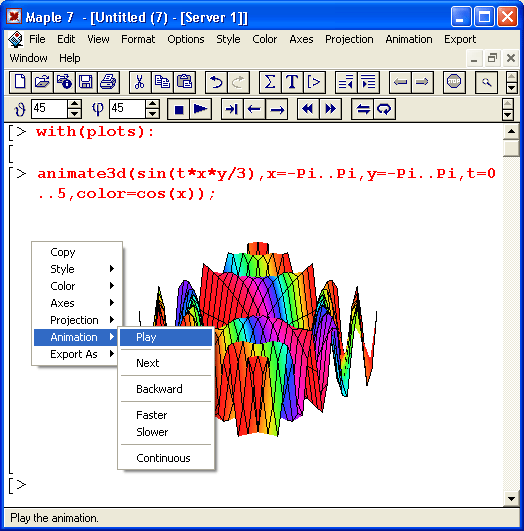
16. Анимация с помощью параметра insequence
Анимация с помощью параметра insequence
Еще один путь получения анимационных рисунков — создание ряда графических объектов pi, р2, рЗ и т. д. и их последовательный вывод с помощью функций display или display3d:
display (pl,p2.p3.....insequence=true)
display3d ( pi. p2. p3..., i nsequence=t rue)
Здесь основным моментом является применение параметра insequence=true. Именно он обеспечивает вывод одного за другим серии графических объектов pi, р2, рЗ и т. д. При этом объекты появляются по одному и каждый предшествующий объект стирается перед появлением нового объекта.
17. Графика пакета plottools
Графика пакета plottools
Инструментальный пакет графики plottools служит для создания графических примитивов, строящих элементарные геометрические объекты на плоскости и в пространстве: отрезки прямых и дуг, окружности, конусы, кубики и т. д. Его применение позволяет разнообразить графические построения и строить множество графиков специального назначения. В пакет входят следующие графические примитивы:
|
arc |
arrow |
circle |
cone |
cuboid |
|
curve |
cutln |
cutout |
cylinder |
disk |
|
dodecahedron |
ellipse |
ellipticArc |
hemisphere |
hexahedron |
|
hyperbola |
icosahedron |
line |
octahedron |
pieslice |
|
point tetrahedron |
polygon torus |
rectangle |
semi torus |
sphere |
ПРИМЕЧАНИЕ
Вызов перечисленных примитивов осуществляется после загрузки пакета в память компьютера командой with(plottools). Только после этого примитивы пакета становятся доступными. Обычно примитивы используются для задания графических объектов, которые затем выводятся функцией display. Возможно применение этих примитивов совместно с различными графиками.
Большинство примитивов пакета plottools имеет довольно очевидный синтаксис. Например, для задания дуги используется примитив агс(с, r, а..b,...), где с — список с координатами центра окружности, к которой принадлежит дуга, г — радиус этой окружности, а.. b — диапазон углов. На месте многоточия могут стоять обычные параметры, задающие цвет дуги, толщину ее линии и т. д. Конус строится примитивом cone(c,r,h...), где с — список с координатами центра, г — радиус основания, h — высота и т. д. Все формы записи графических примитивов и их синтаксис можно найти в справочной системе. В необходимых случаях стоит проверить синтаксис того или иного примитива с помощью справки по пакету plottools.
18. Примеры применения двумерных примитивов пакета plottools
Примеры применения двумерных примитивов пакета plottools
На рис. 12.19 показано применение нескольких примитивов двумерной графики для построения дуги, окружности, закрашенного красным цветом эллипса и отрезка прямой. Кроме того, на графике показано построение синусоиды. Во избежание искажений пропорций фигур надо согласовывать диапазон изменения переменной х. Обычно параметр scalling=constrained выравнивает масштабы и диапазоны по осям координат, что гарантирует отсутствие искажений у окружностей и других геометрических фигур. Однако при этом размеры графика нередко оказываются малыми. Напоминаем, что- этот параметр можно задать и с помощью подменю Projection.
Рис. 12.19. Примеры применения примитивов двумерной графики пакета plottools
Рисунок 12.20 иллюстрирует построение средствами пакета plottools четырех разноцветных стрелок, направленных в разные стороны. Цвет стрелок задан списком цветов с, определенным после команды загрузки пакета. Для построения стрелок используется примитив arrow с соответствующими параметрами.
Рис. 12.20. Построение разноцветных стрелок, направленных в разные стороны
Примитивы могут использоваться в составе графических процедур, что позволяет конструировать практически любые типы сложных графических объектов. В качестве примера на рис. 12.21 представлена процедура SmithChart, которая строит хорошо известную электрикам диаграмму Смита (впрочем, несколько упрощенную). В этой процедуре используется примитив построения дуг arc. При этом задается верхняя часть диаграммы, а нижняя получается ее зеркальным отражением.
ПРИМЕЧАНИЕ
Обратите внимание на то, что, начиная с рис. 12.21, мы не указываем загрузку паета plottools, поскольку она уже была проведена ранее. Однако надо помнить, что все примеры этого раздела предполагают, что такая загрузка обеспечена. Если вы использовали команду restart или только что загрузили систему Maple 7, то для исполнения примера рис. 12.21 и последующих примеров надо исполнить команду with(plottools).
Рис. 12.21. Построение диаграммы Смита
40.gif
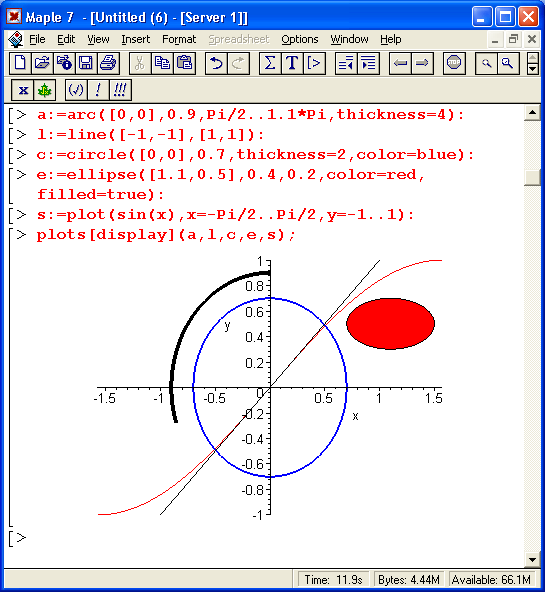
41.gif
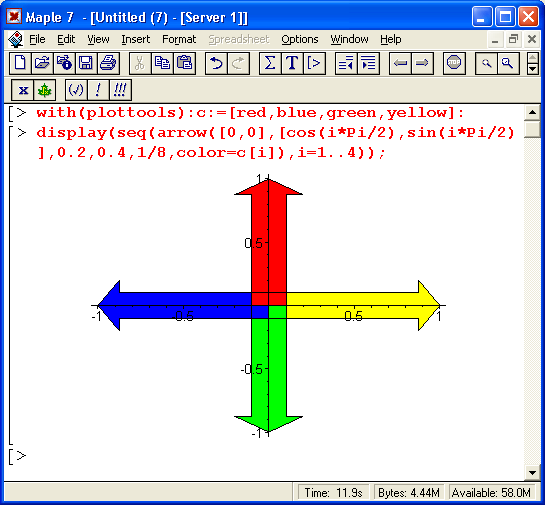
42.gif

19. Примеры применения трехмерных примитивов пакета plottools
Примеры применения трехмерных примитивов пакета plottools
Аналогичным описанному выше образом используются примитивы построения трехмерных фигур. Это открывает возможность создания разнообразных иллюстрационных рисунков и графиков, часто применяемых при изучении курса стереометрии. Могут строиться самые различные объемные фигуры и поверхности — конусы, цилиндры, кубы, полиэдры и т. д. Использование средств функциональной окраски делает изображения очень реалистичными.
Рисунок 12.22 показывает построение цилиндра и двух граненых шаров. Цилиндр строится примитивом cylinder, а граненые шары — примитивом icosahedron.
Другой пример (рис. 12.23) иллюстрирует построение на одном графике двух объемных фигур, одна из которых находится внутри другой фигуры. Этот пример демонстрирует достаточно корректное построение вложенных фигур. На рис. 12.24 показано совместное построение двух пересекающихся кубов и сферы в пространстве. Нетрудно заметить, что графика пакета приблизительно (с точностью до сегмента) вычисляет области пересечения фигур. С помощью контекстно-зависимого меню правой кнопки мыши (оно показано на рис. 12.24) можно устанавливать условия обзора фигур, учитывать перспективу при построении и т. д. В частности, фигуры на рис. 12.24 показаны в перспективе.
Рис. 12.22. Построение цилиндра и двух граненых шаров
Рис. 12.23. Построение двух объемных фигур
Рис. 12.24. Примеры применения примитивов трехмерной графики пакета plottools
Построение еще одной забавной трехмерной фигуры — «шкурки ежа» — демонстрирует рис. 12.25. В основе построения лежит техника создания полигонов. Построение фигур, очень напоминающих улитки, показано на рис. 12.26. При построении этих фигур используется функция tubeplot. Обратите внимание на то, что строятся две входящие друг в друга «улитки».
Наконец, на рис. 12.27 показано построение фигуры — бутылки Клейна. Фигура задана рядом своих фрагментов, определенных в процедуре cleinpoints. Эта процедура является еще одним наглядным примером программирования графических построений с помощью Maple-языка.
С другими возможностями этого пакета читатель теперь справится самостоятельно или с помощью данных справочной системы. Много примеров построения сложных и красочных фигур с применением пакета plottools можно найти в Интернете на сайте фирмы Maple Software, в свободно распространяемой библиотеке пользователей системы Maple и в книгах по этой системе.
43.gif
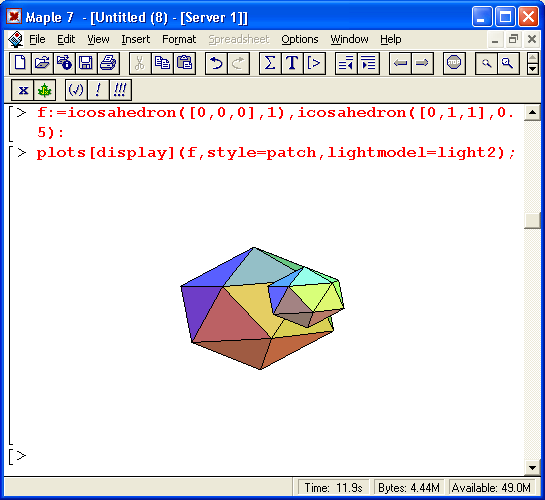
44.gif
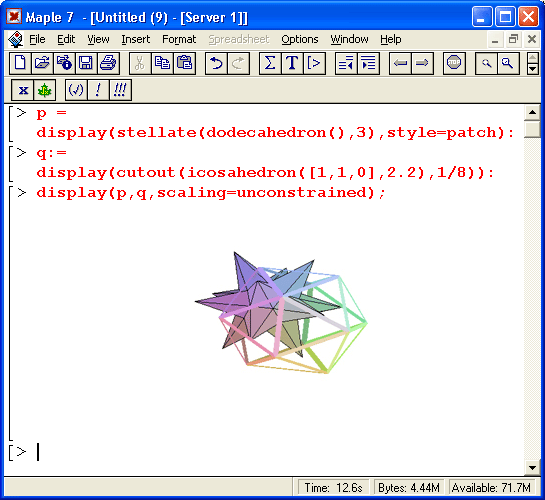
45.gif
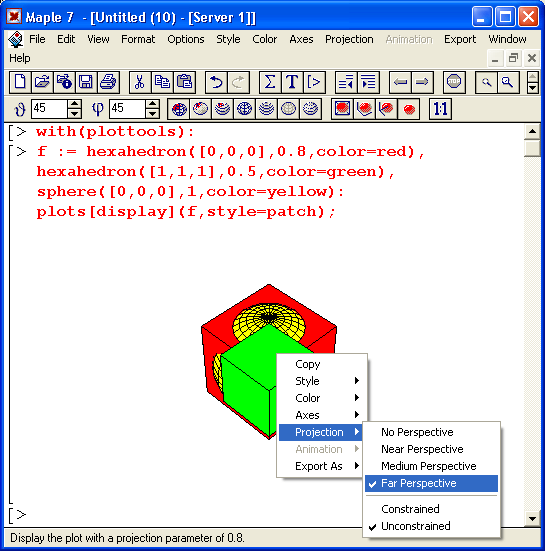
20. Построение графиков из множества фигур
Построение графиков из множества фигур
В ряде случаев бывает необходимо строить графики, представляющие собой множество однотипных фигур. Для построения таких графиков полезно использовать функцию повторения seq(f ,i=a. .b). На рис. 12.28 показано построение фигуры, образованной вращением прямоугольника вокруг одной из вершин.
Рис. 12.25. Построение трехмерной фигуры — «шкурки ежа»
Рис. 12.26. Построение фигуры «улитка»
Рис. 12.27. Построение фигуры «бутылка Клейна»
В этом примере полезно обратить внимание еще и на функцию поворота фигуры — rotate. Именно сочетание этих двух функций (мультиплицирования и поворота базовой фигуры — прямоугольника) позволяет получить сложную фигуру, показанную на рис. 12.28.
46.gif
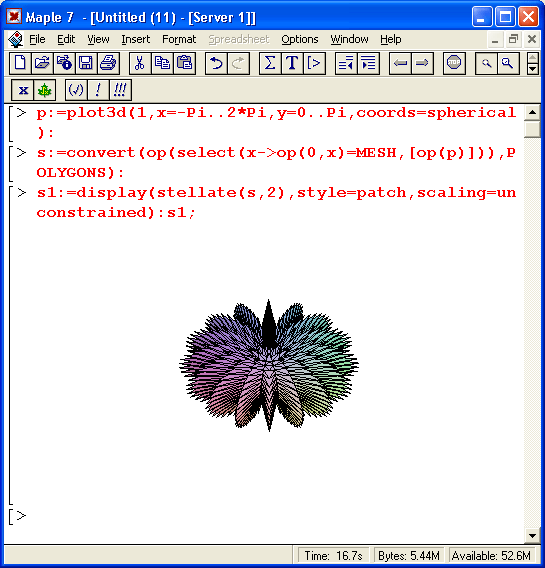
47.gif
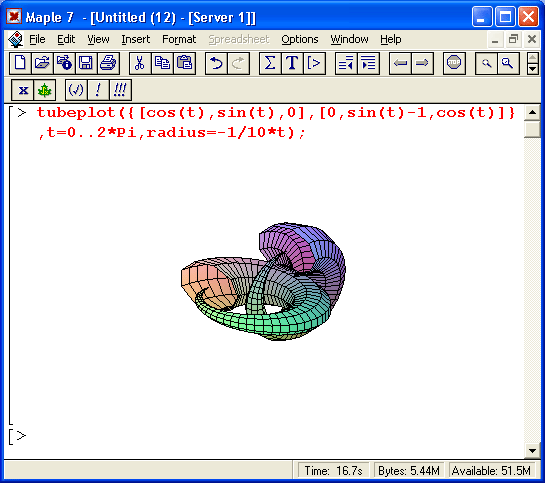
48.gif
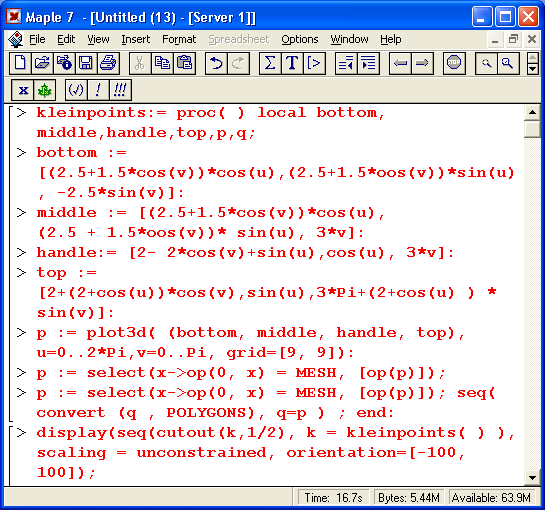
21. Анимация двумерной графики в пакете plottools.
Анимация двумерной графики в пакете plottools
Пакет plottools открывает возможности реализации анимационной графики. Мы ограничимся одним примером анимации двумерных графиков. Этот пример представлен на рис. 12.29. В этом примере показана анимационная иллюстрация решения дифференциального уравнения, описывающего незатухающий колебательный процесс. Строится качающийся объект — стрелка с острием вправо, решение дифференциального уравнения в виде синусоиды и большая стрелка с острием влево, которая соединяет текущую точку графика синусоиды с острием стрелки колеблющегося объекта.
Этот пример наглядно показывает возможности применения анимации для визуализации достаточно сложных физических и математических закономерностей. Перспективы применения системы Maple 7 в создании виртуальных физических и иных лабораторий трудно переоценить.
22. Анимация трехмерной графики в пакете plottools
Анимация трехмерной графики в пакете plottools
Хорошим примером ЗD-анимации является документ, показанный на рис. 12.30. Представленная на нем процедура springPlot имитирует поведение упругой системы, первоначально сжатой, а затем выстреливающей шар, установленный на ее верхней пластине. Упругая система, состоит из неподвижного основания, на котором расположена упругая масса (например, из пористой резины), и верхней пластины.
Рис. 12.28. Построение фигуры, образованной вращением прямоугольника
Рис.12.29. Пример анимации двумерной графики
Рис. 12.30. Имитация отстрела шара сжатой упругой системой
Управление анимацией, реализованной средствами пакета plottools, подобно уже описанному ранее. Последний пример также прекрасно иллюстрирует возможности применения Maple 7 при математическом моделировании различных явлений, устройств и систем.
49.gif
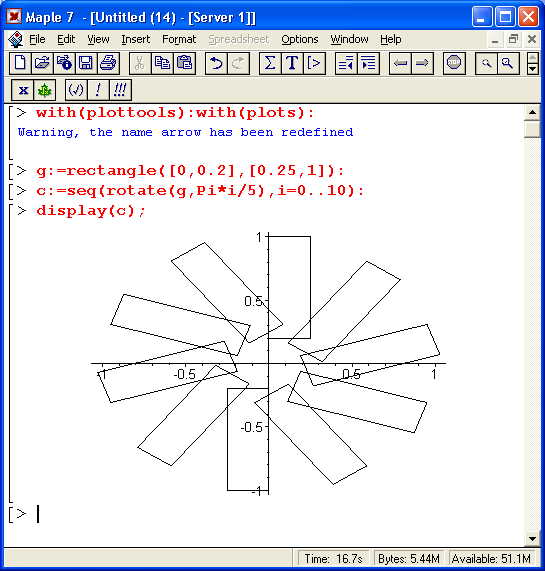
50.gif
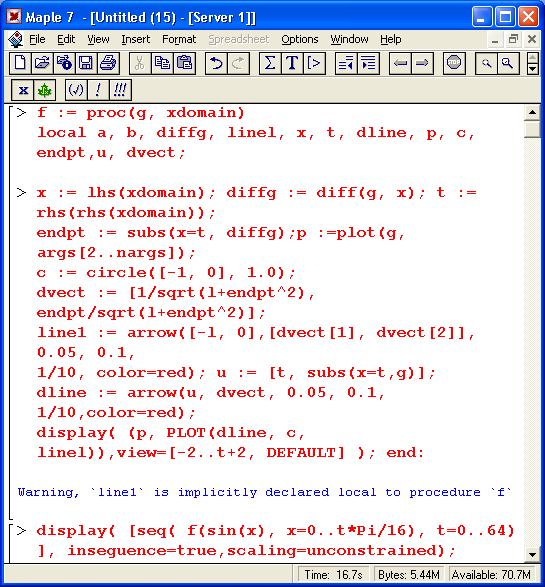
51.gif

23. Расширенные средства графической визуализации
Расширенные средства графической визуализации
Построение ряда графиков, расположенных по горизонтали
Обычно если в строке ввода задается построение нескольких графиков, то в строке вывода все они располагаются по вертикали. Это не всегда удобно, например, при снятии копий экрана с рядом графиков, поскольку экран монитора вытянут по горизонтали, а не по вертикали. Однако при применении функций plots и display можно разместить ряд двумерных графиков в строке вывода по горизонтали. Это демонстрирует пример, показанный на рис. 12.31. Этот пример достаточно прост и нагляден, так что читатель может пользоваться данной возможностью всегда, когда ему это нужно.
Рис. 12.31. Пример расположения трех графиков в строке вывода по горизонтали
52.gif
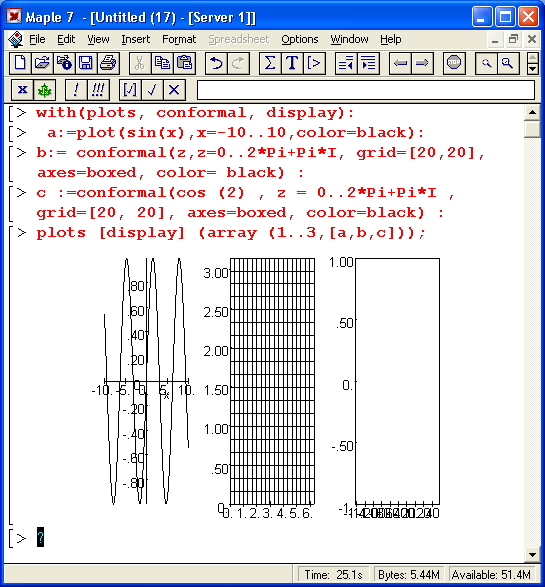
24. Визуализация решения систем линейных уравнений
Визуализация решения систем линейных уравнений
Мы уже не раз использовали графические возможности Maple для визуализации решений математических задач. Так, многие особенности даже функций одной переменной вида f(x) могут быть выявлены с помощью графика этой функции. Затем можно точно вычислить корни функции (точки перехода через 0), экстремумы, "крутизну наклона (производную) в заданных точках и т. д. Еще более информативна в этом отношении трехмерная графика — для большинства функций двух переменных вида z(x, у) нужно очень богатое математическое воображение, чтобы представить их вид — особенно в одной из многих десятков координатных систем.
Однако некоторые виды графиков трудно представить себе даже при наличии такого воображения. В этом отношении Maple 7 предоставляет поистине уникальные возможности, обеспечивая простую и быструю визуализацию решений. Ниже мы рассмотрим несколько наиболее характерных примеров такой визуализации. Системы линейных уравнений могут решаться как с помощью функции solve, так и с помощью матричных методов. Замечательной возможностью функции solve является возможность решения относительно ограниченного числа переменных. Например, систему линейных уравнений с переменными х, у, z, t и v можно решить относительно только первых трех переменных х, у и г. При этом решения будут функциями относительно переменных t и v и можно будет построить наглядный график решения (рис. 12.32).
Рис. 12.32. График, представляющий решения системы линейных уравнений
На рис. 12.32 система задана пятью равенствами: el, е2, еЗ, е4 и е5. Затем функцией solve получено вначале решение для всех переменных (для иллюстрации), а затем для трех переменных х, у и z. Для получения решения в виде списка, а не множества, как в первом случае для всех переменных, использована функция подстановки subs. После этого функция plot3d строит плоскость решения в пространстве.
53.gif
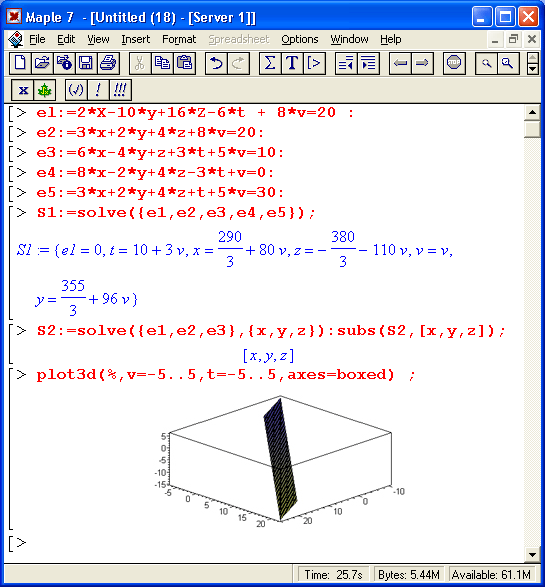
25. Визуализация решения систем неравенств
Визуализация решения систем неравенств
Пожалуй, еще более полезным и наглядным средством является визуализация решения системы уравнений в виде неравенств. В пакете plots имеется специальная графическая функция inequal, которая строит все граничные линии неравенств и позволяет раскрасить разделенные ими области различными цветами:
inequal(ineqs, xspec, yspec, options)
Параметры этой функции следующие: ineqs — одно или несколько неравенств или равенств или список неравенств или равенств; xspec — xvar=min_x. .max_x; yspec — yvar=min_y. .max_y; о — необязательные параметры, например указывающие цвета линий, представляющих неравенства или равенства, и областей, образованных этими линиями и границами графика. Пример применения этой функции представлен на рис. 12,33.
Рис. 12.33. Пример графической интерпретации решения системы неравенств
Обратите внимание на задание цветов: optionsfeasible задает цвет внутренней области, для которой удовлетворяются все неравенства (равенства), optionsopen и optionsdosed задают цвета открытых и закрытых границ областей графика, optionsexcluded используется для цвета внешних областей. График дает весьма наглядную интерпретацию действия ряда неравенств (или равенств).
54.gif
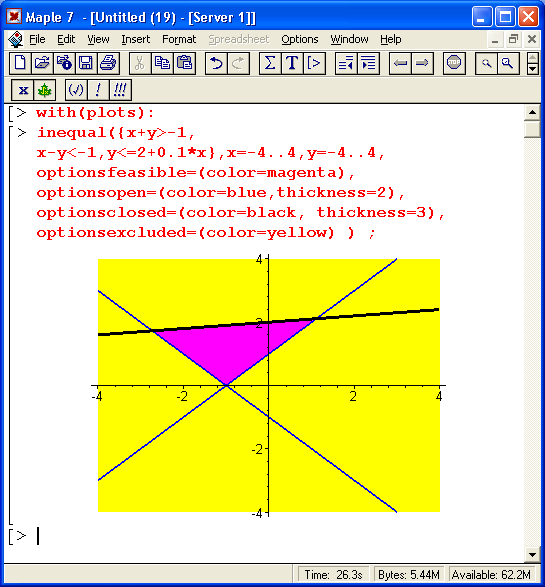
26. Конформные отображения на комплексной плоскости
Конформные отображения на комплексной плоскости
Объем данной книги не позволяет объяснить столь тонкое понятие, как конформные отображения на комплексной плоскости. Ограничимся лишь указанием на то, что в пакете plots имеется функция для таких отображений:
conformal(F,rl,r2,о);
где F — комплексная процедура или выражение; rl, г2 — области, задаваемые в виде а. .Ь или name=a. .b; о — управляющие параметры. Таким образом, для построения нужного графика достаточно задать нужное выражение и области изменения г! и г2. Пример построения конформных изображений для трех выражений дан на рис. 12.34.
Рис. 12.34. Конформное отображение на комплексной плоскости графиков трех зависимостей
Средства конформного отображения в Maple 7, к сожалению, остаются рудиментарными и вряд ли достаточными для специалистов в этой области математики.
55.gif
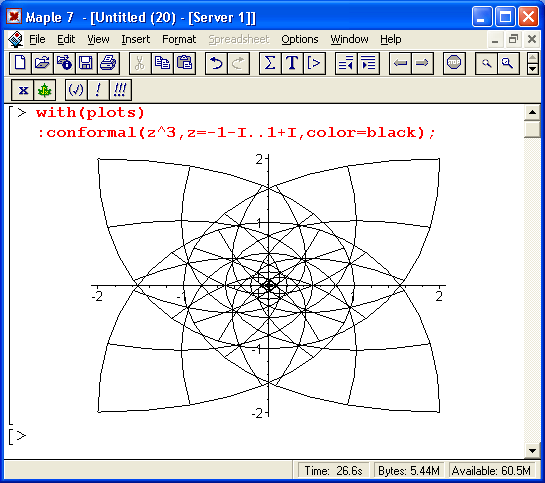
27. Графическое представление содержимого матрицы
Графическое представление содержимого матрицы
Многие вычисления имеют результаты, представляемые в форме матриц. Иногда такие результаты можно наглядно представить графически, например в виде гистограммы. Она представляет собой множество столбцов квадратного сечения, расположенных на плоскости, образованной осями строк (row), и столбцов (column) матрицы. При этом высота столбцов определяется содержимым ячеек матрицы.
Такое построение обеспечивает графическая функция matrixplot из пакета plots. На рис. 12.35 показано совместное применение этой функции с двумя функциями пакета linalg, формирующими две довольно экзотические матрицы А и В.
Рис. 12. 35. Графическое представление матрицы
На рис. 12.35 показана графическая визуализация матрицы, полученной как разность матриц А и В. Для усиления эффекта восприятия применяется функциональная закраска разными цветами. Для задания цвета введена процедура F.
58.gif
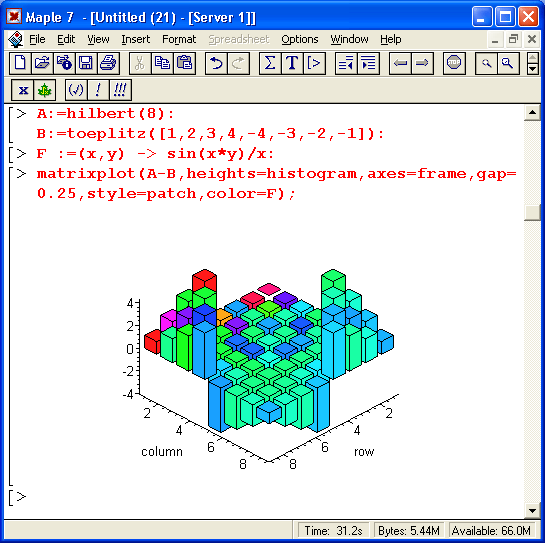
28. Визуализация ньютоновских итераций в комплексной области
Визуализация ньютоновских итераций в комплексной области
Теперь займемся довольно рискованным экспериментом — наблюдением ньютоновских итераций с их представлением на комплексной плоскости. На рис. 12.36 задана функция /(г) комплексного аргумента. Проследить за поведением этой функции на комплексной плоскости в ходе ньютоновских итераций позволяет графическая функция complexplot3d из пакета plots.
Наблюдаемая картина весьма необычна и свидетельствует о далеко не простом ходе итерационного процесса.
Рис. 12.36. Наблюдение за процессом ньютоновских итераций в трехмерном пространстве
ВНИМАНИЕ
Риск работы с этим примером заключается в том, что в системе Maple 7 он иногда вызывает фатальные ошибки, ведущие к прекращению работы с системой. Обычно при запуске этого примера сразу после загрузки системы Maple такого не происходит, но, когда память загружена, сбой вполне возможен. Объективности ради надо заметить, что в системах Maple 6 и 7 подобное поведение системы не было замечено. Тем не менее рекомендуется записывать подобные примеры на диск перед их запуском.
59.gif
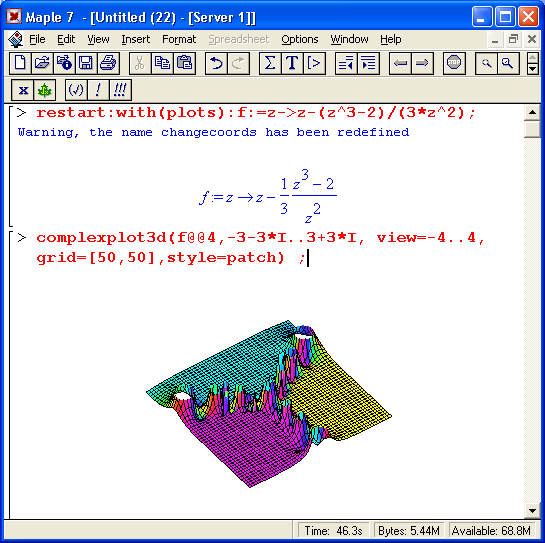
29. Визуализация корней случайных полиномов
Визуализация корней случайных полиномов.
Наряду с традиционной для математических и статистических программ возможностью генерации случайных чисел Maple 7 предоставляет довольно экзотическую возможность генерации случайных полиномов с высокой максимальной степенью. Для этого используется функция:
randpoly(var,o)
Она возвращает случайный полином переменной var, причем максимальная степень полинома птах может указываться параметром о вида degree=nmax.
Приведем примеры генерации случайного полинома с максимальной степенью 50:
С помощью функции аllvalues можно построить список SA корней случайного полинома. А с помощью команды вида:
> with(plots):
complexplot(SA.x=-1.2..1.2.style=point):
построить комплексные корни полученного случайного полинома в виде точек • на комплексной плоскости. Один из таких графиков (их можно построить множество) показан на рис. 12.37.
Рис. 12.37. Расположение корней случайного полинома на комплексной плоскости
Можно заметить любопытную закономерность — точки, представляющие корни случайного полинома, укладываются вблизи окружности единичного радиуса с центром в начале координат. Однако этот пример, приводимый в ряде книг по Maple, показывает, что порою вычисления могут давать довольно неожиданные результаты. Кстати говоря, аналитически можно вычислять корни полинома с максимальной степенью не более четырех.
14.gif
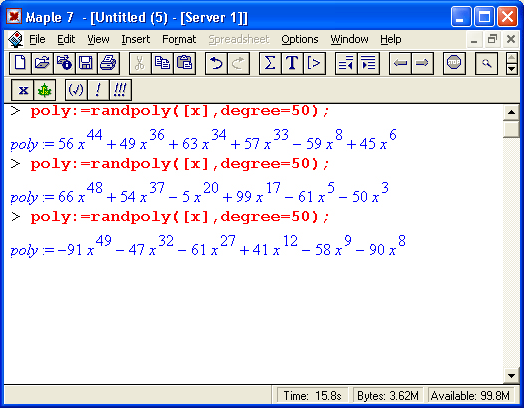
15.gif
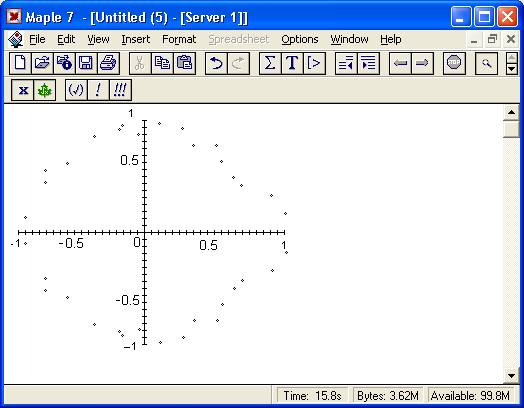
30. Визуализация поверхностей со многими экстремумами
Визуализация поверхностей со многими экстремумами
Maple 7 дает прекрасные возможности для визуализации поверхностей, имеющих множество пиков и впадин, другими словами, экстремумов. Рисунок 12.38 показывает задание «вулканической» поверхности с глубокой впадиной, окруженной пятью пиками. Здесь полезно обратить внимание на способ задания такой поверхности f(a, b, с) как функции трех переменных a, b и с. Он обеспечивает индивидуальное задание координат каждого экстремума и его высоты (отрицательной для впадины).
Рис. 12.38. Построение графика поверхности с множеством экстремумов
Наглядность этого графика усилена за счет применения функциональной окраски и контурных линий, нанесенных на саму поверхность. Все эти возможности обеспечивают параметры основной функции plot3d.
А на рис. 12.39 представлен еще один способ задания поверхности — с помощью функции двух угловых переменных f(theta, phi).
При построении этого рисунка также используются функциональная окраска и построение контурных линий.
61.gif
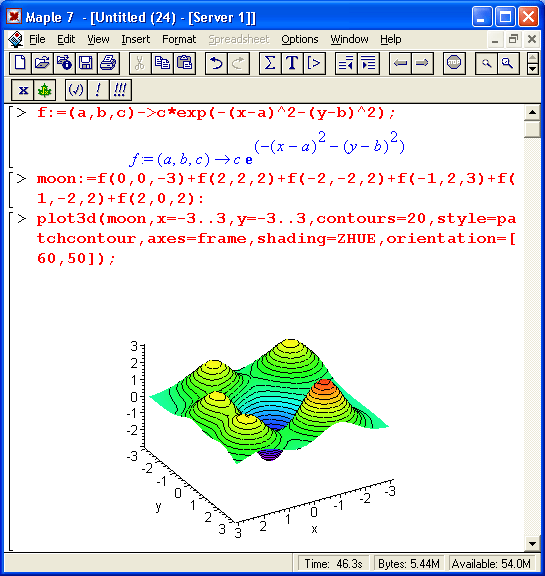
31. Визуализация построения касательной и перпендикуляра
Визуализация построения касательной и перпендикуляра
В ряде геометрических построений нужно отроить касательную и перпендикуляр к кривой, отображающей произвольную функцию f(x) в заданной точке х =а. Рисунок 12.40 поясняет, как это можно сделать. Линии касательной Т(х) и перпендикуляра N(x) определены аналитически через производную в заданной точке.
Во избежание геометрических искажений положения касательной и перпендикуляра при построении графика функцией plot надо использовать параметр scaling=constrained.
Рис. 12.39. Построение графика поверхности, заданной функцией двух угловых переменных
Рис. 12.40. Построение касательной и перпендикуляра к заданной точке графика функции f(x)
60.gif

62.gif
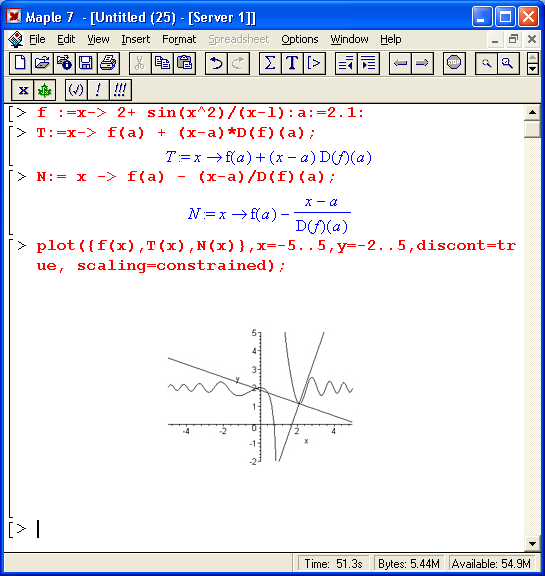
32. Визуализация вычисления определенных интегралов
Визуализация вычисления определенных интегралов
Часто возникает необходимость в геометрическом представлении определенных интегралов в виде алгебраической суммы площадей, ограниченных кривой подынтегральной функции f(x), осью абсцисс х и вертикалями х =а их =b (пределами интегрирования). При этом желательно обеспечение закраски верхней и нижней (отрицательной и положительной) площадей разными цветами, например зеленым для верхней площади и красным для нижней. Как известно, численное значение определенного интеграла есть разность этих площадей.
К сожалению, в Maple 7 нет встроенной функции, явно дающей такое построение. Однако ее несложно создать. На рис. 12.41 представлена процедура a_plot, решающая эту задачу. Параметрами процедуры являются интегрируемая функция/(д:) (заданная как функция пользователя), пределы интегрирования а и b и пределы слева am и справа bm, задающие область построения графика f(x).
Рисунок 12.41 дает прекрасное представление о сущности интегрирования для определенного интеграла. Приведенную на этом рисунке процедуру можно использовать для подготовки Эффектных уроков по интегрированию разных функций.
Рис. 12.41. Графическое представление определенного интеграла
63.gif
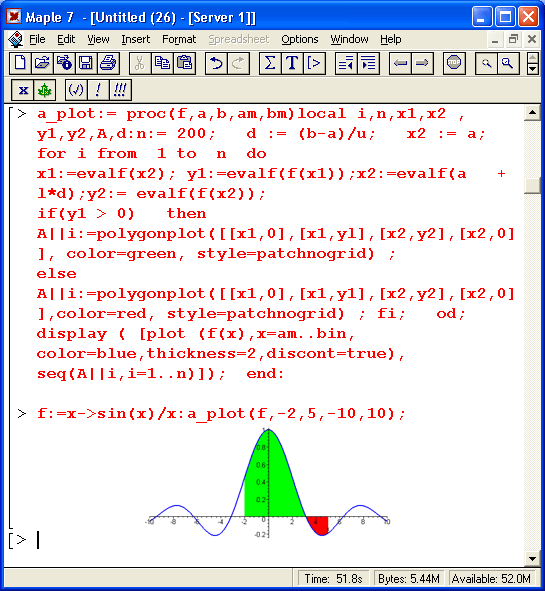
33. Визуализация теоремы Пифагора
Визуализация теоремы Пифагора
Еще один пример наглядного геометрического представления математических понятий — визуализация известной теоремы Пифагора (рис. 12.42).
В этом примере используется функция построения многоугольников. Наглядность построений усиливается выбором разной цветовой окраски треугольников и квадрата.
Рис. 12.42. Графическая иллюстрация к теореме Пифагора
64.gif
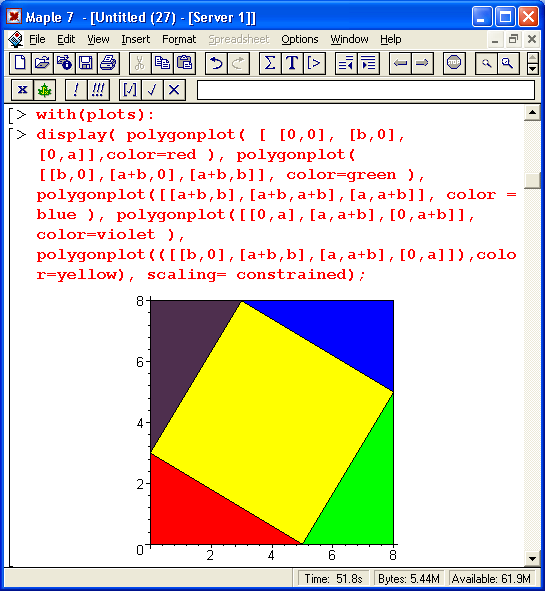
34. Визуализация дифференциальных параметров кривых
Визуализация дифференциальных параметров кривых
Дифференциальные параметры функции f(x), описывающей некоторую кривую, имеют большое значение для анализа ее особых точек и областей существования. Так, точки с нулевой первой производной задают области, где кривая нарастает (первая производная положительна) или убывает (первая производная отрицательна) с ростом аргументах. Нули второй производной задают точки перегиба кривой.
Следующая графическая процедура служит для визуализации поведения кривой /, = /(.г) на отрезке изменениях от а до b:
В этой процедуре заданы следующие цвета (их можно изменить): Таблица 12.1. Цвета при визуализации в процедуре shape_plot
|
Изменение /(х) |
Цвет |
|
Возрастание |
Синий |
|
Убывание |
Красный |
|
Площадь |
Цвет |
|
Над минимумом |
Зеленый |
|
Под максимумом |
Коралловый |
Например, для функции:
построенный график будет иметь вид, представленный на рис. 12.43 (естественно, в книге цвета — лишь оттенки серого).
Рисунок 12.43 дает наглядное представление о поведении заданной функции. Рекомендуется опробовать данную процедуру на других функциях. Следует отметить, что, поскольку процедура использует функции ntiroimize и maximize, она может давать сбои при исследовании сложных функций, содержащих специальные математические функции или особенности. Иногда можно избежать такой ситуации, исключив особенность. Например, для анализа функции sin(x)/x можно записать ее в виде:
>f:=x->if x=0 then 1 else sin(x)/x
end if;
shape_plot(f(x),-10,10);
Исполнение приведенной выше строки ввода дает график, представленный на рис. 12.44.
Рис. 12.43. Визуализация поведения функции f(х)
Рис. 12.44. Визуализация поведения функции sin(x)/x
Данная процедура дает хорошие результаты при анализе функций, представленных полиномами. Вы можете сами убедиться в этом.
16.gif
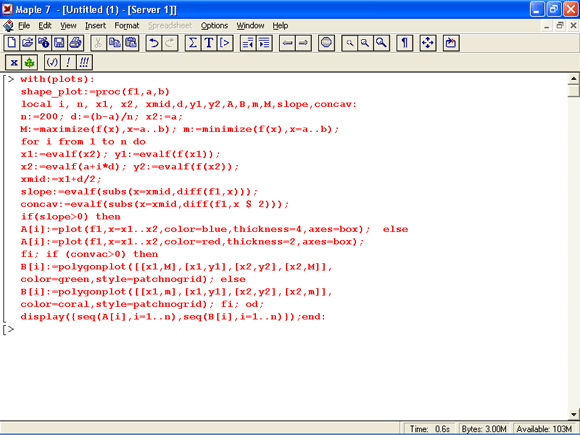
17.gif

18.gif
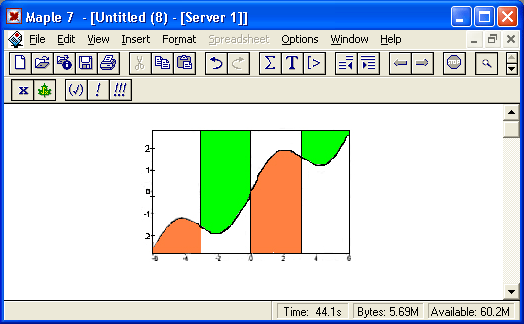
19.gif
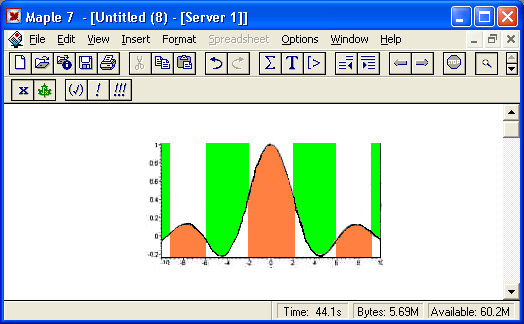
35. Иллюстрация итерационного решения уравнения f(x) = x
Иллюстрация итерационного решения уравнения f (х) = х
Классическим методом решения нелинейных уравнений является сведение их к виду х =f(x) и применение метода простых итераций xk =s(xk-1) при заданном значениих0. Приведем пример такого решения:
>f :=x ->3*1n(x+l);
f:=x-> 3ln(x+1)
>x||0 := 0.5:
x0:=5
>x0 := .5;
x0:=.5
>for k from 1 to 16 do x||k := evalf( f(x||(k-l) )): od;
xl := 1.216395324
x2 := 2.387646445
x3 := 3.660406248
x4:= 4.617307866
x5:= 5.177557566
x6:= 5.462768931
x7:= 5.598173559
x8:= 5.660378631
x9 := 5.688529002
xl0:= 5.701181910
x11 := 5.706851745
x12 := 5.709388956
x13:= 5.710523646
x14 — 5.711030964
xl5:= 5.711257755
x16:= 5.711359134
Нетрудно заметить, что значения xk в ходе итераций явно сходятся к некоторому значению. Проведем проверку решения, используя встроенную функцию solve:
Результат выглядит необычно — помимо довольно "очевидного корнях x= 0 значение другого корня получено в виде специальной функции Ламберта. Впрочем, нетрудно найти и его численное значение:
> evalf(%);
0., 5.711441084
Однако как сделать процесс решения достаточно наглядным? Обычно для этого строят графики двух зависимостей — прямой х и кривой f(x) — и наносят на них ступенчатую линию перемещения точки xk. Специальной функции для графиков подобного рода Maple 7 не имеет. Однако можно составить специальную процедуру для их построения .Ее листинг, заимствованный из примера, описанного в пакете обучения системе Maple 7 - PowerTools, представлен ниже:
Параметрами этой процедуры являются: f1 — функция f(x); а и b — пределы изменениях при построении графика; х0 — значение х, с которого начинаются итерации. Исполнив команду:
>rec_p1ot( f(x), 0, 8, х0):
можно наблюдать график, иллюстрирующий итерационный процесс. Он представлен на рис. 12.45.
Рис. 12.45. Иллюстрация процесса итераций
Нетрудно заметить, что для данной функции процесс итераций хотя и не очень быстро, но уверенно сходится к точке пересечения прямой у = х и кривой y=f(x). Вы можете, меняя зависимость f(x), провести исследования сходимости уравнений х = f(x).
20.gif
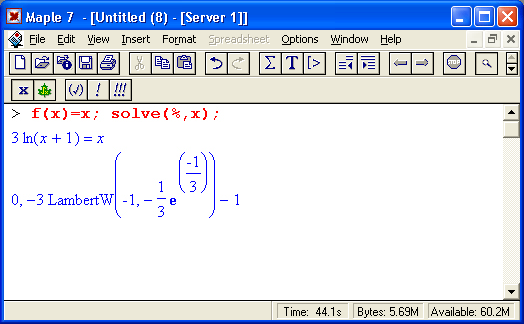
21.gif

22.gif
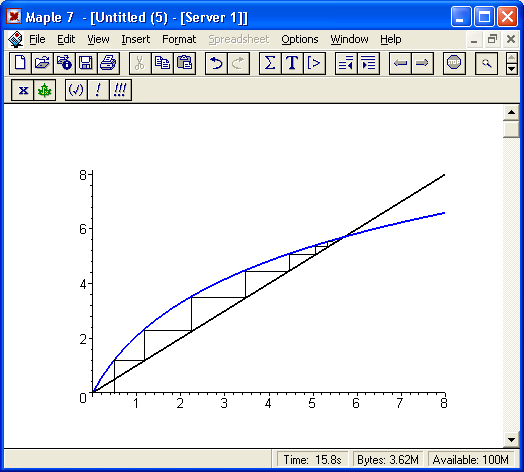
36. Построение сложных фигур в полярной системе координат
Построение сложных фигур в полярной системе координат
Некоторые виды математической графики имеют определенную художественную ценность и фигурируют в символике различных стран и общественных организаций. Остановимся на нескольких таких примерах применительно к графике в полярной системе координат. Представим фигуры, образованные множеством линий на плоскости.
Рисунок 12.46 демонстрирует одну из таких фигур. Это семейство из 10 кардиоид разного размера. Параметр scallIng=constrained обеспечивает правильное отображение фигур — каждая кардиоида вписывается в огибающую ее невидимую окружность. Размер кардиоид задается значением параметра а.
Рис.12.46. Семейство кардиоид на одном графике
Еще одно семейство кардиоид, на сей раз шестилепестковых, представлено на рис. 12.47. Здесь также изменяемым параметром каждой фигуры является ее размер, заданный параметром а.
Фигуре, представленной на рис. 12.48, трудно дать определенное название. Назовем ее волнообразной спиралью.
По образу и подобию приведенных фигур читатель может опробовать свои силы в создании новых красочных фигур в полярной системе координат. Некоторые из них поразительно напоминают снежинки, картинки в калейдоскопе и изображения морских звезд. Если убрать параметр color=black, .введенный ради черно-белой печати картинок в книге, то можно усилить красочность фигур за счет их разноцветной окраски.
Рис. 12.47. Семейство шестилепестковых кардиоид
Рис. 12.48. Фигура— волнообразная спираль
23.gif
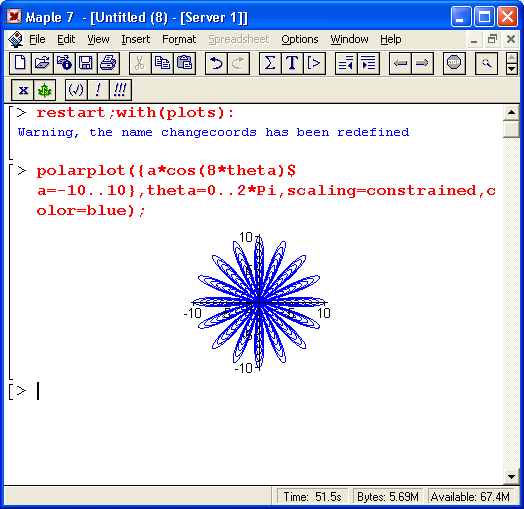
24.gif
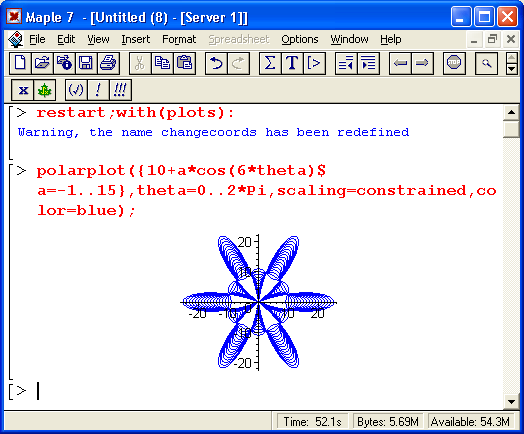
29.gif
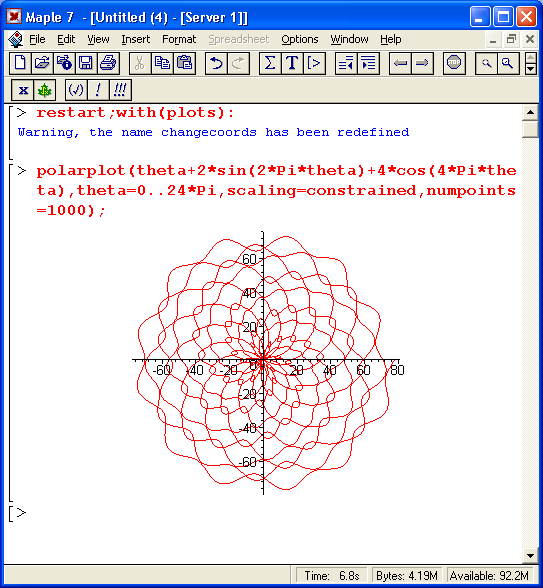
37. Построение сложных фигур импликативной графики
Построение сложных фигур импликативной графики
Импликативные функции (см. урок 7) нередко имеют графики весьма любопытного вида. Ограничимся парой примеров построения таких графиков, представленных на рис. 12.49. Эти фигуры напоминают контурные графики функции двух переменных.
Приведенные примеры дают весьма наглядное представление о больших возможностях визуализации решений самых различных задач в системе Maple V. Можно значительно расширить их, эффектно используя описанные ранее приемы анимации изображений. В целом надо отметить, что графические возможности Maple 7 дают новый уровень качества графики современных математических систем, о котором с десяток лет тому назад можно было только мечтать.
Рис. 12.49. Построение сложных фигур, заданных импликативными функциями
30.gif
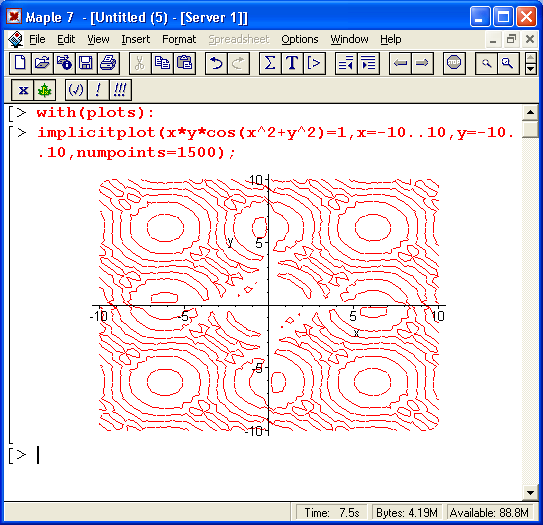
38. Расширенная техника анимации
Расширенная техника анимации
Анимирование разложения импульса в ряд Фурье
Анимирование изображений является одним из самых мощных средств визуализации результатов моделирования тех или иных зависимостей или явлений.
Порою изменение во времени одного из параметров зависимости дает наглядное представление о его математической или физической сути.
Здесь мы расширим представление об анимации и рассмотрим не вполне обычный пример — наблюдение в динамике за гармоническим синтезом некоторой произвольной функции f(x) на отрезке изменения л; от 0 до 1. Значения функции f(x) могут быть одного знака или разных знаков. В этом примере можно наблюдать в динамике синтез заданной функции рядом Фурье с ограниченным числом синусных членов (гармоник) — до 1, 2, 3..JV. На рис. 12.50 представлен документ, реализующий такое разложение и затем синтез для пилообразного линейно нарастающего импульса, описываемого выражением f(x) = -1 + 2 *х. На графике строится исходная функция и результат ее синтеза в динамике анимации.
Рис. 12.50. Один из первых стоп-кадров анимации разложения импульса в ряд Фурье
Рисунок 12.51 показывает завершающий стоп-кадр анимации, когда число гармоник N равно 30. Нетрудно заметить, что такое число гармоник в целом неплохо описывает большую часть импульса, хотя в. его начале и в конце все еще заметны сильные отклонения.
Для f(x) = 1 строится приближение для однополярного импульса с длительностью 1 и амплитудой 1, при f(x) =х — приближение для пилообразного линейно нарастающего импульса, при f(x) =х^2 — приближение для нарастающего по параболе импульса, при f(x)=signum(x-l/2) — приближение для симметричного прямоугольного импульса-меандра и т. д. Фактически можно наблюдать анимационную картину изменения формы импульса по мере увеличения числа используемых для синтеза гармоник. Выбор используемого числа гармоник осуществляет амплитудный селектор — функция a= f(t,k), основанная на применении функции Хевисайда.
Рис. 12.51. Второй (завершающий) кадр анимации
Самым интересным в этом примере оказывается наблюдение за зарождением и эволюцией эффекта Гиббса — так называют волнообразные колебания на вершине импульса, связанные с ограничением числа гармоник при синтезе сигнала. С ростом числа гармоник эффект Гиббса не исчезает, просто обусловленные им выбросы вблизи разрывов импульса становятся более кратковременными. Амплитуда импульсов может достигать 18% от амплитуды перепадов сигнала, что сильно ухудшает приближение импульсных сигналов рядами Фурье и вынуждает математиков разрабатывать особые меры по уменьшению эффекта Гиббса.
Можно ли наблюдать одновременно все фазы анимации? Можно! Для этого достаточно оформить анимационную картину, созданную функцией animate, в виде отдельного графического, объекта например g, после чего можно вывести все его фазы оператором display. Это и иллюстрирует рис. 12.52. На этот раз задано f(x) = signum(x-l/2) и N = 25. Таким образом рассматриваются симметричные прямоугольные импульсы - меандр. У каждого рисунка координатные оси с делениями удалены параметром axes=none.
Рис. 12.52. Иллюстрация получения всех кадров анимации двумерного графика
Любопытно отметить, что при определенных числах гармоник связанная с колебательными процессами неравномерность вершины импульса резко уменьшается. Наблюдение этого явления и является наиболее интересным и поучительным при просмотре данного примера.
При внимательном просмотре рис. 12.52 заметно, что после некоторого периода установления фазы анимационной картинки практически повторяются. Это связано с известным обстоятельством — установившийся спектр меандра содержит только нечетные гармоники. Поэтому, к примеру, вид спектрального разложения при 22 гармониках будет тот же, что и при 21 гармонике, при 24 гармониках тот же, что при 23, и т. д. Однако эта закономерность проявляется только при установившемся (стационарном) спектре.
65.gif
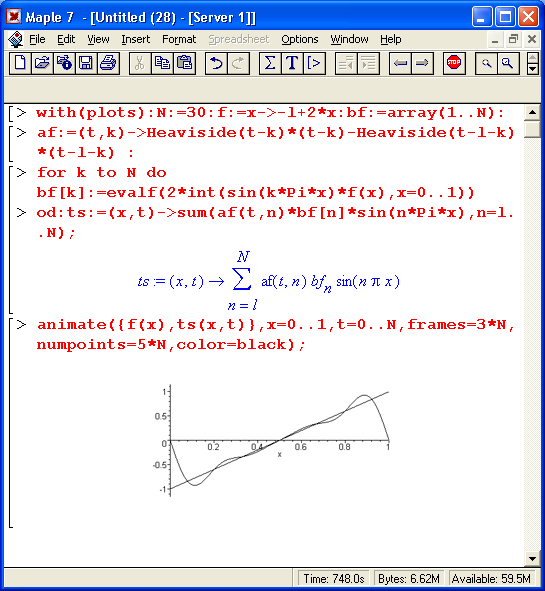
66.gif

67.gif
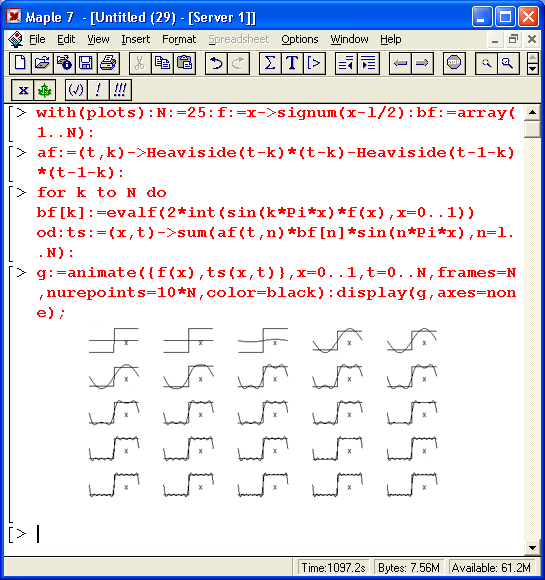
39. Наблюдение кадров анимации поверхности
Наблюдение надрав анимации поверхности
Наблюдение за развитием поверхности производит на многих (особенно на студентов) большое впечатление. Оно позволяет понять детали создания сложных трехмерных графиков и наглядно представить их математическую сущность. Рассмотрим анимацию поверхности на примере рис. 12.18.
Как и для случая анимации двумерного графика, большой интерес представляет построение всех фаз анимации на одном рисунке. Делается это точно так Же, как в двумерном случае. Это иллюстрирует рис. 12.53. На нем представлены 8 фаз анимации трехмерной поверхности cos(t*x*y/3), представленной функцией трех переменных t, х и у. При этом изменение первой переменной создает фазы анимации поверхности.
Рис. 12.53. Фазы анимации трехмерной поверхности
Применение анимации дает повышенную степень визуализации решений ряда задач, связанных с построением двумерных и трехмерных графиков. Следует отметить, что построение анимированных графиков требует дополнительных и достаточно существенных затрат оперативной памяти. Поэтому злоупотреблять числом стоп-кадров таких графиков не стоит.
32.gif
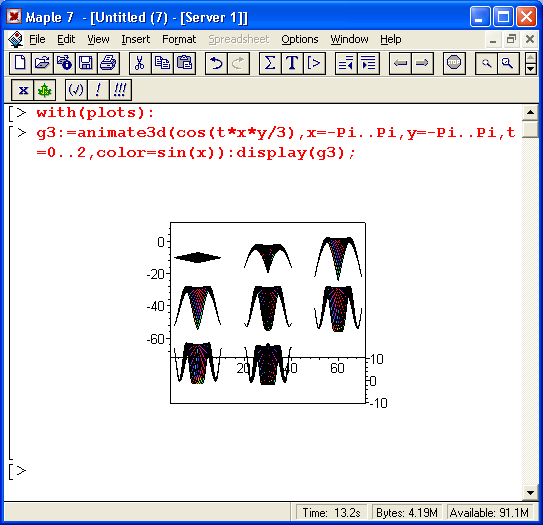
40. Новая функция для построения стрелок arrow
Новая функция для построения стрелок arrow
В пакет plots системы Maple 7 введена новая функция построения стрелок arrow. Она задается в виде arrow(u,[v,]opts) или arrow(U,opts)
Построение стрелок задается одномерными массивами координат начала стрелок и их направления и и v или двумерным массивом U, которые могут быть представлены векторами, списками или множествами. Вид стрелок задается параметром opts, который может иметь значения shape, length, width, head_width, head_length или plane и задает вид стрелок (форму, длину, ширину и т. д.). Детали задания параметров можно найти в справке по данной функции. Рисунок 12.54 дает наглядное представление о ее возможностях.
Рис. 12.54. Построение стрелок с помощью функции arrow
33.gif

41. Построение сложных комбинированных графиков
Построение сложных комбинированных графиков
В заключение этой главы рассмотрим построение с помощью системы Maple 7 достаточно сложных комбинированных графиков, содержащих различные графические и текстовые объекты. Пример построения такого графика представлен на рис. 12.55.
Рис. 12.55. Пример построения сложного объекта, состоящего из 8 графических и текстовых объектов
Представленный на рис. 12.55 объект задает построение восьми графических объектов от р! до р8. Среди них цилиндр, две пересекающие его плоскости и иные (в том числе текстовые) объекты. Обратите внимание на способ вывода этих объектов функцией display3d. Этот пример показывает, что с помощью графических программных средств Maple 7 можно строить достаточно замысловатые графики, которые могут использоваться для визуализации тех или иных геометрических и иных объектов.
68.gif
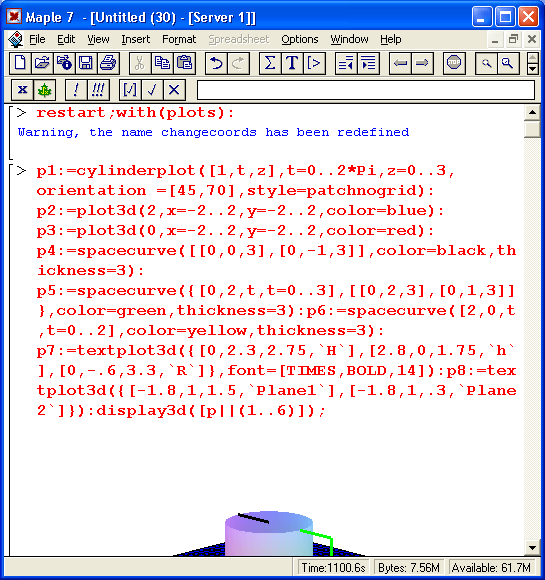
42. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Пользоваться графикой пакета plots.
- Пользоваться техникой анимации графиков пакета plots.
- Применять графику пакета plottools.
- Использовать расширенные средства графической визуализации.
- Использовать расширенную технику создания графической анимации.
- Использовать новую функцию Maple 7 для построения стрелок.
- Строить сложные комбинированные графики.
Урок 13. Решение дифференциальных уравнений
1. Основные средства решения дифференциальных уравнений
Урок 13.
Решение дифференциальных уравнений
Важное место в математических расчетах занимает решение дифференциальных уравнений. К нему, в частности, обычно относится анализ поведения различных систем во времени (анализ динамики), а также вычисление различных полей (тяготения, электрических зарядов и т. д.). Трудно переоценить роль дифференциальных уравнений в моделировании физических и технических объектов и систем, Maple 7 позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Разработчиками системы объявлено о существенном расширении средств решения дифференциальных уравнений и о повышении их надежности в смысле нахождения решений для большинства классов дифференциальных уравнений. Поэтому данный урок целиком посвящен решению уравнений данного класса. Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в разных формах записи:
dsolve(ODE)
dsolve(ODE, y(x), extra_args)
dsolve((ODE, ICs}, y(x), extra_args)
dsolve({sysODE, ICs}, {funcs}, extra_args)
Здесь ODE — одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, у(х) — функция одной переменной, Ics — выражение, задающее начальные условия, {sysODE} —множество дифференциальных уравнений, {funcs} —множество неопределенных функций, extra_argument — опция, задающая тип решения. Параметр extra_argument задает класс решаемых уравнений. Отметим основные значения этого параметра:
- exact — аналитическое решение (принято по умолчанию);
- explicit — решение в явном виде;
- system — решение системы дифференциальных уравнений;
- ICs — решение системы дифференциальных уравнений с заданными начальными условиями;
- formal series — решение в форме степенного многочлена;
- integral transform — решение на основе интегральных преобразований Лапласа, Фурье и др.;
- series — решение в виде ряда с порядком, указываемым значением переменной Order;
- numeric — решение в численном виде.
Для решения задачи Коши в параметры dsolve надо включать начальные условия, а при решении краевых задач — краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньшего порядка системы, то в решении будут появляться неопределенные константы вида _С1, _С2 и т. д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр _Т.
По умолчанию функция dsolve автоматически выбирает наиболее подходящий метод решения дифференциальных уравнений. Однако в параметрах функции dsolve в квадратных скобках можно указать предпочтительный метод решения дифференциальных уравнений. Допустимы следующие методы:
| quadrature | linear | Bernoulli | separable |
|
inverse linear |
homogeneous |
Chini |
lin_sym |
| exact | Abel | pot_sym |
Информацию о каждом методе можно получить, используя команду Tdsolve, method и указав в ней конкретный метод. Например, команда Tdsolve,linear вызовет появление страницы справочной системы с подробным описанием линейного метода решения дифференциальных уравнений.
Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором D. Выражение sysODE должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.
2. Решение ОДУ первого порядка
Решение ОДУ первого порядка
Начнем рассмотрение практических примеров с решения одиночных обыкновенных дифференциальных уравнений (ОДУ) первого порядка:
Следующие примеры иллюстрируют возможность решения одного и того же дифференциального уравнения ode_L разными методами:
Объем данной книги не позволяет остановиться на всех тонкостях аналитического решения дифференциальных уравнений. Множество примеров такого решения дано в справочной базе данных Maple,. 7- К ней нужно обратиться в случае, если решение того или иного дифференциального уравнения выходит за рамки учебного курса.
1.gif
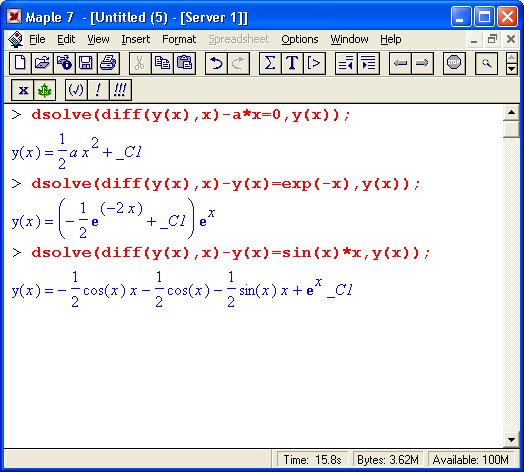
2.gif
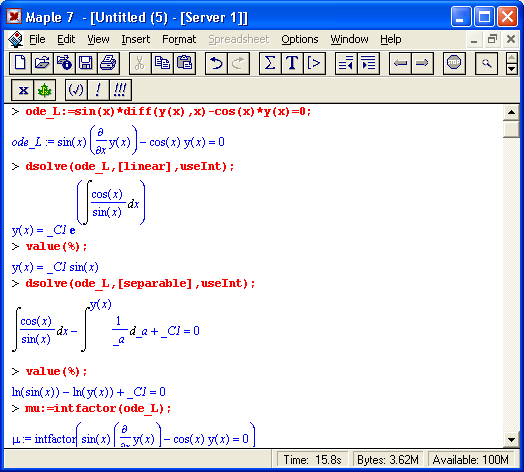
3. Решение дифференциальных уравнений второго порядка
Решение дифференциальных уравнений второго порядка
Здесь видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ можно задать производную более высокого порядка. Ниже представлено решение двух дифференциальных уравнений второго порядка:
Обратите внимание на решение второго из этих уравнений. Здесь использован прием визуализации исходного дифференциального уравнения, и оно задается значением переменной de. Кроме того, и это особенно важно, решение осуществляется при заданных начальных условиях. Именно поэтому в решении отсутствуют произвольные постоянные вида _СN.
3.gif
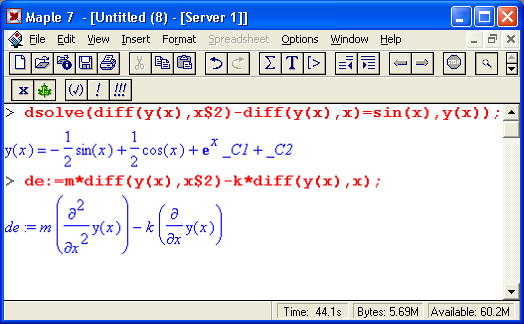
4.gif
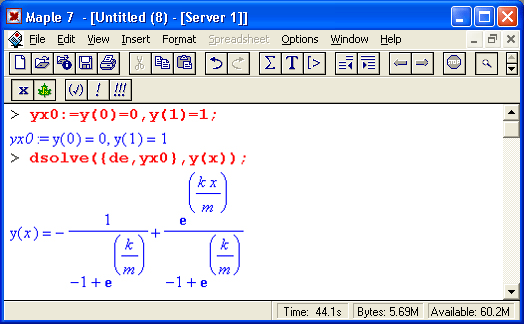
4. Решение систем дифференциальных уравнений
Решение систем дифференциальных уравнений
На рис. 13.1 представлено решение системы из двух дифференциальных уравнений различными методами — в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным. Поэтому полученные в данном случае аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.
Рис. 13.1. Решение системы из двух дифференциальных уравнений различными методами
Следует отметить, что, несмотря на обширные возможности Maple 7 в области аналитического решения дифференциальных уравнений, оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде.
5.gif
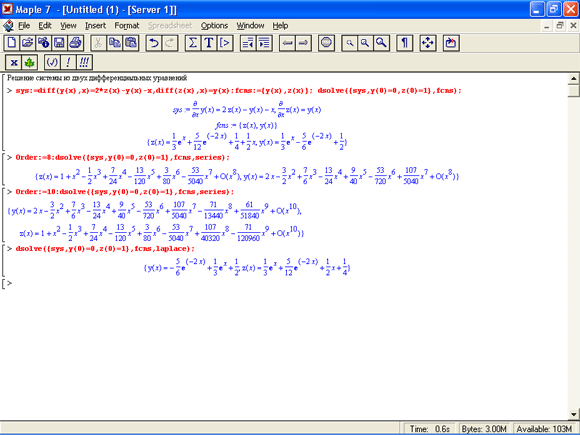
5. Численное решение дифференциальных уравнений
Численное решение дифференциальных уравнений
Большинство нелинейных дифференциальных уравнений не имеет аналитического решения. Кроме того, часто аналитическое решение и не нужно, но требуется получить ответ в виде графических зависимостей.
В таких случаях для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге—Кутта—Фелберга порядков 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения). Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Последнее достаточно наглядно иллюстрирует рис. 13.2.
Рис. 13.2. Решение системы дифференциальных уравнений численным методом rkf45 с выводом графика решения
Указанная процедура возвращает особый тип данных, позволяющих найти решение в любой точке или построить график решения (или решений). Для графического отображения Maple 7 предлагает ряд возможностей, и одна из них представлена на рис. 13.2 — см. последнюю строку ввода. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений.
В список параметров функции dsolve можно явным образом включить указание на метод решения, например опция mathod=dverk78 задает решение непрерывным методом Рунге—Кутта порядка 7 или 8. Вообще говоря, численное решение дифференциальных уравнений можно производить одним из следующих методов:
- classical — одна из восьми версий классического метода, используемого по умолчанию;
- rkf45 — метод Рунге—Кутта 4 или 5 порядка, модифицированный Фелбергом;
- dverk78 — непрерывный метод Рунге—Кутта порядка 7 или 8;
- gear — одна из двух версий одношагового экстраполяционного метода Гира;
- mgear — одна из трех версий многошагового эктраполяционного метода Гира;
- lsode — одна из восьми версий Ливенморского решателя жестких дифференциальных уравнений;
- taylorseries — метод разложения в ряд Тейлора.
Обилие используемых методов расширяет возможности решения дифференциальных уравнений в численном виде. Большинство пользователей Maple 7 вполне устроит автоматический выбор метода решения по умолчанию. Однако в сложных случаях возможна прямая установка одного из указанных выше методов. С деталями реализации методов можно ознакомиться по справочной системе.
С помощью параметра ' abserr' =аеrr можно задать величину абсолютной погрешности решения, а с помощью 'minerr'=mine — минимальную величину погрешности. В большинстве случаев эти величины, заданные по умолчанию, оказываются приемлемыми для расчетов.
Maple 7 реализует адаптируемые к ходу решения методы, при которых шаг решения h автоматически меняется, подстраиваясь под условия решения. Так, если прогнозируемая погрешность решения становится больше заданной, шаг решения автоматически уменьшается. Более того, система Maple способна автоматически выбирать наиболее подходящий для решаемой задачи метод решения.
Еще один пример решения системы дифференциальных уравнений представлен на рис. 13.3. Здесь на одном графике представлены зависимости у(х) и z(х), представляющие полное решение заданной системы. При этом процедура имеет особый вид listprocedure и для преобразования списка выходных данных в векторы решения Y и Z используется функция subs.
Для решения достаточно сложных задач полезны специальная структура DESol для решения дифференциальных уравнений и инструментальный пакет DEtools, содержащий самые изысканные средства для графической визуализации результатов решения дифференциальных уравнений. Эти средства мы более подробно рассмотрим в дальнейшем.
Рис. 13.3. Решение системы дифференциальных уравнений численным методом с выводом всех графиков искомых зависимостей
ВНИМАНИЕ
При решении некоторых задач физики и радиоэлектроники выбираемый поумолчанию шаг изменения аргументах или t - Л может привести к неустойчивости решения. Неустойчивости можно избежать рядом способов. Можно, например, нормировать уравнения, избегая необходимости использования малого шага. А можно задать заведомо малый шаг. Например, при method=classical для этого служит параметр stepsize-h. Примеры такого подхода будут даны в уроке 17 (см. Решение физических задач и моделирование цепи на туннельном диоде).
24.gif
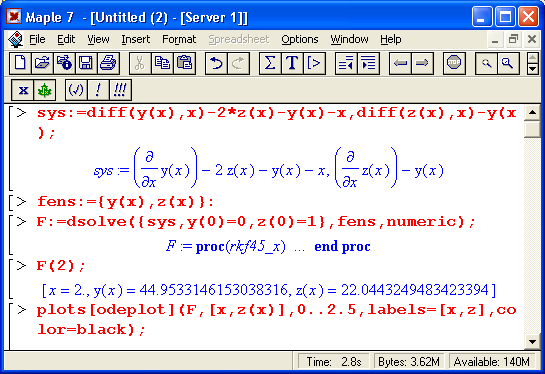
26.gif
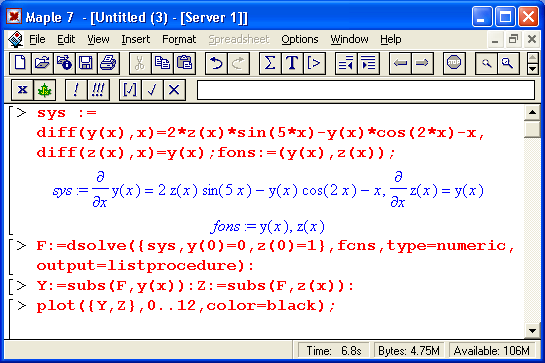
6. Дифференциальные уравнения с кусочными функциями
Дифференциальные уравнения с кусочными функциями
Функции кусочного типа широко используются при математическом моделировании различных физических объектов и систем. В основе такого моделирования обычно лежит решение дифференциальных уравнений, описывающих поведение объектов и систем. Покажем возможность применения кусочных функций для решения дифференциальных уравнений.
Ниже представлено задание дифференциального уравнения первого порядка, содержащего кусочную функцию:
Используя функцию dsolve, выполним решение этого дифференциального уравнения:
Нетрудно заметить, что результат получен также в форме кусочной функции, полностью определяющей решение на трех интервалах изменениях. Приведем пример решения дифференциального уравнения второго порядка с кусочной функцией:
В конце этого раздела приведем пример решения нелинейного дифференциального уравнения Риккати с кусочной функцией:
В ряде случаев желательна проверка решения дифференциальных уравнений. Ниже показано, как она делается для последнего уравнения:
ПРИМЕЧАНИЕ
Как видно из приведенных достаточно простых и наглядных примеров, результаты решения дифференциальных уравнений с кусочными функциями могут быть довольно громоздкими. Это, однако, не мешает эффективному применению функций данного класса.
8.gif
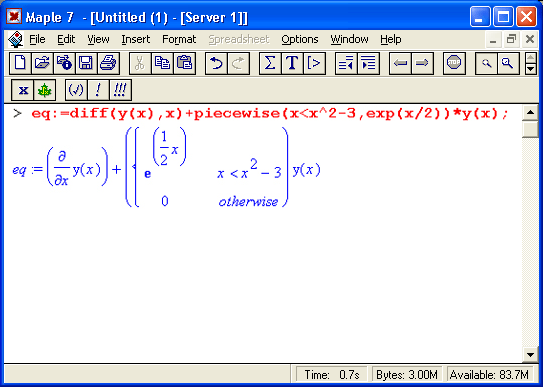
9.gif
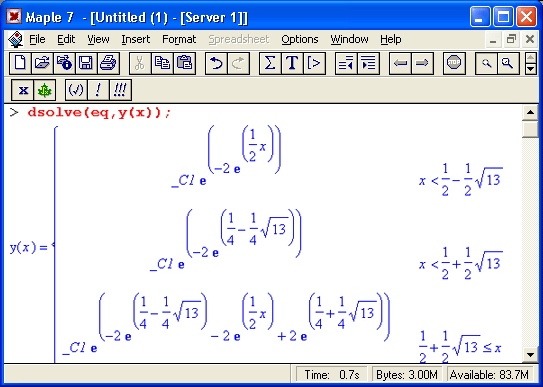
10.gif
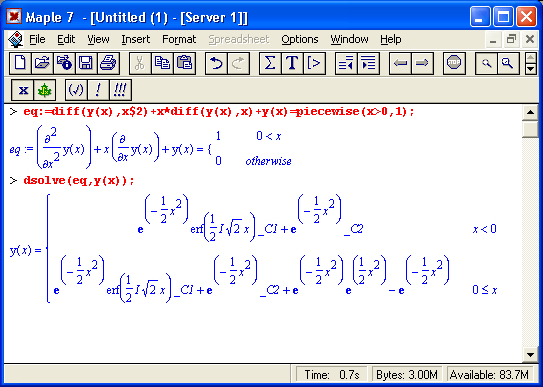
11.gif
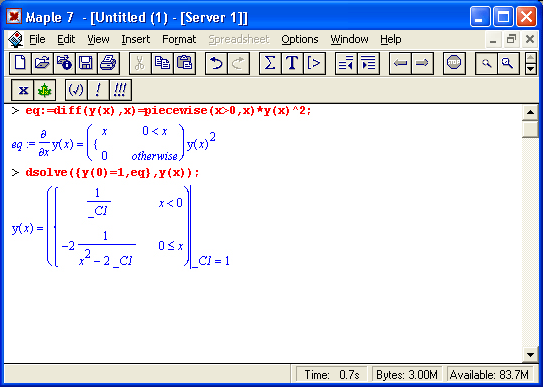
12.gif
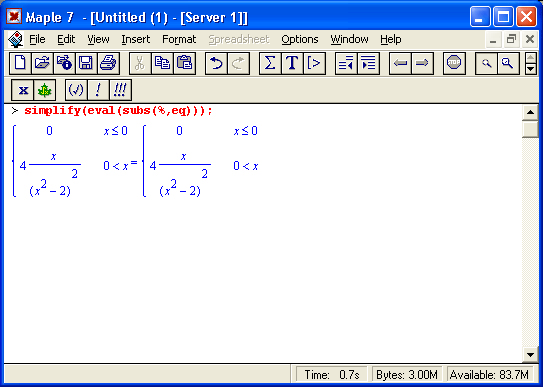
7. Структура неявного представления дифференциальных уравнений — DESol
Структура неявного представления дифференциальных уравнений — DESol
В ряде случаев иметь явное представление дифференциальных уравнений нецелесообразно. Для неявного их представления в Maple 7 введена специальная структура:
DESol(expr.vars)
где exprs — выражение для исходной системы дифференциальных уравнений, vars — заданный в виде опции список переменных (или одна переменная). Структура DESol образует некоторый объект, дающий представление о дифференциальных уравнениях, чем-то напоминающее RootOf. С этим объектом можно обращаться, как с функцией, то есть его можно интегрировать, дифференцировать, получать разложение в ряд и вычислять численными методами. На рис. 13.4 показаны примеры применения структуры DESol. Обратите внимание на последний пример — в нем структура- DESol использована для получения решения дифференциального уравнения в виде степенного ряда.
Рис. 13.4. Примеры применения структуры DESol
13.gif
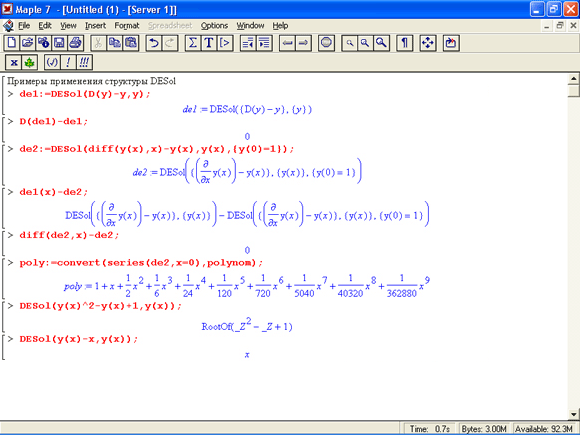
8. Инструментальный пакет решения дифференциальных уравнений DEtools.
Инструментальный пакет решения дифференциальных уравнений DEtools
Решение дифференциальных уравнений самых различных типов — одно из достоинств системы Maple 7. Пакет DEtools предоставляет ряд полезных функций для решения дифференциальных уравнений и систем с такими уравнениями:
> with(DEtools);
Warning, the name adjoint has been redefined
[DEnormal, DEplot, DEplot3d, DEplot_pofygon, DFactor, DFactorLCLM, DFactorsols, Dchangevar, GCRD, LCLM, PDEchangecoords, RiemannPsols, Xchange, Xcommutator, Xgauge, abelsoL, adjoint, autonomous, bernoullisol, buildsol, buildsym, canoni, caseplqt, casesplit, checkrank, chinisol, clairautsol, constcoeffsols, convertAlg, convertsys, dalembertsol, dcoeffs, de2diffop, dfieldplot, diffop2de, dsubs, eigenring, endomorphism_charpoly, equinv, etajc, eulersols, exactsol, expsols, exterior'_power,firint,firtest, formal_sol, gen_exp, generate_ic, genhomosol, gensys, hamilton_eqs, indicialeq, infgen, initialdata, integrate_sols, intfactor, Invariants, kovacicsols, leftdivision, liesol, line_int, linearsol, matrixDE, matrix_riccati, moserjreduce, muchange, mult, mutest, newtonjpolygon, normalG2, odeadvisor, odepde, parametricsol, phaseportrait, poincare, polysols, ratsols, redode, reduceOrder, reduce_order, regular_parts, regularsp, remove_RootOf, riccati_system, riccatisol, rifsimp, rightdivision, rtaylor, separablesol, solvejgroup, super_reduce, symgen, symmetric_po\ver, symmetric^product, symtest, transinv, translate, untranslate, varparam, zoom]
Этот пакет дает самые изысканные средства для аналитического и численного решения дифференциальных уравнений и систем с ними. По сравнению с версией Maple V R5 число функций данного пакета в Maple 7 возросло в несколько раз. Многие графические функции пакета DEtools были уже описаны. Ниже приводятся полные наименования тех функций, которые есть в реализациях R5, 6 и 7 системы Maple:
- DEnormal — возвращает нормализованную форму дифференциальных уравнений;
- DEplot — строит графики решения дифференциальных уравнений;
- DEplot3d — строит трехмерные графики для решения систем дифференциальных уравнений;
- Dchangevar — изменение переменных в дифференциальных уравнениях;
- PDEchangecoords — изменение координатных систем для дифференциальных уравнений в частных производных;
- PDEpTot — построение графиков решения дйффереациальых уравнений в частных производных;
- autonomous — тестирует дифференциальные уравнения на автономность;
- convertAlg — возвращает список коэффициентов для дифференциальных уравнений;
- convertsys — преобразует систему дифференциальных уравнений в систему одиночных уравнений;
- dfieldplot — строит график решения дифференциальных уравнений в виде векторного поля;
- indicialeq — преобразует дифференциальные уравнения в полиномиальные;
- phaseportrait — строит график решения дифференциальных уравнений в форме фазового портрета;
- reduceOrder — понижает порядок дифференциальных уравнений;
- regularsp — вычисляет регулярные особые точки для дифференциальных уравнений второго порядка;
- translate — преобразует дифференциальные уравнения в список операторов;
- untranslate — преобразует список операторов в дифференциальные уравнения;
- varparam — находит общее решение дифференциальных уравнений методом вариации параметров.
Применение этих функций гарантирует совместимость документов реализаций Maple R5, 6 и 7.
9. Основные функции пакета DEtools
Основные функции пакета DEtools
Ввиду обилия функций пакета DEtools дать их полное описание в данной книге не представляется возможным. Поэтому выборочно рассмотрим наиболее важные функции этого пакета. Функция:
autonomous(des.vars,ivar)
тестирует дифференциальное уравнение (или систему) des. Ее параметрами помимо des являются независимая переменная ivar и зависимая переменная dvar. Следующие примеры поясняют применение этой функции:
> automou(sin(z(t)-z(t)^2)*(D@@4)(z)(t)-cos(z(t))-5,z.t);
true
> DE:=diff(x(s),s)-x(s)*cos(arctan(x(s)))=arctan(s):
> autonomous(DE.{x},s);
false
Функция Dchangevar используется для обеспечения замен (подстановок) в дифференциальных уравнениях:
Dchangevar(trans,deqns, c_tvar, rMvar)
Dchangevar(tranl, tran2, .... tranN, deqns, c_ivar, n_ivar)
В первом случае trans — список или множество уравнений, которые подставляются в дифференциальное уравнение, список или множество дифференциальных уравнений deqns. При этом c_ivar — имя текущей переменной, n_ivar — имя новой переменной (его задавать необязательно). Во второй форме для подстановки используются уравнения tranl, tran2, .... Ниже представлены примеры применения функции Dchangevar:
Следует отметить, что подстановки являются мощным средством решения дифференциальных уравнений. Нередки случаи, когда дифференциальное уравнение не решается без их применения. Дополнительные примеры использования подстановок можно найти в справочной базе данных системы Maple 7.
Функция нормализации ОДУ DEnormal синтаксически записывается в виде:
DEnormal(des,ivar,dvar)
где des — система дифференциальных уравнений, 1var — независимая переменная и dvar — зависимая переменная. Применение этой функции поясняют следующие примеры:
Функция convertAlg(des,dvar) возвращает список коэффициентов формы системы дифференциальных уравнений des с зависимыми переменными dvar. Это поясняют следующие примеры:
Для изменения переменных в системах дифференциальных уравнений используется функция convertsys:
convertsys(deqns, inits, vars, ivar, yvec, ypvec)
Здесь deqns — одно дифференциальное уравнение или список (множество), представляющие систему дифференциальных уравнений первого порядка, inits — множество или список начальных условий, vans — зависимые переменные, ivar — независимые переменные, yvec — вектор решений и ypvec — вектор производных. Функция:
indicialeq(des.ivar,alpha.dvar)
обеспечивает полиномиальное представление для линейного однородного дифференциального уравнения второго порядка des. Параметр alpha намечает точку сингулярности.
Функция:
reduceOrder(des.dvar,partsol, solutionForm)
обеспечивает понижение порядка дифференциального уравнения des (или системы уравнений, представленных списком или множеством) при зависимых переменных dvar, частном решении partsol (или списке частных решений) и флаге solutionForm, показывающем, что решение происходит явным методом (explicitly). Для демонстрации действия этой функции воспользуемся примером из ее справочной страницы:
Функция:
regularsp(des,ivar,dvar)
вычисляет регулярные особые (сингулярные) точки для дифференциального уравнения второго порядка или системы дифференциальных уравнений des. Следующий пример поясняет применение данной функции:
> coefs := [21*(х^2 - х + 1),0,100*х^2*(х-1)^2]:
> regularsp(coefs. х);
[0,1]
Еще две функции пакета DEtools:
translate(des,ivar.pt,dvar)
untranslate(des,ivar,pt,dvar)
выполняют особую операцию трансляции дифференциального уравнения (или списка дифференциальных уравнений) из центрированного относительно 0 в центрированное относительно 1 и наоборот. С деталями этого специфического процесса заинтересованный читатель может познакомиться в справочной базе данных. И еще одна полезная функция пакета:
varparam(sols.v.ivar)
находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения; если он равен 0, ищется только частичное решение:
Более подробную информацию об этих функциях читатель найдет в их справочных страницах, а также в информационном документе detdols.mws содержащем систематизированное описание пакета DEtools с многочисленными примерами его применения.
14.gif
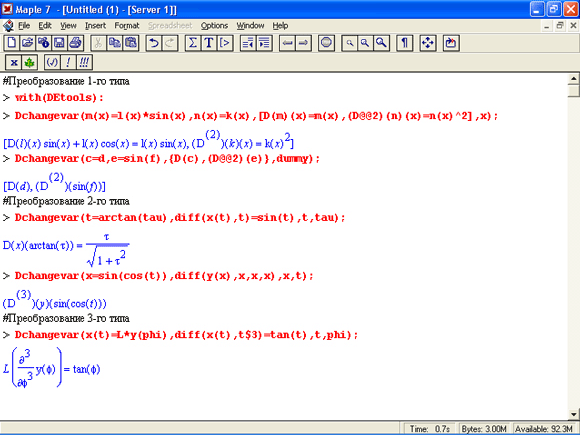
16.gif
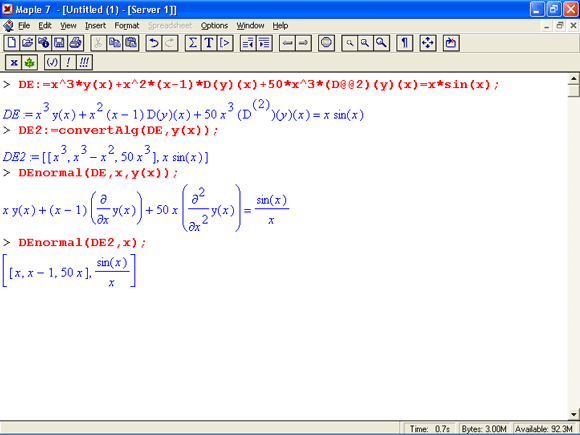
17.gif
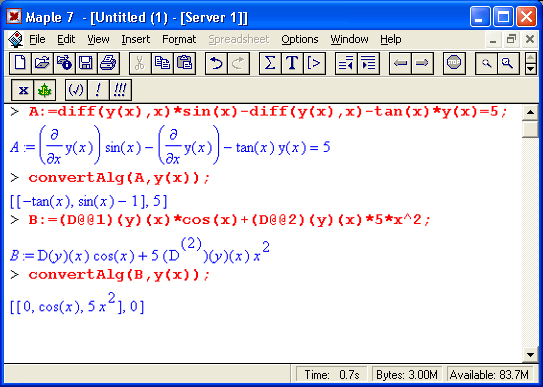
18.gif
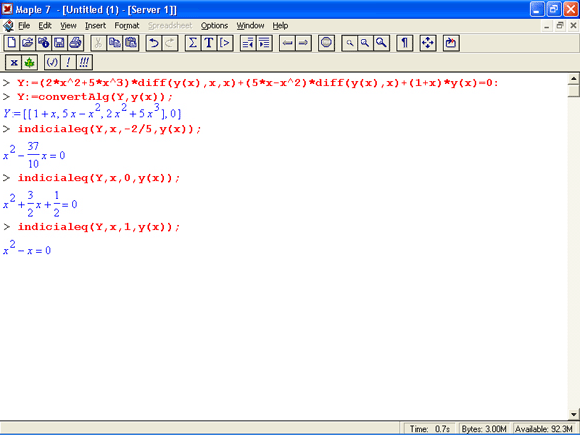
19.gif
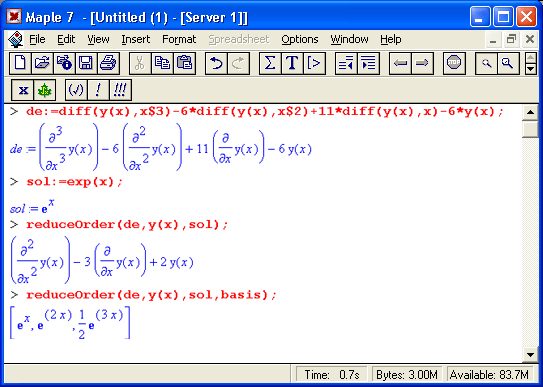
20.gif
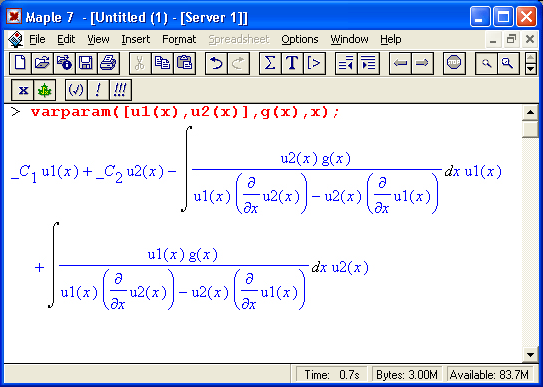
10. Графическое представление решений дифференциальных уравнений
Графическое представление решений дифференциальных уравнений
Применение функции odeplot пакета plots
Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:
odep1ot(s,vars.r,o)
где s — запись (в выходной фирме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, г — параметр, задающий пределы решения (например, а. .Ь), и о — необязательные дополнительные опции.
На рис. 13.5 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.
В этом примере решается дифференциальное уравнение:
y'(x)=cos(x2y(x))
при у(0) = 2 и x, меняющемся от-5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения у(х).
В другом примере (рис. 13.6) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций. —у(х) и z(x).
В этом примере решается система:
у'(х)=z(х),
z'(x) = 3 sin(y(x))
при начальных условиях y(0)=0, z(0) = 1 их, меняющемся от -4 до 4 при числе точек решения, равном 25.
Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 13.7 демонстрирует построение фазового портрета для системы, представленной выше.
Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок; для построения, поэтому возможность Марle 7 быстро строить фазовые портреты трудно переоценить.
Рис. 13.5. Пример решения одиночного дифференциального уравнения
Рис. 13.6. Пример решения системы из двух дифференциальных уравнений
Рис. 13.7. Представление решения системы дифференциальных уравнений в виде фазового портрета
28.gif
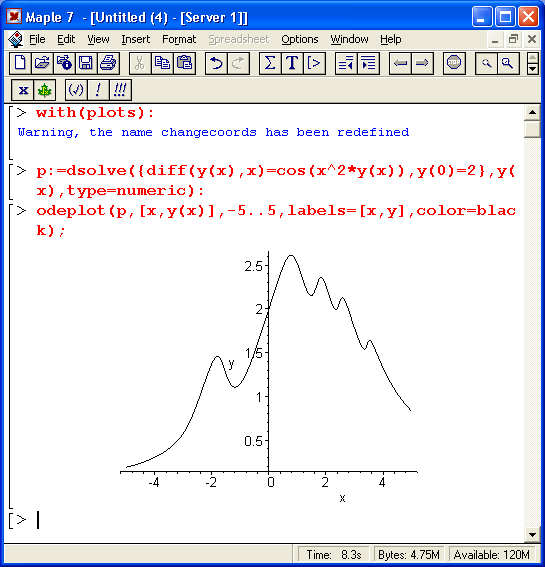
29.gif
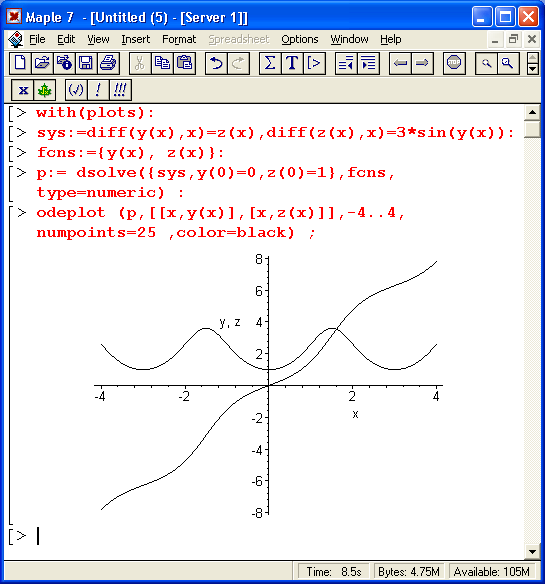
30.gif
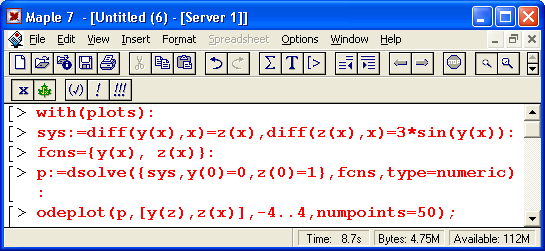
11. Функция DEplotna пакета DEtools
Функция DEplot из пакета DEtools
Специально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot. Функция DEplot может записываться в нескольких формах:
DEplot(deqns, vars. trange. eqns)
DEplot(deqns, vans, trange. inits. eqns)
DEplot(deqns. vars. trange, уrange, xrgnge, eqns) .
DEplot(deqns. vars, trange. Inits, xrange. yrange, eqns)
Здесь deqns — список или множество, содержащее систему дифференциальных уравнений первого порядка или одиночное уравнение любого порядка; vars — зависимая переменная или список либо множество зависимых переменных; trange — область изменения независимой переменной t; Inits — начальные условия для решения; yrange — область изменения для первой зависимой переменной, xrange — область изменения для второй зависимой переменной; eqns — опция, записываемая в виде keyword-value. Замена имен переменных другими в данном случае недопустима.
Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем — только в виде кривых решения. По умолчанию реализуется метод Рунге—Кутта 4-го порядка, что соответствует опции methodiclassical[rk4]. С функцией DEplot могут использоваться следующие параметры:
- arrows = type — тип стрелки векторного поля ('SMALL', 'MEDIUM', 'LARGE', 'LINE'
- или 'NONE');
- colour, color = arrowcolour — цвет стрелок (задается 7 способами);
- dirgrid = [integer,integer] — число линий сетки (по умолчанию [20, 20]);
- iterations = integer — количество итераций, представленное целым числом;
- linесоlor, linecolor = lineinfo — цвет линии (задается 5 способами);
- method='rk4' — задает метод решения ('euler', 'backeuler', 'impeuler' или 'rk4');
- obsrange = TRUE.FALSE — задает (при TRUE) прерывание вычислений, если кривая решения выходит из области обзора;
- scene = [name.name] — задает имена зависимых переменных, для которых строится график;
- stepsize = h — шаг решения, по умолчанию равный abs((b-a))/20 и представленный вещественным значением.
На рис. 13.8 показано решение системы диффкренциальных уравнений
x'(t)=x(t)(1-y(t)
y'(t)= 0,3y(t)(x(t)-1),
описывающих модель Лотки—Вольтерра при заданных в документе изменениях t, x(t) и y(t). Решение представлено в виде векторного поля стрелки которого являются касательными к кривым решения (сами эти кривые не строятся). Обратите внимание на функциональную закраску стрелок векторного поля, делающую решение особенно наглядным (правда, лишь на экране цветного дисплея, а не на страницах книги).
Рис. 13.8. Решение системы дифференциальных уравнений Лотки—Вольтерра , с выводом в виде графика векторного поля
Еще интересней вариант графиков, представленный на рис. 13.9. Здесь помимо векторного поля несколько иного стиля построены фазовые портреты решения с использованием функциональной закраски их линий. Фазовые портреты построены для двух наборов начальных условий:
x(0) = y(0) = 1,2 и x(0) = 1 и у(0)=0,7.
Следует отметить, что функция DEplot может обращаться к другим функциям пакета DEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения.
Рис. 13.9. Пример построения двух фазовых портретов на фоне векторного поля
31.gif
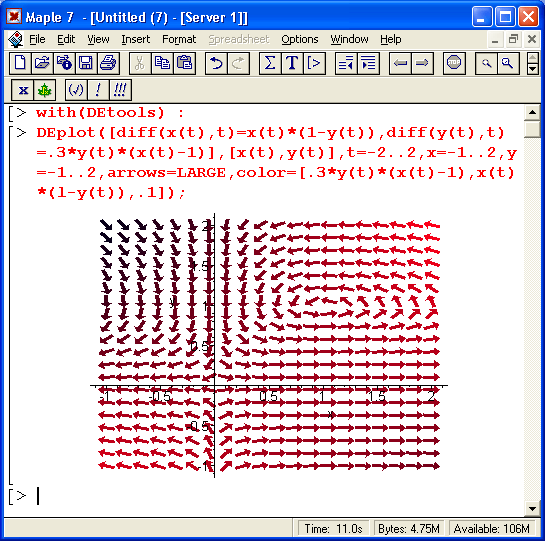
32.gif
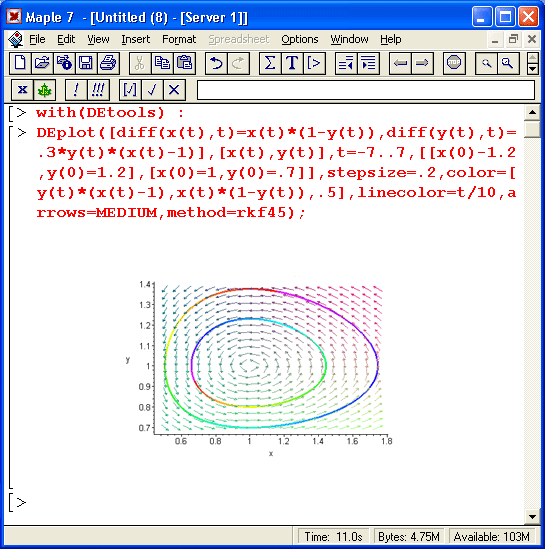
12. Функция DEplot3d из пакета DEtools
Функция DEplotSd из пакета DEtools
В ряде случаев решение систем дифференциальных уравнений удобно представлять в виде пространственных кривых — например, линий равного уровня или просто в виде кривых в пространстве. Для этого служит функция DEplot3d:
DEplot3d(deqns, vars, trarige, initset, о)
DEplot3d(deqns, vars, trang, yrange, xrange, initset, o)
Назначение параметров этой функции аналогично указанному для функции DEplot.
Рисунок 13.10 поясняет применение функции DEPlqt3d для решения системы из двух дифференциальных уравнений с выводом фазового портрета колебаний в виде параметрически заданной зависимости x(t), y(t). В данном случае фазовый портрет строится на плоскости по типу построения графиков/линий равной высоты.
Другой пример (рис. 13.11) показывает решение системы из двух дифференциальных уравнений с построением объемного фазового портрета. В этом случае используется трехмерная координатная система и графические построения соответствуют параметрическим зависимостям x(t), y(t) и z(t). Вид фазового портрета напоминает разворачивающуюся в пространстве объемную, спираль.
Функциональная окраска делает график пикантным.
Рис. 13.10. Пример решения системы из двух дифференциальных уравнений с помощью функции DEptot3d
Возможности функции DEplot3d позволяют решать системы, состоящие более чем из двух дифференциальных уравнений. Однако в этом случае число решений, представляемых графически, выходит за пределы возможного для трехмерной графики. При этом от пользователя зависит, какие из зависимостей опускаются при построении, а какие строятся.
33.gif
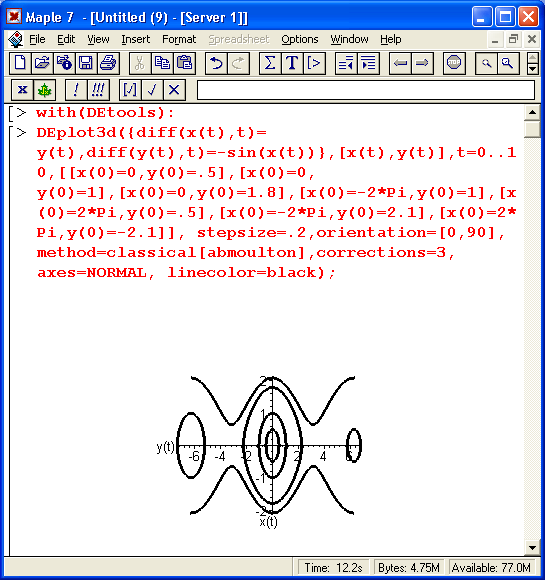
13. Функция PDEplot пакета DEtools.
Функция PDEplot пакета DEtools
Еще одна функция пакета DEtools — DEtools[PDEp1ot] — служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных.
Эта функция используется в следующем виде:
PDEplotCpdiffeq, van, i_curve, srange, о)
PDEplot(pdiffeq, var, i_curve. srange, xrange, yrange, urange, o)
Рис. 13.11. Пример решения системы из двух дифференциальных уравнений с построением трехмерного фазового портрета
Здесь помимо упоминавшихся ранее параметров используются следующие: pdiffeq — квазилинейные дифференциальные уравнения первого порядка (PDE), vans — независимая переменная и i_curve — начальные условия для параметрических кривых трехмерной поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции:
- basechar = TRUE, FALSE. ONLY — устанавливает показ базовых характеристик кривых;
- basecolor, basecolor = b_color — устанавливает цвет базовых характеристик;
- initcolor, initcolor =i_color — инициализация цветов;
- numchar = integer — задает число отрезков кривых, которое не должно быть меньше 4 (по умолчанию 20);
- numsteps = [integerl.integerZ] — задает число шагов интегрирования (по умолчанию [10, 10]).
Рисунок 13.12 демонстрирует применение функции PDEplot. Этот пример показывает, насколько необычным может быть решение даже простой системы дифференциальных уравнений в частных производных.
Рис. 13.12. Пример применения функции PDEplot
В данном случае решение представлено трехмерной фигурой весьма нерегулярного вида.
Другой пример использования функции PDEplot показан на рис. 13.13. Он иллюстрирует комбинированное построение графиков решения разного типа с применением функциональной закраски, реализуемой по заданной формуле с помощью опции initcolor.
Еще раз отметим, что, к сожалению, рисунки в данной книге не дают представления о цвете выводимого Maple графика. Поэтому наглядность решений, видимых на экране монитора, существенно выше.
34.gif
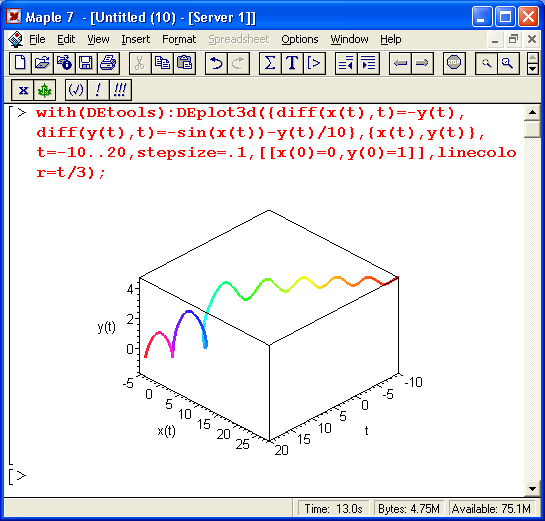
35.gif
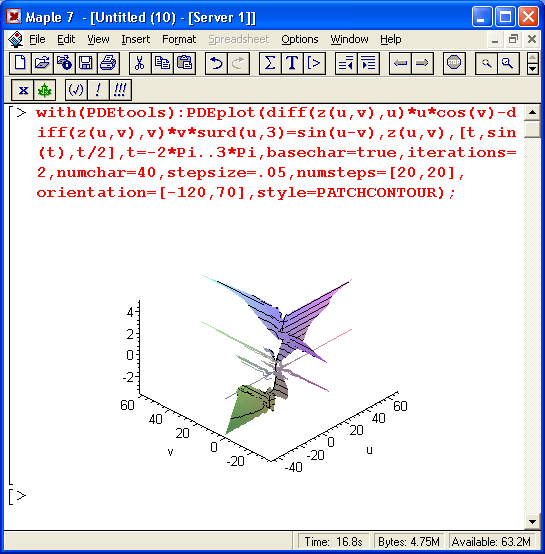
14. Графическая функция dfieldplot
Графическая функция dfieldplot
Графическая функция dfieldplot служит для построения поля направления с помощью векторов по результатам решения дифференциальных уравнений. Фактически эта функция как бы входит в функцию DEplot и при необходимости вызывается последней. Но она может использоваться и самостоятельно, что демонстрирует рис. 13.14, на котором показан пример решения следующей системы дифференциальных уравнений:
x'(t) =x(t)(1- y(t)),
y'(t) = 0,3y(t)(x(t) - 1).
Рис. 13.13. Построение комбинированного графика с помощью функции PDEplot
Обратите внимание на использование опций в этом примере, в частности на вывод надписи на русском языке. В целом список параметров функции phaseportrait аналогичен таковому для функции DEplot (отсутствует лишь задание начальных условий).
36.gif
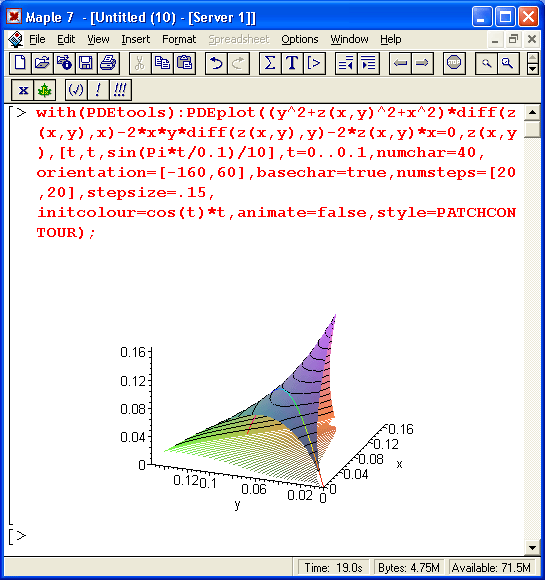
15. Графическая функция phaseportrait
Графическая функция phaseportrait
Графическая функция phaseportrait служит для построения фазовых портретов по результатам решения одного дифференциального уравнения или системы дифференциальных уравнений deqns. Она задается в следующем виде:
phaseportrait(deqns,vars,traf,1n1ts,o)
При задании уравнений достаточно указать их правые части. На рис. 13.15 представлен пример применения функции phaseportrait для решения системы из трех дифференциальных уравнений первого порядка.
В этом примере система дифференциальных уравнений задана с помощью оператора дифференцирования D. Функциональная окраска линии фазового портрета достигается использованием параметра linecolor, в правой части которого задана формула для цвета.
Рис. 13.14. Построение фазового портрета в виде графика векторного поля
Рис. 13.15. Построение фазового портрета с помощью функции phaserportrait
Еще более интересный пример решения дифференциального уравнения представлен на рис. 13.16. Здесь построены фазовые портреты для асимптотических решений.
В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple 7 весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное. В справочной системе можно найти ряд других весьма эффектных решений систем дифференциальных уравнений с визуализацией последних. ,
Рис. 13.16. Построение асимптотического решения на фоне графика векторного поля
37.gif
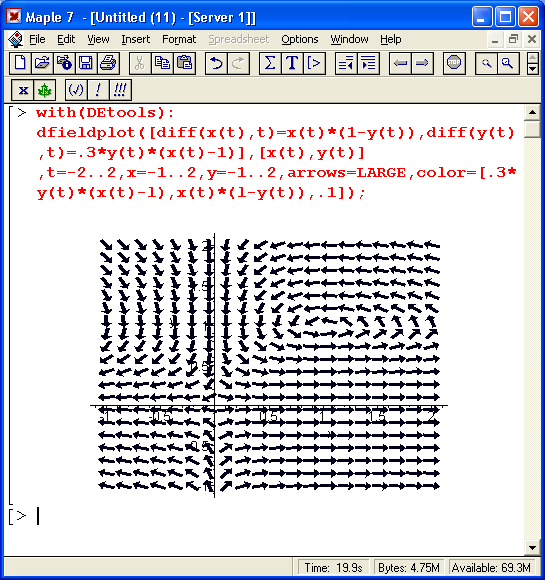
38.gif
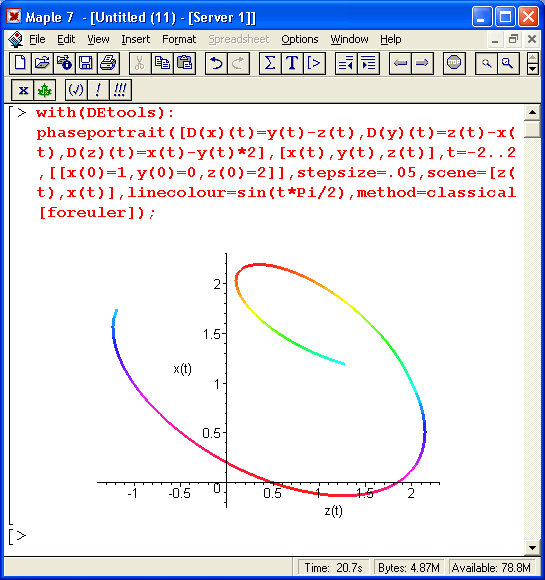
39.gif
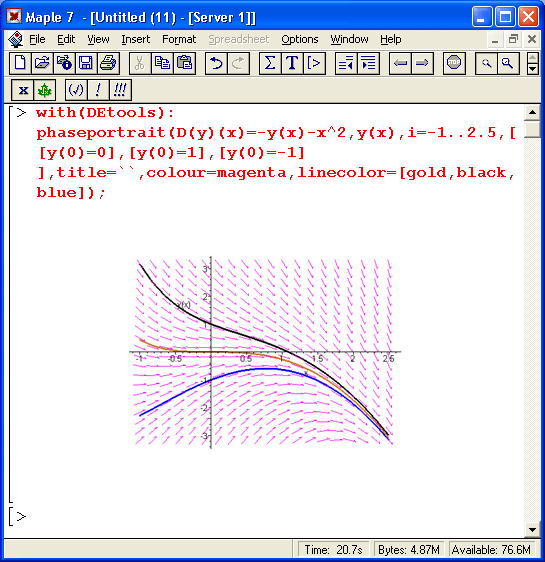
16. Углубленный анализ дифференциальных уравнений
Углубленный анализ дифференциальных уравнений
Задачи углубленного анализа ДУ
Maple 7 существенно доработана по части решения дифференциальных уравнений (ДУ) и систем с ДУ. Эта доработка прежде всего направлена на получение верных решений как можно большего числа ДУ разных классов и систем с ДУ.
В частности, расширен круг нелинейных дифференциальных уравнений, для которых Maple7способна дать аналитические решения.
Весь арсенал средств решения ДУ-и методика их применения вполне заслуживают отражения в отдельной большой книге. Мы ограничимся описанием только трех средств системы Maple 7 - проверки ДУ на автономность, углубленным анализом решения с помощью контроля уровня выхода и получением приближенного полиномиального аналитического решения. Более подробное знакомство с новыми возможностями решения дифференциальных уравнений можно получить из соответствующей статьи справки symbolics в разделе What is new.
17. Проверка ДУ на автономность
Проверка ДУ на автономность
Одиночное дифференциальное уравнение или система дифференциальных уравнений называются автономными, если их правая часть явно не зависит от независимой переменной. Для автономных дифференциальных уравнений или систем при построении графиков решений функцией DEplot не обязательно задавать начальные условия, но нужно указывать диапазон изменения искомых переменных.
Для проверки уравнений (или систем) на автономность используется функция:
autonomous(des,vars,ivar)
где des — заданное дифференциальное уравнение или (в виде списка) система дифференциальных уравнений, vars — зависимые переменные; ivar — независимая переменная. Если система автономна, то эта функция возвращает true, в противном случае false.
Примеры:
В первом случае система дифференциальных уравнений (модель. Лотки-Воль-терра) автономна, а во втором случае дифференциальное уравнение не автономно.
21.gif
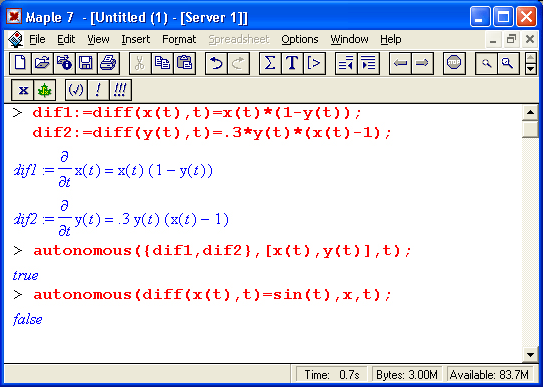
18. Контроль уровня вывода решения ДУ
Контроль уровня вывода решения ДУ
Для углубленного анализа аналитического решения ДУ (или системы ДУ) можно использовать специальную возможность управления уровнем вывода решения с помощью системной переменной infilevel(dsolve)=level. Значение level =all дает обычный вывод решения без Комментариев, уровень 1 зарезервирован для информации, которую может сообщить пользователь, уровень 2 или 3 дает более детальный вывод (включая сообщения об использованном алгоритме и технике решения) и, наконец, уровни 4 и 5 дают наиболее детальную информацию (если тиковая есть в дополнение к той информации, которую дает уровень 2 или 3).
Приведем пример .аналитического решения ДУ третьего порядка с контролем уровня вывода решения:
В данном случае повышение уровня вывода до 4 или 5 бесполезно, поскольку вся информация о решении сообщается уже при уровне 2 (или 3).
22.gif
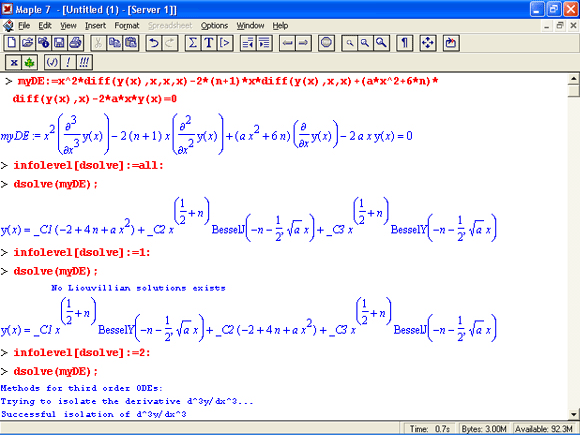
19. Приближенное полиномиальное решение ДУ
Приближенное полиномиальное решение ДУ
Во многих случаях аналитические решения даже простых ДУ оказываются весьма сложными, например содержат специальные математические функции. При этом нередко полезна подмена такого решения другим, тоже аналитическим, но приближенным решением. Наиболее распространенным приближенным решением в этом случае может быть полиномиальное решение, то есть замена реального решения полиномом той или иной степени. При этом порядок полинома задается значением системной переменной Order, а для получения такого решения функция dsolve должна иметь параметр series.
На рис. 13.17 представлено решение ДУ третьего порядка различными методами: точное аналитическое и приближенное в виде полинома с максимальным заданным порядком 10 и 60. График дает сравнение этих решений для зависимости y(t).
Дадим небольшой комментарий. Нетрудно заметить, что точное аналитическое решение весьма сложно и содержит специальные функции Бесселя и гамма- функции. При порядке полинома 8 (он несколько меньше заданного максимального) решение практически совпадает с точным до значений t < 2, а при максимальном заданном порядке 60 область совпадения расширяется до значений t < 5,5. Затем приближенное решение резко отходит от точного.
Этот пример, с одной стороны, иллюстрирует хорошо известный факт — быстрое нарастание погрешности полиномиального приближения за пределами области хорошего совпадения решений. С другой стороны, он показывает, что степень полинома более 60 (и даже выше) вовсе не так уж бесполезна, как это утверждается во многих статьях и книгах по полиномиальному приближению. Точность полиномиальных вычислений Maple 7 достаточно высока, чтобы обеспечить получение приближенных полиномиальных выражений со степенью порядка десятков и иногда даже сотен. Другое дело, что столь «длинный» полином не всегда удобен для аналитических расчетов, даже несмотря на его структурную простоту.
Рис. 13.17. Примеры решения ДУ третьего порядка
40.gif
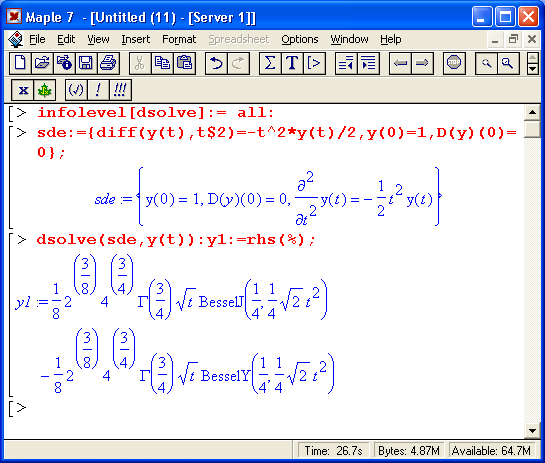
20. Что нового мы узнали?
Что нового мы узнали?
В этим уроке мы научились:
- Использовать основную функцию решения дифференциальных уравнений dsolve.
- Решать дифференциальные уравнения первого порядка. О Решать дифференциальные уравнения второго порядка.
- Решать системы дифференциальных уравнений, .
- Выполнять численное решение дифференциальных уравнений.
- Решать дифференциальные уравнения с кусочными функциями.
- Использовать структуру неявного представления дифференциальных уравнений DESol
- Применять инструментальный пакет решения дифференциальных уравнений DEtools
- Осуществлять графическое представление решений дифференциальных уравнений.
- Осуществлять углубленный анализ аналитических решений дифференциальных уравнений.
Урок 14. Математические пакеты
1. Назначение пакетов расширения и обращение к ним
Урок 14.
Математические пакеты
Как уже отмечалось, некоторые функции системы Maple помимо их нахождения в ядре могут быть расположены в стандартной библиотеке и в пакетах, входящих в поставку системы. Это значит, что их не надо приобретать дополнительно, однако перед использованием таких функций надо загрузить их или отдельно, или вместе с целым пакетом, если большинство его функций представляет интерес для пользователя.
2. Обзор пакетов
Обзор пакетов
В этом уроке дается выборочная информация о функциях, содержащихся в пакетах. Напоминаем, что список пакетов можно получить, используя команду:
>?packages
Этот список приведен ниже:
- DEtools — решение дифференциальных уравнений;
- Domains — создание областей определений в вычислениях;
- GF — поля Галуа;
- Gausslnt — работа с целыми числами Гаусса;
- Groebner — вычисления в базисе Гробнера;
- LREtools — манипуляции с линейными рекуррентными отношениями;
- LinearAlgebra — линейная алгебра;
- Matlab — интеграция с MATLAB;
- Ore_algebra — основные вычисления в алгебре линейных операторов;
- PDEtools — решение дифференциальных уравнений в частных производных;
- Spread — работа с таблицами;
- algcurves — работа с алгебраическими кривыми;
- codegen — генерация кодов;
- combinat — функции комбинаторики;
- combstruct — структуры комбинаторики;
- context — контекстно-зависимые меню;
- diffalg — дифференциальная алгебра;
- difforms — дифференциальные формы;
- finance — финансовые расчеты;
- genfunc — рациональные функции;
- geom3d — трехмерная геометрия Евклида;
- geometry — евклидова геометрия;
- group — представление бесконечных групп;
- inttrans — интегральные преобразования;
- liesymm — симметрия Ли;
- linalg — линейная алгебра и структуры данных массивов;
- networks — графы;
- numapprox — численная аппроксимация;
- numtheory — теория чисел;
- orthopoly — ортогональные полиномы;
- padic — Пи-адические числа;
- plots — расширения графики;
- plottools — создание дополнительных графических объектов; >
- polytools — действия с полиномами;
- powseries — формальные степенные ряды;
- process — мультипроцессы (для операционной системы Unix);
- simplex — линейная оптимизация (симплекс-метод); '
- stats — статистика;
- student — функции в помощь студентам;
- sumtools — определенные и неопределенные суммы;
- tensor — тензоры и теория относительности.
Как следует из просмотра этого обширного списка, пакеты Maple 7 охватывают многие крупные разделы математики и существенно дополняют возможности системы, предоставляемые средствами ее ядра. Пакеты расширения пишутся на Maple-языке программирования, поэтому они могут легко модернизироваться и пополняться. Этим, в частности, объясняется тот факт, что набор пакетов расширения в Maple 7 существенно пополнен по сравнению с предшествующими реализациями системы.
3. Новые пакеты Maple 7
Новые пакеты Maple 7
Система Maple 7 пополнилась рядом новых пакетов:
- CurveFutting — приближение кривых;
- ExternalCalling — внешние вычисления;
- LinearFunctionalSystem — линейные функциональные системы;
- MathML — поддержка средств языка MathML 2.0;
- OrthogonalSeries — серии с ортогональными полиномами;
- PolynomialTools — работа с полиномами.
Из этих пакетов надо особо выделить пакет приближения кривых. Он содержит наиболее важные функции для приближения кривых, которые до сих пор были разбросаны по ряду пакетов. В конце данного урока содержится описание пакета CurveFitting. Там же имеется описание другого нового и полезного пакета — PolynomialTools.
4. Получение информации о конкретном пакете
Получение информации о конкретном пакете
С помощью команды:
>?name_package;
можно получить информацию о любом пакете расширения и найти список входящих в него функций. Названия пакетов были приведены выше.
Для обращения к функциям того или иного пакета используется его полная загрузка командой:
>with(package):[:]
Знак : блокирует вывод списка функций пакета а знак ; указывает вывести этот список.
Если вам необходима какая-то одна функция пакета или небольшая их часть, то не стоит загружать пакет целиком. Это может привести к избыточным затратам памяти компьютера и даже нарушить нормальную работу некоторых функций — следует помнить, что нередко пакеты переопределяют некоторые функции ядра. Для загрузки избранных функций используется команда with в форме
>with(package. fl. f2. ...):
или
>with(package, [fl. f2. ...]):
При этом загружаются функции fl, f2, ... из пакета с именем packages.
Может показаться, что было бы лучше иметь все функции в ядре. Однако создание ядра, реализующего все функции системы (в версии Maple 7 их около 3000), неразумно. Такое ядро занимало бы много места в памяти, имело большое время загрузки и затрудняло бы поиск конкретных нужных функций.
Поэтому ядро Maple 7 содержит определенный (и довольно обширный) минимум хорошо апробированных функций, а большинство других функций размещается в стандартной библиотеке и пакетах. Они готовятся на Maple-языке программирования и могут легко модернизироваться. К тому же пакеты могут модифицироваться (что не очень желательно) или дополняться (что приветствуется) пользователями. Некоторой платой за это является необходимость вызова того или иного пакета или функции перед их применением.
В этом разделе описана структура пакетов Maple 7, имеющих математическую направленность. Ограниченный объем книги и огромное число функций в пакетах не позволяют остановиться даже на описании синтаксических правил применения всех функций этих пакетов. Очевидно, что в этом нет и особого смысла — подавляющее большинство функций представляет малый интерес для конкретного пользователя. Те же, кто ими интересуются, могут легко восполнить пробелы в их описании с помощью справочной системы. Однако в описании состава каждого пакета в данном уроке упомянуты имена всех без исключения его функций. Это позволяет оценить полноту того или иного пакета и без труда вызвать справочные страницы для любой функции. Описание функций пакетов в уроке дано выборочно, при этом предпочтение отдавалось тем функциям, которые используются в массовых математических и научно-технических расчетах и представляют интерес для достаточно широкого круга читателей. Полезно отметить, что большинство функций имеет вполне понятные имена, отражающие их суть и назначение. К примеру, назначение функций animate или даже textplot в пакете plots или Diff, Int и Limit в пакете student понятны, пожалуй, всем. Но и в гораздо более специализированных пакетах имена входящих в них функций в значительной мере знакомы специалистам, поскольку почти всегда ассоциируются с общепринятыми названиями тех или иных специализированных функций или с их комбинациями.
5. Пакеты функций комбинаторики
Пакеты функций комбинаторики
Функции комбинаторики достаточно известны из обычного курса математики. При вызове пакета выводится (если вывод не заблокирован двоеточием) список его функций:
> with(combinat);
Warning, the protected name Chi has been redefined and unprotected
[Chi,bell, binomialcartprod, character, choose, composition, conjpart, decodepart, encodepart,fibonacci,firstpart, graycode, inttovec, lastpart, multinomial, nextpart, numbcomb, numbcomp, numbpart, numbperm, partition, permute, powerset, prevpart, randcomb, randpart, randperm, Stirling], stirling2, subsets, vectoint]
Ввиду важности функций комбинаторики приведем их полные определения:
- Chi(x) — гиперболический косинусный интеграл;
- bell(n) —возвращает число ехр(ехр(х)-1) =sum(ben(n)/n!*x^n, n=0..infinity), причем для вычислении используется рекуррентное соотношение bell(n+1) = (bell(n)+1)^n;
- binomial (n, r) — возвращает биноминальные коэффициенты, причем, если n и r — целые числа, удовлетворяющие условию 0 <= r<= n, то функция возвращает C(n.r)=n!/(r!(n-r)!), а в общем случае С(n, r) = limit(GAMMA(N+D/ GAMMA(R+l)/GAMMA(N-R-t-l),R=r,N=n);
- composition(n, k) — возвращает списки композиций для целых неотрицательных n и k;
- fibonacci(n) — возвращает числа Фибоначчи, вычисляемые по рекуррентной формуле F(n) =F(n - 1) +F(n - 2), где F(0) =0 и F(1) =1;
- fibonacci(n, х) — возвращает значение полинома Фибоначчи F(n, x) =-х F(n - 1,x) + F(n - 2, х), где F(0,x) = 0 и F(l,x) = 1, при этом F(n) = F(n, 1);
- firstpart(n) — возвращает первую часть каноническей последовательности ряда;
- nextpart(l) — возвращает следующую часть канонической последовательности ряда;
- lastpart(n) — возвращает последнюю часть канонической последовательности ряда;
- prevpart(1) — возвращает предыдущую часть канонической последовательности ряда;
- conjpart(l) — возвращает объединенный раздел в канонической последовательности ряда;
- graycode(n) — возвращает список кодов Грея для габитовых чисел;
- multinomial (n, kl, k2, .... km) — возвращает мультиномиальные коэффициенты;
- numbcomb(n) и numbcomb(n. m) — возвращает число комбинаций;
- numbcomp(n, k) — возвращает число композиций;
- numbpart(n) — возвращает список всех возможных сумм, дающих п;
- permute(n) и permute(n, r) — возвращает numbperm(n, r) = nops(permute(n. r));
- powerset(s) — возвращает степень множества в множестве s;
- randcomb(n, m) — возвращает случайную комбинацию;
- randpart(n) — возвращает случайную часть;
- randperm(n) — возвращает случайную композицию;
- stirling(n, m) — возвращает число Стирлинга первого рода;
- stirling2(n, m) — возвращает число Стирлинга второго рода;
- subsets(L) — задает итерационную процедуру над степенями множества или списка L;
- vectoint(l) — возвращает индекс вектора канонического упорядочения 1;
- inttovec(m, n) — возвращает вектор канонического упорядочения для неотрицательных целых чисел тип.
Ниже даны примеры применения некоторых из этих функций:
> choose(4,3);
[[1,2,3],[1,2,4],[1,3,4],[2,3,4]]
> choose([a,a,b,c].3):
[[a,a,b],[a,a,c],[atb,c]]
> composition(3,2):
{[2,1],[1,2]}
> decodepart(4,2);
[1,1,2]
> fibonacci(l0);
55
> seq(fibonacci(1),i-l..l2):
1,1,2,3,5,8,13,21,34,55,89,144
> partition(5);
[[1,1,1,1,1], [1,1,1,2], [1,2,2], [1,1,3], [2,3], [1,4], [5]]
> firstpart(3):
[1,1,1]
> nextpart(%);
[1,2]
> prevpart(%);
[1,1,1]
> 1astpart(3):
[3]
> conjpart(%):
[1,1,1]
> multinomial(8,2,3,3);
560
> numbcomp(8,5):
35
> nuropart(3);
numpart(3)
> numbperm(4);
24
> numbperm([a,b]):
2
> numbperm({a,b,c},2);
6
> permute(3,2);
[[l,-2],[l,3],[2,l],[2,3],[3,l],[3,2]]
> permute([a,a,b],2):
[[a,a],[a,b],(b,a]]
> powerset([a,a,b]):
[[],[а],[b],[а,Ь],[а,а],[а,а,b-]]
> randcomb([a,b,c,d],3):
[a,c,d]
> randcomb([a,b,c,d],3);
[a,b,d]
> randpart(l0);
[2,8]
> randpart(l0):
[10]
> stirling(10,5);
-269325
> stirling2(10,5):
42525
> S:=subsets({l,2}):
> while not S[finished] do S[nextva1ue]() od:
{ }
{1}
{2}
{1,2}
> vectoint([l,0,0]);
1
> inttovec(6,3);
[1,0,1]
Читателю, желающему использовать данный пакет, рекомендуется внимательно ознакомиться с этими простыми примерами и просмотреть примеры из справочной базы данных для имеющихся в пакете функций.
6. Пакет combstruct
Пакет combstruct
Еще девять функций, относящихся к структурам комбинаторики, содержит пакет combstruct:
> with(combstruct):
[allstructs, count, draw,finished, gfeqns, gfseries, gfsolve, iterstritcts, nextstruct]
Эти функции служат для создания случайно однородных объектов, принадлежащих заданному комбинаторному классу. Ограничимся приведением примеров применения этих функций:
> alltructs(Subset({one,two}));
{{ },{one, two}, {two}, {one}}
> anstructs(Permutation([x,y,z]),size=2):
[[x,y],[x,z],[y,x],[y,z],[z,x],[z,y]]
> count(Subset({l,2,3}));
8
> draw(Combiination(5),size=4);
{1,3,4,5}
> count(Permutation([a,a,b])): .
3
> 1t :=iterstructs(Permutation([a,a,b]),size=2);
it := table([finished = false, nextvalue = (pmc() ... endproc )])
> draw(Partition(9));
[2,2,2,3]
> allstructs(Composition(3), size=2):
[[2,l],[l,2]]
Для более полного знакомства с этими специфическими функциями обратитесь к справочной системе.
7. Пакет финансово-экономических функций finance
Пакет финансово-экономических функций finance
Пакет финансово-экономических расчетов открывается командой:
> with(finance)
[amortization, annuity, blackscholes, cashflows, effectiverate,futurevalue, growingannuity, growingperpetuity, levelcoupon, perpetuity, presentvalue, yieldtomaturity]
Этот пакет представлен рядом указанных выше функций в двух формах:
function(args)
finance[function](args).
Благодаря правилам задания аргументов можно реализовать практически все известные финансово-экономические расчеты, такие как амортизация, накопления и платежи по вкладам и т. д. В свете задач рыночной экономики эти функции полезны для приверженцев решения всего на свете без выхода из оболочки Maple. Все же надо отметить, что малозаметные тонкости в определении финансово-экономических функций затрудняют их применение. Есть множество специальных финансово-экономических пакетов, например «Бухгалтерия 1C», которые лучше подходят для наших экономических реалий, чем «заумный» и прозападный Maple 7.
Полный перечень функций можно найти в справке по этому пакету. Ограничимся упоминанием нескольких наиболее характерных функций, связанных с использованием вкладов:
- annuity(cash,rate,nperiods) — вычисление суммы, находящейся на вкладе с начальным значением cash, процентом начисления rate и числом периодов nperiods;
- cashflows(flows,rate) — вычисление общей суммы вклада по списку вложений flows и проценту обесценивания денег rate;
- futurevalue(amount, rate, nperiods) — вычисление будущего значения вклада при начальном вложении amount, проценте начисления rate и числе периодов nperiods;
- presentvalue(amount, rate, nperiods) — вычисление начального вклада для получения суммы в amount при проценте начислений rate и числе вкладов nperiods.
Примеры применения этих функций даны ниже:
Поскольку формулы и обозначения в финансово-экономических расчетах в различной литературе порою заметно различаются (особенно сильны различия между нашей и западной литературой), это может создать серьезные ошибки при вычислениях. К примеру, в формулах Maple на самом деле используются не проценты начислений или обесценивания вкладов, а соответствующие им относительные единицы, например 10% соответствует 0,1.. В нашей литературе проценты обычно задаются в явном виде, то есть rate = 10 при 10%. Надо следить и за знаком величины rate, поскольку она может трактоваться как процент начислений или процент обесценивания денег по вкладам, что соответствует различным ее знакам.
Расчеты такого рода для Maple 7 относятся к достаточно простым, так что даже начинающий пользователь может составить свои функции для таких расчетов по вполне понятным ему и апробированным формулам. Надо отметить, однако, что, используя символьное задание параметров функций, легко получить вывод именно тех формул, которые использует система Maple, и сравнить их со своими формулами. В случае совпадения применение функций Maple возможно и предпочтительно.
ПРИМЕЧАНИЕ
В целом применение Maple 7 как системы с символьной и точной арифметикой весьма предпочтительно в финансово-экономических и статистических расчетах, поскольку обеспечивает принципиально повышенную точность и устойчивость таких расчетов.
1.gif
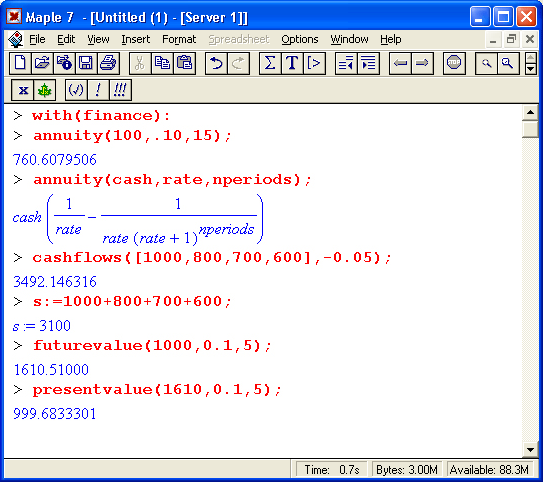
8. Пакет ортогональных многочленов orthopoly
Пакет ортогональных многочленов orthopoly
Ортогональные многочлены (полиномы) находят самое широкое применение в различных математических расчетах. В частности, они широко используются в алгоритмах интерполяции, экстраполяции и аппроксимации различных функциональных зависимостей. В пакете orthopoly задано в функци:
> with(orthopoly);
[G,H,L,P,T,U]
Однобуквенные имена этих функций отождествляются с первой буквой в наименовании ортогональных полиномов. Вопреки принятым в Maple 7 правилам, большие буквы в названиях этих полиномов не указывают на инертность данных функций — все они являются немедленно вычисляемыми. В данном разделе функции этого пакета будут полностью описаны. Отметим определения указанных функций:
- G(n,a,x) — полином Гегенбауэра (из семейства ультрасферических полиномов);
- Н(n,х) — полином Эрмита;
- L(n,x) — полином Лагерра;
- L(n,а,х) — обобщенный полином Лагерра;
- Р(n,х) — полином Лежандра;
- P(n,a,b,x) — полином Якоби;
- Т(n,х) — обобщенный полином Чебышева первого рода;
- U(n,x) — обобщенный полином Чебышева второго рода.
Свойства ортогональных многочленов хорошо известны. Все они характеризуются целочисленным порядком n, аргументом х и иногда дополнительными параметрами а и b. Существуют простые рекуррентные формулы, позволяющие найти полином n-го порядка по значению полинома (n - 1)-го порядка. Эти формулы и используются для вычисления полиномов высшего порядка. Ниже представлены примеры вычисления ортогональных полиномов:
Представляет интерес построение графиков ортогональных многочленов. На рис. 14.1 построены графики ряда многочленов Гегенбауэра и Эрмита.
Рис. 14.1. Графики ортогональных многочленов Гегенбауэра и Эрмита
На рис. 14.2 построены графики ортогональных многочленов Лагерра и Лежандра.
Наконец, на рис. 14.3 даны графики ортогональных многочленов Чебышева Т(n, х) и U(n, х).
Приведенные графики дают начальное представление о поведении ортогональных многочленов.
Рис. 14.2. Графики ортогональных многочленов Лагерра и Лежандра
Рис. 14.3. Графики ортогональных многочленов Чебышева
К примеру, многочлены Чебышева имеют минимальное отклонение от оси абсцисс в заданном интервале изменениях. Это их свойство объясняет полезное применение таких многочленов при решении задач аппроксимации функций. Можно порекомендовать читателю по их образу и подобию построить графики ортогональных многочленов при других значениях параметра и и диапазонах изменения аргумента х.
В отличие от ряда элементарных функций ортогональные многочлены определены только для действительного аргументах. При комплексном аргументе просто повторяется исходное выражение с многочленом:
> eva1f(U(2,2+3*I))):
Р(2,2 + 3I)
> evalf(sqrt(2+3*I)));
1.674149228+ .8959774761I
Ортогональные многочлены неопределены также и для дробного показателя n. Впрочем, надо отметить, что такие многочлены на практике используются крайне редко.
2.gif
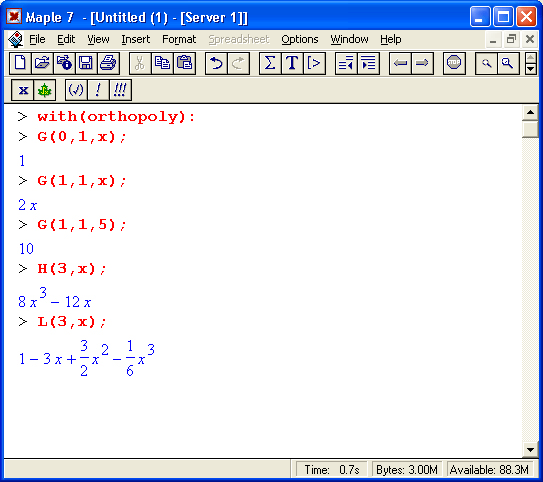
3.gif
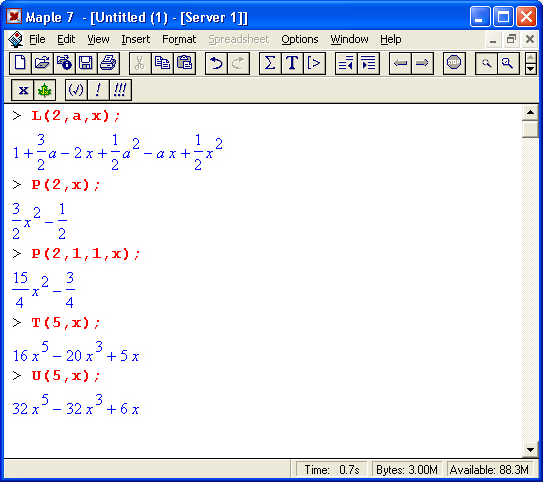
40.gif
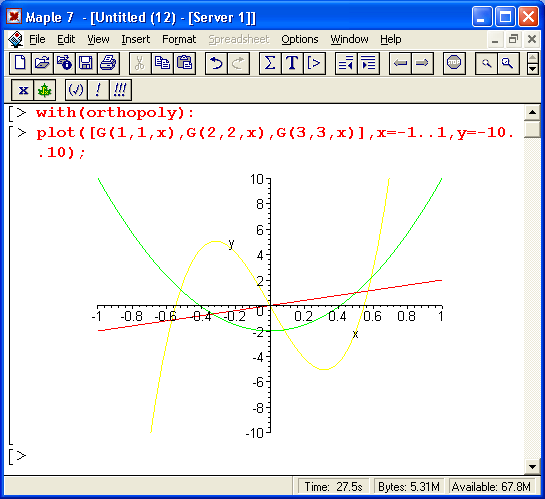
42.gif
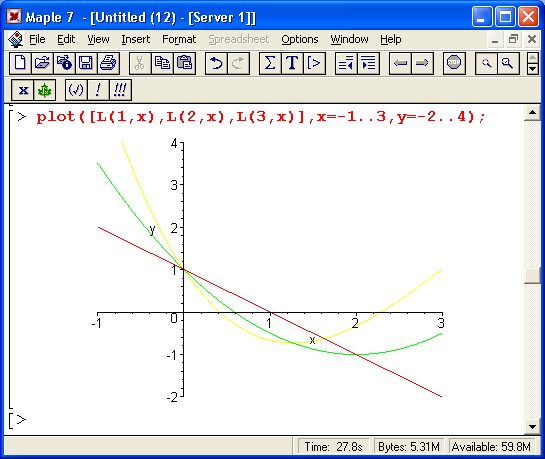
44.gif
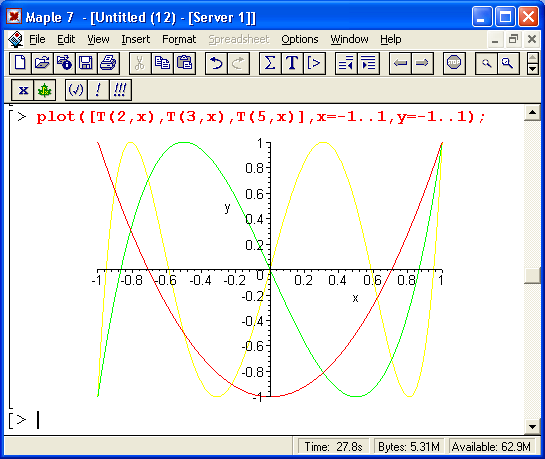
9. Пакет для работы с суммами sumtools
Пакет для работы с суммами sumtools
Этот инструментальный пакет предназначен для работы со специальными суммами. Он содержит указанные ниже функции:
> with(suintools);
[Hypersum, Sumtohyper, extended_gosper, gosper, hyperrecursion, hypersum, hyperterm, simpcomb, sumrecursion, sumtohyper]
Назначение функций данного пакета перечислено ниже:
- hypersum(U, L, z, n) и Hypersum(U, L, z, n) — вычисление гиперсумм;
- sumtohyper(f, k) и Sumtohyper(f, k) — преобразование сумм в гиперсуммы;
- extended_gosper(f, k), extended_gosper(f, k=m..n) и extended_gosper(f, k, j) — реализация расширенного алгоритма Госпера;
- gosper(f, k) и gosper(f, k=m..n) — реализация алгоритма Госпера;
- hyperrecursion(U, L, z, s(n)) — реализация гиперрекурсионного алгоритма;
- hyperterm(U, L, z, k) и Hyperterm(U, L,z, k) — ввод гипергеометрического терма.
10. Работа с пакетом sumtools
7.gif

8.gif
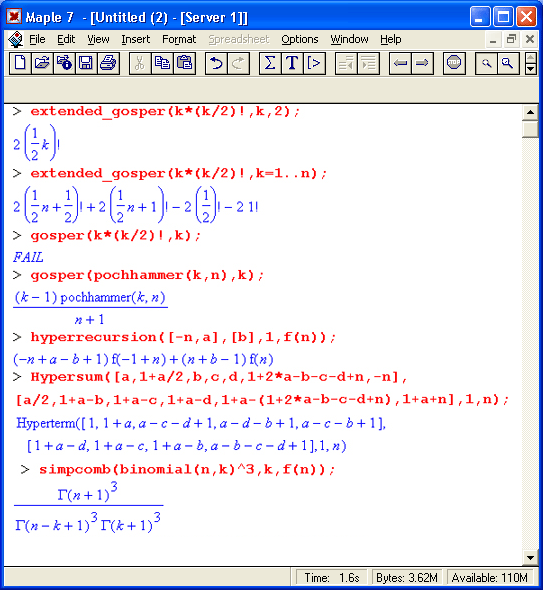
11. Пакет реализации степенных разложений powseries
Пакет реализации степенных разложений powseries
Степенные разложения часто используются в математических расчетах для приближенного представления разнообразных функций и обеспечения единообразия такого представления. В пакете powseries сосредоточены расширенные средства по реализации таких разложений. Они представлены 22 функциями:
> with(powseries);
[compose, evalpow, inverse, multconst, multiply, negative, pawadd, powcos, powcreate, powdijff, powexp, powint, powlog, powpoly, powsin, powsolve, powsqrt, quotient, reversion, subtract, template, tpsform ]
Ниже представлено определение этих функций:
- compose(а,b) — объединяет ряды а и b;
- evalpow(expr) — вычисляет выражение ехрr и возвращает его в виде ряда;
- inverse(р) — инвертирует ряд р;
- mu1tconst(p,const) — умножает ряд р на константу const; ,
- multiply(a,b) — умножает ряд а на ряд b;
- negative(p) — возвращает аддитивный, обратный по отношению к р ряд;
- powadd(a,b,...) — складывает ряды а, b, ...;
- powcreate(expr) — создает ряд для выражения ехрr;
- powpoly(pol ,var) — создает ряд для полинома pol по переменной van;
- powsolve(sys) — создает ряд для решения дифференциальных уравнений sys;
- quotient(a,b) — возвращает частное для а и b в виде ряда;
- reversion(a) — дает обратное к композиции разложение ряда а;
- subtract(а,b) — дает разность рядов а и b.
В выражении ехрr могут использоваться операторы +, -, *, / и ^. С ними могут комбинироваться встроенные функции и функции пользователя, например /(g). Кроме того, могут использоваться следующие функции:
|
Powexp |
powi nv |
powlog |
powneg |
powrev |
|
Powdiff |
powi nt |
powquo |
powsub |
powcos |
|
Powtan |
powsec |
powcsc |
powcot |
powsinh |
|
Powcosh |
powtanh |
powsech |
powcsch |
powcot h. |
|
Powsqrt |
powadd |
multiply |
12. Примеры применения пакета powseries
Примеры применения пакета powseries
Назначение большинства этих функций очевидно из их названий — они возвращают соответствующую функцию (указанную после слова pow в имени) в виде разложения в ряд или полинома. Например, powexp раскладывает выражения с экспоненциальными функциями в ряд.
Получаемые функциями ряды представляются в специальном формате. Поэтому для их применения в обычном виде необходимо использовать функцию tpsform в следующих видах:
- tpsform(p, var, order) — преобразует ряд р в обычную форму с заданием порядка order;
- tpsform(p, var) — преобразует ряд р в обычную форму с порядком, заданным переменной Order.
Здесь р — имя степенного ряда, var.— переменная, относительно которой записан ряд, order — порядок ряда. Если параметр order не указан, используется значение глобальной переменной Order. Ниже даны примеры, иллюстрирующие технику работы со степенными разложениями:
Применение функций этого пакета достаточно просто и прозрачно, так что заинтересованный читатель может сам опробовать на примерах работу тех функций, которые не были использованы в приведенных примерах.
9.gif
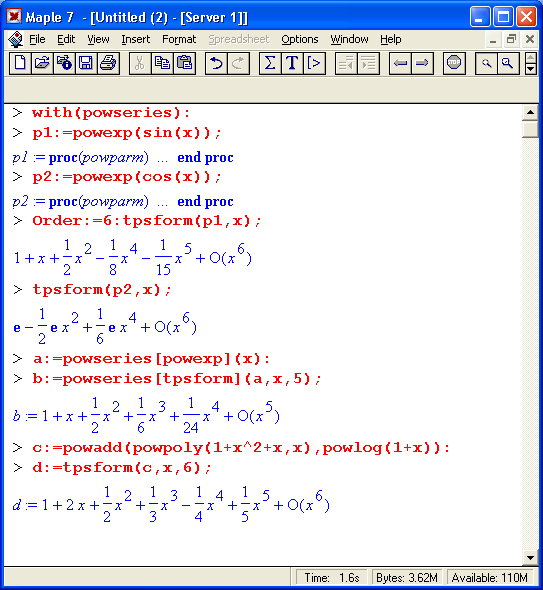
13. Пакет числовой аппроксимации numapprox
Пакет числовой аппроксимации numapprox
Этот пакет содержит небольшое число безусловно очень важных функций:
> with(numapprox);
[chebdeg, chebmult, chebpade, chebsort, chebyshev, confracform, hermite_pade, hornerform, infnorm, laurent, minimax, pade, remez]
В их числе функции интерполяции и аппроксимации полиномами Чебышева, рядом Тейлора, отношением полиномов (Паде-аппроксимация) и др. Все они широко применяются не только в фундаментальной математике, но и при решении многих прикладных задач. Рассмотрим их, начиная с функций аппроксимации аналитических зависимостей.
14. Разложение функции в ряд Лорана
10.gif
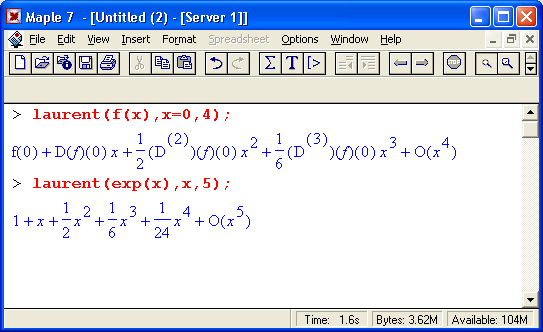
15. Паде-аппроксимация аналитических функций
Паде-аппроксимация аналитических функций
Для аппроксимации аналитических функций одной из лучших является Паде-аппроксимация, при которой заданная функция приближается отношением двух полиномов. Для осуществления такой аппроксимации используется функция pade:
pade(f. x=a, [m.n])
pade(f.,х, [m.n])
Здесь f — аналитическое выражение или функция, х — переменная, относительно которой записывается аппроксимирующая функция, а — координата точки, относительно которой выполняется аппроксимация, m, n — максимальные степени полиномов числителя и знаменателя. Технику аппроксимации Паде поясняет рис. 14.4.
На рис. 14.4 представлена аппроксимация синусоидальной функции, а также построены графики этой функции и аппроксимирующей функции. Под ними дан также график абсолютной погрешности для этого вида аппроксимации. Нетрудно заметить, что уже в интервале [-л, я] погрешность резко возрастает на концах интервала аппроксимации.
Важным достоинством Паде-аппроксимации является возможность довольно точного приближения разрывных функций. Это связано с тем, что нули знаменателя у аппроксимирующего выражения способны приближать разрывы функций, если на заданном интервале аппроксимации число разрывов конечно. На рис. 14.5 представлен пример Паде-аппроксимации функции tan(x) в интервале от -4,5 до 4,5, включающем два разрыва функции.
Как видно из рис. 14.5, расхождение между функцией тангенса и ее аппроксимирующей функцией едва заметно лишь на краях интервала аппроксимации. Оба разрыва прекрасно приближаются аппроксимирующей функцией. Такой характер аппроксимации подтверждается и графиком погрешности, которая лишь на концах интервала аппроксимации [-4,0, 4,0] достигает значений 0,01 (около 1%).
Рис. 14.4. Аппроксимация Паде для синусоидальной функции
Рис. 14.5. Аппроксимация Паде для разрывной функции тангенса
46.gif
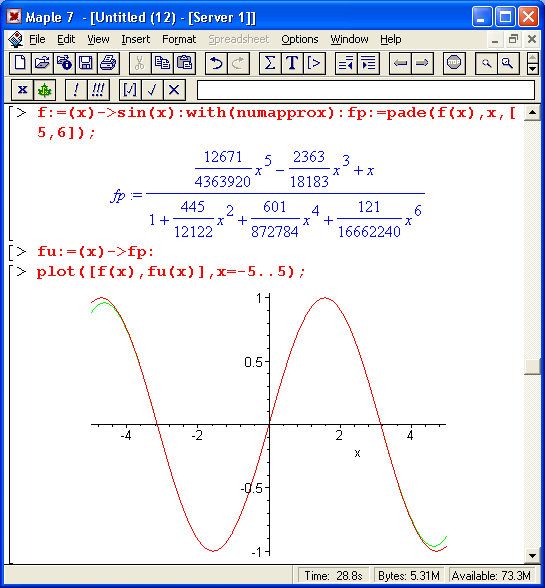
48.gif
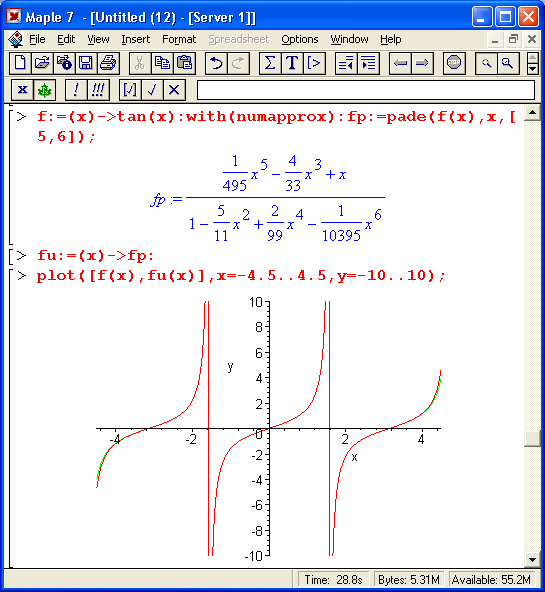
16. Паде-аппроксимация с полиномами Чебышева
Паде-аппроксимация с полиномами Чебышева
Для многих аналитических зависимостей хорошие результаты дает аппроксимация полиномами Чебышева. В общем случае применяется Паде-аппроксимация отношением таких полиномов. Она реализуется функциями chebpade:
chebpade(f, x=a..b, [m.n])
chebpade(f., x, [m.n])
chebpade(f, a..b, [m,n])
Здесь а..b задает отрезок аппроксимации, тип— максимальные степени числителя и знаменателя полиномов Чебышева. Приведенный ниже пример показывает аппроксимацию Паде полиномами Чебышева для функции f=cos(x):
11.gif
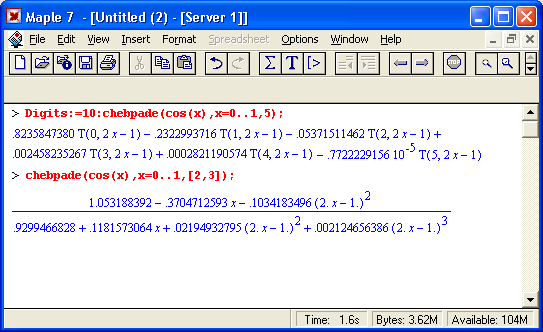
17. Наилучшая минимаксная аппроксимация
Наилучшая минимаксная аппроксимация
Минимаксная аппроксимация отличается от Паде-аппроксимации минимизацией максимальной абсолютной погрешности во всем интервале аппроксимации. Она использует алгоритм Ремеза (см. ниже) и реализуется следующей функцией:
mimmax(f, x=a..b, [m.n], w, 'maxerror')
minimax(f, a..b, [m,n], w, 'maxerror')
Здесь помимо уже отмеченных параметров w — процедура или выражение, maxerror — переменная, которой приписывается значение miniraax-нормы. Ниже дан пример аппроксимации функции cos(x) в интервале [-3, 3]:
12.gif
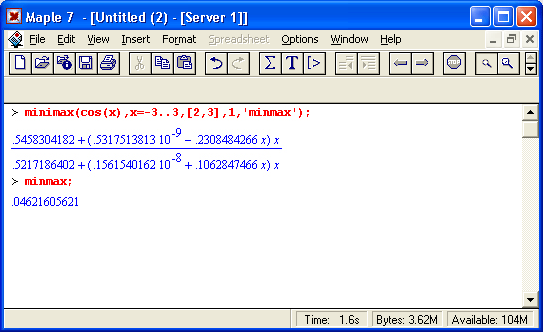
18. Наилучшая минимаксная аппроксимация по алгоритму Ремеза
Наилучшая минимаксная аппроксимация по алгоритму Ремеза
Для получения наилучшей полиномиальной аппроксимации используется алгоритм Ремеза, который реализует следующая функция:
remez(w, f, a, b, m, n,_crit, 'maxerror')
Здесь w — процедура, представляющая функцию w(x) > 0 в интервале [a, b], f — процедура, представляющая аппроксимируемую функцию а и b — числа,' задающие интервал аппроксимации fa,b], m и n — степени числителя и знаменателя аппроксимирующей функции, crit — массив, индексированный от 1 до m + n + 2 и представляющий набор оценок в критических точках (то есть точек максимума/минимума кривых погрешности), mахеrrоr — имя переменной, которой присваивается минимаксная норма w abs(f -r).
Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x):
13.gif
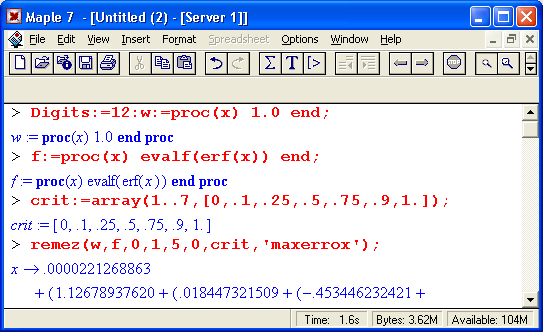
19. Другие функции пакета
Другие функции пакета
Отметим назначение других функций пакета numapprox:
- chebdeg(p) — возвращает степень полинома Чебышева р;
- chebmult(p, q) — умножение полиномов Чебышева р и q;
- chebsort(e) — сортирует элементы ряда Чебышева;
- confracform(r) — преобразует рациональное выражение г в цепную дробь;
- confracform(r, х) — преобразует рациональное выражение г в цепную дробь с независимой переменной х;
- hornerform(r) — преобразует рациональное выражение г в форму Горнера;
- hornerform(r, х) — преобразует рациональное выражение г в форму Горнера с независимой переменной х;
- infnorm(f, x=a...b, 'xmax') — возвращает L-бесконечную норму функции на отрезкех [а, b];
- infnorm(f, a...b, 'xmax') — возвращает L-бесконечную норму функции на отрезке [а, b].
Действие этих функций очевидно, и читатель может самостоятельно опробовать их в работе.
20. Пакет интегральных преобразований inttrans
Пакет интегральных преобразований inttrans
Это один из пакетов, наиболее важных для общематематических и научно-технических приложений. Он содержит небольшой набор функций:
> with(inttrans):
[addtable,fourier,fouriercos,fouriersin, hankel, hilbert, invfourier, invhilbert, invldplace, invmellin, laplace, mellin, savetable]
Однако эти функции охватывают такие практические важные области математики, как ряды Фурье, прямые и обратные преобразования Лапласа и Фурье и ряд других интегральных преобразований. Ниже они обсуждены более подробно.
В предшествующих реализациях системы Maple функции прямого и обратного Z-преобразований также входили в пакет inttrans, однако в Maple 6 и 7 они перенесены в ядро системы.
21. Прямое и обратное преобразования Лапласа
Прямое и обратное преобразования Лапласа
Прямое преобразование Лапсаса заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла
Для осуществления прямого преобразования Лапласа Maple 7 имеет функцию
laplace(expr,t,p)
Здесь ехрr— преобразуемое выражение, t — переменная, относительно которой записано ехрr, и р — переменная, относительно которой записывается результат преобразования.
Обратное преобразование Лапласа означает переход от функции F(p) к функции (t) с помощью формулы
Для вычисления этого интеграла служит функция:
invlaplace(expr,p, t)
где ехрr — выражение относительно переменной р, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение а обратное —оригинал функции. Ниже приведены примеры применения прямого и обратного преобразований Лапласа:
Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t) + acos(t).
14.gif

15.gif
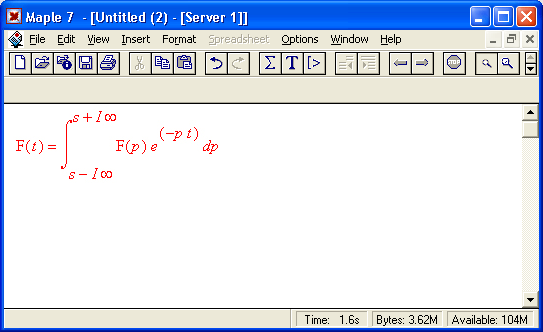
16.gif
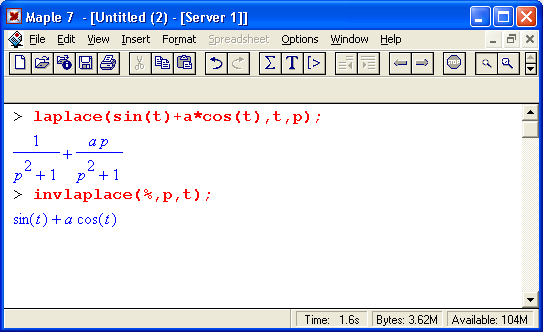
22. Прямое и обратное преобразования Фурье
Прямое и обратное преобразования Фурье
Прямое преобразование Фурье преобразует функцию времени f(t) в функцию частот и заключается в вычислении следующей интегральной функции:
Оно реализуется следующей функцией пакета интегральных преобразований inttrans:
fourier(expr,t,w)
Здесь ехрr — выражение (уравнение или множество), t — переменная, от которой зависит ехрr, и w — переменная, относительно которой записывается результирующая функция. Обратное преобразование Фурье задается вычислением интеграла:
Оно фактически переводит представление сигнала из частотной области во временную. Примеры применения преобразования Фурье представлены ниже:
Обратите внимание на то, что даже в простом первом примере применение обратного преобразования Фурье вслед за прямым не привело к буквальному восстановлению исходной функции sin(t). Потребовалась: команда simplify, чтобы перевести результат в виде представления синуса через экспоненциальные функции к обычному виду sin(t).
17.gif
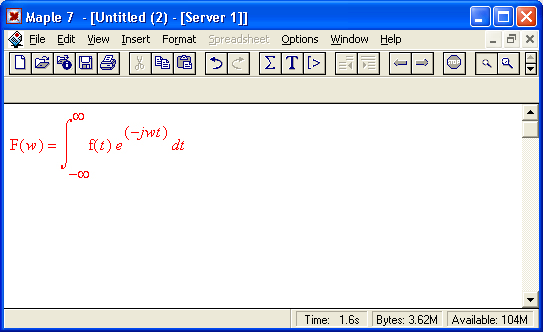
18.gif
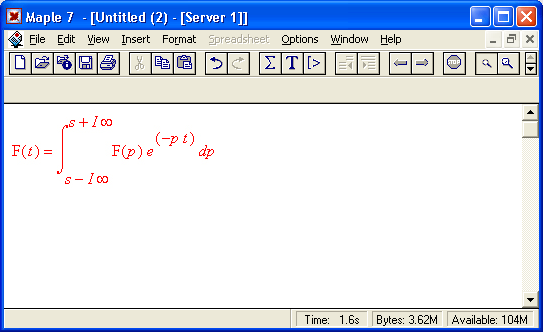
19.gif

23. Вычисление косинусного и синусного интегралов Фурье
Вычисление косинусного и синусного интегралов Фурье
Разложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида:
Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция ./(t). Для вычисления этих интегралов в пакете используются следующие функции:
fouriercos(expr,t,s)
fouriersln(expr,t,s)
Поскольку формат задания этих функций вполне очевиден, ограничимся примерами их применения:
50.gif
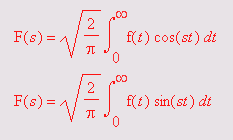
51.gif

24. Интегральное преобразование Ханкеля
Интегральное преобразование Ханкеля
Интегральное преобразование Ханкеля задается следующим выражением:
и выполняется функцией:
hankel(expr, t, s, nu)
Здесь ехрr — выражение, равенство (или множество, или список с выражениями/равенствами), t — переменная в ехрr, преобразуемая в параметр преобразования s, nu— порядок преобразования. Следующий пример демонстрирует применение функции Ханкеля:
20.gif
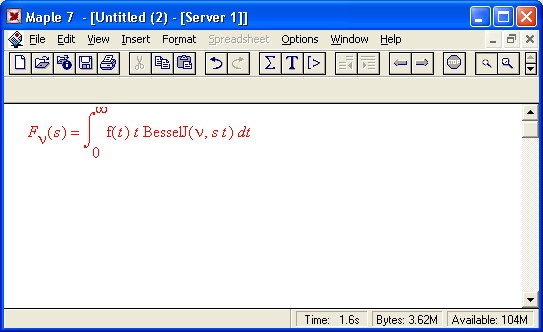
21.gif
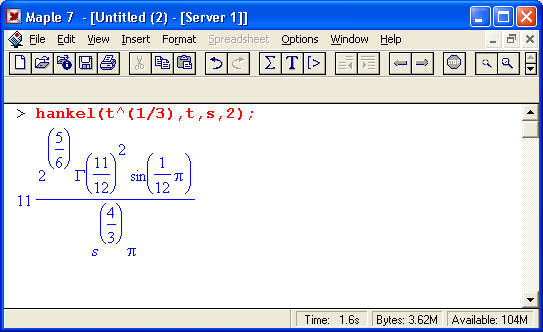
25. Прямое и обратное преобразования Гильберта
Прямое и обратное преобразования Гильберта
Прямое преобразование Гильберта задается следующим выражением:
и превращает функцию f(t) в F(s).
Обратное преобразование Гильберта означает нахождение f(f) по заданной F(s).
Эти преобразования выполняются функциями:
hilbert(expr, t, s)
invhilbert(expr, t,s)
где назначение параметров очевидно.
Приведенные ниже примеры иллюстрируют выполнение этих преобразований:
Как видно из этих примеров, обратное преобразование Гильберта, осуществленное над результатом прямого преобразования, не восстанавливает функцию f(t) буквально.
22.gif

23.gif
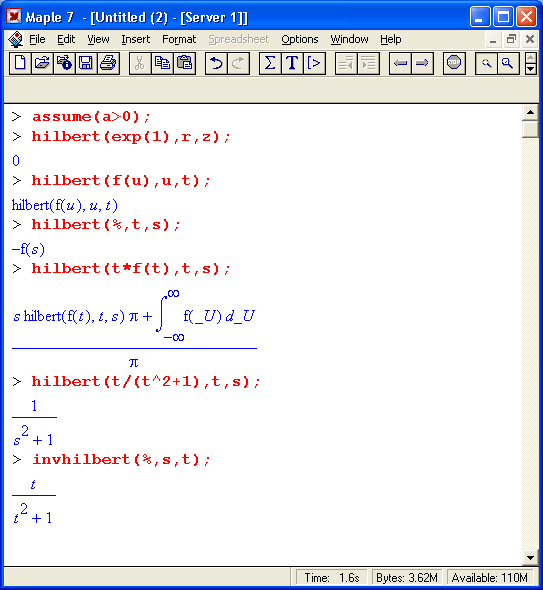
24.gif
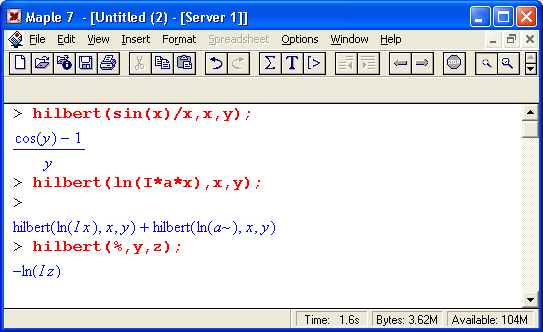
26. Интегральное преобразование Меллина
25.gif
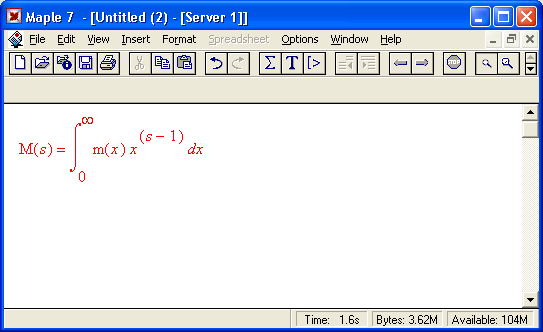
26.gif
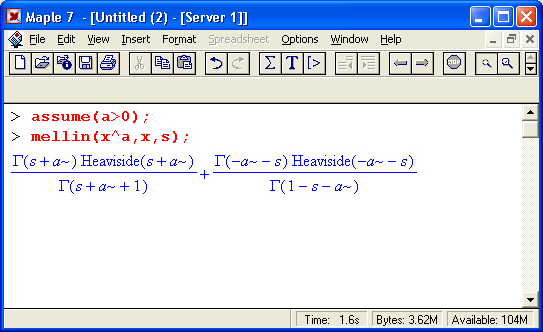
27. Функция addtable
Функция addtable
Как видно из приведенных примеров, не всегда интегральные преобразования дают результат в явном виде. Получить его позволяет вспомогательная функция:
addtable(tname,patt,ехрr,t,s)
где tname — наименование преобразования, для которого образец patt должен быть добавлен к таблице поиска. Остальные параметры очевидны.
Следующие примеры поясняют применение этой функции:
27.gif
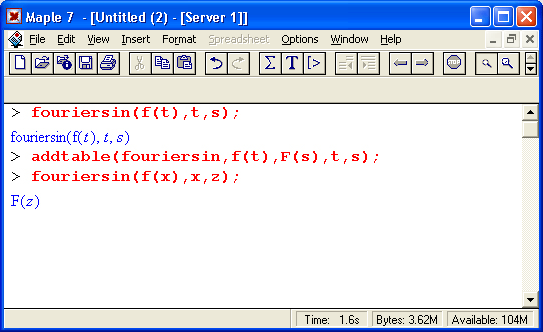
28. Пакет приближения кривых CurveFittirrg
Пакет приближения кривых CurveFitting.
Общая характеристика пакета CurveFitting
Новый пакет приближения кривых CurveFitting весьма полезен тем, кто занимается столь распространенной задачей, как приближение кривых. Он содержит ряд функций:
> with(CurveFitting);
Доступ к функциям пакета возможен с помощью конструкций:
CurveFitting[function](arguments)
function(arguments)
Число функций пакета невелико и все они описаны ниже.
29. Функция вычисления В-сплайнов Bspline.
Функция вычисления В-сплайнов Bspline
Функция BSpline(k, v, opt) служит для вычисления В-сплайнов. Она имеет следующие параметры: k — порядок сплайна (целое число), v— имя и opt — параметр в виде knots=knotlist, где knotlist — спискок из k+1 элементов алгебраического типа. Используя функцию CurveFitting[BSplineCurve], можно строить кривые В-сплайнов. Примеры применения этой функции представлены ниже:
Как нетрудно заметить из этих примеров, функция Bspline возвращает результат в виде кусочных функций типа piecewise.
28.gif
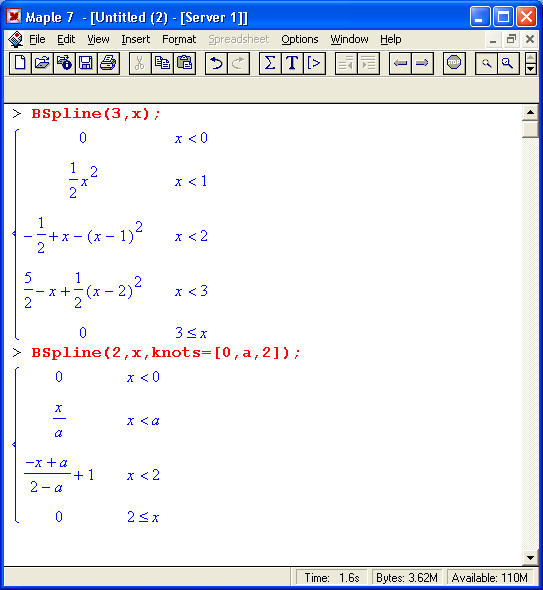
30. Функция построения В-сплайновых кривых BsplineCurve
Функция построения В-сплайновых кривых BsplineCurve
Функция BsplineCurve служит для построения кривых в B-cплайнов. Она Может использоваться в формах:
BSpl1neCurve(xydata, v, opts)
BSpllneCurve (xdata, ydata, v, opts)
Здесь:
xydata — список, массив или матрица точек в форме [[xl.ylj, [х2,у2],..., [хn,уn]];
xdata — список, массив или вектор значений независимой переменной [xl,x2,... ,хn];
ydata — список, массив или вектор значений зависимой переменной в форме [у1,у2,...,уn];
v — имя независимой переменной;
opts — необязательный параметр в форме одного или более выражений вида order=k или knots=knot1ist.
Примеры применения функции BSplineCurve с порядком, заданным по умолчанию, и с третьим порядком (кубический В-сплайн) представлены на рис. 14.6.
Рис. 14.6. Применение функции BSplineCurve
Следует отметить, что при малом, числе точек аппроксимация В-сплайнами дает невысокую точность, что и видно из рис. 14.6
52.gif
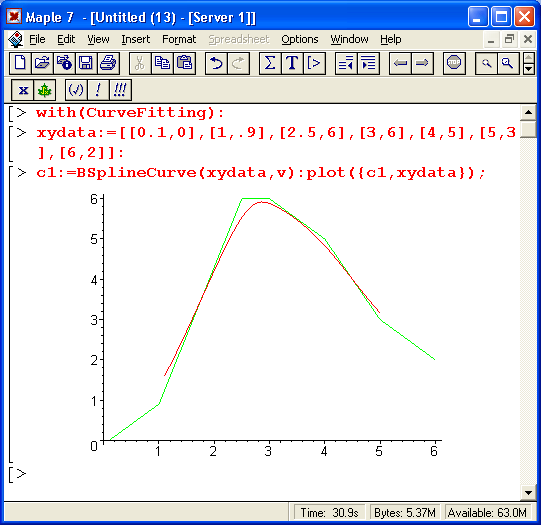
31. Функция реализации метода наименьших квадратов LeastSquares
Функция реализации метода наименьших квадратов LeastSquares
Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов:
LeastSquares (xydata, v, opts)
LeastSquares(xdata, ydata, v.,opts)
Все входящие в нее параметры были определены выше (см. параметры функции BSplineCurve). Параметр opts задается в форме выражений weight=wlist, curve=f или params=pset.
Следующие примеры иллюстрируют применение функции LeastSquares:
29.gif
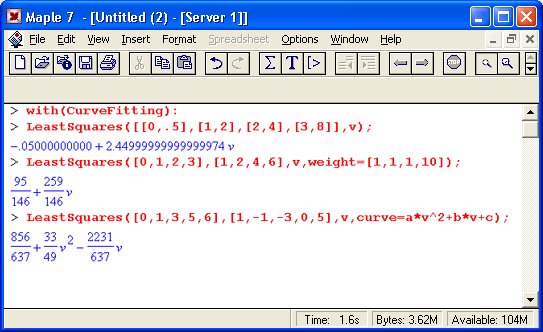
32. Функция полиномиальной аппроксимации Polynomiallnterpolation
Функция полиномиальной аппроксимации PolynomialInterpolation
Функция PolynomialInterpolation реализует полиномиальную интерполяцию и может использоваться в виде:
Polynomiallnterpolation (xydata, v)
Polynomiallnterpolation(xdata, ydata, v)
Параметры функции были определены выше. Параметр v может быть как именем, так и численным значением. Примеры применения функции представлены ниже:
30.gif

33. Функция рациональной аппроксимации Racionallnterpotation
Функция рациональной аппроксимации RacionalInterpolation
Функция рациональной интерполяции задается в Виде:
Rational Interpolation (xydata, z, opts)
RationalInterpolation(xdata, ydata, z, opts)
где необязательный параметр opts задается выражениями methochmethodtype или degrees=[dl,d2]. Функция возвращает результат в виде отношения двух полиномов. Параметр methodtype может иметь значения 4lookaround или subresultant, задающие учет или пропуск сингулярных точек.
Пример применения функции Rational Interpolation (загрузка пакета опущена, но предполагается):
31.gif
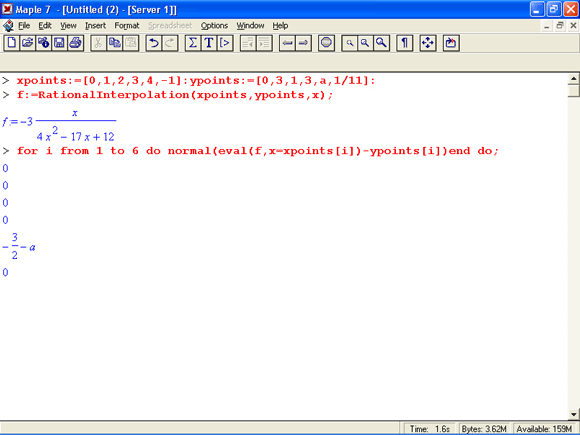
34. Функция вычисления обычных сплайнов Spline
32.gif
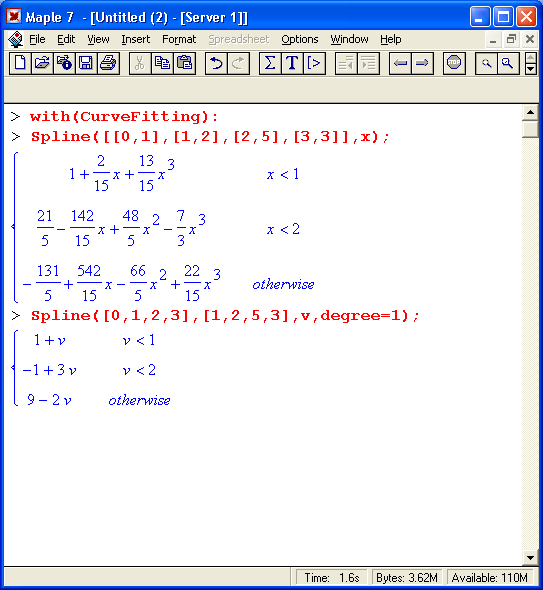
35. Функция аппроксимации непрерывными дробями Thielelnterpolation
Функция аппроксимации непрерывными дробями ThieleInterpolation
Функция ThieleInterpolation осуществляет интерполяцию на основе непрерывных дробей (Thiele's-интерполяцию). Она задается в виде:
Thielelnterpolation (xydata, v)
Thielelnterpolation(xdata, ydata, v)
Примеры применения данной функции представлены ниже:
33.gif
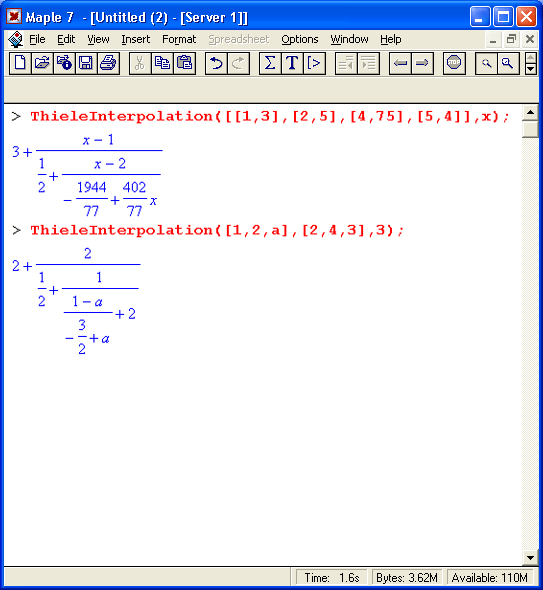
36. Пакет для работы с полиномами PolynomialTools
Пакет для работы с полиномами PolynomialTools
Обзор возможностей пакета PolynomialTools
Пакет для работы с полиномами PolynomialTools предназначен для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами. Этот пакет имеет небольшое число функций:
> with(PolynomialTools):
[IsSelfReciprocal, MinimalPolynomial, PDEToPolynomial, PolynomialToPDE, Shorten, Shorter, Sort, Split, Splits, Translate]
В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др.
37. Функции для работы с полиномами
Функции для работы с полиномами
Рассмотрим несколько функций пакета PolynomialTools общего характера. Примеры применения этой функции представлены ниже:
ПРИМЕЧАНИЕ
Функция IsSelfReciprocat(a, х, 'р') проверяет полином а(х) на условие coeff(a,x,k) =coeff(a,x,d-k) для всех k = 0. .d, где d = degree(a; х) — порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе — false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином Р порядка d/2, такой, что x^(1/2)*P(x+l/x) = а. При нечетном d полином а будет взаимообратным, что подразумевает деление на х+1. В этом случае; если р указано, результат вычисляется в форме а/(х+1).
Функция MinimalPolynomial (r, n, асе) возвращает полином минимальной степени не превышающей n, имеющий корень г. Необязательный аргумент асе задает погрешность приближения. Функция MinimalPolynomia(r, n) использует решетчатый алгоритм и находит полином степени п (или менее) с наименьшими целыми коэффициентами. Корень г может быть действительным или комплексным. Результат зависит от значения переменной окружения Digits. По умолчанию асе задано как 10*(Digits-2). Примеры применения данной функции:
Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — необязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {tl,... ,tm}, таких что полином а расщепляется над K=Q(tl,... ,tm), где Q означает поле рациональных чисел. Примеры:
В пакете определена еще одна подобная функция Splits, с которой можно познакомиться по справке на нее.
Функция Translate(a, х, х0) преобразует полином а(х) с подстановкой х - х + х0, где x0 — константа. Примеры применения этой функции даны ниже:
34.gif
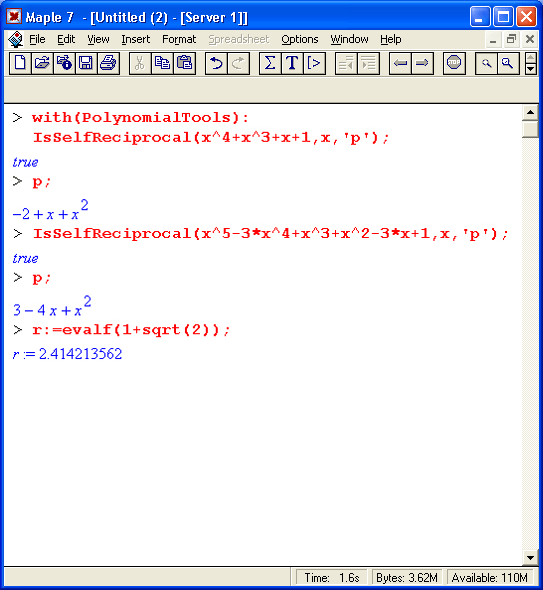
35.gif
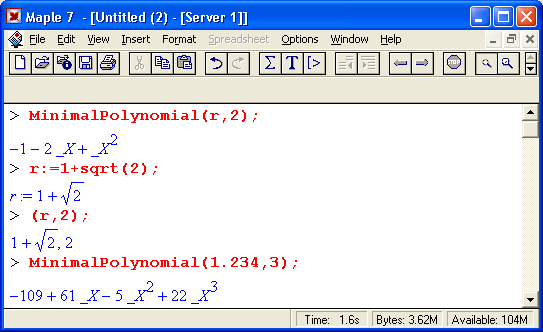
36.gif
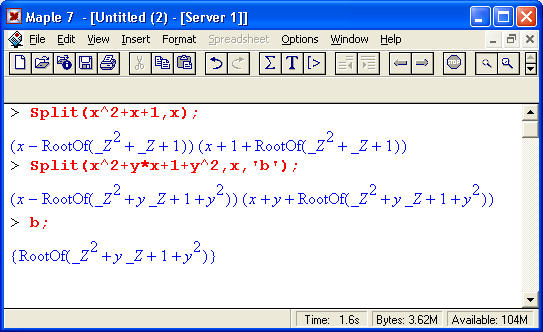
37.gif
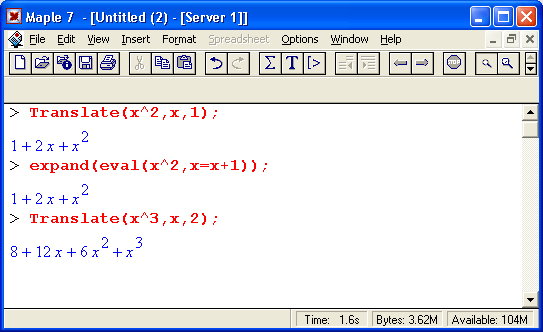
38. Функции сортировки полиномов
Функции сортировки полиномов
Для сортировки полиномов предназначены следующие три функции:
Shorter(f, g, х)
Sort(v, х)
Shorten(f, x)
Здесь f и g полиномы, v — список полиномов их — независимая переменная. Функции отличаются характером сортировки.
Функция Shorter определяет полином f как более короткий, чем g, по следующим признакам: меньшая длина, меньшее имя независимой переменной х, не дробный и меньшая степень других переменных. Функция Sort сортирует лист полиномов х по признакам, определяемым Shorter. Функция Shorten использует преобразования Мебиуса. Многочисленные детали ее применения можно найти в справке по данной функции. Примеры применения функций сортировки:
38.gif
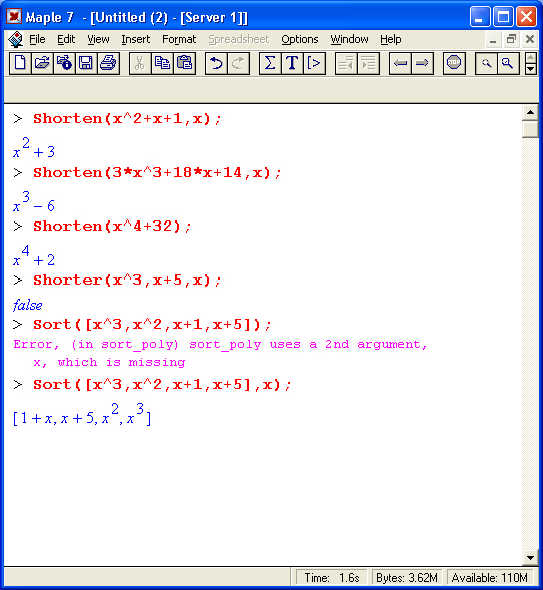
39. Функции преобразования полиномов в РОЕ и обратно
Функции преобразования полиномов в РDЕ и обратно
Функция PolynomialToPDE(polys, vars, depvars) преобразует полиномы polys пo независимым переменным vans в дифференциальные уравнения с частными производными (PDE). Другая функция PDEToPolynomia(pdes, vans, depvars) осуществляет обратное преобразование.
Следующие примеры иллюстрируют применение этих функций:
39.gif
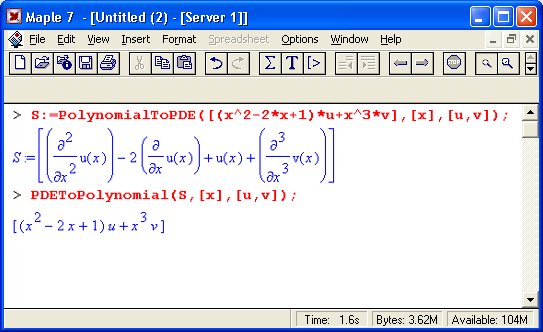
40. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Обращаться к пакетам расширения.
- Пользоваться функциями пакетов комбинаторики.
- Применять пакет финансово-экономических функций.
- Использовать ортогональные многочлены из пакета orthpoly.
- Работать с суммами пакета sumtools.
- Применять степенные разложения пакета powerseries.
- Работать с пакетом численной аппроксимации numapprox.
- Использовать интегральные преобразования пакета inttrans.
- Осуществлять приближение кривых с помощью пакета CurveFitting.
- Использовать пакет работы с полиномами PolynomialTools.
Урок 15. Пакеты линейной алгебры и функциональных систем
1. Основные определения линейной алгебры
Урок 15.
Пакеты линейной алгебры и функциональных систем
Основные определения линейной алгебры
Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple 7 по части решения задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.
Матрица (m х n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).
Квадратная матрица — матрица, у которой число строк m равно числу столбцов n. Пример квадратной матрицы размера 3x3:
Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.
Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4x4:
Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы АТ=А, где Ат - транспонированная матрица А (см. ее определение ниже);Транспонированная матрица — матрица, у которой .столбцы и строки меняются . местами, то есть элементы транспонированной матрицы удовлетворяют условию AT(i,j)=A(j,i). Приведем простой пример. Исходная матрица:
Транспонированная матрица:
Обратная матрица — это матрица М-1, которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.
Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.
Диагональ матрицы — расположенные диагонально элементы Ai,i матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:
Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия под диагоналей (элементы d и k) и над диагоналей (элементы b и f). Матрица, все элементы которой, расположенные кроме как на диагонали, под диагонали и над диагонали, равны нулю, называется ленточной.
Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.
След матрицы — сумма диагональных элементов матрицы.
Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:
где M1<j> — определитель матрицы порядка n - 1, полученной из матрицы А вычеркиванием первой строки и j-гo столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.
Матрица в целой степени — квадратная матрица в степени n (n — целое неотрицательное число), определяемая следующим образом:
М° = Е, М1 = М, М2 = ММ ..., Мn =Мn-1М.
Идемпотентная матрица — матрица, отвечающая условию Р2 = Р.
Симметрическая матрица — матрица, отвечающая условию Ат = А.
Кососимметрическая матрица — матрица, отвечающая условию Ат = -A. Ортогональная матрица — матрица, отвечающая условию Ат =А-1.Нуль-матрица — матрица, все элементы которой равны 0.Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы.
Комплексно-сопряженная матрица — матрица А, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные. Эрмитова матрица — матрица А, удовлетворяющая условию А = А .Собственный вектор квадратной матрицы А — любой вектор х е V", х* О, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.
Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена, — |А - gE|. Собственные значения матрицы — корни ее характеристического многочлена. Норма — обобщенное понятие абсолютной (величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||).
Матричная форма записи системы линейных уравнений — выражение АХ = В, где А — матрица коэффициентов системы, X — вектор неизвестных и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А-1В, где А-1 — обратная матрица.
1.gif

2.gif
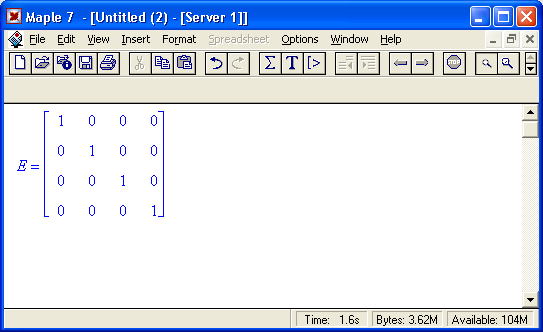
3.gif

4.gif
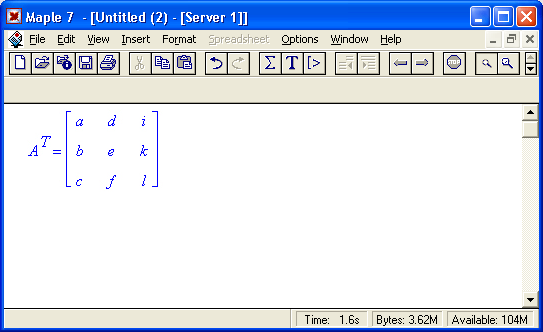
5.gif
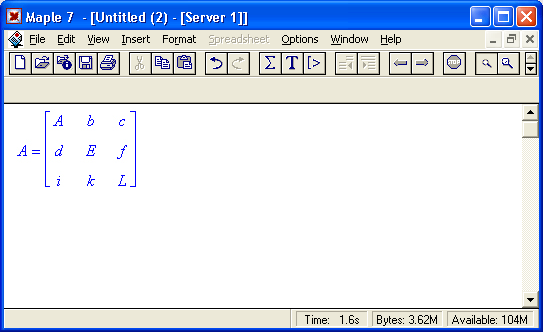
6.gif
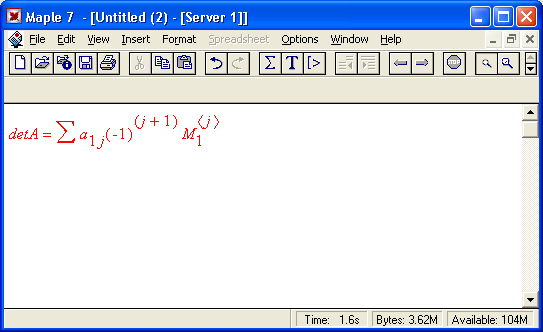
2. Пакет решения задач линейной алгебры linatg
Пакет решения задач линейной алгебры linalg
Несомненно, что уникальной возможностью системы Maple 7, как и других систем компьютерной алгебры, является возможность решения задач линейной алгебры в символьном (формульном, аналитическом) виде. Однако такое решение представляет скорее теоретический, чем практический интерес, поскольку даже при небольших размерах матриц (уже при 4-5 строках и столбцах) символьные результаты оказываются очень громоздкими и труднообозримыми. Они полезны только при решении специфических аналитических задач, например с разреженными матрицами, у которых большинство элементов имеют нулевые значения.
Поэтому разработчики Maple 7 были вынуждены реализовать в своей системе численные методы решения задач линейной алгебры, которые широко используются в основных сферах ее приложения — математическом моделировании систем и устройств, расчетах в электротехнике, механике, астрономии и т. д.
В ядро Maple 7, как отмечалось, введены очень скромные и минимально необходимые средства для решения задач линейной алгебры. Основной упор в их реализации сделан на подключаемые пакеты. Основным из них, унаследованным от предшествующих реализаций системы, является пакет решения задач линейной алгебры Unalg. Это один из самых обширных и мощных пакетов в области решения задач линейной алгебры. Он содержит свыше ста функций:
> with(linalg);
Warning, the names fibonacci, inverse and multiply have been redefined Warning, the protected names norm and trace have been redefined and unprotected[BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp, QRdecomp, Wronskian, addcol, addrow, adj, adjoint, angle, augment, backsub, band, basis, bezout, blockmatrix, charmat, charpoly, cholesky, col, coldim, colspace, colspan, companion, concat, cond, copyinto, crossprod, curl, definite, delcols, delrows, det, diag, diverge, dotprod, eigenvals, eigenvalues, eigenvectors, eigenvects, entermatrix, equal, exponential, extend, ffgausselimfifibonacci,forwardsub,frobenius, gausselim, gaussjord, geneqns, genmatrix, grad, hadamard, hermite, hessian, hilbert,htranspose, thermite, indexfunc, innerprod, intbasis, inverse, ismith, issimilar, iszerojacobian, Jordan, kernel, laplacian, leastsqrs, linsolve,matadd, matrix, minor, minpoly, mulcol, /им/row,multiply, norm, normalize, nullspace, orthog, permanent, pivot, potential, randmatrix, randvector, rank, ratform, row, rowdim, rowspace, rowspan, rref, scalarmul, singularvals, smith, stackmatrix, submatrix, subvector, sumbasis, swapcol, swaprow, Sylvester, toeplitz, trace, transpose, vandermonde, vecpotent, vectdim, vector, wronskian]
Ниже указано назначение тех функций пакета linalg, которые подробно не описаны:
- addcol — добавляет к одному из столбцов другой столбец, умноженный на некоторое число;
- addrow — добавляет к одной из строк другую строку, умноженную на некоторое число;
- angle — вычисляет угол между векторами;
- augment — объединяет две или больше матриц по горизонтали;
- backsub — реализует метод обратной подстановки при решении системы линейных уравнений (см. также forwardsub);
- band — создает ленточную матрицу;
- basis — находит базис векторного пространства;
- bezout — создает Bezout-матрицу двух полиномов; . г
- BlockDiagonal — создает блок-диагональную матрицу;
- blockmatrix — создает блок-матрицу;
- cholesky — декомпозиция Холесского для квадратной положительно определенной матрицы;
- charmat — создает характеристическую матрицу (charmat(M,v) — матрица, вычисляемая как v E-M);
- charpoly — возвращает характеристический полином матрицы;
- colspace — вычисляет базис пространства столбцов;
- colspan — находит базис линейной оболочки столбцов матрицы;
- companion — вычисляет сопровождающую матрицу, ассоциированную с полиномом;
- cond — вычисляет число обусловленности матрицы (cond(M) есть величина norm(M) norm(М-1);
- curl — вычисляет ротор вектора;
- definite — тест на положительную (отрицательную) определенность матрицы;
- diag — создает блок-диагональную матрицу;
- diverge — вычисляет дивергенцию векторной функции;
- eigenvals — вычисляет собственные значения матрицы;
- eigenvects — вычисляет собственные векторы матрицы;
- equal — определяет, являются ли две матрицы равными;
- exponential — создает экспоненциальную матрицу;
- ffgausselim — свободное от дробей Гауссово исключение в матрице;
- fibonacci — матрица Фибоначчи;
- forwardsub — реализует метод прямой подстановки при решении системы линейных уравнений (например, для матрицы L и вектора b
- forwardsub(L, b) возвращает вектор решения х системы линейных уравнений L-x=b);
- frobenius — вычисляет форму Фробениуса (Frobenius) матрицы;
- gausselim — Гауссово исключение в матрице;
- gaussjord — синоним для rref (метод исключения Гаусса—Жордана);
- geneqns — генерирует элементы матрицы из уравнений;
- genmatrix — генерирует матрицу из коэффициентов уравнений;
- grad — градиент векторного выражения;
- GramSchmidt — вычисляет ортогональные векторы;
- hadamard — вычисляет ограничение на коэффициенты детерминанта;
- hessian — вычисляет гессиан-матрицу выражения;
- hilbert — создает матрицу Гильберта;
- htranspose — находит эрмитову транспонированную матрицу;
- ihermite — целочисленная эрмитова нормальная форма;
- indexfunc — определяет функцию индексации массива;
- Innerprod — вычисляет векторное произведение;
- Intbasis — определяет базис пересечения пространств;
- ismith — целочисленная нормальная форма Шмитта;
- iszero — проверяет, является ли матрица ноль-матрицей;
- jacobian —' вычисляет якобиан векторной функции;
- JordanBlock — возвращает блок-матрицу Жордана;
- kernel — находит базис ядра преобразования, соответствующего данной матрице;
- laplacian — вычисляет лапласиан;
- leastsqrs — решение уравнений по методу наименьших квадратов;
- linsolve — решение линейных уравнений;
- LudeComp — осуществляет LU-разложение;
- minpoly — вычисляет минимальный полином матрицы;
- mulcol — умножает столбец матрицы на заданное выражение;
- mulrow — умножает строку матрицы на заданное выражение;
- multiply — перемножение 'матриц или матрицы и вектора;
- normalize — нормализация вектора;
- orthog — тест на ортогональность матрицы;
- permanent — вычисляет перманент матрицы — определитель, вычисляемый без перестановок;
- pivot — вращение относительно элементов матрицы;
- potential — вычисляет потенциал векторного поля;
- Qrdecomp — осуществляет QR-разложение;
- randmatrix — генерирует случайные матрицы;
- randvector — генерирует случайные векторы;
- ratform — вычисляет рациональную каноническую форму;
- references — выводит список основополагающих работ по линейной алгебре;
- rowspace — вычисляет базис пространства строки;
- rowspan — вычисляет векторы охвата для места столбца;
- rref — реализует преобразование Гаусса-Жордана матрицы;
- scalarmul — умножение матрицы или вектора на заданное выражение;
- singval — вычисляет сингулярное значение квадратной матрицы;
- singularvals — возвращает список сингулярных значений квадратной матрицы;
- smith — вычисляет Шмиттову нормальную форму матрицы;
- submatrix — извлекает указанную подматрицу из матрицы;
- subvector — извлекает указанный вектор из матрицы;
- sumbasis — определяет базис объединения системы векторов;
- swapcol — меняет местами два столбца в матрице;
- swaprow — меняет местами две строки в матрице;
- sylvester — создает матрицу Сильвестра из двух полиномов;
- toeplitz — создает матрицу Теплица;
- trace — возвращает след матрицы;
- vandermonde — создает вандермондову матрицу;
- vecpotent — вычисляет векторный потенциал;
- vectdim — определяет размерность вектора;
- wronskian — вронскиан векторных функций.
Ниже мы рассмотрим более подробно наиболее часто используемые функции из этого пакета. С деталями синтаксиса (достаточно разнообразного) для каждой из указанных функций можно ознакомиться в справочной системе Maple. Для этого достаточно использовать команду
?name; где name — имя функции (из приведенного списка).
3. Интерактивный ввод матриц
8.gif

9.gif
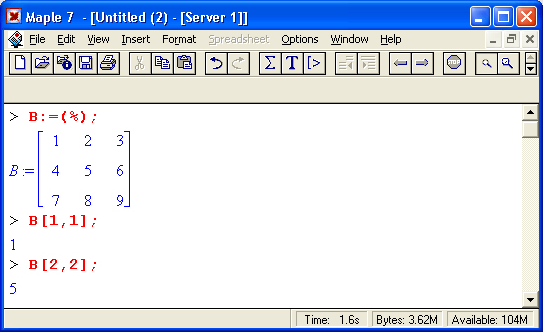
4. Основные функции для задания векторов и матриц
Основные функции для задания векторов и матриц
В библиотечном файле Unalg имеются следующие функции для задания векторов и матриц:
- vector(n,list) — сoздание вектора с n элементами, заданными в списке list;
- matrix(n,m,list) — создание матрицы с числом строк n и столбцов m с элементами, заданными списком list.
Ниже показано применение этих функций:
Обратите внимание на последние примеры — они показывают вызов индексированных переменных вектора и матрицы.
10.gif
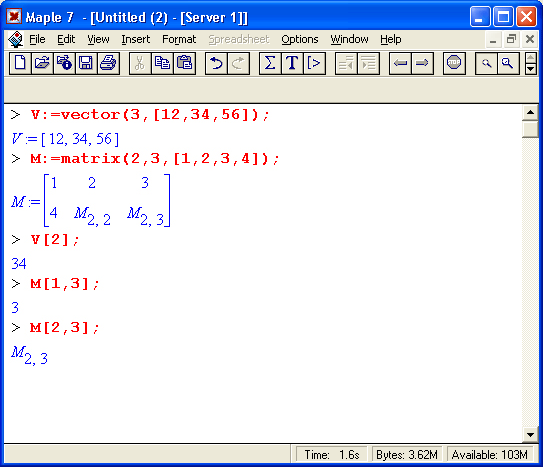
5. Функции для работы, с векторами и матрицами
Функции для работы с векторами и матрицами
Для работы с векторами и матрицами Maple 7 имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории.
Операции со структурой отдельного вектора V и матрицы М:
- coldim(M) — возвращает число столбцов матрицы М;
- rowdim(M) — возвращает число строк матрицы М;
- vectdim(V) — возвращает размерность вектора V;
- col(M,i) — возвращает i-й столбец матрицы М;
- row(M,i) — возвращает i-ю строку матрицы М;
- tninor(M,i, j) — возвращает минор матрицы М для элемента с индексами i и j;
- delcols(M,i.. j) — удаляет столбцы матрицы М от i-roдо j-ro;
- del rows (V,i..j) — удаляет строки матрицы М от i-й до j-й;
- extend (М, т, n,х) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х.
Основные векторные и матричные операции:
- dotprod(U,V) — возвращает скалярное произведение векторов U и V;
- crossprod(U,V) — возвращает векторное произведение векторов U и V;
- norm(V) или norm(M) — возвращает норму вектора или матрицы;
- copyinto(A,B,i, j) — копирует матрицу А в В для элементов последовательно от i до j;
- concat(Ml,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц Ml и М2;
- stack(Ml,M2) — возвращает объединенную матрицу с вертикальным слиянием Ml и М2;
- matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В;
- multlply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В;
- adjoint (М) или adj(M) — возвращает присоединенную матрицу, такую что M?adj(M) дает диагональную матрицу, определитель которой есть det(M);
- charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda;
- det(M) — возвращает детерминант (определитель) матрицы М;
- Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы;
- jordan(M) — возвращает матрицу М в форме Жордана;
- hermite(M) — возвращает матрицу М в эрмитовой форме;
- trace(M) — возвращает след матрицы М;
- rank(M) — возвращает ранг матрицы М;
- transpose(M) — возвращает транспонированную матрицу М;
- inverse(M) или evalm(l/M) — возвращает матрицу, обратную к М;
- singularvals(A) — возвращает сингулярные значения массива или матрицы А.
Приведем примеры применения некоторых из этих функций:
Читатель, понимающий суть матричных вычислений, легко справится с тестированием других функций, входящих в пакет linalg. В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.
11.gif
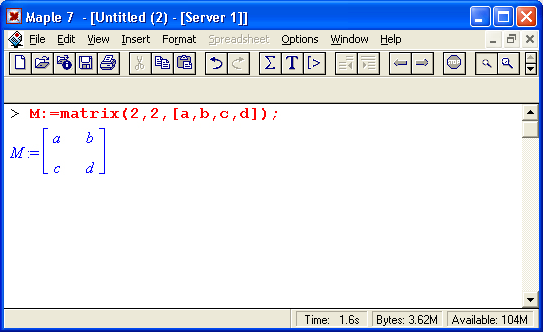
12.gif
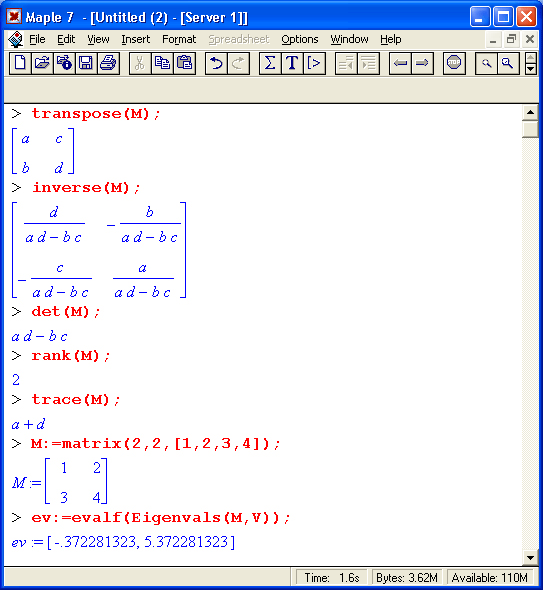
6. Решение систем линейных уравнений.
Решение систем линейных уравнений
Ниже представлен простой пример составления и решения трех систем линейных уравнений с применением функций, входящих в пакет linalg:
А теперь рассмотрим пример решения матричного уравнения в символьном виде:
Следующий пример показывает решение более сложной системы линейных уравнений с комплексными коэффициентами:
На этот раз решение получено использованием функций умножения матриц и вычисления обратной матрицы в виде X = А-1 В, то есть в матричном виде. В конце примера показано преобразование результатов с целью их получения в обычной форме комплексных чисел с частями, представленными в форме чисел с плавающей точкой.
13.gif
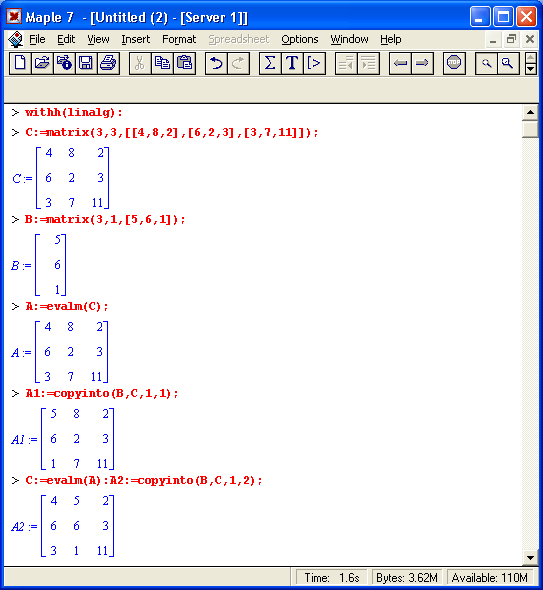
14.gif
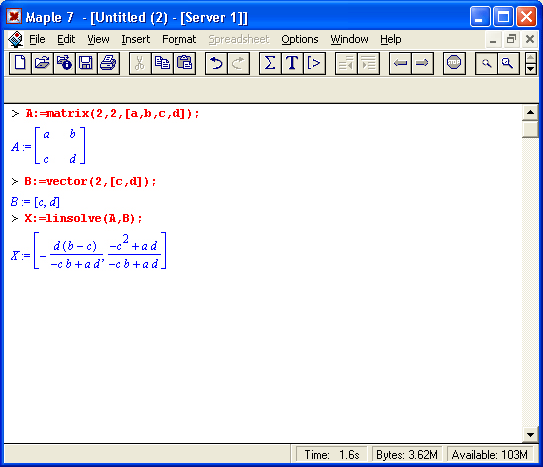
15.gif

7. Пакет линейной алгебры с алгоритмами NAG LinearAlgebra
Пакет линейной алгебры с алгоритмами NAG LinearAlgebra
Назначение и загрузка пакета LinearAlgebra
В последние годы разработчики систем символьной математики осознали, что малая скорость выполнения векторных и матричных операций при решении задач линейной алгебры оборачивается потерей заметной части рынка систем компьютерной математики. Новые версии таких систем (Mathematica 4/4.1 и Maple 6/7) отличаются от прежних прежде всего резким повышением эффективности решения задач линейной алгебры в численном виде.
В новых реализациях систем Maple и MATLAB была сделана ставка на использование давно апробированных быстрых алгоритмов линейной алгебры, предложенных создателями Number Algorithm Group (NAG). Эти алгоритмы издавна применяются на больших ЭВМ и суперкомпьютерах, обеспечивая ускорение численных матричных операций от нескольких раз до нескольких десятков раз. Их применение обеспечивает эффективное использование систем символьной математики в решении задач, сводящихся к задачам линейной алгебры. В числе таких задач многочисленные задачи теоретической электротехники, механики многих объектов, моделирования электронных устройств и т. д. В Maple 7 использование алгоритмов NAG является одной из первых отличительных черт новой версии системы. Оно реализуется новым пакетом LinearAlgebra. Для его загрузки используются следующие команды:
> restart; with(LinearAlgebra):
[Add, Adjoint, BackwardSubstitute, BandMatrix, Basis, BezoutMatrix, BidiagonalForm, BilinearForm, CharacteristicMatrix, CharacteristicPolyhomial, Column, ColumnDimension, ColumnOpemtion, ColumnSpace, CompanionMatrix, CondittonNumber, ConstantMatrix, ConstantVector, CreatePermutation, CrossProduct, DeleteColumn, DeleteRow, Determinant, DiagonalMatrix, Dimension,
Dimensions, DotProduct, Eigenvalues, Eigenvectors, Equql, FonyardSubstitute, FrobeniusForm, GenerateEquations, GenerateMatrix, GetResuNDataType, * GetResultShape, GivensRotationMatrix, GramSchmidt, HarikelMatrix, HermiteForm, HermitianTranspose, HessenbergForm, HilbertMatrix, Households-Matrix, IdentityMatrix, IntersectionBasis, IsDefinite, IsOrthogonal, IsSimilar, IsUnitary,
JordanBlockMatrix, JordanForm, LA_Main, LUDecomposition, LeastSquares, LinearSolve, Map, Map2, MatrixAdd, Matrixlnverse, MatrixMatrixMultiply, MatrixNorm, MatrixScalarMultiply, MatrixVectorMultiply,Minimal/Polynomial, Minor, Multiply, NoUserValue, Norm, Normalize, NullSpace, OuterProductMatrix, Permanent, Pivot, QRDecomposition, RandomMatrix, RandomVector, Rank, Row,
RowDimension, RowOperation, RowSpace, ScalarMatrix, ScalarMultiply, ScalarVector, SchurForm, SingularValues, SmithForm, SubMatrix, SubVector, SumBasis, SylvesterMatrix, ToeplitzMatrix, Trace, Transpose, TridiagonalForm, UnitVector, VandermondeMatrix, VectorAdd, VectorAngle, VectorMatrixMultiply, VectorNorm, VectorScalarMultiply, ZeroMatrix, Zero Vector, Zip ]
> 1nfolevel[LinearA1gebra]:=l:
infolevelLinearAlgebra:=1
Нетрудно заметить, что многие функции этого пакета повторяет по назначению функции более старого пакета linalg, описанного выше. Поэтому мы не будем останавливаться на их повторном описании. Главное то, что эти функции задействуют возможности быстрых алгоритмов NAG и в отличие от функций пакета linalg ориентированы на численные расчеты в формате обработки вещественных чисел, характерном для компьютерной платформы. Знающий матричные методы читатель легко поймет назначение функций пакета LinearAlgebra по их составным названиям. Например, DeleteColumn означает удаление столбца матрицы, ToeplitzMatrix означает создание матрицы Теплица, ZeroMatrix — создание матрицы с нулевыми элементами и т. д. Все имена функций этого пакета начинаются с заглавной буквы.
8. Примеры матричных операций с применением пакета LinearAlgebra
Примеры матричных операций с применением пакета LinearAlgebra
Применение алгоритмов NAG особенно эффективно в том случае, когда используется встроенная в современные микропроцессоры арифметика чисел с плавающей запятой. С помощью специального флага такую арифметику можно отключать или включать:
> UseHardwareFloats := false; # use software floats
UseHardwareFloats :=false
> UseHardwareFloats := true: # default behaviour
UseHardwareFloats :=true
Матрицы в новом пакете линейной алгебры могут задаваться в угловых скобках, как показано ниже:
После этого можно выполнять с ними типовые матричные операции. Например, можно инвертировать (обращать) матрицы:
Обратите внимание, что Maple 7 теперь выдает информационные сообщения о новых условиях реализации операции инвертирования матриц с вещественными элементами, и в частности об использовании алгоритмов NAG и арифметики, встроенной в сопроцессор. (
Следующий пример иллюстрирует создание двух случайных матриц Ml и М2 и затем их умножение:
Параметр inplace в функции умножения обеспечивает помещение результата умножения матриц на место исходной матрицы Ml — излюбленный прием создателей быстрых матричных алгоритмов NAG. Поскольку матрицы Ml и М2 за- -даны как случайные, то при повторении этого примера результаты, естественно, будут иными, чем приведенные.
Следующий пример иллюстрирует проведение хорошо известной операции/ LU-разложения над матрицей М, созданной функцией Matrix:
Конечной целью большинства матричных операций является решение систем линейных уравнений. Для этого пакет LinearAlgebra предлагает великое множество методов и средств их реализации. Мы ограничимся простым примером одновременного решения сразу трех систем уравнений. Дабы не загромождать книгу массивными выражениями, ограничимся решением систем из двух линейных уравнений, матрица коэффициентов у которых одна, а векторы свободных членов разные. Ниже показан пример решения такой системы:
На этом, учитывая ограниченный объем книги, мы завершаем обзор пакета LmearAlgebra. Читатель, познающий или знающий методы линейной алгебры, может опробовать в работе любые функции этого пакета самостоятельно или познакомиться со множеством примеров, размещенных в справочной системе Maple 7. Возможности пакетов linalg и LinearAlgebra удовлетворят самых требовательных специалистов в этой области математики.
16.gif

17.gif
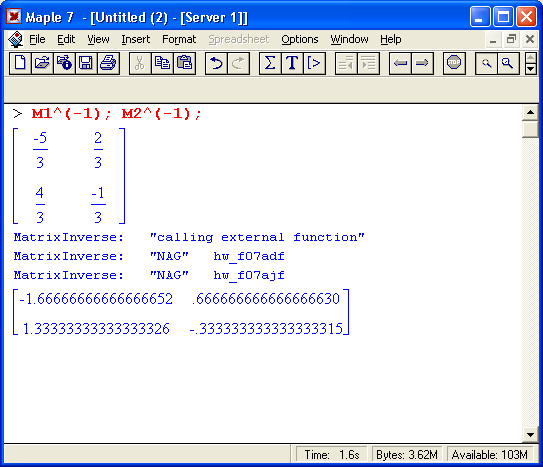
18.gif
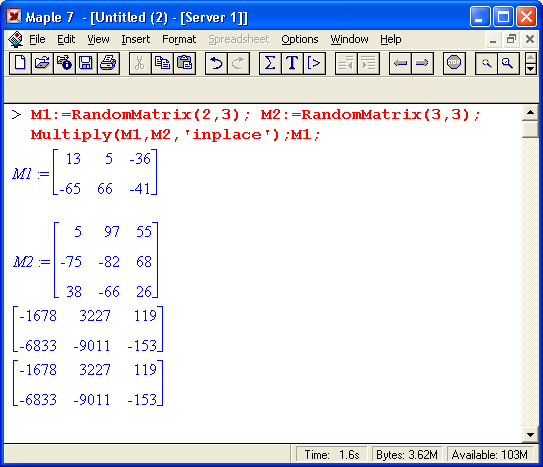
19.gif

30.gif
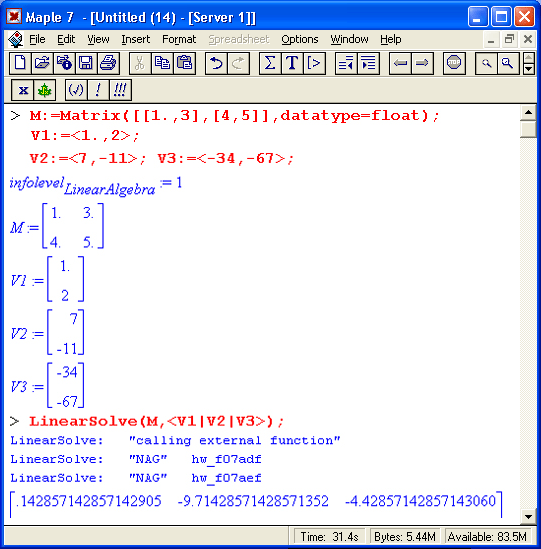
9. Интеграция Maple 7 с MATLAB
Интеграция Maple 7 с MATLAB
Несмотря на обширные средства линейной алгебры (да и многие другие), имеющиеся у системы Maple 7, есть системы компьютерной математики, решающие некоторые классы задач более эффективно, и прежде всего быстрее. В области линейной алгебры к таким системам, безусловно, относится система MATLAB, созданная компанией Math Works, Inc. Ее название происходит именно от слов MATrix LABoratory — матричная лаборатория.
MATLAB содержит в своем ядре многие сотни матричных функций и является одной из лучших матричных систем для персональных компьютеров. Она реализует самые современные алгоритмы матричных операций, включая, кстати, и алгоритмы NAG. Однако главное достоинство MATLAB — наличие множества дополнительных пакетов как по классическим разделам математики, так и по самым новейшим, таким как нечеткая логика, нейронные сети, идентификация систем, обработка сигналов и др. Знаменитым стал пакет моделирования систем и устройств Simulink, включаемый в пакет поставки системы MATLAB. Последней версией системы является MATLAB 6.0. В то же время нельзя не отметить, что MATLAB — одна из самых громоздких математических систем. Инсталляция ее полной версии занимает около 1,5 Гбайт дискового пространства. Несмотря на это, интеграция различных математических систем с данной системой, похоже, становится своеобразной модой. Такая возможность предусмотрена и в системе Maple 7 с помощью пакета Matlab.
10. Загрузка пакета расширения Matlab
Загрузка пакета расширения Matlab
Для загрузки пакета Matlab используется команда: .
> with(Matlab);
[chol, closelink, defined, del, dimensions, eig, evalM,fft, getvar, inv, Iu,ode45, openlink, qr, setvar, size, square, transpose ]
Использование этой команды ведет к автоматическому запуску системы MATLAB (гарантируется работа с версиями MATLAB до 5.3.1 включительно) и установлению необходимой объектной связи между системами Maple 7 и MATLAB.
ПРИМЕЧАНИЕ
Как нетрудно заметить, данный пакет дает доступ всего к 18 функциям системы MATLAB (из многих сотен, имеющихся только в ядре последней системы). Таким образом, есть все основания полагать, что возможности MATLAB в интеграции с системой Maple 7 используются пока очень слабо и носят рудиментарный характер. Стоит ли ради этих функций иметь на компьютере огромную систему MATLAB, пользователи должны решать сами. Если ответ положительный, то, скорее всего, пользователь решает тот класс задач, для которых лучше подходит MATLAB, и надо задуматься уже над тем, нужен ли в этом случае Maple.
11. Типовые матричные операции пакета расширения Matlab
Типовые матричные операции пакета расширения Matlab
Большинство функций пакета Matlab (не путайте с системой MATLAB, имя которой надо записывать прописными буквами) реализуют самые обычные матричные операции, что и иллюстрируют приведенные ниже примеры.
Зададим матрицу М в формате Maple:
Ниже даны примеры транспонирования матрицы, ее инвертирования, вычисления детерминанта и собственных значений матрицы:
Можно проверить, является ли матрица квадратной:
Можно также проверить, является ли данная матрица матрицей системы MATLAB:
Здесь надо иметь в виду, что форматы матриц в системах Maple и MATLAB различны. Выполним LU-преобразование матрицы:
Таким образом, видно, что пакет Maple в данном случае реализует типовые матричные операции, но средствами системы MATLAB. Загрузка последней происходит автоматически при загрузке пакета Matlab. Если система MATLAB не установлена на вашем компьютере, то доступ к функциям пакета Matlab будет отсутствовать, a Maple 7 при попытке использования данных функций будет выдавать сообщения об ошибках.
20.gif
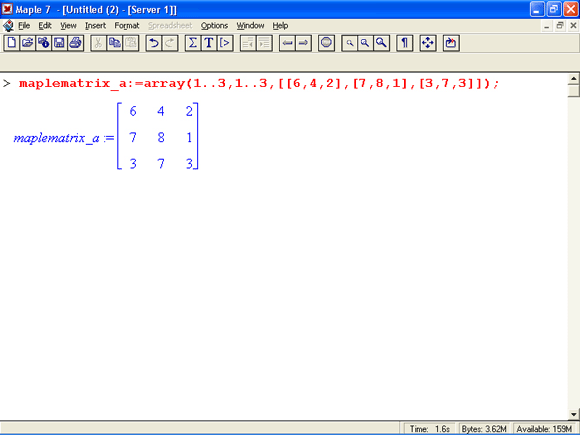
21.gif
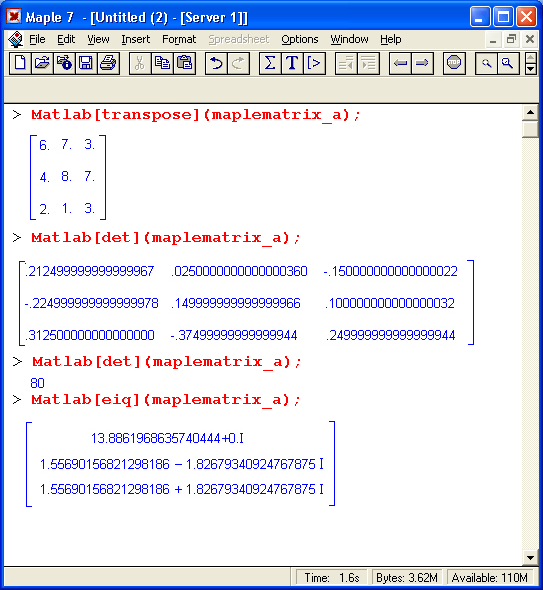
22.gif
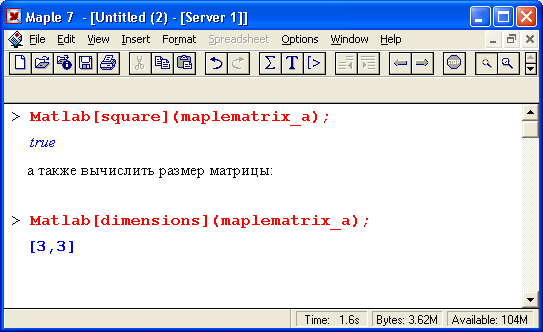
23.gif
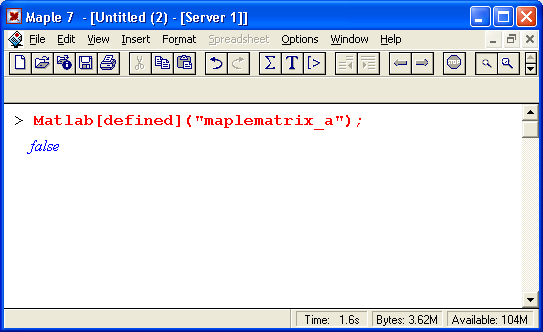
24.gif
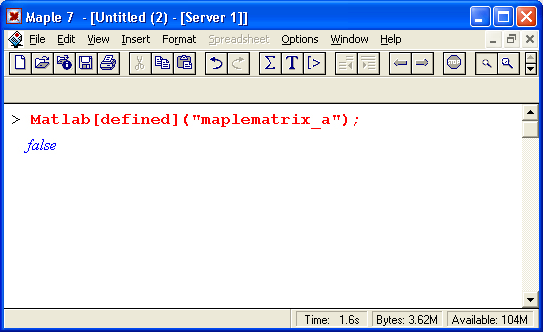
12. Выделение сигнала на фоне шумов
Выделение сигнала на фоне шумов
Среди небольшого числа доступных функций системы MATLAB в пакете Matlab нельзя не выделить особо функции быстрого прямого и обратного преобразований Фурье. В системе MATLAB эти функции реализуют наиболее эффективные алгоритмы быстрого преобразования Фурье (БПФ), обеспечивающие решение крупноразмерных задач (например, обработки сигналов, представленных векторами и матрицами больших размеров) в десятки раз быстрее, чем при обычных методах выполнения преобразований Фурье.
Покажем возможность применения БПФ на ставшем классическим примере — выделении спектра полезного сигнала на фоне сильных помех. Зададим некоторый двухчастотный сигнал, имеющий 1500 точек отсчета:
> num := 1500:
Time := [seq(.03*t. t=1..num)]:
data := [seq((3.6*cos(Time[t]) + cos(6*Time[t])), t=1..num)]:
p1ots[pointp1ot](zip((x,y)->[x,y],Time,data), style=line);
График сигнала представлен на рис. 15.1.
Рис. 15.1. График исходного сигнала
Теперь с помощью генератора случайных чисел наложим на этот сигнал сильный «шум» (слово «шум» взято в кавычки, поскольку речь идет 6 математическом моделировании шума, а не о реальном шуме физической природы):
> tol := 10000:
r := rand(0..to1):
noisyjlata :=[seq(r()/(tol)*data[t], t=l..num)]:
plots[pointp1ot](zip((x,y)->[x,y],T1me,noisy_data), sty1e=1ine);
Нетрудно заметить, что теперь форма сигнала настолько замаскирована шумом (рис. 15.2), что можно лишь с трудом -догадываться, что сигнал имеет периодическую составляющую малой амплитуды. Эта высокочастотная составляющая сигнала скрыта шумом.
Подвергнем полученный сигнал (в виде временной зависимости) прямому преобразованию Фурье, реализованному функцией fft:
> ft := fft(noisy_data):
> VectorOptions(ft, datatype):
complex8
Эта операция переводит задачу из временного представления сигнала в частотное, что позволяет использовать частотные методы анализа сигнала. Выделим, к примеру, действительную и мнимую части элементов вектора ft и проверим его размер:
25.gif
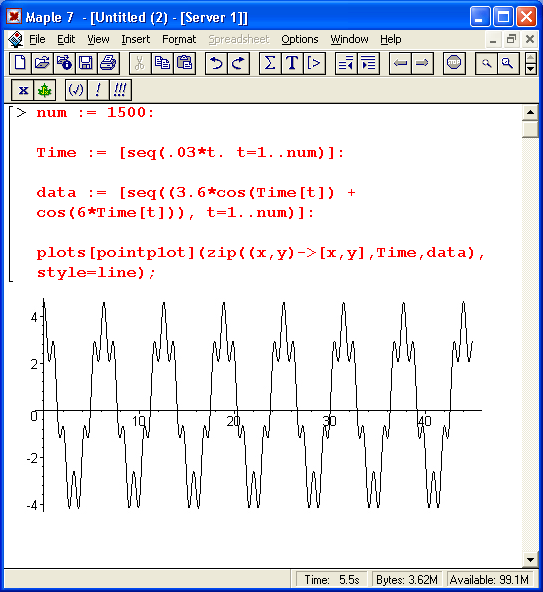
26.gif
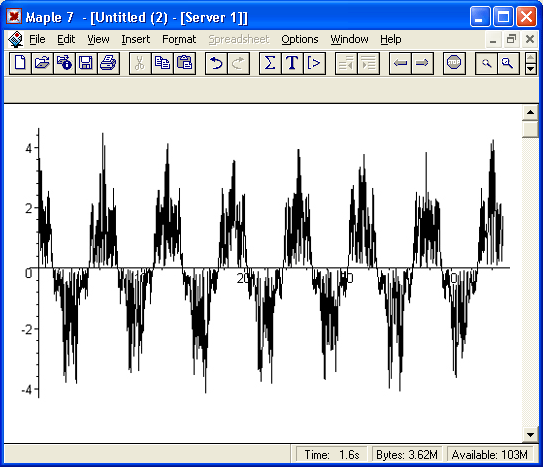
27.gif
13. Пакет анализа линейных функциональных систем LinearFunctionalSystems
Пакет анализа линейных функциональных систем LinearFunctionalSystems
Назначение пакета LinearFunctionalSystems
Пакет LinearFimctionalSystems содержит набор функций для решения задач, связанных с анализом линейных функциональных систем. Обычно такие системы описываются линейными дифференциальными уравнениями, имеющими то или иное решение. Пакет LinearFunctionalSystems позволяет провести тестирование подготовленной системы, оценить ряд ее параметров и получить решение одним из ряда методов.
Вызов всех функций пакета осуществляется командой:
> with(LinearFunctionalSystems):
[AreSameSolution, CanonicalSystem, ExtendSeries, Homogeneous System, IsSolution,
MatrixTriangularization, PolynomialSolution, Properties, RationalSolution,
SeriesSolution, UniversalDenominator]
14. Тестовые функции пакета LinearFunctionalSystems
Тестовые функции пакета LinearFunctionalSystems
Прежде чем рассматривать основные функции пакета, рассмотрим две тестовые функции. Они представлены следующими формами записи:
IsSolution(sol,sys, vars) IsSolution(sol, A, b, x, case)
IsSolution(sol, A, x, case) AreSameSolutior(sol, soil)
В них: sol — тестируемое решение, sys — система функциональных уравнений, х — независимая переменная решения, А и b — матрица и вектор с рациональными элементами, case — имя метода решения ('differential', 'difference' или 'qdifference').
15. Функции решения линейных функциональных систем
Функции решения линейных функциональных систем
Группа основных функций пакета LinearFunctionalSystems имеет идентичный синтаксис и записывается в виде:
name(sys,vars,[method])
или
name(A[.b],x, case, [method]}
Здесь name — одно из следующих имен:
- PolynomialSolution — решение в форме полинома;
- RationalSolution — решение в форме рационального выражения;
- SeriesSolution — решение в виде ряда;
- UniversalDenominator — решение с универсальным знаменателем (и числителем, равным 1).
Система функциональных уравнений задается либо в виде полной системы sys со списком переменных vars, либо в матричном виде с заданием матриц коэффициентов, системы А и вектора свободных членов b (может отсутствовать) с указанием независимой переменной х и параметра case, имеющего значения 'differential', 'difference' или 'qdifference'. Параметр method, задающий метод EG-исключения, может иметь значения 'quasimodular' или 'ordinary'.
16. Вспомогательные функции
Вспомогательные функции
Несколько вспомогательных функций пакета LinearFunctionalSystems представлено ниже:
- MatrixTriangularization(mat, m, n, x, It) — триангуляция матрицы mat размера mxn с указанием типа It ('lead' или 'trail');
- CanonicalSystemCshift, sys. vars) или CanonicalSystemCshift, A[, b]. x, case) — возвращает систему в каноническом виде (параметр shift задается как ' difference' или ' q - difference', назначение других параметров С9ответствует указанным выше для других функций);
- ExtendSeries(sol, deg) — расширяет ряд решения sol до расширенного ряда степени deg;
- HomogeneousSystemChoitio, sys, vars) илиHomogeneousSystemChomo, A[, b], x, case) — преобразует исходную систему в гомогенную с именем homo.
- PropertiesCsys, vars) или Properties(A[. b]. x, case) — возвращает основные свойства системы.
17. Примеры применения пакета LinearFunctiftnalSystems
28.gif
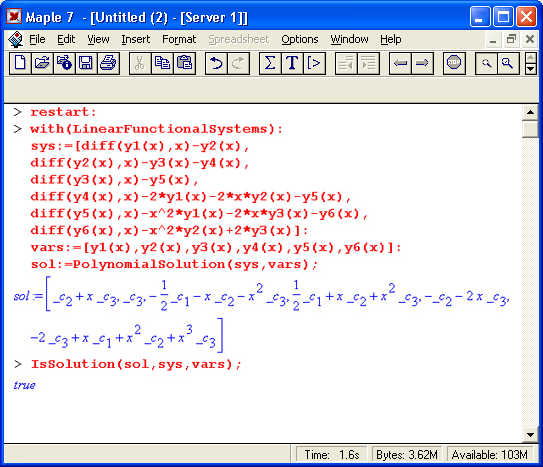
29.gif

18. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Применять основные операции и определения линейной алгебры.
- Использовать пакет решения задач линейной алгебры linalg.
- Использовать пакет линейной алгебры LinearAlgebra с алгоритмами NAG.
- Осуществлять интеграцию системы Maple 7 с матричной системой MATLAB.
- Использовать некоторые функции системы MATLAB при работе в Maple 7.
- Применять функции нового пакета LinearFunctionalSystems.
Урок 16. Обзор пакетов специального назначения
1. Пакет решения задач линейной оптимизации simplex
Урок 16.
Обзор пакетов специального назначения
Задачи линейной оптимизации важны как в фундаментальных, так и в прикладных приложениях математики. В пакете simplex имеется небольшой, но достаточно представительный набор функций и определений для решения таких задач:
> with(simplex);
Warning, the protected names maximize and minimize have been redefined and unprotected
[basis, convexhull, cterm, deftne_zero, display, dual,feasible, maximize, minimize,pivot, pivoteqn, pivotvar, ratio, setup, standardize ]
Приведем краткое назначение этих функций:
- basis — возврат списка основных переменных для множества линейных уравнений;
- convexhull— вычисление выпуклой оболочки для набора точек;
- cterm — задание констант для системы уравнений или неравенств;
- define_zero — определение наименьшего значения, принимаемого за ноль (по
- умолчанию увязано со значением системной переменной Digits);
- display — вывод системы уравнений или неравенств в матричной форме;
- dual — выдача сопряженных выражений; ,
- equality — параметр для функции convert, указывающий на эквивалентность;
- feasible — выяснение возможности решения заданной задачи:
- maximize — вычисление максимума функции;
- minimize — вычисление минимума функции;
- pivot — создание новой системы уравнений с заданным главным элементом;
- pivoteqn — выдача подсистемы уравнений для заданного главного элемента;
- pivotvar — выдача переменных с положительными коэффициентами в целевой функции;
- ratio — выдача отношений для определения наиболее жесткого ограничения;
- setup — задание системы линейных уравнений;
- standardize — приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно».
2. Функции maximize и minimize
Функции maximize и minimize
Главными из этих функций являются maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующих формах:
maximize(f, С)
minimize(f, С)
maximize(f , С, vartype)
nrinimize(f , С, vartype)
maximize(f , С,vartype, 'NewC', 'transform')
m'inimize(f , C, vartype, 'NewC', 'transform')
Здесь f — линейное выражение, С — множество или список условий, vartype — необязательно задаваемый тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны^примеры применения этих функций:
1.gif
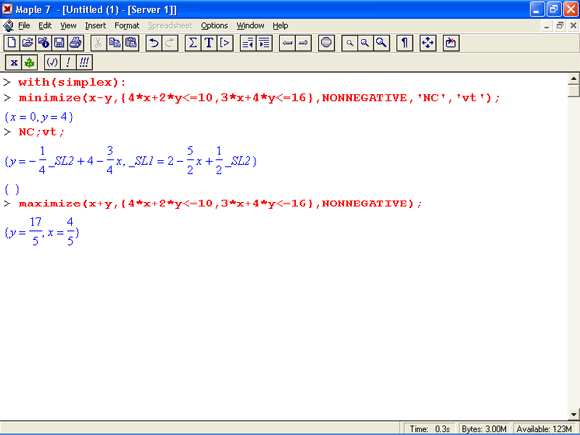
3. Прочие функции пакета simplex.
Прочие функции пакета simplex
Функция basis(C) возвращает базис для системы линейных уравнений С. Например:
> basisC [ х - 2*z+w , z - 2*у - w ] );
[x,z]
Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps:
> convexhum{[0,0],[l,l],[2,-l],[1,1/3],[1,1/2]}):
[[0,0],[2,-1],[1, 1]]
Для определения констант для системы линейных уравнений или неравенств служит функция cterm(C):
> cterm([2*х+у<=6.7*y-z-3-4]);
[6,7]
Функция define_zero(C) возвращает ближайшее ненулевое значение, зависящее от установки переменной Digits:
Функция display(C) имеет еще и форму display(C,[X, у, z]). Она задает вывод линейных уравнений и неравенств в матричной форме:
Функция dual(f, С, у) имеет следующие параметры: f — линейное выражение y, С множество неравенств и у — имя. Эта функция возвращает сопряженное с f выражение:
> dual( x-y,{2*x+3*y<=5.3*x+6*y<=15},z);
115zl +5z2, {1_<3z1+2z2,-l_<6z1+3z2}
Функция feasible может быть задана в трех формах:
feasible(C)
feasible(C,vartype)
feasible(C,vartype,'NewC','Transform')
Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:
> feasible({2*x+3*y<-5, 3*x+6*y<"15}, NONNEGATIVE);
true
> feasib1e({2*x+3*y<-5, 3*х+б*у<—15}, NONNEGATIVE);
false
Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам. Функция pivot (С, х, eqn) конструирует новую систему с заданным главным элементом:
Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С:
> pivoteqnC {_SL1 - 5-3*х-2*у. _SL2 - 4-2*х-2*у}. х );
[_SLl = 5-lx-2y]
Функция pivotvar(f, List) или pivotvar(f) возвращает список переменных, имеющих положительные коэффициенты в выражении для целевой функции:
Функция ratio(C, x) возвращает список отношений, задающих наиболее жесткие ограничения:
Функция setup может иметь три формы:
setup(C)
setup(C, NONNEGATIVE)
setup(C, NONNEGATIVE, 't')
Она обеспечивает конструирование множества уравнений с переменными в левой части:
Последняя функция — standartlze(C) — конвертирует список уравнений (неравенств) в неравенства типа «меньше или равно»:
> standardize({2*x+3*y<-5.3*x+5*yl5});
{2х + Зу<5,Зх + 5у<15,-Зх-5у<-15}
2.gif
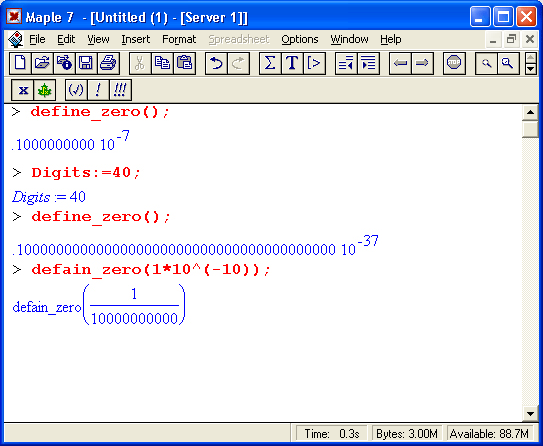
3.gif
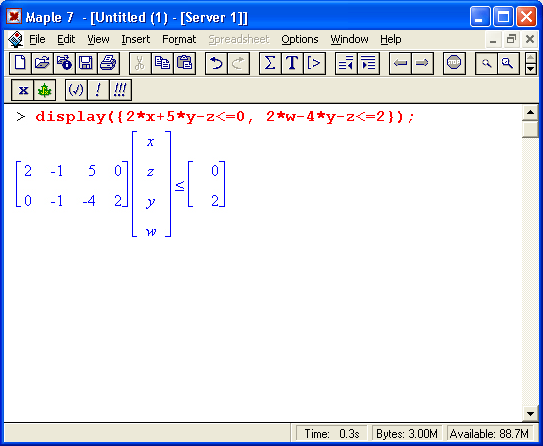
4.gif
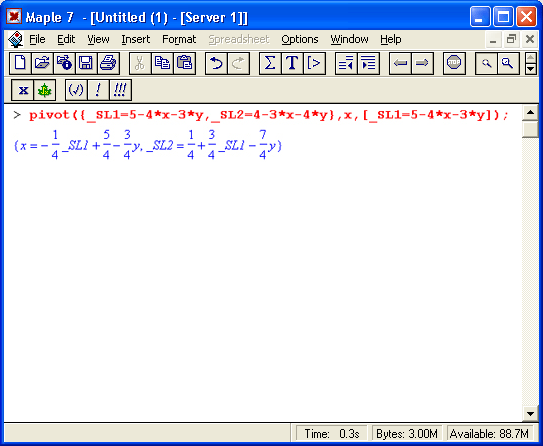
5.gif
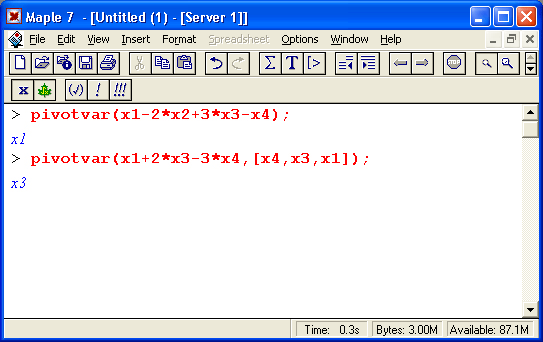
6.gif
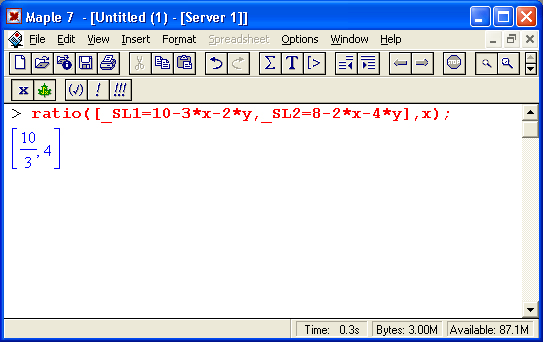
7.gif
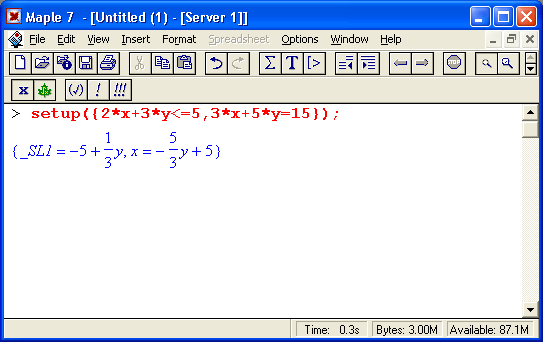
4. Пакет планиметрии geometry
Пакет планиметрии geometry
Пакет геометрических расчетов geometry в системе Maple 7 получил как бы второе рождение число его функций по сравнению с версией этого пакета в системе Maple V R5 возросло в несколько раз. Теперь загрузка пакета возвращает весьма внушительный список из более чем 100 функций:
> with(geometry);
[Appolonius, AreCollinear, AreConcurrent, AreConcyclic, AreConjugate, AreHarmonic, AreOrthogonal, AreParallel, ArePerpendicular, AreSimilar, AreTangent, CirdeQfSimilitude,CrossProduct, CrossRatio, DefinedAs, Equation, EulerCircle, EulerLine, Exterior Angle, ExternalBisector, FindAngle, GergonnePoint, GlideRefledion, HorizontalCoord, HorizontalName, InteriorAngle, IsEquilateral,
IsOnCircle, IsOnLine, IsRightTriangle, MajorAxis, MakeSquare, MinorAxis,NagelPoint, OnSegment, ParallelLine, PedalTriangle, PerpenBisector, PerpendicularLine, Polar, Pole, RadicalAxis, RadicalCenter, RegularPolygon, RegularStarPolygon, SensedMagnitude, SimsonLine, SpiralRotation, StretchReflection, StretchRotation, TangentLine, VerticalCoord, VerticalName,
altitude, apothem, area, asymptotes, bisector, center, centroid, circle, circumcircle, conic, convexhull, coordinates, detail, diagonal, diameter, dilatation, directrix, distance, draw, dsegment, ellipse, excircle, expansion, foci, focus, form, homology, homothety, hyperbola, incircle, inradius, intersection, inversion, line, medial, median, method, midpoint, orthocenter, parabola, perimeter, point, powerpc, projection,
radius, randpoint, reciprocation, reflection, rotation, segment, sides, similitude, slope, square, stretch, tangentpc, translation, triangle, vertex, vertices}
Этот пакет содержит средства расчета основных параметров ряда геометрических объектов. Для каждого объекта возможно задание различных исходных величин, так что пакет охватывает практически все виды классических геометрических расчетов на плоскости. Несомненно, этот пакет заинтересует всех, кто работает в области геометрии и смежных областях.
Обратите внимание на то, что многие функции этого пакета вовсе не рисуют на экране соответствующие фигуры, а лишь выполняют типовые геометрические расчеты. Разумеется, в дальнейшем, используя результаты этих расчетов, можно построить соответствующую фигуру с помощью графических функций.
5. Пример применения расчетных функций пакета geometry
Пример применения расчетных функций пакета geometry
К сожалению, описание всех функций этого пакета потребует привести справочные данные практически по всей геометрии на плоскости, объем которых намного превышает объем данной книги. Учитывая идентичность идеологии при работе с функциями этого пакета, большинство из которых имеет вполне прозрачные имена (правда, англоязычные), работу с пакетом поясним на примере одной из функций — circle. Она позволяет математически задать окружность и определить все ее геометрические параметры. Функция может иметь несколько форм записи. Например, в форме:
circle(c,. [А. В. С], n, 'centername'=m)
она определяет построение окружности, проходящей через три точки А, В и С. Необязательный параметр n — список с именами координатных осей. Параметр ' centername' =m задает имя центра.
В форме circle(c. [А. В], n, 'centername'=m) задается окружность, проходящая через две точки А и В, а в форме circle(c, [A, rad], n, 'centername'=m) задается окружность, проходящая через одну точку А с заданным (и произвольным) радиусом rad и центром с. Наконец, функция circle в форме circle (с, eqn, n, 'centername'=m) позволяет задать окружность по заданным уравнению eqn и центру с. Проиллюстрируем применение функции circle на следующих примерах. Зададим характеристические переменные:
> EnvHorizontalName := m: _EnvVertlcalNane :=n;:
Определим окружность c1, проходящую через три заданные точки А, В и С с указанными после их имен координатами, и найдем координаты центра этой окружности:
Далее найдем радиус окружности:
и уравнение окружности, заданное в аналитическом виде:
Наконец, с помощью функции detail получим детальное описание окружности:
Заинтересованный в таких расчетах читатель может самостоятельно ознакомиться с другими функциями аналогичным образом, тем более, что в справочной системе этого пакета имеется множество примеров работы с его функциями.
8.gif
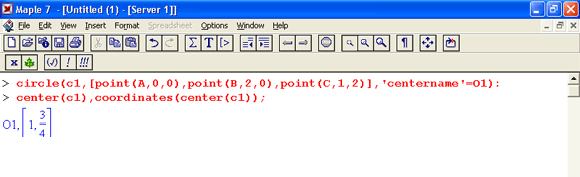
9.gif
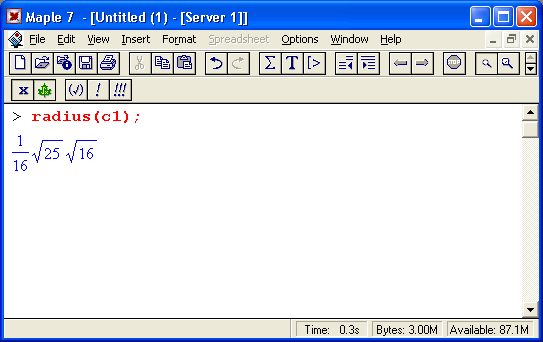
10.gif
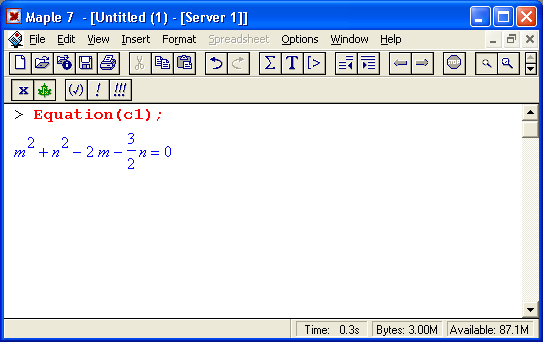
11.gif
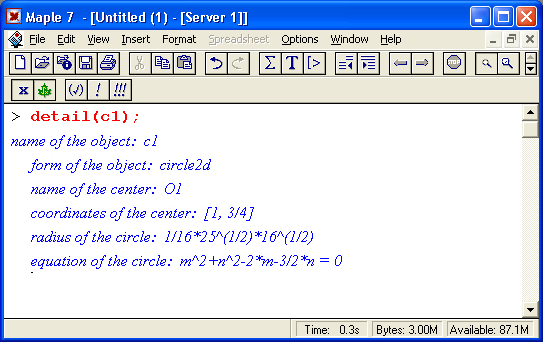
6. Визуализация геометрических объектов с помощью пакета geometry
Визуализация геометрических объектов с помощью пакета geometry
Одно из важных достоинств пакета geometry - возможность наглядной визуализации различных геометрических понятий, например графической иллюстрации доказательства теорем или геометрических преобразований на плоскости. Проиллюстрируем это на нескольких характерных примерах, заодно показывающих технику работы с рядом функций этого пакета.
Рисунок 16.1 показывает построение из множества окружностей фигуры - кардиоиды. Вопреки обычному построению этой фигуры, используется алгоритм случайного (но удовлетворяющего требованиям построения данной фигуры) выбора положений центров и радиусов окружностей.
Рис. 16.1. Построение кардиоиды из окружностей
Рисунок 16.2 дает графическую иллюстрацию к одной из теорем Фейербаха. Здесь эффектно используются средства выделения геометрических фигур цветом, что, увы, нельзя оценить по книжной черно-белой иллюстрации.
На следующем рисунке (рис. 16.3) показано построение фигуры, образованной вращением множества квадратов относительно одной из вершин. Это хороший пример применения функций point, square,.rotation и draw из пакета geometry.
Рисунок 16.4 показывает гомологические преобразования квадрата. Заинтересовавшийся читатель может легко разобраться с деталями простого алгоритма этой программы.
ПРИМЕЧАНИЕ
Обратите особое внимание на последний параметр в функции draw. Он задает построение титульной надписи с заданными шрифтом и размером символов. Сравните титульные надписи на рис. 16.4 и 16.3, где титульная надпись сделана шрифтом, выбранным по умолчанию. Приятно, что в обоих случаях нет преград для использования символов кириллицы и создания надписей на русском языке.
Наконец, на рис. 16.5 показан пример построения трех окружностей, имеющих две общие точки. Обратите внимание на вывод надписей «о», «ol» и «о2», указывающих положение центров окружностей на рисунке.
Рис. 16.2. Графическая иллюстрация к теореме Фейербаха
Рис. 16.3. Фигура, полученная вращением квадрата
Рис. 16.4. Гомологические преобразования квадрата
Рис. 16.5. Три окружности, имеющие две общие точки
Множество примеров применения всех функций пакета geometry дано в справочной системе Maple 7. Рекомендуется просмотреть те из них, которые нужны вам.
27.gif
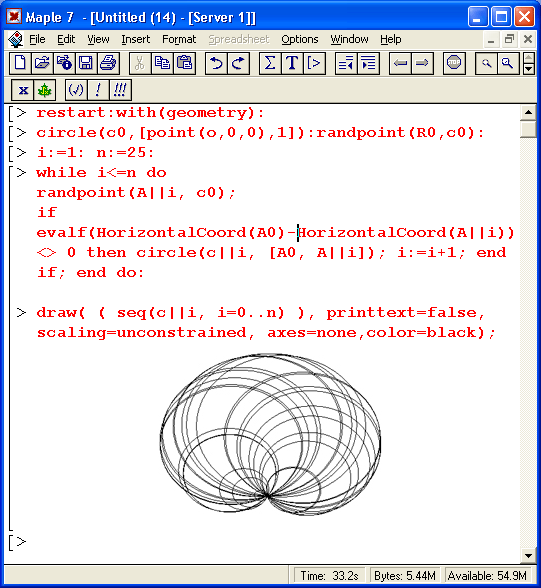
28.gif
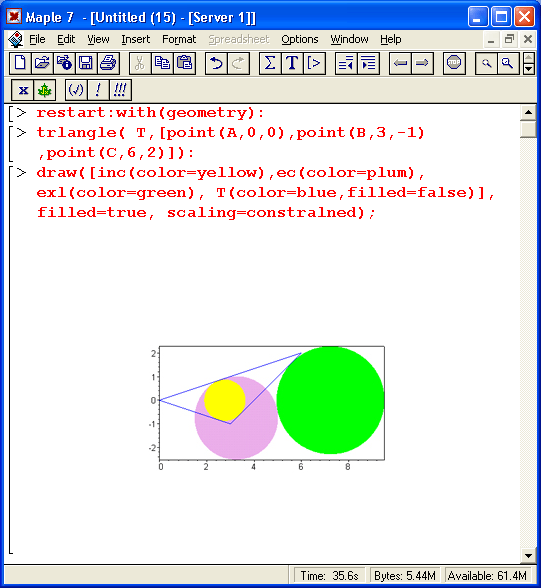
29.gif
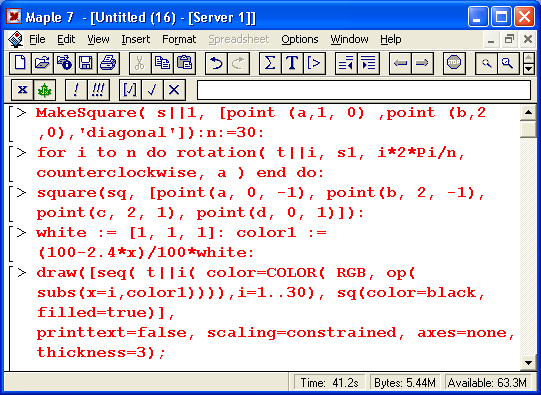
31.gif
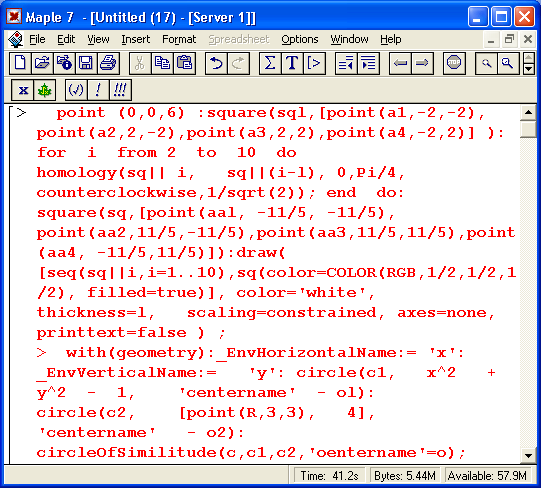
33.gif
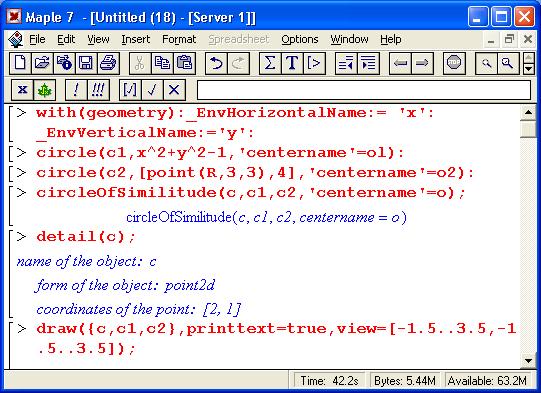
7. Пакет стереометрии geom3
Пакет стереометрии geom3d
Помимо существенного расширения пакета geometry в систему Maple 7 введен новый геометрический пакет geonfld. Он предназначен для решения задач в области трехмерной геометрии. При загрузке пакета появляется доступ к большому (свыше 140) числу новых функций:
> with(geom3d);
[Archimedean, AreCollinear, AreConcurrent, AreConjugate, AreCoplanar, AreDistinct, AreParallel, ArePerpendicular, AreSameObjects, AreSamePlane, AreSkewLines, DefinedAs, DirectionRatios, Equation,'FindAngle, FixedPoint, GlideReflect, GlideReflection, GreatDodeeahedron, Greatlcosahedron, GreatRhombicuboctahedron, GreatRhombiicosidodecahedron,
GreatStellatedDodecahedron,HarmonicConjugate,
HexakisIcosahedron,Hexakis Octahedron, JnRadius,
Is Archimedean, IsEquilateral, IsFacetted,
IsOnObject, IsQuasi,hRegular,
IsRightTriangletIsStellated,IsTangent,
MidRadius, NormalVector, OnSegment, ParallelVector, PentagonalHexacontahedron, PentagonallcositetrahedronjPentakisDodecahedron, QuasiRegularPolyhedron,
RadicalCenter, RadicalLine,RadicalPlane, RegularPolyhedron, RhombicDodecahedron, RhombicTriacontahedron, Rotatory Reflect, Rotatory Reflection, ScrewDisplace, ScrewDisplacement, SmallRhombicubactahedron, SmallRhombiicosidodecahedron, SmallStellatedDodecahedron, SnubCube, SnubDodecahedron, StereographicProjection, StretchRotate, TangentPlane,
TetrakisHexahedron, TrapezoidalHexecontahedron, Trapezoidallcositetrahedron, Triakislcosahedron, TriakisOctahedron, TriakisTetrahedron, TruncatedCuboctahedron, TruncatedDodecahedron,TruncatedHexahedron, Truncatedlcosahedron, Truncatedlcosidodecahedron, TruncatedOctahedron, TruncatedTetrahedron, altitude, area, center, centroid, circle, coordinates, cube,
cuboctahedron, detail, dilate, distance, dodecahedron, draw, dsegment, duality,faces, facet, form, gtetrahedron, hexahedron, homology, homothety, icosahedron, icosidodecahedron, identity, incident, intersection, inverse, inversion, line, midpoint, octahedron, parallel, parallelpiped, plane, point, polar, pole, powerps, projection, radius, rqndpoint, reflect^ reflection, rotate, rotation, schlafli, segment, sides, sphere, stellate, tetrahedron, tname, transform, translate, translation, transprod, triangle, unit, valuesubs, vertices, volume, xcoord, xname, ycoord, yname, zcoord, zname ]
Функции этого пакета обеспечивают задание и определение характеристик и параметров многих геометрических объектов: точек в пространстве, сегментов, отрезков линий и дуг, линий, плоскостей, треугольников, сфер, регулярных и квазирегулярных полиэдров, полиэдров общего типа и др. Для описания функций этого пакета пришлось бы воспроизвести обширное справочное руководство по стереометрии. В то же время назначение функций ясно из их названия, а характер применения тот же, что для функций описанного выше пакета geometry.
8. Пример применения пакета geom3d
Пример применения пакета geom3d
Учитывая сказанное, ограничимся единственным примером применения этого пакета (рис. 16.6).
Рис. 16.6. Иллюстрация применения пакета geom3d
Напоминаем, что цель пакета не в построении рисунков геометрических фигур, а в аналитическом представлении объектов в пространстве. Поэтому в обширной базе данных справочной системы по этому пакету вы встретите очень много рисунков.
35.gif
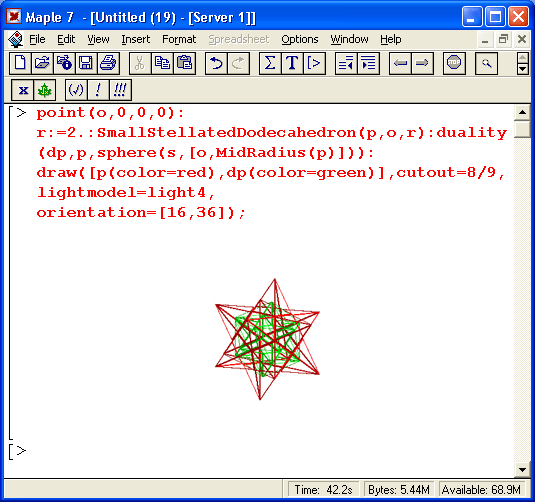
9. Пакет для работы с алгебраическими кривыми algcurves
Пакет для работы с алгебраическими кривыми algcurves
Пакет для работы с алгебраическими кривыми прекрасно дополняет возможности геометрических пакетов. При обращении к нему он дает доступ к полутора десяткам функций:
> restart;with(algcurves);
[Weierstrassform, differentials, genus, homogeneous, homology, integral_basis, isjiyperelliptic, j_invariant, monodromy,parametrization ,periodmatrix,plot_knot,puiseux, singularities ]
Ввиду важности функций пакета и их сравнительно небольшого числа приведем полную форму записи функций и их назначение:
- Weierstrassform(f ,x,y,x0,y0.opt) — вычисление нормальной формы для эллиптических или гиперболических алгебраических кривых;
- differentials(f, x, у, opt) — вычисление голоморфных дифференциалов алгебраических кривых;
- genus(f ,x,y,opt) — проверка подлинности алгебраической кривой;
- homogeneous (f, x, у, z) — создание полинома двух переменных, гомогенного в трех переменных;
- homo!ogy(f, x, у) — нахождение канонического гомологического базиса по алгоритму Треткоффа;
- integral_basis(f, x, у, S) — нахождение интегрального базиса алгебраического поля функции;
- is_hyperelliptic(f. х, у) — тестирование кривой на ее принадлежность к гиперболической;
- j_invariant(f ,x,y) — вычисление инварианта алгебраической кривой;
- monodromy(f, х, у, opt) — вычисляет монодромию алгебраической кривой;
- parametrization(f .x,y,.t) — нахождение параметризации для кривой с родом (даваемым функцией genuc), равным 0;
- periodmatrix(f, х, у, opt) — вычисление периодической матрицы кривой;
- plot_knot(f ,.x,.y,.opt) — построение узла — несамопересекающейся замкнутой кривой в трехмерном евклидовом пространстве;
- puiseux(f ,х=р,у,.n,.Т) — определение Пуизе- расширения алгебраической функции (может иметь и более простые формы записи);
- singularities(f ,x,y) — анализ кривой на сингулярность.
10. Примеры применения пакета algcurves
12.gif
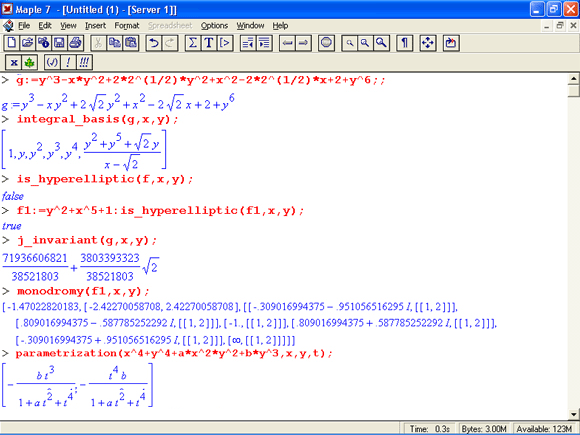
13.gif
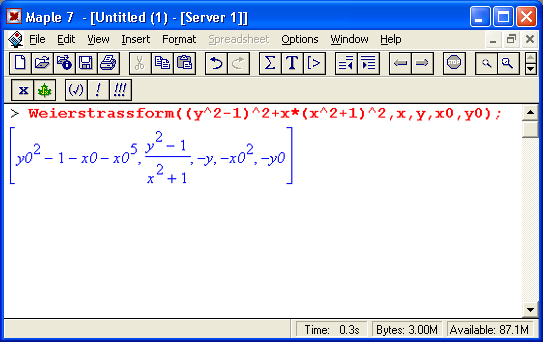
14.gif
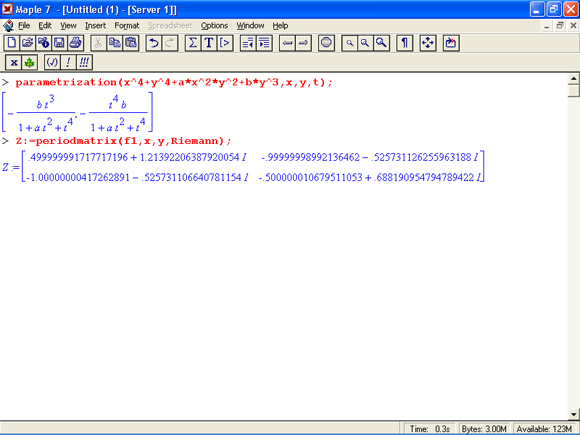
11. Построение алгебраических кривых класса knot
Построение алгебраических кривых класса knot
Функция plot_knot позволяет строить одну или несколько алгебраических кривых — узлов. Пример построения целого семейства узлов показан на рис. 16.7.
Рис. 16.7. Семейство узлов
Для лучшего обзора таких кривых рекомендуется воспользоваться возможностью вращения трехмерных фигур мышью для уточнения угла, под которым рассматривается фигура — в нашем случае семейство алгебраических кривых. Построение на рис. 16.7 выполняется довольно медленно — даже на компьютере с процессором Pentium III 600 МГц оно занимает около минуты.
36.gif
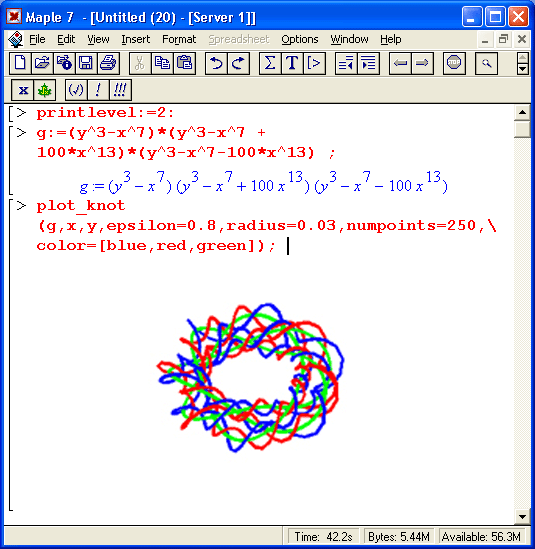
12. Новая функция Maple 7 plot_real_curve
Новая функция Maple 7 plot_real_curve
В пакет расширения algcurves добавлена новая функция импликативной графики plot_real_curve. Она строит алгебраическую кривую для действительной части полиномиального выражения и записывается в виде:
plot_real_curve (p, х, у, opt)
Функция имеет следующие параметры:
- р — полиномиальное выражение переменных х и у задающее алгебраическую кривую;
- opt — параметр, который может быть записан в форме приведенных ниже выражений:
- showArrows = true или false — задает показ стрелок касательных или перпендикулярных к точкам вдоль кривой (по умолчанию false);
- arrowIntervalStep = posint — задает число точек, пропускаемых до показа очередной пары стрелок (по умолчанию 10);
- arrowScaleFactor = positive — задает масштаб для длины стрелок (по умолчанию 1);
- colorOfTangentVector = с — задает цвет касательных стрелок, по умолчанию заданный как зеленный, COLORCRGB,0,1,0);
- colorOfNormalVector = с — задает цвет перпендикулярных стрелок, по умолчанию заданный как красный, COLOR (RGB ,1,0,0);
- colorOf Curve = с — задает цвет кривой, по умолчанию заданный как синий, COLOR(RGB, 0, 0, 1);
- eventTolerance = positive — задает погрешность при представлении сингулярных точек (по умолчанию 0,01);
- NewtonTolerance = positive — задает погрешность при выполнении ньютоновских итераций в ходе построений.
Функция plot_real_curve вычисляет и строит алгебраическую кривую по точкам и может (при использовании параметра opt) строить стрелки-векторы по касательным и перпендикулярным направлениям к каждой точке или к части точек. Возможно задание разных цветов для кривой и стрелок. Применение функции plot_real_curve показывает рис. 16.8.
При задании построения стрелок касательные стрелки строятся по внешней части кривой и указывают направление ее построения. Перпендикулярные стрелки строятся по внутренней части кривой. Нетрудно заметить, что острие стрелки указывается только для длинных стрелок. Короткие стрелки острия не имеют и отображаются как отрезки прямых линий. Построение стрелок оказывается не вполне точным, если разнятся масштабы графика по горизонтали и вертикали, что можно подметить при внимательном рассмотрении графика на рис. 16.8, сверху.
Рис. 16.8. Примеры применения функции plot_real_curve
37.gif
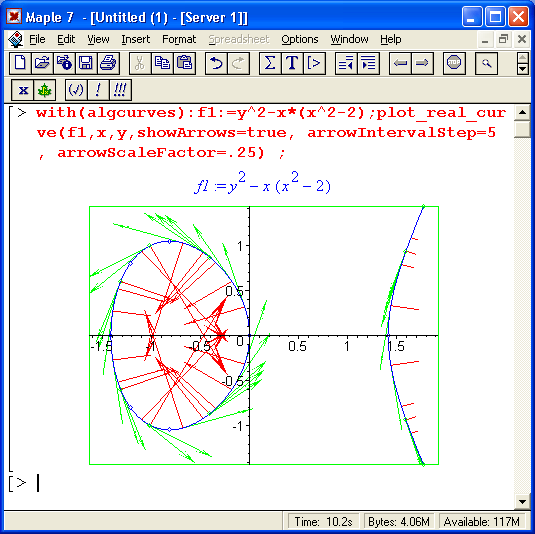
13. Пакет функций теории графов networks
Пакет функций теории графов networks
Графы широко используются при решении многих прикладных и фундаментальных задач. Пользователей, занятых решением таких задач, наверняка порадует пакет networks, содержащий весьма представительный набор функций:
> with(networks);
Warning, the names diameter, draw and vertices have been redefined[acycpoly, addedge, addvertex, adjacency, allpairs, ancestor, arrivals,bicomponents, charpoly, chrompoly, complement, complete, components, connect, connectivity, contract, countcuts, counttrees, cube,cycle, cyclebase, daughter, degreeseq, delete, departures, diameter,dinic, djspantree, dodecahedron, draw, duplicate, edges, ends,eweight,flow,flowpoly,fundcyc, getlabel, girth, graph, graphical,gsimp,gunion,
head, icosahedron, incidence, incident, indegree, induce, isplanar,maxdegree, mincut, mindegree, neighbors, new, octahedron, outdegree,path,petersen, random, rank, rankpoly, shortpathtree, show,shrink, span, spanpoly, spantree, tail, tetrahedron, tuttepoly, vdegree,vertices, void, vweight]
Объективности ради надо отметить, что в Maple 7 из этого пакета удалено несколько второстепенных функций, которые были в версии Maple V R5. Теория графов используется достаточно широко даже при решении прикладных задач — например, для вычисления оптимальных маршрутов движения железнодорожных составов, наиболее целесообразной раскройки тканей и листов из различных материалов и т. д.
14. Примеры применения пакета networks
Примеры применения пакета networks
Рассмотрим некоторые избранные функции этого пакета, которые наиболее часто используются при работе с графами. Детали синтаксиса функций можно найти в справочной базе данных Maple 7.
Функции создания графов:
- new — создает пустой граф (без ребер и узлов);
- void — создает пустой граф (без ребер);
- duplicate — создает копию графа;
- complete — создает полный граф;
- random — возвращает случайный граф;
- petersen — создает граф Петерсена. Функции модификации графов:
- addedges — добавляет в граф ребро;
- addvertex — добавляет в граф вершины;
- connect — соединяет одни заданные вершины с другими;
- delete — удаляет из графа ребро или вершину. Функции контроля структуры графов:
- draw — рисует граф;
- edges — возвращает список ребер графа;
- vertices — возвращает список узлов графа;
- show — возвращает таблицу с полной информацией о графе; .
- ends — возвращает имена вершин графа;
- head — возвращает имя вершины, которая является головой ребер;
- tail — возвращает ими вершины, которая является хвостом ребер;
- incidence — возвращает матрицу инцидентности;
- adjacency — возвращает матрицу смежности;
- eweight — возвращает веса ребер;
- weight — возвращает веса вершин;
- isplanar — упрощает граф, удаляя циклы и повторяющиеся ребра, и проверяет его на планарность (возвращает true, если граф оказался планарным, и false — в противном случае).
Функции с типовыми возможностями графов:
- flow — находит максимальный поток в сети от одной заданной вершины к другой;
- shortpathtree — находит кратчайший путь в графе с помощью алгоритма Дейкстры.
Каждая из этих команд имеет одну или несколько синтаксических форм записи. Их можно уточнить с помощью справочной системы. С ее помощью можно ознакомиться и с назначением других функций этого обширного пакета. Проиллюстрируем его применение на нескольких типичных примерах.
На рис. 16.9 показан пример создания Графа, имеющего четыре вершины, и графа Петерсона с выводом их графиков графической функцией draw.
На рис. 16.10 показан другой пример работы с графами — построение графа функцией complete и затем его преобразование путем удаления части вершин. Исходный и преобразованный графы строятся функцией draw.
В третьем примере (рис. 16.11) граф формируется по частям — вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину а с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления «голов» и «хвостов» графа.
В четвертом примере, представленном на рис.,16.12, показано создание графа G2 (его изображение было приведено на рис. 16.10) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и соmр — принимает значение множества, в котором содержатся вершины, по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В заключительной части этого примера показано применение функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.
Рис. 16.9. Построение графов
Рис. 16.10. Преобразование графа удалением части вершин
Рис. 16.11. Формирование графа и определение его «голов» и «хвостов»
Рис. 16.12. Пример вычисления максимального потока и наиболее коротких путей для заданного графа
39.gif
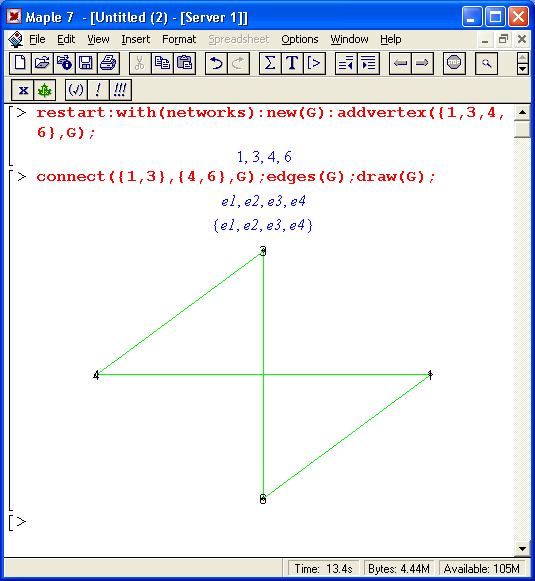
41.gif
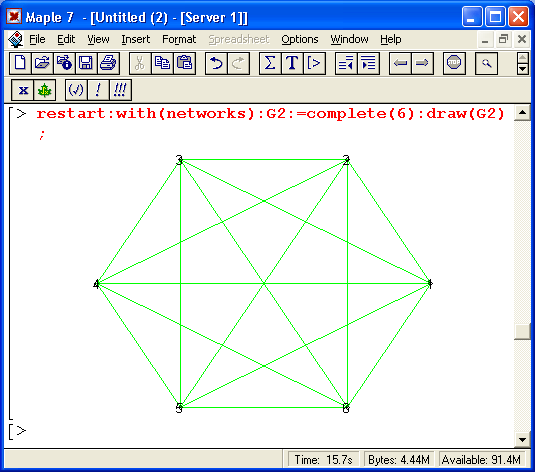
43.gif
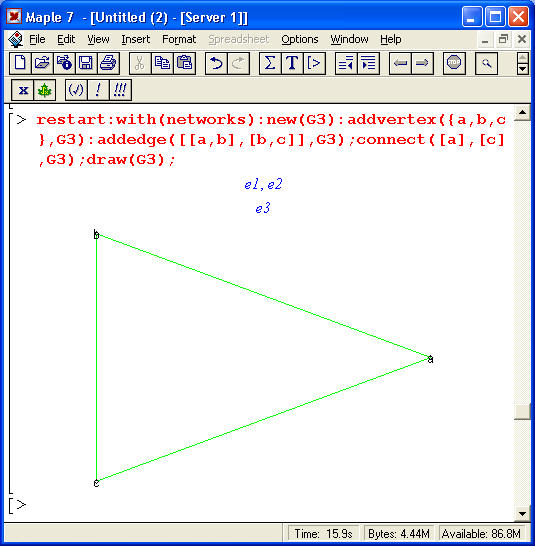
44.gif
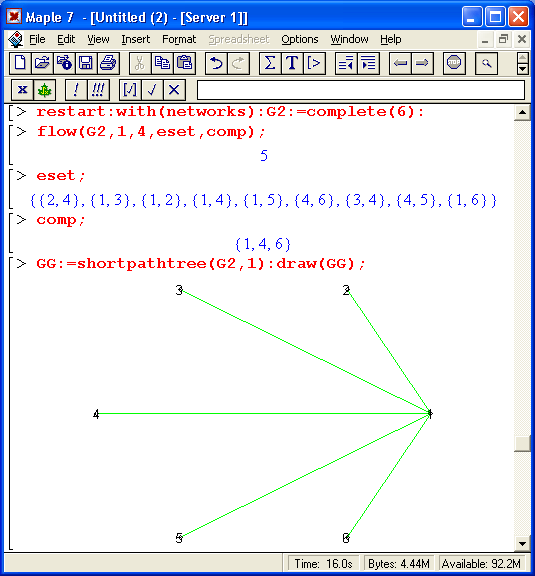
15. Получение информации о графе
Получение информации о графе
Еще один пример, приведенный ниже, иллюстрирует работу функции show, выдающей таблицу с полной информацией о графе, созданном функцией complete:
Разумеется, приведенные примеры далеко не исчерпывают всех задач, которые можно решать с применением графов. Но они наглядно демонстрируют, что для большинства пользователей пакет networks превращает графы из окутанного ореолом таинственности модного средства в простой рабочий инструмент.
15.gif
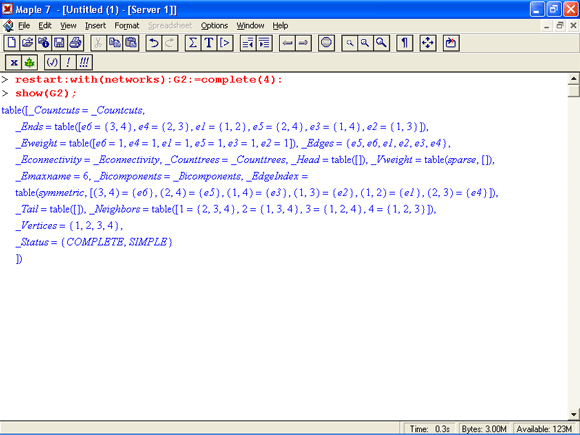
16. Пакет статистических расчетов stats
Пакет статистических расчетов stats
Мир математических систем сейчас насыщен статистическими системами, например такими, как Statistica или StatGraphics. Они прекрасно приспособлены для решения задач статистической обработки обширных массивов данных. Тем не менее проведение статистических расчетов в Maple 7 возможно и в ряде случаев весьма целесообразно — например, когда они являются частью исследовательского проекта.
Пакет stats для таких расчетов представлен всего двумя многоцелевыми статистическими функциями:
stats[subpackage, functionj(args)
subpackage[function](args)
Однако благодаря специальной форме задания параметров (в частности, в виде подпакетов — subpackages) возможно вычисление самых разнообразных статистических функций. Имеются следующие подпакеты:
- anova — вариационный анализ;
- describe — функции распределения вероятности;
- fit — регрессионный анализ;
- random — генерация случайных чисел с различными законами распределения;
- statevalf — вычисление статистических функций и получение оценок для массивов данных;
- statplots — построение графиков статистических функций;
- transform — функции преобразования данных.
17. Генерация случайных чисел с заданным распределением
Генерация случайных чисел с заданным распределением
Основой этого подпакета является функция random:
random[distribution] (quantity,unifarm,method)
или
stats[random, distribution] (quantity,unifofm,method)
где
- distribution — описание закона распределения случайных чисел;
- quantity — положительное число, указывающее на количество получаемых случайных чисел (по умолчанию 1, возможен параметр 'generator');
- uniform — процедура генерации чисел с равномерным распределением или
- ключевое слово 'default' (по умолчанию);
- method — указание на один из трех методов ('auto', 'inverse' или 'builtin').
Возможно задание дискретных и непрерьвных распределений, например binomiald --дискретное биномиальное распределение, discreteumform — дискретное 'равномерное распределение, empirical — дискретное эмпирическое распределение, poisson — дискретное распределение Пуассона, beta — бета-распределение, cauchi — .распределение Коши, exponential — экспоненциальное и др. (есть функции практически для всех известных распределений).
Следующие примеры демонстрируют технику получения случайных чисел с заданным законом распределения;
16.gif
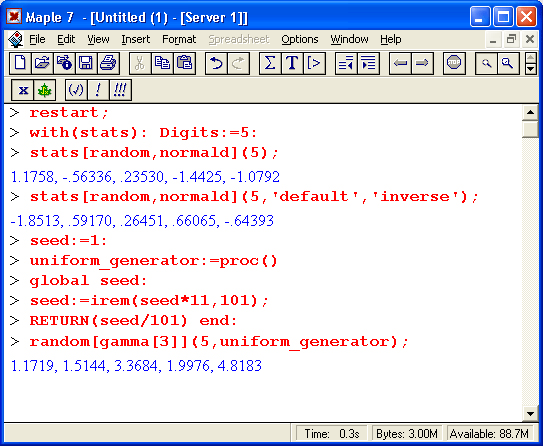
18. Графика статистического пакета stats
Графика статистического пакета stats
Статистический пакет stats имеет свою небольшую библиотечку для построения графиков. Она вызывается в следующем виде:
stats[statplots, function](args)
или
statplots[function](args)
Вид графика задается описанием function: boxplot, histogram, notehedbox, quantile, quantile2, scatterld, scatter2d и symmetry. Данные функции обеспечивают построение типовых графиков, иллюстрирующих статистические расчеты. В качестве примера на рис. 16.13 показано задание множества случайных точек и его отображение на плоскости в ограниченном прямоугольником пространстве.
Рис. 16.13. Создание случайных точек и построение их на плоскости
По равномерности распределения точек можно судить о качестве программного генератора случайных чисел, встроенного в Maple 7.
Довольно часто для визуализации вычислений используется построение гистограмм. Для их создания пакет stats имеет функцию histogram:
stats[statplotsб histogram](data) :
statplots[h1stogram](data)
stats[statplots, histogram[scale](data)
statp1ots[histogram[scale](data)
Здесь data — список данных, scale — число или описатель. Детали применения этой простой функции поясняет рис. 16.14. На нем дан два примера — построение столбцов заданной ширины и высоты и построение гистограммы 100 случайных чисел с нормальным распределением.
Рис. 16.14. Построение гистограмм
Обратите внимание на то, что для второго примера гистограмма будет несколько меняться от пуска к пуску, так как данные для ее построения генерируются случайным образом.
45.gif
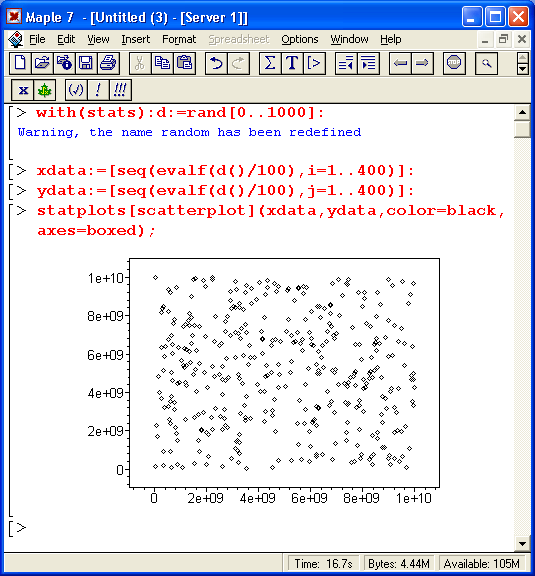
46.gif
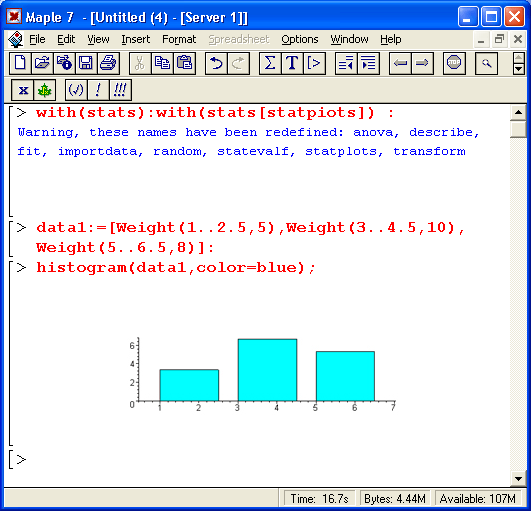
19. Регрессионный анализ
Регрессионный анализ
Под регрессионным анализом (или просто регрессией) обычно подразумевают нахождение некоторой формальной аналитической зависимости, которая приближенно (по критерию минимума среднеквадратической ошибки) аппроксимирует исходную зависимость. Последняя чаще всего бывает представлена некоторым набором точек (например, полученных в результате эксперимента).
Для проведения регрессионного анализа служит функция fit, которая вызывается следующим образом:
stats[fit,leastsquare[vars,eqn.parms]](data)
или
fit[leastsquare[vars,eqn.parms]](data)
где data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями.
На приведенных ниже примерах показано проведение регрессии с помощью функции fit для зависимостей вида у(х):
> with(stats):Digits:=5;
Digits := 5
> fit[leastsquare[[x,y]]]([[l,2,3,4].[3,3.5,3.9,4.6]]);
у = 2.4500 + .52000 х
>fit[leastsquare[[x,y], y=a*x"2+b*x+c]]([[l.2,3.4],[1.8,4.5,10,16.5]]);
2
у = .95000 х + .21000 х + .55000
В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия, и функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией полиномом.
Рисунок 16.15 показывает регрессию для одних и тех же данных Полиномами первой, второй и третьей степени с построением их графиков и точек исходных данных. Нетрудно заметить, что лишь для полинома третьей степени точки исходных данных точно укладываются на кривую полинома, поскольку в этом случае (4 точки) регрессия превращается в полиномиальную аппроксимацию. В других случаях точного попадания точек на линии регрессии нет, но обеспечивается минимум среднеквадратической погрешности для всех точек — следствие реализации метода наименьших квадратов.
Функция fit может обеспечивать регрессию и для функций нескольких переменных. При этом надо просто увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных:
>f:=fit[1eastsquare[[x,y,z],z=-a+b*x+c*y,{a,b,c}]]\
([[l,2,3.5,5],[2.4,6,8.8],[3,5,7,10,Weight(15,2)]]):
f:=z=l + 13/3x-7/6y
> fa:=unapply(rhs(f),x,y);
fa:=(x,y)->l + 13/3x-7/6y
z > fa(1.,2.);
2.999999999
>fa(2,3):
37/6
Рис. 16.15. Примеры регрессии полиномом и первой, второй и третьей степени
В данном случае уравнение регрессии задано в виде z = a + bx + cy. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в не вычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у:
К сожалению, функция fit неприменима для нелинейной регресии. При попытке ее проведения возвращается структура процедуры, но не результат регресии — см. пример ниже:
Для проведения нелинейной регрессии произвольного вида нужно обратиться к средствам нового пакета CurveFitting, включенного в состав Maple 7. Этот пакет был описан в главе 14.
17.gif
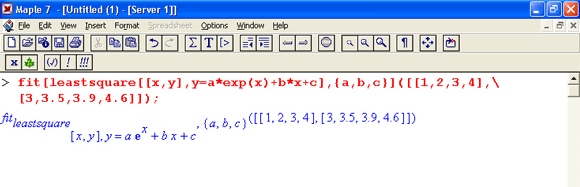
47.gif
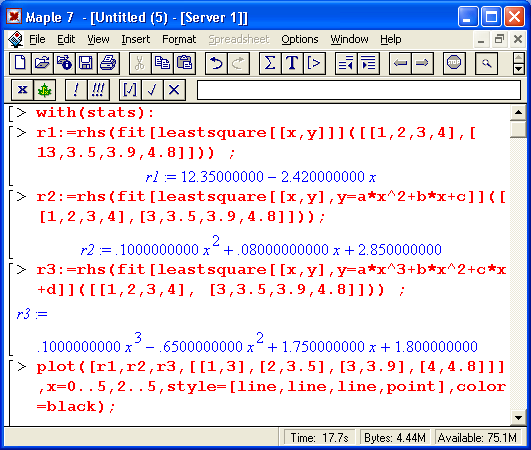
20. Пакет для студентов student
Пакет для студентов student
Пакет student — это, несомненно, один из пакетов, наиболее привлекательных для студентов и аспирантов. В нем собраны наиболее распространенные и нужные функции, которые студенты университетов и иных вузов обычно используют на практических занятиях, при подготовке курсовых и дипломных проектов. Набор этих функций, разумеется, не ограничивается «скромными» потребностями студентов — просто это наиболее распространенные функции, в основном относящиеся к математическому анализу. Наряду со студентами эти функции широко используют профессионалы-математики и ученые, применяющие математические методы в своей работе.
В этом пакете имеется почти полсотни функций:
- D — дифференциальный оператор;
- Diff — инертная форма функции вычисления производной;
- Doubleint — инертная форма функции вычисления двойного интеграла;
- Int — инертная форма функции интегрирования int;
- Limit — инертная форма функции вычисления предела limit;
- Lineint — инертная форма функции вычисления линейного интеграла lineint;
- Point — тестирование объекта на соответствие типу точки (point);
- Product — инертная форма функции вычисления произведения членов последовательности;
- Sum — инертная форма функции вычисления суммы членов последовательности;
- Tripleint — инертная форма функции вычисления тройного интеграла;
- changevar — замена переменной;
- combine — объединение подобных членов;
- completesquare — вычисление полного квадрата (многочлена);
- distance — вычисление расстояния между точками;
- equate — создание системы уравнений из списков, таблицы, массивов;
- extreme — вычисление экстремума выражения;
- integrand — вывод подынтегрального выражения из-под знака инертного интеграла;
- intercept — нахождение точки пересечения двух кривых;
- intparts — интегрирование по частям;
- isolate — выделение подвыражения;
- leftbox — графическая иллюстрация интегрирования методом левых прямоугольников;
- leftsum — числовое приближение к интегралу левыми прямоугольниками;
- makeproc — преобразование выражения в процедуру Maple;
- maximize — вычисление максимума функции;
- middlebox — графическая иллюстрация интегрирования методом центральных прямоугольников;
- middlesum — числовое приближение к интегралу центральными прямоугольниками;
- midpoint — вычисление средней точки сегмента линии;
- minimize — вычисление минимума функции;
- powsubs — подстановка для множителей выражения;
- rightbox — графическая иллюстрация интегрирования методом правых прямоугольников;
- rightsum — числовое приближение к интегралу правыми прямоугольниками;
- showtangent — график функции и касательной линии;
- simpson — числовое приближение к интегралу по методу Симпсона;
- slope — вычисление и построение касательной к заданной точке функции;
- trapezoid — числовое приближение к интегралу методом трапеций;
- value — вычисление инертные функции.
21. Функции интегрирования пакета student.
Функции интегрирования пакета student
В пакетах Maple 7 можно найти множество специальных функций для вычисления интегралов различного типа. Например, в пакете student имеются следующие функции:
- Int(expr,x) — инертная форма вычисления неопределенного интеграла;
- Doubleint(expr,x,y,Domain) — вычисление двойного интеграла по переменным х и у по области Domain;
- Tripleint(expr,x,y,z) — вычисление тройного интеграла;
- intparts(f,u) — интегрирование по частям.
Ниже дан пример применения функции Tripleint пакета student:
Объективности ради надо отметить, что вычисление тройного интеграла с помощью функции Tripleint занимает много времени (около 20 с на компьютере с процессором Pentium II 350 МГц). 'Однако тот же результат (см. последний пример) получается за доли секунды при использовании тройного интегрирования с помощью функции int.
18.gif
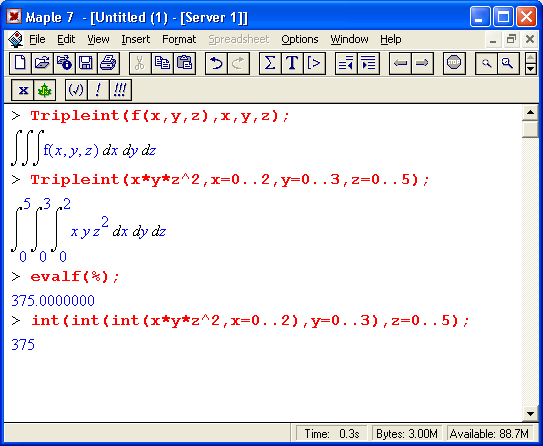
22. Иллюстративная графика пакета student
Иллюстративная графика пакета student
Пакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников:
- leftbox(f(x), x=a..b, о) или leftbox(f(x), x=a..b, n, 'shading'=<color>, о);
- rightbox(f(x), x=a..b, о) или rightbox(f(x), x=a..b, n, о);
- middlebox(f(x), x=a..b, о) или middlebox(f(x), x=a..b, n, o);
Здесь f (x) — функция переменной х, х — переменная интегрирования, а — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — параметры (см. ?plot,options).
Рис. 16.16. Примеры иллюстративной графики пакета student
В этих функциях прямоугольники строятся соответственно слева, справа и по середине относительно узловых точек функции f(x), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х = а для линии, представляющей f(x):
showtangent (f(x), x = а)
Рисунок 16.16 показывает все эти возможности пакета student. Три вида графиков здесь построены в отдельных окнах.
Графические средства пакета student ограничены. Но они предоставляют как раз те возможности, которые отсутствуют в основных средствах построения графиков.
49.gif
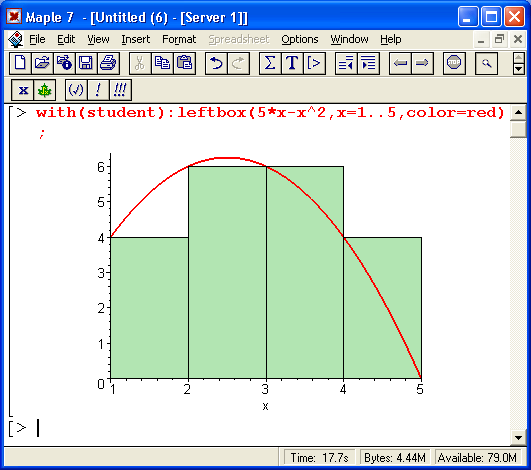
23. Пакет работы с тензорами tensor
Пакет для работы с тензорами tensor
Этот пакет впервые появился в реализации Maple V R5. Он дает средства для работы с тензорами и вычислениями, используемыми в общей теории относительности. В нем использован специальный тип данных tensor_type в виде таблиц с двумя полями: компонентов и характеристик индексов. Поле компонентов — массив с размерностью, эквивалентной рангу объекта. Поле характеристик индексов задается списком чисел 1 и -1. При этом 1 на i-й позиции Означает, что соответствующий индекс контрвариантный, а -1 — что он ковариантный.
Процедура tensor_type возвращает логическое значение true, если ее первый аргумент удовлетворяет свойствам тензора, и false, если он этому свойству не удовлетворяет.
Каждому тензору соответствуют еще две таблицы. Таблица коэффициентов вращения задает коэффициенты вращения Ньюмена—Пенроуза, которые вычисляются функцией tensor[npspin] и индексируются именами греческих букв alpha, beta, gamma, epsilon и т. д. Другая таблица (компонент кривизны) содержит компоненты кривизны Ньюмена—Пенроуза. Они представлены тремя полями: полем Phi в виде массива размерности (0..2.0..2) с компонентами Риччи, поле Psi с массивом размерности (0. .4) с компонентами Вейля и полем R со скаляром Риччи.
Объявление:
> with(tensor);
[Christoffell, Christoffel2, Einstein, Jacobian, Killing_eqns, LevijCivita, Lie_diff, Ricci, Ricciscalar, Riemann, RiemannF, Weyl, act, antisymmetrize, change_basis, commutator,
compare, conj, connexF, contract, convertNP, cov_diff,
create,dlmetric, d2metric, directional_diff, displayGR, display_allGR, dual, entermetric, exteriorjiiff, exterior_prod, frame,geodesic_eqns, get_char, get_compts,get_rank, init, invars, invert, lin_com, lower, npcurve, npspin, partial_diff, permute_indices, petrov, prod, raise, symmetrize, tensorsGR, transform}
дает доступ к следующим функциям пакета:
- Christoffell — вычисление символов Кристоффеля первого рода;
- Christoffel2 — вычисление символов Кристоффеля второго рода;
- Einstein — возвращение тензора Эйнштейна;
- display_alJGR — описывает ненулевые компоненты всех тензоров и параметров, вычисленных командой tensorsGR (общая теория относительности);
- displayGR — описывает ненулевые компоненты конкретного тензора (общая теория относительности);
- Jacobian — Якобиан преобразования координат;
- Killng_eqns — вычисление компонентов для уравнений Киллинга (имеет отношение к симметриям пространства);
- LeviCivita — вычисление ковариантных и контрвариантных псевдотензоров Леви—Чивита;
- Lie_diff — вычисляет производную Ли тензора по отношению к контравариантному векторному полю;
- Ricci — тензор Риччи;
- Ricciscalar — скаляр Риччи;
- Riemann — тензор Римана;
- RiemannF — тензор кривизны Римана в жесткой системе отсчета;
- tensorsGR — вычисляет тензор кривизны в данной системе координат (общая теория относительности);
- Weyl — тензор Вейля;
- act — применяет операции к элементам тензора, таблицам вращений или кривизны;
- antisymmetrize — антисимметризация тензора по любым индексам;
- change_basis — преобразование системы координат;
- commutator — коммутатор двух контравариантных векторных полей;
- compare — сравнивает два тензора, таблицы вращений или кривизны;
- conj — комплексное сопряжение;
- connexF — вычисляет связующие коэффициенты для жесткой системы координат;
- contract — свертка тензора по парам индексов;
- convertNP — преобразует связующие коэффициенты или тензор Римана к формализму Ньюмена—Пенроуза;
- cov_diff — ковариантное дифференцирование;
- create — создает тензорный объект;
- dlmetric — первая частная производная метрики;
- d2metric — вторая частная производная метрики;
- directional_diff — производная по направлению;
- dual — осуществляет дуальную операцию над индексами тензора;
- entermetric — обеспечивает ввод пользователем координатных переменных и ковариантных компонент метрического тензора;
- externor_diff— внешнее дифференцирование полностью антисимметричного ковариантного тензора;
- exterior_prod — внешнее произведение двух ковариантных антисимметричных тензоров;
- frame — задает систему координат, которая приводит метрические компоненты к диагональной сигнатурной матрице (с положительными или отрицательными единицами);
- geodesic_eqns — уравнение Эйлера—Лагранжа для геодезических кривых;
- get_char — возвращает признак (ковариантный/контравариантный) объекта;
- getcompts — возвращает компоненты объекта;
- get_rank — возвращает ранг объекта;
- invars — инварианты тензора кривизны Римана (общая теория относительности);
- invert — обращение тензора второго ранга;
- lincom — линейная комбинация тензорных объектов;
- lower — опускает индексы;
- npcurve — компонента кривизны Ньюмена—Пенроуза в формализме Дебевера (общая теория относительности);
- npspin — компонент вращения Ньюмена—Пенроуза в формализме Дебевера (общая теория относительности);
- partial_diff — частная производная тензора;
- permute_indices — перестановка индексов;
- petrov — классификация Петрова тензора Вейля;
- prod — внутреннее и внешнее тензорные произведения;
- raise — поднятие индекса;
- symmetrize — симметризация тензора по любым индексам;
- transform — преобразование системы координат.
Примеры применения этого пакета можно найти в справочной базе данных системы. Пакет представляет интерес для физиков-теоретиков, работающих в области общей теории относительности и ее приложений/Для них (но не для большинства пользователей) приведенные данные полезны и понятны.
24. Пакет Domains.
Пакет Domains
Этот небольшой пакет служит для создания доменов — таблиц операций для вычислений. При его загрузке появляется сообщение о переопределениях объектов и список из всего лишь шести функций:
>restart;with(Domains):
Domains version 1.0
Initially defined domains are Z and Q the integers and rationale Abbreviations, e.g. DUP for DenseUnivariatePolynomial, also made Warning, the protected names Array, Matrix and Vector have been redefined and unprotected [Array, Matrix, Matrixlnverse, Vector, init, show]
Пакет допускает применение следующих конструкций:
Domains[domain] Doma1ns[evaldomains]
Domains[example] Domains[coding]
Приведенный ниже пример поясняет создание и использование доменов Q (для рациональных
данных) и Z (для целочисленных данных):
> Q['+'](l/2,2/5,3/8);
51/40
> Z[Gcd](660,130);
10
Следующая операция показывает, что домен Z является таблицей:
> type(Z,table);
true
А функция show позволяет вывести полный перечень всех операций, доступных для домена Z:
> show(Z,operations);
Signatures for constructor Z'
note: operations prefixed by -- are not available
*: (Integers,Z) ->Z
* :(Z,Z*) ->Z
+ :(Z,Z*) ->Z
-: (Z,Z) -> Z'
- :Z ->Z
0:Z
1:Z
< :(Z,Z) -> Boolean
<= : (Z.Z) -> Boolean
<> : (Z.Z) -> Boolean
=:(Z.Z) -> Boolean
>: (Z.Z) -> Boolean
>-: (Z.Z) -> Boolean
Abs : Z ->Z
Characteristic : Integers
Coerce : Integers-> Z
Div : (Z.Z) -> Union(Z,.FAIL)
EuclideanNorm : Z -> Integers
Factor : Z -> [Z,.[[Z,Integers]*]]
Gcd : Z* -> Z
Gcdex : (Z,Z,Name) ->Z
Gcdex : (Z,.Z,Name,Name) -> Z
Input : Expression -> Union(Z,.FAIL)
Inv : Z -> Union(Z,FAIL)
Lcm : Z* -> Z
Max : (Z,Z*) -> Z
Min : (Z,.Z*)-> Z
Modp : (Z,.Z) ->Z
Mods : (Z.Z)--> Z
ModularHoraomorphlsm : () -> (Z -> Z.Z)'
Normal : Z -> Z
Output : Z -> Expression
Powmod : (Z,Integers,Z) -> Z
Prime : Z -> Boolean
Quo : (Z,.Z,Name) ->Z
Quo : (Z,.Z) -> Z
Random : О ->Z
RelativelyPrime : (Z,.Z) -> Boolean'
Rem : (Z,.Z,.Name)-> Z
Rera : (Z,Z) -> Z
Sign : Z -> UNIONU,.-l,0)
SmallerEuclideanNorm : (Z,.Z) -> Boolean
Sqrfree : Z ->[Z,.[[Z,.Integers]*]]
Type : Expression -> 'Boolean'
Unit : Z -> Z
UnitNormal : Z -> [Z,.Z,.Z]
Zero : Z -> Boolean
^ : (Z,Integers) -> Z.
Домены позволяют передавать в качестве параметра процедур набор функций в виде единого целою, что и объясняет название этих объектов. Предполагается, что это может привести к заметному сокращению кодов программ вычислений в будущих реализациях системы Maple. Пока же возможности доменов скорее выглядят как очередная экзотика, чем как реальное средство для оптимизации вычислений. Потребуется время, чтобы показать, что это не так.
25. Обзор пакетов узкого назначения
Обзор пакетов узкого назначения
Мы уже не раз обращали внимание читателя на выборочный характер описания системы Maple 7 в данной книге. Хотя она и является одной из самых полных книг по данной системе, книга не претендует на роль детального справочника по Maple 7: Более того, такого справочника в виде книги нет и, вероятно, учитывая быстрые темпы модернизации программы, так и не будет. Для подобного описания Maple пришлось бы подготовить многотомное издание, охватывающее практически все области математики.
Учитывая это, мы вынуждены отказаться от попытки описать ряд пакетов специального назначения. Такими пакетами интересуются серьезные специалисты в области математики и им (не без труда, разумеется) под силу разобраться с назначением функций таких пакетов и примерами их применения, приведенными в справочной системе Maple 7. В связи с выше сказаннным, мы ограничимся перечислением оставшихся неизученными пакетов.
26. Пакет функций теории чисел numtheory
Пакет функций теории чисел numtheory
В этом обширном пакете собрано 46 функций, относящихся к теории чисел:
> with(numtheory);
Warning, the protected rame order has been redefined and unprotected
[GIgcd, bigomega, cfrac, cfracpol, cyclotomic, divisors ;factorEQ,factorset,fermat, imagunit, index, integral_basis, invcfrac, invphi, issqrfree,jacobi, kronecker, Я,legendre, mcombine, mersenne, minkowski, mipolys, mlog, mobius, mroot, msqrt, nearestp, nthconver, nthdenom, nthnumer, nthpow, order,pdexpand, ф,n,pprimroot,primroot, quadres, rootsunity, safeprime, o,sq2factor, sum2sqr, т,thue ]
В новой реализации Maple 7 число функций было уменьшено. Большинство функций этого пакета достаточно просты и заинтересовавшийся читатель вполне в состоянии провести их тестирование самостоятельно.
27. Пакет для работы с р-адическими числами padic
Пакет для работы с р-адическими числами padic
Этот весьма специфический пакет содержит следующие функции для работы с р-адическими числами:
> with(padic);
[arccoshp, arccosp,arccothp, arccotp, arccschp, arccscp, arcsechp, arcsecp, arcsinhp, arcsinp, arctanhp, arctanp, coshp, cosp, cothp, cotp, cschp, cscp, evalp, expansion, expp, Icoeffp, logp, orderp, ordp, ratvaluep, rootp, sechp, seep, sinhp,sinp, sqrtp, tanhp,tanp, valuep]
В Maple 7 число функций этого пакета увеличено почти в четыре раза. Однако ввиду специфичности данных функций их изучение мы оставляем за читателем для самостоятельной работы.
28. Пакет для работы с гауссовыми целыми числами Gausslnt
Пакет для работы с гауссовыми целыми числами Gausslnt
Гауссово целое число — это число вида а + I*b, где а и b — любые целые рациональные числа. Таким образом, они образуют решетку всех точек с целыми координатами на плоскости комплексных чисел. Пакет Gausslnt содержит достаточно представительный набор функций для работы с этими числами:
> with(GaussInt):
Warning, the name GIgcd has been redefined
[GIbasis, Glchrem, GIdivisor, GIfacpoly, GIfacset, GIfactor, GIfactors, GIgcd, GIgcdex, Glhermite, Glissqr, Gllcm, GImcmbine, GInearest, GInodiv, GInorm, Glnormal, Glorder, GIphi, GIprime, Glquadres, Glquo, GIrem, GIroots, GIsieve, GIsmith ,GIsqrfree, GIsqrt, Glunitnormal ]
Нетрудно заметить, что в этот набор входят уже известные числовые функции, к именам которых добавлены буквы 61. Например, функция GIfactor(c) раскладывает гауссово число (в том числе комплексное) на простые множители, GIgcd(cl, с2) находит наибольший общий делитель гауссовых чисел cl и с2 и т. д. Функции этого пакета достаточно просты, так что ограничимся приведенными примерами. Гауссовы целые числа в большинстве научно-технических расчетов встречаются крайне редко. Так что этот пакет рассчитан на специалистов-математиков, работающих в области теории чисел.
29. Пакет алгебры линейных операторов Ore_algebra
Пакет алгебры линейных операторов Ore_algebra
Пакет Ore_algebra содержит набор функций алгебры линейных операторов, состав которого виден после обращения к пакету:
> with(0re_algebra);
[OrejoJDESol, Ore_to_RESol, Orejojdiff, Ore_to_shift, annihilators, applyopr, diff_algebra, poly, algebra, qshiji_algebra, rand_skew_poly, shift_algebra, skew_algebra, skewjslim, skewjgcdex, skewjydiv, skewjxrwer, skew_prem, skew_product]
Этот пакет поддерживает решение задач в области алгебры линейных операторов.
30. Инструментальный пакет для линейных рекуррентных уравнений LREtools
Инструментальный пакет для линейных рекуррентных уравнений LREtools
Этот пакет полезен математикам, часто использующим рекуррентные отношения и формулы. Он дополняет функцию rsolve основной библиотеки и содержит следующие функции: :
> with(LREtools):
[REcontent, REcreate, REplot, REprimpart, REreduceorder, REtoDE,REtodelta, REtoproc, autodispersion, constcoeffsol,
5,dispersion, divconq, firstlin, hypergeomsols, polysols,ratpolysols, riccati, shift]
С назначением функций этого пакета можно познакомиться по справочной системе Maple 7.
31. Пакет функций дифференциальных форм difforms
Пакет функций дифференциальных форм difforms
В пакете дифференциальных форм содержится следующий ряд функций:
> with(difforms);
[&^, d, defform,formpart,parity, scalarpart, simpform, wdegree]
Демонстрационные материалы по применению этого пакета входят в поставку Maple 7.
32. Пакет для работы с рациональными производящими функциями genfunc
Пакет для работы с рациональными производящими функциями genfunc
В пакете genfunc, предназначенном для работы с производящими функциями, содержатся следующие средства:
> with(genfunc);
[rgf_charseq, rgf_encode, rgf_expqnd, rgfjindrecur, rgfjiybrid, rgfjiorm, rgf_pfrac, rgf_relate, rgf_sequence, rgf_simp, rgfjerm,termscale]
Эти функции представляют специальный интерес для пользователей, работающих в области теории чисел и рациональных функций.
33. Пакет операций для работы с конечными группами group
Пакет операций для работы с конечными группами group
Этот пакет содержит довольно представительный набор функций для работы с конечными группами:
> with(group);
[DerivedS, LCS, NormalClosure, RandElement, SnConjugates, Sylow,areconjugate, center,
centralizer, core, cosels, cosrep, derived, elements,groiipmember,grouporder, inter, invperm, isabelian, isnormal,issubgroup, mulperms, normalizer, orbit, parity,
permrep, pres, transgroup ]
Функции этого пакета представляют интерес для математиков, работающих в области конечных групп. Но вряд ли они будут полезны большинству пользователей. Тем не менее, наличие таких функций говорит о полноте функциональных возможностей системы Maple 7.
34. Пакет для работы с симметрией Ли liesymm
Пакет для работы с симметрией Ли liesymm
В этом пакете, являющемся реализацией алгоритма Харрисона-Эстабрука, имеется ряд функций:
> withCllesymm);
Warning, the protected name close has been redefined and unprotected
[ c£A,&mod, H,Lie, Lrank, TD, annul, autosimp, close, d, depvars, determine, dvalue, extgen, extvars, getcoeff, getform, hasclosure, hook, indepvars, makeforms, mixpar, prolong, reduce, setup, translate, vfix, wcollect, wdegree, wedgeset, wsubs]
Эти функции достаточно специфичны и могут пригодиться лишь узким специалистам.
35. Пакет команд для решения уравнений SolveTools
Пакет команд для решения уравнений SolveTools
Пакет команд с весьма многообещающим названием SolveTools на самом деле содержит вовсе не средства для решения уравнений, а несколько весьма специфических функций:
> with(SolveTools):
[Basis, Complexity, GreaterComplexity, RationalCoefficients, SortByComplexity]
Функции этого пакета позволяют найти базис выражений, дескрипторы и рациональные коэффициенты. Примеры применения этого пакета очень просты, и с ними несложно ознакомиться. Однако при этом возникает вопрос «Зачем это надо?», который (увы!) остается без ответа.
36. Пакет для работы с таблицами Spread.
Пакет для работы с таблицами Spread
Загрузка этого пакета дает средства для работы с таблицами:
> with(Spread);
{CopySelection, CreateSpreddsheet,, EvaluateCurrentSelection, EvahiateSpreadsheet,
GetCellFormula, GetCellVabe, GetFormulaeMatrix, GetMaxCok, GetMaxRows, GetSelection, GetValuesMatrix, lnsertMatrixIntoSelection , IsStale, SetCellFormula, SetMatrix, SetSelection]
Функции пакета не имеют самостоятельного значения и призвана поддерживать работу с электронными таблицами, которая уже была подробно описана. Они дают такие средства, как создание в документе шаблона таблиц, проведение операций по заполнению и редактированию ячеек таблиц, копированию содержимого таблиц в буфер памяти и т. д. Назначение функций достаточно очевидно из их составных имен.
37. Пакет генерации кодов codegen
Пакет генерации кодов codegen
Пакет codegen представляет собой набор команд, предназначенных для организации взаимодействия системы Maple 7 с другими программными средствами:
> with(codegen);
[С, GRAD, GRADIENT, HESSIAN, JACOB1AN, cost, declare, dontreturn, eqnjortran, homer, intrep2maple,joinprocs, makeglobal, makeparam, makeproc, makevoid, maple2intrep, optim ize, packargs, packlocals, packparams, prep2trans, renamevar, split, swapargs ]
Этот пакет очень полезен программистам, занимающимся разработкой сложных программных комплексов. Пакет позволяет создавать процедуры на языке Maple 7 и транслировать их в программные модули, записанные на других языках программирования, таких как Фортран или Си.
38. Пакет создания контекстных меню context
Пакет создания контекстных меню context
Пакет context служит для создания контекстных меню. Он содержит небольшое число функций:
> with(context):
[buildcontext, clearlabels, defaultcontext,
display, installcontext, restoredefault,
testactions, troubleshoot]
Этот пакет используется довольно редко и в основном пользователями, решающими в среде Maple не вычислительные, а системные задачи. Описание таких задач выходит за рамки данной книги.
39. Пакет организации многопроцессорной работы process
Пакет организации многопроцессорной работы process )
Этот узкоспециализированный пакет содержит ряд функций по организации работы на нескольких процессорах:
> with(process):
[block, ey.ec, fork, kill, pclose, pipe, popen, wait ]
Данные функции представляют интерес для пользователей операционной системы UNIX, так что в проблематику данной книги не входят.
40. Новые пакеты системы Maple 7
Новые пакеты системы Maple 7
Пакет поддержки вычислений с размерными величинами Units
При выполнении большинства вычислений рекомендуется использовать безразмерные величины. Однако в некоторых областях науки и техники, например в физике, широко используются размерные величины, у которых помимо их значения указываются единицы измерения. Довольно развитую поддержку таких расчетов обеспечивает новый пакет расширения системы Maple 7 — Units. Он содержит следующие функции:
> with(Units);
[AddBaseUnit, AddDimension,AddSystem, AddUnit, Converter, GetDimension, GetDimensions, GetSystem, GetSystems, GetUnit, GetUnits, HasDimension, HasSystem, HasUnit, Natural, RemoveDimension, RemoveSystem, Standard, Unit, UseContexts, UseSystem, UsingContexts, UsingSystem]
Большинство функций этого пакета достаточно просты и даже очевидны. В связи с этим ограничимся несколькими характерными примерами их применения:
19.gif

41. Пакет для работы с рядами ортогональных многочленов OrthogonalSeries.
Пакет для работы с рядами ортогональных многочленов OrthogonalSeries
Новый пакет для работы с рядами ортогональных многочленов OrthogonalSeries имеет довольно представительный набор функций:
> with(OrthogonalSeries);
[Add, Apply Operator, ChangeBasis, Coefficients, ConvertToSum, Copy, Create, Degree, Derivate, DerivativeRepresentation, Evaluate, Getlnfo, Multiply, PolynomialMultiply, ScalarMultiply, SimplifyCoefficients, Truncate]
Поскольку этот пакет представляет интерес в основном для опытных математиков, мы не будем рассматривать его функции (в целом достаточно простые) подробно и ограничимся несколькими примерами. В следующем примере с помощью функции Create создается бесконечный ряд с ортогональным многочленом Эрмита в составе базового выражения ряда:
В другом примере показано представление полиномиального выражения в новом базисе с ортогональными многочленами Чебышева с помощью функции ChangeBasis:
Обратите внимание на то, что новое выражение после исполнения команды Evaluate приняло вид исходного выражения.
Следующий пример демонстрирует создание ряда на основе ортогональных многочленов Чебышева и его копирование с помощью функции Сору:
> S:=Create((-irn/n!,ChebyshevT(n,x));
Вычисление производной от ряда с ортогональными многочленами представлено ниже:
Еще один пример демонстрирует операцию скалярного умножения ряда с помощью функции ScalarMultiply:
Приведенные примеры показывают, что применение этого пакета достаточно просто. С деталями (порой довольно многочисленными) применения функций этого пакета можно познакомиться по справке на данный пакет.
20.gif

21.gif
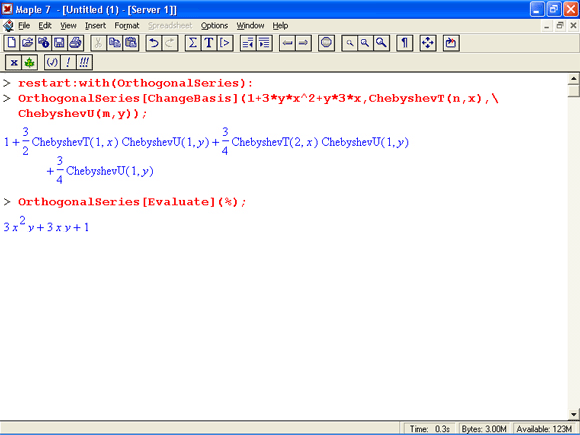
22.gif
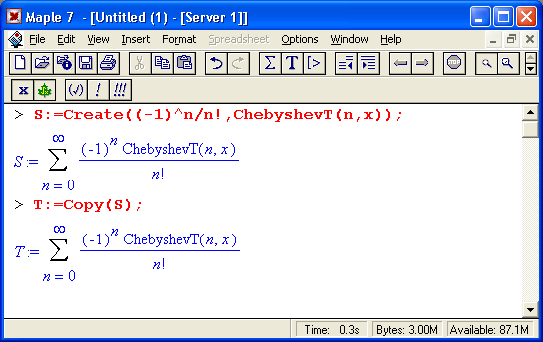
23.gif
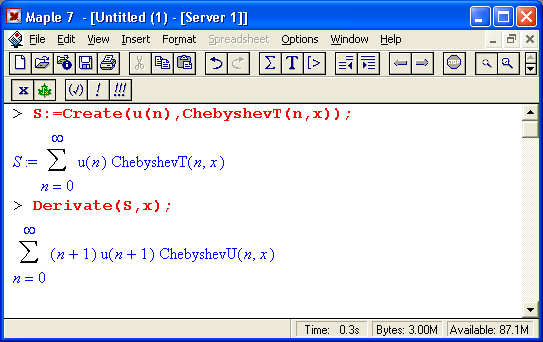
24.gif
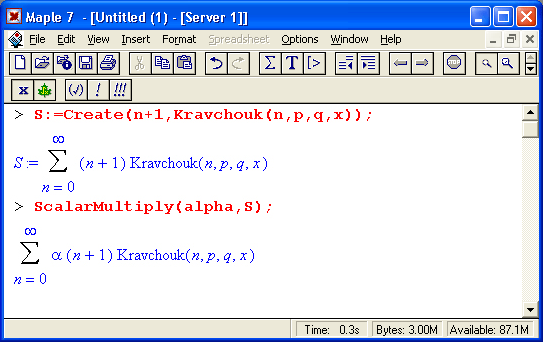
42. Пакет поддержки стандарта MathML
Пакет поддержки стандарта MathML
Для представления математической информации на страницах Интернета в последние годы был создан специальный язык MathML. Пока для большинства пользователей MathML — просто «экзотика», но так как наряду с XML его поддерживает World Wide Web Consortium, его вынуждены поддерживать все солидные фирмы — причем не только создающие системы Компьютерной математики. Среди них такие крупные корпорации, как Intel, IBM и Microsoft. В Maple 7 предусмотрена новая возможность поддержки стандарта MathML 2.O. Для такой поддержки используются MathML Viewer (см. урок 2) и пакет MathML.
Пакет MathML дает минимальный набор функций для использования языка MathML:
> with(HathML);
[Export, ExportContent, ExportPresentation, Import, ImportContent]
В нем всего 5 функций, что позволяет разобрать их достаточно детально. Первые три функции служат для экспорта выражений:
- Export(expr) — преобразует Maple-выражение ехрr в параллельное MathML-выражение;
- ExportContent (expr) — преобразует Maple-выражение ехрr в MathML-выра-жение в формате содержания;
- ExportPresentation (ехрr) -преобразует Maple-выражение expr в MathML-выражение в формате представления.
Еще две функции служат для импорта строки в формате MathML и его преобразования в Maple-выражение:
Import(mnlstring) и ImportConterrt(mmlstnng)
Следующий пример наглядно иллюстрирует применение функций пакета расширения MathML для преобразования математического выражения а*х+b вначале в запись на MathML, а затем преобразование этой записи str в Maple-выражение:
> str:=MathML[Export]
( а*х + b );
str := "<math xmlns-http://www.w3.org/1998/Math/MathML'> <semanticsXmrow xrfe f='id5'xmrow xref='id3'xnii xref='idl '>a</mi><mo>⁢</moXml xref='id2'>x</mi></mrowxmo>+</mo><mixref='id4'>b</mi>
</mrowXannotati on-xml encodrag='MathML-Content'><apply id='id5'><plus/><apply id='id3'xtft mes/xci id='idl'> a</ci><ci id='id2'>x</cix/applyxci id='id4'>b</ci></apply>\ </annotation-xml> <annotationencoding='Maple'> a*x+b </annotationx/semantics\ ></math>" > Import(str):a x + b
Этот пример показателен тем, что дает представление о виде записей на языке MathML. Нетрудно заметить, что это достаточно громоздкий язык. Функции, представленные выше, автоматизируют процесс составления записей на языке MathML обычных математических выражений, что делает доступной для обычных пользователей подготовку публикации в Интернете, содержащей математические выражения.
43. Пакет XMLTools
Пакет ХМLTools
В Maple 7 резко расширены средства интеграции с Интернетом. Это сделано не только на уровне специфических для математических приложений средств, таких как рассмотренный выше пакет MathML, но и на уровне обычных языков сети, таких как HTML и XML.
Пакет XMLTools служит для поддержки средств языка XML. Этот пакет предоставляет весьма внушительное число функций для этого:
> with(XMLTools):
[AddAttribute, AddCfiild, AttrCont, AttributeCount, AttributeNames, AttributeValue, AttributeValueWithDefault, Attributes, CData, CDataData, CleanXML, Comment,
CommentText, ConfentModel, ContentModelCount, Element,
ElementName, ElementStatistics,Equal, FirstChild, FromString, GetAttribute, GetChild, HasAttribute, HasChild,
IsCData, IsComment, IsElement, IsProcessinglnstruction,
IsTree, JoinEntities, LastChild, MakeElement, Print, PrintToFile, PrintToString, ProcessAttributes, ProcessingInstruction, ProcessinglnstructionData, ProcessinglnstructionName, ReadFile, RemoveAttribute, RemoveAttributes, RemoveChild, RemoveContent, SecondChild, Select Attributes, SelectContent, SelectRemoveAttributes, SelectRemoveContent, SeparateEntities, Serialize,
Strip Attributes, StripComments, SubsAttribute, SubsAttributeName, ThirdChild, ToString, WriteFile]
Рассмотрение этих средств (как и средств поддержки HTML) далеко выходит за пределы тематики данной книги, хотя многие из них достаточно просты. Поэтому ограничимся единственным примером применения функции Print для получения программы на языке XML соответствующей программе задания выражения, рассмотренного в предшествующем разделе:
> XMLTools[Print](К );
<math xmlns='http://www.w3.org/1998/Math/MathML1>
<semantics>
<mrowxref='id5'>
mrowxref='id3'>
<mixref='idl'>a</mi>
<mo>⁢</mo>
<mixref='id2'>x</mi>
</mrow> <mo>+</mo>
<mixref='ld4'>b</m1>
</mrow>
<annotation-xml encoding='MathML-Content'>
apply id='id5'>
<plus/>
<apply id='id3'>
<times/>
<ci id='idl'>a</ci>
<ci id='id2'>x</ci>
</apply>
<cild='id4'>b</ci>
</apply>
</annotation-xml>
<annotat1on encoding='Maple'>a*x+b</annotation>
</semantics>
</math>
44. Пакет создания внешних программ ExternatCaUing
Пакет создания внешних программ ExternalCalling
Пакет ExternalCalling служит для создания внешних программ, записанных на языке Maple (или C++). Состав пакета представлен небольшим числом функций:
- DefineExternal(fn,extlib) — используя функцию define_external, Maple 7 задает внешнюю функцию fn в таблице функций внешних библиотек extlib;
- External LibraryName (basename, precision) — задает имя basename функции и точность вычислений precision для функции внешней библиотеки.
Детальное знакомство с этим пакетом мы опускаем. Заинтересованный читатель найдет нужные сведения в справке по этому пакету.
45. Пакет линейных операторов LinearOperators
Пакет линейных операторов Linear-Operators
Пакет линейных операторов LmearOperators — новый пакет, содержащий средства для работы с линейными операторами. Состав пакета виден из его вызова:
> with(LinearOperators);
[Apply, DEToOrePoly, FactoredAnnihilator, FactoredGCRD,
FactoredMinimalAnnihilator,FactoredOrePolyToDE, FactoredOrePolyToOrePoly, FactoredOrePolyToRE, IntegrateSols, MinimalAnnihilator, OrePolyToDE, OrePofyToRE, REToOrePoly, dAlembertianSolver}
Набор функций пакета достаточно представителен. Но, поскольку область применения пакета весьма специфична, рекомендуется знакомиться с его возможностями по справкам на его функции и обзорной статье по нему, имеющейся в обзоре новых пакетов расширения Maple 7 (также размещенной в справочной базе данных пакета).
46. Пакет для работы со случайными объектами RandomTools
Пакет для работы со случайными объектами RandomTools
Пакет для работы со случайными объектами RandomTools служит для расширения базовых возможностей системы Maple 7 (для большинства пользователей и так вполне достаточных) в части генерации различных случайных объектов, таких как числа различных форматов, векторов, матриц, строковых символов, таблиц и т. д. Они образно названы Flavor (в буквальном переводе «букет (вина)»), что подчеркивает возможную сложность структуры создаваемых объектов.
Пакет представлен небольшим числом основных функций:
> with(RandomTools);
[AddFlavor, Generate, GetFlavor, GetFlavors, HasFlavor, RemoveFlavor]
Однако функции AddFlavor и Generate могут использоваться с внушительным набором типов случайных объектов:
|
Choose |
complex |
exprseq |
float |
identical |
|
Integer |
list |
listlist |
negative |
negint |
|
Nonnegative |
nonnegint |
nonposint |
nonpositive |
nonzero |
|
Nonzeroint |
polynom |
posint |
positive |
rational |
|
Set |
structured |
truefalse |
|
|
Действие большинства из них вполне очевидно из названий. Основной функцией является функция генерации случайных объектов Generate(expr). Если тип объекта не задан (например, функцией AddFlavor), то использование функции Generate будет порождать сообщение об ошибке. Примеры применения функций представлены ниже:
Функция GetFlavor(flvr) представляй случайный объект (или объекты) в форме процедуры:
> AddF1avor(a = rand(1..20)):
Generate(a):
15
> GetFlavor(a);
procO localt; global_seed;
_seed := irem(ax_seed,p);
t :=_seed;
toconcats do_seed:=irem(ax_seed,p);
t := sxt + _seed end do ;
irem(t, divisor) +offset endproc
> GetFlavor(integer);
module () localDefaults;
exportMain;
end module
Другая функция GetFlavors () возвращает все типы случайных объектов:
> GetFlavorsO;
a, alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Функция HasFlavor(flvr) служит для проверки наличия объекта данного типа в списке типов объектов, а функция RemoveFl avor(f1vr) — для удаления типа объекта. Следующие примеры иллюстрируют применение этих функций:
> HasFlavor(a):
true
> RemoveFlavor(a);
> HasFlavor(a):
false
> GetFlavors();
alphachar, choose, complex, exprseq, float, integer, list, listlist, negative, negint, nonnegative, nonnegint, nonposint, nonpositive, nonzero, nonzeroint, polynom, posint, positive, rational, set, string, truefalse
Обратите внимание на то, что после уничтожения объекта типа а он исчез из списка, выводимого функцией GetFlavors. Этот пакет, несмотря на довольно специфические возможности, наверняка будет полезен тем читателям, которые всерьез заняты реализацией «продвинутых» методов Монте-Карло, основанных на моделировании случайных объектов и ситуаций. Он служит серьезным дополнением к пакету статистических расчетов stats, описанному в этом уроке выше.
25.gif
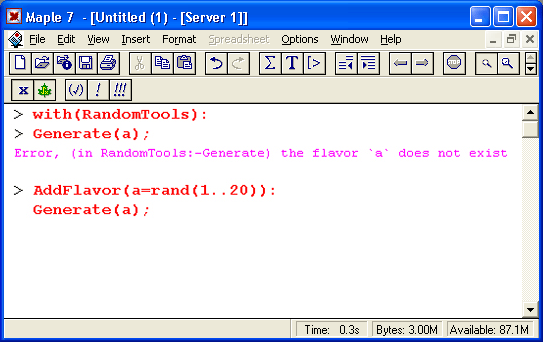
26.gif
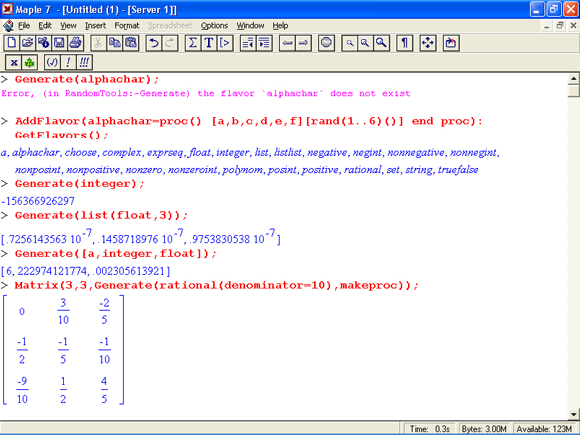
47. Пакет для работы со списками ListTools
Пакет для работы со списками ListTools
Новый пакет ListTools содержит ряд полезных команд для работы со списками. Их набор представлен ниже:
> with(ListTools):
Warning, the assigned name Group now has a global binding
[BinaryPlace, BinarySearch, Categorize, DotProduct, FindRepetitions, Flatten, FlattenOnce, Group, Interleave, Join, JoinSequence, MakeUnique, Pad, PartialSums, Reverse, Rotate, Sorted, Split, Transpose ]
Пакет содержит набор известных функций для работы со списками, например скалярного умножения списков, их обращения, транспонирования, поворота, объединения и т. д. Ограничимся примером на вычисление скалярного произведения векторов:
> L := [0., .84, .91, .14, -.76, -.96, -.28, .66, .99, .41, -.54]:
L := [0., .84, .91, .14, -.76, -.96, -.28, .66, .99, .41, -.54]
> М := [1., .54, -.42, -.99, -.65, .28, .96, .75, -.15, -.91, -.84];
М:= [ 1., .54, -.42, -.99, -.65, .28, .96, .75, -.15, -.91, -.84]
> DotProduct(L, L):
5.0063
> DotProduct(L, M):
.3162
Другие новые пакеты, CurveFitting и LinearFunctionalSystem, мы рассмотрели ранее достаточно подробно (см. уроки 14 и 15). В целом надо отметить, что состав пакетов Maple 7 существенно расширен по сравнению с предшествующими версиями системы. В то же время все пакеты, вошедшие в состав Maple 6, сохранены в новой версии программы — Maple 7, что гарантирует полную совместимость с ней. Практически это было подтверждено проверкой всех (а их многие сотни) примеров применения системы Maple 6 применительно к новой версии Maple 7.
48. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Применять пакет решения задач оптимизации simplex.
- Использовать пакет двумерной геометрии geometry.
- Избранно применять пакет трехмерной геометрии geom3d.
- Использовать пакет для работы с алгебраическими кривыми algcurves.
- Строить и модернизировать графы с помощью пакета networks.
- Использовать возможности пакета статистических расчетов stats.
- Применять пакет для студентов student.
- Использовать средства поддержки MathML.
- Использовать средства ряда новых пакетов Maple 7.
Урок 17. Примеры решения научно-технических задач
1. Небольшое введение
Урок 17.
Примеры решения научно-технических задач
Выше при изложении данного учебного курса приводились многие сотни примеров применения системы Maple 7. При этом намеренно подбирались достаточно простые примеры, занимающие немного места и не требующие чрезмерных ухищрений для решения.
Многие читатели полагают, что системы компьютерной математики хорошо работают на таких простых примерах, но от них мало толку при решении реальных задач математики, физики или радиоэлектроники. Это, конечно, заблуждение. Дело просто в том, что при решении таких задач руководящая роль пользователя сильно возрастает. Вы должны понимать, что не Maple 7 решает вашу задачу, а вы! И система Maple 7 лишь помогает в этом трудном деле. Так что при неудачах в решении своих специфических задач следует прежде всего пенять на себя и на свое незнание возможностей системы Maple 7, а вовсе не на свою помощницу.
В том, что Maple можно успешно использовать при решении вполне конкретных научных и практических задач, призваны убедить примеры, приведенные ниже. Разумеется, и их нельзя отнести к таким сложнейшим задачам, как проектирование ядерного реактора или расчет траектории полета космического корабля, — не стоит забывать, что такие расчеты делают на суперкомпьютерах, а не на домашнем компьютере, который стоит перед вами. И объем материалов по сопровождению и результатам таких расчетов многократно превосходит объем всей этой книги. Тем не менее в этом уроке вы встретите решение вполне реальных и полезных задач в области математики, физики и радиоэлектроники. Почему не в механике, гидродинамике или в оптике? Да потому, как верно сказал наш народный пророк Козьма Прутков: «нельзя объять необъятное». Приведенные примеры отчасти обусловлены личными пристрастиями автора, но они полезны каждому пользователю, желающему всерьез оценить возможности Maple 7.
Описанные в этом уроке задачи являются реальными документами, созданными и отлаженными в среде Maple 7 и лишь затем перенесенными в рукопись книги. Так что они заодно служат примерами того, как надо оформлять такие документы. В то же время от некоторых «излишеств» оформления (например, закрывающихся и открывающихся секций) мы отказались, дабы не усложнять описание документов явно второстепенными деталями. Начнем этот урок с решения весьма актуальной для многих областей применения математики задачи — аппроксимации сложной функции.
2. Выбор аппроксимации для сложной функции
Выбор аппроксимации для сложной функции
Задание исходной функции и построение ее графика
Трудно представить себе область более широкую и>й6читаемую, чем аппроксимация различных функциональных зависимостей. С получения простой аппроксимации сложной зависимости нередко начинаются (а часто и заканчиваются) научные исследования во многих областях как прикладной, так и фундаментальной науки. Покажем возможности в этом системы Maple 7 на одном из примеров, давно помещенных в библиотеку пользователей системы Maple V R2, и переработанных для Maple 7.
Воспользуемся возможностями пакета numapprox, для чего прежде всего подключим его:
> restart:with(numapprox):
[chebdeg,chebmult,chebpade,chebsort,chebyshev, confracform,hermite_pade,hornerform, infnorm,laurent,minimax,pade,remez]
Будем искать приемлемую аппроксимацию для следующей, отнюдь не простой, тестовой функции:
График этой функции представлен на рис. 17.1. С первого взгляда — это простой график, но тут как раз тот случай, когда простота обманчива. Вы сразу Заметите, что график строится необычно медленно, поскольку в каждой из множества его точек системе Maple 7 приходится вычислять значение интеграла с подынтегральной функцией, содержащей довольно каверзную гамма- функцию. И делает это Maple 7 по сложному и медленному алгоритму адаптивного численного интегрирования.
Рис. 17.1. График аппроксимируемой функции
Итак, вычисление f(x) по ее интегральному представлению совершенно не эффективно. Наша цель состоит в разработке процедуры вычислений, которая дала бы 6 точных цифр результата в интервале [0..4] и требовала, по возможности, наименьшего числа арифметических операций для каждого вычисления. Втайне не вредно помечтать о том, чтобы после аппроксимации время вычислений уменьшилось бы хотя в несколько раз. Что получится на деле, вы увидите чуть позже. А пока войдем в дебри аппроксимации.
1.gif
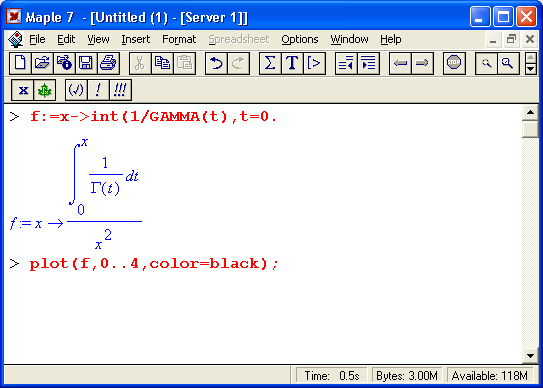
2.gif
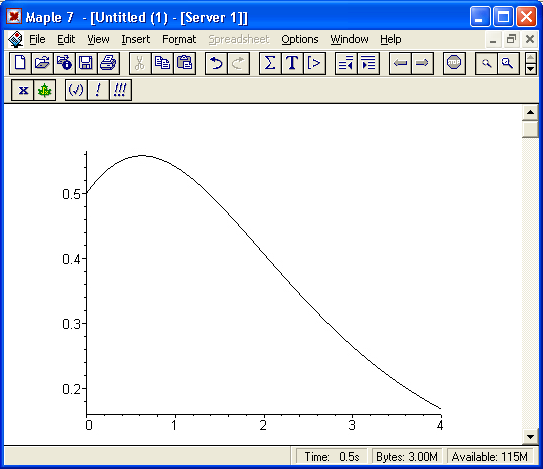
3. Аппроксимации рядом Тейлора
Аппроксимации рядом Тейлора
Начнем с аппроксимации функции хорошо известным рядом Тейлора степени 8 относительно середины интервала (точки с х=2):
Такой ряд позволяет использовать для вычислений только арифметические действия, что само по себе здорово! Для удобства преобразуем аппроксимацию в функцию, чтобы она соответствовала форме, указанной для первоначальной функции f(x). Тогда мы сможем построить график кривой ошибок для аппроксимации полиномом Тейлора:
Кривая ошибок для аппроксимации полиномом Тейлора строится командой:
> plotd(f- TaylorApprox,0..4,.co1or=black);
и имеет вид, представленный на рис. 17.2. Эта кривая нас, прямо скажем, не слишком радует, поскольку погрешность в сотни раз превышает заданную.
Рис. 17.2. Кривая погрешности при аппроксимации рядом Тейлора
Типичное свойство аппроксимации рядом Тейлора состоит в том, что ошибка мала вблизи точки разложения и велика вдали от нее. В данном случае самая большая ошибка имеет место в левой оконечной точке. Чтобы вычислить значение ошибки в точке х =0, что ведет к делению на нуль (см. определение для f(x)), мы должны использовать значение предела:
> maxTaylorError := abs( Limit(f(x), х-0) - ТауlorАрргох(0) );
maxTaylorError := .0015029620
Итак, в самом начале наших попыток мы потерпели полное фиаско. Но отчаиваться не стоит, ибо, как говорят, «даже у хорошей хозяйки первый блин — комом».
3.gif
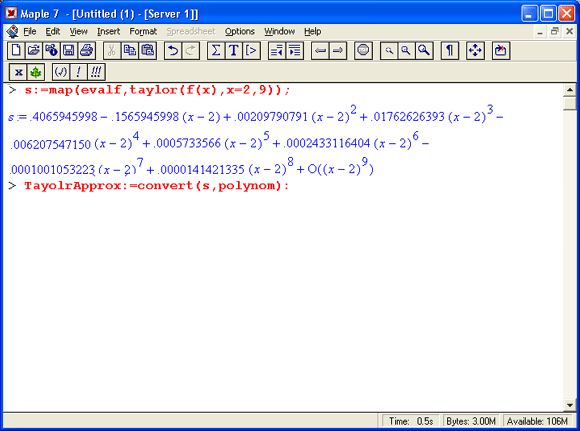
4.gif
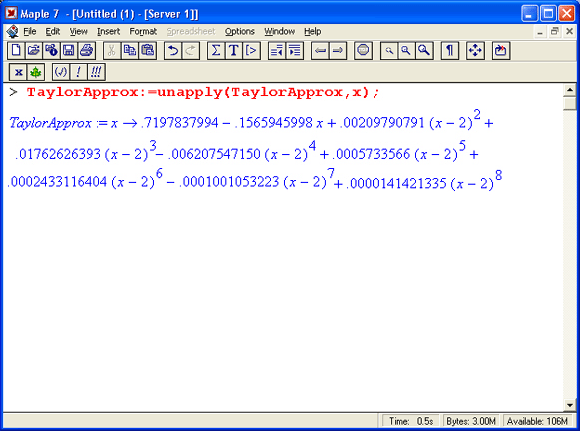
5.gif

4. Паде-аппроксимация
Паде-аппроксимация
Теперь опробуем рациональную аппроксимацию Паде (Fade) функции f(x) степени (4,4). Приближения по этому разложению будут аппроксимировать функцию более точно, и потому ошибки округления в вычислениях станут более заметными. Поэтому зададим еще два дополнительных знака для точности вычислений.
Кривая ошибки для интервала [0, 4] строится командой:
и имеет вид, показанный на рис. 17.3.
Рис. 17.3. Кривая погрешности при Паде- аппроксимации степени (4,4)
Как и при аппроксимации рядом Тейлора, ошибка здесь мала вблизи точки разложения и велика вдали от нее. Мы снова видим из графика, что для указанной функции, самая большая ошибка — в левой оконечной точке. Однако максимальная ошибка в Паде- аппроксимации уже на порядок меньше, чем при аппроксимации полиномом Тейлора:
Это успех, показывающий, что мы на верном пути. Но пока погрешность остается слишком большой по сравнению с заданной.
6.gif
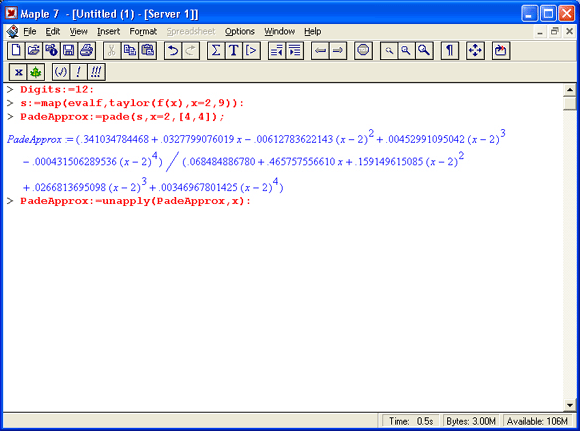
7.gif
8.gif
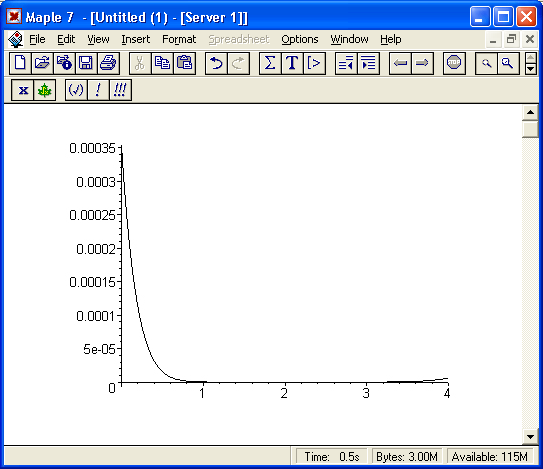
9.gif
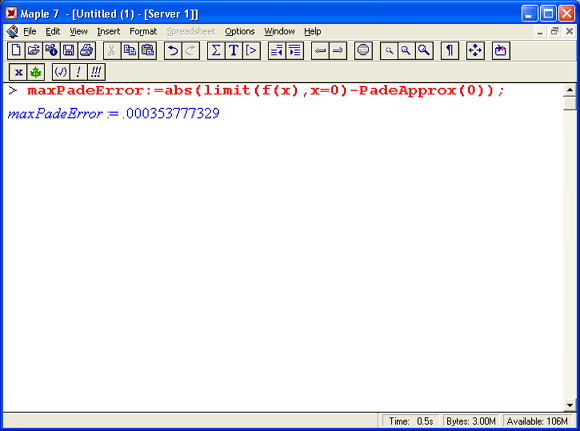
5. Аппроксимация полиномами Чебышева
Аппроксимация полиномами Чебышева
Знатоки техники аппроксимации знают, что лучшие приближения на заданном интервале могут быть получены при использовании разложения в ряд Чебышева. Это связано с тем, что ортогональные полиномы Чебышева позволяют получить аппроксимацию, погрешность которой в заданном диапазоне изменения аргумента распределена более равномерно, чем в предшествующих случаях. Выбросы погрешности на краях интервала аппроксимации в этом случае исключены.
Разложим функцию f(x) на [0, 4] в ряд Чебышева с точностью 1*10-8. Это означает, что все члены с коэффициентами меньше чем эта величина, будут опущены. Такая точность обеспечивается полиномом 13 степени:
Можно проверить для этого примера, что кривая ошибки при аппроксимации рядом Чебышева колеблется. Поскольку ряд Чебышева был оборван на члене 8-й степени (как и полином ряда Тейлора), то максимальная ошибка оказалась равной приблизительно 0,6* 10-5. Эта величина уже на два порядка меньше, чем ошибка при Паде- аппроксимации, вычисленная выше. Но все же немного не дотягивает до наших требований.
Для последующих вычислений полезно заметить, что мы можем использовать процедуру для нахождения численных значений f(x), которая будет намного эффективнее, чем прямое определение, которое требует численного интегрирования для каждого значениях. А именно определим процедуру численной оценки, основанную на разложении в ряд Чебышева степени 13, так как максимальная ошибка при такой аппроксимации меньше чем 10~8, и обеспечивает для нашей цели достаточную точность. Мы определим полином Чебышева Т(х) из пакета orthopoly и затем для эффективной оценки преобразуем его в форму Горнера:
Схема Горнера минимизирует число арифметических операций, заменяя операции возведения в степень операциями последовательного умножения.
10.gif
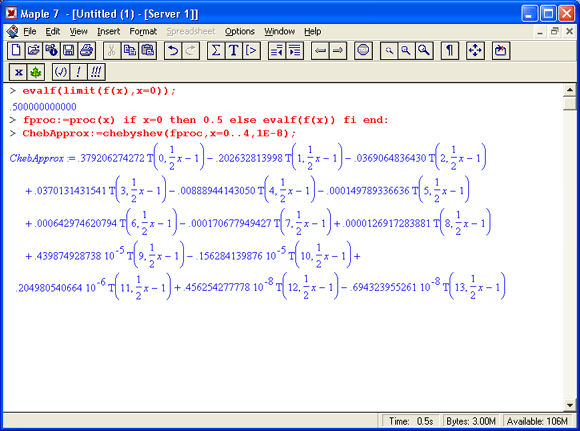
11.gif
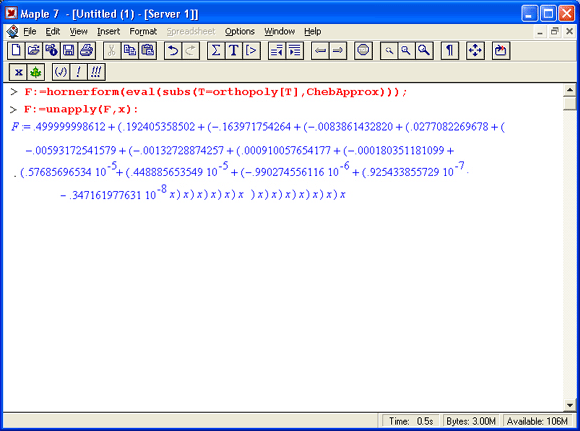
6. Аппроксимация Чебышева-Паде
Аппроксимация Чебышева-Паде
Теперь рассмотрим еще более точную рациональную аппроксимацию Чебышева-Паде. Это такая рациональная функция r[m, n](х) с числителем степени т и знаменателем степени п такой же, как и для разложения в ряд Чебышева. Функция r [m, n](х) согласуется с разложением в ряд Чебышева f(x) членом степени m+n. Мы вычислим аппроксимацию Чебышева-Паде степени (4,4), подобную обычной Паде- аппроксимации, успешно выполненной ранее:
Построим кривую ошибок:
> with(orthopoly, Т):
> plot(F = ChebPadeApprox, 0..4,color=black):
Она представлена на рис. 17.4.
Максимальная ошибка и на этот раз имеет место в левой оконечной точке. Величина максимальной ошибки несколько меньше, чем ошибка при аппроксимации рядом Чебышева. Главное преимущество представления в виде рациональной функции — высокая эффективность вычислений, которая может быть достигнута преобразованием в непрерывную (цепную) дробь (см. ниже). Однако полученная максимальная ошибка чуть-чуть больше заданной:
Рис. 17.4. Кривая ошибки при Паде-Чебышева рациональной аппроксимации
> maxChebPadeError :=abs( F(0) - ChebPadeApprox(O) );
maxChebPadeError= .1236746 10-5
Мы достигли впечатляющего успеха и остается сделать еще один шаг в направлении повышения точности аппроксимации.
12.gif

13.gif
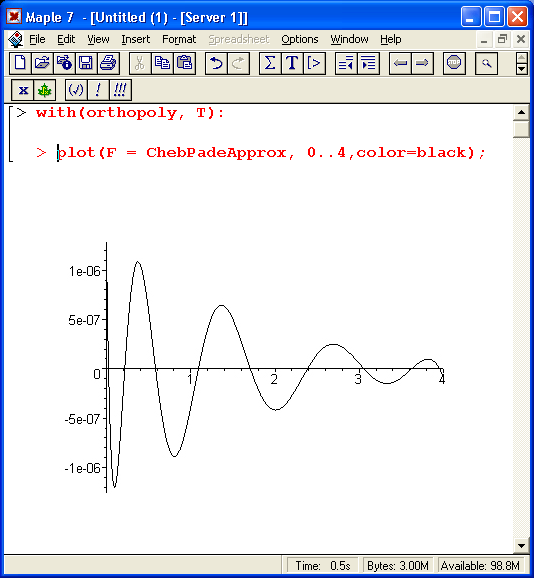
7. Минимаксная аппроксимация
Минимаксная аппроксимация
Классический результат теории аппроксимации заключается в том, что минимакс как наилучшая аппроксимация рациональной функции степени (т, п) достигается, когда кривая ошибки имеет m+n+2 равных по величине колебаний. Кривая ошибки аппроксимации Чебышева-Паде имеет нужное число колебаний, но эта кривая должна быть выровнена (по амплитуде выбросов кривой ошибки) с тем, чтобы обеспечить наилучшее минимаксное приближение. Эта задача решается с помощью функции minimax:
Максимальная ошибка в аппроксимации MinimaxApprox дается значением переменной maxerror. Заметим, что мы наконец достигли нашей цели получения аппроксимации с ошибкой меньшей, чем 1*10-6:
> maxMinimaxError := maxerror;
maxMinimaxError := .585025375366 10-6
Построим график погрешности для данного типа аппроксимации:
> plot(F = MinimaxApprox,0..4,color=black):
График ошибки, представленный на рис. 17.5, показывает равные по амплитуде колебания.
Рис. 17.5. График ошибки при минимаксной аппроксимации
Таким образом, мы добились блестящего успеха в снижении погрешности до требуемого и довольно жесткого уровня. Если бы мы задались целью получить только четыре или пять точных знаков аппроксимации, что в целом ряде случаев вполне приемлемо, то могли бы получить нужный результат гораздо раньше. Нам остается оптимизировать полученную аппроксимацию по минимуму арифметических операций и проверить реальный выигрыш по времени вычислений.
14.gif
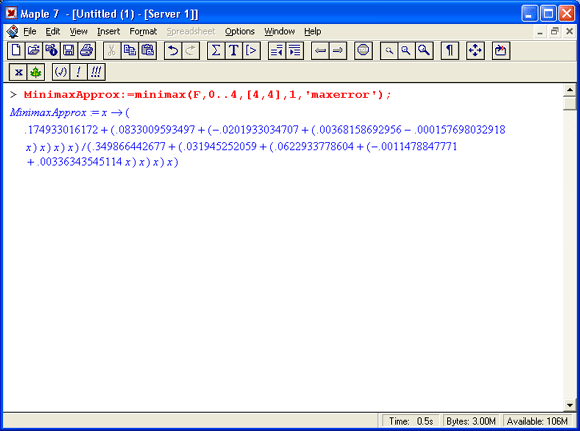
15.gif
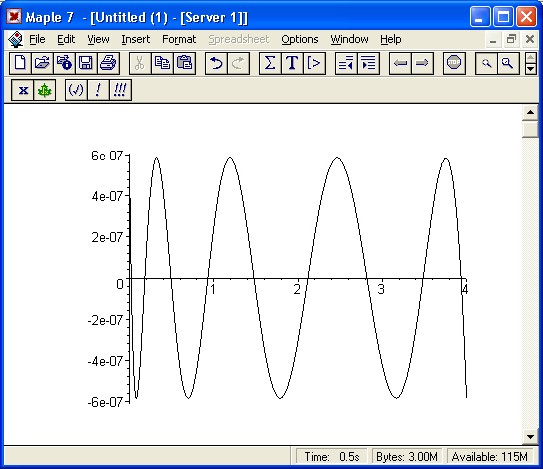
8. Эффективная оценка рациональных функций
Эффективная оценка рациональных функций
Полиномы числителя и знаменателя в минимаксной аппроксимации уже выражены в форме Горнера (то есть в форме вложенного умножения). Оценка полиномом степени п в форме Горнера при n-умножениях и n-суммированиях — это наиболее эффективная схема оценки для полинома в общей форме. Однако для рациональной функции степени (т, п) мы можем делать кое-что даже лучше, чем просто представить выражения числителя и знаменателя в форме Горнера. Мы можем нормализовать рациональную функцию так, что полином знаменателя будет со старшим коэффициентом, равным 1. Мы можем также заметить, что вычисление рациональной функции степени (т, п) в форме Горнера требует выполнения все m+n сложений , m+n-1 умножений и 1 деления. Другими словами, общий индекс действия есть:
- m+n операций умножения/деления;
- m+n операций сложения/вычитания.
Вычисление рациональной функции можно значительно сократить и далее, преобразуя ее в непрерывную (цепную) дробь. Действительно, рациональная функция степени (т, п) может быть вычислена, при использовании только:
- max(m,n) операций умножения/деления;
- m+n операций сложения/вычитания.
Например, если m = n, тогда эта новая схема требует выполнения только поло-, вины числа действий умножения/деления по сравнению с предшествующим методом. Для рациональной функции MlnimaxApprox вычисление в форме, выраженной выше, сводится к 9 действиям умножения/деления и 8 действиям сложения/вычитания. Число операций умножения/деления можно сократить до 8, нормализуя знаменатель к форме monic. Мы можем теперь вычислить непрерывную (цепную) дробь для той же самой рациональной функции. Вычисление по этой схеме, как это можно видеть из вывода Maple, сводятся только к 4 действиям деления и 8 действиям сложения/вычитания:
> MinimaxApprox := confracform(MinimaxApprox):
> lprint(MinimaxApprox(x));
-.468857770747е-1+1.07858705749/(х+4.41994843227+16.1901737091/ (х+4.29121842830+70.1948525272/(х-10.2912843004+ 4.77536150167/(х+1.23883665458))))
9. Сравнение времен вычислений
Сравнение времен вычислений
Теперь определим время, необходимое для вычисления функции/(л:) в 1000 точек, используя первоначальное интегральное определение, и сравним его с временем, требующимся для схемы MinimaxApprox в виде непрерывной дроби. Так как наше приближение будет давать только 6 точных цифр, мы также потребуем 6 точных цифр и от интегрального представления функции:
> Digits :=б: St :=time():
> seq( evalf(f(i/250.0)), i = 1..1000 ):
> oldtime := time() - st;
oldtime-81.805
В процессе вычислений с использованием представления рациональной функции в виде непрерывной дроби иногда требуется внести несколько дополнительных цифр точности для страховки. В данном случае достаточно внести две дополнительные цифры. Итак, новое время вычислений:
> Digits := 8: st := tirae():
> seq( MinimaxApprox(i/250.0), i = 1..1000 ):
> newtime :» time()- st;
newtime:= .694
Ускорение вычисления при аппроксимации есть:
> SpeedUp := oldtime/newtime;
SpeedUp:=U7.S7464
Мы видим, что процедура вычислений, основанная на MinimaxApprox, выполняется почти в 120 раз быстрее процедуры с использованием исходного интегрального определения. Это просто феноменальный успех, полностью оправдывающий время, потерянное на предварительные эксперименты по аппроксимации и ее оптимизации! Разумеется, при условии, что вы будете применять эту аппроксимацию многократно.
10. Преобразование в код Фортрана или С
Преобразование в код Фортрана или С
Один из поводов разработки эффективной аппроксимации для вычисления математической функции заключается в создании библиотек подпрограмм для популярных языков программирования высокого уровня, таких как Фортран или С. В Maple имеются функции преобразования на любой из этих языков. Например, мы можем преобразовывать формулу для минимаксной аппроксимации в код Фортрана.
Итак, нами показано, что правильный выбор аппроксимации для сложной функции обеспечивает уменьшение времени ее вычисления более чем на два порядка (!) при весьма приличной точности в б верных знаков и при использовании для вычислений минимального числа арифметических операций. Применение при этом средств системы Maple 7 позволяет генерировать разложения в различные ряды, быстро вычислять рациональные аппроксимации функций и выполнять преобразования в различные специальные формы, сочетая это с мощными средствами интерактивной работы и графической визуализации, в частности с построением графиков функции и кривых ошибок при разных видах аппроксимации. Все это обеспечивает идеальную среду для решения таких задач.
16.gif
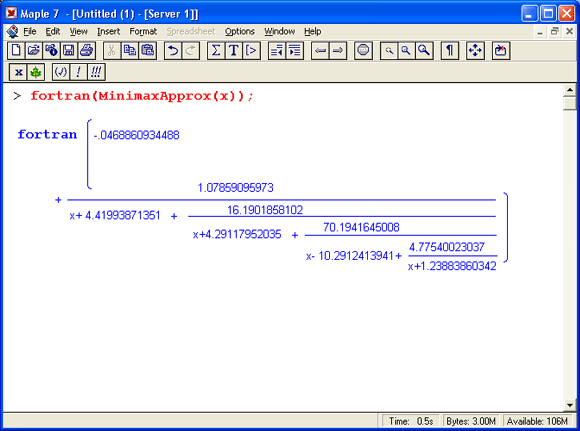
11. Моделирование физических явлений
Моделирование физических явлений
Расчет траектории камня с учетом сопротивления воздуха
Вы хотите метнуть камень в огород вашего вредного соседа? Разумеется, во время его отсутствия. Давайте промоделируем эту ситуацию, предположив два актуальных случая: дело происходит на Луне и на Земле. В первом случае сопротивления воздуха (как и его самого) нет, а в другом — сопротивление воздуха есть и его надо учитывать. Иначе камень упадет в ваш огород, а не в огород соседа!
Итак, пусть подвернувшиеся под руку камни с массой 500 и 100 г брошены под углом 45° к горизонту со скоростью Vo = 20 м/с. Найдем их баллистические траектории, если сила сопротивления воздуха Fтр=А*V, где А=0,1 Н*с/м. Сравним их с траекториями, получающимися без учета сопротивления воздуха.
Начнем с подключения пакета plots, нужного для визуализации данной задачи:
> restart;
> with(plots):
Warning, the name changecoords has been redefined
Составим параметрические уравнения для проекций скорости на оси координат:
> Vox:=Vo*cos(a1pha):Voy:=Vo*sin(alpha):
Vox:= Focos(a)
Voy :=Vo sin(a)
Мы рассматриваем два случая: камень массой 500 г и камень массой 100 г. Поскольку для каждого случая мы предусматриваем расчет в двух вариантах (с учетом сопротивления воздуха и без такого учета), то мы должны составить 4 системы дифференциальных уравнений (ДУ). Каждая система состоит из двух ДУ второго порядка и вид этих систем известен из курса физики. Ниже представлено задание этих систем ДУ (для первой системы дан вывод ее вида):
Зададим исходные числовые безразмерные данные для расчета:
Выполним решение заданных систем ДУ:
Создадим графические объекты — результаты решения систем ДУ:
Построим графики траекторий для первого случая:
Графики траекторий полета камня с массой 500 г представлены на рис. 17.6.
Рис. 17.6. Баллистические траектории камня с массой 500 г
Теперь построим графики траекторий для второго случая:
> display({a3,a4,t1},title='Tpaeкт. полета тела массой 100 г, labels=[x.у], labelfont=[TIMES.ROMAN,14]):
Они представлены на рис. 17.7.
Рис. 17.7. Баллистические траектории камня при массе 100 г
Из проведенных расчетов и графиков видно, что при учете силы сопротивления воздуха дальность и высота полета сильно уменьшаются по сравнению с полетом в вакууме, и эта разница зависит от массы тела, поэтому при небольшой массе тела сопротивлением воздуха пренебрегать нельзя.
17.gif
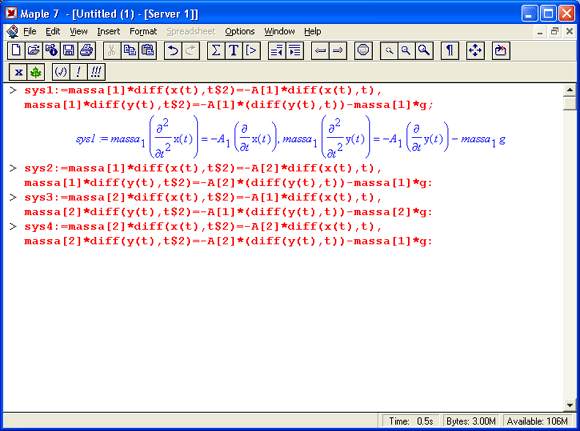
18.gif
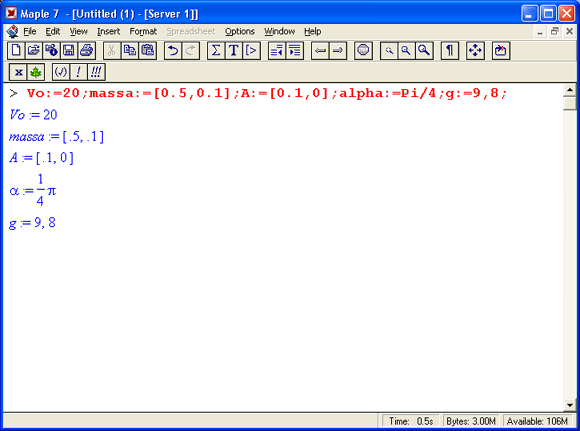
19.gif
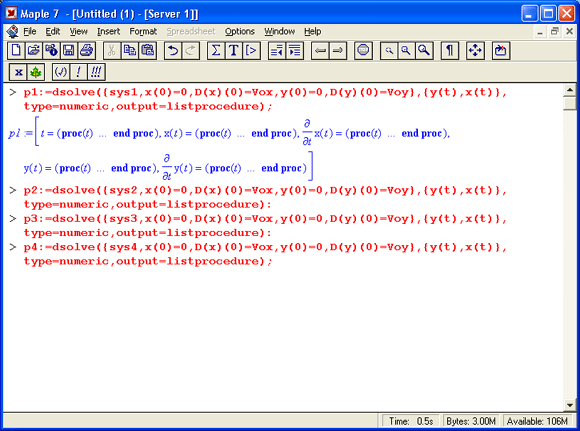
20.gif
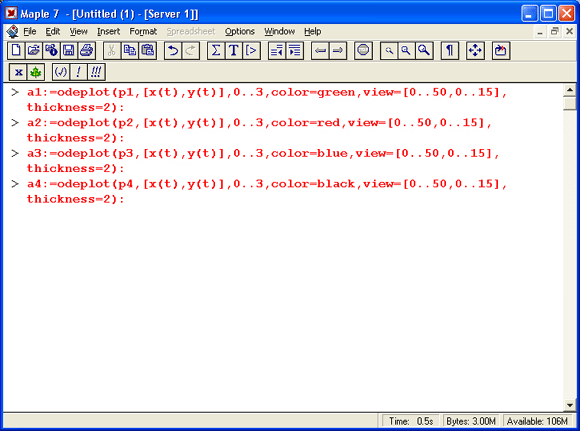
21.gif

22.gif
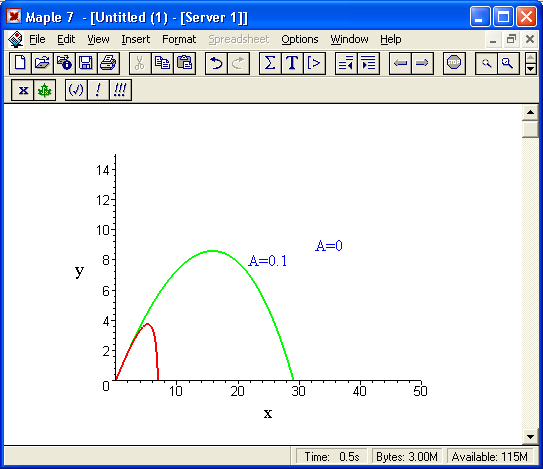
23.gif
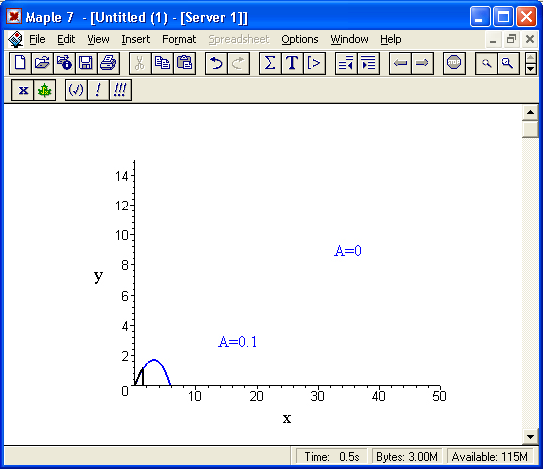
12. Движение частицы в магнитном поле
Движение частицы в магнитном поле
От реального мира перейдем к микромиру. Пусть микрочастица массой 9* 10-31 кг и зарядом +1,6*10"19 Кл влетает в магнитное поле с индукцией В = 0,1 Тл под углом а=80°. Рассчитаем траекторию движения частицы при начальной скорости Vo= 1*107м/с:
> restart;
Сила Лоренца, действующая на движущуюся частицу F = q*(E+[v, В]). Проекции векторного произведения [v, В] на оси х, у, z:
[v.B]x=vy*Bz-vz*By [v,B]y=vz*Bx-vx*Bz [v,B]z=vx*By-vy*Bz
В соответствии с этим известные из курса физики дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:
Зададим исходные числовые данные (опустив размерности):
> q:=-1.6e-19: massa:=9.1e-31: V:=le7: alpha:=80*Pi/180:
> Vx:=V*cos(alpha): Vy:=V*sin(alpha): Ex:=0:Ey:=0:Ez:=0: Bx:=0.1:By:=0: Bz:=0:
Построим траекторию движения частиц в пространстве:
> with(DEtools):DEplot3d({sys},{x(t),y(t),z(t)},t=0..2e-9, [[x(0)=O,D(x)(0)=Vx,y(0)==0,D(y)(0)=Vy,z(0)=0,D(z)(0)=0]], stepsize=le-ll,orientation=[24.117]):
Полученная траектория представлена на рис. 17.8. Она имеет вид спирали в пространстве. При этом скорость движения частицы вдоль оси х неизменна, а вдоль осей у и z имеет характерную колебательную компоненту. Случай явно куда менее тривиальный, чем полет камня, описанный выше.
Рис. 17.8. Траектория движения частицы в магнитном поле
Мы можем найти аналитическое представление для траектории частицы в виде параметрически заданной (с параметром времени t) системы из трех уравнений:
Моделирование движения заряженной частицы в пространстве с магнитным полем показывает, что для принятых для моделирования параметров решаемой задачи, движение частицы происходит по спиралеобразной траектории. Получен как график траектории движения частицы, так и аналитические уравнения, описывающие это движение.
24.gif
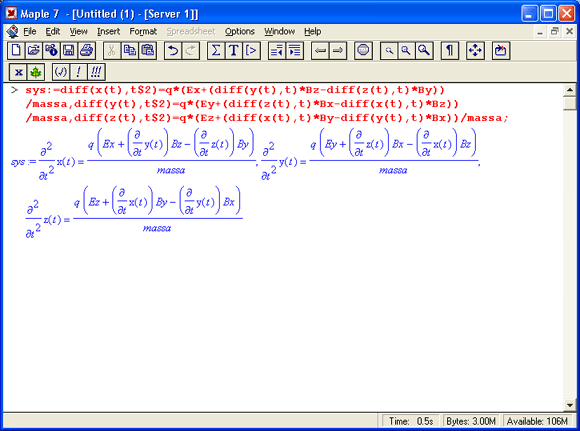
25.gif
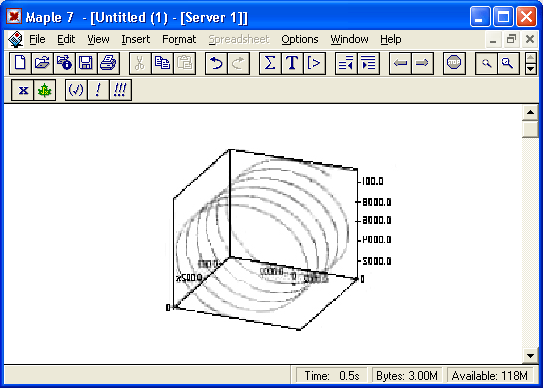
26.gif
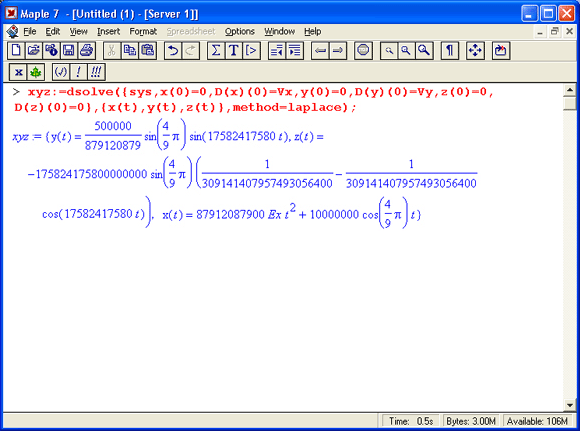
13. Разделение изотопов
Разделение изотопов
Рассмотрим еще одну классическую задачу ядерной физики — разделение изотопов (атомов с одинаковым зарядом ядра, но разной массой). Для этого используют различные способы. В частности, это может быть масс-спектроскопический метод. Из точки А вылетают однозарядные ионы (q = е = 1.6*10-19 Кл) разной массы (от 20 до 23 а.е.м.) и под разными углами в пределах от 80 до 100° к оси х в плоскости ху (рис. 17.9). Вдоль оси z приложено магнитное поле В=10-2 Тл. Рассчитаем траектории полета частиц. Будем надеяться, что это подскажет способ разделения изотопов.
Приступим к решению данной задачи. Сила Лоренца, действующая на движущуюся частицу, F = q*(E+[v, В]). Проекции векторного произведения [v, В] на оси х, у, z заданы выражениями:
[v.B]x-vy*Bz-vz*By [v,B]y-vz*Bx-vx*Bz [v,B]z=vx*By-vy*Bz
Рис. 17.9. Иллюстрация к методу разделения изотопов
В соответствии с этим дифференциальные уравнения, описывающие траекторию полета частицы по осям х, у, z имеют вид:
Зададим исходные числовые данные для расчета:
> q:=1.6e-19:V:=le4:
> Vx:=V*cos(a1pha):Vy:=V*sin(a1pha):Ex:=0:Ey:=0:Ez:=0:Bx:=0: By:=0:Bz:=le-2:
Выполним решение составленной выше системы дифференциальных уравнений:
Построим графики решения:
Эти графики показаны на рис. 17.10.
Рис. 17.10. Траектории движения частиц
Полученные графики (рис. 17.10) наглядно показывают на одну из возможностей разделения изотопов. Как говорится, осталось подставить «стаканчик» в нужное место для ловли нужных изотопов. Разумеется, это только изложение идеи одного из методов разделения изотопов. Увы, на практике приходится использовать сложнейшие и дорогие физические установки для решения этой актуальной задачи.
27.gif
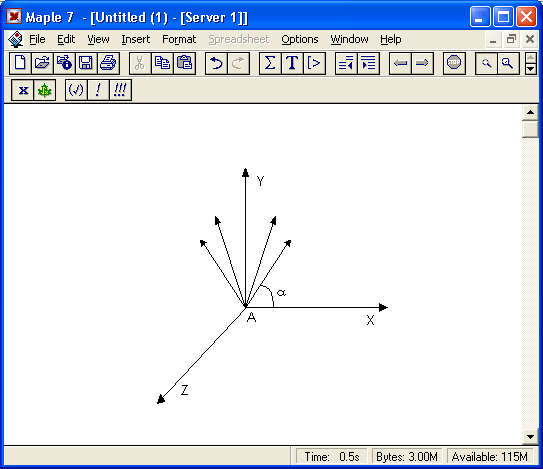
28.gif
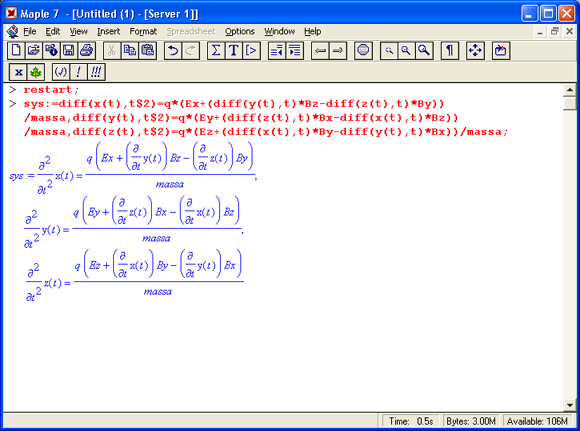
29.gif
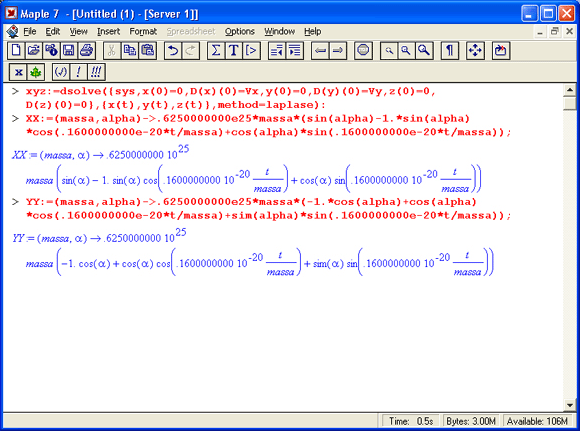
30.gif
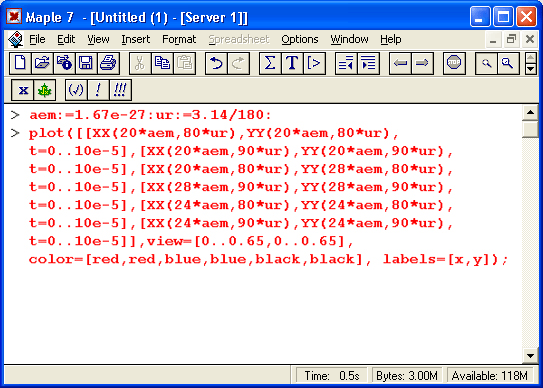
31.gif
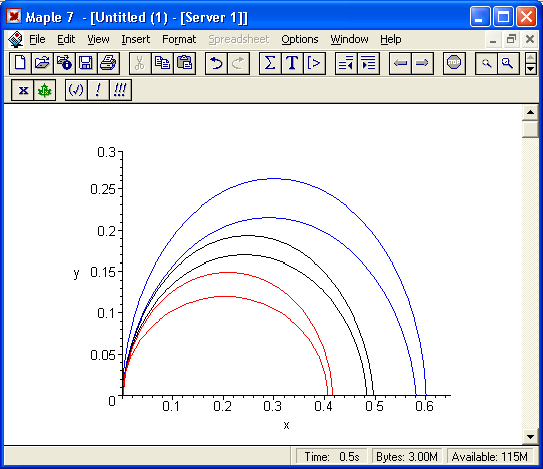
14. Моделирование рассеивания альфа-частиц
Моделирование рассеивания альфа- частиц
Одним из фундаментальных доказательств существования ядра у атомов стал опыт с бомбардировкой тонкой фольги из металла альфа- частицами с высокой энергией. Если бы «массивных» ядер не существовало, то альфа- частицы должны были бы спокойно пролетать сквозь тонкую фольгу, практически не отклоняясь. Однако, как физики и ожидали, некоторая часть частиц испытывала сильное отклонение и даже поворачивала назад. Очевидно, что имели место отскоки (упругие столкновения) с малыми, но массивными ядрами металла фольги.
В нашем распоряжении, увы (а может быть и к счастью), нет ускорителя альфа- частиц. Так что мы, не опасаясь облучения и очередной Чернобыльской катастрофы, сможем смоделировать это интереснейшее физическое явление с помощью математической системы Maple 7. Причем спокойно сидя перед своим домашним компьютером и глубокомысленно наблюдая за траекториями полета альфа- частиц.
Итак, пусть в нашем теоретическом опыте альфа- частицы с энергией 4 МэВ рассеиваются тонкой золотой фольгой. Рассчитать траекторию частицы, приближающейся к ядру атома Аи. Прицельное расстояние р равно 2*10-15 м. Приступим к решению задачи и зададим вначале систему дифференциальных уравнений для траектории альфа- частицы:
Введем исходные числовые данные для вычислений:
> ql:=2*i;6e-19:q2:=79*1.6e-19:massa:=4*1.67e-27:EO:=8.85e-12: a:=4e-13:
p:=5e-15:T:=4e6*1.6e-19:V0x:=sqrt(2*T/massa):
Создадим графическую структуру решения нашей системы дифференциальных уравнений для нескольких расчетных отклонений линии движения альфа- частицы от центра ядра атома, находящегося на ее пути:
> with(DEtools):ss:=DEplot({sys},{y(t),x(t)},t=0..7e-20.
[[x(0)=-a,D(x)(0)=VOx,y(0)=p,D(y)(0)=0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*4.D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*8,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*12,D(y)(0)=0].
[x(0)=-a;D(x)(0)=VOx,y(0)=p*16,D(y)(0)=0],
[x(0)-a.D(x)(0)-VOx.y(0)-p*20,D(y)(0)-0].
[x(0)=-a,D(x)(0)=VOx,y(0)=p*24,D(y)(0)=0],
[x(0)=-a,D(x)(0)=VOx,y(0)=p*28,D(y)(0)=0]],
x(t)=-a..a,scene=[x(t),y(t)],stepsize=le-21,1inecolor=bl ack):
> with(plottools):yy:=circle([0.0],2E-14,color=red,thickness=2):
Warning, the name translate has been redefined
Построим центр ядра (кружок со знаком +) и траектории альфа- частиц:
> ss2:=PLOT(TEXT([0.-0.3e-14],'+'), FONT(HELVETICA, OBLIQUE.14)):
Осталось построить график траекторий движения альфа- частиц вблизи центра атома: i
> with(plots):
Warning, the name changecoords has been redefined
> disp1ay([ss,yy,ss2],tit1e='Pacceивание а-частиц',axes=framed);
График траекторий движения альфа- частиц вблизи ядра представлен на рис. 17.11. Этот график настолько нагляден, что не требует пояснения.
Моделирование движения альфа- частиц вблизи малого и «массивного» ядра атома дает наглядное представление о математической и физической сути данного опыта. Надо лишь помнить, что нельзя нацеливать альфа- частицы прямо в центр ядра. Более сложные, чем приведенные, расчеты показывают, что при этом альфа-частица настолько близко подходит к ядру, что надо учитывать новые факторы, возникающие при близком взаимодействии. Они могут привести к тому, что частица будет поглощена ядром- Но это уже тема нового разговора,, выходящего за рамки данной книги.
Рис. 17.11. Траектории движения альфа- частиц вблизи ядра атома
32.gif
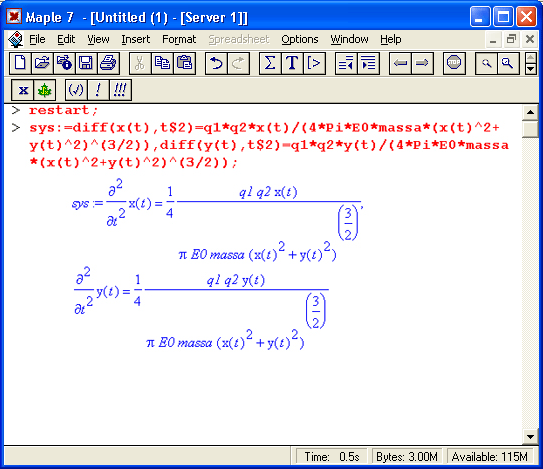
33.gif
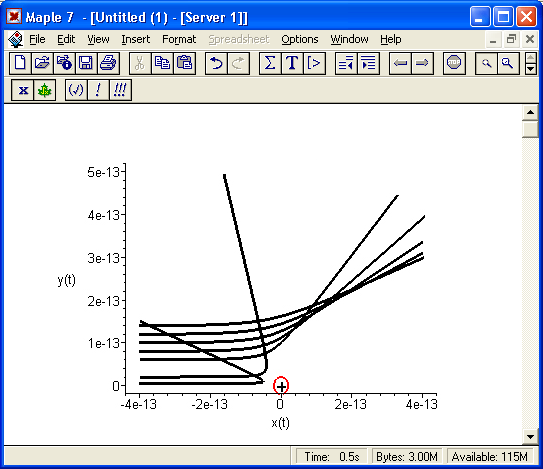
15. Моделирование и расчет электронных схем
Моделирование и расчет электронных схем
Нужно ли применять Maple для моделирования и расчета электронных схем?
Нужно ли применять системы компьютерной математики для анализа, расчета и моделирования электронных схем? Ответ на этот вопрос не так прост, как кажется с первого взгляда. С одной стороны, к услугам пользователя компьютера сейчас имеется ряд программ схемотехнического моделирования, например Micro-CAP, Electronics Workbench, PSpice, Design Labs и др., автоматически составляющих и решающих большие системы уравнений состояния электронных схем и моделирующих работу бесчисленного множества электронных схем без кропотливого «ручного» составления уравнений.
Но, с другой стороны, анализ схем в таких программах настолько автоматизирован, что начисто теряется его физическая и математическая сущность. Это не так уж страшно, когда моделируются типовые схемы на давно известных или, скорее, просто хорошо знакомых электронных приборах. Но это явно плохо, когда объектом исследования и моделирования являются новые нетрадиционные схемы на новых или малоизвестных приборах или когда знание физических и математических основ работы таких схем принципиально необходимо. Например, при изучении их в вузах и университетах. В этом случае применение систем компьютерной математики не только возможно, но и принципиально необходимо.
16. Малосигнальный анализ усилителя на полевом транзисторе
Малосигнальный анализ усилителя на полевом транзисторе
Рассмотрим классический усилительный каскад на полевом транзисторе, схема которого приведена на рис. 17.12, а. Его эквивалентная малосигнальная схема представлена на рис. 17.12, б.
Рис. 17.12. Принципиальная (о) и эквивалентная(6) схемы усилителя на полевом транзисторе
Наша цель заключается в расчете характеристик усилителя операторным методом. Подключим нужный нам пакет plots:
> restart:with(plots):
Warning, the name changecoords has been redefined
Из законов Киргофа вытекает, что сумма токов, втекающих в каждый узел и вытекающих из него равна 0. Следовательно, для узлов эквивалентной схемы рис. 17.12 можно записать следующую систему уравнений в операторной форме:
Переменные напряжения на узлах схемы находятся из аналитического решения данной системы. При этом заблокируем вывод их аналитических значений, поскольку он очень громоздок. Тем не менее вы можете посмотреть на полученные формулы, поставив знак точки с запятой вместо знака двоеточия в приведенных ниже выражениях:
> solve({eql,eq2,eq3.eq4}б{Vl,V2.V3,Vo}):
Обеспечим присвоение переменным Vo, VI, V2 и V3 найденных из решения системы уравнений значений:
> assign(%):
Теперь найдем операторную передаточную функцию в аналитическом виде:
В соответствии с выбранным операторным методом анализа введем обозначения:
Это позволяет найти Н как функцию от частоты f также в аналитическом виде:
Это тоже довольно громоздкое выражение, и его применение при «ручном» анализе потребовало бы от нас немало изобретательности. Между тем Maple 7 позволяет «в два счета» определить из него амплитудно-частотную (AVM) и фазо- частотную (PhaseAV) характеристики усилителя как функции частоты:
> AVM=-evalc(abs(H)):
> PhaseAV:=evalc(argument(H)):
Преобразуем AVD в логарифмическую характеристику, выражающую усиление в децибелах (dB):
> AVdB:=20*1og10(AVM):
Такая характеристика более привычна для специалистов в радиоэлектронике. Соответственно фазо-частотную характеристику выразим в градусах:
> R2D:=evalf(360/(2*Pi));R2D := 57.29577950
> AVdeg:=R2D*PhaseAV:
Теперь можно перейти к обычным численным расчетам. Зададим конкретные значения компонент эквивалентной схемы усилителя:
> Rl:=100: R2:=100000: R3:=1000: R4:=10000: Cl:=1.*10^(-6): С2:=5*10^(-12): СЗ:=1*10^(-6): mu:=50:
Построим амплитудно-частотную характеристику усилителя:
> gaindata:-NULL:
phasedata:=NULL:
for a from 0 to 8 do:
for i from 2*10^a to l(T(a+l) by 10^a do
gaindata:=gaindata, [1. evalf(subs(f=i,AVdB))];
phasedata:=phasedata, [i, eva1f(subs(f=i,AVdeg))]:
od: od:
> 1oglogp1ot([gaindata]. thickness»2, color=black, style=1ine, axes=boxed,
title=`Коэффициент усиления K(f)`,1abels=['Частота (Hz)VK(d8)']):
Она показана на рис. 17.13.
Рис. 17.13. Амплитудно-частотная характеристика усилителя
Далее зададим построение фазо-частотной характеристики усилителя:
> 1og1ogplot([phasedata], thickness=2, color=b1ue, style=line, axes=boxed, title='Фаэовый сдвиг (в градусах)`, labels=['Частота (Hz)','Фаза']);
Она представлена на рис. 17.14.
Рис. 17.14. Фазо-частотная характеристика усилителя
Найдем номинальный коэффициент усиления на частоте f=1000 (Гц):
> AVmid:=eva1f(subs(f=1000, AVdB)):
AVmid=33.12074854
Имея аналитическое выражение для амплитудно-частотной характеристики, можно составить уравнения для вычисления граничных частот (по спаду усиления на -dAV в dB):
> dAV:=3: #Ослабление (в dB на граничных частотах)
> eq5:=AVmid-dAV=20*log10(AVM):
Теперь можно найти эти частоты — нижнюю и верхнюю:
> flow:=fsolve(eq5,f. f-10..2000):flow:= 23.61659476
> fhigh:=fsolve(eqS,f, f-2000..100*10*6);
fliigh := .5737800225 107
Мы можем построить и более наглядную амплитудно-частотную характеристику с точками, соответствующими граничным частотам:
> with(plottools) :h:=log10(AVnvid-dAV):
aplot:= Loglogplot([gaindata], thickness=2, color=b1ack. style=line, axes=boxed,
title='Частоты flow и fhigh среза', labels=['Частота (Hz)VK(dB)']):
bplot:=line([0.1,h], [7.1,h], color=black, linestyle=3):
cplot:=line([log10(flow),0.58],[logHK flow). 1.6], color=blue, linestyle=3):
dplot:=line([log10(fh1gh).0.58],. [log10(fhigh).1.6],. color=red,. 1inestyle=3):
display([aplot.bplot,cplotJ,dplot]):
Эта характеристика показана на рис. 17.15.
На ней проставлены синяя и красная пунктирные вертикали, соответствующие найденным граничным частотам flow и fhigh, а также пунктирная горизонталь, соответствующая коэффициенту усиления на этих частотах. Это позволяет наглядно оценить частотный диапазон работы усилителя.
Таким образом, задача расчета усилителя в малосигнальном режиме полностью решена. Мы получили значение номинального коэффициента усиления, рассчитали нижнюю и верхнюю граничные частоты, получили аналитические выражения для амплитудно-частотной и фазо-частотной характеристик усилителя и построили их наглядные графики.
Рис. 17.15. Амплитудно-частотная характеристика с выделенными точками граничных частот
34.gif
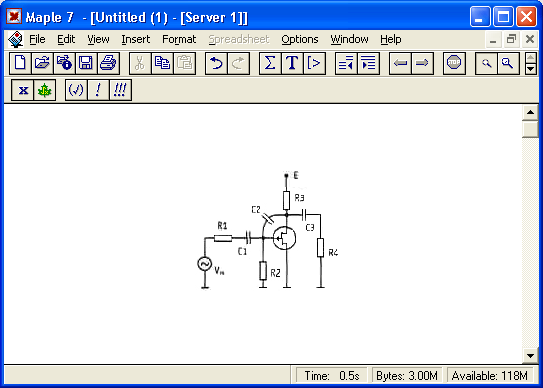
36.gif
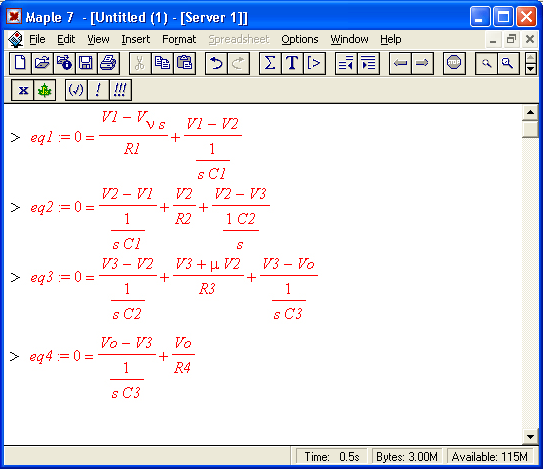
37.gif
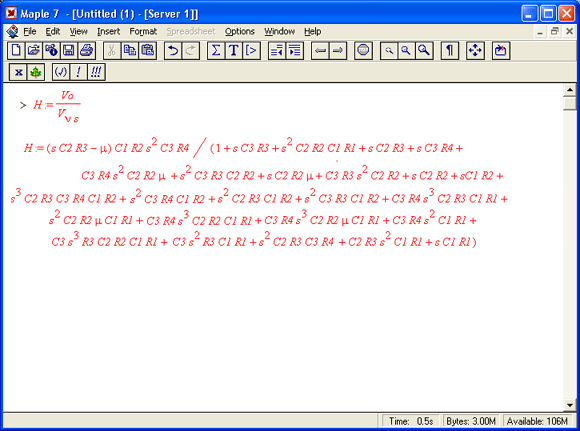
38.gif
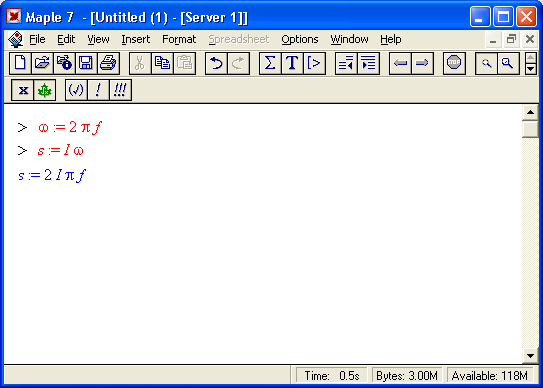
39.gif

40.gif
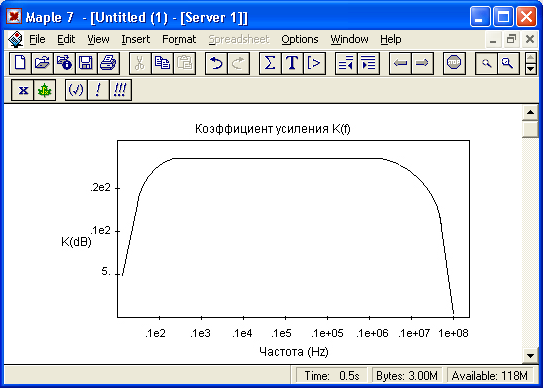
41.gif
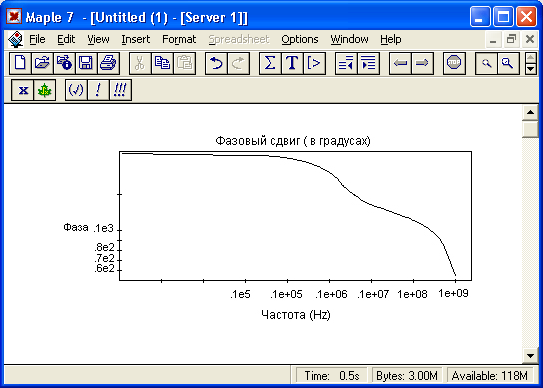
42.gif
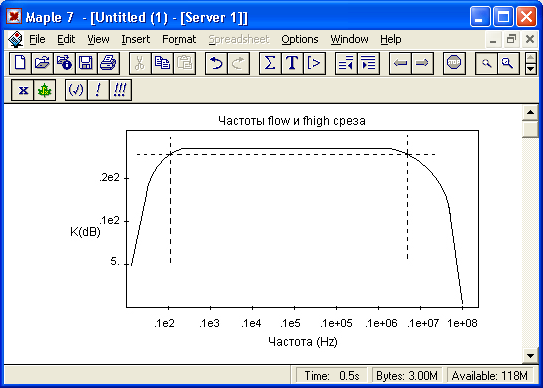
17. Расчет аналогового фильтра на операционном усилителе
Расчет аналогового фильтра на операционном усилителе
Теперь рассмотрим проектирование аналогового полосового фильтра на операционном усилителе, схема которого приведена на рис. 17.16.
Рис. 17.16. Схема полосового фильтра на интегральном операционном усилителе
Подготовимся к расчету фильтра:
> restart:
Зададим основные уравнения, описывающие работу фильтра на малом сигнале:
Введем круговую частоту:
> omega := 2*Pi*f;
W := 2пf
Найдем коэффициент передачи фильтра и его фазо-частотную характеристику как функции от частоты:
> gain := abs(eva1c(Vo/Vi)):
> phase := evalc(op(2,convert(Vo/Vi.polar))):
Для просмотра громоздких аналитических выражений для этих параметров замените знаки двоеточия у выражений для gain и phase на знак точки с запятой. Далее введем конкретные исходные данные для расчета:
> R3 :=1000:
> R4 := 3000:
> СЗ :=0.08*10^(-6):
> С4 := 0.01*10^(-6):
Построим АЧХ фильтра как зависимость коэффициента передачи в децибелах (dB) от частоты f в Гц:
> plot(DogWf), 20*log10(gain), f=[10..50000], color=black, title='Коэффициент передачи dB как функция от частоты f в Гц'):
Эта характеристика представлена на рис. 17.17. Здесь полезно обратить внимание на то, что спад усиления на низких и высоких частотах происходит довольно медленно из-за малого порядка фильтра.
Рис. 17.17. АЧХ фильтра на операционной усилителе
Далее построим фазо-частотную характеристику фильтра как зависимость фазы в радианах от частоты f в Гц:
> plot ([log10(f),phase, f=10..50000], color=black, title=*Фазо-частотная характеристика фильтра*);
Фазо-частотная характеристика (ФЧХ) фильтра показана на рис. 17.18
На ФЧХ фильтра можно заметить характерный разрыв, связанный с превышением фазовым углом граничного значения я. Такой способ представления фазового сдвига общепринят, поскольку его изменения стремятся вписать в диапазон от -я до п.
Рис. 17.18. ФЧХ фильтра на операционном усилителе
43.gif

44.gif
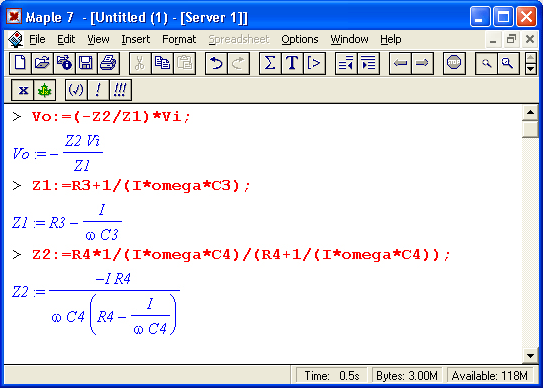
45.gif
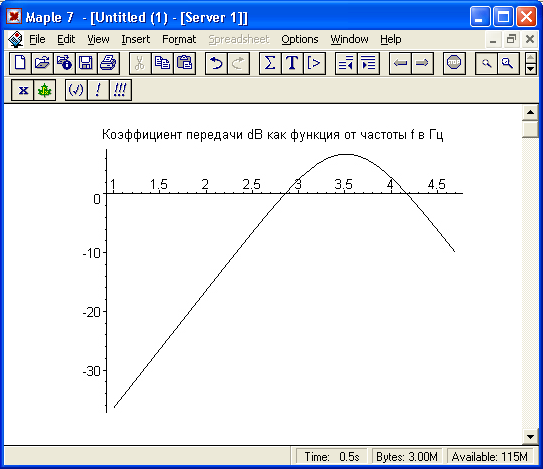
46.gif
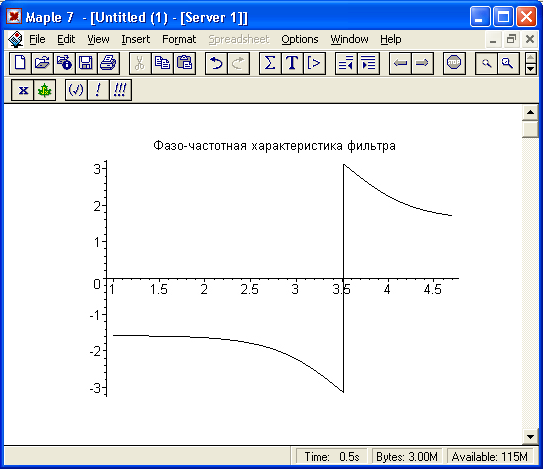
18. Проектирование цифрового фильтра
Проектирование цифрового фильтра
Основной недостаток аналоговых активных фильтров, подобных описанному выше, заключается в их малом порядке. Его повышение за счет применения многих звеньев низкого порядка ведет к значительному повышению габаритов фильтров и их стоимости. От этого недостатка свободны современные цифровые фильтры, число ячеек которых N даже при однокристальном исполнении может достигать десятков и сотен. Это обеспечивает повышенную частотную селекцию.
Спроектируем фильтр N+1-ro порядка класса FIR (Finite Impulse Response или с конечной импульсной характеристикой). Каждая из N ячеек временной задержки фильтра удовлетворяет следующей зависимости выходного сигнала у от входного х вида:
Подключим пакет расширения plots, нужный для графической визуализации проектирования:
> restart:with(p1ots):
Warning, the name changecoords has been redefined
Зададим исходные данные для проектирования полосового цифрового фильтра, выделяющего пятую гармонику из входного сигнала в виде зашумленного меандра с частотой 500 Гц:
> N := 64: # Число секций фильтра (на 1 меньше порядка фильтра)
> fs:= 10000: # Частота квантования
> fl = 2300: # Нижняя граничная частота
> fh = 2700: # Верхняя граничная частота
> m := 10: # 2^m > N - число точек для анализа
Вычислим:
Вычислим FIR-коэффициенты для прямоугольного окна фильтра:
> С :-=(n) -> limit(g,t=n):h := aray(0..N): N2:=N/2:
> for n from 0 to N2 do h[N2-n]:= evalf(C(n)); h[N2+n] := h[N2-n]; od:
Определим массивы входного x(n) и выходного у(n) сигналов:
> х := array(-N..T): y := аггау(0..Т):
Установим значение х(n) равным 0 для времени меньше 0 и 1 для времени >=0:
> for n from -N to -1 do x[n] := 0; od:
> for n from 0 to Т do x[n] := Dirac(n); od:
Вычислим временную зависимость для выходного сигнала:
> for n from 0 to Т do y[n] := sum(h[k]*x[n-k],k=0..N): od:
Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:
> р := [seq([j/fs,y[j]],j=0..T)3:
> plot(p, time=0..3*N/fs, labels=[time,output], axes=boxed, xtickmarks=4, title-'Иипульсная характеристика фильтра',color=black);
Он показан на рис. 17.19. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются несильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.
Рис. 17.19. Импульсная характеристика цифрового фильтра
Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно после подготовки обрабатываемых массивов реализуется функцией FFT:
> rо := array (1..T+1): io := arrayd. .T+l):
> for n from 0 to Т do ro[n+l] :- y[n]; io[n+l] := 0; od:
> FFT(m,ro,io):
Построим график АЧХ фильтра:
> р :=[seq([j*fs/(T+l),abs(ro[j+l]+io[j+l]*I)3,j=O..T/2)]:
> plot(p, frequency=0..fs/2, tabels=[frequency,gain], tit1e='AЧX фильтра',со1ог=black);
Он представлен на рис. 17.20. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).
Рис. 17.20. АЧХ цифрового полосового фильтра
Теперь приступим к тестированию фильтра. Зададим входной сигнал в виде зашумленного меандра с частотой 500 Гц и размахом напряжения 2 В:
> 1 :=round(fs/2/500):
> for n from 0 by 2*1 to Т do
> for n2 from 0 to 1-1 do
> if n+n2 <= Т then
> x[n+n2] := evalf(-l+rand()/10^12-0.5);
> fi:
> if n+n2+1 <= Т then
> x[n+n2-H] :-=eva1f(l+ranoX)/10^12-0.5);
> fi;
> od:
> od:
Временная зависимость синтезированного входного сигнала представлена на рис. 17.21.
Рис. 17.21. Синтезированный входной сигнал
Вычислим реакцию фильтра на входной сигнал:
> for n from 0 to T do
> y[n] := sum(h[k]*x[n-k],k=0..N);
> od:
Построим график выходного сигнала:
> р := [seq([j/fs, x[j]], j=0..T)]:q:= [seq([j/fs , y[j]] , j =0..Т)]:
> plot(p,time=0..T/fs/4,1abels=[time,volts],title='Входной сигнал\сolor=black);
> plot(q,tine=0..T/fs/4,1abels=[tirae,volts], titlе='Выходной сигнал",color=black);
Временная зависимость выходного сигнала показана на рис. 17.22. Нетрудно заметить, что в конце концов выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно заметный переходной процесс. Он связан с узкополосностью данного фильтра.
Рис. 17.22. Временная зависимость выходного сигнала цифрового фильтра
Вычислим спектры входного и выходного сигналов, подготовив массивы выборок сигналов и применив прямое преобразование Фурье с помощью функции FFT:
> Н := array(l..T+l):1i :=array(1..Т+1):
> for n from 0 to T do ,
> ri[n+l] := x[n]*2/T: ii[rn-l] := 0;
> ro[n+l] := y[n]*2/T; Io[rrfl] := 0;
> od:
> FFT(m.ri,ii):rTT(m,ro,io):
Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0,5 В:
> р := [seq([j*fs/(T+l),abs(n[j+l]+ii[j-H]*I)],j=0..T/2)]:
> q := [seq([j*fs/(T-H),abs(ro[j-H]+To[j+l]*I)],j=0..T/2)]:
> plot(p, frequency=0..fs/2,y0..0.5,labe1s=[Частотa.V],title='Частотный спектр входного сигнала',color=black);
Этот график представлен на рис. 17.23. Из него хорошо видно, что спектральный состав входного сигнала представлен только нечетными гармониками, амплитуда которых убывает по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами фильтра 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шума сигнала в пределах полосы прозрачности фильтра.
Теперь построим график спектра выходного сигнала:
> p1ot(q, frequency=0..fs/2,y=0..0.5,labe1s=[Частотa,V], title='Частотный спектр выходного сигнала'бcolor=black);
Он представлен на рис.17.24. Хорошо видно эффективное выделение пятой гармоники сигнала и прилегающей к ней узкой полосы шумового спектра.
Рис. 17.23. Спектрограмма входного сигнала
Рис. 17.24. Спектрограмма выходного сигнала цифрового фильтра
Приведенные данные свидетельствуют, что спроектированный фильтр полностью отвечает заданным требованиям и обеспечивает уверенное выделение пятой гармоники зашумленного меандра. По образу и подобию данного документа можно выполнить проектирование и других видов цифровых фильтров.
47.gif
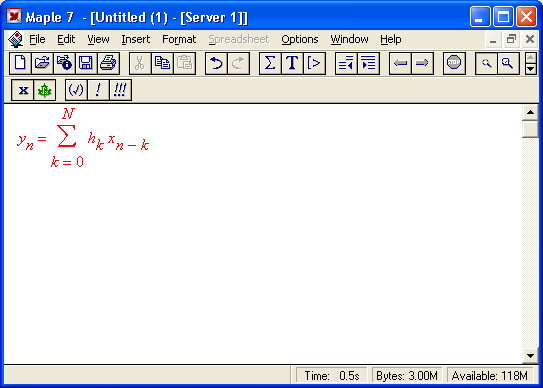
48.gif
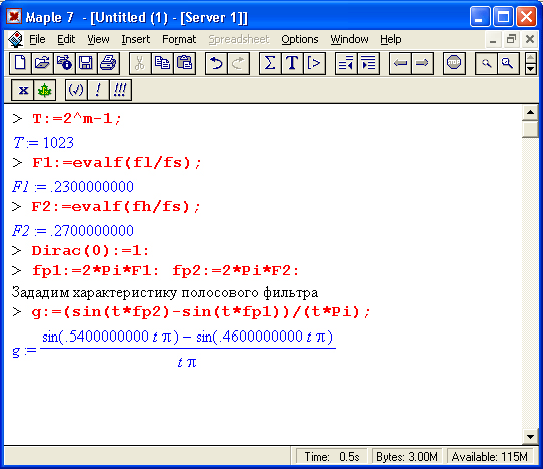
49.gif
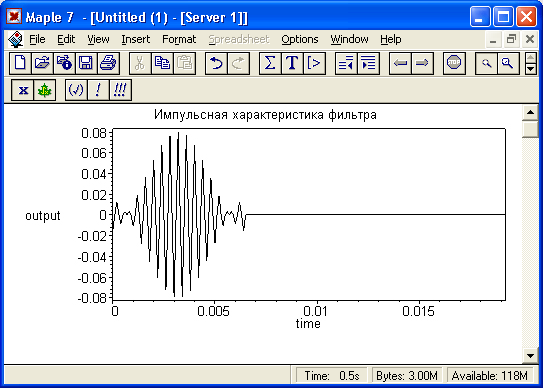
50.gif
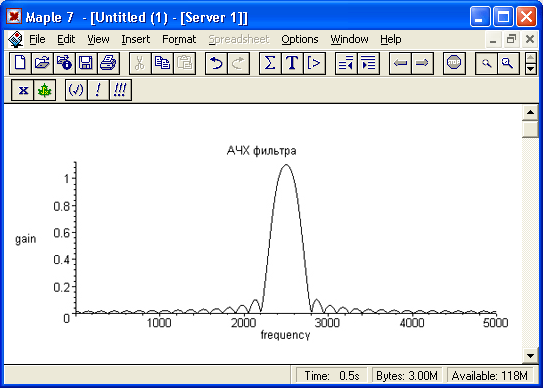
51.gif
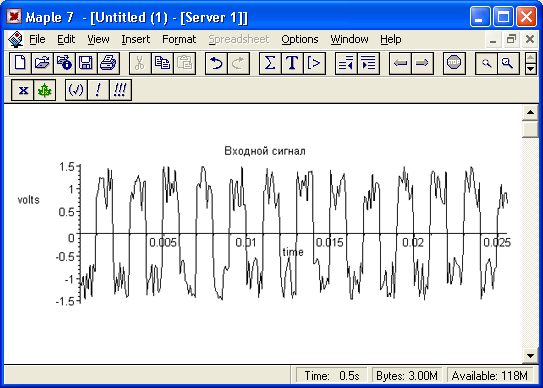
52.gif
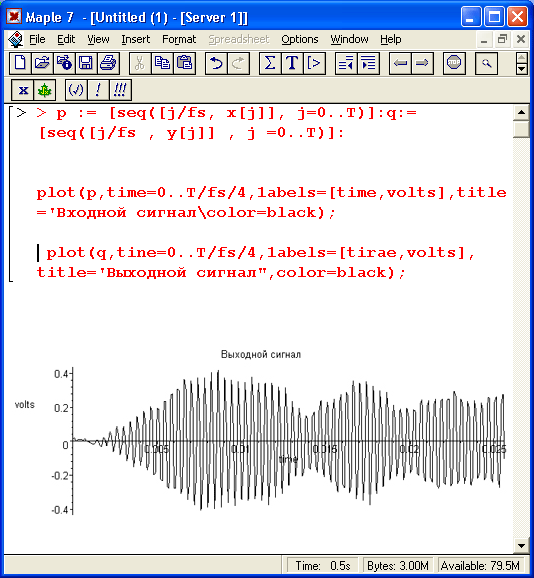
53.gif
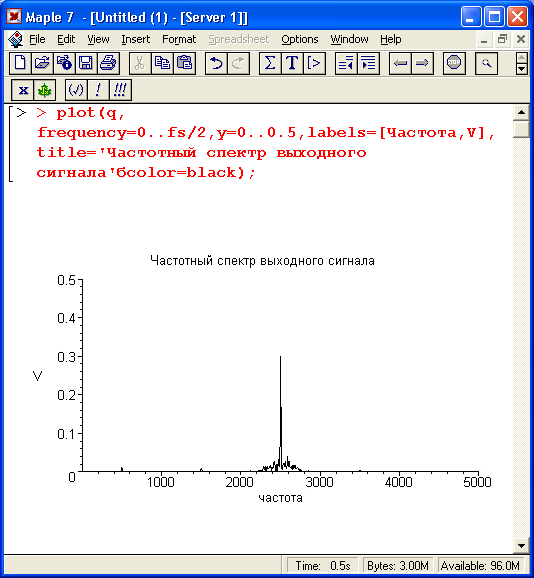
54.gif
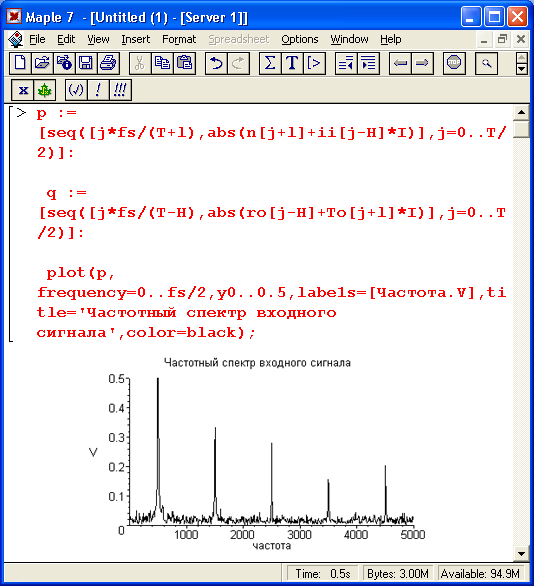
19. Моделирование цепи на туннельном диоде
Моделирование цепи на туннельном диоде
А теперь займемся моделированием явно нелинейной цепи. Выполним его для цепи, которая состоит из последовательно включенных источника напряжения Es, резистора Rs, индуктивности L и туннельного диода, имеющего N-образную вольтамперную характеристику (ВАХ). Туннельный диод обладает емкостью С, что имитируется конденсатором С, подключенным параллельно туннельному диоду. Пусть ВАХ реального туннельного диода задана выражением:
> restart:
> A:=.3t: а:=10: В:=1*10^(-8): b:=20:
> Id:=Ud->A*Ud*exp(-a*Ud)+B*(exp(b*Ud-D):
Id:=Ud->AUde(-aUd)+Be(bUd-1)
Построим график ВАХ:
> plot(Id(Ud), Ud=-.02..0.76,color=black):
Этот график представлен на рис. 17.25. Нетрудно заметить, что ВАХ туннельного диода не только резко нелинейна, но и содержит протяженный участок отрицательной дифференциальной проводимости, на котором ток падает с ростом напряжения. Это является признаком того, что такая цепь способна на переменном токе отдавать энергию во внешнюю цепь и приводить к возникновению колебаний в ней различного типа.
Работа цепи описывается системой из двух дифференциальных уравнений:
di/dt=(Es-i(t)*Rs-u(t))/L
du/dt=(i(t)-Id(u(t))/C
Рис. 17.25. ВАХ туннельного диода
Пусть задано Es = 0,35 В, Rs= 15 Ом, С = 10*10-12, L = 30*10-9 и максимальное время моделирования tm=10*10-9. Итак, задаем исходные данные:
> Es:=.35:Rs:=15:C:=10*10^(-12):L:=30*10^(-6):tm:=10*10^(-9):
Составим систему дифференциальных уравнений цепи и выполним ее решение с помощью функции dsolve:
Поскольку заведомо известно, что схема имеет малые значения L и С, мы задали с помощью параметров достаточно малый шаг решения для функции dsolve — stepsize=l(T(-11) (с). При больших шагах возможна численная неустойчивость решения, искажающая форму колебаний, получаемую при моделировании. Используя функции odeplot и displ ay пакета plots, построим графики решения в виде временных зависимостей u(t) и 10*i (t) и линии, соответствующей напряжению Es источника питания:
> gu:=odeplot(F,[t,u(t)],0,tm,color=black,
labels=['tVu(t),10*i(tr]):
> gi:=odeplot(F,[t,10*i(t)],0..tm.color-black):
> ge:=odeplot(F,[t,Es].0..tm.color=red): .
> display(gu.gi,ge);
Эти зависимости представлены на рис. 17.26. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.
Рис. 17.26. Временные зависимости напряжения на туннельном диоде и тока
Решение можно представить также в виде фазового портрета, построенного на фоне построенных ВАХ и линии нагрузки резистора Rs:
> gv:=plot({Id(Ud),(Es-Ud)/Rs},Ud=-.05..0.75,color=black,
labels=[Ud,Id]):
> gpp:=odeplot(F.[u(t),i(t)],0..tm,color=blue):
> display(gv,gpp);
Фазовый портрет колебаний показан на рис. 17.27.
Рис. 17.27. Фазовый портрет колебаний на фоне ВАХ туннельного диода и линии нагрузки резистора Rs
О том, что колебания релаксационные можно судить по тому, что уже первый цикл колебаний вырождается в замкнутую кривую — предельный цикл, форма которого заметно отличается от эллиптической.
Итак, мы видим, что данная цепь выполняет функцию генератора незатухающих релаксационных колебаний. Хотя поставленная задача моделирования цепи на туннельном диоде успешно решена, в ходе ее решения мы столкнулись с проблемой обеспечения малого шага по времени при решении системы дифференциальных уравнений, описывающих работу цепи. При неудачном выборе шага можно наблюдать явную неустойчивость решения.
55.gif
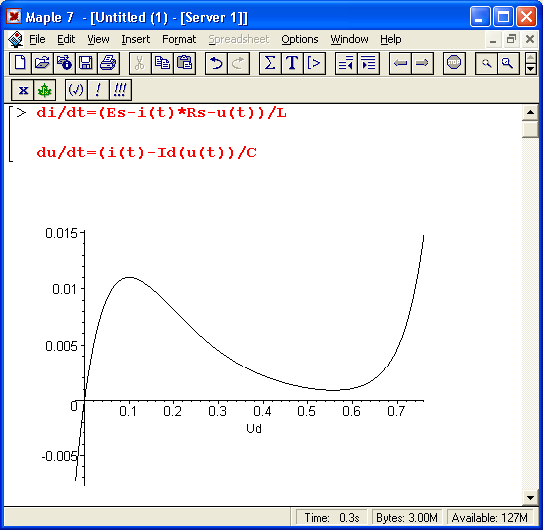
56.gif
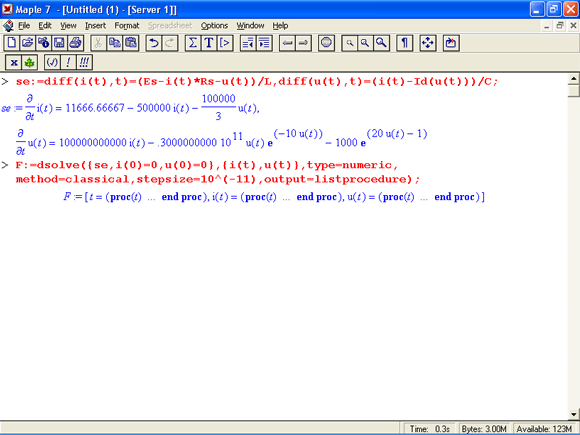
57.gif
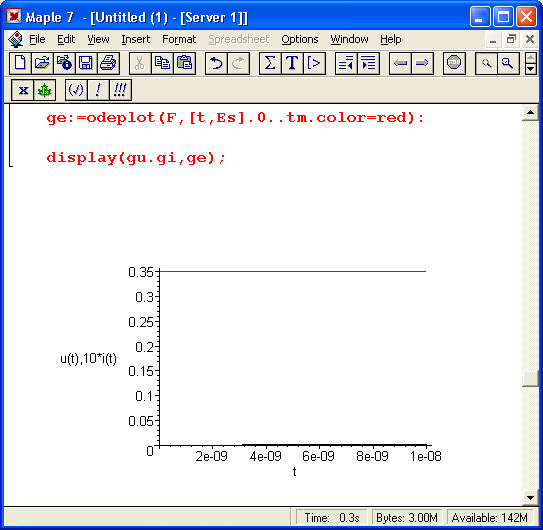
58.gif
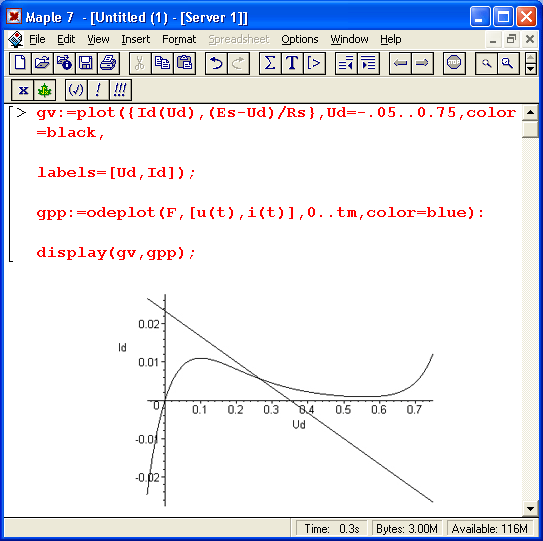
20. Применение интеграла Дюамеля для расчета переходных процессов
Применение интеграла Дюамеля для расчета переходных процессов
Вернемся к линейным цепям и рассмотрим еще один полезный метод расчета электрических цепей — с помощью интеграла Дюамеля. При нем можно рассчитать временную зависимость выходного напряжения u2(t) цепи по известному входному сигналу ul(t) и переходной характеристике цепи a(t). Возьмем в качестве первого классического примера дифференцирующую RC-цепь и вычислим ее реакцию на экспоненциально нарастающий перепад напряжения.
Представлены заданные зависимости ul(t) и a(t), аналитическое выражение для интеграла Дюамеля (одна из 4 форм) и аналитическое выражение для искомой зависимости u2(t). Пока последнее выражение довольно простое. В конце этого фрагмента документа построены графики зависимостей ul(t), a(t) и u2(t).
Обратите внимание на то, что выражение для u2(t), получаемое с помощью интеграла Дюамеля, стало намного сложнее. Тем не менее получено как аналитическое выражение для реакции цепи u2(t), так и графики ul(t), a(t) и u2(t). Они показаны внизу графика.
21. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Оценивать возможности Maple 7 в решении конкретных прикладных задач.
- Выбирать аппроксимацию для сложной функции по заданной точности.
- Моделировать различные физические явления (полет камня, движение частицы в магнитном поле и др.).
- Моделировать и проектировать различные электронные схемы (усилителя, аналогового и цифрового фильтра, нелинейной цепи на туннельном диоде).
- Применять интеграл Дюамеля для расчета переходных процессов в линейных цепях.
Урок 9. Анализ функций и полиномов.
1. Анализ функций
Урок 9.
Анализ функций и полиномов.
Анализ функций
Важным разделом математики является исследование аналитических функций. Оно обычно заключается в определении координат особых точек функции и ее значений в этих точках, а также в выяснении особенностей функции, таких как наличие точек разрыва, асимптот, точек перегибов, разрывов и т. д. К сожалению, пока нет средств, сразу выявляющих все особенности функций, поскольку даже средства, решающие частные задачи анализа функций, довольно сложны и специфичны. Достаточно отметить проблему поиска экстремумов функций (особенно функций нескольких переменных). Поэтому функции приходится анализировать индивидуально.
С помощью функции fsolve легко находятся значения независимой переменной х функций вида f(x), при которых f(x)=0 (корни этого уравнения). При этом данная функция позволяет (в отличие от функции solve) изолировать корни функции f(x) указанием примерного интервала их существования. Ряд функций служит для вычисления экстремумов, максимумов и минимумов функций, а также для определения их непрерывности. Одна из таких функций, extrema, позволяет найти экстремумы выражения ехрr (как максимумы, так и минимумы) при ограничениях constcs и переменных vans, по которым ищется экстремум: extrema(expr. constrs) extrema(expr, constrs, vars) extrematexpr, constrs, vans, V)
Ограничения contrs и переменные vars могут задаваться одиночными объектами или списками ряда ограничений и переменных. Найденные координаты точки экстремума присваиваются переменной 's'. При отсутствии ограничений в виде равенств или неравенств вместо них записывается пустой список {}. Эта функция в предшествующих версиях Maple находилась в стандартной библиотеке и вызывалась командой readlib(extrema). Но в Maple 7 ее можно использовать без предварительного объявления. В этом убеждают приведенные ниже примеры:
Как видно из приведенных примеров, функция extrema возвращает как значения экстремумов, так и значения аргументов, при которых экстремумы наблюдаются.
Для проверки оптимизационных алгоритмов существует ряд тестовых функций. Одна из таких функций — функция двух переменных Розенброка. В представленном ниже примере она задана как rf(x.y):
Как нетрудно заметить, минимум этой функции при значениях х =у = 1, равный О, функцией extrema не обнаружен. Однако это не недостаток данной функции, а просто неудачное ее применение. Функция Розенброка имеет минимум значения, и для его обнаружения надо использовать функцию minimize, описанную ниже.
ПРИМЕЧАНИЕ
Функция extrema дает неплохие результаты при поиске экстремумов простых аналитических функций, не имеющих особенностей. Однако при анализе сложных функций, содержащих функции со сравнением аргумента (например, abs(x), signum(x) и др.), функция extrema часто отказывается работать и просто повторяет запись обращения к ней.
1.gif
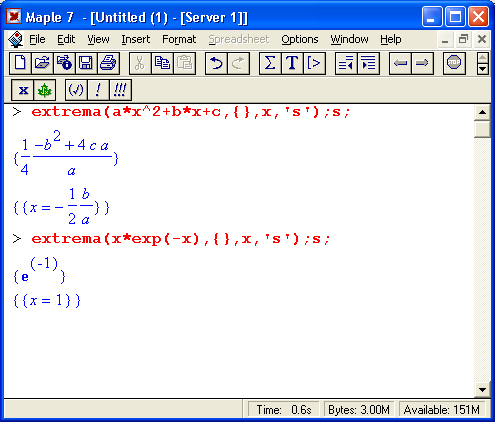
2.gif
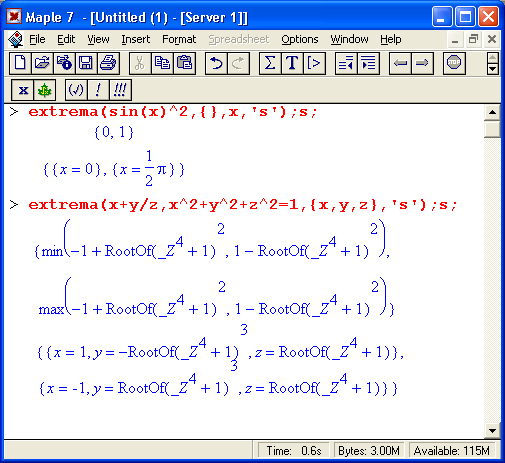
3.gif
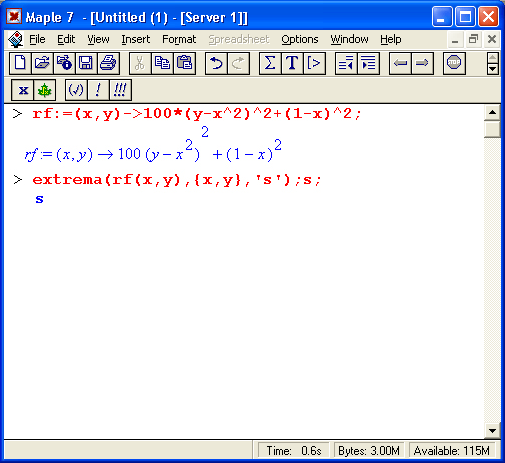
2. Поиск минимумов и максимумов аналитических функций
Поиск минимумов и максимумов аналитических функций
Часто нужно найти минимум или максимум заданной функции. Для поиска минимумов и максимумов выражений (функций) ехрr служат функции стандартной библиотеки:
minimize(expr, optl, opt2, .... optn)
maximize(expr, optl. opt2. .... optn)
Эти функции могут разыскивать максимумы и минимумы для функций как одной, так и нескольких переменных. С помощью опций optl, opt2,..., optn можно указывать дополнительные данные для поиска. Например, параметр `infinity` означает, что поиск минимума или максимума выполняется по всей числовой оси, а параметр location (или locatiorrtrue) дает расширенный вывод результатов поиска — выдается не только значение минимума (или максимума), но и значения переменных в этой точке.
Примеры применения функции minimize приведены ниже:
Приведем подобные примеры и для функции поиска максимума — maximize:
Обратите внимание на то, что в предпоследнем примере Maple 7 явно «оскандалилась» и вместо максимума функции sin(x)/x, равного 1 при х=0, выдал результат в виде бесконечности. Другими словами, система обнаружила, что в данном случае ей незнакомо понятие предела sin(x)/x при х—>0. Эта ситуация кажется более чем странной, если учесть, что в этом примере Maple 6 давал правильный результат.
Применим функцию minimize для поиска минимума функции Розенброка. Рисунок 9.1 показывает, что minimize прекрасно справляется с данной задачей. На рис. 9.1 представлено также построение функции Розенброка, хорошо иллюстрирующее ее особенности.
Рис. 9.1. Поиск минимума функции Розенброка и построение ее графика
Трудность поиска минимума функции Розенброка связана с ее характерными особенностями. Из рис. 9.1 видно, что эта функция представляет собой поверхность типа «глубокого оврага с почти плоским дном», в котором и расположена точка минимума. Такая особенность этой функции существенно затрудняет поиск минимума. То, что система Maple 7 справляется с данной тестовой функцией, вовсе не означает, что трудности в поиске минимума или максимума других функций остаются позади.
4.gif
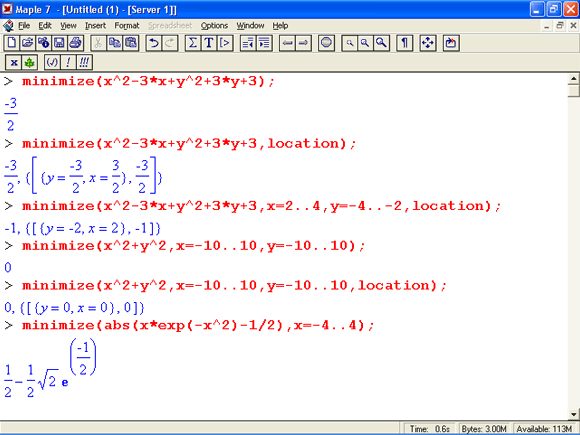
5.gif
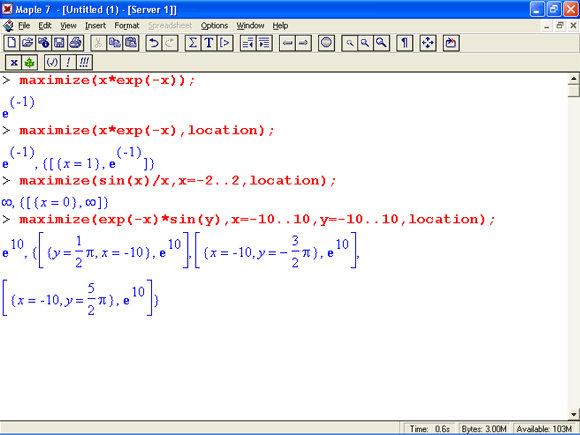
6.gif
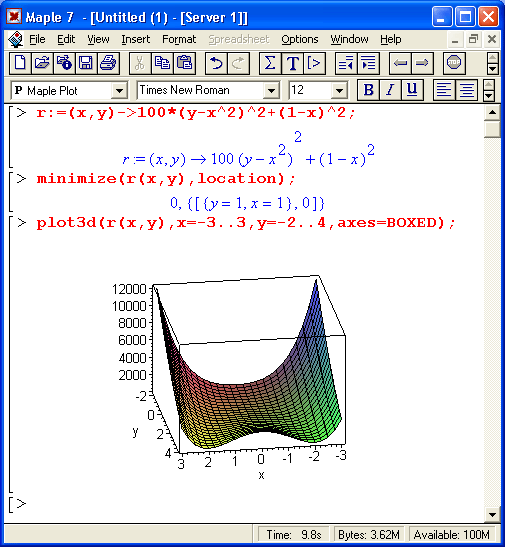
3. Анализ функций на непрерывность
Анализ функций на непрерывность
Для исследования функций на непрерывность Maple 7 имеет функцию iscont, записываемую в ряде форм:
iscont(expr. х - а .. Ь)
iscont(expr. х = а .. b, 'closed')
iscont(expr. х - а .. b, 'open')
Она позволяет исследовать выражение ехрr, заданное в виде зависимости от переменной х, на непрерывность. Если выражение непрерывно, возвращается логическое значение true, иначе — false. Возможен также результат типа FAIL. Параметр 'closed1 показывает, что конечные точки должны также проверяться, а указанный по умолчанию параметр 'open' — что они не должны проверяться.
Работу функции iscont иллюстрируют следующие примеры:
> iscont(l/x^2,x=-l..l);
false
> iscont(l/x^2.x=-l..l,'closed');
false
> iscont(l/x,x-0..1);
true > iscont(l/x,x=0..1.'closed'); ,
false ,--v > iscont(l/(x+a).x=-l..l);
FAIL
Рекомендуется внимательно присмотреться к результатам этих примеров и опробовать свои собственные примеры.
4. Определение точек нарушения непрерывности
Определение точек нарушения непрерывности
Функции, не имеющие непрерывности, доставляют много хлопот. Поэтому важным представляется анализ функций на непрерывность. В Maple 7 функция discont(f,х) позволяет определить точки, в которых нарушается непрерывность функции f(x). Она вычисляет все точки в пределах изменениях от -? до +?. Результаты вычислений могут содержать особые экстра переменные с именами вида _Zn- и _NNn-. В частности, они позволяют оценить периодические нарушения непрерывности функций.
Примеры применения функции discont приведены ниже:
> discont(l/(x-2).x);
{2}
> discont(l/((x-l)*(x-2)*(x-3)).x):
{1,2,3}
> discont(GAMMA(x/2),x):
{-2_NN1~}
Весьма рекомендуется наряду с применением данной функции просмотреть график анализируемой функции.
ПРИМЕЧАНИЕ
В ряде примеров в выводе используются специальные переменные вида _NameN~, где Name — имя переменной иN— ее текущий номер. После выполнения команды restart отсчет N начинается с 1. Если вывод с такими переменными уже применялся, то их текущие номера могут казаться произвольными. Специальные переменные часто используются для упрощения выводимых выражений.
5. Нахождение сингулярных точек функции
Нахождение сингулярных точек функции
Многие операции, такие как интегрирование и дифференцирование, чувствительны к особенностям функций, в частности к их разрывам и особым точкам. Функция singular (ехрr, vars) позволяет найти особые (сингулярные) точки выражения ехрг, в которых она испытывает разрывы. Дополнительно в числе параметров может указываться необязательный список переменных.
Примеры применения этой функции приведены ниже:
7.gif
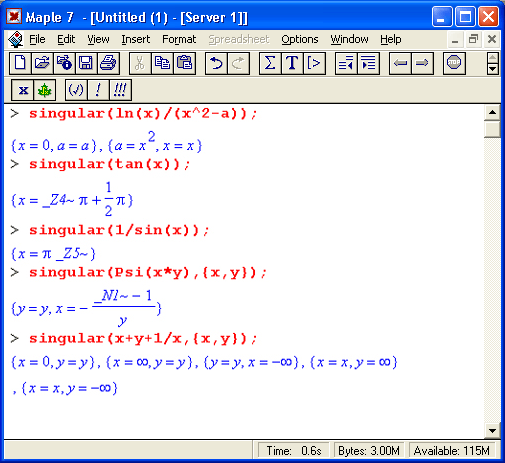
6. Вычисление асимптотических и иных разложений
Вычисление асимптотических и иных разложений
Важным достоинством системы Maple является наличие в ней ряда функций, позволяющих выполнять детальный анализ функций. К такому анализу относится вычисление асимптотических разложений функций, которые представляются в виде рядов (не обязательно с целыми показателями степени). Для этого используется следующая функция:
asympt(f.x) asympt(f,x,n).
Здесь f — функция переменной х или алгебраическое выражение; х — имя переменной, по которой производится разложение; n — положительное целое число (порядок разложения, по умолчанию равный 6). Ниже представлены примеры применения этой функции:
8.gif

9.gif
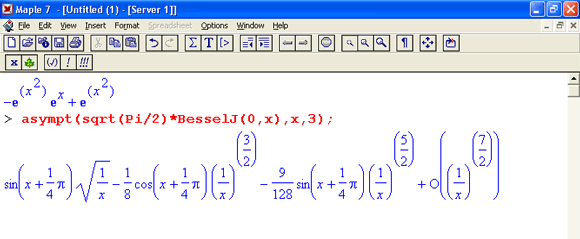
7. Пример анализа сложной функции
Пример анализа сложной функции
Ниже мы рассмотрим типичный анализ достаточно «сложной» функции, имеющей в интересующем нас интервале изменения аргумента х от -4 до 4, нули, максимумы и минимумы. Определение функции f(x), ее графики и график производной dF(x)/dx даны на рис. 9.2. Этот рисунок является началом полного документа, описываемого далее, i
Функция F(x) на первый взгляд имеет не совсем обычное поведение вблизи начала координат (точки с х =у = 0). Для выяснения такого поведения разумно построить график функции при малых х и у. Он также представлен на рис. 9.2 (нижний график) и наглядно показывает, что экстремум вблизи точки (0, 0) является обычным минимумом, немного смещенным вниз и влево от начала координат. Теперь перейдем к анализу функции F(x). Для поиска нулей функции (точек пересечения оси х) удобно использовать функцию f sol ve, поскольку она позволяет задавать область изменениях, внутри которой находится корень. Как видно из приведенных ниже примеров, анализ корней F(x) не вызвал никаких трудностей, и все корни были уточнены сразу: Поиск нулей функции
> fsolve(F(x),x,-2...-l):
-1.462069476 > fso1ve(F(x),x,-.01..0.01);
0.
> fsolve(F(x).x.-.05..0);
-.02566109292
> fsolve(F(x),x,1..2);
1.710986355
> fsolve(F(x),x,2.5..3):
2.714104921
Нетрудно заметить, что функция имеет два очень близких (но различных) корня прих, близких к нулю.
Анализ функции на непрерывность, наличие ее нарушений и сингулярных точек реализуется следующим образом:
Анализ функции на непрерывность, наличие ее нарушений и наличие сингулярных точек
Рис. 9.2. Задание функции F(x) и построение графиков функции и ее производной
Этот анализ не выявляет у заданной функции каких-либо особенностей. Однако это не является поводом для благодушия — попытка найти экстремумы F(x) с помощью функции extrema и минимумы с помощью функции minimize завершаются полным крахом:
Неудачный поиск экстремумов и минимумов функции
>extrema(F(x).{},x, 's');s;
>minimize(F(x),x=-.l...l);
minimize (.05x + xe (-|x|) * sm(2x),x = -.1 .. 1)
>minimize(F(x),x=-2.5..:2);S
minimize (.05x + xe(-|x|) sin(2*),*'=-2.5 ..-2)
Приходится признать, что в данном случае система Maple 7 ведет себя далеко не самым лучшим образом. Чтобы довести анализ F(x) до конца, придется вспомнить, что у функции без особенностей максимумы и минимумы наблюдаются в точках, где производная меняет знак и проходит Через нулевое значение. Таким образом, мы можем найти минимумы и максимумы по критерию равенства производной нулю. В данном случае это приводит к успеху:
Поиск минимумов по критерию равенства нулю производной
> fso1ve(d1ff(F(x),x)=0,x,-.5...5);
-.01274428224
>xm:=%;
хт:= -.0003165288799
>[F(xm),F(xnn-.001),F(xm-.001)]:
[-.00001562612637, .00003510718293, -.00006236451216]
>fsolve(diff(F(x),x)-0.x,-2.5..-2);
-2.271212360 '
>fso1ve(diff(F(x),x)=0,x.2..2.5):
2.175344371
Неудачный поиск максимума
>maximize(F(x) ,x--l.. - .5);
maximize(.05х + хе (-|x|) * sin(2x),x = -l .. -.5)
Поиск максимумов по критерию равенства нулю производной
>fso1ve(diff(F(x).x),x,-l..-.5);
-.8094838517
>fso1ve(diff(F(x),x),x..5..2):
.8602002115
>fsolve(diff(F(x),x),x.-4..-3);
-3.629879137
>fsolve(diff(F(x),x).x,3..4);
3.899664536
Итак, все основные особые точки данной функции (нули, минимумы и максимумы) найдены, хотя и не без трудностей и не всегда с применением специально предназначенных для такого поиска функций. В уроке 12 будет описана процедура, которая автоматизирует процесс анализа не очень сложных функций и обеспечивает его наглядную визуализацию.
10.gif
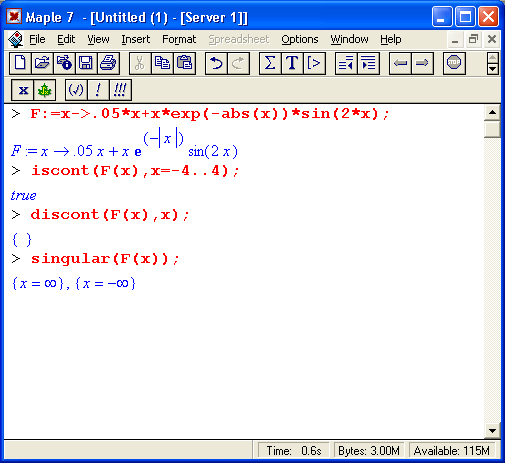
13.gif
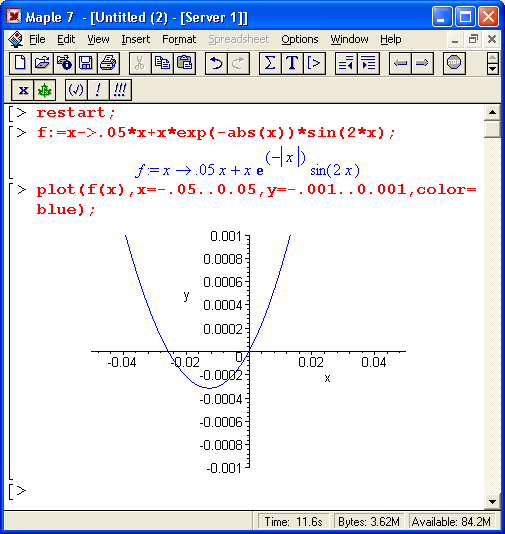
8. Функции из отдельных кусков
Функции из отдельных кусков
Создание функций из отдельных кусков
Для создания функций, составленных из отдельных кусков, Maple 7 располагает интересной функцией:
piecewise(cond_l,f_l. cond_2,f_2. .... cond_n,f_n. f_otherwise)
где f_i — выражение, cond_i — логическое выражение, f_otherwise — необязательное дополнительное выражение. В зависимости от того или иного условия эта функция позволяет формировать соответствующую аналитическую зависимость. К кусочным функциям (подчас в скрытой форме) приводят функции с элементами сравнения аргумента, например abs, signum, max и др. Поэтому в Maple 7 введен достаточно мощный аппарат обработки и преобразований таких функций по частям.
9. Простые примеры применения функции piecewise
Простые примеры применения функции piecewise
Рисунок 9.3 показывает задание функции f(x), содержащей три характерных участка. По определенной через функцию пользователя зависимости f(x) можно, как обычно, построить ее график.
Рис. 9.3. Пример задания и применения функции, составленной из отдельных кусков
Важно отметить, что созданная с помощью функции piecewise зависимость может участвовать в различных преобразованиях. Например, на рис. 9.3 показано, что она легко дифференцируется и можно построить график производной этой функции. При этом каждая часть функции обрабатывается отдельно.
10. Работа с функциями piecewise
Работа с функциями piecewise
С функциями типа piecewise можно работать, как с обычными функциями. При этом необходимые операции и преобразования осуществляются для каждой из частей функции и возвращаются в наглядной форме.
Ниже приведен пример задания функции f в аналитической форме:
Для выявления характера функции воспользуемся функцией convert и создадим объект g в виде кусочной функции:
Выполним дифференцирование и интегрирование функции:
Как нетрудно заметить, результаты получены также в виде кусочных функций. Можно продолжить работу с функцией f и выполнить ее разложение в степенной ряд:
> series(f, х);
-1+.Х + О(x6)
Чтобы убрать член с остаточной погрешностью, можно выполнить эту операцию следующим образом:
> series(g, x);
-1 + х
Обратите внимание на то, что поскольку разложение в ряд ищется (по умолчанию) в окрестности точки х=0, то при этом используется тот кусок функции, в котором расположена эта точка. Читатель может продолжить работу с кусочными функциями и далее.
15.gif

16.gif
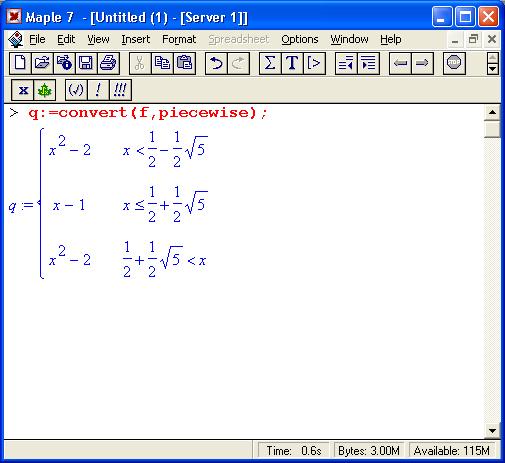
17.gif
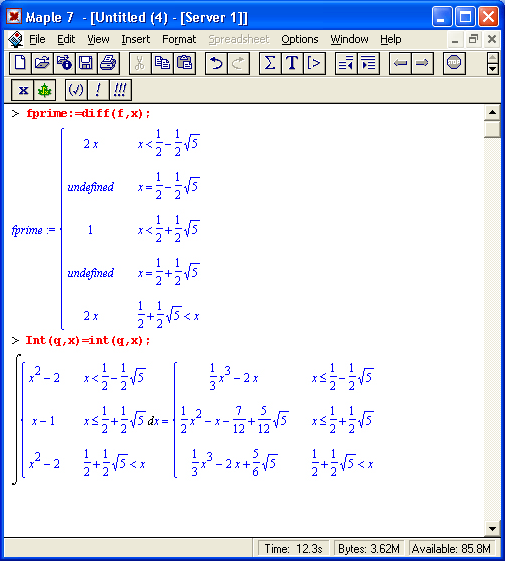
11. Операции с полиномами
Операции с полиномами
К числу наиболее известных и изученных аналитических функций относятся степенные многочлены — полиномы. Графики полиномов описывают огромное разнообразие кривых на плоскости. Кроме того, возможны рациональные полиномиальные выражения в виде отношения полиномов. Таким образом, круг объектов, которые могут быть представлены полиномами, достаточно обширен, и полиномиальные преобразования широко используются на практике, в частности, для приближенного представления других функций.
Под полиномом в системе Maple 7 понимается сумма выражений с целыми степенями. Многочлен для ряда переменных —многомерный полином. К одномерным полиномам относятся степенной многочлен:
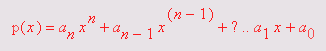
а также отдельная переменная х и константа. Большое достоинство полиномов состоит в том, что они дают единообразное представление многих зависимостей и для своего вычисления требуют только арифметических операций (их число значительно сокращается при использовании хорошо известной схемы Горнера). Производные от полиномов и интегралы с подынтегральными функциями-полиномами легко вычисляются и имеют простой вид. Есть и достаточно простые алгоритмы для вычисления всех (в том числе комплексных) корней полиномов на заданном промежутке.
12. Выделение коэффициентов полиномов
Выделение коэффициентов полиномов
Для выделения коэффициентов полиномов в Maple 7 служат следующие функции:
- coeff(p, х) — возвращает коэффициент при х полинома р;
- coeff(p.x.n) — возвращает коэффициент для члена со степенью n полинома р;
- coeff(p.x^n) — возвращает коэффициенты при х^n полинома р;
- coeffs(p, х, 't') — возвращает коэффициенты полинома нескольких переменных, относящиеся к переменной х (или списку переменных) с опцией ' t', задающей имя переменной;
- collect(p,x) — возвращает полином, объединяя коэффициенты при степенях переменной х.
Ниже даны примеры применения этих функций:
ПРИМЕЧАНИЕ
Следует обратить внимание на то, что при выполнении операции collect в прежних версиях Maple довольно часто возникала фатальная ошибка. Как видно из приведенных примеров, в Maple 7 такой ошибки уже не возникает.
19.gif
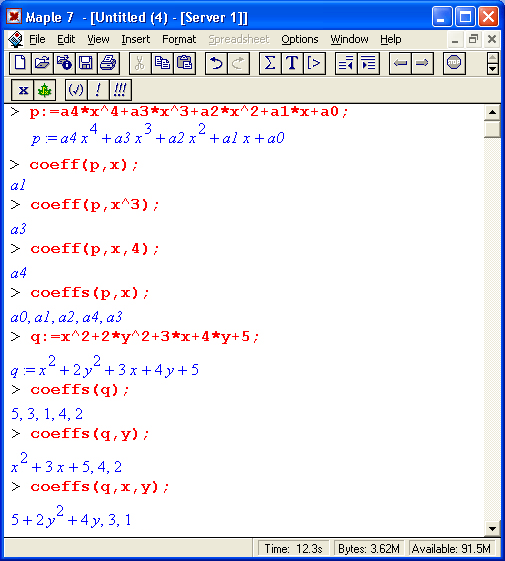
13. Оценка коэффициентов полинома по степеням
Оценка коэффициентов полинома по степеням
Полином может быть неполным, то есть не содержать членов со степенями ниже некоторой. Функция lcoeff возвращает старший, а функция tcoeff — младший коэффициент полинома нескольких переменных. Эти функции задаются в виде:
lcoeff(p) tcoeff(p)
Icoeff(p. x) tcoeff(p, x)
Icoeff(p. x. 't') tcoeff(p, x. 't')
Функции Icoeff и tcoef f возвращают старший (младший) коэффициент полинома р относительно переменной х или ряда переменных при многомерном полиноме. Если х не определено, Icoeff (tcoeff) вычисляет старший (младший) коэффициент относительно всех переменных полинома р. Если третий аргумент t определен, то это имя назначено старшему (младшему) члену р. Если х — единственное неизвестное и d — степень р по х, то lcoeff(p, x) эквивалентно coef f (p. x, d). Если х — список или множество неизвестных, lcoeff (tcoef f) вычисляет старший (младший) коэффициент р, причем р рассматривается как полином многих переменных. Имейте в виду, что р должен быть разложен по степеням неизвестного х до вызова функций lcoeff или tcoef f.
Приведем примеры применения функций lcoeff, tcoef f и coeffs:
20.gif
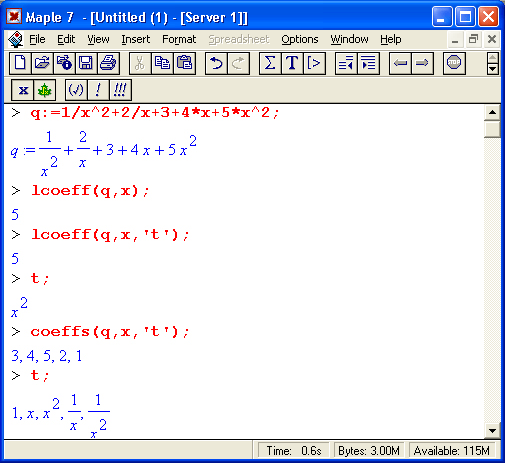
14. Оценка степеней полинома
Оценка степеней полинома
Функция degree возвращает высшую степень полинома, а ldegree — низшую степень. Эти функции задаются следующим образом:
degree(a.x) ldegree(a.x)
Функции degree и ldegree используются, чтобы определить высшую и низшую степени полинома от неизвестного (неизвестных) х, которое чаще всего является единственным, но может быть списком или множеством неизвестных. Полином может иметь отрицательные целые показатели степеней при х. Таким образом, degree и ldegree могут возвратить отрицательное или положительное целое число. Если выражение не является полиномом от х данным параметром, то возвращается FAIL.
Чтобы degree и ldegree возвратили точный результат, полином обязательно должен быть сгруппирован по степеням х. Например, для выражения (х + 1) (х+ 2) - х2 функция degree не обнаружит аннулирование старшего члена и неправильно возвратит результат 2. Во избежание этой проблемы перед вызовом degree следует применять к полиному функции collect или expand. Если х — множество неизвестных, degree/ ldegree вычисляет полную степень. Если х — список неизвестных, degree/ldegree вычисляет векторную степень. Векторная степень определяется следующим образом:
degree(p.[]) =0
degree(p.[xl.x2,...]) =degree(p.xl) degree(lcoeff(p.xl),[x2....])
Полная степень тогда определяется следующим образом:
degree(p.{xl....,xn}) - maximum degree(p.{xl....xn})
или
degree(p,{xl....,xn}) = degree(p.[xl,....xn])
Обращаем внимание на то, что векторная степень зависит от порядка перечисления неизвестных, а полная степень не зависит.
Примеры применения функций degree и ldegree:
21.gif
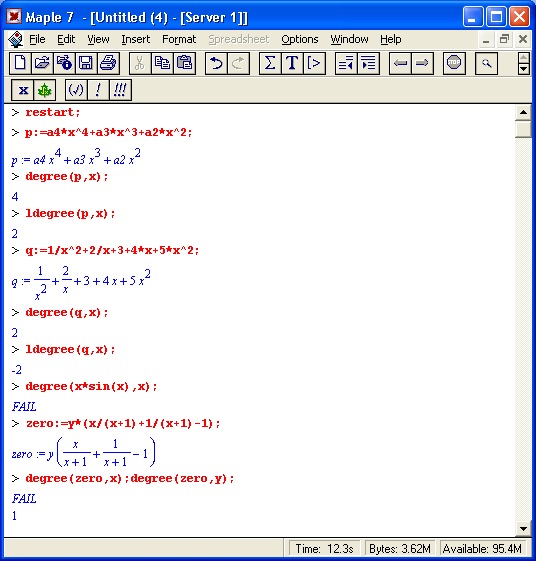
15. Разложение полинома на множители
22.gif
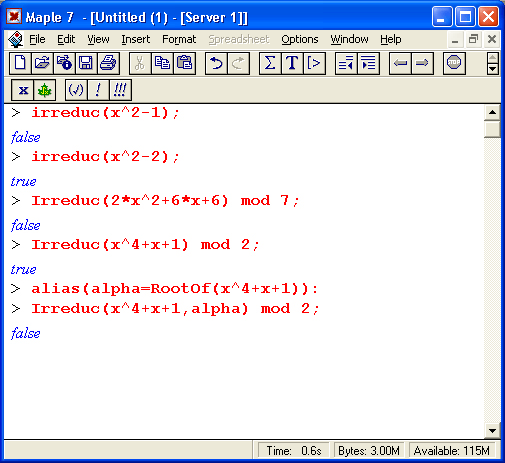
16. Разложение полинома по степеням
Разложение полинома по степеням
Для разложения полинома р по степеням служат инертные функции AFactor(р) и AFactors(p). Полином может быть представлен в виде зависимости от одной или нескольких переменных.
Функция Afactor(p) выполняет полную факторизацию (разложение) полинома р от нескольких переменных с коэффициентами в виде алгебраических чисел над полем комплексных чисел. При этом справедливо отношение evala(AFactor(p) )=factor(p,complex). Таким образом, эта функция является, по существу, избыточной.
В случае одномерного полинома полное разложение на множители является разложением на линейные множители. Функция AFactors аналогична функции Afactor, но создает структуру данных формы [u,[[f[l],e[l]],....[f[n],e[n]]]] так, что p=u*f[l]xe[l]*...*f[n]^e[n], где каждый f[i] — неприводимый полином.
Ниже даны примеры применения функции Afactor:
Нетрудно заметить, что разложение полинома на множители позволяет оценить наличие у него корней. Однако для этого удобнее воспользоваться специальными функциями, рассмотренными ниже.
23.gif
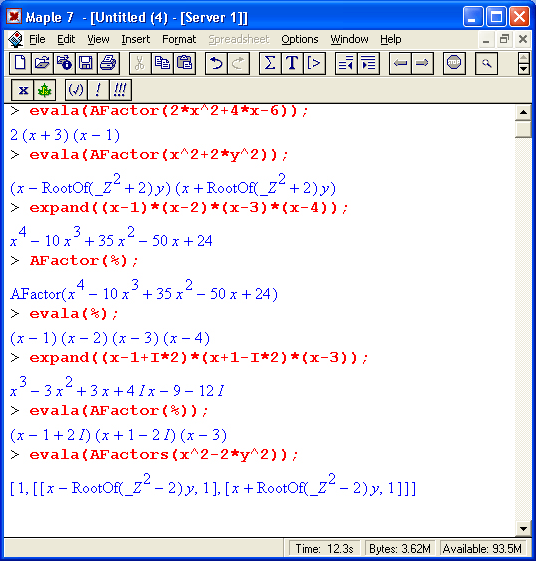
17. Вычисление корней полинома
Вычисление корней полинома
Для вычисления действительных и комплексных корней полиномов служит уже известная нам функция solve(p.x), возвращающая список корней полинома р одной переменной. Кроме того, имеются следующие функции для вычисления корней полиномов:
roots(p) , roots(p. К) ,
roots(p. x), roots(p. x. К)
Эти функции вычисляют точные корни в рациональной или алгебраической области чисел. Корни возвращаются в виде [ [rl.ml], .... [rn.mn] ], где ri — это
корень полинома, a mi — порядковый номер полинома. С действиями этих функций можно разобраться с помощью приведенных ниже примеров:
24.gif
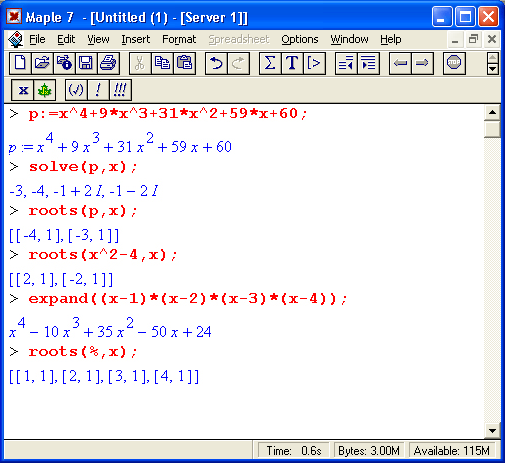
18. Основные операции с полиномами
Основные операции с полиномами
С полиномами могут выполняться различные операции. Прежде всего отметим некоторые функции, которые относятся к одному полиному:
- psqrt(p) — возвращает квадрат полинома;
- proot(p.n) — возвращает n -ю степень полинома;
- realroot(p) — возвращает интервал, в котором находятся действительные корни полинома;
- randpolyCvars, eqns) — возвращает случайный полином по переменным vans (список) с максимальной степенью eqns;
- discrim(p,var) — вычисление дискриминанта полинома по переменной var;
- Primitive(a) mod p — проверка полинома на примитивность (возвращает true, если полином примитивен).
Действие этих функций достаточно очевидно, поэтому ограничимся приведением примеров их использования:
Обратите внимание на то, что для использования некоторых из приведенных функций необходим вызов их из стандартной библиотеки. Для функции randpoly приведенные результаты случайны, так что, скорее всего, их повторение невозможно.
С полиномами можно выполнять обычные операции, используя для этого соответствующие операторы:
В целом надо отметить, что аппарат действий с полиномами в Maple 7 хорошо развит и позволяет выполнять с ними практически любые математические операции. В частности, можно вычислять производные от полиномов и интегралы, у которых полиномы являются подынтегральными функциями:
25.gif
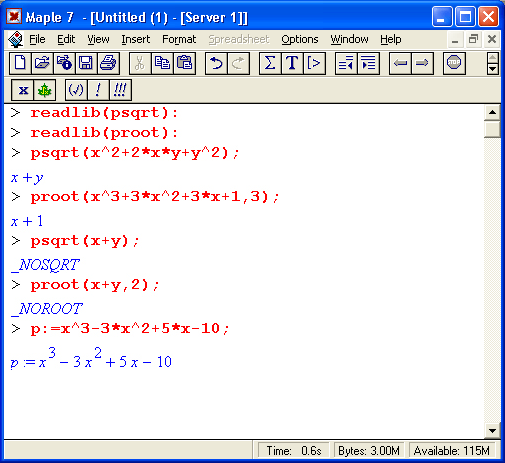
26.gif
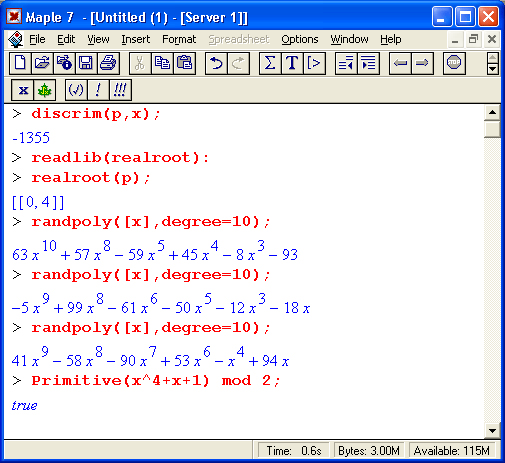
27.gif
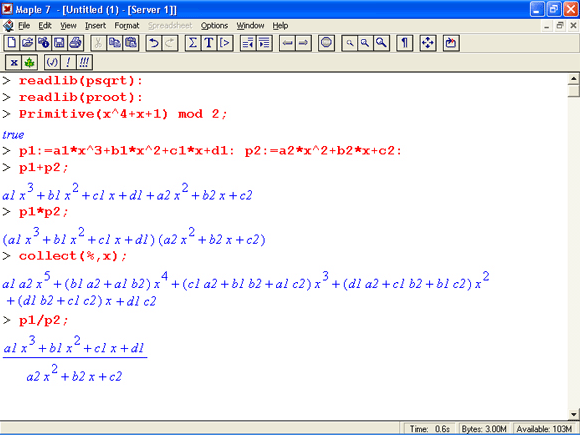
28.gif
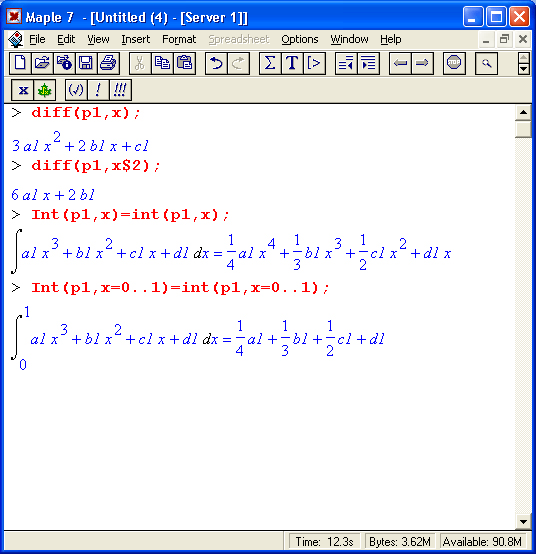
19. Операции над степенными многочленами с отрицательными степенями
Операции над степенными многочленами с отрицательными степенями
Хотя в подавляющем большинстве случаев используются степенные многочлены (полиномы) с положительными степенями, Maple 7 не накладывает особых ограничений и на многочлены с отрицательными степенями. Например, можно задать такой степенной многочлен:
Нетрудно показать, что с ним можно выполнять различные операции:
ПРИМЕЧАНИЕ
Maple 7 не накладывает ограничений на применение степенных многочленов (полиномов) с отрицательными степенями. Однако свойства таких полиномов заметно отличаются от свойств полиномов с положительными степенями, поэтому при применении первых надо проявлять известную осторожность.
29.gif
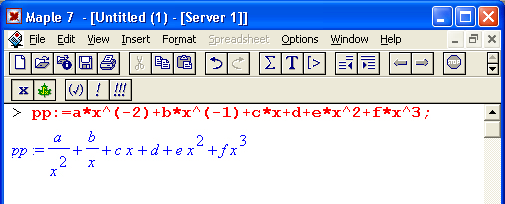
30.gif
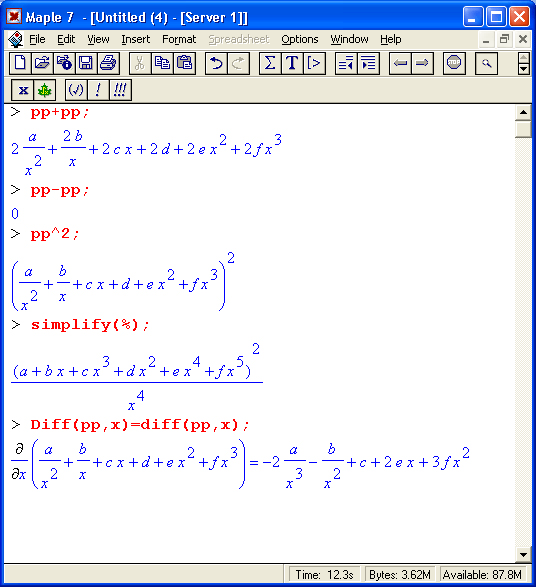
20. Интерполяция и аппроксимация функциональных зависимостей.
Интерполяция и аппроксимация функциональных зависимостей
Интерполяция, экстраполяция и аппроксимация
Вычисление многих функций, особенно специальных, требует больших затрат времени. Поэтому до сих пор широко применяются таблицы таких функций. Достаточно отметить знаменитые на весь мир таблицы в книге «Справочник по специальным функциям с формулами, графиками и таблицами» под редакцией М. Абрамовица и И. Стиган [59].
Если некоторая зависимость у(х) представлена рядом табличных отсчетов y(x), то интерполяцией принято называть вычисление значений у(х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [а,b], то есть при х < а и х > b, вычисление у(х) называют экстраполяцией (или иногда предсказанием значений функции). В данном случае речь идет об одномерной интерполяции, но возможны двумерная интерполяция функций двух переменных z(x, у) и даже многомерная интерполяция для функций многих переменных.
Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой зависимости. Например, если узловые точки функции соединить отрезками прямых, то будем иметь многоинтервальную линейную интерполяцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполяция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функций) также достаточно хорошо известна; она эффективна при интерполяции периодических функций.
Аппроксимацией в системах компьютерной математики обычно называют получение приближенных значений какого-либо выражения. Однако под аппроксимацией функций подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, приближающую заданный ряд узловых точек. Часто для этого используют степенные многочлены — полиномы.
Здесь мы будем рассматривать такие виды аппроксимации, которые дают точные значения функции у(х) в узловых точках в пределах погрешности вычислений по умолчанию. Если аппроксимирующая зависимость выбирается из условия наименьшей среднеквадратической погрешности в узловых точках (метод наименьших квадратов), то мы имеем регрессию или приближение функций по методу наименьших квадратов.
21. Аппроксимация аналитически заданных функций
Аппроксимация аналитически заданных функций
Если функция задана аналитически, то наиболее простым способом нахождения ее аппроксимирующей зависимости является применение функции convert. Это поясняют следующие примеры:
На рис. 9.4 представлен пример полиномиальной аппроксимации хорошо известной статистической функции erfc(x). Для полинома задана максимальная степень 12, но ввиду отсутствия в разложении четных степеней максимальная степень результата оказывается равна 11.
Рис. 9.4. Пример полиномиальной аппроксимации функции erfc(x)
Как видно из приведенного рисунка, в интервале изменениях от -1,5 до 1,5 аппроксимирующее выражение почти повторяет исходную зависимость. Однако затем график аппроксимирующей функции быстро отходит от графика исходной зависимости. При этом он ведет себя иначе даже качественно, никоим образом не показывая асимптотическое поведение, характерное для исходной зависимости.
31.gif

32.gif
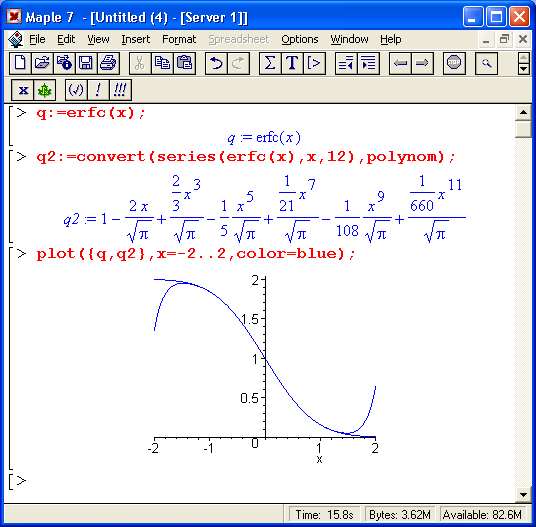
22. Полиномиальная интерполяция табличных данных
Полиномиальная интерполяция табличных данных
Если данные некоторой зависимости у(х) заданы векторами X и Y ее дискретных значений, то для получения интерполяционного степенного многочлена достаточно записать многочлен для всех N пар значений yi(xi) при i=1...N (или i =0...N- 1, если индексы отсчетов начинаются с нуля). Полученная при этом система линейных (относительно коэффициентов полинома) уравнений после решения дает коэффициенты аппроксимирующего полинома. Степень полинома на 1 меньше N, а вычисляемые при х значения у(х) совпадают с табличными (узловыми) в пределах вычислительной погрешности.
На самом деле все это делать не нужно, поскольку Maple 7 имеет реализующую данный алгоритм встроенную функцию interp(X,Y,v) или в инертной форме Interp(X,Y,v).
Переменная v указывает имя переменной интерполяционного полинома. Векторы X и Y должны содержать n + 1 =N координат точек исходной зависимости, где и — степень интерполирующего полинома.
Рисунок 9.5 показывает технику применения полиномиальной аппроксимации на основе функции interp с построением графика исходных точек и аппроксимирующего полинома. Нетрудно заметить, что график полинома проходит точно через исходные точки — они показаны квадратиками.
В этом примере полезно присмотреться к визуализации результатов вычислений и совместному построению графика интерполирующего полинома и исходных точек. В частности, для построения последних использована обычная функция plot, позволяющая выводить на график точки с заданными координатами, причем не только в виде окружностей, но и в виде точек, маленьких крестиков, кружков, квадратов и других фигур. Для выбора типа точек и других параметров графика его надо выделить (установив указатель мыши в поле графика и щелкнув левой кнопкой) и нажать правую кнопку мыши — появится контекстно-зависимое меню с операциями форматирования графика. Это меню показано на рис. 9.5.
Приведем еще несколько примеров использования функции Interp:
Рис. 9.5. Пример осуществления полиномиальной аппроксимации
33.gif
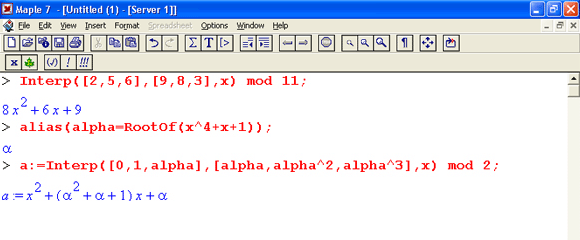
34.gif
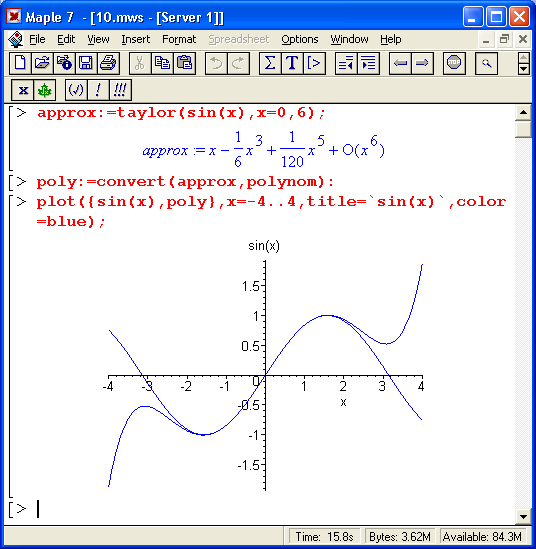
23. Сплайн-интерполяция и аппроксимация
Сплайн-интерполяция и аппроксимация
Точность полиномиальной аппроксимации катастрофически падает при увеличении степени аппроксимирующих полиномов. От этого недостатка можно избавиться, используя для аппроксимации отрезки полиномов невысокой степени, применяемые для представления части узловых точек. Самым известным методом такой аппроксимации является сплайн-аппроксимация на основе применения отрезков кубических полиномов. При этом аппарат сплайн- аппроксимации позволяет получить полиномы, которые дают в узловых точках непрерывность не только представляемой ими функции, но и ее первых и даже вторых производных.
Наглядно сплайн-функцию можно представить в виде гибкой стальной линейки, закрепленной в узловых точках и плавно изгибающейся. Благодаря указанным свойствам сплайнов они неплохо описывают функции, представленные как небольшим числом узловых точек (благодаря плавности сплайн- кривых), так и функции, представляемые очень большим числом узловых точек (поскольку порядок полиномов от этого числа уже не зависит). Недостатком сплайн- аппроксимации является отсутствие общего выражения для всей кривой. Фактически приходится использовать набор сплайн- функций для различных интервалов между узловыми точками.
Для получения сплайн- интерполяций используется Maple-функция spline (X, Y, var, d).
Здесь X и Y — одномерные векторы одинакового размера, несущие значения координат узловых точек исходной функции (причем в произвольном порядке), var — имя переменной, относительно которой вычисляется сплайн-функция, наконец, необязательный параметр d задает вид сплайна. Он может иметь следующие значения: 1inear — линейная функция, или полином первого порядка, quadratic — квадратичная функция, или полином второго порядка, cubic — полином третьего порядка, quartiс — полином четвертого порядка. Если параметр d опущен, то сплайн-функция будет строиться на основе полиномов третьего порядка (кубические сплайны).
Технику сплайновой аппроксимации наглядно поясняет рис. 9.6. На нем представлено задание векторов узловых точек X и Y и четырех сплайновых функций, по которым построены их графики. Для одной из функций (с линейной интерполяцией между узлами) показан вид сплайновой функции.
Рис. 9.6. Задание сплайновой аппроксимации и построение графиков полученных функций
Как видно из рис. 9.6, сплайновая функция представляет собой кусочную функцию, определяемую на каждом отдельном интервале. При этом на каждом участке такая функция описывается отдельным полиномом соответствующей степени. Функция plot «понимает» такие функции и позволяет без преобразования типов данных строить их графики. Для работы с кусочными функциями можно использовать функции convert и piecewise.
35.gif

24. Прямое и обратное Z-преобразования
Прямое и обратное Z-преобразования
Прямое и обратное Z-преобразования функций широко используются при решении задач автоматического управления. Эти преобразования задаются следующими функциями:
- ztrans(f, n, z) — прямое преобразование функции f(n) в f(z);
- invztransCf, z, n) — обратное преобразование f(z) в f(n).
Заметим, что прямое Z-преобразование базируется на соотношении ztrans(f (n) ,n,z)= = sum(f(n)/z~n,n=0. .infinity), записанном на Maple-языке. В первых версиях системы Maple Z-преобразования выполнялись средствами библиотеки и требовали вызова командой readlib(ztrans). Но в Maple 7 они включены в ядро системы и предварительного вызова уже не требуют. В этом убеждают следующие примеры:
Родственные Z-преобразованиям интегральные преобразования Лапласа и Фурье реализуются с помощью пакета inttrans (интегральные преобразования).
36.gif
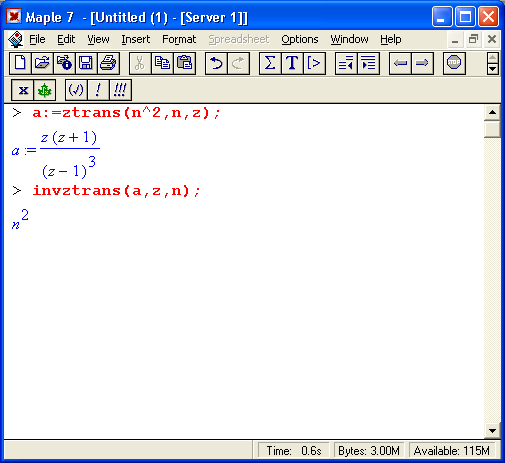
25. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
Выполнять поиск экстремумов функций.
- Осуществлять поиск минимумов и максимумов аналитических функций.
- Анализировать функции на непрерывность.
- Находить сингулярные точки функций.
- Вычислять асимптотические и иные разложения.
- Анализировать сложные функции.
- Работать с кусочными функциями.
- Выполнять операции с полиномами.
- Интерполировать и аппроксимировать функциональные зависимости.
- Вычислять прямые и обратные Z-преобразования.
Заключение
Заключение
Программа Maple корпорации Waterloo Maple Inc. — патриарх в мире систем компьютерной математики. Эта система, снискавшая себе мировую известность и огромную популярность, является одной из лучших среди систем символьной математики, позволяющих решать математические задачи в аналитическом виде. Эта книга познакомила читателей с новейшей версией Maple — Maple 7. Она вобрала в себя не только обширные и мощные возможности- предшествующих реализаций системы, но и предоставила в распоряжение пользователя ряд новых возможностей. Прежде всего это целый букет пакетов: CurveFitting, PolynomialTools, OrthogonalSeries и др.
Maple как система компьютерной математики развивается по ряду характерных направлений. Одно из них — повышение мощности и достоверности аналитических (символьных) вычислений. Это направление представлено в Maple наиболее сильно. Maple 7 уже сегодня способна выполнять сложнейшие аналитические вычисления, которые нередко не под силу даже опытным математикам. Конечно, Maple не способна на «гениальные догадки», но зато рутинные и массовые расчеты система выполняет с блеском. В новой версии ее возможности существенно расширены, особенно в области решений дифференциальных уравнений. : Другое важное направление — повышение эффективности численных расчетов. И тут успехи налицо — начиная с версии Maple 6 в систему включены эффективные алгоритмы группы NAG, лидирующей в области численных расчетов. Повышена эффективность и алгоритмов самой системы Maple 7. В результате этого заметно возросла перспектива использования Maple в численном моделировании и выполнении сложных численных расчетов — в том числе с произвольной точностью.
Интеграция Maple с другими программными средствами — еще одно важное направление развития этой системы. Ядро символьных вычислений Maple уже включено в состав целого ряда систем компьютерной математики — от систем «для всех» класса Mathcad до одной из лучших систем для численных расчетов и моделирования — MATLAB. Имеется целый ряд автоматизированных рабочих мест для математиков на основе ядра системы Maple: Math Office, Scientific Word, Scientific Workplace и др.
Предусмотрена и интеграция Maple 7 с Excel 2000 и MATLAB. Однако альянс Maple 7 с Excel трудно назвать удачным. Во-первых, потому, что куда более распространенная версия Excel 97 связь с Maple 7 не поддерживает. Во-вторых, введенные в Maple 7 средства работы с таблицами (в том числе новые) в большинстве случаев оказываются более удобными, чем обычные средства работы с таблицами у Excel. Достаточно отметить, что таблицы в Maple могут работать с формульными данными и построение рисунков в Maple не требует создания таблицы данных для них, как это нужно в Excel.
Существенно расширена поддержка системы Maple через Интернет. Появление на сайте корпорации Waterloo Maple Inc. массы информационных материалов, и прежде всего обучающих программ и примеров применения Maple, разгрузило саму программу и предоставило ее пользователям обширные возможности в пополнении своих знаний и навыков работы с Maple 7.
С другой стороны, резко повышены возможности Maple 7 для создания web-страниц — основы Интернета. Здесь прежде всего надо отметить включение в пакеты средств поддержки языков HTML, XML и (что особенно важно) MathML.
Все эти возможности в сочетании с прекрасно выполненным и удобным пользовательским интерфейсом и мощной справочной системой делают Maple 7 первоклассной программной средой для решения самых разнообразных математических задач: от самых простых до самых сложных. Особо следует отметить возможность создания превосходных электронных документов, статей, книг и учебников в среде Maple 7 с «живыми» и модифицируемыми примерами.
Maple — быстро развивающаяся система, и работа с ней не только полезна, но и приятна для всех категорий пользователей и учащихся. Автор надеется, что эта книга привлечет внимание наших читателей, и прежде всего специалистов, преподавателей вузов, аспирантов, студентов и даже школьников, к такому уникальному программному продукту, как система компьютерной математики Maple 7, и поможет им в решении учебных и реальных научно-технических задач.