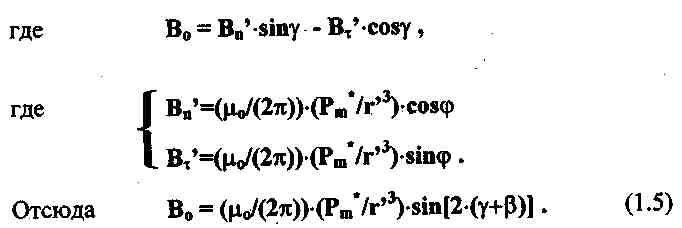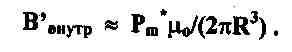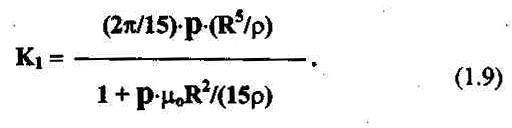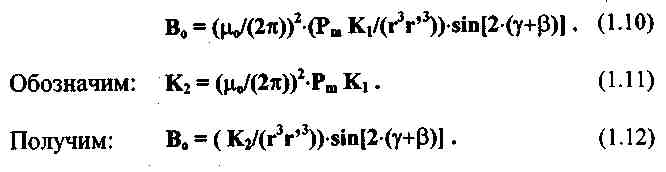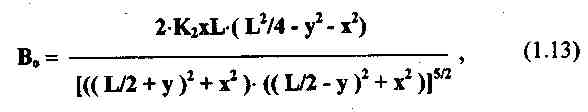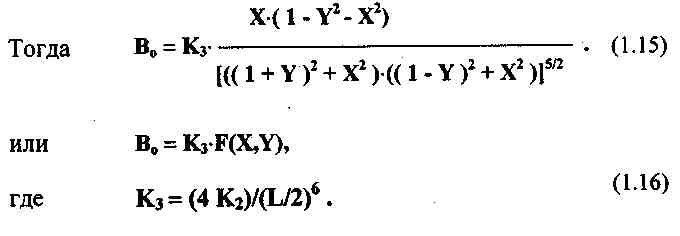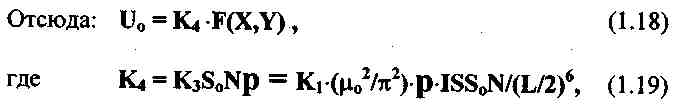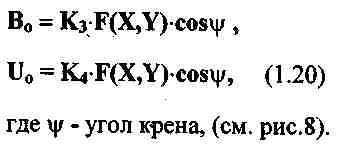Главное меню
Вы здесь
3.1.3.2. Отражение сигнала за счет проводимости объекта
3.1.3.2. Отражение сигнала за счет проводимости объекта
Проводящий металлический объект, размеры которого пока будем также считать небольшими, по крайней мере, не превосходящими r и r' (см. рис.5), с точки зрения переизлучения магнитного поля, можно представить в виде эквивалентной рамки с токомI*, вектор магнитного момента которой Рm* практически параллелен вектору индукции излучающей катушки В.
Величина Рm* зависит от размеров проводящего объекта, его проводимости, от индукции поля в точке расположения объекта, от частоты излучаемого поля. Индукция поля переизлучения имеет в центре приемной катушки ненулевую составляющую Во в направлении вектора нормалиns', что приводит к появлению в этой катушке э.д.с., пропорциональной указанной составляющей:
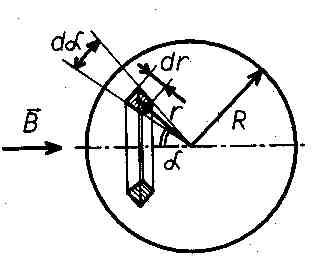
Рис. 6. К расчету магнитного момента эквивалентного шара.
Для того, чтобы вычислить магнитный момент эквивалентной рамкиРm*, необходимо взять интеграл по всему объему проводящего объекта так, чтобы просуммировать вклады всех элементарных кольцевых токов, наведенных полем излучающей катушки, в итоговую величину Рm*. Для простоты будем считать, что магнитное поле по всему объему проводящего объекта однородно, то есть он удален на значительное расстояние от излучающей катушки. Чтобы не возникало проблем с ориентацией объекта, будем пока считать, что он имеет форму однородного шара (см. рис.б). Считая, что проводящий объект удален на значительное расстояние и от приемной катушки, можно записать:
Пренебрегая явлением самоиндукции, влияние которого будет рассмотрено ниже, получаем:
Чтобы учесть явление самоиндукции, предположим для простоты, что переизлученное поле однородновнутри объекта-мишени и, исходя из величины магнитного момента (1.7), составляет:
Подставив в выражение (1.7) В -В'внутр вместо В, получим по-прежнему пропорциональную зависимость Рm* отВ, но с несколько иным коэффициентом K1:
Составляющая индукции в центре приемной катушки:
В системе декартовых координат с началом в середине базы системы катушек (см. рис.7) последнее выражение принимает вид:
Введем нормированные координаты:
Определим с точностью до знака э.д.с., наводимую в приемной катушке:
где So - площадь сечения приемной катушки, N - количество ее витков.
где S - площадь сечения излучающей катушки, I - суммарный ток всех ее витков.
В трехмерном пространстве, когда плоскость XOY не перпендикулярна плоскости приемной рамки,
Рис. 7. Система координат.
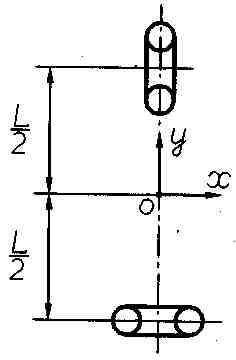
Рис.8. Ориентация объекта по крену.