Главное меню
Вы здесь
11. Функция DEplotna пакета DEtools
Функция DEplot из пакета DEtools
Специально для решения и визуализации решений дифференциальных уравнений и систем с дифференциальными уравнениями служит инструментальный пакет DEtools. В него входит ряд функций для построения наиболее сложных и изысканных графиков решения дифференциальных уравнений. Основной из этих функций является функция DEplot. Функция DEplot может записываться в нескольких формах:
DEplot(deqns, vars. trange. eqns)
DEplot(deqns, vans, trange. inits. eqns)
DEplot(deqns. vars. trange, уrange, xrgnge, eqns) .
DEplot(deqns. vars, trange. Inits, xrange. yrange, eqns)
Здесь deqns — список или множество, содержащее систему дифференциальных уравнений первого порядка или одиночное уравнение любого порядка; vars — зависимая переменная или список либо множество зависимых переменных; trange — область изменения независимой переменной t; Inits — начальные условия для решения; yrange — область изменения для первой зависимой переменной, xrange — область изменения для второй зависимой переменной; eqns — опция, записываемая в виде keyword-value. Замена имен переменных другими в данном случае недопустима.
Эта функция обеспечивает численное решение дифференциальных уравнений или их систем при одной независимой переменной t и строит графики решения. Для автономных систем эти графики строятся в виде векторного поля направлений, а для неавтономных систем — только в виде кривых решения. По умолчанию реализуется метод Рунге—Кутта 4-го порядка, что соответствует опции methodiclassical[rk4]. С функцией DEplot могут использоваться следующие параметры:
- arrows = type — тип стрелки векторного поля ('SMALL', 'MEDIUM', 'LARGE', 'LINE'
- или 'NONE');
- colour, color = arrowcolour — цвет стрелок (задается 7 способами);
- dirgrid = [integer,integer] — число линий сетки (по умолчанию [20, 20]);
- iterations = integer — количество итераций, представленное целым числом;
- linесоlor, linecolor = lineinfo — цвет линии (задается 5 способами);
- method='rk4' — задает метод решения ('euler', 'backeuler', 'impeuler' или 'rk4');
- obsrange = TRUE.FALSE — задает (при TRUE) прерывание вычислений, если кривая решения выходит из области обзора;
- scene = [name.name] — задает имена зависимых переменных, для которых строится график;
- stepsize = h — шаг решения, по умолчанию равный abs((b-a))/20 и представленный вещественным значением.
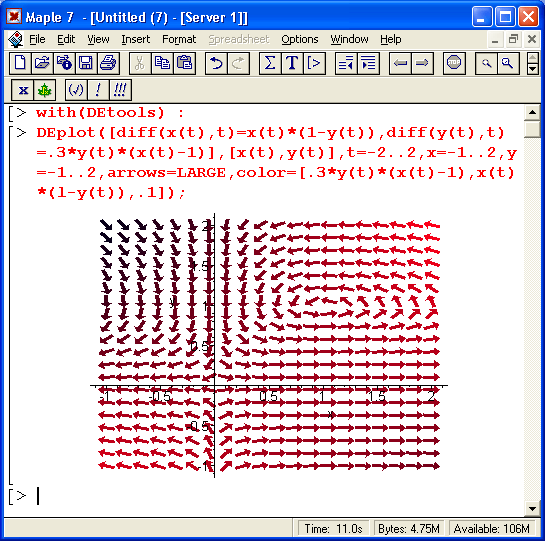
На рис. 13.8 показано решение системы диффкренциальных уравнений
x'(t)=x(t)(1-y(t)
y'(t)= 0,3y(t)(x(t)-1),
описывающих модель Лотки—Вольтерра при заданных в документе изменениях t, x(t) и y(t). Решение представлено в виде векторного поля стрелки которого являются касательными к кривым решения (сами эти кривые не строятся). Обратите внимание на функциональную закраску стрелок векторного поля, делающую решение особенно наглядным (правда, лишь на экране цветного дисплея, а не на страницах книги).
Рис. 13.8. Решение системы дифференциальных уравнений Лотки—Вольтерра , с выводом в виде графика векторного поля
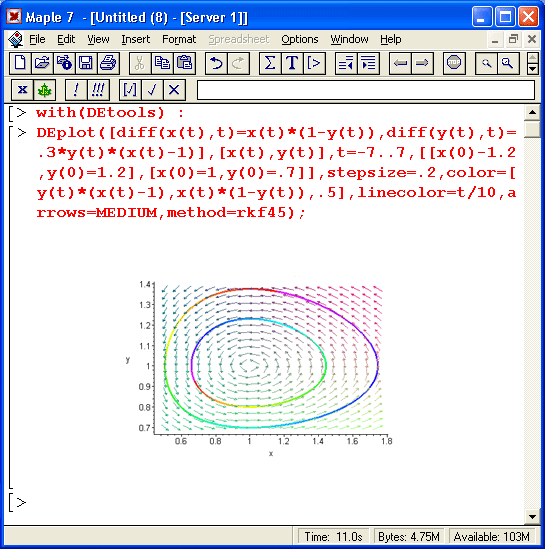
Еще интересней вариант графиков, представленный на рис. 13.9. Здесь помимо векторного поля несколько иного стиля построены фазовые портреты решения с использованием функциональной закраски их линий. Фазовые портреты построены для двух наборов начальных условий:
x(0) = y(0) = 1,2 и x(0) = 1 и у(0)=0,7.
Следует отметить, что функция DEplot может обращаться к другим функциям пакета DEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения.
Рис. 13.9. Пример построения двух фазовых портретов на фоне векторного поля