10. Графическое представление решений дифференциальных уравнений

Графическое представление решений дифференциальных уравнений

Применение функции odeplot пакета plots

Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:

odep1ot(s,vars.r,o) 

где s — запись (в выходной фирме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, г — параметр, задающий пределы решения (например, а. .Ь), и о — необязательные дополнительные опции.

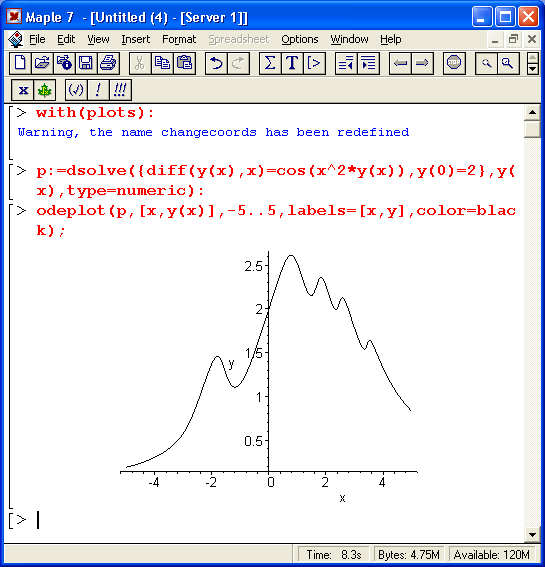
На рис. 13.5 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.

В этом примере решается дифференциальное уравнение:

y'(x)=cos(x²y(x))

при у(0) = 2 и x, меняющемся от-5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения у(х). 

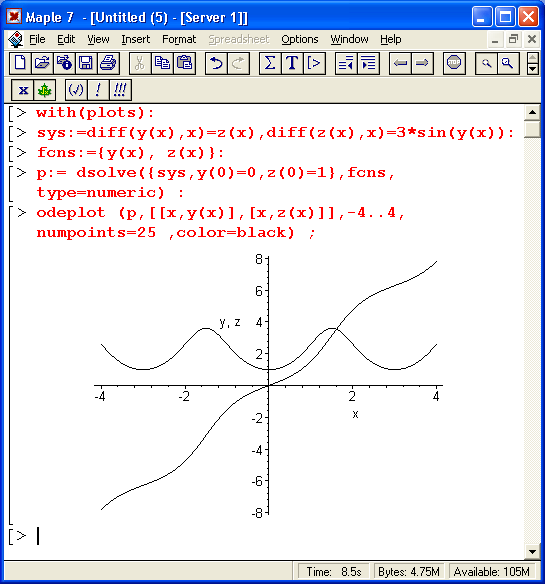
В другом примере (рис. 13.6) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций. —у(х) и z(x).

В этом примере решается система:

у'(х)=z(х),

z'(x) = 3 sin(y(x))

при начальных условиях y(0)=0, z(0) = 1 их, меняющемся от -4 до 4 при числе точек решения, равном 25.

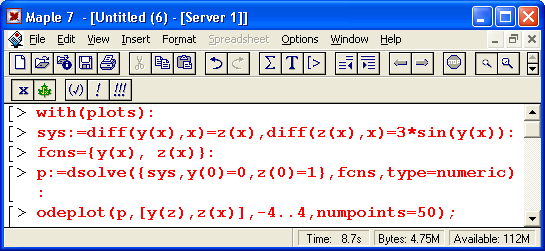
Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 13.7 демонстрирует построение фазового портрета для системы, представленной выше.

Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок; для построения, поэтому возможность Марle 7 быстро строить фазовые портреты трудно переоценить.

Рис. 13.5. Пример решения одиночного дифференциального уравнения

Рис. 13.6. Пример решения системы из двух дифференциальных уравнений

Рис. 13.7. Представление решения системы дифференциальных уравнений в виде фазового портрета