Решение в численном виде — функция fsolve

Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию:

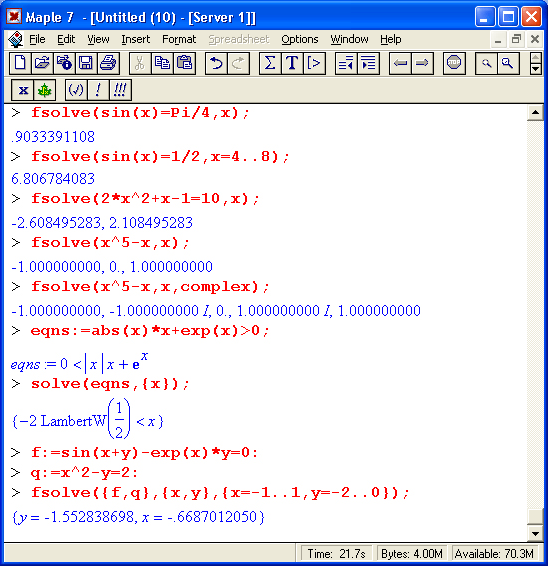
fsolve( eqns. vars. options )

Эта функция может быть использована со следующими параметрами:

•  complex — находит один или все корни полинома в комплексной форме;
•  full digits — задает вычисления для полного числа цифр, заданного функцией Digits;
•  maxsols=n — задает нахождение только n корней;
•  interval — задается в виде а. .b или х=а. .b, или (х=а. .b, y=c. .d, ...} и обеспечивает поиск корней в указанном интервале.

Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры:

 

Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и д.

Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2:

> so1ve(erf(x)=l/2,x);

RootOf(2erf(_Z)-l) 

> fsolve(erf(x)=l/2);

.4769362762

Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve находит обычное приближенное решение.