6. Построение 3D-параметрических графиков — ParametricPlot3D

Построение 3D-параметрических графиков — ParametricPlot3D

Трехмерные графики с параметрически заданными функциями, описывающими положение их точек, относятся к числу наиболее сложных, но в то же время весьма эффектных. В подпакете ParametricPlotSD определены функции, упрощающие подготовку таких графиков:

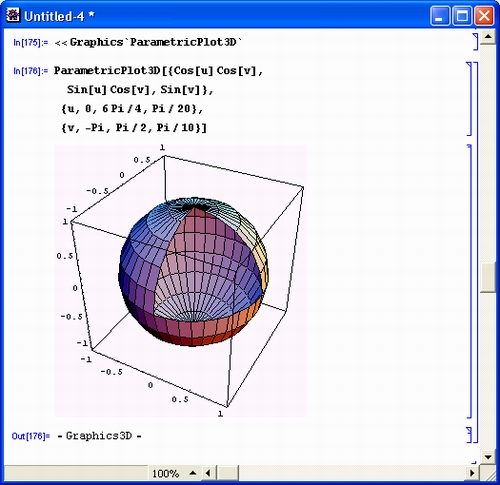
• ParametricPlot3D[{fx,fy,fz},{u,u0,ul,du},{v,c0,vl,dv}] — строит трехмерную поверхность, заданную параметрически функциями f x, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv (рис. 14.60);
• PointParametricPlot3D[ { fx, f у, f z},{u,u0,ul,du}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от одной переменной и с заданным диапазоном изменения и приращением du;
• PointParametricPlot3D[{fx,fy,fz},{u,u0,ul,du),{v,c0,vl,dv}] — строит точками трехмерную поверхность, заданную параметрически функциями fx, f у и f z от переменных и и v с заданными диапазонами изменения и приращениями du и dv.

Рис. 14.60. Пример построения сферы с вырезом с помощью функции ParametricPlot3D

Обратите внимание на то, что выбором диапазона изменения углов можно получить вырез сферы. Окраска поверхности осуществляется автоматически.

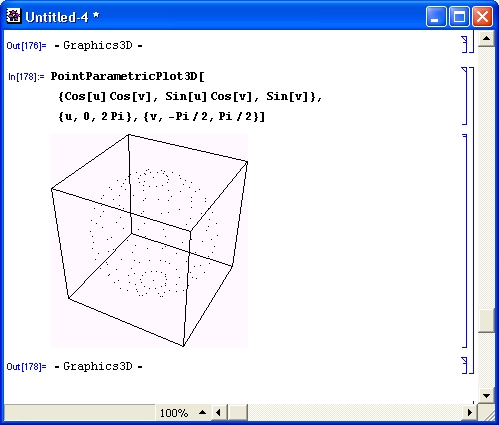
На рис. 14.61 показан пример применения функции PointParametricPlotSD. Здесь сфера построена отдельными точками.

Для построения трехмерных поверхностей в сферической и цилиндрической системах координат служат следующие функции:

• SphericalPlot3D[r, {t, trnin, tmax}, {p,pmin,pmax} ] — построение графика в сферической системе координат;
• CylindricalPlot3D[z,{t,tmin,tmax},{p,pmin,pmax}] — построение графика в цилиндрической системе координат.

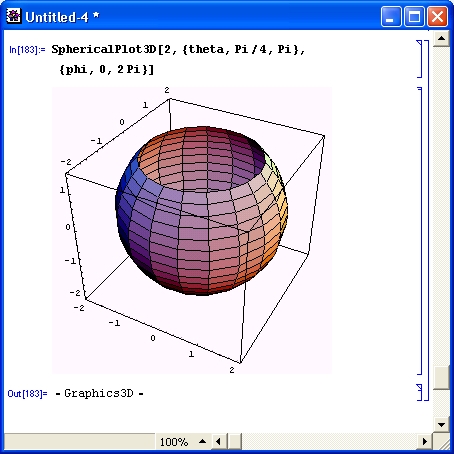
На рис. 14.62 показано построение усеченной сверху сферы с помощью функции SphericalPlot3D. Нетрудно заметить, что применение данной функции — самый простой способ построения сферы. Это естественно, поскольку система координат сферическая.

Риc. 14.61. Пример построения сферы точками

Рис. 14.62. Пример построения сферы с помощью функции SphericolPlot3D

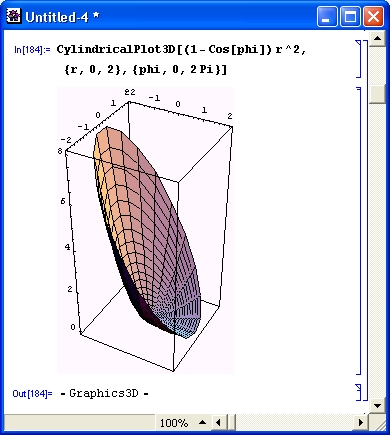
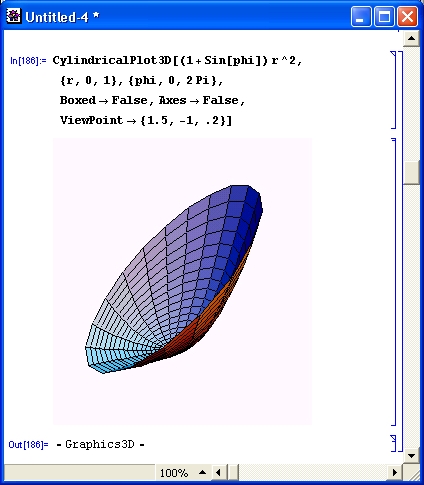
Пример построения поверхности, напоминающей по виду «тарелку» спутниковой антенны, в цилиндрической системе координат дан на рис. 14.63.

С помощью опции Viewpoint можно изменять положение точки, с которой рассматривается фигура. Это существенно меняет ее вид (рис. 14.64).

Еще раз напоминаем, что интерфейс Mathematica предусматривает изменение точки просмотра уже построенной фигуры. При этом Mathematica 4 позволяет вращать фигуру мышью. Рекомендуется просмотреть список опций данных функций, позволяющих в широких пределах менять вид и стиль построения графиков.

Рис. 14.63. Пример построения поверхности в цилиндрической системе координат

Рис. 14.64. Пример построения фигуры, видимой из заданной точки просмотра

Представление полей на плоскости — PlotField

В подпакете PlotField имеются функции, позволяющие строить стрелками графики полей:

• PlotVectorField[ {fx, f у}, {x, xmin, xmax), {y, ymin, ymax} ] —строит плоскость из векторов (стрелок), ограниченную пределами изменения х и у;
• PlotGradientField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) градиента функции f, ограниченную пределами изменения х и у;
• PlotHamiltonianField[f,{x,xmin,xmax},{у,ymin,ymax}] — строит плоскость из векторов (стрелок) гамильтониана функции f, ограниченную пределами изменения х и у;
• PlotPolyaField[f, {х,xmin,xmax}, {у, ymin, ymax} ] — представляет график комплексной функции f(x, у).

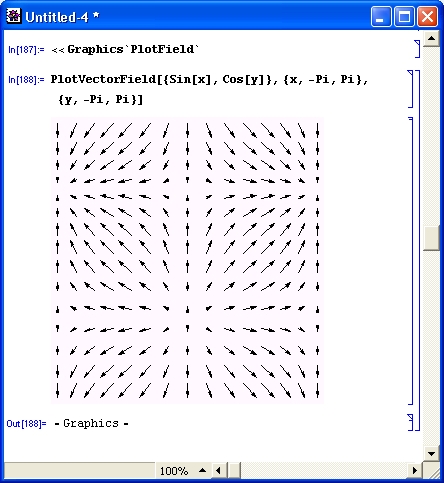
Рисунок 14.65 показывает применение функции PlotVectorField для построения векторного поля согласно параметрически заданной на плоскости функции.

Риc. 14.65. График векторного поля на плоскости

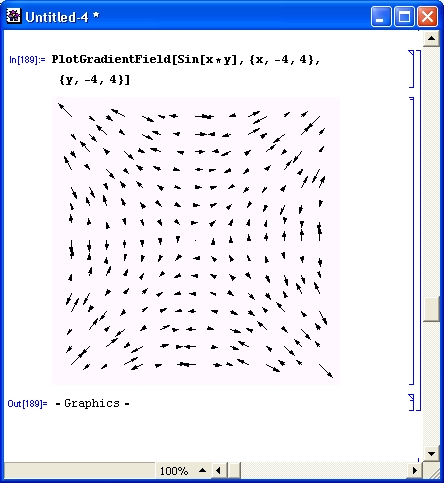
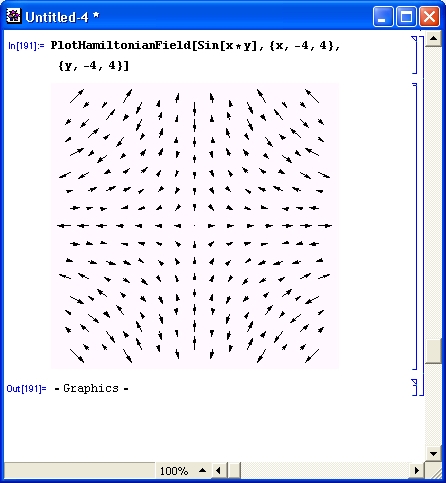
Еще один пример (рис. 14.66), иллюстрирует построение градиента поля с помощью функции PlotGradientField. Применение функции PlotHamiltonianField демонстрирует рис. 14.67.

Указанные функции имеют множество опций. Отметим основные из них (в качестве значений приведены значения по умолчанию):

• ScaleFactor->Automatic — устанавливает размер векторов (стрелок);
• ScaleFunction->None — устанавливает функцию, вычисляющую размер стрелок;
• MaxArrowLenght->None — устанавливает ограничение длины стрелок;
• ColorFunction->None — задает функцию цвета;
• PlotPoints->15 — задает число точек по координатам для построения стрелок.

Рис. 14.66. График градиента поля

Риc. 14.67. Пример применения функции PlotHamiltonianField

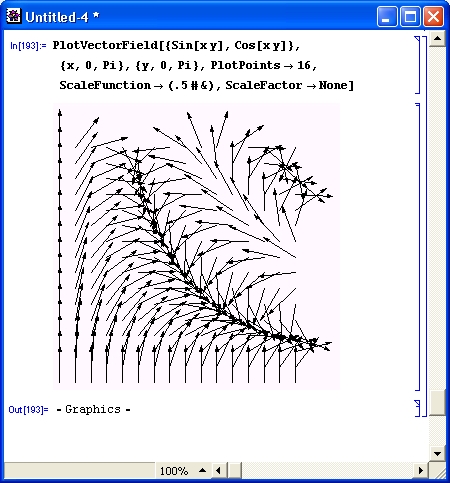
Пример построения сложного графика с применением шестнадцати узловых точек по каждому направлению и использованием опции ScaleFunction показан на рис. 14.68.

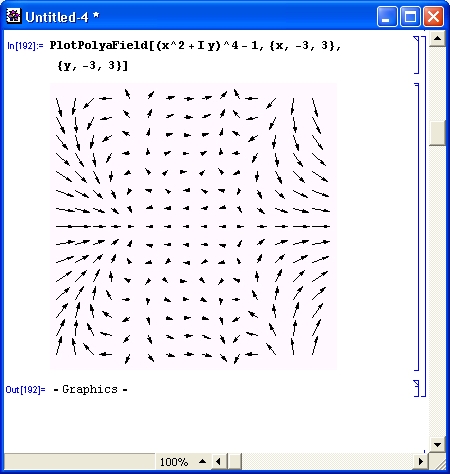
Работу функции PlotPolyaField поясняет рис. 14.69. Обратите внимание на то, что функция в данном случае комплексная.

Рис. 14.68. Пример графика поля с применением нескольких опций

Рис. 14.69. Пример графика поля для комплексной функции

Применение опций позволяет строить самые разнообразные графики различных полей — тепловых, гравитационных, электрических и др.

В подпакете PlotField есть еще одна функция, представляемая в двух формах:

• ListPlotVectorField [ {{vect 11, vect12,...},{vect21, vect22,...},...} ] — строит график векторного поля прямоугольного массива векторов vect _xy ;
• ListPlotVectorField [{{pt1, vect1,...}, (pt2,vect2,...},...}] —строит график векторного поля по списку векторов vect _xy , расположенных в точках pti.

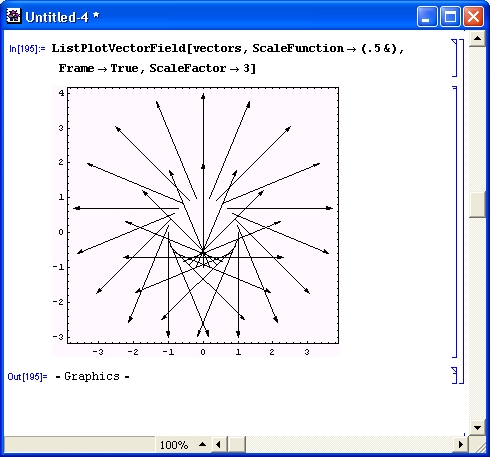
Применение этой функции поясняет график, представленный на рис. 14.70.

Рис. 14.70. Пример построения графика векторного поля с помощью функции ListPlotVectorField

Приведенных примеров вполне достаточно, чтобы судить о возможностях подпа-кета PlotField. В справочной базе данных можно найти другие примеры построения графиков векторных полей.

Представление полей в пространстве — PlotField3D

Для представления векторных полей в пространстве служат функции подпакета PlotField3D:

• PlotVectorField3D[{fx,fy,fz},{x,xmin,xmax},{y,ymin, ymax}, {z, zmin, zmax} ] — строит график векторного поля параметрически заданной трехмерной фигуры;
• PlotGradientField3D[{fx,fy,fz},{x,xmin,xmax},{y,ymin,ymax}, {z, zmin, zmax} ] — строит график градиента векторного поля параметрически заданной трехмерной фигуры.

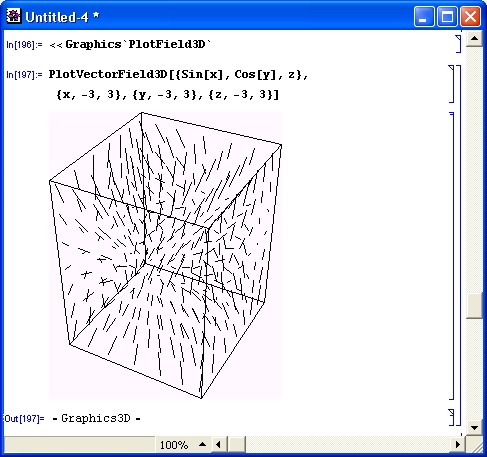
Эти функции подобны описанным в предшествующем разделе, но используются для построения векторных полей не на плоскости, а в пространстве. Рисунок 14.71 показывает пример такого построения.

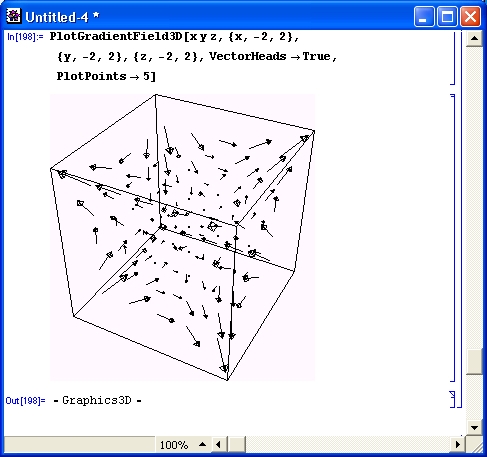
Как видно из рис. 14.71, векторное поле строится отрезками прямых, а не стрелками. Последнее связано с тем, что по умолчанию задана опция VectorHeads-> False. Изменив ее на VectorHeads->True, можно получить представление векторного поля направленными стрелками. Кроме того, используя опцию Plot-Points->n, можно получить заданное число стрелок п по всем направлениям графика. Все это учтено на графике, представленном на рис. 14.72.

Рис. 14.71. Пример построения графика векторного поля в пространстве отрезками прямых

Рис. 14.72. Пример построения графика градиента поля направленными стрелками

В подпакете PlotFieldSD имеется еще одна функция:

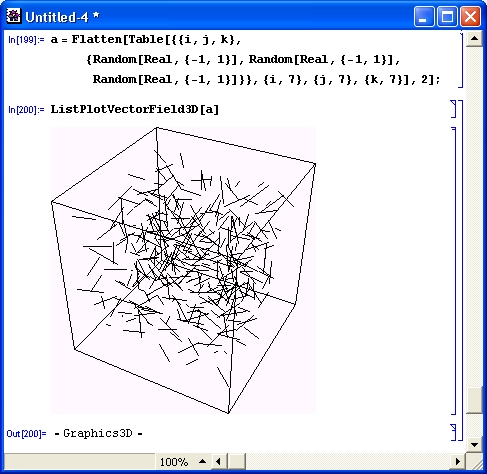
• ListPlotVectorField3D[{ {ptl, vectl}, {pt2, vect2 },...} ] -строит график векторного поля в пространстве по данным векторов vecti, расположенных в точках pti.

Рисунок 14.73 поясняет применение этой функции.

Рис. 14.73. Пример построения графика векторного поля функцией ListPlotVectorReld3D

Нетрудно заметить, что при большом числе векторов в пространстве графики этого типа теряют наглядность. Рекомендуется тщательно отлаживать их, используя весь набор опций (как его получить, описывалось неоднократно).