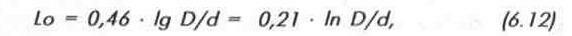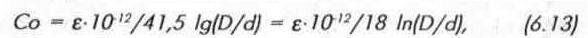6.1. Разновидности линий.
6.1. Разновидности линий.
Существует несколько видов линий передачи высокочастотной энергии. Для выполнения междуэтажных или междурядных соединений в сложных синфазных антеннах применяются двухпроводные воздушные линии (рис. 6.1.).
Рис. 6.1. Поперечное сечение двухпроводной неэкранированной линии из проводов круглого сечения
Интервал величины волнового сопротивления этих линий может быть достаточно широким. Оба провода воздушной симметричной линии должны располагаться строго симметрично относительно друг друга и земли, что является ее недостатком, так как практически трудно выдержать одинаковые расстояния между проводами на протяжении всей длины линии, а также между каждым проводом и землей. Волновое сопротивление для линии из проводов круглого сечения зависит от отношения расстояния между двумя проводниками к их диаметру, и определяется по формуле
Формула справедлива при Ь>3а и d<<a,
где Z — волновое сопротивление полосковой линии, Ом;
e — диэлектрическая проницаемость среды;
а — ширина полосковой линии;
с — расстояние между полосковыми линиями (или толщина диэлектрика);
b — ширина диэлектрика;
d — толщина полоскового проводника.
Рис. 6.2. Схематическое изображение полосковой линии
Зависимость волнового сопротивления полосковых линий от ее геометрических размеров изображена на рис.6.3.
Несимметричные воздушные жесткие линии применяются для изготовления согласующих трансформаторов, фильтров, направленных ответвите-лей и т. д. Воздушная коаксиальная линия изображена на рис. 6.4 [6.2].
Рис. 6.4. Конструктивные варианты воздушных жестких линий:
а — концентрическая (коаксиальная) линия, б — цилиндрический проводник в трубе квадратного сечения.
Волновое сопротивление воздушной коаксиальной линии определяют по формуле
Волновое сопротивление линии, приведенной на рисунке 6.4.6, определяется по формуле
Достоинством воздушных линий является возможность получения . широкого диапазона величины волновых сопротивлений. Для практических целей при их изготовлении можно воспользоваться диаграммой рис.6.5 [6.1].
На графике для сравнения показана зависимость волновых сопротивлений воздушных линий и экранированных линий со сплошным диэлектриком (полиэтиленовой изоляцией, e=2,3 ).
Рис. 6.5. Диаграмма волновых сопротивлений воздушных линий
6.1.1. Резонансные свойства отрезков линий
Линия передачи, длина которой соизмерима с длиной волны распространяющихся в ней электромагнитных колебаний (l=lдл.вол), а расстояние между ее проводниками значительно меньше четверти длины волны, называется длинной линией.
При идеальном согласовании линии с нагрузкой, когда линия нагружена на чисто активное и равное волновому сопротивление (Zн = R = Zв), в линии существуют только падающие волны [волны, распространяющиеся по линии от генератора к нагрузке}. Напряжение и ток вдоль линии передачи имеют одно и то же значение, а фазы волны различны. Отсутствие отраженных волн объясняется тем, что вся подводимая падающими волнами энергия поглощается нагрузкой (рассеивается на ней}. Такая линия называется согласованной с нагрузкой, а режим в линии называют режимом бегущих волн.
Если линия разомкнута (Zн = бесконечности, замкнута накоротко (Zн=O) либо
нагрузка имеет явно выраженный реактивный характер (Zн=jXн), то нагрузка Zн не поглощает энергию, а полностью отражает ее обратно ,к источнику сигнала (генератору). Такой режим в линии характеризуется интерференцией падающих и отраженных волн. Отраженные волны, складываясь с падающими, создают так называемые стоячие волны. В этом случае на линии имеются некоторые точки, в которых напряжение всегда равно нулю: это — узлы напряжения. Точки, где напряжение по амплитуде максимально, называются «пучностями» напряжения.
Входные сопротивления короткозамкнутой и разомкнутой линии имеют реактивный характер и изменяются от длины линии, а в точках, кратных четверти длины волны {l = п * lдл.вол/4), входное сопротивление активное и
имеет значение Z=0 или Z=бесконечности.
Отрезки длинных линий, длина которых кратна четверти длины волны называются РЕЗОНАНСНЫМИ.
В радиотехнике широко используется свойство отрезков длинной линии резонировать на определенных частотах. Геометрическую длину линии можно уменьшить подсоединением конденсатора к ее разомкнутым концам (рис.6.6). Включение конденсатора переменной емкости (варикапа) позволяет настроить отрезок длинной линии (колебательный контур с распределенными параметрами) на необходимую длину волны.
Рис. 6.6. Уменьшение геометрической длины линии
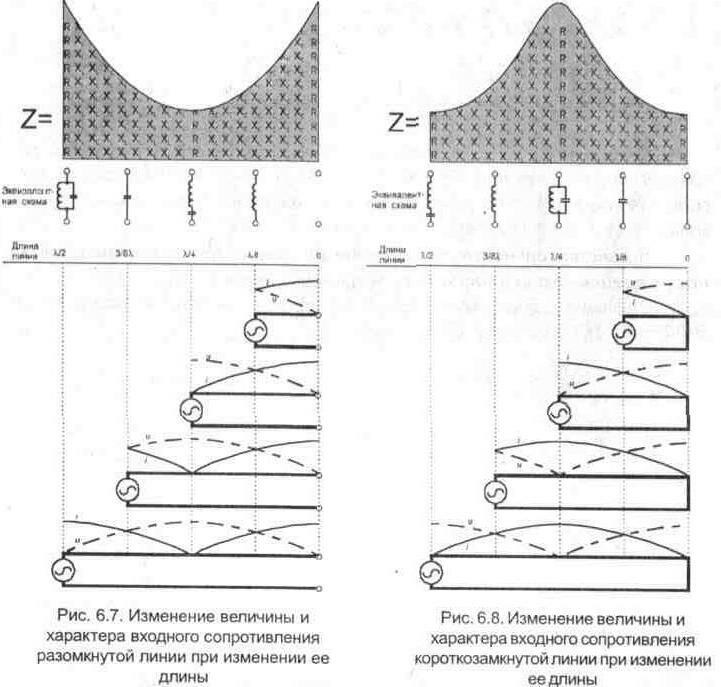
Отрезки длинных линий (замкнутых или разомкнутых на конце} применяют в качестве элементов фильтров резонансных контуров высокочастотных блоков, шлейфов для настройки антенн и т. д. Величина и характер входного сопротивления разомкнутой (рис. 6.7) и замкнутой линии (рис. 6.8) изменяются в зависимости от того, какое количество волн укладывается вдоль линии.
Если нагрузка линии не равна волновому сопротивлению линии, то режим в линии характеризуется одновременным существованием стоячих и бегущих волн. Такой режим в линии называется СМЕШАННЫМ. В таких линиях нет узлов и пучностей напряжения и тока, а есть максимумы и минимумы напряжения и тока. Оценка режима работы линии характеризуется коэффициентом бегущей волны:
КБВ=Umin/Umax (6.6)
где Umin — амплитуда в узле напряжения. В;
Umax, — амплитуда в пучности напряжения, В.
Коэффициент бегущей волны можно определить из соотношений:
K=R/Z при R<Z и K=Z/R при R>Z (6.7)
где Z — волновое сопротивление линии;
R — сопротивление нагрузки линии.
Следовательно, этот коэффициент характеризует собой степень согласования линии с нагрузкой. При R=Z oн равен единице, что означает полное согласование линии с нагрузкой, при котором в линии будет режим бегущей волны.
В действительности такие линии не существуют из-за невозможности идеального согласования нагрузки с линией.
Величина, обратная коэффициенту бегущей волны, называется КОЭФФИЦИЕНТОМ СТОЯЧЕЙ ВОЛНЫ:
КСВ=1/КБВ. (6.8)
Отношение амплитуд напряжения отраженной и падающей волн
называется КОЭФФИЦИЕНТОМ ОТРАЖЕНИЯ, который определяется из формул:
р = (1 -КБВ)/(1 +КБВ) или (6.9) р = (КСВ- 1)/(КСВ+1). (6.10)
Измеряют амплитуды напряжений падающей и отраженной волн с помощью направленных ответвителей.
6.1.2. Параметры фидерных линий
Основными параметрами линии передачи являются волновое сопротивление, погонная емкость, погонное затухание.
ВОЛНОВЫМ СОПРОТИВЛЕНИЕМ ЛИНИИ (Z) называется отношение комплексных амплитуд напряжения к току падающих или отраженных волн. Оно носит комплексный характер и связано с погонной индуктивностью Lo и погонной емкостью линии Со соотношением:
Для коаксиальных кабелей Lo и Со определяются по формулам:
где D — диаметр [внутренний) экрана, мм;
d— диаметр внутреннего проводника, мм.
Погонная емкость кабеля — емкость единицы длины кабеля. Обычно погонная емкость кабеля указывается в пф/м:
где е — диэлектрическая проницаемость изоляции;
D — диаметр (внутренний) экрана, мм;
d—диаметр внутреннего проводника, мм.
Значения диэлектрической проницаемости e материалов приведены в приложении 9.
Волновое сопротивление коаксиального кабеля определяется геометрическими размерами его поперечного сечения и диэлектрической постоянной [см. формулу 6.4).
Электромагнитная волна в фидерной линии с диэлектриком распространяется с меньшей скоростью, чем в свободном пространстве (для вакуума, е = 8,854*10^(-12)). Так, в воздушной линии скорость распространения волны всего на 2-3% меньше, чем в свободном пространстве, а в кабельной линии, заполненной диэлектриком, скорость зависит от диэлектрической проницаемости материала заполнения,
В зарубежной справочной литературе вместо коэффициента укорочения длины волны приводят КОЭФФИЦИЕНТ ЗАМЕДЛЕНИЯ ЛИНИИ ПЕРЕДАЧ, (k = 1/с). Радиоволны в свободном пространстве распространяются со скоростью света ( с = 3*10^8 м/с). В линии передачи их скорость уменьшается в k раз. Значения k меняются в зависимости от конструкции линии.
Типичное значение k составляет:
0,75 — для двухпроводной линии с пластмассовой изоляцией;
0,67 — для коаксиальной линии с твердой пластмассовой изоляцией;
0,85 — для коаксиальной линии с воздушной изоляцией;
0,97 — для открытой воздушной двухпроводной линии. Вследствие потерь электромагнитная волна, распространяясь вдоль линии, уменьшается по величине — затухает. Эффективность прохождения сигнала по линии (фидеру) определяется величиной погонного затухания (Р). ПОГОННОЕ ЗАТУХАНИЕ характеризуется уменьшением напряжения сигнала по мере его распространения вдоль линии на рабочей частоте, приходящееся на единицу длины кабеля. Выражают затухание в децибелах на метр (или неперах на километр).
При небходимости перевода единиц затухания можно воспользоваться следующим соотношением: 1дБ = 0,115 неп (или 1неп = 8,686дВ).
Погонное затухание зависит от материалов, из которых изготовлены проводники и изоляция, их поперечных размеров, частоты измерения и определяется по формуле
Чем выше частота и чем длиннее кабель, тем больше затухание Р фидерной линии.
ПРИМЕР: Определить общее затухание фидерной пинии, выполненной из коаксиального кабеля РК-75-4-11 длиной l=25м для V-TB канала. Из табл. 1.2 находим частоту V-TB канала: Fср=96МГц. По табл. 6.3 определяем затухание кабеля на этой частоте в=0.1 дБ/м. Общее затухание составит T=в*l;T=0.1*25=2.5дБ
Уменьшение напряжения сигнала, по мере его распространения вдоль линии, происходит по экспоненциальному закону:
Затухание сигнала по мощности в фидерной линии определяется формулой
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ линии определяется как отношение мощности на выходе линии к мощности на ее входе:
Из формулы следует, что чем меньше коэффициент погонного затухания линии и меньше ее длина, тем больше КПД.
Рис. 6.1. Поперечное сечение двухпроводной неэкранированной линии из проводов круглого сечения
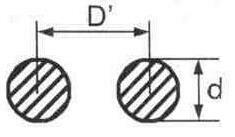
Рис. 6.2. Схематическое изображение полосковой линии
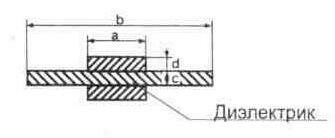
Рис. 6.2. Схематическое изображение полосковой линии
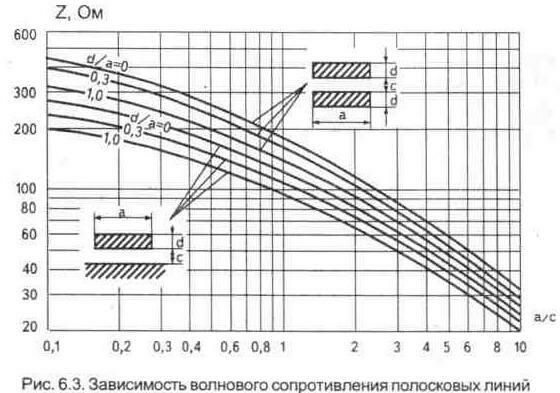
Рис. 6.4. Конструктивные варианты воздушных жестких линий:
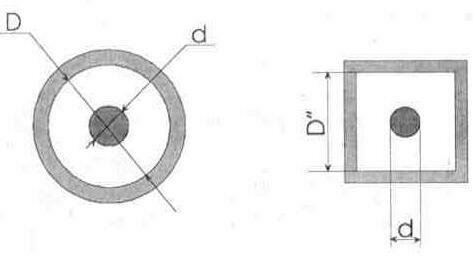
Рис. 6.4. Конструктивные варианты воздушных жестких линий:

Рис. 6.5. Диаграмма волновых сопротивлений воздушных линий
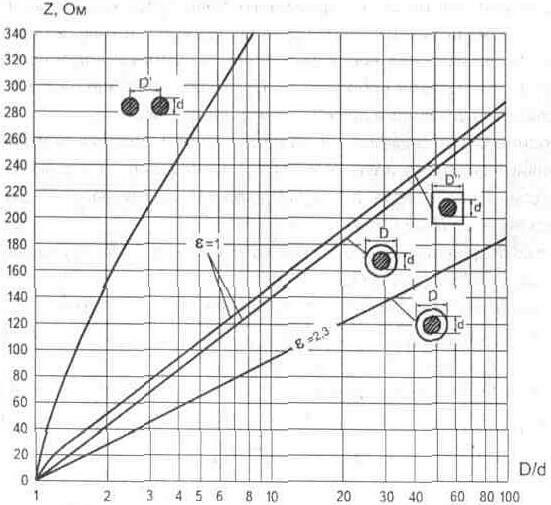
Рис. 6.6. Уменьшение геометрической длины линии
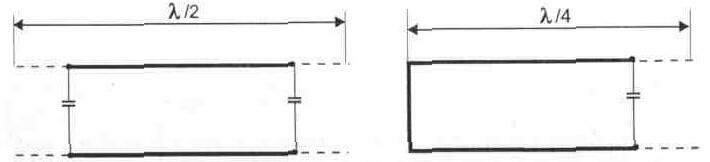
Рис. 6.7. Изменение величины и характера входного сопротивления разомкнутой линии при изменении ее длины
Ф. 6.1. Волновое сопротивление для линии из проводов круглого сечения зависит от отношения расстояния между двумя проводниками к

Ф. 6.11. Связь волнового сопротивления с погонной индуктивностью Lo и погонной емкостью линии Со
Ф. 6.11. Связь волнового сопротивления с погонной индуктивностью Lo и погонной емкостью линии Со коаксиального кабеля
Ф. 6.13. Погонная емкость кабеля указывается в пф/м
Ф. 6.14. Коэффициент укорочения длины фолны в фидерной линии

Ф. 6.17. Погонное затухание зависит от материалов, из которых изготовлены проводники и изоляция, их поперечных размеров, частоты

Ф. 6.18. Уменьшение напряжения сигнала, по мере его распространения вдоль линии, происходит по экспоненциальному закону

Ф. 6.20 Затухание сигнала по мощности в фидерной линии определяется формулой

Ф. 6.21 Коэффициент полезного действия (КПД) линии определяется как отношение мощности на выходе линии к мощности на ее входе

Ф. 6.3. Волновое сопротивление полосоковой линии

Ф. 6.4. Волновое сопротивление воздушной коаксиальной линии