12. Объединяющая идея системы Mathematica

Mathematica построена на постулировании того, что все объекты могут быть представлены как символические выражения.

Все символьные выражения записываются в единой форме head[arg1, arg2, ...].

Список элементов.

{a,b,c}

List[a,b,c]

Алгебраическое выражение.

Plus[Power[x,2],Sqrt[x]]

Уравнение.

x==Sin[x]

Equal[x,Sin[x]]

Логическое выражение.

p&&!q

And[p,Not[q]]

Команда.

AddTo[Part[m,1],a]

Графика.

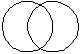
Graphics[{Circle[{1,0},2],Circle[{-1,0},2]}]

Абстрактная математическая запись.

Tilde[CirclePlus[a,b], Subscript[c,Infinity]]

Кнопка.

ButtonBox["Press here"]

Ячейка в документе системы Mathematica, содержащая текст.

A cell containing text

Cell["A cell containing text","Text"]

Единая форма записи символических выражений дает возможность вводить в системе Mathematica любую конструкцию, которая Вам необходима.

Химическая формула.

Chemical[{Hydrogen,1},{Nitrogen,1},{Oxygen,3}]

Электрическая цепь.

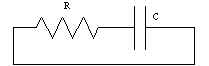
Circuit[{Resistor["R"],Capacitor["C"]}]

Все операции в системе Mathematica в конечном счете - преобразования символических выражений. Mathematica имеет уникальную возможность работы с шаблонами при проведении преобразований.

Команда  /. служит сигналом системе Mathematica применить  подстановку  b - > 1 + x.

{a,b,c,d}/.b->1+x

{a,1+x,c,d}

Каждый символ x_ и y_ замещает любое выражение, так что шаблон x _ + y_ обозначает собой сумму любых двух объектов.

{a + b, c + d, a + c} /. x_ + y_ -> x2 + y2

{a2 + b2, c2 + d2, a2 + c2}

{a + b, c + d, a + c} /. a + x_ -> x3

{b3, c + d, c3}

Mathematica использует шаблоны, чтобы обобщить понятие функции.

Это стандартный способ определения функции для всех значений x.

Изменение общего определения функции при фиксированном значении аргумента.

f[0]:=e

Пример использования определенной выше функции f.

f[6]+f[a+b]+f[0]

Сброс определения функции  f.

Clear[f]

Важная особенность использования шаблонов заключается в том, что они позволяют определять операции, аргументами которых могут выступать любые объекты.

Определение функции g, аргументом которой является список, состоящий из двух элементов.

g[{x_,y_}]:=x+y

g[{4,a b}]

4+a b

Clear[g]

Определение функции, имеющей смысл площади круга, аргументом которой является объект Circle.

area[Circle[{2,3},u]]

Осуществление преобразования  логического правила.

reduce[p_ && q_ || p_]:=p