9. Полосовой фильтр и режекторный фильтр

ЭКСПЕРИМЕНТ 24 Полосовой фильтр и режекторный фильтр

Цели

После проведения данного эксперимента Вы сможете продемонстрировать работу индуктивно-емкостного полосового фильтра и резистивно-емкостного режекторного фильтра.

Необходимые принадлежности

* Осциллограф

* Цифровой мультиметр

* Макетная панель

* Генератор функции

* Элементы:

четыре конденсатора 0,1 мкФ, один конденсатор 0,47 мкФ, одна катушка индуктивности 10 мГн, один резистор 100 Ом, четыре резистора 15 кОм.

ВВОДНАЯ ЧАСТЬ

Полосовой фильтр — это частотночувствительная схема, которая пропускает узкий диапазон. частот в окрестности центральной резонансной частоты (fr)

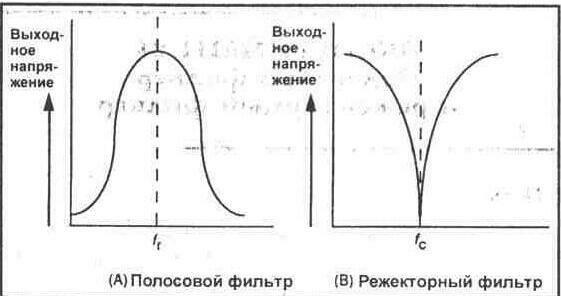
Все другие частоты ниже или выше узкой полосы пропускания значительно подавляются. Типичная характеристика полосового фильтра показана на рисунке 24-1А.

Рис. 24-1.

Режекторный фильтр представляет собой противоположность полосовому фильтру. Он подавляет или устраняет сигналы, частоты которых попадают в узкий диапазон с центральной частотой fc. Все частоты выше и ниже центральной частоты фильтр пропускает с минимальным ослаблением (см. рис. 24-1 В). Режекторный фильтр иногда называют вырезающим фильтром, поскольку этот фильтр используется для вырезания или режекции мешающего сигнала одной частоты.

Краткое содержание

Имеется несколько различных способов схемной реализации полосового фильтра и режекторного фильтра. Индуктивно-емкостные резонансные схемы могут комбинироваться различными методами для создания обоих типов фильтров. В данном эксперименте Вы познакомитесь с полосовым фильтром.

Режекторный фильтр может быть реализован и на базе индуктивно-емкостных схем. Однако в данном эксперименте Вы познакомитесь с популярным и широко используемым двойным Т-образным мостовым фильтром. Это резистивно-емкостной режекторный фильтр, способный подавлять определенную частоту и частоты в ее окрестности. Центральная частота рассчитывается при помощи следующей формулы:

fp = 1/2*3.14RC

Поскольку у Вас нет удобных средств для точного измерения частоты, Вы будете просто варьировать частоту, генерируемую генератором функций, и отмечать при помощи мультиметра выходную характеристику фильтра. Таким образом, можно увидеть, как выходное напряжение изменяется в зависимости от частоты как в случае полосового фильтра, так и в случае режекторного фильтра.

ПРОЦЕДУРА

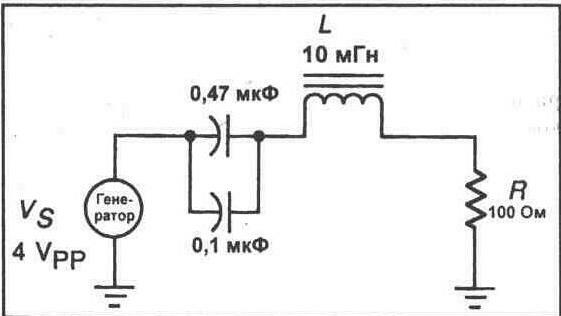
1. Обратитесь к рисунку 24-2. Соберите эту схему полосового фильтра на Вашей макетной панели. Выходное напряжение генератора функций прикладывается к конденсаторам, тогда как выходное напряжение фильтра снимается с резистора 1000м. Заметьте, что общая емкость схемы составлена из двух конденсаторов с емкостью 0,47 мкФ и 0,1 мкФ.

2. Используя значения, показанные на рисунке 24-2, рассчитайте общую емкость схемы и резонансную частоту данной схемы.

Рис. 24-2.

Сt = _______ мкФ

fr=_____Гц

3. Установите регулятором амплитуды генератора функций выходное напряжение размаха 4 В:

Затем установите частоту приблизительно 500 Гц.

4. Подключите осциллограф параллельно выходному резистору 1000м. Медленно увеличивайте частоту на выходе генератора функций и наблюдайте за изменением выходного напряжения схемы. Замечайте вариацию этого напряжения. Изменения частоты выполняйте медленно, чтобы Вы могли получать хорошую индикацию того, как изменяется напряжение, когда частота увеличивается или понижается. Увеличивайте частоту приблизительно до 5 кГц.

5. Регулируйте частоту, наблюдая за выходом фильтра. Настройте генератор функций на пиковое выходное напряжение. Заметьте по генератору функций или измерьте период и частоту при помощи осциллокрафа. f=____Гц

6. Объясните изменения, которые Вы наблюдали в шагах 4 и 5.

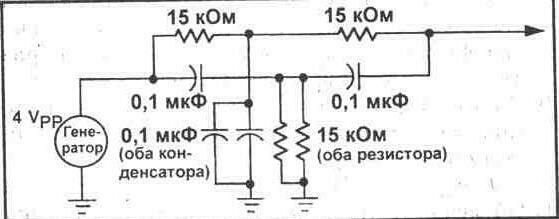
7.Демонтируйте .полосовой фильтр. Вместо него соберите схему двойного Т-образного мостового фильтра, который показан на рисунке 24-3. Будьте внимательны при монтаже схеме, поскольку она несколько сложна, и легко можно сделать ошибку во время монтажа.

Рис. 24-3.

Имеется несколько-важных моментов, которые Вы должны принять во внимание при монтаже данной схемы. Во-первых, значение одного (общего) конденсатора получается комбинированием емкостей двух параллельных конденсаторов 0,1 мкФ. Вспомните, что емкости параллельных конденсаторов складываются, образуя, следовательно. один конденсатор емкостью 0,2 мкФ. Другое значение в данной схеме получается соединением двух параллельных резисторов. Два параллельных резистора с одинаковым сопротивлением имеют общее сопротивление, равное половине сопротивления одного из резисторов. В данном случае два резистора 15 кОм соединены параллельно, чтобы получить сопротивление 7,5 кОм.

8. Используя значения, показанные на рисунке 24-3, рассчитайте частоту режекции или центральную частоту данного фильтра. fc=_____Гц

9. Настройте генератор функций на частоту 10 Гц и размах напряжения 4В. Подключите осциллограф на выход фильтра. Увеличивайте теперь выходную частоту приблизительно до 1000 Гц и наблюдайте за вариацией выходного напряжения фильтра. Повторяйте это несколько раз, чтобы Вы могли наверняка увидеть эффект.

10.Настройте генератор функций на нулевую частоту (минимальное напряжение). Измерьте частоту и запишите. f=_____Гц

11.Объясните полученные Вами результаты в шагах 9 и 10.

ОБЗОРНЫЕ ВОПРОСЫ

1. Режекторный фильтр может быть реализован на базе индуктивно-емкостных схем:

а) высказывание истинно,

б) высказывание ложно.

2. В индуктивно-емкостном полосовом фильтре центральная частота определяется значениями:

а) приложенного напряжения,

б) L и R,

в) R и С,

г) L и С.

3. Полосовой фильтр пропускает:

а) одну частоту,

б) только высокие частоты,

в) узкую полосу частот,

г) все частоты.

4. Двойной Т-образный мостовой фильтр представляет собой:

а) полосовой фильтр,

б) фильтр нижних частот,

в) фильтр верхних частот,

г) режекторный фильтр.

5. Какова центральная частота двойного Т-образного мостового фильтра при значениях R = 10 кОм и С = 0,47 мкФ?

а) 34 Гц,

б) 47 Гц,

в) 68 Гц,

г) 120 Гц.