1. Глава 12. Аксонометрические проекции

Глава 12. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

§ 75. Общие сведения об аксонометрических проекциях

При выполнении технических чертежей в ряде случаев оказывается необходимо наряду с изображением предметов в прямоугольных проекциях иметь и наглядные их изображения. Это необходимо для обеспечения возможности более полно выявить конструктивные решения, заложенные в изображении предмета, правильно представить положение его в пространстве, оценить пропорции его частей и размеры.

Наглядные изображения на некоторых чертежах могут применяться и независимо от прямоугольных изображений, например, при изображении схем электроснабжения и теплоснабжения зданий и сооружений.

Существуют различные способы построения наглядных изображений. Сюда относятся аксонометрические, афинные и векторные проекции, а также ли-

Рис. 156

нейная перспектива. В настоящем учебном пособии рассматриваются только аксонометрические проекции.

Построение аксонометрических проекций заключается в том, что геометрическую фигуру вместе с осями прямоугольных координат, к которым эта фигура отнесена в пространстве, параллельным (прямоугольным или косоугольным) способами проецируют на выбранную плоскость проекций. Таким образом, аксонометрическая проекция — это проекция на одну плоскость. При этом направление проецирования выбирают так, чтобы оно не совпадало ни с одной из координатных осей.

При построении аксонометрических проекций изображаемый предмет жестко связывают с натуральной системой координат Oxyz (см. § 37). В целом аксонометрический чертеж получается состоящим из параллельной проекции предмета, дополненной изображением координатных осей с натуральными масштабными отрезками по этим осям. Название «аксонометрия» и произошло от слов — аксон — ось и метрео — измеряю.

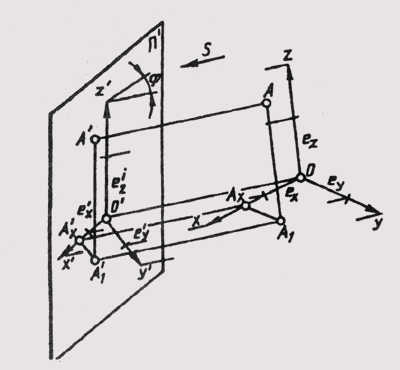
Образование аксонометрической проекции рассмотрим на примере построения аксонометрической точки А, отнесенной к натуральной системе координат Oxyz (рис. 156). Натуральные координаты точки А получаются измерением отрезков координатной ломаной АА₁А_ХО натуральным масштабом е. При параллельном проецировании по направлению S на плоскости аксонометрических проекций Я¹ получим аксонометрическую проекцию А¹ данной точки, аксонометрическую проекцию А¹A¹₁А¹_xО координатной ломаной и аксонометрическую проекцию ОУуУ натуральной системы координат, на осях которой будут находиться единичные аксонометрические масштабные отрезки e¹_xe¹_ye¹_z.

Аксонометрическая проекция А¹₁ горизонтальной проекции точки А (первичной) называется вторичной проекцией точки А. Совокупность всех этих проекций и составляет аксонометрию точки А.

На аксонометрическом чертеже вторичная и аксонометрическая проекции предмета обеспечивают метрическую определенность и обратимость однокартинного изображения.

В аксонометрических проекциях сохраняются все свойства параллельных проекций (см. § 28).

На практике измерения вдоль аксонометрических осей выполняют в одинаковых единицах — миллиметрах, поэтому единичные натуральные масштабные отрезки и их аксонометрию на чертежах не указывают.

Коэффициенты искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине при одинаковых единицах измерения.

Натуральные коэффициенты искажения обозначают: по оси х: и =О¹А¹х/OA_x; по оси у: v =A¹_xА¹₁/A_xA₁;

по оси z: w =A¹₁А₁/A₁A;