2. Выбор аппроксимации для сложной функции

Выбор аппроксимации для сложной функции

Задание исходной функции и построение ее графика

Трудно представить себе область более широкую и>й6читаемую, чем аппроксимация различных функциональных зависимостей. С получения простой аппроксимации сложной зависимости нередко начинаются (а часто и заканчиваются) научные исследования во многих областях как прикладной, так и фундаментальной науки. Покажем возможности в этом системы Maple 7 на одном из примеров, давно помещенных в библиотеку пользователей системы Maple V R2, и переработанных для Maple 7.

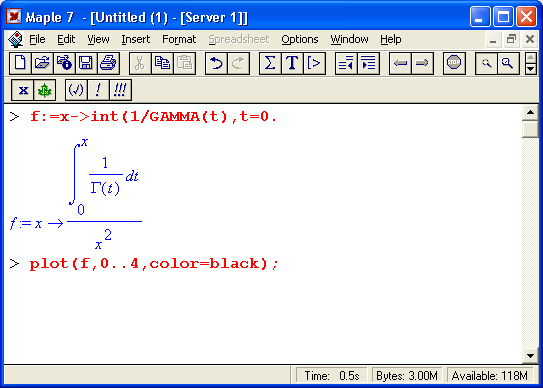
Воспользуемся возможностями пакета numapprox, для чего прежде всего подключим его:

> restart:with(numapprox):

[chebdeg,chebmult,chebpade,chebsort,chebyshev, confracform,hermite_pade,hornerform,   infnorm,laurent,minimax,pade,remez]

Будем искать приемлемую аппроксимацию для следующей, отнюдь не простой, тестовой функции:

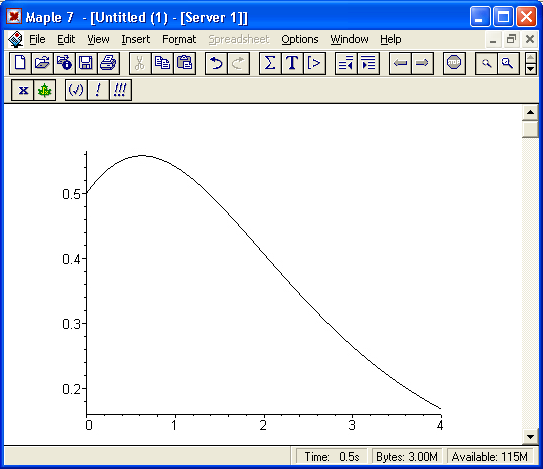
График этой функции представлен на рис. 17.1. С первого взгляда — это простой график, но тут как раз тот случай, когда простота обманчива. Вы сразу Заметите, что график строится необычно медленно, поскольку в каждой из множества его точек системе Maple 7 приходится вычислять значение интеграла с подынтегральной функцией, содержащей довольно каверзную гамма- функцию. И делает это Maple 7 по сложному и медленному алгоритму адаптивного численного интегрирования.

Рис. 17.1. График аппроксимируемой функции

Итак, вычисление f(x) по ее интегральному представлению совершенно не эффективно. Наша цель состоит в разработке процедуры вычислений, которая дала бы 6 точных цифр результата в интервале [0..4] и требовала, по возможности, наименьшего числа арифметических операций для каждого вычисления. Втайне не вредно помечтать о том, чтобы после аппроксимации время вычислений уменьшилось бы хотя в несколько раз. Что получится на деле, вы увидите чуть позже. А пока войдем в дебри аппроксимации.