Главное меню
Вы здесь
21. Прямое и обратное преобразования Лапласа
Прямое и обратное преобразования Лапласа
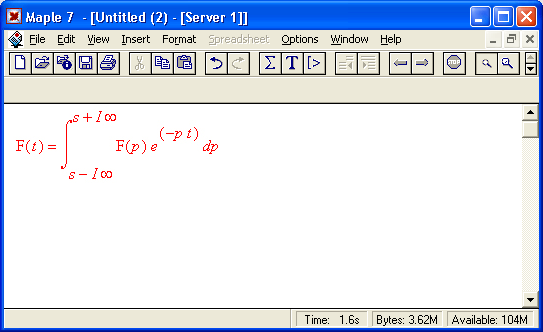
Прямое преобразование Лапсаса заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла
Для осуществления прямого преобразования Лапласа Maple 7 имеет функцию
laplace(expr,t,p)
Здесь ехрr— преобразуемое выражение, t — переменная, относительно которой записано ехрr, и р — переменная, относительно которой записывается результат преобразования.
Обратное преобразование Лапласа означает переход от функции F(p) к функции (t) с помощью формулы
Для вычисления этого интеграла служит функция:
invlaplace(expr,p, t)
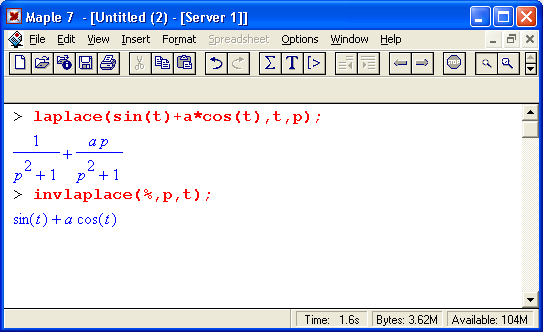
где ехрr — выражение относительно переменной р, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение а обратное —оригинал функции. Ниже приведены примеры применения прямого и обратного преобразований Лапласа:
Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t) + acos(t).