21.1 Задания типа верно — не верно

21.1 Задания типа верно — не верно

В качестве примера, который мы хотим обработать при помощи SPSS, рассмотрим личностный тест, с помощью которого определяется степень любопытства опрашиваемых.

Здесь речь идёт о вопросах, на которые следует давать строго определенные ответы: верно или не верно. Ответ верно соответствует наличию любопытства. Такое же самое значение можно присвоить и ответу не верно; при разработке теста, в него рекомендуется включать и такие вопросы, значимым ответом на которые является отрицательный. Это всегда возможно при соответствующей формулировке.

Если следовать Линерту, то для оценки пригодности отдельных пунктов следует применять нижеследующие два критерия:

Индекс сложности

В простейшем случае он представляет собой долю правильных ответов на данный вопрос, взятую в процентах от общего количества ответов. Для вопросов с несколькими возможными ответами и ступенчатыми ответами существуют модифицированные формулы. Удивительно, но для сложных вопросов индекс сложности принимает малые значения, а для лёгких большие. Вопросы с низким и высоким индексом сложности считаются не желательными.

Коэффициент избирательности

Коэффициентом избирательности, который является важным критерием для оценки применимости вопроса, служит корреляционный коэффициент между ответом на вопрос и суммарным показателем теста. В качестве суммарного показателя теста берётся сумма всех ответов. Это означает, что все правильные ответы должны иметь одинаковый знак! К сожалению, этому важному обстоятельству в справочниках уделяется не достаточно внимания. Для приведенного примера это означает, что пункты 2, 4, 8, 9 и 16 перед анализом должны быть подвергнуты перекодировке.

Для определения корреляционного коэффициента Линерт предлагает различные варианты, так, к примеру, двухрядная поточечная корреляция между заданием с ответом верно — не верно и значением масштаба или ранговая корреляция между заданием со ступенчатым ответом и значением масштаба. Как ни странно: SPSS всегда использует коэффициенты Пирсона.

Непригодные для применения пункты обычно отбираются посредством сравнения индексов сложности и избирательности. Самым простым способом является отбор сначала тех вопросов, которые обладают индексом сложности ниже 20 или выше 80, а затем из списка оставшихся вопросов исключаются те, которые имеют самые низкие коэффициенты избирательности. Линерт предлагает рассчитывать ещё и дополнительные показатели вопросов, такие как: индекс однородности, индекс пригодности, селекционный показатель и (если имеется так называемый внешний критерий) коэффициенты действительности.

Коэффициент пригодности

Коэффициент пригодности является важным критерием для оценки результата теста. Он является мерой точности, с которой проводится тестирование некоторого признака. SPSS предлагает для этой цели множество методов; по умолчанию устанавливается альфа Кронбаха (Cronbach's Alpha) со значением, модуль которого находится между 0 и 1. Обработаем наш пример при помощи SPSS.

•  Откройте файл nuegier.sav.

Помните о том, что вопросы 2, 4, 8, 9 и 16 должны быть перекодированы; их кодовые числа необходимо поменять местами (1 станет 2, 2 станет 1).

•  Это можно сделать при помощи метода, рассмотренного в главе 8, посредством выбора меню Transform (Трансформировать) Recode (Перекодировать) Into same Variables... (В те же переменные)

Можно было бы также воспользоваться и синтаксисом. Для этого необходимо было бы записать следующие инструкции:

RECODE item2, item4,   item8, item9, item16   (1=2) (2=1).  EXECUTE. 

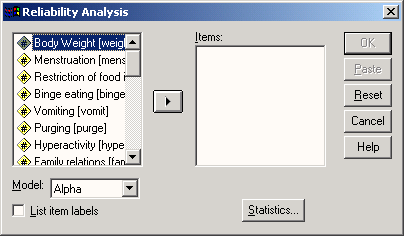
•  После перекодировки выберите в меню Analyze (Анализ) Scale (Масштабировать)  Reliability Analysis... (Анализ пригодности) Откроется диалоговое окно Reliability Analysis (Анализ пригодности).

•  Переменные iteml-itemlS поместите в поле пунктов (Items:). Затем из числа предлагаемых методов расчёта коэффициентов пригодности необходимо выбрать подходящий:

Рис. 21.1: Диалоговое окно Reliability Analysis (Анализ пригодности)

•  Alpha (Альфа): Альфа Кронбаха (при дихотомических пунктах используется формула Кудера-Ричардсона 20 (Kuder-Richardson- Formula 20))

•  Split-half (Расщепление на две половины): Определение пригодности с расщеплением на две половины по Спирману-Брауну (Spearman-Brown)

•  Guttman (Гуттман): Определение нижней границы пригодности Гуттмана

•  Parallel (Парралельно): Оценка максимального правдоподобия пригодности теста при условии наличия одинаковых дисперсий пунктов

•  Strict parallel (Строго параллельно): Оценка максимального правдоподобия пригодности теста при условии наличия одинаковых средних значений пунктов и одинаковых дисперсий пунктов.

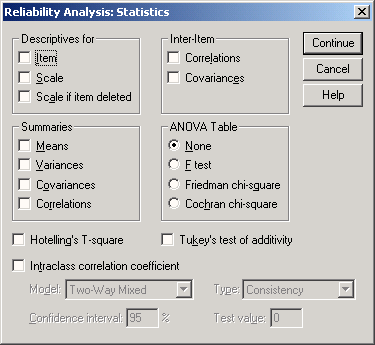
•  Оставьте предварительную установку Alpha (Альфа) и щёлкните на выключателе Statistics...(Статистики). Откроется диалоговое окно Reliability AnalysisStatistics (Анализ пригодности: Статистики).

Вы можете произвести следующие виды расчётов:

•  Descriptives for (Дескриптивные (описательные) статистики для) Item (Пункт): Среднее значение и стандартное отклонение для каждого пункта анкеты или вопроса Scale (Шкала): Среднее значение, дисперсия и стандартное отклонение для значения масштаба

Рис. 21.2: Диалоговое окно Reliability Analysis'.Statistics (Анализ пригодности: Статистики)

Scale if item deleted (Масштабировать, если пункт удалён): Когда при расчёте значения масштаба этот пункт (вопрос) не учитывается, для каждого такого Пункта (ответа на вопрос анкеты), выводятся: среднее значение и дисперсия значения шкалы, корреляция пункта со значением масштаба (то есть избирательность) и альфа Кохрана.

•  Summaries (Итоги, общие сведения) 

Means (Средние значения): Различные виды статистик для средних значений пунктов

Variances (Дисперсия): Различные виды статистик для дисперсий пунктов

Covariances (Ковариации): Различные виды статистик для ковариаций между пунктами

Correlations (Корреляции): Различные виды статистик для корреляций между пунктами.

•  Inter-Item (Между пунктами)

Correlations (Корреляции): Корреляционная матрица Covariances (Ковариации): Ковариационная матрица

•  ANOVA-ТаЫе (Таблица ANOVA)

F test (F тест): Двухфакторный дисперсионный анализ (факторы: наблюдения, пункты) с повторным измерением и одним значением в каждой ячейке Friedman chi-square (Хи-квадрат Фридмана): тест Хи-квадрат Фридмана и коэффициент согласования Кендала (при наличии переменных, относящихся к порядковой шкале)

Cochran chi-square (Хи-квадрат Кохрана): Q Кохрана (при наличии дихотомических переменных).

Далее ещё имеются:

•  Hottelling's T-square (Т-квадрат Хоттелинга): Тест Хоттелинга для проверки утверждения, что средние значения пунктов равны между собой.

•  Tukey's test ofadditivity (Критерий аддитивности Тьюки): Тест Тьюки на аддитивность пунктов.

В случае установки опции Intraclass correlation coefficient (Корреляционный коэффициент внутри класса) речь идёт о расчёте корреляционного коэффициента внутри класса (ICC); информацию по этому поводу Вы найдёте в разделе 15.5.

•  Здесь ограничьтесь активизацией опции Scale if item deleted (Масштабировать, если пункт удалён) и щёлкните на Continue (Далее).

•  Начните расчёт нажатием ОК.

В окне просмотра появятся результаты расчёта. И в 10 версии вывод этих результатов ещё не производится в новой табличной форме.

Коэффициент пригодности, равный 0,7887, является очень высоким. В колонке с названием Corrected Item-Total Correlation (Откорректированный пункт — суммарная корреляция) находятся коэффициенты избирательности. Основываясь на значении этих коэффициентов, пункты 4 и 17 можно считать непригодными для дальнейшего использования, да и пункт 8 должен быть исключён.

•  Мы уже говорили о необходимости проведения расчета индекса сложности. Для расчёта индекса сложности выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)

Процентный показатель частоты появления правильного ответа (кодировка 1) является индексом сложности соответствующего пункта. Все индексы сложности собраны в нижеследующей таблице.

Если следовать рекомендации, сформулированной в начале раздела и исключать пункты с индексом сложности меньшим 20 и большим 80, то помимо пунктов 4, 8 и 17 необходимо исключить из списка и пункт 7.

Если вновь провести анализ пунктов с оставшимися четырнадцатью пунктами, то коэффициент пригодности получится равным 0,8297. Благодаря исключению неподходящих пунктов он стал ещё выше.