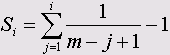Главное меню
Вы здесь
8.6.2 Типы рангов
8.6.2 Типы рангов
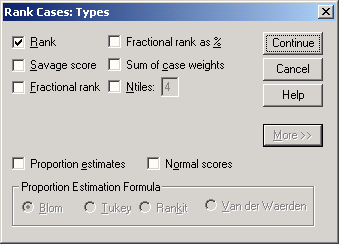
В диалоге Rank Cases можно, щелкнув на кнопке Rank Types... (Типы рангов), от-крыть диалоговое окно Rank Cases: Types (Ранги: Типы). В этом окне представлены шесть типов рангов; щелкнув на кнопке More » (Еще), можно увидеть еще два.
Ниже приведено объяснение различных типы рангов.
-
Rank (Ранг): Абсолютные значения рангов (см. раздел 8.6.1). Это установка по умолчанию.
-
Savage score (Оценка Сэвиджа): Это значения ранга, полученное на основе экспоненциального распределения. При общем количестве значений переменной т оценка Сэвиджа для i-го ранга определяется по формуле
Рис. 8.12: Диалоговое окно Rank Cases: Types
-
Fractional Rank (Относительный ранг): Это значение ранга деленное на количество наблюдений.
-
Fractional Rank as % (Относительный ранг в %): Это численные значения относительных рангов, умноженные на 100. Например, процентный ранг 33,93 означает, что 33,93% всех наблюдений имеют более низкий ранг.
-
Sum of case weights (Сумма весов наблюдений): Эта величина представляет интерес только при определении рангов для подгрупп и является постоянной в каждой подгруппе; она соответствует количеству случаев в подгруппе.
-
Ntiles (N-процентили): Пользователь может задать число групп процентилей, на которые должны быть разбиты наблюдения (по умолчанию 4). Тогда каждому случаю присваивается значение процентильной группы, к которой он принадлежит.
-
Proportion estimates (Долевые оценки): Вычисление накопленной доли при предположении нормальном распределении переменной. Для ранга г и количества наблюдений я соответствующие долевые оценки вычисляются по четырем нижеследующим формулам.
Blom: | (r-3/8)/(n+1/4) |
Tukey: | (r-1/3)/(n+1/3) |
Rankit: | (r-1/2)/n |
Van der Waerden: | r/(n+1) |
-
Normal scores (Нормальные ранги): Значения процентилей, относящиеся к долевым оценкам.
Для перечисленных рангов SPSS автоматически задает имена переменных, которые приведены в нижеследующей таблице. При этом имеет значение, был ли выбран единственный тип ранга или одновременно вычислялись ранги нескольких типов (что является исключением). В последнем случае, для обеспечения однозначности переменных имена должны различаться. В таблице приводятся также принятые в SPSS метки этих переменных. Для долевых оценок и нормальных рангов здесь приведен вариант, когда применяется формула Блома (Blom); при выборе других формул расчета этих рангов метки соответственно изменяются. Имя исходной переменной — lem (в нашем примере — это средняя ожидаемая продолжительность жизни мужчин).
Тип ранга | Единственный тип ранга | Несколько типов | Метка переменной |
Ранг | rlem | rlem | RANK of LEM |
Оценка Сэвиджа | slem | slem | SAVAGE of LEM |
Относительный ранг | rlem | rfrOO-1 | RFRACTION of LEM |
Относительный ранг в % | plem | perOO! | PERCENT of LEM |
Сумма весов наблюдений | nlem | nOOl | N of LEM |
N-процентили | nlem | ntiOOl | NTILES of LEM |
Долевые оценки (по Блому) | plern | plem | PROPORTION of LEM using BLOM |
Нормальные ранги (по Блому) | nlem | nlem | NORMAL of LEM using BLOM |
Если провести ранговые преобразования всех возможных типов и вывести получившиеся значения с помощью средства формирования сводки наблюдений, мы получим следующую таблицу.
Case Processinq Summary3 (Сводка наблюдений)
| LAN | RANK LE | SAVAG of | RFRACT Nof | PERCE of | Nof | NTILES LE | PROPOR Nof using | NORM of usin BLO |
1 | ALB | 3,00 |
| ,107 | 10,7 | 28 | 1 | ,092 |
|
2 | BEL | 11,50 |
| ,410 | 41,0 | 28 | 2 | ,393 |
|
3 | BUL | 15,50 |
| ,553 | 55,3 | 28 | 3 | ,535 | ,088 |
4 | DAE | 24,00 | ,843 | ,857 | 85,7 | 28 | 4 | ,836 | ,979 |
5 | DEU | 13,00 |
| ,464 | 46,4 | 28 | 2 | ,446 |
|
6 | DO | 17,00 |
| ,607 | 60,7 | 28 | 3 | ,588 | ,223 |
7 | FIN | 4,00 |
| ,142 | 14,2 | 28 | 1 | ,128 |
|
8 | FRA | 19.00 | ,098 | ,678 | 67,8 | 28 | 3 | ,659 | ,410 |
9 | GRI | 11,50 |
| ,410 | 41,0 | 28 | 2 | ,393 |
|
10 | GRO | 20,00 | ,209 | ,714 | 71,4 | 28 | 3 | ,694 | ,509 |
11 | IRL | 15,50 |
| ,553 | 55,3 | 28 | 3 | ,535 | ,088 |
12 | ISL | 27,00 | 1,927 | ,964 | 96,4 | 28 | 4 | ,942 | 1,575 |
13 | ITA | 18,00 |
| ,642 | 64,2 | 28 | 3 | ,623 | ,315 |
14 | JUG | 1,00 |
| ,035 | 3,5 | 28 | 1 | ,022 |
|
15 | LUX | 14,00 |
| ,500 | 50,0 | 28 | 2 | ,482 |
|
16 | NIE | 25,00 | 1,093 | ,892 | 89,2 | 28 | 4 | ,871 | 1,134 |
17 | NOR | 28,00 | 2,927 | 1,000 | 100,0 | 28 | 4 | ,977 | 2,011 |
18 | OES | 9,00 |
| ,321 | 32,1 | 28 | 2 | ,305 |
|
19 | POL | 7,00 |
| ,250 | 25,0 | 28 | 1 | ,234 |
|
20 | POR | 2,00 |
| ,071 | 7,1 | 28 | 1 | ,057 |
|
21 | RUM | 6,00 | - | ,214 | 21,4 | 28 | 1 | ,199 |
|
22 | SCH | 26,00 | 1,427 | ,928 | 92,8 | 28 | 4 | ,907 | 1,323 |
23 | SCH | 23,00 | ,643 | ,821 | 82,1 | 28 | 4 | ,800 | ,844 |
24 | sow | 22.00 | ,477 | ,785 | 78,5 | 28 | 4 | ,765 | ,724 |
25 | SPA | 21,00 | ,334 | ,750 | 75,0 | 28 | 3 | ,730 | ,613 |
26 | TSC | 5,00 | - | ,178 | 17,8 | 28 | 1 | ,163 |
|
27 | TUE | 10,00 | - | ,357 | 35,7 | 28 | 2 | ,340 | - |
28 | UNG | 8,00 |
| ,285 | 28,5 | 28 | 2 | ,269 |
|
Total (Всего) N | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
a. Limited to first 100 cases (Ограничено первыми 100 наблюдениями)