9. Подготовка пакетов расширений системы Mathematica

Подготовка пакетов расширений системы Mathematica

Мощным средством расширения возможностей системы Mathematica является подготовка пакетов расширений. Пакеты расширений позволяют создавать новые процедуры и функции и хранить их на диске в виде файлов с расширением . m. После считывания такого пакета с диска все входящие в него определения функций становятся доступными для использования в соответствии с правилами, принятыми для встроенных функций. Текст пакета расширения не выводится после его вызова, чтобы не загромождать документ вспомогательными описаниями. В сущности, пакеты расширения — это просто наборы программ на языке программирования системы Mathematica, подобранные по определенной тематике.

Типовая структура пакетов расширения

Структура пакета расширений (программы) в минимальном виде выглядит следующим образом:

(* Вводный комментарий *)

BeginPackage["Имя_пакета' "]

Mean::usage = "Имя функции[Параметры] Текстовый комментарий"

Begin[" 'Private' "] Unprotected[Список_имен] Определения новых функций

End[ ]

Установка атрибутов защиты EndPackage[ ] (* Завершающий комментарий *)

Особая структура пакетов расширений связана с реализацией описанной выше идеологии контекстов. Пакет открывается необязательным текстовым комментарием, который обрамляется двойными символами « (*» и «*) ». Он может быть как однострочным, так и многострочным. Обычно вводный комментарий включает в себя имя пакета, наименование фирмы и автора — создателей пакета, историю развития, дату создания и т. д. Если вы программируете для себя, можете на первых порах опустить все эти комментарии. Но не забудьте их ввести после отладки пакета, как того требуют культура и дисциплина программирования.

Затем пакет открывается словом BeginPackage. Это слово дается с квадратными скобками, в которых указывается контекст (см. выше) пакета. Обратите внимание на то, что после имени пакета должен стоять апостроф или цепочка символов, обрамленная апострофами. Имя пакета не должно совпадать ни с одним из известных, то есть быть уникальным.

Эта команда изменяет список контекстов, и он принимает вид

{Имя_пакета',System'}.

Таким образом, на первом месте списка контекстов оказывается имя пакета, а на втором — контекст System'. Теперь любой вводимый и не встроенный символ приобретает контекстную приставку с именем данного пакета.

Обратите внимание на то, что контекст System' сохранился в новом списке контекстов, но стал вторым. Это значит, что если вы вводите слова и символы, встроенные в систему, то они будут замещены новыми определениями. К примеру, если вы решили вычислять функцию Sin [x] по новому и ценному для вас алгоритму, то ему будет отдаваться предпочтение при каждом использовании этой функции до тех пор, пока вы работаете с данным пакетом расширения. Однако, как только вы перестанете работать с пакетом, восстановится роль встроенной функции Sin[x].

Следующий блок пакета — сообщения о назначении функций. Эти сообщения выводятся, если после загрузки пакета задать вопросительный знак с последующим именем функции. Эти сообщения не обязательны, но они обеспечивают единство диалога с системой и, безусловно, нужны при профессиональной подготовке пакета. Обычно в этих сообщениях кратко указываются синтаксические правила использования функций и назначение их параметров, указываемых в квадратных скобках.

Затем следует главная часть пакета — определения новых функций. Она открывается определением Begin [" ' Private ' "]. Оно, не меняя список контекстов, устанавливает новый текущий контекст Имя_пакета' Private'. Он присваивается всем ранее не встречавшимся символам. Имя Private принято в пакетах расширения системы Mathematica, хотя, в принципе, может быть любым другим именем. После него следуют сами определения, в которых могут использоваться любые средства, включенные в ядро системы.

В некоторых случаях имена функций могут повторять ранее определенные в ядре системы. Это полезно, если пользователь считает, что введенное им определение уже известной функции более точно или более универсально, чем использованное в системе. В таких случаях перед новым применением идентификатора надо позаботиться о снятии с него защиты с помощью функции Unprotect. Именно эта часть и определяет существо пакета и его ценность.

Завершается эта часть определением End [ ]. При этом восстанавливается контекст, который был до определения Begin [" ' Private' " ], то есть контекст с именем пакета. После этого идет необязательная часть с указанием атрибутов защиты. Пакет завершается определением EndPackage [ ], которое восстанавливает контекст, бывший текущим до загрузки пакета (например Global' ⁴ ), a контекст Имя_пакета ⁴ помещает в начало прежнего списка контекстов..

Контексты в системах Mathematica 3 и 4 идентичны — иначе и быть не может, поскольку всякая старшая версия системы должна обеспечивать совместимость с предшествующей версией. Впрочем, в Mathematica 4 включены два новых контекста, Developer ⁴ и Experimental ⁴ .

Необязательный заключительный комментарий чаще всего дает список тестовых примеров. Он особенно желателен, если пакет содержит определения не вполне очевидных функций. Не забывайте, что этот комментарий не выводится и не исполняется — он нужен лишь на этапе знакомства с пакетом. Разумеется, такое знакомство необходимо при каждой серьезной попытке применения того или иного пакета расширения или применения системы.

В принципе, текстовые комментарии могут вводиться на русском языке. Однако при этом возникают определенные трудности. При выводе комментариев на экран дисплея при работе с оболочкой системы Mathematica могут наблюдаться несоответствия между шрифтами, установленными при вводе комментариев и при их выводе. Поэтому лучше использовать комментарии на английском языке, тем более что комментарии ко всем встроенным функциям и к поставляемым расширениям системы даны, естественно, на английском языке.

Средства создания пакетов расширений

Для создания пакетов расширений в общем случае используются следующие средства системы:

• Begin ["context'"] — устанавливает текущий контекст;
• BeginPackage ["context'"] — делает context единственным активным контекстом. Возможна также форма BeginPackage [ "context" ", { "needl' ", "need2'",...}];'
• Return [ ] — возвращает Null;
• End [ ] — возвращает текущий контекст и переходит к предыдущему;
• EndAdd [ ] — возвращает текущий контекст и переходит к предыдущему, предварительно добавляя текущий контекст к списку контекстов $Context-Path;
• EndPackage [ ] — восстанавливает $Context и $ContextPath в их значениях до предшествующего BeginPackage и добавляет текущий контекст к списку $ContextPath;
• Exit [ ] — завершает сеанс работы Mathematica;
• Goto [tag] —просматривает текущее составное выражение в поиске Label [tag] и передает управление в эту точку;
• Interrupt [ ] — производит прерывание в теле вычислений;
• Label [tag] — представляет точку в составном выражении, в которую управление передается директивой Goto;
• Quit [ ] — завершает сеанс работы Mathematica.

Приведем пример простого фрагмента программы, дающего определение новой функции ExpandBoth с помощью некоторых из представленных средств:

(* :Title: ExpandBoth *)

(* :Context: ProgramminglnMathematica'ExpandBoth" *)

(* : Author: Roman E. Maeder *)

ExpandBoth: : usage = "ExpandBoth [e] expands all numerators and denominators in e."

Begin ["' Private1"]

ExpandBoth [x_Plus] := ExpandBoth /@ x

ExpandBoth [x_] := Expand [ Numerator [x] ] / Expand [ Denominator [x] ]

End [ ] Null

Этот пример настолько прост, что читателю будет нетрудно разобраться с его сутью — расширением выражения по числителю и знаменателю. Ниже представлен сеанс работы с этим пакетом, файл которого expboth.m размещен в каталоге mypack, включенном в общий каталог пакетов расширений:

<<mypack\expboth.m

?ExpandBoth

ExpandBoth [e] expands all numerators and denominators in e.

ExpandBoth [124 /12]

31/3

ExpandBoth [1234/12]

617/6

Мы вернемся к рассмотрению построения пакетов расширений после более детального рассмотрения некоторых деталей этого процесса.

Текстовые сообщения и комментарии

Ценность многих программ на любом языке программирования нередко сводится к нулю из-за отсутствия подробных текстовых комментариев. Из-за этого даже сами разработчики программ через месяц-другой перестают понимать собственные творения. А что говорить о пользователях, рискующих применить такие программы?

Для создания текстовых комментариев различного назначения (как выводимых, так и не выводимых на экран в ходе работы с пакетом) в языке программирования системы Mathematica используются следующие средства:

• (* Comment *) — задание не выводимого на экран текстового комментария, как однострочного, так и многострочного, в любом месте пакета;
• Message [symbol: : tag] — вывод сообщения symbol::tag, если только вывод сообщений не отключен;
• Message [symbol: :tag, e1, e2,...] — выводит сообщение, вставляя значения ei по мере необходимости;
• $MessageList — глобальная переменная, возвращающая список имен сообщений, вырабатываемых во время вычисления текущей входной строки. Имя каждого сообщения заключено в HoldForm [ ]. $MessageList сохраняется в MessageList [n] и переустанавливается в { } после того, как произведена п-я выходная строка;
• MessageList [n] — глобальный объект, который является списком имен (сообщений), которые вырабатываются в процессе обработки п-й входной строки;
• MessageName, применяется в виде symbol: : tag или MessageName [symbol, "tag" ] — имя для сообщения;
• $MessagePrePrint — глобальная переменная, чье значение, если установлено, применяется к выражениям перед тем, как они помещаются в текст сообщений;
• $Messages — возвращает список файлов и каналов, в которые направляется вывод сообщений;
• Messages [symbol] — возвращает все сообщения, присвоенные данному символу symbol.

Следует отметить, что широкое применение комментариев обычно является признаком культуры программирования. Это особенно важно для математических систем, реализующих вычисления по сложным и подчас малопонятным для неспециалистов алгоритмам. Без подробных комментариев пакеты расширений и применений теряют свою практическую полезность и превращаются в ребусы — увы, куда менее интересные, чем те, которые публикуются в газетах и журналах.

Защита идентификаторов от модификации

Атрибут защиты Protected

Как уже отмечалось, система Mathematica позволяет вводить константы, переменные и функции со своими именами — идентификаторами. Между функциями можно задавать различные отношения, в том числе и те, которые не соответствуют правилам, заданным в ядре системы.

Идентификаторы должны быть уникальными, то есть не совпадать с именами встроенных функций, директив, опций, переменных и констант. Однако как быть, если нужно задать новое отношение для уже имеющихся встроенных функций или изменить их определения?

Для решения таких вопросов в систему введена защита идентификаторов от модификации, которая при необходимости может сниматься. Все встроенные в ядро именованные объекты языка программирования системы являются защищенными по умолчанию. Они имеют соответствующий признак — атрибут Protected (защищенный).

Установка и снятие атрибута защиты

Для управления средствами защиты от модификации используются следующие директивы:

• Protect [s1, s2,...] — устанавливает атрибут защиты от модификации (Protected) для перечисленных символов si;
• Protect [\"forml\", \"form2\",...] — устанавливает атрибут защиты от модификации для всех символов, имена которых сопоставимы с любым из указанных строковых шаблонов f ormi;
• Unprotect [s1, s2,...] — удаляет атрибут защиты от модификации (Protected) для символов si, что делает возможной их модификацию;
• Unprotect [\"forml\", \"form2\",...] — снимает защиту всех символов, имена которых текстуально (по буквам) сопоставимы с любым из указанных formi.

Дополнительные функции защиты

Следующие атрибуты и директивы также используются при управлении модификацией:

• NProtectedAll — атрибут, устанавливающий, что ни один из аргументов функции не будет модифицирован при применении N [ ];
• NProtectedFirst — атрибут, указывающий, что первый аргумент функции не будет модифицирован применением N [ ];
• NProtectedRest — атрибут, устанавливающий, что все аргументы после первого аргумента функции не будут модифицированы применением N [ ].

Мы уже рассматривали модификацию функций, в частности снятие и назначение атрибутов защиты. Отметим лишь, что из последующих примеров будет ясно, что эти операции широко применяются в пакетах расширений.

Примеры подготовки пакетов расширений

Наиболее сложным моментом работы с системой Mathematica является разработка пакетов расширения профессионального качества. Именно такие пакеты позволяют приспособить всю мощь системы к решению тех задач, которые полезны конкретному пользователю.

Начать работу с системой можно за несколько часов. Реальное ее освоение потребует нескольких месяцев упорной работы. А подготовка серьезных пакетов, решающих достаточно сложные задачи, может занять и несколько лет. Для облегчения этого процесса рассмотрим основные приемы подготовки пакетов расширений. Напоминаем, что пакеты можно готовить как в оболочке системы (их затем следует записать на диск как файлы с расширением .т), так и с помощью .внешних текстовых редакторов.

В этом разделе представлено несколько примеров построения пакетов расширений системы Mathematica (версии не ниже 3.0), взятых из книги [34], а точнее, из примеров этой книги, включенных в справочную базу данных систем Mathematica. Из примеров удалена большая часть текстовых комментариев, сделанных на английском языке.

Пакет проверки выражений на их алгебраичность

Следующий пакет содержит определение функции AlgExpQ [expr], которая позволяет выяснить, является ли выражение ехрг алгебраическим.

(* :Title: AlgExp *)

(* :Context: Pro gra mminglnMathematica4AlgExp4 *) BeginPackage["ProgramminglnMathematica ' AlgExp '"]

AlgExpQ::usage = "AlgExpQ[expr] returns true if expr is an algebraic expression."

Begin["'Privateч"] SetAttributes[AlgExpQ, bistable]

AlgExpQ[ _Integer ] = True

AlgExpQ[ _Rational ] = True

AlgExpQ[ c_Complex ] := AlgExpQ[Re[c]] && AlgExpQ[Im[c]]

AlgExpQ[ _Symbol ] = True

AlgExpQ[ a_ + b_ ] := AlgExpQ[a] && AlgExpQ[b]

AlgExpQ[ a_ * b_ ] := AlgExpQ[a] && AlgExpQ[b]

AlgExpQ[ a_ ^ b_Integer ] := AlgExpQ[a]

AlgExpQ[ a_ ^ b_Rational ] := AlgExpQ[a]

AlgExpQ[_] = False End[]

EndPackage[]

Если выражение является алгебраическим, то функция AlgExpQ возвращает логическое значение True, иначе она возвращает значение False:

<<mypack\algexp.m

? AlgExpQ

AlgExpQ[expr] returns true

if expr is an algebraic expression.

AlgExpQ [a * x ^ 2 + b * x + c]

True

AlgExpQ[Sqrt[x]]

True

AlgExpQ["x^2+l"]

False

AlgExpQ[1] True AlgExpQ[1.0]

False

Пакет реализации метода Рунге—Кутта

Теперь рассмотрим, как выглядит пакет расширения, решающий систему дифференциальных уравнений хорошо известным численным методом Рунге—Кутта четвертого порядка. Ниже представлена распечатка данного пакета.

(* :Title: RungeKutta *)

(* iContext: ProgramminglnMathematica'RungeKutta' *)

BeginPackage["ProgramminglnMathematica'RungeKutta'"]

RKSolve::usage =

"RKSolve[{el,e2,..}, {yl,y2,..}, {al,a2,..}, {tl, dt}] numerically integrates the ei as functions of the yi with inital values ai.The integration proceeds in steps of dt from 0 to tl.

RKSolve[{el, e2,..},{yl,y2,..},{al,a2,..},{t,t0,tl, dt} ] integrates a time-dependent system from t0 to tl."

Begin["'Private'"]

RKStep[f_, y_, y0_, dt_] :=

Module [{ kl, k2, k3, k4 }, kl = dt N[ f /. Thread[y -> yO] ];

k2 = dt N[ f /. Thread[y -> y0 + kl/2] ];

k3 = dt N[ f /. Thread [y -> yO + k2/2] ] ;

k4 = dt N[ f /. Thread [y -> yO + k3] ] ;

y0 + (kl + 2 k2 + 2 k3 + k4)/6

RKSolve[f_List, y_List, y0_List, {tl_, dt_}] :=

NestList[ RKStepff, y, #, N[dt]]&, N[y0], Round [N [ tl /dt ]] ] /;

Length [f] == Length [y] == Length [y0]

RKSolve [f_List, y_List, y0_List, {t_, t0_, tl_, dt_}] := Module f { res } ,

res = RKSolve [ Append[f, 1], Append[y, t] , Append[y0, t0], {tl-t0, dt} ] ;

Drop[#, -1]& /@ res /;

Length [f] == Length [y] == Length [y0]

End[]

Protect [ RKSolve ]

EndPackage[]

Знающие реализацию этого метода обратят внимание на естественность записи общеизвестных математических операций. Пакет содержит определения двух функций: основной (RKSolve) и вспомогательной (RKStep). Последняя содержит вычисление решения на очередном шаге алгоритма по результатам вычислений на предшествующем шаге. Используется подстановка для переменной х и вычисление решения на очередном шаге по известной формуле Рунге— Кутта четвертого порядка точности.

Теперь рассмотрим, как можно использовать такой пакет, создать который можно в любом текстовом редакторе, например в редакторе NotePad, входящем в состав Windows 95/98. Для удобства работы можно поместить файл этого пакета rk4.m в папку Mypack, расположенную в папке со стандартными пакетами. В этом случае вызов пакета и проверка его загрузки осуществляются следующим образом:

<< mypack\rk4.m

?RKSolve

RKSolve [ {el, e2, ..}, {yl,y2,..}, {al,a2,..}, {tl, dt}] numerically integrates the ei as functions of the yi with inital values ai.The integration proceeds in steps of dt from 0 to tl. RKSolve [ {el, e2, ..}, {yl,y2,..}, {al,a2,..}, {t, t0, tl, dt}] integrates a time-dependent system from t0 to tl .

Итак, при обращении ?RKSolve выводится информация о формате применения функции RKSolve. Она задана на английском языке. Можно записать эту информации и на русском языке, однако при этом возможна нестыковка наборов шрифтов. Поэтому рекомендуется подобную информацию давать на английском языке. В нашем случае решается система дифференциальных уравнений первого порядка в форме Коши, заданная правыми частями {el, е2,...} с переменными {yl, у2,...} и их начальными значениями {al, а2,...} в интервале времени от 0 до .1 при фиксированном шаге dt. Во второй форме записи функции время t может меняться от tO до tl с шагом dt.

Приведенный ниже пример демонстрирует, как этот пакет используется на практике для решения системы дифференциальных уравнений y' = t*y + z и z' = t + y*z при начальных значениях у = z = 1 и t, меняющемся от 1 до 1.5 с шагом 0.1:

RKSolve[{t*y + z, t + y*z}, {у, z}, {1, 1}, {t, 1, 1.5, 0.1}]

{{!., 1.}, {1.22754, 1.22844), {1.52241, 1.53202),

{1.90912, 1.95373}, {2.42456, 2.57444), {3.12741, 3.55937}}

Решение представлено списком значений {yi, zi}, определяющим зависимости y(t) и z(t). Этот пример хорошо иллюстрирует реализацию популярного численного метода для решения систем дифференциальных уравнений.

Пакет символьных преобразований тригонометрических функций

Следующий пакет служит для демонстрации символьных преобразований тригонометрических функций синуса и косинуса.

(* :Title: TrigDefine *)

(* :Context: ProgramminglnMathematica'TrigDefine" *)

BeginPackage["ProgramminglnMathematica' TrigDefine'"]

TrigDefine::usage = "TrigDefine.m defines global rules for putting products of trigonometric functions into normal form."

Begin["'Private'"] (* set the private context *)

(* unprotect any system functions for which rules will be defined *)

protected = Unprotect[ Sin, Cos ] (* linearization *) Sin/: Sin[x_] Cos[y_] := Sin[x+y]/2 + Sin[x-y]/2

Sin/: Sin[x_] Sin[y_] := Cos[x-y]/2 - Cos[x+y]/2 Cos/: Cos[x_] Cos[y_] := Cos[x+y]/2 + Cos[x-y]/2

Sin/: Sin[x_]An_Integer?Positive :=

Expandt (1/2- Cos[2x]/2) Sin [x]^(n-2) ]

Cos/: Cos[x_]An_Integer?Positive :=

Expand[(l/2 + Cos[2x]/2) Cos[x]^(n-2)]

Protect[ Evaluate[protected]](* restore protection of system symbols *)

End[] (* end the private context *) EndPackage[] (* end the package context *)

Данный пакет задает преобразования для произведений sin(x) cos(x), sin(x) sin(y) и cos(x) cos(y), а также для sin(x) ⁿ и cos(x) ⁿ . Следующие примеры наглядно показывают работу с этим пакетом:

<< mypack\trigdefine.m

?Sin

Sin[z] gives the sine of z. Sin[a]*Cos[b]

1/2Sin[a-b] + 1/2 Sin[a+b]

Sin[a]*Sin[b]

1/2Cos[a-b] - 1/2Cos[a+b]

Cos[a]*Cos[b]

1/2 Costa-b] + 1/2Cos[a+b]

Sin[x]^2

1/2-1/2 Cos[2x]

Cos[x]^3

Sec[x]/4 +1/2Cos[2x] Sec[x] + 1/4(1/2 + 1/2 Cos[4x]) Sec[x]

Sin[x]^n

Sin[x]n

Данный пример — наглядная иллюстрация программирования символьных вычислений.

Пакет вычисления функций комплексного переменного

Еще один пакет расширений для вычисления функций комплексного переменного (блок пакетов ALGEBRA) представлен распечаткой, приведенной ниже.

(* :Title: Relm *)

(* :Authors: Roman Maeder and Martin Buchholz *) BeginPackage [ "Algebra 'RelrrT "]

RealValued::usage = "RealValued[f] declares f to be a real-valued function

(for real-valued arguments)."

SBegin["'Private'"]

protected = Unprotect[Re, Im, Abs, Conjugate, Arg] (* test for "reality", excluding numbers *)

realQ[x_] /; !NumberQ[x] := Im[x] == 0 imagQ[x_] /; !NumberQ[x] := Re[x] == 0

(* fundamental rules *)

Re[x_] := x /; realQ[x] Arg[x_] := 0 /; Positive[x] Arg[x_J :=Pi /; Negative[x] Conjugate[x_] := x /; realQ[x] Conjugate[x_] := -x /; imagQ[x]

(* there must not be a rule for Im[x] in terms of Re[x] !! *) (* things known to be real *)

Im[Re[_]] := 0 Im[Im[_]] := 0 Im[Abs[_]] := 0 Im[Arg[_]] := 0 Im[x_?Positive] = 0 Im[x_?Negative] = 0

Im[x_ ^ y_] := 0,/; Positive[x] && Im[y] == 0 Im[Log[r ?Positive]] := 0

(*' arithmetic *)

Re[x_Plus] := Re /@ x Im[x_Plus] := Im /@ x

Re[x_ y_Plus] := Re[Expand[x y]] Im[x_ y_Plus] := Im[Expand[x y]]

Re[x_ y_] := Re[x] Re[y]— Im[x] Im[y] Im[x_ y_] := Re[x] Im[y] + Im[x] Re[y]

(* products *)

Re[(x_?Positive y_) ^k_] := Re[x^k y^k] Im[(x_?Positive y_)^k_] := Im[x^k yAk]

(* nested powers *)

Re[(x_?Positive ^ y_ /; Im[x]==0)^k_] := Re[x^(y k)] Im[(x_?Positive ^ y_ /; Im[x]==0)"kj := Im[хл(у k)]

Re[ l/x_ ] := Re[x] / (Re[x]^2 + Im[х]^2) Im[ l/x_ ] := -Im[x] / (Re[x]"2 + Im[x]A2)

Im[x_^2] := 2 Re[x] Im[x]

Re[ x_^n_Integer ] := Block[{a, b},

a = Round[n/2]; b = n-a;

Re[x^a] Re[x^b] - Im[х^а] 1т[х^b] ]

Im[ x_^n_Integer ] :=Block[{a, b}, a = Round[n/2]; b = n-a; Re[x^a] Im[х^b] + Im[х^a] Re[x^b] ]

Re[x_IntegerAn_Rational] := 0 /; IntegerQ[2n] && Negative[x]

Im[x_IntegerAn_Rational] :=

(-х)лп (-1)л((Numerator[n]-l)/2 /; IntegerQ[2n] && Negative[x]

(* functions *)

Re[Log[r_?Negative]] := Log[-r] Im[Log[r_?Negative]] := Pi Re[Log[z_]] := Log[Abs[z]] /; realQ[z] Re[Log[z_]] := (1/2) Log[Re[z]^2 + Im[z]^2] Im[Log[z_]] := Arg[z]

Re[Log[a_ b_]] := Re[Log[a] + Log[b]]

Im[Log[a_ b_]] := Im[Log[a] + Log[b]]

Re[Log[a_^c_]] := Re[c Log[a]]

Im[Log[a_^c_]] := Im[c Log[a]]

Ке[Е^х_] :=Cos[Im[x]] Exp[Re[x]] Im[Е^х_] := Sin[Im[x]] Exp[Re[x]]

Re[Sin[x_]] := Sin[Re[x]] Cosh[Im[x]] Im[Sin[x_]] :=Cos[Re[x]] Sinh[Im[x]]

Re[Cos[x_]] := Cos[Re[x]] Cosh[Im[x]] Im[Cos[x_]] := -Sin[Re[x]] Sinh[Im[x]]

Re[Sinh[x_]] := Sinh[Re[x]] Cos[Im[x]] Im[Sinh[x_J] := Cosh[Re[x]] Sin[Im[x]]

Re[Cosh[x_]] := Cosh[Re[x]] Cos[Im[x]] Im[Cosh[x_]] := Sinh[Re[x]] Sin[Im[x]]

(* conjugates *)

Re[Conjugate[z_]] := Re[z] Im[Conjugate[z_]] :=

Conjugate[x_Plus]:= Conjugate /@ x Conjugate[x_Times]:= Conjugate /@ x Conjugate[x_^n_Integer]:= Conjugate[x]An Conjugate[Conjugate[x_]]:= x

(* real-valued rules *)

Attributes[RealValued] = {Listable, HoldAll} Attributes[RealValuedQ] = {HoldFirst}

RealValued[f_Symbol] := (f/: RealValuedQ[f] = True; f) RealValued[f ] := RealValued /@ {f}

Im[ (_?RealValuedQ) [_? (Im[#J ==0&)...] ] := 0

(* define built-in function to be real-valued *)

DoRules[flist_] := Block[{protected},

protected = Unprotect[flist];

RealValued[flist];

Protect[Evaluate[protected]]

]

DoRules[{Sin, Cos, Tan, ArcSin, ArcCos, ArcTan, ArcCot, Sinh, Cosh, Tanh, ArcSinh, ArcCosh, ArcTanh, Floor, Ceiling, Round, Sign, Factorial}]

Protect[Evaluate[protected]]

End[]

Protect[RealValued]

EndPackage[]

Как нетрудно заметить, в этом пакете задано вычисление действительной и мнимой частей для ряда тригонометрических, гиперболических и числовых функций.

Пакет расширения графики

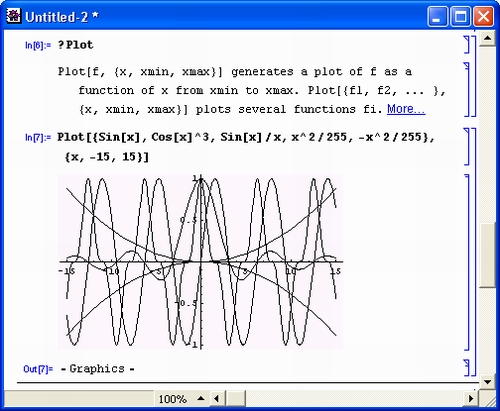
Следующий пример иллюстрирует подготовку графического пакета расширения, который строит графики ряда функций с автоматической установкой стиля линий каждой кривой.

(* :Title: Plot *)

(* :Context: ProgramminglnMathematica"Plot" *)

BeginPackage["ProgramminglnMathematica4 Plot4"]

Plot::usage = Plot::usage <> " If several functions are plotted, different plot styles are chosen automatically."

Begin["'Private'"] protected = Unprotect[Plot]

$PlotActive = True

Plot[f_List, args__]/; $PlotActive := Block[{$PlotActive = False},

With[{styles = NestList[nextStyle, firstStyle, Length[Unevaluated[f]]-1]}, Plot[f, args, PlotStyle -> styles] ] ]

(* style definitions *)

unit = 1/100 max = 5

firstStyle = Dashing[{}]

nextStyle[Dashing[{alpha__, x_, y_, omega__}]] /; x > у + unit :=

Dashing[{alpha, x, у + unit, omega}] nextStyle[Dashing[l_List]] :=

Dashing[Prepend[Table[unit, {Length[1] +1}], max unit]]

Protect! Evaluate[protected] ]

End[]

EndPackage[]

Рисунок 10.6 показывает применение данного пакета.

Пакеты-пустышки

Разумеется, эти примеры не исчерпывают всего разнообразия пакетов расширений. В сущности, они не дают ничего нового, поскольку приведенные листинги являются просто упрощением гораздо более полных и мощных пакетов, уже входящих в систему. В Mathematica 3 и 4 многие функции из пакетов расширения перекочевали в ядро системы, что позволило существенно ускорить вычисления. Поэтому в пакетах расширения можно встретить определения-пустышки, просто сообщающие об этом и не содержащие новых определений функций. Примером такого рода является модуль countroot.m, листинг которого приведен ниже.

Рис. 10.6. Пример применения функции Plot из пакета расширения plot.m (* :Name: Algebra"CountRoots' *)

(* :Copyright: Copyright 1994-1996, Wolfram Research, Inc.*)

(* :Summary:All CountRoots functionality is now provided by Algebra'Rootlsolation". The package Algebra'CountRoots" is obsolete.

*)

Needs["Algebraч Rootlsolation'" ]

CountRoots::obslt =

"All CountRoots functionality is now provided by

Algebra'Rootlsolation'.

The package Algebra'CountRoots" is obsolete."

Message[CountRoots::obslt]

Надо прямо сказать, что в области математики пользователь средней квалификации едва ли может придумать что-либо такое, что еще не включено в ядро или в пакеты расширений системы. Разумно готовить такие пакеты лишь для тех специальных областей применения математики, с которыми работает пользователь, — например в области физики, химии, механики, электротехники и радиотехники и т. д. Однако более вероятно, что пользователь предпочтет готовить не пакеты расширений, а пакеты применений.

Пакеты применений — это группы документов с программами, предназначенные для решения определенного класса математических или научно-технических проблем и задач. В отличие от пакетов расширения, в документах пакетов применений обычно дается подробно комментируемое описание всех основных алгоритмов решения задач. При этом комментарий, как правило, выводится на экран дисплея.

Довольно часто в пакетах применений используется прием объединения ряда ячеек в одну с общим текстовым заголовком. Это особенно полезно для организации вспомогательных и промежуточных вычислений, ячейки которых загромождают экран и лишают текст документа наглядности. Данный прием скрывает такие вычисления, но позволяет в любой момент вывести их на экран дисплея при активизации маленького прямоугольника, отмечающего такие совмещенные ячейки. Тексты документов, поставляемых с системой, являются прекрасными образцами использования этого приема.

Документы пакетов применения — это конечный продукт практического использования системы Mathematica. Поэтому они могут включать в себя все ранее описанные средства системы. Как уже неоднократно отмечалось, документы записываются на диск в виде файлов с расширением .т (в ранних версиях Mathematica — .та), а их полный битовый образ (включающий рисунки) сохраняется во вспомогательных файлах с расширением .mb. При большом числе сложных рисунков в документе эти файлы могут быть весьма большими — сотни килобайт и даже единицы мегабайт.