5. Знакомство с символьными вычислениями

Знакомство с символьными вычислениями

Особенности систем компьютерной математики

Недостатки численных расчетов

Большинство первых CKM (Eureka, Mercury, Excel, Lotus-123, Mathcad для MS-DOS, PC MATLAB и др.) предназначались для численных расчетов. Они как бы превращали компьютер в большой программируемый калькулятор, способный быстро и автоматически (по введенной программе) выполнять арифметические и логические операции над числами или массивами чисел. Их результат всегда конкретен — это или число, или набор чисел, представляющих таблицы, матрицы или точки графиков. Разумеется, компьютер позволяет выполнять такие вычисления с немыслимой ранее скоростью, педантичностью и даже точностью, выводя результаты в виде хорошо оформленных таблиц или графиков.

Однако результаты вычислений редко бывают абсолютно точными в математическом смысле: как правило, при операциях с вещественными числами происходит их округление, обусловленное принципиальным ограничением разрядной сетки компьютера при хранении чисел в памяти. Реализация большинства численных методов (например, решения нелинейных или дифференциальных уравнений) также базируется на заведомо приближенных алгоритмах. Часто из-за накопления погрешностей эти методы теряют вычислительную устойчивость и расходятся, давая неверные решения или даже ведя к полному краху работы вычислительной системы — вплоть до злополучного «зависания».

Условия, при которых это наступает, не всегда известны — их оценка довольно сложна в теоретическом отношении и трудоемка на практике. Поэтому рядовой пользователь, сталкиваясь с такой ситуацией, зачастую становится в тупик или, что намного хуже, неверно истолковывает явно ошибочные результаты вычислений, «любезно» предоставленные ему компьютером. Трудно подсчитать, сколько «открытий» на компьютере было отвергнуто из-за того, что наблюдаемые колебания, выбросы на графиках или асимптоты ошибочно вычисленных функций неверно истолковывались как новые физические закономерности моделируемых устройств и систем, тогда как на деле были лишь грубыми погрешностями численных методов решения вычислительных задач.

Многие ученые справедливо критиковали численные математические системы и программы реализации численных методов за частный характер получаемых с их помощью результатов. Они не давали возможности получить общие формулы, описывающие решение задач. Как правило, из результатов численных вычислений невозможно было сделать какие-либо общие теоретические, а подчас и практические выводы. Поэтому, прежде чем использовать такие системы в реализации серьезных научных проектов, приходилось прибегать к дорогой и недостаточно оперативной помощи математиков-аналитиков. Именно они решали нужные задачи в аналитическом виде и предлагали более или менее приемлемые методы их численного решения на компьютерах.

Понятие о символьных (аналитических) вычислениях

Символьные операции — это как раз то, что кардинально отличает систему Mathematica (и подобные ей символьные математические системы) от систем для выполнения численных расчетов. При символьных операциях, называемых также аналитическими, задания на вычисление составляются в виде символьных (формульных) выражений, и результаты вычислений также получаются в символьном виде. Численные результаты при этом являются частными случаями символьных.

Выражения, представленные в символьном виде, отличаются высокой степенью общности. К примеру, тождество sin(x) ² + соs(x) ² = 1 справедливо при любых значениях аргумента х. Если результат символьной операции равен, к примеру, sin(1), то он и будет выведен как sin(1) — конкретное вещественное число, приближенно представляющее или аппроксимирующее sin(1), вычисляться не будет, ибо носит частный характер.

Результат вычисления sin(х) ² + cos(x) ² можно проверить с помощью систем для численных расчетов, задав ряд конкретных значений х и вычислив сумму квадратов синуса и косинуса. Однако всякий раз мы будем получать частный результат, не имея никакой гарантии того, что он действительно справедлив при любом значении х. К тому же этот результат нередко может оказаться равным 0,9999999 или 1,0000001, так что лишь наша фантазия округляет его до точной единицы. Между тем это как раз то, что абсолютно недопустимо в действиях профессионала — математика-аналитика. Его приведет в ужас малейшее отличие указанного выражения от единицы! Ведь почтенные классики математики давно уже доказали, что этот результат равен в точности единице!

Так чему равна сумма квадратов синуса и косинуса?

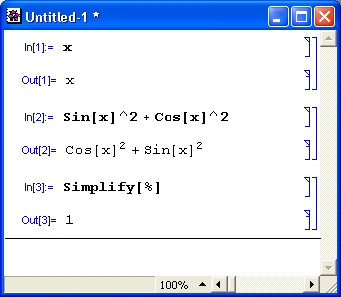
Попытка вычислить в общем виде выражение sin(x) ² + соs(x) ² с помощью численных математических систем или программ на обычных языках программирования к успеху не приведет. Вместо ожидаемого результата появится сообщение об ошибке вида: «Переменная х не определена!». Компьютер будет ждать ввода конкретного значения для х.Так будет независимо от того, запрограммировали вы вычисления на простеньком Бейсике или на языке профессионалов-программистов C++. И лишь системы символьной математики при вычислениях дадут долгожданное и абсолютно точное значение 1 (рис. 1. 3) .

Рис. 1.3. Система Mathematical вычисляет значение sin(x) ² +cos(x) ²

Пока не стоит обращать внимание на то, как получен рис. 1.15 — это окно реально работающей системы Mathematica. Уже при рассмотрении простейшего примера, представленного на этом рисунке, можно сделать несколько характерных выводов. Прежде всего видно, что при выводе неопределенной переменной х мы получаем просто имя этой переменной. Функции sin(х) и cos(х) в системе Mathematica обозначаются как Sin [х] и Cos [х]. Само по себе выражение sin(х) ² + cos(х) ² просто повторяется, а для его вычисления используется функция Simplify (упростить), аргументом которой является знак %, означающий подстановку предшествующего выражения. Два знака % можно использовать для подстановки предшествующего предшествующему выражению и т. д. Для вычисления строки ввода надо нажимать клавиши Shift+Enter, нажатие же одной клавиши Enter просто переводит строку в области ввода, именуемой также ячейкой ввода.

Любопытно, что в начале запуска, сопровождаемого музыкальным звуком, Mathematica выводит чистое окно редактирования документа, в котором нет даже маркера ввода — характерной вертикальной черточки. Этот маркер появится, как только вы введете какой-то первый символ. После получения первого результата появляется и длинная горизонтальная черта, отделяющая выведенные ячейки от свободного поля окна редактирования под ними. Эта черта является признаком возможности ввода очередной ячейки. Ее можно перевести в уже созданную область документа, если вы захотите создать новую ячейку среди уже существующих ячеек ввода.

Обратите внимание на то, что система выделяет ячейки ввода определителем In [N], а ячейки вывода — определителем Out [N], где N — автоматически проставляемый номер строки. Кроме того, в левой части отображаются квадратные скобки с особыми признаками, которые будут описаны в позже. Далее мы, как правило, будем опускать определители ячеек и квадратные скобки и представлять документы в упрощенной и более компактной форме. Например, представленный на рис. 1.15 документ может быть записан в следующем виде:

х

x

Sin[х]^2+Соs[х]^2

Cos[x] ² +Sin[x] ²

Simplify[%]

1

Здесь входные выражения задаются жирным прямым шрифтом, а выходные — прямым шрифтом обычной насыщенности, то есть именно так, как они выглядят при настройке системы по умолчанию. При этом выходные выражения имеют обычный (в терминах системы Mathematica — стандартный) вид, присущий математическим формулам. Все такие выражения в книге представлены путем копирования ячеек ввода и вывода в текст с помощью буфера обмена (Clipboard). Технология такого копирования и ее особенности будут описаны далее.

Ячейки нумеруются по мере их использования. При этом можно с конца документа вернуться к его началу или середине и, изменив содержимое ранее использованных ячеек, снова выполнить вычисления. При этом ячейки меняют номера. При загрузке файла ячейки перенумеруются в строго последовательном порядке. Таким образом, номера ячеек не являются жестко фиксированными, они представляют собой сугубо техническое средство, отражающее работу системы в текущем сеансе — сессии. Это говорит в пользу отказа от вывода определителей ячеек при записи большинства примеров.

Математические системы в образовании и в науке

Можно сказать, что даже самые мощные системы для численных расчетов являются полными «профанами» в символьной математике. Они начисто лишены даже задатков элементарного разума, что видно уже из приведенного примера — даже школьник знает, что сумма квадратов синуса и косинуса равна в точности единице при любом аргументе х. А что говорить о столь распространенных аналитических вычислениях, как упрощение сложных математических формул, осуществление подстановок, вычисление пределов, производных и первообразных функций, разложении их в ряды Тейлора и Фурье, вычислении корней многочленов с буквенными коэффициентами и т. д.?

Такая возможность действительно имеется, однако следует иметь в виду, что векторные графические объекты, скопированные из Mathematica через буфер обмена, не вполне корректно воспринимаются другими приложениями. При верстке данной книги это вызвало очень много проблем.

Трудно сказать, сколько слез пролито школьниками и их матерями по поводу неправильно сделанных математических преобразований на контрольных работах и экзаменах и сколько ребят восприняли математику как заклятого врага из-за первых неудач в ее изучении. Еще больший урон народному хозяйству (то бишь рынку) наносит неумение выпускников школ и вузов применять современные математические методы на практике, хотя именно это является конечной целью фундаментального математического образования. Многие студенты запоминают математические истины от силы на несколько дней во время экзаменов.

Как же найти выход из этого тупика? Одна из возможностей — применение достаточно универсальных СКМ, автоматизирующих большую часть математических вычислений. Такие системы позволяют пользователю — как студенту, так и научному работнику — быстро вспомнить полученные в вузе знания и легко использовать их на практике без этапа нудных и трудоемких рутинных вычислений и преобразований. А заодно и освоить новые для себя методы и разделы современной математики.

К сожалению, за пределами возможностей численных математических систем оказались обширные области математики, связанные с проведением аналитических расчетов — от простых подстановок и сокращений до аналитической обработки математических выражений и функций и обучения компьютера новым математическим закономерностям и соотношениям. Всей этой работой, относящейся в основном к разделам элементарной и высшей алгебры, и были вынуждены заниматься математики-аналитики.

Увы, в нашей системе образования недостаточное знакомство с современными СКМ характерно не только для студентов, но и для доцентов и профессоров вузов. Среди них хорошее владение СКМ скорее исключение, чем правило. Это серьезно препятствует решению ряда первостепенных проблем образования — повышению его фундаментальности и вхождению нашей образовательной системы в общемировую, где компьютерные системы символьной математики в последние годы нашли самое широкое применение.

Очевидно, что чем раньше пользователь ПК начнет знакомиться с СКМ, тем больше математических знаний он получит. Хотя, безусловно, желательно, чтобы такое использование шло под контролем опытного преподавателя.

К сожалению, у нас есть серьезная причина, препятствующая широкому применению СКМ в образовании, — слабость материально-технической базы школ, вузов, да и многих университетов. Классами с современными ПК многие наши образовательные учреждения не обладают. Тем не менее, это чисто техническая проблема, которая постепенно решается.

В новых стандартах образования роль СКМ наконец-то осознана всерьез. По ряду специальностей математического профиля предусмотрено изучение СКМ. Это делает книги, подобные данной, нужными для системы образования.

Разумны ли системы символьной математики?

Математика непрерывно развивается, и ни один самый способный ученик не в состоянии (и слава Богу!) вместить в извилины своего мозга все математические законы и правила, созданные за многовековую историю человечества. Сотни лет назад такие задачи, как решение квадратного уравнения в общем виде, были в числе труднейших математических задач, а сейчас их «щелкают» школьники. Даже многотомные справочники по математике не гарантируют полного описания всех ее возможностей. Так что нет ничего страшного в том, что в наш просвещенный век вычисление производных или первообразных функций в аналитическом виде берет на себя компьютер. И их применение внешне становится таким же простым, как таблица умножения.

Сейчас слова «компьютерный разум» обычно берут в кавычки, всячески подчеркивая, что компьютер сам по себе не способен дать принципиально новые результаты (то есть те, которые не были заранее заложены в него человеком, его создавшим). Для многих, что в целом справедливо, вопрос о том, разумна ли система символьной математики, подобен вопросу о том, разумен ли хороший и полный справочник по математике.

И все же применительно к современным системам символьной математики (и универсальным СКМ) такая аргументация, пожалуй, не вполне приемлема. Да, базовые формулы и правила символьных преобразований в математические системы компьютерной алгебры заложены их создателями. Поэтому принципиально новых научных данных система сама по себе вроде бы и не дает. Но разве не такова в целом и ситуация с обычным использованием математического аппарата любым математиком-аналитиком?

Между тем большинству конкретных пользователей системы символьной математики дают новые знания в виде далеко не очевидных для них математических и иных закономерностей. Результат сложных и многоэтапных рекуррентных символьных преобразований даже по известным правилам может быть действительно новым, то есть ранее не опубликованным, заранее не предсказуемым и далеко не очевидным. Этим системы символьной математики принципиально отличаются от обычных справочников по тем или иным формулам. Они дают сведения не только по жесткому набору формул, но и по тем аналитическим соотношениям, которые в такой набор не вошли.

Подобные результаты нередко могут подтолкнуть серьезного научного работника или педагога к открытию неизвестных закономерностей в исследуемых или изучаемых ими явлениях. К тому же современные системы компьютерной алгебры способны к расширению — в них можно вводить новые закономерности и связи (подчас самые смелые и безумные), а затем исследовать малоизвестные или вообще неизвестные результаты их действия, получаемые в результате сложных аналитических преобразований. Так что вполне допустимо считать такие системы в известной мере разумными и способными помочь пользователю в создании новых теоретических положений и даже научных теорий.

Немаловажный довод в пользу некоторой разумности современных систем символьной математики заключается в особом назначении примеров их применения, которых в справочной базе данных могут насчитываться тысячи. Здесь уместно упомянуть высказывание И . М. Гельфанда: «Теории приходят и уходят, а примеры остаются».

Во всех современных СКМ примеры применения «живые» — вы можете подыскать наиболее близкий к решаемой вами задаче пример и тут же перестроить его под свои нужды. Обычные книги и справочники такой возможности принципиально не дают. Обучение на примерах — один из самых эффективных методических приемов. Он широко используется в данной книге и составляет основу справочной базы данных систем Mathematica.

В свое время нас учили, что количество переходит в качество. Примеров этого в природе превеликое множество. Системы компьютерной математики по обилию встроенных в них функций, правил преобразования и конкретных примеров применения уже вышли за пределы, которые способен оценить индивидуальный пользователь, даже если он достаточно опытный математик. К примеру, ядро Mathematica 4 хранит данные о примерно 5 тысячах интегралов! Это говорит о том, что СКМ находятся уже на пороге того, что их количественные характеристики перерастут в качественные. Среди них может оказаться и разум СКМ — на сей раз без каких-либо оговорок.

Что дает компьютерная математика университетам и школам

В конечном счете, СКМ — не более чем удобный и мощный инструмент для учащегося, педагога, инженера или научного работника. Как его применять (в методическом, научном и практическом отношении), зависит уже от пользователя. Однако важно и ценно то, что системы символьной математики снимают у учащихся психологический барьер в реальном применении математики, особенно высшей.

Тем не менее, многие преподаватели математики опасаются приобщения своих учеников к работе с СКМ. Бывает, что некоторые преподаватели школ и вузов при подготовке массовых заданий по алгебре, тригонометрии и геометрии сами применяют СКМ — например, для подготовки заданий по курсам математики или физики. Но это становится еще одним наивным поводом ограждать учащихся от систем символьной математики и даже запрещать их в учебном процессе. Оно и понятно — ведь школьник или студент, имеющий компьютер с системой компьютерной алгебры, прощелкает все подобные примеры за считанные минуты. Между тем учащихся, столь виртуозно владеющих системами компьютерной математики, надо лишь всячески поощрять! Увы, пока их очень мало...

Надо учитывать, что эффективное применение систем компьютерной алгебры практически невозможно без четкого понимания основ элементарной и высшей математики. Невозможно оно и без творческого участия пользователя как в постановке решения задач, так и в контроле и отборе результатов их решения. В большинстве математических систем используются специальные опции и директивы, направляющие решение в нужное русло. В какое именно — должен определить пользователь, владеющий нужными для этого математическими понятиями. Кроме того, именно пользователю необходимо проверить полученные результаты и убедиться в их достоверности.

Среди части преподавателей вузов существует в корне неверное мнение о том, что не нужно изучать сами СКМ — достаточно использовать доморощенные обучающие программы. Среди таких программ и впрямь есть интересные разработки, но, как правило, они базируются на ядре той или иной символьной СКМ, причем нередко старых версий, применяемых с целью обойти лицензионные ограничения.

По большому счету, такие обучающие системы ничего нового в процесс математических вычислений не вносят. Современные универсальные СКМ намного мощнее подобных программ, имеют более совершенный и более удобный интерфейс пользователя, а главное — только они реально применяются на месте работы будущих специалистов. Поэтому изучение современных СКМ столь же необходимо, как изучение офисных программ, например, того же текстового редактора Word 95/97. Наиболее удобной формой для этого являются спецкурсы, хотя и в ряде обязательных курсов такое изучение предусмотрено новыми учебными программами Министерства образования РФ.

В наших экономических условиях особенно велика роль систем компьютерной математики как мощных электронных справочников. Число издаваемых обычным способом справочников по математике или физике (не говоря уже о инженерных дисциплинах) в последние годы катастрофически упало. Это повышает роль справочников электронных, тем более что справочные базы данных современных систем компьютерной математики обладают рядом очевидных достоинств:

• вмещают в себя объемы информации, эквивалентные порой десяткам книг;
• аккумулируют знания, полученные за многие тысячелетия развития математики;
• имеют безупречное оформление документов (цветные тексты и иллюстрации, всевозможные выделения, качественные иллюстрации и т. д.);
• имеют разную организацию оглавления (индексную, поиск по контексту и т. д.); О отличаются очень быстрым поиском нужной информации по ряду критериев;
• имеют «живые» примеры, которые можно изменять в ходе просмотра справочных данных;
• справочные материалы могут сопровождаться звуковыми и видеокомментариями;
• позволяют готовить высококачественные и наглядные уроки не только по любым разделам математики, но и по многим дисциплинам, базирующимся на применении математического аппарата;
• позволяют быстро размножить интересующие пользователя материалы; 
•  обладают возможностью обновления и пополнения из сети Интернет.

Современные СКМ следует рассматривать не только как электронные справочники нового поколения, но и как системы для самообучения и дистанционного обучения математике. Однако для этого они должны быть снабжены грамотно составленными (прежде всего в методическом отношении) электронными уроками или книгами. Здесь необъятный простор для творчески мыслящих педагогов! В то же время, при отсутствии таких уроков применение математических систем может иметь негативные последствия для образования — опасна подмена обучения основам математики обучением основам работы с математическими системами.

Многие виды вычислений, даже элементарных, довольно трудоемки. Например, построение трехмерной поверхности требует зачастую сотен однообразных вычислений, выполнять которые крайне муторно даже при применении калькуляторов. Современные СКМ (в том числе Mathematica) делают это за считанные секунды, а то и за доли секунды. К тому же они сразу же строят графики поверхностей с разнообразной функциональной окраской и позволяют интерактивно вращать их (Mathematica 4), добиваясь лучшей выразительности и лучшего обзора фигур.

Применение СКМ в образовании избавляет учащихся от массы рутинных вычислений и высвобождает их время для обдумывания алгоритмов решения задач, более обоснованной постановки их решения, многовариантного подхода и представления результатов в наиболее наглядной форме. Высвободившееся время можно использовать для более глубокого изучения математической или физической сущности решаемых задач и их решения различными методами. Таким образом, СКМ не только не лишают учащихся серьезных математических навыков, но, напротив, способны их расширить и углубить.

Немаловажным фактором является то, что новейшие СКМ относятся к самым серьезным программным продуктам, имеющим современный пользовательский интерфейс и мощные средства визуализации всех этапов работы — причем, в области математики более выразительные, чем те, которые дают текстовые процессоры класса Word 95/97. Так что, работая с ними, пользователь поневоле осваивает работу с компьютером и познаёт тонкости интерфейса современных программ.

Кроме того, современные СКМ позволяют готовить и распечатывать документы, затрачивая на это куда меньше времени, чем популярные у математиков системы ТеХ или LaTeX. Впрочем, Mathematica прекрасно сожительствует с ними и позволяет представлять данные в необходимом для этих систем формате. Mathematica 4 поддерживает новейший формат подготовки математических документов для Интернета — MathML.

Работать с современными СКМ просто, приятно и поучительно. Благодаря этому освоение систем Mathematica воспринимается учащимися с большим интересом, что служит побудительным мотивом к их внедрению в систему образования, причем не только высшего, но и среднего, и даже начального (последнему, как отмечалось, фирма Wolfram в последние годы уделяет большое внимание).

Диалог с системой и ее входной язык

Интересно отметить, что, родившись как программа для профессионалов, Mathematica в последние годы упорно позиционируется фирмой Wolfram как система, перспективная не только для высшего, но и для школьного образования. Диалог с системой идет по методу «задал вопрос — получил ответ». Не считая отдельных мелочей, такой диалог вполне понятен не только опытному математику, но и успевающему студенту и даже школьнику.

Впрочем, уже из приведенных простейших примеров видны определенные тонкости записи входных выражений, которые определяются совокупностью правил их ввода, то есть синтаксисом входного языка системы, или (более строго) языка программирования системы. Он будет рассмотрен по мере описания возможностей систем класса Mathematica. Обширные возможности этих систем в решении математических задач придают им функции не только суперкалькуляторов, но и мощных электронных справочников по математике и математическим расчетам.

Даже интуитивно ясно, что осуществление символьных операций — процесс намного более тонкий и сложный, чем реализация даже сложных численных расчетов. В какой-то степени он противен сущности вычислений, реализуемых в современных ЭВМ, — как известно, они работают с «голыми» цифрами и являются «числодробилками». Эти операции сложнее и обычных (довольно примитивных) строковых операций, используемых при обработке текстов. К тому же известно, что одни только таблицы производных, интегралов и формул преобразований занимают многие тома объемных книг. Поэтому высокая эффективность символьных операций реальна только при их реализации на современных высокопроизводительных ПК. Не случайно системы символьной математики получили серьезное развитие лишь в последний десяток лет.

Все сказанное ведет к необходимости символьного представления чисел и использования особых алгоритмов для выполнения операций с ними. Естественно, что реализация символьных операций вначале обеспечивалась за счет снижения эффективности численных расчетов. Тем более приятно, что в новейшей системе Mathematica 4 эта порочная тенденция была решительно остановлена — данная версия системы имеет не только превосходные возможности в части символьных вычислений, но и повышенную эффективность и скорость численных расчетов. Это выдвигает систему Mathematica 4 в число лучших универсальных систем компьютерной математики.

Операции с целыми числами

Продолжим знакомство с возможностями системы Mathematica 4 примерами работы с целыми числами. Несколько таких примеров приведено на рис. 1.4.

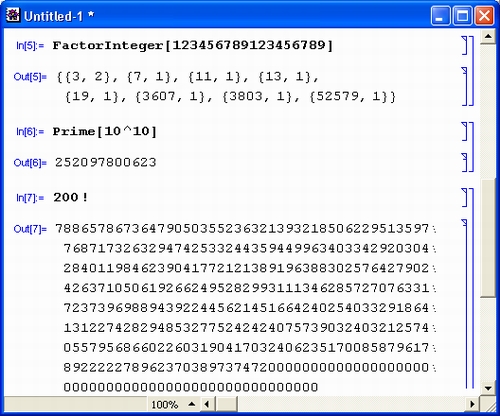
Рис. 1.4. Примеры целочисленных операций

Первая из приведенных операций дает разложение целого числа на простые множители с помощью функции Factorlnteger. Они представлены списками (в фигурных скобках) из двух чисел. Первое число — это множитель, а второе — число его повторений. В считанные секунды Mathematica 4 находит десятибиллионное простое число с помощью функции Prime. Другой характерный пример целочисленных операций — вычисление факториалов (вы можете запросто получить факториал 10 000, но ради сокращения места при описании примера в нем вычислено значение 200! Последний пример показывает отсутствие ошибок при работе с большими целыми числами — и это несмотря на то, что при его выполнении и впрямь дважды вычисляется факториал числа 10 000.

Операции с целыми числами выполняются абсолютно точно. При этом число цифр не ограничено (в разумных пределах).

Арифметика произвольной точности

Арифметика произвольной точности — еще одна из областей применения систем символьной математики (рис. 1. 5).

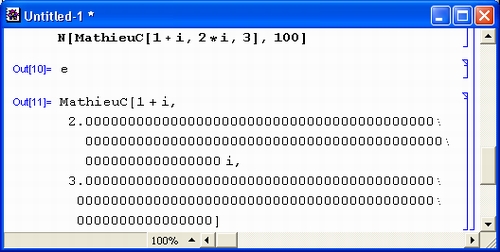
Рис. 1.5. Примеры вычислений с большой точностью

Здесь использована одна из самых распространенных функций системы Mathematica — N[expr, n], дающая результат вычисления выражения ехр r с точностью до n знаков после десятичной точки. Константы я и е вычислены с 500 верными знаками, а новая функция Матье (MathieuC) — с точностью до 200 знаков. Однако в системе Mathematica n может достигать миллиона и более. Ограничения по разрядности чисел и их верхнему и нижнему пределам практически отсутствуют.

Примеры из математического анализа

Разумеется, роль систем символьной математики далеко не исчерпывается приведенными выше примерами. Эти системы способны преобразовывать сложнейшие алгебраические выражения, находить аналитические решения сложных систем линейных, нелинейных и дифференциальных уравнений, манипулировать со степенными многочленами, вычислять производные и интегралы, анализировать функции, находить их пределы и т. д. Это видно уже из примеров, представленных на рис. 1.6 .

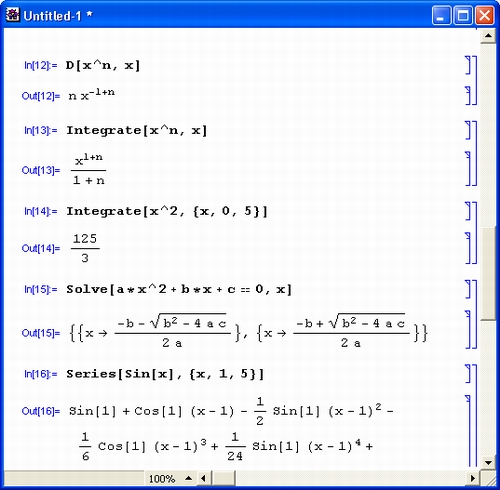
Рис. 1. 6 . Примеры вычислений из области математического анализа

В этих примерах функция D (как приятное исключение из правил, обозначенная одной буквой) вычисляет производную, функция Integrate — интеграл, функция Solve решает нелинейное уравнение (в данном случае квадратное), а функция Series разлагает выражение в ряд относительно заданной переменной и при заданных начальном значении переменной и максимальной степени ряда. В фигурных скобках задаются списки некоторых входных и выходных параметров (аргументов).

Системы символьной математики являются справочниками по многим специальным функциям. При этом они способны давать результаты вычислений в виде специальных функций, что демонстрируют следующие примеры:

Sum[1/k^9,{k,1,n}]

HarmonicNumber [n, 9]

Integrate [Log [x] *Exp [ -х^4 ], {x, 0, Infinity}]

-1/32*Gamma[ 1/4 ] ( 2 EulerGamma + л + Log[64] )

DSolve[y " [t] + y' [t] + y[t]/t = 0, y[t] , t]

{{y[t]->e^-tC[1]+e^-tC[2]Gamma[-1,-t]}}

Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и решения в аналитическом виде дифференциального уравнения. Соответствующие функции будут более подробно описаны в дальнейшем. Обратите внимание на то, что эти примеры даны прямо в тексте книги. Мы будем часто использовать такой прием для представления небольших примеров.

Чем дальше в лес, тем больше дров!

К сожалению, в математике нередко оказывается так, что результирующие выражения быстро нарастают по сложности при, казалось бы, незначительном усложнении или просто изменении условий задачи. Покажем это на примере решения одной из самых часто встречающихся задач — поиска в аналитическом виде корней алгебраического уравнения с целыми степенями членов.

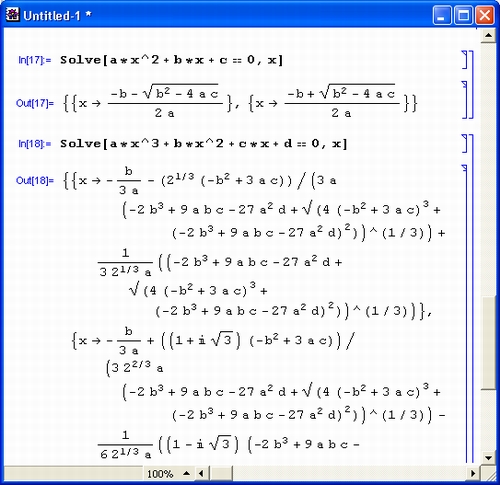
Многие из нас прекрасно помнят формулы для корней квадратного уравнения, которые нам давали еще в школе. Их в точности воспроизвела Mathematica в одном из примеров, приведенных в этом уроке чуть ранее. Это решение еще раз воспроизведено на рис. 1.7 (сверху).

Рис. 1.7. Система Mathematica решает квадратное и кубическое уравнения

Однако едва ли кто вспомнит по памяти формулы аналитического решения кубического уравнения общего вида. Зато система Mathematica играючи справляется с этой задачей с помощью функции Solve, что и показано во втором примере на рис. 1.19. Полученное выражение впечатляет даже студентов университетов, уже изучивших курс математики в полном объеме. Это блестящий пример эффективного представления справочной информации.

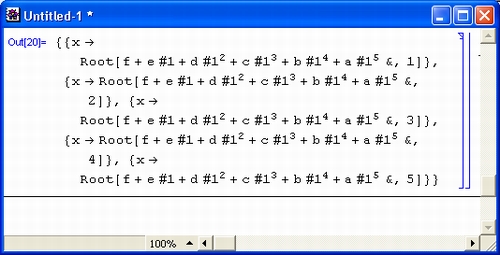
Можно пойти чуть дальше и убедиться в том, что Mathematica решает подобное уравнение даже четвертого порядка. Полученное при этом крайне громоздкое решение (в силу этого оно не приводится) заставит в задумчивости почесать затылок многих любителей математики. Но можно ли продолжать эти вычисления? Увы, классическая математика говорит, что нет! Подобные уравнения порядка выше четвертого современная математика в аналитическом виде не решает. Тем не менее, попытаемся вычислить корни алгебраического уравнения пятой степени в общем виде (рис. 1. 8 ).

Рис. 1.8 . Система Mathematica пытается решить алгебраическое уравнение пятой степени

А вот и сюрприз: Mathematica не только не отказалась решать эту задачу (при отказе она просто повторяет вводимое выражение), но даже подсказала путь ее решения с помощью пятикратного применения функции вычисления корней Root степенных многочленов.

В упомянутых примерах мы сталкиваемся с одной из серьезных проблем символьной математики — разбуханием результатов аналитических преобразований при порой незначительном усложнении решаемых задач. В данном случае это никоим образом не является недостатком систем компьютерной математики как таковых — просто так нарастает сложность решения данной математической задачи в соответствии с канонами абстрактной математики.

Однако нередко разбухание результатов кроется в сложности алгоритмов, особенно рекурсивных. Современные системы символьной математики способны осуществлять весьма глубокую рекурсию, и порой трудно даже предположить, к сколь громоздкому результату это в конечном счете приведет.

Научные работники и инженеры настолько привыкли к упрощению (порой весьма грубому, с точки зрения математиков), что громоздкие решения, получаемые с помощью систем символьной математики, способны их раздражать. Это в определенной мере препятствует применению систем символьной математики на практике и в наши дни.

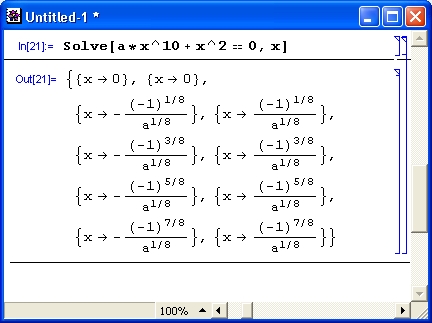
Однако для частных случаев нередко можно получить вполне сносные по виду решения. Вот пример решения неполного алгебраического уравнения десятой степени, при котором Mathematica благополучно возвращает все десять корней довольно простого вида (рис. 1.9 ). 

Примеры такого рода можно встретить повсеместно. Есть множество нелинейных алгебраических или дифференциальных уравнений обманчиво простого вида, но имеющих сложнейшие решения или не имеющих их вовсе. Так что если система символьной математики не находит ответ, это зачастую не является признаком ее слабости — может быть, решения не существует вообще? Порой даже такой отрицательный результат избавляет пользователя от трудоемкого поиска несуществующих решений «в лоб» и направляет его на поиск обходных, порою весьма ценных и полезных методов решения.

Рис. 1.9 . Система Mathematical решает алгебраическое уравнение 10-й степени

Доверяй, но проверяй!

Ситуация с применением математических систем компьютерной алгебры осложняется тем, что они, как и люди-математики, могут давать результаты в различной форме и даже делать ошибки. Вынесенная в заголовок этого подраздела армейская поговорка как нельзя лучше характеризует правильные приемы работы с математическими системами. Если вы получили результат, который не ожидали, — не спешите считать его окончательным и тем более новым. Всегда желательно этот результат сначала проверить. Покажем, как это делается.

Пусть мы решили некоторое уравнение

eqns = х^3 - 3*х + 2 == 0

2-3х+х ³ == 0

и получили его корни

r = Solve[eqns, x]

{{х-> -2), {х^ 1}, {х-> 1}}

Для проверки решения можно использовать операцию подстановки в eqns списка корней г. Эта операция реализуется оператором / ., что иллюстрирует следующий пример:

eqns/.r

{True, True, True}

Результат этой операции — список из трех логических констант True (Истинно). Он означает, что решение верно. Кстати, с помощью этой подстановки можно получить истинный список корней:

х/.r

{-2, 1, 1}

Mathematica имеет и множество иных способов проверки полученных результатов. Но, к сожалению, очень редко встречаются ситуации, когда выданное Mathematica ошибочное или несуществующее решение при подобной проверке дает положительный результат. Как говорится, за что боролись, на то и напоролись! В таких особо каверзных случаях надо ориентироваться на свою интуицию, решение схожей тестовой задачи или решение с помощью других математических систем с иным ядром — например, Derive или Maple V.

Не стоит брезговать проверкой решений даже с помощью менее мощных систем — помните поговорки «Устами младенца глаголет истина!», «Пуля дура — штык молодец», «Мал золотник, да дорог!» и т. д.? Обращайтесь к описанным выше правилам проверки по мере освоения работы с системой Mathematica. При этом вам быстро станут понятными некоторые ее тонкости, которые пока остались «за бортом».