Урок №12.

Функции разреженных матриц

• Элементарные разреженные матрицы

• Преобразование разреженных матриц

• Работа с ненулевыми элементами разреженных матриц

• Визуализация разреженных матриц

• Алгоритмы упорядочения

• Норма, число обусловленности и ранг разреженных матриц

• Разложение Холецкого разреженной матрицы

• LU-разложение разреженной матрицы

• Вычисление собственных значений и сингулярных чисел разреженных матриц

Матрицы без нулевых значений называются полными матрицами. Матрицы, содержащие некоторое число элементов с нулевыми значениями, в MATLAB называются разреженными матрицами. Вообще говоря, разреженными называют те матрицы, для которых разумно использовать численные методы, учитывающие упрощение арифметических операций с нулевыми элементами (например, получение нуля при умножении на нуль или пропуск операций сложения и вычитания при использовании этих операций с нулевыми элементами матриц). Они широко используются при решении прикладных задач. Например, моделировацие электронных и электротехнических линейных цепей часто приводит к появлению в матричном описании топологии схем сильно разреженных матриц. Для таких матриц создан ряд функций, обеспечивающих эффективную работу с ними и устраняющих тривиальные операции с нулевыми элементами матриц.

 

 

Элементарные разреженные матрицы

Вначале рассмотрим элементарные разреженные матрицы и относящиеся к ним функции системы MATLAB.

Функция spdiags расширяет возможности встроенной функции diag. Возможны четыре операции, различающиеся числом входных аргументов:

• [B.d] = spdiags(A) — извлекает все ненулевые диагонали из матрицы А размера mxn. В — матрица размера min(m,n)xp, столбцы которой р являются ненулевыми диагоналями A. d — вектор длины р, целочисленные элементы которого точно определяют номера диагоналей матрицы А (положительные номера — выше главной диагонали, отрицательные — ниже);

• В = spdiags(A.d) — извлекает диагонали, определенные вектором d;

• А = spdiags(B,d,A) — заменяет столбцами матрицы В диагонали матрицы А, определенные вектором d;

• А = spdiags(B,d,m,n) — создает разреженную матрицу размера mxn, размещая соответствующие столбцы матрицы В вдоль диагоналей, определяемых вектором d.

Пример:

» А=[1 3 4 6 8 0 0; 7 8 0 7 0 0 5;

0 0 0 0 0 9 8; 7 6 54 32 0 9 6];

» d=[l 322]

» В = spdlags(A.d)

В =

3644. 0077

0900

0699

• S = speye(m.n) — возвращает разреженную матрицу размера mxn с единицами на главной диагонали и нулевыми недиагональными элементами;

• S = speye(n) — равносильна speye(n.n). Пример:

» S = speye(4)

S =

(1,1)     1

(2.2)     1

(3.3)     1

(4.4)     1

Матрица R = sprand(S) имеет ту же структуру, что и разреженная матрица S, но ее элементы распределены по равномерному закону:

• R = sprand(m,n,density) — возвращает случайную разреженную матрицу размера mxn, которая имеет приблизительно densityxmxn равномерно распределенных ненулевых элементов (0<density<l);

• R = sprand(m,n,density,re) — в дополнение к этому имеет в числе параметров число обусловленности по отношению к операции обращения, приблизительно равное rс. Если вектор гс имеет длину lr (A,r<min(m.n)), то матрица R имеет гс в качестве своих первых 1 r сингулярных чисел, все другие значения равны нулю. В этом случае матрица R генерируется с помощью матриц случайных плоских вращений, которые применяются к диагональной матрице с заданными сингулярными числами. Такие матрицы играют важную роль при анализе алгебраических и топологических структур.

Пример: 

» d=sprand(4,3.0.6) 

d =

(1.1)     0.6614

(2.1)     0.2844

(4,1)     0.0648

(3,3)     0.4692

(4,3)     0.9883

• R = sprandn(S) — возвращает матрицу со структурой разреженной матрицы S, но с элементами, распределенными по нормальному закону с нулевым средним и дисперсией, равной 1;

• R = sprandn(m,n,density) — возвращает случайную разреженную матрицу размера mxn, имеющую примерно densityxmxn нормально распределенных ненулевых элементов (0<density<l);

• R = sprandnCm,n.density,гс) — в дополнение к этому имеет своим параметром число обусловленности по отношению к операции обращения, приблизительно равное rс. Если вектор гс имеет длину 1r (Xr<min(m,n)), то матрица R имеет гс в качестве своих первых 1r сингулярных чисел, все другие значения равны нулю. В этом случае матрица R генерируется с помощью матриц случайных плоских вращений, которые применяются к диагональной матрице с заданными сингулярными числами.

Пример:

» f=sprandn(3,4.0.3) 

f =

(2.1) -0.4326

(2.2) -1.6656

(2.3) 0.1253

(2.4) 0.2877

• sprandsym(S) — возвращает случайную симметрическую матрицу, нижние под-диагонали и главная диагональ которой имеют ту же структуру, что и матрица 5. Элементы результирующей матрицы распределены по нормальному закону со средним, равным 0, и дисперсией, равной 1;

• sprandsym(n,density) — возвращает симметрическую случайную разреженную матрицу размера пхп, которая имеет приблизительно densityxnxn ненулевых элементов; каждый элемент сформирован в виде суммы нормально распределенных случайных чисел (0<density<l);

• R = sprandsym(n,density,гс) — возвращает матрицу с числом обусловленности по отношению к операции обращения, равным гс. Закон распределения не является равномерным; значения случайных элементов симметричны относительно 0 и находятся в пределах [-1, 1]. Если rс — вектор размера п, то матрица R имеет собственные значения, равные элементам вектора rс. Таким образом, если элементы вектора гс положительны, то матрица R является положительно определенной. В любом случае матрица R генерируется с помощью случайного вращения по Якоби диагональных матриц с заданными собственными значениями и числом обусловленности. Такие матрицы играют важную роль при анализе алгебраических и топологических структур;

• R = sprandsym(n.density.rc.klnd) — возвращает положительно определенную матрицу. Аргумент kind может быть следующим:

  • kind=l — матрица R генерируется из положительно определенной диагональной матрицы с помощью случайных вращений Якоби. R имеет точно заданное число обусловленности;

  • kind=2 — матрица R генерируется как смещенная сумма матриц внешних произведений. Число обусловленности матрицы приблизительно, но структура более компактна (по сравнению с предыдущим случаем);

  • kind=3 — генерируется матрица R той же структуры, что и S, а число обусловленности приближенно равно 1/гс. Значение density игнорируется.

Пример:

» a=sprandsym(4,0.3.0.8) 

а =

(1.1) 0.9818

(3.1) 0.0468

(2,2) -0.9283

(1,3) 0.0468

(3.3) 0.8800

(4.4) -0.8000

 

 

П реобразование разреженных матриц

Теперь рассмотрим функции преобразования разреженных матриц. Они представлены ниже:

• k = f ind(X) — возвращает индексы вектора х для его ненулевых элементов. Если таких элементов нет, то find возвращает пустой вектор. find(X>100) возвращает индексы элементов вектора с Х>100;

• [1,j] = find(X) — возвращает индексы строки и столбца для ненулевого элемента матрицы X;

• [1 . j . v] = find(X) — возвращает вектор столбец v ненулевых элементов матрицы X и индексы строки i и столбца j. Вместо X можно вставить (X, операция отношения, параметр), и тогда индексы и вектор-столбец будут отражать элементы матрицы, удовлетворяющие данному отношение. Единственное исключение — f ind(x ~= 0). Индексы те же, что и при исполнении find(X), но вектор v содержит только единицы.

Пример:

» q=sprand(3.4.0.6)

q =

(1.1) 0.7266

(1.2) 0.4120

(3.2) 0.2679

(3.3) 0.4399

(2.4) 0.7446

(3.4) 0.9334

i=

1 

1 

3 

3

2

3

j =

1

2

2

3

4

4

• full(S) — преобразует разреженную матрицу S в полную; если исходная матрица S была полной, то full (S) возвращает S. Пусть X — матрица размера mxn с nz=nnz(X) ненулевыми элементами. Тогда full(X) требует такой объем памяти, чтобы хранить mxn действительных чисел, в то время как sparse(X) требует пространство для хранения лишь nz действительных чисел и (nxz+n) целых чисел — индексов. Большинству компьютеров для хранения действительного числа требуется вдвое больше пространства, чем для целого. Для таких компьютеров sparse(X) требует меньше пространства, чем full(X), если плотность nnz/prod(s1ze(X))<2/3. Выполнение операций над разреженными матрицами, однако, требует больше затрат времени, чем над полными, поэтому для эффективной работы с разреженными матрицами плотность расположения ненулевых элементов должна быть много меньше 2/3.

Примеры:

» q=sprand(3,4,0.6)

q=

(1.1) 0.0129

(1.2) 0.3840 

(2.2) 0.6831 

(3,3) 0.0928 

» d=full(q)

 d =

0.0129     0.3840     0     0 

0              0.6831     0     0 

0               0     0.0928    0

• S=sparse(A) — преобразует полную матрицу в разреженную, удаляя нулевые элементы. Если матрица S уже разреженная, то sparse(S) возвращает S. Функция sparse — это встроенная функция, которая формирует матрицы в соответствии с правилами записи разреженных матриц, принятыми в системе MATLAB;

• S=sparse(i,j,s,m,n,nzmax) — использует векторы 1, j и s для того, чтобы генерировать разреженную матрицу размера mxn с ненулевыми элементами, количество которых не превышает nzmax. Векторы 1 и j задают позиции элементов и являются целочисленными, а вектор s определяет числовое значение элемента матрицы, которое может быть действительным или комплексным. Все элементы вектора s, равные нулю, игнорируются вместе с соответствующими значениями i и j. Векторы i, j и s должны быть одной и той же длины;

• S = sparsed' . j.s.m.n) — использует nzmax=length(s).

• S = sparsed , j .s) — использует m=maxd) и n=max(j). Максимумы вычисляются раньше, чем нулевые строки столбца S будут удалены;

• S = sparse(m.n) равносильно sparse ([ ].[ ].[ ]. m.n, 0). Эта команда генерирует предельную разреженную матрицу, где mxn элементов нулевые.

Все встроенные в MATLAB арифметические, логические и индексные операции могут быть применены и к -разреженным, и к полным матрицам. Операции над разреженными матрицами возвращают разреженные матрицы, а операции над полными матрицами возвращают полные матрицы. В большинстве случаев операции над смешанными матрицами возвращают полные матрицы. Исключение составляют случаи, когда результат смешанной операции явно сохраняет разреженный тип. Так бывает при поэлементном умножении массивов А.*S, где S — разреженный массив.

Пример:

» i=[2,4,3];j=[1,3,8];s=[4,5+5i,9];

t = sparse(i,j,s,5,8)

t =

(2.1) 4.0000

(4.3) 5.0000+5.0000i

(3.8) 9.0000

Функция spconvert используется для создания разреженных матриц из простых разреженных форматов, легко производимых вне средств MATLAB:

• S = spconvert(D) — преобразует матрицу D со строками, содержащими [i.j.r] или [i,j,r.s], где i — индекс ряда, j — индекс строки, г — численное значение, в соответствующую разреженную матрицу. Матрица D может иметь nnz или nnz+1 строк и три или четыре столбца. Три элемента в строке генерируют действительную матрицу, четыре элемента в строке генерируют комплексную матрицу (s преобразуется во мнимую часть значения элемента). Последняя строка массива D типа [m n 0] или [m n 0 0] может быть использована для определения size(S). Команда spconvert может быть использована только после того, как матрица D загружена или из МАТ-файла, или из ASCII-файла при помощи команд load, uiload и т. д.:

»load mydata.dat

»А = spconvert (rnydata);

 

 

Работа с ненулевыми элементами разреженных матриц

Поскольку разреженные матрицы содержат ненулевые элементы, то предусмотрен ряд функций для работы с ними:

• nnz(X) — возвращает число ненулевых элементов матрицы X. Плотность разреженной матрицы определяется по формуле nnz(X)/numel (X). Пример:

h = sparse(hilb(10)); 

» nnz(h) 

ans = 

100

• nonzeros(A) — возвращает полный вектор-столбец ненулевых элементов матрицы А, выбирая их последовательно по столбцам. Эта функция дает только выход s, но не значения i и j из аналогичного выражения [i, j,s]=find(A). Вообще, length(s)=nnz(A)xnzmax(A)xprod(size(A)). Пример:

» g=nonzeros(sparse(hankel([1,2.8])))

g =

1

2

• nzmax(S) — возвращает количество ячеек памяти для ненулевых элементов. Обычно функции nnz(S) и nzmax(S) дают один и тот же результат. Но если S создавалась в результате операции над разреженными матрицами, такой как умножение или LU-разложение, может быть выделено больше элементов памяти, чем требуется, и nzmax(S) отражает это. Если S — разреженная матрица, то nzmax(S) — максимальное количество ячеек для хранения ненулевых элементов. Если S — полная матрица, то nzmax(S)=numel(S).

Пример:

» q=nzmax(sparse(hankel([1.7.23])))

q =

 6

• S=spalloc(m,n,nzmax) — создает массив для разреженной матрицы S размера mxn с пространством для размещения nzmax ненулевых элементов. Затем матрица может быть заполнена по столбцам;

• spalloc(m,n,nzmax) — эквивалентна функции sparse([ ],[ ],[ ],m,n,nzmax).

Пример:

» S = spalloc(5,4,5);

• spfun — вычисление функции для ненулевых элементов. Функция spfun применяется выборочно только к ненулевым элементам разреженной матрицы, сохраняя при этом разреженность исходной матрицы;

• f = spfun(@function,S) — вычисляет function(S) для ненулевых элементов матрицы S. Имя function — это имя m-файла или встроенной в ядро функции. function должна работать с матричным аргументом S и вычислить функцию для каждого элемента матрицы S.

Пример:

» S=spfun(@exp.sprand(4,5,0,4))

S=

(2.2) 1.6864

(2.3) 2.4112

(3.3) 2.6638

(2.4) 1.1888

(3.4) 1.3119

(4.4) 2.4007

(3.5) 1.2870

• R = spones(S) — генерирует матрицу R той же разреженности, что и S, но заменяет на 1 все ненулевые элементы исходной матрицы.

Пример:

» S=sprand(3.2,0.3) 

S=

(3.1) 0.2987 

(1.2) 0.1991 

» spones(S) 

ans =

(3.1) 1 

(1.2) 1

 

 

Визуализация разреженных матриц

Визуализация разреженных матриц нередко позволяет выявить не только любопытные, но и полезные и поучительные свойства тех математических закономерноетей, которые порождают такие матрицы или описываются последними. MATLAB имеет специальные средства для визуализации разреженных матриц, реализованные приведенными ниже командами:

• spy(S) — графически отображает разреженность произвольной матрицы S;

• spy(S.markersize) — графически отображает разреженность матрицы S, выводя маркеры в виде точек точно определенного размера markersize;

• spy(S, 'LineSpec') — отображает разреженность матрицы в виде графика с точно определенным (с помощью параметра LineSpec) цветом линии и маркера. Параметр Linespec определяется так же, как параметр команды plot;

• spy(S. 'LineSpec' .markersize) — использует точно определенные тип, цвет и размер графического маркера. Обычно S — разреженная матрица, но допустимо использование и полной матрицы, когда расположение элементов, отличных от нуля, составляет график.

Пример:

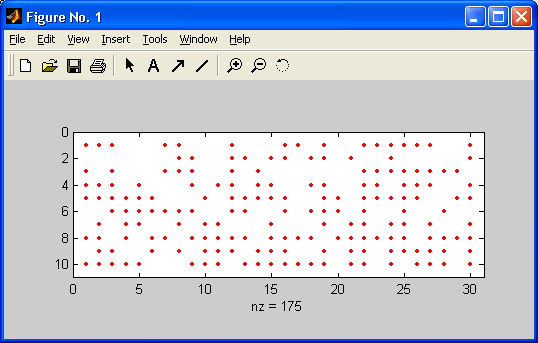
»S=sparse(sprandn(20,30,0.9));spy(S,'-r',6)

Построенный по этому примеру график показан на рис. 12.1.

Рис. 12.1. Визуализация разреженной матрицы

 

 

Алгоритмы упорядочения

Упорядочение — это еще одна характерная для разреженных матриц операция. Ее алгоритм реализуется несколькими функциями:

• р = colmmd(S) — возвращает вектор упорядоченности столбцов разреженной матрицы S. [то nzmax(S) — максимальное количество ячеек для хранения ненулевых элементов. Если S — полная матрица, то nzmax(S)=numel(S).] Для несимметрической матрицы S вектор упорядоченности столбцов р такой, что S(:. р) будет иметь более разреженные L и U в LU-разложении, чем S. Такое упорядочение автоматически применяется при выполнении операций обращения \ и деления /, а также при решении систем линейных уравнений с разреженными матрицами. Можно использовать команду spparms, чтобы изменить некоторые параметры, связанные с эвристикой в алгоритме colmmd;

• j = colperm(S) — возвращает вектор перестановок j, такой что столбцы матрицы S(:. j) будут упорядочены по возрастанию числа ненулевых элементов. Эту функцию полезно иногда применять перед выполнением LU-разложения. Если S — симметрическая матрица, то j=colperm(S) возвращает вектор перестановок j, такой что и столбцы, и строки S(j,j) упорядочены по возрастанию ненулевых элементов. Если матрица S положительно определенная, то иногда полезно применять эту функцию и перед выполнением разложения Холецкого.

Пример:

» S=sparse([2.3.1.4.2].[l,3.2.3.2],[4.3,5.6.7].4.5);full(S) 

ans =

0    5    0    0    0

4    7    0    0    0

0    0    3    0    0

0    0    6    0    0 

» t=colperm(S)

t=
	5	1	2	3
»full(S(;,t))
ans =
0	0	0	5	0
0	0	4	7	0
0	0	0	0	3
0	0	0	0	6

• p = dmperm(A) — возвращает вектор максимального соответствия р такой, что если исходная матрица А имеет полный столбцовый ранг, то А(р.:) — квадратная матрица с ненулевой диагональю. Матрица А(р,:) называется декомпозицией Далмейджа-Мендельсона, или DM-декомпозицией.

Если А — приводимая матрица, [ Квадратная матрица А называется приводимой, если она подобна клеточной матрице, квадратные элементы которой соответствуют индукции линейного оператора А в отдельные подпространства. — Примеч. ред. ]  линейная система Ах=b может быть решена приведением А к верхней блочной треугольной форме с неприводимым диагональным блоком. Решение может быть найдено методом обратной подстановки.

• [p.q.r] = dmperm(A) — находит перестановку строк р и перестановку столбцов q квадратной матрицы А, такую что A(p,q) — матрица в блоке верхней треугольной формы.

Третий выходной аргумент г — целочисленный вектор, описывающий границы блоков. К-й блок матрицы A(p,q) имеет индексы r(k):r(k+l)-l.

• [p.q.r.s] = dmperm(A) — находит перестановки р и q и векторы индексов г и s, так что матрица A(p,q) оказывается в верхней треугольной форме. Блок имеет индексы (r(i):r(i+l)-l,s(i):s(i+l)-l).

В терминах теории графов диагональные блоки соответствуют сильным компонентам Холла графа смежности матрицы А.

Примеры:

» A=sparse([1.2,1.3.2].[3.2.1.1.1].[7.6,4.5,4],3,3)

:full(A) 

ans =

4 0 

4 6 0

5 0 0   

»[p.q.r]=dmperm(A)

Р=

1 2 3

q =

3 2 1 

r =

1 2 3 4 

» fulKA(p.q)) 

ans =

7 0 4

0 6 4

0 0 5

• symmmd(S) — возвращает вектор упорядоченности для симметричной положительно определенной матрицы S, так что S(p,p) будет иметь более разреженное разложение Холецкого, чем S. Иногда symmmd хорошо работает с симметрическими неопределенными матрицами. Такое упорядочение автоматически применяется при выполнении операций \ и /, а также при решении линейных систем с разреженными матрицами [ Функция symamd работает значительно быстрее. — Примеч. ред. ].  

Можно использовать команду spparms, чтобы изменить некоторые опции и параметры, связанные с эвристикой в алгоритме.

Алгоритм упорядочения для симметрических матриц основан на алгоритме упорядочения по разреженности столбцов. Фактически symmmd(S) только формирует матрицу К с такой структурой ненулевых элементов, что К' *К имеет тот же трафик разреженности, что и S, и затем вызывает алгоритм упорядочения по разреженности столбцов для К. На рис. 12.2 приводится пример применения функции symmmd к элементам разреженной матрицы.

Пример:

» B=bucky;p=symmmd(B);

» R=B(p,p);

» subplot(1,2,1),spy(B); subplot(1,2,2).spy(R) ;

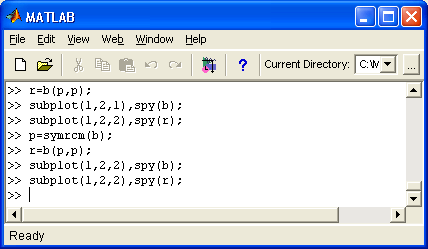
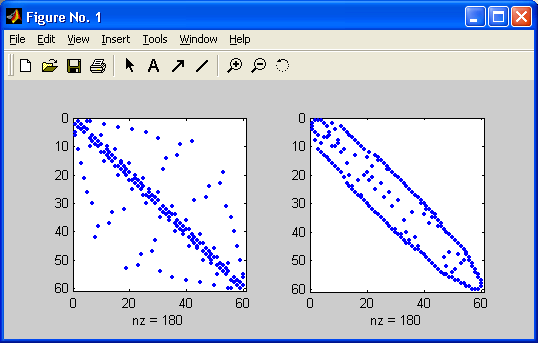
•  r = symrcm(S) — возвращает вектор упорядоченности для симметричной матрицы S и называется упорядочением Катхилла-Макки. Причем формируется такая перестановка г, что S(r.r) будет концентрировать ненулевые элементы вблизи диагонали. Это хорошее упорядочение как перед LU-разложением, так и перед разложением Холецкого. Упорядочение применимо как для симметрических, так и для несимметрических матриц.

Для вещественной симметрической разреженной матрицы S (такой, что S=S ^T ) собственные значения S(r.r) совпадают с собственными значениями S, но для вычисления eig(S(r,r)) требуется меньше времени, чем для вычисления eig(S).

Рис. 12.2. Пример применения функции symmmd

Пример:

» B=bucky;p=symrcm(B);

» R=B(p,p);

» subplot(1,2,1),spy(B);subplot(1,2,2),spy(R) ;

На рис. 12.3 приведен пример концентрации ненулевых элементов разреженной матрицы вблизи главной диагонали.

Рис. 12.3. Пример применения функции symrcm

 

 

Норма, число обусловленности и ранг разреженной матрицы

Ниже представлены функции, позволяющие вычислять числа обусловленности и ранги для разреженных матриц.

• с = condest(A) — использует метод Хейджера в модификации Хаема для оценки числа обусловленности матрицы по первой норме. Вычисленное значение с — нижняя оценка числа обусловленности матрицы А по первой норме. Для повторяемости результатов перед выполнением функции condest нужно обязательно выполнить rand( 'state' ,L), где L -одно и то же целое число;

• с = condest(A.T) — где Т — положительное целое число, чем выше Т, тем выше точность оценки. По умолчанию Т равно 2;

• nrm = normest(S) — возвращает оценку второй нормы матрицы S. Применяется тогда, когда из-за чрезмерного числа элементов в матрице вычисление nrm = norm(S) занимает слишком много времени. Эта функция изначально предназначена для работы с разреженными матрицами, хотя она работает корректно и с большими полными матрицами;

• [c.v] = condestCA) — возвращает число обусловленности с и вектор v, такой, что выполняется условие norm(A*V.l) = norm(A.l)*norm(V.l)/c. Таким образом, для больших значений с вектор V близок к нулевому вектору;

• nrm = normest(S,tol) — использует относительную погрешность tol вместо используемого по умолчанию значения 10- ⁶ ;

• [nrm.count] = normestC...) — возвращает оценку второй нормы и количество использованных операций. Примеры:

» F=wilkinson(150); » condest(sparse(F)) 

ans =

460.2219

» normest(sparse(F)) 

ans =

75.2453

• r=sprank(S) — вычисляет структурный ранг разреженной матрицы S. В терминах теории графов он известен также под следующими названиями: максимальное сечение, максимальное соответствие и максимальное совпадение. Для величины структурного ранга всегда выполняется условие sprank(S)irank(S), а в точной арифметике с вероятностью 1 выполняется условие sprank(S) = rank(sprandnCS)).

Пример:

» S=[3 0004: 54080; 00013]; 

» r=sprank(S)

 

 

Разложение Холецкого разреженных матриц

• choli пс(X,'0') — возвращает неполное разложение Холецкого для действительной симметрической положительно определенной разреженной матрицы [nrm = norm(S) занимает слишком много времени. Эта функция изначально предназначена для работы с разреженными матрицами, хотя она работает корректно и с большими полными матрицами;]. Результат представляет собой верхнюю треугольную матрицу;

• R = cholincCX,'0') — возвращает верхнюю треугольную матрицу, которая имеет такую же разреженную структуру, как и верхний треугольник матрицы действительной положительно определенной матрицы X. Результат умножения R' *R соответствует X по своей разреженной структуре. Положительной определенности матрицы X недостаточно, чтобы гарантировать существование неполного разложения Холецкого, и в этом случае выдается сообщение об ошибке;

• [R,p] = cho!1nc(X, '0') — никогда не выдает сообщение об ошибке в ходе разложения. Если X — положительно определенная матрица, то р=0 и матрица R — верхняя треугольная, в противном случае р — положительное целое число, R — верхняя треугольная матрица размера qxn, где q=p-l. Разреженная структура матрицы R такая же, как и у верхнего треугольника размера qxn матрицы X, и произведение R' *R размера nxn соответствует структуре разреженности матрицы X по ее первым q строкам и столбцам X(l:q,:) и Х(: ,l:q).

• R = cho1inc(X,droptol) — возвращает неполное разложение Холецкого любой квадратной разреженной матрицы, используя положительный числовой параметр droptol. Функция cholinc(X,droptol) возвращает приближение к полному разложению Холецкого, вычисленному с помощью функции chol (X). При меньших значениях droptol аппроксимация улучшается, пока значение droptol не станет равным 0. В этом случае cholinc задает полное преобразование Холецкого (chol(X));

• R = cholinc(X.options) — использует структуру с тремя переменными, которые могут быть использованы в любой из комбинаций: droptol, mi chol, rdi ag. Дополнительные поля игнорируются. Если mi chol =1, chol inc возвращает модифицированное разложение Холецкого. Если rdiag=l, то все нули на диагонали верхней треугольной матрицы заменяются квадратным корнем от произведения droptol и нормы соответствующего столбца матрицы X — sqrt(droptol*norm(X(: ,j))). По умолчанию rdiag=0;

• R = cholinc(X,droptol) и R = cholinc(X.options) — возвращают верхнюю треугольную матрицу R. Результат R'*R — это аппроксимация матрицы;

• R = cholinc(X, 'inf') - возвращает разложение Холецкого в неопределенности, когда не удается получить обычное разложение. Матрица X может быть действительной квадратной положительно полуопределенной.

Пример:

» S = delsqCnumgndCC' .4)) 

S =

(1.1) 4

(2.1) -1

(1.2) -1

(2.2) 4

(3.2) -1

(2.3) -1

(3.3) 4

» RD=cholinc(S,'0')

R0=

(1.1)  2.0000

(1.2)  -0.5000

(2.2) 1.9365

(2.3) -0.5164

(3.3) 1.9322

 

 

LU-разложение разреженных матриц

Функция luinc осуществляет неполное LU-разложение и возвращает нижнюю треугольную матрицу, верхнюю треугольную матрицу и матрицу перестановок для разреженных матриц [ Благодаря LAPACK в MATLAB 6 появилась отсутствующая в прежних версиях возможность использовать команду lu для точного LU-разложения разреженных матриц. — Примеч. ред. ]. Используется в следующих формах:

• luincCX, '0') — возвращает неполное LU-разложение уровня 0 квадратной разреженной матрицы. Треугольные факторы (множители) имеют такую же разреженность (т. е. график разреженности, см. spy), как и матрица перестановок квадратной матрицы X, и их произведение имеет ту же разреженность, что и матрица перестановок X. Функция luinc(X, '0') .возвращает нижнюю треугольную часть нижнего фактора (множителя) и верхний треугольный фактор в одной и той же результирующей матрице. Вся информация о матрице перестановок теряется, но зато число ненулевых элементов результирующей матрицы равно числу ненулевых элементов матрицы X с возможностью исключения некоторых нулей из-за сокращения;

• [L,U] = luincCX. 'О'), где X — матрица размером nхn, возвращает нижнюю треугольную матрицу L и верхнюю треугольную матрицу U. Разреженности матриц L, U и X не сравнимы, но сумма числа ненулевых элементов в матрицах L и U поддерживается равной nnz(X)+n с возможностью исключения некоторых нулей в L и U из-за сокращения;

• [L,U.P]=luinc(X, '0') — возвращает нижнюю треугольную матрицу L, верхнюю треугольную матрицу U и матрицу перестановок Р. Матрица L имеет такую же разреженную структуру, как нижняя треугольная часть перестановленной матрицы X — spones(L)=spones(tril(P*X)), с возможными исключениями единиц на диагонали матрицы L, где Р*Х может быть равно 0;

• luinc(X,droptol) — возвращает неполное LU-разложение любой разреженной матрицы, используя порог droptol. Параметр droptol должен быть неотрицательным числом;
  

• luinc(X,droptol) — возвращает приближение к полному LU-разложению, полученному с помощью функции lu(Х). При меньших значениях droptol аппроксимация улучшается, пока значение droptol не станет равным 0. В этом случае имеет место полное LU- разложение;

• luinc(X,options) — использует структуру с четырьмя переменными, которые могут быть использованы в любой из комбинаций: droptol, milu, udiag, thresh. Дополнительные поля игнорируются. Если miliKL, функция luinc возвращает модифицированное неполное LU-разложение. Если udiag=l, то все нули на диагонали верхней треугольной части заменяются на локальную ошибку droptol;

• luincCX.options) — то же самое, что и luinc(X,droptol), если options содержит только параметр droptol; О [L.U] = luincCX,options) — возвращает перестановку треугольной матрицы L и верхнюю треугольную матрицу U. Результат L*U аппроксимирует X;

• [L.U.P] = luinc(X.options) — возвращает нижнюю треугольную матрицу L, верхнюю треугольную матрицу U и матрицу перестановок Р. Ненулевые входные элементы матрицы U удовлетворяют выражению abs(U(i. j))>=droptol* norm((X:.j)) с возможным исключением диагональных входов, которые были сохранены, несмотря на неудовлетворение критерию;

• [L.U.P] = luincCX,options) — то же самое, что и [L.U.P] = 1uinc(X,dropto1), если options содержит только параметр droptol.

 

 

Вычисление собственных значений  и сингулярных чисел разреженных матриц

Применение функции eigs решает проблему собственных значений, состоящую в нахождении нетривиальных решений системы уравнений, которая может быть интерпретирована как алгебраический эквивалент системы обыкновенных дифференциальных уравнений в явной форме Коши: A*v=l*v.[ Усовершенствованный алгоритм eig позволяет использовать eig для расчета собственных значений и полных, и разреженных матриц, но для получения собственных векторов разреженных матриц по-прежнему желательно использовать именно eigs. — Примеч. ред. ] Вычисляются только отдельные выбранные собственные значения или собственные значения и собственные векторы:

• eigs(A.B) решает проблему обобщенных собственных значений A*V = В* V*D. В должна быть симметрической (или эрмитовой) положительно определенной квадратной матрицей того же размера, что и A. eigs С А, []....) решает стандартную проблему собственных значений A*V = V*D.

• [V,D] = eigs(A) или [V.O] = eigs('Afun',n) — возвращает собственные значения для первого входного аргумента — большой и разреженной квадратной матрицы размера п. Этот параметр может быть как квадратной матрицей, так и строкой, содержащей имя m-файла, который применяет линейный оператор к столбцам данной матрицы. Матрица А — действительная и несимметрическая. Y=Afun(X) должна возвращать Y=A*X.

В случае одного выходного параметра D — вектор, содержащий 6 самых больших собственных значений матрицы А. В случае двух выходных аргументов [V.D] = eigs(A) D — диагональная матрица размера 6x6, содержащая эти 6 самых больших собственных значений, и V — матрица, содержащая б столбцов, являющихся соответствующими собственными векторами. [V.D.flag] = eigs(A) возвращает флаг, равный 0, если все возвращенные собственные значения сходятся, и 1 в противном случае.

1. eigs(A.K) и eigs(A,B,K) возвращают не 6, а К самых больших собственных значений. eigs(A,K,sigma) Heigs(A,B,K.sigma) возвращают не 6, а К собственных значений, выбранных в зависимости от значения параметра sigma;

2. 'lm' — самые большие (как и по умолчанию) по абсолютной величине;

3. ' sm' — самые малые по абсолютной величине;

4. ' l а' и ' sa' — соответственно самые большие и самые малые алгебраически собственные значения для действительных симметрических матриц;

5. 'be' — для действительных симметрических матриц возвращает и самые большие, и самые малые алгебраически собственные значения поровну, но если К нечетное, то самых больших значений на 1 больше, чем самых малых;

6. 'lr' и 'sr' — для несимметрических и комплексных матриц возвращают соответственно собственные значения с самыми большими и самыми малыми действительными частями;

7. '1i' и 'si'— для несимметрических и комплексных матриц возвращают соответственно собственные значения с самыми большими и самыми малыми мнимыми частями;

8. скаляр - ближайшие к величине slgma. В этом случае матрица В может быть только симметрической (или эрмитовой) положительно полуопределенной, а функция Y = AFUN(X) должна возвращать Y = (A-SIGMA*B)\X.

• eigs(A,K,SIGMA,OPTS) и eigs(A,B,K,SIGMA.OPTS) имеют параметры в полях структуры OPTS (в фигурных скобках { } — значения по умолчанию):

1. OPTS.issym: симметрия А или A-SIGMA*B, представленной AFUN [{0} | 1];

2. OPTS.isreal: комплексные А или A-SIGMA*B, представленной AFUN [0 | {1}];

3. OPTS.tol: сходимость: аbs(с1_вычисленное-с1_действительное) < tоl*аbs(с1_вычисленное) [скаляр){eps}];

4. OPTS.maxit: наибольшее число итераций [положительное целое | {300}];

5. OPTS.р: число векторов Ланцо (Lanczos): K+l<p<=N [положительное целое | {2К}];

6. OPTS.v0: начальный вектор [вектор размера N| {произвольно выбирается библиотекой ARPACK}];

7. OPTS.disp: уровень вывода диагностической информации [0 | {1} | 2J;

8. OPTS.cholВ: В — это множитель Холецкого chol (В) [{0} | 1];

9. OPTS.permB: разреженная матрица В равна chol (B(perm(B) .perm(B)) [perm(B) | {1:N}], perm — перестановка.

• eigs(AFUN.N.К,SIGMA,OPTS,PI,...) иeigsCAFUN.N,В.К.SIGMA.OPTS,PI....) предоставляют дополнительные аргументы Р, которые поступают в AFUN(X,P1....).

Функция svds служит для вычисления небольшого числа сингулярных чисел и векторов большой разреженной матрицы. По мере возможности старайтесь использовать svd(fulKA)) вместо svds(A). Если А прямоугольная матрица mxn, svds(A....) манипулирует с несколькими собственными значениями и собственными векторами, возвращенными EIGS(B,...), где В = [SPARSE(М.М) A: A' SPARSE(N.N)]. Положительные собственные значения симметрической матрицы В равны сингулярным числам А.

• svds (А) возвращает 6 самых больших сингулярных чисел А;

• svds (А,К) или svds(A,K.'L') возвращает К самых больших сингулярных чисел;

• S = SVDSCA,К,SIGMA,OPTIONS) устанавливает параметры:

  • OPTIONS.tol — порог чувствительности (по умолчанию le-10), norm(A*V-. -U*S,1) <= tol * norm(A.1);

  • OPTIONS.maxit - наибольшее число итераций (по умолчанию 300);

  • OPTIONS.disp — число значений, показываемых на каждой итерации (по умолчанию 0).

• [U.S.V] = svds(A.k) — возвращает k наибольших сингулярных чисел и соответствующих сингулярных векторов матрицы А. Если А — матрица размера mxn, то U — матрица размера mxk с ортонормальными столбцами, S — диагональная матрица размера kxk, V — матрицы размера nxk с ортонормальными столбцами;

• [U.S.V. flag] = svdsC...) — возвращает флаг, равный 0, если eigs сошлась, и 1 в противном случае;

• [U.S.V] = svds(A.k.sigma) — возвращает k сингулярных чисел, наиболее близких к скаляру sigma, и К сингулярных векторов (при sigma=0 возвращает К наименьших сингулярных чисел и К векторов);

• s = svds(A.k....) — возвращает только вектор сингулярных чисел.

Как видно из приведенного материала, система MATLAB предлагает пользователям уникальный набор матричных операторов и функций, заметно более полный, чем у других математических систем. Это открывает широчайшие возможности в решении всех видов математических задач, в которых используются современные матричные методы.

 

 

Что нового мы узнали?

В этом уроке мы научились:

• Создавать элементарные разреженные матрицы.

• Осуществлять преобразование разреженных матриц.

• Работать с ненулевыми элементами разреженных матриц.

• Осуществлять графическую визуализацию разреженных матриц.

• Использовать функции упорядочения.

• Осуществлять разложение Холецкого разреженных матриц.

• Проводить LU-разложение разреженных матриц.

• Вычислять норму, число обусловленности и ранг разреженных матриц.

• Вычислять собственные значения и сингулярные числа разреженных матриц.