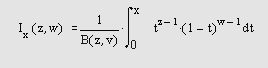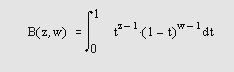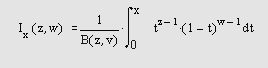4. Бета-функция и ее варианты
Бета-функция и ее варианты
Бета-функция определяется как
где Г (z) — гамма-функция. Неполная бета-функция определяется по формуле
-
beta(Z.W) — возвращает бета-функцию для соответствующих элементов комплексных массивов Z и W. Массивы должны быть одинакового размера (или одна из величин может быть скаляром).
-
beta i nc ( X , Z , W ) — возвращает неполную бета-функцию. Элементы X должны быть в закрытом интервале [0, 1].
-
beta 1 п ( Z , W ) — возвращает натуральный логарифм бета-функции log ( beta ( Z , W ) ) , без вычисления beta(Z.W). Так как сама бета-функция может принимать очень большие или очень малые значения, функция betaln(Z.W) иногда более полезна, так как позволяет избежать переполнения.
Пример:
» format rat;beta((l:10) 4 ,4)
ans=
1/4
1/20
1/60
1/140
1/280
1/504
1/840
1/1320
1/1980
1/2860
21.gif
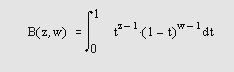
22.gif