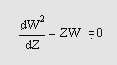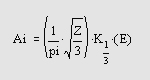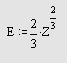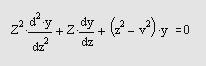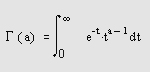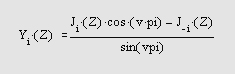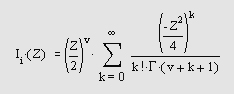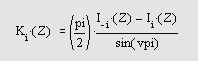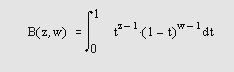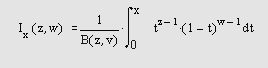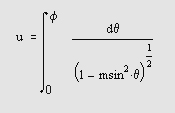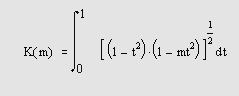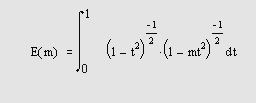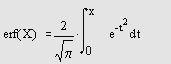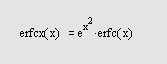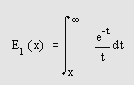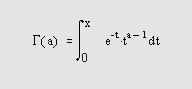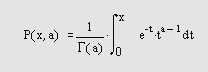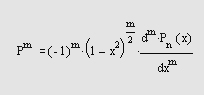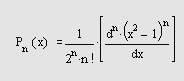Урок 9. Специальные математические функции
1. Урок 9. Специальные математические функции
Урок №9.
Специальные математические функции
-
Функции Эйри
-
Функции Бесселя
-
Бета-функция и ее варианты
-
Эллиптические функции и интегралы
-
Функции ошибки
-
Интегральная показательная функция
-
Гамма-функция и ее варианты
-
Ортогональные полиномы Лежандра
Специальные математические функции являются решениями дифференциальных уравнений специального вида или обозначениями некоторых видов интегралов. Довольно полный обзор специальных функций дается в книгах [55-58], так что ниже мы ограничимся только указанием функций системы MATLAB, реализующих их вычисление. Набор специальных математических функций в системе MATLAB настолько представителен, что позволяет решать практически все задачи, связанные с применением таких функций. Если и обнаруживаются недостающие специальные функции, то пользователь может сам задать их вычисления. Специфика специальных функций в MATLAB та же, что и элементарных, — их аргументами могут быть как одиночные численные значения, так и массивы чисел. В последнем случае функции возвращают массив тех же размерности и размера с преобразованием каждого элемента в соответствии с действием функции. В версии MATLAB 6 вы теперь можете получить справку с записью формул в стандартной математической форме, набрав в командной строке doc function, где function — имя специальной функции.
2. Функции Эйри
Функции Эйри
Функция Эйри формирует пару линейно независимых решений линейного дифференциального уравнения вида
Связь между функцией Эйри и модифицированной функцией Бесселя выражается следующей формулой:
где
- airy(Z) — возвращает функцию Эйри, AKZ), для каждого элемента комплексного массива Z;
- airy(k.Z) — возвращает различные варианты результата в зависимости от значения k:
- k=0 — тот же результат, что и airy(Z);
- k=1 — производную от А1 (Z);
- k=2 — функцию Эйри второго рода, 61 (Z) :
- k=3 — производную от B1(Z). Пример:
D=
1.0000 3.0000 + 2.00001
» S=airy(D)
S =
0.1353 -0.0097 + 0.00551
11.gif
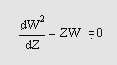
12.gif
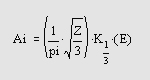
13.gif
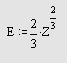
3. Функции Бесселя
Функции Бесселя
Линейное дифференциальное уравнение второго порядка вида
где v — неотрицательная константа, называется уравнением Бесселя, а его решения известны как функции Бесселя. Функции J v (z) и J_ v (z) формируют фундаментальное множество решений уравнения Бесселя для неотрицательных значений п (это так называемые функции Бесселя первого рода): где для гамма-функции используется следующее представление:
Второе решение уравнения Бесселя, линейно независимое от J v (z), определяется как и задает функции Бесселя второго рода Y v (z).
Функции Бесселя третьего рода (функции Ханкеля) и функция Бесселя первого и второго рода связаны следующим выражением:
-
bessel j(nu,Z) — возвращает функцию Бесселя первого рода, J v (z), для каждого элемента комплексного массива Z. Порядок ш может не быть целым, однако должен быть вещественным. Аргумент Z может быть комплексным. Результат вещественный, если Z положительно. Если nu и Z — массивы одинакового размера, то результат имеет тот же размер. Если любая входная величина — скаляр, результат расширяется до размера другой входной величины. Если одна входная величина — вектор-строка, а другая — вектор-столбец, результат представляет собой двумерный массив значений функции.
-
bessely(nu.Z) — возвращает функцию Бесселя второго рода, Y v (z).
-
[J.ierr] = besse1j(nu,Z) и [Y.ierr] = bessely(nu.Z) функции всегда возвращают массив с флагами ошибок:
-
ierr = 1 — запрещенные аргументы;
-
ierr = 2 — переполнение (возвращает Inf);
-
ierr = 3 — некоторая потеря точности при приведении аргумента;
-
ierr = 4 — недопустимая потеря точности: Z или nu слишком велики;
-
ierr = 5 — нет сходимости (возвращает NaN).
-
Примеры:
» S=[2-51.4.7];T=[8.l.3]:g=besselj(T,S)
g=
0.1114-0.05081 -0.0660 -0.1676
» S-[2-5i,4.7];T=[8.1.3J;[g.ierr]=bessely(T,S)
g=
0.1871 - 0.03241 0.3979 0.2681
ierr =
0 0 0
-
besselh(nu,К,Z) — для К=1 или 2 возвращает функцию Бесселя третьего рода (функцию Ханкеля) для каждого элемента комплексного массива Z. Если nu и Z — массивы одинакового размера, то результат имеет тот же размер. Если одна из входных величин — скаляр, результат формируется по размеру другой входной величины. Если одна входная величина — вектор-строка, а другая — вектор-столбец, результат представляет собой двумерный массив значений функции.
-
bessel h(nu.Z) — использует по умолчанию К = 1.
-
besselh(nu.l.Z.l) — масштабирует H (1) v (z) с коэффициентом exp(-i*z).
-
besse1h(nu,2,Z.l) — масштабирует H (2) v (z) с коэффициентом exp(+i*z).
-
[H.ierr] = besselhC...) — всегда возвращает массив с флагами ошибок:
-
ierr = 1 — запрещенные аргументы;
-
ierr = 2 — переполнение (возвращает Inf);
-
ierr = 3 — некоторая потеря точности при приведении аргумента;
-
ierr = 4 — недопустимая потеря точности: Z или nu слишком велики;
-
ierr = 5 — нет сходимости (возвращает NaN).
-
» D=[1.3+2i];F=[3.2]:[K.ierr]=besselk(F,D)
К =
7.1013 -0.0401 - 0.02851
lerr =
0 0
Естественно, что возможно построение графиков специальных функций.
В качестве примера рассмотрим m-файл-сценарий, приведенный ниже:
х=0:0.1:10;
y0=besselj(0.x);
y1=besselj(1.x):
y2=besselj(2.x);
y3=besselj(3.x);
plot(x,y0,.'-m',x,y1,'-r',x,y2,'-.k',x,y3,'-b')
legend('besselj(0.x)'. 'besselj(l.x)' ,'besse1j(2,x)'. ( besselj(3,x)');
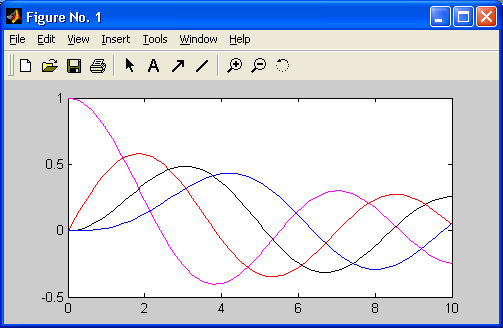
Рис. 9.1 иллюстрирует построение четырех функций Бесселя bessel j(n,x) для п-0, 1, 2 и 3 с легендой, облегчающей идентификацию каждой кривой рисунка.
Рис. 9.1. Графики четырех функций Бесселя besselj(n,x)
Эти графики дают наглядное представление о поведении функций Бесселя, широко используемых при анализе поведения систем, описываемых линейными дифференциальными уравнениями второго порядка.
1a.gif
1b.gif

14.gif
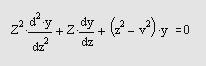
14.gif
16.gif
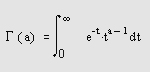
17.gif
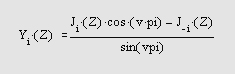
19.gif
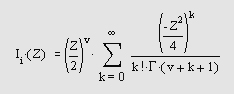
20.gif
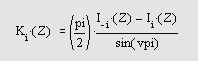
4. Бета-функция и ее варианты
Бета-функция и ее варианты
Бета-функция определяется как
где Г (z) — гамма-функция. Неполная бета-функция определяется по формуле
-
beta(Z.W) — возвращает бета-функцию для соответствующих элементов комплексных массивов Z и W. Массивы должны быть одинакового размера (или одна из величин может быть скаляром).
-
beta i nc ( X , Z , W ) — возвращает неполную бета-функцию. Элементы X должны быть в закрытом интервале [0, 1].
-
beta 1 п ( Z , W ) — возвращает натуральный логарифм бета-функции log ( beta ( Z , W ) ) , без вычисления beta(Z.W). Так как сама бета-функция может принимать очень большие или очень малые значения, функция betaln(Z.W) иногда более полезна, так как позволяет избежать переполнения.
Пример:
» format rat;beta((l:10) 4 ,4)
ans=
1/4
1/20
1/60
1/140
1/280
1/504
1/840
1/1320
1/1980
1/2860
21.gif
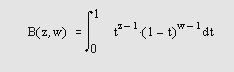
22.gif
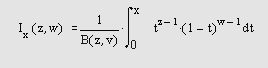
5. Эллиптические функции и интегралы
Эллиптические функции и интегралы
Эллиптические функции Якоби определяются интегралом и соотношениями
сn(u) = cos ф,
cn(u)=cosф,
dn(u) = (1-sin 2 ф) 1/2 ,
аm(u) = ф.
В некоторых случаях при определении эллиптических функций используются модули k вместо параметра гл. Они связаны выражением k = т = sin a .
-
[SN.CN.DN] = ellipj(U.M) — возвращает эллиптические функции Якоби SN, CN и . DN, вычисленные для соответствующих элементов — аргумента U и параметра М. Входные величины U и М должны иметь один и тот же размер (или любая из них может быть скаляром).
-
[SN.CN.DN] = ellipj(U,M,to1) — возвращает эллиптическую функцию Якоби, вычисленную с точностью tol . Значение tol по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:
» [SN.CN.DN]=ellipj([23.1].[0.5.0.2])
|
|
|
|
|
|
|
SN = |
|
|
|
|
474/719 |
1224/1481 |
|
|
|
CN = |
|
|
|
|
1270/1689 |
1457/2588 |
|
|
|
DN = |
|
|
|
|
399/451 |
538/579 |
|
|
|
|
|
|
Полные эллиптические интегралы первого и второго рода определяются следующим образом:
-
ellipke(M) — возвращает полный эллиптический интеграл первого рода для элементов М.
-
[К.Е] = ellipke(M) — возвращает полные эллиптические интегралы первого и второго рода.
-
[К.Е] = ellipke(M.tol) — возвращает эллиптические функции Якоби, вычисленные с точностью tol. Значение по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:
» [f.e]=ellipse([0.2.0.8])
f =
707/426 1018/451
е =
679/456 515/437
Для вычисления этих функций используется итерационный метод арифметико-геометрического среднего (см. детали в Reference Book по системе MATLAB).
18.gif
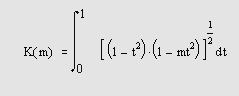
23.gif
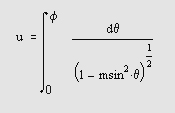
24.gif
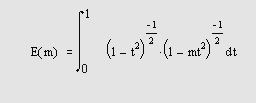
6. Функции ошибки
Функции ошибки
Функция ошибки определяется следующим образом:
-
erf(X) — возвращает значение функции ошибки для каждого элемента вещественного массива X. Дополнительная (остаточная) функция ошибки задается соотношением
-
erfc(X) — возвращает значение остаточной функции ошибки.
-
erfcx(X) — возвращает значение масштабированной остаточной функции ошибки. Эта функция определяется так:
егfсх(х) = е х erfc(x).
-
erfinv(Y) — возвращает значение обратной функции ошибки для каждого элемента массива Y. Элементы массива Y должны лежать в области -1<Y<1. Примеры:
» Y=[0.2,-0.3];a=erf(Y)
а =
0.2227 -0.3286
» b=erfc(Y)
b =
0.7773 1.3286
» c=erfcx(Y)
с =
0.8090 1.4537
» d=erfinv(Y)
d =
0.1791 -0.2725
При вычислении данных функций используется аппроксимация по Чебышеву (см. детали алгоритма в Reference Book no MATLAB).
25.gif
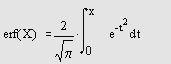
27.gif
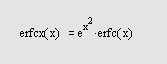
7. Интегральная показательная функция
Интегральная показательная функция
Интегральная показательная функция определяется следующим образом:
-
expint(X) — возвращает интегральную показательную функцию для каждого
элемента X. Пример:
» d=expint([2,3+7i])
d =
0.0489 -0.0013 -0.00601
Для вычисления этой функции используется ее разложение в ряд.
28.gif
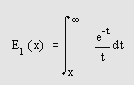
8. Гамма-функция и ее варианты
Гамма-функция и ее варианты
Гамма-функция определяется выражением
Неполная гамма-функция определяется как
-
gamma (А) — возвращает гамма-функцию элементов А. Аргумент А должен быть вещественным.
-
gamma iпс(X,А) — возвращает неполную гамма-функцию соответствующих элементов X и А. Аргументы X и А должны быть вещественными и иметь одинаковый размер (или любой из них может быть скалярным).
gammaln(A) —возвращает логарифмическую гамма-функцию, gammaln(A) = 1og(gamma(A)). Команда gammaln позволяет избежать переполнения, которое может происходить, если вычислять логарифмическую гамма-функцию непосредственно, используя 1og(gamma(A)).
Примеры:
» f=[5.3];d=gamma(f)
d =
24 2 » h=gammaln(f)
h =
3.1781 0.6931
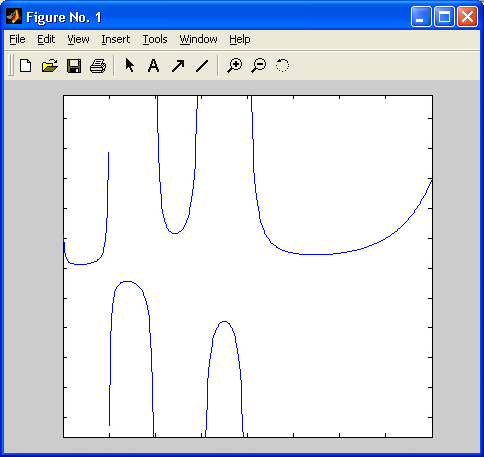
Гамма-функция имеет довольно сложный», график, заслуживающий построения (рис. 9.2).
Рис. 9.2. График гамма-функции
Это можно осуществить с помощью следующего файла-сценария:
%Gamma function graphicclear syms x
ezplot(gamma(x).[-4 4]) grid on
Гамма-функция вычисляется по известному алгоритму W. J. Kody (1989 г.). Для вычисления неполной гамма-функции используются рекуррентные формулы.
2.gif
29.gif
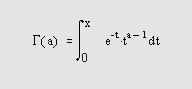
30.gif
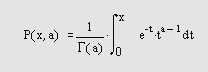
9. Ортогональные полиномы Лежандра
Ортогональные полиномы Лежандра
Функция Лежандра определяется следующим образом:
где Рn(*) — полином Лежандра степени п, рассчитываемый как
-
legendre(n.X) —возвращает функции Лежандра степени п и порядков m = 0,1..... n, вычисленные для элементов X. Аргумент п должен быть скалярным целым числом, не превосходящим 256, а X должен содержать действительные значения в области -UxJl. Возвращаемый массив Р имеет большую размерность, чем X, и каждый элемент P(m+l,dl,d2...) содержит связанную функцию Лежандра степени п и порядка т, вычисленную в точках X(dl,d2...).
-
1egendre(n,X, 'sch') — возвращает квазинормализованные по Шмидту функции Лежандра.
Пример:
» g=rand(3.2);legendre(3,g)
|
|
|
|
|
|
|
|
-0.4469 |
-0.0277 |
0.1534 |
|
|
|
-0.0558 |
1.4972 |
-2.0306 |
|
|
|
5.4204 |
0.2775 |
4.0079 |
|
|
|
-10.5653 |
-14.9923 |
-2.7829 |
|
|
|
|
|
|
|
ans(:.:.2) =
-0.4472-0.34040.0538
0.0150 -1.0567 -1.9562
5.3514 5.7350 4.4289
-10.7782 -7.3449 -3.4148
31.gif
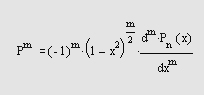
32.gif
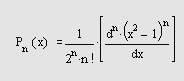
10. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Вычислять функции Эйри.
-
Вычислять функции Бесселя разного рода.
-
Вычислять бета-функцию и ее варианты.
-
Использовать эллиптические функции и интегралы.
-
Вычислять функции ошибки.
-
Вычислять интегральные показательные функции.
-
Вычислять гамма-функцию и ее варианты.
-
Использовать ортогональные полиномы Лежандра.