Урок 8. Операторы и функции
1. Урок 8. Операторы и функции
Урок №8.
Операторы и функции
-
Арифметические и алгебраические операторы и функции
-
Операторы отношения и их функции
-
Логические операторы и функции
-
Специальные символы
-
Системные переменные и константы
-
Функции времени и даты
-
Элементарные функции
-
Тригонометрические и гиперболические функции
-
Функции округления и знака
-
Функции комплексного аргумента
Начиная с этого урока мы переходим к изучению математических и логических возможностей системы MATLAB. Их изучение мы начнем с операторов и функций — тех кирпичиков, из которых строятся математические выражения. Вычисления математических выражений составляют главную цель любой системы, предназначенной для численных расчетов. Здесь мы рассмотрим полный набор операторов входного языка системы MATLAB 6.0 и соответствующих им функций. Напомним, что полный список операторов выводится командой help ops. Операторы и специальные символы системы MATLAB можно разделить на ряд категорий, которые рассматриваются ниже.
2. Арифметические операторы и функции
Арифметические операторы и функции
Арифметические операторы являются самыми распространенными и известными. В отличие от большинства языков программирования в системе MATLAB практически все операторы являются матричными, т. е. предназначены для выполнения операций над матрицами. В табл. 8.1 приводится список арифметических операторов и синтаксис их применения.
Таблица 8.1. Арифметические операторы и функции MATLAB
|
|
|||
|
|
Plus |
Плюс + |
М1+М2 |
|
|
Uplus |
Унарный плюс + |
+М |
|
|
Minus |
Минус |
М1-М2 |
|
|
Uminus |
Унарный минус |
-М |
|
|
Mtimes |
Матричное умножение * |
М1*М2 |
|
|
Times |
Поэлементное умножение массивов .* |
А1*А2 |
|
|
Mpower |
Возведение матрицы в степень |
М1^х |
|
|
Power |
Поэлементное возведение массива в степень |
А1^х |
|
|
Mldivide |
Обратное (справа налево) деление матриц \ |
M1\M2 |
|
|
Mrdivide |
Деление матриц слева направо / |
М1/М2 |
|
|
Ldivide |
Поэлементное деление массивов справа налево . \ |
А1.\А2 |
|
|
Rdivide |
Поэлементное деление массивов слева направо . / |
А1 . /А2 |
|
|
Kron |
Тензорное умножение Кронекера kron |
kron(X.Y) |
|
|
Обратите внимание на то, что каждый оператор имеет аналогичную по назначению функцию. Например, оператору матричного умножения * соответствует функция mtimes(Ml,M2). Примеры применения арифметических операторов уже не раз приводились, так что ограничимся несколькими дополнительными примерами:
» А=[1 2 3];
» В=[4 5 6]:
» В-А
ans=
|
|
3 |
3 3 |
|
|
|
» minus (В. А) |
|
|
|
|
ans = |
|
|
|
|
3 |
3 3 |
|
|
|
» А. ^ 2 |
|
|
|
|
ans = |
|
|
|
|
1 |
4 9 |
|
|
|
» power(A,2) |
|
|
|
|
ans = |
|
|
|
|
1 |
4 9 |
|
|
|
» ДАВ |
|
|
|
|
ans= |
|
|
|
|
4.0000 |
2.5000 2.0000 |
|
|
|
» Idivide(A.B) |
|
|
|
|
ans= |
|
|
|
|
4.0000 |
2.5000 2.0000 |
|
|
|
» rdivide(A.B) |
|
|
|
|
ans= |
|
|
|
|
0.2500 |
0.4000 0.5000 |
|
Соответствие функций операторам и командам в системе MATLAB является одним из основных положений программирования. Оно позволяет одновременно использовать элементы как операторного, так и функционального программирования.
Следует отметить, что в математических выражениях операторы имеют определенный приоритет исполнения. Например, в MATLAB приоритет логических операторов выше, чем арифметических, приоритет возведения в степень выше приоритетов умножения и деления, приоритет умножения и деления выше приоритета сложения и вычитания. Для изменения приоритета операций в математических выражениях используются круглые скобки. Степень вложения скобок не ограничивается.
3. Операторы отношения и их функции
Операторы отношения и их функции
Операторы отношения служат для сравнения двух величин, векторов или матриц. Все операторы отношения имеют два операнда, например х и у, и записываются, как показано в табл. 8.2.
Таблица 8.2. Операторы и функции отношения
| Функция | Название | Оператор | Пример |
| Eq | Равно | = = | x = = y |
| Ne | He равно | ~ = | x ~ = y |
| Lt | Меньше чем | < | x<y |
| Gt | Больше чем | > | x>y |
| Le | Меньше или равно | <= | x<=y |
| Ge | Больше или равно | >= | x>=y |
Данные операторы выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают значение 1 (True), если элементы идентичны, и значение 0 (False) в противном случае. Если операнды — действительные числа, то применение операторов отношения тривиально:
» eq(2.2)
ans =
1
» 2==2
ans =
1
» ne(l,2)
ans =
1
» 2 ~- 2
ans =
0
» 5 > 3
ans =
1
» le(5.3)
ans =
0
Следует отметить, что операторы <, <=, > и >= при комплексных операндах используют для сравнения только действительные части операндов — мнимые отбрасываются. В то же время операторы == и ~= ведут сравнение с учетом как действительной, так и мнимой частей операндов. Следующие примеры поясняют это положение:
» (2+3i)>-(2+i)
ans=
1
» (2+3i)>(2+i)
ans=
0
» abs(2+3i)>abs(2+i)
ans =
1
» (2+3i)—(2+i)
ans =
0
» (2+3i)-(2+i)
ans =
1
Если один из операндов — скаляр, происходит сравнение всех элементов второго операнда-массива со значением этого скаляра:
M=
-1 0
1 2
» М>=0
ans =
0 1
1 1
В общем случае операторы отношения сравнивают два массива одного размера и выдают результат в виде массива того же размера:
» М>[0 1;.1 0]
ans =
0 0
0 1
Таким образом, спектр применения операторов отношения в системе MATLAB шире, чем в обычных языках программирования, поскольку операндами являются не только числа, но и векторы, матрицы и массивы. Возможно применение операторов отношения и к символьным выражениям:
» 'b'>'а'
ans =
1
» 'abc'= ='abc'
ans =
1 1 1
» 'cba'<'abc'
ans =
0 0 1
В этом случае символы, входящие в выражения, представляются своими ASCII-кодами. Строки воспринимаются как векторы, содержащие значения кодов. Все это надо учитывать при использовании управляющих структур языка программирования, в которых широко применяются операторы отношения.
4. Логические операторы
Логические операторы
Логические операторы и соответствующие им функции служат для реализации поэлементных логических операций над элементами одинаковых по размеру массивов (табл. 8.3).
Таблица 8.3. Логические операторы и функции MATLAB
|
And |
Логическое И (AND) & |
|
Or |
Логическое ИЛИ (OR) | |
|
Not |
Логическое НЕ (NOT) ~ |
|
Хог |
Исключающее ИЛИ (EXCLUSIVE OR) |
|
Any |
Верно, если все элементы вектора равны нулю |
|
All |
Верно, если все элементы вектора не равны нулю |
Работа операторов поясняется приведенными ниже примерами:
»А=[1 2 3];
»В=[1 0 0];
» and(A.B)
ans =
1 0 0
» оr(А.В)
ans =
1 1 1
» А&В
ans =
1 0 0
» А|В
ans=
1 1 1
» not(А)
ans =
0 0 0
» not(B)
ans =
0 1 1
» ~B
ans=
0 1 1
» xor(A.B)
ans =
0 1 1
» any(A)
ans =
1
» all([0 0 0])
ans =
0
» all(B)
ans =
0
» and('abc'.'012')
ans =
1 1 1
Обратите внимание, что аргументами логических операторов могут быть числа и строки. При аргументах-числах логический нуль соответствует числовому нулю, а любое отличное от нуля число воспринимается как логическая единица. Для строк действует уже отмеченное правило — каждый символ строки представляется своим ASCII-кодом.
5. Специальные символы
Специальные символы
К классу операторов в системе MATLAB относятся также специальные символы. Они предназначены для создания самых разнообразных объектов входного языка и языка программирования системы и придания им различных форм. В табл. 8.4 представлено описание полного набора специальных символов.
Таблица 8.4. Специальные символы MATLAB
|
: |
Двоеточие |
colon |
|
( ) |
Круглые скобки |
paren |
|
[ ] |
Квадратные скобки |
paren |
|
{ } |
Фигурные скобки |
paren |
|
. |
Десятичная точка |
punct |
|
|
Выделение поля структуры |
punct |
|
|
Родительский каталог |
punct |
|
|
Продолжение строки |
punct |
|
, |
Разделитель |
punct |
|
|
Точка с запятой |
punct |
|
% |
Комментарий |
punct |
|
i |
Вызов команды операционной системы |
punct |
|
= |
Присваивание |
punct |
|
1 |
Кавычка |
punct |
|
1 |
Транспонирование |
transpose |
|
1 |
Транспонирование с комплексным сопряжением |
ctranspose |
|
[,] |
Горизонтальная конкатенация |
horzcat |
|
[;] |
Вертикальная конкатенация |
vertcat |
|
( ).( }.. |
Присваивание подмассива |
subsasgn |
|
( ).{ }.. |
Ссылка на подмассив |
subsref |
|
|
Индекс подмассива |
subsindex |
Теперь рассмотрим их более подробно.
-
: (двоеточие) — формирование подвекторов и подматриц из векторов и матриц. Оператор : — один из наиболее часто используемых операторов в системе MATLAB.
Оператор : использует следующие правила для создания векторов:
-
j:k — то же, что и [j.j+l,...,k];
-
j:k — пустой вектор, если j>k;
-
j:i :k — то же, что и [j, j+i ,j+2i .....k];
-
j:i :k — пустой вектор, если i>0 и j>k или если i<0 и j<k, где 1, j и k — скалярные величины.
Ниже показано, как выбирать с помощью оператора : строки, столбцы и элементы из векторов, матриц и многомерных массивов:
-
А(:, j) — это j-й столбец из А;
-
А(i,:) — это i-я строка из А;
-
А(:,:) — эквивалент двумерного массива. Для матриц это аналогично А;
-
A(j:k) - это A(j), A(j+l),...,A(k);
-
A(:J:k)-это A(:.j),A(:,j+l),...,A(:,k);
-
А(:,: ,k) — это k-я страница трехмерного массива А;
-
A(i.j.k.:) — вектор, выделенный из четырехмерного массива А. Вектор включает элементы А(1, j.k.l), A(i. j,k,2), A(i. j,k.3) и т. д.;
-
А(:) — записывает все элементы массива А в виде столбца.
Символы ( ) (круглые скобки) используются для задания порядка выполнения операций в арифметических выражениях, указания последовательности аргументов функции и указания индексов элемента вектора или матрицы. Если X и V — векторы, то X(V) можно представить как [X(V(D), X(V(2)).....X(V(n))]. Элементы вектора V должны быть целыми числами, чтобы их можно было использовать как индексы элементов массива X. Ошибка генерируется в том случае, если индекс элемента меньше единицы или больше, чем size(X). Такой же принцип индексирования действителен и для матриц. Если вектор V имеет т компонентов, а вектор W — п компонентов, то A(V,W) будет матрицей размера mxn, сформированной из элементов матрицы А, индексы которой — элементы векторов V и W.
Символы [ ] (квадратные скобки) используются для формирования векторов и матриц:
-
[6.9 9.64 sqrt(-l)] — вектор, содержащий три элемента, разделенных пробелами;
-
[6.9. 9.64. i] —такой же вектор;
-
[1+j 2-j 3] и [1 +j 2 -j 3] — разные векторы: первый содержит три элемента, а второй пять;
-
[11 12 13: 21 22 23] — матрица размера 2x3. Точка с запятой разделяет первую и вторую строки.
Еще несколько примеров:
-
А = [ ] — сохраняет пустую матрицу в А;
-
А(m. :) = [] — удаляет строку m из матрицы А;
-
А(: ,n) = [ ] — удаляет столбец n из матрицы А.
Символы { } (фигурные скобки) используются для формирования массивов ячеек. Например, {magic(3) 6.9 'hello'} — массив ячеек с тремя элементами.
Символ . (десятичная точка) используется для отделения дробной части чисел от целой. Например, 314/100, 3.14 и .314е1 — одно и то же число.
Кроме того, символ точки . используется для выделения полей структур. Например, A.(field) и A(i).field, где А — структура, означает выделение поля структуры с именем «field».
Ниже перечислено назначение остальных специальных символов MATLAB:
-
.. (родительский каталог) — переход по дереву каталогов на один уровень вверх;
-
... (продолжение) — три или более точек в конце строки указывают на продолжение строки;
-
; (точка с запятой) — используется внутри круглых скобок для разделения строк матриц, а также в конце операторов для запрета вывода на экран результата вычислений;
-
, (запятая) — используется для разделения индексов элементов матрицы и аргументов функции, а также для разделения операторов языка MATLAB. При разделении операторов в строке запятая может заменяться на точку с запятой с целью запрета вывода на экран результата вычислений;
-
% (знак процента) — используется для указания логического конца строки. Текст, находящийся после знака процента, воспринимается как комментарий и игнорируется (увы, за исключением русскоязычных комментарий, которые нередко ведут к ошибочным командам);
-
! (восклицательный знак) — является указателем ввода команды операционной системы. Строка, следующая за ним, воспринимается как команда операционной системы;
-
= (знак равенства) — используется для присваивания значений в арифметических выражениях;
-
' (одиночная кавычка, апостроф) — текст в кавычках представляется как вектор символов с компонентами, являющимися ASCII-кодами символов. Кавычка внутри строки задается двумя кавычками. Например:
» a-'Hello''my friend'
а =
Hello'my friend
-
' (транспонирование с комплексным сопряжением) — транспонирование матриц, например А' — транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Строки транспонированной матрицы соответствуют столбцам исходной матрицы;
-
.' (транспонирование) — транспонирование массива, например А.' — транспонированный массив А. Для комплексных массивов операция сопряжения не выполняется;
-
[.] — горизонтальная конкатенация. Так, [А.В] — горизонтальная конкатенация (объединение) матриц А и В. А и В должны иметь одинаковое количество строк. [А В] действует аналогично. Горизонтальная конкатенация может быть применена для любого числа матриц в пределах одних скобок: [А,В,С]. Горизонтальная и вертикальная конкатенации могут использоваться одновременно: [А,В:С];
-
[:] — вертикальная конкатенация. Так, [А:В] — вертикальная конкатенация (объединение) матриц А и В. А и В должны иметь одинаковое число столбцов. Вертикальная конкатенация может быть применена для любого числа матриц в пределах одних скобок: [А:В:С]. Горизонтальная и вертикальная конкатенации могут использоваться одновременно: [А;В,С];
-
(),{} — присваивание подмассива. Приведем несколько примеров:
-
А(1)=В — присваивает значения элементов массива В элементам массива А, которые определяются вектором индексов I. Массив В должен иметь такую же размерность, как и массив I, или может быть скаляром;
-
А(I,J)=B — присваивает значения массива В элементам прямоугольной подматрицы А, которые определяются векторами индексов I и J. Массив В должен иметь LENGTH(I) строк и LENGTH(J) столбцов;
-
А{1}=В, где А — массив ячеек и I — скаляр, помещает копию массива В в заданную ячейку массива А. Если I имеет более одного элемента, то появляется сообщение об ошибке.
-
6. Системные переменные и константы
Системные переменные и константы
Как отмечалось ранее, в состав объектов MATLAB входит ряд системных переменных и констант, значения которых устанавливаются системой при ее загрузке или автоматически формируются в процессе вычислений. Описание таких объектов приводится ниже.
-
ans — результат выполнения последней операции. Переменная ans создается автоматически, когда не определены выходные аргументы какого-либо оператора. Пример:
» cos([0:2*pi])
ans =
1.0000 0.5403 -0.4161 -0.9900 -0.6536 0.2837 0.9602
-
computer — возвращает строку с информацией о типе компьютера, на котором установлена система MATLAB;
-
[str.maxsize] = computer — возвращает строку str с информацией о компьютере и целое число maxsize, содержащее максимально допустимое число элементов матрицы для данной версии MATLAB. Пример:
» [str.maxsize] = computer
str =
PCWIN
maxsize =
268435455
-
eps — возвращает интервал между числом 1.0 и следующим ближайшим числом с плавающей запятой, которое воспринимается как отличное от 1.0. Значение eps определяет заданный по умолчанию порог для функций pinv и rank, а также для некоторых других функций. На машинах с арифметикой с плавающей запятой eps = 2 ^ (-52), что приблизительно составляет 2.22е-1б. Пример:
» eps
ans =
2.2204е-016
-
i или j— мнимая единица (равная sqrt(-1)), которая используется для задания мнимой части комплексных чисел. Символ 1 при задании комплексной константы можно использовать без знака умножения. В качестве мнимой единицы можно также использовать символ j. Пример:
» w=3+5i
w =
3.0000 + 5.00001
-
Inf — возвращает представление положительной бесконечности для машинной арифметики. Бесконечность следует из операций, подобных делению на нуль, и переполнения, которое ведет к результатам, слишком большим, чтобы их можно было представить в виде числа с плавающей запятой. Пример:
» 4/0
Warning: Divide by zero.
ans=
Inf
Примечание
Переменным i и j можно задать и иное значение, например, они могут выступать в ка-честве индексов в циклах for. Однако это чревато путаницей, если внутри цикла пользователь задает выражения с комплексными числами.[Используйте как индексы I и J вместо 1 и j.— Примеч. ред.]
-
inputname(argnum) — возвращает в тело функции название переменной рабочей области, соответствующее аргументу с номером argnum. Может использоваться только внутри тела функции. Если входной аргумент не имеет никакого символьного представления (например, если это выражение или функция, дающая на выходе выражение, например а(1), varargin{:}, eval(expr), а не переменная), функция inputname возвращает пустую строку ("");
-
j — мнимая единица. Символ j можно использовать в качестве мнимой единицы наряду с 1. Как мнимая единица (равная sqrt(-D) символ j используется для задания мнимой части комплексных чисел. Все сказанное о символе i относится и к j. Пример:
» s=4-3j
s =
4.0000 - 3.00001
-
NaN — возвращает представление для нечисловых величин, например, в случае операций, которые имеют неопределенные численные результаты. Пример:
» s=0/0
Warning: Divide by zero.
s =NaN
Функция nargchk часто используется внутри m-файлов для проверки соответствия количества входных параметров (аргументов):
-
msg = nargchkOow.high.number) — возвращает сообщение об ошибке, если число number меньше, чем low, или больше, чем high, в противном случае возвращается пустая строка. Пример:
» msg = nargchk(4,9.5)
msg =
[ ]
» msg = nargchk(4.9.2)
msg = Not enough input arguments.
-
msg = nargoutchkdow,high.number) — возвращает сообщение об ошибке, если число number выходных параметров (выходных аргументов в терминологии MATLAB) меньше, чем low, или больше, чем high, в противном случае возвращается пустая строка.
Еще две функции позволяют определить число входных и выходных параметров функции:
-
nargin — возвращает число входных аргументов, определенных для функции. Внутри тела m-файла функции nargin и nargout указывают соответственно количество входных или выходных аргументов, заданных пользователем. Вне тела m-файла функции nargin и nargout показывают соответственно число входных или выходных аргументов для данной функции. Отрицательное число аргументов означает, что функция имеет переменное число аргументов;
-
nargin(@fun) — возвращает число объявленных входных параметров для функции fun. Если функция имеет переменное число входных аргументов, возвращается -1;
-
nargout — возвращает число выходных параметров, определенных для функции;
-
nargout( 'fun') — возвращает число объявленных выходных параметров для функции fun.
Применение этих функций мы рассмотрим немного позже при описании структуры функций.
Продолжаем перечисление системных переменных:
-
pi — число р (отношение длины окружности к ее диаметру), pi возвращает число с плавающей запятой, ближайшее к значению р. Выражения 4*atan(l) и imag(log(-1)) выдают тот же результат. Пример:
» pi
ans = 3.1416
-
real max — возвращает самое большое число в формате с плавающей запятой, соответствующее конкретному компьютеру. Большее значение соответствует системной переменной Inf. Пример:
» n = real max
n =
1.7977е+308
-
real mi n — возвращает наименьшее нормализованное положительное число в формате с плавающей запятой, представимое на конкретном компьютере. Любое меньшее число воспринимается как ноль. Пример:
» n = realmin
n =
2.2251е-308
Переменные varargin и varargout позволяют использовать в функциях переменное число входных и выходных параметров:
-
varargout = foo(n) — возвращает список выходных параметров переменной длины функции foo;
-
у = function bar(varargin) — принимает переменное число аргументов в функцию bar.
Переменные varargin и varargout используются только внутри m-файлов функции для задания произвольных аргументов функции. Эти переменные должны быть последними в списке входов или выходов, а для их обозначения могут использоваться только строчные буквы. Использование этих возможностей мы рассмотрим несколько позже.
7. Функции поразрядной обработки
Функции поразрядной обработки
Ряд функций предназначен для поразрядной логической обработки данных:
-
bitand(A.B) — возвращает поразрядное И двух неотрицательных целых аргументов А и В. Пример:
» f=bitand(7,14)
f =
6
-
bitcmp(A.n) — возвращает поразрядное дополнение аргумента А как n-битовое неотрицательное целое число. Пример:
» g=bitcmp(6,4)
g =
9
-
bitor(A.B) — возвращает поразрядное ИЛИ двух неотрицательных целых аргументов А и В. Пример:
» v=bitor(12.21)
v = 29
-
bitmax — возвращает максимальное целое число без знака, которое может быть представлено в формате чисел с плавающей запятой применительно к используемому компьютеру. Это значение определяется для комбинации, когда все биты установлены. На машинах с IEEE-арифметикой это значение равно 2 53 -1. Пример:
» bitmax
ans =
9.0072е+015
-
bitset(A.bit.v) — устанавливает бит в позиции bit равным значению v, которое должно быть 0 или 1. Пример:
» d=bitset(12.2.1)
d =
14
-
bitshift(A.n) — возвращает значение аргумента А, сдвинутое на п бит. Если n>0, это аналогично умножению на 2" (левый сдвиг). Если n<0, это аналогично делению на 2n (правый сдвиг). Пример:
» f=bitshift(4.3)
f =
32
-
bitset(A.bit) — устанавливает бит в позиции bit аргумента А в единичное значение. Аргумент А должен быть неотрицательным целым, bit — это номер в диапазоне между 1 и числом бит в целом числе, представленном в формате чисел с плавающей запятой.
-
bitget(A.bit) — возвращает значение бита в позиции bit операнда А. Аргумент А должен быть неотрицательным целым числом, bit — это номер между 1 и числом бит в целом числе формата с плавающей запятой. Пример:
» disp(dec2bin(23))
10111
» С = bitget(23.5:-l:l)
С =
1 0 1 1 1
-
bitxor(A, В) — возвращает результат поразрядного исключающего ИЛИ для двух аргументов А и В. Оба аргумента должны быть целыми. Пример:
» x=bitxor(12.31)
х =
19
Чтобы операнды этих функций гарантированно были целыми числами, при их задании рекомендуется использовать функции ceil, fix, floor и round.
8. Функции обработки множеств
Функции обработки множеств
Множество — первичное понятие математики, не имеющее четкого определения. Под множеством подразумевается совокупность некоторых объектов, например книг в библиотеке, людей в зале или элементов вектора. В этом разделе приводятся некоторые функции для обработки множеств, представленных векторами. Они широко используются при анализе и обработке данных.
-
intersect(a.b) — возвращает пересечение множеств для двух векторов а и b, т. е., общие элементы векторов а и b. Результирующий вектор отсортирован по возрастанию. Если входные массивы не являются векторами, то они рассматриваются как совокупность векторов-столбцов а=а(:) или b=b(:);
-
intersect(a,b, 'rows') — возвращает строки, общие для а и b, когда а и b представляют собой матрицы с одинаковым числом столбцов;
-
[c.ia.ib] = intersect(a.b) — также возвращает вектор-столбец индексов ia и ib. но так, что с = a(ia) и с = b(ib) (или с = a(ia.:) ис = b(ib.:)).
Пример:
» А = [1 7 2 6]; В = [7 2 3 4 6 1];
» [c,ia,ib] = intersect(А,В)
1 2 6 7
ia =
1 3 4 2
ib =
6 2 5 1
-
ismember(a.S) — возвращает вектор той же длины, что и исходный а, содержащий логические единицы на месте тех элементов вектора а, которые принадлежат множеству S, и логические нули на месте тех элементов вектора а, которые не принадлежат множеству S;
-
ismember (А. S.' rows') — возвращает вектор, содержащий логические единицы там, где строки матрицы А являются также строками матрицы S, и логические нули в остальных позициях. А и S должны быть матрицами с одним числом столбцов.
Пример:
» set = [0 1 3 5 7 9 11 15 17 19];
» а=[1 2345678];
» k = ismember(a.set)
k =
1 0 1 0 1 0 1 0
-
setdiff(a.b) — возвращает разность множеств, т. е., те элементы вектора а, которые не содержатся в векторе b. Результирующий вектор сортируется по возрастанию;
-
setdiff(a,b, 'rows') — возвращает те строки из матрицы а, которые не содержатся в матрице Ь. Матрицы а и b должны иметь одинаковое число столбцов;
-
[c,i] = setdiff(...) — возвращает также вектор индексов 1, такой что с = а(i) или с = а (i,;).
Если входной массив а является матрицей, то он расценивается как вектор-столбец а(:).
Пример:
» а=[2 3 5 7 8 9 10 13 20];
» b=[1456894]
» с = setdiff(a.b)
с=
2 3 7 10 13 20
-
setxor(a.b) — исключающее ИЛИ для векторов а и b. Результирующий вектор отсортирован;
-
setxor(a,b, 'rows') — возвращает строки, которые не являются пересечениями матриц а и b. Матрицы а и b должны иметь одинаковое число столбцов;
-
[c.ia.ib] = setxor(...) — возвращает также векторы индексов ia и ib так, что с является отсортированной комбинацией элементов с = а(iа)ис = b(ib) или для комбинаций строк с = а(iа,:)ис = b(ib.;).
Если массив а является матрицей, то он расценивается как вектор-столбец а(:).
Пример:
» а = [-1 0 1 Inf -Inf NaN];
» b = [-2 pi 0 Inf];
» с = setxor(a.b)
с =
-Inf -2.0000-1.00001.0000 3.1416 NaN
-
union(a ,b) — возвращает вектор объединенных значений из а и b без повторяющихся элементов. Результирующий вектор сортируется в порядке возрастания;
-
union(a,b, 'rows') — возвращает объединенные строки из а и b, не содержащие повторений (а и b — это матрицы с одинаковым числом столбцов);
-
[c.ia.ib] = unionL.) — дополнительно возвращает i а и i b — векторы индексов, такие что с = a(ia) и c=b(1b), или, для объединенных строк, с = а(1а.:)ис = b(ib,:). Невекторный массив а расценивается как вектор-столбец а(:). Пример:
» а=[2,4,-4,9,0]:b=[2,5,4]:
» [c,ia,ib]=union(a,b)
с =
-4 0 2 4 5 9
ia =
3 5 4
ib =
1 3 2
-
unique(a) — возвращает значения элементов из а, не содержащие повторений. Результирующий вектор сортируется в порядке возрастания. Невекторный массив расценивается как вектор-столбец а=а(: );
-
unique(a, 'rows') — возвращает уникальные строки а;
-
[b.i ,j] = unique(...) — дополнительно возвращает i и j — векторы индексов, такие что b = a(i)na = b(j) (или b = а(1,:) иа = b(j.:)).
Примеры:
» b=[-2,3,5,4,1,-6,2,2,7]
b=
-2 3 5 4 1 -6 2 2 7
» [c,i,j]=unique(b)
с =
|
|
|
-6 |
-2 |
1 2 3 4 |
5 7 |
|
|
|
|
6 |
1 |
5 8 2 4 |
3 9 |
|
|
|
j |
= |
|
|
|
|
|
|
|
2 |
5 |
7 6 3 1 |
4 4 |
|
|
|
» |
a-[-2, |
3.5:4. |
l.-6:2,2.7;-2.3,5J |
|
|
|
|
a |
= |
|
|
|
|
|
|
|
-2 |
3 |
5 |
|
|
|
|
|
4 |
1 |
-6 |
|
|
|
|
|
2 |
2 |
7 |
|
|
|
|
|
-2 |
3 |
5 |
|
|
|
|
» |
c=uniqueCa. ' |
rows ' ) |
|
|
|
|
|
с |
= |
|
|
|
|
|
|
|
-2 |
3 |
5 |
|
|
|
|
|
2 |
2 |
7 |
|
|
|
|
|
4 |
1 |
-6 |
|
|
|
|
|
|||||
9. Функции времени и даты
Функции времени и даты
Ряд функций служит для возврата текущего времени и даты. Они перечислены ниже.
-
calendar(d) — возвращает календарь на месяц, в который попадает день, заданный аргументом d (дни отсчитываются от начала летоисчисления);
-
calendar — возвращает матрицу размером 6x7, содержащую календарь на текущий месяц. Календарь начинается с воскресения (первый столбец) и завершается субботой;
-
calendar(y ,m) — возвращает календарь на месяц, заданный аргументом т, и год, заданный аргументом у;
Вызов функции без присваивания результата выдает календарь на экран. Примеры:
» calendar
Jul 2000
|
S |
М |
Tu |
W |
Th |
F |
S |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
30 |
31 |
0 |
0 |
0 |
0 |
0 |
|
|
|
calendar(700477)
Nov 1917
|
|
||||||||
|
|
S |
M |
Tu |
W |
Th |
F |
S |
|
|
|
0 |
0 |
0 |
0 |
1 |
2 |
3 |
|
|
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
|
25 |
26 |
27 |
28 |
29 |
30 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
-
clock — возвращает вектор из 6 элементов, содержащий текущую дату и время в десятичной форме [год месяц день час минуты секунды]. Первые пять элементов этого вектора — целые числа. Шестой элемент имеет несколько десятичных знаков после запятой. Функция fix(clock) округляет число секунд до целого значения. Пример:
» c=clock
с =
1.0e+003 *
2.0000 0.0070 0.0240 0.0200 0.0120 0.0148
» fix(clock)
ans =
2000 7 24 20 12 26
-
cputime — возвращает время работы процессора (в секундах) , использованное системой MATLAB с момента ее запуска. Это число может выйти за рамки внутреннего представления, и тогда отсчет времени начинается заново. Пример:
» +tl=cputime; w=surf(peaks(30));cputime-tl
ans =
0.2200
-
str = date — возвращает строку, содержащую дату в формате дд-ммм-гггг (день-месяц-год). Пример:
» d = date
d =
24-Jul-2000
-
datenum — преобразует строку даты в порядковый номер даты, который отсчитывается с некоторого начального дня (01.01.00);
-
datenum(str) — преобразует дату, заданную строкой str, в порядковый номер даты. Строка string должна иметь один из следующих форматов: 0, 1, 2, 6, 13, 14, 15 или 16, определенных для функции datestr;
-
datenum(Y.M.D) — возвращает порядковый номер даты для соответствующих массивов элементов Y, М и D (год, месяц, день). Массивы Y, М и D должны иметь одинаковую размерность (при этом любые из них могут быть скалярами);
-
datenum(Y.M.D,H.MI,S) — возвращает порядковый номер даты для соответствующих массивов элементов Y, М, D, H, Ml и S (год, месяц, день, часы, минуты, секунды). Массивы Y, М, D, H, Ml и S должны иметь одинаковую размерность (при этом любые из них могут быть скалярами).
Пример:
» n1 = datenum('26-Nov-1998')
n1 =
730085
» Y=[1998,2000];M-[1,12];D=23;N=datenum(Y,M,D)
N =
729778 730843
-
datestr(D, dateform) — преобразует каждый элемент массива порядковых номеров даты D в строку. Аргумент dateform определяет формат результата; dateform может быть номером или строкой в соответствии с табл. 8.5.
Таблица 8.5. Форматы представления даты
|
Dateform(номер) |
||
|
0 |
'dd-rmiM-yyyy HH:MM:SS' |
1l-Mar-1995 03:45 |
|
1 |
'dd-mmM-yyyy' |
Ol-Mar-1995 |
|
2 |
'mm/dd/yy' |
03/01/95 |
|
3 |
' mmm ' |
Mar |
|
4 |
'm' |
M |
|
5 |
'mm' |
3 |
|
6 |
'mm/dd' |
03/01 |
|
7 |
'dd' |
1 |
|
8 |
'ddd' |
Wed |
|
9 |
'd' |
W |
|
10 |
'УУУУ' |
1995 |
|
11 |
'УУ |
95 |
|
12 |
' mmmyy ' |
Mar95 |
|
13 |
'HH:MM:SS' |
15:45:17 |
-
datevec(A) — преобразует входные величины в массив размерности пхб, каждая строка которого представляет собой вектор [Y,M.D,H,MI,S]. Первые пять элементов вектора — целые числа. Массив А может состоять или из строк, удовлетворяющих формату функции datestr, или из скалярных величин, созданных функциями datenum и now;
-
[Y, M., D, H. MI, S] = datevec (A) — возвращает компоненты вектора даты как индивидуальные переменные.
Любой компонент входного вектора, который не вписывается в нормальный диапазон дат, преобразуется в следующий диапазон (так, например, несуществующая дата June 31 преобразуется в July 1). Допускаются значения нулевого месяца и нулевого дня. Например:
» n = datevecC 11/31/98')
n=
1998 12 1 0 0 0
» n = datevec(710223)
n =
1944 7 10 0 0
О eomday (Y, М) — возвращает последний день года и месяца, заданных соответственно элементами массивов Y и М. Пример (нахождение високосных лет двадцатого столетия):
» у = 1900:1999;
» Е = eomday(y.2);
» y(find(E==29))
ans=
Columns 1 through 6
1904 1908 1912 1916 1920 1924
Columns 7 through 12
1928 1932 1936 1940 1944 1948
Columns 13 through 18
1952 1956 1960 1964 1968 1972
Columns 19 through 24
1976 1980 1984 1988 1992 1996
-
etime(t2,tl) — возвращает длительность промежутка времени (в секундах), задаваемого векторами t1 и t2. Векторы должны удовлетворять формату, выдаваемому функцией clock:
Т = [год месяц день час минуты секунды].
Функция работает некорректно, если в текущий промежуток времени попадут границы месяца или года, что, однако, случается крайне редко и исправляется при повторе операции. Пример (вычисляется время, затрачиваемое на быстрое преобразование Фурье с 2048 точками):
» х = rand(2048,l);t = clock; fft(x); etime(clock.t);etime (clock.t)
ans =
0.0500
-
now — возвращает текущие время и дату в форме числа. Использование rem(now.l) возвращает только время, a floor(now) — только дату. Пример:
» t1 = now, t2 = rem(now,1)
t1 =
7.3009e+005
t2 =
0.6455
-
tic — запускает таймер;
-
toc — выводит время, прошедшее с момента запуска таймера;
-
t = toe — возвращает прошедшее время в переменной t. Пример:
» tic.surf(peaks(50));toc
elapsed_time =
0.7600
-
[N,S] = weekday(D) — возвращает день недели в виде числа N и в виде строки S для каждой даты массива D. Пример:
» D=[728647,735730]:[N.S] = weekday(D)
N =
2 1
S=
Mon Sun
10. Элементарные функции
Элементарные функции
Элементарные функции, пожалуй, наиболее известный класс математических функций. Поэтому, не останавливаясь подробно на их описании, представим набор данных функций, имеющийся в составе системы MATLAB. Функции, перечисленные ниже, сгруппированы по функциональному назначению. В тригонометрических функциях углы измеряются в радианах. Все функции могут использоваться в конструкции вида y=func(x), где func — имя функции. Обычно в такой форме задается информация о функции в системе MATLAB. Мы, однако, будем использовать для функций, возвращающих одиночный результат, более простую форму func(x). Форма [y,z,...]=func(x....) будет использоваться только в тех случаях, когда функция возвращает множественный результат.
11. Алгебраические и арифметические функции
Алгебраические и арифметические функции
В системе MATLAB определены следующие алгебраические и арифметические функции:
-
abs(X) — возвращает абсолютную величину для каждого числового элемента вектора X. Если X содержит комплексные числа, abs(X) вычисляет модуль каждого числа. Примеры:
abs(-5) = 5
abs(3+4i) =5
» abs([1 -2 1 3i 2+3i ])
ans =
1.0000 2.0000 1.0000 3.0000 3.6056
-
ехр(Х) — возвращает экспоненту для каждого элемента X. Для комплексного числа z = х + i*y функция exp(z) вычисляет комплексную экспоненту: exp(z)=exp(x)*(cos(y)+i*sin(y)).
Примеры:
» ехр([1 23])
ans =
2.7183 7.3891 20.0855
» exp(2+3i)
ans =
-7.3151 + 1.0427i
-
factor(n) — возвращает вектор-строку, содержащую простые множители числа п. Для массивов эта функция неприменима. Пример:
f = factor(221)
f =
13 17
-
G=gcd(A, В) — возвращает массив, содержащий наибольшие общие делители соответствующих элементов массивов целых чисел А и В. Функция gcd (0.0) возвращает значение 0, в остальных случаях возвращаемый массив G содержит положительные целые числа;
-
[G, С. D] = gcd(A, В) — возвращает массив наибольших общих делителей G и массивов С и D, которые удовлетворяют уравнению A(i) .*С(1) + B(i) .*D(i) = G(i). Они полезны для выполнения элементарных эрмитовых преобразований. Примеры:
» А=[2 6 9]:
» В=[2 3 3]:
» gcd(A.B)
ans =
2 3 3
» [G.C.D]=gcd(A.B)
G =
2 3 3
C =
0 0 0
D=
1 1 1
-
lcm(A.B) — возвращает наименьшие общие кратные для соответствующих парных элементов массивов А и В. Массивы А и В должны содержать положительные целые числа и иметь одинаковую размерность (любой из них может быть скаляром). Пример:
» А=[1 354];
» В=[2 462];
» lcm(А.В)
ans =
2 12 30 4
-
log (X) — возвращает натуральный логарифм элементов массива X. Для комплексного или отрицательного z, где z = х + y*i, вычисляется комплексный логарифм в виде log(z) = log(abs(z)) + i*atan2(y,x). Функция логарифма вычисляется для каждого элемента массива. Область определения функции включает комплексные и отрицательные числа, что способно привести к непредвиденным результатам при некорректном использовании. Пример:
» Х=[1.2 3.34 5 2.3];
» log(X)
ans=
-0.1823 1.2060 1.6094 0.8329
-
log2(X) — возвращает логарифм по основанию 2 элементов массива X;
-
[F,E] = log2(X) — возвращает массив действительных значений F и массив целых чисел Е. Элементы массива F обычно лежат в диапазоне 0.5 J abs(F) < 1. Для действительных X возвращаемые массивы F удовлетворяют уравнению вида X = F. *2. Е. Для нулевых значений X возвращаются F = 0 и Е = 0.
Пример:
» Х=[2 4.678 5;0.987 1 3];
» [F.E] = log2(Х)
F =
0.5000 0.5847 0.6250
0.9870 0.5000 0.7500
Е =
2 3 3
0 1 2
-
log10(X) — возвращает логарифм по основанию 10 для каждого элемента X. Область функции включает комплексные числа, что способно привести к непредвиденным результатам при некорректном использовании.
Пример:
» Х=[1.4 2.23 5.8 3];
» log10(X)
ans =
0.1461 0.3483 0.7634 0.4771
-
mod(x.y) — возвращает х mod у;
-
mod(X, Y) — возвращает остаток от деления X на Y (т. е., X - Y.*floor(X./Y)) для ненулевого Y, и X в противном случае. Если операнды X и Y имеют одинаковый знак, функция mod(X, Y) возвращает тот же результат, что mod(Х, Y). Однако (для положительных X и Y) mod(-x.y) = rem(-x,y)+y.
Примеры:
» М = mod(5.2)
М =
1
» mod(10.4)
ans =
2
-
pow2(Y) — возвращает массив X, где каждый элемент есть Z Y ;
-
pow2(F.E) — вычисляет Х=Р*2 £ для соответствующих элементов F и Е. Аргументы F и Е — массивы действительных и целых чисел соответственно.
Пример:
» d=pow2(pi/4,2)
d =
3.1416
-
р = nextpow2(A) — возвращает такой показатель степени р, что 2 Р i abs(A). Эта функция эффективно применяется для выполнения быстрого преобразования
Фурье. Если А не является скалярной величиной, то nextpowZ возвращает значение nextpow2(length(A)).
Пример:
» х=[2 678934567784324];
» length(x)
ans =
16
» р = nextpow2(x)
Р =
4
» х=4:
» р = nextpow2(x)
Р =
2
» Х=45;
» р = nextpow2(x)
Р =
6
Функция primes(n) возвращает вектор-строку простых чисел, меньших или равных n. Пример:
» р = primes(25)
Р =
2 3 5 7 11 13 17 19 23
-
[N,D] = rat(X) - возвращает массивы N и D, такие что N./D аппроксимирует X с точностью 1 .е-6*norm(Х(:),!). Даже при том, что все числа с плавающей запятой — рациональные числа, иногда желательно аппроксимировать их дробями, у которых числитель и знаменатель являются по возможности малыми целыми числами. Функция rat пытается это сделать;
-
[N.D] = rat(X.tol) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью tol.
-
rat (X) без выходных параметров просто выдает на экран массив цепных дробей;
-
rats(X.strlen) — возвращает ряд, полученный путем упрощенной рациональной аппроксимации элементов X. Аргумент strlen — длина возвращаемой строки. Функция возвращает знак «*», если полученное значение не может быть напечатано в строке, длина которой задана значением strlen. По умолчанию strlen=13. Тот же алгоритм аппроксимации используется в командном окне MATLAB при задании рационального формата вывода командой format rat.
Пример:
» [g.j]=rat(pi.le-10)
g=
312689
j =
99532
-
sqrt(A) — возвращает квадратный корень каждого элемента массива X. Для отрицательных и комплексных элементов X функция sqrt(X) вычисляет комплексный результат.
Пример:
» А=[25 21.23 55.8 3]:
» sqrt(A)
ans =
5.0 4.6076 7.4699 1.7321
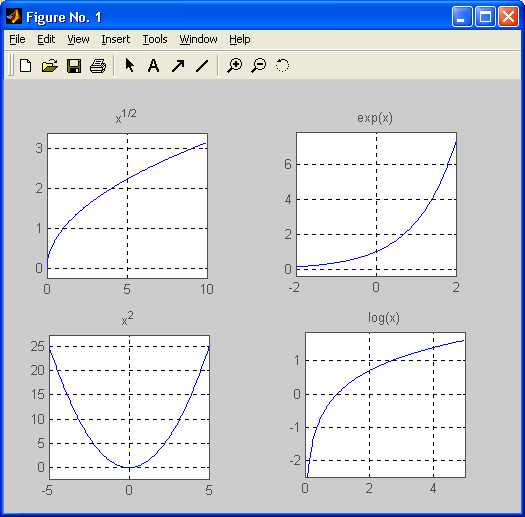
На рис. 8.1 представлены графики ряда распространенных алгебраических функций. Эти графики получены в результате исполнения следующего файла-сценария:
syms x
subplot(2,2.1).ezplot(x*2.[-5 5]).xlabel( " ).grid on
subplot(2,2.2).ezplot(exp(x),[-2 2]),xlabel(").grid on
subplot(2.2.3).ezplot(log(x).[0 5]),grid on
subplot(2.2.4),ezplot(sqrt(x).[0 10]).grid on
Рис. 8.1. Графики ряда алгебраических функций
Графики дают наглядное представление о поведении представленных на них функций. Обратите внимание на применение графической команды ezplot из пакета Symbolic Math ToolBox (она отличается от обычной команды ezplot MATLAB отсутствием заключения символьных переменных в'), команды syms, также входящей в пакет Symbolic Math .Toolbox и задающей символьную переменную х, и несколько необычное применение команды xlabel (''). Эта команда с аргументом в виде пустой строки снимает вывод обозначения горизонтальной оси на двух верхних графиках. Если этого не сделать, то символ «х» окажется наложенным на наименование функций нижних графиков, которое команда ezpl ot выводит над графиками автоматически.
1.gif
12. Тригонометрические и обратные им функции
Тригонометрические и обратные им функции
В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.
Э acos (X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.
Примеры:
»Y = acos (0.5)
1.0472
» acos([0.5 1 2])
ans =
1.0472 0 0 + 1.31701
-
acot (X) — возвращает арккотангенс для каждого элемента X. Пример:
» Y=acot(0.l)
у =
1.4711
-
acsc(X) — возвращает арккосеканс для каждого элемента X. Пример:
» Y= acsc(3)
0.3398
-
asec(X) — возвращает арксеканс для каждого элемента X. Пример:
» Y=asec(0.5)
Y =
0 + 1.31701
-
asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:
» Y= asin (0.278)
Y =
0.2817
-
atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:
» Y=atan(1)
Y =
0.7854
-
atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].
Пример:
» atan2(l,2)
ans =
0.4636
-
cos(X) — возвращает косинус для каждого элемента X. Пример:
»Х=[123];
» cos(X)
ans =
0.5403 -0.4161 -0.9900
-
cot(X) — возвращает котангенс для каждого элемента X. Пример:
» Y = cot(2)
Y =
-0.4577
-
csc(X) — возвращает косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csc(X)
Y =
1.0998 -1.0006 -1.0428
1.1985 1.1884 7.0862
-
sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:
» X=[pi/10 pi/3 pi/5];
» sec(X)
ans =
1.0515 2.0000 1.2361
-
sin(X) — возвращает синус для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sin(X)
ans =
1.0000 0.7071 0.5000 0.0000
-
tan(X) — возвращает тангенс для каждого элемента X.
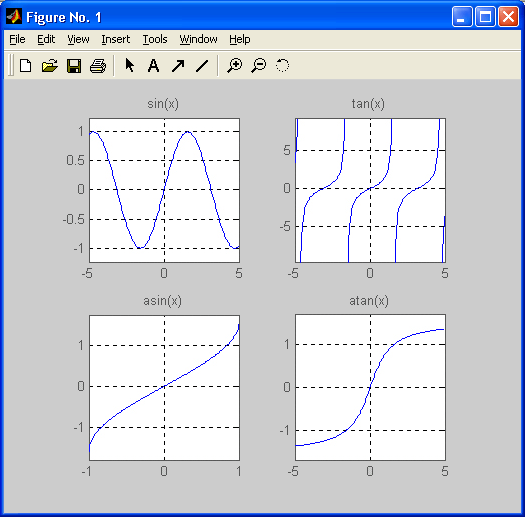
Рис. 8.2. Графики четырех тригонометрических функций
Пример:
» Х=[0.08 0.06 1.09]
X=
0.0800 0.0600 1.0900
» tan(X)
ans=
0.802 0.0601 1.9171
Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):
syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel("),gnd on
subplot(2.2.2),ezp"lot(tan(x).[-5 5]).xlabel(").grid on
subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on
subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on
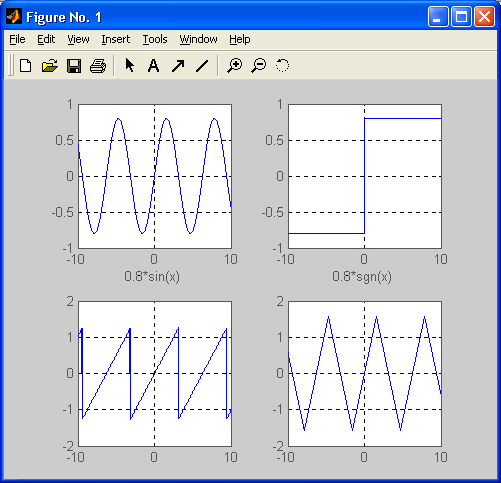
Поскольку многие тригонометрические функции периодичны, появляется возможность формирования из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы, используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных сигнала — прямоугольные, пилообразные и треугольные импульсы:[ В пакете расширения Signal Processing Toolbox есть специальные функции для генерации таких сигналов — square и sawtooth. — Примеч. ред. ]
х=-10:0.01:10;
subplot(2,2.1).plot(x.0.8*sin(x))
.x label('0.8*sin(x)')
subplot(2.2,2).plot(x,0.8*sign(sin(x)))
.x1abel('0.8*sgn(sin(x))')
subplot(2.2.3),plot(x.atan(tan(x/2)))
.xlabel('atan(tan(x/2))')
subplot(2.2.4),plot(x,asin(sin(x)))
.xlabel('asin(sin(x))')
Соответствующие графики представлены на рис. 8.3.
Рис. 8.3. Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний
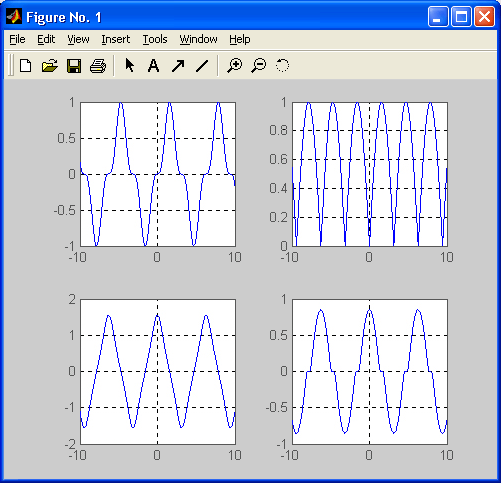
Дополнительный ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:
х=-10:0.01:10;
subplot(2.2.1).plot(x.sin(x). A 3).x1abel('sin(xr3')
subplot(2.2.2).plot(x,abs(s1n(x)))
.xlabel('abs(sin(x))').axis([-10 10 -1 1]),
subplot(2.2,3),plot(x,tan(cos(x)))
.xlabel('tanCcos(x))')
subplot(2.2.4).plot(x.csch(sec(x))),xlabeK'csch(sec(x))')
Рис. 8.4. Графики периодических сигналов без разрывов
Эти графики неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения (или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.
2.gif
3.gif
4.gif
13. Гиперболические и обратные им функции
Гиперболические и обратные им функции
Наряду с тригонометрическими функциями в математических расчетах часто используются и гиперболические функции. Ниже приводится список таких функций, определенных в системе MATLAB. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Все углы в тригонометрических функциях измеряются в радианах.
-
acosh(X) — возвращает гиперболический арккосинус для каждого элемента X. Пример:
»Y= acosh (0.7)
Y =
0 + 0.7954i
-
acoth(X) — возвращает гиперболический арккотангенс для каждого элемента X. Пример:
»Y = acoth (0.1)
Y=
0.1003 + 1.5708i
-
acsch(X) — возвращает гиперболический арккосеканс для каждого элемента X. Пример:
» Y = acsch(1)
Y =
0.8814
-
asech(X) — возвращает гиперболический арксеканс для каждого элемента X. Пример:
» Y = asech(4)
Y =
0 + 1.3181i
-
asinh(X) — возвращает гиперболический арксинус для каждого элемента X. Пример:
» Y = asinh (2.456)
Y =
1.6308
-
atanh(X) — возвращает гиперболический арктангенс для каждого элемента X. Пример:
» Х=[0.84 0.16 1.39];
» atanh (X)
ans =
1.2212 0.1614 0.9065 + 1.5708i
-
cosh(X) — возвращает гиперболический косинус для каждого элемента X. Пример:
» Х=[1 23];
» Cosh(X)
ans =
1.5431 3.7622 10.0677
-
coth(X) — возвращает гиперболический котангенс для каждого элемента X. Пример:
» Y = coth(3.987)
Y =
1.0007
-
csch(x) — возвращает гиперболический косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csch(X)
Y =
0.2757 0.0186 0.0135
0.8656 0.8509 0.0998
-
sech(X) — возвращает гиперболический секанс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sech(X)
ans =
0.3985 0.7549 0.8770 0.0863
-
sinh(X) — возвращает гиперболический синус для каждого элемента X. Пример:
» X=[pi/8 pi/7 pi/5 pi/10];
» sinh(X)
ans =
0.4029 0.4640 0.6705 0.3194
-
tanh(X) — возвращает гиперболический тангенс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi/10];
»tanh(X)
ans =
0.9172 0.6558 0.4805 0.3042
Следующий m-файл-сценарий строит графики ряда гиперболических функций:
syms x
subplot(2,2,l).ezplot(sinh(x).[-4 4]).xlabel(").grid on
subplot(2,2.2).ezplot(cosh(x).[-4 4]).xlabel('').grid on
subp1ot(2.2,3).ezplot(tanh(x).[-4 4]).grid on
subplot(2.2.4).ezplot(sech(x).[-4 4]).grid on
Нетрудно заметить, что гиперболические функции в отличие от тригонометрических не являются периодическими. Выбранные для графического представления функции дают примеры характерных нелинейностей.
В другом файле использованы команды для построения графиков ряда обратных гиперболических функций:
syms x
subplot(2,2.1).ezplot(asinh(x).[-4 4]).xlabel(").grid on
subplot(2.2.2),ezp1ot(acosh(x).[0 4]).xlabel(").grid on
subplot(2,2.3),ezplot(atanh(x).[-l l]).grid on
subplot(2.2.4).ezplot(asech(x).[0 l]).grid on
На этих графиках хорошо видны особенности данного класса функций. Такие функции, как обратный гиперболический синус и тангенс, «ценятся» за симметричный вид их графиков, дающий приближение к ряду типовых нелинейностей.
14. Функции округления и знака
Функции округления и знака
Ряд особых функций служат для выполнения операций округления числовых данных и анализа их знака.
-
fix(A) — возвращает массив А с элементами, округленными до ближайшего к нулю целого числа. Для комплексного А действительные и мнимые части округляются отдельно.
Примеры:
» А=[1/3 2/3: 4.99 5.01]
А =
0.3333 0.6667
4.9900 5.0100
» fix(A)
ans =
0 0
4 5
-
floor(A) — возвращает А с элементами, представляющими ближайшее меньшее или равное соответствующему элементу А целое число. Для комплексного А действительные и мнимые части преобразуются отдельно.
Примеры:
» А=[-1/3 2/3: 4.99 5.01]
А =
-0.33330.6667
4.99005.0100
» floor(А)
ans =
-1 0 4 5
-
ceil (A) — возвращает ближайшее большее или равное А целое число. Для комплексного А действительные и мнимые части округляются отдельно.
Примеры:
» а=-1.789;
» ceil (а)
ans =
-1
» а=-1.789+1*3.908;
» cei l(а)
ans =
-1.0000 + 4.0000i
-
rem(X,Y) — возвращает X - fix(X./Y).*Y, где fix(X./Y) — целая часть от частного X/Y.
Если операнды X и Y имеют одинаковый знак, функция rem(X, Y) возвращает тот же результат, что mod(X.Y). Однако (для положительных X и Y) rem(-x.y) = mod(-x,y)-y. Функция rem возвращает результат, находящийся между 0 и sign(X)*abs(Y). Если Y=0, функция rem возвращает NaN. Аргументы X и Y должны быть целыми числами. Из-за неточного представления в компьютере чисел с плавающей запятой использование вещественных (или комплексных) входных аргументов может привести к непредвиденным результатам.
Пример:
» Х=[25 21 23 55 3];
» Y=[4 8 23 6 4];
» rem(X.Y)
ans=
15013
-
round(X) — возвращает округленные до ближайшего целого элементы массива X. Для комплексного X действительные и мнимые части округляются отдельно.
Пример:
» Х=[5.675 21.6+4.897*1 2.654 55.8765];
» round(X)
ans =
6.0000 22.0000 +5.0000i 3.0000 56.0000
-
sign(X) — возвращает массив Y той же размерности, что и X, где каждый из элементов Y равен:
-
1, если соответствующий элемент X больше 0;
-
0, если соответствующий элемент X равен 0;
-
-1, если соответствующий элемент X меньше 0. Для ненулевых действительных и комплексных X — Sign(X)=X./abs(X).
-
Пример:
» Х=[-5 21 2 0 -3.7]:
» sign(X)
ans =
-1 1 1 0 -1
15. Функции комплексного аргумента
Функции комплексного аргумента
Для работы с комплексными числами и данными в MATLAB используются следующие функции:
-
angle(Z) возвращает аргумент комплексного числа в радианах для каждого элемента массива комплексных чисел Z. Углы находятся в диапазоне [-р; +р]. Для комплексного Z модуль и аргумент вычисляются следующим образом: R = abs(Z) — модуль, theta = angle(Z) — аргумент. При этом формула Z = R.*exp(i*theta) дает переход от показательной формы представления комплексного числа к алгебраической.
Примеры:
» Z=3+i*2
Z =
3.0000 + 2.00001
» theta = angle(Z)
theta =
0.5880
» R = abs(Z)
R =
3.6056
» Z =R.*exp(i*theta)
Z =
3.0000 + 2.00001
-
imag(Z) — возвращает мнимые части всех элементов массива Z. Пример:
» Z-[1+i, 3+2i, 2+3i];
» imag(Z)
ans =
1 2 3
-
real(Z) — возвращает вещественные части всех элементов комплексного массива Z. Пример:
» Z=[1+i. 3+2i 2+3i]:
» real(Z)
ans =
1 3 2
-
conj(Z) — возвращает число, комплексно-сопряженное аргументу Z. Если Z комплексное, то conj(Z) = real(Z) - i *imag (Z). Пример:
» conj(2+31)
ans=
2.0000 - 3.00001
16. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Применять арифметические операторы и функции.
-
Использовать операторы отношения и их функции.
-
Применять логические операторы.
-
Использовать специальные символы.
-
Использовать системные переменные и константы.
-
Работать с функциями поразрядной обработки, множествами, функциями времени и даты.
-
Использовать элементарные функции и строить их графики.
-
Работать с функциями округления и анализа знака.
-
Использовать функции комплексного аргумента.



