4.2.3. Независимые источники сигналов

Стандартные сигналы

Независимые источники напряжения (V) и тока (I) стандартного вида описываются предложениями

Vxxx <+узел> <-узел> [[DC] <значение>] [АС <модуль> [<фаза>]] + [STIMULUS=<имя сигнала>] + [спецификация сигнала]

Ixxx <+узел> <-узел> [[DC] <значение>] [АС <модуль> [<фаза>]] + [STIMULUS=<имя сигнала>] + [спецификация сигнала]

После ключевого слова STIMULUS указывается имя сигнала, созданного с помощью программы Stimulus Editor. При анализе переходных процессов можно использовать один из стандартных сигналов с помощью конструкции <спецификация сигнала>, имеющей вид:

PULSE <параметры> - импульсный сигнал;

SIN <параметры> - синусоидальный сигнал;

ЕХР <параметры> - сигнал экспоненциальной формы;

PWL <параметры> - кусочно-линейный сигнал;

SFFM <параметры> - гармонический сигнал с синусоидальной частотной модуляцией.

Источники могут использоваться во всех видах анализа. По умолчанию все параметры принимают нулевые значения. Параметр DC определяет постоянную составляющую источника напряжения или тока. Для режима АС задаются модуль и фаза (в градусах) источника гармонического сигнала. Приведем примеры:

IBIAS 1302.3MA

VAC 2 3 АС .001

VACPHS 2 3 АС .001 90

13 26 77 DC 0.002 АС 1 SIN(.002 0.05 1.5MEG)

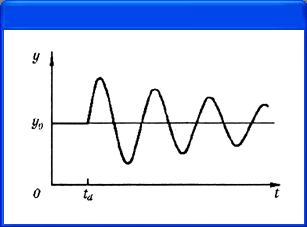
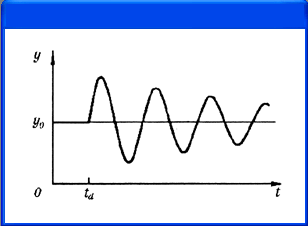
При анализе переходных процессов задаются следующие виды временных зависимостей.

Экспоненциальная функция задается списком параметров

ЕХР (y ₁ у ₂ t _d t _cr t _r t _fr )

и описывается выражением

y, при 0 < t < t _d ;

У1 + (У ₂ -y ₍ ){l-exp[-(t-t _d ) / t _cr ]}uput _d <t<t/, '

y _l+ (y ₂ -y _l ){l-exp[-(t-t _d )/t _CГ }- 1 + exp[-(t - t _r ) / t _lr ]}npu t _r < t < TSTEP.

График этой функции приведен на рис. 4.12, а назначение ее параметров объясняется в табл. 4.20.

Таблица 4.20. Параметры экспоненциального сигнала

Приведем пример описания источника напряжения экспоненциальной формы: V1 3 4 ЕХР (0.02 2NS 20NS 40NS 20NS)

Рис. 4.12. Экспоненциальная функция

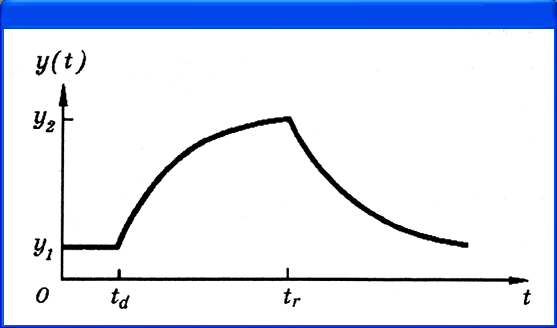
Импульсная функция (рис. 4.13) задается списком параметров

PULSE (y1 y2 t _d t _r t _f т Т)

Смысл ее параметров объясняется в табл. 4.21.

Таблица 4.21. Параметры импульсного сигнала

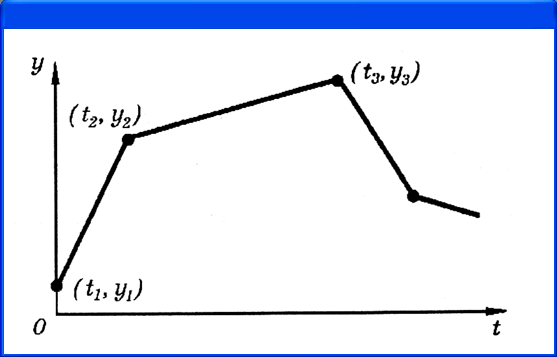
Кусочно-линейная функция задается списком параметров

PWL [TIME_SCALE_FACTOR=<значение>] [VALUE_SCALE_FACTOR=<значе ние>]

+ (точки_отсчета)*

В секции (точки_отсчета) помещаются следующие данные:

• (<t _n .y _n >) - координаты точек;
• FILE <имя файла> - чтение координат точек из файла;
• REPEAT FOR <п> (точки__отсчета)* ENDREPEAT - повторение п раз;
• REPEAT FOREVER (точки_отсчета)* ENDREPEAT -- бесконечное повторение.

PWL представляет собой кусочно-линейную функцию y(t). Соседние точки соединяются прямыми линиями (рис. 4.24). Максимальное количество точек для IBM PC составляет 3995.

Рис. 4.14. Кусочно-линейная функция

Приведем примеры.

1) Ступенчатое напряжение - 10 периодов по 1 мкс:

.PARAM N=1

.STEPPARAMN 1,5,1

V1 1 О PWL TIME_SCALE_FACTOR= 1е-6; Время задано в мкс

+ REPEAT FOR 10

+ (.25, 0) (.26, {N}) (.99, {N}) (1,0)

+ ENDREPEAT .

2) Считывание сигнала из файла:

V2 1 О PWL FILE triangle. in

В текстовом файле triangle. in содержатся значения отсчетов, например

(1ms, 1) (2ms, 0) (3ms, 1) (4ms, 0)

Синусоидальная функция задается списком параметров SIN fo и описывается выражением

Ее параметры описаны в табл. 4.22.

Таблица 4.22. Параметры гармонического сигнала

На рис. 4.15, а приведен график функции при d _f = 0, а на рис. 4.15, б - при d _f >0.

а)

б)

Рис. 4.15. Незатухающая (а) и затухающая (б) синусоидальные функции

Синусоидальная функция с частотной модуляцией задается списком параметров

SFFM (уо у _а f _c m f _m )

и описывается выражением

y(t) = yо ⁺ y _a sin[2nf _c t + msin(2лf _m )]

Ее параметры приведены в табл. 4.23.

Таблица 4.23. Параметры частотно-модулированного сигнала

 

Сигналы произвольной формы

В связи с тем, что программа PSpice имеет довольно бедный набор встроенных источников стандартных сигналов, интересно обсудить возможность генерации сигналов произвольной формы y(t). В этих целях можно использовать генератор цифровых сигналов (разд. 4.3), логические состояния которого при подключении к аналоговой части схемы автоматически преобразуются в импульсное электрическое напряжение, которое может служить источником сигнала. Таким образом, в частности, можно создать генератор псевдослучайных сигналов. При необходимости импульсное напряжение сглаживается аналоговым фильтром. Форма цифрового сигнала задается двояко:

• путем задания дискретных отсчетов (y _i , t _i ,) непосредственно в описании цифрового сигнала (конструкция STIM);
• путем предварительной записи отсчетов (y _i , t _i ) в файл, имя которого указывается в описании цифрового сигнала (конструкция FSTIM).

Второй способ предпочтительнее при формировании длинных отрезков реализаций сигналов сложной формы, в частности случайных сигналов. Отметим, что формируемые таким образом импульсные сигналы имеют постоянное значение на интервале между дискретными отсчетами: y(t)=y(t) при t _i < t < t _i+1 . Тем самым при постоянном шаге дискретизации t = t _i+l - t _t сигнал формируется с запаздыванием на t /2.