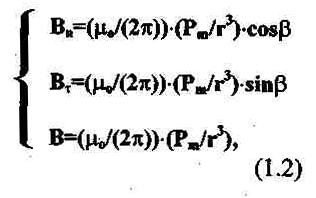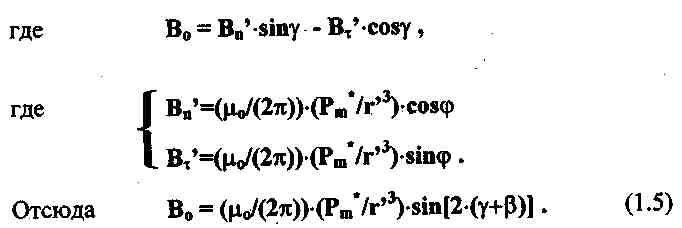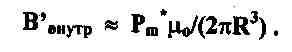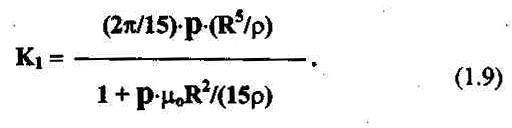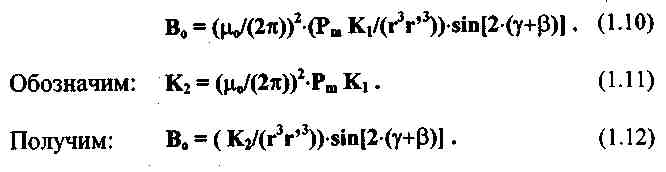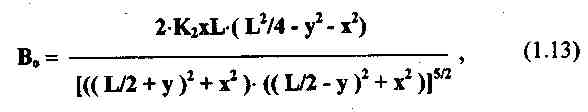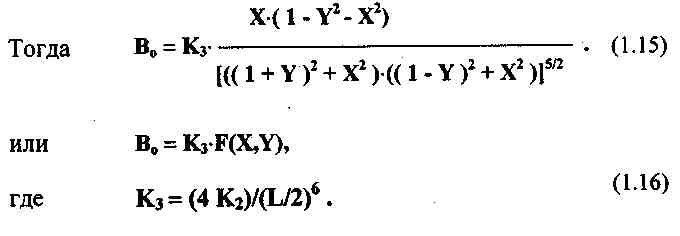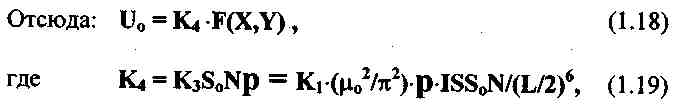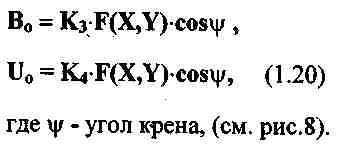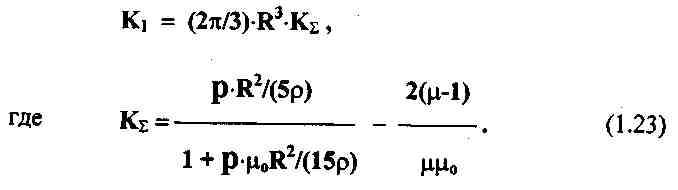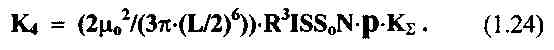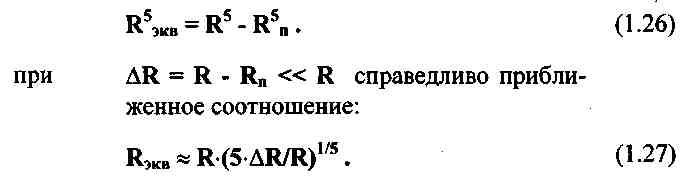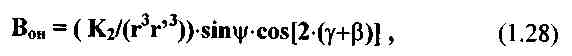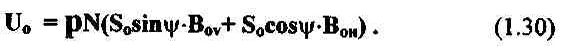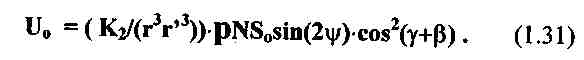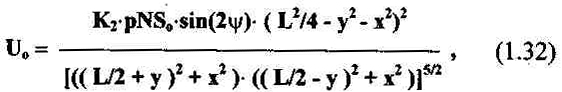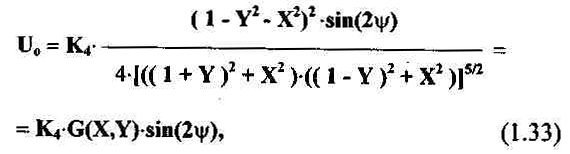3.1 Металлоискатель по принципу "передача-прием"
3.1 МЕТАЛЛОИСКАТЕЛЬ ПО ПРИНЦИПУ "ПЕРЕДАЧА-ПРИЕМ"
Термины "передача-прием" и "отраженный сигнал" в различных поисковых приборах обычно ассоциируются с методами типа импульсной эхо- и радиолокации, что является источником заблуждений, когда речь заходит о металлоискателях. В отличие от различного рода локаторов, в металлоискателях рассматриваемого типа как передаваемый сигнал (излучаемый), так и принимаемый сигнал (отраженный) являются непрерывными, они существуют одновременно и совпадают по частоте.
3.1.1. Принцип действия
3.1.1. Принцип действия
Принцип действия металлоискателей типа "передача-прием" заключается в регистрации сигнала, отраженного (или, как говорят, переизлученного) металлическим предметом (мишенью), см. [32], стр.225-228. Отраженный сигнал возникает вследствие воздействия на мишень переменного магнитного поля передающей (излучающей) катушки металлоискателя. Таким образом, прибор данного типа подразумевает наличие как минимум двух катушек, одна из которых является передающей, а другая приемной.
Основная принципиальная проблема, которая решается в металлоискателях данного типа, заключается в таком выборе взаимного расположения катушек, при котором магнитное поле излучающей катушки в отсутствие посторонних металлических предметов наводит нулевой сигнал в приемной катушке (или в системе приемных катушек). Таким образом, необходимо предотвратить непосредственное воздействие излучающей катушки на приемную. Появление же вблизи катушек металлической мишени приведет к появлению сигнала в виде переменной э.д.с. в приемной катушке.
3.1.2. Схемы датчиков
3.1.2. Схемы датчиков
Поначалу может показаться, что в природе существует всего два варианта взаимного расположения катушек, при котором не происходит непосредственной передачи сигнала из одной катушки в другую (см. рис.1 а и 16) - катушки с перпендикулярными и со скрещивающимися осями.
Рис. 1. Варианты взаимного расположения катушек датика металлоискателя по принципу "передача-прием ".
Более тщательное изучение проблемы показывает, что подобных различных систем датчиков металлоискателей может быть сколь угодно много, однако они будут содержать более сложные системы с количеством катушек больше двух, соответствующим образом включенных электрически. Например, на рис.1 в изображена система из одной излучающей (в центре) и двух приемных катушек, включенных встречно по сигналу, наводимому излучающей катушкой. Таким образом, сигнал на выходе системы приемных катушек в идеале равен нулю, так как наводимые в катушках э.д.с. взаимно компенсируются.
Особый интерес представляют системы датчиков с компланарными катушками (т.е. расположенными в одной плоскости). Это объясняется тем, что с помощью металлоискателей обычно проводят поиск предметов, находящихся в земле, а приблизить датчик на минимальное расстояние к поверхности земли возможно только в том случае, если его катушки компланарны. Кроме того такие датчики обычно компактны и хорошо вписываются в защитные корпуса типа "блина" или "летающей тарелки".
Основные варианты взаимного расположения компланарных катушек приведены на рис.2а и 26. В схеме на рис.2а взаимное расположение катушек выбрано таким, чтобы суммарный поток вектора магнитной индукции через поверхность, ограниченную приемной катушкой, равнялся нулю. В схеме рис.26 одна из катушек (приемная) скручена в виде "восьмерки", так что суммарная э.д.с., наводимая на половинки витков приемной катушки, расположенные в одном крыле "восьмерки", компенсирует аналогичную суммарную э.д.с., наводимую в другом крыле "восьмерки".
Рис. 2. Компланарные варианты взаимного расположения катушек металлоискателя по принципу "передача-прием ".
Возможны и другие разнообразные конструкции датчиков с компланарньми катушками, например рис.2в. Приемная катушка расположена внутри излучающей. Наводимая в приемной катушке э.д.с. компенсируется специальным трансформаторным устройством, отбирающим часть сигнала излучающей катушки.
Рис. 1. Варианты взаимного расположения катушек датика металлоискателя по принципу "передача-прием ".
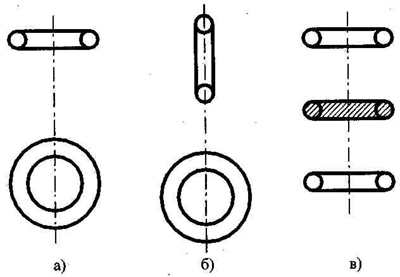
Рис. 2. Компланарные варианты взаимного расположения катушек металлоискателя по принципу "передача-прием ".
3.1.3. Теоретические соображения
3.1.3. Теоретические соображения
3.1.3.1. Система катушек с перпендикулярными осями
3.1.3.1. Система катушек с перпендикулярными осями
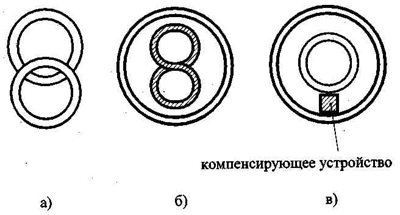
Рассмотрим более подробно взаимодействие датчика металлоискателя с металлической мишенью на примере системы катушек с перпендикулярными осями, рис.1 а. Для простоты рассмотрим систему с катушками, продольными размерами которых можно пренебречь. Будем в дальнейшем считать, что излучающая и приемная катушки представляют собой круглые бесконечно тонкие рамки (см. рис.3). Для такой рамки вектор магнитного момента при протекании тока I имеет вид:
Рис.3. Модель излучающей катушки.
Индукция магнитного поля, создаваемого тауой рамкой на большом расстоянии г от ее центра (см. рис.4), составляет:
Рис. 4. Компоненты вектора индукции магнитного поля излучающей катушки.
полагая ,что r>>ЦS, а индексы "n" и "t" обозначают соответственно нормальную и тангенциальную составляющие вектора магнитной индукции.
Рассмотрим взаимодействие излучающей рамки, приемной рамки и объекта в случае катушек с перпендикулярными осями (см. рис.5).
Рис. 5. Взаимное расположение катушек датчика металлоискателя и объекта (мишени).
Угол между осью симметрии системы катушек и вектором индукции поля В излучающей катушки равен 2р, так как силовые линии вследствие соотношений (1.2) являются окружностями, и ввиду допущения о малых размерах катушек:
где L - так называемая база датчика металлоискателя (см. рис.5).
Рис. 3. Модель излучающей катушки - формулы

Рис. 3. Модель излучающей катушки.
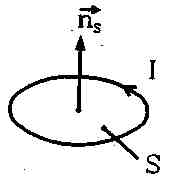
Рис. 4. Компоненты вектора индукции магнитного поля излучающей катушки.
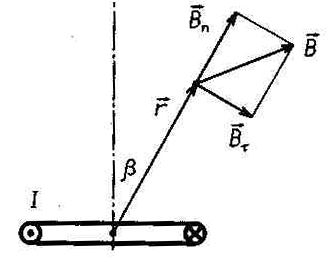
Рис. 5. Взаимное расположение катушек датчика металлоискателя и объекта (мишени).
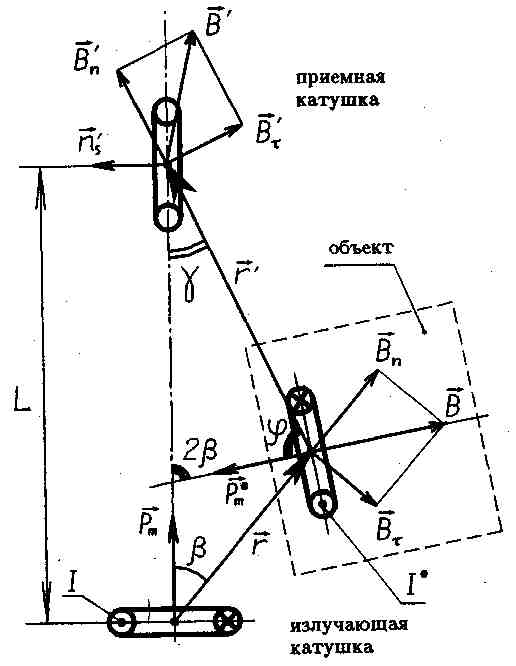
Ф. 1.2 Индукция магнитного поля
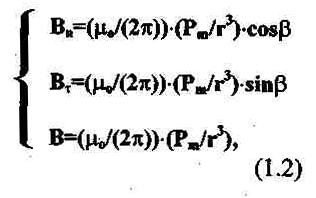
Ф. 1.3 Определение угла между осью симметрии системы катушек и вектором индукции поля В

3.1.3.2. Отражение сигнала за счет проводимости объекта
3.1.3.2. Отражение сигнала за счет проводимости объекта
Проводящий металлический объект, размеры которого пока будем также считать небольшими, по крайней мере, не превосходящими r и r' (см. рис.5), с точки зрения переизлучения магнитного поля, можно представить в виде эквивалентной рамки с токомI*, вектор магнитного момента которой Рm* практически параллелен вектору индукции излучающей катушки В.
Величина Рm* зависит от размеров проводящего объекта, его проводимости, от индукции поля в точке расположения объекта, от частоты излучаемого поля. Индукция поля переизлучения имеет в центре приемной катушки ненулевую составляющую Во в направлении вектора нормалиns', что приводит к появлению в этой катушке э.д.с., пропорциональной указанной составляющей:
Рис. 6. К расчету магнитного момента эквивалентного шара.
Для того, чтобы вычислить магнитный момент эквивалентной рамкиРm*, необходимо взять интеграл по всему объему проводящего объекта так, чтобы просуммировать вклады всех элементарных кольцевых токов, наведенных полем излучающей катушки, в итоговую величину Рm*. Для простоты будем считать, что магнитное поле по всему объему проводящего объекта однородно, то есть он удален на значительное расстояние от излучающей катушки. Чтобы не возникало проблем с ориентацией объекта, будем пока считать, что он имеет форму однородного шара (см. рис.б). Считая, что проводящий объект удален на значительное расстояние и от приемной катушки, можно записать:
Пренебрегая явлением самоиндукции, влияние которого будет рассмотрено ниже, получаем:
Чтобы учесть явление самоиндукции, предположим для простоты, что переизлученное поле однородновнутри объекта-мишени и, исходя из величины магнитного момента (1.7), составляет:
Подставив в выражение (1.7) В -В'внутр вместо В, получим по-прежнему пропорциональную зависимость Рm* отВ, но с несколько иным коэффициентом K1:
Составляющая индукции в центре приемной катушки:
В системе декартовых координат с началом в середине базы системы катушек (см. рис.7) последнее выражение принимает вид:
Введем нормированные координаты:
Определим с точностью до знака э.д.с., наводимую в приемной катушке:
где So - площадь сечения приемной катушки, N - количество ее витков.
где S - площадь сечения излучающей катушки, I - суммарный ток всех ее витков.
В трехмерном пространстве, когда плоскость XOY не перпендикулярна плоскости приемной рамки,
Рис. 7. Система координат.
Рис.8. Ориентация объекта по крену.
Рис. 6. К расчету магнитного момента эквивалентного шара.
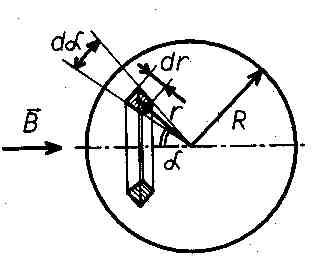
Рис. 7. Система координат.
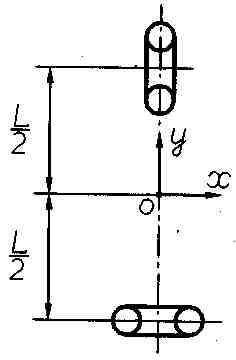
Рис.8. Ориентация объекта по крену.
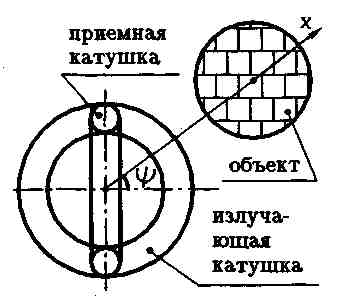
Ф. 1.10 Составляющая индукции в центре приемной катушки
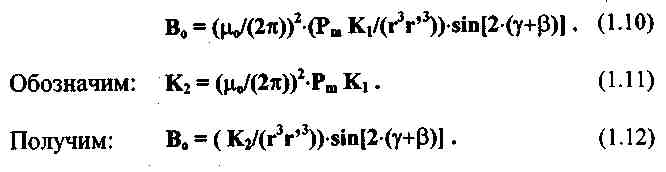
Ф. 1.13 В системе декартовых координат с началом в середине базы системы катушек
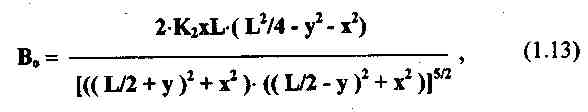
Ф. 1.14 С нормированными координатами

Ф. 1.15 Определение индукции поля
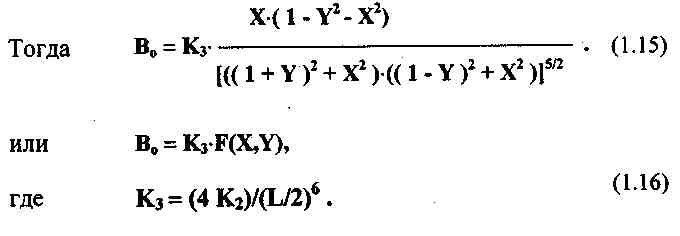
Ф. 1.17 ЭДС наводимая в приемной катушке
Ф. 1.18 ЭДС наводимая в приемной катушке
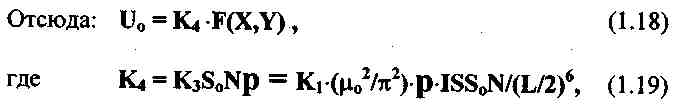
Ф. 1.20 Определение ЭДС
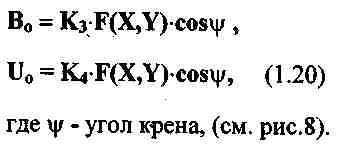
Ф. 1.4 Индукция поля переизлучения
Ф. 1.5 Магнитный момент
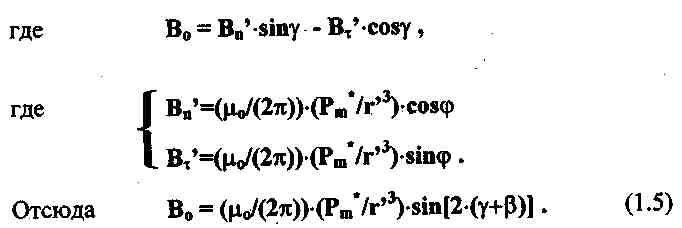
Ф. 1.6 Магнитный момент удаленный на значительное расстояние

Ф. 1.7 Магнитный момент без учета явления самоиндукции

Ф. 1.8 Переизлученное поле однородно внутри объекта-мишени
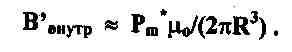
Ф. 1.9 Магнитный момент
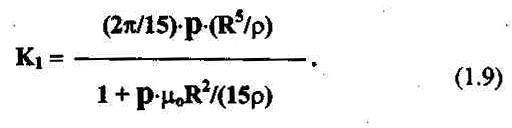
3.1.3.3.Отражение сигнала за счет ферромагнитных свойств объекта
3.1.3.3.Отражение сигнала за счет ферромагнитных свойств объекта
Ферромагнитный объект, размеры которого будем считать также небольшими, по крайней мере, не превосходящими r и rў (см. рис.5), с точки зрения искривления магнитного поля, можно представить в виде эквивалентной рамки с током I*, вектор магнитного момента которойРm*практически параллелен вектору индукции излучающей катушки В.
Величина Рm* зависит от размеров ферромагнитного объекта, его магнитной проницаемости, от индукции поля в точке расположения объекта. Для того, чтобы вычислить магнитный момент эквивалентной рамки Рm*, необходимо взять интеграл по всему объему ферромагнитного объекта так, чтобы просуммировать вклады всех амперовых токов, возникающих в ферромагнетике под действием внешнего поля излучающей катушки.Для шарового однородного объекта получим:
где В - индукция магнитного поля, m - магнитная проницаемость материала объекта, R - радиус объекта - шара.
Все выражения, полученные выше для проводящего объекта, останутся в силе, если в них для данного случая положить:
Ф.1 Сумма всех амперовых токов, возникающих в ферромагнетике под действием внешнего поля излучающей катушки для шарового однород

Ф.2 Преобразованная формула

3.1.3.4.Суперпозиция проводящих и ферромагнитных свойств объекта
3.1.3.4.Суперпозиция проводящих и ферромагнитных свойств объекта
Учет одновременно электропроводных и ферромагнитных свойств объекта в виде шара приводит к следующему значению коэффициента K1:
Нормирующий коэффициент К4, входящий в выражение для напряжения в приемной катушке, составляет:
Численная оценка (1.23) показывает, например, что модули слагаемых в выражении при типовой частоте излучаемого поля 10(кГц) становятся соизмеримы при радиусе шарового объекта порядка 1(см) и при условии наличия у объекта ферромагнитных свойств. Кроме того, зависимость первого слагаемого от оператора Лапласа говорит о том, что фаза отраженного сигнала будет изменяться в зависимости от соотношения у объекта - мишени электропроводных и ферромагнитных свойств, а также от проводимости материала и размеров объекта. На этом явлении основан принцип действия дискриминаторов современных металлоискателей, то есть электронных устройств, позволяющих по фазовому сдвигу отраженного от объекта сигнала оценить свойства объекта (с определенной вероятностью даже тип металла).
Ф.1 Учет электропроводных и ферромагнитных свойств объекта в виде шара
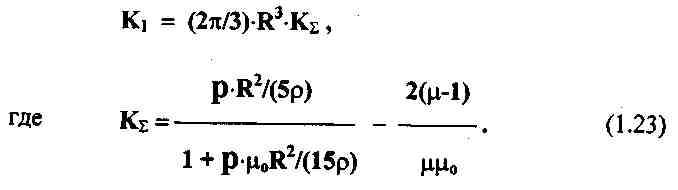
Ф.2 Расчет нормирующего коэффициента
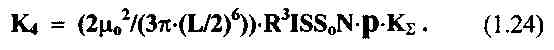
3.1.3.5.Учет формы объекта
3.1.3.5.Учет формы объекта
Полученные ранее выражения, как указывалось, были справедливы только для формы объекта - мишени в виде однородного шара. Очевидно, что воздействие объектов более сложной формы можно свести к воздействию некоторого эквивалентного шара с радиусом Rэкв.
Наведенное в приемной катушке напряжение, обусловленное проявлением только ферромагнитных свойств, для шарового объекта пропорционально его объему (см. выражение (1.22)). Поэтому, для не слишком протяженных объектов более сложной формы, в первом приближении, можно считать эквивалентным такой шар, объем которого совпадает с объемом ферромагнетика у объекта сложной формы. Для этого случая:
где V - объем ферромагнетика.
С напряжением, наведенным в приемной катушке за счет переизлучения от проводящего объекта, ситуация более сложная. В случае больших объектов с хорошей электропроводностью выражение (1.9) и соответственно наведенное в приемной катушке напряжение также пропорционально объему объекта (то естьR^3) и радиус эквивалентного шара также вычисляется по формуле (1.25). В случае небольших объектов с плохой электропроводностью подход иной. В этом случае общее выражение (1.9) вырождается в частный случай (1.8). Рассмотрим вначале влияние шаровой полости с радиусом Rп внутри шарового объекта на Rэкв. Воспользовавшись принципом суперпозиции, представим результат воздействия шарового объекта с полостью как разность результатов воздействия сплошного шара и шара с радиусом Rп. В соответствии с (1.8), имеет место соотношение:
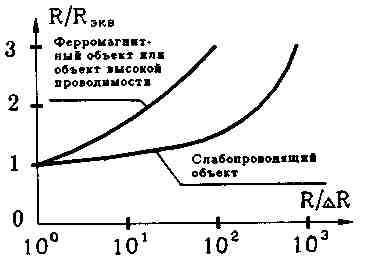
На рис.9 приведены графики зависимости R/Rэкв от R/DR для полого слабоэлектропроводного и для полого ферромагнитного шара. Из графика видно, что для не
Рис.9. Влияние толщины стенки полого шара на эквивалентный радиус.
слишком тонкостенных шаров из слабопроводящего материала Rэкв»R. Следовательно, в отличие от ферромагнитного шара и от шара высокой проводимости, для слабопроводящего шара, в первом приближении, безразлично сплошной он или полый. Его влияние на процесс переизлучения определяется, в основном, линейным размером, то есть R. Поэтому, в случае не слишком протяженных плохопроводящих объектов более сложной формы, в том числе и полой, в первом приближении, можно считать эквивалентным такой шар, радиусRэкв которого равен половине среднего характерного размера объекта.
Приведенный выше вывод хорошо подтверждается на практике в виде существенного отклика металлоискателя от ничтожных по массе обрывков металлической алюминиевой фольги, которая практически попадается везде, где оставила свой след современная цивилизация.
Рис.9. Влияние толщины стенки полого шара на эквивалентный радиус.
Ф. 1.25 Расчет воздействия некоторого эквивалентного шара с радиусом Rэкв
Ф. 1.26 Влияние шаровой полости с радиусом Rп внутри шарового объекта на Rэкв
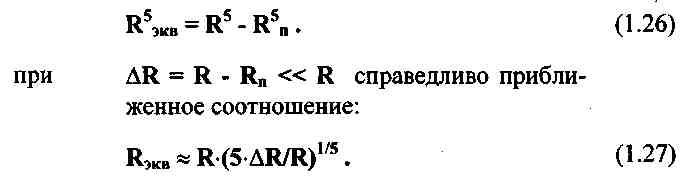
3.1.3.6.Система катушек со скрещенными осями
3.1.3.6.Система катушек со скрещенными осями
Рис. 10. Ориентация датчика по крену.
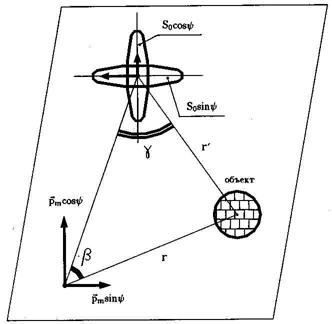
Вид вдоль оси датчика металлоискателя при таком расположении катушек приведен на рис.10. Для расчета такой схемы удобно воспользоваться принципом суперпозиции и разложить вектор магнитного момента излучающей катушки и площадь приемной катушки на вертикальную и горизонтальную составляющие (проекции, см. рис.11).
Для горизонтальной составляющей, проекция индукции поля в приемной катушке Вон будет попрежнему определяться соотношением (1.4). Однако, иная ориентация магнитного момента дает (с точностью до знака) результат:
где К2 определяется по формуле (1.11).
Вертикальная составляющая индукции поля в приемной катушкеBov перпендикулярна векторамr и r' и не зависит в явном виде от углов g и b:
Рис.11. Разложение магнитного момента и площади приемной катушки на составляющие.
ЭДС в приемной катушке Uo , с точностью до знака, составляет:
Отсюда получаем:
В декартовой системе координат с началом в середине базы системы катушек (см. рис.5) получим:
Введя нормированные координаты (1.14), получим:
где К4 вычисляется по формуле (1.19) или (1.24).
Рис. 10. Ориентация датчика по крену.
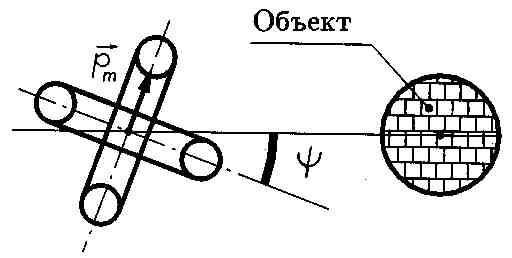
Рис.11. Разложение магнитного момента и площади приемной катушки на составляющие.
Ф. 1.28 Проекция индукции поля в приемной катушке
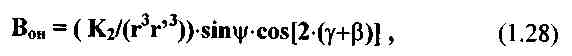
Ф. 1.29 Вертикальная составляющая индукции поля в приемной катушке

Ф. 1.30 ЭДС в приемной катушке Uo
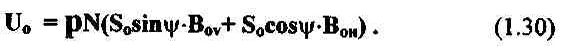
Ф. 1.31 ЭДС в приемной катушке Uo
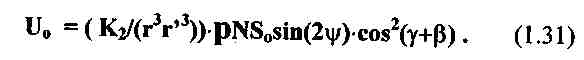
Ф. 1.32 ЭДС в приемной катушке Uo в декартовой системе координат с началом в середине базы системы катушек
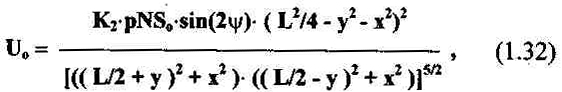
Ф. 1.33 ЭДС в приемной катушке с нормированными резуьтатами
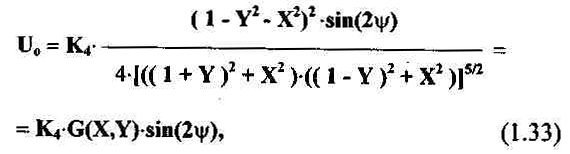
3.1.4. Практические соображения
3.1.4. Практические соображения
Чувствительность металлоискателя зависит, в первую очередь от его датчика. Для рассмотренных вариантов датчиков чувствительность определяется формулами (1.20) и (1.33). При оптимальной для каждого случая ориентации ориентации датчика на объект по углу крена y, она определяется одним и тем же коэффициентом K4 и функциями нормированных координат F(X,Y) иG(X,Y). Для сравнения, в квадрате ХО[-4,4], YО[-4,4], модули этих функций приведены в виде аксонометрического набора сечений в логарифмическом масштабе на рис.12 и рис.13.
Первое, что бросается в глаза - это ярко выраженные максимумы вблизи точек расположения катушек датчика (0,+1) и (0,-1). Максимумы функций F(X,Y) иG(X,Y) не представляют практического интереса и для удобства сравнения функций обрезаны по уровню 0(дБ). Из рисунков и из анализа функций F(X,Y) иG(X,Y) также видно, что в указанном квадрате модуль функции F практически везде немного превосходит модуль функции G, за исключением самых удаленных точек по углам квадрата и за исключением узкой области вблизи Х=0, где у функции F имеет место "овраг".
Асимптотическое поведение указанных функций вдали от начала координат можно проиллюстрировать при Y=0. Оказывается, что модуль функции F убывает с расстоянием пропорционально х^(-7), а модуль функции G - пропорционально х^(-6). К сожалению, преимущество функции G по чувствительности проявляется лишь на больших расстояниях, превышающих практический радиус действия
Рис. 12. График функции F(X,Y).
Рис.13. График функции G(X,Y).
металлоискателя. Одинаковые значения модулей F и G получаются при Х»4,25.
Очень важное практическое значение имеет "овраг" функцииF. Во-первых, он свидетельствует о том, что датчик системы катушек с перпендикулярными осями имеет минимальную (теоретически нулевую) чувствительность к металлическим предметам, расположенным на его продольной оси. Естественно, к этим предметам относятся и многие элементы конструкции самого датчика. Следовательно, отраженный от них бесполезный сигнал будет намного меньше, чем у датчика системы катушек со скрещивающимися осями. Последнее очень важно, учитывая, что отраженный сигнал от металлических элементов самого датчика может на несколько порядков превосходить полезный сигнал (ввиду близости этих элементов к катушкам датчика). Дело не в том, что бесполезный сигнал от металлических элементов конструкции датчика трудно скомпенсировать. Основная сложность заключается в малейших изменениях этих сигналов, которые обычно вызываются тепловыми и особенно механическими деформациями указанных элементов. Эти малейшие изменения могут быть уже сопоставимы с полезным сигналом, что приведет к неверным показаниям или ложным срабатываниям прибора.Во-вторых, если с помощью металлоискателя системы катушек с перпендикулярными осями некоторый небольшой объект уже обнаружен, то направление его точного местонахождения может быть легко "запеленговано" по нулевому значению сигнала металлоискателя при точной ориентации его продольной оси на объект (при любых ориентациях по крену). Учитывая, что площадь "захвата" датчика при поиске может составлять несколько квадратньк метров, последнее качество системы катушек с перпендикулярными осями весьма полезно на практике (меньше бесполезных раскопок).
Следующая особенность графиков функцийF(X,Y) и G(X,Y) - наличие кольцеобразного "кратера" нулевой чувствительности, проходящего через центры катушек (окружность единичноо радиуса с центром в точке (0,0)). На практике эта особенность позволяет определять расстояние до небольших объектов. Если обнаружится, что на некотором конечном расстоянии отраженный сигнал зануляется (при оптимальной ориентации по крену) - значит, расстояние до объекта составляет половину базы прибора, то есть величину L/2.
Необходимо также отметить, чтодиаграммы направленности по углу крена y для датчиков металлоискателей с различным взаимным расположением катушек также различаются. На рис.14б приведена диаграмма направленности прибора с перпендикулярньми осями у катушек, а на рис.14а - со скрещивающимися. Очевидно, что вторая диаграмма более предпочтительна, так имеет меньшее количество зон нечувствительности по крену и меньшее количество лепестков.
Для того, чтобы оценить зависимость наведенного в приемной катушке напряжения от параметров металлоискателя и объекта, надо проанализировать выражение (1.19) для коэффициента К4. Наведенное в приемной катушке напряжение пропорционально (L/2)^6. На величину L/2 нормируются и аргументы функций F и G, убывание которых происходит с 6-й - 7-й степенью расстояния. Поэтому, в первом приближении, при прочих равных условиях,чувствительность металлоискателя не зависит от его базы.
Рис.14. Диаграммы направленности по крену датчиков систем катушек:
- со скрещивающимися осями (а)
- с перпендикулярными осями (б).
Однако, в некоторых случаях конструкция датчика с большей базой может оказаться более предпочтительной, так как в этом случае меньшим будет неизбежное паразитное проникновение сигнала непосредственно из излучающей катушки в приемную.
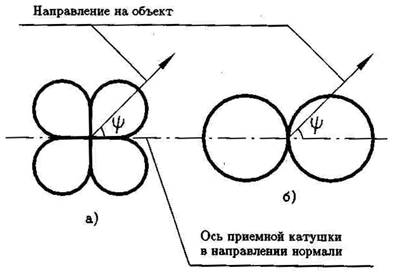
Для того, чтобы проанализировать селективность металлоискателя, то есть его способность различать объекты, изготовленные из различных металлов или сплавов, необходимо обратиться к выражению (1.23). Металлоискатель может различать объекты по фазе отраженного сигнала. Для того, чтобы разрешающая способность прибора по типу металлов была максимальной, необходимо соответствующим образом выбрать частоту сигнала излучающей катушки, так, чтобы фаза отраженного от объектов сигнала составляла около 45°. Это - середина диапазона возможных изменений фазы первого слагаемого выражения (1.23), и там крутизна фазочастотной характеристики максимальна. Второе слагаемое выражения (1.23) считаем нулевым, так как при поиске в первую очередь нас интересует селективность по цветным металлам - неферромагнетикам. Естественно, оптимальный выбор частоты сигнала подразумевает знание типового размера предполагаемых объектов. Практически во всех зарубежных промышленных металлоискателях в качестве такого размера заложен размер монеты. Оптимальная частота составляет:
При типовом диаметре монеты 25(мм) ее объем составляет около 10^(-6) (м^3), что по формуле (1.25) соответствует эквивалентному радиусу около 0,6(см). Отсюда получаем оптимальное значение частоты около 1(кГц) при проводимости материала монеты 20(н0мЧм). В промышленных приборах частота обычно на порядок выше (по технологическим соображениям).
Рис. 12. График функции F(X,Y).
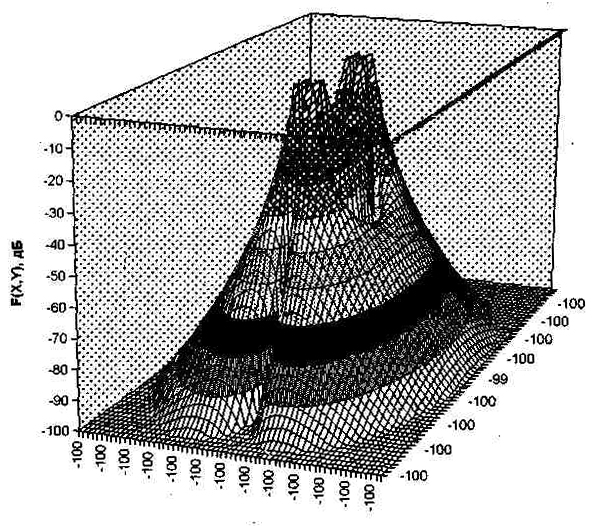
Рис.13. График функции G(X,Y).
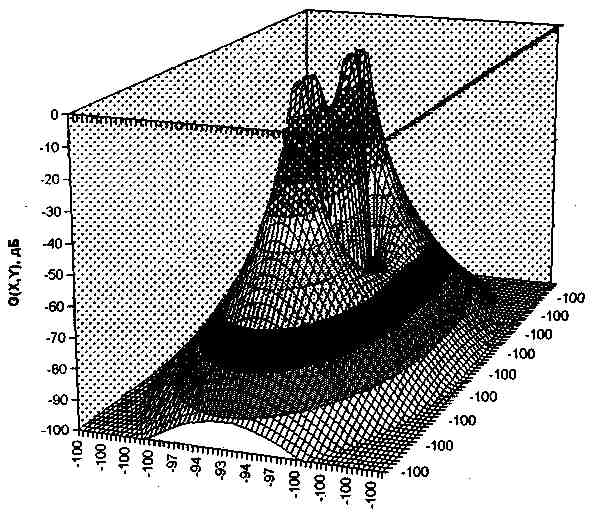
Рис.14. Диаграммы направленности по крену датчиков систем катушек:
Ф. 1.34 Оптимальная частота

3.1.5. Выводы
3.1.5. Выводы
1. По мнению автора, система катушек с перпендикулярными осями предпочтительнее для поиска кладов и реликвий, чем система катушек со скрещивающимися осями. При прочих равных условиях, первая система имеет чувствительность немного выше . Кроме того, с ее помощью гораздо проще определить ("запеленговать") точное направление, в котором следует искать обнаруженный объект.
2. Рассмотренные системы катушек имеют важное свойство, позволяющее оценивать расстояние до небольших объектов по занулению отраженного сигнала при расстоянии до объекта, равном половине базы.
3. При прочих равных условиях (размеры и число витков катушек, чувствительность приемного тракта, величина тока и его частота в излучающей катушке), чувствительность металлоискателя по принципу "передача-прием" практически не зависит от его базы, то есть от расстояния между катушками.