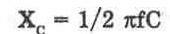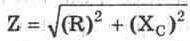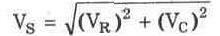5. Конденсаторы и переменный ток
ЭКСПЕРИМЕНТ 20 Конденсаторы и переменный ток
Цели
После проведения данного эксперимента Вы сможете рассчитывать и измерять токи и напряжения в последовательных и параллельных емкостных цепях.
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функций
* Источник постоянного напряжения
* Элементы:
один конденсатор 0, 01 мкф, один резистор, 10 кОм.
ВВОДНАЯ ЧАСТЬ
Когда конденсатор используется в цепи переменного тока, он оказывает определенное противодействие току, которое называется емкостным сопротивлением. Емкостное сопротивление, подобно индуктивному сопротивлению, противодействует протеканию тока, но только в цепи переменного тока. Емкостное сопротивление измеряется в омах и зависит от частоты переменного тока и от емкости конденсатора. Емкостное сопротивление обратно пропорционально частоте (f) и емкости (С). Это
емкостное сопротивление может быть рассчитано при помощи формулы:
Обычно конденсаторы комбинируются с резисторами и другими компонентами в различные последовательные и параллельные цепи для создания фильтров, фазовращателей, цепей связи и прочих схем. Одной из наиболее распространенных конфигураций является последовательная резистивно-емкостная цепь, показанная на рисунке 20-1.
Рис. 20-1.
Исходное напряжение синусоидальной формы (Vs)прикладывается к резистору и конденсатору, включенным последовательно. Полное противодействие протеканию тока в этой цепи является комбинацией емкостного сопротивления и обычного (активного) сопротивления. Резисторы и конденсаторы функционируют различным образом, и поскольку конденсатор порождает сдвиг фаз в цепи на 90 градусов, нельзя непосредственно складывать сопротивление резистора и емкостное сопротивление, чтобы подсчитать общее сопротивление протеканию тока, которое называется полным сопротивлением или импедансом (Z). Для получения полного сопротивления используется приведенная ниже формула:
Теорема Пифагора и полное сопротивление
Это известная теорема Пифагора, используемая для решения прямоугольных треугольников. Сопротивление, емкостное сопротивление и полное сопротивление могут быть представлены сторонами прямоугольного треугольника, как показано на рисунке 20-2А.
Рис. 20-2.
В последовательной цепи один и тот же ток (I) протекает через все компоненты. Это означает,
что ток через конденсатор имеет ту же величину, что и ток через резистор, причем эта величина равна величине тока, потребляемого от источника напряжения. Поскольку ток общий для всех компонентов, мы можем использовать закон Ома и умножить величину тока на величину сопротивления, емкостного сопротивления и полного сопротивления, чтобы вычислить напряжения в цепи.
IR=Vr
IXc= Vc
IZ = Vs
Следовательно, мы можем снова нарисовать треугольник, используя напряжения, полученные нами указанным выше образом (см. рис. 20-2Б). Теперь треугольник представлен напряжением на сопротивлении (Vr), напряжением на конденсаторе (Vc) и напряжением источника питания (Vs). Закон Кирхгофа говорит о том, что сумма падении напряжения на компонентах последовательной цепи равна напряжению источника питания. Это означает, что в том случае, если мы сложим напряжение на резисторе и напряжение на конденсаторе, мы должны получить в результате напряжение источника питания. Однако, как можно видеть на рисунке 20-2Б, напряжения не совпадают по фазе друг с другом. По этой причине напряжения не могут складываться друг с другом непосредственно, и мы должны использовать теорему Пифагора для решения прямоугольного треугольника. Подставляйте поэтому значения из рисунка 20-2Б в формулу
в соответствии с теоремой Пифагора и находите напряжение источника питания следующим образом:
Итак, чтобы найти напряжение источника питания, просто измерьте напряжение на резисторе и напряжение на конденсаторе, возведите каждое значение в квадрат и сложите полученные значения друг с другом. После этого для получения значения напряжения источника питания извлеките корень квадратный из полученной суммы.
Не забывайте, что при известном напряжении источника питания и одном из других напряжений Вы можете вычислить неизвестное напряжение при помощи простого преобразования приведенной выше формулы. Тогда можно получить еще два варианта указанной формулы:
Краткое содержание
В данном эксперименте Вы убедитесь, что конденсатор оказывает противодействие переменному току. Затем Вы соберете последовательную резистивно-емкостную схему, аналогичную приведенной на рисунке 20-2, подсчитаете, а потом измерите все токи и напряжения для проверки существа сказанного ранее.
ПРОЦЕДУРА 1: измерение сдвига фаз
Чтобы завершить данный эксперимент. Вам потребуется измерить сдвиг фаз между двумя
синусоидальными сигналами. Для этого выведите два сигнала на двухканальный осциллограф. Один сигнал, верхняя осциллограмма, используйте в качестве опорного и подключите на вход канала 1 или А. Другой сигнал подведите к каналу 2 или В. После этого проделайте следующее:
1. Отрегулируйте скорость горизонтальной развертки, чтобы можно было видеть один период синусоидального сигнала. Установите непрерывную развертку в состояние калибровки CAL.
2. Измерьте период (t) синусоидальных сигналов, как описано в эксперименте 16.
3. Подсчитайте количество делений между двумя смежными или тремя последовательными положительными пиками синусоидальных сигналов.
4. Рассчитайте смещение во времени (t,) умножением количества делений на настройку скорости горизонтальной развертки.
5. Вычислите сдвиг фаз в градусах при помощи следующей формулы:
360 t1/t градусов
Пример
Период синусоидального сигнала равен 250 мкс. Промежуток между двумя смежными положительными пиками двух синусоидальных сигналов составляет 2,6 деления. Скорость развертки составляет 10 мкс/дел. Смещение во времени равно:
t1= 2,6 х 10 = 26 микросекунд
Сдвиг фаз равен:
360(26)/250 = 37,44 градуса
Процедура 2: резистивно-емкостная схема
1. Соберите резистивно-емкостную схему, показанную на рисунке 20-3.
Рис. 20-3.
2. Отрегулируйте частоту генератора на 600 Гц. Установите величину размаха напряжения на выходе генератора 10В.
3. Проделайте следующие измерения как при помощи осциллографа, так и при использовании мультиметра:
Осциллограф Мулътиметр Vr————В Vr=____В Vc—————В Vc=____В Объясните, почему они различны, но эквиваленты. Нарисуйте прямоугольный треугольник напряжений.
4. Выполните следующие вычисления для схемы на рисунке 20-3.
I=_____мА
Z =_____ Ом
5. Выполните измерение сдвига фаз между входным напряжением и выходным напряжением. _______ градусов
Опережает выходное напряжение или запаздывает по сравнению с выходным напряжением. Почему?
6. Измените входную частоту на 1000 Гц. Убедитесь, что величина размаха напряжения генератора все еще составляет 10 В. Повторите шаги 3, 4 и 5. Сделайте вывод о том, как полное сопротивление и ток варьируются в зависимости от частоты, путем сравнения с Вашими значениями, полученными в шаге 4.
7. Поменяйте местами позиции резистора и конденсатора. Повторите шаг 5. Опережает выходное напряжение или запаздывает по сравнению с выходным напряжением? ______ градусов
8. Найдите частоту, при которой R = Хc. в данной схеме. Сначала частоту вычислите. Затем, используя осциллограф и генератор звуковой частоты, выполните измерения, чтобы проверить Ваши расчеты.
f=_____Гц
Объясните, какую процедуру Вы использовали и почему.
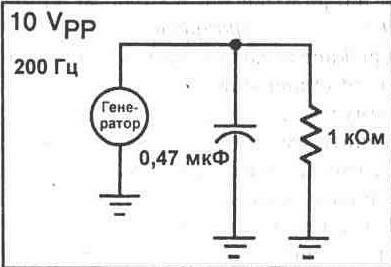
9. Соберите параллельную резистивно-емкостную схему, показанную на рисунке 20-4. Вычислите ее общее активное сопротивление (Rt), общую емкость (Сt) и полное сопротивление (импеданс). Нарисуйте треугольник токов.
Rt = _____ Ом
Сt = _____ мкФ
Z =_____ Ом
Рисунок 20-4.
10.Приложите к схеме напряжение с размахом 10 В и с частотой 200 Гц. Измерьте полный ток в схеме, используя мультиметр. Вычислите импеданс схемы (полное сопротивление). Z=_____Ом
11.Каков сдвиг фаз между полным током и приложенным напряжением? ________градусов
12.Во всех вышеприведенных шагах объясните различия между измеренными и расчетными значениями.
ОБЗОРНЫЕ ВОПРОСЫ
1. При повышении частоты сигнала, приложенного к последовательной резистивно-емкостной схеме, напряжение на конденсаторе соответственно:
а) увеличивается,
б) уменьшается,
в) остается тем же,
г) падает до нуля.
2. При уменьшении емкости конденсатора в последовательной резистивно-емкостной схеме ток схемы соответственно:
а) увеличивается,
б) уменьшается,
в) остается тем же,
г) падает до нуля.
3. Напряжение на резисторе в последовательной резистивно-емкостной схеме имеет значение 3 В. Напряжение на конденсаторе имеет значение 4 В. Напряжение источника питания равно тогда:
а) 1 В,
б) 3,5 В,
в) 5 В,
г) 7 В.
4. Напряжение источника питания в последовательной резистивно-емкостной схеме имеет значение 6 В. Тогда ток в схеме имеет величину:
а) 0.2 Ом,
б) 2 Ом,
в) 20 Ом,
г) 200 Ом.
5. Напряжения на компонентах в последовательной резистивно-емкостной схеме имеют значения: Vr = 5 В и Vc = 4 В. Резистор имеет сопротивление 1,5 кОм. Частота равна 2 кГц. Какова емкость конденсатора?
а) 0,018 мкФ,
б) 0,047 мкФ,
в) 0,066 мкФ,
г) 0,075 мкФ.
Рис. 20-1. Последовательная резистивно-емкостная цепь
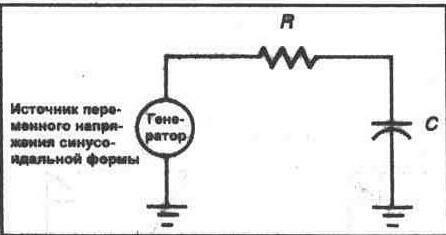
Рис. 20-2. Сопротивление, емкостное сопротивление и полное сопротивление могут быть представлены сторонами прямоугольного треуго
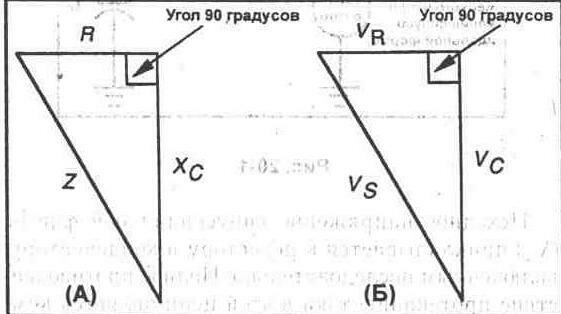
Рис. 20-3. Простая резистивно-емкостная схема
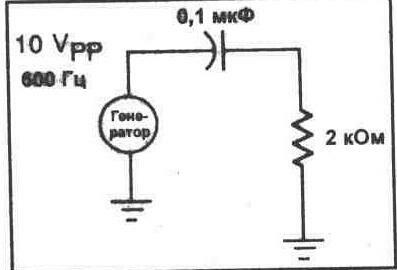
Рисунок 20-4. Параллельная резистивно-емкостная схема