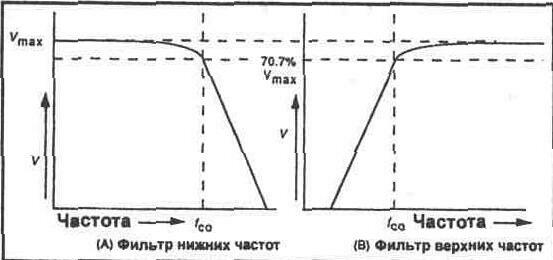
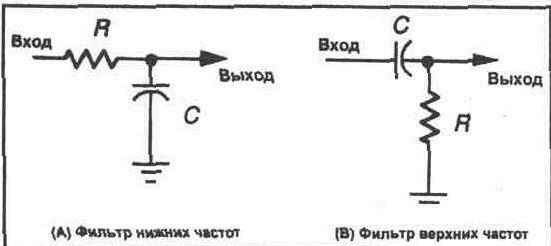
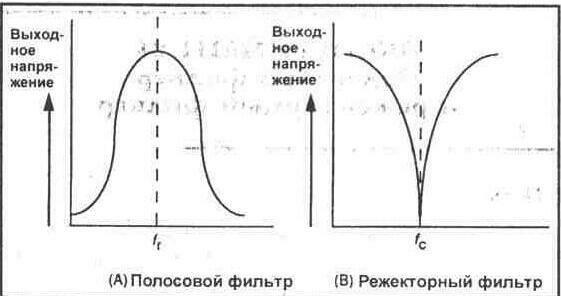
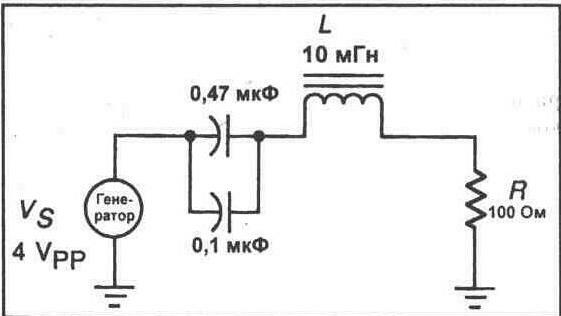
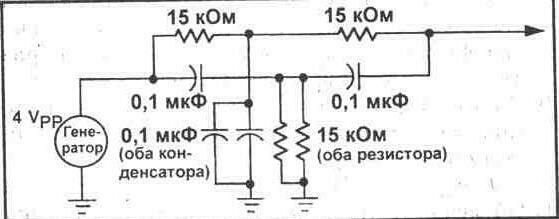
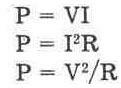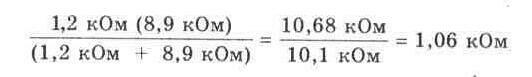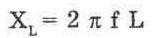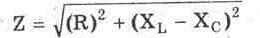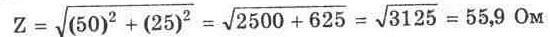4. Раздел 4.
Раздел 4.
Обучение электронного техника не будет полным без приобретения определенных практических навыков использования реальных электронных компонентов, цепей и оборудования. В своей работе в качестве техника Вы будете создавать, тестировать, измерять, обслуживать, ремонтировать, регулировать, монтировать, поддерживать в исправном состоянии, эксплуатировать электронное оборудование и выполнять иные работы. Работа в классах обучения обеспечивает теоретическую базу для понимания оборудования. Лабораторная работа дает опыт в применении теории к аппаратным средствам.
Данное руководство к лабораторным работам содержит ряд экспериментов, которые демонстрируют возможности, содержат процедуры тестирования и измерения и предусматривают прочие действия, которые позволяют на практике проверить и убедиться в правильности теории, изученной Вами в классах. Эксперименты помогут Вам ознакомиться с существенными подробностями в идентификации компонентов, конструкции схем, тестировании схем и в методах измерений при помощи контрольных инструментов, которые Вы будете использовать в своей деятельности.
Данное руководство предназначено для использования почти с любым современным учебником для техников, содержащим основы теории элект
роники и анализ цепей постоянного и переменного тока. В каждом эксперименте представлены учебные цели и вводная часть, в которой указаны те основы, которые Вы изучите в эксперименте. Процедура шаг за шагом проводит ознакомление с процессом создания, демонстрации, анализа и тестирования первичных электронных схем, из которых компонуется вся электронная аппаратура. Вы будете выполнять расчеты, осуществлять измерения и делать заключения в отношении каждой схемы. Раздел каждого эксперимента заканчивается обзорными вопросами, позволяющими Вам лучше запомнить ключевые моменты.
Надеюсь, что Вам доставят удовольствие эксперименты, приведенные в данном руководстве. Проделав их, Вы узнаете много полезного о практической стороне электроники, что обеспечит, в конце концов, успех в работе.
1. Проведение экспериментов
Проведение экспериментов
Для отработки экспериментов, представленных в данном руководстве, Вам потребуются электронные компоненты для конструирования схем, определенная методика соединения компонентов между собой, а также контрольные электронные приборы для осуществления, Ваших измерений. Ниже приводится краткое описание всего необходимого для экспериментов.
Компоненты
Резисторы, конденсаторы, катушки индуктивности и другие детали, требуемые для экспериментов, доступны для Вас в учебной лаборатории. Список деталей и аппаратуры, которые Вам потребуются, представлен в разделе «Необходимые принадлежности» каждого приведенного эксперимента. Указанный список подкрепляется принципиальными схемами экспериментальных цепей, конкретно отражающими потребность в деталях.
Система макетирования
Вам потребуется некоторый способ, чтобы выполнять соединения компонентов между собой. Это обычно осуществляется при помощи системы макетирования. Эта часть оборудования часто называется также тренером или макетирующим устройством. Основной отличительной чертой системы является макетная панель, которая
представляет собой набор металлических соединительных элементов в корпусе из пластика и обеспечивает быстрый, легкий и удобный способ соединения электронных деталей и проводов без всякой пайки. Контактные выводы компонентов вставляются в не требующие пайки соединительные элементы. Ваш инструктор даст Вам пояснения по поводу макетной системы, используемой Вашей школой.
Контрольное оборудование
Для выполнения экспериментов Вам потребуется также определенное контрольное оборудование. Основными элементами такого оборудования являются:
* Цифровой мультиметр (универсальный измерительный прибор)
* Осциллограф
* Генератор функции
* Источник питания
Упомянутые устройства описываются ниже.
Цифровой мультиметр. Цифровой мультиметр является прибором, используемым для измерения напряжений, сопротивлений и токов. Мультиметр подключается к схеме при помощи двух испытательных выводов и выводит измеренное значение на семисегментное цифровое устройство индикации — жидкокристаллическое или на светоизлучающих диодах. Может использоваться и аналоговый мультиметр, который называется также вольтомметром, имеющий шкалу с указателем, хотя точность показании такого прибора хуже, чем у цифрового мультиметра.
Осциллограф.
В осциллографе используется электронно-лучевая трубка для визуализации сигналов
переменного тока. Предпочтительным является осциллограф с двумя входными каналами, позволяющий отображать одновременно два сигнала. Осциллограф дает возможность измерять напряжение, период, частоту и фазовый сдвиг.
Генератор функций. Генератор функций называется также генератором сигналов или генератором гармонических сигналов/звуковым генератором. Он генерирует напряжение синусоидальной формы переменной амплитуды и частоты. Он служит в качестве источника сигналов переменного напряжения для всех экспериментов с переменным током. Генератор функций формирует также сигналы прямоугольной и треугольной формы.
Источник питания. Источник питания может формировать изменяемое постоянное напряжение для питания схем в экспериментах. Большинство лабораторных источников питания позволяют осуществлять плавную регулировку выходного постоянного напряжения от 0 до 15—30 вольт. Многие источники питания содержат также встроенные вольтметры. Предпочтительны источники питания с двумя выходами, поскольку в некоторых экспериментах требуются источники двух независимо регулируемых постоянных напряжений для питания схем.
2. Эксперименты с постоянным током.
Эксперименты с постоянным током.
1. Ознакомление с мультиметром
ЭКСПЕРИМЕНТ 1 Ознакомление с мультиметром
Цели
После проведения данного эксперимента Вы сможете измерять напряжение, ток и сопротивление, используя цифровой мультиметр.
Необходимые принадлежности
* Цифровой мультиметр
* Источник постоянного напряжения
* Одна батарея на 9 вольт
* Один элемент (для карманного фонарика) типоразмера АА, С или D
* Резисторы — 1/2 Вт: один резистор 1 кОм
ВВОДНАЯ ЧАСТЬ
В своей деятельности в качестве техника Вам придется использовать множество контрольных приборов различного типа для тестирования, измерения и обнаружения неисправностей в электронном оборудовании. Мультиметр — это прибор, который будет чаще всего использоваться Вами. Этот прибор предназначен для измерения трех следующих наиболее важных характеристик в любой электронной схеме: напряжение, ток и сопротивление. Большинство мультиметров могут измерять как постоянное, так и переменное (синусоидальное) напряжение, постоянный и переменный ток, а также
сопротивление постоянному току. Два испытательных вывода от мультиметра подключаются к схеме или ее элементу для выполнения этих измерении. Мультиметр является универсальным прибором, который Вы будете использовать практически каждый день в вашей работе. Вы будете использовать мультиметр во всех экспериментах с постоянным током в соответствии с данным руководством по лабораторной практике. Имеется два основных типа мультиметров для общего использования: аналоговый и цифровой.
Аналоговые мультиметры
В аналоговом мультиметре применяется стандартная измерительная шкала с указателем. Значение напряжения, тока или сопротивления отсчитываются от позиции указателя на измерительной шкале. Определение показаний аналогового мультиметра очень похоже на определение времени по стрелкам на часах. В случае часов Вам приходится интерполировать число секунд между маркировками минут. Точно так же при работе с аналоговым мультиметром Вы должны определять или оценивать фактическое значение путем интерполирования между маркировками напряжений, токов или сопротивлений на измерительной шкале.
Аналоговые мультиметры все еще широко используются, поскольку они недороги и надежны в работе. Их основным недостатком является то, что они имеют меньшую точность и больший разброс при измерениях. В большинстве случаев погрешность аналогового мультиметра составляет менее 2% от пределов измерения по шкале прибора, что вполне приемлемо в большинстве практических применении. Тем не менее, во многих случаях желательны более точные измерения.
Цифровые мультиметры
Цифровой мультиметр подобен аналоговому мультиметру в том отношении, что он также является универсальным измерительным прибором, способным измерять напряжение, ток и сопротивление. Основным отличием является то, что результаты измерений выводятся на устройство десятичной цифровой индикации. В большинстве цифровых мультиметров имеется жидкокристаллический индикатор (дисплей), который похож на дисплей, используемый в цифровых электронных часах. Значение тока, напряжения или сопротивления выводится в виде десятичных цифр на семисегментные индикаторы. Индикация в более старых цифровых мультиметрах осуществляется с использованием индикаторов на светоизлучаюших диодах. В некоторых стендовых больших мультиметрах все еще используются светодиодные индикаторы.
В дополнение к удобствам, связанным с использованием десятичных дисплеев, цифровые мультиметры обеспечивают также более высокую точность измерений. Хороший цифровой мультиметр обеспечивает точность измерений от 0, 5% до 1% от фактического значения. Такие точные измерения предпочтительны при тестировании электронных схем, поскольку они дают наилучшую информацию о состояниях схем. Цифровые мультиметры имеют также более высокую разрешающую способность измерительной системы, что обеспечивает более высокоточные измерения с большим числом десятичных разрядов.
Краткое содержание
Мультиметр является измерительным прибором, который при надлежащем его использовании расскажет Вам о состоянии электронной схемы. В данном эксперименте Вы научитесь пользоваться одним из мультиметров Вы научитесь измерять постоянное напряжение, постоянный ток и сопротивление.
ПРОЦЕДУРА
1. Ознакомьтесь с мультиметром. Он должен быть аналоговым или цифровым устройством, в зависимости от того, какой тип имеется в вашей лаборатории. Остановимся на цифровом мультиметре. Исследуйте дисплеи и органы управления. Укажите конкретные особенности мультиметра в предусмотренных полях (см. ниже):
а) тип дисплея ____________________
б) выбор функции измерения (напряжение, ток, сопротивление):
при помощи кнопочных переключателей___ при помощи ползункового переключателя___ при помощи поворотного переключателя ___
в) выбор диапазона измерения:
при помощи кнопочных переключателей ___ при помощи ползункового переключателя___ при помощи поворотного переключателя ___
г) выбор типа измерения (по постоянному току или переменному току):
при помощи кнопочного переключателя ___ при помощи ползункового переключателя __ при помощи поворотного переключателя ___
2. Теперь посмотрите на испытательные выводы мультиметра. Черный вывод называется общим выводом или выводом массы. Красный вывод называется потенциальным выводом. Черный вывод вставляется в гнездо СОМ на передней панели мультиметра. Красный вывод вставляется в отверстие с маркировочными символами оммы и вольты (ft и V). Другое (другие) гнездо (гнезда) на передней панели мультиметра используется (используются) при измерении тока. Черный вывод всегда остается в гнезде СОМ, однако, красный вывод вставляется или в отверстие А, или в отверстие 10А при выполнении измерений тока соответственно до одного ампера или до 10 ампер. Сейчас вставьте красный вывод в гнездо ft/V.
3. Перед тем, как подключать испытательные выводы, в частности, когда измеряемое напряжение или ток неизвестны, желательно устанавливать мультиметр на максимально возможный предел измерений. Это позволяет предотвратить выход мультиметра из строя. Если показание при этом слишком мало, Вы можете шаг за шагом выполнять переключение на более низкие пределы измерений, чтобы получить наиболее оптимальное показание прибора. Когда же диапазон измерения измеряемой величины известен, то для получения наиболее точных значений измерения всегда выбирайте такой предел измерений, который несколько выше измеряемой величины. Например, если Вы желаете измерить напряжение 15 В, установите переключатель на предел измерений 20 В, а не на предел измерений 200 В.
Большинство мультиметров имеют следующие пределы измерений:
» напряжения: 200 мкВ, 2 мВ, 20 м В, 200 м В,
2В, 20В, 200В, 1000В » токи: 200 мкА, 2 мА, 20 мА, 200 мА, 1 А » сопротивления: 2000м, 2 кОм, 20к0м,
200 кОм, 2МОм
Если Ваш мультиметр имеет отличающиеся пределы измерений, запишите их все в только что приведенном формате.
Используя приведенные пределы измерений, укажите оптимальный предел измерения для измерения каждого из следующих электрических сигналов:
а) 120 В = выбрать предел измерения ______
б) 3 мА = выбрать предел измерения ______
в) 470 кОм = выбрать предел измерения ____
4. Чтобы научиться использовать мультиметр, Вы сейчас измерите постоянные напряжения батарей. Мультиметр, установленный для измерения напряжений, называется вольтметром. Включите мультиметр. Установите переключатель пределов измерения и переключатель функций для измерения напряжения батареи 9 В. После этого прикоснитесь пробниками к выводам батареи 9 В. Коснитесь красным выводом к положительному контакту (+) батареи, а черным выводом — к отрицательному контакту (—) батареи. Сосчитайте измеренное напряжение на дисплее прибора и запишите его в предусмотренное ниже поле.
Напряжение батареи = _______ В
5. Поменяйте между собой пробники на контактах батареи 9 В.
Коснитесь черным выводом к положительному контакту (+) батареи, а красным выводом — к отрицательному контакту (—) батареи. Сосчитайте измеренное напряжение на дисплее прибора и запишите его в предусмотренное ниже поле.
Напряжение батареи (при обращении
пробников) = _______ В
Объясните различие между двумя показаниями.
6. Теперь измерьте напряжение стандартного элемента для карманного фонаря. Вы можете использовать элемент большего размера D, меньшего размера С или миниатюрный элемент АА. Прежде чем измерять напряжение элемента, точно определите положительный и отрицательный контакты элемента. После этого измерьте напряжение, подключая пробники прибора к соответствующим контактам элемента. Используйте позицию 20 В на переключателе мультиметра. Поменяйте теперь местами пробники на контактах элемента и снова измерьте напряжение. Запишите оба показания в предусмотренных ниже полях.
Напряжение элемента = _______ В
Напряжение элемента (при обращении пробников) == _______ В
Снова объясните любые отличия, замеченные при измерениях.
7. Установите переключатель мультиметра в позицию 2 В и снова повторите измерение напряжения элемента для карманного фонаря. Запишите полученное значение напряжения. Напряжение элемента = ______ В
Объясните разницу между показаниями, полученными при измерении в диапазонах измерения 2В и 20 В.
8. Далее измерьте напряжение лабораторного источника питания. Большинство таких источников питания имеет изменяемое выходное напряжение.
Включите источник питания и подключите испытательные выводы мультиметра к выходам источника питания. Если источник питания имеет свой собственный встроенный измерительный прибор, установите выходное напряжение 30 В. Если источник питания не может формировать такое большое напряжение, установите его выходное напряжение 14 В. Если источник питания не имеет встроенного измерительного прибора, используйте Ваш мультиметр для измерения выходного напряжения. Установите мультиметр на продел измерения 200 В и измерьте выходное напряжение 30 В. Если на выходе только 14В, используйте 20-вольтовый диапазон измерений мультиметра для измерения этого напряжения. Теперь выполните переключение на следующий более низкий предел измерения (20 В в случае выходного напряжения З0В или 2 В в случае выходного напряжения 14 В). Опишите, что показывает дисплей мультиметра.
9. Теперь Вы будете использовать мультиметр для измерения сопротивлений. В данном режиме мультиметр называется омметром. Установите переключатель мультиметра в положение 2 кОм. Затем дотроньтесь пробниками до двух выводов резистора с номиналом 1 кОм (с цветовым кодом коричневый-черный-красный-золотой). Запишите показание в предусмотренное ниже поле. Значение сопротивления = _______Ом
10. Поменяйте пробники местами и снова измерьте сопротивление. Какое различие Вы заметили, если вообще заметили таковое? 11. Заметьте эффект разомкнутой или замкнутой цепи. При установке мультиметра в режим омметра он может использоваться для измерения так называемой целостности цепи. Другими словами, омметр может обнаруживать разомкнутый контур (бесконечное сопротивление) и замкнутый контур или короткое замыкание (нулевое сопротивление).
При использовании мультиметра, установленного на предел измерения 2 кОм, коснитесь измерительными выводами друг друга. Это состояние представляет собой короткое замыкание. Какое сопротивление Вы измерили при этом?
Сопротивление при коротком
замыкании =_________Ом
Теперь оставьте измерительные выводы открытыми, не касающимися друг друга или чего-нибудь иного. Это соответствует незамкнутому контуру. Что Вы при этом считываете на дисплее мультиметра? Какому сопротивлению это соответствует?
Показание мультиметра =_________
Сопротивление разомкну той цепи =__ Ом 12. Теперь Вы переходите к измерению тока. Мультиметр, используемый таким образом, превращается в амперметр. Для измерения Вам потребуется вставить красный пробник в гнездо с маркировкой А на передней панели Вашего мультиметра. Черным вывод остается соединенным с гнездом СОМ. Установите переключатель мультиметра на предел измерения 20 мА.
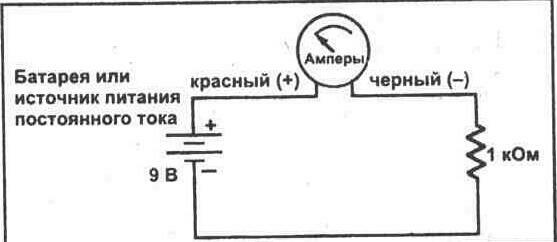
Для измерения тока Вы должны построить простую электрическую схему, через которую должен протекать ток. Вы сделаете это при использовании батареи 9 вольт и резистора 1 кОм. Цепь, которую Вы должны собрать, в схематическом виде представлена на рисунке 1-1. Через эту цепь будет протекать ток величиной в один миллиампер (1 мА) или 0, 001 ампера.
Рис. 1-1. Мультиметр, включенный в цепь в качестве амперметра.
Чтобы собрать цепь, соедините один вывод резистора к отрицательному контакту батареи 9 вольт. После этого коснитесь красным выводом мультиметра к положительному контакту батареи, а черным выводом к свободному выводу резистора 1 кОм. Снимите показание тока на дисплее и запишите это значение. Ток в цепи = _________ мА
Как это согласуется с Вашим расчетным значением? Объясните различия, если таковые имеются.
13. Поменяйте теперь местами пробники мультиметра и повторите шаг 12. Чем отличается новое показание? Объясните.
ОБЗОРНЫЕ ВОПРОСЫ
1. Какой диапазон мультиметра Вы бы использовали для измерения 2, 7 В?
а) 200 мВ,
б) 2 В,
в) 20 В,
г) 200 В.
2. Какое главное преимущество в использовании наименьшего возможного диапазона для измерения электрических величин?
а) предотвращение повреждения мультиметра,
б) более высокая точность представления,
в) более высокая скорость измерения,
г) более высокая точность измерения.
3. Если в показании мультиметра имеется 1 в самой левой позиции (старший значащий разряд) на дисплее, это означает, что Вы:
а) измеряете разомкнутую цепь или бесконечное сопротивление,
б) установили слишком низкий предел измерения для измеряемой величины,
в) имеете случай а и б,
г) имеете случай, отличный и от а и от б.
4. Если при измерении напряжения на дисплее появляется отрицательный знак, это означает, что красный измерительный вывод по отношению к черному пробнику (СОМ) имеет следующую полярность:
а) отрицательную,
б) положительную.
5. Справедливо ли высказывание: Должна соблюдаться правильная полярность измерительных выводов при измерении сопротивления?
а) да,
б) нет.
Рис. 1-1. Мультиметр, включенный в цепь в качестве амперметра.
2. Цветовой код резисторов
ЭКСПЕРИМЕНТ 2 Цветовой код резисторов
Цели
После проведения данного эксперимента Вы сможете понимать цветовой код резисторов, рассчитывать допуски резисторов и измерять сопротивления при помощи омметра.
Необходимые принадлежности
* Цифровой мультиметр
* Резисторы
ВВОДНАЯ ЧАСТЬ
По-видимому, наиболее распространенным электронным компонентом является резистор. Резисторы оказывают определенное противодействие протеканию тока в электронных схемах. Величина этого сопротивления выражается в омах (Ом). Один Ом определяется как величина сопротивления протеканию тока силой в один ампер, когда приложено напряжение величиной один вольт. В электронных схемах резисторы могут иметь величины от доли Ома до нескольких миллионов Ом. Большие значения сопротивления обычно выражаются в килоомах и в мегомах. Килоом — это тысяча Ом. Эта единица измерения обозначается буквой к (кОм). Резистор 10 к имеет величину сопротивления 10х1000 = 100000м. Мегом — это миллион Ом. Данная единица измерения обозначается буквой М (МОм). Следовательно, резистор 2, 2 М имеет величину сопротивления 22000000м.
Резисторы имеют стандартные величины сопротивлений. Значение сопротивления обозначается цветными полосками на корпусе резистора. Вы должны будете только посмотреть на резистор и сразу по его цветовому коду определить фактическую величину его сопротивления.
Цветовой код резисторов
Цветовой код резисторов легко изучается и используется на практике. Как только Вы запомните его, Вы быстро и легко сможете определять величины сопротивлений резисторов. Целью настоящего эксперимента является ознакомление с цветовым кодом резисторов и приобретение опыта в определении величин соответствующих сопротивлений.
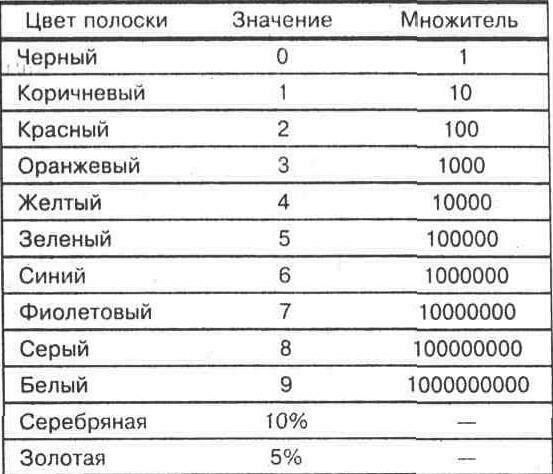
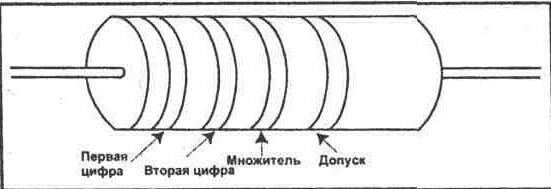
Цветовой код представлен на рисунке 2-1. Первые две цветные полоски на резисторе обозначают цифровые значения. Третья цветная полоска обозначает множитель. Множитель указывает на то, сколько нулей следует добавить после двух цифровых разрядов, чтобы получить окончательную величину сопротивления в омах. Четвертая цветная полоска имеет или серебряный, или золотой цвет, располагается справа и обозначает допуск резистора. Большинство резисторов, которые используются в электронике, имеют допуск или 5%, или 10%, и это означает, что фактическая величина сопротивления может отклоняться от номинального значения, указанного цветовым кодом, на 5% или 10%.
Рис. 2-1. Цветовой код резисторов
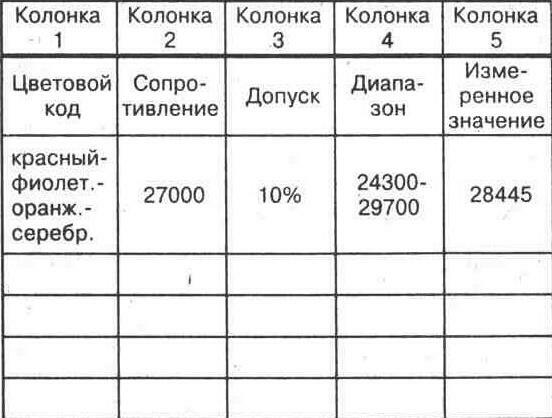
Красный -фиолетовый -оранжевый -серебряный
Рис. 2-2. Пример цветового кода
Величины сопротивлений
Обратитесь к рисунку 2-2. Чтобы определить величину сопротивления, запишите сначала цифры, соответствующие первым двум полоскам. В нашем случае это цифры 2 и 7. Далее запишите количество нулей, указываемое третьей цветной полоской. В данном случае цвет оранжевый, который означает три нуля. Вы теперь определили фактическую величину сопротивления резистора, а именно 270000м. В обычном представлении это записывалось бы как 27 кОм, где к заменяет три нуля.
Наконец, серебряная полоска обозначает допуск 10%. Это означает, что фактическая величина сопротивления резистора может отклоняться от номинального значения, указанного цветовым кодом, на 10%. Десять процентов от 27000 ом составляет:
27000х0, 10=2700 Ом
Следовательно, величина сопротивления варьирует в диапазоне:
27000 - 2700 = 24300 Ом 27000+ 2700=29700 Ом
Таким образом, фактическое значение сопротивления будет находиться в пределах от 24300 до 29700 Ом. Вы можете проверить это, измерив сопротивление резистора при помощи мультиметра.
Резисторы обладают также номинальной мощностью. Эта величина означает, сколько тепла могут безопасно рассеивать резисторы. Резисторы с цветовой кодировкой выпускаются со стандартными номинальными мощностями 1/8, 1/4, 1/2,
1 и 2 ватта (большая часть резисторов имеет номинальную мощность 1/4 ватта). Чем больше резистор, тем больше его способность рассеивать мощность.
Краткое содержание
В данном эксперименте при использовании рисунка 2-3 Вы будете брать резисторы, которые Вам предоставит Ваш инструктор, и определять их сопротивления и допуски. Вы будете также измерять их значения при помощи Вашего мультиметра. Это обеспечит Вас достаточным начальным опытом в определении сопротивления любого резистора, предоставляемого в данной программе.
Рис. 2-3. Таблица для записи значений сопротивления резисторов
ПРОЦЕДУРА
1. Записывайте цветовой код каждого резистора, предоставляемого Вам Вашим инструктором, в левую колонку на рисунке 2-3. Не имеет значения, в каком порядке Вы будете составлять список резисторов. Обеспечивайте, тем не менее, при считывании цветового кода правильное расположение резистора, чтобы Вы правильно считывали этот код — слева направо. Чтобы правильно расположить резистор для считывания цветового кода, необходимо, чтобы золотая или серебряная полоска допуска всегда располагалась справа. Запишите все цветовые коды резисторов в таблицу на рисунке 2-3, прежде чем переходить к следующему шагу. В первом ряду на рисунке 2-3 показан формат записи с использованием примера, приведенного в вводной части данной главы.
2. Преобразуйте цветовой код в соответствующую величину сопротивления. Записывайте значения сопротивлений во вторую колонку на рисунке 2-3. Запишите все значения сопротивлений резисторов, прежде чем переходить к следующему шагу. Допуски следует записать в третью колонку.
3. Используя значения допуска, которые Вы записали в третью колонку, выполните теперь расчет диапазона отклонения от номинала для каждого резистора. То есть, определите верхние и нижние значения диапазонов сопротивлений для всех резисторов по их допуску. Запишите ваши данные в колонку 4 на рисунке 2-3.
4. Далее, используя Ваш цифровой мультиметр, измерьте значение сопротивления каждого резистора. Используйте при этом такой предел измерения для каждого резистора, который обеспечит максимальную точность значения и точность его представления. Каждое измеряемое значение для резисторов записывайте в колонку 5 на рисунке 2-3.
5. Теперь сравните фактически измеренную величину с указанным номинальным сопротивлением резистора и диапазоном допуска. Убедитесь, что измеренное значение находится внутри диапазона допуска. Если какое-либо из измеренных значений находится вне предела допуска, поставьте контрольную отметку рядом с такими резисторами.
ОБЗОРНЫЕ ВОПРОСЫ
1. Краткий способ выразить величину сопротивления 15000000 Ом следующий:
а) 15 кОм,
б) 1. 5 МОм,
в) 1500 кОм,
г) 15 МОм.
2. Резистор с цветовым кодом синий-серый-желтый-серебряный имеет величину:
а) 86 кОм, 5%,
б) 680 кОм, 10%,
в) 860 кОм, 5%,
г) 6, 8 МОм, 10%.
3. Каков диапазон сопротивления резистора с номиналом 2, 2 кОм, 5%?
а) 2090 — 2310 Ом,
б) 1980 — 2420 Ом,
и) 2090 — 2200 Ом,
г) 2200— 2310 Ом.
4. Каким цветом представляется на резисторах множитель 10000000?
а) зеленым,
б) синим,
в) фиолетовым,
г) серым.
5. Размер резистора отражает обычно его:
а) омическое значение,
б) допуск,
в) диапазон сопротивлений,
г) номинальную мощность.
Рис. 2-1. Цветовой код резисторов
Рис. 2-2. Пример цветового кода
Рис. 2-3. Таблица для записи значений сопротивления резисторов
3. Закон Ома
ЭКСПЕРИМЕНТ 3 Закон Ома
Цели
После проведения данного эксперимента Вы сможете рассчитывать и измерять ток, напряжение и сопротивление в электрической схеме для проверки закона Ома.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом, один резистор 680 Ом, один резистор 2, 2 кОм, один резистор 4, 7 кОм.
ВВОДНАЯ ЧАСТЬ
По-видимому, наиболее важным основным принципом в электротехнике является закон Ома. Этот закон отражает связь, которая существует между током, напряжением и сопротивлением в электрической или электронной цепи. Источник напряжения подключается к сопротивлению, что вызывает протекание через него тока. Величина тока определяется величиной приложенного напряжения и величиной сопротивления. Закон Ома утверждает, что на участке цепи ток прямо пропорционален напряжению и обратно пропорционален сопротивлению. Эта связь выражается простой формулой:
I=V/R
В данном выражении: I — ток в амперах, V — напряжение в вольтах, R — сопротивление в омах. Значение тока можно быстро вычислить использовании калькулятора. Например, какой величины ток протекает через резистор 2, 2 кОм, подключенный к источнику напряжения 6В? Ответ таков:
I = 6 В/2, 2 кОм = 6/2200 = 0, 00273 А
Это значение может быть выражено также в миллиамперах, то есть, 2, 73 мА.
Как Вы знаете, основная формула закона Ома может быть преобразована алгебраически, так что Вы сможете определять или напряжение, или сопротивление. Этими другими формулами являются:
V=IxR
R =V/I
В. Вашей работе с электроникой Вам регулярно придется использовать закон Ома; Даже в самых сложных схемах Вы будете применять это соотношение. Важно, чтобы Вы могли проделывать такие расчеты при любых условиях.
Вычисления в соответствии с законом Ома
Для выполнения расчетов в соответствии с законом Ома Вы должны знать две величины из трех. Величины тока, напряжения и сопротивления
могут быть получены различными способами. Величины сопротивлении резисторов могут определяться по их цветовому коду или фактическим измерением сопротивления резистора. Ток обычно определяется путем измерения. Величину напряжения часто бывает легко определить, поскольку напряжение подается от источника питания, выходное напряжение которого фиксированно и известно. Например, если используется батарейка для карманного фонаря, то Вы знаете, что ее напряжение составляет 1, 5 В. Все батареи элементов имеют стандартные значения выходных напряжений, как и многие источники питания. Если напряжение неизвестно, оно может быть, тем не менее, измерено.
Краткое содержание
В данном эксперименте Вы будете собирать некоторые простые электрические схемы и выполнять электрические измерения, в результате чего Вы сможете проводить расчеты в соответствии с законом Ома. Для конкретной схемы Вы научитесь делать расчет необходимых величин. Затем Вы будете конструировать различные схемы и контролировать их величины путем измерении.
ПРОЦЕДУРА
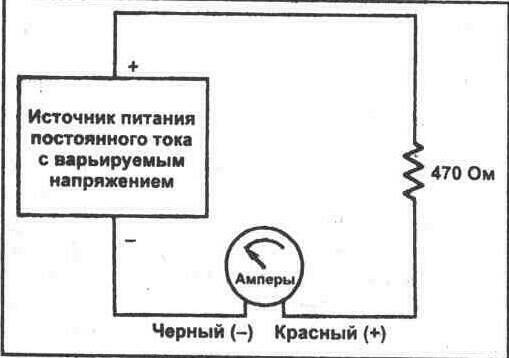
1. Обратитесь к схеме на рисунке 3-1. При известных значениях напряжения и сопротивления рассчитайте величину протекающего в схеме тока. Запишите Ваше полученное значение в предусмотренное поле.
I = ______мА (вычисленное значение)
Рис. 3-1.
2. Соберите схему, показанную на рисунке 3-1. Используйте источник питания постоянного тока, настроенный таким образом, чтобы его выходное напряжение составляло 9 В. Для измерения тока в данной схеме Вы будете использовать мультиметр. Установите предел измерения мультиметра на соответствующее значение, которое основано на Ваших расчетах в шаге 1. Вставьте красный испытательный вывод в гнездо А мультиметра.
3. После того, как Вы собрали схему, коснитесь черным пробником к отрицательному контакту батареи или источника питания, а красным пробником прикоснитесь к неприсоединенному выводу резистора. Прочитайте показание величины тока на мультиметре. Запишите полученное значение.
I = ________мА (измеренное значение)
4. Сравните Ваше расчетное и измеренное значения. Объясните причину различий, если таковые имеются.
5. Удвойте напряжение питания, указанное на рисунке 3-1. Какое теперь новое напряжение питания схемы?
Напряжение питания = ______ вольт
6. Используя величину нового напряжения питания и прежнее сопротивление резистора, рассчитайте величину нового тока.
/ = ______мА (вычисленное значение)
7. Измерьте новый ток, подсоединяя испытательные выводы мультиметра к схеме, как описано ранее.
I =______мА (измеренное значение)
8. Сравните величины токов в шагах 1 и 6 и в шагах 3 и 7. Как изменилась величина тока, когда изменилось напряжение питания? Согласуется ли такое изменение с законом Ома? Объясните.
9. Демонтируйте схему, показанную на рисунке 3-1, и соберите схему, показанную на рисунке 3-2.
Рис. 3-2.
10. Измерьте величину тока, протекающего в схеме, используя процедуру, описанную ранее. Запишите полученное значение.
I= ________мА (измеренное значение)
1. Используя значение измеренного Вами тока, рассчитайте величину сопротивления резистора, применяя для этого закон Ома. Запишите величину сопротивления.
R = ______Ом (вычисленное значение)
12. Теперь по цветовому коду резистора определите его сопротивление и запишите найденное значение. R = _________Ом (определенное по цветовому коду)
13. Сравните значение сопротивления, вычисленное с использованием величины измеренного тока, с величиной сопротивления, определенной по цветовому коду. Объясните любой отличие.
14. Измените величину сопротивления резистора на 2, 2 кОм в схеме на рисунке 3-2.
15. Рассчитайте величину ожидаемого тока. Запишите значение.
I =_______мА (вычисленное значение)
16. Измерьте величину тока, используя процедуру, которая использовалась Вами в предыдущих шагах.
I =_______мА (измеренное значение)
17. Сравните ток, который Вы измерили в шаге 16, с током, измеренным Вами в шаге 10. Как изменился ток после изменения величины сопротивления резистора? Соответствуют л и полученные Вами результаты закону Ома? Объясните.
18. Используйте источник питания постоянного тока с варьируемым напряжением, который Вы применяли в схеме на рисунке 3-2, и резистор 2, 2 кОм. Изменяйте напряжение от 0 до 12 В шагами (дискретами) по 2 В. Измеряйте ток при каждом установленном напряжении.
19. Повторите шаг 18, используя резистор 4700м. Используя данные в шагах 18 и 19, построите графики тока в зависимости от напряжения на миллиметровой бумаге.
ОБЗОРНЫЕ ВОПРОСЫ
1. К резистору 39 кОм был подключен источник питания с неизвестным напряжением. Вы измерили ток и получили величину 0, 31 мА. Приложенное напряжение должно быть порядка:
а) 12 В,
б) 28 В,
в) 57 В,
г) 126 В.
2. Уменьшение напряжения, приложенного к резистору, приводит к:
а) увеличению тока,
б) уменьшению тока,
в) сохранению той же величины тока,
г) падению величины тока до нуля.
3. Уменьшение сопротивления резистора, соединенного с источником питания, приводит к:
а) увеличению тока,
б) уменьшению тока,
в) сохранению той же величины тока,
г) падению величины тока до нуля.
4. Смотрите Ваш график, полученный в шаге 19. Скорость изменения тока по отношению к изменению напряжения:
а) больше при меньшей величине резистора,
б) больше при большей величине резистора,
в) меньше при меньшей величине резистора,
г) та же при любой величине резистора.
5. Для измерения тока при помощи мультиметра как он должен быть подключен к схеме?
а) встречно,
б) параллельно,
в) последовательно,
г) с изменением полярности испытательных выводов.
Рис. 3-1. Схема для измерения закона Ома
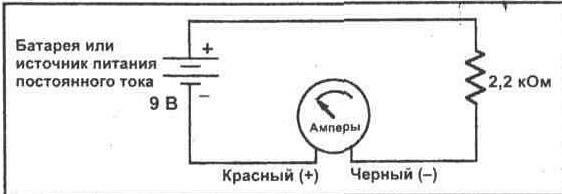
Рис. 3-2. Схема для измерения закона Ома (вариант 2)
4. Последовательные схемы
ЭКСПЕРИМЕНТ 4 Последовательные схемы
Цели
После проведения данного эксперимента Вы сможете рассчитывать общее сопротивление нескольких включенных последовательно резисторов и использовать закон Кирхгофа для напряжений, чтобы осуществлять расчеты и измерения для последовательных схем.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения * Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом,
один резистор 680 Ом,
один резистор 2, 2 кОм,
один резистор 4, 7 кОм,
один светоизлучающий диод (LED).
ВВОДНАЯ ЧАСТЬ
Имеется два основных способа подключения электронных компонентов к источнику питания. При последовательном включении все компоненты подключаются концами друг к другу, образуя простую цепочку, которая соединяется с источником питания. При параллельном включении (эксперимент 5) каждый из отдельных компонентов подключается непосредственно к источнику питания. Естественно, имеются более сложные схемы, в которых используются те или иные комбинации последовательных и параллельных соединений (эксперимент 6). В данном эксперименте Вы узнаете, как выполнять последовательное включение компонентов и осуществлять различные расчеты и измерения.
Сначала познакомимся с тем, как вычислять общее сопротивление последовательной схемы. Если два или более резисторов включены последовательно, общее сопротивление комбинации равно простой сумме отдельных сопротивлений.
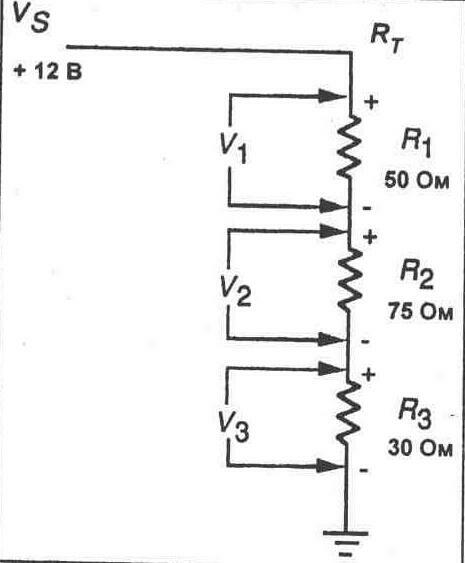
Типичная последовательная схема показана на рисунке 4-1. Общее сопротивление Rт равно сумме отдельных сопротивлений, то есть:
Rт=R1+ R2+ R3
При показанных значениях сопротивлений резисторов общее сопротивление равно:
Rт= 50+ 75+ 30 = 1550м
Три отдельных резистора могут быть заменены единственным резистором с номиналом 155 Ом, при этом никаких изменений в токе схемы не будет.
Падение напряжения
Когда ток протекает через последовательную схему, на каждом сопротивлении происходит падение напряжения. Па рисунке 4-1 показана последовательная схема с напряжениями, указанными для каждого сопротивления. Заметьте полярность падения напряжения на каждом резисторе.
Рис. 4-1.
Конечно, напряжение, падающее на каждом резисторе, может определяться на основании закона Ома. В данном случае общин ток схемы умножается на величину сопротивления каждого резистора для получения соответствующего падения напряжения. Например, напряжение на R2:
V2 = IR2
Исключительно важной характеристикой последовательной схемы, что надо хорошо запомнить,
является то, что сумма отдельных падений напряжения равна напряжению источника. Заметьте на рисунке 4-1, что сумма, полученная сложением напряжений на резисторах R1, R2, и R3 такая же, как и общее приложенное напряжение.
Vs= V1 + V2 + V3
Это основное соотношение известно как закон Кирхгофа для напряжений. Закон этот чрезвычайно полезен при осуществлении расчетов для последовательных схем. При использовании данного соотношения различными способами можно легко выполнять анализ и разработку последовательных схем.
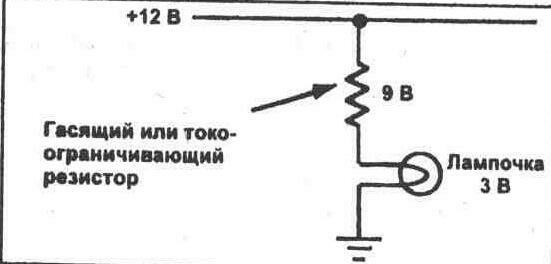
Токоограничивающие резисторы
Примером использования закона Кирхгофа является расчет последовательных гасящих резисторов. Последовательный гасящий резистор — это просто резистор, соединенный последовательно с некоторым устройством с той целью, чтобы понизить напряжение, прилагаемое к данному устройству. Такой резистор называется также токоограничивающим резистором. Часто оказывается необходимым, например, включать лампу накаливания от источника высокого напряжения. Чтобы избежать повреждения устройства при перенапряжении, резистор включается последовательно с устройством, чтобы погасить излишнюю величину напряжения (см. рис. 4-2). Кроме того, может оказаться необходимым включить трехвольтовую лампочку от батареи питания 12 В. Если приложить все напряжение 12 В к лампочке, последняя перегорит. Однако при включении последовательно с лампочкой резистора с правильно выбранным
сопротивлением на резисторе создастся падение излишнего напряжения 9 вольт, тогда как для лампочки останется только 3 вольта необходимого ей напряжения. Короче говоря, резистор выбирается для ограничения тока через лампочку до максимально безопасной величины.
Рис. 4-2.
Краткое содержание
В данном эксперименте Вы убедитесь, что общее сопротивление последовательной схемы равно сумме отдельных сопротивлений включенных последовательно резисторов. Затем Вы проверите справедливость закона Кирхгофа для напряжении. Наконец, Вы рассчитаете последовательный гасящий резистор для светоизлучающего диода.
Рис. 4-3.
ПРОЦЕДУРА
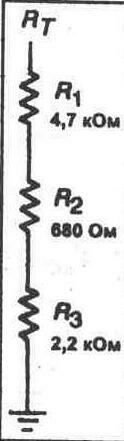
1. Используя значения, указанные на рис. 4-3, рассчитайте общее сопротивление схемы.
Rт= _____Ом (вычисленное значение)
2. Соберите схему, показанную на рисунке 4-3.
3. Используя Ваш мультиметр, измерьте общее сопротивление схемы.
Rт= ______Ом (измеренное значение)
4. Сравните Ваши вычисленное и измеренное значения и объясните возможную разницу.
Рис. 4-4.
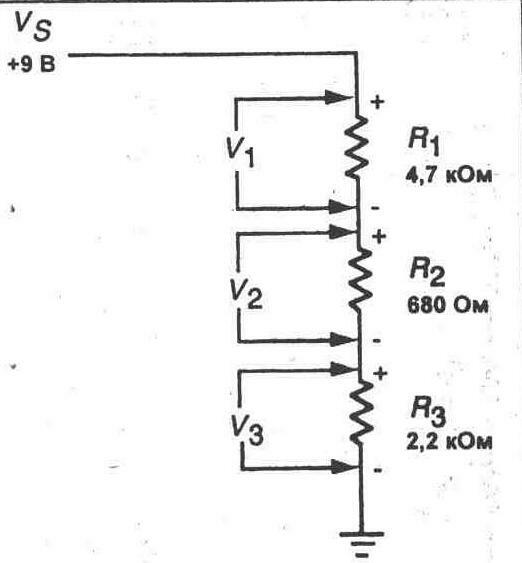
5. Подключите источник питания 9 В к схеме (см. рис. 4-4).
6. Используя значение общего сопротивления, которое Вы подсчитали ранее, рассчитайте и запищите ожидаемый ток в цепи при приложенном напряжении 9 В. I =_____мА
7. Теперь, используя закон Ома, вычислите и запишите напряжение, падающее на каждом резисторе.
V1= _______ В
V2 = _______ В
V3= _______ В
8. Теперь вычислите и запишите сумму отдельных падений напряжения.
Vs=v1+v2+v3___В
9. Используя Ваш мультиметр, измерьте падение напряжения на каждом резисторе. Не забывайте, что Вы измеряете напряжения постоянного тока, и Вам следует прикасаться испытательными выводами мультиметра к выводам резистора в корректном направлении, чтобы получить правильные в отношении полярности показания. Заметьте полярности для падений напряжения в схеме на рисунке 4-4. Запишите Ваши измеренные падения напряжения, а затем вычислите их сумму.
V1=_____В
V2=______В
V3=____в
Vs=______В
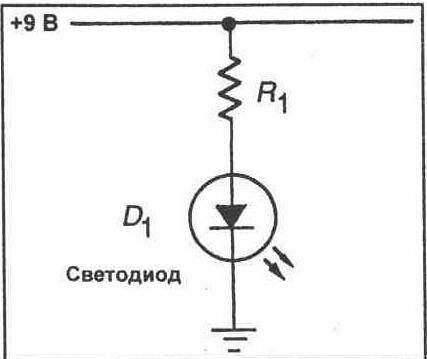
10. Сравните Ваши измеренные и расчетные значения для падений напряжения и общего напряжения. Равна ли сумма падений ли напряжения напряжению источника? 11. Обратитесь к рисунку 4-5. Здесь показан светоизлучающий диод, который должен запитываться от источника питания 9 В. Ваша задача определить сопротивление последовательного гасящего резистора R1. В проводящем состоянии светоизлучающего диода на нем падает напряжение приблизительно 2 В. Ток величиной 15 мА требуется для обеспечения умеренной яркости. Рассчитайте сопротивление потребного последовательного гасящего резистора. Запишите это значение сопротивления. R1= ________ Ом
Рис. 4. 5.
12. Среди имеющихся в Вашей лаборатории резисторов выберите резистор с сопротивлением, ближайшим по величине к найденному Вами. Затем соберите схему, показанную на рисунке 4-5. Обеспечьте соблюдение полярности как для подключения батареи, так и для выводов светоизлучающего диода. При этом отрицательный вывод источника питания должен быть подключен к катодному выводу светодиода (этот вывод идентифицируется плоской стороной на корпусе диода). В символе светодиода стрелка является анодом, тогда как прямая черта соответствует катоду.
13. Если Вы рассчитали и выбрали корректное сопротивление резистора, должен загореться светоизлучающий диод. Измерьте падения напряжения на резисторе R1 и на светоизлучающем диоде (LED).
V1=______В
Vled=_____В
Vs=_______В
14. Равна ли сумма падений напряжения напряжению источника питания? Сравните измеренные и рассчитанные значения. Имеются ли какие-либо отличия? Объясните разницу, если таковая имеется.
ОБЗОРНЫЕ ВОПРОСЫ
1. Два резистора (R1 и R2) соединены последовательно. Сопротивление R1 = 68 Ом. Общее сопротивление R = 150 Ом. Каково значение сопротивления R2?
а) 28 Ом,
б) 82 Ом,
в) 86 Ом,
г) 218 Ом.
2. В последовательной схеме падения напряжений на резисторах равны V1 = 2.5 В, V2, = 1,8 В, V3 = 3,4 В и V4 = 6, 9 В. Каково напряжение источника питания?
а) 10, 3 В,
б) 12, 1 В,
в) 12, 8 В,
г) 14, 6 В.
3. Справедливо ли высказывание: «Ток через все последовательно соединенные резисторы в схеме одинаков»?
а) да,
б) нет.
4. Лампочка напряжением 6 В потребляет ток 0, 15 А. Чтобы подключить ее к источнику питания 15В, Вам требуется последовательный гасящий резистор:
а) 33 Ом,
б) 50 Ом,
в) 60 Ом,
г) 120 Ом.
5. В последовательную цепь включены резисторы 180 Ом, 2, 7 кОм, 5, 6 кОм и 6, 8 кОм. На каком из резисторов будет наименьшее падение напряжения?
а) 180 Ом,
б) 2, 7 кОм,
в) 5, 6 кОм,
г) 6, 8 кОм.
Рис. 4-1. Последовательная схема с напряжениями, указанными для каждого сопротивления
Рис. 4-2. Токоограничивающие резисторы
Рис. 4-3. К закону Кирхгофа для напряжения.
Рис. 4-4. Расчет последовательно соединенных резисторов
Рис. 4.5. Подключение светодиода
5. Параллельные схемы
ЭКСПЕРИМЕНТ 5 Параллельные схемы
Цели
После проведения данного эксперимента Вы, сможете рассчитать общее сопротивление нескольких включенных параллельно резисторов и проверить закон Кирхгофа для тока в параллельных схемах.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 2, 2 кОм, один резистор 4, 7 кОм, один резистор 10 кОм.
ВВОДНАЯ ЧАСТЬ
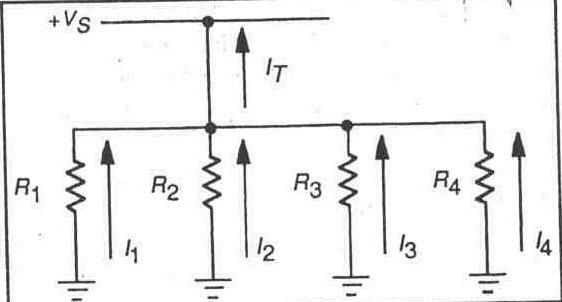
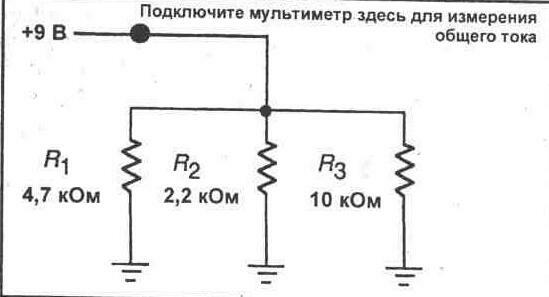
В параллельной схеме все резисторы или другие элементы подключаются непосредственно к источнику питания. На рисунке 5-1 иллюстрируется параллельная схема, в которой четыре резистора подключены непосредственно к источнику питания. Источник питания создает ток, протекающий через каждый резистор. Каждый резистор или иной схемный элемент называется при этом ветвью параллельной схемы.
Рис. 5-1.
Общий ток, потребляемый из источника питания на рисунке 5-1, представляет собой просто сумму токов, протекающих в каждой ветви параллельной схемы. В данном случае общий ток схемы равен:
Iт=I1 + I2 + I3+ I4
Это соотношение известно как закон Кирхгофа для тока в параллельной схеме. Этот закон говорит о том, что сумма токов в отдельных ветвях параллельной схемы равна общему току, потребляемому от источника питания. Закон Кирхгофа для тока позволяет легко осуществлять анализ и разработку параллельных схем.
Общий ток и токи в ветвях параллельной схемы могут вычисляться или измеряться. Тем не менее, имеются некоторые виды схем, когда один из токов в ветвях неизвестен. В подобном случае неизвестный ток в ветви может определяться путем комбинирования вычислений и измерений.
Предположим, например; что ток через R2, и на рисунке 5-1 неизвестен. Вы можете легко определить его, если алгебраически преобразуете основную формулу для отыскания I2,. Вам требуется просто вычесть все известные токи в ветвях от общего тока, чтобы получить неизвестное значение:
I2= It— I1-I3 —I4
или I2=It- (I1+I3+I4)
При измерении и/или вычислении значений неизвестный ток может быть определен.
Чтобы определить полное сопротивление двух или более резисторов, соединенных между собой параллельно, используются специальные формулы. Когда два резистора соединяются параллельно, полное сопротивление их комбинации определяется при помощи простого выражения:
Rt=R1 R2/(R1+R2)
Когда три или больше резисторов соединяются параллельно, может использоваться следующая формула:
Rt= l/(l/R1 + 1/R2 + 1/R3+...)
Хотя эта формула выглядит довольно сложной, ее относительно легко использовать, если у Вас имеется электронный калькулятор. Просто вводите значения и находите их обратные величины. Обратной величиной числа является единица, деленная на это число (1/х). Обратной величиной R1, является 1/R1. После этого все обратные величины складываются, и для нахождения значения полного сопротивления определяется обратная величина полученной суммы.
Краткое содержание
В данном эксперименте Вы приступаете к проверке использования формул для вычисления сопротивлении, включенных параллельно. Затем Вы проделаете расчеты и измерения для типичной параллельной схемы, чтобы проверить закон Кирхгофа для тока.
ПРОЦЕДУРА
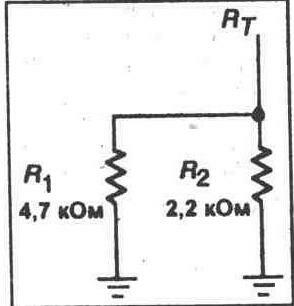
1. Соберите схему, показанную на рисунке 5-2.
2. Используя значения, указанные на рисунке 5-2, рассчитайте полное сопротивление схемы. Rt == _________ Ом
3. Теперь используйте Ваш мультиметр, чтобы измерить полное сопротивление параллельно соединенных резисторов на рисунке 5-2. Rt = _________ Ом
Рис. 5. 2.
4. Сравните Ваши вычисленное и измеренное в шагах 2 и 3 значения и объясните возможную разницу.
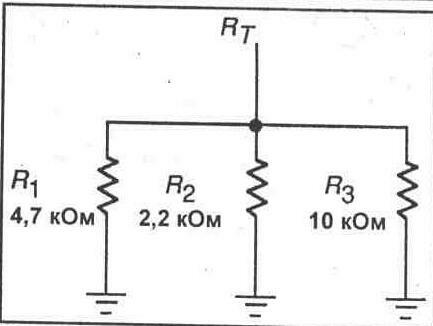
5. Соберите параллельную схему, показанную на рисунке 5-3, присоединяя резистор 10 кОм параллельно к другим двум.
Рис.5.3
6. Используя приведенную выше формулу обратных величин, рассчитайте полное сопротивление параллельно включенных элементов на рисунке 5-3.
Rt = ______ Ом
Рис. 5-4.
7. Используя Ваш мультиметр, измерьте сопротивление схемы на рисунке 5-3. Rt = ______Ом
8. Сравните Ваши вычисленное и измеренное значения и объясните возможную разницу.
9. Подключите источник питания 9 В к параллельной схеме, как показано на рисунке 5-4.
10. Используя значение полного сопротивления, которое Вы вычислили в шаге 6, рассчитайте и запишите ожидаемый общий ток в схеме.
It= _______ мА.
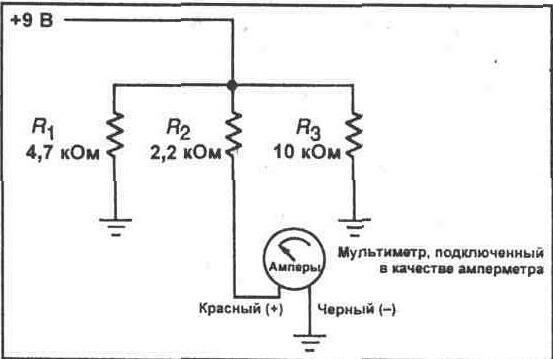
11.Переключите Ваш мультиметр в режим измерения тока в миллиамперном диапазоне. Соедините красный измерительный вывод с гнездом А. Подключите амперметр между положительным выводом источника питания и Вашей параллельной схемой. Не забывайте соблюдать правильную полярность при подключении. Затем измерьте общий ток схемы и запишите его величину.
Iт = _____ мА
12.Отсоедините мультиметр и снова подключите общую точку схемы к положительному выводу источника питания. Затем выполняйте последовательное подключение мультиметра в каждую из параллельных резисторных ветвей и измеряйте ток, протекающий через каждую ветвь. Один из способов такого подключения показан на рисунке 5-5. Просто отсоедините один вывод резистора, ток через который Вы желаете измерить, и включите мультиметр между этим выводом резистора и отрицательным полюсом источника питания. По завершении
измерения тока через каждый резистор снова подключайте данный резистор к отрицательному полюсу источника питания, прежде чем отсоединять другой резистор. Данную процедуру используйте для измерения тока через каждый резистор и запишите все полученные значения.
I1= _______ мА
I2 = ________ мА
I3 = _____ МА
13. Теперь, используя ваши измеренные значения,
вычислите общий ток схемы. It = _____ мА
14.Сравните измеренные значения токов через резисторы со значениями, которые Вы вычислили ранее. Сравните также вычисленное и измеренное значения общего тока в схеме. Объясните возможные отличия.
Рис. 5-5.
ОБЗОРНЫЕ ВОПРОСЫ
1. Пять резисторов 10 кОм соединены параллельно. Общее сопротивление равно:
а) 2 кОм,
б)10 кОм,
в) 25 Ом,
г)50 кОм.
2. В параллельной схеме наибольший ток ветви имеет место через резистор:
а)с наибольшим сопротивлением,
б)с наименьшим сопротивлением.
3. В параллельной схеме полное сопротивление меньше, чем самое маленькое сопротивление отдельной ветви:
а) высказывание верно,
б) высказывание неверно.
4. Параллельная схема имеет две ветви. В одной ветви ток I1= 40 мА. Общий ток в схеме It= 128мА. Ток во второй ветви I2, равен:
а) 51 мА,
б) 68 мА,
в) 88 мА,
г) 168 мА.
5. Если удаляется один резистор из параллельной схемы из четырех резисторов, полное сопротивление схемы:
а) уменьшается до нуля,
б) остается без изменения,
в) уменьшается,
г) увеличивается.
Рис. 5.1. Пример параллельной схемы
Рис. 5.2. Схема для проверки закона Кирхгофа
Рис. 5.3 Схема для расчета обратных величин
Рис. 5.4. Схема для расчета
Рис. 5.5.
6. Комбинация последовательных и параллельных схем
ЭКСПЕРИМЕНТ 6 Комбинация последовательных и параллельных схем
Цели
После проведения данного эксперимента Вы сможете рассчитывать полное сопротивление сложной схемы, состоящей из соединенных последовательно и параллельно резисторов, и определять падение напряжения на любом элементе и ток, протекающий через любой элемент схемы.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Один батарейный зажим с выводами
* Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом, один резистор 680 Ом, один резистор 2, 2 кОм, один резистор 4, 7 кОм, два резистора 10 кОм.
ВВОДНАЯ ЧАСТЬ
Большинство используемых на практике электронных схем часто представляют собой сложные комбинации из последовательных и параллельных схем. Вы должны знать, как рассчитывать нс толь
ко полное сопротивление схемы, но также величину тока через любой компонент или падение напряжения на любом. отдельном компоненте. Производство расчетов для таких цепей должно быть не более сложным, чем расчет простых последовательных и параллельных схем. Смысл этого довольно прост: любая сложная схема может быть легко и просто разбита на несколько более мелких и простых схем. При использовании методов, которые Вы изучили ранее для последовательных и параллельных схем, у Вас не будет проблем при анализе больших и более сложных схем.
Иными словами: для выполнения расчетов в сложной схеме просто смотрите на схему как на несколько небольших и простых схем. Начинайте с расчета тех схем, которые наиболее удалены от источника питания. В расчетах постепенно продвигайтесь вперед к источнику питания, комбинируя Ваши отдельные результаты. Таким образом, постепенно Вы сможете выполнить вычисление эквивалентного полного сопротивления схемы.
После того, как Вам будет уже известно полное сопротивление схемы, рассчитайте полный ток схемы, потребляемый от источника питания. Используя данную величину тока, Вы сможете вычислить падения напряжения при помощи законов Кирхгофа. Применяя законы Ома и Кирхгофа, Вы сможете определить напряжение или ток в любой точке схемы.
Краткое содержание
В данном эксперименте Вы соберете сложную схему, состоящую из соединенных последовательно
и параллельно резисторов. Вы рассчитаете полное сопротивление этой схемы и проверите его измерением. Затем подсчитайте величины тока и напряжения в конкретных точках схемы. И снова сверьте Ваши расчеты с данными фактических измерений.
ПРОЦЕДУРА
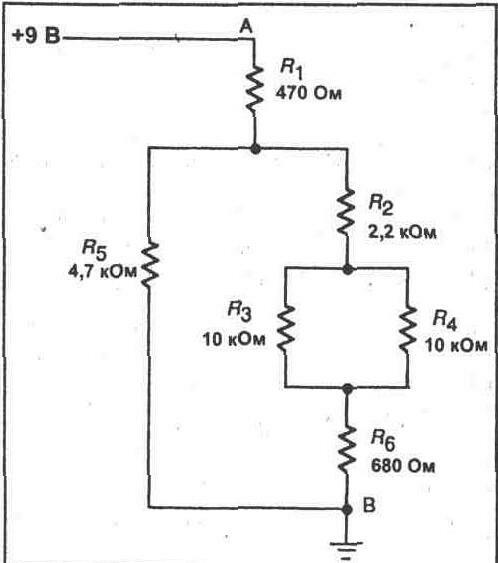
1. Соберите схему, показанную на рисунке 6-1, но не подключайте источник питания до тех пор, пока об этом не будет сказано. Это одна из наиболее сложных схем, которые Вам до сих приходилось собирать, так что будьте предельно внимательны. На данном этапе все еще желательным является использование макетной панели для физической компоновки резисторов с расположением элементов, по возможности наиболее близким к указанному на принципиальной схеме. Это поможет Вам быстро отыскивать каждый резистор и намного облегчит проведение различных измерений токов и напряжении. После того, как Вы завершите монтаж, снова внимательно проконтролируйте его на наличие возможных ошибок.
2. При использовании процедур, которые применялись Вами в предыдущих экспериментах, рассчитайте полное сопротивление схемы между точками А и В. Позже Вы подключите к этим точкам источник питания.
Rt= ____ Ом (расчетное значение)
3. Используя Ваш мультиметр, измерьте общее сопротивление схемы между точками А и В Вашей схемы.
Rt=______ Ом (измеренное значение)
4. Подключите источник питания 9В к схеме в точках А и В.
5. Рассчитайте ток, протекающий через резистор R5
Ir5= ______мА (расчетное значение)
6. Рассчитайте падение напряжения на резисторах R3 и Rt.
Vr3-4= ____ В (расчетное значение)
7. Используя Ваш мультиметр, измерьте ток, протекающий через резистор R5.
Рис. 6-1.
Ir5 = ______ мА (измеренное значение)
8. Измерьте напряжение на резисторах R3 и R4. Vr3-4 =_____В (измеренное значение)
9. Сравните Ваши вычисленные и измеренные значения и объясните возможную разницу в значениях.
ОБЗОРНЫЕ ВОПРОСЫ
1. На рисунке 6-1 какой ток протекает через резистор R3?
а) 0,15 мА,
б) 0,32 мА,
в) 0,44 мА,
г) 0,89 мА.
2. При расчете полного сопротивления схемы, комбинирующей последовательные и параллельные цепи, начните с элементов, наиболее удаленных от источника питания:
а) высказывание справедливо,
б) высказывание несправедливо.
3. Основной причиной различия между расчетными и измеренными значениями является:
а) вариация напряжений,
б) погрешности мультиметра,
в) погрешности вычислений,
г) допуски резисторов.
4. В каком направлении происходит движение электронов через резистор R5, если источник питания подключается к точкам А и В, как показано на рисунке 6-1?
а)сверху вниз,
б) снизу вверх.
5. Какова полярность напряжения на резисторы R.2?
а)вверху +, внизу —;
б)вверху —, внизу +.
Рис. 6-1. Измерения последовательных и параллельных схем
7. Делители напряжения
ЭКСПЕРИМЕНТ 7 Делители напряжения
Цели
После проведения данного эксперимента Вы сможете рассчитать выходное напряжение делителя напряжения с нагрузкой и без таковой, а также продемонстрировать, что потенциометр является варьируемым делителем напряжения.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Один потенциометр 10 кОм
* Резисторы — 1/4 Вт, 5%:
один резистор 220 Ом, один резистор 470 Ом, один резистор 1 к0м, один резистор 2, 2 к0м, один резистор 3, 3 к0м, один резистор 10 к0м, один резистор 100 к0м.
ВВОДНАЯ ЧАСТЬ
Делитель напряжения — это резистивная схема, выходное напряжение которой меньше, чем входное напряжение. В электронных схемах часто оказывается необходимым уменьшить уровень напряжения сигнала. Наиболее легко это можно
осуществить при помощи двухрезисторной схемы, известной как делитель напряжения. Входное напряжение прикладывается параллельно к двум резисторам, а выходное напряжение снимается с одного из этих резисторов. Сопротивления этих резисторов выбираются таким образом, чтобы выходное напряжение составляло некоторую определенную часть от входного напряжения.
Рис. 7-1.
Широко используемый делитель напряжения показан на рисунке 7-1. Вы можете использовать закон Ома для расчета выходного напряжения, если известны входное напряжение и сопротивления резисторов. Тем не менее, следующая формула ускоряет и упрощает процесс вычислений.
Vo = VsR2/(R1 + R2)
Вычисление выходного напряжения в соответствии с приведенной выше формулой предполагает, что в схеме нет нагрузки. Если параллельно
резистору R2 подключена резистивная нагрузка с конечным сопротивлением, выходное напряжение будет меньше, чем вычисленное, по формуле. Если сопротивление нагрузки приближается к сопротивлению R2, нагрузка будет отбирать все больше и больше тока из схемы. Это приведет к перераспределению падений напряжения в схеме, и выходное напряжение будет уже значительно отличаться от рассчитанного в соответствии с приведенной выше формулой напряжения.
Для определения выходного напряжения делителя при наличии нагрузки Вы можете использовать стандартные методы расчетов в соответствии с законами Ома и Кирхгофа, которые уже применялись Вами в предыдущем эксперименте, чтобы дать заключение о выходном напряжении. Во многих приложениях, тем не менее, это не является необходимым. Если сопротивление нагрузки достаточно велико в сравнении со значением R2, выходное напряжение будет почти равным напряжению, значение которого получается в соответствии с приведенной выше формулой. При этом эмпирическим правилом является: сопротивление нагрузки должно в десять или более раз превышать сопротивление R2. Чем выше значение сопротивления нагрузки по отношению к R2, тем ближе выходное напряжение будет к значению, рассчитанному в соответствии с приведенной ранее формулой.
Потенциометр
Одним из наиболее часто используемых электроэлементов является потенциометр, который фактически представляет собой варьируемый делитель напряжения. Потенциометр — это переменный резистор с тремя выводами (см. рис. 7-2). Центральный вывод соединен с подвижным контактом, который может соединяться с любой точкой резистивного элемента, позволяя гасить часть полного приложенного напряжения. Подвижный контакт может перемещаться от одного конца резистивного элемента к другому, позволяя выбирать любое значение напряжения между напряжением входного источника и нулем. Потенциометры широко используются в электронных схемах, поскольку с их помощью удается точно выполнить настройку выходного напряжения, желательного для конкретного применения.
Рис. 7-2.
Краткое содержание
В данном эксперименте Вы соберете и продемонстрируете резистивные делители напряжения, а также покажете изменение выходного напряжения при различных уровнях нагрузки. Вы также
продемонстрируете использование потенциометра в качестве варьируемого делителя напряжения.
ПРОЦЕДУРА
1. Обратитесь к схеме делителя напряжения, показанной на рисунке 7-3. Выполните расчет выходного напряжения с нагрузкой 1 кОм и без нее.
Vo=___В (нагрузка 1 кОм)
Vo = ________ В (без нагрузки)
Рис. 7-3.
2. Соберите схему, показанную на рисунке 7-3. Не присоединяйте резистор 1 кОм. Измерьте выходное напряжение на R2. Это напряжение без нагрузки.
Vo=_______В
3. Присоедините нагрузочный резистор 1 кОм параллельно R2, как показано на рисунке 7-3. Измерьте выходное напряжение с подключенной нагрузкой. После этого отсоедините нагрузку
1 кОм и замените ее резистором 10 кОм. Снова измерьте выходное напряжение. Наконец, замените резистор 10 кОм на резистор 100 кОм. Измерьте выходное напряжение. Запишите значения выходных напряжений в таблицу.
4. Основываясь на данных, накопленных в шаге З, укажите, как варьируется выходное напряжение в зависимости от различных сопротивлений нагрузки.
5. Размонтируйте схему на рисунке 7-3. Смонтируйте потенциометр 10 кОм на Вашей макетной панели. Каждый из контактов должен входить в отверстие на отдельном вертикальном ряду отверстий макетной панели. Центральный контакт — это подвижный контакт. Затем подключите к потенциометру источник питания 9 В, как показано на рисунке 7-4. Вы будете измерять выходное напряжение между отрицательным выводом источника и подвижным контактом потенциометра.
6. Подключите Ваш мультиметр на выход потенциометра для измерения выходного напряжения (Vo). При помощи небольшой отвертки полностью выведите подвижный контакт потенциометра против часовой стрелки. Запишите
полученное выходное напряжение. Затем полностью выведите подвижный контакт потенциометра по часовой стрелке. Снова запишите полученное выходное напряжение.
Vo=___В (против часовой стрелки)
Vo=__В (по часовой стрелке)
7. Теперь контролируйте выходное напряжение потенциометра. Отрегулируйте Ваш потенциометр таким образом, чтобы выходное напряжение составляло половину входного напряжения (напряжения источника питания).
Рис. 7-4.
8. Размонтируйте схему рисунка 7-4.
9. Используя Ваш мультиметр, измерьте сопротивление между центральным выводом (подвижный контакт) и каждым из других выводов потенциометра. Запишите полученные значения. Сопротивление между центральным контактом и одним выводом = ______ Ом
Сопротивление между центральным контактом и другим выводом = ______ Ом
Объясните полученные Вами значения.
Рис. 7-5.
10. Соберите делитель напряжения, показанный на рисунке 7-5. Рассчитайте, в каком диапазоне может варьироваться выходное напряжение при использовании потенциометра.
Vo = __ В (против часовой стрелки)
Vo = _____ В (по часовой стрелке)
11.Подключите схему к источнику питания. Измеряйте теперь выходное напряжение схемы, варьируя положение подвижного контакта потенциометра по всему его диапазону. Запишите предельные значения напряжения.
Vo = __ В (против часовой стрелки) Vo = _____ В (по часовой стрелке)
ОБЗОРНЫЕ ВОПРОСЫ
1. Делитель напряжения, аналогичный показанному на рисунке 7-1, имеет следующие сопротивления резисторов: R1 = 10 кОм и R2 = 1 кОм.
Источник питания дает напряжение 15В. Выходное напряжение составляет:
а) 1, 28 В,
б) 1, 36 В,
в) 1, 5 В,
г) 1, 72 В.
2. Каково минимальное значение сопротивления нагрузки, которая может подключаться к делителю напряжения из вопроса 1, чтобы выходное напряжение не снижалось значительно?
а) 100 Ом,
б) 1 кОм,
в) 10 кОм,
г) 100 кОм.
3. Варьируемый делитель напряжения — это:
а) потенциометр,
б) переменный резистор,
в) реостат,
г) варистор.
4. Постоянное напряжение 6 В приложено к потенциометру. Выходное напряжение может быть установлено на любое значение в диапазоне:
а) от —6 до+ 6 В,
б) от 0 до 6 В,
в) от 0 до 9 В,
г) от 0 до 12 В.
5. Потенциометр из вопроса 4 настроен так, чтобы гасить 85% приложенного напряжения. При этом выходное напряжение составляет:
а) 0, 9 В,
б) 2, 6 В,
в) 4, 3 В,
г) 5, 1 В.
Рис. 7-1. Делитель напряжения — это резистивная схема, выходное напряжение которой меньше, чем входное напряжение.
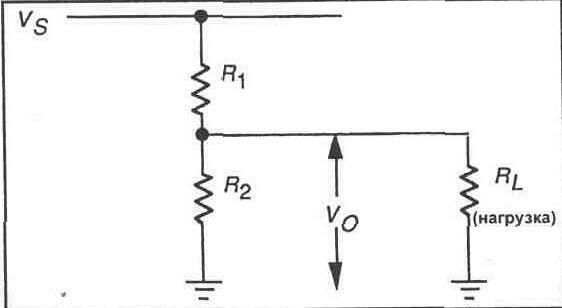
Рис. 7-2. Потенциометр — это переменный резистор с тремя выводами
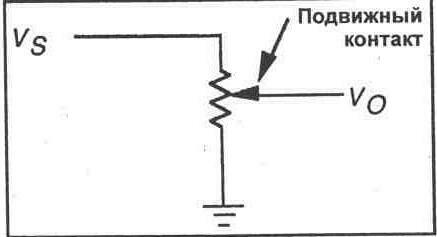
Рис. 7-3. Расчет параметров делителя напряжения
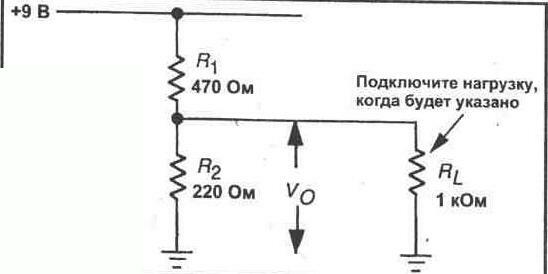
Рис. 7-4. Схема для контроля выходного напряжения потенциометра
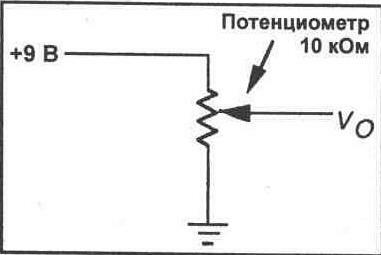
Рис. 7-5. Схема для измерения параметров делителя напряжения
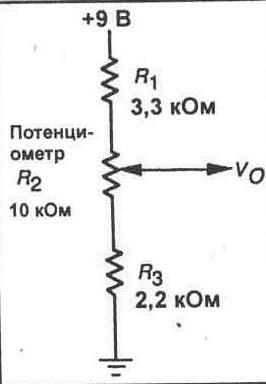
Таблица 1. К измерениям параметров делителя напряжения

8. Мостовые схемы
ЭКСПЕРИМЕНТ 8 Мостовые схемы
Цели
После проведения данного эксперимента Вы сможете распознавать, собирать и уравновешивать мостовую схему.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Один потенциометр 10 кОм * Резисторы — 1/4 Вт, 5%:
один резистор 4, 7 кОм,
один резистор 12 кОм,
один резистор 18 кОм,
один резистор 100 кОм.
Вводная часть
Мостовая схема — это специальное соединение элементов, которое формирует выходное напряжение, сбалансированное относительно массы. Эта схема широко используется в измерительных приборах и во множестве промышленных схем, предназначенных для контроля.
Основная мостовая схема показана на рисунке 8-1А. Схема представлена в типичной ромбовидной конфигурации, чтобы ясно распознавать ее в качестве мостовой схемы. При более детальном рассмотрении Вы можете видеть, что мостовая схема — это по существу два делителя напряжения, параллельно подключенные к источнику питания. Это четко можно видеть по мостовой схеме, представленной в виде, показанном на рисунке 8-1 Б. Заметьте, что выходной сигнал снимается между двумя выходами делителей напряжения (точки А и В).
Рис. 8-1А.
Рис. 8-1 Б.
Обычно выходное напряжение делителя напряжения снимается с точки соединения двух резисторов относительно массы. В мостовой схеме выходное напряжение снимается между двумя выходами делителей напряжения, а не относительно массы. Такой тип выхода называется дифференциальным (или симметричным) выходом.
Равновесие моста
Основное нейтральное состояние в мостовой схеме называется равновесием моста. Уравновешенный мост — это такой мост, выходное напряжение которого равно нулю. Такое состояние имеет место в том случае, когда выходное напряжение одного делителя напряжения равно выходному напряжению другого делителя напряжения, относительно массы. Если ввести в мостовую схему один или больше резистивных элементов с варьируемым сопротивлением, можно легко привести мост к такому уравновешенному состоянию. Равновесие моста имеет место в том случае, если сопротивления моста связаны следующим соотношением:
R1/R2= R3/R4
Иными словами, если отношения резисторов в делителях напряжения одинаковы, мост уравновешен, и выходное напряжение равно нулю.
Мост не уравновешен, если выходное напряжение одного делителя напряжения выше или ниже выходного напряжения другого делителя напряжения. Например, если на рисунке 8-1 напряжение в точке А больше, чем напряжение в точке В,
точка А будет иметь больший положительный потенциал, чем точка В. Если возникнет такое состояние, через нагрузку потечет ток от А к В.
Если же мост нс уравновешен в другом направлении, и напряжение в точке В выше напряжения и точке А, произойдет противоположное, то есть, ток потечет через нагрузку от точки В к точке А.
Краткое содержание
В данной работе Вы соберете мостовую схему и поэкспериментируете с ней. В одном из плечей моста будет использоваться потенциометр для обеспечения различных только что описанных состояний.
ПРОЦЕДУРА
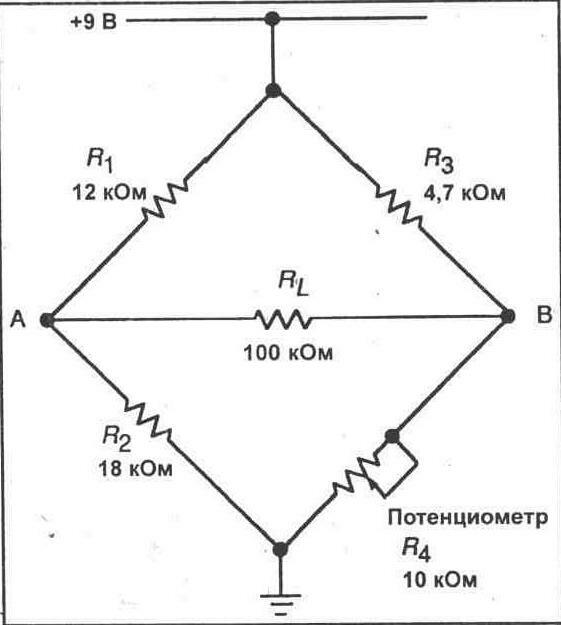
1. Обратитесь к схеме на рисунке 8-2. Значения сопротивлений R1, R2 и R3, заданы. R4 —это потенциометр, подключенный в качестве переменного резистора, который может подстраиваться на любое значение между 0 и 10кОм. Используются только два из трех выводов потенциометра — центральный подвижный и один неподвижный вывод. Используя формулу, приведенную для уравновешенного моста, рассчитайте сопротивление, на которое должен быть установлен потенциометр R4, чтобы уравновесить мост. Для этого преобразуйте формулу, чтобы вычислить R4, и запишите полученное значение.
R4 = _____ Ом
2. Соберите схему, показанную на рисунке 8-2. Установите резистор R4 на середину его диапазона в качестве начальной позиции.
Рис. 8-2.
3. Включите Ваш мультиметр между точками А и В для измерения напряжения. Вы должны сосчитать на индикаторе некоторое значение напряжения. Установите на мультиметре переключатель пределов измерения в позицию для максимальной разрешающей способности.
4. Теперь регулируйте потенциометр R4 до тех пор, пока напряжение между точками А и В не станет
равным нулю. Когда Вы получите нулевое показание, переключите мультиметр на следующий более низкий предел измерения. Вы можете заметить некоторое остаточное напряжение. В данном случае продолжайте точную настройку потенциометром, пока не получите нулевого показания. Это будет уравновешенное состояние моста.
5. При уравновешенном состоянии моста измерьте напряжение в точке А по отношению к массе (в качестве которой служит отрицательный вывод источника питания) и в точке В по отношению к массе. Запишите полученные значения.
Va=_____В
Vв=_____В
6. Удалите потенциометр R4 из макетной панели. Делайте это осторожно, чтобы не нарушить настройку. После того, как Вы удалите потенциометр, измерьте его сопротивление между двумя выводами, которые Вы присоединяли к мостовой схеме. Запишите полученное значение сопротивления. R4 = ____ Ом
7. Сравните ваши расчетное и измеренное значения R4 для уравновешенного моста.
8. Снова включите потенциометр в мостовую схему. При этом Вы должны вставить выводы потенциометра в те же самые отверстия. Выполните измерение напряжения между точками А и В, чтобы убедиться в том, что оно все еще равно нулю. Если это не так, перенастройте R4 таким образом, чтобы обеспечить уравновешенное состояние моста.
9. Непрерывно контролируя напряжение между точками А и В, перемещайте движок потенциометра как в направлении по часовой стрелке, так и против часовой стрелки, из положения, при котором мост уравновешен. Замечайте амплитуду и полярность напряжения во время варьирования. Запишите амплитуду и полярность напряжения в положениях максимального выведения подвижного контакта резистора R4 в направлении по часовой стрелке и против часовой стрелки. Выходное напряжение = _______ В
(макс. против часовой стрелки) Выходное напряжение =_____ В
(макс. по часовой стрелке) 10. Размонтируйте схему.
ОБЗОРНЫЕ ВОПРОСЫ
1. Когда мост уравновешен, выходное напряжение:
а) равно напряжению источника питания,
б)невозможно определить,
в) имеет бесконечную величину,
г) равно нулю.
2. Мостовая схема составлена из двух более простых схем следующего типа:
а) делители напряжения,
б) последовательные схемы,
в) параллельные схемы,
г) делители тока.
3. В мостовой схеме на рисунке 8-1 напряжение между точкой А и массой равно +7,5 В. Напряжение между точкой В и массой равно +4,6 В, В каком направлении будет протекать ток в нагрузке?
а) слева направо,
б) справа налево,
в) ток протекать не будет.
4. В мостовой схеме на рисунке 8-1 сопротивление R1 неизвестно, R2, = 1 кОм, R3 = 3 кОм, R4 = 8 кОм. Каким должно быть сопротивление R1 для равновесия моста?
а) 375 Ом,
б) 1,25 кОм,
в) 2,4 кОм,
г) 2,67 кОм.
5. Один выходной контакт моста соединен с массой:
а) высказывание верно,
б) высказывание неверно.
Рис. 8-1 Б. Мостовая схема — это по существу два делителя напряжения, параллельно подключенные к источнику питания.
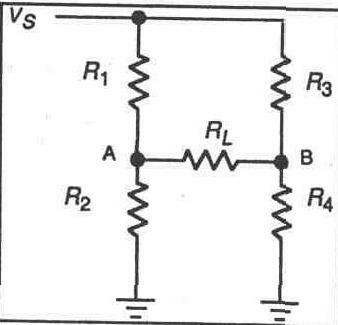
Рис. 8-1А. Основная мостовая схема
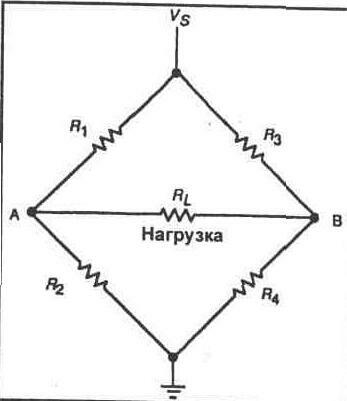
Рис. 8-2. Пример мостовой схемы
9. Терморезисторы
ЭКСПЕРИМЕНТ 9 Терморезисторы
Цели
После проведения данного эксперимента Вы сможете оценивать функционирование схем, содержащих терморезисторы (термисторы).
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Паяльник
* Элементы:
один терморезистор 1 кОм с отрицательным температурным коэффициентом, один резистор — 1/4 Вт, 5%, 1 кОм.
ВВОДНАЯ ЧАСТЬ
Все электрические проводники чувствительны к изменениям температуры. Обычная медная проволока имеет положительный температурный коэффициент; когда она нагревается, ее сопротивление увеличивается. Тем не менее, относительный рост сопротивления очень мал. В большинстве случаев избыток тепла не оказывает значительного влияния на сопротивление.
С другой стороны, имеются типы резисторов, сопротивление которых претерпевает большие изменения при относительно небольших температурных
колебаниях. Такие устройства находят применение.
Прочие типы резисторов
Терморезистор с отрицательным температурным коэффициентом
Специальный резистор, разработанный для больших изменений сопротивления в зависимости от температурных флуктуаций, известен как терморезистор или термистор. Термисторы обычно имеют отрицательный температурный коэффициент (NTC). Это означает, что когда температура терморезистора возрастает, сопротивление его падает, и наоборот. Даже при незначительном изменении температуры происходит значительное изменение сопротивления.
Подобные чувствительные элементы используются для создания различных элементов — от электронных термометров до детекторов — в тех или иных промышленных системах управления, в которых должен осуществляться текущий контроль (мониторинг) и/или управление температурой.
Терморезистор с положительным температурным коэффициентом
Имеются также термисторы с положительным температурным коэффициентом (РТС). Эти устройства увеличивают свое сопротивление при возрастании температуры. При этом их сопротивление изменяется более резко и круто, чем у терморезисторов с отрицательным температурным коэффициентом.
Хорошим примером терморезистора с положительным температурным коэффициентом является нить лампы накаливания. Когда лампа накаливания выключена, нить накала имеет очень низкое значение сопротивления. Однако когда через лампу протекает ток, нить сильно накаляется и быстро нагревается до температуры белого каления. Это значительно увеличивает сопротивление нити. Например, стандартная лампа накаливания 100 Вт имеет в холодном состоянии сопротивление приблизительно 100 м. Когда же на лампу подается напряжение 120 В, нить нагревается с увеличением сопротивления до 1440м, то есть, отмечается рост сопротивления в 14, 4 раза. Характеристики лампы накаливания могут использоваться для целей регулирования в некоторых типах электрических и электронных схем.
Сверхпроводимость
Имеется исключительный случай вариации сопротивления с изменением температуры. А именно, когда температура понижается до очень низкого уровня, сопротивление падает до нуля. Некоторые материалы фактически теряют свое сопротивление, когда их температура понижается до значений, несколько больших абсолютного нуля (-273°С). Это явление известно как сверхпроводимость. Продолжающиеся исследования обнаруживают новые материалы, сопротивление которых устраняется даже при более высоких температурах, что делает их более пригодными для применения на практике.
Краткое содержание
В данном эксперименте Вы поработаете с терморезистором, чтобы разобраться в его термочувствительных характеристиках.
ПРОЦЕДУРА
1. Приготовьте две чашки или два стакана воды. Вы будете использовать их для изменений температуры терморезистора. Один стакан наполните очень горячей водой из-под крана. Другой стакан наполните холодной водой и добавьте в нее кубики льда.
2. Рассмотрите терморезистор. Как Вы можете видеть, это круглый диск из специального резистивного материала. Терморезистор имеет диаметр 1/4 дюйма, а к каждой стороне терморезистора припаяны проволочные выводы. Сначала возьмите терморезистор и измерьте его сопротивление при комнатной температуре при помощи Вашего мультиметра.
R = _ Ом (при комнатной температуре)
3. Закрепите измерительные выводы мультиметра на выводах терморезистора и погрузите корпус терморезистора в горячую воду. Подождите примерно 10 секунд и заметьте сопротивление. R = _____ Ом (в горячей воде)
4. Извлеките терморезистор из горячей воды и сразу же поместите его в стакан с холодной водой. Снова заметьте сопротивление через 10 секунд. R = _____ Ом (в холодной воде)
5. Основываясь на результатах, полученных в двух предыдущих шагах, запишите словами, как изменяется сопротивление в зависимости от изменений температуры.
6. Соберите схему, показанную на рисунке 9-1. Заметьте, что терморезистор подключается вместе с резистором 1 кОм как часть делителя напряжения к источнику питания 9 В. Заметьте, что
Рис. 9-1.
выходное напряжение снимается с выводов термистора. Измерьте теперь выходное напряжение при комнатной температуре.
Vo = __ В (при комнатной температуре)
7. Нагрейте паяльник и поднесите его приблизительно на расстояние 1/4 дюйма от терморезистора. Дайте ему нагревать терморезистор, а в это время следите за изменением напряжения на терморезисторе. Через 10 секунд запишите значение измеренного напряжения.
Vo = __ В (в нагретом состоянии) Дайте затем терморезистору охладиться, прежде чем Вы перейдете к шагу 8.
8. Модифицируйте схему эксперимента так, чтобы она выглядела подобно схеме, показанной на рисунке 9-2. Снова Вы используете терморезистор как часть делителя напряжения. Однако в данной схеме выходное напряжение снимается с резистора 1 кОм, а не с терморезистора.
Рис. 9. 2.
Измерьте и запишите выходное напряжение, снимаемое с резистора 1 кОм, при комнатной температуре.
Vo = __ В (при комнатной температуре)
9. Снова нагрейте паяльник и поднесите его приблизительно на расстояние 1/4 дюйма от терморезистора. Дайте ему нагревать терморезистор, а Вы в это время следите за изменением напряжения на резисторе 1 кОм в течение приблизительно 10 секунд и замечайте, как изменяется напряжение. В конце 10-секундного периода запишите значение измеренного напряжения. Vo = __ В (в нагретом состоянии)
10. Как выходное напряжение варьируется в зависимости от температуры в каждой из схем?
ОБЗОРНЫЕ ВОПРОСЫ
1. Положительный температурный коэффициент означает:
а) когда температура уменьшается, уменьшается сопротивление;
б) когда температура увеличивается, увеличивается сопротивление;
в) когда температура уменьшается, сопротивление увеличивается;
г) когда температура варьируется, сопротивление изменяется.
2. В лампе накаливания сопротивление нити в горячем состоянии ниже, чем сопротивление нити в холодном состоянии:
а) высказывание верно,
б) высказывание неверно.
3. Полная потеря сопротивления при очень низких температурах известна как:
а) сверхсопротивление,
б) экстремальный температурный коэффициент,
в) сверхпроводимость,
г) холодное сопротивление.
4. Чтобы преобразовать изменение сопротивления терморезистора в вариацию напряжения, в какой тип схемы должен быть подключен терморезистор?
а) усилитель,
б) счетчик,
в) фильтр,
г) делитель напряжения.
5. Терморезисторы иногда используются в мостовых схемах:
а) высказывание верно,
б) высказывание неверно.
Рис. 9-1. Подключение терморезистора
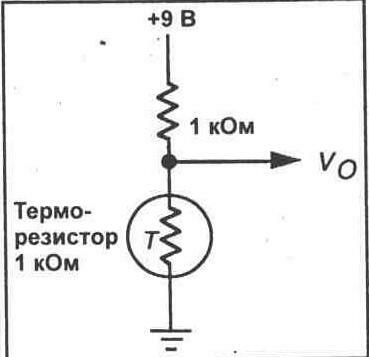
Рис. 9.2. Модифицированная схема подключения терморезистора

10. Мощность в резистивных цепях
ЭКСПЕРИМЕНТ 10 Мощность в резистивных цепях
Цели
После проведения данного эксперимента Вы сможете определять величину мощности, рассеиваемой на резисторе, и выражать связь между сопротивлением нагрузки и внутренним сопротивлением источника для максимальной передачи мощности.
Необходимую принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 120 Ом, один резистор 150 Ом, один резистор 220 Ом, один резистор 470 Ом, два резистора 1 кОм, один резистор 2, 2 кОм, один резистор 4, 7 кОм, один резистор 10 кОм.
ВВОДНАЯ ЧАСТЬ
Объясняя на элементарном уровне, электрическая мощность рассеивается на сопротивлении. Всякий раз, когда через сопротивление протекает ток, расходуется мощность. Эта мощность выделяется в форме тепла. При низких уровнях мощности формируется незначительное количество теплоты. Когда используются более сильные токи, рассеивается больше мощности, и генерируются более значительные уровни тепла. Вот почему многие электроэлементы нагреваются во время работы.
Большая часть электронных компонентов разрабатывается таким образом, что они могут выдерживать только определенную максимальную величину мощности. Это справедливо для резисторов, транзисторов и прочих устройств. Например, стандартные композиционные и пленочные резисторы выпускаются с номинальными значениями мощности 1/8, 1/4, 1/2, 1 и 2 Вт. Чем выше номинальная мощность резистора, тем больше его размер для обеспечения надежного рассеяния этой мощности. Таким образом, номинальная мощность резистера указывает на ту максимальную мощность, которую может надежно рассеивать данный резистор.
Разработка схем
При разработке электронных схем необходимо рассчитывать величину мощности, рассеиваемой резистором, для обеспечения того, чтобы эта мощность была ниже номинальной мощности резистора. Если этого не сделать, резистор может буквально сгореть. Для иллюстрации: для резистора мощностью 1/4 Вт значения тока и напряжения должны быть такими, чтобы полная рассеиваемая резистором мощность была меньше, чем эта номинальная мощность 1/4 Вт.
Формулы мощности
Мощность может рассчитываться при помощи трех следующих основных формул:
Выбирайте формулу, основанную на значениях тока, напряжения или сопротивления, которые Вам известны.
Передача мощности от источника питания к нагрузке
В электрических и электронных системах желательно передавать как можно больше мощности от источника питания к нагрузке. Максимальная передача мощности от генератора, батареи, источника питания или другой электронной схемы имеет место, когда нагрузка согласована с внутренним сопротивлением генератора (рис. 10-1).
На этом рисунке батарея последовательно соединена с резистором Ri, который мы будем называть внутренним сопротивлением источника Ri. Нагрузка, к которой передается мощность, обозначена как RL,. Чтобы к нагрузке передавалась максимальная мощность, сопротивление нагрузки должно быть равно внутреннему сопротивлению генератора. На рисунке 10-1 в нагрузку будет передаваться максимальная мощность, если, например, RL = 1000 Ом и Ri, = 1000 Ом.
Однако поскольку два сопротивления одинаковы, то в каждом из этих сопротивлений будет рас-
Рис.10-1.
сеиваться половина мощности. Это означает, что в случае максимальной передачи мощности как в источнике, так и в нагрузке рассеивается одна и та же величина мощности. Это соответствует эффективности лишь 50%, однако передача максимальной мощности имеет место только при таком условии.
Краткое содержание
В данном эксперименте Вы приступаете к рассмотрению эффекта рассеяния мощности на сопротивлении. Покажите на практике, что формируется тепло. Далее продемонстрируйте режим, при котором имеет место максимальная передача мощности.
ПРОЦЕДУРА
I. Рассмотрите простую схему, показанную на рисунке 10-2. При заданных значениях напряжения и сопротивления, показанных на рисунке, вычислите и запишите величину мощности, рассеиваемой резистором. Р =_____Вт
Рис. 10-2.
2. Соберите схему, показанную на рисунке 10-2. Через несколько секунд дотроньтесь быстро до резистора, чтобы почувствовать нагревание резистора, но будьте очень осторожны. Резистор может очень сильно нагреться. Оставьте резистор на несколько минут подключенным и заметьте эффект протекания через него тока. При условии, что большинство используемых в школьной лаборатории резисторов представляют собой элементы с мощностью 1/4 Вт, укажите, была ли превышена номинальная мощность данного резистора.
Рис. 10-3.
3. Соберите схему, показанную на рисунке 10-3. В ней резистор 1 кОм является имитацией внутреннего сопротивления генератора 9 В, представленного источником питания. В шаге 4 Вы будете подключать резисторы с различными сопротивлениями в качестве нагрузки и определять величину мощности, которая рассеивается в каждом случае.
4. В следующей таблице приведены значения сопротивлений, которые Вы будете использовать в качестве нагрузки. Начиная с самого маленького из указанных значений, подключите этот резистор к схеме, которую Вы только что собрали. Выполните измерение напряжения на сопротивлении, а затем рассчитайте величину рассеиваемой на нем мощности. Повторяйте данный шаг для каждого приведенного в таблице сопротивления и записывайте получаемые значения в таблицу.
5. Обратитесь теперь к Вашим табличным данным. Заметьте, какое сопротивление нагрузки приводит к наибольшей величине мощности рассеяния.
RL == ______ Ом
6. Как это соотносится сравнительно с внутренним сопротивлением генератора?
7. Размонтируйте схему.
ОБЗОРНЫЕ ВОПРОСЫ
1. Мощность, рассеиваемая на резисторе, к которому приложено напряжение 12 В и через который протекает ток 0,15 А, составляет:
а) 1,25 Вт,
б) 1,8 Вт,
в) 12,5 Вт,
г) 80 Вт.
2. Ток, протекающий через резистор 22 Ом, имеет величину ЗА. Рассеиваемая мощность имеет величину:
а) 7,3 Вт,
б) 22 Вт,
в) 66 Вт,
г) 198 Вт.
3. К резистору 4,7 кОм, 1/4 Вт приложено напряжение 40 В. При этом мощность, рассеиваемая на резисторе, превышает номинальную мощность:
а) высказывание верно,
б) высказывание неверно.
4. Мощность рассеивается в виде:
а) света,
б)электрического поля,
в) тепла,
г) магнитного поля.
5. Радиопередатчик имеет выходное сопротивление 500м. Его нагрузкой служит антенна. Антенна для обеспечения максимальной выходной мощности должна иметь сопротивление:
а) 25 Ом,
б) 50 Ом,
в) 100 Ом,
г) 150 Ом.
Рис. 10-1. Максимальная передача мощности имеет место, когда нагрузка согласована с внутренним сопротивлением генератора
Рис. 10-2. К расчету мощности
Рис. 10-3. К расчету мощности
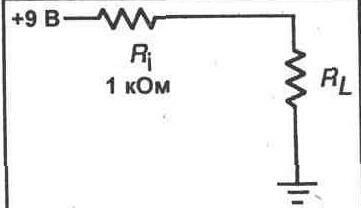
Таблица 1. К измерению параметров мощности
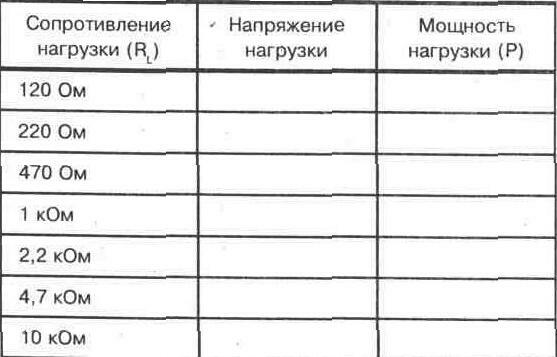
Ф.1 Формула расчета мощности
11. Теорема Тевенина-Гельмгольца
ЭКСПЕРИМЕНТ 11 Теорема Тевенина-Гельмгольца
Цели
После проведения данного эксперимента Вы сможете продемонстрировать и проверить теорему Тевенина-Гельмгольца и использовать ее для анализа схем.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 470 Ом, один резистор 1 кОм, один резистор 2, 2 кОм, один резистор 3, 3 кОм.
ВВОДНАЯ ЧАСТЬ
Теорема Тевенина-Гельмгольца в значительной степени облегчает анализ и разработку электронных схем. Эта теорема позволяет Вам заменить сложную схему, включенную между источником питания и нагрузкой, единственным последовательно включенным резистором. Для примера, предположим, что Вы желаете проанализировать работу схемы, представленной на рисунке 11-1.
Постановка задачи
Конкретно Вы желаете узнать нагрузку или выходное напряжение для различных значений сопротивления нагрузки RL. Всякий раз, когда Вы изменяете RL, Вам надо найти полное сопротивление и общий ток, токи в ветвях и падения напряжения. Этот процесс несложен, но утомителен и требует затрат времени.
Рис. 11-1.
Рис. 11-2.
Решение
Используя теорему Тевенина-Гельмгольца, можно заменить всю сложную схему, включенную между источником питания и нагрузкой, единственным последовательно включенным резистором с сопротивлением, которое называется эквивалентным сопротивлением Тевенина, R . Источник питания заменяется источником питания с другим напряжением, величина которого называется эквивалентным напряжением Тевенина, Vтн (см. рис. 11-2).
В своей совокупности эквивалентное напряжение Тевенина и эквивалентное сопротивление Тевенина формируют напряжение на любой нагрузке и ток в ней с теми же значениями, которые формируются и оригинальной схемой. В результате схемный анализ становится значительно более простым, поскольку весь расчет теперь сводится к расчету простой последовательной схемы.
Шаги
Самый легкий способ для определения эквивалентов Тевенина — это их измерение в конкретной схеме. Чтобы сделать это для рисунка ll-l, удалите нагрузку и, при наличии приложенного
напряжения источника питания, измерьте напряжение между точками включения нагрузки А и В. В результате Вы получаете эквивалентное напряжение Тевенина Vтн.
Далее, при все еще удаленной нагрузке, отсоедините напряжение источника питания и замените его короткозамыкателем (перемычкой). Затем измерьте сопротивление между точками включения нагрузки А и В. В результате Вы получаете эквивалентное сопротивление Тевенина R
После этого Вы можете фактически собрать эквивалентную схему Тевенина с варьируемым источником питания, настроенным на величину напряжения Vтн, и выбрать стандартный резистор с сопротивлением ближайшим к Rтн. Теперь Вы можете подключать различные нагрузки и смотреть, как они работают.
Схемные значения
Другим методом является нахождение величин Vтн и Rтн. Ha основании схемных значений. Сначала удалите резистор нагрузки RL и рассчитайте, напряжение, которое появляется на контактах А и В. Для схемы, представленной на рисунке ll-l, при удалении RL, резисторы R4, R5 и R6 остаются открытыми. Как результат, приложенное к резисторам R2, и R3 напряжение появляется между контактами А и В.
Vтн = Vав = 12 (R2 + R3)/(R1 + R2 + R3) Vтн=Vав = 12 (8,9/10,1) = 12(0,881) = 10,6 В
Далее рассчитывается Rтн. При удаленном R источник питания 12 В заменяется короткозамыкателем. Вычисляется сопротивление между точками А и В.
R4 последовательно с соединенными параллельно резисторами R5 и R6
1,8 кОм + 0,47 кОм = 2,27 кОм
Эквивалентное сопротивление между точками А и В:
Rтн = 2,27 кОм + 1,06 кОм = 3,33 кОм
Эквивалентом Тевенина является источник постоянного напряжения 10,6 В, соединенный последовательно с сопротивлением 3,33 кОм.
Теперь при подключении к этой цепи резистора R, получается полное сопротивление:
910 + 3330 = 4240 Ом
Полный ток, протекающий через схему, имеет величину:
10,6 / 4240 = 0,0025 А = 2,5 мА
А падение напряжения на RL равно:
10,6[910/(910 + 3330)] = 10,6(910/4240) = 2,28 В
Краткое содержание
В данном эксперименте Вы будете использовать процедуру, приведенную ниже.
ПРОЦЕДУРА
1. Обратитесь к схеме, представленной на рисунке 11-3. Используя показанные значения, выполните расчет эквивалентного напряжения и эквивалентного сопротивления Тевенина в точках А и В. Вычислите выходное напряжение для сопротивления нагрузки 3,3 кОм.
Vтн = ____ В Rтн = ______ Ом
VL=____В
Рис. 11-3.
2. Соберите схему, показанную на рисунке ll-З. Включите питание и измерьте эквивалентное выходное напряжение Тевенина на контактах А и В без нагрузки.
Vтн (измеренное) = ______ В
3. Включите нагрузку 3,3 кОм между точками А и В. Измерьте теперь выходное напряжение. Как оно сравнивается с Вашим расчетным значением?
VL (измеренное) = ____ В
4. Выключите питание. Отсоедините источник питания. На его место включите проволочный короткозамыкатель. Отсоедините также нагрузку от контактов А и В. Затем мультиметром
измерьте эквивалентное сопротивление Тевенина на контактах А и В.
Rтн (измеренное) = ____ Ом
5. Нарисуйте эквивалентную схему Тевенина и укажите на ней значения. После этого соберите эту схему, используя источник питания и 'резистор. Используйте такой стандартный резистор, сопротивление которого ближе всего к эквивалентному.
6. Включите питание и измерьте выходное напряжение Тевенина. Отрегулируйте напряжение источника питания, чтобы получить значение, которое Вы рассчитали в шаге 1.
7. Подключите нагрузку 3,3 кОм к эквивалентной схеме и измерьте выходное напряжение. Оно такое же, как и то, которое Вы получили в шаге 3? Объясните.
ОБЗОРНЫЕ ВОПРОСЫ
1. Почему на рисунке 11-1 при удаленном резисторе RL, комбинация резисторов R4-R5-R6 не влияет на выходное напряжение?
а) фактически она влияет на выходное напряжение,
б) в них не протекает ток или на них нет падения напряжения,
в) сопротивление этой комбинации намного меньше, чем сопротивление RL, поэтому нет влияния на выход.
2. Какое значение сопротивления нагрузки создаст максимальную мощность в нагрузке?
а) 910 Ом,
б) 1,06 кОм,
в) 3,33 кОм,
г) 10,6 кОм.
3. Для вычисления Vтн, резистор RL:
а) удаляется или его контакт размыкается,
б) закорачивается.
4. Для вычисления Rтн,источник питания:
а) отключается одним выводом,
б) закорачивается.
5. Теорема Тевенина используется как для схем переменного тока, так и для схем постоянного тока:
а) высказывание истинно,
б) высказывание ложно.
Рис. 11-1. Принципиальная схема для определения теоремы Тевенина-Гельмгольца
Рис. 11-2. Источник питания заменяется источником питания с другим напряжением, величина которого называется эквивалентным напря
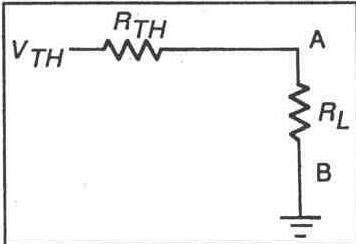
Рис. 11-3. Принципиальная схема для расчета квивалентного напряжения и эквивалентного сопротивления Тевенина в точках А и В
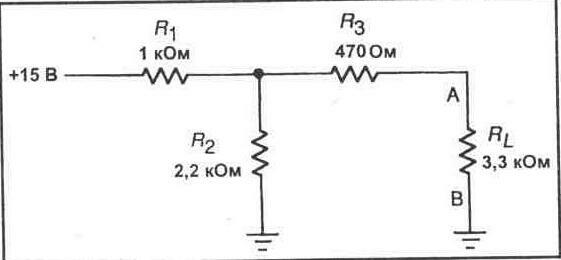
Ф. 1. К расчету сопротивлений между точками А и В
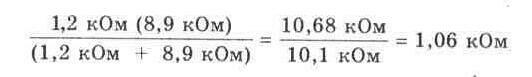
12. Принцип суперпозиции
ЭКСПЕРИМЕНТ 12 Принцип суперпозиции
Цели
После проведения данного эксперимента Вы сможете анализировать схемы, используя принцип суперпозиции.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Два независимых регулируемых источника постоянного напряжения
* Резисторы — 1/4 Вт, 5%:
один резистор 1 кОм, один резистор 1, 5 кОм, один резистор 2, 2 кОм.
ВВОДНАЯ ЧАСТЬ
Принцип суперпозиции — это метод, используемый для анализа сложных схем при использовании двух или более источников питания. Хотя для таких схем могут быть использованы анализ цепей методом контурных токов и другие методы, принцип суперпозиции является более простым и ускоренным.
Для использования принципа суперпозиции при анализе выполняйте три шага:
1) замените все источники напряжения, за исключением одного, короткозамыкателем, а
затем рассчитайте все токи и падения напряжений;
2) замените оставшийся источник напряжения короткозамыкателем и снова сделайте расчет схемы после того, как вновь подключите один из других источников напряжения;
3) алгебраически сложите все токи из Ваших расчетов и подсчитайте все падения напряжения. Пример приводится на рисунке 12-1.
Рис. 12-1.
Примерные шаги
Шаг 1.
Требуется подсчитать напряжение на резисторе R2. Сначала источник V2, заменяется короткозамыкателем. Это приводит к параллельному соединению резисторов R2, и R3
Их эквивалентным сопротивлением является:
180 (330)/(180+ 330) = 59400/510 = 116, 5 Ом
Полное сопротивление составляет:
116, 5+ 750 = 866, 5 Ом
Общий ток, потребляемый от источника питания 12 В, имеет величину:
12/866, 5 = 0, 01385 А = 13, 85 мА
Падение напряжения на резисторе R составляет:
0, 01385 (750) = 10, 39 В
Напряжение на сопротивлениях R2 и R3 имеет величину:
12 - 10,39 = 1,61 В Ток, протекающий через R2 имеет величину:
1,61/330 = 0,0049 А = 4,88 мА Ток, протекающий через R имеет величину:
1,61/180 = 0,00894 А = 8,94 мА
Шаг 2.
Далее источник V1 заменяется короткозамыкателем. Это приводит к параллельному соединению резисторов R1 и R2. Эквивалентным сопротивлением резисторов R1 и R2 является:
750(330)/(750+330)=247500/1080=229,2 Ом
Полное сопротивление составляет:
229,2 + R3 = 229,2 + 180 = 409,2 Ом
Общий ток схемы имеет величину:
12/409,2 = 0,02933 А = 29,33 мА
Падение напряжения на резисторе R3 составляет:
0,02933(180) = 5,28 В
Напряжение на сопротивлениях R1 и R2 имеет величину:
12 - 5,28 = 6,72 В
Ток, протекающий через R1, имеет величину:
6,72/750 - 0,00896 А = 8,96 мА
Ток, протекающий через R2, имеет величину:
6,72/330 = 0,02036 А = 20,36 мА
ШагЗ.
Теперь полный ток через резистор R2 может быть найден сложением токов, которые Вы только что подсчитали. Ток через резистор R2 вызванный напряжением V2 составляет 20,36 мА и протекает сверху вниз (поток электронов). Ток через резистор R2, вызванный напряжением V1, составляет 4,88 мА и протекает снизу вверху. Поскольку два тока противоположно направлены, то результирующим током в цепи является их разность.
20,36 - 4,88 = 15,48 мА
Направление потока электронов такое же, как у тока большей величины (сверху вниз).
Тогда напряжение на резисторе R2, имеет величину:
0,01548(330) = 5,1 В
Это напряжение отрицательно по отношению к массе.
Краткое содержание
В данном эксперименте Вы будете использовать процедуру, приведенную ниже.
ПРОЦЕДУРА
1. Обратитесь к схеме, представленной на рисунке 12-2. Используйте принцип суперпозиции для вычисления всех токов и падений напряжения в схеме. Покажите Вашу работу. Каково падение напряжения на резисторе R2, и какова его полярность?
Vr2=______В
Рис. 12-2.
2. Составьте таблицу, в которой укажите все Ваши расчетные значения, которые относятся к одному только источнику V1, к одному только источнику V2
а также к подключенным одновременно источникам V1 и V2.
3. Соберите схему, показанную на рисунке 12-2. Для данного шага не подключайте V3. А вместо этого вставьте проволочный короткозамыкатель в то место, где показан источник питания V2.
4. Включите питание. Установите источник питания V1 на -15 В. Измерьте все токи через резисторы и соответствующие падения напряжения. Запишите полученные значения в Вашу
таблицу.
5. Выключите питание. Отсоедините проволочный короткозамыкатель и на его место присоедините источник питания V2. Отсоедините источник питания V1, а на его место подключите проволочный короткозамыкатель.
6. Включите питание. Установите источник питания V на +10 В. Измерьте все токи через резисторы и соответствующие падения напряжения. Запишите полученные значения в Вашу таблицу.
7. Выключите питание. Отсоедините проволочный короткозамыкатель и на его место снова присоедините источник питания V1.
8. Включите снова питание. Теперь измерьте все токи и напряжения для данного случая, когда присоединены оба источника питания. Снова запишите полученные значения в Вашу таблицу. Каково напряжение на резисторе R2? Укажите также его полярность.
Vr2=________В
ОБЗОРНЫЕ ВОПРОСЫ
1. Принцип суперпозиции обычно легче использовать, чем метод контурных токов или метод узловых потенциалов:
а) высказывание истинно,
б) высказывание ложно.
2. Принцип суперпозиции используется для анализа схем с одним источником напряжения:
а) высказывание истинно,
б) высказывание ложно.
3. Какова будет полярность падения напряжения на резисторе R, на рисунке 12-2, если изменить полярности обоих источников питания?
а) отрицательная,
б) положительная.
4. Падение напряжения на резисторе R рисунка 12-2 имеет величину:
а) 2, 56 В,
б) 7, 44 В,
в) 12, 44 В,
г) 25, 44 В.
5. Падение напряжения на резисторе R3, рисунка 12-2 имеет величину:
а) 2, 56 В,
б) 8, 44 В,
в) 12, 44 В,
г) 7, 44 В.
Рис. 12-1. Пример к определению принципа суперпозиции
Рис. 12-2. К эксперименту для определения принципа суперпозиции
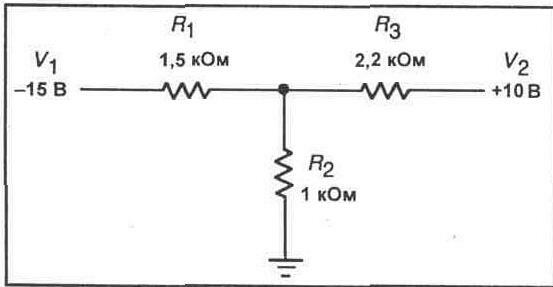
13. Катушки индуктивности и постоянный ток
ЭКСПЕРИМЕНТ 13 Катушки индуктивности и постоянный ток
Цели
После проведения данного эксперимента. Вы сможете продемонстрировать и сформулировать эффект индуктивности в цепи постоянного тока.
Необходимые принадлежности
* Цифровой мультиметр
* Источник постоянного напряжения (от 9 до 15 В)
* Силовой трансформатор
* Неоновая лампа (NE-2) с проволочными выводами
ВВОДНАЯ ЧАСТЬ
Индуктивность — это свойство электронного компонента противодействовать изменениям тока, протекающего через данный компонент.
Индуктивностью обладают компоненты, которые называются катушками индуктивности, соленоидами или дросселями. Если ток, протекающий в катушке индуктивности, изменяется, свойство индуктивности противодействует такому изменению тока. Если ток увеличивается, катушка индуктивности препятствует росту тока. Если ток уменьшается, катушка индуктивности снова пытается сохранить ток без изменения. Эффект индуктивности заметен в первую очередь в тех схемах, где используется переменный ток. Противодействие переменному току, оказываемое катушкой индуктивности, называется индуктивным сопротивлением. Подобно сопротивлению резистора индуктивное сопротивление оказывает фиксированное противодействие, которое контролирует уровень тока в схеме.
В схемах постоянного тока, в которых ток обычно имеет фиксированное значение, определяемое сопротивлениями и напряжениями, катушки индуктивности обычно имеют лишь незначительный эффект или вообще не имеют никакого эффекта. Тем не менее, они оказывают влияние на постоянный ток, и важно ясно представлять себе это явление.
Катушки индуктивности в схемах постоянного тока
Первичным назначением катушки индуктивности в схеме постоянного тока является оказание противодействия в форме сопротивления. Катушки индуктивности обычно представляют собой проволочные спирали, которые создают сопротивление. Хотя резистивное сопротивление катушки индуктивности обычно низко, катушка создает противодействие. В дополнение мощность рассеивается сопротивлением катушки индуктивности.
Эффекты индуктивности проявляются, когда изменяется ток в цепи постоянного тока. Хотя ток обычно имеет фиксированную величину в работающей схеме постоянного тока, не забывайте также, что необходимо еще включать и выключать
схему. Когда ток первоначально подается в схему или удаляется их схемы, имеет место его значительное изменение. Такое изменение тока заставляет катушку индуктивности противодействовать этому изменению. В результате появляется наведенное (индуктированное) напряжение, которое, как и в схеме переменного тока, противодействует изменению тока.
Наиболее значительный эффект достигается в том случае, когда ток через катушку индуктивности внезапно подавляется. Магнитное поле вокруг катушки индуктивности исчезает, индуцируя очень высокое напряжение в катушке. Это напряжение может даже приводить к повреждениям компонентов в некоторых случаях. В других применениях, наоборот, используется преимущество этого эффекта с целью формирования очень высокого напряжения для питания тех или иных специальных компонентов или цепей. Примерами могут служить трансформаторы строчной развертки в телевизионных приемниках и катушки зажигания в системах зажигания автомобилей.
Краткое содержание
В данном эксперименте Вы будете знакомиться с эффектами катушки индуктивности в схеме постоянного тока.
ПРОЦЕДУРА
1. Для данного эксперимента Вы будет использовать первичную обмотку трансформатора. Эта обмотка идентифицируется двумя черными выводами. Все другие выводы игнорируйте.
Измерьте сопротивление катушки индуктивности. Запишите полученное значение.
Сопротивление постоянному току = _____ Ом
2. Предскажите, какой величины ток может быть в катушке индуктивности, если к ней приложить напряжение 15В от источника питания. Ток = ____ мА
3. Подключите источник питания 15 В к катушке индуктивности и измерьте постоянный ток, протекающий через катушку. Обратитесь к рисунку 13-1. Запишите величину протекающего тока.
Измеренный ток = _____ мА
Рис. 13-1. Первичная обмотка, используемая в качестве катушки индуктивности.
4. Какой эффект оказывает источник на катушку индуктивности, и какой эффект оказывает катушка индуктивности на ток в цепи?
5. Рассмотрите неоновую лампу. Это маленькая стеклянная лампочка с тонкими проволочными выводами. Подключите неоновую лампу параллельно с катушкой индуктивности, как показано на рисунке 13-2. Неоновая лампа загорится только в том случае, если напряжение на ее выводах превышает приблизительно 70—90В.
6. Приложите напряжение 15В от источника питания к катушке индуктивности, как показано
на рисунке 13-2. Заметьте состояние неоновой лампы. Включена или выключена неоновая лампа?
Состояние лампы________________
Рис. 13-2.
7. Отсоедините один вывод катушки индуктивности от источника питания и снова заметьте состояние неоновой лампы.
Состояние лампы ________________
8. Повторите шаги 6 и 7 несколько раз, чтобы наверняка увидеть, что происходит.
9. Объясните эффект, который Вы наблюдаете в шагах 7 и 8.
ОБЗОРНЫЕ ВОПРОСЫ
I. Катушка индуктивности противодействует изменениям;
а) напряжения,
б) тока,
в) сопротивления,
г) индуктивности.
2. Другое название для катушки индуктивности:
а) трансформатор,
б) магнит,
в) соленоид,
г) дроссель.
3. Все катушки (соленоиды) имеют сопротивление:
а) высказывание истинно,
б) высказывание ложно.
4. Противодействие постоянному току, оказываемое катушкой индуктивности, называется:
а) индуктивностью,
б) сопротивлением,
в) реактивным сопротивлением,
г) полным сопротивлением.
5. Напряжение 30 вольт подается на 90-вольтовую неоновую лампу. Лампа:
а) включается,
б) не включается.
Рис. 13-1. Первичная обмотка, используемая в качестве катушки индуктивности.
Рис. 13-2. К определению состояния неоновой лампы.
14. Постоянная времени RC-цепи
ЭКСПЕРИМЕНТ 14 Постоянная времени RC-цепи
Цели
После проведения данного эксперимента Вы сможете продемонстрировать, как величины емкости и сопротивления управляют временем заряда и разряда конденсатора.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Источник постоянного напряжения
* Секундомер или часы с секундной стрелкой
* Элементы:
один электролитический конденсатор 22 мкФ, один электролитический конденсатор 100 мкФ, один резистор 33 кОм, 1/4 Вт,
* один резистор 100 кОм, 1/4 Вт, один резистор 220 кОм, 1/4 Вт, один резистор 1 МОм, 1/4 Вт.
ВВОДНАЯ ЧАСТЬ
Конденсатор представляет собой электроэлемент, который накапливает электричество в форме электрического поля. Когда к конденсатору прикладывается постоянное напряжение, электроны покидают одну обкладку конденсатора и скапливаются на другой обкладке под действием
внешней силы напряжения. Это приводит к заряду конденсатора до напряжения, равного приложенному напряжению.
Положительный заряд на одной обкладке конденсатора и отрицательный заряд на другой обкладке конденсатора создают сильное электрическое поле между обкладками в диэлектрике. Такой заряд удерживается даже в том случае, если источник напряжения отсоединяется. Конденсатор может разряжаться соединением его выводов друг с другом для нейтрализации заряда на обкладках.
Зарядка и разрядка конденсатора до определенного напряжения занимает конечный период времени (называемый постоянной времени); это время зависит в основном от емкости конденсатора и включенного последовательно сопротивления. Постоянная времени зарядки — это время, которое требуется конденсатору, чтобы зарядиться до 63, 2% приложенного напряжения. Это время (Т) в секундах выражается так:
Т=RС
Постоянная времени разрядки — это время, которое требуется конденсатору, чтобы разрядиться до 36, 8% от начального заряда.
Время, которое требуется конденсатору, чтобы полностью зарядиться до приложенного напряжения или полностью разрядиться до нуля, приблизительно равно пятикратной постоянной времени, то есть 5Т.
Краткое содержание
Многие электронные схемы основываются на идее использования постоянной времени для своей работы. К таким схемам относятся, например, схемы задержки времени, схемы формирования импульсов и сигналов, а также генераторные схемы. В настоящем эксперименте Вы познакомитесь с постоянной времени заряда и разряда, используя для этого три различных группы резисторов и конденсаторов.
ПРОЦЕДУРА
Процесс зарядки
Резистор 100 кОм; конденсатор 100 мкф
1. Соберите схему, показанную на рисунке 14-1. Соблюдайте полярность при подключении электролитического конденсатора.
Рис. 14-1.
2. Отрегулируйте источник питания на напряжение 12 В.
3. Рассчитайте величину напряжения, которое появится на конденсаторе в течение одной постоянной времени.
Напряжение (Т) = ______ В
4. Рассчитайте постоянную времени, используя значения, показанные на рисунке 14-1. Запишите Ваш результат в колонку 3 на рисунке 14-2. Рассчитайте также значение времени, которое потребуется конденсатору, чтобы полностью зарядиться (5Т). Запишите Ваш результат в колонку 4 на рисунке 14-2.
Рис. 14-2.
5. Соедините измерительные выводы Вашего мультиметра, соблюдая полярность, с выводами конденсатора. Мультиметр должен показать 0 В. Если это не так, на обкладках конденсатора имеется некоторое остаточное напряжение. Удалите его, кратковременно закорачивая выводы конденсатора друг с другом в течение нескольких секунд. Снова выполните измерение напряжения Вашим мультиметром, чтобы убедиться, что напряжение конденсатора равно нулю.
6. Оставьте измерительные выводы мультиметра на выводах конденсатора, свободный конец резистора 100 кОм присоедините к выводу+ 12 В источника питания. В момент присоединения
запустите Ваш секундомер или начните отсчет времени при помощи секундной стрелки Ваших часов. Когда напряжение на конденсаторе начнет расти, замечайте его величину. Когда напряжение на конденсаторе достигнет значения, которое Вы рассчитали в шаге 2, заметьте время по секундомеру или по секундной стрелке. Запишите это значение в качестве измеренной постоянной времени в колонку 5 рисунка 14-2.
ПРИМЕЧАНИЕ: Повторите данный шаг несколько раз, чтобы убедиться в том, что Ваш отсчет времени относительно точен. Ведь Вы пытаетесь наблюдать как за показаниями вольтметра, так и за секундомером, чтобы определить время, необходимое для достижения конкретного уровня напряжения. Это довольно мудреная операция, так что повторите ее несколько раз для большей точности измерений. ВНИМАНИЕ:
если Вам потребуется повторять эксперимент, удаляйте резистор 10кОм и полностью разряжайте конденсатор 100 мкФ, прежде чем приступать к каждому дополнительному измерению. 7. Снова полностью разрядите конденсатор и снова подсоедините измерительные выводы. Коснитесь свободным выводом резистора 100 кОм к выводу +12 В источника питания. На этот раз измерьте время, которое потребуется конденсатору для полной зарядки до величины приложенного напряжения, которое Вы измерили в шаге 1. Как и прежде, начните отсчет времени по секундомеру или по секундной стрелке часов в том момент, когда Вы подаете напряжение на резистор. Запишите это измеренное время,
которое требуется конденсатору для полной зарядки, в колонку 6 рисунка 14-2.
Резистор 11 к0м; конденсатор 22 мкф
8. Повторите шаги с 4 по 7. используя конденсатор 22 мкф и резистор 100 к0м. Заполните поля в таблице на рисунке 14-2, как Вы это делали раньше. Вашими расчетными и измеренными значениями.
Резистор 220 к0м; конденсатор 100 мкф
9. Снова повторите шаги с 4 по 7, но на этот раз используйте конденсатор 100 мкФ и резистор 220 к0м. Запишите Ваши расчетные и измеренные значения в таблицу на рисунке 14-2.
Наблюдение
10. Рассматривая информацию на рисунке 14-2 и замечая различные значения времени, полученные при различных значениях сопротивления и емкости, сделайте Ваше собственное заключение относительно влияния значений сопротивления и емкости на постоянную времени.
Процесс разрядки
Резистор 100 к0м; конденсатор 100 мкф
11. Перекомпонуйте схему, чтобы она соответствовала схеме, показанной на рисунке 14-3. Соблюдайте полярность при подключении электролитического конденсатора. В данной части эксперимента Вы будете демонстрировать процесс разрядки конденсатора. Чтобы сделать это, подключите резистор параллельно конденсатору.
Рис. 14-3.
12. Рассчитайте постоянную времени схемы и время, которое требуется для полной разрядки конденсатора, и запишите Ваши данные в колонку 3 на рисунке 14-4.
Рис. 14-4.
13. Далее определите величину напряжения, до которого разрядится конденсатор за одну постоянную времени. Используйте исходное напряжение
источника питания, которое Вы измерили в шаге 1. Рассчитайте величину напряжения, которое будет присутствовать на Конденсаторе после его разрядки в течение одной постоянной времени.
Напряжение (t) = _______ В
Резистор 100 кОм; конденсатор 22 мкф
14. Подключите измерительные выводы Вашего мультиметра к конденсатору 22 мкф. В данное время напряжение должно равняться нулю, поскольку любой заряд на обкладках конденсатора был устранен в процессе разрядки конденсатора через резистор 1 МОм. Подключите схему к выводу+ 12 В источника питания. Конденсатор заряжается немедленно до напряжения источника питания; последовательно с конденсатором нет подключенного сопротивления.
15. Продолжайте фиксировать измерительные выводы мультиметра параллельно выводам конденсатора. Удалите соединительный провод с вывода+ 12 В источника питания. Одновременно с удалением провода начните отсчет времени по Вашему секундомеру или по секундной стрелке часов. Наблюдайте при этом за напряжением на выводах конденсатора. Когда напряжение достигнет нужного значения, заметьте время. Запишите постоянную времени в колонку 5 таблицы на рисунке 14-4. Как и раньше. Вы можете пожелать повторить шаги 13 и 14 несколько раз, чтобы улучшить точность измерений. Ведь, поскольку Вам приходится наблюдать одновременно за двумя значениями, измерение довольно хитроумно. Усредняя несколько показаний, Вы получите большую точность в измерении.
Резистор 220 кОм; конденсатор 22 мкф
16. Снова повторите шаги с 12 по 15, но на этот раз используйте конденсатор 22 мкф и резистор 220 кОм. Снова рассчитайте значения времени разрядки для одной постоянной времени и для пяти постоянных времени. Запишите все Ваши данные в таблицу на рисунке 14-4.
Наблюдение
17. Рассматривая информацию на рисунке 14-4 и замечая различные значения времени, полученные при различных значениях сопротивления и емкости, сделайте Ваше заключение относительно зависимости между временем разрядки и значениями сопротивления и емкости.
18. На основании сравнения Ваших расчетных и измеренных значений объясните возможные несоответствия.
ОБЗОРНЫЕ ВОПРОСЫ
1. Требуется то же самое время для полной зарядки конденсатора, какое требуется и для полной его разрядки:
а) высказывание истинно,
б) высказывание ложно.
. 2. До какого напряжения зарядится конденсатор 5 мкф через резистор 10кОм за одну постоянную времени при его подключении к источнику питания 6 В?
а) 1, 4 В,
б) 2, 5 В,
в) 3, 8 В,
г) 5 В.
3. Сколько времени потребуется конденсатору из вопроса 2, чтобы полностью разрядиться?
а) 5 мс,
б) 10 мс,
в) 50 мс,
г) 250 мс.
4. Конденсатору требуется 80 миллисекунд, чтобы полностью зарядиться. Поэтому постоянная времени равна:
а) 8 мс,
б) 16 мс,
в) 40 мс,
г) 80 мс.
5. При заданных значениях R (сопротивление) и С (емкость) емкость удваивается, а сопротивление уменьшается в два раза, при этом постоянная времени:
а) остается прежней,
б) удваивается,
в) учетверяется,
г) уменьшается в два раза.
Рис. 14-1. Схема для определения постоянной времени
Рис. 14-2. Таблица для определения времени заряда
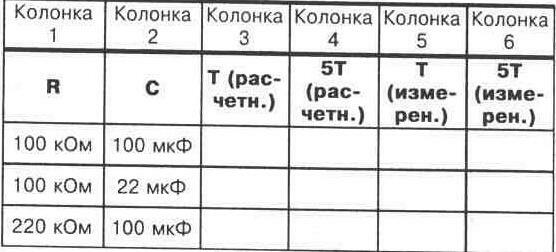
Рис. 14-3. Схема для определения процесса разрядки конденсатора
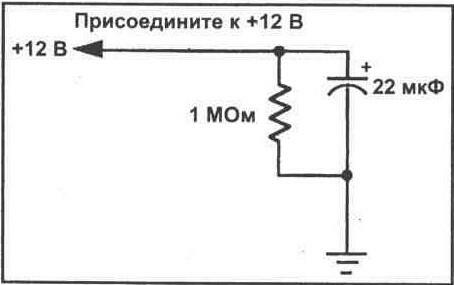
Рис. 14-4. Таблица для определения времени разряда
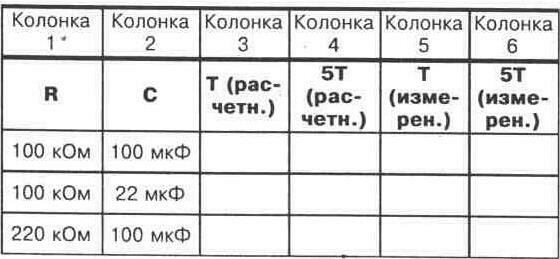
15. Проверка конденсаторов
ЭКСПЕРИМЕНТ 15 Проверка конденсаторов
Цели
После проведения данного эксперимента Вы сможете, используя мультиметр, проверять конденсаторы для выявления дефектных.
Необходимые принадлежности
* Цифровой мультиметр
* Элементы:
один электролитический конденсатор 100 мкФ, один бумажный или пленочный конденсатор 0,47 мкФ, один дисковый конденсатор 0,01 мкФ.
ВВОДНАЯ ЧАСТЬ
Часто появляется необходимость осуществлять проверку конденсаторов во время работ, связанных с поиском неисправностей, ремонтом или разработкой схем. Для данной цели имеются специальные испытательные приборы. У Вас же может не быть под рукой таких приборов, да и особой необходимости в них обычно нет. Для выполнения большинства основных испытаний конденсаторов Вы можете использовать мультиметр, аналоговый или цифровой. В этом эксперименте мы покажем, как использовать Ваш цифровой мультиметр для таких целей.
Выход конденсатора из строя
Имеется три основных пути выхода конденсатора из строя. Во-первых, конденсатор может иметь обрыв. Это означает, что один вывод или даже два вывода могут оторваться от обкладок конденсатора. Схема становится такой, как если бы не было абсолютно никакого электрического соединения.
Другой вид отказа конденсатора — когда он замыкается накоротко. При таком типе неисправности обкладки конденсатора касаются или замыкаются накоротко каким-то другим образом. Короткое замыкание — это соединение с очень незначительным сопротивлением, и эффект такой же, как если бы два вывода конденсатора были соединены непосредственно друг с другом.
Конденсатор может отказать также из-за образовавшейся утечки. Такая утечка происходит вследствие сопротивления, появившегося между обкладками конденсатора. Это проявляется в том, что кажется, будто конденсатор имеет некоторое сопротивление, подключенное к нему параллельно.
Короткие замыкания, обрывы и утечки могут определяться с помощью мультиметра (переключенного в режим измерения сопротивлений, то есть мультиметр при этом используется в качестве омметра).
Проверка конденсатора
Для проверки конденсатора.соедините его выводы параллельно с измерительными выводами мультиметра и измерьте сопротивление конденсатора. Короткое замыкание конденсатора обнаруживается по очень низкому значению сопротивления. Обрыв обнаруживается по всякому отсутствию измерения со стороны мультиметра. Утечка обнаруживается по некоторому определенному значению сопротивления. Запомните также, что в том случае, когда мультиметр «видит» обрыв в схеме, он обычно индицирует единицу в самом левом разряде на жидкокристаллическом дисплее.
О выполнении измерений
Для выполнения измерений значений сопротивления мультиметр должен фактически приложить напряжение к внешнему компоненту. Для этой цели в мультиметре используется внутренний источник. Его напряжение прикладывается к внешнему элементу (резистору или конденсатору) через схемы омметра. Мультиметр, когда он используется для измерения сопротивлений, обращается в омметр. Омметр имеет очень высокое внутреннее сопротивление. Это значение сопротивления определяется пределом измерения, на который устанавливается мультиметр. Чем выше предел измерения сопротивлений, тем больше внутреннее сопротивление мультиметра.
Краткое содержание
Требуется некоторое конечное время для зарядки конденсатора; таким образом, при испытании конденсаторов с большими емкостями Вы заметите варьирование показаний мультиметра. Это происходит, когда конденсатор заряжается до внутреннего напряжения, обеспечиваемого мультиметром. Обычно такая индикация появляется при очень низком начальном значении сопротивления. Постепенно оно увеличивается, пока конденсатор
полностью не зарядится, когда на индикации уже будет показание для незамкнутого контура. В настоящем эксперименте Вы продемонстрируете это явление в следующей процедуре.
ПРОЦЕДУРА
1. Переключите Ваш мультиметр в режим измерения сопротивления постоянному току. Установите предел измерения 200 кОм.
Конденсатор 100 мкф
2. Выберите конденсатор 100 мкф. Кратковременно соедините его выводы, чтобы снять любой заряд, который может остаться в конденсаторе.
3. Коснитесь измерительными выводами мультиметра к выводам конденсатора 100 мкф; красным выводом коснитесь к положительному контакту конденсатора, а черным выводом коснитесь к отрицательному контакту. Обращайте внимание на эффект, который Вы можете наблюдать на жидкокристаллическом дисплее мультиметра. Удерживайте измерительные выводы на выводах конденсатора и следите за показаниями на дисплее, пока не увидите индикации, соответствующей незамкнутой цепи. (Помните: единица в левом разряде индикации.)
4. С учетом изменений в значениях сопротивления, которые Вы заметили во время измерения в шаге 3, объясните, что происходило.
5. Далее разрядите конденсатор, касаясь одним его выводом другого вывода в течение нескольких секунд. Затем установите переключатель диапазонов прибора на предел измерения 2 кОм.
6. Коснитесь измерительными выводами мультиметра к выводам конденсатора; красным выводом — к положительному контакту конденсатора, а черным выводом — к отрицательному контакту. Наблюдайте за эффектом на жидкокристаллическом дисплее мультиметра.
7. Объясните результаты, которые Вы получили в шаге 6, и сравните их с теми результатами, которые были получены Вами в шаге 4.
Конденсатор 0, 47 мкф
8. Выберите конденсатор 0, 47 мкФ. Кратковременно коснитесь друг друга его выводами, чтобы разрядить конденсатор.
9. Установите переключатель диапазонов мультиметра на предел измерения 20МОм. Проверяйте конденсатор, прикоснувшись измерительными выводами мультиметра к выводам конденсатора, обращайте при этом внимание на эффект, который Вы можете наблюдать на жидкокристаллическом дисплее мультиметра.
10. Разрядите конденсатор, касаясь одним его выводом другого вывода в течение нескольких секунд. Затем установите переключатель диапазонов прибора на предел измерения 2 МОм. Затем снова проверьте конденсатор, касаясь измерительными выводами мультиметра выводов конденсатора. Наблюдайте за эффектом на жидкокристаллическом дисплее мультиметра.
Конденсатор 0, 01 мкф
11. Выберите конденсатор 0, 01 мкФ. Кратковременно коснитесь друг друга его выводами, чтобы разрядить конденсатор.
12. Установите переключатель диапазонов мультиметра на предел измерения 2 МОм. Коснитесь измерительными выводами мультиметра к выводам конденсатора и заметьте индикацию мультиметра. ПРИМЕЧАНИЕ: присоединяя измерительные выводы мультиметра к выводам конденсатора, избегайте контакта с Вашими пальцами.
13. Теперь разрядите конденсатор, касаясь одним его выводом другого вывода в течение нескольких секунд. На этот раз присоединяйте измерительные выводы мультиметра к выводам конденсатора, удерживая места соединений Вашими пальцами. Используйте большой и указательный палец каждой руки для прижимания соответствующего измерительного вывода к выводу конденсатора. Наблюдайте за эффектом на жидкокристаллическом дисплее мультиметра.
14. Объясните результаты, которые Вы получили в предыдущих двух шагах.
ОБЗОРНЫЕ ВОПРОСЫ
1. Когда мультиметр переключается в режим омметра, что Вы тестируете?
а) напряжение,
б) ток,
в) сопротивление.
2. Когда мультиметр измеряет незамкнутый контур, на жидкокристаллическом дисплее должно считываться:
а) 0,
б) 1,
и) очень большое значение, г) очень маленькое значение.
3. При проверке конденсатора при помощи мультиметра получено показание 275 кОм. Это означает, что конденсатор:
а) хороший,
б) имеет обрыв,
в) закорочен,
г) имеет утечку.
4. Конденсатор не показывает зарядной индикации на мультиметре. Что может иметь место в подобном случае?
а) конденсатор может иметь очень маленькую величину,
б) используется низкий предел измерения сопротивления,
в) конденсатор может иметь обрыв,
г) все указанное выше,
д) ни одно из указанных выше.
5. Если Вы будете касаться пальцами выводов резистора, конденсатора или измерительных выводов мультиметра, измерения могут оказаться неправильными:
а) высказывание истинно,
б) высказывание ложно.
3. Эксперименты с переменным током.
Эксперименты с переменным током.
1. Ознакомление с осциллографом
ЭКСПЕРИМЕНТ 16 Ознакомление с осциллографом
Цели
После проведения данного эксперимента Вы сможете использовать органы управления осциллографа для вывода на его дисплейный экран осциллограмм сигналов и осуществления измерений амплитуды и частоты для постоянного и перемен-ног» тока.
Необходимые принадлежности
* Осциллограф
* Мультиметр
* Генератор функций
* Источник постоянного напряжения
ВВОДНАЯ ЧАСТЬ
Осциллограф становится относительно простым в использовании прибором после первого знакомства с ним. Затруднение может вызывать лишь изучение и запоминание функции каждого из различных органов управления на передней панели. На передней панели осциллографов имеется множество ручек, лимбов, переключателей, кнопок и соединителей. Для непосвященных это кажется очень трудным. Изучите назначение каждого органа управления и проследите за его действием на дисплее. В результате Вы быстро поймете способ
его использования. Одним из лучших способов изучения функций и методов использования осциллографа является получение по возможности большего опыта во время практической работы.
Осциллограф
Используемый Вами осциллограф, по-видимому, двухканального типа (он позволяет наблюдать одновременно два отдельных сигнала). Следовательно, он имеет два входных кабеля и соединителя. Они обычно маркируются как канал 1 и 2 или А и В. Каждый кабель также имеет наименование; имеются два основных типа — прямой и аттенюаторный.
Кабели осциллографа
Кабель прямого типа является коаксиальным кабелем с двумя выводами, которые обычно имеют концевую заделку посредством зажимов типа «крокодил» для подключения к схеме. В этом кабеле могут использоваться также щуповые наконечники вместо двух зажимов типа «крокодил». В любом случае данный кабель подводит сигнал, который должен воспроизводиться на экране, напрямую (без ослабления) к осциллографу.
С аттенюаторным типом соединителя также используется коаксиальный кабель, но в общем случае применяется щуп вместо зажимов типа «крокодил». Узел щупа содержит последовательный резистор с большим сопротивлением, которое вместе с полным входным сопротивлением осциллографа формирует делитель напряжения. Таким образом, данный щуп и кабель выполняют ослабление (аттенюацию) сигнала в 10 раз.
Преимуществом такого кабеля является то, что он создает меньшую емкостную нагрузку для схем высокой частоты, позволяя визуализировать высокочастотные сигналы и сложные формы сигнала. Тем не менее, взамен имеет место потеря амплитуды сигнала, которая может обычно компенсироваться увеличением усиления осциллографа. Чтобы получить корректное измерение амплитуды сигнала, настройка осциллографа умножается на 10. Такие щупы называются щупами Х10.
Измерение амплитуды
Для амплитудных измерений на осциллографе используется откалиброванная сетка или координатная сетка на экране электронно-лучевой трубки для определения числа делений между максимальным положительным и минимальным отрицательным отклонениями сигнала (такое измерение называется измерением размаха или двойной амплитуды сигнала). Для измерений выполняйте следующие шаги:
Шаги при измерении амплитуды
1. Установите переключатель управления коэффициентом усиления по вертикали для визуализации как можно большего размаха сигнала на координатной сетке.
2. Установите ручку непрерывного управления коэффициентом усиления по вертикали в позицию CAL (калибровка).
3. Подсчитайте количество делений и долей деления между положительным и отрицательным пиками сигнала. Используйте регулятор вертикальной позиции для перемещения осциллограммы сигнала при необходимости. Заметьте, что большая часть осциллографов имеет восемь больших вертикальных делений, разделенных на пять меньших делений.
4. Умножьте число делений на значение установки переключателя коэффициента усиления по вертикали. Вы получаете значение размаха сигнала.
5. Если Вы использовали щуп Х10, умножьте Ваше
значение в шаге 4 на 10. Это даст правильное
значение размаха напряжения.
Пример: Коэффициент усиления по вертикали устанавливается 50 мВ/деление. Это означает, что каждое большое вертикальное деление соответствует 50 мВ. При этом каждое из пяти малых делений соответствует 50/5 = 10 мВ.
Предположим, что амплитуда Вашего сигнала перекрывает 6, 3 делений. Тогда его значение амплитуды равно 50 х 6, 3 = 315 мВ. Если использовался щуп Х10, то амплитуда сигнала равна 315 х 10 = 3150 мВ или 3, 15В.
Измерение частоты
Для измерений частоты (f) на осциллографе сначала измерьте период (t) сигнала. Период — это время одного цикла. Самый простой способ сделать это — подсчитать количество горизонтальных делений между двумя последовательными пиками сигнала. Для измерений выполняйте следующие шаги:
Шаги при измерении частоты
1. Установите переключатель горизонтальной развертки для визуализации одного или двух периодов (циклов) сигнала.
2. Установите ручку непрерывного управления горизонтальной частотной разверткой в положение CAL (калибровка).
3. Подсчитайте количество делений между последовательными пиками сигнала. Используйте регулятор горизонтального сдвига для перемещения осциллограммы сигнала при необходимости.
4. Умножьте число делений на значение установки переключателя горизонтальной развертки. Вы получаете значение периода сигнала (t). 5. Чтобы вычислить частоту сигнала, найдите обратную величину периода: f = 1/t Пример: Переключатель горизонтальной развертки устанавливается на 20 мкс/деление. Предположим, Вы насчитали 4, 4 деления между последовательными пиками сигнала. Тогда его период (1) равен: 4, 4 х 20 = 88 микросекунд. А частота сигнала равна:
f = 1/(88 х 10^-6) = 11363, 64 Гц или 11, 36 кГц
ПРОЦЕДУРА
1. Рассмотрите измерительные выводы осциллографа, чтобы определить, какого они типа. Запишите эти типы:
СН А (канал А. __________
СН В (канал В) __________
2. Включите питание осциллографа при помощи переключателя на передней панели. Дайте электронно-лучевой трубке приблизительно одну минуту, чтобы прогреться:
а) пока электронно-лучевая трубка прогревается, установите переключатель управления режимом развертки в положение Авто;
б) установите селектор источника в положение СН 1 (канал 1) или CН А (канал А);
в) установите регулятор горизонтального сдвига в среднее положение;
г) регулятор вертикального сдвига предусмотрен для обоих входных каналов; установите его также в среднее положение;
д) установите входной переключатель для каждого канала в положение GND (масса);
е) когда осциллограф прогреется, Вы должны видеть яркую горизонтальную линию на экране осциллографа. Поворачивайте регулятор вертикального сдвига, чтобы переместить горизонтальную линию в центр экрана. 3. След на экране должен быть ярким и четким. Если это не так, отрегулируйте его ручками фокусировки и яркости, которые обычно расположены на передней панели осциллографа. Используя регулятор фокусировки, Вы должны попробовать сделать линию размытой, а затем сфокусировать ее до четкого состояния. Попробуйте поработать регулятором яркости, который устанавливает уровень яркости линии. Не делайте линию слишком яркой, ибо в этом случае она будет слишком широкой, что снизит точность Ваших измерений.
ПРИМЕЧАНИЕ: Запомните в качестве основного правила, что яркость делать надо низкой, насколько возможно, лишь бы она обеспечивала удобное наблюдение при нормальном окружающем освещении.
4. Подсоедините щуповой наконечник для канала 1 (СН 1) к небольшому соединителю на передней панели, с маркировкой CAL. Осциллограф содержит встроенный мультивибратор, который работает на частоте 1 кГц и формирует прямоугольное колебание (меандр) с размахом того или иного указанного напряжения. Этот сигнал с внутренней калибровкой позволяет Вам быстро контролировать измерения при помощи осциллографа частоты и амплитуды для корректных калибровок.
CAL (калибровочное) напряжение ___ Vpp
(напряжение размаха). Установите регуляторы передней панели осциллографа таким образом, чтобы регуляторы по горизонтали и вертикали были полностью выведены по часовой стрелке в позиции CAL. Затем установите частоту горизонтальной развертки при помощи переключателя TIME/DIV в положение 0. 1 мс. И, наконец, установите коэффициент усиления по вертикали при помощи переключателя VOLTS/DIV в положение 50 мВ.
5. Если Вы даже подали откалиброванный сигнал на вертикальный вход осциллографа, на его экране не появляется никакого сигнала. Причиной этого является то, что Вы предварительно должны установить входной переключатель в положение GND (масса). Это просто заземлит входную линию и даст Вам опорную позицию нуль вольт для входного сигнала. Вы можете теперь при помощи регулятора вертикального сдвига выполнять перемещение развертки вверх и вниз, чтобы одна из горизонтальных линий на координатной сетке соответствовала положению нуль вольт. Входной переключатель установите в позицию АС (переменный ток). Сразу же Вы должны увидеть прямоугольные колебания на экране. Выполняйте регулирование при помощи регулятора вертикального и горизонтального сдвига, чтобы меандр был четко виден на экране. ПРИМЕЧАНИЕ: Когда Вы устанавливаете входной переключатель в положение АС, последовательно с входной линией включается конденсатор. На основании этого любое постоянное напряжение во входном сигнале блокируется, и на индикацию выводится только переменная составляющая сигнала. В этом случае происходит следующее. Установив линию нуля вольт на центральной горизонтальной линии, Вы заметите, что прямоугольный сигнал коммутируется выше и ниже нулевой линии. Другими словами, блокировочный конденсатор внутри осциллографа подавляет выход постоянного напряжения мультивибратора, так что на экране осциллографа появляется только переменная составляющая сигнала. 6. Далее, используйте регулятор коэффициента усиления по вертикали, чтобы варьировать амплитуду сигнала. По мере вращения регулятора Вы можете заметить, что амплитуда может изменяться в широком диапазоне. Это позволяет Вам удобно разместить сигнал на экране осциллографа для наблюдения за ним. Помните, тем не менее, что для осуществления точных измерений этот регулятор должен быть в полностью выведенном по часовой стрелке положении (CAL).
лишь в этом случае обозначения напряжений на делениях регулятора коэффициента усиления по вертикали корректны. Поворачивайте регулятор горизонтальной развертки. Вы сейчас изменяете скорость развертки внутреннего генератора пилообразного напряжения. Следовательно, Вы можете наблюдать на экране осциллографа больше или меньше периодов сигнала. Таким образом, данный регулятор позволяет Вам удобно отрегулировать количество периодов для индикации. Тем не менее, для измерения периода или других временных параметров сигнала регулятор развертки должен быть в полностью выведенном по часовой стрелке положении (CAL), чтобы значения времени на делениях переключателя были корректны.
7. Установите входной переключатель в положение DC (постоянный ток) и заметьте влияние на форму сигнала. Вам может потребоваться поработать регуляторами вертикального и/или горизонтального сдвига, чтобы снова увидеть форму сигнала. Чтобы временно локализовать и установить нулевую линию, установите входной переключатель назад в положение GND. Затем совместите линию развертки с одной из горизонтальных линий в нижней части экрана. Это опорная линия нулевого напряжения. Теперь установите входной переключатель снова в положение DC. Заметьте, что прямоугольный сигнал появляется выше нулевой линии. Это означает, что прямоугольный сигнал переключается приблизительно от нуля вольт до пикового значения. Заметьте, что когда форма сигнала разворачивается вверх от базисной нулевой линии, она представляет положительное напряжение. Если форма сигнала разворачивается вниз от базисной нулевой линии, она отражает отрицательное напряжение. 8. Измерьте амплитуду сигнала. Обеспечьте, чтобы регулятор коэффициента усиления по вертикали был полностью выведен по часовой Стрелке в положение калибровки. Подсчитайте количество вертикальных делений между основанием прямоугольного колебания и вершиной прямоугольного колебания. Например, если напряжение CAL равно 0, 25В или 250 мВ (размах), Вы должны насчитать 5 делений, когда VOLTS/DIV установлен в. положение 50 мВ. Пять делений по 50 мВ каждое дают напряжение размаха 250 мВ. Если Вы использовали аттенюаторный щуп Х10, установите регулятор коэффициента усиления по вертикали на значение 5 мВ на одно деление, затем умножьте это значение на 10, чтобы получить 250 мВ.
калибровочное напряжение =________ Vpp
Внутренняя схема калибратора недостаточно точна, однако сигнал на экране должен приблизительно соответствовать указанному на передней панели.
9. Измерьте частоту сигнала. Большинство калибраторов используют частоту 1 кГц, однако может использоваться и другое значение. Установите переключатель TIME/DIV в положение 1 мс. Убедитесь, что регулятор развертки находится в положении CAL. Это означает, что каждое горизонтальное деление на экране соответствует одной миллисекунде. Вы должны суметь увидеть, что один период прямоугольного сигнала занимает до одной миллисекунды на экране. Вспомните, что один период состоит из одного развернутого в положительную сторану и одного развернутого в отрицательную сторону импульса.
Установите переключатель TIME/DIV в положение 0, 1 мс. Теперь каждое деление на экране соответствует 0, 1 мс или 100 мкс. Поскольку период сигнала 1 кГц равен 1 миллисекунде, один полный период сигнала должен занимать весь экран (10 горизонтальных делений). Выполняйте перемещение при помощи регулятора горизонтального сдвига туда и сюда, чтобы Вы могли видеть, что положительный фронт импульса на левой стороне экрана начинается у дальней левой вертикальной линии, а затем положительный фронт следующего импульса начинается приблизительно у дальней правой вертикальной линии. Повторите это движение, чтобы Вы могли лучше разобраться в этом. Поскольку калибратор не является чрезмерно точным, длительность одного периода может быть несколько меньше или несколько больше, чем 10 полных делений на экране. Какова измеренная частота калибратора?
частота CAL = ____ Гц
0. Пока Вы рассматриваете эту форму сигнала, установите переключатель MODE в положение NORM. Если картинка исчезает, подстраивайте регулятор порогового уровня до тех пор, пока сигнал не появится снова. Вы используете теперь функцию запускаемой развертки. Вы можете регулировать пусковой
уровень или точку на форме сигнала, где сигнал запускает горизонтальную развертку. Поскольку входной сигнал представляет собой положительный импульс, запуск будет осуществляться по положительному напряжению. Варьируйте регулятором пускового уровня как в направлении по часовой стрелке, так и против часовой стрелки, замечая его влияние на форму сигнала. Установите регулятор пускового уровня таким образом, чтобы, сигнал визуализировался на экране. Вытяните ручку регулятора пускового уровня. Данный переключатель изменяет полярность при запуске. Теперь Вы заметите, что форма сигнала начинается на левой стороне экрана с разворачиванием в отрицательном направлении, а не в положительном, как раньше. Позже, когда Вы будете выводить на экран колебания синусоидальной формы, Вы снова более подробно будете знакомиться с этой пусковой функцией.
11. Подключите кабель осциллографа к выходу генератора функций.
12. Установите генератор функций для формирования синусоидального сигнала с частотой 1 кГц. Поверните регулятор амплитуды или регулятор выходного уровня на генераторе функций до упора по часовой стрелке. Вы должны увидеть синусоидальный сигнал с частотой приблизительно 1 кГц на экране осциллографа. Если на экране ничего нет, переключатель режима MODE может находиться у Вас в положении NORM, а пусковой уровень может быть некорректно отрегулирован.
Регулируйте ручкой пусковой уровень, пока на экране не появится форма сигнала. После этого отрегулируйте положения переключателя коэффициента усиления по вертикали и переключателя горизонтальной развертки таким образом, чтобы Вы могли видеть на экране несколько периодов синусоидального сигнала. Поработайте с регуляторами, пока не получите на экране удовлетворительную картинку. 13. Теперь Вы будете исследовать частотный диапазон генератора функций. На генераторе функций установите переключатель диапазонов в положение самого низкого значения и поверните регулятор частоты в крайнее положение против часовой стрелки. Установите ручку переключателя режима MODE на осциллографе в положение AUTO. Вы видите горизонтальную линию поперек экрана, перемещающуюся вверх и вниз с небольшой скоростью. Скорость небольшая потому, что частота развертки вашего осциллографа слишком быстра для Вас, чтобы визуализировать (то есть, выводить на экран) полный период синусоидального сигнала, генерируемого генератором функций на такой малой частоте. Вы можете получить представление о частоте, если подсчитаете, сколько раз нарастает и убывает синусоидальное колебание. Синусоидальному сигналу должна потребоваться приблизительно 1 секунда, чтобы пройти от самой низкой до самой высокой позиции, а затем вернуться назад. Во время наблюдения за синусоидальным сигналом начните вращать ручку регулятора частоты в направлении по часовой стрелке. Скорость движения вверх и вниз должна возрастать. В некоторый момент Вы должны будете иметь возможность установить переключатель TIME/DIV на большее значение, и Вы будете наблюдать синусоидальный сигнал низкой частоты.
Установите переключатель диапазонов на генераторе функций в положение следующего более высокого значения и заметьте эффект на экране. Частота должна сразу же возрасти до значительно большего значения, и Вы увидите уже больше периодов, визуализируемых на экране. Поверните переключатель TIME/DIV в положение большего значения, и наблюдайте за синусоидальным сигналом на экране. Варьируйте положение регулятора частоты на генераторе функции, чтобы видеть, как изменяется частота.
Продолжайте этот процесс, переключая генератор функций на более высокие частоты и варьируя регулятор частоты по всему его диапазону. Этим Вы будете продолжать увеличивать частоту. При увеличении частоты синусоидальные колебания не будут больше видны, если только Вы нс растянете их при помощи переключателя горизонтальной развертки TIME/ DIV. Всякий раз, когда Вы повышаете частоту. необходимо уменьшать частоту развертки, чтобы наблюдать за формой сигнала. 14. В качестве последнего наблюдения за частотой генератора функций установите переключатель диапазонов на генераторе функций в положение максимального значения и поверните регулятор частоты R полностью выведенное по
часовой стрелке положение. То, что Вы увидите, это сигнал максимальной частоты, которую может обеспечить генератор функций. Используя описанную методику установите переключатель развертки в удобное положение. После этого выполните измерение периода между смежными положительными или отрицательными пиками. Оцените время периода, затем рассчитайте частоту. Какова приблизительно максимальная выходная частота у генератора функций?
Максимальная частота = ___ Гц
15. Пока Вы исследуете максимальную выходную частоту генератора функций, измерьте также амплитуду этого сигнала:
а) обеспечьте, чтобы регулятор амплитуды находился в его полностью выведенном по часовой стрелке положении. Это положение максимального выходного напряжения, которое может быть получено от генератора функций без нагрузки;
б) установите на осциллографе регулятор коэффициента усиления для входного сигнала по, вертикали в полностью выведенное по часовой стрелке положение калибровки;
в) переключатель VOLTS/DIV установите в удобное положение для измерения;
г) используйте регулятор сдвига по вертикали для перемещения сигнала вверх и вниз таким образом, чтобы Вы смогли подсчитать количество делений между отрицательным пиком и положительным пиком сигнала;
д) подсчитайте количество делений и умножьте это число на цену одного деления. Затем снова
умножьте полученное значение на коэффициент 10, если Вы используете аттенюаторный щуп для измерений;
е) какое максимальное выходное напряжение Вы можете получить от генератора функций? Максимальное выходное напряжение = __ В (размах) Наконец, продемонстрируйте, как уменьшить выходное напряжение сигнала с помощью регулятора амплитуды на генераторе функций в направлении против часовой стрелки. Вы должны иметь возможность понизить выходное напряжение до очень низкого уровня, однако это напряжение не опустится полностью до нуля, и при низких амплитудах форма сигнала будет несколько искажена. Однако в любом случае Вы можете варьировать формой выходного сигнала в довольно широком диапазоне.
16. Большинство генераторов функций формируют также прямоугольные сигналы и/или сигналы треугольной формы. Если Вы захотите понаблюдать за другими формами сигналов, формируемыми генератором функций, Вы можете добиться этого настройкой органов управления на передней панели. Рассмотрите сигнал треугольной формы. Какой это сигнал, АС (переменного тока. или DC (постоянного тока)? Рассмотрите сигнал прямоугольной формы. Какой это сигнал, АС (переменного тока. или ОС (постоянного тока)?
Сигнал треугольной формы _________
Сигнал прямоугольной формы _______
ОБЗОРНЫЕ ВОПРОСЫ
1. Щуп х10 осциллографа:
а) ослабляет входной сигнал в 10 раз,
б) усиливает входной сигнал в 10 раз.
2. Расстояние между положительным и отрицательным пиками синусоидального сигнала составляет 6, 4 делений. Регулятор коэффициента усиления по вертикали установлен на 50 мкВ/деление. Используется щуп х10. Значение размаха напряжения составляет:
а) 3, 2 мкВ,
б) 32 мкВ,
в) 320 мкВ,
г) 3, 2 мВ.
3. Расстояние по горизонтали между смежными пиками синусоидального сигнала составляет 4, 7 делений. Скорость развертки составляет 2 мкс/ деление. Частота синусоидального сигнала равна:
а) 63, 5 кГц,
б) 94 кГц,
в) 106, 38 кГц,
г) 176, 24 кГц.
4. Какая форма сигнала обычно не формируется генератором функций?
а) синусоидальный сигнал,
б) пилообразный сигнал,
в) сигнал прямоугольной формы,
г) сигнал треугольной формы.
5. Какой регулятор Вы используете для перемещения сигнала вверх и вниз по экрану? а) регулятор коэффициента усиления по горизонтали,
б) регулятор коэффициента усиления по вертикали,
в) регулятор горизонтального сдвига,
г) регулятор вертикального сдвига.
2. Измерения синусоидальных сигналов
ЭКСПЕРИМЕНТ 17 Измерения синусоидальных сигналов
Цели
После проведения данного эксперимента Вы сможете измерять при помощи мультиметра и осциллографа напряжения синусоидальных сигналов и осуществлять преобразование эффективных значении в значения размаха и наоборот.
Необходимые принадлежности
* Мультиметр (цифровой мультиметр)
* Осциллограф
* Генератор функций
* Источник постоянного напряжения
* Резистор 2,7 кОм
ВВОДНАЯ ЧАСТЬ
Имеется два основных метода измерения напряжений синусоидальных сигналов — при помощи мультиметра и при помощи осциллографа. Если используется мультиметр, показания прибора осуществляются непосредственно в вольтах, которые отмечаются на шкале указателем аналогового прибора или в виде десятичного числа на жидкокристаллическом или светодиодном индикаторе цифрового прибора. При этом представляемое на индикации значение является эффективным значением или среднеквадратическим значением. Оно является также более точным показанием.
Осциллограф визуализирует на экране синусоидальный сигнал. Это наиболее легкий и более точный метод для измерения размаха сигнала. Из двух этих устройств значение мультиметра является более точным, как уже упоминалось. Тем не менее, осциллограф позволяет Вам видеть сигнал, а также любой шум, искажение или помехи, которые могут сопровождать сигнал.
Ограничения приборов
Мультиметр имеет ограничение по высокой частоте. Это предельное значение частоты варьирует от прибора к прибору, однако оно не превышает обычно нескольких тысяч герц. Осциллограф же может выполнять измерения напряжений сигналов с частотой до нескольких мегагерц.
Мультиметр позволяет Вам также измерять ток, тогда как осциллограф нет. При включении мультиметра последовательно с цепью или с компонентом Вы можете получить индикацию эффективной величины тока. Единственным способом измерить ток при помощи осциллографа является косвенный способ, а именно, надо измерить напряжение на резисторе, преобразовать значение размаха в эффективное значение, а затем разделить его на сопротивление резистора.
Формулы преобразования
При выполнении тестов и измерений в электронике обычно является необходимым преобразование
эффективных значении в значения размаха и наоборот. Для преобразования эффективных значении в значения размаха используйте следующие формулы:
Vpp = 2,828 Vrms Ipp = 2,828 Irms
(где: РР — размах, rms — эффективное значение) Для преобразования значений размаха, в эффективные значения используйте следующие формулы:
Vrms= 0,3535 Vpp
Irms= 0,3535 Ipp
Пример: Пусть требуется преобразовать показание 6,3 Vpp в эффективное значение:
Vrms= 0,3535 Vpp = 0,3535 (6,3) = 2,23 В
Пример: Пусть требуется преобразовать эффективное значение тока 7 мА в значение размаха:
Ipp = 2,828 Irms = 2,828 (7) = 19,8 мА
Осциллограф может выполнять также измерения по постоянному току. Смещение горизонтальной линии по вертикали относительно нулевой линии на экране осциллографа представляет собой входной уровень по постоянному току. Для измерения постоянного тока горизонтальную линию развертки совместите с линией координатной сетки, соответствующей нулю. Подайте входной сигнал постоянного тока, затем измерьте смещение по вертикали в делениях и преобразуйте в напряжение.
Краткое содержание
Вы познакомитесь с измерением токов и напряжений синусоидальных сигналов и выполните преобразования единиц в следующей процедуре.
ПРОЦЕДУРА
1. Включите осциллограф и визуализируйте горизонтальную линию.
2. Включите генератор функций, выберите формирование синусоидального сигнала и установите поворотный селектор на 1 кГц. Подключите выход генератора ко входу осциллографа. Визуализируйте сигнал. Отрегулируйте осциллограф для получения стабильной индикации. Отрегулируйте выход генератора до получения значения сигнала 4 V
3. Вычислите эффективное значение (rms) этого синусоидального сигнала. Измерьте эффективное значение при помощи цифрового мультиметра. Сравните Ваши расчетное и измеренное значения.
Vэфф(расчетное) = ______ В
Vэфф (измеренное) = ______ В
4. Измерьте период синусоидального сигнала при помощи осциллографа. Т = _______ секунд
5. Рассчитайте частоту синусоидального сигнала при помощи измеренного Вами периода. Сравните Ваши расчетное и измеренное значения и установку регулятора на генераторе функций.
f = ______ Гц
6. Повторите шаги 2—5 с синусоидальным сигналом 500 мВ на частоте 60 Гц и прямоугольным сигналом 15кГц, 3В Какое значение имеет эффективное напряжение в связи с синусоидальным сигналом?
7. Подключите выход генератора функции к резистору 2, 7 кОм. Отрегулируйте генератор для формирования 9 V с частотой 120 Гц. Проконтролируйте напряжение при помощи осциллографа.
8. Рассчитайте ток через резистор, используя закон Ома.
I = ______ мА
9. Измерьте ток через резистор, используя цифровой мультиметр. Сравните Ваши расчетное и измеренное значения. I = ______ мА
10. Отключите резистор от генератора. Включите один из лабораторных источников постоянного напряжения. Отрегулируйте его на формирование выходного напряжения+ 6 В. Измерьте это выходное напряжение при помощи цифрового мультиметра и осциллографа. Повторите действия для выходного постоянного напряжения-12 В.
11. Подключите выход генератора функций последовательно с источником постоянного напряжения и визуализируйте результирующий сигнал. Установите выходное напряжение источника питания на + 5 В и отрегулируйте генератор функций на 400 Гц и 2 Vpp. Начертите диаграмму комбинированного сигнала.
12. Приведите список источников возможных погрешностей, которые могут быть причиной раз
личий между расчетными и измеренными значениями в предыдущих шагах.
ОБЗОРНЫЕ ВОПРОСЫ
1. Чему равно напряжение размаха 85 мВ в переводе на эффективное значение?
а) 6 мВ,
б) ЗОмВ,
в) 170 мВ,
г) 240 мВ.
2. Чему равно эффективное значение 16 мкА в пересчете на значение размаха?
а) 5, 7 мкА,
б) 11, 3 мкА,
в) 7, 07 мкА,
г) 45, 23 мкА.
3. Мультиметр дает индикацию:
а) значений амплитуды,
б) "значений размаха (двойной амплитуды),
в) эффективных значений,
г) средних значений.
4. Осциллограф может измерять постоянный ток:
а) высказывание истинно,
б) высказывание ложно.
5. Какое устройство дает более точные измерения?
а) осциллограф,
б) мультиметр.
3. Катушки индуктивности и переменный ток
ЭКСПЕРИМЕНТ 18 Катушки индуктивности и переменный ток
Цели
После проведения данного эксперимента Вы сможете объяснить эффект индуктивности в схеме переменного тока и рассчитать значения индуктивности и реактивного сопротивления по результатам измерении.
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Катушка индуктивности 100 мГн
* Генератор функций / сигнал-генератор
ВВОДНАЯ ЧАСТЬ
Когда катушка индуктивности включается в цепь переменного тока, непрерывные изменения напряжения приводят к изменениям тока, которые в свою очередь генерируют то возрастающее, то убывающее магнитное поле. Это магнитное поле индуцирует встречное напряжение в катушке индуктивности, и оно противодействует изменениям тока. В результате имеет место непрерывное противодействие протеканию тока. Это противодействие называется индуктивным сопротивлением (XL).
формула индуктивного сопротивления
Индуктивное сопротивление катушки или дросселя зависит от частоты приложенного переменного напряжения (f) и значения индуктивности (L) в генри. Для вычисления индуктивного сопротивления, выражаемого в омах, служит простая формула:
Индуктивное сопротивление прямо пропорционально частоте и индуктивности. Если известно индуктивное сопротивление, путем преобразования основной формулы может быть найдена или частота, или индуктивность, как показано ниже:
формула полного сопротивления
Вспомните, что чистых индуктивностей нет, поскольку катушки индуктивности сделаны с использованием проволоки, которая имеет сопротивление. Полное сопротивление, оказываемое катушкой индуктивности переменному току, представляет собой, следовательно, комбинацию индуктивного сопротивления и обычного (активного) сопротивления. Это комбинированное противодействие известно как полное сопротивление (или импеданс). Полное сопротивление может быть вычислено при помощи формулы:
Вспомните, что индуктивность приводит к запаздыванию тока относительно напряжения. По
этой причине напряжения на катушке индуктивности и на резисторе сдвинуты по фазе на 90 градусов друг относительно друга. Это как раз и не позволяет нам просто сложить вместе индуктивное сопротивление и активное, сопротивление, чтобы получить величину импеданса.
Если известно полное сопротивление, а индуктивное сопротивление или активное сопротивление неизвестно, предыдущая формула может быть преобразована для их нахождения следующим образом:
Если известно полное сопротивление индуктивной схемы, Вы можете рассчитать ток в схеме, если Вы знаете приложенное напряжение. Это осуществляется применением закона Ома:
I=V/Z
Естественно, эта формула также может быть преобразована для вычисления двух других переменных, если это потребуется:
z=v/I V=IZ
Краткое содержание
В данном эксперименте Вы познакомитесь с эффектом индуктивности в схеме переменного тока.
ПРОЦЕДУРА
1. Измерьте сопротивление обмотки катушки индуктивности при помощи мультиметра.
Сопротивление постоянному току =____ Ом
2. Присоедините катушку индуктивности 100 мГн к сигнал-генератору, формирующему напряжение размаха 4 Vpp с частотой 400 Гц.
3. Теперь измерьте фактическое значение тока первичной обмотки. Вспомните, что амперметр должен включаться последовательно со схемой для выполнения измерения. Подключите мультиметр для измерения переменного тока. Убедитесь, что генератор продолжает формировать 4 Vpp.
Is= _____ МА
4. Используя информацию, которую Вы собрали
в предыдущих шагах, и формулы, приведенные в вводной части, рассчитайте полное сопротивление схемы.
Z = _____ Ом
5. Используя информацию, которую Вы собрали в предыдущих шагах, и формулы, приведенные в вводной части, рассчитайте индуктивность (L) катушки. L = _____ мГн
ОБЗОРНЫЕ ВОПРОСЫ
1. При увеличении частоты переменного тока, пропускаемого через катушку индуктивности, индуктивное сопротивление:
а) возрастает,
б) уменьшается,
в) остается без изменения.
2. При уменьшении величины индуктивности в схеме индуктивное сопротивление:
а) возрастает,
б) уменьшается,
в) остается без изменения.
3. При уменьшении сопротивления катушки индуктивности ее полное сопротивление:
а) возрастает,
б) уменьшается,
в) остается без изменения.
4. Единицей измерения для величины индуктивного сопротивления является:
а) генри,
б) фарада,
в) ватт,
г) ом.
5. Катушка индуктивности имеет (активное) сопротивление 120 Ом. Когда к катушке прикладывается переменное напряжение 24 В с частотой 60Гц, протекает ток 111 мА. Значение индуктивности составляет приблизительно:
а) 0, 12Гн,
б) 0, 35 Гн,
в) 0, 48 Гн,
г) 1, 2 Гн.
Ф.1 Формула индуктивного сопротивления
Ф.2 Определение частоты или индуктивности
Ф.3 Формула полного сопротивления
Ф.4 Определение индуктивного или активного сопротивления
4. Работа трансформатора
ЭКСПЕРИМЕНТ 19 Работа трансформатора
Цели
После проведения данного эксперимента Вы сможете объяснить работу трансформатора в схеме переменного тока и рассчитать значения коэффициента трансформации.
Необходимые принадлежности
* Двухканальный осциллограф
* Цифровой мультиметр
* Силовой трансформатор
* Генератор, функций / сигнал-генератор
* Элементы:
резистор 100 Ом, резистор 1 кОм.
ВВОДНАЯ ЧАСТЬ
Трансформатор — это электронный компонент с одной или несколькими проволочными обмотками обычно на стальном сердечнике или на каркасе. Трансформатор имеет назначение передавать электрическую энергию из одной схемы в другую посредством магнитного поля. Трансформаторы используются для повышения или понижения напряжения, а также для согласования полного сопротивления.
Схема трансформатора
На рисунке 19-1 представлена типичная принципиальная схема трансформатора. Когда переменное напряжение полается на левую на схеме (первичную) обмотку, в ней протекает ток. Ток создает переменное магнитное поле, которое пересекает витки правой на схеме (вторичной) обмотки. Хотя физический контакт между двумя этими обмотками отсутствует, магнитное поле индуцирует (наводит) напряжение во вторичной обмотке. Это напряжение может использоваться затем для питания другой схемы или цепи.
Рис. 19-1.
Величина напряжения, индуцируемого во вторичной обмотке, зависит от количества витков в каждой обмотке. Отношение количества витков во вторичной обмотке (Ns) к количеству витков в первичной обмотке (Np) называется коэффициентом трансформации и выражается математически следующим образом:
Коэффициент трансформации = N = Ns/Np
Определение напряжения
Вы можете определить величину напряжения, создаваемого во вторичной обмотке (Vs), простым
умножением напряжения, подводимого к первичной обмотке (Vp), на коэффициент трансформации. Эта формула такова:
Vs=Vp(Ns/Np)
Если коэффициент трансформации больше 1, напряжение на вторичной обмотке будет больше, чем напряжение на первичной обмотке: повышающий трансформатор. Если коэффициент трансформации меньше 1, напряжение на вторичной обмотке будет меньше, чем напряжение на первичной обмотке: понижающий трансформатор. Коэффициент трансформации и напряжения на обмотках связаны следующим образом:
N= Ns/Np =Vs/Vp
Определение токов. в первичной и вторичной обмотках
Поскольку подводимая мощность трансформатора почти одинаковое выходной мощностью, коэффициент трансформации может быть использован также для определения токов первичной и вторичной обмоток трансформатора (Iр и Is). Здесь имеет место обратная зависимость, как показывает следующее выражение:
Ip/Is=Ns/Np,
Соединения трансформаторной обмотки могут бытъ такими, что выходное напряжение будет в фазе с входным напряжением или различаться по фазе на 180° с ним. Фаза может быть; изменена простым обращением соединений с одной обмоткой. Если соединения трансформатора выполнены
таким образом, чтобы формировать сдвиг по фазе на 180°, говорят, что напряжение на вторичной обмотке этого трансформатора инвертировано.
Некоторые трансформаторы имеют отводы от обмотки, чтобы обеспечить несколько выходных напряжении. Обычным соединением является отвод от средней точки (СТ) вторичной обмотки, который обеспечивает формирование двух напряжений, равных половине полного напряжения на вторичной обмотке (см. рис. 19-1).
Краткое содержание
В данном эксперименте Вы познакомитесь с работой трансформатора. Вы научитесь также измерять напряжения трансформатора и рассчитывать коэффициент трансформации.
ПРОЦЕДУРА
1. Подключите первичную обмотку (черные выводы) трансформатора к выходу сигнал-генератора. Подайте синусоидальное напряжение 100 Гц. Установите величину напряжения на первичной обмотке 10Vpp. Контролируйте сигнал на экране осциллографа.
2. Обратите внимание на три других вывода трансформатора. Два из них имеют один и тот же цвет, обычно желтый или красный. Это выводы от вторичной обмотки. Третий провод имеет другой цвет, обычно синий, и представляет собой отвод от средней точки обмотки. ПРИМЕЧАНИЕ: Концы проводов, по-видимому, неизолированы, так что будьте осторожны, чтобы концы не касались друг друга, в противном случае может иметь место короткое замыкание.
Если выводы вторичной обмотки изолированы, снимите приблизительно 1/2 дюйма изоляции с каждого конца.
3. Включите сигнал-генератор. Используя Ваш мультиметр, измерьте переменное напряжение, создаваемое на двух желтых или красных выводах вторичной обмотки. Не прикасайтесь к выводам при выполнении этого подключения. Запишите полученное напряжение;
Напряжение на вторичной
обмотке (Vs)= ________ В
4. При выполнении Ваших измерений измерьте напряжение между синим выводом и каждым из желтых выводов. Запишите эти значения:
Напряжение между синим выводом
и первым желтым выводом = __________ В
Напряжение между синим выводом и,вторым желтым выводом ==_____ Б
5. Используя полученные Вами в шагах 1 и 3 данные, рассчитайте коэффициент трансформации данного трансформатора,а также токи в первичной и вторичной обмотках. Предполагайте, что нагрузка во вторичной обмотке составляет 100 Ом. Коэффициент трансформации =______
Ip=_____
Is=———————
Какой это трансформатор, повышающий или понижающий?
6. Подключите к выводам вторичной обмотки резистор 1000м. Снова измерьте напряжение на вторичной обмотке. Vs=______В
7. Подключите мультиметр последовательно с вторичной обмоткой. Измерьте ток. 1s = _______ мА
8. Рассчитайте ток в первичной обмотке. 1р = ___ мА
9. Измерьте ток в первичной обмотке. Ip= _______ мА
10.Покажите на экране двухканального осциллографа напряжение на первичной обмотке и напряжение на вторичной обмотке. Какова фазовая зависимость между напряжением на первичной обмотке и напряжением на вторичной обмотке?
11 Обратите (реверсируйте) соединения вторичной обмотки. Какова теперь фазовая зависимость между напряжением на первичной обмотке и напряжением на вторичной обмотке?
12.Отключите резистор 1000м. Реверсируйте первичную и вторичную обмотки. Используйте желтые или красные выводы в качестве выводов первичной обмотки и подключите их к сигнал-генератору. Подключите резистор 1 кОм к вторичной обмотке (теперь это черные выводы).
13.Установите сигнал-генератор на формирование напряжения с размахом 1'2 В на первичной обмотке. Измерьте напряжение на вторичной обмотке:
Vs=_______В
Какой это трансформатор, повышающий или понижающий?
14.Рассчитайте коэффициент трансформации, а также токи в первичной и вторичной обмотках. N =______
Ip=______
Is=_______
15.Подключите мультиметр последовательно с нагрузкой 1 кОм. Измерьте ток во вторичной обмотке.
Is=_______ мА
16.Измерьте ток в первичной обмотке. 1р = _______ мА
ОБЗОРНЫЕ ВОПРОСЫ
1. Трансформатор имеет 1600 витков во вторичной и 500 витков в первичной обмотке. Какого типа этот трансформатор?
а) повышающий,
б) понижающий.
2. Если к первичной обмотке трансформатора, описанного в шаге 6 процедуры, прикладывается напряжение 120 В, каким будет напряжение на вторичной обмотке?
а) 37,5 В,
б) 120 В,
в)384 В,
г) 462 В.
3. В данном эксперименте, если к вторичной обмотке трансформатора в шаге 6 прикладывается напряжение 120 В, какое напряжение Вы измерите в таком случае на первичной обмотке?
а) 14 В.
б) 120 В,
в) 134 В,
г) 1028 В.
4. Переменное напряжение 240В прикладывается к первичной обмотке трансформатора. Напряжение на вторичной обмотке составляет 48 В. Тогда коэффициент трансформации равен:
а) 0,12;
6)0,2;
в) 1,8;
г) 5.
5. Если трансформатор из вопроса 4 имеет отвод от средней точки, каково напряжение на одной половине вторичной обмотки?
а) 24 В,
б) 48 В,
в) 240 В,
г) 600 В.
Рис. 19-1. Схема трансформатора
5. Конденсаторы и переменный ток
ЭКСПЕРИМЕНТ 20 Конденсаторы и переменный ток
Цели
После проведения данного эксперимента Вы сможете рассчитывать и измерять токи и напряжения в последовательных и параллельных емкостных цепях.
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функций
* Источник постоянного напряжения
* Элементы:
один конденсатор 0, 01 мкф, один резистор, 10 кОм.
ВВОДНАЯ ЧАСТЬ
Когда конденсатор используется в цепи переменного тока, он оказывает определенное противодействие току, которое называется емкостным сопротивлением. Емкостное сопротивление, подобно индуктивному сопротивлению, противодействует протеканию тока, но только в цепи переменного тока. Емкостное сопротивление измеряется в омах и зависит от частоты переменного тока и от емкости конденсатора. Емкостное сопротивление обратно пропорционально частоте (f) и емкости (С). Это
емкостное сопротивление может быть рассчитано при помощи формулы:
Обычно конденсаторы комбинируются с резисторами и другими компонентами в различные последовательные и параллельные цепи для создания фильтров, фазовращателей, цепей связи и прочих схем. Одной из наиболее распространенных конфигураций является последовательная резистивно-емкостная цепь, показанная на рисунке 20-1.
Рис. 20-1.
Исходное напряжение синусоидальной формы (Vs)прикладывается к резистору и конденсатору, включенным последовательно. Полное противодействие протеканию тока в этой цепи является комбинацией емкостного сопротивления и обычного (активного) сопротивления. Резисторы и конденсаторы функционируют различным образом, и поскольку конденсатор порождает сдвиг фаз в цепи на 90 градусов, нельзя непосредственно складывать сопротивление резистора и емкостное сопротивление, чтобы подсчитать общее сопротивление протеканию тока, которое называется полным сопротивлением или импедансом (Z). Для получения полного сопротивления используется приведенная ниже формула:
Теорема Пифагора и полное сопротивление
Это известная теорема Пифагора, используемая для решения прямоугольных треугольников. Сопротивление, емкостное сопротивление и полное сопротивление могут быть представлены сторонами прямоугольного треугольника, как показано на рисунке 20-2А.
Рис. 20-2.
В последовательной цепи один и тот же ток (I) протекает через все компоненты. Это означает,
что ток через конденсатор имеет ту же величину, что и ток через резистор, причем эта величина равна величине тока, потребляемого от источника напряжения. Поскольку ток общий для всех компонентов, мы можем использовать закон Ома и умножить величину тока на величину сопротивления, емкостного сопротивления и полного сопротивления, чтобы вычислить напряжения в цепи.
IR=Vr
IXc= Vc
IZ = Vs
Следовательно, мы можем снова нарисовать треугольник, используя напряжения, полученные нами указанным выше образом (см. рис. 20-2Б). Теперь треугольник представлен напряжением на сопротивлении (Vr), напряжением на конденсаторе (Vc) и напряжением источника питания (Vs). Закон Кирхгофа говорит о том, что сумма падении напряжения на компонентах последовательной цепи равна напряжению источника питания. Это означает, что в том случае, если мы сложим напряжение на резисторе и напряжение на конденсаторе, мы должны получить в результате напряжение источника питания. Однако, как можно видеть на рисунке 20-2Б, напряжения не совпадают по фазе друг с другом. По этой причине напряжения не могут складываться друг с другом непосредственно, и мы должны использовать теорему Пифагора для решения прямоугольного треугольника. Подставляйте поэтому значения из рисунка 20-2Б в формулу
в соответствии с теоремой Пифагора и находите напряжение источника питания следующим образом:
Итак, чтобы найти напряжение источника питания, просто измерьте напряжение на резисторе и напряжение на конденсаторе, возведите каждое значение в квадрат и сложите полученные значения друг с другом. После этого для получения значения напряжения источника питания извлеките корень квадратный из полученной суммы.
Не забывайте, что при известном напряжении источника питания и одном из других напряжений Вы можете вычислить неизвестное напряжение при помощи простого преобразования приведенной выше формулы. Тогда можно получить еще два варианта указанной формулы:
Краткое содержание
В данном эксперименте Вы убедитесь, что конденсатор оказывает противодействие переменному току. Затем Вы соберете последовательную резистивно-емкостную схему, аналогичную приведенной на рисунке 20-2, подсчитаете, а потом измерите все токи и напряжения для проверки существа сказанного ранее.
ПРОЦЕДУРА 1: измерение сдвига фаз
Чтобы завершить данный эксперимент. Вам потребуется измерить сдвиг фаз между двумя
синусоидальными сигналами. Для этого выведите два сигнала на двухканальный осциллограф. Один сигнал, верхняя осциллограмма, используйте в качестве опорного и подключите на вход канала 1 или А. Другой сигнал подведите к каналу 2 или В. После этого проделайте следующее:
1. Отрегулируйте скорость горизонтальной развертки, чтобы можно было видеть один период синусоидального сигнала. Установите непрерывную развертку в состояние калибровки CAL.
2. Измерьте период (t) синусоидальных сигналов, как описано в эксперименте 16.
3. Подсчитайте количество делений между двумя смежными или тремя последовательными положительными пиками синусоидальных сигналов.
4. Рассчитайте смещение во времени (t,) умножением количества делений на настройку скорости горизонтальной развертки.
5. Вычислите сдвиг фаз в градусах при помощи следующей формулы:
360 t1/t градусов
Пример
Период синусоидального сигнала равен 250 мкс. Промежуток между двумя смежными положительными пиками двух синусоидальных сигналов составляет 2,6 деления. Скорость развертки составляет 10 мкс/дел. Смещение во времени равно:
t1= 2,6 х 10 = 26 микросекунд
Сдвиг фаз равен:
360(26)/250 = 37,44 градуса
Процедура 2: резистивно-емкостная схема
1. Соберите резистивно-емкостную схему, показанную на рисунке 20-3.
Рис. 20-3.
2. Отрегулируйте частоту генератора на 600 Гц. Установите величину размаха напряжения на выходе генератора 10В.
3. Проделайте следующие измерения как при помощи осциллографа, так и при использовании мультиметра:
Осциллограф Мулътиметр Vr————В Vr=____В Vc—————В Vc=____В Объясните, почему они различны, но эквиваленты. Нарисуйте прямоугольный треугольник напряжений.
4. Выполните следующие вычисления для схемы на рисунке 20-3.
I=_____мА
Z =_____ Ом
5. Выполните измерение сдвига фаз между входным напряжением и выходным напряжением. _______ градусов
Опережает выходное напряжение или запаздывает по сравнению с выходным напряжением. Почему?
6. Измените входную частоту на 1000 Гц. Убедитесь, что величина размаха напряжения генератора все еще составляет 10 В. Повторите шаги 3, 4 и 5. Сделайте вывод о том, как полное сопротивление и ток варьируются в зависимости от частоты, путем сравнения с Вашими значениями, полученными в шаге 4.
7. Поменяйте местами позиции резистора и конденсатора. Повторите шаг 5. Опережает выходное напряжение или запаздывает по сравнению с выходным напряжением? ______ градусов
8. Найдите частоту, при которой R = Хc. в данной схеме. Сначала частоту вычислите. Затем, используя осциллограф и генератор звуковой частоты, выполните измерения, чтобы проверить Ваши расчеты.
f=_____Гц
Объясните, какую процедуру Вы использовали и почему.
9. Соберите параллельную резистивно-емкостную схему, показанную на рисунке 20-4. Вычислите ее общее активное сопротивление (Rt), общую емкость (Сt) и полное сопротивление (импеданс). Нарисуйте треугольник токов.
Rt = _____ Ом
Сt = _____ мкФ
Z =_____ Ом
Рисунок 20-4.
10.Приложите к схеме напряжение с размахом 10 В и с частотой 200 Гц. Измерьте полный ток в схеме, используя мультиметр. Вычислите импеданс схемы (полное сопротивление). Z=_____Ом
11.Каков сдвиг фаз между полным током и приложенным напряжением? ________градусов
12.Во всех вышеприведенных шагах объясните различия между измеренными и расчетными значениями.
ОБЗОРНЫЕ ВОПРОСЫ
1. При повышении частоты сигнала, приложенного к последовательной резистивно-емкостной схеме, напряжение на конденсаторе соответственно:
а) увеличивается,
б) уменьшается,
в) остается тем же,
г) падает до нуля.
2. При уменьшении емкости конденсатора в последовательной резистивно-емкостной схеме ток схемы соответственно:
а) увеличивается,
б) уменьшается,
в) остается тем же,
г) падает до нуля.
3. Напряжение на резисторе в последовательной резистивно-емкостной схеме имеет значение 3 В. Напряжение на конденсаторе имеет значение 4 В. Напряжение источника питания равно тогда:
а) 1 В,
б) 3,5 В,
в) 5 В,
г) 7 В.
4. Напряжение источника питания в последовательной резистивно-емкостной схеме имеет значение 6 В. Тогда ток в схеме имеет величину:
а) 0.2 Ом,
б) 2 Ом,
в) 20 Ом,
г) 200 Ом.
5. Напряжения на компонентах в последовательной резистивно-емкостной схеме имеют значения: Vr = 5 В и Vc = 4 В. Резистор имеет сопротивление 1,5 кОм. Частота равна 2 кГц. Какова емкость конденсатора?
а) 0,018 мкФ,
б) 0,047 мкФ,
в) 0,066 мкФ,
г) 0,075 мкФ.
Рис. 20-1. Последовательная резистивно-емкостная цепь
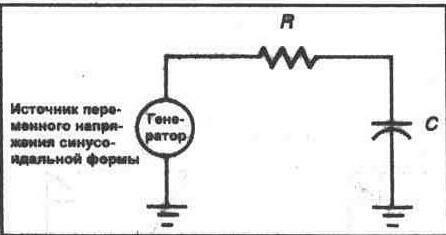
Рис. 20-2. Сопротивление, емкостное сопротивление и полное сопротивление могут быть представлены сторонами прямоугольного треуго
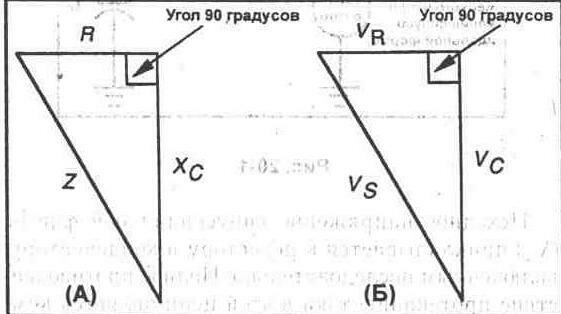
Рис. 20-3. Простая резистивно-емкостная схема
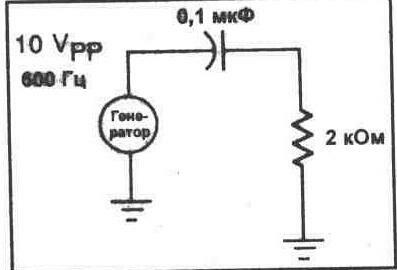
Рисунок 20-4. Параллельная резистивно-емкостная схема
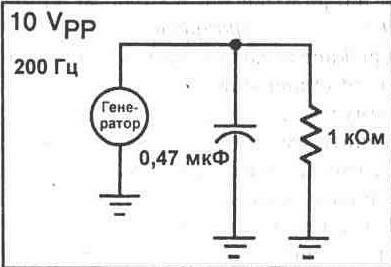
Ф. 1 Емкостное сопротивление обратно пропорционально частоте (f) и емкости (С)
Ф. 2. К определению полного сопротивления или импеданса (Z)
Ф. 3. Нахождение напряжения источника питания
Ф. 4. Нахождение напряжения при помощи простого преобразования
6. Резистивно-индуктивно-емкостные схемы
ЭКСПЕРИМЕНТ 21 Резистивно-индуктивно-емкостные схемы
Цели
После проведения данного эксперимента Вы сможете рассчитывать и измерять все токи, напряжения и полные сопротивления в последовательных LCR-схемах (резистивно-индуктивно-емкостных схемах).
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функции
* Источник постоянного напряжения
* Элементы:
одна катушка индуктивности 100 мГн, один конденсатор 0,1 мкФ, один резистор 4700м.
ВВОДНАЯ ЧАСТЬ
Резистивно-индуктивно-емкостная схема (называемая также LCR-схемой или RLC-схемои) скомбинирована из сопротивления, индуктивности и емкости. Всякий раз, когда катушки и конденсаторы комбинируются в схеме переменного тока,. их реактивные сопротивления гасят друг друга.
Вспомните: катушка индуктивности приводит к запаздыванию тока по отношению к приложенному напряжению на 90 градусов; тогда как конденсатор приводит к тому, что ток опережает напряжение на 90 градусов.
Как результат этого катушка индуктивности аннулирует действие конденсатора, так как их действия противоположны. Аналогично в последовательной схеме, состоящей из индуктивности и емкости, компонент с большей величиной реактивного сопротивления подавляет меньшее реактивное сопротивление.
Рис. 21-1.
Пример. В схеме на рисунке 21-1 катушка индуктивности имеет индуктивное сопротивление 100 Ом, а конденсатор имеет емкостное сопротивление 750м, поэтому емкостное сопротивление аннулируется полностью, и поведение схемы будет таким, как будто она обладает общим индуктивным сопротивлением 100 — 75 = 25 Ом. Это
комбинированное общее (эффективное) реактивное сопротивление и используется при расчете полного сопротивления схемы. Поведение схемы имеет индуктивный характер, поскольку XL, больше, чем Хc.
Определение полного сопротивления
Для получения полного сопротивления последовательной резистивно-индуктивно-емкостной схемы используется приведенная ниже формула:
Следовательно, имеем:
После того, как Вы узнаете полное сопротивление схемы, можно, естественно, рассчитать ток в схеме при помощи закона Ома, в предположении, что известно напряжение источника питания (Vs). Это выполняется при использовании; следующего выражения с подстановкой найденных выше значений:
I=V/Z
I = 100/55,9 = 1,79 А
После этого, зная, что ток в каждом компоненте один и тот же, Вы можете определить падения напряжения на каждом, компоненте. Это снова осуществляется при помощи закона Ома и следующих формул:
Vс = IR = 1,79(50) = 89,5 В
Vс = IXL = 1,79(100) = 179 В
VL= IXc =1,79(75) = 134,25 В
Как и в любой последовательной схеме, значения напряжений распределяются пропорционально значениям активного сопротивления и реактивных сопротивлений: на реактивных сопротивлениях большей величины падают напряжения большей величины. Не забывайте только, что вследствие сдвига фазы, обусловленного типом схемы. Вы не можете попросту складывать непосредственно падения напряжений на компонентах, чтобы получить общее напряжение источника питания. Необходимо при этом выполнять сложение векторных величин. На рисунке 21-2 показано, как это делается при использовании данных предыдущего примера.
Рис. 21-2.
Краткое содержание
В данном эксперименте Вы соберете последовательную резистивно-индуктивно-емкостную схему и сделаете все вычисления, необходимые для расчета схемы. После этого Вы выполните измерения для проверки Ваших расчетов.
ПРОЦЕДУРА
1.Измерьте активное сопротивление катушки индуктивности 100 мГн при помощи вашего мультиметра.
RL =_____Ом
2. Соберите схему, показанную на рисунке 21-3. Отрегулируйте частоту генератора на 1 кГц и установите величину размаха напряжения на выходе генератора 4 В.
Рис. 21-3.
3. Измерьте Vr, Vl, Vc и Q и запишите полученные значения в таблицу. Напомним, что 9 означает
сдвиг фазы тока или V по отношению к приложенному напряжению Vs. 4. Используя табличные данные, вычислите I и Z и запишите их в таблицу. Определите характер схемы (индуктивная или емкостная схема) и отметьте в таблице.
5. Увеличьте частоту генератора до 2 кГц. Сохраняйте величину размаха генератора равной 4 В.
6. Повторите шаги 3 и 4 при этой более высокой частоте. Запишите Ваши данные в таблицу.
7. Нарисуйте эквивалентные схемы для частоты I кГц и частоты 2 кГц и укажите эквивалентные значения реактивных компонентов в мкФ или в мкГн, как это необходимо.
8. Рассчитайте фактическую мощность (Р), рассеиваемую схемой при каждой частоте, и запишите эти значения в таблицу. Назовите компоненты, которые рассеивают мощность, и сделайте пояснения.
ОБЗОРНЫЕ ВОПРОСЫ
I. Резистивно-индуктивно-емкостная схема имеет следующие компоненты: XL = 30 Ом, Хc = 42 Ом, R = 150м. Схема в общем является:
а) индуктивной, XL = 12 Ом,
б) индуктивной, ХL= 72 Ом,
в) емкостной, Хc= 72 Ом,
г) емкостной, Хc = 12 Ом.
2. В схеме, описанной в вопросе 1, наименьшее падение напряжения на:
а) резисторе,
б) катушке индуктивности,
в) конденсаторе.
3. Каково полное сопротивление (импеданс) схемы, описанной в вопросе I?
а) 15 Ом,
б) 19,2 Ом,
в) 72 Ом,
г) 87,5 Ом.
4. Последовательная резистивно-индуктивно-емкостная схема имеет индуктивный характер, если:
а) Хc > XL,
б) Хc > VL
в) VL > Vc, r)XL<Xc.
5. Конденсатор 0,02 мкФ и конденсатор 0,047 мкФ соединены параллельно. Общая эквивалентная емкость равна:
а) 0,0094 мкФ, 6)0,014 мкФ,
в) 0,0335 мкФ,
г) 0,067 мкФ.
Рис. 21-1. Принципиальная схема для определения параметров резистивно-индуктивно-емкостной схемы
Рис. 21-2. Сложение векторных величин
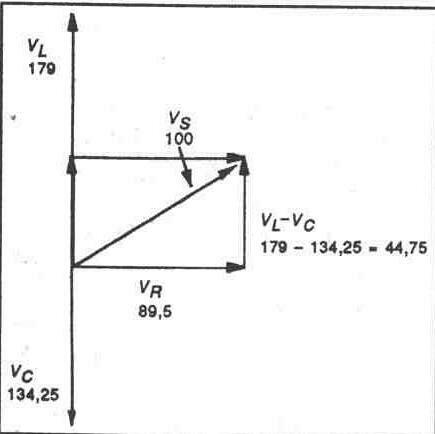
Рис. 21-3. Принципиальная схема для определения параметров резистивно-индуктивно-емкостной схемы
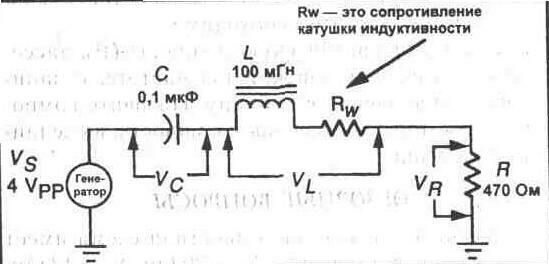
Таблица 1. К измерению параметров резистивно-индуктивно-емкостной схемы

Ф. 1. Полное сопротивление последовательной резистивно-индуктивно-емкостной схемы
Ф. 2. Пример расчета полного сопротивления последовательной резистивно-индуктивно-емкостной схемы
7. Резонанс
ЭКСПЕРИМЕНТ 22 Резонанс
Цели
После проведения данного эксперимента Вы сможете рассчитывать резонансную частоту резистивно-индуктивно-емкостной схемы и выполнять измерения в схеме для определения существования условия резонанса в схеме.
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функций
* Элементы:
одна катушка индуктивности 10 мГн, один конденсатор 0, 22 мкФ, один конденсатор 0, 47 мкФ, один резистор 100 Ом.
ВВОДНАЯ ЧАСТЬ
Резонанс — это такое состояние резистивно-индуктивно-емкостной схемы, когда индуктивное сопротивление и емкостное сопротивление одинаковы. Поскольку эти реактивные сопротивления одинаковы, они полностью компенсируют друг друга. • При резонансе имеют место многие специальные эффекты. Например, в силу того, что реактивные
сопротивления полностью гасят друг друга, схема проявляет себя как полностью резистивная.
Вы сможете обнаружить резонансные схемы почти во всех типах электронного оборудования. Они широко используются для выполнения различных задач настройки и фильтрации в электронном оборудовании. В данном эксперименте Вы рассмотрите эффект резонанса как в параллельных, так и в последовательных схемах.
Последовательный резонансный контур
Последовательный резонансный контур представлен на рисунке 22-1. Вспомните, что при наличии резонанса в схеме индуктивное сопротивление и емкостное сопротивление полностью компенсируют друг друга, и сопротивление току оказывает одно лишь активное сопротивление схемы. В такой схеме полное сопротивление попросту равно значению R плюс сопротивление постоянному току катушки. Главной характеристикой последовательного резонансного контура является то, что его полное сопротивление минимально при резонансе. При настройке частоты на величину, превышающую или лежащую ниже резонансной частоты, полное сопротивление возрастает.
Поскольку при резонансе в последовательном резонансном контуре полное сопротивление минимально, ток в контуре возрастает до пиковой величины. Эта большая величина тока при ее умножении на индуктивное сопротивление и на емкостное сопротивление дает очень высокие падения напряжения на катушке индуктивности и на конденсаторе. В действительности падения напряжения на катушке индуктивности и на конденсаторе
в условиях резонанса часто значительно превышают напряжение питания. Эти необычайно высокие при резонансе напряжения называются скачками напряжения при резонансе или резонансными повышениями напряжения.
Рис. 22-1. Параллельный резонансный контур
Параллельный резонансный контур представлен на рисунке 22-2. Конденсатор и катушка индуктивности соединяются параллельно друг с другом, и вся комбинация иногда соединяется последовательно с резистором. Поскольку при резонансе индуктивное сопротивление и емкостное сопротивление полностью компенсируют друг друга, схема обнаруживает очень значительное активное сопротивление. В такой схеме полное сопротивление параллельного индуктивно-емкостного контура возрастает до многих тысяч Ом при резонансе. При частотах, превышающих или лежащих ниже резонансной частоты, полное сопротивление уменьшается.
Рис. 22-2.
Если Вы измерите линейный ток в резисторе, соединенном последовательно с параллельным резонансным контуром, Вы обнаружите, что ток достигает минимума в условиях резонанса. Это происходит вследствие того, что при резонансе полное сопротивление максимально,и,следовательно, это приводит к формированию минимальной величины тока через контур. При изменении частоты в любую сторону от резонансной частоты полное сопротивление контура уменьшается, и линейный ток возрастает.
Полное сопротивление параллельного резонансного контура вычисляется на основании следующей формулы:
Z=L/CR
В этой формуле: R — сопротивление катушки индуктивности L. Например, если L = 2 мГн, С = 0,05 мкФ и R = 5 Ом, полное сопротивлений Z равно: '
Z = 2 х 10^-3 / (0,05 х 10 ^-6)(5)
Z = 8000 Ом
Вы можете также использовать такую формулу:
Z = Rw(Q^2 + 1)
где: Rw— это сопротивление обмотки катушки индуктивности и Q = Xl/Rw.
Краткое содержание
Как было указано ранее, в данном эксперименте Вы соберете последовательный резонансный контур и параллельный резонансный контур, а также познакомитесь с некоторыми из упомянутых эффектов. Вы практически рассчитаете резонансную частоту (fг ) при заданных значениях индуктивности и емкости. Это осуществляется при помощи следующей формулы:
fr = 1 / 2*3.14(LC)^0.5
ПРОЦЕДУРА
1. Обратитесь к рисунку 22-3. Рассчитайте резонансную частоту при заданных значениях, показанных на рисунке.
Рис. 22-3.
fr=______Гц
2. Прежде чем собирать схему, измерьте сопротивление катушки индуктивности. Это сопротивление оказывает влияние на полное сопротивление схемы.
Активное сопротивление катушки индуктивности = ____ Ом
ПРИМЕЧАНИЕ: Данные, полученные в шагах 3—11, должны заноситься в таблицу на рисунке 22-4, как указано ниже.
3. Вычислите полное сопротивление схемы при резонансе. Запишите Ваш результат.
Рис. 22-4.
4. Далее вычислите полный ток схемы. Запишите его величину.
5. Зная частоту входного сигнала, определите значения индуктивного и емкостного сопротивления. Используя резонансную частоту, которую Вы рассчитали в шаге 1, вычислите определите значения индуктивного и емкостного сопротивления при резонансе. Запишите Ваши результаты.
6. Теперь вычислите падения напряжения на каждом из компонентов схемы на базе значений, полученных в шаге 5. Запишите Ваши результаты.
7. Соберите схему, показанную на рисунке 22-3. При помощи регулятора амплитуды на генераторе функций сформируйте значение размаха напряжения 4 В.
8. При помощи осциллографа осуществляйте мониторинг (текущий контроль) напряжения на резисторе 1000м. Во время мониторинга напряжения добейтесь максимального значения напряжения настройкой регулятора частоты на генераторе функций. Выполняйте Ваши настройки медленно и позволяйте показаниям мультиметра установиться, прежде чем переходить к каждой новой настройке. ПРИМЕЧАНИЕ: настройка на максимальное значение — процесс очень медленный и утомительный, потратьте однако Ваше время, чтобы получить наиболее точные результаты. Продолжайте настройку до тех пор, пока Вы не получите это максимальное напряжение. В результате Вы получили настройку генератора функций на резонансную частоту схемы. Объясните, почему данная процедура используется для нахождения fr .
9. Выполните повторный контроль, чтобы убедиться, что размах выходного напряжения генератора функций составляет 4 В. Если необходимо, снова отрегулируйте выходное напряжение на это значение и повторите при этом шаг 8.
10.После того, как схема настроена в режим резонанса, измерьте падения напряжения на каждом из компонентов. Запишите их значения.
11.Сделайте разрыв в схеме в том месте, где конденсатор 0,22 мкФ соединяется с катушкой, как
Вы это делали в предыдущем эксперименте. Это позволит Вам включить в схему мультиметр для измерения тока в схеме. Переключите Ваш мультиметр для измерения переменного тока. Установите предел измерения 2 мА. Измерьте ток в схеме и запишите Ваш результат.
12. Теперь сравните Ваши расчетные и измеренные значения. Они должны быть одинаковыми или, по крайней мере, очень близкими. Объясните возможные различия.
13. В процессе измерения тока в последовательном резонансном контуре варьируйте выход генератора функций при помощи регулятора частоты. Поворачивайте ручку медленно против часовой стрелки для уменьшения частоты и замечайте влияние на величину тока. Регулировка частоты должна выполняться настолько медленно, чтобы Вы могли наблюдать за изменениями показания мультиметра, так как требуется несколько секунд, чтобы показания установились после каждого нового изменения частоты.
Далее поворачивайте ручку медленно в направлении по часовой стрелке для увеличения частоты и снова замечайте влияние на величину тока. При изменении частоты выше или ниже резонансной частоты Вы обнаружите значительные вариации тока. Во время наблюдения за этими вариациями определяйте сразу, каким образом частота влияет на ток схемы.
14. Снова соедините катушку и конденсатор 0, 22 мкФ.
15. Присоедините измерительные выводы осциллографа к конденсатору и к катушке индуктивности одновременно. Варьируйте частоту при. помощи регулятора частоты на генераторе функций, чтобы получить минимальный уровень напряжения. Когда будет достигнуто минимально возможное напряжение, схема настроена в резонанс. Заметьте положение указателя, регулятора частоты на генераторе функций. Объясните, что Вы здесь получили;
16. Удалите конденсатор 0, 22 мкФ из макетной панели и на его место установите конденсатор 0, 47 мкФ. Вычислите резонансную частоту этой новой комбинации.
fr=____Гц
При увеличении емкости в схеме до 0,47 мкФ резонансная частота:
_________ увеличивается
_________ уменьшается
17.Снова присоедините измерительные выводы осциллографа к комбинации конденсатора и катушки индуктивности. Варьируйте частоту при помощи регулятора частоты на генераторе функций, чтобы получить минимальный уровень напряжения. Когда будет достигнуто минимальное напряжение, заметьте то направление, в котором Вы повернули регулятор генератора функций. Частота в данном случае выше или ниже, чем раньше? _________ выше
_________ ниже
Соответствует это результатам, которые предсказаны Вами в шаге 16?
18.Соберите параллельный резонансный контур, схема которого представлена на рисунке 22-5.
Заметьте, что два конденсатора включены последовательно и их комбинация соединена параллельно с катушкой индуктивности. Это соединение образует параллельный резонансный контур, в котором два последовательно включенных конденсатора имеют единственное эквивалентное значение емкости. Затем параллельный резонансный контур соединен последовательно с резистором 1 кОм, и вся полученная комбинация подключена к генератору функций.
Рис. 22-5.
19. Вычислите резонансную частоту данной схемы. Индуктивность известна, но Вам требуется вычислить полную емкость схемы (Ст). Вспоминая, что Вы узнали ранее о последовательном включении конденсаторов, вычислите сначала полную емкость схемы. Запишите это значение. После этого вычислите резонансную частоту данной схемы и запишите Ваш результат в предусмотренное поле.
Ст = _______мкФ
fr=_______Гц
20.Используя формулу, приведенную ранее для полного сопротивления параллельного резонансного контура, найдите это полное сопротивление. Используйте значение сопротивления катушки, которое Вы измерили в шаге 2.
Z =_______ Ом
21.Подайте на вход схемы синусоидальный сигнал с частотой 3 кГц. При помощи регулятора амплитуды на генераторе функций сформируйте значение размаха напряжения 4 В.
22.Осуществляйте мониторинг напряжения на резисторе 1 кОм при помощи осциллографа. Затем, варьируя частоту при помощи ручки регулятора частоты на генераторе функций, добейтесь минимального напряжения. Как и раньше, делайте это медленно и шагами. Слегка измените частоту и заметьте новое показание напряжения после того, как оно стабилизируется. Продолжайте настройку вперед и назад, пока Вы не добьетесь такой частоты, при которой напряжение минимально. Вы получили при этом резонансную частоту. Запишите в этот момент величину напряжения, которое Вы измерили на резисторе 1 кОм. Vr=_______В
23. Зная значение величины напряжения на резисторе с известным сопротивлением, Вы можете теперь вычислить величину полного тока схемы, используя закон Ома. Сделайте теперь вычисление и запишите значение величины тока.
I =_______ мА
24.Далее измерьте падение напряжения на параллельном резонансном контуре. Самый простой
способ сделать эти — просто прикоснуться испытательными выводами параллельно катушке индуктивности.
VLc=_______В
25.Зная значение величины напряжения на параллельном резонансном контуре и ток, который Вы нашли вычислением в предыдущем шаге, Вы можете теперь вычислить величину полного сопротивления индуктивно-емкостного контура. Сделайте теперь это вычисление и запишите Ваш результат.
Z=_______Ом
Как это значение соответствует значению, которое Вы нашли в шаге 20?
26.Сложите падение напряжения на резисторе 1 кОм и падение напряжения на параллельном резонансном контуре. Равна ли приблизительно эта сумма величине напряжения источника? Объясните Ваш ответ.
27.Соедините измерительные выводы вашего осциллографа с параллельным контуром, прикасаясь ими к двум выводам катушки индуктивности. Вращайте ручку регулятора частоты на генераторе функций в одну и в другую сторону от резонансной частоты и следите за изменением выходного напряжения. Ручку поворачивайте медленно из полностью выведенного в направлении против часовой стрелки положения в полностью выведенное в направлении по часовой стрелке положения, а затем назад, и так несколько раз, чтобы заметить эффект. Объясните вариации напряжения, которые Вы наблюдаете.
28.Выключите генератор функции, но схему пока не разбирайте.
ОБЗОРНЫЕ ВОПРОСЫ
1. Если конденсаторы 0,22 мкф и 0,47 мкФ подключены параллельно к катушке индуктивности 10 мГн, резонансная частота контура составляет:
а)1158 Гц,
б)1406 Гц,
в) 1917 Гц,
г) 2323 Гц.
2. Резонанс в последовательном контуре обнаруживается по:
а) максимальному току,
б) максимальному полному сопротивлению,
в) минимальному току,
г) нулевому току.
3. При резонансе параллельный резонансный контур ведет себя как:
а) резистор с малым сопротивлением,
б) резистор с большим сопротивлением,
в) катушка индуктивности,
г) конденсатор.
4. Каково полное сопротивление параллельного резонансного контура с L = 5 мГн, С == 0,001 мкФ и R =40м?
а) 84 кОм,
б) 125 кОм,
в) 840 кОм,
г) 1,25 МОм.
5. При резонансе в последовательной резистивно-индуктивно-емкостной схеме полное сопротивление равно:
а) XL или Xc
б) сопротивлению катушки индуктивности,
в) XL + Xc,
г) сопротивлению катушки индуктивности плюс сопротивление резистора.
Рис. 22-1. Последовательный резонансный контур
Рис. 22-2. Параллельный резонансный контур
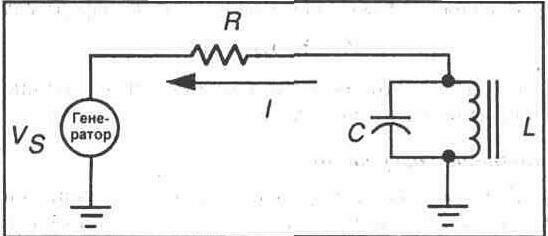
Рис. 22-3. К расчету резонансной частоты последовательного контура
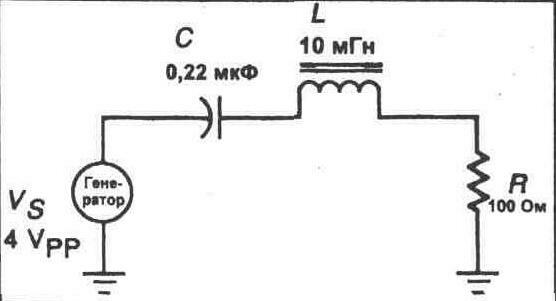
Рис. 22-4. Таблица для записи результатов
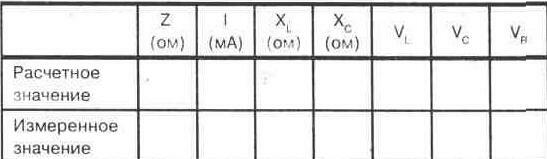
Рис. 22-5. Измерения параллельного резонансного контура
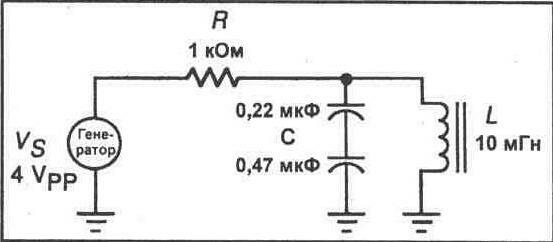
8. Фильтры нижних и верхних частот
ЭКСПЕРИМЕНТ 23 Фильтры нижних и верхних частот
Цели
После проведения данного эксперимента Вы сможете рассчитывать частоту отсечки резистивно-емкостных фильтров нижних и верхних частот, а также познакомитесь с влиянием изменений частоты на выходное напряжение.
Необходимые принадлежности
* Цифровой мультиметр
* Макетная панель
* Генератор функций
* Элементы:
один дисковый конденсатор 0.01 мкФ, один резистор 15 кОм.
ВВОДНАЯ ЧАСТЬ
Фильтр — это частотночувствительная схема, выходная амплитуда которой варьирует в зависимости от частоты на входе.
Фильтр нижних частот — это такой фильтр, который пропускает частоты меньше некоторой определенной частоты отсечки (fco), но подавляет те частоты, которые больше частоты отсечки. Фильтр верхних частот — это такой фильтр, который пропускает частоты, которые больше некоторой определенной частоты отсечки, но подавляет
те частоты, которые меньше частоты отсечки. На рисунке 23-1 представлены выходные характеристики фильтра нижних частот и фильтра верхних частит.
Рис. 23-1.
Фильтры нижних и верхних частот могут быть реализованы различными способами. Простейший фильтр — это резистор и конденсатор, соединенные между собой, как показано на рисунке 23-2.
Рис. 23-2.
Характеристики фильтров
Ключевой характеристикой фильтра нижних частот или фильтра верхних частот является его частота отсечки (fco). Как Вы можете видеть на основании рисунка 23-1, частота отсечки — это такая частота, где выходное напряжение фильтра падает до 70,7% от его максимально возможного выходного напряжения. В фильтре нижних частот выходное напряжение остается относительно постоянным по мере того, как возрастает входная частота. С приближением к частоте отсечки выходное напряжение начинает уменьшаться. Когда достигается частота отсечки,'выходное напряжение понижается до 70,7% от его максимально возможного значения. Выходное напряжение продолжает убывать по мере возрастания частоты.
В фильтре верхних частот выходное напряжение имеет максимальное значение, когда входная частота с запасом превышает частоту отсечки. Когда входная частота постепенно уменьшается, выходное напряжение понижается по мере приближения к частоте отсечки. Когда достигается частота отсечки, выходное напряжение понижается до 70,7% рт его максимально возможного-значения. Выходное напряжение продолжает убывать по мере дальнейшего уменьшения входной частоты.
В фильтре нижних частот сигналы с частотой
ниже fco пропускаются без ослабления или лишь с незначительным ослаблением; сигналы с,частотой выше fco быстро ослабляются. В фильтре верхних частот сигналы с частотой ниже fco значительно подавляются, тогда как сигналы с частотой
выше fco, пропускаются с минимальным противодействием. Снова обратитесь к рисунку 23-1.
Частота отсечки простого резистивно-емкостного фильтра, подобного показанному-на рисунке 23-2, вычисляется при помощи следующей формулы:
fco = 1/2*3.147RC
Пример: Если R = 3,3 кОм и С = 0,15 мкф, частота отсечки равна:
fco = 1/6,28(3300)(0,15 х 10^-6)
fco= 322 Гц
Краткое содержание
В данном эксперименте Вы познакомитесь с действием резистивно-емкостных фильтров верхних и нижних частот. Поскольку в настоящий момент у Вас нет средств для точного измерения частоты, может быть получено лишь общее представление о работе фильтра. Тем не менее, Вы сможете четко показать, что указанные фильтры действительно пропускают некоторые частоты с минимальным ослаблением, тогда как другие частоты ими сильно подавляются.
Рис. 23-3.
ПРОЦЕДУРА
1. Вычислите частоту отсечки фильтра нижних частот, показанного на рисунке 23-3.
fco______Гц
2. Соберите схему, показанную на рисунке 23-3,
при помощи Вашей макетной панели. Подключите резистивно-емкостной фильтр ко входу генератора функций.
3. Установите регулятор частоты генератора функций на частоту 10 Гц. После этого поворачивайте регулятор амплитуды, чтобы подать напряжение с размахом 4 В к схеме.
4. Далее измерьте выходное напряжение фильтра на конденсаторе. Запишите полученное значение.
Выходное напряжение фильтра = ___ В
5. Подключите осциллограф к конденсатору фильтра. При наблюдении за выходным напряжением поворачивайте ручку регулятора частоты, чтобы увеличить частоту до 1000 Гц. Увеличивается или уменьшается выходное напряжение?
________ увеличивается
_________ уменьшается
6. Основываясь на входном значении в шаге 3, вычислите значение выходного напряжения при частоте отсечки.
Напряжение на частоте
отсечки = ________ В
7. Подавайте при помощи генератора функций синусоидальный сигнал в схему на каждой из частот, указанных в приведенной ниже таблице Установите размах напряжения на входе схемы равным 4 В. В процессе изменения частот
снова проконтролируйте входное напряжение, чтобы убедиться, что оно все еще имеет размах 4 В. Измеряйте выходное напряжение фильтра на каждой частоте и записывайте Ваши результаты в следующую таблицу.
|
Входная частота |
Выходное напряжение |
|
10Гц |
|
|
100 Гц |
|
|
200 Гц |
|
|
500 Гц |
|
|
1000 Гц |
|
|
2000 Гц |
|
|
5000 Гц |
|
|
10кГц |
|
|
20 кГц |
8.. Постройте на основании Ваших данных график частотной характеристики на полулогарифмической бумаге.
9. Теперь соберите схему фильтра верхних частот, показанного на рисунке 23-4.
10.Определите частоту отсечки фильтра верхних частот на рисунке 23-4.
fco______Гц
11.Настройте частоту регулятором генератора функций на 10 Гц и величину размаха напряжения на 4 В.
Рис. 23-4.
12.Наблюдайте выходное напряжение фильтра на резисторе 1 кОм. Наблюдая за выходным напряжением на экране осциллографа, повышайте частоту на выходе генератора функций вплоть до 10кГц. Заметьте, как изменяется выходное напряжение по мере повышения частоты. Объясните эти изменения.
13.Как изменяется выходное напряжение с повышением частоты?
__________ увеличивается
__________ уменьшается
14. Подавайте при помощи генератора функций синусоидальный сигнал в схему на каждой из частот, указанных в приведенной ниже таблице. Установите размах напряжения на входе схемы равным 5 В. В процессе изменения частоты при необходимости поддерживайте на входе схемы величину размаха 5 В. Измеряйте выходное напряжение фильтра на резисторе для каждой частоты и записывайте Ваши результаты в таблицу.
|
Входная частота |
Выходное напряжение |
|
10 Гц |
|
|
100 Гц |
|
|
200 Гц |
|
|
500Гц |
|
|
1000 Гц |
|
|
2000 Гц |
|
|
5000 Гц |
|
|
10 кГц |
|
|
20кГц |
15.Постройте на основании Ваших табличных данных график частотной характеристики на полулогарифмической миллиметровой бумаге, как Вы это делали в случае фильтра нижних частот.
ОБЗОРНЫЕ ВОПРОСЫ
1. Резистивно-емкостной фильтр нижних частот имеет частоту отсечки 23222 Гц. Сигнал с частотой 5,5 кГц при этом:
а) пропускается фильтром,
б) подавляется фильтром.
2. Резистивно-емкостной фильтр верхних частот имеет частоту отсечки 15 кГц. Какой сигнал при этом пропускается? а) 6,7 кГц,
б) 36 кГц.
3. Сигнал на входе фильтра нижних частот имеет размах 5 В. Тогда выходное напряжение на резонансной частоте будет равняться:
а) 3,5 В,
б) 4,5 В,
в) 5 В,
г) 7 В.
4. Фильтр нижних частот имеет компоненты с величинами R = 4,7 кОм и С = 0,1 мкФ. Частота отсечки такого фильтра равна:
а) 273 Гц,
б) 339 Гц,
в) 469 Гц,
г) 501 Гц.
5. Внутри мультиметра имеется внутренняя схема, которая заставляет мультиметр действовать как:
а) фильтр нижних частот, 6} фильтр верхних частот.
Рис. 23-1. Выходные характеристики фильтра нижних частот и фильтра высоких частот
Рис. 23-2. Простейший фильтр — это резистор и конденсатор
Рис. 23-3. Эксперимент для оценки характеристик фильтра нижних частот
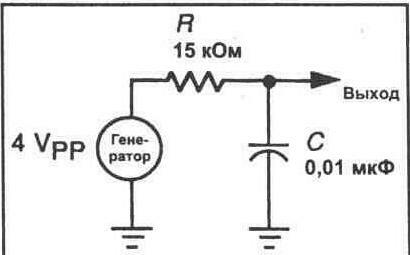
Рис. 23-4. Эксперимент для оценки характеристик фильтра высоких частот
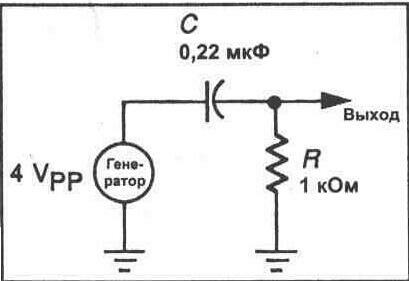
9. Полосовой фильтр и режекторный фильтр
ЭКСПЕРИМЕНТ 24 Полосовой фильтр и режекторный фильтр
Цели
После проведения данного эксперимента Вы сможете продемонстрировать работу индуктивно-емкостного полосового фильтра и резистивно-емкостного режекторного фильтра.
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функции
* Элементы:
четыре конденсатора 0,1 мкФ, один конденсатор 0,47 мкФ, одна катушка индуктивности 10 мГн, один резистор 100 Ом, четыре резистора 15 кОм.
ВВОДНАЯ ЧАСТЬ
Полосовой фильтр — это частотночувствительная схема, которая пропускает узкий диапазон. частот в окрестности центральной резонансной частоты (fr)
Все другие частоты ниже или выше узкой полосы пропускания значительно подавляются. Типичная характеристика полосового фильтра показана на рисунке 24-1А.
Рис. 24-1.
Режекторный фильтр представляет собой противоположность полосовому фильтру. Он подавляет или устраняет сигналы, частоты которых попадают в узкий диапазон с центральной частотой fc. Все частоты выше и ниже центральной частоты фильтр пропускает с минимальным ослаблением (см. рис. 24-1 В). Режекторный фильтр иногда называют вырезающим фильтром, поскольку этот фильтр используется для вырезания или режекции мешающего сигнала одной частоты.
Краткое содержание
Имеется несколько различных способов схемной реализации полосового фильтра и режекторного фильтра. Индуктивно-емкостные резонансные схемы могут комбинироваться различными методами для создания обоих типов фильтров. В данном эксперименте Вы познакомитесь с полосовым фильтром.
Режекторный фильтр может быть реализован и на базе индуктивно-емкостных схем. Однако в данном эксперименте Вы познакомитесь с популярным и широко используемым двойным Т-образным мостовым фильтром. Это резистивно-емкостной режекторный фильтр, способный подавлять определенную частоту и частоты в ее окрестности. Центральная частота рассчитывается при помощи следующей формулы:
fp = 1/2*3.14RC
Поскольку у Вас нет удобных средств для точного измерения частоты, Вы будете просто варьировать частоту, генерируемую генератором функций, и отмечать при помощи мультиметра выходную характеристику фильтра. Таким образом, можно увидеть, как выходное напряжение изменяется в зависимости от частоты как в случае полосового фильтра, так и в случае режекторного фильтра.
ПРОЦЕДУРА
1. Обратитесь к рисунку 24-2. Соберите эту схему полосового фильтра на Вашей макетной панели. Выходное напряжение генератора функций прикладывается к конденсаторам, тогда как выходное напряжение фильтра снимается с резистора 1000м. Заметьте, что общая емкость схемы составлена из двух конденсаторов с емкостью 0,47 мкФ и 0,1 мкФ.
2. Используя значения, показанные на рисунке 24-2, рассчитайте общую емкость схемы и резонансную частоту данной схемы.
Рис. 24-2.
Сt = _______ мкФ
fr=_____Гц
3. Установите регулятором амплитуды генератора функций выходное напряжение размаха 4 В:
Затем установите частоту приблизительно 500 Гц.
4. Подключите осциллограф параллельно выходному резистору 1000м. Медленно увеличивайте частоту на выходе генератора функций и наблюдайте за изменением выходного напряжения схемы. Замечайте вариацию этого напряжения. Изменения частоты выполняйте медленно, чтобы Вы могли получать хорошую индикацию того, как изменяется напряжение, когда частота увеличивается или понижается. Увеличивайте частоту приблизительно до 5 кГц.
5. Регулируйте частоту, наблюдая за выходом фильтра. Настройте генератор функций на пиковое выходное напряжение. Заметьте по генератору функций или измерьте период и частоту при помощи осциллокрафа. f=____Гц
6. Объясните изменения, которые Вы наблюдали в шагах 4 и 5.
7.Демонтируйте .полосовой фильтр. Вместо него соберите схему двойного Т-образного мостового фильтра, который показан на рисунке 24-3. Будьте внимательны при монтаже схеме, поскольку она несколько сложна, и легко можно сделать ошибку во время монтажа.
Рис. 24-3.
Имеется несколько-важных моментов, которые Вы должны принять во внимание при монтаже данной схемы. Во-первых, значение одного (общего) конденсатора получается комбинированием емкостей двух параллельных конденсаторов 0,1 мкФ. Вспомните, что емкости параллельных конденсаторов складываются, образуя, следовательно. один конденсатор емкостью 0,2 мкФ. Другое значение в данной схеме получается соединением двух параллельных резисторов. Два параллельных резистора с одинаковым сопротивлением имеют общее сопротивление, равное половине сопротивления одного из резисторов. В данном случае два резистора 15 кОм соединены параллельно, чтобы получить сопротивление 7,5 кОм.
8. Используя значения, показанные на рисунке 24-3, рассчитайте частоту режекции или центральную частоту данного фильтра. fc=_____Гц
9. Настройте генератор функций на частоту 10 Гц и размах напряжения 4В. Подключите осциллограф на выход фильтра. Увеличивайте теперь выходную частоту приблизительно до 1000 Гц и наблюдайте за вариацией выходного напряжения фильтра. Повторяйте это несколько раз, чтобы Вы могли наверняка увидеть эффект.
10.Настройте генератор функций на нулевую частоту (минимальное напряжение). Измерьте частоту и запишите. f=_____Гц
11.Объясните полученные Вами результаты в шагах 9 и 10.
ОБЗОРНЫЕ ВОПРОСЫ
1. Режекторный фильтр может быть реализован на базе индуктивно-емкостных схем:
а) высказывание истинно,
б) высказывание ложно.
2. В индуктивно-емкостном полосовом фильтре центральная частота определяется значениями:
а) приложенного напряжения,
б) L и R,
в) R и С,
г) L и С.
3. Полосовой фильтр пропускает:
а) одну частоту,
б) только высокие частоты,
в) узкую полосу частот,
г) все частоты.
4. Двойной Т-образный мостовой фильтр представляет собой:
а) полосовой фильтр,
б) фильтр нижних частот,
в) фильтр верхних частот,
г) режекторный фильтр.
5. Какова центральная частота двойного Т-образного мостового фильтра при значениях R = 10 кОм и С = 0,47 мкФ?
а) 34 Гц,
б) 47 Гц,
в) 68 Гц,
г) 120 Гц.
Рис. 24-1. Типичная характеристика полосового и режекторного фильтра
Рис. 24-2. Схема для оценки характеристик фильтров
Рис. 24-3. Схема двойного Т-образного мостового фильтра
4. Приложение
Приложение
ТАБЛИЦА ЗНАЧЕНИЙ ЦВЕТОВОГО КОДА
(ДЛЯ РЕЗИСТОРОВ И КОНДЕНСАТОРОВ)
|
Цвет полоски |
Значение представляемое цветом |
Десятичный множитель |
Процент допуска |
Номинальное напряжение |
% изменений на 1000 операций в тяж.режиме |
|
Черный |
0 |
1 — |
— |
— |
— |
|
Коричневый |
1 |
10 |
1 * |
100 * |
1 % |
|
Красный |
2 |
100 |
2 * |
200 * |
0.1 % |
|
Оранжевый |
3 |
1000 |
3 * |
300 * |
0.01 % |
|
Желтый |
4 |
10000 |
4 * |
400 * |
0.001 % |
|
Зеленый |
5 |
100000 |
5* |
500 * |
— |
|
Синий |
6 |
1000000 |
6 * |
600 * |
— |
|
Фиолетовый |
7 |
10000000 |
7 * |
700 * |
— |
|
Серый |
8 |
100000000 |
8 * |
800* |
— |
|
Белый |
9 |
1000000000 |
9 * |
900 * |
— |
|
Золотой |
— |
0.1 |
5 |
1000 * |
— |
|
Серебряный |
— |
0.01 |
10 |
2000 * |
— |
|
Без цвета |
— |
— |
20 |
500 * |
— |
(*Может применяться только к конденсаторам.)