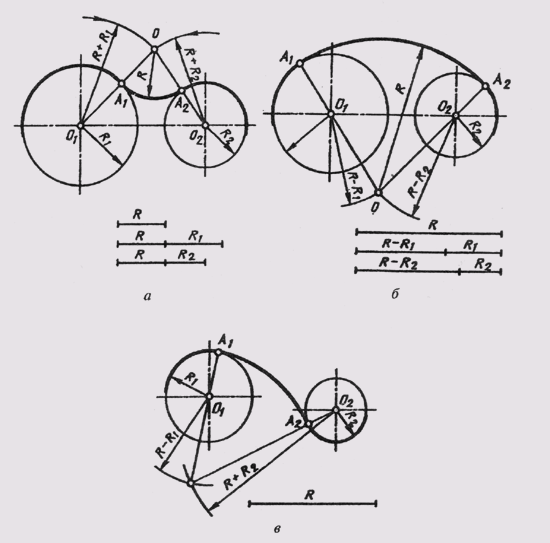8. Иллюстрированный самоучитель по созданию чертежей
|
Иллюстрированный самоучитель по созданию чертежей
|
1. Предисловие
1. Предисловие
ПРЕДИСЛОВИЕ
В учебнике на данном диске отражен опыт графической подготовки специалистов инженерно-технического профиля на кафедре инженерной графики Красноярской государственной академии цветных металлов и золота и более чем 30-летний опыт заведования кафедрой автором.
Впервые учебник под названием «Инженерная графика» авторов Лагеря А.И. и Колесниковой Э.А. был выпущен в 1985 г. издательством «Высшая школа». Второй усовершенствованный и улучшенный вариант был выпущен под тем же названием (автор Лагерь А.И.) издательством Красноярского государственного университета в 1992 г. С учетом использования учебников в вузах страны редакционно-издательский центр Международной профессорской ассоциации (г. Москва) в 1995 г. выпустил учебник под названием «Курс инженерной графики» (автор Лагерь А.И.). Настоящий учебник является вторым изданием последнего, переработанным и дополненным. Из него исключены все специальные вопросы, чтобы сохранить изложение классического курса инженерной графики.
Автор приносит глубокую благодарность официальным рецензентам Астапкович И.И. и Рушелюку К.С. за доброжелательную критику, направленную на совершенствование учебника, а также сотрудникам кафедры Колесниковой Э.А., Гулидовой Л.Н., Новоселовой Н.М., Грубовой Т.С., оказывающих помощь автору на разных этапах подготовки учебников к изданию.
2. Введение
ВВЕДЕНИЕ
Развитие экономики нашей страны предусматривает постоянное ускорение темпов развития промышленности, требующее широкой механизации и автоматизации производственных процессов, внедрения новой техники и технологии, расширения производственной базы. Это связано с разработкой многих проектно-конструкторских, производственных вопросов и вопросов управления, требующих широких знаний графических дисциплин.
Но прежде чем приступить к изготовлению какой-либо детали, механизма, машины, строительству здания или сооружения, проект его изображают на бумаге, т. е. выполняют чертежи.
Выпускаемые в настоящее время вузами инженерные кадры должны быть готовы к решению этих задач. Они должны уметь с помощью чертежа выразить свои теоретические замыслы и технические идеи для последующего их осуществления на практике.
Подготовку специалистов инженерно-технического профиля в вузах по этим вопросам обеспечивает изучение курса «Инженерная графика», который является первой общетехнической дисциплиной, дающей знания, необходимые студенту для изучения последующих общеинженерных и технических дисциплин.
Классический курс инженерной графики включает основные разделы начертательной геометрии и черчения и является также основой, базой для дальнейшего изучения специальных графических курсов: компьютерной графики, строительного, горного, топографического черчения и др.
В учебнике особое внимание уделено новым, современным методам обучения и учету важнейших дидактических принципов, формирующих и развивающих у студентов пространственное представление, являющееся определяющим при изучении графических дисциплин во многих специальностях. Так, например, проектирование и строительство подземного горного предприятия, технически грамотное ведение работ немыслимо без ясного понимания горным специалистом пространственного положения и формы объектов горного производства и правильного их изображения на горных чертежах.
Изложение материала в учебнике базируется на положениях государственных стандартов, введенных и действующих в настоящий момент времени в нашей стране.
В книге выполнен большой объем графического материала, позволяющего использовать его в качестве аналога или прототипа при выполнении эскизов, рабочих чертежей деталей, сборочных чертежей и чертежей для деталирования.
С целью обеспечения самостоятельной работы над изучением курса, особенно при изучении по вечерней и заочной форме, в учебнике после каждой главы приведены вопросы для самоконтроля.
2. Глава 1. Технические средства и приемы выполнения графических работ
1. Часть первая. ОБЩИЕ СВЕДЕНИЯ О ВЫПОЛНЕНИИ ГРАФИЧЕСКИХ РАБОТ
Часть первая.
ОБЩИЕ СВЕДЕНИЯ О ВЫПОЛНЕНИИ ГРАФИЧЕСКИХ РАБОТ
Глава 1. ТЕХНИЧЕСКИЕ СРЕДСТВА И ПРИЕМЫ ВЫПОЛНЕНИЯ ГРАФИЧЕСКИХ РАБОТ
§ 1. Общие сведения
В своей деятельности инженеру приходится работать с большим количеством графических работ, весьма разнообразных по видам, содержанию, назначению, выполнению. Так, чертежи могут быть выполнены вручную и с помощью машин и автоматов, фотографированием, карандашом и тушью, на чертежной бумаге, кальке и миллиметровой бумаге, однотонные, цветные и разноцветные, простые, содержащие изображение одной детали, и сложные сборочные чертежи. Одни чертежи, содержащие изображения машин, аппаратов, автоматов, зданий и сооружений и т. д., выполняются от руки, для выполнения других нужны различные инструменты и приспособления.
Это обусловливает необходимость применения различных материалов, инструментов, приспособлений, машин и автоматов, а также методов выполнения графических работ.
2. Материалы
§2. Материалы
Для выполнения различных видов чертежей карандашом, тушью, красками применяют чертежную бумагу марки О (обычная) и В (высшего качества). Отличительным признаком бумаги высшего качества является наличие на ней водяных знаков, видимых на просвет. Обыкновенная бумага выпускается двух видов: № 1—более высокого качества и № 2 — менее плотная и жесткая.
Для выполнения калькировочных работ с целью размножения чертежей методом светокопирования применяют прозрачную бумагу-кальку, изготовленную на бумажной или полотняной основе, а для бескалькировочного размножения чертежей — кальку карандашную. Для выполнения черновых изображений в масштабе, различных расчетно-графических работ применяют миллиметровую бумагу, а для эскизных работ — белую писчую клетчатую бумагу, обычно с размером клеток 5x5.
Чертежи, выполняемые с помощью графических автоматов и фотографированием, выполняются на листовой или рулонной чертежной бумаге, фотобумаге различных типов или специальной бумаге, изготовленной по отдельным требованиям.
Чертежные карандаши маркируются по твердости стержней от 2Т до 2М. Грифель карандаша тем тверже, чем большая цифра стоит перед буквой Т, и тем мягче, чем большая цифра стоит перед буквой М. Карандаши с грифелем средней твердости имеют обозначение ТМ. На карандашах зарубежного изготовления можно встретить вместо буквы Т буквы Н, а вместо буквы М — В.
Для определенного вида графических работ применяют соответствующую марку карандаша по твердости. Так, для выполнения чертежа в тонких линиях применяют карандаши марки Т, 21, для обводки чертежа — марки М, ТМ, для выполнения рисунков — марки М, 2М. Затачиваются карандаши на конус или «лопаточкой» на длину до 25 мм. При этом графитовый стержень должен выступать из деревянной оправы на 7—9 мм. Заточку карандашей лучше вести с помощью наждачной бумаги.
Некоторые виды чертежей на бумаге, а также чертежи на кальке (упрощенно такие чертежи называют просто кальки) для светокопирования выполняются тушью. Она выпускается, как правило, в флаконах и различается по качеству и цвету. Большинство чертежей выполняется черной тушью. В период работы тушь в флаконах необходимо предохранять от высыхания. Загустевшую тушь разбавляют кипяченой водой или нашатырным спиртом. Качество линий, проведенных тушью, зависит от степени ее разбавления, поэтому, разбавляя тушь, необходимо контролировать качество проводимых линий.
Чертежные резинки применяются двух типов: для стирания линий, выполненных карандашом, и для стирания линий, выполненных тушью. Резинка, применяемая для работы с карандашом, мягкая и при стирании снимает с бумаги только частички графита, не нанося ей значительных повреждений; резинка, применяемая для стирания туши, содержит твердые добавки и при стирании шлифует верхний слой бумаги.
Для получения цветных изображений на чертежах применяют акварельные краски, состоящие из тонкого красящего вещества и связующих. Они разводятся на воде. Особенностью этих красок является то, что при нанесении их слоями один на другой и при смешивании можно получить необходимые оттенки. Иногда применяют краски клеевые и гуашь, которые разводятся на воде. Но они не прозрачные и при наложении одного слоя краски на другой верхний слой полностью скрывает нижний.
3. Инструменты
§ 3. Инструменты
Графические работы выполняются с помощью чертежных инструментов. Набор таких инструментов, размещенный в специальном футляре, называется готовальней. Выпускаются различные типы готовален. Для выполнения чертежно-конструкторских и копировальных работ карандашом и тушью выпускаются универсальные готовальни (У), имеющие в своем наборе различное количество инструментов: У9, У9-Л, У10, У11, У14, У14-Л, У15, У24, У32. Цифра указывает на количество инструментов в наборе.
Для выполнения чертежно-конструкторских работ карандашом выпускаются готовальни: конструкторская (К), конструкторская большая (КБ), конструкторская малая (КМ и КМ-Л). Для выполнения ученических работ выпускают школьные готовальни (Ш). Лучшими считаются наборы чертежных инструментов, изготовленных из латуни (кроме У9, У14, КМ и Ш).
Основными чертежными инструментами в составе готовален являются следующие.
Циркуль чертежный предназначен для проведения окружностей и дуг различных радиусов (не менее 3—4 мм). К циркулю прилагается вставка игольная, рейсфедер циркульный, карандашная ножка и удлинитель, позволяющий осуществлять проведение окружностей диаметром до 450 мм. При работе циркулем иголку и рейсфедер (или карандашную вставку) следует устанавливать перпендикулярно к поверхности бумаги.
Циркуль разметочный предназначен для измерения расстояния и откладывания длин на чертеже. При работе с циркулем иголки обеих ножек должны быть одинаковой высоты.
Кронциркуль падающий служит для вычерчивания окружностей малого диаметра. В нем для удобства работы вращающаяся ножка выполнена свободно перемещающейся вдоль оси кронциркуля. К кронциркулю прилагаются вставка карандашная и рейсфедер циркульный.
Кривоножка служит для проведения кривых линий от руки или под лекало. Состоит из полой пластмассовой ручки, оси с винтом фиксации ножки в неподвижном положении и рейсфедера с кривоножкой.
Рейсфедер с широкими щечками и делительной гайкой применяется для проведения линий толщиной до 1,5 мм. Регулирование толщины линий осуществляется с помощью винта и гайки с делениями. I
Центрик применяется при проведении концентрических окружностей. Он устроен в виде кнопки, в головке которой выполнено углубление для иглы ножки циркуля.
4. Принадлежности и приборы
§ 4. Принадлежности и приборы
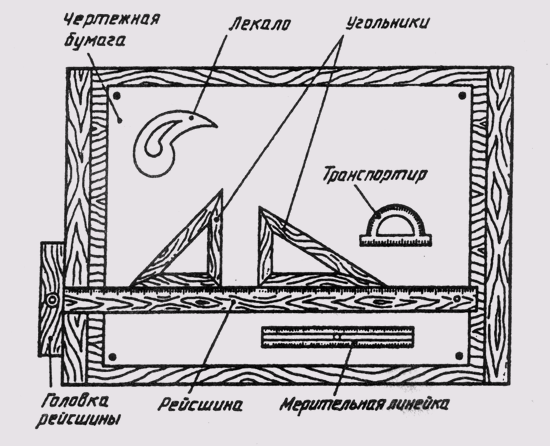
При выполнении графических работ применяют различные принадлежности и приборы, облегчающие труд чертежника, создающие удобства и повышающие производительность труда. На рис. 1 показана чертежная доска с расположенными на ней чертежными принадлежностями.
Чертежная доска служит для прикалывания к ней кнопками бумаги. Она представляет собой деревянный щит, состоящий из продольных дощечек, стянутых торцевыми наружными планками и скрепленных клеем. Рабочую поверхность представляют продольные дощечки, изготовляемые из дерева мягких пород — ольхи или липы. Доски изготовляют различных размеров. Например, чертежная доска №2 имеет длину 1000 мм, ширину 650 мм и толщину 20 мм.
Рейсшина состоит из длинной линейки и двух коротких планок-перекладин. Одна из перекладин соединена с длинной линейкой неподвижно, вторая может быть повернута по отношению к большой линейке на любой угол. Таким образом с помощью рейсшины можно проводить параллельные горизонтальные и наклонные линии.
Рис. 1
Мерительная линейка служит для измерения длин на чертеже. Она изготовляется из твердого дерева и в поперечном сечении имеет форму симметричной трапеции. Линейка снабжена белыми целлулоидными полосками, наклеенными на наклонных ее гранях и имеющими прямолинейную равномерную шкалу с ценой деления 1 мм.
Угольники служат для работы с ними отдельно или в сочетании с рейсшиной. С их помощью можно выполнить различные геометрические построения; проведение ряда параллельных линий, построение взаимно перпендикулярных линий, вычерчивание углов и многоугольников, деление окружности на заданное количество равных участков.
Лекала служат для вычерчивания кривых линий. Они представляют собой тонкие пластинки криволинейного очертания, дающие возможность провести кривые линии, которые не могут быть выполнены с помощью циркуля. Лекала изготовляют с различной кривизной линий. Для вычерчивания лекальной кривой лекало подбирают так, чтобы его кромка совпадала не менее чем с четырьмя точками кривой; при этом соединяют линией только две из них и далее лекало передвигают к последующим точкам.
Транспортир применяют для измерения и откладывания углов на чертеже.
Трафареты и шаблоны применяют для сокращения затрат труда и времени на выполнение отдельных видов графических работ. По форме они могут быть весьма разнообразными в зависимости от их предназначения. С помощью трафаретов и шаблонов могут быть выполнены надписи, вычерчены окружности, прямоугольники, углы, знаки.
Чертежные приборы служат для облегчения труда чертежника, снижения затрат времени на выполнение графических работ. В настоящее время применяются различные конструкции чертежных приборов. Они позволяют заменить одновременно рейсшину, транспортир, угольник, линейку.
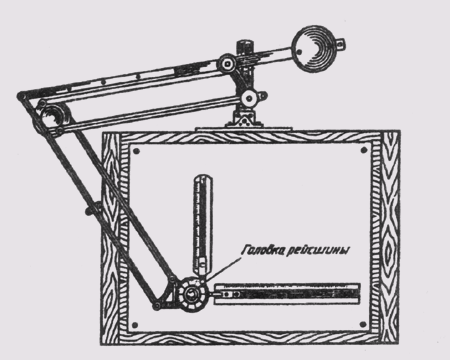
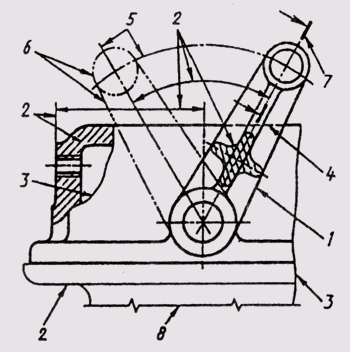
Чертежный прибор (рис. 2) включает две линейки, установленные под углом 90° друг к другу.
С помощью специальной поворотной головки линейки можно расположить под различными углами наклона к заданным линиям. Головка связана системой подвижных рычагов, позволяющей перемещать ее по полю чертежа, с кронштейном-струбциной, с помощью которой и крепится к чертежной доске. Применение такого прибора сокращает затраты времени примерно на одну четверть против выполнения чертежей с применением рейсшины.
Для механизации графических работ применяются также более сложные чертежные станки и комбайны.
Рис. 2
Прибор для штриховки служит для проведения ряда параллельных линий, служащих штриховкой отдельных участков чертежа. Он представляет собой две линейки, одна из которых своим концом шарнирно прикреплена к другой с возможностью перемещения шарнира вдоль второй линейки на заданную величину.
Принадлежности и приборы для создания чертежей
Чертежный прибор включает две линейки
5. Графические автоматы
§ 5. Графические автоматы
В последние годы для решения различных задач инженерной графики применяют ЭВМ различных типов в зависимости от характера решаемой задачи. Для этой цели составляют план решения задачи, алгоритм и пишут на заданном алгоритмическом языке программу. Подготовленные данные вводят в ЭВМ и получают ответ, например в виде координат искомых точек. Такое применение ЭВМ позволяет значительно ускорить решение графических задач, но не решает задачу облегчения чертежно-конструкторского труда.
Для механизации и автоматизации конструкторско-графических работ все более широкое применение находят графические автоматы различных типов. Одни из них позволяют получать и размножать чертежи непосредственно на бумаге (графопостроители), другие — получить их изображение на экране (графические дисплеи). Автоматизированные графические устройства могут работать в индивидуальном режиме с соответствующей подготовкой для этого исходных данных и в режиме связи с ЭВМ, когда проектировщик может выбрать оптимальные варианты решения задач. Графические автоматы находят широкое применение в системах автоматизированного проектирования.
6. Методы выполнения графических работ
§ 6. Методы выполнения графических работ
При выполнении значительного объема графических работ необходимо прежде всего правильно организовать рабочее место чертежника. Чертежная доска, на которой закрепляется бумага, должна быть расположена примерно на 15° в сторону чертежника. При большем наклоне чертежные инструменты могут соскальзывать с чертежной доски.
Перед началом работы следует собрать инструменты, которые будут необходимы для выполнения конкретного чертежа. Их необходимо протереть сухой тряпочкой из хлопчатобумажной ткани. Отобранные инструменты должны располагаться так, чтобы они не мешали работе и в то же время чтобы можно было быстро выбрать среди них необходимый.
До начала выполнения чертежа необходимо заточить несколько карандашей. Это позволит избежать потерь времени на их заточку в процессе работы и работать, не отрываясь от чертежа. Нужно проверить также, чтобы на столе не было ничего лишнего и свет падал с левой стороны.
Прикалывая чертежную бумагу к доске, первую кнопку следует расположить в верхнем левом углу и выровнять верхний срез листа по кромке рейсшины. Второй кнопкой закрепляют правый нижний угол листа, потом закрепляют оставшиеся углы.
Чертежи могут быть выполнены карандашом или тушью. И в том и в другом случае производят подготовку чертежа карандашом и потом обводят его карандашом или тушью.
В производственных условиях чертежи в большинстве случаев выполняют карандашом. Тушью выполняют чертежи в специальных случаях, например для размножения путем светокопирования или фотографирования. К особенностям выполнения чертежей тушью относится то, что на глянцевой бумаге обводить линии тушью более трудно, чем на обычной чертежной бумаге, имеющей шероховатую поверхность. С другой стороны, линии, проведенные тушью, значительно легче подчистить в случае необходимости исправлений.
Обводка чертежа карандашом отличается тем, что чертеж в этом случае трудно сохранить чистым, а вычистить резинкой можно только части поля листа, не занятые изображениями. Это требует в процессе подготовки чертежа тщательного соблюдения чистоты на чертеже и избежания проведения дополнительных, лишних, случайных линий. Недостатком обводки чертежей карандашом является то, что трудно провести линии одинаковой толщины, а также одинаковой черноты с помощью циркуля.
Подготовка чертежа заключается в построении всех его фигур и выполнении надписей тонкими линиями. Для этих работ подбирают твердые карандаши марки 2Т или ЗТ с остро отточенным грифелем.
Далее отбирают характерные точки изображения, соединив которые, можно получить изображаемую фигуру. При нанесении точек с помощью циркуля-измерителя их можно легко накалывать, а при нанесении с помощью линейки отмечать легким уколом карандаша или маленьким кружком. При построении точек циркулем они наносятся в виде засечек. Полученные точки соединяют прямыми или кривыми линиями и получают контур изображения, на который наносят остальные необходимые линии.
После выполнения построения чертеж следует тщательно проверить, выявить и удалить случайные, лишние или неправильные линии. Причем если обводка чертежа будет выполняться карандашом, то удалить эти линии следует до обводки, если же тушью — то после. Перед обводкой тушью их необходимо зачеркнуть карандашом. До обводки чертежа следует только в необходимых случаях пользоваться резинкой, так как это приводит к загрязнению чертежа и повреждению поверхности бумаги, на которую при обводке плохо наносится тушь.
Для ускорения работы по обводке чертежа сначала подряд проводят горизонтальные линии на всех изображениях, потом вертикальные, за ними наклонные одного направления, потом второго и т. д. Сначала проводят сплошные основные толстые линии, за ними, например, штриховые, сплошные тонкие и т. д. В последнюю очередь заполняют графы основной надписи, наносят технические требования и размерные числа.
После окончания обводки чертежа его необходимо снова тщательно проверить для выявления возможных ошибок и упущений. Проверку следует вести по отдельным вопросам в пределах всего чертежа, например, полностью ли обведены нужные линии, везде ли нанесены стрелки на размерных линиях, на всех ли размерных линиях поставлены размеры, не проведены ли лишние линии и др.
Следует отметить, что выполнение графических работ в основной массе осуществляется карандашом, поэтому уместно напомнить несколько общих правил работы с ним. Затачивать карандаш следует с конца свободного от надписи, чтобы сохранить его маркировку.
Подбор твердости грифеля карандаша и правильность его заточки при наличии заданного сорта бумаги должны обеспечивать получение линии четких, хорошо видимых, необходимой толщиной. Нанесение линий плохо видимых, бледных, серых приводит к утомлению зрения чертежника.
Необходимо постоянно следить за сохранением конусности и длины грифеля, постоянно подтачивать его. Укорочение конуса приводит к утолщению линий.
Подбор карандаша при соответствующем сорте бумаги обеспечивает проведение линий, исключающее вдавливание карандаша в бумагу. Это дает возможность при необходимости стереть линию без оставления следов.
При проведении линий карандашом по линейке, рейсшине или угольнику карандаш должен быть расположен в плоскости, перпендикулярной плоскости чертежа или слегка наклонной от себя.
В процессе выполнения чертежа горизонтальные линии рекомендуется проводить по верхней кромке линейки или рейсшины слева направо, а вертикальные — снизу вверх.
При выполнении надписей и размерных цифр на поле чертежа под руку с карандашом необходимо подкладывать чистый лист бумаги, что исключает загрязнение чертежа.
Можно дать некоторые рекомендации и по обводке чертежа тушью, которая осуществляется на чертежной бумаге или на кальке. Обводка на кальке несколько труднее из-за ее глянцевой поверхности. Четкость линии обеспечивается правильной работой с рейсфедером и подбором концентрации туши путем ее разбавки. Выбрав лист бумаги, следует провести на нем несколько пробных линий. Если тушь засыхает в рейсфедере, ее необходимо разбавить, но не доводить до состояния, когда линии будут расплываться.
В заключение можно напомнить также общий ход выполнения чертежа. Начинают выполнять чертеж с вычерчивания рамки формата, выделения поля чертежа и места расположения основной надписи. После этого на поле чертежа намечают расположение изображений — наносят контуры изображения или габаритные очерки. Это дает возможность оценить правильность выбора места расположения изображений и при необходимости внести изменения. Если изображения симметричны, проводят оси симметрии; отмечают центры окружностей штрихпунктирными линиями; наносят остальные элементы изображения. При этом сначала вычерчивают дуги окружностей, а потом линии, касательные к ним.
7. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
19. Общий порядок выполнения чертежа.
3. Глава 2. Оформление чертежей
1. Глава 2. Оформление чертежей
Глава 2. ОФОРМЛЕНИЕ ЧЕРТЕЖЕЙ
§ 7. Общие сведения
Все правила выполнения чертежей, действующие в настоящее время, отражены в государственных стандартах (ГОСТ) Единой системы конструкторской документации (ЕСКД), учитывающей многие рекомендации международных организаций по стандартизации.
Все стандарты, предусмотренные ЕСКД, распределяются по следующим классификационным группам:
0 — общие положения;
1 — основные положения;
2 — классификация и обозначения изделий в конструкторских документах;
3 — общие правила выполнения чертежей;
4 — правила выполнения чертежей в машиностроении и приборостроении;
5 — правила обращения конструкторских документов (учет, хранение, дублирование, внесение изменений);
6 — правила выполнения эксплуатационной и ремонтной документации;
7 — правила выполнения схем;
8 — правила выполнения строительных документов и документов судостроения;
9 — прочие стандарты.
В ЕСКД все стандарты имеют определенную структуру обозначений и названий. Например, ГОСТ 2.303—68 «Линии» означает, что стандарт входит в комплекс ЕСКД, которому присвоен номер 2, номер стандарта — 303 (3 — шифр классификационной группы, 03 — порядковый номер стандарта в группе), год регистрации — 1968, название — «Линии».
В курсе инженерной графики нашли отражения требования стандартов, входящих в группы 1, 2, 3, 4, 7.
Вполне понятно, что все стандарты ЕСКД разработаны для промышленности и не учитывают особенностей выполнения чертежей в учебных заведениях, поэтому при выполнении учебных чертежей допускаются некоторые отклонения от стандартов. При выполнении чертежей необходимо руководствоваться требованиями, установленными «Единой системой конструкторской документации», к форматам, основным надписям, масштабам, линиям, шрифтам и др.
8. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
18. Как обозначают конические фаски на чертеже?
8. Форматы
§ 8. Форматы
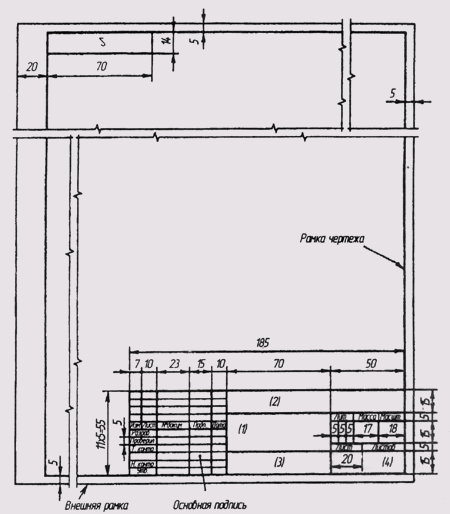
Все чертежи должны выполняться на листах бумаги стандартного формата. Форматы листов бумаги определяются размерами внешней рамки чертежа (рис. 3). Она проводится сплошной тонкой линией. Линия рамки чертежа проводится сплошной толстой основной линией на расстоянии 5 мм от внешней рамки. Слева для подшивки оставляют поле шириной 20 мм. Обозначение и размеры сторон форматов установлены ГОСТ 2.304—68. Данные об основных форматах приведены в табл. 1.
Таблица 1
|
Обозначение формата |
||||
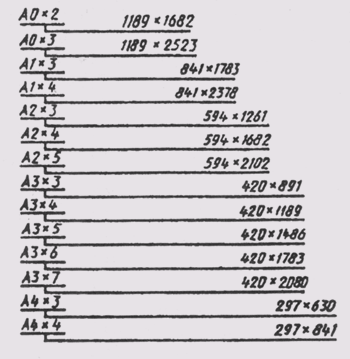
Основные форматы получают из формата АО путем последовательного деления на две равные части параллельно меньшей стороне. При необходимости допускается применять формат А5 с размерами сторон 148 х 210мм. Допускается также применение дополнительных
Рис. 3
форматов. Они образуются увеличением сторон основных форматов на величину, кратную размерам сторон формата А4 (рис. 4).
Допускаются следующие отклоления сторон формата при размерах сторон: до 150 ±1,5, от 150 до 600 ±2,0, свыше 600 ±3,0.
Стандартный бланк чертежа по ГОСТ 2.304—68
9. Основная надпись
§ 9. Основная надпись
Основная надпись чертежа располагается в правом нижнем углу формата (см. рис. 3). Форма, размеры и содержание граф основной надписи установлены ГОСТ 2.104—68. В основной надписи указывают: в графе 1 — наименование изделия; в графе 2 — обозначение чертежа; в графе 3 — материал детали; в графе 4 — наименование предприятия-изготовителя чертежа.
В левом верхнем углу чертежа, в рамке размером 14 х 70 записывается обозначение чертежа, данное в графе 2 рамки основной надписи, повернутое на 180°.
На форматах, больших А4, основная надпись может быть расположена как по короткой, так и по длинной стороне. При расположении основной надписи вдоль короткой стороны повернутое обозначение чертежа располагается в правом верхнем углу по длинной стороне.
Рис. 4
На формате А4 основная надпись располагается только вдоль его короткой стороны.
Рис. 4 Размеры рамки при оформлении чертежа
10. Масштабы
§ 10. Масштабы
Изображение предмета на чертеже может быть выполнено в натуральную величину, уменьшенным или увеличенным. Отношение всех линейных размеров изображения предмета на чертеже к их натуральной величине называется масштабом.
ГОСТ 2.302—68 устанавливает следующий ряд масштабов изображений на чертежах:
масштабы уменьшения —1:2; 1 :2,5; 1:4; 1:5; 1 : 10; 1:15; 1 :20; 1 :25; 1 : 40; 1 : 75; 1 : 100; 1 : 200;
натуральная величина — 1:1;
масштабы увеличения — 2 : 1; 2,5 : 1; 4:1; 5:1; 10 : 1; 40 : 1; 50: 1; 100: 1;
Изображение предмета на чертеже в масштабе увеличения или уменьшения не предусматривает целей определения его размеров, оно вызвано только необходимостью правильного зрительного восприятия формы изображаемого предмета, поэтому, независимо от масштаба изображения, размеры на чертеже проставляются действительные.
Масштаб в основной надписи чертежа обозначается по типу 1:1; 1 : 2; 2 : 1 и т. д. Масштабы изображения, отличающиеся от указанного в основной надписи чертежа, указывают непосредственно после надписи, относящейся к данному изображению, по типу: А (1 : 10), А —А (2:5).
11. Линии
§ 11. Линии
Основными элементами любого чертежа являются линии. В зависимости от их назначения они имеют соответствующие тип и толщину. Изображения предметов на чертеже представляют собой сочетание различных типов линий.
Типы линий, их назначение и толщина установлены ГОСТ 2.303—68 (табл. 2). Сплошная толстая основная линия принята за исходную. Толщина ее S должна выбираться в пределах от 0,6 до 1,5 мм. Она выбирается в зависимости от величины и сложности изображения, формата и назначения чертежа. Исходя из толщины сплошной толстой основной линии выбирают толщину остальных линий при условии, что для каждого типа линий в пределах одного чертежа на всех изображениях она будет одинаковой.
Таблица 2
|
Наименование |
Толщина линии по отношению к толщине основной линии |
Основное назначение |
|
От S/2 до S/2 |
||
|
От S/3 до S/2 |
||
|
От S/3 до S/2 |
||
|
От S/3 до S/2 |
|
От S/3 до (2/3) S |
||
|
От S/3 до S/2 |
||
|
От S/3 до S/2 |
Примечание.
Толщина линий S/3 допускается только для чертежей, выполненных тушью, на форматах с А4 по А2.
В штриховых линиях штрихи должны быть равной длины, а промежутки между ними одинаковыми. Штрихпунктирные линии должны пересекаться и заканчиваться штрихами. Центровые линии должны выходить за очертания окружности на 3...5 мм. Для окружностей, диаметр которых 12 мм и менее, центровые линии вычерчивают сплошными тонкими.
Примеры применения различных типов линий на чертеже приведены на рис. 5.
Линии могут иметь специальное назначение, например, для изображения резьбы, шлицев границ, зон с различной шороховатостью поверхности и др. Их применение регламентируется специальными стандартами ЕСКД.
Качество чертежа в значительной степени зависит от правильного выбора типа линий, соблюдения одинаковой толщины обводки, длины штрихов и расстояния между ними, аккуратности их проведения.
Рис. 5
Рис. 5 Примеры применения различных типов линий на чертеже
12. Надписи на чертежах
§ 12. Надписи на чертежах
Все надписи на чертежах должны выполняться стандартным чертежным шрифтом. Чертежный шрифт применяют также для выполнения надписей на других технических документах. При этом буквы шрифта, цифры, отдельные надписи и текст выполняют от руки. Отдельные надписи могут состоять из одних прописных букв. Цифры, встречающиеся в тексте, также выполняются высотой, равной высоте прописных букв.
Все надписи и размерные числа на чертежах должны быть четкими и ясными. Выполняются надписи шрифтами, предусмотренными ГОСТ 2.304—81 «Шрифты чертежные». Эти шрифты включают русский, латинский и греческий алфавиты, а также арабские и римские цифры.
Стандарт устанавливает следующие размеры шрифта: (1,8); 2,5; 3.5;5;7; 10; 14;20;28;40. Размер шрифта h определяет высоту прописных (заглавных) букв и цифр в миллиметрах.
Данные, касающиеся шрифтов типов A (d = h/14) и Б (d = h/10), приведены соответственно в табл. 3 и 4.
Таблица 3
|
Параметры шрифта |
Обоз- начение |
Относи- тельный размер, d |
Размеры, мм |
||||||
|
h |
14d |
||||||||
|
с |
|||||||||
|
а |
2d |
||||||||
|
d |
22d |
||||||||
|
е |
6d |
||||||||
|
d |
d |
||||||||
Стандартом установлены следующие два типа шрифта в зависимости от толщины d линий шрифта: тип A (d = 1 /14h) без наклона и с наклоном около 75° к горизонтальной строке; тип Б (d= 1/10h) без наклона и с наклоном под 75°. На рис. 6 приведена форма букв русского алфавита и арабских цифр, выполненных шрифтом Б без наклона.
Рис 6.
Таблица 4
|
Параметры шрифта |
Обозна- чение |
Относи- тельный размер, d |
Размеры, мм |
|||||||
|
h |
10d |
|||||||||
|
с |
7d |
|||||||||
|
а |
2d |
|||||||||
|
b |
17d |
|||||||||
|
е |
6d |
|||||||||
|
d |
d |
|||||||||
Примечание. Минимальным расстоянием между словами, разделенным знаком препинания, является расстояние между знаком препинания и следующим за ним словом.
При выполнении надписей на чертежах стандартными шрифтами расстояние а между буквами, соединение линий, которые не параллельны между собой (например, Г и А, А и Т и т. д.), уменьшается на половину, т. е. на толщину плиний шрифта. Для всего текста толщина линий одного шрифта должна быть одинакова.
Выполняемые чертежи часто имеют большое количество буквенных и цифровых надписей. Их необходимо, как правило, располагать горизонтально. Следует избегать расположения надписей внутри контура проекций (кроме размерных чисел). Если надпись наносится под линией или подчеркивается линией, то она должна отстоять от нее примерно на 1 мм.
Если надпись пересекает линию, то в месте пересечения линию необходимо прервать. При заполнении граф основной надписи и других графических документов надпись необходимо располагать по возможности на одинаковом расстоянии от ограничивающих графу линий.
Рис. 6 Форма букв русского алфавита и арабских цифр, выполненных шрифтом без наклона.

13. Основные правила нанесения размеров на чертеже
§ 13. Основные правила нанесения размеров на чертеже
По изображениям предмета на чертеже судят о его величине и величине его отдельных частей. Основанием для этого служат размерные числа, независимо от того, в каком масштабе и с какой точностью
Рис. 7
Рис. 8
Рис. 9
Рис. 10
Рис. 11
Рис. 12
Рис. 13
выполнены изображения. Правила нанесения размеров на чертежах установлены ГОСТ 2.307—68.
Размеры на чертеже указывают размерными числами, размерными и выносными линиями. Размерные числа на чертежах, как правило, указывают в миллиметрах без указания единиц измерения. В тех случаях, когда необходимо применять другие единицы измерения длины, их показывают после размерного числа.
Размерные числа наносят над размерной линией, возможно ближе к ее середине. Зазор между размерным числом и размерной линией должен быть около 1,0 мм. Высоту цифр размерных чисел принимают не менее 3,5 мм (рис. 7).
Размерная линия проводится параллельно отрезку, размер которого над ней наносится. Ее проводят между выносными линиями, проведенными перпендикулярно размерным. Допускается размерные линии проводить непосредственно к линиям видимого контура, осевым и центровым. В отдельных случаях размерная линия может проводиться не перпендикулярно выносной (рис. 8). Размерные линии ограничивают стрелки (рис. 9). В отдельных случаях их проводят не полностью, а с обрывом стрелки с одной стороны (рис. 10). Размер стрелки выбирают от принятой на чертеже толщины сплошной толстой основной линии. В пределах одного чертежа величина стрелок должна быть по возможности одинаковой. Не рекомендуется в качестве размерных линий использовать контурные, осевые, центровые и выносные линии.
Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии, и размеры наносят, как показано на рис. 11.
Выносные линии проводят от границ измерений, они являются вспомогательными и служат для размещения между ними размерных линий. Выносные линии следует по возможности располагать вне контура изображения, перпендикулярно прямолинейному отрезку, размер которого необходимо указать. Выносные линии должны выходить за концы стрелок размерных линий на 1...5 мм (рис. 12).
Минимальное расстояние от размерной линии до параллельной ей линии должно быть 10 мм, а между параллельными размерными линиями — 7 мм.
Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в виде дуги с центром в его вершине. Выносные линии в этом случае проводятся радиально (рис. 13).
При различных наклонах размерных линий размерные числа линейных размеров располагают так, как показано на рис. 14, а, а угловые размеры — как показано на рис. 14, б. Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-выносок (рис. 15).
Если для написания размерного числа мало места над размерной линией или это место занято другими элементами изображения и впи-
Рис. 14
Рис. 15
Рис. 16
Рис. 17
сать в него размерное число невозможно, размерное число наносят по одному из вариантов, приведенных на рис. 16.
С целью упрощения ряда изображений, создания удобств для чтения чертежа стандарт предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. На чертежах применяются
Рис. 18
Рис. 19
Рис. 20
Рис. 21
Рис. 22
Рис. 23
Рис. 24
знаки и буквы для обозначения диаметра и радиуса, длины дуги и квадрата, уклона и конусности, сферы, толщины и длины детали.
Перед размерным числом диаметра наносится знак 0 (рис. 17). Причем между знаком и числом никаких пропусков не предусмотрено. Для окружностей малого диаметра размерные линии стрелки и сам размер наносят по одному из вариантов, приведенных на рис. 18.
Перед размерным числом радиуса дуги всегда ставится знак в виде прописной латинской буквы R. Размерную линию в этом случае проводят по направлению к центру дуги и ограничивают только одной стрелкой, упирающейся в дугу или ее продолжение (рис. 19). Если величина радиуса на чертеже менее 6 мм, стрелку рекомендуется распо-
Рис. 25
лагать с внешней стороны дуги. При необходимости задания положения центра дуги его отмечают пересечением центровых или выносных линий (рис. 20). В тех случаях, когда на чертеже изображена дуга большого радиуса, для которой центр можно не обозначать, размерную линию обрывают, не доводя до центра (рис. 21). Если же в этом случае центр необходимо отметить, допускается приближать его к дуге (рис. 22). Размерная линия в этом случае показывается с изломом 90°, и оба участка размерной линии проводятся параллельно. Не следует располагать на одной прямой размерные линии, выходящие из одного центра и предназначенные для обозначения размерных дуг. Радиусами рекомендуется обозначать дуги до 180°; дуги, величина которых составляет более 180°, обозначаются диаметром.
Знак дуги наносится над размерным числом (рис. 23). Длину дуги задают в линейных единицах, а размерное число, обозначающее дугу, наносится над размерной линией в соответствии с обычными требованиями.
Для простановки размеров квадрата применяют соответствующий знак D, высота которого равна 7/10 высоты размерного числа (рис. 24, а). При ином расположении квадрата наносят размеры его сторон (рис. 24, б). Следует отметить, что знак квадрата наносят только на том изображении, на котором он проецируется в линию.
Знак конусности поверхности наносится на полке линии-выноски, расположенной параллельно оси конуса или на оси конуса (рис. 25, а). Знак конусности располагают так, чтобы его острый угол был направлен в сторону вершины конуса. Величину конусности определяют отношением разности диаметров двух поперечных сечений конуса к расстоянию между этими сечениями, т. е. k = D — dll, где D — диаметр большого сечения; d — диаметр меньшего сечения; l — расстояние между сечениями. Конусность указывают в виде простого дробного числа (рис. 25, б).
Знак уклона прямой указывают на полке линии-выноски. Уклон i представляет собой тангенс угла между данной прямой и горизонтальной или вертикальной прямой (рис. 26, а). Знак уклона располагается
Рис. 26
Рис. 27
Рис. 28
так, чтобы острый угол его был направлен в сторону уклона прямой (рис. 26, б). Уклон, как и конусность, на чертеже задают простой дробью, в процентах или в промилях.
Для обозначения сферы на чертеже применяют знак диаметра или радиуса. В тех случаях, когда по чертежу сферу трудно отличить от других поверхностей, перед знаком радиуса или диаметра допускается добавлять слово «Сфера». Надпись на чертеже выполняется по типу «Сфера диаметр 17» или «Сфера R10» (рис. 27).
Простые плоские детали изображаются в виде одной проекции. В этих случаях ее толщину обозначают строчной буквой s и надпись на чертеже выполняется по типу s2 и располагается на полке линии-выноски (рис. 28, а). Длину предмета указывают буквой / (рис. 28, б).
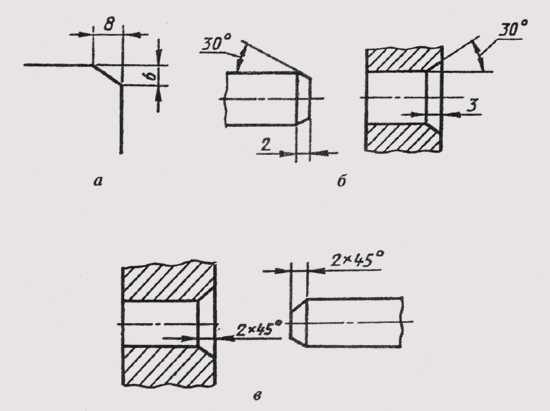
Фаски на чертежах наносят двумя линейными размерами (рис. 29, а) или одним линейным и одним угловым (рис. 29, б). В том случае, если
Рис. 29
угол наклона образующей конуса равен 45°, применяют упрощенное обозначение фаски, когда размерная линия проводится параллельно оси конуса, а надпись выполняется по типу «2 х 45» (рис. 29, в).
Рис. 7 Основные правила нанесения размеров на чертеже
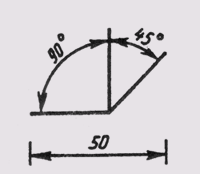
Рис. 8 Размерная линия может проводиться не перпендикулярно выносной
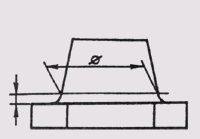
Рис. 9 Размерные линии ограничивают стрелки
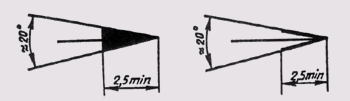
Рис. 10 Размерные линии в отдельных случаях проводят не полностью
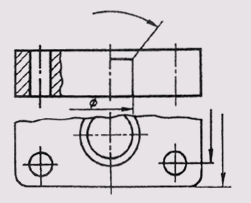
Рис. 11 Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии
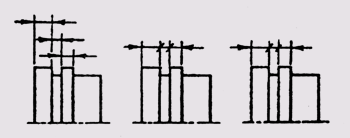
Рис. 12 Выносные линии должны выходить за концы стрелок размерных линий на 1...5 мм
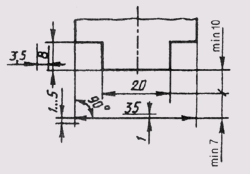
Рис. 13 Выносные линии могут проводиться радиально
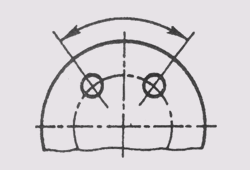
Рис. 14 При различных наклонах размерных линий размерные числа располагаются под углом
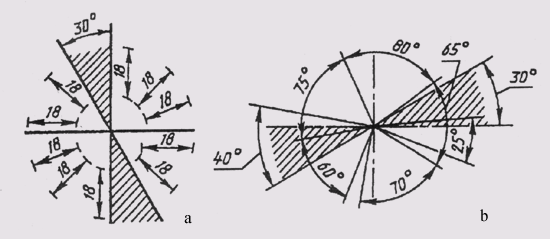
Рис. 15 Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-в
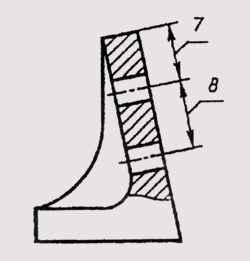
Рис. 16 Сноска размерной линии
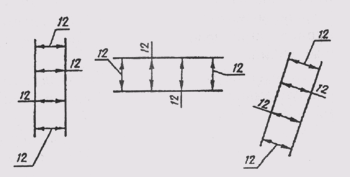
Рис. 17 Перед размерным числом диаметра наносится знак О
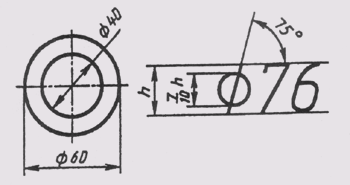
Рис. 18 Для окружностей малого диаметра размерные линии стрелки и сам размер наносят по одному из вариантов
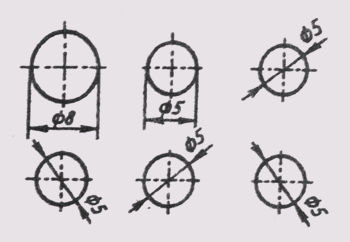
Рис. 19 Перед размерным числом радиуса дуги всегда ставится знак в виде прописной латинской буквы R
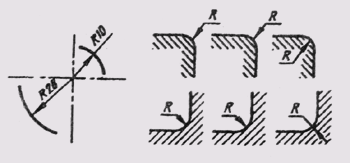
Рис. 20 При необходимости задания положения центра дуги его отмечают пересечением центровых или выносных линий
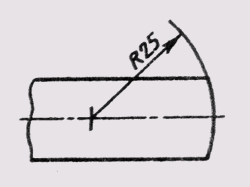
Рис. 21 В тех случаях, когда на чертеже изображена дуга большого радиуса, для которой центр можно не обозначать, размерную линию
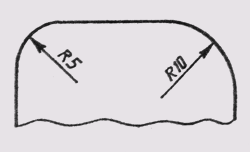
Рис. 22 Допускается приближать центр к дуге
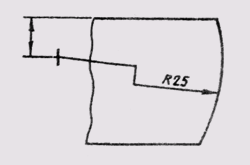
Рис. 23 Знак дуги наносится над размерным числом
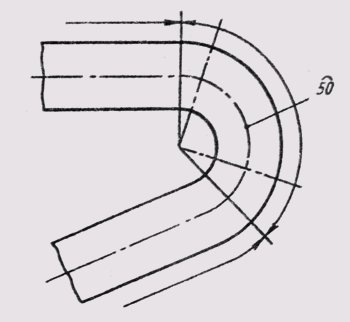
Рис. 24 Для простановки размеров квадрата применяют соответствующий знак D
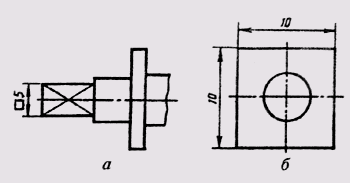
Рис. 25 Знак конусности поверхности наносится на полке линии-выноски
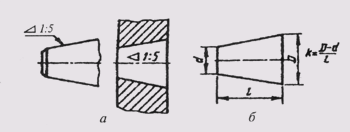
Рис. 26 Знак уклона прямой указывают на полке линии-выноски
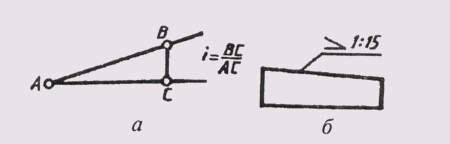
Рис. 27 Надпись на чертеже выполняется по типу «Сфера диаметр 17» или «Сфера R10»
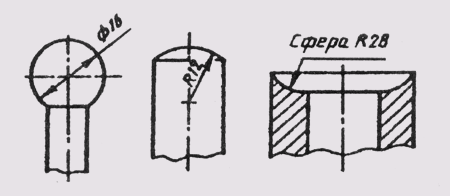
Рис. 28 Простые плоские детали изображаются в виде одной проекции.
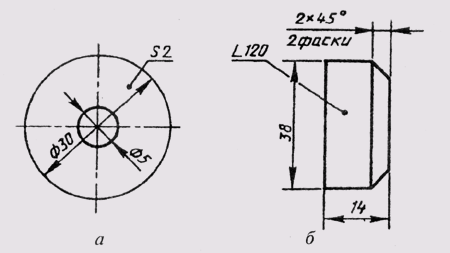
Рис. 29 Фаски на чертежах наносят двумя линейными размерами
4. Глава 3. Некоторые геометрические построения
1. Глава 3. Некоторые геометрические построения
Глава 3. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
§ 14. Общие сведения
При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений прямых с дугами окружностей и дуг окружностей между собой. Сопряжением называют плавный переход дуги окружности в прямую или в дугу другой окружности.
Наиболее часто встречаются задачи на построение следующих сопряжений: двух прямых дугой окружности (скруглением углов); двух дуг окружностей прямой линией; двух дуг окружностей третьей дугой; дуги и прямой второй дугой.
Построение сопряжений связано с графическим определением центров и точек сопряжения. При построении сопряжения широко используются геометрические места точек (прямые, касательные к окружности; окружности, касательные друг к другу). Это объясняется тем, что они основаны на положениях и теоремах геометрии.
10. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
15. Какая плоская кривая называется эвольвентой?
15. Деление отрезка прямой
§ 15. Деление отрезка прямой
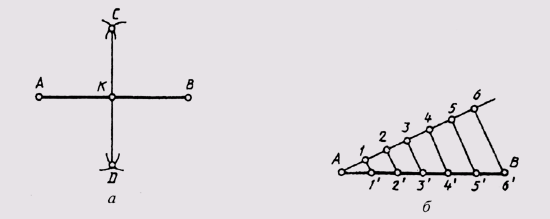
Чтобы разделить заданный отрезок АВ на две равные части, точки его начала и конца принимают за центры, из которых проводят дуги радиусом, по величине превышающим половину отрезка АВ. Дуги проводят до взаимного пересечения, где получают точки С и D. Линия, соединяющая эти точки, разделит отрезок в точке К на две равные части (рис. 30, а).
Рис. 30
Чтобы разделить отрезок АВ на заданное количество равных участков п, под любым острым углом к АВ проводят вспомогательную прямую, на которой из общей заданной прямой точки откладывают п равных участков произвольной длины (рис. 30, б). Из последней точки (на чертеже — шестой) проводят прямую до точки В и через точки 5, 4, 3, 2, 1 проводят прямые, параллельные отрезку 6В. Эти прямые и отсекут на отрезке АВ заданное число равных отрезков (в данном случае 6).
Рис. 30 Деление заданного отрезка АВ на две равные части
16. Деление окружности
§ 16. Деление окружности
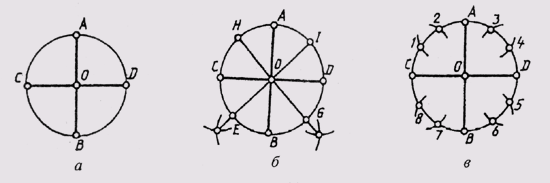
Чтобы разделить окружность на четыре равные части, проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части (рис. 31, а).
Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 31, б).
На двенадцать равных частей окружность делят следующим образом. Делят окружность на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 31, в).
Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7 равных участков.
Рис. 31
Рис. 31 Пользуясь радиусом, нетрудно разделить окружность и на несколько равных участков.
17. Округление углов
§ 17. Скругление углов
Сопряжение двух пересекающихся прямых дугой заданного радиуса называют скруглением углов. Его выполняют следующим образом (рис. 32). Параллельно сторонам угла, образованного данными
Рис. 32
прямыми, проводят вспомогательные прямые на расстоянии, равном радиусу. Точка пересечения вспомогательных прямых является центром дуги сопряжения.
Из полученного центра О опускают перпендикуляры к сторонам данного угла и на пересечении их получают точки сопряжения А а В. Между этими точками проводят сопрягающую дугу радиусом R из центра О.
Рис. 32 Сопряжение двух пересекающихся прямых дугой заданного радиуса называют скруглением углов
18. Сопряжение дуг окружностей прямой линией
§ 18. Сопряжение дуг окружностей прямой линией
При построении сопряжения дуг окружностей прямой линией можно рассмотреть две задачи: сопрягаемая прямая имеет внешнее или внутреннее касание. В первой задаче (рис. 33, а) из центра дуги
Рис. 33
меньшего радиуса R1 проводят касательную вспомогательной окружности, проведенной радиусом R — RI. Ее точку касания Ко используют для построения точки сопряжения А на дуге радиуса R.
Для получения второй точки сопряжения А1 на дуге радиуса R1 проводят вспомогательную линию О1 А1 параллельно О А. Точками A и А1будет ограничен участок внешней касательной прямой.
Задача построения внутренней касательной прямой (рис. 33, б) решается, если вспомогательную окружность построить радиусом, равным R + R1,
Рис. 33 Сопряжение дуг окружностей прямой линией
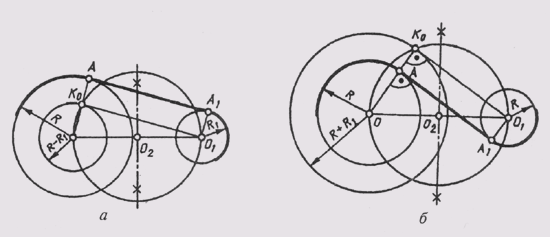
19. Сопряжение двух дуг окружностей третьей дугой
§ 19. Сопряжение двух дуг окружностей третьей дугой
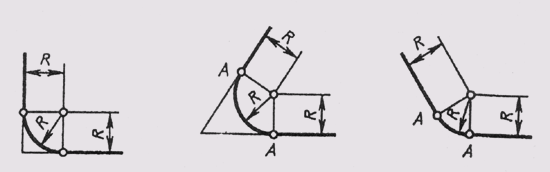
При построении сопряжения двух дуг окружностей третьей дугой заданного радиуса можно рассмотреть три случая: когда сопрягающая дуга радиуса R касается заданных дуг радиусов R1 и R2 с внешней стороны (рис. 34, а); когда она создает внутреннее касание (рис. 34, б); когда сочетаются внутреннее и внешнее касания (рис. 34, в).
Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке: из центра О1 радиусом, равным R + R1, проводят вспомогательную дугу, а из центра O2 проводят вспомогательную дугу радиусом R + R2. На пересечении дуг получают центр О сопрягаемой дуги радиуса R, а на пересечении радиусом R + R1и R + R2 с дугами окружностей получают точки сопряжения А и А1.
Построение центра О при внутреннем касании отличается тем, что из центра О1 проводят вспомогательную окружность радиусом, равным R — R1 а из центра О2 радиусом R — R2. При сочетании внутреннего и внешнего касания из центра О1 проводят вспомогательную окружность радиусом, равным R — R1, а из центра О2 — радиусом, равным R + R2.
20. Сопряжение дуги окружности и прямой линии второй дугой
§ 20. Сопряжение дуги окружности и прямой линии второй дугой
Здесь может быть рассмотрено два случая: внешнее сопряжение (рис. 35, а) и внутреннее (рис. 35, б). В том и в другом случае при построении сопрягающей дуги радиуса R центр сопряжения О лежит на пересечении геометрических мест точек, равно удаленных от прямой и дуги радиуса R на величину R1.
При построении внешнего сопряжения параллельно заданной прямой на расстоянии R1 в сторону окружности проводят вспомогательную прямую, а из центра О радиусом,равным R + R1,— вспомогательную окружность, и на их пересечении получают точку О1 — центр сопрягающей окружности. Из этого центра радиусом R проводят сопрягающую дугу между точками А и А1, построение которых видно из чертежа.
Рис. 34
Рис. 35
Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R — R1.
Рис 34 Внешнее сопряжение дуги окружности и прямой линии второй дугой
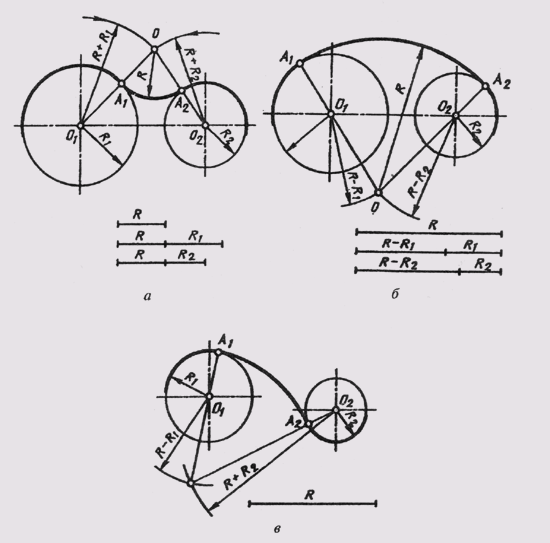
Рис 35 Внутреннее сопряжение дуги окружности и прямой линии второй дугой
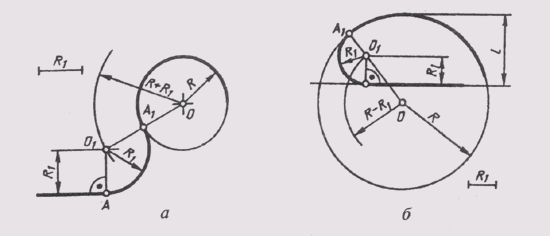
21. Овалы
§21. Овалы
Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами. Овалы состоят из двух опорных окружностей с внутренними сопряжениями между ними.
Различают овалы трехцентровые и многоцентровые. При вычерчивании многих деталей, например кулачков, фланцев, крышек и других, контуры их очерчивают овалами. Рассмотрим пример построения овала по заданным осям. Пусть для четырехцентрового овала, очерченного двумя опорными дугами радиуса R и двумя сопрягающими дугами радиуса r , заданы большая ось АВ и малая ось CD. Величину радиусов R u r надо определить путем построений (рис. 36). Соединим концы большой и малой оси отрезком AС, на котором отложим разность СЕ большой и малой полуосей овала. Проведем перпендикуляр к середине отрезка AF, который пересечет большую и малую оси овала в точках О1 и О2. Эти точки будут центрами сопрягающихся дуг овала, а точка сопряжения будет лежать на самом перпендикуляре.
Рис. 36
Рис. 36 Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами
22. Лекальные кривые
§ 22. Лекальные кривые
Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.
Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее
Рис. 36
Рис. 37
точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.
Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.
Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы.
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.
Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и ну-
Рис. 38
меруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.
Рис. 39
Рис. 40
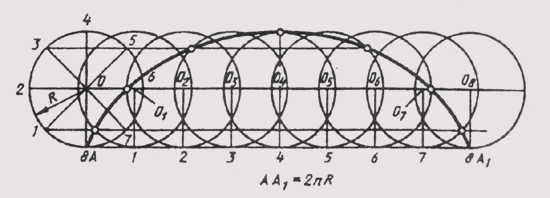
Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
Рис. 41
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 41): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n , на второй — два и т. д.
Полученные точки соединяют плавной кривой и получают эвольвенту окружности.
Рис 36 Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам.

Рис 37 Эллипс представляет собой замкнутую плоскую кривую второго порядка.
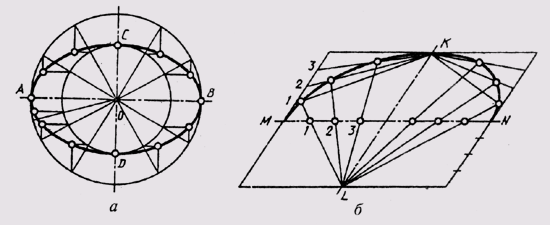
Рис 40 Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла.
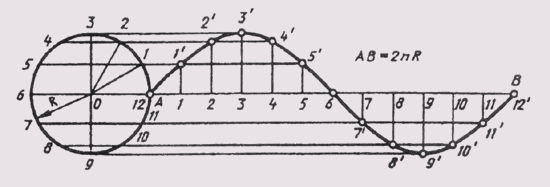
Рис 41 Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без ск
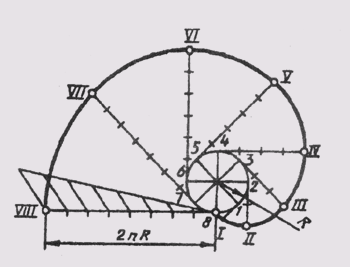
Рис. 38 Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данн
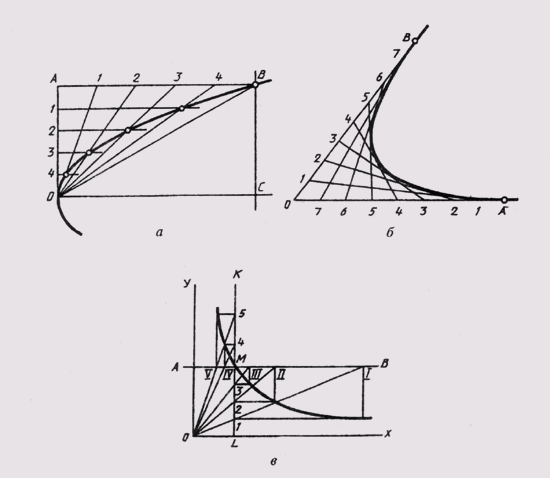
Рис. 39 Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности
5. Глава 4. Общие понятия об образовании чертежа
1. Часть вторая. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЧЕРТЕЖА
Часть вторая.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЧЕРТЕЖА
Глава 4. ОБЩИЕ ПОНЯТИЯ ОБ ОБРАЗОВАНИИ ЧЕРТЕЖА
§ 23. Определение чертежа
Чертежом называют графический документ, содержащий изображения предметов (деталей, узлов, машин, зданий и сооружений и т. д.), выполненных с учетом правил и требований, позволяющих однозначно различать эти предметы. Таким образом, процесс выполнения чертежей основан на знании специальных законов и умении использовать их при выполнении графических работ. Теоретической основой черчения является наука о методах изображения геометрических фигур на плоскости — начертательная геометрия.
К чертежам предъявляют ряд общих требований. Так, чертеж должен быть наглядным и давать четкое представление об изображаемом предмете. Чертеж должен быть обратимым. Это необходимо, чтобы по нему можно было точно воспроизвести форму и размеры изображаемого предмета. Чертеж должен быть простым для графического исполнения и др.
Надо также отметить, что знание графических законов способствует развитию пространственного мышления, являющегося основой технического творчества проектировщиков, конструкторов, изобретателей и рационализаторов.
4. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
12. В чем заключается метод отображения?
24. Основные элементы геометрического пространства
§ 24. Основные элементы геометрического пространства
В инженерной графике геометрическое пространство рассматривается как множество однородных элементов. К основным формообразующим элементам геометрического пространства относятся точки, линии (прямые и кривые), поверхности (плоские и кривые).
Рис. 42
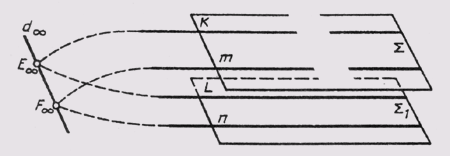
Различают пространство евклидово и неевклидово. Евклидово пространство характеризуется тем, что расположенные в нем параллельные прямые линии или плоскости не пересекаются. Характеристики евклидова пространства не учитывают ряда других геометрических свойств пространства. В более широком понимании эти свойства учитывают проективное пространство, в котором параллельные между собой прямые (плоскости) пересекаются. Эти пересечения происходят в так называемой несобственной точке, которая расположена в бесконечности проективного пространства. Для примера можно привести две параллельные плоскости S и S1 (рис. 42). Проведем в плоскости S прямую К, а в плоскости Si прямую L так, чтобы они были параллельны. В проективном пространстве эти прямые пересекаются вне собственной точки Ебесконечность. Далее в плоскости S проведем прямую т, а в плоскости Si прямую п так, чтобы они были параллельны. Эти прямые также пересекутся вне собственной точки F бесконечность. Нетрудно видеть, что несобственные точки Е бесконечность и F бесконечность определяют несобственную прямую d бесконечность . Учитывая, что несобственные точки принадлежат и плоскости S, и плоскости S1, можно утверждать, что несобственная прямая также принадлежит этим плоскостям. Таким образом, мы имеем случай, когда две параллельные плоскости S и S1пересекаются по бесконечно удаленной несобственной прямой d бесконечность.
Характеристики проективного пространства позволяют в ряде случаев упростить формулировки, принятые для евклидова пространства. Это можно подтвердить следующим примером. В аксиомах евклидова пространства отмечается, что две прямые определяют единственную точку, если они не параллельны. Для проективного пространства оговорка «если они не параллельны» теряет смысл.
В общепринятом смысле пространство можно рассматривать как бесконечное. Однако геометрическое пространство может быть рассмотрено с позиций размерности. Так, множество положений точки, перемещающейся в заданном прямолинейном направлении, образует бесконечную прямую линию, представляющую собой одномерное пространство. Если же прямую перемещать в заданном направлении, не параллельном самой прямой, она образует бесконечную поверхность (в данном случае плоскость), представляющую собой двухмерное пространство. Задав плоскости (поверхности) направление, не параллельное ей и перемещая ее в этом направлении, получим трехмерное пространство. Таким же путем можно получить четырехмерное и в общем виде многомерное пространство.
Примем следующие обозначения элементов пространства. Точки будем обозначать прописными буквами латинского алфавита: А, В, С... или цифрами 1, 2, 3...; прямые — строчными буквами латинского алфавита: а, b, с..., а плоскости — прописными буквами греческого алфавита: Г, Л, П, S, Ф, ¥, Q.
Между элементами пространства существуют следующие отношения.
Тояадественность обозначается знаком ==, например А == В. Это обозначает, что точка А совпадает с точкой В.
Инцидентность (или принадлежность) обозначается знаком ?. Например, А ? а обозначает, что точка А принадлежит (инцидентна) прямой а.
Параллельность обозначается знаком ||. Например, K || L обозначает, что прямая К параллельна прямой
Перпендикулярность обозначается знаком _|_. Например, a _|_ S обозначает, что прямая а перпендикулярна плоскости S.
Над элементами пространства можно выполнить операцию соединение, которую обозначают знаком и. Например, запись А и В ~ а обозначает, что в результате соединения точек А и В получена прямая а. Операцию пересечение обозначают знаком ^. Запись т ^ n = К обозначает, что в результате пересечения прямых тип получена точка К.
Рис. 42 Две параллельные плоскости S и S1
25. Геометрические тела и их отображение
§ 25. Геометрические тела и их отображение
Геометрическое тело рассматривают как множество всех принадлежащих ему точек, связанных между собой и ограниченных в пространстве соответствующим образом. Оно может перемещаться в пространстве без изменения взаимного положения его элементов.
В инженерной графике рассматриваются одномерные тела (отрезок линии), двухмерные (плоская фигура, отсек поверхности), трехмерные (любая объемная фигура). Основными предметами изображения на плоских чертежах являются трехмерные геометрические тела, окружающие нас в реальном трехмерном пространстве.
Сложные геометрические тела можно рассматривать и как состоящие из более простых трехмерных фигур, которые определяются основными формообразующими элементами пространства — точками, линиями, поверхностями.
Геометрические тела на чертежах получают методом отображения. Отображение геометрического тела — это понятие, в соответствии с которым каждой точке трехмерного пространства соответствует конкретная точка двухмерного пространства на чертеже. Отображение геометрических тел может быть выполнено на плоскость или какую-либо другую поверхность. В курсе инженерной графики рассматривается отображение геометрических тел на плоскость. Изображение геометрического тела на плоскости можно получить путем проецирования ее точек на эту плоскость.
Геометрическая связь между геометрическим телом, расположенным в пространстве, и его отображением на чертеже на плоскости устанавливаются по законам проецирования, которые базируются на принципе взаимно-однозначного соответствия.
6. Глава 5. Изображение объектов трехмерного пространства
1. Глава 5. Изображение объектов трехмерного пространства
Глава 5. ИЗОБРАЖЕНИЕ ОБЪЕКТОВ ТРЕХМЕРНОГО ПРОСТРАНСТВА
§ 26. Метод проекций
Теоретические свойства построения чертежа в инженерной графике базируются на правилах построения изображений, основанных на методе проекций. Изображение объектов трехмерного пространства на плоскости получают методом проецирования. Проецирование — это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.
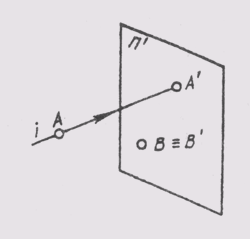
Аппарат проецирования включает в себя изображаемые объекты — точки А, В, проецирующие лучи i и плоскость проекции п', на которой получается изображение объектов (рис. 43). Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А', т. е. [i ~ A; i ^ п' = А']. Проекцией точки В является точка В', хотя проекция точки В, лежащей в плоскости п', совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.
Рис. 43
Изображение объектов трехмерного пространства
7. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
10. Чем характеризуются проекции с числовыми отметками?
27. Способы проецирования
§ 27. Способы проецирования
Построить проекции предметов на чертеже можно двумя способами: центральным и параллельным.
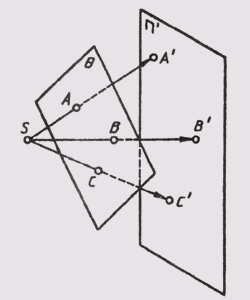
Сущность центрального способа проецирования заключается в том, что все лучи, проецирующие предмет, исходят из одной точки Р, называемой центром проекций (рис. 44). Полученные проекции А', В', С' называются центральными проекциями точек А, В, С.
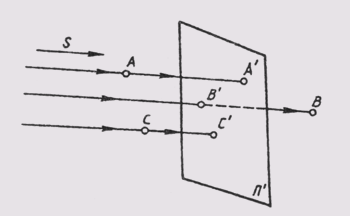
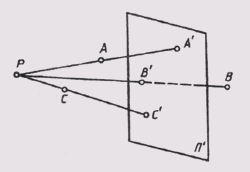
Сущность параллельного способа заключается в том, что все проецирующие лучи проходят параллельно наперед заданному направлению 5, а значит и друг другу (рис. 45). Это можно уподобить случаю центрального способа проецирования, когда центр проекций S удален в бесконечность и все проецирующие лучи становятся параллельны-
Рис. 44
Рис. 45
Рис. 46
Рис. 47
ми. При построении проекций А', В', С' этим способом они называются параллельными проекциями точек А, В, С.
При проецировании совокупность проецирующих лучей образует различные геометрические фигуры. При проецировании прямой линии — это плоскость (рис. 46) при проецировании ломаной линии — поверхность призмы или пирамиды (рис. 47), при проецировании кривой линии — коническая или цилиндрическая поверхность (рис. 48). В отличие от проецируемых фигур эти фигуры называют проецирующими.
45.gif
46.gif
47.gif
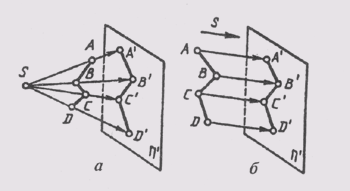
Центральное проецирование
28. Свойства проекций
§ 28. Свойства проекций
Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.
Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п' единственная точка А'. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).
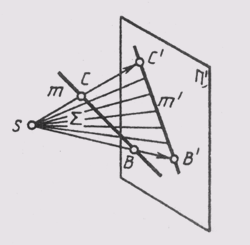
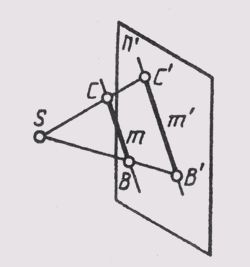
Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п' по линии m', являющейся проекцией на плоскость n'; S ~ т; S п п = т'. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 49). Если в пространстве прямая параллельна плоскости проекции п', то ее проекция параллельна самой прямой (рис. 50). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.
Рис. 49
При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 51):
АВ/ВС = А'В'/В'С.
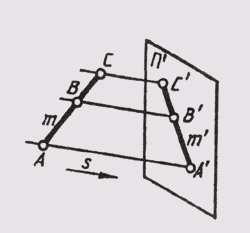
При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 52). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п' получаем т'|| п'.
Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а
Рис. 50
Рис. 51
Рис. 52
Рис. 53
их точки пересечения с плоскостью проекций п' — всю плоскость проекций.
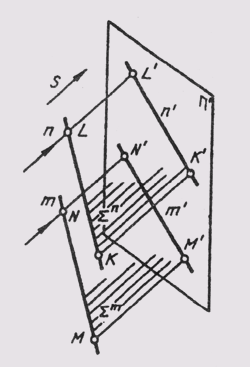
Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 53, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n', которое позволяет определить проекции (рис. 53, б) любой точки D или прямой этой плоскости.
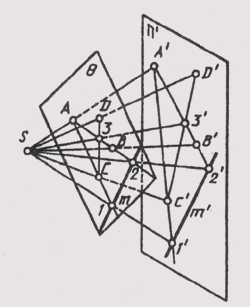
Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 54, а), а при параллельном — равны им (рис. 54,6).
Рис. 54
Рис. 55
Рис. 56
Рис. 57
Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA'B'C', так как АВС бесконечность А'В'С', а на рис. 54, б угол ABC = углу А'В'С', так как АВС = А'В'С'.
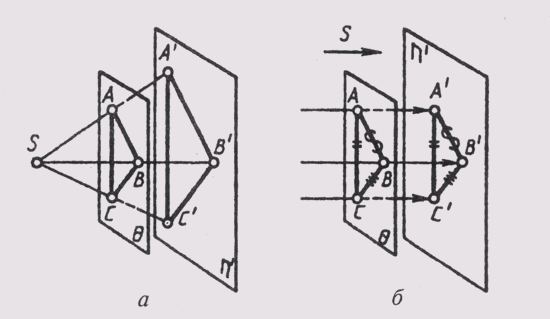
При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 55).
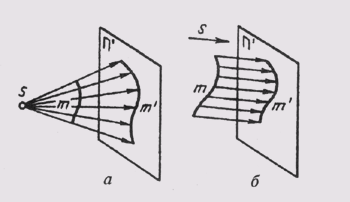
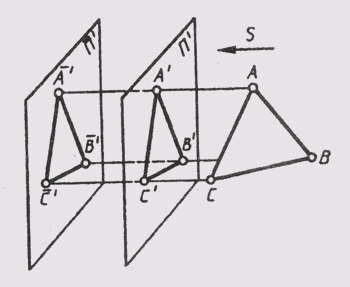
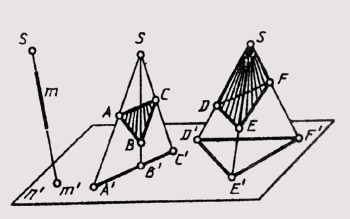
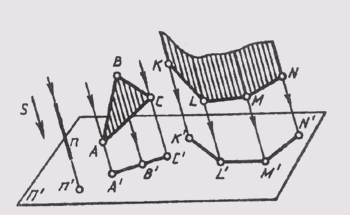
Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).
Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).
49.gif
50.gif
51.gif
52.gif
53a.gif
53b.gif
54.gif
55.gif
56.gif
57.gif
29. Ортогональные проекции
§ 29. Ортогональные проекции
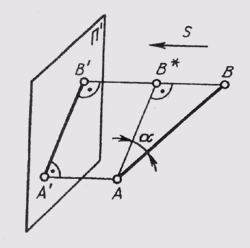
Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка (рис. 58). Это объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А'В' = ABcos a.
При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.
Теорема о проецировании прямого угла. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпенди-
Рис. 58
Рис. 59
кулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой же угол.
Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости п' (рис. 59). Проецирующая плоскость перпендикулярна плоскости п'. Значит, АВ _|_S, так как АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В'С'. Но так какАВ || А'В' _|_ В'С', т. е. на плоскости п' угол между А'В' и В'С равен 90°.
Обратимость чертежа. Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А (см. рис. 53) не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций п'. Любая точка проецирующего луча, проходящего через точку А, будет иметь своей проекцией точку А'. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа. В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрические чертежи).
58.gif
59.gif
30. Аксонометрические проекции
§ 30. Аксонометрические проекции
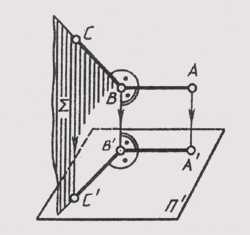
В ряде случаев для пояснения прямоугольных проекций сложных деталей, машин и механизмов применяют аксонометрические проекции. С их помощью получают наглядное изображение предметов. Сущность аксонометрического проектирования заключается в том, что фигуру, связанную с пространственной системой координатных осей, вместе с этими осями координат проецируют на одну плоскость, называемую плоскостью аксонометрических проекций. Подробно аксонометрические проекции рассмотрены в гл. 12.
31. Проекции с числовыми отметками
§31. Проекции с числовыми отметками
Сущность метода проекций с числовыми отметками заключается в том, что любая точка пространства проецируется ортогонально на одну горизонтальную плоскость, называемую плоскостью нулевого уровня. Положение точки по отношению к этой плоскости определяется числовой отметкой, проставляемой у буквенного обозначения проекции точки и представляющую собой число единиц расстояния от точки до плоскости проекций.
7. Глава 6. Проекции точки. Комплексный чертеж
1. Глава 6. Проекции точки. Комплексный чертеж
Глава 6. ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ
§ 32. Комплексный чертеж точки
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
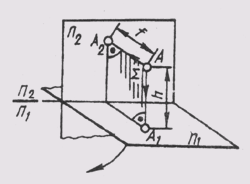
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов
Рис. 60
Рис. 61
пространства на ней будем обозначать с индексом 1 : А1, а1, S1 ... и называть горизонтальными проекциями (точки, прямой, плоскости).
Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П2. Проекции элементов пространства на ней будем обозначать с индексом 2: А2, <a2, S2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.
Спроецируем точку А ортогонально на обе плоскости проекций:
АА1_|_ П1;AА1 ^П1=A1;
АА2_|_ П2;AА2 ^П2=A2;
Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
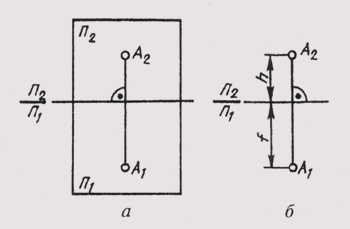
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.
60.gif
61.gif
7. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
4. Как называется расстояние, определяющее положение точки относительно плоскости проекций П1, П2?
7. Как построить дополнительную проекцию точки на плоскости П4 _|_ П2, П4_|_ П1, П5 _|_ П4?
9. Как можно построить комплексный чертеж точки по ее координатам?
33. Элементы трехпроекционного комплексного чертежа точки
§ 33. Элементы трехпроекционного комплексного чертежа точки
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-
Рис. 62
ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-
Рис. 63
ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
62.gif
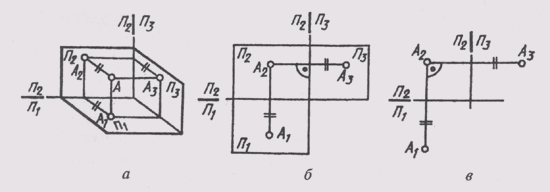
63.gif
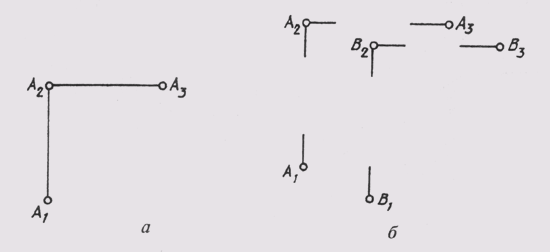
34. Положение точки в пространстве трехмерного угла
§ 34. Положение точки в пространстве трехмерного угла
Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:
- точка расположена в пространстве (см. рис. 62). В этом случае она имеет глубину, высоту и широту;
- точка расположена на плоскости проекций П1 — она не имеет высоты, П2 — не имеет глубины, Пз — не имеет широты;
- точка расположена на оси проекций, П2/П1 не имеет глубины и высоты, П2/П3— не имеет глубины и широты и П1/П3не имеет высоты и широты.
35. Конкурирующие точки
§ 35. Конкурирующие точки
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
Рис. 64
П2 (рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П3 [А3 == B3] (рис. 64, в), они называются профильно конкурирующими.
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.
64.gif
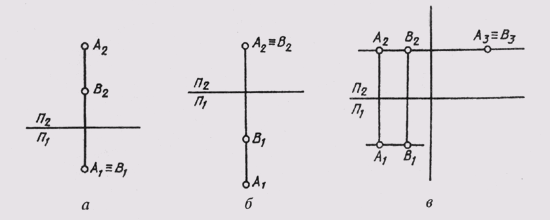
36. Замена плоскостей проекций
§ 36. Замена плоскостей проекций
Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.
На рис. 65, а показаны точка А и ее проекции — горизонтальная А1 и фронтальная А2. По условиям задачи необходимо произвести замену плоскостей П2. Новую плоскость проекции обозначим П4 и расположим перпендикулярно П1. На пересечении плоскостей П1 и П4 получим новую ось П1/П4. Новая проекция точки А4 будет расположена на линии связи, проходящей через точку А1 и перпендикулярно оси П1/П4.
Поскольку новая плоскость П4 заменяет фронтальную плоскость проекции П2, высота точки А изображается одинаково в натуральную величину и на плоскости П2, и на плоскости П4.
Это обстоятельство позволяет определить положение проекции A4, в системе плоскостей П1 _|_ П4 (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
Рис. 65
Рис. 66
Рис. 67
сти проекции П2, отложить ее на новой линии связи от новой оси проекций — и новая проекция точки А4 будет построена.
Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П4 _|_ П2 (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А2А4 _|_. В этом случае глубина точки одинакова и на плоскости П1, и на плоскости П4. На этом основании строят А4 (рис. 66, б) на линии связи А2А4 на таком расстоянии от новой оси П1/П4 на каком А1 находится от оси П2/П1.
Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П5. Ее располагают перпендикулярно уже введенной плоскости П4 (рис. 67, а), т. е. П5П4 и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рис. 67, б на плоскости П1) и откладывают их на новой линии связи А4А5, от новой оси проекций П5/П4. В новой системе плоскостей П4П5 получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А4 и А5, связанных линией связи
A4A5_|_П4/П5
65.gif
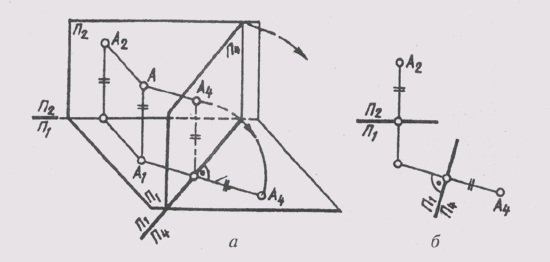
66.gif
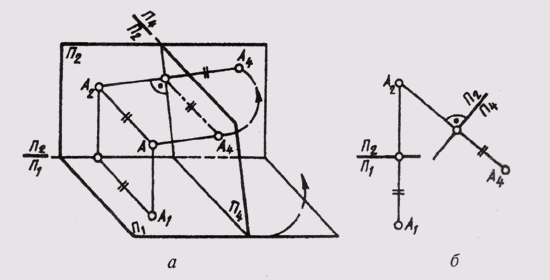
67.gif
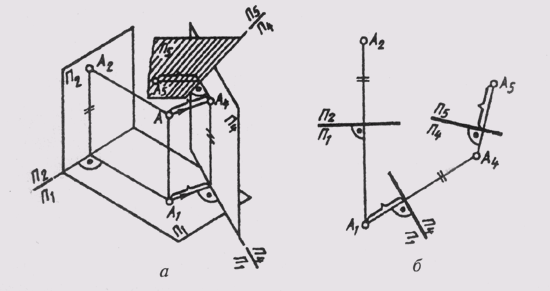
37. Прямоугольные координаты точек
§ 37. Прямоугольные координаты точек
Три основные плоскости проекций (П1_|_П2 _|_ П3) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у,П2/П3 —осью аппликат z.
Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).
Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А1 ортогонально проецировать на ось х в точку Ах. Тогда получим пространственную координатную ломаную АА1АХО, отрезки которой параллельны осям координат и соответственно называются: ОАХ — отрезком абсциссы; АХ А1 — отрезком ординат; А1А — отрезком аппликаты.
Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:
х = OAX абсцисса; у = AxA1— ордината; z = AA1 — аппликата.
Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение
Рис. 68
вертикальной линии связи (рис. 68, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная — величиной аппликаты.
68.gif
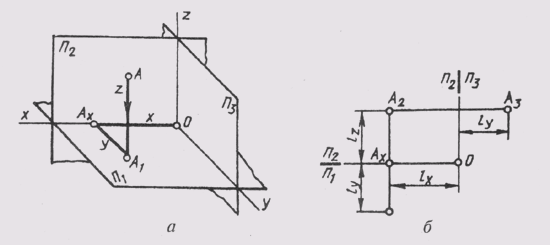
8. Глава 7. Изображение линий на чертеже
1. Глава 7. Изображение линий на чертеже
Глава 7. ИЗОБРАЖЕНИЕ ЛИНИЙ НА ЧЕРТЕЖЕ
§ 38. Образование линий
В общем случае линию можно представить как множество последовательных положений перемещающейся в пространстве точки. Если точка передвигается без изменения направления, образуется прямая линия, если направление движения точки меняется — образуется кривая линия.
Если точка перемещается в одной плоскости, образуется плоская линия, если ее траектория выходит за пределы одной плоскости — такую линию называют пространственной. Пространственные линии не лежат всеми своими точками в одной плоскости. Их называют также линиями двоякой кривизны.
Примерами плоских линий могут быть окружность, эллипс, овал. В качестве примера пространственной линии можно привести винтовую линию.
Плоские линии делят на циркульные, состоящие из сопряженных дуг окружностей, и лекальные — имеющие переменную кривизну. На чертежах циркульные линии проводятся с помощью циркуля, а лекальные — с помощью лекал.
Графически на чертеже линии задаются с помощью проекций. При этом должна быть показана проекционная связь хотя бы одной ее точки, что позволяет избежать неопределенности.
Простейшим видом линии является прямая.
8. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
13. Какие параметры определяют цилиндрическую винтовую линию?
39. Комплексный чертеж прямой линии
§ 39. Комплексный чертеж прямой линии
Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.
На рис. 69, а показаны прямая l и принадлежащие ей точки А и В. Для построения фронтальной проекции прямой l2 достаточно построить фронтальные проекции точек А2 и В2 и соединить их прямой. Аналогично строится горизонтальная проекция, проходящая через горизонтальные проекции точек А1 и В1. После совмещения плоскости П1 с плоскостью П2 получим двухпроекционный комплексный чертеж прямой l (рис. 69, б).
Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.
40. Расположение прямой относительно плоскостей проекций
§ 40. Расположение прямой относительно плоскостей проекций
Относительно плоскостей проекций прямая может занимать различное положение. Прямую, не параллельную ни одной из основных плоскостей проекций (см. рис. 69), называют прямой общего положения. Прямую, параллельную или перпендикулярную одной из плоскостей проекций, называют прямой частного положения.
Прямые, параллельные одной из плоскостей проекций, называют прямыми уровня. Название их зависит от того, какой плоскости они параллельны. Прямую, параллельную горизонтальной плоскости проекций, называют горизонталью и обозначают на чертежах h (рис. 70).
Прямую, параллельную фронтальной плоскости проекций, называют фронталью и обозначают f (рис.71).
Рис. 70
Рис. 71
Рис. 72
Прямую, параллельную профильной плоскости проекций, называют профильной и обозначают р (рис. 72).
У прямой уровня одна проекция параллельна самой прямой и определяет углы наклона этой прямой к двум другим плоскостям проекций.
Параллельность одной из плоскостей проекций определяет расположение двух других проекций прямой уровня:
h2 || П2/П1 ;
h3 _|_ П2/П3 ;
f2 || П2/П1;
f3 _|_ П2/П3 ;
p1 _|_ П2/П1 ;
p2 _|_ П2/П1 ;
Прямые h2 и f1 перпендикулярны вертикальным линиям связи; р1 и р2 располагаются на одной вертикальной линии связи и при двухпроекционном чертеже должны быть определены двумя точками прямой р.
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции параллельны самой
Рис. 73
прямой и совпадают на чертеже с направлением линии связи (рис. 73). Различают горизонтально проецирующие прямые (АВ), фронтально проецирующие прямые (CD) и профильно проецирующие прямые (EF).
69.gif
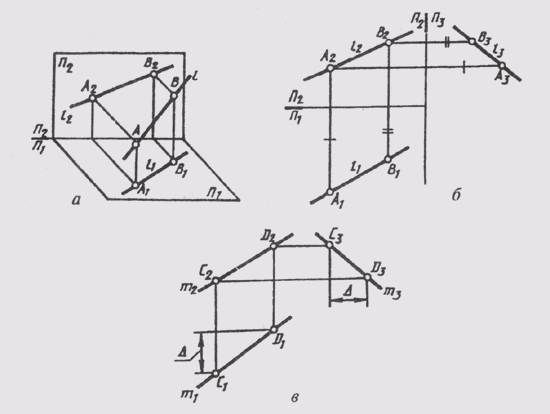
70.gif
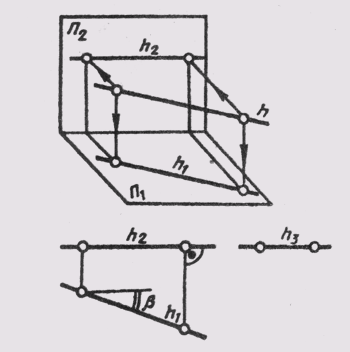
71.gif
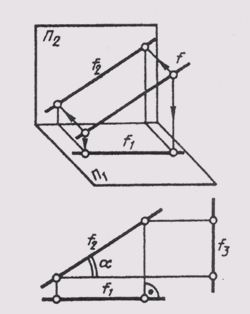
72.gif
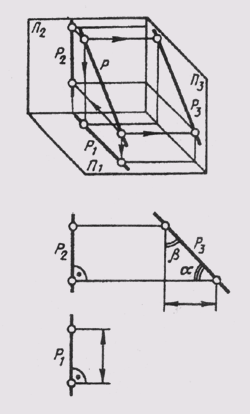
73.gif
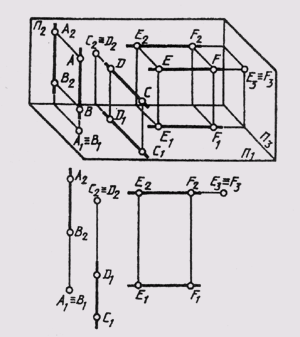
41. Взаимное расположение двух прямых
§ 41. Взаимное расположение двух прямых
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а = b, быть параллельными c|| d, пересекаться т ^ n и скрещиваться (k° / l).
Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):
m^n=M->{m1^n1=M1 или m2^n2= М2}
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):
Рис. 74
Рис. 75
a°/b —> а1 ^ b1 = А1(l1) — горизонтально конкурирующие точки; а2^b1 = В2(l1) — фронтально конкурирующие точки. В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):
k0 /l ->{ k2 ^ l2 или k1 || l1}
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, б) окажутся профильными прямыми, то для определения их взаимного расположения необходимо построить третью, профильную проекцию этих прямых. Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.
Рис. 76
Рис. 77
Рассматривая рис. 76, б можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.
Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а). Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими:
a^b=A->{а2 ^b2=А2 или а1==b1 ,A1~а1(b1)}
Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б). Прямые с и d (рис. 77, в) — фронтально конкурирующие, имеют общую фронтально проецирующую плоскость.
74.gif
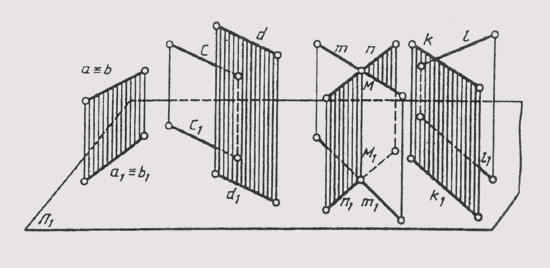
75.gif
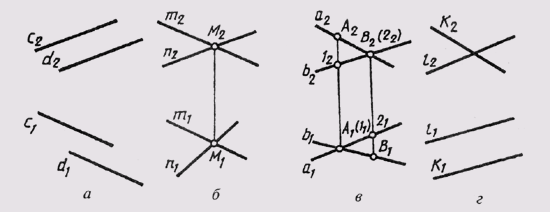
76.gif
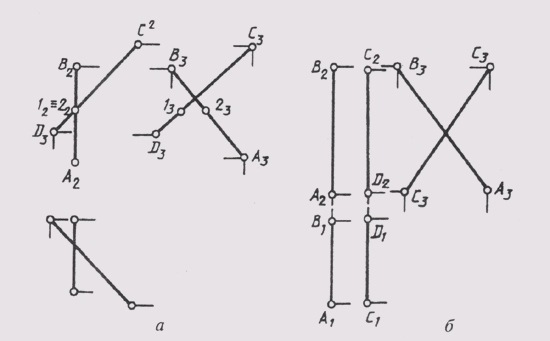
77.gif
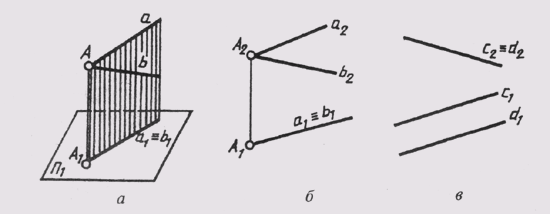
42. Определение натуральной величины отрезка прямой линии
§ 42. Определение натуральной величины отрезка прямой линии
При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.
Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).
Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.
Рис. 78
Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них (см. § 36) или вводом новой плоскости проекций (заменой одной из плоскостей проекций) так, чтобы она была параллельна одной из проекций отрезка (см. §§58, 59).
78.gif
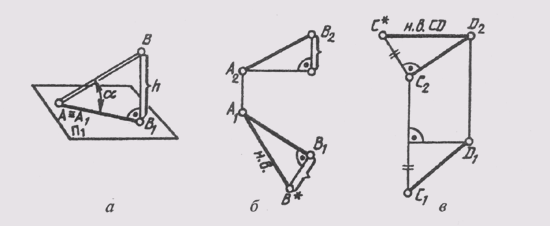
43. Кривые линии
§ 43. Кривые линии
Кривые линии на комплексном чертеже задают своими проекциями, которые строят по проекциям отдельных точек, принадлежащих этой линии. Проекции линий при ортогональном проецировании получают как результат пересечения проецирующих цилиндров с плоскостями проекций (см. § 28); это означает, что проекциями плоских и пространственных кривых линий являются линии плоские. На рис. 79 видно, что секущая т кривой а в общем случае проецируется секущей ее проекции, а касательная/к кривой проецируется касательной к ее проекции.
На комплексном чертеже кривой ее особые точки, к которым относятся точки перегиба, возврата, излома, узловые точки, являются особыми точками и на ее проекции. Это объясняется тем, что особые точки кривых связаны с касательными в этих точках.
Если плоскость кривой занимает проецирующее положение (рис. 80, а), то одна проекция этой кривой имеет форму прямой. У пространственной кривой все ее проекции — кривые линии (рис. 80, б).
Чтобы установить по чертежу, какая задана кривая (плоская или пространственная), необходимо выяснить, принадлежат ли все точки кривой одной плоскости. Заданная на рис. 80, б кривая является пространственной, так как точка D кривой не принадлежит плоскости, определяемой тремя другими точками А, В и Е этой кривой.
Построение и изображение кривых рассматривалось в § 21,22, поэтому приведем пример изображения на чертеже только окружности как плоской кривой и винтовой линии как пространственной кривой.
Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 81, а). Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров. Удобнее всего строить проекции диаметров, параллельных плоскостям проекций: АВ || П1 CD || П2; CD _|_ П1 (рис. 81, б). Фронтальная проекция окружности — эллипс — определяется малой осью эллипса A1B2 = dcos b и большой осью эллипса С2D2=d
Рис. 80
Рис. 81
Если плоскость окружности наклонена ко всем основным плоскостям проекций, то все три ее проекции есть эллипсы, которые можно построить по сопряженным диаметрам, являющимся проекциями тех диаметров окружности, которые параллельны плоскостям проекций (см. рис. 37).
Цилиндрическая винтовая линия (гелиса) — пространственная кривая, представляющая собой траекторию точки, выполняющей винтовое движение. Винтовое движение включает в себя равномерное поступательное движение точки по прямой и равномерное вращательное движение этой прямой с точкой вокруг оси i, которой прямая параллельна. Высота p, на которую точка поднимается по прямой за полный оборот, называется шагом винтовой линии (рис. 82). Если ось i винтовой линии перпендикулярна горизонтальной плоскости проекций, то горизонтальная проекция винтовой линии есть окружность, а фронтальная — синусоида.
Для построения фронтальной проекции винтовой линии при заданном диаметре d и шаге р нужно разделить и окружность, и шаг на равное число частей. Построение проекций точки винтовой линии показано на рис. 82. Цилиндрическую винтовую линию можно развер-
Рис. 82
нуть на плоскость. Развертка ее представляет собой прямую линию с углом подъема а, где tga = P / лd.
79.gif
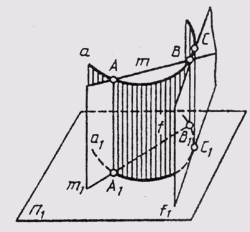
80.gif
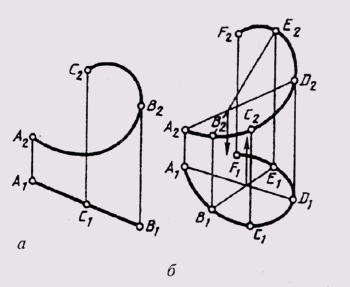
81.gif
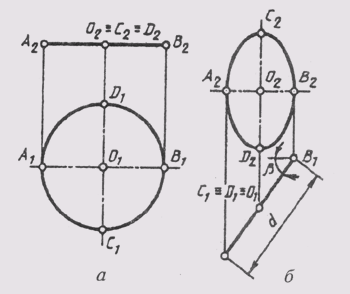
82.gif
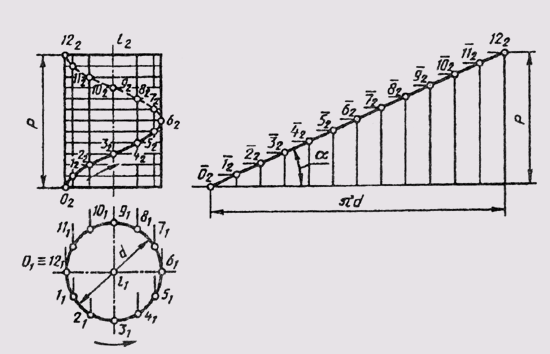
44. Взаимное расположение точки и линии
§ 44. Взаимное расположение точки и линии
Точка в пространстве по отношению к линии может занимать два положения: принадлежать ей или не принадлежать. Если она принадлежит линии, она составляет с ней единое целое и проекции ее на чертеже лежат на соответствующих проекциях линии, а также на одной линии связи.
Если же хотя бы одна из проекций точки не лежит на проекции линии, точка ей не принадлежит. На рис. 83 показан комплексный чертеж линии l, а также ряда точек. Из чертежа видно, что точка А принадлежит линии b, так как горизонтальная ее проекция А1 лежит на горизонтальной проекции линии 11, а фронтальная проекция точки А2 расположена на фронтальной проекции прямой А и ле-
Рис. 83
жит на одной вертикальной линии связи с точкой А1. Точки В и С не принадлежат линии l, так как в первой фронтальная, а во второй горизонтальная проекции не принадлежат соответствующим проекциям линии. Точки D и Е не принадлежат линии l, так как ни одна из их проекций не принадлежит соответствующей проекции линии.
83.gif
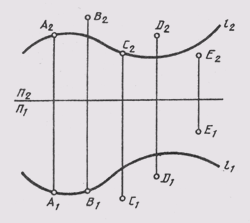
9. Глава 8. Поверхности
1. Глава 8. Поверхности
Глава 8. ПОВЕРХНОСТИ
§ 45. Образование поверхностей
Поверхностью называют множество последовательных положений линий, перемещающихся в пространстве. Эта линия может быть прямой или кривой и называется образующей поверхности. Если образующая кривая, она может иметь постоянный или переменный вид. Перемещается образующая по направляющим, представляющим собой линии иного направления, чем образующие. Направляющие линии задают закон перемещения образующим. При перемещении образующей по направляющим создается каркас поверхности (рис. 84), представляющий собой совокупность нескольких последовательных положений образующих и направляющих. Рассматривая каркас, можно убедиться, что образующие l и направляющие т можно поменять местами, но при этом по верхность получается одна и та же.
Любую поверхность можно получить различными способами. Так, прямой круговой цилиндр (рис. 85) можно создать вращением образующей l вокруг оси г, ей параллельной. Тот же цилиндр образуется
Рис. 84
Рис. 85
перемещением окружности т с центром в точке О, скользящим по оси i. Любая кривая k, лежащая на поверхности цилиндра, образует эту поверхность при своем вращении вокруг оси /'.
На практике из всех возможных способов образования поверхности выбирают наиболее простой.
В зависимости от формы образующей все поверхности можно разделить на линейчатые, у которых образующая прямая линия, и нелинейчатые, у которых образующая кривая линия.
В линейчатых поверхностях выделяют поверхности развертывающиеся, совмещаемые всеми своими точками с плоскостью без разрывов и складок, и неразвертывающиеся, которые нельзя совместить с плоскостью без разрывов и складок.
К развертывающимся поверхностям относятся поверхности всех многогранников, цилиндрические, конические и торсовые поверхности. Все остальные поверхности — неразвертывающиеся. Нелинейчатые поверхности могут быть с образующей постоянной формы (поверхности вращения и трубчатые поверхности) и с образующей переменной формы (каналовые и каркасные поверхности).
Для задания поверхностей выбирают такую совокупность независимых геометрических условий, которая однозначно определяет данную поверхность в пространстве. Эта совокупность условий называется определителем поверхности. Определитель состоит из двух частей: геометрической, в которую входят основные геометрические элементы и соотношения между ними, и алгоритмической, содержащей последовательность и характер операций перехода от основных постоянных элементов и величин к переменным элементам поверхности, т. е. закон построения отдельных точек и линий данной поверхности.
Рис. 86
Рис. 87
Поверхность на комплексном чертеже задается проекциями геометрической части ее определителя с указанием способа построения ее образующих. На чертеже поверхности для любой точки пространства однозначно решается вопрос о принадлежности ее данной поверхности. Графическое задание элементов определителя поверхности обеспечивает обратимость чертежа, но не делает его наглядным. Для наглядности прибегают к построению проекций достаточно плотного каркаса образующих и к построению очерковых линий поверхности (рис. 86). При проецировании поверхности Q на плоскость проекций проецирующие лучи прикасаются к этой поверхности в точках, образующих на ней некоторую линию l, которая называется контурной линией. Проекция контурной линии называется очерком поверхности. На комплексном чертеже любая поверхность имеет: на П1 — горизонтальный очерк, на П2 — фронтальный очерк, на П3 — профильный очерк поверхности. Очерк включает в себя, кроме проекций линии контура, также проекции линий обреза.
Из существенного множества поверхностей в курсе инженерной графики будут рассмотрены все развертывающиеся поверхности, к которым относятся гранные, конические, цилиндрические, торсовые поверхности, некоторые поверхности вращения и винтовые.
Простейшей поверхностью, широко используемой в инженерной графике, является плоскость, представляющая собой поверхность, образованную перемещением прямолинейной образующей (рис. 87) по двум параллельным или пересекающимся прямым m1 и m2.
84.gif
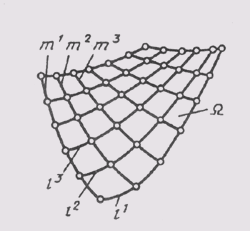
85.gif
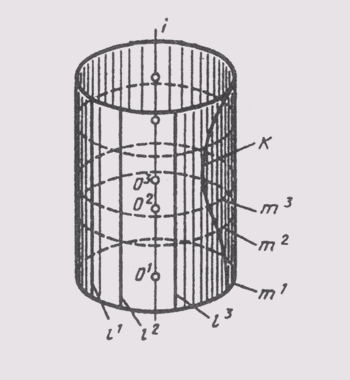
86.gif
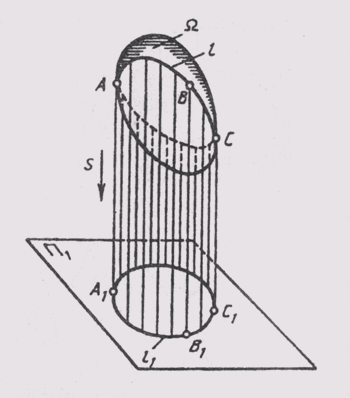
87.gif
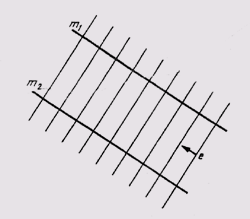
12. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
14. Какие линии характерны для поверхности вращения и какова их роль в построении изображений поверхности?
46. Изображение плоскости на чертеже
§ 46. Изображение плоскости на чертеже
Плоскость на чертеже может быть задана различными способами: тремя точками, не лежащими на одной прямой Q(A, В, С) (рис. 88, а);
прямой и точкой, не лежащей на одной прямой Q(aA; A не принадлежит а) (рис. 88, б);
Рис. 88
двумя пересекающимися прямыми Q(a || b) (рис. 88, в);
двумя параллельными прямыми Q(a ^ b) (рис. 88, г);
любой плоской фигурой, например, треугольником Q(ABC) (рис. 88, д).
Плоскости, заданные на чертеже одним из таких способов, не ограничиваются проекциями определяющих ее элементов.
Рассматривая комплексный чертеж плоскости, можно убедиться, что каждый из названных способов задания ее допускает возможность перехода от одного из них к другому.
88.gif
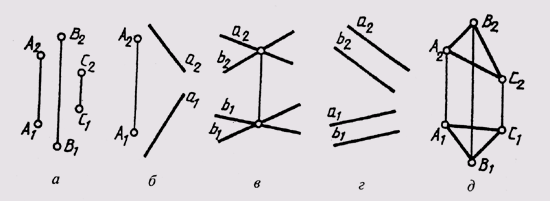
47. Расположение плоскости относительно плоскостей проекций. Взаимное расположение двух плоскостей
§ 47. Расположение плоскости относительно плоскостей проекций. Взаимное расположение двух плоскостей
По расположению относительно плоскостей проекций плоскости делят на плоскости общего и частного положения.
К плоскостям общего положения относятся плоскости, непараллельные и неперпендикулярные ни одной из плоскостей проекций. На комплексном чертеже (см. рис. 88) проекции элементов, которыми задана плоскость, как правило, занимают общее положение.
К плоскостям частного положения относятся плоскости, параллельные или перпендикулярные одной из плоскостей проекций.
Рис. 89
В свою очередь, плоскости частного положения делятся на проецирующие плоскости и плоскости уровня. К проецирующим плоскостям относятся плоскости, перпендикулярные одной из плоскостей проекций. Все проецирующие плоскости будем обозначать буквой Е. Проецирующие плоскости могут быть перпендикулярны П1, П2 или П3. В зависимости от этого различают горизонтально проецирующие плоскости, когда Sum_|_ П1 ; фронтально проецирующие плоскости, когда Sum_|_П2; профильно проецирующие плоскости, когда Sum_|_П3;
Проецирующая плоскость отличается тем, что проекция ее на плоскость проекций, ей перпендикулярную, всегда изображается в виде прямой линии и фигур, лежащих в проецирующей плоскости. Проекция плоскости, выраженной в прямой, вполне определяет положение плоскости относительно плоскостей проекций. Например, на рис. 89, а приведен комплексный чертеж плоскости I, заданной двумя параллельными прямыми. Из рисунка видно, что I (а \\ Ъ) является горизонтально проецирующей плоскостью и расположена под углом Р к фронтальной плоскости проекций и под углом у с фронтальной плоскостью проекций.
На рис. 89, б приведен комплексный чертеж плоскости Sum, составляющей угол а с горизонтальной плоскостью проекций и угол у с фронтальной плоскостью проекций. Это можно записать так: AВС ~ A2 ~ Sum2, B2 ~ Sum2, C2 ~ Sum2.
Наличие вырожденной проекции дает возможность задавать проецирующие плоскости на комплексном чертеже только одной проекцией. На рис. 89, в через точку А проведена профильно проецирующая плоскость (Sum_|_П3) под углом а к П1.
Все изображения, расположенные в заданной плоскости, на плоскости, не перпендикулярные ей, проецируются с искажением.
К плоскостям уровня относятся плоскости, параллельные одной из плоскостей проекций. Их можно считать дважды проецирующими
Рис. 90
плоскостями, так как у них на комплексном чертеже две проекции имеют вид прямой, расположенной под прямым углом к линии связи, а третья проекция дает изображение всех элементов, лежащих в этой плоскости, в натуральную величину. Плоскости уровня обычно обозначаются: Г— горизонтальная плоскость уровня; Ф — фронтальная плоскость уровня; U — профильная
плоскость уровня. На рис. 90, а дан комплексный чертеж плоскости горизонтального уровня (Г || П1); на рис. 90, б приведен комплексный чертеж плоскости фронтального уровня (Ф || П2), Ф э АВС, А2В2С2 — истинная величина треугольника ABC; на рис. 90, в показан комплексный чертеж профильно проецирующей плоскости (U || П3, u аА; А ~ а).
Плоскости уровня отличаются тем, что на плоскости проекций, им перпендикулярную, они проецируются в прямую линию, на которой располагаются точки, прямые и фигуры, расположенные в плоскости уровня. Эти прямые являются вырожденными проекциями заданной плоскости. На плоскость проекций, параллельную заданной плоскости, все изображения этой плоскости проецируются без искажений, т. е. в натуральную величину.
Две плоскости в пространстве могут быть параллельными или пересекаться. Параллельными будут плоскости, если одна из них задана пересекающимися прямыми, параллельными пересекающимся, за-
Рис. 91
дающим вторую плоскость; на рис. 91 показаны параллельные плоскости: Sum (ахb) и Sum2 (cxd), причем а || с, ab || d.
Если плоскости пересекаются, то линия их пересечения — прямая. Плоскости, перпендикулярные между собой, представляют случай их пересечения, когда угол между плоскостями составляет 90°.
Построение линий пересечения плоскостей рассматривается в §62.
89.gif
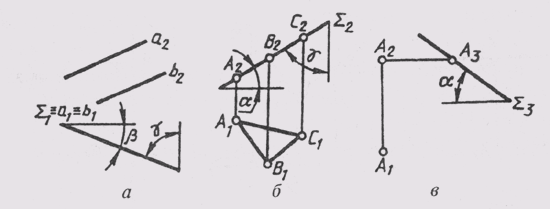
90.gif
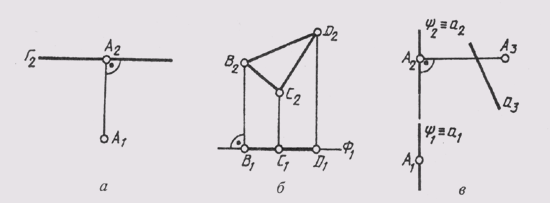
91.gif
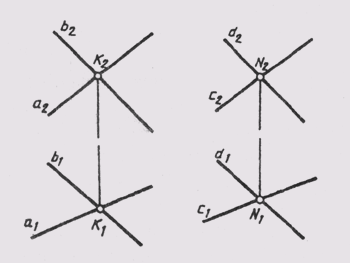
48. Особые линии в плоскости
§ 48. Особые линии в плоскости
К особым линиям в плоскости можно отнести линии, параллельные плоскости проекций. Их называют линиями уровня.
Линию, принадлежащую плоскости и параллельную горизонтальной плоскости проекций, называют горизонталью плоскости (рис. 92, а). Построение горизонтали всегда начинают с ее фронтальной проекции: h(A1 1)~ Q(ABC);h2 ~ A2;h2 _|_ A2Al;h2 ^ B2C2 = l2,l2l1 || A2A1.
Линию, принадлежащую плоскости и параллельную фронтальной плоскости проекций, называют фронталью плоскости (рис. 92, б). Построение фронтали начинают с горизонтальной проекции: f(F1 1) ~ ^(DFE); F1~f1, f1,_|_F1F2; f1^D1E1=l1; l1l2 || F1F2;
l1l2^D2E2=l2^F2=l2.
Рассматривая особые линии в плоскостях частного положения, можно убедиться, что соответствующие линии уровня в этом случае будут и проецирующими.
На рис. 92, в показана горизонталь h фронтально проецирующей плоскости Sum. В данном случае она будет также фронтальной проецирующей прямой, т. е. h э Sum; Sum _|_ П2.
Рис. 92
92.gif
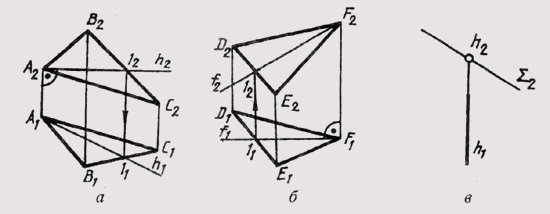
49. Взаимное расположение точки, прямой и плоскости
§ 49. Взаимное расположение точки, прямой и плоскости
Прямая может принадлежать и не принадлежать плоскости. Она принадлежит плоскости, если хотя бы две точки ее лежат на плоскости. На рис. 93 показана плоскость Sum (axb). Прямая l принадлежит плоскости Sum, так как ее точки 1 и 2 принадлежат этой плоскости.
Если прямая не принадлежит плоскости, она может быть параллельной ей или пересекать ее.
Прямая параллельна плоскости, если она параллельна другой пря-
Рис. 93
Рис. 94
мой, лежащей в этой плоскости. На рис. 93 прямая m || Sum, так как она параллельна прямой l, принадлежащей этой плоскости.
Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей. Построение линий пересечения прямой с плоскостью приведено в §61.
Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости. На рис. 94 показан комплексный чертеж плоскости Sum, заданной двумя параллельными прямыми l и п. В плоскости расположена линия m. Точка A лежит в плоскости Sum, так как она лежит на прямой m. Точка В не принадлежит плоскости, так как ее вторая проекция не лежит на соответствующих проекциях прямой.
93.gif
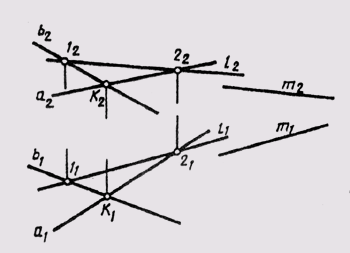
94.gif
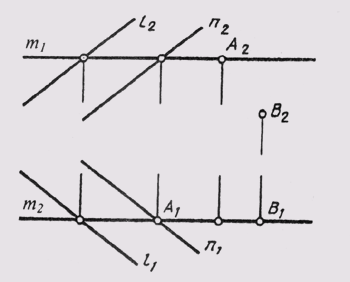
50. Коническая и цилиндрическая поверхности
§ 50. Коническая и цилиндрическая поверхности
К коническим относятся поверхности, образованные перемещением прямолинейной образующей l по криволинейной направляющей m. Особенностью образования конической поверхности является то, что
Рис. 95
Рис. 96
при этом одна точка образующей всегда неподвижна. Эта точка является вершиной конической поверхности (рис. 95, а). Определитель конической поверхности включает вершину S и направляющую m, при этом l'~S; l'^ m.
К цилиндрическим относятся поверхности, образованные прямой образующей /, перемещающейся по криволинейной направляющей т параллельно заданному направлению S (рис. 95, б). Цилиндрическую поверхность можно рассматривать как частный случай конической поверхности с бесконечно удаленной вершиной S.
Определитель цилиндрической поверхности состоит из направляющей т и направления S, образующих l, при этом l' || S; l' ^ m.
Если образующие цилиндрической поверхности перпендикулярны плоскости проекций, то такую поверхность называют проецирующей. На рис. 95, в показана горизонтально проецирующая цилиндрическая поверхность.
На цилиндрической и конической поверхностях заданные точки строят с помощью образующих, проходящих через них. Линии на поверхностях, например линия а на рис. 95, в или горизонтали h на рис. 95, а, б, строятся с помощью отдельных точек, принадлежащих этим линиям.
95.gif
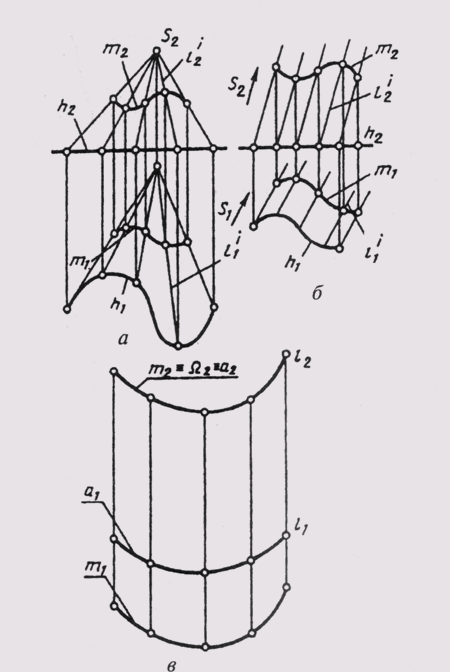
96.gif
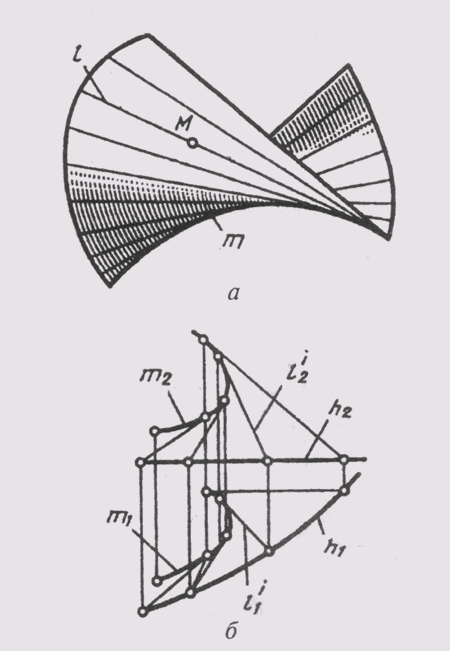
51. Торсовые поверхности
§ 51. Торсовые поверхности
Торсовой называется поверхность, образованная прямолинейной образующей l , касающейся при своем движении во всех своих положениях некоторой пространственной кривой т, называемой ребром возврата (рис. 96). Ребро возврата полностью задает торс и является геометрической частью определителя поверхности. Алгоритмической частью служит указание касательности образующих к ребру возврата.
Коническая поверхность является частным случаем торса, у которого ребро возврата т выродилось в точку S— вершину конической поверхности. Цилиндрическая поверхность — частный случай торса, у которого ребро возврата — точка в бесконечности.
52. Гранные поверхности
§ 52. Гранные поверхности
К гранным относятся поверхности, образованные перемещением прямолинейной образующей l по ломаной направляющей m. При этом если одна точка S образующей неподвижна, создается пирамидальная поверхность (рис. 97), если образующая при перемещении параллельна заданному направлению S, то создается призматическая поверхность (рис. 98).
Элементами гранных поверхностей являются: вершина S (у призматической поверхности она находится в бесконечности), грань (часть плоскости, ограниченная одним участком направляющей m и крайни-
Рис. 97
Рис. 98
Рис. 99
ми относительно него положениями образующей l ) и ребро (линия пересечения смежных граней).
Определитель пирамидальной поверхности включает в себя вершину S, через которую проходят образующие и направляющие: l' ~ S;
l ^ т.
Определитель призматической поверхности, кроме направляющей т, содержит направление S, которому параллельны все образующие l поверхности: l||S; l^ т.
Замкнутые гранные поверхности, образованные некоторым числом (не менее четырех) граней, называются многогранниками. Из числа многогранников выделяют группу правильных многогранников, у которых все грани правильные и конгруэнтные многоугольники, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней. Например: гексаэдр — куб (рис. 99, а), тетраэдр — правильный четырехугольник (рис. 99, 6) октаэдр — многогранник (рис. 99, в). Форму различных многогранников имеют кристаллы.
Пирамида — многогранник, в основании которого лежит произвольный многоугольник, а боковые грани — треугольники с общей вершиной S.
На комплексном чертеже пирамида задается проекциями ее вершин и ребер с учетом их видимости. Видимость ребра определяется с помощью конкурирующих точек (рис. 100).
Призма — многогранник, у которого основание — два одинаковых и взаимно параллельных многоугольника, а боковые грани — параллелограммы. Если ребра призмы перпендикулярны плоскости основания, такую призму называют прямой. Если у призмы ребра перпендикулярны какой-либо плоскости проекций, то боковую поверхность ее называют проецирующей. На рис. 101 дан комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью.
Рис. 100
Рис. 101
При работе с комплексным чертежом многогранника приходится строить на его поверхности линии, а так как линия есть совокупность точек, то необходимо уметь строить точки на поверхности.
Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку. На рис. 100 в грани ACS построена точка М с помощью образующей S-5.
97.gif
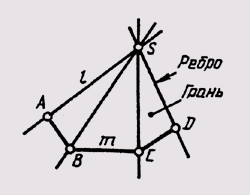
98.gif
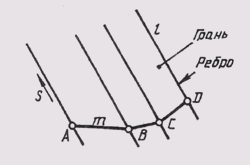
99.gif
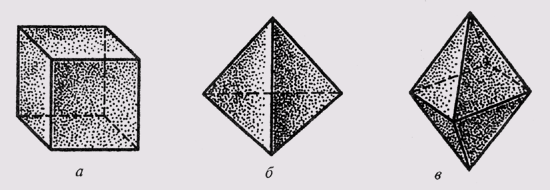
100.gif
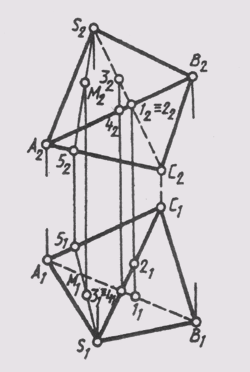
101.gif
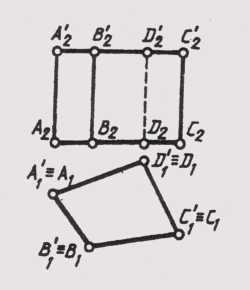
53. Винтовые поверхности
§ 53. Винтовые поверхности
К винтовым относятся поверхности, создаваемые при винтовом движении прямолинейной образующей. Линейчатые винтовые поверхности называют геликоидами.
Прямой геликоид образуется движением прямолинейной образующей i по двум направляющим: винтовой линии т и ее оси i; при этом образующая l пересекает винтовую ось под прямым углом (рис. 102, а). Прямой геликоид используется при создании винтовых лестниц, шнеков, а также силовых резьбах, в станках.
Наклонный геликоид образуется движением образующей по винтовой направляющей т и ее оси i так, что образующая l пересекает ось i под постоянным углом ф, отличным от прямого, т. е. в любом положении образующая l параллельна одной из образующих направляющего конуса с углом при вершине, равным 2ф(рис. 102, б). Наклонные геликоиды ограничивают поверхности витков резьбы.
Рис. 102
Рис. 102 Линейчатые винтовые поверхности - геликоиды.
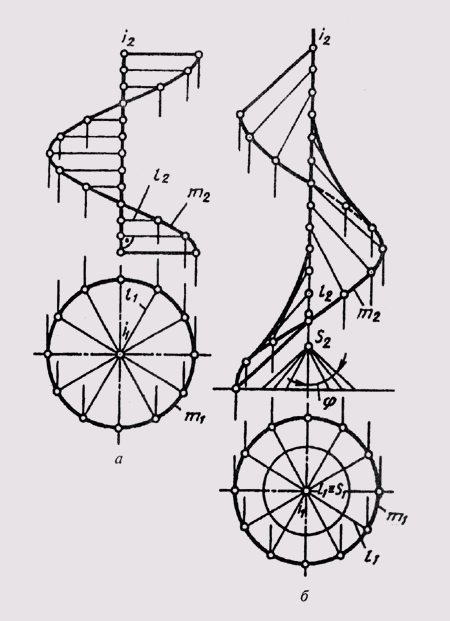
54. Поверхности вращения
§ 54. Поверхности вращения
К поверхностям вращения относятся поверхности, образующиеся вращением линии l вокруг прямой i, представляющей собой ось вращения. Они могут быть линейчатыми, например конус или цилиндр вращения, и нелинейчатыми или криволинейными, например сфера. Определитель поверхности вращения включает образующую l и ось i. Криволинейная поверхность вращения образуется при вращении лю-
Каждая точка образующей при вращении описывает окружность, плоскость которой перпендикулярна оси вращения. Такие окружности поверхности вращения называются параллелями. Наибольшую из параллелей называют экватором. Экватор .определяет горизонтальный очерк поверхности, если i _|_ П1. В этом случае параллелями являются горизонтали h этой поверхности.
Кривые поверхности вращения, образующиеся в результате пересечения поверхности плоскостями, проходящими через ось вращения, называются меридианами. Все меридианы одной поверхности конгруэнтны. Фронтальный меридиан называют главным меридианом; он определяет фронтальный очерк поверхности вращения. Профильный меридиан определяет профильный очерк поверхности вращения.
Строить точку на криволинейных поверхностях вращения удобнее всего с помощью параллелей поверхности. На рис. 103 точка М построена на параллели h4.
Поверхности вращения нашли самое широкое применение в технике. Они ограничивают поверхности большинства машиностроительных деталей.
Коническая поверхность вращения образуется вращением прямой i вокруг пересекающейся с ней прямой — оси i (рис. 104, а). Точка М на поверхности построена с помощью образующей l и параллели h. Эту поверхность называют еще конусом вращения или прямым круговым конусом.
Цилиндрическая поверхность вращения образуется вращением прямой l вокруг параллельной ей оси i (рис. 104, б). Эту поверхность называют еще цилиндром или прямым круговым цилиндром.
Сфера, образуется вращением окружности вокруг ее диаметра (рис. 104, в). Точка A на поверхности сферы принадлежит главному
Рис. 103
Рис. 104
меридиану f, точка В — экватору h, а точка М построена на вспомогательной параллели h'.
Тор образуется вращением окружности или ее дуги вокруг оси, лежащей в плоскости окружности. Если ось расположена в пределах образующейся окружности, то такой тор называется закрытым (рис. 105, а). Если ось вращения находится вне окружности, то такой тор называется открытым (рис. 105, б). Открытый тор называется еще кольцом.
Поверхности вращения могут быть образованы и другими кривыми второго порядка. Эллипсоид вращения (рис. 106, а) образуется вращением эллипса вокруг одной из его осей; параболоид вращения (рис. 106, б) — вращением параболы вокруг ее оси; гиперболоид вращения однополостный (рис. 106, в) образуется вращением гиперболы вокруг мнимой оси, а двуполостный (рис. 106, г) — вращением гиперболы вокруг действительной оси.
В общем случае поверхности изображаются не ограниченными в направлении распространения образующих линий (см. рис. 97, 98). Для решения конкретных задач и получения геометрических фигур ограничиваются плоскостями обреза. Например, чтобы получить круговой цилиндр, необходимо ограничить участок цилиндрической поверхности плоскостями обреза (см. рис. 104, б). В результате получим его верхнее и нижнее основания. Если плоскости обреза перпендикулярны оси вращения, цилиндр будет прямым, если нет — цилиндр будет наклонным.
Рис. 105
Рис. 106
Чтобы получить круговой конус (см. рис. 104, а), необходимо выполнить обрез по вершине и за пределами ее. Если плоскость обреза основания цилиндра будет перпендикулярна оси вращения — конус будет прямой, если нет — наклонный. Если обе плоскости обреза не проходят через вершину — конус получим усеченным.
С помощью плоскости обреза можно получить призму и пирамиду. Например, шестигранная пирамида будет прямой, если все ее ребра имеют одинаковый наклон к плоскости обреза. В других случаях она будет наклонной. Если она выполнена с помощью плоскостей обреза и ни одна из них не проходит через вершину — пирамида усеченная.
Призму (см. рис. 101) можно получить, ограничив участок призматической поверхности двумя плоскостями обреза. Если плоскость обреза перпендикулярна ребрам, например восьмигранной призмы, она прямая, если не перпендикулярна — наклонная.
Выбирая соответствующее положение плоскостей обреза, можно получать различные формы геометрических фигур в зависимости от условий решаемой задачи.
103.gif
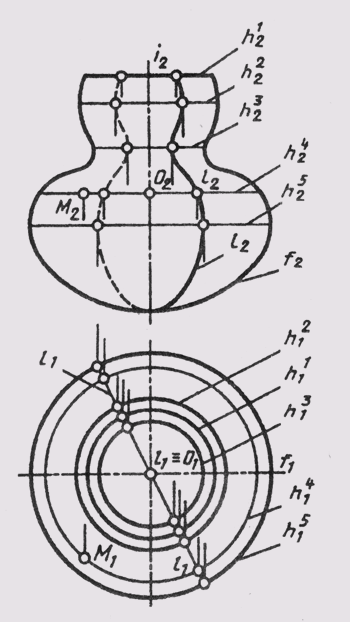
104.gif
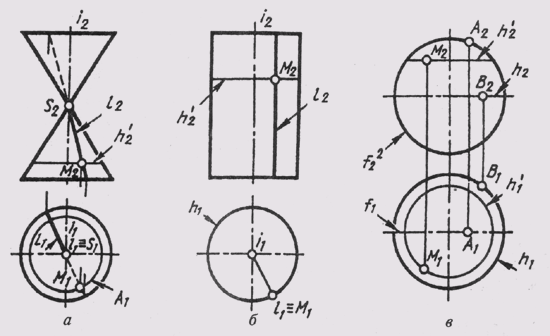
105.gif
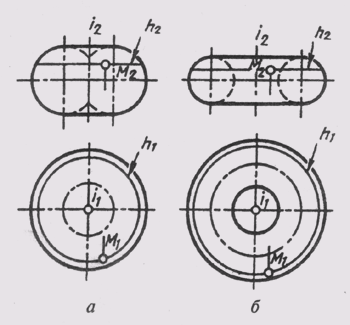
106.gif
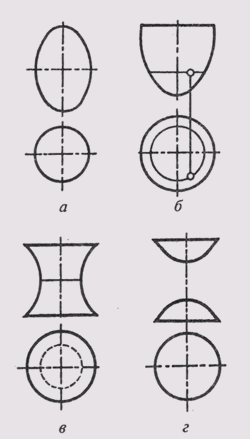
55. Точка и линия на поверхности
§ 55. Точка и линия на поверхности
В общем случае линия может принадлежать поверхности или не принадлежать. Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности (см. рис. 103, линия l). Исключение составляет случай, когда линия представлена прямой, а поверхность — плоскостью. В этом случае для принадлежности прямой плоскости достаточно, чтобы хотя бы две точки ее принадлежали этой поверхности (см. § 49). Задачи построения линий, принадлежащих поверхности, входят составной частью в задачи построения линий пересечения поверхностей плоскостью и пересечения двух поверхностей, которые рассматриваются в §§ 63, 64.
Если линия не принадлежит поверхности, то они пересекаются. Простейшим случаем является пересечение с поверхностью прямой линии. Задача решается путем заключения данной линии в какую-либо проецирующую плоскость и построением натуральной величины сечения, из которого легко определить точку входа и выхода прямой. Задачи такого типа рассматриваются в § 63.
Точка может принадлежать поверхности и не принадлежать. Точка принадлежит поверхности, если она лежит на линии, расположенной на этой поверхности. На рис. 104, в точка М принадлежит сферической поверхности, так как она находится на линии окружности /г', лежащей на этой поверхности. Точки А и В тоже принадлежат сферической поверхности, так как они расположены на линиях очерковых окружностей, принадлежащих сферической поверхности. Примеры принадлежности точки поверхности можно привести и в случае наличия конической поверхности (точка М на рис. 104, а), поверхности тора (точка М на рис. 105) и поверхности более сложной формы (точка М на рис. 103).
Задача определения принадлежности точки поверхности решается следующим способом. Если заданы проекции элементов поверхности и точки, необходимо на одной из плоскостей проекций через заданную точку провести линию, принадлежащую поверхности, и построить проекцию этой линии на одной плоскости проекций. Если вторая проекция пройдет через вторую проекцию точки — точка принадлежит поверхности, если не пройдет — не принадлежит.
Эту задачу можно рассмотреть на примере рис. 104, а. На комплексном чертеже задана коническая поверхность очерковыми линиями. Задана также точка М горизонтальной и фронтальной проекций. Через горизонтальную проекцию точки проведем горизонтальную проекцию h1окружности, принадлежащей конической поверхности. Построив фронтальную проекцию h2 этой окружности, убеждаемся, что она прошла через фронтальную проекцию точки. Это и подтверждает, что точка принадлежит конической поверхности.
Данная задача может быть решена и другим путем. При тех же исходных данных через фронтальную проекцию М1 точки проводим проекцию одной из образующих f Построив горизонтальную проекцию h образующей, убеждаемся, что она прошла через горизонтальную проекцию М1 точки М, и это позволяет сделать вывод о том, что точка М принадлежит конической поверхности.
Принципы построения точек и линий на поверхностях положены в основу построения линий пересечения, срезов, вырезов, проницаний и др., что определяет построение сложных геометрических тел, и в итоге — деталей, узлов, машин, зданий, сооружений.
10. Глава 9. Преобразование комплексного чертежа
1. Глава 9. Преобразование комплексного чертежа
Глава 9. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА
§56. Общие сведения о преобразовании комплексного чертежа
На комплексном чертеже геометрические объекты проецируются так, что многие элементы, составляющие их, например отрезки прямых, углы, плоские фигуры, изображаются с искажением. В то же время при решении многих задач часто возникает необходимость преобразовать комплексный чертеж так, чтобы необходимый элемент расположился параллельно или перпендикулярно одной из плоскостей проекций. Например, необходимо, чтобы отрезок прямой, представляющий собой ребро многогранника, или многоугольник, представляющий собой грань многогранника, расположились параллельно плоскости проекций. В этом случае на эту плоскость они проецируются в натуральную величину.
Решение таких задач в значительной степени упрощается, если интересующие нас элементы пространства занимают частное положение, т. е. располагаются параллельно или перпендикулярно плоскостям проекций. Получающиеся в этом случае «вырожденные» проекции помогают получить ответ на поставленную задачу или упростить ход ее решения. Чтобы добиться такого расположения геометрических элементов, комплексный чертеж преобразуют или перестраивают, исходя из конкретных условий. Преобразование чертежа отображает изменение положения геометрических образов или плоскостей проекций в пространстве. Задача преобразования комплексного чертежа может быть решена перемещением проецирующего тела в пространстве до требуемого положения или изменением в пространстве положения плоскостей проекций относительно геометрического тела. Существует несколько методов решения этих задач. В основном используются способы преобразования чертежа: плоскопараллельный перенос, способ замены плоскостей проекций (см. § 36) и способ вращения.
Так как частных положений у прямых два и у плоскости два, то существуют четыре исходные задачи для преобразования комплексного чертежа:
- прямую общего положения сделать прямой уровня;
- прямую уровня сделать проецирующей;
- плоскость общего положения сделать проецирующей;
- проецирующую плоскость сделать плоскостью уровня.
5. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
12. Как изменяется фронтальная проекция предмета при вращении его вокруг фронтально проецирующей прямой?
57. Способ плоскопараллельного перемещения
§ 57. Способ плоскопараллельного перемещения
Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение. При этом если точка перемещается в плоскости, параллельной П1, то ее фронтальная проекция изображается в виде прямой, параллельной оси П2/П1. Если же точка перемещается в плоскости, параллельной П2, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси.
На рис. 107 показан комплексный чертеж прямой АВ. Прямая не параллельна ни одной из плоскостей проекций. Требуется с помощью плоскопараллельного перемещения задать ей такое положение, чтобы она была параллельна одной из плоскостей проекций, например П2. Через произвольную точку А1, проводим прямую l1 параллельную оси П2/П1, и от этой точки на прямой откладываем отрезок, равный
Рис. 107
А1В1. Из точки А1 проводим вертикальную линию связи, а из точки AT, — горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А2'. Аналогично проведем вертикальную линию связи из точки В1 до пересечения с горизонтальной линией, проведенной из точки B2. Новое положение фронтальной проекции точки В получим на пересечении этих линий в точке В2'.
После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П2, а значит, спроецировалась она на эту плоскость в натуральную величину.
Применяя метод плоскопараллельного перемещения, можно решать многие задачи, связанные с определением натуральной величины отрезков, углов, плоских фигур, а также заданием им нужного положения. Однако он связан с изменением положения геометрической фигуры в пространстве. В практике же встречаются задачи, при решении которых при преобразовании комплексного чертежа удобнее оставить положение проецирующего тела неизменным, а изменить положение плоскостей проекций.
107.gif
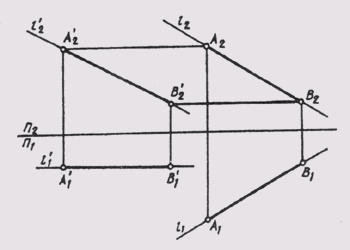
58. Способ замены плоскостей проекций
§ 58. Способ замены плоскостей проекций
Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.
Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.
Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.
1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П4, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П1_|_П2 перейти к системе П4 _|_ П1 или П4 _|_ П2. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П1 _|_ П4, причем П4 || l. Новые линии связи A1A4 и В1В4 проведены
Рис. 108
Рис. 109
Рис. 110
Рис. 111
перпендикулярно новой оси —П1/П4 параллельной горизонтальной проекции l1.
Новая проекция прямой дает истинную величину А4В4 отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L1П1). Угол наклона прямой к фронтальной плоскости проекций (b = L1П2) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П2 (рис. 109).
2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.
Чтобы на новой плоскости проекций изображение прямой было точкой (см. § 10), новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П4_|_ П1. (рис. 110), а фронталь f— на П4_|_ П2
Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П4_|_ П2, расположенной параллельно самой прямой l. В системе плоскостей П2_|_ П4, прямая заняла положение линии l уровня (А2А4 _|_П2/П1;
П2/П4 || l2). Затем от системы П2 _|_ П4 осуществлен переход в систему
Рис. 112
Рис. 113
П4 _|_П5, причем вторая новая плоскость проекций П5 перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П4, то на плоскости П5 получаем изображение прямой в виде точки (А5 = B5 = l5).
3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.
Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости (см. § 47).
На рис. 112 дано построение нового изображения плоскости 0 (ABC) в системе плоскостей П4 _|_П1. Для этого в плоскости 0 построена горизонталь h(A, 1), и новая плоскость проекций П4 расположена перпендикулярно горизонтали h. Графическое решение третьей исходной задачи приводят к построению изображения плоскости в виде прямой линии, угол наклона которой к новой оси проекции П1/П4, определяет угол наклона а плоскости Q(ABC) к горизонтальной плоскости проекций (а = Q ^ П1).
Построив изображение плоскости общего положения в системе П2 _|_П4, (П4 расположить перпендикулярно фронтали плоскости),
Рис. 114
можно определить угол наклона Р этой плоскости к фронтальной плоскости проекций.
4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.
Решение этой задачи позволяет определить величину плоских фигур.
Новую плоскость проекций нужно расположить параллельно заданной плоскости. Если исходное положение плоскости было фронтально проецирующим, то новое изображение строят в системе и П2 _|_П4, а если горизонтально проецирующим, то в системе П1 _|_П4. Новая ось проекций будет расположена параллельно вырожденной проекции проецирующей плоскости (см. § 47). На рис. 113 построена новая проекция А4В4С4 горизонтально проецирующей плоскости Sum (ABC) на плоскости П4 _|_П1
Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3; а затем задачу 4. При первой замене плоскость становится проецирующей, а при второй — плоскостью уровня (рис. 114).
В плоскости А(DEF) проведена горизонталь h (D — 1). По отношению к горизонтали проведена первая ось П1 / П4 _|_h1. Вторая новая ось
проекций параллельна вырожденной проекции плоскости, а новые линии связи — перпендикулярны вырожденной проекции плоскости. Расстояния для построения проекций точек на плоскости П5 нужно замерить на плоскости П1 от оси П1 / П2 и откладывать по новым линиям связи от новой оси П4 /П5. Проекция D5E5F5 треугольника DEF конгруэнтна самому треугольнику ABC.
С применением способа замены плоскостей можно решать ряд других задач как самостоятельных, так и отдельных частей задач, включающих большой объем графических решений.
108.gif
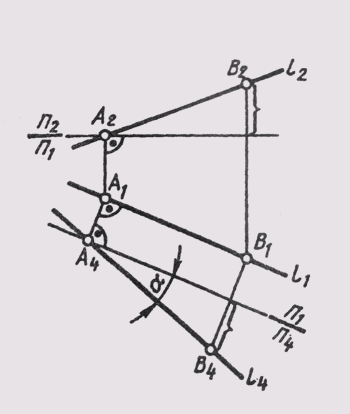
109.gif
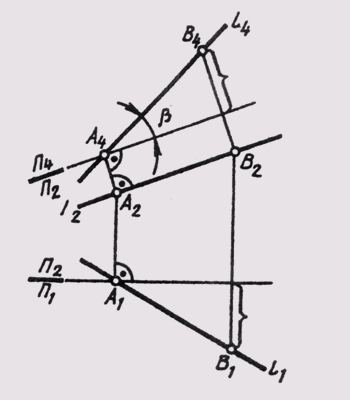
110.gif
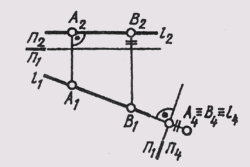
111.gif
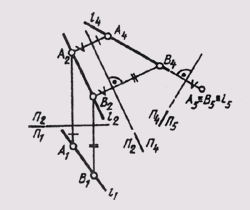
112.gif
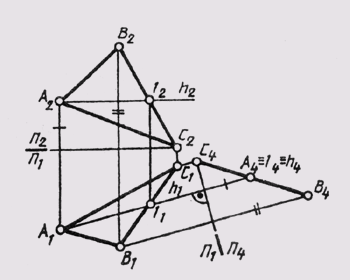
113.gif
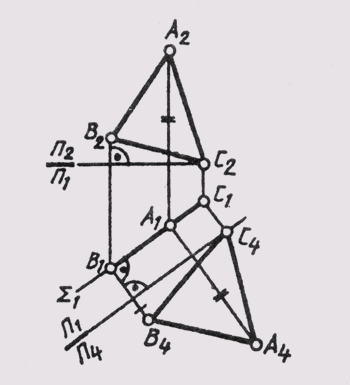
114.gif
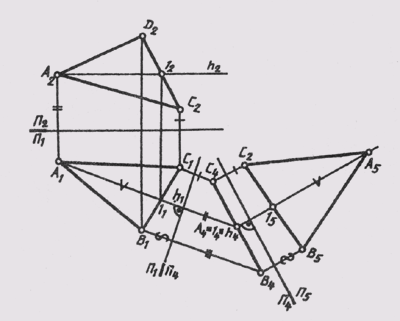
59. Способ вращения
§ 59. Способ вращения
Как уже отмечалось, при преобразовании комплексного чертежа возможно изменение положения заданных геометрических элементов относительно плоскостей проекций при неизменном положении основных плоскостей проекций. Это осуществляется путем вращения этих элементов вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей. Такое преобразование комплексного чертежа носит название способа вращения.
В качестве оси вращения в этом случае удобнее всего выбирать проецирующие прямые или прямые уровни, тогда точка будет вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.
Рис. 115
Рис. 116
При вращении вокруг горизонтально проецирующей прямой горизонтальная проекция А1 точки А перемещается по окружности, а фронтальная AI — по прямой, перпендикулярной фронтальной проекции оси, являющейся фронтальной проекцией плоскости вращения Г2 (рис. 115). При этом расстояние между горизонтальными проекциями двух точек А и В (рис. 116) при их повороте на один и тот же угол со остается неизменным (А1В1 = A1B1).
Аналогичные выводы можно сделать и для вращения вокруг фронтально проецирующей прямой. При вращении плоской фигуры вокруг оси, перпендикулярной плоскости проекций, проекция ее на эту плоскость не изменяется ни по величине, ни по форме, так как не изменяется наклон плоской фигуры к этой плоскости, а меняется лишь положение этой проекции относительно линии связи. Вторая же проекция на плоскости, параллельной оси вращения, изменяется и по форме, и по величине. Проекции точек на этой плоскости проекций находятся на прямых, перпендикулярных исходным линиям связи. Пользуясь этими свойствами, можно применить для преобразования чертежа способ вращения, не задаваясь изображением оси вращения и не устанавливая величину радиуса вращения. Это — способ плоскопараллельного перемещения, при котором все точки геометрической фигуры перемещаются во взаимно параллельных плоскостях без изменения действительного вида и размеров этой фигуры (рис. 117).
Треугольник ABC занимает общее положение. Первым плоскопараллельным перемещением он поставлен во фронтально проецирующее положение с помощью горизонтали h, которую расположим как фронтально проецирующую прямую в ее плоскости вращения Г || П. При этом А1В1С1 = А1В1С1, а плоскости вращения точек В и С параллельны плоскости Г.
Вторым перемещением АВС расположен параллельно плоскости П1. Без изменения оставлена вырожденная фронтальная проекция треугольника (А2В2C2 = А2В2С2), а новая горизонтальная проекция, дающая истинную величину АВС, получена построением новых горизонтальных проекций то-
Рис. 117
Рис. 118
чек А1В1 и С1 в результате их вращения в параллельных фронтальный плоскостях уровня (B2 ~ Ф; B ~ Ф).
На этом примере построено решение третьей и четвертой исходных задач путем преобразования комплексного чертежа плоскости общего положения способом плоскопараллельного перемещения.
Если в качестве оси вращения взять линию уровня, то истинную величину плоской фигуры общего положения можно построить одним поворотом, т. е. избежать двойного преобразования чертежа, что имело место в замене плоскостей проекций и плоскопараллельном перемещении. На рис. 118 построено изображение АВС (А1В1С1) после поворота его вокруг горизонтали h (С, 1) уровня Г ~ h. Так как горизонталь проходит через точку С, то последняя неподвижна при вращении треугольника. Нужно повернуть только точки А и В вокруг горизонтали до совмещения с плоскостью Г || П1. Точка А вращается в горизонтально проецирующей плоскости SumА, перпендикулярной оси вращения. Центр вращения О точки А лежит, на оси вращения. В момент, когда в результате вращения точка А окажется в плоскости Г, т. е. совместится с горизонтальной плоскостью уровня, ее горизонтальная проекция А1 будет удалена от горизонтальной проекции оси вращения h1 на расстояние, равное истинной величине радиуса вращения RА точки А. Натуральную величину RА можно построить как гипотенузу О\А прямоугольного треугольника (см. § 42), одним катетом которого является горизонтальная проекция радиуса A1O1, а вторым — разность высот точек А и О. Построив совмещенную горизонтальную проекцию точки А, легко достроить изображение всего треугольника А1B1C1 в совмещенном с плоскостью Г положении, используя неподвижную точку и плоскость вращения точки В (SumB1 _|_ h1). Фронтальная проекция АВС выродится в прямую и совместится с проекцией Г2 плоскости совмещения.
Аналогичные действия выполняют при вращении плоской фигуры вокруг ее фронтали. Совмещение в этом случае ведется с фронтальной
плоскостью уровня (Ф || П2), проходящей через ось вращения — фронталь.
Способом вращения могут быть решены и другие задачи, применительно к их условиям.
115.gif
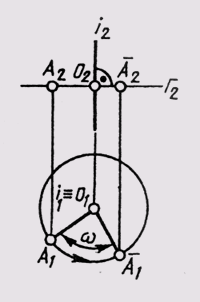
116.gif
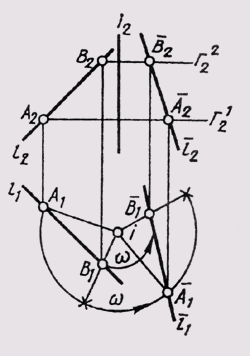
117.gif
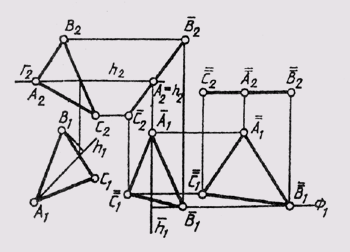
118.gif
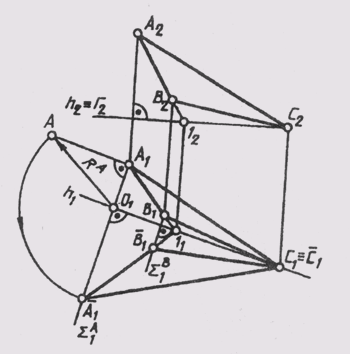
11. Глава 10. Позиционные задачи
1. Глава 10. Позиционные задачи
Глава 10.ПОЗИЦИОННЫЕ ЗАДАЧИ
§ 60. Общие сведения о позиционных задачах
Задачи, связанные с решением вопросов взаимного расположения геометрических фигур на комплексном чертеже, называются позиционными.
Среди позиционных можно выделить две группы задач, представляющих наибольший практический интерес. К ним относятся задачи на взаимную принадлежность и задачи на взаимное перенесение. Задачи первой группы неоднократно упоминались при изучении глав 7 и 8. Это объясняется, тем, что любая линия есть производная точки, а любая поверхность есть производная линии. Конкретно вопросы принадлежности точки прямой рассмотрены в § 44, принадлежности точки и прямой плоскости в § 49, а принадлежности точки и линии поверхности в § 55.
Решение позиционных задач на принадлежность предполагает работу с линиями поверхности графически простыми, например прямой или окружностью. Это необходимо для того, чтобы не усложнять построений на комплексном чертеже. Для правильного выбора этих линий надо знать, какие семейства линий несет на себе та или иная поверхность.
Задачи на взаимное пересечение связаны с построением точек, принадлежащих одновременно двум рассматриваемым геометрическим образам, например прямой и плоскости, двум плоскостям, плоскости и поверхности, двум поверхностям. Каждую из этих точек строят в пересечении двух вспомогательных линий. Эти линии должны быть графически простыми и принадлежать одной вспомогательной плоскости или поверхности. Выбор вспомогательных, поверхностей (посредников), несущих в себе вспомогательные линии, зависит от формы пересекающихся поверхностей. Совокупность построенных общих точек позволяет построить линию пересечения геометрических образов.
9. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
18. Какую линию называют линией перехода и как она вычеркивается при изображении пересекающихся поверхностей?
61. Пересечение прямой с плоскостью
§ 61. Пересечение прямой с плоскостью
Прямая пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют путем построения вспомогательной прямой линии, лежащей в одной проецирующей плоскости с заданной прямой. На рис. 119, а приведен комплексный чертеж прямой l и плоскости 9 (ABC), причем т ~ Q (ABC). Через горизонтальную проекцию прямой l1 проводим проекцию вспомогательной горизонтально проецирующей плоскости Sum1. В пересечении плоскостей Q и Sum получаем линию т, то есть т =Sum ^ Q. Горизонтальная проекция прямой т определяется горизонтальными проекциями точек 1 и 2 пересечения линий ЕС и АС со вспомогательной плоскостью Sum , то есть В1С1 ^ Sum = l1; А1С1 ^ Sum1=21; т1 = l1^21.
Рис. 119
Рис. 120
Рис. 121
Для получения фронтальной проекции линии l построим фронтальные проекции точек 1 и 2, соединив которые, получим фронтальную проекцию m2. В пересечении фронтальных проекций прямых т и l получим фронтальную проекцию точки К, принадлежащей и прямой l, и прямой т, лежащей в плоскости Sum. Значит, точка К и принадлежит плоскости Sum, и является точкой пересечения прямой l с плоскорью Sum.
Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально конкурирующих точек 2 и 3, а видимость относительно фронтальной плоскости проекции — с помощью фронтально конкурирующих точек 3 и 4.
Если плоскость занимает частное положение, то одна проекция точки пересечения прямой с плоскостью определяется сразу в пересечении вырожденной проекции плоскости с соответствующей проекцией прямой (рис. 119, б).
Если прямая пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости на основании теоремы о проецировании прямого угла (см. § 29).
На рис. 120 построены проекции основания М перпендикуляра п, проведенного к плоскости 9 (ABC) из точки К пространства. В AВС имеем: АВ — горизонталь (A2B2 _|_ A2A1), AC — фронталь (А1С1 _|_A1A2). Поэтому проекции перпендикуляра n э К располагаются: п1 _|_A1B1 и n2 _|_ А2С2. Основание перпендикуляра на плоскости построено с помощью вспомогательной линии а плоскости, лежащей в одной с перпендикуляром п горизонтально проецирующей плоскости (а ^ п = М).
Если прямая пересекает плоскость в бесконечности, то имеет место параллельность прямой с плоскостью. На рис. 121 построена прямая т, проходящая через точку N u параллельная плоскости треугольника KLM. На комплексном чертеже параллельность прямой и плоскости доказывается тем, что m1 || а1 и m2 || а2; a ~ KLM.
119.gif
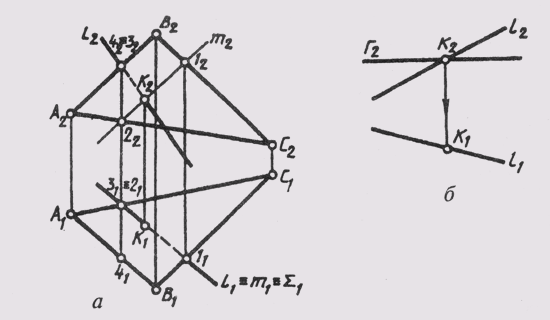
120.gif
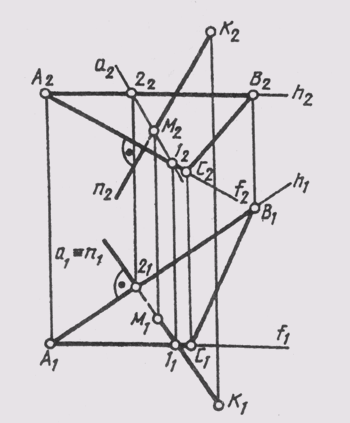
121.gif
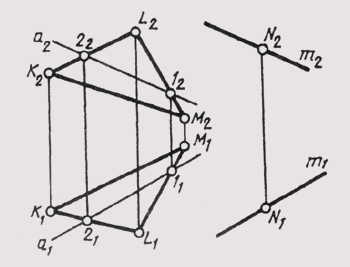
62. Пересечение двух плоскостей
§ 62. Пересечение двух плоскостей
Две плоскости пересекаются по прямой линии. Для построения линии их пересечения необходимо найти две точки, принадлежащие этой линии. Задача упрощается, если одна из пересекающихся плоскостей занимает частное положение. В этом случае ее вырожденная проекция включает в себя проекцию линии пересечения плоскостей.
На рис. 122 приведен комплексный чертеж двух пересекающихся плоскостей £ и 0, причем плоскость Sum частного положения — фронтально проецирующая. Она пересекает линии АВ и АС плоскости 0, данной треугольниками ABC — плоскости общего положения. Точки пересечения 1 и 2 и определяют линию пересечения плоскостей. Соединив их, получаем искомую линию: a(1, 2) = Sum^Q.
Линию пересечения двух плоскостей, занимающих общее положение, можно построить в исходной системе плоскостей проекции. Для этого дважды решают задачу на построение прямой одной плоскости со второй плоскостью. Задачу можно решать в новой системе плоскостей проекции, построив изображение одной из пересекающихся плоскостей как плоскости проецирующей.
На рис. 123, а построена линия пересечения двух треугольников ABC и DEF путем построения точки М пересечения линии АВ с плоскостью DEF и точки N пересечения линии EF с плоскостью АВС:
1) АВ ~ Sum1(Sum1_|_П2), Sum1 ^DEF=l -2(12—22; 11—21), 11—21 ^ А1B1 = М1, M1,M2 || А1A2,М1М2 ^ А2В2 = М2,М(М,М2);
Рис. 122
Рис. 123
2) EF ~ Sum2(Sum2_|_П2), Sum2 ^ ABC = 3—4(32—42; 31—41),31-41 ^ E1F1= = N1, N1N2 || A1,A2; N1N2^ E2F2 = N2; N(N1,N2);
3) M1 U N1, = M1N1, M2 U N2 = M2N2;
4) ABC^DEF = MN.
После построения определяют видимость пересекающихся плоскостей. На фронтальной плоскости она определена с помощью фронтально конкурирующих точек 1 и 5. Для определения видимости на горизонтальной плоскости проекций использованы горизонтально конкурирующие точки 6 и 7.
На рис. 123, б эта же линия пересечения построена с помощью дополнительных проекций данных плоскостей на плоскости П4, относительно которой плоскость DEF занимает проецирующее положение. Дополнительные проекции построены из условия, что горизонталь h ? DEF проецируется в точку на плоскости П4 _|_ h. Новые линии связи проведены .через незаменяемые горизонтальные проекции точек А,
В, С, D, E, F параллельно h1, а новая ось проекций П1/П4 _|_ h1. Замеренные на плоскости П2 высоты точек определили их проекции на плоскости П4.
A4B4C4^ D4E4F4 = M4K4, так как А4В4 ^ D4E4F4 = М4 и В4С4 ^ D4E4F4 = = К4. По направлению новых линий связи определяем горизонтальную проекцию линии МК (М1К1). Отмечаем точку пересечения стороны EF c линией МК: E1F1 ^ M1K1 = N1. Точки отрезка NK не имеют общих точек с плоскостью DEF.
Пересекающиеся плоскости в частном случае могут быть перпендикулярными. Для выявления случаев перпендикулярности надо помнить, что если две плоскости взаимно перпендикулярны, то одна из них проходит через перпендикуляр к другой плоскости. На рис. 122 дан комплексный чертеж взаимно перпендикулярных пересекающихся плоскостей: одна фронтально проецирующая Sum (Sum2), а вторая — общего положения (ABC) — содержит в себе перпендикуляр АВ к плоскости Sum(AB||П2; A2B2Sum2).
Две плоскости в общем случае могут пересекаться в бесконечности. Тогда имеет место параллельность этих плоскостей. При выявлении этого случая следует учитывать, что у параллельных плоскостей две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На рис. 91 плоскость S параллельна плоскости Sum2, так как а || с, b || d.
122.gif
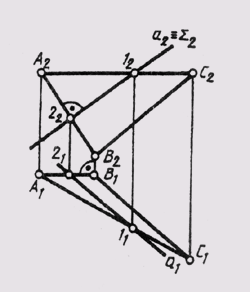
123.gif
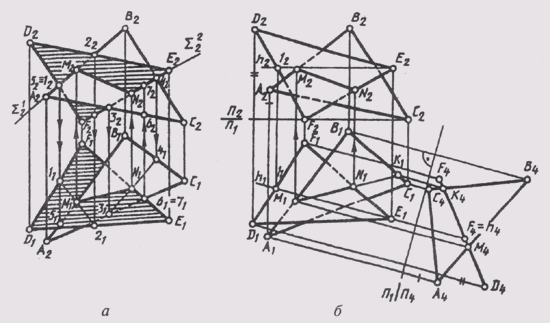
63. Пересечение поверхности с плоскостью. Тела с вырезами.
§ 63. Пересечение поверхности с плоскостью. Тела с вырезами
При пересечении поверхности с плоскостью в сечении получают плоскую линию. Эту линию строят по отдельным точкам. В начале построения сперва выявляют и строят опорные точки, лежащие на контурных линиях поверхности, а также точки на ребрах и линиях основания поверхности. В тех случаях, когда проекция линии пересечения не полностью определяется этими точками, строят дополнительные, промежуточные точки, расположенные между опорными.
В данном разделе рассматриваются случаи пересечения поверхности плоскостями частного положения, так как в случае наличия секущей плоскости общего положения чертеж всегда можно преобразовать так, чтобы секущая плоскость стала проецирующей (см. рис. 129).
В случае пересечения гранной поверхности плоскостью получается плоская ломаная линия. Чтобы построить эту линию, достаточно определить точки пересечения плоскостью ребер и сторон основания, если имеет место пересечение основания, и соединить построенные точки с учетом их видимости (рис. 124, а). Так как в этом случае секущая плоскость Е занимает фронтальное проецирующее положение, то точки пересечения ребер определяются без дополнительных построений:
AS^Sum=1(12; l1); Sum = (22; 21); CS^Sum = 3(32; 31).
Так как грань ACS относительно плоскости П\ невидима, то и линия l1—31 тоже невидима.
Рис. 124
В случае пересечения цилиндрической поверхности вращения плоскостью могут быть получены следующие линии (рис. 124, б):
окружность, если секущая плоскость Г перпендикулярна оси вращения поверхности;
эллипс, если секущая плоскостьSum не перпендикулярна и не параллельна оси вращения;
две образующие прямые, если секущая плоскость U параллельна оси поверхности.
На плоскость П1, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.
При пересечении конической поверхности вращения плоскостью могут быть получены следующие линии (рис. 125, а — д):
окружность, если секущая плоскость Г перпендикулярна оси вращения (а);
эллипс, если секущая плоскость Sum1 пересекает все образующие поверхности (б);
парабола, если секущая плоскость (Sum2) параллельна только одной образующей (S— 1) поверхности (в);
гипербола, если секущая плоскость (Sum3) параллельна двум образующим (S—5 и 5—6) поверхности (г);
две образующие (прямые), если секущая плоскость (Sum4) проходит через вершину S поверхности (д). Проекции кривых линий сечений
Рис. 125
Рис. 126
плоскостью конуса строятся по отдельным точкам (точки 2, 4 на рис. 125, б).
При пересечении сферы плоскостью всегда получается окружность. Если секущая плоскость параллельна какой-либо плоскости проекций, то на эту плоскость окружность сечения проецируется без искажения (рис. 126, а). Если секущая плоскость занимает проецирующее положение, то на плоскости проекций, которой секущая плоскость перпендикулярна (рис. 126, б—на фронтальной), окружность сечения изображается отрезком прямой (12—42), длина которого равна диаметру окружности, а на другой плоскости — эллипсом, большая ось которого (51—61) равна диаметру окружности сечения. Этот эллипс строят по точкам. Точки видимости 2 и 3 относительно плоскости П1 лежат на экваторе сферы.
Рис. 127
Задача построения линии пересечения несколько сложнее при пересечении сферы плоскостью общего положения (рис. 127) Q(a^h).
Этот случай можно свести к предыдущему (см. рис. 126, б), если построить дополнительные изображения сферы и секущей плоскости на плоскости П4 _|_П1, причем П4 _|_h (6). Тогда плоскость в станет проецирующей Q _|_П4 в новой системе плоскостей (см. рис. 127). На чертеже оси проекции проходят через центр сферы. На плоскости П4 отмечаем проекции опорных точек: А4 — самой низкой точки сечения; В4 — самой высокой, дающих величину диаметра d окружности сечения с центром в точке О (О4); Е4 = F4 — на экваторе сферы— точек видимости линии сечения относительно плоскости П1, С4 = D4 = O4 — горизонтального диаметра CD, определяющего большую ось эллипса, — горизонтальной проекции окружности сечения. Горизонтальная проекция сечения — эллипс — легко строится по большой C1D1 и малой А1В1 осям. Фронтальная проекция окружности тоже эллипс, который можно построить по сопряженным диаметрам A2B2 и C2D2 (высоты этих точек отмечены на плоскости П2 и на плоскости П4) с помощью описанного параллелограмма. Видимость окружности сечения относительно плоскости П2 определяется точками G и H, полученными в пересечении главного меридиана сферы f с плоскостью 9. Для этого взята вспомогательная плоскость уровня Ф:
Ф э f; Ф ^ Q = 2—3;
f2^22—32 = H2 и G2.
Линии среза получаются при пересечении поверхности вращения плоскостью, параллельной оси вращения поверхности. Линии среза часто встречаются на поверхностях деталей. На рис. 128 построена линия среза комплексной поверхности, состоящей из поверхностей сферы и конуса, фронтальной плоскостью уровня Ф. Линия среза включает ли-
Рис. 128
Рис. 129
нию пересечения сферы (В2 —А2 — С2) — часть окружности радиуса r — и линию пересечения конуса (В2 — D2 — С2) — ветвь гиперболы, которую строят по отдельным точкам. В качестве вспомогательных секущих плоскостей для построения промежуточных точек берут плоскости, перпендикулярные оси вращения поверхностей.
Пересечение поверхностей геометрических фигур может быть осуществлено не одной, а несколькими секущими плоскостями. Как и в случае пересечения одной плоскостью, построение каждой линии пересечения упрощается, если секущие плоскости являются плоскостями частного положения.
На рис. 129, а по заданной фронтальной проекции выреза, выполненного в правильной треугольной пирамиде тремя фронтально-проецирующими плоскостями, построены горизонтальная и профильная проекции. При решении таких задач вначале анализируют форму каждой грани выреза. Сторонами этих многоугольников будут: 1) линии пересечения граней пирамиды с плоскостями выреза и 2) линии пересечения плоскостей выреза друг с другом. Вершинами: 1) точки пересечения ребер пирамиды с плоскостями выреза и 2) концы отрезков, по которым грани выреза пересекаются друг с другом. На рис. 129, а плоскость I пересекает ребра пирамиды SА и SВ в точках 1 и 2, а с плоскостью III пересекается по отрезку 3—4; таким образом, форма грани 1 — четырехугольник 1—2—3—4. Аналогично в плоскости II получается четырехугольник 5—6—7—8. Вершинами четырехугольника 3—4—8—7 в грани III являются концы отрезков, по которым эта грань пересекается с гранями I и П. Стороны всех этих многоугольников составляют очертания выреза. Для получения их проекций на пл. П1 и П3 сначала нужно отметить фронтальные проекции (12 . . . 82) всех вершин, затем построить горизонтальные и профильные их проекции, после чего соединить на П1 и П3 вершины каждого многоугольника последовательно, с учетом видимости каждого отрезка. Грань I расположена горизонтально, поэтому на П3 проецируется в горизонтальный отрезок. Грань пирамиды SAC профильно-проецирующая, поэтому все линии выреза, полученные в ней, на П3 проецируются в одну линию. При обводке чертежа нужно стереть или оставить тонкими линиями части вырезаемых ребер пирамиды.
На рис. 129, б построены проекции правильной четырехугольной призмы с отверстием, ограниченным фронтально-проецирующими плоскостями.
Каждая грань выреза (I, II, III, IV) представляет собой плоский многоугольник, сторонами которого являются: 1) линии пересечения соответствующей секущей плоскости с гранями призмы и 2) линии пересечения плоскостей выреза друг с другом (отрезки 1—2; 3—4; 5—6; 7—8). Исходя из этого, имеем: грань I — трапеция 1—2—4—3; грань II — трапеция 3—4—6—5; грань III — прямоугольник 5—6—8—7; грань IV — шестиугольник 1—2—10—8—7—9. После анализа формы граней выреза производится построение проекций этих фигур на пл. П1 и П3. На пл. П1 все линии контура совпадают с вырожденными проекциями соответствующих граней. Грани II и IV расположены горизонтально, поэтому на пл. П3 проецируются в виде горизонтальных отрезков.
Рис. 130
На рис. 130, а показано построение выреза в цилиндре. Вырез ограничен тремя гранями. Вертикальная грань ограничена двумя горизонтальными сквозными ребрами 55' и 66' и прямыми 5,6 и 5' 6' на боковой поверхности цилиндра. Наклонную грань ограничивают частью эллипса на боковой поверхности цилиндра и сквозным ребром 55'. Горизонтальная грань представляет собой плоскую фигуру, ограниченную частью окружности и прямой 66'.
Линии выреза, лежащие на боковой поверхности цилиндра, проецируются на окружность основания на П1. Профильная их проекция строится по точкам измерения их глубин относительно плоскости симметрии цилиндра ф. Сквозные ребра 55' и 66' невидимы на П1 и П3
На рис. 130, б приведена задача построения выреза в конусе. Призматическое отверстие в конусе имеет три внутренние стенки, границами между которыми служат ребра АА', BE' и СС', которые перпендикулярны П2i. Правая стенка (АЕ) имеет форму трапеции, так как секущая плоскость этой стенки проходит через вершину S и пересекает конус по образующим SD и SD'. Части этих образующих между точками А (А') и В (В1) дают контур правой стенки. Нижняя стенка (между ребрами ВВ' и СС') представляет собой часть круга, ограниченного параллельно h. Левая стенка (между ребрами АА' и СС') ограничена частью параболы, проекции которой определяются точками F (Р) на профильном меридиане конуса и промежуточными точками К (К') на вспомогательной параллели h'.
Профильный меридиан конуса «вырезан» на участке между точками Е (E') и F (F).
На рис. 130, в построены проекции сферы с вырезом. Призматическое отверстие имеет 4 внутренние стенки, границами между которыми служат ребра АА', ВВ', СС', DD', которые перпендикулярны П2.
Каждая стенка представляет собой часть круга. Верхняя и нижняя параллельны П1 и проецируются на нее в виде части окружности с радиусами, которые определяются по параллелям h и h'.
Экватор вырезан между точками 1,5 и 2,6. Правая и левая стенки выреза параллельны П3 и проецируются на нее в виде частей круга с радиусами, которые определяются окружностями Р и Р'. Профильный меридиан вырезан между точками 3,7 и 4,8.
Приведенные примеры показывают, что, меняя положение секущих плоскостей, можно получить вырезы заданной формы.
124.gif
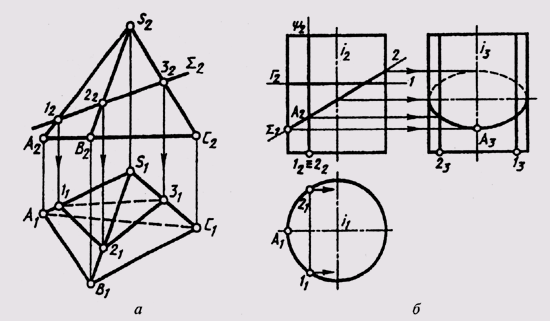
125.gif
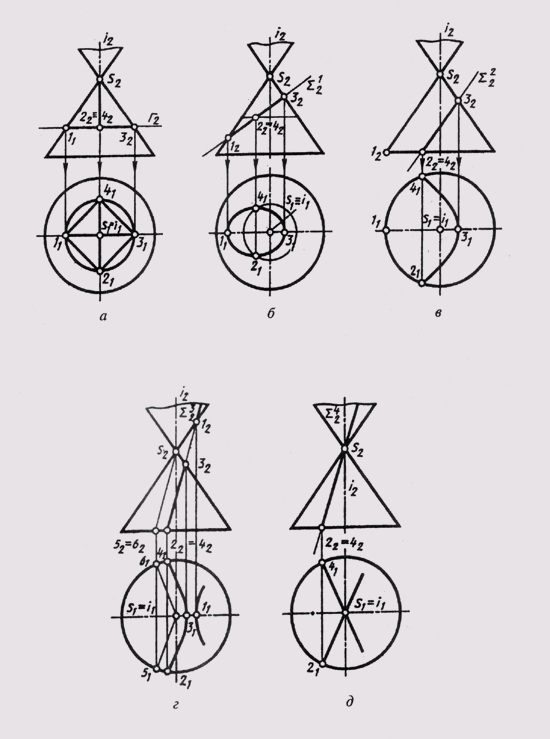
126.gif
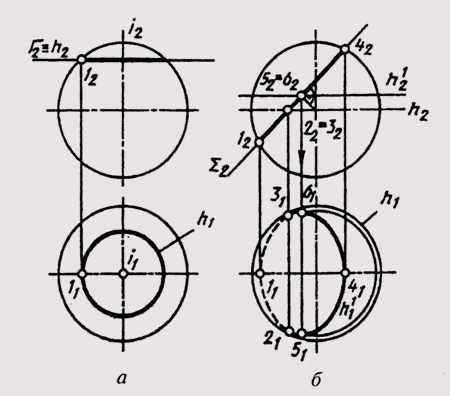
127.gif
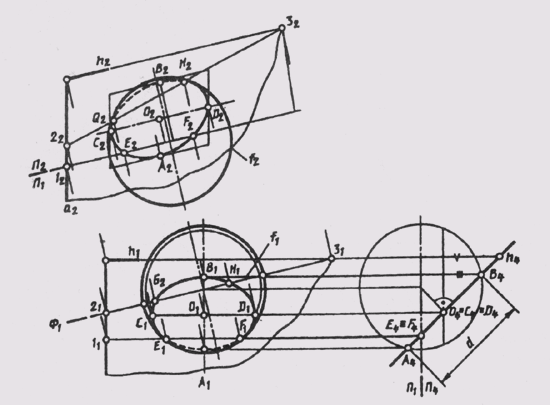
128.gif
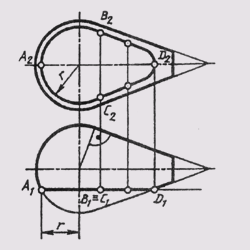
129.gif
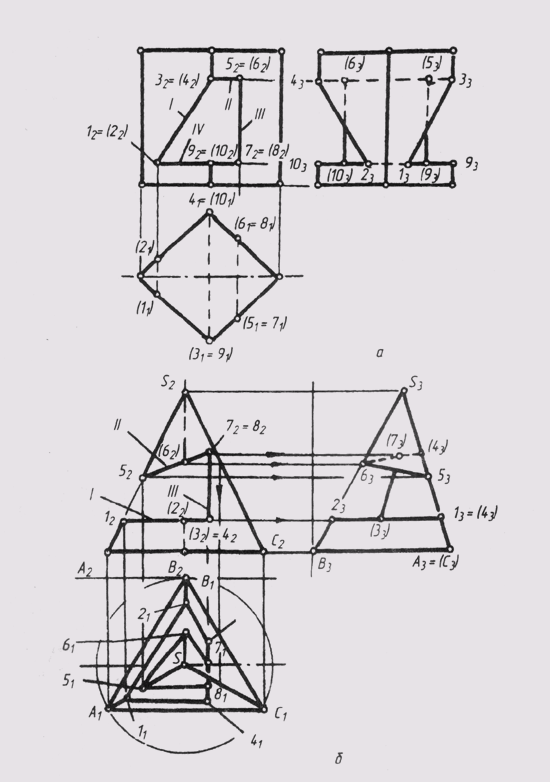
130.gif
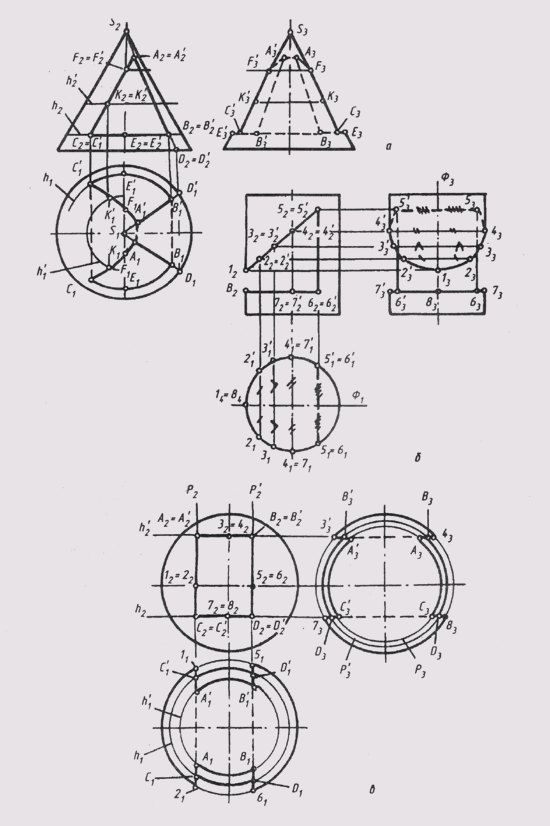
64. Пересечение поверхностей
§ 64. Пересечение поверхностей
При пересечении двух поверхностей образуется линия, в общем виде представляющая собой пространственную кривую, которая может распадаться на две части и более. Причем полученные части могут быть и плоскими, и кривыми.
Если пересекаются гранные поверхности, в общем случае получается пространственная ломаная кривая.
Линию пересечения двух плоскостей строят по отдельным точкам. Сначала в пересечении контурных линий одной поверхности с другой определяют и строят опорные точки. Построение этих точек позволяет видеть, в каких пределах расположены проекции линии пересечения и где между ними имеет смысл построить промежуточные (или случайные) точки. При построении точек пересечения двух поверхностей следует помнить, что проекции этих линий всегда располагаются в пределах площади наложения одноименных проекций пересекающихся плоскостей. На рис. 131 изображены две пересекающиеся поверхности. Площадь сечения — заштрихована. В пределах этой площади и будет расположена линия пересечения заданных поверхностей на данной плоскости проекций.
Рис. 131
Общим способом построения точек линии пересечения двух поверхностей является способ вспомогательных поверхностей — посредников. Посредники пересекают заданные поверхности по линиям, желательно по графически простым. Тогда в пересечении этих линий получаются точки, принадлежащие обеим поверхностям, а значит, и линии их пересечения. В качестве поверхностей-посредников используют или плоскости, или сферы. В зависимости от принятого вида посредника именуют и способ построения линии пересечения: способ вспомогательных секущих плоскостей или способ вспомогательных сфер.
131.gif
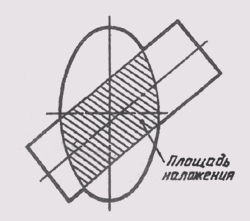
65. Построение линии пересечения поверхностей способом вспомогательных секущих плоскостей
§ 65. Построение линии пересечения поверхностей способом вспомогательных секущих плоскостей
При построении линии пересечения двух поверхностей способом вспомогательных секущих плоскостей секущие плоскости, принятые в качестве посредников, могут быть и общего, и частного положения. Более широкое применение находят плоскости частного положения.
Рис. 132
Рис. 133
Плоскости общего положения применяются в ограниченных случаях. Например, их удобно использовать при построении линии пересечения конических и цилиндрических, а также пирамидальных и призматических поверхностей общего вида, когда основания этих поверхностей расположены в одной и той же плоскости.
Решение задачи построения линии пересечения двух поверхностей способом вспомогательных секущих плоскостей рассмотрим на примере пересечения конуса вращения со сферой. В качестве поверхностей-посредников примем плоскости частного положения— горизонтального уровня. На рис. 132 сначала отметим очевидные общие точки А и В поверхностей в пересечении их главных меридианов f и 1-S-2, так как поверхности имеют общую фронтальную плоскость симметрии Ф(Ф1); f2^S2—S2 = А2(В2); A2Al(B2Bl) || S2S1, A2Al(B2Bl) ^f1 =A1(B1)
Эти опорные точки являются наивысшей А и наинизшей В точками линии пересечения, а также точками видимости линии на плоскости П2.
Брать вспомогательные фронтальные плоскости, параллельные П2, для построения следующих точек неудобно, так как они будут пересекать конус по гиперболам. Графические простые линии (окружности параллелей) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г.
Первую такую вспомогательную плоскость Г1 берем на уровне экватора сферы И. Эта плоскость пересекает конус по параллели h1. В пересечении этих параллелей находятся точки видимости линии пересечения относительно плоскости П1:
h1^h11 = С1(D1); С1С2|| S1S2; С1С2 ^ h2(hl2) = C2(D2).
Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии (рис. 133), то самую высокую А и низкую В точки линии пересечения поверхности легко определить, построив изображения этих поверхностей на плоскости П4, параллельной осевой плоскости Sum (Sum1) данных поверхностей. Можно построить проекции всей линии пересечения в системе плоскостей П1_|_П4, а затем построить ее фронтальную проекцию в проекционной связи с горизонтальной проекцией, замеряя высоты точек на плоскости П4, так, как это показано на рис. 132 для точек А и В.
132.gif
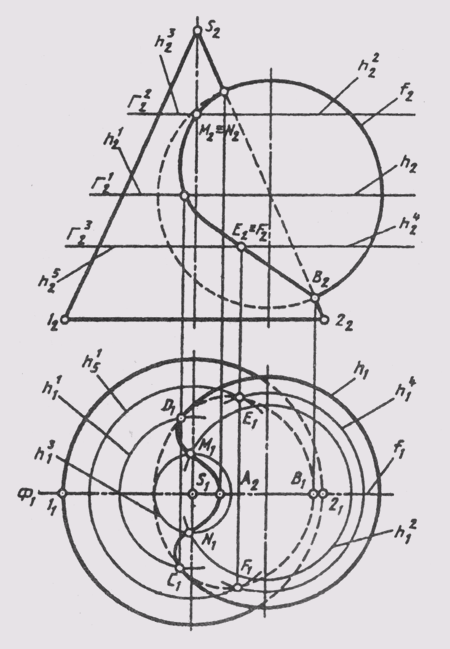
133.gif
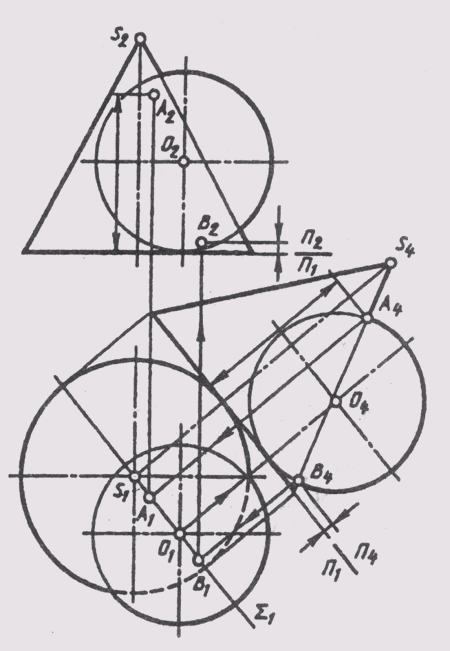
66. Построение линии пересечения поверхностей способом вспомогательных сфер
§ 66. Построение линии пересечения поверхностей способом вспомогательных сфер
При построении линии пересечения поверхностей особенности пересечения соосных поверхностей вращения позволяют в качестве вспомогательных поверхностей-посредников использовать сферы, со-осные с данными поверхностями.
К соосным поверхностям вращения относятся поверхности, имеющие общую ось вращения. На рис. 134 изображены соосные цилиндр и сфера (рис. 134, а), соосные конус и сфера (рис. 134, б) и соосные цилиндр и конус (рис. 134, в).
Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих общих для обеих поверхностей окружностей столько, сколько существует точек пересечения очерковых линий поверхностей. Поверхности на рис. 134 пересекаются по окружностям, создаваемым точками 1 и 2 пересечения их главных меридианов.
Вспомогательная сфера-посредник пересекает каждую из заданных поверхностей по окружности, в пересечении которых получаются точки, принадлежащие и другой поверхности, а значит, и линии пересечения.
Рис. 134
Если оси поверхностей пересекаются, то вспомогательные сферы проводят из одного центра-точки пересечения осей. Линию пересечения поверхностей в этом случае строят способом вспомогательных концентрических сфер.
При построении линии пересечения поверхностей для использования способа вспомогательных концентрических сфер необходимо выполнение следующих условий:
1) пересечение поверхностей вращения;
2) оси поверхностей — пересекающиеся прямые — параллельны одной из плоскостей проекций, т. е. имеется общая плоскость симметрии;
3) нельзя использовать способ вспомогательных секущих плоскостей, так как они не дают графически простых линий на поверхностях.
Обычно способ вспомогательных сфер используется в сочетании со способом вспомогательных секущих плоскостей. На рис. 135 построена линия пересечения двух конических поверхностей вращения с пересекающимися во фронтальной плоскости уровня Ф (Ф1) осями вращения. Значит, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения относительно плоскости П2 или самую высокую А и самую низкую В точки. В пересечении горизонтального меридиана h и параллели h', лежащих в одной вспомогательной секущей плоскости Г(Г2), определены точки видимости С и D линии пересечения относительно плоскости П1. Использовать вспомогательные секущие плоскости для построения дополнительных точек линии пересечения нецелесообразно, так как плоскости, параллельные Ф, будут пересекать обе поверхности по гиперболам, а плоскости, параллельные Г, будут давать в пересечении поверхностей окружности и гиперболы. Вспомогательные горизонтально или фронтально проецирующие плоскости, проведенные через вершину одной из поверхностей, будут пересекать их по образующим и эллипсам. В данном примере выполнены условия, позволяющие применение вспомогательных сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке О (О1; О2), которая является центром вспомогательных сфер, радиус сферы изменяется в пределах
Rmin < R < Rmах- Радиус максимальной сферы определяется расстоянием от центра О наиболее удаленной точки В (Rmax = О2В2), а радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности (по окружности h2) и пересекающей другую (по окружности h3).
Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаем точки Е и F, принадлежащие линии пересечения поверхностей:
Рис. 135
h22 ^ h32 = E2(F2); Е2Е1 || А2А1;
Е2Е1 ^ h21 =E1; F2F ^ h1 = F1
Промежуточная сфера радиуса R пересекает поверхности по окружностям h4 и h5, в пересечении которых находятся точки Ми N:
h42 ^ h52 = M2(N2); M2M1 || А2А1,
М2М1 ^ h41 = М1; N2N1 ^ h41 = N1
Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.
134.gif
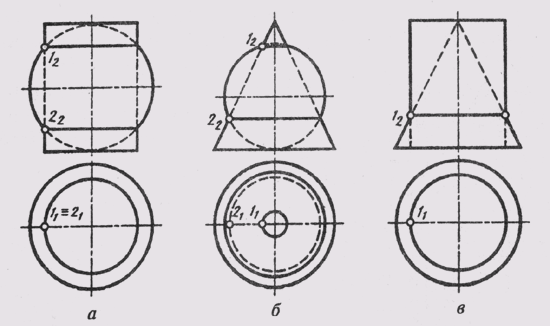
135.gif
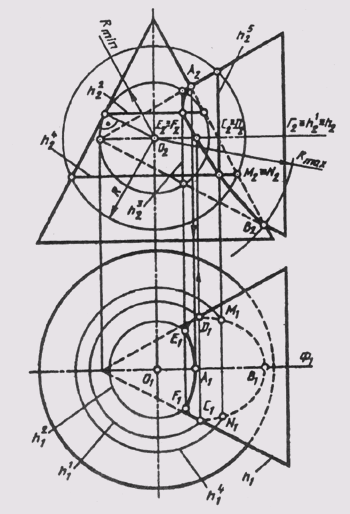
67. Особые случаи построения линии пересечения двух поверхностей вращения
§ 67. Особые случаи построения линии пересечения двух поверхностей вращения
При построении линии пересечения поверхностей вращения — конуса и цилиндра — могут быть различные случаи. На рис. 136 изображены три случая пересечения цилиндра и конуса вращения. В первом случае (рис. 136, а) цилиндр врезается в конус, потому что если вписать в конус сферу с центром в точке пересечения осей поверхностей, то радиус ее будет больше радиуса цилиндра. Все образующие цилиндра пересекаются с поверхностью конуса. Во втором (рис. 136, б) конус врезается в цилиндр, так как сфера, вписанная в цилиндр, пересекает конус. Все образующие конуса пересекают поверхность цилиндра. В третьем (рис. 136, в) сфера, вписанная в одну поверхность, касается второй поверхности, и в пересечении участвуют все образующие и цилиндра, и конуса. В этом случае пространственная линия пересечения поверхностей распадается на две плоские кривые (эллипсы).
Это положение подтверждается теоремой Монжа: если две поверхности второго порядка описаны вокруг третьей поверхности второго порядка, то они пересекаются по двум кривым второго порядка. Такие поверхности имеют две точки, в которых они касаются друг друга, или говорят, что поверхности имеют двойное прикосновение. Линия пересечения двух поверхностей вращения, имеющих двойное прикосновение, распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки прикосновения (рис. 137). Две цилиндрические поверхности вращения одного диаметра касаются друг друга в точках А и В или имеют общие касательные, плоскости Ф1 и Ф2. Линия АВ занимает фронтально проецирующее положение, поэтому плоскости кривых пересечения будут фронтально проецирующими. Эллипсы ACBF и AEBD изображаются
Рис. 136
Рис. 137
Рис. 138
Рис. 139
отрезками прямых на фронтальной плоскости проекций и окружностями, совпадающими с вырожденной проекций вертикального цилиндра, на горизонтальной плоскости проекций. Это положение широко используется при изображении пересекающихся труб или отверстий одного диаметра (рис. 138).
В конструкциях технических деталей часто при пересечении поверхностей вращения используют сопрягающую поверхность, которая осуществляет плавный переход от одной поверхности к другой (рис. 139, а, б, в).
Чтобы не строить две близко расположенные линии пересечения сопрягающей поверхности с основными поверхностями, на чертеже проводят условно одну линию, выполняя ее тонкой сплошной линией.
Эту линию и называют линией перехода. Линия перехода заканчивается в точках пересечения очерковых линий основных поверхностей (рис. 139, а) и заменяется более простыми (циркульными) кривыми.
136.gif
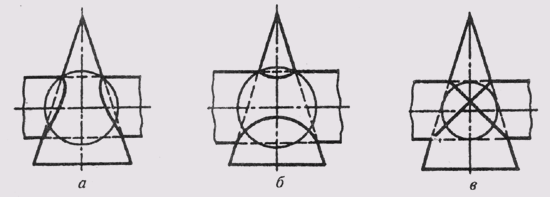
137.gif
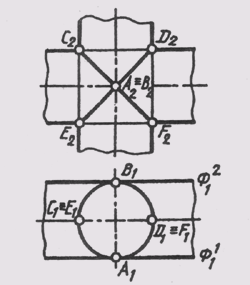
138.gif
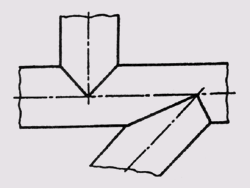
139.gif
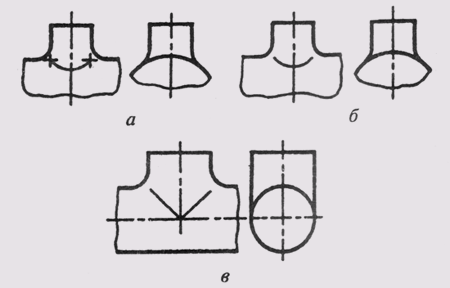
12. Глава 11. Метрические задачи
1. Глава 11. Метрические задачи
Глава 11. МЕТРИЧЕСКИЕ ЗАДАЧИ
§ 68. Общие сведения о метрических задачах
К метрическим относятся задачи, связанные с определением истинных (натуральных) величин расстояний, углов и плоских фигур на комплексном чертеже. Можно выделить три группы метрических задач.
1. Группа задач, включающих в себя определение расстояний от точки до другой точки; от точки до прямой; от точки до плоскости; от точки до поверхности; от прямой до другой прямой; от прямой до плоскости; от плоскости до плоскости. Причем расстояние от прямой до плоскости и между плоскостями измеряется в тех случаях, когда они параллельны.
2. Группа задач, включающая определение углов между пересекающимися или скрещивающимися прямыми, между прямой и плоскостью, между плоскостями (имеется в виду определение величины двухгранного угла).
3. Группа задач, связанная с определением истинной величины плоской фигуры и части поверхности (развертки).
Приведенные задачи могут быть решены с применением различных способов преобразования чертежа. В основе решения метрических задач лежит свойство прямоугольного проецирования, заключающееся в том, что любая геометрическая фигура на плоскость проекций проецируется в натуральную величину, если она лежит в плоскости, параллельной этой плоскости проекций. Решение задач значительно упрощается, если хотя бы одна из геометрических фигур, участвующих в задачах, занимает частное положение. Если одна из геометрических фигур не занимает частного положения, необходимо выполнить определенные построения, позволяющие провести одну из них в это положение.
8. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
13. Как нанести на развертку поверхности точку, ей принадлежащую?
69. Определение истинной величины расстояний
§ 69. Определение истинной величины расстояний
Некоторые задачи на определение расстояний рассматривались в предыдущих разделах. Например, в § 42 определялась натуральная величина отрезка прямой линии методом треугольника, в § 57 определялась натуральная величина отрезка способом плоскопараллельного переноса. Эта задача может быть также решена способом замены плоскостей проекций (см. § 58) или способом вращения (см. § 59). Определение длины отрезка прямой позволяет решить задачу определения расстояния от точки до точки, так как это расстояние и определяется отрезком прямой. Расстояние от точки до прямой измеряется отрезком перпендикуляра, проведенного из точки к прямой. Отрезок этого перпендикуляра изображается в натуральную величину на плоскости в том случае, если он проведен к проецирующей прямой. Значит, нужно преобразовать чертеж данной прямой, сделав ее в новой системе плоскостей проекций проецирующей (см. § 58, задача 2). На рис. 140 определено расстояние от точки М до прямой АВ:
1) П2_|_П1-> П1_|_П4, П4 ||АВ, П1/П4 ||A1B1;
2) П1П4 -> П4_|_П5, П5 _|_AB, П4/П5 _|_A4B4;
3) M5K5 — истинное расстояние от точки М до прямой AB;
4) чтобы построить проекции перпендикуляра МК в исходной системе плоскостей, строят основание перпендикуляра— точку К—на прямой АВ из условия, что в системе П4 _|_П5; он занимает положение линии уровня, т. е.
M4K4_|_A4B4. Горизонтальная и фронтальная проекции точки К определяются по линиям из условия принадлежности ее прямой АВ. Расстояние от точки до плоскости измеряется отрезком перпендикуляра, опущенного из точки на плоскость. Так как перпендикуляр к проецирующей плоскости есть линия уровня, то удобно иметь на чертеже «вырожденную» проекцию данной плоскости, т. е. преобразовать чертеж (см. § 58, задача 3). На рис. 141 построены проекции перпендикуляра МК, отрезок которого определяет расстояние от точки М до плоскости Q(ABC):
Рис. 140
1) П1,П2->П1_|_П4, П4_|_Q, П1 /П4 _|_ h(A, 1)~ 0;
2) М4K4 _|_Q4 — истинная величина расстояний от точки М до плоскости Q;
3)M1K1_|_K4Kl или || П1/ П4;
4) K2 построена с помощью высоты точки К, измеренной на плоскости П4.
Расстояние между параллельными прямыми измеряется отрезком перпендикуляра между ними. На рис. 142 определено расстояние между прямыми а и b путем преобразования чертежа прямых. Сначала построено
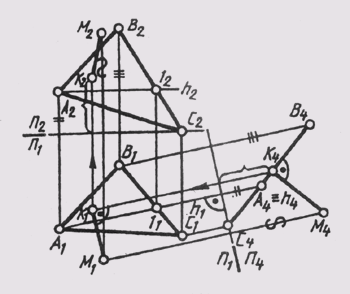
Рис. 141
изображение прямых на плоскости П4_|_П1. В этой системе плоскостей прямые занимают положение линии уровня:
а(b)|| П4; П1 /П4 ||а,(b1).
В системе плоскостей П4 _|_ П5 прямые занимают проецирующее по отношению к плоскости Пз положе-
Рис. 142
ние: П5 _|_ а(b); П4/П5 _|_a(b4) Отрезок M5K5 между вырожденными проекциями прямых определяет истинную величину расстояния между прямыми а и Ъ. Построения проекций перпендикуляра МК в исходной системе плоскостей проекций аналогичны рассмотренным ранее.
Для определения расстояния между скрещивающимися прямыми необходимо одну из прямых сделать проецирующей в новой системе плоскостей проекций.
Расстояние от прямой до плоскости, параллельной прямой, измеряется отрезком перпендикуляра, опущенного из любой точки прямой на плоскость. Значит, достаточно плоскость общего положения преобразовать в положение проецирующей плоскости, взять на прямой точку, и решение задачи будет сведено к определению расстояния от точки до плоскости.
Расстояние между параллельными плоскостями измеряется отрезком перпендикуляра между ними, который легко строится, если плоскости займут проецирующее положение в новой системе плоскостей проекции, т. е. опять используется третья исходная задача преобразования чертежа.
140.gif
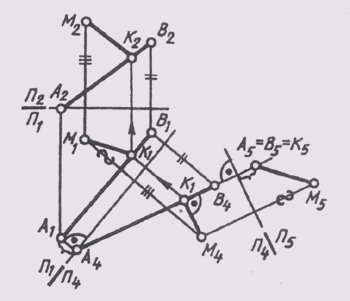
141.gif

142.gif
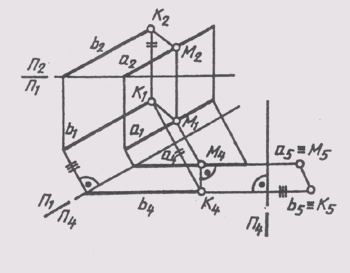
70. Определение истинной величины углов
§ 70. Определение истинной величины углов
Задачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф1), проходящей через
Рис. 143
фронталь f Проекция MI совмещения вершины М угла между прямыми с и d находится на проекции Sum2 фронтально проецирующей плоскости Sum, в которой вращается точка М. Определив с помощью прямоугольного треугольника О2М2М натуральную величину радиуса вращения r и отложив ее на проекции Е2 от фронтальной проекции центра вращения, получаем изображение точки М на плоскости П2 в совмещенном с плоскостью Ф положении. Соединяя фронтальные проекции неподвижных точек 1 и 2 с построенной точкой М, получаем проекции с2 и d2, совмещенных с плоскостью Ф прямых с и d. Угол между прямыми с2 и d2 определяет натуральную величину искомого угла между пересекающимися прямыми с и d.
Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.
Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.
Угол а между прямой l и плоскостью 6 может быть определен через дополнительный угол р между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол Р дополняет искомый угол а до 90°. Определив истинную величину угла Р путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла а между прямой l и плоскостью 0.
Истинная величина двугранного угла — между двумя плоскостями Q и л. — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или если ребро не задано, как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям (см. § 61) из произвольной точки М пространства (см. рис. 145). В плоскости этих перпендикуляров при точке М получаем два плоских
Рис. 144
Рис. 145
угла а и Р, которые соответственно равны линейным углам двух смежных углов (двугранных), образованных плоскостями q и л,. Определив истинную величину углов между перпендикулярными n1 и n2 путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями q и л.
143.gif
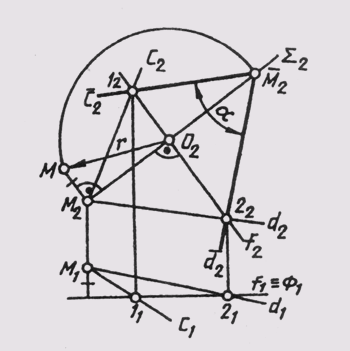
144.gif
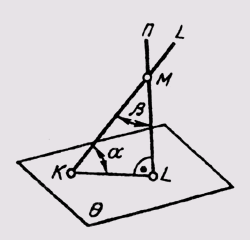
145.gif
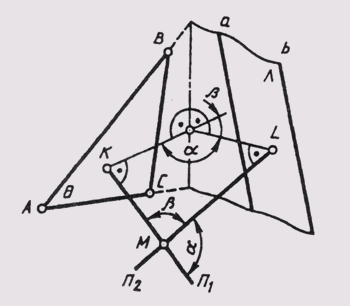
71. Определение истинной величины плоской фигуры
§ 71. Определение истинной величины плоской фигуры
Определение истинной величины плоской фигуры можно осуществить путем преобразования чертежа способом замены плоскостей проекций. На рис. 146, а дан комплексный чертеж прямоугольника ABCD. Ни одна из проекций прямоугольника не занимает частного положения. Задачу решаем последовательным решением третьей и четвертой основных задач. Заменив плоскость П2 на П4, приводим прямоугольник в частное положение, т. е. в виде проецирующей по отношению к П4- Выполнив вторую замену, то есть замену П4 на П5, определяем истинную величину прямоугольника ABC.
Задачу определения истинной величины прямоугольника можно также решить способом вращения вокруг линии уровня плоскости этой фигуры до совмещения с соответствующей плоскостью уровня (рис. 146, б).
В ряду рассматриваемых задач может быть также решена задача на определение истинной величины фигуры сечения поверхности проецирующей плоскостью. В этом случае достаточно одной замены плоскостей проекций (исходная задача 3). В этом случае истинную величину фигуры сечения можно легко построить путем непосредственного замера расстояний точек фигуры «вдоль сечения» и «поперек сечения» (рис. 147).
Длина фигуры сечения АВ изображается в истинную величину на плоскости П2, так как является отрезком фигуры фронтали секущей плоскости. Расстояние между симметричными точками «поперек сечения» изображается в натуральную величину на плоскости П1 так как является отрезками горизонталей секущей плоскости Sum.
72. Построение разверток поверхностей
§ 72. Построение разверток поверхностей
При изготовлении различных конструкций и изделий из листового материала имеет большое значение построение разверток поверхностей. Если представить себе поверхность как гибкую нерастяжимую пленку, то некоторые из них путем изгиба можно совместить с плоскостью без разрывов и деформаций. Такие поверхности относятся к развертывающимся, а полученную в результате развертывания поверхности плоскую фигуру называют разверткой этой фигуры. Те поверхности, которые нельзя совместить без разрывов и деформаций, относятся к неразвертываемым (см. § 45).
В практике возникает необходимость изготовления из листового железа не только развертывающихся плоскостей. Теоретически точно развертываются только гранные поверхности, торсы, конические или цилиндрические поверхности. При развертывании конических и цилиндрических поверхностей общего вида в практике их аппроксимируют вписанными гранными поверхностями. В этом случае чем больше граней содержит вписанная поверхность, тем точнее ее развертка. Построенные таким образом развертки поверхностей называют приближенными.
Чтобы построить развертки неразвертывающихся поверхностей, эти поверхности разбивают на части, которые можно приближенно заменить развертывающимися поверхностями. После этого строят развертки этих частей, которые в сумме дают условную развертку неразвертывающейся поверхности.
73. Развертки пирамидальных и конических поверхностей
§ 73. Развертки пирамидальных и конических поверхностей
При развертывании поверхности на плоскости каждой точке поверхности соответствует единственная точка на развертке: линия поверхности переходит в линию развертки; длины линий, величины плоских углов и площадей, ограниченных замкнутыми линиями, остаются неизмеренными. Таким образом, процесс построения развертки сводится к отыскиванию натуральной (истинной) величины каждого элемента поверхности и изображению их на плоскости.
Рис. 146
Рис. 147
Рис. 148
Рис. 149
Каждая боковая грань на развертке строится как треугольник по трем сторонам. CS — самое короткое боковое ребро, поэтому рациональнее мысленно разрезать пирамиду по этому ребру.
Для нанесения на развертку точек D, Е и F, соответствующих вершинам сечения пирамиды плоскостью Sum, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники АBС и DEF, дающие истинную величину основания и сечения пирамиды.
На рис. 149 способом триангуляции построена развертка конической поверхности, которая заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка представляет собой симметричную фигуру, так как поверхность имеет плоскость симметрии Sum. В этой плоскости лежит самая короткая образующая S-6. По ней и сделан разрез поверхности. Самая длинная образующая S-0 является осью симметрии развертки поверхности.
Натуральные величины образующих определены с помощью прямоугольных треугольников, как в предыдущей задаче на рис. 149. От оси симметрии S-0 строим шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников с общей вершиной S. Каждый из треугольников строим по трем сторонам, при этом две сто-
Рис. 150
роны равны истинным величинам образующих, а третья — хорде, стягивающей дугу окружности основания между соседними точками деления. Построенные на развертке точки О, 1, 2, ... соединяются. Построение развертки значительно упрощается, если поверхность представлена прямой пирамидой правильной формы или прямым круговым конусом. На рис. 150 приведена развертка четырехгранной прямой пирамиды. Построение ее упрощается тем, что образующая пирамиды AS и CS параллельны фронтальной плоскости проекций и на нее спроецировались в натуральную величину. Основание же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости проекций, и на нее проецируется в натуральную величину. Для построения развертки достаточно построить сторону AS и сделать засечки радиусом дуги, равным BS и АВ из точек S и А, соответственно получим точку В и т. д. Основание же в натуральную величину можно построить на базе одной из его сторон (на рис. 150 — на базе стороны АВ). Положение точки на поверхности развертки пирамиды определим в следующем порядке: через фронтальную проекцию точки М (М2) проведем горизонтальную линию до пересечения с ребрами A2S2 и B2S2. Получим точки 11 и 22. На линии AS развертки от точки А отложим отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD на которой нанесем точку М в том положении, которое она занимает на горизонтальной проекции линии 1, 2.
Рис. 151
На рис. 151 приведен пример построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса l на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку. Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из точки M2 проведем горизонтальную линию до пересечения с очерковой образующей L и получим точку M2. Расстояние от основания конуса до точки M2 по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.
146.gif
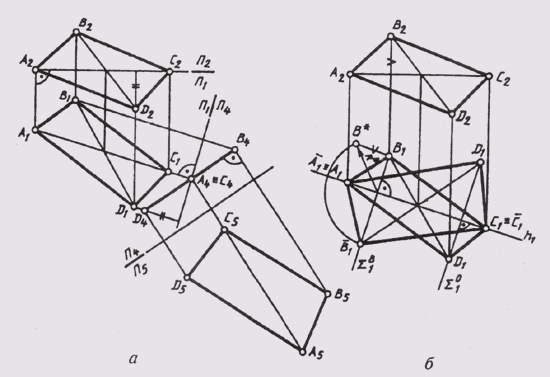
147.gif
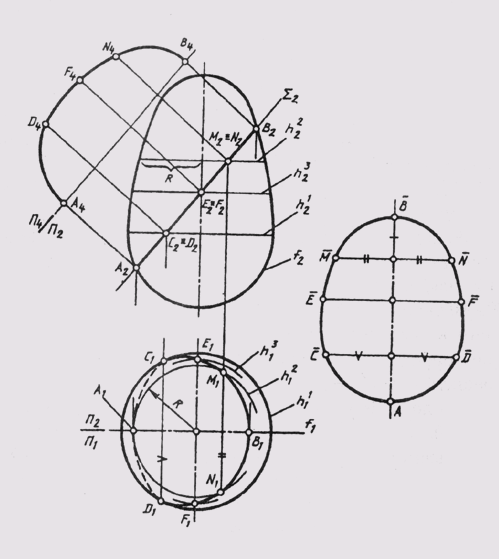
148.gif
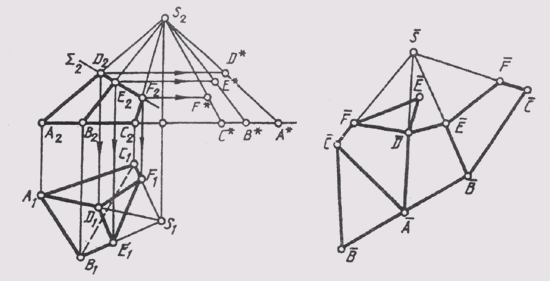
149.gif
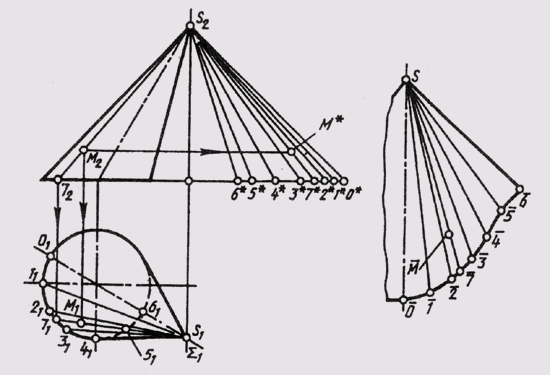
150.gif
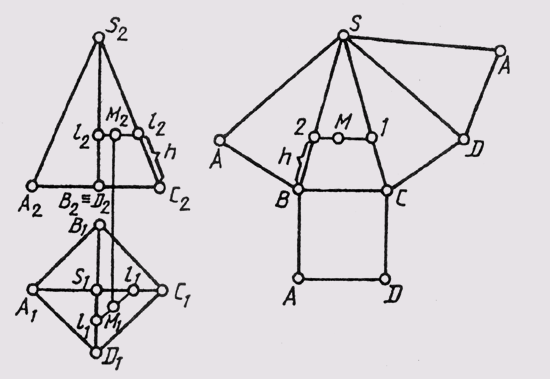
151.gif
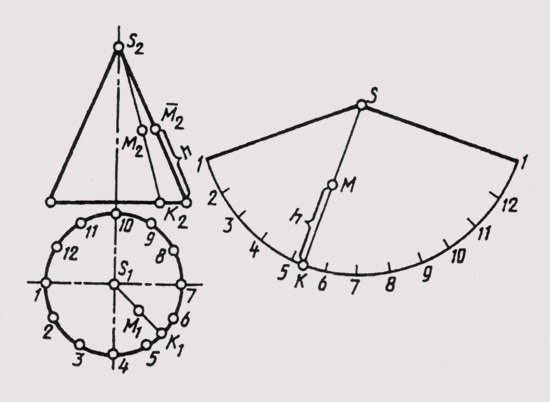
74. Развертки призматических и цилиндрических поверхностей
§ 74. Развертки призматических и цилиндрических поверхностей
Развертки призматических и цилиндрических поверхностей строят способом нормального сечения. Поверхность рассекают плоскостью, перпендикулярной ее образующим (ребрам), и определяют истинную величину нормального сечения. Линию нормального сечения развертывают в прямую. Тогда образующие (ребра) поверхности при развертке ее на плоскость располагаются перпендикулярно развертке линии нормального сечения, которую принимают за базу отсчета размеров образующих (ребер).
На рис. 152 построена полная развертка поверхностей треугольной призмы ABCDEF. Так как боковые ребра призмы BE, AD и CF параллельны плоскости П2, то они в истинную длину изображены на фронтальной плоскости проекций. Плоскость нормального сечения Sum(Sum2) является фронтально проецирующей. Нормальное сечение POR призмы построено в натуральную величину на плоскости П4, параллельной плоскости Sum и перпендикулярной плоскости П2. Линию нормального сечения разворачиваем в прямую и через точки Р, Q, R, и Р проводим прямые, перпендикулярные развертке линии нормального сечения. На каждом из построенных перпендикуляров откладывают по обе стороны от линии Р Р отрезки боковых ребер, измеренные на плоскости П2 (до нормального сечения и после него). Отмечаем точки
Рис. 152
Рис. 153
ребер на развертке А и D; С и F; В и Е, соединяем их отрезками прямых, которые дают истинную величину сторон основания призмы. Присоединяя к разверткебоковой поверхности призмы оба основания (треугольники А В С и DEТ), получаем полную развертку призмы. На развертку призмы нанесена точка М, принадлежащая грани призмы ACFD, с помощью вспомогательной прямой, параллельной ребрам призмы и пересекающей нормальное сечение в точке 1.
На рис. 153 построена развертка боковой поверхности эллиптического цилиндра, в который для построения развертки вписана двенадцатиугольная призма. Поверхность имеет фронтальную плоскость симметрии. Самая длинная образующая — нулевая, самая короткая — шестая, по ней и сделан разрез поверхности. Развертка — фигура симметричная относительно нулевой образующей. Истинная величина половины нормального сечения поверхности плоскостью Sum построена на плоскости П4 — эллипс. Разворачиваем дугу полуэллипса в прямую 0 — 6с помощью хорд 04—14, ... 54 — 64, заменяющих кривые участки эллипса. В точках 0, 1, ... 6 на развертке восстанавливаем перпен-
Рис. 154
Рис. 155
дикуляры, по которым откладываем натуральную длину участков, образующих поверхности (до нормального сечения и после него), измеренную на плоскости П2. Концы отрезков соединяем плавными кривыми, которые являются разверткой оснований поверхности.
С помощью седьмой образующей на развертку нанесена точка поверхности.
Построение разверток призматических и цилиндрических поверхностей значительно упрощается, если они представлены простыми прямыми фигурами. Для примера на рис. 154 приведена развертка трехгранной призы правильной формы. Развертки ее строим, воспользовавшись тем, что ребра ее АА, ВВ, СС параллельны фронтальной плоскости проекций и проецируются на нее в натуральную величину, а нижнее ABC и верхнее А'В'С' основания параллельны горизонтальной плоскости проекций и проецируются на нее в натуральную величину. Точка М на развертке трехгранной призмы строится обычным способом.
На рис. 155 приведен пример построения развертки прямого кругового цилиндра. Ее высота Н на фронтальную плоскость проекций проецируется в натуральную величину, а нижнее и верхнее основания параллельны горизонтальной плоскости проекций и на нее проецируются в натуральную величину. В этом случае развертку цилиндрической поверхности строим с помощью хорд, соединяющих соседние точки деления окружности оснований, в который вписан правильный двенадцатиугольник. В этом случае цилиндрическая поверхность условно заменена поверхностью вписанной правильной двенадцатигранной призмы, и развертка цилиндрической поверхности построена способом триангуляции.
Положение точки М на развертке цилиндрической поверхности определяется обычным способом.
152.gif
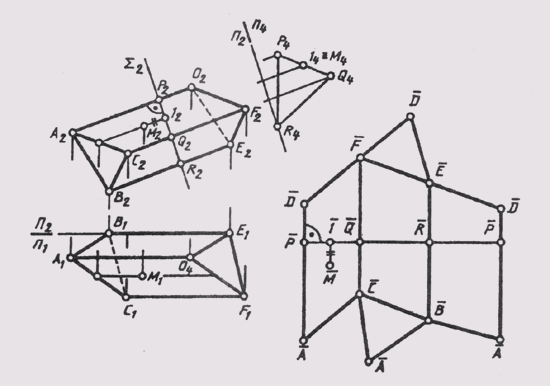
153.gif
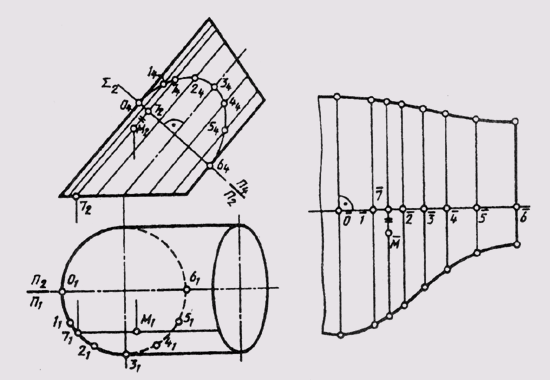
154.gif

155.gif
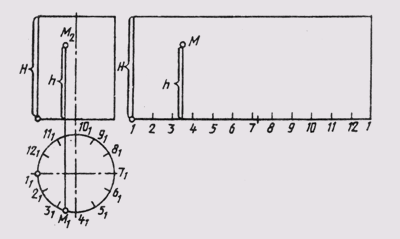
13. Глава 12. Аксонометрические проекции
1. Глава 12. Аксонометрические проекции
Глава 12. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
§ 75. Общие сведения об аксонометрических проекциях
При выполнении технических чертежей в ряде случаев оказывается необходимо наряду с изображением предметов в прямоугольных проекциях иметь и наглядные их изображения. Это необходимо для обеспечения возможности более полно выявить конструктивные решения, заложенные в изображении предмета, правильно представить положение его в пространстве, оценить пропорции его частей и размеры.
Наглядные изображения на некоторых чертежах могут применяться и независимо от прямоугольных изображений, например, при изображении схем электроснабжения и теплоснабжения зданий и сооружений.
Существуют различные способы построения наглядных изображений. Сюда относятся аксонометрические, афинные и векторные проекции, а также ли-
Рис. 156
нейная перспектива. В настоящем учебном пособии рассматриваются только аксонометрические проекции.
Построение аксонометрических проекций заключается в том, что геометрическую фигуру вместе с осями прямоугольных координат, к которым эта фигура отнесена в пространстве, параллельным (прямоугольным или косоугольным) способами проецируют на выбранную плоскость проекций. Таким образом, аксонометрическая проекция — это проекция на одну плоскость. При этом направление проецирования выбирают так, чтобы оно не совпадало ни с одной из координатных осей.
При построении аксонометрических проекций изображаемый предмет жестко связывают с натуральной системой координат Oxyz (см. § 37). В целом аксонометрический чертеж получается состоящим из параллельной проекции предмета, дополненной изображением координатных осей с натуральными масштабными отрезками по этим осям. Название «аксонометрия» и произошло от слов — аксон — ось и метрео — измеряю.
Образование аксонометрической проекции рассмотрим на примере построения аксонометрической точки А, отнесенной к натуральной системе координат Oxyz (рис. 156). Натуральные координаты точки А получаются измерением отрезков координатной ломаной АА1АХО натуральным масштабом е. При параллельном проецировании по направлению S на плоскости аксонометрических проекций Я1 получим аксонометрическую проекцию А1 данной точки, аксонометрическую проекцию А1A11А1xО координатной ломаной и аксонометрическую проекцию ОУуУ натуральной системы координат, на осях которой будут находиться единичные аксонометрические масштабные отрезки e1xe1ye1z.
Аксонометрическая проекция А11 горизонтальной проекции точки А (первичной) называется вторичной проекцией точки А. Совокупность всех этих проекций и составляет аксонометрию точки А.
На аксонометрическом чертеже вторичная и аксонометрическая проекции предмета обеспечивают метрическую определенность и обратимость однокартинного изображения.
В аксонометрических проекциях сохраняются все свойства параллельных проекций (см. § 28).
На практике измерения вдоль аксонометрических осей выполняют в одинаковых единицах — миллиметрах, поэтому единичные натуральные масштабные отрезки и их аксонометрию на чертежах не указывают.
Коэффициенты искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине при одинаковых единицах измерения.
Натуральные коэффициенты искажения обозначают: по оси х: и =О1А1х/OAx; по оси у: v =A1xА11/AxA1;
по оси z: w =A11А1/A1A;
156.gif
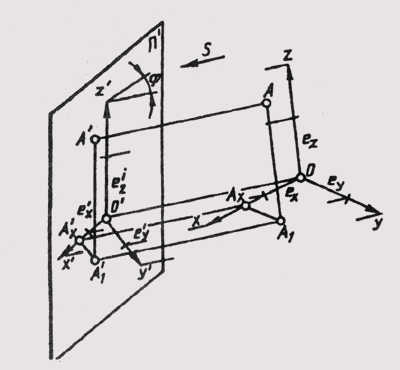
5. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
15. Чему равна большая и малая оси в изометрии и диметрии?
76. Виды аксонометрических проекций
§ 76. Виды аксонометрических проекций
Аксонометрические проекции в зависимости от направления проецирования разделяют на:
косоугольные, когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;
прямоугольные, когда направление проецирования перпендикулярно плоскости аксонометрических проекций.
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
изометрия — все три коэффициента искажения равны между собой (u = v = w);
диметрия — два коэффициента искажения равны между собой и отличаются от третьего (и не равно v = w или и= v не равно w);
триметрия — все три коэффициента искажения не равны между собой (u не равно v не равно w).
Основное предложение аксонометрии сформулировано немецким геометром К. Польке: три произвольной длины отрезка прямых, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных координатных осях от начала.
Согласно этой теореме любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси. Любые произвольной длины отрезки этих прямых, отложенные от точки их пересечения, можно принять за аксонометрические масштабы.
Эта система аксонометрических осей и масштабов является параллельной проекцией некоторой прямоугольной системы координатных
осей и натуральных масштабов, т. е. аксонометрические масштабы можно выдавать совершенно произвольно, а коэффициенты искажения при этом связаны следующим соотношением: u2 + v2 = w2 = 2 + + ctg2(p, где ф — угол между направлением проецирования и плоскостью аксонометрических проекций (рис. 156). Для прямоугольной аксонометрии, когда ф = 90°, это соотношение принимает вид и2 + v2 + w2 = 2 (1), т. е. сумма квадратов коэффициента искажения равна двум.
При прямоугольном проецировании может быть получена только одна изометрическая проекция и бесконечное множество диметрических и триметрических проекций. ГОСТ 2.317—69 предусматривает применение в инженерной графике двух прямоугольных аксонометрии: прямоугольной изометрии и прямоугольной диметрии с коэффициентами искажения и = w = 2v.
77. Прямоугольная изометрия
§ 77. Прямоугольная изометрия
Прямоугольная изометрия характеризуется тем, что коэффициенты искажения составляют 0,82. Их получают из соотношения (1).
Для прямоугольной изометрии из соотношения (1) получаем:
Зu2 = 2, или и = v - w = (2/3)1/2 = 0,82, т. е. отрезок координатной оси
длиной 100 мм в прямоугольной изометрии изобразится отрезком аксонометрической оси длиной 82 мм. При практических построениях пользоваться такими коэффициентами искажения не совсем удобно, поэтому ГОСТ 2.317—69 рекомендует пользоваться приведенными коэффициентами искажения:
и = v = w — 1.
Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т. е. масштаб изображения в прямоугольной изометрии будет МА 1,22: 1.
Аксонометрические оси в прямоугольной изометрии располагаются под углом 120° друг к другу (рис. 157). Изображение окружности в аксонометрии представляет интерес, особен-
Рис. 157
Рис. 158
Рис. 159
но окружностей, принадлежащих координатным или им параллельным плоскостям.
В общем случае окружность проецируется в эллипс, если плоскость окружности расположена под углом к плоскости проекции (см. § 43). Следовательно, аксонометрией окружности будет эллипс. Для построения прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.
В прямоугольной изометрии равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы (рис. 158).
Размеры осей эллипсов при использовании приведенных коэффициентов искажения равны: большая ось 2а= 1,22d, малая ось 2b = 0,71d, где d — диаметр изображаемой окружности.
Диаметры окружностей, параллельных координатным осям, проецируются отрезками, параллельными изометрическим осям, и изображаются равными диаметру окружности: l1=l2 =l3 = d, при этом
l1||x; l2||y; l3||z.
Эллипс, как изометрию окружности, можно построить по восьми точкам, ограничивающим его большую и малую оси и проекции диаметров, параллельных координатным осям.
В практике инженерной графики эллипс, являющийся изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим такие же
Рис. 160
оси: 2a = 1,22d и 2b = 0,71 d. На рис. 159 показано построение осей такого овала для изометрии окружности диаметра d.
Для построения аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения, нужно выделить на окружности некоторое число точек, построить аксонометрию этих точек и соединить их плавной кривой; получим искомый эллипс— аксонометрию окружности (рис. 160).
На окружности, расположенной в горизонтально проецирующей плоскости, взято 8 точек (1,2,... 8). Сама окружность отнесена к натуральной системе координат (рис. 160, а).Проводим оси эллипса прямоугольной изометрии и, используя приведенные коэффициенты искажения, строим вторичную проекцию окружности 11 1,..., 511 по координатам х и у (рис. 160, б). Достраивая аксонометрические координатные ломаные для каждой из восьми точек, получаем их изометрию (11, 21, ... 81). Соединяем плавной кривой изометрические проекции всех точек и получаем изометрию заданной окружности.
Изображение геометрических поверхностей в прямоугольной изометрии рассмотрим на примере построения стандартной прямоугольной изометрии усеченного прямого кругового конуса (рис. 161).
На комплексном чертеже изображен конус вращения, усеченный горизонтальной плоскостью уровня, расположенной на высоте z от нижнего основания, и профильной плоскостью уровня, дающей в се-
Рис. 161
чении на поверхности конуса гиперболу с вершиной в точке А. Проекции гиперболы построены по отдельным ее точкам.
Отнесем конус к натуральной системе координат Oxyz. Построим проекции натуральных осей на комплексном чертеже и отдельно их изометрическую проекцию. Построение изометрии начинаем с построения эллипсов верхнего и нижнего оснований, которые являются изометрическими проекциями окружностей оснований. Малые оси эллипсов совпадают с направлением изометрической оси ОZ (см. рис. 158). Большие оси эллипсов перпендикулярны малым. Величины эллипсов осей определяются в зависимости от величины диаметра окружности (d — нижнего основания и d1 — верхнего основания). Затем строят изометрию сечения конической поверхности профильной плоскости уровня, которая пересекает основание по прямой, отстоящей от начала координат на величину XA и параллельной оси Оу.
Изометрия точек гиперболы строится по координатам, замеряемым на комплексном чертеже, и откладываем без изменения вдоль соответствующих изометрических осей, так как приведенные коэффициенты искажения и = v = w = 1. Изометрические проекции точек гиперболы соединяем плавной кривой. Построение изображения конуса заканчивается проведением очерковых образующих касательной к эллипсам оснований. Невидимая часть эллипса нижнего основания проводится штриховой линией.
157.gif
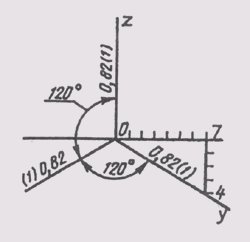
158.gif
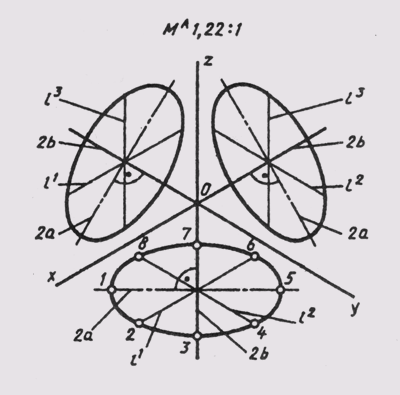
159.gif
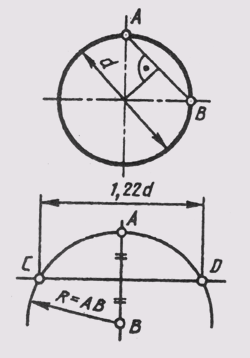
160.gif
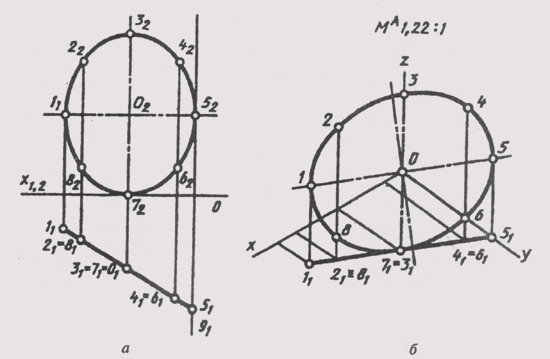
161.gif
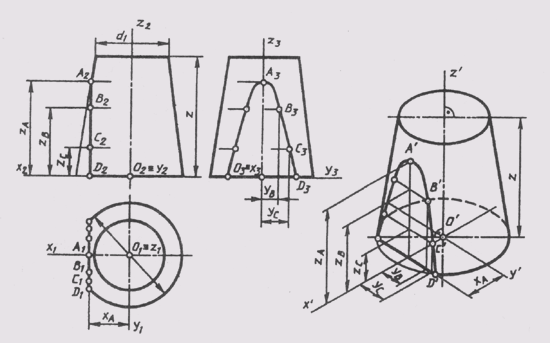
78. Прямоугольная диметрия
§ 78. Прямоугольная диметрия
Прямоугольная диметрия характеризуется тем, что коэффициенты искажения, определенные из выражения (1), и = w = 0,94, a v = 0,47. Определяют их следующим образом:
u2+(u/2)2+u2=2;
u2 =8/9; u = w = (8/9)1/2=0,94; v = 0,47.
В соответствии с ГОСТ 2.317—69 практические построения в прямоугольной диметрии следует выполнять пользуясь приведенными коэффициентами искажения: u = w=1 и v = 0,5.
Расположение осей стандартной прямоугольной диметрии показано на рис. 162. Аксонометрический масштаб для прямоугольной диметрии будет МA 1,06 : 1.
В прямоугольной диметрии равные окружности диаметра d, лежащие в координатных плоскостях хОу и уО, проецируются в равные эллипсы, большая ось которых 2а = 1,06d, а малая — 2b = 0,35d, если пользуемся приведенными коэффициентами искажения. Окружность, расположенная в плоскости xOz, проецируется в эллипс с осями: большая ось которых 2а1 = 1,066d, малая ось — 2b1 = 0,95d (рис. 163). Диаметры.окруж-
Рис. 162
Рис. 163
Рис. 164
ности, параллельные координатным осям, спроецируются в отрезки, параллельные осям диаметрии l1 = l2 = d; l = 0,5d, при этом || Ох; l2 || Оу; l3 || Oz.
Можно построить кроме указанных точек еще четыре точки, симметричные точкам, ограничивающим проекции диаметров, параллельных координатным осям. Тогда эллипс, как диметрию окружности, можно построить по его двенадцати точкам.
Изображение геометрических поверхностей в прямоугольной ди-метрии рассмотрим на примере построения стандартной прямоугольной диметрии прямого кругового цилиндра. На рис. 164 приведен пример комплексного чертежа полого цилиндра высотой Н c наружным d и внутренним d1диаметрами. Цилиндр расположим в натуральную величину в натуральной системе координат Oxyz, относительно которой построим диметрическую его проекцию. Как и в случае построения окружностей в изометрии, в диметрии также начнем построение фигуры с эллипсов верхнего и нижнего оснований цилиндра, которые являются изометрическими проекциями окружностей этих оснований. Окружности основания расположены в плоскостях, параллельных горизонтальной плоскости проекций, поэтому, пользуясь приведенными ранее правилами, определим, что большие оси эллипсов будут перпендикулярны оси Oz. Малые оси эллипсов совпадут с направлением оси Oz. Центры осей эллипсов нижнего и верхнего оснований расположены на расстоянии Я. Величины осей определяем в зависимости от величины наружного и внутреннего диаметров цилиндров. Построив эллипсы, приведем очерковые линии, касательные к внешним эллипсам.
Для наглядности построим вырез четверти цилиндра, построение которого видно из рис. 164. Направление штриховки выреза выберем, как показано на рис. 200. Невидимые линии покажем штриховыми линиями. Для наглядности такими же линиями покажем линии вырезанной части цилиндра. Видимые контурные линии наводят нужной толщиной.
162.gif
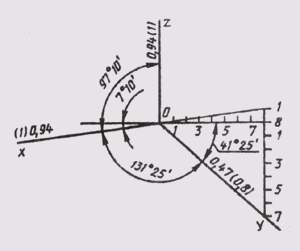
163.gif
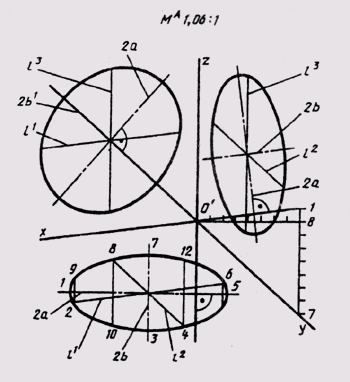
164.gif

14. Глава 13. Изображение предметов
1. Часть третья. ОСНОВЫ МАШИНОСТРОИТЕЛЬНОГО ЧЕРЧЕНИЯ
Часть третья.
ОСНОВЫ МАШИНОСТРОИТЕЛЬНОГО ЧЕРЧЕНИЯ
Глава 13. ИЗОБРАЖЕНИЕ ПРЕДМЕТОВ
§ 79. Общие сведения
Главным элементом в решении графических задач в инженерной графике является чертеж. Под чертежом подразумевают графическое изображение предметов или их частей. Чертежи выполняются в строгом соответствии с правилами проецирования с соблюдением установленных требований и условностей. Причем правила изображения предметов или их составных элементов на чертежах остаются одинаковыми вб всех отраслях промышленности и строительства.
Изображение предмета на чертеже должно быть таким, чтобы по нему можно было установить форму его в целом, форму отдельных его поверхностей, сочетание и взаимное расположение отдельных его поверхностей. Иными словами, изображение предмета должно давать полное представление о его форме, устройстве, размерах, а также о материале, из которого изготовлен предмет, а в ряде случаев включать сведения о способах изготовления предмета. Характеристикой величины предмета на чертеже и его частей являются их размеры, которые наносятся на чертеже. Изображение предметов на чертежах выполняют, как правило", в заданном масштабе.
Изображения предметов на чертеже должны быть размещены так, чтобы поле его было равномерно заполнено. Число изображений на чертеже должно быть достаточным для получения полного и однозначного представления о нем. В то же время на чертеже должно быть только необходимое количество изображений, оно должно быть минимальным, т. е. чертеж должен быть лаконичным и содержать мини-
Рис. 165
мальный объем графических изображений и текста, достаточных для свободного чтения чертежа, а также его изготовления и контроля.
Видимые контуры предметов и их граней на чертежах выполняются сплошной толстой основной линией. Необходимые невидимые части предмета выполняют при помощи штриховых линий. В случае, если изображаемый предмет имеет постоянные или закономерно изменяющиеся поперечные сечения, выполняется в требуемом масштабе и не помещается на поле чертежа заданного формата, его можно показать с разрывами.
Правила построения изображений на чертежах и оформления чертежей приведены и регламентируются комплексом стандартов «Единой системы конструкторской документации» (ЕСКД).
Изображение на чертежах может быть выполнено различными способами. Например, с помощью прямоугольного (ортогонального) проецирования, аксонометрических проекций, линейной перспективы. При выполнении машиностроительных чертежей в инженерной графике чертежи выполняют по методу прямоугольного проецирования. Правила изображения предметов, в данном случае изделий, сооружений или соответствующих составных элементов на чертежах установлены ГОСТ 2.305—68.
При построении изображений предметов методом прямоугольного проецирования предмет располагают между наблюдателем и соответствующей плоскостью проекции. За основные плоскости проекций принимают шесть граней куба, внутри которого располагается изображаемый предмет (рис. 165, а). Грани 1,2 и 3 соответствуют фронтальной, горизонтальной и профильной плоскостям проекций. Грани куба с полученными на них изображениями совмещают с плоскостью чертежа (рис. 165, б). При этом грань 6 можно расположить и рядом с гранью 4.
Изображение на фронтальной плоскости проекций (на грани 1) считается главным. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение давало наиболее полное представление о форме и размерах предмета, несло наибольшую информацию о нем. Это изображение называют главным.
В зависимости от своего содержания изображения предметов разделяют на виды, разрезы, сечения.
165.gif
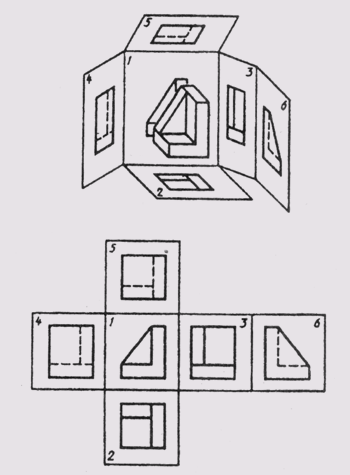
9. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
15. Можно ли на одном изображении соединить часть вида и часть разреза?
25. Какое правило выбора направления штриховки вырезов применяется на аксонометрических изображениях?
80. Построение видов на чертеже
§ 80. Построение видов на чертеже
Изображение обращенной к наблюдателю видимой части поверхности предмета называют видом.
По содержанию и характеру выполнения виды разделяются на основные, дополнительные и местные.
ГОСТ 2.305—68 устанавливает следующее название основных видов, получаемых на основных плоскостях проекций (см. рис. 165): 7 — вид спереди (главный вид); 2 — вид сверху; 3 — вид слева;
4 — вид справа; 5 — вид снизу; б — вид сзади. В практике более широко применяются три вида: вид спереди, вид сверху и вид слева.
Основные виды обычно располагаются в проекционной связи между собой. В этом случае название видов на чертеже надписывать не нужно.
Если какой-либо вид смещен относительно главного изображения, проекционная связь его с главным видом нарушена, то над этим видом выполняют надпись по типу «А» (рис. 166).
Рис. 166
Рис. 167
Рис. 168
Направление взгляда должно быть указано стрелкой, обозначенной той же прописной буквой русского алфавита, что и в надписи над видом. Соотношение размеров стрелок, указывающих направление взгляда, должно соответствовать приведенным на рис. 167.
Если виды находятся в проекционной связи между собой, но разделены какими-либо изображениями или расположены не на одном листе, то над ними также выполняют надпись по типу «А».
Дополнительный вид получается путем проецирования предмета или части его на дополнительную плоскость проекций, не параллельную основным плоскостям (рис. 168). Такое изображение необходимо выполнять в том случае, когда какая-либо часть предмета не изображена без искажения формы или размеров на основных плоскостях проекций. Дополнительная плоскость проекций в этом случае может быть расположена перпендикулярно одной из основных плоскостей проекций.
Когда дополнительный вид расположен в непосредственной проекционной связи с соответствующим основным видом, обозначать его не нужно (рис. 168, а). В остальных случаях дополнительный вид должен быть отмечен на чертеже надписью типа «А» (рис. 168, б), а у свя-
Рис. 169
занного с дополнительным видом изображения нужно поставить стрелку, указывающую направление взгляда, с соответствующим буквенным обозначением.
Дополнительный вид можно повернуть, сохраняя при этом положение, принятое для данного предмета на главном изображении. При этом к надписи нужно добавить знак (рис. 168, в).
Местным видом называется изображение отдельного, ограниченного места поверхности предмета (рис. 169).
Если местный вид расположен в непосредственной проекционной связи с соответствующими изображениями, то его не обозначают. В остальных случаях местные виды обозначаются подобно видам дополнительным, местный вид может быть ограничен линией обрыва («Б» на рис. 169).
166.gif
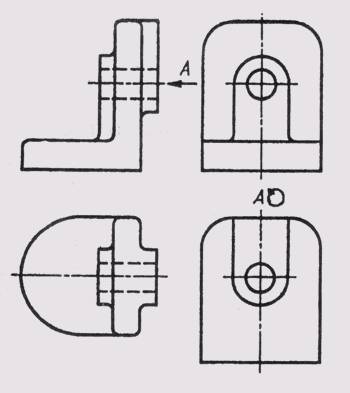
167.gif
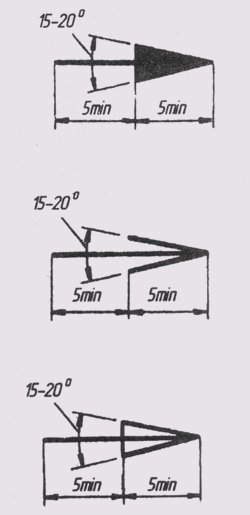
168.gif
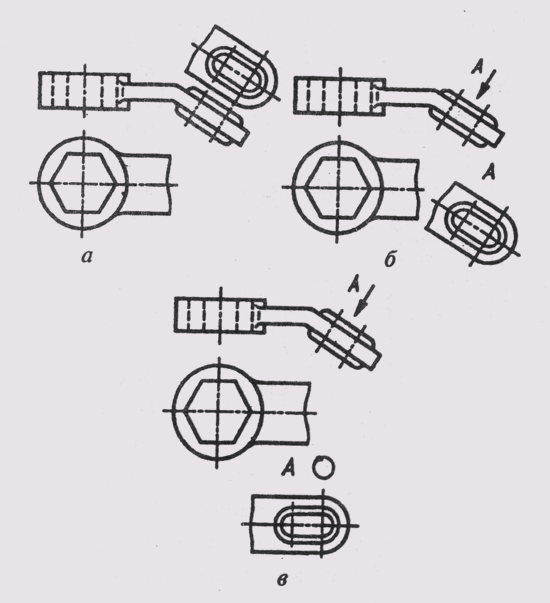
169.gif
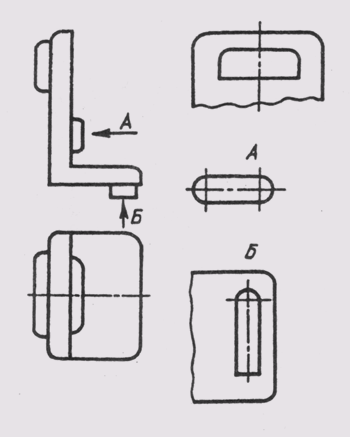
81. Построение третьего вида предмета по двум данным
§ 81. Построение третьего вида предмета по двум данным
Чтобы успешно выполнять и читать чертежи, надо научиться строить третье изображение (обычно — вид слева) предмета по двум данным его изображениям — главному виду и виду сверху, которые заданы на чертеже.
Прежде всего нужно выяснить форму отдельных частей поверхности изображенного предмета. Для этого оба заданных изображения нужно рассматривать одновременно. Полезно при этом иметь в виду, каким поверхностям соответствуют наиболее часто встречающиеся изображения: треугольник, четырехугольник, окружность, шестиугольник и т. д.
На виде сверху в форме треугольника могут изобразиться (рис. 170, а): треугольная призма 1, треугольная 2 и четырехугольная 3 пирамиды, конус вращения 4.
Рис. 170
Изображение в виде четырехугольника (квадрата) могут иметь на виде сверху (рис. 170, б): цилиндр вращения 6, треугольная призма 8, четырехугольные призмы 7 и 10, а также другие предметы, ограниченные плоскостями или цилиндрическими поверхностями 9.
Форму круга могут иметь на виде сверху (рис. 170, в): шар 11, конус 12 и цилиндр 13 вращения, другие поверхности вращения 14.
Вид сверху в форме правильного шестиугольника имеет правильная шестиугольная призма (рис. 170, г), ограничивающая поверхности гаек, болтов и других деталей.
Определив форму отдельных частей поверхности предмета, надо мысленно представить изображение их на виде слева и всего предмета в целом.
Для построения третьего вида необходимо определить, какие линии чертежа целесообразно принять за базовые для отчета размеров изображения предмета. В качестве таких линий применяют обычно осевые линии (проекции плоскостей симметрии предмета и проекции плоскостей оснований предмета). Разберем построение вида слева на примере (рис. 171): по данным главному виду и виду сверху построить вид слева изображенного предмета.
Сопоставив оба изображения, устанавливаем, что поверхность предмета включает в себя поверхности: правильной шестиугольной 1 и четырехугольной 2 призм, двух цилиндров 3 и 4 вращения и усеченного конуса 5 вращения. Предмет имеет фронтальную плоскость симметрии Ф ,которую удобно принять за базу отчета размеров по ширине отдельных частей предмета при построении его вида слева. Высоты отдельных участков предмета отсчитываются от нижнего основания предмета и контролируются горизонтальными линиями связи.
Форма многих предметов усложняется различными срезами, вырезами, пересечением со-
Рис. 172
ставляющих поверхности. Тогда предварительно нужно определить форму линий пересечения, а строить их нужно по отдельным точкам, вводя обозначения проекций точек, которые после выполнения построений могут быть удалены с чертежа.
На рис. 172 построен вид слева предмета, поверхность которого образована поверхностью вертикального цилиндра вращения, с T-образным вырезом в его верхней части и цилиндрическим отверстием с фронтально проецирующей поверхностью. В качестве базовых плоскостей взяты плоскость нижнего основания и фронтальная плоскость симметрии Ф. Изображение Г-образного выреза на виде слева построено с помощью точек контура выреза A В, С, D и Е, а линия пересечения цилиндрических поверхностей — с помощью точек К, L, М и им симметричных. При построении третьего вида учтена симметрия предмета относительно плоскости Ф.
170.gif
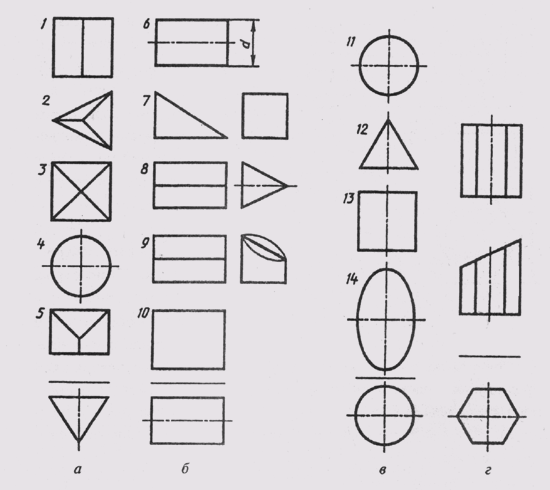
171.gif
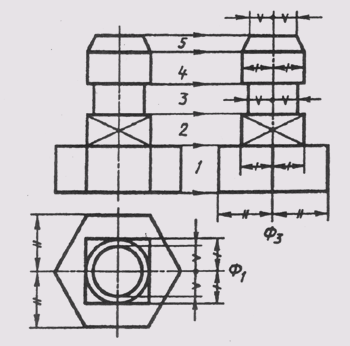
172.gif
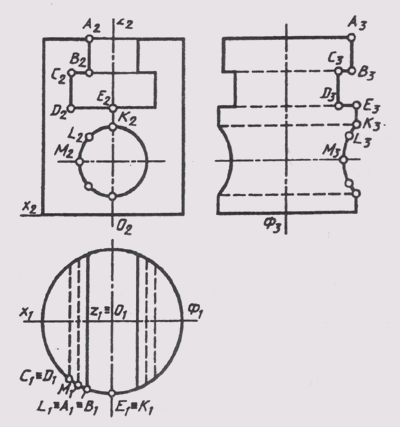
82. Выполнение разрезов на чертеже
§ 82. Выполнение разрезов на чертеже
Изображение предмета, мысленно рассеченного одной или несколькими плоскостями, называют разрезом. Мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений того же предмета. На разрезе показывают то, что получается в секущей плоскости и что расположено за ней.
Разрезы применяются для изображения внутренних поверхностей предмета, чтобы избежать большого количества штриховых линий, которые могут перекрывать друг друга при сложном внутреннем строении предмета и затруднять чтение чертежа.
Чтобы выполнить разрез, необходимо: в нужном месте предмета мысленно провести секущую плоскость (рис. 173, а); часть предмета, находящегося между наблюдателем и секущей плоскостью, мысленно отбросить (рис. 173, б), оставшуюся часть предмета проецировать на соответствующую плоскость проекций, изображение выполнить или на месте соответствующего вида, или на свободном поле чертежа (рис. 173, в); плоскую фигуру, лежащую в секущей плоскости, заштриховать; при необходимости дать обозначение разреза.
В зависимости от числа секущих плоскостей разрезы разделяются на простые — при одной секущей плоскости, сложные — при нескольких секущих плоскостях.
Рис. 173
В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций разрезы разделяются на:
горизонтальные — секущая плоскость параллельна горизонтальной плоскости проекций;
вертикальные — секущая плоскость перпендикулярна горизонтальной плоскости проекций;
наклонные — секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого.
Вертикальный разрез называют фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций, и профильным, если секущая плоскость параллельна профильной плоскости проекций.
Сложные разрезы бывают ступенчатыми, если секущие плоскости параллельны между собой, и ломаными, если секущие плоскости пересекаются между собой.
Разрезы называются продольными, если секущие плоскости направлены вдоль длины или высоты предмета, или поперечными, если секущие плоскости направлены перпендикулярно длине или высоте предмета.
Местные разрезы служат для выявления внутреннего строения предмета в отдельном ограниченном месте. Местный разрез выделяется на виде сплошной волнистой тонкой линией.
Правилами предусмотрено обозначение разрезов.
Рис. 174
Рис. 175
Положение секущей плоскости указывают разомкнутой линией сечения. Начальные и конечные штрихи линии сечения не должны пересекать контур соответствующего изображения. На начальном и конечном штрихах нужно ставить стрелки, указывающие направление взгляда (рис. 174). Стрелки должны наноситься на расстоянии 2...3 мм от внешнего конца штриха. При сложном разрезе штрихи разомкнутой линии сечения проводят также у перегибов линии сечения.
Около стрелок, указывающих направление взгляда с внешней стороны угла, образованного стрелкой и штрихом линии сечения, на горизонтальной строке наносят прописные буквы русского алфавита (рис. 174). Буквенные обозначения присваиваются в алфавитном порядке без повторений и без пропусков, за исключением букв И, О, X, Ъ, Ы, Ь.
Сам разрез должен быть отмечен надписью по типа «А — А» (всегда двумя буквами, через тире).
Если секущая плоскость совпадает с плоскостью симметрии предмета, а разрез выполнен на месте соответствующего вида в проекционной связи и не разделен каким-либо другим изображением, то для горизонтальных, вертикальных и профильных разрезов отмечать положение секущей плоскости не нужно и разрез надписью не сопровождать. На рис. 173 фронтальный разрез не обозначен.
Простые наклонные разрезы и сложные разрезы обозначают всегда.
Рассмотрим характерные примеры построения и обозначения разрезов на чертежах.
На рис. 175 выполнен горизонтальный разрез «А — А» на месте вида сверху. Плоская фигура, лежащая в секущей плоскости,— фигура сечения — заштрихована, а видимые поверхности, расположенные
Рис. 176
Рис. 177
под секущей плоскостью, ограничены контурными линиями и не заштрихованы.
На рис. 176 выполнен профильный разрез на месте вида слева в проекционной связи с главным видом. Секущая плоскость является профильной плоскостью симметрии предмета, поэтому разрез не обозначается.
На рис. 177 выполнен вертикальный разрез «А — А», полученный секущей плоскостью, не параллельной ни фронтальной, ни профильной плоскостям проекций. Такие разрезы можно строить в соответствии с направлением, указанным стрелками (рис. 177), или располагать в любом удобном месте чертежа, а также с поворотом до положения, соответствующего принятому для данного предмета на главном изображении. В этом случае в обозначение разреза добавляется знак O.
Наклонный разрез выполнен на рис. 178. Его можно вычерчивать в
Рис. 178
проекционной связи в соответствии с направлением, указанным стрелками (рис. 178, а), или располагать в любом месте чертежа (рис. 178, б).
На этом же рисунке на главном виде выполнен местный разрез, показывающий сквозные цилиндрические отверстия на основании детали.
Рис. 179
Рис. 180
На рис. 179 на месте главного вида вычерчен сложный фронтальный ступенчатый разрез, выполненный тремя фронтальными параллельными плоскостями. При выполнении ступенчатого разреза все параллельные секущие плоскости мысленно совмещаются в одну, т. е. сложный разрез оформляется как простой. На сложном разрезе переход от одной секущей плоскости к другой не отражается.
При построении ломаных разрезов (рис. 180) одну секущую плоскость располагают параллельно какой-либо основной плоскости проекций, а вторую секущую плоскость поворачивают до совмещения с
Рис. 181
Рис. 182
первой. Вместе с секущей плоскостью поворачивают и расположенную в ней фигуру сечения и разрез выполняют в повернутом положении фигуры сечения.
Соединение части вида с частью разреза в одном изображении предмета согласно ГОСТ 2.305—68 допускается. При этом границей между видом и разрезом служит сплошная волнистая линия или тонкая линия с изломом (рис. 181).
Если соединяются половина вида и половина разреза, каждый из которых является фигурой симметричной, то разделяющей их линией служит ось симметрии. На рис. 182 выполнены четыре изображения детали, причем на каждом из них половина вида соединена с половиной соответствующего разреза. На главном виде и виде слева разрез располагают справа от вертикальной оси симметрии, а на видах сверху и снизу — справа от вертикальной или снизу от горизонтальной оси симметрии.
Рис. 183
Рис. 184
Если контурная линия предмета совпадает с осью симметрии (рис. 183), то границу между видом и разрезом указывают волнистой линией, которую проводят так, чтобы сохранить изображение ребра.
Штриховка фигуры сечения, входящей в разрез, должна выполняться согласно ГОСТ 2.306—68. Цветные, черные металлы и их сплавы обозначают в сечении штриховкой сплошными тонкими линиями толщиной от S/3 до S/2, которые проводят параллельно между собой под углом 45° к линиям рамки чертежа (рис. 184, а). Линии штриховки можно наносить с наклоном влево или вправо, но в одну и ту же сторону на всех изображениях одной и той же детали. Если линии штриховки проведены под углом 45° к линиям рамки чертежа, то можно располагать линии штриховки под углом 30° или 60° (рис. 184, б). Расстояние между параллельными линиями штриховки выбирают в пределах от 1 до 10 мм в зависимости от площади штриховки и необходимости разнообразить штриховку.
Неметаллические материалы (пластмассы, резина и др.) обозначаются штриховкой пересекающимися взаимно перпендикулярными линиями (штриховка «в клетку»), наклонными под углом 45° к линиям рамки (рис. 184, в).
Рассмотрим пример. Выполнив фронтальный разрез, половину профильного разреза соединим с половиной вида слева предмета, заданного на рис. 185, а.
Анализируя данное изображение предмета, приходим к выводу, что предмет представляет собой цилиндр с двумя сквозными призматическими горизонтальными и двумя вертикальными внутренними
Рис. 185
отверстиями, из которых одно имеет поверхность правильной шестиугольной призмы, а второе — цилиндрическую поверхность. Нижнее призматическое отверстие пересекает поверхность наружного и внутреннего цилиндра, а верхнее четырехгранное призматическое отверстие пересекает наружную поверхность цилиндра и внутреннюю поверхность шестигранного призматического отверстия.
Фронтальный разрез предмета (рис. 185, б) выполняется фронтальной плоскостью симметрии предмета и вычерчен на месте главного вида, а профильный разрез — профильной плоскостью симметрией предмета, поэтому ни тот, ни другой обозначать не нужно. Вид слева и профильный разрез представляют собой симметричные фигуры, их половины можно было бы разграничить осью симметрии, если бы не изображение ребра шестигранного отверстия, совпадающего с осевой линией. Поэтому отделяем часть вида слева от профильного разреза волнистой линией, изображая большую часть разреза.
173.gif
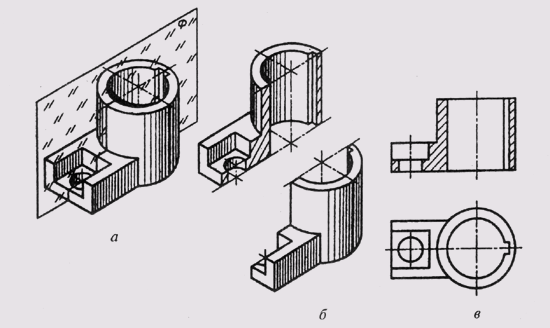
174.gif
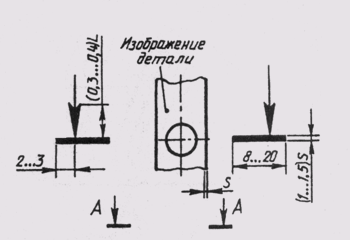
175.gif
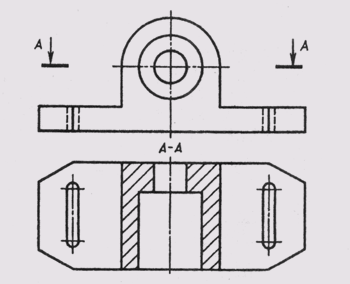
176.gif
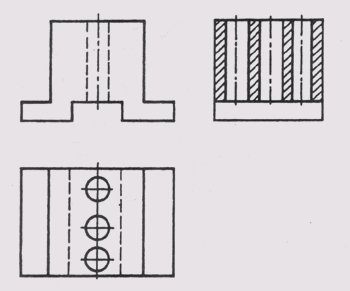
177.gif

178.gif
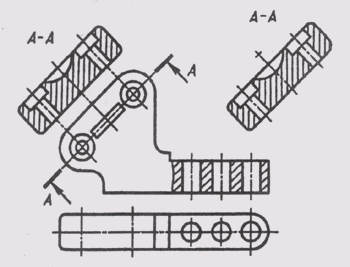
179.gif
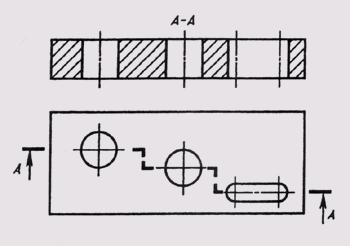
180.gif
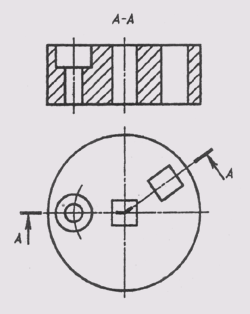
181.gif
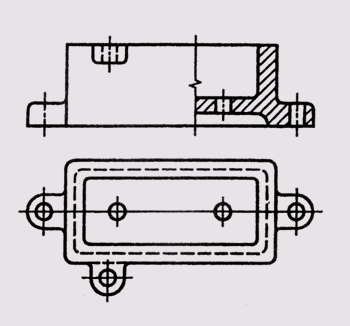
182.gif
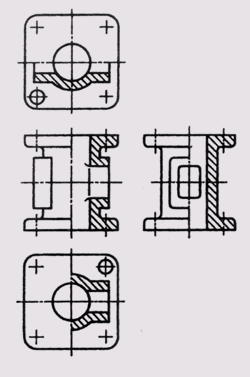
183.gif
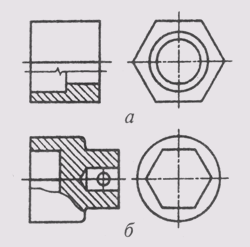
184.gif
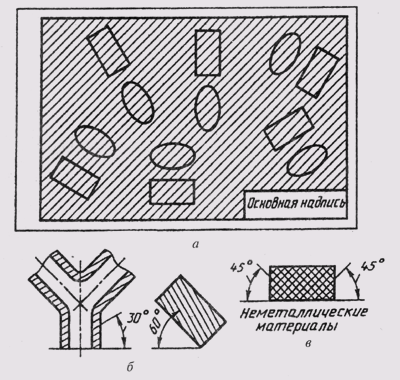
185.gif
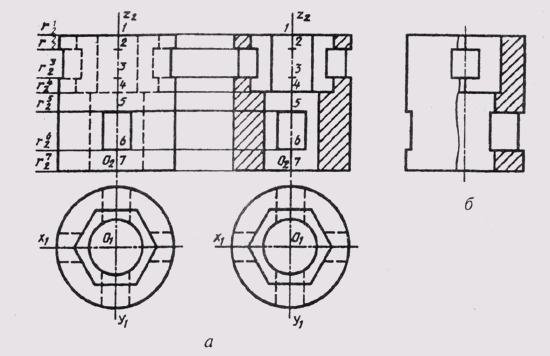
83. Выполнение сечений на чертеже
§ 83. Выполнение сечений на чертеже
Изображение фигуры, получаемой при мысленном рассечении одной или несколькими плоскостями, при условии показа на чертеже только того, что попало в секущую плоскость, называется сечением. Сечение отличается от разреза тем, что на нем изображают только то, что непосредственно попадает в секущую плоскость (рис. 186, а). Сечение, как и разрез,— изображение условное, так как фигура сечения отдельно от предмета не существует: ее мысленно отрывают и изображают на свободном поле чертежа. Сечения входят в состав разреза и существуют как самостоятельные изображения.
Сеченик, не входящие в состав разреза, разделяют на вынесенные (рис. 186, б) и наложенные (рис. 187, а). Предпочтение следует отдать сечениям вынесенным, которые можно располагать в разрезе между частями одного и того же изображения (рис. 187, б).
По форме сечения делят на симметричные (рис. 187, а, б) и несимметричные (рис. 186, б).
Контур вынесенного сечения вычерчивают сплошными
Рис. 186
Рис. 187
Рис. 188
Рис. 189
основными линиями, а наложенного — сплошными тонкими, причем контур основного изображения в месте расположения наложенного сечения не прерывают.
Обозначение сечений в общем случае аналогично обозначению разрезов, т. е. положение секущей плоскости отображают линии сечения, на которых наносят стрелки, дающие направление взгляда и обозначаемые одинаковыми прописными буквами русского алфавита. Над сечением в этом случае выполняют надпись по типу «А — А» (см. рис. 186, б).
Для несимметричных наложенных сечений или выполненных в разрыве основного изображения, линию сечения со стрелками проводят, но буквами не обозначают (рис. 188, а, б). Наложенное симметричное сечение (см. рис. 187, а), симметричное сечение, выполненное в разрыве основного изображения (см. рис. 187, б), вынесенное симметричное сечение, выполненное по следу секущей плоскости (см. рис. 186, а), оформляют без нанесения линии сечения.
Рис. 190
Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, то контур отверстия или углубления вычерчивают полностью (рис. 189, а).
Если секущая плоскость проходит через сквозное некруглое отверстие и сечение получается состоящим из отдельных самостоятельных частей, то следует применять разрезы (рис. 189, б).
Наклонные сечения получаются от пересечения предмета наклонной плоскостью, составляющей с горизонтальной плоскостью проекций угол, отличный от прямого. На чертеже наклонные сечения выполняют по типу вынесенных сечений. Наклонное сечение предмета нужно строить как совокупность наклонных сечений составляющих его геометрических тел. Построение наклонных сечений основано на применении способа замены плоскостей проекций (см. §§ 36, 58).
При вычерчивании наклонного сечения нужно определить, какие поверхности, ограничивающие предмет, рассекаются секущей плоскостью, и какие линии получаются от пересечения этих поверхностей данной секущей плоскостью (см. § 64). На рис. 190 построено наклонное сечение «А — А». Секущая плоскость пересекает основание предмета по трапеции, внутреннюю и наружную цилиндрические поверхности — по эллипсам, центры которых лежат на основной вертикальной оси предмета. Чтение формы наклонного сечения упрощается, если построить горизонтальную проекцию наклонного сечения как наложенное сечение.
186.gif
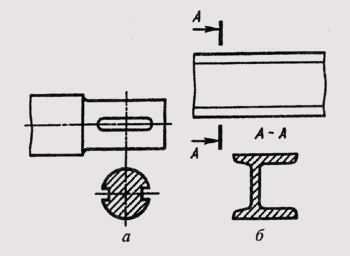
187.gif
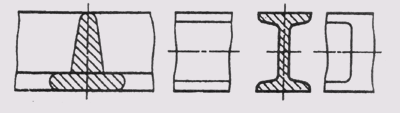
188.gif
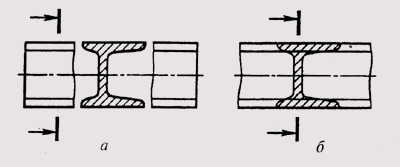
188.gif
190.gif
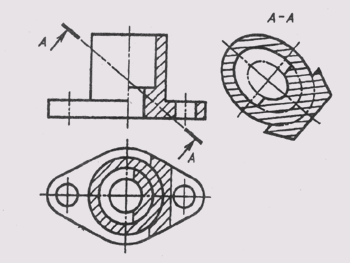
84. Выносные элементы
§ 84. Выносные элементы
При выполнении чертежей в некоторых случаях появляется необходимость в построении дополнительного отдельного изображения какой-либо части предмета, требующей пояснений в отношении формы, размеров или других данных. Такое изображение называется выносным элементом. Его выполняют обычно увеличенным. Выносной элемент может быть выложен как вид или как разрез.
Рис. 191
При построении выносного элемента соответствующее место основного изображения отмечают замкнутой сплошной тонкой линией, обычно овалом или окружностью, и обозначают заглавной буквой русского алфавита на полке линии-выноски. У выносного элемента делается запись по типу А (5 : 1). На рис. 191 приведен пример выполнения выносного элемента. Его располагают возможно ближе к соответствующему месту на изображении предмета.
191.gif
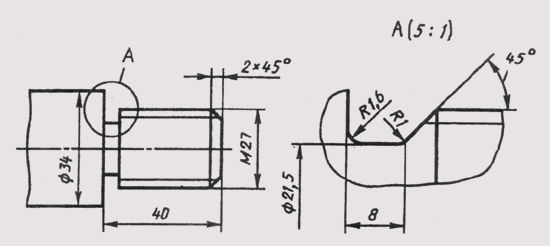
85. Условности и упрощения при изображении предмета
§ 85. Условности и упрощения при изображении предмета
При выполнении различных изображений предмета ГОСТ 2.305—68 рекомендует применять некоторые условности и упрощения, которые, сохраняя ясность и наглядность изображения, сокращают объем графических работ.
Если вид, разрез или сечение являются фигурами симметричными, то можно вычерчивать только половину изображения или немного более половины изображения, ограничивая его волнистой линией (рис. 192).
Допускается упрощение изображать линии среза и линии перехода (см. § 67); вместо лекальных кривых проводят дуги окружности и прямые линии (рис. 193, а), а плавный переход от одной поверхности к другой показывать условно (рис. 193, б) или совсем не показывать (рис. 193, в).
Рис. 192
Рис. 193
Рис. 194
Допускается незначительную конусность или уклон изображать увеличенным. На тех изображениях, где уклон или конусность отчетливо не выявляется, проводят только одну линию, соответствующую меньшему размеру элемента с уклоном (рис. 194, а) или меньшему основанию конуса (рис. 194, б).
При выполнении разрезов показывают нерассеченными непустотелые валы, рукоятки, винты, шпонки, заклепки. Шарики всегда изображают нерассеченными.
Такие элементы, как спицы, тонкие стенки, ребра жесткости, показывают в разрезе незаштрихованными, если секущая плоскость направлена вдоль оси или длинной стороны такого элемента (рис. 195). Если в подобных элементах имеется отверстие или углубление, то делают местный разрез (рис. 196, а).
Отверстия, расположенные на круглом фланце и не попадающие в секущую плоскость, показывают в разрезе так, словно они находятся в секущей плоскости (рис. 196, б).
Рис. 195
Рис. 196
Для сокращения количества изображений допускается часть предмета, расположенную между наблюдателем и секущей плоскостью, изображать штрихпунктирной утолщенной линией (рис. 197).
Более подробно правила изображения предметов изложены в ГОСТ 2.305—68.
Рис. 197
192.gif
193.gif
194.gif
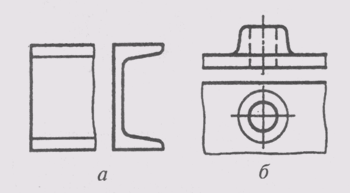
195.gif

196.gif
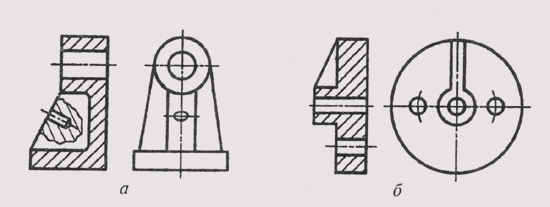
197.gif
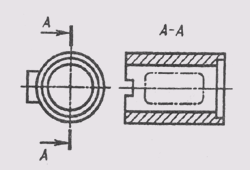
86. Построение наглядного изображения предмета
§ 86. Построение наглядного изображения предмета
Для построения наглядного изображения предмета воспользуемся аксонометрическими проекциями (гл. 12). Выполнить его можно по его комплексному чертежу. Воспользовавшись рис. 172, построим
стандартную прямоугольную изометрию изображенного на нем предмета. Воспользуемся приведенными коэффициентами искажения. Примем расположение начала координат (точка О) — в центре нижнего основания предмета (рис. 198). Вычертив оси изометрии и установив масштаб изображения (МА 1,22 : 1), отмечаем центры окружностей верхнего и нижнего оснований цилиндра, а также окружностей, ограничивающих Т-образный вырез. Вычерчиваем эллипсы, являющиеся изометрией окружностей (см. § 77). Затем проводим линии, параллельные координатным осям, которые ограничивают вырез в цилиндре. Изометрию линии пересечения сквозного цилиндрического отверстия, ось которого
Рис. 198
Рис. 199
параллельна оси Оу с поверхностью основного цилиндра, строим по отдельным точкам, используя те же точки (К, L, М и им симметричные), что и при построении вида слева. Затем удаляем вспомогательные линии и обводим окончательно изображение с учетом видимости отдельных частей предмета.
Для построения аксонометрического изображения предмета с учетом разреза воспользуемся условиями задачи, решение которой отражено на рис. 185, а. На заданном чертеже для построения наглядного изображения отметим положение проекций координатных осей и на сои Oz отметим центры 1,2,..., 7 фигур предмета, расположенных в горизонтальных плоскостях Г1', Т"2, ...,Г7', это верхнее и нижнее основания предмета, основания внутренних отверстий. Для передачи внутренних форм предмета выполним вырез1/4 части предмета координатными плоскостями xOz и yOz.
Рис. 200
Плоские фигуры, получаемые при этом, уже построены на комплексном чертеже, так как они являются половинами фронтального и профильного разреза предметов (рис. 185, б).
Построение наглядного изображения начинаем с проведения осей диметрии и указания масштаба МА 1,06 : 1 (см. § 78). На оси z отмечаем положение центров 1, 2,..., 7 (рис. 199, а); расстояния между ними берем с главного вида предмета. Через отмеченные точки проводим оси диметрии. Затем строим в диметрии фигуры сечения сначала в плоскости xOz, а затем в плоскости yOz. Размеры координатных отрезков берем с комплексного чертежа (рис. 185); при этом размеры по оси у сокращаем в два раза. Выполняем штриховку сечений. Угол наклона линий штриховки в аксонометрии определяется диагоналями параллелограммов, построенных на аксонометрических осях с учетом коэффициентов искажения. На рис. 200, а приведен пример выбора направления штриховки в изометрии, а на рис. 200, б — в диметрии. Далее строим эллипсы — диметрию окружностей, расположенных в горизонтальных плоскостях (см. рис. 199, б). Проводим контурные линии наружного цилиндра, внутренних вертикальных отверстий, строим основание этих отверстий (рис. 199, в); вычерчиваем видимые линии пересечения горизонтальных отверстий с наружной и внутренними поверхностями.
Затем удаляем вспомогательные линии построения, проверяем правильность выполнения чертежа и обводим чертеж линиями требуемой толщины (рис. 199, г).
198.gif
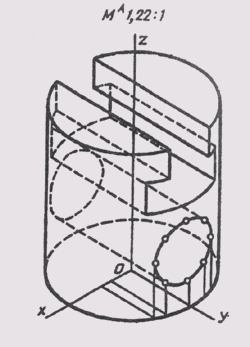
199.gif
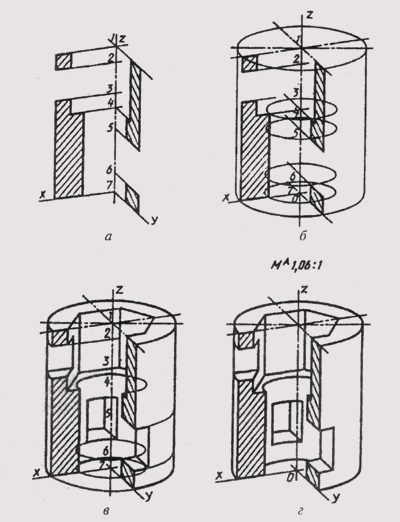
200.gif
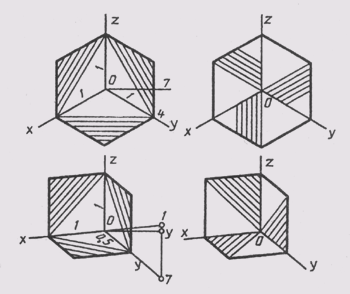
15. Глава 14. Изображение соединений деталей
1. Глава 14. Изображение соединений деталей
Глава 14. ИЗОБРАЖЕНИЕ СОЕДИНЕНИЙ ДЕТАЛЕЙ
§ 87. Общие сведения
Изготовляемые промышленностью машины, станки, приборы и аппараты состоят из различных определенным образом объединенных и взаимосвязанных деталей; которые соединяются между собой различными способами. Соединение деталей обеспечивает их определенное взаимное положение в процессе работы.
Различают разъемные и неразъемные соединения деталей. К разъемным относят соединения, допускающие разборку и повторную сборку соединяемых деталей без разрушения и повреждения. К ним относятся, например, соединения, выполняемые с помощью болта с гайкой.
К неразъемным относят соединения деталей с жесткой механической связью, сохраняющейся в течение всего срока их службы. Разборка таких соединений невозможна без разрушений или повреждений самих деталей или связывающих их элементов. К неразъемным можно отнести, например, соединения деталей сваркой, заклепками, пайкой.
В свою очередь, разъемные соединения делятся на подвижные, допускающие перемещение одной детали относительно другой, и неподвижные, в которых детали не могут перемещаться одна относительно другой. Примером подвижного соединения деталей может быть соединение подвижной гайки с винтом суппорта токарного станка, а неподвижного — соединение деталей при помощи винта.
Выделяют также группы специальных соединений, к которым относятся соединения деталей в передачах у машин, например соединения зубчатых колес. Сюда же относят соединения деталей с помощью пружин, когда после снятия нагрузки детали надо вернуть в исходное положение.
При выполнении на чертежах соединений деталей используют их полные, упрощенные или условные изображения. Иногда (например при обозначении сварки, пайки и др.) применяют дополнительные условные обозначения.
5. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
27. Какие условности применяются при вычерчивании пружин?
88. Разъемные соединения
§ 88. Разъемные соединения
В настоящее время в машиностроении широкое распространение получили разъемные соединения: резьбовые, зубчатые (шлицевые), шпоночные, штифтовые, шплинтовые, клиновые, соединения сочленением.
Большое распространение в современном машиностроении получили разъемные соединения деталей машин, осуществляемые с помощью резьбы. Резьбовое соединение может обеспечивать относительную неподвижность деталей или перемещение одной детали относительно другой. Основным соединяющим элементом в резьбовом соединении является резьба.
Резьбой называется поверхность, образованная при винтовом движении плоского контура по цилиндрической или конической поверхности. При этом образуется винтовой выступ соответствующего профиля, ограниченный винтовыми и цилиндрическими или коническими поверхностями (рис. 201, а).
Рис. 201
Рис. 202
Резьбы классифицируются по форме поверхности, на которой она нарезана (цилиндрические, конические), по расположению резьбы на поверхности стержня или отверстия (наружные, внутренние), по форме профиля (треугольная, прямоугольная, трапецеидальная, круглая), назначению (крепежные, крепежно-уплотнительные, ходовые, специальные и др.), направлению винтовой поверхности (левые и правые) и по числу заходов (однозаходные и многозаходные).
Все резьбы делятся на две группы: стандартные и нестандартные; у стандартных резьб все их параметры определяются стандартами.
Основные параметры резьбы определены ГОСТ 11708—82. Резьбу характеризуют три диаметра: наружный d (D), внутренний d1(D1) и средний d2(D2).
Диаметры наружной резьбы обозначают d, d\, d2, а внутренней резьбы в отверстии — D, D1 и D2.
Наружный диаметр резьбы d (D) — диаметр воображаемого цилиндра, описанного вокруг вершин наружной или впадин внутренней резьбы. Этот диаметр для большинства резьб является определяющим и входит в условное обозначение резьбы.
Рис. 203
Профиль резьбы — контур сечения резьбы плоскостью, проходящей через ее ось (рис. 201, 202).
Угол профиля резьбы — угол между боковыми сторонами профиля (рис. 202).
Шаг резьбы Р — расстояние между соседними одноименными боковыми сторонами профиля в направлении параллельной оси резьбы (рис. 201).
Ход резьбы t— расстояние между ближайшими одноименными боковыми сторонами профиля, принадлежащего одной и той же винтовой поверхности, в направлении, параллельном оси резьбы (рис. 201). В однозаходной резьбе (рис. 201, а) ход равен шагу, а в многозаходной (рис. 201,б) — произведению шага Р на число заходов n(t = лР).
На рис. 203, а — длина резьбы l, длина резьбы с полным профилем l1.
Сбег резьбы — участок неполного профиля в зоне перехода резьбы в главную часть предмета lз.
Недовод резьбы l4 — величина ненарезанной части поверхности между концами сбега и опорной поверхностью детали.
Недорез резьбы /2 включает в себя сбег и недовод резьбы. Чтобы устранить сбег или недорез резьбы, выполняют проточку b (рис. 203, б).
Чтобы облегчить ввинчивание резьбового стержня, на конце резьбы выполняют коническую фаску с под углом 45° (рис. 203, б).
Рассмотрим стандартные резьбы общего назначения.
Резьба метрическая является основной крепежной резьбой. Это резьба однозаходная, преимущественно правая, с крупным или мелким шагом. Профилем метрической резьбы служит равносторонний треугольник. Выступы и выпадины резьбы притуплены (рис. 204) (ГОСТ 9150—81).
Резьба трубная цилиндрическая имеет профиль в виде равнобедренного треугольника с углом при вершине 55° (рис. 205), вершины и впадины скруглены. Эту резьбу применяют в трубопроводах и трубных соединениях (ГОСТ 6351—81).
Рис. 204
Рис. 205
Рис. 206
Рис. 207
Резьба трапецеидальная служит для передачи движения и усилий. Профиль трапецеидальной резьбы — равнобокая трапеция с углом между боковыми сторонами 30° (рис. 206). Для каждого диаметра резьба может быть однозаходной и многозаходной, правой и левой (ГОСТ 9484—81).
Резьба упорная имеет профиль неравнобокой трапеции (рис. 207). Впадины профиля закруглены, для каждого диаметра имеется три различных шага. Служит для передачи движения с большими осевыми нагрузками (ГОСТ. 10177—82).
Резьба круглая для цоколей и патронов, для предохранительных стекол и светильников, для санитарно-технической арматуры (ГОСТ 13536—68) имеет профиль, полученный сопряжением двух дуг одного радиуса (рис. 208) (ГОСТ 13536—68).
Резьба коническая дюймовая с углом профиля 60° (ГОСТ 6111—52) применяется для герметических соединений в трубопроводах машин и станков; нарезается на конической поверхности с конусностью 1 : 16 (рис. 209).
Рис. 208
Рис. 209
Резьба трубная коническая имеет профиль, аналогичный профилю резьбы трубной цилиндрической; применяется в вентилях и газовых баллонах. Возможно соединение труб, имеющих коническую резьбу (конусность 1 : 16), с изделиями, имеющими трубную цилиндрическую резьбу (ГОСТ 6211—81).
Специальные резьбы — это резьбы со стандартным профилем, но отличающиеся от стандартных размеров диаметра или шага резьбы, и резьбы с нестандартным профилем.
Нестандартные резьбы — квадратная и прямоугольная (рис. 210) — изготовляются по индивидуальным чертежам, на которых заданы все параметры резьбы.
Изображение резьбы на чертеже выполняется по ГОСТ 2.311—68. На стержне резьбу изображают сплошными основными линиями по наружному диаметру и сплошными тонкими линиями — по внутреннему диаметру. На рис. 211, а показана резьба на цилиндре, а на рис. 211, б — на конусе.
Рис. 210
Рис. 211
Рис. 212
В отверстии резьбу изображают сплошными основными линиями по внутреннему диаметру и сплошными тонкими линиями — по наружному диаметру. На рис. 212, а резьба показана в отверстии цилиндрическом, а на рис. 212, б — в коническом.
На изображениях, полученных проецированием резьбовой поверхности на плоскость, перпендикулярную ее оси, сплошную тонкую линию проводят дугой на 3/4 длины окружности, разомкнутую в любом месте, но не заканчивающуюся на осях. Сплошную тонкую линию при изображении резьбы проводят на расстоянии не менее 0,8 мм от основной линии и не более величины шага резьбы. Видимая граница резьбы проводится сплошной основной линией в конце полного профиля резьбы до линии наружного диаметра резьбы. Сбег резьбы изображается сплошной тонкой линией, как показано на рис. 213.
Фаски на резьбовом стержне или в резьбовом отверстии, не имеющие специального конструктивного назначения, не изображаются в проекции на плоскость, перпендикулярную оси стержня или отверстия. Сплошная тонкая линия изображения резьбы должна пересекать линию границы фаски (рис. 213, 214). Штриховку в разрезах и сечениях доводят до сплошной основной линии.
Рис. 213
Рис. 214
Рис. 215
Резьбу с нестандартным профилем изображают, как показано на рис. 215, со всеми размерами и дополнительными данными с добавлением слова «резьба».
В резьбовых соединениях резьба условно вычерчивается на стержне, а в отверстии — только та часть резьбы, которая не закрыта стержнем (рис. 216).
Обозначение резьбы включает в себя: вид резьбы, размер, шаг и ход резьбы, поле допуска, класс точности, направление резьбы, номер стандарта.
Вид резьбы условно обозначается:
М — метрическая резьба (ГОСТ 9150—81);
G — трубная цилиндрическая резьба (ГОСТ 6357—81);
Тг — трапецеидальная резьба (ГОСТ 9484—81);
S —упорная резьба (ГОСТ 10177—82);
Rd —круглая резьба (ГОСТ 13536—68);
R — трубная коническая наружная (ГОСТ 6211—81);
Rr — внутренняя коническая (ГОСТ 6211—81);
Rp — внутренняя цилиндрическая (ГОСТ 6211—81);
К — коническая дюймовая резьба (ГОСТ 6111—52).
Размер конических резьб и трубной цилиндрической резьбы условно обозначается в дюймах (1" = 25,4 мм), у всех остальных резьб наружный диаметр резьбы проставляется в миллиметрах.
Шаг резьбы не указывают для метрической резьбы с крупным шагом и для дюймовых
Рис. 216
Рис. 217
резьб, в остальных случаях он указывается. Для многозаходных резьб в обозначение резьбы входит ход резьбы, а шаг проставляется в скобках.
Направление резьбы указывают только для левой резьбы (LH).
Поле допуска и класс точности резьбы на учебных чертежах можно не проставлять.
Примеры обозначения резьб:
М 30 — метрическая резьба с наружным диаметром 30 мм и крупным шагом резьбы;
М 30 х 1,5 — метрическая резьба с наружным диаметром 30 мм, мелким шагом 1,5 мм;
G 1 1/2-A— трубная цилиндрическая резьба с размером 1 1/2", класс точности А;
Тг 40x6 — трапецеидальная резьба однозаходная с наружным диаметром 40 мм и шагом 6 мм;
Тг 20 х 8 (Р4) — трапецеидальная резьба двухзаходная с наружным диаметром 20 мм, ходом 8 мм и шагом 4 мм;
S 80 х 10 — упорная резьба однозаходная с наружным диаметром 80 мм и шагом 10 мм;
S 80 х 20 (Р10) — упорная резьба двухзаходная с наружным диаметром 80 мм, ходом 20 мм и шагом 10 мм;
Rdl6 — резьба круговая с наружным диаметром 16 мм;
Rdil6LH— резьба круглая с диаметром 16 мм, левая;
R 1 1/2— резьба трубная коническая с размером 1 1/2".
К 1 1/2 ГОСТ 6111—52 — резьба коническая дюймовая с размером 1 1/2".
Обозначения резьб согласно ГОСТ 2.311—68 относят к наружному диаметру, как показано на .рис. 217.
Рис. 218
Обозначение конических резьб и трубной цилиндрической резьбы наносят, как показано на рис. 218, а, б, в.
Соединение деталей осуществляют с помощью резьбовых изделий.
К стандартным резьбовым изделиям относятся крепежные резьбовые детали (болты, винты, гайки, шпильки). Техническими требованиями установлены 12 классов точности для винтов, болтов и шпилек и 7 классов точности — для гаек. Установлены также виды и условное обозначение покрытий для крепежных изделий.
Структура условных обозначений крепежных деталей включает в себя:
7 — наименование изделия (болт, винт, и т. д.);
2 — исполнение (исполнение I не указывают);
3 — обозначение резьбы метрической и ее диаметра;
4 — шаг резьбы (для мелкой метрической);
5 — обозначения поля допуска резьбы;
6—длину болта, винта, шпильки в мм; 7—класс точности;
8 — марку стали или сплава;
9 — обозначение вида покрытия;
10 — толщину покрытия в мм;
11 — номер стандарта на конструкции крепежного изделия и его размеры.
На учебных чертежах позиции 5, 7, 8, 9, 10 в курсе инженерной графики можно не включать в условие обозначение изделия, так как назначать обоснованно эти параметры без специальных знаний нельзя.
Болт представляет собой цилиндрический стержень с головкой на одном конце и резьбой на другом конце. Болты используются (вместе с гайками, шайбами) для скрепления двух или нескольких деталей. Существуют различные типы болтов, отличающиеся друг от друга по форме и размерам головки и стержня, по шагу резьбы, по точности изготовления и по исполнению.
Рис. 219
Рис. 220
Болты с шестигранными головками имеют от трех (рис. 219) до пяти исполнений: исполнение 1 — без отверстий (в головке и стержне); исполнение 2 — с отверстием на резьбовой части стержня; исполнение 3 — с двумя отверстиями в головке болта.
При изображении болта на чертеже выполняют два вида (рис. 220) по общим правилам и наносят размеры длины l болта, длины резьбы /о, размер под ключ S и обозначение резьбы Md. Высота H головки в длину болта не включается. Гиперболы, образованные пересечением конической фаски головки болта с ее гранями, заменяются другими окружностями.
Примеры условных обозначений болтов:
Болт Ml2 х 60 ГОСТ 7798—70 — с шестигранной головкой, первого исполнения, с резьбой М12, шаг резьбы крупный, длина болта 60 мм.
Болт 2М12 х 1,25 х 60 ГОСТ 7798—70 — с мелкой метрической резьбой М12х1,25, второго исполнения, длина болта 60 мм.
Винт представляет собой цилиндрический стержень, на одном конце которого выполнена резьба, на другом конце имеется головка. По назначению винты разделяются на крепежные и установочные. Крепежи винтов применяются для соединения деталей путем ввертывания винта резьбовой частью в одну из соединяемых деталей.
Установочные винты используются для взаимного фиксирования деталей. Их стержень нарезан полностью, они имеют нажимной конец цилиндрической или конической формы или плоский конец (рис. 221).
Крепежные винты бывают четырех исполнений; исполнение 1 — диаметр резьбы больше диаметра гладкой части стержня (рис. 222); исполнение 2 — диаметр резьбы равен диаметру гладкой части; исполнение 3 и головка винта имеет крестообразный шлиц для отвертки.
Рис. 221
Рис. 222
В зависимости от условий работы винты изготовляются (рис. 223) с цилиндрической головкой (ГОСТ 1491—80), полукруглой головкой (ГОСТ 17473—80), полупотайной головкой (ГОСТ 17474—80) или потайной головкой (ГОСТ 17475—80) со шлицем, а также с головкой под ключ и с рифлением.
Высота головки в длину винта не входит, исключение составляют винты с потайной головкой (рис. 223).
На чертеже форму винта со шлицем полностью передает одно изображение на плоскости, параллель оси винта. При этом указывают размер резьбы, длину винта, длину нарезанной части (lо = 2d + 6 мм) и условное обозначение винта по соответствующему стандарту.
Примеры условных обозначений винтов:
Винт М12х50 ГОСТ 1491—80 —с цилиндрической головкой, первого исполнения, с резьбой М12 с крупным шагом, длиной 50 мм;
Рис. 224
Винт 2M12x1, 25x50 ГОСТ 17475—80 —с потайной головкой, второго исполнения, с мелкой метрической резьбой диаметром 12 мм и шагом 1,25 мм, длина винта 50 мм.
Шпилька представляет собой цилиндрический стержень с резьбой на обоих концах (рис. 224). Шпилька служит для соединения двух или нескольких деталей. Один конец шпильки 1\ ввертывается в резьбовое отверстие детали, а на другой конец /о навинчивается гайка. Выпускают шпильки с двумя одинаковыми по длине резьбовыми концами для деталей с гладкими сквозными отверстиями. Длина гладкой части стержня шпильки должна быть не менее 0,5d.
Конструкция и размеры шпилек определяются стандартами в зависимости от длины резьбового конца:
ГОСТ 22032—76l1= 1,0d — шпилька ввертывается в сталь, бронзу, латунь;
ГОСТ 22034—76 l1, = 1,25d; ГОСТ 22036—76l1 = 1,6d— шпилька ввертывается в чугун;
ГОСТ 22038—76 l1 = 2d; ГОСТ 22040—76 l1 = 2,5d— шпилька ввертывается в легкие сплавы.
При изображении шпильки вычерчивают только один вид на плоскости, параллельной оси шпильки, и указывают размеры резьбы, длину / шпильки и ее условное обозначение. Примеры условного обозначения шпилек:
Шпилька М8 х 60 ГОСТ 22038—76 — с крупной метрической резьбой диаметром 8 мм, длина шпильки 60 мм, предназначена для ввертывания в легкие сплавы, длина ввинчиваемого конца 16 мм;
Шпилька М8 х 1,0 х 60 ГОСТ 22038—76 — та же, но с мелким шагом резьбы —1,0 мм.
Гайка — крепежная деталь с резьбовым отверстием в центре. Применяется для навинчивания на болт или шпильку до упора в одну из соединяемых деталей. В зависимости от названия и условий работы гайки выполняют шестигранными, круглыми, барашковыми, фасонными и т. д. Наибольшее применение имеют гайки шестигранные. Их изготовляют трех исполнений: исполнение l — с двумя коническими фасками (рис. 225); исполнение 2 — с одной конической фаской; исполнение 3 — без фасок, но с коническим выступом с одного торца.
Форму гайки на чертеже вполне передают два ее вида: на плоскости проекций, параллельной оси гайки, совмещают половину вида с половиной фронтального разреза, и на плоскости, перпендикулярной
Рис. 225
оси гайки, со стороны фаски. На чертеже указывают размер резьбы, размер S под ключ и дают обозначение гайки по стандарту.
Примеры условного обозначения гаек:
Гайка M12 ГОСТ 5915—70 — первого исполнения, с диаметром резьбы 12 мм, шаг резьбы крупный;
Гайка 2М12 х 1,25 ГОСТ 5915—70 — второго исполнения, с мелкой метрической резьбой диаметром 12 мм и шагом 1,25 мм.
Шайба представляет собой точеное или штампованное кольцо, которое подкладывают под гайку, головку винта или болта в резьбовых соединениях. Плоскость шайбы увеличивает опорную поверхность и предохраняет деталь от задиров при завинчивании гайки ключом. С целью предохранения резьбового соединения от самопроизвольного развинчивания в условиях вибрации и знакопеременной нагрузки применяют шайбы пружинные по ГОСТ 6402—70 и шайбы стопорные, имеющие выступы-лапки.
Круглые шайбы по ГОСТ 11371—78 имеют два исполнения (рис. 226): исполнение 1 — без фаски, исполнение 2 — с фаской. Форму круглой шайбы вполне передает одно изображение на плоскости, параллельной оси шайбы.
Внутренний диаметр шайбы обычно на 0,5...2,0 мм больше диаметра стержня болта, на который шайба надевается. В условное обозначение шайбы включается и диаметр резьбы стержня, хотя сама шайба резьбы не имеет.
Примеры условного обозначения шайбы:
Рис. 226
Рис. 227
Шайба 20 ГОСТ 11371—78 — круглая, первого исполнения, для болта с резьбой М20;
Шайба 2.20 ГОСТ 11371—78 — та же шайба, но второго исполнения.
Соединительные детали трубопроводов (муфты, угольники, тройники и т. д.) представляют собой резьбовые соединения, изготовленные из ковкого чугуна и предназначенные для соединения труб в трубопроводах (рис. 227). Трубы используются в коммуникациях, транспортирующих жидкость или газ, а также для прокладки кабеля.
Конструкция и размеры соединительных деталей трубопроводов определены стандартами. Концы труб имеют резьбу наружную, а соединительные детали — внутреннюю. Основным параметром деталей трубных соединений является условный проход Dy — внутренний диаметр труб в миллиметрах. Соединительные детали трубопроводов имеют покрытие в основном цинковое.
Примеры условных обозначений соединительных деталей трубопроводов:
Муфта длинная 20 ГОСТ 8955—75 — прямая, неоцинкованная, для труб с условным проходом 20 мм;
Угольник Ц-25 ГОСТ 8946—75 — прямой, оцинкованный, для труб с условным проходом 25 мм.
Изображения резьбовых соединений на чертежах выполняются в соответствии с требованиями стандартов.
Резьбовые соединения являются неподвижными резьбовыми соединениями. К ним относят соединения деталей с помощью болтов, винтов, шпилек, гаек и соединительных деталей трубопроводов.
Изображение резьбового соединения состоит из изображенных и соединяемых деталей.
Различают конструктивное, упрощенное и условное изображения крепежных деталей и их соединений. При конструктивном изображении
Рис. 228
Рис. 229
размеры деталей и их элементов точно соответствуют стандартам. При упрощенном изображении размеры крепежных деталей определяют по условным соотношениям в зависимости от диаметра резьбы и упрощенно вычерчивают фаски, шлицы, резьбу в глухих отверстиях и т.д.
Условные обозначения используются при диаметрах стержней крепежных деталей 2 мм и менее. Изображения упрощенные и условные крепежных деталей установлены ГОСТ 2.315—68. В настоящем разделе приводятся упрощенные изображения крепежных деталей в резьбовых соединениях, рекомендуемые в учебных чертежах.
Болтовое соединение состоит из болта, гайки, шайбы и соединяемых деталей. В соединяемых деталях просверливают сквозные отверстия диаметром d0 = (1,05...1,10)d, где d — диаметр резьбы болта. В отверстие вставляют болт, надевают на него шайбу и навинчивают до упора гайку (рис. 228).
Длину болта определяют по формуле l = Н1+ Н2 + SШ + Н + К, где H1 и H2— толщина соединяемых деталей; Sm — толщина шайбы, SШ = 0,15d; H—высота гайки, H = 0,8d; К — длина выступающего стержня болта, K = 0,35d.
Расчетную длину болта округляют до ближайшей стандартной длины болта.
На чертеже болтового соединения (рис. 228) выполняют не менее двух изображений — на плоскости проекций, параллельной оси болта, и на плоскости проекций, перпендикулярной его оси (со стороны гайки). При изображении болтового соединения в разрезе болт, гайку и шайбу показывают неразрезанными. Головку болта и гайку на главном виде изображают тремя гранями. Смежные детали штрихуют с наклоном в разные стороны. На чертеже болтового соединения указывают три размера: диаметр резьбы, длину болта и диаметр отверстия под болт.
Условные обозначения болта, гайки и шайбы записываются в спецификации сборочного чертежа (см. § 101).
Шпилечное соединение состоит из шпильки, шайбы, гайки и соединяемых деталей. Соединение деталей шпилькой применяется тогда, когда нет места для головки болта или когда одна из соединяемых деталей имеет значительную толщину. В этом случае экономически нецелесообразно сверлить глубокое отверстие и ставить болт большой длины. Соединение шпилькой уменьшает массу конструкций. Одна из соединяемых шпилькой деталей имеет углубление с резьбой — гнездо под шпильку, которая ввинчивается в него концом l1 (см. рис. 224). Остальные соединяемые детали имеют сквозные отверстия диаметром d0 = (1,05...1,10)d, где d—диаметр резьбы шпильки. Гнездо сначала высверливается на глубину l2, которая на 0,5d больше ввинчиваемого конца шпильки, а затем в гнезде нарезается резьба. На входе в гнездо выполняется фаска с = 0,15d (рис. 229, а). При ввинченной в гнездо шпильке соединение деталей дальше осуществляется как в случае болтового соединения.
Длину шпильки определяют по формуле l = H2 + SШ + Н+ К, где H2 — толщина присоединяемой детали; SШ — толщина шайбы; Н— высота гайки; К—длина выступающего конца над гайкой. Расчетную длину шпильки округляют до стандартного значения.
На чертеже шпилечного соединения линия раздела соединяемых деталей должна совпадать с границей резьбы ввинчиваемого резьбового конца шпильки (рис. 229, б). Гнездо под шпильку оканчивается конической поверхностью с углом 120°. Нарезать резьбу до конца гнезда практически невозможно, но на сборочных чертежах допускается изображать резьбу на всю глубину гнезда. На чертеже шпилечного соединения указывают те же размеры, что и на чертеже болтового соединения. Штриховку в резьбовом соединении шпильки с деталью, в которую шпилька ввинчена, в разрезе доводят до сплошной основной линии резьбы на шпильке и в гнезде.
Рис. 230
Соединение винтом включает соединяемые детали и винт с шайбой. В соединениях винтами с потайной головкой и установочными винтами шайбу не ставят.
У одной из соединяемых деталей должно быть гнездо с резьбой для конца винта, а в другой - гладкое сквозное отверстие диаметром dо= =(1,05...1,10)d. Если применяется винт с потайной или полупотайной головкой, то соответствующая сторона отверстия детали должна быть раз-зенкована под головку винта (рис. 230).
Длина винта определяется по формуле l = Н = SШ + l1, где Н — толщина присоединяемой детали; SШ — толщина шайбы; l1 — длина ввинченного резьбового конца винта, которая назначается для соответствующего материала, как для шпильки.
Расчетная длина винта округляется до стандартного значения длины.
Изображение винтового соединения на чертеже выполняется подобно болтовому соединению по относительным размерам. Относительные размеры головок винта указаны на рис. 231.
На винтовом соединении граница резьбы на стержне винта должна находиться внутри гладкого отверстия, запас резьбы, не использованный при ввинчивании, равен примерно трем шагам резьбы (З.Р). Если диаметр головки винта меньше 12 мм, то шлиц рекомендуется изображать одной утолщенной линией. На виде сверху шлиц в головке показывается повернутым на 45°. На чертеже соединения наносят три размера: диаметр резьбы, длину винта, диаметр отверстия для прохода винта.
Трубное соединение состоит из соединяемых труб и соединительных деталей трубопроводов. При соединении двух труб муфтой кроме муфты в соединение входят контргайка и прокладка (рис. 232).
Чертежи трубных соединений выполняются по размерам их деталей как конструктивные чертежи, без упрощений. Перед тем как приступить к вычерчиванию трубного соединения, необходимо по значе-
Рис. 231
нию условного прохода Dy подобрать по таблицам соответствующих стандартов размеры труб и соединительных частей.
Более подробно правила выполнения чертежей труб и трубопроводов изложены в ГОСТ 2.411—72.
Винтовые (ходовые) соединения относятся к подвижным разъемным соединениям. В этих соединениях одна деталь перемещается относительно другой детали по резьбе. Обычно в этих соединениях применяются резьбы трапецеидальная, упорная, прямоугольная и квадратная. Чертежи винтовых соединений выполняются по общим правилам.
Зубчатое (шлицевое) соединение представляет собой многошпоночное соединение, в котором шпонка выполнена заодно с валом и расположена параллельно его оси. Зубчатые соединения, как и шпоночные, используются для передачи крутящего момента, а также в конст-
Рис. 232
Рис. 233
Рис. 234
рукциях, требующих перемещения деталей вдоль оси вала, например в коробках скоростей.
Благодаря большому числу выступов на валу зубчатое соединение может передавать большие мощности по сравнению со шпоночным соединением и обеспечивать лучшую центровку вала и колеса.
По форме поперечного сечения зубья (шлицы) бывают прямобочные, эвольвентные и треугольные (рис. 233).
ГОСТ 2.409—74 устанавливает условные изображения зубчатых валов, отверстий и их соединений.
Окружности и образующие поверхности выступов (зубьев) валов и отверстий показывают на всем протяжении основными линиями (рис. 234). Окружности и образующие поверхностей впадин показывают сплошными тонкими линиями, а на продольных разрезах — сплошными основными линиями.
При изображении зубчатых соединений и их деталей, имеющих эвольветный или треугольный профиль, делительные окружности и
Рис. 235
образующие делительных поверхностей показывают штрих-пунктирной тонкой линией (рис. 234, б).
На плоскости, перпендикулярной оси зубчатого вала или отверстия, показывают профиль одного зуба (выступа) и двух впадин, а фаски на конце шлицевого вала и в отверстии не показывают.
Границу зубчатой поверхности вала, а также границу между зубьями полного профиля и сбегом показывают сплошной тонкой линией (рис. 234, а).
На продольных разрезах зубья условно совмещают с плоскостью чертежа и показывают нерассеченными, а в соединениях в отверстии показывают только ту часть выступов, которая не закрыта валом (рис. 234, б).
Условное обозначение шлицевого вала или отверстия по соответствующему стандарту помещается в таблице параметров для изготовления и контроля элементов соединения. Условное обозначение соединения допускается указывать на чертеже с обязательной ссылкой на стандарт на полке-выноске, проведенной от наружного диаметра вала (рис. 235).
Соединение шпоночное состоит из вала, колеса и шпонки. Шпонка (рис. 236) представляет собой деталь призматической (шпонки призматические или клиновые) или сегментной (шпонки сегментные) формы, размеры которой определены стандартом. Шпонки применяют для передачи крутящего момента.
В специальную канавку-паз на валу закладывается шпонка. На вал насаживают колесо так, чтобы паз ступицы колеса попал на выступающую часть шпонки. Размеры пазов на валу и в ступице колеса должны соответствовать поперечному сечению шпонки.
Рис. 236
Рис. 237
Размеры призматических шпонок определяются ГОСТ 23360—78; размеры соединений с клиновыми шпонками — ГОСТ 24068—80; размеры соединений с сегментными шпонками — ГОСТ 24071—80.
Шпонки призматические бывают обыкновенные и направляющие. Направляющие шпонки крепят к валу винтами; их применяют, когда колесо перемещается вдоль вала.
По форме торцов шпонки бывают трех исполнений: исполнение
1 — оба торца закруглены; исполнение
2 — один торец закруглен, второй — плоский; исполнение
3 — оба торца плоские.
Рабочими поверхностями у шпонок призматических и сегментных являются боковые грани, а у клиновых верхняя и нижняя широкие грани, одна из которых имеет уклон 1 : 100.
Поперечные сечения всех шпонок имеют форму прямоугольников с небольшими фасками или скругленными. Размеры сечений шпонок выбираются в зависимости от диаметра вала, а длина шпонок — в зависимости от передаваемых усилий.
Условные обозначения шпонок определяются стандартами и включают в себя: наименование, исполнение, размеры, номер стандарта. Пример условного обозначения шпонки:
Шпонка 10 х 8 х 60 ГОСТ 23360—78 — призматическая, первого исполнения, с размерами поперечного сечения 10x8 мм, длина 60 мм.
Чертежи шпоночных соединений выполняются по общим правилам. Шпоночное соединение показывают во фронтальном разрезе осевой плоскостью (рис. 237). Шпонку при этом изображают неразрезанной, на валу выполняют местный разрез. Вторым изображением шпоночного соединения служит сечение плоскостью, перпендикулярной оси вала. Зазор между основаниями паза во втулке (ступице колеса) и шпонкой показывают увеличенным.
Соединение штифтами (рис. 238) — цилиндрическими или коническими — используется для точной взаимной фиксации скрепляемых деталей. Цилиндрические штифты обеспечивают неоднократную сборку и разборку деталей.
Шплинты применяют для ограничения осевого перемещения деталей (рис. 239) стопорения корончатых гаек.
Клиновые соединения (рис. 240) обеспечивают легкую разборку соединяемых деталей. Грани клиньев имеют уклон от 1/5 до1/40
Рис. 238
Рис. 239
Рис. 240
Рис. 241
В соединениях сочленением (рис. 241) выступ одной детали входит в паз или отверстие другой детали; детали поворачиваются одна относительно другой, и тем обеспечивается их соединение.
201.gif
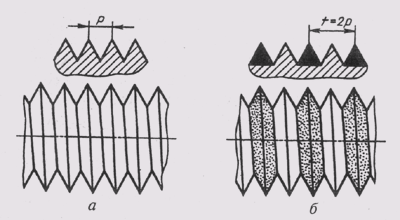
202.gif
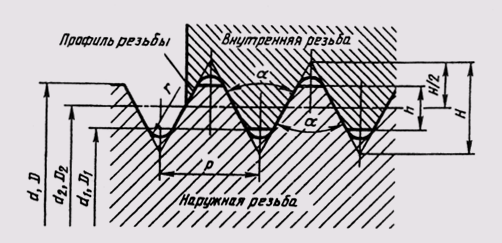
203.gif

204.gif
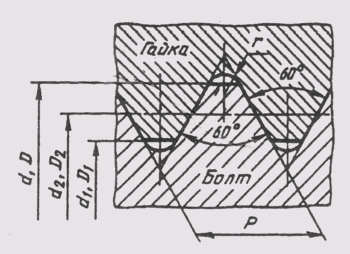
205.gif
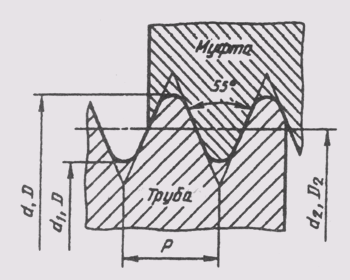
206.gif
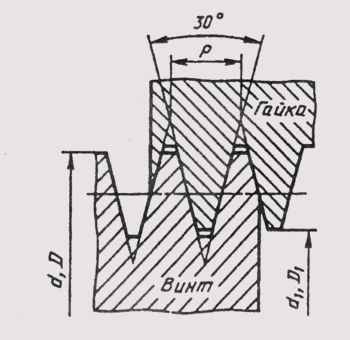
207.gif
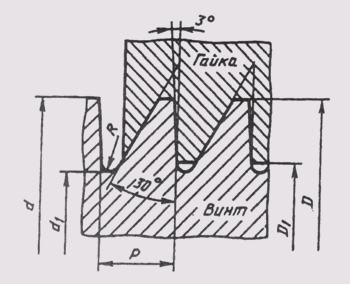
208.gif
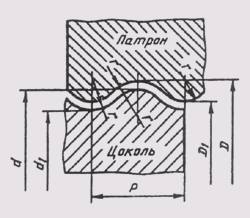
209.gif
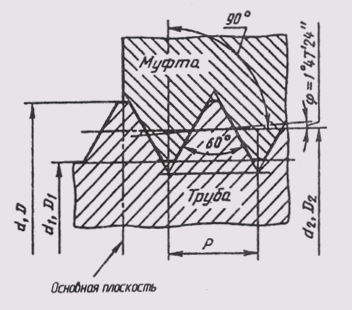
210.gif
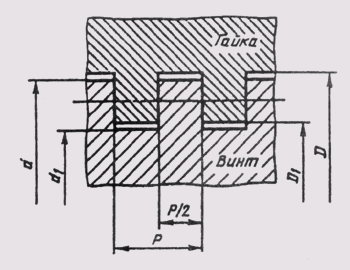
211.gif
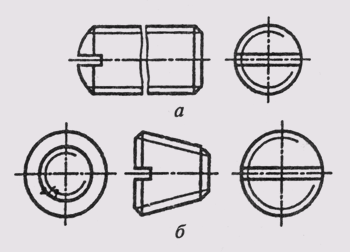
212.gif
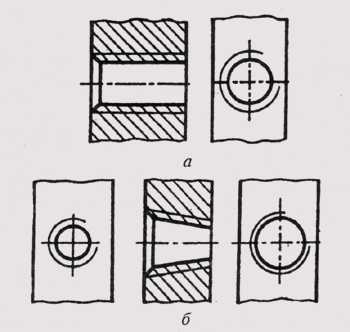
213.gif
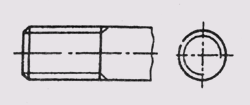
214.gif
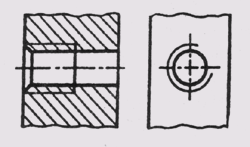
215.gif
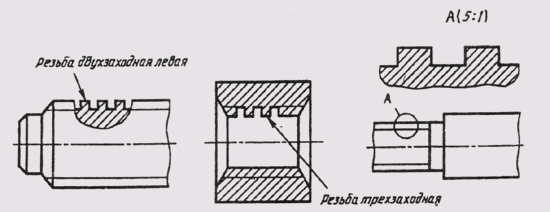
216.gif
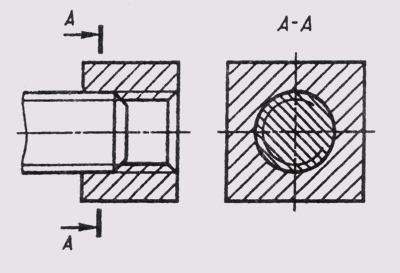
217.gif
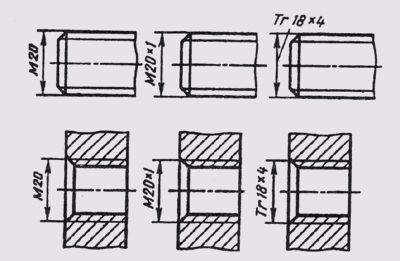
218.gif
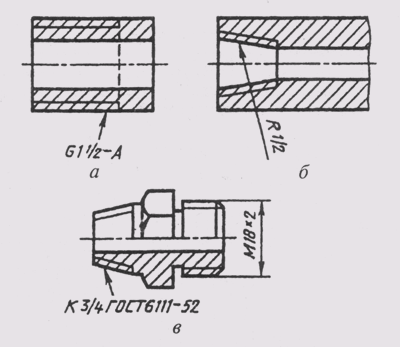
219.gif

220.gif
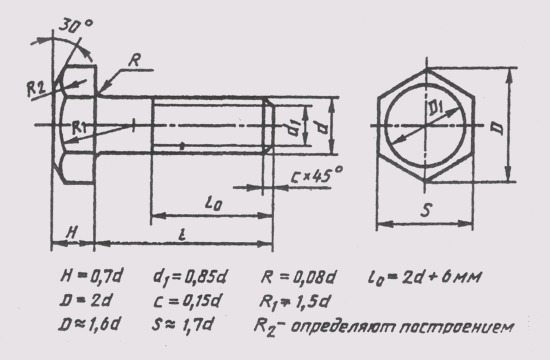
221.gif
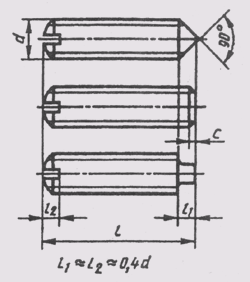
222.gif
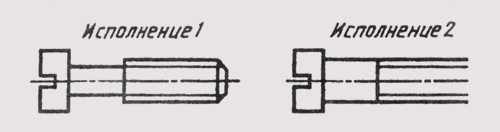
223.gif
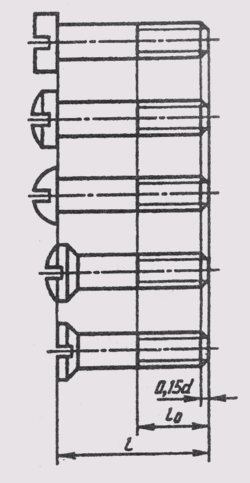
224.gif
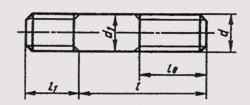
225.gif
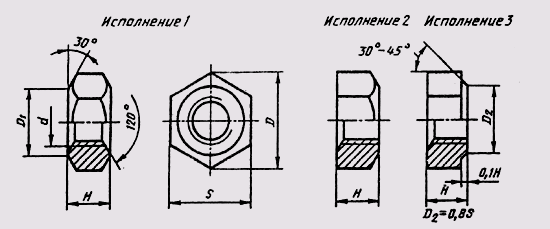
226.gif
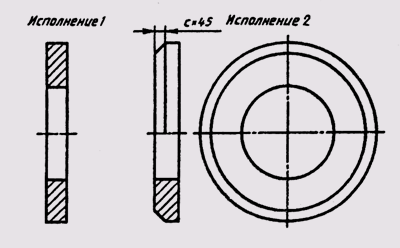
227.gif
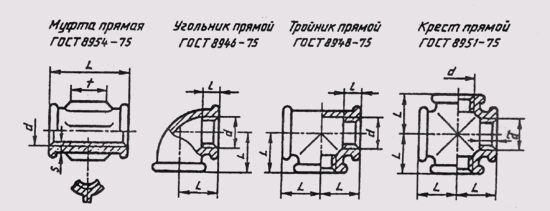
228.gif
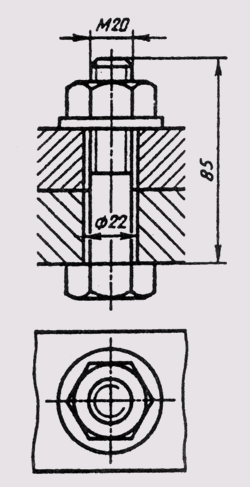
229.gif
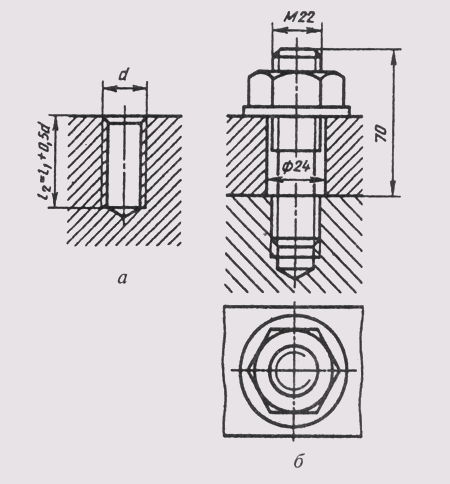
230.gif
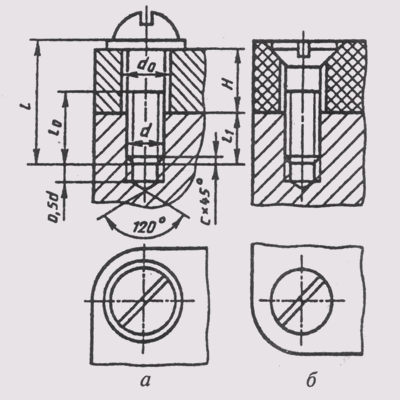
231.gif
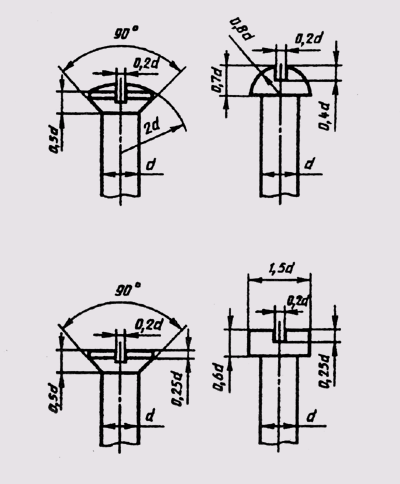
232.gif
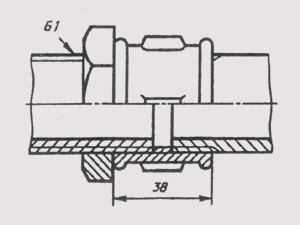
233.gif
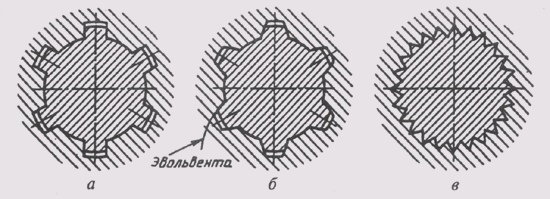
234.gif
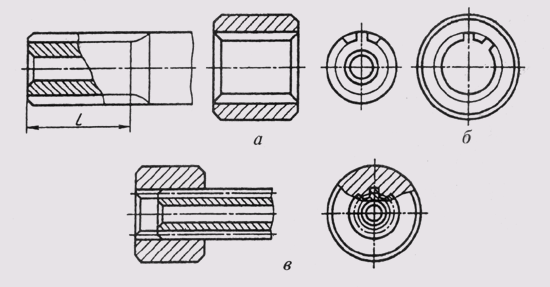
235.gif
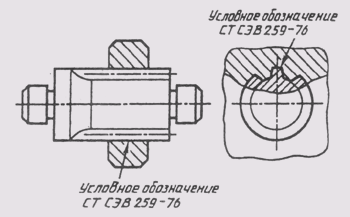
236.gif
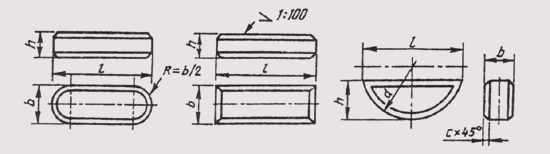
237.gif
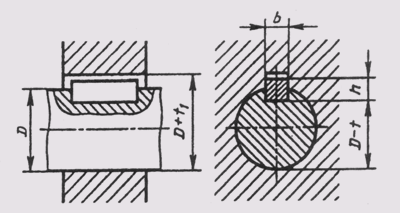
238.gif
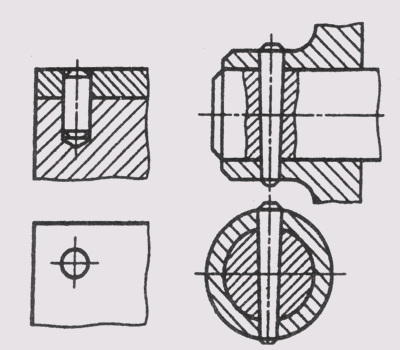
239.gif
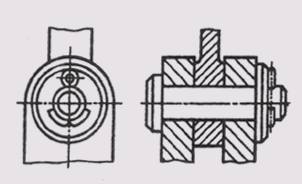
240.gif

241.gif
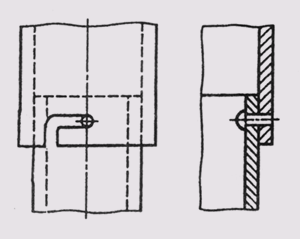
89. Неразъемные соединения
§ 89. Неразъемные соединения
Неразъемные соединения получили широкое распространение в машиностроении. К ним относятся соединения сварные, заклепочные, паяные, клеевые. Сюда относятся также соединения, полученные оп-рессовкой, заливкой, развальцовкой (или завальцовкой), кернением, сшиванием, посадкой с натягом и др.
Сварные соединения получают с помощью сварки. Сваркой называют процесс получения неразъемного соединения твердых предметов, состоящих из металлов, пластмасс или других материалов, путем местного их нагревания до расплавленного или пластического состояния без применения или с применением механических усилий.
Рис. 242
Рис. 243
Сварным соединением называется совокупность изделий, соединенных с помощью сварки.
Сварным швом называется затвердевший после расплавления материал. Металлический сварной шов отличается по своей структуре от структуры металла свариваемых металлических деталей.
По способу взаимного расположения свариваемых деталей различают соединения стыковые (рис. 242, а), угловые (рис. 242, б), тавровые (рис. 242, в) и внахлестку (рис. 242, г). Вид соединения определяет вид сварного шва. Сварные швы подразделяются на: стыковые, угловые (для угловых, тавровых соединений и соединений внахлестку), точечные (для соединений внахлестку, сваркой точками).
По своей протяженности сварные швы могут быть: непрерывными по замкнутому контуру (рис. 243, а) и по незамкнутому контуру (рис. 243, б) и прерывистыми (рис. 243, в). Прерывистые швы имеют равные по длине проваренные участки с равными промежутками между ними. При двусторонней сварке, если заваренные участки расположены друг против друга, такой шов называется цепным (рис. 244, а), если же участки чередуются, то шов называется шахматным (рис. 244, б).
Рис. 244
Рис. 245
Тонколистовые конструкции можно сваривать без предварительной подготовки свариваемых кромок. Форма подготовки кромок зависит от толщины свариваемых деталей, положения шва в пространстве и других данных.
Термины и определения, относящиеся к сварке, установлены ГОСТ 2.601—68. Самым распространенным видом сварки является электросварка, которая может быть ручной, полуавтоматической и автоматической.
Способы сварки, типы и конструктивные элементы сварных швов определяются соответствующими стандартами. Условные изображения и обозначение швов сварных соединений выполняются в соответствии с ГОСТ 2.312—72. Сварные швы изображают сплошными основными линиями, если шов видимый, и штриховыми, если шов невидимый (рис. 245). От изображения шва проводят одностороннюю стрелку с линией-выноской. Условное обозначение сварного шва пишут над полкой линии-выноски, если шов видимый, т. е. показана лицевая сторона шва (рис. 246, а, 6), и под полкой линией-выноской, если шов невидимый, т. е. показана оборотная сторона шва (рис. 246, в, г).
Структура условного обозначения сварного шва приведена на рис. 247, где:
Рис. 246
Рис. 247
1 — вспомогательные знаки, О — шов по замкнутому контуру, | — монтажный шов;
2 — обозначение стандарта на тип и конструктивные элементы шва;
3 — буквенно-цифровое обозначение шва по этому стандарту;
4 — условное обозначение способа сварки по стандарту на данный шов;
5 — вспомогательный знак А — треугольник и размер катета шва;
6 — размеры в мм прерывистого шва со знаками: / — для цепного шва и Z — для шахматного шва или ] — знак незамкнутого контура сварки;
7 — вспомогательные знаки (Q или со) обработки шва;
8 — обозначение шероховатости механически обработанного шва (см. §94);
9 — указание о контроле шва.
Примеры условного обозначения сварных швов:
ГОСТ 14806—80 = Т5 — РиЗ = 1 6—50 Z 100 — шов выполняется электродуговой сваркой алюминия, соединение тавровое Т5, сварка ручная в среде защитных газов РиЗ, катет шва 6 мм А6, шов шахматный, длина провариваемого участка 50 мм, шаг — 100 мм (50 Z 100).
ГОСТ 5264—80—С18 — шов выполняется ручной электродуговой сваркой при монтаже 1, шов стыковой (С 18) по незамкнутому контуру.
При наличии на чертеже нескольких одинаковых швов обозначение наносят только одного шва, и поэтому шву присваивают порядковый номер с указанием количества этих швов у линии-выноски. Все остальные швы этого типа имеют на полке линии-выноски обозначение порядкового номера шва (рис. 248), если указана лицевая сторона шва, и под полкой линии-выноски, если указана оборотная сторона шва. На рис. 248 обозначение № 1 два угловых шва, выполненные ручной электродуговой сваркой, с лицевой стороны усиление шва нужно снять Q механической обработкой, после чего шероховатость шва должна соответствовать шестому классу (Ra = 2,5 мкм).
Рис. 248
Пять швов № 2 выполняются как швы односторонние тавровые Tic катетом 5 мм А5, ручной электродуговой сваркой.
Если все швы на чертеже выполняются по одному стандарту, то его номер не вводят в обозначение шва, а записывают в технических требованиях на поле чертежа по типу «Сварные швы по ГОСТ...».
Если все швы на чертеже одинаковы, то условное обозначение швов можно не наносить на изображениях, а сделать одну запись условного обозначения шва технических требований, например: «Сварные швы по ГОСТ 5264—80—У5—А4».
Клепаные соединения применяются в конструкциях, подверженных действию высокой температуры, коррозии, вибрации, а также в соединениях из плохо сваривающихся металлов или в соединениях металлов с неметаллическими частями. Такие соединения нашли широкое применение в котлах, железнодорожных мостах, некоторых авиационных конструкциях и в отраслях легкой промышленности.
В то же время в ряде отраслей промышленности с усовершенствованием технологии сварного производства объем применения заклепочных соединений постепенно сокращается.
Основным скрепляющим элементом заклепочных соединений является заклепка. Она представляет собой короткий цилиндрический стержень круглого сечения, на одном конце которого находится головка (рис. 249). Головки заклепок могут иметь сферическую, кониче-
Рис. 249
Рис.250
скую или коническо-сферическую форму. В зависимости от этого различают головки полукруглые (рис. 249, а), потайные (рис. 249, б), полупотайные (рис. 249, в), плоские (рис. 249, г).
На сборочных чертежах головки заклепок изображают не по их действительным размерам, а по относительным размерам, в зависимости от диаметра стержня заклепки d.
Технология выполнения заклепочного соединения следующая. В соединяемых деталях выполняют отверстия сверлением или другим способом. В сквозное отверстие соединяемых деталей вставляют до упора головной стержень заклепки. Причем заклепка может быть в горячем или холодном виде. Свободный конец заклепки выходит за пределы детали примерно на 1,5d. Его заклепывают ударами или сильным давлением и создают вторую головку (рис. 250).
Диаметр стержней заклепок выбирают по специальным таблицам. Ориентировочно он принимается равным толщине соединяемых деталей. Длину стержня заклепки принимают также с учетом толщины соединяемых деталей и припуска. Ориентировочно она составляет 1,5d.
Заклепочные швы могут быть однорядными и многорядными. Заклепки обычно располагаются в ряду на одинаковом расстоянии. Расположение заклепок в шве может быть рядовым и шахматным. Соединяемые детали в заклепочных соединениях могут быть выполнены внахлестку или встык с накладками.
На чертежах указывают все конструктивные размеры швов клепаного соединения. При этом не вычерчивают все заклепки соединения. Обычно показывают одну-две из них, а место расположения остальных обозначают пересечением осей (рис. 251).
Заклепочные швы имеют свои обозначения, которые наносятся на чертежах. В обозначении указывают диаметр (d) и длину (/) стержня заклепки, группу металла и номер ГОСТ, определяющего форму головки и покрытие.
Например, заклепка, имеющая полукруглую головку, длину d=25 мм, диаметр стержня d = 10 мм, изготовленная из металла группы ОО, без покрытия имеет обозначение: Заклепка 10x25 ГОСТ 10299—80.
Рис. 251
Рис. 252
Соединения деталей пайкой находят широкое применение в приборостроении, электротехнике. При впайке соединяемые детали нагреваются до температуры, не приводящей к их расплавлению. Зазор между соединяемыми деталями заполняется расплавленным припоем. Припой имеет более низкую температуру плавления, чем соединяемые пайкой материалы. Для пайки используют мягкие припои ПОС — оловянно-свинцовые по ГОСТ 21930—76 и ГОСТ 21931—76 и твердые припои Пер — серебряные по ГОСТ 19738—74.
Припой на видах и разрезах изображают сплошной линией толщиной 2S. Для обозначения пайки используют условный знак (рис. 252, а)— дуга выпуклостью к стрелке, который чертят на линии-выноске, указывающей паяный шов. Если шов выполняется по периметру, то линию-выноску заканчивают окружностью. Номер швов указывают на линии-выноске (рис. 252, б).
Марка припоя записывается или в технических требованиях, или в спецификации в разделе «Материалы» (см. § 101).
Клеевые соединения позволяют соединять разнообразные материалы. Клеевой шов, как и паяный, согласно изображается сплошной линией толщиной 25. На линии-выноске чертят условный знак (рис. 253, а), напоминающий букву К. Если шов выполняется по периметру, то линию-выноску заканчивают окружностью (рис. 253, б). Марка клея записывается или в технических требованиях, или в спецификации в разделе «Материалы».
Опрессовка (армирование) защищает соединяемые элементы от коррозии и химического воздействия вредной среды, выполняет изолирующие функции, позволяет уменьшить массу изделия (рис. 254), экономить материалы.
Рис. 253
Рис. 254
Вальцовка и кернение осуществляется деформацией соединяемых деталей (рис. 255, а, б). Сшивание нитками, металлическими скобками применяется для соединения бумажных листов, картона, различных тканей.
ГОСТ 2.313—82 устанавливают условные обозначения и изображения швов неразъемных соединений, получаемых пайкой, склеиванием, сшиванием.
Соединение деталей путем посадки с натягом обеспечивается системой допусков и посадок определенным температурным режимом перед сваркой деталей.
Рис. 255
242.gif
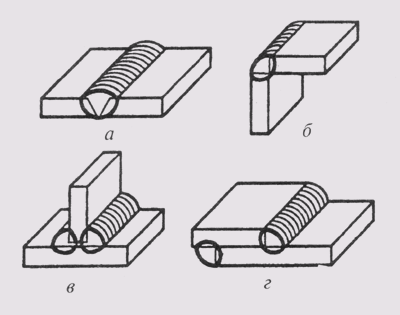
243.gif
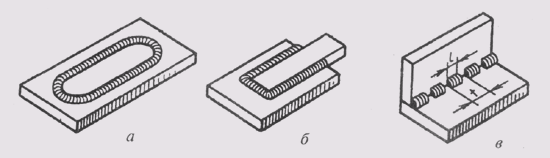
244.gif
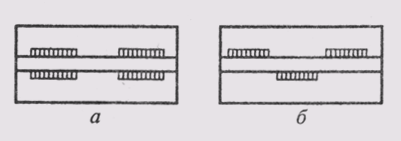
245.gif
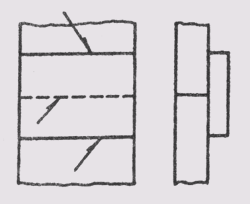
246.gif
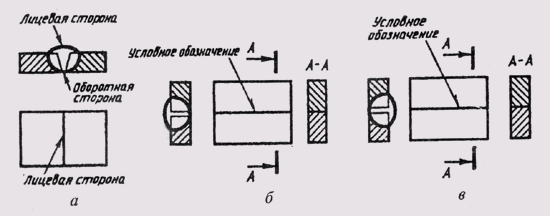
247.gif
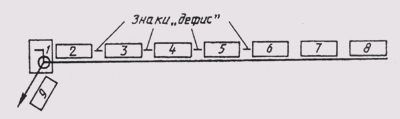
248.gif
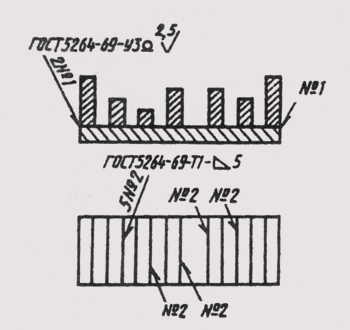
249.gif
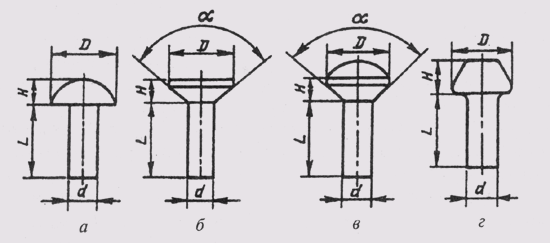
250.gif
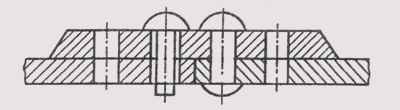
251.gif
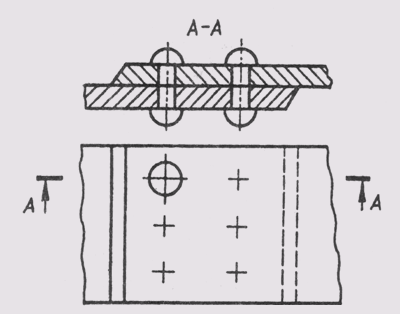
252.gif
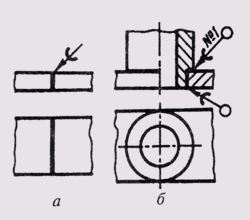
253.gif
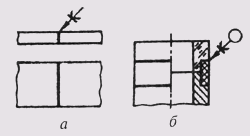
254.gif
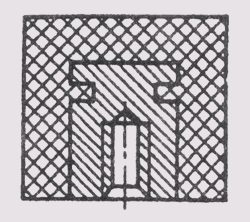
255.gif
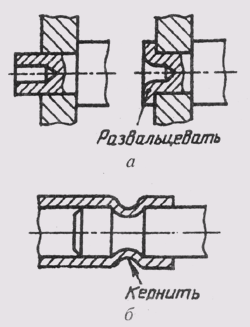
90. Специальные соединения деталей
§ 90. Специальные соединения деталей
К специальным соединениям относятся соединения деталей зубчатыми передачами, пружинами и др. Зубчатые передачи составляют наиболее распространенную группу механических передач и применяются для преобразования и передачи вращательного движения между валами с параллельными (цилиндрические передачи), пересекающимися (конические передачи) и скрещивающимися (червячные передачи) осями, а также для преобразования вращательного движения в поступательное и наоборот (реечные передачи).
В зубчатой передаче передача движения осуществляется за счет непосредственного контакта зубьев колеса и шестерни. Зубчатое колесо с меньшим числом зубьев называется шестерней, а с большим числом — колесом. Основным элементом зубчатого колеса являются зубья. На рис. 256 дано изображение зубчатого колеса с указанием его элементов, терминов и обозначений. Диаметры окружностей впадин
Рис. 256
Рис. 257
df, вершин d3 и делительной окружности d находятся в зависимости от числа зубьев z и шага зацепления Pt. Шаг зацепления определяется длиной дуги делительной окружности между одинаковыми точками двух соседних зубьев. Длина делительной окружности равна лd = zP1, откуда диаметр делительной окружности d = (P1/л) z. Отношение P1/л— Называют модулем зубчатого колеса, обозначают буквой т и измеряют в миллиметрах, т. е. т = P1/л, тогда d = mz. Модуль является основным параметром зубчатого колеса, его величины установлены СТ СЭВ 310—76. Многие размеры зубчатого колеса зависят от величины модуля. Обычно высоту h зуба принимают равной 2,25т, при этом высоту головки ha зуба принимают равной т, а высоту ножки hf зуба — 1,25т. Диаметр окружности вершин da = m(z + 2), диаметр окружности впадин df= m(z + 2,5).
Условные обозначения зубчатых колес определяются ГОСТ 2.402—68.
Окружности и образующие поверхностей выступов зубьев показываются сплошными основными линиями, делительные окружности показывают штрихпунктирными тонкими линиями, окружности и образующие поверхностей впадин зубьев на видах не показывают или изображают сплошной тонкой линией. В разрезах и сечениях образующие поверхностей на
Рис. 258
Рис. 259
всем протяжении изображают сплошными основными линиями (рис. 257, а, б).
Зубья зубчатых колес вычерчивают только в осевых разрезах, условно совмещая их с секущей плоскостью, и показывают нерассеченными. Если необходимо показать профиль зуба, то его показывают на ограниченном участке изображения колеса или применяют выносной элемент (рис. 258).
Рабочие чертежи зубчатых цилиндрических колес выполняются согласно ГОСТ 2.403—75. На чертеже помещают изображение зубчатого колеса и таблицу параметров. На изображение колеса наносят те данные, которые указаны в стандарте. На изображении цилиндрического зубчатого колеса (рис. 259) указывают: диаметр окружности вершин зубьев, ширину венца, размеры фасок и радиусы округлений, шероховатость поверхностей вершин, впадин и боковой поверхности
Рис. 260
зубьев, а также наносят размеры всех конструктивных элементов детали (обода, ступицы, колеса).
Таблицу параметров размещают в правом верхнем углу чертежа (на рис. 259 приведены размеры граф таблиц и их расположение).
Таблица параметров на чертеже цилиндрического зубчатого колеса состоит из трех частей, отделенных друг от друга сплошными основными линиями. В первой (верхней) части содержатся данные для изготовления, во второй — для контроля, в третьей — справочные данные для зубчатого колеса.
Рабочие чертежи деталей зубчатых передач других видов выполняются в соответствии с требованиями ГОСТ 2.405—75 — ГОСТ 2.406—76.
На чертеже зубчатого зацепления вычерчивают не менее двух изображений (рис. 260). На главном виде зацепление может быть показано в разрезе. Тогда зуб ведущего колеса показывается перед зубом ведомого. Контур видимого зуба вычерчивается сплошными основными линиями, а контур невидимого зуба — штриховыми линиями. На чертеже зубчатого зацепления наносят обычно только один размер — величину межосевого расстояния. Правила условных обозначений остальных данных для передач различных типов определяются ГОСТ 2402—68.
Пружины служат для накопления энергии за счет упругой деформации при воздействии внешней нагрузки. С прекращением действия этой нагрузки пружины восстанавливают свою первоначальную форму. По внешней форме (рис. 261) пружины бывают винтовые (цилиндрические и конические) и невинтовые (спиральные, пластинчатые, тарельчатые). По виду деформаций (или нагружения) различают пружины сжатия, растяжения, кручения и изгиба (плоские пружины).
В поперечном сечении витки пружины имеют или круглую (рис. 261, а, б), или прямоугольную (рис. 261, б, г, д) форму. Точное изображение пружин трудоемко и нецелесообразно. ГОСТ 2.401—68 уста-
Рис. 261
навливает условные изображения и правила выполнения чертежей пружин для всех отраслей промышленности.
При изображении цилиндрических пружин (рис. 261, а) сечения витков пружины условно изображают окружностями, а сами витки — прямыми линиями. Крайние витки пружины, работающие на сжатие, не являются рабочими, они поджаты и обработаны с целью обеспечения полного прилегания к опорным поверхностям. Остальные части пружины имеют постоянный шаг, поэтому центры сечений должны располагаться в шахматном порядке. При большом количестве витков их изображают только с концов пружин, пропуская центральную часть. Через центр сечений витков проводят осевую штрих-пунктирную линию. Изображение винтовых пружин на чертеже располагают горизонтально. Пружины вычерчивают в свободном (ненагруженном) состоянии. Пружины, работающие на растяжение, изображаются без просвета между витками.
На чертежах пружин с контролируемыми силовыми параметрами помещают диаграммы испытаний — график нагрузки от деформации или деформации от нагрузки (рис. 262).
На рабочих чертежах изображают пружины только с правой навивкой. Направление навивки указывается в технических требованиях, которые располагают под изображением пружины. Техниче-
Рис. 262
ские требования должны соответствовать ГОСТ 2.401—68.
На учебных чертежах достаточно указать следующие данные:
длина развернутой пружины L, мм;
число рабочих витков п;
число витков полное п1;
направление навивки;
диаметр контрольного стержня Ds, мм, или диаметр контрольной гильзы Dr, мм;
размеры для справок.
Если толщина сечения материала пружины на чертеже 2 мм и менее, то пружину изображают сплошной основной линией толщиной 0,6...1,5 мм (см. рис. 261, г, д).
256.gif
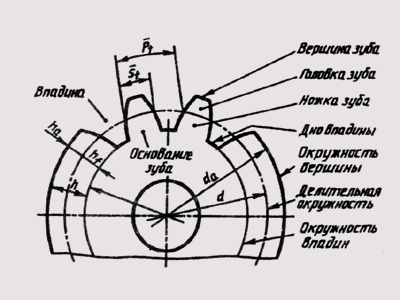
257.gif
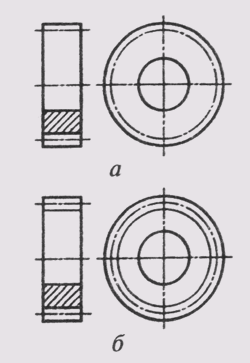
258.gif
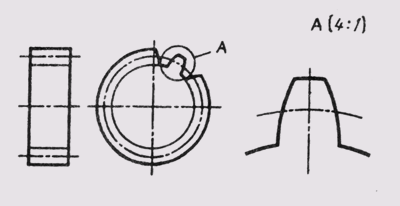
259.gif

260.gif
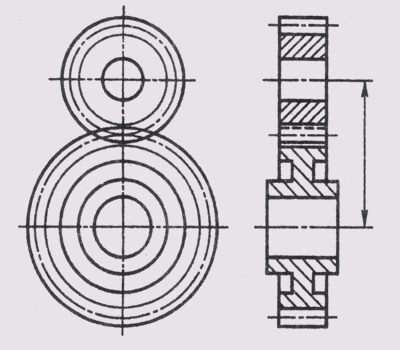
261.gif
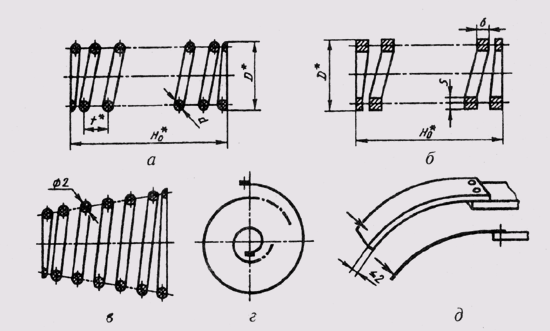
262.gif
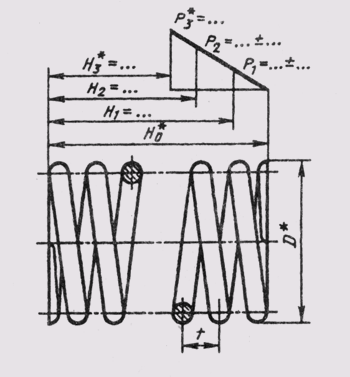
16. Глава 15. Рабочие чертежи деталей
1. Глава 15. Рабочие чертежи деталей
Глава 15. РАБОЧИЕ ЧЕРТЕЖИ ДЕТАЛЕЙ
§ 91. Общие сведения о выполнении и оформлении рабочих чертежей деталей
Деталью называют изделие, изготовленное из однородного по наименованию и марке металла, без применения сборочных операций. Примерами деталей могут быть валик, изготовленный из одного куска металла, болт, шпонка и т. п.
Для изготовления каждой детали нужен ее рабочий чертеж. Рабочим чертежом детали называется документ, содержащий изображение детали, размеры и другие данные, необходимые для изготовления, ремонта и контроля детали. Этот документ содержит данные о материале, шероховатости поверхностей, технические требования и др. Таким образом, рабочий чертеж включает в себя как графическую, так и текстовую часть.
При выполнении рабочего чертежа детали определяют вид, дающий наибольшее представление об ее устройстве (главный вид), и необходимое количество других видов и изображений.
Выбирают необходимый формат бумаги и устанавливают приемлемый масштаб изображений. Далее выполняют компоновку чертежа, т. е. приступают к рациональному размещению изображений на листе. Намечают рамку чертежа и основной надписи. Если изображаются детали, требующие нанесения таблиц параметров, для них предусматривают место в правой верхней части формата. Для других деталей справа оставляют место для записи технических требований к ним, включающим сведения о твердости металла отклонениях оси соосности, радиусы скруглений и др. Далее намечают прямоугольники по размерам, соответствующим габаритным размерам изображений; при этом оставляют необходимый запас площади для нанесения размеров около каждого изображения. В правом верхнем углу оставляют место для нанесения знаков шероховатости.
Надписи на чертежах в технических требованиях и таблицах выполняются в соответствии с ГОСТ 2.316—68. Текстовую часть, надписи и таблицы включают в чертеж, когда содержащиеся в них данные невозможно выразить графически или условными обозначениями. Текст надписи должен быть точным, кратким и располагаться параллельно основной надписи чертежа. Заголовок «Технические требования» пишут. Пункты технических требований должны иметь сквозную нумерацию и группироваться по своему характеру в соответствии с рекомендациями ГОСТ 2.316—68.
Рис. 263
Надписи, относящиеся к изображению, могут содержать не более двух строк, располагаемых над полкой линии-выноски и под ней (рис. 263, а). Линию-выноску заканчивают или точкой на изображении, или стрелкой (рис. 263, б).
Основная надпись выполняется в соответствии с ГОСТ 2.104—68 и 2.107—68 «Основные требования к рабочим чертежам». Наименование деталей записывают в именительном падеже в единственном числе в наименованиях, состоящих из нескольких слов, на первом месте помещают имя существительное, например: «Колесо зубчатое».
263.gif
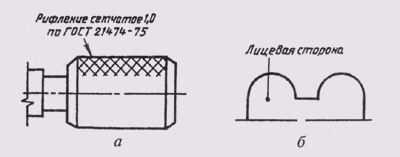
8. Вопросы для самопроверки
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
22. Что такое отгенение? Назовите способы оттенения.
92. Нанесение обозначений материалов на рабочих чертежах деталей
§ 92. Нанесение обозначений материалов на рабочих чертежах деталей
На рабочих чертежах деталей помещают необходимые данные, характеризующие свойства материала готовой детали и материала, из которого деталь должна быть изготовлена.
В основной надписи чертежа детали указывают вид, наименование и марку материала в соответствии со стандартом или другими нормативными документами.
Углеродистую сталь обыкновенного качества обозначают: Ст, Ст. 1, Ст. 2, Ст. 3, Ст. 4, Ст. 5, Ст. 6. В графе 3 основной надписи записывают, например: Ст. 3 ГОСТ 380—88.
В обозначение углеродистой качественной конструкционной стали входят двузначные числа, показывающие содержание углерода в сотых долях процента: 0,5 кп (кипящая), 0,8 кп, 0,8,10 кп, 10,15 кп, 15, 201 20,26,30,35,40 и т. д. В основной надписи записывают, например: «Сталь У25 ГОСТ 1050—88».
Углеродистую инструментальную сталь обозначают буквой «У» с указанием содержания углерода, например У8 ГОСТ 1435—90.
Легированные машиностроительные стали имеют обозначения легирующих элементов: Г — марганец, С — кремний, X — хром, Н — никель, М — молибен и т. д. и процентное содержание этих элементов, например хромоникелевая сталь марки 20 ХН: «Сталь 20ХН ГОСТ 4543—71».
Серый чугун (СЧ) в своем обозначении содержит предел прочности на растяжение (первые две цифры), предел прочности на изгиб (вторые две цифры), например: «СЧ 18—36 ГОСТ 1412—85».
Ковкий чугун (КЧ) в своем обозначении содержит предел прочности на растяжение (первые две цифры) и удлинение в процентах (вторые две цифры), например: «КЧ35—10 ГОСТ 1215—79».
Медь (М) изготовляется марок МО, Ml, М2, МЗ, М4. В основной надписи записывают, например: «М4 ГОСТ 859—78».
Латунь — медно-цинковый сплав, обрабатываемый давлением, изготовляется марок Л96, Л90, Л70, Л А Н. В основной надписи записывают, например: «Л70 ГОСТ 15527—70».
Латунь — медно-цинковый сплав литейный выпускают марок ЛА67-2,5; ЛАЖМц 66-6-3-2; ЛМцС 58-1Н; ЛК80-ЗЛ и др. Первые две цифры означают процентное содержание меди, а остальные — процентное содержание компонентов (алюминия А, железа — Ж, марганца— Мц и др.). В основной надписи записывают, например: «ЛАЖМц 66-6-3-2 ГОСТ 17711—80».
Бронзы оловянные литейные изготовляют марок Бр. ОЦСН 3-7-5-1; БР. ОСЦ 3-12-5; Бр. ОСЦ 5-5-5 и др. Цифры обозначают процентное содержание компонентов (олово — О, цинк — Ц, свинец — Сит. д.), остальное — медь. Пример условной записи: «Бр. ОСЦ 5-5-5 ГОСТ 613—79».
Бронзы безоловянные специальные бывают марок Бр. 45, Бр. А7, Бр АЖН 10-44, Бр. Мц 5 и др. Пример обозначения: «Бр. Мц 5 ГОСТ 18175—78».
Алюминиевые сплавы АЛ, АК, Д1, Д6, Д7 записываются в основной надписи по типу: «АЛ 4 ГОСТ 2685—75; АК 2 ГОСТ 4784—74; Д6 ГОСТ 13722—68».
Все металлы имеют единое условное графическое обозначение (штриховку) на изображениях в разрезах и сечениях (см. ГОСТ 2.306—68). Если деталь изготовляется из сортаментного материала (листа, прутка, проволоки, профиля и т. д.), то обозначают не только материал, но и сортамент с его размерами и номером стандарта на этот сортамент, например:
50ГОСТ2590-88
------------------------ круг;
Ст.3ГОСТ535-88
25 ГОСТ 8560267
----------------------- шестигранник.
45ГОСТ1051-73
Из широко используемых неметаллических материалов можно выделить следующие:
резина листовая техническая по ГОСТ 7338—90;
паронит по ГОСТ 481—80;
винипласт листовой по ГОСТ 9639—71;
текстолит конструкционный;
гетинакс по ГОСТ 2718—74;
полиэтилен по ГОСТ 16338—85;
фторопласт по ГОСТ 14906—77.
Условные обозначения и марки этих материалов определяются их стандартами. Все перечисленные неметаллические материалы имеют единое условное графическое изображение на чертежах (штриховка «в клетку»).
93. Нанесение размеров на рабочих чертежах деталей
§ 93. Нанесение размеров на рабочих чертежах деталей
Вопросы обеспечения рабочего чертежа детали необходимыми размерами продумываются уже по ходу определения необходимого количества и содержания изображений, а непосредственно решаются только тогда, когда изображения детали уже выполнены.
Размеры на рабочем чертеже детали должны быть нанесены так, чтобы обеспечить наименьшую трудоемкость изготовления детали. Неудачное нанесение размеров может привести к выполнению лишних технологических операций и повышению себестоимости детали. Наличие одинаковых размеров у отдельных элементов детали, например, фасок, канавок, проточек, уменьшает число необходимого режущего и измерительного инструмента, что приводит к снижению себестоимости изготовления детали.
Общие вопросы нанесения размеров на чертежах были рассмотрены в § 13. В настоящем параграфе рассматриваются специальные вопросы, учитывающие требования производства при изготовлении деталей.
Нанесение размеров должно соответствовать технологии изготовления детали, т. е. учитывать последовательность операции-обработки заготовки детали и то оборудование, на котором деталь может быть изготовлена.
Все размеры деталей можно разделить на две группы: сопрягаемые и свободные (несопрягаемые).
Сопрягаемые размеры определяют форму поверхности детали, сопрягаемой с поверхностью другой детали в изделии, а также положение этих поверхностей в изделии.
Рис. 264
Поверхности детали, которые не соприкасаются с поверхностями других деталей в изделии, определяются свободными размерами.
Все размеры должны наноситься от базовых поверхностей, линий или точек, относительно которых определяется положение отдельных элементов детали в процессе их изготовления или эксплуатации в готовом изделии. Различают базы конструкторские, технологические, измерительные, сборочные, вспомогательные.
Конструкторские базы определяют положение детали в готовом изделии. На рис. 264 показаны в качестве конструкторских баз плоскость (рис. 264, а), линия (рис. 264, б) и точка (рис. 264, в). По отношению к конструкторской базе ориентируются и другие детали изделия.
Технологические базы определяют положение детали при обработке.
Измерительная (главная) база — это база, от которой производится отсчет размеров при изготовлении и контроле готового изделия (рис. 265). Скрытой измерительной базой является ось вращения детали.
Вспомогательные базы помогают отсчитывать размеры второстепенных элементов детали. Вспомогательные базы должны быть связаны размерами с основной измерительной базой.
В качестве размерных баз должны выбираться более точно обработанные поверхности. Они должны быть обработаны в первую очередь.
Размеры деталей можно наносить от баз тремя способами: цепочкой, координатным и комбинированным способами.
При нанесении размеров цепочкой нужно учитывать, чтобы размерная цепь не была замкнутой. Каждый элемент или ступень детали обрабатывается самостоятельно (рис. 266, а),
Рис. 265
Рис. 266
т. е. сначала обрабатывают ступень диаметра d1 на длину l1 от базы А, затем — ступень диаметра d2 от базы В и т. д. Размер участка диаметром d4 определяется общим габаритным размером 4. Если необходимо указать размеры всех отдельных участков, то габаритный (суммарный) размер должен быть указан, как справочный (размер 84 на рис. 265).
Нанесение размеров цепочкой приводит к суммированию ошибок, появляющихся в процессе изготовления детали, что приводит к более жестким требованиям при контроле суммарных размеров.
Размеры цепочкой наносят в тех случаях, когда требуется точно выдержать размеры отдельных элементов, а не суммарный размер. Цепной способ используется для нанесения размеров межцентровых расстояний при обработке деталей комплектом режущего инструмента и т. д.
При координатном способе размеры наносят от выбранной базы (рис. 266, б). Каждый размер в этом случае является координатной, определяющей положение элемента детали относительно базы. Этот способ позволяет обеспечить высокую точность исполнения размера независимо от исполнения других размеров детали.
Комбинированный способ нанесения размеров (рис. 266, в) нашел самое широкое применение в практике, так как сочетает в себе
Рис. 267
Рис. 268
особенности и цепного, и координатного способов. При этом способе размеры, требующие высокой точности исполнения, можно отделить от других размеров.
Размеры между обрабатываемыми и необрабатываемыми поверхностями детали выделяются в отдельные размерные цепи, которые должны быть связаны между собой одним размером.
При нанесении размеров на рабочих чертежах деталей необходимо соблюдать следующие положения.
1. Чертеж детали должен содержать три группы размеров, необходимых для ее изготовления: габаритные, межосевые и межцентровые размеры и их расстояния до баз, размеры отдельных элементов детали.
2. В ряде случаев проставляют еще и размеры установочные, присоединительные и справочные.
3. Каждый отличный от других элемент детали должен иметь размеры формы и размеры положения его относительно баз. На один и тот же элемент каждый размер проставляется только один раз. При этом для удобства пользования чертежом все размеры, определяющие элемент детали, должны концентрироваться в одном главном для данного элемента изображении. На рис. 267 размер и координаты отверстия диаметром 8 мм даны на виде сверху, а размеры и координаты паза — на главном виде.
4. Нельзя записывать вперемешку размеры наружных и внутренних поверхностей элементов детали (рис. 268). При этом размерные линии предпочтительнее располагать вне контура изображения. Пересечение выносных и размерных линий нежелательно, и категорически воспрещается выносить меньший размер за больший. Простановка размеров от линии невидимого контура не рекомендуется.
Рис. 269
Рис. 270
5. Размеры нескольких одинаковых элементов детали наносят один раз с указанием их количества (рис. 269).
6. При нанесении размеров одинаковых элементов, равномерно расположенных по окружности, вместо угловых размеров, координирующих расположение этих элементов по окружности, можно указывать только их количество (рис. 270).
7. Размеры симметрично расположенных элементов наносят один раз без указания их количества (рис. 271), сгруппировав их в одном месте.
8. Если одинаковые элементы располагаются на разных поверхностях детали и показаны на разных изображениях, то количество этих элементов записывают отдельно для каждой поверхности (рис. 272).
9. На рис. 273 приведены примеры нанесения размеров отверстий в разрезе и на виде, если отсутствует на чертеже разрез по отверстию.
10. Одинаковые радиусы округлений или сгибов могут быть записаны без указания их на изображениях в технических требованиях по типу: «Радиусы скруглений 5 мм»; «Неуказанные радиусы 3 мм»; «Внутренние радиусы сгибов 12 мм».
11. У деталей с резьбой длина резьбового участка включает размер фаски и проточки. Размеры фаски и проточки указываются отдельно внутри размера резьбового участка (рис. 274).
Рис. 271
Рис. 272
Рис. 273
Рис. 274
12. При нанесении размеров необходимо учитывать требования стандартов на нормальные линейные и угловые размеры, а также ГОСТ 2.307—68 и ГОСТ 2.109—73.
264.gif
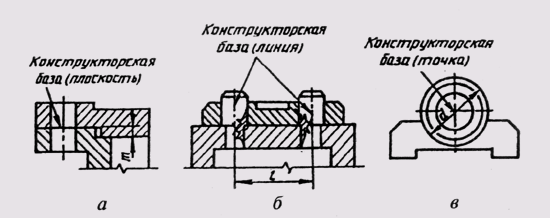
265.gif
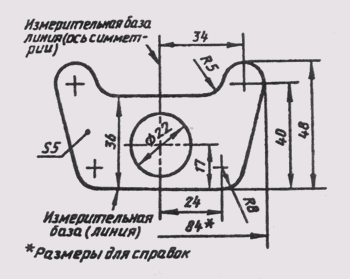
266.gif
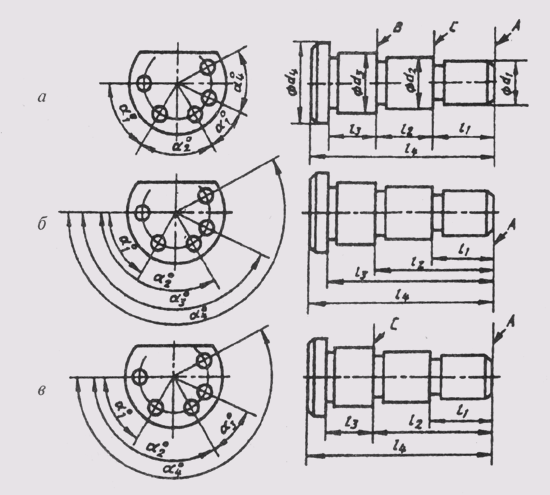
267.gif
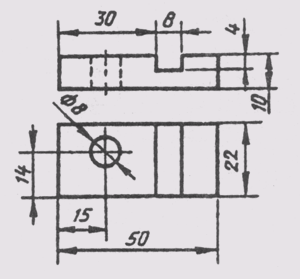
268.gif
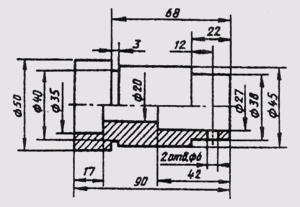
269.gif
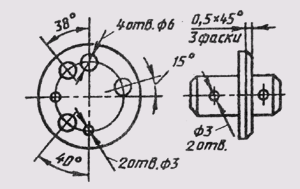
270.gif
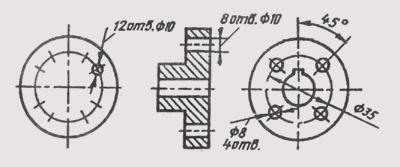
271.gif
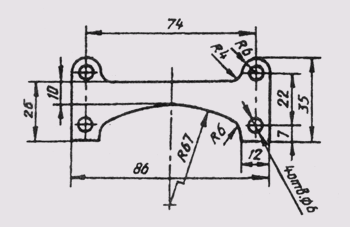
272.gif
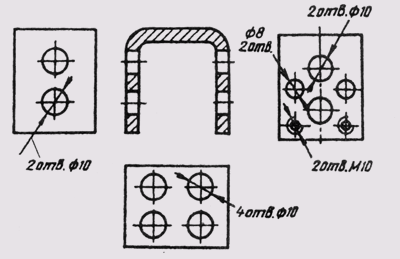
273.gif
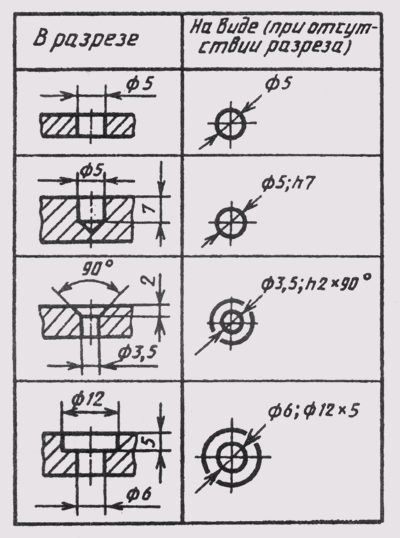
274.gif
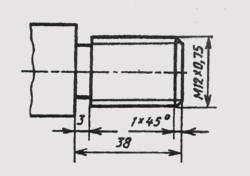
94. Обозначение шероховатости поверхностей на рабочих чертежах деталей
§ 94. Обозначение шероховатости поверхностей на рабочих чертежах деталей
Поверхность любой детали, если даже она очень тщательно обработана, имеет неровности в виде выступов и впадин. Причем такие неровности у некоторых деталей можно обнаружить даже невооружен-
Рис. 275
ным глазом, в других же — только с помощью специальных приспособлений. Величина неровности на поверхности детали измеряется в микрометрах (мкм).
Совокупность неровностей, образующих рельеф поверхности независимо от способа его называют шероховатостью.
Поверхности деталей образуются в результате их обработки. Как правило, рабочие поверхности детали обрабатывают более качественно, чем нерабочие.
Шероховатость поверхности регламентируется ГОСТ 2789—73 и ГОСТ 2.309—73. Стандарт устанавливает следующие параметры для характеристики шероховатости поверхности:
Ra — среднее арифметическое отклонение профиля;
Rz — высота неровностей профиля по десяти точкам;
Rmax — наибольшая высота неровностей профиля;
Sm — средний шаг неровностей;
S — средний шаг неровностей по вершинам и др.
Установлено 14 классов шероховатости поверхностей. Чем меньше шероховатость, тем выше класс шероховатости. Классы шероховатости с первого по пятый, а также классы 13-й и 14-й определяются параметром Rz, все остальные классы (с шестого по двенадцатый включительно) определяются параметром Ra, символ которого не пишется, а пишется только количественная характеристика.
На рис. 275 приведена структура обозначения шероховатости поверхности.
На рис. 276 изображены знаки, которые применяются в обозначении шероховатости. Размер h берется равным высоте размерных чисел на чертеже, а размер Н равен (1, 5, ... 3)h.
Знак на рис. 276, а применяют для обозначения шероховатости поверхности, вид обработки которой конструктором не задается. Знак на рис. 276, б обозначает шероховатость поверхности, образуемой удалением слоя металла (точение, фрезерование, сверление и т. д.). Шероховатость поверхности в состоянии поставки (прокат, поковка, литье и др.) и не обрабатываемой по данному чертежу обозначается знаком, показанным на рис. 276, в.
Обозначения шероховатости поверхностей на изображении детали располагают на линиях контура, выносных линиях или полках ли-
Рис. 276
Рис. 277
Рис. 278
Рис. 279
ний-выносок (рис. 277). Наносят знаки шероховатости на изображении в зависимости от расположения поверхности и наличия полки у знака (рис. 278).
При указании одинаковой шероховатости для всех поверхностей детали обозначение шероховатости помещают в правом верхнем углу чертежа и на изображение не наносят (рис. 279, а). Размеры и толщина линии знака, выносимого в правый верхний угол, должны быть в 1,5 раза больше, чем в обозначениях на изображении.
В случае одинаковой шероховатости для преобладающей части поверхностей детали шероховатость наносится, как показано на рис. 279, б. Это означает, что все поверхности, на которых нет обозначения шероховатости, имеют шероховатость с величиной микронеровностей, указанной в правом верхнем углу чертежа. Размеры знака в скобках должны быть одинаковыми со знаками на изображениях.
Если шероховатость поверхностей, образующих контур детали, должна быть одинаковой, то обозначение шероховатости наносят, как показано на рис. 279, в.
275.gif
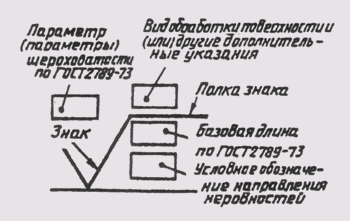
276.gif
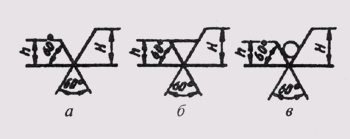
277.gif
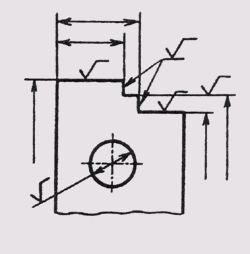
278.gif
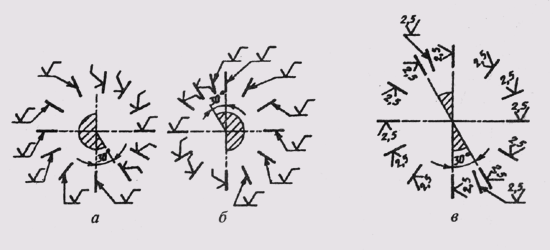
279.gif
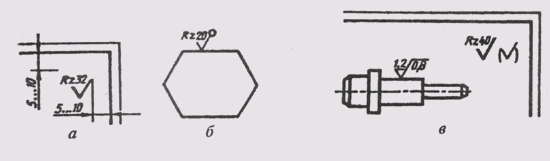
95. Выполнение чертежей оригинальных деталей
§ 95. Выполнение чертежей оригинальных деталей
Все детали можно разделить на три группы: детали стандартные, детали со стандартными изображениями, детали оригинальные.
К стандартным деталям относятся ранее рассмотренные крепежные резьбовые детали (болты, винты, гайки, шпильки), шайбы, штифты, шплинты, шпонки, соединительные детали трубопроводов. Стандарты регламентируют не только форму и размеры этих деталей, но и их изображения 'и нанесение размеров и знаков шероховатости.
Группа стандартов ЕСКД (ГОСТ 2.401—68...ГОСТ 2.426—74) регламентирует только стандартные изображения деталей и указывает правила нанесения размеров на изображениях этих деталей. К таким деталям относятся пружины, зубчатые колеса, рейки, червяки, звездочки и т. д.
К оригинальным деталям относятся такие детали, форма которых отличается от формы деталей первых двух групп. К ним относятся литые детали, детали, изготовляемые штамповкой или ковкой, детали, имеющие форму поверхностей вращения, детали, ограниченные преимущественно плоскостями, и т. д. Форма этих деталей определяется технологией их изготовления и несет в себе элементы, характерные для этой технологии. У литых деталей имеются литейные уклоны и скругления, детали токарной обработки преобладающими имеют поверхности вращения и т. п.
Литые детали нашли очень широкое применение. Это и отдельные детали машин, например маховики, шкивы, цилиндры, крышки, рычаги, это детали типа опор, кронштейнов, это и корпусные коробчатые детали закрытого или открытого типа, имеющие точно обработанные отверстия и плоские наружные поверхности.
Общее количество изображений на чертеже литой детали во многом зависит от правильного выбора главного вида, от разумного ис-
Рис. 280
Рис. 281
пользования допустимых ГОСТ 2.305 — 68 сочетаний видов с разрезами, местных разрезов, сечений выносных элементов, условностей и упрощений.
Корпусные детали коробчатого типа располагают относительно фронтальной плоскости проекций так, чтобы их основные базовые поверхности занимали горизонтальное положение, а детали типа фланцев или шкивов — чтобы их ось проецировалась параллельно основной надписи чертежа, так как такое их расположение соответствует положению детали при ее токарной обработке.
При выполнении чертежей литых деталей нужно учитывать следующие требования.
1 . Литейные уклоны на чертеже не изображают, ограничиваются соответствующей записью в технических требованиях.
2. Для того чтобы деталь не имела внутренних напряжений и литейных дефектов, нужно осуществлять плавный переход от одной толщины стенки к другой по нормам, приведенным на рис. 280, а:
S/S1=<2; r = (0,3...0,4)h;
S/S1>2; l = (4...5)h;
3. Опорные бурты (фланцы) должны быть толще основной части детали. В этом случае нужно предусмотреть плавный переход от стенки к фланцу (рис. 280, б).
4. Обрабатываемые поверхности нужно приподнимать над необрабатываемыми. Это обеспечит свободный выход режущему инструменту и уменьшит площадь механической обработки (рис. 281).
5. Если плита-основание устанавливается на другую деталь, то привалочную плоскость делают несплошной, чтобы уменьшить площадь обработки (рис. 282, а). С этой же целью среднюю часть отвер-
Рис. 282
Рис. 283
стия выполняют большего диаметра, чем концевые работающие части отверстия, где вал сопрягается с отверстием (рис. 282, б).
6. Поверхности, в которых сверлят отверстия, выполняют с приливами, торцевые плоскости которых должны быть перпендикулярны оси отверстия (рис. 283).
При нанесении разрезов на чертежах литых деталей нужно учитывать следующие особенности: а) взаимное положение необрабатываемых поверхностей детали указывают размерами, которые связывают эти поверхности между собой; б) механически обработанные поверхности и необрабатываемые связывают между собой не более чем одним размером по длине, высоте или глубине детали.
Перед нанесением размеров необходимо выбрать основные литейные и конструкторские базы. Литейными базами могут служить оси или плоскости симметрии или необрабатываемые поверхности. От литейных баз наносят размеры, определяющие форму и положение необрабатываемых поверхностей. Отдельно наносят размеры, определяющие форму и положение обрабатываемых поверхностей относительно конструкторских баз.
Размеры на чертежах литых деталей не допускается наносить в виде замкнутой цепи. На рабочем чертеже литой детали должны быть помещены технические требования. На учебных чертежах в технических требованиях можно ограничиться только указанием размеров неуказанных литейных радиусов и размеров для справок.
На рис. 284 показаны изображения и нанесены размеры крышки, полученной путем механической обработки из отливки. В качестве литейных баз были приняты торец детали и ось поверхности выступа диаметр 70, а в качестве конструкторских баз — опорный торец и ось поверхности 0 72, совпадающая с литейной базой. При этом габаритный размер 38 является одновременно размером между литейной и конструкторской базами в продольном направлении.
Детали, имеющие форму тел вращения, обрабатываются в основном на токарных и аналогичных им станках. У таких деталей главное
Рис. 284
Рис. 285
изображение с нанесенными размерами дает полное представление об их форме, поэтому не требуются изображения типа вида слева или вида сверху. Для пояснения отдельных элементов применяют местные разрезы, сечения, выносные элементы.
Детали, ограниченные поверхностями вращения разных диаметров, обычно вычерчивают так, чтобы участки с большими диаметрами находились левее участков с меньшими диаметрами, что соответствует расположению детали на стенке при ее обработке (см. рис. 266).
Если деталь имеет внутренние соосные поверхности вращения, то в качестве главного изображения принимают фронтальный разрез, что дает полное представление о детали и облегчает нанесение размеров (рис. 285, а). При этом ступени отверстия большого диаметра располагают слева.
При выполнении чертежей деталей с преобладающими токарной обработкой поверхностей необходимо учитывать следующие требования.
Рис. 286
1. В местах перехода от одного диаметра вала к другому нужно выполнить скругления галтели (рис. 285, в).
2. Для удобства сборки детали на торцах деталей нужно выполнять фаски (рис. 285, б).
3. На внешних поверхностях рукояток, головок, круглых гаек, завинчиваемых вручную, нужно выполнять рифление по ГОСТ 21474—75 (рис. 286). Условное обозначение рифления наносится прямо на изображении детали на полке линии-выноски и включает наименование, шаг и номер стандарта.
4. Если поверхность детали шлифуется, то необходимо предусмотреть специальную канавку для выхода шлифовального круга. Размеры
Рис. 287
Рис. 288
канавок при круглом и плоском шлифовании определяются стандартом. На рис. 287 приведены изображения канавок для шлифования наружного и внутреннего диаметров и даны рекомендации для их размеров. Размеры канавок в размерные цепи деталей не включают.
Если d = 10..15 мм, то b = 3 мм, d1 =d + + 0,5 мм, h = 0,25 мм, R = 1 мм, R1 = 0,5 мм.
Если d = 50...100 мм, то b = 5 мм, d2 — d + + 1 мм, h = 0,5 мм, R=1,5 мм, R1 = 0,5 мм.
5. Если конструкция детали не предусматривает свободный выход инструмента, то переходная часть ее по своей форме и размерам должна соответствовать форме и размерам этого инструмента (рис. 288).
6. Для установки детали в центрах токарного станка в детали выполняют центровые отверстия, размеры и условные обозначения которых определяются стандартом (рис. 289).
7. Проточки внешние и внутренние для выхода резца при нарезании резьбы вычерчивают укрупненно с помощью выносных элементов (рис. 289).
На рис. 289 выполнен учебный чертеж вала. Сечение А —А выявляет размеры поперечного сечения шпоночной канавки, а сечение Б — Б дает форму и размеры призматической части вала. Центровое отверстие и шпоночная канавка показаны местными разрезами. Выносные элементы I и II помогают выяснить размеры проточки для метрической резьбы и глубину сверления под стопорный винт.
При нанесении размеров по длине вала в качестве основной базы взят правый торец детали. Относительно вспомогательной базы представлены размеры 15, 36 и 70 мм. Обозначение шероховатости поверхностей нанесено с учетом их конструктивного назначения.
Чертежи деталей кроме основных изображений готовой детали содержат полную или частичную развертку этой детали. На изображение развертки наносят только те размеры, которые нельзя указать на изображении готовой детали. Над изображением развертки помещают надпись «Развертка». Изображают развертку сплошными основными линиями (рис. 290). Если необходимо, на развертке указывают линии сгиба и делают соответствующие надписи. Особое внимание нужно обращать на правильное определение размеров в местах сгиба детали.
Рис. 289
Рис. 290
280.gif
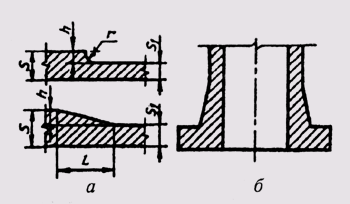
281.gif
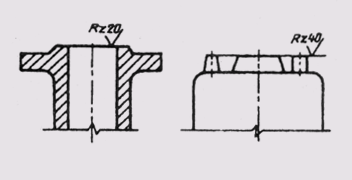
282.gif
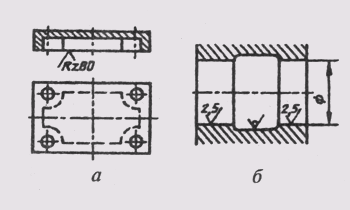
283.gif

284.gif
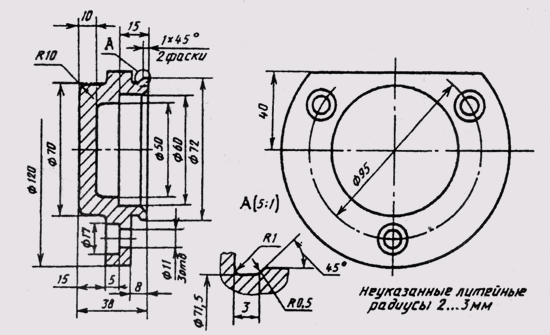
285.gif
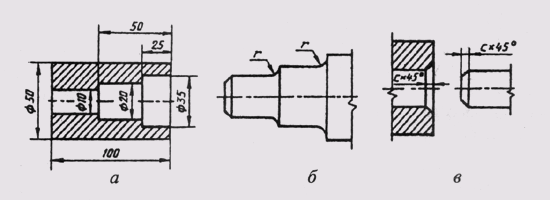
286.gif
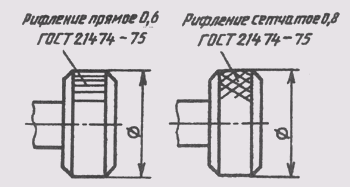
287.gif
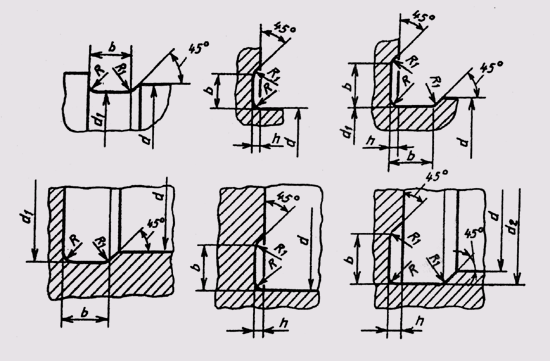
288.gif
289.gif
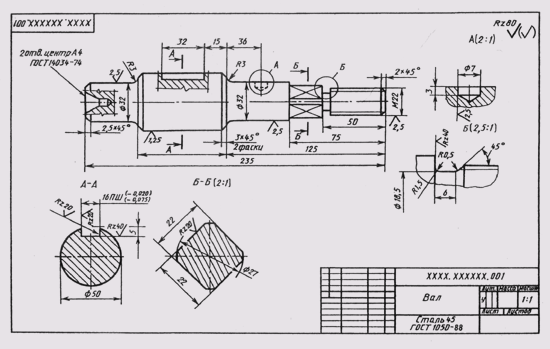
290.gif
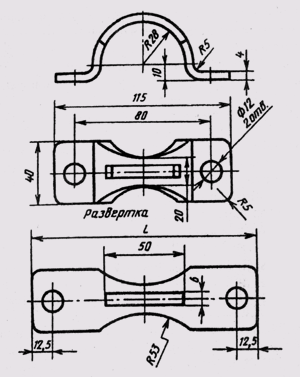
96. Выполнение эскизов деталей
§ 96. Выполнение эскизов деталей
Конструкторские документы для одноразового пользования могут выполняться в виде эскизов. Эскизом называют чертеж, выполненный без применения чертежного инструмента (от руки) и точного соблюдения стандартного масштаба (в глазомерном масштабе). При этом должна сохраняться пропорция в размерах отдельных элементов и всей детали в целом. По содержанию к эскизам предъявляются такие же требования, что и к рабочим чертежам.
Эскизы выполняют в следующих случаях: при разработке новой конструкции, при составлении рабочего чертежа уже имеющейся детали, при необходимости изготовить деталь по самому эскизу.
Эскизы рекомендуется выполнять от руки на листах клетчатой бумаги стандартного формата, мягким карандашом ТМ, М или 2М. Последовательность выполнения эскиза во многом совпадает с последо-
вательностью выполнения рабочего чертежа детали. Выполнение эскиза включает в себя следующие этапы:
подготовительный;
размещение и вычерчивание изображений;
нанесение размеров и знаков шероховатости поверхностей деталей;
выполнение необходимых надписей и окончательное оформление эскиза.
На подготовительном этапе нужно внимательно осмотреть деталь, ознакомиться с ее конструкцией, определить имеющиеся в ней отверстия, канавки, проточки, приливы, выступы, фаски и другие элементы. Мысленно расчленить деталь на простейшие геометрические формы (цилиндр, конус, призма и др.) определить, как эти формы связаны между собой, собраны воедино.
Затем нужно установить материал, из которого деталь изготовлена, и основные технологические операции (резание, штамповка, литье и т. д.), которые использовались при изготовлении детали. Если возможно, устанавливают, частью какого изделия является данная деталь, каково ее назначение в этом изделии.
Затем приступают к выбору главного изображения детали, учитывая некоторые требования конструктивного и технологического порядка. Главное изображение должно давать наибольшую информацию о детали. Определяют, какие целесообразно выполнить разрезы или другие изображения, дополняющие главное изображение. Количество изображений должно быть минимальным, но достаточным для передачи форм детали.
Учитывая сложность детали, ее размеры и размеры листа бумаги, решают вопрос о выборе приблизительного масштаба изображения, чтобы удачно скомпоновать рабочую площадь эскиза. Затем приступают к вычерчиванию изображения. Для этого прежде всего намечают осевые и центровые линии каждого изображения. Осевые и центровые линии проводят с целью выявления или геометрических осей и центров, или проект-плоскостей симметрии детали. Отсутствие осевых и центровых линий затрудняет понимание чертежа, ведет к пропуску необходимых размеров, затрудняет разметку деталей. Затем наносят внешние контуры каждого изображения (рис. 291, а) с конструктивными элементами (фаски, проточки и т. д.), тонкими линиями отмечают контуры необходимых разрезов и сечений. При этом учитывают, что обычно внутренние поверхности параллельны внешним поверхностям детали, оси крепежных отверстий чаще всего располагаются симметрично относительно осей детали или по вершинам правильных многоугольников; острые кромки отлитых элементов должны быть
Рис. 291
скругленными; конструктивные уклоны и конусности должны быть отражены, несмотря на их незначительность.
Проверив выполненные изображения, убирают лишние линии, выполняют штриховку в разрезах и сечениях, обводят видимый контур изображений сплошной линией (рис. 291, б).
На третьем этапе составления эскиза:
намечают размерные базы и проводят выносные и размерные линии для габаритных размеров, межосевых и межцентровых размеров и
Рис. 292
Рис. 293
их расстояний до баз и для размеров отдельных элементов деталей (рис. 291, в);
обмеряют деталь, сопоставляют размеры, полученные обмером, с размерами, рекомендуемыми таблицами размерных рядов, и наносят на эскиз скорректированные, но близкие к измеренным размерам. При этом нужно помнить о сопрягаемых размерах, которые могут быть проверены и уточнены по сопрягаемым с данной поверхностью деталям в готовом изделии;
определяют шероховатость поверхностей детали и наносят на эскиз ее условными обозначениями;
обозначают разрезы, сечения, выносные элементы.
Заключительный этап включает в себя проверку выполненных изображений, заполнение технических требований и основной записи на эскизе, а также таблиц, если они необходимы (рис. 292).
Обмер детали при выполнении ее эскиза с натуры выполняется с помощью различных инструментов, которые выбирают в зависимости от величины и формы детали, а также от требуемой точности определения размеров.
Рис. 294
Рис. 295
Металлическая линейка (рис. 293, а), кронциркуль (рис. 293, б) и нутромер (рис. 293, в) позволяют измерить внешние и внутренние размеры с точностью до 0,1 мм. Штангенциркуль, предельная скоба, калибр, микрометр позволяют выполнить более точный обмер (рис. 294, а, б, в, г). Замер радиусов скруглений производят с помощью радиусных шаблонов (рис. 295, а), а шаги резьбы замеряют с помощью резьбовых шаблонов (рис. 295, б, в).
На рис. 296 показано, как с помощью линейки, кронциркуля и нутромера измеряют линейные размеры детали.
Рис. 296
По размерам наружного или внутреннего диаметра резьбы rto величине шага резьбы, определенного по резьбовому шаблону, подбирают точное значение резьбы по таблицам стандартных резьб.
Если выявится несоответствие шага и диаметра стандарту, то значит резьба нестандартная. В этом случае нужно нанести на эскизе детали шаг резьбы, наружный и внутренний ее диаметры.
291.gif
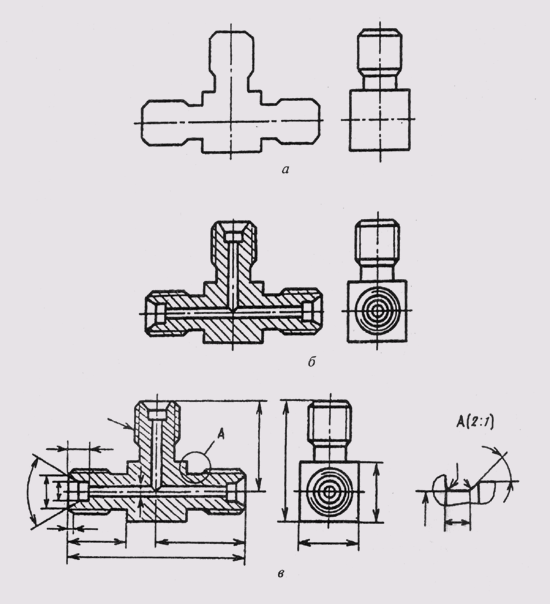
292.gif
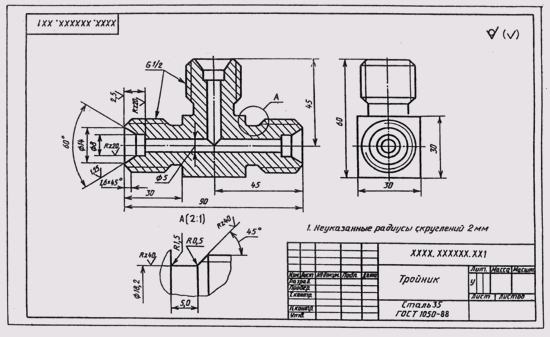
293.gif
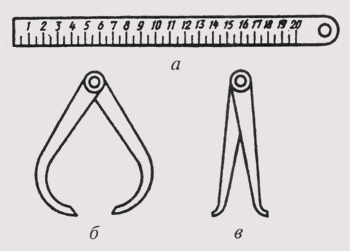
294.gif
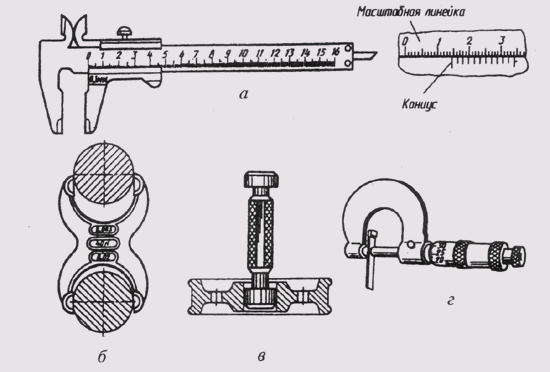
295.gif
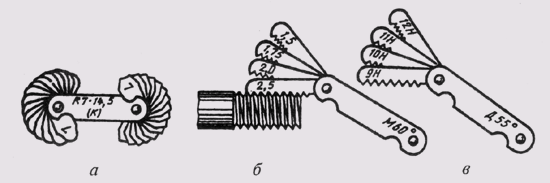
296.gif
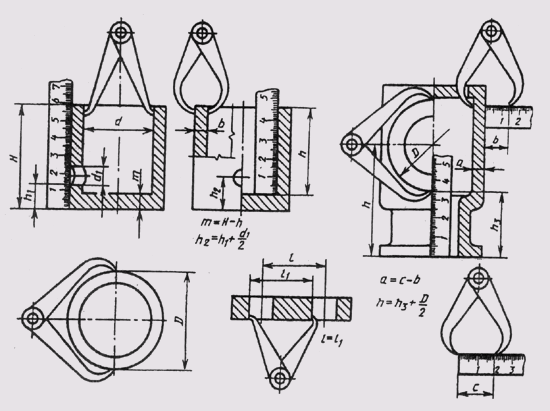
97. Выполнение технических рисунков деталей
§ 97. Выполнение технических рисунков деталей
В тех случаях, когда необходимо быстро пояснить форму рассматриваемого предмета, показать его наглядно, пользуются техническим рисунком. Техническим рисунком называют наглядное изображение имеющегося или проектируемого предмета, выполненное без применения чертежных инструментов, от руки в глазомерном масштабе с соблюдением пропорций и размеров элементов, составляющих его. Технические рисунки, применяемые в конструкторской практике, используют для того, чтобы более быстро выразить свою мысль в наглядной форме. Это дает возможность более доступно, доходчиво пояснить чертежи сложных предметов. Применение технического рисунка позволяет закрепить техническую идею или предложение. Кроме того, применение технического рисунка детали очень полезно при эскизировании деталей с натуры, хотя выполнять технический рисунок можно и по комплексному чертежу предмета.
Важнейшим требованием, предъявляемым к техническому рисунку, является наглядность. Технический рисунок в законченном виде с нанесением тени и штриховки иногда может быть более наглядным, чем аксонометрическое изображение и с нанесенными размерами может заменить чертеж несложной детали, служащей документом для ее изготовления.
Чтобы быстро и правильно выполнить технический рисунок, необходимо получить навыки проведения параллельно расположенных линий под разным наклоном, на разном расстоянии, различной толщины без применения чертежных инструментов, не пользуясь приборами, делить отрезки на равные части, строить наиболее применяемые углы (7,15, 30,41,45,60,90°), делить углы на равные части, строить окружности, овалы и др. Необходимо иметь представление об изображении различных фигур в каждой из плоскостей проекций, уметь выполнить на техническом рисунке изображения наиболее применяемых плоских фигур и простых геометрических форм.
Рис. 297
Рис. 298
Перед началом выполнения технического рисунка решают вопрос о выборе наиболее эффективной системы наглядного изображения. В машиностроительном черчении для этой цели чаще всего используют прямоугольную изометрию. Это объясняется тем, что очертания фигур, расположенных в аксонометрических плоскостях, в изометрии претерпевают одинаковое искажение, что обеспечивает наглядность изображения и сравнительную простоту ее достижения. Находит применение и прямоугольная диметрия.
На рис. 297, а приведен технический рисунок прямоугольного треугольника, расположенного в горизонтальной плоскости проекций и выполненный в прямоугольной изомерии, а на рис. 297, б — технический рисунок прямоугольного треугольника, расположенного во фронтальной плоскости проекций и выполненного в прямоугольной диметрии.
На рис. 298, а показан технический рисунок шестиугольника, расположенного в горизонтальной плоскости проекций и выполненного в прямоугольной изометрии. На рис. 298, б приведен технический рисунок того же шестигранника, выполненный в прямоугольной диметрии. Точно так же выполнен рисунок окружности, расположенной в
Рис. 299
Рис. 300
горизонтальной плоскости проекций (рис. 299, а), и технический рисунок такой же окружности, расположенной во фронтальной плоскости проекций и выполненный с применением правил прямоугольной ди-метрии (рис. 299, б).
Используя правила построения аксонометрических проекций и технических рисунков простейших плоских фигур, можно приступить к выполнению технических рисунков объемных геометрических фигур.
На рис. 300, а приведен технический рисунок прямой четырехгранной пирамиды, выполненный в прямоугольной изомерии, на рис. 300, б — технический рисунок прямой четырехгранной пирамиды, выполненный в прямоугольной диметрии.
Выполнение технических рисунков поверхностей вращения связано с построением эллипсов. На рис. 301, а приведен технический рисунок прямого кругового цилиндра, выполненный в прямоугольной изомерии, а на рис. 301, б — рисунок прямого кругового конуса, выполненный в прямоугольной диметрии.
Рис. 301
Рис. 302
Рис. 303
Далее можно приступить к построению более сложных форм технических деталей.
Технический рисунок может быть выполнен в такой последовательности.
1. В выбранном на чертеже месте строят аксонометрические оси и намечают расположение детали с учетом максимальной ее наглядности (рис. 302, а).
2. Отмечают габаритные размеры детали, начиная с основания, и строят объемный параллелепипед, охвативший всю деталь (рис. 302, б).
3. Габаритный параллелепипед мысленно расчленяют на отдельные геометрические формы, составляющие его, и выделяют их тонкими линиями (рис. 302, в).
4. После проверки и уточнения правильности сделанных наметок обводят линиями необходимой толщины видимые элементы детали (рис. 302, г, д).
5. Выбирают способ оттенения и выполняют соответствующую дорисовку технического рисунка (рис. 302, е). На рис. 302 показана последовательность построения технического рисунка ттетели.
Для повышения наглядности и выразительности на выполненный технический рисунок наносят штриховку сплошными параллельными линиями различной толщины или штриховку в виде сетки. Нанесение на технический рисунок светотени, показывающей распределение света на поверхностях изображаемого предмета, называют оттенением. Оттенение может быть выполнено также с помощью точек. С увеличением освещения расстояние между точками увеличивается. При выполнении оттенения считают, что на изображаемый предмет свет попадает сверху, сзади и слева, поэтому освещенные части делают более светлыми, а правые и нижние части — затемненными. Ближе рас-
положенные части предмета оттеняют светлее, чем участки, расположенные от света дальше. На каждом рисунке применяют один какой-либо способ оттенения, и все поверхности изображаемого предмета оттеняются.
На рис. 303, а приведен технический рисунок цилиндра, на котором оттенение выполнено параллельной штриховкой, на рис. 303, б— траферовкой, а на рис. 303, в — с помощью точек. На рис. 302, е показан технический рисунок детали с оттенением, выполненным параллельной штриховкой.
Оттенение на рабочих чертежах деталей могут быть выполнены также тушевкой — частым, почти сплошным нанесением штрихов в различном направлении, или отмывкой, выполненной тушью или красками.
297.gif
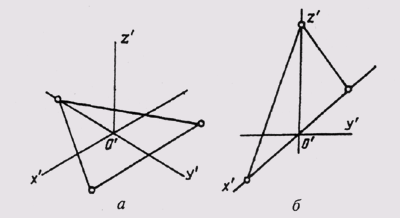
298.gif
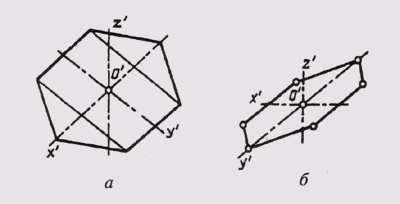
299.gif
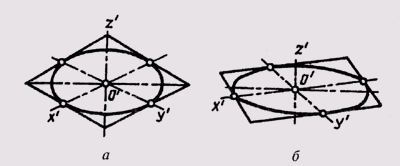
300.gif
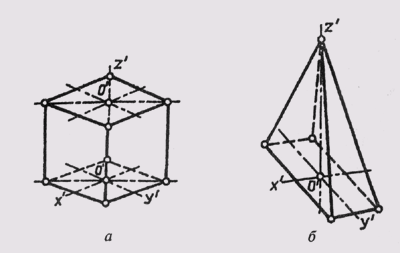
301.gif
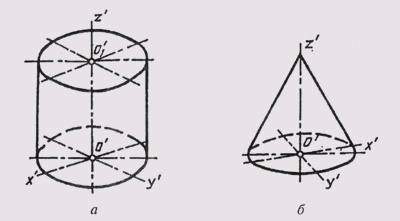
302.gif
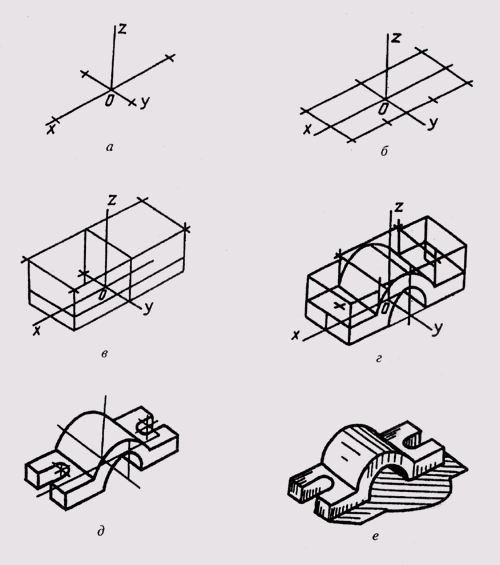
303.gif
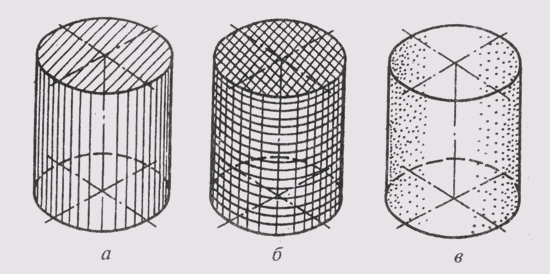
17. Глава 16. Изображение изделий
1. Глава 16. Изображение изделий
Глава 16. ИЗОБРАЖЕНИЕ ИЗДЕЛИЙ
§ 98. Общие сведения об изделиях
В соответствии с ГОСТ 2.101—68 любой предмет или набор предметов производства, подлежащих изготовлению на предприятии, называется изделием. Установлены следующие виды .изделий: сборочные единицы, комплексы, комплекты.
Сборочной единицей называется изделие, составные части которого подлежат соединению между собой сборочными операциями (свинчиванием, сочленением, клепкой, сваркой, пайкой, опрессовкой, развальцовкой, склеиванием, сшивкой, укладкой и т. п.), например станок, редуктор и т. д.
Комплекс включает в себя два и более изделий, не соединенных сборочными операциями, но предназначенных для выполнения взаимосвязанных эксплуатационных функций, например цех-автомат, бурильная установка и др.
В комплекс кроме изделий, выполняющих основные функции, входят детали, сборочные единицы, предназначенные для выполнения вспомогательных функций, например детали и сборочные единицы для монтажа комплекса на месте его эксплуатации и др.
Комплект состоит из двух и более изделий, имеющих общее эксплуатационное значение вспомогательного характера, например комплект запасных частей и т. п.
Сборочные единицы, комплексы и комплекты относятся к специфицированным изделиям, так как включают в себя несколько составных частей, а детали — к неспецифицированным изделиям. Для каждого изделия разрабатывается комплект конструкторских документов, который включает в себя графические и текстовые документы, определяющие состав и устройство изделий и содержащие необходимые данные для его разработки или изготовления, контроля, приемки, эксплуатации и ремонта. ГОСТ 2.102—68 устанавливает 25 видов конструкторских документов. В их число входят чертежи деталей, чертежи сборочные общего вида, габаритные, монтажные; схемы, ведомости, расчеты, пояснительные записки и др. Все они имеют свой шифр.
Каждому изделию и его конструкторским документам присваивается самостоятельное обозначение в соответствии с ГОСТ 2.201—80. Устанавливается следующая структура обозначения изделий и его конструкторского документа:
Четырехзначный код организации-разработчика назначается по специальному кодификатору, а код классификационной характеристики присваивается по классификатору ЕСКД. Структура кода классификационной характеристики:
Порядковый регистрационный номер назначается от 001 до 999. Примеры обозначений документов на изделие: АВГБ. 061341. 021 СБ —сборочный чертеж, АВГБ. 061341. 021—спецификация, АВГБ. 061341. 021 ТУ — технические условия. Структура обозначения эскизных конструкторских документов по ГОСТ 2.201—80:
Сборочные чертежи и эскизы обозначаются подобно структуре обозначения производственной документации в соответствии с ГОСТ 2.201—80.
303.1.gif

303.2.gif
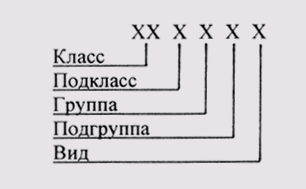
303.3.gif

99. Выполнение чертежа общего вида
§ 99. Выполнение чертежа общего вида
Графический документ, определяющий конструкцию изделия, взаимодействие его основных составных частей и поясняющий принцип работы изделия, называется чертежом общего вида. Чертеж общего вида разрабатывается на первых стадиях проектирования, т. е. на стадии технического предложения, эскизного и технического проектов.
Рис. 304
Чертеж общего вида включает в себя: изображение, виды, разрезы, сечения изделия, надписи и текстовую часть, необходимые для понимания конструктивного устройства изделия, взаимодействия его составных частей и принципа работы изделия; наименование и обозначение составных частей изделия, для которых объясняется принцип работы, приводятся технические характеристики, материалы, количество, и для тех составных частей изделия, с помощью которых описывается принцип действия изделия, поясняются изображения общего вида и состав изделия; необходимые размеры; схему изделия и технические характеристики.
Чертеж общего вида выполняется с соблюдением требований ГОСТ 2.109—73. Составные части изображаются упрощенно. Их можно изображать на одном листе с общим видом или на отдельных последующих листах.
Наименование и обозначение составных частей изделия могут быть указаны одним из следующих способов:
на полках линий-выносок, проведенных от деталей на чертеже общего вида;
в таблице, размещенной на чертеже общего вида (рис. 304);
в таблице, выполненной на отдельных листах формата А4, в качестве следующих листов чертежа общего вида.
Рис. 305
При наличии таблицы порядковый номер составных частей изделия указывается на полках линий-выносок в соответствии с этой таблицей.
Таблицу размещают над основной надписью чертежа.
Текстовую часть в виде технических требований и технической характеристики размещают обязательно на первом листе в виде колонки шириной не более 185 мм. При необходимости текст размещают в одну, две и более колонок. При этом вторая и последняя колонки располагаются слева от основной надписи. Между текстовой частью и таблицей составных частей (или основной надписью) нельзя размещать изображения или другие таблицы.
На чертеже общего вида проставляют габаритные, присоединительные, установочные и необходимые конструктивные размеры (рис. 305).
Необходимые таблицы, в том числе и технические характеристики, оформленные в виде таблицы, размещают на свободном поле чертежа общего вида справа от изображений или ниже их. Если таблиц несколько и на них имеются ссылки в технических требованиях, то таблицы надписывают по типу: «Таблица 1» (без знака №).
Все таблицы заполняются сверху вниз.
304.gif

305.gif
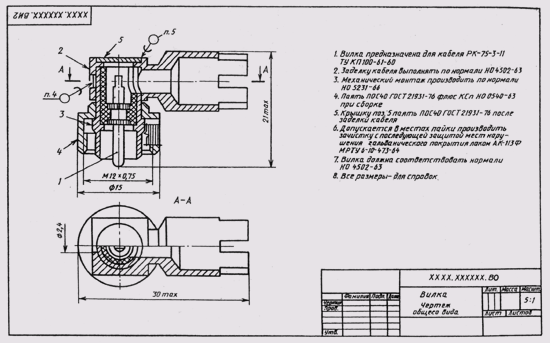
100. Сборочный чертеж
§ 100. Сборочный чертеж
Графический документ, содержащий изображение сборочной единицы и другие данные, необходимые для ее сборки (изготовления) и контроля, называется сборочным чертежом.
Сборочный чертеж выполняется на стадии разработки рабочей-документации на основании чертежа общего вида изделия. На основании ГОСТ 2.109—73 сборочный чертеж должен содержать:
изображение сборочной единицы, дающее представление о расположении и взаимосвязи составных частей, соединяемых по данному чертежу и обеспечивающих возможность осуществления сборки и контроля сборочной единицы;
размеры и другие параметры и требования, которые должны быть выполнены и проконтролированы по данному чертежу;
указания о характере сопряжения разъемных частей изделия, а также указания о способе соединения неразъемных соединений, например сварных, паяных и др.;
номер позиций составных частей, входящих в изделие;
основные характеристики изделия;
размеры габаритные, установочные, присоединительные, а также необходимые справочные размеры.
Количество изображений на сборочном чертеже зависит от сложности конструкций изделия. Учебный сборочный чертеж выполняется обычно в двух или трех основных изображениях с применением разрезов. Рекомендуется соединение половины вида с половиной разреза при наличии симметрии вида и разреза изделия.
Рис. 306
Рис. 307
Разрезы и сечения на сборочных чертежах служат для выявления внутреннего устройства сборочной единицы и взаимосвязи входящих в нее деталей.
Разрез на сборочном чертеже представляет собой совокупность разрезов отдельных частей, входящих в сборочную единицу. Штриховку одной и той же детали в разрезах на разных изображениях выполняют в одну и ту же сторону, выдерживая одинаковое расстояние (шаг) между линиями штриховки. Штриховку смежных деталей из одного материала разнообразят изменением направления штриховки, сдвигом штрихов или изменением шага штриховки (рис. 306). Сварное, паяное или клееное изделия из одного материала, находящиеся в сборе с другими изделиями, в разрезах и сечениях штрихуют как монолитное тело, показывая границы между деталями сварного изделия сплошными основными линиями (рис. 307). Шарики в разрезах и сечениях всегда показывают нерассеченными. Винты, болты, шпильки, штифты, шпонки, шайбы, гайки и другие стандартные крепежные изделия при продольном разрезе показывают нерассеченными. Непустотелые валы, шпиндели, рукоятки, шатуны и т. п. при продольном разрезе также изображают нерассеченными (рис. 308).
На сборочных чертежах допускается не показывать фаски, округления, проточки, углубления, выступы, рифления, оплетку и другие мелкие элементы. Допускается не изображать зазоры между стержнем и отверстием. Если необходимо показать составные части изделия, закрытые крышкой, кожухом, щитом и т. п., то закрывающие изделия можно не изображать, а над изображением выполнить надпись по типу «Крышка поз. 5 не показана».
Изделия из винтовой пружины, изображенной лишь сечением витков, изображают лишь до зоны, условно закрывающей эти изделия и определяемой осевыми линиями сечения витков (рис. 309).
Рис. 308
Рис. 309
При выполнении сборочных чертежей соблюдают условности и упрощения, устанавливаемые стандартами на правила выполнения чертежей различных изделий.
На сборочном чертеже допускается изображать перемещающиеся части изделия в крайнем или промежуточном положении с соответствующими разрезами, используя тонкие штрихпунктирные линии с двумя точками (рис. 310). Для изображения соседних изделий — «обстановки» — используют тонкие сплошные линии (рис. 311).
На сборочных чертежах наносят следующие размеры..
Габаритные размеры, характеризующие три измерения изделия. Если один из размеров является переменным вследствие перемещения движущихся частей изделия, то на чертеже указывают размеры при крайних положениях подвижных частей (рис. 312).
Монтажные размеры, указывающие на взаимосвязь деталей в сборочной единице, например расстояние между осями валов, монтажные зазоры и т. п.
Рис. 310
Рис. 311
Установочные размеры, определяющие величины элементов, на которых изделие устанавливается на месте монтажа или присоединяется к другому изделию, например размеры окружностей и диаметры отверстий под болты, расстояние между осями фундаментных болтов и т. п.
Эксплуатационные размеры, определяющие расчетную, конструктивную характеристику изделия, например диаметры проходных отверстий, размеры резьбы на присоединительных элементах и т. п.
На сборочных чертежах также указывают размеры отверстий под крепежные изделия, если эти отверстия выполняются в процессе сборки.
Все остальные части сборочной единицы нумеруются в соответствии с номерами позиций, указанных в спецификации этой сборочной единицы. Номера позиций указывают на полках линий-выносок, проводимых от точек на изображениях составных частей сборочной единицы, которые проецируются как видимые на основных видах или заменяющих их разрезах.
Номера позиций располагают параллельно основной надписи чертежа вне контура изображения и группируют их в колонку или строчку по возмо:хности на одной линии (рис. 312,313, а). Допускается делать общую линию-выноску с вертикальным расположением позиций (рис. 313,6). Как правило, номер позиции наносят на чертеж один раз. Размер шрифта номеров позиций должен быть на 1—2 размера больше, чем размер шрифта размерных чисел на этом чертеже.
Рис. 311
Рис. 312
Рис. 313
Рис. 314
В процессе сборки изделия выполняются некоторые технологические, так называемые пригоночные, операции. Их выполняют совместной обработкой соединяемых деталей или подгонкой одной детали к другой по месту ее установки. В этих случаях на сборочных чертежах делают текстовые записи, подобные изображенным на рис. 314.
Многие изделия имеют типовые составные части. К ним относятся, например, сальниковые уплотнения (рис. 315). Их мягкая набивка обеспечивает герметичность отверстий, через которые проходят движущиеся части изделия. В качестве набивки используется пеньковое или льняное волокно (рис. 315, а, 6) или набор колец из асбеста, кожи, резины (рис. 315, в). Поджатие набивки осуществляется накидной гайкой (рис. 315, а), резьбовой втулкой (рис. 315, б) или сальниковой крышкой (рис. 315, в). Эти детали на сборочных чертежах изображают в поднятом положении.
Клапаны имеют типовые крепления на штоках или шпинделях. Крепления могут осуществляться или обжимкой клапана (рис. 316, а), или проволочной скобой (рис. 316, б), или кольцом из проволоки (рис. 316, в). Головка шпинделя может крепиться в прорези клапана (рис. 316, г).
Подшипники качения относятся к стандартным изделиям. Их можно изображать на сборочных чертежах упрощенно (рис. 317, а) без указания типа по ГОСТ 2.420—69 или, как показано на рис. 317,б, — с изображением колец и шариков или роликов.
Рис. 315
Рис. 316
Рис. 317
306.gif
307.gif
308.gif
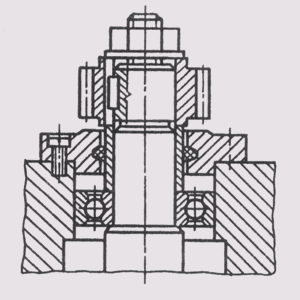
309.gif
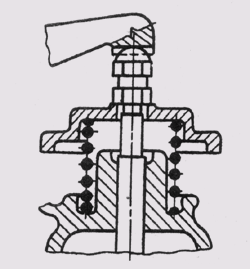
310.gif
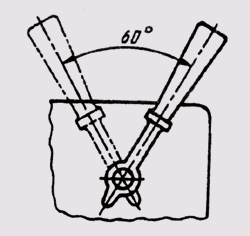
311.gif
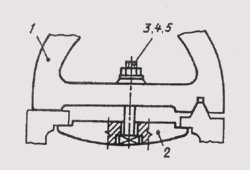
311.gif
312.gif
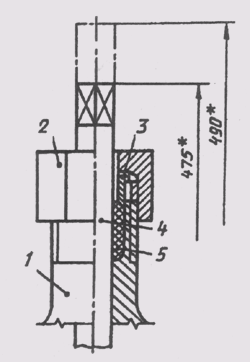
313.gif
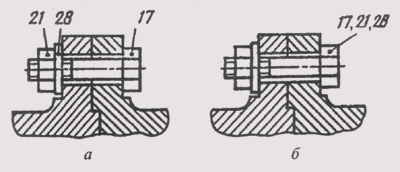
314.gif
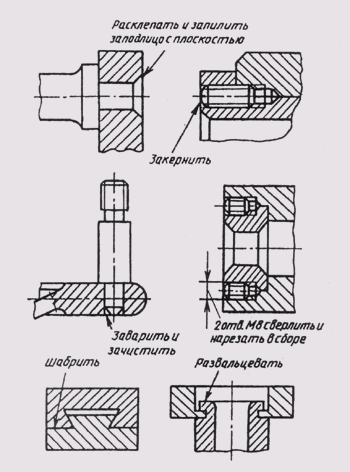
315.gif
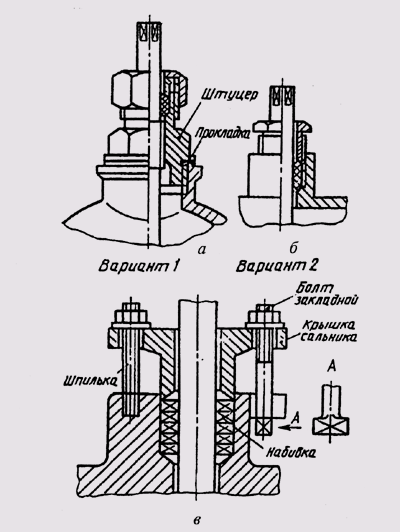
316.gif
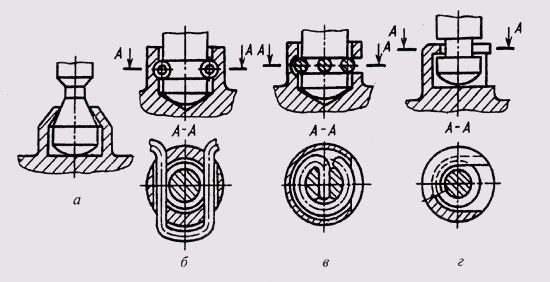
317.gif
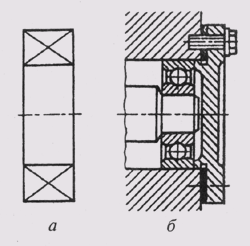
101. Выполнение спецификации к сборочному чертежу
§ 101. Выполнение спецификации к сборочному чертежу
Графический конструкторский документ, определяющий состав сборочной единицы, комплекса или комплекта, называется спецификацией. Спецификация составляется в табличной форме на отдельных листах формата А4 (297 х 210) на каждую сборочную единицу (рис. 318). Основная надпись выполняется размером 40 х 185 в соответствии с ГОСТ 2.104—68.
Форма и порядок выполнения спецификации определяется ГОСТ 2.108—68. Заполняют спецификацию сверху вниз. Разделы спецификации располагаются в такой последовательности: документация, комплексы, сборочные единицы, детали, стандартные изделия, прочие изделия, материалы, комплекты.
Наличие тех или иных разделов определяется составом специфицируемого изделия. Наименование каждого раздела указывают в виде заголовка в графе «Наименование» и подчеркивают сплошной тонкой линией. После каждого раздела оставляют несколько свободных строчек для дополнительных записей.
Графа спецификации заполняется следующим образом.
1. В графе «Формат» указывает форматы документов, обозначения которых записаны в графе «Обозначение». В разделах «Стандартные изделия», «Прочие изделия» и «Материалы» эта графа не заполняется. Для деталей, на которые не выпущены чертежи, в этой графе пишут «БЧ» (без чертежа).
2. В графе «Зона» указывают обозначение зоны в соответствии с ГОСТ 2.104—68. На учебных чертежах эта графа не заполняется.
Рис. 318
3. В графе «Поз.» указывают порядковый номер составных частей, входящих в специфицируемое изделие. В разделах «Документация» и «Комплекты» эта графа не заполняется.
4. В графе «Обозначение» записывается обозначение документа на изделие (сборочную единицу, деталь) в соответствии с ГОСТ 2.201—80. В разделах «Стандартные изделия», «Прочие изделия» и «Материалы» эта графа не заполняется.
5. В графе «Наименование» указывают:
в разделе «Документация» только название документа;
в разделах «Комплекты», «Сборочные изделия», «Детали», «Комплексы» — наименование изделий основной надписью на конструкторских документах этих деталей, например «Колесо зубчатое», «Палец» и т. д.;
в разделе «Стандартные изделия» — наименование и обозначение изделий в соответствии со стандартами на это изделие, например «Болт М 12x70 ГОСТ 7805—70».
В пределах каждой категории стандартов на стандартные изделия запись производят по одноименным группам, в пределах каждой группы — в алфавитном порядке возрастания обозначений стандарта, в порядке возрастания размеров или основных параметров изделия. Например: группу крепежных изделий нужно записывать в такой последовательности: болты, винты, гайки, шайбы, шпильки и т. д.;
в разделе «Материалы» — обозначение материалов, установленных в стандартах и технических условия на эти материалы.
6. В графе «Кол.» указывают количество составных частей в одном специфицируемом изделии, а в разделе «Материалы» — общее количество материалов на одно изделие с указанием единицы измерения.
7. В графе «Примечание» указывают дополнительные сведения для производства, а также для изделий, документов, материалов, внесенных в спецификацию.
318.gif
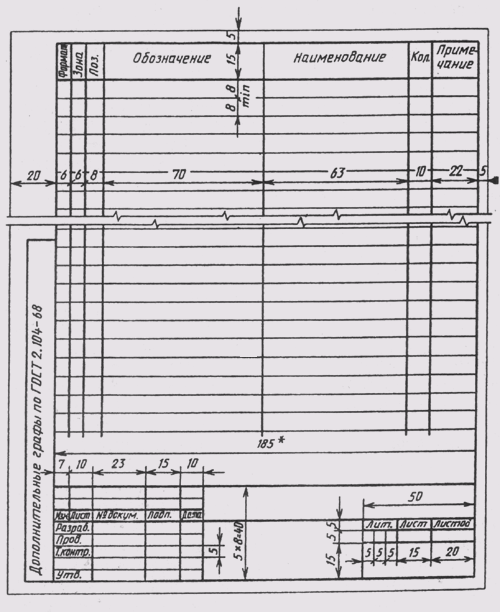
102. Порядок выполнения сборочного чертежа
§ 102. Порядок выполнения сборочного чертежа
Выполнение учебного сборочного чертежа изделия начинается с выяснения назначения этого изделия, его устройства и принципа действия, рабочего положения, способов соединения составных частей, последовательности сборки и разборки.
Для примера рассмотрим вентиль запорный в сборе. Его назначение — обеспечивать доступ рабочей среды (например, жидкости) из одной системы в другую. Открытие и закрытие вентиля обеспечивается вращением маховика соответственно против часовой стрелки и по часовой стрелке.
Вентиль необходимо разобрать на составные части и выделить, если имеются, сборочные единицы. Затем нужно выделить непосредственно входящие в изделие стандартные изделия. Необходимо установить наименование каждой детали, ее назначение в сборочной единице и материал, из которого деталь изготовлена.
Рис. 319
Рис. 320
Рекомендуется составить схему изделия с выделением состава сборочных единиц, наличия деталей стандартных изделий и др. В соответствии со схемой составляют спецификацию (рис. 319). При обозначении составных частей изделия нужно учесть, что три последних знака в обозначении изделия или его документ можно использовать следующим образом:
три нуля и шифр СБ (000СБ) — для обозначения сборочного чертежа изделия;
числа 001,002,003 и т. д. — для обозначения деталей, входящих в это изделие;
числа 100, 200, 300 и т. д. — для обозначения сборочных единиц, входящих в специфицируемое изделие;
числа 101,102,103 и т. д. — для обозначения деталей, входящих в состав сборочной единицы 100, числа 201, 202, 203 и т. д. —для обозначения деталей, входящих в состав сборочной единицы 200 и т. д.
Составлению сборочного чертежа предшествует работа по составлению эскизов всех деталей, входящих в сборочную единицу (см. §96).
Сборочный чертеж изделия вычерчивается по эскизам деталей. При выборе масштаба изображений предпочтение отдается изображению изделия в натуральную величину (М 1:1). Для небольших изделий (как в рассматриваемом примере) следует применять масштаб увеличения, а для изделий больших размеров масштаб уменьшения в соответствии с ГОСТ 2.302—68.
Количество изображений зависит от сложности изделия. Для рассматриваемого предмета достаточно выполнить полный продольный разрез на месте главного вида (рис. 320) и вид сверху.
Построение следует вести одновременно на всех намеченных изображениях, увязывая их друг с другом.Первой вычерчивают основную деталь (обычно это корпус), а затем построенные изображения дополняют изображениями соединяемых с корпусом деталей.
На листе все изображения должны быть размещены свободно, чтобы правильно нанести размеры и номер позиций. Номера позиций проставляют в соответствии с заполненной спецификацией.
На рис. 320 нанесены размеры габаритные (140,100 и 55 мм), установочные (20 и 40 мм) и присоединительные (М27).
В последнюю очередь заполняют основную надпись и выполняют необходимые надписи, располагаемые над основной надписью.
319.gif
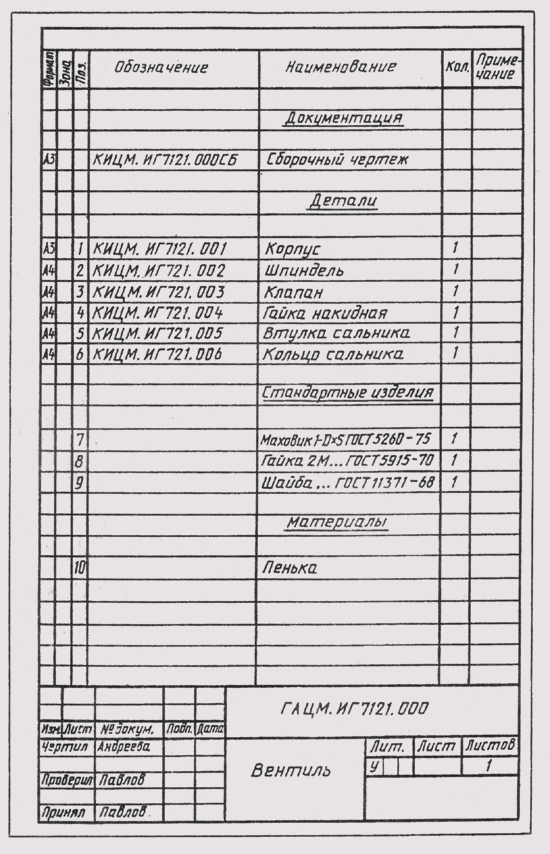
320.gif
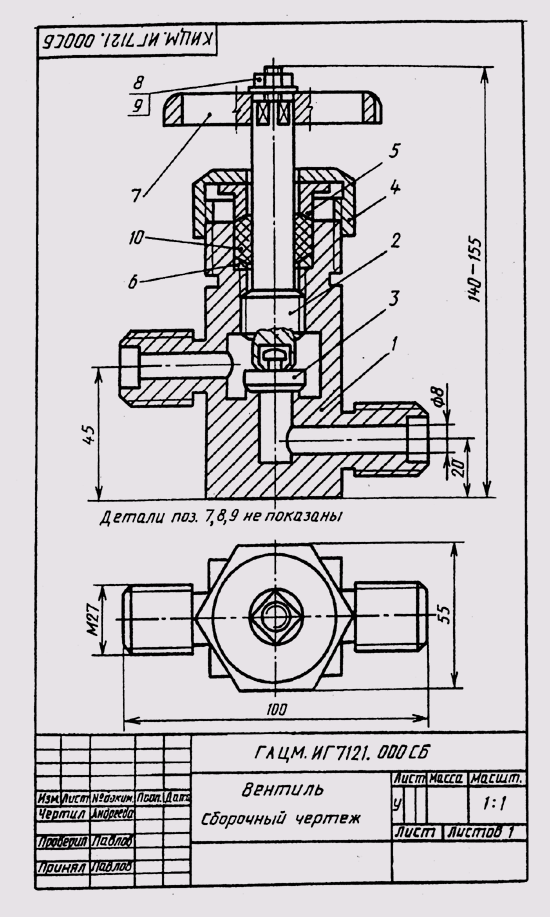
103. Чтение и деталирование сборочного чертежа
§ 103. Чтение и деталирование сборочного чертежа
Чтением сборочного чертежа называют процесс определения конструкции, размеров и принципа работы изделия по его чертежу. Можно рекомендовать такую последовательность чтения сборочного чертежа изделия:
Рис. 321
Рис. 322
по основной надписи определить наименование изделия и масштаб изображения;
по изображениям выяснить, какие виды, разрезы, сечения выполнены на чертеже и каково назначение каждого из них;
прочитать технические требования на чертеже и проставленные размеры;
по спецификации определить назначение каждой детали, положение ее на чертеже;
установить способы соединения деталей между собой и их взаимодействия, определить пределы перемещения подвижных деталей;
последовательно для каждой детали, входящей в сборочную единицу, выяснить ее геометрические формы и размеры, т. е. определить конструкцию детали;
Рис. 323
Рис. 324
мысленно представить внешние, внутренние формы изделия в целом и разобраться в его работе;
определить порядок сборки и разборки изделия, т. е. порядок отделения одной детали от другой, как это делается при демонтаже изделия.
Деталирование — это процесс выполнения рабочих чертежей деталей, входящих в изделие, по сборочному чертежу изделия. Это не простое копирование изображений детали из сборочного чертежа, а работа творческая.
Порядок выполнения рабочего чертежа детали по сборочному чертежу изделия аналогичен выполнению чертежа детали с натуры. При этом формы и размеры детали определяются при чтении сборочного чертежа.
Наименование детали и ее обозначение определяется по спецификации сборочного чертежа, а марка материала — по описанию, приложенному к учебному сборочному чертежу.
Расположение детали относительно фронтальной плоскости проекций, т. е. ее главный вид, выбирается исходя из общих требований, а
Рис. 325
не из расположения ее на сборочном чертеже. Число и содержание изображений детали могут совпадать со сборочным чертежом.
На рабочем чертеже должны быть показаны те элементы детали, которые или совсем не изображены, или изображены упрощенно, условно, схематично на сборочном чертеже. К таким элементам относятся:
литейные и штамповочные скругления, уклоны, конусности;
проточки и канавки для выхода резьбонарезающего и шлифовального инструмента;
внешние, внутренние фаски, облегчающие процесс сборки изделия, и т. п.
Гнезда для винтов и шпилек на сборочных чертежах изображаются упрощенно, а на рабочем чертеже детали гнездо должно быть вычерчено в соответствии с ГОСТ 10549—80.
Размеры детали определяются путем замеров (если они не нанесены на чертеже) по сборочному чертежу. При этом нужно следить, чтобы сопрягаемые размеры не имели расхождений. Размеры конструк-
Рис. 326
тивных элементов (фасок, проточек, уклонов и т. д.) нужно назначать по соответствующим стандартам, а не по сборочному чертежу.
Размеры шпоночных пазов, шлицев, гнезд по шпильки и винты, центровых отверстий и других должны быть взяты из соответствующих стандартов на эти элементы. Диаметры отверстий для прохода крепежных изделий (винтов, болтов, шпилек) должны проставляться с учетом характера сборки.
Шероховатость поверхностей деталей определяется по техническим требованиям, описанию, условиям работы изделия и данной детали в изделии.
Чтобы оценить и проставить на чертеже шероховатость поверхностей детали, нужно определить, сопряженной или свободной является данная поверхность, каков характер эксплуатационных требований к ней и др. Для типовых деталей рекомендуются определенные границы пределов параметров шероховатости.
На рис. 321 выполнен сборочный чертеж обратного двойного клапана, спецификация к нему — на рис. 322.
Принцип действия клапана следующий. Жидкость под давлением поступает в отверстие диаметр 18 верхнего наконечника корпуса 1, сжима-
Рис. 327
ет пружину 3, и в зазор между клапаном 2 и корпусом поступает через отводной (слева) наконечник корпуса в гидравлическую систему. Если снять заглушку 7 с нижнего наконечника корпуса, свинтив накидную гайку 5, можно в корпус через нижнее отверстие подать другую жидкость, подключив клапан ко второму трубопроводу. В этом случае в систему будет поступать смесь жидкостей.
Стандартных деталей клапан не имеет. Сборочный чертеж выполнен в масштабе 1:1.
На месте главного вида выполнен полный продольный разрез клапана фронтальной плоскостью симметрии изделия. Этот разрез позволяет выявить внутреннее строение всех деталей клапана. На месте вида сверху — совмещенное изображение половины вида и половины горизонтального разрезав — А плоскостью, проходящей через ось отводного наконечника корпуса. На виде слева выполнен местный разрез по резьбовому отверстию во фланце корпуса. Кроме этих основных изображений выполнены сечения Б — Б и В — В. Сечение Б — Б показывает отверстия в шестигранной части корпуса для пломбирования клапана после установки его в гидросистеме. Сечение В — В дает представление о сопряжении деталей 1, 2 и 4 и поясняет расположение отверстий в клапане 2.
Рис. 328
На чертеже проставлены габаритные размеры (200 и 100 мм), установочные (75 мм), монтажные (М12 и М 36) и эксплуатационные (диаметр 18) размеры.
Соединения деталей в клапане разъемные, резьбовые. Для обеспечения плотности соединения деталей 2 и 4 в проточку детали 4 заложена прокладка из картона. Наружный диаметр прокладки 48 мм, внутренний 38 мм, толщина 3 мм (см. поз. 7 спецификации на рис. 322). Клапаны и заглушки плотно прилегают к поверхностям корпуса и штуцера (их притирают). Присоединение трубопроводов к корпусу осуществляется с помощью резьбы М 36x2.
Чтобы разобрать клапан, необходимо свинтить накидную гайку 5, а вместе с ней снять заглушку 6, из корпуса вывернуть штуцер 4, снять прокладку 7, через нижнее отверстие в корпусе вынуть оба клапана 2 и пружину 3. Пружина работает на сжатие, ее концы должны быть поджаты и подшлифованы. Сборка клапана производится в обратном порядке.
На рис. 323—328 выполнены рабочие чертежи деталей, входящих в состав обратного клапана (рис. 321).
321.gif
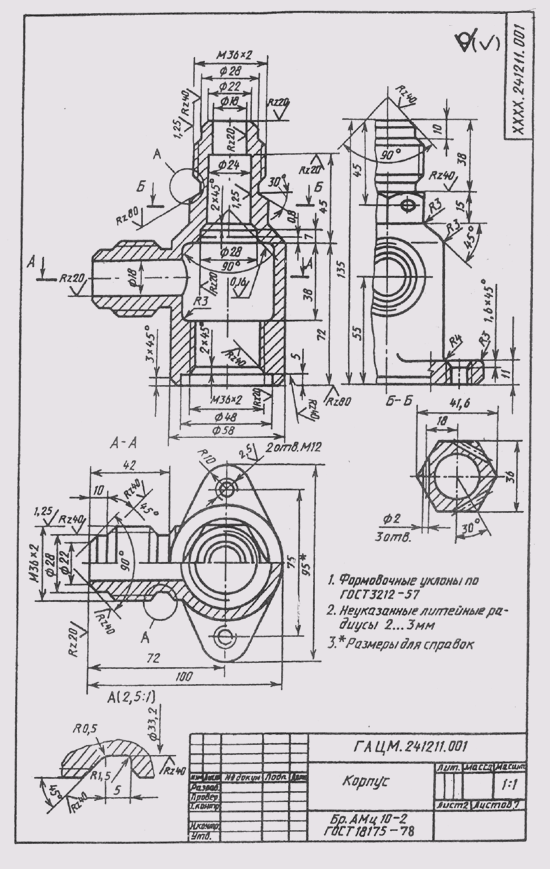
322.gif
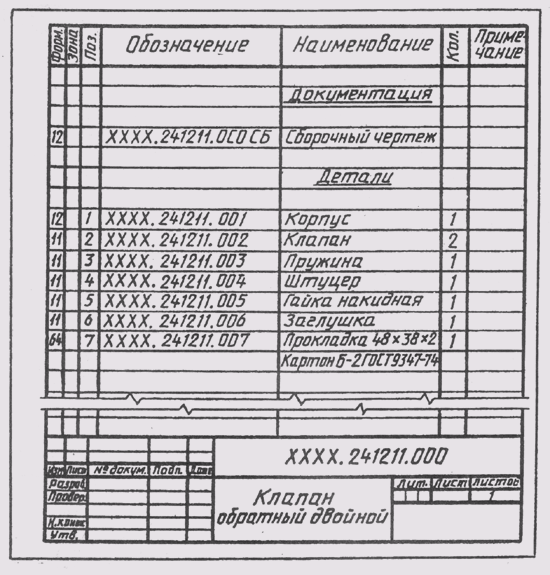
323.gif
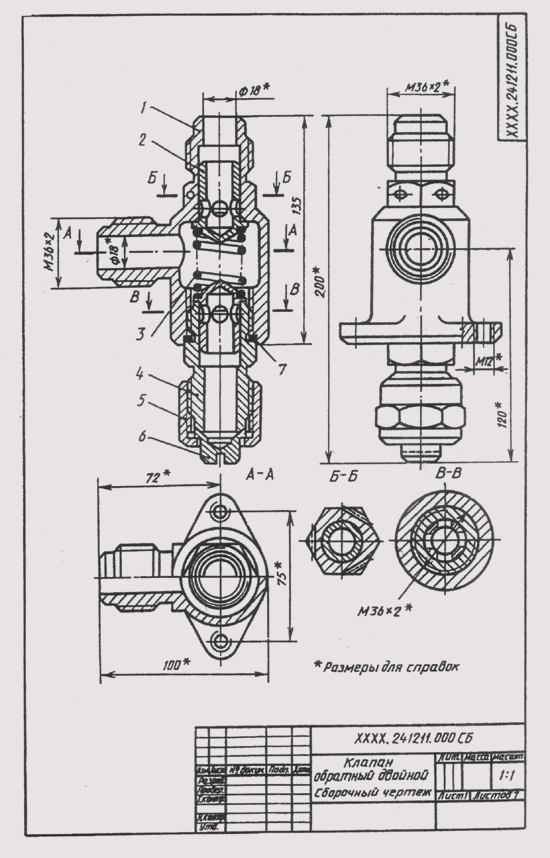
324.gif
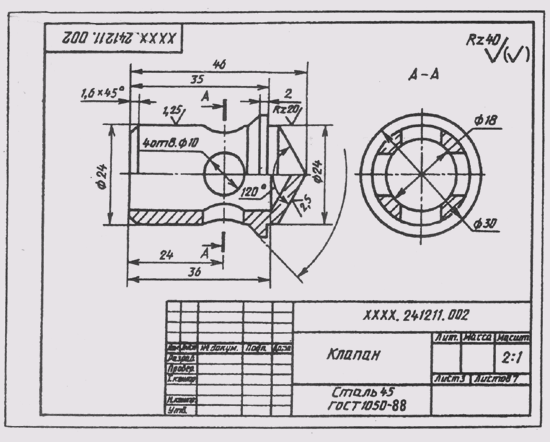
325.gif
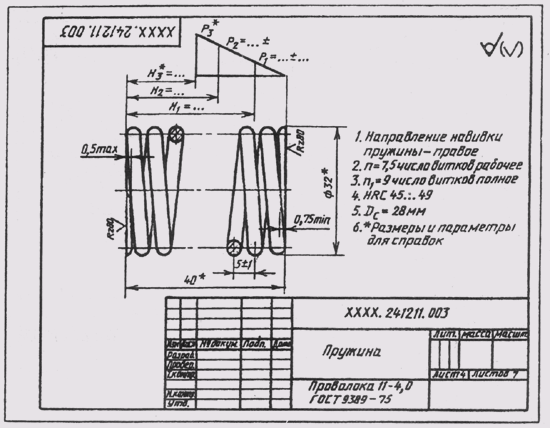
326.gif
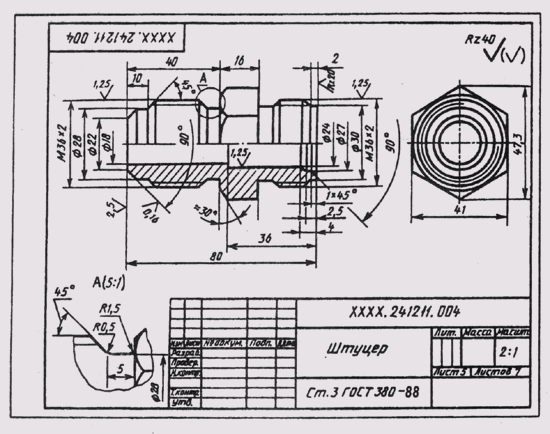
327.gif
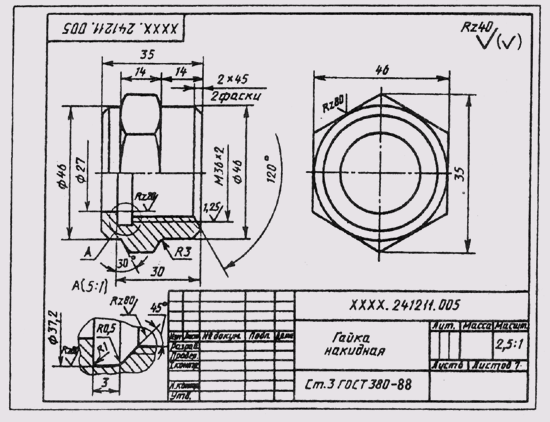
328.gif
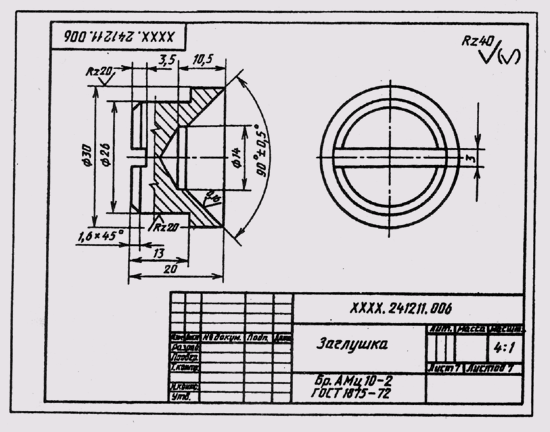
104. Выполнение схем
§ 104. Выполнение схем
Графический документ, на котором показаны в виде условных изображений и обозначений составные части изделия и связи между ними в соответствии с ГОСТ 2.102—68, называют схемой.
Виды и типы схем, общие требования к их выполнению регламентируются ГОСТ 2.701—84.
Схемы облегчают изучение устройства изделия. В зависимости от видов элементов, входящих в состав изделия, и связи между ними схемы разделяют на электрические (Э), гидравлические (Г), пневматические (FT), кинематические (К), оптические (Л) и др.
В зависимости от основного назначения схемы разделяют на следующие типы: структурные (7), функциональные (2), принципиальные (3), соединений (4), подключения (5) и т. д.
Структурная схема определяет основные функциональные части изделия, их назначение и взаимосвязь.
Функциональная схема разъясняет процессы, протекающие в отдельных функциональных цепях изделия или в изделии в целом.
Принципиальная (полная) схема определяет полный состав элементов и связей между ними в изделии, дает детальное представление о принципах работы изделия.
Схема соединений (монтажная) показывает соединения составных частей изделия и определяет провода, кабели, трубопроводы, осуществляющие эти соединения, а также места их присоединения.
Наименование схемы определяется ее видом и типом, а шифр схемы состоит из буквы, определяющей вид схемы, и цифры, обозначающей ее тип. Например, схема электрическая принципиальная имеет шифр ЭЗ. Если приведена схема, у которой в обозначении записан шифр К1, это означает, что выполнена схема кинематическая структурная.
Схемы выполняются без соблюдения масштаба. Линии связи проводят толщиной 0,2...0,4 мм, старясь избежать большого числа их пересечений и изломов. Расстояние между соседними параллельными линиями связи должно быть не менее 3 мм.
Если в условных графических обозначениях имеются утолщенные линии, то их вычерчивают в два раза толще линий связи.
Элементы схемы, составляющие функциональную группу или устройство, не имеющие самостоятельной принципиальной схемы, допускается выделять штрихпунктирными линиями, толщина которых равна толщине принятых линий связи. На схеме указывается наименование этих групп, например коробка скоростей, суппорт и т. п.
Рис. 329
Рис. 330
Элементы схемы, составляющие устройство, имеющие самостоятельную принципиальную схему, выделяют на общей принципиальной схеме сплошной тонкой линией, равной по толщине линиям связи.
На схеме допускается помещать различные технические данные, характеризующие схему в целом и отдельные ее элементы. Эти сведения помещают или около графических обозначений, или над основной надписью.
Электрические принципиальные схемы (ЭЗ) выполняют в соответствии с ГОСТ 2.702—75. Обозначения в электрических схемах установлены ГОСТ 2.721—74 — ГОСТ 2.791—74.
Схемы вычерчивают в отключенном состоянии. Условные знаки на схеме вычерчивают в положении, в котором они изображены в соответствующем стандарте, или повернутыми на угол, кратный 90 , по отношению к этому положению.
Все элементы на схеме должны быть определены однозначно. Для этого данные об элементах записываются в таблицу (рис. 329), которая заполняется сверху вниз и помещается на первом листе или выполняется в виде самостоятельного документа на формате А4.
Каждый элемент схемы должен иметь позиционное обозначение, которое включает в себя буквенное обозначение и порядковый номер (рис. 330). Буквенное обозначение: резистор — R, конденсатор — С, катушка индуктивности — L, амперметр — А, вольтметр—V, генератор— Г, диод полупроводниковый—Д, дроссель—Др, кнопка — Кн, прибор электронный —Д двигатель (мотор) — М, предохранитель— Пр, реле — Р, триод полупроводниковый — Т, трансформатор — Тр и т. д. .
Позиционные обозначения наносят рядом с условным знаком справа от него или над ним. Порядковый номер присваивается в соответствии с последовательностью расположения элементов сверху вниз и справа налево.
Элементы записываются в таблицу группами в порядке расположения их в приложении к ГОСТ 2.702—75, т. е. вначале записывают резисторы, потом — конденсаторы, катушки индуктивности, амперметры и т. д. В пределах каждой группы элементы располагают по возрастанию позиционных номеров. Элементы одного типа с одинаковыми электрическими параметрами, имеющие на схеме последовательные порядковые номера, допускается записывать в графе «Поз.» в одну строчку, по типу: С1...С4, а в графе «Кол.» — общее количество таких элементов.
На схеме рекомендуется указывать характеристики входных и выходных цепей изделия: частоту, напряжение, силу тока и т. п., а также параметры, подлежащие измерению на контрольных контактах, гнездах и т. п. Характеристики входных и выходных цепей изделия записывают в виде таблицы.
На поле электрической принципиальной схемы допускается помещать указания о марках, сечениях и расцветках проводов и кабелей, а также указания о специфических требованиях к электромонтажу изделия.
Кинематические принципиальные схемы (КЗ) показывают последовательность передачи движения от двигателя через передаточный механизм к рабочим органам или инструментам, а также дают возможность судить о способах их регулирования, контроля, управления ими.
Выполняются кинематические схемы в соответствии с ГОСТ 2.703—68. На кинематической схеме показываются все кинематические элементы изделия, отражаются кинематические связи механического и немеханического типа между различными элементами и группами элементов изделия, показывается связь механизма с двигателем.
Элементы кинематических схем обозначаются условно по ГОСТ 2.770—68. К кинематическим элементам относятся валы, оси, подшипники, муфты, тормоза, шкивы, зубчатые колеса, червячные передачи и т. п.
Кинематическая схема вычерчивается в виде развертки и не дает пространственйого (объемного) расположения составных частей изделия. При сложной пространственной кинематике схему рекомендуется изображать в аксонометрических проекциях.
На кинематической схеме можно расположить схему другого вида, непосредственно влияющую на работу изделия.
Каждому кинематическому элементу присваивают порядковый номер, начиная от двигателя. Порядковый номер проставляют на полке линии-выноски, а под полкой указывают основные характеристики и параметры кинематического элемента. Валы нумеруют римскими цифрами, остальные элементы — арабскими.
Рис. 331
Условные знаки на схеме вычерчивают, не придерживаясь масштаба изображения. Однако при повторении одних и тех же знаков выполнять их нужно одинаково. Соотношение размеров условных знаков должно примерно соответствовать действительному соотношению их размеров.
Взаимное расположение элементов на кинематической схеме должно соответствовать исходному, среднему или рабочему положению исполнительных органов. Крайние положения движущихся элементов показывают тонкими штрихпунктирными линиями.
Валы, оси, стержни на кинематических схемах изображают сплошными основными линиями толщиной S; элементы, изображенные внешними очертаниями, зубчатые колеса, червяки, звездочки, шкивы, кулачки — сплошными линиями толщиной 5/2; контур изделия, в который вписана схема, — сплошными тонкими линиями толщиной от 5/3 до 5/2.
На кинематических схемах допускается указывать: наименования каждой группы элементов, имеющей определенное функциональное значение; основные характеристики и параметры кинематических элементов (для двигателя — тип, мощность, скорость вращения, для зубчатых колес — число зубьев и модуль и т. д.); справочные и расчетные данные в виде графиков, диаграмм, таблиц.
Если в схеме есть зубчатые передачи, то колеса считаются как бы прозрачными, и условно предполагается, что они не закрывают друг друга.
Читать кинематическую схему начинают от двигателя, выявляя последовательно по условным обозначениям каждый элемент кинематической цепи, устанавливая его значение и характер передачи движения. Чтение схемы рекомендуется начинать с изучения паспорта данного механизма. На рис. 331 изображена кинематическая схема коробки скоростей токарного станка.
329.gif

330.gif
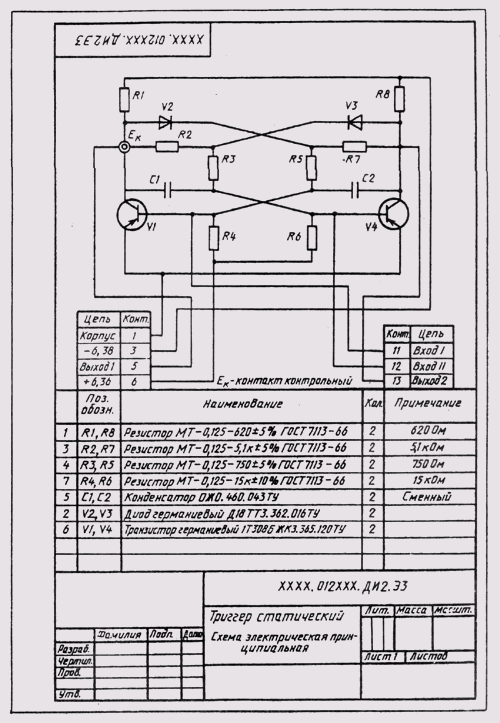
331.gif
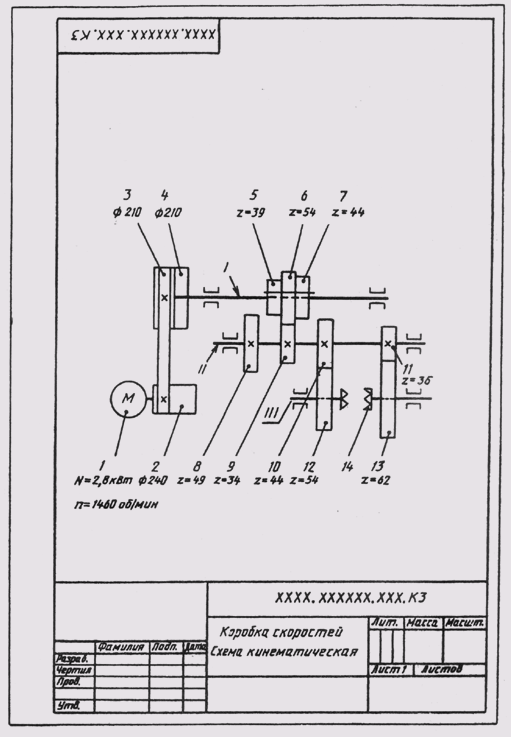
18. Литература
СПИСОК ЛИТЕРАТУРЫ
1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М: Высшая школа, 2000.
2. Гордон В. О., ИвановЮ.Б., Солнцева Т.Е. Сборник задач по курсу начертательной геометрии. М.: Высшая школа, 1998.
3. Иванов Ю.Б. Атлас чертежей общих видов для деталирования. Ч. 1. Технологические приспособления для обработки деталей машин и приборов. М.: Высшая школа, 2000.
4. Лагерь А.И. Курс инженерной графики. М.: Татьянин день, 1995.
5. Лагерь A.M. Инженерная графика. Красноярск: Изд-во Красноярского университета, 1992.
6. Лагерь A.M. Машинная графика. Красноярск: Изд-во Красноярского университета, 1988.
7. Лагерь A.M. Инженерная графика (требования государственных стандартов). Красноярск: Изд-во КГАЦМиЗ, 2000.
8. Левицкий B.C. Машиностроительное черчение и автоматизация выполнения чертежей. М.: Высшая школа, 2000.
9. Локтев О.В. Краткий курс начертательной геометрии. М.: Высшая школа, 2001.
10. Локтев О.В., Числов П.А. Задачник по начертательной геометрии. М.: Высшая школа 2001.
12. Попова Г.Н., Алексеев С.Ю. Машиностроительное черчение: Справочник. СПб.: Политехника, 1994.
13. Чекмарев А.А., Осипов В.К.Справочник по машиностроительному черчению. М.: Высшая школа, 2000.
14. Гардан И., Люка М. Машинная графика и автоматизация конструирования: В 2 т. М., 1987.
15. Чекмарев А.А. Инженерная графика. М.: Высшая школа, 2001.
16. Шипова Г.М., Асташов A.M. Преподавание спецкурса по компьютерной графике на основе системы АшоСаd//Начертательная геометрия, инженерная и компьютерная графика. Нижний Новгород: Изд-во НГСУ, 2000.