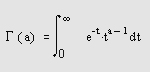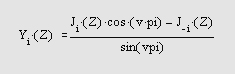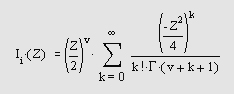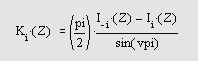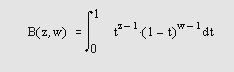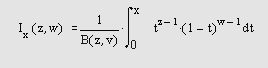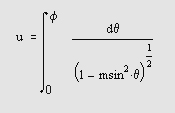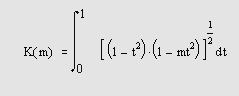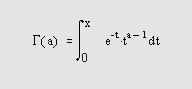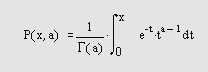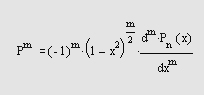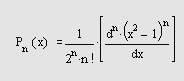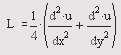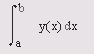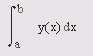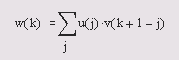Самоучитель по MatLab
Самоучитель по MatLab
|
Введение
Введение
В наши дни компьютерная математика получила должную известность и интенсивно развивается как передовое научное направление на стыке математики и информатики. Это нашло отражение в крупной монографии и в целом ряде книг и обзоров автора данной книги, начавшего осваивать это направление еще в начале 80-х гг. прошлого века.
Программируемые микрокалькуляторы и персональные компьютеры уже давно применяются для математических расчетов. Для подготовки программ использовались различные универсальные языки программирования. В начале 90-х гг. на смену им пришли специализированные системы компьютерной математики (СКМ).
Среди них наибольшую известность получили системы Eureka, Mercury, Mathcad, Derive, Mathematica 2/3/4, Maple V R3/R4/R5 и Maple 6 и др. Каждая из этих систем имеет свои достоинства и недостатки и заслуживает отдельного рассмотрения. Повышенный интерес наших пользователей к подобным системам подтверждают результаты выпуска в последние годы целого ряда книг на русском языке, посвященных указанной теме. В списке литературы данной книги даны лишь основные из этих публикаций. За рубежом по каждой серьезной СКМ на web-сайтах их разработчиков можно найти перечни, включающие сотни наименований книг.
В данной книге рассматривается система MATLAB®, прошедшая многолетний путь развития от узко специализированного матричного программного модуля, используемого только на больших ЭВМ, до универсальной интегрированной СКМ, ориентированной на массовые персональные компьютеры класса IBM PC и Macintosh и рабочие станции UNIX и имеющей мощные средства диалога, графики и комплексной визуализации . MATLAB представляет собой хорошо апробированную и надежную СКМ, рассчитанную на решение самого широкого круга математических задач с представлением данных в универсальной (но не навязываемой пользователям) матричной форме, предложенной фирмой Math Works, Inc.
Система MATLAB предлагается разработчиками (фирма Math Works, Inc.) как лидирующий на рынке, в первую очередь в системе военно-промышленного комплекса, в аэрокосмической отрасли и автомобилестроении, язык программирования высокого уровня для технических вычислений с большим числом стандартных пакетов.прикладных программ. Система MATLAB вобрала в себя не только передовой опыт развития и компьютерной реализации численных методов, накопленный за последние три десятилетия, но и весь опыт становления математики за всю историю человечества. Около миллиона легально зарегистрированных пользователей уже применяют эту систему. Ее охотно используют в своих научных проектах ведущие университеты и научные центры мира. Популярности системы способствует ее мощное расширение Simulink, предоставляющее удобные и простые средства, в том числе визуальное объектно-ориентированное программирование, для моделирования линейных и нелинейных динамических систем, а также множество других пакетов расширения системы.
К сожалению, в России неоправданно мало публикаций по системе MATLAB. Помимо обзоров и первой книги по этой системе, в течение ряда лет серьезных изданий, посвященных MATLAB, практически не было. Наконец, в 1997-1999 гг. появились книги, содержащие перевод части фирменных справочников по системе MATLAB 4.0/5.2. При этом книга описывает лишь отдельные средства упрощенной студенческой версии системы MATLAB 5.0. Стали появляться и книги по пакетам расширения этой системы, и учебные курсы по системе MATLAB. Между тем за рубежом системе MATLAB посвящены сотни книг (их список можно найти на Web-узле фирмы Math Works, Inc., разработавшей эту систему), и еще сотни книг посвящены системе Maple V Release 5, ядро которой входит в состав пакетов расширения MATLAB 6.
Таким образом, интерес к системе MATLAB остается у нас неудовлетворенным. Особенно это относится к учебной литературе по новейшим реализациям системы MATLAB, в первую очередь MATLAB 6. Система MATLAB 6.0 появилась в конце 2000 г., а система MATLAB 6.1 (в которой весьма существенно переработаны пакеты расширения, но в ядро системы добавлены лишь две команды для работы со звуком и команда strfind, дополняющая возможности подробно описанной в книге функции findstr) — в июле 2001 г. MATLAB 6 является последней (на момент подготовки рукописи этой книги) реализацией системы MATLAB. В новой реализации системы не только расширены ее возможности, но и радикально переработан и улучшен интерфейс пользователя, существенно обновился состав пакетов расширений.
Хотя учебный курс по MATLAB 5.3 был выпущен в начале 2001 г., на момент подготовки рукописи данной книги публикаций по новейшей версии MAT-LAB 6 на русском языке вообще не было. Настоящая книга призвана ликвидировать этот пробел. Она подготовлена на основе существенно переработанного учебного курса, но в отличие от него посвящена уже новейшей 12-й реализации системы MATLAB, известной также как MATLAB 6. MATLAB 6 сразу получила широкую известность у нас в России. Как это ни печально, известность пришла во многом благодаря появлению большого числа «пиратских» компакт-дисков, содержащих полные и вполне работоспособные поставки MATLAB 6.0 со всеми ее дорогостоящими пакетами расширения (но, естественно, без русскоязычной документации).Данная книга представляет собой учебный курс по системе MATLAB 6, построенный в виде доступных и органично связанных друг с другом уроков. Описание пакетов расширения MATLAB ввиду большого объема материала по ним было решено вынести в отдельную книгу. При этом предполагаются ее существенно переработанные переиздания, посвященные каждой из версий MATLAB 6. Кроме того, существует учебный курс издательства «Питер» по визуальному моделированию в среде MATLAB, фокусирующийся на средствах Simulink [44]. Впрочем, некоторые примеры применения пакетов расширения в данную книгу включены, как и довольно подробный обзор этих пакетов (урок 23).
Отличия новой реализации MATLAB 6 от предшествующих версий 5.* настолько значительны, что вряд ли стоит пользоваться настоящим изданием для знакомства с предшествующими версиями MATLAB. Читателям, использующим MATLAB 5.*, в том числе любителям Macintosh, VAX/micro VAX и SunOS, можно рекомендовать уже упомянутую ранее изданную литературу по этим системам, все еще верой и правдой служащим многим пользователям. MATLAB 5 — развивающаяся система, которая будет обслуживать пользователей RISC- и VAX-станций Compaq в системах реального времени, пользователей компьютеров Apple, компьютеров на базе процессоров семейства Motorola 68000 и всех тех, кому важна совместимость с Macintosh, Next или RISC-серверами и рабочими станциями под управлением OpenVMS. Новейшие патчи к системам MATLAB 5 можно всегда получить с web-узла фирмы Math Works.
Оглавление книги может служить подробным тематическим указателем, а помещенный в конце книги алфавитный указатель поможет читателю быстро найти интересующие его сведения. Операторы и функции MATLAB 6 описаны настолько подробно, что книга может служить руководством пользователя по этой системе и выполнять функции самоучителя. В целом книга имеет вполне законченный характер и полезна всем, кто собирается изучать или уже использует любую реализацию системы MATLAB 6.
Урок 1. Знакомство с матричной лабораторией MATLAB
1. Урок 1. Знакомство с матричной лабораторией MATLAB
Урок №1.
Знакомство с матричной лабораторией MATLAB
- История появления системы MATLAB
- Возможности систем MATLAB
- Интеграция с другими программными системами
- Ориентация на матричные операции
- Расширяемость системы
- Мощные средства программирования
- Визуализация и графические средства
- Техническая документация по системе
- MATLAB в Интернете
- Данные о системных ресурсах и пакетах расширения
2. История появления системы MATLAB
История появления системы MATLAB
Современная компьютерная математика предлагает целый набор интегрированных программных систем и пакетов программ для автоматизации математических расчетов: Eureka, Gauss, TK Solver!, Derive, Mathcad, Mathematica, Maple V и др. Возникает вопрос: «А какое место занимает среди них система MATLAB?»
MATLAB — одна из старейших, тщательно проработанных и проверенных временем систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Это нашло отражение в названии системы — MATrix LABoratory — матричная лаборатория. Однако синтаксис языка программирования системы продуман настолько тщательно, что эта ориентация почти не ощущается теми пользователями, которых не интересуют непосредственно матричные вычисления.
Матрицы широко применяются в сложных математических расчетах, например при решении задач линейной алгебры и математического моделирования статических и динамических систем и объектов. Они являются основой автоматического составления и решения уравнений состояния динамических объектов и систем. Примером может служить расширение MATLAB — Simulink. Это существенно повышает интерес к системе MATLAB, вобравшей в себя лучшие достижения в области быстрого решения матричных задач.
. Однако в настоящее время MATLAB далеко вышла за пределы специализированной матричной системы и стала одной из наиболее мощных универсальных интегрированных СКМ. Слово «интегрированная» указывает на то, что в этой системе объединены удобная оболочка, редактор выражений и текстовых комментариев, вычислитель и графический программный процессор. В новой версии используются такие мощные типы данных, как многомерные массивы, массивы ячеек, массивы структур, массивы Java и разреженные матрицы, что открывает возможности применения системы при создании и отладке новых алгоритмов матричных и основанных на них параллельных вычислений и крупных баз данных.
В целом MATLAB — это уникальная коллекция реализаций современных численных методов компьютерной математики, созданных за последние три десятка лет. Она вобрала в себя и опыт, правила и методы математических вычислений, накопленные за тысячи лет развития математики. Это сочетается с мощными средствами графической визуализации и даже анимационной графики. Систему с прилагаемой к ней обширной документацией вполне можно рассматривать как фундаментальный многотомный электронный справочник по математическому обеспечению ЭВМ — от массовых персональных компьютеров до супер-ЭВМ.
Увы, пока представленный полностью лишь на английском и частично на японском языках!
Система MATLAB была разработана Молером (С. В. Moler) и с конца 70-х гг. широко использовалась на больших ЭВМ. В начале 80-х гг. Джон Литл (John Little) из фирмы MathWorks, Inc. разработал версии системы PC MATLAB для компьютеров класса IBM PC, VAX и Macintosh. В дальнейшем были созданы версии для рабочих станций Sun, компьютеров с операционной системой UNIX и многих других типов больших и малых ЭВМ. Сейчас свыше десятка популярных компьютерных платформ могут работать с системой MATLAB. К расширению системы были привлечены крупнейшие научные школы мира в области математики, программирования и естествознания. И вот теперь появилась новейшая версия этой системы — MATLAB 6. Одной из основных задач системы было предоставление пользователям мощного языка программирования, ориентированного на математические расчеты и способного превзойти возможности традиционных языков программирования, которые многие годы использовались для реализации численных методов. При этом особое внимание уделялось как повышению скорости вычислений, так и- адаптации системы к решению самых разнообразных задач пользователей.
Возможности MATLAB весьма обширны, а по скорости выполнения задач система нередко превосходит своих конкурентов. Она применима для расчетов практически в любой области науки и техники. Например, очень широко используется при математическом моделировании механических устройств и систем, в частности в динамике, гидродинамике, аэродинамике, акустике, энергетике и т. д. Этому способствует не только расширенный набор матричных и иных операций и функций, но и наличие пакета расширения (toolbox) Simulink, специально предназначенного для решения задач блочного моделирования динамических систем и устройств, а также десятков других пакетов расширений.
В обширном и постоянно пополняемом комплексе команд, функций и прикладных программ (пакетов расширения, пакетов инструментов, (toolbox)) [Пакет инструментов, пакет расширения, прикладная программа — почти синонимы при переводе термина toolbox, но пакет инструментов собственно MATLAB 6 рассматривается как один из toolbox всей системы, включающей MATLAB 6, Simulink и другие пакеты. Редакция старалась максимально сохранить авторский стиль, но следует помнить, что и под прикладной программой, и иод пакетом расширения автор имеет в виду toolbox в терминах MATLAB. — Примеч. ред.
] системы MATLAB содержатся специальные средства для электротехнических и радиотехнических расчетов (операции с комплексными числами, матрицами, векторами и полиномами, обработка данных, анализ сигналов и цифровая фильтрация), обработки изображений, реализации нейронных сетей, а также средства, относящиеся к другим новым направлениям науки и техники. Они иллюстрируются множеством практически полезных примеров. К разработкам расширений для системы MATLAB привлечены многие научные школы мира и руководящие ими крупные ученые и педагоги университетов.
Важными достоинствами системы являются ее открытость и расширяемость. Большинство команд и функций системы реализованы в виде текстовых m-файлов (с расширением .m) и файлов на языке Си, причем все файлы доступны для модификации. Пользователю дана возможность создавать не только отдельные файлы, но и библиотеки файлов для реализации специфических задач.
Поразительная легкость модификации системы и возможность ее адаптации к решению специфических задач науки и техники привели к созданию десятков пакетов прикладных программ (toolbox), намного расширивших сферы применения системы. Некоторые из них, например Notebook (интеграция с текстовым процессором Word и подготовка «живых» электронных книг), Symbolic Math и Extended Symbolic Math (символьные вычисления с применением ядра системы Maple V R5) и Simulink (моделирование динамических систем и устройств, заданных в виде системы блоков), настолько органично интегрировались с системой MATLAB, что стали ее составными частями. Аннотационное описание этих и ряда других пакетов дано в уроке 23. Более подробно, хотя в версиях для выпуска 11.
3. Возможности систем MATLAB
Возможности систем MATLAB
Возможности прежних версий MATLAB 4.x
Уже первые ориентированные на Microsoft Windows версии системы (MATLAB 4.x) обладали мощными средствами. В области математических вычислений:
- матричные, векторные, логические операторы;
- элементарные и специальные функции;
- полиномиальная арифметика;
- многомерные массивы;
- массивы записей;
- массивы ячеек.
В области реализации численных методов:
- дифференциальные уравнения;
- вычисление одномерных и двумерных квадратур;
- поиск корней нелинейных алгебраических уравнений;
- оптимизация функций нескольких переменных;
- одномерная и многомерная интерполяция.
В области программирования:
- свыше 500 встроенных математических функций;
- ввод/вывод двоичных и текстовых файлов;
- применение программ, написанных на Си и ФОРТРАН;
- автоматическая перекодировка процедур MATLAB в тексты программ на языках Си и C++;
- типовые управляющие структуры.
В области визуализации и графики:
- возможность создания двумерных и трехмерных графиков;
- осуществление визуального анализа данных.
Эти средства сочетались с открытой архитектурой систем, позволяющей изменять уже существующие функции и добавлять свои собственные. Входящая в состав MATLAB программа Simulink дает возможность имитировать реальные системы и устройства, задавая их моделями, составленными из функциональных блоков. Simulink имеет обширную и расширяемую пользователями библиотеку блоков и простые средства задания и изменения их параметров.
4. Возможности версий MATLAB 5.x
Возможности версий MATLAB 5.x
В версиях системы MATLAB 5.x введены новые мощные средства. Улучшенная среда программирования:
- профилировщик m-файлов для оценки времени исполнения фрагментов программ;
- редактор/отладчик m-файлов с удобным графическим интерфейсом;
- объектно-ориентированное программирование, включая переназначение функций и операторов;
- средства просмотра содержимого рабочей области и путей доступа;
- конвертирование m-файлов функций в промежуточный р-код.
Графический интерфейс пользователя (GUI):
- интерактивное средство построения графического интерфейса пользователя — GUI;
- новый редактор свойств графических объектов — Handle Graphics Property Editor (редактор свойств дескрипторной графики);
- панели списков, включая списки с множественным выбором;
- форма диалоговых панелей и панелей сообщений;
- многострочный режим редактирования текста;
- запоминание последовательности графических элементов управления;
- расширение параметров элементов управления;
- свойство переносимости между платформами;
- курсор, определяемый пользователем;
- подготовка документов в формате HTML (языка разметки гипертекста Hypertext Mark Up Language) начиная с версии 5.3.
Новые типы данных:
- многомерные массивы;
- массивы структур (записей);
- массивы ячеек данных разного типа;
- массивы символов с 16-разрядной кодировкой;
- массивы с 8-разрядной кодировкой элементов.
Средства программирования:
- списки аргументов переменной длины;
- переназначение функций и операторов;
- применение локальных функций в m-файлах;
- оператор-переключатель switch...case...end;
- оператор wait for;
- функции обработки битов.
Математические вычисления и анализ данных:
- пять новых численных методов решения (solver) обыкновенных дифференциальных уравнений (ОДУ);
ускоренное вычисление функций Бесселя; - вычисление собственных значений и сингулярных чисел для матриц разреженной структуры;
- двумерные квадратурные формулы;
- многомерная интерполяция;
- триангуляция и вывод на терминал данных, определенных на неравномерной сетке;
- анализ и обработка многомерных массивов;
- функции обработки времени и даты.
Новые возможности обычной графики:
- Z-буферизация для быстрой и точной трехмерной визуализации;
- 24-битовая поддержка RGB;
- множественная подсветка поверхностей и полигонов;
- перспективные изображения из произвольной точки;
- новые модели подсветки;
- векторизованные полигоны для больших трехмерных моделей;
- поддержка данных, определенных на неравномерной сетке, включая триангуляционные и сеточные двух- и трехмерные поверхности;
- дескрипторная графика для множественных объектов;
- вывод на терминал, хранение и импорт 8-разрядных изображений;
- дополнительные форматы графических объектов.
Презентационная графика и звук:
- двойные х- и y-оси;
- легенда — пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него;
- управление шрифтом текстовых объектов;
- надстрочные, подстрочные и греческие символы;
- трехмерные диаграммы, поля направлений, ленточные и стержневые графики;
- увеличенное количество стилей для маркировки линий;
- 16-битный стереозвук.
Интерактивная документация:
- возможность просмотра с помощью Netscape Navigator или Microsoft Internet Explorer;
- полная справочная документация в форматах HTML и PDF; О возможность создания «живых» книг с помощью специального приложения
Notebook.
Версия MATLAB 5.3.1 (выпуск 11.1) интегрирует в своем составе 42 программных продукта, среди которых основу составляют базовая система MATLAB и новая реализация пакета расширения Simulink 3.1. В систему введен ряд новых компонентов, включая следующие:
- Data Analysis, Visualization and Application Development — анализ данных, их визуализация и применение;
- Control Design —проектирование устройств управления;
- DSP and Communications System Design — проектирование коммуникационных систем и систем цифровой обработки сигналов;
- Financial Engineering — финансовые расчеты и др.
Из других возможностей версии MATLAB 5.3.1 наиболее значимыми являются следующие:
- существенное обновление пакетов расширения (toolbox) системы MATLAB; О новые улучшенные версии Simulink 3.1 и Real-Time Workshop 3.0;
- Real-Time Windows Target, позволяющая исполнять управляющие программы реального времени на том же компьютере или ноутбуке, где установлены MATLAB, Simulink и Real Time Workshop;
- стандартный пакет расширения хРС для управления системами реального времени на управляющем компьютере (PC) без участия хост-компьютера с установленной системой MATLAB;
- Data Acquisition Toolbox для обмена информацией с блоками сбора данных, подключаемыми к шине компьютера, в реальном масштабе времени;
- новое меню View (Вид), позволяющее выводить или скрывать панель инструментов;
- расширенные возможности работы с целочисленными данными;
- улучшенное окно графики с панелью инструментов;
- возможность вращения графиков в пространстве с помощью мыши в любом направлении простым включением режима вращения с помощью кнопки панели инструментов графического окна;
- поддержка нового стандарта NTSC;
- новый графический интерактивный редактор, облегчающий форматирование графиков;
- обеспечение записи и считывания изображений в формате PNG (Portable Network Graphics) (Переносимая сетевая графика);
- улучшенная визуализация трехмерных скалярных и векторных данных объемных поверхностей;
- новые решатели дифференциальных уравнений и дифференциально-алгебраических уравнений;
- улучшенный редактор и профилировщик m-файлов, содержащий генератор отчетов и поддерживающий HTML (язык разметки гипертекста)-формат записи файлов;
- улучшенная печать, предусматривающая предварительный просмотр печатаемых страниц — команда Print Preview (предварительный просмотр области печати).
5. Возможности новейшей версии MATLAB 6
Возможности новейшей версии MATLAB 6
Новейшая версия системы MATLAB 6 не только имеет перечисленные выше возможности предшествующих версий, но и характеризуется целым рядом новых и важных возможностей:
- доведенное до более чем 600 число встроенных функций и команд;
- новый интерфейс с набором инструментов для управления средой, включающий в себя окно команд (Command Window), окно истории команд (Command History), браузер рабочей области (Workspace Browser) и редактор массивов (Array Editor);
- новые инструменты, позволяющие при помощи мыши интерактивно редактировать и форматировать графики, оптимизировать их коды и затраты памяти на графические команды и атрибуты;
- улучшенные алгоритмы на основе оптимизированной библиотеки LAPACK;
- новая библиотека FFTW (быстрых преобразований Фурье) Массачусетского технологического института Кембриджского университета (США);
- ускоренные методы интегральных преобразований;
- новые, более мощные и точные, алгоритмы интегрирования дифференциальных уравнений и квадратур;
- новые современные функции визуализации: вывод на экран двумерных изображений, поверхностей и объемных фигур в виде прозрачных объектов;
- новая инструментальная панель Camera для управления перспективой и ускорение вывода графики с помощью OpenGL;
- новый интерфейс для вызова Java-процедур и использования Java-объектов непосредственно из MATLAB;
- новые, современные инструменты проектирования графического пользовательского интерфейса;
- обработка (регрессия, интерполяция, аппроксимация и вычисление основных статистических параметров) графических данных прямо из окна графики;
- новое приложение MATLAB для системы разработки Visual Studio, позволяющее автоматически, непосредственно из Microsoft Visual Studio, преобразовывать Си и Си++ коды в выполняемые MATLAB файлы (МЕХ-файлы);
- интеграция с системами контроля версий кода, такими как Visual Source Safe;
- новый интерфейс (последовательный порт) для обмена данными с внешним оборудованием из MATLAB;
- новый пакет управления измерительными приборами (Instrument Control ToolBox) для обмена информацией с приборами, подключенными к Каналу общего пользования (GPIB, HP-IB, IEEE-488)[ Существует аналогичные международные МЭК (IEC) 625.1 и российские государственные стандарты. Несмотря на логическую и электрическую совместимость, международные и отечественные стандарты предполагают использование других разъемов. — Примеч. ред. или к шине VXI через адаптер VXI — GPIB (только в версиях для Windows и Sun Solaris) и последовательному интерфейсу RS-232, RS-422, RS-485 (также и для Linux-версии), в том числе в соответствии со стандартом VISA (Virtual Instruments Systems Application) (Применение виртуальных измерительных приборов);
- существенно обновленные пакеты расширения, в частности новые версии пакета моделирования динамических систем Simulink 4 и Real Time Workshop 4;
- интеграция с системами управления потребностями, например DOORS.
Поставляемый с системой MATLAB 6.0 новый пакет расширения Simulink 4 также имеет ряд новинок. Они перечислены ниже по категориям. - Усовершенствование пользовательского интерфейса:
- новый графический отладчик для интерактивного поиска и диагностики ошибок в модели;
- усовершенствован навигатор моделей (Model Browser, Windows 95/98/Me/ 2000/NT4);
- новый однооконный режим для открытия подсистем;
- контекстное меню для блок-диаграмм (открывается щелчком правой кнопки мыши) как в Windows, так и в Unix версиях;
- новый диалог Finder для поиска моделей и библиотек.
Simulink поступает к пользователям с более 100 встроенными блоками, в состав которых входят наиболее необходимые функции моделирования. Блоки сгруппированы в библиотеки в соответствии с их назначением: источники сигнала, приемники, дискретные, непрерывные, нелинейные, математика, функции и таблицы, сигналы и системы. В дополнение к обширному набору встроенных блоков Simulink имеет расширяемую библиотеку блоков благодаря функции создания пользовательских блоков и библиотек. Вы можете настраивать не только функциональность встроенных и пользовательских блоков, но также пользовательский интерфейс, используя значки и диалоги. Например, вы можете создать блоки для моделирования поведения специальных механических, электрических и программных компонентов, как, например, моторы, преобразователи, серво-клапаны, источники питания, энергетические установки, фильтры, шины, модемы,
- приемники или другие динамические компоненты. Однажды созданные пользовательские блоки могут быть сохранены в библиотеке блоков для использования в будущем. Любые пользовательские блоки или библиотеки блоков могут быть легально распространены в рабочих группах, переданы поставщикам и заказчикам как с исходным кодом, так и без него.
Новые и улучшенные возможности блоков:- наряду с существовавшей ранее поддержкой скалярных и векторных сигналов обеспечена поддержка матричных сигналов многими блоками Simu-link;
- блоки Product, Multiplication, Gain и Math Function теперь поддерживают матричные операции на матричных сигналах;
- Мих и Demux блоки теперь поддерживают мультиплексирование матричных сигналов;
- новый блок Reshape изменяет размер матрицы своего входного сигнала;
- блок Probe теперь по умолчанию выводит размер матрицы сигнала, подаваемого на вход;
- новый блок Bitwise Logical Operator (логические операции по битам) накладывает маску, инвертирует или производит логические операции с отдельными битами целочисленного сигнала без знака;
- четыре новых блока Look-Up Table (просмотра таблиц);
- новый Polynomial блок выводит полиномиальную функцию от входного сигнала.
- Расширенная поддержка для крупных приложений:
- новые объекты данных Simulink позволяют создавать специфические для приложений типы данных MATLAB;
- новый графический пользовательский интерфейс Simulink Explorer для наблюдения и редактирования объектов данных Simulink;
- усовершенствование блока Configurable Subsystems (конфигурируемые подсистемы);
- новое меню выбора блока конфигурируемой подсистемы;
- поддержка защиты интеллектуальной собственности с помощью S-функ-ций, позволяющая не передавать исходный код S-функций (требуется Real-Time Workshop 4.0 (Лаборатория реального времени)) [S-функция — пользовательский программный модуль, который определяет поведение Simulink блока. Simulink содержит шаблоны для создания S-функций с помощью существующих или разработанных заново кодов на Си, Ada (в версии Simulink 4.0/Real Workshop 4.0, нужен отдельный блок Real Workshop Ada Coder), Fortran или MATLAB. Созданную S-функцию вы можете включить в вашу модель, используя соответствующий ей блок Simulink—будь то стандартный или пользовательский. S-функции уменьшают время, необходимое для моделирования крупномасштабных систем, позволяя оперативно вставлять существующие коды в модель. Это, например, особенно важно, если система MATLAB+Simulink+Real Workshop+Real Time Windows Target используется для управления сложными объектами в реальном масштабе времени. Simulink обеспечивает многопортовую и многоскоростную поддержку и разрешает различные интервалы дискретизации (только S-функции на Си и MATLAB). — Примеч. ред.];
- поддержка S-функций, кодируемых на языке ADA (требуется новый отдельный пакет Real Time Workshop Ada Coder);
- улучшенная интеграция со Stateflow — пакетом инструментов моделирования систем, управляемых событиями, значительно усовершенствованный Stateflow Coder для генерации кода;
- run-time сервер MATLAB для запуска программ MATLAB, в том числе в р-кодах, без установленной системы MATLAB;
- улучшенная версия хРС Embedded Target для записи генерируемого кода не только на переносимые носители, но и в постоянные запоминающие устройства, твердотельные диски и на жесткий диск управляющего компьютера. Наряду с хРС поддерживаются другие платформы встроенных управляющих систем, включая VxWorks/Tornado (причем как UNIX, так и Windows хостом с MATLAB), Real Time Windows Target; Lynx Embedded OSEK Target, стандартизированную в автомобилестроении, DOS Target на управляющем компьютере Intel386 и старше (последняя только со снятым с производства компилятором Watcom Си/Си++ с расширителем DOS4GW.exe для DOS и несовместима с приложениями Windows). Но возможность работы без хоста с системой MATLAB (Stand-Alone) имеется только в хРС;
- поддержка хРС Target стандартной полевой шины промышленной автоматизации CAN, возможность синхронизации хРС сигналами, поступающими по этой шине;
- web-сервер, встроенный в хРС Target, позволяющий осуществлять управление встроенными компьютерами и просмотр их состояния при помощи браузеров Интернета (Microsoft Explorer 4.0 и старше и Netscape Navigator 4.5 и старше).
Все это говорит о том, что двенадцатый выпуск системы (MATLAB 6.0 + Simu-link 4.0 + Stateflow 4.0 + ...) подвергся не косметической, а самой серьезной переработке, выдвигающей эту систему на абсолютно новый уровень развития и применения.
6. Интеграция с другими программными системами
Интеграция с другими программными системами
В последние годы разработчики математических систем уделяют огромное внимание их интеграции и совместному использованию. Это не только расширяет класс решаемых каждой системой задач, но и позволяет подобрать для них самые лучшие и наиболее подходящие инструментальные средства. Решение сложных математических задач сразу на нескольких системах существенно повышает вероятность получения корректных результатов — увы, как математики так и математические системы способны ошибаться, особенно при некорректной постановке задач неопытными пользователями.
С системой MATLAB могут интегрироваться такие популярные математические системы, как Mathcad, Maple V и Mathematica. Есть тенденция и к объединению
математических систем с современными текстовыми процессорами. Так, новое средство последних версий MATLAB — Notebook — позволяет готовить документы в текстовом процессоре Word 95/97/2000 [Здесь и далее Word 95 и Word 97 — синонимы соотвественно Microsoft Word 7 из пакета Microsoft Office 95 и Microsoft Word 8 из пакета Microsoft Office 97. — Примеч. ред.] со вставками в виде документов MATLAB и результатов вычислений, представленных в численном, табличном или графическом виде. Таким образом, становится возможной подготовка «живых» электронных книг, в которых демонстрируемые примеры могут быть оперативно изменены. Так, вы можете менять условия задач и тут же наблюдать изменение результатов их решения. В версии MATLAB 6 предусмотрены также улучшенные средства для экспорта графики в слайды презентационной программы Microsoft PowerPoint.
В MATLAB задачи расширения системы решаются с помощью специализированных пакетов расширения — наборов инструментов (Toolbox). Многие из них содержат специальные средства для интеграции с другими программами, поддержки объектно-ориентированного и визуального программирования, для генерации различных приложений. Краткое описание пакетов расширения дано в уроке 23. Кроме того, этой теме посвящены отдельные книги.
В состав системы MATLAB входит ядро одной из самых мощных, популярных и хорошо апробированных систем символьной математики (компьютерной алгебры) Maple V Release 5. Оно используется пакетами расширения Symbolic Math Toolbox и Extended Symbolic Math Toolbox, благодаря которым в среде MATLAB стали доступны принципиально новые возможности символьных и аналитических вычислений.
Новые свойства системе MATLAB придала ее интеграция с программной системой Simulink, созданной для моделирования динамических систем и устройств, заданных в виде системы блоков. Базируясь на принципах визуально-ориентированного программирования, Simulink позволяет выполнять моделирование сложных устройств с высокой степенью достоверности и с прекрасными средствами представления результатов. Помимо естественной интеграции с пакетами расширения Symbolic Math и Simulink MATLAB интегрируется с десятками мощных пакетов расширения, описанными в уроке 23, и значительно более подробно, хотя в версиях для выпуска И, в монографии.
В свою очередь, многие другие математические системы, например Mathcad и Maple, допускают установление объектных и динамических связей с системой MATLAB, что позволяет использовать в них эффективные средства MATLAB для работы с матрицами. Эта прогрессивная тенденция интегрирования компьютерных математических систем, несомненно, будет продолжена.
7. Ориентация на матричные операции
Ориентация на матричные операции
Напомним, что двумерный массив чисел или математических выражений принято называть матрицей. А одномерный массив называют вектором. Примеры векторов и матриц даны ниже:{l, 2, 3, 4} — вектор из 4 элементов;
1 2 3 4
5 6 7 8 матрица размера 3x4;
9 8 7 6
| а | а+b | а+b/с |
| х | у*х | z |
| 1 | 2 | 3 |
матрица с элементами разного типа.
Векторы и матрицы характеризуются размерностью и размером. Размерность определяет структурную организацию массивов в виде строки (размерность 1), страницы (размерность 2), куба (размерность 3) и т. д. Так что вектор является одномерным массивом, а матрица представляет собой двумерный массив с размерностью 2. MATLAB допускает задание и использование многомерных массивов, но в этой главе мы пока ограничимся только одномерными и двумерными массивами — векторами и матрицами.
Размер вектора — это число его элементов, а размер матрицы определяется числом ее строк т и столбцов п. Обычно размер матрицы указывают как тхп. Матрица называется квадратной, если m = n, то есть число строк матрицы равно числу ее столбцов.
Векторы и матрицы могут иметь имена, например V — вектор или М — матрица. В данной книге имена векторов и матриц набираются полужирным шрифтом. Элементы векторов и матриц рассматриваются как индексированные переменные, например:
- V 2 — второй элемент вектора V;
- М 23 — третий элемент второй строки матрицы М.
Система MATLAB выполняет сложные и трудоемкие операции над векторами и матрицами даже в режиме прямых вычислений без какого-либо программирования. Ею можно пользоваться как мощнейшим калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями могут использоваться такие сложные операции, как инвертирование матрицы, вычисление ее собственных значений и принадлежащих им векторов, решение систем линейных уравнений, вывод графиков двумерных и трехмерных функций и многое другое.
Интересно отметить, что даже обычные числа и переменные в MATLAB рассматриваются как матрицы размера 1x1, что дает единообразные формы и методы проведения операций над обычными числами и массивами. Данная операция обычно называется векторизацией. Векторизация обеспечивает и упрощение записи операций, производимых одновременно над всеми элементами вектрров и матриц, и существенное повышение скорости их выполнения. Это также означает, что большинство функций может работать с аргументами в виде векторов и матриц. При необходимости вектора и матрицы преобразуются в массивы, и значения вычисляются для каждого их элемента.
8. Расширяемость системы
Расширяемость системы
Какой бы мощной ни была та или иная математическая система, она не способна включить в себя все средства, которые могут потребоваться сотням тысяч пользователей. Поэтому важно, чтобы система была достаточно гибкой и способной адаптироваться к различным задачам пользователей самых разных категорий — начинающих и опытных математиков, инженеров и научных работников, аспирантов и студентов вузов и даже школьников.
MATLAB — расширяемая система, и ее легко приспособить к решению нужных вам классов задач. Ее огромное достоинство заключается в том, что это расширение достигается естественным путем и реализуется в виде так называемых т-файлов (с расширением .m). Иными словами, расширения системы хранятся на жестком диске компьютера и в нужный момент вызываются для использования точно так же, как встроенные в MATLAB (внутренние) функции и процедуры.
Благодаря текстовому формату m-файлов пользователь может ввести в систему любую новую команду, оператор или функцию и затем пользоваться ими столь же просто, как и встроенными операторами или функциями. При этом в отличие от таких языков программирования, как Бейсик, Си или Паскаль не требуется никакого объявления этих новых функций. Это роднит MATLAB с языками Лого и Форт, имеющими словарную организацию операторов и функций и возможности пополнения словаря новыми определениями-словами. Но, поскольку новые определения в системе MATLAB хранятся в виде файлов на диске, это делает набор операторов и функций практически неограниченным.
В базовый набор слов системы входят спецзнаки, знаки арифметических и логических операций, арифметические, алгебраические, тригонометрические и некоторые специальные функции, функции быстрого преобразования Фурье и фильтрации, векторные и матричные функции, средства для работы с комплексными числами, операторы построения графиков в декартовой и полярной системах координат, трехмерных поверхностей и т. д. Словом, MATLAB предоставляет пользователю обширный набор готовых средств (большая часть из них — это внешние расширения в виде m-файлов).
Дополнительный уровень системы образуют ее пакеты расширения (toolbox). Они позволяют быстро ориентировать систему на решение задач в той или иной предметной области: в специальных разделах математики, в физике и в астрономии, в области нейтронных сетей и средств телекоммуникаций, в математическом моделировании, проектировании событийно-управляемых систем и т. д. Благодаря этому MATLAB обеспечивает высочайший уровень адаптации к решению задач конечного пользователя.
9. Мощные средства программирования
Мощные средства программирования
Многие математические системы создавались исходя из предположения, что пользователь будет решать свои задачи, практически не занимаясь программированием. Однако с самого начала было ясно, что подобный путь имеет недостатки
и, вообще говоря, порочен. Ведь многие задачи нуждаются в развитых средствах программирования, которые упрощают запись алгоритмов задач и порой открывают новые методы создания алгоритмов.
С одной стороны, MATLAB содержит огромное число операторов и функций, которые решают множество практических задач, для чего ранее приходилось готовить достаточно сложные программы. К примеру, это функции обращения или транспонирования матриц, вычисления значений производной или интеграла и т. д. и т. п. Число таких функций с учетом пакетов расширения системы уже достигает многих тысяч и непрерывно увеличивается.
Но, с другой стороны, система MATLAB с момента своего создания создавалась как мощный математико-ориентированный язык программирования высокого уровня. И многие рассматривали это как важное достоинство системы, свидетельствующее о возможности ее применения для решения новых, наиболее сложных математических задач.
Система MATLAB имеет входной язык, напоминающий Бейсик (с примесью Фортрана и Паскаля). Запись программ в системе традиционна и потому привычна для большинства пользователей компьютеров. К тому же система дает возможность редактировать программы с помощью любого привычного для пользователя текстового редактора. Имеет она и собственный редактор с отладчиком. Отказ от присущего системе Mathcad «шика» — задания задач в виде формул — компенсируется заметным увеличением скорости вычислений — при прочих равных условиях она почти на порядок выше, чем у системы Mathcad. А это немаловажное достоинство!
Язык системы MATLAB в части программирования математических вычислений намного богаче любого универсального языка программирования высокого уровня. Он реализует почти все известные средства программирования, в том числе объектно-ориентированное и (средствами Simulink) визуальное программирование. Это дает опытным программистам необъятные возможности для самовыражения.
10. Визуализация и графические средства
Визуализация и графические средства
В последнее время создатели математических систем уделяют огромное внимание визуализации решения математических задач. Говоря проще, это означает, что постановка и описание решаемой задачи и результаты решения должны быть предельно понятными не только тем, кто решает задачи, но и тем, кто в дальнейшем их изучает или просто просматривает. Большую роль в визуализации решения математических задач играет графическое представление результатов, причем как конечных, так и промежуточных.
Визуализация постановки задачи в MATLAB решается применением приложения Notebook и назначением именам функций достаточно ясных имен (идентификаторов). А визуализация результатов вычислений достигается применением обширных средств графики, в том числе анимационной, а также использованием (там, где это нужно) средств символьной математики.
Новая версия MATLAB напрочь избавилась от некоторой примитивности графиков, которая была присуща первым версиям этой системы. Теперь новые графические средства Handle Graphics (дескрипторная или описательная графика) позволяют создавать полноценные объекты графики высокого разрешения, как геометрического, так и цветового. Возможности этой графики поддерживаются объектно-ориентированным программированием, средства которого также имеются в языке программирования системы MATLAB.
Реализуются, причем с повышенной скоростью, построения графиков практически всех известных в науке и технике типов. Широко практикуется функциональная закраска сложных поверхностей, в том числе с интерполяцией по цвету. Возможен учет всевозможных световых эффектов — вплоть до бликов на поверхности сложных фигур при освещении их различными источниками света и с учетом свойств материалов отражающих поверхностей. Применение дескрипторной графики позволяет создавать и типовые элементы пользовательского интерфейса — кнопки, меню, информационные и инструментальные панели и т. д., то есть реализовать элементы визуально-ориентированного программирования.
Графики выводятся отдельно от текстов в отдельных окнах. На одном графике можно представить множество кривых, отличающихся цветом (при цветном дисплее) и отличительными символами (кружками, крестиками, прямоугольниками и т. д.). Графики можно выводить в одно или в несколько окон. Наконец, в статьях и книгах формата Notebook, реализованных при совместной работе системы MATLAB с популярным текстовым процессором Microsoft Word 95/97/2000, графики могут располагаться вместе с текстом, формулами и результатами вычислений (числами, векторами и матрицами, таблицами и т. д.). В этом случае степень визуализации оказывается особенно высокой, поскольку документы класса Notebook по существу являются превосходно оформленными электронными книгами с действующими (вычисляемыми) примерами.
Особенно привлекательной выглядит возможность построения трехмерных поверхностей и фигур. Если в MATLAB 4 рендеринг трехмерных фигур осуществлялся только при помощи фирменного механизма painters, а в MATLAB 5 был добавлен программный рендеринг при помощи Z-буфера, то в MATLAB б основным является индустриальный стандарт Open GL. Он может поддерживаться аппаратно графическими ускорителями. Система автоматически подбирает наиболее оптимальный механизм рендеринга. По сравнению с системой Mathcad построение трехмерных фигур средствами MATLAB происходит почти на порядок быстрее. Кроме того, при построении таких графиков используется достаточно совершенный алгоритм удаления невидимых линий, что наряду с большими размерами графиков и возможностью интерполяции по цвету делает построенные трехмерные поверхности и фигуры весьма эстетичными и наглядными. Фигуры могут быть прозрачными. Уже в ранних версиях была введена эффектная возможность быстрого вращения графиков в любом направлении. В MATLAB 5.3.1 и 6 она улучшена — теперь вращать в пространстве можно даже плоскость с двумерными графиками.
Введен также ряд средств на основе графического интерфейса пользователя (GUI — Graphic User Interface), привычного для операционных систем Windows 95/98/Ме/ 2000/NT4. Это панели инструментов, редактор и отладчик m-файлов, красочная
демонстрация возможностей и т. д. Есть и возможность создавать свои средства пользовательского интерфейса.
11. Техническая документация по системе
Техническая документация по системе
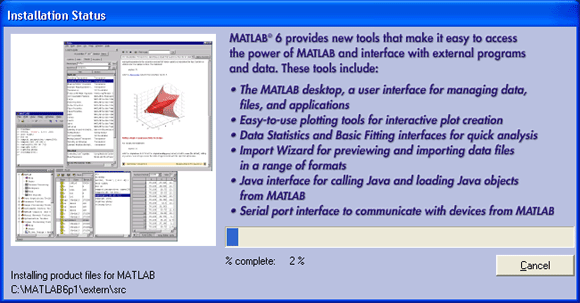
Система MATLAB поставляется с обширной технической документацией и с развитой справочной системой. Система помощи реализована как в стандартном для систем MATLAB варианте — в интерактивном командном режиме, так и в форме гипертекстовых страниц с просмотром их браузером помощи. Кроме того, имеется обширный пакет электронных документов в формате PDF (отдельный компакт-диск в версии 6.0), для просмотра которых используется приложение Acrobat Reader (распространяется бесплатно) или Adobe Acrobat. Ниже перечислены наиболее важные из этих документов (далеко не все) для версии MATLAB 6.0 с указанием их объема в страницах: О «Getting Started with MATLAB» — начальное знакомство с системой MATLAB.
- «Installation Guide for PC» — инсталляция на ПК класса PC.
- «MAT-file format» — описание форматов МАТ-файлов.
- «Release Notes for Release 12» — описание особенностей реализации 12 системы
MATLAB. - «Using MATLAB» — работа с MATLAB в командном и программируемом режимах.
- «Function Reference» — справочник по функциям в трех томах.
том 2 - «Using MATLAB Graphics» — справочник по средствам графики и визуализации.
- «MATLAB Application Program Interface Guide» — описание интерактивного
взаимодействия с языками программирования С и Fortran. - «External Interfaces/API» — описание интерфейса связи с внешними программами API.
- «Creating Graphical User Interface» — создание графического интерфейса пользователя.
Итак, объем фирменной документации только по системе MATLAB 6.0 достигает почти 5000 страниц, что делает ее трудно обозримой. Тем более с учетом того, что эта документация является англоязычной.
Состав документации может несколько меняться в зависимости от типа поставок. Помимо этого, различные поставки системы могут содержать и другую техническую документацию, руководство по работе с системой Simulink, описание пакета символьных вычислений и т. д.
Документацию по системе MATLAB можно рассматривать как многотомный электронный (и обычный) справочник по современным численным методам и средствам их реализации на ЭВМ, включая персональные компьютеры. Одновременно — это одно из самых полных электронных справочных пособий по математике и многочисленным сферам ее применения. К сожалению, пока указанная документация поставляется с системой только на английском и на японском языках. Поскольку эта документация доступна каждому пользователю, рискнувшему установить достаточно полную версию MATLAB 6.0 на свой компьютер, ссылок на нее в списке литературы данного издания нет.
Данная книга дает достаточно полное описание почти всех средств базовой системы MATLAB. Тем не менее настоятельно рекомендуется обращаться к указанной документации всякий раз, когда требуется полное знакомство с той или иной областью применения системы, с ее редкими функциями, операторами или иными средствами, которые не нашли отражения в данной книге ввиду ограниченного (в сравнении с объемом указанной документации) объема.
12. MATLAB в Интернете
MATLAB в Интернете
Представление математических систем в глобальной сети Интернет сегодня становится нормой. Свои сайты (страницы) в Интернете имеют все фирмы-разработчики математических систем.
13. Главная страница фирмы MathWorks
Главная страница фирмы MathWorks
Рис. 1.1. Главная страница web-сайта фирмы MathWorks
Math Works, Inc. — создатель системы MATLAB — также имеет свой, регулярно обновляемый сайт (www.mathworks.com). О важности общения с ним говорит то обстоятельство, что в меню версии MATLAB 6.0 появилась позиция Web, дающая доступ к основным разделам этой страницы. Первая же команда позиции меню The Math Works Web Site дает выход на главную страницу web-сайта фирмы Math Works (рис. 1.2).
Следует отметить, что данная команда исполняется только в том случае, если на компьютере установлен какой-либо из браузеров для работы в сети Интернет, например входящий в состав операционной системы Windows 98 браузер Microsoft Internet Explorer 5.0. Приведенные далее копии экрана, иллюстрирующие отражение MATLAB в Интернете, получены при использовании именно этого браузера. В команной строке можно набрать команду support, которая откроет этот же сайт в окне браузера помощи, входящего в состав самой MATLAB.
Непосредственное подключение к Интернету изначально не требуется. Однако, разумеется, вы можете выйти на web-страницу фирмы Math Works и прямо с помощью браузера даже без установленной на вашем ПК системы MATLAB. Этот процесс подробно описан в книге и в других книгах об Интернете.
1.gif

14. Регистрация через Интернет
Регистрация через Интернет
Если вы удостоились чести стать легальным пользователем системы MATLAB, то первое, что надо сделать, — это установить систему на ваш компьютер и зарегистрироваться в фирме Math Works.
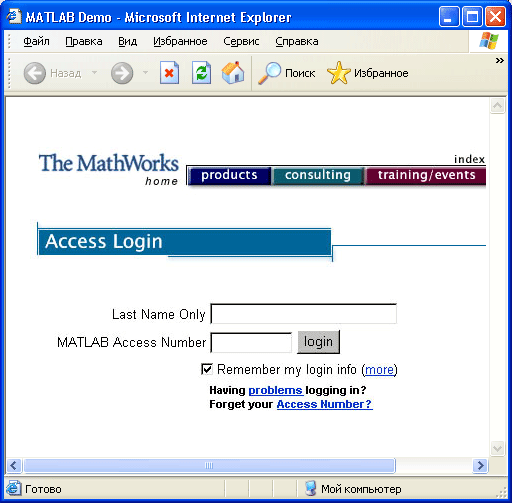
Рис. 1.2. Интернет-страница MATLAB Access фирмы MathWorks
Отдельный урок 2 посвящен тому, как надо устанавливать (инсталлировать) систему. Если система у вас уже установлена, то остается зарегистрироваться. Это можно сделать по телефону (номер указан в документации), по обычной почте (слишком долго и муторно) и через Интернет (проще всего, если есть доступ).
Math Works обычно дает срок в 30 суток для регистрации. До истечения этого срока вы можете ставить систему на свой ПК и спокойно работать с ней, например, оценивая то, нужна ли она вам или нет. Однако спустя этот срок возможность запуска системы будет заблокирована и вам придется вспомнить о необходимости регистрации. Лучше, естественно, сделать это быстрее, не откладывая это не слишком сложное дело на долгий срок.
Для регистрации через Интернет надо исполнить команду Membership в уже упомянутой позиции Web меню. После этого автоматически будет запущена система соединения с вашим Интернет-провайдером и начнется загрузка страницы MATLAB Access (доступ в MATLAB) с указанным адресом. На рис. 1.2 показано, как выглядит эта страница при использовании браузера Microsoft Internet Explorer 5.0.
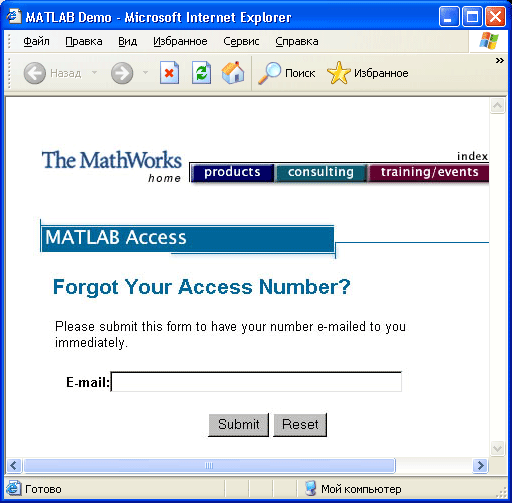
Рис. 1.3. Раздел страницы фирмы MathWorks с регистрационной формой
Эта страница содержит гиперссылки на другие страницы сайта. На ней можно найти и раздел, посвященный регистрации MATLAB (рис. 1.3). Как нетрудно заметить, форма начинается с поля, в которое надо ввести номер лицензии. Он указывается в документации, поставляемой с получаемой системой.
Регистрационную форму следует заполнить, чтобы стать официально зарегистрированным пользователем системы MATLAB. Только в этом случае фирма MathWorks обеспечивает техническую и иную поддержку системы MATLAB. После
регистрации пользователь получает быстрый доступ к ресурсам web-сайта фирмы Math Works. Фамилия пользователя и его данные заносятся в базу данных о пользователях системы, и она появляется над строкой основных гиперссылок основной страницы — рис. 1.4. Разумеется, что фамилия и гиперссылка над ней с именем «access» (доступ) появляются только на странице пользователя, выполнившего регистрацию, и отсутствуют при просмотре web-страницы другими пользователями.
Рис. 1.4. Меню гиперссылок главной страницы Web-сайта фирмы MathWorks с фамилией легального
пользователя системы MATLAB 6.0
Заметим, что основная страница фирмы MathWorks регулярно обновляется и на рис. 1.1 она представлена на момент подготовки рукописи этой книги (март 2001 г.). На ней рекламируется 12-я реализация (12-й выпуск) системы (система MAT-LAB 6.0 с интегрированными пакетами расширения, включая пакет Simulink 4.0).
2.gif

3.gif

4.gif
15. Поддержка системы MATLAB фирмой MathWorks
Поддержка системы MATLAB фирмой MathWorks
Зарегистрированные пользователи (а частично и другие) могут воспользоваться специально организованной фирмой MathWorks службой поддержки системы MATLAB. Для выхода на web-страницу такой поддержки из системы MATLAB достаточно исполнить команду Technical Support Knowledge Base. Будет загружена страница с разделом Support, показанная на рис. 1.5.
На этой странице имеется множество гипертекстовых ссылок (подчеркнутых снизу), открывающих доступ к различным ресурсам web-сайта фирмы MathWorks.
Рис. 1.5. Страница с разделом Support фирмы MathWorks
5.gif

16. MATLAB в образовании
MATLAB в образовании
Как уже отмечалось, MATLAB широко используется в технике, науке и образовании.
Рис. 1.6. Web-страница, посвященная использованию MATLAB в образовании
Рис. 1.7. Web-страница, посвященная книгам по системе MATLAB
В качестве примера на рис. 1.6 показана web-страница, иллюстрирующая применение MATLAB в образовании. На этой странице сообщается о существовании студенческих версий системы MATLAB и специальных академических лицензий для приобретения MATLAB работниками науки и образования по льготным ценам.
Рис. 1.8. Фрагмент web-страницы
На одной из страниц (рис. 1.7) можно найти данные о публикациях по системе MATLAB. (всех версий). Уже из начала этой страницы видно, что число опубликованных книг по этой системе и ее компонентам и расширениям превышает 400. Это говорит об огромном интересе к системе MATLAB во всем мире.
Книги классифицируются по отношению к тому или иному компоненту системы. Есть и раздел по книгам на разных языках (не на английском). Увы, в разделе по русскоязычным книгам имеется только одна книга, показанная на странице, приведенной на рис. 1.8.
На сайте фирмы можно найти информацию как о программных продуктах фирмы, так и о пакетах ее расширения, примеры решения различных задач и т. д.
6.gif
7.gif
8.gif

17. Обновление системы MATLAB через Интернет
Обновление системы MATLAB через Интернет
Интернет позволяет производить обновление программных продуктов. Так, обратившись на сайте фирмы Math Works к странице Downloads (рис. 1.9), вы получите доступ к FTP (File Transfer Protocol) серверу фирмы Math Works и сможете загрузить студенческую версию системы MATLAB.
Рис. 1.9. Web-страница с анкетой, открывающей доступ к разделу Downloads (перекачка файлов)
Можно также получить версии системы с ограниченным 30 днями сроком действия — Trial (Пробные). Однако следует отметить, что перекачка даже упрощенных версий системы по нашему Интернету — большая проблема, поскольку файлы системы очень громоздки, и надо много часов для их перекачки. Вы можете заказать у фирмы компакт-диски с системой. Таким же образом делается обновление прежних версий системы, например MATLAB 5.3.1 до новейшей версии 6.0.
Некоторые пользователи ухитряются растягивать время работы с демонстрационной (и вполне работоспособной) версией MATLAB, переводя часы компьютера на то время, в течение которого доступ к этой версии открыт. Судя по тому что MathWorks снисходительно смотрит на это (допуская такую возможность), то для многих это и впрямь неплохой способ продлить удовольствие от общения с системой MATLAB на длительное время. Однако надо помнить, что в этом случае вы уже лишаетесь официальной технической и прочей поддержки фирмы MathWorks. Да и неудобств от этого более чем достаточно. Не говоря уже о моральной ущербности такого трюка.
9.gif
18. Доступ к FTP-серверу фирмы MathWorks
Доступ к FTP-серверу фирмы MathWorks
Еще одна полезная услуга — доступ к FTP-серверу фирмы MathWorks, на котором хранится великое множество файлов системы MATLAB и файлов с примерами ее применения. Рис. 1.10 показывает одну из страниц FTP-сервера с файлами раз-тела Toolbox системы MATLAB. В этом разделе имеется множество папок с фай-ами. Адрес этой страницы виден в поле адресов браузера.
Рис. 1.10. Страница FTP-сервера фирмы MathWorks
Процесс загрузки файлов хорошо известен пользователям Интернета, и нет смысла описывать его в деталях. Ограничимся примером, показывающим, как можно скачать файл одной из функций Бесселя (рис. 1.11). Этот файл сразу же загружается в редактор m-файлов системы MATLAB и готов к немедленному использованию. Фактически это означает возможность расширения и модификации системы через Интернет.
Эта возможность полезна и в том случае, если вы случайно стерли или неудачно модифицировали какой-то из m-файлов системы. Вы можете получить из Интернета его оригинальную копию и восстановить работу вашей системы MATLAB.
Рис. 1.11. Пример перекачки m-файла системы MATLAB прямо в редактор m-файлов
10.gif
11.gif
19. Данные о системных ресурсах и пакетах расширения
Данные о системных ресурсах и пакетах расширения
Если вас интересуют данные о системных ресурсах или пакетах расширения системы MATLAB, то их тоже нетрудно получить из Интернета.
Страница, показанная на рис. 1.12, дает представление о всех продуктах и услугах фирмы Math Works. Она открывается исполнением команды Product в позиции Web меню системы MATLAB 6.0.
На этой странице есть и данные о многочисленных пакетах расширения системы MATLAB 6.0.
Приведенных данных достаточно для знакомства с Web-узлом фирмы MathWorks и оценки предлагаемых ею услуг по получению и сопровождению программных продуктов.
Версии Windows 98, Millennium Edition, NT4,2000, как и Windows 95 OSR2 и старше, поступают к вам с уже установленным программным обеспечением OpenGL. Но для того, чтобы использовать новый, впервые введенный в MATLAB 6 режим рендеринга графики Open GL, на компьютеры Windows 95 версий ниже OSR2 вам необходимо предварительно установить программное обеспечение Open GL.
Это можно сделать, скачав программу с FTP-сервера фирмы Microsoft_ftp:// ftp.microsoft.com/softlib/msfiles/opengl95.exe или зайдя на web-узел поддерживаемой Silicon Graphics организации Open GL Foundation.www.sgi.com. С MATLAB 6 проверено программное обеспечение Open GL Microsoft для Windows 95 и NT, CosmoGL (версия Open GL компании Cosmo Software — дочерней фирмы Silicon Graphics) и совместимое с OpenGL программное обеспечение Mesa (www.mesa3d.org).
Рис. 1.12. Web-страница с данными о продукции фирмы MathWorks
Но даже.если вы имеете Windows95 OSR2 и старше, вам есть смысл зайти на web-узел www.sgi.com. Там вы сможете установить последние драйверы Open GL для своих видеокарт (в том числе и интегрированных в материнские платы), даже если вы не знаете точное название своей видеокарты.
Теперь для того, чтобы MATLAB 6 могла ненавязчиво продемонстрировать свои новые эффекты трехмерной графики в стиле «Терминатора» и «Парка Юрского периода», вам достаточно щелкнуть на кнопках управления вашей версии Windows Пуск > Настройка > Панель управления > Экран > Настройка > Цветовая палитра > True Color. Приключения начинаются!
12.gif
20. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Разбираться в особенностях различных версий системы MATLAB.
- Понимать возможности систем класса MATLAB и их интеграции с другими программными системами.
- Искать техническую документацию по системе.
- Использовать Интернет-страницы фирмы Math Works, Inc.
- Готовить свой компьютер к использованию новых эффектов трехмерной графики MATLAB 6.
Урок 2. Установка системы и первые навыки работы
1. Урок 2. Установка системы и первые навыки работы
Урок №2.
Установка системы и первые навыки работы
-
Установка и файловая система MATLAB
-
Запуск MATLAB и работа в режиме диалога
-
Первый опыт работы
-
MATLAB в роли суперкалькулятора
-
Числа, константы и системные переменные
-
Текстовые комментарии
-
Переменные, их создание, изменение и уничтожение
-
Операторы и функции
-
Сообщения об ошибках и исправление ошибок
-
Работа с векторами и матрицами
-
Сохранение и загрузка рабочей области сессии
-
Ведение дневника
-
Завершение работы с системой
2. Установка и файловая система MATLAB
Установка и файловая система MATLAB
Новая версия системы MATLAB 6 — весьма громоздкий программный 1 комплекс, который (при полной установке) требует до 1000-1500 Мбайт дисковой памяти (в зависимости от конкретной поставки, полноты справочной системы и числа устанавливаемых пакетов прикладных программ). Поэтому он поставляются исключительно на компакт-дисках. Полный комплект системы размещается на двух компакт-дисках только для чтения (CD-ROM), на одном из которых размещены PDF-файлы документации.
Для успешной установки MATLAB необходимы следующие минимальные средства:
-
компьютер с микропроцессором не ниже Pentium и математическим сопроцессором, рекомендуются процессоры Pentium PRO, Pentium II, Pentium III, Pentium IV или AMD Athlon;
-
устройство считывания компакт дисков (привод CD-ROM) (для установки), мышь, 8-разрядный графический адаптер и монитор, поддерживающие не менее 256 цветов;
-
операционная система Windows 95/98 (оригинальная или второе издание) / Me (Millennium Edition) /2000/ (допускается также NT4 с сервис-пакетами 5 или 6а);
-
ОЗУ емкостью 64 Мбайт для минимального варианта системы (рекомендуется иметь память не менее 128 Мбайт);
-
до 1500 Мбайт дискового пространства при полной установке всех расширений и всех справочных систем.
Для использования расширенных возможностей системы нужны графический ускоритель, Windows-совместимые звуковая карта и принтер, текстовый процессор Microsoft Word 95/97/ 2 2000 для реализации Notebook, компиляторы языков Си/Си++ и/или ФОРТРАН для подготовки собственных файлов расширения и браузер Netscape Navigator 4.0 и выше или Microsoft Internet Explorer 4.0 и выше. Для просмотра файлов справочной системы в формате PDF нужна программа Adobe Reader или Adobe Acrobat 3.0 и выше.
-
Компилятор Compaq Visual Fortran 5.0 или 6.1;
-
Microsoft Visual Си/С++ версий 5.0 или 6.0;
-
Borland Си/С++ версий 5.0, 5.02;
-
Borland C++Builder версий 3.0, 4.0 или 5.0;
-
WATCOM Си/Си++ версий 10.6 или 11 (фирмой Sybase более не поставляется версия этих компиляторов, необходимая для работы управляющих компьютеров под DOS);
-
LCC 2.4 (в комплекте с MATLAB).
Только в Linux версии поддерживается компилятор .GNU C++.
Мы рассматриваем систему, ориентированную на IBM PC (Intel80X86/ Pentium) — совместимые компьютеры под управлением Microsoft Windows как наиболее распространенные. Math Works рекомендует графические видеокарты Accel Eclipse фирмы Accel Graphics для аппаратной поддержки новых, введенных в MATLAB 6, эффектов трехмерной графики (расчет сцены и рендеринг Open GL) на этой платформе. Но наряду с ними MathWorks тщательно протестировала чисто программные драйверы операционных систем Windows. Если ваш графический ускоритель, аппаратно поддерживающий Open GL, другого типа, фирма MathWorks, Inc. его не протестировала со своей обычной легендарной скрупулезностью. Но это не значит, что искажения трехмерной графики неизбежны. Если у вас будут сомнения, вы всегда сможете программно отключить аппаратную поддержку Open GL, прежнему эффективно используя свой графический ускоритель для обработки шгонов, и задействовать только тщательно проверенное MathWorks программное обеспечение Open GL.
Возможна работа MATLAB 6 на ряде других компьютерных платформ: Lintel (ядро Linux 2.2x на Intel Pentium или AMD Athlon), Sun SPARC/UltraSPARC (Solaris 2.6, 2.7, 2.8), Silicon Graphics (рабочие станции на процессорах R12000, R10000, R5000 под IRIX64, IRIX 6.5x), Compaq(DEC) Alpha (Tru64UNIX 4.0f, 5.0), HP (HP700 (HP-UX10.2), HP9000 (HP-UX10.2 или HP-UX11), IBM RS/6000 (AIX 4.3.3). MathWorks протестировала графические ускорители Sun 3D Creator (Solaris 2.6, 2.7, 2.8) и ускорители моделей Silicon Graphics на платформах IRIX/IRIX 64 6.5x для проверки поддержки Open GL на UNIX платформах. Отличия между платформами, таким образом, в основном связаны со скоростью выполнения, в особенности при выводе трехмерной графики при расчете сцены и рендеринге новым, введенным только в данной версии, механизмом Open GL, и с отдельными деталями интерфейса. Как гарантирует MathWorks, отличия совсем (или для платформ HP и IBM почти) не затрагивают базового набора возможностей ядра и пакетов прикладных программ. Например, пользователи Linux Red Hat 7.0 и Slackware 7.0, 7.1, как и пользователи на RISC-платформах IBM и HP, не должны использовать виртуальную машину Java и должны запускать MATLAB 6.0 с параметром nojvm (matl ab-nojvm). Но и это ограничение не распространяется на пользователей RedHat 6.2, Mandrake 7.1, SuSE 6.4, Debian 2.1 и 2.2. Поэтому читатели, работающие с MATLAB 6.0 на любой платформе, могут пользоваться всеми или большей частью материалов данной книги. Для Macintosh поддерживается только версия MATLAB 5.2.1, для пользователей OpenVMS рекомендуется стабилизированная на этой платформе MATLAB 5.2.
Установка системы обычно не имеет никаких специфических особенностей и подобна установке других программных продуктов. Но в среде Windows 2000/NT4 установить и первый раз запустить систему должен администратор системы. От вас требуется задать свое имя (фамилию), сокращенное название организации и пароль, который указывается на установочном компакт-диске или в имеющемся на нем файле. Возможны типичная установка и выборочная, в ходе которой вам предлагается выбор компонентов системы. Последняя предпочтительнее, так как из-за огромного объема системы ее полная установка не всегда возможна.
Прежде чем начинать установку системы, рекомендуется ознакомиться с описанием компонентов. В уроке 23 дается аннотационное (а в монографии — более подробное, хотя в версиях для выпуска 11) описание наиболее важных пакетов прикладных программ — дополнительных компонентов (пакетов инструментов, пакетов расширения, (toolbox)) системы MATLAB. Нет никакого смысла использовать все компоненты, поскольку вы всегда сможете по мере необходимости изменить набор установленных компонентов системы. Установив только нужные компоненты, вы можете уменьшить затраты памяти на жестком диске в несколько раз.
Рис. 2.1. Начало установки — открытие окна Мастера установки
Для установки системы на ПК достаточно вставить первый установочный компакт-диск в устройство считывания компакт-дисков. Диск запускается автома тически, и Мастер установки проверяет, нет ли необходимости обновить или установить виртуальную машину Java фирмы Microsoft. Если такая необходимость есть, то вам надо согласиться с предложением Мастера установки. После того как Мастер установки установит или обновит виртуальную машину Java Microsoft, нужно обязательно ответить согласием на предложение перезагрузить компьютер (restart). Если Мастер установки не предложил вам обновить вашу виртуальную машину Java, но в процессе установки сообщит, что необходимый класс Java отсутствует, не прерывайте установку и не извлекайте компакт-диск. Вам достаточно выбрать Пуск > Выполнить > Обзор, выбрать в папке msutils вашего первого установочного компакт-диска файл msjavx86.exe и запустить его. После установки виртуальной машины Java и перезагрузки компьютера установка MATLAB продолжится автоматически. В самом начале установки собственно MATLAB Мастер установки выводит временное окно — заставку системы. При этом копируются вспомогательные файлы MathWorks Installer (Мастера установки), что показано на рис. 2.1.
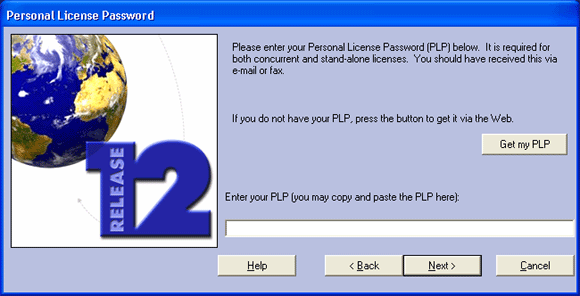
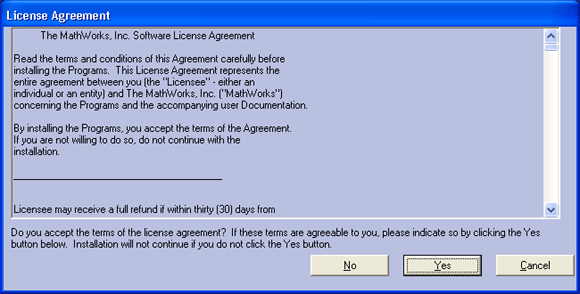
Установка осуществляется с помощью ряда окон Мастера установки. Одно из них и показано на рис. 2.1. Прочтя его текст, надо нажать кнопку Next (Далее). Появится подббное окно с запросом на ввод персонального номера лицензии — рис. 2.2. Введя номер лицензии и подтвердив его щелчком на кнопке Next (Далее), можно получить окно с текстом лицензионного соглашения — рис. 2.3. Если вы с ним согласны, следует вновь щелкнуть кнопку Next (Далее).
Рис. 2.2. Окно с запросом персонального номера лицензии
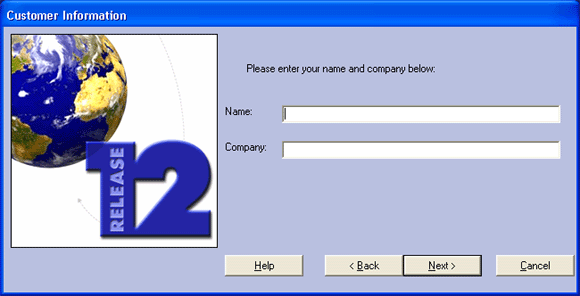
Следующее окно (рис. 2.4) требует ввода пользователем своего имени и названия организации. Их можно сократить, как показано на рис. 2.4.
Рис. 2.3. Окно с текстом лицензии
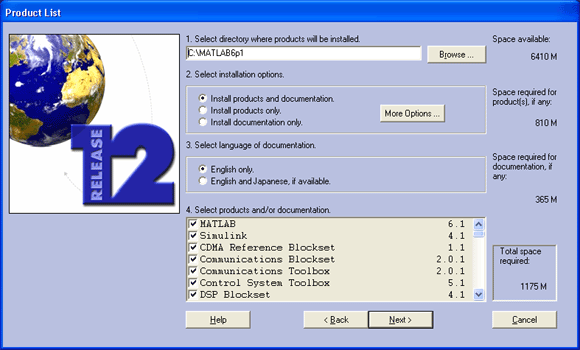
Выполнив эти установки и щелкнув кнопку Next (Далее) (она становится доступной, если данные введены верно), можно получить окно с полем для указания имени папки, в которую будет установлена система, и с полным перечнем компонентов системы. Это окно представлено на рис. 2.5. В нем следует установить флажки напротив названий нужных компонентов.
Рис. 2.4. Окно установки имени пользователя и организации
Рис. 2.5. Окно выбора компонентов системы MATLAB
Здесь обратите особое внимание на указание свободного места в выбранном разделе жесткого диска и на данные о занимаемом системой объеме дискового пространства. Он должен быть заметно меньше, чем объем свободного пространства выбранного раздела диска, поскольку в нем, как правило, размещаются и служебные файлы операционной системы Windows 95/98/Me/ 2000/NT4, в частности временные файлы.
Рис. 2.6. Предупреждение об отсутствии папки для установки системы MATLAB 6.0
Если объема выбранного раздела явно недостаточно, то, во-первых, просмотрите другие разделы жесткого диска, а во-вторых, умерьте свои аппетиты в части установки расширений системы. Скорее всего, большинство этих расширений вам просто не понадобится, поскольку относится к не интересующим вас разделам науки и техники. Кроме того, система помощи может, например, оставаться на компакт-диске, так как вы сможете установить путь к файлам справочной системы на компакт-диске из пользовательского интерфейса после установки системы.
Обратите внимание и на выбор папки для размещения файлов системы MAT-LAB 6.0 — их тысячи! Если вы решили сменить предложенное вам название и место размещения папки для системы, то в случае отсутствия папки, название которой было введено вами, Мастер установки. (MathWorks Installer) выведет окно с сообщением об этом (рис. 2.6).
Вы должны согласиться с предложением о задании новой папки, щелкнув кнопку Yes (Да), или вернуться к окну рис. 2.5, щелкнув кнопку No (Нет). После этого и после выбора необходимых компонентов надо щелкнуть кнопку Next (Далее). Затем начинается самый длительный этап установки. Все файлы системы разар-хивируются и переносятся в создаваемые для них папки. Этот процесс сопровождается контролем по линейным индикаторам (рис. 2.7).
Рис. 2.7. Процесс установки системы MATLAB
Иногда возможно появление окон с сообщением о наличии на вашем компьютере каких-либо файлов, которые входят в состав системы MATLAB. В этом случае вам предоставляется возможность сохранить существующий файл или записать на его место новый файл системы MATLAB. Последнее, пожалуй, более целесообразно, так как MATLAB — очень сложная и объемная система и лучше не рисковать устанавливать ее с «чужими» файлами.
Процесс установки на компьютере Pentium II 350 МГц с 32-скоростным приводом CD-ROM идет довольно медленно и занимает больше часа при полной установке системы. Он может затянуться на несколько часов на менее мощном ПК. После установки надо произвести перезагрузку компьютера или временно отложить ее.
Запуск MATLAB без перезагрузки компьютера не рекомендуется, поскольку может протекать некорректно. Так что если вы отложили перезагрузку компьютера, не забудьте провести ее перед первым запуском системы MATLAB.
Система MATLAB состоит из многих тысяч файлов, находящихся в множестве папок. Полезно иметь представление о содержании основных папок, поскольку это позволяет быстро оценить возможности системы — например, узнать, какие операторы, функции или графические команды входят в систему.
В MATLAB особое значение имеют файлы двух типов — с расширениями .mat и .т. Первые являются бинарными файлами, в которых могут храниться значения переменных. Вторые представляют собой текстовые файлы, содержащие внешние программы, определения команд и функций системы. Именно к ним относится большая часть команд и функций, в том числе задаваемых пользователем для решения своих специфических задач. Нередко встречаются и файлы с расширением .с (коды на языке Си), файлы с откомпилированными кодами MATLAB с расширением .тех и другие. Исполняемые файлы имеют расширение .ехе.
Особое значение имеет папка MATLAB/TOOLBOX/MATLAB. В ней содержится набор стандартных m-файлов системы. Просмотр этих файлов позволяет детально оценить возможности поставляемой конкретной версии системы. Ниже перечислены основные подпапки с этими файлами (деление на категории условно, на самом деле все подпапки находятся в общей папке MATLAB/TOOLBOX/MATLAB).
Подпапка команд общего назначения:
-
General — команды общего назначения: работа со справкой, управление окном MATLAB, взаимодействие с операционной системой и т. д.
Подпапки операторов, конструкций языка и системных функций:
-
ops — операторы и специальные символы;
-
tang — конструкции языка программирования;
-
strfun — строковые функции;
-
iofun — функции ввода/вывода;
-
timefun — функции времени и дат;
-
datatypes — типы и структуры данных.
Подпапки основных математических и матричных функций:
-
elmat — команды создания элементарных матриц и операций с ними;
-
elfun — элементарные математические функции;
-
specfun — специальные математические функции;
-
matfun — матричные функции линейной алгебры;
-
datafun — анализ данных и преобразования Фурье;
-
polyfun — полиномиальные функции и функции интерполяции;
-
funfun — функции функций и функции решения обыкновенных дифференциальных уравнений;
-
soarfun — функции разреженных матриц.
Подпайки команд графики:
-
graph2d — команды двумерной графики;
-
graph3d — команды трехмерной графики;
-
specgraph — команды специальной графики;
-
graphics — команды дескрипторной графики;
-
uitools — графика пользовательского интерфейса.
Полный состав файлов каждой подпапки (их список содержится в файле соп-tents.m) можно вывести на просмотр с помощью команды help имя, где имя — название соответствующей подпапки.
1.gif
2.gif
3.gif
4.gif
5.gif
6.gif

7.gif
3. Запуск MATLAB и работа в режиме диалога
Запуск MATLAB и работа в режиме диалога
В этой книге предполагается, что MATLAB используется в среде операционной системы Windows 95 или Windows 98/Me/2000. Копии сеансов работы MATLAB даны именно для этих случаев. Однако пользователи, работающие с Windows NT4, также могут обращаться к материалам данной книги без каких-либо ограничений, поскольку отличия касаются лишь мелких деталей пользовательского интерфейса. Это справедливо, хотя в меньшей мере, и для пользователей систем MATLAB на иных платформах.
Рис. 2.8. Подготовка к запуску MATLAB
Рис. 2.8 иллюстрирует подготовку к запуску системы MATLAB 6.0 из главного меню операционной системы Windows 98 со стандартным видом рабочего стола, подобным использованному в Windows 95. Для раскрытия главного меню активизируется кнопка Пуск (Start), расположенная внизу рабочего стола слева, или можно щелкнуть на значке с логотипом системы на рабочем столе Windows.
Далее мы не всегда будем повторять полное название системы — MATLAB 6.0 — и ограничимся сокращенным названием MATLAB.
После запуска MATLAB (см. рис. 2.8) на экране появляется основное окно системы MATLAB, показанное на рис. 2.9. Обычно это окно раскрыто не полностью и занимает часть рабочего стола. Вы можете раскрыть окно полностью, щелкнув на средней из трех кнопок, расположенных в конце титульной (верхней) строки окна. Левая кнопка сворачивает окно в кнопку с именем приложения, помещаемую в панель задач Windows 95/98, а правая закрывает окно и прекращает работу с MATLAB. Система готова к проведению вычислений в командном режиме. При этом вы можете не обращать внимания на новации пользовательского интерфейса, привнесенного операционными системами Windows 95 и 98/Me/2000/NT4, в виде расширяемого окна и панели инструментов. Мы обсудим их роль позже. Тем не менее сразу бросается в глаза существенное изменение интерфейса у системы MATLAB 6.0 по сравнению с предшествующей версией MATLAB 5.3.I.
Для уточнения версии системы следует вывести окно с информацией о системе (команда About MATLAB (О MATLAB) в меню Help (Помощь). Это окно представлено на рис. 2.10 в центре. Из него видно, что запущена версия 6.0 (R12) от 22 сентября 2000 г. Поскольку номер лицензии имеет конфиденциальный характер, вместо него на рисунке показан 0.
Рис. 2.9. Окно системы MATLAB после запуска и выполнения простых вычислений
Рис. 2.10. Окно с логотипом системы MATLAB 6.0
Полезно знать, что в начале запуска автоматически выполняется команда rnatl abrc, которая исполняет загрузочный файл matlabrc.m и файл startup.m, если таковой существует. Эти файлы выполняют начальную настройку терминала системы и задают ряд ее параметров. В частности, могут быть заданы пути доступа к другим файлам, необходимым для корректной работы системы MATLAB. Таким образом, опытные пользователи могут выполнить настройку системы под свои запросы. Однако в большинстве случаев особой необходимости в этом нет. Поскольку указанные файлы имеют текстовый формат, их легко просмотреть с помощью какого-либо текстового редактора или с помощью команды type в командном режиме работы MATLAB.
Сеанс работы с MATLAB принято именовать сессией (session). Сессия, в сущности, является текущим документом, отражающим работу пользователя с системой MATLAB. В ней имеются строки ввода, вывода и сообщений об ошибках. Входящие в сессию определения переменных и функций, расположенные в рабочей области памяти, но не саму сессию, можно записать на диск (файлы формата .mat), используя команду save (Сохранить). Команда load (Загрузить) позволяет считать с диска данные рабочей области. Фрагменты сессии можно оформить в виде дневника с помощью команды diary (Дневник). Позже мы обсудим эти команды подробно.
8.gif
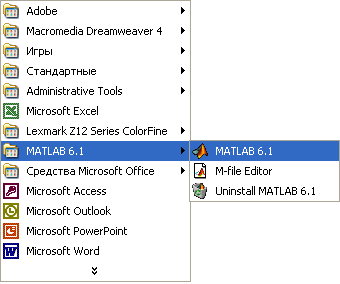
9.gif
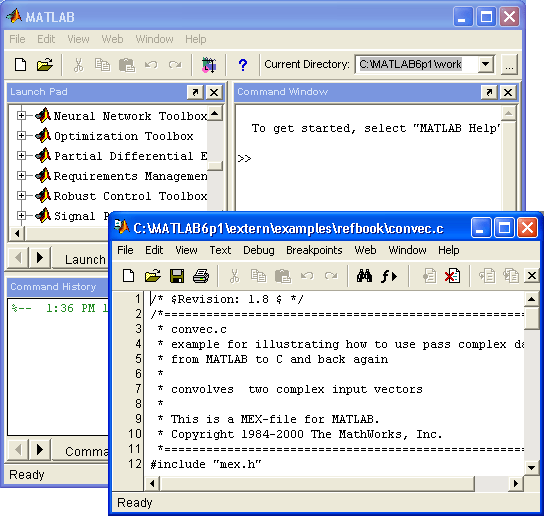
10.gif
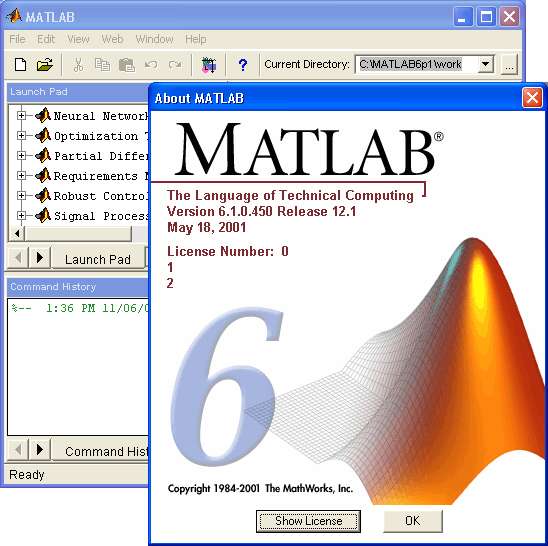
4. Новый и старый облик системы MATLAB 6.0
Новый и старый облик системы MATLAB 6.0
Пользователи, уже имеющие опыт работы с системами MATLAB, будут приятно (а кое-кто, напротив, неприятно) удивлены новациями пользовательского интерфейса системы MATLAB 6.0. В новой версии пользовательского интерфейса не осталось и следа от прежней строгой скромности.
В новой версии вид окна системы (рис. 2.9) уже вполне отвечает канонам современного интерфейса. Пользовательский интерфейс многооконный и имеет ряд средств прямого доступа к различным компонентам системы. Бросается в глаза новый пункт меню — Web. Он дает прямой выход в Интернет (см. урок 1).
В панели инструментов добавлена позиция ввода ранее отмененной операции и меню просмотра файловой системы с кнопкой его открытия. Но самые решительные изменения произошли в левой части общего окна системы — здесь появились окна доступа к компонентам системы Launch Pad/Workspace (Панель запуска/ Рабочая область) и окно Current Directory (текущей папки).
Надо прямо признать, что особой необходимости в этих новациях нет, поскольку старые пользователи уже привыкли к крайней простоте интерфейса систем MATLAB. Учтя это, разработчики системы ввели в позицию View (Вид) меню команду Desktop Layout > Command Windows Only (Только командное окно). Стоит ее исполнить, как вид окна системы будет очень напоминать добрый старый интерфейс версий MATLAB 5.* — рис. 2.11.
Рис. 2.11. Упрощенный интерфейс системы MATLAB 6.0
Если вы все же хотите вкусить прелести нового интерфейса, то исполните в той же позиции меню команду Desktop Layout > Default (Интерфейс по умолчанию). Там же вы найдете и другие возможности модификации вида интерфейса системы MATLAB 6.0.
11.gif
5. Операции строчного редактирования
Операции строчного редактирования
При работе с MATLAB в командном режиме действует простейший строчный редактор. Его команды перечислены в табл. 2.1.
Таблица 2.1. Команды строчного редактора MATLAB
|
Ctrl+b |
Перемещение курсора вправо на один символ |
|
Ctrl+f |
Перемещение курсора влево на один символ |
|
Ctrl +r |
Перемещение курсора вправо на одно слово |
|
Ctrl +1 |
Перемещение курсора влево на одно слово |
|
Home или Ctrl+a |
Перемещение курсора в начало строки |
|
End или Ctrl +e |
Перемещение курсора в конец строки |
|
Ctrl+рu Ctrl+n |
Перелистывание предыдущих команд вверх или вниз для подстановки в строку ввода |
|
Del или Ctrl+d |
Стирание символа справа от курсора |
|
Ctrl+h |
Стирание символа слева от курсора |
|
Ctrl+k |
Стирание до конца строки |
|
Esc |
Очистка строки ввода |
|
Ins |
Включение/выключение режима вставки |
|
PgUp |
Перелистывание страниц сессии вверх |
|
PgDn |
Перелистывание страниц сессии вниз |
Эти возможности кажутся примитивными, но позволяют пользователю быстро работать в стиле первых версий MATLAB для MS-DOS. Они обеспечивают важное свойство новых версий систем — их совместимость со старыми версиями в части преемственности навыков работы. Позже вы увидите, что в новых версиях есть вполне современный редактор со средствами отладки создаваемых документов — m-файлов.
Обратите особое внимание на применение клавиш вверх и вниз. Они используются для подстановки после маркера строки ввода » ранее введенных строк, например для их исправления, дублирования или дополнения. При этом указанные клавиши обеспечивают перелистывание ранее введенных строк снизу вверх или сверху вниз. Такая возможность существует благодаря организации специального стека, хранящего строки с исполненными ранее командами.
6. Команды управления окном
Команды управления окном
Полезно сразу усвоить некоторые команды управления окном командного режима:
-
clс — очищает экран и размещает курсор в левом верхнем углу пустого экрана.
-
home — возвращает курсор в левый верхний угол окна.
-
echo <file_name> on — включает режим вывода на экран текста Script-файла (файла-сценария).
-
echo <file_name> off — выключает режим вывода на экран текста Script-файла.
-
echo <fi1e_name> — меняет режим вывода на противоположный.
-
echo on all — включает режим вывода на экран текста всех m-файлов.
-
echo off all — отключает режим вывода на экран текста всех m-файлов.
-
mоrе on — включает режим постраничного вывода (полезен при просмотре больших m-файлов).
-
mоrе off — отключает режим постраничного вывода (в этом случае для просмотра больших фалов надо пользоваться линейкой прокрутки).
В версии MATLAB 6.0 обе команды clc и home действуют аналогично — очищают экран и помещают курсор в левый верхний угол окна командного режима работы. Команды echo позволяют включать или выключать отображение текстов m-файлов при каждом обращении к ним. Как правило, отображение текста файлов сильно загромождает экран и часто не является необходимым. При больших размерах файлов начало их текста (листинга) убегает далеко за пределы области просмотра (текущего окна командного режима). Поэтому для просмотра длинных листингов файлов полезно включить постраничный вывод командой more on. Различие между m-файлами сценариев и функций мы обсудим позже.
7. MATLAB в роли суперкалькулятора
MATLAB в роли суперкалькулятора
Система MATLAB создана таким образом, что любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькуляторов вычисления (например, выполнять арифметические операции и вычислять элементарные функции), но и операции с векторами и матрицами, комплексными числами, рядами и полиномами. Можно почти мгновенно задать и вывести графики различных функций — от простой синусоиды до сложной трехмерной фигуры.
Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал вопрос, получил ответ». Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командной строке и завершает ввод нажатием клавиши ENTER. В качестве примера на рис. 2.9 уже были показаны простейшие вычисления — вычисление выражения 2+3 и значения sin(l).
Даже из таких простых примеров можно сделать некоторые поучительные выводы:
-
для указания ввода исходных данных используется символ »;
-
данные вводятся с помощью простейшего строчного редактора;
-
для блокировки вывода результата вычислений некоторого выражения после него надо установить знак ; (точка с запятой);
-
если не указана переменная для значения результата вычислений, то MATLAB назначает такую переменную с именем ans;
-
знаком присваивания является привычный математикам знак равенства =, а не комбинированный знак :=, как во многих других языках программирования и математических системах;
-
результат вычислений выводится в строках вывода (без знака »);
-
встроенные функции (например, sin) записываются строчными буквами, и их аргументы указываются в круглых скобках;
-
диалог происходит в стиле «задал вопрос — получил ответ».
Следующий пример (он показан на рис. 2.11) иллюстрирует применение системы MATLAB для выполнения простых векторных операций. В этом примере задается четырехэлементный вектор V со значениями элементов 1, 2, 3 и 4. Далее (сосредоточьте на этом внимание!) вычисляются функции синуса и экспоненты с аргументом в виде вектора, а не скаляра.
Две записи для вектора — V=[l 2 3 4] и V=[1,2,3.4] — являются идентичными. Таким образом, векторы задаются списком своих элементов, разделяемых пробелами или запятыми. Список заключается в квадратные скобки. Для выделения п- го элемента вектора V используется выражение V(n). Оно задает соответствующую индексированную переменную.
В большинстве математических систем вычисление sin(V) и exp(V), где V — вектор, сопровождалось бы выдачей ошибки, поскольку функции sin и ехр должны иметь аргумент в виде скалярной величины. Однако MATLAB — матричная система, а вектор является разновидностью матрицы с размером 1х n. Поэтому в нашем случае результат вычислений будет вектором того же размера, что и аргумент V, но элементы возвращаемого вектора будут синусами или экспонентами от элементов вектора V.
Рис. 2.12. Простейшие операции с матрицей
Еще один пример (рис. 2.12) демонстрирует простейшие операции с матрицей. Здесь задана матрица М с размером 2x2 и вычислена матрица MX=sin(M).
Матрица задается в виде ряда векторов, представляющих ее строки и заключенных в квадратные скобки. Для разделения элементов векторов используется пробелили запятая, а для отделения одного вектора от другого — точка с запятой. Для выделения отдельного элемента матрицы М используется выражение вида M(j,i), где М — имя матрицы, j — номер строки и 1 — номер столбца.
Как видно из приведенных примеров, ввод исходных выражений для вычислений в системе MATLAB осуществляется в самом обычном текстовом формате. В этом же формате выдаются результаты вычислений, за исключением графических. Приведем пример записи вычислений, показанных на рис. 2.8 и 2.9:
То get started, select "MATLAB Help" from the Help menu.
» 2+3
ans=
5
» sin(l)
ans=
0.8415
» type sin
sin is a built-in function.
» help sin
SIN Sine.
SIN(X) is the sine'of the elements of X.
Overloaded methods
help sym/sin.m
» V=[l 2 3 4]
V =
1 2 3 4 » sin(V) ans =
0.8415 0.9093 0.1411 -0.7568
» 3*V
ans =
3 6 9 12
» V^2
??? Error using ==> ^
Matrix must be square.
» V.^2
ans=
1 4 9 16
» V+2
ans =
3 4 5 6
»
Примечание
Обратите внимание на форму ответов при выполнении простых операций без указания переменной, которой присваивается результат. В таких случаях MATLAB сам назначает переменную ans, которой присваивается результат и значение которой затем выводится на экран.
Сравните эти записи с записями в реальных сессиях (рис. 2.9 и 2.11). Вы наверняка отметите, что они практически идентичны. Разве что в текстовых вариантах примеров для экономии бумаги, на которой печаталась эта книга, убраны пропуски между строками. Мы будем показывать представление сессий в виде прямых копий экрана только в том случае, когда это связано со спецификой проведения вычислений, например когда они сопровождаются выводом графиков или демонстрацией элементов пользовательского интерфейса. В остальных случаях будет использоваться представление сессии прямо в тексте книги в представленном выше текстовом формате — основном для командного режима работы с системой MATLAB. При этом строки ввода будут отмечаться маркером ввода » в их начале. Ради компактности записи пустые строки будут опускаться.
12.gif
8. О переносе строки в сессии
О переносе строки в сессии
В некоторых случаях вводимое математическое выражение может оказаться настолько длинным, что для него не хватит одной строки. В этом случае часть выражения можно перенести на новую строку с помощью знака многоточия «...» (3 или более точек), например:
s = 1-1/2 + 1/3- 1/4 + 1/5 - 1/6 + 1/7 ... 1/8 + 1/9 - 1/10 + 1/11 - 1/12:
Этот прием может быть весьма полезным для создания наглядных документов, у которых предотвращается заход строк в невидимую область окна. Вообще говоря, максимальное число символов в одной строке командного режима — 4096, а в m-файле — не ограничено, но со столь длинными строками работать неудобно. В ранних версиях в одной строке было не более 256 символов.
9. Основные объекты MATLAB
Основные объекты MATLAB
Понятие о математическом выражении
Центральным понятием всех математических систем является математическое выражение. Оно задает то, что должно быть вычислено в численном (реже символьном) виде. Вот примеры простых математических выражений:
2+3
2.301*sin(x)
4+ехр(3)/5
sqrt(y)/2
sin(pi/2)
Математические выражения строятся на основе чисел, констант, переменных, операторов, функций и разных спецзнаков. Ниже даются краткие пояснения сути этих понятий.
10. Действительные и комплексные числа
Действительные и комплексные числа
Число — простейший объект языка MATLAB, представляющий количественные данные. Числа можно считать константами, имена которых совпадают с их значениями. Числа используются в общепринятом представлении о них. Они могут быть целыми, дробными, с фиксированной и плавающей точкой. Возможно представление чисел в хорошо известном научном формате с указанием мантиссы и порядка числа.
Ниже приводятся примеры представления чисел:
0
2
-3
2.301 0.00001 123.45бе-24
-234.456е10
Как нетрудно заметить, в мантиссе чисел целая часть отделяется от дробной не запятой, а точкой, как принято в большинстве языков программирования. Для отделения порядка числа от мантиссы используется символ е. Знак «плюс» у чисел не проставляется, а знак «минус» у числа называют унарным минусом. Пробелы между символами в числах не допускаются.
Числа могут быть комплексными: z =Rе(x)+Im(x)*i. Такие числа содержат действительную Re(z) и мнимую Im(z) части. Мнимая часть имеет множитель i или j, означающий корень квадратный из -1:
3i
2j
2+3i
-3.141i
-123.456+2.7e-3i
Функция real (z) возвращает действительную часть комплексного числа, Re(z), a функция imag(z) — мнимую, Im(z). Для получения модуля комплексного числа используется функция abs(z), а для вычисления фазы — angle(Z). Ниже даны простейшие примеры работы с комплексными числами:
»i
ans=
0 +1.0000i
» j
ans =
0 + 1.0000i
» z=2+3i
z =
2.0000 + 3.0000i
» abs(z)
ans =
3.6056
» real(z)
ans=
2
» imag(z)
ans =
3
» angle(z)
ans =
0.9828
В MATLAB не принято делить числа на целые и дробные, короткие и длинные и т. д., как это принято в большинстве языков программирования, хотя задавать числа в таких формах можно. Вообще же операции над числами выполняются в формате, который принято считать форматом с двойной точностью. Такой формат удовлетворяет подавляющему большинству требований к численным расчетам, но совершенно не подходит для символьных вычислений с произвольной (абсолютной) точностью. Символьные вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic Math Toolbox.
11. Константы и системные переменные
Константы и системные переменные
Константа — это предварительно определенное числовое или символьное значение, представленное уникальным именем. Числа (например 1, -2 и 1.23) являются безымянными числовыми константами.
Другие виды констант в MATLAB принято назвать системными переменными, поскольку, с одной стороны, они задаются системой при ее загрузке, а с другой — могут переопределяться. Основные системные переменные, применяемые в системе MATLAB, указаны ниже:
-
i или j — мнимая единица (корень квадратный из -1);
-
pi - число п - 3.1415926...;
-
eps — погрешность операций над числами с плавающей точкой (2- 52 );
-
realmin — наименьшее число с плавающей точкой (2- 1022 );
-
realmax — наибольшее число с плавающей точкой (2 1023 );
-
inf — значение машинной бесконечности;
-
ans — переменная, хранящая результат последней операции и обычно вызывающая его отображение на экране дисплея;
-
NaN — указание на нечисловой характер данных (Not-a-Number).
Вот примеры применения системных переменных:
»
2*pi ans =
6.2832
» eps
ans =
2.2204е-016
» real min
ans=
2.2251e-308
» realmax
ans=
1.7977e+308
» 1/0
Warning: Divide by zero,
ans=
Inf
» 0/0
Warning: Divide by zero,
ans =
NaN
Как отмечалось, системные переменные могут переопределяться. Можно задать системной переменной eps иное значение, например eps=0.0001. Однако важно то, что их значения по умолчанию задаются сразу после загрузки системы. Поэтому неопределенными в отличие от обычных переменных системные переменные не могут быть никогда.
Символьная константа — это цепочка символов, заключенных в апострофы, например:
'Hello my friend!'
'Привет'
'2+3'
Если в апострофы помещено математическое выражение, то оно не вычисляется и рассматривается просто как цепочка символов. Так что ' 2+3' не будет возвращать число 5. Однако с помощью специальных функций преобразования символьные выражения могут быть преобразованы в вычисляемые. Соответствующие функции преобразования будут рассмотрены в дальнейшем.
12. Текстовые комментарии
Текстовые комментарии
Поскольку MATLAB используется для достаточно сложных вычислений, важное значение имеет наглядность их описания. Она достигается, в частности, с помощью текстовых комментариев. Текстовые комментарии вводятся с помощью символа %, например так:
Bit is factorial function
Примечание
В каждой большой программе есть свои «ложки дегтя». В MATLAB 6 такой «ложкой дегтя» является перевод строки при вводе буквы «с» русского алфавита в командной строке. В итоге ввод комментариев в командной строке на русском языке превращается в проблему. Пока автор может порекомендовать заменять русское «с» на английское, что на виде текстового комментария никак не сказывается. Не рекомендуется вводить русскоязычные комментарии и в тесты m-файлов при подготовке их в редакторе/отладчике (он будет описан позже). Это нередко делает программы неработоспособными. Жаловаться тут бесполезно — MATLAB англоязычный продукт и официальной локализованной под Россию версии этой системы пока нет.
Обычно первые строки m-файлов служат для описания их назначения, которое выводится на экран дисплея после команды » help Имя_файла.
Считается правилом хорошего тона вводить в m-файлы достаточно подробные текстовые комментарии. Без таких комментариев даже разработчик программных модулей быстро забывает о сути собственных решений. В текстовых комментариях и в символьных константах могут использоваться буквы русского алфавита — при условии, что установлены содержащие эти буквы наборы шрифтов (см. примечание . выше).
13. Переменные и присваивание им значений
Переменные и присваивание им значений
Переменные — это имеющие имена объекты, способные хранить некоторые, обычно разные по значению, данные. В зависимости от этих данных переменные могут быть числовыми или символьными, векторными или матричными.
В системе MATLAB можно задавать переменным определенные значения. Для этого используется операция присваивания, вводимая знаком равенства =:
Имя_переменной - Выражение
Типы переменных заранее не декларируются. Они определяются выражением, значение которого присваивается переменной. Так, если это выражение — вектор или матрица, то переменная будет векторной или матричной.
Имя переменной (ее идентификатор) может содержать сколько угодно символов, но запоминается и идентифицируется только 31 начальный символ. Имя любой переменной не должно совпадать с именами других переменных, функций и процедур системы, т. е. оно должно быть уникальным. Имя должно начинаться с буквы, может содержать буквы, цифры и символ подчеркивания _. Недопустимо включать в имена переменных пробелы и специальные знаки, например +,.-, *, / и т. д., поскольку в этом случае правильная интерпретация выражений становится невозможной.
Желательно использовать содержательные имена для обозначений переменных, например speed_l для переменной, обозначающей скорость первого объекта. Переменные могут быть обычными и индексированными, то есть элементами векторов или матриц (см. выше). Могут использоваться и символьные переменные, причем символьные значения заключаются в апострофы, например s='Demo'.
14. Уничтожение определений переменных
Уничтожение определений переменных
В памяти компьютера переменные занимают определенное место, называемое рабочей областью (workspace). Для очистки рабочей области используется функция clear в разных формах, например:
-
clear — уничтожение определений всех переменных;
-
clear x — уничтожение определения переменной х;
-
clear a, b, с — уничтожение определений нескольких переменных.
Уничтоженная (стертая в рабочей области) переменная становится неопределенной. Использовать неопределенные переменные нельзя, и такие попытки будут сопровождаться выдачей сообщений об ошибке. Приведем примеры задания и уничтожения переменных:
» x=2*pi
х =
6.2832
» V=[l 2345]
V =
12345
» MAT
??? Undefined function or variable 'MAT'.
» MAT=[1 2 3 4; 5 6 7 8]
MAT=
1234
5678
» clear V
» V
??? Undefined function or variable 'V'.
» clear
» x
??? Undefined function or variable 'x'.
» M
??? Undefined function or variable 'M'.
Обратите внимание на то, что сначала выборочно стерта переменная V, а затем командой clear без параметров стерты все остальные переменные.
15. Операторы и функции
Операторы и функции
Оператор — это специальное обозначение для определенной операции над данными — операндами. Например, простейшими арифметическими операторами являются знаки суммы +, вычитания -, умножения * и деления /. Операторы используются совместно с операндами. Например, в выражении 2+3 знак + является оператором сложения, а числа 2 и 3 — операндами.
Следует отметить, что большинство операторов относится к матричным операциям, что может служить причиной серьезных недоразумений. Например, операторы умножения * и деления / вычисляют произведение и частное от деления двух многомерных массивов, векторов или матриц. Есть ряд специальных операторов, например, оператор \ означает деление справа налево, а операторы . * и . / означают соответственно поэлементное умножение и поэлементное деление массивов.
Следующие примеры поясняют сказанное на примере операций с векторами:
» Vl=[2 4 6 8]
V1=
2468
» V2=[l 2 3 4]
V2 =
1234
» V1/V2
ans =
2
» V1.*V2
ans=
2 8 18 32
» V1./V2
ans =
2 2 2 2
Полный список операторов можно получить, используя команду » help ops. Постепенно мы рассмотрим все операторы системы MATLAB и обсудим особенности их применения. А пока приведем только часть полного списка операторов, содержащую арифметические операторы:
» help ops
Operators and special characters.
Arithmetic operators.
|
|
|
|
|
|
|
|
Plus |
- Plus |
+ |
|
|
|
Up! us |
- Unary plus |
+ |
|
|
|
Minus |
- Minus |
— |
|
|
|
Umlnus |
- Unary minus |
- |
|
|
|
Mtimes |
- Matrix multiply |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
times |
- Array multiply |
* |
|
|
|
mpower |
- Matrix power |
^ |
|
|
|
poWer |
- Array power |
.^ |
|
|
|
mldlvlde |
- Backslash or left matrix divide |
\ |
|
|
|
mrdlvlde |
- Slash or right matrix divide |
/ |
|
|
|
Idi-vide |
- Left array divide |
.\ |
|
|
|
rdlvlde |
- Right array divide |
./ |
|
|
|
kron |
- Kronecker tensor product |
kron |
|
|
|
|
|
|
|
Функции — это имеющие уникальные имена объекты, выполняющие определенные преобразования своих аргументов и при этом возвращающие результаты этих преобразований. Возврат результата — отличительная черта функций. При этом результат вычисления функции с одним выходным параметром подставляется на место ее вызова, что позволяет использовать функции в математических выражениях, например функцию sin в 2*sin(pi/2).
Функции в общем случае имеют список аргументов (параметров), заключенный в круглые скобки. Например, функция Бесселя записывается как bessel(NU.X). В данном случае список параметров содержит два аргумента — NU в виде скаляра и X в виде вектора. Многие функции допускают ряд форм записи, отличающихся списком параметров. Если функция возвращает несколько значений, то она записывается в виде [Yl. Y2....]=func(Xl. X2...)
где Yl. Y2,... — список выходных параметров и XI, Х2.... — список входных аргументов (параметров).
Со списком элементарных функций можно ознакомиться, выполнив команду hel p elfun, а со списком специальных функций — с помощью команды help specfun. Функции могут быть встроенными (внутренними) и внешними, или т-функциями. Так, встроенными являются наиболее распространенные элементарные функции например, sin(x) и ехр(у), тогда как функция sinh(x) является внешней функцией. Внешние функции содержат свои определения в m-файлах. Задание таких функций с помощью специального редактора m-файлов мы рассмотрим в уроке 5. Встроенные функции хранятся в откомпилированном ядре системы MATLAB, в силу чего они выполняются предельно быстро.
16. Применение оператора : (двоеточие)
Применение оператора: (двоеточие)
Очень часто необходимо произвести формирование упорядоченных числовых последовательностей. Такие последовательности нужны для создания векторов или значений абсциссы при построении графиков. Для этого в MATLAB используется оператор : (двоеточие):
Начальное_значение:Шаг:Конечное_значение
Данная конструкция порождает возрастающую последовательность чисел, которая начинается с начального значения, идет с заданным шагом и завершается конечным значением. Если Шаг не задан, то он принимает значение 1. Если конечное значение указано меньшим, чем начальное значение, — выдается сообщение об ошибке. Примеры применения оператора : даны ниже:
» 1:5
ans =
12345
» i=0:2:10
i = 0 2 4 6 8 10
» j=10:-2:2
j =10 8 6 4 2
» V=0:pi/2:2*pi;
» V
V =
0 1.5708 3.1416 4.7124 6.2832
» X= l:-.2:0
X=
1.0000 0.8000 0.6000 0.4000 0.2000 0
» 5:2
ans=
Empty matrix:1-by-0
Как отмечалось, принадлежность MATLAB к матричным системам вносит коррективы в назначение операторов и приводит при неумелом их использовании к казусам. Рассмотрим следующий характерный пример:
» х=0:5
х=
0 1 2 3 4 5
» cos(x)
ans =
1.0000 0.5403 -0.4161 -0.9900 -0.6536 0.2837
» sin(x)/x
ans = -0.0862
Вычисление массива косинусов здесь прошло корректно. А вот вычисление массива значений функции sin(x)/x дает неожиданный, на первый взгляд, эффект — вместо массива с шестью элементами вычислено единственное значение!
Причина «парадокса» здесь в том, что оператор / вычисляет отношение двух матриц, векторов или многомерных массивов. Если они одной размерности, то результат будет одним числом, что в данном случае и выдала система. Чтобы действительно получить вектор значений sin(x) /x, надо использовать специальный оператор поэлементного деления массивов — . /. Тогда будет получен массив чисел:
» sin(x)./x
Warning: Divide by zero.
ans =
NaN 0.8415 0.4546 0.0470 -0.1892-0.1918
Впрочем, и тут без особенностей не обошлось. Так, при х = 0 значение sin(x)/x дает устранимую неопределенность вида 0/0=1. Однако, как и всякая численная система, MATLAB классифицирует попытку деления на 0 как ошибку и выводит соответствующее предупреждение. А вместо ожидаемого численного значения выводится символьная константа NaN, означающая, что неопределенность 0/0 — это все же не обычное число.
Выражения с оператором : могут использоваться в качестве аргументов функций для получения множественных их значений. Например, в приводимом ниже примере вычислены функции Бесселя порядка от 0 до 5 со значением аргумента 0.5:
» bessel(0:l:5,l/2)
ans =
0.9385 0.2423 0.0306 0.0026 0.0002 0.0000
А в следующем примере вычислено шесть значений функции Бесселя нулевого порядка для значений аргумента от 0 до 5 с шагом 1:
» bessel(0.0:1:5)
ans =
1.0000 0.7652 0.2239 -0.2601 -0.3971 -0.1776
Таким образом, оператор : является весьма удобным средством задания регулярной последовательности чисел. Он широко используется при работе со средствами построения графиков. В дальнейшем мы расширим представление о возможностях этого оператора.
17. Сообщения об ошибках и исправление ошибок
Сообщения об ошибках и исправление ошибок
Важное значение при диалоге с системой MATLAB имеет диагностика ошибок. Вряд ли есть пользователь, помнящий точное написание тысяч операторов и функций, входящих в систему MATLAB и в пакеты прикладных программ. Поэтому никто не застрахован от ошибочного написания математических выражений или команд. MATLAB диагностирует вводимые команды и выражения и выдает соответствующие сообщения об ошибках или предупреждения. Пример вывода сообщения об ошибке (деление на 0) только что приводился.
Рассмотрим еще ряд примеров. Введем, к примеру, ошибочное выражение » sqr(2)
и нажмем клавишу ENTER. Система сообщит об ошибке:
??? Undefined function or variable 'sqr'.
Это сообщение говорит о том, что не определена переменная или функция, и указывает, какая именно — sqr. В данном случае, разумеется, можно просто набрать правильное выражение. Однако в случае громоздкого выражения лучше воспользоваться редактором. Для этого достаточно нажать клавишу вниздля перелистывания предыдущих строк. В результате в строке ввода появится выражение » sqr(2)
с курсором в его конце. В версии MATLAB 6 можно теперь нажать клавишу Tab. Система введет подсказку, анализируя уже введенные символы. Если вариантов несколько, клавишу Tab придется нажать еще раз. Из предложенных системой трех операторов выбираем sqrt. Теперь с помощью клавиши вниз вновь выбираем нужную строку и, пользуясь клавишей влево , устанавливаем курсор после буквы г. Теперь нажмем клавишу вверх, а затем клавишу ENTER. Выражение примет следующий вид:
» sqrt(2)
ans= 1.4142
Если бы был только один вариант окончания введенных символов, то после нажатия клавиши Tab система бы закончила наш ввод без перевода строки. Вычисления дают ожидаемый результат — значение квадратного корня из двух.
В системе MATLAB внешние определения используются точно так же, как и встроенные функции и операторы. Никаких дополнительных указаний на их применение делать не надо. Достаточно лишь позаботиться о том, чтобы используемые определения действительно существовали в виде файлов с расширением .m. Впрочем, если вы забудете об этом или введете имя несуществующего определения, то система отреагирует на это звуковым сигналом (звонком) и выводом сообщения об ошибке:
» hsin(1)
??? Undefined function or variable 'hsin'.
» sinh(1)
ans= 1.1752
В этом примере мы забыли (нарочно), какое имя имеет внешняя функция, вычисляющая гиперболический синус. Система подсказала, что функция или переменная с именем hsin не определена ни как внутренняя, ни как m-функция. Зато далее мы видим, что функция с именем sinh есть в составе функций системы MATLAB — она задана в виде М-функции. Между тем в последнем примере мы не давали системе никаких указаний на то, что следует искать именно внешнюю функцию! И это вычисление прошло так же просто, как вычисление встроенной функции, такой как sin. Разумеется, скорость вычислений по внешним определениям несколько ниже, чем по встроенным функциям или операторам.
При этом вычисления происходят следующим образом: вначале система быстро определяет, имеется ли введенное слово среди служебных слов системы. Если да, то нужные вычисления выполняются сразу, если нет, система ищет m-файл с соответствующим именем на диске. Если файла нет, то выдается сообщение об ошибке, и вычисления останавливаются. Если же файл найден, он загружается с жесткого диска в память машины и исполняется. Этот алгоритм аналогичен применяемому в развиваемых и адаптируемых к задачам пользователя языкам программирования ЛОГО и ФОРТ [7, 8].
Иногда в ходе вывода результатов вычислений появляется сокращение NaN (от слов Not a Number — не число). Оно обозначает неопределенность, например вида 0/0 или Inf/Inf, где Inf — системная переменная со значением машинной бесконечности. Могут появляться и различные предупреждения об ошибках (на английском языке). Например, при делении на 0 конечного/ числа появляется предупреждение «Warning: Devide by Zero.» («Внимание: Деление на ноль»). Диапазон чисел, представимых в системе, лежит от 10- 308 до 10+ 308 .
Вообще говоря, в MATLAB надо отличать предупреждение об ошибке от сообщения о ней. Предупреждения (обычно после слова Warning) не останавливают вычисления и лишь предупреждают пользователя о том, что диагностируемая ошибка способна повлиять на ход вычислений. Сообщение об ошибке (после знаков ???) останавливает вычисления.
18. Форматы чисел
Форматы чисел
По умолчанию MATLAB выдает числовые результаты в нормализованной форме с четырьмя цифрами после десятичной точки и одной до нее. Многих такая форма представления не всегда устраивает. Поэтому при работе с числовыми данными можно задавать различные форматы представления чисел. Однако в любом случае все вычисления проводятся с предельной, так называемой двойной, точностью. Для установки формата представления чисел используется команда » format name где name — имя формата. Для числовых данных name может быть следующим сообщением: short — короткое представление в фиксированном формате (5 знаков), short e — короткое представление в экспоненциальном формате (5 знаков мантиссы и 3 знака порядка), long — длинное представление в фиксированном формате (15 знаков), long e — длинное представление в экспоненциальном формате (15 знаков мантиссы и 3 знака порядка), hex — представление чисел в шестнадцатеричной форме; bank — представление для денежных единиц.
Для иллюстрации различных форматов рассмотрим вектор, содержащий два элемента-числа:
х=[4/3 1.2345е-6]
В различных форматах их представления будут иметь следующий вид:
|
|
|
|
|
|
|
|
format short format short e format long format long e format bank |
1.3333 1.3333E+000 1.333333333333338 1.333333333333338E+000 1.33 |
0.0000 1.2345E-006 0.000001234500000 1.234500000000000E-006 0.00 |
|
|
|
|
|
|
|
Задание формата сказывается только на форме вывода чисел. Вычисления все равно происходят в формате двойной точности, а ввод чисел возможен в любом удобном для пользователя виде.
19. Формирование векторов и матриц
Формирование векторов и матриц
Особенности задания векторов и матриц
Описанные выше простые правила вычислений распространяются и на гораздо более сложные вычисления, которые (при использовании обычных языков программирования типа Бейсик или Паскаль) требуют составления специальных программ. MATLAB — система, специально предназначенная для проведения сложных вычислений с векторами, матрицами и массивами. При этом она по умолчанию предполагает, что каждая заданная переменная — это вектор, матрица или массив. Все определяется конкретным значением переменной. Например, если задано Х=1, то это значит, что X —это вектор с единственным элементом, имеющим значение 1. Если надо задать вектор из трех элементов, то их значения следует перечислить в квадратных скобках, разделяя пробелами. Так, например, присваивавание
» V=[l 2 3]
V=
1 2 3
задает вектор V, имеющий три элемента со значениями 1, 2 и 3. После ввода вектора система выводит его на экран дисплея.
Задание матрицы требует указания нескольких строк. Для разграничения строк используется знак ; (точка с запятой). Этот же знак в конце ввода предотвращает вывод матрицы или вектора (и вообще результата любой операции) на экран дисплея. Так, ввод
» М=[1 2 3: 4 5 6; 7 8 9];
задает квадратную матрицу, которую можно вывести:
» M
M =
1 2 3
4 5 6
7 8 9
Возможен ввод элементов матриц и векторов в виде арифметических выражений, содержащих любые доступные системе функции, например:
» V= [2+2/(3+4) exp(5) sqrt(l0)]:
» V
V =
2.2857 148.4132 3.1623
Для указания отдельного элемента вектора или матрицы используются выражения вида V(1) или M(i. j). Например, если задать
» М(2. 2)
arts= 5
то результат будет равен 5. Если нужно присвоить элементу M(i. j) [ В тексте программ MATLAB лучше не использовать i и j как индексы, так как i и j — обозначение квадратного корня из -1. Но можно использовать I и J. — Примеч. ред. ] новое значение х, следует использовать выражение
M(ij)=x
Например, если элементу М(2, 2) надо присвоить значение 10, следует записать
» М(2. 2)=10
Выражение М( i) с одним индексом дает доступ к элементам матрицы, развернутым в один столбец. Такая матрица образуется из исходной, если подряд выписать ее столбцы.
Следующий пример поясняет такой доступ к элементам матрицы М:
» М=[1 2 3: 4 5 6: 7 8 9]
М =
1 2 3
4 5 6
7 8 9
» М(2)
ans =
4
» M(8)
ans =
6
» M(9)
ans =
9
» М(5)=100;
» М
М =
1 2 3
4 100 6
7 8 9
Возможно задание векторов и матриц с комплексными элементами, например:
» i=sqrt(-l):
» СМ =[1 2: 3 4] + i*[5 6: 7 8]
или
» СМ - [1+5*1 2+6*1: 3+7*1 4+8*1]
Это создает матрицу:
CM=
1.0000 + 5.00001 2.0000 + 6.00001
3.0000 + 7.00001 4.0000 + 8.00001
Наряду с операциями над отдельными элементами матриц и векторов система позволяет производить операции умножения, деления и возведения в степень сразу над всеми элементами, т. е. над массивами. Для этого перед знаком операции ставится точка. Например, оператор * означает умножение для векторов или матриц, а оператор .* —поэлементное умножение всех элементов массива. Так, если М — матрица, то М.*2 даст матрицу, все элементы которой умножены на скаляр — число 2. Впрочем, для умножения матрицы,на скаляр оба выражения — М*2 и М.*2 — оказываются эквивалентными.
Имеется также ряд особых функций для задания векторов и матриц. Например, функция magic(n) задает магическую матрицу размера пхп, у которой сумма всех столбцов, всех строк и даже диагоналей равна одному и тому же числу:
» M=magic(4)
М =
|
|
|||||
|
|
16 |
2 |
3 |
13 |
|
|
|
5 |
11 |
10 |
8 |
|
|
|
9 |
7 |
6 |
12 |
|
|
|
4 |
14 |
15 |
1 |
|
» sum(M)
ans=
34 34 34 34
» sum(M')
ans=
34 34 34 34
» sum(diag(M))
ans=
34
» M(1.2)+M(2.2)+M(3.2)+M(4.2)
ans= 34
Уже сама по себе возможность создания такой матрицы с помощью простой функции magic заинтересует любителей математики. Но векторных и матричных функций в системе множество, и мы их детально рассмотрим в дальнейшем. Напомним, что для стирания переменных из рабочей области памяти служит команда clear.
20. Объединение малых матриц в большую
Объединение малых матриц в большую
Описанный способ задания матриц позволяет выполнить операцию конкатенации — объединения малых матриц в большую. Например, создадим вначале магическую матрицу размера 3x3:
» A=magic(3)
А=
|
|
||||
|
|
8 |
1 |
6 |
|
|
|
3 |
5 |
7 |
|
|
|
4 |
9 |
2 |
|
|
|
Теперь можно построить матрицу, содержащую четыре матрицы:
» В-[А А+16:А+32 А+16]
В =
|
|
8 |
1 |
6 |
24 |
17 |
22 |
|
|
|
3 |
5 |
7 |
19 |
21 |
23 |
|
|
|
4 |
9 |
2 |
20 |
25 |
18 |
|
|
|
40 |
33 |
38 |
24 |
17 |
22 |
|
|
|
35 |
37 |
39 |
19 |
21 |
23 |
|
|
|
36 |
41 |
34 |
20 |
25 |
18 |
|
Полученная матрица имеет уже размер 6x6. Вычислим сумму ее столбцов:
» sum(B)
ans =
126 126 126 126 126 126
Любопытно, что она одинакова для всех столбцов. А для вычисления суммы стро! используем команду
» sum(B.')
ans =
78 78 78 174 174 174
Здесь запись В.' означает транспонирование матрицы В, т. е. замену строк столб цами. На этот раз сумма оказалась разной. Это отвергает изначально возникши предположение, что матрица В тоже является магической. Для истинно магической матрицы суммы столбцов и строк должны быть одинаковыми:
» D=magic(6)
D=
|
|
35 |
1 |
6 |
26 |
19 |
24 |
|
|
|
3 |
32 |
7 |
21 |
23 |
25 |
|
|
|
31 |
9 |
2 |
22 |
27 |
20 |
|
|
|
8 |
28 |
33 |
17 |
10 |
15 |
|
|
|
30 |
5 |
34 |
12 |
14 |
16 |
|
|
|
4 |
36 |
29 |
13 |
18 |
11 |
|
|
|
» sum(D)
ans=
111 111 111 111 111 111
» sum(D.')
ans=
111 111 111 111 111 111
Более того, для магической матрицы одинаковой является и сумма элементов по основным диагоналям (главной диагонали и главной антидиагонали).
21. Удаление столбцов и строк матриц
Удаление столбцов и строк матриц
Для формирования матриц и выполнения ряда матричных операций возникает необходимость удаления отдельных столбцов и строк матрицы. Для этого используются пустые квадратные скобки [ ]. Проделаем это с матрицей М:
» М=[1 2 3; 4 5 6; 7 8 9]
М =
|
|
||||
|
|
1 |
2 |
3 |
|
|
|
4 |
5 |
6 |
|
|
|
7 |
8 |
9 |
|
|
|
Удалим второй столбец используя оператор : (двоеточие):
» М(:.2)=[ ]
1 3
4 6
7 9
А теперь, используя оператор : (двоеточие), удалим вторую строку:
» М(2.:)=[ ]
М =
1 3
7 9
22. Операции с рабочей областью и текстом сессии
Операции с рабочей областью и текстом сессии
Дефрагментация рабочей области
По мере задания одних переменных и стирания других рабочая область перестает быть непрерывной и начинает содержать «дыры» и всякий «мусор». Это рано или поздно может привести к ухудшению работы системы или даже к нехватке оперативной памяти. Подобная ситуация становится возможной, если вы работаете с достаточно большими массивами данных.
Во избежание непроизводительных потерь памяти при работе с объемными данными (а векторы, матрицы и массивы относятся к таковым) следует использовать команду pack, осуществляющую дефрагментацию рабочей области. Эта команда переписывает все определения рабочей области на жесткий диск, очищает рабочую область и затем заново считывает все определения без «дыр» и «мусора» в рабочую область.
23. Сохранение рабочей области сессии
Сохранение рабочей области сессии
Переменные и определения новых функций в системе MATLAB хранятся в особой области памяти, именуемой рабочей областью. MATLAB позволяет сохранять значения переменных в виде бинарных файлов с расширением .mat Для этого служит команда save, которая может использоваться в ряде форм:
-
save fname — записывается рабочая область всех переменных в файле бинарного формата с именем fname.mat;
-
save fname X — записывает только значение переменной X;
-
save fname X Y Z — записывает значения переменных X, Y и Z.
После этих параметров можно указать ключи, уточняющие формат записи файлов:
-
-mat — двоичный МАТ-формат, используемый по умолчанию;
-
-ascii — ASCII-формат единичной точности (8 цифр);
-
-ascii -double — ASCII-формат двойной точности (16 цифр);
-
-ascii -double -tabs — формат с разделителем и метками табуляции;
-
V4 — запись МАТ-файла в формате версии MATLAB 4;
-
-append — добавление в существующий МАТ-файл.
Возможно использование слова save и в формате функции, а не команды, например:
save ('fname', 'varT . 'var2')
В этом случае имена файлов и переменных задаются строковыми константами.
Следует отметить, что возможности сохранения всего текста сессии, формируемой в командном режиме, команда save не дает. И не случайно! Дело в том, что сессия является результатом проб и ошибок, и ее текст наряду с правильными определениями содержит сообщения об ошибках, переопределения функций и переменных и много прочей «шелухи». Необходимости сохранять такое «творчество» обычно нет. А если есть — для этого служит команда diary, описанная чуть ниже.
Тем не менее это не значит, что вы не имеете возможности записать только то рациональное зерно, которое родилось в ходе попыток реализации ваших алгоритмов и методов решения задач. Надо просто воспользоваться редактором и отладчиком, которые позволяют (после отладки программы) получить документ в корректной форме без синтаксических и иных ошибок. Такой документ сохраняется в текстовом формате в виде файла с расширением .m.
24. Ведение дневника
Ведение дневника
Мы отмечали, что сессии не записываются на диск стандартной командой save. Однако если такая необходимость есть, можно воспользоваться специальной командой для ведения так называемого дневника сессии:
-
diary filename — ведет запись на диск всех команд в строках ввода и полученных результатов в виде текстового файла с указанным именем;
-
diary off — приостанавливает запись в файл;
-
diary on — вновь начинает запись в файл.
Таким образом, чередуя команды diary off и diary on, можно сохранять нужные фрагменты сессии в их формальном виде. Команду diary можно задать и в виде функции diary('file'), где строка 'file' задает имя файла. Следующий пример поясняет технику применения команды diary:
» diary myfile.m
» 1+2
ans =
3
» diary off
» 2+3
ans =
5
» diary on
» sin(l)
ans =
0.8415
» diary off
Нетрудно заметить, что в данном примере первая операция — 1+2=3 — будет записана в файл myfile.m, вторая — 2+3=5 — не будет записана, третья операция — sin(1)=0.8415 — снова будет записана. Таким образом, будет создан файл сценария (Script-файл) следующего вида:
1+2
ans =
3
diary off sin(1)
ans =
0.8415
diary off
Он приведен в том виде, как записан, т. е. с пробелами между строк. Одна из распространенных ошибок начинающих пользователей — попытка запустить подобный файл в командной строке указанием его имени:
» myfile
??? ans =
|
Missing variable or function.
Error in ==> С:\MATLAB\bin\niyfile.m
On line 3 --> ans =
Обычно это приводит к ошибкам, так как данный файл — это просто текстовая запись команд и результатов их выполнения, не проверяемая на корректность и содержащая ряд строк, ошибочных с позиций синтаксиса языка программирования MATLAB — например, выражения ans =. Зато команда type позволяет просмотреть текст такого файла со всеми записанными действиями:
» type myfile
1+2
ans=
3
diary off.
ans=
0.8415
diary off
Во избежание отмеченных казусов рекомендуется записывать файл с расширением, отличным от .m, например .txt. Это позволит встраивать подобные текстовые файлы дневника сессии в документы, содержащие ее описание.
25. Загрузка рабочей области сессии
Загрузка рабочей области сессии
Для загрузки рабочей области ранее проведенной сессии (если она была сохранена) можно использовать команду load:
-
load fname ... — загрузка ранее сохраненных в файле fname.mat определений со спецификациями на месте многоточия, подобными описанным для команды save (включая ключ -mat для загрузки файлов с расширением .mat обычного бинарного формата, используемого по умолчанию);
-
1oad( 'fname'....) — загрузка файла fname.mat в форме функции.
Если команда (или функция) load используется в ходе проведения сессии, то произойдет замена текущих значений переменных теми значениями, которые были сохранены в считываемом МАТ-файле.
Для задания имен загружаемых файлов может использоваться знак *, означающий загрузку всех файлов с определенными признаками. Например, load demo*.mat означает загрузку всех файлов с началом имени demo, например demol, demo2, demoa, demob и т. д. Имена загружаемых файлов можно формировать с помощью операций над строковыми выражениями.
26. Завершение вычислений и работы с системой
Завершение вычислений и работы с системой
Иногда из-за ошибок в программе или из-за сложности решаемой задачи MATLAB «зацикливается» и перестает выдавать результаты либо непрерывно выдает их, хотя в этом уже нет необходимости. Для прерывания вычислений в этом случае достаточно нажать одновременно клавиши Ctrl и С (латинское).
27. Завершение работы с системой
Завершение работы с системой
Для завершения работы с системой можно использовать команды exit, quit (которые сохраняют содержимое рабочей области и выполняет другие действия в соот ветствии с файлом сценария finish.m) или комбинацию клавиш Ctrl+Q. Если необходимо сохранить значения всех переменных (векторов, матриц) системы, то перед вводом команды exit следует дать команду save нужной формы. Команда load после загрузки системы считывает значения этих переменных и позволяет начать работу с системой с того момента, когда она была прервана.
На этом мы закончим начальную экскурсию в технику матричных вычислений системы MATLAB. Мы расширим представления о ней в последующих уроках.
28. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Устанавливать и запускать систему MATLAB.
-
Редактировать документы и управлять их окном.
-
Выполнять простые расчеты.
-
Работать с числами, константами и переменными разного типа.
-
Задавать текстовые комментарии.
-
Использовать наиболее распространенные операторы и функции.
-
Распознавать сообщения об ошибках и предупреждения.
-
Задавать разные форматы чисел.
-
Осуществлять простые операции с матрицами.
-
Вести дневник сессии.
-
Дефрагментировать, сохранять и загружать рабочую область.
-
Завершать работу с системой.
Урок 3. Основы графической визуализации вычислений
1. Урок 3. Основы графической визуализации вычислений
Урок №3.
Основы графической визуализации вычислений
-
Особенности графики системы MATLAB
-
Построение графика функций одной переменной
-
Столбцовые диаграммы
-
Построение трехмерных графиков
-
Вращение графиков мышью
-
Контекстное меню графиков
-
Управление форматом графиков
2. Особенности графики системы MATLAB
Особенности графики системы MATLAB
Начиная с версии MATLAB 4.0, впервые ориентированной на Windows, графические средства системы MATLAB были существенно улучшены. Основные отличительные черты графики в новой версии MATLAB 6:
-
существенно улучшенный интерфейс графических окон;
-
введение новой панели инструментов Camera для интерактивного изменения условий видимости объекта;
-
расширенные возможности форматирования графики;
-
возможность создания графики в отдельных окнах;
-
возможность вывода нескольких графических окон;
-
возможность перемещения окон по экрану и изменения их размеров;
-
возможность перемещения области графики внутри графического окна;
-
задание различных координатных систем и осей;
-
высокое качество графики;
-
широкие возможности использования цвета;
-
легкость установки графических признаков — атрибутов;
-
снятие ограничений на число цветов;
-
обилие параметров команд графики;
-
возможность получения естественно выглядящих трехмерных фигур и их сочетаний;
-
простота построения трехмерных графиков с их проекцией на плоскость;
-
возможность построения сечений трехмерных фигур и поверхностей плоскостями;
-
функциональная многоцветная и полутоновая окраска;
-
возможность имитации световых эффектов при освещении фигур точечным источником света;
-
возможность создания анимационной графики;
-
возможность создания объектов для типового интерфейса пользователя.
С понятием графики связано представление о графических объектах, имеющих определенные свойства. В большинстве случаев об объектах можно забыть, если только вы не занимаетесь объектно-ориентированным программированием задач графики. Связано это с тем, что большинство команд высокоуровневой графики, ориентированной на конечного пользователя, автоматически устанавливает свойства графических объектов и обеспечивает воспроизведение графики в нужных системе координат, палитре цветов, масштабе и т. д.
На более низком уровне решения задач используется ориентированная на программиста дескрипторная графика (Handle Graphics), при которой каждому графическому объекту в соответствие ставится особое описание — дескриптор, на который возможны ссылки при использовании графического объекта. Дескрипторная графика позволяет осуществлять визуальное программирование объектов пользовательского интерфейса — управляющих кнопок, текстовых панелей и т. д. Команды дескрипторной графики могут использоваться в высокоуровневой графике, например, для удаления осей, изменения цвета и т. д. в уже построенных графических объектах. Эти обширные возможности делают графику MATLAB одной из лучших среди графических подсистем систем компьютерной математики (СКМ).
Несмотря на обилие графических команд, их синтаксис достаточно прост и легко усваивается даже начинающими пользователями. Руководствуясь правилом описания «от простого к сложному», мы рассмотрим сначала графику функций одной переменной, а затем трехмерную графику, специальную, анимационную и, наконец, дескрипторную.
Хотя данная книга не предусматривает исчерпывающе полного описания всех команд графики системы MATLAB, большинство команд графики будет рассмотрено с примерами, которые можно считать дополнительными к тем, которые приведены в документации по системе.
3. Построение графика функций одной переменной
Построение графика функций одной переменной
В режиме непосредственных вычислений доступны практически все возможности системы. Широко используется, например, построение графиков различных функций, дающих наглядное представление об их поведении в широком диапазоне изменения аргумента. При этом графики строятся в отдельных масштабируемых и перемещаемых окнах.
Возьмем вначале простейший пример — построение графика синусоиды. Следует помнить, что MATLAB (как и другие СКМ) строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Зададим интервал изменения аргумента х от 0 до 10с шагом 0.1. Для построения графика достаточно вначале задать вектор х=0:0.1:10, а затем использовать команду построения графиков plot(sin(x)). Это показано на рис. 3.1.
Вектор х задает интервал изменения независимой переменной от 0 до 10 с шагом 0.1. Почему взят такой шаг, а не, скажем, 1? Дело в том, что plot строит не истинный график функции sin(x), а лишь заданное числом элементов вектора х число точек. Эти точки затем просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках полученная кривая глазом воспринимается как вполне плавная, но при 10-20 точках она будет выглядеть состоящей из отрезков прямых.
Графики MATLAB строит в отдельных окнах, называемых графическими окнами. С первого взгляда видны отличия графического окна, показанного на рис. 3.1, от командного окна MATLAB. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 3.1. Средства этой панели (мы их рассмотрим полнее в дальнейшем) позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.
Рис. 3.1. Пример построения графика синусоиды
1.gif
4. Построение в одном окне графиков нескольких функций
Построение в одном окне графиков нескольких функций
Более подробное описание графического окна будет дано в уроке 5. А пока пойдем дальше и попытаемся построить графики сразу трех функций: sin(x), cos(#) и sin (x)/х. Прежде всего отметим, что эти функции могут быть обозначены переменными, не имеющими явного указания аргумента в виде у(х):
»y1=sin(x); y2=cos(x); y3=sin(x)/x;
Такая возможность обусловлена тем, что эти переменные являются векторами — как и переменная х. Теперь можно использовать одну из ряда форм команды
plot: plot(a1.f1.a2.f2.a3.f3,...).
где al, а2, аЗ,.„ — векторы аргументов функций (в нашем случае все они — х), a f1, f2, f3,... —векторы значений функций, графики которых строятся в одном окне. В нашем случае для построения графиков указанных функций мы должны записать следующее:
» plot(x,y1,x,y2,x.y3)
Можно ожидать, что MATLAB в этом случае построит, как обычно, точки графиков этих функций и соединит их отрезками линий. Но, увы, если мы выполним эти команды, то никакого графика не получим вообще. Не исключен даже сбой Б работе программы. Причина этого казуса уже обсуждалась в предыдущем уроке — при вычислении функции y3=sin(x)/x, если х представляет собой массив (вектор), то нельзя использовать оператор матричного деления /.
Этот пример еще раз наглядно указывает на то, что чисто поверхностное применение даже такой мощной системы, как MATLAB, иногда приводит к досадным срывам. Чтобы все же получить график, надо вычислять отношение sin(x) к хс помощью оператора поэлементного деления массивов ./. Этот случай поясняет рис. 3.2.
Рис. 3.2. Построение графиков трех функций
Обратите внимание на то, что хотя на этот раз MATLAB построил графики всех трех функций, в окне командного режима появилось предупреждение о делении на 0 — в момент, когда х=0. Это говорит о том, что piot «не знает» о том, что неопределенность sin(x)/x=0/0 устранимая и дает 1. Это недостаток практически всех систем для численных вычислений.
2.gif
5. Графическая функция fplot
Графическая функция fplot
Разумеется, MATLAB имеет средства для построения графиков и таких функций, как sin(x)/x, которые имеют устранимые неопределенности. Не обсуждая эти средства подробно, просто покажем, как это делается, с помощью другой графической команды —
fplot: fplott'f(x)'. [xmin xmax])
Она позволяет строить функцию, заданную в символьном виде, в интервале изменения аргумента х от xmin до xmax без фиксированного шага изменения х. Один из вариантов ее применения демонстрирует рис. 3.3. Хотя в процессе вычислений предупреждение об ошибке (деление на 0) выводится, но график строится правильно, при х=0 sinx/x=l. Обратите также внимание на две используемые команды: clear (очистить)— очистка графического окна и grid on (сетка)— включение отображения сетки, которая строится пунктирными линиями.
Рис. 3.3. Построение графика sin(x)/x функцией fplot
На рис. 3.3 представлено также меню File (Файл) окна графики. Нетрудно заметить, что оно содержит типовые файловые операции. Однако они относятся не к файлам документов, а к файлам графиков. В частности, можно присваивать имя записываемым на диск рисункам с графиками.
Позже мы более подробно рассмотрим возможности различных графических команд. В частности, покажем, как можно задавать определенный цвет и стиль линий, как менять вывод координатных осей, наносить на графики различные текстовые надписи и выполнять множество иных операций форматирования графиков для придания им более наглядного вида, соответствующего требованиям пользователя. Мы также обсудим множество новых форм применения графических команд, резко расширяющих их возможности построения графиков всех мыслимых типов.
3.gif
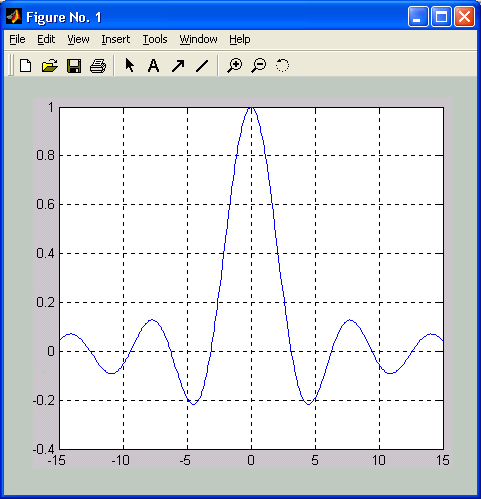
6. Столбцовые диаграммы
Столбцовые диаграммы
В прикладных расчетах часто встречаются графики, именуемые столбцовыми диаграммами, отражающие содержание некоторого вектора V. При этом каждый элемент вектора представляется столбцом, высота которого пропорциональна значению элемента. Столбцы нумеруются и масштабируются по отношению к максимальному значению наиболее высокого столбца. Выполняет построение такого графика команда bar(V) (рис. 3.4).
Столбцовые диаграммы — лишь один из многих типов графиков, которые может строить система MATLAB. Особенно часто столбцовые диаграммы используются при представлении данных финансово-экономических расчетов.
Рис. 3.4 дает также представление о меню Tools (Инструменты) окна графики, появившемся начиная с версии MATLAB 5.3.1 (выпуск 11.1). Нетрудно заметить, что кроме возможности вывода инструментальной панели здесь имеется целый ряд других команд, которые будут рассмотрены в дальнейшем. Это команды вывода свойств графических объектов, изменения масштаба графика, добавления осей и т. д.
Рис. 3.4. Построение столбцовой диаграммы значений элементов вектора
4.gif
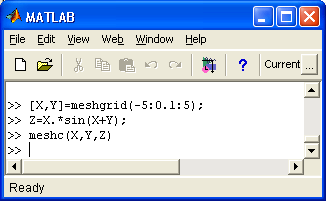
7. Построение трехмерных графиков
Построение трехмерных графиков
Столь же просто обеспечивается построение графиков сложных поверхностей. Надо только знать, какой командой реализуется тот или иной график. Например, для построения графика поверхности и ее проекции в виде контурного графика на плоскость под поверхностью достаточно использовать следующие команды (см. урок 6):
» [X.Y]=meshgrid(-5:0.1:5);
» Z=X.*sin(X+Y);
» meshc(X.Y,Z)
Окно с построенным графиком показано на рис. 3.5.
Рис. 3.5. Окно с графиками поверхности и ее проекции на плоскость под фигурой
Раньше пришлось бы убить много дней на составление и отладку нужной для построения такого графика программы. В MATLAB же можно в считанные секунды изменить задающую поверхность функцию Z(X, Y) и тут же получить новый график поверхности с окраской, в данном случае заданной вектором Z, и с ее проекцией на плоскость XY. На рис. 3.5 показано также открытое меню Help (Помощь) окна трехмерной графики.
Мы ограничимся этими примерами построения графиков как достаточно простыми и типовыми. Из них следует важный вывод — для решения той или иной частной задачи надо знать соответствующие команды и функции. В этом вам помогут как данная книга, так и справочная система MATLAB.
4a.gif
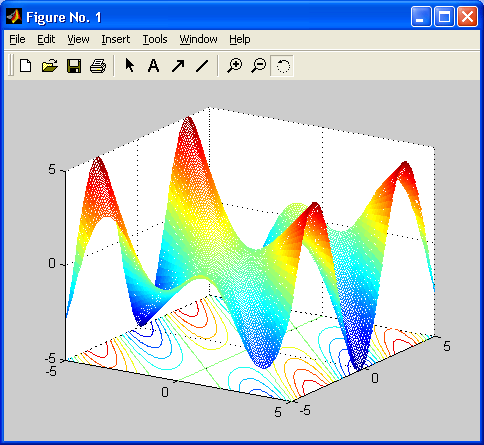
4b.gif
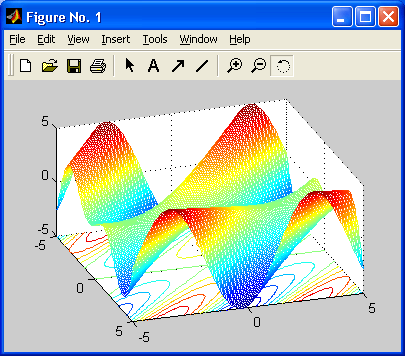
4c.gif
8. Вращение графиков мышью
Вращение графиков мышью
Можно поворачивать построенную фигуру мышью и наблюдать ее под разными углами. Рассмотрим эту возможность на примере построения логотипа системы MATLAB — мембраны. Для этого, введя команду membrane, получим исходный график, представленный на рис. 3.6.
Рис. 3.6. Построение мембраны — логотипа системы MATLAB
Для вращения графика достаточно активизировать последнюю справа кнопку панели инструментов с изображением пунктирной окружности со стрелкой. Теперь, введя курсор мыши в область графика и нажав левую кнопку мыши, можно круговыми движениями заставить график вращаться вместе с обрамляющим его параллелепипедом (рис. 3.7).
Любопытно, что в версии MATLAB 6 вращать можно и двумерные графики, наблюдая поворот плоскости, в которой они построены. Никакого программирования такое вращение не требует.
Рис. 3.7. Вращение трехмерной фигуры мышью
5.gif

6.gif
9. Контекстное меню графиков
Контекстное меню графиков
Для переключения в режим редактирования графика нужно щелкнуть на кнопке Edit Plot (Редактировать график) с изображением курсора-стрелки. В этом режиме графиком можно управлять с помощью контекстного меню, вызываемого щелчком правой кнопки мыши. Вид этого меню при курсоре, расположенном в области трехмерного графика вне построенных трехмерных графических объектов, показан на рис. 3.8. С помощью мыши можно также выделить график. Щелчок левой клавишей выводит рамку вокруг рисунка (см. рис. 3.8). Теперь на график можно наносить стрелки, поясняющие надписи (кнопка с буквой А) и т. д.
Рис. 3.8. График в состоянии редактирования и контекстное меню
7.gif

10. Основы форматирования двумерных графиков
Основы форматирования двумерных графиков
Графики в системе MATLAB строятся обманчиво просто. Связано это с тем, что многие свойства графиков установлены по умолчанию. К таким свойствам относятся вывод или скрытие координатных осей, положение их центра, цвет линии графика, ее толщина и т. д. и т. п. Позже будет показано, как свойства и вид графиков можно менять в широких пределах с помощью параметров команд графики. Однако этот путь требует хорошего знания деталей языка программирования и дескрипторной графики системы MATLAB.
В новой версии MATLAB 6 для изменения свойств графиков (их форматирования) используются принципы визуального контроля за стилем (видом) всех объектов графиков. Это позволяет легко, просто и наглядно придать графикам должный вид перед записью их в виде файлов на диск. Можно сказать, что в этой части реализованы отдельные принципы визуально-ориентированного программирования графических средств.
Здесь мы рассмотрим возможности форматирования графиков, которые, образно говоря, лежат на поверхности. Систематизированное описание интерфейса системы MATLAB 6.0, в том числе интерфейса графических окон, дается в уроке 5.
11. Форматирование линий графиков
Форматирование линий графиков
MATLAB имеет возможность легко настраивать и корректировать свойства графиков с помощью специальных средств. В новой версии MATLAB 6.0 они существенно изменены. Так, в предшествующей версии для настройки (форматирования) графиков использовался специальный редактор свойств — Graphics Properties Editor (Редактор свойств графики). Его можно было вызвать из меню File окна командного режима MATLAB с помощью команды Show Graphics Properties Editor (Показать редактор свойств графики).
В новой версии MATLAB форматирование графиков стало более строгим и удобным. При этом ранее упомянутый редактор свойств графиков перестал так именоваться, и команда Show Graphics Properties в новой версии отсутствует. Ее заменяют команды Figure Properties (свойства фигуры) и Axis Properties (свойства осей) со всеми необходимыми настройками.
При построении графиков появляется графическое окно. Иногда оно бывает скрыто ранее имеющимися окнами как системы MATLAB, так и других работающих в среде Windows 95/98/Me/2000/NT4 приложений. Если вы не увидели графика, заданного для построения, то поищите его в списке открытых окон (приложений), нажимая клавиши Alt + Tab, и выберите из списка нужное окно. Окна графики имеют изображение логотипа системы MATLAB. По умолчанию они выводятся с панелью инструментов с рядом кнопок вполне очевидного назначения.
Щелкнув на кнопке Edit Plot (Редактировать график) в панели инструментов окна графики и щелкнув по графику, можно заметить, что график выделился: вокруг него появилась рамка. Теперь, указав курсором мыши на тот или иной объект графика и щелкнув снова левой клавишей, можно наблюдать выделение объекта и появление окна его форматирования.
Например, указав в режиме редактирования мышью на линию графика (и дважды быстро щелкнув левой клавишей), можно увидеть окно форматирования линий графика, показанное на рис. 3.9 слева. Часть окна графики с выделенным графиком видна справа. Обратите внимание на появление на линии графика ряда черных квадратиков, — они используются для указания курсором мыши именно на линию графика, а не на другие объекты.
Рис. 3.9. Окно графика и окно форматирования линий
В этом окне открыта главная для операций форматирования вкладка — Style (Стиль). Она устанавливает стиль отображения линии, т. е. ее вид (например, сплошная линия или пунктирная), ширину и цвет, а также параметры маркеров, отмечающих опорные точки графиков.
Полезно знать, что кнопка Apply (Применить) позволяет применить сделанные установки к графику до закрытия окна диалога. Кнопка О К вводит сделанные установки и закрывает окно диалога. Назначение других кнопок очевидно.
8a.gif
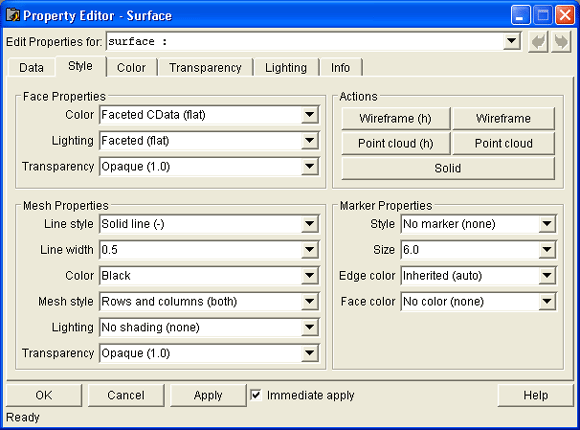
8b.gif
12. Форматирование маркеров опорных точек
Форматирование маркеров опорных точек
В нашем случае опорные точки задаются ранжированной переменной х, имеющей ряд значений от -15 до +15 с шагом 0.1. Эти точки появляются на графике, если в поле свойств маркера Marker Properties (Свойства маркера) из меню Style (Стиль) выбрать стиль маркера. На рис. 3.10, к примеру, показано построение графика с маркерами опорных точек в виде окружностей.
Рис. 3.10. Пример задания параметров маркеров и построения графика с ними
Можно задавать размеры маркеров, цвет их закраски и цвет окантовки. Так, на рис. 3.10 при его просмотре на экране цветного дисплея маркеры имеют вид окружностей с условным размером 4, цветом окантовки красным и цветом закраски желтым. Маркеры можно задавать в виде окружностей, прямоугольников, крестиков, ромбиков и т. д. Применение маркеров делает графики более наглядными.
9.gif
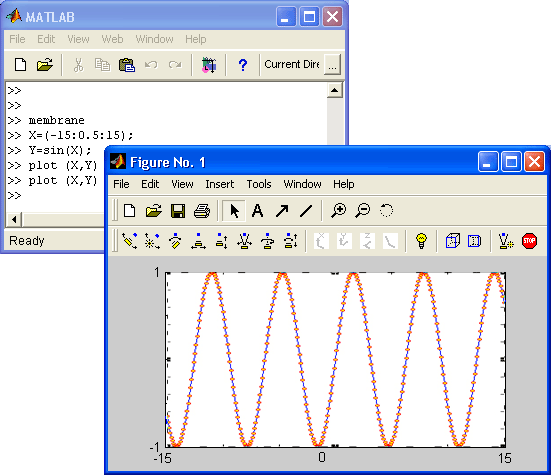
13. Форматирование линий и маркеров для графика нескольких функций
Форматирование линий и маркеров для графика нескольких функций
Если строится график нескольких функций, то можно форматировать линии и маркеры каждой кривой отдельно. Выполним следующие команды:
» х=-6:.1:6;
» plot(x,sin(x),x,sin(x). ^ 3,x,sin(x).^5):
Рис. 3.11 показывает пример такого форматирования для графика, полученного исполнением этих команд.
Кстати, обратите внимание на то, как заданы степени синуса. Записать эти выражения в виде sin(x)^3 и cos(x)^5 будет грубейшей ошибкой, поскольку х здесь вектор. Операторы ^ в данном случае дают поэлементное возведение в степень, что и нужно для построения графиков этих функций.
Рис. 3.11. Пример форматирования для графика трех функций
10a.gif
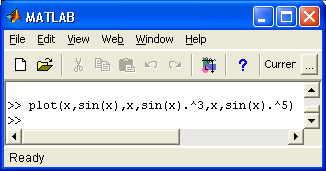
10b.gif
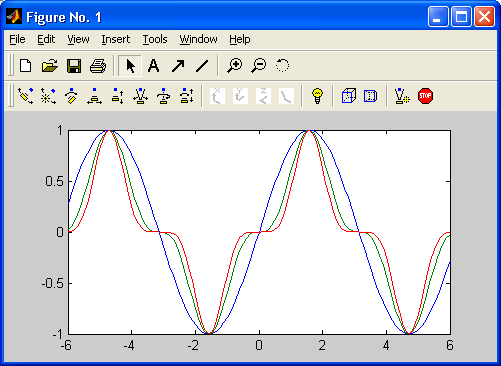
14. Форматирование осей графиков
Форматирование осей графиков
Аналогично описанным выше правилам выполняется форматирование и других объектов графиков. Например, указав курсором мыши на оси графиков (на них тоже есть метки в виде черных квадратиков) и дважды щелкнув левой клавишей мыши, можно увидеть появление окна форматирования объектов дескрипторной графики Property Editor (Редактор свойств, Графический редактор свойств) (рис. 3.12), настроенного на форматирование осей.
Рис. 3.12. Пример форматирования осей графика
Окно графического редактора свойств дескрипторной графики имеет множество вкладок, настройки которых довольно очевидны, и ничто не мешает читателю поэкспериментировать с ними несколько минут. Это позволит понять простоту и одновременно высокую эффективность средств форматирования объектов графики. Например, вы можете задать линейный или логарифмический масштаб осей (вкладка Scale (Масштаб), открытая на рис. 3.12), нормальное или инверсное направление осей ( X, У, а в случае трехмерных графиков и Z), показ сетки (параметр Grid Show), изменить стиль осей и цвета фона (вкладка Style (Стиль)), нанести у осей надписи (вкладка Label (Ярлык)) и пр.
Рис. 3.13 показывает график синусоиды после некоторых операций по форматированию осей. Здесь (кстати, как и на рис. 3.12) задано построение сетки Grid по осям X и Y, построение надписей (просто буквы X и Y) по координатным осям и построение титульной надписи. Заодно на рис. 3.13 показано в открытом виде меню расширенных инструментальных средств графического окна. Его команды подробно обсуждаются в уроке 5. Словом, с объектами графики можно сделать все, что угодно! Некоторые из возможностей форматирования объектов графики мы рассмотрим позже, по мере описания типов графиков.
Рис. 3.13. Пример построения графика синусоиды после форматирования осей
Если компьютер оснащен должным набором шрифтов, то надписи на графиках могут быть сделаны на русском языке — рис. 3.13 хорошо иллюстрирует эту важную для наших пользователей возможность. На нем титульная надпись сделана на русском языке. Средства форматирования надписей дают обширные возможности по выбору набора шрифтов, их стиля, размеров символов и их цвета.
11a.gif

11b.gif
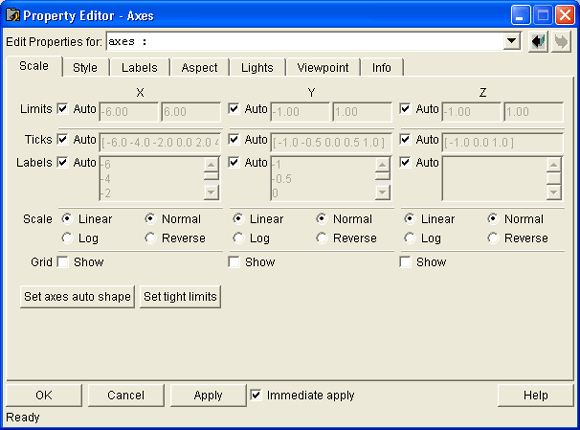
12a.gif
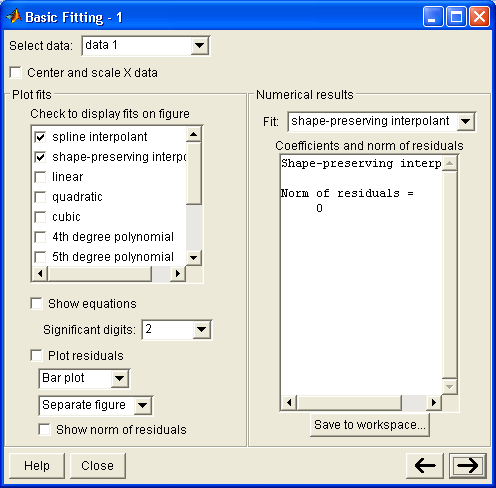
12b.gif
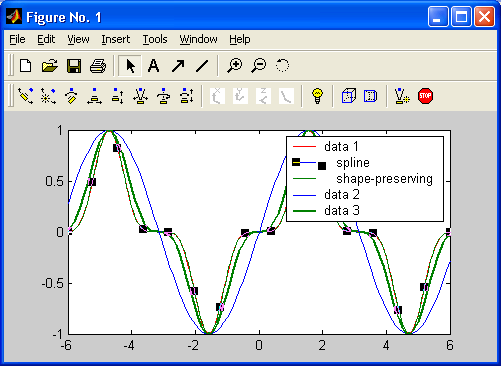
15. Нанесение надписей и стрелок прямо на график
Нанесение надписей и стрелок прямо на график
Дополнительно на график можно нанести надписи с помощью кнопки панели инструментов с буквой А. Место надписи фиксируется щелчком мыши. На рис. 3.14 показан отформатированный график с текстовым блоком, созданным таким образом в левой верхней части поля графика.
Здесь показано контекстное меню правой клавиши мыши, поясняющее выбор размера символов надписи (и другие возможности этого меню). Напоминаем, что это меню появляется при щелчке правой кнопки мыши на заданном объекте. В этом меню имеются все команды, доступные для данного объекта в данной ситуации.
Рис. 3.14. Нанесение надписи на отформатированный график
Полученную таким образом надпись можно выделить и перенести мышью в любое другое место. Рис. 3.15 показывает процесс создания еще двух надписей с переносом их текстового блока в нужное место. Надписи сделаны с разным размером символов и разным стилем. Особенно приятно, что при задании на надписи возведения в степень знаком ^ надпись на экране отображается в естественном математическом виде (степень в виде верхнего индекса).
Рис. 3.15. Окончательно отформатированный график трех функций
На рис. 3.15, в частности, показано задание надписей разным стилем, а также задание стрелки с помощью соответствующей кнопки панели инструментов. Это стрелку в режиме редактирования графика можно перемещать и вращать мышью, а также менять ее длину. Можно также наносить на график и обычные линии (без стрелки).
13.gif
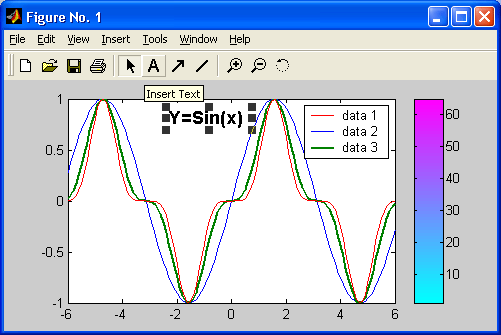
14.gif

16. Построение легенды и шкалы цветов на графике
Построение легенды и шкалы цветов на графике
Дополнительно можно изменить размеры графика (см. меню Tools (Инструменты) и его команды Zoom In (Увеличить)и Zoom Out (Уменьшить)), начать поворот графика мышью (команда Rotate 3D), добавить отрезок прямой или иной графический примитив (подменю Add) и подключить к графику легенду — пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него. Поскольку наш график содержит три кривые, то легенда представляет собой обозначение этих трех линий в правом верхнем углу рисунка (рис. 3.16). Каждая линия имеет тот же цвет, что и на графике (и тот же стиль).
Рис. 3.16. Окончательно сформированный график
Следует еще раз отметить, что все описанные возможности форматирования графиков доступны и программным способом, путем задания соответствующих графических команд, параметров и примитивов. Например команда text(х,у, 'legend') позволяет задать надпись 'legend' с началом, имеющим координаты (х, у). Если после первого апострофа перед текстом поместить параметр \leftarrow, то надпись (легенда) появится после стрелки с острием, обращенным влево. Аналогично параметр \rightarrow после надписи задает вывод стрелки после надписи с острием, обращенным вправо. Эта возможность позволяет помечать не только кривые, но и отдельные точки на них. Возможно также применение команды legend('s1', 's2',...), выводящей легенду обычного вида — отрезки линий графиков с поясняющими надписями 's1', 's2' и т.д.
15.gif
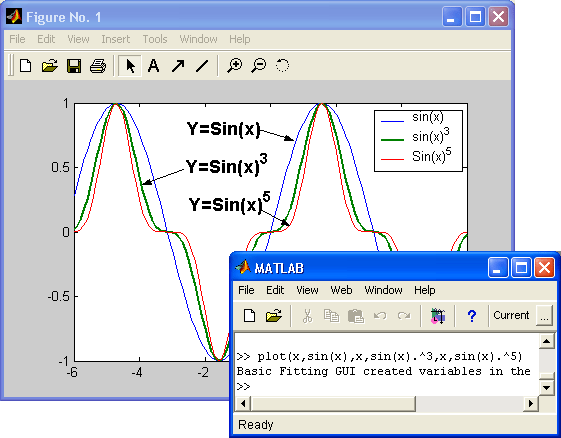
17. Перемещение графика в графическом окне
Перемещение графика в графическом окне
Обычно график занимает фиксированное положение в центре графического окна. Однако в режиме редактирования графиков, когда курсор мыши находится в области графика, в контекстном меню правой клавиши мыши есть команда Unlock Axes Position (Отключить позиционирование осей). Она снимает фиксацию положения координатных осей графика и позволяет двигать его мышью вместе с осями. Это иллюстрирует рис. 3.17.
Рис. 3.17. Пример перемещения графика
Интересно, что при перемещении графика его легенда и цветовая диаграмма остаются на прежнем месте.
16.gif
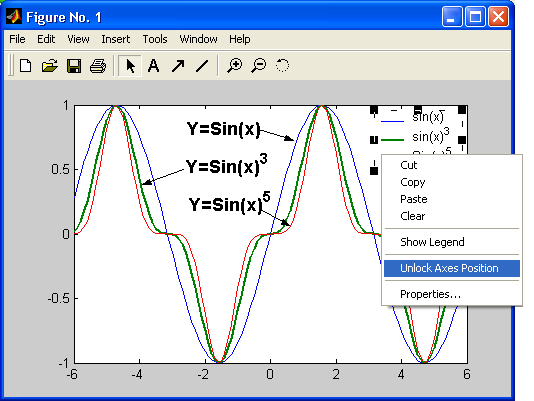
18. Применение графической "лупы"
Применение графической «лупы»
На панели инструментов есть кнопки с изображение лупы и знаками + и -. С их помощью выполняются команды Zoom In (+)(Увеличить) и Zoom Out (-) (Уменьшить). Это позволяет увеличивать или уменьшать масштаб просмотра изображения. При этом команда Zoom In интересна еще одной возможностью — с ее помощью можно выделять часть графика перемещением мыши с нажатой левой клавишей — рис. 3.18.
Рис. 3.18. Пример выделения части графика
Рис. 3.19. Пример просмотра части графика
Область выделения отмечается прямоугольником из тонких точечных линий. Отпустив левую клавишу мыши, можно наблюдать построение выделенной части графика на всем окне — рис. 3.19. С помощью команды Zoom Out можно восстановить график в прежнем масштабе. Таким образом реализуется графическая «лупа».
17.gif
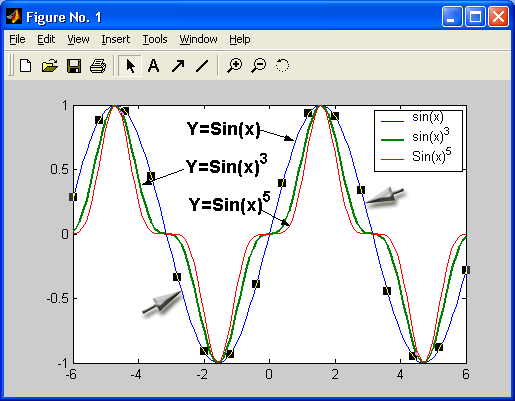
17b.gif
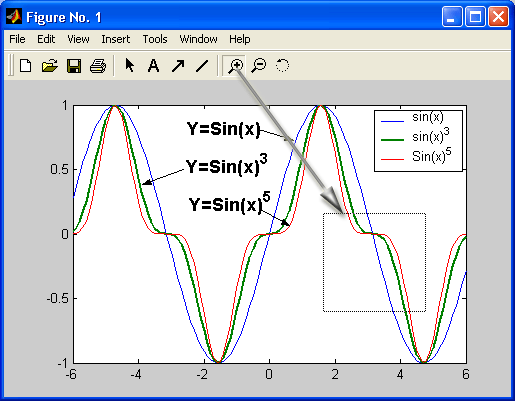
18.gif

19. Работа с камерой ЗD-графики
Работа с камерой 3D-графики
В отличие от двумерных (2D) графиков форматирование трехмерных графиков содержит ряд дополнительных возможностей. Покажем их на простом примере построения 3D-графики с помощью следующих простых команд:
» Z=peaks(40):
» mesh(Z);
Рис. 3.20. Пример построения каркасного 3D-графика
Здесь первая команда создает массив точек поверхности с помощью одного из ряда встроенных в ядро системы MATLAB готовых описаний таких поверхностей.
Рис. 3.21. Пример форматирования трехмерного графика
Вторая команда просто строит эту поверхность по опорным точкам с использованием интерполяции для промежуточных точек. Таким образом создается цветная каркасная поверхность, как бы сотканная из разноцветных проволок. На рис. 3.20 показано построение этой поверхности вместе со специальной панелью инструментов трехмерной графики, названной в оригинале Camera (Камера).
Несмотря на множество кнопок, пользование панелью инструментов 3D-графики достаточно просто, если представить себе, что вы смотрите на предмет через объектив фотокамеры. Наглядные рисунки на кнопках поясняют смысл их действия — это перемещение и вращение 3D-рисунков относительно тех или иных координатных осей, включение отображения перспективы, изменение цветовой схемы и др.
Рис.. 3.22 . Cтоп кадр вращения трехмерного графика
Рис. 3.21 показывает, что приемы форматирования двумерной графики можно использовать при работе с трехмерной графикой — вывод надписи на график, вывод легенды (кстати, теперь объемной) и шкалы цветов.
Для управления положением и вращением трехмерного графика можно использовать клавиши перемещения курсора. Эффект вращения графика иллюстрирует рис. 3.22, где показан график рис. 3.21 после его поворота при нажатой клавише —>. В отличие от поворота мышью (также возможного) перемещение и повороты с помощью клавиш курсора при выбранном типе перемещения дают плавное перемещение или вращение фигуры. Таким образом осуществляется анимация (оживление) трехмерной графики.
19.gif
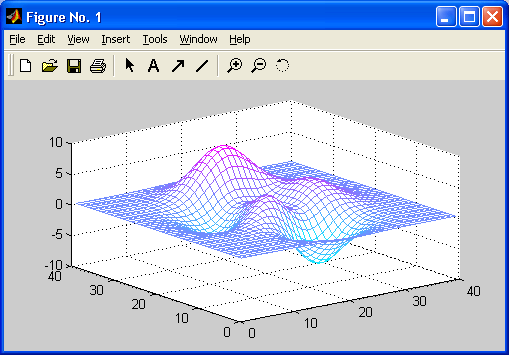
20.gif
21.gif
22.gif
20. Заключительные замечания по графике
Заключительные замечания по графике
Итак, мы рассмотрели основные приемы форматирования графиков, в основном используя средства панели инструментов и отдельные, достаточно очевидные, команды из меню графического окна. Более подробно интерфейс пользователя графического окна будет описан в уроке 5.
Хотя многие приемы форматирования графики заимствованы из технологии визуально-ориентированного программирования, в базовой системе MATLAB (без дополнительных пакетов расширения (toolbox)) все еще отсутствует полноценная возможность такого программирования, даже с учетом расширенных возможностей дескрипторной графики. Это видно уже из того, что вносимые форматированием изменения в графиках не сопровождаются генерацией программных кодов, которые в последующем при их вызове с новыми параметрами порождали бы построение графиков с новыми параметрами. Пользователь может лишь записать на диск копии созданных графиков в формате растрового изображения (.bmp) и использовать их в целях иллюстрации своих материалов.
Однако средства MATLAB позволяют опытным программистам создать расширения системы с визуально-ориентированной технологией программирования. Самым наглядным примером этого является система моделирования динамических объектов Simulink с набором моделей из готовых блоков. При этом автоматически создается не только сложная графическая блок-схема моделируемого устройства, но и система уравнений состояния, решение которой и является основой моделирования.
21. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Строить графики функций одной переменной.
-
Строить столбцовые диаграммы.
-
Строить трехмерные графики.
-
Вращать графики мышью.
-
Использовать контекстное меню графиков.
-
Управлять форматом графиков.
Урок 4. Работа со справкой и примерами
1. Урок 4. Работа со справкой и примерами
Урок №4.
Работа со справкой и примерами
-
Работа с интерактивной справкой
-
Справка по объекту, группе объектов, ключевым словам
-
Просмотр текстов примеров и m-файлов
-
Работа со справочной системой
-
Просмотр документации в формате PDF
-
Демонстрационные примеры
-
Запуск приложения Simulink
2. Интерактивная справка из командной строки
Интерактивная справка из командной строки
Вызов списка разделов интерактивной справки
MATLAB имеет интерактивную систему помощи, которая реализуется в командном режиме с помощью ряда команд. Одной из них является команда
» help
которая выводит весь список папок, содержащих m-файлы с определениями операторов, функций и иных объектов, присущих конкретной реализации системы MATLAB. Ниже приводится этот список для системы MATLAB 6.0:
|
|
HELP topics: |
|
|
|
matlab\general |
- General purpose commands. |
|
|
matlab\ops |
- Operators and special characters. |
|
|
matlab\lang |
- Programming language constructs. |
|
|
matlab\elmat |
- Elementary matrices and matrix manipulation. |
|
|
matlab\elfun |
- Elementary math functions. |
|
|
matlab\specfun |
- Specialized math functions. |
|
|
matlab\matfun |
- Matrix functions - numerical linear algebra. |
|
|
matlab\datafun |
- Data analysis and Fourier transforms. |
|
|
matlab\audio |
- Audio support. |
|
|
matlab\polyfun |
- Interpolation and polynomials. |
|
|
matlab\funfun |
- Function functions and ODE solvers. |
|
|
matlab\sparfun |
- Sparse matrices. |
|
|
matlab\graph2d |
- Two dimensional graphs. |
|
|
matlab\graph3d |
- Three dimensional graphs. |
|
|
matlab\specgraph |
- Specialized graphs. |
|
|
matlab\graphics |
- Handle Graphics. |
|
|
matlab\uitools |
- Graphical user interface tools. |
|
|
matlab\strfun |
- Character strings. |
|
|
matlab\iofun |
- File input/output. |
|
|
matlab\timefun |
- Time and dates. |
|
|
matlab\datatypes |
- Data types and structures. |
|
|
matlab\verctrl |
- Version control . |
|
|
matlab\winfun |
- Windows Operating System Interface Files (DDE/ActiveX) |
|
|
matlab\demos |
- Examples and demonstrations. |
|
|
tool box\ local |
- Preferences . |
|
|
simulink\simulink |
- Simulink |
|
|
simulink\blocks |
- Simulink block library. |
|
|
simulink\simdemos |
- Simulink 4 demonstrations and samples. |
|
|
simdemos\aerospace |
- Simulink: Aerospace model demonstrations and samples. |
|
|
simdemos\automoti ve |
- Simulink: Automotive model demonstrations and samples. |
|
|
||
|
|
s1mdemos\simfeatures - Simulink: Feature demonstrations and samples. |
|
|
|
simdemos\simgeneral |
- Simulink: General model demonstrations and samples. |
|
|
simdemos\simnew |
- Simulink: New features model demonstrations and samples. |
|
|
simulink\dee |
- Differential Equation Editor |
|
|
stateflow\statef1ow |
- Statef low |
|
|
stateflow\sfdemos |
- Statef low demonstrations and samples. |
|
|
statef low\ coder |
- Statef low Coder |
|
|
rtw\rtw |
- Real -Time Workshop |
|
|
rtw\rtwdemos |
- Real -Time Workshop Demonstrations: |
|
|
asap2\asap2 |
- (No table of contents file) |
|
|
asap2\user |
- (No table of contents file) |
|
|
cdma \cdma |
- CDMA Reference Blockset. |
|
|
cdma \cdmamasks |
- CDMA Reference Blockset mask 'helper functions. |
|
|
cdma \cdmamex |
- CDMA Reference Blockset S-Functions. |
|
|
cdma\cdmademos |
- CDMA Reference Blockset demonstrations and examples. |
|
|
commbl ks\commblks |
- Communications Blockset. |
|
|
commbl ks\commmasks |
- Communications Blockset mask helper functions. |
|
|
commbl ks\commmex |
- Communications Blockset S-functions. |
|
|
commbl ks\commbl ksdemos |
- Communications Blockset Demos. |
|
|
commbl ks\commbl ksobsol ete |
- Archived Simulink Files from Communications ToolboxVersion 1.5. |
|
|
||
|
|
comm\comm |
- Communications Toolbox. |
|
|
comm\commdemos |
- Communications Toolbox Demonstrations. |
|
|
comm\commobsolete |
- Archived MATLAB Files from Communications Toolbox Version 1.5. |
|
|
||
|
|
control \control |
- Control System Toolbox. |
|
|
control \ctrlguis |
- Control System Toolbox -- GUI support functions. |
|
|
control \ctrl obsolete |
- Control System Toolbox -- obsolete commands. |
|
|
control \ctrlutll |
- (No table of contents file) |
|
|
control \ctrl demos |
- Control System Toolbox -- Demos. |
|
|
dspblks\dspblks |
- DSP Blockset. |
|
|
dspblks\dspmasks |
- DSP Blocks'et mask helper functions. |
|
|
dspblks\dspmex |
- DSP Blockset S-Function MEX-files. |
|
|
dspblks\dspdemos |
- DSP Blockset demonstrations and examples. |
|
|
dsprtw\ut11_c |
- (No table of contents file) |
|
|
daq\daq |
- Data Acquisition Toolbox. |
|
|
daq\daqdemos |
- Data Acquisition Toolbox - Data Acquisition Demos. |
|
|
database\database |
- Database Toolbox. |
|
|
database\dbdemos |
Database Toolbox Demonstration Functions. |
|
|
database\vqb |
- Visual Query Builder functions. |
|
|
datafeed\datafeed |
- Datafeed Toolbox. |
|
|
datafeed\dfgui |
Datafeed Toolbox Graphical User Interface |
|
|
toolbox\dlals |
- Dials & Gauges Blockset |
|
|
tool box\exl Ink |
- (No table of contents file) |
|
|
fil terdesl gn\ filterdesi gn |
- Filter Design Toolbox. |
|
|
filterdesi gn\quantl zati on |
- (No table of contents file) |
|
|
fi1terdesi gn\ filtdesdemos |
- Filter Design Toolbox Demonstrations. |
|
|
finderiv\finderiv |
- Financial Derivatives Toolbox. |
|
|
ftseries\ftseries |
- Financial Time Series Toolbox |
|
|
ftseries\ftsdemos |
- (No table of contents file) |
|
|
ftseries\ftsdata |
- (No table of contents file) |
|
|
ftseries\ftstutorials |
- (No table of contents file) |
|
|
finance\ finance |
- Financial Toolbox. |
|
|
finance\calendar |
- Financial Toolbox calendar functions. |
|
|
finance\findemos |
- Financial Toolbox demonstration functions. |
|
|
finance\finsupport |
- (No table of contents file) |
|
|
|
|
|
|
|
|
|
|
|
toolbox\fixpo1nt |
- Fixed-Point Blockset |
|
|
|
fixpoint \fxpdemos |
- Fixed- Point Blockset Demos |
|
|
|
f1xpoint\obsolete |
- Obsolete Fixed-Point Blockset |
|
|
|
fuzzy\ fuzzy |
- Fuzzy Logic Toolbox. |
|
|
|
fuzzy \fuzdemos |
- Fuzzy Logic Toolbox Demos. |
|
|
|
garch\garch |
- GARCH Toolbox. |
|
|
|
garch\garchdemos |
- (No table of contents file) |
|
|
|
images\ images |
- Image Processing Toolbox. |
|
|
|
images\imdemos |
- Image Processing Toolbox --- demos and sample images |
|
|
|
instrument\ i nst rument |
- Instrument Control Toolbox. |
|
|
|
i nstrument\ Instrumentdemos |
- (No table of contents file) |
|
|
|
Imi\lmictrl |
- LMI Control Toolbox: Control Applications |
|
|
|
Imi\lmilab |
- LMI Control Toolbox |
|
|
|
toolbox\compiler |
- MATLAB Compiler |
|
|
|
toolbox\rptgen |
- , MATLAB Report Generator |
|
|
|
map\map |
- Mapping Toolbox |
|
|
|
map\mapdisp |
- Mapping Toolbox Map Definition and Display. |
|
|
|
map\mapproj |
- Mapping Toolbox Projections. |
|
|
|
mpc \mpccmds |
- Model Predictive Control Toolbox. |
|
|
|
mpc \mpcdemos |
- Model Predictive Control Toolbox |
|
|
|
motdsp\motdsp |
- Motorola DSP Developer's Kit |
|
|
|
motdsp\motdspmex |
- Motorola DSP Developers Kit |
|
|
|
motdspasm\bin |
- (No table of contents file) |
|
|
|
motdsp\motdspblks |
- Motorola DSP Developers Kit block libraries |
|
|
|
motdsp\motdspmasks |
- Motorola DSP blockset mask helper functions. |
|
|
|
motdsp\motdspdemos |
- MOTDSP Toolbox demonstrations and examples: |
|
|
|
mutools\conmands |
- Mu-Analysis and Synthesis Toolbox. |
|
|
|
mutools\subs |
- Mu-Analysis and Synthesis Toolbox. |
|
|
|
nnet\nnet |
- Neural Network Toolbox. |
|
|
|
nnet\nnutlls |
- (No table of contents file) |
|
|
|
nnet\nncontrol |
- Neural Network Toolbox Control System Functions. |
|
|
|
nnet\nndemos |
- Neural Network Demonstrations. |
|
|
|
nnet\nnobsolete |
- (No table of contents file) |
|
|
|
toolbox\ncd |
- Nonlinear Control Design Blockset |
|
|
|
toolbox\optim |
- Optimization Toolbox. |
|
|
|
toolbox\pde |
- Partial Differential Equation Toolbox. |
|
|
|
powersys\powersys |
- Power System Blockset. |
|
|
|
powersys \ powerdemo |
- Power System Blockset Demos. |
|
|
|
rtw\ada |
- Real -Time Workshop Ada Coder |
|
|
|
targets\ecoder |
- Real -Time Workshop Embedded Coder |
|
|
|
toolbox\reqmgt |
- Requirements Management Interface. |
|
|
|
tool box\ robust |
- Robust Control Toolbox. |
|
|
|
toolbox\sb2sl |
- SB2SL (converts SystemBuild to Simulink) |
|
|
|
signal\signal |
- Signal Processing Toolbox. |
|
|
|
signal \fdatoolgui |
- Signal Processing Toolbox GUI. |
|
|
|
signal \sptoolgul |
- Signal Processing Toolbox GUI |
|
|
|
signal\sigdemos |
- Signal Processing Toolbox Demonstrations. |
|
|
|
rtw\accel |
- Simulink Accelerator |
|
|
|
simulink\mdldiff |
- Model Differencing for Simulink and Stateflow |
|
|
|
simulink\simcoverage |
- Simulink Model Coverage Tool |
|
|
|
toolbox\rptgenext |
- Simulink Report Generator |
|
|
|
toolbox\splines |
- Spline Toolbox. |
|
|
|
toolbox\stats |
- Statistics Toolbox. |
|
|
|
toolbox\symbolic |
- Symbolic Math Toolbox. |
|
|
|
ident\ident |
- System Identification Toolbox. |
|
|
|
ident\idobsolete |
- (No table of contents file) |
|
|
|
|
|
|
|
|
|
|
ident\idguis |
- (No table of contents file) |
|
ident\idutils |
- (No table of contents file) |
|
Ident\iddemos |
- (No table of contents file) |
|
ident\idhelp |
- (No table of contents file) |
|
wavelet\wavelet |
- Wavelet Toolbox. |
|
wavelet\wavedemo |
- Wavelet Toolbox Demonstrations. |
|
xpc\xpc |
- xPC Target |
|
build\xpcblocks |
- (No table of contents file) |
|
xpc\xpcdemos |
- xPC Target -- demos and sample script files. |
|
kernel \embedded |
- xPC Target Embedded Option |
|
MATLABR12\work |
- (No table of contents file) |
|
For more help on |
directory/topic, type "help topic". |
Этот внушительный список дает наглядное представление о пакетах прикладных программ - пакетах инструментов (пакетах расширений) (toolbox), увеличивающих возможности системы MATLAB и содержащих массу серьезных примеров применения системы.
Примечание
Следует отметить, что набор входящих в список средств зависит от набора пакетов расширения, которыми располагает версия системы MATLAB, заказанная или полученная конкретным пользователем. Этот набор может заметно отличаться от приведенного. Кроме того, в MATLAB 6.0 для доступа к пакетам расширения может потребоваться указание пути к их файлам на диске в панели браузера файловой системы.
3. Справка по конкретному объекту
Справка по конкретному объекту
Для получения справки по какому-либо конкретному объекту используются команды
» help имя
или
» doc имя
где имя — имя объекта, для которого требуется вывод справочной информации. Мы уже приводили пример помощи по разделу операторов ops. Ниже дается пример для функции вычисления гиперболического синуса, намеренно введенной с неверным указанием имени:
» help hsln hsin.m
not found.
Нетрудно заметить, что система помощи сообщает, что для функции с именем hsin соответствующий m-файл отсутствует. Введем имя верно:
» help slnh
SINH Hyperbolic sine.
SINH(X) Is the hyperbolic sine of the elements of X.
Overloaded methods
help sym/slnh.m
Теперь полученное сообщение содержит информацию о функции slnh. Хотя имена функций в MATLAB задаются малыми (строчными) буквами, в сообщениях справочной системы имена функций и команд выделяются большими (прописными) буквами. Этот не слишком удачный прием использован для выделения заголовка текста справки в виде имени функции. В данной книге мы отказались от такого приема, вводящего начинающих пользователей в заблуждение.
Аналогичным образом можно получить справку по константам и другим объектам языка MATLAB. Ниже дан пример обращения к справке о числе п:
» help pi
PI 3.1415926535897
PI= 4*atan(1) = imagdog(-l)) = 3.1415926535897
При всей примитивности справки help надо отметить ее высокую эффективность. Особенно популярна интерактивная справка у пользователей, привыкших к работе с языками программирования, которые используются в среде операционной системы MS-DOS. Справка doc имя выводит более полную информацию в окне помощи в формате HTML.
4. Справка по группе объектов
Справка по группе объектов
Пользователя системы MATLAB часто интересует набор функций, команд или иных понятий, относящихся к определенной группе объектов. Выше были указаны имена основных групп объектов системы MATLAB. Ниже дан пример вызова справки по группе объектов timefun:
» help timefun
Time and dates.
Current date and time.
|
|
||
|
|
Now - Current date and time as date number. |
|
|
|
Date - Current date as date string. |
|
|
|
clock - Current date and time as date vector. |
|
|
|
Basic functions. |
|
|
|
datenum - Serial date number. |
|
|
|
datestr - String representation of date. |
|
|
|
datevec - Date components. |
|
|
|
Date functions. |
|
|
|
calendar - Calendar. |
|
|
|
weekday - Day of week. |
|
|
|
eomday - End of month. |
|
|
|
datetick - Date formatted tick labels. |
|
|
|
Timing functions. |
|
|
|
cputime - CPU time in seconds. |
|
|
|
tic. toe - Stop watch timer. |
|
|
|
etime - Elapsed time. |
|
|
|
pause - Wait in seconds. |
|
|
|
После уточнения состава определенной группы объектов можно получить детальную справку по любому выбранному объекту. Как это делается, было описано выше.
5. Справка по ключевому слову
Справка по ключевому слову
Ввиду обилия в системе MATLAB m-функций, число которых около 800, важное значение имеет поиск m-функций по ключевым словам. Для этого служит команда
lookfor Ключевое слово
или
lookfor 'Ключевые слова'
В первом случае ищутся все m-файлы, в заголовках которых встречается заданное ключевое слово, и заголовки обнаруженных файлов выводятся на экран. Следует отметить, что широкий поиск по одному ключевому слову может подчас привести к выводу многих десятков определений и длится довольно долго.
Для уточнения и сокращения зоны поиска следует использовать вторую форму команды lookfor. Вот пример ее применения:
» lookfor 'inverse sin'
ASIN Inverse sine.
ASIN Symbolic inverse sine.
В данном случае для поиска использованы слова ' inverse sin', т. е. задан поиск арксинуса. Система поиска нашла только два вида арксинуса ASIN — обычного и в символьной форме. Число найденных определений зависит от того, с каким числом пакетов прикладных программ (пакетов расширений) поставляется версия системы MATLAB.
В следующей главе мы рассмотрим гораздо более эффектные средства справочной системы, ориентированные на работу в стиле приложений операционных систем Windows 95/98/Me/2000/NT4 с графическим пользовательским интерфейсом.
6. Дополнительные справочные команды
Дополнительные справочные команды
В командном режиме можно получить справочные данные с помощью ряда команд:
-
computer — выводит сообщение о типе компьютера, на котором установлена текущая версия MATLAB;
-
help script — выводит сообщение о назначении m-файлов сценариев (Script-файлов);
-
helрf unction — выводит сообщение о назначении и структуре m-файлов функций;
-
info — выводит информацию о фирме Math Works с указанием адресов электронной почты;
-
subscribe — позволяет создать файл с бланком регистрации;
-
ver — выводит информацию о версиях установленной системы MATLAB и ее компонентов;
-
version — выводит краткую информацию об установленной версии MATLAB,
-
version -Java — выводит информацию об установленной в составе MATLAB версии Ява (Java);
-
what — выводит имена файлов текущего каталога;
-
what name — выводит имена файлов каталога, заданного именем name;
-
whatsnew name — выводит на экран содержимое файлов readme заданного именем name класса для знакомства с последними изменениями в системе и в пакетах прикладных программ;
-
which name — выводит путь доступа к функции с данным именем.
Как правило, эти команды выводят довольно обширные сообщения. Ниже показаны примеры применения отдельных команд этой группы:
» computer
ans=
PCWIN
» version
ans =
6.0.0.88 (R12)
» ver
MATLAB Version 6.0.0.88 (R12) on PCWIN MATLAB License Number: 0
MATLAB Toolbox Version 6.0 (R12) 06-0ct-2000
Simulink Version 4.0 (R12) 16-Jun-2000
Stateflow Version 4.0 (R12) 04-0ct-2000
Приведенный выше сокращенный список пакетов расширения системы MAT-LAB 6.0 дает весьма ценную информацию об их версиях и датах выпуска. Он свидетельствует о весьма существенном обновлении не только базовой системы MATLAB, но и стандартных пакетов расширения (toolbox). Более полный список пакетов расширения дан в уроке 23. Рекомендуем приобрести издание [44] для работы с Simulink и издание [39] для работы с пакетами расширения. В дальнейшем мы рассмотрим и другие команды, которые могут быть отнесены к группе дополнительных справочных команд.
7. Примеры, вызываемые из командной строки
Примеры, вызываемые из командной строки
Вызов списка демонстрационных примеров
Одним из самых эффективных методов знакомства со сложными математическими системами является ознакомление со встроенными примерами их применения.
Система MATLAB содержит многие сотни таких примеров — практически по примеру на каждый оператор или функцию. Наиболее поучительные примеры можно найти в разделе demos, исполнив команду
» help demos
Ниже представлен выводимый этой командой список примеров:
» help demos
Examples and demonstrations.
Type 'demo' at the command line to browse more demos of
MATLAB. the Toolboxes, and SIMULINK.
MATLAB/Introduction.
Demo - Browse demos for MATLAB. Toolboxes, and SIMULINK.
MATLAB/Matrices.
Intro - Introduction to basic matrix operations in MATLAB.
Inverter - Demonstrate the inversion of a matrix.
Buckydem - Connectivity graph of the Buckminster Fuller geodesic dome.
Sparsity - Demonstrate effect of sparsity orderings.
|
|
||
|
|
Matmanip - Introduction to matrix manipulation. |
|
|
|
Eigmovie - Symmetric eigenvalue movie. |
|
|
|
Rrefmovie - Computation of Reduced Row Echelon Form. |
|
|
|
Delsqdemo - Finite difference Laplacian on various domains. |
|
|
|
Sepdemo - Separators for a finite element mesh. |
|
|
|
Airfoil - Display sparse matrix from NASA airfoil. |
|
|
|
Eigshow - Graphical demonstration of matrix eigenvalues. |
|
|
|
Svdshow - Graphical demonstration of matrix singular values. |
|
|
|
MATLAB/Numerics. |
|
|
|
Funfuns - Demonstrate functions that operate on other functions. |
|
|
|
Fitdemo - Nonlinear curve fit with simplex algorithm. |
|
|
|
Sunspots - FFT: the answer is 11.08, what .is the question? |
|
|
|
e2pi - 2D visual solutions: Which is greater. e~pi or pi x e? |
|
|
|
bench - MATLAB Benchmark. |
|
|
|
Fftdemo - Use of the fast finite Fourier transform. |
|
|
|
Census - Try to predict the US population in the year 2000. |
|
|
|
spline2d - Demonstrate GINPUT and SPLINE in two dimensions. |
|
|
|
Lotkademo - An example of ordinary differential equation solution. |
|
|
|
Quaddemo - Adaptive quadrature. |
|
|
|
Zerodemo - Zerofinding with fzero. |
|
|
|
Fplotdemo - Plot a function. |
|
|
|
Quake - Loma Prieta Earthquake. |
|
|
|
Qhulldemo - Tessellation and interpolation of scattered data. |
|
|
|
MATLAB/Visualization. |
|
|
|
graf2d - 2D Plots: Demonstrate XY plots in MATLAB. |
|
|
|
graf2d2 - 3D Plots: Demonstrate XYZ plots in MATLAB. |
|
|
|
Grafcplx - Demonstrate complex function plots in MATLAB. |
|
|
|
Lorenz - Plot the orbit around the Lorenz chaotic attractor. |
|
|
|
Imageext - Image colormaps: changing and rotating colormaps. |
|
|
|
Xpklein - Klein bottle demo. |
|
|
|
Vibes - Vibration movie: Vibrating L-shaped membrane. |
|
|
|
Xpsound - Visualizing sound: Demonstrate MATLAB 's sound capability. |
|
|
|
Imagederno - Demonstrate MATLAB 's image capability. |
|
|
|
Penny - Several views of the penny data. |
|
|
|
Earthmap - View Earth's topography. |
|
|
|
Xfourier - Graphic demo of Fourier series expansion. |
|
|
|
Colormenu - Select color map. |
|
|
|
Cplxdemo - Maps of functions of a complex variable. |
|
|
|
MATLAB/Language. |
|
|
|
Xplang - Introduction to the MATLAB language. |
|
|
|
Hndlgraf - Demonstrate Handle Graphics for line plots. |
|
|
|
grafSd - Demonstrate Handle Graphics for surface plots. |
|
|
|
Hndlaxis - Demonstrate Handle Graphics for axes. |
|
|
|
MATLAB/Differential equations. |
|
|
|
Odedemo - Demo for the MATLAB Differential Equation solvers. |
|
|
|
odeexamples - Browse the MATLAB ODE/DAE/BVP/PDE examples. |
|
|
|
MATLAB/ODEs |
|
|
|
Ballode - Demo of a bouncing ball. |
|
|
|
Brussode - Stiff problem modelling a chemical reaction (Brusselator). |
|
|
|
burgersode - Burger's equation solved using a moving mesh technique. |
|
|
|
femlode - Stiff problem with a time-dependent mass matrix. |
|
|
|
fem2ode - Stiff problem with a constant mass matrix. |
|
|
|
hblode - Stiff problem 1 of Hindmarsh and Byrne. |
|
|
|
Orbitode - Restricted three body problem. |
|
|
|
|
|
|
|
Rigidode - Euler equations of a rigid body without external forces. |
|
|
|
.Vdpode - Parameterizable van der Pol equation (stiff for large mu). |
|
|
|
MATLAB/DAEs |
|
|
|
hbldae - Stiff DAE from a conservation law. |
|
|
|
ampldae - Stiff OAE from an electrical circuit. |
|
|
|
MATLAB/BVPs |
|
|
|
Twobvp - BVP that has exactly two solutions. |
|
|
|
mat4bvp - Find the fourth eigenvalue of the Mathieu's equation. |
|
|
|
Shockbvp - The solution has a shock layer near x = 0. |
|
|
|
MATLAB/PDEs |
|
|
|
pdexl - Example 1 for PDEPE |
|
|
|
pdex2 - Example 2 for PDEPE |
|
|
|
pdex3 - Example 3 for POEPE |
|
|
|
pdex4 - Example 4 for PDEPE |
|
|
|
pdexS - Example 5 for PDEPE |
|
|
|
Extras/Gallery. |
|
|
|
Knot - Tube surrounding a three-dimensional knot. |
|
|
|
Quivdemo - Demonstrate the quiver function. |
|
|
|
kleinl - Construct a Klein bottle. |
|
|
|
Cruller - Construct cruller. |
|
|
|
tori4 - Hoops: Construct four linked tori. |
|
|
|
spharm2 - Construct spherical surface harmonic. |
|
|
|
Modes - Plot 12 modes of the L-shaped membrane. |
|
|
|
Logo - Display the MATLAB L-shaped membrane logo. |
|
|
|
Extras/Games. |
|
|
|
Fifteen - Sliding puzzle. |
|
|
|
Xpbombs - Minesweeper game. |
|
|
|
Life - Conway's Game of Life. |
|
|
|
Soma - Soma cube. |
|
|
|
Extras/Mi seel laneous . |
|
|
|
Truss - Animation of a bending bridge truss. |
|
|
|
Travel . - Traveling salesman problem. |
|
|
|
Spinner - Colorful lines spinning through space. |
|
|
|
Xpquad - Superquadrics plotting demonstration. |
|
|
|
Codec - Alphabet transposition coder/decoder. |
|
|
|
Xphide - Visual perception of objects in motion. |
|
|
|
Makevase - Generate and plot a surface of revolution. |
|
|
|
Wrldtrv - Great circle flight routes around the globe. |
|
|
|
Logospin - Movie of The MathWorks' logo spinning. |
|
|
|
Crulspin - Spinning cruller movie. |
|
|
|
Quatdemo - Quaternion rotation. |
|
|
|
Chaingui - Matrix chain multiplication optimization. |
|
|
|
General Demo/Helper functions. |
|
|
|
Cmdlnwin - Demo gateway routine for playing command line demos. |
|
|
|
Cmdlnbgn - Set up for command line demos. |
|
|
|
Cmdlnend - Clean up after command line demos. |
|
|
|
Finddemo - Find demos available for individual toolboxes. |
|
|
|
Helpfun - Utility function for displaying help text conveniently. |
|
|
|
Pltmat - Display a matrix in a figure window. |
|
|
|
MATLAB/Helper functions. |
|
|
|
Bucky - The graph of the Buckminster Fuller geodesic dome. |
|
|
|
Peaks - A sample function of two variables. |
|
|
|
|
|
Membrane - Generate MathWorks' logo.
See also SIMDEMOS
demos Is both a directory and a function.
DEMOS Demo list for the CDMA Reference Blockset.
Мы настоятельно рекомендуем пользователям системы MATLAB просмотреть с десяток примеров из интересующих их областей. Это займет от силы полчаса или даже меньше, но зато позволит оценить поистине неисчерпаемые возможности системы при решении сложных математических и физических задач, а также превосходные средства графической визуализации решений.
8. Пример - тест на быстродействие компьютера
Пример — тест на быстродействие компьютера
Большинство пользователей, включая автора данной книги, очень ревниво относится к вычислительной мощности своего компьютера. Поэтому в качестве первого демонстрационного примера возьмем тест на сравнительную оценку скорости работы — bench . Исполнив команду » bench можно наблюдать исполнение комплексного теста по оценке быстродействия компьютера при работе с MATLAB. Его итоги представляются в виде столбцовой диаграммы и таблицы, которые показаны на рис. 4.1.
Рис. 4.1 . Результаты тестирования компьютера на быстродеиствие
Увы, в тесте системы MATLAB 6.0 компьютер автора занял последнее место, хотя в тесте системы MATLAB 5.3.1 он занимал достаточно почетное место в середине списка. Однако это вовсе не говорит о снижении производительности данного конкретного компьютера в новой реализации MATLAB. На самом деле производительность даже немного возросла. Просто в новом примере изрядно морально постаревший за год компьютер автора сравнивается с более новыми компьютерами. Кстати, в этом тесте ПК автора переместился на куда более почетное шестое место сверху после замены процессора на Pentium III 600 и установки видеокарты с видеопамятью 32 Мбайта и поддержкой OpenGL.
Приведенные данные говорят о том, что вычислительная мощность современного персонального компьютера (теперь у автора компьютер с процессором Pentium III 600 МГц со 100-мегагерцовой шиной под управлением Windows 98) с системой MATLAB уже приближается к таковой для суперкомпьютеров недавнего прошлого. Новые суперкомпьютеры, разумеется, куда мощнее компьютера с процессором Pentium III и даже Pentium IV, но и для них MATLAB — одна из основных систем для выполнения математических расчетов.
1.gif
1a.gif
1b.gif
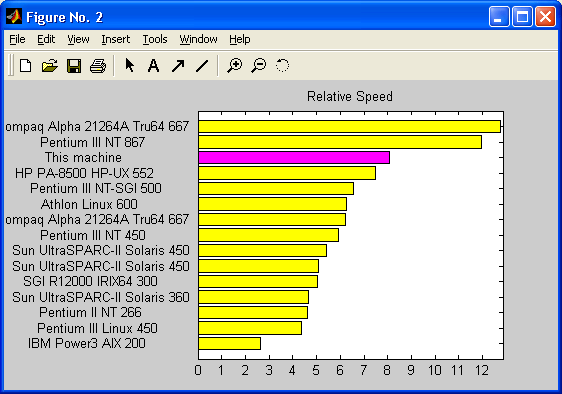
1c.gif

9. Что больше - e^pi или pi^?
Что больше — e ^ pi или pi ^ e?
Рассмотрим еще один простой пример, дающий ответ на сакраментальный вопрос о том, какое значение больше — e^pi или pi^e? Для запуска этого примера надо исполнить команду » e2pi и наблюдать красочное шоу — графики степенных функций х^у и у^х с построением на них линий заданных функций и оценкой их значений. Заключительный слайд этого примера показан на рис. 4.2.
Рис. 4.2. Заключительный слайд примера e2pi
Этот пример — наглядная демонстрация перехода от узких понятий к более широким. Разумеется, вы могли бы вместо приятного обозрения слайд-шоу просто вычислить соответствующие значения:
» e=exp(1)
e =
2.7183
» e ^ pi
ans =
23.1407
» pi^e
ans =
22.4592
Так можно легко убедиться в том, что все же е ^ рi больше, чем pi^e. Но тогда это означало бы, что вы просто технарь или физик-экспериментатор, а не истинный математик. Впрочем, у каждого есть свои взгляды на применение математики. И чьи лучше — вопрос весьма спорный.
2.gif
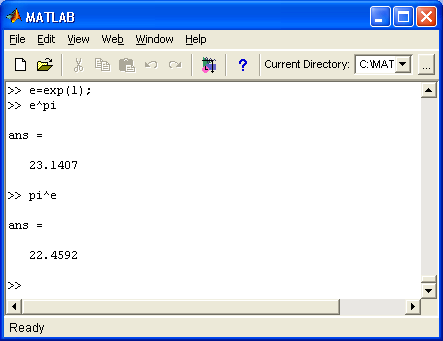
2a.gif
2c.gif
10. Анимация в пространстве - аттрактор Лоренца
Анимация в пространстве — аттрактор Лоренца
Современная трехмерная графика — одна из причин большой популярности системы MATLAB. В этом разделе мы не будем рассматривать конкретные реализации тех или иных видов трехмерной графики. Вы можете самостоятельно вывести на экран дисплея текст (листинг) любого файла примеров трехмерной графики с помощью команды type. Ограничимся лишь тремя примерами визуализации сложных математических задач, когда используется оживление изображений — анимация.
Рис. 4.3. График, иллюстрирующий работу аттрактора Лоренца
На рис. 4.3 показан пример визуализации динамического процесса в так называемом аттракторе Лоренца (пример lorenz) — колебательной системе, создающей хаотические и довольно замысловатые колебания. Наиболее наглядна их визуализация с помощью трехмерного фазового портрета колебаний, который приведен на рис. 4.3. К сожалению, на рис. 4.3 показана лишь завершающая стадия — на экране можно реально видеть движение образующей точки во времени и убедиться в своеобразной хаотичности колебаний. Для запуска анимации надо нажать кнопку Start (Пуск) окна графики.
3a.gif
3b.gif
11. Встроенные фигуры
Встроенные фигуры
MATLAB имеет ряд встроенных фигур, которые можно легко выводить на построение простым указанием их названия. Так, введя команду knot, можно задать построение сложной пространственной фигуры узла с функциональной окраской (рис. 4.4). При запуске этого примера нажатием кнопки Spinmap можно наблюдать изменение окраски, имитирующее как бы движение жидкости внутри замкнутой трубки, образующей данную фигуру.
Рис. 4.4. Построение фигуры-узла
Таким образом, можно сделать вывод о том, что для имитации и моделирования математических и физических задач система MATLAB предоставляет значительные графические возможности — от простейших графиков функций в декартовой системе координат до сложных анимационных графиков с динамической цветной функциональной окраской. Среди множества примеров такой графики всегда можно подобрать наиболее подходящие для решения конкретных задач пользователя, в какой бы области науки, техники или образования он ни работал.
4.gif
12. В паутине нейронных сетей
В паутине нейронных сетей
Даже десятка таких книг, как эта, едва ли хватит для исчерпывающего описания системы MATLAB со всеми ее пакетами расширения. Пакетам расширения посвящена монография [39]. Многие из таких пакетов, например по нейронным сетям, сплайнам, обработке сигналов, проектированию систем управления и т. д., относятся к самым современным и актуальным направлениям науки и техники. Нередко создание таких пакетов для системы MATLAB возглавили основатели указанных научных направлений, и по каждому такому направлению опубликованы десятки научных монографий.
Примером одного из таких направлений является пакет Neural Networks (нейронные сети). Эти сети основаны на аналогии с ячейкой нашего мозга — нейроном. Важное свойство нейрона — возможность к самообучению и распознаванию различных образных представлений и сигналов. В разделе справочной системы Examples and Demos (Примеры и демо) имеется множество конкретных примеров применения нейронных сетей. На рис. 4.5 показан вид демонстрационной панели одного из этих примеров.
Рис. 4.5. Демонстрационная панель примера на применение нейронных сетей
Вы имеете возможность задавать различные параметры нейронной сети, позволяющей распознать букву Т в ее искаженном изображении. Демонстрационная панель построена в виде виртуальной лаборатории и позволяет мышью менять вид образцов (вводя закрашенные квадратики) и оценивать погрешность и вероятность распознавания образа.
5.gif

13. Просмотр текстов примеров и m-файлов
Просмотр текстов примеров и m-файлов
Хотя наблюдение за тем, как MATLAB расправляется со сложными примерами и задачами, само по себе довольно поучительно, жаждущие применить систему на деле пользователи, безусловно, захотят узнать, а как же конкретно реализовано решение той или иной задачи? Для этого вам достаточно просмотреть соответствующий демонстрационный (или любой другой) m-файл. Это можно сделать с помощью любого текстового редактора, редактора и отладчика m-файлов, встроенного в систему, или с помощью команды
type Имя_М-файла
Ниже представлена часть файла демонстрационного примера e2pi:
» type e2pi
function slide=e2pi
% This is a slideshow file for use with playshow.m and makeshow.m
% To see it run. type 'piayshow e2pi',
% ' Copyright 1984-2000 The MathWorks. Inc.
% SRevision: 5.12 $
If nargout<1.
playshow e2pi
else
%========== Slide 1 ==========
slide(l).code={
'x=0:0.16:5;'.
'y=0:0.16:5;'.
'[xx,yy]=meshgrid(x,y);',
'zz=xx.*yy-yy.~xx:',
'h=surf(x.y,zz):'.
'set(h,"EdgeColor".[0.7 0.7 0.7]);',
'view(20.50);',
'colormap(hsv);.' };
slide(l).text={
' Press the "Start" button to see an example of visualization'
' in MATLAB applied to the question:',
' "which is greater, e A pi or pi^e?"'};
Используя команду help, можно получить справку по любой конкретной функции или команде. Ввиду того что текст примера имеет довольно большой объем, мы ограничились приведением только его фрагмента, относящегося к первому слайду. Остальные слайды просто опущены — на их месте стоит многоточие.
14. Справочная система MATLAB 6.0
Справочная система MATLAB 6.0
Основной доступ к справочной информации обеспечивает меню Help (Помощь). Оно открывает доступ к справочным системам MATLAB и к информации о производителе MATLAB. Меню. Help показано на рис. 4.6.
Рис. 4.6. Окно MATLAB 6.0 с открытым меню Help
Основные возможности справочной системы обсуждаются в следующих разделах. Поэтому здесь мы остановимся только на команде About MATLAB. Она выводит окно, содержащее информацию о системе. На рис. 4.7 это окно показано на фоне рабочего окна системы.

Рис. 4.7. Окно со сведениями о системе
В окне About MATLAB можно найти информацию о применяемой версии системы (в нашем случае это 6.0.0.88) и о дате ее создания (22 сентября 2000 г.). Номер лицензии ввиду его конфиденциальности опущен — точнее, заменен нулем.
6.gif
7.gif

15. Запуск справочной системы
Запуск справочной системы
Рис. 4.8. Основное окно справочной подсистемы
Для запуска справочной системы следует использовать одноименную команду Help меню MATLAB. При этом запустится браузер справочной системы (браузер помощи) и откроется ее окно, показанное на рис. 4.8.
Рис. 4.9. Один из документов справочной системы
Бросается в глаза, что справочная система новой версии MATLAB 6.0 существенно переработана даже внешне. Теперь она имеет вполне современный вид электронного документа. В левом окне расположены вкладки разделов справочной системы и дерево ее разделов, в правом — информация о текущем установленном разделе. От использования стандартного Интернет-браузера для вывода справочной информации в новой версии MATLAB отказались. Видимо, мода на всеобщее применение Интернет-браузеров начинает потихоньку отступать.
Каждый небольшой раздел справочной системы представлен в правом окне в виде гипертекстовой ссылки, активизация которой приводит к переходу на соответствующую HTML-страницу. На рис. 4.9 показан один из документов справочной системы, содержащий начальные данные по запуску расширения Simulink.
С помощью линейки прокрутки можно перемещаться по перечню документов справочной системы и выбирать различные темы справки. На рис. 4.10 представлена справка по разделу, посвященному созданию моделей для пакета расширения Simulink.
Несмотря на удобства справочной системы, надо отметить, что ее содержимое во многом дублирует другие справочные подсистемы MATLAB, например справки, вызываемые из командной строки и имеющиеся в виде PDF-файлов. В целом справочная система MATLAB превратилась в монстра — в версии MATLAB 6.0 только для PDF-файлов этой системы пришлось в ее поставку включить отдельный CD-ROM.
Рис. 4.10. Пример просмотра документа, посвященного созданию библиотек расширения Simulink
8.gif

9.gif

10.gif
16. Виды работы справочной системы
Виды работы справочной системы
Как видно из рис. 4.8, окно разделов справочной системы имеет четыре вкладки, соответствующие четырем видам работы справочной системы:
-
Contents (Содержание)— поиск информации по контексту (или попросту по обычному оглавлению с разделами справки);
-
Index (Индекс)— поиск информации по индексному (алфавитному) каталогу;
-
Search (Поиск)— поиск всех тем справки, в которые включена заданная для поиска фраза или отдельное слово;
-
Favorites — доступ к специальным возможностям справочной системы.
Эти виды работы могут применяться в зависимости от конкретных задач пользователя.
17. Работа с индексным каталогом
Работа с индексным каталогом
Мы уже привели пару примеров использования справочной системы по контексту. Теперь рассмотрим работу с индексным каталогом.
Будучи крупной математической системой, MATLAB имеет многие сотни функций, свойства которых запомнить трудно даже пользователю-профессионалу. Да и нужно ли? Справочная система MATLAB позволят найти информацию по нужной функции в считанные секунды.
Если вы знаете имя нужной вам функции, то проще всего воспользоваться индексным каталогом. Откройте в левом окне справки вкладку Index и в поле поиска (сверху) укажите имя нужной вам функции или хотя бы его начальную часть. Нажмите клавишу Enter и через секунду-другую вы получите список всех объектов, включающих заданное имя.
18. Поиск по всей справке
Поиск по всей справке
Еще один полезный вид работы со справочной системой — поиск по заданному слову или фразе. Он происходит почти аналогично ранее приведенному случаю, но при открытой вкладке Search (Поиск) в левом окне справочной системы.
При выдаче данных о функциях используется справочник по ним (Function Reference) и обеспечивается автоматический поиск нужной функции.
19. Новые функции системы MATLAB 6.0
Новые функции системы MATLAB 6.0
Разработчики систем компьютерной математики не очень охотно включают в их состав новые функции, поскольку это чревато несовместимостью новых версий систем с прежними версиями. Тем не менее на это приходится идти.
Какие новые функции включены в систему MATLAB 6.0? Для ответа на этот вопрос просто наберите в поле поиска вкладки Search (Поиск) слово Functions (Функции) в режиме Full Text (полнотекстового поиска). Вы сразу найдете раздел New Functions (Новые функции) в левом окне и, выделив его мышью, получите в правом окне перечень новых функций.
Новых функций в системе MATLAB 6.0 совсем немного — два десятка, и в основном это довольно специфические функции. Но эффективность и возможности старых функций значительно увеличены.
20. Поиск функций по имени
Поиск функций по имени
Если вас не интересует всякая «шелуха», которой сопровождается поиск по заданному слову или фразе (особенно полнотекстовый поиск Full Text), то вы можете перейти к поиску по имени функции — тип поиска Function Name. Это предусмотрено на вкладке Search (Поиск).
Нетрудно заметить, что на этот раз найден только главный раздел функции с именем sin. Остальные разделы отсеяны фильтрами справочной системы.
21. Просмотр документации в формате PDF
Просмотр документации в формате PDF
Описанные выше справочные средства рассчитаны на то, что пользователь уже знаком с системой и желает быстро получить справку по ее конкретным возможностям. Но для общего знакомства с системой они не очень подходят, поскольку много времени занимают «бесконечные» переходы от одного раздела справки к другому. Поэтому хотелось бы обратить внимание читателя на подробные электронные книги, обычно представленные в виде файлов формата PDF, для работы с которыми применяются такие программы, как Acrobat Reader или Adobe Acrobat. Первая позволяет только просматривать материалы книг, а вторая — еще и редактировать их.
Справочная система содержит раздел Favorites с подразделом MATLAB Printable Documentation (печатаемая документация MATLAB), предоставляющим доступ к электронной справочной документации, которая поставляется в виде файлов PDF или PostScript. На рис. 4.11 показано окно этого раздела справки с перечнем документов в формате PDF. Среди документов крупные (сотни страниц) руководства по функциям системы, языку ее программирования, графическим функциям и т. д.
Возможность просмотра документов в этом формате требует наличия программы Adobe Acrobat Reader (можно бесплатно скачать с web-узла фирмы Adobe www.ado-be.com) и файлов самих документов. Не все поставки системы MATLAB имеют эти средства. Полный объем документации по системе MATLAB 6.0 и пакетам прикладных программ уже превышает 600 Мбайт, что делает документацию труднообозримой.
Рис. 4.11. Окно раздела справки с доступом к документам в формате PDF
В качестве примера работы с электронными документами формата PDF рассмотрим просмотр книги-справочника, предназначенной для начального знакомства с системой MATLAB (Getting Started with MATLAB) (Начинаем работу с MATLAB). Его титульная страница показана на рис. 4.12. Заметим, что она появляется после загрузки программы Acrobat Reader (временное окно этой программы не показано).
Рис. 4.12. Начальная страница электронного справочного руководства по MATLAB
Нетрудно заметить, что страница электронного документа в формате PDF содержит древообразный перечень разделов в левой части и большое окно просмотра в правой части. С помощью левого окна можно явно указать раздел справочника, который необходимо просмотреть. Можно также перелистывать материал справочника с помощью линейки прокрутки, расположенной справа в окне просмотра. Таким образом, справочные материалы представлены в типовой форме электронных книг.
Рис. 4.13. Одна из страниц электронного справочника в окне просмотра программы Acrobat Reader
Acrobat Reader — сама по себе серьезная программа, и ее описание в задачи данной книги не входит. Однако надо отметить, что работа с программой интуитивно понятна и не вызывает особых трудностей даже у не очень опытного пользователя. На рис. 4.13 дано представление одной из страниц с некоторым увеличением и в полностью открытом окне просмотра. На ней показан пример построения трехмерного графика с иллюстрацией эффектов освещения построенной поверхности от внешнего источника света. Из рис. 4.13 видно, что качество представления текстов, да и рисунков не очень высокое, даже при увеличении. Тем не менее оно достаточно для просмотра рисунков в обычном масштабе.
Как и все другие виды справочной документации, электронные книги по MATLAB подготовлены на английском языке (и кое-что на японском).
11.gif
12.gif
13.gif
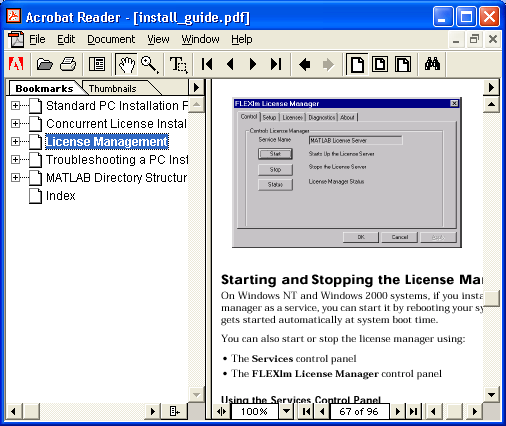
22. Галерея примеров - MATLAB Demos
Галерея примеров — MATLAB Demos
В меню Help имеется команда Demos, дающая доступ к галерее демонстрационных примеров применения системы MATLAB. При запуске этой команды появляется окно демонстрационных примеров MATLAB Demos, показанное на рис. 4.14.
Рис. 4.14. Окно демонстрационных примеров
Это же окно можно вызвать выполнением команды demo в режиме диалога.
В этом окне имеются три панели:
-
левая панель с перечнем разделов, по которым предлагаются примеры;
-
панель с описанием выбранного раздела примеров;
-
панель с перечнем примеров по выбранному разделу.
Выбрав раздел примеров (щелчком мыши), затем следует выбрать нужный пример. На рис. 4.14 показан выбор раздела Gallery и примера Hoops. После этого нажатием кнопки Run можно запустить m-файл с выбранным примером и наблюдать результат его работы (рис. 4.15).
Рис. 4.15. Результат выполнения примера Hoops
Этот пример демонстрирует построение сплетающихся в пространстве нескольких объемных обручей с функциональной цветной окраской. Кнопка Info окна открывает раздел справочной системы с описанием m-файла данного примера.
14a.gif
14b.gif
15.gif
23. Демонстрационные примеры Simulink
Демонстрационные примеры Simulink
Следующий пример, показанный на рис. 4.16, иллюстрирует доступ к примерам пакета системного моделирования Simulink — одного из самых мощных пакетов прикладных программ, расширяющих возможности системы MATLAB. Этот пакет создан для моделирования линейных и нелинейных динамических систем заданием их в виде системы функциональных блоков с автоматическим составлением и решением матричной системы дифференциальных уравнений состояния, описывающей работу созданной модели.
На рис. 4.17 приведен пример просмотра одного из простых примеров — моделирования динамической системы второго порядка, описываемой нелинейными дифференциальными уравнениями Ван-дер-Поля. Сверху показана блок-схема моделируемого объекта, а снизу — результат моделирования его работы. Для пуска моделирования в панели инструментов окна системы Simulink нажимается кнопка пуска с изображением треугольника.
Рис. 4.16. Доступ к примерам пакета Simulink
Окно MAT LAB Demos дает возможность ознакомиться со многими десятками самых серьезных примеров применения системы MATLAB и позволяет убедиться в высоком качестве визуализации их решений. При необходимости всегда можно ознакомиться с файлом любого примера и использовать его для решения схожих задач.
Рис. 4.17. Пример моделирования нелинейной динамической системы второго порядка средствами пакета моделирования Simulink
16.gif
17a.gif

17b.gif
24. Копирование демонстрационных примеров
Копирование демонстрационных примеров
Вполне возможно, что вы захотите воспользоваться каким-либо примером для своих целей. Для этого можно использовать m-файл примера или перенести его текст в командное окно MATLAB, используя буфер обмена. Покажем, как это делается. В нижней части окна примера показано, каким образом осуществляется копирование примера: текст примера выделяется мышью и используется команда Сору (Копировать) меню Edit окна примера, в результате чего текст примера попадет в буфер обмена.
После этого надо вернуться в командное окно MATLAB и, используя команду Paste (Вставить) меню Edit, перенести текст примера из буфера в текущую строку ввода. Выполнив команду (как обычно, клавишей Enter), можно наблюдать исполнение примера, как показано на рис. 4.18.
Трудно сказать почему, но создатели MATLAB в последних версиях отказались от возможности копирования выделенного в примерах окна Demos текста программ с помощью контекстного меню правой клавиши мыши. Зато появилась возможность исполнения выделенных в справке (как на заданную функцию в командном режиме, так и в HTML-браузере справки) примеров с помощью команды Evaluate Selection в контекстном меню правой клавиши мыши в тексте справки.
Остается еще раз отметить, что обилие примеров в системе MATLAB облегчает знакомство с различными аспектами применения системы. Большинство примеров содержат решения отнюдь не тривиальных математических задач и прекрасно иллюстрируют обширные возможности системы. Поэтому работа с демонстрационными примерами — залог успешного освоения системы MATLAB.
Рис. 4.18. Исполнение скопированного примера из командного окна MATLAB
18.gif
25. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Использовать команды справки.
-
Вызывать список демонстрационных примеров.
-
Исполнять примеры и копировать их.
-
Просматривать листинги m-файлов командой type.
-
Работать с различными разделами справочной системы.
-
Просматривать документацию MATLAB в формате PDF.
-
Работать с демонстрационными примерами системы MATLAB.
-
Запускать приложение Simulink.
Урок 5. Пользовательский интерфейс MATLAB
1. Урок 5. Пользовательский интерфейс MATLAB
Урок №5.
Пользовательский интерфейс MATLAB
-
Общая характеристика пользовательского интерфейса
-
Панель инструментов
-
Операции с буфером обмена
-
Браузеры рабочей области и файловой структуры
-
Запуск приложения Simulink
-
Вызов справки по системе MATLAB
-
Меню системы MATLAB
-
Работа с файлами
-
Настройка MATLAB и функция path
-
Обеспечение печати
-
Интерфейс редактора и отладчика т-файлов
-
Файлы сценариев и функций
-
Интерфейс графических окон
-
Общение MATLAB с операционной системой
2. Общая характеристика пользовательского интерфейса
Общая характеристика пользовательского интерфейса
Как видно из материалов предыдущих уроков, в новой версии MATLAB в полной мере сохранен командный интерактивный режим работы. Это старый фасад дворца MATLAB. Командный режим остается одним из наиболее удобных и проверенных методов работы с системой.
Имеются и типовые средства приложений Windows 95/98/Me/2000/NT4 — меню и панель инструментов. Но они по-прежнему выглядят намного скромнее, чем у большинства современных приложений Windows. Видимо, так и должно быть — чем серьезнее математическая система, тем меньше она нуждается в использовании всевозможных кнопок на панели инструментов и тем скромнее может быть ее главное меню.
Рис. 5.1. Окно системы MATLAB
И, тем не менее, пользовательский интерфейс в системе MATLAB 6.0 кардинально переработан. Это видно из рис. 5.1, на котором показано основное полностью открытое окно системы MATLAB 6.0 так, как оно предстает перед пользователем при запуске.
Главными отличиями от весьма скромного интерфейса прежних версий системы MATLAB у новой версии стали:
-
позиция Web меню, открывающая доступ к Интернет ресурсам фирмы Math-Works Inc.;
-
меню используемых разделов текущей папки файловой системы Current Directory в конце панели инструментов справа;
-
окно с вкладками Launch Path (Доступ к частям системы) и Workspace (Рабочая область) в левой части основного окна (сверху);
-
окно с вкладками Command History (Обзор ранее исполненных команд) и Current Directory (Текущая папка) в левой части основного окна (сверху)
-
применение цветового выделения выражений в командной строке, что упрощает оперативный контроль их синтаксиса по мере ввода.
Эти отличия указывают на то, что разработчики новой версии уделили больше внимания оперативному контролю за состоянием системы, который ранее (в прежних версиях) был как бы за кадром.
1.gif
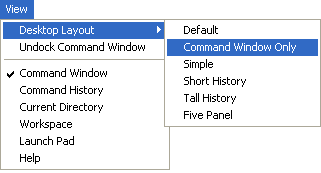
3. Упрощенный интерфейс
Упрощенный интерфейс
Сделав решительный шаг в обновлении интерфейса, разработчики MATLAB 6.0, похоже, испугались недовольства старых пользователей, уже привыкших работать со скромным и отчасти даже ущербным интерфейсом прежних версий MATLAB. А потому они ввели возможности изменения интерфейса системы, в том числе представления его в добром старом виде. Все эти возможности реализуются командами в позиции View (Вид) меню. На рис. 5.1 вкладка View показана в открытом состоянии.
Теперь пользователь может настраивать вид интерфейса и по-разному располагать его окна. В частности, исполнив команду View > Desktop Layout > Command Window Only (Только командное окно) можно получить «старый» вид интерфейса — рис. 5.2. Теперь о новациях в интерфейсе напоминают лишь позиция меню Web и доступ из панели инструментов к папкам файловой системы. Кстати, окно доступа к папкам файловой системы также показано на рис. 5.2.
Нередко MATLAB отказывается исполнять некоторые команды из-за того, что их m-файлов нет в текущей папке. Поэтому обеспечение быстрого доступа к файловой системе из пользовательского интерфейса можно приветствовать.
Для редактирования и отладки m-файлов MATLAB имеет встроенный современный редактор, интерфейс которого выполнен в лучших традициях Windpws-приложений. В том же стиле выполнены окно просмотра ресурсов памяти, окно просмотра путей файловой системы, справочник по возможностям системы и демонстрационные программы. Редактор графики и окно графики со средствами редактирования рисунков уже были описаны.
Рис. 5.2. Упрощенный интерфейс системы MATLAB 6.0
2.gif
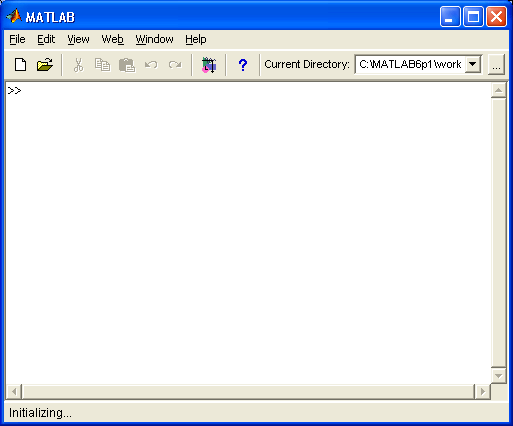
4. Работа с панелью инструментов
Работа с панелью инструментов
Панель инструментов (рис. 5.3) дает наиболее простой и удобный (особенно для начинающих пользователей) способ работы с системой MATLAB. При этом основные команды вводятся указанием курсором мыши на нужную кнопку с нажатием левой клавиши мыши. Кнопки имеют изображение, явно подсказывающее их назначение.
Рис. 5.3. Часть окна системы MATLAB с меню и панелью инструментов
Прежде всего перечислим назначение всех кнопок панели инструментов:
-
New M-file (Новый m-файл) — выводит пустое окно редактора m-файлов;
-
Open file (Открыть файл) — открывает окно для загрузки m-файла;
-
Cut (Вырезать)— вырезает выделенный фрагмент и помещает его в буфер;
-
Сору (Копировать)— копирует выделенный фрагмент в буфер;
Paste (Вставить)— переносит фрагмент из буфера в текущую строку ВВОДА -
Undo (Отменить)— отменяет предшествующую операцию;
-
Redo (Повторить) — восстанавливает последнюю отмененную операцию;
-
Simulink — открывает окно браузера библиотек Simulink;
-
Help (Помощь)— открывает окно справки.
Набор кнопок панели инструментов обеспечивает выполнение наиболее часто необходимых команд и вполне достаточен для повседневной работы с системой.
-
назначении кнопок говорят и всплывающие подсказки, появляющиеся, когда курсор мыши устанавливается на соответствующую кнопку.
-
ни имеют вид желтого прямоугольника с текстом короткой справки — см. пример такой подсказки на рис. 2.12 у кнопки Help панели инструментов. Любопытно отметить, что доступ к браузерам рабочей области и файловой системы из панели инструментов убран.
3.gif
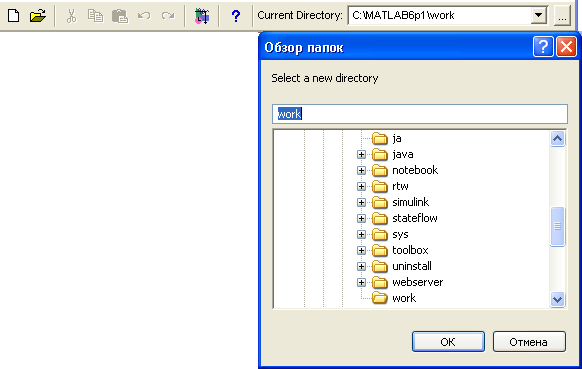
5. Вызов окна открытия нового файла
Вызов окна открытия нового файла
Кнопка New M-file открывает окно редактора/отладчика m-файлов. Это окно показано на рис. 5.4. Работу с этим средством мы обсудим позже.
Рис. 5.4. Пустое окно редактора/отладчика m-файлов
По умолчанию файлу дается имя Untitled (безымянный), которое впоследствии (при записи файла) можно изменить на другое, отражающее тему задачи. Это имя отображается в титульной строке окна редактирования m-файла, которое размещается в окне редактора/отладчика и видно на рис. 5.4. В редакторе/отладчике можно редактировать несколько m-файлов, и каждый из них будет находиться в своем окне редактирования, хотя активным может быть только одно окно, расположенное поверх других окон.
Примечание
Обратите внимание, что панель инструментов является контекстно-зависимой. Для редактора/отладчика m-файлов она имеет несколько иной набор инструментов, чем для окна командного режима работы (см. рис. 5.1). Позже мы уточним эти отличия.
4.gif
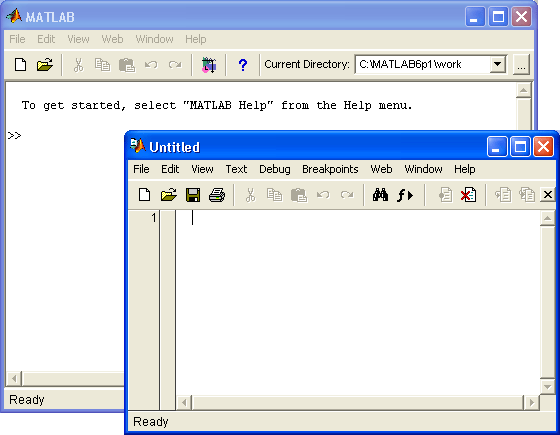
6. Вызов окна загрузки имеющегося файла
Вызов окна загрузки имеющегося файла
Кнопка Open file (Открыть файл) служит для загрузки в редактор/отладчик ранее созданных m-файлов, например входящих в пакет расширения (Toolbox) системы или разработанных пользователем. Она открывает окно, которое является типичным элементом интерфейса Windows-приложений и показано на рис. 5.5 внутри окна редактора/отладчика m-файлов.
Рис. 5.5. Окно загрузки файла в окне редактора/отладчика
В окне загрузки файлов с помощью раскрывающегося списка Папка и вертикальной полосы прокрутки можно «пройтись» по всем дискам, папкам и файлам. Чтобы выбрать нужный файл для загрузки, его требуется выделить мышью. Выбор завершается двойным щелчком на имени файла, нажатием клавиши Enter или щелчком на кнопке Открыть. Любое из этих действий приводит к загрузке документа в текущее окно системы. Кнопка Отмена или клавиша Esc позволяет отказаться от загрузки.
Примечание
Пусть читателя не волнуют внезапно появившиеся русскоязычные надписи на элемен-тах интерфейса окна загрузки файлов. Они говорят лишь о том, что используется окно стандартной русифицированной операционной системы Windows 95/98/Ме, которая обычно устанавливается у наших пользователей.
Для вызова одного из ранее использовавшихся документов достаточно щелкнуть мышью на его имени в списке, находящемся над командой Exit (Выход) в меню File. После загрузки файла с документом его текст появляется в текущем окне — на рис. 5.5 показан текст выбранного файла graf2d.rn (демонстрация возможностей двумерной графики). Его можно начинать редактировать или запускать на исполнение.
5.gif
7. Операции с буфером обмена
Операции с буфером обмена
Кнопки Cut (Вырезать), Сору (Копировать) и Paste (Вставить) реализуют наиболее характерные команды работы с буфером обмена (Clipboard). Первые две операции относятся к выделенным фрагментам сессии или текста m-файлов (если они выполняются в окне редактора/отладчика). Для выделения объектов можно использовать мышь, перемещая курсор по тексту при нажатой левой кнопке, или клавиши со стрелками в комбинации с клавишей Shift.
На рис. 5.6 показан пример выделения содержимого матрицы М в окне документа MATLAB. Эта матрица формируется функцией magiс (n) и называется магической, поскольку сумма элементов любого столбца, любой строки и даже любой диагонали равна одному и тому же числу — 34 для матрицы при n=4.
Рис. 5.6. Окно документа с выделенным содержимым матрицы М
Команда Cut (Вырезать) осуществляет вырезание выделенного фрагмента и размещение его в буфере. При этом вырезанный фрагмент удаляется из текста документа. Команда Сору (Копировать) просто копирует выделенный фрагмент в буфер, сохраняя его в тексте. Команда Paste (Вставить) вызывает объект из буфера (сохраняя объект в буфере) и помещает копию объекта на место в документе, указанное текстовым курсором. Эти операции реализуются как соответствующими кнопками, так и командами меню Edit (Редактировать). В MATLAB можно использовать контекстное меню, появляющееся при нажатии правой кнопки мыши. Например, установив курсор мыши на выделенный фрагмент матрицы М и нажав правую кнопку, можно увидеть меню, показанное на рис. 5.6. В нем, кстати, дублируется позиция с командой Сору (Копировать). Есть и ряд других доступных в данный момент команд. Обратите внимание, что в момент подготовки магической матрицы М ее имя появилось в окне браузера рабочей области — в правой части экрана. При этом матрица представляется изображением таблицы.
Содержимое буфера можно перенести в строку ввода, в окно редактора-отладчика m-файлов или даже в другое приложение. Допустим, мы хотим создать матрицу M1 с содержимым, которое размещено в буфере. Для этого достаточно набрать М1=[ и, нажав правую клавишу мыши, выбрать из появившегося меню команду Paste (Вставить). Этот момент фиксирует рис. 5.7.
Рис. 5.7. Подготовка к вставке данных матрицы из буфера
Исполнив команду Paste, можно увидеть, что данные хранящейся в буфере матрицы появятся после открывающей квадратной скобки. Для создания матрицы Ml остается ввести закрывающую квадратную скобку ] и нажать клавишу Enter. На рис. 5.8 показано, как создается матрица Ml, по содержимому аналогичная матрице М.
Рис. 5.8. Пример создания матрицы M1 с содержимым, взятым из буфера
Разумеется, этот пример является чисто учебным. Не обращаясь к помощи буфера, можно было бы просто записать М1=М. Или М2=М — именно так на рис. 5.8 задана матрица М2. Однако зачастую операции с буфером весьма полезны. Так, все примеры в тексте этой книги получены переносом выделенных фрагментов соответствующей сессии в окно текстового редактора Microsoft Word. Возможен и обратный перенос - записанных в документах редактора Microsoft Word примеров в командную строку MATLAB для исполнения примеров.
Примечание
Обратите внимание на команду Select All в контекстном меню. Эта команда позволяет выделить весь текст текущей сессии-А команда Clear Session очищает окно от содержимого данной сессии.
6a.gif
6b.gif

7.gif

8.gif
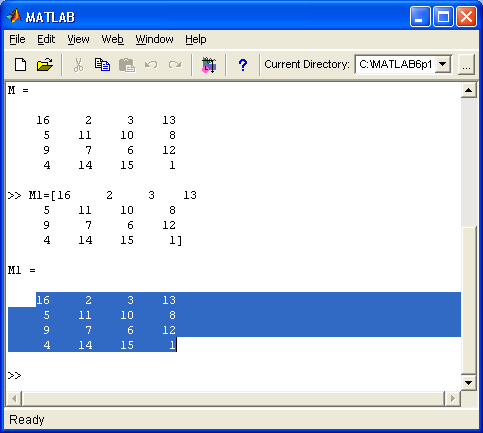
8. Отмена результата предшествующей операции
Отмена результата предшествующей операции
Часто, выполнив какую-то операцию, мы отмечаем, что она оказалась ошибочной. При работе в MATLAB такой ситуации пугаться не стоит, — нажатие кнопки Undo (Отменить) панели инструментов приведет к отмене последнего действия, выполненного в текущей строке. Операции в предыдущих строках документа этой командой не отменяются. Если оказалось, что вы зря произвели отмену последней операции, то ее легко восстановить, введя с панели инструментов операцию Redo (Восстановить).
9. Запуск приложения Simulink
Запуск приложения Simulink
Кнопка Simulink панели инструментов (или команда simulink из строки ввода) запускает одно из самых мощных приложений системы MATLAB — программу моделирования систем, построенных из типовых блоков. Эта система (пакет инструментов (toolbox) Simulink) в данной книге подробно не описывается (см. и описание предшествующей версии в), так что пока отметим лишь, что щелчок на указанной кнопке выводит окно библиотеки типов блоков (рис. 5.9 слева).
В MATLAB 6.0 применена новая версия Simulink 4 с библиотекой блоков Block Library. Эта библиотека содержит существенно расширенный набор компонентов — блоков, объединенных в тематические группы. Чтобы упростить поиск и выбор блоков, окно библиотеки организовано в виде браузера библиотеки, очень напоминающего Проводник (Windows Explorer) операционной системы Windows 95/98/ Me/2000/NT4. Окно браузера показано на рис. 5.9 слева. В нем видно дерево моделей с раскрывающимися ветвями-блоками. Изображение компонентов выделенного блока дерева показывается в поле просмотра в правой части окна браузера.
Для загрузки модели какой либо системы или устройства (в том числе из числа демонстрационных примеров) достаточно активизировать кнопку Ореn.(Открыть), имеющую вид открывающейся папки. При этом появится окно редактора модели программы Simulink, которое показано на рис. 5.9 справа. Это стандартное окно загрузки файлов, принятое во всех приложениях операционной системы Windows 95/98/Ме/2000. В нем можно выбрать и загрузить файл нужной модели или демонстрационного примера.
Рис. 5.9. Окно браузера библиотечных блоков программы Simulink
Рис. 5.10 показывает загруженную в Simulink модель аттрактора Лоренца — демонстрационный файл lorenz. Здесь видно окно с загруженной моделью (она находится слева) и окна встроенного виртуального осциллографа — одного из многих виртуальных регистрирующих устройств, которые имеются в составе Simulink.
Рис. 5.10. Пример работы программы Simulink
Кнопка с треугольником в панели инструментов Simulink запускает процесс моделирования. О его результатах можно судить по показаниям регистрирующих приборов — в частности, упомянутого уже осциллографа. В его окнах появляются сложные и довольно хаотические колебания, характерные для аттрактора Лоренца. Параметры каждого блока можно уточнить или задать с помощью окна параметров блока. На рис. 5.10 снизу справа показано такое окно для блока Beta*z — множительного устройства. Большинство установок параметров блоков довольно очевидны — даже несмотря на то, что их параметры указаны на английском языке.
Кнопка Create a new model (Создать новую модель) в окне библиотек Simulink открывает чистое окно редактора моделей. Любой блок можно перетащить мышью в это окно. Введенные таким образом блоки соединяются друг с другом линиями, для чего используется мышь, с помощью которой указываются точки соединений и осуществляется протягивание соединительных линий.
Таким образом, легко создать новую модель системы. Однако описание подготовки новых моделей для Simulink в тематику данной книги не входит, поскольку книга посвящена лишь описанию базовой системы MATLAB. Заинтересованные читатели могут обратиться к изданиям. Тем не менее приведенные сведения позволят заинтересованному читателю начать работу с Simulink.
9.gif

10.gif
10. Вызов справки MATLAB
Вызов справки MATLAB
Последняя кнопка панели инструментов Help (Помощь) открывает окно с перечнем разделов справочной системы. Это окно было показано на рис. 4.8. В уроке 4 мы подробно ознакомились с работой со справочной системой, так что на этом можно закончить описание средств системы MATLAB, доступ к которым обеспечивает панель инструментов.
11. Средства контроля рабочей области и файловой системы
Средства контроля рабочей области и файловой системы
Векторы и матрицы могут занимать большой объем памяти. Конечно, речь не идет о векторах или матрицах, содержащих несколько элементов или даже несколько десятков элементов. Хотя и в этом случае оценка их размеров полезна при разработке алгоритмов матричных вычислений и оценке их эффективности в части использования памяти.
Как отмечалось, в левой части окна системы MATLAB 6.0 имеется окно специального браузера рабочей области — Workspace Browser. Он служит для просмотра ресурсов рабочей области памяти. Браузер дает наглядную визуализацию содержимого рабочей области. Окно браузера рабочей области выполняет и другие важные функции — позволяет просматривать существующие в памяти объекты, редактировать их содержимое и удалять объекты из памяти. Для вывода содержимого объекта достаточно выделить его имя с помощью мыши и щелкнуть на кнопке
Open (Открыть). Объект можно открыть и двойным щелчком на его имени в списке. Откроется окно редактирования массива Array Editor, показанное на рис. 5.11 применительно к матрице М2.
Рис. 5.11. Пример просмотра содержимого матрицы
Окно редактирования матрицы дает удобный доступ для редактирования любого элемента матрицы по правилам, принятым при работе с электронными таблицами. [ В уроке 23 показано, как использовать Microsoft Excel для ввода матриц. — Примеч. ред. ] . Основное из них — быстрый доступ к любому элементу матрицы. Можно также менять тип значений элементов, выбирая его из списка, предоставляемого меню Numeric format (Формат чисел). В окне также выводятся данные о числе строк и столбцов матрицы.
11.gif
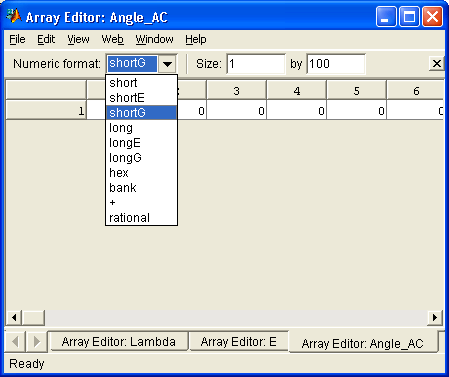
11b.gif

12. Команды просмотра рабочей области who и whos
Команды просмотра рабочей области who и whos
Следует отметить, что просмотр рабочей области возможен и в командном режиме, без обращения к браузеру Workspace Browser. Команда who выводит список определенных переменных, а команда whos — список неременных с указанием их размера и объема занимаемой памяти. Следующие примеры иллюстрируют действие этих команд:
» х=1.234;
» V=[1 2 3 4 5]:
» M=magic(4);
» who
Your variables are:
M V x
|
|
» whos |
|
|
|
|
|
|
Name |
Size |
Bytes |
Class |
|
|
|
M |
4x4 |
128 |
double array |
|
|
|
V |
1x5 |
40 |
double array |
|
|
|
X |
1x1 |
8 |
double array |
|
Если вы хотите просмотреть данные одной переменной, например М, следует использовать команду whos M. Естественно, просмотр рабочей области с помощью браузера рабочей области (Workspace Browser) более удобен и нагляден.
13. Браузер файловой структуры
Браузер файловой структуры
Для просмотра файловой структуры MATLAB служит специальный браузер файловой системы (Path Browser), который запускается при обычной загрузке системы. Если был установлен упрощенный интерфейс, то для запуска браузера файловой системы используется окно Current Directory (Текущая папка). На рис. 5.12 в левой части показано окно этого браузера.
Нетрудно заметить, что браузер файловой системы построен по типу общеизвестного Проводника (Explorer) операционных систем Windows 95/98/Me/2000/NT4. Окно дает возможность просмотра файловой системы ПК и выбора любого файла. Для примера на рис. 5.12 показан выбор m-файла функции синуса.
Исполнив команду Open (Открыть) из контекстного меню правой клавиши мыши или дважды щелкнув по выделенной строке с именем файла, можно ввести этот файл в окно редактора/отладчика m-файлов. При этом редактор запустится автоматически и его окно с готовым для редактирования выбранным файлом появится на экране рис. 5.12.
Рис. 5.12. Пример окна браузера Path Browser
Примечание
Обратите внимание на то, что m-файл функции синуса содержит только комментарии по этой функции, которые используются справочной системой. Самого определения функции синуса на языке программирования системы MATLAB нет. Это связано с тем, что данная функция является встроенной в ядро системы. Так что модифицировать такие функции попросту нельзя. Ничто, однако, не мешает вам создать свой метод (и алгоритм) вычисления встроенных функций и оформить их в виде m-файлов, дав им свои имена — например, mysin.m.
Таким образом, браузер просмотра файловой структуры позволяет детально ознакомиться с файловой системой MATLAB и вывести любой из m-файлов или файлов демонстрационных примеров для просмотра, редактирования и модификации.
12.gif
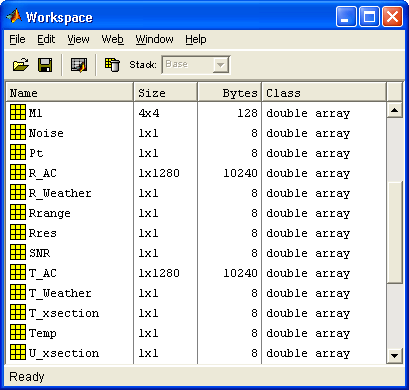
14. Работа с меню
Работа с меню
Открытая позиция строки меню содержит различные операции и команды. Выделенная команда или операция исполняется при нажатии клавиши Enter (Ввод). Выполнение команды можно также осуществить щелчком мыши или нажатием на клавиатуре клавиши, соответствующей выделенному символу в названии команды.
Между командами и операциями нет особых отличий, и в литературе по информатике их часто путают. Мы будем считать командой действие, которое исполняется немедленно. А операцией — действие, которое требует определенной подготовки, например открытие окна для установки определенных параметров.
Параметр (option)— это значение определенной величины, действующее во время текущей сессии. Параметрами обычно являются указания на применяемые наборы шрифтов, размеры окна, цвет фона и т. д.
15. Меню системы
Меню системы
Перейдем к описанию основного меню системы MATLAB 6.0. Это меню (см. рис. 5.1 сверху) выглядит довольно скромно и содержит всего шесть пунктов:
-
File — работа с файлами;
-
Edit — редактирование сессии;
-
View — вывод и скрытие панели инструментов;
-
Web — доступ к Интернет-ресурсам;
-
Windows — установка Windows-свойств окна;
-
Help — доступ к справочным подсистемам.
По сравнению с версией 5.3.1 добавлена единственная позиция Web, дающая доступ к Интернет-ресурсам, описанный в уроке 1.
16. Подменю File
Подменю File
Подменю File содержит ряд операций и команд для работы с файлами. Оно показано на рис. 5.13. Число операций и команд значительно сокращено по сравнению с тем же меню у предшествующей версии системы MATLAB.
Теперь меню File содержит следующие операции:
-
New - открывает подменю с позициями:
-
M-file — открытие окна редактора/отладчика m-файлов;
-
Figure — открытие пустого окна графики;
-
Model — открытие пустого окна для создания Simulink-модели;
-
GUI — открытие окна разработки элементов графического интерфейса пользователя.
-
Open — открывает окно загрузки файла.
-
Close Command Windows — закрывает окно командного режима работы (оно при этом исчезает с экрана).
-
Import data — открывает окно импорта файлов данных.
-
Save Workspace As... — открывает окно записи рабочей области в виде файла с заданным именем.
-
Set Path — открывает окно установки путей доступа файловой системы.
-
Preferences... — открывает окно настройки элементов интерфейса.
-
Print... — открывает окно печати всего текущего документа.
-
Print Selection... — открывает окно печати выделенной части документа.
-
Exit — завершает работу с системой.
Рис. 5.13. Меню файловых операций File
13.gif
17. Открытие окон для подготовки новых файлов
Открытие окон для подготовки новых файлов
Команда New, как отмечено, открывает окна для подготовки новых файлов. Для трех типов файлов (m-файлы, графические файлы и файлы Simulink-моделей) окна их редакторов уже описывались. Новой является позиция GUI подменю File. Она открывает окно редактора элементов пользовательского интерфейса, показанное на рис. 5.14.
Рис. 5.14. Окно редактора элементов GUI
К подробному описанию этого окна мы еще вернемся. А пока отметим, что работа с редактором довольно очевидна.
14.gif
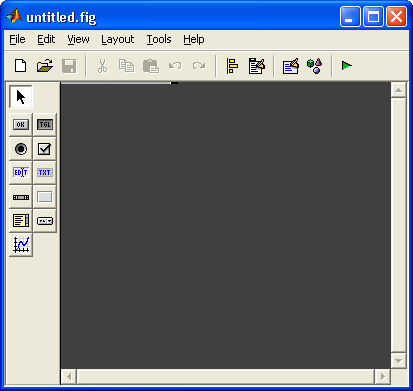
18. Загрузка и сохранение файлов
Загрузка и сохранение файлов
Команды Open... (Открыть) и Import data... (Импортировать данные) выводят стандартные окна (см. рис. 5.5) для загрузки m-файлов и файлов данных. Команда Save Workspace As... (Сохраните рабочую область как...) открывает стандартное окно записи файлов с расширением .mat. Они хранят определения переменных, массивов, функций пользователя и иных объектов, созданных в ходе текущей сессии работы. Эти команды в силу общеизвестности в более подробных комментариях не нуждаются.
19. Установка путей доступа файловой системы
Установка путей доступа файловой системы
Команда Set Path... (Установить путь) открывает окно редактора путей доступа файловой системы. Это окно показано на рис. 5.15.
Окно дает список папок с файлами системы MATLAB. Имеется возможность переноса папок вверх или вниз по списку, уничтожения их и переименования. По умолчанию задается правильная установка путей доступа, так что данными возможностями стоит пользоваться только в особых обстоятельствах, например при случайном переносе папок в другое место или при их переименовании.
Рис. 5.15. Окно редактора путей доступа файловой системы
15.gif
20. Настройка элементов интерфейса
Настройка элементов интерфейса
Окно настройки элементов интерфейса представлено на рис. 5.16.
Рис. 5.16. Окно настройки элементов интерфейса
Интерфейс MATLAB 6.0 стал настолько удобным и даже изысканным, что мало вероятно, что кому-либо захочется менять его в мере, большей, чем это предусмотрено командами подменю View [ Это может потребоваться даже для настройки под особенности операционной системы. Например, для уточнения расположения вашей программы чтения PDF-файлов, вам, возможно, придется вручную удалить апострофы из пути к ее исполняемому файлу. — Примеч. ред. ]. Однако такая возможность есть — команда Preferences... (Предпочтения) выводит окно детальной настройки элементов интерфейса (рис. 5.16). В левой части этого окна имеется древообразный список элементов интерфейса системы, а в правой части—поле задания параметров для выбранного типа элементов. Поскольку изменение параметров производится обычно очень редко, мы не будем детально рассматривать это окно. Заинтересованный читатель наверняка разберется с нужными ему параметрами самостоятельно.
16.gif
21. Обеспечение печати - команды Print и Print Selection
Обеспечение печати — команды Print и Print Selection
В MATLAB для печати используются стандартные средства Windows. Меню File содержит две команды печати. Первая из них — Print — служит для вывода окна печати, показанного на рис. 5.17 применительно к широко распространенному струйному принтеру Epson Stylus COLOR 600. В этом окне также имеется возможность вывода окна со свойствами печати. В нем можно также определить, с какой страницы начинается печать, и задать число страниц при печати, если печатаемый материал не укладывается в одну страницу.
Рис. 5.17. Окно печати
Окно установки свойств печати для данного принтера показано на рис. 5.18. Оно имеет три вкладки для установки соответственно параметров печати, параметров бумаги и использования утилит профилактики принтера. Многие, даже дешевые струйные принтеры обеспечивают печать в цвете, тогда как такую возможность имеют только дорогие лазерные принтеры.
Рис. 5.18. Окно свойств печати
Следует отметить, что окна печати — типичные для операционной системы Windows 95/98/Me/2000/NT4. Их вид зависит от примененного принтера, точнее от установленного для него драйвера. Установки окон довольно очевидны, поэтому более подробно они не описываются. Обратите внимание на полную русификацию окна печати — это связано с тем, что использовалась локализованная для России версия операционной системы Windows 98. В то же время окно свойств принтера русифицировано лишь частично.
Вторая операция — Print Selection — становится доступной, только если в сессии выделен какой-либо фрагмент. На печать при этом выводится только выделенный фрагмент.
Вообще говоря, MATLAB имеет специальные команды для печати, которые вводятся в командной строке, однако возможности Windows настолько удобны, что командными средствами MATLAB для печати приходится пользоваться редко.
17.gif

18.gif
22. Меню Edit - средства редактирования документов
Меню Edit — средства редактирования документов
Меню Edit (рис.5.19) содержит операции и команды редактирования, типичные для большинства приложений Windows:
-
Undo (Отменить) — отмена результата предшествующей операции;
-
Redo (Повторить) — отмена действия последней операции Undo;
-
Cut (Вырезать) — вырезание выделенного фрагмента и перенос его в буфер;
-
Сору (Копировать) — копирование выделенного фрагмента в буфер;
О Paste (Вставить) — вставка фрагмента из буфера в текущую позицию курсора; -
Clear (Очистить) — операция очистки выделенной области;
-
Select All (Выделить) — выделение всей сессии;
-
Delete (Стереть) — уничтожение выделенного объекта;
-
Clear Command Windows (Очистить командное окно) — очистка текста сессии (с сохранением созданных объектов);
-
Clear Command History (Очистить окно истории команд) — очистка окна истории; О Clear Workspace — очистка окна браузера рабочей области.
Рис. 5.19. Меню Edit
Назначение указанных команд и операций уже обсуждалось. Отметим лишь, что команда Clear Command Window очищает окно командного режима работы и помещает курсор в верхний левый угол окна. Однако все определения, сделанные в течение стертых таким образом сессий, сохраняются в памяти компьютера. Для очистки экрана используется также команда clc, вводимая в командном режиме.
19.gif
23. Меню View и Window
Меню View и Window
В MATLAB 6.0, что уже описывалось, набор команд меню View существенно расширен, и теперь с помощью этого меню можно существенно менять вид пользовательского интерфейса.
Меню Window активно только в случае, если в систему загружены файлы. При этом оно имеет единственную команду Close All (закрыть все окна) и открывающийся список всех загруженных файлов. Он позволяет выбрать окно указанного пользователем файла и сделать его открытым.
24. Основы редактирования и отладки m-файлов
Основы редактирования и отладки m-файлов
Интерфейс редактора/отладчика m-файлов
Для подготовки, редактирования и отладки m-файлов служит специальный многооконный редактор. Он выполнен как типичное приложение Windows. Редактор можно вызвать командой edit из командной строки или командой New > M-file из меню File. После этого в окне редактора можно создавать свой файл, пользоваться средствами его отладки и запуска. Перед запуском файла его необходимо записать на диск, используя команду Filе > Save as в меню редактора.
Рис. 5.20. Редактор/отладчик файлов при записи файла на диск
На рис. 5.20 показано окно редактора/отладчика с текстом простого файла в окне редактирования и отладки.
Подготовленный текст файла (это простейшая и наша первая программа на языке программирования MATLAB) надо записать на диск. Для этого используется команда Save As, окно которой видно на рис. 5.20 внутри окна системы редактора/ отладчика. Работа с окном команды Save As уже описывалась.
После записи файла на диск можно заметить, что команда Run в меню Tools (Инструменты) редактора становится активной (до записи файла на диск она пассивна) и позволяет произвести запуск файла. Запустив команду Run, можно наблюдать исполнение m-файла; в нашем случае — это построение рисунка в графическом окне и вывод надписи о делении на ноль в ходе вычисления функции sin(x)/x в командном окне системы (рис. 5.21).
На первый взгляд может показаться, что редактор/отладчик — просто лишнее звено в цепочке «пользователь — MATLAB». И в самом деле, текст файла можно было бы ввести в окно системы и получить тот же результат. Однако на деле редактор/отладчик выполняет важную роль. Он позволяет создать m-файл (программу) без той многочисленной «шелухи», которая сопровождает работу в командном режиме. Далее мы убедимся, что текст такого файла подвергается тщательной синтаксической проверке, в ходе которой выявляются и отсеиваются многие ошибки пользователя. Таким образом, редактор обеспечивает синтаксический контроль файла.
Редактор имеет и другие важные отладочные средства — он позволяет устанавливать в тексте файла специальные метки, именуемые точками прерывания (breakpoints). При их достижении вычисления приостанавливаются, и пользователь может оценить промежуточные результаты вычислений (например, значения переменных), проверить правильность выполнения циклов и т. д. Наконец, редактор позволяет записать файл в текстовом формате и увековечить ваши труды в файловой системе MATLAB.
Для удобства работы с редактором/отладчиком строки программы в нем нумеруются в последовательном порядке. Редактор является многооконным. Окно каждой программы оформляется как вкладка.
Рис. 5.21. Исполнение файла, показанного в окне редактора на рис. 5.20
20.gif
21.gif
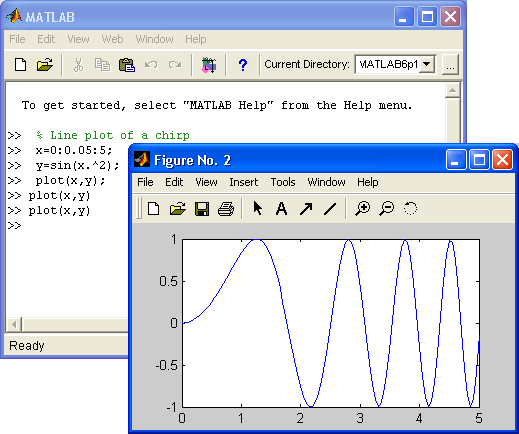
25. Цветовые выделения и синтаксический контроль
Цветовые выделения и синтаксический контроль
Редактор/отладчик m-файлов выполняет синтаксический контроль программного кода по мере ввода текста. При этом используются следующие цветовые выделения:
-
ключевые слова языка программирования — синий цвет;
-
операторы, константы и переменные — черный цвет;
-
комментарии после знака % — зеленый цвет;
-
символьные переменные (в апострофах) — зеленый цвет;
-
синтаксические ошибки — красный цвет.
Благодаря цветовым выделениям вероятность синтаксических ошибок снижается.
Однако далеко не все ошибки диагностируются. Ошибки, связанные с неверным применением операторов или функций (например, применение оператора - вместо + или функции cos(x) вместо sin(x) и т. д.), не способна обнаружить ни одна система программирования. Устранение такого рода ошибок (их называют семантическими) — дело пользователя, отлаживающего свои алгоритмы и программы.
26. Понятие о файлах-сценариях и файлах-функциях
Понятие о файлах-сценариях и файлах-функциях
Здесь полезно отметить, что m-файлы, создаваемые редактором/отладчиком, делятся на два класса:
-
файлы-сценарии, не имеющие входных параметров;
-
файлы-функции, имеющие входные параметры.
Видимый в окне редактора на рис. 5.21 файл является файлом-сценарием, или Script-файлом. Данный файл не имеет списка входных параметров и является примером простой процедуры без параметров. Он использует глобальные переменные, т. е. такие переменные, значения которых могут быть изменены в любой момент сеанса работы и в любом месте программы.
Рис. 5.22. Исполнение файла-сценария из командной строки
Для запуска файла-сценария из командной строки MATLAB достаточно указать его имя в этой строке. Рис. 5.22 поясняет это. Обратите внимание на команду grid on, исполняемую после запуска созданного файла. Эта команда наносит на график сетку из точечных линий.
Файл-функция отличается от файла-сценария прежде всего тем, что созданная им функция имеет входные параметры, список которых указывается в круглых скобках. Используемые в файле-функции переменные являются локальными переменными, изменение значений которых в теле функции никоим образом не влияет на значения, которые те же самые переменные могут иметь за пределами функции.
Иными словами, локальные переменные могут иметь те же имена (идентификаторы), что и глобальные переменные (хотя правила культурного программирования не рекомендуют смешивать имена локальных и глобальных переменных). В дальнейшем мы рассмотрим этот вопрос более подробно, а пока вернемся к теме данного урока — описанию интерфейса компонентов системы MATLAB.
22.gif
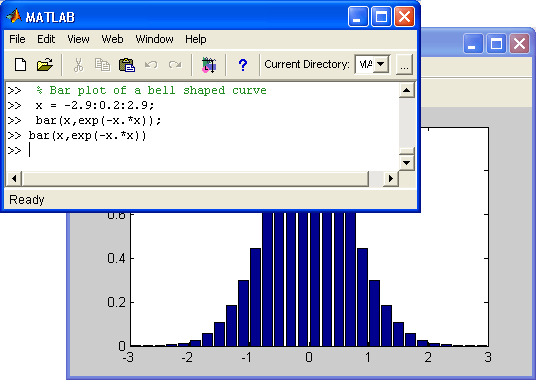
27. Панель инструментов редактора и отладчика
Панель инструментов редактора и отладчика
Редактор имеет свое меню и свою инструментальную панель. Внешний вид инструментальной панели показан на рис. 5.23. По стилю данная панель похожа на панель инструментов окна командного режима работы, но имеет несколько иной набор кнопок.
![]()
Рис. 5.23. Панель инструментов редактора/отладчика m-файлов
Назначение кнопок панели инструментов редактора/отладчика следующее:
-
New — создание нового m-файла;
-
Open — вывод окна загрузки файла;
-
Save — запись файла на диск;
-
Print — печать содержимого текущего окна редактора;
-
Cut — вырезание выделенного фрагмента и перенос его в буфер;
-
Сору — копирование выделенного объекта в буфер;
-
Paste — размещение фрагмента из буфера в позиции текстового курсора;
-
Undo — отмена предшествующей операции;
-
Redo — повтор отмененной операции;
-
Find text — нахождение указанного текста;
-
Show function — показ функции;
-
Set/Clear Breakpoint — установка/сброс точки прерывания;
-
Clear All Breakpoints — сброс всех точек прерывания;
-
Step — выполнение шага трассировки;
-
Step In — пошаговая трассировка с заходом в вызываемые m-файлы;
-
Step Out — пошаговая трассировка без захода в вызываемые m-файлы;
-
Save and Run — запись и сохранение;
-
Exit Debug Mode — выход из режима отладки.
С назначением ряда из этих кнопок вы уже знакомы, поскольку оно аналогично описанному ранее для основного окна MATLAB. А вот о назначении других кнопок надо поговорить.
28. Работа сточками прерывания
Работа с точками прерывания
Основным приемом отладки rn-файлов является установка в их тексте точек прерывания (Breakpoints). Они устанавливаются (и сбрасываются) с помощью кнопки Set/Clear Breakpoint Сброс всех точек прерывания обеспечивается кнопкой Clear All Breakpoints.
Рассмотрим рис. 5.24, на котором в окне редактора/отладчика видна конструкция цикла. Как будет меняться переменная s, значение которой должно давать ряд натуральных чисел?
Прежде всего для отладки надо записать программу на диск, а. затем установить напротив выражения s=s+l точку прерывания — она отчетливо видна на рис. 5.24 как красный кружок. Для установки точки прерывания необходимо поместить текстовый курсор в нужное место (напротив указанного выражения) и щелкнуть на кнопке Set/Clear Breakpoint или щелкнуть справа от номера строки.
Рис. 5.24. Простейший пример на применение точки прерывания в программе
Теперь при пуске программы командой Run она будет исполнена до точки прерывания, после чего текущие значения s будут выведены в окне MATLAB. С помощью кнопки Step (Шаг) можно выполнить очередной шаг вычислений и т. д. Если отпала необходимость останова в точках прерывания, достаточно кнопкой Clear All Breakpoints удалить разом все точки прерывания. Желтая стрелка указывает, в каком месте программы произошла остановка. Обратите внимание на то, что в этом примере каждый шаг исполнения цикла фиксируется в окне командного режима системы MATLAB. При остановке в точке прерывания вы можете провести контроль значений переменных как «вручную», так и с помощью организации вывода на просмотр перед точкой прерывания.
Вы можете задать выполнение программы без остановки при заходе, но с остановкой при выходе (кнопка Step Out), и с остановкой при заходе в вызываемые m-файлы (кнопка Step In). Кнопка Exit Debug Mode (Выход из режима отладки) прекращает операции отладки.
24.gif
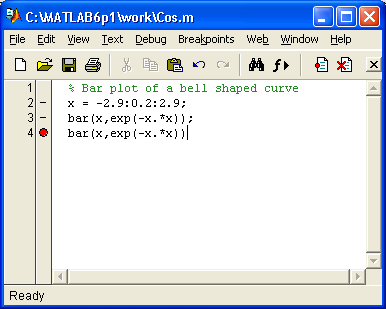
29. Интерфейс графических окон
Интерфейс графических окон
Обзор интерфейса графических окон
В уроке 3 мы уже описывали в общих чертах окно графики. Ниже мы рассмотрим его более детально. Графическое окно MATLAB 6.0 представлено на рис. 5.25. Это обычное масштабируемое и перемещаемое окно Windows-приложений. MATLAB может создавать множество таких окон. Однако размещение графики в окне сессии не предусмотрено. Это возможно в специальном расширении Notebook, позволяющем встраивать объекты MATLAB (тексты, строки ввода и вывода, графики) в документы популярного текстового редактора Word 95/97/2000.
Рис. 5.25. Графическое окно MATLAB
Меню этого окна похоже на меню окна командного режима работы системы MATLAB. Однако при внимательном просмотре заметен ряд отличий.
Прежде всего в меню Edit окна графики наряду со стандартными операциями работы с буфером есть ряд новых команд:
-
Copy Figure (Копировать рисунок) — копирование в буфер рисунка (графика);
-
Copy Options (Копировать параметры) — копирование параметров графика:
-
Figure Properties (Свойства рисунка) — вывод окна свойств графика;
-
Axes Properties (Свойства осей) — вывод окна свойств осей графика;
-
Current Object Properties (Свойства текущего объекта) - вывод окна свойств текущего объекта.
Для вывода свойств графиков, их осей и текущих объектов используется окно свойств графиков с соответствующими вкладками, работа с которым описывалась в уроке 3.
Примечание
Большинство графиков, которые описываются в книге, представлены копиями толь-ко самих графиков, а не всего графического окна. Для получения таких копий использовалась команда Copy Figure из меню Edit окна графики или просто вырезалась нужная часть копии экрана, получаемой нажатием клавиши Print Scrn. Такое представление делает приведенные рисунки одинаковыми для всех версий MATLAB от 5.0 и выше.
25.gif
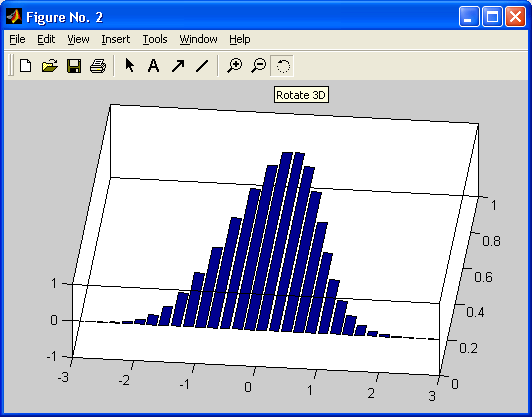
30. Панель инструментов камеры обзора
Панель инструментов камеры обзора
Отличительной особенностью окна графики в версии MATLAB 6.0 стало появление второй инструментальной панели со средствами форматирования трехмерной (3D) графики. Эта панель (она видна на рис. 5.25 под основной панелью инструментов) выводится командой View > Camera Toolbar.
Эта панель управляет некоторой воображаемой фотокамерой (или просто камерой), с помощью которой как бы наблюдается объект. Кнопки имеют наглядные изображения, поясняющие действия кнопок. В связи с этим их подробное описание лишено смысла — проще опробовать их в действии.
31. Меню инструментов Tools
Меню инструментов Tools
Действия кнопок панели инструментов камеры обзора продублированы в меню Tools (Инструменты) — на рис. 5.25 оно представлено в открытом состоянии. Состав команд указанного подменю в версии MATLAB 6.0 существенно изменен и обновлен. Теперь в нем имеются следующие команды:
-
Edit Plot (Редактировать график) — редактирование графика;
-
Zoom In (Увеличение) — увеличение масштаба графика;
-
Zoom Out (Уменьшение) — уменьшение масштаба графика;
-
Rotate 3D (Вращение 3D) — вращение в пространстве;
-
Move Camera (Передвинуть камеру) — установка камеры обзора;
-
Camera Motion (Передвижение камеры) — установка перемещения камеры обзора;
-
Camera Axes (Оси камеры) — установка координатных осей при работе с камерой;
-
Camera Reset (Установка начального состояния камеры) — сброс установок камеры;
-
Basic Fitting — проведение аппроксимации и регрессии;
-
Data Statistics — получение статистических данных для точек графика.
Две последние позиции этого меню дают весьма оригинальные возможности обработки точек графика — выполнение регрессии множеством методов с выводом (где это возможно) уравнения регрессии на график и вычисление статистических параметров для этих точек.
Поскольку эти операции относятся к обработке данных, мы рассмотрим их более детально в уроке 17.
32. Вращение графиков мышью
Вращение графиков мышью
Хорошее впечатление оставляет возможность вращения графиков мышью — прием, введенный в целый ряд систем компьютерной математики (Mathcad, Maple 6 и Mathematica 4). При вводе этой команды вокруг фигуры появляется обрамляющий ее параллелепипед, который можно вращать мышью (при нажатой левой кнопке) в том или ином направлении. Отпустив кнопку мыши, можно наблюдать график в пространстве. Интересно, что эта возможность действует даже в отношении двумерных графиков (см. рис. 5.25).- При этом вращается плоскость, в которой расположен график. Эта плоскость размещается в упомянутом параллелепипеде.
33. Операции вставки
Операции вставки
В уроке 3 мы уже рассматривали операции вставки с помощью основной панели инструментов. Эти возможности продублированы в позиции Insert (Вставка) меню графического окна. Рис. 5.26 показывает пример рисунка, в котором выполнены основные операции вставки с помощью команд меню Insert (Вставка). Это нанесение надписей по осям, титульной надписи, надписи внутри рисунка, стрелки, отрезка прямой, легенды и шкалы цветов. На этом рисунке меню Insert показано в открытом состоянии.
Рис. 5.26. Примеры операций вставки в графическом окне
26.gif
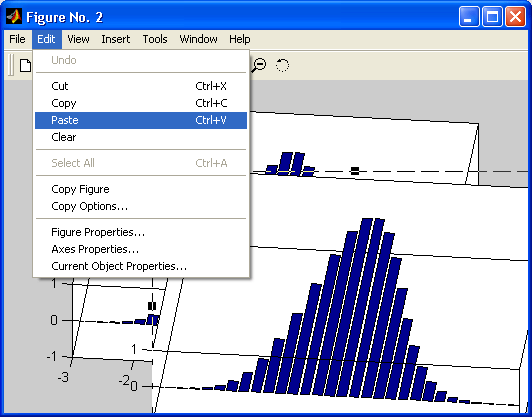
34. Общение MATLAB с операционной системой
Общение MATLAB с операционной системой
Общение системы MATLAB с операционной системой MS-DOS многим покажется рудиментарной возможностью. Так, во время написания данной книги такое общение не потребовалось. [ Это очень важно для систем, работающих в реальном масштабе времени, причем наличие наряду с ! возможности явного задания ОС (dos, unix, vms) позволяет программировать для ОС на управляющем компьютере, отличающемся от ОС пользователя MATLAB.— Примеч. ред. ] . Но, как говорится, из песни слов не выкинешь — MATLAB позволяет из командой строки пользоваться основными услугами старушки MS-DOS и Windows. Есть возможность общения и с другими операционными системами и даже с глобальной сетью Интернет, в том числе и с помощью собственного HTML-браузера MATLAB (браузера помощи).
Для перехода в новую папку служит команда cd:
-
cd wd — переход в указанную папку wd;
-
cd (или произвольное имя переменной ad ad=cd) — возвращает строку с полным именем текущей папки;
-
cd .. — переход к папке, родительской по отношению к текущей.
Примеры (предполагается, что MATLAB установлен на диске Е):
» cd
E:\matlabR12\toolbox
» cd E:\matlabR12\tool
??? Name is nonexistent or not a directory
» cd E:\matlabR12\toolbox\
» cd
E:\matlabR12\toolbox
Для указания пути к текущей папке может использоваться функция pwd:
» pwd
ans =
E:\matlabR12\toolbox
Для получения информации о содержимом текущей папки используется команда dir:
» cd E:\matlabR12\too1box\matlab
» dir
| . | datatypes | funfun graphics | ops | specgraph verctrl |
| .. | demos | general iofun | polyfun | strfun winfun |
| audio | el fun | graph2d lang | sparfun | timefun |
| datafun | elmat | graph3d mat | fun | specfun uitools |
Обратите внимание, что в последнем примере выведено содержимое подпапки matlab одной из самых важных папок системы MATLAB — TOOLBOX. В папке TOOLBOX содержатся 46 самых важных подпапок с хранящимися в них пакетами расширения системы MATLAB, например comm — папка пакета проектирования средств телекоммуникаций, compiler — компилятор программ в коды языка С, symbolic — символьные (аналитические) вычисления и т. д. Впрочем, надо отметить, что в разных поставках системы число подпапок может различаться. Функция dir может использоваться для получения списка файлов в любой папке: files-dir ('путь к папке и имя папки').
35. Выполнение команд !, dos, unix и vms
Выполнение команд !, dos, unix и vms
Из командной строки MATLAB возможно выполнение команд наиболее распространенных операционных систем:
-
! команда — выполнение заданной команды из набора операционной системы; в среде которой установлена MATLAB;
-
unix команда — выполнение заданной команды из операционной системы UNIX или UNIX-подобных систем (версии Linux);
-
vms команда — выполнение заданной команды из операционной системы VMS (Open VMS);
-
dos команда — выполнение заданной команды из набора команд MS-DOS или установленной ОС семейства Windows, в последнем случае команда выполняется в фоновом режиме.
Выведем блокнот Windows для редактирования m-файла:
dos 'notepad myfile.m'
или
[s w]=dos('notepad myfile.m')
s=0, когда команда выполнена успешно, в противном случае s=1, w содержит сообщение DOS.
36. Общение с Интернетом из командной строки
Общение с Интернетом из командной строки
Для общения с Интернетом служит команда web: О web спецификация — дает связь с Web-сервером. [ Те же команды web с параметром —browser (например, web http://www.mathworks.com —browser) вызывают вместо браузера помощи MATLAB браузер HTML, установленный в ваших настройках операционной системы Windows как браузер по умолчанию. В UNIX (Linux) браузер, вызываемый командой web с параметром —browser, определяется командой MATLAB [doccmd.options, ] - docopt, где doccmd — наименование браузера, например netscape, вместо options можно подставить параметры браузера. Можно также отредактировать файл docopt в папке matlabr!2/toolbox/local и указать в нем браузер по умолчанию. — Примеч. ред. ] Примеры применения команды web:
-
web http://www.mathworks.com — загружает Web-страницу MathWorks Web [ Команда support сразу открывает страницу технической поддержки MATLAB. — Примеч. ред. ] в браузер помощи; [ При запуске с параметром —browser можно ввести URL в виде www.mathworks.com, но сайт будет открыт в браузере ОС по умолчанию. — Примеч. ред. ]
-
web mailto:email_address — использует программу для отправки электронной почты, установленную по умолчанию в настройках операционной системы;
-
все формы команды web могут использоваться в функциях. Например, функция s = web('www.mathworks.com', ' -browser') запускает браузер Интернета операционной системы [ Для UNIX и Linux браузера Интернета можно задавать из MATLAB. — Примеч. ред. ] и выдает s=0, если браузер запущен, даже если браузер Интернета открывает страницу в автономном режиме (off-line) или не может ее найти, s=l, если браузер Интернет не был обнаружен, s=2, если браузер был обнаружен, но не был запущен.
Такой выход в Интернет иначе чем экзотикой назвать трудно, благо в Windows 95/ 98/Me/2000/NT4 есть куда более простые способы выхода в Интернет. Отнесем эту возможность к числу приятных мелочей [ Необходимых для работы систем, работающих в реальном масштабе времени. — Примеч. ред. ], которых в MATLAB очень много. Например, приятной мелочью является также собственный web-сервер MATLAB (только в версиях для Microsoft Windows NT4/2000, Linux и Sun Solaris). Доступ к нему может быть ограничен только компьютерами, перечисленными в списке файла hosts.conf.
37. Некоторые другие команды
Некоторые другие команды
Есть еще несколько команд для общения с операционными системами:
-
delete name — стирание файла с заданным именем name (имя записывается по правилам операционной системы);
-
getenvCname') — возвращает значение переменной 'name' среды окружения.
Пример:
» getenv('temp')
ans =
C:\TEMP
Команда tempdir дает информацию о папке для хранения временных файлов:
» tempdir
ans =
С:\ТЕМР\ ...
Еще одна команда — computer — используется в двух формах:
» computer
ans =
PCWIN
и
» [С S]=computer
С = PCWIN
S =
2.1475е+009
Во втором случае помимо сообщения о типе компьютера выводится максимально возможное число элементов в массивах. Оно зависит от объема памяти и свойственных операционной системе ограничений (приведенные данные получены при использовании компьютера с процессором Pentium II, емкостью ОЗУ 128 Мбайт и установленной ОС Windows 98).
Для установки типа терминала может использоваться еще одна команда — terminal. Возможные типы терминалов можно найти в справке по этой команде, выводимой командой help terminal. На этом рассмотрение команд прямого общения с операционными системами можно считать законченным.
38. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Работать с меню, панелями инструментов и буфером обмена.
-
Использовать браузеры рабочего пространства и файловой системы.
-
Запускать примеры приложения Simulink.
-
Осуществлять печать документов.
-
Работать с редактором/отладчиком m-файлов.
-
Различать файлы-сценарии и файлы-функции.
-
Работать с окнами графики.
-
Использовать команды взаимодействия MATLAB с операционной системой и Интернетом.
Урок 6. Обычная графика MATLAB
1. Урок 6. Обычная графика MATLAB
Урок №6.
Обычная графика MATLAB
-
Построение графиков точками и отрезками прямых
-
Графики в логарифмическоми полулогарифмическом масштабе
-
Гистограммы и диаграммы
-
Графики специальных типов
-
Создание массивов данных для трехмерной графики
-
Построение графиков трехмерных поверхностей, сечений и контуров
-
Средства управления подсветкой и обзором фигур
-
Средства оформления графиков
-
Одновременный вывод нескольких графиков
-
Управление цветовой палитрой
-
Окраска трехмерных поверхностей
-
Двумерные и трехмерные графические объекты
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.
2. Построение графиков отрезками прямых
Построение графиков отрезками прямых
Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.
-
plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:
» х=[0 12345];
» Y=[sin(x):cos(x)];
» plot(x.Y)
На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.
Рис. 6.1. Графики двух функций в декартовой системе координат
-
plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.
Вот пример использования команды plot(Y):
» х=2*pi:0.02*pi:2*pi;
» y=sin(x)+i*cos(3*x);
» plot(y)
Соответствующий график показан на рис. 6.2.
Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами
-
plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы.
|
Y |
Желтый |
|
М |
Фиолетовый |
|
С |
Голубой |
|
R |
Красный |
|
G |
Зеленый |
|
В |
Синий |
|
W |
Белый |
|
К |
Черный |
|
|
Точка |
|
0 |
Окружность |
|
X |
Крест |
|
+ |
Плюс |
|
* |
Звездочка |
|
S |
Квадрат |
|
D |
Ромб |
|
V |
Треугольник (вниз) |
|
А |
Треугольник (вверх) |
|
< |
Треугольник (влево) |
|
> |
Треугольник (вправо) |
|
Р |
Пятиугольник |
|
H |
Шестиугольник |
|
- |
Сплошная |
|
|
Двойной пунктир |
|
-. |
Штрих-пунктир |
|
-- |
Штриховая |
Таким образом, с помощью строковой константы S можно изменять цвет линии, представлять узловые точки различными отметками (точка, окружность, крест, треугольник с разной ориентацией вершины и т. д.) и менять тип линии графика.
-
рlot (X1. Y1, S1, Х2, Y2. S2. ХЗ. Y3, S3,...) — эта команда строит на одном графике ряд линий, представленных данными вида (X..Y..S.), где X. и Y. — векторы или матрицы, a S. — строки. С помощью такой конструкции возможно построение, например, графика функции линией, цвет которой отличается от цвета узловых точек. Так, если надо построить график функции линией синего цвета с красными точками, то вначале надо задать построение графика с точками красного цвета (без линии), а затем графика только линии синего цвета (без точек).
При отсутствии указания на цвет линий и точек он выбирается автоматически из таблицы цветов (белый исключается). Если линий больше шести, то выбор цветов повторяется. Для монохромных систем линии выделяются стилем.
Рассмотрим пример построения графиков трех функций с различным стилем представления каждой из них:
» x=-2*pi:0.1*pi:2*pi;
» yl=sin(x);
» y2=sin(x).^2;
» y3=sin(x).^3:
» plot(x.yl.'-m',x,y2.'-.+r'.х.у3,'--ok')
Графики функций для этого примера показаны на рис. 6.3.
Рис. 6.3. Построение графиков трех функций на одном рисунке с разным стилем линий
Здесь график функции yl строится сплошной фиолетовой линией, график у2 строится штрих пунктирной линией с точками в виде знака «плюс» красного цвета, а график уЗ строится штриховой линией с кружками черного цвета. К сожалению, на черно-белых рисунках этой книги вместо разных цветов видны разные градации серого цвета.
1.gif
2.gif
3.gif

3. Графики в логарифмическом масштабе
Графики в логарифмическом масштабе
Для построения графиков функций со значениями х и у, изменяющимися в широких пределах, нередко используются логарифмические масштабы. Рассмотрим команды, которые используются в таких случаях.
-
loglogx(...) — синтаксис команды аналогичен ранее рассмотренному для функции plot(...). Логарифмический масштаб используется для координатных осей X и У. Ниже дан пример применения данной команды:
» x=logspace(-1,3);
» loglog(x.exp(x)./x)
» grid on
На рис. 6.4 представлен график функции ехр(х)/х в логарифмическом масштабе. Обратите внимание на то, что командой grid on строится координатная сетка.
Неравномерное расположение линий координатной сетки указывает на логарифмический масштаб осей.
Рис. 6.4. График функции ехр(x)/x в логарифмическом масштабе
4a.gif
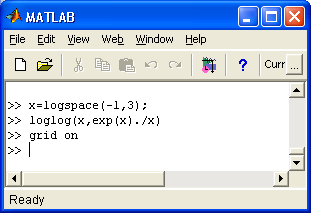
4b.gif
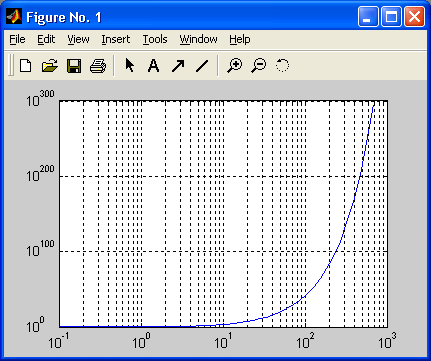
4. Графики в полулогарифмическом масштабе
Графики в полулогарифмическом масштабе
В некоторых случаях предпочтителен полулогарифмический масштаб графиков, когда по одной оси задается логарифмический масштаб, а по другой — линейный.
Для построения графиков функций в полулогарифмическом масштабе используются следующие команды:
-
semilogx(...) — строит график функции в логарифмическом масштабе (основание 10) по оси X и линейном по оси Y;
-
semilоgу (...) — строит график функции в логарифмическом масштабе по оси Y и линейном по оси X.
Рис. 6.5. График экспоненты в полулогарифмическом масштабе
Запись параметров (...) выполняется по аналогии с функцией plot(...). Ниже приводится пример построения графика экспоненциальной функции:
» х=0:0.5:10;
» semilogy(x.exp(x))
График функции при логарифмическом масштабе по оси У представлен на рис. 6.5.
Нетрудно заметить, что при таком масштабе график экспоненциальной функции выродился в прямую линию. Масштабной сетки теперь уже нет.
5.gif
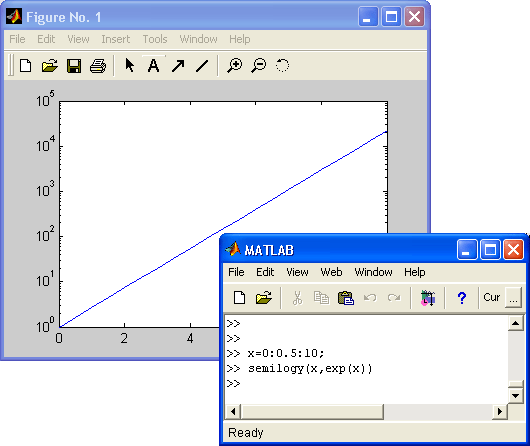
5. Столбцовые диаграммы
Столбцовые диаграммы
Столбцовые диаграммы широко используются в литературе, посвященной финансам и экономике, а также в математической литературе. Ниже представлены команды для построения таких диаграмм.
-
bar(x, Y) — строит столбцовый график элементов вектора Y (или группы столбцов для матрицы Y) со спецификацией положения столбцов, заданной значениями элементов вектора х, которые должны идти в монотонно возрастающем порядке;
-
bar(Y) — строит график значений элементов матрицы Y так же, как указано выше, но фактически для построения графика используется вектор х=1:m;
-
barU.Y,WIDTH) или BAR(Y,WIDTH) — команда аналогична ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По умолчанию задано WIDTH = 0.8.
Возможно применение этих команд и в следующем виде: bаг(.... 'Спецификация') для задания спецификации графиков, например типа линий, цвета и т. д., по аналогии с командой plot. Спецификация 'stacked' задает рисование всех n столбцов в позиции m друг на друге.
Пример построения столбцовой диаграммы матрицы размером 12x3 приводится ниже:
» % Столбцовая диаграмма с вертикальными столбцами
» subplot(2.1.1). bar(rand(12.3).'stacked'), colormap(cool)
На рис. 6.6 представлен полученный график.
Рис. 6.6. Пример построения диаграммы с вертикальными столбцами
Помимо команды bar(...) существует аналогичная ей по синтаксису команда barh(...), которая" строит столбцовые диаграммы с горизонтальным расположением столбцов. Пример, приведенный ниже, дает построения, показанные на рис. 6.7.
» subplot(2.1.1). barh(rand(5.3).'stacked'), colormap(cool)
Рис. 6.7. Пример построения столбцовой диаграммы с горизонтальными столбцами
Какое именно расположение столбцов выбрать, зависит от пользователя, использующего эти команды для представления своих данных.
6a.gif
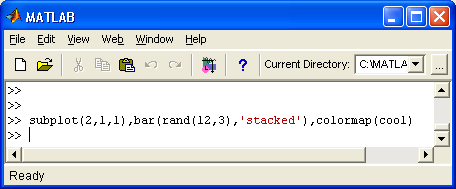
6b.gif
6c.gif
7a.gif

7b.gif
6. Построение гистограмм
Построение гистограмм
Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы служит функция hist, записываемая в следующем виде:
-
N=hist(Y) — возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y — матрица, то выдается массив данных о числе попаданий для каждого из ее столбцов;
-
N=hist(Y,M) — аналогична вышерассмотренной, но используется М интервалов (М — скаляр);
-
N=hist(Y.X) — возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора X;
-
[N,X]=HIST(...) — возвращает числа попаданий в интервалы и данные о центрах интервалов.
Команда hist(...) с синтаксисом, аналогичным приведенному выше, строит график гистограммы. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором х:
» х=-3:0.2:3;
» y=randn(1000,1);
» hist(y,x)
» h=hist(y.x)
h =
Columns 1 through 12
0 0 3 7 8 9 11 23 33 43 57 55
Columns 13 through 24
70 62 83 87 93 68 70 65 41 35 27 21
Columns 25 through 31
12 5 6 3 2 1 0
Построенная гистограмма показана на рис. 6.8.
Рис. 6.8. Пример построения гистограммы
Нетрудно заметить, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно наблюдать еще большее соответствие этому закону.
8.gif
7. Лестничные графики - команды stairs
Лестничные графики — команды stairs
Лестничные графики визуально представляют собой ступеньки с огибающей, представленной функцией у(х). Такие графики используются, например, для отображения процессов квантования функции у(х), представленной рядом своих отсчетов. При этом в промежутках между отсчетами значения функции считаются постоянными и равными величине последнего отсчета.
Для построения лестничных графиков в системе MATLAB используются команды группы stairs:
-
stairs(Y) — строит лестничный график по данным вектора Y;
-
stairs(X.Y) — строит лестничный график по данным вектора Y с координатами х переходов от ступеньки к ступеньке, заданными значениями элементов вектора X;
-
stairs(...,S) — аналогична по действию вышеописанным командам, но строит график линиями, стиль которых задается строками S.
Следующий пример иллюстрирует построение лестничного графика:
» х=0:0.25:10;
» stairs(x,x. ^ 2);
Результат построения представлен на рис. 6.9.
Рис. 6.9. Лестничный график функции х ^ 2
Обратите внимание на то, что отсчеты берутся через равные промежутки по горизонтальной оси. Если, к примеру, отображается функция времени, то stairs имеет вид квантованной по времени функции.
Функция H=stairs(X,Y) возвращает вектор дескрипторов графических объектов.
Функция
[XX,YY]=stairs(X.Y)
сама по себе график не строит, а возвращает векторы XX и YY, которые позволяют построить график с помощью команды plot(XX.YY).
9.gif
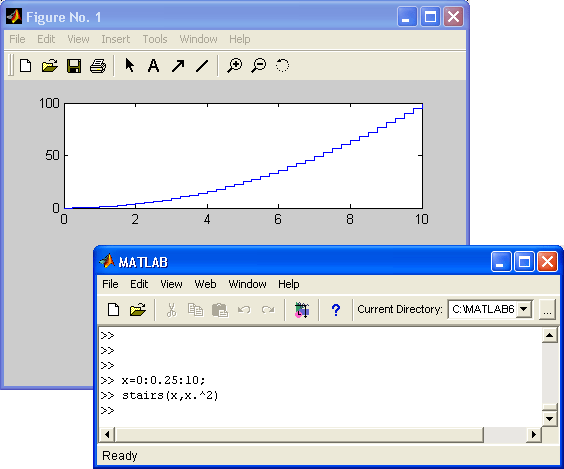
8. Графики с зонами погрешности
Графики с зонами погрешности
Если данные для построения функции определены с заметной погрешностью, то используют графики функций типа errorbar с оценкой погрешности каждой точки путем ее представления в виде буквы I, высота которой соответствует заданной погрешности представления точки. Команда errorbar используется в следующем виде:
-
errorbar(X,Y,L.U) — строит график значений элементов вектора Y в зависимости от данных, содержащихся в векторе X, с указанием нижней и верхней границ значений, заданных в векторах L и U;
-
errorbar(X,Y,E) Herrorbar(Y.E) —строит графики функции Y(X) с указанием этих границ в виде [Y-E Y+E], где Е — погрешность;
-
errorbar(..., 'LineSpec') — аналогична описанным выше командам, но позволяет строить линии со спецификацией 'LineSpec', аналогичной спецификации, примененной в команде plot.
Следующий пример иллюстрирует применение команды errorbar:
» х=2:0.1:2:
» y=erf(x):
» е=rand(size(x))/10;
» errorbar(x.y.e)
Построенный график показан на рис. 6.10.
Рис. 6.10. График функции erf(x) с зонами погрешности
Функция, записываемая в виде H=ERRORBAR(...), возвращает вектор дескрипторов графических объектов.
10.gif
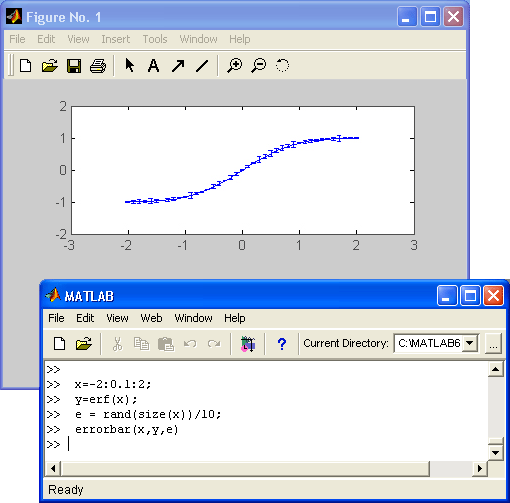
9. График дискретных отсчетов функции
График дискретных отсчетов функции
Еще один вид графика функции у(х) — ее представление дискретными отсчетами. Этот вид графика применяется, например, при описании квантования сигналов. Каждый отсчет представляется вертикальной чертой, увенчанной кружком, причем высота черты соответствует y-координате точки.
Рис. 6.11. График дискретных отсчетов функции
Для построения графика подобного вида используются команды stem(...):
-
stem(X.Y) — строит график отсчетов с ординатами в векторе Y и абсциссами в векторе X;
-
stem(.... 'LINESPEC') — дает построения, аналогичные ранее приведенным командам, но со спецификацией линий 'LINESPEC', подобной спецификации, приведенной для функции plot;
-
stem(Y) — строит график функции с ординатами в векторе Y в виде отсчетов;
-
stem(.... 'filled') — строит график функции с закрашенными маркерами. Следующий пример иллюстрирует применение команды stem:
» х = 0:0.1:4;
» у = sin(x. ^ 2).*exp(-x):
» stem(x.y)
Полученный для данного примера график показан на рис. 6.11.
Функция H=STEM(...) строит график и возвращает вектор дескрипторов графических объектов.
11.gif
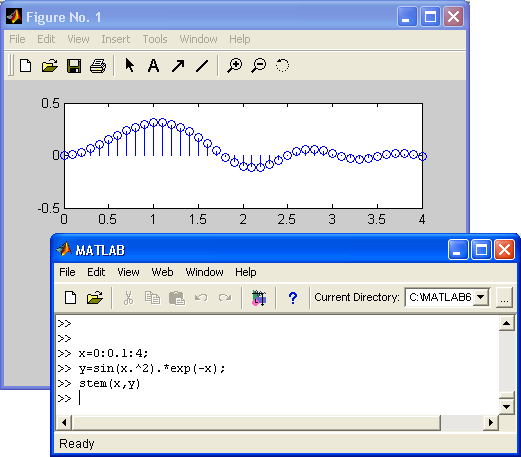
10. Графики в полярной системе координат
Графики в полярной системе координат
В полярной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат, имеющего длину RHO и угол ТНЕТА. Для построения графика функции RHO(THETA) используются приведенные ниже команды. Угол ТНЕТА обычно меняется от 0 до 2*pi. Для построения графиков функций в полярной системе координат используются команды типа polar(...):
-
polarCTHETA, RHO) — строит график в полярной системе координат, представляющий собой положение конца радиус-вектора с длиной RHO и углом ТНЕТА;
-
polarCTHETA,RHO.S) — аналогична предыдущей команде, но позволяет задавать стиль построения с помощью строковой константы S по аналогии с командой plot.
Рис. 6.12 демонстрирует результат выполнения команд:
» t=0:pi/50:2*pi;
» polar(t,sin(5*t))
Рис. 6.12. График функции в полярной системе координат
Графики функций в полярных координатах могут иметь весьма разнообразный вид, порой напоминая такие объекты природы, как снежинки или кристаллики льда на стекле. Вы можете сами попробовать построить несколько таких графиков — многие получают от этого удовольствие.
12.gif
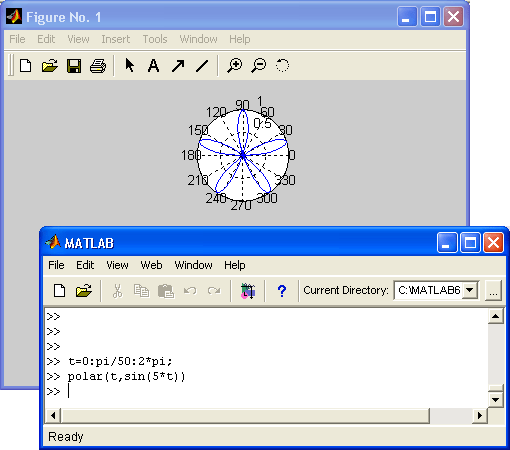
11. Угловые гистограммы
Угловые гистограммы
Угловые гистограммы находят применение в индикаторах радиолокационных станций, для отображения «роз» ветров и при построении других специальных графиков. Для этого используется ряд команд типа rose(...):
-
rose(THETA) — строит угловую гистограмму для 20 интервалов по данным вектора ТНЕТА;
-
rose(ТНЕТА, N) — строит угловую гистограмму для N интервалов в пределах угла от 0 до 2*рi по данным вектора ТНЕТА;
-
rose(ТНЕТА. X) — строит угловую гистограмму по данным вектора ТНЕТА со спецификацией интервалов, указанной в векторе X.
Следующий пример иллюстрирует применение команды rose: » rose(1:100.12)
На рис. 6.13 показан пример построения графика командой rose.
Рис. 6.13. Угловая гистограмма
Функция H=rose(...) строит график и возвращает вектор дескрипторов графических объектов, а функция [T,R]=rose(...) сама по себе график не строит, но возвращает векторы Т и R, которые нужны команде polar (Т. R) для построения подобной гистограммы.
13.gif
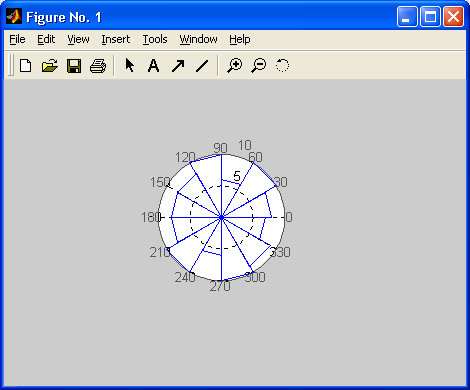
12. Графики векторов
Графики векторов
Иногда желательно представление ряда радиус-векторов в их обычном виде, то есть в виде стрелок, исходящих из начала координат и имеющих угол и длину, определяемые действительной и мнимой частью комплексных чисел, представляющих эти векторы. Для этого служит группа команд compass:
-
compass(U.V) — строит графики радиус-векторов с компонентами (U.V), представляющими действительную и мнимую части каждого из радиус-векторов;
-
compass (Z) — эквивалентно compass (real (Z), imag(Z));
-
compass(U.V,LINESPEC) и Compass(Z.LINESPEC) — аналогичны представленным выше командам, но позволяют задавать спецификацию линий построения LINESPEC, подобную описанной для команды plot.
В следующем примере показано использование команды compass:
» Z=[-1+2i,-2-3i.2+3i.5+2i];
» compass(Z)
Построенный в этом примере график представлен на рис. 6.14.
Рис. 6.14. Построение радиус-векторов
Функция H=COMPASS(...) строит график и возвращает дескрипторы графических объектов.
14.gif
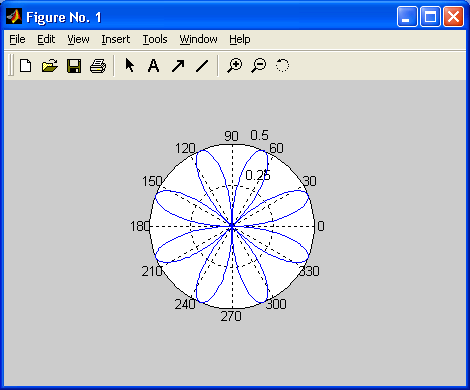
13. График проекций векторов на плоскость
График проекций векторов на плоскость
Иногда полезно отображать комплексные величины вида z = х + yi в виде проекции радиус-вектора на плоскость. Для этого используется семейство графических команд класса feather:
-
feather(U.V) — строит график проекции векторов, заданных компонентами U и V, на плоскость;
-
feather (Z) — для вектора Z с комплексными элементами дает построения, аналогичные feather(REAL(Z),IMAG(Z));
-
feather(..., S) — дает построения, описанные выше, но со спецификацией линий, заданной строковой константой S по аналогии с командой plot.
Пример применения команды feather:
» x=0:0.1*pi:3*pi;
»y=0.05+i;
» z=exp(x*y);
» feather(z)
График, построенный в этом последнем примере, показан на рис. 6.15.
Рис. 6.15. График, построенный функцией feather
Функция Н=РЕАТНЕR(...)строит график и возвращает вектор дескрипторов графических объектов.
15a.gif
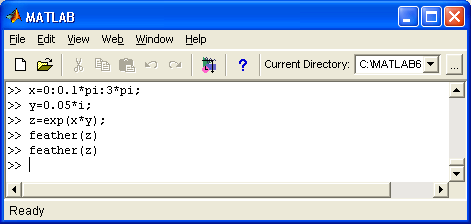
15b.gif
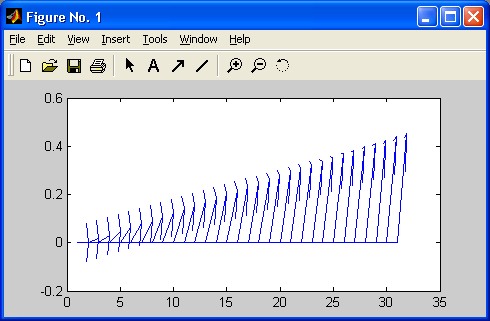
14. Контурные графики
Контурные графики
Контурные графики служат для представления на плоскости функции двух переменных вида z(x, у) с помощью линий равного уровня. Они получаются, если трехмерная поверхность пересекается рядом плоскостей, расположенных параллельно друг другу. При этом контурный график представляет собой совокупность спроецированных на плоскость (х, у) линий пересечения поверхности г(х, у) плоскостями.
Для построения контурных графиков используются команды contour:
-
contour(Z) — строит контурный график по данным матрицы Z с автоматическим заданием диапазонов изменения х и у;
-
contour(X.Y.Z) — строит контурный график по данным матрицы Z с указанием спецификаций для X и Y;О contour(Z.N) и contour(X.Y.Z.N) — дает построения, аналогичные ранее описанным командам, с заданием N линий равного уровня (по умолчанию N=10);
-
contour(Z, V) и contour(X,Y,Z,V) — строят линии равного уровня для высот, указанных значениями элементов вектора V;
-
contour(Z,[v v]) или contour(X.Y,Z.[v v]) — вычисляет одиночный контур для уровня v;
-
[С.Н] = contour (...) — возвращает дескрипторы — матрицу С и вектор-столбец Н. Они могут использоваться как входные параметры для команды clabel;
-
contourC... 'LINESPEC') — позволяет использовать перечисленные выше команды с указанием спецификации линий, которыми идет построение.
Пример построения контурного графика поверхности, заданной функций peaks:
» z=peaks(27);
» contour(z,15)
Построенный в этом примере график показан на рис. 6,16. Заметим, что объект — функция peaks — задан в системе в готовом виде.
Рис. 6.16. Контурный график, построенный с помощью команды contour
Графики этого типа часто используются в топографии для представления на листе бумаги (как говорят математики — на плоскости) объемного рельефа местности. Для оценки высот контурных линий используется их функциональная окраска.
16a.gif

16b.gif
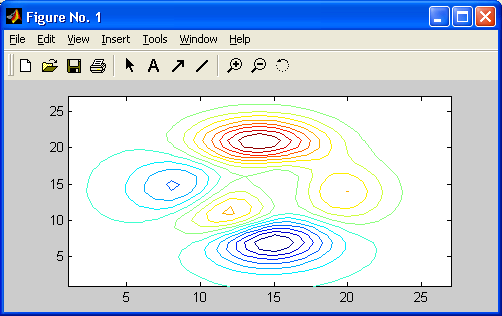
15. Создание массивов данных для трехмерной графики
Создание массивов данных для трехмерной графики
Трехмерные поверхности обычно описываются функцией двух переменных z(x, у). Специфика построения трехмерных графиков требует не просто задания ряда значений х и у, то есть векторов х и у. Она требует определения для X и Y двумерных массивов — матриц. Для создания таких массивов служит функция meshgrid. В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid записывается в следующих формах:
-
[X.Y] = meshgrid(x) — аналогична [X.Y] = meshgrid(x.x);
-
[X.Y.Z] = meshgrid(x.y,z) — возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных графиков;
-
[X.Y] = meshgrid(x.y) — преобразует область, заданную векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора х; а столбцы Y — копиями вектора у.
Пример:
» [X.Y] = meshgnd(l:4.13:17)
X =
|
|
|||||
|
|
1 |
2 |
3 |
4 |
|
|
|
1 |
2 |
3 |
4 |
|
|
|
1 |
2 |
3 |
4 |
|
|
|
1 |
2 |
3 |
4 |
|
|
|
1 |
2 |
3 |
4 |
|
|
|
Y= |
|
|
|
|
|
|
13 |
13 |
13 |
13 |
|
|
|
14 |
14 |
14 |
14 |
|
|
|
15 |
15 |
15 |
15 |
|
|
|
16 |
16 |
16 |
16 |
|
|
|
17 |
17 |
17 |
17 |
|
Приведем еще один пример применения функции meshgrid:
» [X.Y] = meshgrid(-2:.2:2. -2:.2:2);
Такой вызов функции позволяет задать опорную плоскость для построения трехмерной поверхности при изменении дгиг/от-2до2с шагом 0.2. Дополнительные примеры применения функции meshgrid будут приведены далее при описании соответствующих команд. Рекомендуется ознакомиться с также командами surf и slice (ломтик).
Функция ndgrid является многомерным аналогом функции meshgrid:
-
[Х1.Х2.ХЗ,...] = ndgrid(xl,x2,x3....) — преобразует область, заданную векторами xl.x2.x3..., в массивы Х1.Х2.ХЗ..., которые могут быть использованы для вычисления функций нескольких переменных и многомерной интерполяции, i-я размерность выходного массива xi является копией вектора xi;
-
[XI.Х2....] = ndgrid(x) - аналогична [XI.Х2....] = ndgrid(x,x,...). Пример применения функции ndgrid представлен ниже:
»[Х1.'Х2] = ndgrid(-2:.2:2. -2:.2:2);
»Z = XI .* ехр(-Х1."2 - Х2.*2);
»mesh(Z)
Рекомендуем читателю опробовать действие этого примера.
16. Графики поля градиентов quiver
Графики поля градиентов quiver
Для построения графиков полей градиента служат команды quiver:
-
quiver(X.Y.U.V) — строит график поля градиентов в виде стрелок для каждой пары элементов массивов X и Y, причем элементы массивов U и V указывают направление и размер стрелок;
-
qui ver(U, V) — строит векторы скорости в равнорасположенных точках на плоскости (х, у);
-
quiver(U,V,S) или quiver(X,Y.U,V,S) — автоматически масштабирует стрелки по сетке и затем вытягивает их по значению S. Используйте S=0, чтобы построить стрелки без автоматического масштабирования;
-
quiver(...,LINESPEC) — использует для векторов указанный тип линии. Указанные в LINESPEC маркеры рисуются у оснований, а не на концах векторов. Для отмены любого вида маркера используйте спецификацию '.'. Спецификации линий, цветов и маркеров были подробно описаны в разделе, посвященном команде plot;
-
quiver(.... 'filled') — дает график с закрашенными маркерами;
-
H=quiver(...) — строит график и возвращает вектор дескрипторов. Ниже представлен пример применения команды quiver:
» х = -2:.2:2; у = -1:.2:1;
» [хх.уу] = meshgrid(x,y);
» zz = хх.*ехр(-хх. х 2-уу.~2);
» [рх.ру] = gradient(zz..2..2);
» quiver(x.y.px.py,2);
Построенный в этом примере график показан на рис. 6.17.
Рис. 6.17. Пример построения графика поля градиентов
Нетрудно заметить, что представление поля градиентов стрелками дает весьма наглядное представление о линиях поля, указывая области, куда эти линии впадают и откуда они исходят.
17.gif
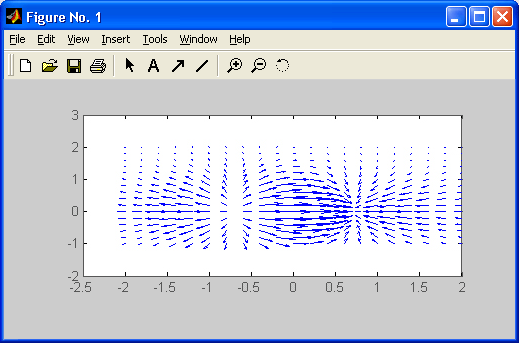
17. Построение графиков поверхностей
Построение графиков поверхностей
Команда plot3(...) является аналогом команды plot (...), но относится к функции двух переменных z(x, у). Она строит аксонометрическое изображение трехмерных поверхностей и представлена следующими формами:
-
plot3(x.y,z) — строит массив точек, представленных векторами х, у и z, соединяя их отрезками прямых. Эта команда имеет ограниченное применение;
-
plot3(X,Y,Z), где X, Y и Z — три матрицы одинакового размера, строит точки с координатами X(i.:), Y(i,:) и Z(i,:) и соединяет их отрезками прямых.
Ниже дан пример построения трехмерной поверхности, описываемой функцией
z(х.у)=х^2+у^2;
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X. ^ 2+Y.^2;
» plot3(X.Y.Z)
График этой поверхности показан на рис. 6.18.
Рис. 6.18. График поверхности, построенный линиями
-
plot3 (X. Y, Z, S) — обеспечивает построения, аналогичные рассмотренным ранее, но со спецификацией стиля линий и точек, соответствующей спецификации команды plot. Ниже дан пример применения этой команды для построения поверхности кружками:
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X. ^ 2+Y.^2;
» plot3(X,Y,Z.'o')
График поверхности, построенный кружками, показан на рис. 6.19.
Рис. 6.19. График поверхности, построенный разноцветными кружками
-
plot3(xl ,yl.zl, sl.х2,у2.z2. s2. хЗ,уЗ.z3,s3,...)— строит на одном рисунке графики нескольких функций zl(xl ,yl), z2(x2,y2) и т. д. со спецификацией линий и маркеров каждой из них.
Пример применения последней команды дан ниже:
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X. ^ 2+Y.^2;
» plot3(X,Y,Z,'-k',Y,X,Z,'-k ' )
График функции, соответствующей последнему примеру, представлен на рис. 6.20.
Рис. 6.20. График функции в сетчатом представлении
В данном случае строятся два графика одной и той же функции с взаимно перпендикулярными образующими линиями. Поэтому график имеет вид сетки без окраски ее ячеек (напоминает проволочный каркас фигуры).
18a.gif

18b.gif
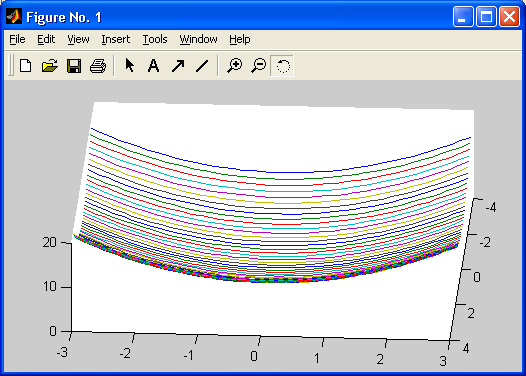
19a.gif
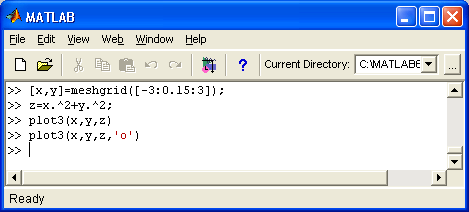
19b.gif
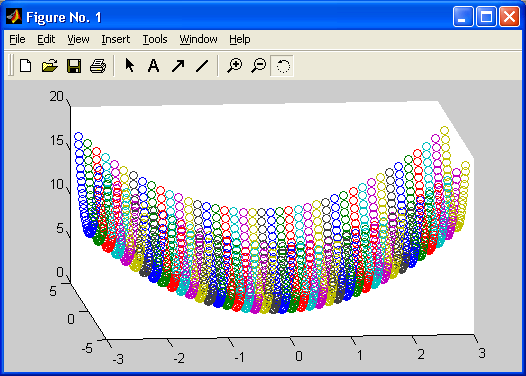
20a.gif

20b.gif
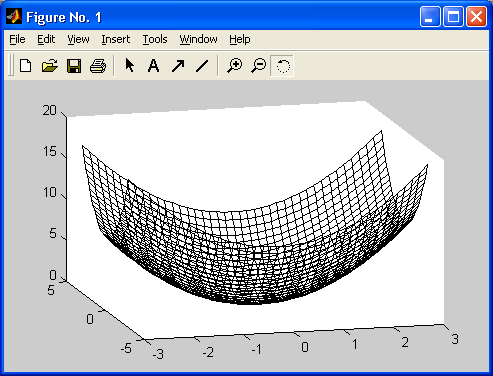
18. Сетчатые 3D-графики с окраской
Сетчатые 3D-графики с окраской
Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. В названии их команд присутствует слово mesh. Имеются три группы таких команд. Ниже приведены данные о наиболее полных формах этих команд. Наличие более простых форм можно уточнить, используя команду help Имя, где Имя — имя соответствующей команды.
-
mesh(X,Y,Z,C) — выводит в графическое окно сетчатую поверхность Z(X.Y) с цветами узлов поверхности, заданными массивом С;
-
mesh(X.Y.Z) — аналог предшествующей команды при C=Z. В данном случае используется функциональная окраска, при которой цвет задается высотой поверхности.
Возможны также формы команды mesh(x,y.Z), mesh(x.y.Z,C), mesh(Z) и mesh(Z.C).
Функция mesh возвращает дескриптор для объекта класса surface. Ниже приводится пример применения команды mesh:
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X.^2+Y.^2;
» mesh(X,Y,Z)
На рис. 6.21 показан график поверхности, созданной командой mesh(X.Y.Z). Нетрудно заметить, что функциональная окраска линий поверхности заметно усиливает наглядность ее представления.
Рис. 6.21. График поверхности, созданный командой mesh(X,Y,Z)
MATLAB имеет несколько графических функций, возвращающих матричный образ поверхностей. Например, функция peaks(N) возвращает матричный образ поверхности с рядом пиков и впадин. Такие функции удобно использовать для проверки работы графических команд трехмерной графики. Для упомянутой функции peaks можно привести такой пример:
» z=peaks(25);
» mesh(z);
График поверхности, описываемой функцией peaks, представлен на рис. 6.22.
Рис. 6.22. График поверхности, описываемой функцией peaks
Рекомендуется ознакомиться с командами и функциями, используемыми совместно с описанными командами: axis, caxis, colormap, hold, shading и view.
21a.gif
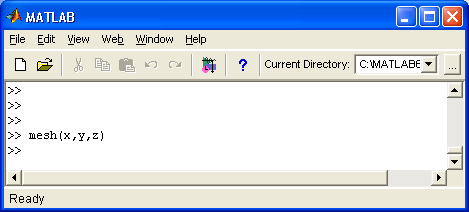
21b.gif
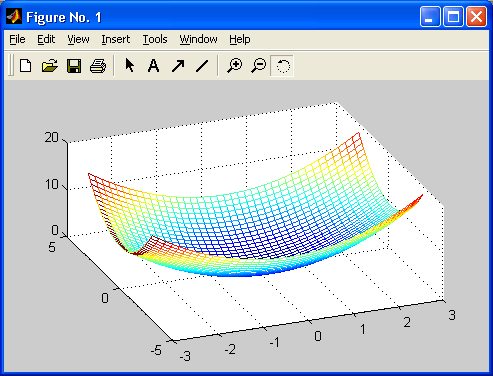
22a.gif

22b.gif
19. Сетчатые 3D-графики с проекциями
Сетчатые 3D-графики с проекциями
Иногда график поверхности полезно объединить с контурным графиком ее проекции на плоскость, расположенным под поверхностью.
Для этого используется команда meshc:
-
meshc(...) — аналогична mesh(...), но помимо графика поверхности дает изображение ее проекции в виде линий равного уровня (графика типа contour).
Ниже дан пример применения этой команды:
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X.^2+Y.^2;
» meshc(X,Y,Z)
Построенный график показан на рис. 6.23.
Рис. 6.23. График поверхности и ее проекции на расположенную ниже плоскость
Нетрудно заметить, что график такого типа дает наилучшее представление об особенностях поверхности.
23a.gif
23b.gif
20. Построение поверхности столбцами
Построение поверхности столбцами
Еще один тип представления поверхности, когда она строится из многочисленных столбцов, дают команды класса meshz:
-
meshz(...) — аналогична mesh(...), но строит поверхность как бы в виде столбиков. Следующий пример иллюстрирует применение команды mesh:
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X.^2+Y.^2;
» meshz(X,Y,Z)
Столбцовый график поверхности показан на рис. 6.24.
Графики такого типа используются довольно редко. Возможно, он полезен архитекторам или скульпторам, поскольку дает неплохое объемное представление о поверхностях.
Рис. 6.24. Построение поверхности столбцами
24a.gif
24b.gif
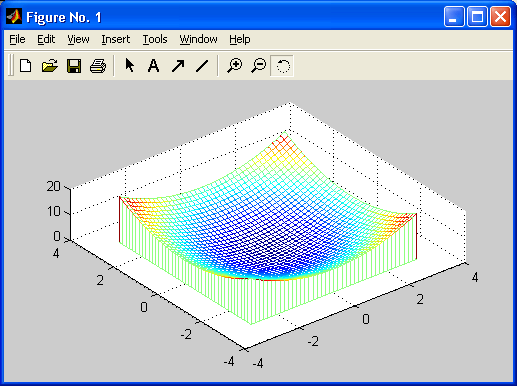
21. Построение поверхности с окраской
Построение поверхности с окраской
Особенно наглядное представление о поверхностях дают сетчатые графики, использующие функциональную закраску ячеек. Например, цвет окраски поверхности z(x, у) может быть поставлен в соответствие с высотой z поверхности с выбором для малых высот темных тонов, а для больших — светлых. Для построения таких поверхностей используются команды класса surf (...):
-
surf (X, Y, Z. С) — строит цветную параметрическую поверхность по данным матриц X, Y и Z с цветом, задаваемым массивом С;
-
surf(X.Y.Z) — аналогична предшествующей команде, где C=Z, так что цвет задается высотой той или иной ячейки поверхности;
-
surf(x.y.Z) и surf(x.y.Z.C) с двумя векторными аргументами х и у — векторы х и у заменяют первых два матричных аргумента и должны иметь длины length(x)=n и length(y)=m, где [m.n]=size(Z). В этом случае вершины областей поверхности представлены тройками координат (x(j), yd), Z(1,j)). Заметим, что х соответствует столбцам Z, а у соответствует строкам;
-
surf(Z) и surf(Z.C) используют х = 1:n и у = 1:m. В этом случае высота Z — однозначно определенная функция, заданная геометрически прямоугольной сеткой;
-
h=surf (...) —строит поверхность и возвращает дескриптор объекта класса surface.
Команды axis, caxis, color-map, hold, shading и view задают координатные оси и свойства поверхности, которые могут использоваться для большей эффектности показа поверхности или фигуры.
Ниже приведен простой пример построения поверхности — параболоида:
» [X.Y]=meshgrid([-3:0.15:3]);
» Z=X.^2+Y.^2;
» Surf(X,Y,Z)
Соответствующий этому примеру график показан на рис. 6.25.
Рис. 6.25. График параболоида с функциональной окраской ячеек
Можно заметить, что благодаря функциональной окраске график поверхности гораздо более выразителен, чем при построениях без такой окраски, представленных ранее (причем даже в том случае, когда цветной график печатается в черно-белом виде).
В следующем примере используется функциональная окраска оттенками серого цвета с выводом шкалы цветовых оттенков:
» [X,Y]=meshgrid([-3:0.1:3]);
» Z=sin(X)./(X.^2+Y.^2+0.3);
» surf(X.Y.Z)
» colormap(gray)
» shading interp
» colorbar
В этом примере команда colormap(gray) задает окраску тонами серого цвета, а команда shading Interp обеспечивает устранение изображения сетки и задает интерполяцию для оттенков цвета объемной поверхности. На рис. 6.26 показан вид графика, построенного в этом примере.
Рис. 6.26. График поверхности с функциональной окраской серым цветом
Обычно применение интерполяции для окраски придает поверхностям и фигурам более реалистичный вид, но фигуры каркасного вида дают более точные количественные данные о каждой точке.
25.gif
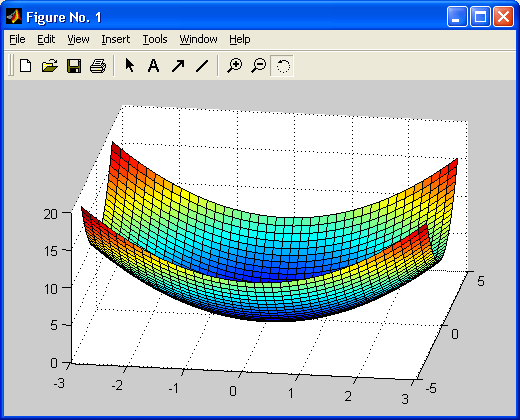
26.gif
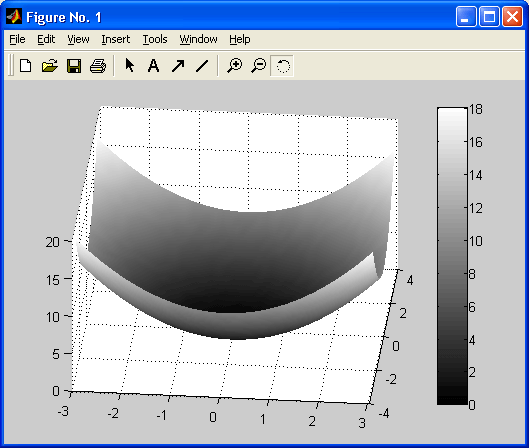
22. Построение поверхности и ее проекции
Построение поверхности и ее проекции
Для повышения наглядности представления поверхностей можно использовать дополнительный график линий равного уровня, получаемый путем проецирования поверхности на опорную плоскость графика (под поверхностью). Для этого используется команда surf с:
-
surfc(...) — аналогична команде surf, но обеспечивает дополнительное построение контурного графика проекции фигуры на опорную плоскость.
Пример применения команды surf с приводится ниже:
» [X.Y]=meshgrid([-3:0.1:3]);
» Z=sin(X)./(X.^2+Y.^2+0.3);
» surfc(X,Y,Z)
На рис. 6.27 показаны графики, построенные в данном примере.
Рис. 6.27. График поверхности и ее проекции на опорную плоскость
Рассмотрим еще один пример применения команды surf с, на этот раз для построения поверхности, описываемой функцией peaks, с применением интерполяции цветов и построением цветовой шкалы:
» [X.Y]=meshgrid([-3:0.1:3]);
» Z=peaks(X,Y);
» surfc(X,Y,Z)
» shading interp
» colorbar
Рис. 6.28 показывает график, построенный в этом примере. И здесь нетрудно заметить, что графики сложных поверхностей с интерполяцией цветовых оттенков выглядят более реалистичными, чем графики сетчатого вида и графики без интерполяции цветов.
Рис. 6.28. График функции peaks с проекцией и шкалой цветов
27.gif

28.gif
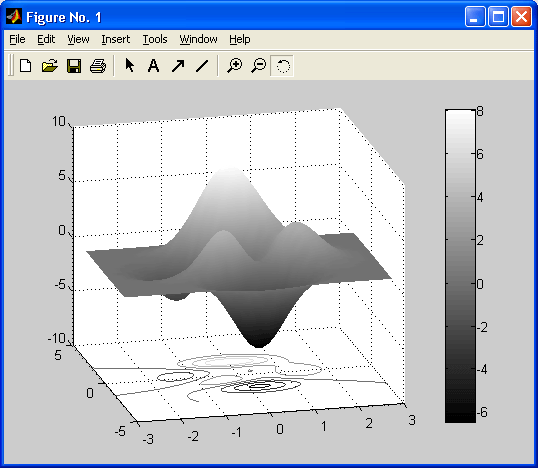
23. Построение освещенной поверхности
Построение освещенной поверхности
Пожалуй, наиболее реалистичный вид имеют графики поверхностей, в которых имитируется освещение от точечного источника света, расположенного в заданном месте координатной системы. Графики имитируют оптические эффекты рассеивания, отражения и зеркального отражения света. Для получения таких графиков используется команда surf 1:
-
surfl(...) — аналогична команде surf (...), но строит график поверхности с подсветкой от источника света;
-
surfl (Z.S) или surfl(X,Y,Z,S) — строит графики поверхности с подсветкой от источника света, положение которого в системе декартовых координат задается вектором S=[Sx,Sy.Sz], а в системе сферических координат — вектором S=[AZ.EL];
-
surfl (..., 'light') — позволяет при построении задать цвет подсветки с помощью объекта Light;
-
surfl (..., 'cdata') — при построении имитирует эффект отражения;
-
surfl(X,Y,Z,S.K) — задает построение поверхности с параметрами, заданными вектором K=[ka,kd,ks.spread], где ka — коэффициент фоновой подсветки, kd — коэффициент диффузного отражения, ks — коэффициент зеркального отражения и spread — коэффициент глянцевитости;
-
H=surf 1 (...) — строит поверхность и возвращает дескрипторы поверхности и источников света.
По умолчанию вектор S задает углы азимута и возвышения в 45°. Используя команды cla, hold on, view(AZ,EL), surfl (...) и hold off, можно получить дополнительные возможности управления освещением. Надо полагаться на упорядочение точек в X, Y, и Z матрицах, чтобы определить внутреннюю и внешнюю стороны параметрических поверхностей. Попробуйте транспонировать матрицы и использовать surfHX' .Y' ,Z'), если вам не понравился результат работы этой команды. Для вычисления векторов нормалей поверхности surf1 требует в качестве аргументов матрицы с размером по крайней мере 3x3.
Ниже представлен пример применения команды surfl:
» [X.Y]=meshgrid([-3:0.1:3]);
» Z=sin(X)./(X. ^ 2+Y.^2+0.3);
» surfl(X,Y,Z)
» colormap(gray)
» shading interp
» colorbar
Построенная в этом примере поверхность представлена на рис. 6.29.
Рис. 6.29. График поверхности с имитацией ее освещения точечным источником
Сравните этот рисунок с рис. 6.26, на котором та же поверхность построена без имитации ее освещения.
Примечание
Нетрудно заметить определенную логику в названиях графических команд. Имя команды состоит из основного слова и суффикса расширения. Например, все команды построения поверхностей имеют основное слово surf (сокращение от surface — поверхность) и суффиксы: с — для контурных линий поверхности, l — для освещенности и т. д. Это правило облегчает запоминание многочисленных команд графики.
29.gif
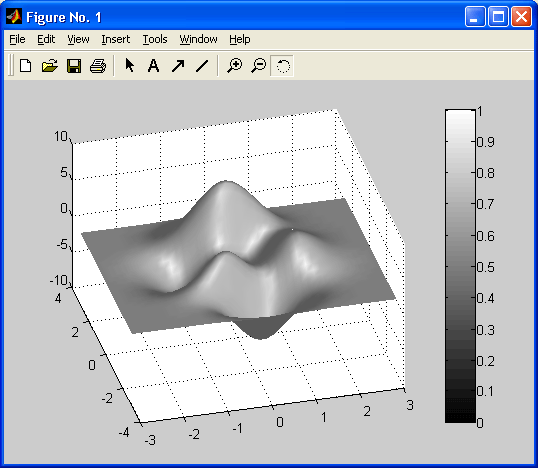
24. Средства управления подсветкой и обзором фигур
Средства управления подсветкой и обзором фигур
Рекомендуется с помощью команды help ознакомиться с командами, задающими управление подсветкой и связанными с ней оптическими эффектами:
-
diffuse — задание эффекта диффузионного рассеяния;
-
lighting — управление подсветкой;
-
material — имитация свойств рассеивания света различными материалами;
-
specular — задание эффекта зеркального отражения.
Следующие три команды позволяют управлять углами просмотра, под которыми рассматривается видимая в графическом окне фигура:
-
view — задание положения точки просмотра;
-
viewmtx — задание и вычисление матрицы вращения;
-
rotateSd — задание поворота трехмерной фигуры.
В ряде случаев применением этих команд можно добиться большей выразительности трехмерных объектов. Скорость построения таких графиков сильно зависит от аппаратной поддержки графики в конкретном ПК. Так, использование современных видеоадаптеров с графическим процессором и поддержкой средств OpenGL позволяет повысить скорость построения трехмерных графиков в несколько раз и добиться большей их выразительности.
25. Построение графиков функций трех переменных
Построение графиков функций трех переменных
Графики сечений функций трех переменных строит команда slice (в переводе — «ломтик»). Она используется в следующих формах:
-
slice(X.Y.Z.V.Sx,Sy,Sz) — строит плоские сечения объемной фигуры V в направлении осей x,y,z c позициями, задаваемыми векторами Sx, Sy, Sz. Массивы X, Y, Z задают координаты для V и должны быть монотонными и трехмерными (как возвращаемые функцией meshgrid) с размером MxNxP. Цвет точек сечений определяется трехмерной интерполяцией в объемной фигуре V;
-
slice(X,Y.Z.V,XI.YI.ZI) — строит сечения объемной фигуры V по поверхности, определенной массивами XI, YI, ZI;
-
slice (... 'method') — при построении задается метод интерполяции, который может быть одним из следующих: 'linear', 'cubic' или 'nearest'. По умолчанию используется линейная интерполяция — 'linear';
-
slice(V.Sx.Sy.Sz) или slice(V.XI.YI.ZI) - подразумевается X=1:N, Y=1:M, Z=1:P;
-
H=slice(...) — строит сечение и возвращает дескриптор объекта класса surface.
График примера, приведенного ниже, представлен на рис. 6.30.
» [x.y.z]= meshgrid(-2:.2:2. -2:.25:2. -2:.16:2);
» v = sin(x) .* ехр(-х.*2 - у. ^ 2 - z. ^ 2);
» slice(x.y.z.v.[-1.2 .8 2].2.[-2 -.2])
26. График трехмерной слоеной поверхности
График трехмерной слоеной поверхности
Иногда бывают полезны графики трехмерных слоеных поверхностей, как бы состоящие из тонких пластинок — слоев. Такие поверхности строит функция water-fall (водопад):
-
waterfal(...) — строит поверхность, как команда mesh(...), но без показа ребер сетки. При ориентации графика относительно столбцов следует использовать запись waterfall(Z 1 ) или waterfall (X ' ,Y' ,Z').
Рассмотрим пример применения команды waterfall:
» [X.Y]=meshgrid([-3:0.1:3]);
» Z=sin(X)./(X.*2+Y.*2+0.3);
» waterfall(X.Y.Z)
» colormap(gray)
» shading interp
Соответствующий график показан на рис. 6.30.
Рис. 6.30. Трехмерная слоеная поверхность
30.gif
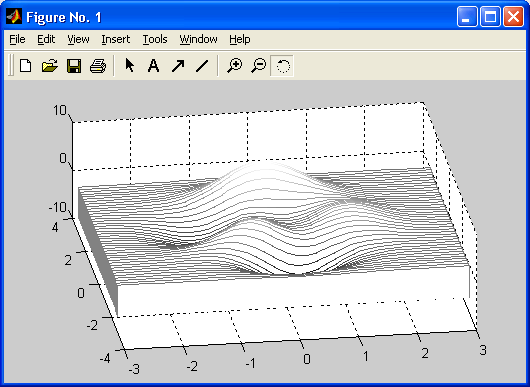
27. Трехмерные контурные графики
Tрехмерные контурные графики
Трехмерный контурный график представляет собой расположенные в пространстве линии равного уровня, полученные при расслоении трехмерной фигуры рядом секущих плоскостей, расположенных параллельно опорной плоскости фигуры.
При этом в отличие от двумерного контурного графика линии равного уровня отображаются в аксонометрии. Для получения трехмерных контурных графиков используется команда contourS:
-
contour3(...) — имеет синтаксис, аналогичный команде contour(...), но строит линии равного уровня в аксонометрии с использованием функциональной окраски (окраска меняется вдоль оси Z).
Полезные частные формы записи этой команды:
-
contour3(Z) — строит контурные линии для поверхности, заданной массивом Z, без учета диапазона изменения х и у;
-
contour3(Z.n) — строит то же, что предыдущая команда, но с использованием п секущих плоскостей (по умолчанию n=10);
-
contour3(X,Y,Z) — строит контурные линии для поверхности, заданной массивом Z, с учетом изменения х и у. Двумерные массивы X и Y создаются с помощью функции meshgrid;
-
contours(X.Y.Z.n) — строит то же, что предыдущая команда, но с использованием п секущих плоскостей.
Пример применения команды contourS:
» contour3(peaks,20)
» colormap(gray)
Соответствующий данному примеру график представлен на рис. 6.31. В данном случае задано построение двадцати линий уровня.
Рис. 6.31. Трехмерный контурный график для функции peaks
С командой contourS связаны следующие одноименные функции (не выполняющие графические построения):
-
C=contour3(...) — возвращает матрицу описания контурных линий С для использования командой clabel;
-
[С, H]=contour3(...) — возвращает массив С и вектор-столбец Н дескрипторов объектов path для каждой линии уровня. Свойство UserData каждого объекта содержит значение высоты для соответствующего контура.
31.gif
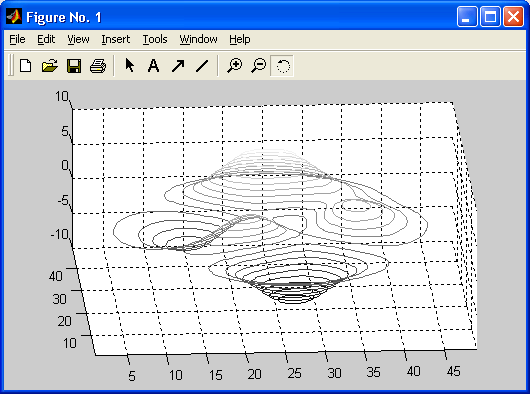
28. Установка титульной надписи
Установка титульной надписи
После того как график уже построен, MATLAB позволяет выполнить его форматирование или оформление в нужном виде. Соответствующие этому средства описаны ниже. Так, для установки над графиком титульной надписи используется следующая команда:
-
title( 'string ' ) — установка на двумерных и трехмерных графиках титульной надписи, заданной строковой константой 'string'.
Пример применения этой команды будет дан в следующем разделе.
29. Установка осевых надписей
Установка осевых надписей
Для установки надписей возле осей х, у и z используются следующие команды:
xlabe('String')
ylabeK ('String')
zlabelС ('String')
Соответствующая надпись задается символьной константой или переменной 'String ' . Пример установки титульной надписи и надписей по осям графиков приводится ниже:
» [X.Y]=meshgrid([-3:0.1:3]);
» Z=sin(X)./(X.^2+Y.^2+0.3);
» surfl(X,Y,Z)
» colorbar
» colormap(gray)
» shading interp
» xlabel'Axis X')
» ylabel'Axis Y')
» zlabel'Axis Z')
» title 'Surface graphic')
Построенный в этом примере график трехмерной поверхности показан на рис. 6.32.
Рис. 6.32. График трехмерной поверхности с титульной надписью и надписями по координатным осям
Сравните его с графиком, показанным на рис. 6.29. Надписи делают рисунок более наглядным.
32.gif
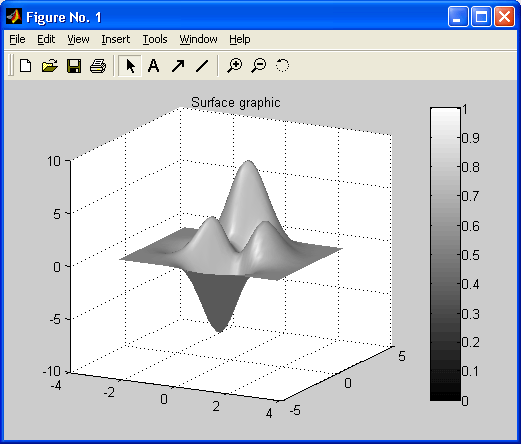
30. Ввод текста в любое место графика
Ввод текста в любое место графика
Часто возникает необходимость добавления текста в определенное место графика, например для обозначения той или иной кривой графика. Для этого используется команда text:
-
text(X.Y. 'string') — добавляет в двумерный график текст, заданный строковой константой 'string', так что начало текста расположено в точке с координатами (X, Y). Если X и Y заданы как одномерные массивы, то надпись помещается во все позиции [x(i) ,y(i)];
-
text(X,Y,Z. 'string') — добавляет в трехмерный график текст, заданный строковой константой 'string', так что начало текста расположено в позиции, заданной координатами X, Y и Z.
В приведенном ниже примере надпись «График функции sin(x ^ 3)» размещается под кривой графика в позиции (-4, 0.7):
» х=10:0.1:10;
» plot(x,sin(x).^3)
» text(-4.0.7,'Graphic sin(x)^3')
График функции с надписью у кривой показан на рис. 6.33.
Рис. 6.33. Пример ввода надписи в поле графика функции
Математически правильной записью была бы sin 3 x.
Попробуйте ввести самостоятельно:
» х=-10:0.1:10;
» plot(x,sin(x).^3)
» text(-4.0.7,'Graphic (sin(х)^3)')
Функция h=text(...) возвращает вектор-столбец h дескрипторов объектов класса text, дочерних для объектов класса axes. Следующий пример вычисляет дескриптор h
» h=text(.25. .5. '\ite^{i\omega\tau} = cos(\omega\tau) + ... i sin(\omega\tau)')
3.0022 и выводит в пустом графике математическую формулу в формате ТеХ вида:
e jwt = cos(wt) + sin(wt)
Пары координат X,Y (или тройки X,Y,Z для трехмерных графиков) могут сопровождаться парами «имя параметра/значение параметра» для задания дополнительных свойств текста. Пары координат X,Y (или тройки X,Y,Z для трехмерных графиков) могут быть полностью опущены, при этом все свойства, в том числе и позиция текста, задаются с помощью пар «имя параметра/значение параметра», заданных по умолчанию.
Используйте функцию get(H), где Н — дескриптор графического объекта (в нашем случае графического объекта класса text), чтобы просмотреть список свойств объекта и их текущие значения. Используйте set(H), чтобы просмотреть список свойств графических объектов и их допустимых значений.
33.gif
31. Позиционирование текста с помощью мыши
Позиционирование текста с помощью мыши
Очень удобный способ ввода текста предоставляет команда gtext:
-
gtext('string') — задает выводимый на график текст в виде строковой константы ' string' и выводит на график перемещаемый мышью маркер в виде крестика. Установив маркер в нужное место, достаточно щелкнуть любой кнопкой мыши для вывода текста;
-
gtext (С) — позволяет аналогичным образом разместить многострочную надпись из массива строковых переменных С.
Пример применения команды gtext:
» х=-15:0.1:15;
» plot(x, sin(x). ^ 3)
» gtext('Function sin(x).^3')
При исполнении этого примера вначале можно увидеть построение графика функции с большим крестом, перемещаемым мышью (рис. 6.34).
Установив перекрестие в нужное место графика, достаточно нажать любую клавишу или любую кнопку мыши, и на этом месте появится надпись (рис. 6.35).
Рис. 6.34. График функции с крестообразным маркером, перемещаемым мышью
Высокая точность позиционирования надписи и быстрота процесса делает данный способ нанесения надписей на графики одним из наиболее удобных.
Рис. 6.35. График функции с надписью, установленной с помощью мыши
34.gif
35a.gif
35b.gif
32. Вывод пояснений
Вывод пояснений
Пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него, называется легендой. Для создания легенды используются различные варианты команды legend:
-
legend(stringl,string2. strings,...) — добавляет к текущему графику легенду в виде строк, указанных в списке параметров;
-
legend (H.stringl,string2. strings,...) — помещает легенду на график, содержащий объекты с дескрипторами Н, используя заданные строки как метки для соответствующих дескрипторов;
-
legend( АХ . ...) — помещает легенду в осях (объект класса axes) с дескриптором АХ;
-
legend (М) — размещает легенду, используя данные из строковой матрицы М;
-
legend OFF — устраняет ранее выведенную легенду;
-
legend — перерисовывает текущую легенду, если таковая имеется;
-
legend( I egendhandl е) — перерисовывает легенду, указанную дескриптором legendhandle;
-
legend (....Pos) — помещает легенду в точно определенное место, специфицированное параметром Pos:
-
Pos=0 — лучшее место, выбираемое автоматически;
-
Pos=l — верхний правый угол;
-
Pos=2 — верхний левый угол;
-
Pos=3 — нижний левый угол;
-
Pos=4 — нижний правый угол;
-
Pos=-l — справа от графика.
-
Чтобы перенести легенду, установите на нее курсор, нажмите левую кнопку мыши и перетащите легенду в необходимую позицию.
-
[legh,objh]=legend(...) — эта функция возвращает дескриптор объекта для легенды (legh) и матрицу objh, содержащую дескрипторы объектов, из которых легенда состоит.
Команда 1 egend может использоваться с двумерной и трехмерной графикой и со специальной графикой — столбцовыми и круговыми диаграммами и т. д. Двойным щелчком можно вывести легенду на редактирование.
Пример, приведенный ниже, строит график трех функций с легендой, размещенной в поле графика:
» x=-2*pi:0.1*pi :2*pi;
» y1=sin(x);
» y2=sin(x).^2;
» plot(x,y1, '-m' ,x,y2 '-.+r')
» legend( 'Function 1', 'Function 2');
Полученный график представлен на рис. 6.36.
Рис. 6.36. График трех функций с легендой в поле графика
Незначительная модификация команды legend (применение дополнительного параметра -1) позволяет построить график трех функций с легендой вне поля графика:
» x=-2*pi:0.1*pi:2*pi;
» yl=sin(x);
» y2=sin(x). ^ 2;
» y3=sin(x). ^ 3;
» plot(x,y1,'-m',x,y2.'-.+r',x,y3,'--ok')
» legend(' Function 1','Function 2','Function 3'.-l);
Соответствующий график показан на рис. 6.37.
Рис. 6.37. График трех функций с легендой, расположенной вне поля графика
В данном случае недостатком можно считать сокращение полезной площади самого графика. Остальные варианты расположения легенды пользователю предлагается изучить самостоятельно. Следует отметить, что применение легенды придает графикам более осмысленный и профессиональный вид. При необходимости легенду можно переместить мышью в подходящее место графика.
36a.gif
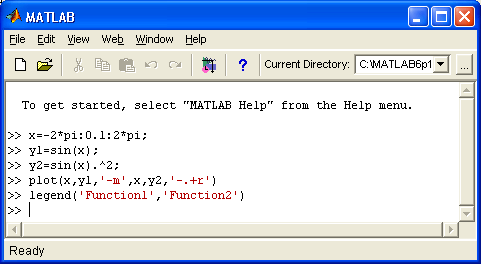
36b.gif
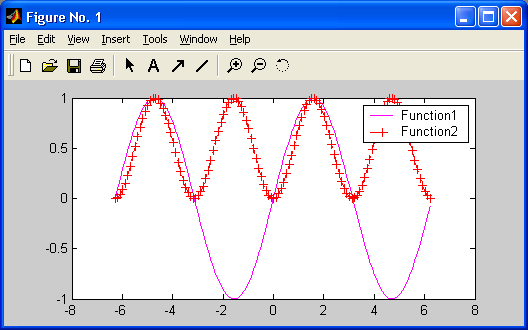
37.gif
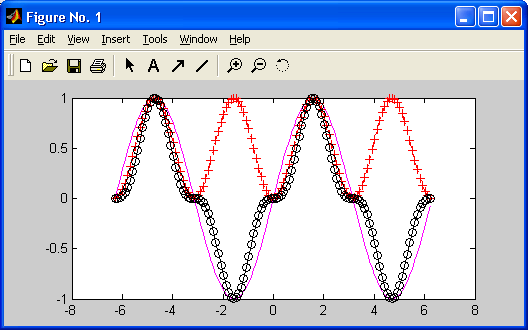
33. Маркировка линий уровня на контурных графиках
Маркировка линий уровня на контурных графиках
К сожалению, контурные графики плохо приспособлены для количественных оценок, если их линии не маркированы. В качестве маркеров используются крестики, рядом с которыми располагаются значения высот. Для маркировки контурных графиков используются команды группы clabel:
-
clabel(CS.H) — маркирует контурный график с данными в контурной матрице CS и дескрипторами объектов, заданными в массиве Н. Метки вставляются в разрывы контурных линий и ориентируются в соответствии с направлением линий;
-
clabel (CS.H, V) — маркируются только те уровни, которые указаны в векторе V. По умолчанию маркируются все контуры. Позиции меток располагаются случайным образом;
-
clabel (CS.H, 'manual') — маркирует контурные графики с установкой положения маркеров с помощью мыши. Нажатие клавиши Enter или кнопки мыши завершает установку маркера. При отсутствии мыши для перехода от одной линии уровня к другой используется клавиша пробела, а для перемещения надписи используются клавиши перемещения курсора;
-
clabel (CS), clabel (CS.V) и clabel (CS. 'manual') — дополнительные возможности маркировки контурных графиков. При отсутствии аргумента h метки не ориентируются вдоль линий контуров; точную позицию метки отмечает значок «+» (далее на рис. 6.39 показан именно этот вариант).
Пример применения команды clabel приводится ниже:
» [X,Y]=meshgrid([-3:0.1:3]);
» Z=sin(X)./(X.^2+Y.^2+0.3);
» C=contour(X.Y.Z.10);
» colormap(gray)
» clabel(С)
Рис. 6.38. Контурный график с маркированными линиями уровня
Рис. 6.38 показывает построение контурного графика с маркированными линиями уровня.
Функция H=cl abel (...) маркирует график и возвращает дескрипторы создаваемых при маркировке объектов класса TEXT (и, возможно, LINE).
38.gif
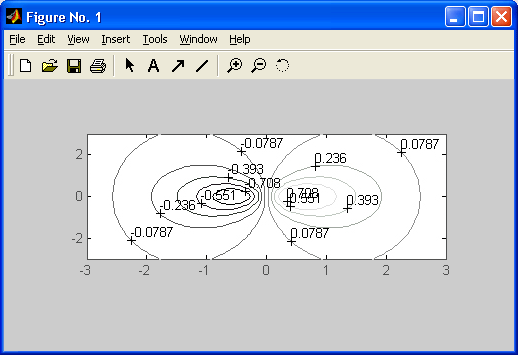
34. Управление свойствами осей графиков
Управление свойствами осей графиков
Обычно графики выводятся в режиме автоматического масштабирования. Следующие команды класса axis меняют эту ситуацию:
-
axis([XMIN XMAX YMIN YMAX]) — установка диапазонов координат по осям х и у для текущего двумерного графика;
-
axis([XMIN XMAX YMIN YMAX ZMIN ZMAX]) - установка диапазонов координат по осям х, у и z текущего трехмерного графика;
-
axis auto — установка параметров осей по умолчанию;
-
axis manual — «замораживает» масштабирование в текущем состоянии, чтобы при использовании команды hold on следующие графики использовали те же параметры осей;
-
axis tight — устанавливает диапазоны координат по осям в соответствии с диапазонами изменения данных;
-
axis ij — задает «матричную» прямоугольную систему координат с началом координат в левом верхнем углу, ось i — вертикальная, размечаемая сверху вниз, ось j — горизонтальная и размечается слева направо;
-
axis xy — устанавливает декартову систему координат с горизонтальной осью х, размечаемой слева направо, и вертикальной осью у, размечаемой снизу вверх. Начало координат размещается в нижнем левом углу;
-
axis equal — включает масштаб с одинаковым расстоянием между метками по осям х, у и z;
-
axis image — устанавливает масштаб, при котором пикселы изображения становятся квадратами;
-
axis square — устанавливает текущие оси в виде квадрата (или куба в трехмерном случае) с одинаковым расстоянием между метками и одинаковой длиной осей;
-
axis normal — восстанавливает масштаб, отменяя установки axis equal и axis square;
-
axis vis3d — «замораживает» пропорции осей для возможности поворота трехмерных объектов;
-
axi s off — убирает с осей их обозначения и маркеры; 0 axis on — восстанавливает ранее введенные обозначения осей и маркеры;
-
V=axis — возвращает вектор-строку, содержащую коэффициенты масштабирования для текущего графика. Если текущий график двумерный, то вектор имеет 4 компонента, если трехмерный — 6 компонентов.
Следующий пример иллюстрирует применение команды axis при построении двумерного графика функции одной переменной:
» х=-5:0.1:5;
» plot(x,sin(x));
» axis([-10 10 -1.5 1.5])
На рис. 6.40 показан график, который строится в этом примере.
Рис. 6.39. Пример задания масштаба осей двумерного графика
Обратите внимание, что теперь масштабы осей заданы командой axis, а не диапазоном изменения значений х и у.
39.gif
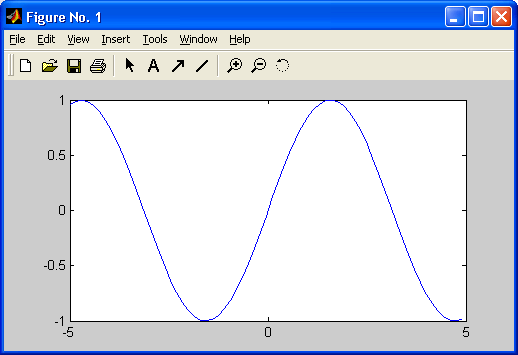
35. Включение и выключение сетки
Включение и выключение сетки
В математической, физической и иной литературе при построении графиков в дополнение к разметке осей часто используют масштабную сетку. Команды grid позволяют задавать построение сетки или отменять это построение:
-
grid on — добавляет сетку к текущему графику;
-
grid off — отключает сетку;
-
grid — последовательно производит включение и отключение сетки.
Рис. 6.40. График синусоиды с сеткой разметки
Команды grid устанавливают свойства объектов XGrid, Ygrid и Zgrid для текущих осей. Ниже приведен пример из предшествующего раздела с добавлением в него команды grid:
» х=-5:0.1:5;
» plot(x,sin(x));
» axis([-10 10 -1.5 1.5])
» grid on
Построенный граф ик показан на рис. 6.40.
Сравните этот график с графиком на рис. 6.39, на котором сетка отсутствует. Нетрудно заметить, что наличие сетки облегчает количественную оценку координат точек графика.
40.gif
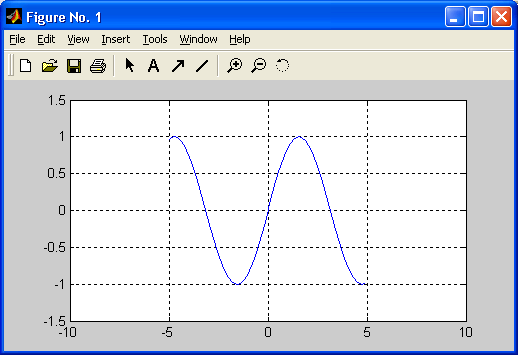
36. Наложение графиков друг на друга
Наложение графиков друг на друга
Во многих случаях желательно построение многих наложенных друг на друга графиков в одном и том же окне. Для этого служит команда продолжения графических построений hold. Она используется в следующих формах:
-
hold on — обеспечивает продолжение вывода графиков в текущее окно, что позволяет добавлять последующие графики к уже существующим;
-
hold off — отменяет режим продолжения графических построений;
-
hold — работает как переключатель, последовательно включая режим продолжения графических построений и отменяя его.
Команда hold on устанавливает значение add для свойства NextPlot объектов figure и axes, a hold off устанавливает для этого свойства значение replace. Рекомендуется также ознакомиться с командами ishold, newplot, figure и axes.
Рис. 6.41. Графики синусоиды и трех параметрических функций в одном окне
Приведенный ниже пример показывает, как с помощью команды hold on на график синусоиды накладываются еще три графика параметрически заданных функций:
& raquo; х--5:0.1:5;
» plot(x,sin(x))
» hold on
» plot(sin(x),cos(x))
» plot(2*sin(x),cos(x))
» plot(4*sin(x),cos(x))
» hold off
Графики построенных функций показаны на рис. 6.42.
В конце приведенного фрагмента программы команда hold off отключает режим добавления графиков к ранее построенным графикам.
41.gif
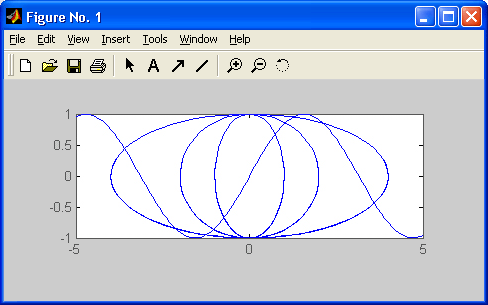
37. Разбиение графического окна
Разбиение графического окна
Бывает, что в одном окне надо расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды subplot, применяемые перед построением графиков:
-
subplot — создает новые объекты класса axes (подокна);
-
subplot(m.n.p) или subplot(mnp) — разбивает графическое окно на тхп подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, а р— номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам);
-
subplot(H), где Н — дескриптор для объекта axes, дает альтернативный способ задания подокна для текущего графика;
-
subplot( 'position',[left bottom width height]) — создает подокно с заданными нормализованными координатами (в пределах от 0.0 до 1.0);
-
subplot(lll) Hclf reset — удаляют все подокна и возвращают графическое окно в обычное состояние.
Рис. 6.42. Четыре графика различного типа, размещенных в подокнах одного окна
Следующий пример иллюстрирует применение команды subplot:
» х=-5:0.1:5;
subplot(2.2.1).plot(x.sin(x))
subplot(2.2.2).plot(sin(5*x).cos(2*x+0.2))
subplot(2.2.3).contour(peaks)
subplot(2.2.4).surf(peaks)
В этом примере последовательно строятся четыре графика различного типа, размещаемых в разных подокнах (рис. 6.42).
Следует отметить, что для всех графиков возможна индивидуальная установка дополнительных объектов, например титульных надписей, надписей по осям и т. д.
42.gif
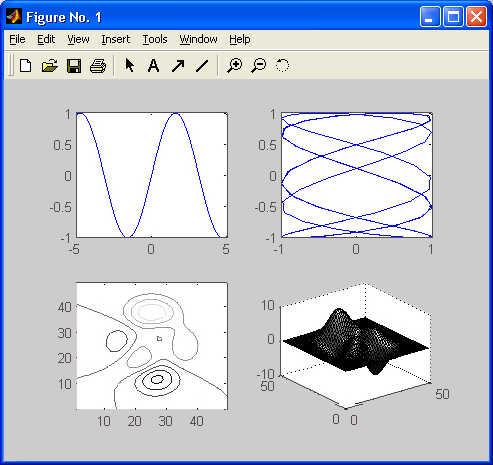
38. Изменение масштаба графика
Изменение масштаба графика
Для изменения масштаба двумерных графиков используются команды класса zoom:
-
zoom — переключает состояние режима интерактивного изменения масштаба для текущего графика;
-
zoom (FACTOR) устанавливает масштаб в соответствии с коэффициентом FACTOR;
-
zoom on — включает режим интерактивного изменения масштаба для текущего графика;
-
zoom off — выключает режим интерактивного изменения масштаба для текущего графика;
-
zoom out — обеспечивает полный просмотр, т. е. устанавливает стандартный масштаб графика;
-
zoom xon или zoom yon — включает режим изменения масштаба только по оси х или по оси у;
-
zoom reset — запоминает текущий масштаб в качестве масштаба по умолчанию для данного графика;
-
zoom(FIG,OPTION) — применяется к графику, заданному дескриптором FIG, при этом OPTION может быть любым из перечисленных выше аргументов.
Команда zoom позволяет управлять масштабированием графика с помощью мыши. Для этого надо подвести курсор мыши к интересующей вас области рисунка. Если команда zoom включена (on), то нажатие левой кнопки увеличивает масштаб вдвое, а правой — уменьшает вдвое. При нажатой левой кнопке мыши можно выделить пунктирным черным прямоугольником нужный участок графика — при отпускании кнопки он появится в увеличенном виде и в том масштабе, который соответствует выделяющему прямоугольнику.
Рассмотрим работу команды zoom на следующем примере:
» х=-5:0.01:5;
» plot(x,sin(x. ^ 5)./(x.^5+eps))
» zoom on
Рис. 6.44 показывает график функции данного примера в режиме выделения его участка с помощью мыши.
После прекращения манипуляций левой кнопкой мыши график примет вид, показанный на рис. 6.44. Теперь в полный размер графического окна будет развернуто изображение, попавшее в выделяющий прямоугольник.
Рис. 6.43. Выделение части графика мышью при использовании команды zoom
Команда zoom, таким образом, выполняет функцию «лупы», позволяющей наблюдать в увеличенном виде отдельные фрагменты сложных графиков. Однако следует учитывать, что для наблюдения фрагментов графиков при высоком увеличении они должны быть заданы большим количеством точек. Иначе вид отдельных фрагментов и тем более особых точек (в нашем случае это точка при х вблизи нуля) будет существенно отличаться от истинного.
Рис. 6.44. График выделенного участка
43.gif
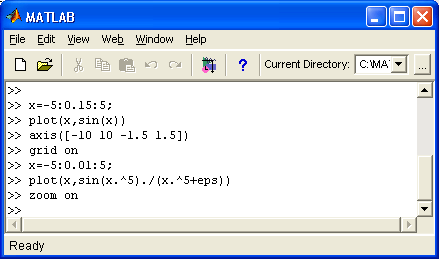
43b.gif
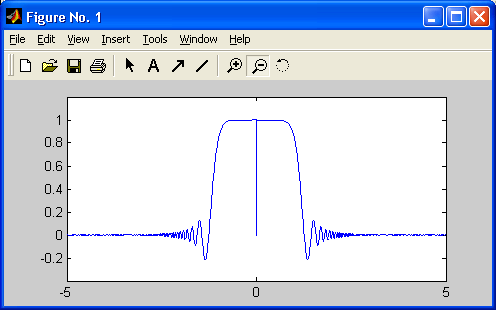
44.gif
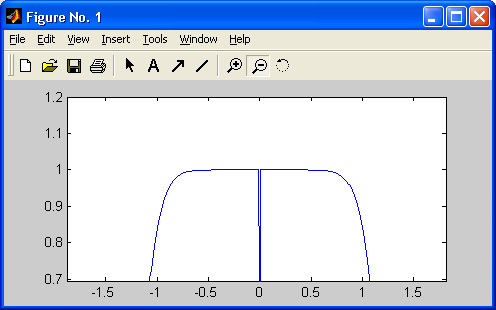
39. Установка палитры цветов
Установка палитры цветов
Поскольку графика MATLAB обеспечивает получение цветных изображений, в ней есть ряд команд для управления цветом и различными световыми эффектами. Среди них важное место занимает установка палитры цветов. Палитра цветов RGB задается матрицей MAP из трех столбцов, определяющих значения интенсивности красного (red), зеленого (green) и синего (blue) цветов. Их интенсивность задается в относительных единицах от 0.0 до 1.0. Например, [0 0 0] задает черный цвет, [1 1 1] — белый цвет, [0 0 1] — синий цвет. При изменении интенсивности цветов в указанных пределах возможно задание любого цвета. Таким образом, цвет соответствует общепринятому формату RGB.
Для установки палитры цветов служит команда colormap, записываемая в следующих формах:
-
colormap( 'default') — устанавливает палитру по умолчанию, при которой распределение цветов соответствует радуге;
-
colormap(MAP) — устанавливает палитру RGB, заданную матрицей MAP;
-
C=colormap — функция возвращает матрицу текущей палитры цветов С. m-файл с именем colormap устанавливает свойства цветов для текущего графика.
Команда help graphSd наряду с прочим выводит полный список характерных палитр, используемых графической системой MATLAB:
-
hsv — цвета радуги;
-
hot — чередование черного, красного, желтого и белого цветов;
-
gray — линейная палитра в оттенках серого цвета;
-
bone — серые цвета с оттенком синего;
-
copper — линейная палитра с оттенками меди;
-
pink — розовые цвета с оттенками пастели;
-
white — палитра белого цвета;
-
flag — чередование красного, белого, синего и черного цветов;
-
lines — палитра с чередованием цветов линий;
-
colorcube — расширенная палитра RGB;
-
jet — разновидность палитры HSV;
-
prism — призматическая палитра цветов;
-
cool — оттенки голубого и фиолетового цветов;
-
autumn — оттенки красного и желтого цветов;
-
spring — оттенки желтого и фиолетового цветов;
-
winter — оттенки синего и зеленого цветов;
-
summer — оттенки зеленого и желтого цветов.
Все эти палитры могут служить параметрами команды colormap, например colormap(hsv) фактически устанавливает то же, что и команда colormap( 'default'). Примеры применения команды colormap будут приведены в следующих разделах.
40. Установка соответствия между палитрой цветов и масштабом осей
Установка соответствия между палитрой цветов и масштабом осей
При использовании функциональной окраски важное значение имеет установка соответствия между палитрой цветов и масштабом координатных осей. Так, выбор ограниченного диапазона интенсивностей цветов может привести к тому, что цветовая гамма будет блеклой и функциональная закраска не будет достигать своих целей. С помощью команды caxis можно обеспечить соответствие между палитрой цветов и масштабом осей:
-
caxis(V) — с помощью двухэлементного вектора V со списком элементов [cmin cmax] устанавливает диапазон используемой палитры цветов для объектов surface и patch, создаваемых такими командами, как mesh, pcolor и surf. Пикселы, цвета которых выходят за пределы [cmin cmax], приводятся к граничным цветам диапазона;
-
caxis('manual') — устанавливает шкалу цветов по текущему интервалу параметра, задающего цвет;
-
caxis('auto') — устанавливает типовое масштабирование шкалы цветов, при котором диапазон используемых цветов соответствует диапазону изменения данных от -Inf до Inf. Линии и грани с цветами, равными NaN, отсекаются.
Функция caxis возвращает двухэлементный вектор с элементами [cmin cmax] для текущего светового эффекта, m-файл с именем caxi s задает свойства dim и CLimMode объекта axes (см. команду help axes).
41. Окраска поверхностей
Окраска поверхностей
Для окраски поверхностей используется команда shading, которая управляет объектами surface (поверхность) и patch (заплата), создаваемыми командами и функциями surf, mesh, pcolor, fill и fill 3. Команда shading (затенение) работает с параметрами и имеет следующий вид:
-
shading flat — задает окраску ячеек или граней в зависимости от текущих данных;
-
shading interp — задает окраску с билинейной интерполяцией цветов;
-
shading faceted — равномерная раскраска ячеек поверхности (принята по умолчанию).
Эти команды устанавливают свойства EdgeColor и FaceColor для графических объектов surface и patch в зависимости от того, какая из команд — mesh (сетчатая поверхность) или surf (затененная поверхность) — используется. Примеры применения команд shading уже приводились.
42. Установка палитры псевдоцветов
Установка палитры псевдоцветов
Довольно часто возникает необходимость представления той или иной матрицы в цветах. Для этого используют псевдоцвета, зависящие от содержимого ячеек. Такое представление реализуют команды класса pcolor:
-
pcolor (С) — задает представление матрицы С в псевдоцвете;
-
pcolor(X,Y,C) — задает представление матрицы С на сетке, формируемой векторами или матрицами X и Y.
Рис. 6.45. Пример применения команды pcolor
Функция pcolor возвращает дескриптор объекта класса surface. Пример применения команды pcolor приводится ниже:
» z=peaks(40);
» colormap(hsv)
» pcolor(z)
График, построенный в этом примере, показан на рис. 6.45.
Характер расцветки поверхности командой pcolor существенно зависит от выбора палитры цветов. В приведенном примере она задается командой colormap.
45.gif
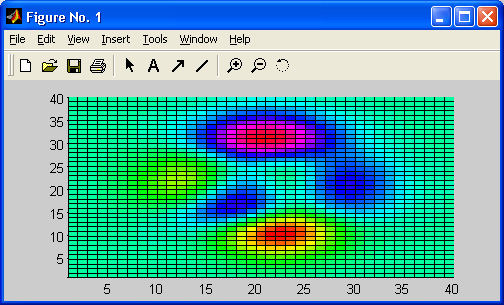
43. Создание закрашенного многоугольника
Создание закрашенного многоугольника
Для создания закрашенного пятна в виде многоугольника может использоваться команда patch:
-
patch(X,Y,C) — создает закрашенный многоугольник, вершины которого заданы векторами X и Y в текущей системе координат, а спецификация окраски задана вектором цветовой палитры С. Можно также задавать цвет с помощью символьной переменной 'color' вида 'г', 'д', 'b', 'с', 'т', 'у', V или V. X и Y могут быть матрицами;
-
patch(X,Y.Z,C) — создает многоугольник в трехмерной системе координат, при этом матрица Z должна иметь тот же размер, что X и Y.
Следующий пример поясняет применение команды patch:
» Х=[1 2 3 2 1];
» Y=[1 2 0 5 1];
» patch(X,Y,[1 0 0])
Построенный многоугольник показан на рис. 6.46.
В данном случае многоугольник окрашен красным цветом, поскольку вектор цветов [1 0 0] указывает на наличие только красной составляющей цвета (другие составляющие представлены относительным уровнем 0).
Рис. 6.46. Многоугольник, построенный командой patch
46a.gif
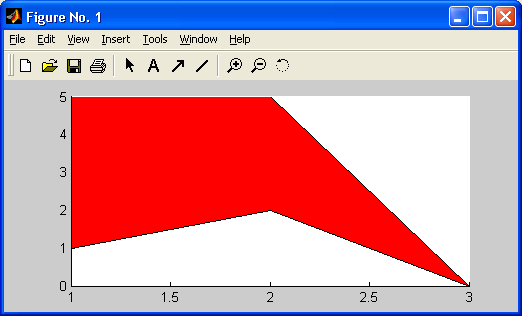
46b.gif
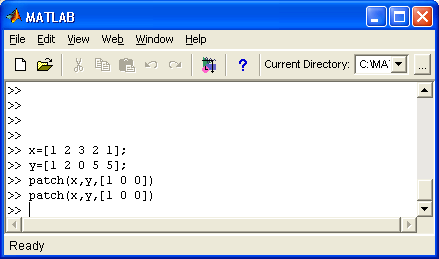
44. Окраска плоских многоугольников
Окраска плоских многоугольников
Для построения окрашенных в заданный цвет плоских многоугольников может использоваться команда fill (заполнить):
-
fill(X.Y.C) — строит закрашенный плоский многоугольник, вершины которого задаются векторами X и Y с цветом, заданным С. Многоугольник должен быть замкнутым. Для построения нескольких прямоугольников параметры команды должны быть матрицами.
-
fill(Xl.Yl,Cl,X2.Y2,C2,...) — представляет собой другой способ построения нескольких закрашенных прямоугольников.
Следующий пример показывает построение четырехугольника, закрашенного синим цветом:
» Х=[1 2 3 2 1];
» Y=[5 0.5 0 4 5]:
» fill(X,Y,[0 0 1])
Построения, реализованные этим примером, показаны на рис. 6.47.
Рис. 6.47. Построение закрашенного четырехугольника на плоскости
Функция H=fill (...) строит график и возвращает вектор-столбец дескрипторов для созданных объектов класса patch по одному дескриптору на каждый объект.
47.gif

45. Вывод шкалы цветов
Вывод шкалы цветов
При использовании функциональной окраски весьма полезным является вывод шкалы цветов командой colorbar. Ее варианты перечислены ниже:
-
colorbar( 'vert') — выводит вертикальную шкалу цветов на текущий график;
-
colorbar( 'horiz') — выводит горизонтальную шкалу цветов на текущий график;
-
colorbar(H) — выводит шкалу цветов на график с дескриптором Н с автоматическим размещением шкалы по вертикали или по горизонтали в зависимости от соотношения размеров графика;
-
colorbar — устанавливает в текущий график новую вертикальную шкалу цветов или обновляет уже имеющуюся.
Следующий пример показывает применение команды colorbar совместно с командой fill3:
» fill3(rand(5,4),rand(5,4),rand(5,4),rand(5,4))
» colorbar('vert')
Более подробно функция f ill3 будет рассмотрена ниже. На рис. 6.48 показана полученная при запуске этого примера картина. Следует отметить, что, поскольку многоугольники строятся со случайными значениями координат вершин, то при каждом запуске будет наблюдаться новая картина.
Рис. 6.48. Случайные многоугольники с функциональной окраской и вертикальной шкалой цветов
Функция H=col orbar(...) возвращает дескриптор для объекта axes со шкалой цветов.
48a.gif
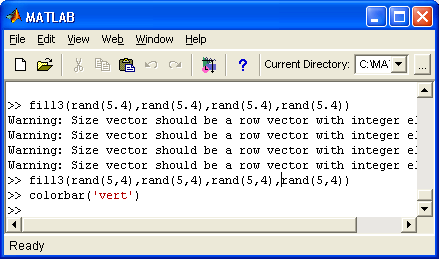
48b.gif
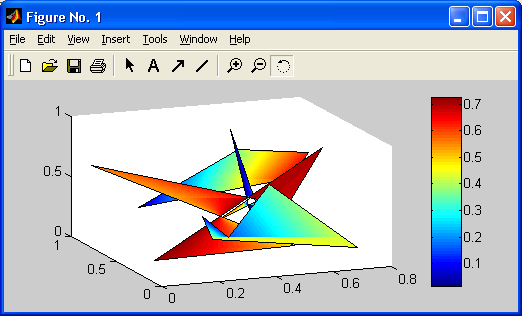
46. Цветные плоские круговые диаграммы
Цветные плоские круговые диаграммы
Закрашенные секторы часто используются для построения круговых диаграмм. Для этого в MATLAB служит команда piе:
-
pie(X) — строит круговую диаграмму по данным нормализованного вектора X/ SUM(X). SUM(X)—сумма элементов вектора. Если SUM(X)<=1.0, то значения в X непосредственно определяют площадь секторов;
-
pie(X.EXPLODE) — строит круговую диаграмму, у которой отрыв секторов от центра задается вектором EXPLODE, который должен иметь тот же размер, что и вектор данных X.
Следующий пример строит цветную круговую диаграмму с пятью секторами, причем последний сектор отделен от остальных:
» Х=[1 2 3 4 5];
» pie(X,[0 0 0 0 2])
Построенная диаграмма показана на рис. 6.49.
Рис. 6.49. Плоская круговая диаграмма
Функция Н=рiе(...) строит график и возвращает вектор дескрипторов созданных объектов классов patch и text.
49a.gif
49b.gif
47. Другие команды управления световыми эффектами
Другие команды управления световыми эффектами
Здесь мы только отметим некоторые дополнительные команды, связанные с управлением цветовыми палитрами:
-
col style — выделение цвета и стиля графика из заданного массива;
-
rgbplot — изображение палитры;
-
hsv2rgb — преобразование палитры HSV в палитру RGB;
-
rgb2hsv — преобразование палитры RGB в палитру HSV;
-
brighten — управление яркостью;
-
contrast — управление контрастом;
-
hidden — управление показом невидимых линий;
-
whitebg — управление цветом фона.
Рекомендуется ознакомиться с этими командами, используя команду help.
48. Окрашенные многоугольники в пространстве
Окрашенные многоугольники в пространстве
Для закраски многоугольников, определенных в пространстве, служит команда f ill3. Ниже представлены основные ее формы:
-
fill3(X,Y,Z,C) — строит закрашенный многоугольник в пространстве с данными вершин, хранящимися в векторах X, Y и Z, и цветом, заданным палитрой С. При построении нескольких закрашенных многоугольников параметры команды должны быть матрицами;
-
fill3(Xl.Yl,Zl,Cl.X2,Y2,Z2,C2,...) — другой вариант построения нескольких закрашенных многоугольников в пространстве;
-
fill 3 — функция, возвращающая вектор-столбец дескрипторов объектов класса patch.
Следующий пример показывает действие команды fill3:
» fill3(rand(5,4),rand(5,4).rand(5.4).rand(5.4))
На рис. 6.50 представлены построенные в этом примере закрашенные многоугольники. Поскольку координаты вершин многоугольников формируются с применением генератора случайных чисел, то наблюдаемая картина оказывается случайной и не будет повторяться при последующих запусках данного примера.
Рис. 6.50. Закрашенные многоугольники в пространстве
Следует обратить внимание на то, что команда pie3 дает функциональную закраску построенных фигур.
50a.gif
50b.gif
50c.gif
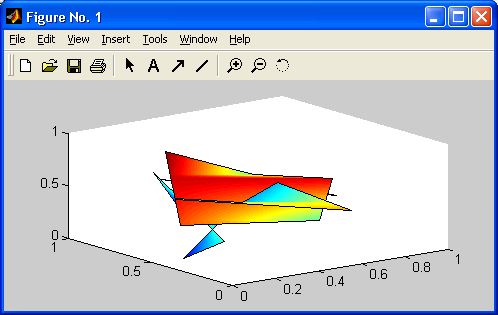
49. Цветные объемные круговые диаграммы
Ц ветные объемные круговые диаграммы
Иногда используются объемные круговые диаграммы. Для их построения служит команда pie3:
-
pie3(...) — аналогична команде pie(...), но дает построение объемных секторов.
В приведенном ниже примере строится объемная диаграмма с отделением двух секторов, показанная на рис. 6.51:
» Х=[1 2 3 4 5];
» pie3(X,[0 0 1 0 1])
Рис. 6.51. Объемная круговая диаграмма
Функция H=pie3(...) строит график и возвращает вектор, содержащий дескрипторы созданных объектов классов patch, surface и text.
51a.gif
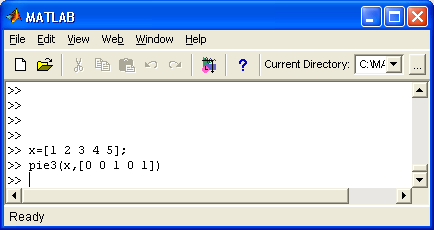
51b.gif
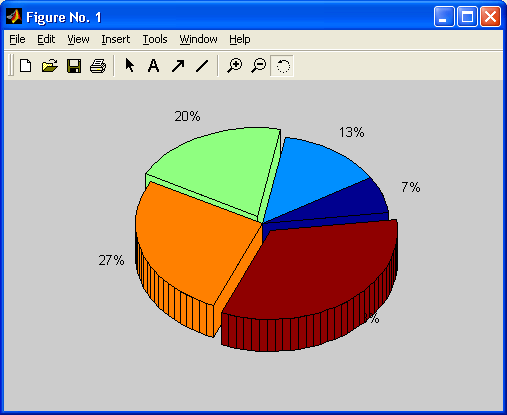
50. Построение цилиндра
Построение цилиндра
Для построения цилиндра в виде трехмерной фигуры применяется функция
cylinder:
-
[X,Y,Z]=cylinder(R,N) — создает массивы X, Y и Z, описывающие цилиндрическую поверхность с радиусом R и числом узловых точек N для последующего построения с помощью функции surf(X.Y.Z);
-
[X,Y,Z]=cyl1nder(R) и [X,Y,Z]=cylinder — подобны предшествующей функции для N=20 и R=[1 1].
Пример построения объемного цилиндра:
» [X,Y,Z]=cylinder(10.30);
» surf(X,Y,Z,X)
На рис. 6.52 показан результат построения цилиндра для данного примера.
Рис. 6.52. Построение цилиндра
Естественность воспроизведения цилиндра существенно зависит от графической команды, используемой для его построения. Команда surf дает возможность задать функциональную окраску с цветом, определяемым вектором X, что делает представление цилиндра достаточно наглядным.
52a.gif
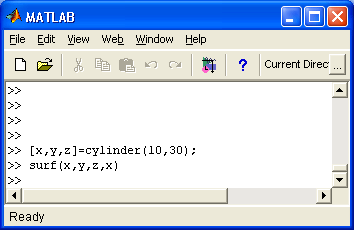
52b.gif
51. Построение сферы
Построение сферы
Для расчета массивов X, Y и Z координат точек сферы как трехмерной фигуры используется функция sphere:
-
[X.Y,Z]=sphere(N) — генерирует матрицы X, Y и Z размера (N+l)x(N+l) для последующего построения сферы с помощью команд surf (X, Y.Z) или surfl (X. Y.Z);
-
[X,Y.Z]=sphere — аналогична предшествующей функции при N=20.
Пример применения этой функции:
» [X,Y,Z]=sphere(30);
» surfl(X,Y,Z)
На рис. 6.53 показана построенная в этом примере сфера. Хорошо видны геометрические искажения (сфера приплюснута), связанные с разными масштабами по координатным осям.
Рис. 6.53. Построение сферы
Обратите внимание на то, что именно функциональная окраска сферы придает ей довольно реалистичный вид. В данном случае цвет задается вектором Z.
53a.gif
53b.gif
52. Трехмерная графика с треугольными плоскостями
Трехмерная графика с треугольными плоскостями
К числу специальных видов графики относится построение объемных фигур с помощью плоских треугольников. Для построения таких фигур в виде каркаса (без окраски и отображения плоскостей) используется команда trimesh:
-
trimesh(TRI,X,Y,Z,C) — построение объемной каркасной фигуры с треугольниками, специфицированными матрицей поверхности TRI, каждая строка которой содержит три элемента и задает одну треугольную грань путем указания индексов, по которым координаты выбираются из векторов X, Y, Z. Цвета ребер задаются вектором С;
-
trimesh(TRI.X.Y.Z) — построение, аналогичное предшествующему при C=Z, т. е. с цветом ребер, зависящим от значений высоты;
-
H=trimesh(...) — строит график и возвращает дескрипторы графических объектов;
-
trimesh(..., 'param'. 'value'. 'param', 'value'...) — добавляет значения 'value' для параметров 'param'.
Рис. 6.54. Одна из объемных фигур, построенных командой trimesh
Следующий пример иллюстрирует применение команды trimesh для построения случайной объемной фигуры, параметры которой задаются с помощью генератора случайных чисел:
» х = rand(1,40);
» у = rand(1,40);
» z = sin(x.^y);
» tri = delaunay(x,y);
» tnmesh(tri .x.y.z)
Рис. 6.55. Один из рисунков, построенных командой trisurf
Одна из построенных фигур показана на рис. 6.54. Другая, абсолютно аналогичная, по заданию входных параметров команда — tnsurf(...) — отличается только закраской треугольных областей, задающих трехмерную фигуру. Если в приведенном выше примере заменить функцию trimesh на trisurf, то можно получить графики, подобные приведенному на рис. 6.55.
Обратите внимание на то, что рис. 6.55 также принадлежит к множеству случайных графических построений. Поэтому возможность его буквального повторения отсутствует.
54a.gif
54b.gif
53. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Строить различные графики функций одной переменной.
-
Строить диаграммы и гистограммы.
-
Строить на плоскости графики специальных типов.
-
Использовать функции задания массивов трехмерной графики.
-
Строить трехмерные графики поверхностей и фигур.
-
Использовать световые эффекты.
-
Наносить на графики надписи и легенды.
-
Маркировать оси и линии графиков, наносить на них сетку.
-
Строить в одном окне несколько графиков и менять их масштаб.
-
Менять палитры цвета и условия освещения.
-
Строить графические объекты на плоскости и в пространстве.
Урок 7. Специальная графика
1. Урок 7. Специальная графика
Урок №7.
Специальная графика
-
Движение точки на плоскости и в пространстве
-
Основные средства анимации
-
Объекты дескрипторной графики
-
Операции над графическими объектами
-
Свойства объектов и управление ими
-
Управление средствами Open GL
-
Управление прозрачностью графических объектов
-
Основные команды для создания пользовательского интерфейса
-
Растровая графика
-
Пакет прикладных программ Images
-
Галерея трехмерной графики
В этом уроке мы рассмотрим некоторые виды специальной графики. Это прежде всего анимационная и дескрипторная (handle) графика.
2. Движение точки на плоскости
Движение точки на плоскости
Для отображения движения точки по траектории используется команда comet. При этом движущаяся точка напоминает ядро кометы с хвостом. Используются следующие формы представления этой команды:
-
comet (Y) — отображает движение «кометы» по траектории, заданной вектором Y;
-
comet (X.Y) — отображает движение «кометы» по траектории, заданной парой векторов Y и X;
-
comet (X.Y.p) — аналогична предшествующей команде, но позволяет задавать длину хвоста кометы (отрезка траектории, выделенного цветом) как p*1ength(Y), где length(Y) - размер вектора Y. а р<1. По умолчанию р = 0.1 [ Обратите внимание, что если Вы используете лупу, как-то иначе пытаетесь изменить размер Вашего рисунка или используете вкладку Copy Figure меню Edit, то график, полученный при использовании comet или cometS, исчезает. — Примеч. ред. ]
Рис. 7.1. Стоп-кадр изображения, полученный из примера использования команды comet
Следующий пример иллюстрирует применение команды comet:
» Х=0:0.01:15;
» comet(X,sin(X) )
Стоп-кадр изображения показан на рис. 7.1. «Хвост кометы» на черно-белом рисунке заметить трудно, поскольку он представляет собой отрезок линии с цветом, отличающимся от цвета линии основной части графика.
1.gif
3. Движение точки в пространстве
Движение точки в пространстве
Есть еще одна команда, которая позволяет наблюдать движение точки, но уже в трехмерном пространстве. Это команда comet3:
-
comet3(Z) — отображает движение точки с цветным «хвостом» по трехмерной кривой, определенной массивом Z;
-
comet3 (X.Y.Z) — отображает движение точки «кометы» по кривой в пространстве, заданной точками [X(i),Y(i),Z(i)];
-
comet3(X,Y,Z,p) — аналогична предшествующей команде с заданием длины «хвоста кометы» как p*1ength(Z). По умолчанию параметр р равен 0.1.
Ниже представлен пример применения команды cometS:
» W=0:pi/500:10*pi;
» comet3(cos(W),sin(W)+W/10.W)
На рис. 7.2 показан стоп-кадр изображения, созданного командой comet().
Рис. 7.2. Стоп-кадр изображения, созданного командой comet3
Разумеется, движение точки по заданной траектории как в двумерном, так и в трехмерном пространстве является самым простейшим примером анимации. Тем не менее эти средства существенно расширяют возможности графической визуализации при решении ряда задач динамики.
2.gif

4. Основные средства анимации
Основные средства анимации
Для более сложных случаев анимации возможно применение техники мультипликации. Она сводится к построению ряда кадров изображения, причем каждый кадр появляется на некоторое время, затем стирается и заменяется на новый кадр, несколько отличающийся от предшествующего. Если это отличие незначительно, то создается иллюзия плавного перемещения объекта.
Отметим кратко основные команды, реализующие анимацию в системе MATLAB:
-
capture — захват видеоизображения;
-
getframe — создание кадра для анимации;
-
moviein — выполнение анимации;
-
rotate — вращение фигуры;
-
frame2im — преобразование кадра в графический образ;
-
im2frame — преобразование графического образа в кадр.
Применение некоторых из этих команд мы рассмотрим далее на конкретных примерах. К сожалению, серьезные задачи анимации обычно требуют применения программных средств — главным образом циклов. Мы рассмотрим их далее, но представляется, что читатели знакомы с понятием циклов, так что приведенные примеры не будут слишком сложны. В крайнем случае, оставьте их разбор до знакомства с основами программирования в системе MATLAB (урок 20).
5. Вращение фигуры - логотипа MATLAB
Вращение фигуры — логотипа MATLAB
Рассмотрим вначале не очень сложный пример вращения сложной трехмерной поверхности — логотипа системы MATLAB, который представлен файлами logo.m и logo.mat. Ниже представлен фрагмент программы, обеспечивающий вращение этой поверхности (фигуры) относительно осей системы координат:
if ~exist('MovieGUIFlag'). figNumber=0; end;
load logo
h=surfl(L.source);
colormap(M);
ax=[7 52 7 52 -.5 .8]:
axis(ax);
axis on:
shading interp;
m=moviein(25):
for n=l:25.
rotate(h.[0 90],15.[21 21 0]);
h=surfl(get(h.'XData'),get(h.'YData').
get(h.'ZData'),source);
axis(ax);
axis on;
shading interp;
m(:,n)=mvframe(figNumber,24); end;
mvstoretfigNumber.m);
Эта программа имеет два блока: в первом задается исходная функция и ее образ, а во втором (с циклом for) выполняется создание кадров и их последовательное воспроизведение, создающее эффект анимации. На рис. 7.3 показан стоп-кадр полученной анимации.
Рис. 7.3. Стоп-кадр программы, обеспечивающей вращение фигуры — логотипа MATLAB
3.gif
6. Волновые колебания мембраны
Волновые колебания мембраны
Принцип мультипликации легко распространить на существенно более сложные задачи анимации. В качестве иллюстрации можно рассмотреть системный пример vibes, демонстрирующий волнообразные колебания тонкой пластины — мембраны. Ниже представлен переработанный файл данного примера, в котором сокращены подробные комментарии на английском языке и введены только для пояснения комментарии на русском языке, их следует изъять при попытке запустить программу:
%Волновые колебания мембраны
%Переработка файла VIBES фирмы MathWorks. Inc.
if~exist('MovieGUIFlag'): figNumber=0; end;
hlpStr= ...
[' Это пример анимации - наблюдение колебаний '
' трехмерной поверхности - мембраны. ']:
mvinit(figNumber.hlpStr):
% Загрузка данных функции
load vibesdat;
[n.n] = size(Ll):
nh = fix(n/2): .
x = (-nh:nh)/nh;
% Вычисление коэффициентов
clear с
for k = 1:12.
eval(['c(k) = L' num2str(k) '(24,13)73:'])
end;
% Установка графических параметров
axis([-11-11-11]); caxis(26.9*[-1.5 1]);
colormap(hot); hold on
% Генерация кадров мультипликации
delt = 0.1;
nf names =12:
M - moviein(nf names):
fon k - l:nf names,
% Коэффициенты
t = k*delt;
s = c.*sin(sqnt(1ambda)*t);
% Амплитуды
L = s(l)*Ll + s(2)*L2 + s(3)*L3 + s(4)*L4 +
s(5)*L5 + s(6)*L6 + .
S(7)*L7 + s(8)*l_8 + s(9)*L9 + s(10)*L10 +
s(ll)*Lll + s(12)*L12;
% Скорость мультипликации
s = s .* lambda;
V = s(l)*Ll + s(2)*L2 +'sC3)*L3 +
s(4)*L4 + s(5)*L5 + s(6)*L6 + ...
s(7)*L7 + s(8)*L8 + s(9)*L9 + s(10)*L10 +
s(11)*L11 + s(12)*L12;
% График поверхности; цвет задается скоростью
V(l:nh.l:nh) = NaN*ones(nh,nh);
Cla
sunf(x.x.L.V);
axis off
% Создание кадров мультипликации
M(:.k) - mvfname(f1gNumben,nfnames): end : hold off
%=======================================
% Запись кадров мультипликации
mvstone( figNumben , M) ;
Этот пример дан с целью иллюстрации, и подробно эту программу мы описывать не будем. К сожалению, в представленном виде (с русскоязычными комментариями), данная программа MATLAB 6 неработоспособна. Чтобы она работала, эти комментарии должны быть убраны или заменены англоязычными. В этом случае проблем с запуском программы не будет.
7. Объекты дескрипторной графики
Объекты дескрипторной графики
Как уже отмечалось, графические средства MATLAB базируются на низкоуровневой графике, которая называется дескрипторной (описательной), или handle графикой. По существу, эта графика обеспечивает объектно-ориентированное программирование как всех рассмотренных выше графических команд, так и пользовательского интерфейса. Графический редактор дескрипторной графики Property Editor в MATLAB 6 является основным редактором графики и нами уже использовался. Хотя обычный пользователь может даже не знать о существовании дескрипторной графики ввиду того, что слово «дескрипторная» в сокращенное название графического редактора не входит, все же надо учитывать, что именно дескрипторная графика дает новые, подчас уникальные возможности создания пользовательских графических программ MATLAB 6, не говоря уже о том, что она помогает понять, каким образом реализованы графические средства системы.
Центральным понятием дескрипторной графики является графический объект. Имеются следующие типы таких объектов:
-
root (корень) — первичный объект, соответствующий экрану компьютера;
-
figure (рисунок) — объект создания графического окна;
-
uicontrol (элемент управления, определенный пользователем) — объект создания элемента пользовательского интерфейса;
-
axes (оси) — объект, задающий область расположения графика в окне объекта figure;
-
uimenu (определенное пользователем меню) — объект создания меню;
-
uicontextmenu (определенное пользователем контекстное меню) - объект создания контекстного меню;
-
image (образ) — объект создания растровой графики;
-
line (линия) — объект создания линии;
-
patch (заплата) — объект создания закрашенных фигур;
-
rectangle (прямоугольник) - объект создания закрашенных прямоугольников;
-
surface (поверхность) — объект создания поверхности;
-
text (текст) — объект создания текстовых надписей;
-
light (свет) — объект создания эффектов освещенности.
Объекты подчас взаимосвязаны и могут обращаться друг к другу для получения того или иного графического эффекта.
8. Создание графического окна и управление им
Создание графического окна и управление им
Прежде чем мы рассмотрим применение дескрипторной графики на реальных примерах, отметим команды и функции, которые предназначены для создания графических окон и управления ими:
-
figure — открыть чистое графическое окно;
-
gcf — получить дескриптор графического окна figure;
-
elf — очистить графическое окно;
-
shg — показать ранее свернутое графическое окно;
-
close (закрыть) — закрыть графическое окно;
-
refresh (обновить) — обновить графическое окно.
Эти команды и функции достаточно очевидны, и мы не будем обсуждать их подробно. Заметим, что команды help name или doc name позволяют уточнить назначение той или иной команды или функции с обобщенным именем name.
9. Создание координатных осей и управление ими
Создание координатных осей и управление ими
Еще одна группа простых команд служит для создания координатных осей и управления ими:
-
axes (оси) — создать оси координат;
-
box (ящик) — построить прямоугольник вокруг рисунка;
-
сlа — убрать построения axes;
-
gса — получить дескриптор графического объекта axes;
-
hold — сохранить оси координат;
-
ishold — проверка статуса hold (1, если оси сохранены, и 0 в противоположном случае).
Эти команды также достаточно очевидны. Заметим, что их можно использовать и в обычной (высокоуровневой) графике, например для устранения осей из уже созданного графика.
10. Пример применения объекта дескрипторной графики
Пример применения объекта дескрипторной графики
Объем и направленность данной книги не позволяют подробно описать все многообразие возможностей дескрипторной графики. Ограничимся пока одним примером. Пусть надо построить линию,-проходящую через три точки с координатами (0,1), (2,4) и (5,-1). Для этого воспользуемся объектом line, который порождается одноименной графической функцией:
» line([0 2 5],[1 4 -1],'color ', 'blue')
На рис. 7.5 построена заданная линия с помощью дескрипторной команды line, которая явно не входит в высокоуровневую графику. Однако нетрудно понять, что именно эта команда составляет основу высокоуровневой команды pi ot, описанной ранее.
Особенность команды 1 i ne заключается в явном задании всех условий построения графика: координат конкретных точек, параметра цвета 'Color' и самого цвета 'blue' (синий). В итоге строятся два отрезка прямой, проходящих через заданные точки и имеющие синий цвет.
Рис. 7.4. Построение отрезков прямой объектом line
4a.gif
4b.gif
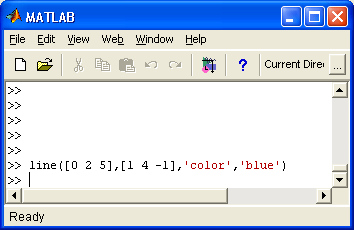
11. Дескрипторы объектов
Дескрипторы объектов
С понятием объектов дескрипторной графики связана особая характеристика объектов — дескриптор (описатель). Его можно понимать как некое число — своеобразный идентификатор («распознаватель») объектов.
Рис. 7.5. Графики пяти функций, представляющих значения элементов магической матрицы magic(5)
Дескриптор объектов root всегда равен 0, а дескриптор объектов figure (рисунок) — это целое число, указывающее на номер графического окна. Дескрипторы других объектов — это числа с плавающей запятой. По значениям дескрипторов MATLAB идентифицирует объекты. Дескриптор одного такого объекта представляет собой одно число, а если объектов несколько — несколько чисел (вектор). Например, следующие команды строят пять графиков, представляющих значения элементов магической матрицы (магического квадрата), в одном окне:
» A=magic(5);
» h=plot(A)
h=
3.0013
101.0009
102.0004
103.0004
104.0004
В данном случае вектор h содержит дескрипторы элементов графика, показанного на рис. 7.5.
Мы еще раз обращаем ваше внимание на то, что дескрипторы дают лишь внутреннее описание того или иного объекта и ассоциировать их явно с привычными параметрами, например координатами или цветом объекта, не следует. Более того, нет никаких оснований считать их одинаковыми для разных версий MATLAB, для разных компьютерных платформ и даже для одинаковых команд, но в разных местах сессии.
5a.gif
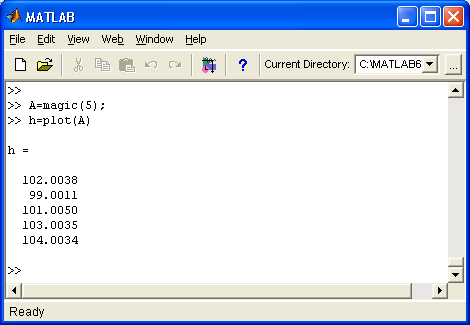
5b.gif
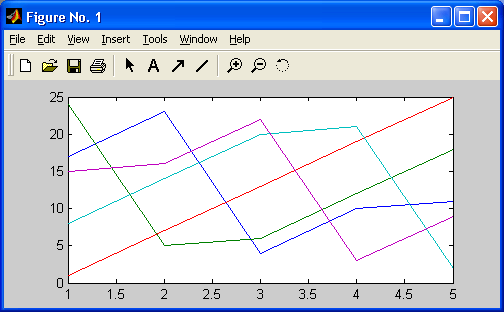
12. Операции над графическими объектами
Операции над графическими объектами
К графическим объектам применяется ряд операций:
-
set — установка свойств (параметров) графического объекта;
-
get — вывод свойств графического объекта;
-
reset — восстановить свойства графического объекта по умолчанию;
-
delete — удалить созданный графический объект;
-
gсо — возвращает дескриптор текущего графического объекта;
-
gcbo — возвращает дескриптор объекта, чья функция в данный момент выполняется;
-
gcbf — возвращает дескриптор окна, содержащего объект, функция которого в данный момент выполняется;
-
drawnow — выполнить очередь задержанных графических команд;
-
findobj — найти объекты с заданными свойствами;
-
copyobj — скопировать объект и порожденные им объекты.
Кроме того, имеются три утилиты, связанные с операциями над объектами:
-
closereq — закрыть окно по запросу;
-
ishandle — проверить дескриптор на истинность;
-
newplot — восстановить свойства объекта, измененные nextPlot.
Назначение большинства этих операций достаточно очевидно. Мы остановимся на двух наиболее важных операциях, связанных с контролем и установкой свойств объектов.
13. Свойства объектов - команда get
Свойства объектов — команда get
Каждый объект дескрипторной графики имеет множество параметров, определяющих его свойства. Вернемся к нашему примеру с построением графика из двух отрезков линии и повторим этот пример в следующем виде:
» h=line([0 2 5].[1 4 -1],'Color','blue')
h =
3.0010
Теперь объект имеет дескриптор h и его значение выведено наряду с построением графика. Команда get (name) выводит свойства объекта с заданным именем. Для нашего объекта это выглядит следующим образом:
» get(h) Color = [001]
EraseMode = normal
LineStyle=-
LineWidth = [0.5]
Marker = none
MarkerSize = [6]
MarkerEdgeColor = auto
MarkerFaceColor = none
XData = [0 2 5]
YData = [14 -1]
ZData - []
BeingDeleted = off
ButtonDownFcn =
Children = []
Clipping = on
CreateFcn =
DeleteFcn =
BusyAction = queue
HandleVisibility = on
HitTest = on
Interruptible = on
Parent = [100.001]
Selected =off
SelectionHighlight = on
Tag =
Type=line
UIContextMenu = []
UserData = []
Visible = on
14. Изменение свойств объекта - команда set
Изменение свойств объекта — команда set
С помощью команды set можно изменить отдельные свойства объекта дескрипторной графики. Эта команда имеет множество параметров, и с ними можно ознакомиться с помощью команд help set или doc set. Ограничимся примером — допустим, нам надо сменить цвет линии с голубого на красный. Для этого достаточно выполнить следующую команду: » set(h,'Color'.'red')
Обратите внимание, что при этом цвет сменится на ранее построенном рисунке с дескриптором h.
15. Управление работой средств OpenGL
Управление работой средств OpenGL
Как уже неоднократно отмечалось, одной из новинок системы MATLAB 6 является поддержка графических средств OpenGL. Эти средства обычно используются чаще всего при реализации трехмерной графики, например при осуществлении сло.жной функциональной окраски поверхностей и трехмерных фигур с учетом характера освещения и структуры материала (рендеринг), при осуществлении анимации для таких объектов, при построении поверхностей из многоугольников, осуществлении эффектов прозрачности и т. д. Целый ряд примеров этого уже приводился как в уроке 6, так и в данном уроке.
Средства OpenGL в MATLAB задействованы автоматически. Это значит, что они будут использованы, если видеокарта компьютера пользователя поддерживает их и если установлены соответствующие драйверы видеоадаптера. На уровне средств стандартной графики MATLAB никаких функций управления OpenGL нет. Однако дескрипторная графика такую возможность предоставляет с помощью команды opengl selectionjnode
Эта команда задает графические режимы осуществления рендеринга. Параметр selectl onjnode может принимать следующие значения:
-
autosel ect — задает автоматическое применение OpenGL и вводит в работу средства OpenGL при наличии возможностей для этого;
-
neverselect — отключает автоматическое применение OpenGL;
-
advise — выводит сообщение о возможности применения OpenGL, но режим рендеринга (RenderMode) устанавливается вручную.
Просто команда opengl выводит сообщение о текущем значении selectionjnode, например:
» opengl
ans =
AutoSelect
А команда opengl info выводит данные о средствах OpenGL ПК, на котором установлена система MATLAB, например:
» opengl info
Version = 1.1.0
Vendor = Microsoft Corporation
Renderer = GDI Generic
MaxTextureSize = 1024
Extensions = GL_WIN_swapJiint GL_EXT_bgra
GL_EXT_paletted_texture
Возможно также управление средствами рендеринга и OpenGL на уровне средств дескрипторной графики с помощью команды set, например: set(gcf.'Renderer','OpenGL')
16. Управление прозрачностью графических объектов
Управление прозрачностью графических объектов
Пожалуй, наиболее впечатляющие и внешне заметные результаты дает применение свойства прозрачности изображений (transparency), доступное только при использовании средств Open GL. Это свойство позволяет строить изображения полупрозрачных струй жидкостей или газов, в которых видны их сгустки или вкрапления твердых тел, изображения галактик со звездными вкраплениями, изображения клеток в биологических объектах и т. д.
В книгу «MATLAB. Using MATLAB Graphics. Version 6.0» введен обширный раздел, посвященный управлению прозрачностью объектов. Ниже представлена краткая «выжимка» из этого раздела.
Свойство прозрачности основано на представлении изображений в виде отдельных слоев, что обычно требует применения многомерных массивов. Данные о прозрачности размещаются в матрице размера mxn AlphaData, элементы которой должны иметь тип double или uint8 (элементы типа NaN недопустимы). Возможности задания прозрачности поддерживаются графическими файлами с расширением PNG. В изображениях, хранящихся в этих файлах, возможна поддержка кодирования цветов с разным разрешением - вплоть до 48 бит при RGB графике.
Для управления прозрачностью служит специальная системная переменная alpha, значение которой лежит в пределах от 0 до 1. Если построенный вами графический объект содержит элементы прозрачности, то для их наблюдения нужно задать команду alpha(x), где х задает уровень прозрачности. Например, задав alpha(0.5), мы получим «полупрозрачное» изображение, на котором будут видны обычно скрытые его детали.
Приведем наглядный пример использования свойств прозрачности из описания графики системы MATLAB, где строится график скорости жидкости на пути ракеты подводного базирования в бесконечной емкости:
[х у z v] = flow;
p=patch(isosurface(x,y,z,v,-3));
isonormals(x,y,z,v,p);
set(p,'facecolor','blue','edgecolor','none');
daspect([1 1 1]);
view(3); axis tight; grid on;
camlight; lighting gouraud;
Здесь строится график трехмерной фигуры flow (течение). Она представлена тремя массивами своих точек х, у и z и дополнительным массивом класса AlphaData — v. При первом построении свойство прозрачности отсутствует (по умолчанию) и построенная фигура будет иметь вид, представленный на рис. 7.6.
Рис. 7.6. Трехмерная фигура в обычном представлении (без свойства прозрачности)
Если исполнить команду alpha(0.5), то в массиве AlphaData будут заданы эле-менхы, обеспечивающие степень прозрачности 0.5. При этом изображение объекта будет иметь вид, представленный на рис. 7.7. Теперь на нем четко видна скрытая ранее твердая сердцевина фигуры и даже проглядывают координатные оси.
Рис. 7.7. Трехмерная фигура с установкой свойства прозрачности
Более подробные сведения об использовании свойства прозрачности можно найти в обширной документации по графике в формате PDF. Эта документация в виде файла graphg.pdf объемом свыше 12 Мбайт поставляется с системой MAT-LAB 6.
6a.gif
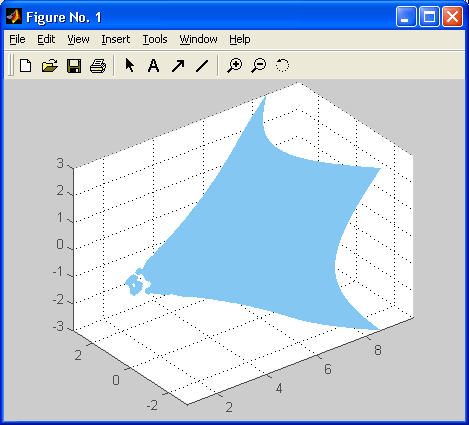
6b.gif
17. Примеры, иллюстрирующие возможности дескрипторной графики
Примеры, иллюстрирующие возможности дескрипторной графики
Теперь рассмотрим более сложные примеры, наглядно демонстрирующие возможности дескрипторной графики. Воспользовавшись File > New > M-File или edit msl.m. создадим файл msl.m следующего содержания:
[х,у] = meshgrid([-2:.4:2]);
Z =sin(x. ^ 2+y.^2);
fh = figureCPosition'.[350 275 400 300].'Color ' . V);
ah = axes('Color'.[.8 .8 .8].'XTick'.[-2 -1 0 1 2]....
'YTick',[-2 -1 0 1 2]};
sh = surfaceCXData'.x.'YData'.y.'ZData'.Z....
'FaceColor',get(ah.'Color')+.....
'EdgeColor'. 'k'.'Marker'.'o'....
'MarkerFaceColor',[.5 1 .85]):
В этом файле заданы три объекта: прямоугольник fh — объект класса figure, оси с метками ah — объект класса axes и трехмерная поверхность sh — объект класса surface. Она является результатом наложения объектов fh и ah друг на друга. При этом объект ah класса axes явно наследует свойства объекта fh класса figure. Наследование здесь проявляется в том, что при задании свойства «цвет граней» (FaceColor) объекта sh используется осветление (добавлением константы 0.1) цвета осей, полученного при помощи функции get (ah. color).
Команда v1ew(3) изменяет точку обзора трехмерной поверхности. Раньше, когда параметры осей были жестко заданы, мы смотрели на поверхность строго сверху. Теперь команда v1ew(3) установила точку обзора трехмерных графиков, принятую по умолчанию.
Теперь создадим второй файл — ms2.m:
h(l) = axes('Position',[0 Oil]);
sphere;
h(2) = axesCPosition'.[0 0 .4 .6]);
peaks:
h(3) = axes('Position'.[0 .5 .5 .5]);
sphere:
h(4) = axes('Position'.[.5 0 .4 .4]);
sphere;
h(5) = axes('Position 1 .[.5 .5 .5 .3]):
cylinder([0 0 0.5]);
set(h,'Visible 1 .'off):
alpha(0.l):
set(gcf.'Renderer'.'opengl')'
Здесь задано 5 трехмерных объектов: три сферы разных размеров, поверхность peaks и цилиндр.
Запустив файл ms2, мы получим еще более интересную картину. Заново будет вычислена величина z, а затем построены изображения пяти фигур:
z = 3*(1-х). ^ 2.*ехр(-(х. ^ 2) - (у+1). ^ 2) ...
- 10*(х/5 - х.'З - у."5).*ехр(-х.^2-у.^2) ...
- 1/3*ехр(-(х+1).^2 - у.^2)
Последовательность наложения фигур, заданных в файле ms2, определяется последовательностью их появления в файле. Любопытен вид цилиндра — похоже, что произошедшее с ним преобразование связано с изменением системы координат с декартовой на сферическую.
Рис. 7.8. Комбинированный рисунок, полученный при запуске файла ms2.m после запуска ms1.m
Чтобы понять, какие из объектов наследуют свойства других объектов, следует рассмотреть диаграмму иерархии объектов дескрипторной графики MATLAB, что объекты surface расположены ниже объектов axes, а те, в свою очередь, расположены ниже объектов класса figure. Поэтому ясно, что в случае запуска файла msl свойства сетки, построенной с применением объекта axes, будут унаследованы объектом sh, построенным командой surface.
[ Обратите внимание, что трехмерная графика в этом примере строится с рендерингом MATLAB 6 ('opengl'). В MATLAB 5.3 без установки патча Open GL по умолчанию был бы выбран рендеринг с использованием Z-буфера и на некоторых компьютерах были бы возможны искажения. Не было бы прозрачной фигуры. В MATLAB 6 при включенном режиме видеоадаптера TrueColor можно пропустить последнюю команду. Но при необходимости вывода изображения на печать set(gcf,'Renderer','opengl') можно быстро отредактировать и заменить на set(gcf,'Renderer', 'painters'). — Примеч. ред. ]
Все объекты второго файла — ms2 — относятся к классу axes. Именно поэтому они строятся поверх объектов, показанных на рис. 7.10. Координаты всех пяти трехмерных фигур (см. рис. 7.11) жестко заданы в соответствующих командах axes. В заключение этого раздела следует еще раз отметить, что дескрипторная графика рассчитана не столько на конкретных пользователей, использующих MATLAB как прикладную программу, сколько на опытных разработчиков программного обеспечения для этой системы. Разумеется, это не исключает полезную возможность изменения параметров графиков путем настройки свойств графических объектов, что особенно наглядно видно из последних приведенных примеров. Многие тайны дескрипторной графики познаются только в ходе практических экспериментов с ней.
7.gif
18. Основные команды для создания пользовательского интерфейса
Основные команды для создания пользовательского интерфейса
Опытные пользователи нередко используют MATLAB для создания своих собственных систем. Этому во многом способствует идеология системы — хранение большей части команд и функций в виде m-файлов. Простота коррекции файлов и отсутствие необходимости явно объявлять создание новых команд и функций привели к появлению множества программных систем на базе MATLAB, особенно в таких областях, как решение задач линейной алгебры, моделирование различных систем и структур и т. д.
В новой версии MATLAB дескрипторная графика позволяет конструировать детали пользовательского интерфейса. Полный список команд и функций для проектирования пользовательского интерфейса можно получить, выполнив команду help uitools.
Ниже перечислены все команды и функции данного назначения. Функции пользовательского интерфейса GUI:
-
ulcontrol — создание управляющего элемента;
-
ulmenu — создание пользовательского меню;
-
ginput — графический ввод с помощью мыши.
Перечень команд и функций пользовательского интерфейса:
-
dragrect — создание выделяющего прямоугольника с помощью мыши;
-
rbbox — растягивание прямоугольника мышью;
-
selectmoveresize — интерактивное выделение, перемещение и копирование объектов с помощью мыши;
-
waitforbuttonpress — ожидание нажатия клавиши клавиатуры или кнопки мыши в окне;
-
waltfor — прекращение выполнения программы в ожидании уничтожения заданного графического объекта или изменения его свойств;
-
uiwait — прекращение выполнения программы в ожидании вызова функции uiresume или закрытия заданного графического окна;
-
inresume — возобновить выполнение после блокировки;
-
uisuspend — прекращение интерактивного состояния фигуры;
-
uirestore — возобновление интерактивного состояния фигуры.
Средства проектирования пользовательского интерфейса:
-
guide — создание GUI;
-
align — выровнять положение объектов интерфейса;
-
cbedit — изменение повторного вызова объектов;
-
menuedit — изменение меню;
-
propedit — изменение свойств объектов.
Средства создания диалоговых окон:
-
dialog — создание диалогового окна;
-
axlimdlg — ограничение размеров диалогового окна;
-
errordlg — создание окна с сообщением об ошибке;
-
helpdlg — создание справочного окна;
-
inputdlg — создание окна диалога ввода;
-
listdlg — создание окна диалога для выбора вариантов параметра из списка;
-
menu — создание меню диалогового ввода;
-
msgbox — создание окна сообщений;
-
questdlg — создание окна запроса;
-
warndlg — создание окна предупреждения;
-
uigetfile — создание стандартного окна открытия файлов;
-
uiputfile — создание стандартного окна записи файлов;
-
uisetcolor — создание окна выбора цвета;
-
uisetfont — создание окна выбора шрифта;
-
pagedlg — создание диалогового окна параметров страницы;
-
printdlg — создание диалогового окна печати;
-
waitbar — создание окна с индикатором прогресса.
Создание меню:
-
makemenu — создать структуры меню;
-
menubar — устанавливать типовые свойства для объекта MenuBar;
-
umtoggle — изменять статус параметра "checked" для объекта uimenu;
-
winmenu — создать подменю для меню Window.
Создание кнопок панели инструментов и управление ими:
-
btngroup — создать кнопку панели инструментов;
-
btnstate — запросить статус кнопки;
-
btnpress — управление кнопкой;
-
btndown — нажать кнопку;
-
btnup — отпустить кнопку
Утилиты задания свойств объектов figure/axes:
-
сlruprop — удалить свойство объекта;
-
getuprop — запросить свойство объекта;
-
setuprop — установить свойство объекта.
Вспомогательные утилиты:
-
all child — запросить все порожденные объекты;
-
findall — найти все объекты;
-
hidegui — скрыть/открыть объекты GUI;
-
edtext — интерактивное редактирование объектов text;
-
getstatus — запросить свойства строки объекта figure;
-
setstatus — установить свойства строки объекта figure;
-
popupstr — запросить свойства строки выпадающего меню;
-
remapflg — изменить положение объекта figure;
-
setptr — установить указатель на объект figure;
-
getptr — получить указатель на объект figure;
-
overobj — запросить дескриптор объекта, над которым находится курсор мыши.
Таким образом, MATLAB содержит обширный набор команд и функций для создания типовых элементов пользовательского интерфейса. Объем данной книги не позволяет останавливаться на детальном описании этих функций, тем более что оно имеется в справочной системе. Поэтому мы ограничимся единственным примером: создание кнопки, на которой можно щелкнуть мышью и перевести ее в нажатое состояние.
19. Пример создания объекта интерфейса
Пример создания объекта интерфейса
Ниже представлена программа (распечатка m-файла с именем ui), которая при запуске создает 4 объекта интерфейса:
k1=uicontrol('Style','pushbutton'....
'Units'.'normalized','Position',[.7 .5 .2 .1],...
'String'.'click here');
k2=ui control('Style'.'pushbutton
'Units'.'normalized','Position',[.6 .3 .2 .1]....
'String'.'click here');
ck = uicontrol('Style', 'pushbutton', 'String', 'Clear'....
'Position', [150 150 100 70], 'Callback', 'da');
hpop = uicontrol('Style', 'popup'....
'String', 'hsv|hot|cool|gray'....
'Position', [30 320 100 50],...
'Callback ' , 'setmap');
Первые два объекта k1 и k2 — это малые кнопки с надписью click here («щелкни здесь»). Объект ck — это большая кнопка Clear (кстати, действующая). Объект hpop — раскрывающийся список (тоже действующий, хотя и содержащий незаполненные поименованные позиции). Для создания всех этих объектов используется команда ui control с соответствующими параметрами, задающими стиль (вид) объекта интерфейса, место его размещения и надпись (на кнопках). На рис. 7.9 построены все эти объекты, причем раскрывающийся список показан в открытом состоянии.
Рис. 7.9. Пример построения объектов пользовательского интерфейса
Дсскрипторная графика MATLAB позволяет создавать любые детали современного пользовательского интерфейса. Однако надо отметить, что пока она не поддерживает визуально-ориентированное программирование, при котором генерация нужных кодов осуществляется автоматически визуальным выбором нужного объекта интерфейса и размещением его в необходимом месте. Такой вид программирования поддерживает пакет Simulink, который в этой книге описан достаточно кратко.
4b.gif
20. Растровая графика
Растровая графика
Одна из отличительных черт системы MATLAB — мощные возможности в реализации обработки изображений (images) класса BitMap (так называемая растровая графика .bmp). Весьма небольшое число команд такой графики включено в ядро системы. Часть из них была рассмотрена выше. Остановимся на некоторых наиболее важных командах.
Команды image(A) и imagesc(A) служат для представления содержимого матрицы А в виде рисунка. Так, исполнив команду
» image(25+5*peaks)
можно наблюдать представление матрицы трехмерной поверхности peaks в наглядном «цветовом» масштабе (рис. 7.10). При этом цвет каждой точки поверхности задается ее высотой.
Рис. 7.10. Представление матрицы peaks в виде растрового рисунка
Для достаточно представительного отображения матрицы peaks в данном случае пришлось ввести нормирующие множитель 5 и слагаемое 25. Другая команда — Imagesc(A) — этого уже не требует. Результат исполнения приведенной ниже команды показан на рис. 7.11:
» imagesc(peaks)
На уровне ядра графических операций поддерживаются довольно очевидные функции преобразования цветовых моделей:
-
RGB=hsv2rgb(HSV) — преобразует матрицу изображения HSV в матрицу изображения RGB;
-
HSV=rgb2hsv(RGB) — преобразует матрицу изображения RGB в матрицу изображения HSV.
Работа этих функций наглядна лишь при цветной графике. Поскольку иллюстрации в книге черно-белые, мы ограничимся лишь упоминанием о данных функциях преобразования.
Рис. 7.11. Представление матрицы с помощью команды imagesc
Для получения детальной информации о графических файлах используется команда imfinfo( 'name'), где name — имя файла с расширением. Пример получения информации о файле saturn.tif (снимок планеты Сатурн) приводится ниже:
» imfinfo('saturn.tif')
ans =
|
ans = |
|
|
Filename : ' E : \MATLABR12\tool box\images\imdemos\saturn .tif ' |
|
|
FileModDate: |
'26-Oct-1996 01:12:02' |
|
FileSize: |
144184 |
|
Format : |
'tif w |
|
FormatVersion: |
[] |
|
Width: |
438 |
|
Height: |
328 |
|
BitOepth: |
8 |
|
Color-Type: |
'grayscale' |
|
FormatSignature: |
[73 73 42 0] |
|
ByteOrder: |
'little-endian' |
|
NewSubfileType: |
0 |
|
BitsPerSample: |
8 |
|
Compression: |
'Uncompressed' |
|
Photomet ri с I nterpretati on : |
'BlacklsZero' |
|
StripOffsets: |
[19x1 double] |
|
SamplesPerPixel : |
1 |
|
RowsPerStrip: |
18 |
|
StripByteCounts: |
[19x1 double] |
|
XResolution: |
72 |
|
YResolution: |
72 |
|
ResolutionUnit: |
'Inch' |
|
Colormap: |
[] |
|
PlanarConfiguration: |
'Chunky' |
|
TileWidth: |
[] |
|
Ti 1 eLength : |
[] |
|
TileOffsets: |
[] |
|
TileByteCounts: |
[] |
|
Orientation: |
1 |
|
Fill Order: |
1 |
|
GrayResponseUnit: |
0.0100 |
|
MaxSampleValue: |
255 |
|
MinSampleValue: |
0 |
|
Thresholding: |
1 |
|
ImageDescription: |
[1x168 char] |
Более интересна работа MATLAB с реальными изображениями. Она положена в основу многочисленных средств создания иллюстраций в пакетах прикладных программ системы MATLAB, и прежде всего специализированного пакета Images (полное название пакета — Image Processing Toolbox (Пакет обработки изображений)).
10a.gif
10b.gif
11a.gif
11b.gif
21. Пакет прикладных программ Images
Пакет прикладных программ Images
Основные средства по обработке изображений входят в пакет прикладных программ Images. С его возможностями можно детально ознакомиться, выполнив следующую команду:
» help images
Image Processing Toolbox.
Version 2.2.2 (R12) 10-Mar-2000
Release information.
Readme = Display information about
versions 2.0. 2.1. and 2.2.
Toolbox preferences.
iptgetpref = Get value of Image Processing
Toolbox preference.
iptsetpref = Set value of Image Processing
Toolbox preference. Demos.
dctdemo- 2-0 DCT image compression demo.
edgedemo - Edge detection demo.
firdemo = 2-D FIR filtering and filter design demo.
imadjdemo - Intensity adjustment and histogram
equalization demo.
landsatdemo = Landsat color composite demo.
nrfiltdemo = Noise reduction filtering demo.
qtdemo = Quadtree decomposition demo.
roidemo = Region-of-interest processing demo.
В обширном списке (выше он дан лишь выборочно) содержится более сотни команд для работы с растровыми изображениями. Эти изображения могут быть получены со сканера, цифрового фотоаппарата либо от видеокамеры, подключенной к компьютеру через видеобластер или подобное устройство.
Пакет Images поддерживает следующие возможности:
-
отображение рисунков различных графических форматов (в том числе с высоким разрешением) на экране дисплея;
-
расширенные функции записи рисунков в файл, считывание их из файла и получение информации о файле;
-
выполнение геометрических операций с графическими объектами, таких как разворот или интерполяция данных;
-
операции на уровне элементарных частей изображений — пикселов;
-
аналитические операции с изображениями;
-
осуществление компрессии и декомпрессии изображений;
-
выполнение различных видов фильтрации изображений и конструирование фильтров;
-
выполнение различных преобразований изображений;
-
поразрядные (битовые) операции с рисунками;
-
операции задания и преобразования цветов;
-
преобразование типов и форматов рисунков;
-
демонстрация возможностей пакета;
-
организация показа слайдов.
Объем данной книги не позволяет описать этот пакет подробно, но в этом нет и особого смысла. Если вы уяснили методы работы с системой MATLAB, вам не составит особого труда ознакомиться с составом всех команд и функций пакета и опробовать их на практике. В связи с этим мы остановимся лишь на нескольких демонстрационных примерах.
22. Примеры применения пакета Images
Примеры применения пакета Images
Есть ряд способов ознакомиться с весьма обширными и впечатляющими возможностями пакета Images: с помощью демонстрационных примеров (Demos) в справочной базе данных системы, путем непосредственного запуска этих примеров (список приводился выше), запуском отдельных команд и т. д.
Пример реконструкции изображений с управлением оригиналом, создаваемым изображением и ошибкой реконструкции представлен в файле dctdemo. Он выводит свое окно со средствами пользовательского интерфейса. Можно задать выбор той или иной исходной картинки, задать степень компрессии изображения и визуально наблюдать за характером преобразований (рис. 7.16). Для просмотра следует нажать кнопку Apply (Применить), кнопка Close (Закрыть) закрывает окно, а кнопка Info выводит информацию о примере.
Другой важной сферой применения пакета Images является фильтрация изображений, например с целью их очистки от шумовых помех. В качестве исходного изображения взят фотоснимок планеты Сатурн, затем с помощью генератора случайных чисел на него нанесены помехи в виде точек. Имеется возможность оценить степень очистки изображения от помех при использовании различных алгоритмов фильтрации, представленных в пакете Images рядом функций.
Следующий пример иллюстрирует возможность изменения яркости изображения. Кривая яркости может устанавливаться перемещением ее точек с помощью мыши. Можно задавать линейный или нелинейный вид этой кривой и тут же наблюдать изменение характеристик изображения. Вид кривой существенно влияет на яркость и контрастность изображений и позволяет выполнять тоновую коррекцию, например осветлять слишком темные изображения или, наоборот, затемнять светлые изображения.
Наконец, последний в этом уроке пример (остальные вы можете просмотреть самостоятельно) показывает действенность алгоритма повышения четкости изображения в произвольной его области. В нашем случае эта область ограничена треугольником. В окне можно наблюдать (и выбирать) исходное изображение, задавать область действия алгоритма и просматривать результирующее изображение.
Даже эти примеры дают возможность оценить обширные возможности пакета Images в технике обработки реальных изображений.
23. Примеры программирования задач со средствами пакета Images
Примеры программирования задач со средствами пакета Images
Вы можете ознакомиться с каждым демонстрационным примером пакета Images, выполнив команду type fname, где fname — имя файла с демонстрационным примером. Однако следует отметить, что демонстрационные программы являются весьма сложными, поскольку создают окна в виде стандартных панелей с современными элементами пользовательского интерфейса и переключателями выбора вариантов. Мы рекомендуем читателю воздержаться от знакомства с этими программами до ознакомления с уроком 20, в котором систематически описаны средства программирования системы MATLAB. А пока мы ограничимся парой характерных примеров, наглядно показывающих, что при работе с системой MATLAB вполне можно руководствоваться народной поговоркой: «Не боги горшки обжигают».
Рассмотрим, к примеру, задачу фильтрации искаженного помехами произвольного изображения, представленного некоторым файлом. Реализующая эту сложную и весьма эффективную операцию программа выглядит следующим образом:
% Picture filter
I = imreadCsaturn.tif);
h = [1 2 1: 0 0 0: -1 -2 -1];
I2 - filter2(h.I);
imshow(I2,[ ]). colorbar
В результате исполнения этой простой и вполне очевидной программы можно получить отфильтрованное изображение из файла saturn.tif . Хотите попробовать обработать какой-либо снимок? Все, что для этого нужно, — подготовить снимок в нужном формате (например, tif) и заменить во второй строке имя демонстрационного файла на имя вашего файла.
Рассмотрим еще один достаточно простой пример — построение сферы в виде глобуса и наклеивание на полушарие этого глобуса изображения карты погоды:
load earth sphere: h - findobjC'Type'.'surface');
hemisphere= [ones(257.125).X.ones(257,125)];
set(h.'CData'.f1i pud(hemi sphere).'FaceColor'.
'texturemap')
colormap(map)
axis equal
view([90 0])
setCgca.'CameraViewAngleMode'.'manual')
view([65 30])
Пакет Images можно рассматривать как полезный инструмент для создания новых алгоритмов и методов обработки изображений и обучения специалистов. Применение его непосредственно для обработки изображений вполне возможно, но все же едва ли целесообразно. Дело в том, что обширнейшие возможности по обработке изображений открывают профессиональные графические пакеты, например Adobe Photoshop, Ulead Photolmpact, Corel Draw и др., в которых реализованы самые современные методы обработки изображений и использованы последние новации пользовательского интерфейса. В этом случае достоинство средств MATLAB проявляется только в математической прозрачности реализаций алгоритмов обработки изображений.
24. Галерея трехмерной графики
Галерея трехмерной графики
Для знакомства с возможностями трехмерной графики и построением пользовательского интерфейса MATLAB имеет галерею (Gallery) в виде профессионально выполненных графических программ. Доступ к ним возможен как из режима демонстрации (команда Examples and Demos в меню Help командного окна MATLAB), так и путем запуска команды из командной строки с указанием имени соответствующего файла.
Галерея представлена фигурами и файлами, список которых приведен в табл. 7.1.
Таблица 7.1. Состав галереи трехмерной графики MATLAB
|
|
|||
|
|
|||
|
|
Knot |
Knot.m |
Завязанный узел |
|
|
Quiver |
Quivdemo. m |
Векторное объемное поле |
|
|
Klein II |
Kleinl. m |
Объемное кольцо |
|
|
Cruller |
Cruller.m |
Объемное кольцо Мебиуса |
|
|
Hoops |
Tory4.m |
Четыре объемных обруча |
|
|
Slosh |
Spharm2.m |
Построение фигуры, напоминающей улитку |
|
|
Modes |
Modes. m |
Демонстрация фаз анимации трехмерной поверхности |
|
|
Logo |
Logo.m |
Построение логотипа системы MATLAB |
Обратите внимание на то, что иногда имя файла не совпадает с именем фигуры в галерее. Некоторые из фигур галереи мы уже описывали — это knot (см. рис. 4.4) и logo . Ниже приведено еще несколько примеров, которые дают наглядное представление о возможностях дескрипторной графики системы MATLAB.
Полезно обратить внимание на то, что в этом примере сам по себе график — двумерный. Объемный вид поверхности достигается сочетанием функциональной окраски с изображением графика векторного поля с помощью стрелок.
Команда kleinl строит график объемной ленты Мебиуса с одним перекручиванием. Этот график хорошо иллюстрирует хотя и одноцветную, но функциональную закраску фигуры с имитацией ее освещения источником света, расположенным вверху справа, и реализацией эффектов отражения света.
Команда cruller строит объемное кольцо Мебиуса с двойным перекручиванием. В данном случае используется обычная функциональная окраска с сохранением линий каркаса фигуры.
Команда tory4 строит четыре переплетающихся друг с другом тора (объемных кольца) в пространстве (рис. 7.25). Наглядности этой картины также способствует функциональная окраска торов и видимые линии каркаса. Обратите внимание, что невидимые линии удалены.
Любопытную фигуру, напоминающую раковину улитки, строит команда spharm2. Здесь интересно применение многоцветной функциональной окраски с использованием интерполяции по цвету, а также имитация эффектов отражения при освещении фигуры источником точечного света. Отчетливо видны зеркальные блики на поверхности фигуры.
Еще одна команда — modes — иллюстрирует построение фаз анимации поверхности . Она генерирует 12 фигур, отражающих положение поверхности в пространстве в различные моменты времени.
В целом указанный набор программ дает хорошее представление о возможностях трехмерной графики системы MATLAB. Команда type name, где name — имя соответствующей команды, выводит полный листинг программы, реализующей построение той или иной фигуры.
25. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Строить графики с анимацией.
-
Использовать простые средства дескрипторной графики.
-
Создавать графические окна и управлять ими.
-
Работать с графическими объектами.
-
Создавать элементы интерфейса.
-
Использовать некоторые средства пакета Images для обработки изображений.
-
Просматривать примеры из галереи трехмерной графики.
Урок 8. Операторы и функции
1. Урок 8. Операторы и функции
Урок №8.
Операторы и функции
-
Арифметические и алгебраические операторы и функции
-
Операторы отношения и их функции
-
Логические операторы и функции
-
Специальные символы
-
Системные переменные и константы
-
Функции времени и даты
-
Элементарные функции
-
Тригонометрические и гиперболические функции
-
Функции округления и знака
-
Функции комплексного аргумента
Начиная с этого урока мы переходим к изучению математических и логических возможностей системы MATLAB. Их изучение мы начнем с операторов и функций — тех кирпичиков, из которых строятся математические выражения. Вычисления математических выражений составляют главную цель любой системы, предназначенной для численных расчетов. Здесь мы рассмотрим полный набор операторов входного языка системы MATLAB 6.0 и соответствующих им функций. Напомним, что полный список операторов выводится командой help ops. Операторы и специальные символы системы MATLAB можно разделить на ряд категорий, которые рассматриваются ниже.
2. Арифметические операторы и функции
Арифметические операторы и функции
Арифметические операторы являются самыми распространенными и известными. В отличие от большинства языков программирования в системе MATLAB практически все операторы являются матричными, т. е. предназначены для выполнения операций над матрицами. В табл. 8.1 приводится список арифметических операторов и синтаксис их применения.
Таблица 8.1. Арифметические операторы и функции MATLAB
|
|
|||
|
|
Plus |
Плюс + |
М1+М2 |
|
|
Uplus |
Унарный плюс + |
+М |
|
|
Minus |
Минус |
М1-М2 |
|
|
Uminus |
Унарный минус |
-М |
|
|
Mtimes |
Матричное умножение * |
М1*М2 |
|
|
Times |
Поэлементное умножение массивов .* |
А1*А2 |
|
|
Mpower |
Возведение матрицы в степень |
М1^х |
|
|
Power |
Поэлементное возведение массива в степень |
А1^х |
|
|
Mldivide |
Обратное (справа налево) деление матриц \ |
M1\M2 |
|
|
Mrdivide |
Деление матриц слева направо / |
М1/М2 |
|
|
Ldivide |
Поэлементное деление массивов справа налево . \ |
А1.\А2 |
|
|
Rdivide |
Поэлементное деление массивов слева направо . / |
А1 . /А2 |
|
|
Kron |
Тензорное умножение Кронекера kron |
kron(X.Y) |
|
|
Обратите внимание на то, что каждый оператор имеет аналогичную по назначению функцию. Например, оператору матричного умножения * соответствует функция mtimes(Ml,M2). Примеры применения арифметических операторов уже не раз приводились, так что ограничимся несколькими дополнительными примерами:
» А=[1 2 3];
» В=[4 5 6]:
» В-А
ans=
|
|
3 |
3 3 |
|
|
|
» minus (В. А) |
|
|
|
|
ans = |
|
|
|
|
3 |
3 3 |
|
|
|
» А. ^ 2 |
|
|
|
|
ans = |
|
|
|
|
1 |
4 9 |
|
|
|
» power(A,2) |
|
|
|
|
ans = |
|
|
|
|
1 |
4 9 |
|
|
|
» ДАВ |
|
|
|
|
ans= |
|
|
|
|
4.0000 |
2.5000 2.0000 |
|
|
|
» Idivide(A.B) |
|
|
|
|
ans= |
|
|
|
|
4.0000 |
2.5000 2.0000 |
|
|
|
» rdivide(A.B) |
|
|
|
|
ans= |
|
|
|
|
0.2500 |
0.4000 0.5000 |
|
Соответствие функций операторам и командам в системе MATLAB является одним из основных положений программирования. Оно позволяет одновременно использовать элементы как операторного, так и функционального программирования.
Следует отметить, что в математических выражениях операторы имеют определенный приоритет исполнения. Например, в MATLAB приоритет логических операторов выше, чем арифметических, приоритет возведения в степень выше приоритетов умножения и деления, приоритет умножения и деления выше приоритета сложения и вычитания. Для изменения приоритета операций в математических выражениях используются круглые скобки. Степень вложения скобок не ограничивается.
3. Операторы отношения и их функции
Операторы отношения и их функции
Операторы отношения служат для сравнения двух величин, векторов или матриц. Все операторы отношения имеют два операнда, например х и у, и записываются, как показано в табл. 8.2.
Таблица 8.2. Операторы и функции отношения
| Функция | Название | Оператор | Пример |
| Eq | Равно | = = | x = = y |
| Ne | He равно | ~ = | x ~ = y |
| Lt | Меньше чем | < | x<y |
| Gt | Больше чем | > | x>y |
| Le | Меньше или равно | <= | x<=y |
| Ge | Больше или равно | >= | x>=y |
Данные операторы выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают значение 1 (True), если элементы идентичны, и значение 0 (False) в противном случае. Если операнды — действительные числа, то применение операторов отношения тривиально:
» eq(2.2)
ans =
1
» 2==2
ans =
1
» ne(l,2)
ans =
1
» 2 ~- 2
ans =
0
» 5 > 3
ans =
1
» le(5.3)
ans =
0
Следует отметить, что операторы <, <=, > и >= при комплексных операндах используют для сравнения только действительные части операндов — мнимые отбрасываются. В то же время операторы == и ~= ведут сравнение с учетом как действительной, так и мнимой частей операндов. Следующие примеры поясняют это положение:
» (2+3i)>-(2+i)
ans=
1
» (2+3i)>(2+i)
ans=
0
» abs(2+3i)>abs(2+i)
ans =
1
» (2+3i)—(2+i)
ans =
0
» (2+3i)-(2+i)
ans =
1
Если один из операндов — скаляр, происходит сравнение всех элементов второго операнда-массива со значением этого скаляра:
M=
-1 0
1 2
» М>=0
ans =
0 1
1 1
В общем случае операторы отношения сравнивают два массива одного размера и выдают результат в виде массива того же размера:
» М>[0 1;.1 0]
ans =
0 0
0 1
Таким образом, спектр применения операторов отношения в системе MATLAB шире, чем в обычных языках программирования, поскольку операндами являются не только числа, но и векторы, матрицы и массивы. Возможно применение операторов отношения и к символьным выражениям:
» 'b'>'а'
ans =
1
» 'abc'= ='abc'
ans =
1 1 1
» 'cba'<'abc'
ans =
0 0 1
В этом случае символы, входящие в выражения, представляются своими ASCII-кодами. Строки воспринимаются как векторы, содержащие значения кодов. Все это надо учитывать при использовании управляющих структур языка программирования, в которых широко применяются операторы отношения.
4. Логические операторы
Логические операторы
Логические операторы и соответствующие им функции служат для реализации поэлементных логических операций над элементами одинаковых по размеру массивов (табл. 8.3).
Таблица 8.3. Логические операторы и функции MATLAB
|
And |
Логическое И (AND) & |
|
Or |
Логическое ИЛИ (OR) | |
|
Not |
Логическое НЕ (NOT) ~ |
|
Хог |
Исключающее ИЛИ (EXCLUSIVE OR) |
|
Any |
Верно, если все элементы вектора равны нулю |
|
All |
Верно, если все элементы вектора не равны нулю |
Работа операторов поясняется приведенными ниже примерами:
»А=[1 2 3];
»В=[1 0 0];
» and(A.B)
ans =
1 0 0
» оr(А.В)
ans =
1 1 1
» А&В
ans =
1 0 0
» А|В
ans=
1 1 1
» not(А)
ans =
0 0 0
» not(B)
ans =
0 1 1
» ~B
ans=
0 1 1
» xor(A.B)
ans =
0 1 1
» any(A)
ans =
1
» all([0 0 0])
ans =
0
» all(B)
ans =
0
» and('abc'.'012')
ans =
1 1 1
Обратите внимание, что аргументами логических операторов могут быть числа и строки. При аргументах-числах логический нуль соответствует числовому нулю, а любое отличное от нуля число воспринимается как логическая единица. Для строк действует уже отмеченное правило — каждый символ строки представляется своим ASCII-кодом.
5. Специальные символы
Специальные символы
К классу операторов в системе MATLAB относятся также специальные символы. Они предназначены для создания самых разнообразных объектов входного языка и языка программирования системы и придания им различных форм. В табл. 8.4 представлено описание полного набора специальных символов.
Таблица 8.4. Специальные символы MATLAB
|
: |
Двоеточие |
colon |
|
( ) |
Круглые скобки |
paren |
|
[ ] |
Квадратные скобки |
paren |
|
{ } |
Фигурные скобки |
paren |
|
. |
Десятичная точка |
punct |
|
|
Выделение поля структуры |
punct |
|
|
Родительский каталог |
punct |
|
|
Продолжение строки |
punct |
|
, |
Разделитель |
punct |
|
|
Точка с запятой |
punct |
|
% |
Комментарий |
punct |
|
i |
Вызов команды операционной системы |
punct |
|
= |
Присваивание |
punct |
|
1 |
Кавычка |
punct |
|
1 |
Транспонирование |
transpose |
|
1 |
Транспонирование с комплексным сопряжением |
ctranspose |
|
[,] |
Горизонтальная конкатенация |
horzcat |
|
[;] |
Вертикальная конкатенация |
vertcat |
|
( ).( }.. |
Присваивание подмассива |
subsasgn |
|
( ).{ }.. |
Ссылка на подмассив |
subsref |
|
|
Индекс подмассива |
subsindex |
Теперь рассмотрим их более подробно.
-
: (двоеточие) — формирование подвекторов и подматриц из векторов и матриц. Оператор : — один из наиболее часто используемых операторов в системе MATLAB.
Оператор : использует следующие правила для создания векторов:
-
j:k — то же, что и [j.j+l,...,k];
-
j:k — пустой вектор, если j>k;
-
j:i :k — то же, что и [j, j+i ,j+2i .....k];
-
j:i :k — пустой вектор, если i>0 и j>k или если i<0 и j<k, где 1, j и k — скалярные величины.
Ниже показано, как выбирать с помощью оператора : строки, столбцы и элементы из векторов, матриц и многомерных массивов:
-
А(:, j) — это j-й столбец из А;
-
А(i,:) — это i-я строка из А;
-
А(:,:) — эквивалент двумерного массива. Для матриц это аналогично А;
-
A(j:k) - это A(j), A(j+l),...,A(k);
-
A(:J:k)-это A(:.j),A(:,j+l),...,A(:,k);
-
А(:,: ,k) — это k-я страница трехмерного массива А;
-
A(i.j.k.:) — вектор, выделенный из четырехмерного массива А. Вектор включает элементы А(1, j.k.l), A(i. j,k,2), A(i. j,k.3) и т. д.;
-
А(:) — записывает все элементы массива А в виде столбца.
Символы ( ) (круглые скобки) используются для задания порядка выполнения операций в арифметических выражениях, указания последовательности аргументов функции и указания индексов элемента вектора или матрицы. Если X и V — векторы, то X(V) можно представить как [X(V(D), X(V(2)).....X(V(n))]. Элементы вектора V должны быть целыми числами, чтобы их можно было использовать как индексы элементов массива X. Ошибка генерируется в том случае, если индекс элемента меньше единицы или больше, чем size(X). Такой же принцип индексирования действителен и для матриц. Если вектор V имеет т компонентов, а вектор W — п компонентов, то A(V,W) будет матрицей размера mxn, сформированной из элементов матрицы А, индексы которой — элементы векторов V и W.
Символы [ ] (квадратные скобки) используются для формирования векторов и матриц:
-
[6.9 9.64 sqrt(-l)] — вектор, содержащий три элемента, разделенных пробелами;
-
[6.9. 9.64. i] —такой же вектор;
-
[1+j 2-j 3] и [1 +j 2 -j 3] — разные векторы: первый содержит три элемента, а второй пять;
-
[11 12 13: 21 22 23] — матрица размера 2x3. Точка с запятой разделяет первую и вторую строки.
Еще несколько примеров:
-
А = [ ] — сохраняет пустую матрицу в А;
-
А(m. :) = [] — удаляет строку m из матрицы А;
-
А(: ,n) = [ ] — удаляет столбец n из матрицы А.
Символы { } (фигурные скобки) используются для формирования массивов ячеек. Например, {magic(3) 6.9 'hello'} — массив ячеек с тремя элементами.
Символ . (десятичная точка) используется для отделения дробной части чисел от целой. Например, 314/100, 3.14 и .314е1 — одно и то же число.
Кроме того, символ точки . используется для выделения полей структур. Например, A.(field) и A(i).field, где А — структура, означает выделение поля структуры с именем «field».
Ниже перечислено назначение остальных специальных символов MATLAB:
-
.. (родительский каталог) — переход по дереву каталогов на один уровень вверх;
-
... (продолжение) — три или более точек в конце строки указывают на продолжение строки;
-
; (точка с запятой) — используется внутри круглых скобок для разделения строк матриц, а также в конце операторов для запрета вывода на экран результата вычислений;
-
, (запятая) — используется для разделения индексов элементов матрицы и аргументов функции, а также для разделения операторов языка MATLAB. При разделении операторов в строке запятая может заменяться на точку с запятой с целью запрета вывода на экран результата вычислений;
-
% (знак процента) — используется для указания логического конца строки. Текст, находящийся после знака процента, воспринимается как комментарий и игнорируется (увы, за исключением русскоязычных комментарий, которые нередко ведут к ошибочным командам);
-
! (восклицательный знак) — является указателем ввода команды операционной системы. Строка, следующая за ним, воспринимается как команда операционной системы;
-
= (знак равенства) — используется для присваивания значений в арифметических выражениях;
-
' (одиночная кавычка, апостроф) — текст в кавычках представляется как вектор символов с компонентами, являющимися ASCII-кодами символов. Кавычка внутри строки задается двумя кавычками. Например:
» a-'Hello''my friend'
а =
Hello'my friend
-
' (транспонирование с комплексным сопряжением) — транспонирование матриц, например А' — транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Строки транспонированной матрицы соответствуют столбцам исходной матрицы;
-
.' (транспонирование) — транспонирование массива, например А.' — транспонированный массив А. Для комплексных массивов операция сопряжения не выполняется;
-
[.] — горизонтальная конкатенация. Так, [А.В] — горизонтальная конкатенация (объединение) матриц А и В. А и В должны иметь одинаковое количество строк. [А В] действует аналогично. Горизонтальная конкатенация может быть применена для любого числа матриц в пределах одних скобок: [А,В,С]. Горизонтальная и вертикальная конкатенации могут использоваться одновременно: [А,В:С];
-
[:] — вертикальная конкатенация. Так, [А:В] — вертикальная конкатенация (объединение) матриц А и В. А и В должны иметь одинаковое число столбцов. Вертикальная конкатенация может быть применена для любого числа матриц в пределах одних скобок: [А:В:С]. Горизонтальная и вертикальная конкатенации могут использоваться одновременно: [А;В,С];
-
(),{} — присваивание подмассива. Приведем несколько примеров:
-
А(1)=В — присваивает значения элементов массива В элементам массива А, которые определяются вектором индексов I. Массив В должен иметь такую же размерность, как и массив I, или может быть скаляром;
-
А(I,J)=B — присваивает значения массива В элементам прямоугольной подматрицы А, которые определяются векторами индексов I и J. Массив В должен иметь LENGTH(I) строк и LENGTH(J) столбцов;
-
А{1}=В, где А — массив ячеек и I — скаляр, помещает копию массива В в заданную ячейку массива А. Если I имеет более одного элемента, то появляется сообщение об ошибке.
-
6. Системные переменные и константы
Системные переменные и константы
Как отмечалось ранее, в состав объектов MATLAB входит ряд системных переменных и констант, значения которых устанавливаются системой при ее загрузке или автоматически формируются в процессе вычислений. Описание таких объектов приводится ниже.
-
ans — результат выполнения последней операции. Переменная ans создается автоматически, когда не определены выходные аргументы какого-либо оператора. Пример:
» cos([0:2*pi])
ans =
1.0000 0.5403 -0.4161 -0.9900 -0.6536 0.2837 0.9602
-
computer — возвращает строку с информацией о типе компьютера, на котором установлена система MATLAB;
-
[str.maxsize] = computer — возвращает строку str с информацией о компьютере и целое число maxsize, содержащее максимально допустимое число элементов матрицы для данной версии MATLAB. Пример:
» [str.maxsize] = computer
str =
PCWIN
maxsize =
268435455
-
eps — возвращает интервал между числом 1.0 и следующим ближайшим числом с плавающей запятой, которое воспринимается как отличное от 1.0. Значение eps определяет заданный по умолчанию порог для функций pinv и rank, а также для некоторых других функций. На машинах с арифметикой с плавающей запятой eps = 2 ^ (-52), что приблизительно составляет 2.22е-1б. Пример:
» eps
ans =
2.2204е-016
-
i или j— мнимая единица (равная sqrt(-1)), которая используется для задания мнимой части комплексных чисел. Символ 1 при задании комплексной константы можно использовать без знака умножения. В качестве мнимой единицы можно также использовать символ j. Пример:
» w=3+5i
w =
3.0000 + 5.00001
-
Inf — возвращает представление положительной бесконечности для машинной арифметики. Бесконечность следует из операций, подобных делению на нуль, и переполнения, которое ведет к результатам, слишком большим, чтобы их можно было представить в виде числа с плавающей запятой. Пример:
» 4/0
Warning: Divide by zero.
ans=
Inf
Примечание
Переменным i и j можно задать и иное значение, например, они могут выступать в ка-честве индексов в циклах for. Однако это чревато путаницей, если внутри цикла пользователь задает выражения с комплексными числами.[Используйте как индексы I и J вместо 1 и j.— Примеч. ред.]
-
inputname(argnum) — возвращает в тело функции название переменной рабочей области, соответствующее аргументу с номером argnum. Может использоваться только внутри тела функции. Если входной аргумент не имеет никакого символьного представления (например, если это выражение или функция, дающая на выходе выражение, например а(1), varargin{:}, eval(expr), а не переменная), функция inputname возвращает пустую строку ("");
-
j — мнимая единица. Символ j можно использовать в качестве мнимой единицы наряду с 1. Как мнимая единица (равная sqrt(-D) символ j используется для задания мнимой части комплексных чисел. Все сказанное о символе i относится и к j. Пример:
» s=4-3j
s =
4.0000 - 3.00001
-
NaN — возвращает представление для нечисловых величин, например, в случае операций, которые имеют неопределенные численные результаты. Пример:
» s=0/0
Warning: Divide by zero.
s =NaN
Функция nargchk часто используется внутри m-файлов для проверки соответствия количества входных параметров (аргументов):
-
msg = nargchkOow.high.number) — возвращает сообщение об ошибке, если число number меньше, чем low, или больше, чем high, в противном случае возвращается пустая строка. Пример:
» msg = nargchk(4,9.5)
msg =
[ ]
» msg = nargchk(4.9.2)
msg = Not enough input arguments.
-
msg = nargoutchkdow,high.number) — возвращает сообщение об ошибке, если число number выходных параметров (выходных аргументов в терминологии MATLAB) меньше, чем low, или больше, чем high, в противном случае возвращается пустая строка.
Еще две функции позволяют определить число входных и выходных параметров функции:
-
nargin — возвращает число входных аргументов, определенных для функции. Внутри тела m-файла функции nargin и nargout указывают соответственно количество входных или выходных аргументов, заданных пользователем. Вне тела m-файла функции nargin и nargout показывают соответственно число входных или выходных аргументов для данной функции. Отрицательное число аргументов означает, что функция имеет переменное число аргументов;
-
nargin(@fun) — возвращает число объявленных входных параметров для функции fun. Если функция имеет переменное число входных аргументов, возвращается -1;
-
nargout — возвращает число выходных параметров, определенных для функции;
-
nargout( 'fun') — возвращает число объявленных выходных параметров для функции fun.
Применение этих функций мы рассмотрим немного позже при описании структуры функций.
Продолжаем перечисление системных переменных:
-
pi — число р (отношение длины окружности к ее диаметру), pi возвращает число с плавающей запятой, ближайшее к значению р. Выражения 4*atan(l) и imag(log(-1)) выдают тот же результат. Пример:
» pi
ans = 3.1416
-
real max — возвращает самое большое число в формате с плавающей запятой, соответствующее конкретному компьютеру. Большее значение соответствует системной переменной Inf. Пример:
» n = real max
n =
1.7977е+308
-
real mi n — возвращает наименьшее нормализованное положительное число в формате с плавающей запятой, представимое на конкретном компьютере. Любое меньшее число воспринимается как ноль. Пример:
» n = realmin
n =
2.2251е-308
Переменные varargin и varargout позволяют использовать в функциях переменное число входных и выходных параметров:
-
varargout = foo(n) — возвращает список выходных параметров переменной длины функции foo;
-
у = function bar(varargin) — принимает переменное число аргументов в функцию bar.
Переменные varargin и varargout используются только внутри m-файлов функции для задания произвольных аргументов функции. Эти переменные должны быть последними в списке входов или выходов, а для их обозначения могут использоваться только строчные буквы. Использование этих возможностей мы рассмотрим несколько позже.
7. Функции поразрядной обработки
Функции поразрядной обработки
Ряд функций предназначен для поразрядной логической обработки данных:
-
bitand(A.B) — возвращает поразрядное И двух неотрицательных целых аргументов А и В. Пример:
» f=bitand(7,14)
f =
6
-
bitcmp(A.n) — возвращает поразрядное дополнение аргумента А как n-битовое неотрицательное целое число. Пример:
» g=bitcmp(6,4)
g =
9
-
bitor(A.B) — возвращает поразрядное ИЛИ двух неотрицательных целых аргументов А и В. Пример:
» v=bitor(12.21)
v = 29
-
bitmax — возвращает максимальное целое число без знака, которое может быть представлено в формате чисел с плавающей запятой применительно к используемому компьютеру. Это значение определяется для комбинации, когда все биты установлены. На машинах с IEEE-арифметикой это значение равно 2 53 -1. Пример:
» bitmax
ans =
9.0072е+015
-
bitset(A.bit.v) — устанавливает бит в позиции bit равным значению v, которое должно быть 0 или 1. Пример:
» d=bitset(12.2.1)
d =
14
-
bitshift(A.n) — возвращает значение аргумента А, сдвинутое на п бит. Если n>0, это аналогично умножению на 2" (левый сдвиг). Если n<0, это аналогично делению на 2n (правый сдвиг). Пример:
» f=bitshift(4.3)
f =
32
-
bitset(A.bit) — устанавливает бит в позиции bit аргумента А в единичное значение. Аргумент А должен быть неотрицательным целым, bit — это номер в диапазоне между 1 и числом бит в целом числе, представленном в формате чисел с плавающей запятой.
-
bitget(A.bit) — возвращает значение бита в позиции bit операнда А. Аргумент А должен быть неотрицательным целым числом, bit — это номер между 1 и числом бит в целом числе формата с плавающей запятой. Пример:
» disp(dec2bin(23))
10111
» С = bitget(23.5:-l:l)
С =
1 0 1 1 1
-
bitxor(A, В) — возвращает результат поразрядного исключающего ИЛИ для двух аргументов А и В. Оба аргумента должны быть целыми. Пример:
» x=bitxor(12.31)
х =
19
Чтобы операнды этих функций гарантированно были целыми числами, при их задании рекомендуется использовать функции ceil, fix, floor и round.
8. Функции обработки множеств
Функции обработки множеств
Множество — первичное понятие математики, не имеющее четкого определения. Под множеством подразумевается совокупность некоторых объектов, например книг в библиотеке, людей в зале или элементов вектора. В этом разделе приводятся некоторые функции для обработки множеств, представленных векторами. Они широко используются при анализе и обработке данных.
-
intersect(a.b) — возвращает пересечение множеств для двух векторов а и b, т. е., общие элементы векторов а и b. Результирующий вектор отсортирован по возрастанию. Если входные массивы не являются векторами, то они рассматриваются как совокупность векторов-столбцов а=а(:) или b=b(:);
-
intersect(a,b, 'rows') — возвращает строки, общие для а и b, когда а и b представляют собой матрицы с одинаковым числом столбцов;
-
[c.ia.ib] = intersect(a.b) — также возвращает вектор-столбец индексов ia и ib. но так, что с = a(ia) и с = b(ib) (или с = a(ia.:) ис = b(ib.:)).
Пример:
» А = [1 7 2 6]; В = [7 2 3 4 6 1];
» [c,ia,ib] = intersect(А,В)
1 2 6 7
ia =
1 3 4 2
ib =
6 2 5 1
-
ismember(a.S) — возвращает вектор той же длины, что и исходный а, содержащий логические единицы на месте тех элементов вектора а, которые принадлежат множеству S, и логические нули на месте тех элементов вектора а, которые не принадлежат множеству S;
-
ismember (А. S.' rows') — возвращает вектор, содержащий логические единицы там, где строки матрицы А являются также строками матрицы S, и логические нули в остальных позициях. А и S должны быть матрицами с одним числом столбцов.
Пример:
» set = [0 1 3 5 7 9 11 15 17 19];
» а=[1 2345678];
» k = ismember(a.set)
k =
1 0 1 0 1 0 1 0
-
setdiff(a.b) — возвращает разность множеств, т. е., те элементы вектора а, которые не содержатся в векторе b. Результирующий вектор сортируется по возрастанию;
-
setdiff(a,b, 'rows') — возвращает те строки из матрицы а, которые не содержатся в матрице Ь. Матрицы а и b должны иметь одинаковое число столбцов;
-
[c,i] = setdiff(...) — возвращает также вектор индексов 1, такой что с = а(i) или с = а (i,;).
Если входной массив а является матрицей, то он расценивается как вектор-столбец а(:).
Пример:
» а=[2 3 5 7 8 9 10 13 20];
» b=[1456894]
» с = setdiff(a.b)
с=
2 3 7 10 13 20
-
setxor(a.b) — исключающее ИЛИ для векторов а и b. Результирующий вектор отсортирован;
-
setxor(a,b, 'rows') — возвращает строки, которые не являются пересечениями матриц а и b. Матрицы а и b должны иметь одинаковое число столбцов;
-
[c.ia.ib] = setxor(...) — возвращает также векторы индексов ia и ib так, что с является отсортированной комбинацией элементов с = а(iа)ис = b(ib) или для комбинаций строк с = а(iа,:)ис = b(ib.;).
Если массив а является матрицей, то он расценивается как вектор-столбец а(:).
Пример:
» а = [-1 0 1 Inf -Inf NaN];
» b = [-2 pi 0 Inf];
» с = setxor(a.b)
с =
-Inf -2.0000-1.00001.0000 3.1416 NaN
-
union(a ,b) — возвращает вектор объединенных значений из а и b без повторяющихся элементов. Результирующий вектор сортируется в порядке возрастания;
-
union(a,b, 'rows') — возвращает объединенные строки из а и b, не содержащие повторений (а и b — это матрицы с одинаковым числом столбцов);
-
[c.ia.ib] = unionL.) — дополнительно возвращает i а и i b — векторы индексов, такие что с = a(ia) и c=b(1b), или, для объединенных строк, с = а(1а.:)ис = b(ib,:). Невекторный массив а расценивается как вектор-столбец а(:). Пример:
» а=[2,4,-4,9,0]:b=[2,5,4]:
» [c,ia,ib]=union(a,b)
с =
-4 0 2 4 5 9
ia =
3 5 4
ib =
1 3 2
-
unique(a) — возвращает значения элементов из а, не содержащие повторений. Результирующий вектор сортируется в порядке возрастания. Невекторный массив расценивается как вектор-столбец а=а(: );
-
unique(a, 'rows') — возвращает уникальные строки а;
-
[b.i ,j] = unique(...) — дополнительно возвращает i и j — векторы индексов, такие что b = a(i)na = b(j) (или b = а(1,:) иа = b(j.:)).
Примеры:
» b=[-2,3,5,4,1,-6,2,2,7]
b=
-2 3 5 4 1 -6 2 2 7
» [c,i,j]=unique(b)
с =
|
|
|
-6 |
-2 |
1 2 3 4 |
5 7 |
|
|
|
|
6 |
1 |
5 8 2 4 |
3 9 |
|
|
|
j |
= |
|
|
|
|
|
|
|
2 |
5 |
7 6 3 1 |
4 4 |
|
|
|
» |
a-[-2, |
3.5:4. |
l.-6:2,2.7;-2.3,5J |
|
|
|
|
a |
= |
|
|
|
|
|
|
|
-2 |
3 |
5 |
|
|
|
|
|
4 |
1 |
-6 |
|
|
|
|
|
2 |
2 |
7 |
|
|
|
|
|
-2 |
3 |
5 |
|
|
|
|
» |
c=uniqueCa. ' |
rows ' ) |
|
|
|
|
|
с |
= |
|
|
|
|
|
|
|
-2 |
3 |
5 |
|
|
|
|
|
2 |
2 |
7 |
|
|
|
|
|
4 |
1 |
-6 |
|
|
|
|
|
|||||
9. Функции времени и даты
Функции времени и даты
Ряд функций служит для возврата текущего времени и даты. Они перечислены ниже.
-
calendar(d) — возвращает календарь на месяц, в который попадает день, заданный аргументом d (дни отсчитываются от начала летоисчисления);
-
calendar — возвращает матрицу размером 6x7, содержащую календарь на текущий месяц. Календарь начинается с воскресения (первый столбец) и завершается субботой;
-
calendar(y ,m) — возвращает календарь на месяц, заданный аргументом т, и год, заданный аргументом у;
Вызов функции без присваивания результата выдает календарь на экран. Примеры:
» calendar
Jul 2000
|
S |
М |
Tu |
W |
Th |
F |
S |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
|
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
30 |
31 |
0 |
0 |
0 |
0 |
0 |
|
|
|
calendar(700477)
Nov 1917
|
|
||||||||
|
|
S |
M |
Tu |
W |
Th |
F |
S |
|
|
|
0 |
0 |
0 |
0 |
1 |
2 |
3 |
|
|
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
|
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
|
25 |
26 |
27 |
28 |
29 |
30 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
-
clock — возвращает вектор из 6 элементов, содержащий текущую дату и время в десятичной форме [год месяц день час минуты секунды]. Первые пять элементов этого вектора — целые числа. Шестой элемент имеет несколько десятичных знаков после запятой. Функция fix(clock) округляет число секунд до целого значения. Пример:
» c=clock
с =
1.0e+003 *
2.0000 0.0070 0.0240 0.0200 0.0120 0.0148
» fix(clock)
ans =
2000 7 24 20 12 26
-
cputime — возвращает время работы процессора (в секундах) , использованное системой MATLAB с момента ее запуска. Это число может выйти за рамки внутреннего представления, и тогда отсчет времени начинается заново. Пример:
» +tl=cputime; w=surf(peaks(30));cputime-tl
ans =
0.2200
-
str = date — возвращает строку, содержащую дату в формате дд-ммм-гггг (день-месяц-год). Пример:
» d = date
d =
24-Jul-2000
-
datenum — преобразует строку даты в порядковый номер даты, который отсчитывается с некоторого начального дня (01.01.00);
-
datenum(str) — преобразует дату, заданную строкой str, в порядковый номер даты. Строка string должна иметь один из следующих форматов: 0, 1, 2, 6, 13, 14, 15 или 16, определенных для функции datestr;
-
datenum(Y.M.D) — возвращает порядковый номер даты для соответствующих массивов элементов Y, М и D (год, месяц, день). Массивы Y, М и D должны иметь одинаковую размерность (при этом любые из них могут быть скалярами);
-
datenum(Y.M.D,H.MI,S) — возвращает порядковый номер даты для соответствующих массивов элементов Y, М, D, H, Ml и S (год, месяц, день, часы, минуты, секунды). Массивы Y, М, D, H, Ml и S должны иметь одинаковую размерность (при этом любые из них могут быть скалярами).
Пример:
» n1 = datenum('26-Nov-1998')
n1 =
730085
» Y=[1998,2000];M-[1,12];D=23;N=datenum(Y,M,D)
N =
729778 730843
-
datestr(D, dateform) — преобразует каждый элемент массива порядковых номеров даты D в строку. Аргумент dateform определяет формат результата; dateform может быть номером или строкой в соответствии с табл. 8.5.
Таблица 8.5. Форматы представления даты
|
Dateform(номер) |
||
|
0 |
'dd-rmiM-yyyy HH:MM:SS' |
1l-Mar-1995 03:45 |
|
1 |
'dd-mmM-yyyy' |
Ol-Mar-1995 |
|
2 |
'mm/dd/yy' |
03/01/95 |
|
3 |
' mmm ' |
Mar |
|
4 |
'm' |
M |
|
5 |
'mm' |
3 |
|
6 |
'mm/dd' |
03/01 |
|
7 |
'dd' |
1 |
|
8 |
'ddd' |
Wed |
|
9 |
'd' |
W |
|
10 |
'УУУУ' |
1995 |
|
11 |
'УУ |
95 |
|
12 |
' mmmyy ' |
Mar95 |
|
13 |
'HH:MM:SS' |
15:45:17 |
-
datevec(A) — преобразует входные величины в массив размерности пхб, каждая строка которого представляет собой вектор [Y,M.D,H,MI,S]. Первые пять элементов вектора — целые числа. Массив А может состоять или из строк, удовлетворяющих формату функции datestr, или из скалярных величин, созданных функциями datenum и now;
-
[Y, M., D, H. MI, S] = datevec (A) — возвращает компоненты вектора даты как индивидуальные переменные.
Любой компонент входного вектора, который не вписывается в нормальный диапазон дат, преобразуется в следующий диапазон (так, например, несуществующая дата June 31 преобразуется в July 1). Допускаются значения нулевого месяца и нулевого дня. Например:
» n = datevecC 11/31/98')
n=
1998 12 1 0 0 0
» n = datevec(710223)
n =
1944 7 10 0 0
О eomday (Y, М) — возвращает последний день года и месяца, заданных соответственно элементами массивов Y и М. Пример (нахождение високосных лет двадцатого столетия):
» у = 1900:1999;
» Е = eomday(y.2);
» y(find(E==29))
ans=
Columns 1 through 6
1904 1908 1912 1916 1920 1924
Columns 7 through 12
1928 1932 1936 1940 1944 1948
Columns 13 through 18
1952 1956 1960 1964 1968 1972
Columns 19 through 24
1976 1980 1984 1988 1992 1996
-
etime(t2,tl) — возвращает длительность промежутка времени (в секундах), задаваемого векторами t1 и t2. Векторы должны удовлетворять формату, выдаваемому функцией clock:
Т = [год месяц день час минуты секунды].
Функция работает некорректно, если в текущий промежуток времени попадут границы месяца или года, что, однако, случается крайне редко и исправляется при повторе операции. Пример (вычисляется время, затрачиваемое на быстрое преобразование Фурье с 2048 точками):
» х = rand(2048,l);t = clock; fft(x); etime(clock.t);etime (clock.t)
ans =
0.0500
-
now — возвращает текущие время и дату в форме числа. Использование rem(now.l) возвращает только время, a floor(now) — только дату. Пример:
» t1 = now, t2 = rem(now,1)
t1 =
7.3009e+005
t2 =
0.6455
-
tic — запускает таймер;
-
toc — выводит время, прошедшее с момента запуска таймера;
-
t = toe — возвращает прошедшее время в переменной t. Пример:
» tic.surf(peaks(50));toc
elapsed_time =
0.7600
-
[N,S] = weekday(D) — возвращает день недели в виде числа N и в виде строки S для каждой даты массива D. Пример:
» D=[728647,735730]:[N.S] = weekday(D)
N =
2 1
S=
Mon Sun
10. Элементарные функции
Элементарные функции
Элементарные функции, пожалуй, наиболее известный класс математических функций. Поэтому, не останавливаясь подробно на их описании, представим набор данных функций, имеющийся в составе системы MATLAB. Функции, перечисленные ниже, сгруппированы по функциональному назначению. В тригонометрических функциях углы измеряются в радианах. Все функции могут использоваться в конструкции вида y=func(x), где func — имя функции. Обычно в такой форме задается информация о функции в системе MATLAB. Мы, однако, будем использовать для функций, возвращающих одиночный результат, более простую форму func(x). Форма [y,z,...]=func(x....) будет использоваться только в тех случаях, когда функция возвращает множественный результат.
11. Алгебраические и арифметические функции
Алгебраические и арифметические функции
В системе MATLAB определены следующие алгебраические и арифметические функции:
-
abs(X) — возвращает абсолютную величину для каждого числового элемента вектора X. Если X содержит комплексные числа, abs(X) вычисляет модуль каждого числа. Примеры:
abs(-5) = 5
abs(3+4i) =5
» abs([1 -2 1 3i 2+3i ])
ans =
1.0000 2.0000 1.0000 3.0000 3.6056
-
ехр(Х) — возвращает экспоненту для каждого элемента X. Для комплексного числа z = х + i*y функция exp(z) вычисляет комплексную экспоненту: exp(z)=exp(x)*(cos(y)+i*sin(y)).
Примеры:
» ехр([1 23])
ans =
2.7183 7.3891 20.0855
» exp(2+3i)
ans =
-7.3151 + 1.0427i
-
factor(n) — возвращает вектор-строку, содержащую простые множители числа п. Для массивов эта функция неприменима. Пример:
f = factor(221)
f =
13 17
-
G=gcd(A, В) — возвращает массив, содержащий наибольшие общие делители соответствующих элементов массивов целых чисел А и В. Функция gcd (0.0) возвращает значение 0, в остальных случаях возвращаемый массив G содержит положительные целые числа;
-
[G, С. D] = gcd(A, В) — возвращает массив наибольших общих делителей G и массивов С и D, которые удовлетворяют уравнению A(i) .*С(1) + B(i) .*D(i) = G(i). Они полезны для выполнения элементарных эрмитовых преобразований. Примеры:
» А=[2 6 9]:
» В=[2 3 3]:
» gcd(A.B)
ans =
2 3 3
» [G.C.D]=gcd(A.B)
G =
2 3 3
C =
0 0 0
D=
1 1 1
-
lcm(A.B) — возвращает наименьшие общие кратные для соответствующих парных элементов массивов А и В. Массивы А и В должны содержать положительные целые числа и иметь одинаковую размерность (любой из них может быть скаляром). Пример:
» А=[1 354];
» В=[2 462];
» lcm(А.В)
ans =
2 12 30 4
-
log (X) — возвращает натуральный логарифм элементов массива X. Для комплексного или отрицательного z, где z = х + y*i, вычисляется комплексный логарифм в виде log(z) = log(abs(z)) + i*atan2(y,x). Функция логарифма вычисляется для каждого элемента массива. Область определения функции включает комплексные и отрицательные числа, что способно привести к непредвиденным результатам при некорректном использовании. Пример:
» Х=[1.2 3.34 5 2.3];
» log(X)
ans=
-0.1823 1.2060 1.6094 0.8329
-
log2(X) — возвращает логарифм по основанию 2 элементов массива X;
-
[F,E] = log2(X) — возвращает массив действительных значений F и массив целых чисел Е. Элементы массива F обычно лежат в диапазоне 0.5 J abs(F) < 1. Для действительных X возвращаемые массивы F удовлетворяют уравнению вида X = F. *2. Е. Для нулевых значений X возвращаются F = 0 и Е = 0.
Пример:
» Х=[2 4.678 5;0.987 1 3];
» [F.E] = log2(Х)
F =
0.5000 0.5847 0.6250
0.9870 0.5000 0.7500
Е =
2 3 3
0 1 2
-
log10(X) — возвращает логарифм по основанию 10 для каждого элемента X. Область функции включает комплексные числа, что способно привести к непредвиденным результатам при некорректном использовании.
Пример:
» Х=[1.4 2.23 5.8 3];
» log10(X)
ans =
0.1461 0.3483 0.7634 0.4771
-
mod(x.y) — возвращает х mod у;
-
mod(X, Y) — возвращает остаток от деления X на Y (т. е., X - Y.*floor(X./Y)) для ненулевого Y, и X в противном случае. Если операнды X и Y имеют одинаковый знак, функция mod(X, Y) возвращает тот же результат, что mod(Х, Y). Однако (для положительных X и Y) mod(-x.y) = rem(-x,y)+y.
Примеры:
» М = mod(5.2)
М =
1
» mod(10.4)
ans =
2
-
pow2(Y) — возвращает массив X, где каждый элемент есть Z Y ;
-
pow2(F.E) — вычисляет Х=Р*2 £ для соответствующих элементов F и Е. Аргументы F и Е — массивы действительных и целых чисел соответственно.
Пример:
» d=pow2(pi/4,2)
d =
3.1416
-
р = nextpow2(A) — возвращает такой показатель степени р, что 2 Р i abs(A). Эта функция эффективно применяется для выполнения быстрого преобразования
Фурье. Если А не является скалярной величиной, то nextpowZ возвращает значение nextpow2(length(A)).
Пример:
» х=[2 678934567784324];
» length(x)
ans =
16
» р = nextpow2(x)
Р =
4
» х=4:
» р = nextpow2(x)
Р =
2
» Х=45;
» р = nextpow2(x)
Р =
6
Функция primes(n) возвращает вектор-строку простых чисел, меньших или равных n. Пример:
» р = primes(25)
Р =
2 3 5 7 11 13 17 19 23
-
[N,D] = rat(X) - возвращает массивы N и D, такие что N./D аппроксимирует X с точностью 1 .е-6*norm(Х(:),!). Даже при том, что все числа с плавающей запятой — рациональные числа, иногда желательно аппроксимировать их дробями, у которых числитель и знаменатель являются по возможности малыми целыми числами. Функция rat пытается это сделать;
-
[N.D] = rat(X.tol) — возвращает массивы N и D, такие что N./D аппроксимирует X с точностью tol.
-
rat (X) без выходных параметров просто выдает на экран массив цепных дробей;
-
rats(X.strlen) — возвращает ряд, полученный путем упрощенной рациональной аппроксимации элементов X. Аргумент strlen — длина возвращаемой строки. Функция возвращает знак «*», если полученное значение не может быть напечатано в строке, длина которой задана значением strlen. По умолчанию strlen=13. Тот же алгоритм аппроксимации используется в командном окне MATLAB при задании рационального формата вывода командой format rat.
Пример:
» [g.j]=rat(pi.le-10)
g=
312689
j =
99532
-
sqrt(A) — возвращает квадратный корень каждого элемента массива X. Для отрицательных и комплексных элементов X функция sqrt(X) вычисляет комплексный результат.
Пример:
» А=[25 21.23 55.8 3]:
» sqrt(A)
ans =
5.0 4.6076 7.4699 1.7321
На рис. 8.1 представлены графики ряда распространенных алгебраических функций. Эти графики получены в результате исполнения следующего файла-сценария:
syms x
subplot(2,2.1).ezplot(x*2.[-5 5]).xlabel( " ).grid on
subplot(2,2.2).ezplot(exp(x),[-2 2]),xlabel(").grid on
subplot(2.2.3).ezplot(log(x).[0 5]),grid on
subplot(2.2.4),ezplot(sqrt(x).[0 10]).grid on
Рис. 8.1. Графики ряда алгебраических функций
Графики дают наглядное представление о поведении представленных на них функций. Обратите внимание на применение графической команды ezplot из пакета Symbolic Math ToolBox (она отличается от обычной команды ezplot MATLAB отсутствием заключения символьных переменных в'), команды syms, также входящей в пакет Symbolic Math .Toolbox и задающей символьную переменную х, и несколько необычное применение команды xlabel (''). Эта команда с аргументом в виде пустой строки снимает вывод обозначения горизонтальной оси на двух верхних графиках. Если этого не сделать, то символ «х» окажется наложенным на наименование функций нижних графиков, которое команда ezpl ot выводит над графиками автоматически.
1.gif
12. Тригонометрические и обратные им функции
Тригонометрические и обратные им функции
В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.
Э acos (X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.
Примеры:
»Y = acos (0.5)
1.0472
» acos([0.5 1 2])
ans =
1.0472 0 0 + 1.31701
-
acot (X) — возвращает арккотангенс для каждого элемента X. Пример:
» Y=acot(0.l)
у =
1.4711
-
acsc(X) — возвращает арккосеканс для каждого элемента X. Пример:
» Y= acsc(3)
0.3398
-
asec(X) — возвращает арксеканс для каждого элемента X. Пример:
» Y=asec(0.5)
Y =
0 + 1.31701
-
asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:
» Y= asin (0.278)
Y =
0.2817
-
atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:
» Y=atan(1)
Y =
0.7854
-
atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].
Пример:
» atan2(l,2)
ans =
0.4636
-
cos(X) — возвращает косинус для каждого элемента X. Пример:
»Х=[123];
» cos(X)
ans =
0.5403 -0.4161 -0.9900
-
cot(X) — возвращает котангенс для каждого элемента X. Пример:
» Y = cot(2)
Y =
-0.4577
-
csc(X) — возвращает косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csc(X)
Y =
1.0998 -1.0006 -1.0428
1.1985 1.1884 7.0862
-
sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:
» X=[pi/10 pi/3 pi/5];
» sec(X)
ans =
1.0515 2.0000 1.2361
-
sin(X) — возвращает синус для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sin(X)
ans =
1.0000 0.7071 0.5000 0.0000
-
tan(X) — возвращает тангенс для каждого элемента X.
Рис. 8.2. Графики четырех тригонометрических функций
Пример:
» Х=[0.08 0.06 1.09]
X=
0.0800 0.0600 1.0900
» tan(X)
ans=
0.802 0.0601 1.9171
Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):
syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel("),gnd on
subplot(2.2.2),ezp"lot(tan(x).[-5 5]).xlabel(").grid on
subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on
subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on
Поскольку многие тригонометрические функции периодичны, появляется возможность формирования из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы, используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных сигнала — прямоугольные, пилообразные и треугольные импульсы:[ В пакете расширения Signal Processing Toolbox есть специальные функции для генерации таких сигналов — square и sawtooth. — Примеч. ред. ]
х=-10:0.01:10;
subplot(2,2.1).plot(x.0.8*sin(x))
.x label('0.8*sin(x)')
subplot(2.2,2).plot(x,0.8*sign(sin(x)))
.x1abel('0.8*sgn(sin(x))')
subplot(2.2.3),plot(x.atan(tan(x/2)))
.xlabel('atan(tan(x/2))')
subplot(2.2.4),plot(x,asin(sin(x)))
.xlabel('asin(sin(x))')
Соответствующие графики представлены на рис. 8.3.
Рис. 8.3. Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний
Дополнительный ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:
х=-10:0.01:10;
subplot(2.2.1).plot(x.sin(x). A 3).x1abel('sin(xr3')
subplot(2.2.2).plot(x,abs(s1n(x)))
.xlabel('abs(sin(x))').axis([-10 10 -1 1]),
subplot(2.2,3),plot(x,tan(cos(x)))
.xlabel('tanCcos(x))')
subplot(2.2.4).plot(x.csch(sec(x))),xlabeK'csch(sec(x))')
Рис. 8.4. Графики периодических сигналов без разрывов
Эти графики неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения (или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.
2.gif
3.gif
4.gif
13. Гиперболические и обратные им функции
Гиперболические и обратные им функции
Наряду с тригонометрическими функциями в математических расчетах часто используются и гиперболические функции. Ниже приводится список таких функций, определенных в системе MATLAB. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Все углы в тригонометрических функциях измеряются в радианах.
-
acosh(X) — возвращает гиперболический арккосинус для каждого элемента X. Пример:
»Y= acosh (0.7)
Y =
0 + 0.7954i
-
acoth(X) — возвращает гиперболический арккотангенс для каждого элемента X. Пример:
»Y = acoth (0.1)
Y=
0.1003 + 1.5708i
-
acsch(X) — возвращает гиперболический арккосеканс для каждого элемента X. Пример:
» Y = acsch(1)
Y =
0.8814
-
asech(X) — возвращает гиперболический арксеканс для каждого элемента X. Пример:
» Y = asech(4)
Y =
0 + 1.3181i
-
asinh(X) — возвращает гиперболический арксинус для каждого элемента X. Пример:
» Y = asinh (2.456)
Y =
1.6308
-
atanh(X) — возвращает гиперболический арктангенс для каждого элемента X. Пример:
» Х=[0.84 0.16 1.39];
» atanh (X)
ans =
1.2212 0.1614 0.9065 + 1.5708i
-
cosh(X) — возвращает гиперболический косинус для каждого элемента X. Пример:
» Х=[1 23];
» Cosh(X)
ans =
1.5431 3.7622 10.0677
-
coth(X) — возвращает гиперболический котангенс для каждого элемента X. Пример:
» Y = coth(3.987)
Y =
1.0007
-
csch(x) — возвращает гиперболический косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csch(X)
Y =
0.2757 0.0186 0.0135
0.8656 0.8509 0.0998
-
sech(X) — возвращает гиперболический секанс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sech(X)
ans =
0.3985 0.7549 0.8770 0.0863
-
sinh(X) — возвращает гиперболический синус для каждого элемента X. Пример:
» X=[pi/8 pi/7 pi/5 pi/10];
» sinh(X)
ans =
0.4029 0.4640 0.6705 0.3194
-
tanh(X) — возвращает гиперболический тангенс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi/10];
»tanh(X)
ans =
0.9172 0.6558 0.4805 0.3042
Следующий m-файл-сценарий строит графики ряда гиперболических функций:
syms x
subplot(2,2,l).ezplot(sinh(x).[-4 4]).xlabel(").grid on
subplot(2,2.2).ezplot(cosh(x).[-4 4]).xlabel('').grid on
subp1ot(2.2,3).ezplot(tanh(x).[-4 4]).grid on
subplot(2.2.4).ezplot(sech(x).[-4 4]).grid on
Нетрудно заметить, что гиперболические функции в отличие от тригонометрических не являются периодическими. Выбранные для графического представления функции дают примеры характерных нелинейностей.
В другом файле использованы команды для построения графиков ряда обратных гиперболических функций:
syms x
subplot(2,2.1).ezplot(asinh(x).[-4 4]).xlabel(").grid on
subplot(2.2.2),ezp1ot(acosh(x).[0 4]).xlabel(").grid on
subplot(2,2.3),ezplot(atanh(x).[-l l]).grid on
subplot(2.2.4).ezplot(asech(x).[0 l]).grid on
На этих графиках хорошо видны особенности данного класса функций. Такие функции, как обратный гиперболический синус и тангенс, «ценятся» за симметричный вид их графиков, дающий приближение к ряду типовых нелинейностей.
14. Функции округления и знака
Функции округления и знака
Ряд особых функций служат для выполнения операций округления числовых данных и анализа их знака.
-
fix(A) — возвращает массив А с элементами, округленными до ближайшего к нулю целого числа. Для комплексного А действительные и мнимые части округляются отдельно.
Примеры:
» А=[1/3 2/3: 4.99 5.01]
А =
0.3333 0.6667
4.9900 5.0100
» fix(A)
ans =
0 0
4 5
-
floor(A) — возвращает А с элементами, представляющими ближайшее меньшее или равное соответствующему элементу А целое число. Для комплексного А действительные и мнимые части преобразуются отдельно.
Примеры:
» А=[-1/3 2/3: 4.99 5.01]
А =
-0.33330.6667
4.99005.0100
» floor(А)
ans =
-1 0 4 5
-
ceil (A) — возвращает ближайшее большее или равное А целое число. Для комплексного А действительные и мнимые части округляются отдельно.
Примеры:
» а=-1.789;
» ceil (а)
ans =
-1
» а=-1.789+1*3.908;
» cei l(а)
ans =
-1.0000 + 4.0000i
-
rem(X,Y) — возвращает X - fix(X./Y).*Y, где fix(X./Y) — целая часть от частного X/Y.
Если операнды X и Y имеют одинаковый знак, функция rem(X, Y) возвращает тот же результат, что mod(X.Y). Однако (для положительных X и Y) rem(-x.y) = mod(-x,y)-y. Функция rem возвращает результат, находящийся между 0 и sign(X)*abs(Y). Если Y=0, функция rem возвращает NaN. Аргументы X и Y должны быть целыми числами. Из-за неточного представления в компьютере чисел с плавающей запятой использование вещественных (или комплексных) входных аргументов может привести к непредвиденным результатам.
Пример:
» Х=[25 21 23 55 3];
» Y=[4 8 23 6 4];
» rem(X.Y)
ans=
15013
-
round(X) — возвращает округленные до ближайшего целого элементы массива X. Для комплексного X действительные и мнимые части округляются отдельно.
Пример:
» Х=[5.675 21.6+4.897*1 2.654 55.8765];
» round(X)
ans =
6.0000 22.0000 +5.0000i 3.0000 56.0000
-
sign(X) — возвращает массив Y той же размерности, что и X, где каждый из элементов Y равен:
-
1, если соответствующий элемент X больше 0;
-
0, если соответствующий элемент X равен 0;
-
-1, если соответствующий элемент X меньше 0. Для ненулевых действительных и комплексных X — Sign(X)=X./abs(X).
-
Пример:
» Х=[-5 21 2 0 -3.7]:
» sign(X)
ans =
-1 1 1 0 -1
15. Функции комплексного аргумента
Функции комплексного аргумента
Для работы с комплексными числами и данными в MATLAB используются следующие функции:
-
angle(Z) возвращает аргумент комплексного числа в радианах для каждого элемента массива комплексных чисел Z. Углы находятся в диапазоне [-р; +р]. Для комплексного Z модуль и аргумент вычисляются следующим образом: R = abs(Z) — модуль, theta = angle(Z) — аргумент. При этом формула Z = R.*exp(i*theta) дает переход от показательной формы представления комплексного числа к алгебраической.
Примеры:
» Z=3+i*2
Z =
3.0000 + 2.00001
» theta = angle(Z)
theta =
0.5880
» R = abs(Z)
R =
3.6056
» Z =R.*exp(i*theta)
Z =
3.0000 + 2.00001
-
imag(Z) — возвращает мнимые части всех элементов массива Z. Пример:
» Z-[1+i, 3+2i, 2+3i];
» imag(Z)
ans =
1 2 3
-
real(Z) — возвращает вещественные части всех элементов комплексного массива Z. Пример:
» Z=[1+i. 3+2i 2+3i]:
» real(Z)
ans =
1 3 2
-
conj(Z) — возвращает число, комплексно-сопряженное аргументу Z. Если Z комплексное, то conj(Z) = real(Z) - i *imag (Z). Пример:
» conj(2+31)
ans=
2.0000 - 3.00001
16. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Применять арифметические операторы и функции.
-
Использовать операторы отношения и их функции.
-
Применять логические операторы.
-
Использовать специальные символы.
-
Использовать системные переменные и константы.
-
Работать с функциями поразрядной обработки, множествами, функциями времени и даты.
-
Использовать элементарные функции и строить их графики.
-
Работать с функциями округления и анализа знака.
-
Использовать функции комплексного аргумента.
Урок 9. Специальные математические функции
1. Урок 9. Специальные математические функции
Урок №9.
Специальные математические функции
-
Функции Эйри
-
Функции Бесселя
-
Бета-функция и ее варианты
-
Эллиптические функции и интегралы
-
Функции ошибки
-
Интегральная показательная функция
-
Гамма-функция и ее варианты
-
Ортогональные полиномы Лежандра
Специальные математические функции являются решениями дифференциальных уравнений специального вида или обозначениями некоторых видов интегралов. Довольно полный обзор специальных функций дается в книгах [55-58], так что ниже мы ограничимся только указанием функций системы MATLAB, реализующих их вычисление. Набор специальных математических функций в системе MATLAB настолько представителен, что позволяет решать практически все задачи, связанные с применением таких функций. Если и обнаруживаются недостающие специальные функции, то пользователь может сам задать их вычисления. Специфика специальных функций в MATLAB та же, что и элементарных, — их аргументами могут быть как одиночные численные значения, так и массивы чисел. В последнем случае функции возвращают массив тех же размерности и размера с преобразованием каждого элемента в соответствии с действием функции. В версии MATLAB 6 вы теперь можете получить справку с записью формул в стандартной математической форме, набрав в командной строке doc function, где function — имя специальной функции.
2. Функции Эйри
Функции Эйри
Функция Эйри формирует пару линейно независимых решений линейного дифференциального уравнения вида
Связь между функцией Эйри и модифицированной функцией Бесселя выражается следующей формулой:
где
- airy(Z) — возвращает функцию Эйри, AKZ), для каждого элемента комплексного массива Z;
- airy(k.Z) — возвращает различные варианты результата в зависимости от значения k:
- k=0 — тот же результат, что и airy(Z);
- k=1 — производную от А1 (Z);
- k=2 — функцию Эйри второго рода, 61 (Z) :
- k=3 — производную от B1(Z). Пример:
D=
1.0000 3.0000 + 2.00001
» S=airy(D)
S =
0.1353 -0.0097 + 0.00551
11.gif
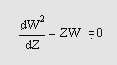
12.gif
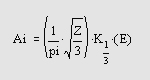
13.gif
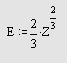
3. Функции Бесселя
Функции Бесселя
Линейное дифференциальное уравнение второго порядка вида
где v — неотрицательная константа, называется уравнением Бесселя, а его решения известны как функции Бесселя. Функции J v (z) и J_ v (z) формируют фундаментальное множество решений уравнения Бесселя для неотрицательных значений п (это так называемые функции Бесселя первого рода): где для гамма-функции используется следующее представление:
Второе решение уравнения Бесселя, линейно независимое от J v (z), определяется как и задает функции Бесселя второго рода Y v (z).
Функции Бесселя третьего рода (функции Ханкеля) и функция Бесселя первого и второго рода связаны следующим выражением:
-
bessel j(nu,Z) — возвращает функцию Бесселя первого рода, J v (z), для каждого элемента комплексного массива Z. Порядок ш может не быть целым, однако должен быть вещественным. Аргумент Z может быть комплексным. Результат вещественный, если Z положительно. Если nu и Z — массивы одинакового размера, то результат имеет тот же размер. Если любая входная величина — скаляр, результат расширяется до размера другой входной величины. Если одна входная величина — вектор-строка, а другая — вектор-столбец, результат представляет собой двумерный массив значений функции.
-
bessely(nu.Z) — возвращает функцию Бесселя второго рода, Y v (z).
-
[J.ierr] = besse1j(nu,Z) и [Y.ierr] = bessely(nu.Z) функции всегда возвращают массив с флагами ошибок:
-
ierr = 1 — запрещенные аргументы;
-
ierr = 2 — переполнение (возвращает Inf);
-
ierr = 3 — некоторая потеря точности при приведении аргумента;
-
ierr = 4 — недопустимая потеря точности: Z или nu слишком велики;
-
ierr = 5 — нет сходимости (возвращает NaN).
-
Примеры:
» S=[2-51.4.7];T=[8.l.3]:g=besselj(T,S)
g=
0.1114-0.05081 -0.0660 -0.1676
» S-[2-5i,4.7];T=[8.1.3J;[g.ierr]=bessely(T,S)
g=
0.1871 - 0.03241 0.3979 0.2681
ierr =
0 0 0
-
besselh(nu,К,Z) — для К=1 или 2 возвращает функцию Бесселя третьего рода (функцию Ханкеля) для каждого элемента комплексного массива Z. Если nu и Z — массивы одинакового размера, то результат имеет тот же размер. Если одна из входных величин — скаляр, результат формируется по размеру другой входной величины. Если одна входная величина — вектор-строка, а другая — вектор-столбец, результат представляет собой двумерный массив значений функции.
-
bessel h(nu.Z) — использует по умолчанию К = 1.
-
besselh(nu.l.Z.l) — масштабирует H (1) v (z) с коэффициентом exp(-i*z).
-
besse1h(nu,2,Z.l) — масштабирует H (2) v (z) с коэффициентом exp(+i*z).
-
[H.ierr] = besselhC...) — всегда возвращает массив с флагами ошибок:
-
ierr = 1 — запрещенные аргументы;
-
ierr = 2 — переполнение (возвращает Inf);
-
ierr = 3 — некоторая потеря точности при приведении аргумента;
-
ierr = 4 — недопустимая потеря точности: Z или nu слишком велики;
-
ierr = 5 — нет сходимости (возвращает NaN).
-
» D=[1.3+2i];F=[3.2]:[K.ierr]=besselk(F,D)
К =
7.1013 -0.0401 - 0.02851
lerr =
0 0
Естественно, что возможно построение графиков специальных функций.
В качестве примера рассмотрим m-файл-сценарий, приведенный ниже:
х=0:0.1:10;
y0=besselj(0.x);
y1=besselj(1.x):
y2=besselj(2.x);
y3=besselj(3.x);
plot(x,y0,.'-m',x,y1,'-r',x,y2,'-.k',x,y3,'-b')
legend('besselj(0.x)'. 'besselj(l.x)' ,'besse1j(2,x)'. ( besselj(3,x)');
Рис. 9.1 иллюстрирует построение четырех функций Бесселя bessel j(n,x) для п-0, 1, 2 и 3 с легендой, облегчающей идентификацию каждой кривой рисунка.
Рис. 9.1. Графики четырех функций Бесселя besselj(n,x)
Эти графики дают наглядное представление о поведении функций Бесселя, широко используемых при анализе поведения систем, описываемых линейными дифференциальными уравнениями второго порядка.
1a.gif
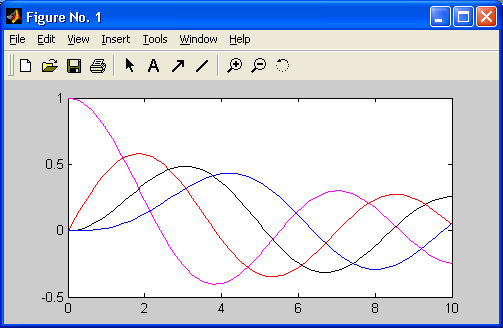
1b.gif

14.gif
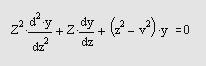
14.gif
16.gif
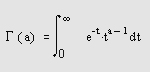
17.gif
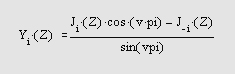
19.gif
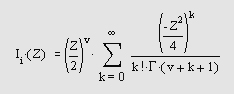
20.gif
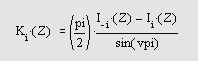
4. Бета-функция и ее варианты
Бета-функция и ее варианты
Бета-функция определяется как
где Г (z) — гамма-функция. Неполная бета-функция определяется по формуле
-
beta(Z.W) — возвращает бета-функцию для соответствующих элементов комплексных массивов Z и W. Массивы должны быть одинакового размера (или одна из величин может быть скаляром).
-
beta i nc ( X , Z , W ) — возвращает неполную бета-функцию. Элементы X должны быть в закрытом интервале [0, 1].
-
beta 1 п ( Z , W ) — возвращает натуральный логарифм бета-функции log ( beta ( Z , W ) ) , без вычисления beta(Z.W). Так как сама бета-функция может принимать очень большие или очень малые значения, функция betaln(Z.W) иногда более полезна, так как позволяет избежать переполнения.
Пример:
» format rat;beta((l:10) 4 ,4)
ans=
1/4
1/20
1/60
1/140
1/280
1/504
1/840
1/1320
1/1980
1/2860
21.gif
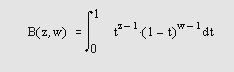
22.gif
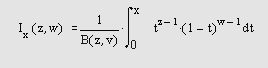
5. Эллиптические функции и интегралы
Эллиптические функции и интегралы
Эллиптические функции Якоби определяются интегралом и соотношениями
сn(u) = cos ф,
cn(u)=cosф,
dn(u) = (1-sin 2 ф) 1/2 ,
аm(u) = ф.
В некоторых случаях при определении эллиптических функций используются модули k вместо параметра гл. Они связаны выражением k = т = sin a .
-
[SN.CN.DN] = ellipj(U.M) — возвращает эллиптические функции Якоби SN, CN и . DN, вычисленные для соответствующих элементов — аргумента U и параметра М. Входные величины U и М должны иметь один и тот же размер (или любая из них может быть скаляром).
-
[SN.CN.DN] = ellipj(U,M,to1) — возвращает эллиптическую функцию Якоби, вычисленную с точностью tol . Значение tol по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:
» [SN.CN.DN]=ellipj([23.1].[0.5.0.2])
|
|
|
|
|
|
|
SN = |
|
|
|
|
474/719 |
1224/1481 |
|
|
|
CN = |
|
|
|
|
1270/1689 |
1457/2588 |
|
|
|
DN = |
|
|
|
|
399/451 |
538/579 |
|
|
|
|
|
|
Полные эллиптические интегралы первого и второго рода определяются следующим образом:
-
ellipke(M) — возвращает полный эллиптический интеграл первого рода для элементов М.
-
[К.Е] = ellipke(M) — возвращает полные эллиптические интегралы первого и второго рода.
-
[К.Е] = ellipke(M.tol) — возвращает эллиптические функции Якоби, вычисленные с точностью tol. Значение по умолчанию — eps; его можно увеличить, тогда результат будет вычислен быстрее, но с меньшей точностью. Пример:
» [f.e]=ellipse([0.2.0.8])
f =
707/426 1018/451
е =
679/456 515/437
Для вычисления этих функций используется итерационный метод арифметико-геометрического среднего (см. детали в Reference Book по системе MATLAB).
18.gif
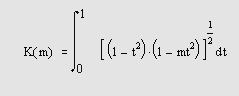
23.gif
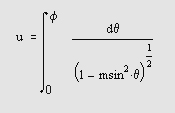
24.gif
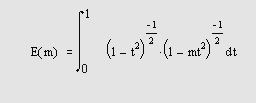
6. Функции ошибки
Функции ошибки
Функция ошибки определяется следующим образом:
-
erf(X) — возвращает значение функции ошибки для каждого элемента вещественного массива X. Дополнительная (остаточная) функция ошибки задается соотношением
-
erfc(X) — возвращает значение остаточной функции ошибки.
-
erfcx(X) — возвращает значение масштабированной остаточной функции ошибки. Эта функция определяется так:
егfсх(х) = е х erfc(x).
-
erfinv(Y) — возвращает значение обратной функции ошибки для каждого элемента массива Y. Элементы массива Y должны лежать в области -1<Y<1. Примеры:
» Y=[0.2,-0.3];a=erf(Y)
а =
0.2227 -0.3286
» b=erfc(Y)
b =
0.7773 1.3286
» c=erfcx(Y)
с =
0.8090 1.4537
» d=erfinv(Y)
d =
0.1791 -0.2725
При вычислении данных функций используется аппроксимация по Чебышеву (см. детали алгоритма в Reference Book no MATLAB).
25.gif
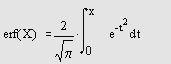
27.gif
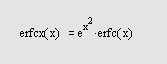
7. Интегральная показательная функция
Интегральная показательная функция
Интегральная показательная функция определяется следующим образом:
-
expint(X) — возвращает интегральную показательную функцию для каждого
элемента X. Пример:
» d=expint([2,3+7i])
d =
0.0489 -0.0013 -0.00601
Для вычисления этой функции используется ее разложение в ряд.
28.gif
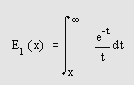
8. Гамма-функция и ее варианты
Гамма-функция и ее варианты
Гамма-функция определяется выражением
Неполная гамма-функция определяется как
-
gamma (А) — возвращает гамма-функцию элементов А. Аргумент А должен быть вещественным.
-
gamma iпс(X,А) — возвращает неполную гамма-функцию соответствующих элементов X и А. Аргументы X и А должны быть вещественными и иметь одинаковый размер (или любой из них может быть скалярным).
gammaln(A) —возвращает логарифмическую гамма-функцию, gammaln(A) = 1og(gamma(A)). Команда gammaln позволяет избежать переполнения, которое может происходить, если вычислять логарифмическую гамма-функцию непосредственно, используя 1og(gamma(A)).
Примеры:
» f=[5.3];d=gamma(f)
d =
24 2 » h=gammaln(f)
h =
3.1781 0.6931
Гамма-функция имеет довольно сложный», график, заслуживающий построения (рис. 9.2).
Рис. 9.2. График гамма-функции
Это можно осуществить с помощью следующего файла-сценария:
%Gamma function graphicclear syms x
ezplot(gamma(x).[-4 4]) grid on
Гамма-функция вычисляется по известному алгоритму W. J. Kody (1989 г.). Для вычисления неполной гамма-функции используются рекуррентные формулы.
2.gif
29.gif
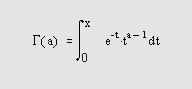
30.gif
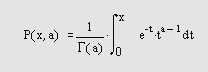
9. Ортогональные полиномы Лежандра
Ортогональные полиномы Лежандра
Функция Лежандра определяется следующим образом:
где Рn(*) — полином Лежандра степени п, рассчитываемый как
-
legendre(n.X) —возвращает функции Лежандра степени п и порядков m = 0,1..... n, вычисленные для элементов X. Аргумент п должен быть скалярным целым числом, не превосходящим 256, а X должен содержать действительные значения в области -UxJl. Возвращаемый массив Р имеет большую размерность, чем X, и каждый элемент P(m+l,dl,d2...) содержит связанную функцию Лежандра степени п и порядка т, вычисленную в точках X(dl,d2...).
-
1egendre(n,X, 'sch') — возвращает квазинормализованные по Шмидту функции Лежандра.
Пример:
» g=rand(3.2);legendre(3,g)
|
|
|
|
|
|
|
|
-0.4469 |
-0.0277 |
0.1534 |
|
|
|
-0.0558 |
1.4972 |
-2.0306 |
|
|
|
5.4204 |
0.2775 |
4.0079 |
|
|
|
-10.5653 |
-14.9923 |
-2.7829 |
|
|
|
|
|
|
|
ans(:.:.2) =
-0.4472-0.34040.0538
0.0150 -1.0567 -1.9562
5.3514 5.7350 4.4289
-10.7782 -7.3449 -3.4148
31.gif
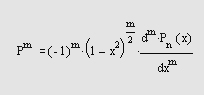
32.gif
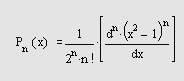
10. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Вычислять функции Эйри.
-
Вычислять функции Бесселя разного рода.
-
Вычислять бета-функцию и ее варианты.
-
Использовать эллиптические функции и интегралы.
-
Вычислять функции ошибки.
-
Вычислять интегральные показательные функции.
-
Вычислять гамма-функцию и ее варианты.
-
Использовать ортогональные полиномы Лежандра.
Урок 10. Операции с векторами и матрицами
1. Урок 10. Операции с векторами и матрицами
Урок №10.
Операции с векторами и матрицами
-
Создание стандартных матриц
-
Создание векторов равноотстоящих точек в линейном и логарифмическом масштабах
-
Создание массивов со случайными элементами
-
Конкатенация матриц
-
Изменение порядка расположения элементов матриц
-
Вычисление сумм и произведений
-
Изменение формы матриц
-
Выделение треугольных частей матриц
-
Вычисление тестовых матриц
-
Матричные функции
Матрицы представляют собой самые распространенные объекты системы MATLAB. Ниже описываются основные операции с матрицами. По обилию матричных операторов и функций MATLAB является лидером среди массовых систем компьютерной математики.
2. Создание матриц с заданными свойствами
Создание матриц с заданными свойствами
Для создания единичной матрицы (она обычно обозначается как Е) служит функция eye:
-
еуе(n) — возвращает единичную матрицу размера nrn;
-
eye(m.n) или еуе([m n]) — возвращают матрицу размера mm с единицами по диагонали и нулями в остальных ячейках;
-
eye(size(A)) — возвращает единичную матрицу того же размера, что и А.
Единичная матрица не определена для многомерных массивов. Так, функция у = eye([2,3,4]) при попытке ее вычисления приведет к ошибке.
Пример использования функции eye:
|
|
» t=eye(4. |
5) |
|
|
|
|
|
|
t = |
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
0 |
0 |
0 |
1 |
0 |
|
3. Создание матрицы с единичными элементами
Создание матрицы с единичными элементами
Для создания матриц, все элементы которых — единицы, используется функция ones:
-
ones(n) — возвращает матрицу размера nхn, все элементы которой — единицы. Если п — не скаляр, то появится сообщение об ошибке;
-
ones(m.n) или ones([m п]) — возвращают матрицу размера mxn, состоящую из единиц;
-
ones(dl.d2,d3....) или ones([dl1 d2 d3...]) — возвращает массив из единиц с размером d1xd2xd3x...;
-
ones(size(A)) — возвращает массив единиц той же размерности и размера, что и А. Матрица с единичными элементами в отличие от единичной матрицы в MATLAB определена и для многомерных массивов.
Пример:
» s=ones(3,4)
s=
1 1 1 1
1 1 1 1
1 1 1 1
4. Создание матрицы с нулевыми элементами
Создание матрицы с нулевыми элементами
Иногда нужны матрицы, все элементы которых — нули. Следующая функция обеспечивает создание таких матриц:
-
zeros(п) — возвращает матрицу размера nхn, содержащую нули. Если n — не скаляр, то появится сообщение об ошибке;
-
zeros(m.n) или zeros([m n]) — возвращают матрицу размера mxn, состоящую из нулей;
-
zeros(d1.d2,d3,...) или zeros([d1.d2.d3...]) — возвращают массив из нулей размера d1xd2xd3x...;
-
zeros(size(A)) — возвращает массив нулей того же размера и размерности, что и А.
Пример:
» D=zeros(3.2)
D=
0 0
0 0
0 0
5. Создание линейного массива равноотстоящих точек
Создание линейного массива равноотстоящих точек
Функция linspace формирует линейный массив равноотстоящих узлов. Это подобно оператору :, но дает прямой контроль над числом точек. Применяется в следующих формах:
-
llnspace(a.b) — возвращает линейный массив из 100 точек, равномерно распределенных между а и b;
-
linspace(a,b,n) — генерирует п точек, равномерно распределенных в интервале от а до b.
Пример:
» M-linspace(4.20.14)
М=
Columns I through 7
4.0000 5.2308 6.4615 7.6923 8.9231 10.153811.3846
Columns 8 through 14
12.615413.846215.076916.307717.538518.769220.0000
6. Создание вектора равноотстоящих в логарифмическом масштабе точек
Создание вектора равноотстоящих в логарифмическом масштабе точек
Функция logspace генерирует вектор равноотстоящих в логарифмическом масштабе точек. Она особенно эффективна при создании вектора частот. Это логарифмический эквивалент оператора : и функции linspace:
-
logspace(a.b) — возвращает вектор-строку из 50 равноотстоящих в логарифмическом масштабе точек между декадами 10^0 и 10^b;
-
logspace(a.b.n) — возвращает n точек между декадами 10^a и 10^b;
-
logspace(a.pi) — возвращает точки в интервале между 10^a и п. Эта функция очень полезна в цифровой обработке сигналов.
Все аргументы функции logspace должны быть скалярными величинами. Пример:
» L=logspaced.2,14)
L =
Columns 1 through 7
10.000011.937814.251017.012520.309224.244628.9427
Columns 8 through 14
34.551141.246349.238858.780270.170483.7678100.0000
7. Создание массивов со случайными элементами
Создание массивов со случайными элементами
-
р = randperm(n) — возвращает случайные перестановки целых чисел 1:n в векторе-строке. Пример:
» randperm(6)
ans =
243651
Функция rand генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке (0, 1):
-
rand(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;
-
rand(m.n) или rand([m п]) — возвращают матрицу размера mxn;
-
rand(m.n,p....) или rand([m n р...]) — возвращает многомерный массив;
-
rand(size(A)) — возвращает массив того же размера и размерности, что и А, с элементами, распределенными по равномерному закону;
-
rand (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет равномерный закон распределения;
-
rand(' state') — возвращает вектор с 35 элементами, содержащий текущее состояние генератора случайных чисел с равномерным распределением. Для изменения состояния генератора можно применять следующие формы этой функции:
-
rand('state' .s) — устанавливает состояние в s;
-
rand( 'state' ,0) — сбрасывает генератор в начальное состояние;
-
rand( 'state'. j) — для целых j, устанавливает генератор в j-е состояние;
-
rand( 'state' ,sum(100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.
-
Пример:
» Y=rand(4,3)
Y=
0.9501 0.8913 0.8214
0.2311 0.7621 0.4447
0.6068 0.4565 0.6154
0.4860 0.0185 0.7919
Проверить равномерность распределения случайных чисел можно, построив большое число точек на плоскости со случайными координатами. Это делается с помощью следующих команд:
» X=rand(1000,1);
» Y=rand(1000,1);
» plot(X,Y,'.')
Полученный при этом график показан на рис. 10.1. Нетрудно заметить, что точки довольно равномерно распределены на плоскости, так что нет оснований не доверять заданному закону распределения координат точек.
Рис. 10.1. Случайные точки с равномерным распределением координат на плоскости
Функция randn генерирует массив со случайными элементами, распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 1:
-
randn(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;
-
randn(m.n) или randn([m n]) — возвращают матрицу размера mxn;
-
randn(m,n,p,...) или randn([m n р...]) — возвращает массив с элементами, значения которых распределены по нормальному закону;
-
randn(size(A)) — возвращает массив того же размера, что и А, с элементами, распределенными по нормальному закону;
-
randn (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет нормальное распределение;
-
randn( 'state') — возвращает двухэлементный вектор, включающий текущее состояние нормального генератора. Для изменения состояния генератора можно применять следующие формы этой функции:
-
randn('state',s) — устанавливает состояние в s;
-
randn('state' ,0) — сбрасывает генератор в начальное состояние;
-
randn('state', j) — для целых j устанавливает генератор в J-e состояние;
-
randn('state', sum( 100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.
-
Пример:
>>Y=randn(4.3)
Y =
-0.4326 -1.1465 0.3273
-1.6656 1.1909 0.1746
0.1253 1.1892 -0.1867
0.2877 -0.0376 0.7258
Проверить распределение случайных чисел по нормальному закону можно, построив гистограмму распределения большого количества чисел. Например, следующие команды
» Y=randn(10000,1);
» hist(Y,100)
строят гистограмму (рис. 10.2) из 100 столбцов для 10 000 случайных чисел с нормальным распределением.
Рис. 10.2. Гистограмма для 10 000 нормально распределенных чисел в 100 интервалах
Из рисунка видно, что огибающая гистограммы действительно близка к нормальному закону распределения.
В пакете расширения Statistics Toolbox можно найти множество статистических функций, в том числе для генерации случайных чисел с различными законами распределения и определения их статистических характеристик.
1.gif
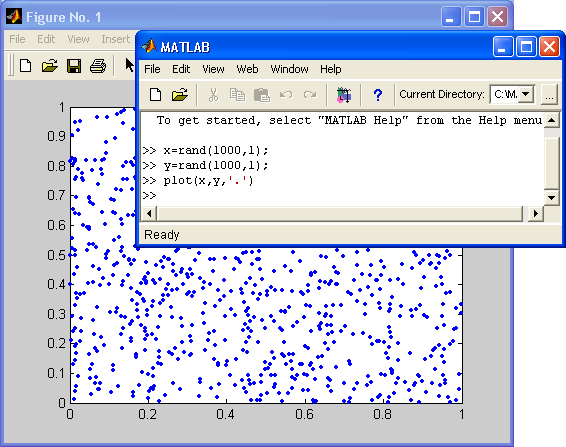
2a.gif
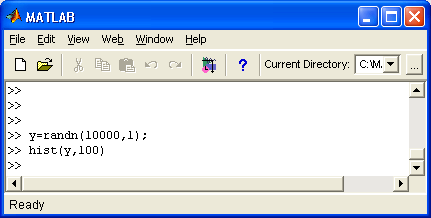
2b.gif
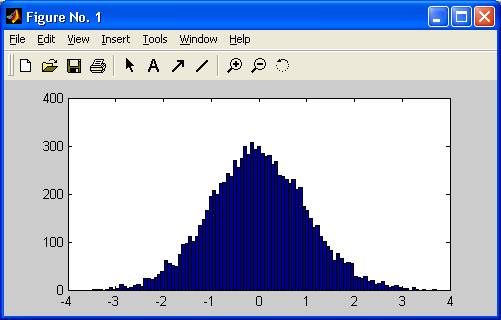
2c.gif

8. Конкатенация матриц
Конкатенация матриц
Конкатенацией называют объединение массивов, которое реализует следующая функция.
-
С = cat (dim, А, В) — объединяет массивы А и В в соответствии со спецификацией размерности dim и возвращает объединенный массив; dim = 1 — горизонтальная конкатенация, dim = 2 — вертикальная, dim = 3 — многомерный массив размерности 3 и т. д.;
-
С = cat(dim,Al,A2,A3,A4,...) объединяет все входные массивы (А1, А2, A3, А4 и т. д.) в соответствии со спецификацией размерности dim и возвращает объединенный массив;
-
cat(2.A,B) — это то же самое, что и [А,В],асаt(,А,В) —то же самое, что и [А; В]. При записи cat (dim, С (:)) или cat (dim, С. field) эта функция применима к массивам ячеек или структур, содержащим численные матрицы. Пример:
» A =[2.4:3,5];B=[8,7;9.0];C=cat(1.A.B)
С =
2 4
3 5
8 7
9 0
9. Создание матриц с заданной диагональю
Создание матриц с заданной диагональю
Свойства матриц сильно зависят от их диагональных элементов. Следующая функция MATLAB позволяет создавать специальные типы матриц с заданными диагональными элементами:
-
X = diag(v.k) — для вектора v, состоящего из п компонентов, возвращает квадратную матрицу X порядка n+abs(k) с элементами v на k-й диагонали, при k=0 -это главная диагональ (из левого верхнего угла матрицы в правый нижний угол), при k>0 — одна из диагоналей (диагональ в терминологии MATLAB — это линия, параллельная главной диагонали) выше главной диагонали, при k<0 — одна из нижних диагоналей. Остальные элементы матрицы — нули;
-
X = diag(v) — помещает вектор v на главную диагональ (то же. что и в предыдущем случае при k=0);
-
v = diag(X.k) — для матрицы X возвращает вектор-столбец, состоящий из элементов n-й диагонали матрицы X;
-
v = diag(X) — возвращает главную диагональ матрицы X (то же, что и в предыдущем случае при k=0).
Примеры:
» v=[2.3];X-d1ag(v.2)
X=
0 0 2 0
0 0 0 3
0 0 0 0
0 0 0 0
» X=[2,5.45,6;3.5.4.9;7.9.4.8;5.66,45.2];
v=diag(X,0)
v =
2
5
4
2
10. Перестановки элементов матриц
Перестановки элементов матриц
Для перестановок элементов матриц служат следующие функции:
-
В = fiiplr(A) — зеркально переставляет столбцы матрицы А относительно вертикальной оси.
Пример:
» F=[1.2.3;5.45,3]
F =
1 2 3
5 45 3
» fliplr(F)
ans=
3 2 1
3 45 5
-
В = flipud(A) — зеркально переставляет строки матрицы А относительно горизонтальной оси.
Пример:
|
|
||||
|
|
F = |
|
|
|
|
|
3 |
2 |
12 |
|
|
|
6 |
3 |
2 |
|
|
|
» flipud(F) |
|
||
|
|
ans = |
|
|
|
|
|
6 |
3 |
2 |
|
|
|
3 |
2 |
12 |
|
|
|
||||
-
perms(v) — возвращает матрицу Р, которая содержит все возможные перестановки элементов вектора v. каждая перестановка в отдельной строке. Матрица Р содержит n! строк и n столбцов.
Пример:
» v=[l 4 6]
v =
1 4 6
P=perms(v)
6 4 1
4 6 1
6 1 4
1 6 4
4 1 6
1 4 6
11. Вычисление произведений
Вычисление произведений
Несколько простых функций служат для перемножения элементов массивов:
-
prod(A) — возвращает произведение элементов массива, если А — вектор, или вектор-строку, содержащую произведения элементов каждого столбца, если А — матрица;
-
prod (A, dim) — возвращает матрицу (массив размерности два) с произведением элементов массива А по столбцам (dim=l), по строкам(dim=2), по иным размерностям в зависимости от значения скаляра dim.
Пример:
|
|
|
|
|
|
|
|
|
» A=[1234; |
2457; |
6 |
|
|
|
|
A |
- |
|
|
|
|
|
|
1 2 |
3 |
4 |
|
|
|
|
2 4 |
5 |
7 |
|
|
|
|
6 8 |
3 |
4 |
|
|
|
>; |
> B=prod(A) |
|
|
|
|
|
В |
= |
|
|
|
|
|
|
12 64 |
45 |
i: |
|
|
|
|
|
|
|
|
- cumprod(A) — возвращает произведение с накоплением. Если А — вектор, cum-prod(A) возвращает вектор, содержащий произведения с накоплением элементов вектора А. Если А — матрица, cumprod(A) возвращает матрицу того же размера, что и А, содержащую произведения с накоплением для каждого столбца матрицы А (Первая строка без изменений, во второй строке произведение первых двух элементов каждого столбца, в третьей строке элементы второй строки матрицы-результата умножаются на элементы третьей строки матрицы входного аргумента по столбцам и т. д.);
- cumprod(A,dim) — возвращает произведение с накоплением элементов по строкам или столбцам матрицы в зависимости от значения скаляра dim.
Примеры:
» А=[1 2 3; 4 5 6; 7 8 9]
А=
1 2 3
4 5 6
7 8 9
» В = cumprod(A)
-
cross(U. V) — возвращает векторное произведение векторов U и V в трехмерном пространстве, т. е. W=UxV. U и V — обязательно векторы с тремя элементами;
-
cross(U,V,dim) — возвращает векторное произведение U и V по размерности, определенной скаляром dim. U и V — многомерные массивы, которые должны иметь одну и ту же размерность, причем размер векторов в каждой размерности size(U.dim) и size(V.dim) должен быть равен 3.
Пример:
» а = [6 5 3]; b= [1 7 6];с = cross(a.b)
с =
9 -33 37
12. Суммирование элементов
Суммирование элементов
Определены следующие функции суммирования элементов массивов:
-
sum(A) — возвращает сумму элементов массива, если А — вектор, или вектор-строку, содержащую сумму элементов каждого столбца, если А — матрица;
-
sum(A.dim) — возвращает сумму элементов массива по столбцам (dim-1), строкам (dim=2) или иным размерностям в зависимости от значения скаляра dim.
Пример:
|
» A=magic(4) |
|
|
|
А = |
|
|
|
16 2 |
3 |
13 |
|
5 11 |
10 |
8 |
|
9 7 |
6 |
12 |
|
4 14 |
15 |
1 |
|
»B=sum(A) |
|
|
|
В = |
|
|
34 34 34 34
-
cumsum(A) — выполняет суммирование с накоплением. Если А — вектор, cumsum(A) возвращает вектор, содержащий результаты суммирования с накоплением элементов вектора А. Если А — матрица, cumsum(A) возвращает матрицу того же размера, что и А, содержащую суммирование с накоплением для каждого столбца матрицы А;
-
cumsum(A.dim) — выполняет суммирование с накоплением элементов по размерности, определенной скаляром dim. Например, cumsum(A.l) выполняет суммирование по столбцам.
Пример:
» A=magic(4)
А =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
» В = cumsum(A)
В =
16 2 3 13
21 13 13 21
30 20 19 33
34 34 34 34
13. Функции формирования матриц
Функции формирования матриц
Для создания матриц, состоящих из других матриц, используются следующие функции:
-
repmat (А, m, п) — возвращает матрицу В, состоящую из mxn копий матрицы А (т. е. в матрице mxn каждый элемент заменяется на копию матрицы А);
-
repmat(А,п) — формирует матрицу, состоящую из пхп копий матрицы А;
-
repmat(A,[m n]) — дает тот же результат, что и repmat(A,m,n);
-
repmat(A,[m п р...]) — возвращает многомерный массив (mxnxp...), состоящий из копий многомерного массива или матрицы А;
-
repmat (A, m, п) — когда А — скаляр, возвращает матрицу размера mxn со значениями элементов, заданных А, Это делается намного быстрее, чем A*ones(m,n).
-
reshape(A,m,n) — возвращает матрицу В размерностью mxn, сформированную из А путем последовательной выборки по столбцам. Если число элементов А не равно mxn, то выдается сообщение об ошибке;
-
reshape(A,m,n,p,...) или В = reshape(A.[m n р...]) — возвращает N-мерный массив с элементами из А, но имеющий размер mxnxp.... Произведение mxnxp... должно быть равно значению prod(size(A)).
-
reshape(A, slz) — возвращает N-мерный массив с элементами из А, но перестроенный к размеру, заданному с помощью вектора siz.
Пример:
» F=[3.2.7.4:4.3.3.2:2.2.5.5]
F =
3 2 7 4
4 3 3 2
2 2 5 5
» reshape(F.2,6)
ans=
3 2 3 7 5 2
4 2 2 3 4 5
14. Поворот матриц
Поворот матриц
Следующая функция обеспечивает поворот матрицы (по расположению элементов): О rot90(A) — осуществляет поворот матрицы А на 90° против часовой стрелки;
-
rot90(A,k) — осуществляет поворот матрицы А на величину 90*k градусов, где k — целое число.
Пример:
» М=[3.2,7;3.3.2:1.1.1]
|
|
|
|
|
|
|
|
|
м= |
|
|
|
|
|
|
|
3 |
2 |
7 |
|
|
|
|
3 |
3 |
2 |
|
|
|
|
1 |
1 |
1 |
|
|
|
» rot90(M) |
|
|||
|
|
ans |
= |
|
|
|
|
|
|
7 |
2 |
1 |
|
|
|
|
2 |
3 |
1 |
|
|
|
|
3 |
3 |
1 |
|
|
|
|
|
|
|
|
15. Выделение треугольных частей матриц
Выделение треугольных частей матриц
При выполнении ряда матричных вычислений возникает необходимость в выделении треугольных частей матриц. Следующие функции обеспечивают такое выделение:
-
tril(X) — возвращает матрицу, все элементы которой выше главной диагонали X заменены нулями, неизменными остаются лишь элементы нижней треугольной части, включая элементы главной диагонали;
-
tril(X.k) — возвращает неизменной нижнюю треугольную часть матрицы X начиная с k-й диагонали. При k=0 это главная диагональ, при k>0 — одна из верхних диагоналей, при k<0 — одна из нижних диагоналей.
Пример:
» М=[3.1.4:8.3.2;8.1.1]
М =
3 1 4
8 3 2
8 1 1
» tril(M)
ans =
3 0 0
8 3 0
8 1 1
-
triu(X) — возвращает неизменной верхнюю треугольную часть матрицы X включая элементы главной диагонали, и заменяет нулями остальные элементы;
-
triu(X.k) — возвращает неизменной верхнюю треугольную часть матрицы X начиная с k-й диагонали. При k=0 — это главная диагональ, при k>0 — одна из верхних диагоналей, при k<0 — одна из нижних диагоналей.
Пример:
м =
3 1 4
8 3 2
8 1 1
» triu(M)
ans =
3 1 4
0 3 2
0 0 1
16. Вычисление сопровождающей матрицы
Вычисление сопровождающей матрицы
Начиная с этого раздела рассматриваются функции, относящиеся к различным специальным матрицам. Они довольно широко используются при решении достаточно серьезных задач матричного исчисления. В связи с тем, что назначение соответствующих функций вытекает из их наименования, мы не будем сопровождать описание вводными комментариями. Соответствующие подробные определения вы найдете в книге. Рекомендуем читателю построить графики, представляющие элементы этих матриц.
-
compan(u) — возвращает сопровождающую матрицу, первая строка которой равна -u (2: n) /u(1), где и — вектор полиномиальных коэффициентов. Собственные значения compan(u) — корни многочлена. Пример: для многочлена х^3+х ^ 2-6х-8 вектор полиномиальных коэффициентов г имеет следующий вид:
» r=[1.1.-6.-8]
r =
1 1 -6 -8
» A=compan(r) % сопровождающая матрица
А =
-1 6 8
1 0 0
0 1 0
» eigtcompan(r)) % корни многочлена
ans =
-2.0000
2.5616
-1.5616
17. Вычисление тестовых матриц
Вычисление тестовых матриц
Для выполнения ряда вычислений в области линейной алгебры создан ряд специальных матриц, именуемых тестовыми матрицами. Такие матрицы создаются указанными ниже средствами.
-
[А.В,С....] = gallerу('tmfun',P1.P2,...) — возвращает тестовые матрицы, определенные строкой tmfun, где tmfun — это имя семейства матриц, выбранное из списка. Р1, Р2,„. — входные параметры, требуемые для конкретного семейства матриц. Число используемых параметров P1, P2,... изменяется от матрицы к матрице. Функция gallery хранит более 50 различных тестовых матричных функций, полезных для тестирования численных алгоритмов и других целей (включая матрицы Коши, Чебышева, фон Неймана, Вандермонде,Уилкинсо-на и т. д.).
Пример:
» A=gallery('dramadah',5.2)
|
|
||||||
|
|
А = |
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
|
|
|
0 |
1 |
1 |
0 |
1 |
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
0 |
0 |
0 |
1 |
1 |
|
|
|
0 |
0 |
0 |
0 |
1 |
|
|
|
18. Матрицы Адамара
Матрицы Адамара
-
Н = hadamard(n) — возвращает матрицу Адамара порядка п. Матрица Адамара — это. квадратная матрица размера п, составленная из значений 1 и — 1, столбцы которой ортогональны, так что справедливо соотношение Н' *Н=n* I, где I = eye (п, п) (единичная квадратная матрица размера п). Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов. Матрица Адамара размера nхn при n>2 существует, только если п делится на 4 без остатка. Алгоритм MATLAB вносит дополнительные ограничения, вычисляя матрицы Адамара только для тех n, когда или n, или n/12, или n/20 являются степенями по основанию 2.
Пример:
|
|
||||
|
|
»Н= |
hadamard(4) |
|
|
|
|
Н = |
|
|
|
|
|
1 |
1 1 |
1 |
|
|
|
1 |
-1 1 |
-1 |
|
|
|
1 |
1 -1 |
-1 |
|
|
|
1 |
-1 -1 |
1 |
|
|
|
|
|
|
|
19. Матрицы Ганкеля
Матрицы Ганкеля
-
hankel(c.r) — возвращает матрицу Ганкеля, первый столбец которой совпадает с вектором с, а последняя строка — с вектором г. Если последний элемент вектора с отличен от первого элемента вектора г, то выдается предупреждение об ошибке, но предпочтение отдается последнему элементу вектора с.
Примеры:
» с=1:4
С=
1 2 3 4
» r=6:10
r =
б 7 8 9 10
» Н - hankel(c.r)
Warning: Column wins anti-diagonal conflict.
H =
1 2 3 4 7
2 3 4 7 8
3 4 7 8 9
4 7 8 9 10
-
hankel (с) — возвращает квадратную матрицу Ганкеля, первый столбец которой совпадает с вектором с и все элементы, лежащие ниже первой антидиагонали (из левого нижнего угла матрицы в правый верхний угол), равны 0.
20. Матрицы Гильберта
Матрицы Гильберта
-
hilb(n) — возвращает матрицу Гильберта порядка п. Матрица Гильберта является примером плохо обусловленной матрицы. Элементы матрицы Гильберта определяются как H(i.j)=l/(i+j-l).
Пример:
» Н = hilb(5)
Н=
1.0000 0.5000 0.3333 0.2500 0.2000
0.5000 0.3333 0.2500 0.2000 0.1667
0.3333 0.2500 0.2000 0.1667 0.1429
0.2500 0.2000 0.1667 0.1429 0.1250
0.2000 0.1667 0.1429 0.1250 0.1111
» cond(hilb(5))
ans =
4.7661е+005
Значение числа обусловленности матрицы Гильберта указывает на очень плохо обусловленную матрицу.
-
invhilb(n) — возвращает матрицу, обратную матрице Гильберта порядка п (п<15). Для п>15 функция invhilb(n) возвращает приближенную матриц. Точная обратная матрица — это матрица с очень большими целочисленными значениями. Эти целочисленные значения могут быть представлены как числа с плавающей запятой без погрешности округления до тех пор, пока порядок матрицы п не превышает 15.
Пример:
»Н=invhilb(S)
Н =
|
|
25 |
-300 |
1050 |
-1400 |
630 |
|
|
|
-300 |
480 |
-18900 |
26880 |
-12600 |
|
|
|
1050 |
18900 |
79380 |
-117600 |
56700 |
|
|
|
-1400 |
26880 |
-117600 |
179200 |
-88200 |
|
|
|
630 |
-12600 |
56700 |
-88200 |
44100 |
|
А вот результат обращения матрицы Гильберта с плавающей запятой:
» inv(hilb(5))
ans =
1.0e+005 *
0.0002 -0.0030 0.0105 -0.0140 0.0063
-0.0030 0.0480 -0.1890 0.2688 -0.1260
0.0105 -0.1890 0.7938 -1.1760 0.5670
-0.0140 0.2688 -1.1760 1.7920 -0.8820
0.0063 -0.1260 0.5670 -0.8820 0.4410
21. Вычисление магического квадрата
Вычисление магического квадрата
-
magic(n) — возвращает матрицу размера nхn, состоящую из целых чисел от 1 до n 2 , в которой суммы элементов по строкам, столбцам и главным диагоналям равны одному и тому же числу. Порядок матрицы должен быть больше или равен 3.
|
|
|||||
|
|
Пример: » M=magic(4) |
|
|||
|
|
м = |
|
|
|
|
|
|
16 |
2 |
3 |
13 |
|
|
|
5 |
11 |
10 |
8 |
|
|
|
9 |
7 |
6 |
12 |
|
|
|
4 |
14 |
15 |
1 |
|
|
|
|
|
|
|
|
22. Матрицы Паскаля
Матрицы Паскаля
-
pascal (n) — возвращает матрицу Паскаля порядка п, т. е. симметрическую положительно определенную матрицу с целочисленными элементами, взятыми из треугольника Паскаля;
-
pascal (n. 1) — возвращает нижний треугольный фактор (до знаков столбцов) Холецкого для матрицы Паскаля. Полученная матрица, все элементы которой выше главной диагонали равны нулю, является своей обратной матрицей, т. е. квадратным корнем из единичной матрицы;
-
pascal(n,2) — возвращает матрицу, полученную в результате транспонирования и перестановок матрицы pascal (n. 1), при этом результат является кубическим корнем из единичной матрицы.
23. Матрицы Теплица
Матрицы Теплица
-
toepl itz(c , r) — возвращает несимметрическую матрицу Топлица, где с — ее первый столбец, а г — первая строка. Если первый элемент столбца с и первый элемент строки г различны, то выдается соответствующее предупреждение, но отдается предпочтение элементу столбца;
-
toeplitz(r) — возвращает симметрическую, или эрмитову, матрицу Топлица, однозначно определяемую вектором r. Пример:
» с=1:3;
» r=1.5:4.0;
» Т= toeplitz(c.r)
Warning: Column wins diagonal conflict.
Т =
1.0000 2.5000 3.5000
2.0000 1.0000 2.5000
3.0000 2.0000 1.0000
24. Матрицы Уилкинсона
Матрицы Уилкинсона
wilkinson(n) — возвращает одну из тестовых матриц Уилкинсона. (Другие матрицы Уилкинсона можно вызвать при помощи функции gallery). Это симметрич-ческая матрица, собственные значения которой попарно близки, но не равны друг другу. Наиболее широко используется wilkinson(21), собственные значения которой (10.746) совпадают до 14-го знака после запятой (различаются с 15-го).
Пример:
W = wilkinson(5)
W=
2 1 0 0 0
1 1 1 0 0
0 1 0 1 0
0 0 1 1 1
0 0 0 1 2
Данные о множестве других тестовых матриц можно найти в справочной системе MATLAB.
25. Матричные функции
Матричные функции
Весьма представителен в MATLAB набор матричных функций. Они перечислены ниже.
-
ехрт(Х) — возвращает е х от матрицы X. Комплексный результат получается, если X имеет неположительные собственные значения. Функция expm является встроенной и использует разложение Паде. Ее вариант в виде m-файла располагается в файле expm1.m. Второй метод вычисления матричной экспоненты использует разложение Тейлора и находится в файле expm2.m. Метод Тейлора не рекомендуется применять как основной, так как он зачастую бывает относительно медленным и неточным. Реализация третьего способа вычисления матричной экспоненты находится в файле ехртЗ.m и использует спектральное разложение матрицы А. Этот метод неудачен, если входная матрица не имеет полного набора линейно независимых собственных векторов.
Пример:
» S-[l.0.3:1.3.1:4.0.0]
S=
1 0 3
1 3 1
4 0 0
>>a=expm(S)
а =
31.2203 0 23.3779
38.965920.0855 30.0593
31.1705 0 23.4277
-
funm(X, @f unction)[ Форма funm(X,@function), как в предыдущих версиях MATLAB, по-прежнему возможна, но не рекомендуется.— Примеч. ред. ]— возвращает любую функцию от квадратной матрицы X, если правильно ввести имя, составленное из латинских букв. Команды funm(X ,@exp), funm(X,@sqrt), funm(X.@log) Hexpm(X),sqrtm(x),logm(X) вычисляют соответственно одинаковые функции, но используют разные алгоритмы. Однако предпочтительнее использовать ехрт(Х), sqrtm(x).logm(X);
-
[Y.esterr] = funm(X.@f uncti on) — не выдает никакого сообщения, но помимо результата вычислений в матрице Y возвращает грубую оценку относительной погрешности результата вычислений funm в esterr. Если матрица X — действительная симметрическая или комплексная эрмитова, то ее форма Шура диагональна и полученный результат может иметь высокую точность.
Примеры:
» S=[1,0.3:1.3.1:4,0.0]
1 0 3
1 3 1
4 0 0
» a=funm(S.@exp)
a=
31.22030.0000 23.3779
38.965920.085530.0593
31.1705-0.000023.4277
-
logm(X) — возвращает логарифм матрицы. Результат получается комплексным, если X имеет отрицательные собственные значения;
-
[Y.esterr]=logm(X) — не выдает какого-либо предупреждающего сообщения, но возвращает оценку погрешности в виде относительной невязки norm(expm(Y)-X)/norm(X);
Если матрица X — действительная симметрическая или комплексная эрмитова, то теми же свойствами обладает и logm(X).
Пример:
а=
31.22030.0000 23.3779
38.965920.085530.0593
31.1705-0.000023.4277
» logm(a)
ans =
1.0000 0.0000 3.0000
1.0000 3.0000 1.0000
4.0000 -0.0000-0.0000
-
sqrtm(X) — возвращает квадратный корень из X, соответствующий неотрицательным действительным частям собственных значений X. Результат получается комплексным, если X имеет отрицательные собственные значения. Если X вырожденная, то выдает предупреждение об ошибке;
-
[Y.resnonii]=sqrtm(X) — не выдает какого-либо предупреждающего сообщения, но возвращает оценку погрешности в виде относительной невязки по нормам Фробениуса (см. урок 11) norm(X-Y ^ 2, ' fro') /norm(X, ' fro') ;
-
[Y. alpha, condest]=sqrtm(X) — с тремя выходными аргументами функция помимо квадратного корня возвращает также фактор стабильности (но не невязку!) и оценку числа обусловленности результирующей матрицы Y.
Пример:
» S=[2.1.0;6,7.-2:3.4.0]; » e=sqrtm(S)
е =
1.2586 0.2334 0.0688
1.6066 2.7006 -0.6043
0.5969 1.1055 0.7918
26. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Создавать матрицы различного вида, включая «магическую» матрицу.
-
Создавать векторы равноотстоящих точек с разным масштабом.
-
Объединять матрицы, используя функцию конкатенации.
-
Создавать матрицы с заданной диагональю.
-
Выполнять перестановки элементов матриц.
-
Вычислять суммы и произведения элементов матриц.
-
Осуществлять поворот матриц и выделение их треугольных частей.
-
Работать с тестовыми матрицами Адамара, Ганкеля, Гильберта, Паскаля, Теплица и Уилкинсона.
-
Работать с различными матричными функциями.
Урок 11. Матричные операции линейной алгебры
1. Урок 11. Матричные операции линейной алгебры
Урок №11.
Матричные операции линейной алгебры
-
Вычисление нормы и чисел обусловленности матрицы
-
Определитель и ранг матрицы
-
Определение нормы вектора
-
Определение ортонормированного базиса матрицы
-
Приведение матрицы к треугольной форме
-
Определение угла между двумя подпространствами
-
Вычисление следа матрицы
-
Разложение Холецкого
-
Обращение матриц
-
LU- и QR-разложения
-
Вычисление собственных значений и сингулярных чисел
-
Приведение матриц к формам Шура и Хессенберга
Линейная алгебра — область, в которой наиболее часто используются векторы и матрицы. Наряду с операциями общего характера, рассмотренными выше, применятся функции, решающие наиболее характерные задачи линейной алгебры. Они и рассмотрены в данном уроке.
2. Вычисление нормы и чисел обусловленности матрицы
Вычисление нормы и чисел обусловленности матрицы
Для понимания всего нижеизложенного материала необходимо учесть, что нормы матриц в MATLAB отличаются от норм векторов.
Пусть А —матрица. Тогда n=norm(A) эквивалентно п=погп(А,2) и возвращает вторую норму, т. е. самое большое сингулярное число А. Функция n=norm(A, 1) возвращает первую норму, т. е. самую большую из сумм абсолютных значений элементов матрицы по столбцам. Норма неопределенности n=norm(A, inf) возвращает самую большую из сумм абсолютных значений элементов матрицы по рядам. Норма Фробениуса (Frobenius) norm(A, 'fro') = sqrt(sum(diag(A'A))).
Пример:
» A=[2.3.1:1.9.4:2.6.7]
A =
2 3 1
1 9 4
2 6 7
» norm(A.l)
ans =
18
Числа обусловленности матрицы определяют чувствительность решения системы линейных уравнений к погрешностям исходных данных. Следующие функции позволяют найти числа обусловленности матриц.
-
cond(X) — возвращает число обусловленности, основанное на второй норме, то есть отношение самого большого сингулярного числа X к самому малому. Значение cond(X), близкое к 1, указывает на хорошо обусловленную матрицу;
-
с = cond(X.p) — возвращает число обусловленности матрицы, основанное на р-норме: norm(X.p)*norm(inv(X),p), где р определяет способ расчета:
-
р=1 — число обусловленности матрицы, основанное на первой норме;
-
р=2 — число обусловленности матрицы, основанное на второй норме;
-
p= 'fro' — число обусловленности матрицы, основанное на норме Фробе-ниуса (Frobenius);
-
р='inf' — число обусловленности матрицы, основанное на норме неопределенности.
-
-
с = cond(X) — возвращает число обусловленности матрицы, основанное на второй норме.
Пример:
» d=cond(hilb(4))
d =
1.5514е+004
-
condeig(A) — возвращает вектор чисел обусловленности для собственных значений А. Эти числа обусловленности — обратные величины косинусов углов между левыми и правыми собственными векторами;
-
[V.D.s] = condeig(A) — эквивалентно [V,D] = eig(A): s = condeig(A);.
Большие числа обусловленности означают, что матрица А близка к матрице с кратными собственными значениями.
Пример:
» d=condeig(rand(4))
d =
1.0766
1.2298
1.5862
1.7540
-
rcond(A) — возвращает обратную величину обусловленности матрицы А по первой норме, используя оценивающий обусловленность метод LAPACK. Если А — хорошо обусловленная матрица, то rcond(A) около 1.00, если плохо обусловленная, то около 0.00. По сравнению с cond функция rcond реализует более эффективный в плане затрат машинного времени, но менее достоверный метод оценки обусловленности матрицы.
Пример:
» s=rcond(hilb(4))
s =
4.6461е-005
3. Определитель и ранг матрицы
Определитель и ранг матрицы
Для нахождения определителя (детерминанта) и ранга матриц в MATLAB имеются следующие функции:
-
det(X) — возвращает определитель квадратной матрицы X. Если X содержит только целые элементы, то результат — тоже целое число. Использование det(X)=0 как теста на вырожденность матрицы действительно только для матрицы малого порядка с целыми элементами.
Пример:
» А=[2,3,6:1.8.4;3.6,7]
А =
|
|
|
|
|
|
|
|
2 |
3 |
6 |
|
|
|
1 |
8 |
4 |
|
|
|
3 |
6 |
7 |
|
|
|
|
|
|
|
» det(A)
ans =
-29
Детерминант матрицы вычисляется на основе треугольного разложения методом исключения Гаусса:
[L.U>lu(A): s=det(L): d=s*prod(diag(U)).
Ранг матрицы определяется количеством сингулярных чисел, превышающих порог
tol=max(size(A))*nprm(A)*eps.
При этом используется следующий алгоритм:
s=svd(A);tol=max(size(A))*npnri(A)*eps;r=sum(s>tol);
Для вычисления ранга используется функция rank:
-
rank (А) — возвращает количество сингулярных чисел, которые являются большими, чем заданный по умолчанию допуск;
-
rank(A.tol) — возвращает количество сингулярных чисел, которые превышают tol. Пример:
» rank(hilbdl))
ans =
10
4. Определение нормы вектора
Определение нормы вектора
Норма вектора — скаляр, дающий представление о величине элементов вектора. Нужно различать норму матрицы и норму вектора. Функция norm определяет, является ли ее аргументом (входным аргументом в терминологии MATLAB) вектор или матрица, и измеряет несколько различных типов норм векторов:
-
norm(X)=norm(X,2) — вторая норма возвращает наибольшее сингулярное число X, max(svd(X));
-
norm(X.p) , где р — целое положительное число, — возвращает корень степени р из суммы абсолютных значений элементов вектора, возведенных в степень р. При р = 1 это может совпадать либо с первой нормой, либо с нормой неопределенности матриц;
-
norm(X, 'inf') возвращает максимальное из абсолютных значений элементов вектора; О norm(X, '-Inf') возвращает минимальное из абсолютных значений элементов вектора.
5. Определение ортонормированного базиса матрицы
Определение ортонормированного базиса матрицы
Вычисление ортонормированного базиса матрицы обеспечивают нижеприведенные функции:
-
В = orth(A) — возвращает ортонормированный базис матрицы А. Столбцы В определяют то же пространство, что и столбцы матрицы А, но столбцы В ортогональны, то есть B*B=eye(rank(A)). Количество столбцов матрицы В равно рангу матрицы А.
Пример:
» А=[2 4 6:9 8 2:12 23 43]
А =
|
|
|
|
|
|
|
|
2 |
4 |
6 |
|
|
|
9 |
8 |
2 |
|
|
|
12 |
23 |
43 |
|
|
|
|
|
|
|
» B=orth(A)
В=
0.1453 -0.0414-0.9885
0.1522 -0.98630.0637
0.9776 0.1597 0.1371
-
null (А) — возвращает ортонормированный базис для нулевого (пустого) пространства А.
Пример:
» null(hilb(11))
ans =
0.0000
-0.0000
0.0009
-0.0099
0.0593
-0.2101
0.4606
-0.6318
0.5276
-0.2453
0.0487
6. Функции приведения матрицы к треугольной форме
Функции приведения матрицы к треугольной форме
Треугольной называется квадратная матрица А, если при l>k (верхняя треугольная матрица) или при к>1(нижняя треугольная матрица) элементы матрицы A(l,k) равны нулю. В строго треугольной матрице нули находятся и на главной диагонали. В линейной алгебре часто используется приведение матриц к той или иной треугольной форме. Оно реализуется следующими функциями:
-
rref (A) — возвращает приведенную к треугольной форме матрицу, используя метод исключения Гаусса с частичным выбором ведущего элемента. По умолчанию принимается значение порога допустимости для незначительного элемента столбца, равное (max(s1ze(A))*eps*norm(A,inf));
-
[R, jb] = rref (A) — также возвращает вектор jb, так что:
-
r = length (jb) может служить оценкой ранга матрицы А;
-
х( jb) — связанные переменные в системе линейных уравнений вида Ах=b;
-
А(:, jb) — базис матрицы А;
-
R(l:r.jb) — единичная матрица размера rхr;
-
-
[R. jb] = rref (A,to!) — осуществляет приведение матрицы к треугольной форме, используя метод исключения Гаусса с частичным выбором ведущего элемента для заданного значения порога допустимости tol;
-
rrefmovie(A) — показывает пошаговое исполнение процедуры приведения матрицы к треугольной.
Примеры:
|
|
|
|
|
|
|
» s=magic(3) |
|
|
|
|
s = |
|
|
|
|
8 1 |
6 |
|
|
|
3 5 |
7 |
|
|
|
4 9 |
2 |
|
|
|
» rref(s) |
|
|
|
|
ans = |
|
|
|
|
1 0 |
0 |
|
|
|
0 1 |
0 |
|
|
|
0 0 |
1 |
|
|
|
|
|
|
7. Определение угла между двумя подпространствами
Определение угла между двумя подпространствами
Угол между двумя подпространствами вычисляет функция subsрасе:
-
theta = subspace(A.B) — возвращает угол между двумя подпространствами, натянутыми на столбцы матриц А и В. Если А и В — векторы-столбцы единичной длины, то угол вычисляется по формуле acos(A'*B). Если некоторый физический эксперимент описывается массивом А, а вторая реализация этого эксперимента — массивом В, то subspace(A.B) измеряет количество новой информации, полученной из второго эксперимента и не связанной со случайными ошибками и флуктуациями.
Пример:
» Н = hadamard(20);A = Н(:.2:4);В = Н(:.5:8);
» subspace(A,B)
ans =
1.5708
8. Вычисление следа матрицы
Вычисление следа матрицы
След матрицы А — это сумма ее диагональных элементов. Он вычисляется функцией trace:
-
trace(A) — возвращает след матрицы. Пример:
» а=[2.3.4:5.6,7;8.9,1]
а =
2 3 4
5 6 7
8 9 1
» trace(a)
ans =
9
9. Разложение Холецкого
Разложение Холецкого
Разложение Холецкого — известный прием матричных вычислений. Функция chol находит это разложение для действительных и комплексных эрмитовых матриц.
-
R = chol(X) — для квадратной матрицы [ Положительно определенной называется действительная симметрическая матрица, все собственные значения которой положительны. Поскольку используется только верхний треугольник матрицы X, матрица X не обязательно должна быть симметрической. — Примеч. ред. ]. X возвращает верхнюю треугольную матрицу R, так что R'*R=X new . Если симметрическая матрица X new , заданная верхней треугольной частью и диагональю матрицы X, не является положительно определенной матрицей, выдает сообщение об ошибке. Разложение Холецкого возможно для действительных и комплексных эрмитовых матриц [ Квадратная матрица с комплексными элементами, комплексно сопряженная матрица которой может быть получена транспонированием, т. е. равна транспонированной матрице (А*=А). — Примеч. ред. ];
-
[R.p] = chol (X) с двумя выходными аргументами никогда не генерирует сообщение об ошибке в ходе выполнения разложения Холецкого квадратной матрицы X. Если верхняя треугольная часть и диагональ X задают положительно определенную матрицу, то р=0, a R совпадает с вышеописанным случаем, иначе р. — положительное целое число, a R — верхняя треугольная матрица порядка q=p-l, такая что R'*R=X(l:q,l:q).
Пример:
» c=chol(pascal(4))
с =
1 1 1 1
0 1 2 3
0 0 1 3
0 0 0 1
10. Обращение матриц - функции inv, pinv
Обращение матриц — функции inv, pinv
Обращение матриц — одна из наиболее распространенных операций матричного анализа. Обратной называют матрицу, получаемую в результате деления единичной матрицы Е на исходную матрицу X. Таким образом, Х^-1=Е/Х. Следующие функции обеспечивают реализацию данной операции:
-
inv(X) — возвращает матрицу, обратную квадратной матрице X. Предупреждающее сообщение выдается, если X плохо масштабирована или близка к вырожденной.
Пример:
» inv(rand(4,4))
ans =
2.2631 -2.3495-0.4696-0.6631
-0.76201.2122 1.7041 -1.2146
-2.04081.4228 1.5538 1.3730
1.3075 -0.0183-2.54830.6344
На практике вычисление явной обратной матрицы не так уж необходимо. Чаще операцию обращения применяют при решении системы линейных уравнений вида Ах=b. Один из путей решения этой системы — вычисление x=inv(A)*b. Но лучшим с точки зрения минимизации времени расчета и повышения точности вычислений является использование оператора матричного деления х=А\b. Эта операция использует метод исключения Гаусса без явного формирования обратной матрицы.
-
В = pinv(A) — возвращает матрицу, псевдообратную матрице А (псевдообращение матрицы по Муру-Пенроузу). Результатом псевдообращения матрицы по Муру-Пенроузу является матрица В того же размера, что и А', и удовлетворяющая условиям А*В*А=А и В*А*В=В. Вычисление основано на использовании функции svd(A) и приравнивании к нулю всех сингулярных чисел, меньших величины tol;
-
В = pinv (A. tol) — возвращает псевдообратную матрицу и отменяет заданный по умолчанию порог, равный max(size(A))*norm(A)*eps.
Пример:
» pinv(rand(4,3))
ans =
-1.3907-0.0485-0.24931.8640
-0.87751.1636 0.6605 -0.0034
2.0906 -0.5921-0.2749-0.5987
11. LU- и QR-разложения
LU- и QR-разложения
Так называемые LU- и QR-разложения реализуются следующими матричными функциями:
Функция 1и выражает любую квадратную матрицу X как произведение двух треугольных матриц, одна из которых (возможно, с перестановками) — нижняя треугольная матрица, а другая — верхняя треугольная матрица[ В MATLAB 6 аргументом (входным аргументом) функции lu может быть и полная прямоугольная матрица. — Примеч. ред. ]. Иногда эту операцию называют LR-разложением. Для выполнения этой операции служит следующая функция:
-
[L,U] = lu(X) — возвращает верхнюю треугольную матрицу U и психологическую нижнюю матрицу L (т. е. произведение нижней треугольной матрицы и матрицы перестановок), так что X=L*U;
-
[L,U,P.] = lu(X) — возвращает верхнюю треугольную матрицу U, нижнюю треугольную матрицу L и сопряженную (эрмитову) матрицу матрицы перестановок Р, так что L*U =Р*Х;
-
lu(Х) — вызванная с одним выходным параметром функция возвращает результат из подпрограмм DGETRF (для действительных матриц) или ZGETRF (для комплексных) известного пакета программ линейной алгебры LAPACK.
-
lu(X, thresh) — где thresh в диапазоне [0...1] управляет центрированием в разреженных матрицах (см. урок 12). Отдельная форма предыдущего случая. Центрирование происходит, если элемент столбца на диагонали меньше, чем произведение thresh и любого поддиагонального элемента. Thresh=l — значение по умолчанию. Thresh=0 задает центрирование по диагонали. Если матрица полная (не разреженная), выводится сообщение об ошибке.
Функция qr выполняет QR-разложепие матрицы. Эта операция полезна для квадратных и треугольных матриц. Она выполняет QR-разложение, вычисляя произведение унитарной [ Квадратная матрица с комплексными элементами, обладающая тем свойством, что обратная матрица ее комплексно сопряженной матрицы равна транспонированной, т. е. (А*)''-А'. — Примеч. ред. ] матрицы и верхней треугольной матрицы. Функция используется в следующих формах: [ Квадратная матрица с комплексными элементами, обладающая тем свойством, что обратная матрица ее комплексно сопряженной матрицы равна транспонированной, т. е. (А*)''-А'. — Примеч. ред. ]
-
[Q.R] = qr(X) — вычисляет верхнюю треугольную матрицу R того же размера, как и у X, и унитарную матрицу Q, так что X=Q*R;
-
[Q.R.E] = qr(X) — вычисляет матрицу перестановок Е, верхнюю треугольную матрицу R с убывающими по модулю диагональными элементами и унитарную матрицу Q, так что X*E=Q*R. Матрица перестановок Е выбрана так, что abs(diag(R)) уменьшается;
-
[Q.R] = qr(X.O) и [Q.R.E] = qr(X,0) — вычисляют экономное разложение, в котором Е — вектор перестановок, так что Q*R=X(: ,Е). Матрица Е выбрана так, что abs(diag(R)) уменьшается;
-
А = qr(X) — возвращает результат из LAPACK. Пример:
» C=rand(5.4)
С=
0.8381 0.5028 0.1934 0.6979
0.0196 0.7095 0.6822 0.3784
0.6813 0.4289 0.3028 0.8600
0.3795 0.3046 0.5417 0.8537
0.8318 0.1897 0.1509 0.5936
» [Q.R]=qr(C)
Q=
-0.5922-0.11140.5197 0.0743 -0.6011
-0.0139-0.9278 -0.0011 -0.34480.1420
-0.4814-0.11730.0699 0.5940 0.6299
-0.2681-0.1525-0.82680.2632 -0.3898
-0.58770.2997 -0.2036-0.67340.2643
R =
-1.4152 -0.7072 -0.5037 -1.4103
0 -0.7541 -0.7274 -0.4819
0 0 -0.3577 -0.4043
0 0 0 0.2573
0 0 0 0
-
[Q,R] = qrdelete(Q,R, j) — изменяет Q и RTaKHM образом, чтобы пересчитать QR-разложение матрицы А для случая, когда в ней удален j-й столбец (А(:, j )=[ ]). Входные значения Q и R представляют QR-разложение матрицы А как результат действия [Q. R]=qr(A)..Аргумент j определяет столбец, который должен быть удален из матрицы А.
Примеры:
» C=rand(3.3)
С =
0.0164 0.0576 0.7176
0.1901 0.3676 0.6927
0.5869 0.6315 0.0841
» [Q.R]=qr(C)
Q=
-0.0265-0.2416-0.9700
-0.3080-0.92120.2378
-0.95100.3051 -0.0500
R =
-0.6171-0.7153-0.3123
0 -0.1599-0.7858
0 0 -0.5356
» [Q1.R1]=qrdelete(Q.R.2)
Q1 =
-0.02650.7459 0.6655
-0.30800.6272 -0.7153
-0.9510-0.22390.2131
R1 =
-0.6171-0.3123
0 0.9510
0 0
-
[Q.R] = qrinsert(Q,R,j,x) — изменяет Q и R таким образом, чтобы пересчитать разложение матрицы А для случая, когда в матрице А перед j-м столбцом вставлен столбец х. Входные значения Q и R представляют QR-разложение матрицы А как результат действия [Q,R]=qr(A). Аргумент х — вектор-столбец, который нужно вставить в матрицу А. Аргумент j определяет столбец, перед которым будет вставлен вектор х.
Примеры:
» C=rand(3.3)
С =
0.1210 0.8928 0.8656
0.4508 0.2731 0.2324
0.7159 0.2548 0.8049
» [Q,R]-qr(c)
Q =
-0.14160.9835 0.1126
-0.52750.0213 -0.8493
-0.8377-0.17970.5157
R =
-0.8546-0.4839-0.9194
0 0.8381 0.7116
0 0 0.3152
» x=[0.5.-0.3.0.2];[Q2.R2]=qrinsert(Q.R.2,x')
Q2 =
-0.14160.7995 -0.5838
-0.5275-0.5600-0.6389
-0.83770.2174 0.5010
R2 =
-0.8546-0.0801-0.4839-0.9194
0 0.6112 0.6163 0.7369
0 0 -0.5681-0.2505
12. Вычисление собственных значений и сингулярных чисел
Вычисление собственных значений и сингулярных чисел
Во многих областях математики и прикладных наук большое значение имеют средства для вычисления собственных значений (собственных чисел, характеристических чисел, решений векового уравнения) матриц, принадлежащих им векторов и сингулярных чисел. В новой версии MATLAB собственные вектора нормализуются, иначе, чем в предыдущих. Основной критерий: либо V'V=I, либо V'BV=I, где V — собственный вектор, I — единичная матрица. Поэтому результаты вычислений в новой версии, как правило, отличаются. Ниже дан список средств решения векового уравнения, реализованных в системе MATLAB.
Несимметрические матрицы могут быть плохо обусловлены при вычислении их собственных значений. Малые изменения элементов матрицы, такие как ошибки округления, могут вызвать большие изменения в собственных значениях. Масштабирование — это попытка перевести каждую плохую обусловленность собственных векторов матрицы в диагональное масштабирование. Однако масштабирование обычно не может преобразовать несимметрическую матрицу в симметрическую, а только пытается сделать (векторную) норму каждой строки равной норме соответствующего столбца. Масштабирование значительно повышает стабильность собственных значений.
-
[D.B] = balance(A) — возвращает диагональную матрицу D, элементы которой являются степенями основания 2, и масштабированную матрицу В, такую, что B=D\A*D, а норма каждого ряда масштабированной матрицы приближается к норме столбца с тем же номером;
-
В = balance(A) — возвращает масштабированную матрицу В. Пример использования функции balance:
» А=[1 1000 10000:0.0001 1 1000:0.000001 0.0001 1]
А =
1.0е+004 *
0.0001 0.1000 1.0000
0.0000 0.0001 0.1000
0.0000 0.0000 0.0001
» [F.G]=balance(A)
F =
1.0е+004 *
3.2768 0 0
0 0.0032 0
0 0 0.0000
G =
1.0000 0.9766 0.0095
0.1024 1.0000 0.9766
1.0486 0.1024 1.0000
Величина, связывающая погрешность вычисления собственных значений с погрешностью исходных данных, называется числом обусловленности (собственных значений) матрицы и вычисляется следующим образом:
cond(V) = norm(V)*norm(inv(V)) где [V.D]=eig(A).[B=D\A*D, а норма каждого ряда масштабированной матрицы приближается к норме столбца с тем же номером;]
-
eig(A) — возвращает вектор собственных значений квадратной полной или симметрической разреженной матрицы А обычно после автоматического масштабирования, но для больших разреженных матриц (в терминологии MATLAB —
это просто полные матрицы со сравнительно большим [ Но небольшим по сравнению с числом нулей разреженной матрицы. Эталонное число нулей разреженной матрицы данного размера можно вычислить, применив к полной матрице этого же размера функцию sparse. — Примеч. ред. ] числом нулей), а также во всех случаях, где помимо собственных значений необходимо получать и собственные вектора разреженной матрицы, вместо нее рекомендовано использовать eigs(A);
-
eig(A.B) - возвращает вектор обобщенных собственных значений квадратных матриц А и В;
-
[V.D] = eig(A.B) — вычисляет диагональную матрицу обобщенных собственных значений D и матрицу V, столбцы которой являются соответствующими собственными векторами (правыми собственными векторами), таким образом что А V = В V D;
-
[V.D] = eig(A) — вычисляет диагональную матрицу собственных значений О матрицы А и матрицу V, столбцы которой являются соответствующими собственными векторами (правыми собственными векторами), таким образом что А V = V D.
-
Нужно использовать [W,D]=e1g(A'); W=W, чтобы вычислить левые собственные вектора, которые соответствуют уравнению W*A=D*W.
[V.D] = eig(A,'nobalance') — находит собственные векторы и собственные значения без предварительного масштабирования. Иногда это улучшает обусловленность входной матрицы, обеспечивая большую точность вычисления собственных векторов для необычно масштабированных матриц;
-
eig(A.B. 'chol') — возвращает вектор, содержащий обобщенные собственные значения, используя разложение матрицы В по методу Холецкого; если А - симметрическая квадратная матрица и В — симметрическая положительно определенная квадратная матрица, то eig(A.B) по умолчанию работает точно так же;
-
eig(A,B, 'qz') — не требует, чтобы матрицы были симметрическими и возвращает вектор, содержащий обобщенные собственные значения, используя QZ-алгоритм; при явном указании этого флага QZ-алгоритм используется вместо алгоритма Холецкого даже для симметрической матрицы и симметрической положительно определенной матрицы В, так как может давать более стабильные значения, чем предыдущий метод. Для несимметрических матриц в MATLAB 6 всегда используется QZ-алгоритм и параметр 'chol' или 'qz' игнорируется;
-
[V.D] = eig(A.B) — возвращает диагональную матрицу обобщенных собственных значений D и матрицу V, чьи столбцы являются соответствующими собственными векторами, так чтобы A*V=B*V*D. Пример:
» В = [3 -12 -.6 2*eps:-2 48 -1 -eps;-eps/8 eps/2 -1 10;-.5 -.5 .3 1]
В =
3.0000 -12.0000 -0.60000.0000
-2.0000 48.0000-1.0000-0.0000
-0.0000 0.0000 -1.0000 10.0000
-0.5000 -0.5000 0.3000 1.0000
» [G.H]=eig(B)
G =
-0.2548 0.7420 -0.4842 0.1956
0.9670 0.0193 -0.0388 0.0276
-0.0015 -0.6181 -0.8575 0.9780
-0.0075 -0.2588 -0.1694 -0.0676
H =
48.5287 0 0 0
0 3.1873 0 0
0 0 0.9750 0
0 0 0 -1.6909
-
svd(X) — возвращает вектор сингулярных чисел. Команда svd выполняет сингулярное разложение матрицы X;
-
[U.S, V] = svd(X) — вычисляет диагональную матрицу S тех же размеров, которые имеет матрица X, с неотрицательными диагональными элементами в порядке их убывания, и унитарные матрицы U и V, так что X=U*S*V ' ;
-
[U.S.V] = svd(X.O) — выполняет экономичное сингулярное разложение. Пример:
» F=[23 12;3 5:6 0]
F =
23 12
3 5
6 0
» [k,l,m]=svd(F)
k=
|
|
|
|
|
|
|
|
0.9628 |
-0.0034 |
-0.2702 |
|
|
|
0.1846 |
0.7385 |
0.6485 |
|
|
|
0.1974 |
-0.6743 |
0.7116 |
|
| l= | ||||
|
|
26.9448 |
0 |
|
|
|
|
0 |
4.1202 |
|
|
|
|
0 |
0 |
|
|
|
|
m= |
|
|
|
0.8863 -0.4630
0.4630 0.8863
13. Приведение матриц к форме Шура и Хессенберга
Приведение матриц к форме Шура и Хессенберга
Ниже приводятся функции, обеспечивающие приведение матриц к специальным формам Шура и Хессенберга:
-
cdf2rdf — преобразование комплексной формы Шура в действительную. Если система [V,D]=eig(X) имеет комплексные собственные значения, объединенные в комплексно-сопряженные пары, то функция cdf2rdf преобразует систему таким образом, что матрица D принимает вещественный диагональный вид с 2x2 вещественными блоками, заменяющими первоначальные комплексные пары.
Конкретные столбцы матрицы V больше не являются собственными векторами, но каждая пара векторов связана с блоком размера 2x2 в матрице D. Пример:
» А-[2 3 6;-4 0 3:1 5 -2]
А =
2 3 6
-4 0 3
1 5 -2
|
|
|
|
|
|
|
|
|
» |
[S.D]=eig(A) |
|
|
|
|
|
S |
= |
|
|
|
|
|
|
0.7081 + 0.32961 |
0.7081 - 0.32961 |
-0.3355 |
|
|
|
|
-0.3456 + 0.36881 |
-0.3456 - 0.36881 |
-0.5721 |
|
|
|
|
0.0837 + 0.35711 |
0.0837 - 0.35711 |
0.7484 |
|
|
|
D |
= |
|
|
|
|
|
|
3.1351 + 4.06031 |
0 |
0 |
|
|
|
|
0 |
3.1351 - 4.06031 |
0 |
|
|
|
|
0 |
0 |
-6.2702 |
|
|
|
» |
[S.D]=cdf2rdf(S.D) |
|
|
|
|
|
S |
= |
|
|
|
|
|
|
0.7081 0.3296 |
-0.3355 |
|
|
|
|
|
-0.3456 0.3688 |
-0.5721 |
|
|
|
|
|
0.0837 0.3571 |
0.7484 |
|
|
|
|
D |
= |
|
|
|
|
|
|
3.1351 4.0603 |
0 |
|
|
|
|
|
-4.0603 3.1351 |
0 |
|
|
|
|
|
0 0 |
-6.2702 |
|
|
|
|
|
|
|
|
|
Функция qz обеспечивает приведение пары матриц к обобщенной форме Шура:
-
[AA.8B.Q.Z.V] = qz(A.B) — возвращает, возможно, комплексные верхние треугольные матрицы АА и ВВ и соответствующие матрицы приведения Q и I, такие что Q*A*Z=AA и Q*B*Z=BB. Функция также возвращает матрицу обобщенных собственных векторов V.
Обобщенные собственные значения могут быть найдены из следующего условия:
A*V*diag(BB) = B*V*diag(AA)
Пример:
» А=[1 2 3:6 3 0;4 7 0];В=[1 1 1:0 7 4:9 4 1];
» [aa.bb.f,g.h]=qz(A.B)
аа =
-2.9395 0.4775 0.8751
0 9.5462 3.5985
0 0 3.2073
bb=
|
|
5.5356 |
3.5345 |
-2.2935 |
|
|
|
0 |
8.4826 |
6.7128 |
|
|
|
0 |
0 |
0.7667 |
|
|
|
-0.0367 |
0.7327 |
-0.6796 |
|
|
|
-0.1052 |
-0.6791 |
-0.7265 |
|
|
|
-0.9938 |
0.0448 |
0.1020 |
|
|
|
-0.7023 -0.7050 -0.0989
0.6867 -0.6343 -0.3552
-0.1877 0.3174 -0.9295
h =
-1.0000 -0.4874 -0.0561
0.9778 -1.0000 0.6238
-0.2673 0.4340 -1.0000
Функция qz(A,B,' real') при заданных матрицах А и В возвращает действительные треугольную матрицу ВВ и квазитреугольную матрицу АА с 2x2 диагональными блоками, соответствующими парам сопряженных комплексных значений. Так как матрица АА квазитреугольная, то необходимо решить проблемы обобщения 2x2 для получения подлинных собственных значений.
Пример:
» А=[1 2 3:6 3 0:4 7 0];В=[1 1 1:0 7 4;9 4 1];
» [aa.bb.f,g.h]=qz(A.B,'real')
аа =
-2.9395 0.4775 0.8751
0 9.5462 3.5985
0 0 3.2073
bb =
5.5356 3.5345 -2.2935
0 8.4826 6.7128
0 0 0.7667
f =
-0.0367 0.7327 -0.6796
-0.1052 -0.6791 -0.7265
-0.9938 0.0448 0.1020
g=
-0.7023 -0.7050 -0.0989
0.6867 -0.6343 -0.3552
-0.1877 0.3174 -0.9295
h =
-1.0000 -0.4874 -0.0561
0.9778 -1.0000 0.6238
-0.2673 0.4340 -1.0000
-
Т = schur(A) — возвращает матрицу Шура Т.
-
[U.T] = schur(A) — возвращает матрицу Шура Т и унитарную матрицу U, такие что A=U Т U и U' и=еуе(51ге(А))(единичная матрица размера А);
-
[U,T] = rsf2csf(u.t)[ В MATLAB 6 в функции schur, если ее входной аргумент — действительная матрица, может использоваться новый параметр 'complex' (schur,'complex'), позволяющий получить комплексную форму Шура без использования функции преобразования rsf2csf. — Примеч. ред. ] — преобразование результатов предыдущей функции (действительной формы Шура) в комплексную форму Шура может использоваться только после вызова [u,t] = schur(A) Комплексная форма Шура — это верхняя треугольная матрица со всеми собственными значениями на диагонали. Действительная форма Шура имеет действительные собственные значения на диагонали, а комплексные собственные значения содержатся в 2x2 блоках, расположенных вдоль диагонали. И входные, и выходные матрицы U, u и Т, tпредставляют собой соответственно унитарные матрицы и матрицы Шура исходной матрицы А, которая удовлетворяет условиям A=UTU' и U' U=eye( si ze(A));
-
Н = hess(A) — находит Н, верхнюю форму Хессенберга для матрицы А;
-
[Р.Н] = hess(A) — возвращает матрицу Хессенберга Н и унитарную матрицу преобразований Р, такую что А=Р*Н*Р' и P'*P=eye(s1ze(A)).
Элементы матрицы Хессенберга, расположенные ниже первой поддиагонали, равны нулю. Если матрица симметричная или эрмитова, то матрица Хессенберга вырождается в трехдиагональную. Эта матрица имеет те же собственные значения, что и оригинал, но для их вычисления необходимо меньшее количество операций. Пример:
» f=magic(4)
f =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
» hess(f)
ans=
16.0000 -8.0577 8.8958 6.1595
-11.0454 24.2131 -8.1984 2.1241
0 -13.5058 -4.3894 -7.8918
0 0 3.2744 -1.8237
14. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Находить числа обусловленности матриц, их определитель, след и ранг.
-
Находить векторную и матричную нормы и различать их.
-
Определять ортонормальный базис матриц.
-
Приводить матрицы к треугольной форме.
-
Определять угол между двумя подпространствами.
-
Осуществлять разложение Холецкого, LU- и QR-разложения матриц.
-
Вычислять обратные матрицы.
-
Находить собственные значения и сингулярные числа матриц.
-
Приводить матрицы к формам Шура и Хессенберга.
Урок 12. Функции разреженных матриц
1. Урок 12. Функции разреженных матриц
Урок №12.
Функции разреженных матриц
-
Элементарные разреженные матрицы
-
Преобразование разреженных матриц
-
Работа с ненулевыми элементами разреженных матриц
-
Визуализация разреженных матриц
-
Алгоритмы упорядочения
-
Норма, число обусловленности и ранг разреженных матриц
-
Разложение Холецкого разреженной матрицы
-
LU-разложение разреженной матрицы
-
Вычисление собственных значений и сингулярных чисел разреженных матриц
Матрицы без нулевых значений называются полными матрицами. Матрицы, содержащие некоторое число элементов с нулевыми значениями, в MATLAB называются разреженными матрицами. Вообще говоря, разреженными называют те матрицы, для которых разумно использовать численные методы, учитывающие упрощение арифметических операций с нулевыми элементами (например, получение нуля при умножении на нуль или пропуск операций сложения и вычитания при использовании этих операций с нулевыми элементами матриц). Они широко используются при решении прикладных задач. Например, моделировацие электронных и электротехнических линейных цепей часто приводит к появлению в матричном описании топологии схем сильно разреженных матриц. Для таких матриц создан ряд функций, обеспечивающих эффективную работу с ними и устраняющих тривиальные операции с нулевыми элементами матриц.
2. Элементарные разреженные матрицы
Элементарные разреженные матрицы
Вначале рассмотрим элементарные разреженные матрицы и относящиеся к ним функции системы MATLAB.
Функция spdiags расширяет возможности встроенной функции diag. Возможны четыре операции, различающиеся числом входных аргументов:
-
[B.d] = spdiags(A) — извлекает все ненулевые диагонали из матрицы А размера mxn. В — матрица размера min(m,n)xp, столбцы которой р являются ненулевыми диагоналями A. d — вектор длины р, целочисленные элементы которого точно определяют номера диагоналей матрицы А (положительные номера — выше главной диагонали, отрицательные — ниже);
-
В = spdiags(A.d) — извлекает диагонали, определенные вектором d;
-
А = spdiags(B,d,A) — заменяет столбцами матрицы В диагонали матрицы А, определенные вектором d;
-
А = spdiags(B,d,m,n) — создает разреженную матрицу размера mxn, размещая соответствующие столбцы матрицы В вдоль диагоналей, определяемых вектором d.
Пример:
» А=[1 3 4 6 8 0 0; 7 8 0 7 0 0 5;
0 0 0 0 0 9 8; 7 6 54 32 0 9 6];
» d=[l 322]
» В = spdlags(A.d)
В =
3644. 0077
0900
0699
-
S = speye(m.n) — возвращает разреженную матрицу размера mxn с единицами на главной диагонали и нулевыми недиагональными элементами;
-
S = speye(n) — равносильна speye(n.n). Пример:
» S = speye(4)
S =
(1,1) 1
(2.2) 1
(3.3) 1
(4.4) 1
Матрица R = sprand(S) имеет ту же структуру, что и разреженная матрица S, но ее элементы распределены по равномерному закону:
-
R = sprand(m,n,density) — возвращает случайную разреженную матрицу размера mxn, которая имеет приблизительно densityxmxn равномерно распределенных ненулевых элементов (0<density<l);
-
R = sprand(m,n,density,re) — в дополнение к этому имеет в числе параметров число обусловленности по отношению к операции обращения, приблизительно равное rс. Если вектор гс имеет длину lr (A,r<min(m.n)), то матрица R имеет гс в качестве своих первых 1 r сингулярных чисел, все другие значения равны нулю. В этом случае матрица R генерируется с помощью матриц случайных плоских вращений, которые применяются к диагональной матрице с заданными сингулярными числами. Такие матрицы играют важную роль при анализе алгебраических и топологических структур.
Пример:
» d=sprand(4,3.0.6)
d =
(1.1) 0.6614
(2.1) 0.2844
(4,1) 0.0648
(3,3) 0.4692
(4,3) 0.9883
-
R = sprandn(S) — возвращает матрицу со структурой разреженной матрицы S, но с элементами, распределенными по нормальному закону с нулевым средним и дисперсией, равной 1;
-
R = sprandn(m,n,density) — возвращает случайную разреженную матрицу размера mxn, имеющую примерно densityxmxn нормально распределенных ненулевых элементов (0<density<l);
-
R = sprandnCm,n.density,гс) — в дополнение к этому имеет своим параметром число обусловленности по отношению к операции обращения, приблизительно равное rс. Если вектор гс имеет длину 1r (Xr<min(m,n)), то матрица R имеет гс в качестве своих первых 1r сингулярных чисел, все другие значения равны нулю. В этом случае матрица R генерируется с помощью матриц случайных плоских вращений, которые применяются к диагональной матрице с заданными сингулярными числами.
Пример:
» f=sprandn(3,4.0.3)
f =
(2.1) -0.4326
(2.2) -1.6656
(2.3) 0.1253
(2.4) 0.2877
-
sprandsym(S) — возвращает случайную симметрическую матрицу, нижние под-диагонали и главная диагональ которой имеют ту же структуру, что и матрица 5. Элементы результирующей матрицы распределены по нормальному закону со средним, равным 0, и дисперсией, равной 1;
-
sprandsym(n,density) — возвращает симметрическую случайную разреженную матрицу размера пхп, которая имеет приблизительно densityxnxn ненулевых элементов; каждый элемент сформирован в виде суммы нормально распределенных случайных чисел (0<density<l);
-
R = sprandsym(n,density,гс) — возвращает матрицу с числом обусловленности по отношению к операции обращения, равным гс. Закон распределения не является равномерным; значения случайных элементов симметричны относительно 0 и находятся в пределах [-1, 1]. Если rс — вектор размера п, то матрица R имеет собственные значения, равные элементам вектора rс. Таким образом, если элементы вектора гс положительны, то матрица R является положительно определенной. В любом случае матрица R генерируется с помощью случайного вращения по Якоби диагональных матриц с заданными собственными значениями и числом обусловленности. Такие матрицы играют важную роль при анализе алгебраических и топологических структур;
-
R = sprandsym(n.density.rc.klnd) — возвращает положительно определенную матрицу. Аргумент kind может быть следующим:
-
kind=l — матрица R генерируется из положительно определенной диагональной матрицы с помощью случайных вращений Якоби. R имеет точно заданное число обусловленности;
-
kind=2 — матрица R генерируется как смещенная сумма матриц внешних произведений. Число обусловленности матрицы приблизительно, но структура более компактна (по сравнению с предыдущим случаем);
-
kind=3 — генерируется матрица R той же структуры, что и S, а число обусловленности приближенно равно 1/гс. Значение density игнорируется.
-
Пример:
» a=sprandsym(4,0.3.0.8)
а =
(1.1) 0.9818
(3.1) 0.0468
(2,2) -0.9283
(1,3) 0.0468
(3.3) 0.8800
(4.4) -0.8000
3. Преобразование разреженных матрицв
П реобразование разреженных матриц
Теперь рассмотрим функции преобразования разреженных матриц. Они представлены ниже:
-
k = f ind(X) — возвращает индексы вектора х для его ненулевых элементов. Если таких элементов нет, то find возвращает пустой вектор. find(X>100) возвращает индексы элементов вектора с Х>100;
-
[1,j] = find(X) — возвращает индексы строки и столбца для ненулевого элемента матрицы X;
-
[1 . j . v] = find(X) — возвращает вектор столбец v ненулевых элементов матрицы X и индексы строки i и столбца j. Вместо X можно вставить (X, операция отношения, параметр), и тогда индексы и вектор-столбец будут отражать элементы матрицы, удовлетворяющие данному отношение. Единственное исключение — f ind(x ~= 0). Индексы те же, что и при исполнении find(X), но вектор v содержит только единицы.
Пример:
» q=sprand(3.4.0.6)
q =
(1.1) 0.7266
(1.2) 0.4120
(3.2) 0.2679
(3.3) 0.4399
(2.4) 0.7446
(3.4) 0.9334
i=
1
1
3
3
2
3
j =
1
2
2
3
4
4
-
full(S) — преобразует разреженную матрицу S в полную; если исходная матрица S была полной, то full (S) возвращает S. Пусть X — матрица размера mxn с nz=nnz(X) ненулевыми элементами. Тогда full(X) требует такой объем памяти, чтобы хранить mxn действительных чисел, в то время как sparse(X) требует пространство для хранения лишь nz действительных чисел и (nxz+n) целых чисел — индексов. Большинству компьютеров для хранения действительного числа требуется вдвое больше пространства, чем для целого. Для таких компьютеров sparse(X) требует меньше пространства, чем full(X), если плотность nnz/prod(s1ze(X))<2/3. Выполнение операций над разреженными матрицами, однако, требует больше затрат времени, чем над полными, поэтому для эффективной работы с разреженными матрицами плотность расположения ненулевых элементов должна быть много меньше 2/3.
Примеры:
» q=sprand(3,4,0.6)
q=
(1.1) 0.0129
(1.2) 0.3840
(2.2) 0.6831
(3,3) 0.0928
» d=full(q)
d =
0.0129 0.3840 0 0
0 0.6831 0 0
0 0 0.0928 0
-
S=sparse(A) — преобразует полную матрицу в разреженную, удаляя нулевые элементы. Если матрица S уже разреженная, то sparse(S) возвращает S. Функция sparse — это встроенная функция, которая формирует матрицы в соответствии с правилами записи разреженных матриц, принятыми в системе MATLAB;
-
S=sparse(i,j,s,m,n,nzmax) — использует векторы 1, j и s для того, чтобы генерировать разреженную матрицу размера mxn с ненулевыми элементами, количество которых не превышает nzmax. Векторы 1 и j задают позиции элементов и являются целочисленными, а вектор s определяет числовое значение элемента матрицы, которое может быть действительным или комплексным. Все элементы вектора s, равные нулю, игнорируются вместе с соответствующими значениями i и j. Векторы i, j и s должны быть одной и той же длины;
-
S = sparsed' . j.s.m.n) — использует nzmax=length(s).
-
S = sparsed , j .s) — использует m=maxd) и n=max(j). Максимумы вычисляются раньше, чем нулевые строки столбца S будут удалены;
-
S = sparse(m.n) равносильно sparse ([ ].[ ].[ ]. m.n, 0). Эта команда генерирует предельную разреженную матрицу, где mxn элементов нулевые.
Все встроенные в MATLAB арифметические, логические и индексные операции могут быть применены и к -разреженным, и к полным матрицам. Операции над разреженными матрицами возвращают разреженные матрицы, а операции над полными матрицами возвращают полные матрицы. В большинстве случаев операции над смешанными матрицами возвращают полные матрицы. Исключение составляют случаи, когда результат смешанной операции явно сохраняет разреженный тип. Так бывает при поэлементном умножении массивов А.*S, где S — разреженный массив.
Пример:
» i=[2,4,3];j=[1,3,8];s=[4,5+5i,9];
t = sparse(i,j,s,5,8)
t =
(2.1) 4.0000
(4.3) 5.0000+5.0000i
(3.8) 9.0000
Функция spconvert используется для создания разреженных матриц из простых разреженных форматов, легко производимых вне средств MATLAB:
-
S = spconvert(D) — преобразует матрицу D со строками, содержащими [i.j.r] или [i,j,r.s], где i — индекс ряда, j — индекс строки, г — численное значение, в соответствующую разреженную матрицу. Матрица D может иметь nnz или nnz+1 строк и три или четыре столбца. Три элемента в строке генерируют действительную матрицу, четыре элемента в строке генерируют комплексную матрицу (s преобразуется во мнимую часть значения элемента). Последняя строка массива D типа [m n 0] или [m n 0 0] может быть использована для определения size(S). Команда spconvert может быть использована только после того, как матрица D загружена или из МАТ-файла, или из ASCII-файла при помощи команд load, uiload и т. д.:
»load mydata.dat
»А = spconvert (rnydata);
4. Работа с ненулевыми элементами разреженных матриц
Работа с ненулевыми элементами разреженных матриц
Поскольку разреженные матрицы содержат ненулевые элементы, то предусмотрен ряд функций для работы с ними:
-
nnz(X) — возвращает число ненулевых элементов матрицы X. Плотность разреженной матрицы определяется по формуле nnz(X)/numel (X). Пример:
h = sparse(hilb(10));
» nnz(h)
ans =
100
-
nonzeros(A) — возвращает полный вектор-столбец ненулевых элементов матрицы А, выбирая их последовательно по столбцам. Эта функция дает только выход s, но не значения i и j из аналогичного выражения [i, j,s]=find(A). Вообще, length(s)=nnz(A)xnzmax(A)xprod(size(A)). Пример:
» g=nonzeros(sparse(hankel([1,2.8])))
g =
1
2
-
nzmax(S) — возвращает количество ячеек памяти для ненулевых элементов. Обычно функции nnz(S) и nzmax(S) дают один и тот же результат. Но если S создавалась в результате операции над разреженными матрицами, такой как умножение или LU-разложение, может быть выделено больше элементов памяти, чем требуется, и nzmax(S) отражает это. Если S — разреженная матрица, то nzmax(S) — максимальное количество ячеек для хранения ненулевых элементов. Если S — полная матрица, то nzmax(S)=numel(S).
Пример:
» q=nzmax(sparse(hankel([1.7.23])))
q =
6
-
S=spalloc(m,n,nzmax) — создает массив для разреженной матрицы S размера mxn с пространством для размещения nzmax ненулевых элементов. Затем матрица может быть заполнена по столбцам;
-
spalloc(m,n,nzmax) — эквивалентна функции sparse([ ],[ ],[ ],m,n,nzmax).
Пример:
» S = spalloc(5,4,5);
-
spfun — вычисление функции для ненулевых элементов. Функция spfun применяется выборочно только к ненулевым элементам разреженной матрицы, сохраняя при этом разреженность исходной матрицы;
-
f = spfun(@function,S) — вычисляет function(S) для ненулевых элементов матрицы S. Имя function — это имя m-файла или встроенной в ядро функции. function должна работать с матричным аргументом S и вычислить функцию для каждого элемента матрицы S.
Пример:
» S=spfun(@exp.sprand(4,5,0,4))
S=
(2.2) 1.6864
(2.3) 2.4112
(3.3) 2.6638
(2.4) 1.1888
(3.4) 1.3119
(4.4) 2.4007
(3.5) 1.2870
-
R = spones(S) — генерирует матрицу R той же разреженности, что и S, но заменяет на 1 все ненулевые элементы исходной матрицы.
Пример:
» S=sprand(3.2,0.3)
S=
(3.1) 0.2987
(1.2) 0.1991
» spones(S)
ans =
(3.1) 1
(1.2) 1
5. Визуализация разреженных матриц
Визуализация разреженных матриц
Визуализация разреженных матриц нередко позволяет выявить не только любопытные, но и полезные и поучительные свойства тех математических закономерноетей, которые порождают такие матрицы или описываются последними. MATLAB имеет специальные средства для визуализации разреженных матриц, реализованные приведенными ниже командами:
-
spy(S) — графически отображает разреженность произвольной матрицы S;
-
spy(S.markersize) — графически отображает разреженность матрицы S, выводя маркеры в виде точек точно определенного размера markersize;
-
spy(S, 'LineSpec') — отображает разреженность матрицы в виде графика с точно определенным (с помощью параметра LineSpec) цветом линии и маркера. Параметр Linespec определяется так же, как параметр команды plot;
-
spy(S. 'LineSpec' .markersize) — использует точно определенные тип, цвет и размер графического маркера. Обычно S — разреженная матрица, но допустимо использование и полной матрицы, когда расположение элементов, отличных от нуля, составляет график.
Пример:
»S=sparse(sprandn(20,30,0.9));spy(S,'-r',6)
Построенный по этому примеру график показан на рис. 12.1.
Рис. 12.1. Визуализация разреженной матрицы
1a.gif
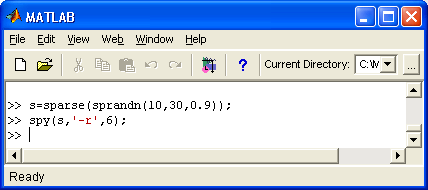
1b.gif
6. Алгоритмы упорядочения
Алгоритмы упорядочения
Упорядочение — это еще одна характерная для разреженных матриц операция. Ее алгоритм реализуется несколькими функциями:
-
р = colmmd(S) — возвращает вектор упорядоченности столбцов разреженной матрицы S. [то nzmax(S) — максимальное количество ячеек для хранения ненулевых элементов. Если S — полная матрица, то nzmax(S)=numel(S).] Для несимметрической матрицы S вектор упорядоченности столбцов р такой, что S(:. р) будет иметь более разреженные L и U в LU-разложении, чем S. Такое упорядочение автоматически применяется при выполнении операций обращения \ и деления /, а также при решении систем линейных уравнений с разреженными матрицами. Можно использовать команду spparms, чтобы изменить некоторые параметры, связанные с эвристикой в алгоритме colmmd;
-
j = colperm(S) — возвращает вектор перестановок j, такой что столбцы матрицы S(:. j) будут упорядочены по возрастанию числа ненулевых элементов. Эту функцию полезно иногда применять перед выполнением LU-разложения. Если S — симметрическая матрица, то j=colperm(S) возвращает вектор перестановок j, такой что и столбцы, и строки S(j,j) упорядочены по возрастанию ненулевых элементов. Если матрица S положительно определенная, то иногда полезно применять эту функцию и перед выполнением разложения Холецкого.
Пример:
» S=sparse([2.3.1.4.2].[l,3.2.3.2],[4.3,5.6.7].4.5);full(S)
ans =
0 5 0 0 0
4 7 0 0 0
0 0 3 0 0
0 0 6 0 0
» t=colperm(S)
|
t= |
|
|
|
|
|
|
5 |
1 |
2 |
3 |
| »full(S(;,t)) | ||||
|
ans = |
|
|
|
|
|
0 |
0 |
0 |
5 |
0 |
|
0 |
0 |
4 |
7 |
0 |
|
0 |
0 |
0 |
0 |
3 |
|
0 |
0 |
0 |
0 |
6 |
|
|
-
p = dmperm(A) — возвращает вектор максимального соответствия р такой, что если исходная матрица А имеет полный столбцовый ранг, то А(р.:) — квадратная матрица с ненулевой диагональю. Матрица А(р,:) называется декомпозицией Далмейджа-Мендельсона, или DM-декомпозицией.
Если А — приводимая матрица, [ Квадратная матрица А называется приводимой, если она подобна клеточной матрице, квадратные элементы которой соответствуют индукции линейного оператора А в отдельные подпространства. — Примеч. ред. ] линейная система Ах=b может быть решена приведением А к верхней блочной треугольной форме с неприводимым диагональным блоком. Решение может быть найдено методом обратной подстановки.
-
[p.q.r] = dmperm(A) — находит перестановку строк р и перестановку столбцов q квадратной матрицы А, такую что A(p,q) — матрица в блоке верхней треугольной формы.
Третий выходной аргумент г — целочисленный вектор, описывающий границы блоков. К-й блок матрицы A(p,q) имеет индексы r(k):r(k+l)-l.
-
[p.q.r.s] = dmperm(A) — находит перестановки р и q и векторы индексов г и s, так что матрица A(p,q) оказывается в верхней треугольной форме. Блок имеет индексы (r(i):r(i+l)-l,s(i):s(i+l)-l).
В терминах теории графов диагональные блоки соответствуют сильным компонентам Холла графа смежности матрицы А.
Примеры:
» A=sparse([1.2,1.3.2].[3.2.1.1.1].[7.6,4.5,4],3,3)
:full(A)
ans =
4 0
4 6 0
5 0 0
»[p.q.r]=dmperm(A)
Р=
1 2 3
q =
3 2 1
r =
1 2 3 4
» fulKA(p.q))
ans =
7 0 4
0 6 4
0 0 5
-
symmmd(S) — возвращает вектор упорядоченности для симметричной положительно определенной матрицы S, так что S(p,p) будет иметь более разреженное разложение Холецкого, чем S. Иногда symmmd хорошо работает с симметрическими неопределенными матрицами. Такое упорядочение автоматически применяется при выполнении операций \ и /, а также при решении линейных систем с разреженными матрицами [ Функция symamd работает значительно быстрее. — Примеч. ред. ].
Можно использовать команду spparms, чтобы изменить некоторые опции и параметры, связанные с эвристикой в алгоритме.
Алгоритм упорядочения для симметрических матриц основан на алгоритме упорядочения по разреженности столбцов. Фактически symmmd(S) только формирует матрицу К с такой структурой ненулевых элементов, что К' *К имеет тот же трафик разреженности, что и S, и затем вызывает алгоритм упорядочения по разреженности столбцов для К. На рис. 12.2 приводится пример применения функции symmmd к элементам разреженной матрицы.
Пример:
» B=bucky;p=symmmd(B);
» R=B(p,p);
» subplot(1,2,1),spy(B); subplot(1,2,2).spy(R) ;
-
r = symrcm(S) — возвращает вектор упорядоченности для симметричной матрицы S и называется упорядочением Катхилла-Макки. Причем формируется такая перестановка г, что S(r.r) будет концентрировать ненулевые элементы вблизи диагонали. Это хорошее упорядочение как перед LU-разложением, так и перед разложением Холецкого. Упорядочение применимо как для симметрических, так и для несимметрических матриц.
Для вещественной симметрической разреженной матрицы S (такой, что S=S T ) собственные значения S(r.r) совпадают с собственными значениями S, но для вычисления eig(S(r,r)) требуется меньше времени, чем для вычисления eig(S).
Рис. 12.2. Пример применения функции symmmd
Пример:
» B=bucky;p=symrcm(B);
» R=B(p,p);
» subplot(1,2,1),spy(B);subplot(1,2,2),spy(R) ;
На рис. 12.3 приведен пример концентрации ненулевых элементов разреженной матрицы вблизи главной диагонали.
Рис. 12.3. Пример применения функции symrcm
2a.gif
2b.gif

3a.gif
3b.gif
7. Норма, число обусловленности и ранг разреженной матрицы
Норма, число обусловленности и ранг разреженной матрицы
Ниже представлены функции, позволяющие вычислять числа обусловленности и ранги для разреженных матриц.
-
с = condest(A) — использует метод Хейджера в модификации Хаема для оценки числа обусловленности матрицы по первой норме. Вычисленное значение с — нижняя оценка числа обусловленности матрицы А по первой норме. Для повторяемости результатов перед выполнением функции condest нужно обязательно выполнить rand( 'state' ,L), где L -одно и то же целое число;
-
с = condest(A.T) — где Т — положительное целое число, чем выше Т, тем выше точность оценки. По умолчанию Т равно 2;
-
nrm = normest(S) — возвращает оценку второй нормы матрицы S. Применяется тогда, когда из-за чрезмерного числа элементов в матрице вычисление nrm = norm(S) занимает слишком много времени. Эта функция изначально предназначена для работы с разреженными матрицами, хотя она работает корректно и с большими полными матрицами;
-
[c.v] = condestCA) — возвращает число обусловленности с и вектор v, такой, что выполняется условие norm(A*V.l) = norm(A.l)*norm(V.l)/c. Таким образом, для больших значений с вектор V близок к нулевому вектору;
-
nrm = normest(S,tol) — использует относительную погрешность tol вместо используемого по умолчанию значения 10- 6 ;
-
[nrm.count] = normestC...) — возвращает оценку второй нормы и количество использованных операций. Примеры:
» F=wilkinson(150); » condest(sparse(F))
ans =
460.2219
» normest(sparse(F))
ans =
75.2453
-
r=sprank(S) — вычисляет структурный ранг разреженной матрицы S. В терминах теории графов он известен также под следующими названиями: максимальное сечение, максимальное соответствие и максимальное совпадение. Для величины структурного ранга всегда выполняется условие sprank(S)irank(S), а в точной арифметике с вероятностью 1 выполняется условие sprank(S) = rank(sprandnCS)).
Пример:
» S=[3 0004: 54080; 00013];
» r=sprank(S)
8. Разложение Холецкого разреженных матриц
Разложение Холецкого разреженных матриц
-
choli пс(X,'0') — возвращает неполное разложение Холецкого для действительной симметрической положительно определенной разреженной матрицы [nrm = norm(S) занимает слишком много времени. Эта функция изначально предназначена для работы с разреженными матрицами, хотя она работает корректно и с большими полными матрицами;]. Результат представляет собой верхнюю треугольную матрицу;
-
R = cholincCX,'0') — возвращает верхнюю треугольную матрицу, которая имеет такую же разреженную структуру, как и верхний треугольник матрицы действительной положительно определенной матрицы X. Результат умножения R' *R соответствует X по своей разреженной структуре. Положительной определенности матрицы X недостаточно, чтобы гарантировать существование неполного разложения Холецкого, и в этом случае выдается сообщение об ошибке;
-
[R,p] = cho!1nc(X, '0') — никогда не выдает сообщение об ошибке в ходе разложения. Если X — положительно определенная матрица, то р=0 и матрица R — верхняя треугольная, в противном случае р — положительное целое число, R — верхняя треугольная матрица размера qxn, где q=p-l. Разреженная структура матрицы R такая же, как и у верхнего треугольника размера qxn матрицы X, и произведение R' *R размера nxn соответствует структуре разреженности матрицы X по ее первым q строкам и столбцам X(l:q,:) и Х(: ,l:q).
-
R = cho1inc(X,droptol) — возвращает неполное разложение Холецкого любой квадратной разреженной матрицы, используя положительный числовой параметр droptol. Функция cholinc(X,droptol) возвращает приближение к полному разложению Холецкого, вычисленному с помощью функции chol (X). При меньших значениях droptol аппроксимация улучшается, пока значение droptol не станет равным 0. В этом случае cholinc задает полное преобразование Холецкого (chol(X));
-
R = cholinc(X.options) — использует структуру с тремя переменными, которые могут быть использованы в любой из комбинаций: droptol, mi chol, rdi ag. Дополнительные поля игнорируются. Если mi chol =1, chol inc возвращает модифицированное разложение Холецкого. Если rdiag=l, то все нули на диагонали верхней треугольной матрицы заменяются квадратным корнем от произведения droptol и нормы соответствующего столбца матрицы X — sqrt(droptol*norm(X(: ,j))). По умолчанию rdiag=0;
-
R = cholinc(X,droptol) и R = cholinc(X.options) — возвращают верхнюю треугольную матрицу R. Результат R'*R — это аппроксимация матрицы;
-
R = cholinc(X, 'inf') - возвращает разложение Холецкого в неопределенности, когда не удается получить обычное разложение. Матрица X может быть действительной квадратной положительно полуопределенной.
Пример:
» S = delsqCnumgndCC' .4))
S =
(1.1) 4
(2.1) -1
(1.2) -1
(2.2) 4
(3.2) -1
(2.3) -1
(3.3) 4
» RD=cholinc(S,'0')
R0=
(1.1) 2.0000
(1.2) -0.5000
(2.2) 1.9365
(2.3) -0.5164
(3.3) 1.9322
9. LU-разложение разреженных матриц
LU-разложение разреженных матриц
Функция luinc осуществляет неполное LU-разложение и возвращает нижнюю треугольную матрицу, верхнюю треугольную матрицу и матрицу перестановок для разреженных матриц [ Благодаря LAPACK в MATLAB 6 появилась отсутствующая в прежних версиях возможность использовать команду lu для точного LU-разложения разреженных матриц. — Примеч. ред. ]. Используется в следующих формах:
-
luincCX, '0') — возвращает неполное LU-разложение уровня 0 квадратной разреженной матрицы. Треугольные факторы (множители) имеют такую же разреженность (т. е. график разреженности, см. spy), как и матрица перестановок квадратной матрицы X, и их произведение имеет ту же разреженность, что и матрица перестановок X. Функция luinc(X, '0') .возвращает нижнюю треугольную часть нижнего фактора (множителя) и верхний треугольный фактор в одной и той же результирующей матрице. Вся информация о матрице перестановок теряется, но зато число ненулевых элементов результирующей матрицы равно числу ненулевых элементов матрицы X с возможностью исключения некоторых нулей из-за сокращения;
-
[L,U] = luincCX. 'О'), где X — матрица размером nхn, возвращает нижнюю треугольную матрицу L и верхнюю треугольную матрицу U. Разреженности матриц L, U и X не сравнимы, но сумма числа ненулевых элементов в матрицах L и U поддерживается равной nnz(X)+n с возможностью исключения некоторых нулей в L и U из-за сокращения;
-
[L,U.P]=luinc(X, '0') — возвращает нижнюю треугольную матрицу L, верхнюю треугольную матрицу U и матрицу перестановок Р. Матрица L имеет такую же разреженную структуру, как нижняя треугольная часть перестановленной матрицы X — spones(L)=spones(tril(P*X)), с возможными исключениями единиц на диагонали матрицы L, где Р*Х может быть равно 0;
-
luinc(X,droptol) — возвращает неполное LU-разложение любой разреженной матрицы, используя порог droptol. Параметр droptol должен быть неотрицательным числом;
-
luinc(X,droptol) — возвращает приближение к полному LU-разложению, полученному с помощью функции lu(Х). При меньших значениях droptol аппроксимация улучшается, пока значение droptol не станет равным 0. В этом случае имеет место полное LU- разложение;
-
luinc(X,options) — использует структуру с четырьмя переменными, которые могут быть использованы в любой из комбинаций: droptol, milu, udiag, thresh. Дополнительные поля игнорируются. Если miliKL, функция luinc возвращает модифицированное неполное LU-разложение. Если udiag=l, то все нули на диагонали верхней треугольной части заменяются на локальную ошибку droptol;
-
luincCX.options) — то же самое, что и luinc(X,droptol), если options содержит только параметр droptol; О [L.U] = luincCX,options) — возвращает перестановку треугольной матрицы L и верхнюю треугольную матрицу U. Результат L*U аппроксимирует X;
-
[L.U.P] = luinc(X.options) — возвращает нижнюю треугольную матрицу L, верхнюю треугольную матрицу U и матрицу перестановок Р. Ненулевые входные элементы матрицы U удовлетворяют выражению abs(U(i. j))>=droptol* norm((X:.j)) с возможным исключением диагональных входов, которые были сохранены, несмотря на неудовлетворение критерию;
-
[L.U.P] = luincCX,options) — то же самое, что и [L.U.P] = 1uinc(X,dropto1), если options содержит только параметр droptol.
10. Вычисление собственных значений и сингулярных чисел разреженных матриц
Вычисление собственных значений и сингулярных чисел разреженных матриц
Применение функции eigs решает проблему собственных значений, состоящую в нахождении нетривиальных решений системы уравнений, которая может быть интерпретирована как алгебраический эквивалент системы обыкновенных дифференциальных уравнений в явной форме Коши: A*v=l*v.[ Усовершенствованный алгоритм eig позволяет использовать eig для расчета собственных значений и полных, и разреженных матриц, но для получения собственных векторов разреженных матриц по-прежнему желательно использовать именно eigs. — Примеч. ред. ] Вычисляются только отдельные выбранные собственные значения или собственные значения и собственные векторы:
-
eigs(A.B) решает проблему обобщенных собственных значений A*V = В* V*D. В должна быть симметрической (или эрмитовой) положительно определенной квадратной матрицей того же размера, что и A. eigs С А, []....) решает стандартную проблему собственных значений A*V = V*D.
-
[V,D] = eigs(A) или [V.O] = eigs('Afun',n) — возвращает собственные значения для первого входного аргумента — большой и разреженной квадратной матрицы размера п. Этот параметр может быть как квадратной матрицей, так и строкой, содержащей имя m-файла, который применяет линейный оператор к столбцам данной матрицы. Матрица А — действительная и несимметрическая. Y=Afun(X) должна возвращать Y=A*X.
В случае одного выходного параметра D — вектор, содержащий 6 самых больших собственных значений матрицы А. В случае двух выходных аргументов [V.D] = eigs(A) D — диагональная матрица размера 6x6, содержащая эти 6 самых больших собственных значений, и V — матрица, содержащая б столбцов, являющихся соответствующими собственными векторами. [V.D.flag] = eigs(A) возвращает флаг, равный 0, если все возвращенные собственные значения сходятся, и 1 в противном случае.
-
eigs(A.K) и eigs(A,B,K) возвращают не 6, а К самых больших собственных значений. eigs(A,K,sigma) Heigs(A,B,K.sigma) возвращают не 6, а К собственных значений, выбранных в зависимости от значения параметра sigma;
-
'lm' — самые большие (как и по умолчанию) по абсолютной величине;
-
' sm' — самые малые по абсолютной величине;
-
' l а' и ' sa' — соответственно самые большие и самые малые алгебраически собственные значения для действительных симметрических матриц;
-
'be' — для действительных симметрических матриц возвращает и самые большие, и самые малые алгебраически собственные значения поровну, но если К нечетное, то самых больших значений на 1 больше, чем самых малых;
-
'lr' и 'sr' — для несимметрических и комплексных матриц возвращают соответственно собственные значения с самыми большими и самыми малыми действительными частями;
-
'1i' и 'si'— для несимметрических и комплексных матриц возвращают соответственно собственные значения с самыми большими и самыми малыми мнимыми частями;
- скаляр - ближайшие к величине slgma. В этом случае матрица В может быть только симметрической (или эрмитовой) положительно полуопределенной, а функция Y = AFUN(X) должна возвращать Y = (A-SIGMA*B)\X.
- eigs(A,K,SIGMA,OPTS) и eigs(A,B,K,SIGMA.OPTS) имеют параметры в полях структуры OPTS (в фигурных скобках { } — значения по умолчанию):
-
OPTS.issym: симметрия А или A-SIGMA*B, представленной AFUN [{0} | 1];
-
OPTS.isreal: комплексные А или A-SIGMA*B, представленной AFUN [0 | {1}];
-
OPTS.tol: сходимость: аbs(с1_вычисленное-с1_действительное) < tоl*аbs(с1_вычисленное) [скаляр){eps}];
-
OPTS.maxit: наибольшее число итераций [положительное целое | {300}];
-
OPTS.р: число векторов Ланцо (Lanczos): K+l<p<=N [положительное целое | {2К}];
-
OPTS.v0: начальный вектор [вектор размера N| {произвольно выбирается библиотекой ARPACK}];
-
OPTS.disp: уровень вывода диагностической информации [0 | {1} | 2J;
-
OPTS.cholВ: В — это множитель Холецкого chol (В) [{0} | 1];
-
OPTS.permB: разреженная матрица В равна chol (B(perm(B) .perm(B)) [perm(B) | {1:N}], perm — перестановка.
-
eigs(AFUN.N.К,SIGMA,OPTS,PI,...) иeigsCAFUN.N,В.К.SIGMA.OPTS,PI....) предоставляют дополнительные аргументы Р, которые поступают в AFUN(X,P1....).
Функция svds служит для вычисления небольшого числа сингулярных чисел и векторов большой разреженной матрицы. По мере возможности старайтесь использовать svd(fulKA)) вместо svds(A). Если А прямоугольная матрица mxn, svds(A....) манипулирует с несколькими собственными значениями и собственными векторами, возвращенными EIGS(B,...), где В = [SPARSE(М.М) A: A' SPARSE(N.N)]. Положительные собственные значения симметрической матрицы В равны сингулярным числам А.
-
svds (А) возвращает 6 самых больших сингулярных чисел А;
-
svds (А,К) или svds(A,K.'L') возвращает К самых больших сингулярных чисел;
-
S = SVDSCA,К,SIGMA,OPTIONS) устанавливает параметры:
-
OPTIONS.tol — порог чувствительности (по умолчанию le-10), norm(A*V-. -U*S,1) <= tol * norm(A.1);
-
OPTIONS.maxit - наибольшее число итераций (по умолчанию 300);
-
OPTIONS.disp — число значений, показываемых на каждой итерации (по умолчанию 0).
-
-
[U.S.V] = svds(A.k) — возвращает k наибольших сингулярных чисел и соответствующих сингулярных векторов матрицы А. Если А — матрица размера mxn, то U — матрица размера mxk с ортонормальными столбцами, S — диагональная матрица размера kxk, V — матрицы размера nxk с ортонормальными столбцами;
-
[U.S.V. flag] = svdsC...) — возвращает флаг, равный 0, если eigs сошлась, и 1 в противном случае;
-
[U.S.V] = svds(A.k.sigma) — возвращает k сингулярных чисел, наиболее близких к скаляру sigma, и К сингулярных векторов (при sigma=0 возвращает К наименьших сингулярных чисел и К векторов);
-
s = svds(A.k....) — возвращает только вектор сингулярных чисел.
Как видно из приведенного материала, система MATLAB предлагает пользователям уникальный набор матричных операторов и функций, заметно более полный, чем у других математических систем. Это открывает широчайшие возможности в решении всех видов математических задач, в которых используются современные матричные методы.
11. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Создавать элементарные разреженные матрицы.
-
Осуществлять преобразование разреженных матриц.
-
Работать с ненулевыми элементами разреженных матриц.
-
Осуществлять графическую визуализацию разреженных матриц.
-
Использовать функции упорядочения.
-
Осуществлять разложение Холецкого разреженных матриц.
-
Проводить LU-разложение разреженных матриц.
-
Вычислять норму, число обусловленности и ранг разреженных матриц.
-
Вычислять собственные значения и сингулярные числа разреженных матриц.
Урок 13. Многомерные массивы
1. Урок 13. Многомерные массивы
Урок №13.
Многомерные массивы
-
Понятие о многомерных массивах
-
Применение оператора «:» в многомерных массивах
-
Доступ к отдельному элементу многомерного массива
-
Удаление размерности в многомерном массиве
-
Создание страниц, заполненных константами и случайными числами
-
Объединение массивов
-
Вычисление числа размерностей массива и определение размера размерностей
-
Перестановки размерностей массивов
-
Сдвиг размерностей массивов
-
Удаление единичных размерностей
В этом уроке мы коснемся вопросов, связанных с более сложными типами данных, к которым относятся многомерные массивы.
2. Понятие о многомерных массивах
Понятие о многомерных массивах
В MATLAB двумерный массив является частным случаем многомерного массива. Многомерные массивы характеризуются размерностью более двух. Таким массивам можно дать наглядную интерпретацию. Так, матрицу (двумерный массив) можно записать на одном листе бумаги в виде строк и столбцов, состоящих из элементов матрицы. Тогда блокнот с такими листками можно считать трехмерным массивом, полку в шкафу с блокнотами — четырехмерным массивом, шкаф со множеством полок — пятимерным массивом и т. д. В этой книге практически нигде, кроме этого раздела, мы не будем иметь дело с массивами, размерность которых выше двух, но знать о возможностях MATLAB в части задания и применения многомерных массивов все же полезно.
В нашей литературе понятия «размер» и «размерность» массивов являются почти синонимами. Однако они имеют явно разный смысл в данной книге, как и в документации и литературе по системе MATLAB. Под размерностью массивов понимается число измерений в пространственном представлении массивов, а под размером — число строк и столбцов (mxn) в каждой размерности массива.
3. Применение оператора ":" в многомерных массивах
Применение оператора «:» в многомерных массивах
При обычном задании массивов (с помощью символа точки с запятой «;») число рядов (строк) массива получается на 1 больше, чем число символов «:», но массив остается двумерным. Оператор «:» (двоеточие) позволяет легко выполнять операции по увеличению размерности массивов. Приведем пример формирования трехмерного массива путем добавления новой страницы. Пусть у нас задан исходный двумерный массив М размером 3x3:
» М=[1 2 3; 4 5 6; 7 8 9]
М =
1 2 3
4 5 6
7 8 9
Для добавления новой страницы с тем же размером можно расширить М следующим образом:
» М(:.:.2)=[10 11 12; 13 14 15; 16 17 18]
M(:.:.l) =
1 2 3
4 5 6
7 8 9
М(:.:.2) =
10 11 12
13 14 15
16 17 18
Посмотрим, что теперь содержит массив М при явном его указании:
» М
М(:,:.1)=
1 2 3
4 5 6
7 8 9
М(:.:.2) =
10 11 12
13 14 15
16 17 18
Как можно заметить, числа в выражениях М(:.:, 1) и М(:,: ,2) означают номер страницы.
4. Доступ к отдельному элементу многомерного массива
Доступ к отдельному элементу многомерного массива
Чтобы вызвать центральный элемент сначала первой, а затем второй страницы, надо записать следующие выражения:
» М(2.2,1)
ans =
5
» МС2.2.2)
ans =
14
Таким образом, в многомерных массивах используется то же правило индексации, что и в одномерных и двумерных. Произвольный элемент, например, трехмерного массива задается как М(1 .j.k), где 1 — номер строки, j — номер столбца и k — номер страницы. Этот элемент можно вывести, а можно присвоить ему заданное значение х: М(1 ,j,k)=x.
5. Удаление размерности в многомерном массиве
Удаление размерности в многомерном массиве
Мы уже отмечали возможность удаления отдельных столбцов присвоением им значений пустого вектора-столбца [ ]. Этот прием нетрудно распространить на страницы и вообще размерности многомерного массива. Например, первую страницу полученного массива М можно удалить следующим образом:
» М(:.:.1)=[ ]
М =
10 11 12
13 14 15
16 17 18
Нетрудно заметить, что в этом массиве осталась только вторая страница и что размерность массива уменьшилась на 1 — он стал двумерным.
6. Создание страниц, заполненных константами и случайными числами
Создание страниц, заполненных константами и случайными числами
Если после знака присваивания стоит численная константа, то соответствующая часть массива будет содержать элементы, содержащие данную константу. Например, создадим из массива М (см. пример выше) массив, у которого вторая страница содержит единицы:
»M(:.:..2)=1
М(:.:,1) =
10 11 12
13 14 15
16 17 18
М(:.:.2) =
1 1 1
1 1 1
1 1 1
А теперь заменим первую страницу массива на страницу с нулевыми элементами:
»M(:.:.1)=0
M(:.:.1)=
0 0 0
0 0 0
0 0 0
М(:.:,2) =
1 1 1
1 1 1
1 1 1
7. Использование функций ones, zeros, rand и randn
Использование функций ones, zeros, rand и randn
Функции ones (создание массивов с единичными элементами), zeros (создание массивов с нулевыми элементами) и rand или randn (создание массивов с элементами — случайными числами с соответственно равномерным и нормальным распределением) могут также использоваться для создания многомерных массивов. Примеры приводятся ниже:
» E=ones(3.3.2)
E(:.:.1)=
1 1 1
1 1 1
1 1 1
E(:.:,2) =
1 1 1
1 1 1
1 1 1
» Z=zeros(2,2,3) Z(:,:.l) =
0 0
0 0
Z(:.:.2) =
0 0
0 0
Z(:.:,3) =
0 0
0 0
» R=randn(3,2.2) R(:.:.l) =
-1.6656-1.1465
0.1253 1.1909
0.2877 1.1892
R(:.:,2) =
-0.0376-0.1867
0.3273 0.7258
0.1746 -0.5883
Эти примеры достаточно очевидны и не требуют особых комментариев. Обратите, однако, внимание на легкость задания размеров массивов для каждой размерности. Кроме того, следует отметить, что если хотя бы одна размерность массива равна нулю, то массив будет пустым:
» A=randn(3,3,3,0)
А =
Empty array: 3-bу-3-bу-3-by-0
Как видно из данного примера, пустой массив возвращается с соответствующим комментарием.
8. Объединение массивов
Объединение массивов
Для создания многомерных массивов служит описанная ранее для матриц специальная функция конкатенации cat:
-
cat(DIM,A,B) — возвращает результат объединения двух массивов А и В вдоль размерности DIM;
-
cat(2.A.B) — возвращает массив [А.В], в котором объединены ряды (горизонтальная конкатенация);
-
cat(1, А.В) — возвращает массив [А:В], в котором объединены столбцы (вертикальная конкатенация);
-
B=cat(DIM.Al,A2,...) — объединяет множество входных массивов Al, A2,... вдоль размерности DIM.
Функции cat(DIM,C{:}) и cat(DIM.C.FIELD) обеспечивают соответственно конкатенацию (объединение) ячеек массива ячеек (см урок 15) или структур массива структур (см. урок 14), содержащих числовые матрицы, в единую матрицу. Ниже приводятся примеры применения функции cat:
» М1=[1 2:3 4]
M1=
1 2
3 4
» М2=[5 6:78]
М2 =
5 6
7 8
» catd.Ml.M2)
ans =
1 2
3 4
5 б
7 8
» cat(2.Ml.M2)
ans=
1 2 5 6
3 4 7 8
» M-cat(3.Ml.M2) M(:,:.l) =
1 2
3 4
М(:,:,2) =
5 6
7 8
9. Работа с размерностями
Работа с размерностями
Вычисление числа размерностей массива
Функция ndims(A) возвращает размерность массива А (если она больше или равна двум). Но если входной аргумент — массив Java или массив массивов Java, то независимо от размерности массива эта функция вернет 2. Следующий пример иллюстрирует применение функции ndims:
» M=rand(2:3:4:5):
» ndims(M)
ans =
4
10. Вычисление размера размерности массива
Вычисление размера размерности массива
Для вычисления размера каждой размерности массива используется функция size:
-
М = size(A.DIM) возвращает размер размерности, указанной скаляром DIM, в виде вектора-строки размером 2. Для двумерного или одномерного массива А size(A.l) возвращает число рядов, a size (А, 2) - число столбцов;
Для N-мерных массивов А при n>2 size(A) возвращает N-мерный вектор-строку, отражающий страничную организацию массива, последняя составляющая этого вектора равна N. В векторе отсутствуют данные о единичных размерностях (тех, где расположены вектор-строка или вектор-столбец, т. е. size(A,DIM)==l). Исключение представляют N-мерные массивы Java массивов javaarray, которые возвращают размер массива самого высокого уровня.
Вообще, когда входным аргументом size является javaarray, то возвращаемое число столбцов всегда 1, а число рядов (строк) равно размеру (длине) javarray.
-
[Ml, М2 ,МЗ,..., MN] = si ze(A) возвращает размер первых N размерностей массива А;
-
D = size (А), для mxn матрицы А возвращает двухэлементный вектор-строку, в котором первая составляющая — число строк т, а вторая составляющая — число столбцов n;
-
[m.n] = size(A) возвращает число рядов и столбцов в разных выходных параметрах (выходных аргументах в терминологии MATLAB) тип.
11. Перестановки размерностей массивов
Перестановки размерностей массивов
Если представить многомерный массив в виде страниц, то их перестановка является перестановкой размерностей массива. Для двумерного массива перестановка часто означает транспонирование — замену строк столбцами и наоборот. Следующие функции обобщают транспонирование матриц для случая многомерных массивов и обеспечивают перестановку размерностей многомерных массивов:
-
permute (A, ORDER) — переставляет размерности массива А в порядке, определяемом вектором перестановок ORDER. Вектор ORDER — одна из возможных перестановок всех целых чисел от 1 до N, где N — размерность массива А;
-
ipermuteCA, ORDER) — операция, обратная permute: permute(permute(A. ORDER), ORDER)=A
Ниже приводятся примеры применения этих функций и функции size:
» А=[1 2: 3 4]:
» В=[5 6; 7 8];
» С=[9 10; И 12];
» D=cat(3.A,B.C)
D(:,:,l) =
1 2
3 4
9 10
11 12
» size(D)
ans =
2 2 3
» size(permute(D.[3 2 1]))
ans=
3 2 2
»size(ipermute(D.[2 1 3]))
ans=
2 2 3
» ipermute(permute(D,[3 2 1]),[3 2 1])
1 2
3 4
ans(:. :,2) =
5 6
78
ans(:.:,3) =
9 10
11 12
12. Сдвиг размерностей массивов
Сдвиг размерностей массивов
Сдвиг размерностей реализуется функцией shiftdim:
-
B=shiftdim(X,N) — сдвиг размерностей в массиве X на величину N. Если М>0, то сдвиг размерностей, расположенных справа, выполняется влево, а N первых слева размерностей сворачиваются в конец массива, т. е. движение размерностей идет по кругу против часовой стрелки. Если М<0, сдвиг выполняется вправо, причем N первых размерностей, сдвинутых вправо, замещаются единичными размерностями;
-
[B,NSHIFTS]=shiftdim(X) — возвращает массив В с тем же числом элементов, что и у массива X, но с удаленными начальными единичными размерностями. Выходной параметр NSHIFTS показывает число удаленных размерностей. Если X — скаляр, функция не изменяет X , В, NSHIFTS.
Следующий пример иллюстрирует применение функции shiftdim:
» A=randn(1,2,3,4);
» [B,N]=shiftdim(A)
B(:.:.1) =
-2.1707-1.01060.5077
-0.05920.6145 1.6924
B(:.:,2) =
0.5913 0.3803 -0.0195
-0.6436-1.0091-0.0482
B(:.:.3) =
0.0000 1.0950 0.4282
-0.3179-1.87400.8956
В(:.:,4) =
0.7310 0.0403 0.5689
0.5779 0.6771 -0.2556
N =
1
13. Удаление единичных размерностей
Удаление единичных размерностей
Функция squeeze(A) возвращает массив, в котором удалены все единичные размерности. Единичной называется размерность, в которой size(A. dim) == 1. Но если
А — одномерный или двумерный массив (матрица или вектор), то функция вернет тот же самый массив А. Следующий пример поясняет работу squeeze:
» A=randn(1.2.1.3.1);
» B=squeeze(A)
В=
0.6145 1.6924 -0.6436
0.5077 0.5913 0.3803
Обратите внимание на то, что пятимерный массив А превращается в массив с размерностью 2 и размером 2x3.
14. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Создавать многомерные массивы.
-
Применять оператор «:» в многомерных массивах.
-
Получать доступ к отдельным элементам многомерных массивов.
-
Удалять размерности у многомерного массива.
-
Создавать массивы, заполненные константами и случайными числами.
-
Осуществлять объединение массивов.
-
Вычислять число размерностей массива и определять размер каждой размерности.
-
Переставлять, сдвигать и удалять единичные размерности в многомерных массивах.
Урок 14. Массивы структур
1. Урок 14. Массивы структур
Урок №14.
Массивы структур
-
Тип данных — структуры
-
Создание структур и доступ к их компонентам
-
Проверка имен полей и структур
-
Функция возврата имен полей
-
Функция возврата содержимого полей структуры
-
Функция присваивания значений полям
-
Удаление полей
2. Тип данных - структуры
Тип данных — структуры
Структуры относятся к сложным типам данных. В предшествующих версиях MATLAB они именовались записями, что приводило к конфликтам в терминологии MATLAB и систем управления базами данных. Этот тип данных стал именоваться структурами после того, как широкое распространение получили средства MATLAB для работы с базами данных с использованием языка запросов Sequential Query Language (SQL).. Структуры MATLAB и их поля в отличие от полей записей баз данных не являются объектами SQL, но зато обращения к структурам могут быть откомпилированы и к ним возможен прямой доступ, минуя сложные и медленные механизмы систем управления базами данных. Структуры могут содержать разнородные данные, относящиеся к некоторому именованному объекту. Например, объект man (человек) может характеризоваться следующими данными:
|
Man(i....) |
|
Имя записи |
|
.name |
Иван |
Имя человека |
|
.surname |
Петров |
Фамилия |
|
.date |
1956 |
Год рождения |
|
.height |
170.5 |
Рост |
|
.weight |
70.34 |
Вес |
Первые два столбца представляют схему структуры. Как нетрудно заметить, каждая i-я структура состоит из ряда полей, имеющих имена, например man(i).name, man(i) .date и т. д. Поля могут содержать данные любого типа — от пустого поля [ ] до массивов. Приведенная выше структура имеет размер 1x1. MATLAB поддерживает и массивы структур, что позволяет создавать мощные базы данных.
Поле структуры может содержать другую вложенную структуру или массив структур. Это позволяет создавать вложенные структуры и даже многомерные массивы структур. Поскольку в данной книге такие структуры не используются, отсылаем заинтересованного читателя к книге [42], где они описаны более подробно.
3. Создание структур и доступ к их компонентам
Создание структур и доступ к их компонентам
Для задания структур на языке MATLAB можно использовать операторы присваивания, что иллюстрирует следующий пример:
» man.name='Иван';
» man.surname-'Петров':
» man.date=1956;
» man.height=170.5;
» man.weight=70.34;
Здесь построена базовая структура без индексного указателя. Теперь можно просмотреть полученную структуру, просто указав ее имя:
» man
man =
name: 'Иван'
surname: 'Петров'
date: 1956
height: 170.5000
weight: 70.3400
Нетрудно догадаться, что компоненты структуры можно вызывать по имени и менять их значения. При этом имя компонента состоит из имени структуры и имени поля, разделенных точкой. Это поясняют следующие примеры:
» man.date
ans =
1956
» man.date=1964
man =
name: 'Иван'
surname: 'Петров'
date: 1964
height: 170.5000
weight: 70.3400
Примечание
Как уже отмечалось, в MATLAB 6.0 существует проблема с записью символов кирилли-цы в командном режиме. Так, в командном режиме нельзя вводить в аргументы структур малую букву «с» русского алфавита — она ведет к переводу строки. Этого ограничения нет при задании структур в программах, хотя и в этом случае ошибки при вводе символов кириллицы не исключены.
Для создания массива структур вводится их индексация. Например, вектор структур можно создать, введя индекс в скобках после имени структуры. Так, для создания новой, второй структуры, можно поступить следующим образом:
»mаn(2).namе='Петр';
»mаn(2).Surnamе='Сидоров';
» man(2).date=1959;
»mаn(2)
ans =
name: 'Петр'
surname: 'Сидоров'
date: 1959
height: [ ]
weight: [ ]
» man(2).surname
ans =
Сидоров
» length(man)
ans = .2
Обратите внимание на то, что не все поля данной структуры заполнены. Поэтому значением двух последних полей структуры 2 оказываются пустые массивы. Число структур в массиве структур позволяет найти функция length (см. последний пример). Эта же функция может использоваться и для нахождения размера любого вектора или размерности многомерного непустого массива, так как length(Х)= MAX(size(X)), если X — непустой массив, и length(X)=0, если Х=[ ].
4. Функция создания структур
Функция создания структур
Для создания структур используется следующая функция:
-
struct('fieldl' .VALUES1, 'field2' .VALUES2,...) — возвращает созданную данной функцией структуру, содержащую указанные в параметрах поля 'fieldn' с их значениями ' VALUESn'. Значением может быть массив ячеек;
-
struct(OBJ) — конвертирует объект OBJ в эквивалентную структуру или массив структур. OBJ может быть объектом или массивом Java.
Пример:
» S=struct('student'.'Иванов'.'group'.2.'estimate','good')
S =
student: 'Иванов'
group: 2
estimate: 'good'
5. Проверка имен полей и структур
Проверка имен полей и структур
Выполнение операций с полями и элементами полей выполняется по тем же правилам, что и при работе с обычными массивами. Однако существует ряд функций, осуществляющих специфические для структур операции [ Помимо функций isstruct и isfields вы можете использовать для тестирования массивов структур функцию isа(имя объекта, 'struct') и команду или функцию whos имя объекта. — Примеч. ред. ].
Приведенные ниже функции служат для тестирования имен полей и структур записей:
-
isfielcKS, 'field') — возвращает логическую 1, если 'field' является именем поля структуры S;
-
isstruct(S) — возвращает логическую 1, если S — структура, и 0 в ином случае. Их применение на примере структуры man показано ниже:
» isfieldCman.'name')
ans =
1
» isfield(man.'family')
ans =
0
» isstruct(man)
ans =
1
» isstruct(many)
??? Undefined function or variable 'many'.
» isstruct('many')
ans =
0
6. Функция возврата имен полей
Функция возврата имен полей
Следующая функция позволяет вывести имена полей заданной структуры:
-
fieldnames (S) — возвращает имена полей структуры S в виде массива ячеек (см. урок 15). Пример:
» fieldnames(man)
ans =
'name'
'surname'
'date'
'height'
'weight'
7. Функция возврата содержимого полей структуры
Функция возврата содержимого полей структуры
В конечном счете работа со структурами сводится к выводу и использованию содержимого полей. Для возврата содержимого поля структуры S служит функция getfield:
-
getfield(S, 'field') — возвращает содержимое поля структуры S, что эквивалентно S. field;
-
getfield(S.{i,j}, 'field', {k}) - 'эквивалентно F=S(i J).field(k). Пример:
» getfield(man(2),'name')
ans =
Петр
8. Функция присваивания значений полям
Функция присваивания значений полям
Для присваивания полям заданных значений используется описанная далее функция selfield:
-
setfielcKS. 'field' ,V) — возвращает структуру S с присвоением полю 'field' значения V, что эквивалентно S.field=V;
-
setfie1d(S,{i .j}, 'field 1 ,{k},V) - эквивалентно S(i ,j).field(k)=V. Пример:
» setfield(man(2).'name'.'Николай')
ans =
name: 'Николай'
surname: 'Сидоров'
date: 1959
height: [ ]
weight: [ ]
9. Удаление полей
Удаление полей
Для удаления полей структуры можно использовать следующую функцию:
-
rmfield(S, 'field') — возвращает структуру S с удаленным полем S.'field';
-
rmfield(S,FIELDS) — возвращает структуру S с несколькими удаленными полями. Список удаляемых полей FIELDS задается в виде массива символов (строки) или строкового массива ячеек.
Пример:
» rmfield(man(2).'surname')
ans =
name: 'Петр'
date: 1959
height: []
weight: []
10. Применение массивов структур
Применение массивов структур
Массивы структур находят самое широкое применение. Например, они используются для представления цветных изображений. Известно, что цветные изображения формата RGB состоят из массивов интенсивности трех цветов - красного R, зеленого G и синего В. При этом каждый массив содержит данные о координатах точки (они определяются целочисленными индексами массива) и о ее яркости (число от 0 до 1 в формате чисел с плавающей запятой). Чтобы некоторое изображение, например pic, несло данные о цвете всех точек, придется представить изображение массивом структур с полями pic.r, pic.g и pic.b.
Еще более сложные структуры (но, в принципе, вполне очевидные) нужны для разработки баз данных, например о работниках предприятия, службах города, городах страны и т. д. Во всех этих случаях особенно важна возможность доступа к отдельным полям структур и возможность присвоения таким полям уникальных имен.
Может показаться, что этот тип данных имеет малое отношение к математическим возможностям системы MATLAB. Однако надо помнить, что поиск информации в больших базах данных, сортировка этой информации и прочие операции, не говоря уже о сложной обработке массивов изображений, — все это примеры явно математических, хотя и достаточно специфических, операций. Причем операций нередко с многомерными структурами. Возможность MATLAB выполнять подобные операции быстро и эффективно (прежде всего с позиций минимальных затрат памяти) открывает перед этой системой очень большие возможности в этой области — впрочем, пока еще ждущие своей реализации. Уже в MATLAB 6.1 возможен одновременный прямой обмен данными между массивами структур MATLAB и множеством записей разных баз данных благодаря Database ToolBox (см. урок 23).
11. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Создавать структуры.
-
Обеспечивать доступ к полям структур.
-
Проверять имена полей и структур.
-
Использовать функции возврата имен полей и их содержимого.
-
Присваивать полям значения и удалять поля.
Урок 15. Массивы ячеек
1. Урок 15. Массивы ячеек
Урок №15.
Массивы ячеек
-
Создание массивов ячеек
-
Создание ячеек с помощью функции cell
-
Визуализация массивов ячеек
-
Создание строкового массива ячеек из массива символов
-
Присваивание с помощью функции deal
-
Функция тестирования имен массивов ячеек
-
Функции преобразования типов данных
-
Многомерные и вложенные массивы ячеек
2. Создание массивов ячеек
Создание массивов ячеек
Массив ячеек — наиболее сложный тип данных в системе MATLAB. Это массив, элементами которого являются ячейки, содержащие любые типы массивов, включая массивы ячеек. Отличительным атрибутом массивов ячеек является задание содержимого последних в фигурных скобках {}. Создавать массивы ячеек можно с помощью оператора присваивания.
Существуют два способа присваивания данных отдельным ячейкам:
-
индексацией ячеек;
-
индексацией содержимого.
Рассмотрим первый способ. Для этого создадим файл-сценарий с именем се.m:
А( 1.1)={'Курить вредно!'};
А(1.2)={[1 2;3 4]};
A(2,1)={2+3i};
А(2.2)={0:0.1:1}
Примечание
Уже отмечалось, что в командном режиме малая русская буква «с» в строках ведет к пе-реводу строки ввода. Однако в m-файлах, создаваемых в редакторе/отладчике М-фай-лов, эта недоработка обычно не проявляется. Хотя гарантии в этом, увы, пока нет.
В этом примере задан массив ячеек с четырьмя элементами: строкой символов, матрицей, комплексным числом и одномерным массивом из 11 чисел. Теперь можно вызвать этот массив:
» се
А =
'Курить вредно!' [2x2 double]
[2.0000+ 3.00001] [1x11 double]
» A(1,1)
ans =
'Курить вредно!'
»А(2.1)
ans =
[2.0000+ 3.00001]
Заметим, что к ячейкам такого массива можно обращаться с помощью индексирования, например в виде А(1,1), А(2,1) и т. д.
При индексации содержимого массив ячеек задается следующим образом:
А{1,1}='Курить вредно!';
А{1,2}-[1 2:3 4];
А{2,1}=2+31;
А{2,2}=0:0.1:1;
Теперь можно ознакомиться с созданным массивом ячеек в командном режиме:
» А
ans =
'Курить вредно! ' [2x2 double]
[2.0000+ 3.0000i] [1x11double]
» А{1,1}
ans =
Курить вредно!
» А{2.1}
ans =
2.0000 + 3.0000i
При серьезной работе с массивами структур (записей) и массивами ячеек полезно иметь дополнительную информацию о списках значений. Для получения такой информации следует выполнить команду help list.
3. Создание ячеек с помощью функции cell
Создание ячеек с помощью функции cell
Для создания массива ячеек может использоваться функция eell :
-
cell(N) — создает массив ячеек из NxN пустых матриц;
-
cell(M.N) или cell([M,N]) — создает массив ячеек из MxN пустых матриц;
-
cell(M.N.P,...) или сеll([М N Р ...]) — создает массив из MxNxPx... пустых матриц;
-
cell (size(A)) — создает массив ячеек из пустых матриц того же размера, что имассив А;
-
cell (объект Java) — автоматически преобразует объекты или массивы Java (javaarray) в массив ячеек, элементы которого являются объектами MATLAB.
Следующие примеры поясняют применение данной функции:
» cell(2)
ans =
[] []
[] []
» C=cell(2.3)
С =
[] [] []
[] [] []
» C0=zeros(2.3)
С0=
0 0 0
0 0 0
» celHsize(CO))
ans =
[] [] []
[] [] []
Образовавшиеся пустые ячейки можно заполнить, используя операции присваивания:
» С{1.1}=1;С{1.2}='Привет':С{2,1}='Неllо':С{2.2}=[1 2; 3 4];
»С
С =
[ 1] 'Привет' []
'Hello ' [2x2 double] []
4. Визуализация массивов ячеек
Визуализация массивов ячеек
Для отображения массива ячеек С служит функция celldlsp(C). Она дает рекурсивное отображение содержимого массива ячеек С. Например, для ранее созданного массива ячеек А получится следующее:
» celldisp(A)
А{1.1}=
Курить вредно!
А{2.1}=
2.0000 + 3.0000i
А{1,2} =
1 2
3 4
А{2,2} -Columns 1 through 7
0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000
Columns 8 through 11
0.7000 0.8000 0.9000 1.0000
Для более наглядного графического представления массива ячеек может использоваться команда cell plot:
5. Создание строкового массива ячеек из массива символов
Создание строкового массива ячеек из массива символов
Для создания из массива символов S строкового массива ячеек может использоваться функция eellstr(S). Каждый ряд массива символов превращается в отдельную ячейку. Следующий пример поясняет применение функции cellstr:
» S={'Привет.'; 'дорогой'; 'друг'};
» C=cellstr(S)
С =
'Привет.'
'дорогой'
'ДРУГ'
Это еще один способ формирования массивов ячеек.
Функция iscellstr(C) равна 1, если ее аргумент С — строковый массив ячеек, и 0, если это неверно.
6. Присваивание с помощью функции deal
Присваивание с помощью функции deal
С помощью функции deal возможно множественное присваивание входных данных выходным:
-
[A.B,C,...]=deal(X,Y,Z,...) — обеспечивает последовательное присваивание входных данных выходным, то есть А=Х, B=Y, C=Z и т. д.;
-
[A,B,C....]=deal(X) — присваивает единственный вход всем выходам, т. е. А=Х, В=Х, С=Х и т. д.
Возможен ряд полезных применений функции deal:
-
[S.FIELD]=deal (X) — присваивает всем полям FIELD структуры S значения X. Если S не существует, то нужно использовать конструкцию [S(1:M)*.FIELD]= deal(X);
-
[X{:}]=dea1 (A. FIELD) — копирует поля FIELD структуры А в массив ячеек X. Если X не существует, следует использовать конструкцию [X{1:M}]=deal (A.FIELD);
-
[A,B,C,...]=deal (X{:}) — копирует содержимое массива ячеек X в отдельные переменные А, В, С,...;
-
[A,B,C,...]=deal(S.FIELD) — копирует содержимое поля FIELD массива структур S в отдельные переменные А, В, С,...;
Следующий пример иллюстрирует применение функции deal:
» [X,Y.Z]=deal(1,2+3i,'Привет!')
X =
1
Y =
2.0000.+ 3.0000i
Z =
Привет!
» [X Y Z]=dealС Привет!')
X =
Привет!
Y =
Привет!
Z =
Привет!
7. Тестирование имен массивов ячеек
Тестирование имен массивов ячеек
Ввиду обилия типов данных в системе MATLAB часто возникает необходимость в их тестировании [ Помимо функций iscell и iscellstr вы всегда можете использовать для тестирования массивов ячеек функцию 15а(имя объекта, 'cell') и команду whos имя объекта. — Примеч. ред. ]. Для тестирования массивов ячеек может использоваться функция is сеll (С), которая возвращает логическое значение 1, если С — массив ячеек, и 0 в противном случае. Это поясняют следующие примеры:
» t=iscell(A)
t =
1
» B=[l 23];
» iscell(B)
ans=
0
8. Функции преобразования типов данных
Функции преобразования типов данных
При обработке сложных данных возникает необходимость в преобразовании их типов. Ниже представлены такие функции, имеющие отношение к массивам ячеек:
-
num2cell (A,DIM) — преобразует массив чисел А в массив ячеек, помещая в одну и ту же ячейку элементы, соответствующие одному значению индекса вдоль измерения, указанного параметром DIM. Например, num2cell (A.2) преобразует каждый ряд массива А в отдельную ячейку. cat(DIM.C{:}) осуществляет обратное преобразование.
-
num2cell (A) — преобразует массив чисел А в массив ячеек и возвращает последний. Каждый элемент А превращается в отдельную ячейку. Возвращаемый массив имеет тот же размер и ту же размерность, что и исходный массив А.
Примеры применения данных функций:
» А=[1 2; 3 4: 5 6]
А=
1 2
3 4
5 6
»С= num2cell(A.2)
С=
[1x2 double]
[1x2 double]
[1x2 double]
»С{1,1}
ans =
1 2
»С{2,1}
ans =
3 4
»С{3,1}
ans =
5 б
» cat(2.C{:})
ans =
1 2 3 4 5 6
ans =
1 2
3 4
5 6
» num2cell(A.[l 2])
ans =
[3x2 double]
-
cell2struct(C. FIELDS. DIM) — преобразует массив ячеек С в массив структур, превращая размерность DIM массива ячеек С в поля структуры S. Размерность 1 — столбцы. Размерность 2 — строки. FILEDS — массив символов или строковый массив ячеек.
Пример преобразования:
» С={' Привет! '.123. 2+31}
С =
'Привет!' [123] [2.0000+3.00001]
» f={ 'name' , 'number' , 'complex'};
» S=cell2struct(C,f,2)
S =
name: 'Привет! '
number: 1 2 3
complex: 2.0000+ 3.0000i
-
struct2cell (S) — преобразует массив структур S размером тхп, в котором содержатся р полей, в массив ячеек, так что возвращаемый массив будет иметь размер рхтхп. Если массив структур многомерный, то возвращаемый массив ячеек будет иметь размер, равный [р size(S)]. Схему структуры с названиями полей возвращаемый массив ячеек не содержит. Пример такого преобразования приводится ниже:
» C=struct2cellS)
С =
'Привет!'
[ 123]
[2.0000+3.0000i]
9. Многомерные массивы ячеек
Многомерные массивы ячеек
С помощью функции cat можно формировать многомерные массивы ячеек. Например, трехмерный массив С формируется следующим образом (m-файл с именем се2.m):
А{1.1}='Курить вредно!';
А{1,2}=[1 2:3 4];
А{2.1}=2+3i;
А{2.2}=0:0.1:1;
В{1,1}='Пить тоже вредно!';
В{1,2}=[1 2 3 4];
В{2.1}=2;
B{2.2}=2*pi;
C=cat(3,A,B);
Теперь можно просмотреть данный массив, имеющий две страницы:
» се2
» С
С(:,:,1) =
'Курить вредно!' [2x2 double]
[2.0000+ 3.0000i] [1x11 double]
С(:.:.2) =
'Пить тоже вредно!' [1x4 double]
[ 2] [ 6.2832]
Доступ к ячейкам многомерных массивов очевиден и поясняется следующими примерами:
» C(l.l.l)
ans =
'Курить вредно!'
» C(1.1.2)
ans =
'Пить тоже вредно!'
10. Вложенные массивы ячеек
Вложенные массивы ячеек
Содержимым ячейки массива ячеек может быть, в свою очередь, произвольный массив ячеек. Таким образом, возможно создание вложенных массивов ячеек — пожалуй, самого сложного типа данных.
В следующем примере показано формирование массива ячеек А с вложенным в него массивом В (он был создан в примере выше):
» clear A;
» A(l.l)={{magic(3).{'Hello!'}}};
»А(1.2)={В};
» А
ans =
{1x2 cell} {2x2 cell}
ans =
[3x3 double] {1x1 cell} >> A{2}
ans =
'Пить тоже вредно!' [1x4 double]
[ 2 ] [ 6.2832]
» cellplot(A)
В данном случае вложенный массив отображается полностью как часть массива А.
11. Что новoго мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Создавать ячейки и массивы ячеек.
-
Осуществлять визуализацию массивов ячеек.
-
Создавать массивы символьных ячеек из массивов строк.
-
Осуществлять присваивание ячейкам значений.
-
Использовать функцию тестирования имен массивов ячеек.
-
Применять функции преобразования типов.
-
Создавать многомерные и вложенные массивы ячеек.
Урок 16. Численные методы
1. Урок 16. Численные методы
Урок №16.
Численные методы
-
Средства решения систем линейных уравнений (СЛУ)
-
Вычисление нулей функции одной переменной
-
Минимизация функции одной и нескольких переменных
-
Аппроксимация Лапласиана
-
Аппроксимация производных конечными разностями
-
Вычисление градиента функции
-
Численное интегрирование
-
Операции с полиномами
-
Решение полиномиальных матричных уравнений
-
Разложение на простые дроби
-
Решение обыкновенных дифференциальных уравнений
-
Информация о пакете для решения уравнений с частными производными
В этом большом уроке описываются функции системы MATLAB, предназначенные для реализации алгоритмов типовых численных методов решения прикладных задач и обработки данных. Наряду с базовыми операциями решения систем линейных и нелинейных уравнений рассмотрены функции вычисления конечных разностей, численного дифференцирования, численного интегрирования, триангуляции, аппроксимации Лапласиана и, наконец, прямого и обратного преобразования Фурье. Отдельные разделы посвящены работе с полиномами и численным методам решения обыкновенных дифференциальных уравнений. Этот большой урок стоит разбить на две-три части или изучать выборочно.
2. Элементарные средства решения СЛУ
Элементарные средства решения СЛУ
Решение систем линейных уравнений (СЛУ) относится к самой массовой области применения матричных методов, описанных в уроках 10-12. В этом разделе вы найдете ответы на вопросы, каким образом применяются указанные методы и какие дополнительные функции имеет система MATLAB для решения систем линейных уравнений.
Как известно, обычная СЛУ имеет вид:
а 11 X 1 , а 12 ,X 2 ..., а 1n X n =b 1
Здесь а 11 , а, 2 ,..., а пп — коэффициенты, образующие матрицу А, которые могут иметь действительные или комплексные значения, x 1 , х 2 ,..., х п — неизвестные, образующие вектор X, и b 1 , b 2 ,..., b п — .свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений, X — искомый вектор неизвестных и В — вектор свободных членов. В зависимости от вида матрицы А и ее характерных особенностей MATLAB позволяет реализовать различные методы решения.
Для реализации различных алгоритмов решения СЛУ и связанных с ними матричных операций применяются следующие операторы: +,-,*,/, \, *, ' . Как отмечалось ранее, MATLAB имеет два различных типа арифметических операций — поэлементные и для массивов (векторов и матриц) в целом. Матричные арифметические операции определяются правилами линейной алгебры.
Арифметические операции сложения и вычитания над массивами выполняются поэлементно. Знак точки «.» отличает операции над элементами массивов от матричных операций. Однако, поскольку операции сложения и вычитания одинаковы для матрицы и элементов массива, знаки «.+» и «.-» не используются. Рассмотрим другие операторы и выполняемые ими операции.
-
* — матричное умножение;
- С = А*В — линейное алгебраическое произведение матриц А и В:
Для случая нескалярных А и В число столбцов матрицы А должно равняться числу строк матрицы В. Скаляр может умножаться на матрицу любого размера.
-
/ — правое деление. Выражение Х=В/А дает решение ряда систем линейных уравнений АХ=В, где А — матрица размера тхп и В — матрица размера nxk;
-
\ — левое деление. Выражение Х=В\А дает решение ряда систем линейных уравнений ХА=В, где А — матрица размера тхп и В — матрица размера nxk. Если А — квадратная матрица, то А\В — примерно то же самое, что и inv(A)*B, в остальных случаях возможны варианты, отмеченные ниже.
Если А — матрица размера пхп, а В — вектор-столбец с п компонентами или матрица с несколькими подобными столбцами, тогда Х=А\В — решение уравнения АХ=В, которое находится хорошо известным методом исключения Гаусса.
Если А — матрица размера тхп и тхп, а В представляет собой вектор-столбец с m компонентами или матрицу с несколькими такими столбцами, тогда система оказывается недоопределенной или переопределенной и решается на основе минимизации второй нормы невязок.
Ранг k матрицы А находится на основе QR-разложения (урок 11) с выбором ведущего элемента. Полученное решение X будет иметь не больше чем k ненулевых компонентов на столбец. Если k<n, то решение, как правило, не будет совпадать с pinv(A)*B, которое имеет наименьшую норму невязок ||Х||.
-
^ — возведение матрицы в степень. Х А р — это X в степени р, если р — скаляр. Если р — целое число, то степень матрицы вычисляется путем умножения X на себя р раз. Если р — целое отрицательное число, то X сначала инвертируется. Для других значений р вычисляются собственные значения и собственные векторы, так что если [V.D]=eig(X), то X*p=V*D. A p/V. Если X — скаляр и Р — матрица, то Х А Р — это скаляр X, возведенный в матричную степень Р. Если X и Р — матрицы, то Х Л Р становится некорректной операцией и система выдает сообщение об ошибке. Возможный вариант решения матричного уравнения АХ=В с применением оператора ^ можно представить как Х=В*А ^ -1.
-
' — транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, А' — транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Транспонирование при решении СЛУ полезно, если в матрице А переставлены местами столбцы и строки.
При записи СЛУ в матричной форме необходимо следить за правильностью записи матрицы А и вектора В. Пример (в виде m-файла):
|
|
|
|
|
|
|
А-[2 1 |
0 |
1: |
|
|
1 -3 |
2 |
4; |
|
|
-5 0 |
-1 |
-7: |
|
|
1 -6 |
2 |
6]: |
|
|
В=[8 9 |
-5 |
0]: |
|
|
Х1=В/А |
|
|
|
|
Х2=В*А ^ -1 |
|
|
|
|
X3=B*inv(A) |
|
|
|
|
|
|
|
Эта программа выдает результаты решения тремя способами:
X1 =
3.0000 -4.0000-1.00001.0000
Х2 =
3.0000 -4.0000-1.00001.0000
X3 =
3.0000 -4.0000-1.00001.0000
Как и следовало ожидать, результаты оказываются одинаковыми для всех трех методов. При решении систем линейных уравнений, особенно с разреженной матрицей коэффициентов, полезно применение функций colmmd (colamd), symmmd (symamd), описанных ранее в уроке 12.
1.gif

3. Функции для решения систем линейных уравнений с ограничениями
Функции для решения систем линейных уравнений с ограничениями
Теперь рассмотрим функции, введенные для решения систем линейных уравнений с ограничениями методом наименьших квадратов:
-
X =lscov(A,B.V) —возвращаетвекторXрешения СЛУ видаА*Х=В+е, гдее — вектор шумов, который имеет ковариационную матрицу V. Реализуется метод наименьших квадратов в присутствии шумов с известной ковариацией. Прямоугольная матрица А должна быть размера тхп, где т>п. При решении минимизируется следующее выражение: (AX-b)'*inv(V)*(AX-b). Решение имеет вид X=inv(A'* inv(V)*A)*A'*inv(V)*B. Алгоритм решения, однако, построен так, что операция инвертирования матрицы V не проводится;
-
[X.dX] = lscov(A,B,V) — возвращает также стандартную погрешность X, помещая ее в переменную dX. Статистическая формула для стандартной погрешности вычисления коэффициентов имеет следующий вид:
mse = B'*(inv(V)-inv(V)*A*inv(A'*inv(V)*A)*A'*inv(V))*B./(m-n)
dX = sqrt(diag(inv(A'*inv(V)*A)*mse))
-
X =isqnonneg(A,B) — решение СЛУ АХ=В методом наименьших квадратов с неотрицательными ограничениями. А — действительная прямоугольная матрица, В — действительный вектор. Вектор X содержит неотрицательные элементы X>=Q, где j = 1, 2,... п. Критерий: минимизация второй нормы вектора В=АХ;
-
X = Isqnonneg(A.B.X0) — решение СЛУ с явно заданным неотрицательным начальным значением X для итераций;
-
[X,W] = Isqnonneg (...) — вместе с решением возвращает вторую норму вектора остатков в квадрате;
-
[X.W.W1] = Isqnonneg(..) — вместе с решением возвращает вторую норму вектора остатков в квадрате и вектор остатков W1;
-
[X.W.Wl.exitflag] = Isqnonneg (...) — вместе с решением возвращает вторую норму вектора остатков в квадрате, вектор остатков W1 и флаг exi tflаg, равный 1, если решение сходится после заданного по умолчанию числа итераций, и 0 — в противном случае;
-
[X.'W.Wl.exitflag,output] = Isqnonneg(...) — дополнительно возвращает число итераций в output;
-
[X.W.Wl.exitflag,output,lambda] = lsqnonneg(...) — дополнительно возвращает вектор lambda, минимизирующий произведение lambda W1 на последнем шаге итераций решения, lambda (i) близко к нулю, когда X(i) положительно, lambda (i) отрицательно, когда Х(1) равно 0;
-
[X.W.Wl.exitflag,output,lambda] = lsqnonneg(A.В,ХО,options) — обычно используется, если при предыдущей попытке решения системы exitflag=l или если необходимо изменить заданный по умолчанию порог отбора по X - tol X. равный 10*max(size(A))*norm(A, l)*eps (произведению первой нормы матрицы, большего из измерений матрицы, машинной точности и 10). Также используется такая форма записи, как X=lsqnonneg(A,B,XO,options). Параметры options должны быть предварительно заданы при помощи функции optimset. Функция Isqnonneg использует только поля 'display' и 'tolX' структуры options. Поэтому наиболее часто используемая вместе с Isqnonneg форма записи функции — options= optimset С tol X'.tol value), где tolvalue — новое значение порога отбора по X.
Применение ограничений позволяет избежать получения отрицательных корней, хотя и ведет к появлению несколько больших погрешностей решения, чем в случае решений без ограничений. Пример:
» С=[4 3:12 5:3 12];b=[1.45,41];D=lsqnonneg(C.b')
D =
2.2242
2.6954
4. Решение СЛУ с разреженными матрицами
Решение СЛУ с разреженными матрицами
Решение СЛУ с разреженными матрицами — хотя и не единственная, но несомненно одна из основных сфер применения аппарата разреженных матриц, описанного в уроке 12. Ниже приведены функции, относящиеся к этой области применения разреженных матриц. Большинство описанных методов относится к итерационным, т. е. к тем, решение которых получается в ходе ряда шагов — итераций, постепенно ведущих к получению результата с заданной погрешностью или с максимальным правдоподобием [33]. Описанные ниже функции MATLAB могут и должны применяться и при решении обычных СЛУ - без разреженных матриц.[ Использование всех этих функций, кроме Isqr, как правило, ограничено системами уравнений, в которых А — нормальная квадратная матрица, т. е. А* А -АА*, где А*— сопряженная (эрмитова) матрица А. — Примеч. ред. ]
5. Точное решение, метод наименьших квадратов и сопряженных градиентов
Точное решение, метод наименьших квадратов и сопряженных градиентов
-
lsqr(A, В)—возвращает точное решение X СЛУ А*Х=В, если матрица последовательная, в противном случае — возвращает решение, полученное итерационным методом наименьших квадратов. Матрица коэффициентов А должна быть прямоугольной размера тхя, а вектор-столбец правых частей уравнений В должен иметь размер т. Условие m>=n может быть и необязательным. Функция 1 sqr начинает итерации от начальной оценки, по умолчанию представляющей собой вектор размером п, состоящий из нулей. Итерации производятся или до сходимости к решению, или до появления ошибки, или до достижения максимального числа итераций (по умолчанию равного min(20, m, n) — либо 20, либо числу уравнений, либо числу неизвестных). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol (по умолчанию 1е-б);
-
lsqr(A.B,tol) — возвращает решение с заданной погрешностью (порогом отбора) tol;
-
lsqr(A,b.tol .maxlt) — возвращает решение при заданном максимальном числе итераций maxit вместо, возможно, чересчур малого числа, заданного по умолчанию;
-
lsqr(A,b.tol .maxit,M) и lsqr(A,b,tol .maxit.Ml.M2) — при решении используются матрица предусловий М или М=М1*М2, так что производится решение системы inv(M)*A*x=inv(M)*b относительно х. Если Ml или М2 — пустые матрицы, то они рассматривается как единичные матрицы, что эквивалентно отсутствию входных условий вообще;
-
lsqr(A.B,tol .maxit.Ml.M2.X0) — точно задается начальное приближение Х0. Если Х0 — пустая матрица, то по умолчанию используется вектор, состоящий из нулей;
-
X = lsqr(A,B.tol .maxit,Ml.M2.X0) — при наличии единственного выходного параметра возвращает решение X. Если метод 1 sqr сходится, выводится соответствующее сообщение. Если метод не сходится после максимального числа итераций или по другой причине, на экран выдается относительный остаток попп(В-А*Х)/ norm(B) и номер итерации, на которой метод остановлен;
-
[X.flag] = lsqr(A.X.tol.maxit.Ml.M2.X0) — возвращает решение X и флаг flag. описывающий сходимость метода;
-
[X.flag.relres] = lsqr(A,X,tol.maxit,Ml.M2.X0) — также возвращает относительную вторую норму вектора остатков rel res=norm(B-A*X)/norm(B). Если флаг flag равен 0, то relres<tol;
-
[X.flag.relres.iter] = bicg(A,B.tol,maxit,Ml,M2.X0) — также возвращает номер итерации, на которой был вычислен X. Значение iter всегда удовлетворяет условию 0<iter<maxit;
-
[X.flag.relres,iter,resvec]= lsqr(A.B.tol.maxit.Ml.M2.X0) — также возвращает вектор вторых норм остатков resvec для каждой итерации начиная с res-vec(l)=norm(B=A*X0). Если флаг flag равен 0, то resvec имеет длину iter+1 и resvec(end)<tol*norm(B). Возможны значения flag, равные 0, 1, 2, 3 и 4. Значения flag предоставляют следующие данные о сходимости решения:
-
flag=0 - решение сходится при заданной точности tol и числе итераций не более заданного maxit;
-
flag=l - число итераций равно заданному maxit, но сходимость не достигнута;
-
flag=2 - матрица предусловий М плохо обусловлена;
-
flag=3 - процедура решения остановлена, поскольку две последовательные оценки решения оказались одинаковыми;
-
fl ag=4 - одна из величин в процессе решения вышла за пределы допустимых величин чисел (разрядной сетки компьютера).
-
Если значение flag больше нуля, то возвращается не последнее решение, а то решение, которое имеет минимальное значение отношения вторых норм векторов norm(B-A*x)/norm(B).
Пример:
» А=[0 012; 1300; 0101; 1010];
» В=[11; 7; 6; 4];
Введенные в этом примере матрица А и вектор В будут использованы и в других примерах данного раздела. В примере процесс итераций сходится на пятом шаге с относительным остатком (отношением вторых норм векторов невязки и свободных членов) 1.9 10- 13 .
Пример:
» lsqr(A,B.1e-6.5)
Isqr converged at iteration 5 to a solution
with relative residual
1.9e-013
ans =
1.0000
2.0000
3.0000
4.0000
6. Двунаправленный метод сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Решение СЛУ с разреженной матрицей возможно также известным двунаправленным методом сопряженных градиентов. Он реализован указанной ниже функцией.
-
biсд(А. В) — возвращает решение X СЛУ А*Х=В. Матрица коэффициентов А должна быть квадратной размера пхп, а вектор-столбец правых частей уравнений В должен иметь длину п. Функция bicg начинает итерации от начальной оценки, по умолчанию представляющей собой вектор размером п, состоящий из нулей. Итерации производятся или до сходимости к решению, или до появления ошибки, или до достижения максимального числа итераций (по умолчанию равно min(20,n) — либо 20, либо числу уравнений). Сходимость достигается, когда относительный остаток norm(B-A*x)/norm(B) меньше или равен погрешности метода (по умолчанию le-6). Благодаря использованию двунаправленного метода сопряженных градиентов bicg сходится за меньшее число итераций, чем lsqr (в нашем примере быстрее на одну итерацию), но требует квадратную матрицу А, отбрасывая информацию, содержащуюся в дополнительных уравнениях, в то время как 1 sqr работает и с прямоугольной матрицей;
-
bicgCA.B.tol) — выполняет и возвращает решение с погрешностью (порогом отбора) tol;
-
bicg(A,b.tol, max it) — выполняет и возвращает решение при заданном максимальном числе итераций maxit;
-
bicgCA.b.tol,maxit,М) и bicg(A,b.tol .maxit,Ml,М2) — при решении используются матрица предусловий М или М=М1*М2, так что производится решение системы inv(M)*A*x=inv(M)*b относительно х. Если Ml или М2 — пустые матрицы, то они рассматривается как единичные матрицы, что эквивалентно отсутствию входных условий вообще;
-
bicgCA.B.tol, maxit. Ml. M2.X0) — точно задается начальное приближение Х0. Если Х0 — пустая матрица, то по умолчанию используется вектор, состоящий из нулей;
-
X = bi eg (А, В, tol, maxit. Ml, M2.X0) — при наличии единственного выходного параметра возвращает решение X. Если метод bicg сходится, выводится соответствующее сообщение. Если метод не сходится после максимального числа итераций или по другой причине, на экран выдается относительный остаток norm(B-A*X)/ norm(B) и номер итерации, на которой метод остановлен;
-
[X.flag.relres] = bicg(A,X,tol .maxit.Ml,M2.X0) — также возвращает относительную вторую норму вектора остатков relres=nQnr)(B-A*X)/norm(B). Если флаг flag равен 0, то rel res<tol;
-
[X, flag, rel res, iter] = bicgCA.B.tol,maxit,Ml,M2.XO) — также возвращает номер итерации, на которой был вычислен X. Значение iter всегда удовлетворяет условию 0<iter<maxit;
-
[X.flag.relres.iter.resvec] = bicgCA.B.tol,maxit,Ml,M2.XO) — также возвращает вектор вторых норм остатков resvec для каждой итерации начиная с res-vec(l)=norm(B-A*X0). Если флаг flag равен 0, то resvec имеет длину iter+1 и resvec(end)<tol*norm(B). Возможны значения flag, равные 0, 1, 2, 3 и 4. Эти значения предоставляют следующие данные о сходимости решения:
-
flag=0 - решение сходится при заданной точности tol и числе итераций не более заданного maxit;
-
flag=l - число итераций равно заданному maxit, но сходимость не достигнута;
-
f l ag=2 - матрица предусловий М плохо обусловлена;
-
fl ag=3 - процедура решения остановлена, поскольку две последовательные оценки решения оказались одинаковыми;
-
fl ag=4 - одна из величин в процессе решения вышла за пределы допустимых величин чисел (разрядной сетки компьютера).
-
Пример:
» bicg(A.B)
BICG converged at iteration 4
to a solution with relative residual
2.3e-015
ans=
1.0000
2.0000
3.0000
4.0000
-
[X.flag] = bicg(A,X.tol ,maxit.Ml,M2,X0) — возвращает решение Х и флаг flag, описывающий сходимость метода.
7. Устойчивый двунаправленный метод
Устойчивый двунаправленный метод
Еще один двунаправленный метод, называемый- устойчивым, реализует функция bicgstab:
-
bicgstab(A.B) — возвращает решение X СЛУ А*Х=В. А — квадратная матрица. Функция bi cgstab начинает итерации от начальной оценки, по умолчанию представляющей собой вектор размером п, состоящий из нулей. Итерации производятся либо до сходимости метода, либо до появления ошибки, либо до достижения максимального числа итераций. Сходимость метода достигается, когда относительный остаток norm(B-A*X)/norm(B) меньше или равен погрешности метода (по умолчанию le-б). Функция bicgstab(...) имеет и ряд других форм записи, аналогичных описанным для функции bi eg (...). Пример:
» bicgstab(A.B)
BICGSTAB converged at iteration 3.5
to a solution with relative residual
6.5e-012
ans =
1.0000
2.0000
3.0000
4.0000
8. Метод сопряженных градиентов
Метод сопряженных градиентов
Итерационный метод сопряженных градиентов реализован функцией peg: О рсд(А.В) — возвращает решение X СЛУ А*Х=В. Матрица А должна быть квадратной, симметрической [ В нашем примере матрица А — несимметрическая, т. е. A(i,j)—*A(j,i). — Примеч. ред. ] и положительно определенной [ Матрица называется положительно определенной, если все ее собственные значения (характеристические числа) действительные и положительные. — Примеч. ред. ]. Функция pcg начинает итерации от начальной оценки, представляющей собой вектор размером п, состоящий из нулей. Итерации производятся либо до сходимости решения, либо до появления ошибки, либо до достижения максимального числа итераций. Сходимость достигается, если относительный остаток norm(b-A*X)/norm(B) меньше или равен погрешности метода (по умолчанию 1е-6). Максимальное число итераций — минимум из п и 20. Функция pcg(...) имеет и ряд других форм записи, описанных для функции bieg(...). Пример:
» pcg(A.B)
Warning: PCG stopped after the maximum 4 iterations
without converging to the desired tolerance le-006
The iterate returned (number 4) has relative residual 0.46
> In C:\MATI_AB\toolbox\matlab\sparfun\pcg.m at line 347
ans =
1.7006
1.2870
-2.0535
8.2912
В данном случае решение к успеху не привело, поскольку матрица А —несимметрическая. Новая функция rrrinres не требует, чтобы матрица А была положительно определенной. Достаточно, чтобы она была квадратной и симметрической. В отличие от peg минимизируется не относительная невязка, а абсолютная. Но и эта функция не может решить наш пример:
» minres(A.В.1е-6.1000000)
minres stopped at iteration 1000000 without converging
to the desired tolerance le-006
because the maximum number of iterations was reached.
The iterate returned (number 1000000) has relative residual 0.011
ans =
1.9669
3.7757
3.0789
1.9367
В MATLAB 6 появилась еще одна новая функция symmlq, которая использует LQ-алгоритм итерационного метода сопряженных градиентов и также не требует, чтобы ее входной аргумент — квадратная симметрическая матрица — была положительно определенной. Эта функция тоже не может решить наш пример, так как наша матрица А — квадратная, но не симметрическая.
9. Квадратичный метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Квадратичный метод сопряженных градиентов реализуется в системе MATLAB с помощью функции cgs:
-
cgs(A.B) — возвращает решение X СЛУ А*Х=В. А — квадратная матрица. Функция cgs начинает итерации от начальной оценки, по умолчанию представляющей собой вектор размера п, состоящий из нулей. Итерации производятся либо до сходимости метода, либо до появления ошибки, либо до достижения максимального числа итераций. Сходимость метода достигается, когда относительный остаток norm(B-A*X)/norm(B) меньше или равен погрешности метода (по умолчанию le-6). Функция cgs(...) имеет и ряд других форм записи, аналогичных описанным для функции bieg(...). Пример:
» cgs(A.B)
CGS converged at iteration 4 to a solution
with relative residual 4e-014
ans =
1.0000
2.0000
3.0000
4.0000
10. Метод минимизации обобщенной невязки
Метод минимизации обобщенной невязки
Итерационный метод минимизации обобщенной невязки также реализован в системе MATLAB. Для этого используется функция gmres:
-
gmres (А, В. restart) — возвращает решение X СЛУ А*Х=В. А —квадратная матрица. Функция gmres начинает итерации от начальной оценки, представляющей собой вектор размера и, состоящий из нулей. Итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций. Сходимость достигается, когда относительный остаток norm(B-A*X)/norm(B) меньше или равен заданной погрешности (по умолчанию 1е-6). Максимальное число итераций — минимум из n/restart и 10. Функция gmres (...) имеет и ряд других форм записи, аналогичных описанным для функции bieg(...). Пример:
» gmres(A.B)
GMRES(4) converged at Iteration 1(4) to a solution with relative residual le-016
ans =
1.0000
2.0000
3.0000
4.0000
11. Квазиминимизация невязки - функция qmr
Квазиминимизация невязки — функция qmr
Метод решения СЛУ с квазиминимизацией невязки реализует функция qmr:
-
qmr (А, В) — возвращает решение X СЛУ А*Х=Ь. Матрица А должна быть квадратной. Функция qmr начинает итерации от начальной оценки, представляющей собой вектор длиной п, состоящий из нулей. Итерации производятся либо до сходимости метода, либо до появления ошибки, либо до достижения максимального числа итераций. Максимальное число итераций — минимум из п и 20. Функция qmr(...) имеет и ряд других форм записи, аналогичных описанным для функции bi eg (...). Пример:
» qmr(A.B)
QMR converged at iteration 4 to a solution
with relative residual 1.1e-014
ans =
1.0000
2.0000
3 .0000
4.0000
12. Вычисление нулей функции одной переменной
Вычисление нулей функции одной переменной
Ряд функций системы MATLAB предназначен для работы с функциями. По аналогии с дескрипторами графических объектов могут использоваться объекты класса дескрипторов функций, задаваемых с помощью символа @, например: » fe=@exp.
Примечание
Подфункциями понимаются как встроенные функции, например sin(x) или ехр(х),так и функции пользователя, например f(x), задаваемые как т-файлы-функции.
Численные значения таких функций, заданных дескрипторами, вычисляются с помощью функции feval:
» feval(fe.1.0)
ans =
2.7183
Для совместимости с прежними версиями можно записывать функции в символьном виде в апострофах, использование функции eval для их вычисления может быть более наглядно, не нужно создавать m-файл, но в учебном курсе мы будем стараться использовать новую нотацию, с использованием дескрипторов функций и feval, так как при этом программирование становится «более объектно-ориентированным», повышается скорость, точность и надежность численных методов. Поэтому, хотя везде в нижеследующем тексте вместо @fun можно подставить и символьное значение функции в апострофах, мы будем использовать нотацию @fun в дидактических целях. Все же иногда в интерактивном режиме можно использовать старую запись, чтобы не создавать m-файл функции.
Довольно часто возникает задача решения нелинейного уравнения вида f(x) = О или/, (г) =/ 2 (дг). Последнее, однако, можно свести к виду f(x) =f 1 (х) - f 2 (х) = 0. Таким образом, данная задача сводится к нахождению значений аргумента х функции f(x) одной переменной, при котором значение функции равно нулю. Соответствующая функция MATLAB, решающая данную задачу, приведена ниже:
-
fzero(@fun,x) — возвращает уточненное значение х, при котором достигается нуль функции fun, представленной в символьном виде, при начальном значении аргумента х. Возвращенное значение близко к точке, где функция меняет знак, или равно NaN, если такая точка не найдена;
-
fzero(@fun,[xl x2]) — возвращает значение х, при котором fun(x)=0 с заданием интервала поиска с помощью вектора x=[xl х2], такого, что знак fun(x(D) отличается от знака fun(x(2)). Если это не так, выдается сообщение об ошибке. Вызов функции fzero с интервалом гарантирует, что fzero возвратит значение, близкое к точке, где fun изменяет знак;
-
fzero(@fun,x.tol) — возвращает результат с заданной погрешностью tol;
-
fzero(@fun,x.tol .trace) — выдает на экран информацию о каждой итерации;
-
fzero(@fun,х.tol .trace,Р1.Р2,...) — предусматривает дополнительные аргументы, передаваемые в функцию fun(x.Pl,P2,...). При задании пустой матрицы для tol или trace используются значения по умолчанию. Пример:
fzero(fun,x,[ ],[ ],Р1).
Для функции fzero ноль рассматривается как точка, где график функции fun пересекает ось х, а не касается ее. В зависимости от формы задания функции fzero реализуются следующие хорошо известные численные методы поиска нуля функции: деления отрезка пополам, секущей и обратной квадратичной интерполяции. Приведенный ниже пример показывает приближенное вычисление р/2 из решения уравнения cos(x)=0 с представлением косинуса дескриптором:
» х= fzero(@cos.[1 3])
x =
1.5708
В более сложных случаях настоятельно рекомендуется строить график функции f(x) для приближенного определения корней и интервалов, в пределах которых они находятся. Ниже дан пример такого рода (следующий листинг представляет собой содержимое m-файла fun1.m):
%Функция, корни которой ищутся
function f=funl(x)
f=0.25*x+sin(x)-1;
» х=0:0.1:10;
» plot(x,funl(x));grid on;
Из рисунка нетрудно заметить, что значения корней заключены в интервалах [0.5 1], [2 3] и [5 6]. Найдем их, используя функцию fzero:
» xl=fzero(@funl.[0.5 1])
xl =
0.8905
» x2=fzero(@funl.[2 3])
x2 =
2.8500
» x3=fzero(@funl,[5.6])
x3 =
5.8128
» x3=fzero(@funl,5,0.001)
x3 =
5.8111
Обратите внимание на то, что корень хЗ найден двумя способами и что его значения в третьем знаке после десятичной точки отличаются в пределах заданной погрешности tol =0.001. К сожалению, сразу найти все корни функция fzero не в состоянии. Решим эту же систему при помощи функции f sol ve из пакета Optimization Toolbox, которая решает систему нелинейных уравнений вида f(x)=0 методом наименьших квадратов, ищет не только точки пересечения, но и точки касания, f solve имеет почти те же параметры (дополнительный параметр — задание якобиана) и почти ту же запись, что и функция lsqnonneg, подробно рассмотренная ранее. Пример:
»fsolve(@funl,0:10 )
ans =
Columns 1 through 7
0.8905 0.8905 2.8500 2.8500 2.8500 5.8128 5.8128
Columns 8 through 11
5.8128 2.8500 2.8500 10.7429
Для решения систем нелинейных уравнений следует также использовать функцию solve из пакета Symbolic Math Toolbox. Эта функция способна выдавать результат в символьной форме, а если такого нет, то она позволяет получить решение в численном виде. Пример:
» solve('0.25*x + sin(x) -1) [ Пакеты расширения Symbolic Math ToolBox и Extended Symbolic Math Toolbox MATLAB 6.0 используют ядро Maple V Release 5 [30-35] и являются поэтому исключением: они пока не поддерживают новую нотацию с использованием дескрипторов функций. — Примеч. ред. ]
ans =
.89048708074438001001103173059554
13. Минимизация функции одной переменной
Минимизация функции одной переменной
Еще одна важная задача численных методов — поиск минимума функции f(x) в некотором интервале изменения х — от х 1 до х 2 . Если нужно найти максимум такой функции, то достаточно поставить знак «минус» перед функцией. Для решения этой задачи используется следующая функция:
[X.fval.exitflag,output] = fminbnd(@fun.x1,x2.options, p1,p2,...)
-
fminbnd(@fun,xl,x2) — возвращает значение х, которое является локальным минимумом функции fun(x) на интервале xl<x<x2;
-
fminbnd(@fun,xl,x2.options) — сходна с описанной выше формой функции, но использует параметры to!X, maxfuneval, maxiter, display из вектора options, предварительно установленные при помощи команды optimset (смотрите описание lsqnonneg);
-
fminbnd(@fun,xl.x2,options.P1.P2...) — сходна с описанной выше, но передает в целевую функцию дополнительные аргументы: Р1, Р2..... Если требуется использовать параметры вычислений по умолчанию, то вместо options перед P1, Р2 необходимо ввести [ ] (пустой массив);
-
[x.fval] = fminbnd(...) — дополнительно возвращает значение целевой функции fval в точке минимума;
-
[x.fval .exitflag] = fminbndL.) —дополнительно возвращает параметр exitflag, равный 1, если функция сошлась с использованием options.tolX, и 0, если достигнуто максимальное число итераций options.maxiter.
В этих представлениях используются следующие обозначения: xl. х2 — интервал, на котором ищется минимум функции; Р1.Р2... — дополнительные, помимо х, передаваемые в функцию аргументы; fun — строка, содержащая название функции, которая будет минимизирована; options — вектор параметров вычислений. В зависимости от формы задания функции fminbnd вычисление минимума выполняется известными методами золотого сечения или параболической интерполяции. Пример:
» options=optimset('tolX',1.е-10):
[x]=fminbnd(@cos.3,4,options)
х =
3.1416
14. Минимизация функции нескольких переменных
Минимизация функции нескольких переменных
Значительно сложнее задача минимизации функций нескольких переменных f(х 1 ,...). При этом значения переменных представляются вектором х, причем начальные значения задаются вектором х 0 Для минимизации функций ряда переменных MATLAB обычно использует разновидности симплекс-метода Нелдера-Мида.
Этот метод является одним из лучших прямых методов минимизации функций ряда переменных, не требующим вычисления градиента или производных функции. Он сводится к построению симплекса в n-мерном пространстве, заданного n+1 вершиной. В двумерном пространстве симплекс является треугольником, а в трехмерном — пирамидой. На каждом шаге итераций выбирается новая точка решения внутри или вблизи симплекса. Она сравнивается с одной из вершин симплекса. Ближайшая к этой точке вершина симплекса обычно заменяется этой точкой. Таким образом, симплекс перестраивается и обычно позволяет найти новое, более точное положение точки решения. Решение повторяется, пока размеры симплекса по всем переменным не станут меньше заданной погрешности решения.
Реализующая симплекс-методы Нелдера-Мида функция записывается в виде:
-
fminsearch(@fun,xO) — возвращает вектор х, который является локальным минимумом функции fun(x) вблизи хО.хО может быть скаляром, вектором (отрезком) при минимизации функции одной переменной или матрицей (для функции нескольких переменных);
-
fminsearch(@fun,xO,options) — аналогична описанной выше функции, но использует вектор параметров options точно так же, как функция fminbnd;
-
fminsearch(@fun,xO,options.P1.P2,...) — сходна с описанной выше функцией, но передает в минимизируемую функцию нескольких переменных fun(x.P1,P2....) ее дополнительные аргументы Р1. Р2,.... Если требуется использовать параметры вычислений по умолчанию, то вместо options перед Р1, Р2 необходимо ввести [ ].;
-
[x.fval] = fminsearchC...) — дополнительно возвращает значение целевой функции fval в точке минимума;
-
[x.fval .exitflag] = fminsearchC...) —дополнительно возвращает параметр exitflag, положительный, если процесс итераций сходится с использованием options. tol X, отрицательный, если итерационный процесс не сходится к полученному решению х, и 0, если превышено максимальное число итераций options. maxi ten;
-
[х. fval .exitflag.output] - fminsearch(...) возвращает структуру (запись) output,
-
output.algorithm — использованный алгоритм;
-
output. funcCount — число оценок целевой функции;
-
output.Iterations — число проведенных итераций.
Классическим примером применения функции fminsearch является поиск минимума тестовой функции Розенброка, точка минимума которой находится в «овраге» с «плоским дном»: rb(x 1 ,x 2 ,а) = 100*(x 2 - x 1 ) 2 + (а - x 1 ) 2 .
Минимальное значение этой функции равно нулю и достигается в точке [ а а 2 ]. В качестве примера уточним значения x 1 и х 2 в точке [-1.2 1]. Зададим функцию (в файле rb.m):
% Тестовая функция Розенброка
function f=rb(x.a)
if nargin<2 a=l: end
f=100*(x(2)-x(i^2) ^ 2+(a-x(l)^2:
Теперь решим поставленную задачу:
»options=optimset( 'tolX',1.e-6):
[xmin. opt, rosexflag, rosout]=fminsearch(@rb.[-1.2 1],options)
xmin =
1.0000 1.0000
opt =
4.1940e-014
rosexflag =
1 rosout =
iterations: 101
funcCount: 189
algorithm: 'Nelder-Mead simplex direct search' .
Для лучшего понимания сути минимизации функции нескольких переменных рекомендуется просмотреть пример минимизации этой функции, имеющийся в библиотеке демонстрационных примеров Demos.
Для минимизации функций нескольких переменных можно использовать также функцию MATLAB fminunc и функцию Isqnonlin из пакета Optimization Toolbox. Первая из них позволяет использовать предварительно заданные командой optimset порог сходимости для значения целевой функции, вектор градиентов opt ions, grad-obj, матрицу Гесса, функцию умножения матрицы Гесса или график разреженности матрицы Гесса целевой функции. Isqnonl in реализует метод наименьших квадратов и, как правило, дает наименьшее число итераций при минимизации. Ограничимся приведением примеров их применения для минимизации функции Розенброка:
» options=optimset('tolX',le-6.'To!Fun'.le-6);
» [xmin. opt. exflag. out, grad, hessian ]=fminunc(@rb,[-1.2 1].options)
Warning: Gradient must be provided for trust-region method;
using line-search method instead.
> In C:\MATLABR12\toolbox\optim\fminunc.m at line 211
Optimization terminated successfully:
Current search direction is a descent direction, and magnitude of directional derivative in search direction less than 2*options.TolFun
xmin =
1.0000 1.0000
opt =
1.9116e-011
exflag=
1
out =
iterations: 26
funcCount: 162
stepsize: 1.2992
firstorderopt: 5.0020e-004
algorithm: 'medium-scale: Quasi-Newton line search'
grad=
l.Oe-003 *
-0.5002
-0.1888
hessian =
820.4028 -409.5496
-409.5496 204.7720
firstorderopt - мера оптимальности для первой нормы градиента целевой функции в найденной точке минимума;
»options=optimset('tolX' Gе-6. 'maxFunEvals' .162):
» [xmin. opt]=lsqnonlin(@rb,[-1.2 1].[0 le-6].[0 le-6],options)
Warning: Large-scale method requires at least as many equations as variables:
switching to line-search method instead. Upper and lower bounds will be ignored.
> In C:\MATLABR12\toolbox\optim\private\lsqncommon.m at line 155
In C:\MATLABR12\toolbox\optim\lsqnonlin.m at line 121
Maximum number of function evaluations exceeded Increase
OPTIONS.maxFunEvals
xmin =
0.6120 0.3715
opt =
0.1446
15. Аппроксимация производных
Аппроксимация производных
Для выполнения аппроксимации Лапласиана в MATLAB используется следующая функция:
-
del 2(11) — возвращает матрицу L дискретной аппроксимации дифференциального оператора Лапласа, примененного к функции U:
![]()
Матрица L имеет тот же размер, что и матрица U, и каждый ее элемент равен разности элемента массива U и среднего значения четырех его соседних элементов (для узлов сетки во внутренней области). Для вычислений используется пятиточечная формула аппроксимации Лапласиана.
Другие формы этой функции также возвращают матрицу L, но допускают дополнительные установки:
-
L = del2(U,h) — использует шаг h для установки расстояния между точками в каждом направлении (h — скалярная величина). По умолчанию h=1;
-
L = de!2(U,hx,hy) — использует hx и hy для точного определения расстояния между точками. Если hx — скалярная величина, то задается расстояние между точками в направлении оси х, если hx — вектор, то он должен иметь размер. равный числу столбцов- матрицы U , и точно определять координаты точек по оси х. Аналогично если hy — скалярная величина, то задается расстояние между точками в направлении оси у, если hy — вектор, то он должен иметь размер. равный числу строк матрицы U, и точно определять координаты точек по оси у:
-
L = del2(U,hx.hy,hz....) — если U является многомерным массивом, то расстояния задаются с помощью параметров hx, hy, hz,.... Пример:
» [х.у]= meshgrid(-5:5.-4:4);
» U =x.*x+y.*y
U =
|
41 |
32 |
25 |
20 |
17 |
16 |
17 |
20 |
25 |
32 |
41 |
|
|
34 |
25 |
18 |
13 |
10 |
9 |
10 |
13 |
18 |
25 |
34 |
|
|
29 |
20 |
13 |
8 |
5 |
4 |
5 |
8 |
13 |
20 |
29 |
|
|
26 |
17 |
10 |
5 |
2 |
1 |
2 |
5 |
10 |
17 |
26 |
|
|
25 |
16 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
16 |
25 |
|
|
26 |
17 |
10 |
5 |
2 |
1 |
2 |
5 |
10 |
17 |
26 |
|
|
29 |
20 |
13 |
8 |
5 |
4 |
5 |
8 |
13 |
20 |
29 |
|
|
34 41 |
25 32 |
18 25 |
13 20 |
10 17 |
9 16 |
10 17 |
13 20 |
18 25 |
25 32 |
34 41 |
|
» V=del2(U)
V =
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 1 |
1 1 1 |
1 |
1 |
1 |
|
» subplot(1,2,1)
» surfl(U)
» subplot(1,2,2)
» surfl(V)
На рис. 16.1 представлены графики поверхностей U и V.
Рис. 16.1. Графики функций U и V
3.gif
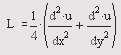
4a.gif
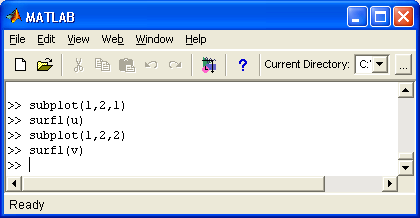
4b.gif
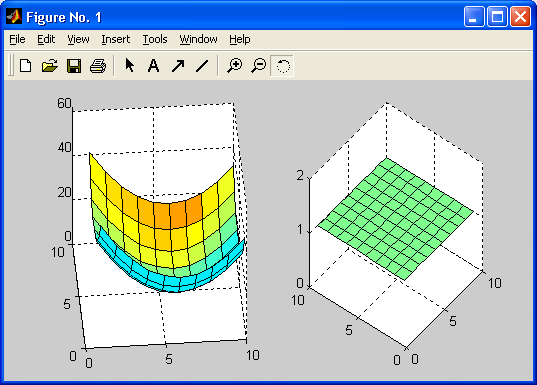
16. Аппроксимация производных конечными разностями
Апроксимация производных конечными разностями
-
diff(X) — возвращает конечные разности смежных элементов массива X. Если X — вектор, то diff(X) возвращает вектор разностей соседних элементов [Х(2)-Х(1) Х(3)-Х(2) ... X(n)-X(n-D], у которого количество элементов на единицу меньше, чем у исходного вектора X. Если X — матрица, то diff(X) возвращает матрицу разностей столбцов: [X(2:m, :)-X(l:m-l. :)];
-
Y = diff(X.n.dim) — возвращает конечные разности для матрицы X по строкам или по столбцам в зависимости от значения параметра dim. Если порядок п равен величине dim или превышает ее, то diff возвращает пустой массив.
Используя функцию diff, можно строить графики производных заданной функции. Пример этого показан ниже:
» Х=0:0.05:10;
» S=sin(X);
» D=diff(S):
» plot(D/0.05)
Для получения приближенных численных значений производной от функции sin(.r) вектор конечно-разностных значений D поделен на шаг точек по х. Как и следовало ожидать, полученный график очень близок к графику функции косинуса (рис. 16.2). Обратите внимание, что по оси х отложены номера элемента* вектора X, а не истинные значения х.
Пакет расширения Symbolic Math Toolbox позволяет выполнять дифференциро вание функций в аналитическом виде, т. е. точно. Это, однако, не всегда нужно
Рис. 16.2. Приближенный график производной от функции sin(x)
5a.gif
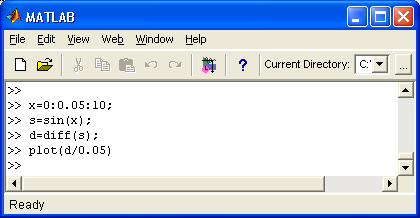
5b.gif

17. Вычисление градиента функции
Вычисление градиента функции
Вычисление конечно-разностным методом градиента функций реализуется следующей функцией:
-
FX = gradient(F) — возвращает градиент функции одной переменной, заданной вектором ее значений F. FX соответствует конечным разностям в направлении х,
-
[FX.FY] = gradient(F) — возвращает градиент функции F(X,Y) двух переменных, заданной матрицей F, в виде массивов FX и FY. Массив FX соответствует конечным разностям в направлении х (столбцов). Массив FY соответствует конечным разностям в направлении у (строк);
-
[FX.FY.FZ,...] = gradient(F) — возвращает ряд компонентов градиента функции нескольких переменных, заданной в виде многомерного массива F;
-
[...] = gradient(F.h) — использует шаг h для установки расстояния между точками в каждом направлении (h — скалярная величина). По умолчанию h=l;
-
[...] = gradient(F.hi,h2,...) — если F является многомерным массивом, то расстояния задаются с помощью параметров h1, h2, h3,....
Пример:
» F=[l 35795678]
F =
135795678
» FX = gradient(F)
FX =
Columns 1 through 7
2.0000 2.0000 2.0000 2.0000 -1.0000-1.50001.0000
Columns 8 through 9
1.0000 1.0000
» F=[l 2 3 6 7 8:1 4 5 7 9 3;5 9 5 2 5 7]
F =
123678
145793
595257
» [FX.FY] = gradient(F)
FX =
1.0000 1.0000 2.0000 2.0000 1.0000 1.0000
.3.0000 2.0000 1.5000 2.0000 -2.0000 -6.0000
4.0000 0 -3.50000 2.5000 2.0000
FY =
0 2.0000 2.0000 1.0000 2.0000-5.0000
2.0000 3.5000 1.0000 -2.0000-1.0000-0.5000
4.0000 5.0000 0 -5.0000-4.0000 4.0000
Функция gradient часто используется для построения графиков полей градиентов.
18. Численное интегрирование
Численное интегрирование
Численное интегрирование традиционно является одной из важнейших сфер применения математического аппарата. В данном разделе приводятся функции для численного интегрирования различными методами. Численное интегрирование заключается в приближенном вычислении определенного интеграла вида
одним из многочисленных численных методов, для вычисления неопределенного интеграла по рекурсивному алгоритму усредняются значения b=a+dn, где d — предельно малая величина.
6.gif
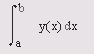
19. Метод трапеций
Метод трапеций
Приведенные ниже функции выполняют численное интегрирование методом трапеций и методом трапеций с накоплением.
-
trapz(Y) — возвращает определенный интеграл, используя интегрирование методом трапеций с единичным шагом между отсчетами. Если Y — вектор, то trapz(Y) возвращает интеграл элементов вектора Y, если Y — матрица, то trapz(Y) возвращает вектор-строку, содержащую интегралы каждого столбца этой матрицы;
-
trapz(X.Y) — возвращает интеграл от функции Y по переменной X, используя метод трапеций (пределы интегрирования в этом случае задаются начальным и конечным элементами вектора X);
-
trapz(...,dim) — возвращает интеграл по строкам или по столбцам для входной матрицы в зависимости от значения переменной dim. Примеры:
»Y=[1.2.3.4]
Y =
1 2 3 4
» trapz(y)
ans =
7.5000
» X=0:pi/70:pi/2;
» Y=cos(X);
» Z = trapz(Y)
Z =
22.2780
-
cumtrapz(Y) — возвращает численное значение определенного интеграла для функции, заданной ординатами в векторе или матрице Y с шагом интегрирования, равным единице (интегрирование методом трапеций с накоплением). В случае когда шаг отличен от единицы, но постоянен, вычисленный интеграл достаточно умножить на величину шага. Для векторов эта функция возвращает вектор, содержащий результат интегрирования с накоплением элементов вектора Y. Для матриц — возвращает матрицу того же размера, что и Y, содержащую результаты интегрирования с накоплением для каждого столбца матрицы Y;
-
cumtrapz(X, Y) — выполняет интегрирование с накоплением от Y по переменной X, используя метод трапеций. X и Y должны быть векторами одной и той же длины или X должен быть вектором-столбцом, a Y — матрицей;
-
cumtrapz(...,dim) — выполняет интегрирование с накоплением элементов по размерности, точно определенной скаляром dim. Длина вектора X должна быть равна size(Y.dim). Примеры:
» cumtrapz(y)
ans=
0 1.5000 4.0000 7.5000
» Y=magic(4)
Y =
162 3 13
5 11 10 8
97 6 12
4 14 15 1
» Z= cumtrapz(Y.l)
Z =
0 0 0 0
10.5000 6.5000 6.5000 10.5000
17.5000 15.500014.500020.5000
24.0000 26.000025.000027.0000
20. Численное интегрирование методом квадратур
Численное интегрирование методом квадратур
Приведенные ниже функции осуществляют интегрирование и двойное интегрирование, используя квадратурную формулу Симпсона или метод Гаусса-Лобатто. Квадратура — численный метод нахождения площади под графиком функции/(т), т. е. вычисление определенного интеграла вида
В приведенных ниже формулах подынтегральное выражение fun обычно задается в форме дескриптора функции, поэтому с дидактическими целями используем нотацию @fun.
Функции quad и quadl используют два различных алгоритма квадратуры для вычисления определенного интеграла. Функция quad выполняет интегрирование по методу низкого порядка, используя рекурсивное правило Симпсона [4, 40]. Но она может быть более эффективной при негладких подынтегральных функциях или при низкой требуемой точности вычислений. Алгоритм quad в MATLAB 6 изменен по сравнению с предшествовавшими версиями, точность по умолчанию по сравнению с версиями 5.3х повышена в 1000 раз (с 10- 3 до 10- 6 ). Новая функция quadl (квадратура Лобатто) использует адаптивное правило квадратуры Гаусса— Лобатто очень высокого порядка. Устаревшая функция quads выполняла интегрирование, используя квадратурные формулы Ньютона—Котеса 8-го порядка [40]. Достижимая точность интегрирования гладких функций в MATLAB 6 поэтому также значительно выше, чем в предшествующих версиях.
-
quad(@fun,a.b) — возвращает численное значение определенного интеграла от заданной функции @fun на отрезке [а Ь]. Используется значительно усовершенствованный в MATLAB 6 адаптивный метод Симпсона;
-
quad(@fun,a.b.tol) — возвращает численное значение определенного интеграла с заданной относительной погрешностью tol. По умолчанию to1=l.e-6. Можно также использовать вектор, состоящий из двух элементов tol =[rel_tol abs_tol], чтобы точно определить комбинацию относительной и абсолютной погрешности;
-
quad(@fun,a.b,tol .trace) — возвращает численное значение определенного интеграла и при значении trace, не равном нулю, строит график, показывающий ход вычисления интеграла;
-
quad(@fun,a,b.tol,trace,PI,P2,...) — возвращает численное значение определенного интеграла по хот подынтегральной функции fun, использует дополнительные аргументы P1, P2,..., которые напрямую передаются в подынтегральную функцию: G=fun(X.Pl,P2,...). Примеры:
» quad('(exp(x)-l)',0,1,1e-5)
ans =
0.7183
» q = quad(@exp,0,2,1e-4)
q =
6.3891
» q = quad(@sin.0,pi,le-3)
q = 2.0000
-
dblquad(@fun,inmin,inmax.outmin,outmax) — вычисляет и возвращает значение двойного интеграла для подынтегральной функции fun (Inner, outer), по умолчанию используя квадратурную функцию quad. Inner — внутренняя переменная, изменяющаяся на закрытом интервале от inmin до inmax, a outer — внешняя переменная, изменяющаяся на закрытом интервале от outmin до outmax. Первый аргумент @fun — строка, описывающая подынтегральную функцию. Этс может быть либо дескриптор функции, либо объект inline (в последнем случае символ «@» в ее записи отсутствует). Обычная запись в апострофах тепер недопустима. Эта функция должна быть функцией двух переменных вид. fout=fun(inner.outer). Функция должна брать вектор inner и скаляр outer возвращать вектор fout, который является функцией, вычисленной в outer и каждом значении inner [ Функция inime('expr', 'argl',...'argn') так же создает объект, но без дескриптора, 'ехрг' — выражеши Строки 'argx' —входные аргументы. При их отсутствии по умолчанию подставляется х. Если вмест 'arg' — скаляр, то он означает количество дополнительных переменных Р. Примеры запис; g = inline(exp); g - inline('t A 2'); g = inline('sin(2*pi*f + theta)'); g = inline('sin(2*pi*f + theta)', : 'theta'); g - inline('x A Pl+P2', 2). - Примеч. ред. ];
-
dblquad(@fun,inmin.inmax.outmin,oiitmax,tol .trace) — передает в функцию dblquad параметры tol и trace. Смотрите справку по функции quad для получения информации о параметрах to! и trace;
-
dblquad(@fun,inmin,inmax,outmin,outmax.tol .trace,order) — передает параметры tol и trace для функции quad или quadl в зависимости от значения строки order. Допустимые значения для параметра order — @quad , @quadl или имя любого определенного пользователем квадратурного метода с таким же вызовом и такими же возвращаемыми параметрами, как у функций quad и quad!. (Например, при проверке старых программ можно использовать @quad8 для большей совместимости с прежними версиями MATLAB). По умолчанию (без параметра order) вызывается @quad. поскольку подинтегральные функции могут быть негладкими.
Пример: пусть m-файл integl.m описывает функцию 2*y*sin(x)+x/2*cos(y), тогда вычислить двойной интеграл от той функции можно следующим образом:
» result = dblquad(@integl,pi,2*pi,0.2*pi)
result =
78.9574
7.gif
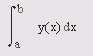
21. Работа с полиномами
Работа с полиномами
Полиномы (у нас их принято называть также степенными многочленами) — широко известный объект математических вычислений и обработки данных. Обычно полином записывается в виде
р(х) = а п х^n + x п-1 x^n -1+ ... + а 2 x^2 + а 1 ^х + а 0 ,
и так обычно принято в MATLAB для п, отрицательных по умолчанию, хотя и возможны иные формы записи, например
р(х) = a 1 x^n + а 2 x^n-1 + ... + а п х + а п+1
Последняя запись обычно принята в MATLAB для n, по умолчанию положительных.
Широкое применение полиномов отчасти обусловлено большими возможностями полиномов в представлении данных, а также их простотой и единообразием вычислений. В этом разделе описаны основные функции для работы с полиномами. При этом полиномы обычно задаются векторами их коэффициентов.
22. Умножение и деление полиномов
Умножение и деление полиномов
Ниже приведены функции, осуществляющие умножение и деление полиномов, или, что то же самое, свертку двух входных векторов, в которых находятся коэффициенты полиномов, и операцию, обратную свертке.
-
w = conv(u.v) — возвращает свертку векторов и и v. Алгебраически свертка — то же самое, что и произведение полиномов, чьи коэффициенты — элементы векторов и и v. Если длина вектора и равна т, а длина вектора v — п, то вектор w имеет длину т+п-1, а его k-й элемент вычисляется по следующей формуле
Пример:
» f=[2.3.5.6];d=[7,8,3]:r=conv(f,d)
r =
14 37 65 91 63 18
-
[q,r] = deconv(v.u) —возвращает результат деления полинома v на полином и. Вектор q представляет собой частное от деления, а г — остаток от деления, так что выполняется соотношение v=conv(u,q)+r.
Пример:
» t=[14,37.65.91,63,18]:r=[7.8.3];[w.e]=deconv(t.r)
w =
2.0000 3.0000 5.0000 6.0000
е =
1.0е-013
0 0 0.1421 -0.1421-0.2132-0.1066
8.gif
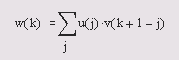
23. Вычисление полиномов
Вычисление полиномов
В этом разделе приведены функции вычисления коэффициентов характеристического полинома, значения полинома в точке и матричного полинома.
-
poly(A) — для квадратной матрицы А размера пхп возвращает вектор-строку размером n+1, элементы которой являются коэффициентами характеристического полинома det(A-sI), где I — единичная матрица, as — оператор Лапласа. Коэффициенты упорядочены по убыванию степеней. Если вектор состоит из п+1 компонентов, то ему соответствует полином вида c 1 s^n+...+c n s+c n+1 ;
-
poly (г) — для вектора г возвращает вектор-строку р с элементами, представляющими собой коэффициенты полинома, корнями которого являются элементы вектора г. Функция roots(p) является обратной, ее результаты, умноженные на целое число, дают poly (r ).
А =
2 3 6
3 8 6
1 7 4
» d=poly(A)
d =
1.0000 -14.0000 -1.0000-40.0000
» А=[3,6.8:12.23.5:11.12.32]
А =
3 6 8
1223 5
1112 32
» poly(A)
ans =
1.0000 -58.0000 681.0000 818.0000
Приведенная ниже функция вычисляет корни (в том числе комплексные) для полинома вида
![]()
-
roots (с) — возвращает вектор-столбец, чьи элементы являются корнями полинома с.
Вектор-строка с содержит коэффициенты полинома, упорядоченные по убыванию степеней. Если с имеет n+1 компонентов, то полином, представленный этим вектором, имеет вид . Пример:
» x=[7.45.12.23];d=roots(x)
d =
-6.2382
-0.0952+0.7195i
-0.0952 -0.7195i
А=[-6.2382 -0.0952+0.71951 -0.0952 -0.71951]:
B=Poly (А)
В=[1.0000 6.4286 1.7145 3.2859]
В*7
ans =
7.0000 45.000212.001523.0013
С погрешностью округления получили тот же вектор.
-
polyval (p,x) — возвращает значения полинома р, вычисленные в точках, заданных в массиве х. Полином р — вектор, элементы которого являются коэффициентами полинома в порядке уменьшения степеней, х может быть матрицей или вектором. В любом случае функция polyval вычисляет значения полинома р для каждого элемента х;
-
[у.delta] = polyval (p. x.S) или [у,delta] = polyval (p.x.S.mu)—использует структуру S, возвращенную функцией polyfit, и данные о среднем значении (mu(l)) и стандартном отклонении (mu(2)) генеральной совокупности для оценки пр-грешности аппроксимации (y+delta).
Пример:
» р=[3,0.4.3]; d=polyval(p,[2,6])
d =
35 675
-
polyvalm(p.X) — вычисляет значения полинома для матрицы. Это эквивалентно подстановке матрицы X в полином р. Полином р — вектор, чьи элементы являются коэффициентами полинома в порядке уменьшения степеней, а X — квадратная матрица.
Пример:
|
|
|
|
|
|
|
|
|
» D=pascal(5) |
|
|||
|
|
D = |
|
|
|
|
|
|
1 1 |
1 |
1 |
1 |
|
|
|
1 2 |
3 |
4 |
5 |
|
|
|
1 3 |
6 |
10 |
15 |
|
|
|
1 4 |
10 |
20 |
35 |
|
|
|
1 5 |
15 |
35 |
70 |
|
|
|
|
|
|
|
|
f=poly(d)
f =
1.0000 -99.0000 626.0000 -626.0000 99.0000-1.0000
» polyvalm(f.D)
ans =
l.0e-006*
-0.0003 -0.0011-0.0038-0.0059-0.0162
-0.0012 -0.0048-0.0163-0.0253-0.0692
-0.0034 -0.0131 -0.0447 -0.0696 -0.1897
-0.0076 -0.0288-0.0983-0.1529-0.4169
-0.0145-0.0551-0.1883-0.2929-0.7984
Данный пример иллюстрирует также погрешности численных методов, поскольку точное решение дает нулевую матрицу.
9.gif

24. Вычисление производной полинома
Вычисление производной полинома
Ниже приведена функция, возвращающая производную полинома р:
-
polyder(p) — возвращает производную полинома р;
-
polyder(a.b) — возвращает производную от произведения полиномов а и b;
-
[q,d] = polyder(b.a) — возвращает числитель q и знаменатель d производной от отношения полиномов b/а.
Примеры:
» a=[3.5.8]:b=[5,3.8]:dp=polyder(a)
dp =
6 5
» dt=polyder(a,b)
dt =
60102 158 64 » [q.p]=polyder(b.a)
q =
1632 -16
p =
9 30 73 80 64
25. Решение полиномиальных матричных уравнений
Решение полиномиальных матричных уравнений
Приведенная ниже функция вычисляет собственные значения матричного полинома.
- [Х.е] = polyeig(AO,Al,...Ap) — решает задачу собственных значений для матричного полинома степени р вида:
где степень полинома р — целое неотрицательное число, а А 0 , А 1 ,..., А p — входные матрицы порядка п. Выходная матрица X размера nхnр содержит собственные векторы в столбцах. Вектор е размером пр содержит собственные значения.
Пример:
» А=[1:4:5:8:9:12:13:16]
А =
|
|
|
|
|
|
|
|
1 2 |
3 4 |
|
|
|
|
5 6 |
7 8 |
|
|
|
|
9 10 |
11 12 |
|
|
|
|
1314 |
15 16 |
|
|
|
|
» В=[4:7 |
;2:5;10:13;23:26] |
|
|
|
|
3 - |
|
|
|
|
|
4 5 |
6 7 |
|
|
|
|
2 3 |
4 5 |
|
|
|
|
1011 |
12 13 |
|
|
|
|
2324 |
25 26 |
|
|
|
|
» [F.a]= |
polyeig(A.B) |
|
|
|
|
F = |
|
|
|
|
|
0.4373 |
0.0689 |
-0.5426 |
-0.7594 |
|
|
-0.3372 |
-0.4969 |
0.6675 |
-0.1314 |
|
|
-0.6375 |
0.7870 |
0.2927 |
-0.1314 |
|
|
0.5374 |
-0.3591 |
- 0.4176 |
0.3771 |
|
|
a = |
|
|
|
|
|
4.4048 |
|
|
|
|
|
0.4425 |
|
|
|
|
|
-0.3229 |
|
|
|
|
|
-1.0000 |
|
|
|
|
|
|
|
||
11.gif

26. Разложение на простые дроби
Разложение на простые дроби
Для отношения полиномов b и а используются следующие функции:
- [r,p,k] = res I due (b, a) — возвращает вычеты, полюса и многочлен целой части отношения двух полиномов b(s) и a(s) в виде
-
[b.a] = residue(r.p.k) — выполняет обратную свертку суммы простых дробей (см. более подробное описание в справочной системе) в пару полиномов с коэффициентами в векторах b и а.
Пример:
» b=[4.3.1]:a=[1.3.7.1]:[r.p,k]=residue(b,a)
r=
1.9484 + 0.80641
1.9484 - 0.80641
0.1033
Р =
-1.4239 + 2.13051
-1.4239 - 2.13051
-0.1523
k =
[ ]
» [bl,al]=residue(r,p,k)
b1=
4.0000 3.0000 1.0000
a1 =
1.0000 3.0000 7.0000 1.0000
12.gif

27. Решение обыкновенных дифференциальных уравнений
Решение обыкновенных дифференциальных уравнений
Анализ поведения многих систем и устройств в динамике, а также решение многих задач в теории колебаний и в поведении упругих: оболочек обычно базируются на решении систем обыкновенных дифференциальных уравнений (ОДУ). Их, как правило, представляют в виде системы из дифференциальных уравнений первого порядка в форме Коши:
с граничными условиями y(t 0 t end , p) = b, где t end , t 0 — начальные и конечные точки интервалов. Параметр t не обязательно означает время, хотя чаще всего решение дифференциальных уравнений ищется во временной области. Вектор b задает начальные и конечные условия.
Ниже коротко описаны численные методы решения обыкновенных дифференциальных уравнений (ОДУ) и некоторые вспомогательные функции, полезные для решения систем ОДУ. Дается представление о пакете расширения, решающем дифференциальные уравнения в частных производных.
13.gif

28. Решатели ОДУ
Решатели ОДУ
Для решения систем ОДУ в MATLAB реализованы различные методы. Их реализации названы решателями ОДУ.
Примечание
В этом разделе обобщенное название sol ver (решатель) означает один из возможных численных методов решения ОДУ: ode45, ode23, ode113, ode15s, ode23s, ode23t , ode23tb, bvp4c или pdepe.
Решатели реализуют следующие методы решения систем дифференциальных уравнений, причем для решения жестких систем уравнений рекомендуется использовать только специальные решатели ode 15s , ode23s, ode23t. ode23tb:
-
ode45 — одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты;
-
ode23 — одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. При умеренной жесткости системы ОДУ и низких требованиях к точности этот мето;. может дать выигрыш в скорости решения;
-
ode113 — многошаговый метод Адамса-Башворта-Мултона переменного порядка Это адаптивный метод, который может обеспечить высокую точность решения
-
ode23tb — неявный метод Рунге-Кутта в начале решения и метод, использующий формулы обратного дифференцирования 2-го порядка в последующем
Несмотря на сравнительно низкую точность, этот метод может оказаться более эффективным, чем ode15s;
-
ode15s — многошаговый метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного дифференцирования. Это адаптивный метод, его стоит применять, если решатель ode45 не обеспечивает решения;
-
ode23s — одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы дифференциальных уравнений;
-
ode23t — метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигналом;
-
bvp4c служит для проблемы граничных значений систем дифференциальных уравнений вида y '== f(t,y), F(y(a), y(b), p) = 0 (краевая задача);
-
pdepe нужен для решения систем параболических и эллиптических дифференциальных уравнений в частных производных, введен в ядро системы для поддержки новых графических функций Open GL, пакет расширения Partial Differential Equations Toolbox содержит более мощные средства.
Все решатели могут решать системы уравнений явного вида у' = F(£, y). Решатели ode15s и ode23t способны найти корни дифференциально-алгебраических уравнений M(t)y' = F(t, у},, где М называется матрицей массы. Решатели ode!5s, ode23s, ode23t и ode23tb могут решать уравнения неявного вида M(t,y) у' = F(t, у). И наконец, все решатели, за исключением ode23s, который требует постоянства матрицы массы, и bvp4c, могут находить корни матричного уравнения вида M(t, у) у' - F(t, у). ode23tb, ode23s служат для решения жестких дифференциальных уравнений . ode15s -жестких дифференциальных и дифференциально-алгебраических уравнений, ode23t -умеренно жестких дифференциальных и дифференциально-алгебраических уравнений.
29. Использование решателей систем ОДУ
Использование решателей систем ОДУ
В описанных далее функциях для решения систем дифференциальных уравнений приняты следующие обозначения и правила:
-
options — аргумент, создаваемый функцией odeset (еще одна функция — odeget или bvpget (только для bvp4c)— позволяет вывести параметры, установленные по умолчанию или с помощью функции odeset /bvpset);
-
tspan — вектор, определяющий интервал интегрирования [tO tfinal]. Для получения решений в конкретные моменты времени t0, tl,..., tfinal (расположенные в порядке уменьшения или увеличения) нужно использовать tspan = [t0 tl ... tfinal];
-
у0 — вектор начальных условий;
-
pi, р2,.„ — произвольные параметры, передаваемые в функцию F;
-
Т, Y — матрица решений Y, где каждая строка соответствует времени, возвращенном в векторе-столбце Т.
Перейдем к описанию функций для решения систем дифференциальных уравнений:
-
[T.Y] = solver(@F,tspan,у0) — где вместо solver подставляем имя конкретного решателя — интегрирует систему дифференциальных уравнений вида у'=F(t,y) на интервале tspan с начальными условиями у0. @F — дескриптор ODE-функции. Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце Т;
-
[T.Y] = solver(@F, tspan, yO. options) — дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Обычно используемые параметры включают допустимое значение относительной погрешности RelTol (по умолчанию le-З) и вектор допустимых значений абсолютной погрешности AbsTol (все компоненты по умолчанию равны 1е-6);
-
[T.Y] = solver(@F,tspan,yO,options,pl,p2...) — дает решение, подобное описанному выше, передавая дополнительные параметры pi, р2,... в m-файл F всякий раз, когда он вызывается. Используйте options=[], если никакие параметры не задаются;
-
[T.Y.TE.YE.IE] = solver(@F.tspan,yO,options) — в дополнение к описанному решению содержит свойства Events, установленные в структуре options ссылкой на функции событий. Когда эти функции событий от (t, у, равны нулю, производятся действия в зависимости от значения трех векторов value, isterminal, di rection (их величины можно установить в m-файлах функций событий). Для i-й функции событий value(i) —значение функции, isterminal (i) — прекратить интеграцию при достижении функцией нулевого значения, direction^) = 0, если все нули функции событий нужно вычислять (по умолчанию), +1 — только те нули, где функция событий увеличивается, -1 — только те нули, где функция событий уменьшается. Выходной аргумент ТЕ — вектор-столбец времен, в которые происходят события (events), строки YE являются соответствующими решениями, а индексы в векторе IE определяют, какая из i функций событий (event) равна нулю в момент времени, определенный ТЕ. Когда происходит вызов функции без выходных аргументов, по умолчанию вызывается выходная функция odeplot для построения вычисленного решения. В качестве альтернативы можно, например, установить свойство OutputFcn в значение ' odephas2' или 'odephas3' для построения двумерных или трехмерных фазовых плоскостей.
-
[T.X.Y] = sim(@model,tspan.-y0.options,ut.p1,р2..„) — использует модель SIMULINK, вызывая соответствующий решатель из нее. Пример:
[T.X.Y] - sim(@model....).
Параметры интегрирования (options) могут быть определены и в m-файле, и в командной строке с помощью команды odeset. Если параметр определен в обоих местах, определение в командной строке имеет приоритет.
Решатели используют в списке параметров различные параметры:
-
NormControl — управление ошибкой в зависимости от нормы вектора решения [on | {off}]. Установите 'on', чтобы norm(e) <= max(RelTol*norm(y), AbsTol). По умолчанию все решатели используют более жесткое управление по каждой из составляющих вектора решения;
-
RelTol — относительный порог отбора [положительный скаляр]. По умолчанию 1е-3 (0.1% точность) во всех решателях; оценка ошибки на каждом шаге интеграции e(i) <= max(RelTol*abs(y(i)), AbsTol(i));
-
AbsTol — абсолютная точность [положительный скаляр или вектор {1е-6}].Скаляр вводится для всех составляющих вектора решения, а вектор указывает на компоненты вектора решения. AbsTol по умолчанию 1е-6 во всех решателях;
-
Refine - фактор уточнения вывода [положительное целое число] — умножает число точек вывода на этот множитель. По умолчанию всегда равен 1, кроме ODE45, где он 4. Не применяется, если tspan > 2;
-
OutputFcn — дескриптор функция вывода [function] — имеет значение в том случае, если решатель вызывается без явного указания функции вывода, OutputFcn по умолчанию вызывает функцию odeplot. Эту установку можно поменять именно здесь;
-
OutputSel — индексы отбора [вектор целых чисел] Установите компоненты, которые поступают в OutputFcn. OutputSel по умолчанию выводит все компоненты;
-
Stats — установите статистику стоимости вычислений [on {off}];
-
Jacobian — функция матрицы Якоби [function constant matrix]. Установите это свойство на дескриптор функции FJac (если FJac(t, у) возвращает dF/dy) или на имя постоянной матрицы dF/dy;
-
Jpattern — график разреженности матрицы Якоби [имя разреженной матрицы]. Матрица S с S(i,j) = 1, если составляющая i F(t, у) зависит от составляющей j величины у, и 0 в противоположном случае;
-
Vectorized — векторизованная ODE-функция [on | {off}]. Устанавливается на 'on', если ODE-функция F F(t,[yl y2...]) возвращает вектор [F(t, yl) F(t, y2) ...];
-
Events — [function] — введите дескрипторы функций событий, содержащих собственно функцию в векторе value, и векторы isterminal и direction (см выше);
-
Mass — матрица массы [constant matrix function]. Для задач М*у' = f(t, у) установите имя постоянной матрицы. Для задач с переменной М введите дескриптор функции, описывающей матрицу массы;
-
MstateDependence — зависимость матрицы массы от у [none | {weak} | strong] — установите 'nоnе' для уравнений M(t)*y' = F(t, у). И слабая ('weak'), и сильная ('strong') зависимости означают M(t, у), но 'weak' приводит к неявным алгоритмам решения, использующим аппроксимации при решении алгебраических уравнений;
-
MassSingular — матрица массы М сингулярная [yes no | {maybe}] (да/нет/может быть);
-
MvPattern — разреженность (dMv/dy), график разреженности (см функцию spy) — введите имя разреженной матрицы S с S(i,j) = 1 для любого k, где (i, k) элемент матрицы массы M(t, у) зависит от проекции] переменной у, и 0 в противном случае;
-
Initial Step — предлагаемый начальный размер шага, по умолчанию каждый решатель определяет его автоматически по своему алгоритму;
-
Initial SI ope — вектор начального уклона ур0 ур0 = F(t0,y0)/M(t0, y0);
-
MaxStep — максимальный шаг, по умолчанию во всех решателях равен одной десятой интервала tspan;
-
BDF (Backward Differentiation Formulas) [on | {off}] — указывает, нужно ли использовать формулы обратного дифференцирования (методы Gear) вместо формул численного дифференцирования, используемых в ode 15s по умолчанию;
-
MaxOrder - Максимальный порядок ODE15S [1 | 2 | 3 4 | {5}].
Решатели используют в списке различные параметры. В приведенной ниже таблице они даны для решателей обычных (в том числе жестких) дифференциальных уравнений.
|
|
|
||||||
|
|
RelTol,AbsTol |
+ |
+ |
+ |
+ |
+ |
|
|
|
OutputFcaOutputSel, Refine, Stats |
+ |
+ |
+ |
+ |
+ |
|
|
|
Events |
+ |
+ |
+ |
+ |
+ |
|
|
|
MaxStep, InitlalStep |
+ |
+ |
+ |
+ |
+ |
|
|
|
Jconstant, Jacobl an, |
|
|
|
|
|
|
|
|
Jpattern, Vectorized |
- |
- |
- |
+ |
+ |
|
|
|
Mass |
- |
- |
- |
+ |
+ |
|
|
|
MassConstant |
- |
- |
- |
+ |
- |
|
|
|
MaxOrder, BOF |
- |
|
- |
+ |
- |
|
Решатель bvp4c имеет очень небольшое число параметров, но можно вводить не только матрицу Якоби интегрируемой функции, но и матрицу Якоби, содержащую частные производные функции граничных условий по границам интервала и по неизвестным параметрам.
Покажем применение решателя ОДУ на ставшем классическом примере — решении уравнения Ван-дер-Поля, записанного в виде системы из двух дифференциальных уравнений:
y' 1= y 2 ;
y' 2= 100*(1-y 1 )^2 * y 2 -y 1
при начальных условиях
y 1 ,(0) = 0;
y 2 (0) = 1.
Перед решением нужно записать систему дифференциальных уравнений в виде ode-функции. Для этого в главном меню выберем File > New > M-File и введем
function dydt = vdp100(t.y)
dydt = zeros(2.1); % a column vector
dydt(l) = y(2);
dydtC2) = 100*(1 -у(1^)2)*у(2) -y(1);
Сохраним m-файл-функцию. Тогда решение решателем ode15s и сопровождающий его график можно получить, используя следующие команды:
» [T,Y]=odel5s(@vdp100.[0 30].[2 0]);
» plot(T.Y)
» hold on:gtext('yl').gtext('y2')
Последние команды позволяют с помощью мыши нанести на графики решений y 1 = y(1) и у 2 = y(2) помечающие их надписи.
30. Описание системы ОДУ
Описание системы ОДУ
Можно использовать m-файл типа odefunction (или m-file типа odefile для совместимости с прежними версиями, но последний случай мы рассматривать не будем, чтобы определить систему дифференциальных уравнений в одной из явных (первая формула) или неявных форм:
y'= F(t, у), My' = F(t, у) или M(t)y' = Y(t, у),
где t — независимая переменная (скаляр), которая обычно представляет время; у — вектор зависимых переменных; F — функция от t и у, возвращающая вектор-столбец такой же длины как и у; М и М(£) — матрицы, которые не должны быть вырожденными. М может быть и константой.
Рассмотрим пример решения уравнения вида
Оно сводится к следующей системе уравнений:
Подготовим m-файл ode-функции vdp.m:
function [outl.out2.out3] = vdp(t.y.flag)
if nargin < 3 | isempty(flag)
outl = [2.*y(2).*(l-y(2). ^ 2)-y(1); y(1)];
else
switch(flag)
case 'inlt' % Return tspan. y0 and options
out1 = [0 20];
out2 = [2; 0];
out3 = [ ];
otherwise
error([' Unknown request ''' flag '''.']);
end
end
Тогда решение системы с помощью решателя ode23 реализуется следующими командами:
» [T.Y] = ode23(@vdp.[0 20]. [2 0]);
Еще проще работать с решателями нового поколения. Рассмотрим систему уравнений: y'+abs(y)=0; y(0)=0; у(4)=-2.
Для решения в пределах отрезка [0; 4] с помощью bvp4c достаточно привести эту систему к виду: y'=-abs(y), y(0)=0; у(4)+2=0. Затем -создаем две ode-функции: twoode и twobc в разных m-файлах:
function dydx = twoode(x,у)
dydx = [ у(2)
-abs(yd))];
function res = twobc(ya.yb) res = [ ya(l)
yb(l) + 2];
Теперь наберите в командной строке type twobvp и посмотрите само решение уравнения, которое содержится в уже имеющемся в системе файле twobvp. А исполнив команду twodvp, можно наблюдать результат решения в виде графиков. В решении вы найдете структуру узлов начальной сетки решения, которая поясняется ниже.
-
solinit — это структура узлов начальной сетки решения (в любой шкале), но такая, что solinit.x=a, solinit.x - b. И функция у, и функция у' должны быть непрерывны на участке [а b]. Дотадка для начальной итерации so1imt=bvpi-mt(x,yinit.params) в bvp4c отличается тем, что ваше начальное представление о функции у yinit можно вводить не только в виде вектора, но и как символьную функцию.
Рекомендуется просмотреть также пример mat4bvp и дополнительные примеры решения систем дифференциальных уравнений, приведенные в файле odedemo. Во многих случаях решение задач, сводящихся к решению систем дифференциальных уравнений, удобнее осуществлять с помощью пакета расширения Simulink.
31. Дескрипторная поддержка параметров решателя
Дескрипторная поддержка параметров решателя
При помощи перечисленных ниже функций можно получить и создать или изменить параметры решателя:
-
o=odeget(options, 'name') — извлекает значение свойства, определенного строкой 'name', из структуры параметров options; возвращает пустую матрицу, если значение данного свойства в структуре options не определено. Можно ввести только первые буквы, которые однозначно определяют имя свойства. Пустая матрица [ ] — допустимый аргумент options;
Пример:
» options = odesetCRelTol' ,[le-6 le-7].'AbsTol' ,6е-3);
» odeget(options.'Rel')
ans =
l.0e-006*
1.0000 0.1000
» odegetCoptions.'Abs')
ans =
0.0060
-
options=odeset( 'namel' .valuel, 'name2' ,value2,...) — создает структуру параметров, в которой указанные свойства по имени ' name...' принимают следующие за ними значения. Вместо 'name...' можно ввести только первые буквы, которые однозначно определяют имя свойства (abs — Abstol, inaxit —maxiter и т. д.);
-
options=odeset (ol dopts, newopts) — изменяет существующую структуру параметров oldopts путем объединения ее с новой структурой newopts. Все новые параметры, не равные пустой матрице, заменяют соответствующие параметры в структуре oldopts;
-
options=odeset(ol dopts, 'namel' .valuel,...) — изменяет в существующей структуре параметров соответствующие значения. Пример:
oldopts
F 1 [ ] 4 'S' 'S' [ ] [ ] [ ]
newopts
Т 3 F [] 'S' [] [] [] []
odeset(oldopts.newopts)
Т 3 F . 4 ' ' 's' [ ] [ ] [ ]
Функция odeset без параметров возвращает все имена свойств и их допустимые значения.
Пример:
» odeset
AbsTol: [ positive scalar or vector {le-6} ]
RelTol: [ positive scalar {le-3} ]
NormControl: [ on | {off} ]
OutputFcn: [ function ]
OutputSel: [ vector of integers ]
Refine: [ positive integer ]
Stats: [ on | {off} ]
InitialStep: [ positive scalar ]
MaxStep: [ positive scalar ]
BDF: [ on | {off} ]
MaxOrder: [ 1 | 2 | 3 | 4 | {5} ]
Jacobian: [ matrix | function ]
JPattern: [ sparse matrix ]
Vectorized: [ on | {off} ]
Mass: [ matrix | function ] MStateOependence: [ none | weak | strong ]
MvPattern: [ sparse matrix ]
MassSingular: [ yes | no | {maybe} ]
InitialSlope: [ vector ] Events: [ function ]
32. Пакет Partial Differential Equations Toolbox
Пакет Partial Differential Equations Toolbox
Специалистов в области численных методов решения дифференциальных уравнений в частных производных несомненно заинтересует обширный пакет Partial Differential Equations Toolbox (PDETB). Хотя этот пакет является самостоятельным приложением и в ядро MATLAB не входит, мы приведем краткое описание некоторых его возможностей с парой примеров. Вы можете вызвать пакет с его графическим интерфейсом командой pdetool.
Поскольку ряд применений пакета -PDETB связан с проблемами анализа и оптимизации трехмерных поверхностей и оболочек, в пакет введены удобные функции для построения их графиков. Они могут использоваться совместно с функцией pdeplot, что иллюстрирует следующий пример:
[p,e,t]=initmesh('Ishapeg');
u=assempde('Ishapeb'p.e.t.1.0,1):
pdeplottp.e.t.'xydata',u.'zdata'.u.'mesh'.'off'):
В состав пакета входит ряд полезных демонстрационных примеров с именами от pdedemol до pdedemo8. Их можно запустить как из командной строки (путем указания имени), так из окна демонстрационных примеров Demos. Рекомендуется, однако, сделать это из командной строки, так как примеры ориентированы на управление в командном режиме — в основном оно сводится к нажатию клавиши Enter для прерывания пауз, введенных для просмотра промежуточных результатов вычислений.
Рассмотрим пример pdedemoS, решающий проблему минимизации параболической поверхности решением дифференциального уравнения
-div( l/sqrt(l+grad|u| ^ 2) * grad(u) ) = 0
при граничном условии u=х*2. Ниже представлен текст файла pdedemo3.m с убранными англоязычными комментариями:
%PDEDEM03 Решение проблемы минимизации параболической поверхности
echo on
clc
g='circleg': % Единичная окружность
b='circleb2': % х ^ 2 - граничное условие
c='l./sqrt(l+ux.*2+uy.*2)':
а=0;
f=0:
rto1=le-3; % Погрешность вычислений решателем
pause % Пауза в вычислениях
clc
% Генерация поверхности
[p,e,t]=initmesh(g); [p,e.t]-refinemesh(g.p.e.t);
% Решение нелинейной проблемы
u=pdenonlin(b.p.e,t.c.a.f,'tol'.rtol);
pdesurf(p.t.u);
pause % Пауза в вычислениях
echo off
Весьма интересны и поучительны примеры с анимацией: pdedemo2 — появление и распространение волн, pdedemoS — вздутие поверхности (пузырек газа), pdedemo6 — колебания плоскости (гиперболическая проблема) и т. д. К сожалению, они представлены слишком объемными файлами, что не позволяет воспроизвести их в книге учебного характера. Однако вам их несомненно стоит просмотреть самостоятельно.
33. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Решать системы линейных уравнений точными и приближенными методами.
-
Решать системы линейных уравнений с разреженными матрицами.
-
Вычислять нули функции одной переменной.
-
Минимизировать функции одной и нескольких переменных.
-
Аппроксимировать производные конечными разностями.
-
Вычислять интегралы численными методами.
-
Выполнять операции с полиномами.
-
Использовать решатели ОДУ.
Урок 17. Обработка данных
1. Урок 17. Обработка данных
Урок №17.
Обработка данных
-
Статистическая обработка массивов
-
Сортировка элементов массивов
-
Триангуляция
-
Преобразования Фурье
-
Свертка и обратная ей операция
-
Дискретная фильтрация
-
Аппроксимация и интерполяция
-
Обработка данных в окне графики
Этот урок посвящен традиционной обработке данных. В нем приведены основные функции для обработки данных, представленных массивами. Они широко используются для анализа данных физических, химических, экономических и иных экспериментов. Это большой урок, рассчитанный на разбиение его на части или выборочное изучение. Последнее более предпочтительно, поскольку урок охватывает данную тему достаточно широко.
2. Статистическая обработка данных
Статистическая обработка данных
Нахождение максимального и минимального элементов массива
Самый простой анализ данных, содержащихся в некотором массиве, заключается в поиске его элементов с максимальным и минимальным значениями. В системе MATLAB определены следующие быстрые функции для нахождения минимальных и максимальных элементов массива:
-
mах(А) — возвращает наибольший элемент, если А — вектор; или возвращает вектор-строку, содержащую максимальные элементы каждого столбца, если А — матрица, в многомерных массивах работает с первой не единичной размерности;
-
mах(А.В) — возвращает массив того же размера, что А и В, каждый элемент которого есть максимальный из соответствующих элементов этих массивов;
-
max(A.[ ],dim) — возвращает наибольшие элементы по столбцам или по строкам матрицы в зависимости от значения скаляра dim. Например, тах(А,[ ],1) возвращает максимальные элементы каждого столбца матрицы А;
-
[C.I] =max(A) — кроме максимальных значений возвращает вектор индексов I этих элементов.
Примеры:
» A=magic(7)
|
30 |
39 |
48 |
1 |
10 |
19 |
28 |
|
38 |
47 |
7 |
9 |
18 |
27 |
29 |
|
46 |
6 |
8 |
17 |
26 |
35 |
37 |
|
5 |
14 |
16 |
25 |
34 |
36 |
45 |
|
13 |
15 |
24 |
33 |
42 |
44 |
4 |
|
21 |
23 |
32 |
41 |
43 |
3 |
12 |
|
22 |
31 |
40 |
49 |
2 |
11 |
20 |
» С = max(A)
С=
46 47 48 49 43 44 45
» С = max(A.[ ].l)
С =
46 47 48 49 43 44 45
» С = max(A.[ ],2)
С =
48
47
46
45
44
43
49
»[C,I]=max(A)
C=
49 43 44 45
I=
7 6 5 4
Для быстрого нахождения элемента массива с минимальным значением служит следующая функция:
-
min(A) — возвращает минимальный элемент, если А — вектор; или возвращает вектор-строку, содержащую минимальные элементы каждого столбца, если А — матрица;
-
min(A.B) — возвращает массив того же размера, что А и В, каждый элемент которого есть минимальный из соответствующих элементов этих массивов;
-
min(A,[ ],dim) — возвращает наименьший элемент по столбцам или по строкам матрицы в зависимости от значения скаляра dim. Например, тах(А,[ ],1) возвращает минимальные элементы каждого столбца матрицы А;
-
[C,I] = min(A) — кроме минимальных значений возвращает вектор индексов этих элементов.
Пример:
» A=magic(4)
А =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
» [C.I] = min(A)
C =
4 2 3 1
I =
4 1 1 4
Работа указанных функций базируется на сравнении численных значений элементов массива А, что и обеспечивает высокую скорость выполнения операций.
3. Нахождение средних, срединных значений массива и стандартных отклонений
Нахождение средних, срединных значений массива и стандартных отклонений
Элементарная статистическая обработка данных в массиве обычно сводится к нахождению их среднего значения, медианы (срединного значения) и стандартного отклонения. Для этого в системе MATLAB определены следующие функции:
-
mean (А) — возвращает арифметическое среднее значение элементов массива, если А — вектор; или возвращает вектор-строку, содержащую средние значения элементов каждого столбца, если А — матрица. Арифметическое среднее значение есть сумма элементов массива, деленная на их число;
-
mean(A.dim) — возвращает среднее значение элементов по столбцам или по строкам матрицы в зависимости от значения скаляра dim (dim=l по столбцам и dim=2 по строкам соответственно).
Примеры:
|
» А = [1 |
2 6 4 |
8; 6 7 |
13 5 4; |
7 9 0] |
|
А = |
|
|
|
|
|
1 |
2 |
6 |
4 |
8 |
|
6 |
7 |
13 |
5 |
4 |
|
7 |
9 |
0 |
8 |
12 |
|
6 |
6 |
7 |
1 |
2 |
|
» mean(A) |
|
|
|
|
|
ans = |
|
|
|
|
|
5.0000 |
6.0000 |
6.5000 |
4.5000 |
6.5000 |
|
»mean(A. |
2) |
|
|
|
|
ans = |
|
|
|
|
|
4.2000 |
|
|
|
|
|
7.0000 |
|
|
|
|
|
7.2000 |
|
|
|
|
|
4.4000 |
|
|
|
|
-
median (A) — возвращает медиану, если А — вектор; или вектор-строку медиан для каждого столбца, если А — матрица;
-
median(A.dim) — возвращает значения медиан для столбцов или строк матрицы в зависимости от значения скаляра dim.
Примеры:
» A=magic(6)
|
35 |
1 |
6 |
26 |
19 |
24 |
|
3 |
32 |
7 |
21 |
23 |
25 |
|
31 |
9 |
2 |
22 |
27 |
20 |
|
8 |
28 |
33 |
17 |
10 |
15 |
|
30 |
5 |
34 |
12 |
14 |
16 |
|
4 |
36 |
29 |
13 |
18 |
11 |
» M=median(A)
М =
19.000018.500018.000019.000018.500018.0000
» M=median(A,2)
М =
21.5000
22.0000
21.0000
16.0000
15.0000
15.5000
-
std(X) — возвращает стандартное отклонение элементов массива, вычисляемое по формуле если X — вектор. Если X — матрица, то std(X) возвращает вектор-строку, содержащую стандартное отклонение элементов каждого столбца (обратите внимание, что оно отличается от среднеквадратического отклонения);
-
std(X.flag) — возвращает то же значение, что и std(X), если flag=0; если flag=l, функция std(X.l) возвращает среднеквадратическое отклонение (квадратный корень из несмещенной дисперсии), вычисляемое по формуле
-
std(X.flag.dim) — возвращает стандартное или среднеквадратическое отклонения по рядам (dim=2) или по столбцам(dim=1) матрицы X в зависимости от значения переменной dim.
Примеры:
» X = linspace(0,3*pi,10)
X = Columns 1 through 7
0 1.0472 2.0944 3.1416 4.1888 5.2360 6.2832
Columns 8 through 10
7.3304 8.3776 9.4248
» s = std(X)
s =
3.1705
4. Функции сортировки элементов массива
Функции сортировки элементов массива
Многие операции статистической обработки данных выполняются быстрее и надежнее, если данные предварительно отсортированы. Кроме того, нередко представление данных в отсортированном виде более наглядно и ценно. Ряд функций служит для выполнения сортировки элементов массива. Они представлены ниже.
-
sort (А) — в случае одномерного массива А сортирует и возвращает элементы по возрастанию их значений; в случае двумерного массива происходит сортировка и возврат элементов каждого столбца. Допустимы вещественные, комплексные и строковые элементы. Если А принимает комплексные значения, то элементы сначала сортируются по абсолютному значению, а затем, если абсолютные значения равны, по аргументу. Если А включает NaN-элементы, sort помещает их в конец;
-
[В. INDEX] = sort(A) — наряду с отсортированным массивом возвращает массив индексов INDEX. Он имеет размер size(A), с помощью этого массива можно восстановить структуру исходного массива.
-
sort(A.dim) — для матриц сортирует элементы по столбцам (dim=l) или по рядам в зависимости от значения переменной dim.
Примеры:
|
» A=magic(5) |
|
||||
|
А = |
|
|
|
|
|
|
17 |
24 |
1 |
8 |
15 |
|
|
23 |
5 |
7 |
14 |
16 |
|
|
4 |
б |
13 |
20 |
22 |
|
|
10 |
12 |
19 |
21 |
3 |
|
|
11 |
18 |
25 |
2 |
9 |
|
|
» [В. B= |
INDEX] |
sort(A) |
|
|
|
|
4 |
5 |
1 |
2 |
3 |
|
|
10 |
6 |
7 |
8 |
9 |
|
|
11 |
12 |
13 |
14 |
15 |
|
|
17 |
18 |
19 |
20 |
16 |
|
|
23 |
24 |
25 |
21 |
22 |
|
|
index= |
|
|
|
|
|
|
|
3 |
2 |
1 |
5 |
4 |
|
|
4 |
3 |
2 |
1 |
5 |
|
|
5 |
4 |
3 |
2 |
1 |
|
|
1 |
5 |
4 |
3 |
2 |
|
|
2 |
1 |
5 |
4 |
3 |
-
sortrows(A) — выполняет сортировку рядов массива А по возрастанию и возвращает отсортированный массив, который может быть или матрицей, или вектором-столбцом;
-
sortrows(A.column) — возвращает матрицу, отсортированную по столбцам, точно указанным в векторе column. Например, sortrows(A,[2 3]) сортирует строки матрицы А сначала по второму столбцу, и затем, если его элементы равны, по третьему;
-
[В, index] = sort rows (А) — также возвращает вектор индексов index. Если А — вектор-столбец, то B=A(index). Если А — матрица размера тхп, то B=A(index.:).
Примеры:
» А=[2 35689: 5 7 1 2 3 5:1 3 2 1 5 1:5 0 8 8 4 3]
А =
|
|
|
||||||
|
|
|
2 |
3 5 |
6 |
8 |
9 |
|
|
|
|
5 |
7 1 |
2 |
3 |
5 |
|
|
|
|
1 |
3 2 |
1 |
5 |
1 |
|
|
|
|
5 |
0 8 |
8 |
4 |
3 |
|
|
|
» |
В= |
sortrows(A) |
|
|
|
|
|
|
в |
= |
|
|
|
|
|
|
|
|
1 |
3 2 |
1 |
5 |
1 |
|
|
|
|
2 |
3 5 |
6 |
3 |
9 |
|
|
|
|
5 |
0 8 |
8 |
4 |
3 |
|
|
|
|
5 |
7 1 |
2 |
3 |
5 |
|
|
|
|
|
|
|
|
|
|
» b = sortrows(A.3)
b=
|
5 |
7 |
1 |
2 |
3 |
5 |
|
1 |
3 |
2 |
1 |
5 |
1 |
|
2 |
3 |
5 |
6 |
8 |
9 |
|
5 |
0 |
8 |
8 |
4 |
3 |
-
cplxpair(A) — сортирует элементы по строкам или столбцам комплексного массива А, группируя вместе комплексно сопряженные пары. Затем найденные пары сортируются по возрастанию действительной части. Внутри пары элемент с отрицательной мнимой частью является первым. Действительные элементы следуют за комплексными парами. Заданный по умолчанию порог 100*eps относительно abs(A(i))) определяет, какие числа являются действительными и какие элементы являются комплексно сопряженными. Если А — вектор, cpl xpair (А) возвращает А вместе с комплексно сопряженными парами. Если А — матрица, cpl xpai r(А) возвращает матрицу А с комплексно сопряженными парами, сортированную по столбцам;
-
cplxpalr(A,tol) — отменяет заданный по умолчанию порог и задает новый tol;
-
cplxpair(A.[].dim) — сортирует матрицу А по строкам или по столбцам в зависимости от значения параметра dim;
-
cplxpair(A,tol ,dim) — сортирует матрицу А по строкам или по столбцам в зависимости от значения параметра dim, используя заданный порог tol.
Пример:
» А=[23+121.34-31.45:23-121.-12.21:-3.34+31.-21]
А =
23.0000 + 12.00001 34.0000 - 3.00001 45.0000
23.0000 - 12.00001 -12.0000 0 + 2.00001
-3.0000 34.0000 + 3.00001 0 - 2.00001
» cplxpair(A)
ans =
23.0000 - 12.00001 34.0000 - 3.00001 0 - 2.00001
23.0000 + 12.00001 34.0000 + 3.00001 0 + 2.00001
-3.0000 -12.0000 45.0000
5. Вычисление коэффициентов корреляции
Вычисление коэффициентов корреляции
Под корреляцией понимается взаимосвязь некоторых величин, представленных данными — векторами или матрицами. Общепринятой мерой линейной корреляции является коэффициент корреляции. Его близость к единице указывает на высокую степень линейной зависимости. Данный раздел посвящен описанию функции для вычисления коэффициентов корреляции и определения ковариационной матрицы элементов массива. Приведенная ниже функция позволяет вычислить коэффициенты корреляции для входного массива данных.
-
corrcoef(X) — возвращает матрицу коэффициентов корреляции для входной матрицы, строки которой рассматриваются как наблюдения, а столбцы — как переменные. Матрица S=corrcoef(X) связана с матрицей ковариаций C=cov(X) следующим соотношением: S(i.j)=C(i.j)/sqrt(C(i.i)C(j.j));
-
Функция S = corrcoef (х,у), где х и у — векторы-столбцы, аналогична функции соггсоеЩх у]). Пример:
|
» M=magic(5) |
|
||||
|
M = |
|
|
|
|
|
|
17 |
24 |
1 |
8 |
15 |
|
|
23 |
5 |
7 |
14 |
16 |
|
|
4 |
6 |
13 |
20 |
22 |
|
|
10 |
12 |
19 |
21 |
3 |
|
|
11 |
18 |
25 |
2 |
9 |
|
» S=corrcoef(M)
S =
1.0000 0.0856 -0.5455 -0.3210 -0.0238
0.0856 1.0000 -0.0981 -0.6731 -0.3210
-0.5455 -0.0981 1.0000 -0.0981 -0.5455
-0.3210 -0.6731 -0.0981 1.0000 0.0856
-0.0238 -0.3210 -0.5455 0.0856 1.0000
В целом, корреляция данных довольно низкая. В данных, расположенных по диагонали — здесь коэффициенты корреляции равны 1, — вычисляется линейная корреляция переменной со своей копией.
6. Вычисление матрицы ковариации
Вычисление матрицы ковариации
Приведенная далее функция позволяет вычислить матрицу ковариации для массива данных.
-
cov(x) — возвращает смещенную дисперсию элементов вектора х. Для матрицы, где каждая строка рассматривается как наблюдение, а каждый столбец — как переменная, cov(x) возвращает матрицу ковариации. diag(cov(x» — вектор смещенных дисперсий для каждого столбца и sqrt(diag(cov(x))) — вектор стандартных отклонений.
-
Функция С = cov(x.y), где х и у — векторы-столбцы одинаковой длины, равносильна функции cov([x у]).
Пример:
» D=[2 -3 6:3 6 -1:9 8 5]:C=cov(D)
С =
14.3333 16.3333 3.6667
16.3333 34.3333 -10.3333
3.6667 -10.3333 14.3333
» diag(cov(D))
ans =
14.3333
34.3333
14.3333
» sqrt(diag(cov(D)))
ans =
3.7859
5.8595
3.7859
» std(D)
ans =
3.7859 5.8595 3.7859
7. Триангуляция
Триангуляция
Далее мы рассмотрим функции геометрического анализа данных. Такой анализ не относится к достаточно распространенным средствам анализа данных, но для специалистов он представляет несомненный интерес.
Пусть есть некоторое число точек. Триангуляция Делоне — это множество линий, соединяющих каждую точку с ее ближайшими соседними точками. Диаграммой Вороного называют многоугольник, вершины которого — центры окружностей, описанных вокруг треугольников Делоне.
8. Расчет триангуляции
Расчет триангуляции
В системе MATLAB определены функции триангуляции Делоне, триангуляции Делоне для ближайшей точки и поиска наилучшей триангуляции. Рассмотрим функции, реализующие триангуляцию Делоне.
-
TRI = delaunay(x.y) — возвращает матрицу размера mх3 множества треугольников (триангуляция Делоне), такую что ни одна из точек данных, содержащиеся в векторах х и у, не попадают внутрь окружностей, проходящих через вершины треугольников. Каждая строка матрицы TRI определяет один такой треугольник и состоит из индексов векторов х и у;
-
TRI = delaunay('x,у.'sorted'-) — при расчетах предполагается, что точки векторов х и у отсортированы сначала по у, затем по х и двойные точки уже устранены. Пример:
» rand('state',0);
» x=rand(1,25);
» y=rand(1,25);
» TRI = delaunay(x,y);
» trimesh(TRI,x,y,zeros(size(x)))
» axis([0 1 0 1]); hold on;
» plot(x,y,'o')
-
dsearch(x.y ,TRI ,xi ,yi) — возвращает индекс точки из числа содержащихся в массивах х и у, ближайшей к точке с координатами (x1,y1), используя массив данных триангуляции TRI (триангуляция Делоне для ближайшей точки);
-
dsearch(x,y,TRI ,x1 ,y1 ,S) — делает то же, используя заранее вычисленную разреженную матрицу триангуляции S: S=sparse(TRI(: ,[1 1 2 2 3 3]), TRK: ,[2 3 1 3 1 2]).1.nxy.nxy), где nxy=prod(size(x));
-
tsearch(x,y.TRI,xi ,yi) — выполняет поиск наилучшей триангуляции, возвращает индексы строк матрицы триангуляции TRI для каждой точки с координатами (xi ,y1). Возвращает NaN для всех точек, находящихся вне выпуклой оболочки.
Триангуляция трехмерных и n-мерных массивов (п>=2) осуществляется при помощи функций delaunayS и delaunayn соответственно. Эти функции используют не алгоритм вычисления диаграмм Вороного, как del aunay, а алгоритм qhul 1 Национального научно-технического и исследовательского центра визуализации и вычисления геометрических структур США [ В MATLAB 6.1 функции delaunay, convhull, griddata, voronoi также используют qhull. - Примеч. ред. ].
Построенная по приведенному ранее примеру диаграмма представлена на рис. 17.1.
Рис. 17.1. Пример применения функции delaunay
1.gif
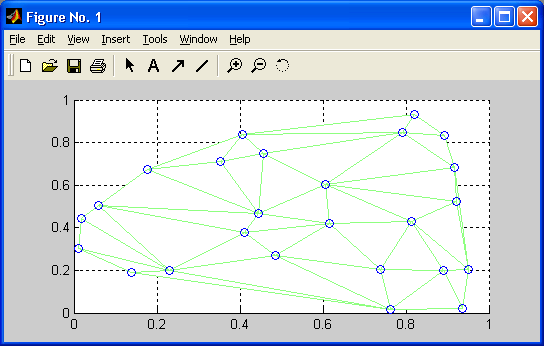
9. Нахождение выпуклой оболочки
Нахождение выпуклой оболочки
В системе MATLAB определена функция вычисления точек выпуклой оболочки:
-
convhull (х,у) — возвращает индексы тех точек, задаваемых векторами х и у, которые лежат на выпуклой оболочке;
-
convhull(x,y,TRI) — использует триангуляцию, полученную в результате применения функции триангуляции Делоне del aunay, вместо того чтобы вычислять ее самостоятельно. Пример:
» хх=-0.8:0.03:0.8;
» уу = abs(sqrt(xx));
» [х,у] = pol2cart(xx,yy);
» k = convhuTI(x,y);
» plot(x(k),y(k).'r:',x,y,'g*')
Рис. 17.2. Пример использования функции convhull
Рис. 17.2 иллюстрирует применение функции convhull для построения выпуклой оболочки. Функция convhulln вычисляет n-мерную выпуклую поверхность, основана на алгоритме qhull.
2.gif
10. Вычисление площади полигона
Вычисление площади полигона
В системе MATLAB определены функции, вычисляющие площадь полигона и анализирующие нахождение точек внутри полигона. Для вычисления площади полигона используется функция polyarea:
-
polyarea(X.Y) — возвращает площадь полигона, заданного вершинами, находящимися в векторах X и Y. Если X и Y — матрицы одного размера, то polyarea возвращает площадь полигонов, определенных столбцами X и Y;
-
polyarea(X.Y.dim) — возвращает площадь полигона, заданного столбцами или строками X и Y в зависимости от значения переменной dim. Пример:
» L = linspace(0.3*pi,10);
» X= sin(L)';
» Y=cos(L)';
» А = polyarea(X.Y)
А =
3.8971
» plot(X.Y.'m')
Рис. 17.3. Область многоугольника, для которого вычислена площадь
Построенный по этому примеру многоугольник представлен на рис. 17.3. В данном примере использована функция linspace(xl.x2,N), генерирующая N точек в промежутке от x1 до х2 с последующим формированием векторов X и Y для построения многоугольника в полярной системе координат.
3a.gif

3b.gif
11. Анализ попадания точек внутрь полигона
Анализ попадания точек внутрь полигона
Функция Inpolygon используется для анализа того, попадают ли заданные точки внутрь полигона:
-
IN=inpolygon(X,Y.xv.yv) — возвращает матрицу IN того же размера, что X и Y. Каждый элемент матрицы IN принимает одно из значений — 1, 0.5 или 0 — в зависимости от того, находится ли точка с координатами (X(p,q),Y(p,q)) внутри полигона, вершины которого определяются векторами xv и yv:
-
IN(p,q) = 1 — если то.чка (X(p.q) ,Y(p,q)) лежит внутри полигона;
-
IN(p,q) = 0.5 — если точка (X(p,q) ,Y(p,q)) лежит на границе полигона;
-
IN(p.q) = 0 — если точка (X(p.q),Y(p,q)) лежит вне полигона. Пример:
-
» L = linspace(0.2*pi,8);
» yv = sin(L)';
» xv= cos(L)';
» x= randn(100,1); у = randn(100,1);
» IN = inpolygon(x,y,xv,yv);
» plot(xv,yv,'k',x(IN),y(IN),'r*',x(~IN),y(~IN),'b*')
Построенные в этом примере массив точек и полигон представлены на рис. 17.4.
Рис. 17.4. Пример применения функции inpolygon
Точки, попавшие внутрь полигона, обозначены символом звездочки, а точки вне полигона обозначены кружками.
4a.gif

4b.gif
12. Построение диаграммы Вороного
Построение диаграммы Вороного
Для построения диаграммы Вороного служат следующие команды:
-
voronoi(x.y) — строит диаграмму Вороного для точек с координатами (х,у). Функция voronoi(х,у,TRI) использует триангуляцию TRI;
-
voronoi (...,' LineSpec') — строит диаграмму с заданным цветом и стилем линий;
-
[vx.vy] = voronoi (...) — возвращает вершины граней Вороного в векторах vx и vy, так что команда plot(vx,vy,'-' ,х.у,'.') создает диаграмму Вороного.
Пример:
» rand('state'.0):
» x = randd.15): у = randd.15):
» TRI = delaunay(x.y);
» subplotd.2,1)....
» trimesh(TRI,x,y,zeros(s1ze(x))); view(2),...
» axis([0 101]); hold on;
» plot(x.y,'o');
» [vx, vy] = voronoi(x.y.TRI);
» subplot(l,2,2)....
» plot(x,y,'r+',vx,vy,'b-'),...
» axis([0 1 0 1])
Рисунок 17.5 (слева) иллюстрирует построение треугольников Делоне. На рисунке справа изображены знаками «плюс» центры окружностей, проведенных вокруг треугольников Делоне.
Функция [V,C]=voronoin(X) служит для построения диаграмм Вороного n-мерных данных. V — массив граней, С —массив клеток диаграмм. При n=2 вершины граней Вороного возвращаются в порядке смежности, при п>2 — в порядке убывания.
Рис. 17.5. Связь триангуляции Делоне с диаграммой Вороного
5.gif
13. Преобразования Фурье
Преобразования Фурье
Разработка преобразований Фурье сыграла огромную роль в появлении и развитии ряда новых областей науки и техники. Достаточно отметить, что электротехника переменного тока, электрическая связь и радиосвязь базируются на спектральном представлении сигналов. Ряды Фурье также можно рассматривать как приближение произвольных функций (определенные ограничения в этом известны) тригонометрическими рядами бесконечной длины. При конечной длине рядов получаются наилучшие среднеквадратические приближения. MATLAB содержит функции для выполнения быстрого одномерного и двумерного быстрого дискретного преобразования Фурье. Для одномерного массива*с длиной N прямое и обратное преобразования Фурье реализуются по следующим формулам:
Прямое преобразование Фурье переводит описание сигнала (функции времени) из временной области в частотную, а обратное преобразование Фурье переводит описание сигнала из частотной области во временную. На этом основаны многочисленные методы фильтрации сигналов.
14. Функции одномерного прямого преобразования Фурье
Функции одномерного прямого преобразования Фурье
В описанных ниже функциях реализован особый метод быстрого преобразования Фурье — Fast Fourier Transform (FFT, или БПФ), позволяющий резко уменьшить число арифметических операций в ходе приведенных выше преобразований. Он особенно эффективен, если число обрабатываемых элементов (отсчетов) составляет 2 т , где т — целое положительное число. Используется следующая функция:
-
fft(X) — возвращает для вектора X дискретное преобразование Фурье, по возможности используя алгоритм быстрого преобразования Фурье. Если X — матрица, функция fft возвращает преобразование Фурье для каждого столбца матрицы;
-
fft(X.n) — возвращает n-точечное преобразование Фурье. Если длина вектора X меньше n, то недостающие элементы заполняются нулями. Если длина X больше п, то лишние элементы удаляются. Когда X — матрица, длина столбцов корректируется аналогично;
-
fft(X,[ Ldirn) и fft(X,n,dim) — применяют преобразование Фурье к одной из размерностей массива в зависимости от значения параметра dim.
Для иллюстрации применения преобразования Фурье создадим трехчастотный сигнал на фоне сильного шума, создаваемого генератором случайных чисел:
»t=0:0.0005:1;
»x=sin(2*pi*200*t)+0.4*sin(2*pi*150*t)
+0.4*sin(2*pi*250*t);
» y=x+2*randn(size(t));
» plot(y(1:100),'b')
Рис. 17.6. Форма зашумленного сигнала
Этот сигнал имеет среднюю частоту 200 рад/с и два боковых сигнала с частотами 150 и 250 рад/с, что соответствует амплитудно-модулированному сигналу с частотой модуляции 50 рад/с и глубиной модуляции 0.8 (амплитуда боковых частот составляет 0.4 от амплитуды центрального сигнала). На рис. 17.6 показан график этого сигнала (по первым 100 отсчетам из 2000). Нетрудно заметить, что из него никоим образом не видно, что полезный сигнал — амплитудно-модулированное колебание, настолько оно забито шумами. Теперь построим график спектральной плотности полученного сигнала с помощью прямого преобразования Фурье, по существу переводящего временное представление сигнала в частотное. Этот график в области частот до 300 Гц (см. рис. 17.6) строится с помощью следующих команд:
» Y=fft(y,1024):
» Pyy=Y.*conj(Y)/1024;
» f=2000*(0:150)/1024;
» plot(f,Pyy(l:151)),grid
График спектральной плотности сигнала, построенный в этом примере, представлен на рис. 17.7. Даже беглого взгляда на рисунок достаточно, чтобы убедиться в том, что спектрограмма сигнала имеет явный пик на средней частоте амплитудно-модулированного сигнала и два боковых пика. Все эти три частотные составляющие сигнала явно выделяются на общем шумовом фоне. Таким образом, данный пример наглядно иллюстрирует технику обнаружения слабых сигналов на фоне шумов, лежащую в основе работы радиоприемных устройств.
Рис. 17.7. График спектральной плотности приведенного на рис. 17.6 сигнала
6a.gif
6b.gif

7a.gif
7b.gif
15. Функции многомерного прямого преобразования Фурье
Функции многомерного прямого преобразования Фурье
Для двумерного прямого преобразования Фурье используется функция fft2:
-
fft2(X) — возвращает для массива данных X двумерное дискретное преобразование Фурье;
-
fft2(X,m.n) — усекает массив X или дополняет его нулями, чтобы перед выполнением преобразования Фурье создать матрицу размера тхп. Результат — матрица того же размера.
Для многомерного прямого преобразования Фурье также существует функция:
-
fftn(X) — возвращает результат N-мерного дискретного преобразования для массива X размерности N. Если X — вектор, то выход будет иметь ту же ориентацию;
-
fftn(X.siz) — возвращает результат дискретного преобразования для массива X с ограничением размера, заданным переменной siz.
16. Функция перегруппировки
Функция перегруппировки
Функция Y = fftshift(X) перегруппировывает выходные массивы функций fft и fft2, размещая нулевую частоту в центре спектра, что иногда более удобно. Если X — вектор, то Y — вектор с циклической перестановкой правой и левой половин исходного вектора. Если X — матрица, то Y — матрица, у которой квадранты I и III меняются местами с квадрантами II и IV [ Для одно- и двумерных массивов функция fftshift(X) эквивалентна функции rot90{X.2) ]. Рассмотрим следующий пример. Вначале построим график спектральной плотности мощности (рис. 17.8) при одномерном преобразовании Фурье:
» rand('state'.0);
» WhO.001:0.512;
» x=sin(2*pi*50*t)+sin(2*pi*120*t);
» y=x+2*randn(size(t))+0.3;
» Y=fft(y);
» Pyy=Y.*conj(Y)/512:
» f=1000*(0:255)/512:
Рис. 17.8. График спектральной плотности сигнала после одномерного преобразования Фурье
Здесь мы ограничились 512 отсчетами, с тем чтобы использовать эффективны!: метод быстрого преобразования Фурье, при котором число отсчетов должно быт: 2 N , где N - целое число. Теперь воспользуемся функцией fftshift:
» Y=fftshift(Y);
» Pyy=Y.*conj(Y)/512;
» p1ot(Pyy).grid
Полученный при этом график представлен на рис. 17.9.
Рис. 17.9. График спектральной плотности того же сигнала после применения функции fftshift
Надо отметить, что этот график дает значения спектральной плотности составляющих спектра не явно от частоты, а как распределение ее значений для элементов вектора Руу.
8.gif
9a.gif
9b.gif
17. Функции обратного преобразования Фурье
Функции обратного преобразования Фурье
Возможно одномерное обратное преобразование Фурье, реализуемое следующими функциями:
-
ifft(F) — возвращает результат дискретного обратного преобразования Фурье вектора F. Если F — матрица, то if ft возвращает обратное преобразование Фурье для каждого столбца этой матрицы;
-
ifft(F.n) — возвращает результат n-точечного дискретного обратного преобразования Фурье вектора F;
-
ifft(F.[ ],dim) иу = ifft(X,n,dim) — возвращают результат обратного дискретного преобразования Фурье массива F по строкам или по столбцам в зависимости от значения скаляра dim.
Для любого X результат последовательного выполнения прямого и обратного преобразований Фурье ifft(fft(x)) равен X с точностью до погрешности округления. Если X — массив действительных чисел, ifft(fft(x)) может иметь малые мнимые части.
Пример:
» V=[l 1110000]:
» fft(V)
ans =
Columns 1 through 4
4.0000 1.0000 - 2.41421 0 1.0000 - 0.41421
Columns 5 through 8
0 1.0000 + 0.41421 0 1.0000 + 2.41421
» 1fft(fft(V))
ans =
1 1 1 1 0 0 0 0
Аналогичные функции есть для двумерного и многомерного случаев:
-
ifft2(F) — производит двумерное дискретное обратное преобразование Фурье для матрицы F;
-
ifft2(F,m,n) — производит обратное преобразование Фурье размерности тхп для матрицы F;
-
ifftn(F) — возвращает результат JV-мерного обратного дискретного преобразования Фурье для N-мерного массива F;
-
ifftn(F.siz) — возвращает результат обратного дискретного преобразования Фурье для массива F с ограничением размера, заданным вектором siz. Если любой элемент siz меньше, чем соответствующая размерность F, то массив F будет урезан до размерности siz.
18. Свертка и дискретная фильтрация
Свертка и дискретная фильтрация
Функция свертки и обратная ей функция
В этом разделе рассмотрены базовые средства для проведения операций свертки и фильтрации сигналов на базе алгоритмов быстрого преобразования Фурье. Многие дополнительные операции, относящиеся к этой области обработки сигналов, можно найти в пакете прикладных программ Signal Processing Toolbox.
Для двух векторов х и у с длиной тип определена операция свертки:
В ее результате получается вектор z с длиной (т+п- 1). Для осуществления свертки используется функция conv(x.y).
Обратная свертке функция определена как [q,r]=deconv(z,x). Она фактически определяет импульсную характеристику фильтра. Если z=conv(x,y), то q=y и г=0. Если х и у — векторы с коэффициентами полиномов, то свертка эквивалентна перемножению полиномов, а обратная операция — их делению. При этом вектор q возвращает частное (фактор), а вектор r - остаток от деления полиномов.
19. Функция свертки двумерных массивов
Функция свертки двумерных массивов
Для двумерных массивов также существует функция свертки: Z=conv2(X.Y) и Z=conv2(X,Y. 'option').
Для двумерных массивов X и Y с размером m хп и тхп соответственно результат двумерной свертки порождает массив размера (т +т -1)х(m +п -1). Во второй форме функции параметр option может иметь следующие значения:
-
' full' — полноразмерная свертка (используется по умолчанию);
-
'same' — центральная часть размера тхп ;
-
'valid' — центральная часть размера (т-т +1)х(п-п +1), еслн (тхп х )>(тхп ).
Возможность изменить решение или трактовку данных с помощью параметров является свойством ряда функций системы MATLAB. Позже мы столкнемся с этой возможностью еще не раз.
20. Дискретная одномерная фильтрация
Дискретная одномерная фильтрация
MATLAB может использоваться для моделирования работы цифровых фильтров. Для обеспечения дискретной одномерной фильтрации используется функция filter в следующих формах записи:
-
filter(B.A.X) — фильтрует одномерный массив данных X, используя дискретный фильтр, описываемый следующим конечноразностным уравнением:
a(l)*y(n) = b(1)*x(n) + b(2)*х(п-1) + ... + b(nb+l)*x(n-nb) -- а(2)*у(п-1) - ... - a(na+l)*y(n-na).
Если а(1) не равно 1, то коэффициенты уравнения нормализуются относительно а (1). Когда X — матрица, функция filten оперирует столбцами X. Возможна фильтрация многомерного (размерности N) массива.
-
[Y. Zf]=fi 1 ten(В, A. X, Zi) — выполняет фильтрацию с учетом ненулевого начального состояния фильтра Zi; возвращает помимо выходного сигнала Y конечное состояние фильтра Zf;
-
filter(B.A.X,[ ].dim) или fi!ter(B.A,X.Zi .dim) — работает в направлении размерности dim
Рассмотрим типовой пример фильтрации гармонического сигнала на фоне других сигналов — файл с именем filtdem.m из пакета расширения Signal Processing Toolbox.
Следующий кадр иллюстрирует конструирование фильтра с достаточно плоской вершиной амплитудно-частотной характеристики (АЧХ) и полосой частот, обеспечивающего выделение сигнала с частотой 15 Гц и подавление сигналов с частотами 5 и 30 Гц. Для формирования полосы пропускания фильтра используется функция el 11 р, а для построения АЧХ — функция freqz (обе — из пакета Signal Processing Toolbox). Это позволяет построить график АЧХ созданного фильтра.
Следующий кадр примера иллюстрирует эффективность выделения сигнала заданной частоты (15 Гц) с помощью операции фильтрации — функции filter, описанной выше. Можно заметить два обстоятельства — полученный стационарный сигнал практически синусоидален, что свидетельствует о высокой степени фильтрации побочных сигналов. Однако нарастание сигнала во времени идет достаточно медленно и занимает несколько периодов частоты полезного сигнала. Характер нарастания сигнала во времени определяется переходной характеристикой фильтра.
Заключительный кадр показывает спектр исходного сигнала и спектр сигнала на выходе фильтра (он показан линиями другого цвета, что, к сожалению, не видно на черно-белом рисунке). Для построения спектров используется прямое преобразование Фурье — функция fft.
Этот пример наглядно иллюстрирует технику фильтрации. Рекомендуется просмотреть дополнительные примеры, которые есть в разделе Demos системы применительно к пакету расширения Signal Processing (если этот пакет установлен).
21. Двумерная фильтрация
Двумерная фильтрация
Для осуществления двумерной фильтрации служит функция filter2:
-
filter2(B.X) — фильтрует данные в двумерном массиве X, используя дискретный фильтр, описанный матрицей В. Результат Y имеет те же размеры, что и X;
-
filter2(B,X, 'option') — выполняет то же, но с опцией, влияющей на размер массива Y:
-
'same' — size(Y)=size(X) (действует по умолчанию);
-
'valid' — size(Y) < size(X), центральная часть двумерной свертки, при вычислении которой не приходится дополнять массивы нулями;
-
'full' — size(Y) > size(X), полная двумерная свертка.
-
22. Функция коррекции фазовых углов unwrap
Функция коррекции фазовых углов unwrap
Фазовые углы одномерных массивов испытывают разрывы при переходе через значения, кратные р. Функции unwrap(P) и unwrap(P,cutoff) устраняют этот недостаток одномерного массива Р, дополняя значения углов в точках разрыва значениями ±2р. Если Р — двумерный массив, то данная функция применяется к столбцам. Параметр cutoff (по умолчанию равный р) позволят назначить любой критический угол в точках разрыва. Функция используется при построении фазочастотных характеристик (ФЧХ) фильтров. Поскольку они строятся редко, оставим за читателем изучение практического применения данной функции.
23. Интерполяция и аппроксимация данных
Интерполяция и аппроксимация данных
Под аппроксимацией обычно подразумевается описание некоторой, порой не заданной явно, зависимости или совокупности представляющих ее данных с помощью другой, обычно более простой или более единообразной зависимости. Часто данные находятся в виде отдельных узловых точек, координаты которых задаются таблицей данных.
Результат аппроксимации может не проходить через узловые точки. Напротив, задача интерполяции — найти данные в окрестности узловых точек. Для этого используются подходящие функции, значения которых в узловых точках совпадают с координатами этих точек. Например, при линейной интерполяции зависимости у(х) узловые точки соединяются друг с другом отрезками прямых и считается, что искомые промежуточные точки расположены на этих отрезках.
Для повышения точности интерполяции применяют параболы (квадратичная интерполяция) или полиномы более высокой степени (полиномиальная интерполяция). Для обработки данных MATLAB использует различные функции интерполяции и аппроксимации данных. Набор таких функций вместе с несколькими вспомогательными функциями описан в этом разделе.
24. Полиномиальная регрессия
Полиномиальная регрессия
Одна из наиболее известных аппроксимаций — полиномиальная. В системе MATLAB определены функции аппроксимации данных полиномами по методу наименьших квадратов — полиномиальной регрессии. Это выполняет функция, приведенная ниже:
-
polyfit(x.y.n) — возвращает вектор коэффициентов полинома р(х) степени п, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х). Результатом является вектор-строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней х и у равно n+1, то реализуется обычная полиномиальная аппроксимация, при которой график полинома точно проходит через узловые точки с координатами (х.у), хранящиеся в векторах х и у. В противном случае точного совпадения графика с узловыми точками не наблюдается;
-
[p.S] = polyflt(x.y.n) — возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предсказания погрешности;
-
[p.S] = polyf1t(x,y,n,mu) возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предска-зния погрешности, но так, что присходит центрирование (нормирование) и масштабирование х, xnorm = (х - mu(l))/mu(2), где mu(l) = mean(x) и mu(2) = std(x). Центрирование и масштабирование не только улучшают свойства степенного многочлена, получаемого при помощи polyval, но и значительно повышают качественные характеристики самого алгоритма аппроксимации.
Рис. 17.10. Пример использования функции polyfit
Пример (полиномиальная регрессия для функции s
» х=(-3:0.2:3)';
y=sin(x);
p=polyflt(x,y,3)
р =
-0.0953 0.0000 0.8651 -0.0000
»x=(-4:0.2:4)';y=sin(x);
» f=polyval(p,x);plot(x,y,'o',x,f)
Рис. 17.14, построенный в этом примере, дает наглядное представление о точности полиномиальной аппроксимации. Следует помнить, что она достаточно точна в небольших окрестностях от точки х = 0, но может иметь большие погрешности за их пределами или в промежутках между узловыми точками.
График аппроксимирующего полинома третьей степени на рис. 17.10 показан сплошной линией, а точки исходной зависимости обозначены кружками. К сожалению, при степени полинома свыше 5 погрешность полиномиальной регрессии (и аппроксимации) сильно возрастает и ее применение без центрирования и масштабирования становится рискованным. Обратите внимание на то, что при полиномиальной регрессии узловые точки не ложатся точно на график полинома, поскольку их приближение к нему является наилучшим в смысле минимального среднеквадратического отклонения. Об этом уже говорилось.
10a.gif
10b.gif
25. Интерполяция периодических функции рядом Фурье
Интерполяция периодических функций рядом Фурье
Под интерполяцией обычно подразумевают вычисление значений функции f(x) в промежутках между узловыми точками. Линейная, квадратичная и полиномиальная интерполяция реализуются при полиномиальной аппроксимации. А вот для периодических (и особенно для гладких периодических) функций хорошие результаты может дать их интерполяция тригонометрическим рядом Фурье. Для этого используется следующая функция:
-
interpft(x.n) — возвращает вектор у, содержащий значения периодической функции, определенные в п равномерно расположенных точках. Если length(x)=rr; и х имеет интервал дискретизации dx, то интервал дискретизации для у составляет dy=dx*m/n, причем п не может быть меньше, чем т. Если X — матрица, interpft оперирует столбцами X, возвращая матрицу Y с таким же числом столбцов, как и у X, но с п строками. Функция y=interpft(x.n.dim) работает либо со строками, либо со столбцами в зависимости от значения параметра dim.
Рис. 17.11. Пример использования функции interpft
Пример:
» x=0:10; y=sin(x).^3;
» x1=0:0.1:10; y1=interpft(y,101);
» x2=0:0.01:10; y2=sin(x2).^3;
» plot(x1,y1, 'r').hold on.plot(x,y, 'b',x2,y2)
Рис. 17.11 иллюстрирует эффективность данного вида интерполяции на примере функции sin(x).^3, которая представляет собой сильно искаженную синусоиду.
Исходная функция на рис. 17.12 представлена сплошной линией с кружками, а интерполирующая функция — штрих-пунктирной линией.
11.gif
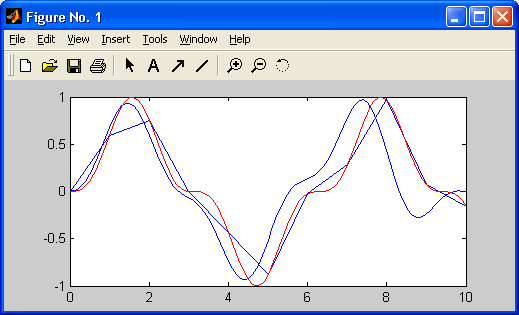
26. Интерполяция на неравномерной сетке
Интерполяция на неравномерной сетке
Для интерполяции на неравномерной сетке используется функция griddata:
-
ZI = griddata(x.y.z.XI.YI) — преобразует поверхность вида z = f(x. у), которая определяется векторами (x.y.z) с (обычно) неравномерно распределенными элементами. Функция griddata аппроксимирует эту поверхность в точках, определенных векторами (XI.YI) в виде значений ZI. Поверхность всегда проходит через заданные точки. XI и YI обычно формируют однородную сетку (созданную с помощью функции meshgrid).
XI может быть вектором-строкой, в этом случае он определяет матрицу с постоянными столбцами. Точно так же YI может быть вектором-столбцом, тогда он определяет матрицу с постоянными строками.
-
[XI.YI.ZI] = griddata(x,y,z,xi ,yi ) — возвращает аппроксимирующую матрицу ZI, как описано выше, а также возвращает матрицы XI и YI, сформированные из вектора-столбца xi и вектора-строки yi . Последние аналогичны матрицам, возвращаемым функцией meshgrid;
-
[...] = griddata (....method) — использует определенный метод интерполяции:
-
'nearest' — ступенчатая интерполяция;
-
'linear' — линейная интерполяция (принята по умолчанию);
-
'cubic' — кубическая интерполяция;
-
' v4 ' — метод, используемый в МATLAB 4.
-
Метод определяет тип аппроксимирующей поверхности. Метод 'cubic 1 формирует гладкие поверхности, в то время как 'linear' и 'nearest' имеют разрывы первых и нулевых производных соответственно. Все методы, за исключением v4, основаны на триангуляции Делоне. Метод ' v4 ' включен для обеспечения совместимости с версией 4 системы MATLAB. Пример:
» x=rand(120.1)*4-2;y=rand(120.1)*4-2;
z=x,*y,*exp(-x.^2-y.^2);
» t=-2:0.1:2;[X,Y]=meshgrid(t,t);
Z=griddata(x.y.z.X.Y);
» mesh(X.Y.Z),hold on;plot3(x.y,z, 'ok')
Функции griddataS и griddatan работают аналогично griddata, но для для трехмерного и n-мерного случая — с использованием алгоритма qhul 1 . Используются, в частности, при трехмерной и n-мерной триангуляции.
Рис. 17.13 иллюстрирует применение функции griddata.
Рис 17.12. Пример использования функции griddata
12.gif
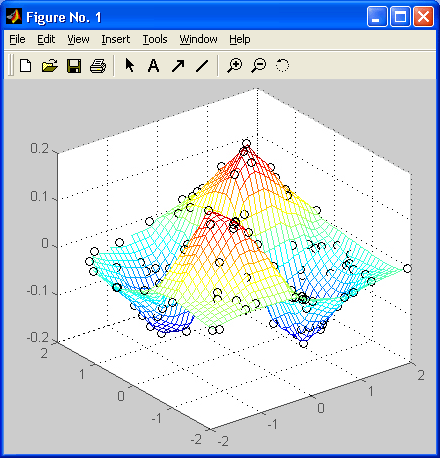
27. Одномерная табличная интерполяция
Одномерная табличная интерполяция
В ряде случаев очень удобна сплайновая интерполяция и аппроксимация таблично заданных функций. При ней промежуточные точки ищутся по отрезкам полиномов третьей степени — это кубическая сплайновая интерполяция. При этом обычно такие полиномы вычисляются так, чтобы не только их значения совпадали с координатами узловых точек, но также чтобы в узловых точках были непрерывны производные первого и второго порядков. Такое поведение характерно для гибкой линейки, закрепленной в узловых точках, откуда и происходит название spline (сплайн) для этого вида интерполяции (аппроксимации). Для одномерной табличной интерполяции используется функция interpl:
-
yi = Interpl(x.Y.xi) — возвращает вектор yi, содержащий элементы, соответствующие элементам xi и полученные интерполяцией векторов х и Y. Вектор х определяет точки, в которых задано значение Y. Если Y — матрица, то интерполяция выполняется для каждого столбца Y и у1 имеет длину length (xi) - by- size (Y. 2);
-
yi = interpl (x.Y.xi .method) — позволяет с помощью параметра method задать метод интерполяции:
-
'nearest' — ступенчатая интерполяция;
-
'linear' — линейная интерполяция (принята по умолчанию);
-
'spline' — кубическая сплайн-интерполяция;
-
'cubic' или 'pchip' — интерполяция многочленами Эрмита;
-
'v5cubic' — кубическая интерполяция MATLAB 5.
-
-
yi = interpl (x.Y.xi .method, значение величин вне пределов изменения х) — позволяет отобразить особенные точки на графике;
-
yi = i nterpl(х, Y, xi.method.' сообщение') — позволяет изменить сообщение об особенных точках на графике.
Все методы интерполяции требуют, чтобы значения х изменялись монотонно. Когда х — вектор равномерно распределенных точек, для более быстрой интерполяции лучше использовать методы '*1inear', '*cubic', '*nearest' или '*spline'. Обратите внимание, что в данном случае наименованию метода предшествует знак звездочки.
Пример (интерполяция функции косинуса):
» x=0:10:y=cos(x);
» xi=0:0.1:10;
» yi=interpl(x,y,xi);
» plot(x,y,'x',xi,yi,'g'),hold on
» yi=interpl(x,y,xi.'spline'):
» plot(x,y,'o ' ,xi,yi,'m').grid,hold off
Узловые точки на рис. 17.17 обозначены кружками с наклонными крестиками. Одна из кривых соответствует линейной интерполяции, другая — сплайн-интерполяции. Нетрудно заметить, что сплайн-интерполяция в данном случае дает гораздо лучшие результаты, чем линейная интерполяция. При последней точки просто соединяются друг с другом отрезками прямых, так что график интерполирующей кривой при линейной интерполяции получается негладким.
28. Двумерная табличная интерполяция
Двумерная табличная интерполяция
Двумерная интерполяция существенно сложнее, чем одномерная, рассмотренная выше, хотя смысл ее тот же — найти промежуточные точки некоторой зависимости z(x, у) вблизи расположенных в пространстве узловых точек. Для двумерной табличной интерполяции используется функция interp2:
-
ZI = interp2(X,Y.Z,XI.YI) — возвращает матрицу ZI, содержащую значения функции в точках, заданных аргументами XI и YI, полученные путем интерполяции двумерной зависимости, заданной матрицами X, Y и Z. При этом X и Y должны быть монотонными и иметь тот же формат, как если бы они были получены с помощью функции meshgrid (строки матрицы X являются идентичными; то же можно сказать о столбцах массива Y). Матрицы X и Y определяют точки, в которых задано значение Z. Параметры XI и YI могут быть матрицами, в этом случае interp2 возвращает значения Z, соответствующие точкам (XI(i,j),YI(i.j)). В качестве альтернативы можно передать в качестве параметров вектор-строку xi и вектор-столбец yi. В этом случае interp2 представляет эти векторы так, как если бы использовалась команда mesh-grid(xi .yi);
-
ZI = interp2(Z,XJ.YI) — подразумевает, что Х=1:n и Y=l:m, где [m.n]=size(Z);
-
ZI = interp2(Z,ntimes) — осуществляет интерполяцию рекурсивным методом с числом шагов ntimes;
-
ZI = interp2(X,Y,Z.XI,YI.method) — позволяет с помощью опции method задать метод интерполяции:
-
'nearest' — интерполяция по соседним точкам;
-
'linear' — линейная интерполяция;
-
'cubic' — кубическая интерполяция (полиномами Эрмита);
-
'spline' — интерполяция сплайнами.
-
Все методы интерполяции требуют, чтобы X и Y изменялись монотонно и имели такой же формат, как если бы они были получены с помощью функции meshgrid. Когда X и Y — векторы равномерно распределенных точек, для более быстрой интерполяции лучше использовать методы '*1inear', '*cubic', или '*nearest'.
Пример:
» [X.Y]=meshgrid(-3:0.25:3);
Z=peaks(X/2.Y*2):
» [Xl,Yl]=meshgrid(-3:0.1:3);
Zl=interp2(X,Y.Z.Xl.Yl) :
» mesh(X.Y,Z).hold on.mesh(Xl.Yl,Zl+15).hold off
Рис. 17.13. Применение функции interpZ
Рис. 17.13 иллюстрирует применение функции interp2 для двумерной интерполяции (на примере функции peaks).
В данном случае поверхность снизу — двумерная линейная интерполяция, которая реализуется по умолчанию, когда не указан параметр method.
13.gif
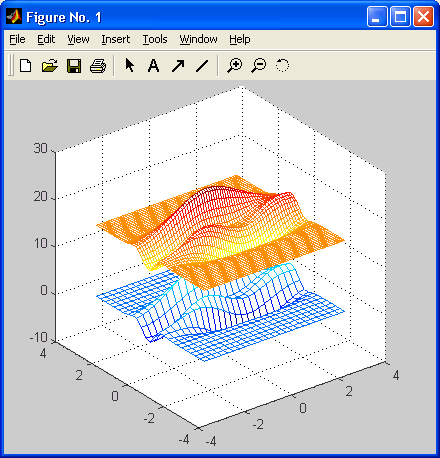
29. Трехмерная табличная интерполяция
Трехмерная табличная интерполяция
Для трехмерной табличной интерполяции используется функция interp3:
-
VI = interp3(X.Y.Z.V.XI,YI.ZI) — интерполирует, чтобы найти VI, значение основной трехмерной функции V в точках матриц XI, YI и ZI. Матрицы X, Y и Z определяют точки, в которых задано значение V. XI, YI и ZI могут быть матрицами, в этом случае InterpS возвращает значения Z, соответствующие точкам (XI (i ,j) ,YI(i. j), ZI (i. j)). В качестве альтернативы можно передать векторы xi, yl и zi. Векторы аргументы, имеющие неодинаковый размер, представляются, как если бы использовалась команда meshgrid;
-
VI = interp3(V.XI.YI.ZI) - подразумевает X=1:N, Y=1:M, Z=1:P, где [M,N.P]=size(V);
-
VI = interpS(V.ntimes) — осуществляет интерполяцию рекурсивным методом с числом шагов ntimes;
-
VI = interp3(... .method) — позволяет задать метод интерполяции:
-
'nearest' — ступенчатая интерполяция;
-
'linear' — линейная интерполяция;
-
'cubic' — кубическая интерполяция (полиномами Эрмита);
-
'spline' — интерполяция сплайнами.
-
Все методы интерполяции требуют, чтобы X, Y и Z изменялись монотонно и имели такой же формат, как если бы они были получены с помощью функции meshgrid. Когда X и Y и Z — векторы равномерно распределенных в пространстве узловых точек, для более быстрой интерполяции лучше использовать методы '*li'near', '*cubic' или '*nearest'.
30. N-мерная табличная интерполяция
N-мерная табличная интерполяция
MATLAB позволяет выполнить даже n-мерную табличную интерполяцию. Для этого используется функция interpn:
-
VI = interpn(X1.X2,X3,... ,V,Y1.Y2.Y3....)- интерполирует, чтобы найти VI, значение основной многомерной функции V в точках массивов Y1, Y2, Y3,.... Функции interpn должно передаваться 2ЛГ+1 аргументов, где N — размерность интерполируемой функции. Массивы X1, Х2, ХЗ,... определяют точки, в которых задано значение V. Параметры Y1, Y2, Y3,... могут быть матрицами, в этом случае interpn возвращает значения VI, соответствующие точкам (YKi, j) ,Y2(i, j), Y3(i, j),...). В качестве альтернативы можно передать векторы yl, y2, уЗ,... В этом случае interpn интерпретирует их, как если бы использовалась команда ndgrid(y1. У2.у3....);
-
VI = interpn(V.Yl,Y2,Y3,...) - подразумевает Xl=1size(V.l), X2=l:size(V,2), X3=l:size(V,3) и т. д.;
-
VI = Interpn(V.ntimes) — осуществляет интерполяцию рекурсивным методом с числом шагов ntimes;
-
VI = interpn(...method) — позволяет указать метод интерполяции:
-
'nearest' — ступенчатая интерполяция;
-
'linear' — линейная интерполяция;
-
'cubic' — кубическая интерполяция.
В связи с редким применением такого вида интерполяции, наглядная трактовка которой отсутствует, примеры ее использования не приводятся.
31. Интерполяция кубическим сплайном
Интерполяция кубическим сплайном
Сплайн-интерполяция используется для представления данных отрезками полиномов невысокой степени — чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Из этого вытекают следующие свойства кубической сплайн-интерполяции:
-
график кусочно-полиномиальной аппроксимирующей функции проходит точно через узловые точки;
-
в узловых точках нет разрывов и резких перегибов функции;
-
благодаря низкой степени полиномов погрешность между узловыми точками обычно достаточно мала;
-
связь между числом узловых точек и степенью полинома отсутствует;
-
поскольку используется множество полиномов, появляется возможность аппроксимации функций с множеством пиков и впадин.
Как отмечалось, в переводе spline означает «гибкая линейка». График интерполирующей функции при этом виде интерполяции можно уподобить кривой, по которой изгибается гибкая линейка, закрепленная в узловых точках. Реализуется сплайн-интерполяция следующей функцией:
-
yi = spline(x,y,xi) — использует векторы х и у, содержащие аргументы функции и ее значения, и вектор xi, задающий новые точки; для нахождения элементов вектора yi используется кубическая сплайн-интерполяция;
-
рр = spline(x.y) — возвращает рр-форму сплайна, используемую в функции ppval и других сплайн-функциях.
Пример:
» х=0:10; y=3*cos(x);
» x1=0:0.1:11;
» y1=spline(x,y.x1);
» plot(x,y,'о',x1,y1,'--')
Сплайн-интерполяция дает неплохие результаты для функций, не имеющих разрывов и резких перегибов. Особенно хорошие результаты получаются для монотонных функций.
Результат интерполяции показан на рис. 17.14.
Рис. 17.14. Пример применения функции spline
Ввиду важности сплайн-интерполяции и аппроксимации в обработке и представлении сложных данных в состав системы MATLAB входит пакет расширения Spline Toolbox, содержащий около 70 дополнительных функций, относящихся к реализации сплайн-интерполяции и аппроксимации, а также графического представления сплайнами их результатов. Для вызова данных об этом пакете (если он установлен) используйте команду help splines.
14a.gif
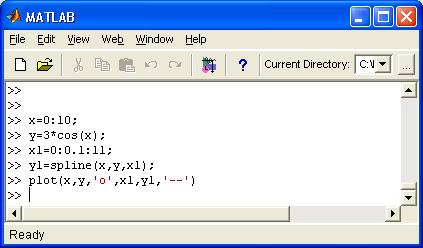
14b.gif
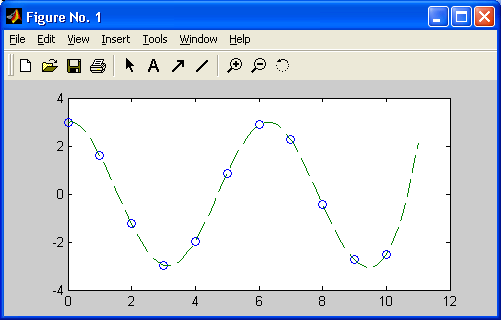
32. Обработка данных в графическом окне
Обработка данных в графическом окне
Средства обработки данных в графическом окне
Решение большинства задач интерполяции и аппроксимации функций и табличных данных обычно сопровождается их визуализацией. Она, как правило, заключается в построении узловых точек функции (или табличных данных) и в построении функции аппроксимации или интерполяции. Для простых видов аппроксимации, например полиномиальной, желательно нанесение на график формулы, полученной для аппроксимации.
В MATLAB 6,0 совмещение функций аппроксимации с графической визуализацией доведено до логического конца — предусмотрена аппроксимация рядом методов точек функции, график которой построен. И все это выполняется прямо в окне редактора графики Property Editor. Для этого в позиции Tools графического окна имеются две новые команды:
-
Basic Fitting - основные виды аппроксимации (регрессии);
-
Data Statistics - статистические параметры данных.
Команда Basic Fitting открывает окно, дающее доступ к ряду видов аппроксима-- ции и регрессии: сплайновой, эрмитовой и полиномиальной со степенями от 1 (линейная аппроксимация) до 10. В том числе со степенью 2 (квадратичная аппроксимация) и 3 (кубическая аппроксимация). Команда Data Statistics открывает окно с результатами простейшей статистической обработки данных.
33. Полиномиальная регрессия для табличных данных
Полиномиальная регрессия для табличных данных
Рассмотрим самый характерный пример обработки данных, примерно представляющих некоторую (например, экспериментальную) зависимость вида у(х). Пусть она задана в табличной форме, причем колонки таблицы соответствуют элементам векторов X и Y одинакового размера в следующем примере:
» Х=[2,4,6,8,10,12,14];
» Y=[3,76,4,4,5,1,5,56,6,6,3,6,7];
» plot(X,Y,'o');
Напомним, что последняя команда строит график узловых точек кружками (без соединения их отрезками прямых).
Примечание
При проведении полиномиальной аппроксимации надо помнить, что максимальная степень полинома на 1 меньше числа точек, т. е. числа элементов в векторах X и Y.
Исполнив команду Tools > Basic Fitting, можно получить окно регрессии. В этом окне птичкой отмечены три вида полиномиальной регрессии — порядка 1 (linear — линейная), 2 (quadratic — квадратичная) и 3 (cubic — кубическая). Стоит отметить какой-либо вид регрессии, как соответствующая кривая функции регрессии (аппроксимации) появится в графическом окне.
Установив птичку у параметра Show equations (Показать уравнения), можно получить в графическом окне запись уравнений регрессии (аппроксимации). Наконец, можно сместить выводимую по умолчанию легенду в место, где она не закрывала бы другие детали графика.
Наконец, исполнив команду Tools > Data Statistics, можно получить окно с рядом статистических параметров данных, представленных векторами X и Y. Отметив птичкой тот или иной параметр в этом окне, можно наблюдать соответствующие построения на графике, например вертикалей с минимальным, средним и максимальных значением у и горизонталей с минимальным, средним и максимальным значением х.
Примечание
Безусловно, эта новинка понравится большинству пользователей системы MATLAB 6.0. Однако нельзя не отметить, что статистические данные более чем скупы.
34. Оценка погрешности аппроксимации
Оценка погрешности аппроксимации
Средства обработки данных из графического окна позволяют строить столбцовый или линейчатый график погрешностей в узловых точках и наносить на эти графики норму погрешности. Норма дает статистическую оценку среднеквадрати-ческой погрешности. Чем она меньше, тем точнее аппроксимация. Для вывода графика погрешности надо установить птичку у параметра Plot residuals (График погрешностей) и в меню ниже этого параметра выбрать тип графика.
Таким образом, интерфейс графического окна позволяет выполнять эффективную обработку данных наиболее распространенными способами.
35. Сплайновая интерполяция в графическом окне
Сплайновая интерполяция в графическом окне
Попытка аппроксимации полиномом 8-й степени не дает положительного результата — кривая проходит внутри облака точек, совершенно не интерполируя это облако.
Однако если применить сплайновую интерполяцию, то картина кардинально меняется. На этот раз кусочная линия интерполяции прекрасно проходит через все точки и поразительно напоминает синусоиду. Даже ее пики со значениями 1 и -1 воспроизводятся удивительно точно, причем и в случаях, когда на них не попадают узловые точки.
Причина столь великолепного результата кроется в уже отмеченных ранее особенностях сплайновой интерполяции - она выполняется по трем ближайшим
точкам, причем эти тройки точек постепенно перемещаются от начала точечного графика функции к ее концу. Кроме того, непрерывность первой и второй производных при сплайновой интерполяции делает кривую очень плавной, что характерно и для первичной функции — синусоиды. Так что данный пример просто является удачным случаем применения сплайновой интерполяции.
Рис. 17.15. Пример сплайновой интерполяции в графическом окне
Мы не можем практически называть этот подход полноценной аппроксимацией, поскольку в данном случае нет единого выражения для аппроксимирующей функции. На каждом отрезке приближения используется кубический полином с новыми коэффициентами. Поэтому и вывода аппроксимирующей функции в поле графика не предусмотрено.
15.gif
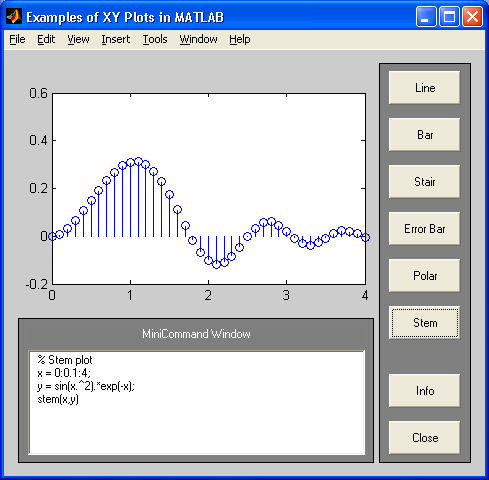
36. Эрмитовая многоинтервальная интерполяция
Эрмитовая многоинтервальная интерполяция
MATLAB 6.0 дает возможность в графическом окне использовать еще один вид многоинтервальной интерполяции на основе полиномов третьей степени Эрмита. Техника интерполяции здесь таже, что и в случае сплайновой интерполяции, (рис. 17.16).
Полиномы Эрмита имеют более гибкие линии, чем сплайны. Они точнее следуют за отдельными изгибами исходной зависимости. Это хорошо показывает рис. 17.16.
Рис. 17.16. Пример эрмитовой интерполяции синусойды в графическом окне
16.gif
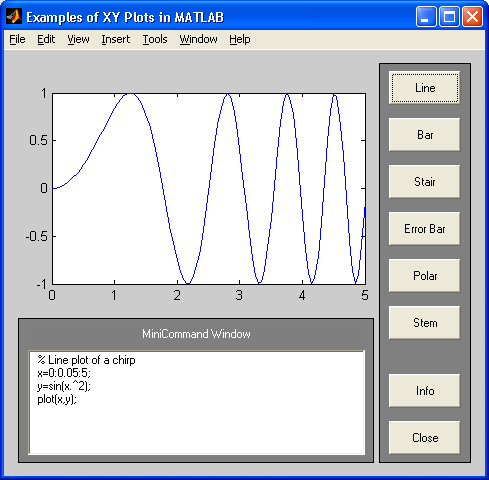
37. Сравнение сплайновой и эрмитовой интерполяции
Сравнение сплайновой и эрмитовой интерполяции
Оба вида интерполяции в данном случае дают превосходные результаты, поскольку представляемая ими кусочная функция практически почти точно проходит через все заданные точки. Однако если учесть, что эти точки принадлежат синусоиде, то в данном случае результаты сплайновой интерполяции оказываются явно лучшими. Особенно это характерно для экстремальных точек.
Поскольку в этих двух методах интерполяции кривая интерполяции проходит точно через узловые точки, в этих точках погрешности интерполяции равны нулю. Вы можете проверить это задав вывод графика погрешности. В целом, можно заключить, что сплайновая интерполяция лучше, когда нужно эффективное сглаживание быстро меняющихся от точки к точке данных и когда исходная зависимость описывается линиями, которые мы наблюдаем при построении их с помощью гибкой линейки. Эрмитова интерполяция лучше отслеживает быстрые изменения исходных данных, но имеет худшие сглаживающие свойства.
Все это говорит о том, что надо внимательно подходить к оценке приемлемости того или иного вида интерполяции (или аппроксимации) для конкретных типов исходных данных.
38. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Выполнять статистическую обработку элементов массивов.
-
Осуществлять триангуляцию и строить диаграммы Вороного.
-
Осуществлять прямое и обратное преобразование Фурье.
-
Осуществлять аппроксимацию и интерполяцию данных.
-
Вести обработку данных в графических окнах.
Урок 18. Работа с символьными данными
1. Урок 18. Работа с символьными данными
Урок №18.
Работа с символьными данными
-
Основные функции символьных данных
-
Операции над строками
-
Преобразование символов и строк
-
Функции преобразования систем счисления
-
Вычисление строковых выражений
Функции обработки массивов символов или рядов этих массивов (строкой в терминологии MATLAB называется любой массив символов или ряд массива символов) для математической системы могут показаться второстепенными. Однако это не так. Строковое представление данных лежит в основе символьной математики, арифметики произвольной точности и многочисленных программных конструкций, не говоря уже о том, что оно широко применяется в базах данных и массивах ячеек. Этот урок посвящен возможностям обработки символьных переменных и выражений в системе MATLAB.
2. Основные функции символьных данных
Основные функции символьных данных
В основе представления символов в строках лежит их кодирование с помощью сменных таблиц кодов. Такие таблицы ставят в однозначное соответствие каждому символу некоторый код со значением от 0 до 255.
Вектор, содержащий строку символов, в системе MATLAB задается следующим образом:
-
S= 'Any Characters' — вектор, компонентами которого являются числовые коды, соответствующие символам [ Символ внутри такой строки дублируется (заменяется на ''). — Примеч. ред. ].
Первые 127 чисел — это коды ASCII, представляющие буквы латинского языка, цифры и спецзнаки. Они образуют основную таблицу кодов. Вторая таблица (коды от 128 до 255) является дополнительной и может использоваться для представления символов других языков, например русского. Длина вектора S соответствует числу символов в строке, включая пробелы. Апостроф внутри строки символов должен вводиться как два апострофа ' '.
К основным строковым функциям относятся следующие:
-
char (X) — преобразует массив X положительных целых чисел (числовых кодов от 0 до 65 535) в массив символов системы MATLAB (причем только первые 127 кодов — английский набор ASCII, со 128 до 255 — расширенный набор ASCII) и возвращает его, на платформе Windows при значении выше 65 535 выдает предупреждение об ошибке, но возвращает русскую букву я (я повторяется так же, как char(255+256rt), где п — целые неотрицательные числа) [ Результат char(x) при х>65535 зависит от платформы, русификации и т. д. — Примеч. ред. ];
Пример:
» X=reshape(32:127,32,3);
» S= char(X')
S=
!"#$*&'()*+.-./0123456789::<=>?
(aABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_
"abcdefghijklmnopqrstuvwxyz{|}-[]
» t1= ' computer'
» t2='for';
» t3='home':
» t4='users':
» S = Char(tl.t2.t3.t4)
S =
computer
for
home
users
-
char (С) — преобразует каждый элемент строкового массива ячеек в ряды массива символов, если строки массива ячеек разного размера, к ним в конце добавляются пробелы (осуществляется набивка (padding) в терминах MATLAB) так чтобы в каждом ряде массива символов было одинаковое число символов;
-
char (Tl, T2, ТЗ), где Т — строки, возвращает массив символов, при этом копии строк T1, T2, Т3 преобразуются в ряды массива символов добавлением при необходимости пробелов в конце рядов массивов символов, как описано ранее;char (java.Tang.string) — преобразует объект класса java.lang. string вмассив символов MATLAB;
-
char (javaarray of java.lang.string) — единственный случай, когда выходным аргументом функции является не массив символов, а строковый массив ячеек, в который преобразуется массив строк Java;
-
double(S) — преобразует символы строки S в числовые коды 0—65535 и возвращает вектор с этими числовыми кодами;
-
ischar'(S) — возвращает логическую единицу, если S является символьной переменной, и логический ноль в противном случае;
-
deblank(str) — возвращает строку, полученную из аргумента — строки str с удаленными из ее конца пробелами;
-
deblank(c) — применяет функцию deblank к каждому элементу строкового массива ячеек с.
Примеры:
» S = 'computer'
S =
computer
» X = double(S)
X =
99 111 109 112 117 116 101 114
» ischar(S)
ans =
1
»c{l,l}='My ';
» c{l,2}='home ';
» c{1.3}='computer ';
» с
с=
'My ' 'home ' 'computer
» с = deblank(c)
с =
'My' 'home' 'computer'
Примечание
Правильная работа строковых функций с дополнительной кодовой таблицей ASCII возможна, но не гарантируется для систем, не прошедших адаптацию под тот или иной язык. В частности, проблемы работы с символами кириллицы (например перевод строки при наборе малой буквы «с» в командной строке) уже обсуждались. Поэтому примеры в этой главе даны для строк с символами основной кодовой таблицы.
3. Операции над строками
Операции над строками
К операциям над строками обычно относят поиск вхождений одних строк в другие, замену регистров символов, объединение строк и т. д. Следующие функции осуществляют операции над строками:
-
findstr(str1,str2) — обеспечивает поиск начальных индексов более короткой строки внутри более длинной и возвращает вектор этих индексов. Индексы указывают положение первого символа более короткой строки в более длинной строке.
Пример:
» strb'Example of the function Is the findstr function';
» str2='the';
» k = findstr(strl,str2)
k =
12 28
-
lower('str') — возвращает строку символов str, в которой символы верхнего регистра переводятся в нижний регистр, а все остальные символы остаются без изменений.
Пример:
» str='Example Of The Function';
» t=lower(str)
t =
example of the function
-
upper( 'str') — возвращает строку символов str, в которой все символы нижнего регистра переводятся в верхний регистр, а все остальные символы остаются без изменений.
Пример:
» str='danger!';
» t = upper(str)
t =
DANGER!
-
strcat(sl,s2,s3,...) — выполняет горизонтальное объединение соответствующих рядов массивов символов s1, s2, s3 и т. д., причем пробелы в конце каждого ряда отбрасываются, и возвращает объединенную строку (ряд) результирующего массива символов, пробелы добавляются заново после анализа строк в полученном массиве. Все входные массивы должны иметь одинаковое число строк (в частном случае должны быть представлены в виде одной строки символов), но если один из входных аргументов — не массив символов, а строковый массив ячеек, то любой из других входных аргументов может быть скаляром или любым массивом той же размерности и того же размера. Если входной массив состоит только из символов, то выходной массив также будет являться массивом символов. Если любой из входных массивов является строковым массивом ячеек, то функция strcat возвращает строковый массив ячеек, сформированный из объединенных соответствующих элементов массивов si, s2, s3. при этом любой из элементов может быть скаляром и т. д.
Примеры:
» sl{1.2}='book' :
» sl sl =
'Home' 'book'
» s2{ 1.1}= 'home ' :
» s2{ 1,2}= 'reading';
» s2 s2 =
'home' 'reading'
» t = strcat(sl.s2)
t =
'Homehome' 'book read ing'
» sl=['wri ']
s1 =wri
» s2=['ter']
s2 =ter
» t = strcat(sl.s2)
t =
writer
-
strvcat(t1,t2,t3....) — выполняет вертикальное объединение строк tl, t2, t3,.. в массив символов S аналогично char(tl,t2.t3....). Пример:
» t1=['string'];
» t2=['concatenation']:
» S = strvcat(tl.t2)
S =
string concatenation
-
strcmp( 'str1' . 'str2') — возвращает логическую единицу, если две сравниваемые строки str1 и str2 идентичны, и логический ноль в противном случае;
-
TF = strcmp(S.T) — возвращает строковый массив ячеек TF, содержащий единицы для идентичных элементов массивов S и Т и нули для всех остальных, причем если один из массивов — не массив символов, а строковый массив ячеек, то перед сравнением из сравниваемых копий рядов массива символов удаляются пробелы в конце строк. Массивы S и Т должны иметь одинаковый размер, или один из них может быть скалярной ячейкой.
Примеры:
» strl='computer';
» str2='computer';
» k = strcmp(strl.str2)
k =
1
» S{l,l}='first';
» S{1,2}='second ' :
» S S =
'first''second'
» T{l.l}='third';
» TF = strcmp(S.T)
TF =
0 0
» T{1.1}='second';
» TF - strcmp(S.T)
TF =
0 1
-
strncmp( 'strT , 'str2' ,n) — возвращает логическую единицу, если две сравниваемые строки strl и str2 содержат n первых идентичных символов, и логический ноль в противном случае. Аргументы strl и str2 могут быть также строковыми массивами ячеек.
-
TF = strncmp(S,T,n) — возвращает строковый массив ячеек TF, содержащий единицы для идентичных (до n символов) элементов массивов S и Т и нули для всех остальных.
Примеры:
» strl='computer'
strl =
computer
» strl='computer for me'
strl =
computer for me
» k = strncmp(strl.str2,3)
k =
1
» k = strncmp(strl,str2.12)
L =
0
-
strmatch( 'str' ,STRS, 'exact') — возвращает только индексы строк символов массива STRS, точно совпадающих со строкой символов str;
-
strjust(S) — возвращает выровненный вправо массив символов (т. е. перемещает пробелы в конце рядов массива символов, если они есть, в начало тех же рядов) [ Функция strjusttS, 'left') возвращает массив символов, где все строки выровнены влево, a strjusttS. 'center') — где все строки выровнены по центру.— Примеч.ред. ];
-
strmatch( 'str' ,STRS) — просматривает массив символов или строковый массив ячеек STRS по строкам, находит строки символов, начинающиеся с строки str, и возвращает соответствующие индексы строк;
Пример:
» STRS{1.1}='character':
» STRS{1.2}='array';
» STRS{2.1}='character array':
» STRS{2.2}='string':
» STRS
STRS =
'character' 'array'
'character array' 'string'
» i = strmatchCcharac'.STRS)
i =
1
2
»i = strmatch('character'.STRS.'exact')
i =
1
-
strrep(strl,str2,str3) — заменяет все подстроки str2, найденные внутри строки символов str1 на строку str3;
-
strrep(strl,str2,str3) — возвращает строковый массив ячеек, полученный в результате выполнения функции strrep над соответствующими рядами входных массивов символов или ячеек, если один из аргументов strl, str2 или str3 — строковый массив ячеек. В этом случае любой из аргументов может быть также скалярной ячейкой.
Пример:
» strl='This is a good example for me.':
» str2='good';
» str3='best';
» str = strrep(strl.str2.str3)
str =
This is a best example for me.
-
strtokCstr' .delimiter) — возвращает часть текстовой строки str, ограниченную с ее конца разделителем del i miter. Символы-разделители в начале строки игнорируются. Вектор delimiter содержит возможные символы-разделители;
-
strtokCstr') — использует символ-разделитель по умолчанию («белое пространство»). Реальными символами-разделителями при этом являются символ табуляции (ASCII-код 9), символ возврата каретки (ASCII-код 13) и пробел (ASCII-код 32);
-
[token,rem]=strtok(...) — возвращает остаток rem исходной строки.
Примеры:
» str='This is a good example for me.':
» token = strtok(str)
token =
This
» token = strtok(str.'f')
token =
This is a good example
» [token,rem] = strtok(str)
token =
This
rem =
is a good example for me.
4. Преобразование символов и строк
Преобразование символов и строк
-
int2str(X) — округляет элементы массива X до целых чисел и возвращает массив символов, содержащих символьные представления округленных целых чисел. Аргумент X может быть скаляром, вектором или матрицей.
Пример:
» X=magic(3)
X =
8 1 б
3 5 7
4 9 2
Х=Х+0.05
X =
8.0500 1.0500 6.0500
3.0500 5.0500 7.0500
4.0500 9.0500 2.0500
» str=int2str(X)
str =
8 1 б 357 492
-
mat2str(A) — преобразует матрицу А в единую строку; если элемент матрицы не скаляр, то он заменяется на [ ], при этом учитываются 15 знаков после десятичной точки;
-
mat2str(A,n) — преобразует матрицу А в строку, используя точность до n цифр после десятичной точки. Функция eval(str) осуществляет обратное преобразование.
Пример:
» randС state');
» A=rand(4.3)
А =
0.9501 0.8913 0.8214
0.2311 0.7621 0.4447
0.6068 0.4565 0.6154
0.4860 0.0185 0.7919
» str = mat2str(A,2)
str =
[0.95 0.89 0.82:0.23 0.76 0.44:0.61 0.46 0.62:0.49 0.019 0.79]
-
num2str(A) — выполняет преобразование массива А в строку символов str с точностью до четырех десятичных разрядов и экспоненциальным представлением, если требуется. Обычно используется при выводе графиков совместно с title, xlabel. ylabel или text;
-
num2str(A,precision) — выполняет преобразование массива А в строку символов str с максимальной точностью, определенной аргументом precision. Аргумент precision определяет число разрядов в выходной строке;
-
num2str(A,format) — выполняет преобразование массива чисел А, используя заданный формат format. По умолчанию принимается формат, который использует четыре разряда после десятичной точки для чисел с фиксированной или плавающей точкой.
Пример:
» str = num2str(pi.7)
str =
3.141593
» randCstate'):
» A=rand(3,5)
A =
0.9501 0.4860 0.4565 0.4447 0.9218
0.2311 0.8913 0.0185 0.6154 0.7382
0.6068 0.7621 0.8214 0.7919 0.1763
» str = num2str(A,l)
str =
1 0.5 0.5 0.4 0.9 0.20.9 0.02 0.6 0.7 0.60.8 0.8 0.8 0.2
-
str2double( 'str') — выполняет преобразование численной строки s, которая представлена в ASCII-символах, в число с двойной точностью. При этом + и -могут быть только в начале строки.
Пример:
» х = str2double('5.45+2.67Г)
5.4500 + 2.67001
Обратите особое внимание на последнюю функцию, поскольку именно она в MATLAB 6 обычно обеспечивает переход от символьного представления математических выражений к их вычисленным численным значениям;
-
str2num(s) — выполняет преобразование численного массива символов — матрицы или строки s, который представлен в ASCII-символах, в матрицу (массив размерности 2).
Пример:
» х = str2num('5.45+2.67')
8.1200
Обратите особое внимание, что при этом можно вводить знаки + и - в любом месте строки. Предыдущая функция выдала бы NaN. Но фирма MathWorks рекомендует использовать str2num с осторожностью и по возможности заменять ее на str2double.
5. Функции преобразования систем счисления
Функции преобразования систем счисления
Некоторые строковые функции служат для преобразования систем счисления. Ниже представлен набор этих функций.
-
bin2dec( 'binarystr') — возвращает десятичное число, эквивалентное строке двоичных символов binarystr.
Пример:
» bin2dec('101')
ans =
5
-
dec2bin(d) — возвращает строку двоичных символов (0 и 1), эквивалентную десятичному числу d. Аргумент d должен быть неотрицательным целым числом, меньшим чем 2 52 ;
-
dec2bin(d.n) — возвращает строку двоичных символов, содержащую по меньшей мере n бит.
Пример:
» str = dec2bin(12)
str =
1100
-
dec2base(d.n) — возвращает строку символов, представляющих десятичное число d как число в системе счисления с основанием n.
Пример:
» str = dec2base(1234.16)
str =
4D2
-
dec2hex(d) — возвращает шестнадцатеричную строку символов, эквивалентную числу d. Аргумент d должен быть неотрицательным целым числом, меньшим чем 2 52 ;
-
str = dec2hex(d.n) — возвращает шестнадцатеричную строку, содержащую по меньшей мере n цифр.
Пример:
» str = dec2hex(1234)
str =
4D2
-
base2dec(S, В) — преобразует строку символов S, представляющих число в системе счисления по основанию В, в символьное представление десятичного числа.
Пример:
» d = base2dec('4D2',16)
d =
1234;
-
hex2dec('hex_value') — возвращает число d, представленное строкой шестнадцатеричных символов hex_value. Если аргумент hex_value является массивоу символов, то каждая строка этого массива интерпретируется как шестнадца-теричное представление числа.
Пример:
» d = hex2dec('4D2')
d =
1234
-
hex2num( 'hex_value') — возвращает десятичное число f с удвоенной точностью, эквивалентное шестнадцатеричному числу, находящемуся в строке символов hex_va1ue.
Пример:
» f = hex2num('4831fb52al8')
f =
6.1189е+039
6. Вычисление строковых выражений
Вычисление строковых выражений
Строковые выражения обычно не вычисляются, так что, к примеру, вывод строки ' 2+3' просто повторяет строку:
» '2+3'
ans =
2+3
Однако с помощью функции eval ('строковое выражение'.) строка, представляющая математическое выражение, может быть вычислена:
» eval C2+3')
ans =
5
» eval('2*sin(l)')
ans =
1.6829
Ниже использование eval возвращает 12 матриц, представляющих магические квадраты чисел от 1 до 12:
for n = 1:12
eval(['IT num2str(n) ' = magic(n)'])
end
eval (SI,S2) — в случае ошибки в вычислении выражения s1 оценивает выражение s2.
T=evalc (S) выполняет то же, что и функция eval(s), но то, что выводится в командное окно, записывается также и в массив Т;
Еще одна функция — feval (@имя_функции,х1,х2,...) — имеет важное достоинство — она позволяет передавать в вычисляемую функцию список ее аргументов. При этом вычисляемая функция задается только своим именем. Это поясняют следующие примеры:
» feval(@prod.[l 23])
ans =
6
Существовавшая в прежних версиях MATLAB форма feval (' иня_функции' ,xl. х2,...) по-прежнему работает, но применять ее не рекомендуется.
» feval(@sum.[l 2 3: 4 5 6].2)
ans =
6
15
Рекомендуется применять функцию feval при вычислении значений функций, записанных в виде строки, вместо eval. m-файлы-функции, содержащие функцию feval, корректно компилируются компилятором системы MATLAB.
Для выполнения вычислений, представленных строкой expression, в заданной рабочей области ws служит функция evalin(ws.expression). Переменная ws может иметь два значения: 'base' — для основной рабочей области и 'caller' — для рабочей области вызванной функции. В приведенном ниже примере в рабочей области записаны переменные а и b и вычисляется символьное значение 'а+b':
» а=2;b=3;
» evalin('base','a+b')
ans =
5
Функция может также записываться в виде [а1.а2,аЗ,...] = eval in(ws, expression), где a1, а2, а3,... — переменные, возвращающие результаты вычислений. А функция evalin(ws,expression, catch_expr) позволяет проверить правильность выражения expression в рабочей области и сформировать сообщение, заданное в строке catch_expr.
Например (в продолжение последнего примера):
» h='Error in expression';
» evalin('base'. 'a+b'. 'h');
ans =
5
» evalinCbase'. 'a+c', 'h'); h = Error in expression
Здесь выражение а+с ошибочно (переменная с не определена), поэтому выдана переменная h с ее значением в виде строки.
7. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Использовать функции строковых данных.
-
Выполнять операции над строками.
-
Преобразовывать символы в строки.
-
Использовать функции преобразования систем счисления.
-
Вычислять строковые выражения.
Урок 19. Работа с файлами
1. Урок 19. Работа с файлами
Урок №19.
Работа с файлами
-
Открытие и закрытие файлов
-
Операции с двоичными файлами
-
Операции над форматированными файлами
-
Позиционирование файла
-
Специализированные файлы
Файлы — это довольно распространенные объекты системы MATLAB. О некоторых типах файлов уже говорилось в предшествующих главах. В этом уроке рассматриваются свойства файлов, которые не зависят от их типа и относятся к любым файлам.
2. Открытие и закрытие файлов
Открытие и закрытие файлов
Файл обычно является некоторой совокупностью данных, объединенных одним именем. Тип файла, как правило, определяется его расширением. Мы рассматриваем файл как некое целое, хотя физически на диске он может быть представлен несколькими областями — говорят, что в этом случае файл фрагментирован.
Перед использованием любого файла он должен быть открыт, а по окончании использования — закрыт. Много файлов может быть открыто и доступно для чтения одновременно. Рассмотрим команды открытия и закрытия файлов.
-
Команда open имя, где имя должно содержать массив символов или символьную переменную, открывает файлы в зависимости от анализа параметра имя и расширения в имени имя:
-
переменная — открывает массив, названный по имени, в редакторе массивов (Array Editor);
-
.mat — открывает файл, сохраняет переменные в структуре в рабочей области;
-
.fig — открывает его в редакторе дескрипторонй графики Property Editor;
-
.m — открывает m-файл в редакторе-отладчике;
-
.mdl - открывает модель в Simulink;
-
.р — открывает, если он есть, m-файл с тем же именем;
-
. html — открывает HTML документ в браузере помощи.
-
Если файлы с расширением существуют в пути MATLAB, то открывается тот файл, который возвращается командой which имя, если нет — то файл из файловой системы. Если файл не имеет расширение имени, то он открывается той программой, формат файлов которой был бы обнаружен функцией игпсИГимя файла') По умолчанию для всех файлов с окончаниями, отличными от вышеперечисленных, вызывается openother. Open вызывает функции орепххх, где ххх — расширение файла. Исключение — переменные рабочей области, для которых вызывается openvar, и рисунки, для работы с которыми вызывается openim. Создавая т-файлы с именем орепххх, пользователи могут изменять обработку файлов и добавлять новые расширения в список. Закрывать файлы, открытые при помощи open, нужно из редакторов, вызываемых ореnххх.
-
[FILENAME, PATHNAME] = uigetfile(FILTERSPEC. Title). Открывает диалог с именем Title и фильтром FILTERSPEC (например, массивом ячеек, содержащим расширения файлов) и возвращает файл, выбранный пользователем, и путь к нему. Возвращает FILENAME=0, если файл не существует или если пользователь нажал на Cancel. [FILENAME, PATHNAME] = uigetfile (FILTERSPEC, Title. X. Y) размещает окно диалога в точке X, Y (координаты в пикселях).
Пример:
[filename, pathname] = uigetfile('*.m;*.fig;*.mat:*.mdl'. 'All MATLAB Files (*.m, *.fig, *.mat. *.mdl)': ...
-
[FILENAME, PATHNAME] = uiputfile(FILTERSPEC. TITLE) сохраняет файл в диалоге, управляемом пользователем. Параметры аналогичны таковым в функции uigetfile.
-
Команда ui open открывает диалог, и если пользователь выбрал файл с известным расширением, вызывает его, используя open, или если имя файла имеет неизвестное расширение, то вызывается uigetfile. Входными аргументами uiopen могут быть mat lab, load, figure, simulink, editor. Без входных аргументов или с входным аргументом matlab в окне диалога предлагается выбрать *.m, *.fig, *.mat, *.mdl (если Simulink установлен) , * . cdr (если state flow установлен) , *.rtw, *.tmf, *.tlc, *.c, *.h, *.ads, *.adb (если установлен Real-Time Workshop). С аргументом load — *.mat. С аргументом figure предлагаются *.fig; simul ink — *.mdl, editor - *.m, *.mdt *.cdr, *.rtw, *.tmf, *.tlc, *.c, *.h, *.ads, *.adb.
Пример:
uiopen figure.
-
Команда uiload открывает файл в диалоге, управляемом пользователем, с использованием команды load.
Функция ui import запускает Мастер импорта (Import Wizard), импортирующий из файла в текущей папке или буфера обмена Windows. Она соответствует выбору Import Data из меню File или выбору Paste Special из меню Edit MATLAB.
-
ui import (FILENAME) — запускает Мастер Импорта, открывая файл FILENAME. Мастер импорта показывает данные для предварительного просмотра. В окне предварительного просмотра появляются данные и их представление в виде переменных MATLAB. Собственно данные, текст и заголовки представляются разными переменными MATLAB. Для данных ASCII вы должны удостовериться, что Мастер импорта распознал разделители столбцов. Самостоятельно он может распознать только символ табуляции, пробел, запятую или точку с запятой. Нужно щелкнуть мышью на кнопке Next и в следующем окне либо подтвердить выбор разделителя, сделанный Мастером, либо выбрать Other и ввести любой разделитель.
-
ui import (' -f i le') — вначале выводит диалог выбора файла.
-
ui import ('-pastespecial') — вначале выводит для предварительного просмотра содержимое буфера обмена Windows.
-
S = ui import (...) хранит результирующие переменные как поля структуры S.
-
Команда uisave — управляемое пользователем сохранение (команда save описана в уроке 2) с Windows диалогом.
-
Функция saveas — сохраняет рисунок или модель Simulink в желаемом формате на носителе информации или на устройстве, разрешенном print.
-
Функция saveas (H, 'FILENAME' ) — сохраняет данные в соответствии с командой дескрипторной графики Н в файле FILENAME. Формат файла определяется расширением имени FILENAME.
-
Функция saveas (H. 'FILENAME' . 'FORMAT' ) — выполняет то же, но с параметром FORMAT (формат задается тем же способом, что и расширение имени файла и может от него отличаться). FORMAT имеет приоритет перед расширением имени файла. Параметры функции:
-
'fig' — сохранить рисунок (график) в двоичном fig-файле;
-
' m ' или ' mf i д ' — сохранить рисунок в двоичном fig-файле и создать m-файл для его загрузки;
-
' mmat ' - сохранить рисунок в m-файле как последовательность команд создания рисунка. Может не поддерживать новейшие графические функции.
-
Примеры:
saveas(gcf. 'output', 'fig') saveas(gcf, 'output', 'bmp')
Команда или функция delete удаляет файл или объект графики.
-
delete имя файла удаляет файл текущей папки. Может быть использована *. Предпочтительно использование с записью в форме функции delete('mw файла'), когда имя файла — строка.
-
delete(H) удаляет графический объект с дескриптором Н. Если этот объект — окно, то оно предварительно закрывается.
-
Функция close(H) закрывает только графические окна. Для закрытия файлов необходимо использовать команду f close.
Для записи файлов на диск служит команда save, используемая в довольно очевидных формах:
save
save filename save filename varl var2 ... save ... option save( ' filename' , ...)
Соответственно для считывания файлов с диска служит команда load:
load
load filename load filename X Y Z
load filename -ascii load filename -mat
S
В этих командах имя файла указывается по правилам, принятым в операционных системах класса MS-DOS. Эти команды обычно дублируются кнопками панелей инструментов и браузером файлов.
3. Операции с двоичными файлами
Операции с двоичными файлами
Двоичными, или бинарными, называют файлы, данные которых представляют собой машинные коды. Основные операции с такими кодами перечислены ниже.
-
fopen(filename, permission) — открывает файл с именем filename и параметром, определенным в permission, и возвращает идентификатор fid со значением: 0 — чтение с клавиатуры (permission установлено в 'r'); 1 — вывод на дисплей (permission установлено в 'а'); 2 — вывод сообщения об ошибке (permission установлен в ' а'); -1 — неудача в открытии файла с выводом сообщения message о типе ошибки. Идентификатор fid часто используется в качестве аргумента другими функциями и программами ввода-вывода. Имя файла filename может содержать путь к файлу.
Если открываемый для чтения файл не найден в текущем каталоге, то функция fopen осуществляет поиск файла по пути, указанном в MATLAB.
Параметр permission может принимать одно из следующих основных значений (другие см. в справочной системе):
-
'r' — открытие файла для чтения (по умолчанию);
-
' r+' — открытие файла для чтения и записи;
-
'w' — удаление содержимого существующего файла или создание нового и открытие его для записи;
-
' а' — создание и открытие нового файла или открытие существующего для записи с добавлением в конец файла.
Добавление к этой строке ' b' (подразумевается по умолчанию) предписывает системе открыть файл в двоичном режиме.
Добавление же вместо b к этой строке ' t', например ' rt', в операционных системах, которые имеют различие между текстовыми и двоичными файлами, предписывает системе открыть файл в текстовом режиме. Например, во всех версиях MATLAB для Windows/MS-DOS и VMS нельзя открыть текстовый файл без параметра ' rt'. При вводе файлов с использованием fopen в текстовом режиме удаляются все символы «возврат каретки» перед символом новой строки.
-
[fid,message] = fopentfilename.permission,format) — открывает файл, как описано выше, возвращая идентификатор файла и сообщение. Кроме того, значение параметра format позволяет точно определить числовой формат. Возможно 8 форматов, описание которых можно найти в справочной системе. В частности, строка format может иметь значения 'native' (формат компьютера, на котором установлена система), 'vax', 'сгау' (компьютеры VAX и Cray) и т. д.
Определенные вызовы функций fread или fwrite могут отменить числовой формат, заданный при вызове функции fopen.
-
fids = fopen С all') — возвращает вектор-строку, содержащую идентификаторы всех открытых файлов, не включая стандартные потоки О, 1 и 2. Число элементов вектора равно числу открытых пользователем файлов;
-
[filename,permission,format] -fopen(fid) — возвращает полное имя файла, строку .permission и строку format. При использовании недопустимых значений fid возвращаются пустые строки для всех выходных аргументов.
Команда fclose закрывает файл. Она имеет следующие варианты.
-
status = fclose(fid) — закрывает файл, если он открыт. Возвращает статус файла status, равный 0, если закрытие завершилось успешно, и -1 в противном случае. Аргумент fid — это идентификатор, связанный с открытым файлом (см. функцию fopen для более подробного описания);
-
status = fclose( 'all') закрывает все открытые файлы. Возвращает 0 в случае успешного завершения и -1 — в противном случае.
Пример открытия и закрытия файла:
» fid=fopen('c:\ex'.'а+') fid = 4
» fclose(4)
ans =
0
-
[A,count] = fread(fid,size,precision) — считывает двоичные данные из заданного файла и помещает их в матрицу А. Выходной аргумент count содержит число удачно считанных элементов. Значение идентификатора fid — это целое число, возвращенное функцией fopen; size — аргумент, определяющий количество считываемых данных. Если аргумент size не определен, функция f read считывает данные до конца файла.
Используются следующие параметры size:
-
n — чтение n элементов в вектор-столбец;
-
inf — чтение элементов до конца файла и помещение их в вектор-столбец, содержащий такое же количество элементов, что и в файле;
-
[m.n] — считывает столько элементов, сколько нужно для заполнения матрицы тхп.
Заполнение происходит по столбцам. Если элементов в файле мало, то матрица дополняется нулями. Если считывание достигает конца файла, не заполнив матрицу необходимого размера, то матрица дополняется нулями. Если происходит ошибка, чтение останавливается на последнем считанном значении. Параметр precision — строка, определяющая числовую точность считывания значений, она контролирует число считанных бит для каждого значения и интерпретирует эти биты как целое число, число с плавающей запятой или как символ
-
[A.count] = fread(fid,size.precision,skip) — включает произвольный аргумент skip, который определяет число байтов, которые необходимо пропустить после каждого считывания. Это может быть полезно при извлечении данных г несмежных областях из записей фиксированной длины. Если precision имеет битовый формат, такой как 'bitN 1 или 'ubitN', значение skip определяется ~ битах. Обширный список возможных значений параметра precision можн найти в справочной системе MATLAB;
-
count=fwrite(fid,A,precision) — записывает элементы матрицы А в файл, представляя их с заданной точностью. Данные записываются в файл по столбцам, выходной аргумент count содержит число удачно записанных элементов. Значение идентификатора fid — это целое число, полученное при использовании функции f open. Добавляет символы «возврат каретки» перед началом новой строки;
-
count=fwrite(fid.A,precision,skip) — делает то же, но включает произвольный аргумент skip, который определяет число байтов, которые надо пропустить перед каждой записью. Это полезно при вставке данных в несмежные области в записях фиксированной длины. Если precision имеет битовый формат, такой как 'bitN' или 'ubitN', значение skip определяется в битах.
Примеры:
» fid = fopen('c:\prim','а+')
fid =
3
» A=magic(7)
А =
|
30 |
39 |
48 |
1 |
10 |
19 |
28 |
|
38 |
47 |
7 |
9 |
18 |
27 |
29 |
|
46 |
6 |
8 |
17 |
26 |
35 |
37 |
|
5 |
14 |
16 |
25 |
34 |
36 |
45 |
|
13 |
15 |
24 |
33 |
42 |
44 |
4 |
|
21 |
23 |
32 |
41 |
43 |
3 |
12 |
|
22 |
31 |
40 |
49 |
2 |
11 |
20 |
» count = fwrite(j.A)
count =
49
» status=fclose(3)
status =
0
» fid
fopen('c:\prim'.'r')
fid =
3
» [B,count] = fread(3.[7.7])
В=
|
30 |
39 |
48 |
1 |
10 |
19 |
28 |
|
|
38 |
47 |
7 |
9 |
18 |
27 |
29 |
|
|
46 |
6 |
8 |
17 |
26 |
35 |
37 |
|
|
5 |
14 |
16 |
25 |
34 |
36 |
45 |
|
|
13 |
15 |
24 |
33 |
42 |
44 |
4 |
|
|
21 |
23 |
32 |
41 |
43 |
3 |
12 |
|
|
22 |
31 |
40 |
49 |
2 |
11 |
20 |
|
|
|
count =
49
4. Операции над форматированными файлами
Операции над форматированными файлами
Файлы, содержащие форматированные данные, называют форматированными файлами. Ниже представлены функции, которые служат для работы с такими файлами.
-
line = fgetl (fid) — возвращает строку из файла с идентификатором fid с удалением символа конца строки. Если функция fgetl обнаруживает конец файла, то она возвращает значение -1 (см. функцию fopen с более подробным описанием fid);
-
line = f gets (fid) — возвращает строку из файла с идентификатором fid, не удаляя символ конца строки. Если функция fgets обнаруживает конец файла, то она возвращает значение -1;
-
line = fgets(fid.nchar) — возвращает не больше чем nchar первых символов строки. После признака конца строки или конца файла никакие дополнительные символы не считываются (см. примеры к функции fscanf);
-
count = fprintf(fid.format,A....) — форматирует данные, содержащиеся в действительной части матрицы А, под контролем строки format и записывает их в файл с идентификатором fid. Функция fprintf возвращает число записанных байтов. Значение идентификатора fid — целое число, возвращаемое функцией fopen.
Если опустить идентификатор fid в списке аргументов функции fprintf, то вывод будет осуществляться на экран, так же как при использовании стандартного вывода (fid=l).
-
fprintf(format,A....) — запись осуществляется на стандартное устройство — экран (но не в файл). Строка format определяет систему счисления, выравнивание, значащие цифры, ширину поля и другие атрибуты выходного формата. Она может содержать обычные буквы алфавита наряду со спецификаторами, знаками выравнивания и т. д.
Таблица 19.1. Специальные символы в строках формата
|
|
||
|
|
\n |
Новая строка |
|
|
\t |
Горизонтальная табуляция |
|
|
\b |
Возврат на один символ |
|
|
\r |
Возврат каретки |
|
|
\f |
Новая страница |
|
|
\\ |
Обратный слеш |
|
|
\" или " |
Одиночная кавычка |
|
|
%% |
Процент |
Функция fprintf ведет себя, как аналогичная функция fprintf О языка ANSI С и с некоторыми исключениями и расширениями. В табл. 19.1 описаны специальные символы, встречающиеся в строке format. Для вывода числовых или символьных данных в строке формата необходимо использовать спецификаторы, перечисленные в табл. 19.2.
Таблица 19.2. Спецификаторы формата вывода данных
|
|
||
| %d | Десятичная система обозначений (со знаком) | |
| %с | Одиночный символ | |
|
%е |
Экспоненциальное представление чисел с использованием символа «е» в нижнем регистре, например 3.1415е + 00 |
|
|
|
%Е |
Экспоненциальное представление чисел с использованием символа «Е» в верхнем регистре, например 3.1415Е + 00 |
|
|
|
%f |
Система обозначений с фиксированной точкой |
|
|
%g |
Наиболее компактный вариант из %е и %f. Незначащие нули не выводятся |
|
|
%G |
То же самое, что и %д, но используется верхний регистр для символа «Е» |
|
|
%о |
Восьмеричная система обозначений (без знака) |
|
|
%s |
Строка символов |
|
|
%u |
Десятичная система обозначений (без знака) |
|
|
%x |
Шестнадцатеричная система обозначений с использованием символов нижнего регистра («a»...«f») |
|
|
|
%X |
Шестнадцатеричная система обозначений с использованием верхнего регистра символов («A»...«F») |
|
Между знаком процента и буквой в спецификатор могут быть вставлены дополнительные символы. Их значение поясняет табл. 19.3.
Таблица 19.3. Параметры спецификаторов формата
|
Знак «минус» (-) |
Выравнивание преобразованных аргументов по левому краю |
%-5.2d |
|
Знак «плюс» (+) |
Всегда печатать знак числа (+ или -) |
%+5.2d |
|
Ноль (0) |
Заполнение нулями вместо пробелов |
%05.2d |
|
Цифры |
Определяет минимальное число знаков, которые будут напечатаны |
%6f |
|
Цифры (после точки) |
Число после точки определяет количество символов, печатаемых справа от десятичной точки |
%6.2f |
-
А = fscanf(fid,format) — читает все данные из файла с идентификатором, fid, преобразует их согласно значению параметра format и возвращает в виде матрицы А. Значение идентификатора fid — целое число, возвращаемое функцией fopen. Параметр format представляет собой строку, определяющую формат данных, которые необходимо прочитать;
-
[A,count] = fscanf(fid.format,size) — считывает количество данных, определенное параметром size, преобразует их в соответствии с параметром format и возвращает вместе с количеством успешно считанных элементов count. Параметр size — это произвольный аргумент, определяющий количество считываемых данных. Допустимы следующие значения:
-
n — чтение п элементов в вектор-столбец;
-
inf — чтение элементов до конца файла и помещение их в вектор-столбец, содержащий такое же количество элементов, что и в файле;
-
[m,n] — считывает столько элементов, сколько требуется для заполнения матрицы размера тхп. Заполнение происходит по столбцам. Величина n (но нет!) может принимать значение Inf.
-
Строка format состоит из обычных символов и (или) спецификаторов. Спецификаторы указывают тип считываемых данных и включают символ %, опцию ширины поля и символы формата. Возможные символы формата перечислены в табл. 19.4.
Таблица 19.4. Символы формата, используемые функцией fscanf
|
|
|
||
|
|
%c |
Последовательность символов; параметр ширины поля определяет количество считываемых символов |
|
|
|
|
||
|
|
%d |
Десятичное число |
|
|
|
%e, %f, %g |
Число с плавающей точкой |
|
|
|
%i |
Целое число со знаком |
|
|
|
%o |
Восьмеричное число со знаком |
|
|
|
%s |
Последовательность непробельных символов |
|
|
|
%u |
Десятичное целое число со знаком |
|
|
|
%x |
Шестнадцатеричное целое число со знаком |
|
|
|
[...] |
Последовательность символов |
|
|
|
|
|
|
Между символом % и символом формата допустимо вставлять следующие символы:
-
звездочка (*) означает, что соответствующее значение не нужно сохранять в выходной матрице;
-
строка цифр задает максимальную ширину поля;
-
буква обозначает размер полученного объекта: h для короткого целого числа (например, %n d), 1 для длинного целого числа (например, %ld) или для числа с двойной точностью с плавающей запятой (например, % lg ).
Примеры:
» х = 0:pi/10:pi:y-[x:sin(x)];
» fid = fopent 'c:\sin.txt'. V);
» fprintf(fid.'X5.3f *10.6f\n'.y):fclose(fid);
0.000 0.000000
0.314 0.309017
0.628 0.587785
0.942 0.809017
1.257 0.951057
1.571 1.000000
1.885 0.951057
2.199 0.809017
2.513 0.587785
2.827 0.309017
3.142 0.000000
» fid = fopen('c:\sin.txt'.'r');
» q=fscanf(fid.'*g'.[2.10]):
» q '
ans =
0 0
0.3140 0.3090
0.6280 0.5878
0.9420 0.8090
1.2570 0.9511
1.5710 1.0000
1.8850 0.9511
2.1990 0.8090
2.5130 0.5878
2.8270 0.3090
» fgetl(fid)
ans =
3.142 0.000000
» fgets(fid)
ans =
-1
» fclose(fid)
ans=
0
5. Позиционирование файла
Позиционирование файла
При считывании и записи файлов они условно представляются в виде линейно расположенных данных, наподобие записи на непрерывной магнитной ленте. Место, с которого идет считывание в данный момент (или позиция, начиная с которой идет запись), определяется специальным указателем. Файлы последовательного доступа просматриваются строго от начала до конца, а в файлах произвольного доступа указатель может быть размещен в любом месте, начиная с которого ведется запись или считывание данных файла.
Таким образом, указатель обеспечивает позиционирование файлов. Имеется ряд функций позиционирования:
-
eofstat = feof(fid) — проверяет, достигнут ли конец файла с идентификатором fid. Возвращает 1, если указатель установлен на конец файла, и 0 — в противном случае;
-
message = ferror(fid) — возвращает сведения об ошибке в виде строки message. Аргумент fid — идентификатор открытого файла (см. функцию fopen с ее подробным описанием);
-
message = f error (f id,'clear') — очищает индикатор ошибки для заданного файла;
-
[message,errnum] = ferror(.) — возвращает номер ошибки errnum последней операции ввода-вывода для заданного файла.
Если последняя операция ввода-вывода, выполненная для определенного значением fid файла, была успешной, значение message — это пустая строка, a errnum принимает значение 0.
Значение errnum, отличное от нуля, говорит о том, что при последней операции ввода-вывода произошла ошибка. Параметр message содержит строку, содержащую информацию о характере возникшей ошибки.
Пример:
» fid=fopen('с:\examplel'.'а+')
fid =
3
» t= fread(3,[4.5])
t =
Empty matrix: 4-by-0
» ferror(3)
ans =
Is the file open for reading? . . .
-
frewind(fid) — устанавливает указатель позиции в начало файла с идентификатором fid;
-
status - fseekCfid,offset,origin) — устанавливает указатель в файле с идентификатором fid в заданную позицию — на байт, указанный параметром offset относительно origin.
Аргументы:
-
fid — идентификатор файла, возвращенный функцией fopen;
-
offset — значение, которое интерпретируется следующим образом:
-
offset>0 — изменяет позицию указателя на offset байт в направлении к концу файла;
-
offset=0 — не меняет позицию указателя;
-
offset<0 — изменяет позицию указателя на offset байт в направлении к началу файла;
-
-
origin — аргумент, принимающий следующие значения:
-
'bof или -1 — начало файла;
-
'cof' или 0 — текущая позиция указателя в файле;
-
' eof' или 1 — конец файла;
-
-
status — выходной аргумент. Принимает значение 0, если операция fseek произошла успешно, и -1 в противном случае. Если произошла ошибка, используйте функцию ferror для получения более подробной информации;
-
position=ftel I (fid) — возвращает позицию указателя для файла с идентификатором fid, полученным с помощью функции fopen. Выходной аргумент position — неотрицательное целое число, определяющее позицию указателя в байтах относительно начала файла. Если запрос был неудачным, position принимает значение -1. Используйте функцию ferror для отображения характера ошибки.
Примеры:
» f id-fopen('с:\example'.'a+')
fid =
3
» count = fwrite(3,magic(6))
count = 36
» ftelK3)
ans =
36
» frewind(3):ftell(3)
ans =
0
» fseek(3.12.0);ftell(3)
ans=
12
» feof(3)
ans =
0
» fclose(3)
ans =
0
-
s=sprintf(format,A,...) — форматирует данные в матрице А в формате, заданном параметром format, и создает из них строковую переменную s;
-
[s.errrmsg] = sprintfCformat,A....) — аналогична ранее описанной функции, но дополнительно возвращает строку ошибки errmsg, если ошибка имела место, или пустую строку в противном случае. Строка format определяет систему счисления, выравнивание, значащие цифры, ширину поля и другие атрибуты выходного формата. Она может содержать обычные символы наряду со спецификаторами, знаками выравнивания и т. д. Функция fprintf ведет себя, как и аналогичная функция fprintf 0 языка ANSI С, с некоторыми исключениями и расширениями.
Примеры:
» sprintf('*0.5g'.(l+sqrt(7))/4)
ans =
0.91144
» sprintfC '%s', 'привет')
ans =
привет
Функция sscanf аналогична функции fscanf за исключением того, что она считывает данные из символьной переменной системы MATLAB, а не из файла.
-
А = sscanf (s,format) — считывает данные из символьной переменной s, преобразует их согласно значению format и создает на основе этих данных матрицу А. Параметр format определяет формат данных, которые нужно считать;
-
А = sscanf(s,format,size) — считывает количество данных, определенное параметром size, и преобразует их согласно строке format. Параметр size представляет собой аргумент, определяющий количество данных для чтения. Допустимы следующие значения:
-
n — чтение п элементов в вектор-столбец;
-
inf — чтение элементов до конца символьной переменной и помещение их в вектор-столбец, содержащий такое же количество элементов, как и в строковой переменной;
-
[m.n] — считывает столько элементов, сколько требуется для заполнения матрицы размера тхп. Заполнение происходит по столбцам. Величина п (но нет!) может принимать значение Inf.
-
-
[A,count,errmsg,nextindex] = sscanf(...) — считывает данные из символьной переменной s, преобразует их согласно значению format и возвращает в матрицу А. Параметр count — выходной.аргумент, который возвращает число успешно считанных элементов; errmsg — выходной аргумент, который возвращает строку ошибки, если ошибка произошла, и пустую строку в противном случае; nextindex — выходной аргумент, который содержит число, на единицу большее, чем количество символов в s.
Строка format состоит из обычных символов и спецификаторов. Спецификаторы указывают тип данных и включают в себя символ %, опцию ширины поля и символы формата. Пояснения можно найти в описании функции fscanf.
Пример:
» s = '4.83 3.16 22 45';
» [A.n,err,next] = sscanf(s. '%f')
А =
4.8300 - 3.1600
22.0000
45.0000
n =
4
еrr=
next =
16
6. Специализированные файлы
Специализированные файлы
Приведенные ниже функции относятся к некоторым специализированным файлам:
-
М = dlmread(filename, delimiter) — считывает данные из файла filename с ASCII-разделителем, используя разделитель delimiter, в массив М. Используйте '\t', i чтобы определить в качестве разделителя символ табуляции;
-
М = dlmreadCfilename.delimiter,г.с) — считывает данные из файла filename с ASCII-разделителем, используя разделитель delimiter, в массив М, начиная со смещения г (по строкам) и с (по столбцам). Параметры r и с отсчитываются начиная с нуля, так что г=0, с=0 соответствует первому значению в файле;
-
М = dlmreadCfilename, deli mi ten, r, с, range) — импортирует индексированный или именованный диапазон данных с разделителями в формате ASCII. Для использования диапазона ячеек нужно определить параметр range в виде range = [ВерхняяСтрока. ЛевыйСтолбец. НижняяСтрока, ПравыйСтолбец].
Аргументы функции dlmread следующие:
-
delimiter — символ, отделяющий отдельные матричные элементы в электронной таблице формата ASCII;
-
(,) — разделитель по умолчанию;
-
r, с — ячейка электронной таблицы, из которой берутся матричные элементы, соответствующие элементам в верхнем левом углу таблицы;
-
range — вектор, определяющий диапазон ячеек электронной таблицы.
Команда dlmwrite преобразует матрицу MATLAB в файл с ASCII-разделителями, читаемый программами электронных таблиц:
-
dl mwri te (f i 1 ename. A. delimiter) — записывает матрицу А в верхнюю левую ячейку электронной таблицы filename, используя разделитель delimiter для отделения элементов матрицы. Используйте ' U' для создания файла с элементами, разделенными табуляцией. Все элементы со значением 0 опускаются. Например, массив [102] появится в файле в виде ' 1., 2' (если разделителем является запятая):
-
dlmwrite(filename,A,delimiter, r,с) — записывает матрицу А в файл filename, начиная с ячейки, определенной r и с, используя разделитель delimiter;
-
info=imfinfo(filename.fmt) — возвращает структуру, поля которой содержат информацию об изображении в графическом файле. Аргумент filename — строка, определяющая имя графического файла, fmt — строка, которая определяет формат файла. Файл должен находиться в текущей директории или в директории, указанной в пути MATLAB. Если imflnfo не может найти файл с именем filename, она ищет файл с именем filename.fmt.
В табл. 19.5 показаны возможные значения для аргумента fmt.
Таблица 19.5. Поддерживаемые графические форматы и их обозначения
|
Формат
|
Тип файла
|
| 'bmp' | Windows Bitmap (BMP) |
| 'hdf ' | Hierarchical Data Format (HDF) |
| 'jpg ' или 'jpeg' | Joint Photographic Experts Group (JPEG) |
| 'pcx' | Windows Paintbrush (PCX) |
| 'tif 'или 'tiff ' | Tagged Image File Format (TIFF) |
| 'xwd' | X Windows Dump (XWD) |
Если filename — TIFF- или HDF-файл, содержащий более одного изображения, то 1 nf о представляет собой массив структур с отдельным элементом (т. е. с индивидуальной структурой) для каждого изображения в файле. Например, info(3) будет в таком случае содержать информацию о третьем изображении в файле. Множество полей в info зависит от конкретного файла и его формата. Однако первые девять полей всегда одинаковы. В табл. 19.6 перечислены эти поля и описаны их значения.
Таблица 19.6. Поля информационной структуры и их значения
|
Поле
|
Значение
|
| Filename | Строка, содержащая имя файла; если файл находится не в текущей директории, строка содержит полный путь к файлу |
| FileModDate | Строка, содержащая дату последнего изменения файла |
| FileSize | Целое число, указывающее размер файла в байтах |
| Format | Строка, содержащая формат файла, заданный параметром fmt; для JPEG- и TIFF-файлов возвращается значение, состоящее из трех символов |
| FormatVersion | Строка или число, описывающее версию формата |
| Width | Целое число, указывающее ширину изображения в пикселях |
| Height | Целое число, указывающее высоту изображения в пикселях |
| BitDepth | Целое число, указывающее число битов на пиксель |
| ColorType | Строка, описывающая тип изображения: 'truecolor' для RGB изображения, 'grayscale' для полутонового изображения или 'indexed' для изображения с индексированными цветами |
-
info = imfinfo(filename) — пытается определить формат файла по содержимому. Пример:
» info = irrifinfo('С:\выставка\Интернет.bmр')
info =
Filename: 'С:\выставка\Интернет.bmр'
FileModDate: '04-Jan-1999 22:35:56'
FileSize: 481078
Format: 'bmp'
FormatVersion: 'Version 3 (Microsoft Windows 3.x)'
или truecolor (RGB) изображение класса uint8, команда imwrite записывает фактические значения массива в файл. Если А имеет класс double, команда imwrite переопределяет значения в массиве перед записью, используя преобразование uint8(round(255*A)). Эта операция преобразует числа с плавающей запятой в диапазоне [0, 1] к 8-битовым целым числам в диапазоне [0, 255]. Допустимые значения параметра ftnt аналогичны тем, что используются в команде imfinfo;
-
imwrite(X,map,filename,fmt) — записывает индексированное изображение, находящееся в массиве X, и соответствующую ему цветовую палитру тар в файл filename. Если X содержит изображение класса uint8, команда imwrite записывает фактические значения массива в файл. Если X имеет класс double, команда imwrite переопределяет значения в массиве перед записью, используя преобразование uintS(X-l). Палитра тар должна иметь класс double; функция imwrite переопределяет значения в тар, используя преобразование uint8(round (255*mар));
-
imwrite (....filename) — записывает изображение в filename в формате, указанном в расширении файла. Расширение может быть одним из допустимых значений параметра fmt;
-
imwrite (....Parameter, Value....) определяет параметры, которые контролируют различные свойства выходного файла. Параметры используются для HDF, JPEG, и TIFF файлов;
-
М = wklread(filename) — считывает электронную таблицу Lotusl23 (WK1) в матрицу М;
-
М = wklread(filename.r.c) — считывает данные, начиная с ячейки, определенной значениями (r,с). Параметры г и с отсчитываются от нуля, так что г=0, с=0 определяют первую ячейку в файле;
-
М = wklread(filename,r,c,range) — считывает диапазон значений, определенный параметром range, где range может быть представлен в одной из следующих форм:
-
вектор с четырьмя элементами, определяющий диапазон ячеек в формате [верхняя_строка. левый_столбец, нижняя_строка, правый_столбец];
-
диапазон ячеек, определенный строкой, например ' А1... С5';
-
имя диапазона, определенное в виде строки, например 'Sales'.
-
-
wklwrite(filename.M) — записывает значения матрицы М в файл filename электронной таблицы Lotus 123 WK1;
-
wklwrite(filename,M,r,c) — записывает данные, начиная с ячейки, определенной значениями (r,с). Параметры г и с отсчитываются от нуля, так что г=0, с=0 определяют первую ячейку в электронной таблице.
В табл. 19.7 представлены форматы изображений, доступных для чтения функцией imread. Списки параметров и их возможных значений для функции imwrite содержатся в табл. 19.8.
Необходимо отметить, что большинство рассмотренных выше функций редко применяются пользователями. Но они довольно широко используются в системных целях и представляют большой интерес для специалистов.
Таблица 19.7. Форматы файлов и их краткое описание
|
Формат
|
Варианты
|
| BMP | 1-битовые, 4-битовые, 8-битовые и 24-битовые несжатые изображения; 4-битовые и 8-битовые изображения со сжатием RLE |
| HDF | 8-разрядные растровые изображения, содержащие или не содержащие цветовую палитру; 24-разрядные растровые изображения |
| JPEG | Любые JPEG-изображения; JPEG-изображения с некоторыми обычно используемыми расширениями |
| PCX | 1-битовые, 8-битовые и 24-битовые изображения |
| TIFF | Любые TIFF-изображения, включая!-битовые, 8-битовые и 24-битовые несжатые изображения; 1-битовые, 8-битовые и 24-битовые изображения с packbit-сжатием; 1-битовые изображения со сжатием CCITT |
| XWD | 1-битовые и 8-битовые Zpixmaps; XYBitmaps; 1-битовые XYPixmaps |
Таблица 19.8. Параметры, используемые при записи графических файлов
| Параметр | Значение | Значение по умолчанию |
| Параметры для HDF-файлов | ||
| 'Compression' | Одно из следующих значений: 'none', Vie', 'jpeg' | 'rle' |
| 'Quality' | Число между 0 и 100; параметр поддерживается для 'Compression'='jpeg'; чем больше число, тем выше качество файла (меньше искажений файла при сжатии) и тем больше его размер | 75 |
| 'WriteMode' | Одно из следующих значений: 'overwrite', 'append' | 'overwrite' |
| Параметры для JPEG-файлов | ||
| 'Quality' | Число между 0 и 100; чем больше число, тем выше качество файла (меньше искажений при сжатии файла) и тем больше его размер. | 75 |
| Параметры для TIFF-файлов | ||
| 'Compression' | Одно из следующих значений: 'none', 'packbits', 'ccitt'; значение 'ccitt' допустимо только для двоичных (двухцветных) изображений | 'ccitt' для двоичных изображений; 'packbits' для всех остальных |
| 'Description' | Любая строка; значение поля ImageDescription возвращается командой imfinfo | Пустая строка |
| 'Resolution' | Скалярное значение для разрешения в направлениях х и у |
72 |
7. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Открывать и закрывать файлы.
-
Выполнять операции с двоичными и форматированными файлами.
-
Осуществлять позиционирование файла.
-
Применять специализированные файлы.
Урок 20. Основы программирования
1. Урок 20. Основы программирования
Урок №20.
Основы программирования
-
Основные понятия программирования
-
Основные типы данных
-
Двойственность операторов, команд и функций
-
Структура и свойства файлов сценариев
-
Структура и свойства файлов функций
-
Статус переменных
-
Использование подфункций
-
Обработка ошибок
-
Функции с переменным числом аргументов
-
Создание Р-кодов
-
Управляющие структуры
-
Диалоговый ввод
-
Условный оператор и циклы
-
Переключатели
-
Средства объектно-ориентированного программирования
2. Основные понятия программирования
Основные понятия программирования
До сих пор мы в основном использовали систему MATLAB в режиме непосредственного счета — в командном режиме. Однако при решении серьезных задач возникает необходимость сохранения используемых последовательностей вычислений, а также их дальнейшей модификации. Иными словами, существует необходимость программирования решения задач.
Это может показаться отходом от важной цели, которая преследуется разработчиками большинства математических систем, — выполнения математических вычислений без использования традиционного программирования. Однако это не так. Выше было показано, что множество математических задач решается в системе MATLAB без программирования. С использованием языков высокого уровня для их решения потребовалось бы написать и оттестировать сотни программ.
Практически невозможно предусмотреть в одной, даже самой большой и мощной, математической системе возможность решения всех задач, которые могут интересовать пользователя. Программирование в системе MATLAB является эффективным средством ее расширения и адаптации к решению специфических проблем. Оно реализуется с помощью языка программирования системы.
Большинство объектов этого языка, в частности все команды, операторы и функции, одновременно являются объектами входного языка общения с системой в командном режиме работы. Так что фактически мы приступили к описанию языка программирования системы MATLAB с первых строк данной книги.
Так в чем же отличие входного языка от языка программирования? В основном — в способе фиксации создаваемых ими кодов. Сессии в командном режиме работы не сохраняются в памяти компьютера (ведение дневника не в счет). Хранятся только определения созданных в ходе их выполнения переменных и функций. А вот программы на языке программирования MATLAB сохраняются в виде текстовых m-файлов. При этом могут сохраняться как целые программы в виде файлов-сценариев, так и отдельные программные модули — функции. Кроме того, важно, что программа может менять структуру алгоритмов вычислений в зависимости от входных данных и данных, создаваемых в ходе вычислений.
С позиций программиста язык программирования системы является типичным проблемно-ориентированным языком программирования высокого уровня. Точнее говоря, это даже язык сверхвысокого уровня, содержащий сложные операторы и функции, реализация которых на обычных языках (например, Бейсике, Паскале или Си) потребовала бы много усилий и времени. К таким функциям относятся матричные функции, функции быстрого преобразования Фурье (БПФ) и др., а к операторам — операторы построения разнообразных графиков, генерации матриц определенного вида и т. д.
3. Основные средства программирования
Основные средства программирования
Итак, программами в системе MATLAB являются m-файлы текстового формата, содержащие запись программ в виде программных кодов. Язык программирования системы MATLAB имеет следующие средства:
-
данные различного типа;
-
константы и переменные;
-
операторы, включая операторы математических выражений;
-
встроенные команды и функции;
-
функции пользователя;
-
управляющие структуры;
-
системные операторы и функции;
-
средства расширения языка.
Коды программ в системе MATLAB пишутся на языке высокого уровня, достаточно понятном для пользователей умеренной квалификации в области программирования. Язык программирования MATLAB является типичным интерпретатором. Это означает, что каждая инструкция программы распознается и тут же исполняется, что облегчает обеспечение диалогового режима общения с системой. Этап компиляции всех инструкций, т. е. полной программы, отсутствует. Высокая скорость выполнения программ обеспечена наличием заведомо откомпилированного ядра, хранящего в себе критичные к скорости выполнения инструкции, такие как базовые математические и иные функции, а также тщательной отработкой системы контроля синтаксиса программ в режиме интерпретации.
Интерпретация означает, что MATLAB не создает исполняемых конечных программ. Они существуют лишь в виде m-файлов. Для выполнения программ необходима среда MATLAB. Однако для программ на языке MATLAB созданы компиляторы, транслирующие программы MATLAB в коды языков программирования С и C++. Это решает задачу создания исполняемых программ, первоначально разрабатываемых в среде MATLAB. Компиляторы для системы MATLAB являются вполне самостоятельными программными средствами и в данной книге не рассматриваются.
Следует особо отметить, что не все инструкции MATLAB могут компилироваться, так что перед компиляцией программы нуждаются в некоторой доработке. Зато скорость выполнения откомпилированных программ порой возрастает в 10-15 раз (правда, это достигается, как правило, для простых примеров с большими циклами).
Начальное представление о переменных, встроенных константах и функциях уже было дано в предшествующих главах. В этой главе эти представления будут существенно расширены с позиций пользователя-программиста.
4. Основные типы данных
Основные типы данных
Структура типов данных системы MATLAB представлена ниже:
Типы данных array и numeric являются виртуальными («кажущимися»), поскольку к ним нельзя отнести какие-либо переменные. Они служат для определения и комплектования некоторых типов данных. Таким образом, в MATLAB определены следующие основные типы данных, в общем случае представляющих собой многомерные массивы:
-
single — числовые массивы с числами одинарной точности;
-
double — числовые массивы с числами удвоенной точности;
-
char — строчные массивы с элементами-символами;
-
sparse — наследует свойства double, разреженные матрицы с элементами-числами удвоенной точности;
-
сеll — массивы ячеек; ячейки, в свою очередь, тоже могут быть массивами;
-
struct — массивы структур с полями, которые также могут содержать массивы;
-
function_handle — дескрипторы функций:
-
int32, uint32 — массивы 32-разрядных чисел со знаком и без знаков;
-
intl6,uint!6 — массивы 16-разрядных целых чисел со знаком и без знаков;
-
int8. uint8 — массивы 8-разрядных целых чисел со знаками и без знаков.
Кроме того, предусмотрен еще один тип данных — UserObject, который относится к типам данных (объектом), определяемым пользователем. Типы данных double, char и sparse были рассмотрены ранее, так что в этой главе будут детально рассмотрены оставшиеся типы. Что касается чисел класса uint8, то они представляют значения от 0 до 255 и занимают в памяти 1/8 часть от размера одного числа с двойной точностью. В основном этот тип данных применяется в служебных целях.
Каждому типу данных можно соотнести некоторые характерные для него операции, называемые методами. Дочерние типы данных, расположенные на приведенной диаграмме ниже родительских типов, наследуют от последних их методы, что является признаком наследования объектов. Поскольку в иерархии типов данных сверху находятся данные типа array, это значит, что все виды данных в MATLAB являются массивами.
5. Виды программирования
Виды программирования
На рынке программного обеспечения система MATLAB позиционируется как язык высокого уровня для научно-технических расчетов. Таким образом, возможность программирования относится к важным достоинствам данного языка, несмотря на обилие средств прямого решения задач. И действительно, именно возможность программирования сложных задач и практически неограниченного расширения системы сделала MATLAB столь почитаемой системой в университетах и крупных научных учреждениях. MATLAB открывает широчайшие возможности реализации новых алгоритмов вычислений, численных методов и методик расчета и проектирования различных систем и устройств.
Язык программирования системы MATLAB вобрал в себя все средства, необходимые для реализации различных видов программирования:
-
процедурного;
-
операторного;
-
функционального;
-
логического;
-
структурного (модульного);
-
объектно-ориентированного;
-
визуально-ориентированного.
В основе процедурного, операторного и функционального типов программирования лежат процедуры, операторы и функции, используемые как основные объекты языка. Эти типы объектов присутствуют в MATLAB. Логическое программирование реализуется в MATLAB с помощью логических операторов и функций. Это позволяет реализовать основные идеи логического программирования, хотя на выдающуюся роль в этом классе языков программирования MATLAB не претендует.
Зато MATLAB представляет собой яркий пример плодотворности структурного программирования. Подавляющее большинство функций и команд языка представляют собой вполне законченные модули, обмен данными между которыми происходит через их входные параметры, хотя возможен обмен информацией и через глобальные переменные. Программные модули оформлены в виде текстовых m-файлов, которые хранятся на диске и подключаются к программам по мере необходимости. Важно отметить, что в отличие от многих языков программирования, применение тех или иных модулей не требует предварительного объявления, а для создания и отладки самостоятельных модулей MATLAB имеет все необходимые средства. Подавляющее большинство команд и функций системы MATLAB поставляется в виде таких модулей.
Объектно-ориентированное программирование также широко представлено в системе MATLAB. Оно особенно актуально при программировании задач графики. Что качается визуально-ориентированного программирования, то в MATLAB оно представлено в основном в пакете моделирования заданных блоками устройств и систем Simulink. Этот пакет будет рассмотрен в конце книги. В ядре системы в данный момент визуально-ориентированное программирование не используется.
6. Двойственность операторов, команд и функций
Двойственность операторов, команд и функций
Для языка системы MATLAB различие между командами (выполняемыми при вводе с клавиатуры) и программными операторами (выполняемыми из программы) является условным. И команды, и программные операторы могут выполняться как из программы, так и в режиме прямых вычислений. Под командами далее в основном понимаются средства, управляющие периферийным оборудованием, под операторами — средства, выполняющие операции с операндами (данными).
Функция преобразует одни данные в другие. Для многих функций характерен возврат значений в ответ на обращение к ним с указанием списка входных параметров — аргументов. Например, говорят, что функция sin(x) в ответ на обращение к ней возвращает значение синуса аргумента х. Поэтому функцию можно использовать в арифметических выражениях, например 2*sin(x+1). Для операторов (и команд), не возвращающих значения, такое применение обычно абсурдно. В данной книге все функции, возвращающие единственное значение (или один массив), записываются малыми (строчными) буквами в виде
f_nаmе(Список_параметров).
Тем самым мы исключаем искусственное выделение имен функций большими (заглавными) буквами, принятое в справочной системе MATLAB. Напоминаем, что как в командной строке, так и в текстах m-файлов функции записываются только малыми буквами. Для функций, возвращающих ряд значений или массивов (например X, Y, Z,...), запись имеет следующий вид: [X. Y, Z. ...]=f_name(Cписок_параметров)
Важное значение имеет двойственность операторов и функций. Многие операторы имеют свои аналоги в виде функций. Так, например, оператор «+» имеет аналог в виде функции sum. Команды, записанные в виде
Command argument
нередко имеют форму записи и в виде функции:
Command(' argument')
Примеры:
» help sin SIN Sine.
SIN(X) is the sine of the elements of X.
Overloaded methods
help sym/sin.m
» help('sin') SIN Sine.
SIN(X) is the sine of the elements of X.
Overloaded methods
help sym/sin.m
» type('sin')
sin is a built-in function.
» type sin
sin is a built-in function.
Указанная двойственность лежит в основе выбора между процедурным и функциональным типами программирования, каждый из которых имеет своих поклонников и противников и может (в той или иной мере) подходить для решения различных классов задач. При этом переход от одного типа программирования к другому возможен в пределах одной программы и происходит настолько естественно, что большинство пользователей даже не задумывается над тем, каким же типом (или стилем) программирования они преимущественно пользуются.
7. Некоторые ограничения
Некоторые ограничения
Поскольку язык программирования системы MATLAB ориентирован на структурное программирование, в нем нет номеров строк (присущих до недавнего времени Бейсику) и программных операторов безусловного перехода GO TO. Имеются лишь управляющие структуры следующих типов: условных выражений if... el se...elseif...end, циклы for...end и while...end. Их форма похожа на ту, которая используется в языке Pascal (т. е. область действия управляющих структур начинается их заголовком, но без слова begin, а заканчивается словом end). С позиций теории структурного программирования этих средств достаточно для решения любых задач. В MATLAB имеются также операторы-переключатели типа case.
Однако в MATLAB исключены те средства, возможности которых можно реализовать уже имеющимися средствами. Зато резко увеличен набор средств программирования для решения математических задач, прежде всего сводящихся к матричным вычислениям и реализации современных численных методов.
Программирование простых задач в среде MATLAB очень напоминает программирование на Бейсике. Во многих случаях программы на Бейсике можно почти дословно перевести на язык системы, учтя небольшие отличия в синтаксисе этих языков. Это нельзя трактовать как отсутствие у языка MATLAB индивидуальных черт. Любители Си, Паскаля или Фортрана также заметят сходство этих языков с языком программирования MATLAB. Так что правильнее считать, что этот язык имеет вполне самостоятельное значение. Он вобрал в себя лучшие средства универсальных языков программирования.
8. М-файлы сценариев и функций
М-файлы сценариев и функций
Структура и свойства файлов сценариев
Итак, мы установили, что работа в командном режиме (сессия) не является программированием. Внешним атрибутом последнего в MATLAB служит задание последовательности действий по программе, записанной в виде m-файла. В уроке 5 было показано, что для создания m-файлов может использоваться как встроенный редактор, так и любой текстовый редактор, поддерживающий формат ASCII. Подготовленный и записанный на диск m-файл становится частью системы, и его можно вызывать как из командной строки, так и из другого m-файла. Есть два типа m-файлов: файлы-сценарии и файлы-функции. Важно, что в процессе своего создания они проходят синтаксический контроль с помощью встроенного в систему MATLAB редактора/отладчика m-файлов.
Файл-сценарий, именуемый также Script-файлом, является просто записью серии команд без входных и выходных параметров. Он имеет следующую структуру:
«Основной комментарий %Дополнительный комментарий Тело файла с любыми выражениями Важны следующие свойства файлов-сценариев:
-
они не имеют входных и выходных аргументов;
-
работают с данными из рабочей области;
-
в процессе выполнения не компилируются;
-
представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, что используется в сессии.
Основным комментарием является первая строка текстовых комментариев, а дополнительным — последующие строки. Основной комментарий выводится при выполнении команд lookfor и help имя_каталога. Полный комментарий выводится при выполнении команды help Имя_файла. Рассмотрим следующий файл-сценарий:
%Plot with color red
%Строит график синусоиды линией красного цвета
%с выведенной масштабной сеткой в интервале [xmin.xmax]
x=xmin:0.1:xmax;
plot(x.sin(x).'r')
grid on
Первые три строки здесь — это комментарий, остальные — тело файла. Обратите внимание на возможность задания комментария на русском языке. Знак % в комментариях должен начинаться с первой позиции строки. В противном случае команда help name не будет воспринимать комментарий (иногда это может понадобиться) и возвратит сообщение вида No help comments found in-name.m.
Обратите внимание на то, что такой файл нельзя запустить без предварительной подготовки, сводящейся к заданию значений переменным xmin и хтах, использованным в теле файла. Это следствие первого свойства файлов-сценариев — они работают с данными из рабочей области. Переменные, используемые в файлах-сценариях, являются глобальными, т. е. они действуют одинаково в командах сессии и внутри программного блока, которым является файл-сценарий. Поэтому заданные в сессии значения переменных используются и в теле файла. Имена файлов-сценариев нельзя использовать в качестве параметров функций, поскольку файлы-сценарии не возвращают значений. Можно сказать, что файл-сценарий — это простейшая программа на языке программирования MATLAB [ Файлы-сценарии нельзя компилировать. Перед компилированием их нужно преобразовать в файлы-функции — Примеч. ред. ].
Рис.20.2. Пример работы с файлом pcr
1.gif
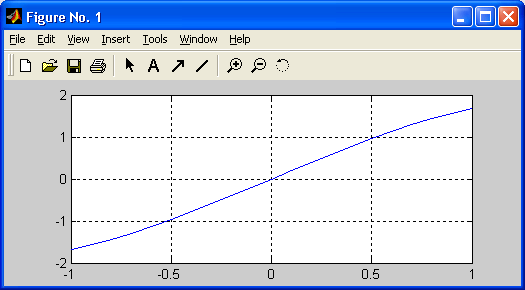
9. Статус переменных в функциях
Статус переменных в функциях
Переменные, указанные в списке параметров функции, являются локальными и служат для переноса значений, которые подставляются на их место при вызовах функций.
Эта особенность переменных-параметров хорошо видна при разборе примера, показанного на рис. 20.3. Здесь (признаемся, что неточно) задана некоторая функция двух переменных fun(x, у).
В этом примере в окне редактора создана функция fun двух переменных х и у, вычисляющая z = х 2 +у 2 . Поскольку переменные х и у указаны как параметры функции fun(x, у), то они являются локальными. В примере вне тела функции им заданы нулевые значения. Очевидно, что при вычислении значения fun(2, 3) в теле функции задается х=2 и у=3. Поэтому результат — z=13. Однако после выхода из тела функции переменные х и у принимают свои исходные значения, равные нулю. Так что эти переменные меняют свои значения на значения параметров функции только локально — в пределах тела функции.
А каков статус переменной z в нашем примере? Она, как и любая переменная, определенная в теле функции, также будет локальной. Изначально ее значение не определено. В теле функции переменная принимает значение z=13. А после возврата из функции, как нетрудно увидеть из рис. 18.2, переменная z, несмотря на ее применение в теле функции, остается неопределенной. На это указывает сообщение, отображаемое после попытки вывода значения переменной z.
Рис. 20.3. Пример, поясняющий действие локальных и глобальных переменных при задании файла-функции
Возврат из функции производится после обработки всего тела функции, т. е. при достижении конца файла функции. При использовании в теле функции условных операторов, циклов или переключателей иногда возникает необходимость осуществить возврат функции раньше, чем будет достигнут конец файла. Для этого служит команда return. В любом случае, результатом, возвращаемым функцией, являются значения выходных параметров (в нашем случае выходным параметром является переменная z), присвоенные им на момент возврата.
У нашей функции имеется один недостаток — вывод на индикацию значения z=13 из тела функции, хотя после этого г остается равным 0. Чтобы убрать побочный эффект вывода значения z, достаточно установить знак ; после математического выражения, определяющего z. Таким образом, окончательно наша функция должна записываться следующим образом:
function z=fun(x,y)
z=x^2+y^2;
Этот пример наглядно показывает, что пропуск любого слова или даже простого оператора (вроде знака :) может привести к не сразу понятным побочным эффектам и даже неверной работе функции. Программирование требует особой точности и педантичности, именно поэтому далеко не все могут быть хорошими программистами.
10. Структура М-файла-функции
Структура М-файла-функции
М-файл-функция является типичным объектом языка программирования системы MATLAB. Одновременно он является полноценным модулем с точки зрения структурного программирования, поскольку содержит входные и выходные параметры и использует аппарат локальных переменных. Структура такого модуля с одним выходным параметром выглядит следующим образом:
function var=f_name(Cnncoк_napaмeтpов)
%Основной комментарий
%Дополнительный комментарий
Тело файла с любыми выражениями
vаr=выражение
М-файл-функция имеет следующие свойства:
-
он начинается с объявления function, после которого указывается имя переменной van — выходного параметра, имя самой функции и список ее входных параметров;
-
функция возвращает свое значение и может использоваться в виде name (Список_параметров) в математических выражениях;
-
все переменные, имеющиеся в теле файла-функции, являются локальными, т. е. действуют только в пределах тела функции;
-
файл-функция является самостоятельным программным модулем, который общается с другими модулями через свои входные и выходные параметры;
-
правила вывода комментариев те же, что у файлов-сценариев;
-
файл-функция служит средством расширения системы MATLAB;
-
при обнаружении файла-функции он компилируется и затем исполняется, а созданные машинные коды хранятся в рабочей области системы MATLAB.
Последняя конструкция vаг=выражение вводится, если требуется, чтобы функция возвращала результат вычислений.
Приведенная форма файла-функции характерна для функции с одним выходным параметром. Если выходных параметров больше, то они указываются в квадратных скобках после слова function. При этом структура модуля имеет следующий вид:
function [varl,var2....]=f_name(Список_параметров)
%Основной комментарий
%Дополнительный комментарий
Тело файла с любыми выражениями
vаг1=выражение
vаг2=выражение
Такая функция во многом напоминает процедуру. Ее нельзя слепо использовать непосредственно в математических выражениях, поскольку она возвращает не единственный результат, а множество результатов — по числу выходных параметров. Если функция используется как имеющая единственный выходной параметр, но имеет ряд выходных параметров, то для возврата значения будет использоваться первый из них. Это зачастую ведет к ошибкам в математических вычислениях. Поэтому, как отмечалось, данная функция используется как отдельный элемент программ вида:
[var1,va2,... ]=f_nаmе(Список_параметров)
После его применения переменные выхода varl, var2,... становятся определенными и их можно использовать в последующих математических выражениях и иных сегментах программы. Если функция используется в виде nаmе(Список_параметров), то возвращается значение только первого выходного параметра — переменной varl.
11. Статус переменных и команда global
Статус переменных и команда global
Итак, из сказанного ясно, что переменные в файлах-сценариях являются глобальными, а в файлах-функциях — локальными. Нередко применение глобальных переменных в программных модулях может приводить к побочным эффектам. Применение локальных переменных устраняет эту возможность и отвечает требованиям структурного программирования.
Однако передача данных из модуля в модуль в этом случае происходит только через входные и выходные параметры, что требует тщательного планирования такой передачи. В жизни мы далеко не всегда едим черную икру (локальные переменные) и часто хотим отведать черного хлебушка (глобальные переменные). Так и при создании файлов-функций порой желательно применение глобальных переменных. Ответственность за это должен брать на себя программист, создающий программные модули.
Команда global varl var2... позволяет объявить переменные модуля-функции глобальными. Таким образом, внутри функции могут использоваться и такие переменные, если это нужно по условиям решения вашей задачи [ Чтобы несколько программных модулей могли совместно использовать глобальную переменную, i идентификатор должен быть объявлен как global во всех модулях. ].
12. Использование подфункций
Использование подфункций
Начиная с версии 5.0 в функции системы MATLAB можно включать подфункции. Они объявляются и записываются в теле основных функций и имеют идентичную им конструкцию. Не следует путать эти функции с внутренними функциями, встроенными в ядро системы MATLAB. Ниже представлен пример функции с подфункцией:
function [mean.stdev] = statv(x)
USTATV Interesting statistics.
%Пример функции с встроенной подфункций
n = length(x);
mean = avg(x.n);
stdev = sqrt(sum((x-avg(x.n)). ^ 2)/n);
%--------------------------------------
function m = avg(x.n) £Mean subfunction m = sum(x)/n;
В этом примере среднее значение элементов вектора х вычисляется с помощью подфункции avg(x.n), тело которой записано в теле основной функции statv. Пример использования функции statv представлен ниже:
» V=[l 2345]
V=
12345
» [a,m]=statv(V)
а =
3
m =
1.4142 » statv(V)
ans =
3
» help statv
STATV Interesting statistics.
Пример функции с встроенной подфункций
Подфункции определены и действуют локально, т. е. только в пределах т-файла, определяющего основную функцию. Команда help пате выводит комментарий, относящийся только к основной функции, тогда как команда type name выводит весь листинг m-файла. Так что заданные в некотором m-файле подфункции нельзя использовать ни в командном режиме работы, ни в других т-файлах. При обращении к функции интерпретатор системы MATLAB прежде всего просматривает m-файл на предмет выявления подфункций. Если они обнаружены, то задаются как локальные функции. Благодаря локальному действию подфункций их имена могут совпадать с именами основных функций системы. Если в функции и подфункциях должны использоваться общие переменные, их надо объявить глобальными как в функции, так и в ее подфункциях.
13. Частные каталоги
Частные каталоги
Для записи m-файлов используются каталоги, называемые родительскими каталогами. Они содержат группы файлов определенного функционального назначения, например по статистическим расчетам, матричным операциям, вычислению определенных классов функций и т. д.
Однако начиная с версии MATLAB 5.0 появилась возможность в родительских каталогах создавать частные каталоги с именем PRIVATE. Расположенные в них m-файлы доступны только файлам родительского каталога. Файлы частных каталогов просматриваются интерпретатором системы MATLAB в первую очередь. Применение частных каталогов позволяет изменять исходные файлы, сохраняя оригиналы в родительском каталоге в неизменном виде.
Если вы решили отказаться от применения измененного файла, достаточно стереть его в частном каталоге. Такая возможность связана с тем, что интерпретатор при поиске m-файла прежде всего просматривает частный каталог и интерпретирует найденный в нем файл. И только если файл не найден, ищется файл в родительском каталоге.
14. Обработка ошибок
Обработка ошибок
Часто в ходе вычислений возникают ошибки. Например, мы уже сталкивались с проблемой вычисления функции sin(x)/x — при х = 0 имеет место ошибка вида «деление на ноль». При появлении ошибки вычисления могут завершиться досрочно с выводом сообщения об ошибке. Следует, однако, отметить, что не все ошибки вызывают остановку вычислений. Некоторые сопровождаются только выдачей предупреждающей надписи.
Такие ситуации должны учитываться программистом, отмечаться как ошибочные и по возможности устраняться. Для вывода сообщения об ошибке служит команда error('Сообщение об ошибке'), при выполнении которой вычисления прерываются и выдается сообщение об ошибке, заданное в апострофах. Ниже дан пример вычисления функции sd(x)=sin(x)/x, в котором задано сообщение об ошибке на русском языке:
function f=sd(x)
if x==0 error('Ошибка - деление на 0'). end
f=sin(x)/x
Для выявления ситуации об ошибке использован оператор условного перехода if, который будет описан детально несколько позднее. Результат выполнения данной функции приводится ниже:
» sd(l)
f =
0.8415
ans =
0.8415
» sd(0)
??? Error using ==> sd Ошибка - деление на 0
Если остановка программы при появлении ошибки нежелательна, то может использоваться команда вывода предупреждающего сообщения warning('Предупреждающее сообщение')
Эта команда выводит стоящее в апострофах сообщение, но не препятствует дальнейшей работе программы. Признаком того, что является ошибкой, а что — предупреждением, являются символы ??? и слово Warning в соответствующих сообщениях.
15. Функция lasterr и обработка ошибок
Функция lasterr и обработка ошибок
Опытные программисты должны предусматривать ситуации с появлением ошибок. К примеру, при х = 0 выражение sin(x)/x = 0/0 = 1 и правильным решением было бы вместо его вычисления использовать значение 1.
В данном простом примере приводится функция sdO, исключающая вычисление sin(x)/x при х = 0:
function f=sdO(x)
if x==0 f=1;
else f=sin(x)/x;
end
return
При этом вычисления пройдут корректно при любом х:
» sd0(l)
ans=
0.8415
»sd0(0)
ans =
1
Для вывода сообщения о последней произошедшей ошибке служит функция lasterr (см. пример ниже):
» ааа
??? Undefined function or variable 'aaa'.
» 2+3
ans =
5
» 1/0
Warning: Divide by zero,
ans =
Inf
» lasterr
ans = Undefined function or variable 'aaa'.
Как нетрудно заметить, функция lasterr возвращает текстовое сообщение, следующее за знаками ??? сообщения об ошибке.
В общем случае программы могут содержать обработчики ошибок, направляющие ход вычислений в нужное русло, даже если появляется ошибка. Но для этого требуются средства индикации и обработки ошибок. Основными из них являются функции eval и l asterr. О функции lasterr уже говорилось, а функция eval (' try', 'catch') в отличие от ранее рассмотренной формы (урок 18) имеет два входных аргумента. Один из них — это строчное выражение, которое преобразуется в исполняемую форму и выполняется при отсутствии ошибки. Если же происходит ошибка, то строка ' catch' вызывает обращение к функции обработки ошибки.
16. Функции с переменным числом аргументов
Функции с переменным числом аргументов
Функции подсчета числа аргументов
При создании функций со специальными свойствами весьма полезны две приведенные ниже функции:
-
nargin — возвращает число входных параметров данной функции;
-
nargout — возвращает число выходных параметров данной функции.
Пусть, к примеру, мы хотим создать функцию, вычисляющую сумму квадратов пяти аргументов xl, х2, хЗ, х4 и х5.
Обычный путь состоит в следующем — создаем функцию с именем sum2_5:
function f=sum2_5(x1,x2,x3,x4,x5) ;
f=x1^2+x2^2+x3^2+x4*2+x5^*2;
Теперь проверим ее в работе:
» sum2_5(l,2.3.4.5)
ans =
55
» sum2_5(l,2)
??? Input argument 'хЗ' is undefined.
Error in ==> C:\MATI_AB\bin\sum2_5.m
On line 2 ==> f=x1^2+x2^2+x3^2+x4^2+x5^2;
Итак, при наличии всех пяти аргументах функция работает корректно. Но если аргументов менее пяти, она выдает сообщение об ошибке. С помощью функции nargin можно создать функцию sum2_5m, которая работает корректно при любом числе заданных входных аргументов в пределах от 1 до 5:
f unction f=sum2m_5(x1 ,x2 , хЗ ,x4 , x5) ;
n=nargin;
if n==1 f=x1^2; end
if n==2 f=x1^2+x2^2;end
if n==3 f=x1^2+x2^2+x3^2; end
if n==4 f=x1^2+x2 ^ 2+x3^2+x4 ^ 2: end
if n==5 f=x1^2+x2^2+x3^2+x
В данной функции используется условный оператор i f...end, который будет детально описан далее. Но и без этого ясно, что благодаря применению функции nargin и условного оператора вычисления всякий раз идут по формуле с числом слагаемых, равным числу входных аргументов — от одного до пяти. Это видно из приведенных ниже примеров:
» sum2_5m(1)
ans =
1
» sum2_5m(1,2)
ans =
5
» sum2_5m( 1,2,3)
ans =
14
» sum2_5m(1,2,3,4)
ans =
30
» sum2_5m(1,2,3,4,5)
ans=
55
» sum2_5m(1,2,3,4,5,6)
??? Error using ==> sum2_5m
Too many input arguments.
Итак, при изменении числа входных параметров от 1 до 5 вычисления проходят корректно. При большем числе параметров выводится сообщение об ошибке. Этс уже действует встроенная в интерпретатор MATLAB система диагностики ошибок
17. Переменные varargin и varargout
Переменные varargin и varargout
Для упрощения записи аргументов функций их можно представить списком, который определяет специальная переменная varargin, являющаяся массивом ячеек. Она должна записываться строчными буквами и может включать в себя как аргументы, так и опции функций. Например, в приведенных ниже примерах:
function myplot(x,varargin)
plot(x,varargin{:}) function [s,varargout] = mysize(x)
nout = max(nargout.1)-1;
s = size(x);
for 1=1:nout, varargout(i) = {s(i)}; end
Эта переменная вбирает в себя все входные параметры и опции начиная со второго аргумента. При обращении к данной функции
myplot(sin(0:.1:1),'color'.[.5 .7 ,3],'linestyle',':')
varargin представляет массив ячеек размера 1x4, включающий а себя значения
'color', [.5 .7 .3], 'linestyle' u ':'.
Аналогично varagin переменная varargout объединяет любое число выходных параметров в массив ячеек. Эта переменная, кстати, как и varargin, должна быть последней в списке аргументов. Обычно эта переменная не создается при вызове функций. Приведенный ниже пример поясняет ее создание с помощью цикла:
function [s,varargout] = rnysize(x)
nout = max(nargout,l)-l:
s = size(x);
for i=1:nout.
varargout(i)= (s(i)}: end
Более подробно циклы будут рассмотрены в дальнейшем описании. В данном случае цикл использован для объединения всех параметров начиная со второго в значение переменной varargout.
18. Комментарии
Комментарии
Как отмечалось, команда help name, где name — имя m-файла, обеспечивает чтение первой строки с текстовым комментарием и тех строк с комментариями, которые следуют непосредственно за первой строкой. Комментарий, расположенный за пределами этой области, не выводится. Это позволяет создавать невыводимый программный комментарий, например: Z=X+Y ^Массив Z является суммой массивов X и Y
Пустая строка прерывает вывод комментария при исполнении команды help name. Команда type name выводит текст программы со всеми комментариями, в том числе и следующими после пустых строк.
Команда help catalog, где catalog — имя каталога с m-файлами, позволяет вывести комментарий, общий для всего каталога. Такой комментарий содержится в файле contents.m, который пользователь может создать самостоятельно с помощью редактора m-файлов. Если такого файла нет, то будет выведен список первых строк комментариев для всех m-файлов каталога.
19. Особенности выполнения m-файлов функций
Особенности выполнения m-файлов функций
М-файлы-функции могут использоваться как в командном режиме, так и вызываться из других M-файлов. При этом необходимо указывать все входные и выходные параметры. Исключением является случай, когда выходной параметр единственный — в этом варианте функция возвращает единственный результат и может использоваться в математических выражениях. При использовании глобальных переменных они должны быть объявлены во всех m-файлах, используемых в решении заданной задачи, и во всех входящих в них встроенных подфункциях.
Имена функций должны быть уникальными. Это связано с тем, что при обнаружении каждого нового имени MATLAB проверяет, относится ли это имя к переменной, подфункции в данном m-файле, частной функции в каталогах PRIVATE или функции в одном из каталогов пути доступа. Если последняя встречается, то будет исполнена именно эта функция. В новой версии MATLAB возможно переопределение функции, но это не рекомендуется делать подавляющему большинству пользователей системы.
Если аргумент функции используется только для вычислений и его значения не меняются, то аргумент передается ссылкой, что уменьшает затраты памяти. В других случаях аргумент передается значением. Для каждой функции выделяется своя (рабочая) область памяти, не входящая в область, предоставляемую системе MAT-LAB. Глобальные переменные принадлежат ряду областей памяти. При их изменении меняется содержимое всех этих областей.
При решении задач с большим объемом данных может ощущаться нехватка оперативной памяти. Признаком этого становится появление сообщения об ошибке «Out of memory».
В этом случае может быть полезным применение следующих мер:
-
стирание ставших ненужными данных, прежде всего больших массивов;
-
увеличение размеров файла подкачки Windows;
-
уменьшение размера используемых данных;
-
снятие ограничений на размеры используемой памяти;
-
увеличение объема физической памяти компьютера.
Чем больше емкость ОЗУ компьютера, на котором используется система MATLAB тем меньше вероятность возникновения указанной ошибки. Опыт показывает, что даже при решении задач умеренной сложности емкость ОЗУ не должна быть менее 16-32 Мбайт.
20. Создание Р-кодов
Создание Р-кодов
Когда встречается сценарий или функция в виде m-файла, то всякий раз выполняется трансляция файлов, создающая так называемые Р-коды (псевдокоды). Она связана с синтаксическим контролем сценария или функции, который несколько замедляет вычисления. Временные Р-коды хранятся в памяти только до использования команды clear или завершения сеанса работы. Кроме того, MATLAB позволяет явно создавать и хранить Р-коды сценариев и функций с помощью команды pcode: pcode имена_М-файлов pcode *.m создает файлы р-кодов для всех m-файлов данной папки, pcode с дополнительным параметром - inplace — хранит эти файлы в тех же папках, что и исходные m-файлы.
Особенно полезно применение этой команды в том случае, когда используется сложная дескрипторная графика и средства создания GUI. В этом случае выигрыш по скорости выполнения вычислений может быть заметным. Переход к Р-кодам полезен, если пользователь желает скрыть созданный им m-файл и реализованные в нем идеи и алгоритмы. Файл с Р-кодами имеет расширение .р. Размер файла с Р-кодами обычно больше, чем размер m-файла.Рассмотрим следующий пример — создадим файл-сценарий pp.m следующего содержания:
told=cputime;
х=-15:.0001:15;
plot(x,sin(x))
t=cputime-told
Эта программа строит график функции sin(x) по большому числу точек. Кроме того, она вычисляет время выполнения данного сценария в секундах. При первом пуске получим:
» рр
t=
0.4400
Теперь выполним создание Р-кодов и вновь запустим программу:
» pcode рр
» рр
t=
0.3900
» рр
t =
0.3300
Нетрудно заметить, что после преобразования в Р-коды время построения графика несколько уменьшилось. Но гораздо важнее то, что теперь вы можете стереть файл pp.m (но оставить рр.р!) и снова запустить программу. Ваши слишком любопытные коллеги едва ли разберутся с тем, что записано в машинных кодах файла рр.р, хотя с помощью специальных программ (декомпиляторов) такая возможность реализуется.
21. Управляющие структуры
Управляющие структуры
Помимо программ с линейной структурой, инструкции которых исполняются строго по порядку, существует множество программ, структура которых нелинейна. При этом ветви программ могут выполняться в зависимости от определенных условий, иногда с конечным числом повторений — циклов, иногда в виде циклов, завершаемых при выполнении заданного условия. Практически любая серьезная программа имеет нелинейную структуру. Для создания таких программ необходимы специальные управляющие структуры. Они имеются в любом языке программирования, и в частности в MATLAB.
22. Диалоговый ввод
Диалоговый ввод
Приведем простой пример диалоговой программы, которую легко поймут приверженцы доброго старого Бейсика:
% Вычисление длины окружности с диалоговым вводом радиуса
r=0;
while r>=0,
r=input('Введите радиус окружностиr=');
if r>=0 disp(' Длина окружности l='); disp(2*pi*r), end
end
Эта программа служит для многократного вычисления длины окружности по вводимому пользователем значению радиуса г. Обратите внимание на то, что здесь мы впервые показываем пример организации простейшего диалога. Он реализован с помощью команды input: MnputCВведите радиус окружности r='):
При выполнении этой команды вначале выводится запрос в виде строки, затем происходит остановка работы программы и ожидается ввод значения радиуса г (в общем случае числа). Ввод, как обычно, подтверждается нажатием клавиши Enter, после чего введенное число присваивается переменной г. Следующая строка
if r>=0 disp(' Длина окружности l = '); disp(2*pi*r);end
с помощью команды disp при r>=0 выводит надпись «Длина окружности 1=» и вычисленное значение длины окружности. Она представляет собой одну из наиболее простых управляющих структур типа if...end. В данном случае она нужна для остановки вычислений, если вводится отрицательное значение г (прием, который любят начинающие программисты).
Приведенные строки включены в управляющую структуру while...end. Это необходимо для циклического повторения вычислений с вводом значений r. Пока r>=0. цикл повторяется. Но стоит задать r<0, вычисление длины окружности перестает выполняться, а цикл завершается.
Если данная программа записана в виде m-файла circ.m, то работа с ней будет выглядеть следующим образом:
» circ
Введите радиус окружности R=1
Длина окружности l=
6.2832
Введите радиус окружности R=2
Длина окружности l=
12.5664
Введите радиус окружности R=-1
»
Итак, на примере даже простой программы мы видим пользу применения управляющих структур типа if...end и whi1e...end, а также функций диалогового ввода input('String') и вывода disp. Обратите внимание на завершение работы программы при вводе любого отрицательного числа для радиуса окружности.
Функция Input может использоваться и для ввода произвольных строковых выражений. При этом она задается в следующем виде:
input('Комментарий'. V)
При выполнении этой функции она останавливает вычисления и ожидает ввода строкового комментария. После ввода возвращается набранная строка. Это иллюстрирует следующий пример:
» S=input('Введите выражение ','s') Введите выражение (Вводим) 2*sin(l)
S =
2*sin(l)
» eval(S)
ans =
1.6829
Обратите внимание на то, что функция eval позволяет вычислить выражение, заданное (полученное от функции input) в символьном виде. Вообще говоря, возможность ввода любого символьного выражения в сочетании с присущими языку программирования MATLAB управляющими структурами открывает путь к созданию диалоговых программ любой сложности [ Нужно проявлять большую осторожность при применении eval и input, так как программы с их с использованием не всегда возможно компилировать. Впрочем, р-коды таких программ можно использовать с сервером run-time. — Примеч. ред. ].
23. Условный оператор
Условный оператор
Условный оператор if в общем виде записывается следующим образом:
if Условие
Инструкции_1
elself Условие
Инструкции_2
else
Инструкции_3
end
Эта конструкция допускает несколько частных вариантов. В простейшем, типа! f...end: if Условие Инструкции end
Пока Условие возвращает логическое значение 1 (то есть «истина»), выполняются Инструкции, составляющие тело структуры if...end. При этом оператор end указывает на конец перечня инструкций. Инструкции в списке разделяются оператором , (запятая) или ; (точка с запятой). Если Условие не выполняется (дает логическое значение 0, «ложь»), то Инструкции также не выполняются.
Еще одна конструкция
if Условие
Инструкции_1
else
Инструкции_2
end
выполняет Инструкции_1, если выполняется Условие, или Инструкции_2 в противном случае.
Условия записываются в виде:
Выражение_1 Оператор_отношения Выражение_2,
причем в качестве Операторов_отношения используются следующие операторы: ==, <, >, <=, >= или ~=. Все эти операторы представляют собой пары символов без пробелов между ними.
Мы уже неоднократно показывали применение этой общеизвестной управляющей структуры в программных модулях. Читателю предлагается опробовать собственные варианты программ с условным оператором.
24. Циклы типа for...end
Циклы типа for...end
Циклы типа for...end обычно используются для организации вычислений с заданным числом повторяющихся циклов. Конструкция такого цикла имеет следующий вид:
for vаг=Выражение. Инструкция. .... Инструкция end
Выражение чаще всего записывается в виде s:d:e, где s — начальное значение переменной цикла var, d — приращение этой переменной и е — конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s :е (в этом случае d=l). Список выполняемых в цикле инструкций завершается оператором end.
Следующие примеры поясняют применение цикла для получения квадратов значений переменной цикла:
» for 1=1:5 i^2. end;
ans =
1
ans =
4
ans =
9
ans =
16
ans =
25
» for x=0:.25:1 Х ^ 2, end:
ans =
0
ans =
0.0625
ans =
0.2500
ans =
0.5625
ans =
1
Оператор continue передает управление в следующую итерацию цикла, пропуская операторы, которые записаны за ним, причем во вложенном цикле он передает управление на следующую итерацию основного цикла. Оператор break может использоваться для досрочного прерывания выполнения цикла. Как только он встречается в программе, цикл прерывается. Возможны вложенные циклы, например:
for i=1:3
for j=l:3
A(1.j)=i+j;
end
end
В результате выполнения этого цикла (файл for2.m) формируется матрица А:
» for2
» А
А =
2 3 4
3 4 5
4 5 6
»
Следует отметить, что формирование матриц с помощью оператора : (двоеточие) обычно занимает намного меньше времени, чем с помощью цикла. Однако применение цикла нередко оказывается более наглядным и понятным. MATLAB допускает использование в качестве переменной цикла массива А размера тхп. При этом цикл выполняется столько раз, сколько столбцов в массиве А, и на каждом шаге переменная var представляет собой вектор, соответствующий текущему столбцу массива А:
» А=[1 2 3:4 5 6]
А =
1 2 3
4 5 6
» for var=A; var, end
var =
1
4
var =
2
5
var=
3
6
25. Циклы типа while...end
Циклы типа while...end
Цикл типа while выполняется до тех пор, пока выполняется Условие:
while Условие Инструкции end
Пример применения цикла while уже приводился. Досрочное завершение циклов реализуется с помощью операторов break или continue.
26. Конструкция переключателя
Конструкция переключателя
Для осуществления множественного выбора (или ветвления) используется конструкция с переключателем типа switch:
switch switch_Bыражение
case саsе_Выражение
Список_инструкций
case {саsе_Выражение1, Саsе_выражение2, саsе_ВыражениеЗ....}
Список_инструкций
otherwise. Список_инструкций end
Если выражение после заголовка switch имеет значение одного из выражений са5е_Выражение..., то выполняется блок операторов case, в противном случае — список инструкций после оператора otherwise. При выполнении блока case исполняются те списки инструкций, для которых сазе_Выражение совпадает со switch_Bbipa-жением. Обратите внимание на то, что сазе_Выражение может быть числом, константой, переменной, вектором ячеек или даже строчной переменной. В последнем случае оператор case истинен, если функция strcmp (значение, выражение) возвращает логическое значение «истине».
Поясним применение оператора switch на примере m-файла swl.m:
switch van
case {1,2,3}
dispCПервый квартал')
case {4,5,6}
disp('Второй квартал')
case {7,8,9}
d.isp( 'Третий квартал')
case {10.11,12}
dispC Четвертый квартал')
otherwise
disp('Ошибка в задании')
end
Эта программа в ответ на значения переменной van — номера месяца — вычисляет, к какому кварталу относится заданный месяц, и выводит соответствующее сообщение:
» var=2;
» swl
Первый квартал
» var=4;swl
Второй квартал
» var=7:swl
Третий квартал
» var=12;swl
Четвертый квартал
» var=-l;swl
Ошибка в задании
27. Конструкция try...catch...end
Конструкция try...catch...end
В MATLAB 6 введена новая конструкция блока вывода ошибок try...catch...end:
try.
Список инструкций
Список инструкций catch.
Список инструкций
...
Список инструкций
end
Эта конструкция выполняет все списки инструкций. Если в каком-то списке до оператора catch появляется ошибка, то выводится сообщение об ошибке, но системная переменная последней ошибки lasterr не меняется. В сообщениях после catch сообщения об ошибке не выводятся.
В следующем примере задано появление ошибки (переменная ааа не определена), после чего выполняется блок try...catch...end:
ааа
??? Undefined function or variable 'ааа'.
try
2+3:
3+4:
2/0: catch
4+5: end:
Warning: Divide by zero.
»lasterr ans = Undefined function or variable 'aaa'.
Обратите внимание, что в конце блока команда lasterr выводит ее начальное значение. А в другом примере ошибка задана в блоке try...catch...end уже после оператора catch:
» try
2+3:
3+4;
4+5: catch
5/0:
end:
» lasterr
ans = Undefined function or variable 'aaa'.
Как нетрудно заметить, на этот раз ошибка в вычислении 5/0 не выводится, а значение lasterr осталось тем, что было изначально.
28. Создание паузы в вычислениях
Создание паузы в вычислениях
Для остановки программы используется оператор pause. Он используется в следующих формах:
-
pause — останавливает вычисления до нажатия любой клавиши;
-
pause(N) — останавливает вычисления на N секунд;
-
pause on — включает режим отработки пауз;
-
pause off — выключает режим отработки пауз.
Следующий пример поясняет применение команды pause:
for i=1:20;
х =rand(1,40);
у =rand(1,40);
z = sin(x.*y);
tri = delaunay(x.y);
trisurf(tri,x,y,z)
paused);
end
Команда paused) здесь обеспечивает показ 20 рисунков — построений трехмерных поверхностей из треугольных окрашенных областей со случайными параметрами.
29. Понятие об объектно-ориентированном программировании
Понятие об объектно-ориентированном программировании
Мы уже много раз упоминали различные объекты языка программирования системы MATLAB. Это является одним из признаков объектно-ориентированного программирования (ООП), причем чисто внешним. В основе объектно-ориентированного программирования лежат три основных положения.
-
Инкапсуляция — объединение данных и программ и передача данных через входные и выходные параметры функций. В результате появляется новый элемент программирования — объект.
-
Наследование — возможность создания родительских объектов и новых дочерних объектов, наследующих свойства родительских объектов. Возможно также множественное наследование, при котором класс наследует свойства нескольких родительских объектов. На наследовании основаны система задания типов данных, дескрипторная графика и многие другие приемы программирования. Примеры наследования мы уже неоднократно отмечали.
-
Полиформизм — присвоение некоторому действию одного имени, которое в дальнейшем используется по всей цепочке создаваемых объектов сверху донизу, причем каждый объект выполняет это действие присущим ему способом.
В дополнение к этим положениям объектно-ориентированное программирование в MATLAB допускает агрегирование объектов, т. е., объединение частей объектов или ряда объектов в одно целое.
Объект можно определить как некоторую структуру, принадлежащую к определенному классу. В MATLAB определены следующие семь основных классов объектов:
-
double — числовые массивы с элементами-числами двойной точности;
-
sparse — двумерные числовые или комплексные разреженные матрицы;
-
char — массивы символов;
-
struct — массивы структур (записей);
-
cell — массивы ячеек;
-
javaarray — массивы Ява;
-
functionjnandle — дескрипторы функций.
С объектами этих классов мы многократно встречались, особо не оговаривая их принадлежность к объектно-ориентированному программированию. Для MATLAB вообще характерно, что никакие классы объектов (в том числе заново создаваемые) не требуют объявления. Например, создавая переменную nаmе='Иван', мы автоматически получаем объект в виде переменной name класса char. Таким образом, для переменных принадлежность к тому или иному классу определяется их значением. Является ли переменная объектом, можно определить при помощи функции isobject(HMfl переменной). Аналогичная функция isjava определяет, является ли переменная объектом Java.
Для создания новых классов объектов служат конструкторы классов. По существу, это m-файлы, имена которых совпадают с именами классов @Имя_класса, но без символа @. Этим символом помечаются подпапки системы MATLAB, в которых имеются конструкторы классов. Множество таких папок с примерами конструкторов классов вы найдете в подпапках MATLAB\TOOLBOX.
В качестве примера рассмотрим поддиректорию @SYM в директории TOOLBOX\ SYMBOLIC. В этой поддиректории можно найти конструкторы для более чем сотни объектов пакета символьной математики. К примеру, конструктор функции, вычисляющей арктангенс, выглядит следующим образом:
» help @sym/atan.m
ATAN Symbolic inverse tangent.
» type @sym/atan,m
function Y = atan(X)
%ATAN Symbolic inverse tangent.
% Copyright (c) 1993-98 by The MathWorks. Inc.
% SRevision: 1.10 $ $Date: 1997/11/29 01:05:16 $
Y = mapleCmap' ,'atan' .X);
В данном случае для конструирования нужного объекта используется функция mapl e, дающая вход в ядро системы символьной математики Maple V R4, которое поставляется в составе системы MATLAB по лицензии фирмы MapleSoft, Inc. Этот пример, кстати, наглядно показывает, что пользователь системы MATLAB может существенно расширить число объектов класса sym, поскольку ядро системы Maple V содержит намного больше определений, чем пакет символьной математики системы MATLAB. Для создания новых классов объектов служит функция class, описанная ниже.
Итак, объектно-ориентированное программирование — это как бы кинжал, закрепленный на вашем поясе. Вы можете и не воспользоваться этим оружием, ощущая при этом его значимость и ценя красоту. Но в альтернативном варианте вы можете использовать его во время ежедневной трапезы в качестве столь необходимого столового ножа. В первом случае вы выступаете в качестве обычного пользователя, а во втором — программиста-профессионала.
Пакеты прикладных программ системы MATLAB позволяют разработчикам с большим успехом использовать возможности объектно-ориентированного программирования путем создания новых классов и объектов. М-файлы системы представляют собой массу наглядных примеров объектно-ориентированного программирования на языке MATLAB. Это дает основание ограничиться справочным описанием основных средств такого программирования с приведением минимума простых примеров.
30. Создание класса или объекта
Создание класса или объекта
Для создания класса объектов или объектов, а также для их идентификации служит функция class. Формы ее применения представлены ниже.
-
class (OBJ) — возвращает класс указанного объекта OBJ. Типы стандартных классов double, sparse, char, cell, struct, functionjiandle были перечислены выше. int8 — 8-разрядный массив целых чисел со знаком; uintS — 8-разрядный массив целых чисел без знака; intlG — 16-разрядный массив целых чисел со знаком; uint!6 — 16-разрядный массив целых чисел без знака; int32 — 32-разрядный массив целых чисел со знаком; uint32 — 32-разрядный массив целых чисел без знака; <class_name> — класс, определенный пользователем; <java_class> — имя класса Ява;
-
OBJ=class(S, 'classjiame' ,PARENT1,PARENT2....) — создает объект класса 'classname' на базе структуры S и родительских объектов PARENT1, PARENT2,... При этом создаваемый объект наследует структуру и поля родительских объектов. Объекту OBJ в данном случае присуще множественное наследование;
-
OBJ=class(struct[ ]. 'classjiame' .PARENT1.PARENT2,...) — не может иметь никаких полей, кроме унаследованных от родительских объектов.
Обратите внимание на то, что эта функция обычно используется в составе m-файлов конструкторов классов объектов.
31. Проверка принадлежности объекта к заданному классу
Проверка принадлежности объекта к заданному классу
Для контроля принадлежности заданного объекта к некоторому классу служит функция isa:
-
isa(OBJ. 'Имя_класса') — возвращает логическую 1, если OBJ принадлежит классу с указанным именем. Дополнительно к вышеописанным выделяет классы numeric и single. Но не обнаруживает класс logical. Нужно использовать функцию islogical, чтобы проверить принадлежность к этому классу.
Примеры применения этой функции:
» Х=[1 2 3];
» isa(X,'char')
ans =
0
» isa(X,'double')
ans =
1
32. Другие функции объектно-ориентированного программирования
Другие функции объектно-ориентированного программирования
Для получения списка методов данного класса объектов сейчас чаще используются функции methodsview и methods. Отличиями от what имя класса является то, что эти функции возвращают информацию также и о классах Java, но информация выводится в отдельном окне, не сообщается информация о папках, все методы из всех папок собраны вместе, и повторяющиеся имена методов удалены:
-
methodsview имя класса или methods имя класса -full — в отдельном окне возвращают полное описание методов класса, включая информацию о наследовании, а для классов Java — и о подписях и атрибутах;
-
M=methods ('имя класса',' -full ') — возвращает ту же информацию в массиве ячеек М;
-
M=methods(' имя класса ') — возвращает массив ячеек с перечислением методов, относящихся к заданному классу объектов;
-
methods имя класса возвращает перечень методов в отдельном окне. Пример:
» methods char Methods for class char: delete diff int
Следующие две функции могут использоваться только внутри конструкторов классов:
inferiorto (' CLASS1'. 'CLASS2'....) и superiortot 'CLASS1', 'CLASS2'....)
Они определяют низший и высший приоритеты классов по отношению к классу конструктора. Для дескрипторов перегружаемых функций существует функция
functions
F=functions(дескриптор функции),
возвращающая массив структур F. METHODS, вложенный в массив F, при этом именем поля в массиве F. METHODS является имя класса, а значением поля — название метода, который вызывается тогда, когда входной аргумент принадлежит этому классу.
Дополнительно functions возвращает следующие поля: F.function — строка, используемая для создания дескриптора функция (существуют также отдельная функция func2str для получения этой информации и обратная ей функция str2func, превращающая строку в дескриптор функции); F.type содержит simple (простая), overloaded (перегружаемая) или subfunction (подфункция), т. е. указывает тип функции; F.default указывает путь к тому файлу, который первый в алгоритме поиска MATLAB и не определен никаким классом.
-
which имя метода — находит загруженный Java класс и все классы MATLAB, которым принадлежит данный метод;
-
which -all имя метода — находит все классы, которым принадлежит данный метод.
Любой оператор в системе MATLAB можно переопределить (т. е. сделать его функцию перегружаемой) путем задания m-файла с новым именем в соответствующем каталоге классов. В частности, в уроке 8 отмечалось, что все арифметические операторы имеют представления в виде соответствующих функций.
При написании книги не ставилась цель детального знакомства с техникой объектно-ориентированного программирования. Дополнительные сведения имеются в книге, содержащей перевод фирменного описания раздела по объектно-ориентированному программированию. Поэтому ограничимся приведенным выше справочным описанием его средств.
33. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Разбираться в видах программирования и его особенностях для MATLAB.
-
Использовать М-файлы сценариев и функций.
-
Выводить сообщения об ошибках и обрабатывать ошибки.
-
Создавать функции с переменным числом аргументов.
-
Использовать комментарии.
-
Создавать Р-коды.
-
Использовать управляющие структуры и функции диалога.
-
Применять условные операторы, циклы и переключатели.
-
Задавать паузы в вычислениях.
-
Использовать некоторые возможности объектно-ориентированного программирования.
Урок 21. Отладка программ
1. Урок 21. Отладка программ
Урок №21.
Отладка программ
-
Общие замечания по отладке m-файлов
-
Вывод листинга m-файла с пронумерованными строками
-
Установка, удаление и просмотр точек прерывания
-
Управление исполнением m-файла
-
Просмотр рабочей области
-
Профилирование m-файлов
-
Работа с системой контроля версий программ
Отладка программ — не менее серьезный этап, чем их подготовка. К сожалению, это редко учитывают начинающие программисты, ослепленные успехом работы первых простеньких программ. Однако по мере усложнения программ необходимость в средствах их отладки возрастает. Этот урок посвящен тем средствам отладки, которые имеются в системе MATLAB.
2. Общие замечания по отладке m-файлов
Общие замечания по отладке m-файлов
Вряд ли существует программа с длиной более десятка строк, которая после запуска сразу бы выдала верный результат. Как правило, любую программу надо отлаживать в интерактивном режиме, запуская и анализируя полученные при каждой модификации результаты. Основным средством отладки m-файлов в системе MATLAB является встроенный редактор/отладчик (M-File Editor/Debuger) с современным графическим интерфейсом. Работа с ним была описана в уроке 5. Однако MATLAB предусматривает основные возможности отладки и в командном режиме. Именно они и рассматриваются в данном разделе.
Вообще говоря, отладка программ — процесс сугубо индивидуальный и творческий. Большинство пользователей средней квалификации обычно отлаживают программы, не обращаясь к специальным средствам отладки, требующим дополнительного времени для освоения и приобретения навыков использования. Если алгоритм решения задачи достаточно прост, то после нескольких модернизаций программы ее удается довести до нужной «кондиции», т. е. заставить работать корректно.
Для этого часто бывает достаточно ввести в программу режим просмотра результатов промежуточных вычислений, разблокировав их вывод снятием операторов ; (точка с запятой) или введя дополнительные переменные, значения которых отражают ход вычислений. После отладки можно вновь ввести блокирующие вывод операторы и убрать указанные переменные.
Серьезная необходимость в применении средств отладки возникает при отладке сложных программ опытными программистами, которые наверняка имеют практику работы с универсальными языками программирования с использованием развитых отладочных средств.
3. Команды отладки программ
Команды отладки программ
Для перехода в командный режим отладки в m-файл следует включить команду keyboard. Ее можно запустить и в командном режиме:
» keyboard
К» type swl
switch var case {1.2,3}
disp('Первый квартал')
case {4.5.6}
dispC Второй квартал')
case {7,8,9}
disp('Третий квартал')
case {10,11.12}
disp('Четвертый квартал')
otherwise
disp('Ошибка в задании')
end
» return
»
Признаком перехода в режим отладки становится появление комбинированного символа К». Он меняется на символ » после возврата командой return в обычный командный режим работы. То же самое происходит при использовании команды dbquit, также прекращающей режим отладки, но прекращающей и выполнение т-файла. Если команда return находится в самом m-файле, она прекратит его выполнение и передаст управление туда, откуда был вызван этот файл.
4. Вывод листинга m-файла с пронумерованными строками
Вывод листинга m-файла с пронумерованными строками
Один из способов отладки m-файлов — размещение в них точек прерывания. Однако в командном режиме нельзя задать установку таких точек с помощью курсора мыши (как в отладчике Windows). Поэтому необходимо иметь листинг программы с пронумерованными строками. Он создается с помощью команды dbtype.
Пример:
» keyboard
К» dbtype sw1
1 switch var
2 case {1.2.3}
3 disp(' Первый квартал')
4 case {4.5,6}
5 disp('Второй квартал')
6 case {7,8.9}
7 disp('Третий квартал')
8 case {10.11,12}
9 disp('Четвертый квартал')
10 otherwise
11 disp('Ошибка в задании')
12 end
K»
5. Установка, удаление и просмотр точек прерывания
Установка, удаление и просмотр точек прерывания
Для установки в тестируемый m-файл точек прерывания используются следующие команды:
-
dbstop In M-file at lineno — установить точку прерывания в заданной строке;
-
dbstop In M-file at subfun — установить точку прерывания в подфункции;
-
dbstop in M-file — установить точку прерывания в m-файле;
-
dbstop if error — установить точку прерывания при сообщении об ошибке, но не при ошибках внутри цикла try...catch;
-
dbstop if all error — установить точку прерывания при сообщении о любой ошибке;
-
dbstop if warning — установить точку прерывания при предупреждении;
-
dbstop if infnan или naninf — установить точку прерывания при результате Inf или NaN.
Можно использовать упрощенный ввод этих команд без использования слов in, at и if. При установке контрольной точки она появляется в окне редактора/отладчика m-файлов. Для удаления точек прерывания используется команда dbclear с тем же синтаксисом, что и dbstop, например:
-
dbclear M-file at 1 ineno — удалить точку прерывания в заданной строке заданного файла.
-
Команда dbstatus выводит список установленных в данной сессии точек прерывания.
Пример:
К» dbstatus
Breakpoint for C:\MATLAB\bin\demol.m is on line 2.
Breakpoint for C:\MATLAB\bin\sd.m is on line 3.
MATLAB 6 значительно изменила синтаксис по сравнению с предыдущими версиями. Поэтому полезно перед отладкой старых программ выполнить команду featureCorAndError' ,0) или просто feature('orAndError') — для выдачи предупреждений об ошибке при выполнении тех конструкций, интерпретация которых в новой версии изменилась. feature('orAndError' ,1) выдает сообщение об ошибке вместо предупреждения об ошибке.
6. Управление исполнением m-файла
Управление исполнением m-файла
После установки точек прерывания начинается собственно процесс тестирования m-файла. Он заключается в исполнении одного или нескольких шагов программы с возможностью просмотра содержимого рабочей области, т. е. значений переменных, меняющихся в ходе выполнения программы. Для пошагового выполнения программы используется команда dbstep в следующих формах:
-
dbstep — выполнение очередного шага;
-
dbstep nlines — выполнение заданного числа строк программы;
-
dbstep In — если следующая выполняемая строка текущего m-файла является вызовом функции из другого m-файла, эта форма позволяет перейти к первой исполняемой строке вызываемой функции и остановиться там;
-
dbstep out — если следующая выполняемая строка текущего m-файла является вызовом функции из другого m-файла, эта форма позволяет перейти к вызываемой функции и остановиться сразу же после ее выполнения.
Для перехода от одной остановки программы к другой используется команда dbcont.
7. Просмотр рабочей области
Просмотр рабочей области
В точках прерывания пользователь имеет возможность просмотреть состояние рабочей области с помощью ранее описанных команд who и whos — см. урок 5. Кроме того, для перемещения по рабочим областям стека вызванных функций вверх или вниз используются следующие команды:
-
dbdown — перемещение в стеке вызываемых функций сверху вниз;
-
dbup — перемещение в стеке вызываемых функций снизу вверх.
Находясь в рабочей области, можно не только просматривать значения переменных, но и менять их в ходе отладки программы. С помощью команды dbstack можно просматривать стек функций. Для завершения отладки используется команда dbquit.
В заключение еще раз обращаем внимание читателя на то, что все возможности отладки реализованы в редакторе/отладчике m-файлов, который характеризуется удобным графическим интерфейсом и средствами визуализации отладки программ. К ним относятся возможность выделения различными цветами элементов m-файла (ключевых слов, переменных, комментариев и т. д.), наглядное представление точек прерывания, простота их установки и т. д. Щелкнув мышью справа от колонки с номерами строк, вы можете установить/снять точку прерывания в окне редактора-отладчика. После остановки в точке прерывания вы можете просмотреть значения всех переменных, подведя курсор мыши к символьному обозначению переменной в окне редактора-отладчика.
В этом отношении некоторые описанные выше приемы отладки в командном режиме выглядят несколько архаично. Скорее всего, они ориентированы на пользователей, привыкших к командному режиму работы с системой.
8. Профилирование m-файлов
Профилирование m-файлов
Вообще говоря, достижение работоспособности программы — лишь один из этапов ее отладки. Не менее важным вопросом является оптимизация программы по минимуму времени исполнения или по минимуму объема кодов. Современные компьютеры, в которых используется система MATLAB, имеют достаточные резервы памяти, так что размеры программы, как правило, не имеют особого значения. Намного важнее проблема оптимизации программы в части быстродействия.
Оценка времени исполнения отдельных частей программы называется ее профилированием. Для выполнения такой процедуры служит команда profile [ Средства профилирования MATLAB позволяют анализировать только m-файлы функций, но не сценариев. Чтобы получить профиль выполнения сценария, приходится преобразовывать его в функции (как правило, не имеющую входных и выходных параметров), добавляя соответствующий заголовок function. ], имеющая ряд опций:
-
profile fun — запуск профилирования для функции fun;
-
profile report — вывод отчета о профилировании;
-
profile plot — графическое представление результатов профилирования в виде диаграммы Парето;
-
profile filename — профилирование файла с заданным именем и путем;
-
prof ile report N — вывод отчета по профилированию заданных N строк;
-
profile report frac — выводит отчет по профилированию тех строк, относительная доля выполнения которых в общем времени выполнения составляет не менее чем frac (от 0.0 до 1.0);
-
profileon — включение профилирования;
-
profile off — выключение профилирования;
-
profile reset — выключение профилирования с уничтожением всех накопленных данных;
-
INFO = profile — возвращает структуру со следующими полями:
-
file — полный путь к профилируемому файлу;
-
interval — интервалы времени в секундах;
-
count — вектор измерений;
-
state — состояние профилировщика: 'on' (включен) или 'off (выключен).
-
Ниже приводится пример на профилирование m-файла ellipj (эллиптическая функция Якоби):
» profile on
» profile ellipj
» ellipj([0:0.01:1].0.5); .
» profile report
Total time in "C:\MATLAB\toolbox\matlab
\specfun\ellipj.m": 0.16 seconds
100% of the total time was spent on lines:
[96 97 86]
85: if -isempty(in)
0.01s. 6% 86: phin(i.in) = 0.5 * ...
87:(asin(c(i+l.in).*sin(rem(phin(i+l.in)
.2*pi))./a(i+l,in))
95: ml = find(m==l):
0.11s. 69% 96: sn(ml) = tanh(u(ml)): 0.04s. 25*97:
cn(ml) = sech(u(ml));
98: dn(ml) = sech(udnl)):
» INFO=profile INFO=file:
'С:\MATLAB\toolboxNmatlab\specfun\el11pj.m'
interval: 0.0100
count: [98x1 double]
state: 'off '
» profile plot
Нетрудно заметить, что при профилировании выводятся номера строк программы, у которых время выполнения превосходит 0.01 с. С использованием этого интервала и оценивается время исполнения программного кода. Последняя команда выводит графическую диаграмму профилирования, показанную на рис. 21.1.
Рис. 21.1. Графическое представление результатов профилирования
При графическом представлении профилирования по горизонтальной оси указываются номера строк, а по вертикальной — время их выполнения. Сначала показываются строки с наибольшим временем выполнения. Таким образом, программист, отлаживающий работу программы, имеет возможность наглядно оценить, где именно находятся критические по быстродействию фрагменты.
1.gif
9. Создание итогового отчета
Создание итогового отчета
Для создания суммарного отчета о профилировании служит команда profsum, которая используется в нескольких формах:
-
profsumm — вывод полного отчета о результатах профилирования т-файла. Выводятся данные о времени выполнения для строк, суммарное время выполнения которых составляет 95% от общего времени (если таких строк много, выводятся данные о 10 строках, выполнение которых заняло наибольшее время);
-
profsumm(FRACTION) — выводит часть отчета для строк, относительное время выполнения которых составляет FRACTION (от 0.0 до 1.0) от общего времени выполнения файла;
-
profsurmi(N) — выводится отчет по N строкам с максимальным временем выполнения;
-
profsumm(STR) — выводит отчет только по тем строкам, в которых встречается строковое выражение STR;
-
profsumm(INFO), profsurmKINFO, FRACTION), profsumm(INFO, N) HprofsummdNFO, STR) -выводят итоговый отчет по строкам, заданным массивом INFO.
Пример применения команды profsumm:
» profile erfcore
» z = erf(0:.01:100):
» profsumm. profile done
Total time in "C:\MATLAB\toolbox\mat1ab
\specfun\erfcore.m": 0.16 seconds
94% of the total time was spent on lines:
[99 109 108 97 95 94 92 86 71 48]
47: %
0.01s. 6*48: k = find((abs(x)
> xbreak) & (abs(x) <= 4.)):
49: if -isempty(k)
70: del = (y-z).*(y+z):
0.01s, 6*71: result(k)
= exp(-z.*z) .* exp(-del) .* result(k)
72: end
85: 0.01s. 6% 86: у = abs(x(k)):
87: z = 1 ./ (y .* y):
91: xnum = (xnum + p(i)) .* z:
0.01s, 6*92: xden = (xden + q(i)) .* z:
93: end
0.01s, 6*94: result(k) =
z .* (xnum + p(5)) ./ (xden + q(5)):
0.01s, 6*95: result(k)
= (1/sqrt(pi) - result(k)) ./y:
96: if jint — 2 0.01s, 6% 97;
z = fix(y*16)/16;
98: del - (y-z).*(y+z):
0.06s. 38*99: result(k) =
exp(-z.*z) .* exp(-del) .* result(k)
100: k - find(~isfinite(result));
107: if jint ==0
0.01s, 6% 108: k = find(x > xbreak);
0.01s, 6% 109: result(k)=
(0.5 - result(k)) + 0.5;
110: k = find(x < -xbreak);
10. Построение диаграмм Парето
Построение диаграмм Парето
Команда profile plot использует для построения графическую команду pareto. Диаграмма Парето представляет собой столбцы, расположенные в порядке убывания отображаемых значений. С другими возможностями команды pareto можно ознакомиться, выполнив команду help pareto.
-
pareto(Y,NAMES) — строит диаграмму Парето с пометкой столбцов значений вектора Y соответствующими именами, содержащимися в векторе NAMES;
-
pareto(Y.X) — строит диаграмму Парето для значений вектора Y в зависимости от значений вектора X;
-
pareti(Y) — строит диаграмму Парето для значений вектора Y в зависимости от индексов его элементов;
-
[H,AX]=pareto(...) — возвращает вектор дескрипторов графических объектов диаграммы Н и их осей АХ.
Пример построения диаграммы Парето был рассмотрен выше (см. рис. 21.1).
11. Работа с системой контроля версий
Работа с системой контроля версий
MATLAB поддерживает системы контроля версий кода Visual Source Safe фирмы Microsoft (поступает вместе с Visual Studio), PVCS фирмы Merant (упрощенные версии этой системы бесплатно поступают с продуктами Borland), Clear Case фирмы Rational Software (в особенности на UNIX-Linux версиях MATLAB), RCS и имеет настраиваемый пользовательский интерфейс, так что вместо вышеперечисленных вы можете подключить свою любимую систему. Функция cmopts выводит информацию об установленной системе контроля версий. Свежеустановленная система MATLAB реагирует следующим образом:
» cmopts
ans =
none
Для подключения PVCS или ее варианта вам нужно отредактировать m-файл cmopts.m в папке C:\matlabrl2\toolbox\local Введите комментарий Ubegin customization section и введите на следующей строчке m-файла, если файл конфигурации проекта Proj.cfg:
DefaultConfigFile=
'с:\\pvcs\pvcsproj\projmgrprj\\Proj.cfg'.
Проверим правильность нашей установки:
»cmopts( 'DefaultConflgFile')
DefaultConfigFile =
с:\\pvcs\pvcsproj\projmgrprj\\Proj.cfg
-
Командаcheckin(f11ename. 'COMMENTS', Текст комментариев, OPTION1, VALUE1.0PTION2, VALUE2.......) включает ваши файлы в систему контроля версий. Filename — полный путь к файлу или строковый массив ячеек, где каждая ячейка указывает путь к файлам, Текст комментариев — массив символов, в данной версии option может быть только lock, value может быть on (замкнута) или off (позволяет доступ к файлу без checkout).
-
Команда checkout(filename, OPTION1, VALUE1.0PTION2. VALUE2.......) извлекает файлы из системы контроля версий. OPTION могут быть lock — аналогично checkin — и ревизия, т. е. указание конкретной версии файла. Команда undocheckout (Filename) — отменяет действие checkout, например замыкание файлов.
12. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Использовать команды отладки.
-
Выводить листинги m-файлов с нумерованными строками.
-
Устанавливать, удалять и просматривать точки прерывания.
-
Осуществлять пошаговое выполнение m-файлов.
-
Просматривать рабочую область.
-
Профилировать m-файлы.
-
Работать с системой контроля версий m-файлов.
Урок 22. Поддержка звуковой системы
1. Урок 22. Поддержка звуковой системы
Урок №22.
Поддержка звуковой системы
-
Средства работы со звуком
-
Демонстрация возможностей работы со звуком
Этот небольшой урок посвящен довольно экзотической возможности математической системы МАТLАВ — работе со звуком. Стоит напомнить, что для этого компьютер должен быть оснащен звуковой картой и звуковыми колонками. Средства поддержки звука в МАТLАВ имеют рудиментарный характер, но все же они есть и позволяют разнообразить выполнение некоторых примеров.
2. Средства работы со звуком
Средства работы со звуком
Начиная с версии МАТЬАВ 5.0 в системе несколько расширены средства для работы со звуком. До этого система имела единственную звуковую команду:
-
sound(Y.Р5) — воспроизводит сигнал из вектора У с частотой дискретизации Р5 с помощью колонок, подключенных к звуковой карте компьютера. Компоненты У могут принимать значения в следующих пределах -1.0<=у<=1.0. Для воспроизведения стереозвука на допускающих это компьютерных платформах У должен быть матрицей размера Мх2;
-
sound(Y) — функционирует аналогично, принимая частоту дискретизации по умолчанию равной 8192 Гц;
-
sound(Y,РS.ВIТS) — функционирует аналогично с заданием разрядности звуковой карты: ВIТS=8 или ВIТ=16.
Теперь появились дополнительные команды воспроизведения звука:
-
sound(Y,...) — масштабирует и воспроизводит сигнал из массива У: По синтаксису команда аналогична-sound( Y,...);
-
soundsc(Y ,...,SLIМ) — аналогична предшествующей команде, но позволяет задать параметр SLIМ = [MIN(Y) MAX(Y)], определяющий тот диапазон значений Y, который будет соответствовать полному динамическому диапазону звука. По умолчанию SLIМ = [МIN(Y) МАХ(У)].
-
Bеер оn или off — соответственно разрешает или запрещает гудок;
-
s=bеер — возвращает состояние оn|off
-
bеер — при s=оn издает гудок.
Кроме того, введены команды для считывания и записи файлов звукового формата .WAV, стандартного для операционных систем класса Windows
-
wavwrite(Y,WAVEFILE_Е) — записывает файл типа WAVE под именем WAVELIFE. Данные по каждому каналу в случае стерео записывются в разных столбцах массива. Величины должны быть в диапазоне [-1; 1];
-
wavwrite(Y.FS.WAVEFILE) — делает то же с заданием частоты дискретизации FS (в герцах);
-
wavwrite(Y,FS,NBITS,WAVEFILE) — делает то же с заданием числа бит на отсчет NBITS, причем NBITS<=16;
-
Y=wavread(FILE) — считывает файл типа WAVE с именем FILE и возвращает данные в массиве Y;
-
[Y,FS,BITS]=wavread(FILE) — считывает файл типа WAVE с именем FILE и возвращает массив данных Y, частоту дискретизации FS (в герцах) и разрядность BITS кодирования звука (в битах);
-
[...]=wavread(FILE.N) — возвращает только первые N отсчетов из каждого канала файла;
-
[...]=wavread(FILE, [N1 N2]) — возвращает только отсчеты с номерами от N1 до N2 из каждого канала;
-
SIZ=wavread(FILE, 'size') — возвращает объем аудиоданных в виде вектора SIZ=[samples channels] (samples — число отсчетов, channels — число каналов);
-
auwrite - записывает файл в соответствии со звуковым форматом фирм Sun и Next; auread воспроизводит файлы в MATLAB 6 на Sun и в MATLAB 5 на Next.
3. Демонстрация возможностей работы со звуком
Демонстрация возможностей работы со звуком
Эта команда служит для комплексной демонстрации возможностей работы со звуком. Она выводит диалоговое окно, которое позволяет выбрать несколько видов звукового сигнала, создать для них массив данных звука и воспроизвести звук (если компьютер оснащен звуковой картой, совместимой с Sound Вlastеr).
Кроме того, имеется возможность графически отобразить временную зависимость звукового сигнала, его частотный спектр и спектрограмму.
Еще один весьма наглядный способ представления массива данных звуковых сигналов — это показ их спектрограммы. Звуковой сигнал при этом делится на множество фрагментов, а спектрограмма дает представление о распределении частот спектра в разные моменты времени. Представление о том, насколько любопытной бывает спектрограмма сложного звукового сигнала, можно получить на примере рис. 22.3. Подобные спектрограммы могут быть использованы при разработке методов распознавания звуков.
Демонстрационные примеры можно просмотреть с помощью команды type xpsound. Вы получите доступ к более подробной информации по работе со звуком в системе MATLAB.
4. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Использовать средства работы со звуком.
-
Запускать демонстрационные примеры работы со звуком.
Урок 23. Знакомство с пакетами расширения MATLAB
1. Урок 23. Знакомство с пакетами расширения MATLAB
Урок №23.
Знакомство с пакетами расширения МАТLАВ
-
Вывод списка пакетов расширения
-
Simulinc for Windows
-
Пакет символьной математики
-
Пакеты математических вычислений
-
Пакеты анализа и синтеза систем управления
-
Пакеты идентификации систем
-
Дополнительные средства пакета Simulinc
-
Пакеты для обработки сигналов и изображений
-
Прочие пакеты прикладных программ
В этом уроке мы кратко ознакомимся с основными средствами профессионального расширения системы и ее адаптации под решение определенных классов математических и научно-технических задач — с пакетами расширения системы MATLAB. Несомненно, что хотя бы части из этих пакетов должен быть посвящен отдельный учебный курс или справочник, быть может, и не один. За рубежом по большинству таких расширений опубликованы отдельные книги, а объем документации по ним составляет сотни мегабайт. К сожалению, объем данной книги позволяет лишь немного пройтись по пакетам расширения, с тем чтобы дать читателю представление о том, в каких направлениях развивается система.
2. Вывод списка пакетов расширения
Вывод списка пакетов расширения
Полный состав системы MATLAB 6.0 содержит ряд компонентов, название, номер версии и дату создания которых можно вывести на просмотр командой ver:
» ver
MATLAB Version 6.0.0.88 (R12) on PCWIN MATLAB License Number: 0
|
|
MATLAB Toolbox |
Version 6.0 |
(R12) |
06-0ct-2000 |
|
|
|
Si mul ink |
Version 4.0 |
(R12) |
16-Jun-2000 |
|
|
|
Stateflow |
Version 4.0 |
(R12) |
04-0ct-2000 |
|
|
|
Stateflow Coder |
Version 4.0 |
(R12) |
04-0ct-2000 |
|
|
|
Real -Time Workshop |
Version 4.0 |
(R12) |
01-Mar-2000 |
|
|
|
COMA Reference Blockset |
Version 1.0.2 |
(R12) |
01-Sep-2000 |
|
|
|
Communications Blockset |
Version 2.0 |
(R12) |
01-Sep-2000 |
|
|
|
Communications Toolbox |
Version 2.0 |
(R12) |
01-Sep-2000 |
|
|
|
Control System Toolbox |
Version 5.0 |
(R12) |
01-Sep-2000 |
|
|
|
DSP Blockset |
Version 4.0 |
(R12) |
01-Sep-2000 |
|
|
|
Data Acquisition Toolbox |
Version 2.0 |
(R12) |
05-0ct-2000 |
|
|
|
Database Toolbox |
Version 2.1 |
(R12) |
18-Jan-2000 |
|
|
|
Datafeed Toolbox |
Version 1.2 |
(R12) |
08-May-2000 |
|
|
|
Dials & Gauges Blockset |
Version 1.1 |
(R12) |
12-May-2000 |
|
|
|
Filter Design Toolbox |
Version 2.0 |
(R12) |
01-Aug-2000 |
|
|
|
Financial Derivatives Toolbox |
Version 1.0 |
(R12) |
14-Aug-2000 |
|
|
|
Financial Time Series Toolbox |
Version 1.0 |
(R12) |
01-Apr-1999 |
|
|
|
Financial Toolbox |
Version 2.1.2 |
(R12) |
01-Sep-2000 |
|
|
|
Fixed-Point Blockset |
Version 3.0 |
(R12) |
26-May-2000 |
|
|
|
Fuzzy Logic Toolbox |
Version 2.1 |
(R12) |
15-Jun-2000 |
|
|
|
GARCH Toolbox |
Version 1.0 |
(R12) |
01-Jun-1999 |
|
|
|
Image Processing Toolbox |
Version 2.2.2 |
(R12) |
10-Mar-2000 |
|
|
|
Instrument Control Toolbox |
Version 1.0 |
(R12) |
01-Sep-2000 |
|
|
|
LMI Control Toolbox |
Version 1.0.6 |
(R12) |
12-Jun-2000 |
|
|
|
MATLAB Compiler |
Version 2.1 |
(R12) |
26-Jul-2000 |
|
|
|
MATLAB Report Generator |
Version 1.1 |
(R12) |
01-Apr-2000 |
|
|
|
Mapping Toolbox |
Version 1.2 |
(R12) |
22-May-2000 |
|
|
|
Model Predictive Control Toolbox |
Version 1.0.5 |
(R12) |
10-May-2000 |
|
|
|
Motorola DSP Developer's Kit |
Version 1.1 |
(R12) |
Ol-Sep-2000 |
|
|
|
Ми-Analysis and Synthesis Toolbox |
Version 3.0.5 |
(R12) |
12-Jun-2000 |
|
|
|
Neural Network Toolbox |
Version 4.0 |
(R12) |
26-May-2000 |
|
|
|
Nonlinear Control Design Blockset |
Version 1.1.4 |
(R12) |
12-Jun-2000 |
|
|
|
Optimization Toolbox |
Version 2.1 |
(R12) |
07-Jun-2000 |
|
|
|
Partial Differential Equation Toolbox |
Version 1.0.3 |
(R12) |
31 -Dec -1999 |
|
|
|
Power System Blockset |
Version 2.1 |
(R12) |
12-Jun-2000 |
|
|
|
Real -Time Workshop Ada Coder |
Version 4.0 |
(R12) |
01-Mar-2000 |
|
|
|
Real -Time Workshop Embedded Coder |
Version 1.0 |
(R12) |
01-Mar-2000 |
|
|
|
Requirements Management Interface |
Version 1.0.1 |
(R12) |
03-Mar-2000 |
|
|
|
Robust Control Toolbox |
Version 2.0.7 |
(R12) |
10-May-2000 |
|
|
|
SB2SL (converts SystemBuild to Simu |
Version 2.1 |
(R12) |
16-Jun-2000 |
|
|
|
Signal Processing Toolbox |
Version 5.0 |
(R12) |
01-Jun-2000 |
|
|
|
Simulink Accelerator |
Version 1.0 |
(R12) |
01-Mar-2000 |
|
|
|
Model Differencing for Simulink and... |
Version 1.0 |
(R12) |
19-Jul-2000 |
|
|
|
Simulink Model Coverage Tool |
Version 1.0 |
(R12) |
02-Jun-2000 |
|
|
|
Simulink Report Generator |
Version 1.1 |
(R12) |
01-Apr-2000 |
|
|
|
Spline Toolbox |
Version 3.0 |
(R12) |
13-Mar-2000 |
|
|
|
Statistics Toolbox |
Version 3.0 |
(R12) |
01-Sep-2000 |
|
|
|
Symbolic Math Toolbox |
Version 2.1.2 |
(R12) |
11-Sep-2000 |
|
|
|
System Identification Toolbox |
Version 5.0 |
(R12) |
27-Aug-2000 |
|
|
|
Wavelet Toolbox |
Version 2.0 |
(R12) |
16-Jun-2000 |
|
|
|
xPC Target |
Version 1.1 |
(R12) |
16-Jun-2000 |
|
|
|
xPC Target Embedded Option |
Version 1.1 |
(R12) |
16-Jun-2000 |
|
Обратите внимание, что практически все пакеты расширения в MATLAB 6.0 обновлены и датируются 2000 годом. Заметно расширено их описание, которое в PDF-формате уже занимает много более десятка тысяч страниц. Ниже дано краткое описание основных пакетов расширения
3. Simulink for Windows
Simulink for Windows
Пакет расширения Simulink служит для имитационного моделирования моделей, состоящих из графических блоков с заданными свойствами (параметрами). Компоненты моделей, в свою очередь, являются графическими блоками и моделями, которые содержатся в ряде библиотек и с помощью мыши могут переноситься в основное окно и соединяться друг с другом необходимыми связями. В состав моделей могут включаться источники сигналов различного вида, виртуальные регистрирующие приборы, графические средства анимации. Двойной щелчок мышью на блоке модели выводит окно со списком его параметров, которые пользователь может менять. Запуск имитации обеспечивает математическое моделирование построенной модели с наглядным визуальным представлением результатов. Пакет основан на построении блочных схем путем переноса блоков из библиотеки компонентов в окно редактирования создаваемой пользователем модели. Затем модель запускается на выполнение. На рис. 23.1 показан процесс моделирования простой системы — гидравлического цилиндра. Контроль осуществляется с помощью виртуальных осциллографов — на рис. 23.1 видны экраны двух таких осциллографов и окно простой подсистемы модели. Возможно моделирование сложных систем, состоящих из множества подсистем.
Simulink составляет и решает уравнения состояния модели и позволяет подключать в нужные ее точки разнообразные виртуальные измерительные приборы. Поражает наглядность представления результатов моделирования. Ряд примеров применения пакета Simulink уже приводился в уроке 4. Предшествующая версия пакета достаточно подробно описана в книгах. Основным нововведением является обработка матричных сигналов. Добавлены отдельные пакеты повышения производительности Simulink, такие как Simulink Accelerator для компиляции кода моделей, Simulink profiler для анализа кода и т. д.
Рис. 23.1. Пример моделирования системы гидравлического цилиндра с помощью расширения Simulink
1.gif
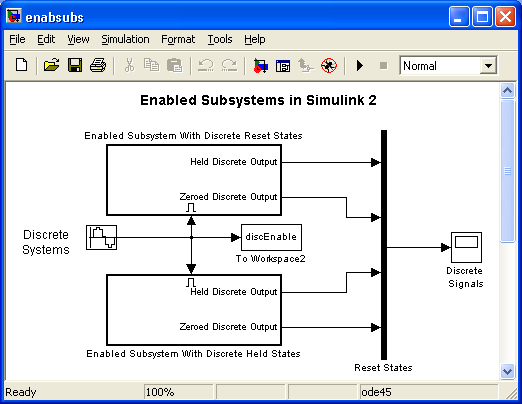
1b.gif
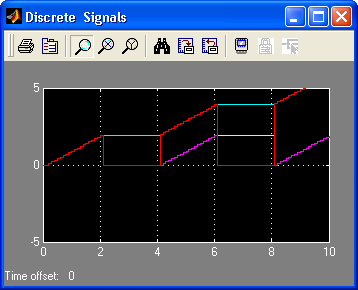
4. Real Time Windows Target и Workshop
Real Time Windows Target и Workshop
Подключающаяся к Simulink мощная подсистема имитационного моделирования в реальном масштабе времени (при наличии дополнительных аппаратных средств в виде плат расширения компьютера), представленная пакетами расширения Real Time Windows Target и Workshop, — мощное средство управления реальными объектами и системами. Кроме того, эти расширения позволяют создавать исполняемые коды моделей. Рис. 4.21 в уроке 4 показывает пример такого моделирования для системы, описываемой нелинейными дифференциальными уравнениями Ван-дер-Поля. Достоинством такого моделирования является его математическая и физическая наглядность. В компонентах моделей Simulink можно задавать не только фиксированные параметры, но и математические соотношения, описывающие поведение моделей.
5. Report Generator для MATLAB и Simulink
Report Generator для MATLAB и Simulink
Генераторы отчетов — средство, введенное еще в MATLAB 5.3.1, дает информацию о работе системы MATLAB и пакета расширения Simulink. Это средство очень полезно при отладке сложных вычислительных алгоритмов или при моделировании сложных систем. Генераторы отчетов запускаются командой Report. Отчеты могут быть представлены в виде программ и редактироваться.
Генераторы отчетов могут запускать входящие в отчеты команды и фрагменты программ и позволяют проконтролировать поведение сложных вычислений.
6. Neural Networks Toolbox
Neural Networks Toolbox
Пакет прикладных программ, содержащих средства для построения нейронных сетей, базирующихся на поведении математического аналога нейрона. Па-кет обеспечивает эффективную поддержку проектирования, обучения и моделирования множества известных сетевых парадигм, от базовых моделей персептрона до самых современных ассоциативных и самоорганизующихся сетей. Пакет может быть использован для исследования и применения нейронных сетей к таким задачам, как обработка сигналов, нелинейное управление и финансовое моделирование. Обеспечена возможность генерации переносимого С-кода с помощью Real Time Workshop.
В пакет включены более 15 известных типов сетей и обучающих правил, позволяющих пользователю выбирать наиболее подходящую для конкретного приложения или исследовательской задачи парадигму. Для каждого типа архитектуры и обучающих правил имеются функции инициализации, обучения, адаптации, создания и моделирования, демонстрации и пример приложения сети.
Для управляемых сетей можно выбрать прямую или рекуррентную архитектуру, используя множество обучающих правил и методов проектирования, таких как персептрон, обратное распространение, обратное распространение Левенберга, сети с радиальным базисом и рекуррентные сети. Вы можете легко изменять любые архитектуры, обучающие правила или переходные функции, добавлять новые, — и все это без написания единой строки на Си или ФОРТРАН. Пример применения пакета для распознавания образа буквы приводился в уроке 4. Детальное описание предшествующей версии пакета можно найти в книге.
7. Fuzzy Logic Toolbox
Fuzzy Logic Toolbox
Пакет прикладных программ Fuzzy Logic относится к теории нечетких (размытых) множеств. Обеспечивается поддержка современных методов нечеткой кластеризации и адаптивных нечетких нейронных сетей. Графические средства пакета позволяют интерактивно отслеживать особенности поведения системы.
Основные возможности пакета:
- определение переменных, нечетких правил и функций принадлежности;
- интерактивный просмотр нечеткого логического вывода;
- современные методы: адаптивный нечеткий вывод с использованием нейронных сетей, нечеткая кластеризация;
- интерактивное динамическое моделирование в Simulink;
-
генерация переносимого Си кода с помощью Real-Time Workshop.
Этот пример наглядно показывает отличия в поведении модели при учете нечеткой логики и без такого учета.
8. Symbolic Math Toolbox
Symbolic Math Toolbox
Пакет прикладных программ, дающих системе MATLAB принципиально новые возможности — возможности решения задач в символьном (аналитическом) виде, включая реализацию точной арифметики произвольной разрядности. Пакет базируется на применении ядра символьной математики одной из самых мощных систем компьютерной алгебры — Maple V R4. Обеспечивает выполнение символьного дифференцирования и интегрирования, вычисление сумм и произведений, разложение в ряды Тейлора и Маклорена, операции со степенными многочленами (полиномами), вычисление корней полиномов, решение в аналитическом виде нелинейных уравнений, всевозможные символьные преобразования, подстановки и многое другое. Имеет команды прямого доступа к ядру системы Maple V.
Пакет позволяет готовить процедуры с синтаксисом языка программирования системы Maple V R4 и устанавливать их в системе MATLAB. К сожалению, по возможностям символьной математики пакет сильно уступает специализированным системам компьютерной алгебры, таким как новейшие версии Maple и Mathematica.
9. Пакеты математических вычислений
Пакеты математических вычислений
В MATLAB входит множество пакетов расширения, усиливающих математические возможности системы, повышающих скорость, эффективность и точность вычислений.
10. NAG Foundation Toolbox
NAG Foundation Toolbox
Одна из самых мощных библиотек математических функций, созданная специальной группой The Numerical Algorithms Group, Ltd. Пакет содержит сотни новых функций. Названия функций и синтаксис их вызова заимствованы из известной библиотеки NAG Foundation Library. Вследствие этого опытные пользователи NAG ФОРТРАН могут без затруднений работать с пакетом NAG в MATLAB. Библиотека NAG Foundation предоставляет свои функции в виде объектных кодов и соответствующих m-файлов для их вызова. Пользователь может легко модифицировать эти МЕХ-файлы на уровне исходного кода.
Пакет обеспечивает следующие возможности:
-
корни многочленов и модифицированный метод Лагерра;
-
вычисление суммы ряда: дискретное и эрмитово-дискретное преобразование Фурье;
-
обыкновенные дифференциальные уравнения: методы Адамса и Рунге-Кутта;
-
уравнения в частных производных;
-
интерполяция;
-
вычисление собственных значений и векторов, сингулярных чисел, поддержка комплексных и действительных матриц;
-
аппроксимация кривых и поверхностей: полиномы, кубические сплайны, полиномы Чебышева;
-
минимизация и максимизация функций: линейное и квадратичное программирование, экстремумы функций нескольких переменных;
-
разложение матриц;
-
решение систем линейных уравнений;
-
линейные уравнения (LAPACK);
-
статистические расчеты, включая описательную статистику и распределения вероятностей;
-
корреляционный и регрессионный анализ: линейные, многомерные и обобщенные линейные модели;
-
многомерные методы: главных компонент, ортогональные вращения;
-
генерация случайных чисел: нормальное распределение, распределения Пуассона, Вейбулла и Кощи;
-
непараметрические статистики: Фридмана, Крускала-Уоллиса, Манна-Уитни; О временные ряды: одномерные и многомерные;
-
аппроксимации специальных функций: интегральная экспонента, гамма-функция, функции Бесселя и Ганкеля.
Наконец, этот пакет позволяет пользователю создавать программы на ФОРТРАН, которые динамически линкуются с MATLAB.
11. Spline Toolbox
Spline Toolbox
Пакет прикладных программ для работы со сплайнами. Поддерживает одномерную, двумерную и многомерную сплайн-интерполяцию и аппроксимацию. Обеспечивает представление и отображение сложных данных и поддержку графики.
Пакет позволяет выполнять интерполяцию, аппроксимацию и преобразование сплайнов из В-формы в кусочно-полиномиальную, интерполяцию кубическими сплайнами и сглаживание, выполнение операций над сплайнами: вычисление производной, интеграла и отображение.
Пакет Spline оснащен программами работы с В-сплайнами, описанными в работе «A Practical Guide to Splines» Карлом Дебуром, создателем сплайнов и автором пакета Spline. Функции пакета в сочетании с языком MATLAB и подробным руководством пользователя облегчают понимание сплайнов и их эффективное применение к решению разнообразных задач.
В пакет включены программы для работы с двумя наиболее широко распространенными формами представления сплайнов: В-формой и кусочно-полиномиальной формой. В-форма удобна на этапе построения сплайнов, в то время как кусочно-полиномиальная форма более эффективна во время постоянной работы со сплайном. Пакет включает функции для создания, отображения, интерполяции, аппроксимации и обработки сплайнов в В-форме и в виде отрезков полиномов.
12. Statistics Toolbox
Statistics Toolbox
Пакет прикладных программ по статистике, резко расширяющий возможности системы MATLAB в области реализации статистических вычислений и статистической обработки данных. Содержит весьма представительный набор средств генерации случайных чисел, векторов, матриц и массивов с различными законами распределения, а также множество статистических функций. Следует отметить, что наиболее распространенные статистические функции входят в состав ядра системы MATLAB (в том числе функции генерации случайных данных с равномерным и нормальным распределением). Основные возможности пакета:
-
описательная статистика;
-
распределения вероятностей;
-
оценка параметров и аппроксимация;
-
проверка гипотез;
-
множественная регрессия;
-
интерактивная пошаговая регрессия;
-
моделирование Монте-Карло;
-
аппроксимация на интервалах;
-
статистическое управление процессами;
-
планирование эксперимента;
-
моделирование поверхности отклика;
-
аппроксимация нелинейной модели;
-
анализ главных компонент;
-
статистические графики;
-
графический интерфейс пользователя.
Пакет включает 20 различных распределений вероятностей, включая t (Стъюдента), F и Хи-квадрат. Подбор параметров, графическое отображение распределений и способ вычисления лучших аппроксимаций предоставляются для всех типов распределений. Предусмотрено множество интерактивных инструментов для динамической визуализации и анализа данных. Имеются специализированные интерфейсы для моделирования поверхности отклика, визуализации распределений, генерации случайных чисел и линий уровня.
13. Optimization Toolbox
Optimization Toolbox
Пакет прикладных задач- для решения оптимизационных задач и систем нелинейных уравнений. Поддерживает основные методы оптимизации функций ряда переменных:
-
безусловная оптимизация нелинейных функций;
-
метод наименьших квадратов и нелинейная интерполяция;
-
решение нелинейных уравнений;
-
линейное программирование;
-
квадратичное программирование;
-
условная минимизация нелинейных функций;
-
метод минимакса;
-
многокритериальная оптимизация.
Разнообразные примеры демонстрируют эффективное применение функций пакета. С их помощью можно также сравнить, как одна и та же задача решается разными методами.
14. Partial Differential Equations Toolbox
Partial Differential Equations Toolbox
Весьма важный пакет прикладных программ, содержащий множество функций для решения систем дифференциальных уравнений в частных производных. Дает эффективные средства для решения таких систем уравнений, в том числе жестких. В пакете используется метод конечных элементов. Команды и графический интерфейс пакета могут быть использованы для математического моделирования уравнений в частных производных применительно к широкому классу инженерных и научных приложений, включая задачи сопротивления материалов, расчеты электромагнитных устройств, задачи тепломассопереноса и диффузии. Основные возможности пакета:
-
полноценный графический интерфейс для обработки уравнений с частными производными второго порядка;
-
автоматический и адаптивный выбор сетки;
-
задание граничных условий: Дирихле, Неймана и смешанных;
-
гибкая постановка задачи с использованием синтаксиса MATLAB;
-
полностью автоматическое сеточное разбиение и выбор величины конечных элементов;
-
нелинейные и адаптивные расчетные схемы;
-
возможность визуализации полей различных параметров и функций решения, демонстрация принятого разбиения и анимационные эффекты.
Пакет интуитивно следует шести шагам решения PDE с помощью метода конечных элементов. Эти шаги и соответствующие режимы пакета таковы: определение геометрии (режим рисования), задание граничных условий (режим граничных условий), выбор коэффициентов, определяющих задачу (режим PDE), дисркре-тизация конечных элементов (режим сетки), задание начальных условий и решение уравнений (режим решения), последующая обработка решения (режим графика).
15. Пакеты анализа и синтеза систем управления
Пакеты анализа и синтеза систем управления
Пакет Control System предназначен для моделирования, анализа и проектирования систем автоматического управления — как непрерывных, так и дискретных. Функции пакета реализуют традиционные методы передаточных функций и современные методы пространства состояний. Частотные и временные отклики, диаграммы расположения нулей и полюсов могут быть быстро вычислены и отображены на экране. В пакете реализованы:
-
полный набор средств для анализа MIMO-систем (множество входов — множество выходов) систем;
-
временные характеристики: передаточная и переходная функции, реакция на произвольное воздействие;
-
частотные характеристики: диаграммы Боде, Николса, Найквиста и др.;
-
разработка обратных связей;
-
проектирование LQR/LQE-регуляторов;
-
характеристики моделей: управляемость, наблюдаемость, понижение порядка моделей;
-
поддержка систем с запаздыванием.
Дополнительные функции построения моделей позволяют конструировать более сложные модели. Временной отклик может быть рассчитан для импульсного входа, единичного скачка или произвольного входного сигнала. Имеются также функции для анализа сингулярных чисел.
Интерактивная среда для сравнения временного и частотного отклика систем предоставляет пользователю графические управляющие элементы для одновременного отображения откликов и переключения между ними. Можно вычислять различные характеристики откликов, такие как время разгона и время регулирования.
Пакет Control System содержит средства для выбора параметров обратной связи. Среди традиционных методов: анализ особых точек, определение коэффициента усиления и затухания. Среди современных методов: линейно-квадратичное регулирование и др. Пакет Control System включает большое количество алгоритмов для проектирования и анализа систем управления. Кроме того, он обладает настраиваемым окружением и позволяет создавать свои собственные m-файлы.
16. Nonlinear Control Design Toolbox
Nonlinear Control Design Toolbox
Nonlinear Control Design (NCD) Blockset реализует- метод динамической оптимизации для проектирования систем управления. Этот инструмент, разработанный для использования с Simulink, автоматически настраивает системные параметры, основываясь на определенных пользователем ограничениях на временные характеристики.
Пакет использует перенос объектов мышью для изменения временных ограничений прямо на графиках, что позволяет легко настраивать переменные и указывать неопределенные параметры, обеспечивает интерактивную оптимизацию, реализует моделирование методом Монте-Карло, поддерживает проектирование SISO- (один вход — один выход) и MIMO-систем управления, позволяет моделировать подавление помех, слежение и другие типы откликов, поддерживает проблемы повторяющегося параметра и задачи управления системами с запаздыванием, позволяет осуществлять выбор между удовлетворенными и недостижимыми ограничениями.
17. Robust Control Toolbox
Robust Control Toolbox
Пакет Robust Control включает средства для проектирования и анализа многопараметрических устойчивых систем управления. Это системы с ошибками моделирования, динамика которых известна не полностью или параметры которых могут изменяться в ходе моделирования. Мощные алгоритмы пакета позволяют выполнять сложные вычисления с учетом изменения множества параметров. Возможности пакета:
-
синтез LQG-регуляторов на основе минимизации равномерной и интегральной нормы;
-
многопараметрический частотный отклик;
-
построение модели пространства состояний;
-
преобразование моделей на основе сингулярных чисел;
-
понижение порядка модели;
-
спектральная факторизация.
Пакет Robust Control базируется на функциях пакета Control System, одновременно предоставляя усовершенствованный набор алгоритмов для проектирования систем управления. Пакет обеспечивает переход между современной теорией управления и практическими приложениями. Он имеет множество функций, реализующих современные методы проектирования и анализа многопараметрических робастных регуляторов.
Проявления неопределенностей, нарушающих устойчивость систем, многообразны — шумы и возмущения в сигналах, неточность модели передаточной функции, немоделируемая нелинейная динамика. Пакет Robust Control позволяет оценить многопараметрическую границу устойчивости при различных неопределенностях. Среди используемых методов: алгоритм Перрона, анализ особенностей передаточных функций и др.
Пакет Robust Control обеспечивает различные методы проектирования обратных связей, среди которых: LQR, LQG, LQG/LTR и др. Необходимость понижения порядка модели возникает в нескольких случаях: понижение порядка объекта, понижение порядка регулятора, моделирование больших систем. Качественная процедура понижения порядка модели должна быть численно устойчива. Процедуры, включенные в пакет Robust Control, успешно справляются с этой задачей.
18. Model Predictive Control Toolbox
Model Predictive Control Toolbox
Пакет Model Predictive Control содержит полный набор средств для реализации стратегии предиктивного (упреждающего) управления. Эта стратегия была разработана для решения практических задач управления сложными многоканальными процессами при наличии ограничений на переменные состояния и управление. Методы предикативного управления используются в химической промышленности и для управления другими непрерывными процессами. Пакет обеспечивает:
-
моделирование, идентификацию и диагностику систем;
-
поддержку MISO (много входов — один выход), MIMO, переходных характеристик, моделей пространства состояний;
-
системный анализ;
-
конвертирование моделей в различные формы представления (пространство состояний, передаточные функции);
-
предоставление учебников и демонстрационных примеров.
Предикативный подход к задачам управления использует явную линейную динамическую модель объекта для прогнозирования влияния будущих изменений управляющих переменных на поведение объекта. Проблема оптимизации формулируется в виде задачи квадратичного программирования с ограничениями, решаемой на каждом такте моделирования заново. Пакет позволяет создавать и тестировать регуляторы как для простых, так и для сложных объектов.
Пакет содержит более полусотни специализированных функций для проектирования, анализа и моделирования динамических систем с использованием предикативного управления. Он поддерживает следующие типы систем: импульсные, непрерывные и дискретные по времени, пространство состояний. Обрабатываются различные виды возмущений. Кроме того, в модель могут быть явно включены ограничения на входные и выходные переменные.
Средства моделирования позволяют осуществлять слежение и стабилизацию. Средства анализа включают вычисление полюсов замкнутого контура, частотного отклика, другие характеристики системы управления. Для идентификации модели в пакете имеются функции взаимодействия с пакетом System Identification. Пакет также включает две функции Simulink, позволяющие тестировать нелинейные модели.
19. мю - Analysis and Synthesis
(Мю)-Analysis and Synthesis
Пакет p-Analysis and Synthesis содержит функции для проектирования устойчивых систем управления. Пакет использует оптимизацию в равномерной норме и сингулярный параметр и. В этот пакет включен графический интерфейс для упрощения операций с блоками при проектировании оптимальных регуляторов. Свойства пакета:
- проектирование регуляторов, оптимальных в равномерной и интегральной норме;
- оценка действительного и комплексного сингулярного параметра мю;
-
D-K-итерации для приближенного мю -синтеза;
-
графический интерфейс для анализа отклика замкнутого контура;
-
средства понижения порядка модели;
-
непосредственное связывание отдельных блоков больших систем.
Модель пространства состояний может быть создана и проанализирована на основе системных матриц. Пакет поддерживает работу с непрерывными и дискретными моделями. Пакет обладает полноценным графическим интерфейсом, включающим в себя: возможность устанавливать диапазон вводимых данных, специальное окно для редактирования свойств D-K итераций и графическое представление частотных характеристик. Имеет функции для матричного сложения, умножения, различных преобразований и других операций над матрицами. Обеспечивает возможность понижения порядка моделей.
20. Stateflow
Stateflow
Stateflow — пакет моделирования событийно-управляемых систем, основанный на теории конечных автоматов. Этот пакет предназначен для использования вместе с пакетом моделирования динамических систем Simulink. В любую Simulink-мо-дель можно вставить Stateflow-диаграмму (или SF-диаграмму), которая будет отражать поведение компонентов объекта (или системы) моделирования. SF-диаграмма является анимационной. По ее выделяющимся цветом блокам и связям можно проследить все стадии работы моделируемой системы или устройства и поставить ее работу в зависимость от тех или иных событий. Рис. 23.6 иллюстрирует моделирование поведения автомобиля при возникновении чрезвычайного обстоятельства на дороге. Под моделью автомобиля видна SF-диаграмма (точнее, один кадр ее работы).
Для создания SF-диаграмм пакет имеет удобный и простой редактор, а также средства пользовательского интерфейса.
21. Quantitative Feedback Theory Toolbox
Quantitative Feedback Theory Toolbox
Пакет содержит функции для создания робастных (устойчивых) систем с обратной связью. QFT (количественная теория обратных связей) — инженерный метод, использующий частотное представление моделей для удовлетворения различных требований к качеству при наличии неопределенных характеристик объекта. В основе метода лежит наблюдение, что обратная связь необходима в тех случаях, когда некоторые характеристики объекта неопределенны и/или на его вход подаются неизвестные возмущения. Возможности пакета:
-
оценка частотных границ неопределенности, присущей обратной связи;
-
графический интерфейс пользователя, позволяющий оптимизировать процесс нахождения требуемых параметров обратной связи;
-
функции для определения влияния различных блоков, вводимых в модель (мультиплексоров, сумматоров, петель обратной связи) при наличии неопределенностей;
-
поддержка моделирования аналоговых и цифровых контуров обратной связи, каскадов и многоконтурных схем;
-
разрешение неопределенности в параметрах объекта с использованием параметрических и непараметрических моделей или комбинации этих типов моделей.
Теория обратных связей является естественным продолжением классического частотного подхода к проектированию. Ее основная цель — проектирование простых регуляторов небольшого порядка с минимальной шириной полосы пропускания, удовлетворяющих качественным характеристикам при наличии неопределенностей.
Пакет позволяет вычислять различные параметры обратных связей, фильтров, проводить тестирование регуляторов как в непрерывном, так и в дискретном пространстве. Имеет удобный графический интерфейс, позволяющий создавать простые регуляторы, удовлетворяющие требованиям пользователя.
QFT позволяет проектировать регуляторы, удовлетворяющие различным требованиям, несмотря на изменения параметров модели. Измеряемые данные могут быть непосредственно использованы для проектирования регуляторов, без необходимости идентификации сложного отклика системы.
22. LMI Control Toolbox
LMI Control Toolbox
Пакет LMI (Linear Matrix Inequality) Control обеспечивает интегрированную среду для постановки и решения задач линейного программирования. Предназначенный первоначально для проектирования систем управления пакет позволяет решать любые задачи линейного программирования практически в любой сфере деятельности, где такие задачи возникают. Основные возможности пакета:
-
решение задач линейного программирования: задачи совместности ограничений, минимизация линейных целей при наличии линейных ограничений, минимизация собственных значений;
-
исследование задач линейного программирования;
-
графический редактор задач линейного программирования;
-
задание ограничений в символьном виде;
-
многокритериальное проектирование регуляторов;
-
проверка устойчивости: квадратичная устойчивость линейных систем, устойчивость по Ляпунову, проверка критерия Попова для нелинейных систем.
Пакет LMI Control содержит современные симплексные алгоритмы для решения задач линейного программирования. Использует структурное представление линейных ограничений, что повышает эффективность и минимизирует требования к памяти. Пакет имеет специализированные средства для анализа и проектирования систем управления на основе линейного программирования.
С помощью решателей задач линейного программирования можно легко выполнять проверку устойчивости динамических систем и систем с нелинейными компонентами. Ранее этот вид анализа считался слишком сложным для реализации. Пакет позволяет даже такое комбинирование критериев, которое ранее считалось слишком сложным и разрешимым лишь с помощью эвристических подходов.
Пакет является мощным средством для решения выпуклых задач оптимизации, возникающих в таких областях, как управление, идентификация, фильтрация,' структурное проектирование, теория графов, интерполяция и линейная алгебра. Пакет LMI Control включает два вида графического интерфейса пользователя: редактор задачи линейного программирования (LMI Editor) и интерфейс Magshape. LMI Editor позволяет задавать ограничения в символьном виде, a Magshape обеспечивает пользователя удобными средствами работы с пакетом.
23. Пакеты идентификации систем
Пакеты идентификации систем
Пакет System Identification содержит средства для создания математических моделей динамических систем на основе наблюдаемых входных и выходных данных. Он имеет гибкий графический интерфейс, помогающий организовать данные и создавать модели. Методы идентификации, входящие в пакет, применимы для решения широкого класса задач, от проектирования систем управления и обработки сигналов до анализа временных рядов и вибрации. Основные свойства пакета:
-
простой и гибкий интерфейс;
-
предварительная обработка данных, включая предварительную фильтрацию, удаление трендов и смещений; О выбор диапазона данных для анализа;
-
методы авторегрессии;
-
анализ отклика во временной и частотной области;
-
отображение нулей и полюсов передаточной функции системы;
-
анализ невязок при тестировании модели;
-
построение сложных диаграмм, таких как диаграмма Найквиста и др.
Графический интерфейс упрощает предварительную обработку данных, а также диалоговый процесс идентификации модели. Возможна также работа с пакетом в командном режиме и с применением расширения Simulink. Операции загрузки и сохранения данных, выбора диапазона, удаления смещений и трендов выполняются с минимальными усилиями и находятся в главном меню.
Представление данных и идентифицированных моделей организовано графически таким образом, что в процессе интерактивной идентификации пользователь легко может вернуться к предыдущему шагу работы. Для новичков существует возможность просматривать следующие возможные шаги. Специалисту графические средства позволяют отыскать любую из ранее полученных моделей и оценить ее качество в сравнении с другими моделями.
Начав с измерения выхода и входа, можно создать параметрическую модель системы, описывающую ее поведение в динамике. Пакет поддерживает все традиционные структуры моделей, включая авторегрессию, структуру Бокса-Дженкинса и др. Он поддерживает линейные модели пространства состояний, которые могут быть определены как в дискретном, так и в непрерывном пространстве. Эти модели могут включать произвольное число входов и выходов. В пакет включены функции, которые можно использовать как тестовые данные для идентифицированных моделей. Идентификация линейных моделей широко используется при проектировании систем управления, когда требуется создать модель объекта. В задачах обработки сигналов модели могут быть использованы для адаптивной обработки сигналов. Методы идентификации успешно применяются и для финансовых приложений.
24. Frequency Domain System Identification Toolbox
Frequency Domain System Identification Toolbox
Пакет Frequency Domain System Identification предоставляет специализированные средства для идентификации линейных динамических систем по их временному или частотному отклику. Частотные методы направлены на идентификацию непрерывных систем, что является мощным дополнением к более традиционной дискретной методике. Методы пакета могут быть применены к таким задачам, как моделирование электрических, механических и акустических систем. Свойства пакета:
-
периодические возмущения, пик-фактор, оптимальный спектр, псевдослучайные и дискретные двоичные последовательности;
-
расчет доверительных интервалов амплитуды и фазы, нулей и полюсов;
-
идентификация непрерывных и дискретных систем с неизвестным запаздыванием;
-
диагностика модели, включая моделирование и вычисление невязок;
-
преобразование моделей в формат System Identification Toolbox и обратно.
Используя частотный подход, можно добиться наилучшей модели в частотной области; избежать ошибок дискретизации; легко выделять постоянную составляющую сигнала; существенно улучшить отношение сигнал/шум. Для получения возмущающих сигналов пакет предоставляет функции генерации двоичных последовательностей, минимизации величины пика и улучшения спектральных характеристик. Пакетом обеспечивается идентификация непрерывных и дискретных линейных статических систем, автоматическая генерация входных сигналов, а также графическое изображение нулей и полюсов передаточной функции результирующей системы. Функции для тестирования модели включают вычисление невязок, передаточных функций, нулей и полюсов, прогонку модели с использованием тестовых данных.
25. Дополнительные пакеты расширения MATLAB
Дополнительные пакеты расширения MATLAB
Пакет прикладных программ для построения и моделирования разнообразных телекоммуникационных устройств: цифровых линий связи, модемов, преобразователей сигналов и др. Имеет богатейший набор моделей самых различных устройств связи и телекоммуникаций. Содержит ряд интересных примеров моделирования коммуникационных средств, например модема, работающего по протоколу v34, модулятора для обеспечения однополосной модуляции и др.
26. Digital Signal Processing (DSP) Blockset
Digital Signal Processing (DSP) Blockset
Пакет прикладных программ для проектирования устройств, использующих процессоры цифровой обработки сигналов. Это прежде всего высокоэффективные цифровые фильтры с заданной или адаптируемой к параметрам сигналов частотной характеристикой (АЧХ). Результаты моделирования и проектирования цифровых устройств с помощью этого пакета могут использоваться для построения высокоэффективных цифровых фильтров на современных микропроцессорах цифровой обработки сигналов.
27. Fixed-Point Blockset
Fixed-Point Blockset
Этот специальный пакет ориентирован на моделирование цифровых систем управления и цифровых фильтров в составе пакета Simulink. Специальный набор компонентов позволяет быстро переключаться между вычислениями с фиксированной и плавающей запятой (точкой). Можно указывать 8-, 16- или 32-битовую длину слова. Пакет обладает рядом полезных свойств:
-
применение беззнаковой или двоичной арифметики;
-
выбор пользователем положения двоичной точки;
-
автоматическая установка положения двоичной точки;
-
просмотр максимального и минимального диапазонов сигнала модели;
-
переключение между вычислениями с фиксированной и плавающей точкой;
-
коррекция переполнения и наличие ключевых компонентов для операций с фиксированной точкой; логические операторы, одно- и двумерные справочные таблицы.
28. Пакеты для обработки сигналов и изображений
Пакеты для обработки сигналов и изображений
Мощный пакет по анализу, моделированию и проектированию устройств обработки всевозможных сигналов, обеспечению их фильтрации и множества преобразований.
Пакет Signal Processing обеспечивает чрезвычайно обширные возможности создания программ обработки сигналов для современных научных и технических приложений. В пакете используется разнообразная техника фильтрации и новейшие алгоритмы спектрального анализа. Пакет содержит модули для разработки линейных систем и анализа временных рядов. Пакет будет полезен, в частности, в таких областях, как обработка аудио- и видеоинформации, телекоммуникации, геофизика, задачи управления в реальном режиме времени, экономика, финансы и медицина. Основные свойства пакета:
-
моделирование сигналов и линейных систем;
-
проектирование, анализ и реализация цифровых и аналоговых фильтров;
-
быстрое преобразование Фурье, дискретное косинусное и другие преобразования;
-
оценка спектров и статистическая обработка сигналов;
-
параметрическая обработка временных рядов;
-
генерация сигналов различной формы.
Пакет Signal Processing — идеальная оболочка для анализа и обработки сигналов. В нем используются проверенные практикой алгоритмы, выбранные по критериям максимальной эффективности и надежности. Пакет содержит широкий спектр алгоритмов для представления сигналов и линейных моделей. Этот набор позволяет пользователю достаточно гибко подходить к созданию сценария обработки сигналов. Пакет включает алгоритмы для преобразования модели из одного представления в другое.
Пакет Signal Processing включает полный набор методов для создания цифровых фильтров с разнообразными характеристиками. Он позволяет быстро разрабатывать фильтры верхних и нижних частот, полосовые пропускающие и задерживающие фильтры, многополосные фильтры, в том числе фильтры Чебышева, Юла-Уолкера, эллиптические и др.
Графический интерфейс позволяет проектировать фильтры, задавая требования к ним в режиме переноса объектов мышью. В пакет включены следующие новые методы проектирования фильтров:
-
обобщенный метод Чебышева для создания фильтров с нелинейной фазовой характеристикой, комплексными коэффициентами или произвольным откликом. Алгоритм разработан Макленаном и Карамом в 1995 г.;
-
метод наименьших квадратов с ограничениями позволяет пользователю явно контролировать максимальную ошибку (сглаживание);
-
метод расчета минимального порядка фильтра с окном Кайзера;
-
обобщенный метод Баттерворта для проектирования низкочастотных фильтров с максимально однородными полосами пропускания и затухания.
Основанный на оптимальном алгоритме быстрого преобразования Фурье пакет Signal Processing обладает непревзойденными характеристиками для частотного анализа и спектральных оценок. Пакет включает функции для вычисления дискретного преобразования Фурье, дискретного косинусного преобразования, преобразования Гильберта и других преобразований, часто применяемых для анализа, кодирования и фильтрации. В пакете реализованы такие методы спектрального анализа как метод Вельха, метод максимальной энтропии и др.
Новый графический интерфейс позволяет просматривать и визуально оценивать характеристики сигналов, проектировать и применять фильтры, производить спектральный анализ, исследуя влияние различных методов и их параметров на получаемый результат. Графический интерфейс особенно полезен для визуализации временных рядов, спектров, временных и частотных характеристик, расположения нулей и полюсов передаточных функций систем.
Пакет Signal Processing является основой для решения многих других задач. Например, комбинируя его с пакетом Image Processing, можно обрабатывать и анализировать двумерные сигналы и изображения. В паре с пакетом System Identification пакет Signal Processing позволяет выполнять параметрическое моделирование систем во временной области. В сочетании с пакетами Neural Network и Fuzzy Logic может быть создано множество средств для обработки данных или выделения классификационных характеристик. Средство генерации сигналов позволяет создавать импульсные сигналы различной формы.
29. Higher-Order Spectral Analysis Toolbox
Higher-Order Spectral Analysis Toolbox
Пакет Higher-Order Spectral Analysis содержит специальные алгоритмы для анализа сигналов с использованием моментов высшего порядка. Пакет предоставляет широкие возможности для анализа негауссовых сигналов, так как содержит алгоритмы, пожалуй, самых передовых методов для анализа и обработки сигналов. Основные возможности пакета:
-
оценка спектров высокого порядка;
-
традиционный или параметрический подход;
-
восстановление амплитуды и фазы;
-
адаптивное линейное прогнозирование;
-
восстановление гармоник;
-
оценка запаздывания;
-
блочная обработка сигналов.
Пакет Higher-Order Spectral Analysis позволяет анализировать сигналы, поврежденные негауссовым шумом, и процессы, происходящие в нелинейных системах. Спектры высокого порядка, определяемые в терминах моментов высокого порядка сигнала, содержат дополнительную информацию, которую невозможно получить, пользуясь только анализом автокорреляции или спектра мощности сигнала. Спектры высокого порядка позволяют:
-
подавить аддитивный цветной гауссов шум;
-
идентифицировать неминимально-фазовые сигналы;
-
выделить информацию, обусловленную негауссовым характером шума;
-
обнаружить и проанализировать нелинейные свойства сигналов.
Возможные приложения спектрального анализа высокого порядка включают акустику, биомедицину, эконометрию, сейсмологию, океанографию, физику плазмы, радары и локаторы. Основные функции пакета поддерживают спектры высокого порядка, взаимную спектральную оценку, линейные модели прогноза и оценку запаздывания.
30. Image Processing Toolbox
Image Processing Toolbox
Пакет Image Processing предоставляет ученым, инженерам и даже художникам широкий спектр средств для цифровой обработки и анализа изображений. Будучи тесно связанным со средой разработки приложений MATLAB, пакет Image Processing Toolbox освобождает вас от выполнения длительных операций кодирования и отладки алгоритмов, позволяя сосредоточить усилия на решении основной научной или практической задачи. Основные свойства пакета:
-
восстановление и выделение деталей изображений;
-
работа с выделенным участком изображения;
-
анализ изображения;
-
линейная фильтрация;
-
преобразование изображений;
-
геометрические преобразования;
-
увеличение контрастности важных деталей;
-
бинарные преобразования;
-
обработка изображений и статистика;
-
цветовые преобразования;
-
изменение палитры;
-
преобразование типов изображений.
Пакет Image Processing дает широкие возможности для создания и анализа графических изображений в среде MATLAB. Этот пакет обеспечивает чрезвычайно гибкий интерфейс, позволяющий манипулировать изображениями, интерактивно разрабатывать графические картины, визуализировать наборы данных и аннотировать результаты для технических описаний, докладов и публикаций. Гибкость, соединение алгоритмов пакета с такой особенностью MATLAB, как матрично-векторное описание делают пакет очень удачно приспособленным для решения практически любых задач по разработке и представлению графики. Примеры применения этого пакета в среде системы MATLAB были даны в уроке 7. В MATLAB входят специально разработанные процедуры, позволяющие повысить эффективность графической оболочки. Можно отметить, в частности, такие особенности:
-
интерактивная отладка при разработке графики;
-
профилировщик для оптимизации времени выполнения алгоритма;
-
средства построения интерактивного графического интерфейса пользователя (GUI Builder) для ускорения разработки GUI-шаблонов, позволяющие настраивать его под задачи пользователя.
Этот пакет позволяет пользователю тратить значительно меньше времени и сил на создание стандартных графических изображений и, таким образом, сконцентрировать усилия на важных деталях и особенностях изображений.
MATLAB и пакет Image Processing максимально приспособлены для развития, внедрения новых идей и методов пользователя. Для этого имеется набор сопрягаемых пакетов, направленных на решение всевозможных специфических задач и задач в нетрадиционной постановке.
Пакет Image Processing в настоящее время интенсивно используется в более чем 4000 компаниях и университетах по всему миру. При этом имеется очень широкий круг задач, которые пользователи решают с помощью данного пакета, например космические исследования, военные разработки, астрономия, медицина, биология, робототехника, материаловедение, генетика и т. д.
31. Wavelet Toolbox
Wavelet Toolbox
Пакет Wavelet предоставляет пользователю полный набор программ для исследования многомерных нестационарных явлений с помощью вейвлетов (коротких волновых пакетов). Сравнительно недавно созданные методы пакета Wavelet расширяют возможности пользователя в тех областях, где обычно применяется техника Фурье-разложения. Пакет может быть полезен для таких приложений, как обработка речи и аудиосигналов, телекоммуникации, геофизика, финансы и медицина. Основные свойства пакета:
-
усовершенствованный графический пользовательский интерфейс и набор команд для анализа, синтеза, фильтрации сигналов и изображений;
-
преобразование многомерных непрерывных сигналов;
-
дискретное преобразование сигналов;
-
декомпозиция и анализ сигналов и изображений;
-
широкий выбор базисных функций, включая коррекцию граничных эффектов;
-
пакетная обработка сигналов и изображений;
-
анализ пакетов сигналов, основанный на энтропии;
-
фильтрация с возможностью установления жестких и нежестких порогов;
-
оптимальное сжатие сигналов.
Пользуясь пакетом, можно анализировать такие особенности, которые упускают другие методы анализа сигналов, т. е. тренды, выбросы, разрывы в производных высоких порядков. Пакет позволяет сжимать и фильтровать сигналы без явных потерь даже в тех случаях, когда нужно сохранить и высоко- и низкочастотные компоненты сигнала. Имеются алгоритмы сжатия и фильтрации и для пакетной обработки сигналов. Программы сжатия выделяют минимальное число коэффициентов, представляющих исходную информацию наиболее точно, что очень важно для последующих стадий работы системы сжатия. В пакет включены следующие базисные наборы вейвлетов: биортогональный, Хаара, «Мексиканская шляпа», Майера и др. Вы также можете добавить в пакет свои собственные базисы.
Обширное руководство пользователя объясняет принципы работы с методами пакета, сопровождая их многочисленными примерами и полноценным разделом ссылок.
32. Прочие пакеты прикладных программ
Прочие пакеты прикладных программ
Довольно актуальный для нашего периода рыночных реформ пакет прикладных программ по финансово-экономическим расчетам. Содержит множество функций по расчету сложных процентов, операций по банковским вкладам, вычисления прибыли и многое другое. К сожалению, из за многочисленных (хотя, в общем-то, не слишком принципиальных) различий в финансово-экономических формулах его применение в наших условиях не всегда разумно — есть множество отечественных программ для таких расчетов, — например «Бухгалтерия 1C». Но если вы хотите подключиться к базам данных агентств финансовых новостей — Bloom-berg, IDC через пакет Datafeed Toolbox MATLAB, то, конечно, обязательно пользуйтесь и финансовыми пакетами расширения MATLAB.
Пакет Financial является основой для решения в MATLAB множества финансовых задач, от простых вычислений до полномасштабных распределенных приложений. Пакет Financial может быть использован для расчета процентных ставок и прибыли, анализа производных доходов и депозитов, оптимизации портфеля инвестиций. Основные возможности пакета:
-
обработка данных;
-
дисперсионный анализ эффективности портфеля инвестиций;
-
анализ временных рядов;
-
расчет доходности ценных бумаг и оценка курсов;
-
статистический анализ и анализ чувствительности рынка;
-
калькуляция ежегодного дохода и расчет денежных потоков;
-
методы начисления износа и амортизационных отчислений.
Учитывая важность даты той или иной финансовой операции, в пакет Financial включены несколько функций для манипулирования датами и временем в различных форматах. Пакет Financial позволяет рассчитывать цены и доходы при инвестициях в облигации. Пользователь имеет возможность задавать нестандартные, в том числе нерегулярные и несовпадающие друг с другом, графики дебитных и кредитных операций и окончательного расчета при погашении векселей. Экономические функции чувствительности могут быть вычислены с учетом разновременных сроков погашения.
Алгоритмы пакета Financial для расчета показателей движения денежных средств и других данных, отражаемых в финансовых счетах, позволяют вычислять, в частности, процентные ставки по займам и кредитам, коэффициенты рентабельности, кредитные поступления и итоговые начисления, оценивать и прогнозировать стоимость инвестиционного портфеля, вычислять показатели износа и т. п. Функции пакета могут быть использованы с учетом положительного и отрицательного денежных потоков (cash-flow) (превышения денежных поступлений над платежами или денежных выплат над поступлениями соответственно).
Пакет Financial содержит алгоритмы, которые позволяют анализировать портфель инвестиций, динамику и экономические коэффициенты чувствительности. В частности, при определении эффективности инвестиций функции пакета позволяют сформировать портфель, удовлетворяющий классической задаче Г. Марковица. Пользователь может комбинировать алгоритмы пакета для вычисления коэффициентов Шарпе и ставок дохода. Анализ динамики и экономических коэффициентов чувствительности позволяет пользователю определить позиции для стреддл-сделок, хеджирования и сделок с фиксированными ставками. Пакет Financial обеспечивает также обширные возможности для представления и презентации данных и результатов в виде традиционных для экономической и финансовой сфер деятельности графиков и диаграмм. Денежные средства могут по желанию пользователя отображаться в десятичном, банковском и процентном форматах.
33. Mapping Toolbox
Mapping Toolbox
Пакет Mapping предоставляет графический и командный интерфейс для анализа географических данных, отображения карт и доступа к внешним источникам данных по географии. Кроме того, пакет пригоден для работы с множеством широко известных атласов. Все эти средства в комбинации с MATLAB предоставляют пользователям все условия для продуктивной работы с научными географическими данными. Основные возможности пакета:
-
визуализация, обработка и анализ графических и научных данных;
-
более 60 проекций карт (прямые и инверсные);
-
проектирование и отображение векторных, матричных и составных карт;
-
графический интерфейс для построения и обработки карт и данных;
-
глобальные и региональные атласы данных и сопряжение с правительственными данными высокого разрешения;
-
функции географической статистики и навигации;
-
трехмерное представление карт со встроенными средствами подсветки и затенения;
-
конвертеры для популярных форматов географических данных: DCW, TIGER, ЕТОРО5.
Пакет Mapping включает более 60 наиболее широко известных проекций, включая цилиндрическую, псевдоцилиндрическую, коническую, поликоническую и псевдоконическую, азимутальную и псевдоазимутальную. Возможны прямые и обратные проекции, а также нестандартные виды проекции, задаваемые пользователем.
В пакете Mapping картой называется любая переменная или множество переменных, отражающих или назначающих численное значение географической точке или области. Пакет позволяет работать с векторными, матричными и смешанными картами данных. Мощный графический интерфейс обеспечивает интерактивную работу с картами, например возможность подвести указатель к объекту и, щелкнув на нем, получить информацию. Графический интерфейс MAPTOOL — полная среда разработки приложений для работы с картами.
Наиболее широко известные атласы мира, Соединенных Штатов, астрономические атласы входят в состав пакета. Географическая структура данных упрощает извлечение и обработку данных из атласов и карт. Географическая структура данных и функции взаимодействия с внешними географическими данными форматов Digital Chart of the World (DCW), TIGER, TBASE и ЕТОРО5 собраны воедино, чтобы обеспечить мощный и гибкий инструмент для доступа к уже существующим и будущим географическим базам данных. Тщательный анализ географических данных часто требует математических методов, работающих в сферической системе координат. Пакет Mapping снабжен подмножеством географических, статистических и навигационных функций для анализа географических данных. Функции навигации дают широкие возможности для выполнения задач перемещения, таких как позиционирование и планирование маршрутов.
34. Power System Blockset
Power System Blockset
Пакет моделирования мощных энергетических (в основном электротехнических) систем, таких как линии передачи, силовые ключи, регуляторы напряжения и тока, устройства управления электродвигателями различного типа и нагревательными системами.
Этот пакет обеспечивает моделирование широкого спектра энергетических систем и устройств — начиная с анализа простейших электрических цепей и кончая моделированием сложных преобразовательных устройств и даже целых электрических систем. Результаты моделирования отображаются разнообразными виртуальными измерительными приборами, такими как графопостроители, осциллографы и др.
35. Data Acquisition Toolbox и Instrument Control Toolbox
Data Acquisition Toolbox и Instrument Control Toolbox
Data Acquisition Toolbox — пакет расширения, относящийся к области сбора данных через блоки, подключаемые к внутренней шине компьютера, функциональных генераторов, анализаторов спектра — словом, приборов, широко используемых в исследовательских целях для получения данных. Они поддержаны соответствующей вычислительной базой. Новый блок Instrument Control Toolbox позволяет подключать приборы и устройства с последовательным интерфейсом и с интерфейсами Канал общего пользования и VXI.
36. Database toolbox и Virtual Reality Toolbox
Database toolbox и Virtual Reality Toolbox
Более чем в 100 раз повышена скорость работы Database toolbox, при помощи которого осуществляется обмен информацией с целым рядом систем управления базами данных через драйверы ODBC или JDBC:
-
Oracle 7.3.3;
-
Access 95 или 97 Microsoft;
-
Microsoft SQL Server 6.5 или 7.0;
-
Sybase Adaptive Server 11;
-
Sybase (бывший Watcom) SQL Server Anywhere 5.0;
-
IBM DB2 Universal 5.0;
-
Informix 7.2.2;
-
Computer Associates Ingres (все версии).
Все данные предварительно преобразуются в массив ячеек в MATLAB 6.0. В MATLAB 6.1 можно использовать и массив структур. Визуальный конструктор (Visual Query Builder) позволяет составлять сколь угодно сложные запросы на диалектах языка SQL этих баз данных даже без знания SQL. В одном сеансе может быть открыто много неоднородных баз данных.
Пакет Virtual Reality Toolbox доступен начиная с версии MATLAB 6.1. Позволяет осуществлять трехмерную анимацию и мультипликацию, в том числе моделей Simulink. Язык программирования — VRML — язык моделирования виртуальной реальности (Virtual Reality Modeling Language). Просмотр анимации возможен с любого компьютера, оснащенного браузером с поддержкой VRML. Подтверждает, что математика — наука о количественных соотношениях и пространственных формах любых действительных или виртуальных миров.
37. Excel Link
Excel Link
Позволяет использовать Microsoft Excel 97 как процессор ввода-вывода MATLAB. Для этого достаточно установить в Excel как add-in функцию поставляемый Math Works файл excllinkxla. В Excel нужно набрать Сервис > Надстройки > Обзор, выбрать файл в каталоге \matlabrl2\toolbox\exlink и установить его. Теперь при каждом запуске Excel появится командное окно MATLAB, а панель управления Excel дополнится кнопками getmatrix, putmatrix, evalstring. Для закрытия MATLAB из Excel достаточно набрать =MLC1ose() в любой ячейке Excel. Для открытия после выполнения этой команды нужно либо щелкнуть мышью на одной из кнопок getmatrix, putmatrix, evalstring, либо набрать в Excel Сервис > Макрос >Выполнить mat! abi ni t. Выделив мышью диапазон ячеек Excel, вы можете щелкнуть на getmatrix и набрать имя переменной MATLAB. Матрица появится в Excel. Заполнив числами диапазон ячеек Excel, вы можете выделить этот диапазон, щелкнуть на putmatrix и ввести имя переменной MATLAB. Работа, таким образом, интуитивно понятна. В отличие от MATLAB Excel Link не чувствителен к регистру: I и i, J и j равноценны.
38. MATLAB Compiler
MATLAB Compiler
Компилятор для программ, создаваемых на языке программирования системы MATLAB. Транслирует коды этих программ в программы на языке Си++. Применение компилятора обеспечивает возможность создания исполняемых кодов (полностью законченных программ), время выполнения которых для программ с большим числом циклических операций уменьшается в 10-15 раз. Может интегрироваться в среду Microsoft Visual Studio и использоваться вместе с Visual C++. Помимо него вы можете использовать и другие компиляторы Си++.
39. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
-
Выводить список пакетов расширения системы MATLAB.
-
Вызывать демонстрационные примеры пакетов расширения.
Приложение
Приложение
Поддержка средств Java в MATLAB 6
Язык программирования Java обычно непосредственно не используется для поддержки математических вычислений в системе MATLAB. Однако этот перспективный язык высокого уровня входит в состав ядра системы и широко применяется для создания средств интерфейса и средств Интернета. Поэтому в новых версиях MATLAB 6.0/6.1 существенно расширена поддержка средств языка Java, который приобрел важное значение для решения задач в области создания электронных и Интернет-документов.
Фактически Java интегрирован в MATLAB и используется для построения его графического интерфейса и справочной системы (наряду с HTML). Кроме того, предусмотрены работа с рядом типов данных, классов и объектов, связанных с Java, и поддержка построенной на Java виртуальной машины. Основной материал по использованию средств языка Java имеется в дополнительном руководстве «MATLAB. External Interfaces. Version 6». Для знакомства с тонкостями программирования на Java рекомендуется обращаться в Интернет-сайт www.javasoft.com, посвященный этому языку. Уточнить версию Java, установленную в системе MATLAB, на вашей компьютерной платформе можно, исполнив команду:
» version -Java ans
Java 1.1.8 from Sun Microsystems Inc.
Вы можете создавать объекты Java в MATLAB с использованием имени класса Java:
» f = java.awt.Frame('My Title')
f =
Java. awt. Frame[f rameO. 0,0, 0x0. i nval i d. hi dden. layout=java. awt. Border-Layout.
resizable.title=my title]
Методы объектов Java могут быть вызваны как с использованием синтаксиса Java, так и с использованием синтаксиса MATLAB:
» setTitle (f. 'new title' )
» t = getTitle(f)
t =
new title
Тот же пример с использованием синтаксиса Java:
» f.setTitle ('modify title' )
» t = f.getTitle
t =
modify title
» whos f
Name Size Bytes Class
f1x1 Java.awt.Frame
Grand total is 1 elements using 0 bytes
Как видно из этого сообщения, в MATLAB поддерживаются Java-классы и Java-объекты.
Для более полного знакомства с возможностями Java в MATLAB можно воспользоваться справочной системой. Правда, в индексном каталоге поиск разделов по имени «Java» к успеху не приводит, но в окне расширенного поиска Search можно найти ряд статей по применению Java.
В окне справки в разделе Calling Java from MATLAB можно найти целый ряд разделов справки, посвященных применению этого языка в системе MATLAB (естественно, на английском языке).
Для получения информации об объектах и методах Java, с которыми может работать MATLAB, нужно исполнить команду:
»methodsview Java.awt.Menultem
Данные окна рис. П2 показывают, что поддержка Java реализована в большом числе объектов и методов системы MATLAB.
При использовании объектов Java пользователь должен учитывать многочисленные отличия в свойствах объектов Java и объектов MATLAB, что ведет к различиям в результатах исполнения многих функций. Например, вот как работает функция определения длины строки в MATLAB:
» s= ' Hellо my friend!'
s =
Hello my friend!
» size(s)
ans =
1 16
Результат означает, что строка s задана как одномерный массив с числом элементов 16. А вот как та же функция работает со строковым массивом Java:
» string=java.lang.Sthng( 'Hello my friend!')
string=
Hello my friend!
» size(string)
ans =
1 1
Нетрудно заметить, что отдельные символы в этом случае не рассматриваются как элементы массива, и строка представлена одномерным массивом единичной длины.
» C=char(string)
С=
Hello my friend!
» [m,n]=size(C)
m =
1
n =
16
» whos С
Name Size Bytes Class
С 1x16 32 char array Grand total is 16 elements using 32 bytes
Использовав преобразование объекта класса java.lang.string в массив символов MATLAB, мы все-таки подсчитали число символов обычными средствами MATLAB. Но в среде MATLAB мы можем сделать это и средствами Java.
» string.length
ans =
16
Или
» e=java.lang.StringBuffer(string)
e =
Hello my friend!
» e.length
ans =
16
Следующий пример показывает создание Java-структуры многоугольника:
» polygon=java.awt.Polygon([14 42 98 124],[55 12 -2 62].4)
polygon =
java.awt.Pol ygon@94067b
Для выявления структуры Java объекта может использоваться функция struct (object), которая преобразует объект в структуру (массив структур) MATLAB с потерей информации о классе.
Пример: .
» struct(string)
ans =
0x0 struct array with fields:» struct(polygon)
ans =
npoints: 4
xpoints: [4x1 int32]
ypoints: [4x1 int32]
Следует отметить, что указание имени объекта с большой буквы (кстати, как это задано в определении класса) ведет к ошибке, поскольку сам объект, преобразуемый в структуру, по правилам MATLAB, где регистр имеет значение, называется
polygon:
» struct(Polygon)
??? Undefined function or variable 'Polygon'.
Эти примеры, и их можно привести множество, свидетельствуют о том, что пользователь, рискнувший применить средства Java в MATLAB на практике, должен хорошо знать как возможности языка Java, так и особенности среды и языка программирования MATLAB. И быть готовым к различным сюрпризам.
Для обычных пользователей системой MATLAB по ее прямому назначению — математические вычисления — большинство возможностей Java представляет ограниченный интерес. Исключением, пожалуй, является работа с такими важными объектами Java, как массивы и классы url. Напомним, что Java-массивы входят в иерархию объектов языка программирования системы MATLAB.
Массивы в Java считаются одномерными (подобными векторам-столбцам MAT-LAB). Однако возможно построение массивов в массивах без ограничения числа уровней вложения. Тем не менее функция ndims MATLAB, если ее входным аргументом является такой «многомерный» массив Java, всегда возвращает 2. Форма таких массивов в общем случае не прямоугольная, т. е. число элементов по рядам и столбцам может различаться. В MATLAB все массивы, кроме массивов Java, могут быть одномерными, двумерными и многомерными. Нумерация элементов Java-массивов в обычных системах программирования на Java идет с нуля. В MATLAB нумерация всех элементов массивов, в том числе и Java-массива (Java-array), начинается с единицы. (База массива равна единице.) Ниже приведен пример задания прямоугольного Java-массива в массиве с числами двойной точности с именем dblArray: dblArray = javaArrayC Java.lang.Double'.3.4);
В следующем фрагменте программы на языке MATLAB с помощью циклов элементам массива присваиваются конкретные значения:
for 1=1:3
for j-l:4 dblArray(i.j) = Java.lang.Double((i*5)+j);
end end
Теперь несложно проверить созданный массив:
dblArray
dblArray =
Java.lang.Double[][]:
|
|
|
|
|
|
|
|
[6] [7] [11] [12] [16] [17] » dblArray(2.3) ans = 13.0 |
[ 8] [13] [18] |
[9] [14] [19] |
|
|
|
|
|
|
|
Из этого примера в целом ясно, что, несмотря на отдельные нюансы, работа с Java-массивами в основном подобна таковой для MATLAB массивов. При этом система MATLAB поддерживает ряд типов преобразований массивов и иных данных из форматов, принятых на языке программирования Java, в форматы MATLAB и наоборот.