Регрессионный анализ

Под регрессионным анализом (или просто регрессией) обычно подразумевают нахождение некоторой формальной аналитической зависимости, которая приближенно (по критерию минимума среднеквадратической ошибки) аппроксимирует исходную зависимость. Последняя чаще всего бывает представлена некоторым набором точек (например, полученных в результате эксперимента).

Для проведения регрессионного анализа служит функция fit, которая вызывается следующим образом: 

stats[fit,leastsquare[vars,eqn.parms]](data)

или

fit[leastsquare[vars,eqn.parms]](data) 

где data — список данных, vars — список переменных для представления данных, eqn — уравнение, задающее аппроксимирующую зависимость (по умолчанию линейную), parms — множество параметров, которые будут заменены вычисленными значениями.

На приведенных ниже примерах показано проведение регрессии с помощью функции fit для зависимостей вида у(х):

> with(stats):Digits:=5;

Digits := 5

> fit[leastsquare[[x,y]]]([[l,2,3,4].[3,3.5,3.9,4.6]]);

у = 2.4500 + .52000 х

>fit[leastsquare[[x,y], y=a*x"2+b*x+c]]([[l.2,3.4],[1.8,4.5,10,16.5]]);

2

у = .95000 х + .21000 х + .55000

В первом примере функция регрессии не задана, поэтому реализуется простейшая линейная регрессия, и функция fit возвращает полученное уравнение регрессии для исходных данных, представленных списками координат узловых точек. Это уравнение аппроксимирует данные с наименьшей среднеквадратичной погрешностью. Во втором примере задано приближение исходных данных степенным многочленом второго порядка. Вообще говоря, функция fit обеспечивает приближение любой функцией полиномом.

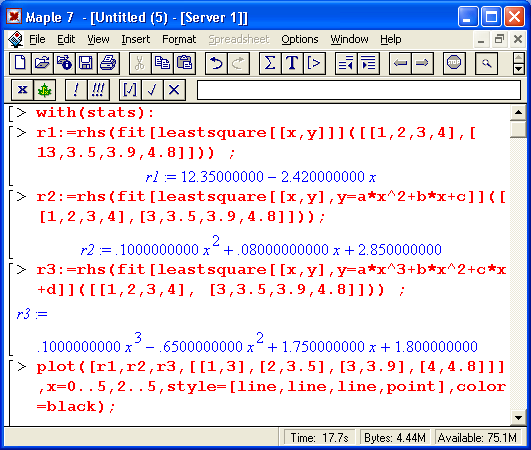
Рисунок 16.15 показывает регрессию для одних и тех же данных Полиномами первой, второй и третьей степени с построением их графиков и точек исходных данных. Нетрудно заметить, что лишь для полинома третьей степени точки исходных данных точно укладываются на кривую полинома, поскольку в этом случае (4 точки) регрессия превращается в полиномиальную аппроксимацию. В других случаях точного попадания точек на линии регрессии нет, но обеспечивается минимум среднеквадратической погрешности для всех точек — следствие реализации метода наименьших квадратов.

Функция fit может обеспечивать регрессию и для функций нескольких переменных. При этом надо просто увеличить размерность массивов исходных данных. В качестве примера ниже приведен пример регрессии для функции двух переменных:

>f:=fit[1eastsquare[[x,y,z],z=-a+b*x+c*y,{a,b,c}]]\

([[l,2,3.5,5],[2.4,6,8.8],[3,5,7,10,Weight(15,2)]]):

f:=z=l + 13/3x-7/6y

> fa:=unapply(rhs(f),x,y);

fa:=(x,y)->l + 13/3x-7/6y

z > fa(1.,2.);

2.999999999

>fa(2,3):

37/6

Рис. 16.15. Примеры регрессии полиномом и первой, второй и третьей степени

В данном случае уравнение регрессии задано в виде z = a + bx + cy. Обратите внимание на важный момент в конце этого примера — применение полученной функции регрессии для вычислений или построения ее графика. Прямое применение функции f в данном случае невозможно, так как она представлена в не вычисляемом формате. Для получения вычисляемого выражения она преобразуется в функцию двух переменных fa(x,y) путем отделения правой части выражения для функции f. После этого возможно вычисление значений функции fa(x,y) для любых заданных значений х и у:

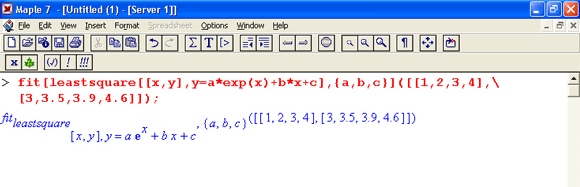
К сожалению, функция fit неприменима для нелинейной регресии. При попытке ее проведения возвращается структура процедуры, но не результат регресии — см. пример ниже:

Для проведения нелинейной регрессии произвольного вида нужно обратиться к средствам нового пакета CurveFitting, включенного в состав Maple 7. Этот пакет был описан в главе 14.