Основные функции пакета DEtools

Ввиду обилия функций пакета DEtools дать их полное описание в данной книге не представляется возможным. Поэтому выборочно рассмотрим наиболее важные функции этого пакета. Функция:

autonomous(des.vars,ivar)

тестирует дифференциальное уравнение (или систему) des. Ее параметрами помимо des являются независимая переменная ivar и зависимая переменная dvar. Следующие примеры поясняют применение этой функции:

> automou(sin(z(t)-z(t)^2)*(D@@4)(z)(t)-cos(z(t))-5,z.t);

true

> DE:=diff(x(s),s)-x(s)*cos(arctan(x(s)))=arctan(s): 

> autonomous(DE.{x},s);

false

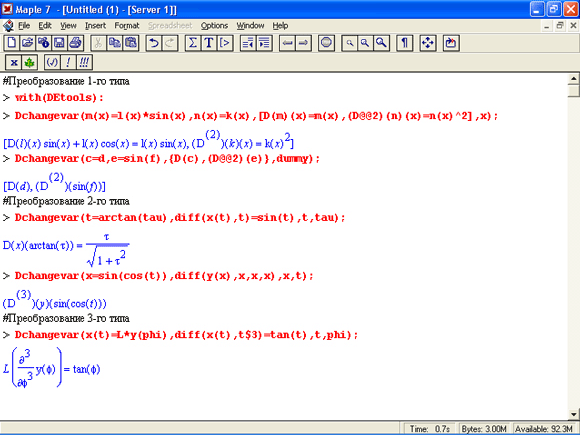
Функция Dchangevar используется для обеспечения замен (подстановок) в дифференциальных уравнениях:

Dchangevar(trans,deqns, c_tvar, rMvar)

Dchangevar(tranl, tran2, .... tranN, deqns, c_ivar, n_ivar)

В первом случае trans — список или множество уравнений, которые подставляются в дифференциальное уравнение, список или множество дифференциальных уравнений deqns. При этом c_ivar — имя текущей переменной, n_ivar — имя новой переменной (его задавать необязательно). Во второй форме для подстановки используются уравнения tranl, tran2, .... Ниже представлены примеры применения функции Dchangevar:

Следует отметить, что подстановки являются мощным средством решения дифференциальных уравнений. Нередки случаи, когда дифференциальное уравнение не решается без их применения. Дополнительные примеры использования подстановок можно найти в справочной базе данных системы Maple 7.

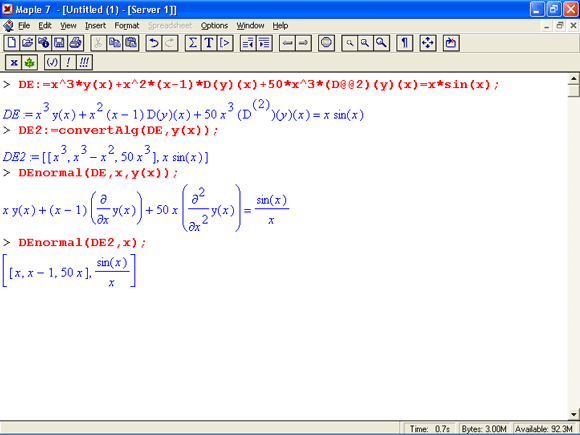
Функция нормализации ОДУ DEnormal синтаксически записывается в виде:

DEnormal(des,ivar,dvar)

где des — система дифференциальных уравнений, 1var — независимая переменная и dvar — зависимая переменная. Применение этой функции поясняют следующие примеры:

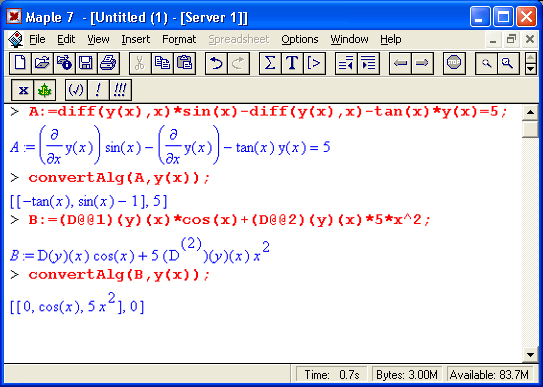
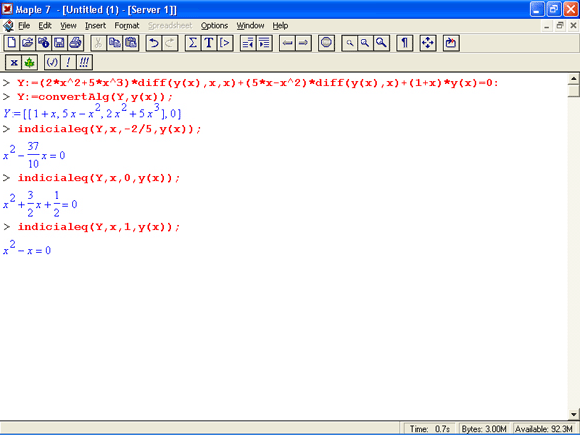
Функция convertAlg(des,dvar) возвращает список коэффициентов формы системы дифференциальных уравнений des с зависимыми переменными dvar. Это поясняют следующие примеры:

Для изменения переменных в системах дифференциальных уравнений используется функция convertsys:

convertsys(deqns, inits, vars, ivar, yvec, ypvec)

Здесь deqns — одно дифференциальное уравнение или список (множество), представляющие систему дифференциальных уравнений первого порядка, inits — множество или список начальных условий, vans — зависимые переменные, ivar — независимые переменные, yvec — вектор решений и ypvec — вектор производных. Функция:

indicialeq(des.ivar,alpha.dvar)

обеспечивает полиномиальное представление для линейного однородного дифференциального уравнения второго порядка des. Параметр alpha намечает точку сингулярности.

Функция:

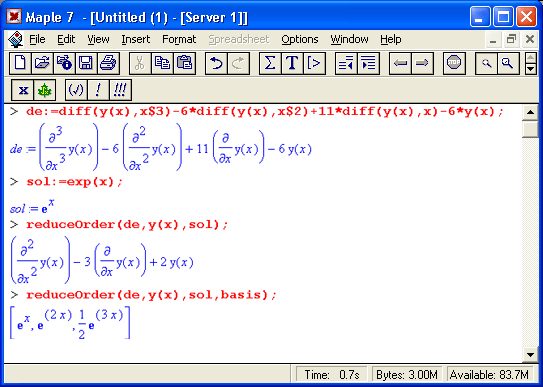
reduceOrder(des.dvar,partsol, solutionForm)

обеспечивает понижение порядка дифференциального уравнения des (или системы уравнений, представленных списком или множеством) при зависимых переменных dvar, частном решении partsol (или списке частных решений) и флаге solutionForm, показывающем, что решение происходит явным методом (explicitly). Для демонстрации действия этой функции воспользуемся примером из ее справочной страницы:

Функция:

regularsp(des,ivar,dvar)

вычисляет регулярные особые (сингулярные) точки для дифференциального уравнения второго порядка или системы дифференциальных уравнений des. Следующий пример поясняет применение данной функции:

> coefs := [21*(х^2 - х + 1),0,100*х^2*(х-1)^2]:

 > regularsp(coefs. х);

[0,1]

Еще две функции пакета DEtools:

translate(des,ivar.pt,dvar) 

untranslate(des,ivar,pt,dvar)

выполняют особую операцию трансляции дифференциального уравнения (или списка дифференциальных уравнений) из центрированного относительно 0 в центрированное относительно 1 и наоборот. С деталями этого специфического процесса заинтересованный читатель может познакомиться в справочной базе данных. И еще одна полезная функция пакета: 

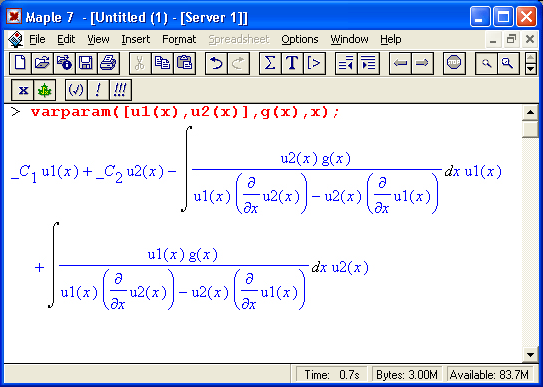
varparam(sols.v.ivar) 

находит общее решение дифференциального уравнения (или системы уравнений) sols методом вариации параметров. Параметр v задает правую часть уравнения; если он равен 0, ищется только частичное решение:

Более подробную информацию об этих функциях читатель найдет в их справочных страницах, а также в информационном документе detdols.mws содержащем систематизированное описание пакета DEtools с многочисленными примерами его применения.