14. Построение двумерных анимированных графиков
Построение двумерных анимированных графиков
Более обширные возможности анимации двумерных графиков обеспечивает функция animate:
ammate(F, х, t)
animate(F,x, t, о)
В ней параметр х задает пределы изменения переменной х, а параметр t — пределы изменения дополнительной переменной t. Суть анимации при использовании данной функции заключается в построении серии кадров (как в мультфильме), причем каждый кадр связан со значением изменяемой во времени переменной t. Если надо явно задать число кадров анимации N, то в качестве о следует использовать frame=N.
Рисунок 12.16 показывает применение функции animate.
Рис. 12.16. Анимация функции sin(i*x)/(i*x) на фоне неподвижной синусоиды
В документе рис. 12.16 строятся две функции — не создающая анимации функция sin(x) и создающая анимацию функция sin(i*x)/(i*x), причем в качестве переменной t задана переменная i. Именно ее изменение и создает эффект анимации. Проигрыватель анимационных клипов и меню, описанные выше, могут использоваться для управления и этим видом анимации. Обратите внимание на вызов графических функций в этом примере командой with и на синтаксис записи этих функций.
К сожалению, картинки в книгах всегда неподвижны и воспроизвести эффект анимации невозможно. Можно лишь представить несколько текущих кадров анимации. Представленная на рис. 12.16 картина соответствует последнему кадру анимации.
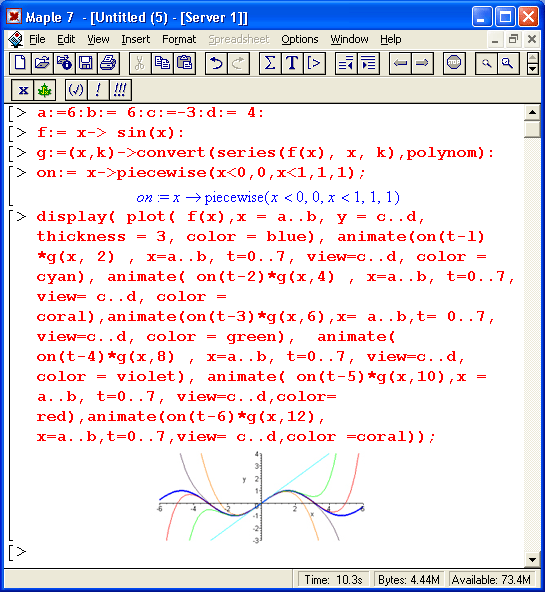
Еще один пример анимации представлен на рис. 12.17. Этот документ показывает кадр анимированного процесса улучшения приближения синусоидальной функции рядом с различным числом членов (и порядком последнего члена ряда). Результирующая картина, изображенная на рис. 12.17, показывает как приближаемую синусоидальную функцию, так и графики всех рядов, которые последовательно выводятся в ходе анимации.
Рис. 12.17. Анимационная демонстрация приближения синусоиды рядом с меняющимся числом членов
Анимация графиков может найти самое широкое применение при создании учебных материалов. С ее помощью можно акцентировать внимание на отдельных параметрах графиков и образующих их функций и наглядно иллюстрировать характер их изменений.
12.gif

39.gif