Глава 21. Анализ пригодности
Глава 21. Анализ пригодности
1. Анализ пригодности
Анализ пригодности
Анализ пригодности (а также: анализ вопросов или анализ заданий) помогает подбирать вопросы (задания) для тестов. При помощи разнообразных критериев а результате такого такой анализа устанавливается, какие задания подходят для определённого теста, а какие нет.
Для этой цели некоторой совокупности (выборке) респондентов предлагают предварительный вариант теста со всеми предполагаемыми заданиями и проводят анализ этих заданий. При помощи этого анализа исключают неподходящие задания, а оставшиеся включают в итоговую форму теста. Тест составленный таким образом должен рассматриваться не как статистический проверочный метод (к примеру, t-тест или U-тест), а как метод исследования личностных признаков.
Более подробную информацию о построении и анализе тестов Вы сможете найти в книге Линерта (Lienert) (см. список литературы). Линерт подразделяет тесты в зависимости от вида исследуемого личностного признака, а именно выделяются тест уровня образованности, тест способностей и личностный тест. Тестовое задание состоит преимущественно из двух частей: проблемы или вопроса и варианта решения проблемы или ответа.
Следует понимать разницу между заданиями, для которых считается правильным только один ответ, а другие — неправильными, и заданиями со ступенчатым ответом. Примерами пунктов, построенными по принципу верно — не верно могут служить следующие пункты:
-
Покупаете ли вы дорогую одежду (да — нет)?
-
Является ли кит представителем семейства млекопитающих (верно — неверно)? Возможны также и задания с множественными ответами:
-
Кем по национальности был Альфред Нобель (немец — швейцарец — швед — австриец — датчанин)?
Задания со ступенчатым вариантом ответа построены иначе. Исследуемый личностный признак оценивается не при помощи ответа верно — не верно, а при помощи ответов, указывающих на силу проявления признака, к примеру:
-
Я теряю самообладание (никогда — редко — иногда — часто).
Для оценки таких ответов каждому варианту ответа присваивается некоторый количественный показатель (как правило, 1, 2, 3 ...).
21.1 Задания типа верно — не верно
21.1 Задания типа верно — не верно
В качестве примера, который мы хотим обработать при помощи SPSS, рассмотрим личностный тест, с помощью которого определяется степень любопытства опрашиваемых.
№ | Вопрос | Правильный ответ |
1 | У Вас много книг? | Да |
2 | Ходите ли Вы за покупками всё время в одни и те же магазины? | Нет |
3 | Считаете ли Вы, что космонавтику развивать необходимо? | Да |
4 | Вас не интересует, почему на вашего соседа одели наручники? | Нет |
5 | Можете ли Вы долго заниматься чем-нибудь одним? | Да |
6 | Регулярно ли Вы смотрите новости? | Да |
7 | Знаете ли Вы, сколько человек живёт в городе, в котором проживаете Вы? | Да |
8 | Ходите ли Вы на работу всегда одной и той же дорогой? | Нет |
9 | Становится ли Вам иногда скучно? | Нет |
10 | Хотели бы Вы полететь на Луну? | Да |
11 | Читаете ли Вы ежедневные газеты регулярно? | Да |
12 | Спрашивали ли Вы уже себя, как будет выглядеть мир через сто лет? | Да |
13 | Замечаете ли вы иногда, что недовольны тем, что Вы можете и знаете? | Да |
14 | Предоставите ли Вы себя для научных экспериментов? | Да |
15 | Интересует ли Вас, сколько зарабатывает ваш сосед? | Да |
16 | Бездельничаете ли Вы во время отпуска? | Нет |
17 | Приятней ли Вам находиться в кругу большого количества друзей, нежели с одним другом? | Да |
18 | Случается ли с вами часто так, что Вы не знаете с чего начать? | Да |
Здесь речь идёт о вопросах, на которые следует давать строго определенные ответы: верно или не верно. Ответ верно соответствует наличию любопытства. Такое же самое значение можно присвоить и ответу не верно; при разработке теста, в него рекомендуется включать и такие вопросы, значимым ответом на которые является отрицательный. Это всегда возможно при соответствующей формулировке.
Если следовать Линерту, то для оценки пригодности отдельных пунктов следует применять нижеследующие два критерия:
Индекс сложности
В простейшем случае он представляет собой долю правильных ответов на данный вопрос, взятую в процентах от общего количества ответов. Для вопросов с несколькими возможными ответами и ступенчатыми ответами существуют модифицированные формулы. Удивительно, но для сложных вопросов индекс сложности принимает малые значения, а для лёгких большие. Вопросы с низким и высоким индексом сложности считаются не желательными.
Коэффициент избирательности
Коэффициентом избирательности, который является важным критерием для оценки применимости вопроса, служит корреляционный коэффициент между ответом на вопрос и суммарным показателем теста. В качестве суммарного показателя теста берётся сумма всех ответов. Это означает, что все правильные ответы должны иметь одинаковый знак! К сожалению, этому важному обстоятельству в справочниках уделяется не достаточно внимания. Для приведенного примера это означает, что пункты 2, 4, 8, 9 и 16 перед анализом должны быть подвергнуты перекодировке.
Для определения корреляционного коэффициента Линерт предлагает различные варианты, так, к примеру, двухрядная поточечная корреляция между заданием с ответом верно — не верно и значением масштаба или ранговая корреляция между заданием со ступенчатым ответом и значением масштаба. Как ни странно: SPSS всегда использует коэффициенты Пирсона.
Непригодные для применения пункты обычно отбираются посредством сравнения индексов сложности и избирательности. Самым простым способом является отбор сначала тех вопросов, которые обладают индексом сложности ниже 20 или выше 80, а затем из списка оставшихся вопросов исключаются те, которые имеют самые низкие коэффициенты избирательности. Линерт предлагает рассчитывать ещё и дополнительные показатели вопросов, такие как: индекс однородности, индекс пригодности, селекционный показатель и (если имеется так называемый внешний критерий) коэффициенты действительности.
Коэффициент пригодности
Коэффициент пригодности является важным критерием для оценки результата теста. Он является мерой точности, с которой проводится тестирование некоторого признака. SPSS предлагает для этой цели множество методов; по умолчанию устанавливается альфа Кронбаха (Cronbach's Alpha) со значением, модуль которого находится между 0 и 1. Обработаем наш пример при помощи SPSS.
-
Откройте файл nuegier.sav.
Помните о том, что вопросы 2, 4, 8, 9 и 16 должны быть перекодированы; их кодовые числа необходимо поменять местами (1 станет 2, 2 станет 1).
-
Это можно сделать при помощи метода, рассмотренного в главе 8, посредством выбора меню Transform (Трансформировать) Recode (Перекодировать) Into same Variables... (В те же переменные)
Можно было бы также воспользоваться и синтаксисом. Для этого необходимо было бы записать следующие инструкции:
RECODE item2, item4, item8, item9, item16 (1=2) (2=1). EXECUTE.
-
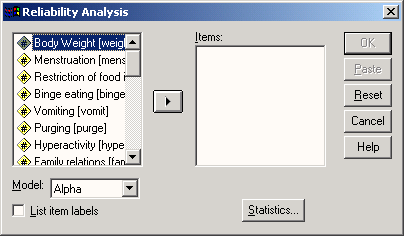
После перекодировки выберите в меню Analyze (Анализ) Scale (Масштабировать) Reliability Analysis... (Анализ пригодности) Откроется диалоговое окно Reliability Analysis (Анализ пригодности).
-
Переменные iteml-itemlS поместите в поле пунктов (Items:). Затем из числа предлагаемых методов расчёта коэффициентов пригодности необходимо выбрать подходящий:
Рис. 21.1: Диалоговое окно Reliability Analysis (Анализ пригодности)
-
Alpha (Альфа): Альфа Кронбаха (при дихотомических пунктах используется формула Кудера-Ричардсона 20 (Kuder-Richardson- Formula 20))
-
Split-half (Расщепление на две половины): Определение пригодности с расщеплением на две половины по Спирману-Брауну (Spearman-Brown)
-
Guttman (Гуттман): Определение нижней границы пригодности Гуттмана
-
Parallel (Парралельно): Оценка максимального правдоподобия пригодности теста при условии наличия одинаковых дисперсий пунктов
-
Strict parallel (Строго параллельно): Оценка максимального правдоподобия пригодности теста при условии наличия одинаковых средних значений пунктов и одинаковых дисперсий пунктов.
-
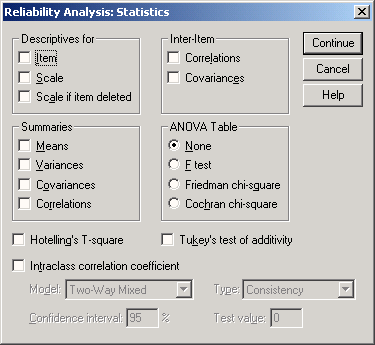
Оставьте предварительную установку Alpha (Альфа) и щёлкните на выключателе Statistics...(Статистики). Откроется диалоговое окно Reliability AnalysisStatistics (Анализ пригодности: Статистики).
Вы можете произвести следующие виды расчётов:
-
Descriptives for (Дескриптивные (описательные) статистики для) Item (Пункт): Среднее значение и стандартное отклонение для каждого пункта анкеты или вопроса Scale (Шкала): Среднее значение, дисперсия и стандартное отклонение для значения масштаба
Рис. 21.2: Диалоговое окно Reliability Analysis'.Statistics (Анализ пригодности: Статистики)
Scale if item deleted (Масштабировать, если пункт удалён): Когда при расчёте значения масштаба этот пункт (вопрос) не учитывается, для каждого такого Пункта (ответа на вопрос анкеты), выводятся: среднее значение и дисперсия значения шкалы, корреляция пункта со значением масштаба (то есть избирательность) и альфа Кохрана.
-
Summaries (Итоги, общие сведения)
Means (Средние значения): Различные виды статистик для средних значений пунктов
Variances (Дисперсия): Различные виды статистик для дисперсий пунктов
Covariances (Ковариации): Различные виды статистик для ковариаций между пунктами
Correlations (Корреляции): Различные виды статистик для корреляций между пунктами.
-
Inter-Item (Между пунктами)
Correlations (Корреляции): Корреляционная матрица Covariances (Ковариации): Ковариационная матрица
-
ANOVA-ТаЫе (Таблица ANOVA)
F test (F тест): Двухфакторный дисперсионный анализ (факторы: наблюдения, пункты) с повторным измерением и одним значением в каждой ячейке Friedman chi-square (Хи-квадрат Фридмана): тест Хи-квадрат Фридмана и коэффициент согласования Кендала (при наличии переменных, относящихся к порядковой шкале)
Cochran chi-square (Хи-квадрат Кохрана): Q Кохрана (при наличии дихотомических переменных).
Далее ещё имеются:
-
Hottelling's T-square (Т-квадрат Хоттелинга): Тест Хоттелинга для проверки утверждения, что средние значения пунктов равны между собой.
-
Tukey's test ofadditivity (Критерий аддитивности Тьюки): Тест Тьюки на аддитивность пунктов.
В случае установки опции Intraclass correlation coefficient (Корреляционный коэффициент внутри класса) речь идёт о расчёте корреляционного коэффициента внутри класса (ICC); информацию по этому поводу Вы найдёте в разделе 15.5.
-
Здесь ограничьтесь активизацией опции Scale if item deleted (Масштабировать, если пункт удалён) и щёлкните на Continue (Далее).
-
Начните расчёт нажатием ОК.
В окне просмотра появятся результаты расчёта. И в 10 версии вывод этих результатов ещё не производится в новой табличной форме.
RЕLIАВILIТУ ANALYSIS SCALE (ALPHA) | ||||
Item-total | Statistics | |||
Scale Mean if Item Deleted | Scale Variance if Item Deleted | Corrected Item-Total Correlation | Alpha if Item Deleted | |
ITEM1 | 24,9333 | 13,5126 | ,5410 | ,7664 |
ITEM2 | 25,0667 | 14,4092 | ,2679 | ,7862 |
ITEM3 | 25,1000 | 13,5414 | ,5097 | ,7684 |
ITEM4 | 25,4333 | 16,0471 - | -,1676 | ,8052 |
ITEMS | 25,2000 | 13,6828 | ,4907 | ,7701 |
ITEM6 | 25,1667 | 14,5575 | ,2358 | ,7883 |
ITEM7 | 25,5000 | 15,2931 | ,1738 | ,7887 |
ITEMS | 24,8000 | 15,1310 | ,1154 | ,7942 |
ITEM9 | 25,2000 | 13,8897 | ,4304 | ,7745 |
ITEM10 | 24,8667 | 13,8437 | ,4732 | ,7717 |
ITEM11 | 25,3667 | 14,2402 | ,4223 | ,7760 |
ITEM12 | 25,0667 | 13,3057 | ,5763 | ,7633 |
ITEM13 | 25,0000 | 13,2414 | ,6017 | ,7615 |
ITEM14 | 24,9667 | 13,8954 | ,4196 | ,7752 |
ITEM15 | 25,0000 | 13,3103 | ,5813 | ,7630 |
ITEM16 | 25,0333 | 14,0333 | ,3713 | ,7787 |
ITEM17 | 24,9667 | 15,3437 | ,0283 | ,8023 |
ITEM18 | 24,9667 | 13,9644 | ,4000 | ,7766 |
Reliability Coefficients | ||||
N of Cases =30,0 | N of Items= 18 | |||
Alpha =,7887 | ||||
Коэффициент пригодности, равный 0,7887, является очень высоким. В колонке с названием Corrected Item-Total Correlation (Откорректированный пункт — суммарная корреляция) находятся коэффициенты избирательности. Основываясь на значении этих коэффициентов, пункты 4 и 17 можно считать непригодными для дальнейшего использования, да и пункт 8 должен быть исключён.
-
Мы уже говорили о необходимости проведения расчета индекса сложности. Для расчёта индекса сложности выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
Процентный показатель частоты появления правильного ответа (кодировка 1) является индексом сложности соответствующего пункта. Все индексы сложности собраны в нижеследующей таблице.
Пункт | Индекс сложности | Пункт | Индекс сложности |
1 | 36,7 | 10 | 30,0 |
2 | 50,0 | 11 | 80,0 |
3 | 53,3 | 12 | 50,0 |
4 | 86,7 | 13 | 43,3 |
5 | 63,3 | 14 | 40,0 |
6 | 60,0 | 15 | 43,3 |
7 | 93,3 | 16 | 46,7 |
8 | 23,3 | 17 | 40,0 |
9 | 63,3 | 18 | 40,0 |
Если следовать рекомендации, сформулированной в начале раздела и исключать пункты с индексом сложности меньшим 20 и большим 80, то помимо пунктов 4, 8 и 17 необходимо исключить из списка и пункт 7.
Если вновь провести анализ пунктов с оставшимися четырнадцатью пунктами, то коэффициент пригодности получится равным 0,8297. Благодаря исключению неподходящих пунктов он стал ещё выше.
1.gif
2.gif
21.2 Задания со ступенчатыми ответами
21.2 Задания со ступенчатыми ответами
В разделе 19.3 была представлена анкета исследования Фрайбургского университета, посвященного отношению респондентов к болезни. Эта анкета охватывает в общей сложности 35 пунктов, отображающих при помощи кодировок 1 = "абсолютно нет" до 5 = "очень сильно" ситуацию, характеризующую то, как пациенты склонны бороться с поразившим их недугом. Пункты были подвергнуты факторному анализу; один из пяти результирующих факторов мы назвали: "Активное действие, направленное на решение проблемы".
В этот фактор вошли следующие переменные:
11 | Искать информацию о заболевании и лечении |
17 | Предпринимать активные действия для решения проблемы |
f8 | Составить план лечения и затем приступить к его реализации |
f13 | Больше себе позволять |
f14 | Пытаться интенсивней жить |
f15 | Решиться на борьбу с болезнью |
f17 | Подбадривать себя |
f18 | Пытаться достичь успеха и самоутверждения |
f19 | Пытаться отвлечься |
110 | Искать уединения |
Эти пункты можно собрать в один тест, который для каждого пациента будет давать некоторое значение на шкале уровня активности его действий. При помощи теста пригодности проверим также реальную пригодность этих пунктов. Так как все пункты имеют положительную кодировку в направлении активного образа действия, в перекодировке, как в разд. 19.1, нет необходимости.
-
Откройте файл fkv.sav.
-
Выберите в меню Analyze (Анализ) Scale (Масштабировать) Reliability Analysis... (Анализ пригодности)
-
Переменные f1, f7, f8, f1З, f14, f15, f17, f18, f19 и f20 поместите в поле, предназначенное для пунктов (вопросов анкеты).
-
Через выключатель Statistics...(Статистики) в группе Descriptives for (Дескриптивные статистики для) активируйте опцию Scale if Item deleted (Масштабировать, если пункт удалён).
В окне просмотра появятся следующие результаты.
RELIABILITY ANALYSIS-SCALE (ALPHA) | |||
Item-total | Statistics | ||
Scale Scale Mean Variance if Item if Item Deleted Deleted | Corrected Item-Total Correlation | Alpha if Item Deleted | |
F1 30,2750 45,5214 | ,4514 | ,8059 | |
F7 30,3937 43,9761 | ,5534 | ,7944 | |
F8 31,0812 43,8990 | ,5453 | ,7953 | |
F13 31,1125 46,1885 | ,4592 | ,8046 | |
F14 30,4250 45,8057 | ,4857 | ,8019 | |
F15 30,2937 45,1899 | ,4351 | ,8084 | |
F17 30,4312 43,4418 | ,6558 | ,7840 | |
F18 30,7000 44,3245 | ,5701 | ,7929 | |
F19 30,5750 46,7491 | ,4632 | ,8042 | |
F20 30,7687 48,2166 | ,3679 | ,8131 | |
Reliability Coefficients | |||
N of Cases = 160,0 | N of Items =10 | ||
Alpha = ,8170 | |||
В колонке Corrected Item-Total Correlation (Откорректированный пункт — суммарная корреляция) приводятся коэффициенты избирательности, а внизу таблицы можно увидеть коэффициент пригодности. В нашем случае он является довольно высоким — значение равно 0,817. На основании получившихся коэффициентов избирательности нет повода для исключения каких-либо пунктов; после любого такого исключения, в рассматриваемом случае, коэффициент пригодности снижался бы, как показано в колонке Alfa if Item Deleted (Альфа, если пункт удалён).
Пригодность всех пунктов не является сюрпризом, т.к., за исключением пункта 20 (который к тому же имеет и наименьшую избирательность), все пункты обладают достаточными факторными нагрузками (> 0,4). Как показывает нижеследующая таблица, большие факторные нагрузки говорят о высоких коэффициентах избирательности.
Избирательность | Факторная нагрузка | |
f1 | 0,6558 | 0,654 |
f7 | 0,5701 | 0,589 |
f8 | 0,5534 | 0,710 |
f13 | 0,5453 | 0,690 |
f14 | 0,4857 | 0,621 |
f15 | 0,4632 | 0,572 |
f17 | 0,4592 | 0,510 |
f18 | 0,4514 | 0,563 |
f19 | 0,4351 | 0,597 |
f20 | 0,3679 | <0,400 |
Что же касается расчёта индекса сложности, то в данном примере он довольно проблематичен; пожалуй, к правильному ответу можно отнести только кодировки 4 и 5.

