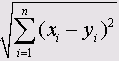20.1 Принцип кластерного анализа
20.1 Принцип кластерного анализа
Для рассмотрения принципа кластерного анализа выберем сначала очень простой пример.
-
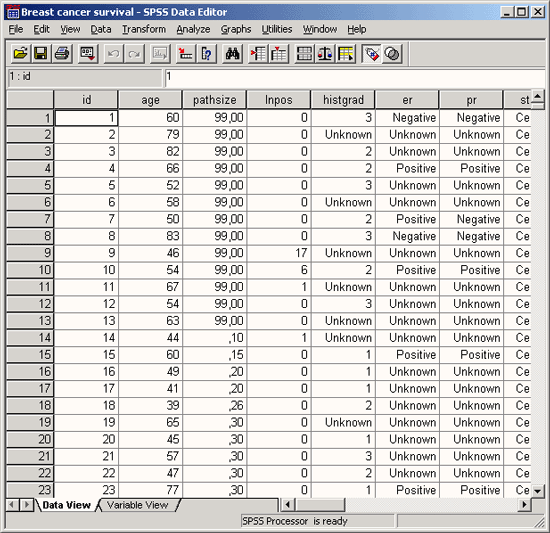
Откройте файл bier.sav, который содержит некоторые данные о 17 сортах пива (см. рис. 20.1).
Рис. 20.1: Данные файла bier.sav в редакторе данных
Переменная herkunft (производитель) указывает на страну-производителя пива, где США закодированы с помощью единицы. Расходы (kosten) приведены в долларах США для ёмкости равной 12 унциям для жидкости (примерно одна треть литра); калорийность указана для одинакового количества пива. Содержание алкоголя приводится в процентах.
Возьмём переменные kalorien (калории) и kosten (расходы) и представим их при помощи простой диаграммы рассеяния.
-
Выберите в меню Graphs (Графики) Scalier... (Диаграмма рассеяния)
-
Переменную kalorien (калории) поместите в поле оси х, а переменную kosten (расходы) в поле оси у, и для обозначения наблюдения используйте переменную bier (пиво).
-
Через кнопку Options... (Опции) активируйте опцию Display Chart with case labels (Показывать график с метками наблюдений).
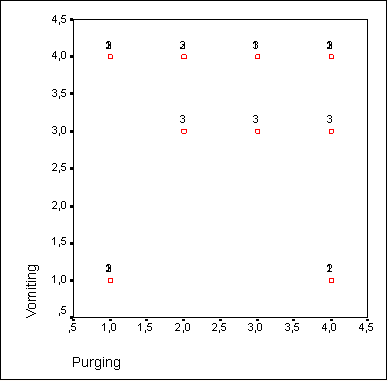
Вы получите диаграмму рассеяния, представленную на рисунке 20.2.
Вы увидите четыре отдельных отчётливых группировки точек, три из них в нижней половине диаграммы и одну в верхнем правом углу. Следовательно, переменные kalorien (калории) и kosten (расходы), явно распадаются на четыре различных кластера по сортам пива.
Сорта пива, которые по значениям двух рассмотренных переменных похожи друг на друга, принадлежат к одному кластеру; сорта пива, находящиеся в различных кластерах, не похожи друг на друга. Решающим критерием для определения схожести и различия двух сортов пива является расстояние между точками на диаграмме рассеяния, соответствующими этим сортам.
Самой распространенной мерой для определения расстояния между двумя точками на плоскости, образованной координатными осями х и у, является евклидова мера:
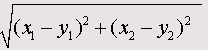
где x1:, и хn — координаты первой точки, у: и уг — координаты второй точки.
Рис. 20.2: Диаграмма рассеяния переменных kalorien (калории) и kosten (расходы)
В соответствии с этой формулой расстояние между сортами пива Budweisei Heineken составляет:
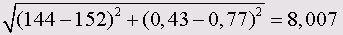
Это расстояние лишь незначительно превосходит то, которое получилось бы, если бы для расчета была взята только одна переменная — kalorien (калории):
|144 - 152 | = 8
Данный эффект можно объяснить тем, что уровни значений переменных kalorien (калории) и kosten (расходы) очень сильно отличаются друг от друга: у переменной kosten (расходы) значения меньше 1, а у переменной kalorien (калории) больше 100. Согласно формуле евклидовой меры, переменная, имеющая большие значения, практически полностью доминирует над переменной с малыми значениями.
Решением этой проблемы является рассмотренное в главе 19.1 z-преобразование (стандартизация) значений переменных. Стандартизация приводит значения всех преобразованных переменных к единому диапазону значений, а именно от —3 до +3.
Если Вы произведёте такое преобразование для переменных kalorien (калории) и kosten (расходы), то для пива Budweiser получите стандартизованные значения равные 0,400 и —0,469 соответственно, а для пива Heineken стандартизированные значения 0,649 и 1,848 соответственно.
Тогда расстояние между двумя сортами пива получится равным
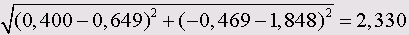
Таким образом, при помощи диаграммы рассеяния для двух переменных: kalorien (калории) и kosten (расходы), мы провели самый простой кластерный анализ. Мы выбрали такой вид графического представления, с помощью которого можно было бы отчётливо распознать группирование в кластеры (четыре в нашем случае).
К сожалению, столь отчётливая картина отношений между переменными, как в приведенном примере, встречается очень редко. Во-первых, структуры кластеров, если вообще таковые имеются, не так чётко разделены, особенно при наличии большого количества наблюдений. Скорее наоборот, кластеры размыты и даже проникают друг в друга. Во-вторых, как правило, кластерный анализ проводится не с двумя, а с намного большим количеством переменных.
При кластерном анализе с тремя переменными можно ввести ещё одну ось — ось z и рассматривать размещение наблюдений, а также проводить расчёт расстояния по формуле евклидовой меры в трёхмерном пространстве.
При наличии более трёх переменных определение расстояния между двумя точками х и у в любом n-мерном пространстве для математиков не представляет особого труда. Формула Евклида в таких случаях приобретает следующий вид:
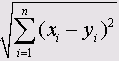
Наряду с евклидовой мерой расстояния, SPSS предлагает и другие дистанционные меры, а также меры подобия. Так что кластерный анализ можно проводить не только с переменными, относящимися к интервальной шкале, как в приведенном случае, но и с дихотомическими переменными, к примеру. В таком ситуации применяется уже другие дистанционные меры и меры подобия (см. разд. 20.3).
При проведении кластерного анализа отдельные кластеры могут формироваться при помощи пошагового слияния, для которого существует ряд различных методов (см. разд. 20.4). Важную роль играют иерархические и партиционные методы, причём последние применяются в подавляющем большинстве случаев. Оба эти метода можно задействовать, если пройти через меню Analyze (Анализ) Classify (Классифицировать)
Они помещены в этом меню под именами Hierarchical Cluster... (Иерархический кластер) и K-Means Cluster... (Кластерный анализ методом к-средних).
Рассмотрим сначала иерархический кластерный анализ, причём начнём с простого примера с 17 сортами пива.
1.gif
2.gif
6.gif