18.1 Пример из области медицины

Обратимся ещё раз к примеру, который уже приводился при рассмотрении логистической регрессии. В этом примере приводятся выборочные данные о пациентах с нарушениями работы легких. Эти данные хранятся в файле lunge.sav. Приведем ещё раз переменные, которые в данном случае будут применяться при дискриминантом анализе:

Имя переменной	Значение
out	Исход (0 = скончался, 1 = выжил)
alter	Возраст
bzeit	Время проведения искусственного дыхания в часах
kob	Концентрация кислорода в смеси для искусственного дыхания
адд	Интенсивность искусственного дыхания
geschl	Пол (1 = мужской, 2 = женский)
gr	Рост

Переменная out делит пациентов на две группы; при помощи остальных переменных предстоит прогнозировать принадлежность к одной из групп.

•  Откройте файл lunge.sav.

•  Выберите в меню Analyze (Анализ) Classify (Классифицировать) Discriminant... (Дискриминантный анализ) 

Откроется диалоговое окно Discriminant Analysis (Дискриминантный анализ).

Рис. 18.1: Диалоговое окно Discriminant Analysis (Дискриминантный анализ).

•  Поместите переменную out в поле, предназначенное для групповых переменных.

•  После щелчка по выключателю Define Range... (Определить промежуток) введите минимальное и максимальное значения этой переменной: 0 и 1.

•  Переменным agg, alter, bzeit, gcschl, gr и kob присвойте статус независимых переменных. Для начала оставим установленный по умолчанию метод: Enter independents together (Одновременный учет всех независимых переменных), при котором в анализе одновременно будут участвовать все независимые переменные.

•  После щелчка по выключателю Statistics... (Статистики) активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты ANOVA), Unstandardized Function Coefficients (Нестандартизированные коэффициенты функции) и Within-groop Correlation Matrice (Корреляционная матрица внутри группы).

•  Через выключатель Classify (Классифицировать) сделайте дополнительно запрос на вывод диаграмм по отдельным группам (Separate-groups Plots), результатов для отдельных наблюдений (Casewise results) и сводной таблицы (Summary table). При выводе результатов для отдельных наблюдений ограничимся первыми двадцатью, поместив этот предел в соответствующую позицию диалогового окна.

Довольно полезный график для объединенных групп, который был реализован в ранних версиях SPSS, и сейчас можно активировать в диалоговом окне, однако вместо графика в окне отображения результатов будет появляться предупреждение о том, что такая гистограмма в анализах более не доступна.

•  При помощи выключателя Save... (Сохранить) активируйте сохранение значения дискриминантной функции в дополнительной переменной (Discriminant Scores).

•  Начните расчёт нажатием ОК.

После вводного обзора действительных и пропущенных значений приводятся средние значения, стандартные отклонения, количество наблюдений для каждой группы в отдельности и суммарные показатели для обеих групп.

Переменная geschl является при этом дихотомической переменной, принадлежащей к номинальной шкале с кодировками: 1 (мужской пол) и 2 (женский пол). Средние значения пола для обоих групп по исходу Легения, кажущиеся на первый взгляд бесполезными, равны 1,63492 и 1,45588; если бы вместо этого переменные были закодированы при помощи 0 и 1, то оба средних значения равнялись бы 0,63492 и 0,45588 соответственно. Для таких дихотомических переменных, кодированных при помощи 0 и 1, среднее значение указывает на долю наблюдений с кодировкой 1. Это означает, что для группы "скончался" доля женщин в процентном отношении составляет 63,492, а для группы "выжил" 45,588.

Group Statistics (Статистики для групп)
Outcome (Исход)		Mean (Среднее значение)	Std. Deviation (Стандартное отклонение)	Valid N (listwise) (Действительные значения (по списку))
				Unwe-ighted (Не взвешено)	Weig-hted (Взве-шено)
gesto-rben (Скон-чался)	Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания)	15,90013	10,90013	63	63,000
	ALTER (Возраст)	31,92063	13,82529	63	63,000
	Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах)	15,36508	10,50085	63	63,000
	Geschlecht (Пол)	1,63492	,48532	63	63,000
	Koerper-groesse (Рост)	165,1429	15,55931	63	63,000
	Sauerstoff-Konzentration (Концент-рация кислорода в смеси для искус-ственного дыхания)	,85952	,14807	63	63,000
ueberlebt (Выжил)	Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания)	11,69699	8,16057	68	68,000
	ALTER (Возраст)	27,97059	10,86411	68	68,000
	Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах)	10,79412	5,10065	68	68,000
	Geschlecht (TlonJ	1,45588	,50175	68	68,000
	Koerpe-rgroesse (Рост)	172,0588	11,01137	68	68,000
	Sauerstoff-Konzentration (Концентрация кислорода в смеси для искус-ственного дыхания)	,80338	,15493	68	68,000
Total	Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания)	13,51843	9,72600	131	131,000
	ALTER (Воз_раст)	29,87023	12,48654	131	131,000
	Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах)	12,99237	8,44120	131	131,000
	Geschlecht (Пол)	1,54198	,50015	131	131,000
	Koerpe-rgroesse (Рост)	168,7328	13,78339	131	131,000
	Sauerstoff-Konzentration (Конце-нтрация кислорода в смеси для искус-ственного дыхания)	,83038	,15369	131	131,000

Затем проводится тест, насколько значимо различаются между собой переменные в обеих группах; наряду с тестовой величиной, в качестве которой служит Лямбда Уилкса ("Wilks-Lambda"), применяется также и простой дисперсионный анализ. Для всех переменных (кроме возраста, для которого однако также просматривается сильная тенденция к значимости) получается значимое различие между обеими группами:

Tests of Equality of Group Means (Тест равенства групповых средних значений)

Wilks Lambda (Лямбда Уилкса)	F	df1	df2	Sig. (Значи-мость)
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,962	5,116	1	129	,025
ALTER (Возраст)	,975	3,331	1	129	,070
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах)	,926	10,273	1	129	,002
Geschlecht (Пол)	,968	4,297	1	129	,040
Koerpergroesse (Рост)	,937	8,722	1	129	,004
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	,966	4,481	1	129	,036

Далее следует корреляционная матрица между всеми переменными, в которой приводятся коэффициенты, осредненные для обеих групп:

Pooled Within-Groims Matrices (Объединённые внутригрупповые матрицы)

		Aggres-sivitaet der Beat-mung (Интен-сивность искус-ственного дыхания)	ALTER (Воз-раст)	Beatmun-gszeit in Std. (Время прове-дения искус-ственного дыхания в часах)	Gesc-hlecht (Пол)	Koerper-groesse (Рост)	Saue-rstoff- Konzen-tration (Концен-трация кисл-орода в смеси для искус-ственного дыхания)
Corre-lation (Корре-пяция)	Aggres-sivitaet der Beatmung (Интен-сивность искус-ственного дыхания)	1,000	-,072	-,058	,141	-,042	,285
	ALTER (Возраст)	-,072	1,000	,093	-,040	,277	-.119
	Beatmu-ngszeit in Std. (Время прове-дения искус-ственного дыхания в часах)	-,058	,093	1,000	,069	-,126	-,089
	Geschlecht (Пол)	.141	-0,40	,069	1,000	-,481	-,066
	Koerpe-rgroesse (Рост)	-,042	,277	-,126	-,481	1,000	,000
	Sauer-stoff-Konze-ntration (Конце-нтрация кисло-рода в смеси для искус-ственного дыхания)	,285	-,119	-,089	-,066	,000	1,000

Следующими шагами являются расчёт и анализ коэффициентов дискриминантной функции. Значения этой функции должны как можно отчётливей разделять обе группы. Мерой удачности этого разделения служит корреляционный коэффициент между рассчитанными значениями дискриминантной функции и показателем принадлежности к группе:

Eigenvalues (Собственные значения)

Function (Функция)	Eigenvalue (Собственное значение)	% of Variance (% дисперсии)	Cumulative % (Сово-купный %)	Canonical Correlation (Канони-ческая корреляция)
1	,256"	100,0	100,0	,452

a. First 1 canonical discriminant functions were used in the analysis (В этом анализе используются первые 1 канонические дискриминантные функции).

Wilks' Lambda (Лямбда Уилкса)

Test of Function(s) (Тест функции (и))	Wilks' Lambda (Лямбда Уилкса)	Chi-square (Хи-квадрат)	df	Sig. (Значимость)
1	,796	28,733	6	,000

Судя по значению коэффициента, равному 0,452, корреляция абсолютно не удовлетворительная. При помощи Лямбда Уилкса производится тест на то, значимо ли в обеих группах отличаются друг от друга средние значения дискриминантной функции; в приводимом примере, значение р < 0,001, указывает на очень значимое различие.

Значение, выводимое под именем "Eigenvalue" (Собственное значение), соответствует отношению суммы квадратов между группами к сумме квадратов внутри групп. Эти две суммы Вы сможете получить, если проведете дисперсионный анализ значений дискриминантной функции (переменная dis1_1) по фактору out (см. гл. 13.3). Большие собственные значения (в данном случае такого, к сожалению, не наблюдается) указывают на "хорошие" (удачно подобранные) дискриминантные функции.

Следующая таблица дает представление о том, как сильно отдельные переменные, применяемые в дискриминантной функции, коррелируют со стандартизированными значениями этой дискриминантной функции. При этом корреляционные коэффициенты были рассчитаны в обеих группах по отдельности и затем усреднены:

Standardized Canonical Discriminant Function Coefficients

(Стандартизиро-ванные канонические коэффициенты дискриминантной функции)
Function (Функция)
1
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,316
ALTER (Возраст)	,494
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах|	,491
Geschlecht (Пол)	,066
Koerpergroesse (Рост)	-,544
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	,385

Structure Matrix 

(Структурная матрица)
Function (Функция)
1
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах)	,558
Koerpergroesse (Рост)	-,514
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,393
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	,368
Geschlecht (Пол)	,361
ALTER (Возраст)	,318

Pooled within-groups correlations between discriminating variables and standardized canonical discriminant functions (Объединённые корреляции внутри групп между диск-риминантными переменными и стандартизированными каноническими дискриминант-ными функциями).

Variables ordered by absolute size of correlation within function (Переменные расположены в соответствии с абсолютными корреляционными величинами внутри функции).

И в заключение, приводятся сами коэффициенты дискриминантной функции:

Canonical Discriminant Function Coefficients

(Канонические коэффициенты дискриминантной функции)
Function (Функция)
1
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания)	,033
ALTER (Возраст)	,040
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах)	,060
Geschlecht (Пол)	,133
Koerpergroesse (Рост)	-,041
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания)	2,539
(Constant)	2,121

Unstandardized coefficients (Нестандартизированные коэффициенты)

Здесь речь идёт о нестандартизированных коэффициентах — это множители при заданных значениях переменных, входящих в дискриминантную функцию. Стандартизированные коэффициенты, которые приводились ранее, основаны на стандартизированных значениях переменных, получаемых с помощью z-преобразования.

Далее приводятся средние значения дискриминантной функции в обеих группах:

Functions at Group Centroids 

(Функции групповых центроидов)
Outcome (Исход)	Function (функция)
	1
gestorben (Скончался)	,522
ueberlebt (Выжил)	-,483

Unstandardized canonical discriminant functions evaluated at group means (Heстандартизированные канонические дискриминантные функции, которые оцениваются по групповым средним значениям).

Далее следует таблица, в которой построчно для каждого наблюдения приводится информация о значении дискриминантной функции и определяется принадлежность к одной из двух групп. Мы здесь ограничились первыми двадцатью наблюдениями.

Группа, к которой фактически принадлежит наблюдение, отображается в колонке с именем "Actual Group" (Фактическая группа). В следующих трёх колонках содержится информация о прогнозе принадлежности к группе, сделанном на основании значения дискриминантной функции. Сначала приводится прогнозируемая принадлежность к группе; если она не соответствует фактической принадлежности, то в колонке "Predicted Group" (Прогнозируемая группа) отображаются две звёздочки (**).

Casewise Statistics 

(Статистики для наблюдений)
	Case Number (Поряд-ковый номер случая)	Actual Group (Факти-ческая груп-па)	Highest Group (Старшая группа)					Second Highest Group (Вторая по старшинству группа)			Discri-minant Scores (Значе-ния дискри-ми- нант-ности)
			Predic-ted Group (Прогно-зируе-мая груп-па)	P(D>d G=g)		P(G=g | D=d)	Squared Maha-lanobis Distance to Centroid (Квадрат рас-стояния Махапа-нобиса до центро-ида)	Group (Груп-па)	P(G=g |D=d)	Squared Maha-lanobis Distance to Centroid (Квадрат рас-стояния Маха-ланобиса до центро-ида)	Function 1 (Фун-кция 1)
				р	df						1
Origi-nal (Перво-нача-льно)	1	0	1"	,727	1	,702	,122	0	,298	1,834	-.833
	2	1	0"	,116	1	,889	2,464	1	,111	6,631	2,092
	3	0	1"	,842	1	,576	,040	0	,424	,650	-,284
	4	1	1	,310	1	,821	1,032	0	,179	4,085	-1,499
	5	1	1	,495	1	,767	,465	0	,233	2,846	-1,165
	6	1	1	,453	1	,779	,563	0	,221	3,081	-1,234
	7	0	1"	,635	1	,728	,225	0	,272	2,189	-,958
	8	1	1	,549	1	,752	,359	0	,248	2,575	-1,083
	9	1	1	,880	1	,587	,023	0	,413	,729	-,332
	10	0	1"	,952	1	,609	,004	0	,391	,893	-,423
	11	0	0	,026	1	,940	4,980	1	,060	10,477	2,753
	12	1	0"	,618	1	,501	,249	1	,499	,256	,023
	13	0	0	,930	1	,603	,008	1	,397	,841	,434
	14	1	1	,817	1	,676	,053	0	,324	1,528	-,714
	15	1	1	,958	1	,611	,003	0	,389	,908	-,431
	16	0	1"	,685	1	,524	,165	0	,476	,359	-,077
	17	1	1	,388	1	,798	,745	0	,202	3,492	-1,347
	18	0	1"	,763	1	,550	,091	0	,450	,496	-,182
	19	1	1	,748	1	,696	,103	0	,304	1,760	-,805
	20	0	0	,308	1	,822	1,037	1	,178	4,095	1,540

** Мisciassiriea case (Неправильно классифицированное наблюдение;

Далее выводятся две вероятности. Вторая из этих двух вероятностей, обозначенная P(G=g|D=d), является мерой принадлежности к одной из двух групп. Это вероятность того, что некоторой наблюдение принадлежит к прогнозированной группе, которая рассчитывается на основе подстановки в дискриминантную функцию значений набора переменных, соответствующих данному наблюдению. Вероятность того, что данный наблюдение принадлежит к другой группе получается вычитанием меры принадлежности из 1. Она приводится в колонке с названием "Second Highest Group" (Вторая по старшинству группа). Если мы рассмотрим первый наблюдение, то здесь вероятность того, что данный пациент выживет, рассчитанная на основании значении исходных переменных, равна 0,702 (в действительности он скончался).

Первую из двух рассмотренных вероятностей, получившую название Р (D>d|G=g), называют ещё и условной вероятностью. Это вероятность того, что пациент, принадлежащий к прогнозируемой группе, действительно имеет значения параметров, соответствующие дискриминантной функции или некоторые другие крайние значения.

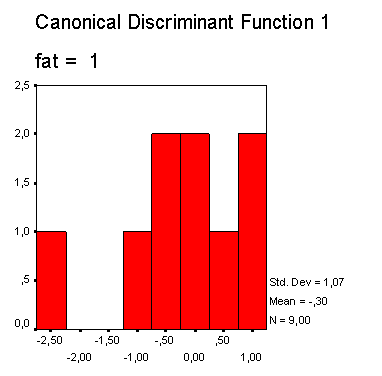
В другой колонке приводится квадрат расстояния Махаланобиса до центроида (среднего значения группы значений дискриминантной функции). В правой колонке таблицы приводится соответствующее значение дискриминантной функции. Распределение значения дискриминантной функции отдельно по группам изображается на двух отдельных гистограммах.

Можно заметить, что значения дискриминантной функции для первой группы (скончался) смещены вправо, а значения второй группы (выжил) — влево, что однако свидетельствует об очень сильном смешении.

В завершении приводится классификационная таблица с указанием достигнутой точности прогнозирования. Значение этой точности равно 68,7 %, что является неудовлетворительным:

Рис. 18.2: Распределение значений дискриминантной функции для группы «скончался»

Рис. 18.3: Распределение значений дискриминантной функции для группы «выжил»

Classification Results 3 

(Классификационные результаты)
Outcome (Исход)	Predicted Group Membership (Предсказанная принадлежность к одной из групп)		Total (Сум-ма)
	gestorben (Сконча-лся)	ueberlebt (Выжил)
Original Перво-начально)	Count (Колич-ество)	gestorben (сконча-лся	38	25	63
		ueberlebt (Выжил)	16	52	68
	%	gestorben (сконча-лся	60,3	39,7	100,0
		ueberlebt (Выжил)	23,5	76,5	100,0

а. 68,7% of original grouped cases correctly classified (68,7 % первоначально сгруппированных наблюдений были классифицированы корректно).

При применении метода логарифмической регрессии (см. гл. 16.4) результат получился немного лучше (доля корректного прогноза 70,99 %).

Для случая, когда пациенту мужского пола, 25 лет, ростом 184 см искусственное дыхание делали на протяжении 5 часов, при концентрации кислорода равной 0,7 и интенсивности соответствующей значению 10, получается следующее значение дискриминантной функции

d = 2,121 + 0,033*10 + 0,04*25 + 0,06*5 + 0,133*1-0,041*184 + 2,539*0,7 = -1,883

Опираясь на распределение значений дискриминантной функции, этого пациента можно отнести к группе выживших.

При выполнении дискриминантного анализа, как и для других многомерных процедур, можно применять и пошаговый образ действий, который как раз и рекомендуется при наличии большого количества независимых переменных. Этот метод похож на многомерный регрессионный анализ, однако переменные при проведении дискриминантного анализа выбираются по другим критериям.

Рассчитаем ещё раз наш пример, но уже с применением пошагового метода.

•  В исходном диалоговом окне дискриминантного анализа активируйте опцию Use stepwse method (Использовать пошаговый метод).

•  Щёлкните на кнопке Method... (Метод)

Откроется диалоговое окно Discriminant Analysis: Step-wise Method (Дискриминантаый анализ: Пошаговый метод).

•  Выберите метод, при помощи которого будет отобрана та переменная, которая увеличивает расстояние Махаланобиса (Mahalanobis) между двумя группами. Эта дистанционная мера базируется на евклидовых расстояниях между нормализованными значениями выборок с учётом корреляции соответствующих переменных.

•  Чтобы искусственно не раздувать объём выводимых результатов, в этот раз через кнопку Classify... (Классифицировать), активируйте опцию Summary table (Сводная таблица).

В рассматриваемом случае мы отказываемся от графического представления результатов. В анализ по очереди будут включены переменные: bzeit, gr, alter и kob; это те же самые переменные, которые использовались при применении метода логистической регрессии. По заключительной классификационной таблице можно сделать вывод о том, что в результате отбрасывания неподходящих переменных доля попаданий слегка выросла. Значение надежности прогноза составило 70,2 %.

Для проведения дискриминантного анализа Вы можете использовать и пример с двумя диагностическими тестами для обнаружения карциномы мочевого пузыря, рассмотренный в главе 16.4. Здесь можно получить более чёткое разделение двух групп (здоров — болен). Точность прогнозирования здесь составляет 82,2 %.