17.3 Многомерный дисперсионный анализ
17.3 Многомерный дисперсионный анализ
Многомерный дисперсионный анализ применяется тогда, когда в одном дисперсионном анализе необходимо одновременно исследовать влияние факторов и возможных ковариации (независимых переменных) на несколько зависимых переменных. Такой многомерный дисперсионный анализ следует предпочесть одномерному тогда (и только тогда), когда зависимые переменные не являются независимыми друг от друга, а наоборот коррелируют между собой.
Если Вы откроете данные из исследования гипертонии (файл hyper.sav) и рассчитаете корреляции между исходными значениями систолического и диастолического давлений, уровнями холестерина и сахара в крови (переменные rrs0, rrd0, cho10 и bz0), то вы заметите, что эти переменные, хотя и не сильно, но всегда значимо коррелируют между собой.
Если Вы хотите узнать, значимо ли отличаются перечисленные переменные для четырёх заданных возрастных групп (переменная ak), то вместо четырёх отдельных одномерных однофакторных дисперсионных анализов Вы должны провести один многомерный однофакторный анализ.
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Multivariate... (Многомерная)
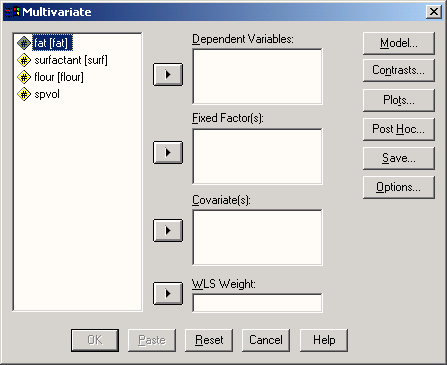
Откроется диалоговое окно Multivariate (Многомерная) (см. рис. 17.8).
Поместите переменные rs0, rrd0, cho10, и bz0 в поле. предусмотренное для зависимых переменных, а переменной ak присвойте статус постоянного фактора.
Под выключателями Contrasts... (Контрасты), Model... (Модель) и Options... (Опции) Вы найдёте множество разнообразных возможностей для задания контрастов, выбора различных вариантов моделей или организации вывода всевозможных дополнительных результатов расчёта; к примеру, здесь можно активировать тесты проверки дисперсии на однородность.
Уже было указано на невозможность в рамках этой книги представить все имеющиеся возможности по отдельности. Чтобы рассмотреть все эти возможности Вам придётся обратиться к оригинальному учебнику по SPSS; опытному же пользователю для понимания будет достаточно просто посмотреть на пункты, имеющиеся в диалоговом окне. В крайнем случае, можно воспользоваться справкой.
-
Оставьте все установки по умолчанию и начните расчёт нажатием ОК.
Рис. 17.8: Диалоговое окно Multivariate (Многомерная)
Появятся довольно обширные результаты расчёта. Важным для нас является в первую очередь глобальный многомерный тест на предмет выявления значимых различий "где-нибудь" между возрастными группами:
Multivariate Tests c (Многомерные тесты)
Effect (Эффект ) | Value (Зна-чение) | F | Hypo-thesis df (Гипо-теза df) | Error df (Ошибка df) | Sig. (Значи-мость) | |
Inte-rcept Отре-зок) | Pillai's Trace (След Пиллая) | ,996 | 9252, 061а | 4,000 | 167,000 | ,000 |
Wilks' Lambda (Лямбда Уилкса) | ,004 | 9252,061 а | 4,000 | 167,000 | ,000 | |
Hotelling's Trace (След Хоттелинга) | 221,606 | 9252, 061а | 4,000 | 167,000 | ,000 | |
Roy's Largest Root 'Макси-мальный характе-ристический корень по методу Роя) | 221,606 | 9252,061 а | 4,000 | 167,000 | ,000 | |
АК | Dillai's Trace (След Пиллая) | ,178 | 2,661 | 12,00ol | 507,00o' | ,002 |
Wilks' Lambda (Лямбда Уилкса) | ,827 | 2,740 | 12,000 | 442,132 | ,001 | |
Hotelling's Trace (След Хоттелинга) | ,203 | ,805 | 12,000 | 197,000 | ,001 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,169 | 7,159Ь | 4,000 | 167,000 | ,000 | |
a. Exact statistic (Точная статистика)
b. The statistic is an upper bound on F that yields a lower bound on the significance level (Статистической характеристикой является верхний придел значения F-распределе-ния, который указывает на нижний предел уровня значимости).
с Design: Intercept+AK (Компоновка: Отрезок + АК)
Здесь производится расчёт величин, традиционных для общей линейной модели. Они уже представлены в главе 17.1.3. Основываясь на критерии "След Пиллая" ("Pillai's Trace"), следует отклонить нулевую гипотезу о том, что между четырьмя возрастными группами не наблюдается различий ни для одной из зависимых переменных (значение р = 0,002).
Для проверки, какие из четырёх зависимых переменных в чем-то различаются между собой, были проведены одномерные тесты. Результаты этих тестов полностью соответствуют результатам отдельного одномерного дисперсионного анализа для каждой зависимой переменной.
Мы здесь воздержимся от подробной расшифровки довольно большой таблицы "Тесты межсубъектных эффектов". Отметим только, что для систолического и диастолического давлений, уровней холестерина и сахара в крови получаются следующие значения вероятности ошибки р: 0,153, 0,002, 0,267 и 0,688 соответственно. Причиной суммарной значимости, поучающейся в результате многомерного теста, являются прежде всего значимые различия для диастолического давления.
Для опытных статистиков, хорошо знакомых с тонкостями многомерных методов, SPSS может предложить избыточное количество разнообразных возможностей в области дисперсионного анализа. В первую очередь можно использовать разнообразные возможности процедуры MANOVA, доступной отныне только через командный синтаксис. Эта процедура позволяет проводить простой и множественный регрессионный анализ, дискриминантный анализ, канонический анализ, анализ главных компонентов и др. Однако сложность работы с заданием параметров может составить некоторые затруднения для менее опытных пользователей. Поэтому в данной книге мы ограничились рассмотрением наиболее часто применяемых компоновок дисперсионного анализа.
10.gif